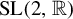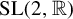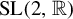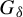1 Introduction
Consider a compact metric space
$\Omega $
and a homeomorphism
$T : \Omega \to \Omega $
. Such a pair
$(\Omega , T)$
will be called a dynamical system in this paper. (It would be more accurate to call it a topological dynamical system, but we hope this slight abuse of language does not lead to any confusion. Given that we are interested in topological notions and quantities, this is the natural setting in which for us to work.) We will freely use standard concepts from the theory of dynamical systems such as minimality and unique ergodicity; see, for example, the textbook [Reference Walters48].
The set of real
$2\times 2$
matrices with determinant equal to one is denoted by
${\mathrm {SL}}(2,{\mathbb R})$
.
Any
$$ \begin{align*} A \in C(\Omega,{\mathrm{SL}}(2,{\mathbb R})) := \{ A : \Omega \to {\mathrm{SL}}(2,{\mathbb R}) : A \mbox{ continuous}\} \end{align*} $$
gives rise to the skew-product
$$ \begin{align*} (T,A) : \Omega \times {\mathbb R}^2 \to \Omega \times {\mathbb R}^2, \quad (\omega,v) \mapsto (T \omega, A(\omega)v), \end{align*} $$
which is usually also referred to as a continuous
${\mathrm {SL}}(2,{\mathbb R}))$
-cocycle. Since the base dynamics T will be fixed throughout, we will sometimes leave it implicit and just refer to
$A \in C(\Omega , {\mathrm {SL}}(2,{\mathbb R}))$
to specify the cocycle it generates. Specifically, by slight abuse of terminology, when we refer to ‘the cocycle A’ below, we really have in mind the map
$(T,A)$
.
For
$n \in {\mathbb Z}$
, define
$A_n : \Omega \to {\mathrm {SL}}(2,{\mathbb R})$
by
$(T,A)^n = (T^n,A_n)$
. A cocycle A is called uniformly hyperbolic if there exists
$L> 0$
with
$$ \begin{align*} \liminf_{n \to \infty} \frac{1}{n}\log\|A_n (\omega)\| \ge L \end{align*} $$
uniformly in
$\omega \in \Omega $
.
One says that A is uniform if there is a number
$L(A)$
such that
$$ \begin{align*} \lim_{n \to \infty} \frac1n \log \|A_n(\cdot)\| = L(A) \end{align*} $$
uniformly. Clearly, any uniform cocycle A with
$L(A)>0$
is uniformly hyperbolic.
A cocycle may or may not be uniform. However, by the subadditive ergodic theorem, once an ergodic measure
$\mu $
is chosen, there is always a (
$\mu $
-dependent)
$L_\mu (A)$
such that
$$ \begin{align*} \lim_{n \to \infty} \frac1n \log \|A_n(\omega)\| = L_\mu(A) \quad \text{for }\mu\text{-almost every } \omega \in \Omega. \end{align*} $$
The numbers
$L(A)$
and
$L_\mu (A)$
are called Lyapunov exponents.
For our actual considerations, a further uniformity property of cocycles will be relevant. A cocycle
$A \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R}))$
is said to have uniform behavior if it is either uniformly hyperbolic, or
$$ \begin{align*} \limsup_{n \to \infty} \frac{1}{n} \log \|A_n (\omega)\| = 0 \end{align*} $$
uniformly in
$\omega \in \Omega $
. Note that this latter condition can also be written as
$\lim _{n \to \infty } ({1}/{n}) \log \|A_n (\omega )\| = 0$
uniformly in
$\omega \in \Omega $
(as
$\|B\|\geq 1$
for any
$B \in {\mathrm {SL}}(2,{\mathbb R})$
, and hence
$\log \|A_n (\omega )\| \geq 0$
).
Remark 1.1. It is known that the property
$$ \begin{align*} \lim_{n \to \infty} \frac{1}{n} \log \|A_n (\omega)\| = 0\quad \text{uniformly in } \omega \in\Omega \end{align*} $$
is equivalent to the simultaneous vanishing of the Lyapunov exponent for all ergodic Borel probability measures
$\mu $
,
$$ \begin{align*} \sup \{ L_\mu(A) : \mu \text{ ergodic} \} = 0; \end{align*} $$
compare [Reference Avila and Bochi1, Proposition 1], [Reference Schreiber42, Theorem 1], and [Reference Sturman and Stark44, Theorem 1.7]. See also [Reference Furman28] for the special case where there is only one ergodic measure and [Reference Bochi and Navas8] for related work.
Let us briefly discuss the relationship between these uniformity notions, see Appendix A for more details. For uniquely ergodic dynamical systems, a continuous cocycle is uniformly hyperbolic if and only if it is uniform with
$L(A)> 0$
. From this, we immediately conclude that for uniquely ergodic dynamical systems, a continuous cocycle is uniform if and only if it has uniform behavior. For general dynamical systems, it is obviously true that a uniform cocycle has uniform behavior. However, the converse does not hold. Indeed, for any non-uniquely ergodic system, there exist uniformly hyperbolic continuous cocycles that are not uniform (see, e.g., Remark A.2).
We will be interested in one-parameter families of cocycles. This is partly motivated by the application of our general results, presented below, to the case of Schrödinger cocycles, which naturally depend on the energy parameter. Let
$I \subseteq {\mathbb R}$
be an interval in
${\mathbb R}$
and equip
$C(I\times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
with the topology of local uniform convergence. Define
$ W(I, \Omega )$
to be the set
$$ \begin{align*} \{ A \in C(I \times \Omega, {\mathrm{SL}}(2,{\mathbb R})) : A(E,\cdot)\text{ has uniform behavior for each }E\in I \}. \end{align*} $$
Then, we have the following result.
Theorem 1.2. Let
$(\Omega ,T)$
be a dynamical system and let
$I \subseteq {\mathbb R}$
be an interval. Then,
$W(I,\Omega )$
is a
$G_\delta $
-set.
Remark 1.3.
-
(a) Of course, the theorem can be applied with I being just one point. This gives that the set of
$A \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R}))$
with uniform behavior is a
$G_\delta $
-set. This particular case was known; see the first paragraph of the proof of [Reference Avila and Bochi1, Theorem 1]. In fact, under suitable assumptions on
$(\Omega ,T)$
, Avila and Bochi even show that it is a dense
$G_\delta $
-set [Reference Avila and Bochi1, Theorem 1]. -
(b) An inspection of the proof shows that I could be chosen as any topological space that is a countable union of compact subspaces. Indeed, the proof proceeds in two steps. In the first step, it is shown that uniformity extends from any E to a suitable neighborhood of it. In the second step, we use that I can be written as a countable union of compact intervals. Both of these steps generalize to the more general setting.
As pointed out above, for uniquely ergodic dynamical systems, a cocycle is uniform if and only if it has uniform behavior, but in general, the set of uniform cocycles may be strictly smaller than the set of cocycles with uniform behavior. This naturally raises the question whether the set of uniform cocycles is a
$G_\delta $
-set in general. Thus, let us consider
$$ \begin{align*} U(I, \Omega) := \{ A \in C(I \times \Omega, {\mathrm{SL}}(2,{\mathbb R})) : A(E,\cdot) \text{ is uniform for each } E \in I \}. \end{align*} $$
The following theorem answers the question affirmatively.
Theorem 1.4. Let
$(\Omega ,T)$
be a dynamical system and let
$I \subset {\mathbb R}$
be an interval. Then,
$U(I,\Omega )$
is a
$G_\delta $
-set.
Remark 1.5.
-
(a) With the obvious modifications, parts (a) and (b) of Remark 1.3 apply here as well.
-
(b) For equicontinuous systems, it is known that the set of uniform cocycles is a dense
$G_\delta $
-set (see [Reference Furman28]).
The results above are relevant in the study of spectral properties of discrete one-dimensional Schrödinger operators with dynamically defined potentials. Operators of this kind arise as follows. The set of continuous
$f : \Omega \longrightarrow {\mathbb R}$
is denoted by
$C(\Omega ,{\mathbb R})$
. Any choice of an
$f\in C(\Omega ,{\mathbb R})$
, commonly referred to as a sampling function, gives rise to potentials
$V_\omega (n) = f(T^n \omega )$
,
$\omega \in \Omega $
,
$n \in {\mathbb Z}$
, and the associated Schrödinger operators
$$ \begin{align*} [H_\omega \psi] (n) = \psi(n+1) + \psi(n-1) + V_\omega(n) \psi(n) \end{align*} $$
in
$\ell ^2({\mathbb Z})$
. The spectral theory of such operators has been reviewed in [Reference Damanik15] and it will be discussed in full detail in the forthcoming monographs [Reference Damanik and Fillman16, Reference Damanik and Fillman17]. We refer to these works for details on the concepts and results discussed next.
If
$\mu $
is a T-ergodic Borel probability measure, then the spectral properties of
$H_\omega $
are
$\mu $
-almost surely independent of
$\omega \in \Omega $
. For example, there are sets
$\Sigma , \Sigma _{\mathrm {ac}}, \Sigma _{\mathrm {sc}}, \Sigma _{\mathrm {pp}}$
such that
$\sigma (H_\omega ) = \Sigma $
and
$\sigma _\bullet (H_\omega ) = \Sigma _\bullet $
,
$\bullet \in \{ \mathrm {ac}, \mathrm {sc}, \mathrm {pp} \}$
for
$\mu $
-almost every
$\omega \in \Omega $
.
Several recent works have investigated the question of which spectral properties are generic. One usually fixes the base dynamics
$(\Omega , T)$
and studies the set of
$f \in C(\Omega ,{\mathbb R})$
for which a certain spectral phenomenon occurs. For example, Avila and Damanik showed in [Reference Avila and Damanik4] that
$\{ f \in C(\Omega ,{\mathbb R}) : \Sigma _{\mathrm {ac}} = \emptyset \}$
is a dense
$G_\delta $
-set for any ergodic
$\mu $
, provided that T is not periodic. (By the standard theory of periodic Schrödinger operators, the result clearly fails if the assumption is dropped.) A companion result was obtained by Boshernitzan and Damanik in [Reference Boshernitzan and Damanik10]:
$\{ f \in C(\Omega ,{\mathbb R}) : \Sigma _{\mathrm {pp}} = \emptyset \}$
is residual (that is, it contains a dense
$G_\delta $
-set), provided that
$(\Omega ,T,\mu )$
has the metric repetition property. See [Reference Boshernitzan and Damanik10, Reference Boshernitzan and Damanik11] for the definition of this property and many examples, including shifts and skew-shifts on tori.
The proofs of the results in [Reference Avila and Damanik4, Reference Boshernitzan and Damanik10] just mentioned rely on approximation of f by functions taking finitely many values. Realizing that the absence of point spectrum, as well as the absence of absolutely continuous spectrum, are phenomena that are quite well understood in the setting of sampling functions taking finitely many values, the results in [Reference Avila and Damanik4, Reference Boshernitzan and Damanik10] then appear to be somewhat natural. (It should be noted, however, that they were both initially quite surprising as one had previously expected the presence of an absolutely continuous spectrum for small quasi-periodic potentials, and the presence of a point spectrum for operators generated by the standard skew-shift
$T(\omega _1,\omega _2) = (\omega _1 + \alpha , \omega _1 + \omega _2)$
.)
Let us discuss some key concepts underlying the general theory and the results just mentioned. A cocycle
$$ \begin{align*} A^g : \omega \mapsto \begin{pmatrix} g(\omega) & -1 \\ 1 & 0 \end{pmatrix} \end{align*} $$
with
$g \in C(\Omega ,{\mathbb R})$
is called a Schrödinger cocycle.
Given an operator family
$\{ H_\omega \}_{\omega \in \Omega }$
as introduced above, the associated one-parameter family of Schrödinger cocycles
$\{ A^{E - f} \}_{E \in {\mathbb R}}$
is intimately related to the study of the solutions of the associated difference equation
$$ \begin{align*} u(n+1) + u(n-1) + V_\omega(n) u(n) = E u(n), \end{align*} $$
and hence provides important information. The parameter E is referred to as the energy in this context.
We write
$$ \begin{align*} \mathcal{UH} & = \{ E \in {\mathbb R} : A^{E-f} \text{ is uniformly hyperbolic} \}, \\ \mathcal{Z} & = \{ E \in {\mathbb R} : L_\mu(A^{E-f}) = 0 \}, \\ \mathcal{NUH} & = {\mathbb R} \setminus (\mathcal{UH} \cup \mathcal{Z} ). \end{align*} $$
Note that
$\mathcal {Z}$
and
$\mathcal {NUH}$
depend on the choice of ergodic measure
$\mu $
, while
$\mathcal {UH}$
does not. This provides a (
$\mu $
-dependent) partition of the energy axis:
${\mathbb R} = \mathcal {UH} \sqcup \mathcal {NUH} \sqcup \mathcal {Z} $
.
Let us now relate the Lyapunov exponents with the spectra mentioned earlier. The Johnson–Lenz theorem [Reference Johnson32, Reference Lenz37] (see also the textbook treatments in [Reference Avila, Bochi and Damanik2, Reference Damanik and Fillman16, Reference Fabbri and Johnson26, Reference Johnson, Obaya, Novo, Núñez and Fabbri33] for applications) states that
$$ \begin{align} \mathcal{Z} \subseteq \Sigma \subseteq \mathcal{Z} \cup \mathcal{NUH}. \end{align} $$
Moreover,
$$ \begin{align} \operatorname{\mathrm{supp}} \mu = \Omega \quad \Rightarrow \quad \Sigma = \mathcal{Z} \cup \mathcal{NUH}. \end{align} $$
Recall that the essential closure of a measurable set
$M \subseteq {\mathbb R}$
is given by
$\overline {M}^{\mathrm {ess}} = \{ E \in {\mathbb R}\hspace{-0.5pt} :\hspace{-0.5pt} {\mathrm {Leb}}(M \cap (E\hspace{-0.5pt} -\hspace{-0.5pt} \varepsilon , E + \varepsilon )\hspace{-0.5pt}>\hspace{-0.5pt} 0 \text { for every } \varepsilon > 0 \}$
. The Ishii–Pastur–Kotani theorem [Reference Ishii31, Reference Kotani and Itô34, Reference Pastur40] (see also [Reference Damanik, Gesztesy, Deift, Galvez, Perry and Schlag14, Reference Kotani36] for an exposition) states that
$$ \begin{align} \Sigma_{\mathrm{ac}} = \overline{\mathcal{Z}}^{\mathrm{ess}}. \end{align} $$
Finally, if the potentials
$\{ V_\omega \}$
take finitely many values and are
$\mu $
-almost surely aperiodic, then by Kotani [Reference Kotani35], we have
$$ \begin{align} {\mathrm{Leb}}(\mathcal{Z}) = 0, \end{align} $$
which by equation (1.3) implies that
$\Sigma _{\mathrm {ac}} = \emptyset $
. The very general result in equation (1.4) was alluded to in the discussion above as one of the general spectral phenomena in the setting of potentials taking finitely many values, and it forms the basis of the generic
$C^0$
result from [Reference Avila and Damanik4] also mentioned above.
Note that under the assumption
$\operatorname {\mathrm {supp}} \mu = \Omega $
(which holds, e.g., when T is minimal), equation (1.2) shows that
$\Sigma = \mathcal {Z}$
if and only if
$\mathcal {NUH} =\emptyset $
. Now, for uniquely ergodic dynamical systems, uniform behavior is equivalent to uniformity, see appendix, and
$L_\mu (A) =0$
if and only if A is uniform with
$L(A) =0$
. Thus, for minimal uniquely ergodic dynamical systems, we have
$$ \begin{align} \Sigma = \mathcal{Z}\ {\Longleftrightarrow}\ \mathcal{NUH}=\emptyset\ {\Longleftrightarrow}\ A^{E-f} \text{ is uniform for all }E\in {\mathbb R}. \end{align} $$
For general systems, it follows from the definitions and Remark 1.1 that
$$ \begin{align*} \{ E \in {\mathbb R} : A^{E-f} \text{ has uniform behavior} \} = \mathcal{UH} \cup \bigcap_{\mu \text{ ergodic}} \mathcal{Z}_\mu.\end{align*} $$
In other words, uniform behavior fails for
$A^{E-f}$
precisely when
$$ \begin{align*} E\in \bigcup_{\mu \text{ ergodic}} \mathcal{NUH}_\mu. \end{align*} $$
This gives
$$ \begin{align*} \mathcal{NUH}_\mu = \emptyset \text{ for each ergodic }\mu &\Longleftrightarrow\ A^{E-f} \text{ has uniform behavior for all } E\in {\mathbb R} \\ &\Longleftrightarrow\ \Sigma_\mu = \mathcal{Z}_{\mathcal{U}}\text{ for each ergodic }\mu. \end{align*} $$
Here,
$$ \begin{align*}\mathcal{Z}_{\mathcal{U}}:=\{ E\in {\mathbb R} : A^{E-f} \text{ is uniform with } L(A^{E-f}) = 0\} = \bigcap_{\mu \text{ ergodic}} \mathcal{Z}_\mu. \end{align*} $$
In any case, if the potentials
$\{ V_\omega \}$
take finitely many values, then equation (1.4) implies zero-measure spectrum whenever one can show that
$\mathcal {NUH} = \emptyset $
. Thus, pursuing a proof of the absence of non-uniformity is a natural approach to a zero-measure spectrum whenever a property such as equation (1.4) is known. This approach is implemented in [Reference Damanik and Lenz21, Reference Lenz37], as well as in the present paper.
Let us mention that the zero-measure spectrum property has been investigated extensively for sampling functions taking finitely many values. From the classical results for the Fibonacci Hamiltonian [Reference Sütő45] or the more general class of operators with Sturmian potentials [Reference Bellissard, Iochum, Scoppola and Testard7] through numerous results for operators with potentials generated by substitutions to the general result [Reference Damanik and Lenz21] by Damanik and Lenz, which covers many examples [Reference Damanik and Lenz22], this is a spectral statement that is quite ubiquitous in this setting.
It has therefore been a very natural open problem to find conditions on the base dynamics
$T : \Omega \to \Omega $
such that
$\{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma ) = 0 \}$
is residual. The paper [Reference Avila, Damanik and Zhang5] by Avila, Damanik, and Zhang discusses this question in the particular case
$T : {\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
,
$\omega \mapsto \omega + \alpha $
,
$\alpha \not \in {\mathbb Q}$
, but fails to answer it. Instead, [Reference Avila, Damanik and Zhang5] proves the weaker result that the singularity of the integrated density of states is generic in this setting.
Not only is the problem open in the case of irrational circle rotations, it is open in any setting and hence one of our goals is to exhibit the first class of base dynamics
$T : \Omega \to \Omega $
for which
$\{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma ) = 0 \}$
is a dense
$G_\delta $
-set. At the same time, we will provide the first class of aperiodic base dynamics for which
$\{ f \in C(\Omega ,{\mathbb R}) : \mathcal {NUH} = \emptyset \}$
or, equivalently,
$\{f\in C(\Omega ,{\mathbb R}) : \Sigma = \mathcal {Z}\}$
is a dense
$G_\delta $
-set. This is of interest as the equality
$\Sigma = \mathcal {Z}$
is known in the periodic case and, hence, aperiodic dynamics giving this feature deserves particular attention.
We will work with aperiodic subshifts that satisfy the Boshernitzan condition. Recall that a subshift is a closed shift-invariant subset
$\Omega $
of
$A^{\mathbb Z}$
, where A is a finite set carrying the discrete topology and
$A^{\mathbb Z}$
is endowed with the product topology. The map
$T : \Omega \to \Omega $
is given by the shift
$(T \omega )_n = \omega _{n+1}$
, and it is clearly a homeomorphism. We say that a subshift
$\Omega $
satisfies the Boshernitzan condition (B) if it is minimal and there is a T-invariant Borel probability measure
$\mu $
such that
$$ \begin{align*} \limsup_{n \to \infty} n \cdot \min \{ \mu([w]) : w \in \Omega_n \}> 0. \end{align*} $$
Here,
$\Omega _n = \{ \omega _1 \cdots \omega _n : \omega \in \Omega \}$
is the set of words of length n that occur in elements of
$\Omega $
and
$[w]$
is the cylinder set
$[w] = \{ \omega \in \Omega : \omega _1 \cdots \omega _n = w \}$
. This condition was introduced by Boshernitzan in [Reference Boshernitzan9] as a sufficient condition for unique ergodicity.
Theorem 1.6. Suppose
$\Omega $
is a subshift that satisfies the Boshernitzan condition
$\mathrm {(B)}$
. Then, the following hold.
-
(a) The set
is a dense
$$ \begin{align*} \{ f \in C(\Omega,{\mathbb R}) : \mathcal{NUH} = \emptyset \} = \{f\in C(\Omega,{\mathbb R}) : \Sigma = \mathcal{Z}\} \end{align*} $$
$G_\delta $
-set.
-
(b) If
$\Omega $
is furthermore aperiodic, then the set is a dense
$$ \begin{align*} \{f\in C(\Omega,{\mathbb R}) : {\mathrm{Leb}}(\Sigma) =0\} \end{align*} $$
$G_\delta $
-set.
The theorem has the following immediate consequence.
Corollary 1.7. Suppose
$\Omega $
is an aperiodic subshift that satisfies the Boshernitzan condition
$\mathrm {(B)}$
. Then, the zero-measure spectrum given by the vanishing set of the Lyapunov exponent is generic, that is,
$$ \begin{align*}\{ f \in C(\Omega,{\mathbb R}) : {\mathrm{Leb}}(\Sigma) = 0 \mbox{ and } \Sigma = \mathcal{Z} \}\end{align*} $$
is a dense
$G_\delta $
-set.
Remark 1.8.
-
(a) It is well known that the spectrum is always closed and, in the dynamically defined setting we consider, it never contains any isolated points. Thus, Corollary 1.7 shows that the Cantor spectrum of zero Lebesgue measure is generic when the base dynamics is given by an aperiodic subshift that satisfies the Boshernitzan condition
$\mathrm {(B)}$
. -
(b) As pointed out above, if the subshift
$\Omega $
satisfies the Boshernitzan condition (B), then it is uniquely ergodic by [Reference Boshernitzan9, Theorem 1.2]. For this reason, there is no ambiguity in writing
$\Sigma $
without specifying
$\mu $
. However, the minimality of
$\Omega $
and the continuity of the sampling functions f in question also imply the independence of the spectrum of
$\omega $
, so that in the setting of Theorem 1.6,
$\sigma (H_\omega ) = \Sigma $
for every
$\omega \in \Omega $
, not merely for
$\mu $
-almost every
$\omega \in \Omega $
. -
(c) Many important classes of subshifts satisfy the Boshernitzan condition (B); see [Reference Damanik and Lenz22] for a detailed discussion.
-
(d) It remains very interesting to clarify whether the zero-measure spectrum is (
$C^0$
-) generic for quasi-periodic potentials, or at least for one-frequency quasi-periodic potentials.
Finally, we note that our general result, Theorem 1.4, can also be seen in the context of a question of Walters on the existence of non-uniform cocycles. Specifically, Walters asks in [Reference Walters, Arnold and Wihstutz47] whether every uniquely ergodic dynamical system (with non-atomic invariant measure) allows for a non-uniform cocycle. Walters discusses some examples, where the answer is affirmative. The question in general seems to still be open with further partial results contained in [Reference Furman28]. In this situation, the following consequence of (the proof of) our spectral results may be of interest.
Corollary 1.9. Suppose
$\Omega $
is an aperiodic subshift that satisfies the Boshernitzan condition
$\mathrm {(B)}$
. Then, the set of uniform cocycles is a dense
$G_\delta $
-set.
Remark 1.10. Based on these considerations, we feel that aperiodic Boshernitzan subshifts are the best candidates for a potential negative answer to Walters’ question, but at this time, we are unable to extend the uniformity result to all continuous cocycles over a Boshernitzan subshift.
The paper is organized as follows. We prove Theorem 1.2 in §2 and Theorem 1.4 in §3. We then provide a result on semicontinuity of the measure of the spectrum for general dynamical systems in §4 and a result on denseness of cocycles for subshifts in §5. In §6, we then derive Theorem 1.6 from results in the earlier sections. Section 6 also contains the proof of Corollary 1.9. Finally, there are two appendices, one discussing the relationships between the uniformity notions we consider, and one discussing a consequence of the avalanche principle that we need in the earlier sections.
2 Cocycles with uniform behavior as a
$G_\delta $
-set
In this section, we prove Theorem 1.2. That is, we show that the set of cocycles with uniform behavior is a
$G_\delta $
-set and, in fact, we prove this result for families of cocycles depending on one real parameter.
We start with a simple observation.
Lemma 2.1. Let
$(\Omega ,T)$
be a dynamical system and
$A \in C(\Omega , {\mathrm {SL}}(2,{\mathbb R}))$
. If there exist
$L> 0$
and
$k \in {\mathbb N}$
with
$M := \max \{ ({1}/{k}) \log \|A_k(\omega )\| : \omega \in \Omega \} < L$
, then
$$ \begin{align*} \frac{1}{n} \log\|A_n (\omega)\| < L \end{align*} $$
for all
$\omega \in \Omega $
and
$$ \begin{align*} n \geq \frac{2 k \max \{ \log \|A(\omega)\| : \omega\in \Omega\}}{L- M}. \end{align*} $$
Proof. Set
$N := {2 k \max \{ \log \|A(\omega )\| : \omega \in \Omega \}}/({L- M})$
. By definition of N, we have
$$ \begin{align} \frac{1}{N} \log \|A_r(\omega)\| \leq \frac{L-M}{2} \end{align} $$
for all
$\omega \in \Omega $
,
$r = 0, \ldots , k$
. Clearly, this estimate continues to hold if N is replaced by any
$n\geq N$
.
Consider now an
$n \in {\mathbb N}$
with
$n \geq N$
. Of course, n can be uniquely written in the form
$n = s k + r$
with
$s \in {\mathbb N}\cup \{0\}$
and
$0 \leq r < k$
. By construction of the cocycle, we obtain
$$ \begin{align*} A_{n}(\omega) = A_r (T^{s k} \omega) A_k (T^{(s-1)k} \omega) \cdots A_k (T^k\omega) A_k(\omega). \end{align*} $$
Taking logarithms and using submultiplicativity of the matrix norm and additivity of the logarithm, we find
$$ \begin{align*} \frac{1}{n}\log\|A_n (\omega)\| & \leq \frac{1}{n} \log\|A_r (T^{sk}\omega)\| + \frac{1}{n}\sum_{j=0}^{s-1} \log\|A_k (T^{jk} \omega)\|\\ & \leq \frac{L-M}{2} + \frac{1}{n}\sum_{j=0}^{s-1} k \frac{\log\|A_k (T^{jk} \omega)\|}{k}\\ & \leq \frac{L-M}{2} + \frac{1}{n}\sum_{j=0}^{s-1} k M\\ & = \frac{L-M}{2} + M \\ & < L. \end{align*} $$
Here, we used equation (2.1) in the second step, the definition of M in the third step,
$sk \le n$
in the fourth step, and
$M < L$
in the last step. This finishes the proof.
Proof of Theorem 1.2
We first consider a compact interval I.
For
$\varepsilon> 0$
, we define
$W_\varepsilon $
to be the set of
$A \in C(I \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
such that for each
$E \in I$
, the cocycle
$A(E,\cdot )$
is uniformly hyperbolic or there exists a
$k \in {\mathbb N}$
with
$({1}/{n}) \log \|A_n (\omega )\| < \varepsilon $
for all
$\omega \in \Omega $
and
$n \geq k$
. Clearly,
$$ \begin{align*} W = \bigcap_{m\in{\mathbb N}} W_{{1}/{m}}. \end{align*} $$
Thus, it suffices to show that
$W_\varepsilon $
is open for any
$\varepsilon> 0$
. To do so, we consider
$E \in I$
arbitrary. There are two cases.
Case 1:
$A(E,\cdot )$
is uniformly hyperbolic. As is well known, the set of uniformly hyperbolic cocycles is open (see, e.g., [Reference Zhang50]). As A is continuous in the first variable, there exists a
$\delta> 0$
such that any
$B \in C(I \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
close enough to A will have the property that
$B(E',\cdot )$
is uniformly hyperbolic for all
$E' \in (E-\delta ,E+\delta ) \cap I$
.
Case 2:
$A(E,\cdot )$
satisfies
$({1}/{k}) \log \|A_k (E,\omega )\| < \varepsilon $
for all
$\omega \in \Omega $
for some
$k \in {\mathbb N}$
. By continuity of A and compactness of
$\Omega $
, there exists a
$\delta> 0$
with
$$ \begin{align*} \sup_{\omega \in \Omega, E' \in (E-\delta, E+\delta) \cap I} \frac{1}{k} \log \|A_k (E',\omega)\| < \varepsilon. \end{align*} $$
This same inequality will then also hold for any
$B \in C(I \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
sufficiently close to A. By Lemma 2.1, there exists then an
$N \in {\mathbb N}$
with
$$ \begin{align*} \frac{1}{n} \log \|B_n (E',\omega)\| < \varepsilon \end{align*} $$
for all
$\omega \in \Omega $
,
$n \geq N$
, and
$E'\in (E - \delta , E + \delta ) \cap I$
for all such B.
So, in both of these two cases, there is an open neighborhood
$(E - \delta , E + \delta ) \cap I$
of E such that any B sufficiently close to A shares the respective property of
$A(E,\cdot )$
for all
$E'$
in this neighborhood. As I is compact, the openness of
$W_\varepsilon $
then follows by standard reasoning.
We now consider an arbitrary interval I in
${\mathbb R}$
. We can write I as a countable union of compact intervals
$I_n$
, that is,
$I = \bigcup _{n \in {\mathbb N}} I_n$
. By what we have shown already,
$W(I_n,\Omega )$
is a
$G_\delta $
-set for each
$n \in {\mathbb N}$
. For any
$n \in {\mathbb N}$
, there is the canonical embedding
$j_n : I_n \times \Omega \longrightarrow I \times \Omega , (E,\omega ) \mapsto (E,\omega )$
, and the associated restriction map
$$ \begin{align*} R_n : C(I\times \Omega,{\mathrm{SL}}(2,{\mathbb R})) \longrightarrow C(I_n \times \Omega, {\mathrm{SL}}(2,{\mathbb R})), \; A \mapsto A \circ j_n. \end{align*} $$
Then,
$R_n$
is continuous. Hence,
$R_n^{-1} (W(I_n,\Omega ))$
is a
$G_\delta $
-set for each
$n \in {\mathbb N}$
(as the inverse image of a
$G_\delta $
-set under a continuous map) and so is then
$$ \begin{align*} W(I,\Omega) = \bigcap_{n \in {\mathbb N}} R_n^{-1} (W(I_n,\Omega)). \end{align*} $$
This finishes the proof.
3 Uniform cocycles are a
$G_\delta $
-set
In this section, we prove Theorem 1.4. A pertinent idea is that for a uniquely ergodic dynamical system
$(\Omega ,T)$
, a continuous
$B : \Omega \to {\mathrm {SL}}(2,{\mathbb R})$
is uniform if and only if
$$ \begin{align} \lim_{n\to \infty} \frac{1}{n} \sup_{\omega, \varrho \in \Omega} |\! \log \|B_n (\omega)\| - \log \|B_n (\varrho)\| | = 0. \end{align} $$
Indeed, it is clear that any uniform B will satisfy equation (3.1). Conversely, any B satisfying equation (3.1) must be uniform as there exists (by the subadditive ergodic theorem) an
$\omega _0 \in \Omega $
with
$\lim _{n \to \infty } ({1}/{n}) \log \|B_n (\omega _0)\| = L(B)$
. Some additional work will be needed to deal with the dependence on the parameter.
We start with two auxiliary statements. For the convenience of the reader, we include sketches of the proofs.
Lemma 3.1. Let
$(\Omega ,T)$
be a dynamical system and
$A \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R})$
be arbitrary.
-
(a) If there exist
$L> 0$
and
$N \in {\mathbb N}$
with
$({1}/{k}) \log \|A_k(\omega )\| < L$
for all
$\omega \in \Omega $
and
$k = N,\ldots , 2N$
, then for all
$$ \begin{align*} \frac{1}{n} \log\|A_n (\omega)\| < L \end{align*} $$
$\omega \in \Omega $
and
$n \geq N$
.
-
(b) Let
$c := \max _{\omega \in \Omega } \{ \log \|A(\omega )\|, \log \|A^{-1}(\omega )\| \}$
. Then, for any
$n \in {\mathbb N}$
,
$$ \begin{align*} \bigg| \frac{\log \|A_{n+1}(\omega)\|}{n+1} - \frac{\log\|A_n (\omega)\|}{n}\bigg| \leq \frac{1}{n+1} \frac{\log\|A_n (\omega)\|}{n} + \frac{c}{n+1}. \end{align*} $$
Proof.
-
(a) Consider
$n \geq N$
. Then, we can uniquely write n in the form
$n = k N + r$
with
$k \in {\mathbb N} \cup \{0\}$
and
$N \leq r \leq 2 N-1$
. Now, the proof follows similar lines as the proof of Lemma 2.1. -
(b) For invertible matrices
$C,B$
, we clearly have
$\|B C\| \leq \|B\| \|C\|$
and
$\|C\| = \|B^{-1} B C\| \leq \|B^{-1}\| \|B C\|$
. Applying this with
$C = A_n (\omega )$
and
$B = A(T^n \omega )$
, we infer part (b) after a short computation.
Remark 3.2. It follows from part (a) of the lemma that for any
$L> 0$
and
$N \in {\mathbb N}$
, the set of
$A \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R}))$
with
$\sup _{\omega \in \Omega , n \geq N} ({1}/{n}) \log \|A_n (\omega )\| < L$
is open.
We now show that the pointwise uniformity of the
$A(E,\cdot )$
appearing in the definition of
$U(I,\Omega )$
can be replaced by a uniform uniformity when I is compact. This is the content of the next proposition.
Proposition 3.3. Let
$(\Omega ,T)$
be a dynamical system. Let
$I \subset {\mathbb R}$
be a compact interval. Consider
$A \in U(I, \Omega )$
. Then, for any
$\varepsilon> 0$
, there exists
$N \in {\mathbb N}$
with
$$ \begin{align*} \frac{1}{n}| \log \|A_n(E,\omega)\| - \log \|A_n (E,\varrho)\| | < \varepsilon \end{align*} $$
for all
$\omega , \varrho \in \Omega $
,
$E \in I$
, and
$n \geq N$
.
Proof. As I is compact, it suffices to find for each
$E \in I$
, a
$\delta> 0$
such that the desired estimate holds in
$(E - \delta , E + \delta ) \cap I$
. We consider two cases.
Case 1:
$A(E,\cdot )$
is uniform with
$L(A(E,\cdot ))> 0$
. The proof follows from Lemma B.1 in the following way. Assume without loss of generality
${\varepsilon }/{46 L} < {1}/{12}$
. By uniformity of
$A(E,\cdot )$
, there exists
$N \in {\mathbb N}$
such that the assumptions of Lemma B.1 will be satisfied with
$L = L(A(E,\cdot ))$
,
$\ell = N$
, and
${\varepsilon }/{ 47 L}< {1}/{12}$
instead of
$\varepsilon $
. Now, as discussed in part (c) of Remark B.2, the assumptions are open assumptions in the following sense. If they are satisfied for the cocycle
$A(E,\cdot )$
with
${\varepsilon }/{ 47 L}$
, then for any
${1}/{12}> \varepsilon ' > {\varepsilon }/{47 L}$
, any B sufficiently close to
$A(E,\cdot )$
will satisfy the assumptions as well with
$\varepsilon '$
instead of
${\varepsilon }/{47 L}$
, and the same L and
$\ell $
. So, the conclusion of the lemma will hold for such B. With
$\varepsilon ' = {\varepsilon }/{46 L}$
, the conclusion of the lemma gives
$$ \begin{align*} L \bigg( 1 - \frac{44}{46 L}\varepsilon \bigg) \leq \frac{1}{n} \log\|B_n (\omega)\| \leq L \bigg( 1 + \frac{\varepsilon}{46 L} \bigg) \end{align*} $$
for all
$n \geq \ell $
and
$\omega \in \Omega $
for any such B. This in turn implies
$$ \begin{align*} \frac{1}{n}|\!\log \|B_n(\omega)\| - \log \|B_n (\varrho)\| | < \varepsilon \end{align*} $$
for all
$\omega \in \Omega $
and
$n \geq \ell = N$
for any such B. By continuity of A (in the first variable), there exists
$\delta> 0$
such that each
$A(E',\cdot )$
with
$E' \in (E - \delta , E + \delta ) \cap I$
is such a B. This gives the desired statement.
Case 2:
$A(E,\cdot )$
is uniform with
$L(A(E,\cdot ))=0$
. In this case, there exists
$N \in {\mathbb N}$
with
$$ \begin{align*} \frac{1}{k} \log \|A_k (E,\omega)\| < \varepsilon / 3 \end{align*} $$
for all
$\omega \in \Omega $
and
$k \geq N$
. By continuity of A, there exists a
$\delta> 0$
with
$$ \begin{align*} \frac{1}{k} \log \|A_k (E',\omega)\| < \varepsilon / 2 \end{align*} $$
for all
$E' \in (E - \delta , E + \delta ) \cap I$
,
$\omega \in \Omega $
and
$k =N,\ldots , 2N$
. By part (a) of Lemma 3.1, we find
$$ \begin{align*} \frac{1}{n} \log \|A_n(E',\omega)\| < \varepsilon / 2 \end{align*} $$
for all
$\omega \in \Omega $
,
$E' \in (E - \delta , E + \delta ) \cap I$
, and
$n \geq N$
, and this easily gives the desired statement in this case.
Whenever
$(\Omega ,T)$
is a dynamical system and I is a compact interval, we define for
$n \in {\mathbb N}$
,
$$ \begin{align*} {\widetilde{\mathrm{Var}}}_n : C(I \times \Omega, {\mathrm{SL}}(2,{\mathbb R})) \longrightarrow [0,\infty) \end{align*} $$
by
$$ \begin{align*} {\widetilde{\mathrm{Var}}}_n (A) := \sup_{E \in I} \sup_{\varrho, \omega \in \Omega} \{ |\!\log \|A_n(E,\omega)\| - \log \|A_n(E,\varrho)\| | \}. \end{align*} $$
By the preceding proposition, any
$A \in U(I,\Omega )$
satisfies
$$ \begin{align*} \lim_{n \to \infty} \frac{1}{n} {\widetilde{\mathrm{Var}}}_n (A) = 0. \end{align*} $$
In fact, also an even stronger converse holds. This is the content of the next proposition.
Proposition 3.4. Let
$(\Omega ,T)$
be a dynamical system. Let
$I \subset {\mathbb R}$
be a compact interval. Then, any
$A \in C(I \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
with
$$ \begin{align*} \liminf_{n \to \infty} \frac{1}{n} {\widetilde{\mathrm{Var}}}_n (A) = 0 \end{align*} $$
belongs to
$U(I,\Omega )$
.
Proof. Choose
$E \in I$
arbitrary and write A instead of
$A(E,\cdot )$
. By the assumption on A, we can find
$n_k \in {\mathbb N}$
with
$$ \begin{align} \delta_k := \frac{1}{n_k} {\widetilde{\mathrm{Var}}}_{n_k} (A) \to 0, \quad k \to \infty. \end{align} $$
We consider two cases.
Case 1: there exists
$\omega _0\in \Omega $
with
$\liminf _{k \to \infty } ({1}/{n_k}) \log \|A_{n_k} (\omega _0)\| = 0$
. Without loss of generality, we can assume
$\lim _{k \to \infty } ({1}/{n_k}) \log \|A_{n_k} (\omega )\| = 0$
. By equation (3.2), this gives
$\lim _{k \to \infty } ({1}/{n_k}) \log \|A_{n_k} (\omega )\| = 0$
uniformly in
$\omega \in \Omega $
. By Lemma 2.1, we infer
$\lim _{n \to \infty } ({1}/{n}) \log \|A_n (\omega )\| = 0$
uniformly.
Case 2: there exists
$\omega _0 \in \Omega $
with
$L := \liminf _{k \to \infty } ({1}/{n_k}) \log \|A_{n_k} (\omega _0)\|> 0 $
. Assume without loss of generality that
$$ \begin{align*} L_k := \frac{1}{n_k} \log\|A_{n_k} (\omega_0)\| \to L, \; k \to \infty. \end{align*} $$
By equation (3.2) and the definition of
${\widetilde {\mathrm {Var}}}_n$
, we then have for all
$\omega \in \Omega $
,
$$ \begin{align} L_k - \delta_k \leq \frac{1}{n_k} \log\|A_{n_k}\| (\omega) < L_k + \delta_k \end{align} $$
with
$\delta _k \to 0$
,
$k \to \infty $
, and
$L_k \to L$
,
$k \to \infty $
. By part (b) of Lemma 3.1, we can assume without loss of generality that each
$n_k$
is even (as we could otherwise replace
$n_k$
by
$n_k +1 $
).
By
$n_k \to \infty $
, Lemma 2.1, and the upper bound in equation (3.3), there exist
$\delta _k'> 0$
with
$\delta _k' \to 0$
,
$k \to \infty $
, and
$$ \begin{align*} \frac{1}{n} \log \|A_{n} (\omega)\| \leq L + \delta_k' \end{align*} $$
for all
$n \geq n_k/2$
. Also, by
$n_k \to \infty $
, we clearly have
$\tfrac 34 L ({n_k}/{2}) \geq \unicode{x3bb} _0$
(with
$\unicode{x3bb} _0$
from Lemma B.1) for all sufficiently large k.
From these considerations, we see that for arbitrary
$\varepsilon < {1}/{12}$
, the assumptions of Lemma B.1 are satisfied with
$\ell = {n_k}/{2}$
, provided that k is sufficiently large. The statement of the lemma then gives the desired uniformity of A.
Proof of Theorem 1.4
It suffices to consider a compact interval I (compare the proof of Theorem 1.2). Set
$$ \begin{align*} U_{n,\varepsilon} := \bigg\{ A \in C(I \times \Omega,{\mathrm{SL}}(2,{\mathbb R})) : \frac{1}{n} {\widetilde{\mathrm{Var}}}_n (A) < \varepsilon \bigg\}. \end{align*} $$
By continuity of A, the set
$U_{n,\varepsilon }$
is open. Hence,
$$ \begin{align*} \widetilde{U}_{N,\varepsilon} := \bigcup_{n \geq N} U_{n,\varepsilon} \end{align*} $$
is open as well. Thus,
$$ \begin{align*} W := \bigcap_{N, k \in {\mathbb N}} \widetilde{U}_{N, {1}/{k}} \end{align*} $$
is a
$G_\delta $
-set.
It remains to show
$W = U(I,\Omega )$
. To show this, we prove two inclusions.
$U(I,\Omega ) \subset W$
: this is a direct consequence of Proposition 3.3.
$W \subset U(I,\Omega )$
: it is not hard to see that
$$ \begin{align*} W = \bigg\{ A \in C(I \times \Omega,{\mathrm{SL}}(2,{\mathbb R})) : \liminf_{n \to \infty} \frac{1}{n} {\widetilde{\mathrm{Var}}}_n (A) = 0 \bigg\}. \end{align*} $$
Now, the inclusion follows from Proposition 3.4.
4 Upper semicontinuity of the measure of the spectrum
In this section, we consider a dynamical system
$(\Omega ,T)$
and the associated Schrödinger operators, and note that the map
$$ \begin{align} M_\Sigma: C(\Omega,{\mathbb R}) \to [0,\infty), \quad f \mapsto {\mathrm{Leb}}(\Sigma_f) \end{align} $$
is upper semi-continuous. The proof uses variations of ideas developed in [Reference Damanik, Fillman and Lukic18] in the context of continuum limit-periodic Schrödinger operators and was suggested to us by Jake Fillman. This will then imply that
$\{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma _f) = 0 \}$
is a
$G_\delta $
-set.
Proposition 4.1. The map
$M_\Sigma $
defined in equation (4.1) is upper semi-continuous, that is, for every
$\delta> 0$
, we have that
$M_\Sigma (\delta ) := \{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma _f) < \delta \}$
is open.
Proof. Let
$\delta> 0$
be given and let us consider
$f \in M_\Sigma (\delta )$
. We have to show that there exists
$\varepsilon> 0$
such that every
$g \in C(\Omega ,{\mathbb R})$
with
$\|f - g\|_\infty < \varepsilon $
belongs to
$M_\Sigma (\delta )$
as well.
By assumption, we have
$\varepsilon ' := \delta - {\mathrm {Leb}}(\Sigma _f)> 0$
. By basic properties of the Lebesgue measure, we can choose finitely many open intervals
$I_1, \ldots , I_m$
with
$$ \begin{align*} \Sigma_f \subset \bigcup_{j = 1}^m I_j \quad \text{and} \quad \sum_{j = 1}^m |I_j| < {\mathrm{Leb}}(\Sigma_f) + \frac{\varepsilon'}{2}. \end{align*} $$
Let us set
$\varepsilon := {\varepsilon '}/{4m}> 0$
. By the well-known properties of the spectrum of a Schrödinger operator with respect to
$\ell ^\infty $
perturbations of the potential, if
$\|f - g\|_\infty < \varepsilon $
, then
$\Sigma _g \subset B_\varepsilon (\Sigma _f)$
(where the latter notation denotes the
$\varepsilon $
neighborhood).
Putting these two ingredients together, we obtain
$$ \begin{align*} \Sigma_g \subset B_\varepsilon \bigg( \bigcup_{j = 1}^m I_j \bigg), \end{align*} $$
and hence,
$$ \begin{align*} {\mathrm{Leb}}(\Sigma_g) \le {\mathrm{Leb}} \bigg( B_\varepsilon \bigg( \bigcup_{j = 1}^m I_j \bigg) \bigg) \le 2m \varepsilon + \sum_{j = 1}^m |I_j| < 2m \varepsilon + {\mathrm{Leb}}(\Sigma_f) + \frac{\varepsilon'}{2} = \delta, \end{align*} $$
as desired. This completes the proof.
Remark 4.2. The statement of the proposition can also be understood as follows. Let
$\mathcal {K}$
be the set of all compact subsets of
${\mathbb R}$
equipped with the Hausdorff metric
$d_H$
and let
$S(\ell ^2 ({\mathbb Z}))$
be the set of bounded self-adjoint operators equipped with the operator norm
$\|\cdot \|$
. Then, the map
$S(\ell ^2({\mathbb Z}))\ni A\mapsto \sigma (A)\in \mathcal {K}$
, mapping a bounded self-adjoint operator to its spectrum, is continuous and, actually, satisfies
$d_H(\sigma (A),\sigma (B))\leq \|A-B\|$
, by the well-known perturbation theory of self-adjoint operators. Moreover, the map
$\mathcal {K}\ni K\mapsto {\mathrm {Leb}}(K)\in [0,\infty )$
is upper semi-continuous, as is certainly well known (and can also be seen from the proof above). Altogether, we find that the map
$S(\ell ^2 ({\mathbb Z}))\longrightarrow [0,\infty ), A\mapsto {\mathrm {Leb}} (\sigma (A))$
is upper semi-continuous. The statement of the proposition then follows by composition as the map
$C(\Omega ,{\mathbb R})\longrightarrow S(\ell ^2({\mathbb Z}))$
,
$f\mapsto H_\omega ^f$
, is continuous with
$\|H_\omega ^f - H_\omega ^g\|\leq \|f-g\|_\infty $
for each
$\omega \in \Omega $
.
Corollary 4.3. Let
$(\Omega ,T)$
be a dynamical system. Then, the set
$\{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma _f) = 0 \}$
is a
$G_\delta $
-set.
Proof. Simply write
$$ \begin{align*} \{ f \in C(\Omega,{\mathbb R}) : {\mathrm{Leb}}(\Sigma_f) = 0 \} = \bigcap_{n \in {\mathbb N}} M_\Sigma \bigg( \dfrac1n \bigg) \end{align*} $$
and use the fact that each
$M_\Sigma (1/n)$
is open by Proposition 4.1.
5 Denseness of locally constant cocycles
In this section, we consider subshifts. Clearly, the set of locally constant cocycles is dense in the set of continuous cocycles over a subshift. Here, we show that a similar result holds for one-parameter families of cocycles.
Lemma 5.1. Let
$(\Omega ,T)$
be a subshift and let I be an interval in
${\mathbb R}$
. Then, the set
$$ \begin{align*} \{A\in C(I \times \Omega,{\mathrm{SL}}(2,{\mathbb R})) : A(E,\cdot) \mbox{ is locally constant for each }E\in I\} \end{align*} $$
is dense in
$C(I\times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
.
Proof. We consider
${\mathrm {SL}}(2,{\mathbb R})$
as a subspace of the space
${\mathrm {M}}(2,{\mathbb R})$
of real
$2\times 2$
-matrices with metric induced by the standard norm on these matrices.
Let
$A : I\times \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
continuous,
$\varepsilon>0$
, and
$J\subset I$
compact be given.
We will construct a continuous
$A' : J\times \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
such that
$A'(E,\cdot )$
is locally constant for each
$E\in J$
, and
$$ \begin{align*} \|A(E,\omega)- A'(E,\omega)\|\leq \varepsilon \end{align*} $$
holds for all
$E\in J$
and
$\omega \in \Omega $
. This
$A'$
can then be extended to a continuous function
$A^* : I\times \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
, which is locally constant in the second argument, by extending it constantly outside of the compact J. Specifically, with
$J=[E_{\min },E_{\max }]$
, we define
$A^*(E,\omega ):= A'(E_{\max },\omega )$
for
$E\geq E_{\max }$
and
$A^*(E,\omega ) = A'(E_{\min },\omega )$
for
$E\leq E_{\min }$
.
As A is continuous, the set
$A(J\times \Omega )\subset {\mathrm {M}}(2,{\mathbb R})$
is compact. Hence, as the determinant is a continuous function on
${\mathrm {M}}(2,{\mathbb R})$
and
$$ \begin{align*} \det C = 1 \quad \text{and} \quad \frac{1}{\sqrt{\det C}} C - C = 0 \end{align*} $$
for any
$C \in A(J\times \Omega )$
(since
$A(J\times \Omega ) \subseteq {\mathrm {SL}}(2,{\mathbb R})$
), there exists a
$\delta>0$
such that
$$ \begin{align*} \det C> 0 \quad \text{and} \quad \bigg\| \frac{1}{\sqrt{\det C}} C - C \bigg\| \leq \frac{\varepsilon}{2} \end{align*} $$
for any
$C\in {\mathrm {M}}(2,{\mathbb R})$
with distance from
$A(J\times \Omega )$
smaller than
$\delta $
. Without loss of generality, we assume
$\delta \leq {\varepsilon }/{2}$
.
By continuity of A again, we can find finitely many open sets
$I_1,\ldots , I_N$
in I with
$$ \begin{align*}J\subset \bigcup_k I_k\end{align*} $$
such that
$$ \begin{align*} \|A(E,\omega) - A(E',\omega)\|< \frac{\delta}{2} \end{align*} $$
for all
$\omega \in \Omega $
whenever
$E',E$
belong to the same
$I_k$
. As locally constant cocycles are dense in
$C(\Omega ,{\mathrm {SL}}(2,{\mathbb R}))$
, we can then choose for each
$k=1,\ldots , N$
, a locally constant
$B_k \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R})$
with
$$ \begin{align*} \|B_k(\omega)- A(E,\omega)\| < \delta \end{align*} $$
for any
$\omega \in \Omega $
and
$E\in I_k$
.
Let
$\varphi _k$
,
$k=1,\ldots , N$
, be a partition of unity subordinate to
$I_1,\ldots , I_N$
. This means that each
$\varphi _k$
is a continuous non-negative function on I with compact support contained in
$I_k$
and
$$ \begin{align*}\sum_{k} \varphi_k (E) =1\end{align*} $$
for each
$E\in J$
. Define
$$ \begin{align*}A_k :J\times \Omega\longrightarrow {\mathrm{M}}(2,{\mathbb R}), (E,\omega)\mapsto \varphi_k (E) B_k (\omega).\end{align*} $$
Then, each
$A_k$
is a continuous function and
$A_k (E,\cdot )$
is locally constant for each
$E\in J$
. Hence,
$$ \begin{align*} \widetilde{A}:=\sum_k A_k \end{align*} $$
is a continuous function on
$J\times \Omega $
and
$\widetilde {A}(E,\cdot )$
is locally constant for each
$E\in J$
. A short computation invoking
$A(E,\omega ) = \sum _k \varphi _k(E) A(E,\omega )$
for all
$E\in J$
and
$\omega \in \Omega $
shows
$$ \begin{align*} \|\widetilde{A}(E,\omega) - A(E,\omega)\| \leq \sum_k \varphi_k (E) \|B_k(\omega) - A(E,\omega)\|< \sum_k \varphi_k(E)\delta = \delta \end{align*} $$
for all
$E\in J$
. Hence, by our choice of
$\delta $
, we infer
for all
$E\in J$
and
$\omega \in \Omega $
. Define
$A'$
on
$J\times \Omega $
by
Then,
$A'$
is continuous with values in
${\mathrm {SL}}(2,{\mathbb R})$
and
$A'(E,\cdot )$
is locally constant (as the determinant of the locally constant
$\widetilde {A}(E,\cdot )$
is locally constant). By construction, we find
$$ \begin{align*} \|A'(E,\omega) - A(E,\omega)\| & \leq \|A'(E,\omega) - \widetilde{A}(E,\omega)\| + \|\widetilde{A}(E,\omega) - A(E,\omega)\|\\ &\leq \frac{\varepsilon}{2} + \delta\\ & \leq \varepsilon, \end{align*} $$
and the proof is finished.
Remark 5.2. The proof carries over directly to any compact topological space I.
From the preceding lemma and our main results, we immediately obtain the following corollary.
Corollary 5.3. Let
$(\Omega ,T)$
be a subshift over a finite alphabet.
-
(a) If all locally constant cocycles on
$\Omega $
have uniform behavior, then for any interval I, the set
$U(I,\Omega )$
is a dense
$G_\delta $
-set. -
(b) If all locally constant cocycles on
$\Omega $
are uniform, then for any interval I, the set
$U(I,\Omega )$
is a dense
$G_\delta $
-set.
6 Generic absence of non-uniform hyperbolicity for Schrödinger operators over Boshernitzan subshifts
In this section, we show that for a generic continuous sampling function over an aperiodic subshift satisfying the Boshernitzan condition, the associated Schrödinger cocycles are uniform for all energies and the associated spectrum is a Cantor set of Lebesgue measure zero equal to the vanishing set of the Lyapunov exponent. That is, we prove Theorem 1.6 (and its corollary). We then also point out a generalization.
Our proof of Theorem 1.6 relies on what we have shown in earlier sections together with the following crucial feature of subshift satisfying the Boshernitzan condition (B).
Lemma 6.1. [Reference Damanik and Lenz21, Reference Damanik and Lenz22]
Let
$(\Omega ,T)$
be a subshift satisfying the Boshernitzan condition (B). Then, any locally constant cocycle is uniform. In particular, if
$(\Omega ,T)$
is additionally assumed to be aperiodic, then
$\Sigma =\mathcal {Z}$
is a Cantor set of Lebesgue measure zero for each Schrödinger operator associated to a locally constant
$f\in C(\Omega ,{\mathbb R})$
.
Proof of Theorem 1.6
(a) Clearly, the map
$$ \begin{align*} S : C(\Omega) \longrightarrow C({\mathbb R} \times \Omega, {\mathrm{SL}}(2,{\mathbb R})), \; f \mapsto ( (E,\omega) \mapsto A^{E - f}(\omega) ) \end{align*} $$
is continuous. Hence, the inverse image under S of any
$G_\delta $
-set in
$C({\mathbb R} \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
is a
$G_\delta $
-set in
$C(\Omega )$
. Thus, the set
$\mathcal {G}$
consisting of
$f \in C(\Omega )$
with
$A(E, \cdot ) := A^{E - f(\cdot )} \in U({\mathbb R}, \Omega )$
is a
$G_\delta $
-set by Theorem 1.4.
Moreover, for subshifts satisfying the Boshernitzan condition (B), it is known that any locally constant
$f \in C(\Omega )$
yields a one-parameter family
$A(E, \cdot ) := A^{E - f(\cdot )} \in U({\mathbb R},\Omega )$
; see Lemma 6.1. As locally constant
$f\in C(\Omega )$
are dense in
$C(\Omega )$
, we infer that the set
$\mathcal {G}$
is dense as well. Altogether, this shows that
$\mathcal {G}$
is a dense
$G_\delta $
-set.
Finally, as mentioned already, any subshift satisfying (B) is uniquely ergodic and minimal. Hence, by the discussion in the introduction and, in particular, by equation (1.5), the Schrödinger operator associated to
$f\in C(\Omega ,{\mathbb R})$
satisfies
$\Sigma = \mathcal {Z}$
if and only if
$\mathcal {NUH} =\emptyset $
holds, and this is the case if and only if the associated Schrödinger cycle is uniform for all
$E\in {\mathbb R}$
, that is, if and only if
$f\in \mathcal {G}$
. As
$\mathcal {G}$
is a
$G_\delta $
-set, this proves part (a).
(b) By Corollary 4.3, the set
$\{ f \in C(\Omega ,{\mathbb R}) : {\mathrm {Leb}}(\Sigma _f) = 0 \}$
is a
$G_\delta $
-set. Moreover, by aperiodicity and the Boshernitzan condition (B), this set is dense by Lemma 6.1. This shows part (b).
As a by-product of the considerations in the preceding proof, we now deal with our result concerning the question of Walters.
Proof of Corollary 1.9
Any locally constant cocycle on a subshift satisfying the Boshernitzan condition (B) is uniform, see Lemma 6.1. Now, the corollary is immediate from part (b) of Corollary 5.3 (applied with an interval I consisting of one point).
Invoking [Reference Avila and Damanik4], we can give also a variant of Theorem 1.6. This variant deals with a more general setting. We formulate it mainly as a reference point for potential future generalizations.
Theorem 6.2. Let
$(\Omega ,T)$
be an aperiodic dynamical system. Assume that the set
$$ \begin{align*} \{ f \in C(\Omega,{\mathbb R}) : A^{E-f} \mbox{ has uniform behavior for all } E \in {\mathbb R} \} \end{align*} $$
is dense in
$C(\Omega ,{\mathbb R})$
. Then, for any ergodic measure
$\mu $
on
$\Omega $
, the set of
$f \in C(\Omega ,{\mathbb R})$
for which we have that
$\mathcal {NUH} = \emptyset $
(and hence
$\Sigma = \mathcal {Z}$
) and
$\Sigma $
is a Cantor set of Lebesgue measure zero is residual (that is, it contains a dense
$G_\delta $
-set).
Proof. Clearly, the map
$$ \begin{align*} S : C(\Omega) \longrightarrow C({\mathbb R} \times \Omega, {\mathrm{SL}}(2,{\mathbb R})), \; f \mapsto ( (E,\omega) \mapsto A^{E - f}(\omega) ) \end{align*} $$
is continuous.
Hence, the inverse image under S of any
$G_\delta $
-set in
$C({\mathbb R} \times \Omega , {\mathrm {SL}}(2,{\mathbb R}))$
is a
$G_\delta $
-set in
$C(\Omega )$
. Thus, the set
$\mathcal {G}$
consisting of
$f \in C(\Omega )$
with
$A(E, \cdot ) := A^{E - f(\cdot )} \in W({\mathbb R}, \Omega )$
is a
$G_\delta $
-set by Theorem 1.2. Moreover, by assumption,
$\mathcal {G}$
is dense. Hence,
$\mathcal {G}$
is a dense
$G_\delta $
-set and for each
$f \in \mathcal {G}$
, we have
$\mathcal {NUH} = \emptyset $
. By equation (1.1), for all
$f \in \mathcal {G}$
, we then have
$\Sigma = \mathcal {Z}$
. Thus, the set of f such that
$\mathcal {NUH} = \emptyset $
and
$\Sigma =\mathcal {Z}$
hold is residual.
Moreover, by [Reference Avila and Damanik4] and our aperiodicity assumption, the set of f with
${\mathrm {Leb}}(\mathcal {Z}) = 0$
is a dense
$G_\delta $
-set and hence residual.
Since the intersection of two residual sets is residual and
${\mathrm {Leb}}(\Sigma ) = 0$
implies that
$\Sigma $
is a Cantor set by general principles (cf. Remark 1.8(a)), we are done.
Remark 6.3.
-
(a) Our proof of Theorem 1.6 works for all uniquely ergodic minimal subshifts for which locally constant cocycles are uniform, as for these subshifts, the conclusions of Lemma 6.1 hold by [Reference Damanik and Lenz21]. Recent results show the uniformity of locally constant cocycles for all simple Toeplitz subshifts [Reference Grigorchuk, Lenz, Nagnibeda and Sell30, Reference Sell43] (see [Reference Liu and Qu39] for related earlier work as well). All simple Toeplitz subshifts are minimal and uniquely ergodic. Hence, the statement of Theorem 1.6 will hold for these subshifts as well. Note that the class of simple Toeplitz subshifts contains examples not satisfying the Boshernitzan condition. A characterization of those simple Toeplitz subshifts satisfying the Boshernitzan condition is contained in [Reference Liu and Qu39].
-
(b) Theorem 6.2 does not require the dynamical system to be a subshift, nor does it require unique ergodicity or minimality. It can be applied to general ergodic dynamical systems. However, so far, the necessary denseness condition is only known for classes of uniquely ergodic minimal subshifts.
-
(c) Theorem 6.2 gives a slightly weaker conclusion than Theorem 1.6 in that the involved sets are shown to be residual rather than dense
$G_\delta $
-sets. The reason is that in the first part of the proof, we obtain the implication
$f \in \mathcal {G}\Longrightarrow \mathcal {NUH} =\emptyset $
, but do not know the converse (as we are dealing with general dynamical systems). If, additionally, the condition of minimality and unique ergodicity is imposed on the dynamical system, the converse holds and we can conclude that the sets in question are
$G_\delta $
-sets (compare the proof of Theorem 1.6 as well). -
(d) The corresponding results hold for non-singular Jacobi operators. The alert reader may point out that in this more general setting, the standard transfer matrices are not given by
${\mathrm {SL}} (2,{\mathbb R})$
cocycles, but rather by
${\mathrm {GL}}(2,{\mathbb R})$
cocycles. However, it is not difficult (see, e.g., [Reference Beckus and Pogorzelski6, Reference Damanik, Killip and Simon20]) to identify an affiliated family of
${\mathrm {SL}} (2,{\mathbb R})$
cocycles whose study via the results above yields the desired conclusions. -
(e) A similar remark applies in the setting of CMV matrices with dynamically defined Verblunsky coefficients. The necessary tools to adapt the present work to that setting are discussed in [Reference Damanik and Lenz23]. The CMV analog of [Reference Avila and Damanik4], as well as the adaptation of Corollary 1.7, have been worked out in [Reference Fang, Damanik and Guo27].
Remark 6.4. We note that our proof of Theorem 1.2 allows for a (semi-) explicit construction of a potential with infinitely many values (and arbitrarily close to any given potential) whose cocycles are uniform for all energies whenever the underlying dynamical system is a subshift
$(\Omega ,T)$
satisfying the Boshernitzan condition (B). The point of the construction is that any finite sum of locally constant functions
$f : \Omega \to {\mathbb R}$
is locally constant again. Here are the details.
Let
$g_0$
be a locally constant function. Let I be a compact interval containing an open neighborhood of the range of
$g_0$
. Let
$g_n$
,
$n\in {\mathbb N}$
, be an arbitrary sequence of locally constant functions on
$\Omega $
with
$\|g_n\| =1$
for each n. Let
$\varepsilon _n\to 0$
.
We now use the
$W_\varepsilon $
from the proof of Theorem 1.2. Consider
$g_0$
. Clearly,
$g_0$
belongs to
$W_{\varepsilon _1}$
(as
$g_0$
is locally constant). As
$W_{\varepsilon _1}$
is open, there exists a
$\delta _1> 0$
such that any perturbation of
$g_0$
with sup norm not exceeding
$\delta _1$
belongs to
$W_{\varepsilon _1}$
as well. Without loss of generality,
$\delta _1 < 1$
. Consider
$g_0 + {\delta _1}/{2} g_1$
. Clearly, this belongs to
$W_{\varepsilon _2}$
(as it is locally constant). As
$W_{\varepsilon _2}$
is open, there exists a
$\delta _2>0$
such that any perturbation of
$g_0 + {\delta _1}/{ 2} g_1$
with sup norm not exceeding
$\delta _2$
belongs to
$W_{\varepsilon _2}$
. Without loss of generality,
$\delta _2 < \delta _1 / 2$
. Inductively, we can then construct for each
$N\in {\mathbb N}$
, a
$\delta _N$
with
$\delta _{N+1} < \delta _{N}/2$
such that any perturbation of
$g_0 + \tfrac 12(\sum _{j=1}^N \delta _j g_j)$
with sup norm not exceeding
$\delta _{N+1}$
belongs to
$W_{\varepsilon _{N+1}}$
. Consider
$$ \begin{align*} g:=g_0 + \lim_{N \to \infty} \bigg( g_1 + \frac {1}{2}\sum_{j=1}^N \delta_j g_{j+1} \bigg). \end{align*} $$
By construction, g belongs to
$W_{\varepsilon _j}$
for any
$j\in {\mathbb N}$
. Now, the intersection of the
$W_{\varepsilon _j}$
is
$W(I,\Omega )$
(by definition of
$W_\varepsilon $
). This easily gives the desired statement. As our choice of
$g_0$
is arbitrary and
$\sum \delta _j$
can be made arbitrarily small by making
$\delta _1$
as small as necessary, the function g can be made arbitrarily close to any given continuous function on
$\Omega $
.
Acknowledgements
Our original version of part (b) of Theorem 1.6 was based on Theorem 6.2. We are indebted to Jake Fillman for pointing out that the ideas in [Reference Damanik, Fillman and Lukic18] should make the proof possible that we now present. D.D. was supported in part by NSF grants DMS–1700131 and DMS–2054752, Simons Fellowship
$\# 669836$
, and an Alexander von Humboldt Foundation research award.
A Appendix. Notions of uniform hyperbolicity
In this section, we discuss various notions of uniform hyperbolicity in the context of continuous
${\mathrm {SL}}(2,{\mathbb R})$
cocycles and the relationships between them. Related discussions can be found in [Reference Damanik, Fillman, Lukic and Yessen19, Reference Viana46, Reference Yoccoz, Brin, Hasselblatt and Pesin49, Reference Zhang50].
Let
$(\Omega ,T)$
be a dynamical system. Denote the projective space over
${\mathbb R}^2$
consisting of lines through the origin by
${\mathbb R} \mathbb {P}^1$
. This is a topological space in a natural way. Then, any
$B\in {\mathrm {SL}} (2,{\mathbb R})$
can be considered as a map on
${\mathbb R} \mathbb {P}^1$
as it maps lines through the origin to lines through the origin. This map on
${\mathbb R} \mathbb {P}^1$
will be denoted by B as well.
Let us consider the following three conditions for a continuous cocycle
$A : \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
.
-
(UH1) There exists
$L> 0$
with
$\liminf _{n \to \infty } ({1}/{n}) \log \|A_n (\omega )\| \geq L$
uniformly in
$\omega \in \Omega $
. -
(UH2) There exists continuous maps
$u, s : \Omega \longrightarrow {\mathbb R} \mathbb {P}^1$
as well as
$\unicode{x3bb}> 1$
and
$C> 0$
with:-
(α)
$A (\omega ) u(\omega ) = u(T\omega ) \mbox { and } A(\omega ) s(\omega ) = s(T\omega )$
for all
$\omega \in \Omega $
; -
(β)
$\| A_n (\omega ) U \|, \|A_{-n} S(\omega )\| \leq C \unicode{x3bb} ^{-n}$
for all
$n \in {\mathbb N}$
,
$\omega \in \Omega $
whenever
$U \in u(\omega )$
and
$S \in s(\omega )$
are normalized.
-
-
(UH3) There exists
$L> 0$
with
$\lim _{n \to \infty } ({1}/{n}) \log \|A_n (\omega )\| = L$
uniformly in
$\omega \in \Omega $
.
Proposition A.1.
-
(a) The conditions
$\mathrm {(UH1)}$
and
$\mathrm {(UH2)}$
are equivalent. -
(b) Condition
$\mathrm {(UH3)}$
implies
$\mathrm {(UH1)}$
. -
(c) If
$(\Omega ,T)$
is uniquely ergodic, then condition
$\mathrm {(UH1)}$
is equivalent to condition
$\mathrm {(UH3)}$
.
Proof.
-
(a) This is well known; see, for example, [Reference Damanik, Fillman, Lukic and Yessen19, Theorem 1.2], [Reference Viana46, Proposition 2.5], [Reference Yoccoz, Brin, Hasselblatt and Pesin49, Proposition 2], and [Reference Zhang50, Corollary 1].
-
(b) This is obvious.
-
(c) By parts (a) and (b), it suffices to show
$\mathrm {(UH2)} / \mathrm {(UH1)} \Longrightarrow \mathrm {(UH3)}$
. This follows by standard methods as discussed, for example, in [Reference Furman28, Reference Lenz38]. More specifically, [Reference Lenz38, Theorem 3] shows that condition
$\mathrm {(UH3)}$
follows from condition
$\mathrm {(UH1)}$
under an additional minimality assumption. This minimality assumption is only used in the proof to ensure
$(\beta )$
of condition
$\mathrm {(UH2)}$
. Hence, the proof carries over to our case.
Remark A.2. It is not hard to see that the implication
$\mathrm {(UH1)} \Longrightarrow \mathrm {(UH3)}$
fails whenever the system is not uniquely ergodic. Indeed, consider a non-uniquely ergodic dynamical system
$(\Omega ,T)$
. Then, there exists a continuous
$f : \Omega \longrightarrow {\mathbb R}$
such that
$$ \begin{align*} \frac{1}{n} \sum_{k=0}^{n-1} f(T^k \omega) \end{align*} $$
does not converge uniformly in
$\omega \in \Omega $
. Without loss of generality, we can assume
$f \geq 1$
(otherwise replace f by
$f + 1 + \|f\|_\infty $
). Set
$h := \exp (f)$
and let
$A : \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
be given by
$$ \begin{align*} A(\omega) = \begin{pmatrix} h(\omega) & 0 \\ 0 & 1/h(\omega) \end{pmatrix}\!. \end{align*} $$
As
$f \geq 1$
, the cocycle A clearly satisfies condition
$\mathrm {(UH1)}$
with
$L = 1$
. However, we have
$$ \begin{align*} \frac{1}{n} \log \|A_n(\omega)\| =\frac{1}{n} \sum_{k=0}^{n-1} f(T^k \omega), \end{align*} $$
which does not converge uniformly, and therefore condition
$\mathrm {(UH3)}$
fails.
Corollary A.3. Let
$(\Omega ,T)$
be uniquely ergodic. Then, an
$A \in C(\Omega ,{\mathrm {SL}}(2,{\mathbb R}))$
is uniform if and only if it has uniform behavior.
Remark A.4. Together with the results from [Reference Avila, Bochi and Damanik2, Reference Avila, Bochi and Damanik3], this corollary shows that for a rather general uniquely ergodic base dynamical system
$(\Omega ,T)$
, the Schrödinger cocycle
$(T, A^{E-f})$
is uniform for any fixed energy
$E \in {\mathbb R}$
and a generic choice of the sampling function f.
B Appendix. A consequence of the avalanche principle
The avalanche principle deals with products of
${\mathrm {SL}}(2,{\mathbb R})$
matrices
$A_N \cdots A_1$
. Roughly stated, it asserts that the norm of this product is large once the norm of each
$A_j$
and of the products
$A_{j+1} A_{j}$
of consecutive matrices are large. It was introduced by Goldstein and Schlag in [Reference Goldstein and Schlag29], and then extended by Bourgain and Jitomirskaya in [Reference Bourgain and Jitomirskaya13]. Subsequently, various further variations and extensions have been found; see, for example, [Reference Bourgain12, Reference Duarte and Klein24, Reference Duarte and Klein25, Reference Schlag41]. For us, the following consequence, essentially taken from [Reference Damanik and Lenz21] and based on [Reference Bourgain and Jitomirskaya13], will be relevant.
Lemma B.1. There exist constants
$\kappa> 0$
and
$\unicode{x3bb} _0> 0$
such that the following holds. Let
$(\Omega ,T)$
be a dynamical system and
$A : \Omega \longrightarrow {\mathrm {SL}}(2,{\mathbb R})$
. Let
$0 < \varepsilon < {1}/{12}$
be arbitrary. Assume that there exist
$\ell \in {\mathbb N}$
and
$L>0$
with:
-
(a1)
$({1}/{n}) \log \|A_n (\omega )\|\leq L(1 + \varepsilon )$
for all
$\omega \in \Omega $
and
$n\geq l$
; -
(a2)
$L (1 - \varepsilon ) \leq ({1}/{2l})\log \|A_{2l} (\omega )\|$
for all
$\omega \in \Omega $
; -
(a3)
$ \tfrac 34 L \ell \geq \unicode{x3bb} _0$
; -
(a4)
$({1}/{\ell }) ({2 \kappa }/{ \exp (\unicode{x3bb} _0)}) < \varepsilon L$
.
Then,
$$ \begin{align*} L (1- 44\varepsilon) \leq \frac{1}{n} \log\|A_n (\omega)\| \leq L (1 + \varepsilon) \end{align*} $$
for all
$\omega \in \Omega $
and
$n \geq \ell $
.
Proof. The assumptions (a1), (a2), (a3), and (a4) of the lemma are just the conditions (I), (II), (III), and (IV) appearing in the proof of [Reference Damanik and Lenz21, Theorem 1]. The lower bound given in the conclusion of the lemma then follows by following this proof verbatim. The upper bound is obvious from the assumptions.
Remark B.2.
-
(a) Let us emphasize that the number L appearing in the lemma is not required to be the Lyapunov exponent of A. It suffices that it is sufficiently close to the actual Lyapunov exponent. This is relevant for an application to families of cocycles.
-
(b) It may be instructive to discuss the assumptions appearing in the lemma. Assumptions (a3) and (a4) are independent of A. For given
$L> 0$
and
$\varepsilon> 0$
, they will be satisfied for all large enough
$\ell $
. For uniquely ergodic systems, assumption (a1) is automatically satisfied for any given
$\varepsilon $
if
$L = L(A)$
and
$\ell $
is large enough. So, in this sense for uniquely ergodic dynamical systems, the crucial condition is assumption (a2). -
(c) Note that the assumptions of the lemma are open conditions in the following sense. Consider an A satisfying the assumptions for
$\ell \in {\mathbb N}$
,
$L> 0$
, and
$\varepsilon> 0$
. Now, let
$\varepsilon '> \varepsilon $
(with
$\varepsilon ' < 1/12$
) be given. Then, any B sufficiently close to A will satisfy the assumptions of the lemma with the same
$\ell $
and L, and
$\varepsilon $
replaced by
$\varepsilon '$
. Indeed, the last two assumptions (a3) and (a4) do not depend on A and are then clearly satisfied for B. The second assumption (a2) is satisfied for B sufficiently close to A due to
$\varepsilon '> \varepsilon $
. Similarly, the first assumption (a1) is satisfied for B sufficiently close to A by part (a) of Lemma 3.1.
