1 INTRODUCTION
Neutron stars (NSs) manifest the most extreme values of many stellar and physical parameters including spin period, orbital parameters, magnetic field, and kick velocity. These are typically old systems (1–10 Gyr) and relatively short timescales (~ 106 yr) (e.g. Yakovlev & Pethick Reference Yakovlev and Pethick2004; Lorimer Reference Lorimer2008) and show a concentration towards the Galactic centre bulge (which is at ~ 8 kpc) and in the globular clusters (Caranicolas & Zotos Reference Caranicolas and Zotos2009; Taani et al. Reference Taani2012a; Kalamkar Reference Kalamkar2013; Taani Reference Taani2016).
It is generally believed that Millisecond Pulsar (MSPs) are very old NSs spun up owing to mass accretion during the phase of mass exchange in binaries (Alpar et al. Reference Alpar1982). These systems are detectable as active radio pulsars only when they recycled (spun up). While the isolated old NSs have not been identified (Haberl Reference Haberl2007; Kaplan Reference Kaplan2008), and we define them here by their steady flux, predominantly thermal X-ray emission, lack of optical or radio counterparts, and the absence of a surrounding pulsar wind nebula (e.g. Ostriker, Rees, & Silk Reference Ostriker, Rees and Silk1970; Shvartsman Reference Shvartsman1971; Neuhäuser & Trümper Reference Neuhäuser and Trümper1999; Treves et al. Reference Treves, Turolla, Zane and Colpi2000; Pavlov, Sanwal, & Teter Reference Pavlov, Sanwal, Teter, Camilo and Gaensler2004; De Luca 2008; Halpern & Gotthelf Reference Halpern and Gotthelf2010). As a consequence, little is known about their physical and statistical properties. One would hope that the isolated old NSs may be detected as soft X-ray sources (0.5–2 keV) in the
![]() $\emph {eRosita}$
all-sky survey (Merloni et al. Reference Merloni2012; Doroshenko et al. Reference Doroshenko, Ducci, Santangelo and Sasaki2014). However, the estimation of the pulsar velocities depends on the direct distance measurements (Hobbs et al. Reference Hobbs, Lorimer, Lyne and Kramer2005) which can be obtained by the dispersion measure and a Galactic density model (Paczyński Reference Paczyński1990; Hansen & Phinney Reference Hansen and Phinney1997; Cordes & Chernoff Reference Cordes and Chernoff1998; Lorimer Reference Lorimer2008; Sartore et al. Reference Sartore, Ripamonti, Treves and Turolla2010). These studies give a mean birth velocity 100–500 km s−1, with possibly a significant population having
$\emph {eRosita}$
all-sky survey (Merloni et al. Reference Merloni2012; Doroshenko et al. Reference Doroshenko, Ducci, Santangelo and Sasaki2014). However, the estimation of the pulsar velocities depends on the direct distance measurements (Hobbs et al. Reference Hobbs, Lorimer, Lyne and Kramer2005) which can be obtained by the dispersion measure and a Galactic density model (Paczyński Reference Paczyński1990; Hansen & Phinney Reference Hansen and Phinney1997; Cordes & Chernoff Reference Cordes and Chernoff1998; Lorimer Reference Lorimer2008; Sartore et al. Reference Sartore, Ripamonti, Treves and Turolla2010). These studies give a mean birth velocity 100–500 km s−1, with possibly a significant population having
![]() $\emph {v}$
⩾ 1 000 km
$\emph {v}$
⩾ 1 000 km
![]() $\text{s}^{-1}$
. Arzoumanian, Chernoff, and Cordes (Reference Arzoumanian, Chernoff and Cordes2002) favour a bimodal pulsar velocity distribution, with peaks around 100 and 500 km
$\text{s}^{-1}$
. Arzoumanian, Chernoff, and Cordes (Reference Arzoumanian, Chernoff and Cordes2002) favour a bimodal pulsar velocity distribution, with peaks around 100 and 500 km
![]() $\text{s}^{-1}$
. However, the mechanisms of high velocity are still open questions (Wang & Han Reference Wang and Han2010).
$\text{s}^{-1}$
. However, the mechanisms of high velocity are still open questions (Wang & Han Reference Wang and Han2010).
Isolated old NSs have attracted much attention because of the hope that their properties could be used to constrain the poorly understood behaviour. Studying their orbital dynamics in known gravitational potential is very significant to our understanding the Galactic gravitational field, as well as the evolution of the Galactic disk structure itself. Paczyński (Reference Paczyński1990) (hereafter P90) simulated the motion of NSs in a galactic potential and calculated the NS space density distribution. In the same work, P90 also suggested a simplified expression for the gravitational potential which is still often applied in the simulation of NS distribution.
This paper is the third in a series of papers. Wei et al. (Reference Wei2010a, hereafter Paper I) used this potential, and they also adopted a Galactic distribution with one-component initial random velocity models. Wei et al. (Reference Wei2010b) investigated the above gravitational potential of the Galactic disk and several prototypical orbits of stars, and found that all of the orbits are symmetric with respect to the galactic plane. Taani et al. (Reference Taani2012b, hereafter Paper II) constructed a phenomenological model with the same gravitational potential, but under a two-component Maxwellian initial random velocity distribution following P90 and Faucher-Giguère & Kaspi (Reference Faucher-Giguère and Kaspi2006). The conclusion was that there are some non-symmetric orbits. When the motion ranges in the vertical direction and hence becomes larger than the one in the radial direction, the orbits become more regular. It was also found that the irregular character of the motion of NSs increases when the vertical direction becomes larger than radial direction. We mean here when the motion is out of the disk plane. The large Galactic radial expansion (understood as
![]() $\emph {R} \sim 15$
Kpc) could give hints to the distribution of NS progenitors. The majority of them (80%) falls within
$\emph {R} \sim 15$
Kpc) could give hints to the distribution of NS progenitors. The majority of them (80%) falls within
![]() $\emph {R}\le$
25 kpc from the Galactic rotation axis.
$\emph {R}\le$
25 kpc from the Galactic rotation axis.
In the present paper, we extend and complete the study of the old NS sample by describing the dynamical orbital evolution of the isolated old NSs. These isolated NSs are evolved under a smooth, time-independent, 3-D axisymmetric gravitational potential that represents a non-rotated galactic disk. In addition, we extend the purpose of the present study to explore the orbital dynamics of realistic triaxial potential in a systematic way. We focus on plotting the 3-D trajectories and their 2-D projections under a variety of initial conditions. These initial conditions are obtained by performing Monte Carlo simulations to develop perturbation approximations of the 3-D orbits.
Our main objective is to investigate the regular or chaotic nature of the computed trajectories. It is noteworthy to mention that Evans (Reference Evans1994) found some semi-stochastic orbits in triaxial potentials, because the chaos was tentatively associated with linear instability of the short- and intermediate-axis orbits, while Goodman & Schwarzschild (Reference Goodman and Schwarzschild1981) discussed the importance of stochastic orbits in triaxial models.
The structure of the paper is as follows. First, we introduce the model and the Monte Carlo technique we have used. Then, we will analyse the dynamical properties of a set of selected initial conditions, including the Poincaré sections, Lyapunov Asymptotic Exponents, and dark triaxial haloes case. Finally, we will end with some conclusions.
2 SIMULATION AND NUMERICAL SETUP
2.1. Galactic gravitational potential
The equations presented in this paper describe how could the motion and position of NSs be affected by the Galactic gravitational potential. We will follow papers I and II in their procedures to introduce the P90 Galactic gravitational potential. This model is time independent and very simple. The integration of the orbit, using this model, is very rapid and can achieve high numerical precision.
It is noteworthy to mention here that the P90 model is taken to be a homogeneous function of the density, and ignore the interstellar friction. This is a reliable approximation for our axisymmetric model, because the steady state distribution of old NSs depends only weakly on the non-homogeneous part of the galactic potential (Frei, Huang, & Paczyński Reference Frei, Huang and Paczyński1992). Using P90 may not be a good approximation when studying non-axisymmetric models, because rotating non-axisymmetric components (like bars or spirals) can introduce resonances (Patsis et al. Reference Patsis2002). This model is time independent and very simple. The integration of the orbit, using this model, is very rapid and can achieve high numerical precision. This model combines three axisymmetric potential-density forms to produce a model of the matter distribution and its gravitational potential of the Milky Way. The basic components of the Milky Way are the visible
![]() $\emph {disk}$
and
$\emph {disk}$
and
![]() $\emph {spheroid}$
, and the invisible dark matter
$\emph {spheroid}$
, and the invisible dark matter
![]() $\emph {halo}$
. For the bulge (spheroid), we adopt a Plummer sphere (Plummer 1911) in order to increase the central mass of the galaxy. For the disk, we adopt Miyamoto–Nagai potential (Miyamoto & Nagai Reference Miyamoto and Nagai1975) which is added in order to reproduce the scale length of the disk corresponding to n = 0. However, Evans & Bowden (Reference Evans and Bowden2014) and Evans & Williams (Reference Evans and Williams2014) presented new analytical families of axisymmetric dark matter haloes, based on interesting modifications of the Miyamoto–Nagai potential, called Miyamoto–Nagai sequence. And for the dark matter halo, we adopt a logarithmic (modified sphere) potential, which produces a flat rotation curve at large radius, since for strongly flattened systems it is more natural to work in cylindrical coordinates R, z, ϕ rather than spherical r, θ, ϕ (Binney, Merrifield, & Shu Reference Binney, Merrifield and Shu1988; Flynn, Sommer-Larsen, & Christensen Reference Flynn, Sommer-Larsen and Christensen1996).
$\emph {halo}$
. For the bulge (spheroid), we adopt a Plummer sphere (Plummer 1911) in order to increase the central mass of the galaxy. For the disk, we adopt Miyamoto–Nagai potential (Miyamoto & Nagai Reference Miyamoto and Nagai1975) which is added in order to reproduce the scale length of the disk corresponding to n = 0. However, Evans & Bowden (Reference Evans and Bowden2014) and Evans & Williams (Reference Evans and Williams2014) presented new analytical families of axisymmetric dark matter haloes, based on interesting modifications of the Miyamoto–Nagai potential, called Miyamoto–Nagai sequence. And for the dark matter halo, we adopt a logarithmic (modified sphere) potential, which produces a flat rotation curve at large radius, since for strongly flattened systems it is more natural to work in cylindrical coordinates R, z, ϕ rather than spherical r, θ, ϕ (Binney, Merrifield, & Shu Reference Binney, Merrifield and Shu1988; Flynn, Sommer-Larsen, & Christensen Reference Flynn, Sommer-Larsen and Christensen1996).
where Φsph, Φhalo, and Φdisk define the spheroid, halo, and disk components, respectively.
The first two components are described by the same law. For the disk component, we follow a Miyamoto–Nagai potential:
where it depends on two variables, namely R, which denotes the radial distance perpendicular to the Galactic central axis, R 2= x 2 + y 2 and z, which denotes the vertical distance from the Galactic plane. The parameter A is a measure of the radial scale length of the disc while the parameter B is a measure of the disc thickness in the z direction. Galactic discs are much larger in the radial than in the vertical directions, thus the values A will be greater than those of the B parameter in our models. The corresponding values for the disk component are A = 3.7 kpc, B = 0.20 kpc, and M disk = 8.01 × 1010 M⊙.
Using Poisson’s equation, ∇2ϕ = 4πρG, we can obtain the expression for the disc density as
Note that when A = 0, the potential reduces to a spherical potential on the galactic plane (z = 0). The spheroid component of the Galactic gravitational potential is similar to the above:
The spheroid component, A = 0.0 kpc, B = 0.28 kpc, and M sph = 1.12 × 1010 M⊙. Here, we must point out, that this potential is not intended to represent a black hole nor any other compact object, but a dense and massive bulge. Therefore, we do not include any relativistic effects (Jung & Zotos Reference Jung and Zotos2015).
Regarding the halo component of the Galactic gravitational potential, is given by the following equation:
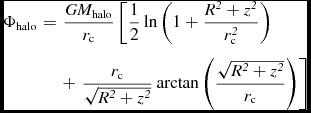 $$\begin{eqnarray}
\Phi \rm _{{\rm halo}}&=&\frac{\it GM\rm _{{\rm halo}}}{\it r_{\text{c}}} \left[\frac{1}{2}\ln \left(1+\frac{\it R^{2}+z^{2}}{\it r_{\text{c}}^{2}}\right) \right.\nonumber\\
&&+ \left.\rm \frac{\it r_{\text{c}}}{\rm \sqrt{\it R^{2}+z^{2}}}\arctan \left(\rm \frac{\rm \rm \sqrt{\it R^{2}+z^{2}}}{\rm \it r_{\text{c}}}\right)\right]
\end{eqnarray}$$
$$\begin{eqnarray}
\Phi \rm _{{\rm halo}}&=&\frac{\it GM\rm _{{\rm halo}}}{\it r_{\text{c}}} \left[\frac{1}{2}\ln \left(1+\frac{\it R^{2}+z^{2}}{\it r_{\text{c}}^{2}}\right) \right.\nonumber\\
&&+ \left.\rm \frac{\it r_{\text{c}}}{\rm \sqrt{\it R^{2}+z^{2}}}\arctan \left(\rm \frac{\rm \rm \sqrt{\it R^{2}+z^{2}}}{\rm \it r_{\text{c}}}\right)\right]
\end{eqnarray}$$
where
![]() $\it r_{{\rm {halo}}}={\rm 12}$
kpc and
$\it r_{{\rm {halo}}}={\rm 12}$
kpc and
![]() $\it M_{\rm {halo}} = {\rm 5.0 \times 10^{10}}$
M⊙.
$\it M_{\rm {halo}} = {\rm 5.0 \times 10^{10}}$
M⊙.
While in a spherically symmetric potential, the x, y, and z components of the angular momentum and the total angular momentum are conserved, out potential only admits two conserved quantities, the total energy E, and the z-component of the angular momentum vector. Therefore, the motion of the objects are in the plane and perpendicular to the vector of the total angular momentum. We assume that the rotation curve is composed of a spheriod, disk, averaged circular velocity, and triaxial halo components in the Galaxy (see Figure 1), and is calculated at any radius by
![]() $v^{2}_{\text{c}}(r) = r\frac{\text{d}\Phi }{\text{d}r}$
. It is clearly seen from the same figure that each contribution prevails in different distances form the galacto-centric R. In particular, at small distances when R ⩾ 3 kpc, the contribution from the spheriod dominates, while at distances of 3 < R < 19 kpc the disk contribution is the dominant factor. On the other hand, at large enough galacto-centric distances, R > 19 kpc, we see that the contribution from the triaxial halo prevails, thus forcing the rotation curve to remain at with increasing distance from the centre (Zotos Reference Zotos2014).
$v^{2}_{\text{c}}(r) = r\frac{\text{d}\Phi }{\text{d}r}$
. It is clearly seen from the same figure that each contribution prevails in different distances form the galacto-centric R. In particular, at small distances when R ⩾ 3 kpc, the contribution from the spheriod dominates, while at distances of 3 < R < 19 kpc the disk contribution is the dominant factor. On the other hand, at large enough galacto-centric distances, R > 19 kpc, we see that the contribution from the triaxial halo prevails, thus forcing the rotation curve to remain at with increasing distance from the centre (Zotos Reference Zotos2014).

Figure 1. Rotation curve of the axisymmetric potential includes a Miyamoto–Nagai disk and spheriod, triaxial halo, and averaged circular velocity in the galactic plane.
2.2. NS initial velocities
The initial velocities of the NSs are calculated as the vector addition of three different velocities: (1) a Maxwellian distribution, (2) a constant kick, and (3) the circular rotation velocities at the birth place. The details on their calculation can be found in Arzoumanian et al. (Reference Arzoumanian, Chernoff and Cordes2002) and Hobbs et al. (Reference Hobbs, Lorimer, Lyne and Kramer2005) and are summarised here.
Concerning the density distribution of the total number of NSs which we used in this simulation, it is about ~ 1 × 107, and it distributes uniformly in the age ⩾ 1 Gyr. This is equivalent to a simulating birthrate of one NS per century (Kulkarni & van Kerkwijk Reference Kulkarni and van Kerkwijk1998; Lyne & smith Reference Lyne and Graham-Smith2007). However, the precise estimates of both the number and lifetime of the NS population are hard to obtain especially at larger distances (see e.g. Keane & Kramer Reference Keane and Kramer2008; Ofek Reference Ofek2009) because they may have been heavily biased by a number of observational selection effects (Lorimer Reference Lorimer2008).
Regarding the kicks simulation, the kick velocity imparted to an NS at birth is one of the major problems in the theory of stellar evolution. However, the physical mechanism that causes this kick is presently unknown and a number of physical models have been described and evaluated (see e.g. Kalogera Reference Kalogera1996; Wang & Han Reference Wang and Han2010; Meng, Chen, & Han Reference Meng, Chen and Han2009). But it is presumably the result of some asymmetry in the core collapse or subsequent SNe explosion (see e.g. Pfahl, Rappaport, & Podsiadlowski, Reference Pfahl, Rappaport and Podsiadlowski2002; Podsiadlowski et al. Reference Podsiadlowski2004). However, the distribution of the kick amplitudes is usually obtained from the analysis of radio pulsar proper motions (Hobbs et al. Reference Hobbs, Lorimer, Lyne and Kramer2005).
The short-lived sudden kick in the phase space has a kick direction uncorrelated with the orientation of the plane and the system velocity that the object acquires because the explosion is also uncorrelated with the rotation in the Galaxy. Therefore, we follow Hansen & Phinney (Reference Hansen and Phinney1997) and find that the distribution is consistent with Maxwellian distribution of kick velocity. Finally, regarding the third element used in the calculation of the initial condition, we choose the initial circular rotation velocity of the NS before a kick. A plot of averaged circular velocity for every parts of our galactic potential model presented is in Figure 1. It rises linearly up to a maximum value and then they become constant for larger radii.
A distinct approach to the analysis of location and velocity of old NSs is based on the Monte Carlo simulation of the evolution of a simulated sample with different initial parameters, and then their orbits are numerically integrated. We would utilise the method of the Poincaré sections to explore their motions. This has been studied in detail in Papers I and II). Once we have selected the above, we can chose a set of initial conditions. We will consider isolated NSs (excluding the MSPs and GCs), being of ages older than 109 yrs and with large radial expansions,
![]() $10 > \emph {R} > 25$
Kpc. The radial distribution has an exponential scale length of λe
−λ|z|, where
$10 > \emph {R} > 25$
Kpc. The radial distribution has an exponential scale length of λe
−λ|z|, where
![]() $\lambda =1/0.07 ~\text{ kpc}^{-1}$
. Here, we assumed a maximum birth height off the plane,
$\lambda =1/0.07 ~\text{ kpc}^{-1}$
. Here, we assumed a maximum birth height off the plane,
![]() $\emph {z}_{\text{max}}$
of 150 pc.
$\emph {z}_{\text{max}}$
of 150 pc.
3 NUMERICAL RESULTS
3.1. Selection of initial conditions
We deal in this section with the analysis of the dynamical evolution of a representative set of NSs’ Orbits in the Galaxy calculated following the previously described distribution of velocities. We aim to obtain a set of different orbits representing NSs at given distances from the axis. Our method follows Arzoumanian (2002). We start by choosing a randomly selected initial position, with boundaries located at the Galacto-centric distance in the r ⩽ 25 kpc.
The initial velocity components of the NSs are also obtained from a random sample, following the vector addition of the three different velocities described in the previous section: the Maxwellian distribution, the constant kick, and the circular motion velocities at the birth place. The direction of the initial velocity vector is chosen randomly within the geometric shape of the potential. We start from a vector based on the circular velocity. Then we add a random kick, in the form of a local perturbation, with modulus following the Maxwellian distribution (Hansen & Phinney Reference Hansen and Phinney1997) and direction to the radial direction. Finally, we add the third vector. This is a velocity vector with a modulus fulfilling a Maxwellian distribution with σv = 265 km s−1 (Hobbs et al. Reference Hobbs, Lorimer, Lyne and Kramer2005; Story & Gonthier Reference Story and Gonthier2007) and σv =190 km s−1 (Hansen & Phinney Reference Hansen and Phinney1997). The direction is given by selecting randomly a direction specified by choosing two angles, 0 < Φ < 360 and − 90 < θ < 90 (Kiel & Hurly 2009).
The equations above were solved numerically in three directions using the -order Runge–Kutta method with adaptive control step sizes (Press et al. Reference Press1992). The initial step size is
![]() ${\text{d}t} = 10^{-4}$
Myr, and calculations of position and velocity in 3-D then continue until 0.1 Myr with adjusted step sizes according to the required accuracy. The data are recorded every 0.1 Myr and the total energy
${\text{d}t} = 10^{-4}$
Myr, and calculations of position and velocity in 3-D then continue until 0.1 Myr with adjusted step sizes according to the required accuracy. The data are recorded every 0.1 Myr and the total energy
![]() $E_{\text{tot}} = \frac{1}{2}(v^{2}_{x} + v^{2}_{y} + v^{2}_{z} ) + \Phi (\emph {R}, \emph {z})$
is checked. The position and velocity then are used for input of the next 0.1 Myr. The procedure used here enabled us to control and achieve required levels of accuracy by using the energy integral.
$E_{\text{tot}} = \frac{1}{2}(v^{2}_{x} + v^{2}_{y} + v^{2}_{z} ) + \Phi (\emph {R}, \emph {z})$
is checked. The position and velocity then are used for input of the next 0.1 Myr. The procedure used here enabled us to control and achieve required levels of accuracy by using the energy integral.
The Monte Carlo simulations were run and the results are given here. One hundred initial conditions were obtained. Different families are identified and we have selected O1, O2, O3. These orbits are listed in Table 1. A periodic orbit is found when the initial and final coordinates coincide with an accuracy at least 10−15. This is a representative set because they show the typical behaviour of the whole distribution, with very large Galactic radial expansion and they are rosette-like type orbits. In addition, the orbits lie essentially in the plane of the long and intermediate axes and so reinforces the shape of the potential to some extent. The most general trajectory for an object in this potential, which allowed us to clarify properties on the structure and configuration of the invariant tori that we encounter in the vicinity of the periodic orbits. The exact initial conditions for the periodic orbit are calculated and listed in Table 1. The trajectories and 2-D projections corresponding to the integration of every initial condition up to a timescale of 108 yr are presented in Figures 2–5.
Table 1. Selected representative orbits, θ and Φ in degrees, |v| in km s−1.


Figure 2. Trajectories corresponding to the different initial conditions of Table 2. These conditions are given in enlarged scale, in order to better view the corresponding morphology. The upper-left panel corresponds to orbit O1. The upper-right panel corresponds to orbit O2. The trajectory is recognised as a precessing banana orbit (see Evans & Bowden Reference Evans and Bowden2014). The bottom-left panel corresponds to orbit O3.

Figure 3. The 3-D Poincaré section x > 0, at y = 0 of the 3-D trajectories corresponding to the selected initial conditions. The upper-left panel corresponds to orbit O1. The upper-right panel corresponds to orbit O2. The bottom left panel corresponds to orbit O3.

Figure 4. The projection on x–z plane of the 3-D Poincaré section. The upper left panel corresponds to orbit O1. The upper right panel corresponds to orbit O2. The bottom left panel corresponds to orbit O3.

Figure 5. The projection on x–vx plane of the 3-D Poincaré section. The upper-left panel corresponds to orbit O1. The upper-right panel corresponds to orbit O2. The bottom left panel corresponds to orbit O3.
As we can see from Figure 2, the different initial heights have an influence on z-direction due to the perturbations and will naturally cause different trajectories, while if the objects are located at different R, trajectories can be less different and may prone to instability through the gravitational perturbation.
It is noteworthy to mention here that if the sun received a kick velocity (50 km s−1) in the Galactic plane (Repetto, Davies, & Sigurdsson Reference Repetto, Davies and Sigurdsson2012), the typical orbit (considered as a circular in the Galactic potential) would turn into a rosette orbit.
3.2. Dynamical analysis
3.2.1. Poincaré sections
In Poincaré sections, periodic orbits appear in the surface of section as a finite set of points. The amount of points depends from the multiplicity of the periodic orbit. This method has been extensively applied to 2-D Hamiltonians in a 2-D plane (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992; Wei et al. Reference Wei2010a; Taani et al. Reference Taani2012b). While in 3-D systems, we have to project the Poincaré surface to spaces with lower dimensions (Contopoulos Reference Contopoulos2004).
By setting
![]() $\emph {y}$
, v
y0 equal to zero at t = 0 (remaining zero at all times) in the Hamiltonian equation, the 3-D Poincaré sections can be found in Figure 3. The points in these figures show the 3-D section. We generate 2 500 consequents of the orbits in 3-D (x, v
x
, z). We find that there are sometimes several orbits from the same family plotted very close to each other. This happens when the sequence of orbits within the family reverses its progression in the x–z plane towards a given direction and very close to the current space position, causing an accumulation of orbits near this position with different local velocities. The stable periodic orbits are surrounded by quasi-periodic orbits that bound to the surface of 3-D tori in a 3-D Hamiltonian system. These quasi-periodic orbits are represented in the surface of section by 2-D tori (Manos, Skokos, & Antonopoulos Reference Manos, Skokos and Antonopoulos2012).
$\emph {y}$
, v
y0 equal to zero at t = 0 (remaining zero at all times) in the Hamiltonian equation, the 3-D Poincaré sections can be found in Figure 3. The points in these figures show the 3-D section. We generate 2 500 consequents of the orbits in 3-D (x, v
x
, z). We find that there are sometimes several orbits from the same family plotted very close to each other. This happens when the sequence of orbits within the family reverses its progression in the x–z plane towards a given direction and very close to the current space position, causing an accumulation of orbits near this position with different local velocities. The stable periodic orbits are surrounded by quasi-periodic orbits that bound to the surface of 3-D tori in a 3-D Hamiltonian system. These quasi-periodic orbits are represented in the surface of section by 2-D tori (Manos, Skokos, & Antonopoulos Reference Manos, Skokos and Antonopoulos2012).
Aiming to gain a better picture, Figure 4 shows the 2-D projection in
![]() $x\text{--}z$
plane, meanwhile Figure 5 shows the 2-D projection in x − vx
. In the first figure, the intersection points distribute in some regular lines on the Poincaré hyper-surface section, while the x − vx
projections are tend to have enclosed curves. This behaviour could indicate a regular motion and a quasi-periodic orbit. All the points along the orbits form ensembles of invariant subset of phase space. The ensemble of old NSs along given orbits for invariant blocks of the galaxy, since the galaxies are seen as built not of stars, but of orbits (Guarinos Reference Guarinos1992).
$x\text{--}z$
plane, meanwhile Figure 5 shows the 2-D projection in x − vx
. In the first figure, the intersection points distribute in some regular lines on the Poincaré hyper-surface section, while the x − vx
projections are tend to have enclosed curves. This behaviour could indicate a regular motion and a quasi-periodic orbit. All the points along the orbits form ensembles of invariant subset of phase space. The ensemble of old NSs along given orbits for invariant blocks of the galaxy, since the galaxies are seen as built not of stars, but of orbits (Guarinos Reference Guarinos1992).
3.2.2. Lyapunov asymptotic exponents
We can conclude from the inspection of these figures all orbits seem to be regular orbits, because they are represented by a tori in the surface of sections (Katsanikas & Patsis Reference Katsanikas, Patsis and Contopoulos2011). In order to crosscheck the results, we have computed the Lyapunov asymptotic exponent for the selected orbits. The ordinary, or asymptotic Lyapunov exponent can be defined as
provided this limit exists (Ott & Yorke Reference Ott and Yorke2008). Here, ϕ(x, t) denotes the solution of the flow equation, such that ϕ(x 0, 0) = x 0, and D is the spatial derivative in the direction of an infinitesimal displacement v.
A system trajectory is chaotic if it shows at least one positive Lyapunov exponent, the movement is confined within certain limited region, and the ω-limit set is not periodic neither composed of equilibrium points (Alligood, Sauer, & Yorke Reference Alligood, Sauer and Yorke1996). Conversely, if the maximum asymptotic Lyapunov exponent is zero, this reflects the existence of a regular motion (that is, a quasi-periodic orbit). Finally, a negative value will reflect the existence of one attractor, but this is not possible in a conservative system like the Hamiltonian we are analysing.
The Lyapunov exponents are computed by calculating the growth rate of the orthogonal semi-axes (equivalent to the initial deviation vectors) of one ellipse centred at the initial position as the system evolves. By solving at the same time, the flow equation and the fundamental equation of the flow (that is, the distortion tensor evolution), we can follow the evolution of the vectors, or axes, along the trajectory, and in turn, their growth rate. This method is described in Benettin et al. (Reference Benettin1980).
The selection of the initial deviation vectors is of importance when computing the Lyapunov exponents during finite integrations, leading to the so-called finite-time Lyapunov exponents (Vallejo, Aguirre, & Sanjuan Reference Vallejo, Aguirre and Sanjuan2003). But when one uses long enough integration times, the axes evolve towards the fastest growing direction and the computation of the growth rates return the asymptotic Lyapunov values (Vallejo, Viana, & Sanjuan Reference Vallejo, Viana and Sanjuan2008).
We have used integration of up T = 105 time-units and the resulting maximal Lyapunov values have been nearly zero in all cases, confirming the analysis done using the Poincaré section methods, it is seen that all orbits retain their regular characteristics along the stellar evolution, the regular orbit bound to the surface of 3-D torus (Kovár et al. Reference Kovár, Kopácek, Karas and Kojima2013) in the phase space forms a narrow curve with zero width. This may be due to a different kick velocities due to SNe mass-loss and natal kicks to the newly formed NS (Podsiadlowski et al. Reference Podsiadlowski2004). By examining the Poincaré section in each case, we found that the system looks integrable and its trajectories lie mostly on tori. These tori are represented by 2-D tori in the surface of section. This is known the KAM (Kolmogorov–Arnold–Moser) theorem (Kolmogorov Reference Kolmogorov1954; Moser Reference Moser1962; Arnold Reference Arnold1963).
3.3. Orbits in the dark triaxial halo case
To investigate the possible effects of spiral structure on the orbital characteristics of trajectory and projections, we adopt the triaxial model of Law, Majewski, & Johnston (Reference Law, Majewski and Johnston2009), that uses a triaxial halo as follows:
where v halo = 128 km s−1, q z represents the flattening perpendicular to the Galactic plane. The various constants C 1, C 2, and C 3 are given by
This potential is triaxial, rotated, and more realistic. As consequent, it reproduces the flat rotation curve for a Milky Way-type galaxy and it can be easily shaped to the axial ratios of the ellipsoidal isopotential surfaces (see Vallejo & Sanjuan Reference Vallejo and Sanjaun2015 for details). We include computations of the three orbits correspondence to O1, O2, and O3 which can be found in realistic galactic-type potentials that incorporates spiral arms (see Figures 6 and 7). The main parameters to play with are the flattening (qz ) and the orientation (ϕ) of the dark halo, since the efficiency of bar formation depends very strongly on the initial orientation of the galaxy disk (Lokas et al. Reference Lokas, Semczuk, Gajda and D’Onghia2015). A lot of work on periodic orbits in the plane of a rotating barred galaxy was carried out by Contopoulos & Papayannopoulos (Reference Contopoulos and Papayannopoulos1980), Papayannopoulos & Petrou (Reference Papayannopoulos and Petrou1983), Mulder & Hooimeyer (Reference Mulder and Hooimeyer1984), Harsoula et al. (Reference Harsoula, Kalapotharakos and Contopoulos2011a, Reference Harsoula, Kalapotharakos and Contopoulos2011b), and Zotos (Reference Zotos2014). All integrable triaxial potentials have a similar orbital structure (e.g. de Zeeuw Reference de Zeeuw1985; Valluri & Merritt 1998; Skokos 2001; Contopoulos Reference Contopoulos2004; Patsis et al. Reference Patsis, Kaufmann, Gottesman and Boonyasait2009; Zotos & Carpintero Reference Zotos and Carpintero2013; Patsis et al. 2014). The plots we delivered were done in spherical coordinates by two different values of the dark halo orientation (ϕ = 0 and ϕ = 90). Figures 6 and 7 (ϕ = 0, q z = 1.25, and λ relatively small value and close to zero for O1) show regular orbits (tube orbits with short and long axes) for oblate and prolate cases, respectively. The effect of spiral structure is presented for all orbits and seems to be chaotic regions on the Poincaré sections (ϕ = 90, q z = 1.5, and λ ⩾ 1 for O2 and O3 in Figures 6 and 7). Thus, NSs in this potential follow harmonic and rotating motion in each of the x, y, z directions independently. These control parameter values are given in Table 2 for all orbits. In Figures 6 and 7 (O1), when ϕ = 0 (stationary) q 1 is then aligned at stable equilibrium point with the Galactic x-axis, and the motion is stable along its axis. The results in this case are comparable with non-triaxial, purely logarithmic potentials. When ϕ = 90, q 1 (see Figures 6 and 7 for O2 and O3) is then aligned with the Galactic y-axis and it takes the role of q 2. We note that tube tori appear in the 3-D projections of the spaces of section as soon as a perturbation is introduced, even if it is a small one (Katsanikas & Patsis Reference Katsanikas, Patsis and Contopoulos2011). At (ϕ, q z ) = (0,1.25) the outer long-axis tube in Figure 6 is wider in the x direction than Figure 7 when seen in projection. It is noteworthy to mention that Figure 6 is symmetric in the v y –y plane, while Figure 7 is not due to the Coriolis force (Gajda, Lokas, & Athanassoula Reference Gajda, Lokas and Athanassoula2016).
Table 2. Maximum asymptotic Lyapunov exponents for the selected representative orbits, two different orientations of dark halo.


Figure 6. Physical trajectories and the corresponding Poincaré sections
![]() $y \text{--} v_y$
, with plane x = 0 and vx
> 0, for the selected representative orbits, for a dark halo orientation of ϕ = 0.
$y \text{--} v_y$
, with plane x = 0 and vx
> 0, for the selected representative orbits, for a dark halo orientation of ϕ = 0.

Figure 7. Physical trajectories and the corresponding Poincaré sections
![]() $y \text{--} v_y$
, with plane x = 0 and vx
> 0, for the selected representative orbits, for a dark halo orientation of ϕ = 90.
$y \text{--} v_y$
, with plane x = 0 and vx
> 0, for the selected representative orbits, for a dark halo orientation of ϕ = 90.
4 CONCLUSIONS
We have found many interesting aspects for simulation of several prototypical orbits of isolated old NSs and their connections with the spatial distribution phenomena, through the long-term stellar dynamics. We employed 3-D Galactic gravitational potential models of normal non-barred galaxies. The models consist of axisymmetric and a triaxial dark halo potentials with three components: bulge, disc, and dark halo. These are relatively simple potentials that can show complex behaviours, which are found in more realistic galactic-type potentials. Then we found that orbits can rotate around the axis of symmetry of the phase space on a surface of section, in the same direction in 3-D and 2-D loops for various values of the initial conditions for the family of axisymmetric and triaxial models. We have used the Poincaré technique to study the 3-D NS trajectories and their 2-D projections. It is shown that both loop and family of orbits arise as a natural consequence of the dynamics of the stable periodic orbits (with regular motion). In addition, the morphology of orbits in triaxial potentials can determine the structure of triaxial galaxy itself. There are 3-D invariant tori containing quasi-periodic motions, these tori are represented by 2-D tori on the surface of the section associated with phase space. In addition, the Lyapunov asymptotic exponent is equal to zero in case of non-triaxial. However, it is clear that the chaotic orbit have a non-zero real exponent, since the finite-time Lyapunov exponents distributions reflect the underlying dynamics (Vallejo et al. Reference Vallejo, Aguirre and Sanjuan2003). We also show that the phase space in triaxial galaxies with a rotated halo is rich in regular and chaotic regions, which is consistent with the analysis done by the Poincaré cross-sections. The results of these motions are strongly affected by the gravitational potential of the galactic disk associated with the effect of kick velocities on the orbital parameters. This can provide us a better visualisation of the old NS dynamics.
The conclusions of the present research are considered as an initial effort and also as a promising step in the task of understanding the underlying dynamics of the phase space by mapping the regular regimes in 3-D axisymmetric potential. Future work will go steps further in detection of the old NSs via accretion of the interstellar medium material which may make them shine, and their weak luminosity could be detected as soft X-ray sources (
![]() $0.5\text{--}2$
keV). However,
$0.5\text{--}2$
keV). However,
![]() $\emph {eROSITA}$
all-sky survey have an excellent capabilities of available survey for this kind of studies, and it should improve our knowledge of Galactic NSs phenomenally for the next decade.
$\emph {eROSITA}$
all-sky survey have an excellent capabilities of available survey for this kind of studies, and it should improve our knowledge of Galactic NSs phenomenally for the next decade.
![]() $\emph {eROSITA}$
will be about 20 times more sensitive than the ROSAT all sky survey in the soft X-ray band (Merloni et al. Reference Merloni2012).
$\emph {eROSITA}$
will be about 20 times more sensitive than the ROSAT all sky survey in the soft X-ray band (Merloni et al. Reference Merloni2012).
ACKNOWLEDGEMENTS
We specifically would like to acknowledge Ying-Chun Wei for his assistance with the simulation code. We are very grateful to Haris Skokos, Panos Patsis, Matthaios Katsanikas, Georgios Contopoulos, Nicola Sartore, Matthew Molloy, Diomar Cesar Lobâo, Barbara Pichardo, and María de los Angeles Perez Villegas for fruitful discussions and useful remarks. A. Taani would like to thank Hamid Al-Naimiy and Awni Al-Khasawneh for their support. The authors would like to thank the anonymous referees for the careful reading of the manuscript and for all suggestions and comments which allowed us to improve both the quality and the clarity of the paper.












