Published online by Cambridge University Press: 14 September 2012
Here we present experimental and theoretical results for how a stratified fluid, initially rotating as a solid body with constant angular velocity, 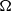 $\Omega $, within a closed cylinder of square cross-section, is spun up when subject to a small, impulsive increase,
$\Omega $, within a closed cylinder of square cross-section, is spun up when subject to a small, impulsive increase, 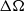 $ \mrm{\Delta} \Omega $, in the cylinder’s rotation rate. The fluid’s adjustment to the new state of solid rotation can be characterized by: (a) an inviscid, horizontal starting flow which conserves the vorticity of the initial condition; (b) the eruption of Ekman layer fluid from the perimeter region of the cylinder’s base and lid; (c) horizontal-velocity Rayleigh layers that grow into the interior from the container’s sidewalls; and (d) the formation and decay of columnar vortices in the vertical corner regions. Asymptotic results describe the inviscid starting flow, and the subsequent interior spin-up that occurs due to the combined effects of Ekman suction through the base and lid Ekman layers, and the growth of the sidewall Rayleigh layers. Attention is focused on the flow development over the spin-up time scale
$ \mrm{\Delta} \Omega $, in the cylinder’s rotation rate. The fluid’s adjustment to the new state of solid rotation can be characterized by: (a) an inviscid, horizontal starting flow which conserves the vorticity of the initial condition; (b) the eruption of Ekman layer fluid from the perimeter region of the cylinder’s base and lid; (c) horizontal-velocity Rayleigh layers that grow into the interior from the container’s sidewalls; and (d) the formation and decay of columnar vortices in the vertical corner regions. Asymptotic results describe the inviscid starting flow, and the subsequent interior spin-up that occurs due to the combined effects of Ekman suction through the base and lid Ekman layers, and the growth of the sidewall Rayleigh layers. Attention is focused on the flow development over the spin-up time scale 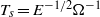 ${T}_{s} = {E}^{\ensuremath{-} 1/ 2} {\Omega }^{\ensuremath{-} 1} $, where
${T}_{s} = {E}^{\ensuremath{-} 1/ 2} {\Omega }^{\ensuremath{-} 1} $, where  $E$ is the Ekman number. (The spin-up process over the much longer diffusive time scale,
$E$ is the Ekman number. (The spin-up process over the much longer diffusive time scale, 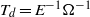 ${T}_{d} = {E}^{\ensuremath{-} 1} {\Omega }^{\ensuremath{-} 1} $, is not considered here.) Experiments were performed using particle imaging velocimetry (PIV) to measure horizontal velocity components at fixed heights within the flow interior and at regular stages during the spin-up period. The velocity data obtained are shown to be in excellent agreement with the asymptotic theory.
${T}_{d} = {E}^{\ensuremath{-} 1} {\Omega }^{\ensuremath{-} 1} $, is not considered here.) Experiments were performed using particle imaging velocimetry (PIV) to measure horizontal velocity components at fixed heights within the flow interior and at regular stages during the spin-up period. The velocity data obtained are shown to be in excellent agreement with the asymptotic theory.