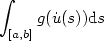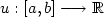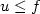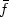Research Article
The Maximum Capacity Shortest Path Problem:Generationof Efficient Solution Sets
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 1-19
-
- Article
- Export citation
On the hardness of approximating the UET-UCT scheduling problem with hierarchical communications
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 21-36
-
- Article
- Export citation
Scheduling multiprocessor taskson two parallel processors
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 37-51
-
- Article
- Export citation
Primal-dual approximation algorithms for a packing-covering pair of problems
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 53-71
-
- Article
- Export citation
Convergence of Prox-Regularization Methods for Generalized Fractional Programming
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 73-94
-
- Article
- Export citation
Generalized Characterizationof the Convex Envelope of a Function
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 95-100
-
- Article
- Export citation
Agrégation des similarités :une solution oubliée
-
- Published online by Cambridge University Press:
- 15 July 2002, pp. 101-108
-
- Article
- Export citation