No CrossRef data available.
Published online by Cambridge University Press: 15 July 2002
We investigate the minima of functionals of the form $$\int_{[a,b]}g(\dot u(s)){\rm d}s$$ 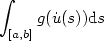 where g is strictly convex. The admissible functions $u:[a,b]\longrightarrow\mathbb{R}$
where g is strictly convex. The admissible functions $u:[a,b]\longrightarrow\mathbb{R}$ 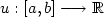 are not necessarily convex and satisfy $u\leq f$
are not necessarily convex and satisfy $u\leq f$ 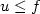 on [a,b], u(a)=f(a), u(b)=f(b), f is a fixed function on [a,b].We show that the minimum is attained by $\bar f$
on [a,b], u(a)=f(a), u(b)=f(b), f is a fixed function on [a,b].We show that the minimum is attained by $\bar f$ 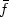 , the convex envelope of f.
, the convex envelope of f.