3.1 Overview

Before elaborating on the model’s details, we provide a summary diagram through Figure 1. The left panel presents some policy interventions that are considered exogenous variables in PPI; for example, reforms to the judicial system to strengthen the rule of law (by modifying the relevant parameter), aligning the countries’ development goals to the SDGs, or promoting synergistic relations between sectors (re-wiring interlinkages). Note that all the interventions take place at the micro-level and, in particular, involve agents in the government arena. Of course, in the long run, and in real life, every aspect of development could be considered endogenous. Here, we have made an exogeneity assumption based on the typical duration of administrative terms (for democratic and semi-democratic governments). In our view, for example, concepts like development goals are more exogenous than indicators. This is so because goals represent the government’s aspirations, and these, in turn, come from much broader processes such as societal consensus, the interests of a small elite, or from the influence of multilateral organizations and international agendas. Endogenizing the formation of aspirations implies modeling cultural and societal changes that involve working on a long-term horizon. Having said that, we should point out that, in contrast to most existing analytic tools that support the 2030 Agenda, PPI focuses on short and midterm analyses. That is, PPI is not designed to forecast indicator levels in 30 or 50 years, but to aid in assessing the feasibility of reaching development goals within a few government terms. Thus, PPI is most useful to national and subnational governments designing development plans; treasuries planning budgets; political parties crafting campaigns; consultants and grading agencies assessing a government’s commitment to development; NGO’s evaluating development strategies; and multilateral organizations coordinating international agendas, to mention a few.

Figure 1. Structure of the PPI model.

The panel at the center of Figure 1 shows that the model makes explicit the linkages between the micro and the macro. At the micro-level, the central authority formulates a strategy and allocates budgetary resources, while the public servants receiving such funds implement the relevant policies (although with objectives that may not coincide with those of the central authority). At the macro level, the network of interdependencies produces spillover effects that contribute, up to a certain extent, to the evolution of the development indicators. In the upward causation component (right vertical arrow), functionaries make effective use of some of the resources they receive from the central government. In the downward causation (left vertical arrow), the overall dynamic produces a continuous reduction in each of the development gaps (i.e., the difference between the goals and the indicators’ current levels). This channel also transmits signals that reflect certain misuse of resources which, in turn, causes the government to penalize inefficient functionaries and reallocate resources. Furthermore, the three circling arrows in the middle of the bottom panel represent a horizontal causation mechanism responsible for social norms of inefficiency that guide the functionaries’ behavior. Finally, the left panel presents the outcomes generated by the model: one observable—the evolution of the indicators—and two non-observable—policy priorities and sectoral inefficiencies.

3.2 Micro-foundations 1: inefficiencies

3.2.1 Public servant benefits

Let us assume that there are $ n $ agents, each in charge of a public policy that is specific to a single policy issue.Footnote ⁵ To implement the mandated policy in a given period $ t $, agent $ i $ receives $ {P}_{i,t} $ resources from the central authority. With these resources, the functionary tries to leverage two potential benefits: (a) the reputation from being a proficient public servant and (b) the utility derived from being inefficient. Proficiency, on the one hand, is beneficial because it signals competence to the central authority and the political system. Therefore, proficient agents gain the political status that may catapult their careers in the future. Inefficiency, on the other hand, is also beneficial because it appeals to the utility derived from private gains.Footnote ⁶ That is, by devoting time and resources to other activities, such as shirking, diverting funds, or benefiting friends (through favorable public tenders), an agent may substitute the benefits from proficiency with the private gains of being inefficient. Of course, there is no free lunch in being inefficient since the central authority exerts monitoring activities and takes punitive actions to increase proficiency. The effectiveness of such mechanisms, however, is bound to the institutional setting of each nation. Accordingly, we elaborate on that below.

We formalize the trade-off between proficiency and inefficiency through

(1)$$ {F}_{i,t+1}=\Delta {I}_{i,t}^{\ast}\frac{C_{i,t}}{P_{i,t}}+\left(1-{\theta}_{i,t}\tau \right)\frac{\left({P}_{i,t}-{C}_{i,t}\right)}{P_{i,t}}, $$

where $ {F}_{i,t+1} $ represents the benefit or utility obtained in the next period. Superficially, equation (1) may suggest that, by specifying the personal gain in absolute terms, the difference $ {P}_{i,t}-{C}_{i,t} $ provides no new information (since proficiency is measured in the same units). As we show ahead, this is not the case because $ {\theta}_{i,t} $ is a function of societal inefficiencies. Therefore, personal gains are a (nonlinear) outcome that depends on the agent and the population’s inefficiencies.

The first summand of equation (1) captures the benefit of being proficient. $ \Delta {I}_{i,t}^{\ast } $ is the change in indicator $ i $ with respect to the previous period (its performance), relative to the changes of all other indicators. More specifically, the relative change in indicator $ i $ is computed as

(2)$$ \Delta {I}_{i,t}^{\ast }=\frac{I_{i,t}-{I}_{i,t-1}}{\sum \limits_j\mid {I}_{j,t}-{I}_{j,t-1}\mid }, $$

and it captures the idea that the central authority evaluates the performance of each policy through development indicators.

Going back to the first summand of equation (1), we find that the relative change in the indicator is pondered by $ \frac{C_{i,t}}{P_{i,t}} $. Here, $ {C}_{i,t} $ is the fraction of the allocated resources $ {P}_{i,t} $ that are effectively used toward the policy. We call it the contribution of agent $ i $. As we will show ahead, $ 0\le {C}_{i,t}\le {P}_{i,t} $, so the factor $ \frac{C_{i,t}}{P_{i,t}} $ represents the efficiency with which resources are being used in policy issue $ i $.

Next, let us focus on the second addend of equation (1), which corresponds to the utility derived from being inefficient. Here, $ {P}_{i,t}-{C}_{i,t} $ is the benefit extracted from not devoting resources to the policy. Thus, when dividing by $ {P}_{i,t} $, it represents the level of inefficiency. We previously mentioned that monitoring and penalties may hinder inefficiencies. This is captured by factor $ \left(1-{\theta}_{i,t}\tau \right) $. Variable $ {\theta}_{i,t} $ is the binary outcome of monitoring inefficiencies. If $ {\theta}_{i,t}=1 $, it means that the government has spotted agent $ i $ in inefficient behavior. In that case, $ i $ is penalized by a factor $ \tau $, such that the benefit from these private gains are reduced. In the literature of public governance, $ \theta $ and $ \tau $ represent two fundamental institutional factors: the potential outcomes of monitoring efforts and the strength of the rule of law. Footnote ⁷

In order to model the binary outcomes of monitoring efforts, we assume that, every period, an independent realization of $ {\theta}_{i,t} $ takes place for each indicator. This is nothing else than a Bernoulli process with a probability of success $ {\lambda}_{i,t} $ determined by

(3)$$ {\lambda}_{i,t}=\frac{\varphi }{1+{e}^{-{D}_{i,t}}}. $$

Parameter $ \varphi $ in equation (3) corresponds to the quality of the monitoring efforts. Note that both $ \varphi \in \left[0,1\right] $ and $ \tau \in \left[0,1\right] $, and that they are time and indicator-independent. This means that these parameters can be directly calibrated from empirical data such as development indicators of public governance.Footnote ⁸

The second factor that determines whether inefficiencies are spotted in equation (3) is $ {D}_{i,t} $. This represents the level of the private gain extracted by agent $ i $, relative to the private gains of all other agents. Formally, this quantity is obtained from

(4)$$ {D}_{i,t}=\frac{\left({P}_{i,t}-{C}_{i,t}\right)-\min \left({P}_{\cdot, t}-{C}_{\cdot, t}\right)}{\max \left({P}_{\cdot, t}-{C}_{\cdot, t}\right)-\min \left({P}_{\cdot, t}-{C}_{\cdot, t}\right)}-\frac{1}{2}, $$

where the term -1/2 is necessary to specify a balanced logistic function in equation (3).

Our motivation to correlate the probability of being spotted with the relative level of inefficiency is rather intuitive. Large inefficiencies, such as corruption scandals, come under the spotlight when they stand out from the norm. Thus, in contrast with the traditional principal-agent view, PPI considers the collective-action problem of social norms that prevent the principal from aligning the agents’ incentives.Footnote ⁹

Now that we have established how the benefit function in equation (1) works, the task of the agent is to determine the level of contribution $ {C}_{i,t} $. Since agents face an environment with uncertainty and, as we will show ahead, there are interdependencies between the indicators, we adopt a robust and empirically validated reinforcement learning model: directed learning (Dhami, Reference Dhami2016).

3.2.2 Public servant learning

The principle behind directed learning is that actions can go in one of two directions: positive or negative; and outcomes encourage or discourage future actions in the same direction.Footnote ¹⁰ For example, if an agent becomes more inefficient and their benefits increase, then, they become even more inefficient in the next period. If, in contrast, the government was able to penalize the agent so that their benefits decreased, they would become more proficient in the next period. Formally, action $ {X}_{i,t} $ of agent $ i $ can be modeled as

(5)$$ {X}_{i,t+1}={X}_{i,t}+\operatorname{sgn}\left(\left({X}_{i,t}-{X}_{i,t-1}\right)\left({F}_{i,t}-{F}_{i,t-1}\right)\right)\mid {F}_{i,t}-{F}_{i,t-1}\mid, $$

where $ \operatorname{sgn}\left(\cdot \right) $ is the sign function.

$ {X}_{i,t} $ is an abstraction of any type of action that an agent may take to be inefficient (e.g., shirking, diverting funds, or favoring friends), so $ X $ may take any real value. In order to map action $ {X}_{i,t} $ into the value of the effective resources, we define

(6)$$ {C}_{i,t}=\frac{P_{i,t}}{1+{e}^{-{X}_{i,t}}}. $$

Equation (6) incorporates the directed learning model into the policymaking process while making sure that $ {C}_{i,t}\le {P}_{i,t} $. This completes the micro-foundations that give place to a specific type of inefficiencies—technical inefficiencies—that arise from the policymaking process.Footnote ¹¹ This part of the model has no free parameters (since $ \varphi $ and $ \tau $ can be imputed from data). Therefore, the learning model does not require calibration.

3.3 Micro-foundations 2: government policy priorities

The policy priorities are represented by the allocation profile $ P={P}_1,\dots {P}_n $. At this point, it is important to introduce a distinction between those indicators that can be intervened via public policies: instrumental; and those that cannot: collateral. An instrumental indicator exists if the government has a policy or program to impact it (i.e., it receives resources). In contrast, a collateral indicator cannot be directly impacted; it is a composite aggregation of various topics, for example, GDP per capita or financial development.Footnote ¹² Naturally, policy priorities can only be defined on the $ n $ instrumental indicators, while there can only be $ n $ public servants (one in charge of each instrumental indicator). When talking about all the indicators together, we say that there are $ N\ge n $ policy issues in total.

While a government determines its policy priorities over the $ n $ instrumental issues, it may have aspirations to improve all $ N $ indicators, even without explicit policy instruments for the collateral ones (political campaigns promising unrealistic GDP growth are a good example). Such aspirations are captured in a vector of goals $ {T}_0,\dots, {T}_N $. Note that we have established a clear difference between goals and priorities, two concepts that are often confused in the literature of sustainable development. Goals, on the one hand, represent the aspirations of a government. They are exogenous variables in PPI and consist of specific values that the central authority wants to reach. Priorities, on the other hand, are not aspirations, but actions. Because of the political economy of the policymaking process, priorities are endogenous variables.

The objective of the government is to close the gap between the goals and the indicators by solving the problem

(7)$$ \min \left[\sum \limits_i^N{\left({T}_i-{I}_{i,t}\right)}^2\right] $$

through the allocation of budgetary resources across policy issues. The central authority achieves this by adapting its allocation profile $ P $. This formulation implies that the government wants to achieve goals for topics in which it may not necessarily have policy instruments. This is why concepts such as accelerators Footnote ¹³ are so important to the 2030 Agenda.

What determines the distribution of resources $ P? $ Different countries and their governments may have various motivations for allocating resources in specific ways. For example, a welfare state may be more welcoming of pro-social policies, such as unemployment benefits and social housing, while a technologically oriented one may prioritize R&D investment. PPI is flexible enough to allow any function or algorithm to model how a government steers its priorities. This, of course, requires certain priors and data. In absence of such information, we remain agnostic about the specificity of each government and provide a simple yet empirically valid policy prioritization heuristic. First, the government agent uses the rule of prioritizing laggard topics because there is a generalized belief that these issues are bottlenecks to development. In fact, this was a promoted approach during the Millennium Development Goals agenda (Garmer, Reference Garmer2017, p. 1). Thus, the government measures the normalized gaps between goals and indicators

(8)$$ {G}_{i,t}=\frac{\left({T}_i-{I}_{i,t}\right)-\min \left({T}_{\cdot }-{I}_{\cdot, t}\right)}{\max \left({T}_{\cdot }-{I}_{\cdot, t}\right)-\min \left({T}_{\cdot }-{I}_{\cdot, t}\right)}. $$

The index with a $ \cdot $ symbol indicates that we perform an operation on one of the indices while holding a specific value for the other. For example, if we want the maximum value across time for the ith quantity of $ I $, then we write $ \max \left({I}_{i,\cdot}\right) $. Similarly, if we want the lowest indicator in a given period $ t $, then we write $ \min \left({I}_{\cdot, t}\right) $.

Besides supporting poorly developed issues, the government avoids systematically allocating resources to inefficient policies. Therefore, our government heuristic also takes into account the normalized history of spotted inefficiencies of each agent, represented by

(9)$$ {H}_{i,t}=\frac{\sum_l^t{\theta}_{i,l}\left({P}_{i,l}-{C}_{i,l}\right)-\min \left[{\sum}_l^t{\theta}_{\cdot, l}\left({P}_{\cdot, l}-{C}_{\cdot, l}\right)\right]}{\max \left[{\sum}_l^t{\theta}_{\cdot, l}\left({P}_{\cdot, l}-{C}_{\cdot, l}\right)\right]-\min \left[{\sum}_l^t{\theta}_{\cdot, l}\left({P}_{\cdot, l}-{C}_{\cdot, l}\right)\right]}. $$

The goal-indicator gap encourages prioritization, while a reputation of inefficiency discourages it. However, international experience suggests that the gaps play a more central role than the inefficiencies (Izquierdo et al., Reference Izquierdo, Pessino and Vuletin2018). Thus, we look for a function where the allocation $ {P}_{i,t} $ depends mainly on $ {G}_{i,t} $ and, in a lesser measure, on $ {H}_{i,t} $. We adopt the functional form.

(10)$$ {q}_{i,t}={G_{i,t}}^{1+{H}_{i,t}}, $$

which can be normalized to obtain the policy priorities

(11)$$ {P}_{i,t}=\frac{q_{i,t}}{\sum_j{q}_{j,t}}. $$

Equation (10) is rather intuitive. In the term $ {G}_{i,t}^{1+{H}_{i,t}} $, the base is always fractional while the exponent is always greater than one. This means that policy issues with more visible inefficiencies will be penalized more. Appendix D.5 shows that the estimated allocation profiles are robust across different functional forms that follow the same logic as equation (10).

Up to this point, it is important to recall that the allocation profile $ P $ refers to transformative resources. Transformative refers to those resources allocated to generate changes in development indicators beyond those already set in motion by committed expenditure (like maintaining highways and hospitals). While there may be committed expenditure that contributes to the natural growth of the indicator, this is accounted for in a growth factor that we explain below. In economic terms, PPI models public expenditure that, on the margin, improves the indicators. That is, $ {P}_{i,t} $ should not be interpreted as an absolute value (and neither monetary), but as the transformative resources currently spent in relation to those historically assigned in policy issue $ i $.Footnote ¹⁴ For example, $ {P}_{i,t}>{P}_{j,t} $ should be interpreted as: policy issue $ i $ receives, in period $ t $, more priority than $ j $ in relation to what each one has been historically allocated.

3.4 Macro-dynamics: development indicators

Now that we have built the micro-foundations of the model, we connect them to the evolution of the development indicators. In doing so, we aim at generating indicator dynamics that resemble empirical data in three aspects: (a) that each indicator starts at a given value and reaches a specific final value and, (b) that all indicators arrive at their final values at the same time, and (3) that these data present a certain level of volatility. We address attribute (a) here and leave (b), and (c) for the calibration procedure explained in Appendix D in the supplemental materials.

3.4.1 Indicator dynamics

From the micro-foundations, we know that a fraction $ {C}_{i,t} $ (the contribution) of an allocation $ {P}_{i,t} $ is used in the implementation of public policies. In conjunction with the incoming spillover effects $ {S}_{i,t} $ (these could be positive or negative), public policies transform the associated indicator $ {I}_{i,t} $. We model this transformation through a random growth process. Let $ {\gamma}_i $ denote a probability associated with the growth process experienced by indicator $ i $. This probability depends on a combination of a parameter $ {\alpha}_i $, network effects, and budgetary allocations. The value of $ {\gamma}_i $ may be above the lower-bound $ {\alpha}_i/\left({\alpha}_i+1\right) $, due to the contributions fostering the public policy, and the existence of incoming spillovers. Therefore, the growth process is modeled as independent Bernoulli trials with a probability of success

(12)$$ {\gamma}_{i,t}=\frac{\alpha_i+{C}_{i,t}/{P}_t^{\ast }}{\alpha_i+{e}^{-\frac{NS_{i,t}}{\sum_j\left({T}_j-{I}_{j,t}\right)/\left({T}_j-{I}_{j,0}\right)}}}, $$

where $ {P}_t^{\ast } $ is the maximum amount of allocated resources across all policy issues in period $ t $. Note that $ \frac{C_{i,t}}{P_t^{\ast }}=\frac{C_{i,t}}{P_{i,t}}\frac{P_{i,t}}{P_t^{\ast }} $, which means that the effect of the contribution is the combination of how efficiently are the resources being used ($ {C}_{i,t}/{P}_{i,t} $) and how much resources policy issue $ i $ receives in comparison with all other issues ($ {P}_{i,t}/{P}_t^{\ast } $). The sum dividing the spillover term $ {S}_{i,t} $ is a correction that we explain ahead.

Next, we define the growth equation of indicator $ i $ as

(13)$$ {I}_{i,t+1}={I}_{i,t}+{\alpha}_i\left({T}_i-{I}_{i,t}\right)\xi \left({\gamma}_{i,t}\right), $$

where $ \xi \left(\cdot \right) $ is the binary outcome (0 or 1) of a growth trial. The growth factor $ {\alpha}_i $ lives in $ \left(0,1\right) $, and it shapes both the probability of success—as indicated in equation (12)—and the amount of growth. We can think of $ {\alpha}_i $ as all the other determinants responsible for an indicator’s growth that are not explicit in the model.Footnote ¹⁵ This factor needs to be calibrated to match the second attribute of the data: all indicators reach their final values at the same time. Note that the gap $ {T}_i-{I}_{i,t} $ shrinks as the indicator grows and that $ {I}_{i,t} $ is always lower than $ {T}_i $. This means that the indicator is guaranteed to converge to $ {T}_i $, which takes care of the first attribute of the data: reaching the indicator’s specific final value. Because of these logistic-like convergence dynamics, the change in the indicator becomes, on average, smaller as it approaches $ {T}_i $, so the magnitude of spillover effects $ {S}_{i,t} $ decreases with time. In order to correct this artifact, equation (12) divides the spillover term, in the exponential function, by the average normalized gap at time $ t $.

Note that the probabilistic nature of equation (13) is consistent with the fact that indicators are not directly manipulable, but rather, governments try to affect them through policy interventions, which sometimes succeed and sometimes fail, depending on the efficiency and efficacy of their implementation. It also implies that the interlinkages do not represent causal relations, but conditional dependencies that increase or decrease the chance of improving an indicator. This is consistent with our earlier point on the impossibility to establish causation in aggregate data. We elaborate on the impossibility of causal networks of development indicators in the next section.

3.4.2 SDG networks and spillovers

Let us define a network with $ N $ nodes, each one corresponding to an indicator. An arrow $ i\to j $ represents a change in indicator $ j $ conditioned by a change by indicator $ i $, not a causal link. That is, the existence of $ i\to j $ means that, if we observe a change in $ j $, a change in $ i $ was likely to have taken place. However, a change in $ i $ does not necessarily trigger a change in $ j $ (otherwise it would be a causal link).Footnote ¹⁶ In terms of the model, a positive edge $ i\to j $ indicates a higher likelihood of $ j $ growing, while a negative one translates into a lower likelihood. This is consistent with conditional dependencies. A further discussion of why SDG networks—by themselves—cannot capture causal relations is provided by Ospina-Forero et al. (Reference Ospina-Forero, Castañeda and Guerrero2020).

We say that a spillover from $ i $ to $ j $ takes place through the interaction of $ i $’s change $ \Delta {I}_{i,t}={I}_{i,t}-{I}_{i,t-1} $ and the intensity of the conditional dependency specified in the adjacency matrix $ \unicode{x1D538} $. Therefore, the incoming spillovers from $ i $ to $ j $ in period $ t $ are

(14)$$ {S}_{i\to j,t}=\Delta {I}_{i,t-1}{\unicode{x1D538}}_{ij}, $$

which can be positive, negative, or zero. We are interested in the strength of incoming spillovers that each node receives. Thus, the relevant measure to consider is the net incoming spillovers

(15)$$ {S}_{j,t}=\sum \limits_i\Delta {I}_{i,t-1}{\unicode{x1D538}}_{ij}, $$

which is one of the determinants of successful growth in equation (12).

3.5 Summary

Appendix B provides a list with all the model variables presented above, specifying whether they are endogenous or exogenous, and the nature of their imputation/calibration. We would like to point out that PPI takes five exogenous sources of information as inputs: (a) initial conditions, (b) spillover network, (c) goals, (d) governance parameters, and (e) growth factors. The first one is usually collected by governments and international organizations. The second one can be estimated via quantitative or qualitative methods (see Ospina-Forero et al., Reference Ospina-Forero, Castañeda and Guerrero2020 for a review on network-estimation methods). The third is an exogenous variable that can be built from societal consensus, political platforms, and public consultations, to mention a few. The fourth can be obtained from international datasets, such as the Worldwide Governance Indicators. The fifth is calibrated (see Appendix D). Algorithm 1 summarizes the model in a few lines. Without priors on the initial values of the endogenous variables, we use random assignments and Monte Carlo simulations. Appendix D.4 elaborates on the stability of simulations in a Monte Carlo setting. Finally, while Algorithm 1 considers four types of exogenous inputs (boundary conditions, edge weights, governance indicators, and growth factors), we should point out that there can be additional sources of information, for example, a vector specifying how flexible are the transformative resources to be reallocated in each policy issue. This is common among federations, where the subnational governments may receive resources from the federal authority with “strings attached”; that is these resources have to be spent in specific topics. Of course, such kind of data may only be available to certain governmental authorities. Nevertheless, the possibility of incorporating them into the analysis of PPI speaks to its flexibility and usefulness.

Algorithm 1. PPI pseudocode.

4.1 Development indicators

We compiled a dataset with 141 national-level development indicators of Mexico, covering the period 2006–2016, such that each SDG contains at least one indicator. Given the current social context of Mexico and the interest of the stakeholders of the project, special attention was given to collecting indicators associated with SDG 16. We split SDG 16 into its two components: peace and justice (SDG 16a) and strong institutions (SDG 16b). This separation is important in the Mexican context as the former covers violence issues while the latter touches on anti-corruption policies. All indicators have been pre-processed so that their values are in the range [0,1], and larger magnitudes denote better outcomes.

A limitation of the official UN SDG database is that many indicators lack comprehensive time coverage. For this reason, we collected data from additional sources and performed a manual classification into the SDGs. Finally, we labeled each indicator as instrumental or collateral according to the inputs received in a stakeholder workshop co-organized with the UNDP and the Mexican National Laboratory for Public Policy. Figure 2 shows the total number of instrumental and collateral indicators by SDG. Accordingly, there are enough instrumental topics to define policy priorities across all the SDGs.

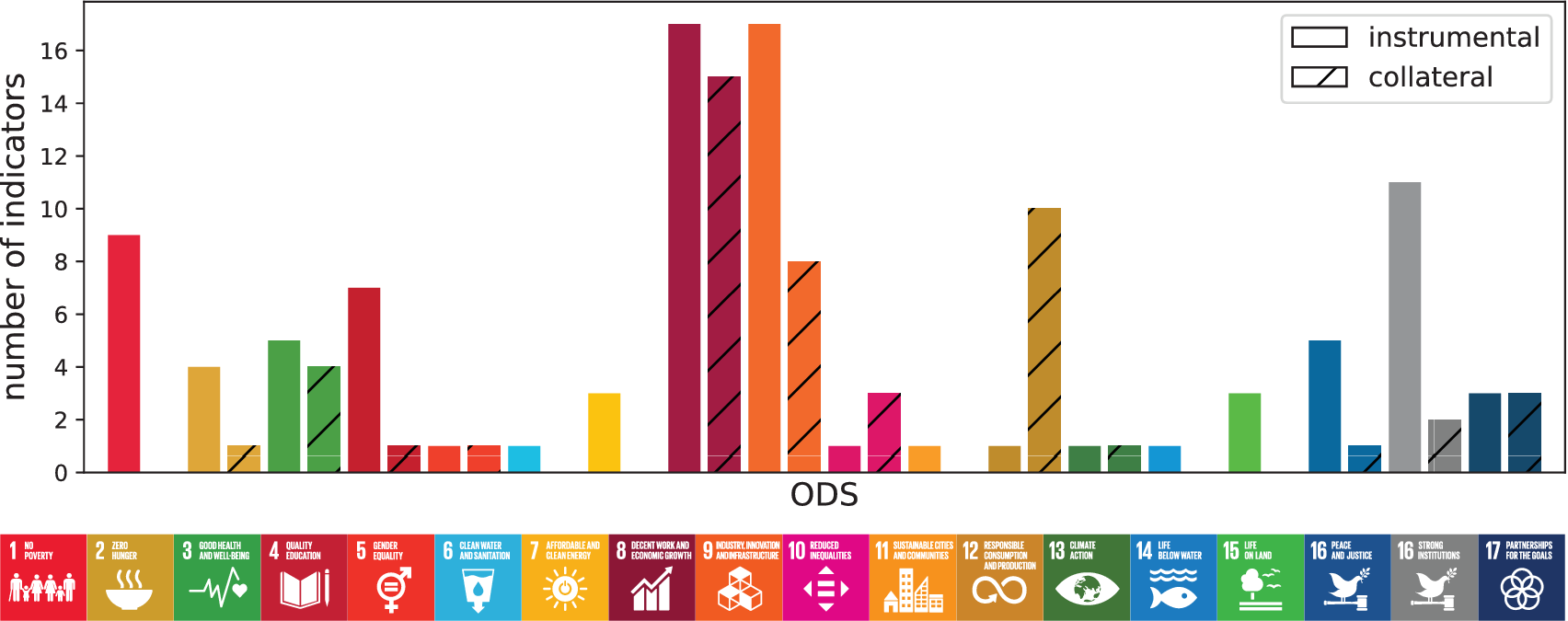
Figure 2. Number of indicators by type and sustainable development goal.

Table 1 shows the summary statistics of the data by source.Footnote ¹⁷ The most salient feature in this table is the relatively large number of missing observations coming from CONEVAL (the watchdog of social policy in Mexico). This is because CONEVAL’s indicators are constructed on a biannual basis. Overall, whenever we encounter missing values, we impute them through linear interpolations. Further details can be found in Appendix A.Footnote ¹⁸

Table 1. Development-indicator data by source

Note. CONEVAL: Mexican institution responsible for the evaluation of social policy. INEGI: Mexican national statistics bureau.

Abbreviations: FAO, Food and Agriculture Organization of the United Nations; SDG, sustainable development goal; UN, United Nations; WDI, World Development Indicators.

4.2 Governance

For the governance parameters related to the quality of monitoring efforts $ \varphi $ and the strength of the rule of law $ \tau $, we use data from the Worldwide Governance Indicators. These indicators reflect the perception of citizens, entrepreneurs, experts in the public/private sector, and NGOs. Although perception-based indices have well-known limitations, they are still one of the best metrics used in corruption studies like those described by Guerrero and Castañeda (Reference Guerrero and Castañeda2019). The indicator of control of corruption reflects the quality of the monitoring efforts by the central authority, which is an important element in the model. The indicator of rule of law, on the other hand, captures the quality of institutions designed to reassure a law-abiding society. Just like with the SDG data, we normalize these indicators across all countries in the sample, and for the years corresponding to the sampling period of the dataset. The normalized values fall within [0,1]. Therefore, the values of $ \varphi $ and $ \tau $ reflect Mexico’s quality of monitoring and rule of law relative to the rest of the world (Appendix G provides a thorough analysis on the relevance of these parameters for curbing inefficiencies).

4.3 Network

The network of conditional dependencies between development indicators can be obtained through various methods, each one implying certain assumptions about the data and its underlying generating mechanisms. Ospina-Forero et al. (Reference Ospina-Forero, Castañeda and Guerrero2020) provide a comprehensive survey on this topic. We must highlight that estimating large networks from time series is a burgeoning research area, so there is no strongly preferred method or accepted gold standard, especially given that development-indicator series tend to be quite short; with generally no more than 10 observations.Footnote ¹⁹ Our method of choice is the Sparse Gaussian Bayesian Networks approach, developed by Aragam et al. (Reference Aragam, Gu and Zhou2019) and accessible through the R package sparsebn. We employ sparsebn to estimate the conditional dependencies network of Mexico using the time series constructed from its development indicators. The method estimates a structural equation model and returns a weighted directed network of conditional dependencies where the edges have been filtered in order to minimize potential overfitting (hence the sparseness of the topology).Footnote ²⁰

The sparsebn method is applied to the first differences of the indicators’ time series (for the period 2006–2016). This is recommended to eliminate potential false positives due to inertial trends that are attributable to the natural temporal evolution of the data (and not to their interdependencies). Next, to improve the estimation, those edges considered—by expert knowledge—to be false positives are removed. Finally, to prevent distorting effects due to extreme values in edge weights (outliers), the magnitude of the maximum and minimum weights is bound by the 95th percentile of the weights’ magnitude distribution (the distribution of the absolute values of the weights).

We represent the network as a matrix $ \unicode{x1D538} $ where the dependencies or edges go from rows to columns. Hence the strength of a dependency $ i\to j $ is indicated by the weight $ {\unicode{x1D538}}_{i,j} $. If the sign of the weight is positive (negative), we have a synergy (trade-off). $ \unicode{x1D538} $ should be interpreted as a stylized fact—a collection of conditional dependencies—that the model takes into account to explain the dynamics of the indicators. Table 2 provides descriptive statistics of the estimated network.

Table 2. Network statistics

Note. The network has been divided into synergies and trade-offs. Due to the uneven distribution of indicators across SDGs, we normalize the statistics by the number of indicators in the relevant SDG. In(out)-degree is the number of incoming(outgoing) connections to(from) a node. The in(out)-strength is the sum of the weights of all incoming(outgoing) connections to(from) a node.

Abbreviations: SDG, sustainable development goal.

4.4 Goals

When calibrating the model to historical data, we can assume that the government’s aspirations or goals are the final values of the indicators. However, for a prospective analysis, the aspirations may be any hypothetical combination of values for the indicators (higher than their initial values). In Mexico, and other Latin American countries, governments are required by law to publish a development plan at the beginning of their term. The purpose of such a document is to provide clarity on development strategies and objectives, as well as to facilitate ex-post evaluations. For the Mexican federal government, this document is the National Development Plan (NDP) and, in its 2019–2024 edition, consists of 234 objectives (i.e., policy issues), 67 of which have concrete development indicators. That is, this document presents the goals that the administration—taking office in 2019—wants to achieve in a 6-year term. Each of these indicators has been assigned a development goal, which is a specific value to be achieved for the indicator. Thus, we use this information as a guideline to conduct the prospective analysis. Figure 3 shows extracts of the Annex XVIII-Bis of the NDP (Cámara de Diputados, Reference de Diputados2019) containing some of its development goals.

Figure 3. Example of official development goals.

Note: Extracts from the Annex XVIII-Bis of Mexico’s National Development Plan. Each box describes an indicator used to evaluate progress in a specific policy issue of the NDP, as well as its baseline value (Línea base) and its goal (Meta). From left to right, the indicators track the following policy issues: carbon emissions from burning fuels; poor access to health services; energetic independence; informal labor. In the same order, the extracts were obtained from pages 187, 103, 166, and 128.

In spite of providing explicit objectives for the NDP indicators, these data do not map directly into the SDG indicators. This is partly because governments evaluate their development through metrics that are specific to their context and needs, meaning that these indicators may not necessarily exist for other countries and, thus, are not part of official international SDG datasets. Nevertheless, the Mexican Treasury has developed a methodology to classify the NDP objectives into the SDGs (SHCP, 2017). The NDP provides the resulting classification of the 67 indicators (Cámara de Diputados, Reference de Diputados2019, pp. 216–19). Thus, to determine the development goals for the prospective analysis, we used the following procedure.

1. 1. Compute the proposed growth rate for each indicator.

2. 2. If an indicator in the SDG database corresponds to one in the NDP, assign the associated growth rate.

3. 3. If an indicator in the SDG database has no corresponding indicator in the NDP, assign the average growth rate of the NDP indicators that are in the same SDG.

4.5 SDG budgeting

An additional innovation of the Treasury’s methodology consists of linking expenditure categories into SDGs (SHCP, 2017). This is something unique to Mexico, and only now it is being emulated by other nations, so our study also provides a first view to cutting-edge open spending data and a framework to exploit it. The SDG-fiscal data consists of more than 1,500 expenditure records, each one categorized into one SDG. Figure 4 shows the distribution of resources allocated through the Mexican budget for 2019 across the 17 SDGs. The fiscal data that have been classified into SDGs do not represent the entire budget of the government because some types of expenditure do not fit any SDG (e.g., expenditure on national defense). Besides, these data do not distinguish between transformative and non-transformative resources. Thus, the exercise to be performed with this information is purely exploratory. Nonetheless, we consider that is important to demonstrate how PPI can exploit expenditure data. Finally, and to avoid any confusions, let us clarify that these budgeting data are only used in one simulation exercise, and are not employed to calibrate the model.

Figure 4. 2019 budget distribution across sustainable development goals. The units in the vertical axis are current Mexican pesos in logarithmic scale.

5.1 Calibration of growth factors and convergence time

In order to infer retrospective policy priorities, we need to calibrate the model’s parameters. The motivation behind such calibration is to generate synthetic indicators that reflect certain features of the historical data by tuning an aggregate quantity (at the level of each indicator) representing the contribution of those factors that the model does not specify explicitly among its agents and processes. More specifically, the growth factors (the free parameter $ {\alpha}_i $) describe the actions of a set of agents that are not made explicit in the model but that exert influence on the evolution of SDG indicators. For instance, private agents (e.g., firms and households) may enable the growth of certain indicators, irrespective of the contributions made by the government. Likewise, the actions of international agents (e.g., multilateral organizations) or events (e.g., a global pandemic) could decelerate development in some issues. Next, we describe how to find the values of these growth factors.

Appendix D, in the supplementary material, presents in detail the different calibration procedures and studies their computational efficiency. To calibrate each individual growth factor in the vector $ {\alpha}_1,\dots, {\alpha}_N $, the method homogenizes convergence times across indicators. This is required because all empirical indicators reach their final values in the same number of periods. Therefore, with the calibration procedure, we are able to preserve this property in the synthetic indicators. In a second step, we find a number of simulated periods under which the calibrated growth factors yield indicator dynamics with similar volatility to the empirical one. This allows us to establish an equivalence between real time and algorithmic time, and then to determine the temporal feasibility of the scenarios proposed via counterfactual simulations.

5.2 Retrospective policy priorities

For the retrospective analysis, we use the development-indicator data, the governance parameters fixed in their historical values, and the estimated network. In other words, PPI’s inputs are: (a) the initial values of the indicators, (b) the network of conditional dependencies, (c) the final values of the development indicators, (d) the parameters that identify the country’s rule of law and the monitoring of corruption, and (e) the growth factors calibrated according to the algorithms developed in Appendix D.

The procedure consists of the following steps:

1. 1. Instantiate the agents with random initial values for the endogenous variables.

2. 2. Impute the values of the indicators from their empirical values in 2006.

3. 3. Impute the vector of development goals from the empirical values of the indicators in 2016.Footnote ²¹

4. 4. Impute the governance parameters $ \varphi $ and $ \tau $ using the empirical values obtained from the data presented in Section 4.2.

5. 5. Impute the vector of $ {\alpha}_i $ using the values calibrated through the algorithm proposed in Appendix D.

6. 6. Run the simulation and stop when all indicators have reached their goals (the ones imputed in step 3).

7. 7. Compute the inter-temporal distribution of resources (further details are explained below) for this specific run.

8. 8. Go back to step 1 and repeat all the steps multiple times, recording the inter-temporal distribution of resources of each run.

9. 9. Compute the average inter-temporal distribution of resources across the multiple runs; this is the retrospective allocation profile (see below).

A clarification is in order with respect to point 3. Because the true development goals of the previous Mexican governments are unknown (beyond vague statements presented in the official discourse), we cannot use the retrospective simulations to produce an ex-post evaluation of these administrations. In other words, we cannot establish, among other things, whether the budgetary priorities were consistent with their development goals. However, setting the goals with the end-values of the indicators is still a useful exercise for two reasons: (a) we can calibrate the model to determine the algorithmic time that takes for the indicators to reach their final values, and (b) we can identify how priorities have to change if goals differ to the observed final values are established in a prospective analysis.

Next, we present the details on how to compute the allocation profile and, then, we describe the results for the retrospective simulations. As mentioned above, the latter are obtained once the growth factors and the algorithmic time for convergence in the historical sample have been calibrated. An allocation profile is estimated with the average distribution of resources across independent Monte Carlo simulations. For a single simulation, we obtain $ n $ synthetic time series of how the government agent allocates resources $ {P}_{i,t} $ across each indicator $ i $ and every period $ t $. The inferred allocation profile is built by, first, computing the inter-temporal mean of allocations for each indicator. It is important to recall that only the instrumental indicators are part of these profiles since their associated government programs receive public funding. Then, by performing $ M $ Monte Carlo independent simulations, we obtain $ M $ vectors $ {P}_{i,\cdot } $ of inter-temporal means. Finally, for each indicator $ i $, we compute the mean allocation across Monte Carlo simulations. Altogether, the inferred allocation to the instrumental indicator $ i $ is given by

(16)$$ {\mathcal{P}}_i=\frac{1}{M}\sum \limits_m^M\frac{1}{L_m}\sum \limits_t^{L_m}{P}_{i,t,m}, $$

where $ {L}_m $ is the number of simulation steps that the $ {m}^{\mathrm{th}} $ simulation took to converge.

Figure 5 shows the inferred policy priorities that the Mexican government established during the sampling period.Footnote ²² According to this exercise, the most prioritized indicators tend to be in SDGs 8, 9, and 16b. The specific definitions of policy issues are presented in Tables 3 and 4, which show the 10 most and least prioritized indicators respectively. The retrospective estimation suggests that the most prioritized issue was building statistical capacity, while the least one was fighting the organized crime. Both cases are consistent with observations by academics, commentators, and public opinion. On the one hand, it is well known that previous governments invested significant resources in creating regulatory organizations to guarantee the generation, transparency, and protection of public data. This is an important part of the statistical capacity of the state. On the other hand, the spike in violence and crime across the country during the last decade speaks to the low priority that this policy issue has received in recent administrations.

Figure 5. Retrospective allocation profile.

Note: Each bar in the left panel can be interpreted as a share of the ratio of transformative resources (expenditure on the margin), so they add up to one. The bars on the right panel are averages of the bars in the left panel, computed for each color.

Table 3. Most prioritized indicators

Note. The indicators have been sorted from top to bottom in descending order of priority. In other words, the first item is the most prioritized.

Abbreviations: SDG, sustainable development goal.

Table 4. Least prioritized indicators

Note. The indicators have been sorted from top to bottom in ascending order of priority. In other words, the first item is the least prioritized.

Abbreviations: SDG, sustainable development goal.

The way to interpret the bars in Figure 5, for the purpose of policy guidance, is in terms of a ranking of budgetary priorities. These priorities are defined as ratios of transformative expenses with respect to the budget assigned to the corresponding programs. In other words, the lack of access to highly disaggregated budgetary data only allows to establish ordinal inferences. However, this shortcoming can be overcome with an alternative version of the model in which budgetary data become an additional input; work that is out of the scope of this paper. Even with just ordinal inferences on policy priorities, PPI provides valuable insights when performing prospective simulations and counterfactual scenarios as shown in the next sections.

6.1 Development goals

Figure 6 presents the development goals of the NDP mapped into the SDG indicators of our database. On average, the proposed growth rate for the indicators is higher than 50%. SDG 16b presents more heterogeneity of goals because it has more direct matches between NDP and SDG indicators. In contrast, the bars that have identical values are the result of assigning the average growth rate of all indicators within the same SDG (because the indicator at stake did not have a direct match with an indicator from the NDP; see Section 4.4 for more details). We build the prospective goals vector $ T $ with this information by taking the final values of the indicators and growing them according to the associated rates.

Figure 6. Prospective development goals.

6.2 Fluid policy priorities

Figure 7 presents fluid policy priorities and compares them with the retrospective ones. The prospective allocation profile should be interpreted as the policy priorities that the Mexican government would establish—under the assumptions previously discussed—if it would truly pursue the proposed goals. Note that, since the goals are based on the NDP, the discrepancies between the prospective and the retrospective profiles allow to answer the following question: how different should policy priorities be (produced by the prospective estimation) from what they have been until now (inferred from the retrospective estimation) if the goals are to be met? From comparing both allocation profiles, we can see important increments in SDGs 1, 3, 9, 10, 12, and 13. On the other hand, the SDGs with a noticeable decrease in priorities are 4, 6, 7, and 16b. Whether the inferred prospective allocations are definitive actions that the government will reflect in its budget is a different story, one that we explore in Section 6.4. The important takeaway from this exercise is that, with this type of simulation exercise, PPI can show that budgetary allocations across government programs can change substantially when there are differences between the goals from the past and new ones (different government agendas).

Figure 7. Prospective policy priorities under perfect fluidity.

Note: Each bar can be interpreted as a share of the ratio of transformative resources (expenditure on the margin), so they add up to one. The left panel corresponds to the retrospective policy priorities presented in Figure 5. The right panel presents the fluid policy priorities inferred from the prospective analysis.

6.3 Feasibility under fluid priorities

The feasibility of a goal usually carries an economic meaning, as it implies achieving something with a limited amount of resources (natural, financial, human, or time-wise). Since PPI assumes a constant expenditure flow (the problem is an allocative one, rather than the size of the overall budget), a natural way to think about feasibility is in terms of how long would it take to achieve a set of goals. Furthermore, given that most governments occupy the office for a limited number of years (at least in democratic regimes), feasibility means being able to reach the government’s goals in such time frame. Nevertheless, one could also think of multi-government feasibility if, for example, a government or political party considers a multi-term strategy. In any case, common sense would suggest that goals that can only be reached in more than two decades are unfeasible for a government strategy. Thus, in this study, we estimate the number of years that it would take the Mexican government to reach the goals proposed in the NDP, and assess their feasibility accordingly.

Before interpreting the results, it is important to point out a caveat in this analysis and its potential solutions. Because there is no one-to-one correspondence between the SDG indicators and the NDP, the way the goals vector was constructed involves computing growth rates from the NDP and mapping them into the SDG indicators. This introduces a bias in those indicators where Mexico lags the most. For instance, if an indicator has a value near zero, it means that, across all the countries in the dataset, Mexico is among the worst performers in this topic. When multiplying that value by 1+growthRate, one would obtain a very low goal, so a minuscule gap to be covered. In reality, the government would not have such a low goal for that indicator (especially under the logic of laggard topics being bottlenecks), but due to the lack of information regarding this goal, its approximation through growth rates is the second best. The consequence is that those indicators with the most modest goals will likely show fast convergence times. To fix this, it is important to obtain development goals in the original units of the data, and this can be done by either selecting indicators for which the goals have been established in their original units (e.g., in official documents) or by working closely with the stakeholders.Footnote ²³ The main implication of this bias is that it underestimates the average convergence time in the prospective analysis. Thus, the interpretation in terms of feasibility might be optimistic.

Figure 8 shows the convergence time of each indicator in years. On average, it would take more than 10 years to reach the goals proposed in the NDP. That is, it would take two administrations to get there. One indicator in SDG 12 stands out as the most difficult to achieve: ethical behavior of firms—not surprisingly, a collateral issue associated with corrupt practices–with almost 25 years of convergence time. Overall, these results suggest that the NDP demands a multi-term strategy to be considered feasible.

Figure 8. Convergence time under fluid priorities.

6.4 Budget and policy coherence

Recall that, according to PPI’s theory, if the government truly wants to achieve the goals proposed in the NDP, it would establish the prospective priorities estimated in Figure 7. We also mentioned that, whether this is reflected in the government’s actions or not is a different question, one that we consider here. Take the budgetary data presented in Section 4.5, and assume that they reflect the policy priorities that the government intends to establish in the next 6 years.Footnote ²⁴ If the budget proposed by the federal government would be coherent with the NDP, then it should resemble the prospective policy priorities. This is so because the prospective priorities are, effectively, a counterfactual of what the government would do under the NDP. Comparing this counterfactual to the fiscal data allows measuring the level of coherence of the budget through an index developed by Guerrero and Castañeda (Reference Guerrero and Castañeda2020).

Figure 9 shows the result of this exercise. The left panel presents the discrepancies between the budget and the priorities, both at the level of the SDGs (because the budgetary data are linked at an aggregate level, not at the indicator level). Let us concentrate on the right-most dot in the panel, which corresponds to SDG 13. The horizontal axis suggests that the government would establish an average allocation of more than 10% to SDG 13. However, the vertical axis shows that the approved budget for such purpose was less than 1%. Thus, the government is under-spending in climate action. Under- or over-expenditures are also called allocative inefficiencies and, together with technical inefficiencies, they are key to understand development (Izquierdo et al., Reference Izquierdo, Pessino and Vuletin2018). The more allocative inefficiencies we find in the plot, the more likely that the coherence index will suggest incoherence between the federal budget and the NDP.

Figure 9. Budget and policy coherence.

The coherence index behaves like a correlation coefficient: positive values indicate coherence, while negative values imply incoherence. An index with value 1 suggests full coherence, meaning that all the dots in the left panel would lie on the dotted line because both the budget and the prospective allocation are identical. The right panel shows the distribution of the coherence index (see Guerrero and Castañeda (Reference Guerrero and Castañeda2020) for details on the estimation procedure). Clearly, the budget is incoherent with the government’s aspirations (at least at the level of the SDGs). Nevertheless, the magnitudes of the indices are not too high, suggesting that moving to the positive side is feasible. Note that the coherence index is specific to the set of indicators, goals, growth factors, and spillover network. Therefore, an incoherent budget may not necessarily mean that the priorities are wrong, it may suggest, instead, that the goals are unrealistic. In any case, the usefulness of PPI becomes evident because it allows assessing both sides of the same coin.

6.5 Rigid policy priorities

Suppose that the budgetary data reflect, indeed, the policy priorities and that the government is not willing to change them throughout its administration. Here, we are in a situation of fiscal rigidities. For PPI, it means that the central authority (i.e., the Treasury) does not adapt its allocations and, instead, establishes a rigid allocation profile (in this case, the budget data). Then, the natural question that arises in this scenario is whether following the approved budget under strict discipline will make the NDP more or less feasible. We can assess this by comparing the convergence times under the budgetary data against the ones obtained from the prospective priorities. New sets of simulations need to be run for (a) taking the budgetary data as the given prioritiesFootnote ²⁵ and, (b) using the prospective priorities obtained in Section 6.2 as the given ones. The reason why we cannot directly compare the convergence times obtained in Section 6.3 is because that exercise assumes fluid priorities while the adoption of the budget assumes rigid ones. Differences in rigidity induce discrepancies in convergence times, as shown by Castañeda and Guerrero (Reference Castañeda and Guerrero2019). Therefore, the correct way to measure delays or savings in this exercise is by having the same level of fiscal rigidity.

The steps to implement this exercise follow those discussed in Section 6, with one exception: the endogenous vector $ P $ is imposed exogenously and remains fixed throughout the simulation. Since we need to perform two sets of simulations, one set fixes $ P $ according to the allocation profile estimated in Section 6.2, and the other set fixes the priorities according to the budgetary data. All other steps remain the same.

Figure 10 shows the difference in convergence time between adopting the federal budget and the prospective allocations. On average, adopting the approved budget would produce an average delay of nearly 2 years with respect to the adoption of the prospective priorities. In some cases, the delays can be of the order of 6 or 7 years. The indicator where the biggest delay takes place is cooperation in labor-employer relations, from SDG 8. We can also observe some savings, especially in the indicators related to SDG 7. Overall, this exercise shows how PPI can be combined with fiscal-SDG linked data, a promising research avenue as more and better public expenditure data become available.

Figure 10. Delays in reaching the development goals.

6.6 Accelerators

The last of our prospective analyses touches a topic that has become highly discussed in the SDG literature: accelerators. According to the UNDP’s SDG Accelerator and Bottleneck Assessment (ABA) tool (Garmer, Reference Garmer2017, p. 6), an accelerator is a “—development policy and/or program areas—that will accelerate progress across the SDGs and the national development goals, and the corresponding drivers that enable their progress”. Thus, the purpose of identifying accelerators is to prioritize them in order to trigger positive multiplicative effects across SDGs. In principle, this very notion appeals to the network of interdependencies. While the ABA tool takes a more qualitative approach, different research groups have emphasized the use of SDG networks to prioritize topics with a high degree of connectivity (Weitz et al., Reference Weitz, Carlsen, Nilsson and Skånberg2018). In this section, we (a) demonstrate that the approach of using networks to identify accelerators is not only naïve but may be outperformed by alternative heuristics and (b) provide a more comprehensive way to identify accelerators by combining PPI with heuristic optimization methods.

What does an accelerator mean in PPI? Under PPI, an accelerator cannot be just an indicator with a high degree of connectivity for the following reasons:

1. 1. Only instrumental indicators can be accelerators because they are the only ones that can be intervened through public policy.

2. 2. The network is not causal, so it is erroneous to assume that one can manipulate the indicators. Instead, one tries to improve them through policy interventions.

3. 3. Given that there always is a budget constraint, when one increases the priority in one topic, it takes away resources from other policy issues. Thus, an accelerator cannot be considered in isolation from those topics that are losing resources; this cannot be accounted for when looking at network interlinkages exclusively.

4. 4. An indicator with high connectivity may be highly inefficient, so allocating more resources without solving the associated public governance problems may result in ineffective policies.

5. 5. Shifting priorities to a node may affect the incentive structure of policy-makers. For example, an agent may become inefficient because it receives more spillovers from the intervened policy issues.

6. 6. Because the relationship between expenditure and development outcomes is nonlinear, the set of accelerators may change with the allocation of transformative resources.

Clearly, in the identification of accelerators, there is more to than meets the eye. Much of this complexity comes from the political economy underlying the policymaking process, and this is something that data, by itself, cannot reveal. Fortunately, the research program of PPI appeals to a generative approach to deal with such complexities, something that we exploit to shed new light on the identification of accelerators. Let us concentrate on the hypothetical case where the policy priorities are given by the budgetary data.

The literature from Political Science and Public Administration suggests that, most of the times, budgetary changes are small (Baumgartner and Jones, Reference Baumgartner and Jones1993; Jones et al., Reference Jones, Baumgartner and True1998). Under normal circumstances (e.g., without a crisis), a 10% change would be considered the upper bound of how large a priority change can be. For the sake of this example, let us assume that the government takes 10% of the budget assigned to each indicator and reallocates it to the accelerators. That is, we choose the accelerators ex-ante and give them the 10% of the budget in equal portions. Finally, we run PPI under full rigidity and obtain the convergence time. Then, the question is: which of the 91 instrumental indicators should be chosen as the accelerators?

6.6.1 Naïve results

Let us begin with the naïve approach, in which the accelerators should be those indicators whose total outgoing weights in the network are positive. That is, these are nodes with net positive conditional dependencies on other nodes; possibly because they have a high degree of positive outgoing links, but also because their positive outgoing edges outweigh their negative ones. We reallocate 10% of the budget to these indicators and run PPI. Then, we compute the difference in convergence speed with respect to the times obtained in Section 6.5 for the budget priorities. Figure 11 shows the result. Overall, the naïve approach identifies 54 accelerators, and generates an average saving of 1.29 months, with individual savings per indicator of up to 8 months. Note, however, how some accelerators generate zero or near-zero savings. This means that the political economy process prevents them from being effective accelerators, despite having net positive outgoing spillovers. From an economic point of view, supporting accelerators that do not improve convergence times is inefficient, unless their spillovers are big enough to outweigh the costs.

Figure 11. Accelerators identified through network connectivity.

6.6.2 PPI results

Given that the naïve approach to accelerators has limitations, how can we find the set of instrumental nodes that can best catalyze development by assigning them the 10% of the budget? A brute force strategy would be to simply enlist all the possible sets of accelerators, run PPI for each one, and select the best-performing set. The problem with this approach is that, given the high-dimensional nature of development, exploring all the possible sets becomes unfeasible very quickly, for example, in this particular study, the number of all possible accelerator sets is $ {2}^{91} $ (that is, approximately a 2 followed by more than 25 zeros). In addition, the “fitness landscape” of this problem is often rough, so traditional optimization methods are bound to fail. Fortunately, heuristic optimization techniques have been designed to deal with this type of problems. In this application, we employ one that stems from Complexity Science: genetic algorithms (Holland, Reference Holland1975). A brief explanation of this algorithm is presented in Appendix I. The left panel in Figure 12 shows the results of our search for accelerators. The genetic algorithm returns a set with 34 accelerators, considerably less than in the naïve approach. In this set, not all the SDGs have accelerators, for example, SDGs 4–7 lack them. Overall, allocating the 10% of the budget to these indicators generates an average saving of 2.25 months, twice as much as the naïve accelerators. Note that all the accelerators lie above the dotted line, and that, in some cases, there are savings of more than 1 year.

Figure 12. Accelerators identified through policy priorities inference and heuristic optimization.

In the right panel, we present a Venn diagram showing the distribution of accelerators across the different types of indicators. Interestingly, 14 out of the 34 accelerators have negative net spillovers—the exact opposite intuition to the naïve approach. This demonstrates how neglecting the political economy process can produce misleading policy prescriptions. Clearly, the identification of accelerators demands a complexity perspective, which is the very essence of the 2030 Agenda. This exercise shows the versatility of PPI and how, when combined with other methods from Complexity Science, it can be used to tackle challenging problems. A more thorough study could explore other heuristic optimization methods, as well as diverse reallocation rules and levels of fiscal rigidity. Here, we have opened the path to explore these possibilities.

7.1 Limitations

First, like with any quantitative model, the quality of the data affects the quality of the outputs. Although, compared to the existing approaches, it can do more with less data, PPI will not fix a government’s data problems. More and better indicators will always be beneficial to any empirical exercise, as they will better capture interdependencies, structural factors, and features of behavioral heuristics.

Second, prospective estimations assume that the main structural issues (the growth factors) remain the same. Likewise, the interlinkages captured by the spillover network are also assumed to remain in place. For this reason, PPI should only be considered for short and midterm studies, even if sensitivity analyses are produced.

Third, although the outputs are obtained from a quantitative model, the inferences drawn from this version of PPI should be interpreted on a more qualitative basis. That is, this implementation is not designed to provide precise estimates on the level of an indicator after a number of years. Instead, it yields the approximate time that it would take to reach a goal, given that the structural factors and theories of change that produced the historical data remain in place. Likewise, priorities should not be interpreted as point estimates, but rather in ordinal terms of which policy issues should receive more or less priority. This, however, may be overcome by introducing granular expenditure data as an input to PPI.

Fourth, the inferences about policy priorities obtained from PPI can only be interpreted at the macro-level. That is, an allocation profile reflects opportunity areas where governments can destine more resources, not the specific policies that should be implemented to improve them. It is assumed that the same policies that have been deployed in the past remain in place. In order to assess micro-level issues, such as choosing better policies and other operative concerns, it is necessary to resort to other methodologies and expert knowledge on those particular topics. Thus, PPI intends to be complementary to the planning process, not a substitute for other approaches or human expertise.