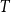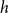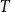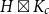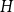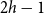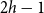1. Introduction
Robertson and Seymour [Reference Robertson and Seymour8] proved that for every tree
$T$
, there is an integer
$c$
such that every
$T$
-minor-free graph has pathwidth at most
$c$
. Bienstock, Robertson, Seymour, and Thomas [Reference Bienstock, Robertson, Seymour and Thomas1] and Diestel [Reference Diestel3] showed the same result with
$c=|V(T)|-2$
, which is best possible, since the complete graph on
$|V(T)|-1$
vertices is
$T$
-minor-free and has pathwidth
$|V(T)|-2$
. Graph product structure theory describes graphs in complicated classes as subgraphs of products of simpler graphs [Reference Campbell, Clinch, Distel, Gollin, Hendrey, Hickingbotham, Huynh, Illingworth, Tamitegama, Tan and Wood2, Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood5, Reference Illingworth, Scott and Wood6]. Inspired by this viewpoint, we prove the following result, where
$H\boxtimes K_c$
is the graph obtained from
$H$
by replacing each vertex of
$H$
by a copy of
$K_c$
and replacing each edge of
$H$
by the join between the corresponding copies of
$K_c$
.
Theorem 1.
For every tree
$T$
of radius
$h$
, there exists
$c\in{\mathbb{N}}$
such that every
$T$
-minor-free graph
$G$
is contained in
$H\boxtimes K_c$
for some graph
$H$
with pathwidth at most
$2h-1$
.
Theorem 1 is a qualitative strengthening of the above-mentioned result of Robertson and Seymour [Reference Robertson and Seymour8] since
$\textrm{pw}(G)\leqslant \textrm{pw}(H\boxtimes K_c) \leqslant c(\textrm{pw}(H)+1)-1 \leqslant 2ch-1$
. Note that the proof of Theorem 1 depends on the above-mentioned result of Robertson and Seymour [Reference Robertson and Seymour8]. The point of Theorem 1 is that
$\textrm{pw}(H)$
only depends on the radius of
$T$
, not on
$|V(T)|$
which may be much greater than the radius. Moreover, radius is the right parameter of
$T$
to consider here, as we now show.
For a tree
$T$
, let
$g(T)$
be the minimum
$k\in{\mathbb{N}}$
such that for some
$c\in{\mathbb{N}}$
every
$T$
-minor-free graph
$G$
is contained in
$H\boxtimes K_c$
where
$\textrm{pw}(H)\leqslant k$
. Theorem 1 shows that if
$T$
has radius
$h$
, then
$g(T)\leqslant 2h-1$
. Now we show a lower bound. The following lemma by Campbell, Clinch, Distel, Gollin, Hendrey, Hickingbotham, Huynh, Illingworth, Tamitegama, Tan, and Wood [Reference Campbell, Clinch, Distel, Gollin, Hendrey, Hickingbotham, Huynh, Illingworth, Tamitegama, Tan and Wood2] is useful, where
$T_{h,d}$
is the complete
$d$
-ary tree of radius
$h$
.
Lemma 2 ([2, v1, Proposition 56]). For any
$h,c\in{\mathbb{N}}$
, there exists
$d\in{\mathbb{N}}$
such that for every graph
$H$
, if
$T_{h,d}$
is contained in
$H\boxtimes K_c$
, then
$\textrm{pw}(H)\geqslant h$
.
Let
$T$
be any tree with radius
$h$
. Thus,
$T$
contains a path on
$2h$
vertices, and
$T_{h-1,d}$
contains no
$T$
-minor, as otherwise
$T_{h-1,d}$
would contain a path on
$2h$
vertices. By Lemma 2, if
$T_{h-1,d}$
is contained in
$H\boxtimes K_c$
, then
$\textrm{pw}(H)\geqslant h-1$
. Hence,
\begin{equation} h-1 \leqslant g(T) \leqslant 2h-1. \end{equation}
This says that the radius of
$T$
is the right parameter to consider in Theorem 1.
Moreover, both the lower and upper bounds in (1) can be achieved, as we now explain. The upper bound in (1) is achieved when
$T$
is a complete ternary tree, as shown by the following result.
Proposition 3.
For all
$h,c\in{\mathbb{N}}$
, there is a
$T_{h,3}$
-minor-free graph
$G$
, such that for every graph
$H$
, if
$G$
is contained in
$H\boxtimes K_c$
, then
$H$
has a clique of size
$2h$
, implying
$\textrm{pw}(H)\geqslant \textrm{tw}(H)\geqslant 2h-1$
.
The next result improves Theorem 1 for an excluded path. It shows that the lower bound in (1) is achieved when
$T$
is a path, since
$P_{2h+1}$
has radius
$h$
, and a graph has no path on
$2h+1$
vertices if and only if it is
$P_{2h+1}$
-minor-free.
Proposition 4.
For any
$h\in{\mathbb{N}}$
, every graph
$G$
with no path on
$2h+1$
vertices is contained in
$H\boxtimes K_{4h}$
for some graph
$H$
with
$\textrm{pw}(H) \leqslant h-1$
.
2. Background
We consider simple, finite, undirected graphs
$G$
with vertex set
$V(G)$
and edge set
$E(G)$
. See [Reference Diestel4] for graph-theoretic definitions not given here. For
$m,n \in \mathbb{Z}$
with
$m \leqslant n$
, let
$[m,n]\,:\!=\,\{m,m+1,\dots,n\}$
and
$[n]\,:\!=\,[1,n]$
.
A graph
$H$
is a minor of a graph
$G$
if
$H$
is isomorphic to a graph that can be obtained from a subgraph of
$G$
by contracting edges. A graph
$G$
is
$H$
-minor-free if
$H$
is not a minor of
$G$
. An
$H$
-model in a graph
$G$
consists of pairwise disjoint vertex subsets
$(W_x \subseteq V(G) \,:\,x\in V(H))$
(called branch sets) such that each subset induces a connected subgraph of
$G$
, and for each edge
$xy\in V(H)$
there is an edge in
$G$
joining
$W_x$
and
$W_y$
. Clearly,
$H$
is a minor of
$G$
if and only if
$G$
contains an
$H$
-model.
A tree decomposition of a graph
$G$
is a collection
$(B_x \,:\,x\in V(T))$
of subsets of
$V(G)$
(called bags) indexed by the vertices of a tree
$T$
, such that (a) for every edge
$uv\in E(G)$
, some bag
$B_x$
contains both
$u$
and
$v$
, and (b) for every vertex
$v\in V(G)$
, the set
$\{x\in V(T)\,:\,v\in B_x\}$
induces a non-empty (connected) subtree of
$T$
. The width of
$(B_x\,:\,x\in V(T))$
is
$\max \{|B_x| \,:\, x\in V(T)\}-1$
. The treewidth of a graph
$G$
, denoted by
$\textrm{tw}(G)$
, is the minimum width of a tree decomposition of
$G$
. A path decomposition is a tree decomposition in which the underlying tree is a path, simply denoted by the sequence of bags
$(B_1,\dots,B_n)$
. The pathwidth of a graph
$G$
, denoted by
$\textrm{pw}(G)$
, is the minimum width of a path decomposition of
$G$
.
The following lemma is folklore (see [Reference Illingworth, Scott and Wood6] for a proof).
Lemma 5.
For every graph
$G$
, for every tree decomposition
$\mathcal{D}$
of
$G$
, for every collection
$\mathcal{F}$
of connected subgraphs of
$G$
, and for every
$\ell \in{\mathbb{N}}$
, either:
-
(a) there are
$\ell$
vertex disjoint subgraphs in
$\mathcal{F}$
, or
-
(b) there is a set
$S\subseteq V(G)$
consisting of at most
$\ell -1$
bags of
$\mathcal{D}$
such that
$S \cap V(F) \neq \varnothing$
for all
$F \in{\mathcal{F}}$
.
The strong product of graphs
$A$
and
$B$
, denoted by
$A \boxtimes B$
, is the graph with vertex set
$V(A) \times V(B)$
, where distinct vertices
$(v,x),(w,y) \in V(A) \times V(B)$
are adjacent if
$v=w$
and
$xy \in E(B)$
, or
$x=y$
and
$vw \in E(A)$
, or
$vw \in E(A)$
and
$xy \in E(B)$
.
Let
$G$
be a graph. A partition of
$G$
is a collection
$\mathcal{P}$
of sets of vertices in
$G$
such that each vertex of
$G$
is in exactly one element of
$\mathcal{P}$
. Each element of
$\mathcal{P}$
is called a part. The width of
$\mathcal{P}$
is the maximum number of vertices in a part. The quotient of
$\mathcal{P}$
(with respect to
$G$
) is the graph, denoted by
$G/\mathcal{P}$
, with vertex set
$\mathcal{P}$
where distinct parts
$A,B\in \mathcal{P}$
are adjacent in
$G/\mathcal{P}$
if and only if some vertex in
$A$
is adjacent in
$G$
to some vertex in
$B$
. An
$H$
-partition of
$G$
is a partition
$\mathcal{P}$
of
$G$
such that
$G/\mathcal{P}$
is contained in
$H$
. The following observation connects partitions and products.
Observation 6 ([Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood5]). For all graphs
$G$
and
$H$
and any
$p\in{\mathbb{N}}$
,
$G$
is contained in
$H\boxtimes K_p$
if and only if
$G$
has an
$H$
-partition with width at most
$p$
.
3. Proofs
We prove the following quantitative version of Theorem 1.
Theorem 7.
Let
$T$
be a tree with
$t$
vertices, radius
$h$
, and maximum degree
$d$
. Then every
$T$
-minor-free graph
$G$
is contained in
$H\boxtimes K_{(d+h-2)(t-1)}$
for some graph
$H$
with pathwidth at most
$2h-1$
.
Recall that
$T_{h,d}$
is the complete
$d$
-ary tree of radius
$h$
. Observation 6 and the next lemma imply Theorem 7, since the tree
$T$
in Theorem 7 is a subtree of
$T_{h,d}$
, and every
$T$
-minor-free graph
$G$
satisfies
$\textrm{tw}(G)\leqslant \textrm{pw}(G)\leqslant t-2$
by the result of Bienstock, Robertson, Seymour, and Thomas [Reference Bienstock, Robertson, Seymour and Thomas1] mentioned in Section 1.
Lemma 8.
For any
$h,d\in{\mathbb{N}}$
with
$d+h\geqslant 3$
, for every
$T_{h,d}$
-minor-free graph
$G$
, for every tree decomposition
$\mathcal{D}$
of
$G$
, and for every vertex
$r$
of
$G$
, the graph
$G$
has a partition
$\mathcal{P}$
such that:
-
• each part of
$\mathcal{P}$
is a subset of the union of at most
$d+h-2$
bags of
$\mathcal{D}$
, -
•
$\{r\}\in \mathcal{P}$
, and
-
•
$G/\mathcal{P}$
has a path decomposition of width at most
$2h-1$
in which the first bag contains
$\{r\}$
.
Proof. We proceed by induction on pairs
$(h,|V(G)|)$
in a lexicographic order. Fix
$h$
,
$d$
,
$G$
,
$\mathcal{D}$
, and
$r$
as in the statement. We may assume that
$G$
is connected. The statement is trivial if
$|V(G)|\leqslant 1$
. Now assume that
$|V(G)|\geqslant 2$
.
For the base case, suppose that
$h=1$
. For
$i\geqslant 0$
, let
$V_i\,:\!=\,\{v\in V(G)\,:\,\textrm{dist}_G(v,r)=i\}$
. So
$V_0=\{r\}$
. If
$|V_i|\geqslant d$
for some
$i\geqslant 1$
, then contracting
$G[V_0\cup \dots \cup V_{i-1}]$
into a single vertex gives a
$T_{1,d}$
-minor. So
$|V_i|\leqslant d-1=d+h-2$
for each
$i\geqslant 0$
. Thus,
$\mathcal{P}\,:\!=\,(V_i\,:\,i\geqslant 0)$
is a partition of
$G$
, and each part of
$\mathcal{P}$
is a subset of the union of at most
$d+h-2$
bags of
$\mathcal{D}$
. Moreover, the quotient
$G/\mathcal{P}$
is a path, which has a path decomposition of width 1, in which the first bag contains
$\{r\}$
.
Now assume that
$h\geqslant 2$
and the result holds for
$h-1$
. Let
$R$
be the neighbourhood of
$r$
in
$G$
. Let
$\mathcal{F}$
be the set of all connected subgraphs of
$G-r$
that contain a vertex from
$R$
and contain a
$T_{h-1,d+1}$
-minor. If there are
$d$
pairwise vertex disjoint subgraphs
$S_1,\ldots,S_d$
in
$\mathcal{F}$
, then we claim that
$G$
contains a
$T_{h,d}$
-minor. Indeed, for each
$i\in [d]$
consider a
$T_{h-1,d+1}$
-model
$(W^i_x\,:\, x\in V(T_{h-1,d+1}))$
in
$S_i$
. Since
$S_i$
is connected, we may assume that all vertices of
$S_i$
are in the model. For each
$i\in [d]$
, let
$y_i$
be a node of
$T_{h-1,d+1}$
such that
$W^i_{y_i}$
contains a vertex from
$R$
, and let
$Y^i$
be the union of
$W^i_x$
for all ancestors
$x$
of
$y_i$
in
$T_{h-1,d+1}$
. Observe that there is a
$T_{h-1,d}$
-model in
$S_i$
such that the root of
$T_{h-1,d}$
is mapped to the set
$Y^i$
. Therefore,
$G-r$
contains
$d$
pairwise disjoint models of
$T_{h-1,d}$
such that each root branch set contains a vertex from
$R$
. So
$G$
contains a model of
$T_{h,d}$
, as claimed.
So
$\mathcal{F}$
contains no
$d$
pairwise vertex disjoint elements. By Lemma 5, there is a minimal set
$X\subseteq V(G-r)$
, such that
$X$
is a subset of the union of
$d-1\leqslant d+h-2$
bags of
$\mathcal{D}$
, and
$G-r-X$
contains no element of
$\mathcal{F}$
.
Let
$G_1,\dots,G_p$
be the components of
$G-r-X$
that contain a vertex from
$R$
. By construction of
$X$
, the graph
$G_i$
contains no
$T_{h-1,d+1}$
-minor. By induction,
$G_i$
has a partition
$\mathcal{P}_i$
such that:
-
• each part of
$\mathcal{P}_i$
is a subset of the union of at most
$(d+1)+(h-1)-2=d+h-2$
bags of
$\mathcal{D}$
, and -
•
$G_i/\mathcal{P}_i$
has a path decomposition
$\mathcal{B}_i$
of width at most
$2h-3$
.
Let
$Z\,:\!=\, V(G-r-X)\setminus V(G_1\cup \dots \cup G_p)$
; that is,
$Z$
is the set of vertices of all components of
$G-r-X$
that have no vertex in
$R$
.
Consider a vertex
$v\in X$
. By the minimality of
$X$
, the graph
$G-r-(X\setminus \{v\})$
contains a connected subgraph
$Y_v$
that contains
$v$
and a vertex
$r_v\in R$
(and contains a
$T_{h-1,d+1}$
-minor). Let
$P_v$
be a path from
$v$
to
$r_v$
in
$Y_v$
plus the edge
$r_vr$
. So
$P_v-\{v,r\}$
is contained in some
$G_i$
, and thus
$P_v$
avoids
$Z$
. So
$\cup \{P_v\,:\,v\in X\}$
is a connected subgraph in
$G-Z$
. Let
$G^{\prime}$
be obtained from
$G$
by contracting
$\cup \{P_v\,:\,v\in X\}$
into a vertex
$r^{\prime}$
, and deleting any remaining vertices not in
$Z$
. So
$V(G^{\prime})=\{r^{\prime}\}\cup Z$
. Since
$G^{\prime}$
is a minor of
$G$
, the graph
$G^{\prime}$
is
$T_{h,d}$
-minor-free. Let
${\mathcal{D}}^{\prime}$
be the tree decomposition of
$G^{\prime}$
obtained from
$\mathcal{D}$
by replacing each instance of each vertex in
$\cup \{P_v\,:\,v\in X\}$
by
$r^{\prime}$
then removing the other vertices in
$V(G)\setminus V(G^{\prime})$
. Observe that for every bag
$B$
in
$\mathcal{D}^{\prime}$
, we have
$B-\{r^{\prime}\}$
contained in some bag of
$\mathcal{D}$
. By induction,
$G^{\prime}$
has a partition
$\mathcal{P}^{\prime}$
such that:
-
• each part of
$\mathcal{P}^{\prime}$
is a subset of the union of at most
$d+h-2$
bags of
${\mathcal{D}}^{\prime}$
, -
•
$\{r^{\prime}\}\in \mathcal{P}^{\prime}$
, and -
•
$G^{\prime}/\mathcal{P}^{\prime}$
has a path decomposition
${\mathcal{B}}^{\prime}$
of width at most
$2h-1$
in which the first bag contains
$\{r^{\prime}\}$
.
Let
$\mathcal{P}\,:\!=\,\{\{r\}\}\cup \{X\}\cup \mathcal{P}_1\cup \dots \cup \mathcal{P}_p \cup (\mathcal{P}^{\prime}\setminus \{\{r^{\prime}\}\})$
. Then
$\mathcal{P}$
is a partition of
$G$
such that each part is a subset of the union of at most
$d+h-2$
bags of
$\mathcal{D}$
. Let
$\mathcal{B}$
be a sequence of subsets of vertices of
$G/\mathcal{P}$
obtained from the concatenation of
$\mathcal{B}_1,\dots,\mathcal{B}_p,$
and
${\mathcal{B}}^{\prime}$
by adding
$\{r\}$
and
$X$
to every bag that comes from
$\mathcal{B}_1,\dots,\mathcal{B}_p$
and replacing
$\{r^{\prime}\}$
by
$X$
. Now we argue that
$\mathcal{B}$
is a path decomposition of
$G/\mathcal{P}$
. Indeed, each part of
$\mathcal{P}$
is contained in consecutive bags of
$\mathcal{B}$
, specifically
$\{r\}$
and
$X$
are added to all bags across
${\mathcal{B}}_1,\ldots,{\mathcal{B}}_p$
, and
$X$
is in the first bag of
${\mathcal{B}}^{\prime}$
. Since
$G_1,\ldots,G_p$
are components of
$G-r-X$
, the neighbourhood in
$G/\mathcal{P}$
of a part in
$\mathcal{P}_i$
is contained in
$\mathcal{P}_i\cup \{\{r\}, X\}$
. Note also that the neigbourhood of
$\{r\}$
in
$G/\mathcal{P}$
is contained in
$\mathcal{P}_1\cup \cdots \cup \mathcal{P}_p\cup \{X\}$
. It follows that
$\mathcal{B}$
is a path decomposition of
$G/\mathcal{P}$
. By construction, the width of
$\mathcal{B}$
is at most
$2h-1$
and the first bag contains
$\{r\}$
, as required.
We now turn to the proof of Proposition 4. We in fact prove a stronger result in terms of tree-depth. A forest is rooted if each component has a root vertex (which defines the ancestor relation). The vertex height of a rooted forest
$F$
is the maximum number of vertices in a root–leaf path in
$F$
. The closure of a rooted forest
$F$
is the graph
$G$
with
$V(G)\,:\!=\,V(F)$
with
$vw\in E(G)$
if and only if
$v$
is an ancestor of
$w$
(or vice versa). The tree-depth of a graph
$G$
is the minimum vertex height of a rooted forest
$F$
such that
$G$
is a subgraph of the closure of
$F$
. It is well known and easily seen that
$\textrm{pw}(G)\leqslant \textrm{td}(G)-1$
for every graph
$G$
. Thus, the following lemma implies Proposition 4 since every
$P_{2h+1}$
-minor-free graph
$G$
has
$\textrm{tw}(G)\leqslant \textrm{pw}(G)\leqslant 2h-1$
by the result of Bienstock, Robertson, Seymour, and Thomas [Reference Bienstock, Robertson, Seymour and Thomas1] mentioned in Section 1.
Lemma 9.
For any
$h,k\in{\mathbb{N}}$
, for every graph
$G$
with no path on
$2h+1$
vertices, for every tree decomposition
$\mathcal{D}$
of
$G$
, the graph
$G$
has a partition
$\mathcal{P}$
such that
$\textrm{td}(G/\mathcal{P}) \leqslant h$
and each part of
$\mathcal{P}$
is a subset of at most two bags of
$\mathcal{D}$
.
Proof. We proceed by induction on
$h$
. For
$h=1$
,
$G$
is the disjoint union of copies of
$K_1$
and
$K_2$
. Let
$\mathcal{P}$
be the partition of
$G$
where the vertex set of each component of
$G$
is a part of
$\mathcal{P}$
. Thus,
$E(G/\mathcal{P})=\varnothing$
and
$\textrm{td}(G/\mathcal{P})=1$
. Each part is a subset of one bag of
$\mathcal{D}$
.
Now assume
$h \geqslant 2$
and the claim holds for
$h-1$
. We may assume that
$G$
is connected. Suppose
$G$
contains three vertex disjoint paths,
$P^{(1)}$
,
$P^{(2)}$
and
$P^{(3)}$
, each with
$2h-1$
vertices. Let
$G^{\prime}$
be the graph obtained by contracting each path
$P^{(i)}$
into a vertex
$v_i$
. Since
$G^{\prime}$
is connected, there is a
$(v_i,v_j)$
-path of length at least
$2$
in
$G^{\prime}$
for some distinct
$i,j\in \{1,2,3\}$
. Without loss of generality,
$i=1$
and
$j=2$
. So there exist vertices
$u\in V(P^{(1)})$
and
$v\in V(P^{(2)})$
together with a
$(u,v)$
-path
$Q$
of length at least
$2$
in
$G$
that internally avoids
$P^{(1)} \cup P^{(2)}$
. Let
$x$
be the endpoint of
$P^{(1)}$
that is furthest from
$u$
(on
$P^{(1)}$
) and let
$y$
be the endpoint of
$P^{(2)}$
that is furthest from
$v$
(on
$P^{(2)}$
). Then
$(xP^{(1)}uQvP^{(2)}y)$
is a path with at least
$2h+1$
vertices, a contradiction.
Now assume that
$G$
contains no three vertex disjoint paths with
$2h-1$
vertices. By Lemma 5, there is a set
$S\subseteq V(G)$
consisting of at most two bags of
$\mathcal{D}$
such that
$G-S$
is
$P_{2h-1}$
-free. By induction,
$G-S$
has a partition
$\mathcal{P}^{\prime}$
such that
$\textrm{td}((G-S)/\mathcal{P}^{\prime}) \leqslant h-1$
and each part of
$\mathcal{P}^{\prime}$
is a subset of at most two bags of
$\mathcal{D}$
. Let
$\mathcal{P}\,:\!=\,\mathcal{P}^{\prime}\cup \{S\}$
. Then,
$\mathcal{P}$
is the desired partition of
$G$
since
$\textrm{td}(G/\mathcal{P})\leqslant \textrm{td}( (G-S)/\mathcal{P}^{\prime}) +1 \leqslant h$
.
We turn to the proof of Proposition 3. It is a strengthening of a similar result by Norin, Scott, Seymour, and Wood [Reference Norin, Scott, Seymour and Wood7, Lemma 13].
Proposition 3.
For all
$h,c\in{\mathbb{N}}$
, there is a
$T_{h,3}$
-minor-free graph
$G$
, such that for every graph
$H$
, if
$G$
is contained in
$H\boxtimes K_c$
, then
$H$
has a clique of size
$2h$
, implying
$\textrm{pw}(H)\geqslant \textrm{tw}(H)\geqslant 2h-1$
.
Proof. We proceed by induction on
$h\geqslant 1$
. First consider the base case
$h=1$
. Let
$G$
be a path on
$n= c+1$
vertices. Thus,
$G$
is
$T_{1,3}$
-minor-free. Suppose that
$G$
is contained in
$H\boxtimes K_c$
. Since
$n\gt c$
and
$G$
is connected,
$|E(H)|\geqslant 1$
and
$H$
has a clique of size 2, as desired.
Now assume
$h\geqslant 2$
and the result holds for
$h-1$
. Let
$t_0\,:\!=\,|V(T_{h-1,3})|$
. By induction, there is a
$T_{h-1,3}$
-minor-free graph
$G_0$
, such that for every graph
$H$
, if
$G_0$
is contained in
$H\boxtimes K_{c}$
, then
$H$
has a clique of size
$2h-2$
. Let
$G$
be obtained from a path
$P$
of length
$c+1$
as follows: for each edge
$vw$
of
$P$
, add
$2c$
copies of
$G_0$
complete to
$\{v,w\}$
.
Suppose for the sake of contradiction that
$G$
contains a
$T_{h,3}$
-model. Let
$X$
be the branch set corresponding to the root of
$T_{h,3}$
. So
$G-X$
contains three pairwise disjoint subgraphs
$Y_1,Y_2,Y_3$
, each containing a
$T_{h-1,3}$
-minor. Each
$Y_i$
intersects
$P$
, otherwise
$Y_i$
is contained in some component of
$G-P$
which is a copy of
$G_0$
. By the construction of
$G$
, each
$Y_i$
intersects
$P$
in a subpath
$P_i$
. Without loss of generality,
$P_1,P_2,P_3$
appear in this order in
$P$
. Since each component of
$G-P$
is only adjacent to an edge of
$P$
, no component of
$G-P_2$
is adjacent to both
$Y_1$
and
$Y_3$
. In particular,
$X$
is not adjacent to both
$Y_1$
and
$Y_3$
, which is a contradiction. Thus
$G$
is
$T_{h,3}$
-minor-free.
Now suppose that
$G$
is contained in
$H\boxtimes K_c$
. Let
$\mathcal{P}$
be the corresponding
$H$
-partition of
$G$
. Since
$|V(P)|\gt c$
there is an edge
$v_1v_2$
of
$P$
with
$v_i\in Q_i$
for some distinct parts
$Q_1,Q_2\in \mathcal{P}$
. At most
$c-1$
of the copies of
$G_0$
attached to
$v_1v_2$
intersect
$Q_1$
, and at most
$c-1$
of the copies of
$G_0$
attached to
$v_1v_2$
intersect
$Q_2$
. Thus, some copy of
$G_0$
attached to
$v_1v_2$
avoids
$Q_1\cup Q_2$
. Let
$H_0$
be the subgraph of
$H$
induced by those parts that intersect this copy of
$G_0$
. So neither
$Q_1$
nor
$Q_2$
is in
$H_0$
. By induction,
$H_0$
has a clique
$C_0$
of size
$2(h-1)$
. Since
$G_0$
is complete to
$v_1v_2$
, we have that
$C_0\cup \{Q_1,Q_2\}$
is a clique of size
$2h$
in
$H$
, as desired.
