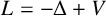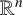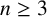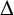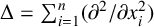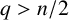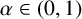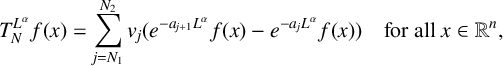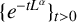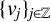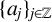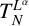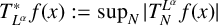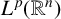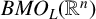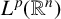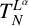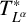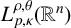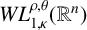1 Introduction
Consider the Schrödinger operator
![]() ${L}=-\Delta +V$
in
${L}=-\Delta +V$
in
![]() ${\mathbb R}^n$
with
${\mathbb R}^n$
with
![]() $n\ge 3$
, where
$n\ge 3$
, where
![]() $ {\Delta = \sum _{j=1}^n({\partial ^2}/ {\partial x^2_j})}$
is the Laplace operator and the nonnegative potential V belongs to the reverse Hölder class
$ {\Delta = \sum _{j=1}^n({\partial ^2}/ {\partial x^2_j})}$
is the Laplace operator and the nonnegative potential V belongs to the reverse Hölder class
![]() $(RH)_q$
: that is, there exists
$(RH)_q$
: that is, there exists
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} \bigg(\frac{1}{|B|}\int_B V(x)^q\,dx\bigg)^{{1}/{q}}\leq \frac{C}{|B|}\int_B V(x)\,dx \end{align*} $$
$$ \begin{align*} \bigg(\frac{1}{|B|}\int_B V(x)^q\,dx\bigg)^{{1}/{q}}\leq \frac{C}{|B|}\int_B V(x)\,dx \end{align*} $$
holds for every ball B in
![]() ${\mathbb R}^{n}$
. In this paper, we mainly focus on the fractional Schrödinger operator
${\mathbb R}^{n}$
. In this paper, we mainly focus on the fractional Schrödinger operator
![]() ${L^\alpha }=(-\displaystyle \Delta +V)^\alpha $
for
${L^\alpha }=(-\displaystyle \Delta +V)^\alpha $
for
![]() $\alpha \in (0,1)$
. When
$\alpha \in (0,1)$
. When
![]() $V=0$
,
$V=0$
,
![]() $L^{\alpha }$
reduces to the fractional Laplace operator
$L^{\alpha }$
reduces to the fractional Laplace operator
![]() $(-\Delta )^{\alpha }$
, which is represented as
$(-\Delta )^{\alpha }$
, which is represented as
where
![]() $\mathcal F$
denotes the Fourier transform defined as
$\mathcal F$
denotes the Fourier transform defined as
for any
![]() $f\in S'$
, where
$f\in S'$
, where
![]() $S'$
denotes the space of tempered distributions. The corresponding fractional heat semigroup is given by
$S'$
denotes the space of tempered distributions. The corresponding fractional heat semigroup is given by
In [Reference Miao, Yuan and Zhang12], by an invariant derivative technique and the Fourier analysis method, Miao, Yuan and Zhang concluded that the convolution kernels of
![]() $\{e^{- {t(-\Delta )^\alpha }}\}_{t>0}$
, denoted by
$\{e^{- {t(-\Delta )^\alpha }}\}_{t>0}$
, denoted by
![]() $K^{-\Delta }_{\alpha , t}(\cdot )$
, satisfy the following pointwise estimate: there exists a positive constant C such that, for any
$K^{-\Delta }_{\alpha , t}(\cdot )$
, satisfy the following pointwise estimate: there exists a positive constant C such that, for any
![]() $(x,t)\in {\mathbb R}_+^{n+1}$
,
$(x,t)\in {\mathbb R}_+^{n+1}$
,
Then, arguing in the same way as in [Reference Ferrari, Miranda, Pallara, Pinamonti and Sire6, Remark 2.2], we also have the lower estimate
Different from the case of
![]() $-\displaystyle \Delta $
, for the Schrödinger operator
$-\displaystyle \Delta $
, for the Schrödinger operator
![]() ${L}$
with the positive potential V, the fractional heat semigroup
${L}$
with the positive potential V, the fractional heat semigroup
![]() $\{e^{- {tL^\alpha }}\}_{t>0}$
with
$\{e^{- {tL^\alpha }}\}_{t>0}$
with
![]() $\alpha \in (0,1)$
generated from
$\alpha \in (0,1)$
generated from
![]() $L^\alpha $
cannot be defined via (1-1). In [Reference Li, Wang, Qian and Zhang10], Li et al. used the subordinative formula to obtain the following pointwise estimate of the integral kernel
$L^\alpha $
cannot be defined via (1-1). In [Reference Li, Wang, Qian and Zhang10], Li et al. used the subordinative formula to obtain the following pointwise estimate of the integral kernel
![]() $K^{L}_{\alpha , t}(\cdot ,\cdot )$
of
$K^{L}_{\alpha , t}(\cdot ,\cdot )$
of
![]() $e^{- {tL^\alpha }}$
: that is, for every
$e^{- {tL^\alpha }}$
: that is, for every
![]() $N>0,$
there exists a positive constant
$N>0,$
there exists a positive constant
![]() $C_N$
such that, for any
$C_N$
such that, for any
![]() $x,y\in \mathbb R^{n}$
,
$x,y\in \mathbb R^{n}$
,
 $$ \begin{align} |K^{L}_{\alpha, t}(x,y)|\leq\frac{C_{N}t}{(t^{1/(2\alpha)}+|x-y|)^{n+2 \alpha }} \bigg(1+\frac{t^{1/(2\alpha)}}{\rho(x)}+\frac{t^{1/(2\alpha)}}{\rho(y)}\bigg)^{-N}. \end{align} $$
$$ \begin{align} |K^{L}_{\alpha, t}(x,y)|\leq\frac{C_{N}t}{(t^{1/(2\alpha)}+|x-y|)^{n+2 \alpha }} \bigg(1+\frac{t^{1/(2\alpha)}}{\rho(x)}+\frac{t^{1/(2\alpha)}}{\rho(y)}\bigg)^{-N}. \end{align} $$
Let
![]() $(\mathbb {X}, \Sigma , m)$
be a complete nonatomic probability space and let
$(\mathbb {X}, \Sigma , m)$
be a complete nonatomic probability space and let
![]() $\tau $
be a measurable, invertible, ergodic measure-preserving point transformation mapping
$\tau $
be a measurable, invertible, ergodic measure-preserving point transformation mapping
![]() $\mathbb {X}$
to itself. For an increasing sequence of positive integers denoted by
$\mathbb {X}$
to itself. For an increasing sequence of positive integers denoted by
![]() $\{n_{k}\}_{k=0}^{\infty }$
, the ergodic average related with
$\{n_{k}\}_{k=0}^{\infty }$
, the ergodic average related with
![]() $\{n_{k}\}^{\infty }_{k=0}$
is defined as
$\{n_{k}\}^{\infty }_{k=0}$
is defined as
 $$ \begin{align*}A_{k}(f)(x):=\frac{1}{n_{k}}\sum^{n_{k}-1}_{j=0}f(\tau^{j}x).\end{align*} $$
$$ \begin{align*}A_{k}(f)(x):=\frac{1}{n_{k}}\sum^{n_{k}-1}_{j=0}f(\tau^{j}x).\end{align*} $$
To investigate the convergence property of the difference average
 $$ \begin{align*}\sum^{\infty}_{k=1}v_{k}(A_{k}(f)(x)-A_{k-1}(f)(x)),\end{align*} $$
$$ \begin{align*}\sum^{\infty}_{k=1}v_{k}(A_{k}(f)(x)-A_{k-1}(f)(x)),\end{align*} $$
Jones and Rosemblatt in [Reference Jones and Rosenblatt9] considered the partial sum
 $$ \begin{align*}T_{n}(f)(x):=\sum^{n}_{k=1}v_{k}(A_{k}(f)(x)-A_{k-1}(f)(x)),\end{align*} $$
$$ \begin{align*}T_{n}(f)(x):=\sum^{n}_{k=1}v_{k}(A_{k}(f)(x)-A_{k-1}(f)(x)),\end{align*} $$
where
![]() $\{v_{k}\}$
is some bounded sequence of real (or complex) numbers. As one of the main results of [Reference Jones and Rosenblatt9], the authors proved that if
$\{v_{k}\}$
is some bounded sequence of real (or complex) numbers. As one of the main results of [Reference Jones and Rosenblatt9], the authors proved that if
![]() $\{n_{k}\}$
is a lacunary sequence of positive integers and
$\{n_{k}\}$
is a lacunary sequence of positive integers and
![]() $v=\{v_{k}\}$
is any sequence such that
$v=\{v_{k}\}$
is any sequence such that
![]() $\|v\|_{\infty }\leq 1$
, then
$\|v\|_{\infty }\leq 1$
, then
![]() $T_{n}(f)$
converges almost everywhere for all functions
$T_{n}(f)$
converges almost everywhere for all functions
![]() $f\in L^{p}$
,
$f\in L^{p}$
,
![]() $1\leq p\leq \infty $
, and converges in
$1\leq p\leq \infty $
, and converges in
![]() $L^p$
norm for all functions
$L^p$
norm for all functions
![]() $f\in L^{p}$
,
$f\in L^{p}$
,
![]() $1< p< \infty $
. In [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3], this method of analyzing the convergence of sequences was applied to differential transforms by Bernardis et al. Based on the idea used in [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3, Reference Jones and Rosenblatt9], in Zhang et al. [Reference Zhang, Ma and Torrea19] and Zhang–Torrea [Reference Zhang and Torrea20], the authors investigated the differential transforms related to the one-sided fractional Poisson-type operator sequence and the heat semigroup, which are generated by the Laplacian and Schrödinger operators, respectively.
$1< p< \infty $
. In [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3], this method of analyzing the convergence of sequences was applied to differential transforms by Bernardis et al. Based on the idea used in [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3, Reference Jones and Rosenblatt9], in Zhang et al. [Reference Zhang, Ma and Torrea19] and Zhang–Torrea [Reference Zhang and Torrea20], the authors investigated the differential transforms related to the one-sided fractional Poisson-type operator sequence and the heat semigroup, which are generated by the Laplacian and Schrödinger operators, respectively.
The aim of this paper is to analyze the behavior of the sum
 $$ \begin{align} \sum_{j\in {\mathbb Z}} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)), \end{align} $$
$$ \begin{align} \sum_{j\in {\mathbb Z}} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)), \end{align} $$
where
![]() $\{v_j\}_{j\in {\mathbb Z}}$
is a bounded sequence of real numbers and
$\{v_j\}_{j\in {\mathbb Z}}$
is a bounded sequence of real numbers and
![]() $\{a_j\}_{j\in {\mathbb Z}}$
is an increasing sequence of positive numbers. It follows from [Reference Zhang and Torrea20] that, in the case
$\{a_j\}_{j\in {\mathbb Z}}$
is an increasing sequence of positive numbers. It follows from [Reference Zhang and Torrea20] that, in the case
![]() $v_j\equiv 1$
, the behavior of the above series coincides with that of
$v_j\equiv 1$
, the behavior of the above series coincides with that of
![]() $e^{-tL^\alpha } f(x)$
. To investigate the behavior of the sum in (1-3), we only need to analyze the ‘partial sums’ of the series in (1-3), which are defined as follows. For each
$e^{-tL^\alpha } f(x)$
. To investigate the behavior of the sum in (1-3), we only need to analyze the ‘partial sums’ of the series in (1-3), which are defined as follows. For each
![]() $N=(N_1,N_2)\in {\mathbb Z}^2$
with
$N=(N_1,N_2)\in {\mathbb Z}^2$
with
![]() $N_1<N_2,$
the corresponding partial sum operators are defined as
$N_1<N_2,$
the corresponding partial sum operators are defined as
 $$ \begin{align} T^{L^\alpha}_N f(x):=\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x))\quad \mbox{for all }x\in \mathbb R^n, \end{align} $$
$$ \begin{align} T^{L^\alpha}_N f(x):=\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x))\quad \mbox{for all }x\in \mathbb R^n, \end{align} $$
and
 $$ \begin{align*} T^{(-\Delta)^{\alpha}}_N f(x):=\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}(-\Delta)^\alpha} f(x)-e^{-a_{j}(-\Delta)^\alpha} f(x))\quad \mbox{for all }x\in \mathbb R^n. \end{align*} $$
$$ \begin{align*} T^{(-\Delta)^{\alpha}}_N f(x):=\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}(-\Delta)^\alpha} f(x)-e^{-a_{j}(-\Delta)^\alpha} f(x))\quad \mbox{for all }x\in \mathbb R^n. \end{align*} $$
We also consider the maximal operators
and
where the supremum is taken over all
![]() $N=(N_1,N_2)\in {\mathbb Z}^2$
with
$N=(N_1,N_2)\in {\mathbb Z}^2$
with
![]() $N_1< N_2$
.
$N_1< N_2$
.
In this paper, we present a detailed study of the convergence of
![]() $T^{L^{\alpha }}_N$
in order to extend the results of [Reference Zhang, Ma and Torrea19, Reference Zhang and Torrea20]. The structure of the paper is as follows. In Section 2, we collect some notation and basic ingredients that are used in what follows. In Section 3, we mainly focus on the boundedness of the operator
$T^{L^{\alpha }}_N$
in order to extend the results of [Reference Zhang, Ma and Torrea19, Reference Zhang and Torrea20]. The structure of the paper is as follows. In Section 2, we collect some notation and basic ingredients that are used in what follows. In Section 3, we mainly focus on the boundedness of the operator
![]() $T^{L^{\alpha }}_N$
. More precisely, we investigate for the first time the integral kernel
$T^{L^{\alpha }}_N$
. More precisely, we investigate for the first time the integral kernel
![]() $K_{N}^{\alpha }(\cdot ,\cdot )$
of
$K_{N}^{\alpha }(\cdot ,\cdot )$
of
![]() $T^{L^{\alpha }}_N$
, and its size description and the smoothness estimates are obtained in Proposition 3.5. Moreover, we investigate the uniform boundedness of
$T^{L^{\alpha }}_N$
, and its size description and the smoothness estimates are obtained in Proposition 3.5. Moreover, we investigate the uniform boundedness of
![]() $T^{L^{\alpha }}_N$
in the BMO-type space denoted by
$T^{L^{\alpha }}_N$
in the BMO-type space denoted by
![]() $BMO_{L}(\mathbb R^{n})$
; see Theorem 3.6. Then with the aid of the vector-valued Calderón–Zygmund theory, we obtain the
$BMO_{L}(\mathbb R^{n})$
; see Theorem 3.6. Then with the aid of the vector-valued Calderón–Zygmund theory, we obtain the
![]() $L^{p}$
-boundedness of
$L^{p}$
-boundedness of
![]() $T^{L^{\alpha }}_N$
. In addition, we get the boundedness of
$T^{L^{\alpha }}_N$
. In addition, we get the boundedness of
![]() $T^{L^{\alpha }}_N$
on the Morrey spaces
$T^{L^{\alpha }}_N$
on the Morrey spaces
![]() $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
and the weak Morrey spaces
$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
and the weak Morrey spaces
![]() $WL^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
; see Theorem 3.7.
$WL^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
; see Theorem 3.7.
In Section 4, our attention shifts to the maximal operator
![]() $T^*_{L^{\alpha }}$
. On the one hand, using a Cotlar-type inequality, the maximal operators and the uniform
$T^*_{L^{\alpha }}$
. On the one hand, using a Cotlar-type inequality, the maximal operators and the uniform
![]() $L^{p}$
-boundedness of
$L^{p}$
-boundedness of
![]() $T^{L^{\alpha }}_N$
, we obtain the
$T^{L^{\alpha }}_N$
, we obtain the
![]() $L^{p}$
-boundedness of
$L^{p}$
-boundedness of
![]() $T^*_{L^{\alpha }}$
and
$T^*_{L^{\alpha }}$
and
![]() $T^*_{(-\Delta )^{\alpha }}$
; see Theorem 4.4. On the other hand, we not only establish the
$T^*_{(-\Delta )^{\alpha }}$
; see Theorem 4.4. On the other hand, we not only establish the
![]() $BMO_{L}$
-boundedness of
$BMO_{L}$
-boundedness of
![]() $T^*_{L^{\alpha }}$
using the
$T^*_{L^{\alpha }}$
using the
![]() $T1$
theorem (see Theorem 4.6), but we also explore the boundedness of
$T1$
theorem (see Theorem 4.6), but we also explore the boundedness of
![]() $T^*_{L^{\alpha }}$
in Morrey spaces (see Theorem 4.7). Finally, Theorem 4.10 analyzes the behavior of
$T^*_{L^{\alpha }}$
in Morrey spaces (see Theorem 4.7). Finally, Theorem 4.10 analyzes the behavior of
![]() $T^*_{L^{\alpha }}$
and
$T^*_{L^{\alpha }}$
and
![]() $T^*_{(-\Delta )^{\alpha }}$
in
$T^*_{(-\Delta )^{\alpha }}$
in
![]() $L^{\infty }$
more deeply. It should be mentioned that some of our results are valid only when the sequence
$L^{\infty }$
more deeply. It should be mentioned that some of our results are valid only when the sequence
![]() $\{a_j\}_{j\in \mathbb Z}$
is lacunary, which means that there exists a
$\{a_j\}_{j\in \mathbb Z}$
is lacunary, which means that there exists a
![]() $\lambda>1$
such that
$\lambda>1$
such that
![]() $\displaystyle {a_{j+1}}/{a_j} \ge \lambda , \, j \in \mathbb {Z}$
.
$\displaystyle {a_{j+1}}/{a_j} \ge \lambda , \, j \in \mathbb {Z}$
.
Throughout this paper, we use c and C to denote positive constants, which are independent of main parameters and may be different at each occurrence. By
![]() $\mathrm {X}\sim \mathrm {Y}$
, we mean that
$\mathrm {X}\sim \mathrm {Y}$
, we mean that
![]() $\mathrm {Y}\lesssim \mathrm {X}\lesssim \mathrm {Y},$
where the second estimate means that there exists a positive constant C, independent of main parameters, such that
$\mathrm {Y}\lesssim \mathrm {X}\lesssim \mathrm {Y},$
where the second estimate means that there exists a positive constant C, independent of main parameters, such that
![]() $\mathrm {X}\leq C\mathrm {Y}.$
Similarly, we write
$\mathrm {X}\leq C\mathrm {Y}.$
Similarly, we write
![]() ${\mathsf V}\gtrsim {\mathsf U}$
for
${\mathsf V}\gtrsim {\mathsf U}$
for
![]() ${\mathsf V}\ge c{\mathsf U}$
.
${\mathsf V}\ge c{\mathsf U}$
.
2 Preliminaries
To investigate estimates of the fundamental solution of Schrödinger operators, Shen in [Reference Shen15] introduced the critical radius function, which is defined as
 $$ \begin{align} \rho(x):=\sup\bigg\{r>0:\frac{1}{r^{n-2}}\int_{B(x,r)}V(y)\,dy\leq1\bigg\}\quad \mbox{for all}\ x\in{\mathbb R}^n, \end{align} $$
$$ \begin{align} \rho(x):=\sup\bigg\{r>0:\frac{1}{r^{n-2}}\int_{B(x,r)}V(y)\,dy\leq1\bigg\}\quad \mbox{for all}\ x\in{\mathbb R}^n, \end{align} $$
where
![]() $B(x,r)$
denotes the ball in
$B(x,r)$
denotes the ball in
![]() $\mathbb {R}^{n}$
centered at x and with radius r. It is well known that the auxiliary function
$\mathbb {R}^{n}$
centered at x and with radius r. It is well known that the auxiliary function
![]() $\rho (x)$
determined by
$\rho (x)$
determined by
![]() $V\in (RH)_{q}$
satisfies
$V\in (RH)_{q}$
satisfies
![]() $0<\rho (x)<\infty $
for any given
$0<\rho (x)<\infty $
for any given
![]() $x\in \mathbb {R}^{n}$
. We need the following known results concerning the critical radius function in (2-1).
$x\in \mathbb {R}^{n}$
. We need the following known results concerning the critical radius function in (2-1).
Lemma 2.1 [Reference Shen15, Lemma 1.4].
There exist constants
![]() $C_{0}\geq 1$
and
$C_{0}\geq 1$
and
![]() $N_{0}>0$
such that, for any x and y in
$N_{0}>0$
such that, for any x and y in
![]() $\mathbb {R}^{n}$
,
$\mathbb {R}^{n}$
,
 $$ \begin{align} \frac{1}{C_{0}}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{-N_{0}}\leq \frac{\rho(y)}{\rho(x)}\leq C_{0}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{{N_{0}}/{(1+N_{0})}}. \end{align} $$
$$ \begin{align} \frac{1}{C_{0}}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{-N_{0}}\leq \frac{\rho(y)}{\rho(x)}\leq C_{0}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{{N_{0}}/{(1+N_{0})}}. \end{align} $$
As a direct consequence of (2-2), we see that, for each fixed
![]() $k\in \mathbb {N}$
, the estimate
$k\in \mathbb {N}$
, the estimate
 $$ \begin{align} \bigg(1+\frac{r}{\rho(x)}\bigg)^{-{N_{0}}/{(1+N_{0})}}\bigg(1+\frac{2^{k}r}{\rho(x)}\bigg)\leq C_{0}\bigg(1+\frac{2^{k}r}{\rho(y)}\bigg) \end{align} $$
$$ \begin{align} \bigg(1+\frac{r}{\rho(x)}\bigg)^{-{N_{0}}/{(1+N_{0})}}\bigg(1+\frac{2^{k}r}{\rho(x)}\bigg)\leq C_{0}\bigg(1+\frac{2^{k}r}{\rho(y)}\bigg) \end{align} $$
holds for any
![]() $y\in B(x,r)$
with
$y\in B(x,r)$
with
![]() $x\in \mathbb {R}^{n}$
and
$x\in \mathbb {R}^{n}$
and
![]() $r\in (0,\infty )$
, where
$r\in (0,\infty )$
, where
![]() $C_{0}$
appears in (2-2).
$C_{0}$
appears in (2-2).
The space
![]() $BMO_{L}({\mathbb R}^n)$
, which was introduced in [Reference Dziubański, Garrigós, Martínez, Torrea and Zienkiewicz5], is defined as the set of locally integrable functions f such that, for all balls
$BMO_{L}({\mathbb R}^n)$
, which was introduced in [Reference Dziubański, Garrigós, Martínez, Torrea and Zienkiewicz5], is defined as the set of locally integrable functions f such that, for all balls
![]() $B= B(x,R)$
,
$B= B(x,R)$
,
 $$ \begin{align*} \begin{cases} \displaystyle \dfrac1{|B|} \int_B\bigg|f(z)- \dfrac1{|B|} \int_B f \bigg| \,dz\le C_1 & \text{if }R \le\rho(x),\\\\[-8pt] \displaystyle \dfrac1{|B|} \int_B |f| \le C_2& \text{if }R>\rho(x). \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \displaystyle \dfrac1{|B|} \int_B\bigg|f(z)- \dfrac1{|B|} \int_B f \bigg| \,dz\le C_1 & \text{if }R \le\rho(x),\\\\[-8pt] \displaystyle \dfrac1{|B|} \int_B |f| \le C_2& \text{if }R>\rho(x). \end{cases} \end{align*} $$
The norm
![]() $\|f\|_{BMO_L(\mathbb {R}^n)}$
is defined as
$\|f\|_{BMO_L(\mathbb {R}^n)}$
is defined as
![]() $\min \{C_1,C_2\}$
, which are given in the above two inequalities.
$\min \{C_1,C_2\}$
, which are given in the above two inequalities.
The classical Morrey spaces
![]() $M^{\lambda }_{p}(\mathbb {R}^{n})$
are defined as follows.
$M^{\lambda }_{p}(\mathbb {R}^{n})$
are defined as follows.
Definition 2.2.
-
(i) Let
 $1\leq p<\infty $
and
$1\leq p<\infty $
and
 $0\leq \lambda \leq n$
. The Morrey space
$0\leq \lambda \leq n$
. The Morrey space
 $M^{\lambda }_{p}(\mathbb {R}^{n})$
is defined as the set of all p-locally integrable functions f on
$M^{\lambda }_{p}(\mathbb {R}^{n})$
is defined as the set of all p-locally integrable functions f on
 $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that  $$ \begin{align*}\|f\|_{M^{\lambda}_{p}(\mathbb{R}^{n})}:=\sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda/p}\|f\|_{L^{p}(B(x,r))}<\infty.\end{align*} $$
$$ \begin{align*}\|f\|_{M^{\lambda}_{p}(\mathbb{R}^{n})}:=\sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda/p}\|f\|_{L^{p}(B(x,r))}<\infty.\end{align*} $$
-
(ii) The weak Morrey space
 $WM^{\lambda }_{1}(\mathbb {R}^{n})$
consists of all measurable functions f on
$WM^{\lambda }_{1}(\mathbb {R}^{n})$
consists of all measurable functions f on
 $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that  $$ \begin{align*} \|f\|_{WM^{\lambda}_{1}(\mathbb{R}^{n})} &:= \sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda}\|f\|_{WL^{1}(B(x,r))} \\ &= \sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda} \sup_{\sigma>0}\sigma|\{y\in B(x,r):|f(y)|>\sigma\}|<\infty. \end{align*} $$
$$ \begin{align*} \|f\|_{WM^{\lambda}_{1}(\mathbb{R}^{n})} &:= \sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda}\|f\|_{WL^{1}(B(x,r))} \\ &= \sup_{x\in\mathbb{R}^{n},r>0}r^{-\lambda} \sup_{\sigma>0}\sigma|\{y\in B(x,r):|f(y)|>\sigma\}|<\infty. \end{align*} $$
The spaces
![]() $M^{\lambda }_{p}(\mathbb {R}^{n})$
, which were originally introduced by Morrey in [Reference Morrey13] as a generalization of Lebesgue spaces, have been studied intensively and widely used in elliptic partial differential equations, calculus of variations and other related fields. For the properties and applications of
$M^{\lambda }_{p}(\mathbb {R}^{n})$
, which were originally introduced by Morrey in [Reference Morrey13] as a generalization of Lebesgue spaces, have been studied intensively and widely used in elliptic partial differential equations, calculus of variations and other related fields. For the properties and applications of
![]() $M^{\lambda }_{p}(\mathbb {R}^{n})$
, we refer the reader to [Reference Adams and Xiao1, Reference Adams and Xiao2, Reference Pan and Tang14, Reference Taylor17] and the references therein. It should be mentioned that
$M^{\lambda }_{p}(\mathbb {R}^{n})$
, we refer the reader to [Reference Adams and Xiao1, Reference Adams and Xiao2, Reference Pan and Tang14, Reference Taylor17] and the references therein. It should be mentioned that
![]() $M^{0}_{p}(\mathbb {R}^{n})=L^{p}(\mathbb {R}^{n})$
and
$M^{0}_{p}(\mathbb {R}^{n})=L^{p}(\mathbb {R}^{n})$
and
![]() $M^{n}_{p}(\mathbb {R}^{n})=L^{\infty }(\mathbb {R}^{n})$
by the Lebesgue differentiation theorem. If
$M^{n}_{p}(\mathbb {R}^{n})=L^{\infty }(\mathbb {R}^{n})$
by the Lebesgue differentiation theorem. If
![]() $\lambda <0$
or
$\lambda <0$
or
![]() $\lambda>n$
, then
$\lambda>n$
, then
![]() $M^{\lambda }_{p}(\mathbb {R}^{n})=\Theta $
, where
$M^{\lambda }_{p}(\mathbb {R}^{n})=\Theta $
, where
![]() $\Theta $
is the set of all functions equivalent to 0 on
$\Theta $
is the set of all functions equivalent to 0 on
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
In [Reference Tang and Dong16], Tang and Dong introduced the following Morrey-type spaces related to L to investigate the boundedness of operators generated by L; for example, Schrödinger-type Calderón–Zygmund operators, Riesz transforms and fractional integrals related to L.
Definition 2.3. Let
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $0\leq \kappa <1$
. For a given
$0\leq \kappa <1$
. For a given
![]() $0<\theta <\infty $
, the Morrey space
$0<\theta <\infty $
, the Morrey space
![]() $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
is defined to be the set of all p-locally integrable functions f on
$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
is defined to be the set of all p-locally integrable functions f on
![]() $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that
 $$ \begin{align} \bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|f(x)|^{p}\,dx\bigg)^{1/p}\leq C\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta} \end{align} $$
$$ \begin{align} \bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|f(x)|^{p}\,dx\bigg)^{1/p}\leq C\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta} \end{align} $$
holds for every ball
![]() $B(x_{0},r)$
in
$B(x_{0},r)$
in
![]() $\mathbb {R}^{n}$
. A norm for
$\mathbb {R}^{n}$
. A norm for
![]() $f\in L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
, denoted by
$f\in L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
, denoted by
![]() $\|f\|_{L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})}$
, is given by the infimum of the constants appearing in (2-4), or, equivalently,
$\|f\|_{L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})}$
, is given by the infimum of the constants appearing in (2-4), or, equivalently,
 $$ \begin{align*}\|f\|_{L^{\rho,\theta}_{p,\kappa}(\mathbb{R}^{n})}:=\sup_{B(x_{0},r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{-\theta}\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}} \int_{B(x_{0},r)}|f(x)|^{p}\,dx\bigg)^{1/p}<\infty,\end{align*} $$
$$ \begin{align*}\|f\|_{L^{\rho,\theta}_{p,\kappa}(\mathbb{R}^{n})}:=\sup_{B(x_{0},r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{-\theta}\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}} \int_{B(x_{0},r)}|f(x)|^{p}\,dx\bigg)^{1/p}<\infty,\end{align*} $$
where the supremum is taken over all balls
![]() $B(x_{0},r)$
in
$B(x_{0},r)$
in
![]() $\mathbb {R}^{n}$
. Define
$\mathbb {R}^{n}$
. Define
Definition 2.4. Let
![]() $p=1$
and
$p=1$
and
![]() $0\leq \kappa <1$
. For a given
$0\leq \kappa <1$
. For a given
![]() $0<\theta <\infty $
, the weak Morrey space
$0<\theta <\infty $
, the weak Morrey space
![]() $WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
is defined to be the set of all measurable functions f on
$WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
is defined to be the set of all measurable functions f on
![]() $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that
 $$ \begin{align*}\frac{1}{|B(x_{0},r)|^{\kappa}}\sup_{\lambda>0}\lambda\cdot|\{x\in B(x_{0},r):|f(x)|>\lambda\}|\leq C\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta}\end{align*} $$
$$ \begin{align*}\frac{1}{|B(x_{0},r)|^{\kappa}}\sup_{\lambda>0}\lambda\cdot|\{x\in B(x_{0},r):|f(x)|>\lambda\}|\leq C\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta}\end{align*} $$
holds for every ball
![]() $B(x_{0},r)$
in
$B(x_{0},r)$
in
![]() $\mathbb {R}^{n}$
. A norm for
$\mathbb {R}^{n}$
. A norm for
![]() $f\in WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
is given by
$f\in WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
is given by
 $$ \begin{align*}\|f\|_{WL^{\rho,\theta}_{1,\kappa}(\mathbb{R}^{n})}:=\sup_{B(x_{0},r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{-\theta}\frac{1}{|B(x_{0},r)|^{\kappa}} \sup_{\lambda>0}\lambda\, |\{x\in B(x_{0},r): |f(x)|>\lambda\}|<\infty.\end{align*} $$
$$ \begin{align*}\|f\|_{WL^{\rho,\theta}_{1,\kappa}(\mathbb{R}^{n})}:=\sup_{B(x_{0},r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{-\theta}\frac{1}{|B(x_{0},r)|^{\kappa}} \sup_{\lambda>0}\lambda\, |\{x\in B(x_{0},r): |f(x)|>\lambda\}|<\infty.\end{align*} $$
Correspondingly, we define
Remark 2.5.
-
(i) It is easy to see that if
 $\theta =0$
or
$\theta =0$
or
 $V=0$
, then the Morrey space
$V=0$
, then the Morrey space
 $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
(or the weak Morrey space
$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
(or the weak Morrey space
 $WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
) is just the Morrey space
$WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
) is just the Morrey space
 $L^{\kappa }_{p}(\mathbb {R}^{n})$
(or the weak Morrey space
$L^{\kappa }_{p}(\mathbb {R}^{n})$
(or the weak Morrey space
 $WL^{\kappa }_{1}(\mathbb {R}^{n})$
), which was defined and studied by Guliyev et al.; see [Reference Guliyev, Eroglu and Mammadov8].
$WL^{\kappa }_{1}(\mathbb {R}^{n})$
), which was defined and studied by Guliyev et al.; see [Reference Guliyev, Eroglu and Mammadov8]. -
(ii) According to the above definitions,
(2-5)and $$ \begin{align} L^{\kappa}_{p}(\mathbb{R}^{n})\subset L^{\rho,\theta_{1}}_{p,\kappa}(\mathbb{R}^{n})\subset L^{\rho,\theta_{2}}_{p,\kappa}(\mathbb{R}^{n}) \end{align} $$
(2-6)whenever
$$ \begin{align} L^{\kappa}_{p}(\mathbb{R}^{n})\subset L^{\rho,\theta_{1}}_{p,\kappa}(\mathbb{R}^{n})\subset L^{\rho,\theta_{2}}_{p,\kappa}(\mathbb{R}^{n}) \end{align} $$
(2-6)whenever $$ \begin{align} WL^{\kappa}_{1}(\mathbb{R}^{n})\subset WL^{\rho,\theta_{1}}_{1,\kappa}(\mathbb{R}^{n})\subset WL^{\rho,\theta_{2}}_{1,\kappa}(\mathbb{R}^{n}), \end{align} $$
$$ \begin{align} WL^{\kappa}_{1}(\mathbb{R}^{n})\subset WL^{\rho,\theta_{1}}_{1,\kappa}(\mathbb{R}^{n})\subset WL^{\rho,\theta_{2}}_{1,\kappa}(\mathbb{R}^{n}), \end{align} $$
 $0<\theta _{1}<\theta _{2}<\infty .$
Hence, for all
$0<\theta _{1}<\theta _{2}<\infty .$
Hence, for all $$ \begin{align*} L^{\kappa}_{p}(\mathbb{R}^{n})\subset L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})\quad \mathrm{and}\quad WL^{\kappa}_{1}(\mathbb{R}^{n})\subset WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n}) \end{align*} $$
$$ \begin{align*} L^{\kappa}_{p}(\mathbb{R}^{n})\subset L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})\quad \mathrm{and}\quad WL^{\kappa}_{1}(\mathbb{R}^{n})\subset WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n}) \end{align*} $$
 $(p,\kappa )\in [1,\infty )\times [0,1)$
.
$(p,\kappa )\in [1,\infty )\times [0,1)$
.
-
(iii) Define a norm on the space
 $L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
. Then this space becomes a Banach space. In view of (2-5), for any given
$L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
. Then this space becomes a Banach space. In view of (2-5), for any given
 $f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
, let
$f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
, let  $$ \begin{align*}\theta^{\ast}:=\inf\{\theta>0:f\in L^{\rho,\theta}_{p,\kappa}(\mathbb{R}^{n})\}.\end{align*} $$
$$ \begin{align*}\theta^{\ast}:=\inf\{\theta>0:f\in L^{\rho,\theta}_{p,\kappa}(\mathbb{R}^{n})\}.\end{align*} $$
Now define the functional
 $\|\cdot \|_{\star }$
by
$\|\cdot \|_{\star }$
by  $$ \begin{align*} \|f\|_{\star}:=\|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}:=\|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}. \end{align*} $$
$$ \begin{align*} \|f\|_{\star}:=\|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}:=\|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}. \end{align*} $$
It is easy to check that this functional
 $\|\cdot \|_{\star }$
satisfies the axioms of a norm.
$\|\cdot \|_{\star }$
satisfies the axioms of a norm. -
(iv) In view of (2-6), for any given
 $f\in WL^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
, let
$f\in WL^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
, let  $$ \begin{align*}\theta^{\ast\ast}:=\inf\{\theta>0:f\in WL^{\rho,\theta}_{1,\kappa}(\mathbb{R}^{n})\}.\end{align*} $$
$$ \begin{align*}\theta^{\ast\ast}:=\inf\{\theta>0:f\in WL^{\rho,\theta}_{1,\kappa}(\mathbb{R}^{n})\}.\end{align*} $$
Similarly, we define the functional
 $\|\cdot \|_{\star \star }$
by
$\|\cdot \|_{\star \star }$
by  $$ \begin{align*}\|f\|_{\star\star}:=\|f\|_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}:=\|f\|_{WL^{\rho,\theta^{\ast\ast}}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\|f\|_{\star\star}:=\|f\|_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}:=\|f\|_{WL^{\rho,\theta^{\ast\ast}}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
By definition, we easily show that this functional
 $\|\cdot \|_{\star \star }$
satisfies the axioms of a (quasi-)norm and that
$\|\cdot \|_{\star \star }$
satisfies the axioms of a (quasi-)norm and that
 $WL^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
is a (quasi-)normed linear space.
$WL^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
is a (quasi-)normed linear space.
Since the Morrey space
![]() $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
(or the weak Morrey space
$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$
(or the weak Morrey space
![]() $WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
) could be viewed as an extension of the Lebesgue spaces (or the weak Lebesgue) on
$WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$
) could be viewed as an extension of the Lebesgue spaces (or the weak Lebesgue) on
![]() $\mathbb {R}^{n}$
, it is natural to investigate the boundedness properties of operators
$\mathbb {R}^{n}$
, it is natural to investigate the boundedness properties of operators
![]() $T^{L^{\alpha }}_{N}$
and
$T^{L^{\alpha }}_{N}$
and
![]() $T^*_{L^{\alpha }}$
in the framework of Morrey spaces.
$T^*_{L^{\alpha }}$
in the framework of Morrey spaces.
3 Boundedness of the operator
 $T^{L^{\alpha }}_N$
$T^{L^{\alpha }}_N$
In this section, as a preparation for Theorem 4.4, we prove the uniform boundedness of the operators
![]() $T^{L^{\alpha }}_N$
, where the standard Calderón–Zygmund theory is a fundamental tool. We refer the reader to [Reference Duoandikoetxea4, Reference Grafakos7] for some basic knowledge about the Calderón–Zygmund theory. The following
$T^{L^{\alpha }}_N$
, where the standard Calderón–Zygmund theory is a fundamental tool. We refer the reader to [Reference Duoandikoetxea4, Reference Grafakos7] for some basic knowledge about the Calderón–Zygmund theory. The following
![]() $L^{2}$
-boundedness of the operator
$L^{2}$
-boundedness of the operator
![]() $T_N^{L^{\alpha }}$
is a direct consequence of the functional calculus and the spectral resolution of L.
$T_N^{L^{\alpha }}$
is a direct consequence of the functional calculus and the spectral resolution of L.
Proposition 3.1. Let
![]() $\alpha \in (0,1)$
. There exists a constant
$\alpha \in (0,1)$
. There exists a constant
![]() $C>0$
, depending on n,
$C>0$
, depending on n,
![]() $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
![]() $\alpha $
(not on N), such that
$\alpha $
(not on N), such that
Proof. Denote by
![]() $dE(\lambda )$
the spectral resolution of the operator L. Since
$dE(\lambda )$
the spectral resolution of the operator L. Since
![]() $L^\alpha $
is a nonnegative, densely defined and self-adjoint operator on
$L^\alpha $
is a nonnegative, densely defined and self-adjoint operator on
![]() $\mathbb {R}^n$
, by spectral analysis,
$\mathbb {R}^n$
, by spectral analysis,
 $$ \begin{align*} e^{- {tL^\alpha}}=\int_0^\infty e^{- {t\lambda^\alpha}}\,dE(\lambda), \end{align*} $$
$$ \begin{align*} e^{- {tL^\alpha}}=\int_0^\infty e^{- {t\lambda^\alpha}}\,dE(\lambda), \end{align*} $$
which is expressed as
 $$ \begin{align*}\langle e^{-t L^\alpha}f,\ g\rangle_{L^2(\mathbb{R}^n)}=\int_0^\infty e^{-t\lambda^\alpha}\,dE_{f,g}(\lambda) \quad \mbox{for all } f, g\in L^2(\mathbb{R}^n),\end{align*} $$
$$ \begin{align*}\langle e^{-t L^\alpha}f,\ g\rangle_{L^2(\mathbb{R}^n)}=\int_0^\infty e^{-t\lambda^\alpha}\,dE_{f,g}(\lambda) \quad \mbox{for all } f, g\in L^2(\mathbb{R}^n),\end{align*} $$
where
![]() $dE_{f,g}(\lambda )$
is a regular Borel complex measure of bounded variation concentrated on the spectrum of
$dE_{f,g}(\lambda )$
is a regular Borel complex measure of bounded variation concentrated on the spectrum of
![]() ${\mathcal L}$
with
${\mathcal L}$
with
![]() $d\vert E_{f,g}\vert (0,\infty )\leq \Vert f\Vert _{L^2({\mathbb R}^n)}\Vert g\Vert _{L^2({\mathbb R}^n)}$
. Therefore, we write
$d\vert E_{f,g}\vert (0,\infty )\leq \Vert f\Vert _{L^2({\mathbb R}^n)}\Vert g\Vert _{L^2({\mathbb R}^n)}$
. Therefore, we write
 $$ \begin{align*} T^{L^{\alpha}}_N =\sum_{j=N_1}^{N_2} v_j\int_0^\infty (e^{-a_{j+1}\lambda^\alpha} -e^{-a_{j}\lambda^\alpha}) \,dE(\lambda) \end{align*} $$
$$ \begin{align*} T^{L^{\alpha}}_N =\sum_{j=N_1}^{N_2} v_j\int_0^\infty (e^{-a_{j+1}\lambda^\alpha} -e^{-a_{j}\lambda^\alpha}) \,dE(\lambda) \end{align*} $$
and we obtain that, for any
![]() $f, g\in L^2(\mathbb {R}^n)$
,
$f, g\in L^2(\mathbb {R}^n)$
,
 $$ \begin{align*} \vert\langle T^{L^{\alpha}}_N f,g\rangle\vert &\le \bigg| \!\sum_{j=N_1}^{N_2} v_j\int_0^\infty \int_{a_j}^{a_{j+1}} \partial_s e^{-s\lambda^\alpha} \,ds \,dE_{f,g}(\lambda)\bigg| \\ &= \bigg|\! \int_0^\infty\sum_{j=N_1}^{N_2} v_j \int_{a_j}^{a_{j+1}} \partial_s e^{-s\lambda^\alpha} \,ds \,dE_{f,g}(\lambda)\bigg| \\ &\le \|v\|_{\ell^\infty(\mathbb Z)} \int_0^\infty \int_{0}^{\infty} \vert\partial_s e^{-s\lambda^\alpha}\vert \,ds ~\vert \,dE_{f,g}\vert(\lambda)\\ &\lesssim \Vert f\Vert_{L^2({\mathbb R}^{n})} \Vert \Vert g\Vert_{L^2({\mathbb R}^{n})}. \end{align*} $$
$$ \begin{align*} \vert\langle T^{L^{\alpha}}_N f,g\rangle\vert &\le \bigg| \!\sum_{j=N_1}^{N_2} v_j\int_0^\infty \int_{a_j}^{a_{j+1}} \partial_s e^{-s\lambda^\alpha} \,ds \,dE_{f,g}(\lambda)\bigg| \\ &= \bigg|\! \int_0^\infty\sum_{j=N_1}^{N_2} v_j \int_{a_j}^{a_{j+1}} \partial_s e^{-s\lambda^\alpha} \,ds \,dE_{f,g}(\lambda)\bigg| \\ &\le \|v\|_{\ell^\infty(\mathbb Z)} \int_0^\infty \int_{0}^{\infty} \vert\partial_s e^{-s\lambda^\alpha}\vert \,ds ~\vert \,dE_{f,g}\vert(\lambda)\\ &\lesssim \Vert f\Vert_{L^2({\mathbb R}^{n})} \Vert \Vert g\Vert_{L^2({\mathbb R}^{n})}. \end{align*} $$
This completes the proof of Proposition 3.1.
Lemma 3.2 [Reference Li, Wang, Qian and Zhang10, Proposition 3.11].
Let
![]() $\alpha \in (0,1)$
. For every
$\alpha \in (0,1)$
. For every
![]() $N>0$
, there exists a constant
$N>0$
, there exists a constant
![]() $C_{N}>0$
such that
$C_{N}>0$
such that
 $$ \begin{align*}|\partial_t K^{L}_{\alpha,t}(x,y)|\leq C_{N}\min\bigg\{\frac{1}{t^{n/2\alpha+1}},\ \frac{t^{N/\alpha}}{|x-y|^{n+2\alpha+2N}}\bigg\}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\bigg(\frac{t^{1/2\alpha}}{\rho(y)}\bigg)^{-N},\end{align*} $$
$$ \begin{align*}|\partial_t K^{L}_{\alpha,t}(x,y)|\leq C_{N}\min\bigg\{\frac{1}{t^{n/2\alpha+1}},\ \frac{t^{N/\alpha}}{|x-y|^{n+2\alpha+2N}}\bigg\}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\bigg(\frac{t^{1/2\alpha}}{\rho(y)}\bigg)^{-N},\end{align*} $$
which further gives
 $$ \begin{align*}|\partial_t K^{L}_{\alpha,t}(x,y)|\leq \frac{C_N}{(t^{1/2\alpha}+|x-y|)^{n+2\alpha}}\bigg(1+\frac{t^{1/2\alpha}}{\rho(x)}+\frac{t^{1/2\alpha}}{\rho(y)}\bigg)^{-N}.\end{align*} $$
$$ \begin{align*}|\partial_t K^{L}_{\alpha,t}(x,y)|\leq \frac{C_N}{(t^{1/2\alpha}+|x-y|)^{n+2\alpha}}\bigg(1+\frac{t^{1/2\alpha}}{\rho(x)}+\frac{t^{1/2\alpha}}{\rho(y)}\bigg)^{-N}.\end{align*} $$
Lemma 3.3 [Reference Li, Wang, Qian and Zhang10, Proposition 3.12].
Let
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $\beta>0$
. Let
$\beta>0$
. Let
![]() $0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
, where
$0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
, where
![]() $\delta _{0}=\min \{1,2-n/q\}$
. For every
$\delta _{0}=\min \{1,2-n/q\}$
. For every
![]() $N>0$
, there exists a constant
$N>0$
, there exists a constant
![]() $C_{N}>0$
such that, for all
$C_{N}>0$
such that, for all
![]() $|h|\leq t^{1/2\alpha }$
,
$|h|\leq t^{1/2\alpha }$
,
 $$ \begin{align*} &|\partial_t K^{L}_{\alpha,t}(x+h,y)-\partial_t K^{L}_{\alpha,t}(x,y)|\\&\quad\leq C_{N}\bigg(\frac{|h|}{\sqrt {t^{1/\alpha}}}\bigg)^{\delta'}\min\bigg\{\frac{1}{t(\sqrt {t^{1/\alpha}})^n},\ \frac{1}{|x-y|^{n+2\alpha}}\bigg\}\bigg(1+\frac{\sqrt {t^{1/\alpha}}}{\rho(x)}+\frac{\sqrt {t^{1/\alpha}}} {\rho(y)}\bigg)^{-N},\end{align*} $$
$$ \begin{align*} &|\partial_t K^{L}_{\alpha,t}(x+h,y)-\partial_t K^{L}_{\alpha,t}(x,y)|\\&\quad\leq C_{N}\bigg(\frac{|h|}{\sqrt {t^{1/\alpha}}}\bigg)^{\delta'}\min\bigg\{\frac{1}{t(\sqrt {t^{1/\alpha}})^n},\ \frac{1}{|x-y|^{n+2\alpha}}\bigg\}\bigg(1+\frac{\sqrt {t^{1/\alpha}}}{\rho(x)}+\frac{\sqrt {t^{1/\alpha}}} {\rho(y)}\bigg)^{-N},\end{align*} $$
which further gives
 $$ \begin{align*}&|\partial_t K^{L}_{\alpha,t}(x+h,y)-\partial_t K^{L}_{\alpha,t}(x,y)|\\ &\quad\leq C_{N}\bigg(\frac{|h|}{\sqrt {t^{1/\alpha}}}\bigg)^{\delta'} \frac{1}{(\!\sqrt {t^{1/\alpha}}+|x-y|)^{n+2\alpha}} \bigg(1+\frac{\sqrt {t^{1/\alpha}}}{\rho(x)}+\frac{\sqrt {t^{1/\alpha}}}{\rho(y)}\bigg)^{-N}. \end{align*} $$
$$ \begin{align*}&|\partial_t K^{L}_{\alpha,t}(x+h,y)-\partial_t K^{L}_{\alpha,t}(x,y)|\\ &\quad\leq C_{N}\bigg(\frac{|h|}{\sqrt {t^{1/\alpha}}}\bigg)^{\delta'} \frac{1}{(\!\sqrt {t^{1/\alpha}}+|x-y|)^{n+2\alpha}} \bigg(1+\frac{\sqrt {t^{1/\alpha}}}{\rho(x)}+\frac{\sqrt {t^{1/\alpha}}}{\rho(y)}\bigg)^{-N}. \end{align*} $$
Lemma 3.4. Assume that
![]() $\delta _{0}=\min \{1,2-n/q\}$
, as in Lemma 3.3.
$\delta _{0}=\min \{1,2-n/q\}$
, as in Lemma 3.3.
-
(i) [Reference Wang, Li and Zhang18, Proposition 7] There exists a constant
 $C>0$
such that
$C>0$
such that  $$ \begin{align*} &|t\partial_{t}K^{L}_{\alpha,t}(x,y)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-y)|\\ &\quad\leq \left\{ \begin{aligned} &C\bigg(\frac{|x-y|}{\rho(x)}\bigg)^{\delta_{0}}\frac{t}{(|x-y|+\sqrt{t^{1/\alpha}})^{n+2\alpha}},& \sqrt{t^{1/\alpha}}\leq |x-y|,\\ &C\bigg(\frac{\sqrt{t^{1/\alpha}}}{\rho(x)}\bigg)^{\delta_{0}}\frac{t}{(|x-y|+\sqrt{t^{1/\alpha}})^{n+2\alpha}},& \sqrt{t^{1/\alpha}}\geq |x-y|. \end{aligned}\right. \end{align*} $$
$$ \begin{align*} &|t\partial_{t}K^{L}_{\alpha,t}(x,y)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-y)|\\ &\quad\leq \left\{ \begin{aligned} &C\bigg(\frac{|x-y|}{\rho(x)}\bigg)^{\delta_{0}}\frac{t}{(|x-y|+\sqrt{t^{1/\alpha}})^{n+2\alpha}},& \sqrt{t^{1/\alpha}}\leq |x-y|,\\ &C\bigg(\frac{\sqrt{t^{1/\alpha}}}{\rho(x)}\bigg)^{\delta_{0}}\frac{t}{(|x-y|+\sqrt{t^{1/\alpha}})^{n+2\alpha}},& \sqrt{t^{1/\alpha}}\geq |x-y|. \end{aligned}\right. \end{align*} $$
-
(ii) [Reference Wang, Li and Zhang18, Proposition 9] For every
 $0<\delta <\min \{2\alpha , \delta _{0}\}$
, there exist constants
$0<\delta <\min \{2\alpha , \delta _{0}\}$
, there exist constants
 $C,c>0$
such that, for
$C,c>0$
such that, for
 $\displaystyle |y-z|<\min \{\rho (x), {|x-y|}/{4}\}$
,
$\displaystyle |y-z|<\min \{\rho (x), {|x-y|}/{4}\}$
,  $$ \begin{align*} &|(t\partial_{t}K^{L}_{\alpha,t}(x,y)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-y)) -(t\partial_{t}K^{L}_{\alpha,t}(x,z)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-z))|\\ &\quad\leq C\bigg(\frac{|y-z|}{\rho(y)}\bigg)^{\delta}\frac{t}{(\!\sqrt {t^{1/\alpha}}+|x-y|)^{n+2\alpha}}. \end{align*} $$
$$ \begin{align*} &|(t\partial_{t}K^{L}_{\alpha,t}(x,y)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-y)) -(t\partial_{t}K^{L}_{\alpha,t}(x,z)-t\partial_{t}K^{-\Delta}_{\alpha,t}(x-z))|\\ &\quad\leq C\bigg(\frac{|y-z|}{\rho(y)}\bigg)^{\delta}\frac{t}{(\!\sqrt {t^{1/\alpha}}+|x-y|)^{n+2\alpha}}. \end{align*} $$
The kernel of
![]() $T^{L^{\alpha }}_N$
can be expressed as
$T^{L^{\alpha }}_N$
can be expressed as
 $$ \begin{align*} K^\alpha_N(x,y) = \sum_{j=N_1}^{N_2}v_j (K^{L}_{\alpha,a_{j+1}} (x,y)-K^{L}_{\alpha,a_{j}} (x,y)). \end{align*} $$
$$ \begin{align*} K^\alpha_N(x,y) = \sum_{j=N_1}^{N_2}v_j (K^{L}_{\alpha,a_{j+1}} (x,y)-K^{L}_{\alpha,a_{j}} (x,y)). \end{align*} $$
The following proposition contains the size descriptions and the smoothness estimates of
![]() $T^{L^{\alpha }}_N$
, which are required in the Calderón–Zygmund theory.
$T^{L^{\alpha }}_N$
, which are required in the Calderón–Zygmund theory.
Proposition 3.5. Let
![]() $\alpha \in (0,1)$
and let
$\alpha \in (0,1)$
and let
![]() $0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
with
$0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
with
![]() $\delta _{0}=\min \{1, 2-n/q\}$
. For every
$\delta _{0}=\min \{1, 2-n/q\}$
. For every
![]() $N>0$
, there exists a constant
$N>0$
, there exists a constant
![]() $C>0$
, depending on
$C>0$
, depending on
![]() $n, \alpha $
and
$n, \alpha $
and
![]() $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
(not on N), such that, for any
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
(not on N), such that, for any
![]() $x\neq y:$
$x\neq y:$
-
(i)
 $$ \begin{align*} | K^\alpha_N(x,y)|\leq \frac{C}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}+\frac{|x-y|}{\rho(y)}\bigg)^{-N}; \mbox{and}\end{align*} $$
$$ \begin{align*} | K^\alpha_N(x,y)|\leq \frac{C}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}+\frac{|x-y|}{\rho(y)}\bigg)^{-N}; \mbox{and}\end{align*} $$
-
(ii)
whenever $$ \begin{align*} | K_N^\alpha(x,y)- K_N^\alpha(x,z)|+|K_N^\alpha(y,x)-K_N^\alpha(z,x)| \leq C\frac{\vert y-z\vert^{\delta'}}{|x-y|^{n+\delta'}}, \end{align*} $$
$$ \begin{align*} | K_N^\alpha(x,y)- K_N^\alpha(x,z)|+|K_N^\alpha(y,x)-K_N^\alpha(z,x)| \leq C\frac{\vert y-z\vert^{\delta'}}{|x-y|^{n+\delta'}}, \end{align*} $$
 $\vert x-y\vert>{2}\vert y-z\vert .$
$\vert x-y\vert>{2}\vert y-z\vert .$
Proof. (i) For the size condition for
![]() $K^{\alpha }_{N}(\cdot ,\cdot )$
, by Lemma 3.2,
$K^{\alpha }_{N}(\cdot ,\cdot )$
, by Lemma 3.2,
 $$ \begin{align*} | K^\alpha_N (x,y)| &\leq \sum_{j=N_1}^{N_2}\vert v_j\vert \vert K^{L}_{\alpha,a_{j+1}}(x,y)-K^{L}_{\alpha,a_{j}} (x,y)\vert\\[5pt] &\le \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \bigg|\!\int_{a_j}^{a_{j+1}}\partial_t K^{L}_{\alpha,t}(x,y) \,dt\bigg|\\[5pt] &\le \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}|\partial_t K^{L}_{\alpha,t}(x,y)| \,dt\\[5pt] &\lesssim \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}}\bigg(1+\frac{t^{1/(2\alpha)}}{\rho(x)}+\frac{t^{1/(2\alpha)}}{\rho(y)}\bigg)^{-N} \,dt\\[5pt] &\lesssim \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}}\,dt. \end{align*} $$
$$ \begin{align*} | K^\alpha_N (x,y)| &\leq \sum_{j=N_1}^{N_2}\vert v_j\vert \vert K^{L}_{\alpha,a_{j+1}}(x,y)-K^{L}_{\alpha,a_{j}} (x,y)\vert\\[5pt] &\le \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \bigg|\!\int_{a_j}^{a_{j+1}}\partial_t K^{L}_{\alpha,t}(x,y) \,dt\bigg|\\[5pt] &\le \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}|\partial_t K^{L}_{\alpha,t}(x,y)| \,dt\\[5pt] &\lesssim \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}}\bigg(1+\frac{t^{1/(2\alpha)}}{\rho(x)}+\frac{t^{1/(2\alpha)}}{\rho(y)}\bigg)^{-N} \,dt\\[5pt] &\lesssim \|v\|_{l^\infty(\mathbb{Z})} \sum_{j=-\infty}^{\infty} \int_{a_j}^{a_{j+1}}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}}\,dt. \end{align*} $$
Since
![]() $\{a_{j}\}_{j\in \mathbb {Z}}$
is an increasing sequence of positive numbers, we see that
$\{a_{j}\}_{j\in \mathbb {Z}}$
is an increasing sequence of positive numbers, we see that
 $$ \begin{align*} | K^\alpha_N (x,y)| &\lesssim \|v\|_{l^\infty(\mathbb{Z})}\int_{0}^{\infty}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \,dt \\[5pt] & \lesssim {1\over {|x-y|^{n}}}. \end{align*} $$
$$ \begin{align*} | K^\alpha_N (x,y)| &\lesssim \|v\|_{l^\infty(\mathbb{Z})}\int_{0}^{\infty}\frac 1{(t^{1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \,dt \\[5pt] & \lesssim {1\over {|x-y|^{n}}}. \end{align*} $$
Furthermore, we also have
 $$ \begin{align*} &| K^\alpha_N (x, y)|& \\[5pt] &\quad\lesssim \int_0^{|x-y|^{2\alpha}}\frac{t^{N/\alpha}}{|x-y|^{n+2\alpha+2N}}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\,dt +\int_{|x-y|^{2\alpha}}^{+\infty}\frac{1}{t^{n/2\alpha+1}}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\,dt\\[5pt] &\quad \lesssim \frac{1}{|x-y|^{n}}\bigg({|x-y|\over \rho(x)}\bigg)^{-N}. \end{align*} $$
$$ \begin{align*} &| K^\alpha_N (x, y)|& \\[5pt] &\quad\lesssim \int_0^{|x-y|^{2\alpha}}\frac{t^{N/\alpha}}{|x-y|^{n+2\alpha+2N}}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\,dt +\int_{|x-y|^{2\alpha}}^{+\infty}\frac{1}{t^{n/2\alpha+1}}\bigg(\frac{t^{1/2\alpha}}{\rho(x)}\bigg)^{-N}\,dt\\[5pt] &\quad \lesssim \frac{1}{|x-y|^{n}}\bigg({|x-y|\over \rho(x)}\bigg)^{-N}. \end{align*} $$
Then, using the symmetry of
![]() $K^{L}_{\alpha ,t}(\cdot , \cdot )$
, we get
$K^{L}_{\alpha ,t}(\cdot , \cdot )$
, we get
 $$ \begin{align*}|{K^\alpha_N(x, y)}|\lesssim \frac{1}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}+\frac{|x-y|}{\rho(y)}\bigg)^{-N}.\end{align*} $$
$$ \begin{align*}|{K^\alpha_N(x, y)}|\lesssim \frac{1}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}+\frac{|x-y|}{\rho(y)}\bigg)^{-N}.\end{align*} $$
(ii) Note that if
![]() $|x-y|>2|y-z|$
, then
$|x-y|>2|y-z|$
, then
![]() $\vert x-y\vert \sim \vert x-z\vert .$
For any
$\vert x-y\vert \sim \vert x-z\vert .$
For any
![]() $0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
, if
$0<\delta '\leq \delta =\min \{2\alpha ,\delta _{0}\}$
, if
![]() $\vert y-z\vert \le {t}^{1/2\alpha }$
, using a similar argument as in (i) and by Lemma 3.3, we get
$\vert y-z\vert \le {t}^{1/2\alpha }$
, using a similar argument as in (i) and by Lemma 3.3, we get
 $$ \begin{align*} &\vert K^\alpha_N(x,y)-K^\alpha_N(x,z)\vert\\ \nonumber &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\int_0^{+\infty}\vert\partial_t K^{L}_{t}(x,y)-\partial_t K^{L}_{t}(x,z)\vert \,dt\\ \nonumber &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\int_0^{|x-y|^{2\alpha}}\frac{1}{|x-y|^{n+2\alpha}}\bigg(\frac{|y-z|}{t^{1/2\alpha}}\bigg)^{\delta'}\,dt +\int_{|x-y|^{2\alpha}}^{+\infty}\bigg(\frac{|y-z|}{t^{1/2\alpha}}\bigg)^{\delta'}\frac{1}{t^{n/2\alpha+1}}\,dt\\ &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\frac{\vert y-z\vert^{\delta'}}{\vert x-y\vert^{n+\delta'}}. \end{align*} $$
$$ \begin{align*} &\vert K^\alpha_N(x,y)-K^\alpha_N(x,z)\vert\\ \nonumber &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\int_0^{+\infty}\vert\partial_t K^{L}_{t}(x,y)-\partial_t K^{L}_{t}(x,z)\vert \,dt\\ \nonumber &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\int_0^{|x-y|^{2\alpha}}\frac{1}{|x-y|^{n+2\alpha}}\bigg(\frac{|y-z|}{t^{1/2\alpha}}\bigg)^{\delta'}\,dt +\int_{|x-y|^{2\alpha}}^{+\infty}\bigg(\frac{|y-z|}{t^{1/2\alpha}}\bigg)^{\delta'}\frac{1}{t^{n/2\alpha+1}}\,dt\\ &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)}\frac{\vert y-z\vert^{\delta'}}{\vert x-y\vert^{n+\delta'}}. \end{align*} $$
If
![]() $\vert y-z\vert>{t}^{1/2\alpha }$
, Lemma 3.2 gives
$\vert y-z\vert>{t}^{1/2\alpha }$
, Lemma 3.2 gives
 $$ \begin{align*} \vert K^\alpha_N(x,y)\vert &\lesssim \int_{0}^{+\infty} |\partial_t K^{L}_{t}(x,y)| \,dt \\ & \lesssim\int_{0}^{+\infty} \bigg(\frac{\vert y-z\vert}{{t}^{1/2\alpha}}\bigg)^{\delta'} \frac{1}{(t^{1/2\alpha}+|x-y|)^{n+2\alpha}}\,dt\\ &\lesssim\frac{\vert y-z\vert^{\delta'}}{\vert x-y\vert^{n+\delta'}}. \end{align*} $$
$$ \begin{align*} \vert K^\alpha_N(x,y)\vert &\lesssim \int_{0}^{+\infty} |\partial_t K^{L}_{t}(x,y)| \,dt \\ & \lesssim\int_{0}^{+\infty} \bigg(\frac{\vert y-z\vert}{{t}^{1/2\alpha}}\bigg)^{\delta'} \frac{1}{(t^{1/2\alpha}+|x-y|)^{n+2\alpha}}\,dt\\ &\lesssim\frac{\vert y-z\vert^{\delta'}}{\vert x-y\vert^{n+\delta'}}. \end{align*} $$
The same bound is valid for
![]() $K^\alpha _N(x,z)$
because
$K^\alpha _N(x,z)$
because
![]() $\vert x-z\vert \sim \vert x-y\vert $
. Then the estimate can be obtained directly owing to the inequality
$\vert x-z\vert \sim \vert x-y\vert $
. Then the estimate can be obtained directly owing to the inequality
The symmetry of the kernel
![]() $K^\alpha _N(x,y)=K^\alpha _N(y,x)$
gives the conclusion of (ii). This completes the proof of Proposition 3.5.
$K^\alpha _N(x,y)=K^\alpha _N(y,x)$
gives the conclusion of (ii). This completes the proof of Proposition 3.5.
The uniform boundedness of
![]() $T^{L^{\alpha }}_N$
in the BMO-type space
$T^{L^{\alpha }}_N$
in the BMO-type space
![]() $BMO_{L}(\mathbb R^{n})$
is as follows.
$BMO_{L}(\mathbb R^{n})$
is as follows.
Theorem 3.6. Let
![]() $\{a_j\}_{j\in \mathbb Z}$
be a positive increasing sequence and let
$\{a_j\}_{j\in \mathbb Z}$
be a positive increasing sequence and let
![]() $T^{L^{\alpha }}_N$
be the operator defined in (1-4) with
$T^{L^{\alpha }}_N$
be the operator defined in (1-4) with
![]() $N=(N_1,N_2)$
.
$N=(N_1,N_2)$
.
-
(i) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^\infty ({\mathbb R}^{n})$
,
$f\in L^\infty ({\mathbb R}^{n})$
,  $$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{BMO_L(\mathbb R^{n})}\leq C\Vert f\Vert_{L^\infty(\mathbb R^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{BMO_L(\mathbb R^{n})}\leq C\Vert f\Vert_{L^\infty(\mathbb R^{n})}.\end{align*} $$
-
(ii) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in BMO_L({\mathbb R}^n)$
,
$f\in BMO_L({\mathbb R}^n)$
,  $$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{BMO_L({\mathbb R}^n)}\le C\Vert f\Vert_{BMO_L({\mathbb R}^n)}.\end{align*} $$
$$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{BMO_L({\mathbb R}^n)}\le C\Vert f\Vert_{BMO_L({\mathbb R}^n)}.\end{align*} $$
The constants C in (i) and (ii) are independent of
 $N.$
$N.$
Proof. Since
![]() $L^\infty ({\mathbb R}^n) \subset BMO_{\mathcal L}({\mathbb R}^n)$
and
$L^\infty ({\mathbb R}^n) \subset BMO_{\mathcal L}({\mathbb R}^n)$
and
![]() $\|f\|_{BMO_{\mathcal L}({\mathbb R}^n)} \le \|f\|_{L^\infty ({\mathbb R}^n)}$
, it is enough to prove that (ii) of Theorem 3.6 holds. We first show that
$\|f\|_{BMO_{\mathcal L}({\mathbb R}^n)} \le \|f\|_{L^\infty ({\mathbb R}^n)}$
, it is enough to prove that (ii) of Theorem 3.6 holds. We first show that
![]() $T_N^{L^{\alpha }} f<\infty $
if
$T_N^{L^{\alpha }} f<\infty $
if
![]() $f\in BMO_L({\mathbb R}^n)$
. Let
$f\in BMO_L({\mathbb R}^n)$
. Let
![]() ${B=B(x_0, \rho (x_0))}$
and
${B=B(x_0, \rho (x_0))}$
and
![]() $B^*=B(x_0, 2C_0\rho (x_0))$
with some
$B^*=B(x_0, 2C_0\rho (x_0))$
with some
![]() $x_0\in {\mathbb R}^{n}$
and
$x_0\in {\mathbb R}^{n}$
and
![]() $C_0>1$
. We decompose f as
$C_0>1$
. We decompose f as
The function
![]() $f_1$
is integrable, and hence
$f_1$
is integrable, and hence
![]() $T^{L^{\alpha }}_N f_1< \infty\ \text{for almost every}\ x\in {\mathbb R}^{n}.$
When
$T^{L^{\alpha }}_N f_1< \infty\ \text{for almost every}\ x\in {\mathbb R}^{n}.$
When
![]() ${x\in B}$
and
${x\in B}$
and
![]() $y\in (B^{*})^{c}$
, we have
$y\in (B^{*})^{c}$
, we have
![]() $|y-x_0|/2\le |x-y|\le 2|y-x_0|$
and
$|y-x_0|/2\le |x-y|\le 2|y-x_0|$
and
![]() $\rho (x)\sim \rho (x_0).$
It can be deduced from Proposition 3.5 and Hölder’s inequality that
$\rho (x)\sim \rho (x_0).$
It can be deduced from Proposition 3.5 and Hölder’s inequality that
 $$ \begin{align*} \vert T^{L^{\alpha}}_N f_2(x)\vert&=\bigg\vert\!\int_{{\mathbb R}^n} K^\alpha_N(x, y)f_2(y)\,dy\bigg\vert\nonumber \\ &\lesssim {\int_{(B^{*})^{c}} {1\over |x-y|^n}{\rho^2(x)\over |x-y|^2 } \vert f_2(y)\vert \,dy}\nonumber \\ &\lesssim {\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} }\vert f(y)\vert \,dy}\nonumber\\ &\lesssim\bigg(\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} } \,dy\bigg)^{1/2}\bigg(\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} }\vert f(y)\vert^2 \,dy\bigg)^{1/2}\nonumber\\ &\lesssim\bigg(\sum_{k=1}^\infty\int_{2^{k+1}B\setminus 2^kB} {\rho^2(x_0)\,dy\over |x_0-y|^{n+2} } \bigg)^{1/2}\bigg(\sum_{k=1}^\infty\int_{2^{k+1}B\setminus 2^kB} {\rho^2(x_0)\vert f(y)\vert^2\over |x_0-y|^{n+2} } \,dy\bigg)^{1/2}\nonumber\\ &\lesssim\bigg(\sum_{k=1}^\infty{\rho^2(x_0)\over (2^kC_0\rho(x_0))^2}{1\over \vert2^{k+1}B\vert}\int_{2^{k+1}B} \vert f(y)\vert^2 \,dy\bigg)^{1/2}\nonumber\\ &\lesssim \bigg(\sum_{k=1}^\infty2^{-2k}\Vert f\Vert^2_{BMO_L({\mathbb R}^n)}\bigg)^{1/2}\nonumber\\ &\lesssim\Vert f\Vert_{BMO_L({\mathbb R}^n)}<\infty.\nonumber \end{align*} $$
$$ \begin{align*} \vert T^{L^{\alpha}}_N f_2(x)\vert&=\bigg\vert\!\int_{{\mathbb R}^n} K^\alpha_N(x, y)f_2(y)\,dy\bigg\vert\nonumber \\ &\lesssim {\int_{(B^{*})^{c}} {1\over |x-y|^n}{\rho^2(x)\over |x-y|^2 } \vert f_2(y)\vert \,dy}\nonumber \\ &\lesssim {\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} }\vert f(y)\vert \,dy}\nonumber\\ &\lesssim\bigg(\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} } \,dy\bigg)^{1/2}\bigg(\int_{(B^{*})^{c}} {\rho^2(x_0)\over |x_0-y|^{n+2} }\vert f(y)\vert^2 \,dy\bigg)^{1/2}\nonumber\\ &\lesssim\bigg(\sum_{k=1}^\infty\int_{2^{k+1}B\setminus 2^kB} {\rho^2(x_0)\,dy\over |x_0-y|^{n+2} } \bigg)^{1/2}\bigg(\sum_{k=1}^\infty\int_{2^{k+1}B\setminus 2^kB} {\rho^2(x_0)\vert f(y)\vert^2\over |x_0-y|^{n+2} } \,dy\bigg)^{1/2}\nonumber\\ &\lesssim\bigg(\sum_{k=1}^\infty{\rho^2(x_0)\over (2^kC_0\rho(x_0))^2}{1\over \vert2^{k+1}B\vert}\int_{2^{k+1}B} \vert f(y)\vert^2 \,dy\bigg)^{1/2}\nonumber\\ &\lesssim \bigg(\sum_{k=1}^\infty2^{-2k}\Vert f\Vert^2_{BMO_L({\mathbb R}^n)}\bigg)^{1/2}\nonumber\\ &\lesssim\Vert f\Vert_{BMO_L({\mathbb R}^n)}<\infty.\nonumber \end{align*} $$
Hence, we have proved that
![]() $T^{L^{\alpha }}_N f(x)<\infty\ \text{for almost every}\ x\in {\mathbb R}^n.$
Then the proof of
$T^{L^{\alpha }}_N f(x)<\infty\ \text{for almost every}\ x\in {\mathbb R}^n.$
Then the proof of
is similar to that for the maximal operator
![]() $T^*_{L^{\alpha }}$
, which can be seen from Theorem 4.6. So we omit the details here.
$T^*_{L^{\alpha }}$
, which can be seen from Theorem 4.6. So we omit the details here.
Theorem 3.7. Let
![]() $\{a_j\}_{j\in \mathbb Z}$
be a positive increasing sequence, let
$\{a_j\}_{j\in \mathbb Z}$
be a positive increasing sequence, let
![]() $0<\kappa <1$
and let
$0<\kappa <1$
and let
![]() $T^{L^{\alpha }}_N$
be the operator defined in (1-4) with
$T^{L^{\alpha }}_N$
be the operator defined in (1-4) with
![]() $N=(N_1,N_2)$
. The following statements hold.
$N=(N_1,N_2)$
. The following statements hold.
-
(i) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
 $\theta $
and
$\theta $
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
,
$f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
,  $$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\leq C\Vert f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\leq C\Vert f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
-
(ii) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
 $\theta $
and
$\theta $
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
,
$f\in L^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
,  $$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\le C\Vert f\Vert_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^{L^{\alpha}}_N f\Vert_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\le C\Vert f\Vert_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
The constants C appearing above are all independent of
 $N.$
$N.$
Proof. We have previously remarked that the constants in the
![]() $L^{p}$
-boundedness only depend on the initial constant in
$L^{p}$
-boundedness only depend on the initial constant in
![]() $L^{p_{0}}(\mathbb {R}^{n})$
(in our case,
$L^{p_{0}}(\mathbb {R}^{n})$
(in our case,
![]() $p_{0}=2$
), the size constant and the smoothness constant of the kernel. Hence, the uniform
$p_{0}=2$
), the size constant and the smoothness constant of the kernel. Hence, the uniform
![]() $L^{p}$
-boundedness of the operators
$L^{p}$
-boundedness of the operators
![]() $T^{L^{\alpha }}_N $
is a direct consequence of the vector-valued Calderón–Zygmund theory.
$T^{L^{\alpha }}_N $
is a direct consequence of the vector-valued Calderón–Zygmund theory.
(i) For any given
![]() $f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
with
$f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
with
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $0<\kappa <1$
, suppose that
$0<\kappa <1$
, suppose that
![]() $f\in L^{\rho ,\theta ^{\ast }}_{p,\kappa }(\mathbb {R}^{n})$
for some
$f\in L^{\rho ,\theta ^{\ast }}_{p,\kappa }(\mathbb {R}^{n})$
for some
![]() $\theta ^{\ast }>0$
, where
$\theta ^{\ast }>0$
, where
Then we only need to prove that, for each ball
![]() $B(x_{0},r)\subset \mathbb {R}^{n}$
, there is some
$B(x_{0},r)\subset \mathbb {R}^{n}$
, there is some
![]() $\nu>0$
such that
$\nu>0$
such that
 $$ \begin{align} \bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f)(x)|^{p}\,dx\bigg)^{1/p}\lesssim \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\nu} \end{align} $$
$$ \begin{align} \bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f)(x)|^{p}\,dx\bigg)^{1/p}\lesssim \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\nu} \end{align} $$
holds for all functions
![]() $f\in L^{\rho ,\theta ^{\ast }}_{p,\kappa }(\mathbb {R}^{n})$
with
$f\in L^{\rho ,\theta ^{\ast }}_{p,\kappa }(\mathbb {R}^{n})$
with
![]() $(p,\kappa )\in (1,\infty )\times (0,1)$
.
$(p,\kappa )\in (1,\infty )\times (0,1)$
.
We first decompose the function f as
 $$ \begin{align*} \begin{cases} f=f_{1}+f_{2}\in L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n}),\\ f_{1}=f\cdot\chi_{2B},\\ f_{2}=f\cdot\chi_{(2B)^{c}}, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} f=f_{1}+f_{2}\in L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n}),\\ f_{1}=f\cdot\chi_{2B},\\ f_{2}=f\cdot\chi_{(2B)^{c}}, \end{cases} \end{align*} $$
where
![]() $2B$
is the ball centered at
$2B$
is the ball centered at
![]() $x_{0}$
of radius
$x_{0}$
of radius
![]() $2r$
,
$2r$
,
![]() $(2B)^{c}=\mathbb {R}^{n}\setminus (2B)$
and
$(2B)^{c}=\mathbb {R}^{n}\setminus (2B)$
and
![]() $\chi _{E}$
denotes the characteristic function of the set E. Then we can write
$\chi _{E}$
denotes the characteristic function of the set E. Then we can write
 $$ \begin{align*}\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f)(x)|^{p}\,dx\bigg)^{1/p}\leq I_{1}+I_{2},\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f)(x)|^{p}\,dx\bigg)^{1/p}\leq I_{1}+I_{2},\end{align*} $$
where
 $$ \begin{align*} \left\{ \begin{aligned} I_{1}:=\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{1})(x)|^{p}\,dx\bigg)^{1/p},\\ I_{2}:=\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{2})(x)|^{p}\,dx\bigg)^{1/p}. \end{aligned} \right.\end{align*} $$
$$ \begin{align*} \left\{ \begin{aligned} I_{1}:=\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{1})(x)|^{p}\,dx\bigg)^{1/p},\\ I_{2}:=\bigg(\frac{1}{|B(x_{0},r)|^{\kappa}}\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{2})(x)|^{p}\,dx\bigg)^{1/p}. \end{aligned} \right.\end{align*} $$
In what follows, we estimate
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
separately. For the term
$I_{2}$
separately. For the term
![]() $I_{1}$
,
$I_{1}$
,
 $$ \begin{align*} I_{1} &\lesssim \frac{1}{|B|^{\kappa/p}}\bigg(\int_{\mathbb{R}^{n}}|f_{1}(x)|^{p}\,dx\bigg)^{1/p} \\ &= \frac{1}{|B|^{\kappa/p}}\bigg(\int_{2B}|f(x)|^{p}\,dx\bigg)^{1/p} \\ &\lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}\frac{|2B|^{\kappa/p}}{|B|^{\kappa/p}}\bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
$$ \begin{align*} I_{1} &\lesssim \frac{1}{|B|^{\kappa/p}}\bigg(\int_{\mathbb{R}^{n}}|f_{1}(x)|^{p}\,dx\bigg)^{1/p} \\ &= \frac{1}{|B|^{\kappa/p}}\bigg(\int_{2B}|f(x)|^{p}\,dx\bigg)^{1/p} \\ &\lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}\frac{|2B|^{\kappa/p}}{|B|^{\kappa/p}}\bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
Moreover, for any fixed
![]() $\theta ^{\ast }>0$
, the inequalities
$\theta ^{\ast }>0$
, the inequalities
 $$ \begin{align} 1\leq \bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}\leq 2^{\theta^{\ast}}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}} \end{align} $$
$$ \begin{align} 1\leq \bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}\leq 2^{\theta^{\ast}}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}} \end{align} $$
further indicate that
 $$ \begin{align*}I_{1}\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}.\end{align*} $$
$$ \begin{align*}I_{1}\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}.\end{align*} $$
Next, we estimate
![]() $I_{2}$
. From Proposition 3.5, we deduce that
$I_{2}$
. From Proposition 3.5, we deduce that
 $$ \begin{align} T^{L^{\alpha}}_{N}(f_{2})(x)\lesssim \int_{(2B)^{c}}\frac{1}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{-N}|f(y)|\,dy. \end{align} $$
$$ \begin{align} T^{L^{\alpha}}_{N}(f_{2})(x)\lesssim \int_{(2B)^{c}}\frac{1}{|x-y|^{n}}\bigg(1+\frac{|x-y|}{\rho(x)}\bigg)^{-N}|f(y)|\,dy. \end{align} $$
Since
![]() $x\in B(x_{0},r)$
and
$x\in B(x_{0},r)$
and
![]() $y\in (2B)^{c}$
, we have
$y\in (2B)^{c}$
, we have
![]() $|x-y|\sim |x_{0}-y|$
. This fact, along with (3-3), implies that, for any
$|x-y|\sim |x_{0}-y|$
. This fact, along with (3-3), implies that, for any
![]() $x\in B(x_{0},r)$
,
$x\in B(x_{0},r)$
,
 $$ \begin{align*} |T^{L^{\alpha}}_{N}(f_{2})(x)| &\lesssim \sum^{\infty}_{k=1}\int_{2^{k}r\leq |x_{0}-y|<2^{k+1}r}\bigg(1+\frac{|x_{0}-y|}{\rho(x)}\bigg)^{-N}\frac{1}{|x_{0}-y|^{n}}|f(y)|\,dy \\ \notag &\lesssim \sum^{\infty}_{k=1}\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{|x_{0}-y|<2^{k+1}r}\bigg(1+\frac{2^{k}r}{\rho(x)}\bigg)^{-N}|f(y)|\,dy. \end{align*} $$
$$ \begin{align*} |T^{L^{\alpha}}_{N}(f_{2})(x)| &\lesssim \sum^{\infty}_{k=1}\int_{2^{k}r\leq |x_{0}-y|<2^{k+1}r}\bigg(1+\frac{|x_{0}-y|}{\rho(x)}\bigg)^{-N}\frac{1}{|x_{0}-y|^{n}}|f(y)|\,dy \\ \notag &\lesssim \sum^{\infty}_{k=1}\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{|x_{0}-y|<2^{k+1}r}\bigg(1+\frac{2^{k}r}{\rho(x)}\bigg)^{-N}|f(y)|\,dy. \end{align*} $$
In view of (2-3) and (3-2), we deduce that
 $$ \begin{align} & |T^{L^{\alpha}}_{N}(f_{2})(x)|\\ \notag &\quad\lesssim \sum^{\infty}_{k=1}\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N}|f(y)|\,dy.\notag \end{align} $$
$$ \begin{align} & |T^{L^{\alpha}}_{N}(f_{2})(x)|\\ \notag &\quad\lesssim \sum^{\infty}_{k=1}\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N}|f(y)|\,dy.\notag \end{align} $$
We consider each term in the sum of (3-4) separately. Using Hölder’s inequality, we deduce that, for each fixed
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
 $$ \begin{align*} \frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}|f(y)|\,dy \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}\frac{|B(x_{0},2^{k+1}r)|^{\kappa/p}}{|B(x_{0},2^{k+1}r)|^{1/p}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
$$ \begin{align*} \frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}|f(y)|\,dy \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})}\frac{|B(x_{0},2^{k+1}r)|^{\kappa/p}}{|B(x_{0},2^{k+1}r)|^{1/p}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
This allows us to obtain
 $$ \begin{align*} I_{2} \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})} \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty}\frac{|B(x_{0},r)|^{(1-\kappa)/p}}{|B(x_{0},2^{k+1}r)|^{(1-k)/p}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N+\theta^{\ast}}. \end{align*} $$
$$ \begin{align*} I_{2} \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{p,\kappa}(\mathbb{R}^{n})} \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty}\frac{|B(x_{0},r)|^{(1-\kappa)/p}}{|B(x_{0},2^{k+1}r)|^{(1-k)/p}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N+\theta^{\ast}}. \end{align*} $$
We can choose N large enough such that
![]() $N\geq \theta ^{\ast }$
and, consequently, the last series is convergent. Then we have
$N\geq \theta ^{\ast }$
and, consequently, the last series is convergent. Then we have
 $$ \begin{align*} I_{2} &\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty} \bigg(\frac{|B(x_{0},r)|}{|B(x_{0},2^{k+1}r)|}\bigg)^{(1-\kappa)/p} \\ &\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}, \end{align*} $$
$$ \begin{align*} I_{2} &\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty} \bigg(\frac{|B(x_{0},r)|}{|B(x_{0},2^{k+1}r)|}\bigg)^{(1-\kappa)/p} \\ &\lesssim \|f\|_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}, \end{align*} $$
where the last inequality follows from the fact that
![]() $1-\kappa>0$
. Summing the above estimates for
$1-\kappa>0$
. Summing the above estimates for
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
, and letting
$I_{2}$
, and letting
![]() $\nu =\max \{\theta ^{\ast },N\cdot ({N_{0}}/{N_{0}+1})\}$
with
$\nu =\max \{\theta ^{\ast },N\cdot ({N_{0}}/{N_{0}+1})\}$
with
![]() $N\geq \theta ^{\ast }$
, we obtain the desired inequality (3-1).
$N\geq \theta ^{\ast }$
, we obtain the desired inequality (3-1).
(ii) According to Definition 2.4, it suffices to prove that, for each given ball
![]() ${B=B(x_{0},r)\subset \mathbb {R}^{n}}$
, there exists some
${B=B(x_{0},r)\subset \mathbb {R}^{n}}$
, there exists some
![]() $\nu>0$
such that
$\nu>0$
such that
 $$ \begin{align} \frac{1}{|B(x_{0},r)|^{\kappa}}\sup_{\lambda>0}\lambda\cdot|\{x\in B(x_{0},r):\ |T^{L^{\alpha}}_{N}(f)(x)|>\lambda\}|\lesssim \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\nu} \end{align} $$
$$ \begin{align} \frac{1}{|B(x_{0},r)|^{\kappa}}\sup_{\lambda>0}\lambda\cdot|\{x\in B(x_{0},r):\ |T^{L^{\alpha}}_{N}(f)(x)|>\lambda\}|\lesssim \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\nu} \end{align} $$
holds for any function
![]() $f\in L^{\rho ,\theta ^{\ast }}_{1,\kappa }(\mathbb {R}^{n})$
with some
$f\in L^{\rho ,\theta ^{\ast }}_{1,\kappa }(\mathbb {R}^{n})$
with some
![]() $\theta ^{\ast }>0$
and
$\theta ^{\ast }>0$
and
![]() $0<\kappa <1$
. We decompose the function f as
$0<\kappa <1$
. We decompose the function f as
 $$ \begin{align*} \begin{cases} f=f_{1}+f_{2}\in L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n}),\\ f_{1}=f\cdot\chi_{2B},\\ f_{2}=f\cdot\chi_{(2B)^{c}}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} f=f_{1}+f_{2}\in L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n}),\\ f_{1}=f\cdot\chi_{2B},\\ f_{2}=f\cdot\chi_{(2B)^{c}}. \end{cases} \end{align*} $$
Then, for any given
![]() $\lambda>0$
, we can write
$\lambda>0$
, we can write
where
 $$ \begin{align*} \left\{ \begin{aligned} J_{1}:= \frac{1}{|B(x_{0},r)|^{\kappa}}\lambda\cdot|\{x\in B(x_{0},r):|T^{L^{\alpha}}_{N}(f_{1})(x)|>\lambda/2\}|,\\ J_{2}:= \frac{1}{|B(x_{0},r)|^{\kappa}}\lambda\cdot|\{x\in B(x_{0},r):|T^{L^{\alpha}}_{N}(f_{2})(x)|>\lambda/2\}|. \end{aligned} \right.\end{align*} $$
$$ \begin{align*} \left\{ \begin{aligned} J_{1}:= \frac{1}{|B(x_{0},r)|^{\kappa}}\lambda\cdot|\{x\in B(x_{0},r):|T^{L^{\alpha}}_{N}(f_{1})(x)|>\lambda/2\}|,\\ J_{2}:= \frac{1}{|B(x_{0},r)|^{\kappa}}\lambda\cdot|\{x\in B(x_{0},r):|T^{L^{\alpha}}_{N}(f_{2})(x)|>\lambda/2\}|. \end{aligned} \right.\end{align*} $$
With the aid of (3-2), we first estimate the term
![]() $J_{1}$
as
$J_{1}$
as
 $$ \begin{align*} J_{1} &\lesssim \frac{1}{|B|^{\kappa}}\bigg(\int_{2B}|f(x)|\,dx\bigg) \\ &\lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})}\frac{|2B|^{\kappa}}{|B|^{\kappa}}\bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}\\ &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
$$ \begin{align*} J_{1} &\lesssim \frac{1}{|B|^{\kappa}}\bigg(\int_{2B}|f(x)|\,dx\bigg) \\ &\lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})}\frac{|2B|^{\kappa}}{|B|^{\kappa}}\bigg(1+\frac{2r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}\\ &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
For the second term
![]() $J_{2}$
, using (3-4) and Chebyshev’s inequality, we have
$J_{2}$
, using (3-4) and Chebyshev’s inequality, we have
 $$ \begin{align}\notag \notag J_{2} &\leq \frac{2}{|B(x_{0},r)|^{\kappa}}\bigg(\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{2})(x)|\,dx\bigg) \\ \notag &\lesssim \frac{|B(x_{0},r)|}{|B(x_{0},r)|^{\kappa}}\sum^{\infty}_{k=1}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N}\\ &\quad \times\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)} |f(y)|\,dy. \end{align} $$
$$ \begin{align}\notag \notag J_{2} &\leq \frac{2}{|B(x_{0},r)|^{\kappa}}\bigg(\int_{B(x_{0},r)}|T^{L^{\alpha}}_{N}(f_{2})(x)|\,dx\bigg) \\ \notag &\lesssim \frac{|B(x_{0},r)|}{|B(x_{0},r)|^{\kappa}}\sum^{\infty}_{k=1}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N}\\ &\quad \times\frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)} |f(y)|\,dy. \end{align} $$
Note that, in (3-6), for each fixed
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
 $$ \begin{align*} \frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}|f(y)|\,dy \lesssim C\|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})}\frac{|B(x_{0},2^{k+1}r)|^{\kappa}}{|B(x_{0},2^{k+1}r)|} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
$$ \begin{align*} \frac{1}{|B(x_{0},2^{k+1}r)|}\int_{B(x_{0},2^{k+1}r)}|f(y)|\,dy \lesssim C\|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})}\frac{|B(x_{0},2^{k+1}r)|^{\kappa}}{|B(x_{0},2^{k+1}r)|} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{\theta^{\ast}}. \end{align*} $$
Consequently,
 $$ \begin{align*} J_{2} \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})} \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty}\frac{|B(x_{0},r)|}{|B(x_{0},r)|^{k}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N+\theta^{\ast}}\frac{|B(x_{0},2^{k+1}r)|^{\kappa}}{|B(x_{0},2^{k+1}r)|}. \end{align*} $$
$$ \begin{align*} J_{2} \lesssim \|f\|_{L^{\rho,\theta^{\ast}}_{1,\kappa}(\mathbb{R}^{n})} \bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty}\frac{|B(x_{0},r)|}{|B(x_{0},r)|^{k}} \bigg(1+\frac{2^{k+1}r}{\rho(x_{0})}\bigg)^{-N+\theta^{\ast}}\frac{|B(x_{0},2^{k+1}r)|^{\kappa}}{|B(x_{0},2^{k+1}r)|}. \end{align*} $$
Therefore, by choosing N large enough such that
![]() $N\geq \theta ^{\ast }$
, we obtain
$N\geq \theta ^{\ast }$
, we obtain
 $$ \begin{align*} J_{2} &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty} \bigg(\frac{|B(x_{0},r)|}{|B(x_{0},2^{k+1}r)|}\bigg)^{1-\kappa} \\[4pt] &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}, \end{align*} $$
$$ \begin{align*} J_{2} &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}\sum_{k=1}^{\infty} \bigg(\frac{|B(x_{0},r)|}{|B(x_{0},2^{k+1}r)|}\bigg)^{1-\kappa} \\[4pt] &\lesssim \|f\|_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\bigg(1+\frac{r}{\rho(x_{0})}\bigg)^{N\cdot({N_{0}}/{N_{0}+1})}, \end{align*} $$
since
![]() $0<\kappa <1$
. Now we choose
$0<\kappa <1$
. Now we choose
![]() $\nu =\max \{\theta ^{\ast },N\cdot ({N_{0}}/{N_{0}+1})\}$
with
$\nu =\max \{\theta ^{\ast },N\cdot ({N_{0}}/{N_{0}+1})\}$
with
![]() $N\geq \theta ^{\ast }$
. Summing the above estimates for
$N\geq \theta ^{\ast }$
. Summing the above estimates for
![]() $J_{1}$
and
$J_{1}$
and
![]() $J_{2}$
and taking the supremum over all
$J_{2}$
and taking the supremum over all
![]() $\lambda>0$
, we obtain the desired inequality (3-5).
$\lambda>0$
, we obtain the desired inequality (3-5).
4 Boundedness of the maximal operator
 $T^*_{L^{\alpha }}$
$T^*_{L^{\alpha }}$
In this section, we give the proof of Theorem 4.4 related to the boundedness of the maximal operator
![]() $T^*_{L^{\alpha }}$
. We first prove the following lemma by adopting the ideas of [Reference Zhang and Torrea20, Lemma 2.3], which is parallel to [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3, Proposition 3.2] or [Reference Zhang, Ma and Torrea19, Proposition 3.1]. Furthermore, the following lemma implies that, without loss of generality, we may assume that
$T^*_{L^{\alpha }}$
. We first prove the following lemma by adopting the ideas of [Reference Zhang and Torrea20, Lemma 2.3], which is parallel to [Reference Bernardis, Lorente, Martín-Reyes, Martínez, Torre and Torrea3, Proposition 3.2] or [Reference Zhang, Ma and Torrea19, Proposition 3.1]. Furthermore, the following lemma implies that, without loss of generality, we may assume that
Lemma 4.1. Given a
![]() $\lambda $
-lacunary sequence
$\lambda $
-lacunary sequence
![]() $\{a_j\}_{j\in \mathbb Z}$
and a multiplying sequence
$\{a_j\}_{j\in \mathbb Z}$
and a multiplying sequence
![]() $\{v_j\}_{j\in \mathbb Z}\in \ell ^\infty (\mathbb Z)$
, we can define a
$\{v_j\}_{j\in \mathbb Z}\in \ell ^\infty (\mathbb Z)$
, we can define a
![]() $\lambda $
-lacunary sequence
$\lambda $
-lacunary sequence
![]() $\{\eta _j\}_{j\in \mathbb Z}$
and
$\{\eta _j\}_{j\in \mathbb Z}$
and
![]() $\{\omega _j\}_{j\in \mathbb Z}\in \ell ^\infty (\mathbb Z)$
verifying the following properties.
$\{\omega _j\}_{j\in \mathbb Z}\in \ell ^\infty (\mathbb Z)$
verifying the following properties.
-
(i)
 $1<\lambda \leq \eta _{j+1}/\eta _j\leq \lambda ^2,\quad \Vert \{\omega _j\}\Vert _{\ell ^\infty (\mathbb Z)}=\Vert \{v_j\}\Vert _{\ell ^\infty (\mathbb Z)}$
.
$1<\lambda \leq \eta _{j+1}/\eta _j\leq \lambda ^2,\quad \Vert \{\omega _j\}\Vert _{\ell ^\infty (\mathbb Z)}=\Vert \{v_j\}\Vert _{\ell ^\infty (\mathbb Z)}$
. -
(ii) For all
 $N=(N_1, N_2)$
, there exists
$N=(N_1, N_2)$
, there exists
 $N'=(N_1', N_2')$
with
$N'=(N_1', N_2')$
with
 $T^{L^{\alpha }}_N=\widetilde {T}^{L^{\alpha }}_{N'},$
where
$T^{L^{\alpha }}_N=\widetilde {T}^{L^{\alpha }}_{N'},$
where
 $\widetilde {T}_{N'}^{L^{\alpha }}$
is the operator defined in (1-4) for the new sequences
$\widetilde {T}_{N'}^{L^{\alpha }}$
is the operator defined in (1-4) for the new sequences
 $\{\eta _j\}_{j\in {\mathbb Z}}$
and
$\{\eta _j\}_{j\in {\mathbb Z}}$
and
 $\{\omega _j\}_{j\in {\mathbb Z}}.$
$\{\omega _j\}_{j\in {\mathbb Z}}.$
Owing to Lemma 4.1, in the rest of this article, we always assume that the lacunary sequence
![]() $\{a_j\}_{j\in \mathbb Z}$
satisfies (4-1) without saying it explicitly.
$\{a_j\}_{j\in \mathbb Z}$
satisfies (4-1) without saying it explicitly.
Lemma 4.2. Let
![]() $\{a_j\}_{j\in \mathbb Z}$
be a
$\{a_j\}_{j\in \mathbb Z}$
be a
![]() $\lambda $
-lacunary sequence and let
$\lambda $
-lacunary sequence and let
![]() $\{v_j\}_{j\in \mathbb Z} \in \ell ^\infty (\mathbb Z)$
.
$\{v_j\}_{j\in \mathbb Z} \in \ell ^\infty (\mathbb Z)$
.
-
(i) For
 $x,y\in \mathbb R^{n}$
,
$x,y\in \mathbb R^{n}$
,  $$ \begin{align*}\displaystyle \bigg\vert\!\sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y)) \bigg\vert \le { {C_{v, \lambda,\alpha, n}} \over a_m^{n/(2\alpha)}}.\end{align*} $$
$$ \begin{align*}\displaystyle \bigg\vert\!\sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y)) \bigg\vert \le { {C_{v, \lambda,\alpha, n}} \over a_m^{n/(2\alpha)}}.\end{align*} $$
-
(ii) If
 $k\ge m$
and
$k\ge m$
and
 $z,y \in \mathbb {R}^n$
with
$z,y \in \mathbb {R}^n$
with
 $|z-y|\ge a_k^{1/(2\alpha )}$
, then
$|z-y|\ge a_k^{1/(2\alpha )}$
, then  $$ \begin{align*} \bigg|\sum_{j=-M}^{m-1}v_j (K^{L}_{\alpha, a_{j+1}}(z,y)-K^{L}_{\alpha, a_{j}}(z,y) ) \bigg|\, \le C_{\lambda, v,\alpha, n}\frac1{a_k^{n/(2\alpha)}}\lambda^{-(k-m+1)}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{j=-M}^{m-1}v_j (K^{L}_{\alpha, a_{j+1}}(z,y)-K^{L}_{\alpha, a_{j}}(z,y) ) \bigg|\, \le C_{\lambda, v,\alpha, n}\frac1{a_k^{n/(2\alpha)}}\lambda^{-(k-m+1)}. \end{align*} $$
Proof. For (i), by the mean value theorem and Lemma 3.2, there exists
![]() $\xi _j\in [a_j, a_{j+1}]$
such that
$\xi _j\in [a_j, a_{j+1}]$
such that
 $$ \begin{align*}&\bigg\vert\!\sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y) ) \bigg\vert\\ &\quad\le C\Vert v\Vert_{l^\infty(\mathbb Z)} \sum_{j=m}^{M} (a_{j+1}-a_j)\vert\partial_t K^{L}_{\alpha, t}(x,y)|_{t=\xi_j}\vert\\ &\quad\le C_{v} \sum_{j=m}^{M} (a_{j+1}-a_j) {\frac 1{(\xi_j^{{1}/{(2\alpha)}}+|x-y|)^{n+2\alpha}}} \\ &\quad\le C_{v} \sum_{j=m}^{M} (\lambda^2-1)a_j ^{-{n/(2\alpha)}}\\ &\quad \le C_{v, \lambda} \frac1{a_m^{n/(2\alpha)}} \sum_{j=m}^{M} \frac1{\lambda^{n(j-m)/(2\alpha)}}\\ &\quad \le C_{v, \lambda,\alpha, n} {1\over a_m^{n/(2\alpha)}}, \end{align*} $$
$$ \begin{align*}&\bigg\vert\!\sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y) ) \bigg\vert\\ &\quad\le C\Vert v\Vert_{l^\infty(\mathbb Z)} \sum_{j=m}^{M} (a_{j+1}-a_j)\vert\partial_t K^{L}_{\alpha, t}(x,y)|_{t=\xi_j}\vert\\ &\quad\le C_{v} \sum_{j=m}^{M} (a_{j+1}-a_j) {\frac 1{(\xi_j^{{1}/{(2\alpha)}}+|x-y|)^{n+2\alpha}}} \\ &\quad\le C_{v} \sum_{j=m}^{M} (\lambda^2-1)a_j ^{-{n/(2\alpha)}}\\ &\quad \le C_{v, \lambda} \frac1{a_m^{n/(2\alpha)}} \sum_{j=m}^{M} \frac1{\lambda^{n(j-m)/(2\alpha)}}\\ &\quad \le C_{v, \lambda,\alpha, n} {1\over a_m^{n/(2\alpha)}}, \end{align*} $$
where we have used the fact that
![]() $\displaystyle \lambda \le {a_{j+1}/ a_j}\le \lambda ^2.$
$\displaystyle \lambda \le {a_{j+1}/ a_j}\le \lambda ^2.$
Now we prove (ii). Using the mean value theorem again, we can see that there exists
![]() $a_j\le \xi _j\le a_{j+1}$
such that
$a_j\le \xi _j\le a_{j+1}$
such that
 $$ \begin{align*} & \bigg\vert\!\sum_{j=-M}^{m-1}v_j (K^{L}_{\alpha, a_{j+1}}(z-y)-K^{L}_{\alpha, a_{j}}(z-y) ) \bigg\vert\\ &\quad\le C\Vert v\Vert_{l^\infty(\mathbb Z)} \sum_{j=m}^{M} (a_{j+1}-a_j)\vert\partial_t K^{L}_{\alpha, t}(x,y)|_{t=\xi_j}\vert\\&\quad\le C_{v,\alpha, n}\sum_{j=-M}^{m-1}(\lambda^2-1)a_j \frac 1{(\xi_j^{ 1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \\&\quad\le C_{\lambda, v,\alpha, n}\sum_{j=-M}^{m-1}{a_j \over (\xi_j^{ 1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \\ &\quad\le C_{\lambda, v,\alpha, n} \sum_{j=-M}^{m-1} {\frac{ a_j }{a_k}}\bigg({1\over a_k^{n/(2\alpha)}}\bigg) \le C_{\lambda, v,\alpha, n} {1\over a_k^{n/(2\alpha)}}\lambda^{-(k-m+1)}, \end{align*} $$
$$ \begin{align*} & \bigg\vert\!\sum_{j=-M}^{m-1}v_j (K^{L}_{\alpha, a_{j+1}}(z-y)-K^{L}_{\alpha, a_{j}}(z-y) ) \bigg\vert\\ &\quad\le C\Vert v\Vert_{l^\infty(\mathbb Z)} \sum_{j=m}^{M} (a_{j+1}-a_j)\vert\partial_t K^{L}_{\alpha, t}(x,y)|_{t=\xi_j}\vert\\&\quad\le C_{v,\alpha, n}\sum_{j=-M}^{m-1}(\lambda^2-1)a_j \frac 1{(\xi_j^{ 1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \\&\quad\le C_{\lambda, v,\alpha, n}\sum_{j=-M}^{m-1}{a_j \over (\xi_j^{ 1/{(2\alpha)}}+|x-y|)^{n+2\alpha}} \\ &\quad\le C_{\lambda, v,\alpha, n} \sum_{j=-M}^{m-1} {\frac{ a_j }{a_k}}\bigg({1\over a_k^{n/(2\alpha)}}\bigg) \le C_{\lambda, v,\alpha, n} {1\over a_k^{n/(2\alpha)}}\lambda^{-(k-m+1)}, \end{align*} $$
since
![]() $k \ge m.$
$k \ge m.$
To prove Theorem 4.4 for
![]() $T^*_{L^{\alpha }}$
, we need the following Cotlar-type inequality to control the operator
$T^*_{L^{\alpha }}$
, we need the following Cotlar-type inequality to control the operator
![]() $T^*_{L^{\alpha },M}$
. This is given precisely in the following theorem.
$T^*_{L^{\alpha },M}$
. This is given precisely in the following theorem.
Theorem 4.3. For each
![]() $q\in (1, +\infty ),$
there exists a positive constant C, depending on
$q\in (1, +\infty ),$
there exists a positive constant C, depending on
![]() $n, \Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$n, \Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
![]() $\lambda $
, such that, for every
$\lambda $
, such that, for every
![]() $x\in {\mathbb R}^n$
and for every
$x\in {\mathbb R}^n$
and for every
![]() $M\in \mathbb Z^+$
,
$M\in \mathbb Z^+$
,
where
and
 $$ \begin{align*} {\mathcal M}_qf(x)=\sup_{r>0} \bigg(\frac{1}{|B(x, r)|}\int_{B(x, r)}\vert f(y)\vert^qdy\bigg)^{1/q}. \end{align*} $$
$$ \begin{align*} {\mathcal M}_qf(x)=\sup_{r>0} \bigg(\frac{1}{|B(x, r)|}\int_{B(x, r)}\vert f(y)\vert^qdy\bigg)^{1/q}. \end{align*} $$
Proof. Observe that, for any
![]() $x_0\in {\mathbb R}^n$
and
$x_0\in {\mathbb R}^n$
and
![]() $N=(N_1, N_2),$
$N=(N_1, N_2),$
with
![]() $-M\le N_1<N_2\le M.$
Then it suffices to estimate
$-M\le N_1<N_2\le M.$
Then it suffices to estimate
![]() $|{T^{L^{\alpha }}_{(m, M)} f(x_0)}|$
for
$|{T^{L^{\alpha }}_{(m, M)} f(x_0)}|$
for
![]() $\vert m\vert \le M$
with constants independent of m and
$\vert m\vert \le M$
with constants independent of m and
![]() $M.$
Denote
$M.$
Denote
![]() $B_k=B(x_0, a_k^{1/(2\alpha )})$
for each
$B_k=B(x_0, a_k^{1/(2\alpha )})$
for each
![]() $k\in \mathbb N$
. We split f as
$k\in \mathbb N$
. We split f as
![]() $f=f\chi _{B_m}+f\chi _{B_m^c}:= f_1+f_2$
. Then
$f=f\chi _{B_m}+f\chi _{B_m^c}:= f_1+f_2$
. Then
![]() $|T^{L^{\alpha }}_{(m,M)} f(x_0)|\le I+II,$
where
$|T^{L^{\alpha }}_{(m,M)} f(x_0)|\le I+II,$
where
 $$ \begin{align*} \left\{\begin{aligned} I&:=\vert T^{L^{\alpha}}_{(m,M)} f_1(x_0)\vert,\\ II&:=\vert T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert. \end{aligned}\right.\end{align*} $$
$$ \begin{align*} \left\{\begin{aligned} I&:=\vert T^{L^{\alpha}}_{(m,M)} f_1(x_0)\vert,\\ II&:=\vert T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert. \end{aligned}\right.\end{align*} $$
By Lemma 4.2(i),
 $$ \begin{align*} I&=\bigg\vert\!\int_{{\mathbb R}^n} \sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x_0,y)- K^{L}_{\alpha, a_{j}}(x_0,y)) f_1(y)\,dy\bigg\vert\\ &\le {C_{n, v, \lambda, \alpha}\over |{a^{n/(2\alpha)}_m}|} \int_{{\mathbb R}^n} \vert f_1(y)\vert \,dy \le C_{v, \lambda, n, \alpha}{\mathcal M} f(x_0). \end{align*} $$
$$ \begin{align*} I&=\bigg\vert\!\int_{{\mathbb R}^n} \sum_{j=m}^{M}v_j (K^{L}_{\alpha, a_{j+1}}(x_0,y)- K^{L}_{\alpha, a_{j}}(x_0,y)) f_1(y)\,dy\bigg\vert\\ &\le {C_{n, v, \lambda, \alpha}\over |{a^{n/(2\alpha)}_m}|} \int_{{\mathbb R}^n} \vert f_1(y)\vert \,dy \le C_{v, \lambda, n, \alpha}{\mathcal M} f(x_0). \end{align*} $$
Also,
 $$ \begin{align*} II&=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha)})} \vert T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert \,dz\leq \sum^{4}_{i=1}A_i, \end{align*} $$
$$ \begin{align*} II&=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha)})} \vert T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert \,dz\leq \sum^{4}_{i=1}A_i, \end{align*} $$
where
 $$ \begin{align*}\left\{\begin{aligned} A_{1}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha) })}\vert T^{L^{\alpha}}_{(-M,M)} f(z)\vert \,dz;\\ A_{2}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(-M,M)} f_1(z)\vert \,dz;\\ A_{3}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(m,M)} f_2(z)-T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert \,dz;\\ A_{4}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(-M,m-1)} f_2(z)\vert \,dz. \end{aligned}\right.\end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} A_{1}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha) })}\vert T^{L^{\alpha}}_{(-M,M)} f(z)\vert \,dz;\\ A_{2}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(-M,M)} f_1(z)\vert \,dz;\\ A_{3}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(m,M)} f_2(z)-T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert \,dz;\\ A_{4}&:=\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/2}a_{m-1}^{1/(2\alpha)})}\vert T^{L^{\alpha}}_{(-M,m-1)} f_2(z)\vert \,dz. \end{aligned}\right.\end{align*} $$
It should be noted that
![]() $A_4=0$
if
$A_4=0$
if
![]() $m+1=-M$
. It is obvious that
$m+1=-M$
. It is obvious that
It follows from the uniform boundedness of
![]() $T^{L^{\alpha }}_{N}$
that
$T^{L^{\alpha }}_{N}$
that
 $$ \begin{align*} A_2&\le \bigg(\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B_{m-1}}\vert T^{L^{\alpha}}_{(-M,M)} f_1(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim \bigg(\frac{1}{a_{m-1}^{n/(2\alpha)}}\int_{\mathbb{R}^n}\vert f_1(z)\vert^q\,dz\bigg)^{1/q}\\ &\thicksim\bigg(\frac{1}{a_{m-1}^{n/(2\alpha)}}\int_{B_{m}}\vert f(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim \bigg(\frac{\lambda^{n/(2\alpha)}}{a_{m}^{n/(2\alpha)}}\int_{B_{m}}\vert f(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim {\mathcal M}_q f(x_0). \end{align*} $$
$$ \begin{align*} A_2&\le \bigg(\frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B_{m-1}}\vert T^{L^{\alpha}}_{(-M,M)} f_1(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim \bigg(\frac{1}{a_{m-1}^{n/(2\alpha)}}\int_{\mathbb{R}^n}\vert f_1(z)\vert^q\,dz\bigg)^{1/q}\\ &\thicksim\bigg(\frac{1}{a_{m-1}^{n/(2\alpha)}}\int_{B_{m}}\vert f(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim \bigg(\frac{\lambda^{n/(2\alpha)}}{a_{m}^{n/(2\alpha)}}\int_{B_{m}}\vert f(z)\vert^q\,dz\bigg)^{1/q}\\ &\lesssim {\mathcal M}_q f(x_0). \end{align*} $$
For the third term
![]() $A_3$
, we can see that
$A_3$
, we can see that
![]() $ A_3\lesssim {\mathcal M} f(x_0)$
, since, for
$ A_3\lesssim {\mathcal M} f(x_0)$
, since, for
![]() $z\in B(x_0, {1\over 2}a_{m-1}^{1/(2\alpha )})$
,
$z\in B(x_0, {1\over 2}a_{m-1}^{1/(2\alpha )})$
,
 $$ \begin{align*} &\vert T^{L^{\alpha}}_{(m,M)} f_2(z)-T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert\\ &\quad\le \int_{B_m^c} \vert K^\alpha_{(m,M)}(z,y)-K^\alpha_{(m,M)}(x_0,y)\vert\vert f(y)\vert \,dy\\ &\quad\le \sum_{j=1}^{+\infty}\int_{B_{2^jm} \setminus B_{2^{j-1}m}}\frac{\vert z-x_0\vert^{\delta'}}{\vert x_0-y\vert^{n+\delta'}}\vert f(y)\vert \,dy\\ &\quad\lesssim\sum_{j=1}^{+\infty}\frac 1{2^{j\delta'}}\frac{a_{m-1}^{\delta'/(2\alpha)}}{a_m^{\delta'/(2\alpha)}}{1\over |2^ja_{m}|^{n/(2\alpha)}}\int_{B_{2^jm}} \vert f(y)\vert \,dy\lesssim {\mathcal M} f(x_0), \end{align*} $$
$$ \begin{align*} &\vert T^{L^{\alpha}}_{(m,M)} f_2(z)-T^{L^{\alpha}}_{(m,M)} f_2(x_0)\vert\\ &\quad\le \int_{B_m^c} \vert K^\alpha_{(m,M)}(z,y)-K^\alpha_{(m,M)}(x_0,y)\vert\vert f(y)\vert \,dy\\ &\quad\le \sum_{j=1}^{+\infty}\int_{B_{2^jm} \setminus B_{2^{j-1}m}}\frac{\vert z-x_0\vert^{\delta'}}{\vert x_0-y\vert^{n+\delta'}}\vert f(y)\vert \,dy\\ &\quad\lesssim\sum_{j=1}^{+\infty}\frac 1{2^{j\delta'}}\frac{a_{m-1}^{\delta'/(2\alpha)}}{a_m^{\delta'/(2\alpha)}}{1\over |2^ja_{m}|^{n/(2\alpha)}}\int_{B_{2^jm}} \vert f(y)\vert \,dy\lesssim {\mathcal M} f(x_0), \end{align*} $$
where
![]() $B_{2^jm}=B(x_0, 2^ja_m^{1/ (2\alpha )})$
for any
$B_{2^jm}=B(x_0, 2^ja_m^{1/ (2\alpha )})$
for any
![]() $j\ge 1$
.
$j\ge 1$
.
For
![]() $A_4,$
we have
$A_4,$
we have
 $$ \begin{align} A_4\le \frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha)})}\int_{B_m^c}\vert K^\alpha_{(-M,m-1)}(z,y) f(y)\vert \,dy\,dz. \end{align} $$
$$ \begin{align} A_4\le \frac{2^{n/2}}{a_{m-1}^{n/(2\alpha)}}\int_{B(x_0, {1/ 2}a_{m-1}^{1/(2\alpha)})}\int_{B_m^c}\vert K^\alpha_{(-M,m-1)}(z,y) f(y)\vert \,dy\,dz. \end{align} $$
For the inner integral in (4-2), since
![]() $z\in B(x_0, {1\over 2}a_{m-1}^{1/(2\alpha )})$
,
$z\in B(x_0, {1\over 2}a_{m-1}^{1/(2\alpha )})$
,
![]() $y\in B_m^c$
and the sequence
$y\in B_m^c$
and the sequence
![]() $\{a_j\}_{j\in \mathbb Z}$
is a
$\{a_j\}_{j\in \mathbb Z}$
is a
![]() $\lambda $
-lacunary sequence, we have
$\lambda $
-lacunary sequence, we have
![]() $\vert z-y\vert \sim \vert y-x_0\vert .$
From the previous arguments and by Lemma 4.2(ii), we get
$\vert z-y\vert \sim \vert y-x_0\vert .$
From the previous arguments and by Lemma 4.2(ii), we get
 $$ \begin{align*} &\int_{B_m^c}\vert K^\alpha_{(-M,m-1)}(z, y) f(y)\vert \,dy\\ &\quad\le C_{\lambda, v,\alpha, n} \sum_{k=m}^{+\infty}\lambda^{-(k-m+1)}\bigg({1\over a_k^{n/(2\alpha)}}\int_{B_{k+1}\setminus B_{k}} \vert f(y)\vert \,dy\bigg)\\ &\quad\le C_{\lambda, v,\alpha, n} {\mathcal M} f(x_0)\sum_{k=m}^{+\infty}\lambda^{-(k-m+1)}\\ &\quad\le C_{\lambda, v,\alpha, n}{\mathcal M} f(x_0), \end{align*} $$
$$ \begin{align*} &\int_{B_m^c}\vert K^\alpha_{(-M,m-1)}(z, y) f(y)\vert \,dy\\ &\quad\le C_{\lambda, v,\alpha, n} \sum_{k=m}^{+\infty}\lambda^{-(k-m+1)}\bigg({1\over a_k^{n/(2\alpha)}}\int_{B_{k+1}\setminus B_{k}} \vert f(y)\vert \,dy\bigg)\\ &\quad\le C_{\lambda, v,\alpha, n} {\mathcal M} f(x_0)\sum_{k=m}^{+\infty}\lambda^{-(k-m+1)}\\ &\quad\le C_{\lambda, v,\alpha, n}{\mathcal M} f(x_0), \end{align*} $$
which implies
![]() $A_4\lesssim {\mathcal M} f(x_0)$
. Combining the above estimates for
$A_4\lesssim {\mathcal M} f(x_0)$
. Combining the above estimates for
![]() $A_i, i=1,2,3,4$
, we get
$A_i, i=1,2,3,4$
, we get
and
Since the constants C appearing above only depend on
![]() $\Vert v\Vert _{l^\infty (\mathbb Z)}$
,
$\Vert v\Vert _{l^\infty (\mathbb Z)}$
,
![]() $\lambda $
,
$\lambda $
,
![]() $\alpha $
and n,
$\alpha $
and n,
This completes the proof of Theorem 4.3.
We now prove the main result of this paper.
Theorem 4.4. Assume that the sequence
![]() $\{a_j\}_{j\in \mathbb Z}$
is a
$\{a_j\}_{j\in \mathbb Z}$
is a
![]() $\lambda $
-lacunary sequence with
$\lambda $
-lacunary sequence with
![]() $\lambda>1$
. Let
$\lambda>1$
. Let
![]() $\mathcal {S}$
be either the operator
$\mathcal {S}$
be either the operator
![]() $T^*_{L^{\alpha }}$
or the operator
$T^*_{L^{\alpha }}$
or the operator
![]() $T^*_{(-\Delta )^{\alpha }}$
defined in (1-5) or (2-3).
$T^*_{(-\Delta )^{\alpha }}$
defined in (1-5) or (2-3).
-
(i) For any
 $1<p<\infty $
, there exists a positive constant C, depending on
$1<p<\infty $
, there exists a positive constant C, depending on
 $n, p, \lambda $
,
$n, p, \lambda $
,
 $\Vert v\Vert _{l^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{l^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^p({\mathbb R}^{n})$
,
$f\in L^p({\mathbb R}^{n})$
,  $$ \begin{align*}\Vert\mathcal{S} f\Vert_{L^p(\mathbb R^{n})}\leq C\Vert f\Vert_{L^p(\mathbb R^{n})}.\end{align*} $$
$$ \begin{align*}\Vert\mathcal{S} f\Vert_{L^p(\mathbb R^{n})}\leq C\Vert f\Vert_{L^p(\mathbb R^{n})}.\end{align*} $$
-
(ii) There exists a positive constant C, depending on
 $n, \lambda $
,
$n, \lambda $
,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^1({\mathbb R}^{n})$
,
$f\in L^1({\mathbb R}^{n})$
,  $$ \begin{align*}|\{x\in {\mathbb R}^{n}:\vert\mathcal{S} f(x)\vert>\sigma\}| \le\frac{ C}{\sigma}\Vert f\Vert_{L^1(\mathbb R^{n})}, \quad \sigma>0,\end{align*} $$
$$ \begin{align*}|\{x\in {\mathbb R}^{n}:\vert\mathcal{S} f(x)\vert>\sigma\}| \le\frac{ C}{\sigma}\Vert f\Vert_{L^1(\mathbb R^{n})}, \quad \sigma>0,\end{align*} $$
Here the constants C appearing in (i) and (ii) above are all independent of N.
Proof. First, it follows from [Reference Duoandikoetxea4, Theorem 2.5] that the maximal operators
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() $ {\mathcal M}_q$
are bounded on
$ {\mathcal M}_q$
are bounded on
![]() $L^p({\mathbb R}^n) $
. On the other hand, since the operators
$L^p({\mathbb R}^n) $
. On the other hand, since the operators
![]() $T^{L^{\alpha }}_N$
are uniformly bounded on
$T^{L^{\alpha }}_N$
are uniformly bounded on
![]() $L^p({\mathbb R}^n)$
,
$L^p({\mathbb R}^n)$
,
 $$ \begin{align*} \Vert T_{L^{\alpha},M}^*f\Vert_{L^p({\mathbb R}^n)}&\leq C \Vert{\mathcal M} (T^{L^{\alpha}}_{(-M, M)} f)\Vert_{L^p({\mathbb R}^n)}+\Vert{\mathcal M}_q f\Vert_{L^p({\mathbb R}^n)}\\&\leq C \Vert T^{L^{\alpha}}_{(-M, M)} f\Vert_{L^p({\mathbb R}^n)}+\Vert f\Vert_{L^p({\mathbb R}^n)}\\ &\leq C\Vert f\Vert_{L^p({\mathbb R}^n)}. \end{align*} $$
$$ \begin{align*} \Vert T_{L^{\alpha},M}^*f\Vert_{L^p({\mathbb R}^n)}&\leq C \Vert{\mathcal M} (T^{L^{\alpha}}_{(-M, M)} f)\Vert_{L^p({\mathbb R}^n)}+\Vert{\mathcal M}_q f\Vert_{L^p({\mathbb R}^n)}\\&\leq C \Vert T^{L^{\alpha}}_{(-M, M)} f\Vert_{L^p({\mathbb R}^n)}+\Vert f\Vert_{L^p({\mathbb R}^n)}\\ &\leq C\Vert f\Vert_{L^p({\mathbb R}^n)}. \end{align*} $$
Note that the constants C appearing above are independent of M. Consequently, letting M increase to infinity yields to the
![]() $L^p$
-boundedness of
$L^p$
-boundedness of
![]() $T^*_{L^{\alpha }}$
. This completes the proof of part (i) of this theorem.
$T^*_{L^{\alpha }}$
. This completes the proof of part (i) of this theorem.
In order to prove (ii), we consider the
![]() $\ell ^\infty (\mathbb Z^2)$
-valued operator
$\ell ^\infty (\mathbb Z^2)$
-valued operator
Since
using (i), we conclude that the operator
![]() $\mathcal {T}$
is bounded from
$\mathcal {T}$
is bounded from
![]() $L^p({\mathbb R}^n) $
into
$L^p({\mathbb R}^n) $
into
![]() $L^p_{\ell ^\infty (\mathbb Z^2)}(\mathbb {R}^n)$
for every
$L^p_{\ell ^\infty (\mathbb Z^2)}(\mathbb {R}^n)$
for every
![]() $1<p<\infty $
. The kernel of
$1<p<\infty $
. The kernel of
![]() $\mathcal {T}$
is given by
$\mathcal {T}$
is given by
![]() $\mathcal {K}(x) = \{ K^\alpha _N(x)\} _{N\in \mathbb Z^2}$
. Therefore, by the vector-valued Calderón–Zygmund theory, the operator
$\mathcal {K}(x) = \{ K^\alpha _N(x)\} _{N\in \mathbb Z^2}$
. Therefore, by the vector-valued Calderón–Zygmund theory, the operator
![]() $\mathcal {T}$
is bounded from
$\mathcal {T}$
is bounded from
![]() $L^1(\mathbb {R}^n)$
into weak-
$L^1(\mathbb {R}^n)$
into weak-
![]() $L^1_{\ell ^\infty (\mathbb Z^2)}(\mathbb {R}^n)$
. Hence, using (4-3) again, we get the proof of (ii).
$L^1_{\ell ^\infty (\mathbb Z^2)}(\mathbb {R}^n)$
. Hence, using (4-3) again, we get the proof of (ii).
We also need the following result established in [Reference Ma, Stinga, Torrea and Zhang11] to prove the boundedness of the maximal operator
![]() $T^*_{L^{\alpha }}$
in the space
$T^*_{L^{\alpha }}$
in the space
![]() $BMO_{L}(\mathbb R^{n})$
. Let f be a locally integrable function on
$BMO_{L}(\mathbb R^{n})$
. Let f be a locally integrable function on
![]() $\mathbb {R}^{n}$
and let
$\mathbb {R}^{n}$
and let
![]() $B=B(x,R)$
be a ball. Let
$B=B(x,R)$
be a ball. Let
 $$ \begin{align*} f(B,V):= \begin{cases} \dfrac{1}{|B|}\displaystyle\int_{B}f(y)\,dy & \mbox{if }R<\rho(x),\\[5pt] 0 & \mbox{if }R\geq\rho(x), \end{cases} \end{align*} $$
$$ \begin{align*} f(B,V):= \begin{cases} \dfrac{1}{|B|}\displaystyle\int_{B}f(y)\,dy & \mbox{if }R<\rho(x),\\[5pt] 0 & \mbox{if }R\geq\rho(x), \end{cases} \end{align*} $$
and let
![]() $0<\gamma \leq 1$
. The space
$0<\gamma \leq 1$
. The space
![]() $BMO_{L}^{\gamma }(\mathbb {R}^{n})$
is defined as the set of all locally integrable functions f satisfying
$BMO_{L}^{\gamma }(\mathbb {R}^{n})$
is defined as the set of all locally integrable functions f satisfying
Lemma 4.5 [Reference Ma, Stinga, Torrea and Zhang11, Theorem 1.2].
Let T be a
![]() $\gamma $
-Schrödinger–Calderón–Zygmund operator for
$\gamma $
-Schrödinger–Calderón–Zygmund operator for
![]() $0\le \gamma <\min \{1,\delta \}$
with the smoothness exponent
$0\le \gamma <\min \{1,\delta \}$
with the smoothness exponent
![]() $\delta>0$
. Then T is a bounded operator from
$\delta>0$
. Then T is a bounded operator from
![]() $BMO_L(\mathbb R^{n})$
into
$BMO_L(\mathbb R^{n})$
into
![]() $BMO_L^\gamma (\mathbb R^{n})$
if and only if there exists a constant C such that
$BMO_L^\gamma (\mathbb R^{n})$
if and only if there exists a constant C such that
for every ball
![]() $B=B(x_0,t)$
,
$B=B(x_0,t)$
,
![]() $x_0\in {\mathbb R}^n$
and
$x_0\in {\mathbb R}^n$
and
![]() $0<t\leq \rho (x_0)/2$
.
$0<t\leq \rho (x_0)/2$
.
![]() $T1$
means that the operator T acts on the constant function 1.
$T1$
means that the operator T acts on the constant function 1.
Theorem 4.6. Let
![]() $\{a_j\}_{j\in \mathbb Z}$
be a
$\{a_j\}_{j\in \mathbb Z}$
be a
![]() $\lambda $
-lacunary sequence and let
$\lambda $
-lacunary sequence and let
![]() $T^*_{L^{\alpha }}$
be the operator defined in (1-5). We have the following statements.
$T^*_{L^{\alpha }}$
be the operator defined in (1-5). We have the following statements.
-
(i) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^\infty ({\mathbb R}^{n})$
,
$f\in L^\infty ({\mathbb R}^{n})$
,  $$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{BMO_L(\mathbb R^{n})}\leq C\Vert f\Vert_{L^\infty(\mathbb R^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{BMO_L(\mathbb R^{n})}\leq C\Vert f\Vert_{L^\infty(\mathbb R^{n})}.\end{align*} $$
-
(ii) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in BMO_L({\mathbb R}^n)$
,
$f\in BMO_L({\mathbb R}^n)$
,  $$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{BMO_L({\mathbb R}^n)}\le C\Vert f\Vert_{BMO_L({\mathbb R}^n)}.\end{align*} $$
$$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{BMO_L({\mathbb R}^n)}\le C\Vert f\Vert_{BMO_L({\mathbb R}^n)}.\end{align*} $$
The constants C appearing in (i) and (ii) are all independent of
 $N.$
$N.$
Proof. By an argument similar to that used in Theorem 3.6, we know that
![]() $ T^*_{L^{\alpha }} f<\infty \text{for almost every}\ x \in \mathbb {R}^{n}$
. Since (i) can be deduced from (ii), we only need to prove (ii). By Theorem 4.4(i) and Proposition 3.5,
$ T^*_{L^{\alpha }} f<\infty \text{for almost every}\ x \in \mathbb {R}^{n}$
. Since (i) can be deduced from (ii), we only need to prove (ii). By Theorem 4.4(i) and Proposition 3.5,
![]() $T^{L^{\alpha }}_N$
and
$T^{L^{\alpha }}_N$
and
![]() ${T}^{*} =\| \, \{ T^{L^{\alpha }}_N\}_{N=(N_1, N_2)}\, \|_{\ell ^\infty (\mathbb Z^2)}$
are
${T}^{*} =\| \, \{ T^{L^{\alpha }}_N\}_{N=(N_1, N_2)}\, \|_{\ell ^\infty (\mathbb Z^2)}$
are
![]() $\gamma $
-Schrödinger–Calderón–Zygmund operators with
$\gamma $
-Schrödinger–Calderón–Zygmund operators with
![]() $\gamma =0$
. Then it is enough to verify that both of the operators satisfy (4-4). More precisely,
$\gamma =0$
. Then it is enough to verify that both of the operators satisfy (4-4). More precisely,
 $$ \begin{align*} | {T}^{*}1(x)-({T}^{*}1)_B | &\le \bigg| {T}^{*}1(x) - \frac1{|B|} \int_B {T}^{*}1(y) \,dy \bigg| \\ & \le \frac1{|B|} \int_B | {T}^{*}1(x) - {T}^{*}1(y) | \,dy \\ &= \frac1{|B|} \int_B | \| \, \{ T^{L^{\alpha}}_N 1(x)\}_N\, \|_{\ell^\infty(\mathbb Z^2)} - \| \, \{ T^{L^{\alpha}}_N 1(y) \}_N\, \|_{\ell^\infty(\mathbb Z^2)} | \, dy \\ & \le \frac1{|B|} \int_B \| \, T^{L^{\alpha}}_N 1(x) - T^{L^{\alpha}}_N 1(y)\, \|_{\ell^\infty(\mathbb Z^2)}\, dy\\ &= \frac1{|B|} \int_B \sup_N | T^{L^{\alpha}}_N 1(x) - T^{L^{\alpha}}_N 1(y)\, | \, dy. \end{align*} $$
$$ \begin{align*} | {T}^{*}1(x)-({T}^{*}1)_B | &\le \bigg| {T}^{*}1(x) - \frac1{|B|} \int_B {T}^{*}1(y) \,dy \bigg| \\ & \le \frac1{|B|} \int_B | {T}^{*}1(x) - {T}^{*}1(y) | \,dy \\ &= \frac1{|B|} \int_B | \| \, \{ T^{L^{\alpha}}_N 1(x)\}_N\, \|_{\ell^\infty(\mathbb Z^2)} - \| \, \{ T^{L^{\alpha}}_N 1(y) \}_N\, \|_{\ell^\infty(\mathbb Z^2)} | \, dy \\ & \le \frac1{|B|} \int_B \| \, T^{L^{\alpha}}_N 1(x) - T^{L^{\alpha}}_N 1(y)\, \|_{\ell^\infty(\mathbb Z^2)}\, dy\\ &= \frac1{|B|} \int_B \sup_N | T^{L^{\alpha}}_N 1(x) - T^{L^{\alpha}}_N 1(y)\, | \, dy. \end{align*} $$
Hence, to prove (4-4), it is sufficient to prove that, for
![]() $0<\delta <\min \{1, 2\alpha , 2-n/q\} $
and for any
$0<\delta <\min \{1, 2\alpha , 2-n/q\} $
and for any
![]() $x, y \in B=B(x_0,t),$
if
$x, y \in B=B(x_0,t),$
if
![]() $t\le \rho (x_0)/2$
, then
$t\le \rho (x_0)/2$
, then
Note that
![]() $\rho (x)\sim \rho (y)\sim \rho (x_0)$
when
$\rho (x)\sim \rho (y)\sim \rho (x_0)$
when
![]() $x, y \in B$
. Since
$x, y \in B$
. Since
![]() $e^{- {t(-\Delta )^\alpha }}f$
is a convolution operator, it follows from (1-1) that
$e^{- {t(-\Delta )^\alpha }}f$
is a convolution operator, it follows from (1-1) that
![]() $(\mathcal {F}K^{-\Delta }_{\alpha , s}(\cdot ))(\xi )=e^{-t|\xi |^{2\alpha }}$
and
$(\mathcal {F}K^{-\Delta }_{\alpha , s}(\cdot ))(\xi )=e^{-t|\xi |^{2\alpha }}$
and
for any
![]() $s>0.$
Then we can write
$s>0.$
Then we can write
 $$ \begin{align*} &\vert T^{L^{\alpha}}_N 1(x)-T^{L^{\alpha}}_N 1(y)\vert\\ &\quad= \bigg|\! \int_{{\mathbb R}^{n}} \sum_{j=N_1}^{N_2}v_j[( (K^{L}_{\alpha, a_{j+1}}(x,z)- K^{-\Delta}_{\alpha, a_{j+1}}(x-z)) -(K^{L}_{\alpha, a_{j}}(x,z) - K^{-\Delta}_{\alpha, a_{j}}(x-z) ) ) \\ &\qquad - ((K^{L}_{\alpha, a_{j+1}}(y,z)- K^{-\Delta}_{\alpha, a_{j+1}}(y-z))- (K^{L}_{\alpha, a_{j}}(y,z) - K^{-\Delta}_{\alpha, a_{j}}(y-z))) ] \,dz\bigg| \\ &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)} \int_{{\mathbb R}^{n}}\int_0^\infty|\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z)) -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz\\ &\quad\lesssim I+II+III, \end{align*} $$
$$ \begin{align*} &\vert T^{L^{\alpha}}_N 1(x)-T^{L^{\alpha}}_N 1(y)\vert\\ &\quad= \bigg|\! \int_{{\mathbb R}^{n}} \sum_{j=N_1}^{N_2}v_j[( (K^{L}_{\alpha, a_{j+1}}(x,z)- K^{-\Delta}_{\alpha, a_{j+1}}(x-z)) -(K^{L}_{\alpha, a_{j}}(x,z) - K^{-\Delta}_{\alpha, a_{j}}(x-z) ) ) \\ &\qquad - ((K^{L}_{\alpha, a_{j+1}}(y,z)- K^{-\Delta}_{\alpha, a_{j+1}}(y-z))- (K^{L}_{\alpha, a_{j}}(y,z) - K^{-\Delta}_{\alpha, a_{j}}(y-z))) ] \,dz\bigg| \\ &\quad\lesssim\Vert v\Vert_{\ell^\infty(\mathbb Z)} \int_{{\mathbb R}^{n}}\int_0^\infty|\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z)) -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz\\ &\quad\lesssim I+II+III, \end{align*} $$
where
 $$ \begin{align*}\left\{\begin{aligned} I&:=\int_{{\mathbb R}^{n}}\int_0^{(2t)^{2\alpha}} |\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz;\\ II&:=\int_{{\mathbb R}^{n}}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz;\\ III&:=\int_{{\mathbb R}^{n}}\int_{\rho^{2\alpha}(x_0)}^\infty |\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz. \end{aligned}\right.\end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} I&:=\int_{{\mathbb R}^{n}}\int_0^{(2t)^{2\alpha}} |\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz;\\ II&:=\int_{{\mathbb R}^{n}}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz;\\ III&:=\int_{{\mathbb R}^{n}}\int_{\rho^{2\alpha}(x_0)}^\infty |\partial_s((K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -(K^{L}_{\alpha, s}(y,z)- K^{-\Delta}_{\alpha, s}(y-z) )\, | \,ds \,dz. \end{aligned}\right.\end{align*} $$
For
![]() $I,$
by Lemma 3.4, we get
$I,$
by Lemma 3.4, we get
![]() $I\leq C(I_{1}+I_{2})$
, where
$I\leq C(I_{1}+I_{2})$
, where
 $$ \begin{align*}\left\{\begin{aligned} I_{1}&:=\int_{{\mathbb R}^{n}} \int_0^{(2t)^{2\alpha}} |\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z) ) |\,ds \,dz;\\ I_{2}&:=\int_{{\mathbb R}^{n}} \int_0^{(2t)^{2\alpha}}| \partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) |\,ds \,dz. \end{aligned}\right.\end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} I_{1}&:=\int_{{\mathbb R}^{n}} \int_0^{(2t)^{2\alpha}} |\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z) ) |\,ds \,dz;\\ I_{2}&:=\int_{{\mathbb R}^{n}} \int_0^{(2t)^{2\alpha}}| \partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) |\,ds \,dz. \end{aligned}\right.\end{align*} $$
For
![]() $I_{1}$
, when
$I_{1}$
, when
![]() $\sqrt {s^{1/\alpha }}\leq |x-z|$
, by choosing
$\sqrt {s^{1/\alpha }}\leq |x-z|$
, by choosing
![]() $\delta _{0}<2\alpha $
, we get
$\delta _{0}<2\alpha $
, we get
 $$ \begin{align*} I_{1} &\lesssim \int^{(2t)^{2\alpha}}_{0}\int_{\mathbb{R}^{n}}\bigg(\frac{|x-z|}{\rho(x)}\bigg)^{\delta_{0}}\frac{1}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\frac{1}{\rho(x_{0})^{\delta_{0}}}\int_{\mathbb{R}^{n}}\frac{|x-z|^{\delta_{0}}}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\bigg(\frac{s^{1/(2\alpha)}}{\rho(x_{0})}\bigg)^{\delta_{0}}\frac{1}{s}\,ds \\ &\lesssim \bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta_{0}}. \end{align*} $$
$$ \begin{align*} I_{1} &\lesssim \int^{(2t)^{2\alpha}}_{0}\int_{\mathbb{R}^{n}}\bigg(\frac{|x-z|}{\rho(x)}\bigg)^{\delta_{0}}\frac{1}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\frac{1}{\rho(x_{0})^{\delta_{0}}}\int_{\mathbb{R}^{n}}\frac{|x-z|^{\delta_{0}}}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\bigg(\frac{s^{1/(2\alpha)}}{\rho(x_{0})}\bigg)^{\delta_{0}}\frac{1}{s}\,ds \\ &\lesssim \bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta_{0}}. \end{align*} $$
When
![]() $\sqrt {s^{1/\alpha }}>|x-z|$
, we obtain
$\sqrt {s^{1/\alpha }}>|x-z|$
, we obtain
 $$ \begin{align*} I_{1} &\lesssim \int^{(2t)^{2\alpha}}_{0}\int_{\mathbb{R}^{n}}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^{\delta_{0}}\frac{1}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\bigg(\frac{s^{1/(2\alpha)}}{\rho(x_{0})}\bigg)^{\delta_{0}}\frac{1}{s}\,ds \\ &\lesssim \bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta_{0}}. \end{align*} $$
$$ \begin{align*} I_{1} &\lesssim \int^{(2t)^{2\alpha}}_{0}\int_{\mathbb{R}^{n}}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^{\delta_{0}}\frac{1}{(|x-z|+s^{1/(2\alpha)})^{n+2\alpha}}\,dz\,ds \\ &\lesssim \int^{(2t)^{2\alpha}}_{0}\bigg(\frac{s^{1/(2\alpha)}}{\rho(x_{0})}\bigg)^{\delta_{0}}\frac{1}{s}\,ds \\ &\lesssim \bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta_{0}}. \end{align*} $$
The proof for
![]() $I_{2}$
is similar to that for
$I_{2}$
is similar to that for
![]() $I_{1}$
, so we omit the details.
$I_{1}$
, so we omit the details.
We have
 $$ \begin{align*} II &= \int_{{\mathbb R}^{n}} \int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)} |\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z) )\\ &\quad-\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z)) | \,ds \,dz\\ &\lesssim II_1+II_2+II_3, \end{align*} $$
$$ \begin{align*} II &= \int_{{\mathbb R}^{n}} \int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)} |\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z) )\\ &\quad-\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z)) | \,ds \,dz\\ &\lesssim II_1+II_2+II_3, \end{align*} $$
where
 $$ \begin{align*}\left\{\begin{aligned} II_{1}&:=\int_{\vert x-z\vert>c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z)) \vert\\ &\quad +\vert\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z))\vert\,ds \,dz; \\ II_{2}&:= \int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -\partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) |\,ds \,dz;\\ II_{3}&:=\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -\partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z))| \,ds \,dz. \end{aligned}\right.\end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} II_{1}&:=\int_{\vert x-z\vert>c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z)) \vert\\ &\quad +\vert\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z))\vert\,ds \,dz; \\ II_{2}&:= \int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -\partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) |\,ds \,dz;\\ II_{3}&:=\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}|\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))\\ &\quad -\partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z))| \,ds \,dz. \end{aligned}\right.\end{align*} $$
For
![]() $II_1$
, noting that
$II_1$
, noting that
![]() $\vert x-y\vert \le 2t\le s^{1/(2\alpha )},$
by Lemma 3.3 and a similar result for the Laplacian as in Lemma 3.3, we have
$\vert x-y\vert \le 2t\le s^{1/(2\alpha )},$
by Lemma 3.3 and a similar result for the Laplacian as in Lemma 3.3, we have
 $$ \begin{align*} II_{11} &\lesssim\int_{\vert x-z\vert>c\rho(x)}{\vert x-y\vert^\delta\over \vert x-z\vert^{2\alpha+n}} \int_{(2t)^{2\alpha}}^ { \rho^{2\alpha}(x_0)}~\frac{1}{s^{\delta/(2\alpha)}}\,ds\,dz\\ &\lesssim\bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta}\int_{\vert x-z\vert>c\rho(x)}\frac{1}{|x-z|^{n+2\alpha}}\rho^{2\alpha}(x_0)\,dz\\ &\lesssim\bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta}. \end{align*} $$
$$ \begin{align*} II_{11} &\lesssim\int_{\vert x-z\vert>c\rho(x)}{\vert x-y\vert^\delta\over \vert x-z\vert^{2\alpha+n}} \int_{(2t)^{2\alpha}}^ { \rho^{2\alpha}(x_0)}~\frac{1}{s^{\delta/(2\alpha)}}\,ds\,dz\\ &\lesssim\bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta}\int_{\vert x-z\vert>c\rho(x)}\frac{1}{|x-z|^{n+2\alpha}}\rho^{2\alpha}(x_0)\,dz\\ &\lesssim\bigg(\frac{t}{\rho(x_{0})}\bigg)^{\delta}. \end{align*} $$
For the term
![]() $II_2$
, in this case,
$II_2$
, in this case,
![]() $|x-y|< c\rho (x)$
and
$|x-y|< c\rho (x)$
and
![]() $\displaystyle |x-y|<{|x-z|/4}$
. By Lemma 3.4, we conclude that, for some
$\displaystyle |x-y|<{|x-z|/4}$
. By Lemma 3.4, we conclude that, for some
![]() $0<\varepsilon <\min \{\alpha ,\delta \}$
small enough,
$0<\varepsilon <\min \{\alpha ,\delta \}$
small enough,
 $$ \begin{align*} II_2&\lesssim\int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)} \bigg({\vert x-y\vert\over \rho(z)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\,ds \,dz\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^\delta \int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)} \frac{1}{s^{n/(2\alpha)+1}} \frac{|x-z|^{\epsilon}\,ds\,dz}{(1+|x-z|/s^{1/(2\alpha)})^{n+2\epsilon}|x-z|^{\epsilon}}\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^\delta\bigg({\rho(x_0) \over\vert x-y\vert}\bigg)^{\varepsilon}\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^{\delta'}. \end{align*} $$
$$ \begin{align*} II_2&\lesssim\int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)} \bigg({\vert x-y\vert\over \rho(z)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\,ds \,dz\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^\delta \int_{4|x-y|<\vert x-z\vert\le c\rho(x)}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)} \frac{1}{s^{n/(2\alpha)+1}} \frac{|x-z|^{\epsilon}\,ds\,dz}{(1+|x-z|/s^{1/(2\alpha)})^{n+2\epsilon}|x-z|^{\epsilon}}\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^\delta\bigg({\rho(x_0) \over\vert x-y\vert}\bigg)^{\varepsilon}\\ &\lesssim\bigg({\vert x-y\vert\over \rho(x_0)}\bigg)^{\delta'}. \end{align*} $$
For the term
![]() $II_3,$
since
$II_3,$
since
![]() $|x-y|\leq 2t\leq s^{1/(2\alpha )}$
, we have
$|x-y|\leq 2t\leq s^{1/(2\alpha )}$
, we have
![]() $|x-z|\leq s^{1/(2\alpha )}$
. By Lemma 3.4,
$|x-z|\leq s^{1/(2\alpha )}$
. By Lemma 3.4,
 $$ \begin{align*} II_3 &\le\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\\&\quad \times \vert{\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))- \partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) }\vert\,ds \,dz\\&\lesssim\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)}\bigg\{\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\\&\quad +\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(y)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|y-z|)^{n+2\alpha}}\bigg\}\,ds \,dz\\&\lesssim\bigg\{\!\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\,ds\,dz\\&\quad +\int_{\vert y-z\vert\le 5|x-y|}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(y)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|y-z|)^{n+2\alpha}}\,ds \,dz\bigg\}\\&\lesssim \int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)} \int_{\vert\xi\vert\le 5{|x-y|/ c}}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|\xi|)^{n+2\alpha}}\, d\xi \,ds\\&\lesssim \int_{(2t)^{2\alpha}}^{+\infty} \bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x_0)}\bigg)^\delta {1\over s^{n/(2\alpha)+1} } |x-y|^n \,ds \\&\lesssim\bigg({t\over \rho(x_0)}\bigg)^{\delta}, \end{align*} $$
$$ \begin{align*} II_3 &\le\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\\&\quad \times \vert{\partial_s(K^{L}_{\alpha, s}(x,z)-K^{-\Delta}_{\alpha, s}(x-z))- \partial_s(K^{L}_{\alpha, s}(y,z)-K^{-\Delta}_{\alpha, s}(y-z)) }\vert\,ds \,dz\\&\lesssim\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)}\bigg\{\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\\&\quad +\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(y)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|y-z|)^{n+2\alpha}}\bigg\}\,ds \,dz\\&\lesssim\bigg\{\!\int_{\vert x-z\vert\le 4|x-y|}\int_{(2t)^{2\alpha}}^{ \rho^{2\alpha}(x_0)}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}}\,ds\,dz\\&\quad +\int_{\vert y-z\vert\le 5|x-y|}\int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(y)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|y-z|)^{n+2\alpha}}\,ds \,dz\bigg\}\\&\lesssim \int_{(2t)^{2\alpha}}^{\rho^{2\alpha}(x_0)} \int_{\vert\xi\vert\le 5{|x-y|/ c}}\bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x)}\bigg)^\delta \frac{1}{(s^{1/(2\alpha)}+|\xi|)^{n+2\alpha}}\, d\xi \,ds\\&\lesssim \int_{(2t)^{2\alpha}}^{+\infty} \bigg(\frac{\sqrt{s^{1/\alpha}}}{\rho(x_0)}\bigg)^\delta {1\over s^{n/(2\alpha)+1} } |x-y|^n \,ds \\&\lesssim\bigg({t\over \rho(x_0)}\bigg)^{\delta}, \end{align*} $$
which gives
![]() $II\lesssim ({t/ \rho (x_0)})^{\delta }$
with
$II\lesssim ({t/ \rho (x_0)})^{\delta }$
with
![]() $0<\delta <2-n/q.$
$0<\delta <2-n/q.$
We next consider the last term
![]() $III$
. Now
$III$
. Now
 $$ \begin{align*} III&\lesssim \int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty}\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z))\vert\,ds \,dz\\ &\quad +\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \vert\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z)) \vert \,ds \,dz. \end{align*} $$
$$ \begin{align*} III&\lesssim \int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty}\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z))\vert\,ds \,dz\\ &\quad +\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \vert\partial_s(K^{-\Delta}_{\alpha, s}(x-z)-K^{-\Delta}_{\alpha, s}(y-z)) \vert \,ds \,dz. \end{align*} $$
In this case, since
![]() $s\ge \rho ^{2\alpha }(x_0)>(2t)^{2\alpha }$
, we have
$s\ge \rho ^{2\alpha }(x_0)>(2t)^{2\alpha }$
, we have
![]() $s^{1/(2\alpha )}>2t>|x-y|$
. Regarding the first term in the summand above, we can apply Lemma 3.3 to deduce that
$s^{1/(2\alpha )}>2t>|x-y|$
. Regarding the first term in the summand above, we can apply Lemma 3.3 to deduce that
 $$ \begin{align*} &{ \int_{{\mathbb R}^{n}}\int_{ \rho^{2\alpha}(x_0)}^{+\infty}{\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z))\vert}\,ds \,dz}\\& \quad \lesssim \int_{\rho^{2\alpha}(x_0)}^{+\infty}{1\over s} \bigg({|x-y|\over s^{1/(2\alpha)}}\bigg)^\delta\bigg(\int_{{\mathbb R}^{n}}\frac{s}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}} \,dz\bigg)\,ds \\& \quad \lesssim \int_{\rho^{2\alpha}(x_0)}^{+\infty}{1\over s} \bigg({|x-y|\over s^{1/(2\alpha)}}\bigg)^\delta\,ds \\& \quad \lesssim\bigg({|x-y|\over \rho(x_0)}\bigg)^\delta \le C\bigg({t\over \rho(x_0)}\bigg)^\delta, \quad 0<\delta<2-n/q. \end{align*} $$
$$ \begin{align*} &{ \int_{{\mathbb R}^{n}}\int_{ \rho^{2\alpha}(x_0)}^{+\infty}{\vert\partial_s(K^{L}_{\alpha, s}(x,z)-K^{L}_{\alpha, s}(y,z))\vert}\,ds \,dz}\\& \quad \lesssim \int_{\rho^{2\alpha}(x_0)}^{+\infty}{1\over s} \bigg({|x-y|\over s^{1/(2\alpha)}}\bigg)^\delta\bigg(\int_{{\mathbb R}^{n}}\frac{s}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}} \,dz\bigg)\,ds \\& \quad \lesssim \int_{\rho^{2\alpha}(x_0)}^{+\infty}{1\over s} \bigg({|x-y|\over s^{1/(2\alpha)}}\bigg)^\delta\,ds \\& \quad \lesssim\bigg({|x-y|\over \rho(x_0)}\bigg)^\delta \le C\bigg({t\over \rho(x_0)}\bigg)^\delta, \quad 0<\delta<2-n/q. \end{align*} $$
For the second part of the summand, by Lemma 3.3, which is also valid for the Laplacian, when
![]() $4|x-y| \le |x-z|$
, we obtain the same estimate as before but with
$4|x-y| \le |x-z|$
, we obtain the same estimate as before but with
![]() $0<\delta <\min \{1, 2-n/q\}$
. If
$0<\delta <\min \{1, 2-n/q\}$
. If
![]() $|x-z| \le 4|x-y|$
, then
$|x-z| \le 4|x-y|$
, then
![]() $|y-z|\le |x-y|+|x-z|\le 5|x-y|$
. Hence,
$|y-z|\le |x-y|+|x-z|\le 5|x-y|$
. Hence,
 $$ \begin{align*} &\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} |\partial_s K^{-\Delta}_{\alpha, s}(x-z)-\partial_s K^{-\Delta}_{\alpha, s}(y-z)| \,ds \,dz\\ &\quad\lesssim\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}} \,ds \,dz\\ &\quad\lesssim \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \frac{|x-y|^n}{s^{n/(2\alpha)+1}} \,ds \le C \frac{|x-y|^n}{\rho^n(x_0)}\\ &\quad\lesssim \bigg({t\over \rho(x_0)}\bigg)^\delta. \end{align*} $$
$$ \begin{align*} &\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} |\partial_s K^{-\Delta}_{\alpha, s}(x-z)-\partial_s K^{-\Delta}_{\alpha, s}(y-z)| \,ds \,dz\\ &\quad\lesssim\int_{{\mathbb R}^{n}} \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \frac{1}{(s^{1/(2\alpha)}+|x-z|)^{n+2\alpha}} \,ds \,dz\\ &\quad\lesssim \int_{ \rho^{2\alpha}(x_0)}^{+\infty} \frac{|x-y|^n}{s^{n/(2\alpha)+1}} \,ds \le C \frac{|x-y|^n}{\rho^n(x_0)}\\ &\quad\lesssim \bigg({t\over \rho(x_0)}\bigg)^\delta. \end{align*} $$
Combining the above estimates for
![]() $I, II$
and
$I, II$
and
![]() $III,$
we have proved (4-5). Hence, we get the estimation (4-4) and the
$III,$
we have proved (4-5). Hence, we get the estimation (4-4) and the
![]() $BMO$
-boundedness of
$BMO$
-boundedness of
![]() $T^{L^{\alpha }}_N$
and
$T^{L^{\alpha }}_N$
and
![]() $T^{*}_{L^{\alpha }}.$
$T^{*}_{L^{\alpha }}.$
For the case
![]() $f\in BMO_L({\mathbb R}^n),$
by (4-5),
$f\in BMO_L({\mathbb R}^n),$
by (4-5),
 $$ \begin{align*} \bigg(\frac{\rho(x_0)}{t}\bigg)^{\gamma}\frac{1}{|B|}\int_B| T_N^{L^{\alpha}} 1(x)-( T_N^{L^{\alpha}} 1)_B|\,dx\lesssim \bigg(\frac{\rho(x_0)}{t}\bigg)^{\delta-\gamma}\le C \end{align*} $$
$$ \begin{align*} \bigg(\frac{\rho(x_0)}{t}\bigg)^{\gamma}\frac{1}{|B|}\int_B| T_N^{L^{\alpha}} 1(x)-( T_N^{L^{\alpha}} 1)_B|\,dx\lesssim \bigg(\frac{\rho(x_0)}{t}\bigg)^{\delta-\gamma}\le C \end{align*} $$
when
![]() $\delta -\gamma \ge 0,$
which can be guaranteed by
$\delta -\gamma \ge 0,$
which can be guaranteed by
![]() $\gamma <\min \{1, 2\alpha , 2-n/q\}$
and choosing
$\gamma <\min \{1, 2\alpha , 2-n/q\}$
and choosing
![]() $\delta \ge \gamma .$
This completes the proof of Theorem 4.6.
$\delta \ge \gamma .$
This completes the proof of Theorem 4.6.
Theorem 4.7. Let
![]() $\{a_j\}_{j\in \mathbb Z}$
a
$\{a_j\}_{j\in \mathbb Z}$
a
![]() $\lambda $
-lacunary sequence, let
$\lambda $
-lacunary sequence, let
![]() $0<\kappa <1$
and let
$0<\kappa <1$
and let
![]() $T^*_{L^{\alpha }}$
be the operator defined in (1-5). We have the following statements.
$T^*_{L^{\alpha }}$
be the operator defined in (1-5). We have the following statements.
-
(i) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
 $\theta $
and
$\theta $
and
 $\alpha $
, such that for all functions
$\alpha $
, such that for all functions
 $f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
,
$f\in L^{\rho ,\infty }_{p,\kappa }(\mathbb {R}^{n})$
,  $$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\leq C\Vert f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}\leq C\Vert f\Vert_{L^{\rho,\infty}_{p,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
-
(ii) There exists a positive constant C, depending on n,
 $\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
$\Vert v\Vert _{\ell ^\infty (\mathbb Z)}$
,
 $\theta $
and
$\theta $
and
 $\alpha $
, such that, for all functions
$\alpha $
, such that, for all functions
 $f\in L^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
,
$f\in L^{\rho ,\infty }_{1,\kappa }(\mathbb {R}^{n})$
,  $$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\le C\Vert f\Vert_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\Vert T^*_{L^{\alpha}} f\Vert_{WL^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}\le C\Vert f\Vert_{L^{\rho,\infty}_{1,\kappa}(\mathbb{R}^{n})}.\end{align*} $$
The constants C appearing in (i) and (ii) are independent of
 $N.$
$N.$
Proof. Using Theorem 4.4 and Proposition 3.5, we deduce the desired results. Since the proofs are similar to those of Theorem 3.6, we omit the details.
The following theorem analyzes the behavior of the functions in
![]() $L^{\infty }$
more deeply.
$L^{\infty }$
more deeply.
Lemma 4.8. Let
![]() $0<\gamma <1/2$
.
$0<\gamma <1/2$
.
-
(i) There exists
 $t_{0}>0$
such that
$t_{0}>0$
such that  $$ \begin{align*}\int^{1}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
$$ \begin{align*}\int^{1}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
-
(ii) Given
 $t_{0}>0$
as before, there exists
$t_{0}>0$
as before, there exists
 $a>1$
large enough such that
$a>1$
large enough such that  $$ \begin{align*}\left\{\begin{aligned} &\frac{1+\gamma}{4}<\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<\int^{1}_{0} K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2;\\[4pt]&\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=\bigg(\int^{1}_{0}-\int^{1}_{1/a}\bigg) K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<\gamma/4;\\[4pt]&\int^{\infty}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz>1/2-\gamma/4. \end{aligned}\right.\end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} &\frac{1+\gamma}{4}<\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<\int^{1}_{0} K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2;\\[4pt]&\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=\bigg(\int^{1}_{0}-\int^{1}_{1/a}\bigg) K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<\gamma/4;\\[4pt]&\int^{\infty}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz>1/2-\gamma/4. \end{aligned}\right.\end{align*} $$
-
(iii) There exists
 $\eta _{0}>0$
such that
$\eta _{0}>0$
such that  $$ \begin{align*}\int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<1/4-\gamma/4.\end{align*} $$
$$ \begin{align*}\int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<1/4-\gamma/4.\end{align*} $$
Proof. By (4-6), we know that
 $$ \begin{align*}K_{\alpha,t^{2\alpha}}^{-\Delta}=\frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-t^{2\alpha}|\xi|^{2\alpha}}e^{ix\xi}d\xi =\frac{1}{t}K_{\alpha,1}^{-\Delta}(x/t)\end{align*} $$
$$ \begin{align*}K_{\alpha,t^{2\alpha}}^{-\Delta}=\frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-t^{2\alpha}|\xi|^{2\alpha}}e^{ix\xi}d\xi =\frac{1}{t}K_{\alpha,1}^{-\Delta}(x/t)\end{align*} $$
and
Moreover,
 $$ \begin{align*} K_{\alpha,1}^{-\Delta}(x) &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-|\xi|^{2\alpha}}e^{ix\xi}d\xi \\ &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-|\eta|^{2\alpha}}e^{i(-x)\eta}d\eta= K_{\alpha,1}^{-\Delta}(-x), \end{align*} $$
$$ \begin{align*} K_{\alpha,1}^{-\Delta}(x) &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-|\xi|^{2\alpha}}e^{ix\xi}d\xi \\ &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{-|\eta|^{2\alpha}}e^{i(-x)\eta}d\eta= K_{\alpha,1}^{-\Delta}(-x), \end{align*} $$
where
![]() $\eta =-\xi $
. Therefore,
$\eta =-\xi $
. Therefore,
 $$ \begin{align*}\int^{\infty}_{0}K_{\alpha,1}^{-\Delta}(x)\,dx=\frac{1}{2}\int_{\mathbb{R}}K_{\alpha,1}^{-\Delta}(x)\,dx=\frac{1}{2}.\end{align*} $$
$$ \begin{align*}\int^{\infty}_{0}K_{\alpha,1}^{-\Delta}(x)\,dx=\frac{1}{2}\int_{\mathbb{R}}K_{\alpha,1}^{-\Delta}(x)\,dx=\frac{1}{2}.\end{align*} $$
Then, there exists
![]() $A>0$
such that
$A>0$
such that
![]() $\int ^{A}_{0}K_{\alpha ,1}^{-\Delta }(w)dw=1/4+\gamma /2.$
Let
$\int ^{A}_{0}K_{\alpha ,1}^{-\Delta }(w)dw=1/4+\gamma /2.$
Let
![]() $w=Az$
. Then,
$w=Az$
. Then,
 $$ \begin{align*} K_{\alpha,1}^{-\Delta}(Az) &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{iAz\xi}e^{-|\xi|^{2\alpha}}d\xi \\ &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{iz\eta}e^{-A^{-2\alpha}|\eta|^{2\alpha}}A^{-1}d\eta=A^{-1}K_{\alpha,A^{-2\alpha}}^{-\Delta}(z), \end{align*} $$
$$ \begin{align*} K_{\alpha,1}^{-\Delta}(Az) &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{iAz\xi}e^{-|\xi|^{2\alpha}}d\xi \\ &= \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}e^{iz\eta}e^{-A^{-2\alpha}|\eta|^{2\alpha}}A^{-1}d\eta=A^{-1}K_{\alpha,A^{-2\alpha}}^{-\Delta}(z), \end{align*} $$
where
![]() $\eta =A\xi $
. So,
$\eta =A\xi $
. So,
 $$ \begin{align*}\int^{1}_{0}K_{\alpha,A^{-2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
$$ \begin{align*}\int^{1}_{0}K_{\alpha,A^{-2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
Assuming that
![]() $A=t_{0}^{-1}$
,
$A=t_{0}^{-1}$
,
 $$ \begin{align*}\int^{1}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
$$ \begin{align*}\int^{1}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz=1/4+\gamma/2.\end{align*} $$
This completes the proof of (i). The proofs of (ii) and (iii) follow easily.
Proposition 4.9. There exist a bounded sequence
![]() $\{v_{j}\}_{j\in \mathbb {Z}}$
, a
$\{v_{j}\}_{j\in \mathbb {Z}}$
, a
![]() $\lambda $
-lacunary sequence
$\lambda $
-lacunary sequence
![]() $\{a_{j}\}_{j\in \mathbb {Z}}$
and
$\{a_{j}\}_{j\in \mathbb {Z}}$
and
![]() $f\in L^{\infty }(\mathbb {R})$
such that
$f\in L^{\infty }(\mathbb {R})$
such that
![]() $T^*_{(-\Delta )^{\alpha }}f(x)=\infty $
for all
$T^*_{(-\Delta )^{\alpha }}f(x)=\infty $
for all
![]() $x\in \mathbb {R}$
.
$x\in \mathbb {R}$
.
Proof. Let
![]() $t_{0}$
and a be as in Lemma 4.8 and let f be the function defined as
$t_{0}$
and a be as in Lemma 4.8 and let f be the function defined as
It is easy to see that
Considering the sequence
![]() $\{a_{j}\}$
with
$\{a_{j}\}$
with
![]() $a_{j}=(t_{0}a^{j})^{2\alpha }$
, we have
$a_{j}=(t_{0}a^{j})^{2\alpha }$
, we have
By (4-7),
 $$ \begin{align*} e^{-a_{j}(-\Delta)^{\alpha}}f(0) =\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-a^{j}z)\,dz =(-1)^{\hspace{1.2pt}j}\int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz. \end{align*} $$
$$ \begin{align*} e^{-a_{j}(-\Delta)^{\alpha}}f(0) =\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-a^{j}z)\,dz =(-1)^{\hspace{1.2pt}j}\int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz. \end{align*} $$
On the other hand, using Lemma 4.8, we get
 $$ \begin{align*} & \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz \\ &\quad= \int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz+\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz + \int^{\infty}_{1}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz \\ &\quad\geq \int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz-\bigg(\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz+ \int^{\infty}_{1}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\bigg) \\ &\quad> \frac{1+\gamma}{4}-\bigg(\frac{\gamma}{4}+\frac{1}{4}-\frac{\gamma}{2}\bigg)=\frac{\gamma}{2}. \end{align*} $$
$$ \begin{align*} & \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz \\ &\quad= \int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz+\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz + \int^{\infty}_{1}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz \\ &\quad\geq \int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz-\bigg(\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz+ \int^{\infty}_{1}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\bigg) \\ &\quad> \frac{1+\gamma}{4}-\bigg(\frac{\gamma}{4}+\frac{1}{4}-\frac{\gamma}{2}\bigg)=\frac{\gamma}{2}. \end{align*} $$
By (4-7), we get
 $$ \begin{align*} &e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x) \\ &\quad= (-1)^{j+1}\bigg\{\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz\bigg\}. \end{align*} $$
$$ \begin{align*} &e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x) \\ &\quad= (-1)^{j+1}\bigg\{\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz\bigg\}. \end{align*} $$
By the dominated convergence theorem, we obtain
 $$ \begin{align*} \lim_{h\rightarrow 0}\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(h-z)\,dz &=\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz \\ &= \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz>\frac{\gamma}{2}. \end{align*} $$
$$ \begin{align*} \lim_{h\rightarrow 0}\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(h-z)\,dz &=\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz \\ &= \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(z)\,dz>\frac{\gamma}{2}. \end{align*} $$
So, there exists
![]() $0<\eta _{0}<1$
such that, for
$0<\eta _{0}<1$
such that, for
![]() $|h|<\eta _{0}$
,
$|h|<\eta _{0}$
,
Then, for each
![]() $x\neq 0$
, we can choose
$x\neq 0$
, we can choose
![]() $j\in \mathbb {Z}$
such that
$j\in \mathbb {Z}$
such that
![]() $|x/a^{j}|<\eta _{0}$
; at this time, there are infinitely many j satisfying this condition, and we get
$|x/a^{j}|<\eta _{0}$
; at this time, there are infinitely many j satisfying this condition, and we get
Choosing
![]() $v_{j}=(-1)^{j+1}$
with
$v_{j}=(-1)^{j+1}$
with
![]() $j\in \mathbb {Z}$
, we have, for any
$j\in \mathbb {Z}$
, we have, for any
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $$ \begin{align*} T^{\ast}_{L^{\alpha},N}f(x) &\geq \sum_{|t/a^{j}|<\eta_{0}}(-1)^{j+1}(e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x)) \\ &\geq \sum_{|t/a^{j}|<\eta_{0}}(-1)^{j+1}\bigg(\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz \\ &\quad+\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz\bigg)=\infty.\\[-42pt] \end{align*} $$
$$ \begin{align*} T^{\ast}_{L^{\alpha},N}f(x) &\geq \sum_{|t/a^{j}|<\eta_{0}}(-1)^{j+1}(e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x)) \\ &\geq \sum_{|t/a^{j}|<\eta_{0}}(-1)^{j+1}\bigg(\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz \\ &\quad+\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz\bigg)=\infty.\\[-42pt] \end{align*} $$
Theorem 4.10. Let
![]() $\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
for some
$\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
for some
![]() $1\leq p\leq \infty $
. We have the following statements.
$1\leq p\leq \infty $
. We have the following statements.
-
(i) Let
 $\{a_{j}\}_{j\in \mathbb {Z}}$
be any increasing sequence and let
$\{a_{j}\}_{j\in \mathbb {Z}}$
be any increasing sequence and let
 $S^{\ast }$
be either
$S^{\ast }$
be either
 $T^{\ast }_{(-\Delta )^{\alpha }}$
or
$T^{\ast }_{(-\Delta )^{\alpha }}$
or
 $T^*_{L^{\alpha }}$
, which is defined in (2-3) or (1-5). Then, for every
$T^*_{L^{\alpha }}$
, which is defined in (2-3) or (1-5). Then, for every
 $f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
$f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
 $B=B(0,1)$
, for any ball
$B=B(0,1)$
, for any ball
 $B_{r}\subset B$
with
$B_{r}\subset B$
with
 $2r<1$
,
$2r<1$
,  $$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|S^{\ast}f(x)|\,dx\lesssim\bigg(\log\frac{2}{r}\bigg)^{1/p'}\|v\|_{l^{p}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|S^{\ast}f(x)|\,dx\lesssim\bigg(\log\frac{2}{r}\bigg)^{1/p'}\|v\|_{l^{p}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
-
(ii) When
 $1< p <\infty $
, for any
$1< p <\infty $
, for any
 $\epsilon>0$
, there exist a
$\epsilon>0$
, there exist a
 $\lambda $
-lacunary sequence
$\lambda $
-lacunary sequence
 $\{a_{j}\}_{j\in \mathbb {Z}}$
, a sequence
$\{a_{j}\}_{j\in \mathbb {Z}}$
, a sequence
 $\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
and a function
$\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
and a function
 $f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
$f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
 $B=B(0,1)$
such that the following statement holds: for any ball
$B=B(0,1)$
such that the following statement holds: for any ball
 $B_{r}\subset B$
with
$B_{r}\subset B$
with
 $2r<1$
,
$2r<1$
,  $$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx\gtrsim\bigg(\log \frac{2}{r}\bigg)^{1/(p-\epsilon)'}\|v\|_{l^{p}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx\gtrsim\bigg(\log \frac{2}{r}\bigg)^{1/(p-\epsilon)'}\|v\|_{l^{p}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
-
(iii) When
 $p=\infty $
, there exist a
$p=\infty $
, there exist a
 $\lambda $
-lacunary sequence
$\lambda $
-lacunary sequence
 $\{a_{j}\}_{j\in \mathbb {Z}}$
, a sequence
$\{a_{j}\}_{j\in \mathbb {Z}}$
, a sequence
 $\{v_{j}\}_{j\in \mathbb {Z}}\in l^{\infty }(\mathbb {Z})$
and
$\{v_{j}\}_{j\in \mathbb {Z}}\in l^{\infty }(\mathbb {Z})$
and
 $f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
$f\in L^{\infty }(\mathbb {R}^{n})$
with support in the unit ball
 $B=B(0,1)$
such that the following statement holds: for any ball
$B=B(0,1)$
such that the following statement holds: for any ball
 $B_{r}\subset B$
with
$B_{r}\subset B$
with
 $2r<1$
,
$2r<1$
,  $$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx\gtrsim\bigg(\log\frac{2}{r}\bigg)\|v\|_{l^{\infty}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
$$ \begin{align*}\frac{1}{|B_{r}|}\int_{B_{r}}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx\gtrsim\bigg(\log\frac{2}{r}\bigg)\|v\|_{l^{\infty}(\mathbb{Z})}\|f\|_{L^{\infty}(\mathbb{R}^{n})}.\end{align*} $$
In the statements above,
![]() $p'={p}/{(p-1)}$
, and if
$p'={p}/{(p-1)}$
, and if
![]() $p=1$
, then
$p=1$
, then
![]() $p'=\infty $
.
$p'=\infty $
.
Proof. For (i), we prove this theorem only for the case
![]() $1<p<\infty $
and in the Schrödinger setting. For the cases
$1<p<\infty $
and in the Schrödinger setting. For the cases
![]() $p=1$
and
$p=1$
and
![]() $p=\infty $
, the proof follows by introducing the obvious changes. Since
$p=\infty $
, the proof follows by introducing the obvious changes. Since
![]() $2r<1$
, we know that
$2r<1$
, we know that
![]() $B\setminus B_{2r}\neq \varnothing $
. Let
$B\setminus B_{2r}\neq \varnothing $
. Let
![]() $f=f_{1}+f_{2}$
, where
$f=f_{1}+f_{2}$
, where
![]() $f_{1}=f\chi _{B_{2r}}$
and
$f_{1}=f\chi _{B_{2r}}$
and
![]() $f_{2}=f\chi _{B\setminus B_{2r}}$
. Then,
$f_{2}=f\chi _{B\setminus B_{2r}}$
. Then,
By Theorem 4.4,
 $$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f_{1}(x)|\,dx &\leq\bigg(\frac{1}{|B_{r}|}\int_{B_{r}} | T^*_{L^{\alpha}} f_{1}(x)|^{2}\,dx\bigg)^{1/2} \\ &\lesssim \bigg(\frac{1}{|B_{r}|}\int_{\mathbb{R}^{n}}|f_{1}(x)|^{2}\,dx\bigg)^{1/2}\lesssim\|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
$$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f_{1}(x)|\,dx &\leq\bigg(\frac{1}{|B_{r}|}\int_{B_{r}} | T^*_{L^{\alpha}} f_{1}(x)|^{2}\,dx\bigg)^{1/2} \\ &\lesssim \bigg(\frac{1}{|B_{r}|}\int_{\mathbb{R}^{n}}|f_{1}(x)|^{2}\,dx\bigg)^{1/2}\lesssim\|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
We should note that, for any
![]() $j\in \mathbb {Z}$
, by (1-2),
$j\in \mathbb {Z}$
, by (1-2),
 $$ \begin{align} &\int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)|\,dy \notag \\\notag &\quad\leq \int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j+1}}(x,y)|\,dy+\int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j}}(x,y)|\,dy \\\notag &\quad\lesssim\int_{\mathbb{R}^{n}}\frac{a_{j+1}}{(a_{j+1}^{1/(2\alpha)}+|x-y|)^{n+2\alpha}}\,dy+ \int_{\mathbb{R}^{n}}\frac{a_{j}}{(a_{j}^{1/(2\alpha)}+|x-y|)^{n+2\alpha}}\,dy \\&\quad= C. \end{align} $$
$$ \begin{align} &\int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)|\,dy \notag \\\notag &\quad\leq \int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j+1}}(x,y)|\,dy+\int_{\mathbb{R}^{n}}|K^{L}_{\alpha, a_{j}}(x,y)|\,dy \\\notag &\quad\lesssim\int_{\mathbb{R}^{n}}\frac{a_{j+1}}{(a_{j+1}^{1/(2\alpha)}+|x-y|)^{n+2\alpha}}\,dy+ \int_{\mathbb{R}^{n}}\frac{a_{j}}{(a_{j}^{1/(2\alpha)}+|x-y|)^{n+2\alpha}}\,dy \\&\quad= C. \end{align} $$
For
![]() $1<p<\infty $
and any
$1<p<\infty $
and any
![]() $N=(N_{1},N_{2})$
, by Hölder’s inequality, (4-8) and Fubini’s theorem, we can use Proposition 3.5 to obtain
$N=(N_{1},N_{2})$
, by Hölder’s inequality, (4-8) and Fubini’s theorem, we can use Proposition 3.5 to obtain
 $$ \begin{align*} &\bigg|\hspace{-1.4pt}\sum^{N_{2}}_{j=N_{1}}v_{j}(e^{-a_{j+1}L^{\alpha}}f_{2}(x)-e^{-a_{j}L^{\alpha}}f_{2}(x))\bigg| \\&\quad\lesssim \sum^{N_{2}}_{j=N_{1}}\bigg|v_{j}\int_{\mathbb{R}^{n}}(K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y))f_{2}(y)\,dy\bigg| \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\,dy\bigg)^{p'}\bigg)^{1/p'} \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|^{p'}\,dy\bigg) \\&\qquad\times \bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)|\,dy\bigg)^{p'/p}\bigg)^{1/p'} \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\bigg)\,dy^{1/p'}\\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\int_{\mathbb{R}^{n}}\sum^{+\infty}_{j=-\infty}|K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\,dy\bigg)^{1/p'} \\&\quad\lesssim\|v\|_{l^{p}(\mathbb{Z})}\bigg(\int_{\mathbb{R}^{n}}\frac{1}{|x-y|^{n}}|f_{2}(y)|^{p'}\,dy\bigg)^{1/p'}. \end{align*} $$
$$ \begin{align*} &\bigg|\hspace{-1.4pt}\sum^{N_{2}}_{j=N_{1}}v_{j}(e^{-a_{j+1}L^{\alpha}}f_{2}(x)-e^{-a_{j}L^{\alpha}}f_{2}(x))\bigg| \\&\quad\lesssim \sum^{N_{2}}_{j=N_{1}}\bigg|v_{j}\int_{\mathbb{R}^{n}}(K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y))f_{2}(y)\,dy\bigg| \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\,dy\bigg)^{p'}\bigg)^{1/p'} \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|^{p'}\,dy\bigg) \\&\qquad\times \bigg(\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)|\,dy\bigg)^{p'/p}\bigg)^{1/p'} \\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\sum^{N_{2}}_{j=N_{1}}\int_{\mathbb{R}^{n}} |K^{L}_{\alpha, a_{j+1}}(x,y)-K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\bigg)\,dy^{1/p'}\\&\quad\lesssim \|v\|_{l^{p}(\mathbb{Z})}\bigg(\int_{\mathbb{R}^{n}}\sum^{+\infty}_{j=-\infty}|K^{L}_{\alpha, a_{j+1}}(x,y)- K^{L}_{\alpha, a_{j}}(x,y)||f_{2}(y)|\,dy\bigg)^{1/p'} \\&\quad\lesssim\|v\|_{l^{p}(\mathbb{Z})}\bigg(\int_{\mathbb{R}^{n}}\frac{1}{|x-y|^{n}}|f_{2}(y)|^{p'}\,dy\bigg)^{1/p'}. \end{align*} $$
For
![]() $y\in B\setminus B_{2r}$
and
$y\in B\setminus B_{2r}$
and
![]() $x\in B_{r}$
, we have
$x\in B_{r}$
, we have
![]() $r\leq |x-y|\leq 2$
. Then,
$r\leq |x-y|\leq 2$
. Then,
 $$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f_{2}(x)|\,dx &\lesssim\frac{1}{|B_{r}|}\int_{B_{r}}\bigg(\int_{\mathbb{R}^{n}}\frac{1}{|x-y|^{n}}|f_{2}(y)|^{p'}\,dy\bigg)^{1/p'}\,dx \\ &\lesssim \frac{\|f\|_{L^{\infty}(\mathbb{R}^{n})}}{|B_{r}|}\int_{B_{r}}\bigg(\int_{r\leq |x-y|\leq 2}\frac{1}{|x-y|^{n}}\,dy\bigg)^{1/p'}\,dx \\ &\sim \bigg(\log\frac{2}{r}\bigg)^{1/p'} \|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
$$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f_{2}(x)|\,dx &\lesssim\frac{1}{|B_{r}|}\int_{B_{r}}\bigg(\int_{\mathbb{R}^{n}}\frac{1}{|x-y|^{n}}|f_{2}(y)|^{p'}\,dy\bigg)^{1/p'}\,dx \\ &\lesssim \frac{\|f\|_{L^{\infty}(\mathbb{R}^{n})}}{|B_{r}|}\int_{B_{r}}\bigg(\int_{r\leq |x-y|\leq 2}\frac{1}{|x-y|^{n}}\,dy\bigg)^{1/p'}\,dx \\ &\sim \bigg(\log\frac{2}{r}\bigg)^{1/p'} \|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
Hence,
 $$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f(x)|\,dx\ {\lesssim}\ \, \bigg(1+\bigg(\log\frac{2}{r}\bigg)^{1/p'}\bigg)\|f\|_{L^{\infty}(\mathbb{R}^{n})} \lesssim\bigg(\log\frac{2}{r}\bigg)^{1/p'}\|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
$$ \begin{align*} \frac{1}{|B_{r}|}\int_{B_{r}}| T^*_{L^{\alpha}} f(x)|\,dx\ {\lesssim}\ \, \bigg(1+\bigg(\log\frac{2}{r}\bigg)^{1/p'}\bigg)\|f\|_{L^{\infty}(\mathbb{R}^{n})} \lesssim\bigg(\log\frac{2}{r}\bigg)^{1/p'}\|f\|_{L^{\infty}(\mathbb{R}^{n})}. \end{align*} $$
For (ii), we only need to consider the case
![]() $n=1$
as the multidimensional cases are similar. In what follows, we assume that
$n=1$
as the multidimensional cases are similar. In what follows, we assume that
![]() $1<p<\infty $
and we choose
$1<p<\infty $
and we choose
![]() $\epsilon $
such that
$\epsilon $
such that
![]() $0<\epsilon <p-1$
. Let
$0<\epsilon <p-1$
. Let
 $$ \begin{align*}f(x)=\sum^{0}_{k=-\infty}(-1)^{k}\chi_{(-a^{k},-a^{k-1}]}(x),\end{align*} $$
$$ \begin{align*}f(x)=\sum^{0}_{k=-\infty}(-1)^{k}\chi_{(-a^{k},-a^{k-1}]}(x),\end{align*} $$
where
![]() $a>1$
is the constant defined in Lemma 4.8. We check that
$a>1$
is the constant defined in Lemma 4.8. We check that
 $$ \begin{align*}f(a^{j}x)=(-1)^{j}f(x)+(-1)^{j}\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}(x)\end{align*} $$
$$ \begin{align*}f(a^{j}x)=(-1)^{j}f(x)+(-1)^{j}\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}(x)\end{align*} $$
when
![]() $j\leq 0$
. We always assume that
$j\leq 0$
. We always assume that
![]() $j\leq 0$
in what follows.
$j\leq 0$
in what follows.
Choose a lacunary sequence
![]() $\{a_{j}\}_{j\in \mathbb {Z}}$
with
$\{a_{j}\}_{j\in \mathbb {Z}}$
with
![]() $a_{j}=(t_{0}a^{\,j})^{2\alpha }$
,
$a_{j}=(t_{0}a^{\,j})^{2\alpha }$
,
![]() $j\in \mathbb {Z}$
. Then, similarly to the proof of Proposition 4.9, we have
$j\in \mathbb {Z}$
. Then, similarly to the proof of Proposition 4.9, we have
 $$ \begin{align*} &e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x) \\&\quad= C(-1)^{j+1}\bigg(\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz \\&\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}\bigg(\frac{x}{a^{j+1}}-z\bigg)\,dz \\&\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}\bigg(\frac{x}{a^{j}}-z\bigg)\,dz\bigg). \end{align*} $$
$$ \begin{align*} &e^{-a_{j+1}(-\Delta)^{\alpha}}f(x)-e^{-a_{j}(-\Delta)^{\alpha}}f(x) \\&\quad= C(-1)^{j+1}\bigg(\int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j+1}-z)\,dz+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(x/a^{j}-z)\,dz \\&\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}\bigg(\frac{x}{a^{j+1}}-z\bigg)\,dz \\&\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]}\bigg(\frac{x}{a^{j}}-z\bigg)\,dz\bigg). \end{align*} $$
Using Lemma 4.8, we obtain
 $$ \begin{align*} & \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz \\ &\quad= \bigg\{\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz+\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz\bigg\}\\ &\quad\geq \int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz-\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\\ & \quad>{(1+\gamma)}/{4}-{\gamma}/{4}={1}/{4}. \end{align*} $$
$$ \begin{align*} & \int^{\infty}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz \\ &\quad= \bigg\{\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz+\int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)f(-z)\,dz\bigg\}\\ &\quad\geq \int^{1}_{1/a}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz-\int^{1/a}_{0}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\\ & \quad>{(1+\gamma)}/{4}-{\gamma}/{4}={1}/{4}. \end{align*} $$
Therefore, there exists
![]() $0<\eta _{0}<1$
small enough such that, for
$0<\eta _{0}<1$
small enough such that, for
![]() $|h|<\eta _{0}$
,
$|h|<\eta _{0}$
,
Moreover, using Lemma 4.8 again, we can choose the last
![]() $\eta _{0}$
small enough such that
$\eta _{0}$
small enough such that
 $$ \begin{align} \int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<{(1-\gamma)}/{4}. \end{align} $$
$$ \begin{align} \int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz<{(1-\gamma)}/{4}. \end{align} $$
For the given
![]() $\eta _{0}$
in (4-10), let
$\eta _{0}$
in (4-10), let
![]() $2r<1$
be such that
$2r<1$
be such that
![]() $r<\eta _{0}^{2}$
and
$r<\eta _{0}^{2}$
and
![]() $r\sim a^{\mathrm {J}_{0}}\eta _{0}$
for a certain negative integer
$r\sim a^{\mathrm {J}_{0}}\eta _{0}$
for a certain negative integer
![]() $\mathrm {J}_{0}$
. If
$\mathrm {J}_{0}$
. If
![]() $\mathrm {J}_{0}\leq j\leq 0$
, we have
$\mathrm {J}_{0}\leq j\leq 0$
, we have
![]() $r/a^{j}<\eta _{0}$
. And, for any
$r/a^{j}<\eta _{0}$
. And, for any
![]() $-r\leq x\leq r$
, we get
$-r\leq x\leq r$
, we get
 $$ \begin{align*}-1\cdot\chi_{[1-\eta_{0},+\infty)}(z)\leq\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j+1}}-z\bigg)\leq \chi_{[a-\eta_{0},+\infty)}(z)\end{align*} $$
$$ \begin{align*}-1\cdot\chi_{[1-\eta_{0},+\infty)}(z)\leq\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j+1}}-z\bigg)\leq \chi_{[a-\eta_{0},+\infty)}(z)\end{align*} $$
and
 $$ \begin{align*}-1\cdot\chi_{[1-\eta_{0},+\infty)}(u)\leq\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j}}-z\bigg)\leq \chi_{[a-\eta_{0},+\infty)}(z).\end{align*} $$
$$ \begin{align*}-1\cdot\chi_{[1-\eta_{0},+\infty)}(u)\leq\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}}\chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j}}-z\bigg)\leq \chi_{[a-\eta_{0},+\infty)}(z).\end{align*} $$
Then, by (4-9),
 $$ \begin{align*} & \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j+1}}-z\bigg)\,dz \\[5pt] &\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j}}-z\bigg)\,dz \\[5pt] &\quad\geq -2\int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\geq \frac{\gamma-1}{2}. \end{align*} $$
$$ \begin{align*} & \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j-1}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j+1}}-z\bigg)\,dz \\[5pt] &\qquad+ \int_{\mathbb{R}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\sum^{-j}_{\mathrm{l}=1}(-1)^{\mathrm{l}} \chi_{(-a^{\mathrm{l}},-a^{\mathrm{l}-1}]} \bigg(\frac{x}{a^{j}}-z\bigg)\,dz \\[5pt] &\quad\geq -2\int^{\infty}_{1-\eta_{0}}K_{\alpha,t_{0}^{2\alpha}}^{-\Delta}(z)\,dz\geq \frac{\gamma-1}{2}. \end{align*} $$
So, for any
![]() $t\in [-r,r]$
and
$t\in [-r,r]$
and
![]() $\mathrm {J}_{0}\leq j\leq 0$
, combining (4-9) with (4-10) yields
$\mathrm {J}_{0}\leq j\leq 0$
, combining (4-9) with (4-10) yields
Choose a sequence
![]() $\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
, where
$\{v_{j}\}_{j\in \mathbb {Z}}\in l^{p}(\mathbb {Z})$
, where
![]() $v_{j}=(-1)^{j+1}(-j)^{-{1}/{(p-\epsilon )}}$
. Then, for
$v_{j}=(-1)^{j+1}(-j)^{-{1}/{(p-\epsilon )}}$
. Then, for
![]() $N=(\mathrm {J}_{0},0)$
,
$N=(\mathrm {J}_{0},0)$
,
 $$ \begin{align*} \frac{1}{2r}\int_{[-r,r]}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx &\geq \frac{1}{2r}\int_{[-r,r]}|T^{(-\Delta)^{\alpha}}_{N}f(x)|\,dx \\[5pt] &\geq\frac{C\gamma}{4r}\int_{[-r,r]}\sum^{-1}_{j=\mathrm{J}_{0}}((-j)^{-{1}{(p-\epsilon)}})\,dx \\[5pt] &\geq C\cdot(-\mathrm{J}_{0})^{{1}/{(p-\epsilon)^{'}}}\sim \bigg(\log\frac{2}{r}\bigg)^{{1}/{(p-\epsilon)^{'}}}. \end{align*} $$
$$ \begin{align*} \frac{1}{2r}\int_{[-r,r]}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx &\geq \frac{1}{2r}\int_{[-r,r]}|T^{(-\Delta)^{\alpha}}_{N}f(x)|\,dx \\[5pt] &\geq\frac{C\gamma}{4r}\int_{[-r,r]}\sum^{-1}_{j=\mathrm{J}_{0}}((-j)^{-{1}{(p-\epsilon)}})\,dx \\[5pt] &\geq C\cdot(-\mathrm{J}_{0})^{{1}/{(p-\epsilon)^{'}}}\sim \bigg(\log\frac{2}{r}\bigg)^{{1}/{(p-\epsilon)^{'}}}. \end{align*} $$
For (iii), let
![]() $v_{j}=(-1)^{j+1}, a_{j}=(t_{0}a^{j})^{2}$
and
$v_{j}=(-1)^{j+1}, a_{j}=(t_{0}a^{j})^{2}$
and
![]() $0<\eta _{0}<1$
as fixed in the proof of (ii). Consider the same function f as in (ii). Then
$0<\eta _{0}<1$
as fixed in the proof of (ii). Consider the same function f as in (ii). Then
![]() $\|v\|_{l^{\infty }(\mathbb {Z})}=1$
and
$\|v\|_{l^{\infty }(\mathbb {Z})}=1$
and
![]() $\|f\|_{L^{\infty }(\mathbb {R})}=1$
. By the same arguments as in (ii), with
$\|f\|_{L^{\infty }(\mathbb {R})}=1$
. By the same arguments as in (ii), with
![]() $N=(\mathrm {J}_{0},0)$
,
$N=(\mathrm {J}_{0},0)$
,
 $$ \begin{align*} \frac{1}{2r}\int_{[-r,r]}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx &\geq \frac{1}{2r}\int_{[-r.r]}|T^{(-\Delta)^{\alpha}}_{N}f(x)|\,dx\\&\geq \frac{C}{2r}\int_{[-r,r]}\sum^{0}_{j=\mathrm{J}_{0}}C_{1}\,dx \\[-2pt]&\geq C\cdot C_{1}\cdot(-\mathrm{J}_{0})\sim \log\frac{2}{r}.\\[-38.5pt] \end{align*} $$
$$ \begin{align*} \frac{1}{2r}\int_{[-r,r]}|T^{\ast}_{(-\Delta)^{\alpha}}f(x)|\,dx &\geq \frac{1}{2r}\int_{[-r.r]}|T^{(-\Delta)^{\alpha}}_{N}f(x)|\,dx\\&\geq \frac{C}{2r}\int_{[-r,r]}\sum^{0}_{j=\mathrm{J}_{0}}C_{1}\,dx \\[-2pt]&\geq C\cdot C_{1}\cdot(-\mathrm{J}_{0})\sim \log\frac{2}{r}.\\[-38.5pt] \end{align*} $$