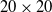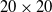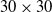1. Introduction
Cable trenches are critical components of the power transmission system [Reference Xie, Sun, Zhang, Ye, Fan and Zhu1]. To ensure the safe operation of the power grid, regular inspection and maintenance of cable trenches are essential. Currently, these inspections are primarily performed manually, which is labor-intensive and challenging due to the potential presence of toxic and hazardous gases within the trenches [Reference Khan, Malik, Al-Arainy and Alghuwainem2]. This not only complicates manual inspection but also poses significant safety risks.
Replacing manual inspection with robots can significantly improve the quality and efficiency of inspections [Reference Dong, Chen, Liang, Li, Yan and Zhang3, Reference Jia, Tian, Liu and Fan4], aligning with future development trends. Given the complex environment of cable trenches, robots must be equipped with mechanical arms capable of interacting with cables or equipment within the trenches and must possess strong obstacle-crossing capabilities. In our previous work, we designed a tracked inspection robot for cable trenches, equipped with a six-degree-of-freedom mechanical arm and high climbing and obstacle-crossing performance [Reference Dong, Zhang, Liu, Li, Wang and Mengqian5]. Additionally, to achieve automated and intelligent inspection, the robot must possess robust path planning and trajectory tracking capabilities [Reference Al-Araji6].
Robot path planning includes both global and local path planning. Common algorithms for global path planning include bio-inspired algorithms, sampling-based algorithms, and grid-based search algorithms [Reference Ding, Zhou, Huang, Song, Lu and Wang7]. Bio-inspired algorithms are inspired by animal self-organization behavior, natural evolution, and biological neural systems [Reference Li, Yang and Xu8], such as genetic algorithms (GAs) [Reference Ismail, Sheta and Al-Weshah9] and ant colony algorithms [Reference Tan, Ouyang, Zhang, Lao and Wen10]. These are suitable for solving and optimizing complex problems but are limited by slow processing speeds and susceptibility to local optima [Reference Miao, Chen, Yan and Wu11, Reference Elhoseny, Tharwat and Hassanien12]. Sampling-based algorithms, like the well-known Rapidly-exploring Random Tree (RRT) algorithm [Reference Qi, Yang and Sun13], iteratively add random nodes to draw edges and use collision detection to validate edge effectiveness, performing well in high-dimensional configuration spaces. However, traditional RRT algorithms face limitations such as slow convergence and fluctuating path quality [Reference Elbanhawi and Simic14]. Grid-based search algorithms, typically represented by A* [Reference Duchoň, Babinec, Kajan, Beňo, Florek, Fico and Jurišica15], offer advantages in real-time performance and optimization [Reference Li, Dong, Chen, Mu, Fan, Wang and Chen16]. O. A. R. Abdul Wahhab et al. [Reference Razzaq Abdul Wahhab and Al-Araji17] employed three optimization algorithms, including A*, to address the issues of obstacle avoidance and minimizing path length in path planning, achieving promising results. Building on the minimum cost equation of the A* algorithm, Liu et al. [Reference Liu, Liu and Xiao18] further enhanced the fitness function of the Improved Gray Wolf Optimization algorithm. This resulted in a fast iterative path planning method tailored for parking lots. To enhance the performance of the A* algorithm, many researchers have proposed improvements. Wang et al. [Reference Wang, Lou, Jing, Wang, Liu and Liu19] introduced distance expansion from obstacles, bidirectional search, and smoothing processes to increase search efficiency, reduce redundant path points, and decrease path turns. Li et al. [Reference Li, Huang, Ding, Song and Lu20] introduced a bidirectional search strategy with weighted heuristic functions using exponential decay and incorporated path node filtering, improving search efficiency, reducing redundant nodes, and minimizing turning angles. To address the issues of excessive node searches and low computational efficiency in end-effector path planning for robotic arms using the traditional A* algorithm, Tang et al. [Reference Tang, Zhou and Xu21] proposed an improved A* algorithm. This method incorporates a novel node search strategy and local path optimization technique, significantly reducing the number of searched nodes and enhancing search efficiency. Further considering robot motion constraints, Chen et al. [Reference Y., W., L. and Z.22] guided hybrid A* for secondary path planning, optimizing the algorithm path, eliminating redundant nodes, and ensuring safe and smooth robot movement. However, the standard A* algorithm often encounters difficulties when dealing with dynamic obstacles and may generate suboptimal paths in certain environments.
Common methods for local path planning include the Artificial Potential Field (APF) [Reference Khatib23, Reference Ding, Zheng, Liu, Guo and Guo24] and Dynamic Window Approach (DWA) algorithms. The APF algorithm is prone to local optima and oscillations, insufficiently considers dynamic constraints, and handles dynamic obstacles poorly. The DWA algorithm samples the current environment, including robot speed, motion parameters, and position. Although the DWA algorithm is capable of handling dynamic obstacles, it may become trapped in local optima and has limitations in generating smooth paths. To improve the performance of the DWA algorithm, many researchers have proposed enhancements. Kobayashi et al. [Reference Kobayashi and Motoi25] combined DWA with a virtual manipulator (VM) to create DWV, generating path candidates using variable speeds adjusted by the VM and predicted positions of static and dynamic obstacles. Sun et al. [Reference Sun, Wang, Xu, Huang, Shi, Zou and Chen26] optimized the evaluation function’s sub-functions using fuzzy control logic by dynamically modifying weight coefficients and selecting critical points on the global path as key sub-targets in the local motion planning phase, reducing planning time and shortening the planned path length. Dobrevski et al. [Reference Dobrevski and Skočaj27] utilized neural networks to model the motion trajectories of dynamic obstacles and predict corresponding adjustments to the DWA weights, thereby enabling safe local navigation for robots in dynamic environments.
Building upon prior research [Reference Dong, Zhang, Liu, Li, Wang and Mengqian5], this study further optimizes robot path planning by developing an enhanced integrated global and local path planning algorithm based on traditional A* and DWA methods. Compared to traditional algorithms, the enhanced A* algorithm improves the smoothness of the robot’s path and accelerates global exploration efficiency, while the optimized DWA enhances the robot’s ability to avoid both static and dynamic obstacles in local environments. The integration of these two algorithms results in significant improvements in planning efficiency, safety, and path smoothness. Additionally, a robot obstacle-crossing motion planning strategy is devised specifically for convex obstacle scenarios where avoidance is not feasible. Simulation and experimental results demonstrate that the proposed robot path planning algorithm reduces path length and enhances both path search efficiency and path smoothness compared to other common algorithms. The obstacle-crossing motion planning strategy effectively guides the robot in overcoming convex obstacles.
2. Robot path planning and obstacle-crossing strategy
2.1. Cable trench inspection robot
The path planning algorithm and obstacle-crossing motion planning strategy designed in this paper are applied to the cable trench inspection robot, as shown in Fig. 1. The robot features a structure comprising a six-degree-of-freedom robotic arm and a quadrupedal six-track walking mechanism. It is equipped with sensors including a 32-line laser radar and integrated infrared and visible light cameras. Detailed design parameters of the robot and its control system can be found in our previous work [Reference Dong, Zhang, Liu, Li, Wang and Mengqian5].

Figure 1. Cable trench inspection robot.
2.2. Improved global path planning algorithm based on A*
Automated inspection in cable trenches requires robots to autonomously plan a safe and efficient path on a predefined grid map to reach their destinations. The A* algorithm provides advantages in search efficiency and path length optimization. Traditional A* integrates optimal path search principles from Dijkstra algorithm with heuristic strategies akin to greedy algorithms [Reference Liu, Wang, Yang, Liu, Li and Wang28]. Equation (1) defines the evaluation function used to estimate the anticipated total distance from the starting node to the target node, guiding the search toward nodes closer to the projected goal.
In this context,
![]() $F(n)$
represents the estimated total cost from the initial node through node
$F(n)$
represents the estimated total cost from the initial node through node
![]() $n$
to the target node;
$n$
to the target node;
![]() $G(n)$
is the actual cost from the initial node to node
$G(n)$
is the actual cost from the initial node to node
![]() $n$
; and
$n$
; and
![]() $H(n)$
is the heuristic estimate cost from node
$H(n)$
is the heuristic estimate cost from node
![]() $n$
to the target node, typically calculated using Euclidean distance, Manhattan distance, or Chebyshev distance. The traditional A* algorithm is constrained by its inherent algorithmic nature and the discrete nature of grid-based maps, resulting in planned paths that may include unnecessary turns and risks approaching obstacles diagonally. To address the inefficiencies, lack of smoothness, and safety concerns in traditional A* path planning, this study optimizes the traditional A* algorithm based on its evaluation function as follows.
$n$
to the target node, typically calculated using Euclidean distance, Manhattan distance, or Chebyshev distance. The traditional A* algorithm is constrained by its inherent algorithmic nature and the discrete nature of grid-based maps, resulting in planned paths that may include unnecessary turns and risks approaching obstacles diagonally. To address the inefficiencies, lack of smoothness, and safety concerns in traditional A* path planning, this study optimizes the traditional A* algorithm based on its evaluation function as follows.
2.2.1. Adaptive neighborhood expansion
To accommodate the uneven distribution of obstacles in the environment and enhance the accuracy of shortest path estimation, we introduce the concept of adaptive “step size.” This approach involves dynamically adjusting the obstacle probability
![]() $P$
to effectively manage the complexity of the current map environment.
$P$
to effectively manage the complexity of the current map environment.
![]() $P$
is defined as the proportion of obstacle grid units in the local environment formed by the current point and the target point. Assuming
$P$
is defined as the proportion of obstacle grid units in the local environment formed by the current point and the target point. Assuming
![]() $N$
is the number of obstacle grid units in this local environment, with current coordinates
$N$
is the number of obstacle grid units in this local environment, with current coordinates
![]() $(x_{cur}, y_{cur})$
and goal coordinates
$(x_{cur}, y_{cur})$
and goal coordinates
![]() $(x_{goal}, y_{goal})$
, the expression for obstacle probability
$(x_{goal}, y_{goal})$
, the expression for obstacle probability
![]() $P$
is presented in Eq. (2).
$P$
is presented in Eq. (2).
Based on obstacle probability
![]() $P$
, dynamically adjust the node neighborhood expansion method, and search step size: in densely populated obstacle areas, employ a conservative neighborhood expansion strategy to decrease the search step size and minimize collision risks; in sparsely populated obstacle areas, employ a more aggressive neighborhood expansion strategy to increase the search step size and enhance search speed.
$P$
, dynamically adjust the node neighborhood expansion method, and search step size: in densely populated obstacle areas, employ a conservative neighborhood expansion strategy to decrease the search step size and minimize collision risks; in sparsely populated obstacle areas, employ a more aggressive neighborhood expansion strategy to increase the search step size and enhance search speed.
2.2.2. Optimization of evaluation function
The search performance of the traditional A* algorithm is influenced by the heuristic function
![]() $H(n)$
, where varying weights of
$H(n)$
, where varying weights of
![]() $H(n)$
may increase the planned path length [Reference Min, Pan, Dai, Kawsar, Li and Wang29]. By incorporating obstacle probability
$H(n)$
may increase the planned path length [Reference Min, Pan, Dai, Kawsar, Li and Wang29]. By incorporating obstacle probability
![]() $P$
into
$P$
into
![]() $F(n)$
, dynamically adjusting the weight of
$F(n)$
, dynamically adjusting the weight of
![]() $H(n)$
based on obstacle probability, we adapt the A* search process accordingly. The enhanced evaluation function is presented in Eq. (3).
$H(n)$
based on obstacle probability, we adapt the A* search process accordingly. The enhanced evaluation function is presented in Eq. (3).
When obstacles are scarce, lowering obstacle probability
![]() $P$
increases the weight of
$P$
increases the weight of
![]() $H(n)$
, thereby accelerating the A* algorithm’s search process. Conversely, in densely populated obstacle areas, raising obstacle probability
$H(n)$
, thereby accelerating the A* algorithm’s search process. Conversely, in densely populated obstacle areas, raising obstacle probability
![]() $P$
decreases the weight of
$P$
decreases the weight of
![]() $H(n)$
, improving the accuracy of the A* algorithm’s search. Integrating obstacle probability
$H(n)$
, improving the accuracy of the A* algorithm’s search. Integrating obstacle probability
![]() $P$
for search preference adjustment enhances the efficiency and adaptability of the A* algorithm across diverse map environments.
$P$
for search preference adjustment enhances the efficiency and adaptability of the A* algorithm across diverse map environments.
2.2.3. Optimization of child node selection
During the A* algorithm’s search process, it is critical to avoid paths that diagonally traverse through obstacle vertices, as this increases collision risks. Therefore, it is essential to evaluate the spatial relationship between child nodes and obstacles during their generation to prevent paths from diagonally crossing obstacle vertices.
The specific improvement in child node selection is depicted in Fig. 2. When encountering obstacles along the search path, an obstacle repulsive field, inspired by the artificial potential field method, is introduced. This mechanism causes nodes approaching obstacles to experience repulsive forces, prompting the algorithm to reevaluate and adjust path nodes, thereby ensuring the discovery of safer paths.

Figure 2. Optimizing child node selection using artificial potential fields.
2.2.4. Path smoothing
Paths generated by traditional A* algorithms often lack optimality and include multiple turning points, which can hinder actual robot movement. Therefore, additional path smoothing is necessary. This process involves extracting key path points and eliminating redundant path segments to improve the overall smoothness of the planned path, thereby reducing energy consumption during robot motion.
The specific process of extracting key points from the path is illustrated in Fig. 3: Suppose the initial path planned by the A* algorithm is
![]() $Q_{start} - Q_1 - Q_2 - Q_3 - Q_4 - Q_5 - Q_6 - Q_7 - Q_8 - Q_{goal}$
. This process involves removing intermediate points along the straight segments of the path, retaining only the starting point, path turning points, and the endpoint. This results in a streamlined path such as
$Q_{start} - Q_1 - Q_2 - Q_3 - Q_4 - Q_5 - Q_6 - Q_7 - Q_8 - Q_{goal}$
. This process involves removing intermediate points along the straight segments of the path, retaining only the starting point, path turning points, and the endpoint. This results in a streamlined path such as
![]() $Q_{start} - Q_3 - Q_4 - Q_5 - Q_7 - Q_{goal}$
. This approach significantly reduces pauses in robot motion, stabilizes movement, and prevents excessive acceleration and deceleration that could lead to impact loads.
$Q_{start} - Q_3 - Q_4 - Q_5 - Q_7 - Q_{goal}$
. This approach significantly reduces pauses in robot motion, stabilizes movement, and prevents excessive acceleration and deceleration that could lead to impact loads.

Figure 3. Extracting key points of the path.
The specific process of removing redundant path points is depicted in Fig. 4: Starting from the initial point, the path following the extraction of key points is evaluated. It checks whether there are obstacles between
![]() $Q_{start}$
and
$Q_{start}$
and
![]() $Q_4$
. If no obstacles exist,
$Q_4$
. If no obstacles exist,
![]() $Q_4$
is removed. The process continues to evaluate whether obstacles exist between
$Q_4$
is removed. The process continues to evaluate whether obstacles exist between
![]() $Q_{start}$
and
$Q_{start}$
and
![]() $Q_5$
. If obstacles are present, this node is retained as an intermediate point, and the search continues from this node as the new starting point to find the next intermediate node until reaching the endpoint. This iterative process results in a streamlined path such as
$Q_5$
. If obstacles are present, this node is retained as an intermediate point, and the search continues from this node as the new starting point to find the next intermediate node until reaching the endpoint. This iterative process results in a streamlined path such as
![]() $Q_{start} - Q_5 - Q_{goal}$
, effectively reducing the path length.
$Q_{start} - Q_5 - Q_{goal}$
, effectively reducing the path length.

Figure 4. Removing redundant points from the path.
2.3. Improved local path planning algorithm based on DWA
Global path planning provides the robot with a path to the target point in a static map. However, the environment in cable trenches may change, potentially obstructing previously accessible paths with obstacles. Therefore, enhancing the robot’s capability for local path planning is crucial. This paper improves upon the traditional DWA algorithm to achieve effective local path planning for the robot. The principle of traditional DWA [Reference Yang, Fu, Li, Mao and Guo30] involves sampling multiple sets of velocities
![]() $(\nu, \omega )$
at a specific resolution in velocity space and simulating the trajectories of these velocities over a specified time period. After obtaining feasible trajectories, these trajectories are evaluated using the scoring function in Eq. (4), and the optimal trajectory corresponding to
$(\nu, \omega )$
at a specific resolution in velocity space and simulating the trajectories of these velocities over a specified time period. After obtaining feasible trajectories, these trajectories are evaluated using the scoring function in Eq. (4), and the optimal trajectory corresponding to
![]() $(\nu, \omega )$
is selected to drive the robot’s motion.
$(\nu, \omega )$
is selected to drive the robot’s motion.
Here,
![]() ${heading}(\nu, \omega ) = 180^\circ - |\theta _{da}|$
represents the heading evaluation function.
${heading}(\nu, \omega ) = 180^\circ - |\theta _{da}|$
represents the heading evaluation function.
![]() $\theta _{da}$
denotes the robot’s orientation angle, which is the angle between the direction of motion and the line connecting the robot’s geometric center to the target point. The distance function
$\theta _{da}$
denotes the robot’s orientation angle, which is the angle between the direction of motion and the line connecting the robot’s geometric center to the target point. The distance function
![]() ${dist}(\nu, \omega ) = \sqrt{(x_{pred} - x_{obs})^2 + (y_{pred} - y_{obs})^2}$
serves as a safety metric, indicating the distance between the predicted path endpoint and the nearest obstacle, where
${dist}(\nu, \omega ) = \sqrt{(x_{pred} - x_{obs})^2 + (y_{pred} - y_{obs})^2}$
serves as a safety metric, indicating the distance between the predicted path endpoint and the nearest obstacle, where
![]() $(x_{pred}, y_{pred})$
are the coordinates of the predicted path endpoint and
$(x_{pred}, y_{pred})$
are the coordinates of the predicted path endpoint and
![]() $(x_{obs}, y_{obs})$
are the coordinates of the nearest obstacle. The velocity function
$(x_{obs}, y_{obs})$
are the coordinates of the nearest obstacle. The velocity function
![]() ${velocity}(\nu, \omega ) = \nu$
represents the speed, indicating the linear velocity of the robot in the current sampling space.
${velocity}(\nu, \omega ) = \nu$
represents the speed, indicating the linear velocity of the robot in the current sampling space.
![]() $\sigma$
,
$\sigma$
,
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
, and
$\beta$
, and
![]() $\gamma$
are weight coefficients that influence the overall effectiveness of the algorithm.
$\gamma$
are weight coefficients that influence the overall effectiveness of the algorithm.
To prevent discontinuities caused by a single function dominating the overall evaluation function, it is necessary to normalize the evaluation function as shown in Eq. (5).
 \begin{equation} \left \{\begin{aligned}{heading}_{normal}(m) & =\frac{{heading}(m)}{\sum _{i=1}^n{heading}(m)} \\[3pt] {dist}_{normal}(m) & =\frac{{dist}(m)}{\sum _{i=1}^n{dist}(m)} \\[3pt] {velocity}_{normal}(m) & =\frac{{velocity}(m)}{\sum _{i=1}^n{velocity}(m)} \end{aligned}\right . \end{equation}
\begin{equation} \left \{\begin{aligned}{heading}_{normal}(m) & =\frac{{heading}(m)}{\sum _{i=1}^n{heading}(m)} \\[3pt] {dist}_{normal}(m) & =\frac{{dist}(m)}{\sum _{i=1}^n{dist}(m)} \\[3pt] {velocity}_{normal}(m) & =\frac{{velocity}(m)}{\sum _{i=1}^n{velocity}(m)} \end{aligned}\right . \end{equation}
where
![]() $n$
represents the number of velocity and angular velocity combinations that satisfy the constraints and
$n$
represents the number of velocity and angular velocity combinations that satisfy the constraints and
![]() $m$
denotes the current path being evaluated.
$m$
denotes the current path being evaluated.
Although the DWA algorithm achieves path planning by selecting the optimal velocity combinations, it may fall into local optima and is highly dependent on the choice of evaluation function weights. To improve path smoothness, reduce robot impacts, and minimize energy consumption, the path length constraints, as shown in Eq. (6), are integrated into the evaluation function.
 \begin{equation} \begin{aligned}{DIST}(\nu, \omega )= &\, \sqrt{\left (y_{pred }-y_{start}\right )^2+\left (x_{pred}-x_{start}\right )^2} \\[3pt] & -\sqrt{\left (y_{cur}-y_{start}\right )^2+\left (x_{cur }-x_{start}\right )^2} \end{aligned} \end{equation}
\begin{equation} \begin{aligned}{DIST}(\nu, \omega )= &\, \sqrt{\left (y_{pred }-y_{start}\right )^2+\left (x_{pred}-x_{start}\right )^2} \\[3pt] & -\sqrt{\left (y_{cur}-y_{start}\right )^2+\left (x_{cur }-x_{start}\right )^2} \end{aligned} \end{equation}
where
![]() $(x_{cur}, y_{cur})$
denotes the current coordinates of the robot’s position.
$(x_{cur}, y_{cur})$
denotes the current coordinates of the robot’s position.
Introducing the
![]() ${DIST}(\nu, \omega )$
function accelerates the robot’s search speed toward the target point, thereby shortening the path length. Therefore, by incorporating path length constraints, the evaluation function of the DWA algorithm can be enhanced as shown in Eq. (7).
${DIST}(\nu, \omega )$
function accelerates the robot’s search speed toward the target point, thereby shortening the path length. Therefore, by incorporating path length constraints, the evaluation function of the DWA algorithm can be enhanced as shown in Eq. (7).
2.4. Obstacle-crossing motion planning for the robot
Path planning algorithms enable the automated operation of robots. However, when encountering convex obstacles that cannot be avoided along the path, the robot must cross them to continue its inspection tasks. Obstacles of different heights require different strategies for crossing actions. This paper categorizes obstacles into three height classes and develops corresponding crossing strategies, detailed in Table I.
Table I. Obstacle classification and obstacle-crossing strategies.


Figure 5. Obstacle-crossing motion planning for strategy 1.
In Table I,
![]() $h$
represents the height of obstacles, and
$h$
represents the height of obstacles, and
![]() $h_{max}$
denotes the maximum obstacle height the robot can traverse. According to the analysis and testing documented in [Reference Dong, Zhang, Liu, Li, Wang and Mengqian5], the maximum obstacle height
$h_{max}$
denotes the maximum obstacle height the robot can traverse. According to the analysis and testing documented in [Reference Dong, Zhang, Liu, Li, Wang and Mengqian5], the maximum obstacle height
![]() $h_{max}$
that the robot designed in this study can traverse is 300 mm.
$h_{max}$
that the robot designed in this study can traverse is 300 mm.
This paper is based on the principle of smooth obstacle-crossing, aiming to maintain stable variation of the robot’s center of mass during the obstacle-crossing process.
When
![]() $h \lt h_{max} / 2$
, strategy 1 is employed for obstacle-crossing motion planning, with specific steps detailed in Fig. 5. The process unfolds as follows:
$h \lt h_{max} / 2$
, strategy 1 is employed for obstacle-crossing motion planning, with specific steps detailed in Fig. 5. The process unfolds as follows:
-
(a) The robot halts its forward movement at an appropriate distance from the vertical face of the obstacle.
-
(b) Lower the front flipper until its end rests on the edge of the convex surface, simultaneously pressing down the rear flipper to maintain ground contact.
-
(c) Further lower the front flipper to elevate the robot until the lower edge of the front flipper’s track is level.
-
(d) Proceed by advancing until the robot’s front wheels are positioned on the edge of the convex surface, then stop.
-
(e) Lower the front flipper to maintain contact with the ground, reducing the risk of the robot tipping as its center of gravity crosses the vertical face of the convex surface.
-
(f) Continue moving forward until the robot’s center of gravity completely crosses the convex surface and then stop.
-
(g) Raise the front flipper to level the robot, ensuring full ground contact with its tracks while pressing down the rear flipper.
-
(h) Finally, continue forward motion until no longer suspended, retracting both front and rear flippers to complete the obstacle-crossing action.
When
![]() $h_{max} / 2 \lt h \lt h_{max}$
, strategy 2 is employed for obstacle-crossing motion planning, with specific steps detailed in Fig. 6:
$h_{max} / 2 \lt h \lt h_{max}$
, strategy 2 is employed for obstacle-crossing motion planning, with specific steps detailed in Fig. 6:
-
(a) The robot halts its forward movement at an appropriate distance from the vertical face of the convex surface.
-
(b) Lower the front flipper until its end rests on the edge of the convex surface, while simultaneously lowering the rear flipper to maintain ground contact.
-
(c) Continue lowering the front flipper to lift the robot until the lower edge of the front flipper’s track is level with the robot.
-
(d) Lower the rear flipper to further lift the robot, ensuring it remains perpendicular to the ground, achieving a greater obstacle-crossing height.
-
(e) The robot then advances until its front wheels are on the edge of the convex obstacle, then stops.
-
(f) Lower the front flipper to maintain contact with the ground, minimizing the risk of the robot tipping as its center of gravity crosses the vertical face of the convex surface.
-
(g) Continue forward until the robot’s center of gravity completely crosses the convex surface, then stop.
-
(h) Lift the front flipper to level the robot, ensuring full ground contact with its tracks.
-
(i) Finally, continue forward while retracting both front and rear flippers to complete the obstacle-crossing action.

Figure 6. Obstacle-crossing motion planning for strategy 2.

Figure 7. Path planning using improved A* compared to traditional A*.
3. Simulation and experimental testing
To evaluate the effectiveness of the improved robot path planning algorithm and obstacle-crossing motion planning strategy proposed in this paper, simulations of the path planning algorithm and experimental tests of the robot’s obstacle-crossing maneuvers were conducted.
3.1. Simulation of global path planning based on A* algorithm
Initially, a
![]() $20 \times 20$
grid map is constructed, where red squares represent obstacles and white squares denote navigable areas for the robot. The complexity of the obstacle distribution on this map is designed to reflect the real working environment of a robot at the interface between cable trenches and substations, making the simulation results applicable to real-world scenarios. On this map, the improved A* algorithm proposed in this paper is compared with the traditional A* algorithm for path planning. The simulation results are depicted in Fig. 7, where the red dot denotes the starting position, the green dot denotes the target position, and the solid blue line illustrates the globally planned path by the algorithm.
$20 \times 20$
grid map is constructed, where red squares represent obstacles and white squares denote navigable areas for the robot. The complexity of the obstacle distribution on this map is designed to reflect the real working environment of a robot at the interface between cable trenches and substations, making the simulation results applicable to real-world scenarios. On this map, the improved A* algorithm proposed in this paper is compared with the traditional A* algorithm for path planning. The simulation results are depicted in Fig. 7, where the red dot denotes the starting position, the green dot denotes the target position, and the solid blue line illustrates the globally planned path by the algorithm.
We compared the performance of the path planning algorithms across four aspects: the number of nodes, path length, number of turns, and total degree of turns. The results are presented in Table II.
Table II. Performance comparison between traditional A* algorithm and improved A* algorithm proposed in this paper.

Table II shows that the improved A* algorithm in this paper exhibits significant improvements over the traditional A* algorithm in terms of node count, path length, number of turns, and degree. Specifically, the node count has been reduced by 58%, the path length has been shortened by 6.1%, the number of turns decreased by 50%, and the total degree of turns reduced by 55%. To further validate the performance of the improved A* algorithm proposed in this study, simulations were conducted to compare its results with those of other algorithms such as Ant Colony Optimization (ACO), ACO combined with GA (ACO + GA), Sparrow Search Algorithm (SSA), and Improved Sparrow Search Algorithm (ISSA), as depicted in Fig. 8. Performance comparison of path planning algorithms is shown in Table III.
From Table III, it is evident that the improved A* algorithm presented in this study exhibits the shortest search time among the five tested algorithms, reducing the search duration by 97% compared to the ISSA algorithm, which had the shortest search time among the other methods. Additionally, the path length is reduced by 0.8% compared to ISSA. This demonstrates that the enhanced A* algorithm developed in this study possesses superior search efficiency. Although the search path length of the improved A* algorithm is approximately 1% longer than that of ACO + GA, its search time is significantly shorter. Therefore, the proposed improved A* algorithm demonstrates excellent performance and holds substantial practical value.
3.2. Simulation of integrated global and local path planning
To enhance the robot’s navigation through cable trenches and its resilience to disturbances, we utilize a fusion algorithm that integrates the improved A* algorithm with enhanced DWA for path planning. The fusion algorithm is implemented by first employing the improved A* algorithm to discover an initial path. Subsequently, the nodes from this path serve as critical waypoints for real-time dynamic obstacle avoidance using the enhanced DWA algorithm. The improved DWA algorithm utilizes the robot’s perceived surrounding information along with its kinematic and dynamic models to plan the robot’s path within a local range, thereby enabling it to effectively avoid dynamic obstacles. Consequently, the simulation experiments conducted in this study are based on the assumption that the robot can accurately acquire environmental information. In the subsequent simulation experiments, the robot’s maximum speed is set to 1 m/s, the maximum angular velocity is set to 0.23 rad/s, the acceleration is set to
![]() $0.1 \, \text{m/s}^2$
, the angular acceleration is set to
$0.1 \, \text{m/s}^2$
, the angular acceleration is set to
![]() $0.57 \, \text{rad/s}^2$
, the velocity resolution is set to 0.03 m/s, and the angular velocity resolution is set to 0.0175 rad/s.
$0.57 \, \text{rad/s}^2$
, the velocity resolution is set to 0.03 m/s, and the angular velocity resolution is set to 0.0175 rad/s.
Table III. Comparison of simulation results from multiple algorithms.


Figure 8. Path planning results of ACO, ACO + GA, SSA, and ISSA algorithms.

Figure 9. Integrated global and local path planning.
To validate the effectiveness of the path planning approach based on the improved A* algorithm and enhanced DWA algorithm, we conducted fusion path planning simulations on three different grid maps: map1, a
![]() $20 \times 20$
grid with simple obstacles; map2, a
$20 \times 20$
grid with simple obstacles; map2, a
![]() $30 \times 30$
grid with complex obstacles; and map3, which features a different obstacle configuration from map2. In these maps, red squares represent known obstacles, white squares denote navigable areas, gray squares indicate unknown static obstacles, and yellow squares represent dynamic obstacles. The complexity of the obstacle distribution on these maps is slightly higher than that of the robot’s actual working environment at the interface between cable trenches and substations, making the test results applicable to real-world robot scenarios. Each of the three maps was tested using both the improved A* algorithm combined with traditional DWA and the improved A* algorithm combined with the enhanced DWA. In the enhanced DWA, the coefficients for the heading evaluation function, obstacle distance evaluation function, and current velocity evaluation function were set to 0.25, 0.14, and 0.23, respectively, with the prediction time set to 3 s. Additionally, the minimum safe distance between the robot and obstacles was set to 0.65 m. The simulation results are shown in Fig. 9, where the globally planned path is represented by a blue dashed line, the robot’s actual trajectory by a blue solid line, and the trajectories of obstacles by red solid lines. The fusion path planning algorithms were evaluated based on the length of the final planned path, with the results detailed in Table IV.
$30 \times 30$
grid with complex obstacles; and map3, which features a different obstacle configuration from map2. In these maps, red squares represent known obstacles, white squares denote navigable areas, gray squares indicate unknown static obstacles, and yellow squares represent dynamic obstacles. The complexity of the obstacle distribution on these maps is slightly higher than that of the robot’s actual working environment at the interface between cable trenches and substations, making the test results applicable to real-world robot scenarios. Each of the three maps was tested using both the improved A* algorithm combined with traditional DWA and the improved A* algorithm combined with the enhanced DWA. In the enhanced DWA, the coefficients for the heading evaluation function, obstacle distance evaluation function, and current velocity evaluation function were set to 0.25, 0.14, and 0.23, respectively, with the prediction time set to 3 s. Additionally, the minimum safe distance between the robot and obstacles was set to 0.65 m. The simulation results are shown in Fig. 9, where the globally planned path is represented by a blue dashed line, the robot’s actual trajectory by a blue solid line, and the trajectories of obstacles by red solid lines. The fusion path planning algorithms were evaluated based on the length of the final planned path, with the results detailed in Table IV.
Table IV. Length comparison of integrated global and local path planning.

From the simulation results presented in Table IV, it is evident that our improved A* algorithm, when integrated with the enhanced DWA algorithm, reduces the robot’s path length by 3.2% in the
![]() $20 \times 20$
obstacle map (map1) compared to integration with the traditional DWA algorithm. Additionally, in the
$20 \times 20$
obstacle map (map1) compared to integration with the traditional DWA algorithm. Additionally, in the
![]() $30 \times 30$
obstacle maps (map2 and map3) with different obstacle configurations, the path lengths are reduced by 3.5% and 3.6%, respectively. The simulation results across different map sizes and varying obstacle configurations demonstrate the superior global and local path planning capabilities of our improved A* algorithm when combined with the enhanced DWA algorithm.
$30 \times 30$
obstacle maps (map2 and map3) with different obstacle configurations, the path lengths are reduced by 3.5% and 3.6%, respectively. The simulation results across different map sizes and varying obstacle configurations demonstrate the superior global and local path planning capabilities of our improved A* algorithm when combined with the enhanced DWA algorithm.
3.3. Experimental validation of robot obstacle-crossing motion planning strategies
To validate the obstacle-crossing motion planning strategies proposed in this paper, as depicted in Fig. 10, the robot was operated by trained personnel to test obstacle crossing over convex obstacles of heights 10 cm and 20 cm. Strategy 1 was employed for overcoming the 10 cm obstacles, while strategy 2 was applied for the 20 cm obstacles.

Figure 10. Experimental validation of robot obstacle-crossing motion planning strategies.
During the obstacle-crossing process, the robot’s pitch angle
![]() $\theta _1$
and the absolute displacement
$\theta _1$
and the absolute displacement
![]() $(x, y, z)$
of a target ball (placed above the robot’s rear axle with the ground as the
$(x, y, z)$
of a target ball (placed above the robot’s rear axle with the ground as the
![]() $xy$
-plane) were real-time collected using IMU and a laser tracker. The relationship between the robot’s pitch angle
$xy$
-plane) were real-time collected using IMU and a laser tracker. The relationship between the robot’s pitch angle
![]() $\theta _1$
and the
$\theta _1$
and the
![]() $z$
-direction displacement over time is illustrated in Fig. 11.
$z$
-direction displacement over time is illustrated in Fig. 11.

Figure 11. Experimental results of robot obstacle-crossing motion planning strategies.
From Fig. 11, it can be observed that the robot successfully navigates 10 cm and 20 cm convex obstacles using strategy 1 and strategy 2, respectively. This demonstrates that the obstacle-crossing motion planning strategies designed in this study meet the robot’s obstacle-crossing requirements, suitable for assisting in the automated inspection of cable trenches. Additionally, Fig. 11(b) reveals that during the traversal of a 20 cm obstacle, despite efforts by the operator to maintain smooth obstacle-crossing, the robot’s pitch angle tends to increase with the height of the convex obstacle.
4. Conclusion
To address the challenges of automated inspection for cable trench inspection robots, we have researched and designed an integrated global and local path planning algorithm, along with obstacle-crossing motion strategies. First, we enhanced the traditional A* algorithm to achieve global path planning. Compared to the traditional A* algorithm, the improved A* algorithm reduces the number of search nodes by 58% and the path length by 6.1% in complex obstacle environments, while also minimizing the number of turns and turning angles. Second, we integrated an improved DWA for dynamic obstacle avoidance. Simulation tests confirmed the superiority of this integrated algorithm. Results indicate that the improved A* algorithm combined with the enhanced DWA reduces path lengths by 3.2%, 3.5%, and 3.6% on the
![]() $20 \times 20$
grid map and two
$20 \times 20$
grid map and two
![]() $30 \times 30$
grid maps with different obstacle configurations, respectively, compared to integration with the traditional DWA. This integrated algorithm significantly enhances the efficiency of robot navigation. Furthermore, to tackle the challenges posed by convex obstacles during real inspections, we proposed practical scenario-based obstacle-crossing motion planning strategies. Experimental tests on convex obstacles of 10 cm and 20 cm in height confirmed the robot’s ability to successfully cross these obstacles, demonstrating the effectiveness and feasibility of the proposed strategies.
$30 \times 30$
grid maps with different obstacle configurations, respectively, compared to integration with the traditional DWA. This integrated algorithm significantly enhances the efficiency of robot navigation. Furthermore, to tackle the challenges posed by convex obstacles during real inspections, we proposed practical scenario-based obstacle-crossing motion planning strategies. Experimental tests on convex obstacles of 10 cm and 20 cm in height confirmed the robot’s ability to successfully cross these obstacles, demonstrating the effectiveness and feasibility of the proposed strategies.
Future research will focus on optimizing the robot’s path planning algorithm performance, particularly in environments with varying terrain and dynamic obstacles. The research outcomes are expected to be applicable to industrial inspection in complex environments, such as oil refineries, cable trenches, or urban infrastructure where obstacles and challenging terrain are common. Integrating the path planning algorithm and obstacle-crossing motion planning strategies into the robot’s autonomous control system will enhance its adaptability and operational efficiency in these scenarios. Additionally, to facilitate the deployment of the algorithm on the robot, future work will incorporate advanced sensing technologies, such as LiDAR and 3D vision systems, to enable more accurate obstacle detection and path planning. Finally, further research will explore the application of these strategies in dynamic environments, particularly in scenarios where multiple obstacles may move unpredictably, thereby enhancing the robot’s autonomy and flexibility.
Author contributions
Linjie Dong and Junfei Wang designed and improved the path planning algorithm. Renfei Zhang and Jie Li conducted simulation tests and data collection. Junfei Wang and Shanshan Wang performed simulation result analysis. Linjie Dong, Junfei Wang, and Renfei Zhang conducted experimental tests. Linjie Dong and Xingsong Wang wrote the article.
Financial support
This work is supported by the National Key R&D Program of China (grant no. 2021YFF0500900), the Natural Science Foundation of Jiangsu Province, China (grant no. BK202300367), the Natural Science Foundation of the Jiangsu Higher Education (grant no. 23KJB510016), and Science and Technology Project of the State Administration for Market Regulation, China (grant no. 2023MK040).
Competing interests
The authors declare no conflicts of interest exist.
Ethical approval
None.