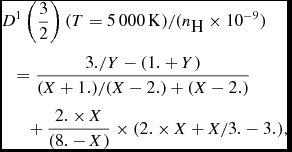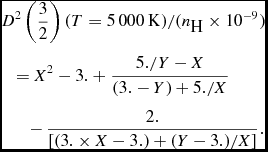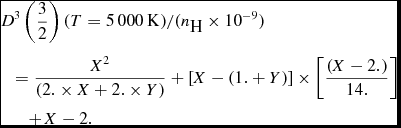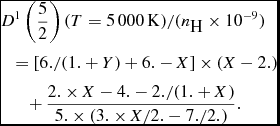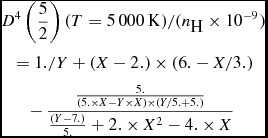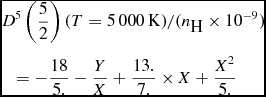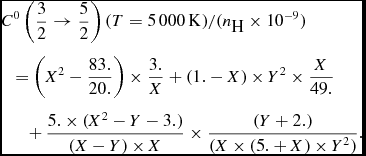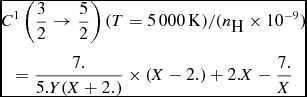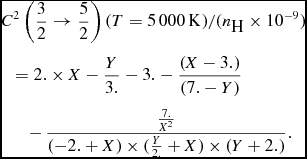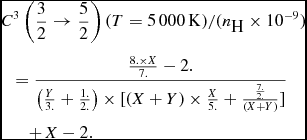1 INTRODUCTION
The second solar spectrum (SSS) is the spectrum of the scattering linear polarisation observed close to the limb of the quiet Sun where the anisotropy of the radiation is maximum. The SSS is depolarised by turbulent solar magnetic fields via the Hanle effect and by isotropic collisions with neutral hydrogen. The Hanle depolarisation allows diagnostics of the magnetic fields by confronting the discrepancy between the polarisation modelled in the absence of magnetic fields and the observed polarisation (e.g. Stenflo Reference Stenflo1982; Landi Degl’Innocenti Reference Landi Degl’Innocenti1983; Sahal-Bréchot, Malinovsky, & Bommier Reference Sahal-Bréchot, Malinovsky and Bommier1986; Stenflo Reference Stenflo2004; Trujillo Bueno, Shchukina, & Asensio Ramos Reference Trujillo Bueno, Shchukina and Asensio Ramos2004; Derouich et al. Reference Derouich, Bommier, Malherbe and Degl’Innocenti2006; Faurobert et al. Reference Faurobert, Derouich, Bommier and Arnaud2009).
The study of the widths, shifts, and (de)polarisation of spectral lines under the influence of collisions with neutral perturbers has already been the subject of numerous studies (e.g. Lemaire, Chotin, & Rostas Reference Lemaire, Chotin and Rostas1985; Baird, Eckart, & Sanderman Reference Baird, Eckart and Sanderman1979; Monteiro et al. 1988; Chambaud & Lévy Reference Chambaud and Lévy1989; Anstee & O’Mara Reference Anstee and O’Mara1991; Spielfiedel et al. 1991; Krsljanin & Peach Reference Krsljanin and Peach1993; Leininger, Gadéa, & Dickinson Reference Leininger, Gadéa and Dickinson2000; Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b; Derouich, Radi, & Barklem Reference Derouich, Radi and Barklem2015, see also Barklem Reference Barklem2016 and references therein). In addition, Anstee, Barklem and O’Mara (ABO) developed a powerful semi-classical theory during the 1990s for collisional line broadening by neutral hydrogen (Anstee & O’Mara Reference Anstee and O’Mara1991, Reference Anstee and O’Mara1995; Anstee Reference Anstee1992; Anstee, O’Mara, & Ross Reference Anstee, O’Mara and Ross1997; Barklem Reference Barklem1998; Barklem & O’Mara Reference Barklem and O’Mara1997; Barklem, Anstee, & O’Mara Reference Barklem, Anstee and O’Mara1998). The ABO theory has been generalised successfully by Derouich, Sahal-Bréchot, and Barklem (DSB) to obtain the depolarisation and polarisation transfer rates by collisions with neutral hydrogen (see, for example, Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b and Derouich Reference Derouich2004).
In this context, we developed an original collisional code which enables us to provide a large amount of the collisional depolarisation and polarisation transfer rates (e.g. Derouich et al. Reference Derouich, Radi and Barklem2015, Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b). As done in most semi-classical collisional approaches, the approximation of the rectilinear trajectories is adopted in the collisional method of this work. This approximation was validated by several works (see, for example, Smith, Vidal, & Cooper Reference Smith, Vidal and Cooper1969; Allard & Kielkopf Reference Allard and Kielkopf1982). Furthermore, we assume that the impact approximation is valid where we consider only the binary collisions which are well separated and uncorrelated. This approximation is well satisfied in the solar conditions (see, e.g., Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b and Derouich Reference Derouich2004).
The DSB and ABO theories allowed us to obtain widespread collisional data for neutral atoms (Derouich et al. Reference Derouich, Radi and Barklem2015). Therefore, depolarisation and polarisation transfer rates can be determined from general relationships without the requirement to utilise the collisional numerical code level by level. Unfortunately, this is not possible to do for ionised atoms where one must proceed level by level. Thus, any calculation of the depolarisation and transfer of polarisation rates is limited to a given level of a given ionised atom.
Recently, Derouich (Reference Derouich2017) removed this limitation in the case of p-levels of ions. In this paper, we intend to extend the results of Derouich (Reference Derouich2017) to the case of d-states.
The paper is organised as follows. Section 2 states the problem to be treated. In Section 3, we describe the numerical work and provide the general relationships for the d-states of simple ions. Atoms with hyperfine structure and complex atoms are presented in Sections 4 and 5. Finally, the conclusions of the paper are presented in Section 6.
2 STATEMENT OF THE PROBLEM
For neutral atoms, the Unsöld energy E p has a constant value Ep = − 4/9 a.u. (see, e.g., Anstee Reference Anstee1992, Barklem & O’Mara Reference Barklem and O’Mara1998; Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b). The constant Ep = − 4/9 a.u. is used in the expression of the interaction potential which, in turn, is used to calculate the collisional rates for any level on any atom. On the other hand, for ionised atoms, the Unsöld energy is not constant and one has to determine the value of Ep for each case (Derouich, Sahal-Bréchot, & Barklem Reference Derouich, Sahal-Bréchot and Barklem2004). After that the code of collisions should be run to get the collisional rates level by level. This is a strong restriction which hinders the generalisation of the DSB results published in Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004). That restriction has been removed for the p-states of ions in the recent paper of Derouich (Reference Derouich2017). The model presented in Derouich (Reference Derouich2017) is extended here to d (l = 2) ionic levels.
We can summarise the calculations of the collisional depolarisation rates for the levels of ionised atoms in two main stages. In the first stage, one calculates the value of E p for the ionic state under study. This calculation requires summation over values of the dipole oscillator strengths of all transitions to the level of interest for the perturbed ion and to the ground state for the neutral hydrogen atom (see Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004 and references therein). Then, in the second stage, the calculated value of Ep is injected in the code of collisions to determine the interaction potential. Once the interaction potential is obtained, it is introduced in the formalism treating the dynamics of collisions in order to calculate the probabilities of collisions on the tensorial basis [see equation (10) of Derouich, Sahal-Bréchot, & Barklem (Reference Derouich, Sahal-Bréchot and Barklem2003a)]. Depolarisation rates are obtained after integrating the probabilities of collisions, firstly over the impact-parameter b and secondly over a Maxwell distribution of velocities f(v), for a local temperature T of the solar atmosphere.
In practise, solar physicists can obtain the value of E p (stage 1) but it is difficult for them to determine the interaction potential and treat the dynamics of collisions in order to obtain the collisional depolarisation rates (stage 2). Our problem can be stated as how to use powerful numerical methods in order to overcome the difficulty raised in the stage 2. The essential contribution of this paper is to allow solar community to compute easily the collisional rates for the d-states of any ion by completing only stage 1.
3 GENERAL RELATIONSHIPS FOR d-STATES OF SIMPLE IONS
3.1 Definitions and notations
Polarisation of atomic levels quantifies the population differences and the interferences between the magnetic sublevels. The values of the polarisation of J-levels are typically presented by the values of the elements J ρ k q of the density matrix—the index k gives the tensorial order inside the level where 0 ⩽ k ⩽ 2J and q concerns the interferences between the sublevels, − k ⩽ q ⩽ +k.
The tensorial order and thus the polarisation of atomic levels can be generated by anisotropic illumination. Consequently, one receives polarised light emitted by ions containing these levels. To obtain theoretically the Stokes parameters characterising the radiation (I, Q, U, and V), one needs to solve the radiative transfer problem coupled to the statistical equilibrium equations (SEE) for the elements J ρ k q (see, e.g., Landi Degl’Innocenti & Landolfi 2004). The elements J ρ k q at each point of the LOS are the unknowns of the problem. To obtain these elements precisely, one must solve the SSE and take into account all relevant processes intervening in the time of the polarised line formation. These processes are mainly the collisional interactions, magnetic fields effects, and radiative transfer effects.
As it is showed in equation (1) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), the variation of ρ k q (J) due to isotropic collisions is
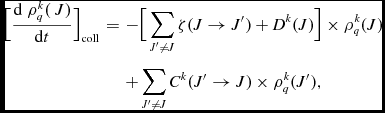 $$\begin{eqnarray}
\big [\frac{{\rm d} \; \rho _q^{k} (\ J)}{{\rm d}t}\big ]_{{\rm coll}} & = & - \big [\sum _{J^{\prime } \ne J} \zeta (J \rightarrow J^{\prime }) + D^k(J) \big ] \times \rho _q^{k} (J) \nonumber \\
&& + \sum _{J^{\prime } \ne J} C^k(J^{\prime } \rightarrow J) \times \rho _q^{k} (J^{\prime }),
\end{eqnarray}$$
$$\begin{eqnarray}
\big [\frac{{\rm d} \; \rho _q^{k} (\ J)}{{\rm d}t}\big ]_{{\rm coll}} & = & - \big [\sum _{J^{\prime } \ne J} \zeta (J \rightarrow J^{\prime }) + D^k(J) \big ] \times \rho _q^{k} (J) \nonumber \\
&& + \sum _{J^{\prime } \ne J} C^k(J^{\prime } \rightarrow J) \times \rho _q^{k} (J^{\prime }),
\end{eqnarray}$$
where ζ(J → J′) are the fine structure transfer rates given by [equation (2) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2003a)]
In the absence of the polarisation, k = 0 and q = 0 and using the general density matrix formalism one shows that the unknowns of the problem become ρ0 0(αJ) which are simply proportional to the populations of the levels as in spectroscopic studies (e.g., Asplund Reference Asplund2005).
In the solar photosphere where the SSS is originated, the isotropic collisions with neutral hydrogen dominate any other kind of collisions. These collisions occur inside the same electronic ionic level. The depolarisation and polarisation transfer rates are q-independent because the collisions are isotropic (e.g., Sahal-Bréchot Reference Sahal-Bréchot1977; Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b).
We denote the depolarisation rates due to purely elastic collisions occurring in only one J-level by Dk (J); the expression of Dk is given by equations (7) and (9) of Derouich et al. (Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b). The Ck (J → J′) indicate the polarisation transfer rates due to collisions between the initial level (J) and the final level (J′) (see Equation (3) of Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2003a).
Our results are concentrated on the d-states with orbital momentum l=2. The spin of the optical electron is s=1/2. The total angular momentum is J = l+s and thus one has J=3/2 or J=5/2. As a result, there are two fine structure states
![]() $^2D_{J=\frac{3}{2}}$
and
$^2D_{J=\frac{3}{2}}$
and
![]() $^2D_{J=\frac{5}{2}}$
.
$^2D_{J=\frac{5}{2}}$
.
Throughout this paper, all the collisional rates are given in s−1. In the framework of the impact approximation, the rates are proportional to the neutral hydrogen density in cm−3 denoted by
![]() $n_{\textrm {H}}$
and they depend on the temperature T given in Kelvins. We showed in our previous works that the collisional rates can be expressed as (e.g., Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2003a; Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004)
$n_{\textrm {H}}$
and they depend on the temperature T given in Kelvins. We showed in our previous works that the collisional rates can be expressed as (e.g., Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2003a; Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004)
where T = 5000K and λ is the so-called velocity exponent. Both DSB and ABO found that collisional rates have typical temperature dependence of T
0.38 which means that
![]() $\lambda \eqsim 0.25$
.
$\lambda \eqsim 0.25$
.
3.2 Numerical results
The numerical code of collisions is updated in order to make it useful for calculations of large number of collisional rates of ionic d-states. Using this code, collisional rates are obtained at T = 5000K for effective principal quantum number n* in the interval [2.5, 4]. Furthermore, we computed for each value of n*, grids of collisional rates for each Unsöld energy E p which is in the typical interval [ − 2, − 0.6] (in atomic units). We adopt a step size of 0.1 in the variation of n* and E p. Consequently, we obtain three-dimensional tables containing the collisional rates with the parameters n* and E p.
Based on these tables, we used our Genetic Programming (GP) method of fitting in order to provide analytically general relationships between collisional rates, n* and E p. This method has been used successfully in Derouich et al. (Reference Derouich, Radi and Barklem2015) and in Derouich (Reference Derouich2017). The GP method minimises the summed square of the difference between the tabulated rates and rates obtained from the GP relationships. The relationships predicted by the GP-based model are compared with the available data of the d-states of the Ca ii, Ba ii, and Sr ii in order to estimate their precision.
The following equations show the relationships between the collisional depolarisation/transfer of polarisation rates of the left-hand side and the n* and E
p in the right-hand side. Let us recall that, for
![]() $J=\frac{3}{2}$
, 0 ⩽ k ⩽ 3 and for
$J=\frac{3}{2}$
, 0 ⩽ k ⩽ 3 and for
![]() $J=\frac{5}{2}$
, 0 ⩽ k ⩽ 5. In particular, by definition, D
k = 0(J)=0. In the following, we provide the non-zero depolarisation and polarisation transfer rates associated to the levels
$J=\frac{5}{2}$
, 0 ⩽ k ⩽ 5. In particular, by definition, D
k = 0(J)=0. In the following, we provide the non-zero depolarisation and polarisation transfer rates associated to the levels
![]() $^2D_{J=\frac{3}{2}}$
and
$^2D_{J=\frac{3}{2}}$
and
![]() $^2D_{j=\frac{5}{2}}$
.
$^2D_{j=\frac{5}{2}}$
.
3.2.1 Depolarisation rates of the level
 $^2D_{J=\frac{3}{2}}$
$^2D_{J=\frac{3}{2}}$
-
•
(5)where X = n*p and Y = −E p > 0. $$\begin{eqnarray}
&&D^{1}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K})/(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad =\frac{3./Y-(1.+Y)}{(X+1.)/(X-2.)+(X-2.)} \nonumber \\
&&\qquad+\, \frac{2. \times X}{(8.-X)} \times (2. \times X+X/3.-3.),
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{1}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K})/(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad =\frac{3./Y-(1.+Y)}{(X+1.)/(X-2.)+(X-2.)} \nonumber \\
&&\qquad+\, \frac{2. \times X}{(8.-X)} \times (2. \times X+X/3.-3.),
\end{eqnarray}$$
In order to compare with published results, let us consider the case of the d-state of the Ca II where n*d = 2.315 and E p= − 1.2. According to the equation (14) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), the reference value of
 $D^{1}(\frac{1}{2}) (T=5\,000\,{\rm K})$
/
$D^{1}(\frac{1}{2}) (T=5\,000\,{\rm K})$
/
 $(n_{\textrm {H}} \times 10^{-9})$
=1.9904 s−1=
$(n_{\textrm {H}} \times 10^{-9})$
=1.9904 s−1=
 $D_\textrm {reference}$
. The GP methods provide equation (2) which implies that
$D_\textrm {reference}$
. The GP methods provide equation (2) which implies that
 $D^{1}(\frac{1}{2}) (T=5\,000\,{\rm K})$
/
$D^{1}(\frac{1}{2}) (T=5\,000\,{\rm K})$
/
 $(n_{\textrm {H}} \times 10^{-9})$
=1.98365 s−1=
$(n_{\textrm {H}} \times 10^{-9})$
=1.98365 s−1=
 $D_\textrm {GP}$
. Thus, the relative error is
(6)which demonstrates how good is the precision of the GP method of fitting.
$D_\textrm {GP}$
. Thus, the relative error is
(6)which demonstrates how good is the precision of the GP method of fitting. $$\begin{eqnarray}
re\textrm {(Ca II)}= \frac{|D_\textrm {reference}-D_\textrm {GP}|}{D_\textrm {reference}} \times 100=0.5\%
\end{eqnarray}$$
$$\begin{eqnarray}
re\textrm {(Ca II)}= \frac{|D_\textrm {reference}-D_\textrm {GP}|}{D_\textrm {reference}} \times 100=0.5\%
\end{eqnarray}$$
-
•
(7)With respect to the reference value given in equation (14) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), $$\begin{eqnarray}
&&D^{2}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=X^2-3. + \frac{5./Y-X}{(3.-Y)+5./X} \nonumber\\
&&\qquad -\, \frac{2.}{[(3. \times X-3.) +(Y-3.)/X]}.
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{2}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=X^2-3. + \frac{5./Y-X}{(3.-Y)+5./X} \nonumber\\
&&\qquad -\, \frac{2.}{[(3. \times X-3.) +(Y-3.)/X]}.
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 10%, in the case of the d-state of the Ca ii. In addition, in the case of the d-state of the Sr ii,
$re\textrm {(Ca \textsc {ii})}$
≃ 10%, in the case of the d-state of the Ca ii. In addition, in the case of the d-state of the Sr ii,
 $re\textrm {(Sr \textsc {ii})}$
≃ 23%. For the Ba ii of the d-state,
$re\textrm {(Sr \textsc {ii})}$
≃ 23%. For the Ba ii of the d-state,
 $re\textrm {(Ba \textsc {ii})}$
≃ 7%. To determine the error bars for the Sr ii and Ba ii, we compared with the results obtained by Derouich (Reference Derouich2008) and Deb & Derouich (Reference Deb and Derouich2014).
$re\textrm {(Ba \textsc {ii})}$
≃ 7%. To determine the error bars for the Sr ii and Ba ii, we compared with the results obtained by Derouich (Reference Derouich2008) and Deb & Derouich (Reference Deb and Derouich2014).
-
•
(8)By comparing with the reference value of $$\begin{eqnarray}
&&D^{3}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&& \quad=\frac{X^2}{(2. \times X+2. \times Y)}+[X-(1.+Y)] \times \left[\frac{(X-2.)}{14.}\right] \nonumber \\
&&\qquad +\,X-2.
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{3}\left(\frac{3}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&& \quad=\frac{X^2}{(2. \times X+2. \times Y)}+[X-(1.+Y)] \times \left[\frac{(X-2.)}{14.}\right] \nonumber \\
&&\qquad +\,X-2.
\end{eqnarray}$$
 $D^{3}(\frac{3}{2}) (T=5\,000\,{\rm K})$
given in equation (14) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), we get
$D^{3}(\frac{3}{2}) (T=5\,000\,{\rm K})$
given in equation (14) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), we get
 $re\textrm {(Ca \textsc {ii})}$
% ≃ 0.25%.
$re\textrm {(Ca \textsc {ii})}$
% ≃ 0.25%.
3.2.2 Depolarisation rates of the level
 $^2D_{J=\frac{5}{2}}$
$^2D_{J=\frac{5}{2}}$
-
•
(9)At T = 5000K, $$\begin{eqnarray}
&& D^{1}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
& &\quad= [6./(1.+Y)+6.-X] \times (X-2.)\nonumber \\
& &\qquad +\,\frac{2.\times X-4.-2./(1.+X)}{5. \times (3. \times X/2.-7./2.)}.
\end{eqnarray}$$
$$\begin{eqnarray}
&& D^{1}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
& &\quad= [6./(1.+Y)+6.-X] \times (X-2.)\nonumber \\
& &\qquad +\,\frac{2.\times X-4.-2./(1.+X)}{5. \times (3. \times X/2.-7./2.)}.
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 11% for the level 2
D
5/2 of the Ca ii.
$re\textrm {(Ca \textsc {ii})}$
≃ 11% for the level 2
D
5/2 of the Ca ii.
-
•
(10)We find that, $$\begin{eqnarray}
&&D^{2}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {\scriptsize H}} \times 10^{-9}) \nonumber \\
&&\quad= (4./5. -7./X+3. \times X) \nonumber\\
&&\qquad-\, \frac{3. \times X}{X^2-3.+X}-\frac{(5.-X/Y)}{(7./3.+2./Y)}.
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{2}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {\scriptsize H}} \times 10^{-9}) \nonumber \\
&&\quad= (4./5. -7./X+3. \times X) \nonumber\\
&&\qquad-\, \frac{3. \times X}{X^2-3.+X}-\frac{(5.-X/Y)}{(7./3.+2./Y)}.
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 20% for Ca ii,
$re\textrm {(Ca \textsc {ii})}$
≃ 20% for Ca ii,
 $re\textrm {(Ba \textsc {ii})}$
≃ 12% for Ba ii, and
$re\textrm {(Ba \textsc {ii})}$
≃ 12% for Ba ii, and
 $re\textrm {(Sr \textsc {ii})}$
≃ 1.3% for Sr ii.
$re\textrm {(Sr \textsc {ii})}$
≃ 1.3% for Sr ii.
-
•
(11)where $$\begin{eqnarray}
&&D^{3}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=11./80. \times X^2 \times (X+2.) \nonumber \\
&&\qquad -\, \frac{Y}{(X-Y/7.-7./(X \times 4.))},
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{3}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=11./80. \times X^2 \times (X+2.) \nonumber \\
&&\qquad -\, \frac{Y}{(X-Y/7.-7./(X \times 4.))},
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
is less than 0.1%.
$re\textrm {(Ca \textsc {ii})}$
is less than 0.1%.
-
•
(12)with $$\begin{eqnarray}
&&D^{4}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=1./Y+(X-2.) \times (6.-X/3.)\nonumber\\
&&\qquad-\,\frac{\frac{5.}{(5. \times X-Y \times X) \times (Y/5.+5.)}}{\frac{(Y-7.)}{5.}+2. \times X^2-4. \times X}
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{4}\left(\frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=1./Y+(X-2.) \times (6.-X/3.)\nonumber\\
&&\qquad-\,\frac{\frac{5.}{(5. \times X-Y \times X) \times (Y/5.+5.)}}{\frac{(Y-7.)}{5.}+2. \times X^2-4. \times X}
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 5%.
$re\textrm {(Ca \textsc {ii})}$
≃ 5%.
-
•
(13)and $$\begin{eqnarray}
&&D^{5}\left(\frac{5}{2}\right) (T=5\,000\,\textrm {K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=-\frac{18}{5.}-\frac{Y}{X} + \frac{13.}{7.} \times X +\frac{X^2}{5.}
\end{eqnarray}$$
$$\begin{eqnarray}
&&D^{5}\left(\frac{5}{2}\right) (T=5\,000\,\textrm {K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=-\frac{18}{5.}-\frac{Y}{X} + \frac{13.}{7.} \times X +\frac{X^2}{5.}
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
is less than 3%.
$re\textrm {(Ca \textsc {ii})}$
is less than 3%.
3.2.3 Polarisation transfer rates between the levels
 $^2D_{J=\frac{3}{2}}$
and
$^2D_{J=\frac{3}{2}}$
and
 $^2D_{J=\frac{5}{2}}$
$^2D_{J=\frac{5}{2}}$
Concerning the non-zero polarisation transfer rates between the levels
![]() $^2D_{J=\frac{3}{2}}$
and
$^2D_{J=\frac{3}{2}}$
and
![]() $^2D_{J=\frac{5}{2}}$
, only the rates
$^2D_{J=\frac{5}{2}}$
, only the rates
![]() $C^{0}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
$C^{0}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
![]() $C^{1}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
$C^{1}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
![]() $C^{2}(\frac{3}{2} \rightarrow \frac{5}{2})$
, and
$C^{2}(\frac{3}{2} \rightarrow \frac{5}{2})$
, and
![]() $C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
are non-zero.
$C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
are non-zero.
-
•
(14)By comparing to the reference value of $$\begin{eqnarray}
&&C^{0}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=\left(X^2-\frac{83.}{20.}\right) \times \frac{3.}{X}+(1.-X) \times Y^2 \times \frac{X}{49.} \nonumber \\
&&\qquad+\,\frac{5. \times (X^2-Y-3.) }{(X-Y) \times X} \times \frac{(Y+2.)}{(X \times (5.+X) \times Y^2)}.\nonumber \\
\end{eqnarray}$$
$$\begin{eqnarray}
&&C^{0}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=\left(X^2-\frac{83.}{20.}\right) \times \frac{3.}{X}+(1.-X) \times Y^2 \times \frac{X}{49.} \nonumber \\
&&\qquad+\,\frac{5. \times (X^2-Y-3.) }{(X-Y) \times X} \times \frac{(Y+2.)}{(X \times (5.+X) \times Y^2)}.\nonumber \\
\end{eqnarray}$$
 $C^{0}(\frac{3}{2} \rightarrow \frac{5}{2}) (T=5\,000\,{\rm K}))$
given in equation (17) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), we found that
$C^{0}(\frac{3}{2} \rightarrow \frac{5}{2}) (T=5\,000\,{\rm K}))$
given in equation (17) of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), we found that
 $re\textrm {(Ca \textsc {ii})}$
≃ 2%,
$re\textrm {(Ca \textsc {ii})}$
≃ 2%,
 $re\textrm {(Ba \textsc {ii})}$
≃ 19%,
$re\textrm {(Ba \textsc {ii})}$
≃ 19%,
 $re\textrm {(Sr \textsc {ii})}$
≃ 4%. Note that in Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), the polarisation transfer rates are denoted by Dk
(J′ → J, T) instead of the notation Ck
(J′ → J, T) adopted here.
$re\textrm {(Sr \textsc {ii})}$
≃ 4%. Note that in Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004), the polarisation transfer rates are denoted by Dk
(J′ → J, T) instead of the notation Ck
(J′ → J, T) adopted here.
-
•
(15)We notice that $$\begin{eqnarray}
&&C^{1}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad =\frac{7.}{5.Y(X+2.) } \times (X-2.) +2. X-\frac{7.}{X}
\end{eqnarray}$$
$$\begin{eqnarray}
&&C^{1}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad =\frac{7.}{5.Y(X+2.) } \times (X-2.) +2. X-\frac{7.}{X}
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 1%.
$re\textrm {(Ca \textsc {ii})}$
≃ 1%.
-
•
(16)We notice that $$\begin{eqnarray}
&&C^{2}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=2. \times X-\frac{Y}{3.}-3.- \frac{(X-3.)}{(7.-Y)} \\
&&\qquad-\, \frac{\frac{7.}{X^2}}{(-2.+X) \times (\frac{Y}{2.}+X) \times (Y+2.)}.
\end{eqnarray}$$
$$\begin{eqnarray}
&&C^{2}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=2. \times X-\frac{Y}{3.}-3.- \frac{(X-3.)}{(7.-Y)} \\
&&\qquad-\, \frac{\frac{7.}{X^2}}{(-2.+X) \times (\frac{Y}{2.}+X) \times (Y+2.)}.
\end{eqnarray}$$
 $re\textrm {(Ca \textsc {ii})}$
≃ 5%,
$re\textrm {(Ca \textsc {ii})}$
≃ 5%,
 $re\textrm {(Ba \textsc {ii})}$
≃ 3%, and
$re\textrm {(Ba \textsc {ii})}$
≃ 3%, and
 $re\textrm {(Sr \textsc {ii})}$
≃ 26%.
$re\textrm {(Sr \textsc {ii})}$
≃ 26%.
-
•
(17)When we compare a direct calculation of $$\begin{eqnarray}
&&C^{3}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=\frac{ \frac{8. \times X}{7.}-2. }{\left(\frac{Y}{3.}+\frac{1.}{2.}\right) \times [(X+Y) \times \frac{X}{5.}+ \frac{\frac{7.}{2.}}{(X+Y)}]} \nonumber\\
&&\qquad+\,X-2.
\end{eqnarray}$$
$$\begin{eqnarray}
&&C^{3}\left(\frac{3}{2} \rightarrow \frac{5}{2}\right) (T=5\,000\,{\rm K}) /(n_{\textrm {H}} \times 10^{-9}) \nonumber \\
&&\quad=\frac{ \frac{8. \times X}{7.}-2. }{\left(\frac{Y}{3.}+\frac{1.}{2.}\right) \times [(X+Y) \times \frac{X}{5.}+ \frac{\frac{7.}{2.}}{(X+Y)}]} \nonumber\\
&&\qquad+\,X-2.
\end{eqnarray}$$
 $C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
and its calculation via equation (17), we find that
$C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
and its calculation via equation (17), we find that
 $re\textrm {(Ca \textsc {ii})}$
≃ 7%.
$re\textrm {(Ca \textsc {ii})}$
≃ 7%.
Only the excitation collisional transfer rates
![]() $C^{0}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
$C^{0}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
![]() $C^{1}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
$C^{1}(\frac{3}{2} \rightarrow \frac{5}{2})$
,
![]() $C^{2}(\frac{3}{2} \rightarrow \frac{5}{2})$
, and
$C^{2}(\frac{3}{2} \rightarrow \frac{5}{2})$
, and
![]() $C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
are given here. However, it is straightforward to retrieve the values of the de-excitation collisional rates
$C^{3}(\frac{3}{2} \rightarrow \frac{5}{2})$
are given here. However, it is straightforward to retrieve the values of the de-excitation collisional rates
![]() $C^{0}(\frac{5}{2} \rightarrow \frac{3}{2})$
,
$C^{0}(\frac{5}{2} \rightarrow \frac{3}{2})$
,
![]() $C^{1}(\frac{5}{2} \rightarrow \frac{3}{2})$
,
$C^{1}(\frac{5}{2} \rightarrow \frac{3}{2})$
,
![]() $C^{2}(\frac{5}{2} \rightarrow \frac{3}{2})$
, and
$C^{2}(\frac{5}{2} \rightarrow \frac{3}{2})$
, and
![]() $C^{3}(\frac{5}{2} \rightarrow \frac{3}{2})$
by applying the detailed balance relation:
$C^{3}(\frac{5}{2} \rightarrow \frac{3}{2})$
by applying the detailed balance relation:
 $$\begin{eqnarray}
&&C^k(J_u \rightarrow J_l, T) \nonumber\\
&&\quad= \frac{2J_l+1}{2J_u+1} \exp \left(\frac{E_{J_u}-E_{J_l}}{k_{\rm B}T}\right) \; \; C^k_I(J_l \rightarrow J_u, T),
\end{eqnarray}$$
$$\begin{eqnarray}
&&C^k(J_u \rightarrow J_l, T) \nonumber\\
&&\quad= \frac{2J_l+1}{2J_u+1} \exp \left(\frac{E_{J_u}-E_{J_l}}{k_{\rm B}T}\right) \; \; C^k_I(J_l \rightarrow J_u, T),
\end{eqnarray}$$
where Jl =3/2 (lower level) and Ju =5/2 (upper level); EJ being the energy of the level (J) and k B the Boltzmann constant.
Thanks to the relationships given here, any collisional rates can be obtained by simply determining the value of n* and E p.
4 HYPERFINE STRUCTURE COLLISIONAL RATES
The procedure for calculating the hyperfine structure rates consists of following steps:
-
• Determination of the hyperfine eigenstates after diagonalisation of the Hamiltonian.
-
• Calculation of the interaction potential which is expressed in the basis of the set of the hyperfine eigenstates.
-
• Calculation of the collisional scattering matrix in the same hyperfine structure basis by solving the Schrödinger equation.
-
• Finally, one must perform the integrations over the impact parameters and the relative velocities.
This is what we will call ‘direct method’. There is also an ‘indirect’ and more practical method that allows the calculation of the hyperfine depolarisation and polarisation transfer rates via the values of the collisional rates associated to the fine structure, Dk (J) and Ck (J → J′).
4.1 On the possibility of the direct method of the calculations of the hyperfine structure rates
There are two types of problems in the direct calculations of the hyperfine collisional rates, first one corresponds to the zero-magnetic field case and second one corresponds to non-zero magnetic field case.
-
1. Zero magnetic field case: Giving a real numerical prediction in the cases where the coherences (interferences) between different hyperfine levels are taken into account is a complicated problem which would be taken up in the future. In fact, one needs a full study based on accurate interaction potentials and close coupling dynamical description that fully accounts for the collision channels associated to the hyperfine levels and the coherences between them. In particular, the interaction potential, the wavefunctions, and the Hamiltonian must be expressed in a basis vectors formed from the complete set of hyperfine eigenstates which take into account the coherences. The fact that the magnetic field is zero implies that the basis is uniquely determined and the good quantum numbers of the basis remain unchangedFootnote 1 which makes the calculations of the hyperfine structure rates possible but rather complicated.
-
2. Non-zero magnetic field case: In a magnetised medium like the solar atmosphere and especially in the so-called Paschen–Back effect regime, the hyperfine eigenstates of the total Hamiltonian can be changed according to the value of the magnetic field. Thus, total Hamiltonian should be diagonalised for each magnetic field to yield the hyperfine eigenstates (e.g., Landi Degl’Innocenti & Landolfi 2004) and, after that, the interaction potential and the dynamics of collisions have to be treated in the basis of the set of the obtained hyperfine eigenstatesFootnote 2 .
Inversion of the scattering polarisation including a proper treatment of elastic and inelastic collisions in the presence of strong magnetic field cannot be performed at least in the near future. The main reason is that the magnetic field is unknown before the interpretation of the scattering polarisation and thus cannot be considered in the collisional problem. In fact, the magnetic field is typically invoked as free fitting parameter to superpose theoretical Stokes profiles to observed ones; however, the collisional rates have to be obtained and introduced in the SEE before the fitting.
A possible solution of this problem is to perform the calculations of the collisional rates for expected range of magnetic field values in order to determine an empirical law of the variation of the collisional cross-section as a function of the magnetic field (e.g., Volpi & Bohn Reference Volpi and Bohn2002).
The solar physicist should be aware that using collisional rates calculated in zero magnetic field are suitable only for the Hanle effect regime. It should be sufficient to observe that magnetic-induced crossing interferences in the
 $^2P_{\frac{3}{2}}$
level of Na I would set on for ~ 10 Gauss implying the change of the eigenstates of the total Hamiltonian. It is worth noting that Kerkeni & Bommier (Reference Kerkeni and Bommier2002) unawarely used collisional rates for the
$^2P_{\frac{3}{2}}$
level of Na I would set on for ~ 10 Gauss implying the change of the eigenstates of the total Hamiltonian. It is worth noting that Kerkeni & Bommier (Reference Kerkeni and Bommier2002) unawarely used collisional rates for the
 $^2P_{\frac{3}{2}}$
level of Na I which are calculated in the limit of zero magnetic field. This would induce errors in their modelling of the atomic polarisation of the
$^2P_{\frac{3}{2}}$
level of Na I which are calculated in the limit of zero magnetic field. This would induce errors in their modelling of the atomic polarisation of the
 $^2P_{\frac{3}{2}}$
level considering that the strength of magnetic fields in the quiet Sun can be tenths of Gauss.
$^2P_{\frac{3}{2}}$
level considering that the strength of magnetic fields in the quiet Sun can be tenths of Gauss.
4.2 Calculation of the hyperfine structure rates by using the indirect method: the frozen nuclear spin approximation
It is worth noticing that the indirect method can be used only for zero magnetic field case.
The (de)polarisation rates obtained in this paper (i.e., Dk (J) and Ck (J → J′)) can be utilised only in zero magnetic field case or in Hanle effect regime. In addition, we do not obtain directly the collisional rates for the hyperfine levels. We neglect the effect of the hyperfine structure during the collision.
In the DSB approach, our aim was to propose a general method, i.e., which can be applied to any ion. Thus, we tried to neglect, whenever possible, the parts of the interaction potential which are specific to a given ion. We compared our results to those obtained with quantum chemistry methods and showed that the precision of the DSB method is sufficient for correctly studying the SSS (see Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b, Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004). We notice that those quantum-chemistry methods take into account spin–orbit interactions but not the hyperfine structure effects.
Our numerical results are obtained for the depolarisation and polarisation transfer rates for fine structure J-levels. In order to obtain the collisional rates for the hyperfine levels, the frozen nuclear spin approximation must be applied. The frozen approximation means that during the collision the nuclear spin of the perturbed ion is conserved. This would be the case if
ΔE
HFS is the energy of the hyperfine structure and
![]() $ \displaystyle \tau$
is the typical time duration of a collision. Equation (19) is typically satisfied in the solar conditions (e.g., Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b).
$ \displaystyle \tau$
is the typical time duration of a collision. Equation (19) is typically satisfied in the solar conditions (e.g., Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003b).
In the typical solar conditions, it is easy to show that 1/τ ~ 1013 s−1 (i.e., 1/τ ~ 334 cm−1). In these conditions, the hyperfine splitting is usually much smaller than 1/τ and therefore one can assume that the nuclear spin is conserved during the collision. It is important, however, to not confuse this condition with the fact that the SEE must be solved for the hyperfine levels when the inverse of the lifetime of the level is smaller than the hyperfine splitting, i.e., the hyperfine levels are separated.
Our relationships given by the equations (2)– (17) can be used to easily derive the hyperfine depolarisation rates and polarisation transfer rates for any singly ionised atom. This is the indirect method which is based on the frozen core approximation. According to this method, the hyperfine collisional rates are given as a linear combination of the fine structure rates, first obtained by Nienhuis (Reference Nienhuis1976) and Omont (Reference Omont1977).
5 COMPLEX ATOMS
5.1 Why treating complex atoms?
The important aspect of the DSB method is its extension to the cases of complex atoms and ions. Originally, this extension was presented and explained in detail by Derouich, Sahal-Bréchot, & Barklem (Reference Derouich, Sahal-Bréchot and Barklem2005b). Its importance appeared especially in the atlas of the linearly polarised solar-limb spectrum published by Gandorfer (Reference Gandorfer2000, Reference Gandorfer2002, Reference Gandorfer2005), where the linear polarisation of the lines of complex atoms/ions is particularly interesting. In fact, among atomic polarised lines presented in Gandorfer (Reference Gandorfer2000), there are 38% of polarised Fe i lines and 13% for Ti i. The observations of the linear polarisation reported by Gandorfer (Reference Gandorfer2000, Reference Gandorfer2002, Reference Gandorfer2005) show polarisation peaks in many spectral lines of complex ions, e.g., Nd ii 5249 Å, Eu ii 4129 Å, Ce ii 4062 Å, Ce ii 4083 Å, Zr ii 5350 Å, etc. (e.g. Manso Sainz, Landi Degl’Innocenti, & Trujillo Bueno Reference Manso Sainz, Degl’Innocenti and Bueno2006).
Depolarising collision rates of complex ions are vital for a reliable interpretation of such lines and can be theoretically obtained only via our semi-classical theory with good accuracy. It is important to notice that it is very difficult or even impossible to treat collisional processes, involving complex neutral and ionised atoms, by standard quantum chemistry methods. Our results allowed us to calculate, for the first time, the (de)polarisation rates of the levels associated to complex atoms (Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2005b).
5.2 Accuracy of the calculations
The results given by the equations (2)–(17) are concerned with simple atoms. The electronic configuration of the complex ion has one optical electron above an incomplete (i.e., open) subshell which has a non-zero angular momentum. To derive the collisional rates of levels of complex ions from those of simple ions, we consider that only the valence electron can undergo perturbations due to collisions with hydrogen atoms. This is the frozen core approximation. This approximation has been adopted in our calculations of the depolarisation and polarisation transfer rates, but also it has been used by ABO semi-classical theory for collisional line broadening by neutral hydrogen.
ABO have tested the results for both complex atoms like Fe i (Multiplets 1146 and 1165) and simple atoms (Multiplets 7, 9, and 11 of Mg i; Multiplet 4 of Na i; Ca ii infrared triplet). They estimated the accuracy of their theory to be around 20% or better (Barklem Reference Barklem1998).
ABO used two methods in testing the collisional rates. The rates were used to fit the spectrum of selected solar lines and the derived abundance was compared with meteoritic abundance of the emitting atoms or the solar abundance obtained by other authors. Alternatively, they adopted meteoritic abudance or previously determined solar abudance to obtain empirically collisional broadening cross-sections by fitting the line profile. In either method, a single parameter is adjusted to achieve the best possible match between the observed solar spectrum and the synthesised spectrum (Barklem Reference Barklem1998).
In the description of the complex or simple atom/ion, we adopt the same description used by ABO. For example, calculations of (de)polarisation rates and broadening rates associated with Fe I lines are based on the same interaction potential and the same dynamics of collisions. There are no additional conceptual approximations to extend the ABO theory to the calculations of the depolarisation rates performed by DSB. Thus, the conclusions of ABO concerning the accuracy remain valid for the case of (de)polarisation rates. This means that for complex atoms/ions, the accuracy of the (de)polarisation rates must be around 20% or better.
The main idea which allowed the extension of the results obtained for simple atoms/ions to complex atoms/ions is the use of the frozen core approximation. This allows treatment of heavy and/or complex atoms/ions like Fe i, Ti i, Nd ii, Eu ii, Ce ii, Zr ii, etc., whose collisional rates cannot be presently calculated via quantum chemistry methods. The spectral lines of such atoms/ions show significant polarisation peaks in many spectral lines (see the atlases by Gandorfer Reference Gandorfer2000, Reference Gandorfer2002, Reference Gandorfer2005).
In Section 2 of Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2005b), the DSB model for complex atom/ion was explained. According to the DSB model, the electronic coonfiguration of a complex atom/ion is composed of three parts which were fully explained by Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2005b). As a result, it was possible to show how to derive the depolarisation and polarisation transfer rates of complex ions from the rates associated to simple ions—the (de)polarisation rate of a complex atom can be written as a linear combination of the (de)polarisation rates of simple atom. Thus, the relationships given in this paper are easily applicable to the case of complex ions.
6 CONCLUSIONS
This paper completes the previous work of Derouich (Reference Derouich2017) which was devoted to the case of the polarisation of the p-states of ions. The scattering polarisation profiles of the solar ions have been (and are still) widely investigated both from theoretical and observational points of view. To gain complete understanding of the scattering polarisation in the photosphere of the Sun, one should obtain collisional rates for ion–hydrogen interactions. Calculations of the (de)polarisation collisional rates affecting the levels of the solar ions, first require the calculation of the atomic wavefunctions and interaction potentials. Second, the time-dependent Schrödinger equations have to be solved on the basis of the set of eigenfunctions. This is a complicated problem which we show that could be avoided by applying general relationships provided in this paper.
In fact, in this paper, we provide useful relationships which allow the calculations of any depoalrisation and polarisation transfer rates of the d-states of complex and simple ions. The hyperfine levels are also treated in this work. The establishment of the relationships was possible, thanks to the general nature of the DSB approach, but also to the very powerful GP methods.
ACKNOWLEDGEMENTS
This work was supported by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (D-049-130-1437). The authors, therefore, gratefully acknowledge the DSR technical and financial support.