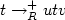We give an explicit criterionfor unavoidability of word sets. We characterize extendible, finitelyand infinitely as well, elements in them. We furnish a reasonable upperbound and an exponential lower bound on the maximum leghth of words in a reduced unavoidable set of agiven cardinality.

Using an inductive definition of normal terms of thetheory of Cartesian ClosedCategories with a given graph of distinguished morphisms, we give a reduction freeproof of the decidability of this theory. This inductive definition enables us toshow via functional completeness that extensions of such a theory by new constants (“indeterminates”) are conservative.

Under the assumption that the Polynomial-TimeHierarchy does not collapsewe show for a regular language L:the unbalanced polynomial-time leaf language class determined by L equals  iff L is existentially but notquantifierfree definable in FO[<, min, max, +1, −1].Furthermore, no suchclass lies properly between NP and co-1-NP or NP⊕co-NP. The proofs rely on a result of Pin and Weilcharacterizing the automata of existentially first-order definable languages.

In this paper we show that neither the set of all valid equationsbetween shuffle expressions nor the set of schemas of valid equations isrecursively enumerable. Thus, neither of the sets can be recursivelygenerated by any axiom system.

String rewriting reductions of the form $t\to_R^+ utv$ , called loops, are the most frequent cause of infinite reductions (non-termination). Regarded as a model of computation, infinite reductions are unwanted whence their static detection is important. There are string rewriting systems which admit infinite reductions although they admit no loops. Their non-termination is particularly difficult to uncover. We present a few necessary conditions for the existence of loops, and thus establish a means to recognize the difficult case. We show in detail four relevant criteria: (i) the existence of loops is characterized by the existence of looping forward closures; (ii) dummy elimination, a non-termination preserving transformation method, also preserves the existence of loops; (iii) dummy introduction, a transformation method that supports subsequent dummy elimination, likewise preserves loops; (iv) bordered systems can be reduced to smaller systems on a larger alphabet, preserving the existence and the non-existence of loops. We illustrate the power of the four methods by giving a two-rule string rewriting system over a two-letter alphabet which admits an infinite reduction but no loop. So far, the least known such system had three rules.

In [6] it was shown that shuffle languagesare contained in one-way-NSPACE(log n) and in P.In this paper we show that nondeterministic one-way logarithmic spaceis in some sense the lower bound for accepting shuffle languages.Namely, we show that there exists a shuffle language which is notaccepted by any deterministic one-way Turing machine with space bounded bya sublinear function, and that there exists a shuffle language which isnot accepted with less than logarithmic space even if we allow two-waynondeterministic Turing machines.