Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-06T08:27:27.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Looping String Rewriting

Published online by Cambridge University Press:  15 August 2002

Alfons Geser  and
Hans Zantema
Alfons Geser
Affiliation:
Alfons Geser, Symbolisches Rechnen, Wilhelm-Schickard-Institut für Informatik, Universität Tübingen, Sand 13, 72076 Tübingen, Germany
Hans Zantema
Affiliation:
Department of Computer Science, Universiteit Utrecht, P.O. Box 80.089, 3508 TB Utrecht, The Netherlands
Get access

Abstract

String rewriting reductions of the form $t\to_R^+ utv$ 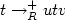, called loops, are the most frequent cause of infinite reductions (non-termination). Regarded as a model of computation, infinite reductions are unwanted whence their static detection is important. There are string rewriting systems which admit infinite reductions although they admit no loops. Their non-termination is particularly difficult to uncover. We present a few necessary conditions for the existence of loops, and thus establish a means to recognize the difficult case. We show in detail four relevant criteria: (i) the existence of loops is characterized by the existence of looping forward closures; (ii) dummy elimination, a non-termination preserving transformation method, also preserves the existence of loops; (iii) dummy introduction, a transformation method that supports subsequent dummy elimination, likewise preserves loops; (iv) bordered systems can be reduced to smaller systems on a larger alphabet, preserving the existence and the non-existence of loops. We illustrate the power of the four methods by giving a two-rule string rewriting system over a two-letter alphabet which admits an infinite reduction but no loop. So far, the least known such system had three rules.

Keywords

string rewritingsemi-thue systemterminationloopterm rewritingtransformation orderingdummy introductiondummy eliminationoverlap closureforward closure.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 33 , Issue 3 , May 1999 , pp. 279 - 301
Copyright
© EDP Sciences, 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adjan, S. and Oganesjan, G., Problems of equality and divisibility in semigroups with a single defining relation. Mat. Zametki 41 (1987) 412-421.
R. Book and F. Otto, String-rewriting systems. Texts and Monographs in Computer Science. Springer, New York (1993).
Dershowitz, N., Termination of linear rewriting systems. In Proc. of the 8th International Colloquium on Automata, Languages and Programming (ICALP81), Springer, Lecture Notes in Computer Science 115 (1981) 448-458. CrossRef
Dershowitz, N., Termination of rewriting. J. Symb. Comput. 3 (1987) 69-115; Corrigendum 4 (1987) 409-410. CrossRef
Dershowitz, N. and Hoot, C., Natural termination. Theoret. Comput. Sci. 142 (1995) 179-207. CrossRef
Ferreira, M. and Zantema, H., Dummy elimination: Making termination easier. In Proc. 10th Conf. Fundamentals of Computation Theory, H. Reichel, Ed., Springer, Lecture Notes in Computer Science 965 (1995) 243-252. CrossRef
A. Geser, Termination of one-rule string rewriting systems ℓ → r where |r| ≤ 9. Tech. Rep., Universität Tübingen, D (Jan. 1998).
Guttag, J.V., Kapur, D. and Musser, D.R., On proving uniform termination and restricted termination of rewriting systems. SIAM J. Comput. 12 (1983) 189-214. CrossRef
G. Huet and D.S. Lankford, On the uniform halting problem for term rewriting systems. Rapport Laboria 283, INRIA (1978).
M. Jantzen, Confluent string rewriting, Vol. 14 of EATCS Monographs on Theoretical Computer Science. Springer, Berlin (1988).
Y. Kobayashi, M. Katsura and K. Shikishima-Tsuji, Termination and derivational complexity of confluent one-rule string rewriting systems. Tech. Rep., Dept. of Computer Science, Toho University, JP (1997).
W. Kurth, Termination und Konfluenz von Semi-Thue-Systemen mit nur einer Regel. Dissertation, Technische Universität Clausthal, Germany (1990).
Kurth, W., One-rule semi-Thue systems with loops of length one, two, or three. RAIRO Theoret. Informatics Appl. 30 (1995) 415-429. CrossRef
D.S. Lankford and D.R. Musser, A finite termination criterion. Tech. Rep., Information Sciences Institute, Univ. of Southern California, Marina-del-Rey, CA (1978).
Y. Matiyasevitch and G. Sénizergues, Decision problems for semi-Thue systems with a few rules. In IEEE Symp. Logic in Computer Science'96 (1996).
R. McNaughton, The uniform halting problem for one-rule Semi-Thue Systems. Tech. Rep. 94-18, Dept. of Computer Science, Rensselaer Polytechnic Institute, Troy, NY, Aug. 1994. See also ``Correction to The Uniform Halting Problem for One-rule Semi-Thue Systems'', personal communication (Aug. 1996).
R. McNaughton, Well-behaved derivations in one-rule Semi-Thue Systems. Tech. Rep. 95-15, Dept. of Computer Science, Rensselaer Polytechnic Institute, Troy, NY (Nov. 1995).
R. McNaughton, Semi-Thue Systems with an inhibitor. Tech. Rep. 97-5, Dept. of Computer Science, Rensselaer Polytechnic Institute, Troy, NY (1997).
Otto, F., The undecidability of self-embedding for finite semi-Thue and Thue systems. Theoret. Comput. Sci. 47 (1986) 225-232. CrossRef
Rosen, B.K., Tree-manipulating systems and Church-Rosser Theorems. J. ACM 20 (1973) 160-187. CrossRef
Shikishima-Tsuji, K., Katsura, M. and Kobayashi, Y., On termination of confluent one-rule string rewriting systems. Inform. Process. Lett. 61 (1997) 91-96. CrossRef
C. Wrathall, Confluence of one-rule Thue systems. In Word Equations and Related Topics, K.U. Schulz, Ed., Springer, Lecture Notes in Computer Science 572 (1991).
H. Zantema and A. Geser, A complete characterization of termination of 0 p 1 q → 1 r 0 s .Applicable Algebra in Engineering, Communication, and Computing. In print.
Zantema, H. and Geser, A., A complete characterization of termination of 0 p 1 q → 1 r 0 s . In Proc. of the 6th Conference on Rewriting Techniques and Applications, J. Hsiang, Ed., Springer, Lecture Notes in Computer Science 914 (1995) 41-55. CrossRef