Introduction
Active ice streams of the West Antarctic ice sheet exhibit high flow velocities, despite small gravitational driving stresses (Reference Whillans, Bentley, van der Veen, Alley and BindschadlerWhillans and others, 2001). Several studies have shown that the high surface velocities are primarily due to basal motion, with ice deformation playing an insignificant role in comparison (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986; Reference Frolich, Vaughan and DoakeFrolich and others, 1989; Reference Kamb, Alley and BindschadlerKamb, 2001). Basal conditions therefore control, to a large extent, the flow rates of ice streams. It has been argued that driving stress within ice streams may be balanced in parts by localized ‘sticky spots’, i.e. places where resistance to basal sliding is significantly higher than over the surrounding areas (Reference AlleyAlley, 1993; Reference Joughin, MacAyeal and TulaczykJoughin and others, 2004, Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyeal2006). This suggests that short-term (<100 years) future changes in ice flux may arise due to changes in the spatial configuration and the degree of basal lubrication of such local pinning points. However, if these pinning points are local undulations and bumps in bed geometry, the potential for such future changes in ice flux is more limited.
The goal of this study is to estimate spatial variations in basal slipperiness and the reasons for short-scale (<10h, where h is mean ice thickness) variations in surface velocity and surface topography. The motivation for doing this is to assess, in general terms, the potential for future changes in the contribution of Rutford Ice Stream to global sea-level change due to changes in local basal conditions.
We employ Bayesian inference to update estimates of both basal slipperiness and bed geometry. Our estimate of basal properties combines information extracted from the measurements with other available information obtained independently of the measurements. This combined estimate is referred to as the a posteriori estimate, while the estimate obtained independently, and possibly prior to the measurements, is referred to as the a priori estimate. The estimates are given in the form of probability density functions (PDFs) describing the probability of a given distribution of basal slipperiness and bed geometry. The distribution that maximizes the a posteriori probability is referred to as the ‘maximum a posteriori estimate’. The term ‘Bayesian inference’ derives from the use of Bayes’s theorem in calculating the conditional probability of the estimate, m, given the measurements, d, i.e. the probability, P(m|d). The methodology used is outlined below and described in more detail by Reference Gudmundsson and RaymondGudmundsson and Raymond (2008) and Reference Raymond and GudmundssonRaymond and Gudmundsson (2009).
Methodology
Notation
We denote vectors by boldface italic letters (e.g. d), and matrices by bold upper-case letters (e.g. C). The notation P(m|d) indicates the multidimensional PDF of the vector m conditional on d. In d = g(m), the forward function, g, is vector-valued and returns the vector d for a given value of the vector m. Superscript ‘T’ means transposition, here to column vectors. The subscript ‘prior’ denotes a prior estimate, while a hat (e.g. 
) indicates a maximum a posteriori (MAP) estimate.
Inverse method
To estimate the basal properties of Rutford Ice Stream, we perform a nonlinear Bayesian inverse calculation consisting of determining P(m|d), the probability density for the system state, m, i.e. the basal properties, conditional on the surface measurement vector, d. This probability distribution is termed the ‘a posteriori distribution’ and can be written using Bayes’s rule as
As a function of the system state, m, the a posteriori distribution is the product of two terms: the likelihood function, P(d |m), and the a priori estimate of the system state, P(m|m prior). The likelihood function measures the probability of observing the data, d, if the system state were m, while the a priori probability density incorporates information that is known independently of the data.
We assume in the following that both the measurement errors and the prior estimate can be described by multidimensional Gaussian distributions, i.e. the likelihood function is given by
while the a priori probability distribution is given by
The function g represents the numerical forward ice-stream model that calculates the surface components given a discretized system state, m = [b C]T, where b and C are the basal topography and basal slipperiness vectors of gridpoint values, respectively. The observed surface data, d = [s u w]T, consists of the surface topography, s, horizontal surface velocity, u, and vertical surface velocity, w. CD is the data covariance matrix, CM is the model covariance matrix and m prior the centre of the a priori probability density.
Taking the negative of the logarithm of the product of Equations (2) and ( 3) results in the cost function
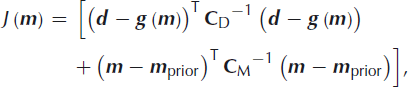
from which we single out the system state with the largest probability, 
, referred to as the MAP estimate. The maximum a posteriori model is derived from an iterative optimization process of the objective function, Equation (4), that minimizes J(m).
We have used a nonlinear Gauss–Newton method in the minimization (Reference Raymond and GudmundssonRaymond and Gudmundsson, 2009). The Fréchet derivatives, which are the first derivatives of the forward model with respect to the model parameters, are approximated with analytical transfer functions (Reference GudmundssonGudmundsson, 2003). These transfer functions are valid for linear media and small-amplitude variations of the basal disturbances. They are functions of the wavenumber vector, k, and of a set of zeroth-order parameters that describe the mean state of the glacier, i.e. surface slope, a, slip ratio, C (0), mean ice thickness, h (0), and mean deformational surface velocity, u d. Approximating the Fréchet derivatives by the analytical transfer functions greatly enhances the numerical efficiency of the method. Reference Raymond and GudmundssonRaymond and Gudmundsson (2009) show that this approximation is suitable for both nonlinear finite-amplitude effects and rheological nonlinearities
Using the transfer function formulation, the minimization of the objective function, Equation (4), is most conveniently done in Fourier space. Thus, all vector components entering the objective function, Equation (4), i.e. surface fields, a priori and covariance matrices, are transformed into frequency space. The correct matrix transpose is the Hermitian transpose, here denoted by the superscript ‘H’. The covariance matrices for the data and model parameters, CD and CM, are transformed into Fourier space by the relation FCFH, where F is the discrete Fourier transform matrix and C the matrix to be transformed. The transformation of the above components into frequency space requires them to be first interpolated onto an equidistant grid. This gives rise to interpolation errors and some spatial correlation between interpolated values, both of which can be estimated using geostatistical interpolation methods.
Inverse procedure
The estimation procedure is described in detail by Reference Raymond and GudmundssonRaymond and Gudmundsson (2009) and Reference Gudmundsson and RaymondGudmundsson and Raymond (2008). The main steps involved in the iterative optimization by which the objective function, J(m), is minimized, are:
Initialization step: Define initial distributions for bedrock topography and basal slipperiness. Here we use the a priori estimate, m prior, as a starting point for the optimization of the objective function.
Forward step: Calculate the steady-state surface response, g(m i ), for the given bedrock and the distribution of the basal slipperiness with the forward finite-element (FE) model. i indicates the ith iterate with m i = 0 = m prior.
Convergence step: The convergence test reads J(m
i
) − J(m
i−
1) ≪ 3N. This criterion is based on the fact that 3N corresponds theoretically to the expected value of 
(Reference TarantolaTarantola, 2005). Once the stopping criterion is satisfied, stop the iteration procedure, else
Inversion step: Determine incremental corrections to the prior bedrock profile and distribution of the basal slipperiness by inversion. Return to Forward step.
Quantifying uncertainties
Data uncertainties
The covariance matrix, CD, defines the uncertainties in the data. The matrix CD is a block diagonal matrix consisting of the matrices describing the uncertainties in the surface topography, Cs, horizontal velocity, Cu, and vertical velocity, Cw, along the main diagonal. The off-diagonal blocks are zero matrices, since no cross-correlation between the surface fields is considered. The elements along the main diagonal of the block matrices are the variances of the individual measurements about the mean of the multidimensional Gaussian probability, and the off-diagonal elements show to what extent these individual measurements are correlated
The covariance matrices for Cs, Cu and Cw used in the inversion result from an interpolation of the original surface data onto the nodes of the FE forward model using a best linear unbiased estimator (Reference KitanidisKitanidis, 1997).
Uncertainties in the model parameters
The prior probability, Equation (3), is represented by a Gaussian PDF, characterized by the mean and the covariance matrix. The mean, m prior, contains both a prior bed topography and a prior basal slipperiness distribution, (m prior = [b prior C prior ]T). The covariance matrix, CM, is of block diagonal form and consists of the matrices CB and CC describing the uncertainties in the prior bedrock topography and the prior basal slipperiness along the main diagonal, respectively. No cross-correlation between prior estimates of bed topography and basal slipperiness is considered, hence
The estimation of the covariance matrices, CB and CC, is described below.
Forward ice-stream model
We use a commercial FE program, MSC-MARC (MSC Software Corporation, 2000), to model the ice dynamics along the flowline on Rutford Ice Stream shown in Figure 1. The forward model is two-dimensional and plane-strain. Four-node, isoparametric, quadrilateral Hermann elements are used. A mixed semi-implicit Lagrangian–Eulerian approach is employed to determine the transient evolution of the surface (Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson, 2004; Reference RaymondRaymond, 2007). The coordinates are (x, z), where x is taken in the direction of the flowline and z is the vertical. The surface and the bed are given by z = s(x, t) and z = b(x), respectively, and t represents time. u and w denote the horizontal and vertical velocity components, respectively.
Fig. 1. Location map. A Landsat image showing the flowline on Rutford Ice Stream, West Antarctica, selected for the inversion as a thick solid line running down the centre of the ice stream (http://landsat.gsfc.nasa.gov/).
The numerical model solves the full equilibrium equations and the mass-conservation equation for incompressible ice. These equations read σij ,j = −ρgi and vi ,i = 0, respectively, where σij are the components of the Cauchy stress tensor, ρ is the ice density, g is the acceleration due to gravity and vi are the components of the velocity vector. The constitutive law is Glen’s flow law, extended following Reference HutterHutter (1983) with a linear term to avoid the singularity in viscosity as the deviatoric stress goes to zero:
In this equation, A is the rate factor, n is the stress exponent and 
, 
and τ are the strain rate, the deviatoric stress tensors and the effective shear stress, respectively. The parameter τ
0 is the crossover stress at which the linear and exponential terms contribute equally to the total strain rate. In this study, n = 3 and the rate factor, A = A
0
B(T), is temperature-dependent. The rate factor is expressed as the product of a constant rate factor, A
0, at a reference temperature and a parameter, B(T), describing the temperature dependence. The parameter B(T) follows a double exponential fit derived by Reference Smith and MorlandSmith and Morland (1981),
where T is the temperature (°C). The temperature profile is assumed to increase linearly from a mean surface temperature of T s = −25°C to T b = 0°C at the bed.
Boundary conditions
At the upstream and downstream model ends, velocities are prescribed. Along the bed, we prescribe a sliding relation of the form 
, which relates the basal shear stress, τ
b, to the basal sliding velocity, u
b. C(x) is the sliding coefficient and m is the sliding-law exponent, m = 1 in this study. Basal sliding is introduced in the numerical model by adding a uniform thin layer with the viscosity which gives a surface-parallel velocity at its top equal to the required sliding velocity.
The ice surface is stress-free and evolves with time according to the kinematic boundary condition. The kinematic boundary condition reads
where s(x, t) describes the surface elevation, t is the time, u and w are the horizontal and vertical surface velocities, respectively, and 
is the accumulation rate function.
Parameterization of side drag
We assume plane-strain conditions 
, absence of any transverse vertical shear 
and no along-flow variation in horizontal shear 
. It follows that the equilibrium conditions, σij
,j
+ ρgi
= 0, can be written as
Note that the ‘side-drag term’, ∂yσxy , can be interpreted as a fictitious body-force term. The size of this term can be estimated from measurements of surface velocity using
where η is the effective viscosity and u and v are the x and y components of the velocity vector. Alternatively, the size of this term can be varied in the numerical model until the calculated basal shear stress is comparable to previous estimates of basal stress obtained from surface measurements. Such previous estimates of basal shear stress on Rutford Ice Stream include those of Reference Frolich, Mantripp, Vaughan and DoakeFrolich and others (1987) who conducted a force-balance study of the ice stream using measurements of surface topography and surface velocities, Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others (2006) who estimated the basal stress distribution from satellite measurements of surface velocities, and Reference GudmundssonGudmundsson (2007) who estimated basal stress from measurements of tidal response. Despite using very different methods and different datasets, all these authors concluded that the basal shear stress of Rutford Ice Stream is ∼20 kPa. Given this good agreement between previous estimates of basal shear stress, we parameterized the side drag by introducing the side-drag terms as a fictitious body-force term in the x-direction, and set the size of this term to give a basal shear stress of ∼20 kPa.
Rutford Ice Stream Inversion
The goal of the inversion is to determine both bed topography and basal slipperiness from surface data. The surface datasets are measurements of surface topography, surface velocity, surface mass balance and rate of surface elevation change.
In an initial inversion experiment (experiment A), the basal properties are estimated using only surface measurements of horizontal (u) and vertical (w) velocity, without imposing any constraints on rates of surface elevation change, ∂s/∂t, and using a model surface geometry derived from measurements. The MAP estimate is found by minimizing the cost function (Equation (4)), where the measurement vector, d, includes measurements of both u and w. As the model surface geometry is based directly on measurements and is not changed during the experiment, the misfit between measured and modelled surface geometry is always equal to zero.
In a second inversion experiment (experiment B), estimates for both bed and surface geometry, as well as for the basal slipperiness, are updated. The modelled surface topography is allowed to evolve with time toward a steady state for a given surface mass-balance distribution. The measured surface topography is now included in the measurement vector, and the difference between measured and calculated surface geometry enters the cost function (in experiment A this difference is always equal to zero). Experiment B gives rates of elevation change that are close to zero, and, if fully successful, a surface topography profile that is within expected errors of measurements of surface topography.
Inversion experiment B is motivated by the fact that measured surface velocities on Rutford Ice Stream have not changed significantly over the past 25 years Reference Gudmundsson and Jenkins(Gudmundsson and Jenkins, 2009). Repeated GPS elevation measurements also show no significant temporal changes in surface elevation. It therefore appears that Rutford Ice Stream is close to a steady state.
Using the kinematic boundary condition at the surface, the rate of elevation change can be determined from surface slope, surface velocity and surface mass balance:
If perfectly accurate measurements of u, w, b and s were available everywhere along the profile, the rate of elevation change could be calculated using the above equation. Hence, there would be no additional information contained in the estimates of the rate of elevation change, and the results of experiments A and B would be identical. However, for inaccurate measurements available at discrete locations, having estimates of ∂s/∂t gives, in general, some additional information. This can be utilized to improve the retrieval of basal properties and for model validation purposes. We show below that, in our case, the two inversion experiments result in significantly different estimates of basal properties.
Data
The selected flowline on Rutford Ice Stream is shown in Figure 1. Surface and bedrock topography data are based on airborne radar soundings (personal communication from H. Corr, 2008). The horizontal and vertical velocity data are a combination of surveyed stake movements made in 1978/79 and 1979/80 (Reference Stephenson and DoakeStephenson and Doake, 1982) and in 1984/85 and 1985/86 (Reference Frolich, Mantripp, Vaughan and DoakeFrolich and others, 1987) and data collected by G.H. Gudmundsson in three field seasons between 2002 and 2006. Analysing this dataset, Reference Gudmundsson and JenkinsGudmundsson and Jenkins (2009) found no evidence for any velocity changes on Rutford Ice Stream over the past 25 years.
We opt to use these ground-based stake velocity measurements rather than satellite-derived velocities for two reasons. First, the ground-based dataset is very comprehensive and gives velocities directly along the medial flowline. We see no reason why satellite data would significantly improve our knowledge of the velocity along the flowline. Second, the ground-based data give additional information about vertical velocity which is generally not available from satellite measurements.
Surface accumulation data based on polarization of 4.3 cm wavelength microwave emission were provided by Reference Arthern, Winebrenner and VaughanArthern and others (2006). All raw datasets are presented in Figure 2. Horizontal surface velocities increase from 0.8 m d−1 at the start of the upper end of the flowline to 1.1 m d−1 at the grounding line.
Fig. 2. Rutford Ice Stream data. (a) Surface and bedrock topography measured from airborne radar, (b) horizontal surface velocity, (c) vertical surface velocity and (d) water equivalent accumulation rate along the profile shown in Figure 1. The grounding line is located at the end of the profile at x ≈ 300 km.
Data errors and covariance models for the original datasets were estimated from experimental variograms. All datasets were interpolated to the nodal points of the forward FE model using a best linear unbiased estimator (BLUE). The BLUE covariance matrices were calculated and used to define the various covariance matrices used in the inverse calculation. The interpolated datasets with error bars are shown in Figure 3. The error bars are the square roots of the main diagonal elements of the corresponding covariance matrices. Even for uncorrelated data errors, interpolating the data onto the FE grid introduces some spatial correlations in the resulting dataset. These correlations are described by the BLUE covariance matrices. As a consequence, the covariance matrices describing the surface data errors are not diagonal matrices.
Fig. 3. The data and estimated data errors after interpolation onto the nodal points of the FE forward model. (a) Surface and bedrock topography with dots denoting the error range, (b) horizontal and (c) vertical surface velocities and corresponding error bars and (d) water equivalent accumulation rate.
Prior model parameters
For the inversion of the Rutford surface data, the prior estimate for the bedrock topography, b prior, was obtained by interpolating the radar measurements shown in Figure 2a onto an equidistant grid using BLUE. The resulting b prior is shown in Figures 3a and 4a (dashed curves). The prior basal slipperiness, C prior (Fig. 4b), was estimated from the basal shear stress, τ b, computed from the local ice thickness and surface slope and from the basal velocity on Rutford Ice Stream by the relation C prior = u b/τ b. The basal velocity is taken here to be the surface velocity, since the deformational ice velocity is generally small on Rutford Ice Stream. The a priori distributions for basal properties are used as a starting point for the inversion.
Fig. 4. Inversion experiment A. Solid curves show inferred (a) bedrock topography and (b) basal slipperiness distribution for the selected flowline on Rutford Ice Stream. The dashed curves show (a) the prior bedrock distribution obtained by interpolating the airborne radar data using BLUE to the forward FE grid and (b) the prior basal slipperiness distribution.
The transfer functions give the surface response to basal disturbances around a uniformly inclined slab of constant thickness. Hence, we need to define a local slope and thickness to calculate the transfer functions. These zeroth-order parameters entering the transfer functions were determined by applying a 40 km low-pass Lanczos filter on the respective input and output fields of the forward FE model. The exact value used for the cut-off wavelength of the Lanczos filter (e.g. 40 km) has no effect on the final results. Only the convergence rate of the nonlinear inversion procedure may have been affected by the value used.
Inversion experiment A
We start by estimating basal properties (bed topography and basal slipperiness) along the selected flowline without explicitly constraining the rate of change of the surface topography, ∂s/∂t. In this experiment, the surface geometry of the FE forward model is fixed, i.e. estimates of surface geometry are not updated.
The measurement vector, d, entering the cost function, Equation (4), contains measurements of horizontal and vertical components of the surface velocity only. Note that the measured surface geometry could also have been considered as a part of the measurement vector. However, as the surface geometry of the numerical model is based on interpolation of direct measurements and is not updated in the course of the inversion, the corresponding residuals between modelled and measured quantities are automatically equal to zero. A detailed explanation of the inversion procedure is given by Reference Raymond and GudmundssonRaymond and Gudmundsson (2009).
A total of 14 iterations were needed for convergence. Figure 4 shows the maximum a posteriori solution for the bedrock and basal slipperiness distribution for the selected flowline on Rutford Ice Stream (solid curves). The prior distributions are shown for comparison (dashed curves). Figure 4a shows that for the upper half of the flowline (150 < x < 220 km), the final estimated bedrock shape is close to the initial prescribed bedrock topography derived from interpolated radar measurements. Over the lower half, however, the final estimated bed topography is ∼75 m higher than radar measurements suggest. The basal slipperiness distribution shows little short-scale (<10h) spatial variability. From x = 150 km to x ≈ 230 km, C varies by less than a factor of two. The most conspicuous feature of the basal slipperiness distribution in Figure 4b is the pronounced broad peak at x = 245 km where C increases by a factor of ∼20.
Figure 5 shows a comparison between observed and inferred surface data along the flowline. The figure shows that the forward model reproduces the horizontal velocity rather well apart from the region 220 < x < 260 km, where modelled surface velocities are consistently lower than indicated by observations. The vertical velocities are reproduced less precisely and are clearly often over- or underestimated. A clear indication that the results of the inversion are less than satisfactory comes from an inspection of calculated rates of surface elevation change shown in Figure 6. As the figure shows, the calculated rates of surface elevation change vary strongly along the profile between about −0.02 and 0.02 m d − 1 . There are no long-term estimates of surface elevation change on Rutford Ice Stream. However, surface velocities have changed by <0.1% a − 1 over the past 25 years (Reference Gudmundsson and JenkinsGudmundsson and Jenkins, 2009), and repeated GPS kinematic profiling over a 3 year period showed no significant changes in surface elevation. It therefore seems likely that Rutford Ice Stream is close to a steady state. Available kinematic GPS data give an upper limit of |∂s/∂t| = 0.2 m a − 1, although quite possibly the actual rate is considerably smaller. A modelled rate of 0.02 m d − 1 corresponds to a rate of elevation change of ∼7.3 m a − 1. Hence, the modelled rates shown in Figure 6 are at least two, if not three, orders of magnitude too large. We conclude that the results of inversion experiment A are clearly incompatible with the available data.
Fig. 5. Inversion experiment A: comparison between observed (crosses) and inferred (dashes) data along the flowline on Rutford Ice Stream. (a) Horizontal and (b) vertical velocity. The inferred surface data shown are the results of a forward step using the basal properties shown in Figure 4.
Fig. 6. Inversion experiment A: inferred rates of surface elevation change.
Inversion experiment B
The surface of the forward FE model is now allowed to esurface data shown are the results of a forward step using the basal olve with time until a steady state is reached (Equation (9)). Hence, we look for basal conditions that give zero rates of surface elevation change. Starting from the interpolated measured surface topography, the forward model calculates the surface evolution toward a steady state. Basal properties are then estimated through a minimization of Equation (4) where the measurement vector, d, now contains measurements of horizontal and vertical components of the surface velocity, and of surface topography. Note that in this inversion experiment the final surface topography can differ from the measured one. However, because the errors in the measured surface elevation are small (∼1 m), the result of a successful inversion is a distribution of basal properties (topography, slipperiness) forwhich theforward model gives a steady-state surface topography quite similar to the measured topography. The deviation of the modelled surface geometry from that measured is used for model verification purposes to test the correctness of model assumptions, in particular that of steady flow conditions.
Figure 7 shows the estimated bedrock topography and basal slipperiness distribution along the flowline (solid curves) and, for comparison, the corresponding a priori distributions (dashed curves). Over the whole length of the profile the overall shape of the inferred bed topography is similar to the initial estimate based on radar sounding. For 230 < x < 260 km the retrieved bed is ∼100 m less deep, resulting in ∼5% less total ice thickness in that area. The estimated basal slipperiness, C (Fig. 7b), shows a gradual increase in C toward the grounding line on which is superimposed a strong local increase at x ≈ 245 km. Apart from the sharp increase in slipperiness at ∼245 km, there are almost no clear signs of any short-scale (<10h) spatial variations in slipperiness.
Fig. 7. Inversion experiment B: estimated (a) bedrock topography and (b) basal slipperiness distribution along the medial flowline of Rutford Ice Stream. The dashed curves correspond to (a) the prior bedrock distribution and (b) the prior basal lubrication distribution. The MAP solution is shown as a solid curve.
Figure 8 shows residuals between measured and modelled surface data. In Figure 9 the datasets of measured and modelled surface data are plotted together for further comparison. As Figures 8a and 9a show, the surface topography is reproduced almost perfectly. For 150 < x < 220 km the residuals, Δs, are close to the error level. For the remaining part of the profile, the residuals between modelled and measured surface topography are up to ∼20 m. The residuals between modelled and measured horizontal velocities tell a similar story (Figs 8b and 9b). For 150 < x < 220 km the residuals are of similar size to measurement errors, while further downstream some systematic differences are observed. These systematic differences are at most ∼10% of the mean surface value. Vertical residuals (Figs 8c and 9c) are small over the whole profile and only larger than the measurement errors at a few locations. The calculated rates of surface elevation change are shown in Figure 10. Along the whole of the profile the rates of surface elevation change are, within numerical errors, equal to zero.
Fig. 8. Inversion experiment B: residuals between observations along the flowline on Rutford Ice Stream and FE model predictions for (a) surface topography, (b) horizontal and (c) vertical velocity. The solid curves show the residuals for the prior distribution, and the dashed curves those for the MAP solution. The dotted curves show the measurement errors, defined as the square roots of the main diagonal of the data covariance matrix, CD. The residuals are not detrended and are set artificially to zero at the upstream and downstream model boundaries to stabilize the inversion step.
Fig. 9. Inversion experiment B: comparison between observed (solid curve in (a) and crosses in (b) and (c)) and inferred data (dashed curves) along the flowline on Rutford Ice Stream. (a) Surface topography, (b) horizontal and (c) vertical velocity. The inferred data correspond to the FE prediction for the MAP solution shown in Figure 7.
Fig. 10. Inversion experiment B: inferred rates of surface elevation change.
Discussion
Inversion experiment A did not result in realistic rates of surface elevation change. For that reason alone the model can be unequivocally rejected and will not be discussed further. The experiment shows that it is possible to find distributions of basal properties (topography and slipperiness) that give a reasonably good fit with discrete measurements of horizontal and vertical surface velocities but unrealistic rates of surface elevation change.
Inversion experiment B gave more encouraging results. For the upper half of the profile all residuals are close to measurement errors. Over the lower half, however, residuals are generally significantly larger than measurement errors and are also clearly not randomly distributed.
That the model fails for the lower half of the profile is understandable. At x ≈ 250 km a bedrock ridge aligned with the flow rises ∼400 m above the surrounding part of the bed floor. The ridge is a few kilometres wide and runs down the whole remaining part of the profile toward the grounding line at x ≈ 300 km. Upstream from the head of the ridge, both published measurements of surface velocities by Reference Frolich, Mantripp, Vaughan and DoakeFrolich and others (1987, Reference Frolich, Vaughan and Doake1989) and a more detailed unpublished dataset by Gudmundsson show a strong transverse surface extension, which is followed by a corresponding transverse compression a few tens of kilometres further downstream. In the surface topography two prominent knolls, marking the upper and lower limits of the bedrock ridge, are clearly visible in satellite imagery. Strain rates calculated from stake measurements show that, for x > 230 km, transverse strain rates are comparable to or larger than the longitudinal strain rates (Reference Frolich, Mantripp, Vaughan and DoakeFrolich and others, 1987). Hence, the assumption of plane strain does not hold for this part of the profile and the failure of the model to produce acceptable results for this region is reassuring.
Having rejected modelling results for the region x > 230 km, we now focus on results from the upper half of the profile where residuals are small and almost randomly distributed. In this part of the profile the final estimate for the bedrock topography is everywhere within 50 m of that derived from the airborne radar survey, with no significant spatial variations in basal slipperiness. The calculated steady-state surface topography is within a few metres of the measured topography. Modelled horizontal velocities agree with measured values to within a few per cent, and modelled vertical velocities agree with measured velocities within measurement errors.
One of the key findings of this study is that surface properties appear to be entirely controlled by basal topography. There is no need to introduce any spatial variations in basal slipperiness to reproduce short-scale (<10 h) variation in surface topography and surface velocity. The localized peak in slipperiness at x ≈ 245 km is a modelling artefact related to three-dimensional effects not accounted for in the model. The only significant variation in slipperiness is an overall gradual increase in slipperiness toward the grounding line. This general increase in slipperiness is a robust model feature. From the onset area toward the grounding line, ice thicknesses decrease from ∼2300 to 1700 m, slope decreases from ∼0.0025 to 0.0017 while surface speed increases from 0.8 m d − 1 to 1.1 m d − 1 . Driving stress therefore decreases with distance while flow velocity increases. Hence the general increases in basal slipperiness toward the grounding line.
Although we find no evidence for significant short-scale variations in basal slipperiness from our analysis of surface data, we do not rule out the possibility of a variation in basal slipperiness. As shown by Reference Gudmundsson and RaymondGudmundsson and Raymond (2008), the spatial resolution of a slipperiness retrieval is limited. It is therefore possible that the smoothness of the retrieved basal slipperiness distribution is due to the limited spatial resolving power of the inversion method rather than the absence of any short-scale variations in basal slipperiness.
Our finding that short-scale variations in surface topography and surface velocity are strongly related to basal topography is, in some ways, not surprising. As we have shown before (e.g. Reference GudmundssonGudmundsson, 2003, Reference Gudmundsson2008; Reference RaymondRaymond and Gudmundsson, 2005), basal topography exerts strong control on surface flow and surface topography whenever the ratio between basal sliding and deformational velocity is large (>100), as is the case on Rutford Ice Stream.
The fact that the modelled steady-state geometry is in almost perfect agreement with the measured surface topography suggests that Rutford Ice Stream is currently in a steady state. This result concurs with the conclusions of Reference Gudmundsson and JenkinsGudmundsson and Jenkins (2009), that flow velocities on Rutford Ice Stream are stable over decadal timescales. The only significant temporal changes in flow appear to be those related to tidal forcing (Reference Gudmundsson and KnightGudmundsson, 2006).
Summary and Conclusions
Using a nonlinear Bayesian inverse method, we have estimated both bedrock topography and basal slipperiness along a flowline on Rutford Ice Stream from observed surface topography and surface velocities. We first inferred basal properties from measurements of surface horizontal and vertical velocity for a given surface geometry without constraining the rates of surface elevation change (inversion experiment A). Comparison between measured and calculated rates of surface elevation changes revealed large and significant differences. Therefore, in a second step (inversion experiment B), the modelled surface topography was chosen to be in steady state with given basal conditions. Using this approach, we determined basal conditions that are consistent with all surface observations, i.e. surface topography, surface velocities and rates of surface elevation change.
The retrieved basal slipperiness distribution is smooth, with no localized sticky or slippery spots. The only area for which the inverse model predicts a significant perturbation in slipperiness is characterized by strong transverse gradients in flow. This is also an area where the plane-strain model that we use in this study clearly is not adequate to describe the flow regime. Hence, we do not have confidence in this result, and consider it to be an artefact of the modelling approach.
Apart from an overall gradual increase in slipperiness with distance along the profile toward the grounding line, we therefore find no evidence for any localized spatial variations in basal slipperiness. Although it seems unlikely that short-scale spatial variation in basal slipperiness is completely absent, our results show that, if they are present at all, their amplitudes are too small to have any significant effect on flow velocities. Hence, our modelling suggests that localized variations in surface velocity are primarily caused by basal topography, with short-scale variation in basal slipperiness playing no significant role. We conclude that the potential for future changes in the flow rates of Rutford Ice Stream due to changes in local bed conditions is limited.
Acknowledgements
This study was supported by UK Natural Environment Research Council (NERC) Geophysical Equipment Facility (GEF) grant No. 711 and ETH research grant No. 0-20054-02. We thank two anonymous reviewers for constructive and helpful reviews.
