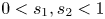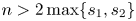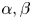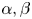1. Introduction
In this paper, we study anti-symmetric solutions about the hyperplane $\{x_n=0\}$![]() for the following system involving fractional Laplacian
for the following system involving fractional Laplacian

where $s_1,s_2\in (0,1)$![]() , $n>\max \{2s_1,2s_2\}$
, $n>\max \{2s_1,2s_2\}$![]() , $\mathbb {R}_+^n=\{x=(x',x_n)\in \mathbb {R}^n|x_n>0\}$
, $\mathbb {R}_+^n=\{x=(x',x_n)\in \mathbb {R}^n|x_n>0\}$![]() and $x'=(x_1,x_2,\ldots,x_{n-1})$
and $x'=(x_1,x_2,\ldots,x_{n-1})$![]() .
.
The fractional Laplacian $(-\Delta )^s \, (0< s<1)$![]() is a nonlocal operator defined by
is a nonlocal operator defined by
where $P.V.$![]() stands for the Cauchy principal value and $C(n,s)=(\int _{\mathbb {R}^n}\frac {1-\cos \xi }{|\xi |^{n+2s}}\,{\rm d}\xi )^{-1}$
stands for the Cauchy principal value and $C(n,s)=(\int _{\mathbb {R}^n}\frac {1-\cos \xi }{|\xi |^{n+2s}}\,{\rm d}\xi )^{-1}$![]() (see [Reference Caffarelli and Silvestre2, Reference Di Nezza, Palatucci and Valdinoci11]). Let
(see [Reference Caffarelli and Silvestre2, Reference Di Nezza, Palatucci and Valdinoci11]). Let
Then for $u\in L_{2s}, (-\Delta )^su$![]() can be defined in distributional sense (see [Reference Silvestre34])
can be defined in distributional sense (see [Reference Silvestre34])
Moreover, $(-\Delta )^su$![]() is well defined for $u\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$
is well defined for $u\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$![]() . We call $(u,v)$
. We call $(u,v)$![]() a classical solution of (1.1) if $(u,v)\in ( L_{2s_1}\cap C^{1,1}_{loc}(\mathbb {R}_+^n)\cap C(\mathbb {R}^n)) \times (L_{2s_2}\cap C^{1,1}_{loc}(\mathbb {R}_+^n)\cap C(\mathbb {R}^n))$
a classical solution of (1.1) if $(u,v)\in ( L_{2s_1}\cap C^{1,1}_{loc}(\mathbb {R}_+^n)\cap C(\mathbb {R}^n)) \times (L_{2s_2}\cap C^{1,1}_{loc}(\mathbb {R}_+^n)\cap C(\mathbb {R}^n))$![]() and satisfies (1.1).
and satisfies (1.1).
As is well known, the method of moving planes and moving spheres play an important role in proving the nonexistence of solutions. Chen et al. [Reference Chen, Li and Li3, Reference Chen, Li and Zhang4] introduced a direct method of moving planes and moving spheres for fractional Laplacian, which have been widely applied to derive the symmetry, monotonicity and nonexistence and even a prior estimates of solutions for some equations involving fractional Laplacian. In such process, some suitable forms of maximum principles are the key ingredients. The method of moving planes in integral forms is also a vital tool for classification of solutions (see [Reference Chen, Li and Ou5]).
Recently, Li and Zhuo [Reference Li and Zhuo20] classified anti-symmetric classical solutions of Lane–Emden system (1.1) in the case of $s_1=s_2=:s\in (0,1)$![]() and $\alpha =\beta =0$
and $\alpha =\beta =0$![]() . They established the following Liouville type theorem.
. They established the following Liouville type theorem.
Proposition 1.1 ([Reference Li and Zhuo20])
Given $0< p,q\leq \frac {n+2s}{n-2s},$![]() assume that $(u, v)$
assume that $(u, v)$![]() is an anti-symmetric classical solution of system (1.1). If $0 < pq < 1$
is an anti-symmetric classical solution of system (1.1). If $0 < pq < 1$![]() or $p + 2s > 1$
or $p + 2s > 1$![]() and $q + 2s > 1$
and $q + 2s > 1$![]() , then $(u,v)\equiv (0,0)$
, then $(u,v)\equiv (0,0)$![]() .
.
As a corollary of proposition 1, the nonexistence results in the larger space $L_{2s+1}$![]() follows immediately for the case $p+2s>1$
follows immediately for the case $p+2s>1$![]() , $q+2s>1$
, $q+2s>1$![]() .
.
Proposition 1.2 ([Reference Li and Zhuo20])
Assume that $u$![]() and $v \in L_{2s+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n)$
and $v \in L_{2s+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n)$![]() satisfy system (1.1). Then if $0 < p, q \leq \frac {n+2s}{n-2s}$
satisfy system (1.1). Then if $0 < p, q \leq \frac {n+2s}{n-2s}$![]() , $p+2s > 1$
, $p+2s > 1$![]() and $q + 2s > 1$
and $q + 2s > 1$![]() , $(u,v)\equiv (0,0)$
, $(u,v)\equiv (0,0)$![]() is the only solution.
is the only solution.
The nonexistence of anti-symmetric classical solutions to the corresponding scalar problem were given in [Reference Zhuo and Li37].
The following Hardy–Hénon system with homogeneous Dirichlet boundary conditions has been investigated widely

There are enormous nonexistence results of (1.2) for the case $\Omega =\mathbb {R}^n$![]() . We list some main results as follows.
. We list some main results as follows.
If $s_1=s_2=1$![]() , for $\alpha,\beta \geq 0$
, for $\alpha,\beta \geq 0$![]() , system (1.2) is the well-known Hénon–Lane–Emden system. It has been conjectured that the Sobolev's hyperbola
, system (1.2) is the well-known Hénon–Lane–Emden system. It has been conjectured that the Sobolev's hyperbola
is the critical dividing curve between existence and nonexistence of solutions to (1.2). Particularly, the Hénon–Lane–Emden conjecture states that system (1.2) admits no nonnegative non-trivial solutions if $p>0$![]() , $q>0$
, $q>0$![]() and $\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}>n-2$
and $\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}>n-2$![]() . For $\alpha =\beta =0$
. For $\alpha =\beta =0$![]() , this conjecture has been completely proved for radial solutions (see [Reference Mitidieri23, Reference Serrin and Zou32]). However, for non-radial solutions, the conjecture is only fully answered when $n\leq 4$
, this conjecture has been completely proved for radial solutions (see [Reference Mitidieri23, Reference Serrin and Zou32]). However, for non-radial solutions, the conjecture is only fully answered when $n\leq 4$![]() (see [Reference Poláčik, Quittner and Souplet29, Reference Serrin and Zou33, Reference Souplet35]). In higher dimensions, the conjecture was partially solved. Figueiredo and Felmer [Reference de Figueiredo and Felmer14] showed that system (1.2) admits no classical positive solutions if
(see [Reference Poláčik, Quittner and Souplet29, Reference Serrin and Zou33, Reference Souplet35]). In higher dimensions, the conjecture was partially solved. Figueiredo and Felmer [Reference de Figueiredo and Felmer14] showed that system (1.2) admits no classical positive solutions if
Busca and Manásevich [Reference Busca and Manásevich1] proved the conjecture if
where
When $\alpha,\beta >0$![]() , Fazly and Ghoussoub [Reference Fazly and Ghoussoub13] showed that the conjecture holds for dimension $n = 3$
, Fazly and Ghoussoub [Reference Fazly and Ghoussoub13] showed that the conjecture holds for dimension $n = 3$![]() under the assumption of the boundedness of positive solutions, Li and Zhang [Reference Li and Zhang22] removed this assumption and proved this conjecture for dimension $n = 3$
under the assumption of the boundedness of positive solutions, Li and Zhang [Reference Li and Zhang22] removed this assumption and proved this conjecture for dimension $n = 3$![]() . When $\min \{\alpha,\beta \}>-2$
. When $\min \{\alpha,\beta \}>-2$![]() , the conjecture is proved for bounded solutions in $n=3$
, the conjecture is proved for bounded solutions in $n=3$![]() (see [Reference Phan27]).
(see [Reference Phan27]).
If $s_1=s_2=:s\in (0,1), \alpha, \beta \geq 0$![]() , there are fewer nonexistence results of solutions to system (1.2) in the case of $p>0$
, there are fewer nonexistence results of solutions to system (1.2) in the case of $p>0$![]() , $q>0$
, $q>0$![]() and $\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}>n-2s$
and $\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}>n-2s$![]() , namely the case that $(p,q)$
, namely the case that $(p,q)$![]() locates at bottom left of the fractional Sobolev's hyperbola $\left \{p>0,q>0:\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}=n-2s\right \}$
locates at bottom left of the fractional Sobolev's hyperbola $\left \{p>0,q>0:\frac {n+\alpha }{p+1}+\frac {n+\beta }{q+1}=n-2s\right \}$![]() . For $\alpha =\beta =0$
. For $\alpha =\beta =0$![]() , Quaas and Xia in [Reference Quaas and Xia30] proved that there exist no classical positive solutions to (1.2) provided that
, Quaas and Xia in [Reference Quaas and Xia30] proved that there exist no classical positive solutions to (1.2) provided that
where
Note that region (1.3) of $(p,q)$![]() contains the following region:
contains the following region:
As $\min \{\alpha,\beta \}>-2s$![]() , Peng [Reference Peng26] derived that system (1.2) admits no nonnegative classical solutions if $0< p<\frac {n+2s+2\alpha }{n-2s}$
, Peng [Reference Peng26] derived that system (1.2) admits no nonnegative classical solutions if $0< p<\frac {n+2s+2\alpha }{n-2s}$![]() and $0< q<\frac {n+2s+2\beta }{n-2s}$
and $0< q<\frac {n+2s+2\beta }{n-2s}$![]() .
.
For scalar equation (i.e. $s_1=s_2:=s, \alpha =\beta, p=q, u=v$![]() ), in the Laplacian case, if $\alpha =0$
), in the Laplacian case, if $\alpha =0$![]() , a celebrated Liouville type theorem was showed by Gidas and Spruck [Reference Gidas and Spruck17] for $1< p<\frac {n+2}{n-2}$
, a celebrated Liouville type theorem was showed by Gidas and Spruck [Reference Gidas and Spruck17] for $1< p<\frac {n+2}{n-2}$![]() ; if $\alpha \leq -2$
; if $\alpha \leq -2$![]() and $p>1$
and $p>1$![]() , there is no any positive solution (see [Reference Gidas and Spruck16, Reference Ni25]); if $\alpha >-2$
, there is no any positive solution (see [Reference Gidas and Spruck16, Reference Ni25]); if $\alpha >-2$![]() and $1< p<\frac {n+2+2\alpha }{n-2}$
and $1< p<\frac {n+2+2\alpha }{n-2}$![]() , Phan and Souplet [Reference Phan and Souplet28] derived a Liouville theorem for bounded solutions; if $0 < p \leq 1$
, Phan and Souplet [Reference Phan and Souplet28] derived a Liouville theorem for bounded solutions; if $0 < p \leq 1$![]() , the nonexistence result was proved by Dai and Qin [Reference Dai and Qin8] for any $\alpha$
, the nonexistence result was proved by Dai and Qin [Reference Dai and Qin8] for any $\alpha$![]() . We also refer to [Reference Gabriele15, Reference Mitidieri and Pokhozhaev24] and references therein. For the scalar fractional Laplacian case, Chen et al. [Reference Chen, Li and Li3], Jin et al. [Reference Jin, Li and Xiong18] proved the nonexistence results for $\alpha =0$
. We also refer to [Reference Gabriele15, Reference Mitidieri and Pokhozhaev24] and references therein. For the scalar fractional Laplacian case, Chen et al. [Reference Chen, Li and Li3], Jin et al. [Reference Jin, Li and Xiong18] proved the nonexistence results for $\alpha =0$![]() and $0< p<\frac {n+ 2s}{n-2s}.$
and $0< p<\frac {n+ 2s}{n-2s}.$![]() If $\alpha >-2s$
If $\alpha >-2s$![]() , Dai and Qin [Reference Dai and Qin9] showed a Liouville type theorem for optimal range $0< p<\frac {n+2s+2\alpha }{n-2s}$
, Dai and Qin [Reference Dai and Qin9] showed a Liouville type theorem for optimal range $0< p<\frac {n+2s+2\alpha }{n-2s}$![]() .
.
For the case $\Omega =\mathbb {R}^n_+$![]() , the following several main results exist.
, the following several main results exist.
If $s_1=s_2=1$![]() , $\alpha =\beta =0$
, $\alpha =\beta =0$![]() , $\min \{p,q\}>1$
, $\min \{p,q\}>1$![]() , a Liouville theorem is proved for bounded solutions by Chen et al. [Reference Chen, Lin and Zou6]. If $s_1=s_2=:s \in (0,1)$
, a Liouville theorem is proved for bounded solutions by Chen et al. [Reference Chen, Lin and Zou6]. If $s_1=s_2=:s \in (0,1)$![]() , for $\alpha =\beta =0$
, for $\alpha =\beta =0$![]() , the nonexistence of positive viscosity-bounded solutions to system (1.2) was showed by Quaas and Xia in [Reference Quaas and Xia31]. For $\alpha,\beta >-2s$
, the nonexistence of positive viscosity-bounded solutions to system (1.2) was showed by Quaas and Xia in [Reference Quaas and Xia31]. For $\alpha,\beta >-2s$![]() , if $p\geq \frac {n+2s+\alpha }{n-2s}$
, if $p\geq \frac {n+2s+\alpha }{n-2s}$![]() and $q\geq \frac {n+2s+\beta }{n-2s}$
and $q\geq \frac {n+2s+\beta }{n-2s}$![]() , Duong and Le [Reference Duong and Le12] obtained the nonexistence of solutions satisfying the following decay at infinity:
, Duong and Le [Reference Duong and Le12] obtained the nonexistence of solutions satisfying the following decay at infinity:
For general $s_1, s_2\in (0,1)$![]() , Le in [Reference Le19] concluded a Liouville type theorem. Precisely, they obtained that if $1\leq p\leq \frac {n+2s_1+2\alpha }{n-2s_2}$
, Le in [Reference Le19] concluded a Liouville type theorem. Precisely, they obtained that if $1\leq p\leq \frac {n+2s_1+2\alpha }{n-2s_2}$![]() , $1\leq q\leq \frac {n+2s_2+2\alpha }{n-2s_1}$
, $1\leq q\leq \frac {n+2s_2+2\alpha }{n-2s_1}$![]() and $(p,q)\neq (\frac {n+2s_1+2\alpha }{n-2s_2},\frac {n+2s_2+2\alpha }{n-2s_1}$
and $(p,q)\neq (\frac {n+2s_1+2\alpha }{n-2s_2},\frac {n+2s_2+2\alpha }{n-2s_1}$![]() ), $\alpha >-2s_1$
), $\alpha >-2s_1$![]() and $\beta >-2s_2$
and $\beta >-2s_2$![]() , then $(u,v)\equiv (0,0)$
, then $(u,v)\equiv (0,0)$![]() is the only nonnegative classical solutions to system (1.2). More nonexistence results for general nonlinearities in a half space can be seen in [Reference Dai and Peng10, Reference Zhang, Yu and He36]. For the corresponding scalar problem of (1.2) with Laplacian and $\alpha =\beta =0$
is the only nonnegative classical solutions to system (1.2). More nonexistence results for general nonlinearities in a half space can be seen in [Reference Dai and Peng10, Reference Zhang, Yu and He36]. For the corresponding scalar problem of (1.2) with Laplacian and $\alpha =\beta =0$![]() , Gidas and Spruck [Reference Gidas and Spruck17] obtained the nonexistence of nontrivial nonnegative classical solution of (1.2) for $1< p\leq \frac {n+2}{n-2}$
, Gidas and Spruck [Reference Gidas and Spruck17] obtained the nonexistence of nontrivial nonnegative classical solution of (1.2) for $1< p\leq \frac {n+2}{n-2}$![]() . For the corresponding scalar problem (1.2) with fractional Laplacian and $\alpha =\beta =0$
. For the corresponding scalar problem (1.2) with fractional Laplacian and $\alpha =\beta =0$![]() , Chen et al. [Reference Chen, Li and Li3] showed that $u\equiv 0$
, Chen et al. [Reference Chen, Li and Li3] showed that $u\equiv 0$![]() is the only nonnegative solution to (1.2) for $1< p\leq \frac {n+2s}{n-2s}$
is the only nonnegative solution to (1.2) for $1< p\leq \frac {n+2s}{n-2s}$![]() . Recently, a Liouville type theorem of the corresponding scalar problem for $1< p<\frac {n+2s+2\alpha }{n-2s}, \alpha >-2s$
. Recently, a Liouville type theorem of the corresponding scalar problem for $1< p<\frac {n+2s+2\alpha }{n-2s}, \alpha >-2s$![]() and $s\in (0,1]$
and $s\in (0,1]$![]() was established by Dai and Qin in [Reference Dai and Qin9].
was established by Dai and Qin in [Reference Dai and Qin9].
In this paper, we will study nonexistence of anti-symmetric classical solutions to system (1.1) for general $\alpha, \beta, p, q$![]() .
.
For $\alpha >-2s_1$![]() and $\beta >-2s_2$
and $\beta >-2s_2$![]() , we denote
, we denote

Note that for the case $s_1=s_2$![]() , the set $\mathcal {R}_{sub}$
, the set $\mathcal {R}_{sub}$![]() locates at bottom left of the preceding fractional Sobolev's hyperbola.
locates at bottom left of the preceding fractional Sobolev's hyperbola.
Throughout this paper, we always assume $s_1,s_2\in (0,1)$![]() , $n>\max \{2s_1,2s_2\}$
, $n>\max \{2s_1,2s_2\}$![]() and use $C$
and use $C$![]() to denote a general positive constant whose value may vary from line to line even the same line. Our main results are as follows.
to denote a general positive constant whose value may vary from line to line even the same line. Our main results are as follows.
Theorem 1.1 For $(p,q)\in \mathcal {R}_{sub}$![]() , assume that $(u,v)$
, assume that $(u,v)$![]() is a classical solution of system (1.1). For either one of the following two cases:
is a classical solution of system (1.1). For either one of the following two cases:
(i) $\min \{p+2s_1,p+2s_1+\alpha \}>1$
 and $\min \{q+2s_2,q+2s_2+\beta \}>1$
and $\min \{q+2s_2,q+2s_2+\beta \}>1$ ,
,(ii) $0< pq<1$
 with $\alpha \geq -2s_1pq$
with $\alpha \geq -2s_1pq$ , $\beta \geq -2s_2pq$
, $\beta \geq -2s_2pq$ ,
,we have that $(u,v)=(0,0)$
 .
.
The nonexistence results (i) of theorem 1 can be extended to a larger space.
Theorem 1.2 Assume that $(p,q)\in \mathcal {R}_{sub}$![]() and $(u,v)\in (L_{2s_1+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n))\times (L_{2s_2+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n))$
and $(u,v)\in (L_{2s_1+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n))\times (L_{2s_2+1}\cap C^{1,1}_{loc}(\mathbb {R}^n_+)\cap C(\mathbb {R}^n))$![]() satisfies system (1.1). Then for the case that $\min \{p+2s_1,p+2s_1+\alpha \}>1$
satisfies system (1.1). Then for the case that $\min \{p+2s_1,p+2s_1+\alpha \}>1$![]() and $\min \{q+2s_2,q+2s_2+\beta \}>1$
and $\min \{q+2s_2,q+2s_2+\beta \}>1$![]() , $(u,v)\equiv (0,0)$
, $(u,v)\equiv (0,0)$![]() is the only solution.
is the only solution.
Combining our anti-symmetric property, in the proof of theorem 1.1, we only utilized the extended spaces $L_{2s_1+1}, L_{2s_2+1}$![]() instead of the usual spaces $L_{2s_1}, L_{2s_2}$
instead of the usual spaces $L_{2s_1}, L_{2s_2}$![]() in the case that $\min \{p+2s_1,p+2s_1+\alpha \}>1$
in the case that $\min \{p+2s_1,p+2s_1+\alpha \}>1$![]() and $\min \{q+2s_2,q+2s_2+\beta \}>1$
and $\min \{q+2s_2,q+2s_2+\beta \}>1$![]() . One can see that theorem 1.2 is a direct corollary of (i) of theorem 1.1.
. One can see that theorem 1.2 is a direct corollary of (i) of theorem 1.1.
Remark 1.1 Our results of theorems 1.1 and 1.2 are the extension to general $s_1,s_2,\alpha,\beta$![]() of the nonexistence results of Li and Zhuo [Reference Li and Zhuo20] (see preceding propositions 1.1 and 1.2) except one critical point of $(p,q)$
of the nonexistence results of Li and Zhuo [Reference Li and Zhuo20] (see preceding propositions 1.1 and 1.2) except one critical point of $(p,q)$![]() .
.
Remark 1.2 When $s_1=s_2$![]() , $p=q$
, $p=q$![]() , $\alpha =\beta$
, $\alpha =\beta$![]() and $u=v$
and $u=v$![]() , the results of theorems 1.1 and 1.2 are the nonexistence of nontrivial classical solutions to the corresponding scalar problem.
, the results of theorems 1.1 and 1.2 are the nonexistence of nontrivial classical solutions to the corresponding scalar problem.
Under appropriate decay conditions of $u$![]() and $v$
and $v$![]() at infinity, we can extend the nonexistence result of classical solutions of (1.1) to an unbounded domain of $(p,q)$
at infinity, we can extend the nonexistence result of classical solutions of (1.1) to an unbounded domain of $(p,q)$![]() . Particularly, this unbounded domain, except at most a bounded sub-domain, locates at above the preceding fractional Sobolev's hyperbola for the case $s_1=s_2$
. Particularly, this unbounded domain, except at most a bounded sub-domain, locates at above the preceding fractional Sobolev's hyperbola for the case $s_1=s_2$![]() .
.
Theorem 1.3 Suppose $p\geq \frac {n+2s_1+\alpha }{n-2s_2}$![]() , $q\geq \frac {n+2s_2+\beta }{n-2s_1}$
, $q\geq \frac {n+2s_2+\beta }{n-2s_1}$![]() , $\alpha >-2s_2$
, $\alpha >-2s_2$![]() , $\beta >-2s_1$
, $\beta >-2s_1$![]() . Assume $(u,v)$
. Assume $(u,v)$![]() is a classical solution of system (1.1) satisfying
is a classical solution of system (1.1) satisfying
for some $C>0$![]() , where $a=-\frac {2s_1+2s_2+\beta }{q-1}$
, where $a=-\frac {2s_1+2s_2+\beta }{q-1}$![]() and $b=-\frac {2s_1+2s_2+\alpha }{p-1}$
and $b=-\frac {2s_1+2s_2+\alpha }{p-1}$![]() . Then $(u,v)\equiv (0,0)$
. Then $(u,v)\equiv (0,0)$![]() .
.
Remark 1.3 The results of theorem 1.3 are new even if for the corresponding scalar problem with $\alpha =0$![]() .
.
Remark 1.4 When $\alpha,\beta$![]() are positive, define the region
are positive, define the region

Note that $\mathcal {R}_{sup}$![]() is contained in the nonexistence region of $(p,q)$
is contained in the nonexistence region of $(p,q)$![]() obtained in theorem 1.1. Hence, if $(p,q)\in \mathcal {R}_{sup}$
obtained in theorem 1.1. Hence, if $(p,q)\in \mathcal {R}_{sup}$![]() , theorem 1.1 tells us that the results of theorem 1.3 still hold true without the decay conditions.
, theorem 1.1 tells us that the results of theorem 1.3 still hold true without the decay conditions.
2. Preliminaries
In this section, we introduce and prove some necessary lemmas.
Proposition 2.1 ([Reference Duong and Le12])
Let $s\in (0,1)$![]() and $w(y)\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$
and $w(y)\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$![]() satisfy $w(y)=-w(y^-_\lambda )$
satisfy $w(y)=-w(y^-_\lambda )$![]() , where $y^-_\lambda =(y', 2\lambda -y_n)$
, where $y^-_\lambda =(y', 2\lambda -y_n)$![]() for any real number $\lambda$
for any real number $\lambda$![]() . Assume there exists $x\in \Sigma _\lambda$
. Assume there exists $x\in \Sigma _\lambda$![]() such that
such that
where $\Sigma _\lambda =\{x\in \mathbb {R}^n|x_n<\lambda \}$![]() . Then we have the following claims:
. Then we have the following claims:
(i) if
\[\mathop{\lim\inf}\limits_{|x|\to \infty }|x|^{2s}c(x)\geq0, \]there exists a constant $R_0>0$
 (depending on c, but independent of $w$
(depending on c, but independent of $w$ ) such that
\[ |x|< R_0, \]
) such that
\[ |x|< R_0, \]
(ii) if $c$
 is bounded below in $\Sigma _\lambda$
is bounded below in $\Sigma _\lambda$ , there exists a constant $\ell >0$
, there exists a constant $\ell >0$ (depending on the lower bound of $c$
(depending on the lower bound of $c$ , but independent of $w$
, but independent of $w$ ) such that
\[ {\rm d}(x,T_\lambda)> \ell, \]where $T_\lambda =\{x\in \mathbb {R}^n|x_n=\lambda \}$
) such that
\[ {\rm d}(x,T_\lambda)> \ell, \]where $T_\lambda =\{x\in \mathbb {R}^n|x_n=\lambda \}$
 .
.
We want to point out that the constant $\ell$![]() is non-increasing about $\lambda$
is non-increasing about $\lambda$![]() , since $\ell$
, since $\ell$![]() is non-decreasing about the lower bound of $c$
is non-decreasing about the lower bound of $c$![]() , which can be seen from the proof of proposition 2.1 in [Reference Duong and Le12].
, which can be seen from the proof of proposition 2.1 in [Reference Duong and Le12].
In order to apply the method of moving planes to prove the nonexistence, we need to establish the following estimate.
Lemma 2.1 Let $s\in (0,1)$![]() and $w(y)\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$
and $w(y)\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}^n)$![]() satisfy $w(y)=-w(y^-_\lambda )$
satisfy $w(y)=-w(y^-_\lambda )$![]() . Assume there exists $x\in \Sigma _\lambda$
. Assume there exists $x\in \Sigma _\lambda$![]() such that $w(x)=\mathop {\inf }\nolimits _{\Sigma _\lambda }w(y)<0$
such that $w(x)=\mathop {\inf }\nolimits _{\Sigma _\lambda }w(y)<0$![]() . Then we have
. Then we have

where $d=d(x,T_\lambda )$![]() and the constant $C(n,s)$
and the constant $C(n,s)$![]() is positive.
is positive.
Proof. Applying the definition of fractional Laplacian, we have

By an elementary calculation (see [Reference Cheng, Huang and Li7]), we derive
Hence, combining this and (2.1), we complete the proof of lemma 2.1.
In order to apply the method of moving spheres to prove the nonexistence, we need to establish a similar estimate as that of lemma 2.1. To this end, we need to introduce some notations. For any real number $\lambda >0$![]() , we denote
, we denote
Let $x^\lambda =\frac {\lambda ^2x}{|x|^2}$![]() be the inversion of the point $x=(x', x_n)$
be the inversion of the point $x=(x', x_n)$![]() about the sphere $S_\lambda$
about the sphere $S_\lambda$![]() and $x^*=(x', -x_n)$
and $x^*=(x', -x_n)$![]() . Denote
. Denote
Lemma 2.2 Let $w(x)\in L_{2s}\cap C_{loc}^{1,1}(\mathbb {R}_+^n)$![]() satisfy
satisfy
Assume there exists $\tilde {x}\in B_\lambda ^+$![]() such that $w(\tilde {x})=\inf _{B_\lambda ^+}w(x)<0$
such that $w(\tilde {x})=\inf _{B_\lambda ^+}w(x)<0$![]() . Then we have
. Then we have

where $h_\lambda (\tilde {x},y)=\frac {1}{|\tilde {x}-y|^{n+2s}}-\frac {1}{|\frac {|y|}{\lambda }\tilde {x}-\frac {\lambda }{|y|}y|^{n+2s}}+ \frac {1}{|\frac {|y|}{\lambda }\tilde {x}-\frac {\lambda }{|y|}y^*|^{n+2s}}-\frac {1}{|\tilde {x}-y^*|^{n+2s}}>0$![]() for $\tilde {x},y\in B_\lambda ^+$
for $\tilde {x},y\in B_\lambda ^+$![]() , $\delta =\min \{\tilde {x}_n,\lambda -|\tilde {x}|\}$
, $\delta =\min \{\tilde {x}_n,\lambda -|\tilde {x}|\}$![]() and $C(n,s)$
and $C(n,s)$![]() is a positive constant.
is a positive constant.
Proof. By the definition of fractional Laplacian and assumptions (2.2), we derive

Using similar arguments in [Reference Li and Zhuo21], we can obtain that $h_\lambda (x,y)>0$![]() for $x,y\in B_\lambda ^+$
for $x,y\in B_\lambda ^+$![]() .
.
Furthermore, choose $r<\tilde {x}_n$![]() small such that $H:=\{x\in B_\delta (\tilde {x})|x_n>\tilde {x}_n\}\subset \{x\in \mathbb {R}^n|x_n>\tilde {x}_n\}\subset (B_r^+(0))^C$
small such that $H:=\{x\in B_\delta (\tilde {x})|x_n>\tilde {x}_n\}\subset \{x\in \mathbb {R}^n|x_n>\tilde {x}_n\}\subset (B_r^+(0))^C$![]() where $\delta =\min \{\tilde {x}_n,\lambda -|\tilde {x}|\}$
where $\delta =\min \{\tilde {x}_n,\lambda -|\tilde {x}|\}$![]() , then we calculate
, then we calculate

From the definition $\delta =\min \{\tilde {x}_n,\lambda -|\tilde {x}|\}$![]() , we have $|\tilde {x}-y^*|< C\tilde {x}_n$
, we have $|\tilde {x}-y^*|< C\tilde {x}_n$![]() for any $y\in B_\delta ^+(\tilde {x})$
for any $y\in B_\delta ^+(\tilde {x})$![]() . Simple calculations imply that
. Simple calculations imply that
It is easy to see that

Lemma 2.3 Let $\alpha,\beta >-n$![]() . Suppose that $(u,v)$
. Suppose that $(u,v)$![]() is a nonnegative classical solution for the following system:
is a nonnegative classical solution for the following system:

Then for $x\in \mathbb {R}^n_+$![]() , we have
, we have

where $C$![]() is a positive constant.
is a positive constant.
Proof. Define a cut-off function $\eta (x)\in C_0^{\infty }(\mathbb {R}^n)$![]() satisfying $\eta (x)=0$
satisfying $\eta (x)=0$![]() for $|x|>1$
for $|x|>1$![]() and $\eta (x)=1$
and $\eta (x)=1$![]() for $|x|<\frac {1}{2}$
for $|x|<\frac {1}{2}$![]() . Denote $\eta _R(x)=\eta (\frac {x}{R})$
. Denote $\eta _R(x)=\eta (\frac {x}{R})$![]() for large $R$
for large $R$![]() and
and

Note that $(u_R(x), v_R(x))$![]() is a solution for the following system:
is a solution for the following system:

Let $U_R(x)=u(x)-u_R(x)$![]() and $V_R(x)=v(x)-v_R(x)$
and $V_R(x)=v(x)-v_R(x)$![]() . From (2.7) and (2.8), we derive
. From (2.7) and (2.8), we derive

By the definitions of $U_R(x)$![]() and $V_R(x)$
and $V_R(x)$![]() , obviously, for $x\in \mathbb {R}^n_+$
, obviously, for $x\in \mathbb {R}^n_+$![]() ,
,
where we used the assumptions $\alpha,\beta >-n$![]() .
.
Next, we claim that $U_R(x)\geq 0$![]() and $V_R(x)\geq 0$
and $V_R(x)\geq 0$![]() for $x\in \mathbb {R}_+^n$
for $x\in \mathbb {R}_+^n$![]() . If not, from (2.10) we know that there exists some $\hat {x}\in \mathbb {R}_+^n$
. If not, from (2.10) we know that there exists some $\hat {x}\in \mathbb {R}_+^n$![]() such that $U_R(\hat {x})=\mathop {\inf }\nolimits _{\mathbb {R}_+^n}U_R(x)<0$
such that $U_R(\hat {x})=\mathop {\inf }\nolimits _{\mathbb {R}_+^n}U_R(x)<0$![]() . Then,
. Then,

This leads a contradiction with the first equation in (2.9). Thus, $U_R(x)\geq 0$![]() holds true for any $x\in \mathbb {R}_+^n$
holds true for any $x\in \mathbb {R}_+^n$![]() , that is, $u(x)\geq u_R(x)$
, that is, $u(x)\geq u_R(x)$![]() in $\mathbb {R}_+^n$
in $\mathbb {R}_+^n$![]() . Letting $R \to \infty$
. Letting $R \to \infty$![]() , we obtain
, we obtain

Similarly, one has

3. Proof of theorem 1.1
In this section, we are ready to prove theorem 1.1. For (i) of theorem 1.1, namely the case $\min \{p+2s_1,p+2s_1+\alpha \}>1$![]() and $\{q+2s_2,q+2s_2+\beta \}>1$
and $\{q+2s_2,q+2s_2+\beta \}>1$![]() , we use the method of moving spheres to derive a lower bound for $u(x)$
, we use the method of moving spheres to derive a lower bound for $u(x)$![]() and $v(x)$
and $v(x)$![]() . Then, lemma 2.3 and a ‘bootstrap’ iteration process will give the better lower-bound estimates which can imply the nonexistence result. For (ii) of theorem 1.1, namely the case $0< pq<1$
. Then, lemma 2.3 and a ‘bootstrap’ iteration process will give the better lower-bound estimates which can imply the nonexistence result. For (ii) of theorem 1.1, namely the case $0< pq<1$![]() , $\alpha \geq -2s_1pq$
, $\alpha \geq -2s_1pq$![]() and $\beta \geq -2s_2pq$
and $\beta \geq -2s_2pq$![]() , a direct application of lemma 2.3 and iteration technique may give its proof.
, a direct application of lemma 2.3 and iteration technique may give its proof.
3.1 Proof of (i) of theorem 1.1
Proof. By contradiction, assume that $(u,v) \not \equiv (0,0)$![]() , then we can derive that $u>0$
, then we can derive that $u>0$![]() and $v>0$
and $v>0$![]() in $\mathbb {R}^n_+$
in $\mathbb {R}^n_+$![]() . Indeed, if there exists some $\hat {x}\in \mathbb {R}_+^n$
. Indeed, if there exists some $\hat {x}\in \mathbb {R}_+^n$![]() such that $u(\hat {x})=0$
such that $u(\hat {x})=0$![]() , from the anti-symmetry of $u$
, from the anti-symmetry of $u$![]() , we have
, we have
which contradicts with the equation
Thus $u(x)>0,$![]() and using the same arguments as above, we easily obtain $v(x)>0$
and using the same arguments as above, we easily obtain $v(x)>0$![]() . Therefore, we may assume that $u(x)>0$
. Therefore, we may assume that $u(x)>0$![]() and $v(x)>0$
and $v(x)>0$![]() in the rest proof of (i) of theorem 1.
in the rest proof of (i) of theorem 1.
Let $u_\lambda (x)$![]() and $v_\lambda (x)$
and $v_\lambda (x)$![]() be the Kelvin transform of $u(x)$
be the Kelvin transform of $u(x)$![]() and $v(x)$
and $v(x)$![]() centred at origin, respectively
centred at origin, respectively

for arbitrary $x\in \mathbb {R}^n\setminus \{0\}$![]() . By an elementary calculation, $u_\lambda (x)$
. By an elementary calculation, $u_\lambda (x)$![]() and $v_\lambda (x)$
and $v_\lambda (x)$![]() satisfy the following system:
satisfy the following system:

where
Note that both $\tau _1$![]() and $\tau _2$
and $\tau _2$![]() are nonnegative and they will not be zero simultaneously, since $(p,q)\in \mathcal {R}_{sub}$
are nonnegative and they will not be zero simultaneously, since $(p,q)\in \mathcal {R}_{sub}$![]() .
.
Denote
By elementary calculations and the mean value theorem, for $x\in B_\lambda ^+$![]() , there holds
, there holds

where $\xi _\lambda (x)$![]() is between $v(x)$
is between $v(x)$![]() and $v_\lambda (x)$
and $v_\lambda (x)$![]() , $\eta _\lambda (x)$
, $\eta _\lambda (x)$![]() is between $u(x)$
is between $u(x)$![]() and $u_\lambda (x)$
and $u_\lambda (x)$![]() . Note that
. Note that
Next, we will use the method of moving spheres to claim that $U_\lambda (x)\geq 0$![]() and $V_\lambda (x)\geq 0$
and $V_\lambda (x)\geq 0$![]() in $B_\lambda ^+$
in $B_\lambda ^+$![]() for any $\lambda >0$
for any $\lambda >0$![]() .
.
Step 1. Give a start point. We show that for sufficiently small $\lambda >0$![]() ,
,
Suppose (3.4) is not true, there must exist a point $\bar {x}\in B_\lambda ^+$![]() such that at least one of $U_\lambda (\bar {x})$
such that at least one of $U_\lambda (\bar {x})$![]() and $V_\lambda (\bar {x})$
and $V_\lambda (\bar {x})$![]() is negative at this point. Without loss of generality, we assume
is negative at this point. Without loss of generality, we assume
We will obtain contradictions for all four possible cases, respectively.
Case 1. $(p,q)\in \mathcal {R}_{sub}$![]() and $p\geq 1, q\geq 1$
and $p\geq 1, q\geq 1$![]() . Due to $p\geq 1$
. Due to $p\geq 1$![]() , by the convexity of the function $f(t)=t^p$
, by the convexity of the function $f(t)=t^p$![]() , then we can take $\xi _\lambda (x)=v(x)$
, then we can take $\xi _\lambda (x)=v(x)$![]() in (3.1). From equation (3.1) and lemma 2.2, we have
in (3.1). From equation (3.1) and lemma 2.2, we have

Hence,

If $\delta =\min \{\lambda -|\bar {x}|,\bar {x}_n\}=\lambda -|\bar {x}|$![]() , which implies that $\lambda -|\bar {x}|\leq \bar {x}_n\leq |\bar {x}|$
, which implies that $\lambda -|\bar {x}|\leq \bar {x}_n\leq |\bar {x}|$![]() , using the fact and (3.6), we obtain
, using the fact and (3.6), we obtain
As $\lambda \to 0$![]() , the right-hand side of (3.7) will go to infinity since $\alpha >-2s_1$
, the right-hand side of (3.7) will go to infinity since $\alpha >-2s_1$![]() . This is impossible.
. This is impossible.
If $\delta =\min \{\lambda -|\bar {x}|,\bar {x}_n\}=\bar {x}_n$![]() , from $\bar {x}_n\leq |\bar {x}|$
, from $\bar {x}_n\leq |\bar {x}|$![]() and (3.6), we derive
and (3.6), we derive
which is also impossible.
Case 2. $0< p,q<1$![]() . Due to $p<1$
. Due to $p<1$![]() , we can take $\xi _\lambda (x) =v_\lambda (x)$
, we can take $\xi _\lambda (x) =v_\lambda (x)$![]() . From equation (3.1) and lemma 2.2, we have
. From equation (3.1) and lemma 2.2, we have

Analogous to (3.7) and (3.8), there holds
or
Applying lemma 2.3 and the mean value theorem, we obtain that for $x\in B_1^+$![]() ,
,

For $x\in (B_1^+)^C$![]() , we derive
, we derive

Similarly, we have

Then by the definition of $v_\lambda (x)$![]() , we obtain
, we obtain

If $\delta =\lambda -|\bar {x}|\leq \bar {x}_n$![]() , that is, $|\bar {x}|\geq \frac {\lambda }{2}$
, that is, $|\bar {x}|\geq \frac {\lambda }{2}$![]() , combining (3.11) and (3.12), we conclude that for $\bar {x}\in B_\lambda ^+$
, combining (3.11) and (3.12), we conclude that for $\bar {x}\in B_\lambda ^+$![]() and sufficiently small $\lambda$
and sufficiently small $\lambda$![]() ,
,
which gives that
Due to $\min \{p+2s_1, p+2s_1+\alpha \}>1$![]() and $\frac {\lambda }{|\bar {x}|}\leq 2$
and $\frac {\lambda }{|\bar {x}|}\leq 2$![]() , inequality (3.13) is impossible as $\lambda >0$
, inequality (3.13) is impossible as $\lambda >0$![]() sufficiently small.
sufficiently small.
If $\delta =\bar {x}_n$![]() , it follows from (3.10) and (3.12) that
, it follows from (3.10) and (3.12) that
which implies that
Either one of the two inequalities will yield a contradiction since the left terms go to infinity as $\min \{p+2s_1,p+2s_1+\alpha \}>1$![]() and $\lambda >0$
and $\lambda >0$![]() small enough.
small enough.
For case 3: $(p,q)\in \mathcal {R}_{sub}, p\geq 1, 0< q<1$![]() and case 4: $(p,q)\in \mathcal {R}_{sub}, 0< p<1, q\geq 1$
and case 4: $(p,q)\in \mathcal {R}_{sub}, 0< p<1, q\geq 1$![]() , similar argument as that of cases 1 and 2 can show that $U_\lambda (x)\geq 0$
, similar argument as that of cases 1 and 2 can show that $U_\lambda (x)\geq 0$![]() and $V_\lambda (x)\geq 0$
and $V_\lambda (x)\geq 0$![]() in $B_\lambda ^+$
in $B_\lambda ^+$![]() for sufficiently small $\lambda >0$
for sufficiently small $\lambda >0$![]() . Therefore, (3.4) holds.
. Therefore, (3.4) holds.
Step 2. Now we move the sphere $S_\lambda$![]() outwards as long as (3.4) holds. Define
outwards as long as (3.4) holds. Define
We will show that $\lambda _0=+\infty$![]() . Suppose on the contrary that $0<\lambda _0<+\infty$
. Suppose on the contrary that $0<\lambda _0<+\infty$![]() . We want to show that there exists some small $\varepsilon >0$
. We want to show that there exists some small $\varepsilon >0$![]() such that for any $\lambda \in (\lambda _0,\lambda _0+\varepsilon )$
such that for any $\lambda \in (\lambda _0,\lambda _0+\varepsilon )$![]() ,
,
This implies that the plane $S_{\lambda _0}$![]() will be moved outwards a little bit further, which contradicts with the definition of $\lambda _0$
will be moved outwards a little bit further, which contradicts with the definition of $\lambda _0$![]() .
.
Firstly, we claim that
Indeed, if there exists some point $x^0\in B_{\lambda _0}^+$![]() such that $U_{\lambda _0}(x^0)= 0$
such that $U_{\lambda _0}(x^0)= 0$![]() , we have
, we have
On the other hand, it is easy to get that

If $\tau _1>0$![]() , then $(-\Delta )^{s_1}U_{\lambda _0}(x^0)>0$
, then $(-\Delta )^{s_1}U_{\lambda _0}(x^0)>0$![]() , where we use the facts that $V_{\lambda _0}\geq 0$
, where we use the facts that $V_{\lambda _0}\geq 0$![]() and $v>0$
and $v>0$![]() in $\mathbb {R}^n_+$
in $\mathbb {R}^n_+$![]() . If $\tau _1=0$
. If $\tau _1=0$![]() , then we have that $\tau _2>0$
, then we have that $\tau _2>0$![]() . Moreover, $V_{\lambda _0}(x^0)=0$
. Moreover, $V_{\lambda _0}(x^0)=0$![]() follows from (3.16) and (3.17). Using an argument similar to (3.16) and (3.17), we derive
follows from (3.16) and (3.17). Using an argument similar to (3.16) and (3.17), we derive

which is absurd. Thus, $U_{\lambda _0}(x)> 0$![]() is proved. Similarly, we derive that $V_{\lambda _0}(x)> 0$
is proved. Similarly, we derive that $V_{\lambda _0}(x)> 0$![]() . Hence, (3.15) holds.
. Hence, (3.15) holds.
Next, we will show that the sphere can be moved further outwards. The continuity of $u(x)$![]() and (3.15) yield that there exists some sufficiently small $l\in (0,\frac {\lambda _0}{2})$
and (3.15) yield that there exists some sufficiently small $l\in (0,\frac {\lambda _0}{2})$![]() and $\varepsilon _1\in (0,\frac {\lambda _0}{2})$
and $\varepsilon _1\in (0,\frac {\lambda _0}{2})$![]() such that for $\lambda \in (\lambda _0,\lambda _0+\varepsilon _1)$
such that for $\lambda \in (\lambda _0,\lambda _0+\varepsilon _1)$![]() ,
,
For $x\in B_\lambda ^+\setminus B_{\lambda _0-l}^+$![]() , using the similar proof of (3.4), we can deduce that
, using the similar proof of (3.4), we can deduce that
Note that the distance between $\bar {x}$![]() and $S_\lambda$
and $S_\lambda$![]() , i.e. $\lambda -|\bar {x}|$
, i.e. $\lambda -|\bar {x}|$![]() , plays an important role in this process.
, plays an important role in this process.
Hence, it follows from (3.18) and (3.19) that for all $\lambda \in (\lambda _0,\lambda _0+\varepsilon _1)$![]() ,
,
Similarly, we can also prove that there exists $\varepsilon _2>0$![]() such that for all $\lambda \in (\lambda _0, \lambda _0+\varepsilon _2)$
such that for all $\lambda \in (\lambda _0, \lambda _0+\varepsilon _2)$![]() ,
,
Let $\varepsilon =\min \{\varepsilon _1,\varepsilon _2\}$![]() , therefore, (3.14) can be completely concluded. This contradicts with the definition of $\lambda _0$
, therefore, (3.14) can be completely concluded. This contradicts with the definition of $\lambda _0$![]() . So $\lambda _0=+\infty$
. So $\lambda _0=+\infty$![]() .
.
Then, we have for every $\lambda >0$![]() ,
,
which gives that,
For any given $|x|\geq 1$![]() , let $\lambda =\sqrt {|x|}$
, let $\lambda =\sqrt {|x|}$![]() , then it follows from (3.20) that
, then it follows from (3.20) that

and similarly from (3.21), we obtain
Now we make full use of the above properties to derive some lower-bound estimates of solutions to (1.1) through iteration technique.
Let $\theta _0=\frac {n-2s_1}{2}+1$![]() , $\sigma _0=\frac {n-2s_2}{2}+1$
, $\sigma _0=\frac {n-2s_2}{2}+1$![]() . From lemma 2.3, inequality (3.23) and the mean value theorem, we have for $x_n>1$
. From lemma 2.3, inequality (3.23) and the mean value theorem, we have for $x_n>1$![]() ,
,

Similarly, we have
Denote $\theta _1=p(\sigma _0-1)-(\alpha +2 s_1)+1$![]() and $\sigma _1=q(\theta _0-1)-(\beta +2s_2)+1$
and $\sigma _1=q(\theta _0-1)-(\beta +2s_2)+1$![]() . Repeat the above process replacing (3.23) by (3.25), then we have
. Repeat the above process replacing (3.23) by (3.25), then we have

and analogously,
where $\theta _2=p(\sigma _1-1)-\alpha -2s_1+1$![]() and $\sigma _2=q(\theta _1-1)-\beta -2s_2+1$
and $\sigma _2=q(\theta _1-1)-\beta -2s_2+1$![]() .
.
After such $k$![]() iteration steps, we derive
iteration steps, we derive
where $\theta _{k+1}=p(\sigma _{k}-1)-\alpha -2s_1+1$![]() and $\sigma _{k+1}=q(\theta _{k}-1)-\beta -2s_2+1$
and $\sigma _{k+1}=q(\theta _{k}-1)-\beta -2s_2+1$![]() . Elementary calculations give that
. Elementary calculations give that

where $m=0,1,2,\ldots$![]() .
.
For the case $pq\geq 1$![]() , we claim that both $\{\theta _k\}$
, we claim that both $\{\theta _k\}$![]() and $\{\sigma _k\}$
and $\{\sigma _k\}$![]() are decreasing sequences and unbounded from below. Denote
are decreasing sequences and unbounded from below. Denote

Note that $A_e,A_o\leq 0$![]() and they will not be zero simultaneously, since $(p,q)\in \mathcal {R}_{sub}$
and they will not be zero simultaneously, since $(p,q)\in \mathcal {R}_{sub}$![]() . By elementary calculations, we have
. By elementary calculations, we have

Hence, the sequence $\{\theta _k\}$![]() is decreasing.
is decreasing.
Combining the above properties of $A_e, A_o$![]() , the assumption $pq\geq 1$
, the assumption $pq\geq 1$![]() and (3.29), we deduce that $\theta _k\to -\infty$
and (3.29), we deduce that $\theta _k\to -\infty$![]() as $k\to +\infty$
as $k\to +\infty$![]() . Similarly, we can show that $\{\sigma _k\}$
. Similarly, we can show that $\{\sigma _k\}$![]() is also decreasing and $\sigma _k\to -\infty$
is also decreasing and $\sigma _k\to -\infty$![]() . These and (3.27) indicate that $u(x)$
. These and (3.27) indicate that $u(x)$![]() and $v(x)$
and $v(x)$![]() do not belong to any $L_{2s}$
do not belong to any $L_{2s}$![]() . Hence, the solutions $(u,v)\equiv (0,0)$
. Hence, the solutions $(u,v)\equiv (0,0)$![]() when $pq\geq 1$
when $pq\geq 1$![]() .
.
Next, we consider the case $pq<1$![]() . From (3.28), we can conclude that
. From (3.28), we can conclude that
Since $p+2s_1+\alpha >1$![]() and $q+2s_2+\beta >1$
and $q+2s_2+\beta >1$![]() , we have
, we have
Hence, from (3.30) and (3.27), we have for $x_n>1$![]() ,
,
Combining this with lemma 2.3, we have

Let $x'-y'=(x_n+y_n)z'$![]() , we have
, we have

Let $y_n=x_nz_n$![]() , one has
, one has

Due to $p+2s_1+\alpha >1$![]() and $q+2s_2+\beta >1$
and $q+2s_2+\beta >1$![]() , we have $\frac {q(2s_1+\alpha )+(2s_2+\beta )}{1-pq}>1$
, we have $\frac {q(2s_1+\alpha )+(2s_2+\beta )}{1-pq}>1$![]() , which implies that
, which implies that
This yields that the right-hand side of (3.32) is infinity, which is impossible. Hence, for $pq<1$![]() we also obtain $(u,v)\equiv (0,0).$
we also obtain $(u,v)\equiv (0,0).$![]()
In sum, we conclude that there is no nontrivial classical solutions to system (1.1) for the case that $(p,q)\in \mathcal {R}_{sub}$![]() , $\min \{p+2s_1, p+2s_1+\alpha \}>1$
, $\min \{p+2s_1, p+2s_1+\alpha \}>1$![]() , $\min \{q+2s_2,q+2s_2+\beta \}>1$
, $\min \{q+2s_2,q+2s_2+\beta \}>1$![]() .
.
3.2 Proof of (ii) of theorem 1.1
Proof. Assume that $(u,v) \not \equiv (0,0)$![]() , from the proof of (i), we know that $u>0$
, from the proof of (i), we know that $u>0$![]() and $v>0$
and $v>0$![]() in $\mathbb {R}_+^n$
in $\mathbb {R}_+^n$![]() . Applying lemma 2.3, for $x_n>\min \{2,\frac {|x'|}{10}\}$
. Applying lemma 2.3, for $x_n>\min \{2,\frac {|x'|}{10}\}$![]() , we have
, we have

Similarly, for $x_n>\min \{2,\frac {|x'|}{10}\}$![]() , we have
, we have
Iterating (3.33) with (3.34), for $x_n>\min \{2,\frac {|x'|}{10}\}$![]() , we get
, we get

Using the same argument as that of (3.35), for $x_n>\min \left \{2,\frac {|x'|}{10}\right \}$![]() , we obtain
, we obtain
After $k$![]() iteration steps, it is easy to see that for $|x|$
iteration steps, it is easy to see that for $|x|$![]() large and $x_n>\min \left \{2,\frac {|x'|}{10}\right \}$
large and $x_n>\min \left \{2,\frac {|x'|}{10}\right \}$![]() ,
,
Here,
where
Simple calculations imply that

where $m=0,1,2,\ldots.$![]()
From $0< pq<1$![]() , we obtain
, we obtain
This yields that for $|x|$![]() large,
large,
as $k\to +\infty$![]() . Due to $0< pq<1$
. Due to $0< pq<1$![]() and $\alpha \geq -2s_1pq$
and $\alpha \geq -2s_1pq$![]() , $\beta \geq -2s_2pq$
, $\beta \geq -2s_2pq$![]() , we have
, we have
This contradicts with the assumptions that $u(x)\in L_{2s_1}$![]() and $v(x)\in L_{2s_2}$
and $v(x)\in L_{2s_2}$![]() . Hence, $(u,v)\equiv (0,0)$
. Hence, $(u,v)\equiv (0,0)$![]() .
.
4. Proof of theorem 1.3
In this section, we give the proof of theorem 1.3 by using the method of moving planes.
Proof. Suppose on the contrary that $(u,v) \not \equiv (0,0)$![]() , we know that $u>0$
, we know that $u>0$![]() and $v>0$
and $v>0$![]() in $\mathbb {R}_+^n$
in $\mathbb {R}_+^n$![]() . Let $\bar {u}(x)$
. Let $\bar {u}(x)$![]() and $\bar {v}(x)$
and $\bar {v}(x)$![]() be the Kelvin transform of $u(x)$
be the Kelvin transform of $u(x)$![]() and $v(x)$
and $v(x)$![]() centred at origin, respectively
centred at origin, respectively

for arbitrary $x\in \mathbb {R}^n\setminus \{0\}$![]() . Then, $\bar {u}(x)$
. Then, $\bar {u}(x)$![]() and $\bar {v}(x)$
and $\bar {v}(x)$![]() satisfy the following system:
satisfy the following system:

where
Note that $\bar {\tau }_1\leq 0$![]() and $\bar {\tau }_2\leq 0$
and $\bar {\tau }_2\leq 0$![]() due to $p\geq \frac {n+2s_1+\alpha }{n-2s_2}$
due to $p\geq \frac {n+2s_1+\alpha }{n-2s_2}$![]() and $q\geq \frac {n+2s_2+\beta }{n-2s_1}$
and $q\geq \frac {n+2s_2+\beta }{n-2s_1}$![]() . Obviously, for $|x|$
. Obviously, for $|x|$![]() large enough,
large enough,
For any real number $\rho >0$![]() and $x\in \Sigma _\rho$
and $x\in \Sigma _\rho$![]() , define
, define
where $\Sigma _\rho$![]() , $T_\rho$
, $T_\rho$![]() and $x^-_\rho$
and $x^-_\rho$![]() are defined as in proposition 2.1. Then, for $x\in \Sigma _\rho \cap \mathbb {R}^n_+$
are defined as in proposition 2.1. Then, for $x\in \Sigma _\rho \cap \mathbb {R}^n_+$![]() , we have
, we have

where we use the fact $p>1$![]() in the last inequality. Similarly,
in the last inequality. Similarly,
Step 1. We claim that for $\rho >0$![]() sufficiently small,
sufficiently small,
Otherwise, from (4.1), there exists some $\bar {x}\in \Sigma _\rho \cap \mathbb {R}_+^n$![]() such that at least one of $\bar {U}_\rho (x)$
such that at least one of $\bar {U}_\rho (x)$![]() , $\bar {V}_\rho (x)$
, $\bar {V}_\rho (x)$![]() is negative. Without loss of generality, we may assume that
is negative. Without loss of generality, we may assume that
Combining equation (4.2) and lemma 2.1, we deduce

This yields that
Observe that (4.1) and the decay conditions of $u$![]() and $v$
and $v$![]() in theorem 1.3 ensure that
in theorem 1.3 ensure that
where we used the assumption $\alpha >-2s_2$![]() . Hence, inequality (4.6) is impossible as $\rho >0$
. Hence, inequality (4.6) is impossible as $\rho >0$![]() is sufficiently small. Therefore, (4.4) holds.
is sufficiently small. Therefore, (4.4) holds.
Step 2. Move the plane $T_\rho$![]() upwards along the $x_n$
upwards along the $x_n$![]() -axis as long as (4.4) holds. Let
-axis as long as (4.4) holds. Let
We will show that $\rho _0=+\infty$![]() by contradiction arguments.
by contradiction arguments.
Suppose on the contrary that $0<\rho _0<+\infty$![]() . We will verify that
. We will verify that
Then using the above equalities (4.7), we immediately obtain
which is impossible. Thus $\rho _0=+\infty$![]() must hold.
must hold.
Therefore, our goal is to prove (4.7). Suppose that (4.7) does not hold, then we deduce that
Otherwise, there exists some point $\tilde {x}\in \Sigma _{\rho _0}\cap \mathbb {R}^n_+$![]() such that $\bar {U}_{\rho _0}(\tilde {x})=0$
such that $\bar {U}_{\rho _0}(\tilde {x})=0$![]() . We have
. We have
On the contrary, it is easy to get that

where we use the fact $\bar {V}_{\rho _0}\geq 0$![]() . This leads to a contradiction. Hence, (4.8) holds.
. This leads to a contradiction. Hence, (4.8) holds.
Now we show that the plane $T_{\rho _0}$![]() can be moved upwards a little bit further and hence obtain a contradiction with the definition of $\rho _0$
can be moved upwards a little bit further and hence obtain a contradiction with the definition of $\rho _0$![]() . Precisely, we will verify that there exists some small $\varepsilon >0$
. Precisely, we will verify that there exists some small $\varepsilon >0$![]() such that for any $\rho \in (\rho _0,\rho _0+\varepsilon )$
such that for any $\rho \in (\rho _0,\rho _0+\varepsilon )$![]() ,
,
where $\varepsilon$![]() is determined later.
is determined later.
If (4.9) is not true, then for any $\varepsilon _k\to 0$![]() as $k\to +\infty$
as $k\to +\infty$![]() , there exists $\rho _k\in (\rho _0,\rho _0+\varepsilon _k)$
, there exists $\rho _k\in (\rho _0,\rho _0+\varepsilon _k)$![]() and $x_k\in \mathbb {R}_+^n\cap \Sigma _{\rho _k}$
and $x_k\in \mathbb {R}_+^n\cap \Sigma _{\rho _k}$![]() such that
such that
Similar argument as that of (4.5) gives that
where $c(x)=-|x|^{-\bar {\tau }_1} p\bar {v}^{p-1}(x)$![]() . From (4.1) and the decay conditions of $u$
. From (4.1) and the decay conditions of $u$![]() and $v$
and $v$![]() , we deduce that
, we deduce that
where we used the assumption $\alpha >-2s_2$![]() . Then from proposition 2.1 we know that there exists $\ell _k>0$
. Then from proposition 2.1 we know that there exists $\ell _k>0$![]() and $R_0>0$
and $R_0>0$![]() such that
such that
Denote $\ell _0 (>0)$![]() as the constant given in proposition 2.1 corresponding to the half space $\Sigma _{\rho _0+1}$
as the constant given in proposition 2.1 corresponding to the half space $\Sigma _{\rho _0+1}$![]() . Combining the remark about the monotonicity of $\ell$
. Combining the remark about the monotonicity of $\ell$![]() with respect to $\lambda$
with respect to $\lambda$![]() below proposition 2.1, (4.13) and the fact that $\varepsilon _k\to 0$
below proposition 2.1, (4.13) and the fact that $\varepsilon _k\to 0$![]() , we have that
, we have that
If $\rho _0-\frac {\ell _0}{2}\leq 0$![]() , then (4.14) contradicts with the fact that $x_k\in \mathbb {R}^n_+$
, then (4.14) contradicts with the fact that $x_k\in \mathbb {R}^n_+$![]() . If $\rho _0-\frac {\ell _0}{2}>0$
. If $\rho _0-\frac {\ell _0}{2}>0$![]() , due to (4.8) and continuity of $\bar {u}$
, due to (4.8) and continuity of $\bar {u}$![]() , we know that there exists $\varepsilon '\in (0,\frac {\ell _0}{2})$
, we know that there exists $\varepsilon '\in (0,\frac {\ell _0}{2})$![]() such that for any $\varepsilon _k\leq \varepsilon '$
such that for any $\varepsilon _k\leq \varepsilon '$![]() and $\rho \in (\rho _0,\rho _0+\varepsilon _k)$
and $\rho \in (\rho _0,\rho _0+\varepsilon _k)$![]() ,
,
This contradicts with (4.14) and (4.10). Hence, we derive that for any $\rho \in (\rho _0, \rho _0+\varepsilon ')$![]() with $\varepsilon '>0$
with $\varepsilon '>0$![]() small enough,
small enough,
Similarly, we may verify that there exists $\varepsilon ''>0$![]() such that for any $\rho \in (\rho _0, \rho _0+\varepsilon '')$
such that for any $\rho \in (\rho _0, \rho _0+\varepsilon '')$![]() the inequality holds
the inequality holds
Let $\varepsilon =\min \{\varepsilon ',\varepsilon ''\}$![]() , then (4.9) follows immediately and hence (4.7) holds, which yields that $\rho _0=+\infty$
, then (4.9) follows immediately and hence (4.7) holds, which yields that $\rho _0=+\infty$![]() .
.
The result $\rho _0=+\infty$![]() indicates that both $\bar {u}(x)$
indicates that both $\bar {u}(x)$![]() and $\bar {v}(x)$
and $\bar {v}(x)$![]() are monotone increasing along the $x_n$
are monotone increasing along the $x_n$![]() -axis. This contradicts with the asymptotic behaviours (4.1). Therefore, $(\bar {u},\bar {v})=(0,0)$
-axis. This contradicts with the asymptotic behaviours (4.1). Therefore, $(\bar {u},\bar {v})=(0,0)$![]() , which yields that $(u,v)=(0,0)$
, which yields that $(u,v)=(0,0)$![]() . We complete the proof of theorem 1.3.
. We complete the proof of theorem 1.3.
Acknowledgements
The authors are supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2022JJ30118).