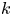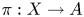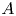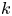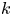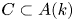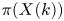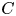1. Introduction
Let ![]() $X$ be a ramified cover of an abelian variety over a number field
$X$ be a ramified cover of an abelian variety over a number field ![]() $K$, i.e. there is a finite surjective non-étale morphism
$K$, i.e. there is a finite surjective non-étale morphism ![]() $X\to A$ with
$X\to A$ with ![]() $X$ normal and irreducible. The aim of this paper is to prove novel results on the distribution of rational points on
$X$ normal and irreducible. The aim of this paper is to prove novel results on the distribution of rational points on ![]() $X$.
$X$.
In this work we are guided by Lang's conjectures on varieties of general type, and by a question of Serre on covers of abelian varieties. By Kawamata's structure result for ramified covers of abelian varieties [Reference KawamataKaw81], for every ramified cover ![]() $X\to A$ of an abelian variety
$X\to A$ of an abelian variety ![]() $A$ over a number field
$A$ over a number field ![]() $K$, there is a finite field extension
$K$, there is a finite field extension ![]() $L/K$ and finite étale cover
$L/K$ and finite étale cover ![]() $X'\to X_L$ such that
$X'\to X_L$ such that ![]() $X'$ dominates a positive-dimensional variety of general type over
$X'$ dominates a positive-dimensional variety of general type over ![]() $L$. Assuming Lang's conjecture [Reference JavanpeykarJav20, Reference LangLan86], it follows that the
$L$. Assuming Lang's conjecture [Reference JavanpeykarJav20, Reference LangLan86], it follows that the ![]() $K$-rational points
$K$-rational points ![]() $X(K)$ are not Zariski-dense in
$X(K)$ are not Zariski-dense in ![]() $X$. Despite Faltings’ deep finiteness theorems for integral (and rational) points on subvarieties of abelian varieties [Reference FaltingsFal94], we are far from proving such desired non-density results for rational points on ramified covers of abelian varieties (even in dimension two) over number fields.
$X$. Despite Faltings’ deep finiteness theorems for integral (and rational) points on subvarieties of abelian varieties [Reference FaltingsFal94], we are far from proving such desired non-density results for rational points on ramified covers of abelian varieties (even in dimension two) over number fields.
Lang's aforementioned conjecture predicts that, for any abelian variety ![]() $A$ over a number field
$A$ over a number field ![]() $K$ with
$K$ with ![]() $A(K)$ dense and any ramified cover
$A(K)$ dense and any ramified cover ![]() $\pi :X\to A$, the set
$\pi :X\to A$, the set ![]() $A(K)\setminus \pi (X(K))$ is again dense. Motivated by the inverse Galois problem, Serre also raised a related question [Reference SerreSer08, § 5.4, Problem], a positive answer to which would lead to the same conclusion. Our main results stated in the following (see Theorems 1.3 and 1.4) confirm the density of
$A(K)\setminus \pi (X(K))$ is again dense. Motivated by the inverse Galois problem, Serre also raised a related question [Reference SerreSer08, § 5.4, Problem], a positive answer to which would lead to the same conclusion. Our main results stated in the following (see Theorems 1.3 and 1.4) confirm the density of ![]() $A(K)\setminus \pi (X(K))$ unconditionally for all abelian varieties, and thereby provide novel evidence for Lang's conjectures on rational points and answer, in part, Serre's question.
$A(K)\setminus \pi (X(K))$ unconditionally for all abelian varieties, and thereby provide novel evidence for Lang's conjectures on rational points and answer, in part, Serre's question.
We stress that there are no prior results concerning the distribution of rational points on ramified covers of abelian varieties, except for some very special cases, and the same goes for integral points on ramified covers of ![]() $\mathbb {G}_m^n$. Our current work provides the first step towards understanding the Diophantine properties of ramified covers of abelian varieties.
$\mathbb {G}_m^n$. Our current work provides the first step towards understanding the Diophantine properties of ramified covers of abelian varieties.
The conclusion of our main theorem that ![]() $A(K)\setminus \pi (X(K))$ is dense bears a strong resemblance to the geometric formulation of Hilbert's irreducibility theorem. In fact, this point of view is quite fruitful and key to many of the results of this paper.
$A(K)\setminus \pi (X(K))$ is dense bears a strong resemblance to the geometric formulation of Hilbert's irreducibility theorem. In fact, this point of view is quite fruitful and key to many of the results of this paper.
In its simplest form, Hilbert's irreducibility theorem states that, given a number field ![]() $K$ and an irreducible polynomial
$K$ and an irreducible polynomial ![]() $p(t,x_1,\ldots,x_s)$ with coefficients in
$p(t,x_1,\ldots,x_s)$ with coefficients in ![]() $K$, there exist infinitely many
$K$, there exist infinitely many ![]() $a \in K$ such that the specialization
$a \in K$ such that the specialization ![]() $p(a,x_1,\ldots,x_s)$ is an irreducible polynomial in the variables
$p(a,x_1,\ldots,x_s)$ is an irreducible polynomial in the variables ![]() $x_1,\ldots,x_s$. A similar statement applies to the simultaneous specialization of finitely many irreducible polynomials.
$x_1,\ldots,x_s$. A similar statement applies to the simultaneous specialization of finitely many irreducible polynomials.
Following the work of several authors, Hilbert's irreducibility theorem has been recast in geometric language as follows. An irreducible polynomial ![]() $p(t,x)$ defines in a natural way an irreducible cover (that is, a finite surjective morphism) of an open subvariety of
$p(t,x)$ defines in a natural way an irreducible cover (that is, a finite surjective morphism) of an open subvariety of ![]() $\mathbb {P}_1$ over
$\mathbb {P}_1$ over ![]() $K$: this is obtained simply by projecting the zero locus of
$K$: this is obtained simply by projecting the zero locus of ![]() $p$ on the
$p$ on the ![]() $t$-line. Hilbert's irreducibility theorem can then be interpreted as stating that ‘many’ fibres of this cover are irreducible over
$t$-line. Hilbert's irreducibility theorem can then be interpreted as stating that ‘many’ fibres of this cover are irreducible over ![]() $K$ and hence, in particular, that they have no
$K$ and hence, in particular, that they have no ![]() $K$-rational points; in turn, this is also equivalent to ‘many’ rational points of
$K$-rational points; in turn, this is also equivalent to ‘many’ rational points of ![]() $\mathbb {P}_1$ not being the image of rational points in the zero locus of
$\mathbb {P}_1$ not being the image of rational points in the zero locus of ![]() $p$. Similar constructions can be made in the case of several variables, and this point of view is encapsulated in the following definition of Serre (for this and much more about the Hilbert property we refer the reader to the books of Serre [Reference SerreSer08, Chapter 3] and Fried and Jarden [Reference Fried and JardenFJ08]).
$p$. Similar constructions can be made in the case of several variables, and this point of view is encapsulated in the following definition of Serre (for this and much more about the Hilbert property we refer the reader to the books of Serre [Reference SerreSer08, Chapter 3] and Fried and Jarden [Reference Fried and JardenFJ08]).
Definition 1.1 An integral, quasi-projective variety ![]() $X$ over a field
$X$ over a field ![]() $k$ satisfies the Hilbert property over
$k$ satisfies the Hilbert property over ![]() $k$ if, for every finite collection of finite surjective morphisms
$k$ if, for every finite collection of finite surjective morphisms ![]() $(\pi _i:Y_i\to X)_{i=1}^n$ with
$(\pi _i:Y_i\to X)_{i=1}^n$ with ![]() $Y_i$ a normal (integral) variety over
$Y_i$ a normal (integral) variety over ![]() $k$ and
$k$ and ![]() $\deg \pi _i \geq 2$, the set
$\deg \pi _i \geq 2$, the set ![]() $X(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is dense in
$X(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is dense in ![]() $X$.
$X$.
In this language, Hilbert's irreducibility theorem states that every projective space over a number field ![]() $K$ has the Hilbert property. As the Hilbert property is a birational invariant, it follows that every rational variety over
$K$ has the Hilbert property. As the Hilbert property is a birational invariant, it follows that every rational variety over ![]() $K$ has the Hilbert property.
$K$ has the Hilbert property.
The arithmetic nature of the ground field is of course essential for the truth of Hilbert's irreducibility theorem, and a field ![]() $k$ is called Hilbertian if
$k$ is called Hilbertian if ![]() $\mathbb {P}_1$ has the Hilbert property over
$\mathbb {P}_1$ has the Hilbert property over ![]() $k$ (or equivalently, if
$k$ (or equivalently, if ![]() $\mathbb {P}_n$ has the Hilbert property over
$\mathbb {P}_n$ has the Hilbert property over ![]() $k$ for every
$k$ for every ![]() $n$). In this paper we focus on the case of finitely generated fields of characteristic zero, which are known to be Hilbertian.
$n$). In this paper we focus on the case of finitely generated fields of characteristic zero, which are known to be Hilbertian.
Clearly not every variety has the Hilbert property: for example, in [Reference Corvaja and ZannierCZ17] it is shown that, as a consequence of the Chevalley–Weil theorem, a smooth proper variety over a number field with the Hilbert property is geometrically simply connected. Nonetheless, the literature is by now very rich with examples of varieties with the Hilbert property. Several proofs exist for the case of projective space (see, for example, [Reference Bombieri and GublerBG06, § 9.6], [Reference Fried and JardenFJ08, Chapter 11], [Reference SchinzelSch00, § 4.4], [Reference SerreSer97, Chapter 9], [Reference SerreSer08, Chapter 3] and [Reference VölkleinVöl96]). Note that connected reductive algebraic groups have been shown in [Reference Colliot-Thélène and SansucCTS87] to have the Hilbert property over Hilbertian fields; note that these varieties are rational over ![]() $\overline {k}$, but not necessarily over
$\overline {k}$, but not necessarily over ![]() $k$). Some sporadic examples of varieties with the Hilbert property are also known (such as the K3 surface
$k$). Some sporadic examples of varieties with the Hilbert property are also known (such as the K3 surface ![]() $x^4+y^4 = z^4+w^4 \subset \mathbb {P}_{3,\mathbb {Q}}$, which is not even geometrically unirational [Reference Corvaja and ZannierCZ17, Theorem 1.4]; see also [Reference DemeioDem19] and [Reference DemeioDem20]).
$x^4+y^4 = z^4+w^4 \subset \mathbb {P}_{3,\mathbb {Q}}$, which is not even geometrically unirational [Reference Corvaja and ZannierCZ17, Theorem 1.4]; see also [Reference DemeioDem19] and [Reference DemeioDem20]).
Hilbert's irreducibility theorem and its extensions have led to a number of applications (see, for example, [Reference Dvornicich and ZannierDZ07, Reference ZannierZan00]), typically motivated by the following observation: if a certain desired object can be realized geometrically, and if the base space of the geometric construction has the Hilbert property, then the situation can be specialized to an arithmetic one. The point is of course that various tools are available on the geometric side that might make certain constructions more natural than they would be if they were carried out directly on the arithmetic side. Concretely, this has been implemented for example by Néron [Reference NéronNér52], who used this idea to construct elliptic curves defined over ![]() $\mathbb {Q}$ of large rank. By far the most important such application is to the inverse Galois problem (this was also Hilbert's original motivation): if a group
$\mathbb {Q}$ of large rank. By far the most important such application is to the inverse Galois problem (this was also Hilbert's original motivation): if a group ![]() $G$ can be realized as the Galois group of a cover
$G$ can be realized as the Galois group of a cover ![]() $Y \to X$ defined over
$Y \to X$ defined over ![]() $\mathbb {Q}$, with
$\mathbb {Q}$, with ![]() $X$ having the Hilbert property, then
$X$ having the Hilbert property, then ![]() $G$ is a Galois group over
$G$ is a Galois group over ![]() $\mathbb {Q}$. Noether famously used this idea to prove that
$\mathbb {Q}$. Noether famously used this idea to prove that ![]() $S_n$ is a Galois group over
$S_n$ is a Galois group over ![]() $\mathbb {Q}$ for all
$\mathbb {Q}$ for all ![]() $n$.
$n$.
Given the significance of the Hilbert property for number-theoretical questions, one would wish to extend Hilbert's theorem to other classes of varieties in addition to the rational varieties. However, there are serious restrictions to possible generalizations of the classical results, starting with the aforementioned fact that the Hilbert property can only hold for geometrically simply connected varieties [Reference Corvaja and ZannierCZ17].
Nevertheless, it is conjectured that, for a variety ![]() $X$ over a finitely generated field
$X$ over a finitely generated field ![]() $k$ of characteristic zero with
$k$ of characteristic zero with ![]() $X(k)$ Zariski-dense, the only obstruction to the Hilbert property should indeed come from unramified covers (see Conjecture 1.7 for a precise statement). Further taking into account that the original version of Hilbert's irreducibility theorem does not need to contend with any unramified covers at all (since
$X(k)$ Zariski-dense, the only obstruction to the Hilbert property should indeed come from unramified covers (see Conjecture 1.7 for a precise statement). Further taking into account that the original version of Hilbert's irreducibility theorem does not need to contend with any unramified covers at all (since ![]() $\mathbb {P}_n$ is geometrically simply connected), it seems natural to rule out such covers at the outset. This leads to the following notion.
$\mathbb {P}_n$ is geometrically simply connected), it seems natural to rule out such covers at the outset. This leads to the following notion.
Definition 1.2 (Corvaja–Zannier)
A smooth proper variety ![]() $X$ over a field
$X$ over a field ![]() $k$ has the weak-Hilbert property over
$k$ has the weak-Hilbert property over ![]() $k$ if, for all finite collections of finite surjective ramified morphisms
$k$ if, for all finite collections of finite surjective ramified morphisms ![]() $(\pi _i:Y_i\to X)_{i=1}^n$ with each
$(\pi _i:Y_i\to X)_{i=1}^n$ with each ![]() $Y_i$ an integral normal variety over
$Y_i$ an integral normal variety over ![]() $k$, the set
$k$, the set ![]() $X(k) \setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is Zariski-dense in
$X(k) \setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is Zariski-dense in ![]() $X$.
$X$.
Note that we restrict ourselves to finite surjective morphisms, as opposed to Corvaja and Zannier who considered dominant rational maps of finite degree in their definition of the weak-Hilbert property (see [Reference Corvaja and ZannierCZ17, § 2.2]). By a standard argument using Stein factorization, one can easily show that these two definitions are equivalent (see, for example, the proof of Theorem 7.11). In addition, we stress that the weak-Hilbert property is a birational invariant amongst smooth proper varieties (see Proposition 3.1). As a consequence, all our results concerning this property automatically propagate between smooth proper varieties within the same birational equivalence class.
The weak-Hilbert property can be applied to the inverse Galois problem similarly as the classical Hilbert property; see Remark 1.5. It is studied (using some of the results of this paper) in [Reference Bary-Soroker, Fehm and PetersenBSFP22, Reference JavanpeykarJav22, Reference Gvirtz-Chen and MezzedimiGCM21].
Our main (though not only) focus in this paper is the weak-Hilbert property for abelian varieties over finitely generated fields of characteristic zero.
Theorem 1.3 Let ![]() $k$ be a finitely generated field of characteristic zero, let
$k$ be a finitely generated field of characteristic zero, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\Omega \subset A(k)$ be a Zariski-dense subgroup, and let
$\Omega \subset A(k)$ be a Zariski-dense subgroup, and let ![]() $(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of ramified covers with each
$(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of ramified covers with each ![]() $Y_i$ a normal integral variety. Then, there is a finite index coset
$Y_i$ a normal integral variety. Then, there is a finite index coset ![]() $C\subset \Omega$ such that, for every
$C\subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$ and every
$C$ and every ![]() $i=1,\ldots, n$, the scheme
$i=1,\ldots, n$, the scheme ![]() $Y_{i,c}$ has no
$Y_{i,c}$ has no ![]() $k$-points. In particular, if
$k$-points. In particular, if ![]() $A(k)$ is dense, then
$A(k)$ is dense, then ![]() $A$ has the weak-Hilbert property over
$A$ has the weak-Hilbert property over ![]() $k$.
$k$.
We prove a stronger conclusion on the scheme-theoretic fibres ![]() $Y_{i,c}$, assuming however in addition that the ramified covers
$Y_{i,c}$, assuming however in addition that the ramified covers ![]() $\pi _i:Y_i\to A$ do not have any non-trivial étale subcovers. Here, we say that
$\pi _i:Y_i\to A$ do not have any non-trivial étale subcovers. Here, we say that ![]() $Y_i\to A$ has no non-trivial étale subcovers if, for every cover
$Y_i\to A$ has no non-trivial étale subcovers if, for every cover ![]() $X_i\to A$ of degree greater than one such that
$X_i\to A$ of degree greater than one such that ![]() $Y_i\to A$ factors over
$Y_i\to A$ factors over ![]() $X_i\to A$, we have that
$X_i\to A$, we have that ![]() $X_i\to A$ is ramified. Note that such a covering
$X_i\to A$ is ramified. Note that such a covering ![]() $Y_i\to A$ is ramified if it is of degree greater than one. Indeed, otherwise
$Y_i\to A$ is ramified if it is of degree greater than one. Indeed, otherwise ![]() $Y_i\to A$ would be an étale subcover of itself.
$Y_i\to A$ would be an étale subcover of itself.
Theorem 1.4 Let ![]() $k$ be a finitely generated field of characteristic 0, let
$k$ be a finitely generated field of characteristic 0, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\Omega \subset A(k)$ be a Zariski-dense subgroup and, for
$\Omega \subset A(k)$ be a Zariski-dense subgroup and, for ![]() $i=1,\ldots, n$, let
$i=1,\ldots, n$, let ![]() $Y_i$ be a normal integral variety, and let
$Y_i$ be a normal integral variety, and let ![]() $\pi _i:Y_i \to A$ be a finite surjective morphism with no non-trivial étale subcovers. Then, there is a finite index coset
$\pi _i:Y_i \to A$ be a finite surjective morphism with no non-trivial étale subcovers. Then, there is a finite index coset ![]() $C\subset \Omega$ such that, for every
$C\subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$ and every
$C$ and every ![]() $i=1,\ldots, n$, the
$i=1,\ldots, n$, the ![]() $k$-scheme
$k$-scheme ![]() $Y_{i,c}$ is integral.
$Y_{i,c}$ is integral.
Remark 1.5 (Inverse Galois problem)
Let ![]() $G$ be a finite group, let
$G$ be a finite group, let ![]() $X$ be a normal geometrically integral variety over
$X$ be a normal geometrically integral variety over ![]() $\mathbb {Q}$, and let
$\mathbb {Q}$, and let ![]() $X\to A$ be a
$X\to A$ be a ![]() $G$-Galois cover of an abelian variety
$G$-Galois cover of an abelian variety ![]() $A$ over
$A$ over ![]() $\mathbb {Q}$ with no non-trivial étale subcovers. Then, if
$\mathbb {Q}$ with no non-trivial étale subcovers. Then, if ![]() $A(\mathbb {Q})$ is dense, by our version of Hilbert's irreducibility theorem for abelian varieties (Theorem 1.4), there is a Galois number field
$A(\mathbb {Q})$ is dense, by our version of Hilbert's irreducibility theorem for abelian varieties (Theorem 1.4), there is a Galois number field ![]() $K$ with Galois group
$K$ with Galois group ![]() $G$.
$G$.
Note that Theorems 1.3 and 1.4 represent the usual parallelism between irreducible fibres and fibres with no rational points. In addition, as alluded to previously, one can easily extend these results to obtain similar conclusions for finite collections of dominant rational maps of finite degree (see Theorem 7.11). Furthermore, we stress that the assumption that the subgroup ![]() $\Omega$ is Zariski-dense in Theorems 1.3 and 1.4 can not be weakened to the assumption that
$\Omega$ is Zariski-dense in Theorems 1.3 and 1.4 can not be weakened to the assumption that ![]() $\Omega$ is merely infinite (see Remark 7.9).
$\Omega$ is merely infinite (see Remark 7.9).
The two results directly generalize [Reference ZannierZan10, Theorem 2] in which the case of an abelian variety isomorphic to a power of a non-CM elliptic curve was handled. In addition, we stress that in Theorem 1.3 one cannot expect the integrality of the fibres ![]() $Y_{i,c}$. Indeed, the presence of non-trivial étale subcovers obstructs the desired integrality; see Remark 7.8 for a precise statement.
$Y_{i,c}$. Indeed, the presence of non-trivial étale subcovers obstructs the desired integrality; see Remark 7.8 for a precise statement.
Remark 1.6 (About our proofs)
Working with pairs ![]() $(A,\Omega )$ in Theorems 1.3 and 1.4 has several technical advantages. For example, an induction argument allows one to reduce from a finite collection of covers to just a single cover (Lemma 4.14). Moreover, by a specialization argument, we can easily pass from number fields to arbitrary finitely generated fields of characteristic zero (see § 7.1). Furthermore, using local–global arguments, it suffices to construct a single point in
$(A,\Omega )$ in Theorems 1.3 and 1.4 has several technical advantages. For example, an induction argument allows one to reduce from a finite collection of covers to just a single cover (Lemma 4.14). Moreover, by a specialization argument, we can easily pass from number fields to arbitrary finitely generated fields of characteristic zero (see § 7.1). Furthermore, using local–global arguments, it suffices to construct a single point in ![]() $\Omega$ over which the fibre is integral (Corollary 5.4). Finally, using structure results for vertically ramified covers (Lemma 2.17), we establish a product theorem for pairs
$\Omega$ over which the fibre is integral (Corollary 5.4). Finally, using structure results for vertically ramified covers (Lemma 2.17), we establish a product theorem for pairs ![]() $(A,\Omega )$ which allows us to consider only pairs
$(A,\Omega )$ which allows us to consider only pairs ![]() $(A,\Omega )$ with
$(A,\Omega )$ with ![]() $\Omega$ cyclic; see § 5.2 for precise statements.
$\Omega$ cyclic; see § 5.2 for precise statements.
As already hinted at, the weak-Hilbert property is conjectured to hold as soon as the ‘obvious’ necessary conditions are met; more precisely, one has the following (see [Reference CampanaCam11, § 4] for the definition of a ‘special’ smooth proper connected variety).
Conjecture 1.7 (Campana, Corvaja–Zannier)
Let ![]() $X$ be a smooth proper geometrically connected variety over a finitely generated field
$X$ be a smooth proper geometrically connected variety over a finitely generated field ![]() $k$ of characteristic zero. Then the following are equivalent.
$k$ of characteristic zero. Then the following are equivalent.
1. There is a finite field extension
 $L/k$ such that
$L/k$ such that  $X_L$ has the weak-Hilbert property over
$X_L$ has the weak-Hilbert property over  $L$.
$L$.2. There is a finite field extension
 $M/k$ such that
$M/k$ such that  $X(M)$ is dense in
$X(M)$ is dense in  $X$.
$X$.3. The smooth proper connected variety
 $X_{\overline {k}}$ is special (in the sense of Campana [Reference CampanaCam11, § 4]).
$X_{\overline {k}}$ is special (in the sense of Campana [Reference CampanaCam11, § 4]).
Frey and Jarden [Reference Frey and JardenFJ74] proved that an abelian variety ![]() $A$ over a finitely generated field
$A$ over a finitely generated field ![]() $k$ of characteristic zero admits a finite extension
$k$ of characteristic zero admits a finite extension ![]() $L/k$ such that
$L/k$ such that ![]() $A(L)$ is Zariski-dense in
$A(L)$ is Zariski-dense in ![]() $A$ (see also [Reference JavanpeykarJav21a, § 3] and [Reference Hassett and TschinkelHT00]). As abelian varieties are special [Reference CampanaCam11, § 4], by combining Frey and Jarden's result with Theorem 1.3 we obtain a proof of Conjecture 1.7 for any variety which is birational to a smooth projective connected variety with trivial tangent bundle.
$A$ (see also [Reference JavanpeykarJav21a, § 3] and [Reference Hassett and TschinkelHT00]). As abelian varieties are special [Reference CampanaCam11, § 4], by combining Frey and Jarden's result with Theorem 1.3 we obtain a proof of Conjecture 1.7 for any variety which is birational to a smooth projective connected variety with trivial tangent bundle.
Corollary 1.8 Let ![]() $k$ be a finitely generated field of characteristic zero. Let
$k$ be a finitely generated field of characteristic zero. Let ![]() $X$ be a smooth proper geometrically connected variety over
$X$ be a smooth proper geometrically connected variety over ![]() $k$ which is birational to a smooth proper variety with trivial tangent bundle. Then
$k$ which is birational to a smooth proper variety with trivial tangent bundle. Then ![]() $X_{\overline {k}}$ is special [Reference CampanaCam11, § 4], and there is a finite field extension
$X_{\overline {k}}$ is special [Reference CampanaCam11, § 4], and there is a finite field extension ![]() $L/k$ such that
$L/k$ such that ![]() $X_L$ has the weak-Hilbert property over
$X_L$ has the weak-Hilbert property over ![]() $L$.
$L$.
Note that in view of Campana's perspective on special varieties, it is natural to study the influence of some positivity condition on the tangent bundle; the varieties under consideration in this work being precisely those with trivial tangent bundle. According to a classical theorem of Mori, a smooth projective variety with ample tangent bundle is geometrically isomorphic to a projective space, so that the Hilbert property for such varieties follows from Hilbert's original irreducibility theorem (after a possible field extension).
Motivated by Conjecture 1.7 and inspired by fundamental properties of special varieties [Reference CampanaCam11] and of varieties with a dense set of rational points, we establish several basic facts about the class of varieties with the weak-Hilbert property in § 3, first and foremost among them the following product theorem.
Theorem 1.9 Let ![]() $X$ and
$X$ and ![]() $Y$ be smooth proper varieties over a finitely generated field
$Y$ be smooth proper varieties over a finitely generated field ![]() $k$ of characteristic zero with the weak-Hilbert property over
$k$ of characteristic zero with the weak-Hilbert property over ![]() $k$. Then
$k$. Then ![]() $X\times Y$ has the weak-Hilbert property over
$X\times Y$ has the weak-Hilbert property over ![]() $k$.
$k$.
Theorem 1.9 was obtained jointly by the third-named author and Olivier Wittenberg, and we are grateful to Olivier Wittenberg for allowing us to include this result here.
It seems worthwhile pointing out that Theorem 1.9 is the ‘weak-Hilbert’ analogue of Bary-Soroker, Fehm and Petersen's product theorem for the (usual) Hilbert property [Reference Bary-Soroker, Fehm and PetersenBSFP14]. This product theorem was stated by Serre as a problem in [Reference SerreSer08, § 3.1].
Note that Theorem 1.9 actually reproves the product theorem of [Reference Bary-Soroker, Fehm and PetersenBSFP14] when the base field is finitely generated and of characteristic zero. Indeed, if ![]() $X$ and
$X$ and ![]() $Y$ satisfy the Hilbert property (hence, weak-Hilbert property) over a finitely generated field
$Y$ satisfy the Hilbert property (hence, weak-Hilbert property) over a finitely generated field ![]() $k$ of characteristic zero, then
$k$ of characteristic zero, then ![]() $X\times Y$ has the weak-Hilbert property over
$X\times Y$ has the weak-Hilbert property over ![]() $k$ by Theorem 1.9. However, because
$k$ by Theorem 1.9. However, because ![]() $X$ and
$X$ and ![]() $Y$ are geometrically simply connected (by Corvaja and Zannier's theorem [Reference Corvaja and ZannierCZ17, Theorem 1.6]), it follows that
$Y$ are geometrically simply connected (by Corvaja and Zannier's theorem [Reference Corvaja and ZannierCZ17, Theorem 1.6]), it follows that ![]() $X\times Y$ is geometrically simply connected (by the product property for étale fundamental groups). Thus, the smooth proper variety
$X\times Y$ is geometrically simply connected (by the product property for étale fundamental groups). Thus, the smooth proper variety ![]() $X\times Y$ is geometrically simply connected and has the weak-Hilbert property over
$X\times Y$ is geometrically simply connected and has the weak-Hilbert property over ![]() $k$. Therefore, by definition, it has the Hilbert property over
$k$. Therefore, by definition, it has the Hilbert property over ![]() $k$.
$k$.
In addition to proving Theorem 1.9, in § 3 we also show that the weak-Hilbert property of a variety ![]() $X$ is inherited by both its étale covers and its surjective images under some natural assumptions (in particular, including smooth surjective images), thus building a toolkit that simplifies proving new instances of the weak-Hilbert property.
$X$ is inherited by both its étale covers and its surjective images under some natural assumptions (in particular, including smooth surjective images), thus building a toolkit that simplifies proving new instances of the weak-Hilbert property.
To conclude this introduction we describe the ingredients that go into the proof of Theorem 1.3, which is the main result of this paper. Our argument follows the same broad lines as the proof of [Reference ZannierZan10, Theorem 2], which handled the special case of ![]() $A=E^n$ being the power of a non-CM elliptic curve with a non-degenerate point
$A=E^n$ being the power of a non-CM elliptic curve with a non-degenerate point ![]() $P$, that is, a rational point
$P$, that is, a rational point ![]() $P$ generating a Zariski-dense subgroup. The method is based on the following idea, which we simplify slightly for ease of exposition. Suppose that
$P$ generating a Zariski-dense subgroup. The method is based on the following idea, which we simplify slightly for ease of exposition. Suppose that ![]() $A$ is defined over a number field
$A$ is defined over a number field ![]() $K$. Given a cover
$K$. Given a cover ![]() $\pi : Y \to A$, one proves that there is a prime
$\pi : Y \to A$, one proves that there is a prime ![]() $\mathfrak {p}$ of
$\mathfrak {p}$ of ![]() $\mathcal {O}_K$ and a torsion point
$\mathcal {O}_K$ and a torsion point ![]() $\zeta \in A(\mathcal {O}_K/\mathfrak {p})$ that does not lift to
$\zeta \in A(\mathcal {O}_K/\mathfrak {p})$ that does not lift to ![]() $Y(\mathcal {O}_K/\mathfrak {p})$. Any rational point
$Y(\mathcal {O}_K/\mathfrak {p})$. Any rational point ![]() $Q \in A(K)$ reducing to
$Q \in A(K)$ reducing to ![]() $\zeta$ modulo
$\zeta$ modulo ![]() $\mathfrak {p}$ then also does not lift to
$\mathfrak {p}$ then also does not lift to ![]() $Y(K)$, and, because this condition is adelically open and using the group structure on
$Y(K)$, and, because this condition is adelically open and using the group structure on ![]() $A$, we get the desired Zariski-dense subset of points that do not lift to
$A$, we get the desired Zariski-dense subset of points that do not lift to ![]() $Y$. Naturally this requires that there is at least one
$Y$. Naturally this requires that there is at least one ![]() $Q \in A(K)$ reducing to
$Q \in A(K)$ reducing to ![]() $\zeta$: the last task remaining is then to prove the existence of such a point
$\zeta$: the last task remaining is then to prove the existence of such a point ![]() $Q$.
$Q$.
Despite the basic strategy being the same, however, we need to introduce several new ingredients with respect to [Reference ZannierZan10], and to reinterpret various parts of Zannier's approach in a more general context. We now briefly describe where the main novelties lie.
Some technical reductions, carried out in § 4, show that multiple variants of the weak-Hilbert property for abelian varieties are essentially all equivalent. These variants describe how the weak-Hilbert property interacts with the group structure of ![]() $A$, and allow us to pass from statements about fibres of covers having no
$A$, and allow us to pass from statements about fibres of covers having no ![]() $k$-rational points to statements about fibres being irreducible over
$k$-rational points to statements about fibres being irreducible over ![]() $k$. The core argument of our proof is contained in § 6, where we study the case of abelian varieties possessing a non-degenerate point. Unlike in the case of
$k$. The core argument of our proof is contained in § 6, where we study the case of abelian varieties possessing a non-degenerate point. Unlike in the case of ![]() $A=E^n$, which can essentially be reduced to the analysis of a single elliptic curve, we do not have at our disposal the full strength of Serre's open image theorem [Reference SerreSer72]. In addition, some explicit computations with torsion points that are accessible in dimension one would become extremely cumbersome in general. We bypass these problems by giving a more streamlined construction of the torsion point
$A=E^n$, which can essentially be reduced to the analysis of a single elliptic curve, we do not have at our disposal the full strength of Serre's open image theorem [Reference SerreSer72]. In addition, some explicit computations with torsion points that are accessible in dimension one would become extremely cumbersome in general. We bypass these problems by giving a more streamlined construction of the torsion point ![]() $\zeta$ (see § 6.1) and by replacing the open image theorem by an appeal to several deep results in the Kummer theory of abelian varieties (see § 6.2).
$\zeta$ (see § 6.1) and by replacing the open image theorem by an appeal to several deep results in the Kummer theory of abelian varieties (see § 6.2).
All that is left to do is then to extend the result to all abelian varieties. Up to ![]() $k$-isogeny, any abelian variety
$k$-isogeny, any abelian variety ![]() $A$ over
$A$ over ![]() $k$ is a direct product of
$k$ is a direct product of ![]() $k$-simple abelian varieties
$k$-simple abelian varieties ![]() $A_i$, and if
$A_i$, and if ![]() $A(k)$ is Zariski-dense, then
$A(k)$ is Zariski-dense, then ![]() $A_i(k)$ is Zariski-dense for all
$A_i(k)$ is Zariski-dense for all ![]() $i$. As any point of infinite order on a simple abelian variety is non-degenerate, defining
$i$. As any point of infinite order on a simple abelian variety is non-degenerate, defining ![]() $\Omega _i = \langle P_i\rangle$ for
$\Omega _i = \langle P_i\rangle$ for ![]() $P_i$ a point of infinite order in
$P_i$ a point of infinite order in ![]() $A_i(k)$, we may conclude at this point that, for every
$A_i(k)$, we may conclude at this point that, for every ![]() $i$, the pair
$i$, the pair ![]() $(A_i,\Omega _i)$ satisfies the conclusion of Theorem 1.3. The results of § 3 (in particular, Theorem 1.9) can then be used to show that
$(A_i,\Omega _i)$ satisfies the conclusion of Theorem 1.3. The results of § 3 (in particular, Theorem 1.9) can then be used to show that ![]() $A$ has the weak-Hilbert property over
$A$ has the weak-Hilbert property over ![]() $k$. However, the more precise version given by Theorem 1.3 (or Theorem 1.4) does not follow as easily. This is why in § 5.2 we extend the techniques developed in § 3 to prove a more specific version of Theorem 1.9, in which the factors are abelian varieties and we also take into account a (Zariski-dense) subgroup
$k$. However, the more precise version given by Theorem 1.3 (or Theorem 1.4) does not follow as easily. This is why in § 5.2 we extend the techniques developed in § 3 to prove a more specific version of Theorem 1.9, in which the factors are abelian varieties and we also take into account a (Zariski-dense) subgroup ![]() $\Omega$. A key observation in this section is that, given a cover
$\Omega$. A key observation in this section is that, given a cover ![]() $Z\to A$, the existence of a single point
$Z\to A$, the existence of a single point ![]() $P\in \Omega$ for which the fibre
$P\in \Omega$ for which the fibre ![]() $Z_P$ is integral implies that there is a finite index coset
$Z_P$ is integral implies that there is a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that, for every
$\Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$, the fibre over
$C$, the fibre over ![]() $c$ has no
$c$ has no ![]() $K$-points; see Corollary 5.4. Using the invariance of the weak-Hilbert property under isogeny, it is then a fairly straightforward matter to deduce from this the general case of our result for
$K$-points; see Corollary 5.4. Using the invariance of the weak-Hilbert property under isogeny, it is then a fairly straightforward matter to deduce from this the general case of our result for ![]() $k$ a number field. Finally, we use a specialization argument to reduce from finitely generated fields of characteristic zero to number fields.
$k$ a number field. Finally, we use a specialization argument to reduce from finitely generated fields of characteristic zero to number fields.
Outline of paper
In § 2 we gather some preliminaries. Notably, we provide a structure result for vertically ramified covers of products (Lemma 2.17). In the following section we prove that the class of varieties over a finitely generated field of characteristic zero with the weak-Hilbert property is closed under products, finite étale covers, and smooth images. In § 4 we introduce the class of (PB)-covers, i.e. ramified covers of abelian varieties with no non-trivial étale subcovers. We prove several basic properties of (PB)-covers, and provide links between variants of the Hilbert property for abelian varieties. In § 5 we prove a product theorem, analogous to that obtained in § 3, that applies to a variant of the weak-Hilbert property specific to abelian varieties. Then, in § 6, we prove that this property holds for abelian varieties over number fields endowed with a non-degenerate point. Finally, in § 7 we prove the theorems stated in the introduction: the results of the previous sections suffice to handle the case of the ground field being a finite extension of ![]() $\mathbb {Q}$, and the general case is then proven by reduction to the number field case.
$\mathbb {Q}$, and the general case is then proven by reduction to the number field case.
2. Preliminaries
2.1 Notation
Throughout the paper we let ![]() $K$ denote a number field, whereas we write
$K$ denote a number field, whereas we write ![]() $k$ for a general field (unless otherwise specified). For a number field
$k$ for a general field (unless otherwise specified). For a number field ![]() $K$, we denote by
$K$, we denote by ![]() $M_K$ the set of its places, and by
$M_K$ the set of its places, and by ![]() $M_K^{\operatorname {fin}}$ the subset of finite places.
$M_K^{\operatorname {fin}}$ the subset of finite places.
A variety over a field ![]() $k$ is an integral separated scheme of finite type over
$k$ is an integral separated scheme of finite type over ![]() $k$. If
$k$. If ![]() $X$ is a variety over
$X$ is a variety over ![]() $k$ and
$k$ and ![]() $A\subset k$ is a subring, we define a model for
$A\subset k$ is a subring, we define a model for ![]() $X$ over
$X$ over ![]() $A$ to be a pair
$A$ to be a pair ![]() $(\mathcal {X},\phi )$, where
$(\mathcal {X},\phi )$, where ![]() $\mathcal {X}$ is a separated scheme of finite type over
$\mathcal {X}$ is a separated scheme of finite type over ![]() $A$ and
$A$ and ![]() $\phi :\mathcal {X}\times _A k\to X$ is an isomorphism; we often omit
$\phi :\mathcal {X}\times _A k\to X$ is an isomorphism; we often omit ![]() $\phi$ from the notation.
$\phi$ from the notation.
A morphism ![]() $\pi :Y\to X$ of normal varieties over
$\pi :Y\to X$ of normal varieties over ![]() $k$ is a cover of
$k$ is a cover of ![]() $X$ (over
$X$ (over ![]() $k$) if
$k$) if ![]() $\pi$ is finite and surjective.
$\pi$ is finite and surjective.
For a morphism ![]() $f:Y \rightarrow X$ of schemes, and a point
$f:Y \rightarrow X$ of schemes, and a point ![]() $c \in X$, we denote the scheme-theoretic fibre of
$c \in X$, we denote the scheme-theoretic fibre of ![]() $f$ over
$f$ over ![]() $c$ by
$c$ by ![]() $Y_c$, or by
$Y_c$, or by ![]() $f^{-1}(c)$ when we need to specify the morphism to avoid ambiguity.
$f^{-1}(c)$ when we need to specify the morphism to avoid ambiguity.
Let ![]() $A$ be an abelian variety over a field
$A$ be an abelian variety over a field ![]() $k$. For a prime
$k$. For a prime ![]() $\ell$ different from the characteristic of
$\ell$ different from the characteristic of ![]() $k$, we let
$k$, we let ![]() $T_{\ell } A := \varprojlim _{n \to \infty } A[\ell ^n]$ denote the
$T_{\ell } A := \varprojlim _{n \to \infty } A[\ell ^n]$ denote the ![]() $\ell$-adic Tate module of
$\ell$-adic Tate module of ![]() $A$, where
$A$, where ![]() $A[\ell ^n]$ is, by convention, the full geometric torsion subgroup
$A[\ell ^n]$ is, by convention, the full geometric torsion subgroup ![]() $A[\ell ^n](\overline {k})$. We similarly denote by
$A[\ell ^n](\overline {k})$. We similarly denote by ![]() $A[\ell ^\infty ]$ the union of all
$A[\ell ^\infty ]$ the union of all ![]() $A[\ell ^n](\overline {k})$ for
$A[\ell ^n](\overline {k})$ for ![]() $n \geq 1$. We denote by
$n \geq 1$. We denote by ![]() $\operatorname {Gal}(k'/k)$ the Galois group of a (possibly infinite) Galois field extension
$\operatorname {Gal}(k'/k)$ the Galois group of a (possibly infinite) Galois field extension ![]() $k'/k$, and simply by
$k'/k$, and simply by ![]() $\Gamma _k$ the absolute Galois group of
$\Gamma _k$ the absolute Galois group of ![]() $k$, namely
$k$, namely ![]() $\Gamma _{k} = \operatorname {Gal}(\overline {k}/k)$. For a rational (respectively,
$\Gamma _{k} = \operatorname {Gal}(\overline {k}/k)$. For a rational (respectively, ![]() $\ell$-adic) number
$\ell$-adic) number ![]() $a\neq 0$, we define
$a\neq 0$, we define ![]() $v_{\ell }(a)$ to be the unique integer such that
$v_{\ell }(a)$ to be the unique integer such that ![]() $a={a_1}/{a_2}\cdot \ell ^{v_{\ell }(a)}$, with
$a={a_1}/{a_2}\cdot \ell ^{v_{\ell }(a)}$, with ![]() $a_1, a_2 \in \mathbb {Z}$ (respectively,
$a_1, a_2 \in \mathbb {Z}$ (respectively, ![]() $a_1, a_2 \in \mathbb {Z}_\ell$) and
$a_1, a_2 \in \mathbb {Z}_\ell$) and ![]() $\ell \nmid a_i, \ i=1,2$. If
$\ell \nmid a_i, \ i=1,2$. If ![]() $a=0$, we let
$a=0$, we let ![]() $v_{\ell }(a):= \infty$ by convention.
$v_{\ell }(a):= \infty$ by convention.
2.2 Unramified morphisms
As regards unramified morphisms, we follow the conventions of the Stacks project [Sta20, Tag 02G3]: in particular, a morphism of schemes ![]() $Y\to X$ is unramified if and only if it is locally of finite type and its diagonal is an open immersion [Sta20, Tag 02GE]. We say that a morphism locally of finite type (e.g. a cover
$Y\to X$ is unramified if and only if it is locally of finite type and its diagonal is an open immersion [Sta20, Tag 02GE]. We say that a morphism locally of finite type (e.g. a cover ![]() $Y \to X$) is ramified if it is not unramified. We need the following lemma.
$Y \to X$) is ramified if it is not unramified. We need the following lemma.
Lemma 2.1 Let ![]() $f:X\to S$ be a morphism of normal proper varieties over a field
$f:X\to S$ be a morphism of normal proper varieties over a field ![]() $k$ and let
$k$ and let ![]() $\pi :Z\to X$ be a finite surjective ramified morphism. Assume that the branch locus
$\pi :Z\to X$ be a finite surjective ramified morphism. Assume that the branch locus ![]() $D$ of
$D$ of ![]() $\pi :Z\to X$ dominates
$\pi :Z\to X$ dominates ![]() $S$ (i.e.
$S$ (i.e. ![]() $f(D) = S$). Then, for every point
$f(D) = S$). Then, for every point ![]() $s$ in
$s$ in ![]() $S$, the morphism
$S$, the morphism ![]() $Z_s\to X_s$ is finite surjective ramified.
$Z_s\to X_s$ is finite surjective ramified.
Proof. A morphism of varieties ![]() $V\to W$ over
$V\to W$ over ![]() $k$ is unramified if and only if, for every
$k$ is unramified if and only if, for every ![]() $w$ in
$w$ in ![]() $W$, the morphism
$W$, the morphism ![]() $V_w\to \operatorname {Spec} k(w)$ is unramified (i.e. étale); see [Sta20, Tag 00UV]. Now, let
$V_w\to \operatorname {Spec} k(w)$ is unramified (i.e. étale); see [Sta20, Tag 00UV]. Now, let ![]() $s$ be a point of
$s$ be a point of ![]() $S$. To show that the finite surjective morphism
$S$. To show that the finite surjective morphism ![]() $Z_s\to X_s$ is ramified, let
$Z_s\to X_s$ is ramified, let ![]() $d\in D$ be a point lying over
$d\in D$ be a point lying over ![]() $s$. Then, by the definition of the branch locus,
$s$. Then, by the definition of the branch locus, ![]() $Z_d\to \operatorname {Spec} k(d)$ is ramified. Note that
$Z_d\to \operatorname {Spec} k(d)$ is ramified. Note that ![]() $Z_d = Z_s\times _{X_s} d$ as schemes over
$Z_d = Z_s\times _{X_s} d$ as schemes over ![]() $d=\operatorname {Spec} k(d)$. As the fibre of
$d=\operatorname {Spec} k(d)$. As the fibre of ![]() $Z_s\to X_s$ over
$Z_s\to X_s$ over ![]() $d$ is ramified, it follows that
$d$ is ramified, it follows that ![]() $Z_s\to X_s$ is ramified.
$Z_s\to X_s$ is ramified.
An unramified cover ![]() $X\to Y$ of varieties might not be étale [Reference CutkoskyCut18, Exercise 21.89], but this holds whenever the target is geometrically unibranch [Sta20, Tag 0BQ2], as we now show. (Recall that a scheme
$X\to Y$ of varieties might not be étale [Reference CutkoskyCut18, Exercise 21.89], but this holds whenever the target is geometrically unibranch [Sta20, Tag 0BQ2], as we now show. (Recall that a scheme ![]() $Y$ is equidimensional if every irreducible component has the same dimension.)
$Y$ is equidimensional if every irreducible component has the same dimension.)
Lemma 2.2 Let ![]() $X$ be a geometrically unibranch integral scheme and let
$X$ be a geometrically unibranch integral scheme and let ![]() $\pi :Y\to X$ be a finite surjective unramified morphism of schemes with
$\pi :Y\to X$ be a finite surjective unramified morphism of schemes with ![]() $Y$ equidimensional. Then
$Y$ equidimensional. Then ![]() $\pi$ is étale.
$\pi$ is étale.
Proof. By [Sta20, Tag 04HJ], there is a surjective étale morphism ![]() $f:U\to X$ such that
$f:U\to X$ such that ![]() $Y_U :=Y\times _{\pi, X, f} U$ has a finite disjoint union decomposition
$Y_U :=Y\times _{\pi, X, f} U$ has a finite disjoint union decomposition
such that each ![]() $V_j\to U$ is a closed immersion. Refining this decomposition if necessary, we may assume that each
$V_j\to U$ is a closed immersion. Refining this decomposition if necessary, we may assume that each ![]() $V_j$ is connected. As
$V_j$ is connected. As ![]() $X$ is a geometrically unibranch integral scheme and
$X$ is a geometrically unibranch integral scheme and ![]() $U\to X$ is a surjective étale morphism, it follows that
$U\to X$ is a surjective étale morphism, it follows that ![]() $U$ is a disjoint union of integral schemes. Indeed, each connected component of
$U$ is a disjoint union of integral schemes. Indeed, each connected component of ![]() $U$ is reduced because
$U$ is reduced because ![]() $U \to X$ is étale and
$U \to X$ is étale and ![]() $X$ is integral, hence reduced. Furthermore, each connected component of
$X$ is integral, hence reduced. Furthermore, each connected component of ![]() $U$ is irreducible, for two irreducible components would meet at some point
$U$ is irreducible, for two irreducible components would meet at some point ![]() $u$, and the local ring at
$u$, and the local ring at ![]() $u$ would have two minimal primes, contradicting the fact that
$u$ would have two minimal primes, contradicting the fact that ![]() $X$ is geometrically unibranch [Sta20, Tag 06DM]. Let
$X$ is geometrically unibranch [Sta20, Tag 06DM]. Let ![]() $U_i$ be the connected component containing the image of
$U_i$ be the connected component containing the image of ![]() $V_j \to U$. Then the restriction of the closed immersion
$V_j \to U$. Then the restriction of the closed immersion ![]() $V_j\to U$ to the integral scheme
$V_j\to U$ to the integral scheme ![]() $U_i$ is a dominant closed immersion, as
$U_i$ is a dominant closed immersion, as ![]() $V_j \hookrightarrow Y_U$ is an open and closed immersion,
$V_j \hookrightarrow Y_U$ is an open and closed immersion, ![]() $Y_U \to U$ is finite surjective and
$Y_U \to U$ is finite surjective and ![]() $Y_U$ is equidimensional (because
$Y_U$ is equidimensional (because ![]() $Y$ is equidimensional). It follows that each non-trivial
$Y$ is equidimensional). It follows that each non-trivial ![]() $V_j\to U_i$ is an isomorphism. This implies that
$V_j\to U_i$ is an isomorphism. This implies that ![]() $Y_U\to U$ is étale, so that
$Y_U\to U$ is étale, so that ![]() $Y\to X$ is étale by étale descent.
$Y\to X$ is étale by étale descent.
The following consequence is well known and used repeatedly throughout the paper.
Lemma 2.3 Let ![]() $X$ be an integral normal noetherian scheme, and let
$X$ be an integral normal noetherian scheme, and let ![]() $\pi : Y \to X$ be a finite surjective morphism of integral schemes. Then
$\pi : Y \to X$ be a finite surjective morphism of integral schemes. Then ![]() $\pi$ is either ramified or étale.
$\pi$ is either ramified or étale.
2.3 Galois closures
Let ![]() $\pi : Y \to X$ be a cover of normal varieties over a field
$\pi : Y \to X$ be a cover of normal varieties over a field ![]() $k$ of characteristic zero, and let
$k$ of characteristic zero, and let ![]() $G(Y/X)$ be the automorphism group of
$G(Y/X)$ be the automorphism group of ![]() $Y$ over
$Y$ over ![]() $X$. The arguments in the proof of [Reference CutkoskyCut18, Proposition 21.67] show the following.
$X$. The arguments in the proof of [Reference CutkoskyCut18, Proposition 21.67] show the following.
Proposition 2.4 The canonical homomorphism ![]() $G(Y/X) \to \operatorname {Aut}(k(Y) / k(X))^{\operatorname {opp}}$ is an isomorphism.
$G(Y/X) \to \operatorname {Aut}(k(Y) / k(X))^{\operatorname {opp}}$ is an isomorphism.
The cover ![]() $\pi : Y \to X$ is called Galois if
$\pi : Y \to X$ is called Galois if ![]() $\#G(Y/X) = \deg \pi$. In this case we also write
$\#G(Y/X) = \deg \pi$. In this case we also write ![]() $\operatorname {Gal}(Y/X)$ for
$\operatorname {Gal}(Y/X)$ for ![]() $G(Y/X)$. We let
$G(Y/X)$. We let ![]() $\widehat {Y}\to X$ be the normalization of
$\widehat {Y}\to X$ be the normalization of ![]() $X$ in the Galois closure of
$X$ in the Galois closure of ![]() $k(Y)$ over
$k(Y)$ over ![]() $k(X)$; we note that the composed cover
$k(X)$; we note that the composed cover ![]() $\widehat {Y}\to X$ (which we commonly refer to as the Galois closure of
$\widehat {Y}\to X$ (which we commonly refer to as the Galois closure of ![]() $\pi : Y\to X$) is Galois. By Proposition 2.4, the morphism
$\pi : Y\to X$) is Galois. By Proposition 2.4, the morphism ![]() $\pi : Y \to X$ is Galois if and only if the field extension
$\pi : Y \to X$ is Galois if and only if the field extension ![]() $k(Y) / k(X)$ is. Moreover, if
$k(Y) / k(X)$ is. Moreover, if ![]() $\pi : Y \to X$ is étale, then
$\pi : Y \to X$ is étale, then ![]() $\pi$ is Galois if and only if it is Galois in the sense of [Sta20, Tag 03SF].
$\pi$ is Galois if and only if it is Galois in the sense of [Sta20, Tag 03SF].
Definition 2.5 If ![]() $\pi : Y \to X$ is Galois with Galois group
$\pi : Y \to X$ is Galois with Galois group ![]() $G=\mathrm {Gal}(Y/X)$ and
$G=\mathrm {Gal}(Y/X)$ and ![]() $H$ is a subgroup of
$H$ is a subgroup of ![]() $G$, we let
$G$, we let ![]() $Y/H$ be the normalization of
$Y/H$ be the normalization of ![]() $X$ in
$X$ in ![]() $k(Y)^H$, where
$k(Y)^H$, where ![]() $k(Y)^H$ is the subfield of
$k(Y)^H$ is the subfield of ![]() $k(Y)$ fixed by
$k(Y)$ fixed by ![]() $H$. Note that
$H$. Note that ![]() $Y/H$ is a normal (integral) variety over
$Y/H$ is a normal (integral) variety over ![]() $k$, and that one could equivalently describe
$k$, and that one could equivalently describe ![]() $Y/H$ as the (geometric) quotient of
$Y/H$ as the (geometric) quotient of ![]() $Y$ by
$Y$ by ![]() $H$.
$H$.
By Galois theory for ![]() $k(X)\subset k(Y)$ and Zariski's main theorem that a birational cover of a normal variety is an isomorphism, we have the following geometric version of Galois correspondence.
$k(X)\subset k(Y)$ and Zariski's main theorem that a birational cover of a normal variety is an isomorphism, we have the following geometric version of Galois correspondence.
Proposition 2.6 Assume that ![]() $\pi : Y \to X$ is a Galois cover with group
$\pi : Y \to X$ is a Galois cover with group ![]() $G$. There is a bijection between subgroups
$G$. There is a bijection between subgroups ![]() $H$ of
$H$ of ![]() $G$ and intermediate covers
$G$ and intermediate covers ![]() $Y \to Z \to X$ with
$Y \to Z \to X$ with ![]() $Z$ normal and integral. The correspondence is given by
$Z$ normal and integral. The correspondence is given by ![]() $H \mapsto [Y \to Y/H \to X]$.
$H \mapsto [Y \to Y/H \to X]$.
Remark 2.7 (i) Let ![]() $k \subset F \subset F'$ be field extensions such that
$k \subset F \subset F'$ be field extensions such that ![]() $\overline {k} \cap F'=k$ (i.e.
$\overline {k} \cap F'=k$ (i.e. ![]() $\overline {k}$ and
$\overline {k}$ and ![]() $F'$ are linearly disjoint over
$F'$ are linearly disjoint over ![]() $k$) and
$k$) and ![]() $F'/F$ is finite. Let
$F'/F$ is finite. Let ![]() $\widehat {F'}/F$ be the Galois closure of
$\widehat {F'}/F$ be the Galois closure of ![]() $F'/F$, let
$F'/F$, let ![]() $M/F{\overline {k}}$ be the Galois closure of
$M/F{\overline {k}}$ be the Galois closure of ![]() $F'{\overline {k}}/F{\overline {k}}$ and write
$F'{\overline {k}}/F{\overline {k}}$ and write ![]() $L = \widehat {F'} \cap \overline {k}$. Note that
$L = \widehat {F'} \cap \overline {k}$. Note that ![]() $L$ is a finite extension of
$L$ is a finite extension of ![]() $k$. Then
$k$. Then ![]() $\widehat {F'}$ is also the Galois closure of
$\widehat {F'}$ is also the Galois closure of ![]() $F'L$ over
$F'L$ over ![]() $FL$; hence, in particular, we have
$FL$; hence, in particular, we have ![]() $\widehat {F'} \otimes _{L} \overline {k} \cong \widehat {F'} \overline {k} = M$.
$\widehat {F'} \otimes _{L} \overline {k} \cong \widehat {F'} \overline {k} = M$.
(ii) Proposition 2.4 and remark (i) have the following immediate consequence. If ![]() $W \xrightarrow {\phi } V$ is a cover of varieties over
$W \xrightarrow {\phi } V$ is a cover of varieties over ![]() $k$,
$k$, ![]() $\widehat {W} \rightarrow V$ is the Galois closure of
$\widehat {W} \rightarrow V$ is the Galois closure of ![]() $\phi$, and
$\phi$, and ![]() $\operatorname {Spec} L /\operatorname {Spec} k$ is the normalization of
$\operatorname {Spec} L /\operatorname {Spec} k$ is the normalization of ![]() $\operatorname {Spec} k$ in
$\operatorname {Spec} k$ in ![]() $\widehat {W}$, then
$\widehat {W}$, then ![]() $\widehat {W} \times _{\operatorname {Spec} L} \operatorname {Spec} \overline {k}$ is the Galois closure of
$\widehat {W} \times _{\operatorname {Spec} L} \operatorname {Spec} \overline {k}$ is the Galois closure of ![]() $W \times _k \overline {k} \xrightarrow {\phi } V\times _k \overline {k}$.
$W \times _k \overline {k} \xrightarrow {\phi } V\times _k \overline {k}$.
Remark 2.8 Let ![]() $E'/E$ be a finite separable extension, and
$E'/E$ be a finite separable extension, and ![]() $\widehat {E'}/E$ be its Galois closure, of Galois group
$\widehat {E'}/E$ be its Galois closure, of Galois group ![]() $G$, and let
$G$, and let ![]() $H$ be such that
$H$ be such that ![]() $\widehat {E'}^H = E'$. Then
$\widehat {E'}^H = E'$. Then ![]() $\widehat {E'}\otimes _E E' \cong \oplus _{r \in G/H} \widehat {E'}$ as
$\widehat {E'}\otimes _E E' \cong \oplus _{r \in G/H} \widehat {E'}$ as ![]() $\widehat {E'}$-algebras.
$\widehat {E'}$-algebras.
The following proposition and its corollary tell us how Galois closure of covers behaves under smooth base change.
Proposition 2.9 Let ![]() $F/E$ be a finite separable field extension, let
$F/E$ be a finite separable field extension, let ![]() $E'/E$ be a field extension and let
$E'/E$ be a field extension and let ![]() $\widehat {F}/F$ be the Galois closure of
$\widehat {F}/F$ be the Galois closure of ![]() $F$ over
$F$ over ![]() $E$. Assume that
$E$. Assume that ![]() $F_{E'}:= E' \otimes _E F$ is a field, and let
$F_{E'}:= E' \otimes _E F$ is a field, and let ![]() $\widehat {F_{E'}}$ be the Galois closure of
$\widehat {F_{E'}}$ be the Galois closure of ![]() $E' \otimes _E F$ over
$E' \otimes _E F$ over ![]() $E'$. There exists a surjective morphism
$E'$. There exists a surjective morphism ![]() $E' \otimes _E \widehat {F} \rightarrow \widehat {F_{E'}}$ that restricts to the identity on
$E' \otimes _E \widehat {F} \rightarrow \widehat {F_{E'}}$ that restricts to the identity on ![]() $E'\otimes _E F$.
$E'\otimes _E F$.
Proof. There is a canonical embedding ![]() $\iota :F \hookrightarrow E' \otimes _E F \hookrightarrow \widehat {F_{E'}}$ that is the identity on
$\iota :F \hookrightarrow E' \otimes _E F \hookrightarrow \widehat {F_{E'}}$ that is the identity on ![]() $E$. The field
$E$. The field ![]() $\widehat {F_{E'}}$ is normal over
$\widehat {F_{E'}}$ is normal over ![]() $E'$, and contains
$E'$, and contains ![]() $F$ (through the embedding
$F$ (through the embedding ![]() $\iota$). Hence, there exists an embedding
$\iota$). Hence, there exists an embedding ![]() $\widehat {F}\hookrightarrow \widehat {F_{E'}}$ which restricts to the identity on
$\widehat {F}\hookrightarrow \widehat {F_{E'}}$ which restricts to the identity on ![]() $E$. Consider the morphism
$E$. Consider the morphism ![]() $\varphi : E' \otimes _E \widehat {F} \rightarrow \widehat {F_{E'}}$ which, by the universal property of the tensor product, is induced by the embedding
$\varphi : E' \otimes _E \widehat {F} \rightarrow \widehat {F_{E'}}$ which, by the universal property of the tensor product, is induced by the embedding ![]() $E'\hookrightarrow E' \otimes _E F \hookrightarrow \widehat {F_{E'}}$ and the natural embedding
$E'\hookrightarrow E' \otimes _E F \hookrightarrow \widehat {F_{E'}}$ and the natural embedding ![]() $\widehat {F} \hookrightarrow \widehat {F_{E'}}$. The field
$\widehat {F} \hookrightarrow \widehat {F_{E'}}$. The field ![]() $\widehat {F}$ is generated over
$\widehat {F}$ is generated over ![]() $E$ by the roots
$E$ by the roots ![]() $\alpha _1,\ldots,\alpha _n$ of a separable polynomial with coefficients in
$\alpha _1,\ldots,\alpha _n$ of a separable polynomial with coefficients in ![]() $E$, and these same roots also generate
$E$, and these same roots also generate ![]() $\widehat {F_{E'}}$ over
$\widehat {F_{E'}}$ over ![]() $E'$. As both
$E'$. As both ![]() $E'$ and
$E'$ and ![]() $\alpha _1,\ldots,\alpha _n$ are contained in the image of
$\alpha _1,\ldots,\alpha _n$ are contained in the image of ![]() $\varphi$, this shows that
$\varphi$, this shows that ![]() $\varphi$ is surjective as desired.
$\varphi$ is surjective as desired.
Corollary 2.10 Let ![]() $Z \rightarrow X$ be a cover of normal varieties over
$Z \rightarrow X$ be a cover of normal varieties over ![]() $k$, let
$k$, let ![]() $X'\to X$ be a smooth morphism of varieties over
$X'\to X$ be a smooth morphism of varieties over ![]() $k$, and let
$k$, and let ![]() $\widehat {Z} \rightarrow Z \rightarrow X$ be the Galois closure of
$\widehat {Z} \rightarrow Z \rightarrow X$ be the Galois closure of ![]() $Z\to X$. Then
$Z\to X$. Then ![]() $Z' := Z \times _X X'$ and
$Z' := Z \times _X X'$ and ![]() $\widehat {Z} \times _X X'$ are normal. Assume that
$\widehat {Z} \times _X X'$ are normal. Assume that ![]() $Z' := Z \times _X X'$ is connected. Then
$Z' := Z \times _X X'$ is connected. Then ![]() $Z'$ is an integral normal scheme and, if
$Z'$ is an integral normal scheme and, if ![]() $Z''\rightarrow Z' \rightarrow X'$ is the Galois closure of
$Z''\rightarrow Z' \rightarrow X'$ is the Galois closure of ![]() $Z' \rightarrow X'$, then there is an open and closed embedding
$Z' \rightarrow X'$, then there is an open and closed embedding ![]() $Z'' \rightarrow \widehat {Z} \times _X X'$ that commutes with projection to
$Z'' \rightarrow \widehat {Z} \times _X X'$ that commutes with projection to ![]() $Z'$.
$Z'$.
Proof. By [Sta20, Tag 034F], the schemes ![]() $Z'$ and
$Z'$ and ![]() $\widehat {Z} \times _X X'$ are normal. In particular, if
$\widehat {Z} \times _X X'$ are normal. In particular, if ![]() $Z'$ is connected, then it is integral (as it is connected and normal). Define
$Z'$ is connected, then it is integral (as it is connected and normal). Define
Note that
The result now follows from Proposition 2.9 and the universal property of normalization.
2.4 Action on the fibres
Let ![]() $X$ be a normal variety over a field
$X$ be a normal variety over a field ![]() $k$. Let
$k$. Let ![]() $G$ be a finite group and let
$G$ be a finite group and let ![]() $\phi :Y \rightarrow X$ be an étale (right)
$\phi :Y \rightarrow X$ be an étale (right) ![]() $G$-torsor over
$G$-torsor over ![]() $X$, so that
$X$, so that ![]() $Y$ is also normal. In this section we discuss various properties of the action of
$Y$ is also normal. In this section we discuss various properties of the action of ![]() $G$ on the fibres of
$G$ on the fibres of ![]() $\phi$. Let
$\phi$. Let ![]() $\overline {y_0}: \operatorname {Spec} \overline {k}\rightarrow Y$ be a geometric point of
$\overline {y_0}: \operatorname {Spec} \overline {k}\rightarrow Y$ be a geometric point of ![]() $Y$ and let
$Y$ and let ![]() $\overline {x_0} = \phi \circ \overline {y_0}$ be the corresponding geometric point of
$\overline {x_0} = \phi \circ \overline {y_0}$ be the corresponding geometric point of ![]() $X$.
$X$.
The left  $G$-action
$G$-action
There is a left ![]() $G$-action on
$G$-action on ![]() $Y_{\overline {x_0}}$, defined as follows:
$Y_{\overline {x_0}}$, defined as follows:
This induces a morphism ![]() $\iota _{\overline {y_0}}:G \rightarrow \operatorname {Aut}(Y_{\overline {x_0}})$. It is straightforward to check that
$\iota _{\overline {y_0}}:G \rightarrow \operatorname {Aut}(Y_{\overline {x_0}})$. It is straightforward to check that ![]() $\iota _{\overline {y_0}}(G)$ consists of the group
$\iota _{\overline {y_0}}(G)$ consists of the group ![]() $\operatorname {Aut}_G(Y_{\overline {x_0}})$ of all automorphisms of
$\operatorname {Aut}_G(Y_{\overline {x_0}})$ of all automorphisms of ![]() $Y_{\overline {x_0}}$ that commute with the right
$Y_{\overline {x_0}}$ that commute with the right ![]() $G$-action.
$G$-action.
Decomposition group
There is a natural left ![]() $\Gamma _{k(x_0)}$-action on
$\Gamma _{k(x_0)}$-action on ![]() $Y_{\overline {x_0}}$ given by
$Y_{\overline {x_0}}$ given by
where ![]() ${{^\gamma }{\overline {y'}}{}}$ denotes the composition
${{^\gamma }{\overline {y'}}{}}$ denotes the composition ![]() $\operatorname {Spec} \overline {k(x_0)} \xrightarrow {\gamma } \operatorname {Spec} \overline {k(x_0)} \xrightarrow {\overline {y'}} Y$. As the
$\operatorname {Spec} \overline {k(x_0)} \xrightarrow {\gamma } \operatorname {Spec} \overline {k(x_0)} \xrightarrow {\overline {y'}} Y$. As the ![]() $G$-action is defined over
$G$-action is defined over ![]() $k$, the action (2) commutes with the right
$k$, the action (2) commutes with the right ![]() $G$-action, hence yields a morphism
$G$-action, hence yields a morphism ![]() $\Gamma _{k(x_0)} \rightarrow \operatorname {Aut}_G(Y_{\overline {x_0}})$. Composing with the inverse of the isomorphism
$\Gamma _{k(x_0)} \rightarrow \operatorname {Aut}_G(Y_{\overline {x_0}})$. Composing with the inverse of the isomorphism ![]() $\iota _{\overline {y_0}} : G \to \operatorname {Aut}_G(Y_{\overline {x_0}})$ we get a morphism
$\iota _{\overline {y_0}} : G \to \operatorname {Aut}_G(Y_{\overline {x_0}})$ we get a morphism
called the decomposition morphism of ![]() $\overline {y_0}$ under
$\overline {y_0}$ under ![]() $\phi$. The image of
$\phi$. The image of ![]() $\mathfrak {D}_{\overline {y_0}}$ is called the decomposition group of
$\mathfrak {D}_{\overline {y_0}}$ is called the decomposition group of ![]() $\overline {y_0}$ and denoted by
$\overline {y_0}$ and denoted by ![]() $D_{\overline {y_0}}$. Finally, if
$D_{\overline {y_0}}$. Finally, if ![]() $P$ is an
$P$ is an ![]() $L$-rational point of
$L$-rational point of ![]() $X$ for some field
$X$ for some field ![]() $k \subseteq L \subseteq \overline {k}$, a decomposition group of
$k \subseteq L \subseteq \overline {k}$, a decomposition group of ![]() $P$ under
$P$ under ![]() $\phi$ is any subgroup of the form
$\phi$ is any subgroup of the form ![]() $D_{\overline {y_0}}$ for some geometric point
$D_{\overline {y_0}}$ for some geometric point ![]() $\overline {y_0}$ of
$\overline {y_0}$ of ![]() $Y$ whose image in
$Y$ whose image in ![]() $X(\overline {k})$ is the geometric point corresponding to
$X(\overline {k})$ is the geometric point corresponding to ![]() $P$.
$P$.
Remark 2.11 Note that the morphism ![]() $\mathfrak {D}_{\overline {y_0}}$ is the unique morphism that sends
$\mathfrak {D}_{\overline {y_0}}$ is the unique morphism that sends ![]() $\gamma \in \Gamma _{k(x_0)}$ to the unique element
$\gamma \in \Gamma _{k(x_0)}$ to the unique element ![]() $g \in G$ such that
$g \in G$ such that ![]() ${{^\gamma }{\overline {y_0}}{}} = \overline {y_0} \cdot g$.
${{^\gamma }{\overline {y_0}}{}} = \overline {y_0} \cdot g$.
Compatibility with subcovers
Let ![]() $Y_1 \xrightarrow {\phi _1} Y_2 \xrightarrow {\phi _2} X$ be finite étale morphisms of
$Y_1 \xrightarrow {\phi _1} Y_2 \xrightarrow {\phi _2} X$ be finite étale morphisms of ![]() $k$-schemes of finite type such that the composition
$k$-schemes of finite type such that the composition ![]() $\phi := \phi _2 \circ \phi _1$ is an étale
$\phi := \phi _2 \circ \phi _1$ is an étale ![]() $G$-torsor. Suppose that
$G$-torsor. Suppose that ![]() $Y_2 = Y_1/H$ for some subgroup
$Y_2 = Y_1/H$ for some subgroup ![]() $H\subset G$. (By Proposition 2.6, the latter is automatically satisfied if
$H\subset G$. (By Proposition 2.6, the latter is automatically satisfied if ![]() $Y_1$ and
$Y_1$ and ![]() $Y_2$ are integral normal schemes.) Again let
$Y_2$ are integral normal schemes.) Again let ![]() $\overline {y_0}$ be a geometric point of
$\overline {y_0}$ be a geometric point of ![]() $Y_1$ and
$Y_1$ and ![]() $\overline {x_0}$ be its image in
$\overline {x_0}$ be its image in ![]() $X$. By our discussion of the left
$X$. By our discussion of the left ![]() $G$-action, we have a commutative diagram:
$G$-action, we have a commutative diagram:

where the map in the upper row is the left ![]() $G$-action (1).
$G$-action (1).
Observe that ![]() $\phi _2^{-1}(\overline {x_0})$ is isomorphic to
$\phi _2^{-1}(\overline {x_0})$ is isomorphic to ![]() $G/H$, with the isomorphism preserving the left
$G/H$, with the isomorphism preserving the left ![]() $G$-action. The commutativity of (3) implies the following lemma.
$G$-action. The commutativity of (3) implies the following lemma.
Lemma 2.12 The fibre ![]() $\phi _2^{-1}(\overline {x_0})$ contains no
$\phi _2^{-1}(\overline {x_0})$ contains no ![]() $k$-rational points if and only if the decomposition group
$k$-rational points if and only if the decomposition group ![]() $D_{\overline {y_0}}$ acts with no fixed points on
$D_{\overline {y_0}}$ acts with no fixed points on ![]() $\phi _2^{-1}(\overline {x_0})$. Moreover,
$\phi _2^{-1}(\overline {x_0})$. Moreover, ![]() $D_{\overline {y_0}}$ acts with no fixed points on
$D_{\overline {y_0}}$ acts with no fixed points on ![]() $\phi _2^{-1}(\overline {x_0})$ if and only if
$\phi _2^{-1}(\overline {x_0})$ if and only if ![]() $D_{\overline {y_0}} \subset G$ acts with no fixed points on
$D_{\overline {y_0}} \subset G$ acts with no fixed points on ![]() $G/H$.
$G/H$.
The irreducibility of a fibre of a Galois cover is equivalent to the absence of rational points on the fibres of certain subcovers, as is shown implicitly in [Reference SerreSer08, Proposition 3.3.1].
Proposition 2.13 Let ![]() $\pi : Y \to X$ be a Galois cover with group
$\pi : Y \to X$ be a Galois cover with group ![]() $G$, and let
$G$, and let ![]() $x \in X(k)$ be a rational point. Suppose that
$x \in X(k)$ be a rational point. Suppose that ![]() $\pi$ is étale at
$\pi$ is étale at ![]() $x$. The scheme
$x$. The scheme ![]() $Y_x$ is reducible over
$Y_x$ is reducible over ![]() $k$ if and only if there is a subgroup
$k$ if and only if there is a subgroup ![]() $H \subsetneq G$ such that the fibre of
$H \subsetneq G$ such that the fibre of ![]() $Y/H \to X$ over
$Y/H \to X$ over ![]() $x$ has a
$x$ has a ![]() $k$-rational point.
$k$-rational point.
Specialization
From now on, we assume that ![]() $k$ is a number field
$k$ is a number field ![]() $K$. Given an étale
$K$. Given an étale ![]() $G$-torsor
$G$-torsor ![]() $\phi :Y\to X$ as before and a place
$\phi :Y\to X$ as before and a place ![]() $v \in M_{K}^{\operatorname {fin}}$, we say that a point
$v \in M_{K}^{\operatorname {fin}}$, we say that a point ![]() $x_0 \in X(K_v)$ is of good reduction for
$x_0 \in X(K_v)$ is of good reduction for ![]() $\phi$ if there exists an étale
$\phi$ if there exists an étale ![]() $G$-torsor
$G$-torsor ![]() $\psi :\mathcal {Y}\rightarrow \mathcal {X}$ over
$\psi :\mathcal {Y}\rightarrow \mathcal {X}$ over ![]() $\operatorname {Spec} \mathcal {O}_{K_v}$ extending
$\operatorname {Spec} \mathcal {O}_{K_v}$ extending ![]() $\phi$ such that
$\phi$ such that ![]() $x_0$ extends to a morphism
$x_0$ extends to a morphism ![]() $\operatorname {Spec} \mathcal {O}_{K_v} \rightarrow \mathcal {X}$, where
$\operatorname {Spec} \mathcal {O}_{K_v} \rightarrow \mathcal {X}$, where ![]() $\mathcal {O}_{K_v}$ is the ring of integers of
$\mathcal {O}_{K_v}$ is the ring of integers of ![]() $K_v$. We fix a geometric point
$K_v$. We fix a geometric point ![]() $\overline {y_0} \in Y$ lying over
$\overline {y_0} \in Y$ lying over ![]() $x_0$, and have a commutative diagram:
$x_0$, and have a commutative diagram:

where ![]() $\mathcal {O}_{K_v^{\operatorname {ur}}}$ denotes the ring of integers of the maximal unramified extension
$\mathcal {O}_{K_v^{\operatorname {ur}}}$ denotes the ring of integers of the maximal unramified extension ![]() $K_v^{\operatorname {ur}} \subset \overline {K_v}$ of
$K_v^{\operatorname {ur}} \subset \overline {K_v}$ of ![]() $K_v$. Diagram (4) induces morphisms:
$K_v$. Diagram (4) induces morphisms:

where the isomorphism ![]() $\widehat {\mathbb {Z}} \cong \Gamma _{\mathbb {F}_v}$ sends the topological generator
$\widehat {\mathbb {Z}} \cong \Gamma _{\mathbb {F}_v}$ sends the topological generator ![]() $1 \in \widehat {\mathbb {Z}}$ to the Frobenius
$1 \in \widehat {\mathbb {Z}}$ to the Frobenius ![]() $x \mapsto x^{\# \mathbb {F}_v}$.
$x \mapsto x^{\# \mathbb {F}_v}$.
Proposition 2.14 There exists a morphism ![]() $\operatorname {Gal}(K_v^{\operatorname {ur}}/K_v) \to G$ such that the following diagram commutes.
$\operatorname {Gal}(K_v^{\operatorname {ur}}/K_v) \to G$ such that the following diagram commutes.

Proof. The fibres of ![]() $\psi : \mathcal {Y} \to \mathcal {X}$ over
$\psi : \mathcal {Y} \to \mathcal {X}$ over ![]() $\psi (\overline {y_0})$ and over
$\psi (\overline {y_0})$ and over ![]() $\psi (\overline {y_0}_v)$ are both identified with
$\psi (\overline {y_0}_v)$ are both identified with ![]() $G$, hence with each other, in a
$G$, hence with each other, in a ![]() $G$-equivariant way.
$G$-equivariant way.
The image of ![]() $1 \in \widehat {\mathbb {Z}}$ under
$1 \in \widehat {\mathbb {Z}}$ under ![]() $\mathfrak {D}_{{\overline {y_0}_v}}$ is known as the Frobenius element of
$\mathfrak {D}_{{\overline {y_0}_v}}$ is known as the Frobenius element of ![]() $\overline {y_0}_v$, and is denoted by
$\overline {y_0}_v$, and is denoted by ![]() $\operatorname {Fr}_{\phi,\overline {y_0}_v}$. We also use the notation
$\operatorname {Fr}_{\phi,\overline {y_0}_v}$. We also use the notation ![]() $\operatorname {Fr}_{\phi,\overline {y_0}}:= \operatorname {Fr}_{\phi,\overline {y_0}_v}$; note that this is well defined. If
$\operatorname {Fr}_{\phi,\overline {y_0}}:= \operatorname {Fr}_{\phi,\overline {y_0}_v}$; note that this is well defined. If ![]() $\overline {y}^1_v$ and
$\overline {y}^1_v$ and ![]() $\overline {y}^2_v$ lie above the same point
$\overline {y}^2_v$ lie above the same point ![]() $x_v \in \mathcal {X}(\mathbb {F}_v)$, and
$x_v \in \mathcal {X}(\mathbb {F}_v)$, and ![]() $\overline {y}^2_v=\overline {y}^1_v \cdot g$, then we have that
$\overline {y}^2_v=\overline {y}^1_v \cdot g$, then we have that ![]() $\operatorname {Fr}_{\phi,\overline {y}^2_v}=g^{-1}\cdot \operatorname {Fr}_{\phi,\overline {y}^1_v}\cdot g$. In particular, the conjugacy class of
$\operatorname {Fr}_{\phi,\overline {y}^2_v}=g^{-1}\cdot \operatorname {Fr}_{\phi,\overline {y}^1_v}\cdot g$. In particular, the conjugacy class of ![]() $\operatorname {Fr}_{\phi,\overline {y_0}_v}$ depends only on the base point
$\operatorname {Fr}_{\phi,\overline {y_0}_v}$ depends only on the base point ![]() $x_v$. Thus, when there is no risk of confusion, we also use the notation
$x_v$. Thus, when there is no risk of confusion, we also use the notation ![]() $\operatorname {Fr}_{x_v}$ to indicate the Frobenius element
$\operatorname {Fr}_{x_v}$ to indicate the Frobenius element ![]() $\operatorname {Fr}_{\phi,\overline {y_0}_v}$ of any geometric point
$\operatorname {Fr}_{\phi,\overline {y_0}_v}$ of any geometric point ![]() $\overline {y_0}_v$ above
$\overline {y_0}_v$ above ![]() $x_v$. If
$x_v$. If ![]() $x_0 \in X(K_v)$ reduces to
$x_0 \in X(K_v)$ reduces to ![]() $x_v$ in
$x_v$ in ![]() $\mathcal {X}({\mathbb {F}_v})$, we also use the notation
$\mathcal {X}({\mathbb {F}_v})$, we also use the notation ![]() $\operatorname {Fr}_{x_0}:= \operatorname {Fr}_{x_v}$.
$\operatorname {Fr}_{x_0}:= \operatorname {Fr}_{x_v}$.
Proposition 2.15 Let ![]() $\phi :Y \rightarrow X$ be an étale cover of (normal) varieties over
$\phi :Y \rightarrow X$ be an étale cover of (normal) varieties over ![]() $K$, whose Galois closure
$K$, whose Galois closure ![]() $\widehat {Y}\rightarrow X$ has Galois group
$\widehat {Y}\rightarrow X$ has Galois group ![]() $G$, and let
$G$, and let ![]() $H \subset G$ be such that
$H \subset G$ be such that ![]() $Y \cong \widehat {Y}/H$ as
$Y \cong \widehat {Y}/H$ as ![]() $X$-covers. Let
$X$-covers. Let ![]() $v$ be a finite place of
$v$ be a finite place of ![]() $\mathcal {O}_{K}$ and
$\mathcal {O}_{K}$ and ![]() $x_0 \in X(K_v)$ be a point with good reduction for
$x_0 \in X(K_v)$ be a point with good reduction for ![]() $\phi$. Then,
$\phi$. Then, ![]() $\phi ^{-1}(x_0)(K_v) \neq \emptyset$ if and only if
$\phi ^{-1}(x_0)(K_v) \neq \emptyset$ if and only if ![]() $\operatorname {Fr}_{{x_0}}$ acts on
$\operatorname {Fr}_{{x_0}}$ acts on ![]() $G/H$ with at least one fixed point (note that, for
$G/H$ with at least one fixed point (note that, for ![]() $g \in G$, the condition that
$g \in G$, the condition that ![]() $g$ acts with at least one fixed point on
$g$ acts with at least one fixed point on ![]() $G/H$ depends only on the conjugacy class of
$G/H$ depends only on the conjugacy class of ![]() $g$).
$g$).
Proof. Let ![]() $\overline {x_0}:\operatorname {Spec} \overline {K_v} \to {x_0} \rightarrow X$ be a geometric point lying over
$\overline {x_0}:\operatorname {Spec} \overline {K_v} \to {x_0} \rightarrow X$ be a geometric point lying over ![]() $x_0$. We have that
$x_0$. We have that ![]() $\phi ^{-1}(x_0)(K_v)\neq \emptyset$ if and only if there exists a point in
$\phi ^{-1}(x_0)(K_v)\neq \emptyset$ if and only if there exists a point in ![]() $\phi ^{-1}(\overline {x_0})$ fixed by
$\phi ^{-1}(\overline {x_0})$ fixed by ![]() $\operatorname {Fr}_{{x_0}}$. By Lemma 2.12 and Proposition 2.14, such a point exists if and only if
$\operatorname {Fr}_{{x_0}}$. By Lemma 2.12 and Proposition 2.14, such a point exists if and only if ![]() $\operatorname {Fr}_{{x_0}}$ acts with at least one fixed point on
$\operatorname {Fr}_{{x_0}}$ acts with at least one fixed point on ![]() $G/H$.
$G/H$.
2.5 Vertically ramified covers
The following structure result shows that, roughly speaking, a cover of ![]() $X\times Y$ which is ‘vertically ramified’ splits as a product, up to a finite étale cover. The fact that such a structure result might be true was first observed after many fruitful discussions between the third-named author and Olivier Wittenberg.
$X\times Y$ which is ‘vertically ramified’ splits as a product, up to a finite étale cover. The fact that such a structure result might be true was first observed after many fruitful discussions between the third-named author and Olivier Wittenberg.
The following structure result is used twice in this paper. First, we use it to prove the product property for varieties with the weak-Hilbert property (Theorem 1.9). We then use it to prove a similar product property of a variant of the Hilbert property for abelian varieties (see Proposition 5.6).
Definition 2.16 Let ![]() $X, Y$ be proper smooth varieties over
$X, Y$ be proper smooth varieties over ![]() $k$ and
$k$ and ![]() $\pi : Z \to X \times Y$ be a ramified cover. We say that
$\pi : Z \to X \times Y$ be a ramified cover. We say that ![]() $\pi$ is vertically ramified over
$\pi$ is vertically ramified over ![]() $X$ if there exists a dense open subscheme
$X$ if there exists a dense open subscheme ![]() $U \subset X$ such that
$U \subset X$ such that ![]() $\pi$ is unramified (hence, étale; see Lemma 2.3) over
$\pi$ is unramified (hence, étale; see Lemma 2.3) over ![]() $U \times Y$.
$U \times Y$.
Lemma 2.17 Let ![]() $X,Y$ be proper smooth varieties over
$X,Y$ be proper smooth varieties over ![]() $k$ and
$k$ and ![]() $\pi : Z \to X \times Y$ be a ramified cover. Let
$\pi : Z \to X \times Y$ be a ramified cover. Let ![]() $U \subset X$ be a dense open subscheme such that
$U \subset X$ be a dense open subscheme such that ![]() $\pi$ is unramified over
$\pi$ is unramified over ![]() $U \times Y$ (so that
$U \times Y$ (so that ![]() $\pi$ is vertically ramified over
$\pi$ is vertically ramified over ![]() $X$). Assume, furthermore, that the geometric fibres of the composition
$X$). Assume, furthermore, that the geometric fibres of the composition ![]() $Z \to X \times Y \xrightarrow {p_1} X$ are connected and
$Z \to X \times Y \xrightarrow {p_1} X$ are connected and ![]() $U(k) \neq \emptyset$. Then there exists a commutative diagram
$U(k) \neq \emptyset$. Then there exists a commutative diagram

where:
(1)
 $X', Y', Z'$ are normal varieties over
$X', Y', Z'$ are normal varieties over  $k$;
$k$;(2)
 $X' \to X$ is a ramified cover;
$X' \to X$ is a ramified cover;(3)
 $Z' \to Z$ and
$Z' \to Z$ and  $Y' \to Y$ are finite étale;
$Y' \to Y$ are finite étale;(4)
 $Z'$ is a connected component of the fibred product
$Z'$ is a connected component of the fibred product  $Z \times _Y Y'$; in particular, if
$Z \times _Y Y'$; in particular, if  $Z \times _Y Y'$ is connected, the upper square is Cartesian;
$Z \times _Y Y'$ is connected, the upper square is Cartesian;(5)
 $Z' \rightarrow X' \rightarrow X$ is the Stein factorization of
$Z' \rightarrow X' \rightarrow X$ is the Stein factorization of  $Z' \rightarrow X$.
$Z' \rightarrow X$.
Proof. Let ![]() $x\in U(k)$ be a
$x\in U(k)$ be a ![]() $k$-rational point. Then
$k$-rational point. Then ![]() $Z_x\to \{x\} \times Y$ is a finite étale morphism. Let
$Z_x\to \{x\} \times Y$ is a finite étale morphism. Let ![]() $Y'\to Z_x\to Y$ be the Galois closure of
$Y'\to Z_x\to Y$ be the Galois closure of ![]() $Z_x\to Y$, and observe, in particular, that
$Z_x\to Y$, and observe, in particular, that ![]() $Y' \to Y$ is finite étale. Let
$Y' \to Y$ is finite étale. Let ![]() $Z' \subset Z\times _{Y} Y'$ be a connected component of the pull-back of
$Z' \subset Z\times _{Y} Y'$ be a connected component of the pull-back of ![]() $Z\to Y$ along
$Z\to Y$ along ![]() $Y'\to Y$.
$Y'\to Y$.
There are natural maps ![]() $Z' \to Z \to X \times Y \to X$ and
$Z' \to Z \to X \times Y \to X$ and ![]() $Z' \to Y'$ which induce a morphism
$Z' \to Y'$ which induce a morphism ![]() $Z' \to X \times Y'$. Let
$Z' \to X \times Y'$. Let ![]() $Z'\to X'\to X$ be the Stein factorization of the composed morphism
$Z'\to X'\to X$ be the Stein factorization of the composed morphism ![]() $Z'\to X\times Y'\to X$, which (together with the obvious map
$Z'\to X\times Y'\to X$, which (together with the obvious map ![]() $Z' \to Y'$) gives a natural morphism
$Z' \to Y'$) gives a natural morphism ![]() $Z'\to X'\times Y'$. We claim that this map is an isomorphism.
$Z'\to X'\times Y'$. We claim that this map is an isomorphism.
To prove this, note that ![]() $Z'$ is normal, as
$Z'$ is normal, as ![]() $Z'\subset Z \times _Y Y'\to Z$ is finite étale and
$Z'\subset Z \times _Y Y'\to Z$ is finite étale and ![]() $Z$ is normal. Moreover, the morphism
$Z$ is normal. Moreover, the morphism ![]() $Z'\to X'\times Y'$ is finite and surjective. By [Reference GrothendieckGro71, Proposition X.1.2], the Stein factorization of
$Z'\to X'\times Y'$ is finite and surjective. By [Reference GrothendieckGro71, Proposition X.1.2], the Stein factorization of ![]() $Z'\to X$ is étale over
$Z'\to X$ is étale over ![]() $U\subset X$. By [Reference GrothendieckGro63, Corollaire 7.8.7], over the étale locus the Stein factorization commutes with taking fibres, so the Stein factorization of
$U\subset X$. By [Reference GrothendieckGro63, Corollaire 7.8.7], over the étale locus the Stein factorization commutes with taking fibres, so the Stein factorization of ![]() $Z'_x\to \operatorname {Spec} k(x)$ is given by
$Z'_x\to \operatorname {Spec} k(x)$ is given by ![]() $\operatorname {Spec} \Gamma (Z'_x, \mathcal {O}_{Z'_x})$. As
$\operatorname {Spec} \Gamma (Z'_x, \mathcal {O}_{Z'_x})$. As ![]() $Z'_{x} = Z_{x} \times _Y Y'$ is a disjoint union of copies of
$Z'_{x} = Z_{x} \times _Y Y'$ is a disjoint union of copies of ![]() $Y'$ (as it follows from Remark 2.8 and a standard normalization argument, noting that
$Y'$ (as it follows from Remark 2.8 and a standard normalization argument, noting that ![]() $Y'\to Z_{x} \to Y$ is the Galois closure of
$Y'\to Z_{x} \to Y$ is the Galois closure of ![]() $Z_x \to Y$), we see that
$Z_x \to Y$), we see that ![]() $Z'_x \to X'_x \times Y'$ is an isomorphism (as it is a finite surjective morphism between the same number of copies of
$Z'_x \to X'_x \times Y'$ is an isomorphism (as it is a finite surjective morphism between the same number of copies of ![]() $Y'$). It follows that
$Y'$). It follows that ![]() $Z'\to X'\times Y'$ is an isomorphism over a dense open subset, hence it is a birational morphism. As
$Z'\to X'\times Y'$ is an isomorphism over a dense open subset, hence it is a birational morphism. As ![]() $Z'$ and
$Z'$ and ![]() $X'\times Y'$ are integral normal varieties over
$X'\times Y'$ are integral normal varieties over ![]() $k$, it follows as claimed that
$k$, it follows as claimed that ![]() $Z'\to X'\times Y'$ is an isomorphism by Zariski's main theorem (see [Reference GrothendieckGro61, Corollaire 4.4.9]).
$Z'\to X'\times Y'$ is an isomorphism by Zariski's main theorem (see [Reference GrothendieckGro61, Corollaire 4.4.9]).
We have thus constructed the desired diagram and shown parts (1) and (3). Parts (4) and (5) are true by construction. As for part (2), we already know that ![]() $X' \to X$ is finite (it arises as the finite part of the Stein factorization of
$X' \to X$ is finite (it arises as the finite part of the Stein factorization of ![]() $Z' \to X$) and surjective because
$Z' \to X$) and surjective because ![]() $Z' \to X$ is. It remains to show that
$Z' \to X$ is. It remains to show that ![]() $X' \to X$ is ramified; if it were not,
$X' \to X$ is ramified; if it were not, ![]() $Z' \to X \times Y' \to X \times Y$ would be étale, hence also
$Z' \to X \times Y' \to X \times Y$ would be étale, hence also ![]() $Z' \to Z \to X \times Y$ would be étale. As we already know that
$Z' \to Z \to X \times Y$ would be étale. As we already know that ![]() $Z' \to Z$ is surjective and étale, by the cancellation property for étale morphisms we would get that
$Z' \to Z$ is surjective and étale, by the cancellation property for étale morphisms we would get that ![]() $\pi : Z \to X \times Y$ is also étale, a contradiction.
$\pi : Z \to X \times Y$ is also étale, a contradiction.
3. The weak-Hilbert property
Throughout this section, we let ![]() $k$ be a field of characteristic zero, unless otherwise specified. The goal of this section is to prove that the class of varieties with the (potential) weak-Hilbert property (Definition 1.2) has several features in common with Campana's class of special varieties [Reference CampanaCam11].
$k$ be a field of characteristic zero, unless otherwise specified. The goal of this section is to prove that the class of varieties with the (potential) weak-Hilbert property (Definition 1.2) has several features in common with Campana's class of special varieties [Reference CampanaCam11].
We begin by showing that the weak-Hilbert property is a birational invariant among smooth proper geometrically connected varieties.
Proposition 3.1 (Birational invariance)
Let ![]() $X$ and
$X$ and ![]() $X'$ be smooth proper geometrically connected varieties over
$X'$ be smooth proper geometrically connected varieties over ![]() $k$. Suppose that
$k$. Suppose that ![]() $X$ and
$X$ and ![]() $X'$ are birational over
$X'$ are birational over ![]() $k$. Then
$k$. Then ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $k$ if and only if
$k$ if and only if ![]() $X'$ has the weak-Hilbert property over
$X'$ has the weak-Hilbert property over ![]() $k$.
$k$.
Proof. We denote by ![]() $\operatorname {Cov}(X)$ (respectively,
$\operatorname {Cov}(X)$ (respectively, ![]() $\operatorname {Cov}(X')$) the category of covers of
$\operatorname {Cov}(X')$) the category of covers of ![]() $X$ (respectively,
$X$ (respectively, ![]() $X'$).
$X'$).
As ![]() $X$ and
$X$ and ![]() $X'$ are birational over
$X'$ are birational over ![]() $k$, we may choose:
$k$, we may choose:
(i) a dense open subscheme
 $U$ of
$U$ of  $X$ with
$X$ with  $\mathrm {codim}_X(X\setminus U)\geq 2$;
$\mathrm {codim}_X(X\setminus U)\geq 2$;(ii) a dense open subscheme
 $U'$ of
$U'$ of  $X'$ with
$X'$ with  $\mathrm {codim}_{X'}(X'\setminus U')\geq 2$; and
$\mathrm {codim}_{X'}(X'\setminus U')\geq 2$; and(iii) an isomorphism
 $\sigma : U' \to U$ with inverse
$\sigma : U' \to U$ with inverse  $\sigma ' : U \to U'$.
$\sigma ' : U \to U'$.
We let ![]() $\eta _X, \eta _{X'}$ be the generic points of
$\eta _X, \eta _{X'}$ be the generic points of ![]() $X, X'$, and we denote the isomorphism
$X, X'$, and we denote the isomorphism ![]() $\sigma '|_{\eta _X}:\eta _X \rightarrow \eta _{X'}$ as
$\sigma '|_{\eta _X}:\eta _X \rightarrow \eta _{X'}$ as ![]() $\iota$.
$\iota$.
We define the functor ![]() $N\sigma ^*:\operatorname {Cov}(X) \rightarrow \operatorname {Cov}(X')$ (respectively,
$N\sigma ^*:\operatorname {Cov}(X) \rightarrow \operatorname {Cov}(X')$ (respectively, ![]() $N(\sigma ')^*:\operatorname {Cov}(X') \rightarrow \operatorname {Cov}(X)$) as sending a cover
$N(\sigma ')^*:\operatorname {Cov}(X') \rightarrow \operatorname {Cov}(X)$) as sending a cover ![]() $Y \to X$ to the relative normalization
$Y \to X$ to the relative normalization ![]() $Y' \to X'$ of
$Y' \to X'$ of ![]() $X'$ in the cover
$X'$ in the cover ![]() $\iota _*( Y|_{\eta _X}) \rightarrow \eta _{X'}$ (respectively, in the cover
$\iota _*( Y|_{\eta _X}) \rightarrow \eta _{X'}$ (respectively, in the cover ![]() $\iota ^*( Y|_{\eta _X}) \rightarrow \eta _{X'}$).
$\iota ^*( Y|_{\eta _X}) \rightarrow \eta _{X'}$).
Clearly, ![]() $N(\sigma ')^*$ and
$N(\sigma ')^*$ and ![]() $N\sigma ^*$ are inverse natural equivalences. We claim that these functors send étale covers to étale covers.
$N\sigma ^*$ are inverse natural equivalences. We claim that these functors send étale covers to étale covers.
Let ![]() $Y \to X$ be an étale cover. We then have that
$Y \to X$ be an étale cover. We then have that ![]() $\sigma ^*Y\rightarrow U'$ is étale as well. As
$\sigma ^*Y\rightarrow U'$ is étale as well. As ![]() $U'$ is normal, it follows that
$U'$ is normal, it follows that ![]() $\sigma ^*Y$ is normal as well. Hence,
$\sigma ^*Y$ is normal as well. Hence, ![]() $((N\sigma ^*)Y)|_{U'}\cong \sigma ^*Y$ as
$((N\sigma ^*)Y)|_{U'}\cong \sigma ^*Y$ as ![]() $U'$-schemes. In particular,
$U'$-schemes. In particular, ![]() $(N\sigma ^*)Y \rightarrow X'$ is finite and étale over the complement of a codimension-two closed subscheme of the base. As
$(N\sigma ^*)Y \rightarrow X'$ is finite and étale over the complement of a codimension-two closed subscheme of the base. As ![]() $X'$ is smooth and
$X'$ is smooth and ![]() $(N\sigma ^*)Y$ is normal, by Zariski–Nagata purity [Reference GrothendieckGro71, Théorème X.3.1],
$(N\sigma ^*)Y$ is normal, by Zariski–Nagata purity [Reference GrothendieckGro71, Théorème X.3.1], ![]() $(N\sigma ^*)Y \rightarrow X'$ is étale, which concludes the proof of the claim (the proof for
$(N\sigma ^*)Y \rightarrow X'$ is étale, which concludes the proof of the claim (the proof for ![]() $N(\sigma ')^*$ being analogous).
$N(\sigma ')^*$ being analogous).
Therefore, because ![]() $N(\sigma ')^*$ and
$N(\sigma ')^*$ and ![]() $N\sigma ^*$ are natural inverses, Lemma 2.3 implies that ramified covers
$N\sigma ^*$ are natural inverses, Lemma 2.3 implies that ramified covers ![]() $\pi : Y \to X$ give rise to ramified covers of
$\pi : Y \to X$ give rise to ramified covers of ![]() $X'$ (through
$X'$ (through ![]() $N\sigma ^*$), and conversely (through
$N\sigma ^*$), and conversely (through ![]() $N(\sigma ')^*$), which immediately implies that
$N(\sigma ')^*$), which immediately implies that ![]() $X$ has the weak-Hilbert property if and only if
$X$ has the weak-Hilbert property if and only if ![]() $X'$ does.
$X'$ does.
Remark 3.2 Let ![]() $X$ be a smooth proper variety over
$X$ be a smooth proper variety over ![]() $k$ with the weak-Hilbert property over
$k$ with the weak-Hilbert property over ![]() $k$, let
$k$, let ![]() $U$ be a dense open of
$U$ be a dense open of ![]() $X$. Then, for every finite collection of ramified covers
$X$. Then, for every finite collection of ramified covers ![]() $(Z_i \xrightarrow {\pi _i} U)_i$, we have that
$(Z_i \xrightarrow {\pi _i} U)_i$, we have that ![]() $U(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in
$U(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in ![]() $U$. Indeed, letting
$U$. Indeed, letting ![]() $Z'_i$ be the normalization of
$Z'_i$ be the normalization of ![]() $X$ in
$X$ in ![]() $Z_i$, this becomes an immediate consequence of applying the definition of the weak-Hilbert property to
$Z_i$, this becomes an immediate consequence of applying the definition of the weak-Hilbert property to ![]() $X$ and the family of ramified covers
$X$ and the family of ramified covers ![]() $(Z'_i \xrightarrow {\pi '_i} X)_i$.
$(Z'_i \xrightarrow {\pi '_i} X)_i$.
Remark 3.3 If ![]() $Y \xrightarrow {\pi } X$ is a cover of varieties over
$Y \xrightarrow {\pi } X$ is a cover of varieties over ![]() $k$ and
$k$ and ![]() $Y$ is not geometrically connected, then
$Y$ is not geometrically connected, then ![]() $Y(k)= \emptyset$, so that
$Y(k)= \emptyset$, so that ![]() $\pi (Y(k))=\emptyset$. In particular, when studying the weak-Hilbert property for
$\pi (Y(k))=\emptyset$. In particular, when studying the weak-Hilbert property for ![]() $X$, one may always restrict to covers
$X$, one may always restrict to covers ![]() $Y\to X$ with
$Y\to X$ with ![]() $Y$ geometrically connected (hence, geometrically integral).
$Y$ geometrically connected (hence, geometrically integral).
3.1 Images of varieties with the weak-Hilbert property
In this subsection we show that, under suitable assumptions on a map of varieties ![]() $X \to Y$, if the variety
$X \to Y$, if the variety ![]() $X$ has the weak-Hilbert property then so does
$X$ has the weak-Hilbert property then so does ![]() $Y$.
$Y$.
Proposition 3.4 (Finite étale images)
Let ![]() $X\xrightarrow {\phi } Y$ be a finite étale morphism of smooth proper varieties over
$X\xrightarrow {\phi } Y$ be a finite étale morphism of smooth proper varieties over ![]() $k$. If
$k$. If ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $k$, then
$k$, then ![]() $Y$ has the weak-Hilbert property over
$Y$ has the weak-Hilbert property over ![]() $k$.
$k$.
Proof. As ![]() $X$ and
$X$ and ![]() $Y$ are integral, it follows that
$Y$ are integral, it follows that ![]() $\phi$ is surjective. Let
$\phi$ is surjective. Let ![]() $( \pi _i : Z_i \to Y)_{i=1,\ldots,n}$ be a finite collection of ramified covers over
$( \pi _i : Z_i \to Y)_{i=1,\ldots,n}$ be a finite collection of ramified covers over ![]() $k$. By base change, we obtain finite surjective morphisms
$k$. By base change, we obtain finite surjective morphisms ![]() $\varphi _i : Z_i \times _Y X \to X$.
$\varphi _i : Z_i \times _Y X \to X$.
Let ![]() $Z'$ be a connected component of
$Z'$ be a connected component of ![]() $Z_i \times _Y X$. As
$Z_i \times _Y X$. As ![]() $Z'\subset Z_i\times _Y X$ is open and closed, the morphism
$Z'\subset Z_i\times _Y X$ is open and closed, the morphism ![]() $Z'\to Z_i$ is finite étale, hence surjective (by connectivity of
$Z'\to Z_i$ is finite étale, hence surjective (by connectivity of ![]() $Z'$ and
$Z'$ and ![]() $Z_i$). It follows that
$Z_i$). It follows that ![]() $\dim Z'=\dim Z_i = \dim Y = \dim X$. In particular, because
$\dim Z'=\dim Z_i = \dim Y = \dim X$. In particular, because ![]() $\varphi _i|_{Z'}:Z'\to X$ is finite, it is also surjective. Furthermore, the morphism
$\varphi _i|_{Z'}:Z'\to X$ is finite, it is also surjective. Furthermore, the morphism ![]() $\varphi _i|_{Z'}:Z'\to X$ is ramified. Indeed, because
$\varphi _i|_{Z'}:Z'\to X$ is ramified. Indeed, because ![]() $X$ is smooth, if
$X$ is smooth, if ![]() $Z' \to X$ is unramified, then it is étale (Lemma 2.3). It follows that, as
$Z' \to X$ is unramified, then it is étale (Lemma 2.3). It follows that, as ![]() $Z'\to X$ is étale and
$Z'\to X$ is étale and ![]() $X\to Y$ is étale, the composition
$X\to Y$ is étale, the composition ![]() $Z' \to X \to Y$ is étale, which by the surjectivity of
$Z' \to X \to Y$ is étale, which by the surjectivity of ![]() $Z' \to Z_i$ implies that
$Z' \to Z_i$ implies that ![]() $Z_i \to Y$ is étale, contradicting our assumption that it is ramified.
$Z_i \to Y$ is étale, contradicting our assumption that it is ramified.
Let ![]() $Z'_{ij}$ be the connected components of
$Z'_{ij}$ be the connected components of ![]() $Z_i \times _Y X$. We may apply the weak-Hilbert property of
$Z_i \times _Y X$. We may apply the weak-Hilbert property of ![]() $X$ to the ramified covers
$X$ to the ramified covers ![]() $\varphi _{i}|_{Z'_{ij}} : Z'_{ij} \to X$ to see that
$\varphi _{i}|_{Z'_{ij}} : Z'_{ij} \to X$ to see that ![]() $X(k) \setminus \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$ is dense in
$X(k) \setminus \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$ is dense in ![]() $X$. Applying the surjective morphism
$X$. Applying the surjective morphism ![]() $\phi$ to this dense set of rational points we get a dense set of rational points on
$\phi$ to this dense set of rational points we get a dense set of rational points on ![]() $Y$. We claim that this dense set is contained in
$Y$. We claim that this dense set is contained in ![]() $Y(k)\setminus \bigcup _i \pi _i(Z_i(k))$. Indeed, suppose by contradiction that there is a point
$Y(k)\setminus \bigcup _i \pi _i(Z_i(k))$. Indeed, suppose by contradiction that there is a point ![]() $Q \in X(k)\setminus \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$ such that
$Q \in X(k)\setminus \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$ such that ![]() $\phi (Q)\in \pi _i(Z_i(k))$ for some
$\phi (Q)\in \pi _i(Z_i(k))$ for some ![]() $i$. Then, by the universal property of the product
$i$. Then, by the universal property of the product ![]() $Z_i \times _Y X$, the point
$Z_i \times _Y X$, the point ![]() $Q$ belongs to
$Q$ belongs to ![]() $\varphi _i((Z_i \times _Y X) (k)) \subset \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$, contradicting our assumption.
$\varphi _i((Z_i \times _Y X) (k)) \subset \bigcup _{i,j} \varphi _i(Z'_{ij}(k))$, contradicting our assumption.
Remark 3.5 The converse to Proposition 3.4 is false. Indeed, let ![]() $E$ be an elliptic curve over
$E$ be an elliptic curve over ![]() $\mathbb {Q}$ with
$\mathbb {Q}$ with ![]() $E(\mathbb {Q})$ dense, and let
$E(\mathbb {Q})$ dense, and let ![]() $E'\to E$ be a finite étale morphism with
$E'\to E$ be a finite étale morphism with ![]() $E'(\mathbb {Q})=\emptyset$; such data are easily seen to exist. Then
$E'(\mathbb {Q})=\emptyset$; such data are easily seen to exist. Then ![]() $E$ has the weak-Hilbert property over
$E$ has the weak-Hilbert property over ![]() $\mathbb {Q}$ by Faltings’ theorem, whereas
$\mathbb {Q}$ by Faltings’ theorem, whereas ![]() $E'$ has no
$E'$ has no ![]() $\mathbb {Q}$-points and, thus, does not have the weak-Hilbert property over
$\mathbb {Q}$-points and, thus, does not have the weak-Hilbert property over ![]() $\mathbb {Q}$. However, there is a number field
$\mathbb {Q}$. However, there is a number field ![]() $K$ such that
$K$ such that ![]() $E_K'$ has the weak-Hilbert property over
$E_K'$ has the weak-Hilbert property over ![]() $K$. More generally, assuming
$K$. More generally, assuming ![]() $k$ is a finitely generated field of characteristic zero, we show a converse to Proposition 3.4 in which we allow an extension of the base field; see Theorem 3.16 for a precise statement.
$k$ is a finitely generated field of characteristic zero, we show a converse to Proposition 3.4 in which we allow an extension of the base field; see Theorem 3.16 for a precise statement.
A surjective morphism ![]() $f:X\to Y$ of varieties over
$f:X\to Y$ of varieties over ![]() $k$ is said to have no multiple fibres in codimension one if, for every point
$k$ is said to have no multiple fibres in codimension one if, for every point ![]() $y$ in
$y$ in ![]() $Y$ of codimension one, the scheme-theoretic fibre
$Y$ of codimension one, the scheme-theoretic fibre ![]() $X_y$ has an irreducible component which is reduced.
$X_y$ has an irreducible component which is reduced.
Proposition 3.6 (Fibrations with no multiple fibres)
Let ![]() $X\xrightarrow {\phi } Y$ be a surjective morphism of smooth proper varieties over
$X\xrightarrow {\phi } Y$ be a surjective morphism of smooth proper varieties over ![]() $k$ with geometrically connected generic fibre and no multiple fibres in codimension one. If
$k$ with geometrically connected generic fibre and no multiple fibres in codimension one. If ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $k$, then
$k$, then ![]() $Y$ has the weak-Hilbert property over
$Y$ has the weak-Hilbert property over ![]() $k$.
$k$.
Proof. Let ![]() $( \pi _i : Z_i \to Y)_{i=1,\ldots,n}$ be a finite collection of ramified covers of
$( \pi _i : Z_i \to Y)_{i=1,\ldots,n}$ be a finite collection of ramified covers of ![]() $Y$ over
$Y$ over ![]() $k$. To prove the statement, we have to show that
$k$. To prove the statement, we have to show that ![]() $Y(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in
$Y(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in ![]() $Y$. Let
$Y$. Let ![]() $V \subset X$ be the smooth locus of
$V \subset X$ be the smooth locus of ![]() $\phi$, and let
$\phi$, and let ![]() $U$ be the image
$U$ be the image ![]() $\phi (V)$. Note that
$\phi (V)$. Note that ![]() $V$ is a dense open subscheme of
$V$ is a dense open subscheme of ![]() $X$, so that
$X$, so that ![]() $U \subset Y$ is also an open subscheme. Let
$U \subset Y$ is also an open subscheme. Let ![]() $\psi :V\to U$ denote the induced (smooth) morphism. As
$\psi :V\to U$ denote the induced (smooth) morphism. As ![]() $\phi$ has no multiple fibres in codimension one, the complement of
$\phi$ has no multiple fibres in codimension one, the complement of ![]() $U$ in
$U$ in ![]() $Y$ is of codimension at least two. As
$Y$ is of codimension at least two. As ![]() $V\xrightarrow {\phi |_{V}}Y$ is smooth, the morphism
$V\xrightarrow {\phi |_{V}}Y$ is smooth, the morphism ![]() $Z_i\times _Y V\rightarrow Z_i$ is smooth. In particular, by [Sta20, Tag 034F] and the normality of
$Z_i\times _Y V\rightarrow Z_i$ is smooth. In particular, by [Sta20, Tag 034F] and the normality of ![]() $Z_i$, the scheme
$Z_i$, the scheme ![]() $W_i:=Z_i\times _Y V$ is normal.
$W_i:=Z_i\times _Y V$ is normal.
We claim that ![]() $W_i$ is integral. Since
$W_i$ is integral. Since ![]() $k$ is of characteristic zero and
$k$ is of characteristic zero and ![]() $X$ is smooth, the generic fibre
$X$ is smooth, the generic fibre ![]() $X_{ {k(Y)}}$ of
$X_{ {k(Y)}}$ of ![]() $\phi :X\to Y$ is smooth. As
$\phi :X\to Y$ is smooth. As ![]() $X_{ {k(Y)}}$ is geometrically connected (by assumption),
$X_{ {k(Y)}}$ is geometrically connected (by assumption), ![]() $X_{ {k(Y)}}$ is geometrically integral. It follows that the same is true for the generic fibre of
$X_{ {k(Y)}}$ is geometrically integral. It follows that the same is true for the generic fibre of ![]() $V \to Y$. In particular, the generic fibre of
$V \to Y$. In particular, the generic fibre of ![]() $W_i=Z_i\times _Y V\to Z_i$, being the base change of the generic fibre of
$W_i=Z_i\times _Y V\to Z_i$, being the base change of the generic fibre of ![]() $V \to Y$, is geometrically integral as well. Applying [Reference LiuLiu06, Proposition 3.8] to
$V \to Y$, is geometrically integral as well. Applying [Reference LiuLiu06, Proposition 3.8] to ![]() $(W_i)_{\overline {k}}\to (Z_i)_{\overline {k}}$, we deduce that
$(W_i)_{\overline {k}}\to (Z_i)_{\overline {k}}$, we deduce that ![]() $W_i$ is integral.
$W_i$ is integral.
Define ![]() $\pi '_i:W_i \rightarrow V$ to be the natural projection. We claim that
$\pi '_i:W_i \rightarrow V$ to be the natural projection. We claim that ![]() $\pi '_i$ is ramified. In fact, assume by contradiction that it is not. We have the following commutative diagram, which is Cartesian in the upper left corner.
$\pi '_i$ is ramified. In fact, assume by contradiction that it is not. We have the following commutative diagram, which is Cartesian in the upper left corner.

As ![]() $\pi '_i$ and
$\pi '_i$ and ![]() $\psi$ are both smooth, so is the morphism
$\psi$ are both smooth, so is the morphism ![]() $W_i \to U$. Moreover,
$W_i \to U$. Moreover, ![]() $W_i \to Z_i|_{U}$ is smooth and surjective (being a base change of the smooth surjective morphism
$W_i \to Z_i|_{U}$ is smooth and surjective (being a base change of the smooth surjective morphism ![]() $\psi$). Hence, applying [Sta20, Tag 02K5] to
$\psi$). Hence, applying [Sta20, Tag 02K5] to ![]() $(f,q,p)=(W_i \to Z_i|_{U}, \pi _i|_{U}, W_i \to U)$, we obtain that
$(f,q,p)=(W_i \to Z_i|_{U}, \pi _i|_{U}, W_i \to U)$, we obtain that ![]() $\pi _i|_{U}$ is smooth, hence étale, which by the Zariski–Nagata theorem implies that
$\pi _i|_{U}$ is smooth, hence étale, which by the Zariski–Nagata theorem implies that ![]() $\pi _i$ is étale: contradiction.
$\pi _i$ is étale: contradiction.
As ![]() $X$ has the weak-Hilbert property, by Remark 3.2, the set
$X$ has the weak-Hilbert property, by Remark 3.2, the set ![]() $S:=V(k)\setminus \bigcup _{i=1}^n \pi '_i(W_i(k))$ is dense in
$S:=V(k)\setminus \bigcup _{i=1}^n \pi '_i(W_i(k))$ is dense in ![]() $X$. By the universal property of the fibred product
$X$. By the universal property of the fibred product ![]() $W_i=Z_i\times _Y V$, following the same argument used at the end of the proof of Proposition 3.4, we conclude that
$W_i=Z_i\times _Y V$, following the same argument used at the end of the proof of Proposition 3.4, we conclude that ![]() $\psi (S) \subset Y(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in
$\psi (S) \subset Y(k) \setminus \bigcup _i \pi _i(Z_i(k))$ is Zariski-dense in ![]() $Y$, as required.
$Y$, as required.
Theorem 3.7 (Smooth images)
Let ![]() $X\xrightarrow {\phi } Y$ be a smooth proper morphism of smooth proper varieties over
$X\xrightarrow {\phi } Y$ be a smooth proper morphism of smooth proper varieties over ![]() $k$. If
$k$. If ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $k$, then
$k$, then ![]() $Y$ has the weak-Hilbert property over
$Y$ has the weak-Hilbert property over ![]() $k$.
$k$.
Proof. Let ![]() $X\to X'\to Y$ be the Stein factorization of
$X\to X'\to Y$ be the Stein factorization of ![]() $\phi :X\to Y$. Note that
$\phi :X\to Y$. Note that ![]() $X\to X'$ is a smooth proper morphism and that
$X\to X'$ is a smooth proper morphism and that ![]() $X'\to Y$ is finite étale. In particular, because
$X'\to Y$ is finite étale. In particular, because ![]() $X\to X'$ has no multiple fibres in codimension one, it follows that
$X\to X'$ has no multiple fibres in codimension one, it follows that ![]() $X'$ has the weak-Hilbert property over
$X'$ has the weak-Hilbert property over ![]() $k$ by Proposition 3.6. Then, as
$k$ by Proposition 3.6. Then, as ![]() $X'$ has the weak-Hilbert property over
$X'$ has the weak-Hilbert property over ![]() $k$ and
$k$ and ![]() $X'\to Y$ is a finite étale morphism of smooth proper varieties over
$X'\to Y$ is a finite étale morphism of smooth proper varieties over ![]() $k$, we conclude that
$k$, we conclude that ![]() $Y$ has the weak-Hilbert property over
$Y$ has the weak-Hilbert property over ![]() $k$ (Proposition 3.4), as required.
$k$ (Proposition 3.4), as required.
3.2 Arithmetic refinements
An arithmetic refinement of a variety ![]() $Z$ over
$Z$ over ![]() $k$ is the data of a finite index set
$k$ is the data of a finite index set ![]() $J$ and, for every
$J$ and, for every ![]() $j$ in
$j$ in ![]() $J$, a cover
$J$, a cover ![]() $\psi _j:W_j\to Z$ with
$\psi _j:W_j\to Z$ with ![]() $W_j$ normal and geometrically integral, with the property that
$W_j$ normal and geometrically integral, with the property that ![]() $Z(k)\subset \bigcup _{j\in J}\psi _j(W_j(k))$. When ‘testing’ the weak-Hilbert property for a variety
$Z(k)\subset \bigcup _{j\in J}\psi _j(W_j(k))$. When ‘testing’ the weak-Hilbert property for a variety ![]() $X$, one can replace a given cover by arithmetic refinements. Let us be more precise.
$X$, one can replace a given cover by arithmetic refinements. Let us be more precise.
Let ![]() $n\geq 1$ be an integer and, for
$n\geq 1$ be an integer and, for ![]() $i=1,\ldots, n$, let
$i=1,\ldots, n$, let ![]() $\pi _i:Z_i\to X$ be a ramified cover of normal projective geometrically integral varieties over
$\pi _i:Z_i\to X$ be a ramified cover of normal projective geometrically integral varieties over ![]() $k$. For every
$k$. For every ![]() $i$, let
$i$, let ![]() $J_i$ be a finite set. For
$J_i$ be a finite set. For ![]() $i=1,\ldots, n$ and
$i=1,\ldots, n$ and ![]() $j$ in
$j$ in ![]() $J_i$, let
$J_i$, let ![]() $\psi _{i,j}:W_{ij}\to Z_j$ be a cover. Assume that, for
$\psi _{i,j}:W_{ij}\to Z_j$ be a cover. Assume that, for ![]() $i=1,\ldots, n$, the collection
$i=1,\ldots, n$, the collection ![]() $\{\psi _{i,j}:W_{ij}\to Z_i\}_{j\in J_i}$ is an arithmetic refinement of
$\{\psi _{i,j}:W_{ij}\to Z_i\}_{j\in J_i}$ is an arithmetic refinement of ![]() $Z_i$. Then
$Z_i$. Then
 \[ X(k)\setminus \bigcup_{i=1}^n \bigcup_{j\in J_i} \pi_i(\psi_{i,j}(W_{ij}(k))) = X(k) \setminus \bigcup_{i=1}^n \pi_i(Z_i(k)). \]
\[ X(k)\setminus \bigcup_{i=1}^n \bigcup_{j\in J_i} \pi_i(\psi_{i,j}(W_{ij}(k))) = X(k) \setminus \bigcup_{i=1}^n \pi_i(Z_i(k)). \]
Thus, when ‘testing’ the weak-Hilbert property for a variety (Definition 1.2), one may replace each cover ![]() $Z_i\to X$ in a given finite collection of covers
$Z_i\to X$ in a given finite collection of covers ![]() $(Z_i\to X)_i$ by an arithmetic refinement of
$(Z_i\to X)_i$ by an arithmetic refinement of ![]() $Z_i$.
$Z_i$.
3.3 Chevalley–Weil for finitely generated fields of characteristic zero
Let ![]() $f:X\to Y$ be a finite étale surjective morphism of proper schemes over a field
$f:X\to Y$ be a finite étale surjective morphism of proper schemes over a field ![]() $k$. When
$k$. When ![]() $k$ is a number field, a classical result (which goes back to Chevalley and Weil [Reference Chevalley and WeilCW32]) shows that there exists a finite extension
$k$ is a number field, a classical result (which goes back to Chevalley and Weil [Reference Chevalley and WeilCW32]) shows that there exists a finite extension ![]() $L$ of
$L$ of ![]() $k$ such that every
$k$ such that every ![]() $k$-rational point of
$k$-rational point of ![]() $Y$ lifts to an
$Y$ lifts to an ![]() $L$-rational point of
$L$-rational point of ![]() $X$. The same statement holds when
$X$. The same statement holds when ![]() $k$ is a finitely generated field of characteristic zero; because we were unable to find this precise statement in the literature, we include a short proof.
$k$ is a finitely generated field of characteristic zero; because we were unable to find this precise statement in the literature, we include a short proof.
Theorem 3.8 If ![]() $f : X \to Y$ is a finite étale surjective morphism of proper schemes over a finitely generated field
$f : X \to Y$ is a finite étale surjective morphism of proper schemes over a finitely generated field ![]() $k$ of characteristic zero, then there is a finite field extension
$k$ of characteristic zero, then there is a finite field extension ![]() $L/k$ such that
$L/k$ such that ![]() $Y(k)\subset f(X(L))$.
$Y(k)\subset f(X(L))$.
Proof. By standard spreading out arguments, we may choose a regular ![]() $\mathbb {Z}$-finitely generated integral domain
$\mathbb {Z}$-finitely generated integral domain ![]() $A\subset k$, a proper model
$A\subset k$, a proper model ![]() $\mathcal {X}$ for
$\mathcal {X}$ for ![]() $X$ over
$X$ over ![]() $A$, a proper model
$A$, a proper model ![]() $\mathcal {Y}$ for
$\mathcal {Y}$ for ![]() $Y$ over
$Y$ over ![]() $A$, and a finite étale surjective morphism
$A$, and a finite étale surjective morphism ![]() $F:\mathcal {X}\to \mathcal {Y}$ extending
$F:\mathcal {X}\to \mathcal {Y}$ extending ![]() $f$. By properness of
$f$. By properness of ![]() $\mathcal {Y}$ over
$\mathcal {Y}$ over ![]() $A$, for every
$A$, for every ![]() $k$-point
$k$-point ![]() $y:\operatorname {Spec} k\to Y$, there exist a dense open subscheme
$y:\operatorname {Spec} k\to Y$, there exist a dense open subscheme ![]() $U_y\subset \operatorname {Spec} A$ whose complement in
$U_y\subset \operatorname {Spec} A$ whose complement in ![]() $\operatorname {Spec} A$ is of codimension at least two and a morphism
$\operatorname {Spec} A$ is of codimension at least two and a morphism ![]() $U_y\to \mathcal {Y}$ extending the morphism
$U_y\to \mathcal {Y}$ extending the morphism ![]() $y:\operatorname {Spec} k\to Y$. Pulling back
$y:\operatorname {Spec} k\to Y$. Pulling back ![]() $U_y\to \mathcal {Y}$ along
$U_y\to \mathcal {Y}$ along ![]() $F:\mathcal {X}\to \mathcal {Y}$, we obtain a finite étale surjective morphism
$F:\mathcal {X}\to \mathcal {Y}$, we obtain a finite étale surjective morphism ![]() $V_y:= U_y\times _{\mathcal {Y}} \mathcal {X}\to U_y$ of degree
$V_y:= U_y\times _{\mathcal {Y}} \mathcal {X}\to U_y$ of degree ![]() $\deg (f)$. By purity of the branch locus [Reference GrothendieckGro71, Théorème X.3.1], the finite étale morphism
$\deg (f)$. By purity of the branch locus [Reference GrothendieckGro71, Théorème X.3.1], the finite étale morphism ![]() $V_y\to U_y$ extends to a finite étale morphism
$V_y\to U_y$ extends to a finite étale morphism ![]() $\overline {V_y}\to \operatorname {Spec} A$. Since the set of isomorphism classes of finite étale covers of
$\overline {V_y}\to \operatorname {Spec} A$. Since the set of isomorphism classes of finite étale covers of ![]() $\operatorname {Spec} A$ with bounded degree is finite by the Hermite–Minkowski theorem for arithmetic schemes [Reference Harada and HiranouchiHH09], the set of isomorphism classes of the
$\operatorname {Spec} A$ with bounded degree is finite by the Hermite–Minkowski theorem for arithmetic schemes [Reference Harada and HiranouchiHH09], the set of isomorphism classes of the ![]() $\overline {V_y}$ (and, thus,
$\overline {V_y}$ (and, thus, ![]() $V_y$) appearing above (with
$V_y$) appearing above (with ![]() $y\in Y(k)$) is finite. In particular, we may choose a finite field extension
$y\in Y(k)$) is finite. In particular, we may choose a finite field extension ![]() $L/k$ such that, for all
$L/k$ such that, for all ![]() $k$-points
$k$-points ![]() $y:\operatorname {Spec} k\to Y$ and every connected (hence, irreducible) component
$y:\operatorname {Spec} k\to Y$ and every connected (hence, irreducible) component ![]() $V'$ of
$V'$ of ![]() $V_y$, the function field
$V_y$, the function field ![]() $K(V')$ of
$K(V')$ of ![]() $V'$ is contained in
$V'$ is contained in ![]() $L$. This readily implies that
$L$. This readily implies that ![]() $Y(k)\subset f(X(L))$, as required.
$Y(k)\subset f(X(L))$, as required.
3.4 Applying the Chevalley–Weil theorem
Let ![]() $X$ and
$X$ and ![]() $Y$ be smooth projective geometrically connected varieties over
$Y$ be smooth projective geometrically connected varieties over ![]() $k$. We stress that projectivity is only assumed for technical reasons, as it is used to ensure the existence of certain Weil restrictions in the proof of Theorem 3.9.
$k$. We stress that projectivity is only assumed for technical reasons, as it is used to ensure the existence of certain Weil restrictions in the proof of Theorem 3.9.
Let ![]() $\pi :Z\to X\times Y$ be a cover which is vertically ramified (see Definition 2.16) over
$\pi :Z\to X\times Y$ be a cover which is vertically ramified (see Definition 2.16) over ![]() $X$. We apply the Chevalley–Weil theorem (Theorem 3.8) and use Weil's restriction of scalars to construct suitable arithmetic refinements of the vertically ramified morphism
$X$. We apply the Chevalley–Weil theorem (Theorem 3.8) and use Weil's restriction of scalars to construct suitable arithmetic refinements of the vertically ramified morphism ![]() $Z\to X\times Y$. The precise statement we prove reads as follows.
$Z\to X\times Y$. The precise statement we prove reads as follows.
Theorem 3.9 (Arithmetic refinement)
Let ![]() $k$ be a finitely generated field of characteristic zero. Let
$k$ be a finitely generated field of characteristic zero. Let ![]() $X$ and
$X$ and ![]() $Y$ be smooth projective geometrically connected varieties over
$Y$ be smooth projective geometrically connected varieties over ![]() $k$. Let
$k$. Let ![]() $\pi :Z\to X\times Y$ be a cover which is vertically ramified over
$\pi :Z\to X\times Y$ be a cover which is vertically ramified over ![]() $X$. Assume that
$X$. Assume that ![]() $Z(k)$ is dense in
$Z(k)$ is dense in ![]() $Z$, so that, in particular,
$Z$, so that, in particular, ![]() $X(k)$ and
$X(k)$ and ![]() $Y(k)$ are dense in
$Y(k)$ are dense in ![]() $X$ and
$X$ and ![]() $Y$, respectively. There exists an arithmetic refinement
$Y$, respectively. There exists an arithmetic refinement ![]() $\{f_j:W_j\to Z\}_{j\in J}$ of
$\{f_j:W_j\to Z\}_{j\in J}$ of ![]() $Z$ such that, for every
$Z$ such that, for every ![]() $j$ in
$j$ in ![]() $J$, the Stein factorization of
$J$, the Stein factorization of ![]() $W_j\to X\times Y\to X$ is ramified over
$W_j\to X\times Y\to X$ is ramified over ![]() $X$.
$X$.
Proof. Let ![]() $Z\to S\to X$ be the Stein factorization of the composed map
$Z\to S\to X$ be the Stein factorization of the composed map ![]() $Z\to X\times Y\to X$ and note that
$Z\to X\times Y\to X$ and note that ![]() $S$ is a normal geometrically integral variety over
$S$ is a normal geometrically integral variety over ![]() $k$. If
$k$. If ![]() $S\to X$ is ramified, there is no need to replace
$S\to X$ is ramified, there is no need to replace ![]() $Z\to X\times Y$ by an arithmetic refinement, and we are done. Thus, we may and do assume that
$Z\to X\times Y$ by an arithmetic refinement, and we are done. Thus, we may and do assume that ![]() $S\to X$ is unramified, hence étale (Lemma 2.3). Note that the finite surjective morphism
$S\to X$ is unramified, hence étale (Lemma 2.3). Note that the finite surjective morphism ![]() $Z\to X\times Y$ factors over a finite surjective morphism
$Z\to X\times Y$ factors over a finite surjective morphism ![]() $Z\to S\times Y$ which is vertically ramified with respect to
$Z\to S\times Y$ which is vertically ramified with respect to ![]() $S\times Y\to S$ (note that
$S\times Y\to S$ (note that ![]() $S \rightarrow X$ is étale). As the geometric fibres of the composed morphism
$S \rightarrow X$ is étale). As the geometric fibres of the composed morphism ![]() $Z\to S\times Y\to S$ are connected and
$Z\to S\times Y\to S$ are connected and ![]() $S(k)$ is dense, it follows from Lemma 2.17 that there is the following commutative diagram.
$S(k)$ is dense, it follows from Lemma 2.17 that there is the following commutative diagram.

Here ![]() $S' \to S$ is a ramified cover,
$S' \to S$ is a ramified cover, ![]() $Y' \to Y$ is finite étale and
$Y' \to Y$ is finite étale and ![]() $\psi :Z'\cong S'\times Y'\to Z$ is finite étale. In particular, because
$\psi :Z'\cong S'\times Y'\to Z$ is finite étale. In particular, because ![]() $k$ is a finitely generated field of characteristic zero, it follows from the Chevalley–Weil theorem (Theorem 3.8) that there is a finite field extension
$k$ is a finitely generated field of characteristic zero, it follows from the Chevalley–Weil theorem (Theorem 3.8) that there is a finite field extension ![]() $L/k$ such that
$L/k$ such that ![]() $Z(k)\subset \psi (Z'(L))$.
$Z(k)\subset \psi (Z'(L))$.
Consider the induced morphism of Weil restriction of scalars ![]() $R_{L/k}(\psi _L):R_{L/k} Z'_L \to R_{L/k} Z_L$; see [Reference Bosch, Lütkebohmert and RaynaudBLR90, Chapter 7.6]. Let
$R_{L/k}(\psi _L):R_{L/k} Z'_L \to R_{L/k} Z_L$; see [Reference Bosch, Lütkebohmert and RaynaudBLR90, Chapter 7.6]. Let ![]() $\Delta :Z\to R_{L/k} Z_L$ be the diagonal morphism. Let
$\Delta :Z\to R_{L/k} Z_L$ be the diagonal morphism. Let ![]() $(W_j)_{j\in J}$ be the connected components of
$(W_j)_{j\in J}$ be the connected components of ![]() $Z\times _{\Delta, R_{L/k} Z_L} R_{L/k} Z'_L$ such that
$Z\times _{\Delta, R_{L/k} Z_L} R_{L/k} Z'_L$ such that ![]() $W_j(k)\neq \emptyset$ and let
$W_j(k)\neq \emptyset$ and let ![]() $f_j:W_j\to Z$ be the natural morphism. As
$f_j:W_j\to Z$ be the natural morphism. As ![]() $W_j$ is normal connected and with a
$W_j$ is normal connected and with a ![]() $k$-rational point, it is geometrically integral. Moreover, note that, by the defining properties of the Weil restriction of scalars, the finite set of covers
$k$-rational point, it is geometrically integral. Moreover, note that, by the defining properties of the Weil restriction of scalars, the finite set of covers ![]() $\{f_j:W_j\to Z\}_{j\in J}$ is an arithmetic refinement of
$\{f_j:W_j\to Z\}_{j\in J}$ is an arithmetic refinement of ![]() $Z$.
$Z$.
After base change to ![]() $\overline {k}$, the fibre product
$\overline {k}$, the fibre product ![]() $Z\times _{\Delta, R_{L/k} Z_L} R_{L/k} Z'_L$ is given by
$Z\times _{\Delta, R_{L/k} Z_L} R_{L/k} Z'_L$ is given by ![]() $Z'_{\overline {k}}\times _{Z_{\overline {k}}} \ldots \times _{Z_{\overline {k}}} Z'_{\overline {k}}$. Hence, the morphism
$Z'_{\overline {k}}\times _{Z_{\overline {k}}} \ldots \times _{Z_{\overline {k}}} Z'_{\overline {k}}$. Hence, the morphism ![]() $(W_j)_{\overline {k}} \rightarrow X_{\overline {k}}$ factors as
$(W_j)_{\overline {k}} \rightarrow X_{\overline {k}}$ factors as ![]() $(W_j)_{\overline {k}} \rightarrow Z'_{\overline {k}} \rightarrow Z_{\overline {k}} \rightarrow X_{\overline {k}}$, with the morphism
$(W_j)_{\overline {k}} \rightarrow Z'_{\overline {k}} \rightarrow Z_{\overline {k}} \rightarrow X_{\overline {k}}$, with the morphism ![]() $(W_j)_{\overline {k}} \rightarrow Z'_{\overline {k}}$ being finite étale. From this it follows that the Stein factorization of
$(W_j)_{\overline {k}} \rightarrow Z'_{\overline {k}}$ being finite étale. From this it follows that the Stein factorization of ![]() $(W_j)_{\overline {k}}\to X_{\overline {k}}$ factors over the Stein factorization of
$(W_j)_{\overline {k}}\to X_{\overline {k}}$ factors over the Stein factorization of ![]() $Z'_{\overline {k}} = S'_{\overline {k}}\times Y'_{\overline {k}}\to X_{\overline {k}}$ which implies that the Stein factorization of
$Z'_{\overline {k}} = S'_{\overline {k}}\times Y'_{\overline {k}}\to X_{\overline {k}}$ which implies that the Stein factorization of ![]() $(W_j)_{\overline {k}}\to X_{\overline {k}}$ is ramified over
$(W_j)_{\overline {k}}\to X_{\overline {k}}$ is ramified over ![]() $X_{\overline {k}}$. As Stein factorization commutes with flat base change (in particular, base change to
$X_{\overline {k}}$. As Stein factorization commutes with flat base change (in particular, base change to ![]() $\overline {k}$ in our case), we deduce that the Stein factorization of
$\overline {k}$ in our case), we deduce that the Stein factorization of ![]() $W_j\to X$ is ramified over
$W_j\to X$ is ramified over ![]() $X$, as required.
$X$, as required.
Example 3.10 (Wittenberg)
It can happen that the geometric fibres of ![]() $Z\to X$ are connected. Indeed, let
$Z\to X$ are connected. Indeed, let ![]() $E'\to E$ be a degree-two isogeny between elliptic curves over
$E'\to E$ be a degree-two isogeny between elliptic curves over ![]() $k$, and let
$k$, and let ![]() $G$ be its kernel. Let
$G$ be its kernel. Let ![]() $G$ act on
$G$ act on ![]() $E'$ by translation and on
$E'$ by translation and on ![]() $\mathbb {P}_{1,k}$ by the involution
$\mathbb {P}_{1,k}$ by the involution ![]() $x\mapsto -x$. Define
$x\mapsto -x$. Define
The natural morphism ![]() $Z\to X\times Y$ is a finite surjective ramified morphism of degree two which is vertically ramified with respect to
$Z\to X\times Y$ is a finite surjective ramified morphism of degree two which is vertically ramified with respect to ![]() $X\times Y\to X$. In fact, the branch locus of
$X\times Y\to X$. In fact, the branch locus of ![]() $Z\to X\times Y$ lies over precisely two points of
$Z\to X\times Y$ lies over precisely two points of ![]() $X$. Note that the geometric fibres of
$X$. Note that the geometric fibres of ![]() $Z\to X\times Y\to X$ are connected, so that the Stein factorization of
$Z\to X\times Y\to X$ are connected, so that the Stein factorization of ![]() $Z\to X$ is étale (even an isomorphism) over
$Z\to X$ is étale (even an isomorphism) over ![]() $X$. Define
$X$. Define ![]() $Z' = E'\times \mathbb {P}_{1,k}$. Then
$Z' = E'\times \mathbb {P}_{1,k}$. Then ![]() $Z'\to Z$ is a finite étale morphism (as the action of
$Z'\to Z$ is a finite étale morphism (as the action of ![]() $G$ on
$G$ on ![]() $E'\times \mathbb {P}_{1,k}$ is free), and the Stein factorization of the composed morphism
$E'\times \mathbb {P}_{1,k}$ is free), and the Stein factorization of the composed morphism ![]() $Z'\to Z\to X\times Y\to X$ is given by
$Z'\to Z\to X\times Y\to X$ is given by ![]() $Z\to X'\to X$. Note that
$Z\to X'\to X$. Note that ![]() $X'\to X$ is ramified (as the action of
$X'\to X$ is ramified (as the action of ![]() $G$ on
$G$ on ![]() $X'$ is not free). This example shows that it is necessary to pass to a finite étale cover of
$X'$ is not free). This example shows that it is necessary to pass to a finite étale cover of ![]() $Z$ to guarantee that the Stein factorization is ramified over the base.
$Z$ to guarantee that the Stein factorization is ramified over the base.
3.5 Products
We are now ready to show that a product of varieties satisfying the weak-Hilbert property over a finitely generated field ![]() $k$ of characteristic zero has the weak-Hilbert property over
$k$ of characteristic zero has the weak-Hilbert property over ![]() $k$.
$k$.
Proof of Theorem 1.9 Let ![]() $X$ and
$X$ and ![]() $Y$ be smooth proper varieties over
$Y$ be smooth proper varieties over ![]() $k$ with the weak-Hilbert property over
$k$ with the weak-Hilbert property over ![]() $k$. We may assume, without loss of generality, by Chow's lemma and Proposition 3.1, that
$k$. We may assume, without loss of generality, by Chow's lemma and Proposition 3.1, that ![]() $X$ and
$X$ and ![]() $Y$ are projective (so that we may appeal to Theorem 3.9). We aim to show that
$Y$ are projective (so that we may appeal to Theorem 3.9). We aim to show that ![]() $X\times Y$ has the weak-Hilbert property over
$X\times Y$ has the weak-Hilbert property over ![]() $k$. For
$k$. For ![]() $i=1,\ldots, n$, let
$i=1,\ldots, n$, let ![]() $\pi _i:Z_i\to X\times Y$ be a ramified cover with
$\pi _i:Z_i\to X\times Y$ be a ramified cover with ![]() $Z_i$ a normal proper geometrically integral variety over
$Z_i$ a normal proper geometrically integral variety over ![]() $k$ (we remind the reader of Remark 3.3). Let
$k$ (we remind the reader of Remark 3.3). Let ![]() $\psi _i:S_i\to X$ denote the Stein factorization of
$\psi _i:S_i\to X$ denote the Stein factorization of ![]() $Z_i\to X\times Y\to X$, so that
$Z_i\to X\times Y\to X$, so that ![]() $Z_i\to S_i$ has geometrically connected fibres. By Theorem 3.9 we may replace each vertically ramified cover
$Z_i\to S_i$ has geometrically connected fibres. By Theorem 3.9 we may replace each vertically ramified cover ![]() $Z_i \rightarrow X \times Y$ with an arithmetic refinement
$Z_i \rightarrow X \times Y$ with an arithmetic refinement ![]() $W_{i,j} \rightarrow Z_i \rightarrow X \times Y$. Therefore, reindexing if necessary, we may assume that there exists
$W_{i,j} \rightarrow Z_i \rightarrow X \times Y$. Therefore, reindexing if necessary, we may assume that there exists ![]() $1 \leq m \leq n$ such that:
$1 \leq m \leq n$ such that:
(i)
 $\psi _i$ is ramified for
$\psi _i$ is ramified for  $i=1,\ldots, m$;
$i=1,\ldots, m$;(ii)
 $\psi _i$ is étale (see Lemma 2.3) and the branch locus of
$\psi _i$ is étale (see Lemma 2.3) and the branch locus of  $Z_i \rightarrow X \times Y$ dominates
$Z_i \rightarrow X \times Y$ dominates  $X$ for
$X$ for  $i=m+1,\ldots, n$.
$i=m+1,\ldots, n$.
We define
 \[ \Sigma:=X(k)\setminus \bigcup_{i=1}^m \psi_i(S_i(k)), \]
\[ \Sigma:=X(k)\setminus \bigcup_{i=1}^m \psi_i(S_i(k)), \]
which is Zariski-dense in ![]() $X$ because
$X$ because ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $k$. Moreover, we define
$k$. Moreover, we define
 \begin{align*} \Psi := \bigcup_{x \in \Sigma} \biggl( \{x\} \times \biggl(Y(k) \setminus \bigcup_{i=m+1}^n \pi_{i,x}(Z_{i,x}(k)) \biggr) \biggr)&= ( \Sigma \times Y(k) ) \setminus \bigcup_{i=m+1}^n\pi_{i}(Z_{i}(k))\\ &\subseteq (X(k) \times Y(k)) \setminus \bigcup_{i=1}^n\pi_{i}(Z_{i}(k)). \end{align*}
\begin{align*} \Psi := \bigcup_{x \in \Sigma} \biggl( \{x\} \times \biggl(Y(k) \setminus \bigcup_{i=m+1}^n \pi_{i,x}(Z_{i,x}(k)) \biggr) \biggr)&= ( \Sigma \times Y(k) ) \setminus \bigcup_{i=m+1}^n\pi_{i}(Z_{i}(k))\\ &\subseteq (X(k) \times Y(k)) \setminus \bigcup_{i=1}^n\pi_{i}(Z_{i}(k)). \end{align*}
To conclude the proof it suffices to show that ![]() $\Psi$ is dense in
$\Psi$ is dense in ![]() $X \times Y$. By [Reference GrothendieckGro66, Theorem 12.2.4 (iv)] and [Reference GrothendieckGro65, Theorem 6.9.1], there is a dense open subscheme
$X \times Y$. By [Reference GrothendieckGro66, Theorem 12.2.4 (iv)] and [Reference GrothendieckGro65, Theorem 6.9.1], there is a dense open subscheme ![]() $U\subset X$ such that, for every
$U\subset X$ such that, for every ![]() $x$ in
$x$ in ![]() $U(k)$, the fibre
$U(k)$, the fibre ![]() $Z_x$ of
$Z_x$ of ![]() $Z\to X\times Y\to X$ over
$Z\to X\times Y\to X$ over ![]() $x$ is a normal (not necessarily connected) scheme. As
$x$ is a normal (not necessarily connected) scheme. As ![]() $\Sigma \cap U$ is dense in
$\Sigma \cap U$ is dense in ![]() $U$, to show the density of
$U$, to show the density of ![]() $\Psi$ it suffices to prove that, for every
$\Psi$ it suffices to prove that, for every ![]() $x$ in
$x$ in ![]() $U(k)$, the set
$U(k)$, the set ![]() $Y(k) \setminus \bigcup _{i=m+1}^n\pi _{i,x}(Z_{i,x}(k))$ is dense in
$Y(k) \setminus \bigcup _{i=m+1}^n\pi _{i,x}(Z_{i,x}(k))$ is dense in ![]() $Y$. To do so, it suffices to show that, for
$Y$. To do so, it suffices to show that, for ![]() $m+1 \leq i\leq n$ and
$m+1 \leq i\leq n$ and ![]() $x$ in
$x$ in ![]() $U(k)$, and for every connected component
$U(k)$, and for every connected component ![]() $Z'$ of
$Z'$ of ![]() $Z_{i,x}$, the restriction of the morphism
$Z_{i,x}$, the restriction of the morphism ![]() $\pi _{i,x}:Z_{i,x}\to \{x\} \times Y\cong Y$ to
$\pi _{i,x}:Z_{i,x}\to \{x\} \times Y\cong Y$ to ![]() $Z'$ is a ramified cover.
$Z'$ is a ramified cover.
Let ![]() $i\in \{m+1,\ldots, n\}$ and fix
$i\in \{m+1,\ldots, n\}$ and fix ![]() $x$ in
$x$ in ![]() $U(k)$. Let
$U(k)$. Let ![]() $\psi _i^{-1}(x)=s_1 \sqcup \cdots \sqcup s_r$ (where the
$\psi _i^{-1}(x)=s_1 \sqcup \cdots \sqcup s_r$ (where the ![]() $s_i$ are the points in the fibre). Then the normal scheme
$s_i$ are the points in the fibre). Then the normal scheme ![]() $Z_{i,x}$ decomposes as a disjoint union
$Z_{i,x}$ decomposes as a disjoint union ![]() $Z_{i,x} = Z_{i,s_1}\sqcup \cdots \sqcup Z_{i,s_r}$ of normal connected varieties. Recall that the branch locus
$Z_{i,x} = Z_{i,s_1}\sqcup \cdots \sqcup Z_{i,s_r}$ of normal connected varieties. Recall that the branch locus ![]() $D_i$ of
$D_i$ of ![]() $\pi _i:Z_i\to X\times Y$ dominates
$\pi _i:Z_i\to X\times Y$ dominates ![]() $X$. We have the following commutative diagram of morphisms.
$X$. We have the following commutative diagram of morphisms.

As the branch locus ![]() $D_i$ of
$D_i$ of ![]() $\pi _i$ dominates
$\pi _i$ dominates ![]() $X$, it follows that the branch locus
$X$, it follows that the branch locus ![]() $D_{i,S_i}$ of
$D_{i,S_i}$ of ![]() $\pi _{i,S_i}:Z_{i,S_i}\to S_i\times Y$ dominates
$\pi _{i,S_i}:Z_{i,S_i}\to S_i\times Y$ dominates ![]() $S_i$. This implies that, for all
$S_i$. This implies that, for all ![]() $s$ in
$s$ in ![]() $S_i$, the morphism
$S_i$, the morphism ![]() $Z_{i,s} \to \{s\} \times Y$ is ramified (Lemma 2.1), hence so is the composition
$Z_{i,s} \to \{s\} \times Y$ is ramified (Lemma 2.1), hence so is the composition ![]() $Z_{i,s} \to \{s\} \times Y \to \{\psi _i(s)\} \times Y$, as required.
$Z_{i,s} \to \{s\} \times Y \to \{\psi _i(s)\} \times Y$, as required.
Remark 3.11 If ![]() $X$ and
$X$ and ![]() $Y$ are special varieties over
$Y$ are special varieties over ![]() $k$, then
$k$, then ![]() $X\times Y$ is special [Reference CampanaCam11]. Thus, the product theorem for the weak-Hilbert property is in accordance with the conjecture of Campana and Corvaja and Zannier (Conjecture 1.7) that a variety is special if and only if it has the weak-Hilbert property over some finite field extension of the base.
$X\times Y$ is special [Reference CampanaCam11]. Thus, the product theorem for the weak-Hilbert property is in accordance with the conjecture of Campana and Corvaja and Zannier (Conjecture 1.7) that a variety is special if and only if it has the weak-Hilbert property over some finite field extension of the base.
Remark 3.12 Note that Theorem 1.9 improves on the main result of [Reference JavanpeykarJav21b] over finitely generated fields of characteristic zero. Indeed, in [Reference JavanpeykarJav21b] it is proven that ![]() $X\times Y$ has the ‘very-weak-Hilbert property’ (see [Reference JavanpeykarJav21b, Definition 1.1]), albeit without any assumption on the base field. The main novelty of our current approach is Theorem 3.9, in which we deal with ‘vertically ramified’ covers.
$X\times Y$ has the ‘very-weak-Hilbert property’ (see [Reference JavanpeykarJav21b, Definition 1.1]), albeit without any assumption on the base field. The main novelty of our current approach is Theorem 3.9, in which we deal with ‘vertically ramified’ covers.
Example 3.13 New examples of varieties with the weak-Hilbert property can be given by taking products. For example, let ![]() $X$ be the K3 surface defined by
$X$ be the K3 surface defined by ![]() $x^4+y^4=z^4+w^4$ in
$x^4+y^4=z^4+w^4$ in ![]() $\mathbb {P}_{3,\mathbb {Q}}$, and note that
$\mathbb {P}_{3,\mathbb {Q}}$, and note that ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $\mathbb {Q}$ (see [Reference Corvaja and ZannierCZ17, Theorem 1.4]). Let
$\mathbb {Q}$ (see [Reference Corvaja and ZannierCZ17, Theorem 1.4]). Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $\mathbb {Q}$ with
$\mathbb {Q}$ with ![]() $A(\mathbb {Q})$ dense, so that
$A(\mathbb {Q})$ dense, so that ![]() $A$ has the weak-Hilbert property (Theorem 1.3). Then, for every positive integer
$A$ has the weak-Hilbert property (Theorem 1.3). Then, for every positive integer ![]() $m$, because
$m$, because ![]() $\mathbb {P}_{n,\mathbb {Q}}$ has the (weak-)Hilbert property over
$\mathbb {P}_{n,\mathbb {Q}}$ has the (weak-)Hilbert property over ![]() $\mathbb {Q}$, the variety
$\mathbb {Q}$, the variety ![]() $A\times \mathbb {P}_{n,\mathbb {Q}}\times X^{m}$ has the weak-Hilbert property over
$A\times \mathbb {P}_{n,\mathbb {Q}}\times X^{m}$ has the weak-Hilbert property over ![]() $\mathbb {Q}$ by Theorem 1.9.
$\mathbb {Q}$ by Theorem 1.9.
3.6 Finite étale covers and extending the base field
We now adapt the arguments in the proof of Theorem 3.9 to prove that the (potential) weak-Hilbert property of a variety ![]() $X/k$ is inherited by every base change
$X/k$ is inherited by every base change ![]() $X_L$ with
$X_L$ with ![]() $L/k$ finite, as well as its étale covers when
$L/k$ finite, as well as its étale covers when ![]() $k$ is finitely generated over
$k$ is finitely generated over ![]() $\mathbb {Q}$. We use the following technical lemma in both situations.
$\mathbb {Q}$. We use the following technical lemma in both situations.
Lemma 3.14 Let ![]() $L/k$ be a finite extension of fields of characteristic zero, let
$L/k$ be a finite extension of fields of characteristic zero, let ![]() $X$ be a smooth proper geometrically connected variety over
$X$ be a smooth proper geometrically connected variety over ![]() $L$, let
$L$, let ![]() $Y$ be a smooth proper geometrically connected variety over
$Y$ be a smooth proper geometrically connected variety over ![]() $k$ and let
$k$ and let ![]() $\pi :X\to Y$ be a finite étale morphism. Assume that the variety
$\pi :X\to Y$ be a finite étale morphism. Assume that the variety ![]() $Y$ has the weak-Hilbert property over
$Y$ has the weak-Hilbert property over ![]() $k$, and that
$k$, and that ![]() $Y(k)\subset \pi (X(L))$. Then
$Y(k)\subset \pi (X(L))$. Then ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $L$.
$L$.
Proof. As ![]() $X$ is geometrically connected and
$X$ is geometrically connected and ![]() $X\to Y$ is surjective, it follows that
$X\to Y$ is surjective, it follows that ![]() $Y$ is geometrically connected over
$Y$ is geometrically connected over ![]() $k$.
$k$.
We now explain how to reduce to the case that ![]() $Y$ (hence,
$Y$ (hence, ![]() $X$) is projective over
$X$) is projective over ![]() $k$. To do so, let
$k$. To do so, let ![]() $Y'\to Y$ be a proper birational surjective morphism with
$Y'\to Y$ be a proper birational surjective morphism with ![]() $Y'$ a smooth projective geometrically connected variety over
$Y'$ a smooth projective geometrically connected variety over ![]() $k$. Define
$k$. Define ![]() $X':=X\times _Y Y'$ and note that the natural projection
$X':=X\times _Y Y'$ and note that the natural projection ![]() $\pi ':X'\to Y'$ is finite étale (surjective), as it is the base change of
$\pi ':X'\to Y'$ is finite étale (surjective), as it is the base change of ![]() $\pi :X\to Y$ along
$\pi :X\to Y$ along ![]() $Y'\to Y$. In particular, because
$Y'\to Y$. In particular, because ![]() $X'$ is finite étale over the smooth variety
$X'$ is finite étale over the smooth variety ![]() $Y'$ over
$Y'$ over ![]() $k$, the scheme
$k$, the scheme ![]() $X'$ is a smooth projective geometrically connected variety over
$X'$ is a smooth projective geometrically connected variety over ![]() $L$. As
$L$. As ![]() $X'\to X$ is a proper birational surjective morphism, to show that
$X'\to X$ is a proper birational surjective morphism, to show that ![]() $X$ has the weak-Hilbert property over
$X$ has the weak-Hilbert property over ![]() $L$, by Proposition 3.1, it suffices to show that
$L$, by Proposition 3.1, it suffices to show that ![]() $X'$ has the weak-Hilbert property over
$X'$ has the weak-Hilbert property over ![]() $L$. Finally, because
$L$. Finally, because ![]() $Y(k)\subset \pi (X(L))$, it readily follows from the universal property of fibre products that
$Y(k)\subset \pi (X(L))$, it readily follows from the universal property of fibre products that ![]() $Y'(k)\subset \pi '(X'(L))$. Thus, replacing
$Y'(k)\subset \pi '(X'(L))$. Thus, replacing ![]() $X$ by
$X$ by ![]() $X'$ and
$X'$ and ![]() $Y$ by
$Y$ by ![]() $Y'$ if necessary, we may and do assume that
$Y'$ if necessary, we may and do assume that ![]() $X$ and
$X$ and ![]() $Y$ are projective over
$Y$ are projective over ![]() $k$.
$k$.
Now, let ![]() $Z$ be a normal proper variety over
$Z$ be a normal proper variety over ![]() $L$ and let
$L$ and let ![]() $Z\to X$ be a ramified cover. As
$Z\to X$ be a ramified cover. As ![]() $X$ and
$X$ and ![]() $Y_L$ are projective over
$Y_L$ are projective over ![]() $L$, we may consider the Weil restrictions
$L$, we may consider the Weil restrictions ![]() $R_{L/k}(Z)\to R_{L/k}(X)\to R_{L/k}(Y_L)$ and the diagonal map
$R_{L/k}(Z)\to R_{L/k}(X)\to R_{L/k}(Y_L)$ and the diagonal map ![]() $Y \xrightarrow {\Delta } R_{L/k}(Y_L)$. Let
$Y \xrightarrow {\Delta } R_{L/k}(Y_L)$. Let ![]() $Z' := R_{L/k}(Z) \times _{R_{L/k}(Y_L)} Y$ and write
$Z' := R_{L/k}(Z) \times _{R_{L/k}(Y_L)} Y$ and write ![]() $Z'=\bigcup _i Z'_i$ for its decomposition in irreducible components. We note that, for each
$Z'=\bigcup _i Z'_i$ for its decomposition in irreducible components. We note that, for each ![]() $i$, the natural morphism
$i$, the natural morphism ![]() $Z_i'\to Y$ is finite.
$Z_i'\to Y$ is finite.
We claim that, if the morphism ![]() $Z'_i \rightarrow Y$ is surjective, then the composed morphism
$Z'_i \rightarrow Y$ is surjective, then the composed morphism ![]() $\widetilde {Z_i}'\to Y$ is ramified, where
$\widetilde {Z_i}'\to Y$ is ramified, where ![]() $\widetilde {Z_i}'$ is the normalization of
$\widetilde {Z_i}'$ is the normalization of ![]() $Z_i'$. To prove this, it suffices to show that
$Z_i'$. To prove this, it suffices to show that ![]() $\widetilde {Z_i}'_L \rightarrow Y_L$ is ramified. We have the following commutative diagram:
$\widetilde {Z_i}'_L \rightarrow Y_L$ is ramified. We have the following commutative diagram:

where the composition of the maps in the lower row is the identity. As the composition ![]() $(Z'_i)_L \rightarrow Z \rightarrow Y_L$ is finite surjective and
$(Z'_i)_L \rightarrow Z \rightarrow Y_L$ is finite surjective and ![]() $Z$ is connected, we have that
$Z$ is connected, we have that ![]() $(Z'_i)_L \rightarrow Z$ is surjective. In particular, because
$(Z'_i)_L \rightarrow Z$ is surjective. In particular, because ![]() $Z \rightarrow Y_L$ (which is equal to the composition
$Z \rightarrow Y_L$ (which is equal to the composition ![]() $Z \rightarrow X \rightarrow Y_L$) is ramified, it follows that the composition
$Z \rightarrow X \rightarrow Y_L$) is ramified, it follows that the composition ![]() $\widetilde {Z_i}'_L \rightarrow Z \rightarrow Y_L$ is ramified. (Indeed, if it were unramified, then it would be étale by Lemma 2.3 which would contradict the fact that
$\widetilde {Z_i}'_L \rightarrow Z \rightarrow Y_L$ is ramified. (Indeed, if it were unramified, then it would be étale by Lemma 2.3 which would contradict the fact that ![]() $Z\to Y_L$ is ramified, as
$Z\to Y_L$ is ramified, as ![]() $Z$ is normal.)
$Z$ is normal.)
Now, by the weak-Hilbert property for ![]() $Y$ over
$Y$ over ![]() $k$, there is a Zariski-dense subset
$k$, there is a Zariski-dense subset ![]() $C\subset Y(k)$ of points not lifting to
$C\subset Y(k)$ of points not lifting to ![]() $k$-points in
$k$-points in ![]() $Z'$. Let
$Z'$. Let ![]() $\Omega \subset X(L)$ be the inverse image of
$\Omega \subset X(L)$ be the inverse image of ![]() $C$ in
$C$ in ![]() $X(L)$ via
$X(L)$ via ![]() $\pi : X(L) \to Y(L)$. Note that the assumption
$\pi : X(L) \to Y(L)$. Note that the assumption ![]() $Y(k) \subseteq \pi (X(L))$ ensures that
$Y(k) \subseteq \pi (X(L))$ ensures that ![]() $\pi (\Omega )=C$, hence
$\pi (\Omega )=C$, hence ![]() $\Omega$ is a dense subset of
$\Omega$ is a dense subset of ![]() $X$. We claim that, for every
$X$. We claim that, for every ![]() $c$ in
$c$ in ![]() $\Omega$, the fibre
$\Omega$, the fibre ![]() $Z_c$ has no
$Z_c$ has no ![]() $L$-point. Indeed, such an
$L$-point. Indeed, such an ![]() $L$-point would induce a
$L$-point would induce a ![]() $k$-point of
$k$-point of ![]() $R_{L/k}(Z)$ and a
$R_{L/k}(Z)$ and a ![]() $k$-point of
$k$-point of ![]() $Y$ and, thus, a
$Y$ and, thus, a ![]() $k$-point of
$k$-point of ![]() $Z'$ mapping to
$Z'$ mapping to ![]() $\pi (c) \in Y(k)$: contradiction.
$\pi (c) \in Y(k)$: contradiction.
As a first direct consequence, we deduce that the weak-Hilbert property persists along finite extensions of the field of definition.
Proposition 3.15 (Base change)
Let ![]() $L/k$ be a finite extension of fields of characteristic zero and let
$L/k$ be a finite extension of fields of characteristic zero and let ![]() $V$ be a smooth proper (geometrically) connected variety over
$V$ be a smooth proper (geometrically) connected variety over ![]() $k$ with the weak-Hilbert property over
$k$ with the weak-Hilbert property over ![]() $k$. Then
$k$. Then ![]() $V_L$ has the weak-Hilbert property over
$V_L$ has the weak-Hilbert property over ![]() $L$.
$L$.
Proof. Define ![]() $X:=V_L$ and
$X:=V_L$ and ![]() $Y:=V$. As the morphism
$Y:=V$. As the morphism ![]() $\pi :X=V_L\to V=Y$ is finite étale and
$\pi :X=V_L\to V=Y$ is finite étale and ![]() $Y(k)=V(k)\subset V(L)= \pi (X(L))$, the proposition follows from Lemma 3.14.
$Y(k)=V(k)\subset V(L)= \pi (X(L))$, the proposition follows from Lemma 3.14.
Theorem 3.16 Let ![]() $k$ be a finitely generated field of characteristic zero. Let
$k$ be a finitely generated field of characteristic zero. Let ![]() $f:V\to U$ be a finite étale morphism of smooth proper geometrically connected varieties over
$f:V\to U$ be a finite étale morphism of smooth proper geometrically connected varieties over ![]() $k$. If
$k$. If ![]() $U$ has the weak-Hilbert property over
$U$ has the weak-Hilbert property over ![]() $k$, then there is a finite field extension
$k$, then there is a finite field extension ![]() $L/k$ such that
$L/k$ such that ![]() $V_L$ has the weak-Hilbert property over
$V_L$ has the weak-Hilbert property over ![]() $L$.
$L$.
Proof. As ![]() $f:V\to U$ is a finite étale morphism and
$f:V\to U$ is a finite étale morphism and ![]() $k$ is a finitely generated field of characteristic zero, by the Chevalley–Weil theorem (Theorem 3.8), there is a finite extension
$k$ is a finitely generated field of characteristic zero, by the Chevalley–Weil theorem (Theorem 3.8), there is a finite extension ![]() $L/k$ such that
$L/k$ such that ![]() $U(k)\subset f(V(L))$. Define
$U(k)\subset f(V(L))$. Define ![]() $X:=V_L$ and
$X:=V_L$ and ![]() $Y=U$, and let
$Y=U$, and let ![]() $\pi :X\to Y$ be the composed morphism
$\pi :X\to Y$ be the composed morphism ![]() $V_L\to V\to U$. Note that
$V_L\to V\to U$. Note that ![]() $Y(k)=U(k)\subset f(V(L))=\pi (X(L))$. Thus, by Lemma 3.14, the weak-Hilbert property holds for
$Y(k)=U(k)\subset f(V(L))=\pi (X(L))$. Thus, by Lemma 3.14, the weak-Hilbert property holds for ![]() $X=V_L$ over
$X=V_L$ over ![]() $L$.
$L$.
4. Variants of the Hilbert property for abelian varieties
With a view towards proving that the weak-Hilbert property holds for abelian varieties with a dense set of rational points (Theorem 1.3) we study properties and relations between variants of the Hilbert property for abelian varieties over an arbitrary field ![]() $k$ of characteristic zero.
$k$ of characteristic zero.
Definition 4.1 Let ![]() $\pi :Y\to A$ be a cover of an abelian variety
$\pi :Y\to A$ be a cover of an abelian variety ![]() $A$ over
$A$ over ![]() $k$. The cover
$k$. The cover ![]() $\pi$ satisfies:
$\pi$ satisfies:
(PB) for pullback, if, for every positive integer
 $m$, the scheme
$m$, the scheme  $[m]^* {Y} = Y\times _{\pi, A, [m]} A$ is geometrically integral;
$[m]^* {Y} = Y\times _{\pi, A, [m]} A$ is geometrically integral;(GPB) for Galois pullback, if the Galois closure of
 $\pi$ is a (PB)-cover; and
$\pi$ is a (PB)-cover; and(Ram) for ramified, if
 $\pi$ is ramified.
$\pi$ is ramified.
As we show later in Lemma 4.4, a cover ![]() $\pi :Y\to A$ of an abelian variety
$\pi :Y\to A$ of an abelian variety ![]() $A$ over
$A$ over ![]() $k$ satisfies (PB) if and only if it has no non-trivial étale subcovers.
$k$ satisfies (PB) if and only if it has no non-trivial étale subcovers.
Note that, if ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $k$ and
$k$ and ![]() $\pi :Y\to A$ is a cover of
$\pi :Y\to A$ is a cover of ![]() $A$ which satisfies the property (PB), then the scheme
$A$ which satisfies the property (PB), then the scheme ![]() $[m]^*{Y}$ is a geometrically integral normal projective variety over
$[m]^*{Y}$ is a geometrically integral normal projective variety over ![]() $k$ for every positive integer
$k$ for every positive integer ![]() $m$. We stress that the properties (PB) and (Ram) are central to our paper, whereas the notion (GPB) is introduced only for technical purposes.
$m$. We stress that the properties (PB) and (Ram) are central to our paper, whereas the notion (GPB) is introduced only for technical purposes.
Definition 4.2 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\pi : Y \to A$ be a cover of
$\pi : Y \to A$ be a cover of ![]() $A$ over
$A$ over ![]() $k$, and let
$k$, and let ![]() $\Omega \subseteq A(k)$ be a finitely generated Zariski-dense subgroup. We say that the pair
$\Omega \subseteq A(k)$ be a finitely generated Zariski-dense subgroup. We say that the pair ![]() $(\pi, \Omega )$ satisfies:
$(\pi, \Omega )$ satisfies:
(PF) for pointless (reduced) fibres, if either
 $\deg \pi =1$ or there is a finite-index coset
$\deg \pi =1$ or there is a finite-index coset  $C \subseteq \Omega$ such that, for every
$C \subseteq \Omega$ such that, for every  $c$ in
$c$ in  $C$, the scheme
$C$, the scheme  $\pi ^{-1}(c)$ is reduced and has no
$\pi ^{-1}(c)$ is reduced and has no  $k$-rational points;
$k$-rational points;(IF) for integral fibres, if there is a finite-index coset
 $C \subseteq \Omega$ such that, for every
$C \subseteq \Omega$ such that, for every  $c$ in
$c$ in  $C$, the scheme
$C$, the scheme  $\pi ^{-1}(c)$ is integral.
$\pi ^{-1}(c)$ is integral.
In addition, we say that property (PF), respectively property (IF), holds for ![]() $\pi$ (without specifying
$\pi$ (without specifying ![]() $\Omega$) if property (PF), respectively property (IF), holds for all pairs
$\Omega$) if property (PF), respectively property (IF), holds for all pairs ![]() $(\pi, \Omega )$ with
$(\pi, \Omega )$ with ![]() $\Omega$ a finitely generated Zariski-dense subgroup of
$\Omega$ a finitely generated Zariski-dense subgroup of ![]() $A(k)$. Let
$A(k)$. Let ![]() $r$ be a positive integer. We say that property (PF), respectively property (IF), holds for
$r$ be a positive integer. We say that property (PF), respectively property (IF), holds for ![]() $\pi$ up to rank
$\pi$ up to rank ![]() $r$ if property (PF), respectively property (IF), holds for all pairs
$r$ if property (PF), respectively property (IF), holds for all pairs ![]() $(\pi, \Omega )$ with
$(\pi, \Omega )$ with ![]() $\Omega$ a finitely generated Zariski-dense subgroup of
$\Omega$ a finitely generated Zariski-dense subgroup of ![]() $A(k)$ of rank at most
$A(k)$ of rank at most ![]() $r$.
$r$.
We say that a property ![]() $(\star )$ in the list of Definition 4.1 implies property (PF), respectively property (IF), for a pair
$(\star )$ in the list of Definition 4.1 implies property (PF), respectively property (IF), for a pair ![]() $(A, \Omega )$ if the following holds: for every cover
$(A, \Omega )$ if the following holds: for every cover ![]() $\pi : Y \to A$ such that
$\pi : Y \to A$ such that ![]() $\pi$ satisfies property
$\pi$ satisfies property ![]() $(\star )$, the pair
$(\star )$, the pair ![]() $(\pi, \Omega )$ also satisfies property (PF), respectively property (IF).
$(\pi, \Omega )$ also satisfies property (PF), respectively property (IF).
We record the following obvious observation.
Remark 4.3 Let ![]() $Z \rightarrow A$ be a cover that factors through a subcover
$Z \rightarrow A$ be a cover that factors through a subcover ![]() $Z \rightarrow Z' \xrightarrow {\psi } A$ with
$Z \rightarrow Z' \xrightarrow {\psi } A$ with ![]() $\deg \psi \geq 2$. If
$\deg \psi \geq 2$. If ![]() $Z' \rightarrow A$ satisfies property (PF), then so does
$Z' \rightarrow A$ satisfies property (PF), then so does ![]() $Z \rightarrow A$.
$Z \rightarrow A$.
As we show in the following lemma, a cover of an abelian variety has property (PB) if and only if it has no étale subcovers; this generalizes [Reference ZannierZan10, Proposition 2.1] to non-algebraically closed fields.
Lemma 4.4 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$. Let
$k$. Let ![]() $\pi :Z \rightarrow A$ be a cover with
$\pi :Z \rightarrow A$ be a cover with ![]() $Z$ geometrically integral over
$Z$ geometrically integral over ![]() $k$. Then there is a factorization
$k$. Then there is a factorization
where ![]() $\phi _{\overline {k}}$ has property (PB) and
$\phi _{\overline {k}}$ has property (PB) and ![]() $\lambda$ is unramified. In particular,
$\lambda$ is unramified. In particular, ![]() $\pi$ is a (PB)-cover if and only if it has no étale subcovers.
$\pi$ is a (PB)-cover if and only if it has no étale subcovers.
Proof. The maximal étale subcover of ![]() $Z \rightarrow A$ is unique up to unique isomorphism (as a subcover of
$Z \rightarrow A$ is unique up to unique isomorphism (as a subcover of ![]() $Z\to A$), so that, by Galois descent, the morphism
$Z\to A$), so that, by Galois descent, the morphism ![]() $Z \rightarrow A$ factors through a non-trivial étale subcover if and only if
$Z \rightarrow A$ factors through a non-trivial étale subcover if and only if ![]() $Z_{\overline {k}}\rightarrow A_{\overline {k}}$ does. The lemma now follows from [Reference ZannierZan10, Proposition 2.1] (where the base field is assumed to be algebraically closed).
$Z_{\overline {k}}\rightarrow A_{\overline {k}}$ does. The lemma now follows from [Reference ZannierZan10, Proposition 2.1] (where the base field is assumed to be algebraically closed).
In fact, [Reference ZannierZan10, Proposition 2.1] also proves that a cover satisfies property (PB) if its total space remains geometrically integral after pull-back along multiplication by the degree of the cover.
Lemma 4.5 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, and
$k$, and ![]() $\phi :X \rightarrow A$ be a cover of degree
$\phi :X \rightarrow A$ be a cover of degree ![]() $d$ with
$d$ with ![]() $X$ a geometrically integral variety over
$X$ a geometrically integral variety over ![]() $k$. Then
$k$. Then ![]() $\phi$ has property (PB) if and only if the fibre product
$\phi$ has property (PB) if and only if the fibre product ![]() $X \times _{\phi, A,[d]}A$ is geometrically integral.
$X \times _{\phi, A,[d]}A$ is geometrically integral.
4.1 Avoiding the branch locus
We now show that, given a Zariski-dense subgroup ![]() $\Omega$ of
$\Omega$ of ![]() $A(k)$, one may always find a finite-index coset
$A(k)$, one may always find a finite-index coset ![]() $C$ of
$C$ of ![]() $\Omega$ that avoids any given (proper) closed subscheme of
$\Omega$ that avoids any given (proper) closed subscheme of ![]() $A$. In particular, given a cover
$A$. In particular, given a cover ![]() $\pi : Y \to A$, there exists a finite-index coset of
$\pi : Y \to A$, there exists a finite-index coset of ![]() $\Omega$ that is disjoint from the branch locus of
$\Omega$ that is disjoint from the branch locus of ![]() $\pi$. This gives us an ample supply of points of
$\pi$. This gives us an ample supply of points of ![]() $\Omega$ over which the fibre of
$\Omega$ over which the fibre of ![]() $\pi$ is unramified; we use this fact in several of our subsequent proofs.
$\pi$ is unramified; we use this fact in several of our subsequent proofs.
Lemma 4.6 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and let
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and let ![]() $Z\subsetneq A$ be a closed subscheme. Then there exists a finite index coset
$Z\subsetneq A$ be a closed subscheme. Then there exists a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that
$\Omega$ such that ![]() $C \cap Z = \emptyset$.
$C \cap Z = \emptyset$.
Proof. As ![]() $\Omega$ is Zariski-dense, there exists
$\Omega$ is Zariski-dense, there exists ![]() $P \in \Omega$ such that
$P \in \Omega$ such that ![]() $P \notin Z$. Now, by standard spreading out arguments, we may choose the following data:
$P \notin Z$. Now, by standard spreading out arguments, we may choose the following data:
(1) a
 $\mathbb {Z}$-finitely generated subring
$\mathbb {Z}$-finitely generated subring  $R\subset k$, an abelian scheme
$R\subset k$, an abelian scheme  $\mathcal {A}$ over
$\mathcal {A}$ over  $R$ and an isomorphism
$R$ and an isomorphism  $\mathcal {A}\times _R k \cong A$ such that
$\mathcal {A}\times _R k \cong A$ such that  $\Omega \subset A(k)$ lies in the subgroup
$\Omega \subset A(k)$ lies in the subgroup  $\mathcal {A}(R)\subset A(k)$;
$\mathcal {A}(R)\subset A(k)$;(2) a closed subscheme
 $\mathcal {Z}\subset \mathcal {A}$ defining
$\mathcal {Z}\subset \mathcal {A}$ defining  $Z\subset A$ over
$Z\subset A$ over  $R$;
$R$;(3) a section
 $\sigma _P:\operatorname {Spec} R \to \mathcal {A}$ which coincides with
$\sigma _P:\operatorname {Spec} R \to \mathcal {A}$ which coincides with  $P$ in
$P$ in  $A(k)$.
$A(k)$.
As ![]() $P \notin Z$, we have that
$P \notin Z$, we have that ![]() $\sigma _P^*\mathcal {Z} \subsetneq \operatorname {Spec} R$ is a proper closed subset. In particular, there exists a closed point
$\sigma _P^*\mathcal {Z} \subsetneq \operatorname {Spec} R$ is a proper closed subset. In particular, there exists a closed point ![]() $v \in \operatorname {Spec} R$ such that
$v \in \operatorname {Spec} R$ such that ![]() $P \bmod v=\sigma _P(\operatorname {Spec} \mathbb {F}_v)\notin \mathcal {Z}$. As
$P \bmod v=\sigma _P(\operatorname {Spec} \mathbb {F}_v)\notin \mathcal {Z}$. As ![]() $\mathcal {A}(\operatorname {Spec} \mathbb {F}_v)$ is a finite group, the kernel
$\mathcal {A}(\operatorname {Spec} \mathbb {F}_v)$ is a finite group, the kernel ![]() $\Omega '$ of the specialization map
$\Omega '$ of the specialization map ![]() $\mathcal {A}(R)\to \mathcal {A}(\mathbb {F}_v)$ is of finite index. In particular, for each
$\mathcal {A}(R)\to \mathcal {A}(\mathbb {F}_v)$ is of finite index. In particular, for each ![]() $c$ in the finite index coset
$c$ in the finite index coset ![]() $C:= P + \Omega '$ of
$C:= P + \Omega '$ of ![]() $\Omega$, we have that
$\Omega$, we have that ![]() $P \equiv c \bmod v$. Finally, for each
$P \equiv c \bmod v$. Finally, for each ![]() $c \in C$, the element
$c \in C$, the element ![]() $c \bmod v$ does not lie in the closed subscheme
$c \bmod v$ does not lie in the closed subscheme ![]() $\mathcal {Z} \subset \mathcal {A}$, hence
$\mathcal {Z} \subset \mathcal {A}$, hence ![]() $c \notin Z=\mathcal {Z}\cap A$.
$c \notin Z=\mathcal {Z}\cap A$.
Corollary 4.7 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and let
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and let ![]() $\phi :Y \rightarrow A$ be a ramified cover. Then there exists a finite index coset
$\phi :Y \rightarrow A$ be a ramified cover. Then there exists a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that, for each
$\Omega$ such that, for each ![]() $c \in C$, the scheme
$c \in C$, the scheme ![]() $\phi ^{-1}(c)$ is étale over
$\phi ^{-1}(c)$ is étale over ![]() $k$.
$k$.
Proof. Let ![]() $B\subset A$ be the branch locus of
$B\subset A$ be the branch locus of ![]() $\phi$. As
$\phi$. As ![]() $A$ is normal, by Lemma 2.3, the morphism
$A$ is normal, by Lemma 2.3, the morphism ![]() $\phi$ is étale over
$\phi$ is étale over ![]() $U := A \setminus B$. Moreover, by Lemma 4.6, there is a finite index coset
$U := A \setminus B$. Moreover, by Lemma 4.6, there is a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that
$\Omega$ such that ![]() $C \cap B= \emptyset$. In particular, for every
$C \cap B= \emptyset$. In particular, for every ![]() $c \in C$, we have that
$c \in C$, we have that ![]() $c \in U$ and
$c \in U$ and ![]() $\phi$ is étale over
$\phi$ is étale over ![]() $c$.
$c$.
4.2 Base change of (PB)-covers
The first basic observation is that the total space of a cover ![]() $Y\to A$ which has property (PB) remains connected after pull-back along étale covers of
$Y\to A$ which has property (PB) remains connected after pull-back along étale covers of ![]() $A$.
$A$.
Lemma 4.8 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$ and let
$k$ and let ![]() $\pi :Y\to A$ be a cover of
$\pi :Y\to A$ be a cover of ![]() $A$. Then
$A$. Then ![]() $\pi$ satisfies property (PB) if and only if, for every isogeny
$\pi$ satisfies property (PB) if and only if, for every isogeny ![]() $\phi :A'\to A_{\overline {k}}$ of abelian varieties over
$\phi :A'\to A_{\overline {k}}$ of abelian varieties over ![]() $\overline {k}$, the fibre product
$\overline {k}$, the fibre product ![]() $Y_{\overline {k}}\times _{\overline {\pi },A_{\overline {k}}, \phi } A'$ is connected.
$Y_{\overline {k}}\times _{\overline {\pi },A_{\overline {k}}, \phi } A'$ is connected.
Proof. We note that ![]() $Y_{\overline {k}}\times _{\overline {\pi },A_{\overline {k}}, \phi } A'$, being étale over
$Y_{\overline {k}}\times _{\overline {\pi },A_{\overline {k}}, \phi } A'$, being étale over ![]() $Y_{\overline {k}}$, which is normal, is itself normal. The ‘if’ direction follows because
$Y_{\overline {k}}$, which is normal, is itself normal. The ‘if’ direction follows because ![]() $[N]$ is, in particular, an isogeny and normal connected schemes are integral. For the ‘only if’ direction, observe that given any isogeny
$[N]$ is, in particular, an isogeny and normal connected schemes are integral. For the ‘only if’ direction, observe that given any isogeny ![]() $\phi : A' \to A_{\overline {k}}$ we may find another isogeny
$\phi : A' \to A_{\overline {k}}$ we may find another isogeny ![]() $\psi : A_{\overline {k}} \to A'$ such that
$\psi : A_{\overline {k}} \to A'$ such that ![]() $\phi \circ \psi = [\deg \phi ]$. As
$\phi \circ \psi = [\deg \phi ]$. As ![]() $\pi$ satisfies property (PB), the fibre product
$\pi$ satisfies property (PB), the fibre product ![]() $Y_{\overline {k}} \times _{\overline {\pi }, A_{\overline {k}}, [\deg \phi ]} A_{\overline {k}}$ is integral. The claim follows from the commutative diagram
$Y_{\overline {k}} \times _{\overline {\pi }, A_{\overline {k}}, [\deg \phi ]} A_{\overline {k}}$ is integral. The claim follows from the commutative diagram

where both squares are Cartesian, the horizontal morphisms are surjective, and ![]() $Y_{\overline {k}} \times _{\overline {\pi }, A_{\overline {k}}, [\deg \phi ]} A_{\overline {k}}$ is irreducible, hence so is
$Y_{\overline {k}} \times _{\overline {\pi }, A_{\overline {k}}, [\deg \phi ]} A_{\overline {k}}$ is irreducible, hence so is ![]() $Y_{\overline {k}} \times _{\overline {\pi },A_{\overline {k}}, \phi } A'$ as desired.
$Y_{\overline {k}} \times _{\overline {\pi },A_{\overline {k}}, \phi } A'$ as desired.
Remark 4.9 Let ![]() $f:X \rightarrow Y$ be a continuous, surjective and open morphism of topological spaces. Assume that
$f:X \rightarrow Y$ be a continuous, surjective and open morphism of topological spaces. Assume that ![]() $Y$ is connected and that, for all points
$Y$ is connected and that, for all points ![]() $y \in Y$, the fibre
$y \in Y$, the fibre ![]() $X_{y}$ is connected. Then
$X_{y}$ is connected. Then ![]() $X$ is connected. Indeed, assume by contradiction that
$X$ is connected. Indeed, assume by contradiction that ![]() $X = U_1 \sqcup U_2$, with
$X = U_1 \sqcup U_2$, with ![]() $U_1$ and
$U_1$ and ![]() $U_2$ non-empty open subsets of
$U_2$ non-empty open subsets of ![]() $X$. Then
$X$. Then ![]() $Y=f(U_1)\cup f(U_2)$. As
$Y=f(U_1)\cup f(U_2)$. As ![]() $f$ is open,
$f$ is open, ![]() $f(U_1)$ and
$f(U_1)$ and ![]() $f(U_2)$ are open, and, because
$f(U_2)$ are open, and, because ![]() $Y$ is connected,
$Y$ is connected, ![]() $f(U_1)\cap f(U_2)\neq \emptyset$. Let
$f(U_1)\cap f(U_2)\neq \emptyset$. Let ![]() $y \in f(U_1)\cap f(U_2)$. Then
$y \in f(U_1)\cap f(U_2)$. Then ![]() $X_y = (X_y \cap U_1) \sqcup (X_y \cap U_2)$, and both
$X_y = (X_y \cap U_1) \sqcup (X_y \cap U_2)$, and both ![]() $X_y \cap U_1$ and
$X_y \cap U_1$ and ![]() $X_y \cap U_2$ are non-empty: contradiction.
$X_y \cap U_2$ are non-empty: contradiction.
As a consequence of Lemma 4.8 and Remark 4.9, we show that a (PB)-cover remains a (PB)-cover after pull-back along any dominant morphism of abelian varieties. In other words, the property of being a (PB)-cover of an abelian variety commutes with dominant base change.
Lemma 4.10 Let ![]() $\phi :Z \rightarrow A$ be a (PB)-cover of an abelian variety
$\phi :Z \rightarrow A$ be a (PB)-cover of an abelian variety ![]() $A$ over
$A$ over ![]() $k$, and let
$k$, and let ![]() $\lambda :A' \rightarrow A$ be a dominant morphism of abelian varieties. Then
$\lambda :A' \rightarrow A$ be a dominant morphism of abelian varieties. Then ![]() $\lambda ^*Z:=A'\times _{\lambda, A,\phi } Z$ is geometrically integral and
$\lambda ^*Z:=A'\times _{\lambda, A,\phi } Z$ is geometrically integral and ![]() $\lambda ^* Z\to A'$ is a (PB)-cover.
$\lambda ^* Z\to A'$ is a (PB)-cover.
Proof. Let ![]() $n\geq 1$ be an integer and let
$n\geq 1$ be an integer and let ![]() $\mu := [n]_{A'}$ be multiplication by
$\mu := [n]_{A'}$ be multiplication by ![]() $n$ on
$n$ on ![]() $A'$. By using properties of Stein factorization, we may factor the morphism
$A'$. By using properties of Stein factorization, we may factor the morphism ![]() $\lambda \circ \mu$ as
$\lambda \circ \mu$ as
where ![]() $\lambda _2$ has geometrically integral fibres and
$\lambda _2$ has geometrically integral fibres and ![]() $\lambda _1$ is an isogeny. Note that
$\lambda _1$ is an isogeny. Note that ![]() $(\lambda \circ \mu )^*Z \cong \lambda _2^*\lambda _1^*Z$. Moreover, because
$(\lambda \circ \mu )^*Z \cong \lambda _2^*\lambda _1^*Z$. Moreover, because ![]() $\phi$ satisfies property (PB), by Lemma 4.8, the morphism
$\phi$ satisfies property (PB), by Lemma 4.8, the morphism ![]() $\lambda _1^*Z\rightarrow A''$ is a (PB)-cover, so that
$\lambda _1^*Z\rightarrow A''$ is a (PB)-cover, so that ![]() $\lambda _1^*Z$ is geometrically connected. As
$\lambda _1^*Z$ is geometrically connected. As ![]() ${\lambda _2}$ is smooth and has geometrically connected fibres, the morphism
${\lambda _2}$ is smooth and has geometrically connected fibres, the morphism ![]() ${\lambda _2}^* ({\lambda _1}^*{Z}) \rightarrow {\lambda _1}^*{Z}$ is smooth and has geometrically connected fibres. As
${\lambda _2}^* ({\lambda _1}^*{Z}) \rightarrow {\lambda _1}^*{Z}$ is smooth and has geometrically connected fibres. As ![]() ${\lambda _1}^*{Z}$ is geometrically connected and smooth morphisms are flat, hence open, we have that
${\lambda _1}^*{Z}$ is geometrically connected and smooth morphisms are flat, hence open, we have that ![]() ${\lambda _2}^*({\lambda _1}^*{Z})$ is geometrically connected by Remark 4.9. As
${\lambda _2}^*({\lambda _1}^*{Z})$ is geometrically connected by Remark 4.9. As ![]() ${\lambda _1}^*{Z}$ is normal (hence, geometrically normal),
${\lambda _1}^*{Z}$ is normal (hence, geometrically normal), ![]() ${\lambda _2}^*({\lambda _1}^*{Z})$ is geometrically normal by [Sta20, Tag 034F]. As
${\lambda _2}^*({\lambda _1}^*{Z})$ is geometrically normal by [Sta20, Tag 034F]. As ![]() $\lambda _2^*(\lambda _1^*Z)$ is geometrically normal and connected, it is geometrically integral. Therefore,
$\lambda _2^*(\lambda _1^*Z)$ is geometrically normal and connected, it is geometrically integral. Therefore, ![]() $(\lambda \circ \mu )^*Z\cong \lambda _2^*\lambda _1^*Z$ is as well. As this holds for every integer
$(\lambda \circ \mu )^*Z\cong \lambda _2^*\lambda _1^*Z$ is as well. As this holds for every integer ![]() $n\geq 1$, this proves that
$n\geq 1$, this proves that ![]() $\lambda ^*Z$ is geometrically integral and that
$\lambda ^*Z$ is geometrically integral and that ![]() $\lambda ^\ast Z\to A'$ satisfies the property (PB).
$\lambda ^\ast Z\to A'$ satisfies the property (PB).
4.3 Spreading out (PB)-covers
We now show that a cover of an abelian variety over a function field which satisfies property (PB) can be spread out to a cover of an abelian scheme which fibrewise satisfies property (PB).
Lemma 4.11 Let ![]() $S$ be an integral scheme of characteristic zero with function field
$S$ be an integral scheme of characteristic zero with function field ![]() $k(S)$ and let
$k(S)$ and let ![]() $\mathcal {A}\to S$ be an abelian scheme. Let
$\mathcal {A}\to S$ be an abelian scheme. Let ![]() $Z\to \mathcal {A}$ be a finite surjective morphism such that
$Z\to \mathcal {A}$ be a finite surjective morphism such that ![]() $Z_{k(S)}\to \mathcal {A}_{k(S)}$ is a (PB)-cover of
$Z_{k(S)}\to \mathcal {A}_{k(S)}$ is a (PB)-cover of ![]() $\mathcal {A}_{k(S)}$ over
$\mathcal {A}_{k(S)}$ over ![]() $k(S)$. Then, there exists a dense open subscheme
$k(S)$. Then, there exists a dense open subscheme ![]() $U \subset S$ such that, for every
$U \subset S$ such that, for every ![]() $u \in U$, the morphism
$u \in U$, the morphism ![]() $Z_u \to \mathcal {A}_u$ is a (PB)-cover of
$Z_u \to \mathcal {A}_u$ is a (PB)-cover of ![]() $\mathcal {A}_u$ over
$\mathcal {A}_u$ over ![]() $k(u)$.
$k(u)$.
Proof. Let ![]() $d$ be the degree of
$d$ be the degree of ![]() $Z$ over
$Z$ over ![]() $\mathcal {A}$. The isomorphism
$\mathcal {A}$. The isomorphism ![]() $[d]^* Z_{k(S)} \cong ( [d]^*Z ) \times _S k(S)$ and the assumption that
$[d]^* Z_{k(S)} \cong ( [d]^*Z ) \times _S k(S)$ and the assumption that ![]() $Z_{k(S)} \to \mathcal {A}_{k(S)}$ is a (PB)-cover show that the generic fibre of
$Z_{k(S)} \to \mathcal {A}_{k(S)}$ is a (PB)-cover show that the generic fibre of ![]() $[d]^*Z \to \mathcal {A}$ is geometrically irreducible. Since
$[d]^*Z \to \mathcal {A}$ is geometrically irreducible. Since ![]() $Z$ is normal and
$Z$ is normal and ![]() $S$ is of characteristic zero, the scheme
$S$ is of characteristic zero, the scheme ![]() $Z_{k(S)}$ is normal. By spreading out (see [Reference GrothendieckGro65, Théorème 6.9.1] and [Reference GrothendieckGro66, Théorème 9.7.7(iv) and Théorème 12.2.4(iv)]), there is a dense open subscheme
$Z_{k(S)}$ is normal. By spreading out (see [Reference GrothendieckGro65, Théorème 6.9.1] and [Reference GrothendieckGro66, Théorème 9.7.7(iv) and Théorème 12.2.4(iv)]), there is a dense open subscheme ![]() $U$ of
$U$ of ![]() $S$ such that, for all
$S$ such that, for all ![]() $u \in U$, the scheme
$u \in U$, the scheme ![]() $[d]^*Z_u$ is normal and geometrically irreducible over
$[d]^*Z_u$ is normal and geometrically irreducible over ![]() $k(u)$. In particular, by Lemma 4.5, for every
$k(u)$. In particular, by Lemma 4.5, for every ![]() $u \in U$, the cover
$u \in U$, the cover ![]() $Z_u \to \mathcal {A}_u$ of degree
$Z_u \to \mathcal {A}_u$ of degree ![]() $d$ is a (PB)-cover, as required.
$d$ is a (PB)-cover, as required.
4.4 Invariance under translation
Since the class of (PB)-covers (respectively, ramified covers) is invariant by translation on ![]() $A$, we obtain the following proposition.
$A$, we obtain the following proposition.
Proposition 4.12 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, and let
$k$, and let ![]() $r$ be a positive integer. Then the following two statements are equivalent.
$r$ be a positive integer. Then the following two statements are equivalent.
(1) For every non-trivial (PB)-cover
 $Z \rightarrow A$ and every finitely generated Zariski-dense subgroup
$Z \rightarrow A$ and every finitely generated Zariski-dense subgroup  $\Omega \subset A(k)$ of rank at most
$\Omega \subset A(k)$ of rank at most  $r$, there exists a finite index coset
$r$, there exists a finite index coset  $C$ of
$C$ of  $\Omega$ such that, for every
$\Omega$ such that, for every  $c \in C$, the scheme
$c \in C$, the scheme  $Z_c$ is étale over
$Z_c$ is étale over  $k$ and has no
$k$ and has no  $k$-points (respectively, is integral).
$k$-points (respectively, is integral).(2) For every non-trivial (PB)-cover
 $Z \rightarrow A$, for every
$Z \rightarrow A$, for every  $b\in A(k)$, and every finitely generated Zariski-dense subgroup
$b\in A(k)$, and every finitely generated Zariski-dense subgroup  $\Omega \subset A(k)$ of rank at most
$\Omega \subset A(k)$ of rank at most  $r$, there exists a finite index coset
$r$, there exists a finite index coset  $C$ of
$C$ of  $\Omega$ such that, for every
$\Omega$ such that, for every  $c \in C$, the scheme
$c \in C$, the scheme  $Z_{b+c}$ is étale over
$Z_{b+c}$ is étale over  $k$ and has no
$k$ and has no  $k$-points (respectively, is integral).
$k$-points (respectively, is integral).
The same equivalence holds with (PB) replaced by (Ram).
Remark 4.13 In the case of (Ram) we actually only care about the equivalence of statements (1) and (2) for property (PF) because, by Remark 7.8, the fibres ![]() $\phi ^{-1}(c)$ will rarely be integral.
$\phi ^{-1}(c)$ will rarely be integral.
4.5 From one cover to many covers
Lemma 4.14 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, and let
$k$, and let ![]() $r$ be a positive integer. Then the following statements hold.
$r$ be a positive integer. Then the following statements hold.
(1) Suppose that every (PB)-cover of
 $A$ satisfies property (IF) (respectively, property (PF)) up to rank
$A$ satisfies property (IF) (respectively, property (PF)) up to rank  $r$. Then, for any finite collection
$r$. Then, for any finite collection  $(\pi _i : Y_i \to A)_{i=1,\ldots,n}$ of non-trivial (PB)-covers and for every finitely generated Zariski-dense subgroup
$(\pi _i : Y_i \to A)_{i=1,\ldots,n}$ of non-trivial (PB)-covers and for every finitely generated Zariski-dense subgroup  $\Omega \subset A(k)$ of rank at most
$\Omega \subset A(k)$ of rank at most  $r$, there is a finite-index coset
$r$, there is a finite-index coset  $C$ of
$C$ of  $\Omega$ such that, for every
$\Omega$ such that, for every  $c \in C$ and
$c \in C$ and  $i \in \{1,\ldots,n\}$, the scheme
$i \in \{1,\ldots,n\}$, the scheme  $\pi _i^{-1}(c)$ is integral (respectively, reduced with no
$\pi _i^{-1}(c)$ is integral (respectively, reduced with no  $k$-rational points).
$k$-rational points).(2) Suppose that every (Ram)-cover of
 $A$ satisfies property (PF) up to rank
$A$ satisfies property (PF) up to rank  $r$. Then, for any finite collection
$r$. Then, for any finite collection  $(\pi _i : Y_i \to A)_{i=1,\ldots,n}$ of ramified covers and for every finitely generated Zariski-dense subgroup
$(\pi _i : Y_i \to A)_{i=1,\ldots,n}$ of ramified covers and for every finitely generated Zariski-dense subgroup  $\Omega \subset A(k)$ of rank at most
$\Omega \subset A(k)$ of rank at most  $r$, there is a finite-index coset
$r$, there is a finite-index coset  $C$ of
$C$ of  $\Omega$ such that, for every
$\Omega$ such that, for every  $c \in C$ and
$c \in C$ and  $i \in \{1,\ldots,n\}$, the scheme
$i \in \{1,\ldots,n\}$, the scheme  $\pi _i^{-1}(c)$ is reduced and has no
$\pi _i^{-1}(c)$ is reduced and has no  $k$-rational points.
$k$-rational points.
Proof. We argue by induction on ![]() $n$; the case
$n$; the case ![]() $n=1$ being true by assumption. Suppose now the claim is true for
$n=1$ being true by assumption. Suppose now the claim is true for ![]() $n-1$; we prove it for
$n-1$; we prove it for ![]() $n$. Let
$n$. Let ![]() $\pi _1,\ldots,\pi _n$ be non-trivial covers of
$\pi _1,\ldots,\pi _n$ be non-trivial covers of ![]() $A$ that satisfy property (PB) (respectively, property (Ram)) and let
$A$ that satisfy property (PB) (respectively, property (Ram)) and let ![]() $\Omega$ be a Zariski-dense subgroup of
$\Omega$ be a Zariski-dense subgroup of ![]() $A(k)$ of rank at most
$A(k)$ of rank at most ![]() $r$. By the inductive hypothesis, there exists a finite-index coset
$r$. By the inductive hypothesis, there exists a finite-index coset ![]() $C_{n-1} \subseteq \Omega$ such that, for every
$C_{n-1} \subseteq \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C_{n-1}$ and
$C_{n-1}$ and ![]() $i\in \{1,\ldots,n-1\}$, the scheme
$i\in \{1,\ldots,n-1\}$, the scheme ![]() $\pi _i^{-1}(c)$ is integral (respectively, is reduced and has no
$\pi _i^{-1}(c)$ is integral (respectively, is reduced and has no ![]() $k$-rational points). Let
$k$-rational points). Let ![]() $\Omega '\subset \Omega$ be a finite index (Zariski-dense) subgroup (of rank at most
$\Omega '\subset \Omega$ be a finite index (Zariski-dense) subgroup (of rank at most ![]() $r$) and let
$r$) and let ![]() $c_{n-1}\in A$ be such that
$c_{n-1}\in A$ be such that ![]() $C_{n-1} = c_{n-1} + \Omega '$. By Proposition 4.12, there is a finite-index coset
$C_{n-1} = c_{n-1} + \Omega '$. By Proposition 4.12, there is a finite-index coset ![]() $C$ of
$C$ of ![]() $\Omega '$ such that, for every
$\Omega '$ such that, for every ![]() $c$ in
$c$ in ![]() $C$, the fibre
$C$, the fibre ![]() $\pi _n^{-1}(c)$ is integral (respectively, is reduced and has no
$\pi _n^{-1}(c)$ is integral (respectively, is reduced and has no ![]() $k$-rational points). It is immediate to check that
$k$-rational points). It is immediate to check that ![]() $C$ is a finite-index coset of
$C$ is a finite-index coset of ![]() $\Omega$ with the desired properties.
$\Omega$ with the desired properties.
4.6 Invariance under isogeny
The analogue of Proposition 3.4 in the context of the Hilbert property for pairs ![]() $(A,\Omega )$ reads as follows.
$(A,\Omega )$ reads as follows.
Proposition 4.15 Let ![]() $\phi :A\to B$ be an isogeny of abelian varieties over
$\phi :A\to B$ be an isogeny of abelian varieties over ![]() $k$. If every (PB)-cover of
$k$. If every (PB)-cover of ![]() $A$ has property (PF), then every (PB)-cover of
$A$ has property (PF), then every (PB)-cover of ![]() $B$ has property (PF).
$B$ has property (PF).
Proof. Let ![]() $\pi : Z\to B$ be a non-trivial (PB)-cover and let
$\pi : Z\to B$ be a non-trivial (PB)-cover and let ![]() $\Omega \subset B(k)$ be a finitely generated Zariski-dense subgroup. To show that there is a finite index coset
$\Omega \subset B(k)$ be a finitely generated Zariski-dense subgroup. To show that there is a finite index coset ![]() $C\subset \Omega$ such that
$C\subset \Omega$ such that ![]() $\pi ^{-1}(c)$ has no
$\pi ^{-1}(c)$ has no ![]() $k$-rational points for every
$k$-rational points for every ![]() $c\in C$, replacing
$c\in C$, replacing ![]() $\Omega$ by a finite-index subgroup if necessary, we may and do assume that
$\Omega$ by a finite-index subgroup if necessary, we may and do assume that ![]() $\Omega$ is in the image of
$\Omega$ is in the image of ![]() $A(k) \xrightarrow {\phi } B(k)$. Then
$A(k) \xrightarrow {\phi } B(k)$. Then ![]() $\Omega ':=\phi ^{-1}\Omega \cap A(k)$ is a finitely generated Zariski-dense subgroup of
$\Omega ':=\phi ^{-1}\Omega \cap A(k)$ is a finitely generated Zariski-dense subgroup of ![]() $A$. Moreover, let
$A$. Moreover, let ![]() $\pi ':Z'\to A$ be the pull-back of
$\pi ':Z'\to A$ be the pull-back of ![]() $\pi :Z\to B$ along
$\pi :Z\to B$ along ![]() $\phi :A\to B$. As
$\phi :A\to B$. As ![]() $Z\to B$ is a (PB)-cover, it follows that
$Z\to B$ is a (PB)-cover, it follows that ![]() $Z'$ is integral (Lemma 4.8). Moreover, because
$Z'$ is integral (Lemma 4.8). Moreover, because ![]() $Z'\to Z$ is finite étale, we see that
$Z'\to Z$ is finite étale, we see that ![]() $Z'$ is normal. In particular, again by Lemma 4.8, it follows that the cover
$Z'$ is normal. In particular, again by Lemma 4.8, it follows that the cover ![]() $Z'\to A$ is a non-trivial (PB)-cover. As every (PB)-cover of
$Z'\to A$ is a non-trivial (PB)-cover. As every (PB)-cover of ![]() $A$ has property (PF), the (non-trivial) cover
$A$ has property (PF), the (non-trivial) cover ![]() $Z' \to A$ satisfies property (PF). In particular, we can choose a finite-index coset
$Z' \to A$ satisfies property (PF). In particular, we can choose a finite-index coset ![]() $C'$ of
$C'$ of ![]() $\Omega '$ such that, for all
$\Omega '$ such that, for all ![]() $c$ in
$c$ in ![]() $C'$, the fibre
$C'$, the fibre ![]() $(\pi ')^{-1}(c)$ has no
$(\pi ')^{-1}(c)$ has no ![]() $k$-rational points and is reduced. The universal property of fibre products then implies that
$k$-rational points and is reduced. The universal property of fibre products then implies that ![]() $(\pi ')^{-1}(c) \cong \pi ^{-1}(\phi (c))$, so that for every
$(\pi ')^{-1}(c) \cong \pi ^{-1}(\phi (c))$, so that for every ![]() $c$ in the finite-index coset
$c$ in the finite-index coset ![]() $C:=\phi (C') \subseteq \Omega$ the fibre
$C:=\phi (C') \subseteq \Omega$ the fibre ![]() $\pi ^{-1}(c)$ has no
$\pi ^{-1}(c)$ has no ![]() $k$-rational points and is reduced. This proves that
$k$-rational points and is reduced. This proves that ![]() $\pi : Z \to B$ satisfies property (PF) as desired.
$\pi : Z \to B$ satisfies property (PF) as desired.
4.7 A special class of products
Lemma 4.16 Assume that for all positive integers ![]() $r$, for all abelian varieties
$r$, for all abelian varieties ![]() $A_1, \ldots, A_r$ over
$A_1, \ldots, A_r$ over ![]() $k$, and for all cyclic, Zariski-dense subgroups
$k$, and for all cyclic, Zariski-dense subgroups ![]() $\Omega _i\subset A_i(k)$ (for
$\Omega _i\subset A_i(k)$ (for ![]() $i=1,\ldots,r$) property (PB) implies property (IF) for the pair
$i=1,\ldots,r$) property (PB) implies property (IF) for the pair ![]() $( \prod _{i=1}^r A_i, \prod _{i=1}^r \Omega _i)$. Then property (PB) implies property (IF) for all pairs
$( \prod _{i=1}^r A_i, \prod _{i=1}^r \Omega _i)$. Then property (PB) implies property (IF) for all pairs ![]() $(A,\Omega )$, where
$(A,\Omega )$, where ![]() $A$ is an abelian variety
$A$ is an abelian variety ![]() $A$ over
$A$ over ![]() $k$ and
$k$ and ![]() $\Omega$ is a finitely generated Zariski-dense subgroup of
$\Omega$ is a finitely generated Zariski-dense subgroup of ![]() $A(k)$.
$A(k)$.
Proof. Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$,
$k$, ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup, and ![]() $\phi :Z \rightarrow A$ a (PB)-cover. We want to prove that there exists a finite index coset
$\phi :Z \rightarrow A$ a (PB)-cover. We want to prove that there exists a finite index coset ![]() $C \subset \Omega$ such that, for every
$C \subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$, the scheme
$C$, the scheme ![]() $\phi ^{-1}(c)$ is integral. As every finitely generated abelian group contains a free abelian subgroup of finite index, we can assume, up to replacing
$\phi ^{-1}(c)$ is integral. As every finitely generated abelian group contains a free abelian subgroup of finite index, we can assume, up to replacing ![]() $\Omega$ with a finite-index subgroup, that
$\Omega$ with a finite-index subgroup, that ![]() $\Omega = \bigoplus _{i=1}^r \Omega _i$, with
$\Omega = \bigoplus _{i=1}^r \Omega _i$, with ![]() $\Omega _i= \langle \omega _i \rangle \subset \Omega$ cyclic of infinite order. Moreover, we can assume without loss of generality (up to replacing
$\Omega _i= \langle \omega _i \rangle \subset \Omega$ cyclic of infinite order. Moreover, we can assume without loss of generality (up to replacing ![]() $\Omega$ with a finite-index subgroup again) that the Zariski closure
$\Omega$ with a finite-index subgroup again) that the Zariski closure ![]() $A_i$ of
$A_i$ of ![]() $\Omega _i$ is irreducible and, hence, an abelian subvariety of
$\Omega _i$ is irreducible and, hence, an abelian subvariety of ![]() $A$. Let
$A$. Let ![]() $\lambda : \bigoplus _{i=1}^rA_i \rightarrow A$ be the natural surjective morphism (defined by the colimit property of the direct sum). It follows from Lemma 4.10 that
$\lambda : \bigoplus _{i=1}^rA_i \rightarrow A$ be the natural surjective morphism (defined by the colimit property of the direct sum). It follows from Lemma 4.10 that ![]() $\lambda ^*Z$ is a (PB)-cover of
$\lambda ^*Z$ is a (PB)-cover of ![]() $\bigoplus _{i=1}^rA_i$. Moreover,
$\bigoplus _{i=1}^rA_i$. Moreover, ![]() ${\lambda }|_{\oplus _i \Omega _i}: \bigoplus _{i=1}^r \Omega _i \rightarrow \Omega$ is an isomorphism.
${\lambda }|_{\oplus _i \Omega _i}: \bigoplus _{i=1}^r \Omega _i \rightarrow \Omega$ is an isomorphism.
Let ![]() $C'$ be a finite index coset of
$C'$ be a finite index coset of ![]() $\bigoplus _{i=1}^r \Omega _i \subset \bigoplus _{i=1}^rA_i$ such that, for each
$\bigoplus _{i=1}^r \Omega _i \subset \bigoplus _{i=1}^rA_i$ such that, for each ![]() $c$ in
$c$ in ![]() $C'$, the scheme
$C'$, the scheme ![]() $(\lambda ^*\phi )^{-1}(c)$ is integral. Then
$(\lambda ^*\phi )^{-1}(c)$ is integral. Then ![]() $C:=\lambda (C')$ is a finite index coset of
$C:=\lambda (C')$ is a finite index coset of ![]() $\Omega$. Moreover, because
$\Omega$. Moreover, because ![]() $(\lambda ^*\phi )^{-1}(c) \cong \phi ^{-1}({\lambda (c)})$ for every
$(\lambda ^*\phi )^{-1}(c) \cong \phi ^{-1}({\lambda (c)})$ for every ![]() $c$ in
$c$ in ![]() $C'$, it follows that, for every
$C'$, it follows that, for every ![]() $c$ in
$c$ in ![]() $C$, the scheme
$C$, the scheme ![]() $\phi ^{-1}(c)$ is integral, as required.
$\phi ^{-1}(c)$ is integral, as required.
4.8 From (PB)-covers to ramified covers
The following proposition shows that, when studying the weak-Hilbert property for abelian varieties, it is natural to only consider (PB)-covers.
Proposition 4.17 Suppose that, for every abelian variety ![]() $B$ over
$B$ over ![]() $k$, every (PB)-cover
$k$, every (PB)-cover ![]() $\pi :Y \to B$ has property (PF). Then, for every abelian variety
$\pi :Y \to B$ has property (PF). Then, for every abelian variety ![]() $A$ over
$A$ over ![]() $k$, every (Ram)-cover
$k$, every (Ram)-cover ![]() $\psi : Z \to A$ has property (PF).
$\psi : Z \to A$ has property (PF).
Proof. Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\psi :Z\to A$ be a ramified cover and let
$\psi :Z\to A$ be a ramified cover and let ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup. To prove the proposition, by Corollary 4.7, translating the origin on
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup. To prove the proposition, by Corollary 4.7, translating the origin on ![]() $A$ and replacing
$A$ and replacing ![]() $\Omega$ by a finite index subgroup if necessary, we may and do assume that
$\Omega$ by a finite index subgroup if necessary, we may and do assume that ![]() $\psi :Z\to A$ is étale over every
$\psi :Z\to A$ is étale over every ![]() $c$ in
$c$ in ![]() $\Omega$.
$\Omega$.
By Lemma 4.4, there exists a factorization
where ![]() $\lambda$ is étale and
$\lambda$ is étale and ![]() $\psi _0$ is a non-trivial (PB)-cover. If
$\psi _0$ is a non-trivial (PB)-cover. If ![]() $A'(k) = \emptyset$, then the claim trivially holds, so that we can assume that
$A'(k) = \emptyset$, then the claim trivially holds, so that we can assume that ![]() $A'(k) \neq \emptyset$ and that
$A'(k) \neq \emptyset$ and that ![]() $\lambda$ is an isogeny. We define
$\lambda$ is an isogeny. We define ![]() $\Omega ' := \lambda ^{-1}(\Omega ) \cap A'(k)$ and
$\Omega ' := \lambda ^{-1}(\Omega ) \cap A'(k)$ and ![]() $N := A'(k) \cap \operatorname {Ker} \lambda$, and note that
$N := A'(k) \cap \operatorname {Ker} \lambda$, and note that ![]() $N$ is a finite group. We have a natural exact sequence
$N$ is a finite group. We have a natural exact sequence
Note that the cokernel of the last morphism is finite, as every isogeny between abelian varieties is a left and right factor of multiplication by some integer ![]() $m \in \mathbb {N}_{>0}$.
$m \in \mathbb {N}_{>0}$.
For each ![]() $n$ in the finite group
$n$ in the finite group ![]() $N$, we define
$N$, we define ![]() $\psi _n$ to be the cover of
$\psi _n$ to be the cover of ![]() $A'$ given by the composition
$A'$ given by the composition ![]() $Z \xrightarrow {\psi _0} A' \xrightarrow {+n} A'$. By Lemma 4.14, as every
$Z \xrightarrow {\psi _0} A' \xrightarrow {+n} A'$. By Lemma 4.14, as every ![]() $\psi _n$ is a (PB)-cover, there exists a finite index coset
$\psi _n$ is a (PB)-cover, there exists a finite index coset ![]() $C \subset \Omega '$ such that, for every
$C \subset \Omega '$ such that, for every ![]() $n \in N$ and every
$n \in N$ and every ![]() $c \in C$, the scheme
$c \in C$, the scheme ![]() $\psi _n^{-1}(c)$ has no
$\psi _n^{-1}(c)$ has no ![]() $k$-points. Let
$k$-points. Let ![]() $c \in \lambda (C) \subset \Omega$, and choose a representative
$c \in \lambda (C) \subset \Omega$, and choose a representative ![]() $c_0 \in C$ such that
$c_0 \in C$ such that ![]() $\lambda (c_0)=c$. We have
$\lambda (c_0)=c$. We have
and, by construction, this is étale and has no ![]() $k$-points. As
$k$-points. As ![]() $\lambda (C) \subset \Omega$ is a coset of finite index, this concludes the proof.
$\lambda (C) \subset \Omega$ is a coset of finite index, this concludes the proof.
4.9 Galois closures and (PB)-covers
The next proposition is very close in spirit to the first part of the proof of [Reference ZannierZan10, Theorem 1].
Proposition 4.18 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$ and let
$k$ and let ![]() $r$ be a positive integer.
$r$ be a positive integer.
(1) Suppose that, for every finite field extension
 $L/k$, every (GPB)-cover
$L/k$, every (GPB)-cover  $\pi : Y \to A_L$ of
$\pi : Y \to A_L$ of  $A_L$ has property (IF) up to rank
$A_L$ has property (IF) up to rank  $r$ over
$r$ over  $L$. Then, for every finite field extension
$L$. Then, for every finite field extension  $M/k$, every (PB)-cover
$M/k$, every (PB)-cover  $\pi : Y \to A_M$ of
$\pi : Y \to A_M$ of  $A_M$ has property (IF) up to rank
$A_M$ has property (IF) up to rank  $r$ over
$r$ over  $M$.
$M$.(2) Suppose that, for every finite field extension
 $L/k$, every (GPB)-cover
$L/k$, every (GPB)-cover  $\pi : Y \to A_L$ of
$\pi : Y \to A_L$ of  $A_L$ has property (PF) up to rank
$A_L$ has property (PF) up to rank  $r$ over
$r$ over  $L$. Then, for every finite field extension
$L$. Then, for every finite field extension  $M/k$, every (PB)-cover
$M/k$, every (PB)-cover  $\pi : Y \to A_M$ of
$\pi : Y \to A_M$ of  $A_M$ has property (PF) up to rank
$A_M$ has property (PF) up to rank  $r$ over
$r$ over  $M$.
$M$.
Proof. We only prove part (1), as the proof of part (2) is essentially identical. First, we may and do assume that ![]() $M=k$. Thus, let
$M=k$. Thus, let ![]() $\pi :Y\to A$ be a (PB)-cover of
$\pi :Y\to A$ be a (PB)-cover of ![]() $A$, and let
$A$, and let ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup of rank at most
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup of rank at most ![]() $r$. Define
$r$. Define ![]() $B:=(\deg \pi )!$ and consider
$B:=(\deg \pi )!$ and consider ![]() $[B]^\ast \pi :[B]^*Y \to A$. To prove that
$[B]^\ast \pi :[B]^*Y \to A$. To prove that ![]() $(A,\Omega )$ has property (IF), replacing
$(A,\Omega )$ has property (IF), replacing ![]() $\Omega$ with its finite-index subgroup
$\Omega$ with its finite-index subgroup ![]() $[B]\Omega = \{[B]\omega : \omega \in \Omega \}$, we may assume that the image of
$[B]\Omega = \{[B]\omega : \omega \in \Omega \}$, we may assume that the image of ![]() $A(k) \xrightarrow {[B]} A(k)$ contains
$A(k) \xrightarrow {[B]} A(k)$ contains ![]() $\Omega$. Let
$\Omega$. Let ![]() $[B]^*\Omega =\{x \in A(k): Bx \in \Omega \}$.
$[B]^*\Omega =\{x \in A(k): Bx \in \Omega \}$.
We now choose a finite field extension ![]() $L/k$ such that, if
$L/k$ such that, if ![]() $\widehat {Y_L}\to Y_L\to A_L$ is the Galois closure of
$\widehat {Y_L}\to Y_L\to A_L$ is the Galois closure of ![]() $Y_L\to A_L$, then
$Y_L\to A_L$, then ![]() $\widehat {Y_L}$ is geometrically integral over
$\widehat {Y_L}$ is geometrically integral over ![]() $L$. Replacing
$L$. Replacing ![]() $L$ by a finite field extension if necessary, let
$L$ by a finite field extension if necessary, let ![]() $\psi :A'\to A_L$ be an isogeny of abelian varieties such that
$\psi :A'\to A_L$ be an isogeny of abelian varieties such that ![]() $\widehat {Y_L}\to A'\to A_L$ is the (PB)-factorization of
$\widehat {Y_L}\to A'\to A_L$ is the (PB)-factorization of ![]() $\widehat {Y_L}\to A_L$ (see Lemma 4.4). Replacing
$\widehat {Y_L}\to A_L$ (see Lemma 4.4). Replacing ![]() $L$ by a finite field extension if necessary, we may suppose that
$L$ by a finite field extension if necessary, we may suppose that ![]() $\ker \psi$ is
$\ker \psi$ is ![]() $L$-rational. We observe that
$L$-rational. We observe that ![]() $\deg \psi$ divides the degree of
$\deg \psi$ divides the degree of ![]() $\widehat {Y_L}\to A_L$, which divides
$\widehat {Y_L}\to A_L$, which divides ![]() $(\deg \pi )!=B$. Consider the following diagram in which every square is Cartesian.
$(\deg \pi )!=B$. Consider the following diagram in which every square is Cartesian.

As we observed previously, ![]() $[B]$ kills
$[B]$ kills ![]() $\operatorname {Ker} \psi$. It follows that
$\operatorname {Ker} \psi$. It follows that ![]() $\psi$ is an isogeny factor of
$\psi$ is an isogeny factor of ![]() $[B]$, which gives the identity at the center of the diagram. Note that the composed morphism
$[B]$, which gives the identity at the center of the diagram. Note that the composed morphism ![]() $A_L\cong A_L\times \{0\}\to A_L\times \ker \psi \to A'$ is an isogeny. Therefore, because
$A_L\cong A_L\times \{0\}\to A_L\times \ker \psi \to A'$ is an isogeny. Therefore, because ![]() $\widehat {Y_L}\to A'$ is a (PB)-cover, it follows from Lemma 4.10 that
$\widehat {Y_L}\to A'$ is a (PB)-cover, it follows from Lemma 4.10 that ![]() $V\to A_L$ is a (PB)-cover, so that, in particular,
$V\to A_L$ is a (PB)-cover, so that, in particular, ![]() $V$ is geometrically integral over
$V$ is geometrically integral over ![]() $L$.
$L$.
We now apply Corollary 2.10 to see that the composed morphism ![]() $V\to [B]^\ast Y_L\to A_L$ is a Galois closure of the morphism
$V\to [B]^\ast Y_L\to A_L$ is a Galois closure of the morphism ![]() $[B]^\ast Y_L\to A_L$. Explicitly, applying Corollary 2.10 with
$[B]^\ast Y_L\to A_L$. Explicitly, applying Corollary 2.10 with
and with ![]() $X'\to X$ given by multiplication with
$X'\to X$ given by multiplication with ![]() $B$, we deduce that the Galois closure
$B$, we deduce that the Galois closure ![]() $\widehat {[B]^*Y_L}$ of
$\widehat {[B]^*Y_L}$ of ![]() $[B]^*Y_L \rightarrow A_L$ embeds as a connected component of
$[B]^*Y_L \rightarrow A_L$ embeds as a connected component of ![]() $\widehat {Y_L}\times _{A_L, [B]} A_L$, and the embedding commutes with projection to
$\widehat {Y_L}\times _{A_L, [B]} A_L$, and the embedding commutes with projection to ![]() $A_L$. As
$A_L$. As ![]() $\operatorname {Ker} \psi (\overline {K})= \operatorname {Ker} \psi (K)$, all connected components of
$\operatorname {Ker} \psi (\overline {K})= \operatorname {Ker} \psi (K)$, all connected components of ![]() $\widehat {Y_L}\times _{A_L, [B]} A_L$ are isomorphic, over
$\widehat {Y_L}\times _{A_L, [B]} A_L$ are isomorphic, over ![]() $A_L$, to
$A_L$, to ![]() $V$. Hence, we deduce that there exists an isomorphism
$V$. Hence, we deduce that there exists an isomorphism ![]() $\widehat {[B]^*Y_L}\cong V$ which commutes with projection to
$\widehat {[B]^*Y_L}\cong V$ which commutes with projection to ![]() $A_L$. As
$A_L$. As ![]() $V\to A_L$ is a (PB)-cover, we conclude that
$V\to A_L$ is a (PB)-cover, we conclude that ![]() $[B]^\ast Y_L\to A_L$ is a (GPB)-cover of
$[B]^\ast Y_L\to A_L$ is a (GPB)-cover of ![]() $A_L$.
$A_L$.
For ![]() $x \in A_L(L)$ we have the following Cartesian diagram:
$x \in A_L(L)$ we have the following Cartesian diagram:

and, hence, a canonical isomorphism of schemes (with Galois action),
As every (GPB)-cover of ![]() $A_L$ has property (IF) up to rank
$A_L$ has property (IF) up to rank ![]() $r$ over
$r$ over ![]() $L$, there is a finite-index coset
$L$, there is a finite-index coset ![]() $C$ of
$C$ of ![]() $[B]^*\Omega$ such that the fibre of
$[B]^*\Omega$ such that the fibre of ![]() $[B]^*\pi _L$ over every
$[B]^*\pi _L$ over every ![]() $c \in C$ is integral. The previous isomorphism shows that
$c \in C$ is integral. The previous isomorphism shows that ![]() $[B]C$ is a finite-index coset of
$[B]C$ is a finite-index coset of ![]() $\Omega$ such that the fibre of
$\Omega$ such that the fibre of ![]() $\pi : Y_L \to A_L$ over any
$\pi : Y_L \to A_L$ over any ![]() $[B]c \in [B]C$ is integral, hence
$[B]c \in [B]C$ is integral, hence ![]() $(\pi _L:Y_L\to A_L,\Omega )$ has property (IF) over
$(\pi _L:Y_L\to A_L,\Omega )$ has property (IF) over ![]() $L$. This implies (readily) that
$L$. This implies (readily) that ![]() $(\pi :Y\to A, \Omega )$ has property (IF) over
$(\pi :Y\to A, \Omega )$ has property (IF) over ![]() $k$, as required.
$k$, as required.
Proposition 4.19 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, and let
$k$, and let ![]() $r$ be a positive integer. Suppose that, for every finite field extension
$r$ be a positive integer. Suppose that, for every finite field extension ![]() $L/k$, every (GPB)-cover
$L/k$, every (GPB)-cover ![]() $\pi : Y \to A_L$ of
$\pi : Y \to A_L$ of ![]() $A_L$ has property (PF) up to rank
$A_L$ has property (PF) up to rank ![]() $r$ over
$r$ over ![]() $L$. Then, for every finite field extension
$L$. Then, for every finite field extension ![]() $M/k$, every (PB)-cover
$M/k$, every (PB)-cover ![]() $\pi : Y \to A_M$ of
$\pi : Y \to A_M$ of ![]() $A_M$ has property (IF) up to rank
$A_M$ has property (IF) up to rank ![]() $r$ over
$r$ over ![]() $M$.
$M$.
Proof. By Proposition 4.18(1), it suffices to prove that, for every finite field extension ![]() $L/k$, every (GPB)-cover
$L/k$, every (GPB)-cover ![]() $\pi : Y \to A_L$ has property (IF) up to rank
$\pi : Y \to A_L$ has property (IF) up to rank ![]() $r$ over
$r$ over ![]() $L$. To do so, let
$L$. To do so, let ![]() $\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup of rank at most
$\Omega \subset A(k)$ be a finitely generated Zariski-dense subgroup of rank at most ![]() $r$, let
$r$, let ![]() $\pi : Y \to A_L$ be a (GPB)-cover of
$\pi : Y \to A_L$ be a (GPB)-cover of ![]() $A_L$, and let
$A_L$, and let ![]() $\widehat {\pi } : \widehat {Y} \to A_L$ be its Galois closure with group
$\widehat {\pi } : \widehat {Y} \to A_L$ be its Galois closure with group ![]() $G$.
$G$.
Let ![]() $H_1:=\{e\}, \ldots, H_{s}$ be an enumeration of the proper subgroups of
$H_1:=\{e\}, \ldots, H_{s}$ be an enumeration of the proper subgroups of ![]() $G$. By our definition of (GPB)-cover, the cover
$G$. By our definition of (GPB)-cover, the cover ![]() $\widehat {\pi }$ satisfies property (PB), hence for each
$\widehat {\pi }$ satisfies property (PB), hence for each ![]() $i=1,\ldots, s$ so does its subcover
$i=1,\ldots, s$ so does its subcover ![]() $\widehat {Y}_{H_i} \to A_L$. By Proposition 4.18(2), the hypothesis implies that every (PB)-cover
$\widehat {Y}_{H_i} \to A_L$. By Proposition 4.18(2), the hypothesis implies that every (PB)-cover ![]() $\pi : Y \to A_L$ has property (PF) up to rank
$\pi : Y \to A_L$ has property (PF) up to rank ![]() $r$, so that by Lemma 4.14 there is a finite-index coset
$r$, so that by Lemma 4.14 there is a finite-index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that, for each
$\Omega$ such that, for each ![]() $c \in C$ and each
$c \in C$ and each ![]() $i=1,\ldots,s$, the fibre of
$i=1,\ldots,s$, the fibre of ![]() $\widehat {Y}_{H_i} \to A_L$ over
$\widehat {Y}_{H_i} \to A_L$ over ![]() $c$ has no
$c$ has no ![]() $L$-rational points and is reduced. As
$L$-rational points and is reduced. As ![]() $\widehat {Y} = \widehat {Y}_{H_1} \to A_L$ is étale over the points of
$\widehat {Y} = \widehat {Y}_{H_1} \to A_L$ is étale over the points of ![]() $C$, by Proposition 2.13, we conclude that the fibre
$C$, by Proposition 2.13, we conclude that the fibre ![]() $\widehat {\pi }^{-1}(c)$ is integral, as required.
$\widehat {\pi }^{-1}(c)$ is integral, as required.
5. A product theorem for abelian varieties
Throughout this section we let ![]() $K$ be a number field.
$K$ be a number field.
5.1 Local considerations
Lemma 5.1 If ![]() $E/K$ is a non-trivial finite extension of number fields, then there exist infinitely many places
$E/K$ is a non-trivial finite extension of number fields, then there exist infinitely many places ![]() $v$ of
$v$ of ![]() $K$ such that
$K$ such that ![]() $(\operatorname {Spec} E)(K_v)=\emptyset$.
$(\operatorname {Spec} E)(K_v)=\emptyset$.
Proof. We may and do assume that ![]() $E$ is Galois over
$E$ is Galois over ![]() $K$. By Chebotarev's density theorem, the set of finite places
$K$. By Chebotarev's density theorem, the set of finite places ![]() $v$ of
$v$ of ![]() $K$ which are unramified and not totally split in
$K$ which are unramified and not totally split in ![]() $E$ is infinite. As
$E$ is infinite. As ![]() $E$ over
$E$ over ![]() $K$ is Galois, for any of the (infinitely many) finite places
$K$ is Galois, for any of the (infinitely many) finite places ![]() $v$ of
$v$ of ![]() $K$ unramified and not totally split in
$K$ unramified and not totally split in ![]() $E$, the
$E$, the ![]() $K_v$-algebra
$K_v$-algebra ![]() $E\otimes _K K_v$ is isomorphic to the power
$E\otimes _K K_v$ is isomorphic to the power ![]() $M^\ell$ of a non-trivial extension
$M^\ell$ of a non-trivial extension ![]() $M$ of
$M$ of ![]() $K_v$ (with
$K_v$ (with ![]() $\ell \geq 1$ an integer). For such a
$\ell \geq 1$ an integer). For such a ![]() $v$, because
$v$, because ![]() $M$ is non-trivial over
$M$ is non-trivial over ![]() $K_v$, we have that
$K_v$, we have that
This concludes the proof.
For the next two propositions we let ![]() $\mathbb {A}^{\operatorname {fin}}_{K}$ be the ring of finite adèles of
$\mathbb {A}^{\operatorname {fin}}_{K}$ be the ring of finite adèles of ![]() $K$. We also implicitly consider
$K$. We also implicitly consider ![]() $K$ as embedded diagonally in
$K$ as embedded diagonally in ![]() $\mathbb {A}^{\operatorname {fin}}_{K}$.
$\mathbb {A}^{\operatorname {fin}}_{K}$.
Recall that, for a finite-type separated scheme ![]() $X$ over
$X$ over ![]() $K$, the adelic topology is defined as follows. Fix a model
$K$, the adelic topology is defined as follows. Fix a model ![]() $\mathcal {X}$ (separated, of finite type) of
$\mathcal {X}$ (separated, of finite type) of ![]() $X$ over
$X$ over ![]() $\operatorname {Spec} \mathcal {O}_K$. The adelic topology on
$\operatorname {Spec} \mathcal {O}_K$. The adelic topology on ![]() $X(\mathbb {A}_K^{\operatorname {fin}})\subseteq \prod _{v \in M_K^{\operatorname {fin}}} X(K_v)$ is by definition the topology generated by all subsets of the form
$X(\mathbb {A}_K^{\operatorname {fin}})\subseteq \prod _{v \in M_K^{\operatorname {fin}}} X(K_v)$ is by definition the topology generated by all subsets of the form
where ![]() $S$ is a finite subset of
$S$ is a finite subset of ![]() $M_K^{\operatorname {fin}}$, each
$M_K^{\operatorname {fin}}$, each ![]() $U_v$ is an open subset of
$U_v$ is an open subset of ![]() $X(K_v)$ (for its natural
$X(K_v)$ (for its natural ![]() $v$-adic topology) and
$v$-adic topology) and ![]() $\mathcal {O}_v$ is the ring of integers of
$\mathcal {O}_v$ is the ring of integers of ![]() $K_v$. One checks that this definition is independent of the choice of model
$K_v$. One checks that this definition is independent of the choice of model ![]() $\mathcal {X}$. When
$\mathcal {X}$. When ![]() $X$ is proper over
$X$ is proper over ![]() $K$, the valuative criterion for properness easily implies that
$K$, the valuative criterion for properness easily implies that ![]() $X(\mathbb {A}_K^{\operatorname {fin}}) = \prod _{v \in M_K^{\operatorname {fin}}} X(K_v)$ as topological spaces.
$X(\mathbb {A}_K^{\operatorname {fin}}) = \prod _{v \in M_K^{\operatorname {fin}}} X(K_v)$ as topological spaces.
Proposition 5.2 If ![]() $f:Z' \rightarrow Z$ is a projective morphism of separated schemes of finite type over
$f:Z' \rightarrow Z$ is a projective morphism of separated schemes of finite type over ![]() $K$, then the induced morphism
$K$, then the induced morphism ![]() $f:Z'(\mathbb {A}_K^{\operatorname {fin}}) \rightarrow Z(\mathbb {A}_K^{\operatorname {fin}})$ is closed.
$f:Z'(\mathbb {A}_K^{\operatorname {fin}}) \rightarrow Z(\mathbb {A}_K^{\operatorname {fin}})$ is closed.
Proof. Let ![]() $v$ be a finite place of
$v$ be a finite place of ![]() $K$. As
$K$. As ![]() $f$ is projective, there exists
$f$ is projective, there exists ![]() $n \in \mathbb {N}$ such that
$n \in \mathbb {N}$ such that ![]() $f$ factors as
$f$ factors as ![]() $X \hookrightarrow \mathbb {P}_{n,Y} \rightarrow Y$, where
$X \hookrightarrow \mathbb {P}_{n,Y} \rightarrow Y$, where ![]() $X \hookrightarrow \mathbb {P}_{n,Y}$ is a closed embedding and
$X \hookrightarrow \mathbb {P}_{n,Y}$ is a closed embedding and ![]() $\mathbb {P}_{n,Y} \rightarrow Y$ is the standard projection. It is straightforward to see that
$\mathbb {P}_{n,Y} \rightarrow Y$ is the standard projection. It is straightforward to see that ![]() $X(K_v) \hookrightarrow \mathbb {P}_{n,Y}(K_v)$ is a closed embedding, hence it is a proper map of topological spaces. Moreover, because
$X(K_v) \hookrightarrow \mathbb {P}_{n,Y}(K_v)$ is a closed embedding, hence it is a proper map of topological spaces. Moreover, because ![]() $\mathbb {P}_n(K_v)$ is compact, the composed map
$\mathbb {P}_n(K_v)$ is compact, the composed map ![]() $\mathbb {P}_{n,Y}(K_v)= \mathbb {P}_n(K_v) \times Y(K_v) \rightarrow Y(K_v)$ is proper. As composition of proper maps is proper, the map
$\mathbb {P}_{n,Y}(K_v)= \mathbb {P}_n(K_v) \times Y(K_v) \rightarrow Y(K_v)$ is proper. As composition of proper maps is proper, the map ![]() $f_{K_v}:Z'(K_v) \rightarrow Z(K_v)$ is proper, hence closed. Choose a finite set of finite places
$f_{K_v}:Z'(K_v) \rightarrow Z(K_v)$ is proper, hence closed. Choose a finite set of finite places ![]() $S$ of
$S$ of ![]() $K$ and a proper morphism
$K$ and a proper morphism ![]() $\phi :\mathcal {Z}' \rightarrow \mathcal {Z}$ of finite-type separated
$\phi :\mathcal {Z}' \rightarrow \mathcal {Z}$ of finite-type separated ![]() $\mathcal {O}_{K,S}$-schemes extending
$\mathcal {O}_{K,S}$-schemes extending ![]() $f:Z'\to Z$ over
$f:Z'\to Z$ over ![]() $\mathcal {O}_{K,S}$. By the valuative criterion for properness, for all
$\mathcal {O}_{K,S}$. By the valuative criterion for properness, for all ![]() $v \notin S$, we have
$v \notin S$, we have ![]() $\phi (\mathcal {Z}'(\mathcal {O}_v))=f({Z}'(K_v)) \cap \mathcal {Z}(\mathcal {O}_v)$. It is now a straightforward verification to see that
$\phi (\mathcal {Z}'(\mathcal {O}_v))=f({Z}'(K_v)) \cap \mathcal {Z}(\mathcal {O}_v)$. It is now a straightforward verification to see that ![]() $f:Z'(\mathbb {A}_K^{\operatorname {fin}}) \rightarrow Z(\mathbb {A}_K^{\operatorname {fin}})$ is closed.
$f:Z'(\mathbb {A}_K^{\operatorname {fin}}) \rightarrow Z(\mathbb {A}_K^{\operatorname {fin}})$ is closed.
Corollary 5.3 Let ![]() $\phi :Z \rightarrow A$ be a cover of normal varieties over
$\phi :Z \rightarrow A$ be a cover of normal varieties over ![]() $K$, and let
$K$, and let ![]() $P \in A(K)$ such that
$P \in A(K)$ such that ![]() $\phi$ is étale over
$\phi$ is étale over ![]() $P$. Suppose that one of the following conditions hold:
$P$. Suppose that one of the following conditions hold:
(1) the set
 $Z_P(\mathbb {A}_K^{\operatorname {fin}})$ is empty;
$Z_P(\mathbb {A}_K^{\operatorname {fin}})$ is empty;(2) the morphism
 $\phi$ is Galois and
$\phi$ is Galois and  $Z_P(K)=\emptyset$;
$Z_P(K)=\emptyset$;(3) the scheme
 $Z_P$ is integral and
$Z_P$ is integral and  $\deg \phi >1$.
$\deg \phi >1$.
Then there is an adelic open neighbourhood ![]() $U_P \subset A(\mathbb {A}_K^{\operatorname {fin}})$ of
$U_P \subset A(\mathbb {A}_K^{\operatorname {fin}})$ of ![]() $P$ such that, for every
$P$ such that, for every ![]() $Q$ in
$Q$ in ![]() $U_P \cap A(K)$, the set
$U_P \cap A(K)$, the set ![]() $Z_Q(\mathbb {A}_K^{\operatorname {fin}})$ is empty.
$Z_Q(\mathbb {A}_K^{\operatorname {fin}})$ is empty.
Proof. We first show that condition (2) implies condition (1) and condition (3) implies condition (1), respectively. Indeed, if ![]() $\phi$ is Galois, because
$\phi$ is Galois, because ![]() $\phi$ is étale over
$\phi$ is étale over ![]() $P$, the scheme
$P$, the scheme ![]() $Z_P$ is a Galois étale cover of
$Z_P$ is a Galois étale cover of ![]() $P \cong \operatorname {Spec} K$. Therefore, if
$P \cong \operatorname {Spec} K$. Therefore, if ![]() $Z_P(K)=\emptyset$, then
$Z_P(K)=\emptyset$, then ![]() $Z_P \cong \operatorname {Spec} E \sqcup \cdots \sqcup \operatorname {Spec} E$, where
$Z_P \cong \operatorname {Spec} E \sqcup \cdots \sqcup \operatorname {Spec} E$, where ![]() $E$ is a finite non-trivial Galois extension of
$E$ is a finite non-trivial Galois extension of ![]() $K$. By Lemma 5.1, there is a finite place
$K$. By Lemma 5.1, there is a finite place ![]() $v$ of
$v$ of ![]() $K$ such that
$K$ such that ![]() $Z_P(K_v)=\emptyset$. In particular, the set
$Z_P(K_v)=\emptyset$. In particular, the set ![]() $Z_P(\mathbb {A}_K^{\operatorname {fin}})$ is empty. This shows that condition (2) implies condition (1).
$Z_P(\mathbb {A}_K^{\operatorname {fin}})$ is empty. This shows that condition (2) implies condition (1).
Now, assume condition (3) holds, so that ![]() $Z_P$ is integral. Then, because
$Z_P$ is integral. Then, because ![]() $Z_P\to \operatorname {Spec} K$ has degree greater than one (as
$Z_P\to \operatorname {Spec} K$ has degree greater than one (as ![]() $\deg \phi >1$ and
$\deg \phi >1$ and ![]() $Z_P$ is integral), by Lemma 5.1, there exists a finite place
$Z_P$ is integral), by Lemma 5.1, there exists a finite place ![]() $v$ of
$v$ of ![]() $K$ such that
$K$ such that ![]() $Z_P(K_v)=\emptyset$, so that again
$Z_P(K_v)=\emptyset$, so that again ![]() $Z_P(\mathbb {A}_K^{\operatorname {fin}})=\emptyset$. This shows that condition (3) implies condition (1).
$Z_P(\mathbb {A}_K^{\operatorname {fin}})=\emptyset$. This shows that condition (3) implies condition (1).
Thus, to prove the corollary, we may assume that condition (1) holds. As ![]() $\phi$ is finite, hence projective [Sta20, Tag 0B3I], the subset
$\phi$ is finite, hence projective [Sta20, Tag 0B3I], the subset ![]() $\phi (Z(\mathbb {A}_K^{\operatorname {fin}})) \subset A(\mathbb {A}_K^{\operatorname {fin}})$ is closed by Proposition 5.2. Moreover, as
$\phi (Z(\mathbb {A}_K^{\operatorname {fin}})) \subset A(\mathbb {A}_K^{\operatorname {fin}})$ is closed by Proposition 5.2. Moreover, as ![]() $\phi (Z(\mathbb {A}_K^{\operatorname {fin}}))$ does not contain
$\phi (Z(\mathbb {A}_K^{\operatorname {fin}}))$ does not contain ![]() $P$ by condition (1), the corollary follows by taking
$P$ by condition (1), the corollary follows by taking ![]() $U_P$ to be the complement of
$U_P$ to be the complement of ![]() $\phi (Z(\mathbb {A}_K^{\operatorname {fin}}))$ in
$\phi (Z(\mathbb {A}_K^{\operatorname {fin}}))$ in ![]() $A(\mathbb {A}_K^{\operatorname {fin}})$.
$A(\mathbb {A}_K^{\operatorname {fin}})$.
Corollary 5.4 Let ![]() $\phi : Z \rightarrow A$ be a cover of an abelian variety
$\phi : Z \rightarrow A$ be a cover of an abelian variety ![]() $A$ over
$A$ over ![]() $K$ with
$K$ with ![]() $\deg \phi >1$, and let
$\deg \phi >1$, and let ![]() $\Omega \subset A(K)$ be a subgroup. If there is a point
$\Omega \subset A(K)$ be a subgroup. If there is a point ![]() $P \in \Omega$ such that
$P \in \Omega$ such that ![]() $Z_P$ is integral, then there exists a finite index coset
$Z_P$ is integral, then there exists a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that, for each
$\Omega$ such that, for each ![]() $c$ in
$c$ in ![]() $C$, the set
$C$, the set ![]() $Z_c(K)$ is empty.
$Z_c(K)$ is empty.
Proof. By Corollary 5.3, there is an open adelic neighbourhood ![]() $U_P \subset A(\mathbb {A}_K^{\operatorname {fin}})$ of
$U_P \subset A(\mathbb {A}_K^{\operatorname {fin}})$ of ![]() $P$ such that the set
$P$ such that the set ![]() $\phi ^{-1}(U_P)(\mathbb {A}_K^{\operatorname {fin}})$ is empty. As
$\phi ^{-1}(U_P)(\mathbb {A}_K^{\operatorname {fin}})$ is empty. As ![]() $A$ is proper over
$A$ is proper over ![]() $K$, the adelic topology on
$K$, the adelic topology on ![]() $A(\mathbb {A}_K^{\operatorname {fin}})=\prod _{v \in M_K^{\operatorname {fin}}}A(K_v)$ coincides with the product topology. Therefore, we may assume that there is a finite subset of finite places
$A(\mathbb {A}_K^{\operatorname {fin}})=\prod _{v \in M_K^{\operatorname {fin}}}A(K_v)$ coincides with the product topology. Therefore, we may assume that there is a finite subset of finite places ![]() $V := \{v_1, \ldots, v_r\} \subset M_K^{\operatorname {fin}}$ and, for each
$V := \{v_1, \ldots, v_r\} \subset M_K^{\operatorname {fin}}$ and, for each ![]() $i=1,\ldots, r$, an open subset
$i=1,\ldots, r$, an open subset ![]() $U_i \subset A(K_{v_i})$ containing
$U_i \subset A(K_{v_i})$ containing ![]() $P$ such that
$P$ such that
 \[ \prod_{i=1}^r U_i \times \prod_{v \notin V} A(K_v) \subset U_P. \]
\[ \prod_{i=1}^r U_i \times \prod_{v \notin V} A(K_v) \subset U_P. \]
For ![]() $i=1,\ldots, r$, let
$i=1,\ldots, r$, let ![]() $W_i := -P + U_i \subset A(K_{v_i})$, and note that
$W_i := -P + U_i \subset A(K_{v_i})$, and note that ![]() $W_i$ is an open subset of
$W_i$ is an open subset of ![]() $A(K_{v_i})$ containing the identity.
$A(K_{v_i})$ containing the identity.
Let ![]() $p_i$ be the residue characteristic of
$p_i$ be the residue characteristic of ![]() $v_i$. By [Reference MattuckMat55], the topological group
$v_i$. By [Reference MattuckMat55], the topological group ![]() $A(K_{v_i})$ contains a finite index open subgroup isomorphic to the additive group
$A(K_{v_i})$ contains a finite index open subgroup isomorphic to the additive group ![]() $\mathcal {O}_{v_i}^{\dim A}$. Let
$\mathcal {O}_{v_i}^{\dim A}$. Let ![]() $t_i:=[A(K_{v_i}): \mathcal {O}_{v_i}^{\dim A}]$. Then, for
$t_i:=[A(K_{v_i}): \mathcal {O}_{v_i}^{\dim A}]$. Then, for ![]() $n_i$ sufficiently large, the subgroup
$n_i$ sufficiently large, the subgroup ![]() $(p_i^{n_i} t_i) \Omega$ is contained in
$(p_i^{n_i} t_i) \Omega$ is contained in ![]() $W_i$. Define
$W_i$. Define ![]() $N:=\prod _{i=1}^r p_i^{n_i} t_i$, and
$N:=\prod _{i=1}^r p_i^{n_i} t_i$, and ![]() $\omega := N\Omega$. As
$\omega := N\Omega$. As ![]() $\Omega$ is a finitely generated abelian group (by Mordell–Weil), the subgroup
$\Omega$ is a finitely generated abelian group (by Mordell–Weil), the subgroup ![]() $\omega$ is of finite index, so that the finite index coset
$\omega$ is of finite index, so that the finite index coset ![]() $C := \omega + P$ of
$C := \omega + P$ of ![]() $\Omega$ satisfies the condition in the statement.
$\Omega$ satisfies the condition in the statement.
5.2 Products of abelian varieties
The main result of this section (Corollary 5.7) will allow us to reduce the proof of Hilbert's irreducibility theorem for pairs ![]() $(A,\Omega )$ to the case that
$(A,\Omega )$ to the case that ![]() $\Omega$ is cyclic.
$\Omega$ is cyclic.
Lemma 5.5 Let ![]() $A, B$ be abelian varieties over
$A, B$ be abelian varieties over ![]() $K$. Let
$K$. Let ![]() $\pi : Z \rightarrow A \times B$ be a (PB)-cover of
$\pi : Z \rightarrow A \times B$ be a (PB)-cover of ![]() $A\times B$, and let
$A\times B$, and let ![]() $Z \rightarrow S \xrightarrow {\phi } A$ be the Stein factorization of
$Z \rightarrow S \xrightarrow {\phi } A$ be the Stein factorization of ![]() $p_1 \circ \pi$, where
$p_1 \circ \pi$, where ![]() $p_1: A \times B \rightarrow A$ denotes the projection. Then
$p_1: A \times B \rightarrow A$ denotes the projection. Then ![]() $\phi$ is a (PB)-cover of
$\phi$ is a (PB)-cover of ![]() $A$.
$A$.
Proof. By the universal property of fibre products, if ![]() $S\to S'\to A$ is a non-trivial étale subcover of
$S\to S'\to A$ is a non-trivial étale subcover of ![]() $S\to A$, the finite étale morphism
$S\to A$, the finite étale morphism ![]() $S'\times B \to A\times B$ is a non-trivial étale subcover of
$S'\times B \to A\times B$ is a non-trivial étale subcover of ![]() $Z\to A\times B$. Therefore, the result follows from Lemma 4.4.
$Z\to A\times B$. Therefore, the result follows from Lemma 4.4.
Proposition 5.6 Let ![]() $A, B$ be abelian varieties over
$A, B$ be abelian varieties over ![]() $K$, and
$K$, and ![]() $\Omega _A \subset A(K), \ \Omega _B \subset B(K)$ be Zariski-dense subgroups. Suppose that, for every finite extension
$\Omega _A \subset A(K), \ \Omega _B \subset B(K)$ be Zariski-dense subgroups. Suppose that, for every finite extension ![]() $L$ of
$L$ of ![]() $K$, property (PB) implies property (IF) for both
$K$, property (PB) implies property (IF) for both ![]() $(A_L,\Omega _A)$ and
$(A_L,\Omega _A)$ and ![]() $(B_L,\Omega _B)$. Then property (PB) implies property (PF) for
$(B_L,\Omega _B)$. Then property (PB) implies property (PF) for ![]() $(A \times B, \Omega _A \times \Omega _B)$.
$(A \times B, \Omega _A \times \Omega _B)$.
Proof. Let ![]() $\pi : Z \to A \times B$ be a (PB)-cover, which we may assume to be of degree at least two. By Corollary 4.7, there exist finite index cosets
$\pi : Z \to A \times B$ be a (PB)-cover, which we may assume to be of degree at least two. By Corollary 4.7, there exist finite index cosets ![]() $C_A\subset \Omega _A$ and
$C_A\subset \Omega _A$ and ![]() $C_B\subset \Omega _B$ such that
$C_B\subset \Omega _B$ such that ![]() $\pi$ is étale over
$\pi$ is étale over ![]() $C_A \times C_B$. To prove the proposition, up to composing with a translation of
$C_A \times C_B$. To prove the proposition, up to composing with a translation of ![]() $A \times B$, we may and do assume that
$A \times B$, we may and do assume that ![]() $C_A$ and
$C_A$ and ![]() $C_B$ are actually subgroups. Therefore, replacing
$C_B$ are actually subgroups. Therefore, replacing ![]() $\Omega _A$ (respectively,
$\Omega _A$ (respectively, ![]() $\Omega _B$) with
$\Omega _B$) with ![]() $C_A$ (respectively,
$C_A$ (respectively, ![]() $C_B$), we may assume that
$C_B$), we may assume that ![]() $\pi$ is étale over
$\pi$ is étale over ![]() $\Omega _A \times \Omega _B$.
$\Omega _A \times \Omega _B$.
Let ![]() $Z \to S \to A$ be the Stein factorization of the composition
$Z \to S \to A$ be the Stein factorization of the composition ![]() $Z \to A \times B \to A$ as follows.
$Z \to A \times B \to A$ as follows.

We note that ![]() $S \to A$ has property (PB) by Lemma 5.5. Note that
$S \to A$ has property (PB) by Lemma 5.5. Note that ![]() $S \to A$ could be an isomorphism.
$S \to A$ could be an isomorphism.
We now distinguish two cases.
(1) Assume ![]() $S \to A$ is not an isomorphism. Applying the assumption to the (PB)-cover
$S \to A$ is not an isomorphism. Applying the assumption to the (PB)-cover ![]() $\phi : S \to A$ and to the (finitely generated) subgroup
$\phi : S \to A$ and to the (finitely generated) subgroup ![]() $\Omega _A$, we get a finite-index coset
$\Omega _A$, we get a finite-index coset ![]() $C \subseteq \Omega _A$ with the property that, for every
$C \subseteq \Omega _A$ with the property that, for every ![]() $c \in C$, the fibre
$c \in C$, the fibre ![]() $\phi ^{-1}(c)$ has no
$\phi ^{-1}(c)$ has no ![]() $K$-rational points. It follows immediately that
$K$-rational points. It follows immediately that ![]() $C \times \Omega _B$ is a finite-index coset of
$C \times \Omega _B$ is a finite-index coset of ![]() $\Omega _A \times \Omega _B$ such that, for any
$\Omega _A \times \Omega _B$ such that, for any ![]() $(c,b) \in C \times \Omega _B$, we have
$(c,b) \in C \times \Omega _B$, we have ![]() $\pi ^{-1}((c,b))(K) \subseteq \psi ^{-1} \phi ^{-1}(c) (K) = \emptyset$. As
$\pi ^{-1}((c,b))(K) \subseteq \psi ^{-1} \phi ^{-1}(c) (K) = \emptyset$. As ![]() $\pi ^{-1}((c,b))$ is reduced by assumption, this proves that
$\pi ^{-1}((c,b))$ is reduced by assumption, this proves that ![]() $\pi :Z\to A\times B$ has property (PF) in this case.
$\pi :Z\to A\times B$ has property (PF) in this case.
(2) Assume that ![]() $S \to A$ is an isomorphism, so that
$S \to A$ is an isomorphism, so that ![]() $Z \to A$ has geometrically connected fibres. As
$Z \to A$ has geometrically connected fibres. As ![]() $K$ is of characteristic zero and
$K$ is of characteristic zero and ![]() $Z$ is a normal geometrically integral variety over
$Z$ is a normal geometrically integral variety over ![]() $K$,
$K$, ![]() $Z_{\overline {K}}$ is normal by [Sta20, Tag 034F]. Hence, the generic fibre of
$Z_{\overline {K}}$ is normal by [Sta20, Tag 034F]. Hence, the generic fibre of ![]() $Z_{\overline {K}} \rightarrow {A}_{\overline {K}}$ is normal and integral by a simple localization argument. Therefore, by [Reference GrothendieckGro66, Theorem 12.2.4(iv)] and [Reference GrothendieckGro65, Theorem 6.9.1], there is a dense open subscheme
$Z_{\overline {K}} \rightarrow {A}_{\overline {K}}$ is normal and integral by a simple localization argument. Therefore, by [Reference GrothendieckGro66, Theorem 12.2.4(iv)] and [Reference GrothendieckGro65, Theorem 6.9.1], there is a dense open subscheme ![]() $\mathcal {U}$ of
$\mathcal {U}$ of ![]() $A$ over which the geometric fibres of
$A$ over which the geometric fibres of ![]() $Z \to A$ are normal (integral) varieties. In particular, for every
$Z \to A$ are normal (integral) varieties. In particular, for every ![]() $a \in \mathcal {U}(K)$, the morphism
$a \in \mathcal {U}(K)$, the morphism ![]() $Z_a \rightarrow \{a\} \times B$ is a cover of
$Z_a \rightarrow \{a\} \times B$ is a cover of ![]() $B$ over
$B$ over ![]() $K$.
$K$.
Let ![]() $\eta _A \in A$ be the generic point. By Lemma 4.4, there is a finite étale cover
$\eta _A \in A$ be the generic point. By Lemma 4.4, there is a finite étale cover ![]() $\widetilde {B}\to B_{\eta _A}$ and a cover
$\widetilde {B}\to B_{\eta _A}$ and a cover ![]() $Z_{\eta _A}\to \widetilde {B}$ such that
$Z_{\eta _A}\to \widetilde {B}$ such that ![]() $Z_{\eta _A}\to B_{\eta _A}$ factors as
$Z_{\eta _A}\to B_{\eta _A}$ factors as
and the morphism ![]() $Z_{\overline {K(A)} }\to \widetilde {B}_{\overline {K(A)}}$ is a (PB)-cover of the abelian variety
$Z_{\overline {K(A)} }\to \widetilde {B}_{\overline {K(A)}}$ is a (PB)-cover of the abelian variety ![]() $\widetilde {B}_{\overline {K(A)}}$. Let
$\widetilde {B}_{\overline {K(A)}}$. Let ![]() $\tilde {Z}$ be the normalization of
$\tilde {Z}$ be the normalization of ![]() $A \times B$ in (the function field of)
$A \times B$ in (the function field of) ![]() $\widetilde {B}$. Note that
$\widetilde {B}$. Note that ![]() $\tilde {Z}$ is a normal variety over
$\tilde {Z}$ is a normal variety over ![]() $K$ and that the factorization 9 induces a factorization
$K$ and that the factorization 9 induces a factorization
with ![]() $\tilde {Z}_{\eta _A}= \widetilde {B}$. By construction
$\tilde {Z}_{\eta _A}= \widetilde {B}$. By construction ![]() $\lambda$ is vertically ramified over
$\lambda$ is vertically ramified over ![]() $A$ (see Definition 2.16). Moreover,
$A$ (see Definition 2.16). Moreover, ![]() $\lambda$ is a (PB)-cover of
$\lambda$ is a (PB)-cover of ![]() $A\times B$, as it is a factor of the (PB)-cover
$A\times B$, as it is a factor of the (PB)-cover ![]() $Z \to A \times B$.
$Z \to A \times B$.
(a) Suppose that
 $\tilde {Z}=A \times B$ (i.e.
$\tilde {Z}=A \times B$ (i.e.  $\deg \lambda =1$), so that
$\deg \lambda =1$), so that  $Z_{\eta _A}\to B_{\eta _A}$ is a (PB)-cover. Therefore, by applying Lemma 4.11 to the abelian scheme
$Z_{\eta _A}\to B_{\eta _A}$ is a (PB)-cover. Therefore, by applying Lemma 4.11 to the abelian scheme  $\mathcal {A} := A\times B\to A=:S$, there is a dense open subscheme
$\mathcal {A} := A\times B\to A=:S$, there is a dense open subscheme  $U\subset A$ such that, for every
$U\subset A$ such that, for every  $a$ in
$a$ in  $U(K)$, the morphism
$U(K)$, the morphism  $Z_a \to \{a\} \times B$ is (PB)-cover of
$Z_a \to \{a\} \times B$ is (PB)-cover of  $B$. As
$B$. As  $\Omega _A$ is dense in
$\Omega _A$ is dense in  $A$, there is a
$A$, there is a  $K$-rational point
$K$-rational point  $a$ of
$a$ of  $U$ contained in
$U$ contained in  $\Omega _A$. In particular, the assumption on
$\Omega _A$. In particular, the assumption on  $(B,\Omega _B)$ implies that there is a finite-index coset
$(B,\Omega _B)$ implies that there is a finite-index coset  $C$ of
$C$ of  $\Omega _B$ such that, for every
$\Omega _B$ such that, for every  $c$ in
$c$ in  $C$, the scheme
$C$, the scheme  $\pi ^{-1}((a,c))$ is integral. By Corollary 5.4, the existence of such a point implies that
$\pi ^{-1}((a,c))$ is integral. By Corollary 5.4, the existence of such a point implies that  $(\pi, \Omega _A \times \Omega _B)$ satisfies property (PF) as desired.
$(\pi, \Omega _A \times \Omega _B)$ satisfies property (PF) as desired.(b) Suppose that
 $\deg \lambda \geq 2$. Then, property (PF) for
$\deg \lambda \geq 2$. Then, property (PF) for  $(\pi, \Omega _A \times \Omega _B)$ is implied by property (PF) for
$(\pi, \Omega _A \times \Omega _B)$ is implied by property (PF) for  $(\lambda, \Omega _A \times \Omega _B)$ (see Remark 4.3). Thus, we may and do assume that
$(\lambda, \Omega _A \times \Omega _B)$ (see Remark 4.3). Thus, we may and do assume that  $\tilde {Z}=Z$, so that
$\tilde {Z}=Z$, so that  $\pi :Z \to A \times B$ is vertically ramified over
$\pi :Z \to A \times B$ is vertically ramified over  $A$. Applying Lemma 2.17 to
$A$. Applying Lemma 2.17 to  ${\pi }_{\overline {K}}: Z_{\overline {K}} \rightarrow A_{\overline {K}} \times B_{\overline {K}}$ yields the existence of a commutative diagram
(11)where:
${\pi }_{\overline {K}}: Z_{\overline {K}} \rightarrow A_{\overline {K}} \times B_{\overline {K}}$ yields the existence of a commutative diagram
(11)where:
(i)
 $\overline {S'}, \overline {B'}, \overline {Z'}$ are normal varieties over
$\overline {S'}, \overline {B'}, \overline {Z'}$ are normal varieties over  $\overline {K}$;
$\overline {K}$;(ii)
 $\overline {S'} \to A_{\overline {K}}$ is a ramified cover;
$\overline {S'} \to A_{\overline {K}}$ is a ramified cover;(iii)
 $\overline {Z'} \to Z_{\overline {K}}$ and
$\overline {Z'} \to Z_{\overline {K}}$ and  $\phi _B:\overline {B'} \to B_{\overline {K}}$ are finite étale; in particular, we may fix a structure of abelian variety on
$\phi _B:\overline {B'} \to B_{\overline {K}}$ are finite étale; in particular, we may fix a structure of abelian variety on  $\overline {B'}$ that makes
$\overline {B'}$ that makes  $\phi _B$ an isogeny;
$\phi _B$ an isogeny;(iv)
 $\overline {Z'}$ is a connected component of the fibred product
$\overline {Z'}$ is a connected component of the fibred product  $Z_{\overline {K}} \times _{B_{\overline {K}}} \overline {B'}$; in particular, because
$Z_{\overline {K}} \times _{B_{\overline {K}}} \overline {B'}$; in particular, because  $Z_{\overline {K}} \times _{B_{\overline {K}}} \overline {B'}$ is connected by Lemma 4.8, the square is Cartesian;
$Z_{\overline {K}} \times _{B_{\overline {K}}} \overline {B'}$ is connected by Lemma 4.8, the square is Cartesian;(v)
 $\overline {Z'} \to \overline {S'} \to A_{\overline {K}}$ is the Stein factorization of
$\overline {Z'} \to \overline {S'} \to A_{\overline {K}}$ is the Stein factorization of  $\overline {Z'} \to A_{\overline {K}}$; hence
$\overline {Z'} \to A_{\overline {K}}$; hence  $\overline {S'} \to A_{\overline {K}}$ is a (PB)-cover by Lemma 5.5.
$\overline {S'} \to A_{\overline {K}}$ is a (PB)-cover by Lemma 5.5.
We choose a finite extension
 $L/K$ over which the entire diagram (11) is defined. More precisely, we let
$L/K$ over which the entire diagram (11) is defined. More precisely, we let  $S', Z'$ be varieties over
$S', Z'$ be varieties over  $L$ and
$L$ and  $B'$ be an abelian variety over
$B'$ be an abelian variety over  $L$ such that
$L$ such that  $S'_{\overline {K}}\cong \overline {S'}$,
$S'_{\overline {K}}\cong \overline {S'}$,  $B'_{\overline {K}}\cong \overline {B'}$ (as abelian varieties over
$B'_{\overline {K}}\cong \overline {B'}$ (as abelian varieties over  $\overline {K}$), and
$\overline {K}$), and  $Z'_{\overline {K}}\cong \overline {Z'}$. Moreover, let
$Z'_{\overline {K}}\cong \overline {Z'}$. Moreover, let  $\phi ':S' \to A_L$ be a morphism such that
$\phi ':S' \to A_L$ be a morphism such that  $\phi '_{\overline {K}}=\overline {\phi '}$. In addition, replacing
$\phi '_{\overline {K}}=\overline {\phi '}$. In addition, replacing  $L$ by a finite extension if necessary, we have that
$L$ by a finite extension if necessary, we have that  $\Omega _B \subset \phi _B(B'(L))$.
$\Omega _B \subset \phi _B(B'(L))$.As
 $S' \to A_L$ is a non-trivial (PB)-cover of
$S' \to A_L$ is a non-trivial (PB)-cover of  $A_L$, our assumption on
$A_L$, our assumption on  $(A_L,\Omega _A)$ implies that there is a finite-index coset
$(A_L,\Omega _A)$ implies that there is a finite-index coset  $C \subseteq \Omega _A \subset A_L(L)$ such that, for every
$C \subseteq \Omega _A \subset A_L(L)$ such that, for every  $c \in C$, the scheme
$c \in C$, the scheme  $(\phi ')^{-1}(c)$ is integral. In particular, as the degree of
$(\phi ')^{-1}(c)$ is integral. In particular, as the degree of  $\phi '$ is at least two, the set
$\phi '$ is at least two, the set  $((\phi ')^{-1}(c))(L)$ is empty. Thus, for every
$((\phi ')^{-1}(c))(L)$ is empty. Thus, for every  $(c,b)$ in the finite index coset
$(c,b)$ in the finite index coset  $C\times \Omega _B$ of
$C\times \Omega _B$ of  $\Omega _A\times \Omega _B$, we have that
$\Omega _A\times \Omega _B$, we have that  $\pi _L^{-1}((c,b))(L)$ (hence
$\pi _L^{-1}((c,b))(L)$ (hence  $\pi ^{-1}((c,b))(K)$) is empty. It follows that
$\pi ^{-1}((c,b))(K)$) is empty. It follows that  $\pi$ satisfies property (PF) as desired.
$\pi$ satisfies property (PF) as desired.
This concludes the proof.
Corollary 5.7 Let ![]() $A, B$ be abelian varieties over
$A, B$ be abelian varieties over ![]() $K$, and
$K$, and ![]() $\Omega _A \subset A(K), \ \Omega _B \subset B(K)$ be Zariski-dense subgroups. Suppose that, for every finite extension
$\Omega _A \subset A(K), \ \Omega _B \subset B(K)$ be Zariski-dense subgroups. Suppose that, for every finite extension ![]() $L$ of
$L$ of ![]() $K$, property (PB) implies property (IF) for both
$K$, property (PB) implies property (IF) for both ![]() $(A_L,\Omega _A)$ and
$(A_L,\Omega _A)$ and ![]() $(B_L,\Omega _B)$. Then, for every finite extension
$(B_L,\Omega _B)$. Then, for every finite extension ![]() $E$ of
$E$ of ![]() $K$, property (PB) implies property (IF) for
$K$, property (PB) implies property (IF) for ![]() $(A_E \times B_E, \Omega _A \times \Omega _B)$.
$(A_E \times B_E, \Omega _A \times \Omega _B)$.
Proof. Note that ![]() $\Omega _A$ and
$\Omega _A$ and ![]() $\Omega _B$ are finitely generated by the Mordell–Weil theorem. We know by Proposition 5.6 that, for all finite extensions
$\Omega _B$ are finitely generated by the Mordell–Weil theorem. We know by Proposition 5.6 that, for all finite extensions ![]() $E/K$, property (PB) implies property (PF) for
$E/K$, property (PB) implies property (PF) for ![]() $(A_E \times B_E, \Omega _A \times \Omega _B)$. Applying, for all finite extensions
$(A_E \times B_E, \Omega _A \times \Omega _B)$. Applying, for all finite extensions ![]() $E/K$ and all
$E/K$ and all ![]() $r \geq 1$, Proposition 4.19 to
$r \geq 1$, Proposition 4.19 to ![]() $(A_E \times B_E, \Omega _A \times \Omega _B)$, we deduce that property (PB) implies property (IF) for
$(A_E \times B_E, \Omega _A \times \Omega _B)$, we deduce that property (PB) implies property (IF) for ![]() $(A_E \times B_E, \Omega _A \times \Omega _B)$.
$(A_E \times B_E, \Omega _A \times \Omega _B)$.
6. Abelian varieties with a non-degenerate point
The main result of this section (Theorem 6.15) says, roughly speaking, that an abelian variety over a number field endowed with a non-degenerate point has the weak-Hilbert property. We prove this theorem using Kummer theory for abelian varieties.
6.1 Constructing a suitable torsion point
Proposition 6.1 Let ![]() $A$ be an abelian variety over a finite field
$A$ be an abelian variety over a finite field ![]() $\mathbb {F}_q$ of cardinality
$\mathbb {F}_q$ of cardinality ![]() $q$, and let
$q$, and let ![]() $\ell$ be a rational prime coprime with
$\ell$ be a rational prime coprime with ![]() $q$. Then
$q$. Then
where ![]() $\operatorname {Fr}_q\in \Gamma _{\mathbb {F}_q}$ is the Frobenius of
$\operatorname {Fr}_q\in \Gamma _{\mathbb {F}_q}$ is the Frobenius of ![]() $\mathbb {F}_q$ and
$\mathbb {F}_q$ and ![]() $\rho : \Gamma _{\mathbb {F}_q} \rightarrow T_\ell A$ is the Galois action on the
$\rho : \Gamma _{\mathbb {F}_q} \rightarrow T_\ell A$ is the Galois action on the ![]() $\ell$-adic Tate module.
$\ell$-adic Tate module.
Proof. It follows from the standard theory of abelian varieties and Tate modules that, if ![]() $\phi :A \rightarrow A$ denotes the Frobenius endomorphism, then
$\phi :A \rightarrow A$ denotes the Frobenius endomorphism, then ![]() $\det (\rho (\operatorname {Fr}_q)-1)=\deg (\phi -1)= \# \operatorname {Ker}(\phi -1)$. As
$\det (\rho (\operatorname {Fr}_q)-1)=\deg (\phi -1)= \# \operatorname {Ker}(\phi -1)$. As ![]() $\operatorname {Ker}(\phi -1)=A(\mathbb {F}_q)$, the proposition follows.
$\operatorname {Ker}(\phi -1)=A(\mathbb {F}_q)$, the proposition follows.
The following elementary result in group theory goes back to Jordan [Reference JordanJor72].
Proposition 6.2 Let ![]() $G$ be a group acting transitively on a set
$G$ be a group acting transitively on a set ![]() $X$. If
$X$. If ![]() $|X| \geq 2$, then there exists
$|X| \geq 2$, then there exists ![]() $g \in G$ that acts on
$g \in G$ that acts on ![]() $X$ with no fixed points.
$X$ with no fixed points.
We recall that throughout this paper, we let ![]() $K$ denote a number field. The main result of this subsection is the following lemma which gives a torsion point
$K$ denote a number field. The main result of this subsection is the following lemma which gives a torsion point ![]() $\zeta$ over which the fibre has no
$\zeta$ over which the fibre has no ![]() $K(\zeta )$-points.
$K(\zeta )$-points.
Lemma 6.3 Let ![]() $\phi :Y \rightarrow A$ be a non-trivial (GPB)-cover of an abelian variety
$\phi :Y \rightarrow A$ be a non-trivial (GPB)-cover of an abelian variety ![]() $A$ over
$A$ over ![]() $K$ with Galois closure
$K$ with Galois closure ![]() $\widehat {\phi }:\widehat {Y} \to A$ and Galois group
$\widehat {\phi }:\widehat {Y} \to A$ and Galois group ![]() $G$. For every finite set
$G$. For every finite set ![]() $S$ of prime numbers, there exists a torsion point
$S$ of prime numbers, there exists a torsion point ![]() $\zeta \in A(\overline {K})_{\operatorname {tors}}$ such that
$\zeta \in A(\overline {K})_{\operatorname {tors}}$ such that ![]() $\operatorname {ord} (\zeta )$ is coprime with all the finite primes in
$\operatorname {ord} (\zeta )$ is coprime with all the finite primes in ![]() $S$, the fibre
$S$, the fibre ![]() $\phi ^{-1}(\zeta )$ is étale over
$\phi ^{-1}(\zeta )$ is étale over ![]() $K(\zeta )$ and there exists an element
$K(\zeta )$ and there exists an element ![]() $g$ in a decomposition group at
$g$ in a decomposition group at ![]() $\zeta$ for
$\zeta$ for ![]() $\widehat {\phi }$ such that
$\widehat {\phi }$ such that ![]() $g$ acts with no fixed points on the geometric fibre
$g$ acts with no fixed points on the geometric fibre ![]() $\phi ^{-1}(\overline {\zeta })$.
$\phi ^{-1}(\overline {\zeta })$.
Proof. By Remark 2.7(ii), the Galois closure of ![]() $Y_{\overline {K}} \to A_{\overline {K}}$ is the base change to
$Y_{\overline {K}} \to A_{\overline {K}}$ is the base change to ![]() $\overline {K}$ of the Galois closure of
$\overline {K}$ of the Galois closure of ![]() $Y \to A$, hence the Galois closure of
$Y \to A$, hence the Galois closure of ![]() $Y_{\overline {K}} \to A_{\overline {K}}$ is a (PB)-cover.
$Y_{\overline {K}} \to A_{\overline {K}}$ is a (PB)-cover.
Choose a finite set of places ![]() $S' \subset M_K^{\operatorname {fin}}$ and an abelian scheme
$S' \subset M_K^{\operatorname {fin}}$ and an abelian scheme ![]() $\mathcal {A}\to \operatorname {Spec}_{\mathcal {O}_{K,S'}}$ extending
$\mathcal {A}\to \operatorname {Spec}_{\mathcal {O}_{K,S'}}$ extending ![]() $A \to \operatorname {Spec} K$; this is possible by spreading out. After possibly enlarging
$A \to \operatorname {Spec} K$; this is possible by spreading out. After possibly enlarging ![]() $S'$, we may choose a normal integral model
$S'$, we may choose a normal integral model ![]() $\mathcal {Y}$ of
$\mathcal {Y}$ of ![]() $Y$ over
$Y$ over ![]() $\mathcal {O}_{K,S'}$ and a finite surjective morphism
$\mathcal {O}_{K,S'}$ and a finite surjective morphism ![]() $\psi :\mathcal {Y} \rightarrow \mathcal {A}$ extending
$\psi :\mathcal {Y} \rightarrow \mathcal {A}$ extending ![]() $\phi$. We let
$\phi$. We let ![]() $\mathcal {B} \subset \mathcal {A}$ denote the branch locus of
$\mathcal {B} \subset \mathcal {A}$ denote the branch locus of ![]() $\psi$; note that
$\psi$; note that ![]() $\mathcal {B}$ is a closed subscheme of
$\mathcal {B}$ is a closed subscheme of ![]() $\mathcal {A}$ of pure codimension one by [Reference GrothendieckGro71, Théorème X.3.1]. As
$\mathcal {A}$ of pure codimension one by [Reference GrothendieckGro71, Théorème X.3.1]. As ![]() $\mathcal {A}$ is normal and
$\mathcal {A}$ is normal and ![]() $\psi$ is finite surjective, the morphism
$\psi$ is finite surjective, the morphism ![]() $\psi$ is étale precisely where it is unramified (Lemma 2.3), hence
$\psi$ is étale precisely where it is unramified (Lemma 2.3), hence ![]() $\psi |_{\psi ^{-1}(\mathcal {A}\setminus \mathcal {B})}$ is étale. We define
$\psi |_{\psi ^{-1}(\mathcal {A}\setminus \mathcal {B})}$ is étale. We define ![]() $\mathcal {U} := \mathcal {A} \setminus \mathcal {B}$ and
$\mathcal {U} := \mathcal {A} \setminus \mathcal {B}$ and ![]() $\mathcal {V}:= \psi ^{-1}(\mathcal {U})$. In addition, we define
$\mathcal {V}:= \psi ^{-1}(\mathcal {U})$. In addition, we define ![]() $U:=\mathcal {U}_K$ and
$U:=\mathcal {U}_K$ and ![]() $V:=\mathcal {V}_K$.
$V:=\mathcal {V}_K$.
Let now ![]() $\hat {\psi }:\hat {\mathcal {V}} \rightarrow \mathcal {U}$ be a Galois closure of the finite étale morphism
$\hat {\psi }:\hat {\mathcal {V}} \rightarrow \mathcal {U}$ be a Galois closure of the finite étale morphism ![]() $\mathcal {V} \rightarrow \mathcal {U}$ (with Galois group
$\mathcal {V} \rightarrow \mathcal {U}$ (with Galois group ![]() $G$) and let
$G$) and let ![]() $\hat {V} := \hat {\mathcal {V}}_{K}$. As
$\hat {V} := \hat {\mathcal {V}}_{K}$. As ![]() $\hat {\mathcal {V}}$ is regular and connected, it is integral. We let
$\hat {\mathcal {V}}$ is regular and connected, it is integral. We let ![]() $H \subset G$ be the subgroup corresponding to
$H \subset G$ be the subgroup corresponding to ![]() $\mathcal {V}$ by Galois theory [Sta20, Tag 0BND], so that
$\mathcal {V}$ by Galois theory [Sta20, Tag 0BND], so that ![]() $\hat {\mathcal {V}}/H \rightarrow \mathcal {V}$ is an isomorphism.
$\hat {\mathcal {V}}/H \rightarrow \mathcal {V}$ is an isomorphism.
As ![]() $G$ acts transitively on
$G$ acts transitively on ![]() $G/H$, by Proposition 6.2 there exists an element
$G/H$, by Proposition 6.2 there exists an element ![]() $g \in G$ that acts with no fixed points on
$g \in G$ that acts with no fixed points on ![]() $G/H$.
$G/H$.
If ![]() $v$ is a finite place of
$v$ is a finite place of ![]() $K$ not in
$K$ not in ![]() $S'$ and
$S'$ and ![]() $\zeta _v \in \mathcal {U}({\mathbb {F}_v})$ is a torsion point of order
$\zeta _v \in \mathcal {U}({\mathbb {F}_v})$ is a torsion point of order ![]() $m$ coprime with
$m$ coprime with ![]() $S$ such that a Frobenius of
$S$ such that a Frobenius of ![]() $\zeta _v$ for
$\zeta _v$ for ![]() $\hat {\psi }$ is
$\hat {\psi }$ is ![]() $g$, then any
$g$, then any ![]() $\zeta \in \mathcal {A}[m](K_v)$ that reduces to
$\zeta \in \mathcal {A}[m](K_v)$ that reduces to ![]() $\zeta _v$ modulo
$\zeta _v$ modulo ![]() $v$ is such that
$v$ is such that ![]() $\psi ^{-1}(\zeta )$ has no
$\psi ^{-1}(\zeta )$ has no ![]() $K_v$-points by Proposition 2.15. In particular, for such
$K_v$-points by Proposition 2.15. In particular, for such ![]() $v, \zeta _v$ and
$v, \zeta _v$ and ![]() $\zeta$, the fibre
$\zeta$, the fibre ![]() $\psi ^{-1}(\zeta )$ is reduced and has no
$\psi ^{-1}(\zeta )$ is reduced and has no ![]() $K(\zeta )$-points. Thus, to prove the lemma it suffices to show that there exist
$K(\zeta )$-points. Thus, to prove the lemma it suffices to show that there exist ![]() $v$ and
$v$ and ![]() $\zeta _v$ as above.
$\zeta _v$ as above.
For each prime number ![]() $\ell$, we denote by
$\ell$, we denote by ![]() $\rho _\ell : \Gamma _K \to \operatorname {Aut}(T_\ell (A))$ the natural
$\rho _\ell : \Gamma _K \to \operatorname {Aut}(T_\ell (A))$ the natural ![]() $\ell$-adic Galois representation attached to
$\ell$-adic Galois representation attached to ![]() $A$. For every positive integer
$A$. For every positive integer ![]() $C$ we define the following open subset of
$C$ we define the following open subset of ![]() $\Gamma _K$:
$\Gamma _K$:
We claim that there exists a positive integer ![]() $C$ such that
$C$ such that ![]() $\square _C \neq \emptyset$. To see this, choose a finite place
$\square _C \neq \emptyset$. To see this, choose a finite place ![]() $w_0$ of
$w_0$ of ![]() $K$ at which
$K$ at which ![]() $A$ has good reduction and that does not lie over any prime in
$A$ has good reduction and that does not lie over any prime in ![]() $S$. Let now
$S$. Let now ![]() $\operatorname {Fr}_{w_0} \in \Gamma _{K}$ be a Frobenius element corresponding to a place of
$\operatorname {Fr}_{w_0} \in \Gamma _{K}$ be a Frobenius element corresponding to a place of ![]() $\overline {K}$ lying over
$\overline {K}$ lying over ![]() $w_0$, and let
$w_0$, and let ![]() $C := \prod _{\ell _i \in S} \{\det (\rho _{\ell _i}(\operatorname {Fr}_{w_0})-1)\}_{\ell _i}$ (where, for a rational number
$C := \prod _{\ell _i \in S} \{\det (\rho _{\ell _i}(\operatorname {Fr}_{w_0})-1)\}_{\ell _i}$ (where, for a rational number ![]() $q \in \mathbb {Q}$ and a rational prime
$q \in \mathbb {Q}$ and a rational prime ![]() $\ell$,
$\ell$, ![]() $\{q\}_\ell := \ell ^{v_\ell (q)}$). By Proposition 6.1, this number is non-zero, and
$\{q\}_\ell := \ell ^{v_\ell (q)}$). By Proposition 6.1, this number is non-zero, and ![]() $\operatorname {Fr}_{w_0} \in \square _C$, so that the claim holds. We fix from now on a value of
$\operatorname {Fr}_{w_0} \in \square _C$, so that the claim holds. We fix from now on a value of ![]() $C$ for which
$C$ for which ![]() $\square _C \neq \emptyset$.
$\square _C \neq \emptyset$.
Let ![]() $M$ be a finite Galois extension of
$M$ be a finite Galois extension of ![]() $K$ such that
$K$ such that ![]() $\square _C= \pi _{{\overline {K}/M}}^{-1}(\square '_C)$ for some subset
$\square _C= \pi _{{\overline {K}/M}}^{-1}(\square '_C)$ for some subset ![]() $\square '_C \subset \operatorname {Gal}(M/K)$, where
$\square '_C \subset \operatorname {Gal}(M/K)$, where ![]() $\pi _{\overline {K}/M} : \Gamma _{K} \rightarrow \operatorname {Gal}(M/K)$ denotes the natural projection. By enlarging
$\pi _{\overline {K}/M} : \Gamma _{K} \rightarrow \operatorname {Gal}(M/K)$ denotes the natural projection. By enlarging ![]() $S'$ if necessary, we may assume that it contains all the places that ramify in the extension
$S'$ if necessary, we may assume that it contains all the places that ramify in the extension ![]() $M/K$. Fix an element
$M/K$. Fix an element ![]() $\gamma _0 \in \square '_C$ and consider the following Cartesian diagram.
$\gamma _0 \in \square '_C$ and consider the following Cartesian diagram.

As ![]() $\widehat {Y}\to A$ is a (PB)-cover, it follows that
$\widehat {Y}\to A$ is a (PB)-cover, it follows that ![]() $[C]^*\hat {Y}$ and, thus,
$[C]^*\hat {Y}$ and, thus, ![]() $[C]^*\hat {V}$, is geometrically integral over
$[C]^*\hat {V}$, is geometrically integral over ![]() $K$. Consider the finite étale Galois morphism
$K$. Consider the finite étale Galois morphism
where ![]() ${[C]^*\hat {\mathcal {V}}} \times _{\mathcal {O}_{K,S'}} {\mathcal {O}_{M,S'}}$ is integral. Note that the Galois group
${[C]^*\hat {\mathcal {V}}} \times _{\mathcal {O}_{K,S'}} {\mathcal {O}_{M,S'}}$ is integral. Note that the Galois group ![]() $G'$ of
$G'$ of ![]() $r$ can be identified with
$r$ can be identified with ![]() $\operatorname {Gal}(M/K) \times G$. Let
$\operatorname {Gal}(M/K) \times G$. Let ![]() $\gamma :=(\gamma _0, g)$ in
$\gamma :=(\gamma _0, g)$ in ![]() $G'$.
$G'$.
By the geometric Chebotarev theorem [Reference PinkPin97, Theorem B.9] there exist a finite place ![]() $v$ of
$v$ of ![]() $K$ not in
$K$ not in ![]() $S'$ and a point
$S'$ and a point ![]() $P_v \in [C]^{-1}\mathcal {U}(\mathbb {F}_v)$ such that a Frobenius at
$P_v \in [C]^{-1}\mathcal {U}(\mathbb {F}_v)$ such that a Frobenius at ![]() $P_v$ for
$P_v$ for ![]() $r$ is
$r$ is ![]() $\gamma$. As the residue field at
$\gamma$. As the residue field at ![]() $P_v$ is
$P_v$ is ![]() $\mathbb {F}_v$, and because
$\mathbb {F}_v$, and because ![]() $\gamma _0$ is an element of
$\gamma _0$ is an element of ![]() $\square '_C$, by Proposition 6.1 we have
$\square '_C$, by Proposition 6.1 we have ![]() $\{ \# \mathcal {A}(\mathbb {F}_v)\}_{\ell _i} \mid C$ for every
$\{ \# \mathcal {A}(\mathbb {F}_v)\}_{\ell _i} \mid C$ for every ![]() $\ell _i \in S$. In particular, for every element
$\ell _i \in S$. In particular, for every element ![]() $P \in \mathcal {A}(\mathbb {F}_v)$ and every
$P \in \mathcal {A}(\mathbb {F}_v)$ and every ![]() $\ell _i \in S$, the
$\ell _i \in S$, the ![]() $\ell _i$ part of the order of
$\ell _i$ part of the order of ![]() $P$ (which is a divisor of
$P$ (which is a divisor of ![]() $\# \mathcal {A}(\mathbb {F}_v)$) divides
$\# \mathcal {A}(\mathbb {F}_v)$) divides ![]() $C$, hence the order of
$C$, hence the order of ![]() $[C]P$ is not divisible by any prime in
$[C]P$ is not divisible by any prime in ![]() $S$. The place
$S$. The place ![]() $v$ and the point
$v$ and the point ![]() $\zeta _v:= [C] P_v$ satisfy all the conditions we need:
$\zeta _v:= [C] P_v$ satisfy all the conditions we need: ![]() $v$ is not in
$v$ is not in ![]() $S'$, the order of
$S'$, the order of ![]() $\zeta _v$ is not divisible by any prime in
$\zeta _v$ is not divisible by any prime in ![]() $S$, and a Frobenius at
$S$, and a Frobenius at ![]() $\zeta _v$ for
$\zeta _v$ for ![]() $\psi$ is the projection of
$\psi$ is the projection of ![]() $\gamma$ to
$\gamma$ to ![]() $G$, which by definition is
$G$, which by definition is ![]() $g$.
$g$.
6.2 Kummer theory
Let ![]() $A$ be an abelian variety over the number field
$A$ be an abelian variety over the number field ![]() $K$. Recall that a point
$K$. Recall that a point ![]() $P\in A(K)$ is said to be non-degenerate if the set
$P\in A(K)$ is said to be non-degenerate if the set ![]() $\mathbb {Z} P := \{nP : n \in \mathbb {Z}\}$ is dense in
$\mathbb {Z} P := \{nP : n \in \mathbb {Z}\}$ is dense in ![]() $A$. We fix throughout a non-degenerate point
$A$. We fix throughout a non-degenerate point ![]() $P\in A(K)$.
$P\in A(K)$.
The aim of this section is to construct a finite place ![]() $v$ of
$v$ of ![]() $K$ and a finite index coset
$K$ and a finite index coset ![]() $C$ of
$C$ of ![]() $\mathbb {Z} P$ whose elements all reduce modulo
$\mathbb {Z} P$ whose elements all reduce modulo ![]() $v$ to the torsion point
$v$ to the torsion point ![]() $\zeta$ constructed in Lemma 6.3.
$\zeta$ constructed in Lemma 6.3.
For every positive integer ![]() $m$, we set
$m$, we set ![]() $K_{m} := K(A[m])$ and
$K_{m} := K(A[m])$ and ![]() $K_{P,m} := K(A[m], [m]^{-1}P)$, where
$K_{P,m} := K(A[m], [m]^{-1}P)$, where
The extensions ![]() $K_{P,m}/K_m$,
$K_{P,m}/K_m$, ![]() $K_{P,m}/K$ and
$K_{P,m}/K$ and ![]() $K_m/K$ are all Galois. Note that the extension of
$K_m/K$ are all Galois. Note that the extension of ![]() $K$ generated by all
$K$ generated by all ![]() $m$-division points of
$m$-division points of ![]() $P$ also contains all (the coordinates of the)
$P$ also contains all (the coordinates of the) ![]() $m$-torsion points of
$m$-torsion points of ![]() $A$, because every
$A$, because every ![]() $m$-torsion point is the difference of two
$m$-torsion point is the difference of two ![]() $m$-division points of
$m$-division points of ![]() $P$. The Galois group
$P$. The Galois group ![]() $G_m := \operatorname {Gal}(K_{P,m}/K)$ sits in the obvious exact sequence
$G_m := \operatorname {Gal}(K_{P,m}/K)$ sits in the obvious exact sequence
where ![]() $H_m = \operatorname {Gal}(K_m/K)$ and
$H_m = \operatorname {Gal}(K_m/K)$ and ![]() $N_m=\operatorname {Gal}(K_{P,m}/K_m)$. Fix once and for all a compatible system
$N_m=\operatorname {Gal}(K_{P,m}/K_m)$. Fix once and for all a compatible system ![]() $(P_m)_{m \geq 1}$ of points of
$(P_m)_{m \geq 1}$ of points of ![]() $A(\overline {K})$ that satisfy
$A(\overline {K})$ that satisfy ![]() $nP_m = P_{{m}/{n}}$ for all positive integers
$nP_m = P_{{m}/{n}}$ for all positive integers ![]() $n \mid m$. This choice allows us to interpret
$n \mid m$. This choice allows us to interpret ![]() $G_m$ as a subgroup of
$G_m$ as a subgroup of ![]() $A[m] \rtimes \operatorname {Aut} A[m]$ via the map
$A[m] \rtimes \operatorname {Aut} A[m]$ via the map
In this way, ![]() $H_m$ gets identified with a subgroup of
$H_m$ gets identified with a subgroup of ![]() $\operatorname {Aut} A[m]$, and the kernel
$\operatorname {Aut} A[m]$, and the kernel ![]() $N_m$ with a subgroup of
$N_m$ with a subgroup of ![]() $A[m]$.
$A[m]$.
Restricting our attention to positive integers ![]() $m$ of the form
$m$ of the form ![]() $m=\ell ^n$, where
$m=\ell ^n$, where ![]() $\ell$ is a fixed prime, and passing to the limit
$\ell$ is a fixed prime, and passing to the limit ![]() $n \to \infty$ in (13), we obtain an injection
$n \to \infty$ in (13), we obtain an injection
where ![]() $\ell ^{-\infty } P := \{ x \in A(\overline {K}) : \ell ^nx = P \text { for some }n \geq 1\}$. We may therefore write elements of
$\ell ^{-\infty } P := \{ x \in A(\overline {K}) : \ell ^nx = P \text { for some }n \geq 1\}$. We may therefore write elements of ![]() $G_{\ell ^\infty }$ as pairs
$G_{\ell ^\infty }$ as pairs ![]() $(t, M)$ with
$(t, M)$ with ![]() $t \in T_\ell (A)$ and
$t \in T_\ell (A)$ and ![]() $M \in \operatorname {Aut} T_\ell (A)$. As previously, note that
$M \in \operatorname {Aut} T_\ell (A)$. As previously, note that ![]() $K(A[\ell ^\infty ])$ is a subfield of
$K(A[\ell ^\infty ])$ is a subfield of ![]() $K( \ell ^{-\infty }P)$.
$K( \ell ^{-\infty }P)$.
Finally, there are obvious variants of this construction where one works with finitely many primes ![]() $\ell _1,\ldots,\ell _r$. In this case, the Galois group of
$\ell _1,\ldots,\ell _r$. In this case, the Galois group of ![]() $K(\ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)$ over
$K(\ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)$ over ![]() $K$ embeds into
$K$ embeds into ![]() $\prod _{i=1}^r T_{\ell _i}(A) \rtimes \prod _{i=1}^r \operatorname {Aut}(T_{\ell _i}(A))$ by passing to the inverse limit in (13) over positive integers
$\prod _{i=1}^r T_{\ell _i}(A) \rtimes \prod _{i=1}^r \operatorname {Aut}(T_{\ell _i}(A))$ by passing to the inverse limit in (13) over positive integers ![]() $m$ all of whose prime factors lie in
$m$ all of whose prime factors lie in ![]() $\{\ell _1,\ldots,\ell _r\}$. Moreover,
$\{\ell _1,\ldots,\ell _r\}$. Moreover, ![]() $K(A[\ell _1^\infty ], \ldots, A[\ell _r^\infty ])$ is a subfield of
$K(A[\ell _1^\infty ], \ldots, A[\ell _r^\infty ])$ is a subfield of ![]() $K( \ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)$, and the Galois group
$K( \ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)$, and the Galois group ![]() $\operatorname {Gal}\big (K(\ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)/K(A[\ell _1^\infty ], \ldots, A[\ell _r^\infty ]) \big )$ is identified with a subgroup of
$\operatorname {Gal}\big (K(\ell _1^{-\infty }P, \ldots, \ell _r^{-\infty }P)/K(A[\ell _1^\infty ], \ldots, A[\ell _r^\infty ]) \big )$ is identified with a subgroup of ![]() $\prod _{i=1}^r T_{\ell _i}(A)$.
$\prod _{i=1}^r T_{\ell _i}(A)$.
6.2.1 The  $\ell$-part of the reductions of
$\ell$-part of the reductions of  $P$
$P$
Let ![]() $S^b$ be the set of finite places of bad reduction of
$S^b$ be the set of finite places of bad reduction of ![]() $A$, define
$A$, define ![]() $\mathcal {U}=\operatorname {Spec} \mathcal {O}_{K,S^b}$ and let
$\mathcal {U}=\operatorname {Spec} \mathcal {O}_{K,S^b}$ and let ![]() $\mathcal {A}$ be the (smooth proper) Néron model of
$\mathcal {A}$ be the (smooth proper) Néron model of ![]() $A$ over
$A$ over ![]() $\mathcal {U}$. The point
$\mathcal {U}$. The point ![]() $P$ gives rise to a point of infinite order of
$P$ gives rise to a point of infinite order of ![]() $\mathcal {A}(\mathcal {U})$ that we still denote by
$\mathcal {A}(\mathcal {U})$ that we still denote by ![]() $P$. For a finite place
$P$. For a finite place ![]() $v$ of
$v$ of ![]() $K$ at which
$K$ at which ![]() $A$ has good reduction we may then consider the image of
$A$ has good reduction we may then consider the image of ![]() $P$ in
$P$ in ![]() $\mathcal {A}(\mathbb {F}_v)$, where
$\mathcal {A}(\mathbb {F}_v)$, where ![]() $\mathbb {F}_v$ is the residue field at
$\mathbb {F}_v$ is the residue field at ![]() $v$. For the sake of simplicity, we denote this image by
$v$. For the sake of simplicity, we denote this image by ![]() $P \bmod v$, and we abuse notation and write simply
$P \bmod v$, and we abuse notation and write simply ![]() $A(\mathbb {F}_v)$ instead of
$A(\mathbb {F}_v)$ instead of ![]() $\mathcal {A}(\mathbb {F}_v)$.
$\mathcal {A}(\mathbb {F}_v)$.
We need the following notion of the ![]() $\ell$ part of an element in an abelian group.
$\ell$ part of an element in an abelian group.
Definition 6.4 Let ![]() $B$ be an abelian group and
$B$ be an abelian group and ![]() $g \in B$ be an element of finite order. The subgroup of
$g \in B$ be an element of finite order. The subgroup of ![]() $B$ generated by
$B$ generated by ![]() $g$ is a finite abelian group that we may write as the (internal) direct product of its Sylow subgroups: let
$g$ is a finite abelian group that we may write as the (internal) direct product of its Sylow subgroups: let
where the ![]() $\ell _i$ are pairwise distinct prime numbers and
$\ell _i$ are pairwise distinct prime numbers and ![]() $S_{\ell _i}$ is the corresponding Sylow subgroup. Given a prime
$S_{\ell _i}$ is the corresponding Sylow subgroup. Given a prime ![]() $\ell$, the
$\ell$, the ![]() $\ell$ part of
$\ell$ part of ![]() $g$ is the projection of
$g$ is the projection of ![]() $g$ on
$g$ on ![]() $S_{\ell }$ (which may be trivial). We denote it by
$S_{\ell }$ (which may be trivial). We denote it by ![]() $[g]_\ell$.
$[g]_\ell$.
Remark 6.5 An equivalent construction of the ![]() $\ell$ part of
$\ell$ part of ![]() $g$ is as follows. Let
$g$ is as follows. Let ![]() $m=\operatorname {ord}(g)$ and let
$m=\operatorname {ord}(g)$ and let ![]() $\ell ^e$ be the exact power of
$\ell ^e$ be the exact power of ![]() $\ell$ that divides
$\ell$ that divides ![]() $m$. Write
$m$. Write ![]() $m=\ell ^e q$ and choose an integer
$m=\ell ^e q$ and choose an integer ![]() $s$ with
$s$ with ![]() $s \equiv 1 \pmod {\ell ^e}, s \equiv 0 \pmod {q}$. The
$s \equiv 1 \pmod {\ell ^e}, s \equiv 0 \pmod {q}$. The ![]() $\ell$ part of
$\ell$ part of ![]() $g$ is then
$g$ is then ![]() $s \cdot g$.
$s \cdot g$.
Let ![]() $v$ be a finite place of good reduction for
$v$ be a finite place of good reduction for ![]() $A$. We may then consider the
$A$. We may then consider the ![]() $\ell$ part of
$\ell$ part of ![]() $P \bmod v$, where we (equivalently) view
$P \bmod v$, where we (equivalently) view ![]() $P \bmod v$ as a point of finite order of either
$P \bmod v$ as a point of finite order of either ![]() $A(\mathbb {F}_v)$ or
$A(\mathbb {F}_v)$ or ![]() $A(\overline {\mathbb {F}_v})$. We now wish to describe
$A(\overline {\mathbb {F}_v})$. We now wish to describe ![]() $[P \bmod v]_\ell$ in terms of Kummer theory. Note that
$[P \bmod v]_\ell$ in terms of Kummer theory. Note that ![]() $[P \bmod v]_{\ell }$ is an element of
$[P \bmod v]_{\ell }$ is an element of ![]() $A(\mathbb {F}_v)[\ell ^\infty ] \subseteq A(\overline {\mathbb {F}_v})[\ell ^\infty ]$, and that, provided that
$A(\mathbb {F}_v)[\ell ^\infty ] \subseteq A(\overline {\mathbb {F}_v})[\ell ^\infty ]$, and that, provided that ![]() $\ell$ is different from the residue characteristic of
$\ell$ is different from the residue characteristic of ![]() $v$, there is a canonical identification
$v$, there is a canonical identification ![]() $A(\overline {K})[\ell ^\infty ] \cong A(\overline {\mathbb {F}_v})[\ell ^\infty ]$ given by reduction modulo (a place of
$A(\overline {K})[\ell ^\infty ] \cong A(\overline {\mathbb {F}_v})[\ell ^\infty ]$ given by reduction modulo (a place of ![]() $\overline {K}$ over)
$\overline {K}$ over) ![]() $v$: indeed, for any positive integer
$v$: indeed, for any positive integer ![]() $n$ coprime with the residue characteristic of
$n$ coprime with the residue characteristic of ![]() $v$, the
$v$, the ![]() $n$-torsion subscheme of
$n$-torsion subscheme of ![]() $\mathcal {A}$ is finite étale over
$\mathcal {A}$ is finite étale over ![]() $\mathcal {O}_{K_v}$. We may therefore also view
$\mathcal {O}_{K_v}$. We may therefore also view ![]() $[P \bmod v]_{\ell }$ as an element of
$[P \bmod v]_{\ell }$ as an element of ![]() $A(\overline {K})[\ell ^\infty ]$. Recall, on the other hand, that we have a canonical identification
$A(\overline {K})[\ell ^\infty ]$. Recall, on the other hand, that we have a canonical identification
It will be useful to make this identification more explicit.
Remark 6.6 Representing points in ![]() $T_\ell (A)$ as compatible sequences
$T_\ell (A)$ as compatible sequences ![]() $(t_0, t_1,t_2,\ldots )$ of torsion points (with
$(t_0, t_1,t_2,\ldots )$ of torsion points (with ![]() $t_i \in A[\ell ^i]$ and
$t_i \in A[\ell ^i]$ and ![]() $\ell t_i = t_{i-1}$) and elements of
$\ell t_i = t_{i-1}$) and elements of ![]() $V_\ell (A)$ as
$V_\ell (A)$ as ![]() $\ell ^{-n} (t_0, t_1,t_2,\ldots )$, the torsion point corresponding to
$\ell ^{-n} (t_0, t_1,t_2,\ldots )$, the torsion point corresponding to ![]() $\ell ^{-n} (t_0, t_1,t_2,\ldots ) \bmod T_\ell (A)$ is simply
$\ell ^{-n} (t_0, t_1,t_2,\ldots ) \bmod T_\ell (A)$ is simply ![]() $t_{n}$. The inverse map, from
$t_{n}$. The inverse map, from ![]() $A(\overline {K})[\ell ^\infty ]$ to
$A(\overline {K})[\ell ^\infty ]$ to ![]() $V_\ell (A)/T_\ell (A)$, may be described as follows. Let
$V_\ell (A)/T_\ell (A)$, may be described as follows. Let ![]() $t \in A(\overline {K})[\ell ^\infty ]$ be a torsion point of exact order
$t \in A(\overline {K})[\ell ^\infty ]$ be a torsion point of exact order ![]() $\ell ^n$ and choose
$\ell ^n$ and choose ![]() $t_{n+1}, t_{n+2}, \ldots \in A(\overline {K})[\ell ^\infty ]$ with the property that
$t_{n+1}, t_{n+2}, \ldots \in A(\overline {K})[\ell ^\infty ]$ with the property that ![]() $\ell ^i t_{n+i}=t$ and
$\ell ^i t_{n+i}=t$ and ![]() $\ell t_{n+i+1} = t_{n+i}$ for all
$\ell t_{n+i+1} = t_{n+i}$ for all ![]() $i\geq 1$. The element
$i\geq 1$. The element
is then well-defined up to addition of elements of ![]() $T_\ell (A)$, and its image via
$T_\ell (A)$, and its image via ![]() $\pi _\ell$ is
$\pi _\ell$ is ![]() $t$.
$t$.
A general principle of Kummer theory is that all the information about the ![]() $\ell$-part of the reductions of
$\ell$-part of the reductions of ![]() $P$ should be captured by the Galois group
$P$ should be captured by the Galois group ![]() $G_{\ell ^\infty }$. In our context, using the above identification
$G_{\ell ^\infty }$. In our context, using the above identification ![]() $\pi _\ell$, this has been made concrete by Pink as follows.
$\pi _\ell$, this has been made concrete by Pink as follows.
Theorem 6.7 [Reference PinkPin04, Proposition 3.2]
Let ![]() $v$ be a finite place of
$v$ be a finite place of ![]() $K$ at which
$K$ at which ![]() $A$ has good reduction and let
$A$ has good reduction and let ![]() $\ell$ be a prime different from the residue characteristic of
$\ell$ be a prime different from the residue characteristic of ![]() $v$. Let
$v$. Let ![]() $\operatorname {Fr}_v \in G_{\ell ^\infty }$ be a Frobenius element at
$\operatorname {Fr}_v \in G_{\ell ^\infty }$ be a Frobenius element at ![]() $v$ for the extension
$v$ for the extension ![]() $K( \ell ^{-\infty }P)/K$. Writing
$K( \ell ^{-\infty }P)/K$. Writing ![]() $\operatorname {Fr}_v=(t,M) \in T_\ell (A) \rtimes \operatorname {Aut} T_\ell (A)$, we have
$\operatorname {Fr}_v=(t,M) \in T_\ell (A) \rtimes \operatorname {Aut} T_\ell (A)$, we have
Remark 6.8 Note that, as a consequence of the Weil conjectures, the eigenvalues of ![]() $M$ (as in Theorem 6.7) are all of absolute value
$M$ (as in Theorem 6.7) are all of absolute value ![]() $\sqrt {\#\mathbb {F}_v}$. In particular,
$\sqrt {\#\mathbb {F}_v}$. In particular, ![]() $M-\operatorname {Id} : V_\ell (A) \to V_\ell (A)$ is invertible. Also note that, in general,
$M-\operatorname {Id} : V_\ell (A) \to V_\ell (A)$ is invertible. Also note that, in general, ![]() $(M-\operatorname {Id})^{-1}t$ is an element of
$(M-\operatorname {Id})^{-1}t$ is an element of ![]() $V_\ell (A) := T_\ell (A) \otimes _{\mathbb {Z}_\ell } \mathbb {Q}_\ell$, but not necessarily of
$V_\ell (A) := T_\ell (A) \otimes _{\mathbb {Z}_\ell } \mathbb {Q}_\ell$, but not necessarily of ![]() $T_\ell (A)$. Finally, to make the connection between our language and that of [Reference PinkPin04], note that
$T_\ell (A)$. Finally, to make the connection between our language and that of [Reference PinkPin04], note that
 \[ \begin{array}{cccc} \lambda : & \mathbb{Z}[1/\ell] & \to & A(\overline{K}) \\ & \dfrac{b}{\ell^k} & \mapsto & b P_{\ell^k} \end{array} \]
\[ \begin{array}{cccc} \lambda : & \mathbb{Z}[1/\ell] & \to & A(\overline{K}) \\ & \dfrac{b}{\ell^k} & \mapsto & b P_{\ell^k} \end{array} \]is a special splitting in the sense of [Reference PinkPin04, § 2].
6.2.2 6.2.2 Adelic Kummer theory for abelian varieties
We now review the last result we need from Kummer theory. The following theorem is essentially due to Ribet [Reference RibetRib79]; for the version quoted here see Hindry [Reference HindryHin88, § 2, Proposition 1] or Bertrand [Reference BertrandBer88, Theorem 1].
Theorem 6.9 Let ![]() $A$ be an abelian variety over a number field
$A$ be an abelian variety over a number field ![]() $K$ and let
$K$ and let ![]() $P \in A(K)$ be a non-degenerate point. There is a constant
$P \in A(K)$ be a non-degenerate point. There is a constant ![]() $c=c(A/K, P)$, which only depends on
$c=c(A/K, P)$, which only depends on ![]() $K$,
$K$, ![]() $A$ and
$A$ and ![]() $P$, such that, for every integer
$P$, such that, for every integer ![]() $m$, the index of
$m$, the index of ![]() $N_m$ in
$N_m$ in ![]() $A[m]$ (under the identification given by (13)) is bounded by
$A[m]$ (under the identification given by (13)) is bounded by ![]() $c$.
$c$.
Remark 6.10 Proposition 1 of [Reference HindryHin88, § 2] is stated under the assumption that ![]() $P$ be indivisible in
$P$ be indivisible in ![]() $A(K)$; the conclusion is then that the constant
$A(K)$; the conclusion is then that the constant ![]() $c(A/K, P)$ is independent of
$c(A/K, P)$ is independent of ![]() $P$. One may readily check that (allowing
$P$. One may readily check that (allowing ![]() $c$ to also depend on
$c$ to also depend on ![]() $P$) the hypothesis that
$P$) the hypothesis that ![]() $P$ be indivisible may be removed; this is also the statement given in [Reference BertrandBer88].
$P$ be indivisible may be removed; this is also the statement given in [Reference BertrandBer88].
We use this result in the form of the following obvious corollary.
Corollary 6.11 Let ![]() $c$ be as in Theorem 6.9. Then, for any choice of primes
$c$ be as in Theorem 6.9. Then, for any choice of primes ![]() $\ell _1, \ldots, \ell _r$, all strictly larger than
$\ell _1, \ldots, \ell _r$, all strictly larger than ![]() $c$, the Galois group of
$c$, the Galois group of
is isomorphic to ![]() $\prod _{i=1}^r T_{\ell _i}(A)$ under the injection induced by (13).
$\prod _{i=1}^r T_{\ell _i}(A)$ under the injection induced by (13).
Proof. It suffices to show that for each ![]() $m=\ell _1^{e_1} \cdots \ell _r^{e_r}$ the image of
$m=\ell _1^{e_1} \cdots \ell _r^{e_r}$ the image of ![]() $N_m$ via (13) is all of
$N_m$ via (13) is all of ![]() $A[m] \rtimes \{1\}$. If this were not the case, then by our assumption that
$A[m] \rtimes \{1\}$. If this were not the case, then by our assumption that ![]() $\ell _1,\ldots, \ell _r >c$, the index
$\ell _1,\ldots, \ell _r >c$, the index ![]() $[A[m] : N_m]$ would be at least
$[A[m] : N_m]$ would be at least ![]() $\min \{\ell _i\} > c$, which contradicts Theorem 6.9.
$\min \{\ell _i\} > c$, which contradicts Theorem 6.9.
6.3 The case of a cyclic dense subgroup
Let ![]() $A$ be an abelian variety over a number field
$A$ be an abelian variety over a number field ![]() $K$ and let
$K$ and let ![]() $P \in A(K)$ be a non-degenerate point. Let
$P \in A(K)$ be a non-degenerate point. Let ![]() $c=c(A/K, P)$ be as in Theorem 6.9 (and Corollary 6.11) and fix a positive integer
$c=c(A/K, P)$ be as in Theorem 6.9 (and Corollary 6.11) and fix a positive integer ![]() $d$; when applying the results of this section to our study of covers of abelian varieties, the integer
$d$; when applying the results of this section to our study of covers of abelian varieties, the integer ![]() $d$ will represent the degree of a cover. We define
$d$ will represent the degree of a cover. We define
Note that ![]() $S$ is clearly finite; it is the set of ‘bad’ primes we will have to avoid in our arguments. Let
$S$ is clearly finite; it is the set of ‘bad’ primes we will have to avoid in our arguments. Let ![]() $\zeta \in A(\overline {K})$ be a torsion point of order
$\zeta \in A(\overline {K})$ be a torsion point of order ![]() $m=\ell _1^{e_1} \cdots \ell _r^{e_r}$, and assume that each prime factor
$m=\ell _1^{e_1} \cdots \ell _r^{e_r}$, and assume that each prime factor ![]() $\ell _i$ is not in
$\ell _i$ is not in ![]() $S$. Let
$S$. Let ![]() $L$ be a finite Galois extension of
$L$ be a finite Galois extension of ![]() $K(\zeta )$ of degree dividing
$K(\zeta )$ of degree dividing ![]() $d!$ and write
$d!$ and write ![]() $\Delta$ for the Galois group of
$\Delta$ for the Galois group of ![]() $L$ over
$L$ over ![]() $K(\zeta )$. Finally fix a non-empty conjugacy-stable subset
$K(\zeta )$. Finally fix a non-empty conjugacy-stable subset ![]() $\delta \subseteq \Delta$. The following proposition and corollary show that, given such a torsion point
$\delta \subseteq \Delta$. The following proposition and corollary show that, given such a torsion point ![]() $\zeta$, one can find a finite place
$\zeta$, one can find a finite place ![]() $v$ of
$v$ of ![]() $K(\zeta )$ and a finite index coset
$K(\zeta )$ and a finite index coset ![]() $C$ of
$C$ of ![]() $\langle P\rangle$ such that every
$\langle P\rangle$ such that every ![]() $c$ in
$c$ in ![]() $C$ is congruent to
$C$ is congruent to ![]() $\zeta$ modulo
$\zeta$ modulo ![]() $v$, whilst simultaneously fixing the Frobenius conjugacy class of
$v$, whilst simultaneously fixing the Frobenius conjugacy class of ![]() $v$ in the extension
$v$ in the extension ![]() $L/K(\zeta )$.
$L/K(\zeta )$.
Proposition 6.12 With the notation as before, there is a positive density set of finite places ![]() $v$ of
$v$ of ![]() $K(\zeta )$ with the following properties:
$K(\zeta )$ with the following properties:
(1)
 $v$ is unramified in
$v$ is unramified in  $L$, and the corresponding Frobenius element in
$L$, and the corresponding Frobenius element in  $\Delta$ lies in
$\Delta$ lies in  $\delta$;
$\delta$;(2)
 $A \times _K K(\zeta )$ has good reduction at
$A \times _K K(\zeta )$ has good reduction at  $v$, and
$v$, and  $v$ does not divide
$v$ does not divide  $m=\operatorname {ord}(\zeta )$;
$m=\operatorname {ord}(\zeta )$;(3) the
 $\ell _i$-part of
$\ell _i$-part of  $P \bmod v$ is equal to the
$P \bmod v$ is equal to the  $\ell _i$-part of
$\ell _i$-part of  $\zeta$ for all
$\zeta$ for all  $i=1,\ldots,r$.
$i=1,\ldots,r$.
Before proving the proposition we briefly pause to explain its role in our approach. Given a (GPB)-cover ![]() $\phi : Y \to A$, Lemma 6.3 will provide us with a torsion point
$\phi : Y \to A$, Lemma 6.3 will provide us with a torsion point ![]() $\zeta \in A(\overline {K})$ that does not lift to
$\zeta \in A(\overline {K})$ that does not lift to ![]() $Y(K(\zeta ))$. Fix in addition a Zariski-dense cyclic subgroup
$Y(K(\zeta ))$. Fix in addition a Zariski-dense cyclic subgroup ![]() $\Omega \subseteq A(K)$. We use Proposition 6.12 to show that there is a finite index coset of
$\Omega \subseteq A(K)$. We use Proposition 6.12 to show that there is a finite index coset of ![]() $\Omega$ all of whose points reduce to
$\Omega$ all of whose points reduce to ![]() $\zeta$ modulo a suitable place
$\zeta$ modulo a suitable place ![]() $v$ of
$v$ of ![]() $K(\zeta )$: the idea is then to show that the points in this coset do not lift to
$K(\zeta )$: the idea is then to show that the points in this coset do not lift to ![]() $Y$. In order to draw this conclusion we also need to impose some additional conditions related to the behaviour of the place
$Y$. In order to draw this conclusion we also need to impose some additional conditions related to the behaviour of the place ![]() $v$ in the field over which the fibre
$v$ in the field over which the fibre ![]() $\phi ^{-1}(\zeta )$ splits: in the present setting, such conditions are encapsulated by the field
$\phi ^{-1}(\zeta )$ splits: in the present setting, such conditions are encapsulated by the field ![]() $L$ and by the conjugacy class
$L$ and by the conjugacy class ![]() $\delta$. Finally, we point out that this result has no analogue in [Reference ZannierZan10], and replaces a completely different argument that used Serre's open image theorem for elliptic curves, a tool that is not available to us in the context of general abelian varieties.
$\delta$. Finally, we point out that this result has no analogue in [Reference ZannierZan10], and replaces a completely different argument that used Serre's open image theorem for elliptic curves, a tool that is not available to us in the context of general abelian varieties.
Proof. Let ![]() $K_{P,\infty }$ be the extension of
$K_{P,\infty }$ be the extension of ![]() $K$ generated by
$K$ generated by ![]() $\ell _i^{-\infty } P$ for all
$\ell _i^{-\infty } P$ for all ![]() $i=1,\ldots,r$ and
$i=1,\ldots,r$ and ![]() $K_\infty = K(A[\ell _i^\infty ] : i =1,\ldots, r)$. Note that
$K_\infty = K(A[\ell _i^\infty ] : i =1,\ldots, r)$. Note that ![]() $K_{\infty } = K(\zeta )(A[\ell _i^\infty ] : i =1,\ldots, r)$ and similarly for
$K_{\infty } = K(\zeta )(A[\ell _i^\infty ] : i =1,\ldots, r)$ and similarly for ![]() $K_{P,\infty }$. Letting
$K_{P,\infty }$. Letting ![]() $G=\operatorname {Gal}(K_{P,\infty }/K(\zeta ))$,
$G=\operatorname {Gal}(K_{P,\infty }/K(\zeta ))$, ![]() $H=\operatorname {Gal}\big ( K_\infty /K(\zeta )\big )$ and
$H=\operatorname {Gal}\big ( K_\infty /K(\zeta )\big )$ and ![]() $N = \operatorname {Gal}(K_{P,\infty } / K_\infty )$, we have the exact sequence
$N = \operatorname {Gal}(K_{P,\infty } / K_\infty )$, we have the exact sequence
Writing ![]() $T := \prod _{i=1}^r T_{\ell _i}(A)$, by passing to the limit in (13) we may identify
$T := \prod _{i=1}^r T_{\ell _i}(A)$, by passing to the limit in (13) we may identify ![]() $G$ with a subgroup of
$G$ with a subgroup of ![]() $T \rtimes \operatorname {Aut}(T)$. As every prime
$T \rtimes \operatorname {Aut}(T)$. As every prime ![]() $\ell _i$ is strictly larger than
$\ell _i$ is strictly larger than ![]() $c$, by Corollary 6.11, the subgroup
$c$, by Corollary 6.11, the subgroup ![]() $N$ can be identified with
$N$ can be identified with ![]() $T \rtimes \{1\}$. We write
$T \rtimes \{1\}$. We write ![]() $t_i$ for the projection of an element
$t_i$ for the projection of an element ![]() $t \in T$ to
$t \in T$ to ![]() $T_{\ell _i}(A)$.
$T_{\ell _i}(A)$.
It will also be useful to fix ![]() $\mathbb {Z}_{\ell _i}$-bases of the Tate modules
$\mathbb {Z}_{\ell _i}$-bases of the Tate modules ![]() $T_{\ell _i}(A)$ as follows. For each prime divisor
$T_{\ell _i}(A)$ as follows. For each prime divisor ![]() $\ell _i$ of
$\ell _i$ of ![]() $m$, write
$m$, write ![]() $[\zeta ]_{\ell _i}$ as
$[\zeta ]_{\ell _i}$ as ![]() $n_i\zeta$, and note that it is a torsion point of order
$n_i\zeta$, and note that it is a torsion point of order ![]() $\ell _i^{e_i}$. For every such
$\ell _i^{e_i}$. For every such ![]() $\ell _i$, fix a basis
$\ell _i$, fix a basis ![]() $v_{i,1},\ldots,v_{i,2g}$ of
$v_{i,1},\ldots,v_{i,2g}$ of ![]() $T_{\ell _i}(A)$ with the property that
$T_{\ell _i}(A)$ with the property that ![]() $\pi _{\ell _i}(\ell _i^{-e_i} v_{i,1}) = n_i\zeta$, where
$\pi _{\ell _i}(\ell _i^{-e_i} v_{i,1}) = n_i\zeta$, where ![]() $\pi _{\ell _i}$ is defined by (14). This is possible because
$\pi _{\ell _i}$ is defined by (14). This is possible because ![]() $n_i\zeta$ is a torsion point of exact order
$n_i\zeta$ is a torsion point of exact order ![]() $\ell ^{e_i}_i$. We use these bases to identify
$\ell ^{e_i}_i$. We use these bases to identify ![]() $T \cong \prod _{i=1}^r T_{\ell _i}(A)$ with
$T \cong \prod _{i=1}^r T_{\ell _i}(A)$ with ![]() $\prod _{i=1}^r \mathbb {Z}_{\ell _i}^{2g}$ and
$\prod _{i=1}^r \mathbb {Z}_{\ell _i}^{2g}$ and ![]() $\operatorname {Aut}(T)$ with
$\operatorname {Aut}(T)$ with ![]() $\prod _{i=1}^r \operatorname {GL}_{2g}(\mathbb {Z}_{\ell _i})$. By the definition of
$\prod _{i=1}^r \operatorname {GL}_{2g}(\mathbb {Z}_{\ell _i})$. By the definition of ![]() $\pi _{\ell _i}$ in (14) and Remark 6.6, we see that a representative in
$\pi _{\ell _i}$ in (14) and Remark 6.6, we see that a representative in ![]() $V_{\ell _i}(A) \cong \mathbb {Q}_{\ell _i}^{2g}$ of
$V_{\ell _i}(A) \cong \mathbb {Q}_{\ell _i}^{2g}$ of ![]() $n_i\zeta$ is
$n_i\zeta$ is ![]() $\ell _i^{-e_i} (1 \ 0 \ \ldots 0)^{\rm T}$.
$\ell _i^{-e_i} (1 \ 0 \ \ldots 0)^{\rm T}$.
Let ![]() $F$ be the extension of
$F$ be the extension of ![]() $K$ generated by
$K$ generated by ![]() $K_{P,\infty }$ and by
$K_{P,\infty }$ and by ![]() $L$. The Galois group
$L$. The Galois group ![]() $G_1$ of
$G_1$ of ![]() $F$ over
$F$ over ![]() $K(\zeta )$ injects into
$K(\zeta )$ injects into ![]() $\Delta \times G \subseteq \Delta \times (T \rtimes \operatorname {Aut}(T))$. We represent elements
$\Delta \times G \subseteq \Delta \times (T \rtimes \operatorname {Aut}(T))$. We represent elements ![]() $g_1$ of
$g_1$ of ![]() $G_1$ as triples
$G_1$ as triples ![]() $(\gamma, (t,M))$ with
$(\gamma, (t,M))$ with ![]() $\gamma \in \Delta$,
$\gamma \in \Delta$, ![]() $t \in T$ and
$t \in T$ and ![]() $M \in \operatorname {Aut}(T)$. Note that
$M \in \operatorname {Aut}(T)$. Note that ![]() $M$ corresponds to a collection
$M$ corresponds to a collection ![]() $(M_1,\ldots,M_r)$ of matrices with
$(M_1,\ldots,M_r)$ of matrices with ![]() $M_i \in \operatorname {\operatorname {GL}}_{2g}(\mathbb {Z}_{\ell _i})$ or, equivalently,
$M_i \in \operatorname {\operatorname {GL}}_{2g}(\mathbb {Z}_{\ell _i})$ or, equivalently, ![]() $M$ is a matrix in
$M$ is a matrix in ![]() $\operatorname {\operatorname {GL}}_{2g}(\prod _{i=1}^r \mathbb {Z}_{\ell _i})$. It thus makes sense to compute the determinant of
$\operatorname {\operatorname {GL}}_{2g}(\prod _{i=1}^r \mathbb {Z}_{\ell _i})$. It thus makes sense to compute the determinant of ![]() $M$ as an element of the ring
$M$ as an element of the ring ![]() $\prod _{i=1}^r \mathbb {Z}_{\ell _i}$ (independent of the choice of basis); equivalently,
$\prod _{i=1}^r \mathbb {Z}_{\ell _i}$ (independent of the choice of basis); equivalently, ![]() $\det (M)$ is the collection
$\det (M)$ is the collection ![]() $(\det (M_1),\ldots, \det (M_r))$.
$(\det (M_1),\ldots, \det (M_r))$.
We claim that ![]() $G_1$ contains
$G_1$ contains ![]() $\{1\} \times (T \rtimes \{1\})$. On the one hand, multiplication by
$\{1\} \times (T \rtimes \{1\})$. On the one hand, multiplication by ![]() $\#\Delta$ is invertible on the profinite abelian group
$\#\Delta$ is invertible on the profinite abelian group ![]() $T$ (because, by assumption,
$T$ (because, by assumption, ![]() $\#\Delta$ is relatively prime to the order of any finite quotient of
$\#\Delta$ is relatively prime to the order of any finite quotient of ![]() $T$), so, given
$T$), so, given ![]() $t \in T$, we may find
$t \in T$, we may find ![]() $t' \in T$ such that
$t' \in T$ such that ![]() $[\#\Delta ] t' =t$. On the other hand, basic Galois theory shows that
$[\#\Delta ] t' =t$. On the other hand, basic Galois theory shows that ![]() $G_1$ surjects onto
$G_1$ surjects onto ![]() $G$, which contains
$G$, which contains ![]() $T \rtimes \{1\}$. Therefore, given any
$T \rtimes \{1\}$. Therefore, given any ![]() $t \in T$, we know that
$t \in T$, we know that ![]() $G_1$ contains an element of the form
$G_1$ contains an element of the form ![]() $g_1=(\gamma, (t',1))$ for some
$g_1=(\gamma, (t',1))$ for some ![]() $\gamma \in \Delta$ and
$\gamma \in \Delta$ and ![]() $t' \in T$ such that
$t' \in T$ such that ![]() $[\#\Delta ] t'=t$. It follows that
$[\#\Delta ] t'=t$. It follows that ![]() $G_1$ contains
$G_1$ contains ![]() $g_1^{\#\Delta }=(1,(t,1))$, which proves the claim.
$g_1^{\#\Delta }=(1,(t,1))$, which proves the claim.
We now consider
 \[ U = \left\{ (\gamma, (t,M)) \in G_1 \left\vert \begin{array}{c@{}} \det(M_i-\operatorname{Id}) \neq 0 \ \text{for all } i=1,\ldots,r \\ \gamma \in \delta \\ \pi_{\ell_i}( ((M-\operatorname{Id})^{-1} t)_i ) = [\zeta]_{\ell_i},\quad \text{ for } i=1,\ldots,r \end{array}\right. \right\}. \]
\[ U = \left\{ (\gamma, (t,M)) \in G_1 \left\vert \begin{array}{c@{}} \det(M_i-\operatorname{Id}) \neq 0 \ \text{for all } i=1,\ldots,r \\ \gamma \in \delta \\ \pi_{\ell_i}( ((M-\operatorname{Id})^{-1} t)_i ) = [\zeta]_{\ell_i},\quad \text{ for } i=1,\ldots,r \end{array}\right. \right\}. \]
Note that ![]() $U$ is open in
$U$ is open in ![]() $G_1$: indeed, the first condition is clearly open, whereas the condition
$G_1$: indeed, the first condition is clearly open, whereas the condition ![]() $\gamma \in \delta$ factors via the finite quotient
$\gamma \in \delta$ factors via the finite quotient ![]() $G_1 \twoheadrightarrow \Delta$. Finally,
$G_1 \twoheadrightarrow \Delta$. Finally, ![]() $(\gamma, (t,M)) \mapsto \pi _{\ell _i}(((M-\operatorname {Id})^{-1}t)_i)=\pi _{\ell _i}( (M_i-\operatorname {Id})^{-1} t_i )$ is a continuous function with values in the discrete set
$(\gamma, (t,M)) \mapsto \pi _{\ell _i}(((M-\operatorname {Id})^{-1}t)_i)=\pi _{\ell _i}( (M_i-\operatorname {Id})^{-1} t_i )$ is a continuous function with values in the discrete set ![]() $A[\ell _i^\infty ]$, hence it is locally constant. As we are imposing only finitely many of these conditions,
$A[\ell _i^\infty ]$, hence it is locally constant. As we are imposing only finitely many of these conditions, ![]() $U$ is the finite intersection of open subsets of
$U$ is the finite intersection of open subsets of ![]() $G_1$ and is therefore open.
$G_1$ and is therefore open.
To prove the proposition, it suffices to show that ![]() $U$ is non-empty. To see this, note that the Chebotarev density theorem yields the existence of a positive density set of places unramified in
$U$ is non-empty. To see this, note that the Chebotarev density theorem yields the existence of a positive density set of places unramified in ![]() $L$ and whose corresponding Frobenius conjugacy class lies in
$L$ and whose corresponding Frobenius conjugacy class lies in ![]() $U$. Discarding the finitely many places that do not satisfy condition (2) still leaves us with a positive density set of places that satisfy all conditions in the statement (note that all places whose Frobenius belongs to
$U$. Discarding the finitely many places that do not satisfy condition (2) still leaves us with a positive density set of places that satisfy all conditions in the statement (note that all places whose Frobenius belongs to ![]() $U$ satisfy condition (3) thanks to Theorem 6.7). Thus, it suffices to show that
$U$ satisfy condition (3) thanks to Theorem 6.7). Thus, it suffices to show that ![]() $U$ is non-empty.
$U$ is non-empty.
We start by choosing an element ![]() $g_1=(\gamma,(t,M)) \in G_1$ with
$g_1=(\gamma,(t,M)) \in G_1$ with ![]() $\gamma \in \delta$ and
$\gamma \in \delta$ and ![]() $\det (M_i-\operatorname {Id}) \neq 0$ for every
$\det (M_i-\operatorname {Id}) \neq 0$ for every ![]() $i=1,\ldots, r$. To see that such an element exists, note first that
$i=1,\ldots, r$. To see that such an element exists, note first that ![]() $G_1 \to \Delta$ is surjective, and that by the Chebotarev density theorem (applied to the extension
$G_1 \to \Delta$ is surjective, and that by the Chebotarev density theorem (applied to the extension ![]() $F/K(\zeta )$, with Galois group
$F/K(\zeta )$, with Galois group ![]() $G_1$) we may find an element
$G_1$) we may find an element ![]() $g_1$ whose image in
$g_1$ whose image in ![]() $\Delta$ lies in
$\Delta$ lies in ![]() $\delta$ and which is the Frobenius of some place
$\delta$ and which is the Frobenius of some place ![]() $w$ of
$w$ of ![]() $K(\zeta )$. As a consequence of the Weil conjectures, all the eigenvalues of
$K(\zeta )$. As a consequence of the Weil conjectures, all the eigenvalues of ![]() $M_i$ (which corresponds to the action of a Frobenius at
$M_i$ (which corresponds to the action of a Frobenius at ![]() $w$ on
$w$ on ![]() $T_{\ell _i}(A)$) then have absolute value
$T_{\ell _i}(A)$) then have absolute value ![]() $\sqrt {\#\mathbb {F}_w} \neq 1$, which ensures that
$\sqrt {\#\mathbb {F}_w} \neq 1$, which ensures that ![]() $\det (M_i-\operatorname {Id})$ is non-zero for all
$\det (M_i-\operatorname {Id})$ is non-zero for all ![]() $i$.
$i$.
The fact that ![]() $g_1=(\gamma, (t,M))$ fixes
$g_1=(\gamma, (t,M))$ fixes ![]() $\zeta$ (recall that
$\zeta$ (recall that ![]() $g_1 \in G_1 = \operatorname {Gal}(F/K(\zeta ))$) translates into the following condition. Write as before
$g_1 \in G_1 = \operatorname {Gal}(F/K(\zeta ))$) translates into the following condition. Write as before ![]() $M=(M_1,\ldots,M_r)$ with
$M=(M_1,\ldots,M_r)$ with ![]() $M_i \in \operatorname {\operatorname {GL}}_{2g}(\mathbb {Z}_{\ell _i})$. Reducing
$M_i \in \operatorname {\operatorname {GL}}_{2g}(\mathbb {Z}_{\ell _i})$. Reducing ![]() $M_i$ modulo
$M_i$ modulo ![]() $\ell _i^{e_i}$ gives the action of
$\ell _i^{e_i}$ gives the action of ![]() $g_1$ on
$g_1$ on ![]() $A[\ell _i^{e_i}]$, which must be trivial on the first basis element because
$A[\ell _i^{e_i}]$, which must be trivial on the first basis element because ![]() $G_1$ fixes
$G_1$ fixes ![]() $\zeta$ (hence, also
$\zeta$ (hence, also ![]() $n_i\zeta$). It follows that we have
$n_i\zeta$). It follows that we have
 \begin{equation} M_i \equiv \begin{pmatrix} 1 & * & \cdots & * \\ 0 & * & \cdots & * \\ \vdots & \vdots & \cdots & \vdots \\ 0 & * & \cdots & * \end{pmatrix} \pmod{\ell^{e_i}_i} \end{equation}
\begin{equation} M_i \equiv \begin{pmatrix} 1 & * & \cdots & * \\ 0 & * & \cdots & * \\ \vdots & \vdots & \cdots & \vdots \\ 0 & * & \cdots & * \end{pmatrix} \pmod{\ell^{e_i}_i} \end{equation}
where each entry ![]() $*$ may in principle be arbitrary. We now construct an element of
$*$ may in principle be arbitrary. We now construct an element of ![]() $U$ as a product
$U$ as a product ![]() $(1,(t',1)) \cdot g_1$ for a suitable
$(1,(t',1)) \cdot g_1$ for a suitable ![]() $t' \in T$. We have already observed that all elements of the form
$t' \in T$. We have already observed that all elements of the form ![]() $(1,(t',1))$ are in
$(1,(t',1))$ are in ![]() $G_1$, and
$G_1$, and ![]() $g_1$ is in
$g_1$ is in ![]() $G_1$ by construction, so for any choice of
$G_1$ by construction, so for any choice of ![]() $t'$ we do indeed get an element of
$t'$ we do indeed get an element of ![]() $G_1$. For
$G_1$. For ![]() $t'\in T$ (to be determined later), consider the element
$t'\in T$ (to be determined later), consider the element
Note that its image in ![]() $\Delta$ is
$\Delta$ is ![]() $\gamma \in \delta$, and that
$\gamma \in \delta$, and that ![]() $\det (M_i-\operatorname {Id})\neq 0$ for all
$\det (M_i-\operatorname {Id})\neq 0$ for all ![]() $i =1,\ldots, r$ by our choice of
$i =1,\ldots, r$ by our choice of ![]() $M$. Hence, for this element to lie in
$M$. Hence, for this element to lie in ![]() $U$, we only need to ensure that we can satisfy the conditions
$U$, we only need to ensure that we can satisfy the conditions
This condition is implied by the equality (which we write in the coordinates chosen previously)
As ![]() $M_i-\operatorname {Id}$ is invertible, the latter equality is, in turn, equivalent to
$M_i-\operatorname {Id}$ is invertible, the latter equality is, in turn, equivalent to
This equation clearly has the unique solution
in ![]() $V_{\ell _i}(A)$, and we claim that this element
$V_{\ell _i}(A)$, and we claim that this element ![]() $t'_i$ lies in
$t'_i$ lies in ![]() $T_{\ell _i}(A)$. Indeed, the congruence in (15) ensures that the first column of
$T_{\ell _i}(A)$. Indeed, the congruence in (15) ensures that the first column of ![]() $M_i - \operatorname {Id}$ is an integral multiple of
$M_i - \operatorname {Id}$ is an integral multiple of ![]() $\ell _i^{e_i}$, so that the vector
$\ell _i^{e_i}$, so that the vector ![]() $(M_i-\operatorname {Id}) \ell _i^{-e_i} (1 \ 0 \ \ldots \ 0)^{\rm T}$ (which is simply
$(M_i-\operatorname {Id}) \ell _i^{-e_i} (1 \ 0 \ \ldots \ 0)^{\rm T}$ (which is simply ![]() $\ell _i^{-e_i}$ times the first column of
$\ell _i^{-e_i}$ times the first column of ![]() $M_i - \operatorname {Id}$) has integral coordinates; equivalently, given our identifications, it corresponds to an element of
$M_i - \operatorname {Id}$) has integral coordinates; equivalently, given our identifications, it corresponds to an element of ![]() $T_{\ell _i}(A)$. We may then take
$T_{\ell _i}(A)$. We may then take ![]() $t'=(t'_1,\ldots,t'_r)$, where each
$t'=(t'_1,\ldots,t'_r)$, where each ![]() $t_i'$ is as constructed previously, to obtain as desired that the product
$t_i'$ is as constructed previously, to obtain as desired that the product ![]() $(1,(t',1)) \cdot g_1$ lies in
$(1,(t',1)) \cdot g_1$ lies in ![]() $U$. This proves that
$U$. This proves that ![]() $U$ is non-empty, which by our previous remarks finishes the proof of the proposition.
$U$ is non-empty, which by our previous remarks finishes the proof of the proposition.
Corollary 6.13 Let ![]() $v$ be as in Proposition 6.12. Then there exist integers
$v$ be as in Proposition 6.12. Then there exist integers ![]() $s$ and
$s$ and ![]() $q$ such that every
$q$ such that every ![]() $Q$ in the coset
$Q$ in the coset ![]() $sP + \mathbb {Z} (mq P)$ of
$sP + \mathbb {Z} (mq P)$ of ![]() $\mathbb {Z}P$ is congruent to
$\mathbb {Z}P$ is congruent to ![]() $\zeta$ modulo
$\zeta$ modulo ![]() $v$.
$v$.
Proof. Let ![]() $n=\operatorname {ord}(P \bmod v)$. As the
$n=\operatorname {ord}(P \bmod v)$. As the ![]() $\ell$-parts of
$\ell$-parts of ![]() $(P \bmod v)$ and
$(P \bmod v)$ and ![]() $\zeta$ agree for all prime divisors
$\zeta$ agree for all prime divisors ![]() $\ell$ of
$\ell$ of ![]() $m=\operatorname {ord}(\zeta )$, we see, in particular, that for all
$m=\operatorname {ord}(\zeta )$, we see, in particular, that for all ![]() $\ell \mid m$ we have
$\ell \mid m$ we have ![]() $v_\ell (m) = v_\ell (n)$. This shows that
$v_\ell (m) = v_\ell (n)$. This shows that ![]() $m \mid n$ and that writing
$m \mid n$ and that writing ![]() $n=mq$ we have
$n=mq$ we have ![]() $(m,q)=1$. By the Chinese remainder theorem, there is an integer
$(m,q)=1$. By the Chinese remainder theorem, there is an integer ![]() $s$ such that
$s$ such that ![]() $s\equiv 0 \bmod q$ and
$s\equiv 0 \bmod q$ and ![]() $s\equiv 1 \bmod m$. As the order of
$s\equiv 1 \bmod m$. As the order of ![]() $sP \bmod v$ equals
$sP \bmod v$ equals ![]() $m$ and, for every prime divisor
$m$ and, for every prime divisor ![]() $\ell$ of
$\ell$ of ![]() $m$,
$m$,
it follows that ![]() $sP$ is congruent to
$sP$ is congruent to ![]() $\zeta$ modulo
$\zeta$ modulo ![]() $v$. As
$v$. As ![]() $mqP$ reduces to the trivial element modulo
$mqP$ reduces to the trivial element modulo ![]() $v$, the integers
$v$, the integers ![]() $q$ and
$q$ and ![]() $s$ have the desired property.
$s$ have the desired property.
6.4 Main theorem: cyclic case
Proposition 6.14 Let ![]() $A$ be an abelian variety over a number field
$A$ be an abelian variety over a number field ![]() $K$. Let
$K$. Let ![]() $\Omega =\langle P \rangle \subset A(K)$ be a Zariski-dense cyclic subgroup of
$\Omega =\langle P \rangle \subset A(K)$ be a Zariski-dense cyclic subgroup of ![]() $A$. Then property (GPB) implies property (PF) for
$A$. Then property (GPB) implies property (PF) for ![]() $(A, \Omega )$.
$(A, \Omega )$.
Proof. Let ![]() $\phi :Y \rightarrow A$ be a (GPB)-cover of
$\phi :Y \rightarrow A$ be a (GPB)-cover of ![]() $A$ of degree
$A$ of degree ![]() $d$,
$d$, ![]() $\hat {\phi }:\hat {Y}\rightarrow A$ be the Galois closure of
$\hat {\phi }:\hat {Y}\rightarrow A$ be the Galois closure of ![]() $\phi$, and
$\phi$, and ![]() $G$ be its Galois group. We have to prove that there is a finite index coset
$G$ be its Galois group. We have to prove that there is a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that, for each
$\Omega$ such that, for each ![]() $c \in C$, the fibre
$c \in C$, the fibre ![]() $\phi ^{-1}(c)$ is reduced and has no
$\phi ^{-1}(c)$ is reduced and has no ![]() $K$-rational points.
$K$-rational points.
First, we choose a finite set ![]() $S^b$ of finite places of
$S^b$ of finite places of ![]() $K$, an abelian scheme
$K$, an abelian scheme ![]() $\mathcal {A}$ over
$\mathcal {A}$ over ![]() $A$ extending
$A$ extending ![]() $A$ over
$A$ over ![]() $\mathcal {O}_{K,S^b}$, a normal proper model
$\mathcal {O}_{K,S^b}$, a normal proper model ![]() $\mathcal {Y}$ for
$\mathcal {Y}$ for ![]() $Y$ over
$Y$ over ![]() $\mathcal {O}_{K,S^b}$ and a finite surjective morphism
$\mathcal {O}_{K,S^b}$ and a finite surjective morphism ![]() $\psi :\mathcal {Y}\to \mathcal {A}$ extending
$\psi :\mathcal {Y}\to \mathcal {A}$ extending ![]() $\phi :Y\to A$ over
$\phi :Y\to A$ over ![]() $\mathcal {O}_{K,S^b}$. Now, we let
$\mathcal {O}_{K,S^b}$. Now, we let ![]() $c(A/K, P)$ be the constant of Theorem 6.9, and let
$c(A/K, P)$ be the constant of Theorem 6.9, and let ![]() $S$ be a finite set of rational primes containing
$S$ be a finite set of rational primes containing ![]() $\{\ell \bigm \vert \ell \leq \max \{c(A/K, P),d\}\}$. By Lemma 6.3, there is a torsion point
$\{\ell \bigm \vert \ell \leq \max \{c(A/K, P),d\}\}$. By Lemma 6.3, there is a torsion point ![]() $\zeta \in A(\overline {K})$ with the following properties:
$\zeta \in A(\overline {K})$ with the following properties:
(1) the order of
 $\zeta$ is coprime with
$\zeta$ is coprime with  $S$;
$S$;(2) the fibre
 $\phi ^{-1}(\zeta )$ is étale over
$\phi ^{-1}(\zeta )$ is étale over  $\operatorname {Spec} K(\zeta )$;
$\operatorname {Spec} K(\zeta )$;(3) if
 $\Delta \subset G$ is a decomposition group for
$\Delta \subset G$ is a decomposition group for  $\zeta$ (associated with an implicit choice of a geometric point
$\zeta$ (associated with an implicit choice of a geometric point  $\overline {y_0} \in \hat {\phi }^{-1}(\zeta )(\overline {K})$ lying over
$\overline {y_0} \in \hat {\phi }^{-1}(\zeta )(\overline {K})$ lying over  $\zeta$), there exists an element
$\zeta$), there exists an element  $\delta _0 \in \Delta$ such that
$\delta _0 \in \Delta$ such that  $\delta _0$ acts with no fixed points on
$\delta _0$ acts with no fixed points on  $\phi ^{-1}(\overline {\zeta })$.
$\phi ^{-1}(\overline {\zeta })$.
We define ![]() $K_0 := K(\zeta )$. Let
$K_0 := K(\zeta )$. Let ![]() $\mathcal {U}$ be a dense open subscheme of
$\mathcal {U}$ be a dense open subscheme of ![]() $\mathcal {A}$ such that
$\mathcal {A}$ such that ![]() $\psi$ is étale over
$\psi$ is étale over ![]() $\mathcal {U}$ and
$\mathcal {U}$ and ![]() $\mathcal {U}(K_0)$ contains
$\mathcal {U}(K_0)$ contains ![]() $\zeta$. After possibly enlarging
$\zeta$. After possibly enlarging ![]() $S^b$, we may assume that the Zariski closure
$S^b$, we may assume that the Zariski closure ![]() $\overline {\{\zeta \}} \subset \mathcal {A}$ is contained in
$\overline {\{\zeta \}} \subset \mathcal {A}$ is contained in ![]() $\mathcal {U}$. Write
$\mathcal {U}$. Write ![]() $\mathcal {V} := \psi ^{-1}(\mathcal {U})$, so that
$\mathcal {V} := \psi ^{-1}(\mathcal {U})$, so that ![]() $\psi |_{\mathcal {V}}:\mathcal {V}\to \mathcal {U}$ is finite étale. Let
$\psi |_{\mathcal {V}}:\mathcal {V}\to \mathcal {U}$ is finite étale. Let ![]() $\hat {\psi }:\hat {\mathcal {V}} \rightarrow \mathcal {U}$ be the Galois closure of
$\hat {\psi }:\hat {\mathcal {V}} \rightarrow \mathcal {U}$ be the Galois closure of ![]() $\psi |_{\mathcal {V}}$, and note that its Galois group is
$\psi |_{\mathcal {V}}$, and note that its Galois group is ![]() $G$.
$G$.
Let ![]() $L/K_0$ be the finite Galois extension corresponding to
$L/K_0$ be the finite Galois extension corresponding to ![]() $\operatorname {Ker}(\mathfrak {D}_{\zeta }:\Gamma _{K_0} \rightarrow G)$. The canonical identification of
$\operatorname {Ker}(\mathfrak {D}_{\zeta }:\Gamma _{K_0} \rightarrow G)$. The canonical identification of ![]() $\mathrm {Gal}(L/K_0)$ with
$\mathrm {Gal}(L/K_0)$ with ![]() $\Delta$ provided by
$\Delta$ provided by ![]() $\mathfrak {D}_{\zeta }$ allows us to assume, with a slight abuse of notation, that these two groups are the same.
$\mathfrak {D}_{\zeta }$ allows us to assume, with a slight abuse of notation, that these two groups are the same.
Note that ![]() $L$ is the Galois closure over
$L$ is the Galois closure over ![]() $K_0$ of the minimal field of definition of
$K_0$ of the minimal field of definition of ![]() $\overline {y_0}$, so that
$\overline {y_0}$, so that ![]() $L/K_0$ has degree dividing
$L/K_0$ has degree dividing ![]() $d!$. In particular, we may apply Proposition 6.12 and Corollary 6.13 to see that there exist a finite place
$d!$. In particular, we may apply Proposition 6.12 and Corollary 6.13 to see that there exist a finite place ![]() $v \in M_{K_0}$ not lying over any place of
$v \in M_{K_0}$ not lying over any place of ![]() $S^b$, and a finite index coset
$S^b$, and a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega$ such that each
$\Omega$ such that each ![]() $c \in C$ reduces to
$c \in C$ reduces to ![]() $\zeta \bmod v$ and such that a Frobenius (after implicitly fixing a place
$\zeta \bmod v$ and such that a Frobenius (after implicitly fixing a place ![]() $w \in M_{\overline {K}}$ lying over
$w \in M_{\overline {K}}$ lying over ![]() $v$) for
$v$) for ![]() $v \in M_{K_0}$ in
$v \in M_{K_0}$ in ![]() $\Delta$ is
$\Delta$ is ![]() $\delta _0$. In particular, for each
$\delta _0$. In particular, for each ![]() $c$ in
$c$ in ![]() $C$, a decomposition group for
$C$, a decomposition group for ![]() $c$ contains the Frobenius
$c$ contains the Frobenius ![]() $\delta _0=\operatorname {Fr}_{\overline {y_0}, w, \hat {\psi }} \in \Delta$. The latter acts without fixed points on
$\delta _0=\operatorname {Fr}_{\overline {y_0}, w, \hat {\psi }} \in \Delta$. The latter acts without fixed points on ![]() $\psi ^{-1}(c) \bmod v$, so that by Lemma 2.12 the
$\psi ^{-1}(c) \bmod v$, so that by Lemma 2.12 the ![]() $\mathcal {O}_{K_{v}}$-scheme
$\mathcal {O}_{K_{v}}$-scheme ![]() $\psi ^{-1}(c)_{\mathcal {O}_{K_v}}$ has no
$\psi ^{-1}(c)_{\mathcal {O}_{K_v}}$ has no ![]() $\mathbb {F}_v$-points. As the
$\mathbb {F}_v$-points. As the ![]() $\mathcal {O}_{K_{v}}$-scheme
$\mathcal {O}_{K_{v}}$-scheme ![]() $\psi ^{-1}(c)_{\mathcal {O}_{K_v}}$ is finite over
$\psi ^{-1}(c)_{\mathcal {O}_{K_v}}$ is finite over ![]() $\mathcal {O}_{K_v}$, it has no
$\mathcal {O}_{K_v}$, it has no ![]() $K_v$-points either. Therefore, the scheme
$K_v$-points either. Therefore, the scheme ![]() $\phi ^{-1}(c)$ has no
$\phi ^{-1}(c)$ has no ![]() $K$-points, as required. This concludes the proof.
$K$-points, as required. This concludes the proof.
Theorem 6.15 Let ![]() $A$ be an abelian variety over a number field
$A$ be an abelian variety over a number field ![]() $K$. Let
$K$. Let ![]() $\Omega =\langle P \rangle \subset A(K)$ be a Zariski-dense cyclic subgroup of
$\Omega =\langle P \rangle \subset A(K)$ be a Zariski-dense cyclic subgroup of ![]() $A$. Then, for every (PB)-cover
$A$. Then, for every (PB)-cover ![]() $\pi : Y \to A$ the pair
$\pi : Y \to A$ the pair ![]() $(\pi,\Omega )$ satisfies property (IF).
$(\pi,\Omega )$ satisfies property (IF).
Proof. It immediately follows from Proposition 6.14 that, for every number field ![]() $K$, every abelian variety
$K$, every abelian variety ![]() $A$ over
$A$ over ![]() $K$, and every finitely generated Zariski-dense subgroup
$K$, and every finitely generated Zariski-dense subgroup ![]() $\Omega$ of rank one, we have that property (GPB) implies property (PF) for
$\Omega$ of rank one, we have that property (GPB) implies property (PF) for ![]() $(A,\Omega )$. Therefore, the result follows from Proposition 4.19 (with
$(A,\Omega )$. Therefore, the result follows from Proposition 4.19 (with ![]() $r=1$).
$r=1$).
7. Proof of the main results
If ![]() $k$ is a finitely generated field of characteristic zero and
$k$ is a finitely generated field of characteristic zero and ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $k$, then
$k$, then ![]() $A(k)$ is a finitely generated abelian group [Reference ConradCon06, Corollary 7.2]. Therefore, the results of § 4 apply to every subgroup
$A(k)$ is a finitely generated abelian group [Reference ConradCon06, Corollary 7.2]. Therefore, the results of § 4 apply to every subgroup ![]() $\Omega$ of
$\Omega$ of ![]() $A(k)$.
$A(k)$.
7.1 From number fields to finitely generated fields over  $\mathbb {Q}$
$\mathbb {Q}$
We deduce the weak-Hilbert property for all abelian varieties over finitely generated fields by a specialization argument to number fields (see Proposition 7.6). For the proof we rely on a general result essentially due to Serre, for which we need some notation. Let ![]() $S$ be a variety over a number field
$S$ be a variety over a number field ![]() $K$, with generic point
$K$, with generic point ![]() $\eta$, and let
$\eta$, and let ![]() $\mathcal {A} \to S$ be an abelian scheme.
$\mathcal {A} \to S$ be an abelian scheme.
Definition 7.1 For positive integers ![]() $d$ and
$d$ and ![]() $h$, we let
$h$, we let ![]() $S(d,h)$ be the set of closed points of
$S(d,h)$ be the set of closed points of ![]() $S$ of degree at most
$S$ of degree at most ![]() $d$ over
$d$ over ![]() $K$ and of logarithmic height at most
$K$ and of logarithmic height at most ![]() $h$ (after some appropriate embedding
$h$ (after some appropriate embedding ![]() $S \hookrightarrow \mathbb {P}_{N, K}$ has been chosen).
$S \hookrightarrow \mathbb {P}_{N, K}$ has been chosen).
Theorem 7.2 There exist an integer ![]() $d_0$ and constant
$d_0$ and constant ![]() $c>0$ such that the set
$c>0$ such that the set
has cardinality at least ![]() $e^{ch}$ for
$e^{ch}$ for ![]() $h \gg 1$, and the set
$h \gg 1$, and the set ![]() $\bigcup _{h\geq 1} S(d_0,h)_{\mathrm {End}}$ is Zariski-dense in
$\bigcup _{h\geq 1} S(d_0,h)_{\mathrm {End}}$ is Zariski-dense in ![]() $S$.
$S$.
Proof. This can be deduced from the main results of Masser [Reference MasserMas96] or upon combining work of Serre [Reference SerreSer00, Letter to Ken Ribet of January 1st, 1981, § 1] and Noot [Reference NootNoo95, Corollary 1.5], as we now explain.
Fix an auxiliary prime ![]() $\ell$. Serre constructs the following data:
$\ell$. Serre constructs the following data:
(1) a dense open
 $X_0 \subset \mathbb {A}^{\dim S}_{\mathbb {Q}}$;
$X_0 \subset \mathbb {A}^{\dim S}_{\mathbb {Q}}$;(2) a dense open
 $X\subset S$ and a finite étale morphism
$X\subset S$ and a finite étale morphism  $\pi :X\to X_0$;
$\pi :X\to X_0$;(3) an étale cover
 $X^*\to X$,
$X^*\to X$,
such that, if ![]() $B_0$ is the set of points
$B_0$ is the set of points ![]() $x_0 \in X_0(\mathbb {Q})$ for which the fibre of
$x_0 \in X_0(\mathbb {Q})$ for which the fibre of ![]() $X^* \to X_0$ is irreducible, and
$X^* \to X_0$ is irreducible, and ![]() $B$ is its inverse image under
$B$ is its inverse image under ![]() $\pi$, then the images of the
$\pi$, then the images of the ![]() $\ell$-adic Galois representations attached to
$\ell$-adic Galois representations attached to ![]() $\mathcal {A}_s$ are equal to those attached to
$\mathcal {A}_s$ are equal to those attached to ![]() $\mathcal {A}_\eta$ for all
$\mathcal {A}_\eta$ for all ![]() $s \in B$. Note that, by Hilbert's (classical) irreducibility theorem,
$s \in B$. Note that, by Hilbert's (classical) irreducibility theorem, ![]() $B_0$ is the complement of a thin set.
$B_0$ is the complement of a thin set.
Let ![]() $k= k(\eta )$ be the function field of
$k= k(\eta )$ be the function field of ![]() $S$. Then, for all
$S$. Then, for all ![]() $s$ in
$s$ in ![]() $B$, we have
$B$, we have
By Tate's conjecture on endomorphisms (which holds for all finitely generated fields of characteristic zero; see [Reference FaltingsFal84]) we thus obtain ![]() $\operatorname {End}_{k}( \mathcal {A}_\eta ) \otimes \mathbb {Q}_\ell \cong \operatorname {End}_{k(s)}(\mathcal {A}_s) \otimes \mathbb {Q}_\ell$. As the inclusion
$\operatorname {End}_{k}( \mathcal {A}_\eta ) \otimes \mathbb {Q}_\ell \cong \operatorname {End}_{k(s)}(\mathcal {A}_s) \otimes \mathbb {Q}_\ell$. As the inclusion ![]() $\operatorname {End}_{k}( \mathcal {A}_\eta ) \hookrightarrow \operatorname {End}_{k(s)}(\mathcal {A}_s)$ has torsion-free cokernel, we see that all points in
$\operatorname {End}_{k}( \mathcal {A}_\eta ) \hookrightarrow \operatorname {End}_{k(s)}(\mathcal {A}_s)$ has torsion-free cokernel, we see that all points in ![]() $B$ satisfy the desired property concerning endomorphisms and have bounded degree over
$B$ satisfy the desired property concerning endomorphisms and have bounded degree over ![]() $\mathbb {Q}$ (we take, in particular,
$\mathbb {Q}$ (we take, in particular, ![]() $d_0 = \deg \pi$). Note that
$d_0 = \deg \pi$). Note that ![]() $B$ is Zariski dense, so that
$B$ is Zariski dense, so that ![]() $\bigcup _{h\geq 1} S(d_0,h)_{\mathrm {End}}$ is Zariski dense. To conclude the proof, it only remains to show that the cardinality of
$\bigcup _{h\geq 1} S(d_0,h)_{\mathrm {End}}$ is Zariski dense. To conclude the proof, it only remains to show that the cardinality of ![]() $S(d_0,h)_{\mathrm {End}}$ grows exponentially in
$S(d_0,h)_{\mathrm {End}}$ grows exponentially in ![]() $h$. This follows from the fact that the complement of a thin set of
$h$. This follows from the fact that the complement of a thin set of ![]() $\mathbb {A}_{\mathbb {Q}}^{\dim S}$ contains
$\mathbb {A}_{\mathbb {Q}}^{\dim S}$ contains ![]() $\gg e^{ch}$ points of logarithmic height
$\gg e^{ch}$ points of logarithmic height ![]() $h$ for some positive constant
$h$ for some positive constant ![]() $c$ (see [Reference SerreSer08, Theorem 3.4.4]).
$c$ (see [Reference SerreSer08, Theorem 3.4.4]).
Lemma 7.3 Let ![]() $\Omega \subset \mathcal {A}(S)$ be a Zariski-dense subgroup. There exists a Zariski-dense set of closed points
$\Omega \subset \mathcal {A}(S)$ be a Zariski-dense subgroup. There exists a Zariski-dense set of closed points ![]() $s \in S$ of bounded degree over
$s \in S$ of bounded degree over ![]() $K$ such that the image
$K$ such that the image ![]() $\Omega _s := \operatorname {Im}_{\mathcal {A}(S)\rightarrow \mathcal {A}(k(s))}(\Omega )$ is Zariski-dense in
$\Omega _s := \operatorname {Im}_{\mathcal {A}(S)\rightarrow \mathcal {A}(k(s))}(\Omega )$ is Zariski-dense in ![]() $\mathcal {A}_s$ and the restriction morphism
$\mathcal {A}_s$ and the restriction morphism ![]() $\Omega \rightarrow \Omega _s$ is an isomorphism.
$\Omega \rightarrow \Omega _s$ is an isomorphism.
Proof. We need the following observation, which follows at once from Poincaré's reducibility theorem for abelian varieties: if ![]() $A$ is an abelian variety over a field
$A$ is an abelian variety over a field ![]() $k$, and
$k$, and ![]() $B\subset A$ is an abelian subvariety, there exists an endomorphism
$B\subset A$ is an abelian subvariety, there exists an endomorphism ![]() $\phi :A \rightarrow A$ such that
$\phi :A \rightarrow A$ such that ![]() $B \subset \operatorname {Ker} \phi$, and the quotient
$B \subset \operatorname {Ker} \phi$, and the quotient ![]() $(\operatorname {Ker} \phi )/B$ is finite. In particular, a finitely generated subgroup
$(\operatorname {Ker} \phi )/B$ is finite. In particular, a finitely generated subgroup ![]() $\langle Q_1,\ldots,Q_r\rangle \subset A(k)$ is Zariski-dense in
$\langle Q_1,\ldots,Q_r\rangle \subset A(k)$ is Zariski-dense in ![]() $A$ if and only if there does not exist any non-zero endomorphism
$A$ if and only if there does not exist any non-zero endomorphism ![]() $\phi \in \operatorname {End}_{k}(A)$ such that
$\phi \in \operatorname {End}_{k}(A)$ such that ![]() $\phi (Q_i)=0$ for all
$\phi (Q_i)=0$ for all ![]() $i=1,\ldots,r$.
$i=1,\ldots,r$.
As ![]() $\Omega$ is finitely generated (see [Reference ConradCon06, Corollary 7.2]), we may write
$\Omega$ is finitely generated (see [Reference ConradCon06, Corollary 7.2]), we may write ![]() $\Omega =\langle P_1,\ldots,P_r \rangle$. Let
$\Omega =\langle P_1,\ldots,P_r \rangle$. Let ![]() $\Gamma := \operatorname {End}_{S}(\mathcal {A})\cdot \Omega \subset \mathcal {A}(S)$. By the main theorem of [Reference MasserMas89], the cardinality of the set of
$\Gamma := \operatorname {End}_{S}(\mathcal {A})\cdot \Omega \subset \mathcal {A}(S)$. By the main theorem of [Reference MasserMas89], the cardinality of the set of ![]() $s \in S(d_0,h)$ such that the reduction morphism
$s \in S(d_0,h)$ such that the reduction morphism ![]() $\Gamma \rightarrow \mathcal {A}_s(k(s))$ is not injective is bounded above by
$\Gamma \rightarrow \mathcal {A}_s(k(s))$ is not injective is bounded above by ![]() $C\cdot h^k$, for some
$C\cdot h^k$, for some ![]() $k \in \mathbb {N}$ and
$k \in \mathbb {N}$ and ![]() $C \in \mathbb {R}_{>0}$. Defining
$C \in \mathbb {R}_{>0}$. Defining
we claim that ![]() $\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$ is Zariski-dense in
$\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$ is Zariski-dense in ![]() $S$. Indeed, let
$S$. Indeed, let ![]() $U \subset S$ be a dense open subset. By Theorem 7.2, there exist an integer
$U \subset S$ be a dense open subset. By Theorem 7.2, there exist an integer ![]() $d_0$ and a constant
$d_0$ and a constant ![]() $c>0$ (possibly depending on
$c>0$ (possibly depending on ![]() $U$) such that, for every
$U$) such that, for every ![]() $h\geq 1$, the set
$h\geq 1$, the set
has cardinality at least ![]() $e^{ch}$. By comparing cardinality bounds, because
$e^{ch}$. By comparing cardinality bounds, because ![]() $e^{ch} > C \cdot h^k$ for
$e^{ch} > C \cdot h^k$ for ![]() $h$ sufficiently large, there is an integer
$h$ sufficiently large, there is an integer ![]() $h\geq 1$ such that the intersection of
$h\geq 1$ such that the intersection of ![]() $U$ and
$U$ and ![]() $S(d_0,h)_{\text {good}}$ is non-empty, so that
$S(d_0,h)_{\text {good}}$ is non-empty, so that ![]() $\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$ meets all open dense subschemes
$\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$ meets all open dense subschemes ![]() $U$ as desired.
$U$ as desired.
We claim that, for a point ![]() $s$ in
$s$ in ![]() $\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$, the reduction
$\bigcup _{h\geq 1}S(d_0,h)_{\text {good}}$, the reduction ![]() $\Omega _s= \langle \overline {P_1},\ldots,\overline {P_r} \rangle$ is Zariski-dense in
$\Omega _s= \langle \overline {P_1},\ldots,\overline {P_r} \rangle$ is Zariski-dense in ![]() $\mathcal {A}_s$, where
$\mathcal {A}_s$, where ![]() $\overline {P_i}$ denotes the reduction of
$\overline {P_i}$ denotes the reduction of ![]() $P_i \in \mathcal {A}(S)$ in
$P_i \in \mathcal {A}(S)$ in ![]() $\mathcal {A}_s(k(s))$.
$\mathcal {A}_s(k(s))$.
Assume, by contradiction, that this does not hold. By the observation in the first paragraph, there exists a non-zero endomorphism ![]() $\bar {\phi } \in \operatorname {End}_{k(s)}(\mathcal {A}_s)$ such that
$\bar {\phi } \in \operatorname {End}_{k(s)}(\mathcal {A}_s)$ such that ![]() $\bar {\phi }(\overline {P_i})=0$ for each
$\bar {\phi }(\overline {P_i})=0$ for each ![]() $i=1,\ldots, r$. As
$i=1,\ldots, r$. As ![]() $\operatorname {End}_{\eta }\mathcal {A}_{\eta } \xrightarrow {\sim } \operatorname {End}_{k(s)}\mathcal {A}_s$, the endomorphism
$\operatorname {End}_{\eta }\mathcal {A}_{\eta } \xrightarrow {\sim } \operatorname {End}_{k(s)}\mathcal {A}_s$, the endomorphism ![]() $\bar {\phi }$ is the reduction of some (necessarily non-zero)
$\bar {\phi }$ is the reduction of some (necessarily non-zero) ![]() $\phi \in \operatorname {End}_{\eta }(\mathcal {A}_{\eta })$. As
$\phi \in \operatorname {End}_{\eta }(\mathcal {A}_{\eta })$. As ![]() $\Gamma \rightarrow \mathcal {A}_s(k(s))$ is injective, we obtain
$\Gamma \rightarrow \mathcal {A}_s(k(s))$ is injective, we obtain ![]() $\phi (P_i)=0$ for each
$\phi (P_i)=0$ for each ![]() $i=1,\ldots,r$. In particular, we see that
$i=1,\ldots,r$. In particular, we see that ![]() $\Omega \subset \operatorname {Ker} \phi$, contradicting the Zariski-density of
$\Omega \subset \operatorname {Ker} \phi$, contradicting the Zariski-density of ![]() $\Omega$.
$\Omega$.
Remark 7.4 Lemma 7.3 can also be deduced from Néron's [Reference NéronNér52, Théorème 6].
Remark 7.5 A different proof of Lemma 7.3 can also be obtained by combining Silverman's specialization theorem [Reference SilvermanSil83], which gives boundedness of height for the points ![]() $s \in S^{(0)}$ for which the specialization map
$s \in S^{(0)}$ for which the specialization map ![]() $\mathcal {A}(S) \to \mathcal {A}_s(k(s))$ is not injective, with a weaker version of Theorem 7.2, where we only require that the set in question be infinite.
$\mathcal {A}(S) \to \mathcal {A}_s(k(s))$ is not injective, with a weaker version of Theorem 7.2, where we only require that the set in question be infinite.
Proposition 7.6 Assume that, for every number field ![]() $L$, every abelian variety
$L$, every abelian variety ![]() $A$ over
$A$ over ![]() $L$, and every Zariski-dense subgroup
$L$, and every Zariski-dense subgroup ![]() $\Omega \subset A(L)$, we have that property (PB) implies property (IF) for
$\Omega \subset A(L)$, we have that property (PB) implies property (IF) for ![]() $(A,\Omega )$. Then, for every finitely generated field
$(A,\Omega )$. Then, for every finitely generated field ![]() $k$ of characteristic zero, every abelian variety
$k$ of characteristic zero, every abelian variety ![]() $A'$ over
$A'$ over ![]() $k$, and every Zariski-dense subgroup
$k$, and every Zariski-dense subgroup ![]() $\Omega '\subset A'(k)$, we have that property (PB) implies property (IF) for
$\Omega '\subset A'(k)$, we have that property (PB) implies property (IF) for ![]() $(A',\Omega ')$.
$(A',\Omega ')$.
Proof. Let ![]() $A$ be an abelian variety defined over a finitely generated field
$A$ be an abelian variety defined over a finitely generated field ![]() $k$ of characteristic zero, and let
$k$ of characteristic zero, and let ![]() $\Omega \subset A(k)$ be a Zariski-dense (finitely generated) subgroup. Let
$\Omega \subset A(k)$ be a Zariski-dense (finitely generated) subgroup. Let ![]() $S$ be a smooth geometrically connected variety over a number field
$S$ be a smooth geometrically connected variety over a number field ![]() $K$ such that
$K$ such that ![]() $K(S)=k$, and let
$K(S)=k$, and let ![]() $\eta \in S$ be its generic point. As
$\eta \in S$ be its generic point. As ![]() $\Omega$ is finitely generated, by spreading out (and possibly restricting
$\Omega$ is finitely generated, by spreading out (and possibly restricting ![]() $S$), we may assume that
$S$), we may assume that ![]() $A$ extends to an abelian scheme
$A$ extends to an abelian scheme ![]() $\mathcal {A} \rightarrow S$ with generic fibre
$\mathcal {A} \rightarrow S$ with generic fibre ![]() $\mathcal {A}_{\eta }=A$, and that
$\mathcal {A}_{\eta }=A$, and that ![]() $\Omega \subset \mathcal {A}(S)$. Let us show that property (PB) implies property (IF) for
$\Omega \subset \mathcal {A}(S)$. Let us show that property (PB) implies property (IF) for ![]() $(A,\Omega )$.
$(A,\Omega )$.
Let ![]() $\phi :X \rightarrow A$ be a (PB)-cover. Replacing
$\phi :X \rightarrow A$ be a (PB)-cover. Replacing ![]() $S$ by a dense open subscheme if necessary, we may assume that
$S$ by a dense open subscheme if necessary, we may assume that ![]() $\phi :X\to A$ extends to a finite surjective morphism
$\phi :X\to A$ extends to a finite surjective morphism ![]() $\psi :\mathcal {X} \rightarrow \mathcal {A}$. By Lemma 4.11, replacing
$\psi :\mathcal {X} \rightarrow \mathcal {A}$. By Lemma 4.11, replacing ![]() $S$ by a dense open subscheme if necessary, for every
$S$ by a dense open subscheme if necessary, for every ![]() $s$ in
$s$ in ![]() $S$, the specialization
$S$, the specialization ![]() $\psi _s :\mathcal {X}_s\rightarrow \mathcal {A}_s$ is a (PB)-cover of the abelian variety
$\psi _s :\mathcal {X}_s\rightarrow \mathcal {A}_s$ is a (PB)-cover of the abelian variety ![]() $\mathcal {A}_s$ over
$\mathcal {A}_s$ over ![]() $\kappa (s)$.
$\kappa (s)$.
For ![]() $s$ in
$s$ in ![]() $S$, let
$S$, let ![]() $\mathrm {red}_s:\mathcal {A}(S)\to \mathcal {A}_s(\kappa (s))$ denote the reduction map. Then, by Lemma 7.3, there exists a closed point
$\mathrm {red}_s:\mathcal {A}(S)\to \mathcal {A}_s(\kappa (s))$ denote the reduction map. Then, by Lemma 7.3, there exists a closed point ![]() $s \in S$ such that the specialization
$s \in S$ such that the specialization ![]() $\Omega _s:= \mathrm {red}_s(\Omega )$ is isomorphic to
$\Omega _s:= \mathrm {red}_s(\Omega )$ is isomorphic to ![]() $\Omega$ and Zariski-dense in
$\Omega$ and Zariski-dense in ![]() $\mathcal {A}_s$. In particular, by our assumption on the pair
$\mathcal {A}_s$. In particular, by our assumption on the pair ![]() $(\mathcal {A}_s, \Omega _s)$ over the number field
$(\mathcal {A}_s, \Omega _s)$ over the number field ![]() $\kappa (s)$, there exists a finite index coset
$\kappa (s)$, there exists a finite index coset ![]() $C$ of
$C$ of ![]() $\Omega _s \cong \Omega$ such that, for all
$\Omega _s \cong \Omega$ such that, for all ![]() $c \in C$, the scheme
$c \in C$, the scheme ![]() $\psi _s^{-1}(c) \cong \psi ^{-1}(c)$ is integral.
$\psi _s^{-1}(c) \cong \psi ^{-1}(c)$ is integral.
Define ![]() $C':=\mathrm {red}_s^{-1}(C)$ to be the inverse image of
$C':=\mathrm {red}_s^{-1}(C)$ to be the inverse image of ![]() $C$ in
$C$ in ![]() $\Omega$, and note that
$\Omega$, and note that ![]() $C'\subset \Omega$ is a finite index coset. Let
$C'\subset \Omega$ is a finite index coset. Let ![]() $c$ be an element of
$c$ be an element of ![]() $C'\subset \mathcal {A}(S)$. The
$C'\subset \mathcal {A}(S)$. The ![]() $c(S)$-scheme
$c(S)$-scheme ![]() $\mathcal {X}|_{c(S)}$ is connected, and finite étale over the point
$\mathcal {X}|_{c(S)}$ is connected, and finite étale over the point ![]() $c(s)$. In particular, the fibre of
$c(s)$. In particular, the fibre of ![]() $\mathcal {X}|_{c(S)} \to c(S)$ over
$\mathcal {X}|_{c(S)} \to c(S)$ over ![]() $c(\eta )$ is étale and integral. Thus, for every
$c(\eta )$ is étale and integral. Thus, for every ![]() $c$ in the finite index coset
$c$ in the finite index coset ![]() $C'$ of
$C'$ of ![]() $\Omega$, the scheme
$\Omega$, the scheme ![]() $\phi ^{-1}(c)=\psi ^{-1}(\eta _{c})$ is integral. We conclude that property (IF) holds for
$\phi ^{-1}(c)=\psi ^{-1}(\eta _{c})$ is integral. We conclude that property (IF) holds for ![]() $(A, \Omega )$.
$(A, \Omega )$.
7.2 Main results
We now show that every (PB)-cover ![]() $Y \to A$ of an abelian variety over a finitely generated field of characteristic zero satisfies property (IF), and that every (Ram)-cover
$Y \to A$ of an abelian variety over a finitely generated field of characteristic zero satisfies property (IF), and that every (Ram)-cover ![]() $Y \to A$ satisfies property (PF).
$Y \to A$ satisfies property (PF).
Theorem 7.7 Let ![]() $k$ be a finitely generated field of characteristic zero, let
$k$ be a finitely generated field of characteristic zero, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$, let
$k$, let ![]() $\Omega \subset A(k)$ be a Zariski-dense subgroup and let
$\Omega \subset A(k)$ be a Zariski-dense subgroup and let ![]() $(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of (PB)-covers. Then, there is a finite index coset
$(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of (PB)-covers. Then, there is a finite index coset ![]() $C\subset \Omega$ such that, for every
$C\subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$ and every
$C$ and every ![]() $i=1,\ldots, n$, the scheme
$i=1,\ldots, n$, the scheme ![]() $Y_{i,c}$ is integral.
$Y_{i,c}$ is integral.
Proof. By Lemma 4.14(1), we may and do assume that ![]() $n=1$. By Proposition 7.6, it suffices to prove that property (PB) implies property (IF) for all covers
$n=1$. By Proposition 7.6, it suffices to prove that property (PB) implies property (IF) for all covers ![]() $Y \to A$ and all
$Y \to A$ and all ![]() $\Omega \subseteq A(K)$, where
$\Omega \subseteq A(K)$, where ![]() $K$ is a number field,
$K$ is a number field, ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $K$ and
$K$ and ![]() $\Omega$ is a (finitely generated) Zariski-dense subgroup of
$\Omega$ is a (finitely generated) Zariski-dense subgroup of ![]() $A(K)$. By Lemma 4.16 it then suffices to prove this statement for
$A(K)$. By Lemma 4.16 it then suffices to prove this statement for ![]() $(A,\Omega ) = (\prod A_i, \prod \Omega _i)$, where each
$(A,\Omega ) = (\prod A_i, \prod \Omega _i)$, where each ![]() $\Omega _i$ is cyclic and Zariski-dense in
$\Omega _i$ is cyclic and Zariski-dense in ![]() $A_i$. By Theorem 6.15, for every finite field extension
$A_i$. By Theorem 6.15, for every finite field extension ![]() $L/K$, we know that property (PB) implies property (IF) over
$L/K$, we know that property (PB) implies property (IF) over ![]() $L$ for every pair
$L$ for every pair ![]() $((A_i)_L,\Omega _i)$. Therefore, the statement follows from Corollary 5.7 and an immediate induction.
$((A_i)_L,\Omega _i)$. Therefore, the statement follows from Corollary 5.7 and an immediate induction.
Proof of Theorem 1.3 It suffices to prove the first statement. To do so, note that, by Lemma 4.14(2), we may assume that ![]() $n=1$. The result then follows from Proposition 4.17 and Theorem 7.7.
$n=1$. The result then follows from Proposition 4.17 and Theorem 7.7.
Proof of Theorem 1.4 This is Theorem 7.7, as (PB)-covers are precisely covers with no non-trivial étale subcovers (Lemma 4.4).
Remark 7.8 Note that property (Ram) does not imply property (IF) in general. Indeed, if ![]() $\phi : A \to A'$ is a non-trivial isogeny of abelian varieties such that all points in
$\phi : A \to A'$ is a non-trivial isogeny of abelian varieties such that all points in ![]() $\ker \phi$ are defined over
$\ker \phi$ are defined over ![]() $k$, and
$k$, and ![]() $X \to A$ is any ramified cover, then the composition
$X \to A$ is any ramified cover, then the composition ![]() $\pi : X \to A'$ is ramified. However, for every
$\pi : X \to A'$ is ramified. However, for every ![]() $P$ in the subgroup
$P$ in the subgroup ![]() $\Omega :=\mathrm {Im}(A(k)\to A'(k))$, the fibre of
$\Omega :=\mathrm {Im}(A(k)\to A'(k))$, the fibre of ![]() $\pi$ over
$\pi$ over ![]() $P$ splits into at least
$P$ splits into at least ![]() $\#\ker \phi$ components.
$\#\ker \phi$ components.
Remark 7.9 (Necessity of density)
In Theorems 1.3 and 1.4 it is necessary to assume that the subgroup ![]() $\Omega$ be Zariski-dense. Indeed, let
$\Omega$ be Zariski-dense. Indeed, let ![]() $E$ be an elliptic curve over a number field
$E$ be an elliptic curve over a number field ![]() $K$ with
$K$ with ![]() $E(K)$ infinite. Let
$E(K)$ infinite. Let ![]() $\pi :C\to E$ be a ramified double cover with
$\pi :C\to E$ be a ramified double cover with ![]() $C$ a smooth projective connected curve of genus at least two such that
$C$ a smooth projective connected curve of genus at least two such that ![]() $0_E \in \pi (C(K))$. Let
$0_E \in \pi (C(K))$. Let ![]() $\Omega = E(K) \times \{0\}$. Note that
$\Omega = E(K) \times \{0\}$. Note that ![]() $\Omega$ is an infinite (non-dense) subgroup of
$\Omega$ is an infinite (non-dense) subgroup of ![]() $A:=E\times E$. Define
$A:=E\times E$. Define ![]() $Y:= E\times C$ and note that
$Y:= E\times C$ and note that ![]() $Y\to A$ is a ramified (PB)-cover. Note that
$Y\to A$ is a ramified (PB)-cover. Note that ![]() $\Omega \setminus \pi (Y(K))$ is empty. Thus, the group
$\Omega \setminus \pi (Y(K))$ is empty. Thus, the group ![]() $\Omega$ does not contain a finite index coset (nor even a non-empty subset)
$\Omega$ does not contain a finite index coset (nor even a non-empty subset) ![]() $C$ such that
$C$ such that ![]() $Y_c$ has no
$Y_c$ has no ![]() $K$-points.
$K$-points.
Proof of Theorem 1.8 As the weak-Hilbert property is a birational invariant among smooth proper varieties (Proposition 3.1), we may and do assume that ![]() $X$ has trivial tangent bundle. In particular, because
$X$ has trivial tangent bundle. In particular, because ![]() $k$ is of characteristic zero, there is a finite field extension
$k$ is of characteristic zero, there is a finite field extension ![]() $L/k$ such that
$L/k$ such that ![]() $X_L$ is an abelian variety (see [Reference BrionBri12, Corollary 2.3]). Replacing
$X_L$ is an abelian variety (see [Reference BrionBri12, Corollary 2.3]). Replacing ![]() $L$ by a finite field extension if necessary, by the potential density of rational points on abelian varieties (see [Reference JavanpeykarJav21a, § 3]), we may assume that
$L$ by a finite field extension if necessary, by the potential density of rational points on abelian varieties (see [Reference JavanpeykarJav21a, § 3]), we may assume that ![]() $X(L)$ is Zariski-dense in
$X(L)$ is Zariski-dense in ![]() $X$. It then follows from Theorem 1.3 that
$X$. It then follows from Theorem 1.3 that ![]() $X_L$ has the weak-Hilbert property over
$X_L$ has the weak-Hilbert property over ![]() $L$. Finally, it is shown in [Reference CampanaCam11] that
$L$. Finally, it is shown in [Reference CampanaCam11] that ![]() $X_{\overline {k}}$ is special. This concludes the proof.
$X_{\overline {k}}$ is special. This concludes the proof.
We record the following consequence of Theorem 1.3 which, roughly speaking, says that abelian varieties also satisfy a version of the Hilbert property with respect to the complex-analytic topology.
Remark 7.10 (Zariski density versus complex-analytic density)
Let ![]() $k$ be a finitely generated field of characteristic zero, let
$k$ be a finitely generated field of characteristic zero, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$ and let
$k$ and let ![]() $(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of ramified covers. Choose an embedding
$(\pi _i:Y_i \to A)_{i=1}^n$ be a finite collection of ramified covers. Choose an embedding ![]() $k\to \mathbb {C}$ and assume that
$k\to \mathbb {C}$ and assume that ![]() $A(k)$ is dense in
$A(k)$ is dense in ![]() $A(\mathbb {C})$ with respect to the complex-analytic topology on
$A(\mathbb {C})$ with respect to the complex-analytic topology on ![]() $A(\mathbb {C})$. Then, because
$A(\mathbb {C})$. Then, because ![]() $A(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ contains a finite index coset of
$A(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ contains a finite index coset of ![]() $A(k)$ (by Theorem 1.3), the subset
$A(k)$ (by Theorem 1.3), the subset ![]() $A(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is complex-analytically dense in
$A(k)\setminus \bigcup _{i=1}^n \pi _i(Y_i(k))$ is complex-analytically dense in ![]() $A(\mathbb {C})$. (Indeed, a finite index coset
$A(\mathbb {C})$. (Indeed, a finite index coset ![]() $C$ of a complex-analytically dense subgroup
$C$ of a complex-analytically dense subgroup ![]() $\Omega$ of
$\Omega$ of ![]() $A(\mathbb {C})$ is complex-analytically dense.)
$A(\mathbb {C})$ is complex-analytically dense.)
We conclude our paper by showing that our main results concerning rational points on ramified covers of abelian varieties can be used to obtain similar conclusions for rational points on varieties which only admit a dominant generically finite rational map to an abelian variety.
Theorem 7.11 (Improving Theorem 1.4)
Let ![]() $k$ be a finitely generated field of characteristic zero, let
$k$ be a finitely generated field of characteristic zero, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$ and let
$k$ and let ![]() $\Omega \subset A(k)$ be a Zariski-dense subgroup. For
$\Omega \subset A(k)$ be a Zariski-dense subgroup. For ![]() $i=1,\ldots, n$, let
$i=1,\ldots, n$, let ![]() $Z_i$ be a normal projective variety and let
$Z_i$ be a normal projective variety and let ![]() $\pi _i:Z_i \dashrightarrow A$ be a dominant generically finite rational map which does not (rationally) dominate any non-trivial étale cover of
$\pi _i:Z_i \dashrightarrow A$ be a dominant generically finite rational map which does not (rationally) dominate any non-trivial étale cover of ![]() $A$. Then, there is a finite index coset
$A$. Then, there is a finite index coset ![]() $C\subset \Omega$ such that, for every
$C\subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$ and every
$C$ and every ![]() $i=1,\ldots, n$, the rational map
$i=1,\ldots, n$, the rational map ![]() $\pi _i$ is defined above
$\pi _i$ is defined above ![]() $c$ and the
$c$ and the ![]() $k$-scheme
$k$-scheme ![]() $Z_{i,c}$ is integral.
$Z_{i,c}$ is integral.
Proof. For ![]() $i=1,\ldots, n$, let
$i=1,\ldots, n$, let ![]() $W_i$ be a normal projective variety over
$W_i$ be a normal projective variety over ![]() $k$ and let
$k$ and let ![]() $W_i\to Z_i$ be a proper birational surjective morphism such that the composed rational map
$W_i\to Z_i$ be a proper birational surjective morphism such that the composed rational map ![]() $W_i\to Z_i\dashrightarrow A$ is a (proper surjective generically finite) morphism. Let
$W_i\to Z_i\dashrightarrow A$ is a (proper surjective generically finite) morphism. Let ![]() $W_i\to Y_i\to A$ be the Stein factorization of
$W_i\to Y_i\to A$ be the Stein factorization of ![]() $W_i\to A$, so that
$W_i\to A$, so that ![]() $Y_i$ is a normal projective variety,
$Y_i$ is a normal projective variety, ![]() $Y_i\to A$ is a finite morphism and
$Y_i\to A$ is a finite morphism and ![]() $W_i\to Y_i$ is a proper birational surjective morphism. As
$W_i\to Y_i$ is a proper birational surjective morphism. As ![]() $W_i\to Z_i$ and
$W_i\to Z_i$ and ![]() $W_i\to Y_i$ are proper birational surjective morphisms, we can choose a closed subset
$W_i\to Y_i$ are proper birational surjective morphisms, we can choose a closed subset ![]() $W_i^0\subset W_i$ such that
$W_i^0\subset W_i$ such that ![]() $W_i\to Z_i$ and
$W_i\to Z_i$ and ![]() $W_i\to Y_i$ are isomorphisms away from
$W_i\to Y_i$ are isomorphisms away from ![]() $W_i^0$. Let
$W_i^0$. Let ![]() $Z\subset A$ be the image of
$Z\subset A$ be the image of ![]() $\bigcup _{i=1}^n W_i^0$ in
$\bigcup _{i=1}^n W_i^0$ in ![]() $A$. By Lemma 4.6, replacing
$A$. By Lemma 4.6, replacing ![]() $\Omega$ by a finite index coset if necessary and translating the origin of
$\Omega$ by a finite index coset if necessary and translating the origin of ![]() $A$, we may and do assume that
$A$, we may and do assume that ![]() $\Omega \cap Z=\emptyset$.
$\Omega \cap Z=\emptyset$.
As ![]() $Z_i \dashrightarrow A$ does not (rationally) dominate any non-trivial étale cover of
$Z_i \dashrightarrow A$ does not (rationally) dominate any non-trivial étale cover of ![]() $A$, it follows that
$A$, it follows that ![]() $Y_i\to A$ has no non-trivial étale subcovers. In particular, by Theorem 1.4, there is a finite index coset
$Y_i\to A$ has no non-trivial étale subcovers. In particular, by Theorem 1.4, there is a finite index coset ![]() $C\subset \Omega$ such that, for every
$C\subset \Omega$ such that, for every ![]() $c$ in
$c$ in ![]() $C$ and every
$C$ and every ![]() $i=1,\ldots, n$, the
$i=1,\ldots, n$, the ![]() $k$-scheme
$k$-scheme ![]() $Y_{i,c}$ is integral. As
$Y_{i,c}$ is integral. As ![]() $C\cap Z=\emptyset$, it follows that
$C\cap Z=\emptyset$, it follows that ![]() $Z_{i,c} = W_{i,c} = Y_{i,c}$ is integral, as required.
$Z_{i,c} = W_{i,c} = Y_{i,c}$ is integral, as required.
Acknowledgements
A.J. is grateful to R. van Dobben de Bruyn for a helpful discussion on Stein factorizations, and D. Holmes for a helpful discussion on unramified morphisms. A.J. gratefully acknowledges support from the IHES and the University of Paris–Saclay. We are also most grateful to Olivier Wittenberg for allowing us to include Theorem 1.9 and Example 3.10, as they were obtained in collaboration with him. We are most grateful to the referees for their comments and suggestions. We thank David McKinnon for asking a question which led to Remark 7.10. The senior authors Corvaja and Zannier are grateful to the junior authors for their strength in making what was a mere project into this paper.