Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T07:31:23.036Z Has data issue: false hasContentIssue false
  • English
  • Français

On the logarithmic region in wall turbulence

Published online by Cambridge University Press:  28 January 2013

Ivan Marusic ,
Jason P. Monty ,
Marcus Hultmark  and
Alexander J. Smits
Ivan Marusic*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, Victoria 3010, Australia
Jason P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, Victoria 3010, Australia
Marcus Hultmark
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Alexander J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

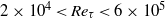Considerable discussion over the past few years has been devoted to the question of whether the logarithmic region in wall turbulence is indeed universal. Here, we analyse recent experimental data in the Reynolds number range of nominally $2\times 1{0}^{4} \lt {\mathit{Re}}_{\tau } \lt 6\times 1{0}^{5} $ for boundary layers, pipe flow and the atmospheric surface layer, and show that, within experimental uncertainty, the data support the existence of a universal logarithmic region. The results support the theory of Townsend (The Structure of Turbulent Shear Flow, Vol. 2, 1976) where, in the interior part of the inertial region, both the mean velocities and streamwise turbulence intensities follow logarithmic functions of distance from the wall.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R3
Copyright
©2013 Cambridge University Press

References

Andreas, E. L., Claffey, K. J., Jordan, R. E., Fairall, C. W., Guest, P. S., Persson, P. O. G. & Grachev, A. A. 2006 Evaluations of the von Kármán constant in the atmospheric surface layer. J. Fluid Mech. 559, 117–149.CrossRefGoogle Scholar
Bailey, S.C.C., Kunkel, G.J., Hultmark, M., Vallikivi, M., Hill, J.P., Meyer, K.A., Tsay, C., Arnold, C.B. & Smits, A.J. 2010 Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid Mech. 663, 160–179.CrossRefGoogle Scholar
Chauhan, K., Ng, H. C. H. & Marusic, I. 2010 Empirical mode decomposition and Hilbert transforms for analysis of oil-film interferograms. Meas. Sci. Tech. 21, 105405, 1–13.CrossRefGoogle Scholar
Coles, D. E. & Hirst, E. A. 1969 Compiled data. In Proceedings of Computation of Turbulent Boundary Layers, AFOSR-IFP Stanford Conference 1968, Vol.II.Google Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20, 125101.CrossRefGoogle Scholar
Hultmark, M. 2012 A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707, 575–584.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.CrossRefGoogle ScholarPubMed
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
von Kármán, T. 1930 Mechanische ähnlichkeit und turbulenz. Gött. Nachr. 58–76.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME J. Fluids Engng 132, 094001.Google Scholar
Klewicki, J. C., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.CrossRefGoogle Scholar
Kulandaivelu, V. 2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, University of Melbourne.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.CrossRefGoogle Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81, 115–130.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461–2464.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows: recent advances and key issues. Phys. Fluids 22, 065103.CrossRefGoogle Scholar
Marusic, I. & Perry, A. E. 1995 A wall wake model for the turbulent structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Marusic, I., Uddin, M. & Perry, A. E 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 12, 3718–3726.CrossRefGoogle Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google ScholarPubMed
McKeon, B. J., Li, J., Jiang, W., Morrison, J. & Smits, A. J. 2004 Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.CrossRefGoogle Scholar
Millikan, C. M. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics, Harvard and MIT, 12–26 September. Wiley.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-contained high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.Google Scholar
Monty, J. P. 2005 Developments in smooth wall turbulent duct flows. PhD thesis, University of Melbourne.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755.Google Scholar
Ng, H. C. H., Marusic, I., Monty, J. P., Hutchins, N. & Chong, M. S. 2007 Oil-film interferometry in high Reynolds number turbulent boundary layers. In Proceedings of the 16th Australasian Fluid Mechanics Conference, Gold Coast, Australia.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. M. & Chong, M. S. 2005 Evidence of the ${k}^{- 1} $ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.CrossRefGoogle Scholar
Perry, A. E. & Abell, C. J. 1977 Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech. 79, 785–799.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached eddy hypothesis in zero pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Prandtl, L. 1925 Bericht über untersuchungen zur ausgebildeten turbulenz. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2, 1–219.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Smits, A. J., Monty, J. P., Hultmark, M., Bailey, S. C. C., Hutchins, N. & Marusic, I. 2011 Spatial resolution correction for wall-bounded turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.). pp. 253–272. Computational Mechanics Publications.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, Vol. 2. Cambridge University Press.Google Scholar
Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements using a nanoscale thermal anemometry probe. Exp. Fluids 51 (6), 1521–1527.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. C. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Winkel, E. S., Cutbirth, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2012 Turbulence profiles from a smooth flat-plate turbulent boundary layer at high Reynolds number. Exp. Therm. Fluid Sci. 40, 140–149.CrossRefGoogle Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar