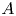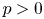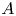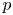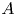1. Introduction
1.1 Main results
Let ![]() $p$ be an odd prime and let
$p$ be an odd prime and let ![]() $\mathcal {A}_2$ denote the moduli stack of principally polarized abelian surfaces over
$\mathcal {A}_2$ denote the moduli stack of principally polarized abelian surfaces over ![]() $\mathbb {F}_p$. We view
$\mathbb {F}_p$. We view ![]() $\mathcal {A}_2$ as (the special fiber of the canonical integral model of) a GSpin Shimura variety and let
$\mathcal {A}_2$ as (the special fiber of the canonical integral model of) a GSpin Shimura variety and let ![]() $Z(m)$ denote the Heegner divisors in
$Z(m)$ denote the Heegner divisors in ![]() $\mathcal {A}_2$ for an integer
$\mathcal {A}_2$ for an integer ![]() $m\geq 1$; more precisely,
$m\geq 1$; more precisely, ![]() $Z(m)$ parametrizes abelian surfaces with a special endomorphism
$Z(m)$ parametrizes abelian surfaces with a special endomorphism ![]() $s$ such that
$s$ such that ![]() $s\circ s$ is the endomorphism given by multiplication by
$s\circ s$ is the endomorphism given by multiplication by ![]() $m$ (see § 2.2).
$m$ (see § 2.2).
Theorem 1 Assume ![]() $p\geq 5$. Let
$p\geq 5$. Let ![]() $C$ be an irreducible smooth quasi-projective curve with a finite morphism
$C$ be an irreducible smooth quasi-projective curve with a finite morphism ![]() $C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$. Assume that the generic point of
$C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$. Assume that the generic point of ![]() $C$ corresponds to an ordinary abelian surface.
$C$ corresponds to an ordinary abelian surface.
(1) If the image of
 $C$ is not contained in any Heegner divisor
$C$ is not contained in any Heegner divisor  $Z(m)$, and if
$Z(m)$, and if  $C$ is projective, then there exist infinitely many
$C$ is projective, then there exist infinitely many  $\bar {\mathbb {F}}_p$-points on
$\bar {\mathbb {F}}_p$-points on  $C$ which correspond to non-simple abelian surfaces.
$C$ which correspond to non-simple abelian surfaces.(2) If the image of
 $C$ is contained in some
$C$ is contained in some  $Z(m)$ such that
$Z(m)$ such that  $p\nmid m$, then there exist infinitely many
$p\nmid m$, then there exist infinitely many  $\bar {\mathbb {F}}_p$-points on
$\bar {\mathbb {F}}_p$-points on  $C$ which correspond to abelian surfaces isogenous to self-products of elliptic curves.
$C$ which correspond to abelian surfaces isogenous to self-products of elliptic curves.
In Theorem 1(2), note that the elliptic curve may vary for these points. An equivalent statement is that there exist infinitely many ![]() $\bar {\mathbb {F}}_p$-points on
$\bar {\mathbb {F}}_p$-points on ![]() $C$ which correspond to abelian surfaces whose Néron–Severi ranks are strictly larger than that of the generic point of
$C$ which correspond to abelian surfaces whose Néron–Severi ranks are strictly larger than that of the generic point of ![]() $C$. Note that in case (2), any irreducible component of
$C$. Note that in case (2), any irreducible component of ![]() $Z(m)\subset \mathcal {A}_2$ is an irreducible component of a Hecke translate of some Hilbert modular surface associated to the real quadratic field
$Z(m)\subset \mathcal {A}_2$ is an irreducible component of a Hecke translate of some Hilbert modular surface associated to the real quadratic field ![]() $F=\mathbb {Q}(\sqrt {m})$ (if
$F=\mathbb {Q}(\sqrt {m})$ (if ![]() $m$ is a square number, then we obtain a Hecke translate of the self-product of the modular curve).
$m$ is a square number, then we obtain a Hecke translate of the self-product of the modular curve).
Remark 2 The assumption that the generic point is ordinary is necessary (especially if we formulate the theorem in terms of the Néron–Severi rank). For instance, in case (2), we may take ![]() $C$ to be an irreducible component of the non-ordinary locus. If
$C$ to be an irreducible component of the non-ordinary locus. If ![]() $p$ is inert in
$p$ is inert in ![]() $F$, then all the points on
$F$, then all the points on ![]() $C$ are supersingular and the Néron–Severi rank does not jump. If
$C$ are supersingular and the Néron–Severi rank does not jump. If ![]() $p$ is split in
$p$ is split in ![]() $F$, then the only points where the Néron–Severi rank jumps are the finitely many supersingular points.
$F$, then the only points where the Néron–Severi rank jumps are the finitely many supersingular points.
Remark 3 We make the (technical) assumption that ![]() $C$ is projective in case (1) because the Heegner divisors
$C$ is projective in case (1) because the Heegner divisors ![]() $Z(m)$ are all non-compact and we plan to remove this assumption in future work. On the other hand, the Hilbert modular surfaces considered in case (2) do contain compact special divisors (see the second half of § 2.2 for the definitions of special divisors in the Hilbert case, and § 4.3.3 for a criterion of when these special divisors are compact) the
$Z(m)$ are all non-compact and we plan to remove this assumption in future work. On the other hand, the Hilbert modular surfaces considered in case (2) do contain compact special divisors (see the second half of § 2.2 for the definitions of special divisors in the Hilbert case, and § 4.3.3 for a criterion of when these special divisors are compact) the ![]() $\bar {\mathbb {F}}_p$-points of which parameterize abelian surfaces isogenous to a self-product of elliptic curves. By working exclusively with these compact special divisors, we no longer need assume that
$\bar {\mathbb {F}}_p$-points of which parameterize abelian surfaces isogenous to a self-product of elliptic curves. By working exclusively with these compact special divisors, we no longer need assume that ![]() $C$ is projective.
$C$ is projective.
Remark 4 A modification of our argument shows that with the same assumption as in case (1), for a fixed real quadratic number field ![]() $F$, there are infinitely many ordinary
$F$, there are infinitely many ordinary ![]() $\bar {\mathbb {F}}_p$-points on
$\bar {\mathbb {F}}_p$-points on ![]() $C$ such that the corresponding abelian surfaces admit real multiplication by
$C$ such that the corresponding abelian surfaces admit real multiplication by ![]() $F$.Footnote 1 Here we need to assume
$F$.Footnote 1 Here we need to assume ![]() $p\geq 7$ if
$p\geq 7$ if ![]() $p$ is ramified in
$p$ is ramified in ![]() $F$. Otherwise,
$F$. Otherwise, ![]() $p\geq 5$ is enough.
$p\geq 5$ is enough.
The proof of Theorem 1(1) applies to the case when ![]() $p$ is split in
$p$ is split in ![]() $F/\mathbb {Q}$; and for the other cases, one needs to carry out a more general study of the local behavior at supersingular points (see the arXiv version [Reference Maulik, Shankar and TangMST18, § 9, Appendix A] for details).
$F/\mathbb {Q}$; and for the other cases, one needs to carry out a more general study of the local behavior at supersingular points (see the arXiv version [Reference Maulik, Shankar and TangMST18, § 9, Appendix A] for details).
To prove Theorem 1(1), we consider the intersection number of ![]() $C$ and
$C$ and ![]() $Z(\ell ^2)$, where
$Z(\ell ^2)$, where ![]() $\ell$ is a varying prime number. If we consider
$\ell$ is a varying prime number. If we consider ![]() $Z(\ell )$ with
$Z(\ell )$ with ![]() $\ell \equiv 3 \bmod 4$ instead, we prove the following theorem.
$\ell \equiv 3 \bmod 4$ instead, we prove the following theorem.
Theorem 5 Suppose we have the same assumptions as in Theorem 1(1). Then there are infinitely many ordinary ![]() $\bar {\mathbb {F}}_p$-points on
$\bar {\mathbb {F}}_p$-points on ![]() $C$ such that, for each of these points, the corresponding abelian surface admits real multiplication by the ring of integers of some real quadratic field (note that the quadratic fields may vary for these points).
$C$ such that, for each of these points, the corresponding abelian surface admits real multiplication by the ring of integers of some real quadratic field (note that the quadratic fields may vary for these points).
It would be interesting to find ![]() $\bar {\mathbb {F}}_p$-points of complex multiplication by maximal orders, but our current method only asserts real multiplication by maximal orders.
$\bar {\mathbb {F}}_p$-points of complex multiplication by maximal orders, but our current method only asserts real multiplication by maximal orders.
1.2 Previous work and heuristics
Theorem 1 is a generalization of [Reference Chai and OortCO06, Proposition 7.3], where Chai and Oort proved Theorem 1(2) with ![]() $\mathcal {A}_1 \times \mathcal {A}_1$ taking the place of a Hilbert modular surface. Their proof crucially uses the product structure of the Shimura variety, as well as the product structure of the Frobenius morphism. Following the discussion in § 7 of [Reference Chai and OortCO06], Theorem 1 is related to a bi-algebraicity conjecture. See § 1.4 for more details.
$\mathcal {A}_1 \times \mathcal {A}_1$ taking the place of a Hilbert modular surface. Their proof crucially uses the product structure of the Shimura variety, as well as the product structure of the Frobenius morphism. Following the discussion in § 7 of [Reference Chai and OortCO06], Theorem 1 is related to a bi-algebraicity conjecture. See § 1.4 for more details.
We offer the following heuristic for Theorem 1(1). Using Honda and Tate's classification of ![]() $\mathbb {F}_q^n$-isogeny classes of abelian varieties in terms of Weil-
$\mathbb {F}_q^n$-isogeny classes of abelian varieties in terms of Weil-![]() $q^n$ numbers, the number of
$q^n$ numbers, the number of ![]() $\mathbb {F}_{q^n}$-isogeny classes of abelian varieties is seen to equal
$\mathbb {F}_{q^n}$-isogeny classes of abelian varieties is seen to equal ![]() $q^{n(3/2 + o(1))}$. Similarly, the number of split
$q^{n(3/2 + o(1))}$. Similarly, the number of split ![]() $\mathbb {F}_{q^n}$-isogeny classes in
$\mathbb {F}_{q^n}$-isogeny classes in ![]() $\mathcal {A}_2$ is seen to equal
$\mathcal {A}_2$ is seen to equal ![]() $q^{n(1 + o(1))}$. If we treat the map from
$q^{n(1 + o(1))}$. If we treat the map from ![]() $C(\mathbb {F}_{q^n})$ to the set of
$C(\mathbb {F}_{q^n})$ to the set of ![]() $\mathbb {F}_{q^n}$-isogeny classes as a random map, we expect that the number of
$\mathbb {F}_{q^n}$-isogeny classes as a random map, we expect that the number of ![]() $\mathbb {F}_{q^n}$ points of
$\mathbb {F}_{q^n}$ points of ![]() $C$ which are not simple is around
$C$ which are not simple is around ![]() $q^{n/2(1 + o(1))}$. Letting
$q^{n/2(1 + o(1))}$. Letting ![]() $n$ approach infinity, this heuristic suggests that infinitely many points of
$n$ approach infinity, this heuristic suggests that infinitely many points of ![]() $C(\bar {\mathbb {F}}_q)$ that are split. There are analogous questions in other settings. For the case of equicharacteristic
$C(\bar {\mathbb {F}}_q)$ that are split. There are analogous questions in other settings. For the case of equicharacteristic ![]() $0$, these results are well known (for instance, the density of Noether–Lefschetz loci is discussed in [Reference VoisinVoi02, Proposition 17.20]). In mixed characteristic, the analogue of Theorem 1(2) is treated in [Reference CharlesCha18, Reference Shankar and TangST20]. The major difference between Theorem 1 and these other cases is that the ordinary generic point assumption is crucial because the result is simply false otherwise (as remarked in § 1.1).
$0$, these results are well known (for instance, the density of Noether–Lefschetz loci is discussed in [Reference VoisinVoi02, Proposition 17.20]). In mixed characteristic, the analogue of Theorem 1(2) is treated in [Reference CharlesCha18, Reference Shankar and TangST20]. The major difference between Theorem 1 and these other cases is that the ordinary generic point assumption is crucial because the result is simply false otherwise (as remarked in § 1.1).
Indeed, this difference hints at the key difficulty in our setting, which is that the local intersection number at a supersingular point is of the same magnitude as the total intersection number, which makes the approach more complicated than that of [Reference Shankar and TangST20]; we discuss this in more detail in § 1.3.
1.3 Proof of the main results
We view both Hilbert modular surfaces and the Siegel three-fold as GSpin Shimura varieties attached to a quadratic space ![]() $(V,Q)$. In each setting, we have a notion of special endomorphisms and special divisors and, for simplicity, we use the same notation
$(V,Q)$. In each setting, we have a notion of special endomorphisms and special divisors and, for simplicity, we use the same notation ![]() $Z(m)$.
$Z(m)$.
The main idea of the proof is to compare the global and local intersection numbers ofFootnote 2 ![]() $C. Z(m)$ for appropriate sequences of
$C. Z(m)$ for appropriate sequences of ![]() $m$ and show it is not possible for finitely many points to account for the total global intersection as
$m$ and show it is not possible for finitely many points to account for the total global intersection as ![]() $m$ increases.
$m$ increases.
More precisely:
(1) the global intersection number
 $I(m) := C . Z(m)$ is controlled by Borcherds theory [Reference BorcherdsBor98] (see also [Reference MaulikMau14] and [Reference Howard and Madapusi PeraHMP20]);
$I(m) := C . Z(m)$ is controlled by Borcherds theory [Reference BorcherdsBor98] (see also [Reference MaulikMau14] and [Reference Howard and Madapusi PeraHMP20]);(2) we prove that as
 $m\rightarrow \infty$, the total local contribution from supersingular points is at most
$m\rightarrow \infty$, the total local contribution from supersingular points is at most  $\frac {11}{12}I(m)$ by studying special endomorphisms;Footnote 3
$\frac {11}{12}I(m)$ by studying special endomorphisms;Footnote 3(3) we prove that the local contribution from a non-supersingular point is
 $o(I(m))$ as
$o(I(m))$ as  $m\rightarrow \infty$.
$m\rightarrow \infty$.
This allows us to conclude that, as ![]() $m\rightarrow \infty$, more and more points of
$m\rightarrow \infty$, more and more points of ![]() $C$ contribute to the intersection
$C$ contribute to the intersection ![]() $C . Z(m)$. To prove Theorem 1(1), the sequence of
$C . Z(m)$. To prove Theorem 1(1), the sequence of ![]() $m$ will consist only of squares, and to prove Theorem 5, the sequence will consist only of primes. Note that in
$m$ will consist only of squares, and to prove Theorem 5, the sequence will consist only of primes. Note that in ![]() $\mathcal {A}_2$, the Heegner divisor
$\mathcal {A}_2$, the Heegner divisor ![]() $Z(m)$ for square
$Z(m)$ for square ![]() $m$ parametrizes abelian surfaces which are not geometrically simple, thereby allowing us to deduce Theorem 1(1). Similar arguments allow us to deduce Theorem 1(2), and also Theorem 5.
$m$ parametrizes abelian surfaces which are not geometrically simple, thereby allowing us to deduce Theorem 1(1). Similar arguments allow us to deduce Theorem 1(2), and also Theorem 5.
Compared with the number field situation, the main difficulty of the positive characteristic function field case is that the local contributions at supersingular points are of the same magnitude as the global contribution. More precisely, taking the Hilbert case as an example, Borcherds theory implies that the generating series of ![]() $Z(m)$ is a non-cuspidal modular form of weight
$Z(m)$ is a non-cuspidal modular form of weight ![]() $2$; on the other hand, the theta series attached to the special endomorphism lattice at a supersingular point is also a non-cuspidal weight
$2$; on the other hand, the theta series attached to the special endomorphism lattice at a supersingular point is also a non-cuspidal weight ![]() $2$ modular form because the lattice is of rank
$2$ modular form because the lattice is of rank ![]() $4$. Therefore, even without considering higher intersection multiplicities, the local intersection number of
$4$. Therefore, even without considering higher intersection multiplicities, the local intersection number of ![]() $C.Z(m)$ at a supersingular point is also of the same magnitude as the growth rate of Fourier coefficients of an Eisenstein series of weight
$C.Z(m)$ at a supersingular point is also of the same magnitude as the growth rate of Fourier coefficients of an Eisenstein series of weight ![]() $2$.
$2$.
Bounding the local contribution from a supersingular point
Let ![]() $A \rightarrow C$ denote the family of principally polarized abelian surfaces induced from a morphism
$A \rightarrow C$ denote the family of principally polarized abelian surfaces induced from a morphism ![]() $C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$, and let
$C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$, and let ![]() $\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \rightarrow C$ denote the formal neighborhood of a supersingular point. For a special endomorphism
$\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \rightarrow C$ denote the formal neighborhood of a supersingular point. For a special endomorphism ![]() $s$ such that
$s$ such that ![]() $s\circ s=m$, we say that
$s\circ s=m$, we say that ![]() $s$ is of norm
$s$ is of norm ![]() $m$.
$m$.
The local contribution to ![]() $C . Z(m)$ from this supersingular point equals
$C . Z(m)$ from this supersingular point equals ![]() $\sum _{n=0}^{\infty } r_n(m)$, where
$\sum _{n=0}^{\infty } r_n(m)$, where ![]() $r_n(m)$ is the number of special endomorphisms of
$r_n(m)$ is the number of special endomorphisms of ![]() $A \mod t^{n+1}$ with norm
$A \mod t^{n+1}$ with norm ![]() $m$. Therefore, in order to bound the local contribution, it suffices to prove that, as
$m$. Therefore, in order to bound the local contribution, it suffices to prove that, as ![]() $n\rightarrow \infty$, there are many special endomorphisms of
$n\rightarrow \infty$, there are many special endomorphisms of ![]() $A \mod t^n$ which decay rapidly enough (see Definition 5.1.1 and Theorem 5.1.2 for precise statements).
$A \mod t^n$ which decay rapidly enough (see Definition 5.1.1 and Theorem 5.1.2 for precise statements).
A similar decay result appears in the mixed characteristic setting (see [Reference Shankar and TangST20]), by a straightforward application of Grothendieck–Messing theory. In the equicharacteristic case, however, proving our decay results is much more involved. In particular, we need to use Kisin's description [Reference KisinKis10, § 1.4, 1.5] of the ![]() $F$-crystal associated to a certain automorphic vector bundle
$F$-crystal associated to a certain automorphic vector bundle ![]() $\mathbb {L}_\mathrm {cris}$, whose
$\mathbb {L}_\mathrm {cris}$, whose ![]() $F$-invariant part is the lattice of special endomorphisms, in order to prove the required decay. See § 3.1.5 and the proof of Theorem 5.1.2 for more details.
$F$-invariant part is the lattice of special endomorphisms, in order to prove the required decay. See § 3.1.5 and the proof of Theorem 5.1.2 for more details.
We focus on the Siegel case from now on. Let ![]() $L_0$ denote the lattice of special endomorphisms of
$L_0$ denote the lattice of special endomorphisms of ![]() $A \mod t$, and let
$A \mod t$, and let ![]() $L_n \subset L_0$ be the lattice of special endomorphisms of
$L_n \subset L_0$ be the lattice of special endomorphisms of ![]() $A \mod t^{n+1}$. These lattices are of rank
$A \mod t^{n+1}$. These lattices are of rank ![]() $5$ and are equipped with natural quadratic forms such that
$5$ and are equipped with natural quadratic forms such that ![]() $A \mod t^{n+1}$ admits a special endomorphism of norm
$A \mod t^{n+1}$ admits a special endomorphism of norm ![]() $m$ if and only if
$m$ if and only if ![]() $m$ is represented by
$m$ is represented by ![]() $L_n$. Broadly speaking, we can bound the local contribution by using geometry-of-numbers techniques. To obtain the desired estimate, we choose the sequence
$L_n$. Broadly speaking, we can bound the local contribution by using geometry-of-numbers techniques. To obtain the desired estimate, we choose the sequence ![]() $m$ as follows. We first prove the existence of a rank
$m$ as follows. We first prove the existence of a rank ![]() $2$ sublattice
$2$ sublattice ![]() $P_n \subset L_n$ that has the following property: for all
$P_n \subset L_n$ that has the following property: for all ![]() $m$ bounded by an appropriate function of
$m$ bounded by an appropriate function of ![]() $n$, the abelian surface
$n$, the abelian surface ![]() $A \mod t^{n+1}$ has a special endomorphism of norm
$A \mod t^{n+1}$ has a special endomorphism of norm ![]() $m$ only if the quadratic form restricted to
$m$ only if the quadratic form restricted to ![]() $P_n$ represents
$P_n$ represents ![]() $m$. This fact follows from the existence of a rank
$m$. This fact follows from the existence of a rank ![]() $3$ submodule of special endomorphisms which decay rapidly (Theorem 5.1.2). Furthermore, the discriminant of
$3$ submodule of special endomorphisms which decay rapidly (Theorem 5.1.2). Furthermore, the discriminant of ![]() $P_n$ goes to infinity as
$P_n$ goes to infinity as ![]() $n\rightarrow \infty$. Therefore, the density of numbers (or primes, or prime-squares) represented by the binary quadratic form
$n\rightarrow \infty$. Therefore, the density of numbers (or primes, or prime-squares) represented by the binary quadratic form ![]() $P_n$ approaches zero, as
$P_n$ approaches zero, as ![]() $n\rightarrow \infty$. We now pick a sequence of prime-squares
$n\rightarrow \infty$. We now pick a sequence of prime-squares ![]() $m$ none of which are represented by
$m$ none of which are represented by ![]() $P_n$ defined by the finitely many supersingular points on
$P_n$ defined by the finitely many supersingular points on ![]() $C$.
$C$.
The non-ordinary locus is singular at superspecial points. This allows us to prove the existence of a special endomorphism that decays ‘more rapidly than expected’ (see Definition 5.1.1(3)). Consequently, by the explicit formula of Eisenstein series in these cases by [Reference Bruinier and KussBK01], we prove that the sum of local contributions at supersingular points is at most ![]() $11/12$ of the global contribution.
$11/12$ of the global contribution.
We remark that our proof is more involved than the proof of [Reference Chai and OortCO06, Proposition 7.3] because the intersection theory on Hilbert modular surfaces and Siegel three-folds is more complicated than that on the product of ![]() $j$-lines.
$j$-lines.
1.4 Additional remarks
The key difference between the number field and function field situation is the following. Let ![]() $A$ be an abelian surface over
$A$ be an abelian surface over ![]() $\mathcal {O}_K$, where
$\mathcal {O}_K$, where ![]() $K$ is a local field. The
$K$ is a local field. The ![]() $\mathbb {Z}_p$-module of special endomorphisms of
$\mathbb {Z}_p$-module of special endomorphisms of ![]() $A[p^{\infty }]$ has rank at most 3. This rank equals 3 if and only if
$A[p^{\infty }]$ has rank at most 3. This rank equals 3 if and only if ![]() $A$ can be realized as the limit point (in the analytic topology) of a sequence of CM points. This can happen in the mixed characteristic case, but not in the equicharacteristic
$A$ can be realized as the limit point (in the analytic topology) of a sequence of CM points. This can happen in the mixed characteristic case, but not in the equicharacteristic ![]() $p$ case unless
$p$ case unless ![]() $A$ is defined over a finite field.Footnote 4 Thus, we have a rank
$A$ is defined over a finite field.Footnote 4 Thus, we have a rank ![]() $3$ decay in the Decay Lemma (Theorem 5.1.2).
$3$ decay in the Decay Lemma (Theorem 5.1.2).
In the setting of higher-dimensional GSpin Shimura varieties, for the same reason, we expect that generalizations of the Decay Lemma will only yield a rank-![]() $3$
$3$ ![]() $\mathbb {Z}_p$-module that decays rapidly. This has the consequence of the existence of formal curves, such that the module of special endomorphisms of the
$\mathbb {Z}_p$-module that decays rapidly. This has the consequence of the existence of formal curves, such that the module of special endomorphisms of the ![]() $p$-divisible group over these formal curves have large rank. An interesting bi-algebraicity question is whether such formal curves can be algebraic without being special. In the ordinary case, Chai has the following conjecture.
$p$-divisible group over these formal curves have large rank. An interesting bi-algebraicity question is whether such formal curves can be algebraic without being special. In the ordinary case, Chai has the following conjecture.
Conjecture 6 [Reference ChaiChai03, Conjecture 7.2, Remark 7.2.1, Proposition 5.3, and Remark 5.3.1]
Let ![]() $X$ be a subvariety in a mod
$X$ be a subvariety in a mod ![]() $p$ Shimura variety passing through an ordinary point
$p$ Shimura variety passing through an ordinary point ![]() $P$. Assume that the formal germ of
$P$. Assume that the formal germ of ![]() $X$ at
$X$ at ![]() $P$ is a formal torus in the Serre–Tate coordinates. Then
$P$ is a formal torus in the Serre–Tate coordinates. Then ![]() $X$ is a Shimura subvariety.
$X$ is a Shimura subvariety.
1.5 Organization of the paper
In § 2, we recall the notion of special endomorphisms, special divisors and crystalline realization ![]() $\mathbb {L}_\mathrm {cris}$ of the automorphic vector bundle of special endomorphisms. In § 3, we recall the lattices of special endomorphisms of a supersingular point and compute
$\mathbb {L}_\mathrm {cris}$ of the automorphic vector bundle of special endomorphisms. In § 3, we recall the lattices of special endomorphisms of a supersingular point and compute ![]() $\mathbb {L}_{\mathrm {cris}}$ on its deformation space. In § 4, we recall Borcherds theory and the explicit formula for the Fourier coefficients of vector-valued Eisenstein series due to Bruinier and Kuss; we use them to compare the global intersection number and the
$\mathbb {L}_{\mathrm {cris}}$ on its deformation space. In § 4, we recall Borcherds theory and the explicit formula for the Fourier coefficients of vector-valued Eisenstein series due to Bruinier and Kuss; we use them to compare the global intersection number and the ![]() $\bmod \, t$ local intersection number at a supersingular point. Sections 5 and 6 are the key technical part of the paper. We prove the decay theorems for special endomorphisms, which we use to bound the higher local intersection multiplicities at supersingular points. Section 7 provides the outline of the main proofs and by geometry-of-numbers arguments, we prove Theorem 1(2) in § 8 and prove Theorems 1(1) and 5 in § 9.
$\bmod \, t$ local intersection number at a supersingular point. Sections 5 and 6 are the key technical part of the paper. We prove the decay theorems for special endomorphisms, which we use to bound the higher local intersection multiplicities at supersingular points. Section 7 provides the outline of the main proofs and by geometry-of-numbers arguments, we prove Theorem 1(2) in § 8 and prove Theorems 1(1) and 5 in § 9.
To get the main idea of the proof, the reader may focus on Theorem 1(2) and start from §§ 7 and 8 and refer back to §§ 3–5 when necessary.
1.6 Notation
We write ![]() $f\asymp g$ if
$f\asymp g$ if ![]() $f=O(g)$,
$f=O(g)$, ![]() $g=O(f)$. Throughout the paper,
$g=O(f)$. Throughout the paper, ![]() $p$ is an odd prime.
$p$ is an odd prime.
2. Special endomorphisms
In this section, we first introduce quadratic lattices ![]() $(L,Q)$ such that the associated GSpin Shimura varieties will be
$(L,Q)$ such that the associated GSpin Shimura varieties will be ![]() $\mathcal {A}_2$ and certain Hilbert modular surfaces related to the Heegner divisors
$\mathcal {A}_2$ and certain Hilbert modular surfaces related to the Heegner divisors ![]() $Z(m)$. The definition of special endomorphisms and Heegner divisors are given in § 2.2.
$Z(m)$. The definition of special endomorphisms and Heegner divisors are given in § 2.2.
2.1 The global lattice  $L$
$L$
For a quadratic ![]() $\mathbb {Z}$-lattice
$\mathbb {Z}$-lattice ![]() $(L,Q)$, let
$(L,Q)$, let ![]() $C(L)$ (respectively,
$C(L)$ (respectively, ![]() $C^+(L)$) denote the (respectively, even) Clifford algebra of
$C^+(L)$) denote the (respectively, even) Clifford algebra of ![]() $L$. Let
$L$. Let ![]() $(-)'$ denote the standard involution on
$(-)'$ denote the standard involution on ![]() $C(L)$ fixing all elements in
$C(L)$ fixing all elements in ![]() $L$ given by
$L$ given by ![]() $(v_1\cdots v_n)'=v_n\cdots v_1$ for
$(v_1\cdots v_n)'=v_n\cdots v_1$ for ![]() $v_i\in L$. Let
$v_i\in L$. Let ![]() $V$ denote
$V$ denote ![]() $L\otimes \mathbb {Q}$ endowed with the quadratic form
$L\otimes \mathbb {Q}$ endowed with the quadratic form ![]() $Q$. There is a bilinear form
$Q$. There is a bilinear form ![]() $[-,-]$ on
$[-,-]$ on ![]() $V$ given by
$V$ given by ![]() $[x,y]:=Q(x+y)-Q(x)-Q(y)$.
$[x,y]:=Q(x+y)-Q(x)-Q(y)$.
Let ![]() $L_{\rm S}$ be the rank-
$L_{\rm S}$ be the rank-![]() $5$
$5$ ![]() $\mathbb {Z}$-lattice endowed with the quadratic form
$\mathbb {Z}$-lattice endowed with the quadratic form ![]() $Q(x)=x_0^2+x_1x_2-x_3x_4$ for
$Q(x)=x_0^2+x_1x_2-x_3x_4$ for ![]() $x=(x_0, \ldots, x_4)\in \mathbb {Z}^5$. This quadratic form has signature
$x=(x_0, \ldots, x_4)\in \mathbb {Z}^5$. This quadratic form has signature ![]() $(3,2)$ and
$(3,2)$ and ![]() $L_{\rm S}$ is an even lattice, maximal among
$L_{\rm S}$ is an even lattice, maximal among ![]() $\mathbb {Z}$-valued sublattices in
$\mathbb {Z}$-valued sublattices in ![]() $L_{\rm S}\otimes \mathbb {Q}$. For
$L_{\rm S}\otimes \mathbb {Q}$. For ![]() $p>2$,
$p>2$, ![]() $L_{\rm S}$ is self-dual at
$L_{\rm S}$ is self-dual at ![]() $p$. A direct computation shows that
$p$. A direct computation shows that ![]() $C^+(L_{\rm S})\cong M_4(\mathbb {Z})$. Let
$C^+(L_{\rm S})\cong M_4(\mathbb {Z})$. Let
Then ![]() $\delta :=v_0\cdots v_4 \in C(L_{\rm S})$ lies in the center of
$\delta :=v_0\cdots v_4 \in C(L_{\rm S})$ lies in the center of ![]() $C(L_{\rm S})$ and
$C(L_{\rm S})$ and ![]() $\delta '=\delta, \delta ^2=1$. Therefore, there is an isomorphism between quadratic spaces given by
$\delta '=\delta, \delta ^2=1$. Therefore, there is an isomorphism between quadratic spaces given by ![]() $L_{\rm S}\xrightarrow []{\simeq } \delta L_{\rm S} \subset C^+(L_{\rm S})$. (See, for instance, [Reference Kudla and RapoportKR00, App. A].)
$L_{\rm S}\xrightarrow []{\simeq } \delta L_{\rm S} \subset C^+(L_{\rm S})$. (See, for instance, [Reference Kudla and RapoportKR00, App. A].)
Given a vector ![]() $x\in L_{\rm S}$ such that
$x\in L_{\rm S}$ such that ![]() $Q(x)=m, m\in \mathbb {Z}_{>0}$, the orthogonal complement
$Q(x)=m, m\in \mathbb {Z}_{>0}$, the orthogonal complement ![]() $x^\perp \subset L_{\rm S}$ endowed with the restriction of
$x^\perp \subset L_{\rm S}$ endowed with the restriction of ![]() $Q$ on
$Q$ on ![]() $x^\perp$ is a quadratic
$x^\perp$ is a quadratic ![]() $\mathbb {Z}$-lattice of signature
$\mathbb {Z}$-lattice of signature ![]() $(2,2)$ and let
$(2,2)$ and let ![]() $L_{\rm H}\subset x^\perp \otimes \mathbb {Q}$ be a maximal lattice containing
$L_{\rm H}\subset x^\perp \otimes \mathbb {Q}$ be a maximal lattice containing ![]() $x^\perp$. If
$x^\perp$. If ![]() $m$ is not a perfect square, let
$m$ is not a perfect square, let ![]() $F$ denote the real quadratic field
$F$ denote the real quadratic field ![]() $\mathbb {Q}(\sqrt {m})$. A direct computation shows that there is an isomorphism
$\mathbb {Q}(\sqrt {m})$. A direct computation shows that there is an isomorphism ![]() $L_{\rm H}\otimes \mathbb {Q}\cong \mathbb {Q}^2\oplus F$ such that
$L_{\rm H}\otimes \mathbb {Q}\cong \mathbb {Q}^2\oplus F$ such that ![]() $Q((a,b,\gamma ))=ab+\operatorname {Nm}_{F/\mathbb {Q}}\gamma$ (see, for instance, [Reference Howard and YangHY12, Proposition 2.2.2 (3)] and its proof).Footnote 5 The assumption
$Q((a,b,\gamma ))=ab+\operatorname {Nm}_{F/\mathbb {Q}}\gamma$ (see, for instance, [Reference Howard and YangHY12, Proposition 2.2.2 (3)] and its proof).Footnote 5 The assumption ![]() $p\nmid m$ and
$p\nmid m$ and ![]() $p>2$ implies that
$p>2$ implies that ![]() $x^\perp$ and, hence,
$x^\perp$ and, hence, ![]() $L_{\rm H}$ are self-dual at
$L_{\rm H}$ are self-dual at ![]() $p$.
$p$.
Now let ![]() $(L,Q)$ have signature
$(L,Q)$ have signature ![]() $(n,2)$, and let
$(n,2)$, and let ![]() $p$ be a prime such
$p$ be a prime such ![]() $(L,Q)$ is self-dual at
$(L,Q)$ is self-dual at ![]() $p$. As in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, §§ 4.1 and 4.2] and [Reference Kudla and RapoportKR00, § 1], there is a GSpin Shimura variety
$p$. As in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, §§ 4.1 and 4.2] and [Reference Kudla and RapoportKR00, § 1], there is a GSpin Shimura variety ![]() $M$ attached to
$M$ attached to ![]() $(L,Q)$ and this Shimura variety also admits a smooth integral model
$(L,Q)$ and this Shimura variety also admits a smooth integral model ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathbb {Z}_{(p)}$ because
$\mathbb {Z}_{(p)}$ because ![]() $L$ is self-dual at
$L$ is self-dual at ![]() $p$; the Shimura variety (and its integral model) recovers the moduli space of principally polarized abelian surfaces when
$p$; the Shimura variety (and its integral model) recovers the moduli space of principally polarized abelian surfaces when ![]() $L=L_{\rm S}$ (see Remark 2.2.2 for details) and it is a Hilbert modular surface when
$L=L_{\rm S}$ (see Remark 2.2.2 for details) and it is a Hilbert modular surface when ![]() $L=L_{\rm H}$ (see, for instance, [Reference Howard and YangHY12, §§ 2.2 and 3.1]). We may write
$L=L_{\rm H}$ (see, for instance, [Reference Howard and YangHY12, §§ 2.2 and 3.1]). We may write ![]() $M_L$ and
$M_L$ and ![]() $\mathcal {M}_L$ to emphasis on the dependence on
$\mathcal {M}_L$ to emphasis on the dependence on ![]() $L$.
$L$.
To prove Theorems 1(1) and 5 we take ![]() $L=L_{\rm S}$ and to prove Theorem 1(2) we take
$L=L_{\rm S}$ and to prove Theorem 1(2) we take ![]() $L=L_{\rm H}$.
$L=L_{\rm H}$.
2.2 Special endomorphisms and special divisors
We first introduce the notion of special endomorphisms when ![]() $L=L_{\rm S}$ and
$L=L_{\rm S}$ and ![]() $\mathcal {M}$ is the moduli space of principally polarized abelian surfaces. Given an
$\mathcal {M}$ is the moduli space of principally polarized abelian surfaces. Given an ![]() $\mathcal {M}$-scheme
$\mathcal {M}$-scheme ![]() $S$, let
$S$, let ![]() $A_S$ denote the pull-back of the universal principally polarized abelian surface on
$A_S$ denote the pull-back of the universal principally polarized abelian surface on ![]() $\mathcal {M}$ via
$\mathcal {M}$ via ![]() $S\rightarrow \mathcal {M}$; let
$S\rightarrow \mathcal {M}$; let ![]() ${\dagger}$ denote the Rosati involution on
${\dagger}$ denote the Rosati involution on ![]() $A_S$.
$A_S$.
Definition 2.2.1 A special endomorphism of ![]() $A_S$ is an element
$A_S$ is an element ![]() $s\in \operatorname {End}(A_S)$ such that
$s\in \operatorname {End}(A_S)$ such that ![]() $s^{\dagger} =s$ and
$s^{\dagger} =s$ and ![]() $\operatorname {Tr} s=0$, where
$\operatorname {Tr} s=0$, where ![]() $\operatorname {Tr}$ is the reduced trace on the semisimple algebra
$\operatorname {Tr}$ is the reduced trace on the semisimple algebra ![]() $\operatorname {End}(A_S)\otimes \mathbb {Q}$.
$\operatorname {End}(A_S)\otimes \mathbb {Q}$.
Remark 2.2.2 Our definition of special endomorphisms is essentially the same as the one given by Kudla and Rapoport [Reference Kudla and RapoportKR00, Definition 2.1 and (2.21)]. Indeed, as in [Reference Kudla and RapoportKR00, §§ 1 and 2], the moduli problem indicates that every ![]() $\mathcal {M}$-scheme
$\mathcal {M}$-scheme ![]() $S$ gives rise to a principally polarized abelian scheme
$S$ gives rise to a principally polarized abelian scheme ![]() $B_S$ over
$B_S$ over ![]() $S$ with
$S$ with ![]() $\iota : C^+(L)\hookrightarrow \operatorname {End}(B_S)$ and a polarization such that the induced Rosati involution
$\iota : C^+(L)\hookrightarrow \operatorname {End}(B_S)$ and a polarization such that the induced Rosati involution ![]() ${\dagger}$ satisfies
${\dagger}$ satisfies ![]() $\iota (c)^{\dagger} =\iota (c^T)$, where
$\iota (c)^{\dagger} =\iota (c^T)$, where ![]() $(-)^T$ is the transpose on
$(-)^T$ is the transpose on ![]() $C^+(L)\simeq M_4(\mathbb {Z})$ (see condition (iii) and the first paragraph of [Reference Kudla and RapoportKR00, p. 701]); moreover, for each
$C^+(L)\simeq M_4(\mathbb {Z})$ (see condition (iii) and the first paragraph of [Reference Kudla and RapoportKR00, p. 701]); moreover, for each ![]() $\ell \neq p$, there is an isomorphism
$\ell \neq p$, there is an isomorphism ![]() $C^+(L)\otimes \mathbb {Z}_\ell \simeq T_\ell (B_S)$, where
$C^+(L)\otimes \mathbb {Z}_\ell \simeq T_\ell (B_S)$, where ![]() $T_\ell$ denotes the
$T_\ell$ denotes the ![]() $\ell$-adic Tate module, compatible with the
$\ell$-adic Tate module, compatible with the ![]() $C^+(L)$-action (it acts on itself via left multiplication; see [Reference Kudla and RapoportKR00, p. 703]).Footnote 6 Therefore, via
$C^+(L)$-action (it acts on itself via left multiplication; see [Reference Kudla and RapoportKR00, p. 703]).Footnote 6 Therefore, via ![]() $\iota$, we have
$\iota$, we have ![]() $B_S\cong A_S^4$, where
$B_S\cong A_S^4$, where ![]() $A_S$ is an abelian surface and by the compatibility of the polarization with
$A_S$ is an abelian surface and by the compatibility of the polarization with ![]() $\iota$ (see also [Reference Kudla and RapoportKR00, Equations (1.9) and (1.10)]), and the polarization on
$\iota$ (see also [Reference Kudla and RapoportKR00, Equations (1.9) and (1.10)]), and the polarization on ![]() $B_S$ is induced by the self-product of a principal polarization on
$B_S$ is induced by the self-product of a principal polarization on ![]() $A_S$. Hence,
$A_S$. Hence, ![]() $\mathcal {M}$ parameterizes principally polarized abelian surfaces. Moreover, an element
$\mathcal {M}$ parameterizes principally polarized abelian surfaces. Moreover, an element ![]() $s_B$ in
$s_B$ in ![]() $\operatorname {End}(B_S)\cong M_4(\operatorname {End}(A_S))$ commuting with
$\operatorname {End}(B_S)\cong M_4(\operatorname {End}(A_S))$ commuting with ![]() $\iota (C^+(L))$ is of form
$\iota (C^+(L))$ is of form ![]() $\operatorname {diag}(s,s,s,s)$, where an endomorphism
$\operatorname {diag}(s,s,s,s)$, where an endomorphism ![]() $s$ of
$s$ of ![]() $A_S$. In the sense of Kudla and Rapoport, such
$A_S$. In the sense of Kudla and Rapoport, such ![]() $s_B$ is special if and only if it is traceless and fixed by the Rosati involution on
$s_B$ is special if and only if it is traceless and fixed by the Rosati involution on ![]() $B_S$; this is equivalent to that
$B_S$; this is equivalent to that ![]() $s$ is traceless and fixed by the Rosati involution on
$s$ is traceless and fixed by the Rosati involution on ![]() $A_S$. Therefore, our definition is the same as that of Kudla and Rapoport.
$A_S$. Therefore, our definition is the same as that of Kudla and Rapoport.
Definition 2.2.3 Let ![]() $\mathbb {D}$ denote the Dieudonné crystal over
$\mathbb {D}$ denote the Dieudonné crystal over ![]() $\mathcal {M}_{\mathbb {F}_p}$ (i.e. the first relative crystalline homology of the universal family of principally polarized abelian surface over
$\mathcal {M}_{\mathbb {F}_p}$ (i.e. the first relative crystalline homology of the universal family of principally polarized abelian surface over ![]() $\mathcal {M}_{\mathbb {F}_p}$). Let
$\mathcal {M}_{\mathbb {F}_p}$). Let ![]() $\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of trace
$\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of trace ![]() $0$ elements fixed by the Rosati involution.Footnote 7
$0$ elements fixed by the Rosati involution.Footnote 7
By definition, when ![]() $S$ is a
$S$ is a ![]() $\mathcal {M}_{\mathbb {F}_p}$-scheme, an element
$\mathcal {M}_{\mathbb {F}_p}$-scheme, an element ![]() $s\in \operatorname {End}(A_S)$ is a special endomorphism if and only if the crystalline realization of
$s\in \operatorname {End}(A_S)$ is a special endomorphism if and only if the crystalline realization of ![]() $s\in \operatorname {End}(\mathbb {D}_S)$ lies in
$s\in \operatorname {End}(\mathbb {D}_S)$ lies in ![]() $\mathbb {L}_{\mathrm {cris},S}$.
$\mathbb {L}_{\mathrm {cris},S}$.
Definition 2.2.4 For the ![]() $p$-divisible group
$p$-divisible group ![]() $A_S[p^\infty ]$, we say
$A_S[p^\infty ]$, we say ![]() $s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of
$s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of ![]() $s$ in
$s$ in ![]() $\operatorname {End}(\mathbb {D}_S)$ lies in
$\operatorname {End}(\mathbb {D}_S)$ lies in ![]() $\mathbb {L}_{\mathrm {cris},S}$.
$\mathbb {L}_{\mathrm {cris},S}$.
Remark 2.2.5 In [Reference Madapusi PeraMP16, § 4.14], there is a definition of ![]() $\mathbb {L}_\mathrm {cris}$ as a direct summand of the endomorphism of the first relative crystalline cohomology of the Kuga–Satake abelian scheme over
$\mathbb {L}_\mathrm {cris}$ as a direct summand of the endomorphism of the first relative crystalline cohomology of the Kuga–Satake abelian scheme over ![]() $\mathcal {M}_{\mathbb {F}_p}$. More precisely, the left multiplication of
$\mathcal {M}_{\mathbb {F}_p}$. More precisely, the left multiplication of ![]() $\operatorname {GSpin}(V,Q)\subset C^+(V)^\times$ acting on
$\operatorname {GSpin}(V,Q)\subset C^+(V)^\times$ acting on ![]() $C(V)$ induces a variation of Hodge structures on
$C(V)$ induces a variation of Hodge structures on ![]() $C(V)$ over
$C(V)$ over ![]() $M$; this gives rise to the Kuga–Satake abelian scheme
$M$; this gives rise to the Kuga–Satake abelian scheme ![]() $A^{\mathrm {KS}}$ over
$A^{\mathrm {KS}}$ over ![]() $M$ and the Kuga–Satake abelian scheme extends over
$M$ and the Kuga–Satake abelian scheme extends over ![]() $\mathcal {M}$. The
$\mathcal {M}$. The ![]() $8$-dimensional abelian scheme considered by Kudla and Rapoport is a sub abelian scheme of
$8$-dimensional abelian scheme considered by Kudla and Rapoport is a sub abelian scheme of ![]() $A^{\mathrm {KS}}$ via the natural embedding
$A^{\mathrm {KS}}$ via the natural embedding ![]() $C^+(V)\subset C(V)$. (Note that in [Reference Kudla and RapoportKR00],
$C^+(V)\subset C(V)$. (Note that in [Reference Kudla and RapoportKR00], ![]() $\gamma \in \operatorname {GSpin}(V,Q)$ acts on
$\gamma \in \operatorname {GSpin}(V,Q)$ acts on ![]() $C^+(V)$ by the right multiplication by
$C^+(V)$ by the right multiplication by ![]() $\gamma$ and
$\gamma$ and ![]() $C^+(V)$ acts on
$C^+(V)$ acts on ![]() $C^+(V)$ by left multiplication, which is opposite to the convention in [Reference Madapusi PeraMP16]. This difference is due to the different choices of the symplectic pairing on
$C^+(V)$ by left multiplication, which is opposite to the convention in [Reference Madapusi PeraMP16]. This difference is due to the different choices of the symplectic pairing on ![]() $C^+(V)$ and
$C^+(V)$ and ![]() $C(V)$ in [Reference Kudla and RapoportKR00, (1.9)] and [Reference Madapusi PeraMP16, § 1.6]. If we use the symplectic pairing in [Reference Madapusi PeraMP16] for the discussion in [Reference Kudla and RapoportKR00], then we obtain similar results as in [Reference Kudla and RapoportKR00] but with the convention consistent with that in [Reference Madapusi PeraMP16].)
$C(V)$ in [Reference Kudla and RapoportKR00, (1.9)] and [Reference Madapusi PeraMP16, § 1.6]. If we use the symplectic pairing in [Reference Madapusi PeraMP16] for the discussion in [Reference Kudla and RapoportKR00], then we obtain similar results as in [Reference Kudla and RapoportKR00] but with the convention consistent with that in [Reference Madapusi PeraMP16].)
Let ![]() $\mathbb {D}^{\mathrm {KS}}$ denote the Dieudonné crystal of
$\mathbb {D}^{\mathrm {KS}}$ denote the Dieudonné crystal of ![]() $A^{\mathrm {KS}}$ over
$A^{\mathrm {KS}}$ over ![]() $\mathcal {M}_{\mathbb {F}_p}$; Madapusi Pera defined
$\mathcal {M}_{\mathbb {F}_p}$; Madapusi Pera defined ![]() $\mathbb {L}_\mathrm {cris} \subset \operatorname {End} (\mathbb {D}^{\mathrm {KS}})$ by the crystalline realization of the absolute Hodge cycle induced by the
$\mathbb {L}_\mathrm {cris} \subset \operatorname {End} (\mathbb {D}^{\mathrm {KS}})$ by the crystalline realization of the absolute Hodge cycle induced by the ![]() $\operatorname {GSpin}(V,Q)$-invariant idempotent which realizes
$\operatorname {GSpin}(V,Q)$-invariant idempotent which realizes ![]() $V\subset \operatorname {End}(C(V))$ as a direct summand. As the element
$V\subset \operatorname {End}(C(V))$ as a direct summand. As the element ![]() $\delta$ given in § 2.1 lies in the center of
$\delta$ given in § 2.1 lies in the center of ![]() $C(L)$, then it induces an isomorphism
$C(L)$, then it induces an isomorphism ![]() $\operatorname {End}(C(L))\supset L \cong \delta L \subset \operatorname {End}(C^+(L))$ compatible with
$\operatorname {End}(C(L))\supset L \cong \delta L \subset \operatorname {End}(C^+(L))$ compatible with ![]() $\operatorname {GSpin}(V,Q)$-action. Therefore,
$\operatorname {GSpin}(V,Q)$-action. Therefore, ![]() $\delta$ induces an isomorphism between the crystals
$\delta$ induces an isomorphism between the crystals ![]() $\mathbb {L}_\mathrm {cris}$ in our sense and that in the sense of Madapusi Pera; in particular, the notions of special endomorphisms coincide under the identification via
$\mathbb {L}_\mathrm {cris}$ in our sense and that in the sense of Madapusi Pera; in particular, the notions of special endomorphisms coincide under the identification via ![]() $\delta$. In addition, for a special endomorphism
$\delta$. In addition, for a special endomorphism ![]() $s$ in both cases,
$s$ in both cases, ![]() $s\circ s$ is a scalar multiple
$s\circ s$ is a scalar multiple ![]() $Q(s)$ on the suitable abelian scheme; because
$Q(s)$ on the suitable abelian scheme; because ![]() $\delta ^2=1$, hence
$\delta ^2=1$, hence ![]() $Q(s)$ remains the same for images of
$Q(s)$ remains the same for images of ![]() $s$ under various identification of special endomorphisms. By [Reference Madapusi PeraMP16, Lemma 5.2],
$s$ under various identification of special endomorphisms. By [Reference Madapusi PeraMP16, Lemma 5.2], ![]() $Q(s)>0$ for all non-zero special endomorphism
$Q(s)>0$ for all non-zero special endomorphism ![]() $s$.
$s$.
Definition 2.2.6 For ![]() $m\in \mathbb {Z}_{>0}$, the special divisor
$m\in \mathbb {Z}_{>0}$, the special divisor ![]() $\mathcal {Z}(m)$ is the Deligne–Mumford stack over
$\mathcal {Z}(m)$ is the Deligne–Mumford stack over ![]() $\mathcal {M}$ with functor of points
$\mathcal {M}$ with functor of points ![]() $\mathcal {Z}(m)(S) = \{s\in \operatorname {End}(A_S) \text { special } |\ Q(s) = m\}$ for any
$\mathcal {Z}(m)(S) = \{s\in \operatorname {End}(A_S) \text { special } |\ Q(s) = m\}$ for any ![]() $\mathcal {M}$-scheme
$\mathcal {M}$-scheme ![]() $S$. We use the same notation for the image of
$S$. We use the same notation for the image of ![]() $\mathcal {Z}(m)$ in
$\mathcal {Z}(m)$ in ![]() $\mathcal {M}$. By, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8],
$\mathcal {M}$. By, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8], ![]() $\mathcal {Z}(m)$ is flat over
$\mathcal {Z}(m)$ is flat over ![]() $\mathbb {Z}_{(p)}$ and hence
$\mathbb {Z}_{(p)}$ and hence ![]() $\mathcal {Z}(m)_{\mathbb {F}_p}$ is still a divisor of
$\mathcal {Z}(m)_{\mathbb {F}_p}$ is still a divisor of ![]() $\mathcal {M}_{\mathbb {F}_p}$; we denote
$\mathcal {M}_{\mathbb {F}_p}$; we denote ![]() $\mathcal {Z}(m)_{\mathbb {F}_p}$ by
$\mathcal {Z}(m)_{\mathbb {F}_p}$ by ![]() $Z(m)$.
$Z(m)$.
Lemma 2.2.7 Every ![]() $\bar {\mathbb {F}}_p$-point of
$\bar {\mathbb {F}}_p$-point of ![]() $Z(m^2)$ corresponds to a geometrically non-simple abelian surface.
$Z(m^2)$ corresponds to a geometrically non-simple abelian surface.
Proof. Let ![]() $s$ be a special endomorphism of an abelian surface
$s$ be a special endomorphism of an abelian surface ![]() $A$ such that
$A$ such that ![]() $s\circ s=[m^2]$. Then
$s\circ s=[m^2]$. Then ![]() $(s-[m])\circ (s+[m])=0$. As
$(s-[m])\circ (s+[m])=0$. As ![]() $\operatorname {Tr} s=0$, then
$\operatorname {Tr} s=0$, then ![]() $s\pm [m]\neq 0$ and, hence,
$s\pm [m]\neq 0$ and, hence, ![]() $s\pm [m]$ are not invertible. Then
$s\pm [m]$ are not invertible. Then ![]() $\ker (s-[m])$ defines a non-trivial sub abelian scheme of
$\ker (s-[m])$ defines a non-trivial sub abelian scheme of ![]() $A$.
$A$.
We now discuss the case when ![]() $L=L_{\rm H}$. We keep the same notation as in § 2.1. For simplicity, we first discuss the case when
$L=L_{\rm H}$. We keep the same notation as in § 2.1. For simplicity, we first discuss the case when ![]() $L_{\rm H}=x^\perp$, where
$L_{\rm H}=x^\perp$, where ![]() $x\in L_{\rm S}$ and
$x\in L_{\rm S}$ and ![]() $Q(x)=m$ with
$Q(x)=m$ with ![]() $p\nmid m$; for the general case, the following discussion still holds true when replacing endomorphisms with suitable elements in
$p\nmid m$; for the general case, the following discussion still holds true when replacing endomorphisms with suitable elements in ![]() $\operatorname {End} \otimes \mathbb {Q}$ (see the end of this subsection). When
$\operatorname {End} \otimes \mathbb {Q}$ (see the end of this subsection). When ![]() $L_{\rm H}=x^\perp \subset L_{\rm S}$, the Shimura variety (and its integral model)
$L_{\rm H}=x^\perp \subset L_{\rm S}$, the Shimura variety (and its integral model) ![]() $\mathcal {M}_{L_{\rm H}}$ defined by
$\mathcal {M}_{L_{\rm H}}$ defined by ![]() $L_{\rm H}$ is naturally a sub-Shimura variety of
$L_{\rm H}$ is naturally a sub-Shimura variety of ![]() $\mathcal {M}_{L_{\rm S}}$, the moduli space of principally polarized abelian surfaces and, hence, a point on
$\mathcal {M}_{L_{\rm S}}$, the moduli space of principally polarized abelian surfaces and, hence, a point on ![]() $\mathcal {M}_{L_{\rm H}}$ corresponds to a polarized abelian surface with real multiplication by
$\mathcal {M}_{L_{\rm H}}$ corresponds to a polarized abelian surface with real multiplication by ![]() $\mathcal {O}:=\mathbb {Z}[x]/(x^2-m)$. Let
$\mathcal {O}:=\mathbb {Z}[x]/(x^2-m)$. Let ![]() $\sigma$ denote the ring automorphism on
$\sigma$ denote the ring automorphism on ![]() $\mathcal {O}$ satisfying
$\mathcal {O}$ satisfying ![]() $x^{\sigma } = -x$. As before, let
$x^{\sigma } = -x$. As before, let ![]() $S$ be a
$S$ be a ![]() $\mathcal {M}_{L_{\rm H}}$-scheme, and let
$\mathcal {M}_{L_{\rm H}}$-scheme, and let ![]() $A_S$ denote the abelian surface over
$A_S$ denote the abelian surface over ![]() $S$ with real multiplication by
$S$ with real multiplication by ![]() $\mathcal {O}$.
$\mathcal {O}$.
Definition 2.2.8 [Reference Howard and YangHY12, § 3.1, p. 26]
A special endomorphism (respectively, special quasi- endomorphism) of ![]() $A_S$ is an element
$A_S$ is an element ![]() $s\in \operatorname {End}(A_S)$ (respectively,
$s\in \operatorname {End}(A_S)$ (respectively, ![]() $s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$) such that
$s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$) such that ![]() $s^{\dagger} =s$ and
$s^{\dagger} =s$ and ![]() $s\circ f =f^\sigma \circ s$ for all
$s\circ f =f^\sigma \circ s$ for all ![]() $f\in \mathcal {O}$.
$f\in \mathcal {O}$.
We still use ![]() $\mathbb {D}$ to denote the pull-back to
$\mathbb {D}$ to denote the pull-back to ![]() $\mathcal {M}_{L_{\rm H}, \mathbb {F}_p}$ the Dieudonné crystal over
$\mathcal {M}_{L_{\rm H}, \mathbb {F}_p}$ the Dieudonné crystal over ![]() $\mathcal {M}_{L_{\rm S}, \mathbb {F}_p}$ in Definition 2.2.3; since the abelian surfaces over
$\mathcal {M}_{L_{\rm S}, \mathbb {F}_p}$ in Definition 2.2.3; since the abelian surfaces over ![]() $\mathcal {M}_{L_{\rm H}}$ admit an
$\mathcal {M}_{L_{\rm H}}$ admit an ![]() $\mathcal {O}$-action, the Dieudonné crystal
$\mathcal {O}$-action, the Dieudonné crystal ![]() $\mathbb {D}$ is also endowed with an
$\mathbb {D}$ is also endowed with an ![]() $\mathcal {O}$-action.
$\mathcal {O}$-action.
Definition 2.2.9 Let ![]() $\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of elements
$\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of elements ![]() $v$ fixed by Rosati involution and
$v$ fixed by Rosati involution and ![]() $s\circ f=f^\sigma \circ s$ for all
$s\circ f=f^\sigma \circ s$ for all ![]() $f\in \mathcal {O}$. For the
$f\in \mathcal {O}$. For the ![]() $p$-divisible group
$p$-divisible group ![]() $A_S[p^\infty ]$, we say
$A_S[p^\infty ]$, we say ![]() $s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of
$s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of ![]() $s$ in
$s$ in ![]() $\operatorname {End}(\mathbb {D}_S)$ lies in
$\operatorname {End}(\mathbb {D}_S)$ lies in ![]() $\mathbb {L}_{\mathrm {cris},S}$.
$\mathbb {L}_{\mathrm {cris},S}$.
Remark 2.2.10 By Remark 2.2.5 and [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP17, Proposition 2.5.1 and Prop. 2.6.4], to show that the above definitions of special endomorphisms and ![]() $\mathbb {L}_\mathrm {cris}$ can be identified with those by Madapusi Pera, we only need to show that for an endomorphism
$\mathbb {L}_\mathrm {cris}$ can be identified with those by Madapusi Pera, we only need to show that for an endomorphism ![]() $s$ (of either the abelian surface or of its Dieudonné crystal
$s$ (of either the abelian surface or of its Dieudonné crystal ![]() $\mathbb {D}$) fixed by the Rosati involution is traceless and orthogonal to
$\mathbb {D}$) fixed by the Rosati involution is traceless and orthogonal to ![]() $x$ if and only if
$x$ if and only if ![]() $s\circ x=-x\circ s$. To see this, note that if
$s\circ x=-x\circ s$. To see this, note that if ![]() $\operatorname {Tr} s=0$, then
$\operatorname {Tr} s=0$, then ![]() $s\perp x$ if and only if
$s\perp x$ if and only if ![]() $Q(s+x)-Q(s)-Q(x)=s\circ x+x\circ s=0$; on the other hand, if
$Q(s+x)-Q(s)-Q(x)=s\circ x+x\circ s=0$; on the other hand, if ![]() $s\circ x=-x\circ s$, then
$s\circ x=-x\circ s$, then ![]() $x^{-1}\circ s \circ x =-s$ and, hence,
$x^{-1}\circ s \circ x =-s$ and, hence, ![]() $\operatorname {Tr} s=0$.
$\operatorname {Tr} s=0$.
2.2.11
In general (i.e. when ![]() $x^\perp \subsetneq L_{\rm H}$), we may still use the same definition for
$x^\perp \subsetneq L_{\rm H}$), we may still use the same definition for ![]() $\mathbb {L}_\mathrm {cris}$ and special endomorphisms of
$\mathbb {L}_\mathrm {cris}$ and special endomorphisms of ![]() $p$-divisible groups, as
$p$-divisible groups, as ![]() $x^\perp$ is self-dual at
$x^\perp$ is self-dual at ![]() $p$ and, hence,
$p$ and, hence, ![]() $x^\perp \otimes \mathbb {Z}_p = L_{\rm H} \otimes \mathbb {Z}_p$. On the other hand, we consider special quasi-endomorphisms
$x^\perp \otimes \mathbb {Z}_p = L_{\rm H} \otimes \mathbb {Z}_p$. On the other hand, we consider special quasi-endomorphisms ![]() $s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$ which satisfy the following integrality condition: the
$s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$ which satisfy the following integrality condition: the ![]() $\ell$-adic realizations of
$\ell$-adic realizations of ![]() $s$ lie in
$s$ lie in ![]() $L_{\rm H}\otimes \mathbb {Z}_\ell \subset \operatorname {End}(T_\ell (A_S)\otimes \mathbb {Q}_\ell )$ for all
$L_{\rm H}\otimes \mathbb {Z}_\ell \subset \operatorname {End}(T_\ell (A_S)\otimes \mathbb {Q}_\ell )$ for all ![]() $\ell \neq p$ and the crystalline realizations of
$\ell \neq p$ and the crystalline realizations of ![]() $s$ lie in
$s$ lie in ![]() $\mathbb {L}_{\mathrm {cris}, S}$. As in Definition 2.2.6, the special divisor
$\mathbb {L}_{\mathrm {cris}, S}$. As in Definition 2.2.6, the special divisor ![]() $\mathcal {Z}(m)$ is the Deligne–Mumford stack over
$\mathcal {Z}(m)$ is the Deligne–Mumford stack over ![]() $\mathcal {M}_{L_{\rm H}}$ with
$\mathcal {M}_{L_{\rm H}}$ with ![]() $\mathcal {Z}(m)(S)$ given by
$\mathcal {Z}(m)(S)$ given by
 \begin{align*} &\big\{s\in \operatorname{End}(A_S)\otimes\mathbb{Q} \text{ special quasi-endomorphism satisfying the integrality condition above }\\ &\quad \mid Q(s)=m\big\} \end{align*}
\begin{align*} &\big\{s\in \operatorname{End}(A_S)\otimes\mathbb{Q} \text{ special quasi-endomorphism satisfying the integrality condition above }\\ &\quad \mid Q(s)=m\big\} \end{align*}
for any ![]() $\mathcal {M}$-scheme
$\mathcal {M}$-scheme ![]() $S$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8], where they used [Reference Madapusi PeraMP16, Proposition 5.21],
$S$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8], where they used [Reference Madapusi PeraMP16, Proposition 5.21], ![]() $\mathcal {Z}(m)$ is flat over
$\mathcal {Z}(m)$ is flat over ![]() $\mathbb {Z}_p$. We use
$\mathbb {Z}_p$. We use ![]() $Z(m)$ to denote the image of
$Z(m)$ to denote the image of ![]() $\mathcal {Z}(m)_{\mathbb {F}_p}$ in
$\mathcal {Z}(m)_{\mathbb {F}_p}$ in ![]() $\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$, which is a divisor in
$\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$, which is a divisor in ![]() $\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$.
$\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$.
2.3 Lattices of special endomorphisms of supersingular points
For a fixed supersingular point, let ![]() $A$ denote the abelian surface attached to this point.
$A$ denote the abelian surface attached to this point.
Definition 2.3.1 Let ![]() $L''$ denote the
$L''$ denote the ![]() $\mathbb {Z}$-lattice of special endomorphisms of
$\mathbb {Z}$-lattice of special endomorphisms of ![]() $A$ (respectively, special quasi-endomorphisms when
$A$ (respectively, special quasi-endomorphisms when ![]() $L=L_{\rm H}$). Let
$L=L_{\rm H}$). Let ![]() $L''\subset L'\subset L''\otimes \mathbb {Q}$ be a
$L''\subset L'\subset L''\otimes \mathbb {Q}$ be a ![]() $\mathbb {Z}$-lattice which is maximal at all
$\mathbb {Z}$-lattice which is maximal at all ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $L''\otimes \mathbb {Z}_p=L'\otimes \mathbb {Z}_p$. Let
$L''\otimes \mathbb {Z}_p=L'\otimes \mathbb {Z}_p$. Let ![]() $Q'$ denote the natural quadratic form on
$Q'$ denote the natural quadratic form on ![]() $L'$ given by
$L'$ given by ![]() $s\circ s=[Q'(s)]\in \operatorname {End}(A)\otimes \mathbb {Q}$. By the positivity of the Rosati involution,
$s\circ s=[Q'(s)]\in \operatorname {End}(A)\otimes \mathbb {Q}$. By the positivity of the Rosati involution, ![]() $Q'$ is positive definite (see, for instance, [Reference Madapusi PeraMP16, Lemma 5.12]).
$Q'$ is positive definite (see, for instance, [Reference Madapusi PeraMP16, Lemma 5.12]).
Even though there seem to be choices involved here, we see that for our computation, these choices do not matter and the result only depends on the Ekedahl–Oort stratum that the supersingular point lies in. The information of ![]() $L'\otimes \mathbb {Z}_p$ is provided in § 3.
$L'\otimes \mathbb {Z}_p$ is provided in § 3.
Lemma 2.3.2 We have ![]() $(L'\otimes \mathbb {Z}_\ell, Q')\cong (L\otimes \mathbb {Z}_\ell, Q)$ for
$(L'\otimes \mathbb {Z}_\ell, Q')\cong (L\otimes \mathbb {Z}_\ell, Q)$ for ![]() $\ell \neq p$.
$\ell \neq p$.
Proof. Both lattices shall be maximal at ![]() $\ell$ and by [Reference Howard and PappasHP17, Remark 7.2.5],
$\ell$ and by [Reference Howard and PappasHP17, Remark 7.2.5], ![]() $(L'\otimes \mathbb {Q}_\ell, Q')\cong (L\otimes \mathbb {Q}_\ell, Q)$. Then we conclude by the fact that there is a unique isometry class of
$(L'\otimes \mathbb {Q}_\ell, Q')\cong (L\otimes \mathbb {Q}_\ell, Q)$. Then we conclude by the fact that there is a unique isometry class of ![]() $\mathbb {Z}_\ell$-maximal sublattices of a given
$\mathbb {Z}_\ell$-maximal sublattices of a given ![]() $\mathbb {Q}_\ell$-quadratic space (see, for instance, [Reference Howard and PappasHP17, Theorem A.1.2]).
$\mathbb {Q}_\ell$-quadratic space (see, for instance, [Reference Howard and PappasHP17, Theorem A.1.2]).
Remark 2.3.3 Actually, for the case of Hilbert modular surfaces, the essential part of the above lemma is [Reference Howard and YangHY12, Proposition 3.1.3]. For the ![]() $\mathcal {A}_2$ case, we can explicitly compute
$\mathcal {A}_2$ case, we can explicitly compute ![]() $L''$ as follows and it is maximal. By [Reference EkedahlEke87, Proposition 5.2], for any
$L''$ as follows and it is maximal. By [Reference EkedahlEke87, Proposition 5.2], for any ![]() $\ell \neq p$, there is a unique class (up to
$\ell \neq p$, there is a unique class (up to ![]() $\operatorname {GL}_4(\mathbb {Z}_\ell )$-conjugation) of principal polarizations on the Tate module
$\operatorname {GL}_4(\mathbb {Z}_\ell )$-conjugation) of principal polarizations on the Tate module ![]() $T_\ell (A)$. Therefore, to compute
$T_\ell (A)$. Therefore, to compute ![]() $L''\otimes \mathbb {Z}_\ell$, we may assume that
$L''\otimes \mathbb {Z}_\ell$, we may assume that ![]() $A=E^2$ and endowed with the product principal polarization, where
$A=E^2$ and endowed with the product principal polarization, where ![]() $E$ is a supersingular elliptic curve. Hence, the quadratic form on the lattice
$E$ is a supersingular elliptic curve. Hence, the quadratic form on the lattice ![]() $L''$, which is the trace
$L''$, which is the trace ![]() $0$ part of
$0$ part of ![]() $H^2(A)$, is given by
$H^2(A)$, is given by ![]() $x_0^2+\operatorname {Nm}$, where
$x_0^2+\operatorname {Nm}$, where ![]() $\operatorname {Nm}$ is the quadratic form given by the reduced norm on the quaternion algebra
$\operatorname {Nm}$ is the quadratic form given by the reduced norm on the quaternion algebra ![]() $\operatorname {End}(E)$.
$\operatorname {End}(E)$.
3. The  $F$-crystals
$F$-crystals  $\mathbb {L}_{\mathrm {cris}}$ on local deformation spaces of supersingular points
$\mathbb {L}_{\mathrm {cris}}$ on local deformation spaces of supersingular points
Let ![]() $p$ be an odd prime. In this section, we compute the lattices (
$p$ be an odd prime. In this section, we compute the lattices (![]() $L''\otimes \mathbb {Z}_p$ in Definition 2.3.1) of special endomorphisms of supersingular points with the natural quadratic forms following Howard and Pappas [Reference Howard and PappasHP17, §§ 5 and 6].Footnote 8 In conjunction with [Reference KisinKis10, § 1], we then obtain
$L''\otimes \mathbb {Z}_p$ in Definition 2.3.1) of special endomorphisms of supersingular points with the natural quadratic forms following Howard and Pappas [Reference Howard and PappasHP17, §§ 5 and 6].Footnote 8 In conjunction with [Reference KisinKis10, § 1], we then obtain ![]() $\mathbb {L}_{\mathrm {cris}}$ (see Definitions 2.2.3 and 2.2.9) on the formal neighborhoods of supersingular points in the Shimura variety
$\mathbb {L}_{\mathrm {cris}}$ (see Definitions 2.2.3 and 2.2.9) on the formal neighborhoods of supersingular points in the Shimura variety ![]() $\mathcal {M}$. As a direct consequence, we obtain the local equation of the non-ordinary locus in § 3.4. These are the key inputs to §§ 5–6; in particular, we use the explicit descriptions of this section to prove our decay results.
$\mathcal {M}$. As a direct consequence, we obtain the local equation of the non-ordinary locus in § 3.4. These are the key inputs to §§ 5–6; in particular, we use the explicit descriptions of this section to prove our decay results.
3.1 A brief review of the work of Howard and Pappas and Kisin
As both [Reference Howard and PappasHP17] and [Reference KisinKis10] apply to GSpin Shimura varieties of any dimension, we first recall their results in the general setting.
Let ![]() $(V,Q)$ denote a quadratic
$(V,Q)$ denote a quadratic ![]() $\mathbb {Q}$-vector space of signature
$\mathbb {Q}$-vector space of signature ![]() $(n,2)$ and let
$(n,2)$ and let ![]() $L\subset V$ be a maximal even lattice which is self-dual at
$L\subset V$ be a maximal even lattice which is self-dual at ![]() $p$. Let
$p$. Let ![]() $\mathcal {M}$ denote the smooth canonical integral model over
$\mathcal {M}$ denote the smooth canonical integral model over ![]() $\mathbb {Z}_p$ of the GSpin Shimura variety attached to
$\mathbb {Z}_p$ of the GSpin Shimura variety attached to ![]() $(L,Q)$ in [Reference KisinKis10].
$(L,Q)$ in [Reference KisinKis10].
Set ![]() $k=\bar {\mathbb {F}}_p, W=W(k), K=W[1/p]$. In this section, we consider a fixed supersingular point
$k=\bar {\mathbb {F}}_p, W=W(k), K=W[1/p]$. In this section, we consider a fixed supersingular point ![]() $P\in \mathcal {M}(k)$. In the case of abelian surfaces considered in § 2 (with
$P\in \mathcal {M}(k)$. In the case of abelian surfaces considered in § 2 (with ![]() $L=L_{\rm S}$ or
$L=L_{\rm S}$ or ![]() $L_{\rm H}$),
$L_{\rm H}$), ![]() $P$ supersingular means the corresponding abelian surface over
$P$ supersingular means the corresponding abelian surface over ![]() $P$ is supersingular. This, in turn, is equivalent to the action of the crystalline Frobenius
$P$ is supersingular. This, in turn, is equivalent to the action of the crystalline Frobenius ![]() $\varphi$ on
$\varphi$ on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ being pure, with slope
$\mathbb {L}_{\mathrm {cris},P}(W)$ being pure, with slope ![]() $0$. In the general setting, let
$0$. In the general setting, let ![]() $\mathbb {D}$ denote the Dieudonné crystal of the universal Kuga–Satake abelian variety over
$\mathbb {D}$ denote the Dieudonné crystal of the universal Kuga–Satake abelian variety over ![]() $\mathcal {M}_{\mathbb {F}_p}$ and let
$\mathcal {M}_{\mathbb {F}_p}$ and let ![]() $\mathbb {L}_{\mathrm {cris}}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal corresponding to
$\mathbb {L}_{\mathrm {cris}}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal corresponding to ![]() $L\subset C(L)$ defined in [Reference Madapusi PeraMP16, § 4.14].Footnote 9 Let
$L\subset C(L)$ defined in [Reference Madapusi PeraMP16, § 4.14].Footnote 9 Let ![]() $\varphi$ denote the crystalline Frobenius on
$\varphi$ denote the crystalline Frobenius on ![]() $\mathbb {D}_P(W)$ and
$\mathbb {D}_P(W)$ and ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$. Then we say
$\mathbb {L}_{\mathrm {cris},P}(W)$. Then we say ![]() $P$ is supersingular if
$P$ is supersingular if ![]() $\varphi$ acts on
$\varphi$ acts on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ with pure slope
$\mathbb {L}_{\mathrm {cris},P}(W)$ with pure slope ![]() $0$ (see, for instance, [Reference Howard and PappasHP17, Lemma 4.2.4, § 7.2.1]).
$0$ (see, for instance, [Reference Howard and PappasHP17, Lemma 4.2.4, § 7.2.1]).
By Dieudonné theory, we have ![]() $L''\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$. To compute
$L''\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$. To compute ![]() $L''\otimes \mathbb {Z}_p$ and the
$L''\otimes \mathbb {Z}_p$ and the ![]() $\varphi$-action on
$\varphi$-action on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$, we introduce another free
$\mathbb {L}_{\mathrm {cris},P}(W)$, we introduce another free ![]() $W$-module
$W$-module ![]() $\mathbb {L}^\#_P(W)$ following [Reference Howard and PappasHP17, § 6.2.1].Footnote 10
$\mathbb {L}^\#_P(W)$ following [Reference Howard and PappasHP17, § 6.2.1].Footnote 10
Definition 3.1.1 The filtration on ![]() $\mathbb {D}_P(W)$ is given by
$\mathbb {D}_P(W)$ is given by ![]() $\operatorname {Fil}^1 \mathbb {D}_P(W):=\varphi ^{-1}(p\mathbb {D}_P(W))$. We define
$\operatorname {Fil}^1 \mathbb {D}_P(W):=\varphi ^{-1}(p\mathbb {D}_P(W))$. We define ![]() $\mathbb {L}^\#_P(W):=\{v\in \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K \mid v\operatorname {Fil}^1 \mathbb {D}_P(W)\subset \operatorname {Fil}^1 \mathbb {D}_P(W)\}$.
$\mathbb {L}^\#_P(W):=\{v\in \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K \mid v\operatorname {Fil}^1 \mathbb {D}_P(W)\subset \operatorname {Fil}^1 \mathbb {D}_P(W)\}$.
3.1.2
By [Reference Howard and PappasHP17, Theorem 7.2.4], studying supersingular points and their formal neighborhood in ![]() $\mathcal {M}$ reduces to study the points and their formal neighborhood in the associated Rapoport–Zink spaces and hence we use results in [Reference Howard and PappasHP17, §§ 5 and 6].
$\mathcal {M}$ reduces to study the points and their formal neighborhood in the associated Rapoport–Zink spaces and hence we use results in [Reference Howard and PappasHP17, §§ 5 and 6].
By [Reference Howard and PappasHP17, Proposition 5.2.2], ![]() $\varphi (\mathbb {L}^\#_P(W))=\mathbb {L}_{\mathrm {cris},P}(W)$. In particular,
$\varphi (\mathbb {L}^\#_P(W))=\mathbb {L}_{\mathrm {cris},P}(W)$. In particular,
Recall that in Definition 2.3.1, we endow ![]() $V':=L''\otimes \mathbb {Q}_p$ with a quadratic form
$V':=L''\otimes \mathbb {Q}_p$ with a quadratic form ![]() $Q'$; let
$Q'$; let ![]() $[-,-]'$ denote the bilinear form on
$[-,-]'$ denote the bilinear form on ![]() $V'$ given by
$V'$ given by ![]() $[x,y]'=Q'(x+y)-Q'(x)-Q'(y)$. Hence
$[x,y]'=Q'(x+y)-Q'(x)-Q'(y)$. Hence
Since ![]() $P$ is supersingular, we have
$P$ is supersingular, we have ![]() $n=\operatorname {rk}_W \mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {rk}_{\mathbb {Z}_p} L''=\dim _{\mathbb {Q}_p}V'$.
$n=\operatorname {rk}_W \mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {rk}_{\mathbb {Z}_p} L''=\dim _{\mathbb {Q}_p}V'$.
Let ![]() $\Lambda _P\subset V'$ denote the dual of
$\Lambda _P\subset V'$ denote the dual of ![]() $L''\otimes \mathbb {Z}_p$ with respect to
$L''\otimes \mathbb {Z}_p$ with respect to ![]() $[-,-]'$. Then by [Reference Howard and PappasHP17, Propositions 5.2.2 and 6.2.2],
$[-,-]'$. Then by [Reference Howard and PappasHP17, Propositions 5.2.2 and 6.2.2], ![]() $\Lambda _P$ is a vertex lattice, i.e.
$\Lambda _P$ is a vertex lattice, i.e. ![]() $\Lambda _P$ is a
$\Lambda _P$ is a ![]() $\mathbb {Z}_p$-lattice in
$\mathbb {Z}_p$-lattice in ![]() $V'$ such that
$V'$ such that ![]() $p\Lambda _P\subset \Lambda _P^\vee \subset \Lambda _P$. The type
$p\Lambda _P\subset \Lambda _P^\vee \subset \Lambda _P$. The type ![]() $t_P$ of
$t_P$ of ![]() $\Lambda _P$ is defined to be
$\Lambda _P$ is defined to be ![]() $\dim _{\mathbb {F}_p}(\Lambda _P/\Lambda _P^\vee )$. By [Reference Howard and PappasHP17, Proposition 5.1.2, (1.2.3.1)], there is
$\dim _{\mathbb {F}_p}(\Lambda _P/\Lambda _P^\vee )$. By [Reference Howard and PappasHP17, Proposition 5.1.2, (1.2.3.1)], there is ![]() $t_{\rm max}\in 2 \mathbb {Z}$ which only depends on
$t_{\rm max}\in 2 \mathbb {Z}$ which only depends on ![]() $n$ and
$n$ and ![]() $\det (V')=\det (V_{\mathbb {Q}_p})$Footnote 11 such that
$\det (V')=\det (V_{\mathbb {Q}_p})$Footnote 11 such that ![]() $t_P\in 2\mathbb {Z}$ and
$t_P\in 2\mathbb {Z}$ and ![]() $2\leq t_P \leq t_{\rm max}$. Moreover, there exists a vertex lattice
$2\leq t_P \leq t_{\rm max}$. Moreover, there exists a vertex lattice ![]() $\Lambda \subset V'$ of type
$\Lambda \subset V'$ of type ![]() $t_{\rm max}$ such that
$t_{\rm max}$ such that ![]() $\Lambda _P\subset \Lambda$. Indeed, the proof of [Reference Howard and PappasHP17, Proposition 5.1.2] constructs all possible isometry classes of
$\Lambda _P\subset \Lambda$. Indeed, the proof of [Reference Howard and PappasHP17, Proposition 5.1.2] constructs all possible isometry classes of ![]() $\Lambda$ (with the quadratic form) for all
$\Lambda$ (with the quadratic form) for all ![]() $(V,Q)$ (note that in [Reference Howard and PappasHP17], they proved that for given
$(V,Q)$ (note that in [Reference Howard and PappasHP17], they proved that for given ![]() $(V,Q)$, the isometry class of
$(V,Q)$, the isometry class of ![]() $\Lambda$ is unique).
$\Lambda$ is unique).
Therefore, given ![]() $(V,Q)$, we first obtain the isometry class of
$(V,Q)$, we first obtain the isometry class of ![]() $\Lambda$ of type
$\Lambda$ of type ![]() $t_{\rm max}$ and then all isometry classes of the lattices of special endomorphisms
$t_{\rm max}$ and then all isometry classes of the lattices of special endomorphisms ![]() $L''\otimes \mathbb {Z}_p$ attached to all supersingular points are given by the duals of the vertex lattices contained in
$L''\otimes \mathbb {Z}_p$ attached to all supersingular points are given by the duals of the vertex lattices contained in ![]() $\Lambda$.
$\Lambda$.
From ![]() $\Lambda$, we may compute all possible isomorphism classes of
$\Lambda$, we may compute all possible isomorphism classes of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ and
$\mathbb {L}_{\mathrm {cris},P}(W)$ and ![]() $\mathbb {L}_P^\#(W)$ as rank-
$\mathbb {L}_P^\#(W)$ as rank-![]() $n$ free
$n$ free ![]() $W$-modules endowed with a quadratic form/bilinear form and a
$W$-modules endowed with a quadratic form/bilinear form and a ![]() $\sigma$-linear Frobenius
$\sigma$-linear Frobenius ![]() $\varphi$ (here we use
$\varphi$ (here we use ![]() $\sigma$ to denote the Frobenius action on
$\sigma$ to denote the Frobenius action on ![]() $W$) following [Reference Howard and PappasHP17, Proposition 6.2.2, § 5.3.1]. Indeed,
$W$) following [Reference Howard and PappasHP17, Proposition 6.2.2, § 5.3.1]. Indeed, ![]() $\mathbb {L}^\#_P(W)\subset \Lambda \otimes _{\mathbb {Z}_p}W=:\Lambda _W$ is the preimage of a Lagrangian
$\mathbb {L}^\#_P(W)\subset \Lambda \otimes _{\mathbb {Z}_p}W=:\Lambda _W$ is the preimage of a Lagrangian ![]() $\overline {L}^\#_P\subset \Lambda _W/\Lambda _W^\vee$ with respect to the quadratic form
$\overline {L}^\#_P\subset \Lambda _W/\Lambda _W^\vee$ with respect to the quadratic form ![]() $pQ'\bmod p$ such that
$pQ'\bmod p$ such that
where we use ![]() $\varphi$ to denote the
$\varphi$ to denote the ![]() $\sigma$-linear map on
$\sigma$-linear map on ![]() $\Lambda _W$ given by
$\Lambda _W$ given by ![]() $\operatorname {Id} \otimes \sigma$ and
$\operatorname {Id} \otimes \sigma$ and ![]() $\bar {\varphi }(\bar {v}):=\overline{\varphi (v)}$ is well-defined for
$\bar {\varphi }(\bar {v}):=\overline{\varphi (v)}$ is well-defined for ![]() $\bar {v}\in \Lambda _W/\Lambda _W^\vee$ with a lift
$\bar {v}\in \Lambda _W/\Lambda _W^\vee$ with a lift ![]() $v\in \Lambda _W$. The quadratic form and
$v\in \Lambda _W$. The quadratic form and ![]() $\varphi$-action on
$\varphi$-action on ![]() $\mathbb {L}^\#_P(W)$ are the restrictions of the quadratic forms and
$\mathbb {L}^\#_P(W)$ are the restrictions of the quadratic forms and ![]() $\varphi$-action on
$\varphi$-action on ![]() $\Lambda _W$. We then obtain
$\Lambda _W$. We then obtain ![]() $\mathbb {L}_{\mathrm {cris},P}(W)=\varphi (\mathbb {L}^\#_P(W))$. Note that by [Reference Howard and PappasHP17, Proposition 5.1.2], the even-dimensional
$\mathbb {L}_{\mathrm {cris},P}(W)=\varphi (\mathbb {L}^\#_P(W))$. Note that by [Reference Howard and PappasHP17, Proposition 5.1.2], the even-dimensional ![]() $\mathbb {F}_p$-quadratic space
$\mathbb {F}_p$-quadratic space ![]() ${(\Lambda /\Lambda ^\vee, pQ'\bmod p)}$ does not have a Lagrangian defined over
${(\Lambda /\Lambda ^\vee, pQ'\bmod p)}$ does not have a Lagrangian defined over ![]() $\mathbb {F}_p$ and, hence, is non-split; see [Reference Howard and PappasHP14, §§ 3.2-3.3] for a discussion on how to find all such
$\mathbb {F}_p$ and, hence, is non-split; see [Reference Howard and PappasHP14, §§ 3.2-3.3] for a discussion on how to find all such ![]() $\overline {L}^\#_P$.
$\overline {L}^\#_P$.
Definition 3.1.3 For a supersingular point ![]() $P$, we say
$P$, we say ![]() $P$ is superspecial if
$P$ is superspecial if ![]() $t_P=2$;Footnote 12 we say
$t_P=2$;Footnote 12 we say ![]() $P$ is supergeneric if
$P$ is supergeneric if ![]() $t_P=t_{\rm max}\neq 2$.
$t_P=t_{\rm max}\neq 2$.
By [Reference Howard and PappasHP17, Proposition 5.2.2], ![]() $P$ is superspecial if and only if
$P$ is superspecial if and only if
By [Reference Howard and PappasHP17, (1.2.3.1)], in the setting of § 2, we have ![]() $t_{\rm max}\leq 4$ and, hence, the supersingular points in question are either superspecial or supergeneric.
$t_{\rm max}\leq 4$ and, hence, the supersingular points in question are either superspecial or supergeneric.
Remark 3.1.4 By [Reference Madapusi PeraMP16, Proposition 4.7(iii) and (iv)], ![]() $\operatorname {GSpin}(L,Q)_W$ acts on
$\operatorname {GSpin}(L,Q)_W$ acts on ![]() $\mathbb {D}_P(W)$ and
$\mathbb {D}_P(W)$ and ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$; moreover, as
$\mathbb {L}_{\mathrm {cris},P}(W)$; moreover, as ![]() $W$-quadratic spaces,
$W$-quadratic spaces, ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\cong L\otimes W$ (we use
$\mathbb {L}_{\mathrm {cris},P}(W)\cong L\otimes W$ (we use ![]() $Q_W$ to denote the quadratic form on
$Q_W$ to denote the quadratic form on ![]() $L''\otimes \mathbb {Z}_p$) and for
$L''\otimes \mathbb {Z}_p$) and for ![]() $x\in \mathbb {L}_{\mathrm {cris},P}(W), x\circ x = Q_W(x)\cdot \operatorname {Id} \in \operatorname {End}(\mathbb {D}_P(W))$. Therefore,
$x\in \mathbb {L}_{\mathrm {cris},P}(W), x\circ x = Q_W(x)\cdot \operatorname {Id} \in \operatorname {End}(\mathbb {D}_P(W))$. Therefore, ![]() $Q'$ on
$Q'$ on ![]() $L''\otimes \mathbb {Z}_p$ is the restriction of
$L''\otimes \mathbb {Z}_p$ is the restriction of ![]() $Q$ on
$Q$ on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ to
$\mathbb {L}_{\mathrm {cris},P}(W)$ to ![]() $L''\otimes \mathbb {Z}_p$. We introduce the notation
$L''\otimes \mathbb {Z}_p$. We introduce the notation ![]() $Q'$ to emphasize that
$Q'$ to emphasize that ![]() $Q'$ and
$Q'$ and ![]() $Q$ (as
$Q$ (as ![]() $\mathbb {Z}_p$-quadratic forms) are restrictions of
$\mathbb {Z}_p$-quadratic forms) are restrictions of ![]() $Q_W$ to
$Q_W$ to ![]() $\mathbb {Z}_p$-lattices in different
$\mathbb {Z}_p$-lattices in different ![]() $\mathbb {Q}_p$-subspaces. Hence,
$\mathbb {Q}_p$-subspaces. Hence, ![]() $\operatorname {GSpin}(L,Q)_W=\operatorname {GSpin} (\mathbb {L}_{\mathrm {cris},P}(W),Q')$.
$\operatorname {GSpin}(L,Q)_W=\operatorname {GSpin} (\mathbb {L}_{\mathrm {cris},P}(W),Q')$.
3.1.5
We now describe the ![]() $F$-crystal
$F$-crystal ![]() $\mathbb {L}_{\mathrm {cris}}$ over the formal completion
$\mathbb {L}_{\mathrm {cris}}$ over the formal completion ![]() $\widehat {\mathcal {M}}_{P}$ along the supersingular point
$\widehat {\mathcal {M}}_{P}$ along the supersingular point ![]() $P$ following [Reference KisinKis10, §§ 1.4 and 1.5] and [Reference MoonenMoo98, § 4.5]; see also [Reference Howard and PappasHP17, §§ 3.1.4 and 3.1.6].
$P$ following [Reference KisinKis10, §§ 1.4 and 1.5] and [Reference MoonenMoo98, § 4.5]; see also [Reference Howard and PappasHP17, §§ 3.1.4 and 3.1.6].
The Hodge filtration ![]() $\operatorname {Fil}^1 \mathbb {D}_P(W) \bmod p \subset \mathbb {D}_P(k)$ corresponds to a cocharacter
$\operatorname {Fil}^1 \mathbb {D}_P(W) \bmod p \subset \mathbb {D}_P(k)$ corresponds to a cocharacter ![]() $\bar {\mu }: \mathbb {G}_{m,k}\rightarrow \operatorname {GSpin} (L,Q)_k$ and we pick a cocharacter
$\bar {\mu }: \mathbb {G}_{m,k}\rightarrow \operatorname {GSpin} (L,Q)_k$ and we pick a cocharacter ![]() $\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {GSpin} (L,Q)_W$ which lifts
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {GSpin} (L,Q)_W$ which lifts ![]() $\bar {\mu }$. Let
$\bar {\mu }$. Let ![]() $U_P\subset \operatorname {GSpin}(L,Q)_W$ denote the opposite unipotent of the parabolic subgroup defined by
$U_P\subset \operatorname {GSpin}(L,Q)_W$ denote the opposite unipotent of the parabolic subgroup defined by ![]() $\mu$; and let
$\mu$; and let ![]() $\widehat {U_P}$ denote the formal completion of
$\widehat {U_P}$ denote the formal completion of ![]() $U_P$ along the identity. Pick coordinates and write
$U_P$ along the identity. Pick coordinates and write ![]() $\widehat {U_P}=\operatorname {Spf} W[[x_1,\ldots, x_d]]$ such that
$\widehat {U_P}=\operatorname {Spf} W[[x_1,\ldots, x_d]]$ such that ![]() $x_1=\cdots =x_d=0$ defines the identity element in
$x_1=\cdots =x_d=0$ defines the identity element in ![]() $U_P$. Let
$U_P$. Let ![]() $\sigma$ denote the Frobenius action on
$\sigma$ denote the Frobenius action on ![]() $W[[x_1,\ldots, x_d]]$ which lifts the
$W[[x_1,\ldots, x_d]]$ which lifts the ![]() $\sigma$-action on
$\sigma$-action on ![]() $W$ and for which
$W$ and for which ![]() $\sigma (x_i)=x_i^p$.
$\sigma (x_i)=x_i^p$.
Let ![]() $R$ denote
$R$ denote ![]() $\widehat {\mathcal {O}}_{\mathcal {M},P}$, the complete local ring of
$\widehat {\mathcal {O}}_{\mathcal {M},P}$, the complete local ring of ![]() $\mathcal {M}$ at
$\mathcal {M}$ at ![]() $P$. Then there exists an isomorphism from
$P$. Then there exists an isomorphism from ![]() $\operatorname {Spf} R$ to
$\operatorname {Spf} R$ to ![]() $\widehat {U_P}$ (and we still use
$\widehat {U_P}$ (and we still use ![]() $\sigma$ to denote the Frobenius action on
$\sigma$ to denote the Frobenius action on ![]() $R$ via the identification to
$R$ via the identification to ![]() $W[[x_1,\ldots, x_d]]$) such that:
$W[[x_1,\ldots, x_d]]$) such that:
(1)
 $\mathbb {D}(R)=\mathbb {D}_P(W)\otimes _W R$ and
$\mathbb {D}(R)=\mathbb {D}_P(W)\otimes _W R$ and  $\mathbb {L}_{\mathrm {cris}}(R)=\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W R$ as
$\mathbb {L}_{\mathrm {cris}}(R)=\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W R$ as  $R$-modules; and
$R$-modules; and(2) under the above identifications, the
 $\sigma$-linear Frobenius action, denoted by
$\sigma$-linear Frobenius action, denoted by  $\operatorname {Frob}$, on
$\operatorname {Frob}$, on  $\mathbb {D}(R)$ and
$\mathbb {D}(R)$ and  $\mathbb {L}_{\mathrm {cris}}(R)$ is given by
$\mathbb {L}_{\mathrm {cris}}(R)$ is given by  $u\cdot (\varphi \otimes \sigma )$, where
$u\cdot (\varphi \otimes \sigma )$, where  $u$ denotes the universal
$u$ denotes the universal  $W[[x_1,\ldots, x_d]]$-point in
$W[[x_1,\ldots, x_d]]$-point in  $\widehat {U_P}$ and
$\widehat {U_P}$ and  $\varphi$ is the crystalline Frobenius on
$\varphi$ is the crystalline Frobenius on  $\mathbb {D}_P(W)$ or
$\mathbb {D}_P(W)$ or  $\mathbb {L}_{\mathrm {cris},P}(W)$ given in § 3.1.2.
$\mathbb {L}_{\mathrm {cris},P}(W)$ given in § 3.1.2.
On ![]() $\mathbb {L}_{\mathrm {cris}}$, the
$\mathbb {L}_{\mathrm {cris}}$, the ![]() $\operatorname {GSpin}(L,Q)_W$ action factors through the quotient
$\operatorname {GSpin}(L,Q)_W$ action factors through the quotient ![]() $\operatorname {SO}(L,Q)_W$. Thus, from now on, because we only care about
$\operatorname {SO}(L,Q)_W$. Thus, from now on, because we only care about ![]() $\operatorname {Frob}$ on
$\operatorname {Frob}$ on ![]() $\mathbb {L}_{\mathrm {cris}}$, then by Remark 3.1.4, we work with
$\mathbb {L}_{\mathrm {cris}}$, then by Remark 3.1.4, we work with ![]() $\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$ and
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$ and ![]() $U_P$ the opposite unipotent of
$U_P$ the opposite unipotent of ![]() $\mu$ in
$\mu$ in ![]() $\operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$.
$\operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$.
In the rest of this section, we apply §§ 3.1.2 and 3.1.5 to the setting in § 2 and we work with the coordinates on ![]() $\widehat {U_P}$. When
$\widehat {U_P}$. When ![]() $L=L_{\rm H}$, we write
$L=L_{\rm H}$, we write ![]() $\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ and when
$\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ and when ![]() $L=L_{\rm S}$, we write
$L=L_{\rm S}$, we write ![]() $\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$. We use
$\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$. We use ![]() $\epsilon \in \mathbb {Z}_p^\times$ to denote an element which is not a perfect square in
$\epsilon \in \mathbb {Z}_p^\times$ to denote an element which is not a perfect square in ![]() $\mathbb {Z}_p$. Let
$\mathbb {Z}_p$. Let ![]() $\mathbb {Z}_{p^2}$ (respectively,
$\mathbb {Z}_{p^2}$ (respectively, ![]() $\mathbb {Q}_{p^2}$) denote
$\mathbb {Q}_{p^2}$) denote ![]() $W(\mathbb {F}_{p^2})$ (respectively,
$W(\mathbb {F}_{p^2})$ (respectively, ![]() $W(\mathbb {F}_{p^2})[1/p]$) and let
$W(\mathbb {F}_{p^2})[1/p]$) and let ![]() $\lambda \in \mathbb {Z}_{p^2}^\times$ be an element such that
$\lambda \in \mathbb {Z}_{p^2}^\times$ be an element such that ![]() $\sigma (\lambda )=-\lambda$ (for instance, we can take
$\sigma (\lambda )=-\lambda$ (for instance, we can take ![]() $\lambda$ to be a root in
$\lambda$ to be a root in ![]() $\mathbb {Z}_{p^2}$ of
$\mathbb {Z}_{p^2}$ of ![]() $x^2-\epsilon =0$). We use
$x^2-\epsilon =0$). We use ![]() $\{v_i\}_{i=1}^{n+2}$ to denote a
$\{v_i\}_{i=1}^{n+2}$ to denote a ![]() $W$-basis of
$W$-basis of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ and
$\mathbb {L}_{\mathrm {cris},P}(W)$ and ![]() $\{w_i\}_{i=1}^{n+2}$ to denote a
$\{w_i\}_{i=1}^{n+2}$ to denote a ![]() $\mathbb {Z}_p$-basis of
$\mathbb {Z}_p$-basis of ![]() $\Lambda _P^\vee =\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$; note that
$\Lambda _P^\vee =\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$; note that ![]() $\operatorname {Span}_W\{w_i\}$ is a
$\operatorname {Span}_W\{w_i\}$ is a ![]() $W$-sublattice of
$W$-sublattice of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$.
$\mathbb {L}_{\mathrm {cris},P}(W)$.
3.2 The Hilbert case  $L=L_{\rm H}$
$L=L_{\rm H}$
Recall that as in Theorem 1(2), we have ![]() $p\nmid m\in \mathbb {Z}_{>0}$.
$p\nmid m\in \mathbb {Z}_{>0}$.
3.2.1
Assume that ![]() $p$ is inert in
$p$ is inert in ![]() $\mathbb {Q}(\sqrt {m})$;Footnote 13 then we have
$\mathbb {Q}(\sqrt {m})$;Footnote 13 then we have ![]() $t_{\rm max}=4$.
$t_{\rm max}=4$.
The vertex lattice with type ![]() $t_{\rm max}$ is
$t_{\rm max}$ is ![]() $\Lambda =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$, where
$\Lambda =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$, where
Hence, ![]() $\Lambda ^\vee =p\Lambda$. Set
$\Lambda ^\vee =p\Lambda$. Set ![]() $e_2=(1\otimes 1+ (1/\lambda ) \otimes \lambda )/2, f_2=(1\otimes 1+ (-1/\lambda ) \otimes \lambda )/2 \in \mathbb {Z}_{p^2}\otimes _{\mathbb {Z}_p} Z$. Then, as elements in
$e_2=(1\otimes 1+ (1/\lambda ) \otimes \lambda )/2, f_2=(1\otimes 1+ (-1/\lambda ) \otimes \lambda )/2 \in \mathbb {Z}_{p^2}\otimes _{\mathbb {Z}_p} Z$. Then, as elements in ![]() $\Lambda _W$,
$\Lambda _W$,
All possible ![]() $\overline {L}^\#_P$ are given by two families of Lagrangians in
$\overline {L}^\#_P$ are given by two families of Lagrangians in ![]() $k$-quadratic space spanned by
$k$-quadratic space spanned by ![]() $\bar {e}_1,\bar {e}_2,\bar {f}_1,\bar {f}_2\in \Lambda _W/\Lambda _W^\vee$ with quadratic form
$\bar {e}_1,\bar {e}_2,\bar {f}_1,\bar {f}_2\in \Lambda _W/\Lambda _W^\vee$ with quadratic form ![]() $pQ$ satisfying (3.1.1):
$pQ$ satisfying (3.1.1):
where ![]() $\bar {c}\in k$.Footnote 14 Therefore, we have that
$\bar {c}\in k$.Footnote 14 Therefore, we have that
or
where ![]() $c\in W$.Footnote 15 Moreover, by (3.1.2),
$c\in W$.Footnote 15 Moreover, by (3.1.2), ![]() $P$ is superspecial if and only if
$P$ is superspecial if and only if ![]() $\sigma ^{-1}(c)-\sigma (c)\in pW$, which is equivalent to the Teichmüller lift of
$\sigma ^{-1}(c)-\sigma (c)\in pW$, which is equivalent to the Teichmüller lift of ![]() $\bar {c}$ lying in
$\bar {c}$ lying in ![]() $\mathbb {Z}_{p^2}$. Note that if
$\mathbb {Z}_{p^2}$. Note that if ![]() $c-c'\in pW$, then
$c-c'\in pW$, then ![]() $c,c'$ define the same
$c,c'$ define the same ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$. Therefore, without loss of generality, from now on, we only work with
$\mathbb {L}_{\mathrm {cris},P}(W)$. Therefore, without loss of generality, from now on, we only work with ![]() $c\in W$ which is the Teichmüller lifting of
$c\in W$ which is the Teichmüller lifting of ![]() $\bar {c}\in k$. Hence,
$\bar {c}\in k$. Hence, ![]() $P$ is superspecial if and only if there exists
$P$ is superspecial if and only if there exists ![]() $c\in \mathbb {Z}_{p^2}$ such that
$c\in \mathbb {Z}_{p^2}$ such that ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ is given by the above form.
$\mathbb {L}_{\mathrm {cris},P}(W)$ is given by the above form.
To compute the ![]() $F$-crystal
$F$-crystal ![]() $\mathbb {L}_{\mathrm {cris}}$, we pick the following
$\mathbb {L}_{\mathrm {cris}}$, we pick the following ![]() $W$-basis
$W$-basis ![]() $\{v_1,\ldots, v_4\}$ of
$\{v_1,\ldots, v_4\}$ of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ such that the Gram matrix of
$\mathbb {L}_{\mathrm {cris},P}(W)$ such that the Gram matrix of ![]() $[-,-]'$ with respect to this basis is
$[-,-]'$ with respect to this basis is ![]() $\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$, where
$\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$, where ![]() $I$ denotes the
$I$ denotes the ![]() $2\times 2$ identity matrix. For the first family, take
$2\times 2$ identity matrix. For the first family, take
for the second family, take
Then on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$, with respect to
$\mathbb {L}_{\mathrm {cris},P}(W)$, with respect to ![]() $\{v_1,\ldots,v_4\}$, we have
$\{v_1,\ldots,v_4\}$, we have
 \[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0\\ 0 & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 \end{bmatrix}. \]
\[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0\\ 0 & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 \end{bmatrix}. \]
The filtration on ![]() $\mathbb {L}_{\mathrm {cris},P}(k)$ is given by
$\mathbb {L}_{\mathrm {cris},P}(k)$ is given by
so we may choose ![]() $\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be ![]() $t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1)$. Then
$t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1)$. Then ![]() $\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ with the universal point
$\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ with the universal point
 \[ u= \begin{bmatrix} 1 & x & -xy & y\\ 0 & 1 & -y & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -x & 1 \end{bmatrix} \quad \text{and} \quad \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -xy/p-ay/p & a+x & p & y\\ -y/p & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ -x/p-a/p & 0 & 0 & 1 \end{bmatrix}, \]
\[ u= \begin{bmatrix} 1 & x & -xy & y\\ 0 & 1 & -y & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -x & 1 \end{bmatrix} \quad \text{and} \quad \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -xy/p-ay/p & a+x & p & y\\ -y/p & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ -x/p-a/p & 0 & 0 & 1 \end{bmatrix}, \]
where ![]() $a=\sigma (c)-\sigma ^{-1}(c)$; we have
$a=\sigma (c)-\sigma ^{-1}(c)$; we have ![]() $a=0$ if
$a=0$ if ![]() $P$ is superspecial and
$P$ is superspecial and ![]() $a\in W^\times$ if
$a\in W^\times$ if ![]() $P$ is supergeneric.
$P$ is supergeneric.
When ![]() $P$ is superspecial,
$P$ is superspecial, ![]() $\{w_1=pv_1+v_3,w_2=\lambda (pv_1-v_3),w_3=v_2,w_4=v_4 \}$ is a
$\{w_1=pv_1+v_3,w_2=\lambda (pv_1-v_3),w_3=v_2,w_4=v_4 \}$ is a ![]() $\mathbb {Z}_p$-basis of
$\mathbb {Z}_p$-basis of ![]() $L''\otimes \mathbb {Z}_p$. Using
$L''\otimes \mathbb {Z}_p$. Using ![]() $\{w_1,\ldots, w_4\}$ as a
$\{w_1,\ldots, w_4\}$ as a ![]() $K$-basis of
$K$-basis of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)[1/p]$, we have
$\mathbb {L}_{\mathrm {cris},P}(W)[1/p]$, we have
 \begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} -\dfrac{xy}{2p} & \dfrac{\lambda xy}{2p} & \dfrac{x}{2p} & \dfrac{y}{2p}\\ -\dfrac{xy}{2\lambda p} & \dfrac{xy}{2p} & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} \\ -y & \lambda y & 0 & 0 \\ -x & \lambda x & 0 & 0\end{bmatrix}\right) \circ \sigma. \end{equation}
\begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} -\dfrac{xy}{2p} & \dfrac{\lambda xy}{2p} & \dfrac{x}{2p} & \dfrac{y}{2p}\\ -\dfrac{xy}{2\lambda p} & \dfrac{xy}{2p} & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} \\ -y & \lambda y & 0 & 0 \\ -x & \lambda x & 0 & 0\end{bmatrix}\right) \circ \sigma. \end{equation} When ![]() $P$ is supergeneric,
$P$ is supergeneric, ![]() $\left\{ {w_1=v_4, w_2=pv_1+v_3+(c+\sigma ^{-1}(c))v_4, w_3} \right.$
$\left\{ {w_1=v_4, w_2=pv_1+v_3+(c+\sigma ^{-1}(c))v_4, w_3} \right.$ ![]() $\left. {=\lambda (pv_1-v_3+(c-\sigma ^{-1}(c))v_4), w_4=pv_2-cv_3-p\sigma ^{-1}(c)v_1-c\sigma ^{-1}(c)v_4} \right\}$ is a
$\left. {=\lambda (pv_1-v_3+(c-\sigma ^{-1}(c))v_4), w_4=pv_2-cv_3-p\sigma ^{-1}(c)v_1-c\sigma ^{-1}(c)v_4} \right\}$ is a ![]() $\mathbb {Z}_p$-basis of
$\mathbb {Z}_p$-basis of ![]() ${L''\otimes \mathbb {Z}_p}$ and with respect to this basis,
${L''\otimes \mathbb {Z}_p}$ and with respect to this basis, ![]() $\operatorname {Frob}=(I+({y}/{p})A+xB)\circ \sigma$, where
$\operatorname {Frob}=(I+({y}/{p})A+xB)\circ \sigma$, where
 \[ A\!=\!\begin{bmatrix} -c & -c^2 & -\lambda c^2 & 0\\ 1/2 & 0 & \lambda c & c^2/2\\ 1/(2\lambda) & c/\lambda & 0 & -c^2/(2\lambda) \\ 0 & -1 & \lambda & c \end{bmatrix}, \quad B\!=\!\begin{bmatrix} 0 & -1\!+\!cy/p & \lambda cy/p \!+\!\lambda & -c^2y/p\\ 0 & -y/(2p) & \lambda y/(2p) & 1/2\!+\!cy/(2p)\\ 0 & -y/(2\lambda p) & y/(2p) & 1/(2\lambda) \!+\!cy/(2p\lambda)\\ 0 & 0 & 0 & 0 \end{bmatrix}. \]
\[ A\!=\!\begin{bmatrix} -c & -c^2 & -\lambda c^2 & 0\\ 1/2 & 0 & \lambda c & c^2/2\\ 1/(2\lambda) & c/\lambda & 0 & -c^2/(2\lambda) \\ 0 & -1 & \lambda & c \end{bmatrix}, \quad B\!=\!\begin{bmatrix} 0 & -1\!+\!cy/p & \lambda cy/p \!+\!\lambda & -c^2y/p\\ 0 & -y/(2p) & \lambda y/(2p) & 1/2\!+\!cy/(2p)\\ 0 & -y/(2\lambda p) & y/(2p) & 1/(2\lambda) \!+\!cy/(2p\lambda)\\ 0 & 0 & 0 & 0 \end{bmatrix}. \]3.2.2
Assume that ![]() $p$ is split in
$p$ is split in ![]() $\mathbb {Q}(\sqrt {m})$; then we have
$\mathbb {Q}(\sqrt {m})$; then we have ![]() $t_{\rm max}=2$ and, hence, every
$t_{\rm max}=2$ and, hence, every ![]() $P$ is superspecial.
$P$ is superspecial.
The vertex lattice with type ![]() $t_{\rm max}$ is
$t_{\rm max}$ is ![]() $\Lambda =\{(x_1,x_2,x_3,x_4)\in \mathbb {Z}_p^4\}$ with
$\Lambda =\{(x_1,x_2,x_3,x_4)\in \mathbb {Z}_p^4\}$ with
we have ![]() $\Lambda ^\vee =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,e_2, pe_3, pe_4\}$, where
$\Lambda ^\vee =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,e_2, pe_3, pe_4\}$, where ![]() $e_i$ is the vector with
$e_i$ is the vector with ![]() $x_i=1$ and
$x_i=1$ and ![]() $x_j=0$ for
$x_j=0$ for ![]() $j\neq i$. Recall that we take
$j\neq i$. Recall that we take ![]() $\epsilon =\lambda ^2$; we then haveFootnote 16 that
$\epsilon =\lambda ^2$; we then haveFootnote 16 that
 \begin{align*} \mathbb{L}_{\mathrm{cris},P}(W)&=\operatorname{Span}_W\bigl \{v_1= \tfrac{1}{2} (e_3+\lambda^{-1}e_4), v_2= \tfrac{1}{2} (e_1+\lambda^{-1}e_2), v_3=- \tfrac{1}{2} (pe_3-\lambda^{-1}pe_4),\\ &\quad v_4=\tfrac{1}{2}(e_1-\lambda^{-1}e_2) \bigr\}. \end{align*}
\begin{align*} \mathbb{L}_{\mathrm{cris},P}(W)&=\operatorname{Span}_W\bigl \{v_1= \tfrac{1}{2} (e_3+\lambda^{-1}e_4), v_2= \tfrac{1}{2} (e_1+\lambda^{-1}e_2), v_3=- \tfrac{1}{2} (pe_3-\lambda^{-1}pe_4),\\ &\quad v_4=\tfrac{1}{2}(e_1-\lambda^{-1}e_2) \bigr\}. \end{align*}
The Gram matrix is ![]() $\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$ and on
$\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$ and on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$, the Frobenius
$\mathbb {L}_{\mathrm {cris},P}(W)$, the Frobenius ![]() $\varphi =b\sigma$ with
$\varphi =b\sigma$ with
 \[ b=\begin{bmatrix}0 & 0 & -p & 0\\ 0 & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{bmatrix}. \]
\[ b=\begin{bmatrix}0 & 0 & -p & 0\\ 0 & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{bmatrix}. \]
The filtration on ![]() $\mathbb {L}_{\mathrm {cris},P}(k)$ given by
$\mathbb {L}_{\mathrm {cris},P}(k)$ given by ![]() $\varphi$ is the same as in § 3.2.1 and, hence, we may use the same
$\varphi$ is the same as in § 3.2.1 and, hence, we may use the same ![]() $\mu$ and
$\mu$ and ![]() $u$ there. Therefore, on
$u$ there. Therefore, on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, we have
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, we have
 \[ \operatorname{Frob}=ub\sigma, \text{ with } ub=\begin{bmatrix}xy/p & y & -p & x\\ y/p & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ x/p & 1 & 0 & 0\end{bmatrix}. \]
\[ \operatorname{Frob}=ub\sigma, \text{ with } ub=\begin{bmatrix}xy/p & y & -p & x\\ y/p & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ x/p & 1 & 0 & 0\end{bmatrix}. \]
Moreover, ![]() $\{w_1=pv_1-v_3, w_2=\lambda (pv_1+v_3), w_3=v_2+v_4, w_4=\lambda (v_4-v_2)\}$ is a
$\{w_1=pv_1-v_3, w_2=\lambda (pv_1+v_3), w_3=v_2+v_4, w_4=\lambda (v_4-v_2)\}$ is a ![]() $\mathbb {Z}_p$-basis of
$\mathbb {Z}_p$-basis of ![]() ${L''\otimes \mathbb {Z}_p}$ and with respect to this basis,
${L''\otimes \mathbb {Z}_p}$ and with respect to this basis,
 \begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}\right) \circ \sigma. \end{equation}
\begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}\right) \circ \sigma. \end{equation}3.3 The Siegel case  $L=L_{\rm S}$
$L=L_{\rm S}$
We now compute ![]() $\mathbb {L}_{\mathrm {cris}}$ for Theorems 1(1) and 5. In this case, we have
$\mathbb {L}_{\mathrm {cris}}$ for Theorems 1(1) and 5. In this case, we have ![]() $t_{\rm max}=4$.
$t_{\rm max}=4$.
The vertex lattice with type ![]() $t_{\rm max}$ is
$t_{\rm max}$ is ![]() $\Lambda = \operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1 \} \oplus Z_S$, where
$\Lambda = \operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1 \} \oplus Z_S$, where ![]() $Z_S=\{(x_1,x_2,x_3)\in \mathbb {Z}_p^3\}$
$Z_S=\{(x_1,x_2,x_3)\in \mathbb {Z}_p^3\}$
 \begin{gather*} [Z_S, e_1]'=[Z_S,f_1]'=[e_1,e_1]'=[f_1,f_1]'=0,\quad [e_1,f_1]'=1/p,\\ Q'((x_1,x_2,x_3))=c(-\epsilon x_1^2-p^{-1} x_2^2 +\epsilon p^{-1} x_3^2), \end{gather*}
\begin{gather*} [Z_S, e_1]'=[Z_S,f_1]'=[e_1,e_1]'=[f_1,f_1]'=0,\quad [e_1,f_1]'=1/p,\\ Q'((x_1,x_2,x_3))=c(-\epsilon x_1^2-p^{-1} x_2^2 +\epsilon p^{-1} x_3^2), \end{gather*}
for some ![]() $c\in \mathbb {Z}_p^\times$. As
$c\in \mathbb {Z}_p^\times$. As ![]() $\det \Lambda =\det L \in \mathbb {Q}_p^\times /(\mathbb {Q}_p^\times )^2$ and
$\det \Lambda =\det L \in \mathbb {Q}_p^\times /(\mathbb {Q}_p^\times )^2$ and ![]() $\det L=2$, we have
$\det L=2$, we have ![]() $c=-1$. Let
$c=-1$. Let ![]() $g=(1,0,0)\in Z_S$ and
$g=(1,0,0)\in Z_S$ and ![]() $Z=\operatorname {Span}_{\mathbb {Z}_p}\{(0,1,0), (0,0,1)\}\subset Z_S$. Then
$Z=\operatorname {Span}_{\mathbb {Z}_p}\{(0,1,0), (0,0,1)\}\subset Z_S$. Then ![]() $\Lambda /\Lambda ^\vee =\operatorname {Span}_{\mathbb {F}_p}\{\overline {e}_1,\overline {f}_1\}\oplus Z/Z^\vee$. Note that
$\Lambda /\Lambda ^\vee =\operatorname {Span}_{\mathbb {F}_p}\{\overline {e}_1,\overline {f}_1\}\oplus Z/Z^\vee$. Note that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$ is exactly the same quadratic
$\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$ is exactly the same quadratic ![]() $\mathbb {Z}_p$-lattice which is denoted by
$\mathbb {Z}_p$-lattice which is denoted by ![]() $\Lambda$ in § 3.2.1; hence, the same computation there applies to find
$\Lambda$ in § 3.2.1; hence, the same computation there applies to find ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\subset \Lambda \otimes W$. More precisely, there exist
$\mathbb {L}_{\mathrm {cris},P}(W)\subset \Lambda \otimes W$. More precisely, there exist ![]() $v_1,\ldots, v_4\in \operatorname {Span}_W\{e_1,f_1\}\oplus Z\otimes W$ and
$v_1,\ldots, v_4\in \operatorname {Span}_W\{e_1,f_1\}\oplus Z\otimes W$ and ![]() $c\in W$ which is the Teichmüller lift of
$c\in W$ which is the Teichmüller lift of ![]() $\bar {c}\in k$ such that
$\bar {c}\in k$ such that
(1)
 $\mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {Span}_W\{v_1,\ldots,v_4,v_5\}$, where
$\mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {Span}_W\{v_1,\ldots,v_4,v_5\}$, where  $v_5=g$;
$v_5=g$;(2) the Gram matrix of
 $[-,-]'$ with respect to
$[-,-]'$ with respect to  $\{v_1,\ldots,v_5\}$ is
where
$\{v_1,\ldots,v_5\}$ is
where \[ \begin{bmatrix}0 & I & 0\\ I & 0 & 0\\ 0 & 0 & 2\epsilon\end{bmatrix}, \]
\[ \begin{bmatrix}0 & I & 0\\ I & 0 & 0\\ 0 & 0 & 2\epsilon\end{bmatrix}, \] $I$ is the
$I$ is the  $2\times 2$ identity matrix;
$2\times 2$ identity matrix;(3) the Frobenius
 $\varphi$ on
$\varphi$ on  $\mathbb {L}_{\mathrm {cris},P}(W)$ with respect to the basis
$\mathbb {L}_{\mathrm {cris},P}(W)$ with respect to the basis  $\{v_i\}$ is
$\{v_i\}$ is
 \[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 1/p & 0 & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}; \]
\[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 1/p & 0 & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}; \](4)
 $P$ is superspecial if and only if
$P$ is superspecial if and only if  $\sigma ^2(c)=c$.
$\sigma ^2(c)=c$.
We may choose ![]() $\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be ![]() $t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1, 1)$. Then
$t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1, 1)$. Then ![]() $\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$ with the universal point
$\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$ with the universal point
 \[ u= \begin{bmatrix} 1 & x & -xy-\dfrac{z^2}{4\epsilon} & y & z\\ 0 & 1 & -y & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -x & 1 & 0\\ 0 & 0 & -\dfrac{z}{2\epsilon} & 0 & 1 \end{bmatrix}\]
\[ u= \begin{bmatrix} 1 & x & -xy-\dfrac{z^2}{4\epsilon} & y & z\\ 0 & 1 & -y & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -x & 1 & 0\\ 0 & 0 & -\dfrac{z}{2\epsilon} & 0 & 1 \end{bmatrix}\]and
 \[ \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -\dfrac{1}{p}\left(xy+\dfrac{z^2}{4\epsilon}\right)-\dfrac{ay}{p} & a+x & p & y & z\\ -\dfrac{y}{p} & 1 & 0 & 0 & 0\\ \dfrac{1}{p} & 0 & 0 & 0 & 0\\ -\dfrac{x+a}{p} & 0 & 0 & 1 & 0\\ -\dfrac{z}{2\epsilon p} & 0 & 0 & 0 & 1 \end{bmatrix} \]
\[ \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -\dfrac{1}{p}\left(xy+\dfrac{z^2}{4\epsilon}\right)-\dfrac{ay}{p} & a+x & p & y & z\\ -\dfrac{y}{p} & 1 & 0 & 0 & 0\\ \dfrac{1}{p} & 0 & 0 & 0 & 0\\ -\dfrac{x+a}{p} & 0 & 0 & 1 & 0\\ -\dfrac{z}{2\epsilon p} & 0 & 0 & 0 & 1 \end{bmatrix} \]
acting on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$, where
$\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$, where ![]() $a=\sigma (c)-\sigma ^{-1}(c)$; note that
$a=\sigma (c)-\sigma ^{-1}(c)$; note that ![]() $a=0$ if and only if
$a=0$ if and only if ![]() $P$ is superspecial.
$P$ is superspecial.
For the proofs of Theorems 1(1) and 5, we only need to study superspecial points so we only give the matrix of ![]() $\operatorname {Frob}$ with respect to a basis of
$\operatorname {Frob}$ with respect to a basis of ![]() $\mathbb {L}_{\mathrm {cris}} \otimes _W K$ consisting of elements in
$\mathbb {L}_{\mathrm {cris}} \otimes _W K$ consisting of elements in ![]() $L''\otimes \mathbb {Z}_p$ when
$L''\otimes \mathbb {Z}_p$ when ![]() $P$ is superspecial; we refer the reader to the appendix for the discussion when
$P$ is superspecial; we refer the reader to the appendix for the discussion when ![]() $P$ is supergeneric.
$P$ is supergeneric.
We now assume that ![]() $P$ is superspecial. Let
$P$ is superspecial. Let ![]() $w_1=\lambda (pv_1-v_3), w_2=pv_1+v_3, w_3=v_2, w_4=v_4, w_5=v_5$. Then
$w_1=\lambda (pv_1-v_3), w_2=pv_1+v_3, w_3=v_2, w_4=v_4, w_5=v_5$. Then ![]() $L''\otimes \mathbb {Z}_p=\operatorname {Span}_{\mathbb {Z}_p}\{w_1,\ldots, w_5\}$. We view
$L''\otimes \mathbb {Z}_p=\operatorname {Span}_{\mathbb {Z}_p}\{w_1,\ldots, w_5\}$. We view ![]() $\{w_i\}_{i=1}^5$ as a
$\{w_i\}_{i=1}^5$ as a ![]() $K$-basis of
$K$-basis of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\otimes K$, then the Frobenius on
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes K$, then the Frobenius on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$ is given by
$\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$ is given by
 \begin{equation} \operatorname{Frob}=\left(I+ \begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p}\\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}\right) \circ \sigma. \end{equation}
\begin{equation} \operatorname{Frob}=\left(I+ \begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p}\\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}\right) \circ \sigma. \end{equation}3.4 Equation of non-ordinary locus
We now use the computation in §§ 3.2 and 3.3 to obtain the local equation of the non-ordinary locus in a formal neighborhood of a supersingular point ![]() $P$ using results in [Reference OgusOgu01]. Although [Reference OgusOgu01] only focuses on the case of K3 surfaces, the results that we recall here apply to any GSpin Shimura varieties. We follow the notation in § 3.1. For a perfect field
$P$ using results in [Reference OgusOgu01]. Although [Reference OgusOgu01] only focuses on the case of K3 surfaces, the results that we recall here apply to any GSpin Shimura varieties. We follow the notation in § 3.1. For a perfect field ![]() $k'$ of characteristic
$k'$ of characteristic ![]() $p$, for
$p$, for ![]() $P'\in \mathcal {M}(k')$, we say
$P'\in \mathcal {M}(k')$, we say ![]() $P$ is ordinary if the slopes of the crystalline Frobenius
$P$ is ordinary if the slopes of the crystalline Frobenius ![]() $\varphi$ on
$\varphi$ on ![]() $\mathbb {L}_{\mathrm {cris},P'}(W)$ are
$\mathbb {L}_{\mathrm {cris},P'}(W)$ are ![]() $-1,1$ with multiplicity
$-1,1$ with multiplicity ![]() $1$ and
$1$ and ![]() $0$ with multiplicity
$0$ with multiplicity ![]() $n$.Footnote 17
$n$.Footnote 17
The cocharacter ![]() $\bar {\mu }$ defines a filtration
$\bar {\mu }$ defines a filtration ![]() $\operatorname {Fil}^i, i=-1,0,1$ on
$\operatorname {Fil}^i, i=-1,0,1$ on ![]() $\mathbb {L}_{\mathrm {cris},P}(k)$, which is the Hodge filtration in [Reference OgusOgu01] and, in particular,
$\mathbb {L}_{\mathrm {cris},P}(k)$, which is the Hodge filtration in [Reference OgusOgu01] and, in particular, ![]() $\dim \operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)=1$,
$\dim \operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)=1$, ![]() $\dim \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)=n+1$,
$\dim \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)=n+1$, ![]() $\dim \operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris},P}(k)=n+2$ and the annihilator of
$\dim \operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris},P}(k)=n+2$ and the annihilator of ![]() $\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)$ in
$\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)$ in ![]() $\mathbb {L}_{\mathrm {cris},P}(k)$ with respect to
$\mathbb {L}_{\mathrm {cris},P}(k)$ with respect to ![]() $Q$ is
$Q$ is ![]() $\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)$.Footnote 18 The Hodge filtration over the mod
$\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)$.Footnote 18 The Hodge filtration over the mod ![]() $p$ complete local ring
$p$ complete local ring ![]() $R\otimes _W k$ at
$R\otimes _W k$ at ![]() $P$ is given by
$P$ is given by ![]() $\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris},P}(k)\otimes _k (R\otimes k)$. Note that
$\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris},P}(k)\otimes _k (R\otimes k)$. Note that ![]() $\operatorname {Frob} (\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k) )\subset \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$, so we have a well-defined map
$\operatorname {Frob} (\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k) )\subset \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$, so we have a well-defined map ![]() $p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)\rightarrow \operatorname {gr}_{-1}{\mathbb{L}_{\mathrm {cris}}(R\otimes _W k)}$, where
$p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)\rightarrow \operatorname {gr}_{-1}{\mathbb{L}_{\mathrm {cris}}(R\otimes _W k)}$, where ![]() $\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)/\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$.
$\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)/\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$.
Lemma 3.4.1 (Ogus)
For a supersingular point ![]() $P$, The non-ordinary locus (over
$P$, The non-ordinary locus (over ![]() $k$) in the formal neighborhood of
$k$) in the formal neighborhood of ![]() $P$ is given by the equation
$P$ is given by the equation
Proof. By [Reference OgusOgu01, Proposition 11], the discussion of the conjugate filtration on [Reference OgusOgu01, pp. 333–334], and the fact that the annihilator of ![]() $\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ in
$\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ in ![]() $\mathbb {L}_{\mathrm {cris}}(R\otimes k)$ with respect to
$\mathbb {L}_{\mathrm {cris}}(R\otimes k)$ with respect to ![]() $Q$ is
$Q$ is ![]() $\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$, we have that the equation defining the non-ordinary locus is the projection of the conjugate filtration (denoted by
$\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$, we have that the equation defining the non-ordinary locus is the projection of the conjugate filtration (denoted by ![]() $F^2_{con}$ in [Reference OgusOgu01]) to
$F^2_{con}$ in [Reference OgusOgu01]) to ![]() $\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes k)$. By definition,
$\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes k)$. By definition, ![]() $F^2_{con}=p\operatorname {Frob} \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ and then the lemma follows.
$F^2_{con}=p\operatorname {Frob} \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ and then the lemma follows.
Corollary 3.4.2 When ![]() $L=L_{\rm H}$, the local equation of the non-ordinary locus in a formal neighborhood of a supersingular point
$L=L_{\rm H}$, the local equation of the non-ordinary locus in a formal neighborhood of a supersingular point ![]() $P$ is
$P$ is ![]() $xy=0$ if
$xy=0$ if ![]() $P$ is superspecial and is
$P$ is superspecial and is ![]() $y=0$ if
$y=0$ if ![]() $P$ is supergeneric; when
$P$ is supergeneric; when ![]() $L=L_{\rm S}$, the local equation is
$L=L_{\rm S}$, the local equation is ![]() $xy+z^2/(4\epsilon )=0$ if
$xy+z^2/(4\epsilon )=0$ if ![]() $P$ is a superspecial point and
$P$ is a superspecial point and ![]() $(x+a)y+z^2/(4\epsilon )=0$ if
$(x+a)y+z^2/(4\epsilon )=0$ if ![]() $P$ supergeneric, where
$P$ supergeneric, where ![]() $a\in W(k)^\times$ depends on
$a\in W(k)^\times$ depends on ![]() $P$.
$P$.
Proof. We prove this corollary in the case ![]() $L = L_{\rm S}$, because the other case is handled the same way. Recall we have the basis
$L = L_{\rm S}$, because the other case is handled the same way. Recall we have the basis ![]() $v_1 \ldots v_5$ of
$v_1 \ldots v_5$ of ![]() $\mathbb {L}_{\mathrm {cris}}$, with
$\mathbb {L}_{\mathrm {cris}}$, with ![]() $\operatorname {Fil}^-{1} = \mathbb {L}_{\mathrm {cris}}$ and
$\operatorname {Fil}^-{1} = \mathbb {L}_{\mathrm {cris}}$ and ![]() $\operatorname {Fil}^0$ being spanned by
$\operatorname {Fil}^0$ being spanned by ![]() $v_2,v_3,v_4$ and
$v_2,v_3,v_4$ and ![]() $v_5$. Therefore, using the explicit formulas from the previous section, we see the map
$v_5$. Therefore, using the explicit formulas from the previous section, we see the map ![]() $p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k) \rightarrow \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$ is given by
$p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k) \rightarrow \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$ is given by ![]() $p\operatorname {Frob}(v_1) = -(xy + {z^2}/{4\epsilon } + ay)v_1$. Our result now follows from Ogus's description of the non-ordinary locus.
$p\operatorname {Frob}(v_1) = -(xy + {z^2}/{4\epsilon } + ay)v_1$. Our result now follows from Ogus's description of the non-ordinary locus.
4. Arithmetic Borcherds theory, Siegel mass formula, and Eisenstein series
We use arithmetic Borcherds theory [Reference Howard and Madapusi PeraHMP20] to control the global intersection number of a curve ![]() $C$ with special divisors. More precisely, we use the work of Bruinier and Kuss in [Reference Bruinier and KühnBK03] to study the Fourier coefficients of the Eisenstein part of the (vector-valued) modular form arising from Borcherds theory. To compare the global intersection number with the local contribution later in the paper, we also apply the computations in [Reference Bruinier and KühnBK03] and the Siegel mass formula to the Eisenstein part of the theta series attached to a supersingular point and reduce the question to a computation of local densities and determinants of the lattices
$C$ with special divisors. More precisely, we use the work of Bruinier and Kuss in [Reference Bruinier and KühnBK03] to study the Fourier coefficients of the Eisenstein part of the (vector-valued) modular form arising from Borcherds theory. To compare the global intersection number with the local contribution later in the paper, we also apply the computations in [Reference Bruinier and KühnBK03] and the Siegel mass formula to the Eisenstein part of the theta series attached to a supersingular point and reduce the question to a computation of local densities and determinants of the lattices ![]() $L$ and
$L$ and ![]() $L'$ introduced in § 2.1 and Definition 2.3.1 (in § 4.2, we summarize the properties of
$L'$ introduced in § 2.1 and Definition 2.3.1 (in § 4.2, we summarize the properties of ![]() $L'$). We use Hanke's method in [Reference HankeHan04] to compute the local densities. Throughout this section,
$L'$). We use Hanke's method in [Reference HankeHan04] to compute the local densities. Throughout this section, ![]() $p$ is an odd prime such that
$p$ is an odd prime such that ![]() $L$ is self-dual at
$L$ is self-dual at ![]() $p$. For a prime
$p$. For a prime ![]() $\ell$, we use
$\ell$, we use ![]() $v_\ell : \mathbb {Z}_\ell \backslash \{0\}\rightarrow \mathbb {Z}_{\geq 0}$ to denote the
$v_\ell : \mathbb {Z}_\ell \backslash \{0\}\rightarrow \mathbb {Z}_{\geq 0}$ to denote the ![]() $\ell$-adic valuation.
$\ell$-adic valuation.
4.1 Arithmetic Borcherds theory and the explicit formula for the Eisenstein series
Recall the special divisors ![]() $Z(m)$ from Definition 2.2.6 and § 2.2.11. The following modularity result is the key input to the estimate of the intersection number
$Z(m)$ from Definition 2.2.6 and § 2.2.11. The following modularity result is the key input to the estimate of the intersection number ![]() $Z(m).C$.
$Z(m).C$.
To state the result using vector-valued modular forms, for ![]() $\mu \in L^\vee /L,\ m\in \mathbb {Q}_{>0}$, let
$\mu \in L^\vee /L,\ m\in \mathbb {Q}_{>0}$, let ![]() $\mathcal {Z}(m,\mu )$ denote the special divisors over
$\mathcal {Z}(m,\mu )$ denote the special divisors over ![]() $\mathbb {Z}$ in
$\mathbb {Z}$ in ![]() $\mathcal {M}$ defined in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, § 4.5, Definition 4.5.6]. By definition,
$\mathcal {M}$ defined in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, § 4.5, Definition 4.5.6]. By definition, ![]() $\mathcal {Z}(m,0)$ is the divisor
$\mathcal {Z}(m,0)$ is the divisor ![]() $\mathcal {Z}(m)$ defined in § 2.2; and roughly speaking,
$\mathcal {Z}(m)$ defined in § 2.2; and roughly speaking, ![]() $\mathcal {Z}(m,\mu )$ parametrizes abelian surfaces
$\mathcal {Z}(m,\mu )$ parametrizes abelian surfaces ![]() $A$ with a special quasi-endomorphism
$A$ with a special quasi-endomorphism ![]() $s$ such that
$s$ such that ![]() $Q(s)=m$ and the
$Q(s)=m$ and the ![]() $\ell$-adic and crystalline realizations of
$\ell$-adic and crystalline realizations of ![]() $s$ lie in the image of
$s$ lie in the image of ![]() $(\mu +L)\otimes \mathbb {Z}_\ell$ and
$(\mu +L)\otimes \mathbb {Z}_\ell$ and ![]() $(\mu +L)\otimes \mathbb {Z}_p$ in
$(\mu +L)\otimes \mathbb {Z}_p$ in ![]() $\operatorname {End}(T_\ell (A)\otimes \mathbb {Q}_\ell )$ and
$\operatorname {End}(T_\ell (A)\otimes \mathbb {Q}_\ell )$ and ![]() $\operatorname {End}(\mathbb {D}\otimes _W W[1/p])$, respectively, where
$\operatorname {End}(\mathbb {D}\otimes _W W[1/p])$, respectively, where ![]() $\mathbb {D}$ is the Dieudonné module of
$\mathbb {D}$ is the Dieudonné module of ![]() $A$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8] and [Reference Madapusi PeraMP16, Proposition 5.21], the assumption that
$A$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8] and [Reference Madapusi PeraMP16, Proposition 5.21], the assumption that ![]() $L$ is self-dual at
$L$ is self-dual at ![]() $p$ implies that
$p$ implies that ![]() $\mathcal {Z}(m,\mu )$ is flat over
$\mathcal {Z}(m,\mu )$ is flat over ![]() $\mathbb {Z}_p$. Let
$\mathbb {Z}_p$. Let ![]() $Z(m,\mu )$ denote
$Z(m,\mu )$ denote ![]() $\mathcal {Z}(m,\mu )_{\mathbb {F}_p}$. Let
$\mathcal {Z}(m,\mu )_{\mathbb {F}_p}$. Let ![]() $(\mathfrak {e}_\mu )_{\mu \in L^\vee /L}$ denote the standard basis of
$(\mathfrak {e}_\mu )_{\mu \in L^\vee /L}$ denote the standard basis of ![]() $\mathbb {C}[L^\vee /L]$. Let
$\mathbb {C}[L^\vee /L]$. Let ![]() $\omega \in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ denote the Hodge line bundle in the
$\omega \in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ denote the Hodge line bundle in the ![]() $\mathbb {Q}$-Picard group of
$\mathbb {Q}$-Picard group of ![]() $\mathcal {M}_{\mathbb {F}_p}$; in other words,
$\mathcal {M}_{\mathbb {F}_p}$; in other words, ![]() $\omega$ is the line bundle of weight
$\omega$ is the line bundle of weight ![]() $1$ modular forms (see, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Theorem 4.4.6] for a definition of
$1$ modular forms (see, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Theorem 4.4.6] for a definition of ![]() $\omega$).
$\omega$).
Theorem 4.1.1 (Borcherds, Howard–Madapusi Pera)
Assume ![]() $(L,Q)$ is a maximal quadratic lattice of signature
$(L,Q)$ is a maximal quadratic lattice of signature ![]() $(n,2)$ such that
$(n,2)$ such that ![]() $L$ is self-dual at
$L$ is self-dual at ![]() $p$. The generating series
$p$. The generating series
lies in ![]() $M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$. Here,
$M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$. Here, ![]() $\rho _L$ denotes the Weil representation on
$\rho _L$ denotes the Weil representation on ![]() $\mathbb {C}[L^\vee /L]$ and
$\mathbb {C}[L^\vee /L]$ and ![]() $M_{1+{n}/{2}}(\rho _L)$ denotes the space of vector-valued modular forms of
$M_{1+{n}/{2}}(\rho _L)$ denotes the space of vector-valued modular forms of ![]() $\operatorname {Mp}_2(\mathbb {Z})$ with respect to
$\operatorname {Mp}_2(\mathbb {Z})$ with respect to ![]() $\rho _L$ of weight
$\rho _L$ of weight ![]() $1+{n}/{2}$.Footnote 19 In particular, for any
$1+{n}/{2}$.Footnote 19 In particular, for any ![]() $\mathbb {Q}$-linear functional
$\mathbb {Q}$-linear functional ![]() $\alpha : \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}\rightarrow \mathbb {C}$, the vector-valued power series
$\alpha : \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}\rightarrow \mathbb {C}$, the vector-valued power series
is the Fourier expansion of an element of ![]() $M_{1+{n}/{2}}(\rho _L)$.
$M_{1+{n}/{2}}(\rho _L)$.
Proof. By abuse of notation, we also use ![]() $\omega$ to denote the Hodge line bundle over
$\omega$ to denote the Hodge line bundle over ![]() $\mathcal {M}$. By [Reference Howard and Madapusi PeraHMP20, Theorem B], the generating series
$\mathcal {M}$. By [Reference Howard and Madapusi PeraHMP20, Theorem B], the generating series ![]() $\omega ^{-1}\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}\mathcal {Z}(m,\mu ) q^m \mathfrak {e}_\mu \in M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M})_{\mathbb {Q}}$. As
$\omega ^{-1}\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}\mathcal {Z}(m,\mu ) q^m \mathfrak {e}_\mu \in M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M})_{\mathbb {Q}}$. As ![]() $\mathcal {Z}(m,\mu )$ are flat over
$\mathcal {Z}(m,\mu )$ are flat over ![]() $\mathbb {Z}_p$, then the desired assertion follows from intersecting with
$\mathbb {Z}_p$, then the desired assertion follows from intersecting with ![]() $\mathcal {M}_{\mathbb {F}_p}$.
$\mathcal {M}_{\mathbb {F}_p}$.
4.1.2
In the setting of Theorem 1(2) (i.e. the case when ![]() $L=L_{\rm H}$), we work with curves
$L=L_{\rm H}$), we work with curves ![]() $C$ that are not necessarily proper. We therefore need a version of the above modularity result that holds for the special fiber a toroidal compactification of
$C$ that are not necessarily proper. We therefore need a version of the above modularity result that holds for the special fiber a toroidal compactification of ![]() $\mathcal {M}$. To that end, let
$\mathcal {M}$. To that end, let ![]() $\mathcal {M}^{\textrm {tor}}$ denote a toroidal compactification of
$\mathcal {M}^{\textrm {tor}}$ denote a toroidal compactification of ![]() $\mathcal {M}$, and let
$\mathcal {M}$, and let ![]() $D_1,\ldots, D_k$ denote irreducible components of the boundary
$D_1,\ldots, D_k$ denote irreducible components of the boundary ![]() $\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}\setminus \mathcal {M}_{\mathbb {F}_p}$. In [Reference Bruinier, Burgos Gil and KühnBBGK07, Theorem 6.2], the authors prove the modularity result for
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}\setminus \mathcal {M}_{\mathbb {F}_p}$. In [Reference Bruinier, Burgos Gil and KühnBBGK07, Theorem 6.2], the authors prove the modularity result for ![]() $\mathcal {M}^{\textrm {tor}}$, which will directly imply the modularity result for
$\mathcal {M}^{\textrm {tor}}$, which will directly imply the modularity result for ![]() $\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$. The constant term is still given by the Hodge line bundle, still denoted by
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$. The constant term is still given by the Hodge line bundle, still denoted by ![]() $\omega$, on
$\omega$, on ![]() $\mathcal {M}^{\rm {tor}}_{\mathbb {F}_p}$ and the special divisors
$\mathcal {M}^{\rm {tor}}_{\mathbb {F}_p}$ and the special divisors ![]() $Z(m,\mu )$ are replaced byFootnote 20
$Z(m,\mu )$ are replaced byFootnote 20 ![]() $Z'(m,\mu ) + E(m,\mu )$, where
$Z'(m,\mu ) + E(m,\mu )$, where ![]() $Z'(m,\mu )$ is the Zariski-closure of
$Z'(m,\mu )$ is the Zariski-closure of ![]() $Z(m,\mu )$ in
$Z(m,\mu )$ in ![]() $\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$, and
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$, and ![]() $E(m,\mu )$ is a ‘correction term’, and has as its irreducible components the
$E(m,\mu )$ is a ‘correction term’, and has as its irreducible components the ![]() $D_i$ with appropriate multiplicity. Crucially, when
$D_i$ with appropriate multiplicity. Crucially, when ![]() $Z(m,\mu )$ is proper (see § 4.3.3 for when this happens), the multiplicities of the
$Z(m,\mu )$ is proper (see § 4.3.3 for when this happens), the multiplicities of the ![]() ${D_i}$ in correction term
${D_i}$ in correction term ![]() $E(m,\mu )$ are all zero and, hence,
$E(m,\mu )$ are all zero and, hence, ![]() $E(m,\mu )$ is trivial. Therefore, compact special divisors stay as they are in the modularity theorem for
$E(m,\mu )$ is trivial. Therefore, compact special divisors stay as they are in the modularity theorem for ![]() $\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$.Footnote 21
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$.Footnote 21
4.1.3
Recall that we have a finite morphism ![]() $\pi : C\rightarrow \mathcal {M}_{\bar {\mathbb {F}}_p}$. When
$\pi : C\rightarrow \mathcal {M}_{\bar {\mathbb {F}}_p}$. When ![]() $C$ is proper, for
$C$ is proper, for ![]() $Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$, we define
$Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$, we define ![]() $C.Z$ as the degree of
$C.Z$ as the degree of ![]() $\pi ^* Z \in \operatorname {Pic}(C)_{\mathbb {Q}}$. For Theorem 1(2), we pick a toroidal compactification
$\pi ^* Z \in \operatorname {Pic}(C)_{\mathbb {Q}}$. For Theorem 1(2), we pick a toroidal compactification ![]() $\mathcal {M}^{\rm {tor}}$ of the Hilbert modular surface
$\mathcal {M}^{\rm {tor}}$ of the Hilbert modular surface ![]() $\mathcal {M}$ and let
$\mathcal {M}$ and let ![]() $C'$ denote the smooth compactification of
$C'$ denote the smooth compactification of ![]() $C$ and the finite morphism
$C$ and the finite morphism ![]() $\pi$ extends to a finite morphism
$\pi$ extends to a finite morphism ![]() $\pi ': C'\rightarrow \mathcal {M}^{\rm {tor}}_{\bar {\mathbb {F}}_p}$. Then for a proper divisor
$\pi ': C'\rightarrow \mathcal {M}^{\rm {tor}}_{\bar {\mathbb {F}}_p}$. Then for a proper divisor ![]() $Z$ in
$Z$ in ![]() $\mathcal {M}_{\mathbb {F}_p}$, we use
$\mathcal {M}_{\mathbb {F}_p}$, we use ![]() $C.Z$ to denote
$C.Z$ to denote ![]() $\deg _{C'}(\pi ^*Z)$; because
$\deg _{C'}(\pi ^*Z)$; because ![]() $Z$ is proper,
$Z$ is proper, ![]() $C'\cap Z=C\cap Z$ so we only need to consider points in
$C'\cap Z=C\cap Z$ so we only need to consider points in ![]() $\mathcal {M}_{\bar {\mathbb {F}}_p}$.
$\mathcal {M}_{\bar {\mathbb {F}}_p}$.
4.1.4
We apply Theorem 4.1.1 and § 4.1.2 to ![]() $\alpha (Z):=C.Z$ defined in § 4.1.3 for
$\alpha (Z):=C.Z$ defined in § 4.1.3 for ![]() $Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ (and we further assume that
$Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ (and we further assume that ![]() $Z$ is proper when
$Z$ is proper when ![]() $L=L_{\rm H}$). We decompose the modular form
$L=L_{\rm H}$). We decompose the modular form ![]() $-(\omega.C)\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}Z(m,\mu ).C q^m \mathfrak {e}_\mu$ as
$-(\omega.C)\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}Z(m,\mu ).C q^m \mathfrak {e}_\mu$ as ![]() $E(q)+G(q)$, where
$E(q)+G(q)$, where ![]() $E(q)\in M_{1+{n}/{2}}(\rho _L)$ is an Eisenstein series and
$E(q)\in M_{1+{n}/{2}}(\rho _L)$ is an Eisenstein series and ![]() $G(q)\in M_{1+{n}/{2}}(\rho _L)$ is a cusp form. Note that the constant term of
$G(q)\in M_{1+{n}/{2}}(\rho _L)$ is a cusp form. Note that the constant term of ![]() $E(q)$ is
$E(q)$ is ![]() $-(\omega.C)\mathfrak {e}_0$.
$-(\omega.C)\mathfrak {e}_0$.
We now recall the vector-valued Eisenstein series ![]() $E_0(\tau )\in M_{1+{n}/{2}}(\rho _L)$ which has constant term
$E_0(\tau )\in M_{1+{n}/{2}}(\rho _L)$ which has constant term ![]() $\mathfrak {e}_0$. This Eisenstein series has been studied in [Reference BruinierBru02, § 1.2.3], [Reference Bruinier and KussBK01, § 4], and [Reference Bruinier and KühnBK03, § 3]. Here we follow [Reference BruinierBru17, § 2.1] as we use the same convention of quadratic forms. We denote an element in
$\mathfrak {e}_0$. This Eisenstein series has been studied in [Reference BruinierBru02, § 1.2.3], [Reference Bruinier and KussBK01, § 4], and [Reference Bruinier and KühnBK03, § 3]. Here we follow [Reference BruinierBru17, § 2.1] as we use the same convention of quadratic forms. We denote an element in ![]() $\operatorname {Mp}_2(\mathbb {Z})$ by
$\operatorname {Mp}_2(\mathbb {Z})$ by ![]() $(g,\sigma )$, where
$(g,\sigma )$, where ![]() $g=\big [\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\big ]\in \operatorname {SL}_2(\mathbb {Z})$ and
$g=\big [\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\big ]\in \operatorname {SL}_2(\mathbb {Z})$ and ![]() $\sigma$ is a choice of the square root of
$\sigma$ is a choice of the square root of ![]() $\tau \mapsto c\tau +d$. Let
$\tau \mapsto c\tau +d$. Let ![]() $\Gamma '_\infty \subset \operatorname {Mp}_2(\mathbb {Z})$ denote the stabilizer of
$\Gamma '_\infty \subset \operatorname {Mp}_2(\mathbb {Z})$ denote the stabilizer of ![]() $\infty$. Then for
$\infty$. Then for ![]() $n\geq 3$, the following summation converges on the upper half plane and we define
$n\geq 3$, the following summation converges on the upper half plane and we define
When ![]() $n=2$, we define
$n=2$, we define ![]() $E_0(\tau )$ use analytic continuation following [Reference Bruinier and KühnBK03, § 3]. Write
$E_0(\tau )$ use analytic continuation following [Reference Bruinier and KühnBK03, § 3]. Write ![]() $\tau =x+iy$ and define for
$\tau =x+iy$ and define for ![]() $s\in \mathbb {C}$,
$s\in \mathbb {C}$,
which converges on the upper half plane for ![]() $s$ with
$s$ with ![]() $\Re s>0$ (
$\Re s>0$ (![]() $n=2$ here). By [Reference Bruinier and KühnBK03, p. 1697],
$n=2$ here). By [Reference Bruinier and KühnBK03, p. 1697], ![]() $E_0(\tau,s)$ has meromorphic continuation in
$E_0(\tau,s)$ has meromorphic continuation in ![]() $s$ to the entire
$s$ to the entire ![]() $\mathbb {C}$ and it is holomorphic at
$\mathbb {C}$ and it is holomorphic at ![]() $s=0$ and we define
$s=0$ and we define ![]() $E_0(\tau )$ to be the value at
$E_0(\tau )$ to be the value at ![]() $s=0$ of the meromorphic continuation of
$s=0$ of the meromorphic continuation of ![]() $E_0(\tau,s)$. Moreover, by [Reference Bruinier and KühnBK03, p. 1697],
$E_0(\tau,s)$. Moreover, by [Reference Bruinier and KühnBK03, p. 1697], ![]() $E_0(\tau )$ is holomorphic and, hence, lies in
$E_0(\tau )$ is holomorphic and, hence, lies in ![]() $M_{1+{n}/{2}}(\rho _L)$ if
$M_{1+{n}/{2}}(\rho _L)$ if ![]() $\rho _L$ does not contain the trivial representation as a subquotient. In the proof of Theorem 1(2), we work with
$\rho _L$ does not contain the trivial representation as a subquotient. In the proof of Theorem 1(2), we work with ![]() $L=L_{\rm H}$ and this condition for
$L=L_{\rm H}$ and this condition for ![]() $\rho _L$ is always satisfied as far as the
$\rho _L$ is always satisfied as far as the ![]() $m$ in the statement of Theorem 1(2) is not a perfect square, that is,
$m$ in the statement of Theorem 1(2) is not a perfect square, that is, ![]() $\mathcal {M}$ is not the product of modular curves.
$\mathcal {M}$ is not the product of modular curves.
We denote the ![]() $q$-expansion of
$q$-expansion of ![]() $E_0(\tau )$ as
$E_0(\tau )$ as ![]() $\sum _{m\geq 0,\, m\in \mathbb {Z}+Q(\mu )}q_L(m,\mu )q^m \mathfrak {e}_\mu$ and set
$\sum _{m\geq 0,\, m\in \mathbb {Z}+Q(\mu )}q_L(m,\mu )q^m \mathfrak {e}_\mu$ and set ![]() $q_L(m):=q_L(m,0)$ for
$q_L(m):=q_L(m,0)$ for ![]() $m\in \mathbb {Z}_{>0}$.
$m\in \mathbb {Z}_{>0}$.
4.1.5
We fix some notation before we state the explicit formula of ![]() $q_L(m)$ given by Bruinier and Kuss. Given a quadratic lattice
$q_L(m)$ given by Bruinier and Kuss. Given a quadratic lattice ![]() $L$ (not necessarily the lattice
$L$ (not necessarily the lattice ![]() $L_{\rm H},L_{\rm S}$), we write
$L_{\rm H},L_{\rm S}$), we write ![]() $\det (L)$ for the determinant of its Gram matrix. We have
$\det (L)$ for the determinant of its Gram matrix. We have ![]() $|L^\vee /L|=|\!\det (L)|$.
$|L^\vee /L|=|\!\det (L)|$.
For a rational prime ![]() $\ell$, we use
$\ell$, we use ![]() $\delta (\ell, L,m)$ to denote the local density of
$\delta (\ell, L,m)$ to denote the local density of ![]() $L$ representing
$L$ representing ![]() $m$ over
$m$ over ![]() $\mathbb {Z}_\ell$. More precisely,
$\mathbb {Z}_\ell$. More precisely, ![]() $\delta (\ell, L,m)=\lim _{a\rightarrow \infty } \ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$. Here [Reference Bruinier and KussBK01, Lemma 5] asserts that the limit is stable once
$\delta (\ell, L,m)=\lim _{a\rightarrow \infty } \ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$. Here [Reference Bruinier and KussBK01, Lemma 5] asserts that the limit is stable once ![]() $a\geq 1+2v_\ell (2m)$. In particular, if
$a\geq 1+2v_\ell (2m)$. In particular, if ![]() $m$ is representable by
$m$ is representable by ![]() $(L\otimes \mathbb {Z}_\ell, Q)$, then
$(L\otimes \mathbb {Z}_\ell, Q)$, then ![]() $\delta (\ell,L,m)>0$.
$\delta (\ell,L,m)>0$.
Given ![]() $0\neq D\in \mathbb {Z}$ such that
$0\neq D\in \mathbb {Z}$ such that ![]() $D\equiv 0,1 \bmod 4$, we use
$D\equiv 0,1 \bmod 4$, we use ![]() $\chi _D$ to denote the Dirichlet character
$\chi _D$ to denote the Dirichlet character ![]() $\chi _D(a)=(\frac {D}{a})$, where
$\chi _D(a)=(\frac {D}{a})$, where ![]() $(\frac {\cdot }{\cdot })$ is the Kronecker symbol. For a Dirichlet character
$(\frac {\cdot }{\cdot })$ is the Kronecker symbol. For a Dirichlet character ![]() $\chi$, we set
$\chi$, we set ![]() $\sigma _s(m,\chi )=\sum _{d|m}\chi (d)d^s$.
$\sigma _s(m,\chi )=\sum _{d|m}\chi (d)d^s$.
Theorem 4.1.6 (Bruinier and Kuss; see also [Reference BruinierBru17, Theorems 2.3 and 2.4])
Consider ![]() $L\,{=}\,L_{\rm H},$
$L\,{=}\,L_{\rm H},$ ![]() $L_{\rm S}$ defined in § 2.1 and
$L_{\rm S}$ defined in § 2.1 and ![]() $m\in \mathbb {Z}_{>0}$.
$m\in \mathbb {Z}_{>0}$.
(1) For
 $L=L_{\rm H}$, the Fourier coefficient
$L=L_{\rm H}$, the Fourier coefficient  $q_L(m)$ is
$q_L(m)$ is
 \[ -\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L})}{\sqrt{|L^\vee/L|}L(2,\chi_{4\det L})}\prod_{\ell \mid 2\det(L)}\delta(\ell, L, m). \]
\[ -\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L})}{\sqrt{|L^\vee/L|}L(2,\chi_{4\det L})}\prod_{\ell \mid 2\det(L)}\delta(\ell, L, m). \](2) For
 $L=L_{\rm S}$, write
$L=L_{\rm S}$, write  $m=m_0f^2$, where
$m=m_0f^2$, where  ${\rm {gcd}}(f,2\det L)=1$ and
${\rm {gcd}}(f,2\det L)=1$ and  $v_\ell (m_0)\in \{0,1\}$ for all
$v_\ell (m_0)\in \{0,1\}$ for all  ${\ell \nmid 2\det L}$. Then the Fourier coefficient
${\ell \nmid 2\det L}$. Then the Fourier coefficient  $q_L(m)$ is
where
$q_L(m)$ is
where \[ -\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}})}{3\sqrt{|L^\vee/L|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\prod_{\ell\mid 2\det L}\big(\delta(\ell,L,m)/(1-\ell^{-4})\big), \]
\[ -\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}})}{3\sqrt{|L^\vee/L|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\prod_{\ell\mid 2\det L}\big(\delta(\ell,L,m)/(1-\ell^{-4})\big), \] $\mu$ is the Mobius function and
$\mu$ is the Mobius function and  $\mathcal {D}=-2m_0\det L$.Footnote 22
$\mathcal {D}=-2m_0\det L$.Footnote 22
Proof. When ![]() $L=L_{\rm S}$, this is [Reference Bruinier and KussBK01, Theorem 11]. When
$L=L_{\rm S}$, this is [Reference Bruinier and KussBK01, Theorem 11]. When ![]() $L=L_{\rm H}$, one modifies the proof of [Reference Bruinier and KussBK01, Theorem 11] as follows. Using [Reference Bruinier and KühnBK03, Proposition 3.1] instead of [Reference Bruinier and KussBK01, Proposition 2], we obtain [Reference Bruinier and KussBK01, Proposition 3] because Shintani's formula works in general. To express the formula in [Reference Bruinier and KussBK01, Proposition 3] as a product of local terms, we use [Reference IwaniecIwa97, § 11.5, p. 196]. The rest of the proof, which computes the local terms at
$L=L_{\rm H}$, one modifies the proof of [Reference Bruinier and KussBK01, Theorem 11] as follows. Using [Reference Bruinier and KühnBK03, Proposition 3.1] instead of [Reference Bruinier and KussBK01, Proposition 2], we obtain [Reference Bruinier and KussBK01, Proposition 3] because Shintani's formula works in general. To express the formula in [Reference Bruinier and KussBK01, Proposition 3] as a product of local terms, we use [Reference IwaniecIwa97, § 11.5, p. 196]. The rest of the proof, which computes the local terms at ![]() $\ell \nmid 2\det L$, works in the same way (see also [Reference IwaniecIwa97, Equations (11.71)–(11.74)]).
$\ell \nmid 2\det L$, works in the same way (see also [Reference IwaniecIwa97, Equations (11.71)–(11.74)]).
If ![]() $Z(m)\neq \emptyset$, then
$Z(m)\neq \emptyset$, then ![]() $m$ is representable by
$m$ is representable by ![]() $(L,Q)$ and, in particular, for every
$(L,Q)$ and, in particular, for every ![]() $\ell$,
$\ell$, ![]() $m$ is representable by
$m$ is representable by ![]() $(L\otimes \mathbb {Z}_\ell,Q)$ and, hence,
$(L\otimes \mathbb {Z}_\ell,Q)$ and, hence, ![]() $\delta (\ell, L,m)>0$. By Theorem 4.1.6, we have
$\delta (\ell, L,m)>0$. By Theorem 4.1.6, we have ![]() $q_L(m)<0$ when
$q_L(m)<0$ when ![]() $Z(m)\neq \emptyset$.
$Z(m)\neq \emptyset$.
4.2 The lattice  $L'$ and the Siegel mass formula
$L'$ and the Siegel mass formula
4.2.1
For a supersingular point ![]() $P\in \mathcal {M}(k)$, we defined
$P\in \mathcal {M}(k)$, we defined ![]() $L''$, the lattice of special endomorphisms, in Definition 2.3.1 and picked
$L''$, the lattice of special endomorphisms, in Definition 2.3.1 and picked ![]() $L'\supset L''$ which is maximal at all
$L'\supset L''$ which is maximal at all ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$. Though there may be choices for
$L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$. Though there may be choices for ![]() $L'$, the local lattices
$L'$, the local lattices ![]() $L'\otimes \mathbb {Z}_\ell$ are well-defined up to isometry. More precisely, for
$L'\otimes \mathbb {Z}_\ell$ are well-defined up to isometry. More precisely, for ![]() $\ell \neq p$,
$\ell \neq p$, ![]() $L'\otimes \mathbb {Z}_\ell$ is given by Lemma 2.3.2; and for
$L'\otimes \mathbb {Z}_\ell$ is given by Lemma 2.3.2; and for ![]() $\ell =p$,
$\ell =p$, ![]() $L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$ is computed in §§ 3.2–3.3. Note that given
$L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$ is computed in §§ 3.2–3.3. Note that given ![]() $L$, the isometry class of the quadratic lattice
$L$, the isometry class of the quadratic lattice ![]() $L'\otimes \mathbb {Z}_p$ only depends on whether
$L'\otimes \mathbb {Z}_p$ only depends on whether ![]() $P$ is superspecial or supergeneric; indeed, following the notation in § 3.1.2, if
$P$ is superspecial or supergeneric; indeed, following the notation in § 3.1.2, if ![]() $t_P=t_{\rm max}$ (for instance, when
$t_P=t_{\rm max}$ (for instance, when ![]() $P$ is supergeneric), then
$P$ is supergeneric), then ![]() $\Lambda _P$ is a maximal lattice with respect to
$\Lambda _P$ is a maximal lattice with respect to ![]() $pQ'$ and, hence, its isometry class (and, thus, the isometry class of
$pQ'$ and, hence, its isometry class (and, thus, the isometry class of ![]() $L'\otimes \mathbb {Z}_p=\Lambda _P^\vee$) is unique; if
$L'\otimes \mathbb {Z}_p=\Lambda _P^\vee$) is unique; if ![]() $t_P=2$, that is,
$t_P=2$, that is, ![]() $P$ is superspecial, then
$P$ is superspecial, then ![]() $\Lambda _P^\vee$ is a maximal lattice with respect to
$\Lambda _P^\vee$ is a maximal lattice with respect to ![]() $Q'$ and, hence, is unique up to isometry.
$Q'$ and, hence, is unique up to isometry.
To compute the local intersection number of ![]() $Z(m).C$ at
$Z(m).C$ at ![]() $P$, we also need to consider sublattices
$P$, we also need to consider sublattices ![]() $L'''$ of
$L'''$ of ![]() $L'$ such that
$L'$ such that ![]() $L'''\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$ for all
$L'''\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$ for all ![]() $\ell \neq p$ (more precisely, we take
$\ell \neq p$ (more precisely, we take ![]() $L'''$ to be the lattices defined in § 7.2.3). In particular,
$L'''$ to be the lattices defined in § 7.2.3). In particular, ![]() $\det L'''=p^{2a} \det L'$ for some
$\det L'''=p^{2a} \det L'$ for some ![]() $a\in \mathbb {Z}_{\geq 0}$.
$a\in \mathbb {Z}_{\geq 0}$.
Let ![]() $\theta _{L'''}(q)$ denote the theta series of the positive-definite lattice
$\theta _{L'''}(q)$ denote the theta series of the positive-definite lattice ![]() $L'''$, which is a modular form of weight
$L'''$, which is a modular form of weight ![]() $\operatorname {rk} L'/2$; we decompose
$\operatorname {rk} L'/2$; we decompose ![]() $\theta _{L'''}(q)=E_{L'''}(q)+G_{L'''}(q)$, where
$\theta _{L'''}(q)=E_{L'''}(q)+G_{L'''}(q)$, where ![]() $E_{L'''}$ is an Eisenstein series and
$E_{L'''}$ is an Eisenstein series and ![]() $G_{L'''}$ is a cusp form. Let
$G_{L'''}$ is a cusp form. Let ![]() $q_{L'''}(m)$ denote the
$q_{L'''}(m)$ denote the ![]() $m$th Fourier coefficients of
$m$th Fourier coefficients of ![]() $E_{L'''}$ (at the cusp
$E_{L'''}$ (at the cusp ![]() $\infty$). The following theorem asserts that
$\infty$). The following theorem asserts that ![]() $q_{L'''}(m)$ only depends on the genus of
$q_{L'''}(m)$ only depends on the genus of ![]() $L'''$ and gives explicit formula for
$L'''$ and gives explicit formula for ![]() $q_{L'''}(m)$. In particular, when we consider the theta series for
$q_{L'''}(m)$. In particular, when we consider the theta series for ![]() $L'$, we have that
$L'$, we have that ![]() $q_{L'}(m)$ is independent of the choice of
$q_{L'}(m)$ is independent of the choice of ![]() $L'$ above and it only depends on
$L'$ above and it only depends on ![]() $L$ and whether
$L$ and whether ![]() $P$ is superspecial or supergeneric.
$P$ is superspecial or supergeneric.
Theorem 4.2.2 (Siegel mass formula)
Notation as in § 4.2.1. The Eisenstein series ![]() $E_{L'''}$ only depends on the genus of
$E_{L'''}$ only depends on the genus of ![]() $L'''$. Moreover, for
$L'''$. Moreover, for ![]() $m\in \mathbb {Z}_{>0}$:
$m\in \mathbb {Z}_{>0}$:
(1) when
 $L=L_{\rm H}$,
$L=L_{\rm H}$,
 \[ q_{L'''}(m)=\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L'})}{\sqrt{|L'''^\vee/L'''|}L(2, \chi_{4\det L'})}\prod_{\ell \mid 2 det L'}\delta(\ell, L''',m); \]
\[ q_{L'''}(m)=\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L'})}{\sqrt{|L'''^\vee/L'''|}L(2, \chi_{4\det L'})}\prod_{\ell \mid 2 det L'}\delta(\ell, L''',m); \](2) when
 $L=L_{\rm S}$,
where we write
$L=L_{\rm S}$,
where we write \begin{align*} q_{L'''}(m)&=\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}'})}{3\sqrt{|L'''^\vee/L'''|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}'}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\\ &\quad \times\prod_{\ell\mid 2\det L'}\big(\delta(\ell,L''',m)/(1-\ell^{-4})\big), \end{align*}
\begin{align*} q_{L'''}(m)&=\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}'})}{3\sqrt{|L'''^\vee/L'''|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}'}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\\ &\quad \times\prod_{\ell\mid 2\det L'}\big(\delta(\ell,L''',m)/(1-\ell^{-4})\big), \end{align*} $m=m_0f^2$ with
$m=m_0f^2$ with  ${\rm {gcd}}(f,2\det L')=1$ and
${\rm {gcd}}(f,2\det L')=1$ and  $v_\ell (m_0)\in \{0,1\}$ for all
$v_\ell (m_0)\in \{0,1\}$ for all  $\ell \nmid 2\det L'$ and
$\ell \nmid 2\det L'$ and  $\mathcal {D}'=-2 m_0 \det L'$
$\mathcal {D}'=-2 m_0 \det L'$
Proof. The first assertion follows from the Siegel mass formula; see, for instance, [Reference Iwaniec and KowalskiIK04, Theorem 20.9, (20.121), and pp. 479-480]. To obtain the formula above, we note that the proof of [Reference Bruinier and KussBK01, Theorem 11] using [Reference Bruinier and KussBK01, Theorem 6] also applies to ![]() $L'''$ and, hence, we conclude that the formula in [Reference BruinierBru17, Theorems 2.3 and 2.4] also applies to
$L'''$ and, hence, we conclude that the formula in [Reference BruinierBru17, Theorems 2.3 and 2.4] also applies to ![]() $L'''$ and obtain the formulas in the theorem with all
$L'''$ and obtain the formulas in the theorem with all ![]() $L'$ replaced by
$L'$ replaced by ![]() $L'''$. Note that by the computations in §§ 3.2–3.3, we have
$L'''$. Note that by the computations in §§ 3.2–3.3, we have ![]() $p\mid \det L'$ and, hence,
$p\mid \det L'$ and, hence, ![]() $\ell \mid 2 \det L'''$ if and only if
$\ell \mid 2 \det L'''$ if and only if ![]() $\ell \mid 2 \det L'$; also
$\ell \mid 2 \det L'$; also ![]() $\chi _{4 \det L'''}=\chi _{4 \det L'}$ and
$\chi _{4 \det L'''}=\chi _{4 \det L'}$ and ![]() $\chi _{D'}=\chi _{-2m_0 \det L'''}$. Hence, using
$\chi _{D'}=\chi _{-2m_0 \det L'''}$. Hence, using ![]() $L'$ (instead of
$L'$ (instead of ![]() $L'''$) for
$L'''$) for ![]() $\chi, \mathcal {D}'$ and the product
$\chi, \mathcal {D}'$ and the product ![]() $\ell \mid 2 \det L'$ yields the same formulas.
$\ell \mid 2 \det L'$ yields the same formulas.
4.3 The asymptotic of  $q_L(m)$
$q_L(m)$
The discussion of this subsection also applies to ![]() $q_{L'''}(m)$ when
$q_{L'''}(m)$ when ![]() $m$ is representable by
$m$ is representable by ![]() $(L''',Q')$, but we only focus on
$(L''',Q')$, but we only focus on ![]() $q_L(m)$ here.
$q_L(m)$ here.
4.3.1
Assume that ![]() $m$ is representable by
$m$ is representable by ![]() $(L\otimes \mathbb {Z}_\ell,Q)$ for every prime
$(L\otimes \mathbb {Z}_\ell,Q)$ for every prime ![]() $\ell$. We also assume that, as
$\ell$. We also assume that, as ![]() $m$ varies within a specified set
$m$ varies within a specified set ![]() $T$, there exists an absolute constant
$T$, there exists an absolute constant ![]() $C>0$ such that for all
$C>0$ such that for all ![]() $\ell \mid 2 \det L$, we have
$\ell \mid 2 \det L$, we have ![]() $v_\ell (m)\leq C$. As we shall see in § 4.3.3, we will always be in this situation.
$v_\ell (m)\leq C$. As we shall see in § 4.3.3, we will always be in this situation.
For a given ![]() $\ell \mid 2 \det L$, as in [Reference BruinierBru17, proof of Proposition 2.5], by [Reference Bruinier and KussBK01, Lemma 5], we have
$\ell \mid 2 \det L$, as in [Reference BruinierBru17, proof of Proposition 2.5], by [Reference Bruinier and KussBK01, Lemma 5], we have ![]() $\delta (\ell,L,m)=\ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$ with
$\delta (\ell,L,m)=\ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$ with ![]() $a=1+2C+2v_\ell (2)$ and, hence,
$a=1+2C+2v_\ell (2)$ and, hence, ![]() $\ell ^{a(1-\operatorname {rk} L)}\leq \delta (\ell,L,m)\leq \ell ^a$.Footnote 23
$\ell ^{a(1-\operatorname {rk} L)}\leq \delta (\ell,L,m)\leq \ell ^a$.Footnote 23
Therefore, given ![]() $(L,Q)$, by Theorem 4.1.6, we have that
$(L,Q)$, by Theorem 4.1.6, we have that ![]() $|q_L(m)|\asymp m \sigma _{-1}(m, \chi _{4\det L})$ and, hence,
$|q_L(m)|\asymp m \sigma _{-1}(m, \chi _{4\det L})$ and, hence, ![]() $m^{1-\epsilon }\ll _\epsilon |q_L(m)|\ll _\epsilon m^{1+\epsilon }$ for
$m^{1-\epsilon }\ll _\epsilon |q_L(m)|\ll _\epsilon m^{1+\epsilon }$ for ![]() $L=L_{\rm H}$; and
$L=L_{\rm H}$; and
for ![]() $L=L_{\rm S}$. As in the proof of [Reference BruinierBru17, Proposition 2.5], we have
$L=L_{\rm S}$. As in the proof of [Reference BruinierBru17, Proposition 2.5], we have ![]() $\sum _{d\mid f}\mu (d)\chi _{\mathcal {D}}(d)d^{-2}\sigma _{-3}(f/d)\geq 1/5$ and
$\sum _{d\mid f}\mu (d)\chi _{\mathcal {D}}(d)d^{-2}\sigma _{-3}(f/d)\geq 1/5$ and
moreover, by [Reference BruinierBru17, Proposition 2.5], ![]() $L(2,\chi _D)\geq \zeta (4)/\zeta (2)$ and
$L(2,\chi _D)\geq \zeta (4)/\zeta (2)$ and ![]() $L(2,\chi _D)\leq \prod _{p} (1-p^{-2})^{-1}=\zeta (2)$. Hence,
$L(2,\chi _D)\leq \prod _{p} (1-p^{-2})^{-1}=\zeta (2)$. Hence, ![]() $|q_L(m)|\asymp m^{3/2}$ when
$|q_L(m)|\asymp m^{3/2}$ when ![]() $L=L_{\rm S}$.
$L=L_{\rm S}$.
Lemma 4.3.2 We fix the same assumptions as in § 4.3.1. For ![]() $m\gg 1$, we have
$m\gg 1$, we have ![]() $Z(m)\neq \emptyset$ and the intersection number
$Z(m)\neq \emptyset$ and the intersection number ![]() $Z(m).C = -q_L(m)(\omega. C)+o(|q_L(m)|)$. More precisely, when
$Z(m).C = -q_L(m)(\omega. C)+o(|q_L(m)|)$. More precisely, when ![]() $L=L_{\rm H}$, the error term can be bounded by
$L=L_{\rm H}$, the error term can be bounded by ![]() $O_\epsilon (m^{1/2+\epsilon })$ and when
$O_\epsilon (m^{1/2+\epsilon })$ and when ![]() $L=L_{\rm S}$, the error term can be bounded by
$L=L_{\rm S}$, the error term can be bounded by ![]() $O(m^{5/4})$.
$O(m^{5/4})$.
Proof. We follow the discussion in § 4.1.4. Let ![]() $g(m), m\in \mathbb {Z}_{>0}$ denote the
$g(m), m\in \mathbb {Z}_{>0}$ denote the ![]() $m$th Fourier coefficients of
$m$th Fourier coefficients of ![]() $\mathfrak {e}_0$-component of
$\mathfrak {e}_0$-component of ![]() $G(q)$, which is also a cusp form of weight
$G(q)$, which is also a cusp form of weight ![]() $1+{n}/{2}$ with respect to a certain subgroup of
$1+{n}/{2}$ with respect to a certain subgroup of ![]() $\operatorname {Mp}_2(\mathbb {Z})$ which is the preimage of a congruence subgroup of
$\operatorname {Mp}_2(\mathbb {Z})$ which is the preimage of a congruence subgroup of ![]() $\operatorname {SL}_2(\mathbb {Z})$ depending on
$\operatorname {SL}_2(\mathbb {Z})$ depending on ![]() $L$. When
$L$. When ![]() $L=L_{\rm H}$, by Deligne's bound [Reference DeligneDel73, Reference DeligneDel74], we have
$L=L_{\rm H}$, by Deligne's bound [Reference DeligneDel73, Reference DeligneDel74], we have ![]() $|g(m)|\ll m^{1/2}\sigma _0(m)\ll _\epsilon m^{1/2+\epsilon }=o_\epsilon (m^{1-\epsilon })=o(|q_L(m)|)$ for any
$|g(m)|\ll m^{1/2}\sigma _0(m)\ll _\epsilon m^{1/2+\epsilon }=o_\epsilon (m^{1-\epsilon })=o(|q_L(m)|)$ for any ![]() $0<\epsilon <1/4$. When
$0<\epsilon <1/4$. When ![]() $L=L_{\rm S}$, the trivial bound yields
$L=L_{\rm S}$, the trivial bound yields ![]() $|g(m)|\ll m^{5/4}=o(m^{3/2})$ (see [Reference SarnakSar90, Proposition 1.3.5]). Therefore, by Theorem 4.1.1,
$|g(m)|\ll m^{5/4}=o(m^{3/2})$ (see [Reference SarnakSar90, Proposition 1.3.5]). Therefore, by Theorem 4.1.1, ![]() $Z(m).C=-q_L(m)(\omega.C)+o(|q_L(m)|)$; in particular, for
$Z(m).C=-q_L(m)(\omega.C)+o(|q_L(m)|)$; in particular, for ![]() $m\gg 1$,
$m\gg 1$, ![]() $Z(m).C>0$ and, hence,
$Z(m).C>0$ and, hence, ![]() $Z(m)\neq \emptyset$.
$Z(m)\neq \emptyset$.
4.3.3
When ![]() $L=L_{\rm S}$, recall from § 2.1 that the quadratic form is
$L=L_{\rm S}$, recall from § 2.1 that the quadratic form is ![]() $Q(x)=x_0^2+x_1x_2-x_3x_4$ and hence every
$Q(x)=x_0^2+x_1x_2-x_3x_4$ and hence every ![]() $m\in \mathbb {Z}_{>0}$ is representable by
$m\in \mathbb {Z}_{>0}$ is representable by ![]() $(L,Q)$. In particular,
$(L,Q)$. In particular, ![]() $Z(m)\neq \emptyset$ and
$Z(m)\neq \emptyset$ and ![]() $\delta (\ell,L,m)>0$ for all
$\delta (\ell,L,m)>0$ for all ![]() $\ell$. Moreover, in order to prove Theorem 1(1) and Remark 4, we work with
$\ell$. Moreover, in order to prove Theorem 1(1) and Remark 4, we work with ![]() $m\in T:=\{Dq^2\mid q \text { prime and }q\neq p \}$, where we take
$m\in T:=\{Dq^2\mid q \text { prime and }q\neq p \}$, where we take ![]() $D=1$ for Theorem 1(1) and
$D=1$ for Theorem 1(1) and ![]() $D$ being the discriminant of the real quadratic field in Remark 4; and for Theorem 5, we work with
$D$ being the discriminant of the real quadratic field in Remark 4; and for Theorem 5, we work with ![]() $m\in T: = \{ q{\rm \mid }q{\rm prime and }q\ne p,q$
$m\in T: = \{ q{\rm \mid }q{\rm prime and }q\ne p,q$ ![]() ${\rm is a quadratic residue}\,\bmod \,p,{\rm and }q\equiv 3\,\bmod \,4\}$. In particular, for all such
${\rm is a quadratic residue}\,\bmod \,p,{\rm and }q\equiv 3\,\bmod \,4\}$. In particular, for all such ![]() $m$, we have
$m$, we have ![]() $v_\ell (m)\leq 2+v_\ell (D)$ and, hence, the assumptions in § 4.3.1 are satisfied.
$v_\ell (m)\leq 2+v_\ell (D)$ and, hence, the assumptions in § 4.3.1 are satisfied.
When ![]() $L=L_{\rm H}$, because
$L=L_{\rm H}$, because ![]() $L$ is maximal and isotropic, we have that the quadratic form on
$L$ is maximal and isotropic, we have that the quadratic form on ![]() $L\otimes \mathbb {Z}_\ell$ is given by
$L\otimes \mathbb {Z}_\ell$ is given by ![]() $xy+Q_1(z)$, where
$xy+Q_1(z)$, where ![]() $x,y \in \mathbb {Z}_\ell$,
$x,y \in \mathbb {Z}_\ell$, ![]() $z\in \mathbb {Z}_\ell ^2$, and
$z\in \mathbb {Z}_\ell ^2$, and ![]() $Q_1$ is some quadratic form. Then
$Q_1$ is some quadratic form. Then ![]() $\delta (\ell, L,m)>0$ for all
$\delta (\ell, L,m)>0$ for all ![]() $\ell$; indeed, by [Reference HankeHan04, Definition 3.1 and Lemma 3.2],
$\ell$; indeed, by [Reference HankeHan04, Definition 3.1 and Lemma 3.2], ![]() $\delta (\ell,L,m)>0$ if there exists
$\delta (\ell,L,m)>0$ if there exists ![]() $x,y \in \mathbb {Z}/\ell ^{1+2v_\ell (2)}$ such that
$x,y \in \mathbb {Z}/\ell ^{1+2v_\ell (2)}$ such that ![]() $xy\equiv m \bmod \ell ^{1+2v_\ell (2)}$ and
$xy\equiv m \bmod \ell ^{1+2v_\ell (2)}$ and ![]() $x\not \equiv 0\bmod \ell$ (by the terminology in [Reference HankeHan04], this construct a good type solution (taking
$x\not \equiv 0\bmod \ell$ (by the terminology in [Reference HankeHan04], this construct a good type solution (taking ![]() $z=0$) for
$z=0$) for ![]() $(L,Q)\bmod \ell ^{1+2v_\ell (2)}$, which can be lifted to
$(L,Q)\bmod \ell ^{1+2v_\ell (2)}$, which can be lifted to ![]() $\mathbb {Z}/\ell ^k$ for any
$\mathbb {Z}/\ell ^k$ for any ![]() $k\geq 1+2v_\ell (2)$). Such
$k\geq 1+2v_\ell (2)$). Such ![]() $x,y$ always exists and, hence, every
$x,y$ always exists and, hence, every ![]() $m\in \mathbb {Z}_{>0}$ is representable by
$m\in \mathbb {Z}_{>0}$ is representable by ![]() $(L\otimes \mathbb {Z}_\ell,Q)$ for all
$(L\otimes \mathbb {Z}_\ell,Q)$ for all ![]() $\ell$ and, hence, by Lemma 4.3.2, there exists
$\ell$ and, hence, by Lemma 4.3.2, there exists ![]() $N\in \mathbb {Z}_{>0}$ such that for all
$N\in \mathbb {Z}_{>0}$ such that for all ![]() $m>N$,
$m>N$, ![]() $m$ is representable by
$m$ is representable by ![]() $(L,Q)$. For the proof of Theorem 1(2), we work with
$(L,Q)$. For the proof of Theorem 1(2), we work with ![]() $m$ in
$m$ in
where ![]() $F$ is the real quadratic field attached to the Hilbert modular surface and the constant
$F$ is the real quadratic field attached to the Hilbert modular surface and the constant ![]() $C$ is chosen so that this set is non-empty. The existence of
$C$ is chosen so that this set is non-empty. The existence of ![]() $q$ implies that
$q$ implies that ![]() $m\neq \operatorname {Nm}_{F/\mathbb {Q}}\gamma$ for any
$m\neq \operatorname {Nm}_{F/\mathbb {Q}}\gamma$ for any ![]() $\gamma \in F$ and, hence, for any
$\gamma \in F$ and, hence, for any ![]() $v\in L_{\rm H}\otimes \mathbb {Q}$ such that
$v\in L_{\rm H}\otimes \mathbb {Q}$ such that ![]() $Q(v)=m$, we have
$Q(v)=m$, we have ![]() $v^\perp \subset L_{\rm H}\otimes \mathbb {Q}$ is anisotropic. Note that if
$v^\perp \subset L_{\rm H}\otimes \mathbb {Q}$ is anisotropic. Note that if ![]() $Z(m)$ is non-compact in
$Z(m)$ is non-compact in ![]() $\mathcal {M}_{\mathbb {F}_p}$, then
$\mathcal {M}_{\mathbb {F}_p}$, then ![]() $Z(m)$ parametrizes abelian surfaces which are isogenous to the self-product of elliptic curves and then
$Z(m)$ parametrizes abelian surfaces which are isogenous to the self-product of elliptic curves and then ![]() $v^\perp$ is isotropic. Therefore, for any
$v^\perp$ is isotropic. Therefore, for any ![]() $m\in T$, we have that
$m\in T$, we have that ![]() $Z(m)$ is compact in
$Z(m)$ is compact in ![]() $\mathcal {M}_{\mathbb {F}_p}$. Note that
$\mathcal {M}_{\mathbb {F}_p}$. Note that ![]() $T\subset \mathbb {Z}_{>0}$ is of positive density.
$T\subset \mathbb {Z}_{>0}$ is of positive density.
Lemma 4.3.4 For ![]() $L=L_{\rm H}$ and
$L=L_{\rm H}$ and ![]() $M>0$, we have
$M>0$, we have ![]() $\sum _{1\leq m \leq M,\, m\in T}|q_L(m)|\asymp M^2$.
$\sum _{1\leq m \leq M,\, m\in T}|q_L(m)|\asymp M^2$.
Proof. By §§ 4.3.1 and 4.3.3, we have for ![]() $m\in T$,
$m\in T$, ![]() $|q_L(m)|\asymp m\sigma _{-1}(m,\chi )$, where
$|q_L(m)|\asymp m\sigma _{-1}(m,\chi )$, where ![]() $\chi =\chi _{4\det L}$. We write
$\chi =\chi _{4\det L}$. We write
 \begin{align*} \sum_{1\leq m \leq M,\, m\in T} m\sigma_{-1}(m,\chi) & = \sum_{1\leq m\leq M,\, m\in T}\sum_{d\mid m}d\cdot \chi(m/d)= \sum_{1\leq d\leq M,\, 1\leq f\leq M,\, df\leq M, df\in T} d\cdot \chi(f)\\ &= \sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)+\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T}d\\ &\quad -\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr). \end{align*}
\begin{align*} \sum_{1\leq m \leq M,\, m\in T} m\sigma_{-1}(m,\chi) & = \sum_{1\leq m\leq M,\, m\in T}\sum_{d\mid m}d\cdot \chi(m/d)= \sum_{1\leq d\leq M,\, 1\leq f\leq M,\, df\leq M, df\in T} d\cdot \chi(f)\\ &= \sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)+\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T}d\\ &\quad -\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr). \end{align*}Note that
 \begin{gather*} \biggl|\sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)\biggr| \leq \sum_{1\leq d\leq M^{1/2}}d\cdot (M/d)=O(M^{3/2}),\\ \biggl|\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr)\biggr|\leq \biggl(\sum_{1\leq d\leq M^{1/2}}d\biggr)\cdot \biggl(\sum_{1\leq f\leq M^{1/2}}1\biggr)=O( M^{3/2}). \end{gather*}
\begin{gather*} \biggl|\sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)\biggr| \leq \sum_{1\leq d\leq M^{1/2}}d\cdot (M/d)=O(M^{3/2}),\\ \biggl|\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr)\biggr|\leq \biggl(\sum_{1\leq d\leq M^{1/2}}d\biggr)\cdot \biggl(\sum_{1\leq f\leq M^{1/2}}1\biggr)=O( M^{3/2}). \end{gather*}
The second term is the main term. First, let ![]() $T':=\{m\in \mathbb {Z}\mid m>N, p\nmid m, v_\ell (m)\leq C,\forall \ell \mid 2\det L\}$, then
$T':=\{m\in \mathbb {Z}\mid m>N, p\nmid m, v_\ell (m)\leq C,\forall \ell \mid 2\det L\}$, then
because ![]() $v_\ell (df)\leq C \iff v_\ell (d)\leq C, \forall \ell \mid 2 \det L$ when
$v_\ell (df)\leq C \iff v_\ell (d)\leq C, \forall \ell \mid 2 \det L$ when ![]() $v_\ell (f)=0, \forall \ell \mid 2 \det L$ and if
$v_\ell (f)=0, \forall \ell \mid 2 \det L$ and if ![]() $v_\ell (f)>0$ for some
$v_\ell (f)>0$ for some ![]() $\ell \mid 2 \det L$, then
$\ell \mid 2 \det L$, then ![]() $\chi (f)=0$. As
$\chi (f)=0$. As ![]() $\sum _{1\leq d\leq M/f,\, p\nmid d,\, v_\ell (d)\leq C,\,\forall \ell \mid 2 \det L}d=C_1 ({M^2}/{f^2})+O(M)$, where
$\sum _{1\leq d\leq M/f,\, p\nmid d,\, v_\ell (d)\leq C,\,\forall \ell \mid 2 \det L}d=C_1 ({M^2}/{f^2})+O(M)$, where ![]() $C_1$ and the implicit constant only depend on
$C_1$ and the implicit constant only depend on ![]() $C,L,p$. Hence,
$C,L,p$. Hence,
To finish the proof, we only need to show that
 \[ \displaystyle\biggl|\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T'\setminus T}d\biggr|=o(M^2). \]
\[ \displaystyle\biggl|\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T'\setminus T}d\biggr|=o(M^2). \] As ![]() $M/f\geq M^{1/2}$, by the definition of
$M/f\geq M^{1/2}$, by the definition of ![]() $T$,
$T$, ![]() $\#\{d\mid 1\leq d \leq M/f, df\in T'\setminus T\}=o(M/f)$ with implicit constant independent of
$\#\{d\mid 1\leq d \leq M/f, df\in T'\setminus T\}=o(M/f)$ with implicit constant independent of ![]() $f$ and, hence, we obtain the desired bound.Footnote 24
$f$ and, hence, we obtain the desired bound.Footnote 24
4.4 Local densities at  $p$ and the ratios of Fourier coefficients
$p$ and the ratios of Fourier coefficients
We set the same notation as in § 4.2.1. Theorems 4.1.6 and 4.2.2 reduce the comparison between ![]() $q_L(m)$ and
$q_L(m)$ and ![]() $q_{L'''}(m)$ to the computation of the local density
$q_{L'''}(m)$ to the computation of the local density ![]() $\delta (p,L''',m)$, which we now compute following [Reference HankeHan04, § 3]. Recall that
$\delta (p,L''',m)$, which we now compute following [Reference HankeHan04, § 3]. Recall that ![]() $p$ is an odd prime and
$p$ is an odd prime and ![]() $v_p(m)\leq 1$ for all
$v_p(m)\leq 1$ for all ![]() $m\in T$ defined in § 4.3.3. For an arbitrary quadratic lattice
$m\in T$ defined in § 4.3.3. For an arbitrary quadratic lattice ![]() $(L,Q)$, let
$(L,Q)$, let ![]() $\alpha (p,L,m):=p^{1-\operatorname {rk} L}\#\{v\in L/pL \mid Q(v)\equiv m \bmod p\}$; if we diagonalize
$\alpha (p,L,m):=p^{1-\operatorname {rk} L}\#\{v\in L/pL \mid Q(v)\equiv m \bmod p\}$; if we diagonalize ![]() $L\otimes \mathbb {Z}_p$ such that
$L\otimes \mathbb {Z}_p$ such that ![]() $Q$ is given by
$Q$ is given by ![]() $\sum _{i=1}^{\operatorname {rk} L} a_i x_i^2$ with
$\sum _{i=1}^{\operatorname {rk} L} a_i x_i^2$ with ![]() $a_i\in \mathbb {Z}_p$, then we define
$a_i\in \mathbb {Z}_p$, then we define
 \begin{align*} \alpha^*(p,L,m)&:=p^{1-\operatorname{rk} L}\#\big\{v=(x_1,\ldots, x_{\operatorname{rk} L})\in L/pL \mid Q(v)\equiv m, \exists i \text{ such that }v_p(a_i)=0,\\ &\qquad\qquad\qquad x_i \not\equiv 0 \bmod p\big\}. \end{align*}
\begin{align*} \alpha^*(p,L,m)&:=p^{1-\operatorname{rk} L}\#\big\{v=(x_1,\ldots, x_{\operatorname{rk} L})\in L/pL \mid Q(v)\equiv m, \exists i \text{ such that }v_p(a_i)=0,\\ &\qquad\qquad\qquad x_i \not\equiv 0 \bmod p\big\}. \end{align*}Lemma 4.4.1 (Hanke)
If ![]() $p\nmid m$, we have
$p\nmid m$, we have
if ![]() $v_p(m)=1$, we have
$v_p(m)=1$, we have
where if we write ![]() $(L'''\otimes \mathbb {Z}_p, Q')$ into diagonal form
$(L'''\otimes \mathbb {Z}_p, Q')$ into diagonal form ![]() $\sum _{i=1}^{\operatorname {rk} L'''}a_i x_i^2$ with
$\sum _{i=1}^{\operatorname {rk} L'''}a_i x_i^2$ with ![]() $a_i\in \mathbb {Z}_p$, we define
$a_i\in \mathbb {Z}_p$, we define ![]() $s_0=\#\{a_i \mid v_p(a_i)=0\}$ and
$s_0=\#\{a_i \mid v_p(a_i)=0\}$ and ![]() $L'''_I$ is the quadratic lattice with quadratic form
$L'''_I$ is the quadratic lattice with quadratic form ![]() $\sum _{i=1}^{\operatorname {rk} L'''}a'_i x_i^2$, where
$\sum _{i=1}^{\operatorname {rk} L'''}a'_i x_i^2$, where ![]() $a'_i =p a_i$ if
$a'_i =p a_i$ if ![]() $v_p(a_i)=0$ and
$v_p(a_i)=0$ and ![]() $a'_i=p^{-1} a_i$ if
$a'_i=p^{-1} a_i$ if ![]() $v_p(a_i)\geq 1$.
$v_p(a_i)\geq 1$.
Proof. If ![]() $p\nmid m$, the assertion follows from [Reference HankeHan04, Remark 3.4.1(a) and Lemma 3.2]; if
$p\nmid m$, the assertion follows from [Reference HankeHan04, Remark 3.4.1(a) and Lemma 3.2]; if ![]() $v_p(m)=1$, then we only have good type and bad type I solutions in the sense of [Reference HankeHan04, Definition 3.1, p. 360] and the assertion follows from [Reference HankeHan04, Lemma 3.2, p. 360, and Remark 3.4.1(a)].
$v_p(m)=1$, then we only have good type and bad type I solutions in the sense of [Reference HankeHan04, Definition 3.1, p. 360] and the assertion follows from [Reference HankeHan04, Lemma 3.2, p. 360, and Remark 3.4.1(a)].
We first compute ![]() $\delta (p,L',m)$ by Lemma 4.4.1. We always pick
$\delta (p,L',m)$ by Lemma 4.4.1. We always pick ![]() $\epsilon \in \mathbb {Z}_p^\times \backslash (\mathbb {Z}_p^\times )^2$ as in § 3.1.2.
$\epsilon \in \mathbb {Z}_p^\times \backslash (\mathbb {Z}_p^\times )^2$ as in § 3.1.2.
4.4.2
Consider ![]() $L=L_{\rm H}$ and recall that
$L=L_{\rm H}$ and recall that ![]() $p\nmid m, \ \forall m \in T$. Let
$p\nmid m, \ \forall m \in T$. Let ![]() $F$ denote the real quadratic field attached to the Hilbert modular surface defined by
$F$ denote the real quadratic field attached to the Hilbert modular surface defined by ![]() $L_{\rm H}$.
$L_{\rm H}$.
(1) Assume that
 $p$ is inert in
$p$ is inert in  $F$ and
$F$ and  $P$ is supergeneric. By § 3.2.1,
$P$ is supergeneric. By § 3.2.1,  $L'\otimes \mathbb {Z}_p=\Lambda ^\vee =p\Lambda$ and, hence,
$L'\otimes \mathbb {Z}_p=\Lambda ^\vee =p\Lambda$ and, hence,  $p\mid Q'(v),\forall v\in L'$; in particular,
$p\mid Q'(v),\forall v\in L'$; in particular,  $\delta (p,L',m)=0$.
$\delta (p,L',m)=0$.(2) Assume that
 $p$ is inert in
$p$ is inert in  $F$ and
$F$ and  $P$ is superspecial. By § 3.2.1,
$P$ is superspecial. By § 3.2.1,  $Q'(v)=xy+p(z^2-\epsilon w^2)$, where
$Q'(v)=xy+p(z^2-\epsilon w^2)$, where  $w_i$ are given right above (3.2.1) and
$w_i$ are given right above (3.2.1) and  $v=xw_3+yw_4+zw_1+ww_2$ with
$v=xw_3+yw_4+zw_1+ww_2$ with  $x,y,z,w\in \mathbb {Z}_p$. Hence,
$x,y,z,w\in \mathbb {Z}_p$. Hence,  $\delta (p,L',m)=\alpha (p,L',m)=1-1/p$.
$\delta (p,L',m)=\alpha (p,L',m)=1-1/p$.(3) Assume that
 $p$ is split in
$p$ is split in  $F$; hence,
$F$; hence,  $P$ is superspecial. By § 3.2.2,
$P$ is superspecial. By § 3.2.2,  $L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ with
$L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ with  $Q'(v)= x^2-\epsilon y^2-pz^2+\epsilon pw^2$, where
$Q'(v)= x^2-\epsilon y^2-pz^2+\epsilon pw^2$, where  $v=xe_1+ye_2+z(pe_3)+w(pe_4)$ with
$v=xe_1+ye_2+z(pe_3)+w(pe_4)$ with  $x,y,z,w\in \mathbb {Z}_p$. Hence,
$x,y,z,w\in \mathbb {Z}_p$. Hence,  $\delta (p,L',m)=\alpha (p,L',m)=1+1/p$.
$\delta (p,L',m)=\alpha (p,L',m)=1+1/p$.
4.4.3
Consider ![]() $L=L_{\rm S}$.
$L=L_{\rm S}$.
(1) Assume that
 $P$ is superspecial. By § 3.3, we have
$P$ is superspecial. By § 3.3, we have  $Q'(v)=xy+\epsilon z^2+pw^2-p\epsilon u^2$, where
$Q'(v)=xy+\epsilon z^2+pw^2-p\epsilon u^2$, where  $v=xw_3+yw_4+zw_5+ww_2+uw_1$ with
$v=xw_3+yw_4+zw_5+ww_2+uw_1$ with  $x,y,z,w,u\in \mathbb {Z}_p$ and
$x,y,z,w,u\in \mathbb {Z}_p$ and  $w_i$ are given right above (3.3.1). Hence, if
$w_i$ are given right above (3.3.1). Hence, if  $p\nmid m$, then
$p\nmid m$, then  $\delta (p,L',m)=\alpha (p,L',m)\leq 1+1/p$ by [Reference HankeHan04, Table 1]. If
$\delta (p,L',m)=\alpha (p,L',m)\leq 1+1/p$ by [Reference HankeHan04, Table 1]. If  $v_p(m)=1$, then the quadratic form of
$v_p(m)=1$, then the quadratic form of  $L'_I$ is
$L'_I$ is  $p(xy+\epsilon z^2)+ w^2-\epsilon u^2$ and, hence,
$p(xy+\epsilon z^2)+ w^2-\epsilon u^2$ and, hence,  $\delta (p,{L}^{\prime},m) = \alpha ^*(p,{L}^{\prime},m) + p^{-2}\alpha (p,{{L}^{\prime}}_I,m/p)$
$\delta (p,{L}^{\prime},m) = \alpha ^*(p,{L}^{\prime},m) + p^{-2}\alpha (p,{{L}^{\prime}}_I,m/p)$  $= (1-p^{-2}) + p^{-2}(1 + p^{-1}) = 1 + p^{-3}$.
$= (1-p^{-2}) + p^{-2}(1 + p^{-1}) = 1 + p^{-3}$.(2) Assume that
 $P$ is supergeneric. By § 3.3,
$P$ is supergeneric. By § 3.3,  $L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ and, hence, the quadratic form is
$L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ and, hence, the quadratic form is  $pxy+\epsilon z^2+pw^2-p\epsilon u^2$. If
$pxy+\epsilon z^2+pw^2-p\epsilon u^2$. If  $p\nmid m$, then
$p\nmid m$, then  $\delta (p,L',m)=\alpha (p,L',m)=0 \text { or } 2$; if
$\delta (p,L',m)=\alpha (p,L',m)=0 \text { or } 2$; if  $v_p(m)=1$, then the quadratic form of
$v_p(m)=1$, then the quadratic form of  $L'_I$ is
$L'_I$ is  $p\epsilon z^2+xy+ w^2-\epsilon u^2$ and, hence,
$p\epsilon z^2+xy+ w^2-\epsilon u^2$ and, hence,  $\delta (p,L',m)=\alpha ^*(p,L',m)+\alpha (p,L'_I,m/p)=0+1+p^{-2}=1+p^{-2}$ by [Reference HankeHan04, Table 1].
$\delta (p,L',m)=\alpha ^*(p,L',m)+\alpha (p,L'_I,m/p)=0+1+p^{-2}=1+p^{-2}$ by [Reference HankeHan04, Table 1].
We now estimate ![]() $\delta (p,L''',m)$ for sublattices lattices
$\delta (p,L''',m)$ for sublattices lattices ![]() $L'''$ of
$L'''$ of ![]() $L'$ defined in § 4.2.1.
$L'$ defined in § 4.2.1.
Lemma 4.4.4 If ![]() $p\nmid m$, then
$p\nmid m$, then ![]() $\delta (p,L''',m)\leq 2$.
$\delta (p,L''',m)\leq 2$.
Proof. By Lemma 4.4.1, ![]() $\delta (p,L''',m)=\alpha (p,L''',m)$. Write the quadratic form
$\delta (p,L''',m)=\alpha (p,L''',m)$. Write the quadratic form ![]() $Q'$ on
$Q'$ on ![]() $L'''$ into the diagonal form
$L'''$ into the diagonal form ![]() $\sum _{i=1}^{\operatorname {rk} L'''} a_i x_i^2$ with
$\sum _{i=1}^{\operatorname {rk} L'''} a_i x_i^2$ with ![]() $a_i\in \mathbb {Z}_p$ and we may assume that there exists
$a_i\in \mathbb {Z}_p$ and we may assume that there exists ![]() $a_i$ such that
$a_i$ such that ![]() $p\nmid a_i$; otherwise
$p\nmid a_i$; otherwise ![]() $\delta (p,L''',m)=0$, then we are done. Now let
$\delta (p,L''',m)=0$, then we are done. Now let ![]() $\tilde {L}'''$ denote the quadratic form
$\tilde {L}'''$ denote the quadratic form ![]() $\sum _{1\leq i\leq \operatorname {rk} L''',\, p\nmid a_i} a_i x_i^2$. Then by definition,
$\sum _{1\leq i\leq \operatorname {rk} L''',\, p\nmid a_i} a_i x_i^2$. Then by definition, ![]() $\alpha (p,L''',m)=\alpha (p, \tilde {L}''',m)$. Since
$\alpha (p,L''',m)=\alpha (p, \tilde {L}''',m)$. Since ![]() $p\mid \operatorname {disc} L'$, then
$p\mid \operatorname {disc} L'$, then ![]() $p\mid \operatorname {disc} L'''$ and
$p\mid \operatorname {disc} L'''$ and ![]() $\operatorname {rk} \widetilde {L'''}\leq \operatorname {rk} L'''-1\leq 4$. Then by [Reference HankeHan04, Table 1],
$\operatorname {rk} \widetilde {L'''}\leq \operatorname {rk} L'''-1\leq 4$. Then by [Reference HankeHan04, Table 1], ![]() $\alpha (p, \tilde {L}''',m)\leq 2$ and hence
$\alpha (p, \tilde {L}''',m)\leq 2$ and hence ![]() $\delta (p,L''',m)\leq 2$.
$\delta (p,L''',m)\leq 2$.
Lemma 4.4.5 Assume that ![]() $L=L_{\rm S}$ and
$L=L_{\rm S}$ and ![]() $v_p(m)=1$. We have
$v_p(m)=1$. We have ![]() $\delta (p,L''',m)\leq 2+2p$. Moreover, if
$\delta (p,L''',m)\leq 2+2p$. Moreover, if ![]() $P$ is superspecial and
$P$ is superspecial and ![]() $[L':L''']=p$, then
$[L':L''']=p$, then ![]() $\delta (p,L''',m)\leq 4$.
$\delta (p,L''',m)\leq 4$.
Proof. By Lemma 4.4.1, ![]() $\delta (p,L''',m)=\alpha ^*(p,L''',m)+p^{1-s_0}\alpha (p,L'''_I,m/p)\leq \alpha (p,L''',m)+p\alpha (p,L'''_I,m/p)$. By the proof of Lemma 4.4.4, we have
$\delta (p,L''',m)=\alpha ^*(p,L''',m)+p^{1-s_0}\alpha (p,L'''_I,m/p)\leq \alpha (p,L''',m)+p\alpha (p,L'''_I,m/p)$. By the proof of Lemma 4.4.4, we have ![]() $\alpha (p,L''',m)=\alpha (p,\tilde {L}''',m)\leq 2$. The same argument implies that
$\alpha (p,L''',m)=\alpha (p,\tilde {L}''',m)\leq 2$. The same argument implies that ![]() $\alpha (p,L'''_I,m/p)\leq 2$ if
$\alpha (p,L'''_I,m/p)\leq 2$ if ![]() $\operatorname {rk}(\tilde {L}''')\leq 4$. If
$\operatorname {rk}(\tilde {L}''')\leq 4$. If ![]() $\operatorname {rk}(\tilde {L}''')=5$, then it is isotropic and we write the quadratic form as
$\operatorname {rk}(\tilde {L}''')=5$, then it is isotropic and we write the quadratic form as ![]() $xy+Q_1(z)$. The equation
$xy+Q_1(z)$. The equation ![]() $xy+Q_1(z)\equiv (m/p) \bmod p$ has
$xy+Q_1(z)\equiv (m/p) \bmod p$ has ![]() $(p-1)p^3$ solutions in
$(p-1)p^3$ solutions in ![]() $\mathbb {F}_p^5$ with
$\mathbb {F}_p^5$ with ![]() $x\neq 0$ and has at most
$x\neq 0$ and has at most ![]() $p^4$ solutions with
$p^4$ solutions with ![]() $x=0$. Hence
$x=0$. Hence ![]() $\alpha (p, L''',m/p)=\alpha (p, \tilde {L}''',m/p)<2$. Therefore,
$\alpha (p, L''',m/p)=\alpha (p, \tilde {L}''',m/p)<2$. Therefore, ![]() $\delta (p,L''',m)\leq 2+2p$.
$\delta (p,L''',m)\leq 2+2p$.
If ![]() $P$ is superspecial and
$P$ is superspecial and ![]() $[L':L''']=p$, then
$[L':L''']=p$, then ![]() $s_0\geq 1$ and, hence,
$s_0\geq 1$ and, hence, ![]() $\delta (p,L''',m)\leq \alpha ^*(p,L''',m)+\alpha (p,L'''_I,m/p)\leq 4$.
$\delta (p,L''',m)\leq \alpha ^*(p,L''',m)+\alpha (p,L'''_I,m/p)\leq 4$.
The following lemma, which is the main goal of this subsection, will be used to compare the local intersection number at a supersingular point ![]() $P$ with the global intersection number.
$P$ with the global intersection number.
Lemma 4.4.6 Notation as in § 4.2.1 and consider ![]() $m\in T$ (defined in § 4.3.3).
$m\in T$ (defined in § 4.3.3).
(1) If
 $P$ is superspecial or
$P$ is superspecial or  $L=L_{\rm H}$, then
$L=L_{\rm H}$, then
 \[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{1}{p-1}. \]
\[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{1}{p-1}. \](2) If
 $L=L_{\rm S}$ and
$L=L_{\rm S}$ and  $P$ is supergeneric, then
$P$ is supergeneric, then
 \[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{2}{p^2-1}. \]
\[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{2}{p^2-1}. \](3) If
 $p\nmid m$, then
$p\nmid m$, then
 \[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}. \]
\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}. \](4) Assumption as in Lemma 4.4.5, then
moreover, if \[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2p}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-1})}; \]
\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2p}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-1})}; \] $P$ is superspecial and
$P$ is superspecial and  $[L':L''']=p$, then
$[L':L''']=p$, then
 \[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{4}{p^2-1}. \]
\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{4}{p^2-1}. \]
Proof. Recall from § 4.2.1 that ![]() $L'''\otimes \mathbb {Z}_\ell \cong L\otimes \mathbb {Z}_\ell, \forall \ell \neq p$; hence, for
$L'''\otimes \mathbb {Z}_\ell \cong L\otimes \mathbb {Z}_\ell, \forall \ell \neq p$; hence, for ![]() $\ell \neq p$, we have
$\ell \neq p$, we have ![]() $\delta (\ell,L''',m)=\delta (\ell,L,m)$ and
$\delta (\ell,L''',m)=\delta (\ell,L,m)$ and ![]() $\det L'''=p^k \det L$ for some
$\det L'''=p^k \det L$ for some ![]() $k\in \mathbb {Z}_{\geq 0}$. As
$k\in \mathbb {Z}_{\geq 0}$. As ![]() $L$ is self-dual at
$L$ is self-dual at ![]() $p$, then
$p$, then ![]() $p\nmid \det L$; by § 3.1.2,
$p\nmid \det L$; by § 3.1.2, ![]() $\det L'=p^{2b} \det L$ for some
$\det L'=p^{2b} \det L$ for some ![]() $b\in \mathbb {Z}_{>0}$ (concretely, one may deduce this fact by the explicit formula of
$b\in \mathbb {Z}_{>0}$ (concretely, one may deduce this fact by the explicit formula of ![]() $Q'$ in §§ 4.4.2–4.4.3) and, hence,
$Q'$ in §§ 4.4.2–4.4.3) and, hence, ![]() $k\in 2 \mathbb {Z}_{>0}$. Thus,
$k\in 2 \mathbb {Z}_{>0}$. Thus, ![]() $\chi _{4 \det L}(d)=\chi _{4 \det L'}(d)$ and
$\chi _{4 \det L}(d)=\chi _{4 \det L'}(d)$ and ![]() $\chi _{-2 m_0 \det L}(d)=\chi _{-2 m_0 \det L'}(d)$ if
$\chi _{-2 m_0 \det L}(d)=\chi _{-2 m_0 \det L'}(d)$ if ![]() $p\nmid d$.
$p\nmid d$.
Therefore, by Theorems 4.1.6 and 4.2.2, we have that for ![]() $L=L_{\rm H}$,
$L=L_{\rm H}$, ![]() $p\nmid m$,
$p\nmid m$,
 \begin{align*} \frac{q(m)_{L'''}}{-q(m)_L}&=\frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-\chi_{4\det L}(p)p^{-2})}\\ &\leq \frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}; \end{align*}
\begin{align*} \frac{q(m)_{L'''}}{-q(m)_L}&=\frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-\chi_{4\det L}(p)p^{-2})}\\ &\leq \frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}; \end{align*}
for ![]() $L=L_{\rm S}$,
$L=L_{\rm S}$, ![]() $v_p(m)\leq 1$, we observe that
$v_p(m)\leq 1$, we observe that ![]() $m_0$ remains the same for
$m_0$ remains the same for ![]() $L$ and
$L$ and ![]() $L'''$ and
$L'''$ and ![]() $p\nmid f$ and, hence,
$p\nmid f$ and, hence,
Therefore, parts (1) and (2) follow from §§ 4.4.2–4.4.3; part (3) follows from Lemma 4.4.4; part (4) follows from Lemma 4.4.5.
5. The decay lemma for supersingular points and its proof in the Hilbert case
The goal of this section is to prove that special endomorphisms ‘decay rapidly’. More precisely, consider a generically ordinary two-dimensional abelian scheme over ![]() $\bar {\mathbb {F}}_p[[t]]$ whose special fiber is supersingular. We consider the lattice of special endomorphisms of the abelian scheme mod
$\bar {\mathbb {F}}_p[[t]]$ whose special fiber is supersingular. We consider the lattice of special endomorphisms of the abelian scheme mod ![]() $t^N$ as
$t^N$ as ![]() $N$ varies, and establish bounds for the covolume of these lattices. These bounds are exactly what we need to bound the local intersection multiplicity
$N$ varies, and establish bounds for the covolume of these lattices. These bounds are exactly what we need to bound the local intersection multiplicity ![]() $\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \cdot Z(m)$: see Lemma 7.2.1. The precise definitions and results are in Definition 5.1.1 and Theorem 5.1.2.
$\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \cdot Z(m)$: see Lemma 7.2.1. The precise definitions and results are in Definition 5.1.1 and Theorem 5.1.2.
Throughout this section, as in § 3, ![]() $k=\bar {\mathbb {F}}_p$,
$k=\bar {\mathbb {F}}_p$, ![]() $W=W(k)$, and
$W=W(k)$, and ![]() $K=W[1/p]$. We focus on the behavior of the curve
$K=W[1/p]$. We focus on the behavior of the curve ![]() $C$ in Theorems 1 and 5 in a formal neighborhood of a supersingular point
$C$ in Theorems 1 and 5 in a formal neighborhood of a supersingular point ![]() $P$, so we may let
$P$, so we may let ![]() $C = \operatorname {Spf} k[[t]]$ denote a generically ordinary formal curve in
$C = \operatorname {Spf} k[[t]]$ denote a generically ordinary formal curve in ![]() $\mathcal {M}_k$ which specializes to
$\mathcal {M}_k$ which specializes to ![]() $P$. As in § 3.1.5,
$P$. As in § 3.1.5, ![]() $\sigma$ denote both the Frobenius on
$\sigma$ denote both the Frobenius on ![]() $K$ and the Frobenius on the coordinate rings
$K$ and the Frobenius on the coordinate rings ![]() $W[[x,y], W[[x,y,z]]$ of
$W[[x,y], W[[x,y,z]]$ of ![]() $\widehat {\mathcal {M}}_{P}$, which is the unique extension of the Frobenius action on
$\widehat {\mathcal {M}}_{P}$, which is the unique extension of the Frobenius action on ![]() $W$ for which
$W$ for which ![]() $\sigma (x)=x^p$,
$\sigma (x)=x^p$, ![]() $\sigma (y)=y^p$, and
$\sigma (y)=y^p$, and ![]() $\sigma (z)=z^p$. For a matrix
$\sigma (z)=z^p$. For a matrix ![]() $M$ with entries in
$M$ with entries in ![]() $K[[x,y]]$ or
$K[[x,y]]$ or ![]() $K[[x,y,z]]$, we use
$K[[x,y,z]]$, we use ![]() $M^{(n)}$ to denote
$M^{(n)}$ to denote ![]() $\sigma ^n(M)$. Also recall we set
$\sigma ^n(M)$. Also recall we set ![]() $\lambda \in \mathbb {Z}_{p^2}^\times$ such that
$\lambda \in \mathbb {Z}_{p^2}^\times$ such that ![]() $\sigma (\lambda ) = - \lambda$. We use
$\sigma (\lambda ) = - \lambda$. We use ![]() $\sigma _t$ to denote the Frobenius on
$\sigma _t$ to denote the Frobenius on ![]() $K[[t]]$ which extends
$K[[t]]$ which extends ![]() $\sigma$ on
$\sigma$ on ![]() $K$ and sends
$K$ and sends ![]() $t$ to
$t$ to ![]() $t^p$.
$t^p$.
5.1 Statement of the decay lemma and the first reduction step
The map ![]() $C\rightarrow \mathcal {M}_k$ gives rise to a local ring homomorphism from
$C\rightarrow \mathcal {M}_k$ gives rise to a local ring homomorphism from ![]() $k[[x,y]] \rightarrow k[[t]]$ (in the Hilbert case) or
$k[[x,y]] \rightarrow k[[t]]$ (in the Hilbert case) or ![]() $k[[x,y,z]]\rightarrow k[[t]]$ (in the Siegel case), and we denote by
$k[[x,y,z]]\rightarrow k[[t]]$ (in the Siegel case), and we denote by ![]() $x(t)$,
$x(t)$, ![]() $y(t)$, and
$y(t)$, and ![]() $z(t)$ the images of
$z(t)$ the images of ![]() $x$,
$x$, ![]() $y$, and
$y$, and ![]() $z$, respectively. Let
$z$, respectively. Let ![]() $v_t$ denote the
$v_t$ denote the ![]() $t$-adic valuation map on
$t$-adic valuation map on ![]() $k[[t]]$. Let
$k[[t]]$. Let ![]() $A$ denote the
$A$ denote the ![]() $t$-adic valuation of the local equation defining the non-ordinary locus in Corollary 3.4.2. More precisely, if
$t$-adic valuation of the local equation defining the non-ordinary locus in Corollary 3.4.2. More precisely, if ![]() $P$ superspecial, then
$P$ superspecial, then ![]() $A=v_t(xy)$ in the Hilbert case and
$A=v_t(xy)$ in the Hilbert case and ![]() $A=v_t(xy+{z^2}/{4\epsilon })$ in the Siegel case.
$A=v_t(xy+{z^2}/{4\epsilon })$ in the Siegel case.
Definition 5.1.1 Let ![]() $w$ denote a special endomorphism of the
$w$ denote a special endomorphism of the ![]() $p$-divisible group at
$p$-divisible group at ![]() $P$ (i.e.
$P$ (i.e. ![]() $w$ is an element in
$w$ is an element in ![]() $L'\otimes \mathbb {Z}_p$; see Definitions 2.2.4 and 2.2.9).
$L'\otimes \mathbb {Z}_p$; see Definitions 2.2.4 and 2.2.9).
(1) We say that
 $w$ decays rapidly if
$w$ decays rapidly if  $p^n w$ does not lift to an endomorphism modulo
$p^n w$ does not lift to an endomorphism modulo  $t^{A_n+1}$ for all
$t^{A_n+1}$ for all  $n\in \mathbb {Z}_{\geq 0}$, where
$n\in \mathbb {Z}_{\geq 0}$, where  $A_n:=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$; here
$A_n:=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$; here  $[x]$ denotes the maximal integer
$[x]$ denotes the maximal integer  $y$ such that
$y$ such that  $y\leq x$.
$y\leq x$.(2) We say that a
 $\mathbb {Z}_p$-submodule of
$\mathbb {Z}_p$-submodule of  $L'\otimes \mathbb {Z}_p$ decays rapidly if every primitive vector in the submodule decays rapidly.
$L'\otimes \mathbb {Z}_p$ decays rapidly if every primitive vector in the submodule decays rapidly.(3) We say that
 $w$ decays very rapidly if
$w$ decays very rapidly if  $p^n w$ does not lift to an endomorphism modulo
$p^n w$ does not lift to an endomorphism modulo  $t^{A_{n-1} + ap^n+1}$ for some constant
$t^{A_{n-1} + ap^n+1}$ for some constant  $a \leq A/2$ (independent of
$a \leq A/2$ (independent of  $n$), for all
$n$), for all  $n\in \mathbb {Z}_{\geq 0}$, where
$n\in \mathbb {Z}_{\geq 0}$, where  $A_n$ is defined in part (1) and we define
$A_n$ is defined in part (1) and we define  $A_{-1}=[A/p]$.
$A_{-1}=[A/p]$.
We remark that the value ![]() $a$ will be one of the valuations of a local coordinate equation, used to prove Proposition 5.1.3.
$a$ will be one of the valuations of a local coordinate equation, used to prove Proposition 5.1.3.
Theorem 5.1.2 (Decay lemma)
Assume ![]() $P$ is superspecial. There exists a rank-
$P$ is superspecial. There exists a rank-![]() $3$
$3$ ![]() $\mathbb {Z}_p$-submodule of
$\mathbb {Z}_p$-submodule of ![]() $L'\otimes \mathbb {Z}_p$ which decays rapidly and furthermore, there is a primitive vector in this submodule which decays very rapidly.
$L'\otimes \mathbb {Z}_p$ which decays rapidly and furthermore, there is a primitive vector in this submodule which decays very rapidly.
Here we only state the decay lemma for a superspecial point because we do not need to work with supergeneric points to prove Theorems 1 and 5. We refer the reader to the appendix of [Reference Maulik, Shankar and TangMST18] for a decay lemma when ![]() $P$ is supergeneric.
$P$ is supergeneric.
Proposition 5.1.3 Assume ![]() $P$ is superspecial. With respect to the
$P$ is superspecial. With respect to the ![]() $w_i$-basis in §§ 3.2–3.3, there exists a rank-
$w_i$-basis in §§ 3.2–3.3, there exists a rank-![]() $3$
$3$ ![]() $\mathbb {Z}_p$-submodule of
$\mathbb {Z}_p$-submodule of ![]() $L'\otimes \mathbb {Z}_p$ such that for every primitive
$L'\otimes \mathbb {Z}_p$ such that for every primitive ![]() $w$ in this submodule, the coefficients of
$w$ in this submodule, the coefficients of ![]() $1=t^0, \ldots,t^{A(1+p+\cdots +p^n)}$ in the power series
$1=t^0, \ldots,t^{A(1+p+\cdots +p^n)}$ in the power series ![]() $p^n\tilde {w}\in (K[[t]])^4$ (or
$p^n\tilde {w}\in (K[[t]])^4$ (or ![]() $(K[[t]])^5$) do not all lie in
$(K[[t]])^5$) do not all lie in ![]() $W^4$ (or
$W^4$ (or ![]() $W^5$) for all
$W^5$) for all ![]() $n\in \mathbb {Z}_{\geq 0}$ (property DR); moreover, there exist
$n\in \mathbb {Z}_{\geq 0}$ (property DR); moreover, there exist ![]() $a\leq A/2$ (independent of
$a\leq A/2$ (independent of ![]() $n$) and a primitive
$n$) and a primitive ![]() $w$ in the rank-
$w$ in the rank-![]() $3$ submodule such that the coefficients of
$3$ submodule such that the coefficients of ![]() $1,\ldots, t^{A(1+p+\cdots +p^{n-1})+ap^n}$ in
$1,\ldots, t^{A(1+p+\cdots +p^{n-1})+ap^n}$ in ![]() $p^n\tilde {w}\in (K[[t]])^4$ (or
$p^n\tilde {w}\in (K[[t]])^4$ (or ![]() $(K[[t]])^5$) do not all lie in
$(K[[t]])^5$) do not all lie in ![]() $W^4$ (or
$W^4$ (or ![]() $W^5$) for all
$W^5$) for all ![]() $n\in \mathbb {Z}_{\geq 0}$ (property DvR).
$n\in \mathbb {Z}_{\geq 0}$ (property DvR).
We now prove the decay lemma assuming the above proposition holds.
Proof of Theorem 5.1.2 assuming Proposition 5.1.3 holds To ease exposition we focus on the Hilbert case and the proof holds verbatim for the Siegel case. For ![]() $m\in \mathbb {Z}_{\geq 0}$, let
$m\in \mathbb {Z}_{\geq 0}$, let ![]() $S_m$ denote
$S_m$ denote ![]() $\operatorname {Spec} k[t]/(t^m)$ and let
$\operatorname {Spec} k[t]/(t^m)$ and let ![]() $D_m$ denote the
$D_m$ denote the ![]() $p$-adic completion of the PD enveloping algebra of the ideal
$p$-adic completion of the PD enveloping algebra of the ideal ![]() $(t^m,p)$ in
$(t^m,p)$ in ![]() $W[[t]]$. Let
$W[[t]]$. Let ![]() $\iota _m$ denote the composite map
$\iota _m$ denote the composite map ![]() $S_m \rightarrow \operatorname {Spf} k[[t]] \rightarrow \operatorname {Spf} k[[x,y]]$. Then by [Reference de JongdJ95, § 2.3], there exists a functor from the category of
$S_m \rightarrow \operatorname {Spf} k[[t]] \rightarrow \operatorname {Spf} k[[x,y]]$. Then by [Reference de JongdJ95, § 2.3], there exists a functor from the category of ![]() $p$-divisible groups over
$p$-divisible groups over ![]() $S_m$ to the category Dieudonné modules over
$S_m$ to the category Dieudonné modules over ![]() $D_m$. More precisely, a special endomorphism
$D_m$. More precisely, a special endomorphism ![]() $\tilde {w}_m$ of the
$\tilde {w}_m$ of the ![]() $p$-divisible group over
$p$-divisible group over ![]() $S_m$ which specializes to
$S_m$ which specializes to ![]() $w\in L'\otimes \mathbb {Z}_p$ gives rise to an endomorphism of the Dieudonné module which specializes to
$w\in L'\otimes \mathbb {Z}_p$ gives rise to an endomorphism of the Dieudonné module which specializes to ![]() $w$. By functoriality of Dieudonné modules, images of special endomorphisms are horizontal sections of
$w$. By functoriality of Dieudonné modules, images of special endomorphisms are horizontal sections of ![]() $\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ stable under the Frobenius action; here the connection on
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ stable under the Frobenius action; here the connection on ![]() $\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back of the connection on
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back of the connection on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ by a ring homomorphism
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ by a ring homomorphism ![]() $W[[x,y]]\rightarrow W[[t]]$ which liftsFootnote 25
$W[[x,y]]\rightarrow W[[t]]$ which liftsFootnote 25 ![]() $k[[x,y]]\rightarrow k[[t]]$ given by
$k[[x,y]]\rightarrow k[[t]]$ given by ![]() $C$ and the
$C$ and the ![]() $\sigma _t$-linear Frobenius is given in [Reference MoonenMoo98, § 4.3.3].Footnote 26
$\sigma _t$-linear Frobenius is given in [Reference MoonenMoo98, § 4.3.3].Footnote 26
The connection on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ gives rise to a connection on
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ gives rise to a connection on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]\supset \mathbb {L}_{\mathrm {cris}}(W[[x,y]])$. Let
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]\supset \mathbb {L}_{\mathrm {cris}}(W[[x,y]])$. Let ![]() $\tilde {w}$ denote the horizontal section in
$\tilde {w}$ denote the horizontal section in ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]$ extending
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]$ extending ![]() $w\in L'\otimes \mathbb {Z}_p\subset \mathbb {L}_{\mathrm {cris},P}(W)$. As the image of
$w\in L'\otimes \mathbb {Z}_p\subset \mathbb {L}_{\mathrm {cris},P}(W)$. As the image of ![]() $\tilde {w}_m$ in
$\tilde {w}_m$ in ![]() $\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is horizontal and the connection on
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is horizontal and the connection on ![]() $\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back connection, then
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back connection, then ![]() $\tilde {w}_m=\iota _m^* \tilde {w}$. Therefore, if
$\tilde {w}_m=\iota _m^* \tilde {w}$. Therefore, if ![]() $w$ lifts to a special endomorphism in
$w$ lifts to a special endomorphism in ![]() $S_m$, then
$S_m$, then ![]() $\iota _m^* \tilde {w} \in \iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)\subset \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[t]]$.
$\iota _m^* \tilde {w} \in \iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)\subset \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[t]]$.
The section ![]() $\tilde {w}$ is constructed in [Reference KisinKis10, § 1.5.5] as follows. Recall from §§ 3.2–3.3, the Frobenius on
$\tilde {w}$ is constructed in [Reference KisinKis10, § 1.5.5] as follows. Recall from §§ 3.2–3.3, the Frobenius on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, with respect to a
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, with respect to a ![]() $\varphi$-invariant basis
$\varphi$-invariant basis ![]() $\{w_i\}$, is given by
$\{w_i\}$, is given by ![]() $(I+F)\circ \sigma$ for some matrix
$(I+F)\circ \sigma$ for some matrix ![]() $F$ with entries in
$F$ with entries in ![]() $(x,y)K[x,y]$. We define
$(x,y)K[x,y]$. We define ![]() $F_{\infty }$ to be the infinite product
$F_{\infty }$ to be the infinite product ![]() $\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where
$\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where ![]() $F^{(i)}$ is the
$F^{(i)}$ is the ![]() $i$th
$i$th ![]() $\sigma$-twist of
$\sigma$-twist of ![]() $F$ (recall
$F$ (recall ![]() $\sigma (x)=x^p, \sigma (y)=y^p$). As
$\sigma (x)=x^p, \sigma (y)=y^p$). As ![]() $v_t(y), v_t(x)\geq 1$, the product is well-defined and the entries of
$v_t(y), v_t(x)\geq 1$, the product is well-defined and the entries of ![]() $F_{\infty }$ are power series valued in
$F_{\infty }$ are power series valued in ![]() $K[[t]]$. The
$K[[t]]$. The ![]() $\mathbb {Q}_p$-span of the columns of
$\mathbb {Q}_p$-span of the columns of ![]() $F_{\infty }$ are vectors of
$F_{\infty }$ are vectors of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)\otimes K[[x,y]]$ which are Frobenius stable and horizontal. Then
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes K[[x,y]]$ which are Frobenius stable and horizontal. Then ![]() $\tilde {w}$ is the unique vector in the above
$\tilde {w}$ is the unique vector in the above ![]() $\mathbb {Q}_p$-span which specializes to
$\mathbb {Q}_p$-span which specializes to ![]() $w$ modulo
$w$ modulo ![]() $(x,y)$; in other words,
$(x,y)$; in other words, ![]() $\tilde {w}=F_{\infty } w$.
$\tilde {w}=F_{\infty } w$.
Now we are ready to reduce to the proof of the decay lemma to the following proposition. Indeed, by Proposition 5.1.3, with respect to ![]() $\{w_i\}$, there exists a rank-
$\{w_i\}$, there exists a rank-![]() $3$
$3$ ![]() $\mathbb {Z}_p$-submodule of
$\mathbb {Z}_p$-submodule of ![]() $L'\otimes \mathbb {Z}_p$ such that for every primitive
$L'\otimes \mathbb {Z}_p$ such that for every primitive ![]() $w$ in this submodule, the coefficient of
$w$ in this submodule, the coefficient of ![]() $t^{k_n}$ for some
$t^{k_n}$ for some ![]() $k_n\leq A(1+p+\cdots +p^{n+1})$ in
$k_n\leq A(1+p+\cdots +p^{n+1})$ in ![]() $p^n \tilde {w}$ does not lie in
$p^n \tilde {w}$ does not lie in ![]() $(p^{-1}W)^4$; because
$(p^{-1}W)^4$; because ![]() $p\mathbb {L}_{\mathrm {cris},P}(W)\subset L'\otimes W$, with respect to a
$p\mathbb {L}_{\mathrm {cris},P}(W)\subset L'\otimes W$, with respect to a ![]() $W$-basis of
$W$-basis of ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$, the coefficient of
$\mathbb {L}_{\mathrm {cris},P}(W)$, the coefficient of ![]() $t^{k_n}$ in
$t^{k_n}$ in ![]() $p^n \tilde {w}$ does not lie in
$p^n \tilde {w}$ does not lie in ![]() $W^4$. On the other hand, for any
$W^4$. On the other hand, for any ![]() $N< p(A_n+1)$, we have
$N< p(A_n+1)$, we have ![]() $p^{-1}t^N\notin D_{A_n+1}$. Note that
$p^{-1}t^N\notin D_{A_n+1}$. Note that ![]() $p(A_n+1)>p A(p^n+\cdots + 1/p)=A(p^{n+1}+\cdots +1)\geq k_n$. Hence,
$p(A_n+1)>p A(p^n+\cdots + 1/p)=A(p^{n+1}+\cdots +1)\geq k_n$. Hence, ![]() $p^n \tilde {w}$ does not extend to a special endomorphism over
$p^n \tilde {w}$ does not extend to a special endomorphism over ![]() $S_{A_n+1}$. Thus, this rank-
$S_{A_n+1}$. Thus, this rank-![]() $3$ submodule decays rapidly. Moreover, the existence of a vector decaying very rapidly follows by the second assertion of Proposition 5.1.3 via the same argument and the fact that
$3$ submodule decays rapidly. Moreover, the existence of a vector decaying very rapidly follows by the second assertion of Proposition 5.1.3 via the same argument and the fact that ![]() $p(A_{n-1}+ap^n+1)>p( A(p^{n-1}+\cdots + 1/p)+ap^n)=A(p^{n}+\cdots +1)+ap^{n+1}$.
$p(A_{n-1}+ap^n+1)>p( A(p^{n-1}+\cdots + 1/p)+ap^n)=A(p^{n}+\cdots +1)+ap^{n+1}$.
By a slight abuse of terminology, if a submodule of ![]() $L'\otimes \mathbb {Z}_p$ satisfies the property DR (with respect to basis
$L'\otimes \mathbb {Z}_p$ satisfies the property DR (with respect to basis ![]() $\{w_i\}$), we also say that this submodule decays rapidly; if a primitive vector satisfies property DvR, we also say that this vector decays very rapidly. By the proof of Theorem 5.1.2 above, property DR (respectively, DvR) implies decaying (respectively, very) rapidly in the sense of Definition 5.1.1.
$\{w_i\}$), we also say that this submodule decays rapidly; if a primitive vector satisfies property DvR, we also say that this vector decays very rapidly. By the proof of Theorem 5.1.2 above, property DR (respectively, DvR) implies decaying (respectively, very) rapidly in the sense of Definition 5.1.1.
The rest of this section is devoted to prove Proposition 5.1.3 for the Hilbert case and its proof for the Siegel case is given in § 6. In the following, the split/inert case means that ![]() $p$ is split/inert in the real quadratic field attached to the Hilbert modular surface.
$p$ is split/inert in the real quadratic field attached to the Hilbert modular surface.
In the Hilbert case, by Corollary 3.4.2, the non-ordinary locus is cut out by the equation ![]() $xy = 0$. As in the proof of reducing Theorem 5.1.2 to Proposition 5.1.3, we pick a lift
$xy = 0$. As in the proof of reducing Theorem 5.1.2 to Proposition 5.1.3, we pick a lift ![]() $W[[x,y]]\rightarrow W[[t]]$ of the local ring homomorphism
$W[[x,y]]\rightarrow W[[t]]$ of the local ring homomorphism ![]() $k[[x,y]]\rightarrow k[[t]]$ defined by
$k[[x,y]]\rightarrow k[[t]]$ defined by ![]() $C$. As
$C$. As ![]() $C$ is generically ordinary, we have that both
$C$ is generically ordinary, we have that both ![]() $x$ and
$x$ and ![]() $y$ map to power series in
$y$ map to power series in ![]() $W[[t]]$ which are non-zero
$W[[t]]$ which are non-zero ![]() $\bmod \, p$. Without loss of generality, we assume that
$\bmod \, p$. Without loss of generality, we assume that ![]() $v_t(x) \leq v_t(y)$, and that
$v_t(x) \leq v_t(y)$, and that ![]() $x(t) = t^a + \cdots$ and
$x(t) = t^a + \cdots$ and ![]() $y(t) = \alpha t^b + \cdots$, where
$y(t) = \alpha t^b + \cdots$, where ![]() $\alpha \in W^\times$. We will see that the value
$\alpha \in W^\times$. We will see that the value ![]() $a = v_t(x)$ will be the one that is used in the statement of Proposition 5.1.3.
$a = v_t(x)$ will be the one that is used in the statement of Proposition 5.1.3.
5.2 Decay in the split case
Notation as in the proof of Theorem 5.1.2. We first compute ![]() $F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.2),
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.2),
 \begin{align*} F=\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}. \end{align*}
\begin{align*} F=\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}. \end{align*}
We remind the reader that ![]() $(I+F)\circ \sigma = \operatorname {Frob}$.
$(I+F)\circ \sigma = \operatorname {Frob}$.
Let ![]() $F_{\infty }(1)$ and
$F_{\infty }(1)$ and ![]() $F_{\infty }(2)$ denote the top-left and top-right
$F_{\infty }(2)$ denote the top-left and top-right ![]() $2 \times 2$ blocks of
$2 \times 2$ blocks of ![]() $F_{\infty }$ respectively. To simplify the notation, defineFootnote 27
$F_{\infty }$ respectively. To simplify the notation, defineFootnote 27
 \begin{align*} G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_u = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_l = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \end{align*}
\begin{align*} G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_u = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_l = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \end{align*}
and let ![]() $F_t$,
$F_t$, ![]() $F_u$ and
$F_u$ and ![]() $F_l$ denote the top-left, top-right, and bottom-left
$F_l$ denote the top-left, top-right, and bottom-left ![]() $2 \times 2$ blocks of
$2 \times 2$ blocks of ![]() $F$. The product expansion of Frobenius
$F$. The product expansion of Frobenius ![]() $F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$ allows for
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$ allows for ![]() $F_{\infty }$ to be expressed as an infinite sum of finite products of
$F_{\infty }$ to be expressed as an infinite sum of finite products of ![]() $\sigma$-twists of
$\sigma$-twists of ![]() $F_t$,
$F_t$, ![]() $F_u$, and
$F_u$, and ![]() $F_l$. The following elementary lemma picks out the terms in
$F_l$. The following elementary lemma picks out the terms in ![]() $F_{\infty }(1), F_{\infty }(2)$ with the desired
$F_{\infty }(1), F_{\infty }(2)$ with the desired ![]() $p$-power on the denominators.
$p$-power on the denominators.
Lemma 5.2.1
(1) We have that
 $F_{\infty }(1)$ is a sum of products of the form
$F_{\infty }(1)$ is a sum of products of the form  $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here
$\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here  $X_i$ is
$X_i$ is  $F_t$,
$F_t$,  $F_u$, or
$F_u$, or  $F_l$,Footnote 28
$F_l$,Footnote 28  $m_1 + 1$ is the number of occurrences of
$m_1 + 1$ is the number of occurrences of  $F_t$, and
$F_t$, and  $m_2$ is the number of occurrences of the pair
$m_2$ is the number of occurrences of the pair  $F_u, F_l$ and
$F_u, F_l$ and  $n_i$ is a strictly increasing sequence of non-negative integers. The
$n_i$ is a strictly increasing sequence of non-negative integers. The  $p$-adic valuation of
$p$-adic valuation of  $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is
$\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is  $-(n+1)$, where
$-(n+1)$, where  $n = m_1 + m_2$. The analogous statement holds for
$n = m_1 + m_2$. The analogous statement holds for  $F_{\infty }(2)$.
$F_{\infty }(2)$.(2) Fix values of
 $m_1,m_2$ as above. Among all the terms in the above sum, those with minimal
$m_1,m_2$ as above. Among all the terms in the above sum, those with minimal  $t$-adic valuation only occur when
$t$-adic valuation only occur when  $n_i = i$, and either when
$n_i = i$, and either when  $X_0 = X_1 = \cdots = X_{m_1} = F_t$ or
$X_0 = X_1 = \cdots = X_{m_1} = F_t$ or  $X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for
$X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for  $F_{\infty }(2)$.
$F_{\infty }(2)$.(3) (For
 $F_{\infty }(1)$) The product
$F_{\infty }(1)$) The product  $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)}$ (modulo terms with smaller
$\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)}$ (modulo terms with smaller  $p$-power in denominatorsFootnote 29) equals
$p$-power in denominatorsFootnote 29) equals
 \[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 -1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p})^{(m_1 + 2i + 1)}. \]
\[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 -1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p})^{(m_1 + 2i + 1)}. \](4) (For
 $F_{\infty }(2)$) The product
$F_{\infty }(2)$) The product  $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ (modulo terms with smaller
$\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ (modulo terms with smaller  $p$-power in denominators) equals
$p$-power in denominators) equals
 \[ \displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 - 1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p} )^{(m_1 + 2i + 1)} \cdot F_u^{(m_1 + 2m_2 + 1)}. \]
\[ \displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 - 1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p} )^{(m_1 + 2i + 1)} \cdot F_u^{(m_1 + 2m_2 + 1)}. \]
5.2.2 Notation. We make the following definition to further lighten the notation.
Let ![]() $P(1)_{m_2,n}$ denote the product
$P(1)_{m_2,n}$ denote the product
 \[ \displaystyle \prod_{i=0}^{m_1} G^{(i)}\prod_{i=0}^{m_2-1}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i + 2)}. \]
\[ \displaystyle \prod_{i=0}^{m_1} G^{(i)}\prod_{i=0}^{m_2-1}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i + 2)}. \]
Recall that ![]() $A = a + b$ denotes the
$A = a + b$ denotes the ![]() $t$-adic valuation
$t$-adic valuation ![]() $v_t(xy)$ of
$v_t(xy)$ of ![]() $xy$ and let
$xy$ and let ![]() $B$ denote
$B$ denote ![]() $v_t(x^{p+1} + y^{p+1})$. Note that
$v_t(x^{p+1} + y^{p+1})$. Note that ![]() $B \geq a(p+1)$ and the equality holds unless
$B \geq a(p+1)$ and the equality holds unless ![]() $a = b$.
$a = b$.
To prove Proposition 5.1.3, we consider the following case-by-case analysis depending on the relation between ![]() $a$ and
$a$ and ![]() $b$. The following elementary lemmas will be used in the case-by-case analysis.
$b$. The following elementary lemmas will be used in the case-by-case analysis.
Lemma 5.2.3 Let ![]() $n, e, f$ be in
$n, e, f$ be in ![]() $\mathbb {Z}_{\geq 0}$.
$\mathbb {Z}_{\geq 0}$.
(1) The kernel of the
 $2 \times 2$ matrix
$2 \times 2$ matrix  $P(1)_{e,n}$ modulo
$P(1)_{e,n}$ modulo  $p$ is defined over
$p$ is defined over  $\mathbb {F}_{p^2}$ but not over
$\mathbb {F}_{p^2}$ but not over  $\mathbb {F}_p$.
$\mathbb {F}_p$.(2) The reductions of
 $P(1)_{e,n}$ and
$P(1)_{e,n}$ and  $P(1)_{f,n}$ modulo
$P(1)_{f,n}$ modulo  $p$ are not scalar multiples (over
$p$ are not scalar multiples (over  $k$) of each other if
$k$) of each other if  $e \not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if
$e \not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if  $f = e \pm 1$.
$f = e \pm 1$.
Proof. As the entries of ![]() $G$,
$G$, ![]() $H_u$, and
$H_u$, and ![]() $H_l$ are all in
$H_l$ are all in ![]() $W(\mathbb {F}_{p^2})[1/p]$, it follows that
$W(\mathbb {F}_{p^2})[1/p]$, it follows that ![]() $G^{(2m)} = G$ and
$G^{(2m)} = G$ and ![]() $G^{(2m+1)} = G^{(1)}$ (and the analogous statements hold for
$G^{(2m+1)} = G^{(1)}$ (and the analogous statements hold for ![]() $H_u$ and
$H_u$ and ![]() $H_l$). A direct computation shows that
$H_l$). A direct computation shows that ![]() $GG^{(1)}G = G$,
$GG^{(1)}G = G$, ![]() $H_uH_l^{(1)}H_uH_l^{(1)} = H_uH_l^{(1)}$, and
$H_uH_l^{(1)}H_uH_l^{(1)} = H_uH_l^{(1)}$, and ![]() $H_u^{(1)}H_lH_u^{(1)}H_l= H_u^{(1)}H_l$. Therefore, if
$H_u^{(1)}H_lH_u^{(1)}H_l= H_u^{(1)}H_l$. Therefore, if ![]() $n-e$ is odd, then
$n-e$ is odd, then ![]() $P(1)_{e,n}$ simplifies to
$P(1)_{e,n}$ simplifies to ![]() $GG^{(1)}H_uH_l^{(1)}$,
$GG^{(1)}H_uH_l^{(1)}$, ![]() $GG^{(1)}$, or
$GG^{(1)}$, or ![]() $H_uH_l^{(1)}$; if
$H_uH_l^{(1)}$; if ![]() $n-e$ is even,
$n-e$ is even, ![]() $P(1)_{e,n}$ simplifies to
$P(1)_{e,n}$ simplifies to ![]() $G$ or
$G$ or ![]() $GH_u^{(1)}H_l$. A direct computation shows that the matrices
$GH_u^{(1)}H_l$. A direct computation shows that the matrices ![]() $GG^{(1)}$,
$GG^{(1)}$, ![]() $H_uH_l^{(1)}$ and
$H_uH_l^{(1)}$ and ![]() $GG^{(1)}H_uH_l^{(1)}$ (respectively,
$GG^{(1)}H_uH_l^{(1)}$ (respectively, ![]() $G$ and
$G$ and ![]() $GH_u^{(1)}H_l$) are equal to
$GH_u^{(1)}H_l$) are equal to
 \[ \begin{bmatrix} \dfrac{1}{2} & \dfrac{\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{1}{2}\\ \end{bmatrix}\quad \left(\text{respectively, }\begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2}\\ \end{bmatrix}\right). \]
\[ \begin{bmatrix} \dfrac{1}{2} & \dfrac{\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{1}{2}\\ \end{bmatrix}\quad \left(\text{respectively, }\begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2}\\ \end{bmatrix}\right). \] In either case, because ![]() $\lambda \in W(\mathbb {F}_{p^2})\backslash \mathbb {Z}_p$, there is no non-trivial
$\lambda \in W(\mathbb {F}_{p^2})\backslash \mathbb {Z}_p$, there is no non-trivial ![]() $\mathbb {F}_p$-linear combination of the columns modulo
$\mathbb {F}_p$-linear combination of the columns modulo ![]() $p$ which equals zero; this implies part (1). Furthermore, the above matrices are clearly not scalar multiples of each other, whence part (2) follows.
$p$ which equals zero; this implies part (1). Furthermore, the above matrices are clearly not scalar multiples of each other, whence part (2) follows.
Lemma 5.2.4 Let ![]() $n, e, f$ be in
$n, e, f$ be in ![]() $\mathbb {Z}_{\geq 0}$.
$\mathbb {Z}_{\geq 0}$.
(1) The kernel of the
 $2 \times 2$ matrix
$2 \times 2$ matrix  $P(1)_{e,n-1}\cdot H_u^{(n+e)}$ modulo
$P(1)_{e,n-1}\cdot H_u^{(n+e)}$ modulo  $p$ is defined over
$p$ is defined over  $\mathbb {F}_{p^2}$ but not
$\mathbb {F}_{p^2}$ but not  $\mathbb {F}_p$.
$\mathbb {F}_p$.(2) The reductions of
 $P(1)_{e,n-1} \cdot H_u^{(n+e)}$ and
$P(1)_{e,n-1} \cdot H_u^{(n+e)}$ and  $P(1)_{f,n-1}\cdot H_u^{(n+f)}$ modulo
$P(1)_{f,n-1}\cdot H_u^{(n+f)}$ modulo  $p$ are not scalar multiples of each other if
$p$ are not scalar multiples of each other if  $e\not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if
$e\not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if  $f = e \pm 1$.
$f = e \pm 1$.
Proof. We argue along the lines of the proof of Lemma 5.2.3. Indeed, if ![]() $n-e$ is odd (respectively, even), we are reduced to the cases of
$n-e$ is odd (respectively, even), we are reduced to the cases of ![]() $GG^{(1)}H_uH_l^{(1)}H_u$,
$GG^{(1)}H_uH_l^{(1)}H_u$, ![]() $GG^{(1)}H_u$,
$GG^{(1)}H_u$, ![]() $H_uH_l^{(1)}H_u$, and
$H_uH_l^{(1)}H_u$, and ![]() $H_u$ (respectively,
$H_u$ (respectively, ![]() $GH_u^{(1)}H_lH_u^{(1)}$ and
$GH_u^{(1)}H_lH_u^{(1)}$ and ![]() $GH_u^{(1)}$). The rest of the argument is similar.
$GH_u^{(1)}$). The rest of the argument is similar.
We now prove Proposition 5.1.3 when ![]() $p$ is split in the real quadratic field defining the Hilbert modular surface. The proof is a case-by-case study in the following four cases based on the relation of
$p$ is split in the real quadratic field defining the Hilbert modular surface. The proof is a case-by-case study in the following four cases based on the relation of ![]() $a=v_t(x)$ and
$a=v_t(x)$ and ![]() $b=v_t(y)$. The idea is to pick out the term(s) with minimal
$b=v_t(y)$. The idea is to pick out the term(s) with minimal ![]() $t$-adic valuation among all the terms with the same
$t$-adic valuation among all the terms with the same ![]() $p$-power denominators given in Lemma 5.2.1. Case 4 is the generic case and it is easy to pick out such terms so we give the proof directly. In Cases 1–3, we first state the lemmas on the terms with minimal
$p$-power denominators given in Lemma 5.2.1. Case 4 is the generic case and it is easy to pick out such terms so we give the proof directly. In Cases 1–3, we first state the lemmas on the terms with minimal ![]() $t$-adic valuation and then prove the decay lemma. For the convenience of the reader, we summarize the desired vectors which decay rapidly enough at the beginning of each case.
$t$-adic valuation and then prove the decay lemma. For the convenience of the reader, we summarize the desired vectors which decay rapidly enough at the beginning of each case.
Case 1:  $a = b$
$a = b$
Recall that ![]() $A=v_t(xy)=a+b=2a$.
$A=v_t(xy)=a+b=2a$.
We prove that every vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly, where
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly, where ![]() $w_i = w_4$ if the
$w_i = w_4$ if the ![]() $t$-adic valuation of
$t$-adic valuation of ![]() $x - y$ is
$x - y$ is ![]() $> a$, and
$> a$, and ![]() $w_i = w_3$ otherwise. Moreover,
$w_i = w_3$ otherwise. Moreover, ![]() $w_i$,
$w_i$, ![]() $i=3,4$ respectively, decays very rapidly.
$i=3,4$ respectively, decays very rapidly.
Lemma 5.2.5
(1) Among the terms appearing in
 $F_{\infty }(1)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal  $t$-adic valuation is
$t$-adic valuation is
 \[ P(1)_{0,n}(xy)^{1 + p + \cdots + p^{n}}. \]
\[ P(1)_{0,n}(xy)^{1 + p + \cdots + p^{n}}. \](2) Among the terms appearing in
 $F_{\infty }(2)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal  $t$-adic valuation is
$t$-adic valuation is
 \[ P(1)_{0,n-1}\cdot F_u^{(n )} (xy)^{1 + p + \cdots + p^{n-1}}. \]
\[ P(1)_{0,n-1}\cdot F_u^{(n )} (xy)^{1 + p + \cdots + p^{n-1}}. \]
This lemma follows directly from Lemma 5.2.1 and the assumption that ![]() $a = b$.
$a = b$.
Proof of Proposition 5.1.3 in this case We first prove that every primitive vector ![]() $w\in \operatorname {Span}_{\mathbb {Z}_p} \{w_1,w_2\}$ decays rapidly. Indeed, write
$w\in \operatorname {Span}_{\mathbb {Z}_p} \{w_1,w_2\}$ decays rapidly. Indeed, write ![]() $w=cw_1+dw_2$, by Lemmas 5.2.3(1) and 5.2.5(1), there is a unique (non-vanishing) term in
$w=cw_1+dw_2$, by Lemmas 5.2.3(1) and 5.2.5(1), there is a unique (non-vanishing) term in ![]() $F_{\infty }(1)w$ with denominator
$F_{\infty }(1)w$ with denominator ![]() $1/p^{n+1}$ and minimal
$1/p^{n+1}$ and minimal ![]() $t$-adic valuation
$t$-adic valuation ![]() $A(1+p+\cdots + p^n)$ given by
$A(1+p+\cdots + p^n)$ given by ![]() $P(1)_{0,n}[c\quad d]^{\rm T} (xy)^{1+p+\cdots +p^n}$. Hence, modulo
$P(1)_{0,n}[c\quad d]^{\rm T} (xy)^{1+p+\cdots +p^n}$. Hence, modulo ![]() $t^{A(1+p+\cdots + p^n)+1}$, the horizontal section
$t^{A(1+p+\cdots + p^n)+1}$, the horizontal section ![]() $p^n\tilde {w}=F_{\infty }(p^nw)$ does not lie in
$p^n\tilde {w}=F_{\infty }(p^nw)$ does not lie in ![]() $W[[t]]$ and, hence,
$W[[t]]$ and, hence, ![]() $w$ decays rapidly.
$w$ decays rapidly.
Second, let ![]() $i\in \{3,4\}$ be defined as above and we show that
$i\in \{3,4\}$ be defined as above and we show that ![]() $w_i$ decays very rapidly. Note that our definition of
$w_i$ decays very rapidly. Note that our definition of ![]() $w_i$ implies that the first two entries of the
$w_i$ implies that the first two entries of the ![]() $i$th row of
$i$th row of ![]() $F$ have
$F$ have ![]() $t$-adic valuation equalling
$t$-adic valuation equalling ![]() $a$. Furthermore, by Lemma 5.2.3(1),
$a$. Furthermore, by Lemma 5.2.3(1), ![]() $P(1)_{0,n-1} \cdot v \neq 0$ mod
$P(1)_{0,n-1} \cdot v \neq 0$ mod ![]() $p$, where
$p$, where ![]() $v$ is the
$v$ is the ![]() $n$th Frobenius twist of either column of
$n$th Frobenius twist of either column of ![]() $H_u$. Therefore, among the terms in the
$H_u$. Therefore, among the terms in the ![]() $i$th column of
$i$th column of ![]() $F_{\infty }$ with denominator
$F_{\infty }$ with denominator ![]() $p^{n+1}$, the term with minimal
$p^{n+1}$, the term with minimal ![]() $t$-adic valuation has
$t$-adic valuation has ![]() $t$-adic valuation
$t$-adic valuation ![]() $2a(1 + p + \cdots + p^{n-1}) + ap^n$. Hence,
$2a(1 + p + \cdots + p^{n-1}) + ap^n$. Hence, ![]() $w_i$ decays very rapidly since
$w_i$ decays very rapidly since ![]() $a\leq (2a)/2=A/2$.
$a\leq (2a)/2=A/2$.
Finally, we show that every vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly. Let
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly. Let ![]() $w_u$ denote a primitive vector in the span of
$w_u$ denote a primitive vector in the span of ![]() $w_1,w_2$. It suffices to show that every vector which either has the form
$w_1,w_2$. It suffices to show that every vector which either has the form ![]() $p^m w_u + w_i$ or
$p^m w_u + w_i$ or ![]() $w_u + p^m w_i$ decays rapidly, where
$w_u + p^m w_i$ decays rapidly, where ![]() $m \geq 0$. We first prove that every vector which has the form
$m \geq 0$. We first prove that every vector which has the form ![]() $p^m w_u + w_i$ decays rapidly where
$p^m w_u + w_i$ decays rapidly where ![]() $m \geq 0$. Indeed, consider the two-dimensional vector whose entries are the first two entries of
$m \geq 0$. Indeed, consider the two-dimensional vector whose entries are the first two entries of ![]() $F_{\infty } \cdot p^m w_u$. The
$F_{\infty } \cdot p^m w_u$. The ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{n+1}$ equals
$1/p^{n+1}$ equals ![]() $2a(1 + p + \cdots + p^{n+m})$. Similarly, consider the two-dimensional vector whose entries are the first two entries of
$2a(1 + p + \cdots + p^{n+m})$. Similarly, consider the two-dimensional vector whose entries are the first two entries of ![]() $F_{\infty } \cdot w_i$. The
$F_{\infty } \cdot w_i$. The ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{n+1}$ equals
$1/p^{n+1}$ equals ![]() $2a(1 + p + \cdots + p^{n-1}) + ap^n$. Regardless of the value of
$2a(1 + p + \cdots + p^{n-1}) + ap^n$. Regardless of the value of ![]() $m$, the latter quantity is always smaller than the former quantity, whence it follows that
$m$, the latter quantity is always smaller than the former quantity, whence it follows that ![]() $p^mw_u + w$ decays rapidly. Now, consider a vector of the form
$p^mw_u + w$ decays rapidly. Now, consider a vector of the form ![]() $w_u + p^m w_i$, where
$w_u + p^m w_i$, where ![]() $m > 0$. Analogous to the previous case, consider the two-dimensional vector whose entries are the first two entries of
$m > 0$. Analogous to the previous case, consider the two-dimensional vector whose entries are the first two entries of ![]() $F_{\infty } \cdot w_u$. The
$F_{\infty } \cdot w_u$. The ![]() $t$-adic valuation of the sum of all terms with denominator
$t$-adic valuation of the sum of all terms with denominator ![]() $p^{n+1}$ equals
$p^{n+1}$ equals ![]() $2a(1 + p + \cdots + p^n)$. Similarly, consider the two-dimensional vector whose entries are the first two entries of
$2a(1 + p + \cdots + p^n)$. Similarly, consider the two-dimensional vector whose entries are the first two entries of ![]() $F_{\infty } \cdot p^m w_i$. The
$F_{\infty } \cdot p^m w_i$. The ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{n+1}$ equals
$1/p^{n+1}$ equals ![]() $2a(1 + p + \cdots + p^{n+m-1}) + ap^{n+m}$. Regardless of the value of
$2a(1 + p + \cdots + p^{n+m-1}) + ap^{n+m}$. Regardless of the value of ![]() $m$ (recall that
$m$ (recall that ![]() $m>0$), the latter quantity is always greater than the former quantity, whence it follows that
$m>0$), the latter quantity is always greater than the former quantity, whence it follows that ![]() $p^mw_u + w$ decays rapidly.
$p^mw_u + w$ decays rapidly.
Case 2:  $b = p^{2e}a$ for some
$b = p^{2e}a$ for some  $e\in \mathbb {Z}_{\geq 1}$
$e\in \mathbb {Z}_{\geq 1}$
We prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly where
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly where ![]() $w$ is some primitive vector in
$w$ is some primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$. We further prove that
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$. We further prove that ![]() $w$ decays very rapidly.
$w$ decays very rapidly.
Lemma 5.2.6
(1) Among the terms appearing in
 $F_{\infty }(1)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal  $t$-adic valuation is
$t$-adic valuation is
 \[ P(1)_{e,n}(xy)^{1 + p + \cdots + p^{n-e}}x^{p^{n - e + 1} + p^{n-e+2} + \cdots + p^{n + e}}. \]
\[ P(1)_{e,n}(xy)^{1 + p + \cdots + p^{n-e}}x^{p^{n - e + 1} + p^{n-e+2} + \cdots + p^{n + e}}. \](2) Among the terms appearing in
 $F_{\infty }(2)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, there are exactly two terms with minimal
$p^{n+1}$, there are exactly two terms with minimal  $t$-adic valuation, and they are
and
$t$-adic valuation, and they are
and \[ P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-2}}, \]
\[ P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-2}}, \] \[ P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}. \]
\[ P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}. \]
Proof. In the following, we prove part (1); part (2) follows by an identical argument.
Note that the ![]() $t$-adic valuation of all the entries of
$t$-adic valuation of all the entries of ![]() $F(1)$ is
$F(1)$ is ![]() $a+b$, and the
$a+b$, and the ![]() $t$-adic valuation of the entries of
$t$-adic valuation of the entries of ![]() $F_u$ and
$F_u$ and ![]() $F_l$ is
$F_l$ is ![]() $a$. Let
$a$. Let ![]() $k,l$ be in
$k,l$ be in ![]() $\mathbb {Z}_{\geq 0}$ such that
$\mathbb {Z}_{\geq 0}$ such that ![]() $k + l = n+1$. Consider the following terms of
$k + l = n+1$. Consider the following terms of ![]() $F_{\infty }(1)$ with denominator exactly
$F_{\infty }(1)$ with denominator exactly ![]() $p^{n+1}$:
$p^{n+1}$:
Similar to Lemma 5.2.1(2), we observe that among all the terms of ![]() $F_{\infty }(1)$ with denominator exactly
$F_{\infty }(1)$ with denominator exactly ![]() $p^{n+1}$ given in Lemma 5.2.1(1), for each other term
$p^{n+1}$ given in Lemma 5.2.1(1), for each other term ![]() $X$ not listed above, there exists at least one
$X$ not listed above, there exists at least one ![]() $X_{k,l}$ (as
$X_{k,l}$ (as ![]() $k$ and
$k$ and ![]() $l$ vary over all non-negative integers constrained by
$l$ vary over all non-negative integers constrained by ![]() $k + l = n+1$) such that
$k + l = n+1$) such that ![]() $v_t(X_{k,l})< v_t(X)$. Therefore, to prove part (1), it suffices to show that
$v_t(X_{k,l})< v_t(X)$. Therefore, to prove part (1), it suffices to show that ![]() $v_t(X_{k,l})$ with
$v_t(X_{k,l})$ with ![]() $k = n - e + 1$ and
$k = n - e + 1$ and ![]() $l = e$ is less than
$l = e$ is less than ![]() $v_t(X_{k,l})$ with any other choice of
$v_t(X_{k,l})$ with any other choice of ![]() $k,l$.
$k,l$.
As ![]() $b = ap^{2e}$ and
$b = ap^{2e}$ and ![]() $k + l = n+1$, then
$k + l = n+1$, then
and we need to prove that ![]() $k = n-e +1$ minimizes this expression as
$k = n-e +1$ minimizes this expression as ![]() $k$ ranges over
$k$ ranges over ![]() $\mathbb {Z} \cap [0,n+1]$. Note that if we allow
$\mathbb {Z} \cap [0,n+1]$. Note that if we allow ![]() $k$ to take all real values in the interval
$k$ to take all real values in the interval ![]() $[0,n+1]$, a direct computation shows that
$[0,n+1]$, a direct computation shows that ![]() $f$ is convex (i.e.
$f$ is convex (i.e. ![]() $f''(k)>0$). Therefore, it suffices to show that
$f''(k)>0$). Therefore, it suffices to show that ![]() $f(n-e+1)< f(n-e)$ and
$f(n-e+1)< f(n-e)$ and ![]() $f(n-e+1) < f(n-e+2)$. These claims can be verified directly and, hence, we prove part (1).
$f(n-e+1) < f(n-e+2)$. These claims can be verified directly and, hence, we prove part (1).
Proof of Proposition 5.1.3 in this case We first prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Indeed, let
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Indeed, let ![]() $w'$ be a primitive vector in
$w'$ be a primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$. Lemma 5.2.3(1) implies that
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$. Lemma 5.2.3(1) implies that ![]() $P(1)_{e,n} \cdot w'$ mod
$P(1)_{e,n} \cdot w'$ mod ![]() $p$ is non-zero. This fact taken in conjunction with Lemma 5.2.6(1) yields that
$p$ is non-zero. This fact taken in conjunction with Lemma 5.2.6(1) yields that ![]() $w'$ decays rapidly.
$w'$ decays rapidly.
Second, we prove that there exists a primitive vector ![]() $w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ (independent of
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ (independent of ![]() $n$) which decays very rapidly. Set
$n$) which decays very rapidly. Set
 \begin{align*} Y_{e,n}&:= P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots +p^{n + e-2}}\\ &\quad + P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}, \end{align*}
\begin{align*} Y_{e,n}&:= P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots +p^{n + e-2}}\\ &\quad + P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}, \end{align*}
which is the sum of the two terms with minimal ![]() $t$-adic valuation listed in Lemma 5.2.6(2). The sum
$t$-adic valuation listed in Lemma 5.2.6(2). The sum ![]() $Y_{e,n}$ is non-zero modulo
$Y_{e,n}$ is non-zero modulo ![]() $p$ by Lemma 5.2.3(2). Furthermore, up to Frobenius twists and multiplication by scalars, the matrix
$p$ by Lemma 5.2.3(2). Furthermore, up to Frobenius twists and multiplication by scalars, the matrix ![]() $Y_{e,n}\, \bmod p$ is independent of
$Y_{e,n}\, \bmod p$ is independent of ![]() $n$. Therefore, there exists a vector
$n$. Therefore, there exists a vector ![]() $w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which is independent of
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which is independent of ![]() $n$ and does not lie in the kernel of
$n$ and does not lie in the kernel of ![]() $Y_{e,n}\,\bmod p$. The very rapid decay of
$Y_{e,n}\,\bmod p$. The very rapid decay of ![]() $w$ follows from this observation and Lemma 5.2.6(2).
$w$ follows from this observation and Lemma 5.2.6(2).
Finally, a valuation-theoretic argument analogous to Case 1 shows that every primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly, thereby establishing Proposition 5.1.3 in this case.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly, thereby establishing Proposition 5.1.3 in this case.
Case 3:  $b = p^{2e + 1} a$ for some
$b = p^{2e + 1} a$ for some  $e\in \mathbb {Z}_{\geq 0}$
$e\in \mathbb {Z}_{\geq 0}$
We prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w\}$ decays rapidly where
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w\}$ decays rapidly where ![]() $w$ is some primitive vector in
$w$ is some primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and that
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly.
Lemma 5.2.7
(1) Among the terms appearing in
 $F_{\infty }(2)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal  $t$-adic valuation is
$t$-adic valuation is
 \[ P(1)_{e,n-1}\cdot H_u^{(n+e)}(xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e}}. \]
\[ P(1)_{e,n-1}\cdot H_u^{(n+e)}(xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e}}. \](2) Among the terms appearing in
 $F_{\infty }(1)$ described in Lemma 5.2.1 with denominator
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator  $p^{n+1}$, there are exactly two terms with minimal
$p^{n+1}$, there are exactly two terms with minimal  $t$-adic valuation, and they are
$t$-adic valuation, and they are
 \[ P(1)_{e,n} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-1}}, \]
\[ P(1)_{e,n} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-1}}, \] \[ P(1)_{e+1,n} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e}}. \]
\[ P(1)_{e+1,n} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e}}. \]
Proof. The proof of this lemma is identical to that of Lemma 5.2.6, so we omit the details.
Proof of Proposition 5.1.3 in this case Analogous to Case 2, Lemmas 5.2.4 and 5.2.7(2) imply the existence of a primitive ![]() $w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ that decays rapidly; and by Lemmas 5.2.4(1) and 5.2.7(1),
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ that decays rapidly; and by Lemmas 5.2.4(1) and 5.2.7(1), ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation-theoretic argument shows that every primitive vector in
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation-theoretic argument shows that every primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w,w_3,w_4\}$ decays rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w,w_3,w_4\}$ decays rapidly.
Case 4:  $b \neq a p^e$ for any value of
$b \neq a p^e$ for any value of  $e$
$e$
Proof of Proposition 5.1.3 As this is the easiest case, we are content with merely sketching a proof. Analogous to Lemmas 5.2.6 and 5.2.7, it is easy to see that in this case there are unique terms with minimal ![]() $t$-adic valuations with denominator
$t$-adic valuations with denominator ![]() $p^{n+1}$ occurring in both
$p^{n+1}$ occurring in both ![]() $F_{\infty }(1)$ and
$F_{\infty }(1)$ and ![]() $F_{\infty }(2)$. It follows that every primitive vector in
$F_{\infty }(2)$. It follows that every primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly and every vector in
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly and every vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation theoretic argument similar to Case 1 shows that every vector in the span of
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation theoretic argument similar to Case 1 shows that every vector in the span of ![]() $w_1,w_2,w_3,w_4$ does decay rapidly, finishing the proof of Proposition 5.1.3.
$w_1,w_2,w_3,w_4$ does decay rapidly, finishing the proof of Proposition 5.1.3.
5.3 Decay in the inert case
Notation as in the proof of Theorem 5.1.2 and § 3.2.1. Recall that ![]() $P$ is superspecial and we show that the
$P$ is superspecial and we show that the ![]() $\mathbb {Z}_p$-span of
$\mathbb {Z}_p$-span of ![]() $w_1,w_2,w_3$ decays rapidly, and the vector
$w_1,w_2,w_3$ decays rapidly, and the vector ![]() $w_3$ decays very rapidly.
$w_3$ decays very rapidly.
Proof of Proposition 5.1.3 The proof goes along the same lines as the proof of the decay lemma for split Hilbert modular varieties, so we are content with just outlining the salient points.
We first compute ![]() $F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.1), with respect to the basis
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.1), with respect to the basis ![]() $\{w_1,w_2,w_3,w_4 \}$,
$\{w_1,w_2,w_3,w_4 \}$, ![]() $F=\big (\begin {smallmatrix} F_t & F_u\\ F_l & 0 \end {smallmatrix}\big )$, where
$F=\big (\begin {smallmatrix} F_t & F_u\\ F_l & 0 \end {smallmatrix}\big )$, where
Recall that the non-ordinary locus is cut out by the equation ![]() $xy = 0$ and
$xy = 0$ and ![]() $a = v_t(x)$,
$a = v_t(x)$, ![]() $b = v_t(y)\in \mathbb {Z}_{>0}$.
$b = v_t(y)\in \mathbb {Z}_{>0}$.
Similar to Lemma 5.2.1, it is easy to see that the top-left ![]() $2\times 2$ block of
$2\times 2$ block of ![]() $F_{\infty }$ with
$F_{\infty }$ with ![]() $p$-adic valuation
$p$-adic valuation ![]() $-(n+1)$ has a term of the form
$-(n+1)$ has a term of the form ![]() $F_t F_t^{(1)} \ldots F_t^{(n)}$, and this term is the unique term with minimal
$F_t F_t^{(1)} \ldots F_t^{(n)}$, and this term is the unique term with minimal ![]() $t$-adic valuation (equalling
$t$-adic valuation (equalling ![]() $(a + b)(1 + p + \cdots +p^n)$). Similarly, the top-right
$(a + b)(1 + p + \cdots +p^n)$). Similarly, the top-right ![]() $2\times 2$ block of
$2\times 2$ block of ![]() $F_{\infty }$ with
$F_{\infty }$ with ![]() $p$-adic valuation
$p$-adic valuation ![]() $-(n+1)$ has a term of the form
$-(n+1)$ has a term of the form ![]() $F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$, and this term is the unique term with minimal
$F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$, and this term is the unique term with minimal ![]() $t$-adic valuation (equaling
$t$-adic valuation (equaling ![]() $(a + b)(1 + p + \cdots + p^{n-1}) + ap^n$).
$(a + b)(1 + p + \cdots + p^{n-1}) + ap^n$).
Arguments identical to Lemmas 5.2.3 and 5.2.4 yield that every primitive vector in the ![]() $\mathbb {Z}_p$ span of
$\mathbb {Z}_p$ span of ![]() $w_1,w_2$ (and in the span of
$w_1,w_2$ (and in the span of ![]() $w_3$) decays rapidly (very rapidly, in the case of
$w_3$) decays rapidly (very rapidly, in the case of ![]() $w_3$). Further, as the
$w_3$). Further, as the ![]() $t$-adic valuation of
$t$-adic valuation of ![]() $F_t F_t^{(1)} \ldots F_t^{(m)}$ is different from the
$F_t F_t^{(1)} \ldots F_t^{(m)}$ is different from the ![]() $t$-adic valuation of
$t$-adic valuation of ![]() $F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$ for every pair of integers
$F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$ for every pair of integers ![]() $n,m$, it follows that
$n,m$, it follows that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_3\}$ also decays rapidly. The argument is elaborated on in the last paragraph of the proof for Case 1 in § 5.2.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_3\}$ also decays rapidly. The argument is elaborated on in the last paragraph of the proof for Case 1 in § 5.2.
6. Proof of the decay lemma in the Siegel case
In this section, we prove Proposition 5.1.3 and, hence, Theorem 5.1.2 (for superspecial points) in the Siegel case. We refer the reader to the appendix for a decay lemma for supergeneric points. The main idea of the proof is similar to that of the Hilbert case in § 5.
6.1 Preparation of the proof
We follow the notation in § 5, ![]() $k=\bar {\mathbb {F}}_p$,
$k=\bar {\mathbb {F}}_p$, ![]() $W=W(k)$,
$W=W(k)$, ![]() $K=W[1/p]$,
$K=W[1/p]$, ![]() $\lambda \in \mathbb {Z}_{p^2}^\times$ such that
$\lambda \in \mathbb {Z}_{p^2}^\times$ such that ![]() $\sigma (\lambda ) = - \lambda$, and
$\sigma (\lambda ) = - \lambda$, and ![]() $C = \operatorname {Spf} k[[t]]$ a generically ordinary formal curve in
$C = \operatorname {Spf} k[[t]]$ a generically ordinary formal curve in ![]() $\mathcal {M}_k$ which specializes to a superspecial point
$\mathcal {M}_k$ which specializes to a superspecial point ![]() $P$. This gives rise to a local ring homomorphism
$P$. This gives rise to a local ring homomorphism ![]() $k[[x,y,z]]\rightarrow k[[t]]$ and we pick a lift
$k[[x,y,z]]\rightarrow k[[t]]$ and we pick a lift ![]() $W[[x,y,z]]\rightarrow W[[t]]$ (still a ring homomorphism), and we denote by
$W[[x,y,z]]\rightarrow W[[t]]$ (still a ring homomorphism), and we denote by ![]() $x(t)$,
$x(t)$, ![]() $y(t)$, and
$y(t)$, and ![]() $z(t)$ the images of
$z(t)$ the images of ![]() $x$,
$x$, ![]() $y$, and
$y$, and ![]() $z$, respectively.
$z$, respectively.
Let ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$ denote the
$c$ denote the ![]() $t$-adic valuations of
$t$-adic valuations of ![]() $x(t)$,
$x(t)$, ![]() $y(t)$, and
$y(t)$, and ![]() $z(t)$, respectively. We adopt the convention that
$z(t)$, respectively. We adopt the convention that ![]() $a,b,c$ may take on the value
$a,b,c$ may take on the value ![]() $\infty$ if the corresponding power series is
$\infty$ if the corresponding power series is ![]() $0$. As before,
$0$. As before, ![]() $v_t$ denotes the
$v_t$ denotes the ![]() $t$-adic valuation map on
$t$-adic valuation map on ![]() $K[[t]]$ or
$K[[t]]$ or ![]() $k[[t]]$.
$k[[t]]$.
Also recall that ![]() $\sigma$ denotes both the Frobenius on
$\sigma$ denotes both the Frobenius on ![]() $K$ and the Frobenius on the coordinate rings
$K$ and the Frobenius on the coordinate rings ![]() $W[[x,y,z]]$ with
$W[[x,y,z]]$ with ![]() $\sigma (x)=x^p, \sigma (y)=y^p$,
$\sigma (x)=x^p, \sigma (y)=y^p$, ![]() $\sigma (z)=z^p$; and for a matrix
$\sigma (z)=z^p$; and for a matrix ![]() $M$ with entries in
$M$ with entries in ![]() $K[[x,y,z]]$,
$K[[x,y,z]]$, ![]() $M^{(n)}$ denotes
$M^{(n)}$ denotes ![]() $\sigma ^n(M)$.
$\sigma ^n(M)$.
The preparation lemmas of the Siegel case are very similar to that of the split Hilbert case in the beginning of § 5.2.
6.1.1
Notation. Recall that ![]() $F_{\infty }=\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.3.1), with respect to the basis
$F_{\infty }=\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.3.1), with respect to the basis ![]() $\{w_1,\ldots, w_5\}$,
$\{w_1,\ldots, w_5\}$,
 \[ F=\begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p} \\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}, \]
\[ F=\begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p} \\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}, \]
where ![]() $\epsilon =\lambda ^2\in \mathbb {Z}_p^\times$. We denote by
$\epsilon =\lambda ^2\in \mathbb {Z}_p^\times$. We denote by ![]() $F_t$,
$F_t$, ![]() $F_u$, and
$F_u$, and ![]() $F_l$ the top-left
$F_l$ the top-left ![]() $2 \times 2$ block, the top-right
$2 \times 2$ block, the top-right ![]() $2 \times 3$ block, and the bottom-left
$2 \times 3$ block, and the bottom-left ![]() $3 \times 2$ block of
$3 \times 2$ block of ![]() $F$, respectively. Define
$F$, respectively. Define
 \[ G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-1}{2 \lambda}\\ \dfrac{\lambda}{2} & \dfrac{-1}{2} \end{bmatrix},\quad H_u = \begin{bmatrix} \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda}\\ \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2} \end{bmatrix}, \quad \text{and} \quad H_l = \begin{bmatrix} \lambda & -1\\ \lambda & -1\\ \lambda & -1 \end{bmatrix}. \]
\[ G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-1}{2 \lambda}\\ \dfrac{\lambda}{2} & \dfrac{-1}{2} \end{bmatrix},\quad H_u = \begin{bmatrix} \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda}\\ \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2} \end{bmatrix}, \quad \text{and} \quad H_l = \begin{bmatrix} \lambda & -1\\ \lambda & -1\\ \lambda & -1 \end{bmatrix}. \]
Let ![]() $F_{\infty }(1)$ and
$F_{\infty }(1)$ and ![]() $F_{\infty }(2)$ denote the top-left
$F_{\infty }(2)$ denote the top-left ![]() $2 \times 2$ block and top-right
$2 \times 2$ block and top-right ![]() $2 \times 3$ of
$2 \times 3$ of ![]() $F_{\infty }$, respectively.
$F_{\infty }$, respectively.
By Corollary 3.4.2, the non-ordinary locus is cut out by the equation ![]() $xy + z^2/(4\epsilon ) = 0$. Let
$xy + z^2/(4\epsilon ) = 0$. Let ![]() $\eta t^A$ and
$\eta t^A$ and ![]() $\mu t^B$ denote the leading terms of
$\mu t^B$ denote the leading terms of ![]() $xy + z^2 /(4\epsilon )$ and
$xy + z^2 /(4\epsilon )$ and ![]() $xy^p + x^p y + z^{1 + p}/(2\epsilon )$, respectively. In particular,
$xy^p + x^p y + z^{1 + p}/(2\epsilon )$, respectively. In particular, ![]() $A=v_t(xy + z^2/(4 \epsilon ))$ and
$A=v_t(xy + z^2/(4 \epsilon ))$ and ![]() $B=v_t(xy^p + x^p y + z^{1 + p}/(2\epsilon ))$.
$B=v_t(xy^p + x^p y + z^{1 + p}/(2\epsilon ))$.
As in the Hilbert case, the product expansion of Frobenius ![]() $F_{\infty } = \prod _{i=0}^\infty (1+F^{(i)})$ allows for
$F_{\infty } = \prod _{i=0}^\infty (1+F^{(i)})$ allows for ![]() $F_{\infty }$ to be expressed as an infinite sum of finite products of
$F_{\infty }$ to be expressed as an infinite sum of finite products of ![]() $\sigma$-twists of
$\sigma$-twists of ![]() $F_t$,
$F_t$, ![]() $F_u$, and
$F_u$, and ![]() $F_l$. The following lemma picks out the terms in
$F_l$. The following lemma picks out the terms in ![]() $F_{\infty }(1),F_{\infty }(2)$ with the desired
$F_{\infty }(1),F_{\infty }(2)$ with the desired ![]() $p$-power denominators, analogous to Lemma 5.2.1 in the Hilbert case.
$p$-power denominators, analogous to Lemma 5.2.1 in the Hilbert case.
Lemma 6.1.2
(1) We have that
 $F_{\infty }(1)$ is a sum of products of the form
$F_{\infty }(1)$ is a sum of products of the form  $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here,
$\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here,  $X_i$ is
$X_i$ is  $F_t$,
$F_t$,  $F_u$, or
$F_u$, or  $F_l$,Footnote 30
$F_l$,Footnote 30  $m_1 + 1$ is the number of occurrences of
$m_1 + 1$ is the number of occurrences of  $F_t$, and
$F_t$, and  $m_2$ is the number of occurrences of the pair
$m_2$ is the number of occurrences of the pair  $F_u,F_l$, and
$F_u,F_l$, and  $\{n_i\}_{i=0}^{m_1+2m_2}$ is a strictly increasing sequence of non-negative integers. The
$\{n_i\}_{i=0}^{m_1+2m_2}$ is a strictly increasing sequence of non-negative integers. The  $p$-adic valuation of
$p$-adic valuation of  $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is
$\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is  $-(n+1)$, where
$-(n+1)$, where  $n = m_1+m_2$. The analogous statement holds for
$n = m_1+m_2$. The analogous statement holds for  $F_{\infty }(2)$.
$F_{\infty }(2)$.(2) Fix values of
 $m_1,m_2$ as above. Among all the terms in the above sum, those with minimal
$m_1,m_2$ as above. Among all the terms in the above sum, those with minimal  $t$-adic valuation only occur when
$t$-adic valuation only occur when  $n_i = i$ for all
$n_i = i$ for all  $i$, and either when
$i$, and either when  $X_0 = X_1 = \cdots = X_{m_1} = F_t$ or
$X_0 = X_1 = \cdots = X_{m_1} = F_t$ or  $X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for
$X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for  $F_{\infty }(2)$.
$F_{\infty }(2)$.(3) (For
 $F_{\infty }(1)$) The product
$F_{\infty }(1)$) The product  $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 1 + 2i)}F_l^{(m_1 + 2i + 2)}$ equals
$\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 1 + 2i)}F_l^{(m_1 + 2i + 2)}$ equals
 \[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2 -1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}. \]
\[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2 -1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}. \](4) (For
 $F_{\infty }(2)$) The product
$F_{\infty }(2)$) The product  $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ equals
$\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ equals
 \begin{align*} &\displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2-1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}\\ &\qquad \cdot F_u^{(m_1 + 2m_2 + 1)}. \end{align*}
\begin{align*} &\displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2-1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}\\ &\qquad \cdot F_u^{(m_1 + 2m_2 + 1)}. \end{align*}
6.1.3
Notation. Let ![]() $P(1)_{m_2,n}$ denote the product
$P(1)_{m_2,n}$ denote the product  $\displaystyle \prod _{i =0}^{m_1}G^{(i)} \prod _{i = 0}^{m_2 -1} \frac {1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}$.
$\displaystyle \prod _{i =0}^{m_1}G^{(i)} \prod _{i = 0}^{m_2 -1} \frac {1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}$.
The following will play a similar role as Lemma 5.2.3.
Lemma 6.1.4 The kernel of ![]() $P(1)_{g,f+g} \bmod p$ does not contain any non-zero vector defined over
$P(1)_{g,f+g} \bmod p$ does not contain any non-zero vector defined over ![]() $\mathbb {F}_p.$ Moreover, if
$\mathbb {F}_p.$ Moreover, if ![]() $f$ is odd (respectively, even), the kernel of
$f$ is odd (respectively, even), the kernel of ![]() $P(1)_{g,f+g} \bmod p$ does not contain the vector
$P(1)_{g,f+g} \bmod p$ does not contain the vector ![]() $\big [\begin {smallmatrix} \lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$ (respectively,
$\big [\begin {smallmatrix} \lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$ (respectively, ![]() $\big [\begin {smallmatrix} -\lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$).
$\big [\begin {smallmatrix} -\lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$).
Proof. We prove the assertions by explicit computation as in Lemmas 5.2.3 and 5.2.4. Note that
Both these matrices satisfy the relation ![]() $X^2 = -X$ and, hence,
$X^2 = -X$ and, hence, ![]() $\prod _{i=0}^{m_2-1}H_u^{(m_1+2i+1)}H_l^{(m_1+2i+2)}$ equals, up to a multiple of
$\prod _{i=0}^{m_2-1}H_u^{(m_1+2i+1)}H_l^{(m_1+2i+2)}$ equals, up to a multiple of ![]() $\pm 1$, one of these matrices depending on the parity of
$\pm 1$, one of these matrices depending on the parity of ![]() $m_1$. Similarly, we have
$m_1$. Similarly, we have
Therefore, ![]() $P(1)_{g,f+g}$ equals
$P(1)_{g,f+g}$ equals ![]() $\pm \frac {1}{2} \big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ]$ if
$\pm \frac {1}{2} \big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ]$ if ![]() $f$ is odd, and equals
$f$ is odd, and equals ![]() $\pm \frac {1}{2}\big [\begin {smallmatrix} 1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]$ if
$\pm \frac {1}{2}\big [\begin {smallmatrix} 1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]$ if ![]() $f$ is even. The lemma then follows immediately.
$f$ is even. The lemma then follows immediately.
For fixed ![]() $n$, among the terms listed in Lemma 6.1.2 with denominator
$n$, among the terms listed in Lemma 6.1.2 with denominator ![]() $p^{n+1}$, the number of terms with equal minimal
$p^{n+1}$, the number of terms with equal minimal ![]() $t$-adic valuation depends on certain numerical relation between
$t$-adic valuation depends on certain numerical relation between ![]() $A$ and
$A$ and ![]() $B$. We then perform the following case-by-case analysis in §§ 6.2–6.4 to prove the decay lemma. The first case, while technically the easiest, holds the main ideas in general.
$B$. We then perform the following case-by-case analysis in §§ 6.2–6.4 to prove the decay lemma. The first case, while technically the easiest, holds the main ideas in general.
6.2 Case 1:  $A < B$
$A < B$
Note that if ![]() $a + b \neq 2c$ or, more generally, if the leading terms of
$a + b \neq 2c$ or, more generally, if the leading terms of ![]() $xy$ and
$xy$ and ![]() $z^2/(4\epsilon )$ do not cancel, then
$z^2/(4\epsilon )$ do not cancel, then ![]() $A< B$.
$A< B$.
Proof of Proposition 5.1.3 in this case For the ease of exposition, we assume that ![]() $a \leq b \leq c$. Note that this forces
$a \leq b \leq c$. Note that this forces ![]() $2a \leq A$. Even though the statement of Proposition 5.1.3 is not symmetric in
$2a \leq A$. Even though the statement of Proposition 5.1.3 is not symmetric in ![]() $a,b,c$, an identical argument as that below suffices to deal with all the other cases.
$a,b,c$, an identical argument as that below suffices to deal with all the other cases.
We prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly. For a primitive vector
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly. For a primitive vector ![]() $w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$, write
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$, write ![]() $w = \alpha _u w_u + \alpha _l w_3$, where
$w = \alpha _u w_u + \alpha _l w_3$, where ![]() $w_u$ is a primitive vector in
$w_u$ is a primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$, and
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$, and ![]() $\alpha _u,\alpha _l \in \mathbb {Z}_p$. As
$\alpha _u,\alpha _l \in \mathbb {Z}_p$. As ![]() $w$ is primitive, then either
$w$ is primitive, then either ![]() $\alpha _u$ or
$\alpha _u$ or ![]() $\alpha _l$ is a
$\alpha _l$ is a ![]() $p$-adic unit. We may assume that
$p$-adic unit. We may assume that ![]() $\alpha _u$ is a unit: the other case is entirely analogous to this one. Suppose that the
$\alpha _u$ is a unit: the other case is entirely analogous to this one. Suppose that the ![]() $p$-adic valuation of
$p$-adic valuation of ![]() $\alpha _l$ is
$\alpha _l$ is ![]() $m \geq 0$.
$m \geq 0$.
Consider the terms appearing in ![]() $F_{\infty }(1)$ described in Lemma 6.1.2 with denominator
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator ![]() $p^{n+1}$. As
$p^{n+1}$. As ![]() $A < B$, the one with minimal
$A < B$, the one with minimal ![]() $t$-adic valuation is
$t$-adic valuation is ![]() $P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$, and this is the unique term with this property. Similarly, consider the terms appearing in
$P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$, and this is the unique term with this property. Similarly, consider the terms appearing in ![]() $F_{\infty }(2)$ with denominator
$F_{\infty }(2)$ with denominator ![]() $p^{n+1 + m}$. As
$p^{n+1 + m}$. As ![]() $A < B$, the unique term whose first column has minimal
$A < B$, the unique term whose first column has minimal ![]() $t$-adic valuation is
$t$-adic valuation is ![]() $P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$.
$P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$.
Let ![]() $P$ denote the
$P$ denote the ![]() $2 \times 3$ matrix whose first two columns equal
$2 \times 3$ matrix whose first two columns equal ![]() $P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$ (part of
$P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$ (part of ![]() $F_{\infty }(1)$), and whose last column is the first column of
$F_{\infty }(1)$), and whose last column is the first column of ![]() $P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$ (part of
$P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$ (part of ![]() $F_{\infty }(2)$). As
$F_{\infty }(2)$). As ![]() $1\leq a < A$, then for any
$1\leq a < A$, then for any ![]() $m\in \mathbb {Z}_{\geq 0}$, we have
$m\in \mathbb {Z}_{\geq 0}$, we have ![]() $A(1 + \cdots + p^n)\neq A(1 + \cdots + p^{n+m-1}) + ap^{m+n}$. Therefore, regardless of the value of
$A(1 + \cdots + p^n)\neq A(1 + \cdots + p^{n+m-1}) + ap^{m+n}$. Therefore, regardless of the value of ![]() $m$, the
$m$, the ![]() $t$-adic valuation of entries of the first two columns of
$t$-adic valuation of entries of the first two columns of ![]() $P$ are different from the
$P$ are different from the ![]() $t$-adic valuation of the last column of
$t$-adic valuation of the last column of ![]() $P$.
$P$.
To prove that ![]() $w$ decays rapidly, it suffices to prove that among the monomials in
$w$ decays rapidly, it suffices to prove that among the monomials in ![]() $P w$ with
$P w$ with ![]() $p$-adic valuation equalling
$p$-adic valuation equalling ![]() $-(n+1)$, there exists a monomial with
$-(n+1)$, there exists a monomial with ![]() $t$-adic valuation
$t$-adic valuation ![]() $\leq A(1 + \cdots + p^n)$. By the proof of Proposition 5.1.3 in Case 1 in § 5.2, this, in turn, reduces to proving the following statement: if
$\leq A(1 + \cdots + p^n)$. By the proof of Proposition 5.1.3 in Case 1 in § 5.2, this, in turn, reduces to proving the following statement: if ![]() $m \geq 1$, then
$m \geq 1$, then ![]() $w_u \bmod p$ is not in the kernel of
$w_u \bmod p$ is not in the kernel of ![]() $P(1)_{0,n}\bmod p$; and if
$P(1)_{0,n}\bmod p$; and if ![]() $m = 0$, the vector
$m = 0$, the vector ![]() $\big [\begin {smallmatrix} (\lambda ^{-1})^{(n)}\\ 1 \end {smallmatrix}\big ] \bmod p$ is not in the kernel of
$\big [\begin {smallmatrix} (\lambda ^{-1})^{(n)}\\ 1 \end {smallmatrix}\big ] \bmod p$ is not in the kernel of ![]() $P(1)_{0,n-1}\bmod p$. Both statements follow from Lemma 6.1.4, establishing the decay of the rank-
$P(1)_{0,n-1}\bmod p$. Both statements follow from Lemma 6.1.4, establishing the decay of the rank-![]() $3$ submodule
$3$ submodule ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$.
Proposition 5.1.3 in this case follows from the observation that because ![]() $2a\leq A$, then
$2a\leq A$, then ![]() $w_3$ decays very rapidly.
$w_3$ decays very rapidly.
6.3 Case 2:  $A \geq B, a \neq b$
$A \geq B, a \neq b$
Note that if ![]() $A \geq B$, then
$A \geq B$, then ![]() $a + b = 2c$ (as the only way this can happen is if
$a + b = 2c$ (as the only way this can happen is if ![]() $xy$ has the same
$xy$ has the same ![]() $t$-adic valuation as
$t$-adic valuation as ![]() $z^2/(4\epsilon )$). We may, therefore, assume without loss of generality that
$z^2/(4\epsilon )$). We may, therefore, assume without loss of generality that ![]() $a < b$. It follows then that
$a < b$. It follows then that ![]() $a < c < b$. Within this case, we need to consider the following two subcases.
$a < c < b$. Within this case, we need to consider the following two subcases.
Subcase  $(2.1)_e$:
$(2.1)_e$:  $B (1 + p^{2e-1}) < A(1+p) < B(1 + p^{2e + 1})$ for some
$B (1 + p^{2e-1}) < A(1+p) < B(1 + p^{2e + 1})$ for some  $e\in \mathbb {Z}_{\geq 1}$
$e\in \mathbb {Z}_{\geq 1}$
In this subcase, we prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly, where
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly, where ![]() $i\in \{3,4,5 \}$ will be chosen depending on the values of
$i\in \{3,4,5 \}$ will be chosen depending on the values of ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$.
$c$.
The following lemma, in conjunction with Lemma 6.1.4, implies (as in Case 1) that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. It can be proved by the same argument as in the proof of Lemma 5.2.6(1), so we omit its proof.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. It can be proved by the same argument as in the proof of Lemma 5.2.6(1), so we omit its proof.
Lemma 6.3.1 Among the terms appearing in ![]() $F_{\infty }(1)$ described in Lemma 6.1.2 with denominator
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator ![]() $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal ![]() $t$-adic valuation is
$t$-adic valuation is
The ![]() $t$-adic valuation of this term is
$t$-adic valuation of this term is ![]() $A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
The following lemmas will be used to show that one of ![]() $w_3,w_4,w_5$ also decays rapidly. These lemmas imply that among the terms appearing in
$w_3,w_4,w_5$ also decays rapidly. These lemmas imply that among the terms appearing in ![]() $F_{\infty }(2)$ with denominator
$F_{\infty }(2)$ with denominator ![]() $p^{n+1}$, for at least one of the columns of this matrix, there exists a unique term with minimum
$p^{n+1}$, for at least one of the columns of this matrix, there exists a unique term with minimum ![]() $t$-adic valuation.
$t$-adic valuation.
Lemma 6.3.2 Given ![]() $g\in \mathbb {Z}_{\geq 1}, n\in \mathbb {Z}_{\geq 0}$, consider the multiset consisting of numbers of the form
$g\in \mathbb {Z}_{\geq 1}, n\in \mathbb {Z}_{\geq 0}$, consider the multiset consisting of numbers of the form ![]() $A(1 + \cdots + p^{n - f -1}) + B(p^{n - f} + p^{n-f + 2} + \cdots + p^{n+f -2}) + gp^{n+f}$, as
$A(1 + \cdots + p^{n - f -1}) + B(p^{n - f} + p^{n-f + 2} + \cdots + p^{n+f -2}) + gp^{n+f}$, as ![]() $f$ varies over
$f$ varies over ![]() ${\mathbb {Z}\cap [0, n]}$. If the minimal number in this multiset occurs more than once, then it must occur for consecutive values of
${\mathbb {Z}\cap [0, n]}$. If the minimal number in this multiset occurs more than once, then it must occur for consecutive values of ![]() $f$.
$f$.
Proof. For any choice of ![]() $f$, let us denote the expression by
$f$, let us denote the expression by ![]() $v(f)$. It suffices to prove the following statement: for
$v(f)$. It suffices to prove the following statement: for ![]() $f_1 < f_2-1$, if
$f_1 < f_2-1$, if ![]() $v(f_1) = v(f_2)$, then
$v(f_1) = v(f_2)$, then ![]() $v(f_2) > v(f_2 -1)$. To that end, suppose that
$v(f_2) > v(f_2 -1)$. To that end, suppose that ![]() $v(f_1) = v(f_2)$. Then
$v(f_1) = v(f_2)$. Then ![]() $A(1 + p + \cdots + p^{f_2-f_1-1}) = B(p^{f_2-f_1}-1)(p^{f_2 + f_1} +1)/(p^2-1)+gp^{f_2}(p^{f_2}-p^{f_1})$.
$A(1 + p + \cdots + p^{f_2-f_1-1}) = B(p^{f_2-f_1}-1)(p^{f_2 + f_1} +1)/(p^2-1)+gp^{f_2}(p^{f_2}-p^{f_1})$.
To prove ![]() $v(f_2)>v(f_2-1)$, note that
$v(f_2)>v(f_2-1)$, note that ![]() $p^{-(n-f_2)}(v(f_2) - v(f_2-1)) = B(p^{2f_2-1}+1)/(p+1) + gp^{2f_2-1}(p-1) - A$. Multiplying this by
$p^{-(n-f_2)}(v(f_2) - v(f_2-1)) = B(p^{2f_2-1}+1)/(p+1) + gp^{2f_2-1}(p-1) - A$. Multiplying this by ![]() $(1 + p + \cdots + p^{f_2-f_1})$ and applying the relation of
$(1 + p + \cdots + p^{f_2-f_1})$ and applying the relation of ![]() $A$ and
$A$ and ![]() $B$ above, we have
$B$ above, we have
 \begin{align*} \frac{1 + p + \cdots + p^{f_2-f_1-1}}{p^{n-f_2}}(v(f_2) - v(f_2-1))&=\frac{B(p^{f_2-f_1} - 1)(p^{2f_2 -1} - p^{f_1 + f_2})}{p^2-1}\\ &\quad + g(p^{f_2 -f_1} -1)(p^{2f_2 -1} - p^{f_1 + f_2}), \end{align*}
\begin{align*} \frac{1 + p + \cdots + p^{f_2-f_1-1}}{p^{n-f_2}}(v(f_2) - v(f_2-1))&=\frac{B(p^{f_2-f_1} - 1)(p^{2f_2 -1} - p^{f_1 + f_2})}{p^2-1}\\ &\quad + g(p^{f_2 -f_1} -1)(p^{2f_2 -1} - p^{f_1 + f_2}), \end{align*}
which is positive because ![]() $f_2 > f_1+1$. The lemma follows.
$f_2 > f_1+1$. The lemma follows.
Lemma 6.3.3 There are at most two numbers ![]() $g$ in the set
$g$ in the set ![]() $\{a,b,c\}$ such that there exists an integer
$\{a,b,c\}$ such that there exists an integer ![]() $f$ (
$f$ (![]() $f$ is allowed to depend on the choice of
$f$ is allowed to depend on the choice of ![]() $g$) with
$g$) with ![]() $A(1 + \cdots + p^{n-f-1}) + B(p^{n-f} + p^{n-f + 2} + \cdots + p^{n + f-2}) + gp^{n + f}$
$A(1 + \cdots + p^{n-f-1}) + B(p^{n-f} + p^{n-f + 2} + \cdots + p^{n + f-2}) + gp^{n + f}$ ![]() $= A(1 + \cdots + p^{n-f}) + B(p^{n-f + 1} + p^{n-f + 1} + \cdots + p^{n + f-3}) + gp^{n + f-1}$.Footnote 31
$= A(1 + \cdots + p^{n-f}) + B(p^{n-f + 1} + p^{n-f + 1} + \cdots + p^{n + f-3}) + gp^{n + f-1}$.Footnote 31
Proof. Suppose there existed choices of ![]() $f\in \mathbb {Z}_{\geq 0}$ for all three choices of
$f\in \mathbb {Z}_{\geq 0}$ for all three choices of ![]() $g$. Let
$g$. Let ![]() $f_1,f_2,f_3$ be the choices for
$f_1,f_2,f_3$ be the choices for ![]() $f$. Then, by the proof of Lemma 6.3.2, we have that
$f$. Then, by the proof of Lemma 6.3.2, we have that ![]() $ap^{2f_1-1}(p-1) = A - B(1 + p^{2f_1 -1})/(1+p)$, and similarly
$ap^{2f_1-1}(p-1) = A - B(1 + p^{2f_1 -1})/(1+p)$, and similarly ![]() $bp^{2f_2-1}(p-1) = A-B(1 + p^{2f_2-1})/(1 + p),$
$bp^{2f_2-1}(p-1) = A-B(1 + p^{2f_2-1})/(1 + p),$ ![]() $cp^{2f_3-1}(p-1) = A-B(1 + p^{2f_3-1})/(1 + p)$. Substituting these expressions in the equality
$cp^{2f_3-1}(p-1) = A-B(1 + p^{2f_3-1})/(1 + p)$. Substituting these expressions in the equality ![]() $a + b = 2c$ yields the equation
$a + b = 2c$ yields the equation
As ![]() $A\geq B\geq p+1$, we have
$A\geq B\geq p+1$, we have ![]() $A\neq B/(p+1)$ and hence
$A\neq B/(p+1)$ and hence ![]() $p^{1-2f_1}+p^{1-2f_2}-2p^{1-2f_3}=0$. As
$p^{1-2f_1}+p^{1-2f_2}-2p^{1-2f_3}=0$. As ![]() $f_1,f_2,f_3\in \mathbb {Z}_{\geq 1}$, we must have
$f_1,f_2,f_3\in \mathbb {Z}_{\geq 1}$, we must have ![]() $f_1=f_2=f_3$ and, hence,
$f_1=f_2=f_3$ and, hence, ![]() $a=b=c$, which is a contradiction.
$a=b=c$, which is a contradiction.
Proof of Proposition 5.1.3 in this case Let ![]() $h \in \{a,b,c\}$ be such that there is no
$h \in \{a,b,c\}$ be such that there is no ![]() $f$ which satisfies the hypothesis of Lemma 6.3.3 (indeed, the lemma guarantees the existence of such an
$f$ which satisfies the hypothesis of Lemma 6.3.3 (indeed, the lemma guarantees the existence of such an ![]() $h$).
$h$).
We first show the existence of a rank-![]() $3$ submodule which decays rapidly. Without loss of generality, we may assume that
$3$ submodule which decays rapidly. Without loss of generality, we may assume that ![]() $h =a$ and we prove that
$h =a$ and we prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly (if
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly (if ![]() $h = b$ or
$h = b$ or ![]() $c$, the identical proof will show sufficient decay, with
$c$, the identical proof will show sufficient decay, with ![]() $w_4$ or
$w_4$ or ![]() $w_5$ taking the place of
$w_5$ taking the place of ![]() $w_3$).
$w_3$).
As in Case 1, Lemmas 6.3.1 and 6.1.4–6.3.3 imply that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3\}$ both decay rapidly. Therefore, it suffices to show that
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3\}$ both decay rapidly. Therefore, it suffices to show that ![]() $\alpha _u w_u + \alpha _3 w_3$ decays rapidly, where
$\alpha _u w_u + \alpha _3 w_3$ decays rapidly, where ![]() $w_u$ is a primitive vector in the span of
$w_u$ is a primitive vector in the span of ![]() $w_1,w_2$, and either
$w_1,w_2$, and either ![]() $\alpha _u$ or
$\alpha _u$ or ![]() $\alpha _3$ in
$\alpha _3$ in ![]() $\mathbb {Z}_p$ is a
$\mathbb {Z}_p$ is a ![]() $p$-adic unit.
$p$-adic unit.
By Lemma 6.3.1, the ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{n+1}$ of
$1/p^{n+1}$ of ![]() $F_{\infty } w_u$ is
$F_{\infty } w_u$ is ![]() $d(n) = A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1}+ p^{n-e+3} + \cdots + p^{n+e-1})$. Similarly, the
$d(n) = A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1}+ p^{n-e+3} + \cdots + p^{n+e-1})$. Similarly, the ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{m+1}$ of
$1/p^{m+1}$ of ![]() $F_{\infty } \cdot w_3$ is
$F_{\infty } \cdot w_3$ is ![]() $c(m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2}) + ap^{m + f}$ for some
$c(m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2}) + ap^{m + f}$ for some ![]() $f\in \mathbb {Z}\cap [0,n]$. As in Case 1, it suffices to prove that
$f\in \mathbb {Z}\cap [0,n]$. As in Case 1, it suffices to prove that ![]() $d(n)$ is never equal to
$d(n)$ is never equal to ![]() $c(m)$, regardless of the values of
$c(m)$, regardless of the values of ![]() $n$ and
$n$ and ![]() $m$.
$m$.
Let ![]() $c(f',m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f' }+ p^{m-f'+2} + \cdots + p^{m+f'-2}) + ap^{m + f'}$, for any value of
$c(f',m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f' }+ p^{m-f'+2} + \cdots + p^{m+f'-2}) + ap^{m + f'}$, for any value of ![]() $f' \leq m$. By the definition of
$f' \leq m$. By the definition of ![]() $f$,
$f$, ![]() $c(m) = c(f,m)$, and
$c(m) = c(f,m)$, and ![]() $f' = f$ minimizes the value of
$f' = f$ minimizes the value of ![]() $c(f',m)$.
$c(f',m)$.
If ![]() $n \geq m$, because
$n \geq m$, because ![]() $a< A$, then
$a< A$, then ![]() $d(n) > c(e,m) \geq c(f,m) = c(m)$, as required. On the other hand, if
$d(n) > c(e,m) \geq c(f,m) = c(m)$, as required. On the other hand, if ![]() $m > n$, we have
$m > n$, we have ![]() $c(m) > A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2})\geq d(n)$, where the last inequality follows from Lemma 6.3.1.
$c(m) > A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2})\geq d(n)$, where the last inequality follows from Lemma 6.3.1.
Finally, we treat the question of very rapid decay. If we may take ![]() $h = a$ or
$h = a$ or ![]() $h = c$, the very rapid decay of
$h = c$, the very rapid decay of ![]() $w_3$ or
$w_3$ or ![]() $w_5$ is established by the inequality
$w_5$ is established by the inequality ![]() $2 a < 2c \leq A$. Otherwise,
$2 a < 2c \leq A$. Otherwise, ![]() $h$ must be
$h$ must be ![]() $b$ and for both
$b$ and for both ![]() $a,c$, there exist
$a,c$, there exist ![]() $f_1,f_3$ satisfying the equation in Lemma 6.3.3. As
$f_1,f_3$ satisfying the equation in Lemma 6.3.3. As ![]() $a\neq c$, then
$a\neq c$, then ![]() $f_1\neq f_3$ and at least one
$f_1\neq f_3$ and at least one ![]() $f_i\geq 2$. By the proof of Lemma 6.3.3, we have
$f_i\geq 2$. By the proof of Lemma 6.3.3, we have ![]() $A-B(1+p^{2f_i-1})/(p+1)>0$ and, hence,
$A-B(1+p^{2f_i-1})/(p+1)>0$ and, hence, ![]() $A\geq 7B >2b$. Thus,
$A\geq 7B >2b$. Thus, ![]() $w_4$ decays very rapidly.
$w_4$ decays very rapidly.
Subcase  $(2.2)_e$:
$(2.2)_e$:  $A(1+p) = B(1 + p^{2e - 1})$ for some
$A(1+p) = B(1 + p^{2e - 1})$ for some  $e\in \mathbb {Z}_{\geq 1}$
$e\in \mathbb {Z}_{\geq 1}$
In this subcase, we prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly. We first need the following lemma.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly. We first need the following lemma.
Lemma 6.3.4 Among the terms appearing in ![]() $F_{\infty }(2)$ described in Lemma 6.1.2 with denominator
$F_{\infty }(2)$ described in Lemma 6.1.2 with denominator ![]() $p^{n+1}$, the unique term with minimal
$p^{n+1}$, the unique term with minimal ![]() $t$-adic valuation is
$t$-adic valuation is
The ![]() $t$-adic valuation of the
$t$-adic valuation of the ![]() $i$th column term is
$i$th column term is ![]() $A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-3}) + gp^{n+e-1},$ where
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-3}) + gp^{n+e-1},$ where ![]() $g$ is
$g$ is ![]() $a$,
$a$, ![]() $b$, or
$b$, or ![]() $c$ depending on whether
$c$ depending on whether ![]() $i$ is
$i$ is ![]() $1$,
$1$, ![]() $2$, or
$2$, or ![]() $3$.
$3$.
Proof. It suffices to prove that choice of ![]() $f = e$ minimizes the expression
$f = e$ minimizes the expression ![]() $A(1 + p + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n+f-3}) + gp^{n+f-1}$, where
$A(1 + p + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n+f-3}) + gp^{n+f-1}$, where ![]() $f$ is allowed to range between
$f$ is allowed to range between ![]() $0$ and
$0$ and ![]() $n$. This can be verified by direct calculation.
$n$. This can be verified by direct calculation.
Proof of Proposition 5.1.3 in this case It follows from Lemmas 6.3.4 and 6.1.4 that ![]() $w_3$,
$w_3$, ![]() $w_4$, and
$w_4$, and ![]() $w_5$ individually decay rapidly, and that
$w_5$ individually decay rapidly, and that ![]() $w_3$ decays very rapidly. In order to show that
$w_3$ decays very rapidly. In order to show that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly, it suffices to show that the
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly, it suffices to show that the ![]() $t$-adic valuations of the coefficients
$t$-adic valuations of the coefficients ![]() $1/p^{l+1},1/p^{m+1}, 1/p^{n+1}$ of
$1/p^{l+1},1/p^{m+1}, 1/p^{n+1}$ of ![]() $F_{\infty }(w_3),F_{\infty }(w_4),F_{\infty }(w_5)$ are always distinct, regardless of the values of
$F_{\infty }(w_3),F_{\infty }(w_4),F_{\infty }(w_5)$ are always distinct, regardless of the values of ![]() $l,m,n$. By Lemma 6.3.4, these quantities equal
$l,m,n$. By Lemma 6.3.4, these quantities equal ![]() $A(1 + p + \cdots + p^{l-e}) + B(p^{l-e+1} + p^{l-e + 3} + \cdots + p^{l+e-3}) + ap^{l+e-1}$,
$A(1 + p + \cdots + p^{l-e}) + B(p^{l-e+1} + p^{l-e + 3} + \cdots + p^{l+e-3}) + ap^{l+e-1}$, ![]() $A(1 + p + \cdots + p^{m-e}) + B(p^{m-e+1} + p^{m-e + 3} + \cdots + p^{m+e-3}) + bp^{m+e-1}$ and
$A(1 + p + \cdots + p^{m-e}) + B(p^{m-e+1} + p^{m-e + 3} + \cdots + p^{m+e-3}) + bp^{m+e-1}$ and ![]() $A(1 + p + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n+e-3}) + cp^{n+e-1}$.
$A(1 + p + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n+e-3}) + cp^{n+e-1}$.
As ![]() $a,b,c$ are all strictly less than
$a,b,c$ are all strictly less than ![]() $B$, these quantities will all be different unless two of
$B$, these quantities will all be different unless two of ![]() $l,m,n$ are equal. In this case, the quantities still differ, because
$l,m,n$ are equal. In this case, the quantities still differ, because ![]() $a,b,c$ are all distinct integers by assumption. Therefore,
$a,b,c$ are all distinct integers by assumption. Therefore, ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly.
6.4 Case 3:  $A \geq B$ and
$A \geq B$ and  $a = b$
$a = b$
In this case, ![]() $a = b = c$. We may assume that
$a = b = c$. We may assume that ![]() $x(t) = t^a$,
$x(t) = t^a$, ![]() $y(t) = \beta t^a + \sum _{i=a+1}^\infty \beta _i t^i$, and
$y(t) = \beta t^a + \sum _{i=a+1}^\infty \beta _i t^i$, and ![]() $z(t) = \gamma t^a + \sum _{i=a+1}^\infty \gamma _i t^i$. As
$z(t) = \gamma t^a + \sum _{i=a+1}^\infty \gamma _i t^i$. As ![]() $A\geq B$, we have
$A\geq B$, we have ![]() $\beta + \gamma ^2 /(4\epsilon ) =0$. We break the proof of the decay lemma into two subcases and the following lemma is used in both cases.
$\beta + \gamma ^2 /(4\epsilon ) =0$. We break the proof of the decay lemma into two subcases and the following lemma is used in both cases.
Lemma 6.4.1 Suppose that ![]() $\gamma \in \mathbb {F}_p$. Let
$\gamma \in \mathbb {F}_p$. Let ![]() $a' > a$ denote the smallest integer such that either
$a' > a$ denote the smallest integer such that either ![]() $\beta _{a'}\neq 0$ or
$\beta _{a'}\neq 0$ or ![]() $\gamma _{a'}\neq 0$. Then both
$\gamma _{a'}\neq 0$. Then both ![]() $\beta _{a'}$ and
$\beta _{a'}$ and ![]() $\gamma _{a'}$ are non-zero and, moreover,
$\gamma _{a'}$ are non-zero and, moreover, ![]() $B \geq (p-1)a + 2 a'$.
$B \geq (p-1)a + 2 a'$.
Proof. As ![]() $\gamma \in \mathbb {F}_p$ and
$\gamma \in \mathbb {F}_p$ and ![]() $\beta +\gamma ^2/(4\epsilon )=0$, then
$\beta +\gamma ^2/(4\epsilon )=0$, then ![]() $\beta \in \mathbb {F}_p$. Therefore, in
$\beta \in \mathbb {F}_p$. Therefore, in ![]() $k[[t]]$,
$k[[t]]$,
 \begin{align*} xy + z^2/(4\epsilon) &= \sum_{i \geq a'} (\beta_i + \gamma \gamma_i/(2\epsilon))t^{i+a} + (4\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j t^{i+j},\\ xy^p + x^p y + z^{1+p}/(2\epsilon)& = \sum_{i \geq a'}(\beta_i + \gamma \gamma_i/(2\epsilon))t^{i + pa}\\ &\quad + \sum_{i\geq a'}(\beta_i^p + \gamma \gamma_i^p/(2\epsilon)) t^{pi + a} + (2\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j^p t^{i + jp}. \end{align*}
\begin{align*} xy + z^2/(4\epsilon) &= \sum_{i \geq a'} (\beta_i + \gamma \gamma_i/(2\epsilon))t^{i+a} + (4\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j t^{i+j},\\ xy^p + x^p y + z^{1+p}/(2\epsilon)& = \sum_{i \geq a'}(\beta_i + \gamma \gamma_i/(2\epsilon))t^{i + pa}\\ &\quad + \sum_{i\geq a'}(\beta_i^p + \gamma \gamma_i^p/(2\epsilon)) t^{pi + a} + (2\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j^p t^{i + jp}. \end{align*} If one of ![]() $\beta _{a'}$ and
$\beta _{a'}$ and ![]() $\gamma _{a'}$ were zero, then
$\gamma _{a'}$ were zero, then ![]() $A = a' + a$, whereas
$A = a' + a$, whereas ![]() $B\geq a'+pa$; this contradicts with the assumption that
$B\geq a'+pa$; this contradicts with the assumption that ![]() $A\geq B$. Hence, we obtain the first assertion of the lemma.
$A\geq B$. Hence, we obtain the first assertion of the lemma.
Let ![]() $a'' \geq a'$ denote the smallest integer such that
$a'' \geq a'$ denote the smallest integer such that ![]() $\beta _i + \gamma \gamma _i/(2\epsilon ) \neq 0$. Then by applying the Frobenius action, we have
$\beta _i + \gamma \gamma _i/(2\epsilon ) \neq 0$. Then by applying the Frobenius action, we have ![]() $\beta _{a''}^p+\gamma \gamma _{a''}^p/(2\epsilon )\neq 0$ and
$\beta _{a''}^p+\gamma \gamma _{a''}^p/(2\epsilon )\neq 0$ and ![]() $B \geq \min \{(p+1)a',a'' + pa \}$. If
$B \geq \min \{(p+1)a',a'' + pa \}$. If ![]() $B \geq (p+1)a'$, then the second assertion of the lemma follows.
$B \geq (p+1)a'$, then the second assertion of the lemma follows.
Therefore, we assume that ![]() $B = a'' + pa < (p+1)a'$. The expansion of
$B = a'' + pa < (p+1)a'$. The expansion of ![]() $xy + z^2/(4\epsilon )$ above has a non-zero term of the form
$xy + z^2/(4\epsilon )$ above has a non-zero term of the form ![]() $(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$. As
$(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$. As ![]() $A\geq B$, the term
$A\geq B$, the term ![]() $(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$ has to be cancelled out by a term of the form
$(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$ has to be cancelled out by a term of the form ![]() $(4\epsilon )^{-1}\sum _{i + j = a + a'',\, i,j \geq a'}\gamma _i\gamma _j t^{i+j}$. Therefore, it follows that
$(4\epsilon )^{-1}\sum _{i + j = a + a'',\, i,j \geq a'}\gamma _i\gamma _j t^{i+j}$. Therefore, it follows that ![]() $2a' \leq a + a''$ and, hence,
$2a' \leq a + a''$ and, hence, ![]() $B = a'' + pa\geq (p-1)a+2a'$.
$B = a'' + pa\geq (p-1)a+2a'$.
Case  $(3.1)_e$:
$(3.1)_e$:  $B(1 + p^{2e-1}) < (p+1)A < B(1 + p^{2e + 1})$ for some
$B(1 + p^{2e-1}) < (p+1)A < B(1 + p^{2e + 1})$ for some  $e\in \mathbb {Z}_{\geq 1}$
$e\in \mathbb {Z}_{\geq 1}$
The same argument as in Case 2.1 suffices to prove Proposition 5.1.3, unless ![]() $A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$. Therefore, we assume that this is the case.
$A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$. Therefore, we assume that this is the case.
Lemma 6.4.2 Among the terms appearing in ![]() $F_{\infty }(2)$ described in Lemma 6.1.2 with denominator
$F_{\infty }(2)$ described in Lemma 6.1.2 with denominator ![]() $p^{n+1}$, there are exactly two with minimal
$p^{n+1}$, there are exactly two with minimal ![]() $t$-adic valuation. They are
$t$-adic valuation. They are
 \begin{align*} &P(1)_{e-1,n-1}F_u^{(n+e-1)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e + 1} + p^{n - e + 3 } + \cdots + p^{n + e -3}},\\ &P(1)_{e,n-1}F_u^{(n+e)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e -1})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e } + p^{n - e + 2 } + \cdots + p^{n + e -2}}. \end{align*}
\begin{align*} &P(1)_{e-1,n-1}F_u^{(n+e-1)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e + 1} + p^{n - e + 3 } + \cdots + p^{n + e -3}},\\ &P(1)_{e,n-1}F_u^{(n+e)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e -1})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e } + p^{n - e + 2 } + \cdots + p^{n + e -2}}. \end{align*}
Both the terms have ![]() $t$-adic valuation
$t$-adic valuation ![]() $A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1} + p^{n - e + 3} + \cdots + p^{n + e -3}) + ap^{n + e -1}$.
$A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1} + p^{n - e + 3} + \cdots + p^{n + e -3}) + ap^{n + e -1}$.
Proof. This lemma follows from a similar argument as Lemma 5.2.6(2) and the proofs of Lemmas 6.3.2 and 6.3.3, so we omit the details.
Proof of Proposition 5.1.3 in this case We show that either ![]() $w_3$ or
$w_3$ or ![]() $w_5$ decays very rapidly. There are two terms with minimal
$w_5$ decays very rapidly. There are two terms with minimal ![]() $t$-adic valuation as in Lemma 6.4.2, appearing in the coefficient of
$t$-adic valuation as in Lemma 6.4.2, appearing in the coefficient of ![]() $1/p^{n+1}$ of
$1/p^{n+1}$ of ![]() $F_{\infty }(w_3)$ and
$F_{\infty }(w_3)$ and ![]() $F_{\infty }(w_5)$. A direct computation yields that the sum of these two terms equals by
$F_{\infty }(w_5)$. A direct computation yields that the sum of these two terms equals by
where
(i)
 $u(t)$ denotes either
$u(t)$ denotes either  $x(t)$ or
$x(t)$ or  $z(t)$, according to whether we work with
$z(t)$, according to whether we work with  $w_3$ or
$w_3$ or  $w_5$;
$w_5$;(ii)
 $X(t) = pF_u\cdot F_l^{(1)}\cdot pF_u^{(2)} \cdots F_l^{(2e-1)} \cdot [(\lambda ^{-1})^{(2e)},1]^{\textrm {T}}$; and
$X(t) = pF_u\cdot F_l^{(1)}\cdot pF_u^{(2)} \cdots F_l^{(2e-1)} \cdot [(\lambda ^{-1})^{(2e)},1]^{\textrm {T}}$; and(iii)
 $Y(t) = pF_t \cdot pF_u^{(1)} \cdot F_l^{(2)} \cdots pF_u^{(2e-3)} \cdot F_l^{(2e -2)} \cdot [(\lambda ^{-1})^{(2e-1)},1]^{\textrm {T}}$; the superscript T denotes transpose.
$Y(t) = pF_t \cdot pF_u^{(1)} \cdot F_l^{(2)} \cdots pF_u^{(2e-3)} \cdot F_l^{(2e -2)} \cdot [(\lambda ^{-1})^{(2e-1)},1]^{\textrm {T}}$; the superscript T denotes transpose.
The decay of ![]() $w_3$ and
$w_3$ and ![]() $w_5$ is determined by the
$w_5$ is determined by the ![]() $t$-adic valuation of the entries of
$t$-adic valuation of the entries of ![]() $X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. For the rest of the proof, it suffices to focus on the second row of
$X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. For the rest of the proof, it suffices to focus on the second row of ![]() $X(t), Y(t)$ and, hence, we view them as functions. We prove the very rapid decay of
$X(t), Y(t)$ and, hence, we view them as functions. We prove the very rapid decay of ![]() $w_3$ or
$w_3$ or ![]() $w_5$ in two cases. (1) Both
$w_5$ in two cases. (1) Both ![]() $\beta,\gamma \in \mathbb {F}_p$. In this case, we claim that the
$\beta,\gamma \in \mathbb {F}_p$. In this case, we claim that the ![]() $t$-adic valuation of
$t$-adic valuation of ![]() $X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$ is at most
$X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$ is at most ![]() $A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$ for at least one choice of
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$ for at least one choice of ![]() $u(t)$ between
$u(t)$ between ![]() $x(t)$ and
$x(t)$ and ![]() $z(t)$, where
$z(t)$, where ![]() $a'$ is defined in Lemma 6.4.1. This claim implies that the
$a'$ is defined in Lemma 6.4.1. This claim implies that the ![]() $t$-adic valuation of the coefficient of
$t$-adic valuation of the coefficient of ![]() $1/p^{n+1}$ of
$1/p^{n+1}$ of ![]() $F_{\infty }(w_3)$ or
$F_{\infty }(w_3)$ or ![]() $F_{\infty }(w_5)$ is at most
$F_{\infty }(w_5)$ is at most ![]() $A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n + e -3}) + a'p^{n+e-1}$. This is sufficient to prove the rapid decay of
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n + e -3}) + a'p^{n+e-1}$. This is sufficient to prove the rapid decay of ![]() $w_3$ or
$w_3$ or ![]() $w_5$. Indeed, this quantity is strictly less than
$w_5$. Indeed, this quantity is strictly less than ![]() $A(1 + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n + f -3}) + ap^{n+f-1}$ for all values of
$A(1 + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n + f -3}) + ap^{n+f-1}$ for all values of ![]() $f \neq e,e+1$ by Lemma 6.4.1 and, hence, the sum of the two terms in Lemma 6.4.2 gives the minimal
$f \neq e,e+1$ by Lemma 6.4.1 and, hence, the sum of the two terms in Lemma 6.4.2 gives the minimal ![]() $t$-adic valuation term of the coefficient of
$t$-adic valuation term of the coefficient of ![]() $1/p^{n+1}$ in
$1/p^{n+1}$ in ![]() $F_{\infty }(w_3)$ or
$F_{\infty }(w_3)$ or ![]() $F_{\infty }(w_5)$. Moreover, the bounds on
$F_{\infty }(w_5)$. Moreover, the bounds on ![]() $a'$ in Lemma 6.4.1 proves that
$a'$ in Lemma 6.4.1 proves that ![]() $w_3$ or
$w_3$ or ![]() $w_5$ decays very rapidly.
$w_5$ decays very rapidly.
We now prove the claim by contradiction. Suppose that ![]() $X(t)x(t)^{p^{2e}} + Y(t)x(t)^{p^{2e-1}}$ has
$X(t)x(t)^{p^{2e}} + Y(t)x(t)^{p^{2e-1}}$ has ![]() $t$-adic valuation greater than
$t$-adic valuation greater than ![]() $A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$. As
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$. As ![]() $z(t) = \gamma x(t) + \gamma _{a'}t^{a'} + \cdots$ with
$z(t) = \gamma x(t) + \gamma _{a'}t^{a'} + \cdots$ with ![]() $\gamma \in \mathbb {F}_p$,
$\gamma \in \mathbb {F}_p$, ![]() $\gamma _{a'}\neq 0$ and we have assumed that
$\gamma _{a'}\neq 0$ and we have assumed that ![]() $A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$, it follows that there is a unique monomial in
$A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$, it follows that there is a unique monomial in ![]() $X(t)z(t)^{p^{2e}} + Y(t)z(t)^{p^{2e-1}}$ with
$X(t)z(t)^{p^{2e}} + Y(t)z(t)^{p^{2e-1}}$ with ![]() $t$-adic valuation
$t$-adic valuation ![]() $A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$, thereby establishing the claim for
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$, thereby establishing the claim for ![]() $u(t)=z(t)$. (2) Either
$u(t)=z(t)$. (2) Either ![]() $\beta$ or
$\beta$ or ![]() $\gamma$ is not in
$\gamma$ is not in ![]() $\mathbb {F}_p$. In this case, as
$\mathbb {F}_p$. In this case, as ![]() $\beta + \gamma ^2/(4\epsilon ) = 0$, we may assume that
$\beta + \gamma ^2/(4\epsilon ) = 0$, we may assume that ![]() $\gamma \notin \mathbb {F}_p$. We again consider the function
$\gamma \notin \mathbb {F}_p$. We again consider the function ![]() $X(t)u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. Suppose that the leading coefficient of
$X(t)u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. Suppose that the leading coefficient of ![]() $X(t)$ is
$X(t)$ is ![]() $\mu _X$ and that of
$\mu _X$ and that of ![]() $Y(t)$ is
$Y(t)$ is ![]() $\mu _Y$. Then, the terms of minimal equal
$\mu _Y$. Then, the terms of minimal equal ![]() $t$-adic valuations cancel out in the case when
$t$-adic valuations cancel out in the case when ![]() $u(t) = x(t)$ only if
$u(t) = x(t)$ only if ![]() $\mu _X + \mu _Y = 0$, otherwise, by the same idea as in part (1),
$\mu _X + \mu _Y = 0$, otherwise, by the same idea as in part (1), ![]() $w_3$ decays very rapidly. Therefore, we may assume that
$w_3$ decays very rapidly. Therefore, we may assume that ![]() $\mu _X + \mu _Y = 0$. However, in this case, if we pick
$\mu _X + \mu _Y = 0$. However, in this case, if we pick ![]() $u(t) = z(t)$, then the terms with minimal equal
$u(t) = z(t)$, then the terms with minimal equal ![]() $t$-adic valuations cancel out only if
$t$-adic valuations cancel out only if ![]() $\mu _X \gamma ^{p^{2e}} + \mu _Y \gamma ^{p^{2e-1}} = 0$, which is not possible as
$\mu _X \gamma ^{p^{2e}} + \mu _Y \gamma ^{p^{2e-1}} = 0$, which is not possible as ![]() $\gamma ^{p^{2e}} \neq \gamma ^{p^{2e-1}}$. In other words, we show that in this case,
$\gamma ^{p^{2e}} \neq \gamma ^{p^{2e-1}}$. In other words, we show that in this case, ![]() $w_5$ decays very rapidly.
$w_5$ decays very rapidly.
As in Case 2.1, ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly, and also every vector that can be written as
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly, and also every vector that can be written as ![]() $\alpha _u w_u + \alpha _iw_i$ with
$\alpha _u w_u + \alpha _iw_i$ with ![]() $\alpha _i\in \mathbb {Z}_p^\times$ (
$\alpha _i\in \mathbb {Z}_p^\times$ (![]() $i = 3,5$ depending on whether
$i = 3,5$ depending on whether ![]() $w_3$ or
$w_3$ or ![]() $w_5$ decays) decays very rapidly. The latter statement follows by the same valuation-theoretic argument as in the proof of Case 2.1, which also proves that
$w_5$ decays) decays very rapidly. The latter statement follows by the same valuation-theoretic argument as in the proof of Case 2.1, which also proves that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly.
Case  $(3.2)_e: A(1+p)=B(1+p^{2e-1})$ for some
$(3.2)_e: A(1+p)=B(1+p^{2e-1})$ for some  $e\in \mathbb {Z}_{\geq 1}$
$e\in \mathbb {Z}_{\geq 1}$
Lemma 6.4.3 Among the terms appearing in ![]() $F_{\infty }(1)$ described in Lemma 6.1.2 with denominator
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator ![]() $p^{n+1}$, there are exactly two with minimal
$p^{n+1}$, there are exactly two with minimal ![]() $t$-adic valuation. They are
$t$-adic valuation. They are
 \begin{align*} & P(1)_{e,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+1} + p^{n-e+3} + \cdots +p^{n+e-1}},\\ & P(1)_{e-1,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e+1}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+2} + p^{n-e+4} + \cdots +p^{n+e-2}}. \end{align*}
\begin{align*} & P(1)_{e,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+1} + p^{n-e+3} + \cdots +p^{n+e-1}},\\ & P(1)_{e-1,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e+1}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+2} + p^{n-e+4} + \cdots +p^{n+e-2}}. \end{align*}
Both these terms have ![]() $t$-adic valuation
$t$-adic valuation ![]() $A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
As we have seen many lemmas of this flavor, we omit the proof.
This lemma shows that there are two terms with the same ![]() $t$-adic valuation, which could, therefore, lead to cancellation, and such phenomenon prevents us from proving that
$t$-adic valuation, which could, therefore, lead to cancellation, and such phenomenon prevents us from proving that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Nevertheless, the following lemma shows that there is at least a saturated rank-1 submodule of
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Nevertheless, the following lemma shows that there is at least a saturated rank-1 submodule of ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
Lemma 6.4.4 There is a vector ![]() $w_0$ in
$w_0$ in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
Proof. By Lemma 6.4.3 and the proof of Lemma 6.1.4, the coefficient (viewed as a power series in ![]() $t$) of the sum of the two terms with minimal
$t$) of the sum of the two terms with minimal ![]() $t$-adic valuation among the terms with denominator
$t$-adic valuation among the terms with denominator ![]() $p^{n+1}$ is of the form
$p^{n+1}$ is of the form ![]() $\mu _1 M_1 + \mu _2 M_2$, for some
$\mu _1 M_1 + \mu _2 M_2$, for some ![]() $p$-adic units
$p$-adic units ![]() $\mu _i$, where
$\mu _i$, where ![]() $\{M_1,M_2\}=\big \{\big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ], \big [\begin {smallmatrix}1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]\big \}$.
$\{M_1,M_2\}=\big \{\big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ], \big [\begin {smallmatrix}1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]\big \}$.
As ![]() $M_1 \bmod p$ and
$M_1 \bmod p$ and ![]() $M_2 \bmod p$ are not scalar multiples of each other, the linear combination
$M_2 \bmod p$ are not scalar multiples of each other, the linear combination ![]() $\mu _1 M_1 + \mu _2 M_2 \bmod p$ is non-zero. Therefore, there exists a vector
$\mu _1 M_1 + \mu _2 M_2 \bmod p$ is non-zero. Therefore, there exists a vector ![]() $\bar {w}_0$ defined over
$\bar {w}_0$ defined over ![]() $\mathbb {F}_p$ which does not lie in
$\mathbb {F}_p$ which does not lie in ![]() $\ker (\mu _1 M_1 + \mu _2 M_2 \bmod p)$. Choosing
$\ker (\mu _1 M_1 + \mu _2 M_2 \bmod p)$. Choosing ![]() $w_0\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which lifts
$w_0\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which lifts ![]() $\bar {w}_0$ finishes the proof of this lemma.
$\bar {w}_0$ finishes the proof of this lemma.
We are now ready to prove the last remaining case of Proposition 5.1.3 (and also the decay lemma Theorem 5.1.2).
Proof of Proposition 5.1.3 We first prove that there is a rank-![]() $2$ submodule of
$2$ submodule of ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ which decays rapidly. For ease of notation, let
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ which decays rapidly. For ease of notation, let ![]() $\bar {F_u}$ denote the matrix
$\bar {F_u}$ denote the matrix ![]() $({1}/{t^a})F_u$ evaluated at
$({1}/{t^a})F_u$ evaluated at ![]() $t=0$.
$t=0$.
Let ![]() $K$ denote
$K$ denote ![]() $\ker (P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p)\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4,w_5\}$. If
$\ker (P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p)\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4,w_5\}$. If ![]() $\dim _{\mathbb {F}_p}K\leq 1$, then lifting two linearly independent
$\dim _{\mathbb {F}_p}K\leq 1$, then lifting two linearly independent ![]() $\mathbb {F}_p$-vectors
$\mathbb {F}_p$-vectors ![]() $\notin K$ gives the desired rank
$\notin K$ gives the desired rank ![]() $2$ submodule. Therefore, we assume that
$2$ submodule. Therefore, we assume that ![]() $\dim _{\mathbb {F}_p}K=2$ (note that because
$\dim _{\mathbb {F}_p}K=2$ (note that because ![]() $P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p$ is not the zero matrix, so
$P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p$ is not the zero matrix, so ![]() $\dim _{\mathbb {F}_p}K\neq 3$). It follows that
$\dim _{\mathbb {F}_p}K\neq 3$). It follows that ![]() $\beta,\gamma \in \mathbb {F}_p$.
$\beta,\gamma \in \mathbb {F}_p$.
We prove that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly. First, because
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly. First, because ![]() $K\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4\}=\operatorname {Span}_{\mathbb {F}_p}\{\beta w_3-w_4\}$, then any primitive vector in
$K\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4\}=\operatorname {Span}_{\mathbb {F}_p}\{\beta w_3-w_4\}$, then any primitive vector in ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which modulo
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which modulo ![]() $p$ is not a multiple of
$p$ is not a multiple of ![]() $\beta w_3 - w_4$ must decay rapidly. Now we consider
$\beta w_3 - w_4$ must decay rapidly. Now we consider ![]() $\beta w_3 - w_4$. Up to constants, the coefficient of the
$\beta w_3 - w_4$. Up to constants, the coefficient of the ![]() $1/p^{n+1}$ part of the first entry of
$1/p^{n+1}$ part of the first entry of ![]() $F_{\infty }(\beta w_3 - w_4)$ equals
$F_{\infty }(\beta w_3 - w_4)$ equals ![]() $\beta _{a'} t^{A(1 + \cdots +p^{n-e}) + B(p^{n-e+1} + p^{n-e+2} + \cdots + p^{n+e-3}) + a' p^{n+e -1}}$. Lemma 6.4.1 establishes the required decay as follows: first, as
$\beta _{a'} t^{A(1 + \cdots +p^{n-e}) + B(p^{n-e+1} + p^{n-e+2} + \cdots + p^{n+e-3}) + a' p^{n+e -1}}$. Lemma 6.4.1 establishes the required decay as follows: first, as ![]() $a' \leq B \leq A$, we have that the vector
$a' \leq B \leq A$, we have that the vector ![]() $\beta w_3 - w_4$ decays rapidly; second, the exact bound for
$\beta w_3 - w_4$ decays rapidly; second, the exact bound for ![]() $a'$ in Lemma 6.4.1 implies (as in the proof in Case 2.1) that
$a'$ in Lemma 6.4.1 implies (as in the proof in Case 2.1) that ![]() $\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly; finally, the very rapid decay of
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly; finally, the very rapid decay of ![]() $w_3$,
$w_3$,![]() $w_4$ follows from the bound
$w_4$ follows from the bound ![]() $2a' \leq B \leq A$.
$2a' \leq B \leq A$.
Then, Proposition 5.1.3 follows by an argument analogous to that in Case 2.1 with Lemma 6.4.4.
7. The setup of the main proofs
In this section, we provide the general setup of the proofs of Theorems 1 and 5. As mentioned in § 1.3, the proofs consist of the following parts:
(1) the sum of the local contributions at supersingular points is at most
 $11/12$ of the global contribution; and
$11/12$ of the global contribution; and(2) the local contribution from non-supersingular points is of smaller magnitude.
Proposition 7.2.5 makes part (1) precise, and is stated in § 7.2. We prove Proposition 7.2.5 and part (2) in § 8 for the Hilbert case and in § 9 for the Siegel case. The idea involved in the statement of Proposition 7.2.5 is that we break the global intersection number ![]() $C . Z(m)$ into pieces, one for each non-ordinary point on
$C . Z(m)$ into pieces, one for each non-ordinary point on ![]() $C$, by using the relation between the Hasse invariant and the Hodge line bundle in § 7.1. We also relate the local intersection multiplicity at a point to a lattice-point count.
$C$, by using the relation between the Hasse invariant and the Hodge line bundle in § 7.1. We also relate the local intersection multiplicity at a point to a lattice-point count.
7.1 The global contribution and its decomposition
Recall that in § 4.3.3, we list the set ![]() $T$ of
$T$ of ![]() $m\in \mathbb {Z}_{>0}$ for which we will study
$m\in \mathbb {Z}_{>0}$ for which we will study ![]() $C.Z(m)$ to prove our main theorems. To study the asymptotic behavior, we define
$C.Z(m)$ to prove our main theorems. To study the asymptotic behavior, we define ![]() $T_M=\{m\in T\mid m\leq M\}$ for
$T_M=\{m\in T\mid m\leq M\}$ for ![]() $M\in \mathbb {Z}_{>0}$. Moreover, in §§ 8–9, we construct a subset
$M\in \mathbb {Z}_{>0}$. Moreover, in §§ 8–9, we construct a subset ![]() $S_M\subset T_M$ which consists of bad values of
$S_M\subset T_M$ which consists of bad values of ![]() $m$ that we want to rule out. The total global intersection number that we consider is
$m$ that we want to rule out. The total global intersection number that we consider is ![]() $\sum _{m\in T_M-S_M} C.Z(m)$. We sum over
$\sum _{m\in T_M-S_M} C.Z(m)$. We sum over ![]() $m$ instead of working with individual
$m$ instead of working with individual ![]() $m$ because geometry-of-numbers techniques which we use to bound the local intersection multiplicity (for cumulative
$m$ because geometry-of-numbers techniques which we use to bound the local intersection multiplicity (for cumulative ![]() $m$) do not work for individual
$m$) do not work for individual ![]() $m$. The following lemma gives the asymptotics of the global term using results in § 4.
$m$. The following lemma gives the asymptotics of the global term using results in § 4.
Lemma 7.1.1 Assume that ![]() $\#S_M=O(M^{1-\epsilon })=O(\# T_M^{1-\epsilon })$ for some
$\#S_M=O(M^{1-\epsilon })=O(\# T_M^{1-\epsilon })$ for some ![]() $\epsilon >0$ if
$\epsilon >0$ if ![]() $L=L_{\rm H}$ and that
$L=L_{\rm H}$ and that ![]() $\#S_M=o(\# T_M)$ if
$\#S_M=o(\# T_M)$ if ![]() $L=L_{\rm S}$. Then
$L=L_{\rm S}$. Then
 \[ \sum_{m\in T_M-S_M} C.Z(m)=(\omega.C)\sum_{m\in T_M-S_M} |q_L(m)|+o\biggl(\sum_{m\in T_M-S_M} |q_L(m)|\biggr). \]
\[ \sum_{m\in T_M-S_M} C.Z(m)=(\omega.C)\sum_{m\in T_M-S_M} |q_L(m)|+o\biggl(\sum_{m\in T_M-S_M} |q_L(m)|\biggr). \]
Moreover, we have, for Theorem 1(2), ![]() $\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2$; for Theorem 1(1) and Remark 4,
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2$; for Theorem 1(1) and Remark 4, ![]() $\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2/\log M$; for Theorem 5,
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2/\log M$; for Theorem 5, ![]() $\sum _{m\in T_M-S_M} C.Z(m)\asymp M^{5/2}/\log M$.
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^{5/2}/\log M$.
Proof. By § 4.3.1 and the assumption on ![]() $S_M$, we have
$S_M$, we have ![]() $\sum _{m\in S_M}|q_L(m)|=o(\sum _{m\in T_M}|q_L(m)|)$. Then the assertions follow from § 4.3.1, Lemmas 4.3.2 and 4.3.4, and the prime number theorem.
$\sum _{m\in S_M}|q_L(m)|=o(\sum _{m\in T_M}|q_L(m)|)$. Then the assertions follow from § 4.3.1, Lemmas 4.3.2 and 4.3.4, and the prime number theorem.
For each non-ordinary point ![]() $P$ on
$P$ on ![]() $C\cap Z(m)$, we introduce the notion of global intersection number
$C\cap Z(m)$, we introduce the notion of global intersection number ![]() $g_P(m)$ at
$g_P(m)$ at ![]() $P$ using the following (well-known) relation between the non-ordinary locus and the divisor class of the Hodge bundle. Note that in the proof we only use the notion
$P$ using the following (well-known) relation between the non-ordinary locus and the divisor class of the Hodge bundle. Note that in the proof we only use the notion ![]() $g_P(m)$ for a supersingular point.
$g_P(m)$ for a supersingular point.
Lemma 7.1.2 The non-ordinary locus in ![]() $\mathcal {M}_k$ and
$\mathcal {M}_k$ and ![]() $\mathcal {M}^{\rm {tor}}_k$ is cut out by a Hasse-invariant
$\mathcal {M}^{\rm {tor}}_k$ is cut out by a Hasse-invariant ![]() $H$, which is a section of
$H$, which is a section of ![]() $\omega ^{p-1}$ and, hence, the number of non-ordinary points (counted with multiplicity) on
$\omega ^{p-1}$ and, hence, the number of non-ordinary points (counted with multiplicity) on ![]() $C$ is given by
$C$ is given by ![]() $(p-1)(C.\omega )$.
$(p-1)(C.\omega )$.
See, for instance, [Reference BoxerBox15, §§ 1.4 and 1.5, Theorem 6.2.3] for an explanation of this fact (and we use the fact that the ordinary Newton stratum coincides with the ordinary Ekedahl–Oort stratum). For the last assertion in the lemma, we remark that when ![]() $L=L_{\rm H}$, the boundary
$L=L_{\rm H}$, the boundary ![]() $\mathcal {M}^{\rm {tor}}_k\setminus \mathcal {M}_k$ is ordinary and, hence, the intersection of
$\mathcal {M}^{\rm {tor}}_k\setminus \mathcal {M}_k$ is ordinary and, hence, the intersection of ![]() $C'$ (in § 4.1.3) with the non-ordinary locus is the same as the intersection of
$C'$ (in § 4.1.3) with the non-ordinary locus is the same as the intersection of ![]() $C$ with the non-ordinary locus.
$C$ with the non-ordinary locus.
Definition 7.1.3 Let ![]() $t$ be the local coordinate at
$t$ be the local coordinate at ![]() $P$ (i.e.
$P$ (i.e. ![]() $\hat {C}_{P}=\operatorname {Spf} k[[t]]$) and let
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$) and let ![]() $A=v_t(H)$. We define
$A=v_t(H)$. We define ![]() $g_P(m)=({A}/({p-1}))|q_L(m)|$.
$g_P(m)=({A}/({p-1}))|q_L(m)|$.
Note that by the above lemmas, we have the following decomposition
 \begin{align*} \sum_{P\in C \text{ non-ord}}\sum_{m\in T_M-S_M}g_P(m)&=\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\\ &=\sum_{m\in T_M-S_M} C.Z(m) + o\biggl(\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\biggr). \end{align*}
\begin{align*} \sum_{P\in C \text{ non-ord}}\sum_{m\in T_M-S_M}g_P(m)&=\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\\ &=\sum_{m\in T_M-S_M} C.Z(m) + o\biggl(\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\biggr). \end{align*}7.2 The lattices and the outline of the proof
Let ![]() $B \rightarrow \operatorname {Spf} k[[t]]$ denote the generically ordinary abelian surface given by pulling back the universal family over
$B \rightarrow \operatorname {Spf} k[[t]]$ denote the generically ordinary abelian surface given by pulling back the universal family over ![]() $\mathcal {M}_k$ to
$\mathcal {M}_k$ to ![]() $\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for some point
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for some point ![]() $P\in C$. Recall the notion of special endomorphisms from § 2.2 and by a slight abuse of terminology, when
$P\in C$. Recall the notion of special endomorphisms from § 2.2 and by a slight abuse of terminology, when ![]() $L=L_{\rm H}$, we also refer to a special quasi-endomorphism with certain integrality condition in § 2.2.11 as a special endomorphism. For any
$L=L_{\rm H}$, we also refer to a special quasi-endomorphism with certain integrality condition in § 2.2.11 as a special endomorphism. For any ![]() $n\in \mathbb {Z}_{>0}$, the lattice is special endomorphisms of
$n\in \mathbb {Z}_{>0}$, the lattice is special endomorphisms of ![]() $B \bmod t^n$ is a sublattice of
$B \bmod t^n$ is a sublattice of ![]() $B\bmod t$, which is equipped with a positive definite quadratic form
$B\bmod t$, which is equipped with a positive definite quadratic form ![]() $Q'$ (see Definition 2.3.1).
$Q'$ (see Definition 2.3.1).
Lemma 7.2.1 The local intersection multiplicity of ![]() $C.Z(m)$ at
$C.Z(m)$ at ![]() $P$, denoted by
$P$, denoted by ![]() $l_P(m)$, equals
$l_P(m)$, equals
 \[ \sum_{n = 1} ^ {\infty} \#\{ \textrm{Special endomorphisms } s \textrm{ of }B \bmod t^n \textrm{ with } Q'(s)=m\}. \]
\[ \sum_{n = 1} ^ {\infty} \#\{ \textrm{Special endomorphisms } s \textrm{ of }B \bmod t^n \textrm{ with } Q'(s)=m\}. \] The lemma follows directly from the moduli interpretation of ![]() $Z(m)$. Note that as
$Z(m)$. Note that as ![]() $B$ generically has no special endomorphisms, this infinite sum can actually be truncated at some finite stage (which will depend on
$B$ generically has no special endomorphisms, this infinite sum can actually be truncated at some finite stage (which will depend on ![]() $m$).
$m$).
Remark 7.2.2 Given ![]() $B$, the lattices of special endomorphisms of
$B$, the lattices of special endomorphisms of ![]() $B\bmod t^n$ have the same rank for all
$B\bmod t^n$ have the same rank for all ![]() $n\in \mathbb {Z}_{>0}$. Indeed, the work of de Jong, Moonen, and Kisin cited in the proof of Theorem 5.1.2 applies to any
$n\in \mathbb {Z}_{>0}$. Indeed, the work of de Jong, Moonen, and Kisin cited in the proof of Theorem 5.1.2 applies to any ![]() $P$ and for any special endomorphism
$P$ and for any special endomorphism ![]() $w$ of
$w$ of ![]() $B\bmod t$, we have the parallel extension
$B\bmod t$, we have the parallel extension ![]() $\tilde {w}\in (K[[t]])^4$ (or
$\tilde {w}\in (K[[t]])^4$ (or ![]() $(K[[t]])^5$), which is invariant under the Frobenius on
$(K[[t]])^5$), which is invariant under the Frobenius on ![]() $\mathbb {L}_{\mathrm {cris}}(W[[t]])$. By de Jong's theory (here we need the fully faithfulness of the Dieudonné functor, see [Reference de JongdJ95, Corollary 2.4.9]), whether
$\mathbb {L}_{\mathrm {cris}}(W[[t]])$. By de Jong's theory (here we need the fully faithfulness of the Dieudonné functor, see [Reference de JongdJ95, Corollary 2.4.9]), whether ![]() $w$ extends over
$w$ extends over ![]() $\bmod t^n$ depends on the
$\bmod t^n$ depends on the ![]() $p$-powers in the denominators of the coefficients of
$p$-powers in the denominators of the coefficients of ![]() $\tilde {w}$. Therefore, given
$\tilde {w}$. Therefore, given ![]() $n$, there exists
$n$, there exists ![]() $N$ such that
$N$ such that ![]() $p^Nw$ extends over
$p^Nw$ extends over ![]() $\bmod t^n$ and, hence, these lattices tensor
$\bmod t^n$ and, hence, these lattices tensor ![]() $\mathbb {Z}_\ell, \ell \neq p$ are all isomorphic and, in particular, the rank of the lattices is independent of
$\mathbb {Z}_\ell, \ell \neq p$ are all isomorphic and, in particular, the rank of the lattices is independent of ![]() $n$.
$n$.
Motivated by the decay lemma Theorem 5.1.2, we define the following lattices for supersingular points (note that the notation is slightly different from that in the introduction and we use the notation in this section for the rest of the paper).
7.2.3
Assume ![]() $P$ is superspecial and recall that
$P$ is superspecial and recall that ![]() $A=v_t(H)$, where
$A=v_t(H)$, where ![]() $H$ is the Hasse invariant and we use the constants
$H$ is the Hasse invariant and we use the constants ![]() $a$ and
$a$ and ![]() $A_n=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$ as in Definition 5.1.1.
$A_n=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$ as in Definition 5.1.1.
Define ![]() $L_{0,1}$,
$L_{0,1}$, ![]() $L_{n,1}, n\in \mathbb {Z}_{>0}$, and
$L_{n,1}, n\in \mathbb {Z}_{>0}$, and ![]() $L_{n,2}, n\in \mathbb {Z}_{\geq 0}$ to be the lattices of special endomorphisms of
$L_{n,2}, n\in \mathbb {Z}_{\geq 0}$ to be the lattices of special endomorphisms of ![]() $B$ mod
$B$ mod ![]() $t$, mod
$t$, mod ![]() $t^{A_{n-1}+1}$, and mod
$t^{A_{n-1}+1}$, and mod ![]() $t^{A_{n-1}+ap^n+1}$, respectively. As in Definition 2.3.1, we pick a lattice
$t^{A_{n-1}+ap^n+1}$, respectively. As in Definition 2.3.1, we pick a lattice ![]() $L'_{n,i}\subset L'$ such that
$L'_{n,i}\subset L'$ such that ![]() $L_{n,i}\subset L'_{n,i}$ and for
$L_{n,i}\subset L'_{n,i}$ and for ![]() $\ell \neq p$,
$\ell \neq p$, ![]() $L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$, and
$L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$, and ![]() $L'_{n,i}\otimes \mathbb {Z}_p=L_{n,i}\otimes \mathbb {Z}_p$. In particular,
$L'_{n,i}\otimes \mathbb {Z}_p=L_{n,i}\otimes \mathbb {Z}_p$. In particular, ![]() $L'_{0,1}=L'$ and by Theorem 5.1.2, we have
$L'_{0,1}=L'$ and by Theorem 5.1.2, we have ![]() $[L'_{n,1}: L'_{n,2}]\geq p$ and
$[L'_{n,1}: L'_{n,2}]\geq p$ and ![]() $[L':L'_{n,1}]\geq p^{3n}$.
$[L':L'_{n,1}]\geq p^{3n}$.
As we assume that ![]() $C$ does not admit any global special endomorphisms, we have
$C$ does not admit any global special endomorphisms, we have ![]() ${\bigcap _{n=0}^\infty L_{n,i}=\{0\}}$. By Remark 7.2.2, the difference between
${\bigcap _{n=0}^\infty L_{n,i}=\{0\}}$. By Remark 7.2.2, the difference between ![]() $L'_{n,i}$ and
$L'_{n,i}$ and ![]() $L_{n,i}$ is the same as that between
$L_{n,i}$ is the same as that between ![]() $L_{0,i}$ and
$L_{0,i}$ and ![]() $L'$, we also have
$L'$, we also have ![]() $\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$.
$\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$.
Corollary 7.2.4 If ![]() $P$ is superspecial, then
$P$ is superspecial, then
 \[ l_P(m)\leq \frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m)), \]
\[ l_P(m)\leq \frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m)), \]
where ![]() $r_{n,i}(m)=\#\{s\in L'_{n,i}\mid Q'(s)=m\}$.
$r_{n,i}(m)=\#\{s\in L'_{n,i}\mid Q'(s)=m\}$.
Proof. By Lemma 7.2.1 and § 7.2.3, we have that for ![]() $P$ superspecial,
$P$ superspecial,
 \begin{align*} l_P(m) & \leq (A_{-1}+a)r_{0,1}(m)+(A_0-A_{-1}-a) r_{0,2}(m)\\ &\quad + \sum_{n=1}^\infty (ap^n r_{n,1}(m) + (A_n-A_{n-1}-ap^n) r_{n,2}(m))\\ & =A_{-1}(r_{0,1}(m)-r_{0,2}(m)) + a\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))+\sum_{n=0}^\infty A_n (r_{n,2}(m)-r_{n+1,2}(m))\\ & \leq \frac{A}{p}(r_{0,1}(m)-r_{0,2}(m)) + \frac{A}{2}\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))\\ &\quad +\sum_{n=0}^\infty (A(p^n+\cdots +1+ p^{-1}) (r_{n,2}(m)-r_{n+1,2}(m)), \end{align*}
\begin{align*} l_P(m) & \leq (A_{-1}+a)r_{0,1}(m)+(A_0-A_{-1}-a) r_{0,2}(m)\\ &\quad + \sum_{n=1}^\infty (ap^n r_{n,1}(m) + (A_n-A_{n-1}-ap^n) r_{n,2}(m))\\ & =A_{-1}(r_{0,1}(m)-r_{0,2}(m)) + a\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))+\sum_{n=0}^\infty A_n (r_{n,2}(m)-r_{n+1,2}(m))\\ & \leq \frac{A}{p}(r_{0,1}(m)-r_{0,2}(m)) + \frac{A}{2}\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))\\ &\quad +\sum_{n=0}^\infty (A(p^n+\cdots +1+ p^{-1}) (r_{n,2}(m)-r_{n+1,2}(m)), \end{align*}
where the last equality follows from the facts that ![]() $r_{n,1}(m)\geq r_{n,2}(m)$,
$r_{n,1}(m)\geq r_{n,2}(m)$, ![]() $r_{n,2}(m)\geq r_{n+1,2}(m)$ and
$r_{n,2}(m)\geq r_{n+1,2}(m)$ and ![]() $a\leq A/2$,
$a\leq A/2$, ![]() $A_n\leq A(p^n+\cdots + p^{-1})$. We then obtain the assertion in part (1) by rearranging the summations.
$A_n\leq A(p^n+\cdots + p^{-1})$. We then obtain the assertion in part (1) by rearranging the summations.
The main task of the next two sections is to prove the following proposition.
Proposition 7.2.5 Given ![]() $C$, there exists
$C$, there exists ![]() $S_M$ satisfying the assumption in Lemma 7.1.1 such that for every supersingular point
$S_M$ satisfying the assumption in Lemma 7.1.1 such that for every supersingular point ![]() $P$ on
$P$ on ![]() $C$, we have
$C$, we have
 \[ \sum_{m\in T_M-S_M}l_P(m)\leq \frac{11}{12}\sum_{m\in T_M-S_M}g_P(m)+o\biggl(\sum_{m\in T_M-S_M}g_P(m)\biggr). \]
\[ \sum_{m\in T_M-S_M}l_P(m)\leq \frac{11}{12}\sum_{m\in T_M-S_M}g_P(m)+o\biggl(\sum_{m\in T_M-S_M}g_P(m)\biggr). \] Once we have this proposition, we prove that the local contribution from non-supersingular points have smaller order of magnitude, whence we conclude that there are infinitely many non-supersingular points on ![]() $C$ which lie in the desired special divisors.
$C$ which lie in the desired special divisors.
7.3 Ordinary points
To bound ![]() $l_P(m)$, we need the following decay lemma for ordinary points, which follows directly from Serre–Tate theory. We thank Keerthi Madapusi Pera for pointing this out to us. Let
$l_P(m)$, we need the following decay lemma for ordinary points, which follows directly from Serre–Tate theory. We thank Keerthi Madapusi Pera for pointing this out to us. Let ![]() $B \rightarrow \operatorname {Spf} k[[t]]$ denote the abelian surface with ordinary reduction given by pulling back the universal family over
$B \rightarrow \operatorname {Spf} k[[t]]$ denote the abelian surface with ordinary reduction given by pulling back the universal family over ![]() $\mathcal {M}_k$ to
$\mathcal {M}_k$ to ![]() $\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for an ordinary point
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for an ordinary point ![]() $P$.
$P$.
Lemma 7.3.1 Let ![]() $A$ be an integer such that
$A$ be an integer such that ![]() $w$ is not a special endomorphism for the
$w$ is not a special endomorphism for the ![]() $p$-divisible group
$p$-divisible group ![]() $B[p^\infty ] \bmod t^{A+1}$. Then,
$B[p^\infty ] \bmod t^{A+1}$. Then, ![]() $pw$ is not a special endomorphism for
$pw$ is not a special endomorphism for ![]() $B[p^\infty ]\bmod t^{pA+1}$.
$B[p^\infty ]\bmod t^{pA+1}$.
Proof. Note that an endomorphism of ![]() $B[p^\infty ] \bmod t^n$ is special if and only if its reduction on
$B[p^\infty ] \bmod t^n$ is special if and only if its reduction on ![]() $B[p^\infty ]\bmod t$ is special. Hence, we only need to consider the deformation of endomorphisms. The statement now follows directly from [Reference KatzKat81, Theorem 2.1]
$B[p^\infty ]\bmod t$ is special. Hence, we only need to consider the deformation of endomorphisms. The statement now follows directly from [Reference KatzKat81, Theorem 2.1]
Lemma 7.3.2 Let ![]() $L_0, L_n, n\in \mathbb {Z}_{>0}$ be the lattices of special endomorphisms of
$L_0, L_n, n\in \mathbb {Z}_{>0}$ be the lattices of special endomorphisms of ![]() $B\bmod t$ and
$B\bmod t$ and ![]() $B\bmod t^{Ap^{n-1}+1}$, respectively, where
$B\bmod t^{Ap^{n-1}+1}$, respectively, where ![]() $A\in \mathbb {Z}_{>0}$. Then:
$A\in \mathbb {Z}_{>0}$. Then:
(1) for any
 $A$, we have
$A$, we have  $\operatorname {rk}_{\mathbb {Z}}L_n\leq 2$ if
$\operatorname {rk}_{\mathbb {Z}}L_n\leq 2$ if  $L=L_{\rm H}$ and
$L=L_{\rm H}$ and  $\operatorname {rk}_{\mathbb {Z}}L_n\leq 3$ if
$\operatorname {rk}_{\mathbb {Z}}L_n\leq 3$ if  $L=L_{\rm S}$;
$L=L_{\rm S}$;(2) there exist a constant
 $A$ and a
$A$ and a  $\mathbb {Z}_p$-lattice
$\mathbb {Z}_p$-lattice  $\Lambda$ (depending on
$\Lambda$ (depending on  $P$) with
$P$) with  $\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 1$ when
$\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 1$ when  $L=L_{\rm H}$ and
$L=L_{\rm H}$ and  $\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 2$ when
$\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 2$ when  $L=L_{\rm S}$ such that
$L=L_{\rm S}$ such that  $L_n\subset (\Lambda +p^{n-1} L_1\otimes \mathbb {Z}_p)\cap L_0$.
$L_n\subset (\Lambda +p^{n-1} L_1\otimes \mathbb {Z}_p)\cap L_0$.
In particular, if ![]() $\operatorname {rk}_{\mathbb {Z}}L_n=3$ when
$\operatorname {rk}_{\mathbb {Z}}L_n=3$ when ![]() $L=L_{\rm S}$ or
$L=L_{\rm S}$ or ![]() $\operatorname {rk}_{\mathbb {Z}}L_n=2$ when
$\operatorname {rk}_{\mathbb {Z}}L_n=2$ when ![]() $L=L_{\rm H}$, then
$L=L_{\rm H}$, then ![]() $(\operatorname {disc} L_n)^{1/2}\geq p^{n-1}$.
$(\operatorname {disc} L_n)^{1/2}\geq p^{n-1}$.
Proof. Note that ![]() $L_n\subset L_n\otimes \mathbb {Z}_p\subset L_0\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$, where
$L_n\subset L_n\otimes \mathbb {Z}_p\subset L_0\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$, where ![]() $\mathbb {L}_{\mathrm {cris},P}$ is the fiber of the
$\mathbb {L}_{\mathrm {cris},P}$ is the fiber of the ![]() $F$-crystal
$F$-crystal ![]() $\mathbb {L}_{\mathrm {cris}}$ defined in Definitions 2.2.3 and 2.2.9 and
$\mathbb {L}_{\mathrm {cris}}$ defined in Definitions 2.2.3 and 2.2.9 and ![]() $\varphi$ is the Frobenius action. As
$\varphi$ is the Frobenius action. As ![]() $P$ is ordinary, then
$P$ is ordinary, then ![]() $\varphi$ acts on
$\varphi$ acts on ![]() $\mathbb {L}_{\mathrm {cris},P}(W)$ with slope
$\mathbb {L}_{\mathrm {cris},P}(W)$ with slope ![]() $-1,1,0,0$ (Hilbert case) or
$-1,1,0,0$ (Hilbert case) or ![]() $-1,1,0,0,0$ (Siegel case) and hence part (1) follows.
$-1,1,0,0,0$ (Siegel case) and hence part (1) follows.
Let ![]() $\Lambda '$ be the
$\Lambda '$ be the ![]() $\mathbb {Z}_p$-lattice of special endomorphisms of
$\mathbb {Z}_p$-lattice of special endomorphisms of ![]() $B[p^\infty ]$. As
$B[p^\infty ]$. As ![]() $\hat {C}_{P}$ is not contained in any special divisor,Footnote 32
$\hat {C}_{P}$ is not contained in any special divisor,Footnote 32 ![]() $B[p^\infty ]$ admits at most a rank-
$B[p^\infty ]$ admits at most a rank-![]() $2$ (respectively, rank-
$2$ (respectively, rank-![]() $1$) module of special endomorphisms when
$1$) module of special endomorphisms when ![]() $L=L_{\rm S}$ (respectively,
$L=L_{\rm S}$ (respectively, ![]() $L=L_{\rm H}$); indeed, if
$L=L_{\rm H}$); indeed, if ![]() $\operatorname {rk}_{\mathbb {Z}_p}\Lambda '=3$ (respectively,
$\operatorname {rk}_{\mathbb {Z}_p}\Lambda '=3$ (respectively, ![]() $2$), then
$2$), then ![]() $\Lambda '\otimes \mathbb {Q}_p=L_0\otimes \mathbb {Q}_p$ and, thus,
$\Lambda '\otimes \mathbb {Q}_p=L_0\otimes \mathbb {Q}_p$ and, thus, ![]() $B$ admits special endomorphisms.
$B$ admits special endomorphisms.
We now mimic the proof of [Reference Shankar and TangST20, Theorem 4.1.1] using Lemma 7.3.1 instead of [Reference Shankar and TangST20, Lemma 4.1.2(2)]. Let ![]() $\Lambda \subset L_0\otimes \mathbb {Z}_p$ be the saturation of
$\Lambda \subset L_0\otimes \mathbb {Z}_p$ be the saturation of ![]() $\Lambda '$ in
$\Lambda '$ in ![]() $L_0\otimes \mathbb {Z}_p$; then there exists
$L_0\otimes \mathbb {Z}_p$; then there exists ![]() $\Lambda _0\subset L_0\otimes \mathbb {Z}_p$ such that
$\Lambda _0\subset L_0\otimes \mathbb {Z}_p$ such that ![]() $L_0\otimes \mathbb {Z}_p=\Lambda \oplus \Lambda _0$. Let
$L_0\otimes \mathbb {Z}_p=\Lambda \oplus \Lambda _0$. Let ![]() $\Lambda _n$ denote
$\Lambda _n$ denote ![]() $(L_n\otimes \mathbb {Z}_p+\Lambda )\cap \Lambda _0$; then
$(L_n\otimes \mathbb {Z}_p+\Lambda )\cap \Lambda _0$; then ![]() $L_n\otimes \mathbb {Z}_p+\Lambda =\Lambda \oplus \Lambda _n$. It suffices to show that there exists
$L_n\otimes \mathbb {Z}_p+\Lambda =\Lambda \oplus \Lambda _n$. It suffices to show that there exists ![]() $A$ such that
$A$ such that ![]() $\Lambda _n\subset p\Lambda _{n-1}$ (and this implies that
$\Lambda _n\subset p\Lambda _{n-1}$ (and this implies that ![]() $\Lambda _n\subset p^{n-1}\Lambda _1$).
$\Lambda _n\subset p^{n-1}\Lambda _1$).
By definition, none of the elements in ![]() $\Lambda _0$ extend to
$\Lambda _0$ extend to ![]() $\operatorname {Spf} k[[t]]$, then there exists
$\operatorname {Spf} k[[t]]$, then there exists ![]() $A$ such that
$A$ such that ![]() $\Lambda _1\subset p\Lambda _0$. For
$\Lambda _1\subset p\Lambda _0$. For ![]() $n\geq 2$, assume for contradiction that there exists
$n\geq 2$, assume for contradiction that there exists ![]() $\alpha \in \Lambda _n\backslash p\Lambda _{n-1}$. If
$\alpha \in \Lambda _n\backslash p\Lambda _{n-1}$. If ![]() $\alpha \in p\Lambda _{n-2}$, then write
$\alpha \in p\Lambda _{n-2}$, then write ![]() $\alpha =p\beta$ with
$\alpha =p\beta$ with ![]() $\beta \in \Lambda _{n-2}$. As
$\beta \in \Lambda _{n-2}$. As ![]() $p\beta =\alpha \in \Lambda _n$, then by Lemma 7.3.1,
$p\beta =\alpha \in \Lambda _n$, then by Lemma 7.3.1, ![]() $\beta \in \Lambda _{n-1}$, which contradicts with the assumption that
$\beta \in \Lambda _{n-1}$, which contradicts with the assumption that ![]() $\alpha \notin p\Lambda _{n-1}$. Thus we have
$\alpha \notin p\Lambda _{n-1}$. Thus we have ![]() $\alpha \notin p\Lambda _{n-2}$; by iterating the argument, we have
$\alpha \notin p\Lambda _{n-2}$; by iterating the argument, we have ![]() $\alpha \notin p\Lambda _0$. This is a contradiction because
$\alpha \notin p\Lambda _0$. This is a contradiction because ![]() $\alpha \in \Lambda _n\subset \Lambda _1\subset p\Lambda _0$.
$\alpha \in \Lambda _n\subset \Lambda _1\subset p\Lambda _0$.
8. Proof of Theorem 1(2)
In this section, we use the results proved in §§ 4 and 5 to prove Proposition 7.2.5 in the case of Hilbert modular surfaces. This, in conjunction with Lemma 8.1.2, yields Theorem 1(2).
8.1 The bad set  $S_M$ and the local intersection multiplicities at non-supersingular points
$S_M$ and the local intersection multiplicities at non-supersingular points
We first construct the set ![]() $S_M$; the following lemma only concerns ordinary and superspecial points because we only need to consider such
$S_M$; the following lemma only concerns ordinary and superspecial points because we only need to consider such ![]() $P$ for the proof of Theorem 1(2). Indeed, if
$P$ for the proof of Theorem 1(2). Indeed, if ![]() $P\in Z(m)$, then
$P\in Z(m)$, then ![]() $P$ is either ordinary or supersingular and if
$P$ is either ordinary or supersingular and if ![]() $P\in Z(m), p\nmid m$, then by § 4.4.2(1),
$P\in Z(m), p\nmid m$, then by § 4.4.2(1), ![]() $P$ is not supergeneric. Therefore for
$P$ is not supergeneric. Therefore for ![]() $P\in Z(m), m\in T$,
$P\in Z(m), m\in T$, ![]() $P$ is either superspecial or ordinary.
$P$ is either superspecial or ordinary.
Lemma 8.1.1 Notation is as in §§ 7.1 and 7.2.3 and Lemma 7.3.2. Given a finite set ![]() $\{P_i\}\subset (C\cap (\bigcup _{m\in \mathbb {Z}_{>0}} Z(m)))(k)$, there exists
$\{P_i\}\subset (C\cap (\bigcup _{m\in \mathbb {Z}_{>0}} Z(m)))(k)$, there exists ![]() $S_M\subset T_M$ with
$S_M\subset T_M$ with ![]() $\#S_M=O(M^{1-\epsilon })$ for some
$\#S_M=O(M^{1-\epsilon })$ for some ![]() $0<\epsilon <1/6$ such that for all
$0<\epsilon <1/6$ such that for all ![]() $i$:
$i$:
(1) if
 $P_i$ is superspecial, then
$P_i$ is superspecial, then  $\{s\in L'_{N,1} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where
$\{s\in L'_{N,1} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where  $N=(({1+\epsilon })/{3})\log _p M$;
$N=(({1+\epsilon })/{3})\log _p M$;(2) if
 $P_i$ is ordinary, then
$P_i$ is ordinary, then  $\{s\in L_{N} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where
$\{s\in L_{N} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where  $N=\epsilon \log _p M$.
$N=\epsilon \log _p M$.
Proof. As the union of finitely many sets with cardinality ![]() $O(M^{1-\epsilon })$ still has cardinality to be
$O(M^{1-\epsilon })$ still has cardinality to be ![]() $O(M^{1-\epsilon })$, it suffices to prove the assertion for each
$O(M^{1-\epsilon })$, it suffices to prove the assertion for each ![]() $P_i$ separately. We follow the idea of the proof of [Reference Shankar and TangST20, Theorem 4.3.3].
$P_i$ separately. We follow the idea of the proof of [Reference Shankar and TangST20, Theorem 4.3.3].
If ![]() $P_i$ is superspecial, we take
$P_i$ is superspecial, we take ![]() $S_M=\{m\in T_M\mid \exists s\in L'_{N,1} \text { with } Q'(s)=m\}$ and then it satisfies part (1) by definition. Note that
$S_M=\{m\in T_M\mid \exists s\in L'_{N,1} \text { with } Q'(s)=m\}$ and then it satisfies part (1) by definition. Note that ![]() $\#S_M\leq \#\{s\in L'_{N,1}\mid Q'(s)\leq M\}$. Then by a geometry-of-numbers argument (see, for instance, [Reference Shankar and TangST20, Lemma 4.2.1]) and Theorem 5.1.2, we have
$\#S_M\leq \#\{s\in L'_{N,1}\mid Q'(s)\leq M\}$. Then by a geometry-of-numbers argument (see, for instance, [Reference Shankar and TangST20, Lemma 4.2.1]) and Theorem 5.1.2, we have
where ![]() $d_N$ is the first successive minimum of
$d_N$ is the first successive minimum of ![]() $L'_{N,1}$ and
$L'_{N,1}$ and ![]() $d_N\rightarrow \infty$ as
$d_N\rightarrow \infty$ as ![]() $N\rightarrow \infty$ because
$N\rightarrow \infty$ because ![]() $\cap L'_{N,1}=\{0\}$. Then
$\cap L'_{N,1}=\{0\}$. Then ![]() $\#S_M=O(M^{1-\epsilon })$ by the definition of
$\#S_M=O(M^{1-\epsilon })$ by the definition of ![]() $N$.
$N$.
If ![]() $P_i$ is ordinary, then
$P_i$ is ordinary, then ![]() $\operatorname {rk} L_N=2$ by Lemma 7.3.2 and the fact that
$\operatorname {rk} L_N=2$ by Lemma 7.3.2 and the fact that ![]() $\operatorname {rk} L_N=\operatorname {rk} L_0$ is even by the Tate conjecture. Similar to the superspecial case, we take
$\operatorname {rk} L_N=\operatorname {rk} L_0$ is even by the Tate conjecture. Similar to the superspecial case, we take ![]() $S_M=\{m\in T_M \mid \exists s\in L_{N} \text { with } Q'(s)=m\}$ and then by Lemma 7.3.2,
$S_M=\{m\in T_M \mid \exists s\in L_{N} \text { with } Q'(s)=m\}$ and then by Lemma 7.3.2, ![]() $\#S_M=O(M/p^N+M^{1/2}/d_N)=O(M^{1-\epsilon })$.
$\#S_M=O(M/p^N+M^{1/2}/d_N)=O(M^{1-\epsilon })$.
Lemma 8.1.2 Notation as in Lemma 8.1.1. For an ordinary point ![]() $P=P_i\in C(k)$, we have
$P=P_i\in C(k)$, we have
Proof. By Lemmas 7.2.1, 7.3.2, and 8.1.1,
 \[ \sum_{m\in T_M-S_M}l_P(m)=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^N(p^n-p^{n-1})r_n(m))\leq A\sum_{n=0}^N p^n\sum_{m=1}^M r_n(m), \]
\[ \sum_{m\in T_M-S_M}l_P(m)=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^N(p^n-p^{n-1})r_n(m))\leq A\sum_{n=0}^N p^n\sum_{m=1}^M r_n(m), \]
where ![]() $r_n(m)=\#\{s\in L_n\mid Q'(s)=m\}$. By a geometry-of-numbers argument and Lemma 7.3.2, we have
$r_n(m)=\#\{s\in L_n\mid Q'(s)=m\}$. By a geometry-of-numbers argument and Lemma 7.3.2, we have ![]() $\sum _{m=1}^M r_n(m)=O(M/p^n+M^{1/2}/d_n)$, where
$\sum _{m=1}^M r_n(m)=O(M/p^n+M^{1/2}/d_n)$, where ![]() $d_n$ is the first successive minimum of
$d_n$ is the first successive minimum of ![]() $L_n$ and the implicit constant here only depends on
$L_n$ and the implicit constant here only depends on ![]() $p$. Thus,
$p$. Thus, ![]() $\sum _{m\in T_M-S_M}l_P(m)=O(NM+p^N M^{1/2})=O(M^{1+\epsilon })$.
$\sum _{m\in T_M-S_M}l_P(m)=O(NM+p^N M^{1/2})=O(M^{1+\epsilon })$.
8.2 Proof of Proposition 7.2.5 in the Hilbert case
We follow the notation in Lemma 8.1.1 and ![]() $P=P_i$ superspecial. We break
$P=P_i$ superspecial. We break ![]() $\sum _{m\in T_M-S_M}l_P(m)$ into two parts and are treated in the following lemmas.
$\sum _{m\in T_M-S_M}l_P(m)$ into two parts and are treated in the following lemmas.
Lemma 8.2.1 Notation as in Corollary 7.2.4. For any ![]() $\epsilon >0$, there exists
$\epsilon >0$, there exists ![]() $c\in \mathbb {Z}_{>0}$ which only depends on
$c\in \mathbb {Z}_{>0}$ which only depends on ![]() $P$ and
$P$ and ![]() $\epsilon$ such that
$\epsilon$ such that
 \[ \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\leq \epsilon M^2 + o(M^2). \]
\[ \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\leq \epsilon M^2 + o(M^2). \]Proof. By Lemma 8.1.1, ![]() $r_{n,i}(m)=0$ for
$r_{n,i}(m)=0$ for ![]() $n>N=(({1+\epsilon })/{3})\log _p M$ and, hence,
$n>N=(({1+\epsilon })/{3})\log _p M$ and, hence,
 \begin{align*} \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))&=\sum_{m\in T_M-S_M}\sum_{n=c}^N \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\leq \sum_{n=c}^N\sum_{m=1}^M Ap^n r_{n,1}(m) \end{align*}
\begin{align*} \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))&=\sum_{m\in T_M-S_M}\sum_{n=c}^N \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\leq \sum_{n=c}^N\sum_{m=1}^M Ap^n r_{n,1}(m) \end{align*}
because ![]() $r_{n,1}(m)\geq r_{n,2}(m)$.
$r_{n,1}(m)\geq r_{n,2}(m)$.
By a geometry-of-numbers argument, ![]() $\sum _{m=1}^M r_{n,1}(m)\leq c_2(M^2/p^{3n}+M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n)$, where
$\sum _{m=1}^M r_{n,1}(m)\leq c_2(M^2/p^{3n}+M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n)$, where ![]() $c_2$ is an absolute constant and
$c_2$ is an absolute constant and ![]() $d_n$ is the first successive minimum of
$d_n$ is the first successive minimum of ![]() $L'_{n,1}$. Hence,
$L'_{n,1}$. Hence,
 \[ \sum_{n=c}^N Ap^n \sum_{m=1}^M r_{n,1}(m)\leq Ac_2M^2\sum_{n=c}^N 1/p^{2n}+\sum_{n=c}^N Ap^nc_2(M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n). \]
\[ \sum_{n=c}^N Ap^n \sum_{m=1}^M r_{n,1}(m)\leq Ac_2M^2\sum_{n=c}^N 1/p^{2n}+\sum_{n=c}^N Ap^nc_2(M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n). \]
Note that ![]() $Ac_2\sum _{n=c}^N\leq Ac_2 (p^{2c}(1-p^{-2}))^{-1}$, which goes to zero as
$Ac_2\sum _{n=c}^N\leq Ac_2 (p^{2c}(1-p^{-2}))^{-1}$, which goes to zero as ![]() $c\rightarrow \infty$ and the second term is
$c\rightarrow \infty$ and the second term is
 \[ O( M^{3/2})+O((\log M)M)+O(M^{1/2})\sum_{n=c}^N p^n=O(M^{3/2}). \]
\[ O( M^{3/2})+O((\log M)M)+O(M^{1/2})\sum_{n=c}^N p^n=O(M^{3/2}). \]Thus, we obtain the desired estimate.
Lemma 8.2.2 Notation as in Corollary 7.2.4. For any ![]() $c\in \mathbb {Z}_{>0}$, we have
$c\in \mathbb {Z}_{>0}$, we have
 \begin{align*} &\sum_{m\in T_M-S_M}\biggl(\frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^c \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\biggr)\\ &\qquad \leq \alpha \sum_{m\in T_M-S_M} g_P(m)+o(M^2), \end{align*}
\begin{align*} &\sum_{m\in T_M-S_M}\biggl(\frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^c \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\biggr)\\ &\qquad \leq \alpha \sum_{m\in T_M-S_M} g_P(m)+o(M^2), \end{align*}
where ![]() $\alpha <11/12$ is an absolute constant.
$\alpha <11/12$ is an absolute constant.
Proof. Let ![]() $\theta _{n,i}$ denote the theta series attached to the lattice
$\theta _{n,i}$ denote the theta series attached to the lattice ![]() $L'_{n,i}$. We decompose
$L'_{n,i}$. We decompose ![]() $\theta _{n,i}=E_{n,i}+G_{n,i}$, where
$\theta _{n,i}=E_{n,i}+G_{n,i}$, where ![]() $G_{n,i}$ is a cusp form and
$G_{n,i}$ is a cusp form and ![]() $E_{n,i}$ is an Eisenstein series as in § 4.2 and follow the proof of Lemma 4.3.2.
$E_{n,i}$ is an Eisenstein series as in § 4.2 and follow the proof of Lemma 4.3.2.
Let
 \begin{align*} E&=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G&=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{align*}
\begin{align*} E&=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G&=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{align*} Note that ![]() $G$ is a weight-
$G$ is a weight-![]() $2$ cusp form and by Deligne's Weil bound, we have that its
$2$ cusp form and by Deligne's Weil bound, we have that its ![]() $m$th Fourier coefficient
$m$th Fourier coefficient ![]() $q_G(m)=O(m^{1/2+\epsilon })$. Hence, the total contribution from the cusp form
$q_G(m)=O(m^{1/2+\epsilon })$. Hence, the total contribution from the cusp form ![]() $G$ is
$G$ is ![]() $\sum _{m\in T_M-S_M}q_G(m)=O(M^{3/2+\epsilon })$.
$\sum _{m\in T_M-S_M}q_G(m)=O(M^{3/2+\epsilon })$.
Let ![]() $q_{n,i}(m)$ and
$q_{n,i}(m)$ and ![]() $q(m)$ denote the
$q(m)$ denote the ![]() $m$th Fourier coefficient of
$m$th Fourier coefficient of ![]() $E_{n,i}$ and
$E_{n,i}$ and ![]() $E$ respectively. Recall that for
$E$ respectively. Recall that for ![]() $p\nmid m$ for
$p\nmid m$ for ![]() $m\in T_M$, by Lemma 4.4.6 and the fact that
$m\in T_M$, by Lemma 4.4.6 and the fact that ![]() $|L'^\vee /L'|=p^2$, we have for any
$|L'^\vee /L'|=p^2$, we have for any ![]() $n,i$ that
$n,i$ that
Recall from § 7.2.3 that ![]() $[L':L'_{n,1}]\geq p^{3n}$ and
$[L':L'_{n,1}]\geq p^{3n}$ and ![]() $[L':L'_{n,1}]\geq p^{3n+1}$; therefore,
$[L':L'_{n,1}]\geq p^{3n+1}$; therefore,
 \begin{align*} \frac{q(m)}{|q_L(m)|}&\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^c\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\\ &\leq \frac{A}{p-1}\biggl(\frac{p+2}{2p}+\frac{p}{p^2-1}\biggr). \end{align*}
\begin{align*} \frac{q(m)}{|q_L(m)|}&\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^c\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\\ &\leq \frac{A}{p-1}\biggl(\frac{p+2}{2p}+\frac{p}{p^2-1}\biggr). \end{align*}
Take ![]() $\alpha =({p+2})/{2p}+{p}/({p^2-1})$, which is
$\alpha =({p+2})/{2p}+{p}/({p^2-1})$, which is ![]() $<11/12$ when
$<11/12$ when ![]() $p\geq 5$. We have the left-hand side equals
$p\geq 5$. We have the left-hand side equals
 \[ \sum_{m\in T_M-S_M}(q(m)+q_G(m))\leq \sum_{m\in T_M-S_M}\frac{\alpha A}{p-1}|q_L(m)|+O(M^{3/2+\epsilon}), \]
\[ \sum_{m\in T_M-S_M}(q(m)+q_G(m))\leq \sum_{m\in T_M-S_M}\frac{\alpha A}{p-1}|q_L(m)|+O(M^{3/2+\epsilon}), \]
which gives the desired estimate by the definition of ![]() $g_P(m)$.
$g_P(m)$.
Proof Proof of Proposition 7.2.5 when  $L=L_{\rm H}$
$L=L_{\rm H}$
The set ![]() $S_M$ is constructed by Lemma 8.1.1 and taking
$S_M$ is constructed by Lemma 8.1.1 and taking ![]() $\{P_i\}$ to contain all of (the finitely many) supersingular points in
$\{P_i\}$ to contain all of (the finitely many) supersingular points in ![]() $C\cap (\bigcup _{p\nmid m}Z(m))$. Then the desired estimate follows from Lemmas 8.2.1 and 8.2.2 by taking
$C\cap (\bigcup _{p\nmid m}Z(m))$. Then the desired estimate follows from Lemmas 8.2.1 and 8.2.2 by taking ![]() $c$ such that
$c$ such that ![]() $\epsilon <\frac {11}{12}-\alpha$.
$\epsilon <\frac {11}{12}-\alpha$.
Proof of Theorem 1(2) If ![]() $C$ is contained in
$C$ is contained in ![]() $Z(m)$ with
$Z(m)$ with ![]() $m$ being a perfect square, then by applying suitable Hecke translates, we may assume that
$m$ being a perfect square, then by applying suitable Hecke translates, we may assume that ![]() $C$ is contained in the product of modular curves and then the assertion is a special case of [Reference Chai and OortCO06, Proposition 7.3]. Now for the rest of the proof, we may assume that
$C$ is contained in the product of modular curves and then the assertion is a special case of [Reference Chai and OortCO06, Proposition 7.3]. Now for the rest of the proof, we may assume that ![]() $C$ is contained in some Hilbert modular surface and we use
$C$ is contained in some Hilbert modular surface and we use ![]() $Z(m)$ to denote special divisors on the Hilbert modular surface. Note that any point on
$Z(m)$ to denote special divisors on the Hilbert modular surface. Note that any point on ![]() $Z(m)$ corresponds to an abelian surface isogenous to the self-product of an elliptic curve. Thus, we assume for contradiction that there are only finitely many points on
$Z(m)$ corresponds to an abelian surface isogenous to the self-product of an elliptic curve. Thus, we assume for contradiction that there are only finitely many points on ![]() $C\cap (\bigcup _{m\in T}Z(m))$ and take
$C\cap (\bigcup _{m\in T}Z(m))$ and take ![]() $\{P_i\}$ to be this finite set and apply Lemma 8.1.1 to construct
$\{P_i\}$ to be this finite set and apply Lemma 8.1.1 to construct ![]() $S_M$. As all
$S_M$. As all ![]() $Z(m)$ are compact, it makes sense to consider
$Z(m)$ are compact, it makes sense to consider ![]() $C.Z(m)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, and Lemma 8.1.2.
$C.Z(m)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, and Lemma 8.1.2.
9. Proofs of Theorems 1(1) and 5
In this section, we prove all of Theorems 1 and 5. Section 9.1 consists of results pertaining to squares represented by positive-definite quadratic forms.Footnote 33 In § 9.2, we prove Proposition 7.2.5 by combining results proved in §§ 4, 6, and 9.1. Finally, we deal with the intersection multiplicities at non-supersingular points in § 9.3 to finish the proof of the main theorem.
We now set up notation that we use for § 9. For superspecial points ![]() $P$, recall that we defined
$P$, recall that we defined ![]() $L'_{n,i}$ in § 7.2.3. Let
$L'_{n,i}$ in § 7.2.3. Let ![]() $l(n)_i,\ i=1,\ldots, 5$, denote the
$l(n)_i,\ i=1,\ldots, 5$, denote the ![]() $i$th successive minimum of the quadratic form
$i$th successive minimum of the quadratic form ![]() $Q'$ restricted to
$Q'$ restricted to ![]() $L'_{n,1}$. Let
$L'_{n,1}$. Let ![]() $P_n$ denote a rank two sublattice of
$P_n$ denote a rank two sublattice of ![]() $L'_{n,1}$ with minimal discriminant. Note that
$L'_{n,1}$ with minimal discriminant. Note that ![]() $l(n)_1l(n)_2\asymp d_n$, where
$l(n)_1l(n)_2\asymp d_n$, where ![]() $d_n$ denotes the root discriminant of
$d_n$ denotes the root discriminant of ![]() $P_n$. Moreover, because
$P_n$. Moreover, because ![]() $\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$, we have
$\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$, we have ![]() $l(n)_1\rightarrow \infty$ as
$l(n)_1\rightarrow \infty$ as ![]() $n\rightarrow \infty$.
$n\rightarrow \infty$.
9.1 Preparation
We need the following results to prove Proposition 7.2.5. Although Lemma 9.1.2 is stated for the rank-![]() $5$ lattices
$5$ lattices ![]() $L'_{n,1}$, the proof does not use the assumption on rank and, hence, it holds for the lattices
$L'_{n,1}$, the proof does not use the assumption on rank and, hence, it holds for the lattices ![]() $L_n$ for ordinary points (notation as in Lemma 7.3.2) when
$L_n$ for ordinary points (notation as in Lemma 7.3.2) when ![]() $\operatorname {rk}_{\mathbb {Z}}L_0=3$; see § 9.3 for details.
$\operatorname {rk}_{\mathbb {Z}}L_0=3$; see § 9.3 for details.
Lemma 9.1.1 We have ![]() $l(n)_1l(n)_2\cdots l(n)_i\gg p^{(i-2)n}$ for
$l(n)_1l(n)_2\cdots l(n)_i\gg p^{(i-2)n}$ for ![]() $i\geq 3$.
$i\geq 3$.
Proof. Note that if we have two lattices ![]() $L_1\supset L_2$, then the successive minima of
$L_1\supset L_2$, then the successive minima of ![]() $L_2$ give upper bounds of that of
$L_2$ give upper bounds of that of ![]() $L_1$. Thus, we may enlarge
$L_1$. Thus, we may enlarge ![]() $L'_{n,i}$ and prove the assertion for the enlarged lattices.
$L'_{n,i}$ and prove the assertion for the enlarged lattices.
We enlarge ![]() $L'_{n,i}$ as follows. For
$L'_{n,i}$ as follows. For ![]() $\ell \neq p$, we still require
$\ell \neq p$, we still require ![]() $L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$; at
$L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$; at ![]() $p$, let
$p$, let ![]() $\Lambda _0$ denote the rank-
$\Lambda _0$ denote the rank-![]() $3$ submodule of
$3$ submodule of ![]() $L'\otimes \mathbb {Z}_p$ which decays rapidly in the decay lemma (Theorem 5.1.2), then we enlarge
$L'\otimes \mathbb {Z}_p$ which decays rapidly in the decay lemma (Theorem 5.1.2), then we enlarge ![]() $L'_{n,1}$ such that
$L'_{n,1}$ such that ![]() $L'_{n,1}\otimes \mathbb {Z}_p=p^n \Lambda _0+L'\otimes \mathbb {Z}_p$.
$L'_{n,1}\otimes \mathbb {Z}_p=p^n \Lambda _0+L'\otimes \mathbb {Z}_p$.
For the enlarged ![]() $L'_{n,1}$, we have
$L'_{n,1}$, we have
where the implied constants only depend on the lattice ![]() $L'$. Thus, the assertion follows.
$L'$. Thus, the assertion follows.
Lemma 9.1.2 Suppose that ![]() $d_n^2M=o(p^{2n})$ as
$d_n^2M=o(p^{2n})$ as ![]() $n\rightarrow \infty$. Then, for any vector
$n\rightarrow \infty$. Then, for any vector ![]() $v \in L'_{n,1}$ such that
$v \in L'_{n,1}$ such that ![]() $Q(v) \leq M$, we have that
$Q(v) \leq M$, we have that ![]() $v \in P_n$ for
$v \in P_n$ for ![]() $n\gg 1$. In particular, if
$n\gg 1$. In particular, if ![]() $d_n \leq p^{n / 2}$, then for any vector
$d_n \leq p^{n / 2}$, then for any vector ![]() $v\in L'_{n,1}$ such that
$v\in L'_{n,1}$ such that ![]() $Q'(v) < p^{n - \epsilon }$ for some absolute constant
$Q'(v) < p^{n - \epsilon }$ for some absolute constant ![]() $\epsilon >0$, we have that
$\epsilon >0$, we have that ![]() $v \in P_n$ for
$v \in P_n$ for ![]() $n\gg 1$. (All the implicit constants here are independent of
$n\gg 1$. (All the implicit constants here are independent of ![]() $n,M$.)
$n,M$.)
Proof. Recall that ![]() $l(n)_1 \cdot l(n)_2 \asymp d_n$. Thus, by Lemma 9.1.1, we have
$l(n)_1 \cdot l(n)_2 \asymp d_n$. Thus, by Lemma 9.1.1, we have
In other words, for any vector ![]() $v$ linearly independent to
$v$ linearly independent to ![]() $P_n$, we have
$P_n$, we have ![]() $Q'(v)\geq l(n)_3^2\gg p^{2n}/d_n^2$. Then the first assertion follows. The second assertion follows directly from the first assertion by taking
$Q'(v)\geq l(n)_3^2\gg p^{2n}/d_n^2$. Then the first assertion follows. The second assertion follows directly from the first assertion by taking ![]() $M=p^{n-\epsilon }$.
$M=p^{n-\epsilon }$.
Proposition 9.1.3 Fix ![]() $D\in \mathbb {Z}_{>0}$. Recall
$D\in \mathbb {Z}_{>0}$. Recall ![]() $r_{n,i}(m)$ from Corollary 7.2.4. Then we have the following two bounds:
$r_{n,i}(m)$ from Corollary 7.2.4. Then we have the following two bounds:
(1)
 $\displaystyle \sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_{n,1}(m) = O_\epsilon \biggl (\frac {M^{2+\epsilon }}{p^{2n}} + \frac {M^{3/2 +\epsilon }}{p^{n}} + M^{1 + \epsilon } \biggr )$;
$\displaystyle \sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_{n,1}(m) = O_\epsilon \biggl (\frac {M^{2+\epsilon }}{p^{2n}} + \frac {M^{3/2 +\epsilon }}{p^{n}} + M^{1 + \epsilon } \biggr )$;(2)
 $\displaystyle \sum _{m=D\ell ^2,\, m\leq M, \ell \text { prime }} r_{n,1}(m)$ and
$\displaystyle \sum _{m=D\ell ^2,\, m\leq M, \ell \text { prime }} r_{n,1}(m)$ and  $\displaystyle \sum _{\ell \leq M,\, \ell \text { prime }} r_{n,1}(\ell )$ are both
$\displaystyle \sum _{\ell \leq M,\, \ell \text { prime }} r_{n,1}(\ell )$ are both
 \begin{equation*} O \biggl (\frac{M^{5/2}}{p^{3n}} + \frac{M^{2}}{p^{2n}} + \frac{M^{3/2}}{p^{n}} + \frac{M}{d_n} + \frac{M^{1/2}}{l(n)_1} \biggr). \end{equation*}
\begin{equation*} O \biggl (\frac{M^{5/2}}{p^{3n}} + \frac{M^{2}}{p^{2n}} + \frac{M^{3/2}}{p^{n}} + \frac{M}{d_n} + \frac{M^{1/2}}{l(n)_1} \biggr). \end{equation*}
Proof. In the proof, for the simplicity of notation, we write ![]() $L'_n, r_n(m)$ for
$L'_n, r_n(m)$ for ![]() $L'_{n,1}, r_{n,1}(m)$.
$L'_{n,1}, r_{n,1}(m)$.
We note that bound (2) is a trivial upper bound from a geometry-of-numbers argument. Indeed, both ![]() $\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)$ and
$\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)$ and ![]() $\sum _{\ell \leq M,\, \ell \text { prime }} r_n(\ell )$ are no greater than
$\sum _{\ell \leq M,\, \ell \text { prime }} r_n(\ell )$ are no greater than ![]() $\sum _{m=1}^M r_n(m)$; we then obtain the desired bound by [Reference Shankar and TangST20, Lemma 4.2.1] and Lemma 9.1.1.
$\sum _{m=1}^M r_n(m)$; we then obtain the desired bound by [Reference Shankar and TangST20, Lemma 4.2.1] and Lemma 9.1.1.
Now we prove part (1). We may assume that there exists a vector ![]() $v_0\in L'_0$ such that
$v_0\in L'_0$ such that ![]() $Q'(v_0)=D\ell _0^2$ for some prime
$Q'(v_0)=D\ell _0^2$ for some prime ![]() $\ell _0$. Otherwise
$\ell _0$. Otherwise ![]() $r_n(m)=0$ for all
$r_n(m)=0$ for all ![]() $m=D\ell ^2$ for any prime
$m=D\ell ^2$ for any prime ![]() $\ell$. Let
$\ell$. Let ![]() $e_1$ denote a primitive vector in
$e_1$ denote a primitive vector in ![]() $L'_n$ such that
$L'_n$ such that ![]() $e_1=p^k v_0$ for some
$e_1=p^k v_0$ for some ![]() $k\in \mathbb {Z}_{\geq 0}$. By definition,
$k\in \mathbb {Z}_{\geq 0}$. By definition, ![]() $p^nL'_0\subset L'_n$ and, thus,
$p^nL'_0\subset L'_n$ and, thus, ![]() $p^nv_0\in L'_n$. Therefore,
$p^nv_0\in L'_n$. Therefore, ![]() $k\leq n$. As
$k\leq n$. As ![]() $e_1$ is primitive in
$e_1$ is primitive in ![]() $L'_n$, we extend it into a basis
$L'_n$, we extend it into a basis ![]() $\{e_1,e_2,\ldots, e_5\}$ of
$\{e_1,e_2,\ldots, e_5\}$ of ![]() $L'_n$. Let
$L'_n$. Let ![]() $\widetilde {L'}_n$ denote the sublattice of
$\widetilde {L'}_n$ denote the sublattice of ![]() $L'_0$ spanned by
$L'_0$ spanned by ![]() $f'_1:=v_0 = e_1/p^k,e_2,\ldots, e_5$; since
$f'_1:=v_0 = e_1/p^k,e_2,\ldots, e_5$; since ![]() $\widetilde {L'}_n$ is a sublattice of
$\widetilde {L'}_n$ is a sublattice of ![]() $L'_0$, then
$L'_0$, then ![]() $Q'|_{\widetilde {L'}_n}$ is still
$Q'|_{\widetilde {L'}_n}$ is still ![]() $\mathbb {Z}$-valued. We have
$\mathbb {Z}$-valued. We have ![]() $Q'(f'_1)=D\ell _0^2=:N$. Let
$Q'(f'_1)=D\ell _0^2=:N$. Let ![]() $f_1 = {f'_1}/{2N}$, and let
$f_1 = {f'_1}/{2N}$, and let ![]() $f_i = e_i - f_1\cdot [f'_1,e_i]'$ for
$f_i = e_i - f_1\cdot [f'_1,e_i]'$ for ![]() $i>1$. As
$i>1$. As ![]() $[f'_1, e_i]\in \mathbb {Z}$ for
$[f'_1, e_i]\in \mathbb {Z}$ for ![]() $i\geq 2$, we then have
$i\geq 2$, we then have ![]() $f_1,f_2, \ldots, f_5 \in (2N)^{-1}\widetilde {L'}_n$ with
$f_1,f_2, \ldots, f_5 \in (2N)^{-1}\widetilde {L'}_n$ with ![]() $[f_i,f_1]'=0$ for
$[f_i,f_1]'=0$ for ![]() $i\geq 2$, and
$i\geq 2$, and ![]() $\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}\supset \widetilde {L'}_n$.
$\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}\supset \widetilde {L'}_n$.
Let ![]() $\widetilde {Q'}$ denote the restriction of
$\widetilde {Q'}$ denote the restriction of ![]() $Q'\otimes \mathbb {Q}$ to
$Q'\otimes \mathbb {Q}$ to ![]() $\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}\subset L'_0\otimes \mathbb {Q}$. By the definition of
$\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}\subset L'_0\otimes \mathbb {Q}$. By the definition of ![]() $f_i$, we have
$f_i$, we have ![]() $\widetilde {Q'}$ is a
$\widetilde {Q'}$ is a ![]() $(2N)^{-1}\mathbb {Z}$-valued quadratic form. Let
$(2N)^{-1}\mathbb {Z}$-valued quadratic form. Let ![]() $\widetilde {l(n)}_1,\ldots, \widetilde {l(n)}_4$ denote the successive minima of
$\widetilde {l(n)}_1,\ldots, \widetilde {l(n)}_4$ denote the successive minima of ![]() $\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}$. As
$\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}$. As ![]() $(2N)^{-1}\widetilde {L'}_n=(2N)^{-1}L'_n+(2N)^{-1}p^{-k}\mathbb {Z} e_1$, then
$(2N)^{-1}\widetilde {L'}_n=(2N)^{-1}L'_n+(2N)^{-1}p^{-k}\mathbb {Z} e_1$, then ![]() $\widetilde {l(n)}_1\cdots \widetilde {l(n)}_i\gg p^{(i-1)n-k}\geq p^{(i-2)n}$ for
$\widetilde {l(n)}_1\cdots \widetilde {l(n)}_i\gg p^{(i-1)n-k}\geq p^{(i-2)n}$ for ![]() $i\geq 2$ (note that
$i\geq 2$ (note that ![]() $k\leq n$ and
$k\leq n$ and ![]() $N$ is absorbed in the implicit constant as
$N$ is absorbed in the implicit constant as ![]() $N$ is independent of
$N$ is independent of ![]() $n,k$). Then the standard geometry-of-numbers argument gives
$n,k$). Then the standard geometry-of-numbers argument gives
On the other hand, on ![]() $\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, for
$\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, for ![]() $v=xf_1+y_2f_2+\cdots + y_5f_5$, we have
$v=xf_1+y_2f_2+\cdots + y_5f_5$, we have ![]() $Q'(v)=({1}/{4D\ell _0^2}) x^2 +\widetilde {Q'}(v_y)$, where
$Q'(v)=({1}/{4D\ell _0^2}) x^2 +\widetilde {Q'}(v_y)$, where ![]() $v_y=y_2f_2+\cdots + y_5f_5$. If
$v_y=y_2f_2+\cdots + y_5f_5$. If ![]() $Q'(v)=D\ell ^2\leq M$, then
$Q'(v)=D\ell ^2\leq M$, then ![]() $\widetilde {Q'}(v_y)\leq Q'(v)\leq M$ and
$\widetilde {Q'}(v_y)\leq Q'(v)\leq M$ and ![]() $4D\ell _0^2\widetilde {Q'}(v_y)=(2D\ell _0\ell -x)(2D\ell _0\ell + x)$. For a given
$4D\ell _0^2\widetilde {Q'}(v_y)=(2D\ell _0\ell -x)(2D\ell _0\ell + x)$. For a given ![]() $v_y$ with
$v_y$ with ![]() $\widetilde {Q'}(v_y)\leq M$, there are at most
$\widetilde {Q'}(v_y)\leq M$, there are at most ![]() $O_\epsilon (M^\epsilon )$ ways to factor
$O_\epsilon (M^\epsilon )$ ways to factor ![]() $4 D\ell _0^2\widetilde {Q'}(v_y)$ into two factors (recall that
$4 D\ell _0^2\widetilde {Q'}(v_y)$ into two factors (recall that ![]() $N=D\ell _0^2$ is independent of
$N=D\ell _0^2$ is independent of ![]() $n,M$ and, hence, gets absorbed in the implicit constant) and, thus, there are at most
$n,M$ and, hence, gets absorbed in the implicit constant) and, thus, there are at most ![]() $O_\epsilon (M^\epsilon )$ possible
$O_\epsilon (M^\epsilon )$ possible ![]() $x$ such that for
$x$ such that for ![]() $v=xf_1+v_y$, we have
$v=xf_1+v_y$, we have ![]() $Q'(v)=D\ell ^2\leq M$ for some prime
$Q'(v)=D\ell ^2\leq M$ for some prime ![]() $\ell$. As
$\ell$. As ![]() $L'_n\subset \operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, then
$L'_n\subset \operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, then ![]() $\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)=O_\epsilon (M^\epsilon Y_n)$, which gives bound (1) by the above bound for
$\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)=O_\epsilon (M^\epsilon Y_n)$, which gives bound (1) by the above bound for ![]() $Y_n$.
$Y_n$.
Proposition 9.1.4 Fix ![]() $D\in \mathbb {Z}_{>0}$. The proportion of primes
$D\in \mathbb {Z}_{>0}$. The proportion of primes ![]() $\ell \leq (M/D)^{1/2}$ such that
$\ell \leq (M/D)^{1/2}$ such that ![]() $D\ell ^2$ is represented by the quadratic form restricted to
$D\ell ^2$ is represented by the quadratic form restricted to ![]() $P_n$ goes to zero as
$P_n$ goes to zero as ![]() $n\rightarrow \infty$.
$n\rightarrow \infty$.
Proof. Let ![]() $R_n$ denote the imaginary quadratic ring with discriminant
$R_n$ denote the imaginary quadratic ring with discriminant ![]() $-d_n^2$. The class group of
$-d_n^2$. The class group of ![]() $R_n$ is in bijection with equivalence classes of binary quadratic forms of discriminant
$R_n$ is in bijection with equivalence classes of binary quadratic forms of discriminant ![]() $-d_n^2$. Let
$-d_n^2$. Let ![]() $\mathfrak {a}$ denote the ideal corresponding to
$\mathfrak {a}$ denote the ideal corresponding to ![]() $Q'$ restricted to
$Q'$ restricted to ![]() $P_n$. Recall that
$P_n$. Recall that ![]() $l(n)_1\rightarrow \infty$ as
$l(n)_1\rightarrow \infty$ as ![]() $n\rightarrow \infty$. Thus, for
$n\rightarrow \infty$. Thus, for ![]() $n\gg 1$, we have that
$n\gg 1$, we have that ![]() $\mathfrak {a}$ is not equivalent to any ideal whose norm is
$\mathfrak {a}$ is not equivalent to any ideal whose norm is ![]() $D$, that is,
$D$, that is, ![]() $(P_n,Q')$ does not represent
$(P_n,Q')$ does not represent ![]() $D$. Note that it suffices to deal with primes
$D$. Note that it suffices to deal with primes ![]() $\ell$ which are relatively prime to
$\ell$ which are relatively prime to ![]() $Dd_n^2$.
$Dd_n^2$.
The correspondence between ideal classes and binary quadratic forms yields that the integer ![]() $D\ell ^2$ is represented by
$D\ell ^2$ is represented by ![]() $(P_n,Q')$ if and only if there exists an invertible ideal
$(P_n,Q')$ if and only if there exists an invertible ideal ![]() $\mathfrak {b}$ equivalent to
$\mathfrak {b}$ equivalent to ![]() $\mathfrak {a}$ with
$\mathfrak {a}$ with ![]() $\operatorname {Nm} \mathfrak {b} = D\ell ^2$. This implies that
$\operatorname {Nm} \mathfrak {b} = D\ell ^2$. This implies that ![]() $\ell = \mathfrak {c}_1 \mathfrak {c}_2$ (i.e. the prime
$\ell = \mathfrak {c}_1 \mathfrak {c}_2$ (i.e. the prime ![]() $\ell$ splits in
$\ell$ splits in ![]() $R_n$), and that
$R_n$), and that ![]() $\mathfrak {b} = \mathfrak {d}\mathfrak {c}_1^2$ or
$\mathfrak {b} = \mathfrak {d}\mathfrak {c}_1^2$ or ![]() $\mathfrak {b} = \mathfrak {d}\mathfrak {c}_2^2$, where
$\mathfrak {b} = \mathfrak {d}\mathfrak {c}_2^2$, where ![]() $\mathfrak {d}$ is some ideal such that
$\mathfrak {d}$ is some ideal such that ![]() $\operatorname {Nm} \mathfrak {d}=D$ (the case
$\operatorname {Nm} \mathfrak {d}=D$ (the case ![]() $\mathfrak {b} = \mathfrak {c}_1 \mathfrak {c}_2$ is ruled out by the above discussion that
$\mathfrak {b} = \mathfrak {c}_1 \mathfrak {c}_2$ is ruled out by the above discussion that ![]() $\mathfrak {a}$ and, therefore,
$\mathfrak {a}$ and, therefore, ![]() $\mathfrak {b}$ is not equivalent to any ideal whose norm is
$\mathfrak {b}$ is not equivalent to any ideal whose norm is ![]() $D$). In other words,
$D$). In other words, ![]() $Q'$ restricted to
$Q'$ restricted to ![]() $P_n$ represents
$P_n$ represents ![]() $D\ell ^2$ if and only if there exist some ideals
$D\ell ^2$ if and only if there exist some ideals ![]() $\mathfrak {c},\mathfrak {d}$ such that
$\mathfrak {c},\mathfrak {d}$ such that ![]() $\operatorname {Nm} \mathfrak {c}=\ell$,
$\operatorname {Nm} \mathfrak {c}=\ell$, ![]() $\operatorname {Nm} \mathfrak {d}=D$, and
$\operatorname {Nm} \mathfrak {d}=D$, and ![]() $\mathfrak {c}^2\mathfrak {d}$ is equivalent to
$\mathfrak {c}^2\mathfrak {d}$ is equivalent to ![]() $\mathfrak {a}$.
$\mathfrak {a}$.
Let ![]() $C$ denote the equivalence classes of ideals
$C$ denote the equivalence classes of ideals ![]() $\mathfrak {c}$ such that
$\mathfrak {c}$ such that ![]() $\mathfrak {c}^2$ is equivalent to
$\mathfrak {c}^2$ is equivalent to ![]() $\mathfrak {a}\mathfrak {d}^{-1}$ for some
$\mathfrak {a}\mathfrak {d}^{-1}$ for some ![]() $\mathfrak {d}$ with
$\mathfrak {d}$ with ![]() $\operatorname {Nm} \mathfrak {d}=D$. As
$\operatorname {Nm} \mathfrak {d}=D$. As ![]() $D$ is fixed, then
$D$ is fixed, then ![]() $C$ is a finite (independent of
$C$ is a finite (independent of ![]() $n$) union of torsors for the
$n$) union of torsors for the ![]() $2$-torsion of the class group of
$2$-torsion of the class group of ![]() $R_n$, when
$R_n$, when ![]() $C$ is non-empty. By genus theory, the cardinality of the two-torsion of the class group of
$C$ is non-empty. By genus theory, the cardinality of the two-torsion of the class group of ![]() $R_n$ is bounded above by the number of divisors of
$R_n$ is bounded above by the number of divisors of ![]() $d_n^2$; this is classical and dates back to Gauss in the case when
$d_n^2$; this is classical and dates back to Gauss in the case when ![]() $R_n$ is the maximal order in its field of fractions, and can be deduced for non-maximal orders from [Reference NeukirchNeu99, Proposition 12.9]. Thus,
$R_n$ is the maximal order in its field of fractions, and can be deduced for non-maximal orders from [Reference NeukirchNeu99, Proposition 12.9]. Thus, ![]() $\# C=O_\epsilon (d_n^{\epsilon })$.
$\# C=O_\epsilon (d_n^{\epsilon })$.
We finish the proof in two cases.
(1) If ![]() $d_n \leq (\log M)^2$, it follows by [Reference Thorner and ZamanTZ18, Corollary 1.3] that the proportion of primes represented by the quadratic form associated to any ideal class
$d_n \leq (\log M)^2$, it follows by [Reference Thorner and ZamanTZ18, Corollary 1.3] that the proportion of primes represented by the quadratic form associated to any ideal class ![]() $\mathfrak {c}$ is
$\mathfrak {c}$ is ![]() $1/d_n$ because
$1/d_n$ because ![]() $d_n\asymp$ the class number of
$d_n\asymp$ the class number of ![]() $R_n$. Thus, the total proportion of
$R_n$. Thus, the total proportion of ![]() $\ell$ such that
$\ell$ such that ![]() $D\ell ^2$ is representable is
$D\ell ^2$ is representable is ![]() $\#C/d_n=O_\epsilon (d_n^{\epsilon -1})$, which goes to zero as
$\#C/d_n=O_\epsilon (d_n^{\epsilon -1})$, which goes to zero as ![]() $d_n\rightarrow \infty$.
$d_n\rightarrow \infty$.
(2) If ![]() $d_n \geq (\log M)^2$, let
$d_n \geq (\log M)^2$, let ![]() $f_{\mathfrak {c}}$ denote the binary quadratic form associated to
$f_{\mathfrak {c}}$ denote the binary quadratic form associated to ![]() $\mathfrak {c}$. Then as in the proof of [Reference Shankar and TangST20, Claim 3.1.9], we have
$\mathfrak {c}$. Then as in the proof of [Reference Shankar and TangST20, Claim 3.1.9], we have
 \begin{align*} \#\{\ell \mid \ell & <(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\leq \#\{m \mid m<(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\\ & =O(M^{1/2}/d_n+M^{1/4}). \end{align*}
\begin{align*} \#\{\ell \mid \ell & <(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\leq \#\{m \mid m<(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\\ & =O(M^{1/2}/d_n+M^{1/4}). \end{align*}Thus, by the above discussion,
which finishes the proof.
The following result gives a bound of Fourier coefficients of the cuspidal part of our theta series in terms of the discriminant of the quadratic lattice.
Proposition 9.1.5 (Duke and Waibel)
Let ![]() $S$ be a fixed finite set of primes. Let
$S$ be a fixed finite set of primes. Let ![]() $\theta$ be the theta series attached to a positive definite quadratic lattice of rank-
$\theta$ be the theta series attached to a positive definite quadratic lattice of rank-![]() $5$ with discriminant
$5$ with discriminant ![]() $D_\theta$ such that all prime factors of
$D_\theta$ such that all prime factors of ![]() $D_\theta$ lie in
$D_\theta$ lie in ![]() $S$. Write
$S$. Write ![]() $\theta =E+G$, where
$\theta =E+G$, where ![]() $E$ is an Eisenstein series and
$E$ is an Eisenstein series and ![]() $G$ is a cusp form. Then, there exist absolutely bounded positive constants
$G$ is a cusp form. Then, there exist absolutely bounded positive constants ![]() $N_0$ and
$N_0$ and ![]() $C$ such that for all
$C$ such that for all ![]() $m\in T$ (the set
$m\in T$ (the set ![]() $T$ defined in § 4.3.3), the
$T$ defined in § 4.3.3), the ![]() $m$th Fourier coefficient
$m$th Fourier coefficient ![]() $q_G(m)$ of
$q_G(m)$ of ![]() $G$ satisfies that
$G$ satisfies that ![]() $q_G(m) \leq CD_\theta ^{N_0} m^{1 + 1/4}$.
$q_G(m) \leq CD_\theta ^{N_0} m^{1 + 1/4}$.
By Remark 7.2.2, we have that ![]() $\operatorname {disc} L'_{n,i}$ are independent of
$\operatorname {disc} L'_{n,i}$ are independent of ![]() $n,i$ away from
$n,i$ away from ![]() $p$ and hence all the theta series attached to these lattices satisfy the assumption on
$p$ and hence all the theta series attached to these lattices satisfy the assumption on ![]() $D_\theta$.
$D_\theta$.
An analogous result of Proposition 9.1.5 was proved by Duke in the case of ternary quadratic forms. The main steps of his proof carry through in this case too, so we will be content with just sketching his proof.
Proof. The proof of [Reference DukeDuk05, Lemma 1] and the discussion on [Reference DukeDuk05, p.40] apply to rank-![]() $5$ quadratic forms (with suitable modification of the power of
$5$ quadratic forms (with suitable modification of the power of ![]() $D_\theta$) and we have that the Petersson norm of
$D_\theta$) and we have that the Petersson norm of ![]() $G$ satisfies
$G$ satisfies ![]() $\|G\|=O(D_\theta ^{N_1})$ for some absolute constant
$\|G\|=O(D_\theta ^{N_1})$ for some absolute constant ![]() $N_1$ (here we use the fact that the level
$N_1$ (here we use the fact that the level ![]() $N_\theta$ of
$N_\theta$ of ![]() $G$ is
$G$ is ![]() $O(D_\theta )$.
$O(D_\theta )$.
Thus, to obtain a bound for ![]() $q_G(m)$, we only need to bound the Fourier coefficients
$q_G(m)$, we only need to bound the Fourier coefficients ![]() $a_j(m)$ for an orthonormal basis of the space of cusp forms of weight
$a_j(m)$ for an orthonormal basis of the space of cusp forms of weight ![]() $5/2$ and level
$5/2$ and level ![]() $N_\theta$ (with respect to certain quadratic character determined by
$N_\theta$ (with respect to certain quadratic character determined by ![]() $\theta$). Now we apply [Reference WaibelWai18, Theorem 1]. Using the notation there, we have that if
$\theta$). Now we apply [Reference WaibelWai18, Theorem 1]. Using the notation there, we have that if ![]() $m=\ell$, then
$m=\ell$, then ![]() $t=\ell$,
$t=\ell$, ![]() $v=1$,
$v=1$, ![]() $w=1$,
$w=1$, ![]() $(m,N_\theta )=O(1)$; if
$(m,N_\theta )=O(1)$; if ![]() $m=D\ell ^2$, then
$m=D\ell ^2$, then ![]() $t=D, v\asymp 1, w\asymp \ell, (m,N_\theta )=O(1)$. Thus,
$t=D, v\asymp 1, w\asymp \ell, (m,N_\theta )=O(1)$. Thus, ![]() $|a_j(m)|\ll _\epsilon m^{{27}/{28}+\epsilon }D_\theta ^\epsilon$ for
$|a_j(m)|\ll _\epsilon m^{{27}/{28}+\epsilon }D_\theta ^\epsilon$ for ![]() $m=\ell$ and
$m=\ell$ and ![]() $|a_j(m)|\ll _\epsilon m^{{3}/{4}+\epsilon }D_\theta ^\epsilon$, which gives the desired bound once we combine with the above estimate of
$|a_j(m)|\ll _\epsilon m^{{3}/{4}+\epsilon }D_\theta ^\epsilon$, which gives the desired bound once we combine with the above estimate of ![]() $\|G\|$.
$\|G\|$.
9.2 Proof of Proposition 7.2.5 in the Siegel case
Notation as in § 7.2.3 and Corollary 7.2.4. For a supersingular point ![]() $P$ with non-zero local intersection number, we first prove that it must be superspecial in the settings of Theorems 1 and 5 and Remark 4 when
$P$ with non-zero local intersection number, we first prove that it must be superspecial in the settings of Theorems 1 and 5 and Remark 4 when ![]() $p$ splits in
$p$ splits in ![]() $F$ and then estimate
$F$ and then estimate ![]() $\sum _{m\in T_M-S_M}r_{n,i}(m)$ with respect to different ranges of
$\sum _{m\in T_M-S_M}r_{n,i}(m)$ with respect to different ranges of ![]() $n$.
$n$.
Definition 9.2.1 Given absolute constants ![]() $\epsilon _0,\epsilon _1>0$ (we choose
$\epsilon _0,\epsilon _1>0$ (we choose ![]() $\epsilon _0,\epsilon _1$ in the proof of Proposition 7.2.5), the ranges of
$\epsilon _0,\epsilon _1$ in the proof of Proposition 7.2.5), the ranges of ![]() $n$ are defined as follows:
$n$ are defined as follows:
(i)
 $n$ is small if
$n$ is small if  $n \leq \epsilon _0 \log _p M$;
$n \leq \epsilon _0 \log _p M$;(ii)
 $n$ is in the lower medium range if
$n$ is in the lower medium range if  $\epsilon _0 \log _p M < n \leq \frac {3}{4} \log _p M$;
$\epsilon _0 \log _p M < n \leq \frac {3}{4} \log _p M$;(iii)
 $n$ is in the upper medium range if
$n$ is in the upper medium range if  $\frac {3}{4} \log _p M < n \leq (1 + \epsilon _1)\log _p M$;
$\frac {3}{4} \log _p M < n \leq (1 + \epsilon _1)\log _p M$;(iv)
 $n$ is large if
$n$ is large if  $n > (1 + \epsilon _1)\log _p M$.
$n > (1 + \epsilon _1)\log _p M$.
Proof Proof of Proposition 7.2.5 for Theorem 1(1) and Remark 4 with  $p$ split in
$p$ split in  $F$
$F$
For ![]() $m\in T_M$, we have
$m\in T_M$, we have ![]() $m=D\ell ^2$, where
$m=D\ell ^2$, where ![]() $D$ is a non-zero quadratic residue mod
$D$ is a non-zero quadratic residue mod ![]() $p$. Then by § 4.4.3(2), any supergeneric point does not lie on
$p$. Then by § 4.4.3(2), any supergeneric point does not lie on ![]() $Z(m)$. Hence, we only consider
$Z(m)$. Hence, we only consider ![]() $P$ superspecial.
$P$ superspecial.
Recall from Lemma 7.1.1 that for any ![]() $S_M$ such that
$S_M$ such that ![]() $\#S_M=o(\# T_M)$, we have
$\#S_M=o(\# T_M)$, we have
We first prove that there exists ![]() $S_M$ such that
$S_M$ such that ![]() $\#S_M=o(\# T_M)$ and the contribution from
$\#S_M=o(\# T_M)$ and the contribution from ![]() $n\geq \epsilon _0 \log _p M$ is
$n\geq \epsilon _0 \log _p M$ is ![]() $o(M^2/\log M)$.
$o(M^2/\log M)$.
The lower medium range. By Proposition 9.1.3(1),
 \begin{align*} & \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{m=D\ell^2,\, m\leq M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} Ap^n r_{n,1}(m)\\ &\quad = A\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} p^n O_\epsilon (M^{2+\epsilon}/p^{2n} + M^{3/2+\epsilon}/p^n + M^{1+\epsilon})\\ &\quad=O_\epsilon(M^{2+\epsilon-\epsilon_0} + M^{3/2 + \epsilon} \log M + M^{7/4 + \epsilon}), \end{align*}
\begin{align*} & \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{m=D\ell^2,\, m\leq M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} Ap^n r_{n,1}(m)\\ &\quad = A\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} p^n O_\epsilon (M^{2+\epsilon}/p^{2n} + M^{3/2+\epsilon}/p^n + M^{1+\epsilon})\\ &\quad=O_\epsilon(M^{2+\epsilon-\epsilon_0} + M^{3/2 + \epsilon} \log M + M^{7/4 + \epsilon}), \end{align*}
which is ![]() $o(M^2/\log M)$ once we take
$o(M^2/\log M)$ once we take ![]() $\epsilon <\min \{\epsilon _0,1/4\}$.
$\epsilon <\min \{\epsilon _0,1/4\}$.
The upper medium range. We treat this part in two ways according to whether ![]() $d_{n_0} \leq M^{1/8}$, where
$d_{n_0} \leq M^{1/8}$, where ![]() $n_0 = \lceil \frac {3}{4}\log _p M\rceil$.
$n_0 = \lceil \frac {3}{4}\log _p M\rceil$.
(1) If ![]() $d_{n_0} \geq M^{1/8}$, then we bound this part using geometry-of-numbers. As
$d_{n_0} \geq M^{1/8}$, then we bound this part using geometry-of-numbers. As ![]() $L'_{n,1}\subset L'_{n_0,1}$ for all
$L'_{n,1}\subset L'_{n_0,1}$ for all ![]() $n\geq n_0$, then, by definition,
$n\geq n_0$, then, by definition, ![]() $d_n\geq d_{n_0}\geq M^{1/8}$. By Proposition 9.1.3(2), we have that
$d_n\geq d_{n_0}\geq M^{1/8}$. By Proposition 9.1.3(2), we have that
 \begin{align*} &\sum_{m\in T_M-S_M}\sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\sum_{m=D\ell^2,\, m\leq M} Ap^n r_{n,1}(m)\\ &\quad = O((M + M^{5/4} + M^{3/2} + M^{15/8 + \epsilon_1} + M^{3/2 + \epsilon_1})\log M), \end{align*}
\begin{align*} &\sum_{m\in T_M-S_M}\sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\sum_{m=D\ell^2,\, m\leq M} Ap^n r_{n,1}(m)\\ &\quad = O((M + M^{5/4} + M^{3/2} + M^{15/8 + \epsilon_1} + M^{3/2 + \epsilon_1})\log M), \end{align*}
which is ![]() $o(M^2/\log M)$ once we take
$o(M^2/\log M)$ once we take ![]() $\epsilon _1<1/8$.
$\epsilon _1<1/8$.
(2) If ![]() $d_{n_0} < M^{1/8}$, we control this part by putting
$d_{n_0} < M^{1/8}$, we control this part by putting ![]() $m$ in this range into
$m$ in this range into ![]() $S_M$. More precisely, consider
$S_M$. More precisely, consider ![]() $R_M:=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. By our assumption,
$R_M:=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. By our assumption, ![]() $d_{n_0}^2M< M^{5/4}=o(p^{2n_0})$ and by Lemma 9.1.2, for
$d_{n_0}^2M< M^{5/4}=o(p^{2n_0})$ and by Lemma 9.1.2, for ![]() $M\gg 1$, if
$M\gg 1$, if ![]() $m\in R_M$, then
$m\in R_M$, then ![]() $m$ is represented by
$m$ is represented by ![]() $Q'\!\mid _{P_{n_0}}$, which is a binary quadratic form. Then by Proposition 9.1.4 (note that
$Q'\!\mid _{P_{n_0}}$, which is a binary quadratic form. Then by Proposition 9.1.4 (note that ![]() $n_0\rightarrow \infty$ as
$n_0\rightarrow \infty$ as ![]() $M\rightarrow \infty$),
$M\rightarrow \infty$), ![]() $\#R_M=o(M^{1/2}/\log M)=o(\# T_M)$. Thus, we may choose
$\#R_M=o(M^{1/2}/\log M)=o(\# T_M)$. Thus, we may choose ![]() $S_M$ such that
$S_M$ such that ![]() $S_M\supset R_M$ and then
$S_M\supset R_M$ and then
 \[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\frac{3}{4}\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\frac{3}{4}\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
The large ![]() $n$. Let
$n$. Let ![]() $n_0=\lceil (1+\epsilon _1)\log _p M\rceil$ and let
$n_0=\lceil (1+\epsilon _1)\log _p M\rceil$ and let ![]() $R_M':=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. We show that
$R_M':=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. We show that ![]() $\#R'_M=o(M^{1/2}/\log M)$ and, thus, we may choose
$\#R'_M=o(M^{1/2}/\log M)$ and, thus, we may choose ![]() $S_M$ such that
$S_M$ such that ![]() $S_M\supset R'_M$ and then
$S_M\supset R'_M$ and then
 \[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
We bound the size of ![]() $R'_M$ case by case depending on the size of
$R'_M$ case by case depending on the size of ![]() $d_{n_0}, l(n_0)_1$.
$d_{n_0}, l(n_0)_1$.
Case (1): ![]() $d_{n_0} \leq M^{1/2+\epsilon _2}$ for some absolute constant
$d_{n_0} \leq M^{1/2+\epsilon _2}$ for some absolute constant ![]() $\epsilon _2<\epsilon _1/2$. Then
$\epsilon _2<\epsilon _1/2$. Then ![]() $d_{n_0}\leq M^{1/2+\epsilon _2}< p^{n_0/2}$ and
$d_{n_0}\leq M^{1/2+\epsilon _2}< p^{n_0/2}$ and ![]() $M< p^{n_0-\epsilon _1}$. By Lemma 9.1.2, for
$M< p^{n_0-\epsilon _1}$. By Lemma 9.1.2, for ![]() $M\gg 1$, if
$M\gg 1$, if ![]() $m\in R'_M$, then
$m\in R'_M$, then ![]() $m$ is represented by
$m$ is represented by ![]() $Q'\!\mid _{P_{n_0}}$. By Proposition 9.1.4,
$Q'\!\mid _{P_{n_0}}$. By Proposition 9.1.4, ![]() $\#R'_M=o(M^{1/2}/\log M)$.
$\#R'_M=o(M^{1/2}/\log M)$.
Case (2): ![]() $d_{n_0} > M^{1/2+\epsilon _2}$ for all
$d_{n_0} > M^{1/2+\epsilon _2}$ for all ![]() $\epsilon _2<\epsilon _1/2$ and
$\epsilon _2<\epsilon _1/2$ and ![]() $l(n_0)_1>M^{\epsilon _3}$ for some absolute constant
$l(n_0)_1>M^{\epsilon _3}$ for some absolute constant ![]() $\epsilon _3>0$. We have
$\epsilon _3>0$. We have ![]() $\#R'_M\leq \#\{v\in L'_{n_0,1}\mid Q'(v)\in T_M\}$, which is
$\#R'_M\leq \#\{v\in L'_{n_0,1}\mid Q'(v)\in T_M\}$, which is ![]() $O(M^{1/2-\epsilon _1}+M^{1/2-\epsilon _2}+M^{1/2}/l(n_0)_1)=o(M^{1/2}/\log M)$ by Proposition 9.1.3(2).
$O(M^{1/2-\epsilon _1}+M^{1/2-\epsilon _2}+M^{1/2}/l(n_0)_1)=o(M^{1/2}/\log M)$ by Proposition 9.1.3(2).
Case (3): ![]() $d_{n_0} > M^{1/2+\epsilon _2}$ for some
$d_{n_0} > M^{1/2+\epsilon _2}$ for some ![]() $\epsilon _2<\epsilon _1/2$ and
$\epsilon _2<\epsilon _1/2$ and ![]() $l(n_0)_1\leq M^{\epsilon _3}$ for some
$l(n_0)_1\leq M^{\epsilon _3}$ for some ![]() $\epsilon _3<\epsilon _2$. Then
$\epsilon _3<\epsilon _2$. Then ![]() $l(n_0)_2=d_{n_0}/l(n_0)_1>M^{1/2}$. In other words, any vector
$l(n_0)_2=d_{n_0}/l(n_0)_1>M^{1/2}$. In other words, any vector ![]() $v\in L'_{n_0,1}$ which is not a scalar multiple of the chosen vector
$v\in L'_{n_0,1}$ which is not a scalar multiple of the chosen vector ![]() $v_0$ of the minimum length has
$v_0$ of the minimum length has ![]() $Q'_{n_0}(v)\leq l(n_0)_2^2>M$. Therefore, any
$Q'_{n_0}(v)\leq l(n_0)_2^2>M$. Therefore, any ![]() $m\in R'_M$ has to be represented by the rank-
$m\in R'_M$ has to be represented by the rank-![]() $1$ quadratic form spanned by
$1$ quadratic form spanned by ![]() $v_0$. As
$v_0$. As ![]() $M\rightarrow \infty$, we have
$M\rightarrow \infty$, we have ![]() $l(n_0)_1\rightarrow \infty$. Thus, once
$l(n_0)_1\rightarrow \infty$. Thus, once ![]() $M$ is large enough such that
$M$ is large enough such that ![]() $l(n_0)_1^2>D$, then this rank-
$l(n_0)_1^2>D$, then this rank-![]() $1$ quadratic form would represent at most one element in
$1$ quadratic form would represent at most one element in ![]() $T_M$ and, hence,
$T_M$ and, hence, ![]() $\#R'_M=o(\# T_M)$.
$\#R'_M=o(\# T_M)$.
In conclusion, taking ![]() $S_M=R_M\cup R'_M$, we have
$S_M=R_M\cup R'_M$, we have ![]() $\#S_M=o(\# T_M)$ and
$\#S_M=o(\# T_M)$ and
 \[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{\infty}\!\!\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=o(M^2/\log M). \]
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{\infty}\!\!\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=o(M^2/\log M). \]
The small ![]() $n$. We follow the notation and the idea of the proof in Lemma 8.2.2.
$n$. We follow the notation and the idea of the proof in Lemma 8.2.2.
We enlarge ![]() $L'_{n,1}$ as in the proof of Lemma 9.1.1; also let
$L'_{n,1}$ as in the proof of Lemma 9.1.1; also let ![]() $w$ be the vector which decays very rapidly in the decay lemma for superspecial points, then we enlarge
$w$ be the vector which decays very rapidly in the decay lemma for superspecial points, then we enlarge ![]() $L'_{n,2}$ such that
$L'_{n,2}$ such that ![]() $L'_{n,2}\otimes \mathbb {Z}_p=L'_{n,1}\otimes \mathbb {Z}_p+p^{n+1}\mathbb {Z}_pw$. Then
$L'_{n,2}\otimes \mathbb {Z}_p=L'_{n,1}\otimes \mathbb {Z}_p+p^{n+1}\mathbb {Z}_pw$. Then ![]() $\operatorname {disc} L'_{n,i}\asymp p^{6n}$ with the implicit constant only depending on
$\operatorname {disc} L'_{n,i}\asymp p^{6n}$ with the implicit constant only depending on ![]() $P$. Note that Corollary 7.2.4 still holds with the new definitions of
$P$. Note that Corollary 7.2.4 still holds with the new definitions of ![]() $L'_{n,i}$.
$L'_{n,i}$.
Let
 \begin{gather*} E=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{gather*}
\begin{gather*} E=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{gather*}
Note that here the Eisenstein series ![]() $E$ and the cusp form
$E$ and the cusp form ![]() $G$ depend on
$G$ depend on ![]() $M$.
$M$.
As ![]() $\operatorname {disc} L'_{n,i}=O(p^{6\epsilon _0 \log _p M})=O(M^{6\epsilon _0})$ for
$\operatorname {disc} L'_{n,i}=O(p^{6\epsilon _0 \log _p M})=O(M^{6\epsilon _0})$ for ![]() $n\leq \epsilon _0 \log _p M$, then by Proposition 9.1.5, the
$n\leq \epsilon _0 \log _p M$, then by Proposition 9.1.5, the ![]() $m$th Fourier coefficient
$m$th Fourier coefficient
 \[ q_G(m)\ll (M^{6\epsilon_0})^{N_0}m^{5/4}\sum_{n=0}^{[\epsilon_0 \log M]}p^n\ll M^{(6N_0+1)\epsilon_0} m^{5/4} \]
\[ q_G(m)\ll (M^{6\epsilon_0})^{N_0}m^{5/4}\sum_{n=0}^{[\epsilon_0 \log M]}p^n\ll M^{(6N_0+1)\epsilon_0} m^{5/4} \]
and ![]() $\sum _{m\in T_M-S_M} q_G(m)=O(M^{(6N_0+1)\epsilon _0+7/4})=o(M^2/\log M)$ once we take
$\sum _{m\in T_M-S_M} q_G(m)=O(M^{(6N_0+1)\epsilon _0+7/4})=o(M^2/\log M)$ once we take ![]() $\epsilon _0<(24N_0+4)^{-1}$.
$\epsilon _0<(24N_0+4)^{-1}$.
The computation for the Eisenstein part is the same as in the proof of Lemma 8.2.2. More precisely, because ![]() $p\nmid m$, by Lemma 4.4.6(1) and (3), we have
$p\nmid m$, by Lemma 4.4.6(1) and (3), we have
 \[ \frac{q(m)}{|q_L(m)|}\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^{[\epsilon_0 \log M]}\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\leq \frac{11}{12}\cdot\frac{A}{p-1}. \]
\[ \frac{q(m)}{|q_L(m)|}\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^{[\epsilon_0 \log M]}\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\leq \frac{11}{12}\cdot\frac{A}{p-1}. \]Thus, we finish the proof by putting all parts together and using Corollary 7.2.4.
Proof of Proposition 7.2.5 for Theorem 5 As every ![]() $m\in T_M$ in this case is a non-zero quadratic residue
$m\in T_M$ in this case is a non-zero quadratic residue ![]() $\bmod p$, hence by § 4.4.3(2), all supersingular points on
$\bmod p$, hence by § 4.4.3(2), all supersingular points on ![]() $Z(m)$ are superspecial. The idea of the proof is similar to the case of Theorem 1(1).
$Z(m)$ are superspecial. The idea of the proof is similar to the case of Theorem 1(1).
By Lemma 7.1.1, we have ![]() $\sum _{m\in T_M-S_M}g_P(m)\asymp M^{5/2}(\log M)^{-1}$. We construct
$\sum _{m\in T_M-S_M}g_P(m)\asymp M^{5/2}(\log M)^{-1}$. We construct ![]() $S_M$ by large
$S_M$ by large ![]() $n$. More precisely, we set
$n$. More precisely, we set ![]() $S_M=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$, where
$S_M=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$, where ![]() $n_0=\lceil (1+\epsilon _1)\log _p M\rceil$. Then
$n_0=\lceil (1+\epsilon _1)\log _p M\rceil$. Then
 \begin{align*} \#S_M \leq \#\{v\in L'_{n_0,1}\mid Q'(v)\leq M\}&=O(M^{5/2}/p^{3n_0}+M^2/p^{2n_0}+M^{3/2}/p^{n_0}+M/d_{n_0}+M^{1/2})\\ &=O(M^{1/2}+M/d_{n_0}), \end{align*}
\begin{align*} \#S_M \leq \#\{v\in L'_{n_0,1}\mid Q'(v)\leq M\}&=O(M^{5/2}/p^{3n_0}+M^2/p^{2n_0}+M^{3/2}/p^{n_0}+M/d_{n_0}+M^{1/2})\\ &=O(M^{1/2}+M/d_{n_0}), \end{align*}
which is ![]() $o(M/\log M)=o(\# T_M)$ if there exists an absolute constant
$o(M/\log M)=o(\# T_M)$ if there exists an absolute constant ![]() $\epsilon >0$ such that
$\epsilon >0$ such that ![]() ${d_{n_0}\gg M^\epsilon}$. If not, then by Lemma 9.1.2, we have that for
${d_{n_0}\gg M^\epsilon}$. If not, then by Lemma 9.1.2, we have that for ![]() $M\gg 1$, all
$M\gg 1$, all ![]() $m\in S_M$ representable by the binary quadratic form
$m\in S_M$ representable by the binary quadratic form ![]() $Q'|_{P_{n_0}}$. As
$Q'|_{P_{n_0}}$. As ![]() $d_{n_0}\rightarrow \infty$, the density of primes representable by
$d_{n_0}\rightarrow \infty$, the density of primes representable by ![]() $Q'|_{P_{n_0}}$ goes to zero, that is, we still have
$Q'|_{P_{n_0}}$ goes to zero, that is, we still have ![]() $\#S_M=o(\# T_M)$. With this choice of
$\#S_M=o(\# T_M)$. With this choice of ![]() $S_M$, we have
$S_M$, we have
 \[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
For ![]() $n$ in the medium range,
$n$ in the medium range,
 \[ \sum_{m\in T_M-S_M}\sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\ll \sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\!\! p^n \sum_{m\leq M} r_{n,1}(m)=o(M^{5/2}/\log M) \]
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\ll \sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\!\! p^n \sum_{m\leq M} r_{n,1}(m)=o(M^{5/2}/\log M) \]
because ![]() $\sum _{m\leq M} r_{n,1}(m)=O(M^{5/2}/p^{3n}+M^2/p^{2n}+M^{3/2}/p^n+M)$. The estimate for small
$\sum _{m\leq M} r_{n,1}(m)=O(M^{5/2}/p^{3n}+M^2/p^{2n}+M^{3/2}/p^n+M)$. The estimate for small ![]() $n$ is exactly as in the case for Theorem 1(1) above and, thus, we finish the proof.
$n$ is exactly as in the case for Theorem 1(1) above and, thus, we finish the proof.
9.3 Contribution from non-supersingular points and conclusions
To finish the proof, we only need to show that ![]() $\sum _{m\in T_M-S_M} l_P(m)$ for non-supersingular points
$\sum _{m\in T_M-S_M} l_P(m)$ for non-supersingular points ![]() $P$ are
$P$ are ![]() $o(\sum _{m\in T_M-S_M}C.Z(m))$, which is
$o(\sum _{m\in T_M-S_M}C.Z(m))$, which is ![]() $o(M^2/\log M)$ for Theorem 1(1) and Remark 4 and is
$o(M^2/\log M)$ for Theorem 1(1) and Remark 4 and is ![]() $o(M^{5/2}/\log M)$ for Theorem 5. We use the notation in Lemma 7.3.2 for ordinary points.
$o(M^{5/2}/\log M)$ for Theorem 5. We use the notation in Lemma 7.3.2 for ordinary points.
Recall that an abelian surface is ordinary, almost ordinary (i.e. its Newton polygon has slopes ![]() $0,1/2,1$), or supersingular.
$0,1/2,1$), or supersingular.
Lemma 9.3.1 If ![]() $P$ is almost ordinary or if
$P$ is almost ordinary or if ![]() $P$ is ordinary with
$P$ is ordinary with ![]() $\operatorname {rk}_{\mathbb {Z}} L_0\neq 3$, then
$\operatorname {rk}_{\mathbb {Z}} L_0\neq 3$, then
 \[ \sum_{m\in T_M-S_M} l_P(m)=o\biggl(\sum_{m\in T_M-S_M}C.Z(m)\biggr). \]
\[ \sum_{m\in T_M-S_M} l_P(m)=o\biggl(\sum_{m\in T_M-S_M}C.Z(m)\biggr). \]Proof. By the classification of endomorphism rings of char ![]() $p$ abelian surfaces (see, for instance, [Reference TateTat71, Theorem 1]), we see that if the abelian surface corresponding to
$p$ abelian surfaces (see, for instance, [Reference TateTat71, Theorem 1]), we see that if the abelian surface corresponding to ![]() $P$ has almost ordinary reduction, then its lattice of special endomorphisms has rank at most
$P$ has almost ordinary reduction, then its lattice of special endomorphisms has rank at most ![]() $1$. On the other hand, if
$1$. On the other hand, if ![]() $P$ is ordinary, then
$P$ is ordinary, then ![]() $\operatorname {rk}_{\mathbb {Z}} L_0$ is odd and, hence,
$\operatorname {rk}_{\mathbb {Z}} L_0$ is odd and, hence, ![]() $\operatorname {rk}_{\mathbb {Z}} L_0=1$. In both cases, let
$\operatorname {rk}_{\mathbb {Z}} L_0=1$. In both cases, let ![]() $a_n x^2$ denote the quadratic form with one variable given by
$a_n x^2$ denote the quadratic form with one variable given by ![]() $Q'$ restricted to the lattice of special endomorphisms of the abelian surface mod
$Q'$ restricted to the lattice of special endomorphisms of the abelian surface mod ![]() $t^n$. As the lattice mod
$t^n$. As the lattice mod ![]() $t^{n+1}$ is a sublattice of that mod
$t^{n+1}$ is a sublattice of that mod ![]() $t^n$, we have
$t^n$, we have ![]() $a_n\mid a_{n+1}$.
$a_n\mid a_{n+1}$.
As ![]() $C$ does not have any global special endomorphisms, we have
$C$ does not have any global special endomorphisms, we have ![]() $a_n\rightarrow \infty$ and, hence,
$a_n\rightarrow \infty$ and, hence, ![]() $a_nx^2$ does not represent any element in
$a_nx^2$ does not represent any element in ![]() $T_M\subset \{D\ell ^2\mid \ell \text { prime}\}$ or
$T_M\subset \{D\ell ^2\mid \ell \text { prime}\}$ or ![]() $T_M\subset \{\ell \mid \ell \text { prime}\}$ once
$T_M\subset \{\ell \mid \ell \text { prime}\}$ once ![]() $n\gg 1$ (with then implicit constant only depending on
$n\gg 1$ (with then implicit constant only depending on ![]() $P$).
$P$).
Thus, ![]() $\sum _{m\in T_M-S_M} l_P(m)=\sum _{m\in T_M-S_M} O(M^{1/2})=o(\sum _{m\in T_M-S_M}C.Z(m))$.
$\sum _{m\in T_M-S_M} l_P(m)=\sum _{m\in T_M-S_M} O(M^{1/2})=o(\sum _{m\in T_M-S_M}C.Z(m))$.
Now it only remains to treat the case when ![]() $P$ is ordinary and
$P$ is ordinary and ![]() $\operatorname {rk}_{\mathbb {Z}}L_0=3$. We first construct
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. We first construct ![]() $S_M$ for such
$S_M$ for such ![]() $P$.
$P$.
Lemma 9.3.2 Given ![]() $M$, set
$M$, set ![]() $n_0=\lceil (1+\epsilon _0)\log _p M\rceil$ and
$n_0=\lceil (1+\epsilon _0)\log _p M\rceil$ and ![]() $S_M=\{m\in T_M\mid \exists v\in L_{n_0} \text { with} Q'(v)=m\}$. Then
$S_M=\{m\in T_M\mid \exists v\in L_{n_0} \text { with} Q'(v)=m\}$. Then ![]() $\#S_M=o(\# T_M)$.
$\#S_M=o(\# T_M)$.
Proof. By a geometry-of-numbers argument and Lemma 7.3.2, we have
where ![]() $a_{n_0}$ is the minimal length of a non-zero vector in
$a_{n_0}$ is the minimal length of a non-zero vector in ![]() $L_{n_0}$ and
$L_{n_0}$ and ![]() $b_{n_0}$ is the minimal root discriminant of a rank
$b_{n_0}$ is the minimal root discriminant of a rank ![]() $2$ sublattice in
$2$ sublattice in ![]() $L_{n_0}$. Since
$L_{n_0}$. Since ![]() $C$ does not have any global special endomorphisms, we have
$C$ does not have any global special endomorphisms, we have ![]() $a_{n_0},b_{n_0}\rightarrow \infty$ as
$a_{n_0},b_{n_0}\rightarrow \infty$ as ![]() $M\rightarrow \infty$. Fix
$M\rightarrow \infty$. Fix ![]() $0<\epsilon _1<\epsilon _0/4$. We prove the desired estimate by a case-by-case discussion based on the size of
$0<\epsilon _1<\epsilon _0/4$. We prove the desired estimate by a case-by-case discussion based on the size of ![]() $a_{n_0},b_{n_0}$.
$a_{n_0},b_{n_0}$.
Case (1): ![]() $a_{n_0}< M^{\epsilon _1}$ and
$a_{n_0}< M^{\epsilon _1}$ and ![]() $b_{n_0}>M^{1/2+2\epsilon _1}$. Then we conclude as in the proof Proposition 7.2.5 for Theorem 1(1) for large
$b_{n_0}>M^{1/2+2\epsilon _1}$. Then we conclude as in the proof Proposition 7.2.5 for Theorem 1(1) for large ![]() $n$ case (3). More precisely, all
$n$ case (3). More precisely, all ![]() $v\in L_{n_0}$ with
$v\in L_{n_0}$ with ![]() $Q'(v)\leq M$ lie in a rank-
$Q'(v)\leq M$ lie in a rank-![]() $1$ sublattice of
$1$ sublattice of ![]() $L_{n_0}$ and, thus, the total number of such
$L_{n_0}$ and, thus, the total number of such ![]() $v$ is
$v$ is ![]() $o(\# T_M)$.
$o(\# T_M)$.
Case (2): ![]() $a_{n_0}\geq M^{\epsilon _1}$ and
$a_{n_0}\geq M^{\epsilon _1}$ and ![]() $b_{n_0}>M^{1/2+2\epsilon _1}$. Then
$b_{n_0}>M^{1/2+2\epsilon _1}$. Then
Case (3): ![]() $b_{n_0}\leq M^{1/2+2\epsilon _1}$. Then
$b_{n_0}\leq M^{1/2+2\epsilon _1}$. Then ![]() $p^{n_0/2}=M^{1/2+\epsilon _0/2}\geq b_{n_0}$ and by Lemma 9.1.2 (note the proof of this lemma applies to this case), for
$p^{n_0/2}=M^{1/2+\epsilon _0/2}\geq b_{n_0}$ and by Lemma 9.1.2 (note the proof of this lemma applies to this case), for ![]() $M\gg 1$, if
$M\gg 1$, if ![]() $m\in S_M$, then
$m\in S_M$, then ![]() $m$ is represented by the binary quadratic form given by restricting
$m$ is represented by the binary quadratic form given by restricting ![]() $Q'$ to the rank-
$Q'$ to the rank-![]() $2$ sublattice in
$2$ sublattice in ![]() $L_{n_0}$ with minimal discriminant(=
$L_{n_0}$ with minimal discriminant(=![]() $b_{n_0}^2$). As
$b_{n_0}^2$). As ![]() $b_{n_0}\rightarrow \infty$, then we conclude by Proposition 9.1.4 for Theorem 1(1) and Remark 4 and by the fact that the density of primes represented by such quadratic forms goes to zero for Theorem 5.
$b_{n_0}\rightarrow \infty$, then we conclude by Proposition 9.1.4 for Theorem 1(1) and Remark 4 and by the fact that the density of primes represented by such quadratic forms goes to zero for Theorem 5.
Now we estimate the total local contribution at an ordinary point with ![]() $\operatorname {rk}_{\mathbb {Z}}L_0=3$.
$\operatorname {rk}_{\mathbb {Z}}L_0=3$.
Proposition 9.3.3 Assume ![]() $P$ is ordinary with
$P$ is ordinary with ![]() $\operatorname {rk}_{\mathbb {Z}}L_0=3$. After possible enlarging
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. After possible enlarging ![]() $S_M$ in Lemma 9.3.2 (still with
$S_M$ in Lemma 9.3.2 (still with ![]() $\#S_M=o(\#T_M)$), we have
$\#S_M=o(\#T_M)$), we have
 \[ \sum_{m\in T_M-S_M} l_P(m)=o \biggl (\sum_{m\in T_M-S_M}C.Z(m) \biggr ). \]
\[ \sum_{m\in T_M-S_M} l_P(m)=o \biggl (\sum_{m\in T_M-S_M}C.Z(m) \biggr ). \]Proof. Notation as in Lemma 7.3.2. By Lemmas 7.2.1, 7.3.2, and 9.3.2, we have
 \begin{align*} \sum_{m\in T_M-S_M} l_P(m)&=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^{[(1+\epsilon_0)\log_p M]}(p^n-p^{n-1})r_n(m))\\ &\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n \sum_{m\in T_M-S_M} r_n(m). \end{align*}
\begin{align*} \sum_{m\in T_M-S_M} l_P(m)&=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^{[(1+\epsilon_0)\log_p M]}(p^n-p^{n-1})r_n(m))\\ &\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n \sum_{m\in T_M-S_M} r_n(m). \end{align*}
Notation is as in Lemma 9.3.2. We have ![]() $\sum _{m=1}^M r_n(m)=O(M^{3/2}/p^n+M/b_n+M^{1/2}/a_n)$.
$\sum _{m=1}^M r_n(m)=O(M^{3/2}/p^n+M/b_n+M^{1/2}/a_n)$.
For Theorem 5, we have
 \[ \sum_{m\in T_M-S_M} l_P(m)\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M)=O(M^{2+\epsilon_0})=o(M^{5/2}/\log M), \]
\[ \sum_{m\in T_M-S_M} l_P(m)\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M)=O(M^{2+\epsilon_0})=o(M^{5/2}/\log M), \]
when we take ![]() $\epsilon _0<1/2$.
$\epsilon _0<1/2$.
For Theorem 1(1) and Remark 4, set ![]() $n_1=\lceil ({3}/{4})\log _p M\rceil$. First,
$n_1=\lceil ({3}/{4})\log _p M\rceil$. First,
 \[ \sum_{n=0}^{n_1} p^n \sum_{m\in T_M-S_M} r_n(m)\ll \sum_{n=0}^{n_1}p^n(M^{3/2}/p^n+M)=O(M^{7/4})=o(M^2/\log M). \]
\[ \sum_{n=0}^{n_1} p^n \sum_{m\in T_M-S_M} r_n(m)\ll \sum_{n=0}^{n_1}p^n(M^{3/2}/p^n+M)=O(M^{7/4})=o(M^2/\log M). \]
Second, for ![]() $\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]} p^n \sum _{m\in T_M-S_M}r_n(m)$, we bound it by studying the following two cases separately.
$\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]} p^n \sum _{m\in T_M-S_M}r_n(m)$, we bound it by studying the following two cases separately.
Case (1): ![]() $b_{n_1}\geq M^{1/8}$. As in the first part, we have
$b_{n_1}\geq M^{1/8}$. As in the first part, we have
 \[ \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]}p^n \sum_{m\in T_M-S_M}r_n(m)\ll \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M/b_n+M^{1/2}), \]
\[ \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]}p^n \sum_{m\in T_M-S_M}r_n(m)\ll \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M/b_n+M^{1/2}), \]
which is ![]() $O(M^{3/2}\log M + M^{2+\epsilon _0-1/8}+M^{3/2+\epsilon _0})=o(M^2/\log M)$ once we take
$O(M^{3/2}\log M + M^{2+\epsilon _0-1/8}+M^{3/2+\epsilon _0})=o(M^2/\log M)$ once we take ![]() $\epsilon _0<1/8$.
$\epsilon _0<1/8$.
Case (2): ![]() $b_{n_1} < M^{1/8}$. We are going to enlarge
$b_{n_1} < M^{1/8}$. We are going to enlarge ![]() $S_M$ to be
$S_M$ to be ![]() $\{m\in T_M\mid \exists v\in L_{n_1} \text { with } Q'(v)=m\}$. As
$\{m\in T_M\mid \exists v\in L_{n_1} \text { with } Q'(v)=m\}$. As ![]() $b_{n_1}^2 M < M^{5/4}=o(p^{2n_1})$, then we conclude, as in the upper medium range Case (2) in the proof of Proposition 7.2.5 for Theorem 1(1), by Lemma 9.1.2 and Proposition 9.1.4 that
$b_{n_1}^2 M < M^{5/4}=o(p^{2n_1})$, then we conclude, as in the upper medium range Case (2) in the proof of Proposition 7.2.5 for Theorem 1(1), by Lemma 9.1.2 and Proposition 9.1.4 that ![]() $\#S_M=o(\#T_M)$ and
$\#S_M=o(\#T_M)$ and ![]() $\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]}p^n \sum _{m\in T_M-S_M}r_n(m)=0$.
$\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]}p^n \sum _{m\in T_M-S_M}r_n(m)=0$.
Proof Proof of Theorem 1(1), Remark 4 with  $p$ split in
$p$ split in  $F$, and Theorem 5
$F$, and Theorem 5
Assume for contradiction that there are only finitely many points on ![]() $C\cap (\bigcup _{m\in T}Z(m))$. Then we construct
$C\cap (\bigcup _{m\in T}Z(m))$. Then we construct ![]() $S_M$ by taking the union of the
$S_M$ by taking the union of the ![]() $S_M$ in Proposition 7.2.5 for supersingular points and that in Lemma 9.3.2 and Proposition 9.3.3 for ordinary points with
$S_M$ in Proposition 7.2.5 for supersingular points and that in Lemma 9.3.2 and Proposition 9.3.3 for ordinary points with ![]() $\operatorname {rk}_{\mathbb {Z}}L_0=3$. As it is a finite union, we still have
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. As it is a finite union, we still have ![]() $\#S_M=o(\#T_M)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, Lemma 9.3.1, and Proposition 9.3.3.
$\#S_M=o(\#T_M)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, Lemma 9.3.1, and Proposition 9.3.3.
Acknowledgements
We thank Johan de Jong, Keerthi Madapusi Pera, Arul Shankar, Salim Tayou, and Jacob Tsimerman for helpful discussions. D.M. is partially supported by NSF FRG grant DMS-1159265. A.N.S. is partially supported by the NSF grant DMS-2100436. Y.T. is partially supported by the NSF grant DMS-1801237. We would like to thank the anonymous referees for thorough readings and valuable suggestions which have greatly helped improve this paper.