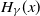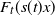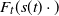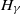1. Introduction
Extreme value theory (EVT) develops probabilistic models and methods for describing the random behaviour of extreme observations that occur rarely. These theoretical foundations are very important for studying practical problems in environmental, climate, insurance, and financial fields (e.g. [Reference Dey and Yan5, Reference Embrechts, Klüppelberg and Mikosch6, Reference Kulik and Soulier10]), to name a few.
In the univariate setting, the most popular approaches for statistical analysis are the so-called block maxima (BM) and peaks over threshold (POT) (see, e.g., [Reference Bücher and Zhou3] for a review). Let
![]() $X_1,\ldots,X_n$
be independent and identically distributed (i.i.d.) random variables according to a common distribution F. The first approach concerns the modelling of k sample maxima derived over blocks of a certain size m, i.e.
$X_1,\ldots,X_n$
be independent and identically distributed (i.i.d.) random variables according to a common distribution F. The first approach concerns the modelling of k sample maxima derived over blocks of a certain size m, i.e.
![]() $M_{m,i}=\max\!(X_{(i-1)m+1},\ldots,X_{im})$
,
$M_{m,i}=\max\!(X_{(i-1)m+1},\ldots,X_{im})$
,
![]() $i\in\{1,\ldots,k\}$
. In this case, under some regularity conditions (e.g. [Reference de Haan and Ferreira4, Chapter 1]), the weak limit theory establishes that
$i\in\{1,\ldots,k\}$
. In this case, under some regularity conditions (e.g. [Reference de Haan and Ferreira4, Chapter 1]), the weak limit theory establishes that
![]() $F^m(a_mx+b_m)$
converges pointwise to
$F^m(a_mx+b_m)$
converges pointwise to
![]() $G_\gamma(x)$
as
$G_\gamma(x)$
as
![]() $m\to\infty$
for every continuity point x of
$m\to\infty$
for every continuity point x of
![]() $G_\gamma$
, where
$G_\gamma$
, where
![]() $ G_\gamma$
is the generalised extreme value (GEV) distribution,
$ G_\gamma$
is the generalised extreme value (GEV) distribution,
![]() $a_m>0$
and
$a_m>0$
and
![]() $b_m$
are suitable norming constants for each
$b_m$
are suitable norming constants for each
![]() $m=1,2,\ldots$
, and
$m=1,2,\ldots$
, and
![]() $\gamma\in\mathbb{R}$
is the so-called tail index, which describes the tail heaviness of F (e.g. [Reference de Haan and Ferreira4, Chapter 1]). The second method concerns the modelling of k random variables out of the n available that exceed a high threshold t, or, equivalently, of k threshold excesses
$\gamma\in\mathbb{R}$
is the so-called tail index, which describes the tail heaviness of F (e.g. [Reference de Haan and Ferreira4, Chapter 1]). The second method concerns the modelling of k random variables out of the n available that exceed a high threshold t, or, equivalently, of k threshold excesses
![]() $Y_j$
,
$Y_j$
,
![]() $j=1,\ldots,k$
, which are i.i.d. copies of
$j=1,\ldots,k$
, which are i.i.d. copies of
![]() $Y=X-t\mid X>t$
. In this context, the generalised Pareto (GP) distribution, say
$Y=X-t\mid X>t$
. In this context, the generalised Pareto (GP) distribution, say
![]() $H_\gamma$
, appears as the weak limit law of appropriately normalised high threshold exceedances, i.e.
$H_\gamma$
, appears as the weak limit law of appropriately normalised high threshold exceedances, i.e.
![]() $F_t(s(t)x)$
converges pointwise to
$F_t(s(t)x)$
converges pointwise to
![]() $H_{\gamma}(x)$
as
$H_{\gamma}(x)$
as
![]() $t\to x^*$
for all the continuity points x of
$t\to x^*$
for all the continuity points x of
![]() $H_\gamma(x)$
, where
$H_\gamma(x)$
, where
![]() $F_t(x)=\mathbb{P}(Y\leq x)$
and
$F_t(x)=\mathbb{P}(Y\leq x)$
and
![]() $s(t)>0$
is a suitable scaling function for any
$s(t)>0$
is a suitable scaling function for any
![]() $t\leq x^*$
, with
$t\leq x^*$
, with
![]() $x^*=\sup(x \;:\; F(x)<\infty)$
. This result motivates the POT approach, which was introduced decades ago by the seminal paper [Reference Balkema and de Haan1]. Since then, few other convergence results have emerged. For instance, the uniform convergence of
$x^*=\sup(x \;:\; F(x)<\infty)$
. This result motivates the POT approach, which was introduced decades ago by the seminal paper [Reference Balkema and de Haan1]. Since then, few other convergence results have emerged. For instance, the uniform convergence of
![]() $F_t(s(t)\, \cdot \,)$
to
$F_t(s(t)\, \cdot \,)$
to
![]() $H_\gamma$
and the corresponding convergence rate have been derived by [Reference Pickands11, Reference Raoult and Worms12], respectively. Similar results but in Wasserstein distance have recently been established by [Reference Bobbia, Dombry and Varron2]. As for the GEV distribution, more results are available. In particular, there are sufficient conditions to ensure, in addition to weak convergence, that
$H_\gamma$
and the corresponding convergence rate have been derived by [Reference Pickands11, Reference Raoult and Worms12], respectively. Similar results but in Wasserstein distance have recently been established by [Reference Bobbia, Dombry and Varron2]. As for the GEV distribution, more results are available. In particular, there are sufficient conditions to ensure, in addition to weak convergence, that
![]() $F^m(a_m\, \cdot \, +b_m)$
converges to
$F^m(a_m\, \cdot \, +b_m)$
converges to
![]() $G_\gamma$
, for example, uniformly and in variational distance, and the density of
$G_\gamma$
, for example, uniformly and in variational distance, and the density of
![]() $F^m(a_m\, \cdot \, +b_m)$
converges pointwise, locally uniformly, and uniformly to that of
$F^m(a_m\, \cdot \, +b_m)$
converges pointwise, locally uniformly, and uniformly to that of
![]() $G_\gamma$
(e.g. [Reference Falk, Hüsler and Reiss7, Chapter 2]; [Reference Resnick13, Chapter 2]).
$G_\gamma$
(e.g. [Reference Falk, Hüsler and Reiss7, Chapter 2]; [Reference Resnick13, Chapter 2]).
The main contribution of this article is to provide new convergence results that can be useful in practical problems for the POT approach. Motivated by the utility in the statistical field of assessing the asymptotic accuracy of estimation procedures, we study stronger forms of convergence than the pointwise one, as
![]() $\lim_{t\to x^*}{\mathscr{D}}(F_t(s(t)\, \cdot \,) ;\; H_{\gamma})=0$
, where
$\lim_{t\to x^*}{\mathscr{D}}(F_t(s(t)\, \cdot \,) ;\; H_{\gamma})=0$
, where
![]() ${\mathscr{D}}(\cdot \,;\, \cdot)$
is either the variational distance, the Hellinger distance, or the Kullback–Leibler divergence. In particular, we provide upper bounds for the rate of convergence to zero of
${\mathscr{D}}(\cdot \,;\, \cdot)$
is either the variational distance, the Hellinger distance, or the Kullback–Leibler divergence. In particular, we provide upper bounds for the rate of convergence to zero of
![]() ${\mathscr{D}}(F_t(s(t)\,\cdot);\; H_{\gamma})$
in the case that
${\mathscr{D}}(F_t(s(t)\,\cdot);\; H_{\gamma})$
in the case that
![]() ${\mathscr{D}}(\cdot \,;\, \cdot)$
is the variational and Hellinger distance, and further translate them into bounds on Kullback–Leibler divergence between the densities of
${\mathscr{D}}(\cdot \,;\, \cdot)$
is the variational and Hellinger distance, and further translate them into bounds on Kullback–Leibler divergence between the densities of
![]() $F_t(s(t)\,\cdot\,)$
and
$F_t(s(t)\,\cdot\,)$
and
![]() $H_{\gamma}$
, respectively. We also pinpoint cases where recentering of exceedances is necessary to reach the optimum rate, namely where
$H_{\gamma}$
, respectively. We also pinpoint cases where recentering of exceedances is necessary to reach the optimum rate, namely where
![]() $F_t(s(t)\cdot+c(t))$
has to be considered in place of
$F_t(s(t)\cdot+c(t))$
has to be considered in place of
![]() $F_t(s(t)\,\cdot\,)$
, for a suitable real valued function c(t).
$F_t(s(t)\,\cdot\,)$
, for a suitable real valued function c(t).
The article is organised as follows. Section 2 provides a brief summary of the probabilistic context on which our results are based. Section 3 provides our new results on strong convergence to a GP distribution. Section 4 provides the proofs of the main results.
2. Background
Let X be a random variable with a distribution function F that is in the domain of attraction of the GEV distribution
![]() $G_\gamma$
, denoted as
$G_\gamma$
, denoted as
![]() $F\in\mathcal{D}(G_\gamma)$
. This means that there are norming constants
$F\in\mathcal{D}(G_\gamma)$
. This means that there are norming constants
![]() $a_m>0$
and
$a_m>0$
and
![]() $b_m\in\mathbb{R}$
for
$b_m\in\mathbb{R}$
for
![]() $m=1,2,\ldots$
such that
$m=1,2,\ldots$
such that
for all
![]() $x\in\mathbb{R}$
such that
$x\in\mathbb{R}$
such that
![]() $1+\gamma x>0$
, where
$1+\gamma x>0$
, where
![]() $\gamma\in\mathbb{R}$
, and this is true if only if there is a scaling function
$\gamma\in\mathbb{R}$
, and this is true if only if there is a scaling function
![]() $s(t)>0$
with
$s(t)>0$
with
![]() $t< x^*$
such that
$t< x^*$
such that
(e.g. [Reference de Haan and Ferreira4, Theorem 1.1.6]). The densities of
![]() $H_\gamma$
and
$H_\gamma$
and
![]() $G_\gamma$
are
$G_\gamma$
are
![]() $h_\gamma(x)=\left(1+\gamma x \right)^{-(1/\gamma+1)}$
and
$h_\gamma(x)=\left(1+\gamma x \right)^{-(1/\gamma+1)}$
and
![]() $g_{\gamma}(x)=G_\gamma(x)h_\gamma(x)$
, respectively. Let
$g_{\gamma}(x)=G_\gamma(x)h_\gamma(x)$
, respectively. Let
![]() $U(v)\;:\!=\;F^{\leftarrow}(1-1/v)$
for
$U(v)\;:\!=\;F^{\leftarrow}(1-1/v)$
for
![]() $v\geq 1$
, where
$v\geq 1$
, where
![]() $F^{\leftarrow}$
is the left-continuous inverse function of F and
$F^{\leftarrow}$
is the left-continuous inverse function of F and
![]() $G^{\leftarrow}(\exp\!(\!-\!1/x))=(x^\gamma-1)/\gamma$
. Then, we recall that the first-order condition in (2.1) is equivalent to the limit result
$G^{\leftarrow}(\exp\!(\!-\!1/x))=(x^\gamma-1)/\gamma$
. Then, we recall that the first-order condition in (2.1) is equivalent to the limit result
for all
![]() $x>0$
, where
$x>0$
, where
![]() $a(v)>0$
is a suitable scaling function. In particular, we can set
$a(v)>0$
is a suitable scaling function. In particular, we can set
![]() $s(t)= a(1/(1-F(t)))$
; see [Reference de Haan and Ferreira4, Chapter 1] for possible selections of the function a.
$s(t)= a(1/(1-F(t)))$
; see [Reference de Haan and Ferreira4, Chapter 1] for possible selections of the function a.
A stronger convergence form than that in formula (2.2) is the uniform one, i.e.
In the case of distributions F with finite end-point
![]() $x^*$
, the following slightly more general form of convergence is also of interest
$x^*$
, the following slightly more general form of convergence is also of interest
for a centering function c(t) satisfying
![]() $c(t)/s(t)\to0$
as
$c(t)/s(t)\to0$
as
![]() $t\to x^*$
. To establish the speed at which
$t\to x^*$
. To establish the speed at which
![]() $F_t(s(t) x)$
or
$F_t(s(t) x)$
or
![]() $F_t(s(t)x+c(t))$
converges uniformly to
$F_t(s(t)x+c(t))$
converges uniformly to
![]() $H_\gamma(x)$
, [Reference Raoult and Worms12] relied on a specific formulation of the well-known second-order condition. In its general form, the second-order condition requires the existence of a positive function a and a positive or negative function A, named the rate function, such that
$H_\gamma(x)$
, [Reference Raoult and Worms12] relied on a specific formulation of the well-known second-order condition. In its general form, the second-order condition requires the existence of a positive function a and a positive or negative function A, named the rate function, such that
![]() $\lim_{v\to \infty}|A(v)|=0$
and
$\lim_{v\to \infty}|A(v)|=0$
and
where D is a non-null function which is not a multiple of
![]() $(x^\gamma-1)/\gamma$
[Reference de Haan and Ferreira4, Definition 2.3.1]. The rate function A is necessarily regularly varying at infinity with index
$(x^\gamma-1)/\gamma$
[Reference de Haan and Ferreira4, Definition 2.3.1]. The rate function A is necessarily regularly varying at infinity with index
![]() $\rho\leq0$
, named the second-order parameter [Reference de Haan and Ferreira4, Theorem 2.3.3]. In the following, we use the same specific form of second-order condition of [Reference Raoult and Worms12] to obtain decay rates for stronger metrics than uniform distance between distribution functions.
$\rho\leq0$
, named the second-order parameter [Reference de Haan and Ferreira4, Theorem 2.3.3]. In the following, we use the same specific form of second-order condition of [Reference Raoult and Worms12] to obtain decay rates for stronger metrics than uniform distance between distribution functions.
3. Strong results for POT
In this section we discuss strong forms of convergence for the distribution of renormalised exceedances over a threshold. First, in Section 3.1, we discuss convergence to a GP distribution in variational and Hellinger distance, drawing a connection with known results for density convergence of normalized maxima. In Section 3.2 we quantify the speed of convergence in variational and Hellinger distance. Moreover, we show how these can be used to also bound Kullback–Leibler divergences. Throughout, for a twice-differentiable function W(x) on
![]() $\mathbb{R}$
, we denote by
$\mathbb{R}$
, we denote by
![]() $W'(x)=(\partial/\partial x)W(x)$
and
$W'(x)=(\partial/\partial x)W(x)$
and
![]() $W''(x)=(\partial^2/\partial x^2)W(x)$
the first- and second-order derivatives, respectively.
$W''(x)=(\partial^2/\partial x^2)W(x)$
the first- and second-order derivatives, respectively.
3.1. Strong convergence under classical assumptions
Let the distribution function F be twice differentiable. We write
![]() $f=F'$
,
$f=F'$
,
![]() $g_m=(F^m(a_m\,\cdot \,+b_m))'$
, and
$g_m=(F^m(a_m\,\cdot \,+b_m))'$
, and
![]() $f_t=F'_{\!\!t}$
. Under the classical von Mises-type conditions
$f_t=F'_{\!\!t}$
. Under the classical von Mises-type conditions
 \begin{alignat}{2} \lim_{x\to\infty}\frac{xf(x)}{1-F(x)} & = \frac{1}{\gamma}, \qquad & \gamma & > 0, \nonumber \\[5pt] \lim_{x\to x^*}\frac{(x^*-x)f(x)}{1-F(x)} & = -\frac{1}{\gamma}, & \gamma & < 0, \\[5pt] \lim_{x\to x^*}\frac{f(x)\int_x^{x^*}(1-F(v))\,\textrm{d}v}{(1-F(x))^2} & = 0, & \gamma & = 0, \nonumber\end{alignat}
\begin{alignat}{2} \lim_{x\to\infty}\frac{xf(x)}{1-F(x)} & = \frac{1}{\gamma}, \qquad & \gamma & > 0, \nonumber \\[5pt] \lim_{x\to x^*}\frac{(x^*-x)f(x)}{1-F(x)} & = -\frac{1}{\gamma}, & \gamma & < 0, \\[5pt] \lim_{x\to x^*}\frac{f(x)\int_x^{x^*}(1-F(v))\,\textrm{d}v}{(1-F(x))^2} & = 0, & \gamma & = 0, \nonumber\end{alignat}
we know that the first-order condition in (2.3) is satisfied, and that
locally uniformly for
![]() $(1+\gamma x) >0$
. Since the equality
$(1+\gamma x) >0$
. Since the equality
![]() $g_m(x)=F^{m-1}(a_mx+b_m) h_m(x)$
holds with
$g_m(x)=F^{m-1}(a_mx+b_m) h_m(x)$
holds with
![]() $b_m=U(m)$
,
$b_m=U(m)$
,
![]() $a_m=a(m)$
, and
$a_m=a(m)$
, and
![]() $h_m(x)=ma_mf(a_m x +b_m)$
, and since
$h_m(x)=ma_mf(a_m x +b_m)$
, and since
![]() $F^{m-1}(a_mx+b_m)$
converges to
$F^{m-1}(a_mx+b_m)$
converges to
![]() $G_\gamma(x)$
locally uniformly as
$G_\gamma(x)$
locally uniformly as
![]() $m\to\infty$
, the convergence result in (3.2) thus implies that
$m\to\infty$
, the convergence result in (3.2) thus implies that
![]() $g_m(x)$
converges to
$g_m(x)$
converges to
![]() $g_\gamma(x)$
locally uniformly [Reference Resnick13, Section 2.2].
$g_\gamma(x)$
locally uniformly [Reference Resnick13, Section 2.2].
On the other hand, the density pertaining to
![]() $F_t(s(t)x)$
is
$F_t(s(t)x)$
is
and, setting
![]() $v=1/(1-F(t))$
, we have
$v=1/(1-F(t))$
, we have
![]() $a(v)=s(t)$
and
$a(v)=s(t)$
and
![]() $v\to \infty$
as
$v\to \infty$
as
![]() $t\to x^*$
. Therefore, a further implication of the convergence result in (3.2) is that
$t\to x^*$
. Therefore, a further implication of the convergence result in (3.2) is that
![]() $l_t(x)$
converges to
$l_t(x)$
converges to
![]() $h_\gamma(x)$
locally uniformly for
$h_\gamma(x)$
locally uniformly for
![]() $x>0$
if
$x>0$
if
![]() $\gamma \geq 0$
, or for
$\gamma \geq 0$
, or for
![]() $x\in (0,-1/\gamma)$
if
$x\in (0,-1/\gamma)$
if
![]() $\gamma <0$
.
$\gamma <0$
.
In turn, by Scheffe’s lemma we have
![]() $\lim_{t\to x^*}{\mathscr{V\,}}({\mathcal{P}}_t, {\mathscr{P}})=0$
, where
$\lim_{t\to x^*}{\mathscr{V\,}}({\mathcal{P}}_t, {\mathscr{P}})=0$
, where
![]() ${\mathscr{V\,}}({\mathcal{P}}_t ;\; {\mathscr{P}})=\sup_{B\in\mathbb{B}}\left|{\mathcal{P}}_t(B) - {\mathscr{P}}(B)\right|$
is the total variation distance between the probability measures
${\mathscr{V\,}}({\mathcal{P}}_t ;\; {\mathscr{P}})=\sup_{B\in\mathbb{B}}\left|{\mathcal{P}}_t(B) - {\mathscr{P}}(B)\right|$
is the total variation distance between the probability measures
![]() ${\mathcal{P}}_t(B)\;:\!=\;\mathbb{P}(({X-t})/{s(t)}\in B \mid X>t)$
and
${\mathcal{P}}_t(B)\;:\!=\;\mathbb{P}(({X-t})/{s(t)}\in B \mid X>t)$
and
![]() ${\mathscr{P}}(B)\;:\!=\;\mathbb{P}(Z\in B)$
, and where Z is a random variable with distribution
${\mathscr{P}}(B)\;:\!=\;\mathbb{P}(Z\in B)$
, and where Z is a random variable with distribution
![]() $H_\gamma$
and B is a set in the Borel
$H_\gamma$
and B is a set in the Borel
![]() $\sigma$
-field of
$\sigma$
-field of
![]() $\mathbb{R}$
, denoted by
$\mathbb{R}$
, denoted by
![]() $\mathbb{B}$
. Let
$\mathbb{B}$
. Let
![]() ${\mathscr{H}\;\,}^2(l_t;\; h_\gamma)\;:\!=\;\int \big[\sqrt{l_t(x)}-\sqrt{h_\gamma(x)}\big]^2\, \mathrm{d} x$
be the square of the Hellinger distance. It is well known that the Hellinger and total variation distances are related as
${\mathscr{H}\;\,}^2(l_t;\; h_\gamma)\;:\!=\;\int \big[\sqrt{l_t(x)}-\sqrt{h_\gamma(x)}\big]^2\, \mathrm{d} x$
be the square of the Hellinger distance. It is well known that the Hellinger and total variation distances are related as
(see, e.g., [Reference Ghosal and van der Vaart9, Appendix B]). Therefore, the conditions in (3.1) ultimately entail that the Hellinger distance between the density of rescaled peaks over a threshold
![]() $l_t$
and the GP density
$l_t$
and the GP density
![]() $h_\gamma$
also converges to zero as
$h_\gamma$
also converges to zero as
![]() $t \to x^*$
. In the next subsection we introduce a stronger assumption, allowing us to also quantify the speed of such convergence.
$t \to x^*$
. In the next subsection we introduce a stronger assumption, allowing us to also quantify the speed of such convergence.
3.2. Convergence rates
As in [Reference Raoult and Worms12] we rely on the following assumption, in order to derive the convergence rate for the variational and Hellinger distances.
Condition 3.1.
Assume that F is twice differentiable. Moreover, assume that there exists
![]() $\rho\leq 0$
such that
$\rho\leq 0$
such that
defines a function of constant sign near infinity, whose absolute value
![]() $|A(v)|$
is regularly varying as
$|A(v)|$
is regularly varying as
![]() $v\to\infty$
with index of variation
$v\to\infty$
with index of variation
![]() $\rho$
.
$\rho$
.
When Condition 3.1 holds then the classical von Mises conditions in (3.1) are also satisfied for the cases where
![]() $\gamma$
is positive, negative, or equal to zero, respectively. Furthermore, Condition 3.1 implies that an appropriate scaling function for the exceedances of a high threshold
$\gamma$
is positive, negative, or equal to zero, respectively. Furthermore, Condition 3.1 implies that an appropriate scaling function for the exceedances of a high threshold
![]() $t<x^*$
, which complies with the equivalent first-order condition (2.2), is defined as
$t<x^*$
, which complies with the equivalent first-order condition (2.2), is defined as
![]() $s(t)=(1-F(t))/f(t)$
. With such a choice of the scaling function s, we establish the following results.
$s(t)=(1-F(t))/f(t)$
. With such a choice of the scaling function s, we establish the following results.
Theorem 3.1.
Assume Condition 3.1 is satisfied. Then, there exist constants
![]() $c>0$
,
$c>0$
,
![]() $\alpha_j>0$
with
$\alpha_j>0$
with
![]() $j=1,2$
,
$j=1,2$
,
![]() $K>0$
, and
$K>0$
, and
![]() $t_0 < x^*$
, depending on
$t_0 < x^*$
, depending on
![]() $\gamma$
, such that
$\gamma$
, such that
for all
![]() $t\geq t_0$
, where
$t\geq t_0$
, where
![]() $v=1/(1-F(t))$
,
$v=1/(1-F(t))$
,
 \begin{align*} \tilde{l}_t = \begin{cases} l_t, & \gamma \geq 0, \\[5pt] l_t( \cdot \, + ({x^*-t})/{s(t)} + {1}/{\gamma}), & \gamma < 0, \end{cases} \end{align*}
\begin{align*} \tilde{l}_t = \begin{cases} l_t, & \gamma \geq 0, \\[5pt] l_t( \cdot \, + ({x^*-t})/{s(t)} + {1}/{\gamma}), & \gamma < 0, \end{cases} \end{align*}
and
![]() $S(v) = 1-|A(v)|^{\alpha_1 }+4 \exp\!(c |A(v)|^{\alpha_2})$
.
$S(v) = 1-|A(v)|^{\alpha_1 }+4 \exp\!(c |A(v)|^{\alpha_2})$
.
Note that
![]() $\tilde{l}_t$
is the density of
$\tilde{l}_t$
is the density of
![]() $F_t(s(t) \cdot +c(t))$
, with centring function
$F_t(s(t) \cdot +c(t))$
, with centring function
 \begin{equation} c(t) \;:\!=\; \begin{cases} 0, & \gamma \geq 0, \\[5pt] x^*-t +\gamma^{-1}s(t), & \gamma < 0, \end{cases}\end{equation}
\begin{equation} c(t) \;:\!=\; \begin{cases} 0, & \gamma \geq 0, \\[5pt] x^*-t +\gamma^{-1}s(t), & \gamma < 0, \end{cases}\end{equation}
for
![]() $t<x^*$
. Given the relationship between the total variation and Hellinger distances in (3.3), with obvious adaptations when a non-null recentring is considered, the following result is a direct consequence of Theorem 3.1.
$t<x^*$
. Given the relationship between the total variation and Hellinger distances in (3.3), with obvious adaptations when a non-null recentring is considered, the following result is a direct consequence of Theorem 3.1.
Corollary 3.1.
Under the assumptions of Theorem 3.1, for all
![]() $t\geq t_0$
,
$t\geq t_0$
,
![]() ${\mathscr{V\,}}(\widetilde{{\mathcal{P}}}_t ;\; {\mathscr{P}})\leq |A(v)| \sqrt{K S(v)}$
, with
${\mathscr{V\,}}(\widetilde{{\mathcal{P}}}_t ;\; {\mathscr{P}})\leq |A(v)| \sqrt{K S(v)}$
, with
![]() $\widetilde{\mathcal{P}}_t$
the probability measure pertaining to
$\widetilde{\mathcal{P}}_t$
the probability measure pertaining to
![]() $\tilde{l}_t$
.
$\tilde{l}_t$
.
Theorem 3.1 implies that when
![]() $\gamma \geq 0$
the Hellinger and variational distances of the probability density and measure of rescaled exceedances from their GP distribution counterparts are bounded from above by
$\gamma \geq 0$
the Hellinger and variational distances of the probability density and measure of rescaled exceedances from their GP distribution counterparts are bounded from above by
![]() $C_1 |A(v)|$
, for a positive constant
$C_1 |A(v)|$
, for a positive constant
![]() $C_1$
, as the threshold t approaches the end-point
$C_1$
, as the threshold t approaches the end-point
![]() $x^*$
. Since, for a fixed
$x^*$
. Since, for a fixed
![]() $x \in \cap_{t\geq t_0}(0,({x^*-t})/{s(t)})$
,
$x \in \cap_{t\geq t_0}(0,({x^*-t})/{s(t)})$
,
![]() $|F_t(s(t)x)-H_\gamma(x)| \leq {\mathscr{V\,}}({\mathcal{P}}_t;\; {\mathscr{P}})$
, and since [Reference Raoult and Worms12, Theorem 2(i)] implies that
$|F_t(s(t)x)-H_\gamma(x)| \leq {\mathscr{V\,}}({\mathcal{P}}_t;\; {\mathscr{P}})$
, and since [Reference Raoult and Worms12, Theorem 2(i)] implies that
![]() $|F_t(s(t)x)-H_\gamma(x)|/|A(v)|$
converges to a positive constant, there also exists
$|F_t(s(t)x)-H_\gamma(x)|/|A(v)|$
converges to a positive constant, there also exists
![]() $C_0>0$
such that, for all large t,
$C_0>0$
such that, for all large t,
![]() $C_0|A(v)|$
is a lower bound for the variational and Hellinger distances. Therefore, since
$C_0|A(v)|$
is a lower bound for the variational and Hellinger distances. Therefore, since
![]() $C_0|A(v)|\leq {\mathscr{V\,}}({\mathcal{P}}_t;\; {\mathscr{P}})\leq {\mathscr{H}\;}(l_t;\; h_\gamma) \leq C_1|A(v)|$
, the decay rate of the variational and Hellinger distances is precisely
$C_0|A(v)|\leq {\mathscr{V\,}}({\mathcal{P}}_t;\; {\mathscr{P}})\leq {\mathscr{H}\;}(l_t;\; h_\gamma) \leq C_1|A(v)|$
, the decay rate of the variational and Hellinger distances is precisely
![]() $|A(v)|$
as
$|A(v)|$
as
![]() $t\to x^*$
. When
$t\to x^*$
. When
![]() $\gamma <0$
, analogous considerations apply to
$\gamma <0$
, analogous considerations apply to
![]() $\tilde{l}_t$
and
$\tilde{l}_t$
and
![]() $\widetilde{{\mathcal{P}}}_t$
. With the following results, we give precise indications of when a recentred version of
$\widetilde{{\mathcal{P}}}_t$
. With the following results, we give precise indications of when a recentred version of
![]() $l_t$
is necessary to achieve the optimal rate.
$l_t$
is necessary to achieve the optimal rate.
Proposition 3.1.
Under the assumptions of Theorem 3.1, when
![]() $\gamma <0$
there are constants
$\gamma <0$
there are constants
![]() $c_j$
,
$c_j$
,
![]() $j=1,2$
, and
$j=1,2$
, and
![]() $t_1 < x^*$
, depending on
$t_1 < x^*$
, depending on
![]() $\gamma$
, such that, for all
$\gamma$
, such that, for all
![]() $t >t_1$
,
$t >t_1$
,
where
![]() $\mu_t\;:\!=\;c(t)/s(t)$
and c(t) is as in the second line of (3.4).
$\mu_t\;:\!=\;c(t)/s(t)$
and c(t) is as in the second line of (3.4).
Corollary 3.2. Under the assumptions of Theorem 3.1:
-
(i) when
 $-1/2 \leq \gamma <0$
, there are constants
$-1/2 \leq \gamma <0$
, there are constants
 $c_3>0$
and
$c_3>0$
and
 $t_2 < x^*$
, depending on
$t_2 < x^*$
, depending on
 $\gamma$
, such that, for all
$\gamma$
, such that, for all
 $t>t_2$
,
$t>t_2$
,
 ${\mathscr{H}\;}(l_t;\; h_\gamma) \leq c_3 |A(v)|$
;
${\mathscr{H}\;}(l_t;\; h_\gamma) \leq c_3 |A(v)|$
; -
(ii) when
 $ \gamma <-1/2$
, there are constants
$ \gamma <-1/2$
, there are constants
 $c_4>0$
and
$c_4>0$
and
 $t_3 < x^*$
, depending on
$t_3 < x^*$
, depending on
 $\gamma$
, such that, for all
$\gamma$
, such that, for all
 $t>t_3$
,
$t>t_3$
,
 ${\mathscr{H}\;}(l_t;\; h_\gamma) \geq c_4 |A(v)|^{-1/2\gamma}$
.
${\mathscr{H}\;}(l_t;\; h_\gamma) \geq c_4 |A(v)|^{-1/2\gamma}$
.
According to Corollary 3.2(ii), the density
![]() $l_t$
of rescaled exceedances
$l_t$
of rescaled exceedances
![]() $Y/s(t)$
does not achieve the optimal convergence rate
$Y/s(t)$
does not achieve the optimal convergence rate
![]() $|A(V)|$
whenever
$|A(V)|$
whenever
![]() $\gamma <-1/2$
, in which case the rate is only of order
$\gamma <-1/2$
, in which case the rate is only of order
![]() $|A(v)|^{-1/2\gamma}$
. In simple terms, this is due to the fact that, when
$|A(v)|^{-1/2\gamma}$
. In simple terms, this is due to the fact that, when
![]() $\gamma$
is negative, the supports of
$\gamma$
is negative, the supports of
![]() $l_t$
and
$l_t$
and
![]() $h_\gamma$
can be different and the approximation error is affected by the amount of probability mass in the unshared region of points. Indeed, we recall that the end-point
$h_\gamma$
can be different and the approximation error is affected by the amount of probability mass in the unshared region of points. Indeed, we recall that the end-point
![]() $(x^*-t)/{s}(t)$
of
$(x^*-t)/{s}(t)$
of
![]() $l_t$
converges to
$l_t$
converges to
![]() $-1/{\gamma}$
as t approaches
$-1/{\gamma}$
as t approaches
![]() $x^*$
at rate A(v) (see, e.g., [Reference de Haan and Ferreira4, Lemma 4.5.4]). Nevertheless, for
$x^*$
at rate A(v) (see, e.g., [Reference de Haan and Ferreira4, Lemma 4.5.4]). Nevertheless, for
![]() $t<x^*$
it can be that
$t<x^*$
it can be that
![]() $(x^*-t)/{s}(t)>-1/\gamma$
or
$(x^*-t)/{s}(t)>-1/\gamma$
or
![]() $(x^*-t)/{s}(t)<-1/\gamma $
. In turn, when
$(x^*-t)/{s}(t)<-1/\gamma $
. In turn, when
![]() $\gamma$
is smaller than
$\gamma$
is smaller than
![]() $-1/2$
, the approximation error due to support mismatch has a dominant effect. However, if scaled exceedances are shifted by subtracting the quantity
$-1/2$
, the approximation error due to support mismatch has a dominant effect. However, if scaled exceedances are shifted by subtracting the quantity
![]() $\mu_t$
, in this case the upper end-point of the density
$\mu_t$
, in this case the upper end-point of the density
![]() $\tilde{l}_t$
is the same of that of
$\tilde{l}_t$
is the same of that of
![]() $h_\gamma$
, hence no support mismatch occurs and the optimal convergence rate is also achieved in the case where
$h_\gamma$
, hence no support mismatch occurs and the optimal convergence rate is also achieved in the case where
![]() $\gamma <-1/2$
.
$\gamma <-1/2$
.
A further implication of Theorem 3.1 concerns the speed of convergence to zero of the Kullback–Leibler divergence
![]() ${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)\;:\!=\; \int\ln\lbrace\tilde{l}_t(x)/h_\gamma(x)\rbrace\tilde{l}_t(x)\, \mathrm{d} x$
, and the divergences of higher order
${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)\;:\!=\; \int\ln\lbrace\tilde{l}_t(x)/h_\gamma(x)\rbrace\tilde{l}_t(x)\, \mathrm{d} x$
, and the divergences of higher order
![]() $p\geq 2$
,
$p\geq 2$
,
![]() ${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)\;:\!=\; \int|\ln\lbrace\tilde{l}_t(x)/h_\gamma(x)\rbrace|^p\tilde{l}_t(x)\, \mathrm{d} x$
. Using the uniform bound on density ratio provided in Lemma 4.7 we are able to translate the upper bounds on the squared Hellinger distance
${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)\;:\!=\; \int|\ln\lbrace\tilde{l}_t(x)/h_\gamma(x)\rbrace|^p\tilde{l}_t(x)\, \mathrm{d} x$
. Using the uniform bound on density ratio provided in Lemma 4.7 we are able to translate the upper bounds on the squared Hellinger distance
![]() ${\mathscr{H}\;\,}^2(\tilde{l}_t;\; h_\gamma)$
into upper bounds on the Kullback–Leibler divergence
${\mathscr{H}\;\,}^2(\tilde{l}_t;\; h_\gamma)$
into upper bounds on the Kullback–Leibler divergence
![]() ${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)$
and higher-order divergences
${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)$
and higher-order divergences
![]() ${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)$
.
${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)$
.
Corollary 3.3.
Under the assumptions of Theorem 3.1, in particular with
![]() $\rho < 0$
and
$\rho < 0$
and
![]() $\gamma \neq 0$
, there exist constants
$\gamma \neq 0$
, there exist constants
![]() $M>0$
and
$M>0$
and
![]() $t_4<x^*$
, depending on
$t_4<x^*$
, depending on
![]() $\gamma$
, such that, for all
$\gamma$
, such that, for all
![]() $t\geq t_4$
,
$t\geq t_4$
,
-
(i)
 ${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)\leq 2M K S(v) |A(v)|^2$
;
${\mathscr{K}\;}(\tilde{l}_t;\; h_\gamma)\leq 2M K S(v) |A(v)|^2$
; -
(ii)
 ${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)\leq 2 p! K S(v) |A(v)|^2$
, with
${\mathscr{D}}_p(\tilde{l}_t;\; h_\gamma)\leq 2 p! K S(v) |A(v)|^2$
, with
 $p\geq 2$
.
$p\geq 2$
.
To extend the general results in Lemma 4.7 and Corollary 3.3 to the case of
![]() $\gamma=0$
seems to be technically over-complicated. Nevertheless, there are specific examples where the properties listed in such lemmas are satisfied, such as the following.
$\gamma=0$
seems to be technically over-complicated. Nevertheless, there are specific examples where the properties listed in such lemmas are satisfied, such as the following.
Example 3.1. Let
![]() $F(x)=\exp\!(\!-\!\exp\!(\!-\!x))$
,
$F(x)=\exp\!(\!-\!\exp\!(\!-\!x))$
,
![]() $x\in \mathbb{R}$
, be the Gumbel distribution function. In this case, Condition 3.1 is satisfied with
$x\in \mathbb{R}$
, be the Gumbel distribution function. In this case, Condition 3.1 is satisfied with
![]() $\gamma=0$
and
$\gamma=0$
and
![]() $\rho=-1$
, so that Theorem 3.1 applies to this example, and, for an arbitrarily small
$\rho=-1$
, so that Theorem 3.1 applies to this example, and, for an arbitrarily small
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $l_t(x)/h_0(x)\leq \exp\!(\!\exp\!(\!-\!t))<1+\varepsilon$
for all
$l_t(x)/h_0(x)\leq \exp\!(\!\exp\!(\!-\!t))<1+\varepsilon$
for all
![]() $x>0$
and suitably large t. Hence, the bounded density ratio property is satisfied and it is still possible to conclude that
$x>0$
and suitably large t. Hence, the bounded density ratio property is satisfied and it is still possible to conclude that
![]() ${\mathscr{D}}_p({l}_t;\; h_0)/|A(v)|^2$
and
${\mathscr{D}}_p({l}_t;\; h_0)/|A(v)|^2$
and
![]() ${\mathscr{K}\;}({l}_t;\; h_0)/|A(v)|^2$
can be bounded from above as in Corollary 3.3.
${\mathscr{K}\;}({l}_t;\; h_0)/|A(v)|^2$
can be bounded from above as in Corollary 3.3.
4. Proofs
4.1. Additional notation
For
![]() $y >0$
we write
$y >0$
we write
![]() $T(y)=U(e^y)$
and, for
$T(y)=U(e^y)$
and, for
![]() $t < x^*$
, we define the functions
$t < x^*$
, we define the functions
 \begin{align*}p_t(y) =\begin{cases} ({T(y+T^{-1}(t))-t})/{s(t)} - ({e^{\gamma y}-1})/{\gamma}, & \gamma > 0, \\[5pt] ({T(y+T^{-1}(t))-t})/{s(t)}-y, & \gamma = 0, \\[5pt] ({T(y+T^{-1}(t))-x^* -\gamma^{-1}s(t)})/{s(t)} - ({e^{\gamma y}-1})/{\gamma}, & \gamma < 0,\end{cases} \end{align*}
\begin{align*}p_t(y) =\begin{cases} ({T(y+T^{-1}(t))-t})/{s(t)} - ({e^{\gamma y}-1})/{\gamma}, & \gamma > 0, \\[5pt] ({T(y+T^{-1}(t))-t})/{s(t)}-y, & \gamma = 0, \\[5pt] ({T(y+T^{-1}(t))-x^* -\gamma^{-1}s(t)})/{s(t)} - ({e^{\gamma y}-1})/{\gamma}, & \gamma < 0,\end{cases} \end{align*}
with
![]() $s(t)=(1-F(t))/f(t)$
, and
$s(t)=(1-F(t))/f(t)$
, and
 \begin{align*}q_t(y) =\begin{cases} ({1}/{\gamma})\ln[1+\gamma \mathrm{e}^{-\gamma y} p_t(y)], & \gamma \neq 0, \\[5pt] p_t(y), & \gamma = 0.\end{cases} \end{align*}
\begin{align*}q_t(y) =\begin{cases} ({1}/{\gamma})\ln[1+\gamma \mathrm{e}^{-\gamma y} p_t(y)], & \gamma \neq 0, \\[5pt] p_t(y), & \gamma = 0.\end{cases} \end{align*}
Moreover, for
![]() $t<x^*$
we set
$t<x^*$
we set
 \begin{align*}\tilde{x}_t^* =\begin{cases} ({x^*-t})/{{s}(t)}, & \gamma \geq 0, \\[5pt] -{1}/{\gamma}, & \gamma < 0.\end{cases} \end{align*}
\begin{align*}\tilde{x}_t^* =\begin{cases} ({x^*-t})/{{s}(t)}, & \gamma \geq 0, \\[5pt] -{1}/{\gamma}, & \gamma < 0.\end{cases} \end{align*}
Furthermore, for
![]() $x \in (0, x^*-t)$
, we let
$x \in (0, x^*-t)$
, we let
![]() $\phi_t(x)=T^{-1}(x+t)-T^{-1}(t)$
. Finally, for
$\phi_t(x)=T^{-1}(x+t)-T^{-1}(t)$
. Finally, for
![]() $x \in \mathbb{R}$
,
$x \in \mathbb{R}$
,
![]() $\gamma \in \mathbb{R}$
, and
$\gamma \in \mathbb{R}$
, and
![]() $\rho \leq 0$
, we set
$\rho \leq 0$
, we set
 \begin{align*}I_{\gamma,\rho}(x)=\begin{cases} \int_0^x \mathrm{e}^{\gamma s}\int_0^s \mathrm{e}^{\rho z}\, \mathrm{d} z\, \mathrm{d} s, & \gamma \geq 0, \\[5pt] -\int_x^\infty \mathrm{e}^{\gamma s} \int_0^s \mathrm{e}^{\rho z}\, \mathrm{d} z\, \mathrm{d} s, & \gamma < 0.\end{cases} \end{align*}
\begin{align*}I_{\gamma,\rho}(x)=\begin{cases} \int_0^x \mathrm{e}^{\gamma s}\int_0^s \mathrm{e}^{\rho z}\, \mathrm{d} z\, \mathrm{d} s, & \gamma \geq 0, \\[5pt] -\int_x^\infty \mathrm{e}^{\gamma s} \int_0^s \mathrm{e}^{\rho z}\, \mathrm{d} z\, \mathrm{d} s, & \gamma < 0.\end{cases} \end{align*}
4.2. Auxiliary results
In this section we provide some results which are auxiliary to the proofs of the main ones, presented in Section 3. Throughout, for Lemmas 4.1–4.6, Condition 3.1 is implicitly assumed to hold. The proofs are provided in the Supplementary Material. In particular, Lemmas 4.1 and 4.2 are used directly in the proof of our main result, Theorem 3.1.
Lemma 4.1.
For every
![]() $\varepsilon>0$
and every
$\varepsilon>0$
and every
![]() $\alpha>0$
, there exist
$\alpha>0$
, there exist
![]() $x_1 < x^*$
and
$x_1 < x^*$
and
![]() $\kappa_1>0$
(depending on
$\kappa_1>0$
(depending on
![]() $\gamma$
) such that, for all
$\gamma$
) such that, for all
![]() $t \geq x_1$
and
$t \geq x_1$
and
![]() $y \in (0, -\alpha \ln \vert A(\mathrm{e}^{T^{-1}(t)})\vert)$
,
$y \in (0, -\alpha \ln \vert A(\mathrm{e}^{T^{-1}(t)})\vert)$
,
Lemma 4.2.
For every
![]() $\varepsilon>0$
and every
$\varepsilon>0$
and every
![]() $\alpha>0$
, there exist
$\alpha>0$
, there exist
![]() $x_2 < x^*$
and
$x_2 < x^*$
and
![]() $\kappa_2>0$
(depending on
$\kappa_2>0$
(depending on
![]() $\gamma$
) such that, for all
$\gamma$
) such that, for all
![]() $t \geq x_2$
and
$t \geq x_2$
and
![]() $y \in (0,-\alpha \ln \vert A(\mathrm{e}^{T^{-1}(t)}) \vert )$
,
$y \in (0,-\alpha \ln \vert A(\mathrm{e}^{T^{-1}(t)}) \vert )$
,
Lemma 4.3.
If
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $\rho<0$
, there exists a regularly varying function
$\rho<0$
, there exists a regularly varying function
![]() $\mathcal{R}$
with negative index
$\mathcal{R}$
with negative index
![]() $\varrho$
such that, defining the function
$\varrho$
such that, defining the function
as
![]() $v\to\infty$
,
$v\to\infty$
,
![]() $\eta(U(v))=O(\mathcal{R}(v))$
.
$\eta(U(v))=O(\mathcal{R}(v))$
.
Lemma 4.4.
If
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $\rho<0$
, there exists
$\rho<0$
, there exists
![]() $x_3\in(0,\infty)$
and
$x_3\in(0,\infty)$
and
![]() $\delta >0$
such that, for all
$\delta >0$
such that, for all
![]() $x\geq x_3$
,
$x\geq x_3$
,
![]() $f(x) = h_\gamma(x)[1+O(\{1-H_\gamma(x)\}^\delta)]$
.
$f(x) = h_\gamma(x)[1+O(\{1-H_\gamma(x)\}^\delta)]$
.
Lemma 4.5.
If
![]() $\gamma<0$
and
$\gamma<0$
and
![]() $\rho<0$
, there exists a a regularly varying function
$\rho<0$
, there exists a a regularly varying function
![]() $\tilde{\mathcal{R}}$
with negative index
$\tilde{\mathcal{R}}$
with negative index
![]() $\tilde{\varrho}=(\!-\!1)\vee(\!-\!\rho/\gamma)$
such that, defining the function
$\tilde{\varrho}=(\!-\!1)\vee(\!-\!\rho/\gamma)$
such that, defining the function
as
![]() $y\to\infty$
,
$y\to\infty$
,
![]() $\tilde{\eta}(y)=O(\tilde{\mathcal{R}}(y))$
.
$\tilde{\eta}(y)=O(\tilde{\mathcal{R}}(y))$
.
Lemma 4.6.
If
![]() $\gamma<0$
and
$\gamma<0$
and
![]() $\rho<0$
, there exist
$\rho<0$
, there exist
![]() $\tilde{\delta}>0$
such that, as
$\tilde{\delta}>0$
such that, as
![]() $y\to \infty$
,
$y\to \infty$
,
Finally, in order to exploit Theorem 3.1 to give bounds on Kullback–Leibler and higher-order divergences, we introduce by the next lemma a uniform bound on density ratios.
Lemma 4.7.
Under the assumptions of Theorem 3.1, if
![]() $\rho <0$
and
$\rho <0$
and
![]() $\gamma \neq 0$
, then there exist a
$\gamma \neq 0$
, then there exist a
![]() $t^* <x^*$
and a constant
$t^* <x^*$
and a constant
![]() $M \in (0,\infty)$
such that
$M \in (0,\infty)$
such that
4.3. Proof of Theorem 3.1
Proof of Theorem
3.1. For every
![]() $x_t>0$
,
$x_t>0$
,
 \begin{align*} & {\mathscr{H}\;\,}^2(l_t;\; h_\gamma) \\ & = \int_0^{x_t} + \int_{x_t}^\infty \Big[\sqrt{f_t}(x)-\sqrt{h_\gamma({(x-c(t))}/s(t))/s(t)}\Big]^2\,\mathrm{d} x \\[5pt] & \leq \int_{0}^{\phi_t(x_t)}\mathrm{e}^{-y} \Big[1-\sqrt{\mathrm{e}^{-q_t(y)}(1+q'_{\!\!t}(y))}\Big]^2\,\mathrm{d} y + \Bigg[\sqrt{1-F_t(x_t)} + \sqrt{1-{H_\gamma\bigg(\frac{x_t-c(t)}{s(t)}\bigg)}}\Bigg]^2 \\[5pt] & \;=\!:\; \mathcal{I}_1(t)+\mathcal{I}_2(t). \end{align*}
\begin{align*} & {\mathscr{H}\;\,}^2(l_t;\; h_\gamma) \\ & = \int_0^{x_t} + \int_{x_t}^\infty \Big[\sqrt{f_t}(x)-\sqrt{h_\gamma({(x-c(t))}/s(t))/s(t)}\Big]^2\,\mathrm{d} x \\[5pt] & \leq \int_{0}^{\phi_t(x_t)}\mathrm{e}^{-y} \Big[1-\sqrt{\mathrm{e}^{-q_t(y)}(1+q'_{\!\!t}(y))}\Big]^2\,\mathrm{d} y + \Bigg[\sqrt{1-F_t(x_t)} + \sqrt{1-{H_\gamma\bigg(\frac{x_t-c(t)}{s(t)}\bigg)}}\Bigg]^2 \\[5pt] & \;=\!:\; \mathcal{I}_1(t)+\mathcal{I}_2(t). \end{align*}
Let
![]() $x_t$
be such that
$x_t$
be such that
![]() $\phi_t(x_t)=-\alpha \ln \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert$
for a positive constant
$\phi_t(x_t)=-\alpha \ln \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert$
for a positive constant
![]() $\alpha$
to be specified later. Then, by Lemmas 4.1 and 4.2, for a suitably small
$\alpha$
to be specified later. Then, by Lemmas 4.1 and 4.2, for a suitably small
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\kappa_3>0$
such that, for all sufficiently large t,
$\kappa_3>0$
such that, for all sufficiently large t,
where
![]() $\alpha_1\;:\!=\;\alpha(1-4\varepsilon)$
is positive. Moreover, on one hand we have the identity
$\alpha_1\;:\!=\;\alpha(1-4\varepsilon)$
is positive. Moreover, on one hand we have the identity
![]() $1-F_t(x_t)=\vert A(\mathrm{e}^{T^{-1}(t)})\vert^\alpha$
. On the other hand, for some constant
$1-F_t(x_t)=\vert A(\mathrm{e}^{T^{-1}(t)})\vert^\alpha$
. On the other hand, for some constant
![]() $\kappa_5>0$
we have the inequality
$\kappa_5>0$
we have the inequality
 \begin{align*} 1- {H_\gamma\bigg(\frac{x_t-c(t)}{s(t)}\bigg)} & = \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha \exp\big\lbrace -q_t\big({-}\alpha\ln\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert\big)\big\rbrace \\[5pt] & \leq \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha \exp\big\lbrace\kappa_5\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^{1-2\varepsilon\alpha}\big\rbrace. \end{align*}
\begin{align*} 1- {H_\gamma\bigg(\frac{x_t-c(t)}{s(t)}\bigg)} & = \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha \exp\big\lbrace -q_t\big({-}\alpha\ln\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert\big)\big\rbrace \\[5pt] & \leq \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha \exp\big\lbrace\kappa_5\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^{1-2\varepsilon\alpha}\big\rbrace. \end{align*}
Consequently,
Now, we can choose
![]() $\alpha >2$
and
$\alpha >2$
and
![]() $\varepsilon$
small enough that
$\varepsilon$
small enough that
![]() $\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha < \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^2$
and
$\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^\alpha < \big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert^2$
and
![]() $\alpha_2 \;:\!=\; 1-2\varepsilon\alpha > 0$
. The conclusion then follows noting that
$\alpha_2 \;:\!=\; 1-2\varepsilon\alpha > 0$
. The conclusion then follows noting that
![]() $T^{-1}(t)=-\!\ln\!(1-F(t))$
and, in turn,
$T^{-1}(t)=-\!\ln\!(1-F(t))$
and, in turn,
![]() $\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert = \vert A(v)\vert$
.
$\big\vert A(\mathrm{e}^{T^{-1}(t)})\big\vert = \vert A(v)\vert$
.
4.4. Proof of Proposition 3.1
Proof of Proposition
3.1. Assume first that, for all large t,
![]() $\mu_t=({x^*-t})/{s(t)}+{1}/{\gamma}$
is positive. In this case, we have the following identities:
$\mu_t=({x^*-t})/{s(t)}+{1}/{\gamma}$
is positive. In this case, we have the following identities:
 \begin{align*} {\mathscr{H}\;\,}^2(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) & = \int_0^{-1/\gamma}\Big[\sqrt{h_\gamma(x)}-\sqrt{h_\gamma(x-\mu_t)}\Big]^2\,\mathrm{d} x + 1 - H_\gamma\bigg({-}\frac{1}{\gamma}-\mu_t\bigg) \\[5pt] & = \int_0^\infty\mathrm{e}^{-s}\Bigg[\sqrt{\frac{\exp\{-({1}/{\gamma})\ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t)\}} {1-\gamma\mathrm{e}^{-\gamma s}\mu_t}} - 1\Bigg]^2\, \mathrm{d} s + (\!-\!\gamma \mu_t)^{-1/\gamma}. \end{align*}
\begin{align*} {\mathscr{H}\;\,}^2(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) & = \int_0^{-1/\gamma}\Big[\sqrt{h_\gamma(x)}-\sqrt{h_\gamma(x-\mu_t)}\Big]^2\,\mathrm{d} x + 1 - H_\gamma\bigg({-}\frac{1}{\gamma}-\mu_t\bigg) \\[5pt] & = \int_0^\infty\mathrm{e}^{-s}\Bigg[\sqrt{\frac{\exp\{-({1}/{\gamma})\ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t)\}} {1-\gamma\mathrm{e}^{-\gamma s}\mu_t}} - 1\Bigg]^2\, \mathrm{d} s + (\!-\!\gamma \mu_t)^{-1/\gamma}. \end{align*}
Concerning the first term on the right-hand side, for all
![]() $s>0$
as
$s>0$
as
![]() $t\to x^*$
we have
$t\to x^*$
we have
![]() $0 \leq \ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t) \leq \ln\!(1-\gamma\mu_t) = O(\mu_t)$
and
$0 \leq \ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t) \leq \ln\!(1-\gamma\mu_t) = O(\mu_t)$
and
where, for a positive constant
![]() $\tau$
,
$\tau$
,
![]() ${\mu_t}$
satisfies
${\mu_t}$
satisfies
![]() ${\mu_t}/{|A(v)|} = (1+o(1))\tau$
(see, e.g., [Reference de Haan and Ferreira4, Lemma 4.5.4]). Then, as
${\mu_t}/{|A(v)|} = (1+o(1))\tau$
(see, e.g., [Reference de Haan and Ferreira4, Lemma 4.5.4]). Then, as
![]() $t \to x^*$
,
$t \to x^*$
,
 \begin{equation*} \int_0^\infty\mathrm{e}^{-s}\Bigg[\sqrt{\frac{\exp\{-({1}/{\gamma})\ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t)\}} {1-\gamma\mathrm{e}^{-\gamma s}\mu_t}}-1\Bigg]^2\, \mathrm{d} s = O(\mu_t^2) = O(|A(v)|^2). \end{equation*}
\begin{equation*} \int_0^\infty\mathrm{e}^{-s}\Bigg[\sqrt{\frac{\exp\{-({1}/{\gamma})\ln\!(1-\gamma\mathrm{e}^{-\gamma s}\mu_t)\}} {1-\gamma\mathrm{e}^{-\gamma s}\mu_t}}-1\Bigg]^2\, \mathrm{d} s = O(\mu_t^2) = O(|A(v)|^2). \end{equation*}
Concerning the second term, as
![]() $t \to x^*$
,
$t \to x^*$
,
![]() $(\!-\!\gamma\mu_t)^{-1\gamma} = (\!-\!\gamma)^{-1/\gamma}(1+o(1))\tau^{-1/\gamma}|A(v)|^{-1/\gamma}$
. The result now follows for the case where
$(\!-\!\gamma\mu_t)^{-1\gamma} = (\!-\!\gamma)^{-1/\gamma}(1+o(1))\tau^{-1/\gamma}|A(v)|^{-1/\gamma}$
. The result now follows for the case where
![]() $\mu_t$
is ultimately positive. When it is ultimately negative, simply note that
$\mu_t$
is ultimately positive. When it is ultimately negative, simply note that
and proceed as above, but replacing
![]() $\mu_t$
with
$\mu_t$
with
![]() $-\mu_t$
.
$-\mu_t$
.
4.5. Proof of Corollary 3.2
Proof of Corollary
3.2. Observe that, for
![]() $\gamma <0$
,
$\gamma <0$
,
![]() ${\mathscr{H}\;}(l_t;\; h_\gamma) = {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t))$
. Moreover, note that, by the triangular inequality and the first identity in (4.1),
${\mathscr{H}\;}(l_t;\; h_\gamma) = {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t))$
. Moreover, note that, by the triangular inequality and the first identity in (4.1),
 \begin{align*} {\mathscr{H}\;}(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) - {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) & \leq {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) \\[5pt] & \leq {\mathscr{H}\;}(h_\gamma;h_\gamma(\cdot \, - \mu_t)) + {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)). \end{align*}
\begin{align*} {\mathscr{H}\;}(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) - {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) & \leq {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) \\[5pt] & \leq {\mathscr{H}\;}(h_\gamma;h_\gamma(\cdot \, - \mu_t)) + {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)). \end{align*}
Whenever
![]() $\gamma \geq -1/2$
, by Theorem 3.1 and Proposition 3.1, the term on the second line is of order
$\gamma \geq -1/2$
, by Theorem 3.1 and Proposition 3.1, the term on the second line is of order
![]() $O(|A(v)|)$
as
$O(|A(v)|)$
as
![]() $t \to x^*$
. Instead, if
$t \to x^*$
. Instead, if
![]() $\gamma <-1/2$
, by Theorem 3.1 and Proposition 3.1, as
$\gamma <-1/2$
, by Theorem 3.1 and Proposition 3.1, as
![]() $t\to x^*$
the term on the left-hand side of the first line satisfies
$t\to x^*$
the term on the left-hand side of the first line satisfies
 \begin{align*} {\mathscr{H}\;}(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) - {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) & \geq c_3 |A(v)|^{-1/2\gamma} - O(|A(v)|) \\[5pt] & = c_3 |A(v)|^{-1/2\gamma}(1+o(1)). \end{align*}
\begin{align*} {\mathscr{H}\;}(h_\gamma;\; h_\gamma(\cdot \, - \mu_t)) - {\mathscr{H}\;}(\tilde{l}_t;\; h_\gamma(\cdot\, +\mu_t)) & \geq c_3 |A(v)|^{-1/2\gamma} - O(|A(v)|) \\[5pt] & = c_3 |A(v)|^{-1/2\gamma}(1+o(1)). \end{align*}
The result now follows.
4.6. Proof of Corollary 3.3
Proof of Corollary 3.3. By [Reference Ghosal, Ghosh and van der Vaart8, Lemma 8.2],
Moreover, by [Reference Ghosal and van der Vaart9, Lemma B.3], for
![]() $p\geq 2$
,
$p\geq 2$
,
The conclusion now follows by combining the above inequalities and applying Theorem 3.1 and Lemma 4.7.
Acknowledgements
Simone Padoan is supported by the Bocconi Institute for Data Science and Analytics (BIDSA), Italy.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/jpr.2023.53