Introduction
Reference NyeNye (1965) examined the steady rectilinear flow of a Glen material in channels of prescribed cross-section: rectangular, elliptic, and parabolic, under a zero-velocity basal condition. The analysis consisted necessarily of a fully numerical solution of the partial differential equations. Nye also presented two analytical solutions for flow in an infinitely wide channel of uniform depth and in a semi-circular filled channel. He also presented an analytical solution due to W. Chester (private communication between Chester and Nye) for a slightly elliptic channel obtained by a standard perturbation of the solution for a semicircular channel. Finally, he noted that a standard perturbation could not be performed on the solution for the infinitely wide channel of uniform depth.
The emphasis here will be on analytical solutions because such solutions are more adaptable for qualitative studies. Although we shall again assume a zero-velocity basal condition, the techniques exhibited can be applied to other basal conditions such as a Reference WeertmanWeertman (1957, Reference Weertman1964) sliding law. There are two reasons why we restrict the study to the non-sliding case. First, a direct comparison with Nye’s work is then possible. Second, the whole subject of sliding laws is currently at issue.
For brevity, Nye’s assumptions, notation, coordinate system, and sign conventions (his fig. 1a and b) are used throughout. We are concerned with the steady cylindrical flow of a homogeneous, isotropic Glen material. In addition, we assume that the xy plane is a plane of symmetry. (The x-axis lies on the ice surface and points down-slope with the y-axis into the bed through the thalweg.)

Fig. 1. The right half of six basal profiles corresponding to a Newtonian material and null-velocity basal condition. Parameter values are:
Curve A: b = a, C1 = 0.6668;
Curve B: b = 2a, C1 = 0.5429;
Curve C: b = 3a, C1 = 0.5242;
Curve D: b = a, C1 = 0.95254;
Curve E: b = 2a, C1 = 0.92033;
Curve F: b = 3a, C1 = 0.9146.
The equilibrium equations reduce to the single equation

where α is the bed slope. Glen’s flow law reduce to

where ![]() . We shall consider two cases:
. We shall consider two cases:
n = 1, a Newtonian material, and n = 3, which is a popular but not universal choice to represent ice. Under assumptions invoked here, A is a constant.
A solution involves finding the two stress components τ xy, τ xz and longitudinal velocity u which satisfy (1) and (2) along with certain boundary conditions. The boundary conditions consist of the free surface condition
and the null-velocity condition u = 0 on a basal profile as yet to be determined. In addition, symmetry implies that
In cases of flows periodic in z condition, (4) is replaced by
Analysis for a Newtonian Material
Most creep data for ice apply above 1 bar. At this high stress range there is considerable variation in values of n measured in the laboratory and calculated from field measurements, (see, for example, Reference PatersonPaterson (1981).) However, there is no ambiguity in the conclusion that n > 1, i.e. the behaviour is non-Newtonian.
Laboratory tests carried out at small total creep strains and at low stresses show n ≈ 1, (see, e.g. Reference LandauerLandauer, 1955; Reference Jellinek and BrillJellinek and Brill, 1956; Reference Bromer and KingeryBromer and Kingery, 1968; Reference Mellor and TestaMellor and Testa, 1969; and Reference Colbeck and EvansColbeck and Evans, 1973). However, Reference Weertman, Whalley, Whalley, Jones and GoldWeertman (1973) offers the explanation that, because the total creep strains are so small in these experiments, it is unlikely that the dislocation density has reached the steady-state value. Values of n calculated from field observation at low stresses vary, but in general exceed unity. Reference Shreve and SharpShreve and Sharp (1970) from analysis of bore-hole data, Reference NyeNye (1953) from tunnel closure, and Reference ThomasThomas (1971) and Reference DorrerDorrer (1971) from ice shelf spreading support a value n ≈ 3. On the other hand, Reference Gerrard, Gerrard, Perutz and RochGerrard and others (1952) from bore-hole data as reexamined by Reference NyeNye (1957) indicates a lower value n ≈ 2. (This is my calculation from Nye’s figure 6, Curve T1 taken at the base of the glacier.)

Fig. 6. Dimensionless velocity profiles U and boundary associated effective stresses Ta for the case c = 2. b/a = 08. ∈ = – 0.235. The tick marks indicate equal stress increase over intervals CC’. C’E. and EO. T0 – 0 on OC. The key stresses are: 0: Ta = 0; C’: Ta = 1.028; ∈: Ta = 0898.
The situation involving the measurement of the index n at low stresses is further clouded by the fact that there are no field measurements at stresses as low as 0.25 bar. In addition, as pointed out by Reference PatersonPaterson (1981) and by Reference Morland and ShoemakerMorland and Shoemaker (1982) for the case of ice shelves, there are serious difficulties involved in calculating n from any field data. It would seem that until this ambiguity is removed in favour of a value of n much greater than one there is justification for treating the linear case here.
Consider the following class of functions as prospective velocity field in Equation (2):

Here, K = ρga sin α is a characteristic stress as used by Nye, the basal stress for an infinitely wide channel of depth a. Coefficient b is a horizontal length scale. Coefficients Bi and Ci are arbitrary at this stage. For the special case Bi = Ci = 0, all i. Equation (5) reduces to the velocity field for an infinitely wide channel of depth a (Reference NyeNye, 1965).
Flow Equations (2) with n = 1 determine the associated stress components


Equilibrium Equation (1) is satisfied identically by Equations (6), as are the boundary conditions Equation (3) and Equation (4).
Rather than attempting to choose coefficients so that the null velocity condition is satisfied on a predetermined basal profile, it is easier and far more flexible to adopt an inverse approach, thus assigning coefficients and determining the resultant null velocity profile. To this end we shall examine two special cases which will prove to be sufficiently general to illustrate the possibilities of the method.
Basal Profiles Intersecting z-Axis
If C1, is the only non-zero coefficient in Equation (5) the null-velocity profile is determined as the solution to

With the characteristic length a fixed, Equation (7) contains two parameters. It is a simple numerical task to determine the ranges of b and C1 which place the thalweg at z = 0 as required.
Figure 1 graphs the right half of six basal profiles on axes y/a, z/a; three intersect the y/a axis at 0.3 and three at 0.7. The profiles resemble ellipses. Our primary interest is in shape modification, not scale. Scale can always be adjusted by varying the constant a. With scale removed from consideration, two parameters remain for shape modification and this is reduced to one if the width/depth ratio of the channel is specified.
To illustrate the flexibility of a one-parameter modification to shape with a fixed width/depth ratio we consider basal profile families which have the same intercepts on y/yi, z/yi axes, where yi is the yi intercept of any curve. Let c = zi/yi be the fixed ratio of the intercepts. Substituting the intercepts (0, cyi) and (yi,0) into Equation (7) gives
With a = 1, and b and c assigned, yi is determined from Equation (9) and C1, from Equation (8). The basal profiles are then found from Equation (7) as before.
Figure 2 illustrates profiles corresponding to c = 1 and c = 2. It is clear that the single parameter which governs shape affords considerable variation. Velocity and stress results are not illustrated; these are easily obtained from Equation (5) and (6) and are qualitatively similar to Nye’s results.

Fig. 2. The right half of seven basal profiles plotted on y/yi, z/yi axes. Parameter values are:
Curve A: b = 0.95a, C1 = 0.9024;
Curve B: b = 0.8a, C1 = 0.6381;
Curve C: b = 0.7a, C1 = 0.4855;
Curve D: b = 1.55, C1 = 0.9555;
Curve E: b = 1.5a, C1 = 0.8859;
Curve F: b = a, C1 = 0.3271;
Curve G: b = 0.75a, C1 = 0.1454.
Basal Profiles Not Intersecting z-Axis
If B1 is the only non-zero coefficient in Equation (5), the null-velocity profile is determined as the solution to

Profiles of this class are periodic in z and may not intersect the z-axis. In that event exact solutions are provided for Newtonian flow in overfilled channels (an ice sheet flowing over a periodic array of cylindrical channels in the direction of the cylindrical axes). Since this problem has not been previously considered, we illustrate some details of the velocity and stress fields.
Figure 3 graphs families of half wavelength basal profiles plotted on axes y/yi, z/yi – similar to Figure 2. Profiles are shown for c = 1 and c = 2 where c is the ratio of the half wavelength to ice depth at the thalweg. With c and b/a given, the dimensionless half wavelength zi/a is found from the condition cos zi/b = 1 or
The dimensionless intercept yi/a is then given by
Finally, B1 is found from Equation (10) which gives
Note that all basal profiles are smooth and intersect the y/yi axis orthogonally. Thus, curve A approximates a V-shaped profile but the bottom is actually rounded at the thalweg.

Fig. 3. The right half of seven periodic basal profiles plotted on y/yi, z/yi coordinates. The ice surface corresponds to the top of the box. Parameter values are:
Curve A: b/a = 0.53, B1 = −0.1529;
Curve B: b/a = 0.45, B1 = −0.0861;
Curve C: b/a= 0.40, B1 = −0.0500;
Curve D: b/a = 0.32, B1 = −0.000011852;
Curve E: b/a = 1.175, B1 = −0.9591;
Curve F: b/a = 0.8, B1 = −0.2308;
Curve G: b/a = 0.65, B1 = −0.016929.
Figure 4 illustrates dimensionless velocity profiles and dimensionless boundary stresses corresponding to curve E of Figure 3. Dimensionless velocity is defined by

where aAK/2 is the surface velocity in an infinitely wide channel of uniform depth a for a linear material. In terms of dimensionless variables Y = y/yi, Z = z/yi-where yi is given by Equation (12)

In Figure 4, since b/a = 1.175 and c = 2 the channel depth at the thalweg is yi/a = 1.85 from Equation (12). Thus, the maximum channel depth is greater than a which explains why values of U exceed unity.

Fig. 4. Dimensionless velocity profiles U at intervals of 0.2 and dimensionless boundary stresses T for the case c = 2 b/a = 1.175. B1 = −0.9591. The inner boundary tick marks indicate equal stress increments over intervals OB, BC, CC′; C′D, DE, and EO on which stress varies monotonically. (The increments are not the same for all intervals.) Key stresses are:
O: T = 0.0, B: T = 0.408, C: T = 0.0, C′: T = 0.230, D: T = 1.23, E: T = 0.906.
Dimensionless effective stress is defined by

In dimensionless variables (Y, Z) this becomes

where τ xy and τxz are computed from Equation (6).
Because T is proportional to grad U for a linear material one can visualize the profiles of T from the boundary values of T and profiles of U illustrated. The boundary stresses are given by the tic marks on the inner boundary which are spaced at equal increments of T over arcs OB, BC, CC’, C’D, DE, and EO on which stress varies monotonically. The increments are not the same for all intervals. The key stresses are: O: T = 0.0, B: T = 0.408, C: T = 0.0, C: T = 0.230, D: T = 1.23, E: T = 0.906. Thus, T has an overall maximum at point D and a relative maximum at point B. The boundary stress on OBC is sinusoidal as can be seen from Equation (15’). The fact that T = 0 at point C follows from the symmetry of the periodic channel array. The stress would not vanish at C nor be sinusoidal on the free surface for an isolated valley.
The Nye shape factor is easily computed. Thus, the dimensionless shear stress at the thalweg, assuming plane flow, is equal to the dimensionless ice depth, or 1.85. The actual dimensionless stress is 0.906. Thus, the Nye shape factor value is f = 0.49.
Profiles for n = 3 Not Intersecting z-Axis
For a non-linear material it is difficult to produce an interesting class of velocity fields which is associated with an equilibrium stress field through Glen’s flow law. Taking a new approach we consider the equilibrium stress field


where b/a and ϵ are parameters and unknown function f must satisfy the condition that f’ bounded. Equation (16) are substituted into Glen’s flow law (2) with n = 3. This gives


Equations (17) thus result in expansions in powers of ϵ out to ϵ3. Provided conditions can be established such that the ϵ2 and ϵ3 terms are uniformly dominated by the ϵ° and ϵ1 terms (better yet, that the ϵ2 and ϵ3 terms are also uniformly dominated by the ϵ1 term), for suitably small ϵ the ϵ2 and ϵ3 terms may be neglected. (These conditions will be considered later.) Equations (17) may then be integrated, yielding a velocity field which is associated with the equilibrium stress field through the flow law only out to the first order ϵ term.
The velocity field resulting from this procedure is

The constant of integration was determined by the condition that for ϵ = 0 the velocity be that of an n = 3 Glen material flowing in a uniform channel of depth a.
The procedure also produces a differential equation for the determination of f(y) in Equations (16) and (18). Thus,

Letting f′ = g gives a form of the modified Bessel equation which has the regular solution

Note that lim f’  ; thus f and f′ are bounded. Moreover, from Equation (16b) τxz(0,z) = 0 which was not a required condition. The boundary condition τxz(y,0) = 0 is satisfied by Equation (16b) while the other boundary condition τxy(0,z) = 0 is satisfied by Equation (16a).
; thus f and f′ are bounded. Moreover, from Equation (16b) τxz(0,z) = 0 which was not a required condition. The boundary condition τxz(y,0) = 0 is satisfied by Equation (16b) while the other boundary condition τxy(0,z) = 0 is satisfied by Equation (16a).
The quantity 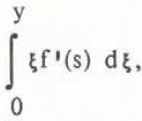 , necessary for determining τxy in equation (16a), is found by integration using (20). This gives
, necessary for determining τxy in equation (16a), is found by integration using (20). This gives

The constant C1 is determined by the condition that for | ϵ | = 1 the ϵ° terms in Equations (16a and b) are just sufficient to dominate the ϵ1 terms throughout the flow field. It is fairly easy to show that

Here yi is the y-intercept of the zero-velocity basal profile which is yet to be determined. With C1, yi/a, b/a, and ϵ given, the stress and velocity fields are known. The analysis is valid for | ϵ | small compared with unity but because the bounding procedure leading to Equation (22) was fairly crude it is expected that the useful range of | ϵ | will be somewhat larger.
We illustrate results in Figure 5 for fixed aspect ratio c defined as previously for the Newtonian material leading to Figure 3. With c prescribed, the intercepts zi/a and yi/a are again given by Equations (11) and (12), respectively. Substituting the intercept (yi,0) into Equation (18) with u = 0 and solving for ϵ results in

At this stage with the input parameters c and b/a prescribed and zi/a, yi/a determined from Equation (11) and (12), C1, is found from Equation (22), ϵ from Equation (23). f’ from Equation (20) and 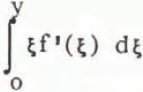 from Equation (21). Velocity is then given by Equation (18) and the stress components by Equation (16).
from Equation (21). Velocity is then given by Equation (18) and the stress components by Equation (16).

Fig. 5. The right half of six periodic basal profiles for an n = 3 Glen material. Parameters are:
Curve A: b/a = 0.4, ϵ = −0.470;
Curve B: b/a = 0.35, ∈ = −0.248;
Curve C: b/a = 0.9, ϵ = −0.294;
Curve D: b/a = 0.7, ϵ = –0.124;
Curve E: b/a = 1.3, ϵ = –0.186;
Curve F: b/a = 1.0, ϵ = –0.441.
It is evident from Equations (16) and (18), noting that f’ is bounded, that the perturbation on stress and velocity is not felt at the free surface y = 0. This property is built into the general expansions (17) for ∂u/∂y and ∂u/∂z before truncation; thus, both ∂u/∂y and ∂u/∂z approach zero to order y3 at y = 0. This behaviour is appropriate if the basal profile is a perturbation on a horizontal base.
Note that with C1 given by Equation (22), uniform domination of the ϵ1 terms by the ϵ° terms is assured for | ϵ | ≤ 1. However, there is no assurance of a similar uniform domination of the ϵ2 and ϵ3 terms. A practical numerical measure of this domination will be discussed later.
Again, defining a dimensionless velocity by U = 4u/Ak3a where AK3a is the free-surface velocity in a channel of depth a and using dimensionless variables Y = y/yi, Z = z/yi, the dimensionless velocity field from Equations (18) and (20) is

(Note that C1, from Equation (22), has the dimension [length]3).
Figure 5 graphs the right half of a range of zero-velocity basal profiles determined for fixed c and b/a with ϵ and C1 determined by the previously outlined procedures. The profiles are found by setting U = 0 in Equation (24). The results indicate that | ϵ | increases rapidly as c decreases. Also, the cusp-line behaviour at the y-intercept, noted previously for the n = 1 material in Figure 3, again appears for c = 1 as | ϵ | increases. For c = 2 and 3 deep valley profiles (not illustrated) can be produced corresponding to the range |ϵ | < 0.5. Solutions for such cases should be useful for approximating Nye shape factors.
The dimensionless effective stress T defined by Equation (15) becomes

Because stresses and velocities are associated through the flow law only to the first power of ϵ, relative errors in the velocity-stress relation of order ϵ2 are present in Equations (24) and (25). To remove this undesirable feature of the solution we can, alternatively, regard Equation (24) as a given velocity field. Stresses can then be derived by inverting Glen’s flow law, Equation (2). This results in the associated stress field

This stress field satisfies equilibrium only out to first order e and differs by order ϵ3 from the original stress field. In terms of the dimensionless variables Y = y/yi, Z = z/yi, the dimensionless associated effective stress becomes

Several numerical examples suggest the following conclusions: (i) T and Ta differ uniformly by well less than| ϵ |, (ii) the values of Ta/T tend to oscillate slowly about unity, (iii) the relative error | (T–Ta)/T |, for fixed z/yi, is minimized at the base and maximized near the free surface, (iv) overall equilibrium is satisfied to at least two figures. This latter conclusion is arrived at by numerical integration of the basal drag, (v) Finally, comparison of T and Ta values for several numerical examples supports the conclusion that there is satisfactory domination of the ϵ2 and ϵ3 terms in Equation (17) provided | ϵ | is small compared to unity.
Figure 6 illustrates profiles of U and boundary values of Ta corresponding to b/a = 0.8, c = 2, ϵ = – 02352. Here, yi = 1.257 a, computed from Equation (12), is the maximum ice depth at z = 0; the minimum ice depth is 0.886 a at z/yi = ± 2 This represents a perturbation between + 25% to – 11% on the depth of a uniform channel. The ratio of the half width of the glacier valley to the depth of valley at the thalweg is w/2h = 2/0.295 ≃ 7, a value which is well within the range of actual glacier valleys. (Reference ShoemakerShoemaker (in press) presents w/2h values for various glacier and fjord valleys which correspond to the range 1 ≤ w/2h ≤ 10).
The Nye shape factor for the example is f = 0.71. This can be compared to the value f = 0.73 corresponding to a linear material flowing in profile F of Figure 3, a very similar but slightly deeper profile. Thus, the Nye shape factor is very insensitive to the non-linear flow law. The velocity profiles corresponding to profile F of Figure 3, however, are qualitatively dissimilar to those of Figure 6. Rather, they are similar to Figure 4 in that they intersect the free surface; the dimensionless velocity U varies between 1.23 and 0.769 on the free surface of profile F of Figure 3. Moreover, the velocity gradients corresponding to Figure 6 are much steeper near the base and much less steep near the free surface as compared with the linear case. This result is, of course, consistent with the flow law.
Profiles for n = 3 Intersecting z-Axis
Reference NyeNye (1965) presented an analytical solution due to W. Chester for a slightly elliptic channel, A standard perturbation technique was employed. We shall again consider a multi-parameter inverse technique which will involve four independent small parameters. Nye’s solution will be obtained by setting three of the parameters, equal to zero. The emphasis will be upon exhibiting a variety of channel shapes for which exact solutions can be obtained corresponding to a zero-velocity basal condition.
The single equilibrium equation in cylindrical coordinates is

We consider the stress field


which reduces to the stress field for flow in a semicircular channel of radius a if ϵ2j = 0. As before, K. is the basal shear stress in a channel of uniform depth a.
The free-surface boundary condition is
and symmetry implies that
Both boundary conditions are satisfied by Equation (30).
Substitution of Equations (29) and (30) into (28) determines functions g2j in terms of f2j such that equilibrium is satisfied. Thus

Glen’s flow law (2) in cylindrical coordinates is

The stress field given by Equations (29) and (30) along with (33) is substituted into Equation (2’). This results in an expansion in e out to third powers. Truncating the higher powers enables one to obtain a velocity field which is associated with the stress field out to first power of ϵ. Differential equations also result for the determination of f2j. These are

with the regular solutions

The resultant velocity field is

where the constant of integration was determined by the condition that Equation (36), if ϵ2j = 0 reduces to Nye’s solution for flow in a semicircular channel. The stress fields will not be investigated here but are easily obtained by substitution of Equation (35) into Equations (29) and (30).
The restriction of “small perturbations” are satisfied if the coefficients in Equation (36), e.g. | ϵ6| 2/9| ϵ6| (−1 + ![]() ) are small compared with unity. These coefficients
) are small compared with unity. These coefficients ![]() , and
, and ![]() are the effective small parameters.
are the effective small parameters.
To within the accuracy of the perturbation scheme Nye’s solution for an elliptic channel is obtained if E4 = E6 = E8 = 0.
Figure 7 illustrates various basal profiles which satisfy the small parameter restriction. The values of the effective small parameters for the four cases where there is only one non-zero E2j are: ![]() ,
, ![]() . Thus, the solution corresponding to the ellipse-like channel, which is similar to Nye’s solution, may violate the small-parameter restriction. Parameter values are acceptably small for the other examples. The effect of ϵ4, ϵ6, and ϵ8 upon shape may be ascertained by comparison of the profiles. By using even higher-order terms it should be possible to match profiles which are of particular interest. However, it must be noted that all such profiles must satisfy the condition that | w2/h − 1 | be small compared to unity. Most glacier valleys fall outside this range.
. Thus, the solution corresponding to the ellipse-like channel, which is similar to Nye’s solution, may violate the small-parameter restriction. Parameter values are acceptably small for the other examples. The effect of ϵ4, ϵ6, and ϵ8 upon shape may be ascertained by comparison of the profiles. By using even higher-order terms it should be possible to match profiles which are of particular interest. However, it must be noted that all such profiles must satisfy the condition that | w2/h − 1 | be small compared to unity. Most glacier valleys fall outside this range.

Fig. 7. Five profile perturbations on a semicircular filled channel.
Conclusion
The inverse technique exhibited here was developed by the author primarily for use in obtaining exact solutions where a sliding law is included, an extension of Reference ShoemakerShoemaker (in press). In the form exhibited here, the technique is applicable to cold-based glaciers. The flow law, however, is restricted to be homogenous.
Acknowledgements
The author wishes to thank Vincent Ng for doing the numerical calculations and the NSERC of Canada for financial support.









