Research Article
An Index of Regional Snow-Pack Stability based on Natural Slab Avalanches
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 67-73
-
- Article
-
- You have access
- HTML
- Export citation
Frazil Formation in Water of Different Salinities and Supercoolings
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 74-85
-
- Article
-
- You have access
- HTML
- Export citation
Flood and Landslide Events, Peyto Glacier Terminus, Alberta, Canada, 11–14 July 1983
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 86-91
-
- Article
-
- You have access
- HTML
- Export citation
Determination of the Flow Properties at Dye 3, South Greenland, by Bore-Hole-Tilting Measurements and Perturbation Modelling
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 92-98
-
- Article
-
- You have access
- HTML
- Export citation
The Dynamics of Ice-Sheet Outlets
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 99-107
-
- Article
-
- You have access
- HTML
- Export citation
Spatial and Temporal Variations in Electrical Conductivity in a Pro-Glacial Stream System
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 108-114
-
- Article
-
- You have access
- HTML
- Export citation
Adjusting Two-Dimensional Velocity Data to Obey Continuity
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 115-119
-
- Article
-
- You have access
- HTML
- Export citation
Normal Stress Effects in the Creep of Ice
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 120-126
-
- Article
-
- You have access
- HTML
- Export citation
Growth Forms of Large Frost Crystals in the Antarctic
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 127-135
-
- Article
-
- You have access
- HTML
- Export citation
Audibility within and Outside Deposited Snow
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 136-142
-
- Article
-
- You have access
- HTML
- Export citation
Bedrock Control on Glacial Limits: Examples from the Ladakh and Zanskar Ranges, North-Western Himalaya, India
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 143-149
-
- Article
-
- You have access
- HTML
- Export citation
Changes in Texture and Fabric of Particles in Glacial Traction with Distance from Source, Mỳrdalsjökull, Iceland
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 150-156
-
- Article
-
- You have access
- HTML
- Export citation
The Internal Structure and Ice Crystallography of Seasonal Frost Mounds
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 157-162
-
- Article
-
- You have access
- HTML
- Export citation
Mixing Formulae and Experimental Results for the Dielectric Constant of Snow
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 163-170
-
- Article
-
- You have access
- HTML
- Export citation
Measurement of the Fracture Toughness of Glacier Ice
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 171-176
-
- Article
-
- You have access
- HTML
- Export citation
Cylindrical Flow in and Over Channels of Irregular Shape
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 177-184
-
- Article
-
- You have access
- HTML
- Export citation
Short Notes
A Reconstruction of Snow-Avalanche Characteristics in Montana, U.S.A., Using Vegetative Indicators
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 185-187
-
- Article
-
- You have access
- HTML
- Export citation
The Diurnal Hysteresis of Snow Albedo
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 188-189
-
- Article
-
- You have access
- HTML
- Export citation
Preferential Discharge of Pollutants During Snowmelt in Scotland
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 190-193
-
- Article
-
- You have access
- HTML
- Export citation
A Note on the Density Distribution of Dry Snow
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 194-195
-
- Article
-
- You have access
- HTML
- Export citation

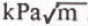 . This is half the value typically obtained by other workers in laboratory tests. The results are compared with other data and the reasons for the disagreement discussed.
. This is half the value typically obtained by other workers in laboratory tests. The results are compared with other data and the reasons for the disagreement discussed.