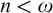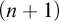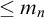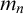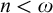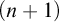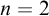1. Introduction
A Heyting algebra
$(H,\land ,\lor ,\to ,0,1)$
is a bounded distributive lattice with a binary operation
$\to $
such that
$$\begin{align*}a\land b \leq c \Longleftrightarrow a \leq b\to c, \end{align*}$$
for every
$a,b,c\in H$
[Reference Balbes and Dwinger1, Reference Chagrov and Zakharyaschev7, Reference Esakia9, Reference Rasiowa and Sikorski16]. Heyting algebras appear naturally in many areas of mathematics. For instance, the lattice of open sets of a topological space forms a Heyting algebra. The subobject classifier of a topos can also be endowed with the structure of a Heyting algebra. Lastly, every distributive algebraic lattice is a Heyting algebra.
In this paper we focus on finitely generated Heyting algebras. We recall that an algebra A is said to be n-generated when there is a subset
$X \subseteq A$
of size
$\leq n$
such that the least subalgebra of A containing X is A itself. Accordingly, we say that A is finitely generated when it is n-generated for some
$n < \omega $
. A class of similar algebras that can be axiomatised by (universally quantified) equations is called a variety. Examples of varieties include the class of all Heyting algebras, as well as that of all Boolean algebras. A variety is said to be n-finite when its n-generated members are finite, and locally finite when it is n-finite for every
$n < \omega $
. We call a variety strictly n-finite if it is n-finite, but not
$(n+1)$
-finite.
Dual characterisations of finitely generated Heyting algebras were obtained in [Reference Esakia and Grigolia10] (see also [Reference Bezhanishvili5, Section 3.1]), while locally finite varieties of Heyting algebras were studied by G. Bezhanishvili and R. Grigolia in [Reference Bezhanishvili and Grigolia4]. In the same paper, they raise the following question [Reference Bezhanishvili and Grigolia4, Problem 2.4]: is it true that a variety of Heyting algebras is locally finite iff it is 2-finite? While this holds in the restrictive context of varieties of Heyting algebras of width two [Reference Benjamins2], in this paper we establish that for any
$n<\omega $
there exists an infinite
$(n+1)$
-generated Heyting algebra
$H_n$
whose n-generated subalgebras are of size
$\leq m_n$
for some
$m_n < \omega $
. From this we deduce the main result of this article: for every
$n<\omega $
the variety generated by
$H_n$
fails to be locally finite, although it is n-finite (Theorem 5.1). For
$n=2$
this provides a negative answer to Bezhanishvili and Grigolia’s question.
From the viewpoint of propositional logic, the key importance of varieties of Heyting algebras is that they provide an algebraic semantics to the axiomatic extensions of the intuitionistic propositional calculus, i.e., superintuitionistic logics. As a consequence of this fact, properties of varieties of Heyting algebras correspond to properties of superintuitionistic logics, and vice versa. It thus follows immediately from the main result of this paper that, for every
$n<\omega $
, there exists a superintuitionistic logic with only finitely many formulas up to logical equivalence in n variables, but which has infinitely many non-equivalent formulas in
$(n+1)$
variables. In Remark 5.5 we additionally make explicit that this logic can be chosen to be finitely axiomatisable.
The structure of this article is based around the proof of Theorem 5.1. In Section 2 we recall the Esakia duality between the category of Heyting algebras with homomorphisms and the category of Esakia spaces with Esakia morphisms. In Section 3 we introduce the notion of colouring of a poset, which is the essential combinatorial tool in the proof of our main result. We believe that everything from Section 3 is essentially folklore, or a slight variation on the standard ideas from bisimulations and back-and-forth systems, but we provide details of every proof as the finitary version of these claims are not common in the literature. In Section 4 we introduce the counterexamples to the question of Bezhanishvili and Grigolia. We describe for every
$n<\omega $
an Esakia Space
$X_n$
and we use the Colouring Theorem to show that its dual
$H_n$
is an infinite
$(n+1)$
-generated Heyting algebra, but every n-generated subalgebras of
$H_n$
is bounded in size by some
$m_n < \omega $
. Finally, in Section 5 we use standard arguments from universal algebra to establish the main result of the article (Theorem 5.1) and we point out some immediate corollaries.
This result was first established in 2020, although it never appeared in print [Reference Martins and Moraschini14]. Independently, the first and fourth authors discovered an alternative simpler proof in 2023 [Reference Hyttinen and Quadrellaro13]. To make the result available, we decided to publish the latter together.
2. Esakia duality
We review in this section the Esakia duality [Reference Esakia8, Reference Esakia9] between Heyting algebras and Esakia spaces. We start by fixing some notation: whenever
$(X,\leq )$
is a poset and
$Y\subseteq X$
we let
$$ \begin{align*} {\uparrow}Y = \{ x\in X \mid \exists y \in Y \text{ and } y \leq x \} \, \, \text{ and } \, \, {\downarrow} Y = \{ x\in X \mid \exists y \in Y \text{ and } y \geq x \}. \end{align*} $$
For
$x\in X$
, we write
${\uparrow } x$
and
${\downarrow } x$
for the sets
$ {\uparrow } \{x\}$
and
$ {\downarrow } \{x\}$
, respectively. A subset
$Y \subseteq X$
is said to be an upset when
$U = {\uparrow } U$
. We write
$\mathsf {Up}(X)$
for the set of upsets of a poset X. Also, given any subset
$Y\subseteq X$
we write
$Y^c$
for its complement
$X\smallsetminus Y$
. If
$x\in {\downarrow } U$
, we often say that x sees U. We will always use the convention that the “arrow operators” defined above bind stronger than other set theoretic operations. For example, the expressions
${\uparrow } U \smallsetminus V$
and
${\downarrow } U \cap V$
are to be read as
$({\uparrow } U) \smallsetminus V$
and
$({\downarrow } U) \cap V$
, respectively.
We recall that an Esakia space is a triple
$X =(X,\tau ,\leq )$
, where
$(X,\tau )$
is a compact topological space and
$(X,\leq )$
a poset satisfying the following conditions:
-
(i) Priestley separation axiom: For all
$x,y\in X$
such that
$x\nleq y$
, there is a clopen upset U such that
$x\in U$
and
$y\notin U$
. -
(ii) If U is clopen, then also
${\downarrow } U$
is clopen.
Given Esakia spaces X and Y, an Esakia morphism
$p \colon X \to Y$
is a continuous map satisfying the two following conditions:
-
(i) For all
$x, y \in X$
if
$x \leq y$
, then
$p(x) \leq p(y)$
. -
(ii) For all
$x \in X$
and
$y \in Y$
such that
$p(x) \leq y$
, there exists
$z \in X$
such that
$x \leq z$
and
$p(z) = y$
.
Esakia duality is a dual categorical equivalence between the category of Heyting algebras with homomorphisms and the category of Esakia spaces with Esakia morphisms, which generalizes Stone duality. We shall review the definition of the two contravariant functors
$(-)^\ast $
and
$(-)_\ast $
witnessing Esakia duality. On the one hand, with every Heyting algebra H we associate an Esakia space
$H_\ast $
as follows. A prime filter F of H is a proper filter for which
$x\lor y\in F$
entails
$x\in F$
or
$y\in F$
. Then the Esakia space
$H_\ast $
is obtained by endowing the poset of prime filters of H ordered under the inclusion relation with the topology generated by the subbasis
$$\begin{align*}\{ \phi(a) \,|\, a\in H \} \cup \{ \phi(a)^c \,| \, a\in H \}, \end{align*}$$
where
$\phi (a)$
is the set of prime filters of H containing a. Furthermore, every homomorphism
$h:H\to H'$
between Heyting algebras is associated with the Esakia morphism
$h_*:H^{\prime }_\ast \to H_\ast $
defined as
$h_*(F)=h^{-1}[F]$
. On the other hand, with every Esakia space X we associate a Heyting algebra
$X^\ast $
as follows. Let
$\mathsf {ClUp}(X)$
be the set of clopen upsets of X. Then
$$\begin{align*}X^\ast = (\mathsf{ClUp}(X), \cap, \cup, \to, \emptyset, X), \end{align*}$$
where
$\to $
is defined by letting
$U\to V = ({\downarrow } (U\smallsetminus V))^c$
. Furthermore, every Esakia morphism
$p:X\to Y$
is associated with the homomorphism
$p^*:Y^\ast \to X^\ast $
defined as
$p^*(U)=p^{-1}[U]$
.
3. Poset colourability
We introduce in this section the colouring technique, which is the key combinatorial technique used in our subsequent proofs. The first item in the next definition exemplifies the idea of a back-and-forth system, and can also be seen as a version of the notion of layered bisimulation from [Reference Visser18]. The connection between back and forth systems and types goes back to Fraïssé [Reference Fraïsse11].
Remark 3.1. In this paper, we always identify natural numbers with finite ordinals, i.e., we identify each natural number
$n<\omega $
with the set
$\{ m\in \omega \mid m<n\}$
. In particular, we stress that when we write
$n < \omega $
, it may be the case that
$n=0$
.
Definition 3.2. Let X be a poset and
$G\subseteq \mathsf {Up}(X)$
.
-
(i) For every
$n < \omega $
we define recursively an equivalence relation
${\sim }^G_n$
on X as follows: for every
$x, y \in X$
, Moreover, we consider the following equivalence relation on X:
$$ \begin{align*} x {\sim}^G_0 y \; &\;\Longleftrightarrow \; \forall g\in G \; (x\in g \iff y\in g); \\ x{\sim}^G_{n+1} y \; &\;\Longleftrightarrow \; \forall z\geq x \; \exists v\geq y \; (z{\sim}^G_{n} v) \; \land \; \forall v\geq y \; \exists z\geq x \; (z{\sim}^G_{n} v). \end{align*} $$
$$\begin{align*}{\sim}^G_{\omega} =\bigcap_{n\in\omega} {\sim}^G_{n}. \end{align*}$$
-
(ii) The n-type and the
$\omega $
-type over G of an element
$x \in X$
are, respectively, the sets
$$\begin{align*}\{ y\in X \mid x{\sim}^G_n y\} \, \, \text{ and } \, \, \{ y\in X \mid x{\sim}^G_\omega y\}. \end{align*}$$
-
(iii) We say an element
$x\in X$
is G-isolated if
$x{\sim }^G_{\omega }y$
entails
$x=y$
. -
(iv) We say that X is G-coloured (or coloured by G) if every element of X is G-isolated.
Lemma 3.3. Let X be a poset. For every
$G\subseteq \mathsf {Up}(X)$
and
$n<\omega $
, the equivalence relation
${\sim }^G_{n+1}$
refines
${\sim }^G_{n}$
.
Proof. We proceed by induction. For
$n=0$
we assume
$x {\nsim }^G_0 y$
. Without loss of generality there is some
$g\in G$
such that
$x\in g$
and
$y\notin g$
. Since g is an upset, it follows that
$z\in g$
for every
$z\geq x$
but
$y\notin g$
, showing
$x {\nsim }^G_1 y$
.
For
$n=m+1$
assume
$x {\nsim }^G_{n} y$
. Without loss of generality there is some
$z\geq x$
such that for all
$v\geq y$
it holds
$z\nsim ^G_{n-1} v$
. Hence, by the induction hypothesis, we obtain
$z\nsim ^G_{n}v$
and therefore
$x {\nsim }^G_{n+1} y$
.
By a term we understand a first-order term in the language of Heyting algebras.
Definition 3.4. The implication rank
$\mathsf {rank}(\phi )$
of a term
$\phi $
is defined as follows:
-
(i) If
$\phi $
is a constant or a variable, then
$\mathsf {rank}(\phi )=0$
; -
(ii)
$\mathsf {rank}(\psi \land \chi )=\text {max}\{\mathsf {rank}(\psi ),\mathsf {rank}(\chi ) \}$
; -
(iii)
$\mathsf {rank}(\psi \lor \chi )=\text {max}\{\mathsf {rank}(\psi ),\mathsf {rank}(\chi ) \}$
; -
(iv)
$\mathsf {rank}(\psi \to \chi )=\text {max}\{\mathsf {rank}(\psi ),\mathsf {rank}(\chi ) \}+1$
.
Let H be a Heyting algebra. Given a subset
$G \subseteq H$
, we denote by
$\langle G \rangle $
the subalgebra of H generated by G. We recall that the universe of
$\langle G \rangle $
is
$$\begin{align*}\{ \phi^H(\vec{g}) \mid \vec{g} \in G \text{ and }\phi \text{ is a term}\}, \end{align*}$$
where
$\phi ^H(\vec {g})$
is the interpretation of
$\phi $
in H under the assignment
$\vec {g}$
.
Definition 3.5. Let X be an Esakia space and
$G = \{ g_i \mid i < k \} \subseteq X^\ast $
. The implication rank
$\mathsf {rank}(U)$
of an element
$U \in \langle G \rangle $
is
$$\begin{align*}\min \{ \mathsf{rank}(\phi) \mid \phi \text{ is a term such that }U = \phi^{X^\ast}(g_0,\dots,g_{k-1})\}. \end{align*}$$
In addition, with every U as above we associate a term
$\phi _U(x_0, \dots , x_{k-1})$
such that
$U = \phi _U^{X^\ast }(g_0, \dots , g_{k-1})$
and
$\mathsf {rank}(U) = \mathsf {rank}(\phi )$
.
The following lemma and the subsequent Colouring Theorem generalize [Reference Grilletti and Quadrellaro12, Proposition 34] and are essentially a reformulation of [Reference Bezhanishvili5, Theorem 3.1.5]. The relation between the implication rank of a term and the existence of a back-and-forth system of corresponding length was established in [Reference Visser18, Theorems 4.7 and 4.8].
Lemma 3.6. Let X be an Esakia space and
$x,y\in X$
. The following condition holds for every finite
$G\subseteq X^\ast $
:
$$ \begin{align*} x {\sim}^G_{n} y & \Longleftrightarrow \forall U \in \langle G \rangle \text{ with } \mathsf{rank}(U)\leq n: (x \in U \iff y \in U). \end{align*} $$
Proof. We fix an enumeration
$G=\{g_i \mid i< k\}$
and let
$\vec {g} = (g_0, \dots , g_{n-1})$
. Moreover, given a term
$\phi (x_0, \dots , x_{n-1})$
, we will write
$\phi (\vec {g})$
as a shorthand for
$\phi ^{X^\ast }(\vec {g})$
. Both implications in the statement will be proven by induction on n.
$(\Rightarrow )$
For the case where
$n=0$
, suppose that
$x {\sim }^G_{0} y$
and consider
$U \in \langle G \rangle $
such that
$\mathsf {rank}(U)=0$
. Then we may assume that
$\phi _U$
is a meet of joins of constants and variables. If
$\phi _U=0$
or
$\phi _U=1$
, then
$U=\emptyset $
or
$U=X$
and the claim follows immediately. On the other hand, if
$\phi _U=g_i$
for some
$i<k$
, we have that
$x\in g_i$
if and only if
$y\in g_i$
by the definition of
${\sim }^G_{0}$
. As
$\phi _U$
is a meet of joins of constants and variables, this implies that the claim holds.
Then we consider the case where
$n = m+1$
. Suppose that
$x {\sim }^G_{m+1} y$
and consider
$U \in \langle G \rangle $
such that
$\mathsf {rank}(U) \leq m+1$
. First suppose that
$\mathsf {rank}(U) \leq m$
. By Lemma 3.3 we have
$x {\sim }^G_{m} y$
and, therefore, the claim holds by the induction hypothesis. Then we consider the case where
$\mathsf {rank}(U) = m+1$
. We may assume that
$\phi _U$
is a conjunction of disjunctions of terms of the form
$\alpha \to \beta $
of implication rank
$\leq m+1$
and with variables among
$x_0, \dots , x_{n-1}$
.
For each of these implications
$\alpha \to \beta $
, let
We will show that
$x \in U_{\alpha \beta }$
if and only if
$y \in U_{\alpha \beta }$
. By symmetry, it suffices to prove the implication from right to left. Accordingly, suppose
$x\notin ({\downarrow } (\alpha (\vec {g})\smallsetminus \beta (\vec {g})))^c$
. Then there is some
$z\geq x$
such that
$z\in \alpha (\vec {g})\smallsetminus \beta (\vec {g})$
and, since
$x {\sim }^G_{m+1} y$
, there is some
$v\geq y $
such that
$z {\sim }^G_{m} v$
. As
$\alpha (\vec {g}), \beta (\vec {g}) \in \langle G \rangle $
and
$\mathsf {rank}(\alpha (\vec {g})), \mathsf {rank}(\alpha (\vec {g})) \leq m$
, we can apply the induction hypothesis obtaining
$v\in \alpha (\vec {g})\smallsetminus \beta (\vec {g})$
. Hence, we conclude that
$y\notin ({\downarrow } (\alpha (\vec {g})\smallsetminus \beta (\vec {g})))^c = U_{\alpha \beta }$
.
Since U is a meet of joins of sets of the form
$U_{\alpha \beta }$
, the claim follows from the fact no
$U_{\alpha \beta }$
separates x and y.
$(\Leftarrow )$
For the case where
$n=0$
, suppose that
$x {\nsim }^G_0 y$
. Without loss of generality, we may assume that there is some
$g_i\in G$
such that
$x\in g_i$
and
$y\notin g_i$
. Since
$\mathsf {rank}(g_i)=0$
, the claim follows immediately.
For the case where
$n=m+1$
, suppose that
$x\nsim ^G_{m+1} y$
. We may assume that there is
$z\geq x$
such that for all
$v\geq y$
we have
$z\nsim ^G_{m} v$
. By the induction hypothesis, for every
$v\geq y$
, there is either
$\psi _v(\vec {g})\in \langle G \rangle $
such that
$z\in \psi _v(\vec {g})$
and
$v\notin \psi _v(\vec {g})$
, or
$\chi _v\in \langle G \rangle $
such that
$z\notin \chi _v(\vec {g})$
and
$v\in \chi _v(\vec {g})$
, with
$\mathsf {rank}(\psi _v),\mathsf {rank}(\chi _v)\leq m$
. We let
$$ \begin{align*} I_0&:=\{v \in {\uparrow} y \;|\;z\in \psi_v(\vec{g}) \text{ and } v\notin \psi_v(\vec{g}) \}; \\ I_1&:=\{v \in {\uparrow} y \;|\;z\notin \chi_v(\vec{g}) \text{ and } v\in \chi_v(\vec{g}) \}. \end{align*} $$
By construction we have
${\uparrow } y = I_0 \cup I_1$
. Then we define
Notice that by the previous direction the number of terms of rank
$\leq m$
is finite, whence the intersections and unions above are finitary and thus Z is a well-defined element of
$\langle G \rangle $
. Furthermore,
$\mathsf {rank}(Z) \leq m+1$
because each
$\psi _v$
and
$\chi _v$
has implication rank
$\leq m$
. Therefore, to conclude the proof, it suffices to show that
$x \notin Z$
and
$y \in Z$
.
Since for every
$v\in I_0$
we have
$z\in \psi _v(\vec {g})$
and for every
$v\in I_1$
we have
$z\notin \chi _v(\vec {g})$
, it follows that
$z\in \bigcap _{v\in I_0} \psi _v(\vec {g}) \smallsetminus \bigcup _{v\in I_1} \chi _v(\vec {g})$
. As
$x \leq z$
, we obtain
$$\begin{align*}x\notin \bigg({\downarrow} \bigg( \bigcap_{v\in I_0} \psi_v(\vec{g}) \smallsetminus \bigcup_{v\in I_1} \chi_v(\vec{g}) \bigg)\bigg)^c = Z. \end{align*}$$
To prove that
$y\in Z$
, suppose the contrary. Then there is some
$w\geq y$
such that
$w\in \bigcap _{v\in I_0} \psi _v(\vec {g}) \smallsetminus \bigcup _{v\in I_1} \chi _v(\vec {g})$
. As
$w \geq y$
and
${\uparrow } y = I_0 \cup I_1$
, either
$w \in I_0$
or
$w \in I_1$
. If
$w\in I_0$
, then
$w\notin \psi _w(\vec {g})$
. While if
$w\in I_1$
, then
$w\in \chi _w(\vec {g})$
. In both cases, we obtain
$w\notin \bigcap _{v\in I_0} \psi _v(\vec {g}) \smallsetminus \bigcup _{v\in I_1} \chi _v(\vec {g})$
, a contradiction.
Let X be an Esakia space and
$G \subseteq X^\ast $
. In view of Esakia duality, the subalgebra
$\langle G \rangle $
of
$X^\ast $
is proper if and only if the relation
$$\begin{align*}R = \{ \langle x, y \rangle \in X \times X \mid x \in U \text{ iff }y \in U, \text{ for every }U \in \langle G \rangle \} \end{align*}$$
differs from the identity relation on X (see, e.g., [Reference Bezhanishvili5, Corollary 2.3.10]). As a consequence, we deduce the following:
Lemma 3.7. Let X be an Esakia space and
$G \subseteq X^\ast $
. Then
$X^\ast = \langle G \rangle $
if and only if for every
$x, y \in X$
,
$$\begin{align*}\{ U \in \langle G \rangle \mid x \in U \} = \{ U \in \langle G \rangle \mid y \in U \} \text{ implies }x = y. \end{align*}$$
In view of the next result, the concept of subalgebra generation can be studied through that of colouring.
Colouring Theorem 3.8. Let X be an Esakia space and
$G\subseteq X^\ast $
finite. Then
$X^\ast = \langle G \rangle $
if and only if X is G-coloured.
Proof.
$(\Rightarrow )$
To prove that every element of X is G-isolated, it suffices to show that for every pair of distinct
$x, y \in X$
we have
$x\nsim ^G_\omega y$
. Accordingly, consider two distinct
$x, y \in X$
. By symmetry we may assume that
$x \nleq y$
. The Priestley separation axiom implies that there is
$U \in X^\ast $
such that
$x\in U$
and
$y\notin U$
. From the assumption that
$X^\ast =\langle G \rangle $
it follows that
$U\in \langle G \rangle $
. By Lemma 3.6 we obtain that
$x\nsim ^G_n y$
for
$n = \mathsf {rank}(U)$
. Therefore, the definition of
$ {\sim }^G_\omega $
guarantees that
$x\nsim ^G_\omega y$
.
$(\Leftarrow )$
By Lemma 3.7 it suffices to prove that if
$x, y \in X$
are such that
$\{ U \in \langle G \rangle \mid x \in U \} = \{ U \in \langle G \rangle \mid y \in U \}$
, then
$x = y$
. Together with Lemma 3.6, the assumption that
$\{ U \in \langle G \rangle \mid x \in U \} = \{ U \in \langle G \rangle \mid y \in U \}$
implies
$x {\sim }^G_\omega y$
. Since X is G-coloured, we conclude that
$x = y$
.
For the following definition to make sense, recall that we always identify natural numbers with finite ordinals, i.e., we identify
$n<\omega $
with the set
$\{ m\in \omega \mid m<n\}$
.
Definition 3.9. Let X be an Esakia space.
-
(i) A colouring of X is a function
$c \colon n \to X^\ast $
where
$n < \omega $
and X is coloured by
$c[n]$
; -
(ii) X is said to be n-colourable if there is a colouring
$c: n \to X^\ast $
.
The following is an immediate consequence of the Colouring Theorem 3.8:
Corollary 3.10. An Esakia space X is n-colourable if and only if
$X^\ast $
is n-generated.
4. The counterexamples
Our aim is to construct for each
$n < \omega $
an infinite
$(n+1)$
-generated Heyting algebra whose n-generated subalgebras are of size
$\leq m_n$
for some
$m_n < \omega $
. We will do this by exhibiting their dual Esakia spaces
$X_n$
.
Definition 4.1. For every
$n<\omega $
, let
$X_n = (X_n, \tau , \leq )$
be the ordered topological space where
$$ \begin{align*} X_n &= \{x^l_{i} \mid l\leq 2^n \text{ and } i<\omega \}\cup \{x_\infty\},\\ \tau &= \{ U \in \wp(X_n) \mid \text{if }x_\infty \in U\text{, then }U \text{ is cofinite}\}, \end{align*} $$
and
$\leq $
is the unique partial order with minimum
$x_\infty $
such that for every
$x^l_{i}, x^{l'}_{i'} \in X_n$
,
$$\begin{align*}x^l_{i} \leq x^{l'}_{i'} \Longleftrightarrow \text{either }i \geq i'+2 \text{ or }(i = i'+1 \text{ and }l'\neq l+1). \end{align*}$$
Lastly, for each
$i<\omega $
we let
$L^i_n = \{ x^l_{i} \mid l\leq 2^n \}$
and we refer to this as the ith level/layer of
$X_n$
.
Notice that
$X_0$
is the dual of the Rieger–Nishimura lattice, i.e., the free Heyting algebra on one generator [Reference Nishimura15, Reference Rieger17]. On the other hand,
$X_2$
is depicted in Figure 1 as an exemplification.
Figure 1 The Esakia space
$X_2$
.
Lemma 4.2. For every
$n<\omega $
,
$X_n$
is an Esakia space.
Proof. First,
$X_n$
is compact because it is the Alexandroff extension of the countable discrete space
$X_n \smallsetminus \{ x_\infty \}$
. To prove that the Priestley separation axiom holds, consider
$x, y \in X_n$
such that
$x \nleq y$
. Then x differs from the minimum
$x_\infty $
. Consequently,
${\uparrow } x$
is finite and omits
$x_\infty $
. It follows that
${\uparrow } x$
is a clopen upset which, obviously, omits y. It only remains to prove that the downset of a nonempty clopen set U is clopen. Since U is open and nonempty, the definition of the topology guarantees that U contains an element of the form
$x^l_i$
. Therefore,
${\downarrow } U$
contains
$X_n \smallsetminus (L_n^0 \cup \dots \cup L_n^{i+1})$
. It follows that
${\downarrow } U$
is cofinite and contains
$x_\infty $
, whence it is clopen.
By the previous lemma, the dual Heyting algebra
$X_n^\ast $
of
$X_n$
is well-defined. The goal of this section is to show that
$X_n^\ast $
is an infinite
$(n+1)$
-generated Heyting algebra whose n-generated subalgebras are of size
$\leq m_n$
, for some
$m_n < \omega $
which depends only on n. Firstly, notice that to prove that
$X_n^\ast $
is
$(n+1)$
-generated, it suffices by Corollary 3.10 to show that
$X_n$
is
$(n+1)$
-colourable. Intuitively, the latter holds because of two reasons. On the one hand, since
$X_n$
has strictly less than
$2^{n+1}$
maximal elements, we can assign to each maximal element a different subset of colours. On the other hand, the construction of
$X_n$
makes sure any two points at level
$i+1$
see different elements at level i, and thus have different
$\omega $
-types. We make this intuition precise in the proof of the next proposition.
Proposition 4.3. The Esakia space
$X_n$
is
$ (n+1) $
-colourable.
Proof. Since
$n<n+1$
there is an injection
$e:2^{n}+1\to \wp (n+1)$
. Then let
$c:n+1\to X_n^\ast $
be the map defined by letting
$$\begin{align*}c(k)=\{x_0^l\in X_n \mid k\in e(l) \}. \end{align*}$$
By the definition of
$X_n$
we have
$$\begin{align*}X_n = \{ x_\infty \} \cup \bigcup_{i < \omega}L_n^i. \end{align*}$$
Therefore, to prove that
$X_n$
is
$ (n+1) $
-colourable, it suffices to show that for every
$i < \omega $
the points in
$L_n^i$
are all
$c[n+1]$
-isolated. We proceed by induction on i, noting that, by the definition of c and of
${\sim }_0^{c[n+1]}$
, it is clear that every point in
$L_n^0$
is
$c[n+1]$
-isolated. Now, let
$i>0$
and assume that, for all
$j <i$
, every point in
${L_n^{j}}$
is
$c[n+1]$
-isolated.
Let us first show that
$x_i^l {\nsim }_\omega ^{c[n+1]} x_i^{l'}$
, for every
$l \neq l' \leq 2^n$
. By the construction of
$X_n$
we can suppose, without loss of generality, that there exists
$z \in L_n^{i-1}$
lying above
$x_i^l$
but not above
$x_i^{l'}$
. As z is
$c[n+1]$
-isolated by our induction hypothesis, it follows that for all
$v \geq x_i^{l'}$
, there exists
$m_v$
satisfying
$z {\nsim }_{m_v}^{c[n+1]} v$
. Take 
, which exists, as
${\uparrow } x_i^{l'}$
is finite. By Lemma 3.3 we have that
$z{\nsim }_{m}^{c[n+1]} v$
for every
$v\geq x_i^{l'}$
. It is now clear that
$x_i^l {\nsim }_{m+1}^{c[n+1]}x_i^{l'}$
, thus
$x_i^l{\nsim }_\omega ^{c[n+1]} x_i^{l'}$
.
Next we show that, given
$l \leq 2^n$
, then for every
$t> i$
and
$y \in L_n^t$
, we have
$x_i^l{\nsim }_\omega ^{c[n+1]}y$
. By the construction of
$X_n$
we know that
$x_i^{l'}> y$
, for some
$l\neq l'\leq 2^n$
. It follows from our induction hypothesis and from what we just proved above that for every
$z \geq x_i^l$
, there exists
$m_z \in \omega $
such that
$z{\nsim }_{m_z}^{c[n+1]} x_i^{l'}$
. As
${\uparrow } x_i^{l}$
is finite, taking 
and applying Lemma 3.3 yields
$z{\nsim }_{m'}^{c[n+1]} x_i^{l'}$
for every
$z \geq x_i^l$
. Since
$x_i^{l'} \geq y$
, this implies
$x_i^l {\nsim }_{m'+1}^{c[n+1]} y$
, hence also
$x_i^l{\nsim }_\omega ^{c[n+1]}y$
.
Again using our induction hypothesis, we can now conclude that every point in
$L_n^i$
is
$c[n+1]$
-isolated.
Corollary 4.4. The Heyting algebra
$X_n^\ast $
is infinite and
$(n+1)$
-generated.
Proof. Since
$X_n$
is infinite, the Heyting algebra
$X_n^\ast $
is also infinite. Furthermore, it is
$(n+1)$
-generated by Corollary 3.10 and Proposition 4.3.
Therefore, it only remains to prove that the n-generated subalgebras of
$X_n^\ast $
are of size
$\leq m_n$
for some
$m_n < \omega $
. This result follows from two facts. Firstly, in Lemmas 4.5 and 4.7, we show that for every n-colouring
$c:n\to X_n^\ast $
we can find a level
$j<\omega $
such that at least two elements of
$L_n^j$
have the same type under
$c[n]$
and every element in
${\downarrow } L_n^{j+1}$
has the same
$0$
-type. Then, in Lemma 4.9, we use the specific configuration of
$X_n$
to show that there is a level
$j'>j$
such that every element in
${\downarrow } L_n^{j'}$
has the same
$\omega $
-type under
$c[n]$
. We then conclude in Proposition 4.10 that every subalgebra of
$X_n^\ast $
is bounded in size by some
$m_n<\omega $
depending only on n. We will now proceed to prove three technical lemmas.
Lemma 4.5. Let
$c:m\to X_n^\ast $
be a function and
$i, k < \omega $
such that the following conditions hold:
-
(i)
$|L_n^{i}/{\sim }_\omega ^{c[m]}| \leq k\leq 2^n$
. -
(ii) For all
$x,y\in L_n^{i+1}$
we have
$x{\sim }^{c[m]}_{0}y$
.
Then
$|L_n^{i+1}/{\sim }_\omega ^{c[m]}| \leq k\leq 2^n$
.
Proof. By condition (i) we can enumerate
$L_n^{i}/{\sim }_\omega ^{c[m]}$
as
$\{ A_j \mid j< k \}$
. Recall that we say that an element
$x \in L_n^{i+1}$
sees some
$A_j$
when
$x \in {\downarrow } A_j$
.
Claim 4.6. If two elements of
$L_n^{i+1}$
see the same
$A_j$
’s, then they have the same
$\omega $
-type.
Proof of the claim
Consider
$x, y \in L_n^{i+1}$
and suppose that they see the same
$A_j$
’s. We need to show that
$x {\sim }_p^{c[m]} y$
for every
$p < \omega $
. The proof proceeds by induction on p. The case where
$p = 0$
holds by condition (ii). For the case where
$p = q+1$
, the induction hypothesis guarantees that
$x {\sim }_q^{c[m]} y$
. Then consider some
$z \geq x$
. We need to find some
$v \geq y$
such that
$z {\sim }_q^{c[m]} v$
. If
$z = x$
, then we are done taking 
. Then we consider the case where
$x < z$
. If
$z \in {\uparrow } L_n^{i-1}$
, the definition of
$X_n$
and the assumption that
$x, y \in L_n^{i+1}$
guarantee that
$y \leq z$
, in which case we take 
. It only remains to consider the case where
$z \in L_n^{i}$
. Clearly, there exists
$j < k$
such that
$z \in A_j$
. Therefore, x sees
$A_j$
and so does y by assumption. Let
$v \in A_j$
be such that
$y \leq v$
. As
$z, v \in A_j$
, the elements z and v have the same
$\omega $
-type, whence
$z {\sim }_q^{c[m]} v$
.
Now, observe that if
$A_j$
contains at least two elements of
$L_n^{i}$
, then every element of
$L_n^{i+1}$
sees
$A_j$
because of the structure of
$X_n$
. Furthermore, as
$L_n^{i}$
has
$2^n + 1$
elements and the
$A_j$
’s are exactly
$k \leq 2^n$
, we may assume without loss of generality that
$A_{k-1}$
contains at least two elements of
$L_n^{i}$
. Together with the claim, this implies that if two elements of
$L_n^{i+1}$
see the same elements of
$\{ A_j \mid j < k-1 \}$
, then they have the same
$\omega $
-type. As the structure of
$X_n$
guarantees that every element of
$L_n^{i+1}$
sees every
$A_j$
except possibly one, we conclude that
$L_{n}^{i+1} / {{\sim }}_\omega ^{c[m]}$
has
$\leq k$
elements.
Lemma 4.7. For every function
$c:n\to X_n^\ast $
, there is
$j<\omega $
such that at least two elements in
$L_n^j$
have the same
$ \omega $
-type and every element in
${\downarrow } L_n^{j+1}$
has the same 0-type.
Proof. For each
$l < n$
, let 
. We may assume without loss of generality that every
$U_l$
is finite and nonempty, for otherwise the topology of
$X_n$
would yield
$U_l=\emptyset $
or
$U_l=X_n$
, in which case
$U_l$
does not contribute to distinguish between the
$\omega $
-type or
$0$
-type of the elements of
$X_n$
. Furthermore, for each
$l<n$
we denote by
$i_l$
the least i such that
$U_l\cap L^{i+1}_n=\emptyset $
, which exists because
$U_l$
is finite. Lastly, we may assume without loss of generality that
$i_l\leq i_{l'}$
for each
$l<l'$
.
Claim 4.8. For each
$l<n$
, the number of distinct
$\omega $
-types over
$c[l+1]$
of the elements of
$L_n^{i_{l}}$
is bounded above by
$2^{l+1}$
. Furthermore, every member of
${\downarrow } L_n^{i_{l}+1}$
has the same 0-type over
$c[l+1]$
.
Proof of the claim
From the definition of
$i_0, \dots , i_l$
and the assumption that
$i_0 \leq \dots \leq i_l$
it follows that
${\downarrow } L_n^{i_{l}+1} \cap (U_0 \cup \dots \cup U_{l}) = \emptyset $
. Therefore, the last part of the claim holds. We prove the first part of the claim by induction on l.
Induction Base. We need to prove that the number of distinct
$\omega $
-types over
$c[1]=\{U_0\}$
of the elements of
$L_n^{i_{0}}$
is
$\leq 2$
. It suffices to show that
$$\begin{align*}(x \in U_0 \Longleftrightarrow y \in U_0) \text{ implies }x {\sim}_\omega^{c[1]} y, \end{align*}$$
for every pair of distinct
$x, y \in L_n^{i_{0}}$
. If
$i_0 = 0$
, this is clear, as the sole possible
$\omega $
-types over
$\{ U_0 \}$
of the elements of
$L_n^0$
are
$U_0$
and
$\{ x \in X_n \mid {\uparrow } x \cap U_0 = \emptyset \}$
. Then we consider the case where
$i_0> 0$
. Clearly, if
$x, y \in U_0$
, the
$\omega $
-type over
$\{ U_0 \}$
of x and y is
$U_0$
. Then we consider the case where
$x, y \notin U_0$
. If
$L_n^{i_0 -1} \subseteq U_0$
, then
$x, y \notin U_0$
, but
${\uparrow } x\smallsetminus \{ x \}, {\uparrow } y\smallsetminus \{ y \} \subseteq U_0$
, so that
$x {\sim }_\omega ^{c[1]} y$
. Then we consider the case where
$L_n^{i_0 -1} \nsubseteq U_0$
. By assumption there is an element
$z \in U_0 \cap L_n^{i_0}$
. The definition of
$X_n$
guarantees that the set
${\uparrow } z \cap L_n^{i_0 -1}$
is either
$L_n^{i_0 -1}$
or
$L_n^{i_0 -1} \smallsetminus \{ v \}$
for some
$v \in X_n$
. Since
${\uparrow } z \subseteq U_0$
and
$L_n^{i_0 -1} \nsubseteq U_0$
, we obtain
$U_0 \cap L_n^{i_0 -1} = L_n^{i_0 -1} \smallsetminus \{ v \}$
for some
$v \in X_n$
. As x and y are distinct from z (because
$x, y \notin U_0$
and
$z \in U_0$
) and
$z \nleq v \in L_{n}^{i_0 -1}$
, the definition of
$X_n$
guarantees that
$x, y < v$
. As
$x, y, v \notin U_0$
and
${\uparrow } x \smallsetminus \{ x, v \}, {\uparrow } y \smallsetminus \{ y, v \} \subseteq {\uparrow } z \subseteq U_0$
, we conclude that
$x {\sim }_\omega ^{c[1]} y$
as desired.
Induction Step. Suppose that the statement holds for l, i.e., that the number of distinct
$\omega $
-types over
$c[l+1]$
of the elements of
$L_n^{i_{l}}$
is bounded above by
$2^{l+1}$
. We will prove that this also holds when l is replaced by
$l+1$
. If
$i_{l+1}=0$
, this is clear, as the sole possible
$\omega $
-types over
$\{ U_0, \dots , U_{l+1} \}$
of the elements of
$L_n^{i_{l+1}} = L_n^0$
are the sets of the form
$\bigcap _{j \in J} U_j \cap \bigcap _{j \notin J} U_j^c $
for some
$J \subseteq l+1$
. Thus we may assume that
$i_{l+1}>0$
.
We will prove that the number of distinct
$\omega $
-types over
$c[l+1]$
of the elements of
$L^{i_{l+1}-1}_n$
is at most
$2^{l+1}$
, that is,
$$ \begin{align} |L^{i_{l+1}-1}_n/{\sim}_\omega^{c[l+1]}|\leq 2^{l+1}. \end{align} $$
We have two cases: either
$i_l<i_{l+1}$
or
$i_l = i_{l+1}$
. Suppose first that
$i_l<i_{l+1}$
. If
$i_l = i_{l+1}-1$
we are done by the inductive assumption. Then we may assume that
$i_l < i_{l+1}-1$
. Recall that
$i_0 \leq \dots \leq i_l < i_l +1 \leq i_{l+1}$
. Moreover, from the definition of
$i_0, \dots , i_l$
it follows
$$\begin{align*}(U_0 \cup \dots \cup U_l) \cap {\downarrow} L_n^{i_{l}+1} = \emptyset. \end{align*}$$
Therefore, for each
$x, y \in {\downarrow } L_n^{i_{l}+1}$
it holds
$x {\sim }_0^{c[l+1]} y$
. Consequently, the result follows from the induction hypothesis and
$i_{l+1} - i_l$
applications of Lemma 4.5. It only remains to consider the case where
$i_l=i_{l+1}$
.
Let m be the greatest integer such that
$i_m < i_l=i_{l+1}$
, if it exists, or
$-1$
otherwise. If
$m\neq -1$
, then
$m < l$
and by the induction hypothesis, the number of distinct
$\omega $
-types over
$c[m+1]$
of the elements of
$L_n^{i_m}$
is at most
$2^{m+1}$
. Since
$$\begin{align*}(U_0 \cup \dots \cup U_{i_m}) \cap {\downarrow} L_n^{i_m+1} = \emptyset, \end{align*}$$
by the definition of the
$i_t$
’s and by the structure of
$X_n$
, it follows from
$i_l - 1 - i_m$
applications of Lemma 4.5 that
$|L_n^{i_l -1}/{\sim }_\omega ^{c[m+1]}| \leq 2^{m+1}$
.
Now, for an arbitrary m satisfying the above definition, notice that if
$m < k <l+1$
, then
$i_k = i_l = i_{l+1}$
. Again by the definition of the
$i_t$
’s, it follows that, for any such k, we have that
$L_n^j\subseteq U_k=c(k)$
, for every
$j < i_l-1$
. As
$m < m+1 < l+1$
because
$m < l$
, the
$\omega $
-type of an element x of
$L_n^{i_l-1}$
over
$c[l+1]$
is totally determined by its
$\omega $
-type over
$c[m+1]$
(of which there are none if
$m\,{=}\,{-}1$
, and at most
$2^{m+1}$
otherwise, by above) together with whether or not x belongs to
$U_k$
, for each
$m < k < l+1$
. Thus, there are at most
$ 2^{m+1} \cdot 2^{l-m} = 2^{l+1}$
possible
$\omega $
-types over
$c[l+1]$
that
$x \in L_n^{i_l-1}$
can have, as desired. This concludes the proof of condition (1).
To conclude the proof of the claim, it is convenient to separate the following cases.
Case A. Suppose that
$L_n^{i_{l+1}-1} \subseteq U_{l+1}$
. This entails that the
$\omega $
-types over
$c[l+2]$
of the elements in
$L_n^{i_{l+1}-1}$
are the same as those over
$c[l+1]$
. Hence, the elements from
$L^{i_{l+1}}_n$
which see the same
$\omega $
-types over
$c[l+1]$
from
$ L^{i_{l+1}-1}_n $
also see the same
$\omega $
-types over
$c[l+2]$
from
$ L^{i_{l+1}-1}_n $
. Consequently, the
$\omega $
-types over
$c[l+2]$
of the elements in
$L^{i_{l+1}}_n$
are determined by their
$\omega $
-types over
$c[l+1]$
(of which there are at most
$2^{l+1}$
, by induction hypothesis and by possibly repeatedly applying Lemma 4.5 if
$i_l<i_{l+1}$
) together with whether or not they belong to the set
$U_{l+1}\cap L^{i_{l+1}}_n$
, in the sense that for
$x,y\in L^{i_{l+1}}_n$
,
$$\begin{align*}x{\sim}^{c[l+2]}_{\omega} y \Longleftrightarrow x{\sim}^{c[l+1]}_{\omega} y \text{ and }x{\sim}^{\{U_{l+1}\}}_{0} y. \end{align*}$$
This gives us at most
$2^{l+2}$
possible
$\omega $
-types over
$c[l+2]$
for elements of
$L^{i_{l+1}}_n$
.
Case B. Suppose that
$L_n^{i_{l+1}-1} \nsubseteq U_{l+1}$
. Recall that
$U_{l+1} \cap L_n^{i_{l+1}} \ne \emptyset $
by the definition of
$i_{l+1}$
. Moreover, by the definition of
$X_n$
the upset generated by any pair of distinct elements of
$L_n^{i_{l+1}}$
contains the whole
$L_n^{i_{l+1}-1}$
. Therefore, the assumption that
$L_n^{i_{l+1}-1} \nsubseteq U_{l+1}$
allows us to assume, without loss of generality, that
$ L_n^{i_{l+1}}\cap U_{l+1}=\{x_{i_{l+1}}^0\}$
and
$L_n^{i_{l+1}-1} \cap U_{l+1} =L_n^{i_{l+1}-1}\smallsetminus \{x_{i_{l+1}-1}^1\}$
. By condition (1), the elements in
$L_n^{i_{l+1}-1} \cap U_{l+1} =\{ x^t_{i_{l+1}-1} \mid t\neq 1 \}$
have at most
$2^{l+1}$
different
$\omega $
-types over
$c[l+1]$
and, since they all belong to
$U_{l+1}$
, they have at most
$2^{l+1}$
different
$\omega $
-types also over
$c[l+2]$
.
Now, the definition of
$X_n$
guarantees that for every
$m>0$
we have that
$x^m_{i_{l+1}}\leq x^1_{i_{l+1}-1}$
. Furthermore,
$x^m_{i_{l+1}}$
does not belong to
$U_{l+1}$
because
$ L_n^{i_{l+1}}\cap U_{l+1}=\{x_{i_{l+1}}^0\}$
. Therefore, the
$\omega $
-type over
$c[l+2]$
of an element of the form
$x^m_{i_{l+1}}$
with
$m> 0$
is determined by the fact that
$x^m_{i_{l+1}}$
does not belong to
$U_{l+1}$
and by the elements of
$L_n^{i_{l+1}-1}$
with distinct
$\omega $
-types over
$c[l+2]$
it sees. Since
$x^m_{i_{l+1}}$
sees all but possibly one of the element of
$L_n^{i_{l+1}-1}$
and the elements of
$L_n^{i_{l+1}-1}$
have at most
$2^{l+1}$
different
$\omega $
-types, this implies that
$$\begin{align*}\vert L_n^{i_{l+1}} \smallsetminus \{ x_{i_{l+1}}^0 \} / {\sim}^{c[l+2]}_{\omega} \vert \leq 2^{l+1}+1. \end{align*}$$
Consequently,
$$\begin{align*}\vert L_n^{i_{l+1}} / {\sim}^{c[l+2]}_{\omega} \vert \leq 2^{l+1}+2 \leq 2^{l+2}, \end{align*}$$
thus finishing the proof of the claim.
From the claim it follows that the number of
$\omega $
-types of the elements in
$L^{i_{n-1}}_{n}$
over
$c[n]$
is bounded above by
$2^{n}$
. Since
$L^{i_{n-1}}_{n}$
has
$2^{n}+1$
elements, it follows that at least two elements of
$L^{i_{n-1}}_{n}$
have the same
$\omega $
-type. Moreover, the second part of the claim guarantees that every element of
${\downarrow } L^{i_{n-1}+1}_n$
has the same 0-type over
$c[n]$
. Thus, the statement holds for 
.
The proof of the following lemma shows concretely why, in the Esakia space
$X_n$
, we defined each element
$x^{2^n}_{i+1}$
so that it sees every element at level
$L^{i}_{n}$
. The key point is that, if two elements at level i have the same
$\omega $
-type, then
$x^{2^n+1}_{i+1}$
will have exactly the same type of some other element at level
$i+1$
. Proceeding inductively, we find a level from which every element has the same type under the given colouring. We make this reasoning explicit in the next proof.
Lemma 4.9. Let
$c \colon m\to X_n^\ast $
be a function and
$i < \omega $
. Suppose two distinct elements of
$L_n^{i}$
have the same
$\omega $
-type over
$c[m]$
and that for every
$q> i$
the elements of
$L_n^{q}$
have the same 0-type over
$c[m]$
. Then every element of
${\downarrow } L_n^{i+2^n+1}$
has the same
$\omega $
-type over
$c[m]$
.
Proof. Since two distinct elements of
$L_n^{i}$
have the same
$\omega $
-type over
$c[m]$
and all the elements of
$L_n^{i+1}$
have the same
$0$
-type over
$c[m]$
, then it follows from the construction of
$X_n$
that
$x^{2^n}_{i+1}{\sim }^{c[m]}_{\omega } x^j_{i+1}$
for some
$j<2^n$
. Therefore, the construction of
$X_n$
guarantees that the elements
$x^{2^n-1}_{i+2}$
and
$x^{2^n}_{i+2}$
see the same equivalence classes of
$L_n^{i+1} / {\sim }_\omega ^{c[m]}$
. Since by assumption
$x^{2^n-1}_{i+2}$
and
$x^{2^n}_{i+2}$
have the same
$0$
-type over
$c[m]$
, this implies that
$x^{2^n-1}_{i+2}{\sim }^{c[m]}_{\omega } x^{2^n}_{i+2}$
. For the same reason, we have that
$x^{2^n-2}_{i+3}{\sim }^{c[m]}_{\omega }x^{2^n-1}_{i+3}{\sim }^{c[m]}_{\omega } x^{2^n}_{i+3}$
. By proceeding in this way, we obtain that every element of
$L_n^{i+2^n+1}$
has the same
$\omega $
-type over
$c[m]$
. Since for
$t\geq i+2^n+1$
every element of
$L^{t}_n$
has the same
$0$
-type over
$c[m]$
, this is enough to conclude that every element of
${\downarrow } L_n^{i+2^n+1}$
has the same
$\omega $
-type over
$c[m]$
.
We can now conclude by showing that the Heyting algebra
$X^\ast _n$
satisfies the desired property.
Proposition 4.10. There exists
$m_n < \omega $
such that the n-generated subalgebras of
$X_n^\ast $
are of size
$\leq m_n$
.
Proof. We begin by the following observation.
Claim 4.11. There exists
$k < \omega $
such that for every function
$c \colon n \to X_n^*$
the number of
$\omega $
-types over
$c[n]$
of elements of
$X_n$
is
$\leq k$
.
Proof of the claim
Recall the definition of the integers
$i_0, \dots , i_{n-1}$
associated with c in the proof of Lemma 4.7. In view of Claim 4.8 and the fact that each
$L_n^{i_l}$
has
$2^n +1$
elements, we obtain that for each
$i_l$
at least two elements of
$L_n^{i_l}$
have the same
$\omega $
-type over
$c[l+1]$
and every point in
${\downarrow } L_n^{i_l+1}$
has the same
$0$
-type over
$c[l+1]$
. Hence, it follows from Lemma 4.9 that all the elements of
${\downarrow } L_n^{i_l+2^n+1}$
have the same
$\omega $
-type over
$c[l+1]$
. Furthermore, from the construction of
$X_n$
and the definition of
$i_l$
it follows that the upset
${\uparrow } L_n^{i_l-2}$
(which is the emptyset if
$i_l \leq 1$
) is contained in 
. Let us partition
$X_n$
as the union
$$\begin{align*}{\uparrow} L_n^{i_l-2} \cup L_n^{i_l-1} \cup L_n^{i_l} \cup \dots \cup L_n^{i_l+2^n} \cup {\downarrow} L_n^{i_l+2^n+1}, \end{align*}$$
and note that the above discussion entails that the effect of the clopen
$U_l$
in the determination of the
$\omega $
-type over
$c[n]$
of a point x is trivial if
$x\in {\uparrow } L_n^{i_l-2} \cup {\downarrow } L_n^{i_l+2^n+1}$
, and noticeable only if
$x\in L_n^{i_l-1} \cup L_n^{i_l} \cup \dots \cup L_n^{i_l+2^n}$
. Since each of these
$(i_l+2^n)-(i_l-2)=2^n+2$
layers has
$2^n+1$
many elements, we conclude that the clopen
$U_l$
can only contribute to distinguish at most
$(2^n+1)(2^n+2)+2$
$\omega $
-types over
$c[n]$
in
$X_n$
.
Since the
$i_l$
in the above argument was arbitrary, it now follows that each clopen in
$c[n]=\{U_0,\dots , U_{n-1}\}$
can only contribute to distinguish at most
$(2^n+1)(2^n+2)+2$
$\omega $
-types over
$c[n]$
in
$X_n$
. Therefore, there are at most 
distinct
$\omega $
-types over
$c[n]$
in
$X_n$
. As this bound is independent of the choice of the function c, we have found the desired uniform upper bound.
In order to conclude the proof, it suffices to show that the n-generated subalgebras of
$X_n^\ast $
are of size
$\leq 2^{k}$
, for in this case the statement holds for 
. Suppose, on the contrary, that there is an n-generated subalgebra of
$X_n^\ast $
containing distinct elements
$U_0, \dots , U_{2^k}$
. Moreover, let
$m < \omega $
be such that
$\mathsf {rank}(U_i) \leq m$
for every
$i \leq 2^k$
. Since every family of
$2^k +1$
distinct subsets of a set Y separates at least
$k+1$
elements of Y, there are distinct
$x_0, \dots , x_k \in X_n$
that are separated by
$U_0, \dots , U_{2^k}$
. By Lemma 3.6 the elements
$x_0, \dots , x_k$
are unrelated by
${\sim }_m^{c[n]}$
. By the definition of
${\sim }_\omega ^{c[n]}$
, this implies that
$x_0, \dots , x_k$
are also unrelated by
${\sim }_\omega ^{c[n]}$
. Therefore, there are
$k+1$
distinct
$\omega $
-types over
$c[n]$
(that is,
$x_0 / {\sim }_\omega ^{c[n]}, \dots , x_k/ {\sim }_\omega ^{c[n]}$
), but this contradicts Claim 4.11.
5. The main result
Given a class
$\mathsf {K}$
of similar algebras, we let
The aim of this section is to establish the main result of the paper, namely:
Theorem 5.1. For each
$n < \omega $
, the variety
$\mathbb {V}(X^\ast _n)$
is strictly n-finite, i.e., it is n-finite but contains an infinite
$(n+1)$
-generated algebra.
In particular, the variety
$\mathbb {V}(X^\ast _n)$
is n-finite, but not locally finite. For the case where
$n = 2$
, this provides a negative answer to [Reference Bezhanishvili and Grigolia4, Problem 2.4]. The proof of Theorem 5.1 relies on the next observation [Reference Berman3, Lemma 1.3].
Proposition 5.2. Let
$\mathsf {K}$
be a variety and
$Var$
a set of variables. Moreover, let
$\{ v_i \mid i \in I \}$
be a family of functions
$v_i \colon Var \to A_i$
with
$A_i \in \mathsf {K}$
such that for every pair of terms
$\varphi $
and
$\psi $
with variables in
$Var$
it holds that
$$\begin{align*}\mathsf{K} \nvDash \varphi \thickapprox \psi \text{ implies that there exists } i \in I \text{ such that }\varphi^{A_i}(v_i(\vec{x})) \ne \psi^{A_i}(v_i(\vec{x})). \end{align*}$$
Then the n-generated free algebra of
$\mathsf {K}$
embeds into the direct product
$\prod _{i \in I}A_i$
.
As a consequence, we deduce the following:
Corollary 5.3. Let
$\mathsf {K}$
be a class of similar algebras of finite type and
$n < \omega $
. If the cardinality of the n-generated members of
$\mathbb {S}(\mathsf {K})$
is bounded above by some
$m_n < \omega $
, then
$\mathbb {V}(\mathsf {K})$
is n-finite.
Proof. Since the type of
$\mathsf {K}$
is finite and the cardinality of the n-generated members of
$\mathbb {S}(\mathsf {K})$
is bounded above by some
$m_n < \omega $
, up to isomorphism there are only finitely many n-generated algebras in
$\mathbb {S}(\mathsf {K})$
, all of whom are finite. We enumerate them as
$H_0, \dots , H_k$
.
Now, consider the set of variables 
. Clearly, if two terms
$\varphi $
and
$\psi $
with variables in
$Var$
differ when interpreted in the variety
$\mathbb {V}(\mathsf {K})$
, then there exist some
$i \leq k$
and a function
$v \colon Var \to H_i$
such that
$\varphi ^{H_i}(v(\vec {x})) \ne \psi ^{H_i}(v(\vec {x}))$
. Therefore, we can apply Proposition 5.2 obtaining that the free n-generated algebra
$F_n$
of
$\mathbb {V}(\mathsf {K})$
embeds into 
. Since both
$Var$
and each
$H_i$
are finite, so is H and, therefore,
$F_n$
. As every n-generated member of
$\mathbb {V}(\mathsf {K})$
is a homomorphic image of
$F_n$
, we conclude that
$\mathbb {V}(\mathsf {K})$
is n-finite.
We are now ready to prove Theorem 5.1.
Proof. By Corollary 4.4 the Heyting algebra
$X_n^\ast $
is infinite and
$(n+1)$
-generated. As
$X_n^\ast \in \mathbb {V}(X_n^\ast )$
, it only remains to prove that the variety
$\mathbb {V}(X_n^\ast )$
is n-finite. But this is an immediate consequence of Proposition 4.10 and Corollary 5.3.
Remark 5.4. In view of Theorem 5.1, for each
$n < \omega $
there is an n-finite variety of Heyting algebras that contains an infinite
$(n+1)$
-generated algebra. We will prove that such a variety can be chosen finitely axiomatisable.
First, recall from Theorem 5.1 that
$\mathbb {V}(X_n^\ast )$
is n-finite. Therefore, there is some
$m <\omega $
such that every n-generated member of
$\mathbb {V}(X_n^\ast )$
has size
$\leq m$
(for instance, m can be taken to be the size of the free n-generated algebra of
$\mathbb {V}(X_n^\ast )$
). This property can be expressed by a first-order sentence, namely,
$$ \begin{align*} \theta_n= \forall (x_i)_{i<n} \exists (y_j)_{j<m} \; & \bigg( \bigg( \bigwedge_{i<n} x_i=y_i \bigg) \land \bigg(\bigvee_{j<m} y_j=0 \bigg) \land \bigg (\bigvee_{j<m} y_j=1 \bigg ) \land \\ &\bigg ( \bigwedge_{\odot\in \{\land,\lor,\to \}} \bigwedge_{i,i'<m} \bigvee_{j<m} y_i\odot y_{i'}= y_{j} \bigg ) \Big ). \end{align*} $$
Then, let
$\Sigma _n$
be the set of universally quantified equations valid in
$\mathbb {V}(X_n^\ast )$
. Since
$\mathbb {V}(X_n^\ast )$
is a variety, it is axiomatized by
$\Sigma _n$
. Together with the fact that every n-generated member of
$\mathbb {V}(X_n^\ast )$
has size
$\leq m$
, this implies
$\Sigma _n\models \theta _n$
(where
$\models $
stands for the consequence relation of first-order logic). By the compactness theorem there is a finite
$T\subseteq \Sigma _n$
such that
$T\models \theta _n$
. Let
$\mathcal {V}$
be the class of all the Heyting algebras satisfying T. Clearly,
$\mathcal {V}$
is a variety of Heyting algebras. Furthermore, from
$T\subseteq \Sigma _n$
it follows immediately that
$X_n^\ast \in \mathcal {V}$
. Therefore,
$\mathcal {V}$
contains an infinite
$(n+1)$
-generated algebra, namely,
$X_n^\ast $
(Corollary 4.4). Lastly,
$\mathcal {V}$
is n-finite because
$T\models \theta _n$
and, therefore, every n-generated algebra in
$\mathcal {V}$
is of size
$\leq m$
.
Remark 5.5. From a logical standpoint, the importance of Heyting algebras is that they algebraize the intuitionistic propositional calculus
$\mathsf {IPC}$
in the sense of [Reference Blok and Pigozzi6]. As a consequence, the axiomatic extensions of
$\mathsf {IPC}$
(known as superintuitionistic logics, or si-logics for short) form a lattice that is dually isomorphic to that of varieties of Heyting algebras (see, e.g., [Reference Chagrov and Zakharyaschev7]). Because of this, Remark 5.4 can be rephrased as follows: for every
$n < \omega $
there is a finitely axiomatisable si-logic that has only finitely many formulas in variables
$x_{0}, \dots , x_{n-1}$
up to logical equivalence, but that has infinitely many nonequivalent formulas in variables
$x_0, \dots , x_n$
.
Funding
The second author was supported by the grant 2023.03419.BD from the Portuguese Foundation for Science and Technology (FCT). The third author was supported by the proyecto PID
$2022$
-
$141529$
NB-C
$21$
de investigación financiado por MICIU/AEI/
$10$
.
$13039$
/
$501100011033$
y por FEDER, UE. He was also supported by the Research Group in Mathematical Logic,
$2021$
SGR
$00348$
funded by the Agency for Management of University and Research Grants of the Government of Catalonia. The fourth author was supported by grant 336283 of the Academy of Finland and has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 101020762).
Open access
