Article contents
Strong coupling of flow structure and heat transport in liquid metal thermal convection
Published online by Cambridge University Press: 17 November 2023
Abstract
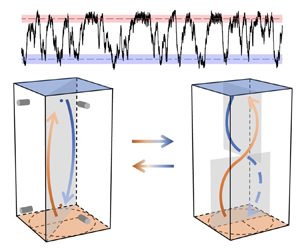
A typical feature of thermal convection is the formation of large-scale flow (LSF) structures of the order of system size. How this structure affects global heat transport is an important issue in the study of thermal convection. We present an experimental study of the coupling between the flow structure and heat transport in liquid metal convection with different degrees of spatial confinement, characterized by the aspect ratio  $\varGamma$ of the convection cell. Combining measurements in two convection cells with
$\varGamma$ of the convection cell. Combining measurements in two convection cells with  $\varGamma =1.0$ and 0.5, the study shows that a large-scale circulation (LSC) transports
$\varGamma =1.0$ and 0.5, the study shows that a large-scale circulation (LSC) transports  ${\sim }35\,\%$ more heat than a twisted LSC. It is further found that when the LSF is in the form of the LSC state, the system is in a fully developed turbulence state with a
${\sim }35\,\%$ more heat than a twisted LSC. It is further found that when the LSF is in the form of the LSC state, the system is in a fully developed turbulence state with a  $Nu\sim Ra^{0.29}$ scaling for the heat transport. However, the twisted LSC state with a heat transport scaling of
$Nu\sim Ra^{0.29}$ scaling for the heat transport. However, the twisted LSC state with a heat transport scaling of  $Nu\sim Ra^{0.37}$ appears when the system is not in the fully developed turbulence state. Bistability is observed when the system evolves from the twisted-LSC-dominated to the LSC-dominated state.
$Nu\sim Ra^{0.37}$ appears when the system is not in the fully developed turbulence state. Bistability is observed when the system evolves from the twisted-LSC-dominated to the LSC-dominated state.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by



