1. Introduction
Mass changes in the Greenland ice sheet (GIS) are of considerable interest because of their sensitivity to climate change, the mass-loss contribution to sea-level rise, and the likelihood of an increasing rate of mass loss with climate warming. In recent years, the GIS has experienced increased surface melting from increasing temperatures (Reference Hall, Williams, Luthcke and DigirolamoHall and others, 2008; Reference Box, Yang, Bromwich and BaiBox and others, 2009), increased snow accumulation from increasing precipitation (Reference BoxBox and others, 2006; Reference HannaHanna and others, 2008), accelerated ice flow from melt/acceleration effects (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002b; Reference Joughin, Das, King, Smith, Howat and MoonJoughin and others, 2008b; Reference Van de WalVan de Wal and others, 2008; Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010) and increased discharge from accelerating outlet glaciers due to warming ocean waters (Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference StraneoStraneo and others, 2010). In response, the GIS has been thinning at the margins and growing in its interior (Reference KrabillKrabill and others, 2000; Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others, 2005; Reference ZwallyZwally and others, 2005; Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). The net rate of ice loss appears to have accelerated in recent years compared with the 1990s, but published values of the rate of mass loss and changes with time have differed widely (Reference Alley, Spencer and AnandakrishnanAlley and others, 2007; Reference Shepherd and WinghamShepherd and Wingham, 2007; Reference Monitoring and ProgrammeAMAP, 2009).
Estimates of input and output (Reference Monitoring and ProgrammeAMAP, 2009) for the GIS for a state of near balance give a mass gain of 550 Gt a−1 from precipitation (less evaporation), which is balanced by mass loss through meltwater and blowing snow (370 Gt a−1) and glacier discharge (180 Gt a−1). However, these values have large uncertainties and significant interannual variations. Variations in precipitation, temperature and other factors cause variations in the mass exchange at the surface and in the dynamics of ice flow toward the margins on land and through outlet glaciers into the ocean.
A review (Reference Shepherd and WinghamShepherd and Wingham, 2007) said ‘it is reasonable… to conclude the GIS is losing about 100 Gt a−1’, which was consistent with the high-resolution analysis of Gravity Recovery and Climate Experiment (GRACE) data (Reference LuthckeLuthcke and others, 2006) that gave a net mass loss of 101 Gt a−1 for the period 2003–05. Furthermore, a 122 ± 47 Gt a−1 increase in loss rate by 2005 compared with 1996 based on a mass flux analysis (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006) is approximately consistent with the increase shown by the GRACE results for 2003–05 compared by Reference LuthckeLuthcke and others (2006) with the near balance for 1992–2002 from satellite-radar and airborne-laser altimetry (Reference ZwallyZwally and others, 2005).
This paper focuses on the GIS mass balance for 2003–07 and the changes since 1992–2002, including the spatial distributions of mass balance and changes by drainage system and elevation. Our 2003–07 results are derived from the Ice, Cloud and land Elevation Satellite (ICESat)’s laser altimeter measurements (Reference ZwallyZwally and others, 2002a) of surface elevations using some of the methodology previously applied (Reference ZwallyZwally and others, 2005) to data from European Remote-sensing Satellite (ERS) radar altimetry and airborne laser altimetry (Airborne Topographic Mapper (ATM)). Significant improvements for determining mass changes, dM/dt, from elevation changes, dH/dt, for both the 1992–2002 and 2003–07 periods are (1) calculation of the appropriate densities to apply to changes in the thickness of the firn–ice column and (2) partitioning of dH/dt and dM/dt into components driven by accumulation variations and those driven by melting and ice dynamics. For 1992–2002, we use the previous dH/dt (Reference ZwallyZwally and others, 2005) calculated from elevation changes, dh/dt, calculated at crossovers where ERS satellite tracks cross on consecutive ascending and descending passes, with ATM data (Reference AbdalatiAbdalati and others, 2001) added to fill in gridcells on outlet glaciers. For 2003–07, we calculate dH/dt from dh/dt calculated from ICESat data collected on successive satellite passes along closely spaced ground tracks (‘repeat tracks’), which significantly increases the along-track spatial resolution and the density of derived dh/dt compared with crossover analysis.
2. Elevation Change, dh/dt, from Repeat-Track Analysis of Icesat Data
Our repeat-track analysis to derive dh/dt from ICESat data is enabled by ICESat’s capability to point the laser beam to reference tracks over the ice sheets to ±100 m (1σ). However, because the tracks do not repeat exactly, the surface elevation, h(x, y, ti ), measured along a repeat pass (y direction) at time ti depends on the cross-track surface slope, α, and the cross-track distance, x, as well as actual elevation changes with time. This mixing of apparent height changes caused by cross-track displacements and real height changes, h(ti ), is illustrated in Figure 1 and by
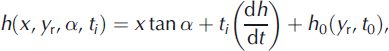
where h 0 is the elevation at the position, y r, of the reference track at t 0. Use of Equation (1) assumes the cross-track surface slope is constant over distances of ∼200 m and that dh/dt is constant with time, i.e. h(t) changes are linear. Although important seasonal and interannual variations in h(x, y, α, t) are ignored in this solution, departures from linearity are nevertheless retained in the height residuals relative to the linear solution and can be further analyzed. Measured h(x, y, α, t) are first interpolated to equally spaced (172 m) reference points along each track. We then solve Equation (1) by least-squares methods for three parameters, α, dh/dt, h 0, at each reference point, which requires data on at least N = 4 along-track repeats. For solutions with N = 10 repeats, for example, we obtain an accuracy, σ dh/dt , for dh/dt of better than 25 cm a−1 for α < 2° at one-point along-track solutions (Fig. 2a). The resulting standard errors, σ dH/dt and σα , on dh/dt and α decrease with increasing N by 1/(N−3)1/2 as expected. We use data from 12 laser campaigns (also designated as Laser 2a, 2b, 2c, 3a, 3b, 3c, 3d, 3e, 3f, 3g, 3h and 3i) from the fall of 2003 to the fall of 2007, i.e. F03, W04, S04, F04, W05, S05, F05, W06, S06, F06, W07 and F07, where F indicates boreal fall, W indicates boreal winter, S indicates boreal spring and 03 indicates 2003, etc. The effective length of each campaign was 33 to ∼36 days. (F03 was 45 days, but the additional ground tracks were not covered in subsequent campaigns.) However, data are not continuous along each track due to losses in thick-cloud cover, so N varies with location from a maximum of 12. The data versions are all release 428, except for S04, which is release 128. Data can be obtained from NASA’s archive at the US National Snow and Ice Data Center (http://nsidc.org/data/icesat/index.html).
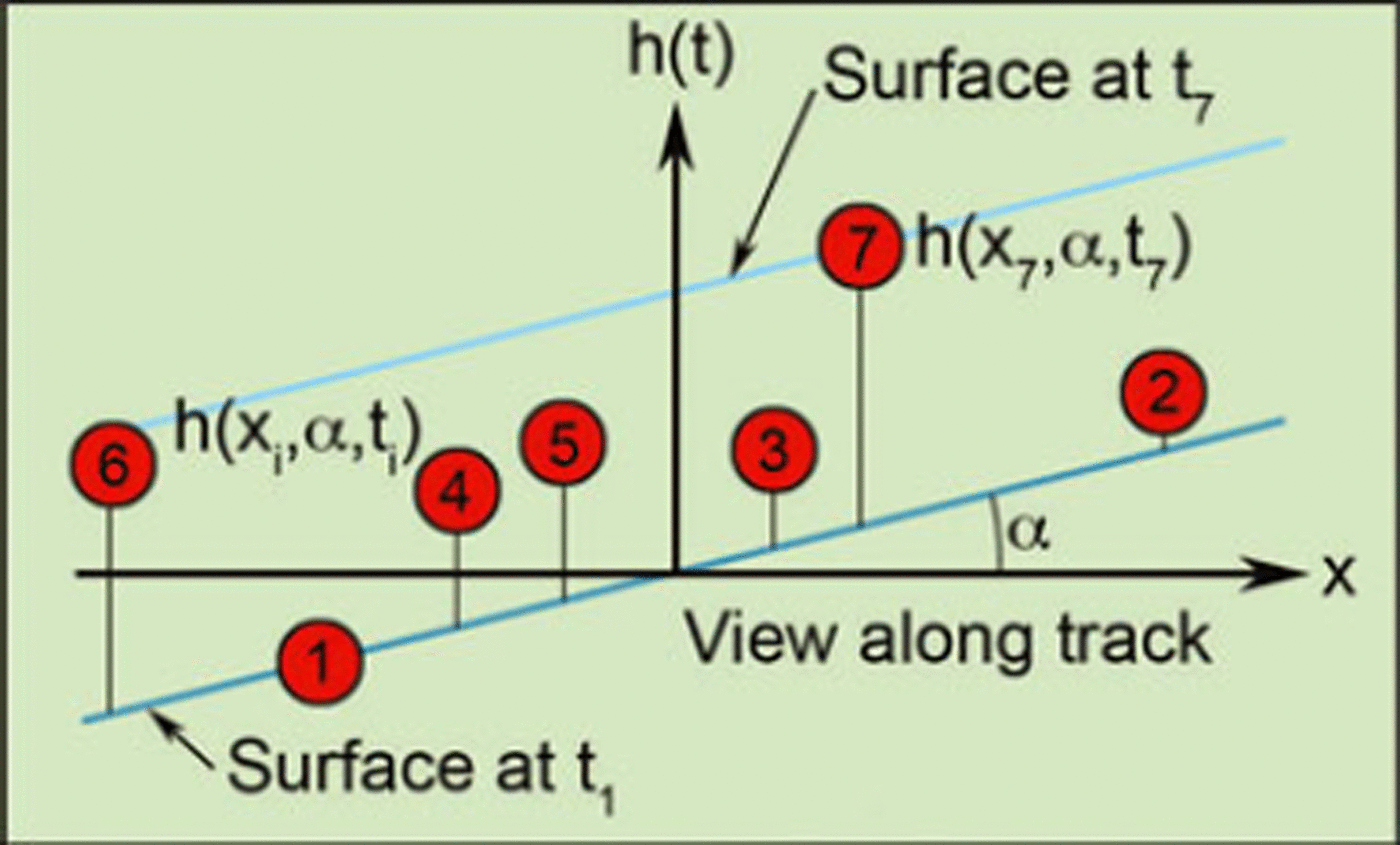
Fig. 1. Schematic of elevations h(xi , α, ti ) for successive data collected on repeat tracks at times ti along an ICESat reference track with cross-track slope α and distance xi from the reference track. h is shown increasing with time.
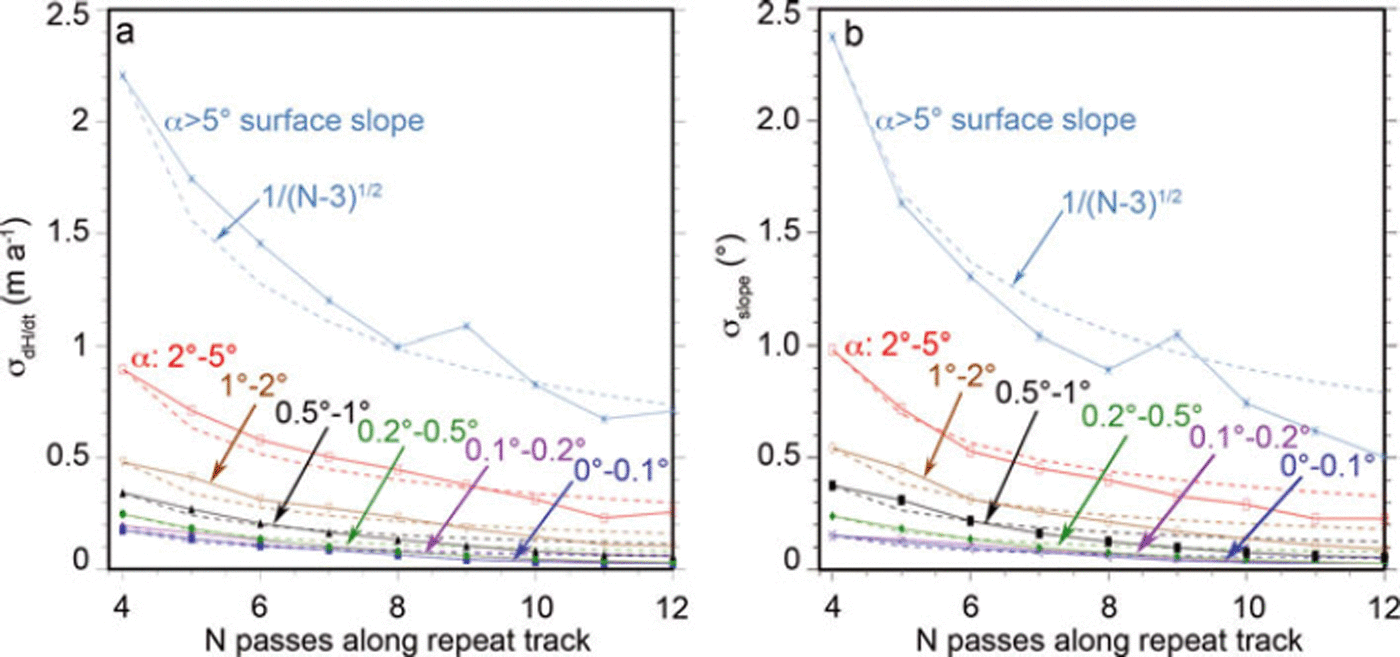
Fig. 2. (a) Error on ICESat dh/dt (m a−1)as a function of the number of repeats, N, used in the solution at each along-track location separated by 172 m. 0.25 m a−1 accuracy is achieved for N ≥ 10 repeats for slopes <2°. Dashed curves are 1/(N−3)1/2 fits to the errors. (b) Error on slope α as a function of N. Slope error is about ±20% for N = 10.
The dh/dt results are improved by a seven-point solution that uses data at three points on either side of each reference point, i.e. strips that are ∼1 km along track, and a quadratic surface in the along-track y direction that is derived from multiple repeats. The maximum number of h(x, y, α, t) values used in the seven-point solutions is 84. We obtain seven-point solutions at 97% of the locations. For the other 3%, which are mostly near the edge of the ice sheet where a satisfactory seven-point solution cannot be obtained, we use one-point solutions. The formal σ
dh/dt
on dh/dt from the seven-point solutions are multiplied by ![]() to account for the non-independence of consecutive along-track solutions.
to account for the non-independence of consecutive along-track solutions.
We further improve the relative accuracy to the cm level for each of the 12 campaigns by referencing to the ocean surface, i.e. the open water within sea ice, on the Arctic Ocean. This reduces inter-campaign range biases. We empirically determine an elevation correction, d, from the time variation of the average mean sea surface over the Arctic Ocean using the methods described by Reference Zwally, Yi, Kwok and ZhaoZwally and others (2008). Although the magnitude of d is spatially variable, its time variation appears to be the same over the Arctic Ocean, so we take it to be applicable to Greenland as well. The respective values of d for the 12 periods are −0.049, 0.045, 0.132, −0.061, −0.104, 0.021, 0.011, 0.014, 0.012, 0.074, 0.004 and 0.043 m. We reduce the time variation of these d values by 0.003 m a−1 to account for the current rate of sea-level rise, and then subtract the reduced d values from the measured elevations. The linear trend in the reduced d is 0.006 m a−1, which averaged over all of Greenland increases the overall mass loss by ∼9 Gt a−1 compared with data without the d correction applied.
2.2. Characteristics of dh/dt on Jakobshavn Isbræ
We select Jakobshavn Isbræ, west-central Greenland, to show the characteristics of the dh/dt derived from ICESatmeasured surface elevations, h, in Figure 3a, including the small σ dh/dt relative to dh/dt, the details of the oscillations in the h and dh/dt profiles, the consistency of the oscillations on consecutive profiles, and the small variation from linearity in the h(t) at different locations. Jakobshavn is of particular interest because of its rapid speed-up and increased thinning rate inland of the grounding line as the floating ice tongue thinned and broke away during 1996–2004 (Reference JoughinJoughin and others, 2008a; Reference Thomas, Frederick, Krabill, Manizade and MartinThomas and others, 2009). Profiles of h for 12 ICESat repeats along track 419 (T419) relative to the first pass in fall 2003 are shown in Figure 3a along with dh/dt, its formal error, σ dh/dt , and elevation in Figure 3b (track locations are shown in Fig. 14 further below).
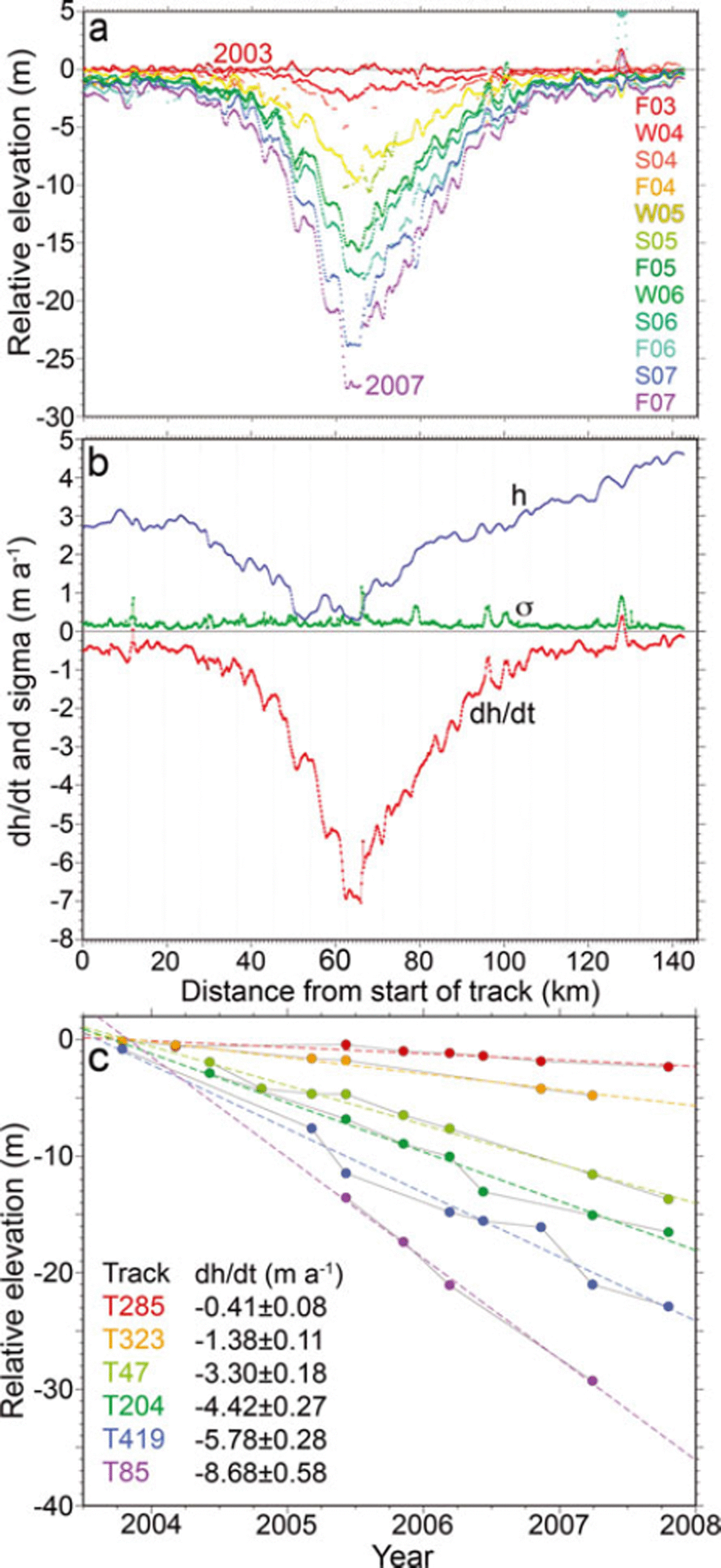
Fig. 3. (a) ICESat surface elevation (h) profiles (ten-point smoothing) relative to the first profile from fall 2003 across Jakobshavn Isbræ along T419 (Fig. 14). Maximum surface lowering is 27.6 m in 4 years. F03 is fall 2003, W04 is winter 2004, S04 is spring 2004, etc. (b) Profiles of h from 1030 to 1465 m, derived dh/dt, and σ dh/dt from along-track solutions at 172 m spacing. Units of h are from 1000 m (0 on y-axis) to 1500 m (5 on y-axis). Maximum dh/dt is 7 m a−1 near the center of the glacier. Matching peaks in h and dh/dt indicate oscillations are growing with time. (c) h(t) at crossings of ICESat tracks with a flowline near the center of the glacier (Fig. 14). Over 4 years, h(t) is close to linear.
The largest dh/dt derived in this region is 11.3 m a−1 at the end (69.17° N, 49.32° W) of the discontinuous T85, near the center of the glacier downstream from T419. The linear character of h(t) in Figure 3c at six crossings of ICESat tracks with a flowline down the center of the glacier (Fig. 14), where dh/dt values range from −8.7 to −0.1 m a−1 below and above the EL, shows that the glacier’s thinning rate is nearly constant during 2003–07. Therefore, any residual effects from removal of the ice tongue do not appear to be causing either a significant increase or decrease in the thinning rate in this portion of the glacier.
3. Mapping of dh/dt
We average the derived ICESat dh/dt values over ∼50 km gridcells to obtain the average elevation change, dH/dt, in each cell (Fig. 4a), along with the formal error, σ dH/dt , of the average dH/dt (Fig. 5a). The dH/dt values in Figure 4a are similar to the map of along-track dh/dt derived from ICESat data as shown in figure 2 of Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others (2009), which described the patterns of dynamic thinning but did not calculate dM/dt, as we do in section 4. The ICESat σ dH/dt are approximately one-third of the corresponding values of those for ERS radar altimetry (Fig. 5b), which are computed from the time-series analysis of crossover differences (Reference ZwallyZwally and others, 2005). The smaller σ dH/dt for ICESat reflects the higher accuracy of the laser versus radar altimetry and possibly the higher accuracy of the repeat-track analysis (even though data collection was not continuous).
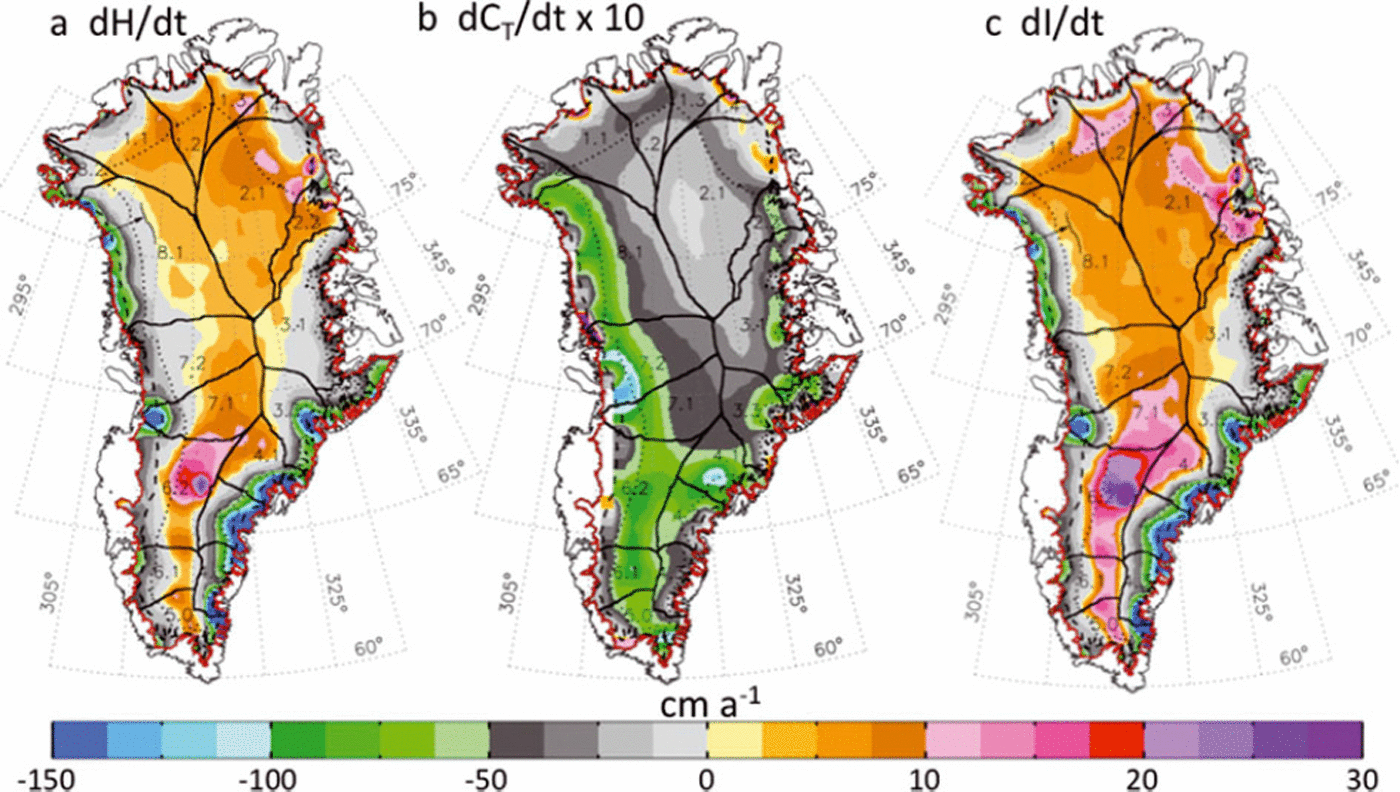
Fig. 4. (a) ICESat dH/dt = 〈dh/dt〉 averaged in ∼50 km gridcells. (b) Temperature-driven part of the firn compaction dCT /dt times 10. (c) dl/dt = (dH/dt) − (dCT /dt) − (dB/dt). Although dCT /dt is generally smaller than dH/dt, it shifts the dH/dt = 0 line by ∼100 km in the northwest as shown by the arrows. In addition to the delineation of the drainage systems (black curves), the 2000 m contour (dotted curve), the EL (dashed curve) and the ice-sheet boundary (red curve) are shown here and in Figures 5–9.
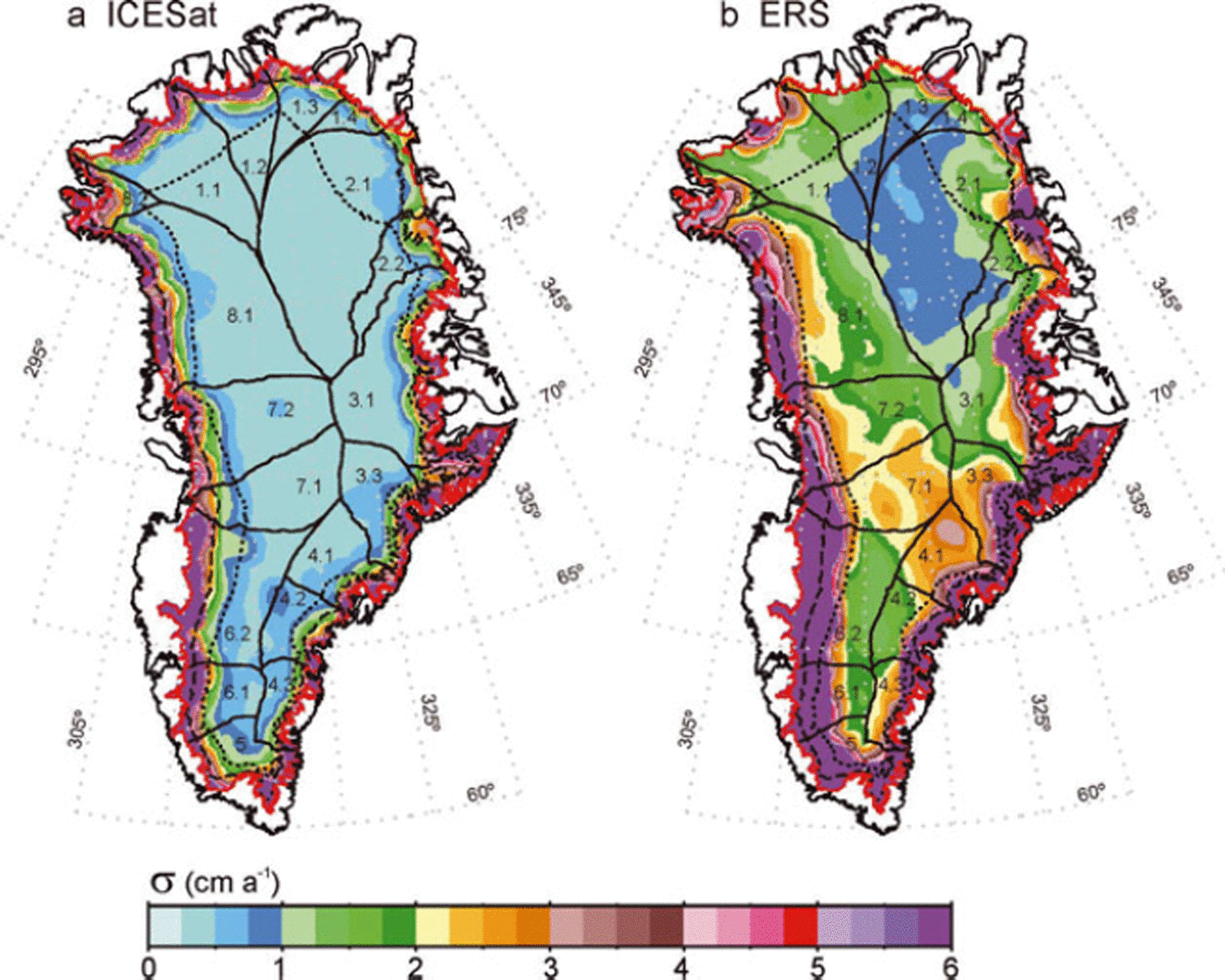
Fig. 5. (a) Maps of σ dH/dt for ICESat 2003–07 computed from the cell-average dH/dt of the dh/dt solutions at the individual reference points. (b) σ dH/ dt for ERS 1992–2002 is computed from time-series analysis of crossover differences (Reference ZwallyZwally and others, 2005).
The dM/dt, area and other parameter calculations in the following sections are made using the 50 km gridcell averages. However, at the edges of the ice sheet, the 50 km gridcells are split into portions lying on and off the ice sheet, using an ice-sheet boundary with 1–2 km resolution. For the dH/dt from ICESat data, only dh/dt data within the portion of the cells lying on the ice sheet are used in the calculations. For the dH/dt from ERS/ATM, the procedures for selection of crossovers, the use of ATM data, and optimal interpolation to fill in missing cells were given by Reference ZwallyZwally and others (2005); here we also weight all the boundary cells by the fraction of the cell area lying within the boundary. An important correction to dH/dt from radar altimetry is the backscatter correction previously applied (Reference ZwallyZwally and others, 2005), which empirically corrects for variations in the effective backscattering depth in the firn and is similar to that applied by Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) and Reference Wingham, Shepherd, Muir and MarshallWingham and others (2006).
4. Derivation of Ice-Mass Changes, dm/dt, from Elevation Changes, dh/dt
Derivation of dM/dt from dH/dt requires consideration (Reference Zwally and LiZwally and Li, 2002) of the surface mass balance, firn compaction, dynamics, and underlying bedrock motion:
where A(t) is the snow accumulation rate, ρ sf is the density of near-surface firn (typically 0.33), V fc(t) is the velocity of firn compaction at the surface, A b(t) is the ablation rate, ρ i = 0.90 is the density of glacier ice, V ice is the vertical velocity of the ice at the firn/ice transition, and dB/dt is the vertical bedrock motion. In steady state with a long-term average accumulation rate of 〈A〉, V ice = 〈A〉/ρ i in the accumulation zone and V fc = 1.7V ice using ρ sf = 0.33 and ρ i = 0.90. The units of A(t) and A b(t) are cm w.e.a−1, the units of velocities and elevation changes are cm a−1, and all densities are relative to ρ water = 1. H, A and dB/dt are positive upward and V fc, A b and V ice are positive downward as commonly defined for these parameters.
For non-steady state, we rewrite the ice-sheet terms in Equation (2) as perturbations from steady state, assuming that dB/dt is constant during the time of the measurements:
where dH a/dt = (A(t) − 〈A〉)/ρ sf is the direct change caused by A(t), dCAT /dt = −(V fc(t) − 〈V fc〉) is the change in firn-compaction rate driven by both A(t) and temperature T(t), dH b/dt = −(A b(t) − 〈A b〉/ρ i is driven by changes in the ablation rate, dH d/dt = −(V ice(t) − 〈V ice〉) is driven by dynamic changes in the ice flow relative to the long term, 〈A〉, and 〈〉 indicates long-term averages of the various parameters. All terms in Equation (3) are positive upward and are defined as averages over some area, which in our following analyses are 50 km gridcells.
Positive values of dH d/dt indicate that the ice flow is less than that required to balance the long-term average 〈A〉, which is described as dynamic thickening in the same manner as negative dH d/dt is described as dynamic thinning. However, dH d/dt includes not only long-term changes in the ice dynamics, but also short-term changes. For example, if dH d/dt is determined during two different periods at an interval of 10 years, then both values of dH d/dt would include multi-decadal dynamic imbalances compared with the multi-decadal average 〈A〉, and their difference would indicate the sub-decadal dynamic changes (see section 6.3).
4.1. Separation of accumulation and temperature effects on firn compaction
The firn-compaction (dCAT /dt) and dB/dt terms in Equation (3) change dH/dt but not dM/dt. Both dH a/dt and dCAT /dt are affected by A(t), and dCAT /dt depends strongly on T(t) as previously used (Reference ZwallyZwally and others, 2005) to calculate dM/ dt. Importantly, dCAT /dt depends on the time history of both A(t) and T(t) as their effects propagate into the firn. We assume the compaction effects of A(t) and T(t) are separable
so that
which should be valid at least for small A(t) and T(t) perturbations. The total elevation change from both A(t) and T(t) perturbations becomes
where dH a CA /dt is the total change caused by A(t), including the direct change and the change induced in the compaction rate. Equation (3) then gives
where dl/dt is an approximation of the change in thickness of the ice column, defined by treating dB/dt and dCT /dt as corrections to dH/dt.
In Equation (6), the three terms on the right-hand side involve changes in mass, and
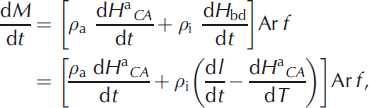
where ρ a is the appropriate density for the A(t)-driven changes, ρ i is the density of ice appropriate for the ablation and dynamic terms (combined as dH bd/dt ≡ (dH b/dt) + (dH d/ dt)), Ar is the area of a firn/ice column or map gridcell, and f is the fraction of the cell inside the ice-sheet boundary. We use ρ i = 0.90 for the typical density of glacier ice in the ablation zone and 0.91 in the accumulation zone, taking into account small variations from the 0.917 density of solid ice due to air content. dM/dt is also used in units of mass change per unit area, which is defined as the surface flux equivalent (SFE). The SFE is equal to the negative of the mass-flux change at the surface that would be required for the ice column to be in balance. Maps of dM/dt are presented in SFE units of Gt a−1 (100 km)−2, where Gt a−1 (100 km)−2 = 100 kg a−1 m−2.
4.2. Separation of accumulation and melting/icedynamic driven mass changes
An important aspect of our formulation is the separation of total dM/dt into two components: dM a/dt = ρ adH a CA /dt, which is driven by A(t) perturbations, and dM bd/dt = ρ i(dH bd/dt), which is driven by ice dynamics and by ice ablation below the equilibrium line (EL). The EL varies from ∼1000 m in the south, to 1600 m around 72° N, to 200 m in the north (Reference Zwally and GiovinettoZwally and Giovinetto, 2001). Above the EL, dH b/dt = 0 and we use dH bd/dt = dH d/dt.
The primary value in Equations (6) and (7) is dH/dt measured over some time, Δt. For dB/dt, we use the radial components of three models of isostatic rebound (Reference Ivins, Wu, Raymond, Yoder, James and SiderisIvins and others, 2001; Reference HuybrechtsHuybrechts, 2002; Reference PeltierPeltier, 2004), labeled (dB/ dt)I,H,P respectively, interpolated to our gridpoints. As in Reference ZwallyZwally and others (2005), we weight these models to account for distributions that showed similar patterns, specifically dB/dt = [(dB/dt)P/4] + [(dB/dt)H/4] + [(dB/dt)I/2]. We obtain the values of ρ a, dH a CA /dt and dCT /dt from our firn-compaction model (Reference Zwally and LiZwally and Li, 2002), which was modified to include the effects of surface melting and percolation (Reference Li, Zwally and ComisoLi and others, 2007) and is further modified here to include a variable accumulation rate, A(t), as described in more detail by Li and Zwally (in press). The model is driven by a T(t) temperature record from 1982 to the present as derived from Advanced Very High Resolution Radiometer (AVHRR) satellite measurements (Reference ComisoComiso, 2003) with values extended and updated using new calibrations.
We parameterize the accumulation perturbations, A(t) − 〈A〉, as a function of T(t) using a sensitivity of (5 ± 1.5)% δA K−1. The Intergovernmental Panel on Climate Change (IPCC) report (Reference SolomonSolomon and others, 2007) summarized the sensitivity of accumulation rate to temperature with a range of 4.7–8.5% δA K−1. Data from Greenland ice cores (Reference Clausen, Gundestrup, Johnsen, Bindschadler and ZwallyClausen and others, 1988) give a range of 4–6% δA K−1 using a sensitivity of δ18O to temperature of 0.69‰ K−1 (Reference Zwally and GiovinettoZwally and Giovinetto, 1997). For 1988–2005, our T(t) data and A(T(t)) parameterization give an A(t) increase of 0.6% a−1. This rate is close to the 0.7% a−1 we calculate for 1988–2004 from results of a regional-climate and surface mass-balance model using linear fits to the trends in the percolation and dry-snow zones given in figure 11a of Reference BoxBox and others (2006) with zone areas weighted by 30% and 70%.
4.3. Density, ρ a, for accumulation-driven mass changes
Our compaction model first calculates dH a CAT /dt using both T(t) and A(t), and then calculates dCT /dt using T(t) with constant 〈A〉. Equation (5) then gives the dH a CA/dt, and dH bd/dt is the residual part of dH/dt according to Equation (6). Equation (6) gives dl/dt for calculation of dM/dt in Equation (7), with all values calculated as averages over Δt. The average ρ a is calculated over Δt from ρ a = ΔMA /ΔH a CA , where ΔMA and ΔH a CA are the integrals over Δt of (A(t) − 〈A〉 and dH a CA/dt. Our calculated ρ a is 0.525 for 1992–2002 and 0.527 for 2003–07, averaged over the ice sheet above the EL. The distribution of ρ a in Figure 7c shows that ρ a is generally smaller (e.g. <0.5) in the northern part of the ice sheet and toward higher elevations where lower A reduces the rate of firn compaction. The largest values of ρ a (e.g. >0.65) are in the areas with high A at lower elevations mostly in the southern part.
Previous estimates of dM/dt from dH/dt made by various authors assumed there is an effective density, ρ eff, so that dM/dt = ρ effdI/dt, or when firn compaction terms are neglected dM/dt = ρ eff(dH/dt−dB/dt). For example, we previously used a density of 0.90, which is appropriate for solid ice if all the dH/dt is from long-term changes, and we illustrated a lower dM/dt estimate using ρ = 0.4, which is appropriate if all the dH/dt is from the addition or depletion of the upper part of the firn (Reference ZwallyZwally and others, 2005). Other authors used values ranging from 0.35 to 0.917 (e.g. 0.35 in Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005); 0.300 for the‘interior’ and 0.900 to ‘seaward’ in Reference Thomas, Frederick, Krabill, Manizade and MartinThomas and others (2006); and 0.350 and 0.917 in Reference Wingham, Shepherd, Muir and MarshallWingham and others (2006)). However, Equation (7) shows that ρ eff is strictly valid only if A(t) is constant, so that dH a CA/dt = 0 and ρ eff = 0.9. Calculations of dM/dt using Equation (7) show that in some locations ρ eff values calculated using (dM/dt)/(dI/dt) are unrealistically outside the 0.3–0.91 range for firn/ice densities. Therefore, using a fixed value of ρ eff is only valid if A(t) variations are insignificant (i.e when dH a CA/dt = 0 and ρ eff = 0.9). Consistent with this conclusion, Reference HelsenHelsen and others (2008) used a compaction model based on the model of Reference Zwally and LiZwally and Li (2002) and showed that a significant portion of the dH/dt observed in East Antarctica can be caused by temporal variations in accumulation.
5. Results
The spatial distributions of our calculated dCT /dt and dl/dt for 2003–07 are given in Figure 4b and c. Although dCT /dt is generally smaller than dH/dt, the larger values of dl/dt evident at higher elevations, in particular, are a result of warmer temperatures increasing the rate of firn compaction. We also recalculate dCT /dt and dl/dt for the 1992–2002 period using the dH/dt from Reference ZwallyZwally and others (2005), and compare the dl/dt for the two periods in Figure 6a and b, with their difference in Figure 6c. To compare the rates of ice-sheet thickness change, the comparison of dl/dt is more meaningful than comparison of dH/dt maps, because of the magnitude of dCT /dt that changed with climate warming between the respective periods.
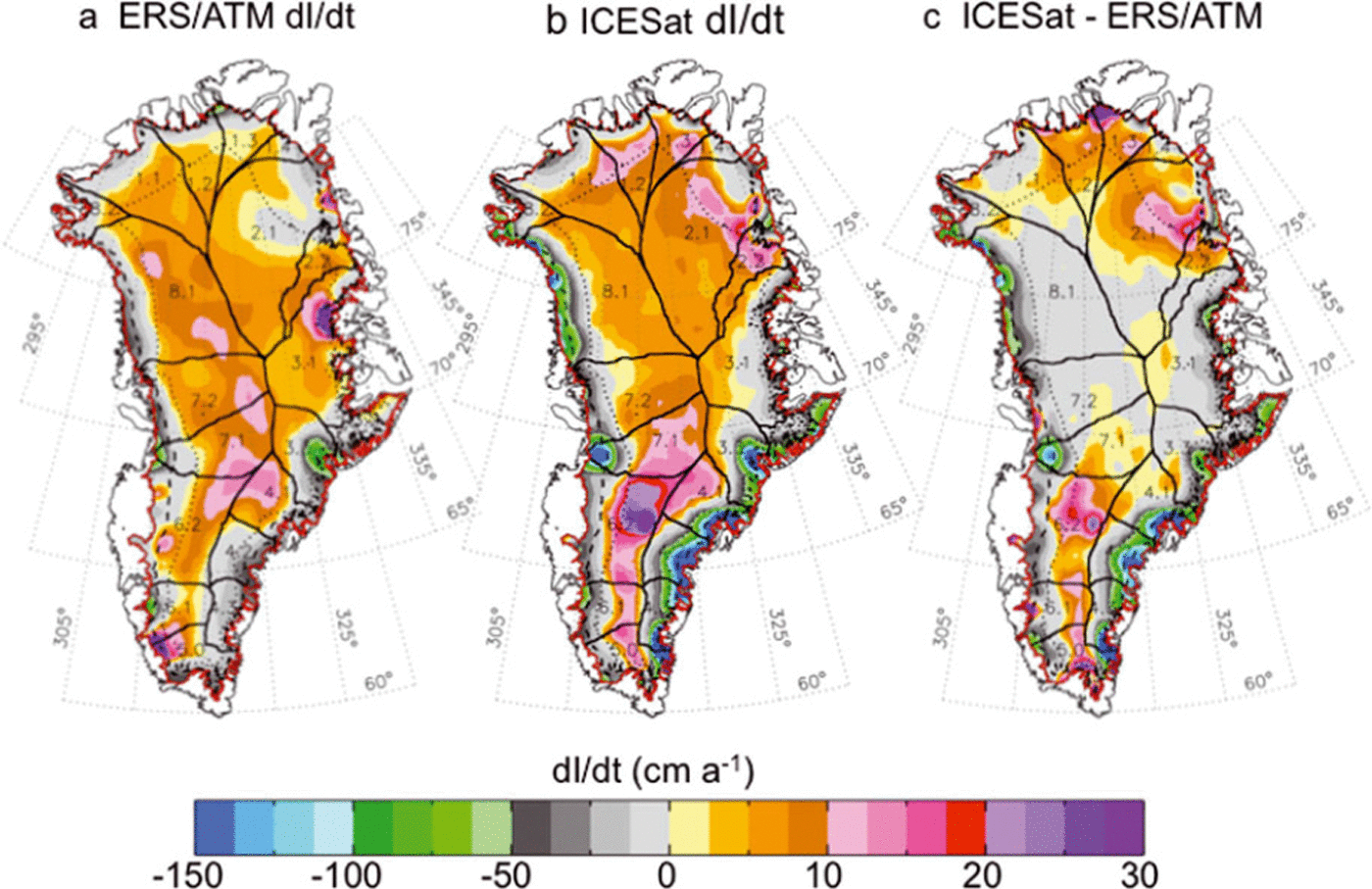
Fig. 6. (a) Distribution of dl/dt for 1992–2002 derived from ERS/ATM (Reference ZwallyZwally and others, 2005). (b) Distribution of dl/dt for 2003–07 from ICESat. (c) Change in dl/dt between 1992–2002 and 2003–07. Increased thinning is evident around most of the margins. Increased thickening is shown in the northern drainage systems (DS1 and DS2) and at higher elevations in the south (DS5 and DS6). The central region has a small thinning above ∼2000 m in the latter period.
During 1992–2002, much of the ice sheet was shown to be thinning below 2000 m elevation and thickening above 2000 m. During 2003–07, the largest changes in dl/dt are the increases in thinning along most of the ice-sheet margin below the EL and below 2000 m. Above 2000 m, increased thickening is observed in the southwest drainage systems (DS5 and DS6) and in the northeast (DS1.2, DS1.3 and DS2). However, this increased thickening is mostly counterbalanced by a large area of small thinning in the central region.
The distributions of dH
a
CA/dt, dH
bd/dt and ρ
a for 2003– 07 are shown in Figure 7a–c. The resulting distribution of dM/dt is in Figure 8, and the map of the calculated error, σ
dM/dt
, is in Figure 9a, along with the σ
dM/dt
for 1992–2002 in Figure 9b. σ
dM/dt
is calculated using propagation of errors, ![]() , which applied to Equation (7) gives
, which applied to Equation (7) gives
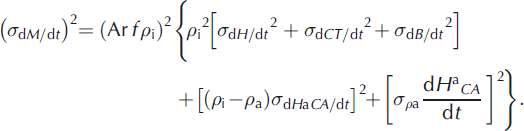
For ICESat, σ
dH/dt
in Figure 5a is computed from the cell-average dH/dt of the dh/dt solutions at the individual reference points. For ERS, σ
dH/dt
in Figure 5b is computed from the time-series analysis of crossover differences (Reference ZwallyZwally and others, 2005).
σ
dCT/dt
is calculated from the fit of CT
(t) for the appropriate period (October 2003–October 2007 for ICESat and April 1992–October 2001 for ERS), as the uncertainty in the time derivative in CT
(t) = a + (dCT
/dt)t + csin(ωt)+dcos(ωt), where ω = 2π/365.25 and t is in days. σ
dB/dt
is computed as half the difference between the similar and different values used to compute dB/dt. ![]() is the difference between dH
a
CA
/dt for the cases where accumulation changes at a rate of 5% K−1 and 8% K−1. σρ
a is the standard deviation of the distribution of ρ
a.
is the difference between dH
a
CA
/dt for the cases where accumulation changes at a rate of 5% K−1 and 8% K−1. σρ
a is the standard deviation of the distribution of ρ
a.
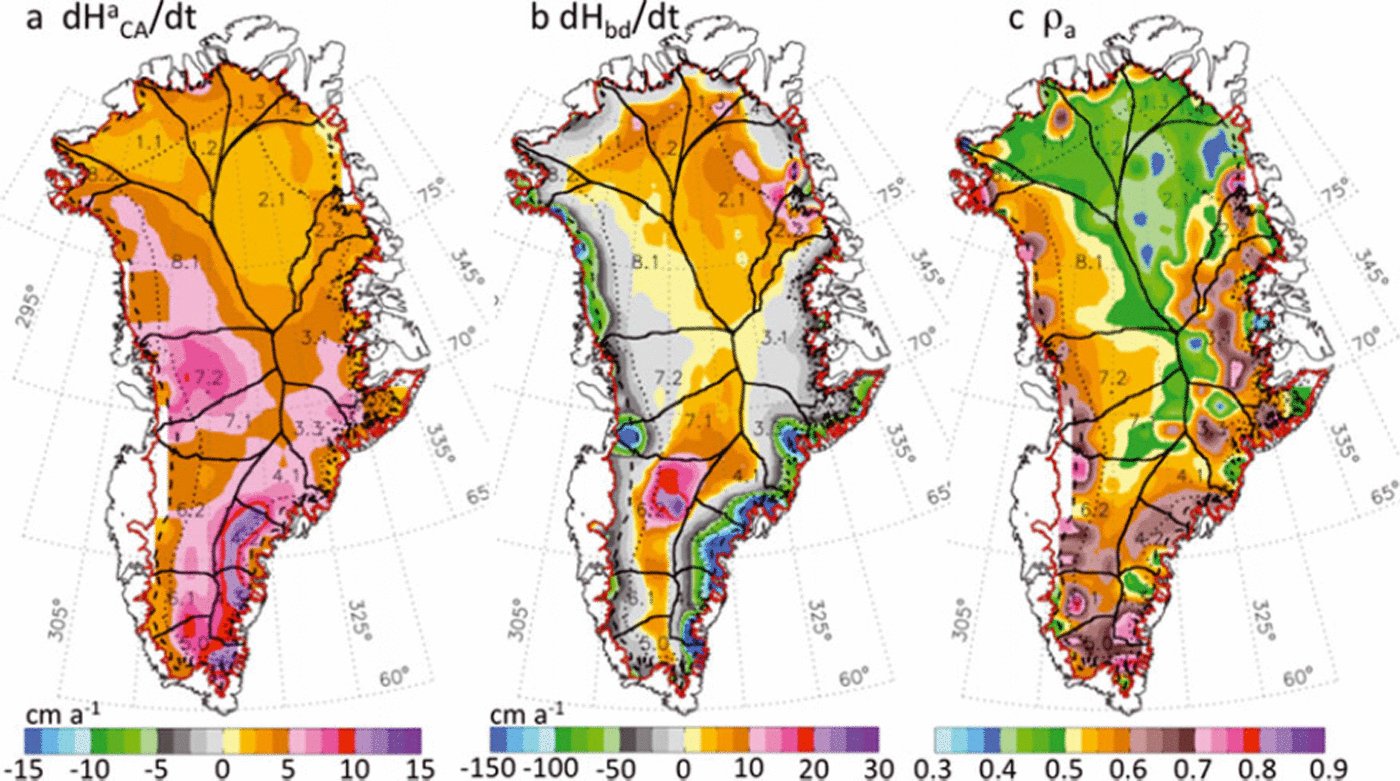
Fig. 7. Maps for the 2003–07 period. (a) Accumulation-driven elevation change, dH a CA /dt. (b) Ablation- and dynamic-driven elevation change, dH bd/dt. (c) Relative density, ρ A, of the firn for the dH a CA /dt component.
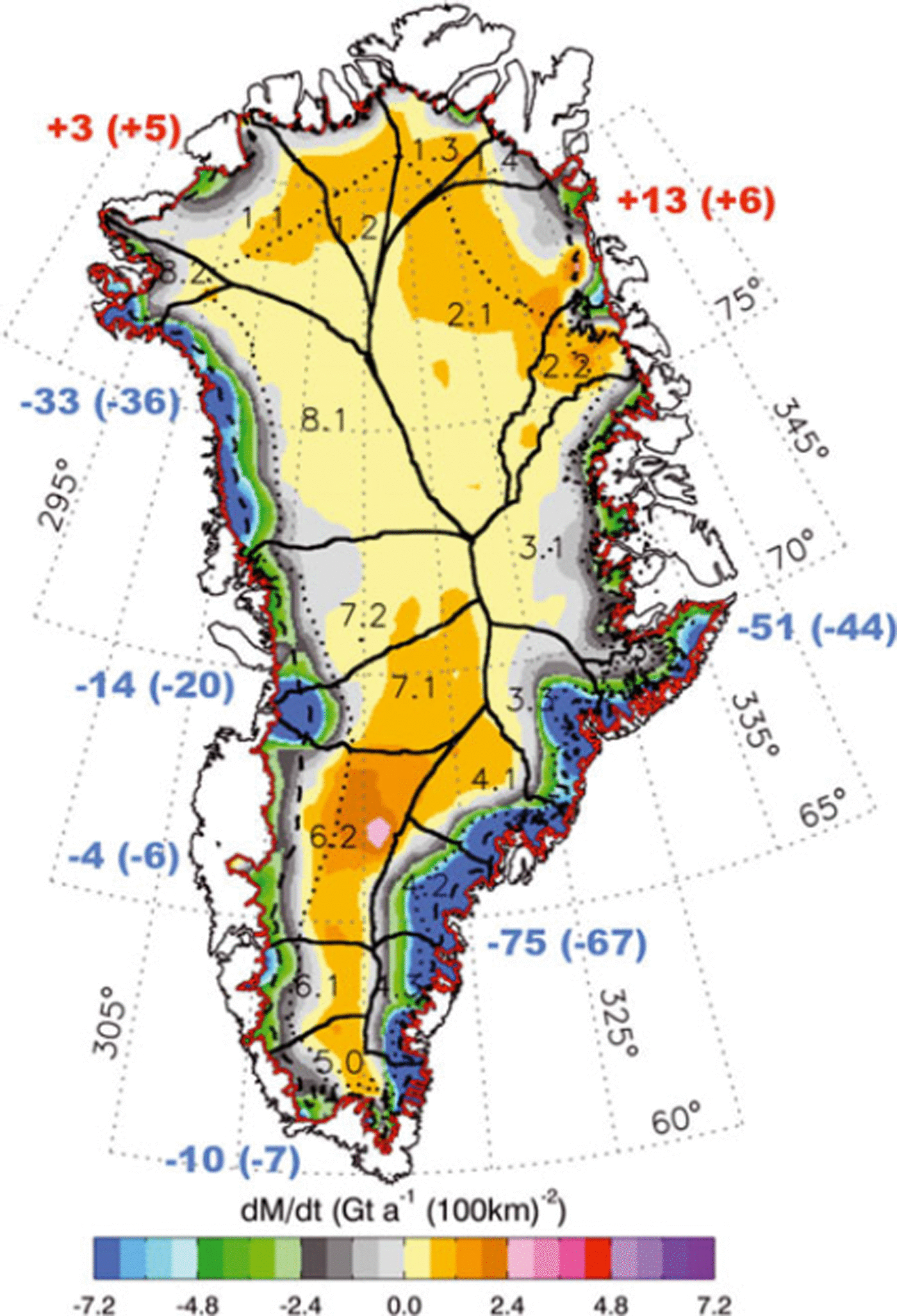
Fig. 8. Map of dM/dt (Gt a−1 (100 km)−2) for 2003–07 derived from ICESat data. The numbers around the map are the net gains (red) or losses (blue) (Gt a−1) for the DS1–DS7. The numbers in parentheses are the changes from the 1992–2002 period. All drainage systems except DS5 are divided into subsystems (e.g. DS1.1, etc.). The largest increases in the rates of mass loss are in the west central region and the southeast. The northern DS1 and DS2 are gaining mass. Most of the areas above and below 2000 m (dotted curve) are gaining and losing mass, respectively. Mass losses below the EL (dashed curve) are from a combination of increased melting and acceleration of outlet glaciers.
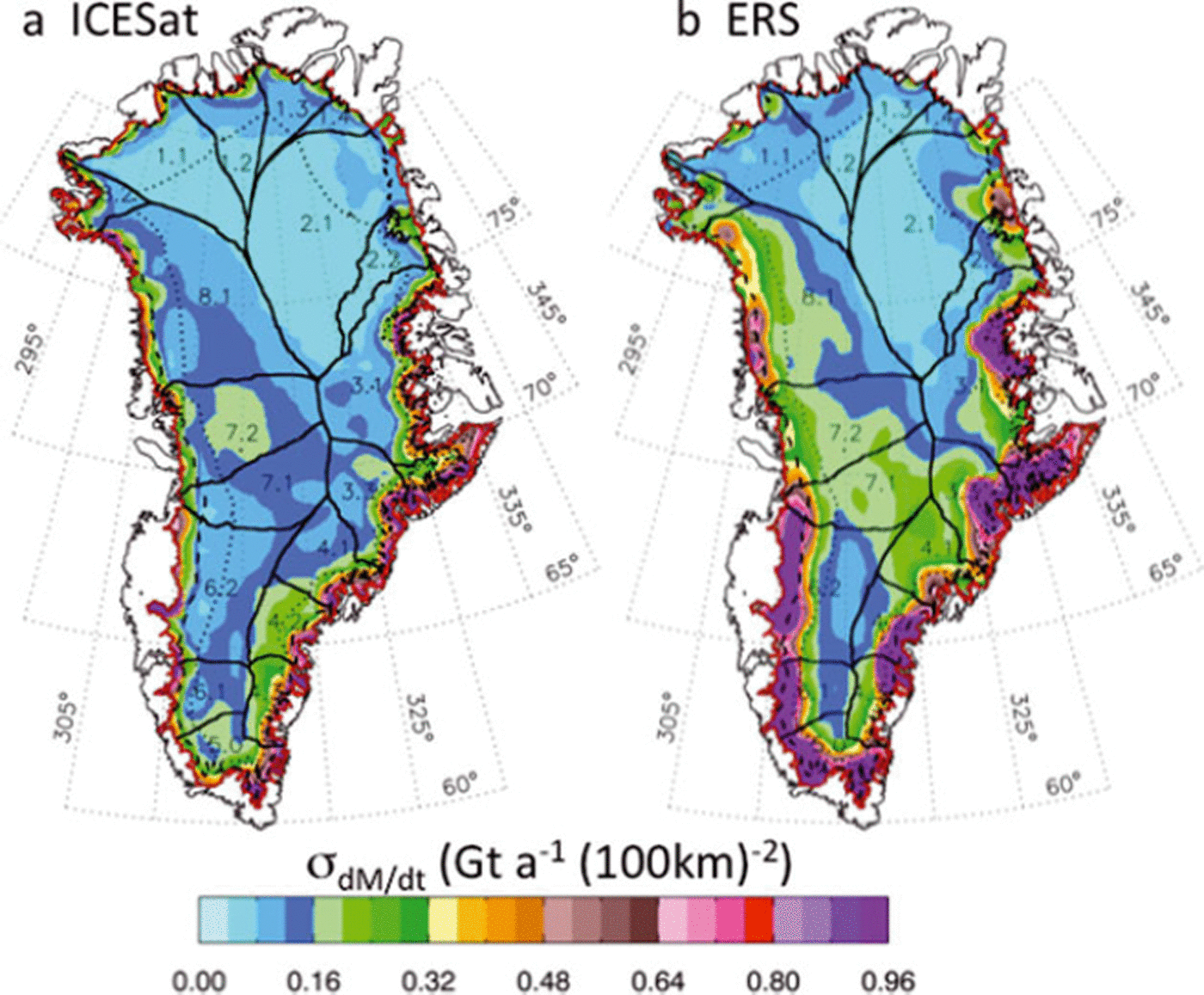
Fig. 9. (a) Maps of σ dM/dt (a) for 2003–07 from ICESat data and (b) for 1992–2002 from ERS and ATM data.
The values of dH/dt, dCT /dt, dl/dt, dH a CA /dt and dH bd/dt as functions of elevation averaged over the ice sheet are shown in Figure 10. The importance of dCT /dt as a correction to dH/dt is illustrated by the close agreement between dl/dt values (5.2 vs 4.9 cm a−1) for 1992–2002 and 2003–07 respectively at elevations above 2200 m, in contrast to the large difference between the dH/dt values (4.9 vs 1.0 cm a−1 ). Without dCT /dt, which is larger for the warmer 2003–07 period, the dH/dt alone would have incorrectly suggested that the ice-sheet thickening of ∼5 cm a−1 at higher elevations (Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others, 2005; Reference ZwallyZwally and others, 2005) had significantly diminished. The average dCT /dt over the accumulation zone are −0.2 and −4.1 cm a−1 for 1992– 2002 and 2003–07 respectively, and the associated volume changes of −3 km3 a−1 and −59 km3 a−1 would lower the derived dM/dt by 3 Gt a−1 and 54 Gt a−1 if the dCT /dt correction to dH/dt were not applied.
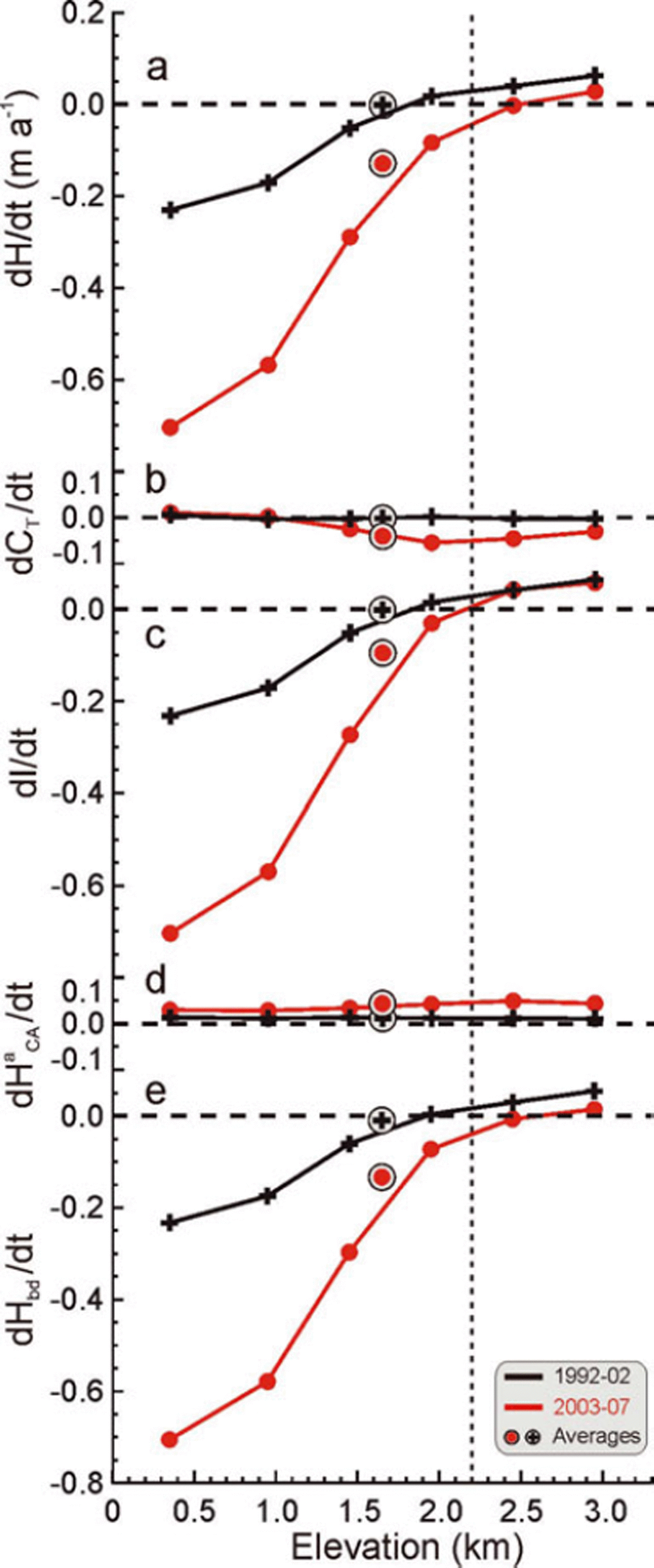
Fig. 10. All parameters averaged in 500 m elevation bands over the ice sheet versus elevations for 1992–2002 and 2003–07. Averages are over all elevations weighted by area. (a) Measured dH/dt decreased with time at all elevations. (b) Firn-compaction correction dCT /dt driven by temperature variations only. (c) dl/dt = (d H/dt) − (dCT /dt) − (dB/dt) shows little change with time above 2200 m. (d) dH a CA/dt, the portion of dl/dt driven by accumulation variations, increased slightly at all elevations. (e) dH bd/dt, the portion of dl/dt driven by changes in ablation (below EL only) and ice dynamics, decreased at all elevations. The increased thinning below the EL is from increased melting and acceleration of outlet glaciers. The increase in dynamic thinning extends inland to the highest elevations.
The average dB/dt is 0.06 cm a−1, which adjusts dM/dt by −1 Gt a−1. The close agreement of dl/dt at high elevations averaged over the ice sheet between the two periods suggests that the laser and radar results are actually quite comparable, despite the time difference between the measurements and technical differences between the laser and radar measurements. There is also close agreement (Fig. 11) between the two periods in both the derived dM bd/dt and the dM/dt at all elevations in four (DS1, DS2, DS5 and DS6) of the eight drainage systems, with average values being slightly higher in DS1 and DS2 and slightly lower in DS5 and DS6 in the latter period.
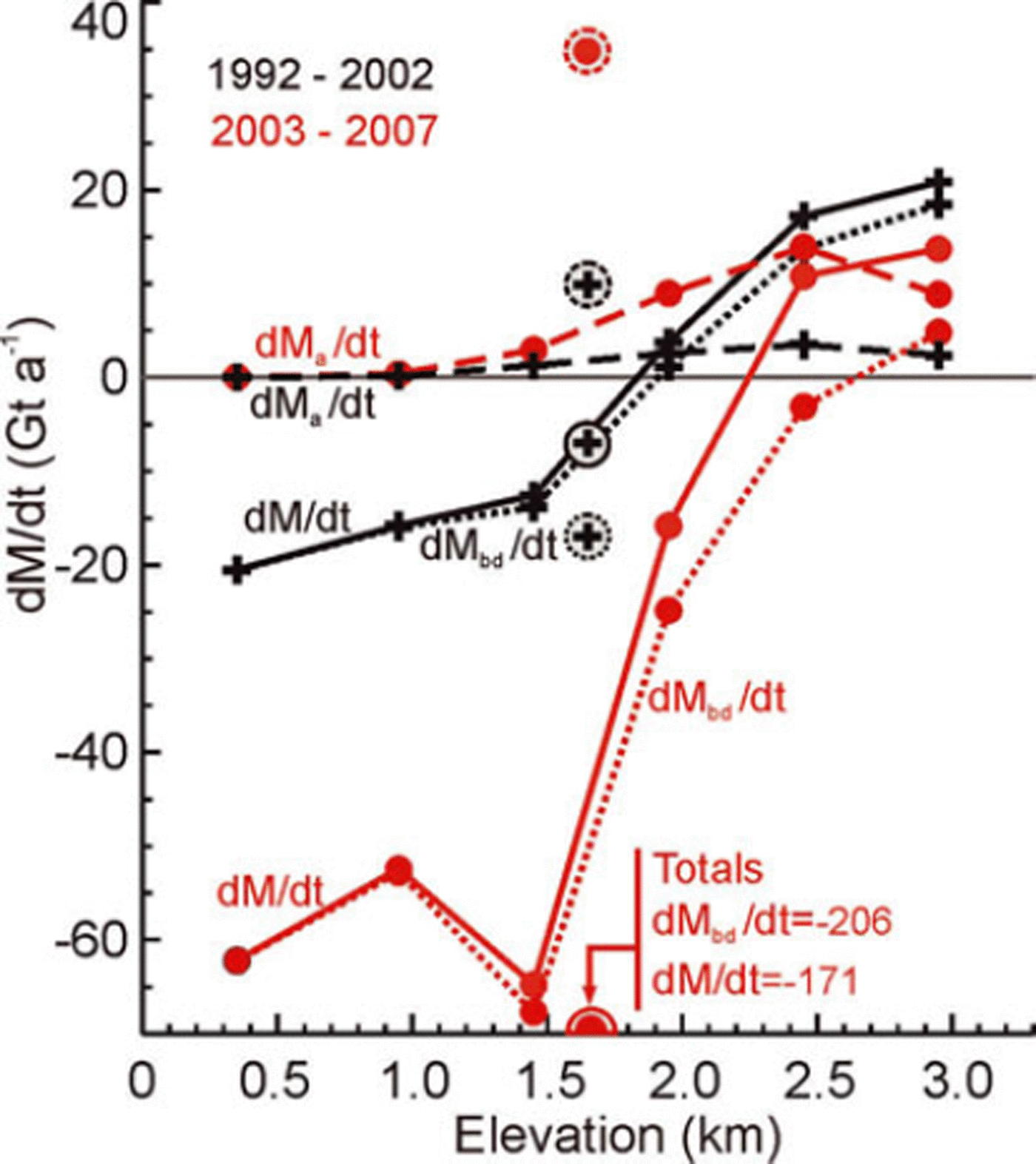
Fig 11. dM/dt is total rate of mass change, dM a/dt is the component driven by temporal variations in snow accumulation, and dM bd/dt is the component driven by ablation and ice dynamics, all averaged by 500 m elevation bands over the ice sheet for the 1992–2002 and 2003–07 periods. Circled symbols are totals for all elevations weighted by area.
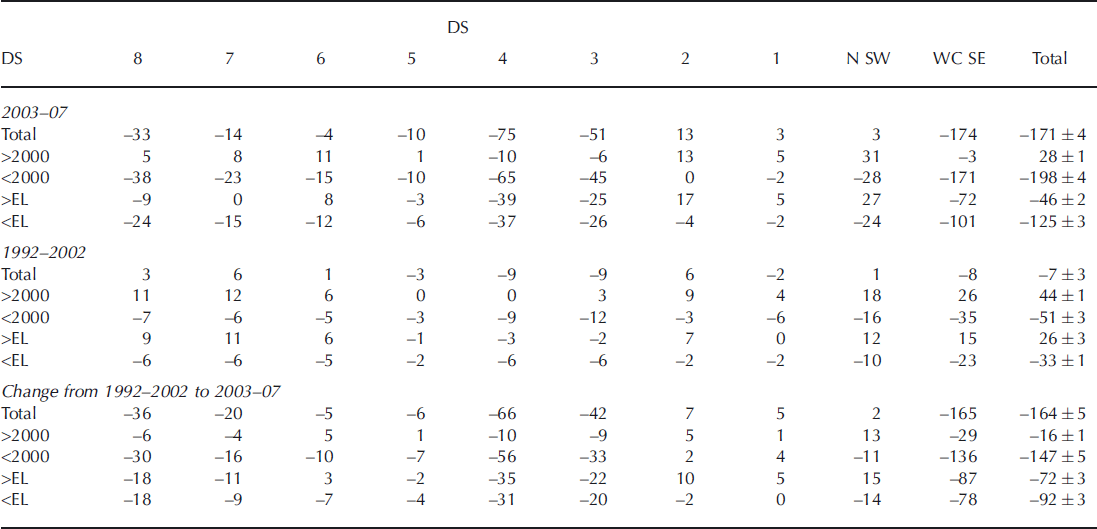
The distribution of dM/dt (Figs 8 and 11; Table 1) shows that during 2003–07 most of the GIS above 2000 m was gaining mass (+28 ± 1 Gt a−1) and most of it below 2000 m was losing mass (−198 ± 4 Gt a−1). Both these rates are lower than the 1992–2002 values of +44 ± 1 Gt a−1 and −51 ± 3 Gt a−1. The total loss of 171 ± 4 Gt a−1 during 2003– 07 is in close agreement with two GRACE-based loss rates for similar time periods of 158 ± 8 Gt a−1 for October 2003–November 2007 (Reference LuthckeLuthcke and others, 2009) and 179 ± 25 Gt a−1 for February 2003–January 2008 (Reference Wouters, Chambers and SchramaWouters and others, 2008). Our derived mass loss of 171 ± 4 Gt a−1 represents an increased loss rate of 164 ± 5 Gt a−1 compared with the near-balance conditions during 1992–2002, for which we obtain a revised small loss of 7 ± 3 Gt a−1. The previous small gain (Reference ZwallyZwally and others, 2005) of 11 Gt a−1 is revised here due to several factors: −13.8 Gt a−1 change is from improvements in the firn-compaction model, −9.2 Gt a−1 from use of recalibrated T(t) data, +11.9 Gt a−1 from changes in the grid-map projection and use of partial gridcells at the ice edge, and 7.8 Gt a−1 from partitioning of the height changes into accumulation-driven changes with an average density of 0.53 and ablation-/dynamic-driven changes with an average density of 0.9.
Table 1. dM/dt (Gt a−1) by drainage system (DS): four DS in north and southwest (N SW; 1, 2, 5, 6), four DS in west central and southeast (WC SE; 3, 4, 7, 8) and totals. (Totals are rounded to integers after summation of values by DS before rounding)
Our partitioning of the dM/dt gives an accumulation-driven gain (dM a/dt) of 35 Gt a−1 for 2003–07, compared with a gain of 10 Gt a−1 during 1992–2002 (Fig. 11). The derived ablation–dynamic loss rate (dM bd/dt) of 206 Gt a−1 for 2003–07 is much larger than the corresponding loss rate of 17 Gt a−1 during 1992–2002. Although both components of dM/dtare larger in the later period, the increase in the loss term (−189 Gt a−1) from melting and ice dynamics strongly dominates the increase in the gain term (+25 Gt a−1) from snow accumulation. For comparison, if none of the mass change were ascribed to changes in accumulation, then net rate of mass loss for 2003–07 would be <171 Gt a−1 (i.e. less negative than −171 Gt a−1), because the positive dH a CA/dt component of observed elevation change would have an associated density of 0.91 instead of 0.527.
To calculate a sensitivity of the derived dM/dt to our parameterization of A(t), we ran the firn compaction for the 2003–07 period using a parameterization of 8% δA K−1 instead of 5% δA K−1, which changed dM/dt by 11 Gt a−1, giving a sensitivity of −3.7 Gt a−1 (% δA K)−1. For 2003–07, the sensitivity can also be estimated by noting that a dM a/dt value of 35 Gt a−1 would be ∼60 Gt a−1 (i.e. (35 × 2.91)/0.527) if part of the measured elevation changes were not ascribed to increasing A(t), giving a sensitivity of (35 − 60)/5 = −5.0 Gt a−1 (% δA K)−1. For 1992–2002, the dM a/dt of 10 Gt a−1 would be 17 Gt a−1, giving −1.4 Gt a−1 (% δA K)−1. Therefore, the sensitivity appears to depend somewhat on the specific A(T(t)) variability history.
The relative values of the dM a/dt and dM bd/dt components of dM/dt vary significantly from one drainage system to another, as do their changes with time (Fig. 12). In the northern drainage systems (DS1 and DS2), dM bd/dt values are essentially the same in both time periods, indicating little change in either the dynamics or the ablation in those systems. Also, dM bd/dt is not large compared with dM a/dt in these drainage systems as it is in the southeast DS3 and DS4 and in the upper western DS7 and DS8 (note the dM bd/dt scale is ten times the dM a/dt scale in Fig. 12). Although dM a/dt increases with time in all drainage systems, consistent with the increase in A(t), the increase in dM bd/dt from dynamic thinning and ablation dominates those increases in dM a/dt in all drainage systems except the northern DS1 and DS2.
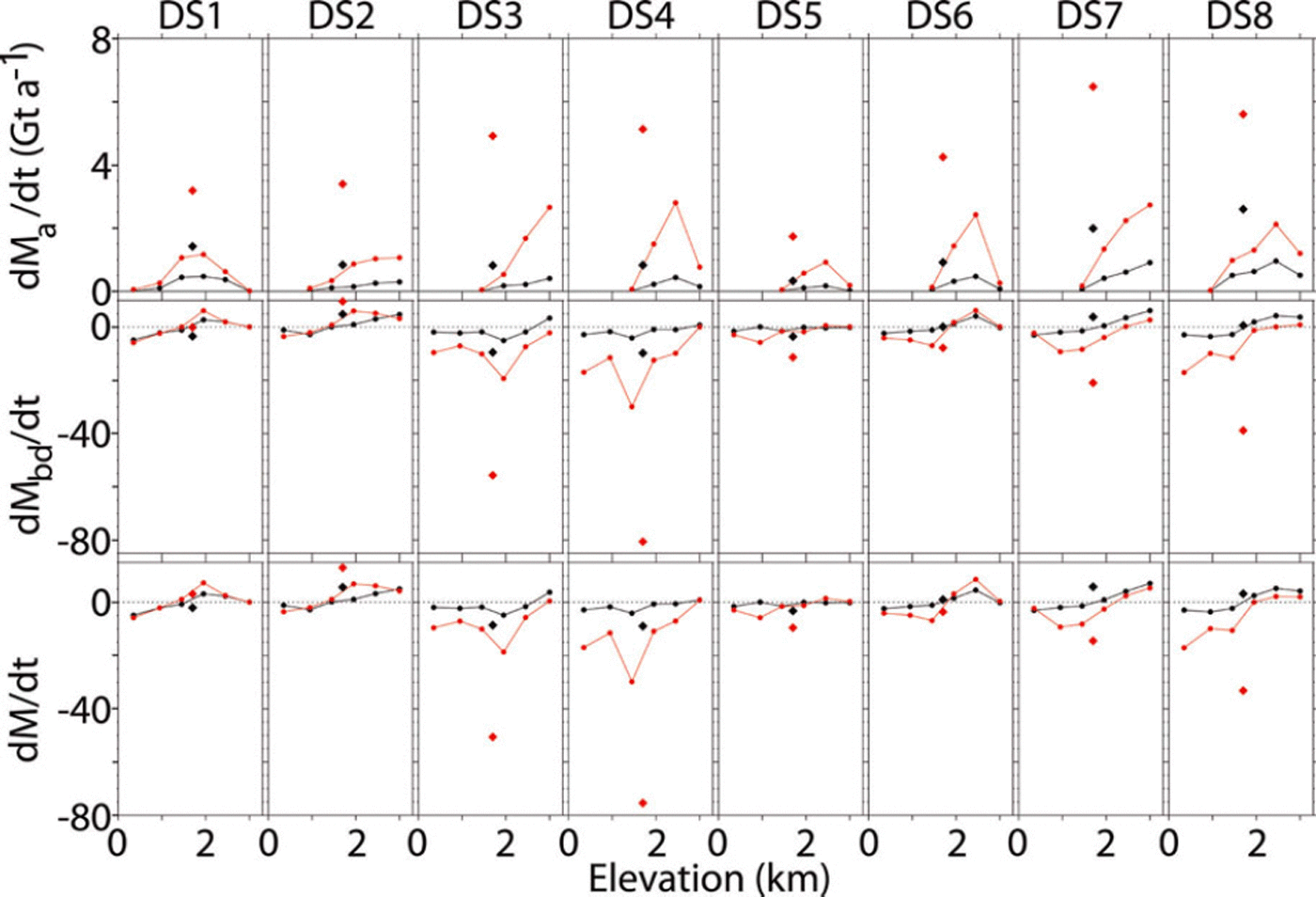
Fig. 12. Components of mass change by drainage system. dM a/dt, dM bd/dt, dM/dt (Gt a−1)averaged over 500 m elevation bands for the eight drainage systems for 1992–2002 (black) and 2003–07 (red) with totals for 1992–2002 (black symbols) and 2003–07 (red symbols). Accumulation-driven mass increases are largest in DS3, DS4, DS7 and DS8, and dynamic-/ablation-driven thinning is largest in DS3, DS4 and DS8 and very small in DS1, DS2, DS5 and DS6.
6. Discussion
6.1. Ice-sheet interior
Our results show that the part of the accumulation zone above 2000 m (60.8% by area) is thickening on average during both periods by similar amounts, as shown by a dl/dt value of +4.78 cm a−1 during 2003–07 and the slightly larger value of +5.10 cm a−1 during 1992–2002 (Fig. 10). Although dl/dt is similar in both periods, the accumulation-driven part (dH a CA/dt) increased from +1.13 to +4.68 cm a−1 while the dynamic driven part (dH d/dt) decreased from +3.96 to +0.10 cm a−1. Therefore, the changes at higher elevations (>2000 m) are a combination of ice thickening of 3.55 cm a−1 from increased A(t) and an approximately equal increase in dynamic thinning of 3.86 cm a−1.
If the resulting dl/dt decrease of 0.32 cm a−1 were not partitioned between dH a CA/dt and dH d/dt, it would imply a decrease in the rate of mass gain of only 2 or 3 Gt a−1. However, the partitioning gives a dM a/dt increase of 20 Gt a−1 (i.e. gaining lower-density firn) and a larger dM d/dt decrease of 36 Gt a−1 (i.e. losing higher-density ice), giving a net change of −16.5 Gt a−1 above 2000 m. Therefore, although the accumulation-driven thickening approximately balances the dynamic thinning (in terms of cm a−1), the net effect is a decrease in the rate of mass gain from 44 to 28 Gt a−1.
The map of the dM/dt distribution (Fig. 8), Table 1 and Figure 13 show that the northern DS1 and DS2 have net mass gains and have become slightly more positive during 2003–07 compared with 1992–2002. The four drainage systems in the north and southwest (DS1, DS2, DS5 and DS6) show increased mass-gain rates above 2000 m (+18 to +31 Gt a−1), suggesting increases in rates of ice accumulation, and small increased loss rates at lower elevations (−15 to −25 Gt a−1 ). Overall, the major changes toward increased losses are in southeast DS3 and DS4 and west central DS7 and DS8 in regions with accelerating glaciers (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006). These four drainage systems have small negative changes above 2000 m (+26 to −2 Gt a−1), but large changes at lower elevations (−32 to −156 Gt a−1).
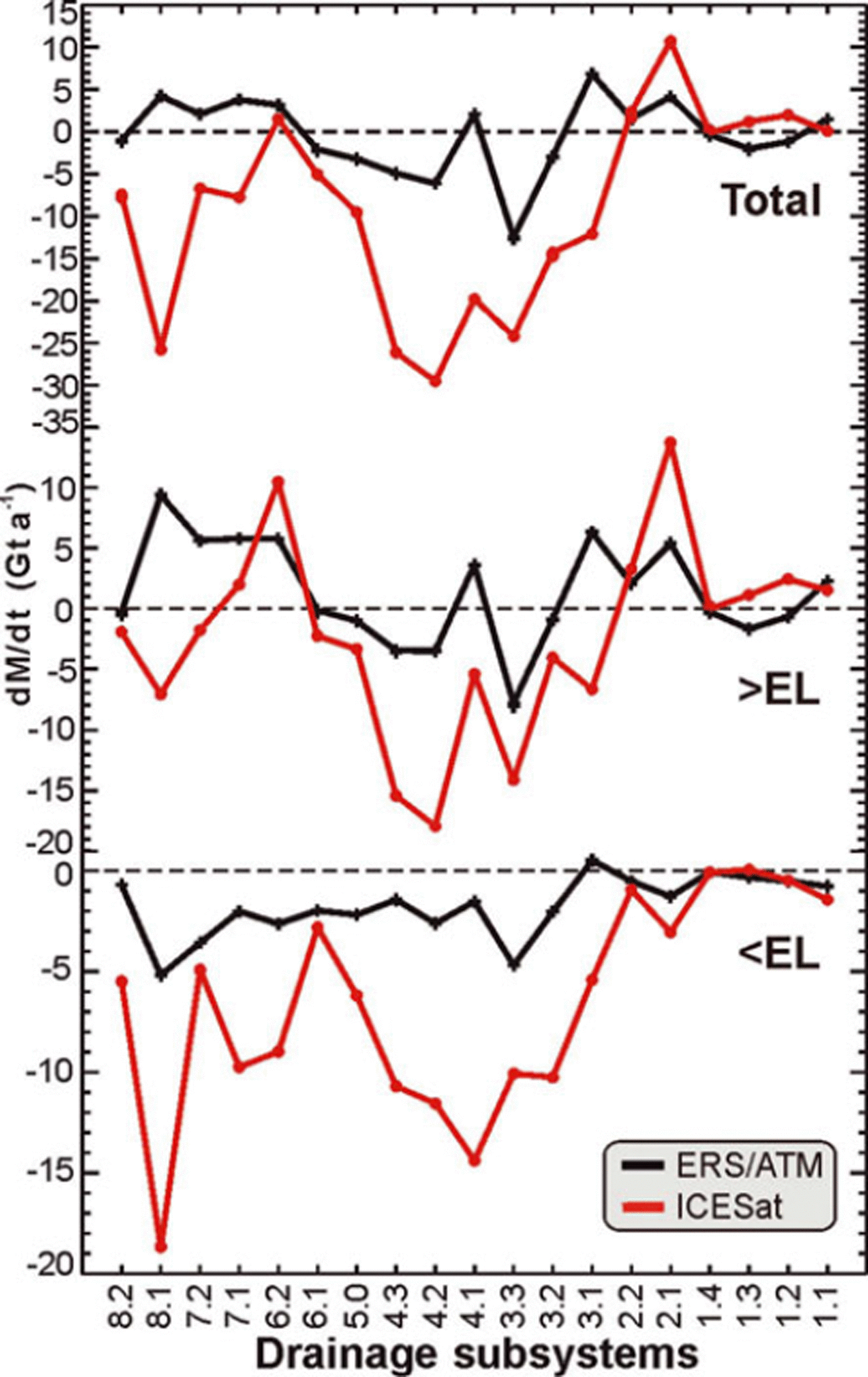
Fig. 13. Total rate of mass change and rates above and below EL by drainage subsystems.
6.2. Ice-sheet margins and outlet glaciers
Only 11.2% of the GIS area lies below the EL, and 39.2% lies below 2000 m, but the change in mass loss at these lower elevations, from −33 to −125 Gt a−1 below the EL and from −51 to −198 Gt a−1 below 2000 m (Table 1), dominates the total mass balance for the whole ice sheet. Therefore, the lower elevations of the GIS have been mostly thinning, and this thinning has increased significantly in the later period (Figs 10–12). However, the increases below the EL in the northern DS1 and DS2 are small or near zero (Fig. 13).
The only locations around the margins that show thickening at lower elevations (Fig. 8) are the southeast corners of DS2.1 and DS2.2, a small area near Petermann Gletscher at the boundary between DS1.1 and DS1.2 and the small ice dome extending westward from the GIS at 66° N in DS6.2. In contrast, during 1992–2002, the pattern of thickening and thinning around the margin was more mixed, with areas of significant thickening in DS3.1 and DS5. Also, the thinning in the western ablation zone in DS6.2, DS7.2 and DS8.1 was small in 1992–2002 compared with 2003–07.
About 25 Gt a−1 or 5% of the total mass flux from the GIS is through Jakobshavn Isbræ (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006), in DS7.1. During the 1990s, the mass gain of 5.8 Gt a−1 above the EL in DS7.1 exceeded the loss of 2.0 Gt a−1 below the EL. For 2003–07, the gain above the EL reduced to 2.0 Gt a−1, and the loss below increased to 9.7 Gt a−1. Therefore, the net balance changed from a gain of 3.8 Gt a−1 in the 1990s to a loss of 7.8 Gt a−1, which accounts for ∼7% of the total increase in dM/dt between the two periods.
Figures 14a, 15a, 16a and 17a show dH/dt maps of four outlet glaciers kriged from the along-track dh/dt at higher resolution (10 km, 5 km, 500 m and 500 m, respectively) than the 50 km used for dM/dt calculations and analysis. Figures 14b, 15b, 16b and 17b show a comparison between the dh/dt at intersections of a central flowline with the ICESat tracks and dH/dt interpolated from the higher-resolution maps. These maps provide a high-resolution pictorial representation of the topography on these outlet glaciers but are not used in our dM/dt calculations.
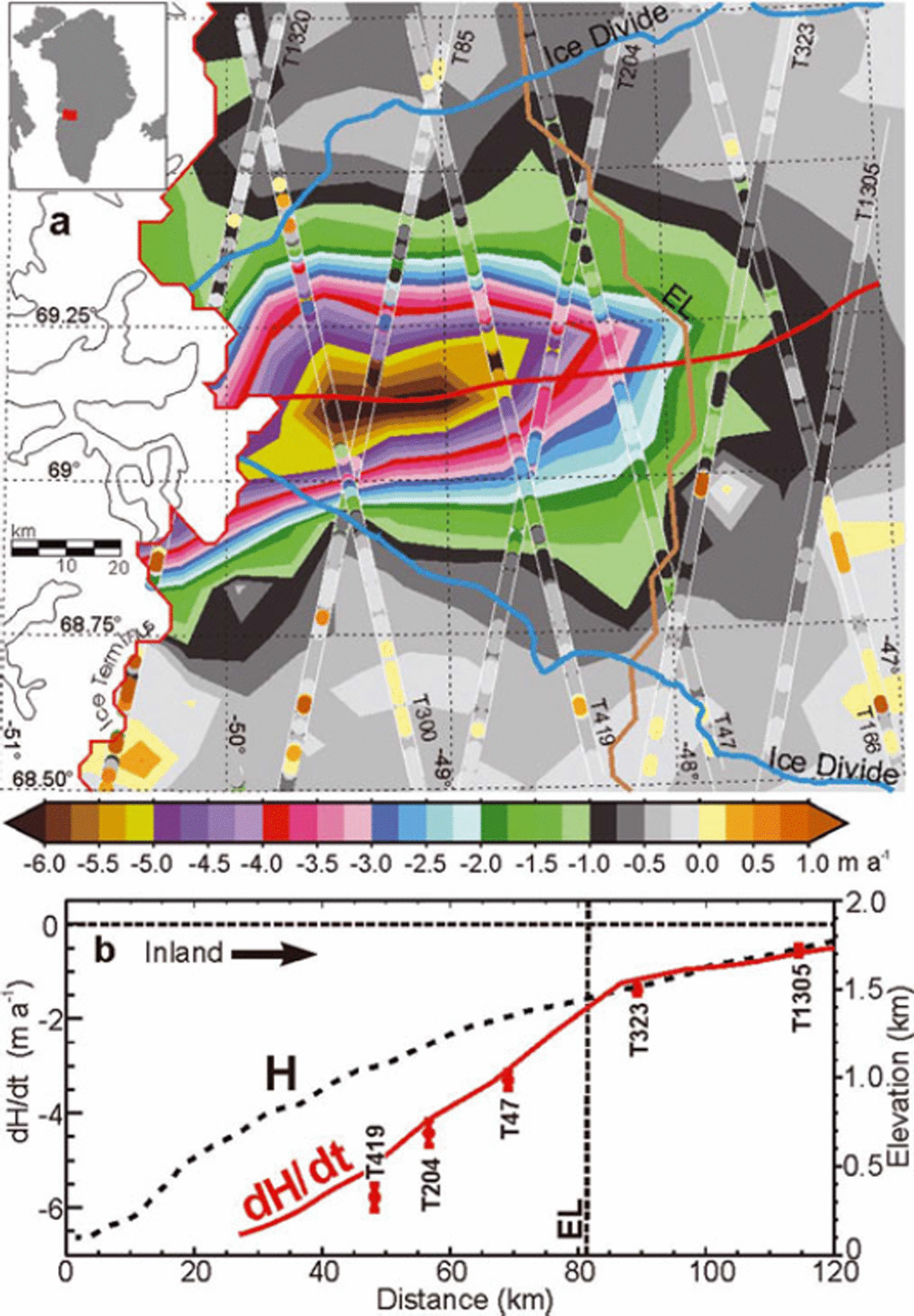
Fig. 14. (a) dH/dt map of Jakobshavn Isbræ kriged on a 10 km grid from the along-track dh/dt plotted on the tracks. (b) dH/dt profile (interpolated from dH/dt map) and H profile along a central flowline (red curve in (a)). Red symbols are dh/dtf ± σ dh/dt at points where the flowline crosses the ICESat tracks. Steep increase in dH/dt below the EL indicates effect of increased melting as well as thinning from glacier acceleration.
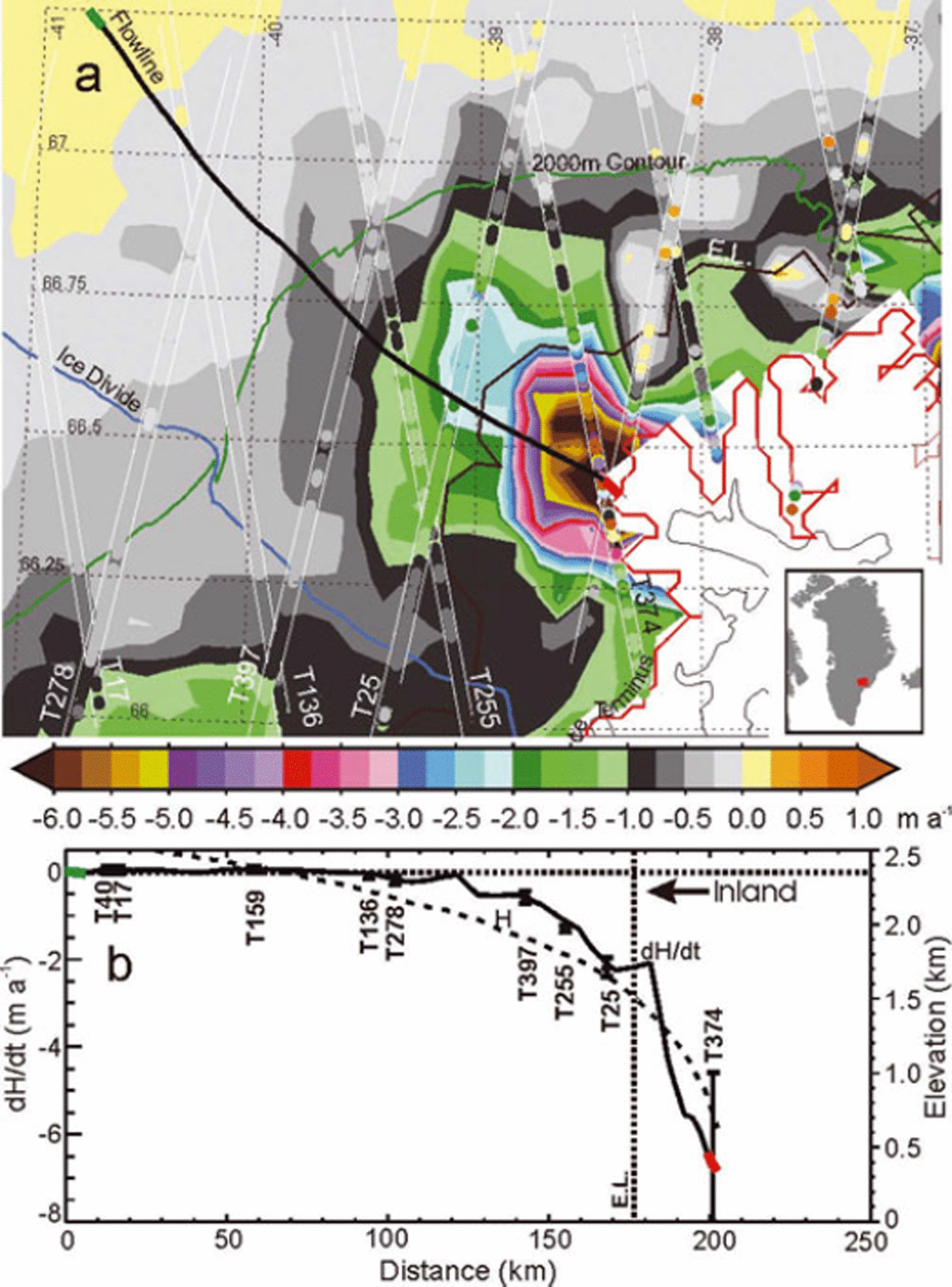
Fig. 15. (a) dH/dt map of Helheimgletscher kriged on a 5 km grid from along-track dh/dt plotted on the tracks. (b) dH/dt profile (interpolated from dH/dt map) and H profile along a central flowline (black curve in (a)). Black symbols are dh/dt ± σ dh/dt at points where the flowline crosses the ICESat tracks. Red and green segments in (a) indicate the ends of flowline.
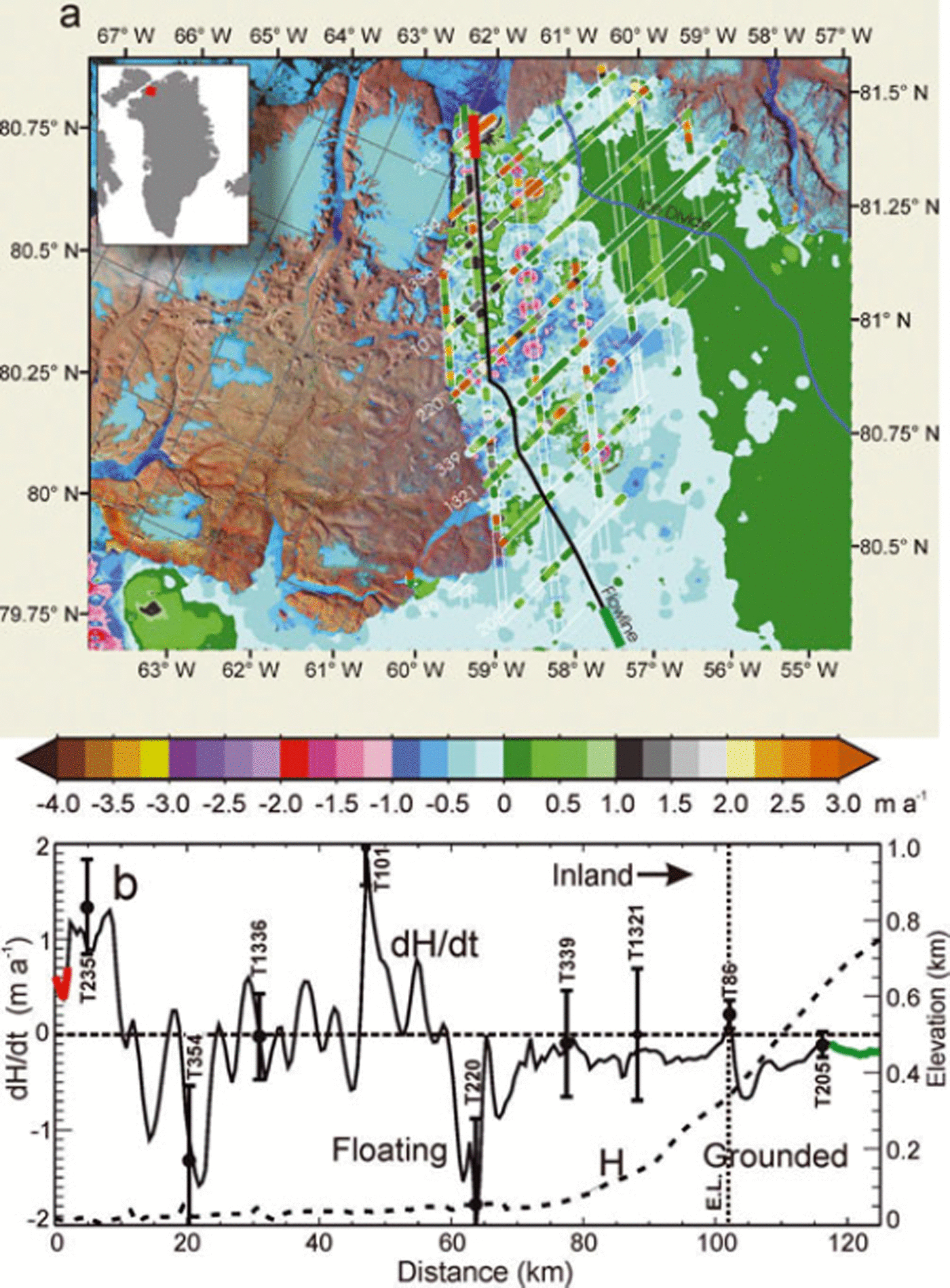
Fig. 16. (a) dH/dt map of Petermann Gletscher kriged on a 500 m grid from along-track dh/dt plotted on the tracks. (b) dH/dt profile (interpolated from dH/dt map) and H profile along a central flowline (black curve in (a)). Black symbols are dh/dt ± σ dh/dt at points where the flowline crosses the ICESat tracks. Red and green segments in (a) indicate the ends of flowline.
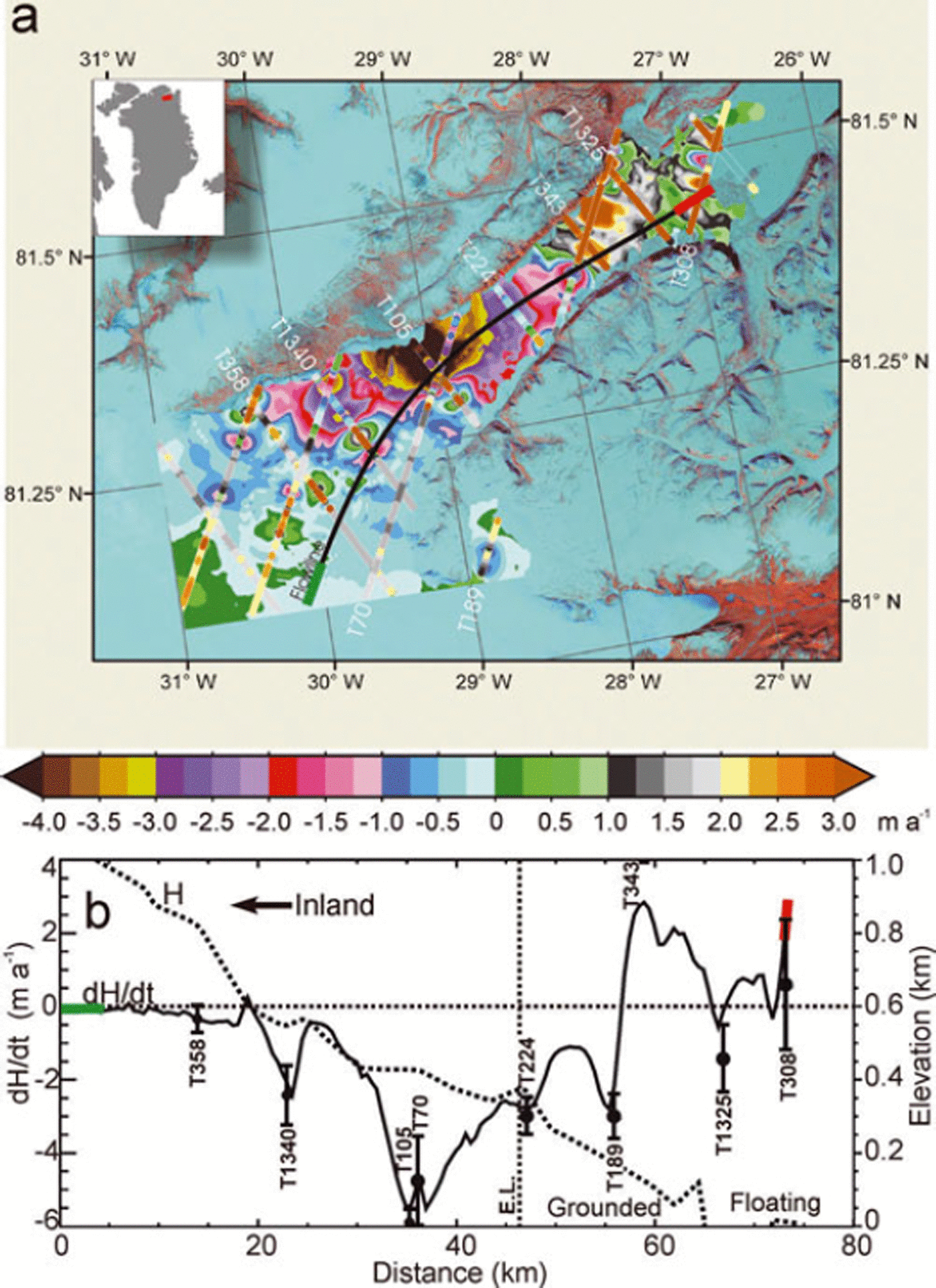
Fig. 17. (a) dH/dt map of Hagen Bræ kriged on a 500 m grid from along-track dh/dt plotted on the tracks. (b) dH/dt profile (interpolated from dH/dt map) and H profile along a central flowline (black curve in (a)). Black symbols are dh/dt ± σ dh/dt at points where the flowline crosses the ICESat tracks. Red and green segments in (a) indicate the ends of flowline.
The acceleration of Jakobshavn Isbræ (Reference JoughinJoughin and others, 2008a) as the floating ice tongue thinned and broke away during 1996–2004 certainly contributes to this increased rate of mass loss. However, the near-linear change in h(t) over 4 years, as shown in Figure 3c at six locations on Jakobshavn, suggests that the rate of thinning changed little during 2003–07. The rate of glacier thinning along the flowline (Fig. 14) shows a marked break at the EL (1440 m), with increasingly larger rates of thinning at lower elevations downstream of the EL (slope of 1.08 m a−1 (100 m)−1. Above the EL the slope of the thinning rate is 0.38 m a−1 (100 m)−1, or only one-third of that below the EL. Because the location of the EL is determined by the surface mass balance, and not by ice dynamics, this change at the EL cannot be explained by a change in the rate of dynamic thinning at this location. Assuming that the thinning above the EL is all caused by ice dynamics, extension of the 0.38 m a−1 (100 m)−1 thinning rate to below the EL suggests that at 1000 m elevation, for example, about half of the ∼6 m a−1 thinning is from dynamics and the other half is from increased melting. Therefore, increased melting and flow acceleration appear to be contributing similar amounts to the current thinning on the lower part of the glacier. Similarly, Helheimgletscher on the east coast also shows a break in the thinning rate near the EL (Fig. 15).
Two northern glaciers with floating ice tongues are Petermann Gletscher in the northeast corner of DS1.1 (Fig. 16) and Hagen Bræ in the northeast corner of DS1.3 (Fig. 17). dH/dt on the floating part of Petermann shows an oscillating mixture of thickening and thinning, with an average close to zero, thinning inland of the grounding line to ∼1400 m, and thickening at higher elevations (Figs 16 and 4c). The pattern of dH/dt on Hagen Bræ is thickening on the floating part, strong thinning to about 600 m, and thickening inland to ∼1000 m. This pattern of thinning of grounded ice inland of ice tongues that are not significantly thinning suggests that factors other than a decrease in the buttressing effect (Reference Thomas, Rignot, Kanagaratnam, Krabill and CasassaThomas and others, 2004) of floating ice are affecting the thinning of the grounded ice on these glaciers.
6.3. Dynamic thinning and inland coupling
The increase in dH bd/dt in 2003–07 compared with 1992– 2002 (Fig. 10) is large below the EL (−19 to −72 cm a−1), where it is a combination of local ablation changes and dynamic thinning (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). Above the EL, the dynamic thinning (dH d/dt) decreases with increasing elevation and becomes zero or slightly positive above ∼2300 m in averages over the GIS (Fig. 10e). The marked increase in dynamic thinning in 2003–07 extends into the GIS interior, decreasing with elevation (−6 to −30 cm a−1 between 1200 and 1700 m and 5 to 1 cm a−1 above 2700 m).
The increase in dynamic thinning during the later period indicates that the effects of increased melting and accelerating glaciers, which are occurring at the margins, are dynamically extending inland to the highest elevations in some drainage systems. The increased thinning rate between 1500 and 2000 m, for example, cannot be significantly affected dynamically by local changes in the surface mass balance, because the resulting changes in driving stresses from A(t) are small. Also, this inland extension occurs relatively fast (decadal-scale response).
However, the inland extension of dynamic thinning is not the same in all drainage systems. The largest changes and inland extension are in DS4 in the southeast, followed by DS7, DS3, DS5, DS6 and DS8 (as shown by dM bd/dt in Fig. 12). The response time for inland dynamic coupling should be fastest in DS4 (as observed; Fig. 12) where the ice is warmer and deforms more easily and where the slopes are steep and the distance from the margin to the ice divide is smaller, i.e. 100–200 km. In contrast, dH bd/dt is nearly the same in both time periods in DS1 and DS2 in the north, where the ice is colder and the slopes are less steep.
6.4. Response to climate change
Changes in A(t) and T(t) on the GIS have immediate effects on the surface mass balance, the surface elevation and ice thickness, D, and the surface slope, α. Changes in D and α also change the driving stresses that force the ice flow, but these changes are generally expected to affect the ice dynamics only on timescales of centuries (Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999). Two mechanisms for rapid response of the ice dynamics to climate that have been observed in Greenland are changes in buttressing of outlet glaciers caused by removal of their floating ice tongues (Reference Thomas, Rignot, Kanagaratnam, Krabill and CasassaThomas and others, 2004; Reference Nick, Vieli, Howat and JoughinNick and others, 2009) and changes in basal lubrication and sliding from the melt/acceleration effect (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002b; Reference Joughin, Das, King, Smith, Howat and MoonJoughin and others, 2008b; Reference Van de WalVan de Wal and others, 2008; Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010).
The observed increase of 164 Gt a−1 in dM/dtto 171 Gt a−1 suggests that the GIS is responding to enhanced climate warming in the Arctic (Reference Monitoring and ProgrammeAMAP, 2009), and that mass-exchange processes and ice dynamics causing greater mass loss are dominating those of mass gain. The thinning at the margins and thickening inland during the 1990s was already consistent with a response to a warmer climate, even though the mass balance then was close to zero. From 1997 to 2007, the 10 year trend in our AVHRR temperature record is +1.7 K (10 a)−1, which compares with a 2.7 K(10 a)−1 increase (Reference Hall, Williams, Luthcke and DigirolamoHall and others, 2008) for 2000–06 and a 1.8 K (10 a)−1 increase (Reference Box, Yang, Bromwich and BaiBox and others, 2009) for 1994–2007. Our corresponding increase in A(T(t)) is 8.5% (10 a)−1, which compares with 7% (10 a)−1 for 1988–2004 and 3.3% (10 a)−1 for 1958–2003 from regional-climate surface mass-balance models (Reference Hanna, Huybrechts, Janssens, Cappelen, Steffen and StephensHanna and others, 2005; Reference BoxBox and others, 2006).
The increased mass loss is partly due to changes in surface mass balance and partly to changes in the ice dynamics. Since temperature increase is the primary forcing for these changes, including the variation of A(t) with T(t), it might be expected that an additional warming of 3.4 K in another two decades would increase the rate of loss to 500 Gt a−1 (1.4 mm a−1 sea-level rise), assuming a linear relationship between temperature increase and mass loss. Numerical models of ice-sheet response to climate change in the next century generally account for changes in surface mass balance, but either neglect the effects of surface changes on the ice dynamics or only consider local changes in the driving forces. Most models do not include higher-order stress couplings within the ice, melt/acceleration effects, or the acceleration of outlet glaciers. The observed increase in dynamic thinning in 2003–07 and the dynamic coupling inland on decadal timescales is a new indication of how the GIS is responding to climate change that needs to be accounted for in predicting ice-sheet behavior.
7. Summary
The mass changes of the GIS that we derive for two periods (1992–2002 and 2003–07) show a significant increase in the rate of mass loss (from 7 ± 3 Gt a−1 to 171 ± 4 Gt a−1) during a period of significant climate warming in Greenland (∼2 K (10 a)−1 ). From 1992–2002 to 2003–07, the contribution of the GIS to sea-level rise changed from essentially zero to 0.5 mm a−1, ∼15% of the recent rate of sea-level rise (Reference SolomonSolomon and others, 2007). Even though the GIS was close to mass balance during the 1990s, it was already showing characteristics of responding to a warmer climate, specifically thinning at the margins and thickening inland at higher elevations. Our results show that increased ice thinning due to increases in melting and acceleration of outlet glaciers during 2003–07 now strongly exceeds the inland thickening from increases in accumulation. Over the entire GIS, the mass loss between the two periods, from increased melting and ice dynamics, increased from 17 to 206 Gt a−1 while the mass gain, from increased precipitation and accumulation, increased from 10 to 25 Gt a−1. These results provide new quantitative information on how the competing mass-exchange processes that affect ice-sheet growth or shrinkage evolve with time in a changing climate. Understanding this evolution is important for the future, because the climate affecting the Greenland and Antarctic ice sheets is predicted to continue warming as the build-up of CO2 and other greenhouse gases in the Earth’s atmosphere continues at an increasing rate (Reference SolomonSolomon and others, 2007).
Our separation of the mass changes, dM a/dt, driven by accumulation variability, from the changes, dM bd/dt, driven by changes in ablation and ice dynamics is enabled by a new formulation of the elevation changes as perturbations from steady state. This formulation, as applied to measurements over two time periods (1992–2002 and 2003–07) with midpoints separated by 8 years, also provides a new determination of the changes in the dynamic thickening or dynamic thinning, and how the changes at the margins are propagating inland on decadal timescales.
Our detailed distributions derived for dH a CA/dt and dH bd/dt in Figure 7a and b and for dM a/dt, dM bd/dt and dM/dt (as a function of elevation and by drainage system in Figure 12) show how these parameters vary significantly among the different climate regimes of the GIS. The eight drainage systems have significant differences in important parameters that affect the surface balance and ice dynamics, including surface temperature, accumulation rate, internal ice temperature, basal melting or freezing, number of outlet glaciers with or without floating ice tongues, and the length of the ice margin terminating on land versus ocean. For example, the northern DS1 and DS2 have lower temperatures, lower accumulation rates and smaller ablation zones than the more southerly systems. Also, the drainage systems on the west coast have wide ablation zones with low slopes, and most of DS5 and DS6 terminate on land, whereas the east central DS3, the southeast DS4 and the west central DS7 and DS8 have many outlet glaciers terminating in the ocean and some with floating ice tongues. Our results provide a new description of the behavior of the GIS in these differing climate and glaciological regimes and therefore an improved basis for testing models of the ice response to climate change.
Acknowledgements
This research was supported by NASA’s ICESat Project Science funding. We thank two anonymous reviewers and the scientific editor, H.A. Fricker, for helpful suggestions and comments, and the European Space Agency for providing radar altimeter data from ERS-1 and -2. We also thank R. Alley for his suggestion of using a relationship between accumulation rate and temperature to model the effects of accumulation variations on firn compaction. We are also grateful to all the engineers, scientists, and managers who contributed so much to making ICESat a very successful, pioneering space mission.




















