Control parameters of GLE

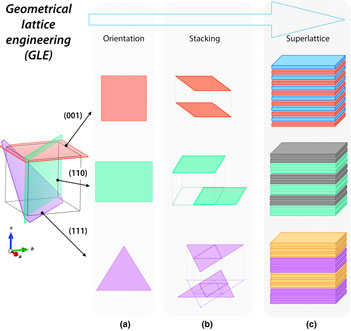
In general, the GLE concept is comprised of three controllable stages throughout the process of heteroepitaxial fabrication. Here, we use a 3D simple cubic unit-cell model to schematically illustrate these control parameters, as shown in Fig. 1.

1. A. Growth orientation: Starting with the same bulk compound, its 3D crystal structure is viewed as a stacking of atomic layers with different in-plane lattice geometries along different directions. For example, as shown in Fig. 1, while the (001) planes have square symmetry, the (110) and (111) planes have rectangular and triangular geometries, respectively. The required in-plane lattice geometry by design can be thus determined by selecting the proper structure and orientation of the substrate surface, which acts as a guiding template during the initial stage of nucleation and growth. A typical example for this case is the realization of 2D magnetically frustrated lattices derived from ultra-thin (111)-oriented spinel-type structure AB ₂O₄ (for more details see section “Geometrically frustrated lattices”).

2. B. Out-of-plane stacking sequence: In a bulk crystal, the periodicity of the atomic layers to fulfill the requirement of translational symmetry as well as the relative atomic positions in neighboring lattice planes vary dramatically with the specific choice of the crystallographic direction. For instance, the stacking of the adjacent layers can be either right on top of each other [the (001) stacking in Fig. 1], or shifted [the (110) stacking], or even entirely inversed [the (111) stacking]. This observation is of paramount importance for the design of artificial heterostructures since by controlling the number of stacking layers within that period one can devise unique quasi-2D lattices that cannot be obtained in the naturally formed crystals. Among the prominent example of GLE we cite the generalized graphene lattice, which can be obtained by digitally tuning the number of atomic layers of (111)-oriented ABO₃ perovskite-type structures for searching potential topological phases with and without spin–orbit active ions (for more details see section “Generalized graphene lattice from ABO₃ perovskites”).

3. C. Isostructural superlattices approach: Combining isostructural materials together to establish superlattice structures via digital control over the individual number of layers adds another practical dimension to the application of GLE. This approach can be very useful for the purpose of achieving materials with complex chemical compositions or even thermodynamically unstable phases in the bulk form. A representative test case is the fabrication of (111)-oriented 1ABO₃/1AB′O₃ superlattices [here “1” refers to single pc/cubic unit cell], giving rise to A ₂ BB′O₆ double perovskite. Further examples can be found in section “Artificial double-perovskite lattice”.

Figure 1. Schematic illustration of the idea about geometrical lattice engineering, which has three control parameters named as orientation, stacking, and superlattice throughout its entire process.

In what follows, we discuss in some details how the control parameters of GLE can be experimentally realized in the fabrication of complex oxide thin films and superlattices.

Geometrically frustrated lattices

Various geometrically frustrated magnetic systems, including spin ice, spin glass, and spin liquid have been studied over several decades.^[ Reference Mila ^{29 –} Reference Binder and Young ^{34 ]} In such systems, the exchange interaction between nearest neighbor ions is typically antiferromagnetic (for spin ice, the exchange interaction is ferromagnetic) and the peculiar geometries of the lattices (triangular and kagome lattice for the 2D case, or pyrochlore and hyper-kagome lattice for the 3D case) render the magnetic bonds impossible to be satisfied simultaneously. These geometrically frustrated lattices, especially the 2D ones have an excellent potential to host various intriguing exotic phenomena such as quantum spin liquid, topological phases, kinetic ferromagnetism, and chiral superconducting state to list a few.^[ Reference Han, Helton, Chu, Nocera, Rodriguez-Rivera, Broholm and Lee ^{16 ,} Reference Punk, Chowdhury and Sachdev ^{35 –} Reference Yu and Li ^{37 ]} The fabrication of a 2D geometrically frustrated lattice, however, has proven to be rather challenging. For example, even though several metal–organic hybrid counterparts were synthesized by chemical methods, structural disorder, and strong lattice distortions remained a persistent hindrance.^[ Reference Liu, Kravstsov, Beauchamp, Eubank and Eddaoudi ^{38 ,} Reference Nytko, Helton, Müller and Nocera ^{39 ]} Alternatively, the GLE approach offers a promising way to generate such frustrated lattice by growing ultra-thin spinels along the [111] crystallographic axis, as shown in Fig. 2.

Figure 2. The conventional unit cell of a normal spinel structure. The corresponding (111) ionic planes are marked in the figures. Note, the A ionic planes only form the triangle planes, while the B ionic planes form both the triangle planes and also the kagome planes.

First we recap that the general chemical formula of the spinel structure can be written as A _{1− δ} Β_δ [Α _δ Β _2−δ ]O₄; with δ = 0, it is known as normal spinel AB ₂O₄, in which all A-site cations are tetrahedrally coordinated, while all B-site cations are octahedrally coordinated. Next we point out that the normal spinel shows a structurally unique feature when viewed along the [111] crystallographic axis. Specifically, the crystal structure can be regarded as a stacking of alternative lattice planes, each of which is composed of single kind of ions (see Fig. 2). In this stacking, the O sublattice has the cubic close packing (CCP) atomic arrangement. In contrast, the A and B ionic planes show three distinct types of geometrically frustrated lattices: triangular A plane (T plane), triangular B plane (T′ plane), and kagome B plane (K plane) as displayed in Fig. 2. In the bulk, totally 18 ionic planes complete a full periodicity in the form of [O–K–O–T–T′–T]₃ ^[ Reference Vaz, Henrich, Ann and Altman ^{40 ]} with [O–K–O–T–T′–T] as the basic repeat unit. For the rest of this paper such a basic repeat unit is referred as “1 monolayer” of the (111)-oriented normal spinel.

From the synthesis point of view, there are two main issues one needs to overcome to obtain high-quality (111)-oriented normal spinel heterostructures. First, due to the limited availability of isostructural/isosymmetric substrates, large lattice mismatch (>5%) between the film and the substrate generally leads to incoherent or inhomogeneous growth. Secondly, a magnetically passive spacer in the superlattice has to be chemically stable and lattice symmetry compatible with the spinel structure. A complete solution to these issues has been recently demonstrated by Liu et al.^[ Reference Liu, Choudhury, Cao, Middey, Kareev, Meyers, Kim, Ryan and Chakhalian ^{24 ]} in the epitaxial growth of (111)-oriented CoCr₂O₄/Al₂O₃ (CCO/AlO) heterostructures. For this system, AlO was selected as both the substrate and spacer because: (1) AlO is a non-magnetic insulator with a large band gap of about 9 eV and (2) since along the (0001)-direction the oxygen sublattice consists of hexagonal close packing (HCP) arrangement, it has an in-plane lattice geometry, which almost perfectly matches the CCP arrangement of spinel [see Fig. 3(a)]. In addition, a fairly small lattice mismatch of ~3% can be obtained when we compare the respective in-plane O–O distances (AlO: 2.74 Å; CCO: 2.82 Å).

Figure 3. (111)-oriented CoCr₂O₄/Al₂O₃ (CCO/AlO) heterostructures. (a) Epitaxial relationship between CCO and AlO. The hexagonal close packing of AlO oxygen sublattice is labeled as AB in black, while the CCP of CCO oxygen sublattice is labeled as ABC in brown. (b)–(d) RHEED images during the growth of each component. The half-order reflections (marked by pink solid circles) observed on CCO layer is due to the double expansion of the in-plane unit cell. Reproduced from Ref. Reference Liu, Choudhury, Cao, Middey, Kareev, Meyers, Kim, Ryan and Chakhalian24, with the permission of AIP Publishing.

The spinel-based heterostructures were fabricated layer-by-layer using the pulsed laser deposition (PLD) technique. The structural properties of the resultant samples were characterized by X-ray reflectivity (XRR) and X-ray diffraction (XRD) measurements with the results for two prototypical samples [a thicker (2CCO/2AlO)₁₀ and an ultra-thin (2CCO/1AlO)₄] shown in Fig. 4. As seen, according to the XRR scans with fittings from Fig. 4(a), 1CCO has a thickness of ~4.93 Å, while 1AlO ~13.5 Å and the average interface roughness is about 3 Å. On the other hand, the XRD 2θ–ω scans shown in Fig. 4(b) in the vicinity of the substrate (006) reflection confirm that the films are grown along the (111)-direction with no additional peaks from impurity phase. In particular, besides the film's (222) main reflection (labeled as 0th), the superlattice's satellite peaks labeled as ±1st were clearly distinguishable and the number of the thickness fringes between the main peak and the satellite peak agrees quite well with the superlattice repeat pattern. These observations provide a solid evidence that growth of the geometrically engineered spinel-type structures along (111) is experimentally feasible.

Figure 4. (a) X-ray reflectivity and (b) x-ray diffraction curves of 2CCO/nAlO (n = 1 and 2) superlattices. Both the thickness fringes and the superlattice satellite peaks are clearly seen from the graphs. (c, d) x-ray absorption spectra of the CCO/AlO superlattices on the L _2,3 edges of Co and Cr, respectively. The spectra of CCO powders with normal spinel structure are plotted as references [Figs4(a) and 4(b) adapted with permission of AIP Publishing from Ref. Reference Chopdekar, Liberati, Takamura, Kourkoutis, Bettinger, Nelson-Cheeseman, Arenholz, Doran, Scholl, Muller and Suzuki46].

Another important issue is related to cation disorder or a mixture of various cation valences that can occur during the growth of spinel films^[ Reference Liu, Kareev, Cao, Liu, Middey, Meyers, Freeland and Chakhalian ^{41 –} Reference Chopdekar, Liberati, Takamura, Kourkoutis, Bettinger, Nelson-Cheeseman, Arenholz, Doran, Scholl, Muller and Suzuki ^{46 ]} and if present it may potentially destroy the expected normal spinel stacking patterns. Thus, it was necessary to investigate the chemical states and environments of both Co and Cr ions in the films. Such information can be readily probed by soft x-ray absorption spectroscopy (XAS) measurements. This synchrotron-based technique is extremely sensitive to the local electronic properties of a specific chemical element. The dataset was collected on the L _3,2 absorption edge of both Co and Cr elements of a representative 2CCO/2AlO superlattice in the total electron yield. As seen in Figs. 4(c) and 4(d), both the Co and Cr XAS of the 2CCO/2AlO sample have lineshapes (including the peak positions as well as the fine multiplet features) almost identical to those of the CCO bulk samples implying the absence of any detectable cation distribution disorder or mixture of chemical valences. This result further confirmed that the normal spinel structure was indeed maintained in the superlattice (i.e., Co²⁺ ions were tetrahedrally coordinated, while Cr³⁺ ions were octahedrally coordinated).

It is worth noting that in addition to sandwiching the ultrathin spinel structure toward 2D limit with magnetically inactive spacers^[ Reference Liu, Choudhury, Cao, Middey, Kareev, Meyers, Kim, Ryan and Chakhalian ^{24 ,} Reference Yahiro, Tanaka, Yamamoto and Kawai ^{47 ]}, it may be also interesting to explore (111)-oriented all magnetic spinel superlattices. To illustrate this idea we note that since magnetic properties of spinels strongly depend on the exchange interaction between A and B sites, the periodic modulation of the exchange interaction in artificial superlattices can give rise to novel properties not existing in either the single composition or the solid solution. Murata et al.^[ Reference Murata, Kozuka, Uchida and Kawasaki ^{48 ]} recently reported the growth of such ZnFe₂O₄/ZnCr₂O₄ superlattices on MgAl₂O₄ (111) substrates. Both of the constituent layers have a normal spinel structure with non-magnetic A sites (Zn²⁺, S = 0) and magnetic B sites (Fe³⁺, S = 5/2; Cr³⁺, S = 3/2). The effect of GLE was investigated by measuring zero field cooling (ZFC) and field cooling (FC) magnetic susceptibilities of the ZnFe₂O₄ and the ZnCr₂O₄ thin films, the Zn(CrFe)O₄ solid solution, and the mZnFe₂O₄/mZnCr₂O₄ (m = 1, 2, 4, and 10) superlattices. In the bulk, both materials are characterized by large and negative Curie–Weiss temperatures; the ZnFe₂O₄ film shows spin–glass behavior below ~17 K, while ZnCr₂O₄ film shows antiferromagnetic ordering below 13 K. In contrast to this, the Zn(CrFe)O₄ solid solution exhibits a distinct spin–glass behavior below 28 K. This higher transition temperature T _g is attributed to the random distributions of the Fe³⁺ and Cr³⁺ ions on the B sites causing spatially inhomogeneous exchange interactions. On the other hand, the spin–glass behavior was also observed for all of the superlattice films with a non-monotonic variation of T _g with the layer thickness m. These experimental results were interpreted as the result of a periodic modulation of the exchange coupling between the B site ions across the interfaces. As the thickness of both layers becomes smaller, the number of the bulk-like Cr³⁺–O–Cr³⁺ as well as the Fe³⁺–O–Fe³⁺ magnetic bonds decreases. At the same time, more ZnFe₂O₄/ZnCr₂O₄ interfaces appear where artificially induced antiferromagnetic Cr³⁺–O–Fe³⁺ interaction starts to compete with the bulk-like magnetic interactions. As the result of such competition, the formation of a long-range magnetic ordering is suppressed and the spin–glass behavior gradually arises. In addition, once the layer thickness of each composition decreases below a certain critical limit (m = 4), the material can be viewed as mainly being made of the interfaces where the induced Cr³⁺–O–Fe³⁺ interaction is dominant and a new magnetic state dramatically different from the bulk appears in the superlattice. The suppression of the spin–glass behavior for 1 < m < 4 was interpreted originating from some new type of short-range magnetic clusters induced by the Cr³⁺–O–Fe³⁺ interaction, which again does not exist in the constituent bulk compounds. These examples corroborate that apart from chemical doping and epitaxial strain, GLE of the stacking layers as well as their sequences in the heterostructures is an effective way to alter electronic and magnetic behaviors.

Generalized graphene lattice from ABO₃ perovskites

Perovskite oxides are the host of diverse properties including metal–insulator transition, magnetism, superconductivity, charge, and orbital orderings, multiferroicity, etc. These infinite layer ABO₃ perovskite compounds consist of alternating AO/BO₂, ABO/O₂, and AO₃/B atomic planes along the pc [001], [110], and [111] directions, respectively. Thus, the precise control during the growth of two or three pc unit cells of ABO₃ along the (111) orientation leads to new lattice geometries with vertically shifted triangular planes of B sites and results in buckled honeycomb lattice^[ Reference Xiao, Zhu, Ran, Nagaosa and Okamoto ^{10 –} Reference Rüegg and Fiete ^{12 ]} and dice lattice^[ Reference Wang and Ran ^{49 ]} respectively as shown in Fig. 5. The emergence of striking topological phases including anomalous quantum Hall state was originally predicted in a honeycomb lattice by Haldane^[ Reference Haldane ^{50 ]}, and recently initiated active searches for artificially stabilized graphene like quasi-2D lattice that can provide an ideal playground for interacting topological phases in complex oxides^[ Reference Xiao, Zhu, Ran, Nagaosa and Okamoto ^{10 –} Reference Rüegg and Fiete ^{12 ,} Reference Wang, Wang, Fang and Dai ^{14 ,} Reference Okamoto ^{19 –} Reference Lado, Pardo and Baldomir ^{21 ,} Reference Rüegg, Mitra, Demkov and Fiete ^{51 –} Reference Okamoto, Zhu, Nomura, Arita, Xiao and Nagaosa ^{59 ]}. Here we describe the case of rare-earth nickelates that vividly illustrates the opportunities for designer topological phases by GLE.

Figure 5. Buckled honeycomb lattice and Dice lattice geometry can be generated by epitaxial growth of perovskite system along the [111] direction. A sites are not shown for Dice lattice due to visual clarity.

The first member of rare earth nickelates series, LaNiO₃ is a paramagnetic metal. The other members (RENiO₃ with RE = Pr, Nd,…,Lu, and Y) in the bulk form exhibit metal–insulator transition, E′-type antiferromagnetic ordering, charge ordering and structural transition with a strong dependence of the transition temperature on the size of RE ions^[ Reference Medarde ^{60 ,} Reference Catalan ^{61 ]}. The possibility of realizing cuprate-like Fermi surface has led to a rapid development and study of (001)-oriented ultra-thin films and superlattices of various members of the RENiO₃ family (see Ref. [Reference Middey, Chakhalian, Mahadevan, Freeland, Millis and Sarma62] for review). Several theoretical works^[ Reference Yang, Zhu, Xiao, Okamoto, Wang and Ran ^{11 ,} Reference Rüegg and Fiete ^{12 ,} Reference Rüegg, Mitra, Demkov and Fiete ^{51 –} Reference Doennig, Pickett and Pentcheva ^{53 ]} further emphasized the possibility of realizing interaction-driven topological phases without spin-orbit (e.g., Dirac half semimetal phase, quantum anomalous Hall insulator phase, or ferromagnetic nematic phase) in the weakly correlated limit on the buckled honeycomb lattice of RENiO₃. Moreover, in contrast to the bulk LaNiO₃, where orbital ordering is not present, theoretical modeling in strongly correlated limit predicted the presence of an orbitally ordered magnetic phase as the ground state^[ Reference Rüegg and Fiete ^{12 ,} Reference Rüegg, Mitra, Demkov and Fiete ^{51 –} Reference Doennig, Pickett and Pentcheva ^{53 ]} for the buckled honeycomb lattice of LaNiO₃.

Despite the conceptual simplicity, growth of perovskites along the [111]-direction presents formidable challenge. Contrary to the [001]_pc-direction, the epitaxial stabilization along [111]_pc direction is far less explored due to unavoidable surface/chemical reconstruction effects as all perovskite substrates are strongly polar along this direction, e.g., SrTiO₃: [SrO₃]⁴⁻, Ti⁴⁺; LaAlO₃:[LaO₃]³⁻, Al³⁺, and so on. While growing a metallic buffer layer at the very beginning of growth may help to avoid this polarity problem by effective screening of dipoles^[ Reference Blok, Wan, Koster, Blank and Rijnders ^{63 ]}, one should pay particular attention as unwanted interfacial (between buffer layer and desired material) effects may have significant influence on the buffered heterostructure. As the reconstruction effect often appears only at the substrate–vacuum interface, the choice of a substrate with the same charge per plane sequence as that of the desired material can be another solution to this problem, which does not require to grow a buffer layer. To investigate this, Middey et al.^[ Reference Middey, Rivero, Meyers, Kareev, Liu, Cao, Freeland, Barraza-Lopez and Chakhalian ^{64 ]} have grown LaNiO₃ films on SrTiO₃ [with polar jump at film/substrate interface: see the upper panel of Fig. 6(a)] and LaAlO₃ [without any polar jump at film/substrate interface: see lower panel of Fig. 6(a)] (111) substrate using pulsed laser interval deposition. The growth was monitored by in situ high-pressure reflection high-energy electron diffraction (RHEED). It was shown that while thick bulk-like LaNiO₃ film is metallic and can effectively screen charge dipoles, a few unit-cell thin LNO film is insulating because of quantum confinement^[ Reference Middey, Meyers, Kareev, Moon, Gray, Liu, Freeland and Chakhalian ^{23 ]}, and does require additional effects to avoid polar catastrophe. Specifically, in sharp contrast to the film grown on LAO (111), the presence of additional Bragg reflections [inset in Fig. 6(b)] for the 5 uc film on STO (111) confirmed the appearance of an additional non-perovskite phase during the initial stage of LNO growth. This secondary chemical phase was identified as La₂Ni₂O₅ from the XRD, which was further corroborated by the observation of dominant contribution from Ni²⁺ ions in XAS spectrum [Fig. 6(b)]. Similar secondary phase formation has been also reported for the LNO film on STO (111), grown by molecular beam epitaxy^[ Reference Freeland, Tung, Luo, Zhou, Lee, Chang, Morgan, Bedzyk and Fong ^{65 ]}. With the increase of LNO film thickness, the increased metallicity screens the effect of polar jump and the relative amount of Ni³⁺ ions increases for the expense of Ni²⁺. Finally, stoichiometric LaNiO₃ along [111] was obtained at about 15 uc. On the other hand, Ni³⁺ was stabilized from the very initial stage of growth of LNO on the LAO (111) substrate and thus confirmed that the absence of a polar jump at the film/substrate interface was critically important for the epitaxial stabilization along [111]. As a result, the desired generalized graphene-like crystal of RENiO₃ with RE = La to Nd was successfully achieved on the LAO (111) substrate^[ Reference Middey, Meyers, Kareev, Moon, Gray, Liu, Freeland and Chakhalian ^{23 ]}.

Figure 6. (a) Schematics (assuming pure ionic picture) to demonstrate the presence (absence) of polar jump for RENiO3 on SrTiO₃ (LaAlO₃) (111) substrate^[ Reference Catalan ^{61 ]}. (b) XAS of 5 uc LNO films on LAO and STO (111) have been compared with bulk Ni²⁺O, and LaNi³⁺O₃. RHEED pattern of these films, recorded along pc [1−1 0]. For details, see Ref. Reference Blok, Wan, Koster, Blank and Rijnders63. (c) Experimental arrangement for measuring XLD of (111)-oriented superlattice (upper panel) and XA spectra recorded for a [2NdNiO₃/4LaAlO₃]×3 SL grown on LAO (111) using vertically (V) and horizontally (H) polarized x-ray and their difference are plotted in lower panel. Due to strong overlap of Ni L ₃ edge with La M ₄ edge (from the substrate and spacer layer LAO), only Ni L ₂ edge is shown. Panel(c) adapted with permission from Ref. Reference Middey, Meyers, Doennig, Kareev, Liu, Cao, Yang, Shi, Gu, Ryan, Pentcheva, Freeland and Chakhalian25. Copyrighted by the American Physics Society.

According to the theoretical calculations^[ Reference Rüegg and Fiete ^{12 ,} Reference Rüegg, Mitra, Demkov and Fiete ^{51 ]}, the QAH topological phases should be accompanied by spontaneous ferromagnetism. X-ray resonant magnetic scattering measurements on 2NdNiO₃/4LaAlO₃ (111) (denoted as 2NNO/4LAO) superlattice, however, ruled out the possibility of a long-range ferromagnetic ground state and instead established the presence of antiferromagnetic correlations. In addition, XAS measurements using linearly polarized x-rays found the presence of large (about 9%) X-ray linear dichroism (XLD) on Ni L ₂ edge, as shown in Fig. 6(c). This XLD signal together with the ab intio calculations concludes an unusual antiferro-orbital-ordered state, which does not exist in either bulk or (001)-oriented nickelate thin films or heterostructures^[ Reference Middey, Meyers, Doennig, Kareev, Liu, Cao, Yang, Shi, Gu, Ryan, Pentcheva, Freeland and Chakhalian ^{25 ]}. In short, the artificially stabilized buckled honeycomb lattice structure for various other perovskite-based transition metal oxides can be a very promising route for realizing new types of correlated Mott phases or interacting topological phases. In addition, very recently the fabrications of (111)-oriented bilayers and trilayers of transition metal perovskites SrIrO₃ have been reported^[ Reference Hirai, Matsuno and Takagi ^{26 ,} Reference Anderson, Ryu, Zhou, Xie, Podkaminer, Ma, Irwin, Pan, Rzchowski and Eom ^{27 ]} with the goal to access new topological phases.

Another interesting application of GLE is connected to designer magnetic phases by layering along [111]. For example, LNO has been heterostructured with LaMnO₃ (LMO) along the [111]-direction^[ Reference Gibert, Zubko, Scherwitzl, Íñiguez and Triscone ^{66 ]}. Although bulk LNO is paramagnetic and bulk LMO is antiferromagnetic, the (111)-oriented LNO/LMO superlattices found to exhibit strong exchange bias (EB) effect. We note that EB is generally observed for ferromagnetic/antiferromagnetic or ferromagnetic/spin–glass interface.^[ Reference Nogués, Sort, Langlais, Skumryev, Suriñach, Muñoz and Baró ^{67 ,} Reference Ali, Adie, Marrows, Greig, Hickey and Stamps ^{68 ]} This surprising result was attributed to the quantum confinement effect^[ Reference Dong and Dagotto ^{69 ]} and charge transfer between Ni and Mn^[ Reference Lee and Han ^{70 ]}, which are more effective for (111) orientation compared with (001). Very recent XAS experiments confirmed the larger electron transfer across the interface for (111) heterostructures.^[ Reference Piamonteze, Gibert, Heidler, Dreiser, Rusponi, Brune, Triscone, Nolting and Staub ^{71 ]}.

Artificial double-perovskite lattice

In the past decade, ordered double-perovskite oxides with the chemical formula A ₂ BB′O₆ (A is an alkali-earth ion, and B and B′ are two different transition metal ions) have motivated plethora of research activities.^[ Reference Anderson, Greenwood, Taylor and Poeppelmeier ^{72 ]} In this family, the B and B′ ions are naturally ordered by forming a rock salt sublattice with B–O–B′ super-exchange that can generate rich magnetic and topological behaviors depending on the choice of the transition metal elements. Thus, the ordered double perovskites offer an excellent engineering playground for which potential functionalities can be predicted and explored^[ Reference Anderson, Greenwood, Taylor and Poeppelmeier ^{72 –} Reference Serrate, De Teresa and Ibarra ^{76 ]}. From the synthesis perspective, in the bulk the formation of an ordered double perovskite requires a relatively large difference between the chemical valences of B and B′ ions. Moreover, the ionic radii difference between those ions must be within a limited range often preventing synthesis of a variety interesting structures.^[ Reference Anderson, Greenwood, Taylor and Poeppelmeier ^{72 ]} Consequently, there are formidable challenges for the bulk synthesis of many theoretically proposed ordered double-perovskite materials, which are expected to host many interesting phenomena^[ Reference Cook and Paramekanti ^{20 ,} Reference Zhang, Huang, Haule and Vanderbilt ^{77 –} Reference Liu, Fuh and Wang ^{79 ]}

With the recent advances in thin-film growth techniques, it was noticed that there is another way to overcome those limitations.^[ Reference Gibert, Zubko, Scherwitzl, Íñiguez and Triscone ^{66 ,} Reference Ichikawa, Arai, Imai, Hagiwara, Sakama, Azuma, Shimakawa, Takano, Kotaka, Yonetani, Fujisawa, Shimizu, Ishikawa and Cho ^{80 –} Reference Chang, Lee, Jun, Kwon, Kim and Kim ^{83 ]} As illustrated in Fig. 7, the structure of an ordered double-perovskite A ₂ BB′O₆ consists of alternating monolayers of ABO₃ and AB′O₃ placed along the (111) orientation. By epitaxially growing (111)-oriented 1ABO₃/1AB′O₃ superlattices, it is now possible to design a wide range of ordered double-perovskite compounds that have never been realized through traditional bulk synthesis. In contrast to the artificial graphene-like lattices, here the out-of-plane stacking sequence of each perovskite composition has to be maintained with a monolayer precision to realize the required double-perovskite structure.

Figure 7. B-site ordered double perovskites viewed along the conventional (001) and the unconventional (111) direction, respectively. The (001) rock-salt arrangement of the B and B′ sites is equivalent to (111) BO₆ and B′O₆ superlattice.

Following this idea, a series of artificial double-perovskite La₂ BB′O₆ (B and B′ = Fe, Cr, Mn, and Ni) in the thin film form were obtained by PLD^[ Reference Gibert, Zubko, Scherwitzl, Íñiguez and Triscone ^{66 ,} Reference Ueda, Tabata and Kawai ^{81 ,} Reference Ueda, Tabata and Kawai ^{82 ]}. Among these materials, the artificial La₂FeCrO₆ (1LaFeO₃–1LaCrO₃) system has been extensively investigated and yet some controversy about its electronic and magnetic structure remained due to complexity of Fe³⁺–O–Cr³⁺ superexchange.^[ Reference Kanamori ^{84 ]}. Ueda et al.^[ Reference Ueda, Tabata and Kawai ^{81 ]} grew the artificial La₂FeCrO₆ (LFCO) films for the first time and found the samples to show ferromagnetic behavior. However, the small magnetic moment of only ~0.009 µ _B at 0.1 T raised questions about the true nature of the magnetic ordering; to complicate the case both canted antiferromagnetic and ferrimagnetic ground states have been theoretically predicted.^[ Reference Pickett ^{85 ]}

To resolve the controversy, Gray et al.^[ Reference Gray, Lee, Liu, Chakhalian and Freeland ^{86 ]} synthesized artificial La₂FeCrO₆ and performed XAS and X-ray magnetic circular dichroism (XMCD) measurements at the L-edge of both Fe and Cr ions to probe the electronic and magnetic properties of each transition metal element. The corresponding absorption data shown in Fig. 8 confirmed that in the artificial LFCO compound both Fe and Cr are trivalent with high-spin configurations (Fe³⁺, S = 5/2; Cr³⁺, S = 3/2). In addition, the XMCD spectra of both elements revealed that the magnetic moments of Fe³⁺ and Cr³⁺ ions are parallel to each other. The estimated magnetic moments were about 0.3 µ _B/Cr and 0.2 µ _B/Fe at 5 T and appeared to be much smaller than the expected saturated values (3 µ _B/Cr and 5 µ _B/Fe). Furthermore, no detectable XMCD signal was observed for either ion under 0.1 T. Based on those observations, the artificial La₂FeCrO₆ was claimed to have a canted AFM ground state. Chakraverty et al.^[ Reference Chakraveerty, Ohtomo, Okuyama, Saito, Okude, Kumai, Arima, Tokura, Tsukimoto, Ikuhara and Kawasaki ^{87 ]} studied the relation between the degree of B-site disorder and the corresponding magnetic state on a series of thick LFCO films (up to a few hundred nanometers) that were synthesized with a LFCO polycrystalline target. They observed that only the high-quality B-site ordered sample show the expected saturated magnetization of ~2 µ _B per LFCO formula, consistent with a ferrimagnetic ordering picture in which the local spin moment of Cr and Fe ions are anti-aligned, while the samples with sizable B, B′-site cation disorder show strong suppression of the total magnetic moment.

Figure 8. XAS and XMCD spectra on the L edge of (a) Fe and (b) Cr of the (111)-oriented 1LaFeO₃/1LaCrO₃ superlattice. Both spectra were measured at 10 K with an external magnetic field ~5 T applied parallel to the film surface. Data were collected in the total electron yield mode. Adapted from Ref. Reference Gray, Lee, Liu, Chakhalian and Freeland86, with the permission of AIP Publishing.

In addition, 1BiFeO₃/1BiCrO₃ (BFCO) artificial double-perovskite superlattice was also developed by Ichikawa et al.^[ Reference Ichikawa, Arai, Imai, Hagiwara, Sakama, Azuma, Shimakawa, Takano, Kotaka, Yonetani, Fujisawa, Shimizu, Ishikawa and Cho ^{80 ]} on STO (111) substrate and room temperature multiferroic behavior was observed on this system. Interestingly, the saturated magnetic moment per formula unit of the superlattice was much stronger than the signal of the film grown from the BFCO sputtering target^[ Reference Nechache, Carignan, Gunawan, Harnagea, Botton and Menard ^{88 ]}. This enhanced magnetization due to GLE sheds additional light on its potential for the development of new magnetic materials for application.

Summary and outlook

In the previous sections, the current status of GLE is discussed mainly with emphasis on the system layered along the cubic (or pc) (111) orientation of perovskites and spinels. However, the GLE concept is certainly not restricted to those systems and its realization opens wide opportunities for experimentalists to fabricate other interesting lattices in the heterostructured form. For instance, apart from spinel-type compounds, 2D frustrated lattices also appear in ultra-thin (111)-oriented pyrochlore (chemical formula: A ₂ B ₂O₇) structures (Fig. 9, right panel on the top). This can be easily understood since the B sublattice in the pyrochlore structure is identical to that of spinel. Several theoretical works^[ Reference Rüegg and Fiete ^{12 ,} Reference Guo and Franz ^{17 ,} Reference Hu, Zhong and Fiete ^{18 ,} Reference Yang and Nagaosa ^{89 ]} have predicted the emergence of topological states with different B cations, while the experimental work on fabricating (111) pyrochlore films have been recently initiated^[ Reference Fujita, Kozuka, Uchida, Tsukazaki, Arima and Kawasaki ^{90 –} Reference Chu, Riggs, Shapiro, Liu, Serero, Yi, Melissa, Suresha, Frontera, Vishwanath, Marti, Fisher and Ramesh ^{93 ]}. Additionally, it was theoretically proposed that a monolayer of corundum-type (chemical formula: M₂O₃) structure grown along the (0001) direction could also form the graphene-like honeycomb lattice geometry^[ Reference Afonso and Pardo ^{94 ]} analogous to the perovskite (111) bilayers (Fig. 9, left panel on the top).

Figure 9. Summary and outlook on GLE. The upper panel displays other possible routines to topological phase and frustrated magnetism by applying pure GLE. The bottom panel presents the combination of GLE with IE or SE to establish new systems with intriguing physics such as quasi-particle excitation and emergent phenomena.

To push this field further, one can envision that a combination of GLE with other engineering approaches should allow for even more exotic phases. A fusion of GLE and IE may enable new tailor-made phenomena since for heterostructures the mismatches at the interface should be profoundly altered by the epitaxial orientation. For instance, while the basic scenario of two-dimensional electron gas (2DEG) at the interface between two insulating complex oxides has been interpreted within the “polar discontinuity” model^[ Reference Ohtomo and Hwang ^{95 ,} Reference Nakagawa, Hwang and Muller ^{96 ]}, the polar mismatch patterns vary with the orientation of the heterostructure. This can be utilized to tune the carrier density and mobility of the 2DEG. Toward experimental realization of this idea a pioneering work has been reported on the growth of the prototypical LaAlO₃/SrTiO₃ system with (001), (110), and (111) interfaces (Fig. 9, right panel on the bottom)^[ Reference Herranz, Sánchez, Dix, Scigaj and Fontcuberta ^{97 ]}. Another interesting theory proposal is the study on the interface between (100)-oriented high-temperature superconducting cuprate YBa₂Cu₃O₇ (YBCO) and colossal magnetoresistance manganite La _x Ca_1−x MnO₃ (LCMO).^[ Reference Takei, Fregoso, Galitski and Sarma ^{98 ]} Compared to the extensively investigated (001) YBCO/LCMO interface^[ Reference Chakhalian, Freeland, Habermeier, Cristiani, Khaliullin, van Veenendaal and Keimer ^{99 ]} where the nodes of Cu d _x2–y2 orbital are in the a–b plane, the (100)-oriented YBCO has nodes of the d _x2–y2 orbital out of the CuO₂ plane (see Fig. 9, left panel on the bottom). This unique orbital coupling pattern is crucial for the emergence of exotic Majorana states^[ Reference Catalano, Gibert, Bisogni, He, Sutarto, Viret, Zubko, Scherwitzl, Sawatzky, Schmitt and Triscone ^{100 ]}. Furthermore, the combination of GLE and SE may open another interesting dimension for controlled modifications of the bond-length and bond-angle in structural units by epitaxial strain along the unconventional crystallographic axes.^[ Reference Catalano, Gibert, Bisogni, He, Sutarto, Viret, Zubko, Scherwitzl, Sawatzky, Schmitt and Triscone ^{100 –} Reference Kim, Puggioni, Yuan, Xie, Zhou, Campbell, Ryan, Choi, Kim, Patzner, Ryu, Podkaminer, Irwin, Ma, Fennie, Rzchowski, Pan, Gopalan, Rondinelli and Eom ^{102 ]}

To summarize, with the modern state-of-the-art thin-film fabrication methods, the notion of GLE can be experimentally realized and used as another control knob. Despite the challenges of layering with atomic precision along unconventional crystallographic directions, GLE has excellent potential for the discovery of novel electronic, magnetic, and topological phases with complex oxides.