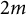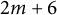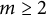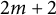1 Introduction
There is a very famous theorem in projective geometry known as Poncelet’s closure theorem or Poncelet’s porism, first introduced in [Reference Poncelet15]. Let
![]() $\mathbb {P}^2(=\mathbb {C}\mathbb {P}^2) $
be the complex projective plane and let
$\mathbb {P}^2(=\mathbb {C}\mathbb {P}^2) $
be the complex projective plane and let
![]() $C_1, C_2\subset \mathbb {P}^2$
be smooth conics that intersect transversely. Given a general point
$C_1, C_2\subset \mathbb {P}^2$
be smooth conics that intersect transversely. Given a general point
![]() $P_1\in C_1$
, let
$P_1\in C_1$
, let
![]() $L_1$
be a line passing through
$L_1$
be a line passing through
![]() $P_1$
and tangent to
$P_1$
and tangent to
![]() $C_2$
. Then
$C_2$
. Then
![]() $L_1$
intersects
$L_1$
intersects
![]() $C_1$
at another point
$C_1$
at another point
![]() $P_2$
, and we can choose a line
$P_2$
, and we can choose a line
![]() $L_2$
passing through
$L_2$
passing through
![]() $P_2$
and tangent to
$P_2$
and tangent to
![]() $C_2$
. By repeating this process, we obtain a sequence
$C_2$
. By repeating this process, we obtain a sequence
![]() $(P_1, L_1), (P_2, L_2), \ldots $
of pairs of points
$(P_1, L_1), (P_2, L_2), \ldots $
of pairs of points
![]() $P_i\in C_1$
and tangent lines
$P_i\in C_1$
and tangent lines
![]() $L_i \in C_2^\ast $
such that
$L_i \in C_2^\ast $
such that
![]() $P_i\in L_i$
, where
$P_i\in L_i$
, where
![]() $C_2^\ast $
is the dual curve of
$C_2^\ast $
is the dual curve of
![]() $C_2$
. Such a sequence is called a Poncelet transverse originating at
$C_2$
. Such a sequence is called a Poncelet transverse originating at
![]() $P_1$
. Poncelet’s closure theorem can be stated as follows:
$P_1$
. Poncelet’s closure theorem can be stated as follows:
Theorem 1.1 [Reference Poncelet15]
Let
![]() $C_1$
,
$C_1$
,
![]() $C_2$
be as above. If there exists a point
$C_2$
be as above. If there exists a point
![]() $P\in C_1$
such that the Poncelet transverse originating at P is periodic with period n, then for any
$P\in C_1$
such that the Poncelet transverse originating at P is periodic with period n, then for any
![]() $Q\in C_1$
, the Poncelet transverse originating at
$Q\in C_1$
, the Poncelet transverse originating at
![]() $Q\in C_1$
is also periodic with period n.
$Q\in C_1$
is also periodic with period n.
A modern proof in terms of torsion points of elliptic curves was given by P. Griffiths and J. Harris in [Reference Griffiths and Harris10]. We call a Poncelet transverse
![]() $\sqcap _n$
with minimum period n an n-sided Poncelet transverse and denote it by a sequence
$\sqcap _n$
with minimum period n an n-sided Poncelet transverse and denote it by a sequence
![]() $\sqcap _n:(P_1, L_1), \ldots , (P_n, L_n)$
of n pairs. Sometimes, we omit “n-sided Poncelet” and simply use “transverse” when it is evident from the context that we are talking about an n-sided Poncelet transverse. For a general choice of origin
$\sqcap _n:(P_1, L_1), \ldots , (P_n, L_n)$
of n pairs. Sometimes, we omit “n-sided Poncelet” and simply use “transverse” when it is evident from the context that we are talking about an n-sided Poncelet transverse. For a general choice of origin
![]() $P_1\in C_1$
, an n-sided Poncelet transverse will consist of n distinct points
$P_1\in C_1$
, an n-sided Poncelet transverse will consist of n distinct points
![]() $P_1, \ldots , P_n$
and n distinct lines
$P_1, \ldots , P_n$
and n distinct lines
![]() $L_1, \ldots , L_n$
and can be viewed as an n-gon with these points and lines as vertices and edges that is inscribed in
$L_1, \ldots , L_n$
and can be viewed as an n-gon with these points and lines as vertices and edges that is inscribed in
![]() $C_1$
and circumscribed about
$C_1$
and circumscribed about
![]() $C_2$
. Poncelet’s theorem also holds for special choices of origins, where
$C_2$
. Poncelet’s theorem also holds for special choices of origins, where
![]() $\sqcap _n$
will involve intersection points of
$\sqcap _n$
will involve intersection points of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
and/or bitangent lines of
$C_2$
and/or bitangent lines of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
and can be viewed as a degenerated n-gon having double edges. In this paper, we consider curves arising from
$C_2$
and can be viewed as a degenerated n-gon having double edges. In this paper, we consider curves arising from
![]() $2m$
-sided Poncelet transverses (
$2m$
-sided Poncelet transverses (
![]() $m\geq 2$
) and construct a new infinite sequence of curves that are interesting with regard to their embedded topology.
$m\geq 2$
) and construct a new infinite sequence of curves that are interesting with regard to their embedded topology.
The embedded topology of an algebraic plane curve
![]() $\mathcal {C}\subset \mathbb {P}^2(=\mathbb {C}\mathbb {P}^2)$
, which is defined over the field of complex numbers
$\mathcal {C}\subset \mathbb {P}^2(=\mathbb {C}\mathbb {P}^2)$
, which is defined over the field of complex numbers
![]() $\mathbb {C}$
, is the homeomorphism class of the pair
$\mathbb {C}$
, is the homeomorphism class of the pair
![]() $(\mathbb {P}^2, \mathcal {C})$
of topological spaces. One of the main objectives in this area of research is to give a complete classification of the embedded topology of plane curves. It is known that for two plane curves
$(\mathbb {P}^2, \mathcal {C})$
of topological spaces. One of the main objectives in this area of research is to give a complete classification of the embedded topology of plane curves. It is known that for two plane curves
![]() $\mathcal {C}_1, \mathcal {C}_2\subset \mathbb {P}^2$
, if
$\mathcal {C}_1, \mathcal {C}_2\subset \mathbb {P}^2$
, if
![]() $(\mathbb {P}^2, \mathcal {C}_1)$
and
$(\mathbb {P}^2, \mathcal {C}_1)$
and
![]() $(\mathbb {P}^2, \mathcal {C}_2)$
are homeomorphic as pairs, then
$(\mathbb {P}^2, \mathcal {C}_2)$
are homeomorphic as pairs, then
![]() $\mathcal {C}_1$
and
$\mathcal {C}_1$
and
![]() $\mathcal {C}_2$
have the same combinatorial type. Here, the combinatorial type of plane curves is data consisting of the number of irreducible components, the degrees and the topological types of singularities, and configuration of irreducible components (see [Reference Bartolo, Cogolludo and Tokunaga5], [Reference Bartolo, Bannai, Shirane and Tokunaga2] for details). However, the converse is not true because there exist pairs of plane curves
$\mathcal {C}_2$
have the same combinatorial type. Here, the combinatorial type of plane curves is data consisting of the number of irreducible components, the degrees and the topological types of singularities, and configuration of irreducible components (see [Reference Bartolo, Cogolludo and Tokunaga5], [Reference Bartolo, Bannai, Shirane and Tokunaga2] for details). However, the converse is not true because there exist pairs of plane curves
![]() $\mathcal {C}_1, \mathcal {C}_2$
that have the same combinatorial type, but the homeomorphism classes of
$\mathcal {C}_1, \mathcal {C}_2$
that have the same combinatorial type, but the homeomorphism classes of
![]() $(\mathbb {P}^2, \mathcal {C}_1)$
and
$(\mathbb {P}^2, \mathcal {C}_1)$
and
![]() $(\mathbb {P}^2, \mathcal {C}_2)$
are distinct. The first example of such pairs
$(\mathbb {P}^2, \mathcal {C}_2)$
are distinct. The first example of such pairs
![]() $(\mathcal {C}_1, \mathcal {C}_2)$
was given by Zariski in [Reference Zariski17], and the name Zariski pair was coined by E. Artal in [Reference Bartolo1] (see [Reference Zariski17], [Reference Bartolo1], [Reference Bartolo, Cogolludo and Tokunaga5] for precise definitions and details).
$(\mathcal {C}_1, \mathcal {C}_2)$
was given by Zariski in [Reference Zariski17], and the name Zariski pair was coined by E. Artal in [Reference Bartolo1] (see [Reference Zariski17], [Reference Bartolo1], [Reference Bartolo, Cogolludo and Tokunaga5] for precise definitions and details).
Remark 1.2 It is known that the combinatorial type of a plane curve is equivalent to the embedded topology in its regular neighborhood (cf. [Reference Bartolo, Cogolludo and Tokunaga5]). Furthermore, the study of Zariski pairs can be regarded as an algebraic analogue of the study of surface-knots.
Understanding what causes the differences in the embedded topology of Zariski pairs should lead to a better understanding of the embedded topology of plane curves in general and hence is important. Concerning Zariski pairs of reducible plane curves with irreducible components of small degree, the following results are known. In the case where
![]() $\mathcal {C}_i$
are line arrangements, it is known that Zariski pairs do not exist for
$\mathcal {C}_i$
are line arrangements, it is known that Zariski pairs do not exist for
![]() $\deg \mathcal {C}_i\leq 9$
(see [Reference Nazir and Yoshinaga13]). Also, it is known that there exists a Zariski pair of line arrangements of
$\deg \mathcal {C}_i\leq 9$
(see [Reference Nazir and Yoshinaga13]). Also, it is known that there exists a Zariski pair of line arrangements of
![]() $\deg \mathcal {C}_i=11$
(see [Reference Bartolo, Ruber, Cogolludo-Agustín and Buzunáriz4]). However, the case of
$\deg \mathcal {C}_i=11$
(see [Reference Bartolo, Ruber, Cogolludo-Agustín and Buzunáriz4]). However, the case of
![]() $\deg \mathcal {C}_i=10$
is open. In the case of conic-line arrangements (i.e., reducible curves whose irreducible components are lines and smooth conics), the existence of a Zariski pair of degree
$\deg \mathcal {C}_i=10$
is open. In the case of conic-line arrangements (i.e., reducible curves whose irreducible components are lines and smooth conics), the existence of a Zariski pair of degree
![]() $7$
consisting of curves with two conics and three lines as irreducible components is known (see [Reference Tokunaga16]). Also, a Zariski pair of degree
$7$
consisting of curves with two conics and three lines as irreducible components is known (see [Reference Tokunaga16]). Also, a Zariski pair of degree
![]() $6$
consisting of curves with three conics as irreducible components is known (see [Reference Oka14]). It would be interesting to find a Zariski pair of conic-line arrangements of low degree consisting of curves with a single conic and additional lines.
$6$
consisting of curves with three conics as irreducible components is known (see [Reference Oka14]). It would be interesting to find a Zariski pair of conic-line arrangements of low degree consisting of curves with a single conic and additional lines.
Now, we explain our main result. Note that in the following, we work over the field of complex numbers
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $C_1$
,
$C_1$
,
![]() $C_2$
be smooth conics intersecting transversely that admit a
$C_2$
be smooth conics intersecting transversely that admit a
![]() $2m$
-sided Poncelet transverse. Let
$2m$
-sided Poncelet transverse. Let
![]() $L_1, \ldots , L_{2m}$
be distinct lines forming a nondegenerated
$L_1, \ldots , L_{2m}$
be distinct lines forming a nondegenerated
![]() $2m$
-sided Poncelet transverse
$2m$
-sided Poncelet transverse
![]() $\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
, where
$\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
, where
![]() $L_1, \ldots , L_{2m}$
are tangent lines of
$L_1, \ldots , L_{2m}$
are tangent lines of
![]() $C_2$
and the points
$C_2$
and the points
![]() $P_{1}=L_{2m}\cap L_1$
and
$P_{1}=L_{2m}\cap L_1$
and
![]() $P_i=L_{i-1}\cap L_{i}$
(
$P_i=L_{i-1}\cap L_{i}$
(
![]() $2\leq i \leq 2m$
) lie on
$2\leq i \leq 2m$
) lie on
![]() $C_1$
. Let
$C_1$
. Let
![]() $\mathcal {P}_{2m}:=\sum _{i=1}^{2m} L_i$
be the union of the lines and let
$\mathcal {P}_{2m}:=\sum _{i=1}^{2m} L_i$
be the union of the lines and let
![]() $T_1, T_2, T_3, T_4$
be the four bitangent lines of
$T_1, T_2, T_3, T_4$
be the four bitangent lines of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
. The curves that we are interested in are reducible curves of the form
$C_2$
. The curves that we are interested in are reducible curves of the form
having two conics and
![]() $2m+2$
lines as irreducible components. We consider the double covers of
$2m+2$
lines as irreducible components. We consider the double covers of
![]() $\mathbb {P}^2$
branched along the
$\mathbb {P}^2$
branched along the
![]() $2m+2$
lines
$2m+2$
lines
![]() $\mathcal {P}_{2m}+T_i+T_j$
and see how
$\mathcal {P}_{2m}+T_i+T_j$
and see how
![]() $C_1+C_2$
behaves under these double covers. Namely, we calculate the splitting types of
$C_1+C_2$
behaves under these double covers. Namely, we calculate the splitting types of
![]() $C_1+C_2$
with respect to these double covers. (See Section 2 and [Reference Bannai6] for details on splitting types.) This will be done by studying the invertible sheaves
$C_1+C_2$
with respect to these double covers. (See Section 2 and [Reference Bannai6] for details on splitting types.) This will be done by studying the invertible sheaves
![]() $\mathcal {F}$
of order 2 on
$\mathcal {F}$
of order 2 on
![]() $C_1+C_2$
, or equivalently, torsion points of order 2 of the Jacobian
$C_1+C_2$
, or equivalently, torsion points of order 2 of the Jacobian
![]() $J(C_1+C_2)$
of the singular curve
$J(C_1+C_2)$
of the singular curve
![]() $C_1+C_2$
. As an application of these calculations, we obtain the following theorem.
$C_1+C_2$
. As an application of these calculations, we obtain the following theorem.
Theorem 1.3 Under the above notation, it is possible to choose labels of
![]() $T_1, \ldots , T_4$
so that the pair
$T_1, \ldots , T_4$
so that the pair
![]() $(\mathcal {C}_{ij}, \mathcal {C}_{kl})$
is a Zariski pair if
$(\mathcal {C}_{ij}, \mathcal {C}_{kl})$
is a Zariski pair if
![]() $\{i, j\}=\{1,2\}$
or
$\{i, j\}=\{1,2\}$
or
![]() $\{3, 4\}$
and
$\{3, 4\}$
and
![]() $\{k, l\}\not =\{1,2\}, \{3, 4\}$
.
$\{k, l\}\not =\{1,2\}, \{3, 4\}$
.
We note that in the above setting,
![]() $C_1, C_2$
admits two degenerated
$C_1, C_2$
admits two degenerated
![]() $2m$
-sided Poncelet transverses each having two bitangent lines as edges. The differences of the curves
$2m$
-sided Poncelet transverses each having two bitangent lines as edges. The differences of the curves
![]() $\mathcal {C}_{ij}$
and
$\mathcal {C}_{ij}$
and
![]() $\mathcal {C}_{kl}$
in the theorem are whether the two bitangent lines lie in the same degenerated Poncelet transverse or not. Although the curves that are proven to be Zariski pairs in Theorem 1.3 are conic-line arrangements of
$\mathcal {C}_{kl}$
in the theorem are whether the two bitangent lines lie in the same degenerated Poncelet transverse or not. Although the curves that are proven to be Zariski pairs in Theorem 1.3 are conic-line arrangements of
![]() $\deg \mathcal {C}_{ij}\geq 10$
, we believe that our method of systematically constructing Zariski pairs from Poncelet transverses is in itself interesting and worth sharing. We hope this topological viewpoint is new and will add to the already rich literature on curves related to Poncelet’s closure theorem.
$\deg \mathcal {C}_{ij}\geq 10$
, we believe that our method of systematically constructing Zariski pairs from Poncelet transverses is in itself interesting and worth sharing. We hope this topological viewpoint is new and will add to the already rich literature on curves related to Poncelet’s closure theorem.
Similar studies relating torsion elements of the Jacobian
![]() $J(C)$
and the embedded topology of reducible curves having C as an irreducible component have been done in [Reference Bannai and Tokunaga8], [Reference Bartolo, Bannai, Shirane and Tokunaga2], [Reference Bartolo, Bannai, Shirane and Tokunaga3] when C is a smooth curve. This paper can be considered as a variation of these works in the case where C is reducible and singular.
$J(C)$
and the embedded topology of reducible curves having C as an irreducible component have been done in [Reference Bannai and Tokunaga8], [Reference Bartolo, Bannai, Shirane and Tokunaga2], [Reference Bartolo, Bannai, Shirane and Tokunaga3] when C is a smooth curve. This paper can be considered as a variation of these works in the case where C is reducible and singular.
This paper is organized as follows: In Section 2, we review the definition of splitting types and state the proposition that is used in distinguishing the embedded topology. In Section 3, we give a discussion on unramified double covers of conic-line arrangements, especially in the case of two transversal conics. In Section 4, we study n-sided Poncelet transverses and double covers related to them. Finally, in Section 5, we give the proof of our main result, Theorem 1.3.
2 Splitting types
In this section, we review the notion of splitting types of plane algebraic curves with respect to a double cover, which will be used to distinguish the embedded topology of the curves that we are interested in. We refer the reader to [Reference Bannai6] for details. Let
![]() $\pi _{\mathcal {B}}:S'\rightarrow \mathbb {P}^2$
be a double cover branched along a curve
$\pi _{\mathcal {B}}:S'\rightarrow \mathbb {P}^2$
be a double cover branched along a curve
![]() $\mathcal {B}\subset \mathbb {P}^2$
of even degree and let
$\mathcal {B}\subset \mathbb {P}^2$
of even degree and let
![]() $C\subset \mathbb {P}^2$
be an irreducible plane curve. The preimage
$C\subset \mathbb {P}^2$
be an irreducible plane curve. The preimage
![]() $\pi _{\mathcal {B}}^{-1}(C)$
can be either reducible or irreducible, depending on the relation between C and the branch locus
$\pi _{\mathcal {B}}^{-1}(C)$
can be either reducible or irreducible, depending on the relation between C and the branch locus
![]() $\mathcal {B}$
. In the former case where
$\mathcal {B}$
. In the former case where
![]() $\pi _{\mathcal {B}}^{-1}(C)$
is reducible,
$\pi _{\mathcal {B}}^{-1}(C)$
is reducible,
![]() $\pi _{\mathcal {B}}^{-1}(C)$
will have two irreducible components since
$\pi _{\mathcal {B}}^{-1}(C)$
will have two irreducible components since
![]() $\pi _{\mathcal {B}}^{-1}$
is a double cover. In this case, we say that C is a splitting curve with respect to
$\pi _{\mathcal {B}}^{-1}$
is a double cover. In this case, we say that C is a splitting curve with respect to
![]() $\pi _{\mathcal {B}}$
or
$\pi _{\mathcal {B}}$
or
![]() $\mathcal {B}$
. Let
$\mathcal {B}$
. Let
![]() $C_1, C_2$
be splitting curves with respect to
$C_1, C_2$
be splitting curves with respect to
![]() $\mathcal {B}$
and let
$\mathcal {B}$
and let
![]() $\pi _{\mathcal {B}}^{-1}(C_i)=C_i^++C_i^-$
,
$\pi _{\mathcal {B}}^{-1}(C_i)=C_i^++C_i^-$
,
![]() $(i=1, 2)$
. The relation between the components
$(i=1, 2)$
. The relation between the components
![]() $C_1^\pm $
,
$C_1^\pm $
,
![]() $C_2^\pm $
reflects how the curves
$C_2^\pm $
reflects how the curves
![]() $\mathcal {B}, C_1, C_2$
are “intertwined” in
$\mathcal {B}, C_1, C_2$
are “intertwined” in
![]() $\mathbb {P}^2$
and hence gives information about the embedded topology of the reducible curve
$\mathbb {P}^2$
and hence gives information about the embedded topology of the reducible curve
![]() $\mathcal {C}=\mathcal {B}+C_1+C_2$
. The information can be formulated as follows:
$\mathcal {C}=\mathcal {B}+C_1+C_2$
. The information can be formulated as follows:
Definition 2.1 Let
![]() $\mathcal {B}, C_1, C_2$
be as above. For integers
$\mathcal {B}, C_1, C_2$
be as above. For integers
![]() $m_1\leq m_2$
, we say that the triple
$m_1\leq m_2$
, we say that the triple
![]() $(C_1, C_2; \mathcal {B})$
has splitting type
$(C_1, C_2; \mathcal {B})$
has splitting type
![]() $(m_1, m_2)$
, if
$(m_1, m_2)$
, if
![]() $C_1^+\cdot C_2^+=m_1$
and
$C_1^+\cdot C_2^+=m_1$
and
![]() $C_1^+\cdot C_2^-=m_2$
for a suitable choice of labels.
$C_1^+\cdot C_2^-=m_2$
for a suitable choice of labels.
The splitting types can be used to distinguish the embedded topology of reducible plane curves by the following proposition.
Proposition 2.2 [Reference Bannai6, Proposition 2.5]
Let
![]() $\mathcal {B}_1$
,
$\mathcal {B}_1$
,
![]() $\mathcal {B}_2$
be plane curves of degree
$\mathcal {B}_2$
be plane curves of degree
![]() $2d$
and let
$2d$
and let
![]() $C_{i1}, C_{i2}$
be splitting curves with respect to
$C_{i1}, C_{i2}$
be splitting curves with respect to
![]() $\mathcal {B}_i$
,
$\mathcal {B}_i$
,
![]() $(i=1, 2)$
. Suppose that
$(i=1, 2)$
. Suppose that
![]() $C_{i1}\cap C_{i2}\cap \mathcal {B}_i=\emptyset $
,
$C_{i1}\cap C_{i2}\cap \mathcal {B}_i=\emptyset $
,
![]() $C_{i1}$
and
$C_{i1}$
and
![]() $C_{i2}$
intersect transversely and that
$C_{i2}$
intersect transversely and that
![]() $(C_{11}, C_{12};\mathcal {B}_1)$
and
$(C_{11}, C_{12};\mathcal {B}_1)$
and
![]() $(C_{21}, C_{22}; \mathcal {B}_2)$
have distinct spitting types. Then a homeomorphism
$(C_{21}, C_{22}; \mathcal {B}_2)$
have distinct spitting types. Then a homeomorphism
![]() $h:\mathbb {P}^2\rightarrow \mathbb {P}^2$
such that
$h:\mathbb {P}^2\rightarrow \mathbb {P}^2$
such that
![]() $h(\mathcal {B}_1)=\mathcal {B}_2$
and
$h(\mathcal {B}_1)=\mathcal {B}_2$
and
![]() $\{h(C_{11}), h(C_{12})\}=\{C_ {21}, C_{22}\}$
does not exist.
$\{h(C_{11}), h(C_{12})\}=\{C_ {21}, C_{22}\}$
does not exist.
Remark 2.3 It is known that Definition 2.1 and Proposition 2.2 can be modified to a more general version (see [Reference Bannai, Shirane and Tokunaga7]), but the above version is enough for our purposes.
Later, we will calculate the splitting types of pairs of conics
![]() $C_1, C_2$
with respect to various double covers in order to prove our main theorem.
$C_1, C_2$
with respect to various double covers in order to prove our main theorem.
3 Line bundles of order two and unramified double covers of conic-line arrangements with simple nodes
In this section, we briefly recall the theory of double covers. We will especially consider the case of conic-line arrangements with simple nodes for later use. We refer the reader to [Reference Harris11, Section 2, Section 3] for details and arguments in a more general setting.
First, we consider topological (unramified) double covers. Let
![]() $\mathcal {C}=C_1+\dots +C_k$
be a conic-line arrangement with simple nodes (i.e., each irreducible component
$\mathcal {C}=C_1+\dots +C_k$
be a conic-line arrangement with simple nodes (i.e., each irreducible component
![]() $C_i$
of
$C_i$
of
![]() $\mathcal {C}$
is either a line or a smooth conic, and all intersection points are ordinary double points). Let
$\mathcal {C}$
is either a line or a smooth conic, and all intersection points are ordinary double points). Let
![]() $\varphi : \mathcal {C}'\rightarrow \mathcal {C}$
be a topological double cover of
$\varphi : \mathcal {C}'\rightarrow \mathcal {C}$
be a topological double cover of
![]() $\mathcal {C}$
. Then, since
$\mathcal {C}$
. Then, since
![]() $C_i\cong \mathbb {P}^1$
and is simply connected,
$C_i\cong \mathbb {P}^1$
and is simply connected,
![]() $\varphi ^{-1}(C_i)$
splits into two disjoint sets
$\varphi ^{-1}(C_i)$
splits into two disjoint sets
![]() $C_i^\pm \subset \mathcal {C}'$
. We fix a labeling
$C_i^\pm \subset \mathcal {C}'$
. We fix a labeling
![]() $C_i^\pm $
for the meantime. Let
$C_i^\pm $
for the meantime. Let
![]() $Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, and let
$Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, and let
![]() $C_i, C_j$
be the irreducible components intersecting at Q. Then
$C_i, C_j$
be the irreducible components intersecting at Q. Then
![]() $C_i^+$
will intersect with either
$C_i^+$
will intersect with either
![]() $C_j^+$
or
$C_j^+$
or
![]() $C_j^-$
over Q. We say that
$C_j^-$
over Q. We say that
![]() $\mathcal {C}'$
is glued by
$\mathcal {C}'$
is glued by
![]() $+$
over Q if
$+$
over Q if
![]() $C_i^+$
intersects
$C_i^+$
intersects
![]() $C_j^+$
and is glued by
$C_j^+$
and is glued by
![]() $-$
over Q if
$-$
over Q if
![]() $C_i^+$
intersects
$C_i^+$
intersects
![]() $C_j^-$
. We summarize this data in the form of a map defined as below.
$C_j^-$
. We summarize this data in the form of a map defined as below.
Definition 3.1 A gluing data of order two on
![]() $\mathcal {C}$
is a map
$\mathcal {C}$
is a map
![]() $\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
. If there is no confusion, we simply call it a gluing data. The gluing data
$\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
. If there is no confusion, we simply call it a gluing data. The gluing data
![]() $\kappa _{\varphi }$
of a topological double cover
$\kappa _{\varphi }$
of a topological double cover
![]() $\varphi :\mathcal {C}'\rightarrow \mathcal {C}$
is a gluing data on
$\varphi :\mathcal {C}'\rightarrow \mathcal {C}$
is a gluing data on
![]() $\mathcal {C}$
defined by
$\mathcal {C}$
defined by
![]() $\kappa _{\varphi }(Q)=+$
if
$\kappa _{\varphi }(Q)=+$
if
![]() $\mathcal {C}'$
is glued by
$\mathcal {C}'$
is glued by
![]() $+$
over Q and
$+$
over Q and
![]() $\kappa _{\varphi }(Q)=-$
if
$\kappa _{\varphi }(Q)=-$
if
![]() $\mathcal {C}'$
is glued by
$\mathcal {C}'$
is glued by
![]() $-$
over Q.
$-$
over Q.
If we reverse the labeling of
![]() $C_i^\pm $
of
$C_i^\pm $
of
![]() $\pi ^{-1}(C_i)$
, then all of the signs for
$\pi ^{-1}(C_i)$
, then all of the signs for
![]() $Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\cap C_i$
will be reversed. Namely, for a gluing data
$Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\cap C_i$
will be reversed. Namely, for a gluing data
![]() $\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
and each
$\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
and each
![]() $i=1,\dots ,k$
, a new gluing data
$i=1,\dots ,k$
, a new gluing data
![]() $\kappa _{i}$
is obtained by
$\kappa _{i}$
is obtained by
 $$ \begin{align} \kappa_{i}(Q):=\left\{ \begin{array}{ll} -\kappa(Q) & \text{if }Q\in C_i, \\ \kappa(Q) & \text{otherwise} \end{array} \right. \end{align} $$
$$ \begin{align} \kappa_{i}(Q):=\left\{ \begin{array}{ll} -\kappa(Q) & \text{if }Q\in C_i, \\ \kappa(Q) & \text{otherwise} \end{array} \right. \end{align} $$
for each
![]() $Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
. We say that two gluing data
$Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
. We say that two gluing data
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa '$
are equivalent, and write
$\kappa '$
are equivalent, and write
![]() $\kappa \sim \kappa '$
, if
$\kappa \sim \kappa '$
, if
![]() $\kappa '$
can be constructed from
$\kappa '$
can be constructed from
![]() $\kappa $
by a finite number of the above operations. In this way, we have a map from the set of topological double covers
$\kappa $
by a finite number of the above operations. In this way, we have a map from the set of topological double covers
![]() $\varphi : \mathcal {C}'\rightarrow \mathcal {C}$
to the set of equivalence classes of gluing data
$\varphi : \mathcal {C}'\rightarrow \mathcal {C}$
to the set of equivalence classes of gluing data
![]() $\kappa _{\varphi }$
on
$\kappa _{\varphi }$
on
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 3.2 Let
![]() $\mathcal {C}=C_1+\dots +C_k$
be a conic-line arrangement with simple nodes. The following map
$\mathcal {C}=C_1+\dots +C_k$
be a conic-line arrangement with simple nodes. The following map
![]() $\Psi $
from the set of homeomorphism classes of topological double covers of
$\Psi $
from the set of homeomorphism classes of topological double covers of
![]() $\mathcal {C}$
to the set of equivalence classes of gluing data on
$\mathcal {C}$
to the set of equivalence classes of gluing data on
![]() $\mathcal {C}$
is well-defined and one-to-one:
$\mathcal {C}$
is well-defined and one-to-one:

where
![]() $\kappa _\varphi $
is the gluing data of the topological double cover
$\kappa _\varphi $
is the gluing data of the topological double cover
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {C}$
. In particular, any continuous deformation
$\mathcal {C}$
. In particular, any continuous deformation
![]() $\varphi _t:\mathcal {C}^{\prime }_t\to \mathcal {C}$
(
$\varphi _t:\mathcal {C}^{\prime }_t\to \mathcal {C}$
(
![]() $t\in \Delta $
) of topological double covers of
$t\in \Delta $
) of topological double covers of
![]() $\mathcal {C}$
is constant, where
$\mathcal {C}$
is constant, where
![]() $\Delta \subset \mathbb {C}$
is a small neighborhood of the origin.
$\Delta \subset \mathbb {C}$
is a small neighborhood of the origin.
Proof Suppose that
![]() $h:\mathcal {C}'\to \mathcal {C}"$
is a homeomorphism over
$h:\mathcal {C}'\to \mathcal {C}"$
is a homeomorphism over
![]() $\mathcal {C}$
of topological double covers
$\mathcal {C}$
of topological double covers
![]() $\varphi ':\mathcal {C}'\to \mathcal {C}$
and
$\varphi ':\mathcal {C}'\to \mathcal {C}$
and
![]() $\varphi ":\mathcal {C}"\to \mathcal {C}$
. Put
$\varphi ":\mathcal {C}"\to \mathcal {C}$
. Put
![]() ${\varphi '}^{-1}(C_i)={C'}_i^++{C'}_i^-$
and
${\varphi '}^{-1}(C_i)={C'}_i^++{C'}_i^-$
and
![]() ${\varphi "}^{-1}(C_i)={C_i"}^++{C_i"}^-$
. Note that h satisfies
${\varphi "}^{-1}(C_i)={C_i"}^++{C_i"}^-$
. Note that h satisfies
![]() $h({\varphi '}^{-1}(C_i))={\varphi "}^{-1}(C_i)$
, but there may be
$h({\varphi '}^{-1}(C_i))={\varphi "}^{-1}(C_i)$
, but there may be
![]() $1\leq i\leq k$
such that
$1\leq i\leq k$
such that
![]() $h({C'}_i^+)= {C_i"}^-$
depending on how the components are labeled by
$h({C'}_i^+)= {C_i"}^-$
depending on how the components are labeled by
![]() $\pm $
. Since h is a homeomorphism,
$\pm $
. Since h is a homeomorphism,
![]() $\kappa _{\varphi "}$
can be obtained from
$\kappa _{\varphi "}$
can be obtained from
![]() $\kappa _{\varphi '}$
by applying the operations (3.1) to
$\kappa _{\varphi '}$
by applying the operations (3.1) to
![]() $\kappa _{\varphi '}$
for
$\kappa _{\varphi '}$
for
![]() $1\leq i\leq k$
with
$1\leq i\leq k$
with
![]() $h({C'}_i^+)= {C_i"}^-$
, which corresponds to exchanging
$h({C'}_i^+)= {C_i"}^-$
, which corresponds to exchanging
![]() ${C'}_i^+$
and
${C'}_i^+$
and
![]() ${C'}_i^-$
. Hence, the gluing data
${C'}_i^-$
. Hence, the gluing data
![]() $\kappa _{\varphi "}$
is equivalent to
$\kappa _{\varphi "}$
is equivalent to
![]() $\kappa _{\varphi '}$
, and the map
$\kappa _{\varphi '}$
, and the map
![]() $\Psi $
is well-defined.
$\Psi $
is well-defined.
Let
![]() $\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
be a gluing data on
$\kappa :\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
be a gluing data on
![]() $\mathcal {C}$
. For each
$\mathcal {C}$
. For each
![]() $i=1,\dots ,k$
, let
$i=1,\dots ,k$
, let
![]() $C_i^+\sqcup C_i^-$
be the disjoint union of two copies
$C_i^+\sqcup C_i^-$
be the disjoint union of two copies
![]() $C_i^\pm $
of
$C_i^\pm $
of
![]() $C_i$
, and let
$C_i$
, and let
![]() $\varphi _i:C_i^+\sqcup C_i^-\to C_i$
be the projection, which is the topological double cover of
$\varphi _i:C_i^+\sqcup C_i^-\to C_i$
be the projection, which is the topological double cover of
![]() $C_i$
. We construct a topological space
$C_i$
. We construct a topological space
![]() $\mathcal {C}^{\prime }_\kappa $
by gluing
$\mathcal {C}^{\prime }_\kappa $
by gluing
![]() $C_i^\pm \cap \varphi _i^{-1}(Q)$
to
$C_i^\pm \cap \varphi _i^{-1}(Q)$
to
![]() $C_j^\pm \cap \varphi _j^{-1}(Q)$
if
$C_j^\pm \cap \varphi _j^{-1}(Q)$
if
![]() $\kappa (Q)=+$
, and to
$\kappa (Q)=+$
, and to
![]() $C_j^\mp \cap \varphi _j^{-1}(Q)$
if
$C_j^\mp \cap \varphi _j^{-1}(Q)$
if
![]() $\kappa (Q)=-$
, for each
$\kappa (Q)=-$
, for each
![]() $1\leq i<j\leq k$
and
$1\leq i<j\leq k$
and
![]() $Q\in C_i\cap C_j$
. Then the topological double covers
$Q\in C_i\cap C_j$
. Then the topological double covers
![]() $\varphi _i$
induce a topological double cover
$\varphi _i$
induce a topological double cover
![]() $\varphi _\kappa :{\mathcal {C}'}_\kappa \to \mathcal {C}$
. Since the operation (3.1) corresponds to replacing
$\varphi _\kappa :{\mathcal {C}'}_\kappa \to \mathcal {C}$
. Since the operation (3.1) corresponds to replacing
![]() $C_i^+$
and
$C_i^+$
and
![]() $C_i^-$
, the map
$C_i^-$
, the map
![]() $\lbrack \kappa \rbrack \mapsto \lbrack \varphi _\kappa \rbrack $
is well-defined, and is the inverse map of
$\lbrack \kappa \rbrack \mapsto \lbrack \varphi _\kappa \rbrack $
is well-defined, and is the inverse map of
![]() $\Psi $
. Hence,
$\Psi $
. Hence,
![]() $\Psi $
is one-to-one.
$\Psi $
is one-to-one.
Let
![]() $\varphi _t:\mathcal {C}^{\prime }_t\to \mathcal {C}$
(
$\varphi _t:\mathcal {C}^{\prime }_t\to \mathcal {C}$
(
![]() $t\in \Delta $
) be a continuous deformation of topological double covers, and let
$t\in \Delta $
) be a continuous deformation of topological double covers, and let
![]() $\Phi :\overline {\mathcal {C}}'\to \Delta \times \mathcal {C}$
be the continuous family of the topological double covers
$\Phi :\overline {\mathcal {C}}'\to \Delta \times \mathcal {C}$
be the continuous family of the topological double covers
![]() $\varphi _t$
, where
$\varphi _t$
, where
![]() $\overline {\mathcal {C}}':=\{(t, P')\mid t\in \Delta ,\ {P'}\in {\mathcal {C}}^{\prime }_t \}$
and
$\overline {\mathcal {C}}':=\{(t, P')\mid t\in \Delta ,\ {P'}\in {\mathcal {C}}^{\prime }_t \}$
and
![]() $\Phi (t,P'):=(t,\varphi _t({P'}))$
. Then
$\Phi (t,P'):=(t,\varphi _t({P'}))$
. Then
![]() $\Phi $
is a topological double cover of
$\Phi $
is a topological double cover of
![]() $\Delta \times \mathcal {C}$
. Since
$\Delta \times \mathcal {C}$
. Since
![]() $\Delta \times C_i$
is simply connected for each irreducible component
$\Delta \times C_i$
is simply connected for each irreducible component
![]() $C_i\subset \mathcal {C}$
, the preimage
$C_i\subset \mathcal {C}$
, the preimage
![]() $\Phi ^{-1}(\Delta \times C_i)$
consists of two connected components
$\Phi ^{-1}(\Delta \times C_i)$
consists of two connected components
![]() $\overline {C}_i^{\,\pm }$
. For each
$\overline {C}_i^{\,\pm }$
. For each
![]() $Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, the preimage
$Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, the preimage
![]() $\Phi ^{-1}(\Delta \times \{Q\})$
also consists of two components
$\Phi ^{-1}(\Delta \times \{Q\})$
also consists of two components
![]() $\Delta _Q^\pm $
. For each
$\Delta _Q^\pm $
. For each
![]() $t\in \Delta $
, we define a gluing data
$t\in \Delta $
, we define a gluing data
![]() $\kappa _t:\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
by, for each
$\kappa _t:\mathop {\mathrm {Sing}}\nolimits (\mathcal {C})\to \{+,-\}$
by, for each
![]() $Q\in C_i\cap C_j$
(
$Q\in C_i\cap C_j$
(
![]() $i\ne j$
),
$i\ne j$
),
![]() $\kappa _t(Q)=+$
if
$\kappa _t(Q)=+$
if
![]() $\Delta _Q^+\subset \overline {C}_i^{\,+}\cap \overline {C}_j^{\,+}$
, and
$\Delta _Q^+\subset \overline {C}_i^{\,+}\cap \overline {C}_j^{\,+}$
, and
![]() $\kappa _t(Q)=-$
otherwise. This
$\kappa _t(Q)=-$
otherwise. This
![]() $\kappa _t$
coincides with the gluing data
$\kappa _t$
coincides with the gluing data
![]() $\kappa _{\varphi _t}$
of
$\kappa _{\varphi _t}$
of
![]() $\varphi _t$
for any
$\varphi _t$
for any
![]() $t\in \Delta $
. Since
$t\in \Delta $
. Since
![]() $\kappa _t$
is constant under t, all topological double covers
$\kappa _t$
is constant under t, all topological double covers
![]() $\varphi _t$
are homeomorphic.
$\varphi _t$
are homeomorphic.
Next, we consider the relation between unramified double covers of
![]() $\mathcal {C}$
and invertible sheaves of order
$\mathcal {C}$
and invertible sheaves of order
![]() $2$
on
$2$
on
![]() $\mathcal {C}$
following [Reference Harris11]. Let
$\mathcal {C}$
following [Reference Harris11]. Let
![]() $\mathcal {C}$
be a reduced curve and let
$\mathcal {C}$
be a reduced curve and let
![]() $\mathcal {F}$
be an invertible sheaf of order
$\mathcal {F}$
be an invertible sheaf of order
![]() $2$
on
$2$
on
![]() $\mathcal {C}$
(i.e.,
$\mathcal {C}$
(i.e.,
![]() $\mathcal {F}\otimes \mathcal {F} \cong \mathcal {O}_{\mathcal {C}}$
, where
$\mathcal {F}\otimes \mathcal {F} \cong \mathcal {O}_{\mathcal {C}}$
, where
![]() $\mathcal {O}_{\mathcal {C}}$
is the structure sheaf of, and, by abuse of terminology, the structure sheaf is considered as order 2
$\mathcal {O}_{\mathcal {C}}$
is the structure sheaf of, and, by abuse of terminology, the structure sheaf is considered as order 2
![]() $\mathcal {C}$
). Let
$\mathcal {C}$
). Let
![]() $p_{\mathcal {F}}:\boldsymbol {L}_{\mathcal {F}}\rightarrow \mathcal {C}$
be the line bundle corresponding to
$p_{\mathcal {F}}:\boldsymbol {L}_{\mathcal {F}}\rightarrow \mathcal {C}$
be the line bundle corresponding to
![]() $\mathcal {F}$
and let
$\mathcal {F}$
and let
![]() $t\in \Gamma (\boldsymbol {L}_{\mathcal {F}}, p_{\mathcal {F}}^\ast \mathcal {F})$
be the tautological section. Then, since we have assumed that
$t\in \Gamma (\boldsymbol {L}_{\mathcal {F}}, p_{\mathcal {F}}^\ast \mathcal {F})$
be the tautological section. Then, since we have assumed that
![]() $\mathcal {F}\otimes \mathcal {F} \cong \mathcal {O}_{\mathcal {C}}$
, the zero divisor of
$\mathcal {F}\otimes \mathcal {F} \cong \mathcal {O}_{\mathcal {C}}$
, the zero divisor of
![]() $t^2-1$
in
$t^2-1$
in
![]() $\boldsymbol {L}_{\mathcal {F}}$
gives an unramified double cover
$\boldsymbol {L}_{\mathcal {F}}$
gives an unramified double cover
![]() $\varpi _{\mathcal {F}}:\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
$\varpi _{\mathcal {F}}:\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
![]() $\mathcal {C}$
. Note that the construction is algebraic, but since it is unramified,
$\mathcal {C}$
. Note that the construction is algebraic, but since it is unramified,
![]() $\varpi _{\mathcal {F}}$
is also a topological double cover. It is known that this relation induces a one-to-one correspondence between isomorphism classes of invertible sheaves
$\varpi _{\mathcal {F}}$
is also a topological double cover. It is known that this relation induces a one-to-one correspondence between isomorphism classes of invertible sheaves
![]() $\mathcal {F}$
of order 2, and isomorphism classes of unramified double covers
$\mathcal {F}$
of order 2, and isomorphism classes of unramified double covers
![]() $\varpi _{\mathcal {F}}:\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
$\varpi _{\mathcal {F}}:\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
![]() $\mathcal {C}$
. In the case where
$\mathcal {C}$
. In the case where
![]() $\mathcal {C}$
is a conic-line arrangement with simple nodes, the relation between invertible sheaves of order 2 and unramified double covers can be described using the gluing data as follows: Let
$\mathcal {C}$
is a conic-line arrangement with simple nodes, the relation between invertible sheaves of order 2 and unramified double covers can be described using the gluing data as follows: Let
![]() $\mathcal {F}$
be an invertible sheaf of order 2 on
$\mathcal {F}$
be an invertible sheaf of order 2 on
![]() $\mathcal {C}$
. Then, since the components of
$\mathcal {C}$
. Then, since the components of
![]() $\mathcal {C}$
are isomorphic to
$\mathcal {C}$
are isomorphic to
![]() $\mathbb {P}^1$
and
$\mathbb {P}^1$
and
![]() $\mathop {\mathrm {Pic}}\nolimits (\mathbb {P}^1)$
is torsion free, the restrictions
$\mathop {\mathrm {Pic}}\nolimits (\mathbb {P}^1)$
is torsion free, the restrictions
![]() $\mathcal {F}|_{C_i}$
are isomorphic to the trivial sheaf
$\mathcal {F}|_{C_i}$
are isomorphic to the trivial sheaf
![]() $\mathcal {O}_{C_i}$
. Given a node
$\mathcal {O}_{C_i}$
. Given a node
![]() $Q\in C_i\cap C_j$
, the line bundle
$Q\in C_i\cap C_j$
, the line bundle
![]() $\mathcal {F}$
and its transition functions give the data of gluing of the trivial sheaves
$\mathcal {F}$
and its transition functions give the data of gluing of the trivial sheaves
![]() $\mathcal {F}|_{C_i}$
and
$\mathcal {F}|_{C_i}$
and
![]() $\mathcal {F}|_{C_j}$
over Q which is given by multiplication with
$\mathcal {F}|_{C_j}$
over Q which is given by multiplication with
![]() $1$
or
$1$
or
![]() $-1$
, since
$-1$
, since
![]() $\mathcal {F}$
is of order 2. Conversely, an invertible sheaf of order 2 can be constructed by assigning this gluing data
$\mathcal {F}$
is of order 2. Conversely, an invertible sheaf of order 2 can be constructed by assigning this gluing data
![]() $\pm 1$
of the trivial sheaves at each node Q. In this way, we can associate a gluing data
$\pm 1$
of the trivial sheaves at each node Q. In this way, we can associate a gluing data
![]() $\kappa _{\mathcal {F}}$
to
$\kappa _{\mathcal {F}}$
to
![]() $\mathcal {F}$
. Again, changing the signs of the gluing data at every node in an irreducible component
$\mathcal {F}$
. Again, changing the signs of the gluing data at every node in an irreducible component
![]() $C_i$
will result in an isomorphic sheaf. Hence, we have the following Lemma:
$C_i$
will result in an isomorphic sheaf. Hence, we have the following Lemma:
Lemma 3.3 Let
![]() $\mathcal {C}=C_1+\cdots +C_k$
be a conic-line arrangement with simple nodes. Then, there is a one-to-one correspondence between the set of invertible sheaves
$\mathcal {C}=C_1+\cdots +C_k$
be a conic-line arrangement with simple nodes. Then, there is a one-to-one correspondence between the set of invertible sheaves
![]() $\mathcal {F}$
of order
$\mathcal {F}$
of order
![]() $2$
on
$2$
on
![]() $\mathcal {C}$
and the set of equivalence classes of gluing data on
$\mathcal {C}$
and the set of equivalence classes of gluing data on
![]() $\mathcal {C}$
. Furthermore, this correspondence is compatible with the correspondence between the unramified double cover
$\mathcal {C}$
. Furthermore, this correspondence is compatible with the correspondence between the unramified double cover
![]() $\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
$\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
of
![]() $\mathcal {C}$
associated to
$\mathcal {C}$
associated to
![]() $\mathcal {F}$
and its gluing data. Namely, if
$\mathcal {F}$
and its gluing data. Namely, if
![]() $\kappa _{\mathcal {F}}$
is the gluing data of
$\kappa _{\mathcal {F}}$
is the gluing data of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\kappa _{\varpi _{\mathcal {F}}}$
is the gluing data of
$\kappa _{\varpi _{\mathcal {F}}}$
is the gluing data of
![]() $\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
, then
$\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}$
, then
![]() $\kappa _{\mathcal {F}} \sim \kappa _{\varpi _{\mathcal {F}}}$
.
$\kappa _{\mathcal {F}} \sim \kappa _{\varpi _{\mathcal {F}}}$
.
Proof The first part follows from the discussion stated before the lemma. See also [Reference Harris11, Section 2b]. For the second part, let
![]() $\mathcal {F}$
be an invertible sheaf of order 2 and let
$\mathcal {F}$
be an invertible sheaf of order 2 and let
![]() ${\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}}$
be the associated unramified double cover. The preimage of
${\mathcal {C}^{\prime }_{\mathcal {F}}\rightarrow \mathcal {C}}$
be the associated unramified double cover. The preimage of
![]() $C_i$
in
$C_i$
in
![]() $\mathcal {C}^{\prime }_{\mathcal {F}}$
consists of disjoint copies
$\mathcal {C}^{\prime }_{\mathcal {F}}$
consists of disjoint copies
![]() $C_i^+$
and
$C_i^+$
and
![]() $C_i^-$
of
$C_i^-$
of
![]() $C_i$
corresponding to the decomposition
$C_i$
corresponding to the decomposition
![]() ${t_i^2-1=(t_i-1)(t_i+1)}$
, where
${t_i^2-1=(t_i-1)(t_i+1)}$
, where
![]() $t_i$
is the tautological section of
$t_i$
is the tautological section of
![]() $p^\ast (\mathcal {F}|_{C_i})$
. The gluing data of
$p^\ast (\mathcal {F}|_{C_i})$
. The gluing data of
![]() $\mathcal {F}$
at a node
$\mathcal {F}$
at a node
![]() $Q\in C_i\cap C_j$
tells us how the tautological sections
$Q\in C_i\cap C_j$
tells us how the tautological sections
![]() $t_i, t_j$
are related and in turn how
$t_i, t_j$
are related and in turn how
![]() $C_i^\pm $
and
$C_i^\pm $
and
![]() $C_j^\pm $
intersect as curves in
$C_j^\pm $
intersect as curves in
![]() $\boldsymbol {L}_{\mathcal {F}}$
. If the sheaves
$\boldsymbol {L}_{\mathcal {F}}$
. If the sheaves
![]() $\mathcal {F}|_{C_i}$
and
$\mathcal {F}|_{C_i}$
and
![]() $\mathcal {F}|_{C_j}$
are glued by multiplication by
$\mathcal {F}|_{C_j}$
are glued by multiplication by
![]() $1$
over Q, then
$1$
over Q, then
![]() $t_i=t_j$
over Q and
$t_i=t_j$
over Q and
![]() $C_i^+$
intersects
$C_i^+$
intersects
![]() $C_j^+$
over Q. If they are glued by
$C_j^+$
over Q. If they are glued by
![]() $-1$
, then
$-1$
, then
![]() $t_i=-t_j$
over Q and
$t_i=-t_j$
over Q and
![]() $C_i^+$
intersects
$C_i^+$
intersects
![]() $C_j^-$
over Q. Hence, the gluing data
$C_j^-$
over Q. Hence, the gluing data
![]() $\kappa _{\mathcal {F}}$
of
$\kappa _{\mathcal {F}}$
of
![]() $\mathcal {F}$
as a sheaf and the gluing data
$\mathcal {F}$
as a sheaf and the gluing data
![]() $\kappa _{\varpi _{\mathcal {F}}}$
of the topological unramified double cover
$\kappa _{\varpi _{\mathcal {F}}}$
of the topological unramified double cover
![]() $\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}} \to \mathcal {C}$
associated to
$\varpi _{\mathcal {F}}: \mathcal {C}^{\prime }_{\mathcal {F}} \to \mathcal {C}$
associated to
![]() $\mathcal {F}$
coincide.
$\mathcal {F}$
coincide.
Furthermore, given two invertible sheaves
![]() $\mathcal {F}_1, \mathcal {F}_2$
that are each of order
$\mathcal {F}_1, \mathcal {F}_2$
that are each of order
![]() $2$
, the product
$2$
, the product
![]() $\mathcal {F}_1\otimes \mathcal {F}_2$
is again of order
$\mathcal {F}_1\otimes \mathcal {F}_2$
is again of order
![]() $2$
. The gluing data of
$2$
. The gluing data of
![]() $\mathcal {F}_1\otimes \mathcal {F}_2$
is given by simply taking the products of the gluing data of
$\mathcal {F}_1\otimes \mathcal {F}_2$
is given by simply taking the products of the gluing data of
![]() $\mathcal {F}_1$
and
$\mathcal {F}_1$
and
![]() $\mathcal {F}_2$
at each
$\mathcal {F}_2$
at each
![]() $Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, as the transition functions of
$Q\in \mathop {\mathrm {Sing}}\nolimits (\mathcal {C})$
, as the transition functions of
![]() $\mathcal {F}_1\otimes \mathcal {F}_2$
are given by products of the transition function of
$\mathcal {F}_1\otimes \mathcal {F}_2$
are given by products of the transition function of
![]() $\mathcal {F}_1$
and
$\mathcal {F}_1$
and
![]() $\mathcal {F}_2$
. The gluing data of the unramified double cover associated to
$\mathcal {F}_2$
. The gluing data of the unramified double cover associated to
![]() $\mathcal {F}_1\otimes \mathcal {F}_2$
can also be obtained likewise.
$\mathcal {F}_1\otimes \mathcal {F}_2$
can also be obtained likewise.
Understanding and calculating the structure of the unramified double covers through this gluing data is useful and will be used in the proof of the main theorem. Also, in some cases where
![]() $\mathcal {C}\subset \mathbb {P}^2$
, and the unramified double cover of
$\mathcal {C}\subset \mathbb {P}^2$
, and the unramified double cover of
![]() $\mathcal {C}$
is induced by a (possibly ramified) double cover of
$\mathcal {C}$
is induced by a (possibly ramified) double cover of
![]() $\mathbb {P}^2$
, the structure of the former can be deduced from the latter as follows: Let
$\mathbb {P}^2$
, the structure of the former can be deduced from the latter as follows: Let
![]() $\pi :S'\to \mathbb {P}^2$
be a double cover branched along a plane curve
$\pi :S'\to \mathbb {P}^2$
be a double cover branched along a plane curve
![]() $\mathcal {B}\subset \mathbb {P}^2$
of degree
$\mathcal {B}\subset \mathbb {P}^2$
of degree
![]() $2d$
, and let
$2d$
, and let
![]() $F\in \Gamma (\mathbb {P}^2,\mathcal {O}_{\mathbb {P}^2}(2d))$
be a defining polynomial of
$F\in \Gamma (\mathbb {P}^2,\mathcal {O}_{\mathbb {P}^2}(2d))$
be a defining polynomial of
![]() $\mathcal {B}$
. Assume that there is an effective divisor D on the curve
$\mathcal {B}$
. Assume that there is an effective divisor D on the curve
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $\mathcal {B}|_{\mathcal {C}}=2D$
and
$\mathcal {B}|_{\mathcal {C}}=2D$
and
![]() $\mathop {\mathrm {Supp}}\nolimits D\cap \mathop {\mathrm {Sing}}\nolimits \mathcal {C}=\emptyset $
(i.e.,
$\mathop {\mathrm {Supp}}\nolimits D\cap \mathop {\mathrm {Sing}}\nolimits \mathcal {C}=\emptyset $
(i.e.,
![]() $\mathcal {C}$
intersects with
$\mathcal {C}$
intersects with
![]() $\mathcal {B}$
at smooth points of
$\mathcal {B}$
at smooth points of
![]() $\mathcal {C}$
with even multiplicities). Put
$\mathcal {C}$
with even multiplicities). Put
![]() $\mathcal {L}:=\mathcal {O}_{\mathbb {P}^2}(d)$
, and let
$\mathcal {L}:=\mathcal {O}_{\mathbb {P}^2}(d)$
, and let
![]() $p_{\mathcal {L}}:\boldsymbol {L}_{\mathcal {L}}\to \mathbb {P}^2$
be the line bundle corresponding to
$p_{\mathcal {L}}:\boldsymbol {L}_{\mathcal {L}}\to \mathbb {P}^2$
be the line bundle corresponding to
![]() $\mathcal {L}$
, where
$\mathcal {L}$
, where
![]() $\boldsymbol {L}_{\mathcal {L}}:=\mathrm {Spec}\,S(\mathcal {L}^{-1})$
is the spectrum of the symmetric algebra
$\boldsymbol {L}_{\mathcal {L}}:=\mathrm {Spec}\,S(\mathcal {L}^{-1})$
is the spectrum of the symmetric algebra
![]() $S(\mathcal {L}^{-1})$
of
$S(\mathcal {L}^{-1})$
of
![]() $\mathcal {L}^{-1}$
. Let
$\mathcal {L}^{-1}$
. Let
![]() $t\in \Gamma (\boldsymbol {L}_{\mathcal {L}},p_{\mathcal {L}}^\ast \mathcal {L})$
be the tautological section. Then
$t\in \Gamma (\boldsymbol {L}_{\mathcal {L}},p_{\mathcal {L}}^\ast \mathcal {L})$
be the tautological section. Then
![]() $S'$
can be regarded as the subvariety of
$S'$
can be regarded as the subvariety of
![]() $\boldsymbol {L}_{\mathcal {L}}$
defined by
$\boldsymbol {L}_{\mathcal {L}}$
defined by
![]() $t^2-F=0$
, and
$t^2-F=0$
, and
![]() $\pi =p_{\mathcal {L}}|_{S'}$
. Since
$\pi =p_{\mathcal {L}}|_{S'}$
. Since
![]() $\mathop {\mathrm {Supp}}\nolimits D$
is contained in the smooth part of
$\mathop {\mathrm {Supp}}\nolimits D$
is contained in the smooth part of
![]() $\mathcal {C}$
, D corresponds to a Cartier divisor on
$\mathcal {C}$
, D corresponds to a Cartier divisor on
![]() $\mathcal {C}$
, and there is a section
$\mathcal {C}$
, and there is a section
![]() $s_D\in \Gamma (\mathcal {C},\mathcal {O}_{\mathcal {C}}(D))$
defining D and satisfying
$s_D\in \Gamma (\mathcal {C},\mathcal {O}_{\mathcal {C}}(D))$
defining D and satisfying
![]() $s_D^2=F|_{\mathcal {C}}$
. Put
$s_D^2=F|_{\mathcal {C}}$
. Put
![]() $\mathcal {F}:=\mathcal {L}|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-D)$
and let
$\mathcal {F}:=\mathcal {L}|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-D)$
and let
![]() $p_{\mathcal {F}}:\boldsymbol {L}_{\mathcal {F}}\to \mathcal {C}$
be the line bundle corresponding to
$p_{\mathcal {F}}:\boldsymbol {L}_{\mathcal {F}}\to \mathcal {C}$
be the line bundle corresponding to
![]() $\mathcal {F}$
. Note that
$\mathcal {F}$
. Note that
![]() $\mathcal {F}$
is of order
$\mathcal {F}$
is of order
![]() $2$
, and
$2$
, and
![]() $\frac {t|_{\mathcal {C}}}{s_D}$
can be regarded as a section of
$\frac {t|_{\mathcal {C}}}{s_D}$
can be regarded as a section of
![]() $\Gamma (\boldsymbol {L}_{\mathcal {F}},p_{\mathcal {F}}^\ast \mathcal {F})$
. We say that the unramified double cover
$\Gamma (\boldsymbol {L}_{\mathcal {F}},p_{\mathcal {F}}^\ast \mathcal {F})$
. We say that the unramified double cover
![]() $\varpi :\mathcal {C}_{\mathcal {F}}'\to \mathcal {C}$
given by
$\varpi :\mathcal {C}_{\mathcal {F}}'\to \mathcal {C}$
given by
 $$\begin{align*}\left( \frac{t|_{\mathcal{C}}}{s_D} \right)^2 - 1=0 \end{align*}$$
$$\begin{align*}\left( \frac{t|_{\mathcal{C}}}{s_D} \right)^2 - 1=0 \end{align*}$$
in
![]() $\boldsymbol {L}_{\mathcal {F}}$
and
$\boldsymbol {L}_{\mathcal {F}}$
and
![]() $\varpi :=p_{\mathcal {F}}|_{\mathcal {C}'}$
is induced by
$\varpi :=p_{\mathcal {F}}|_{\mathcal {C}'}$
is induced by
![]() $\pi $
. The morphism
$\pi $
. The morphism
![]() $\mathcal {F}\to \mathcal {L}|_{\mathcal {C}}$
given by multiplication of
$\mathcal {F}\to \mathcal {L}|_{\mathcal {C}}$
given by multiplication of
![]() $s_D$
induces the morphism
$s_D$
induces the morphism
![]() $\boldsymbol {L}_{\mathcal {F}}\to \boldsymbol {L}_{\mathcal {L}}|_{\mathcal {C}}$
over
$\boldsymbol {L}_{\mathcal {F}}\to \boldsymbol {L}_{\mathcal {L}}|_{\mathcal {C}}$
over
![]() $\mathcal {C}$
, which is given by multiplication of the value of
$\mathcal {C}$
, which is given by multiplication of the value of
![]() $s_D$
to each fiber coordinate of
$s_D$
to each fiber coordinate of
![]() $\boldsymbol {L}_{\mathcal {F}}$
. This morphism induces
$\boldsymbol {L}_{\mathcal {F}}$
. This morphism induces
![]() $\mathcal {C}^{\prime }_{\mathcal {F}}\to \pi ^{-1}(\mathcal {C})$
, which is isomorphic over
$\mathcal {C}^{\prime }_{\mathcal {F}}\to \pi ^{-1}(\mathcal {C})$
, which is isomorphic over
![]() $\mathcal {C}\setminus \mathop {\mathrm {Supp}}\nolimits D$
. Hence, we can deduce the structure of
$\mathcal {C}\setminus \mathop {\mathrm {Supp}}\nolimits D$
. Hence, we can deduce the structure of
![]() $\mathcal {C}^{\prime }_{\mathcal {F}}$
by studying
$\mathcal {C}^{\prime }_{\mathcal {F}}$
by studying
![]() $\pi ^{-1}(\mathcal {C})$
. In the above cases, explicit calculations of transition functions may be avoided when calculating the gluing data, which we see in the following example.
$\pi ^{-1}(\mathcal {C})$
. In the above cases, explicit calculations of transition functions may be avoided when calculating the gluing data, which we see in the following example.
Example 3.4 Let
![]() $C_1, C_2\subset \mathbb {P}^2$
be smooth conics intersecting transversely,
$C_1, C_2\subset \mathbb {P}^2$
be smooth conics intersecting transversely,
![]() $T_1$
,
$T_1$
,
![]() $T_2$
,
$T_2$
,
![]() $T_3$
,
$T_3$
,
![]() $T_4$
be the four bitangent lines to
$T_4$
be the four bitangent lines to
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and
$C_2$
, and
![]() $P_{ik}=T_i\cap C_k$
be the tangent points. Since
$P_{ik}=T_i\cap C_k$
be the tangent points. Since
![]() $T_i+T_j$
has degree 2 and
$T_i+T_j$
has degree 2 and
![]() $(T_i+T_j)|_{\mathcal {C}}=2(P_{i1}+P_{i2}+P_{j1}+P_{j2})$
, the ramified double cover
$(T_i+T_j)|_{\mathcal {C}}=2(P_{i1}+P_{i2}+P_{j1}+P_{j2})$
, the ramified double cover
![]() $\pi _{ij}:S^{\prime }_{ij}\rightarrow \mathbb {P}^2$
of
$\pi _{ij}:S^{\prime }_{ij}\rightarrow \mathbb {P}^2$
of
![]() $\mathbb {P}^2$
branched along
$\mathbb {P}^2$
branched along
![]() $T_i+T_j$
induces an unramified double cover
$T_i+T_j$
induces an unramified double cover
![]() $\varpi _{ij}: \mathcal {C}^{\prime }_{ij}\rightarrow \mathcal {C}$
of
$\varpi _{ij}: \mathcal {C}^{\prime }_{ij}\rightarrow \mathcal {C}$
of
![]() $\mathcal {C}=C_1+C_2$
as explained above by taking
$\mathcal {C}=C_1+C_2$
as explained above by taking
![]() $\mathcal {B}=T_i+T_j$
and
$\mathcal {B}=T_i+T_j$
and
![]() $D=P_{i1}+P_{i2}+P_{j1}+P_{j2}$
. Note again that the covers
$D=P_{i1}+P_{i2}+P_{j1}+P_{j2}$
. Note again that the covers
![]() $\varpi _{ij}$
and
$\varpi _{ij}$
and
![]() $\pi _{ij}|_{\pi _{ij}^{-1}(\mathcal {C})}$
of
$\pi _{ij}|_{\pi _{ij}^{-1}(\mathcal {C})}$
of
![]() $\mathcal {C}$
are isomorphic outside the points
$\mathcal {C}$
are isomorphic outside the points
![]() $\{P_{i1}, P_{i2}, P_{j1}, P_{j2}\}$
. Now let
$\{P_{i1}, P_{i2}, P_{j1}, P_{j2}\}$
. Now let
![]() $S_{ij}\rightarrow S_{ij}^\prime $
be the canonical resolution of
$S_{ij}\rightarrow S_{ij}^\prime $
be the canonical resolution of
![]() $\pi _{ij}$
. Then
$\pi _{ij}$
. Then
![]() $S_{ij}\cong \Sigma _2$
, where
$S_{ij}\cong \Sigma _2$
, where
![]() $\Sigma _2$
is the Hirzebruch surface of degree 2, and we have the following diagram:
$\Sigma _2$
is the Hirzebruch surface of degree 2, and we have the following diagram:

where
![]() $\sigma _{ij}$
is the blow-up at the intersection point
$\sigma _{ij}$
is the blow-up at the intersection point
![]() $T_i\cap T_j$
. The pencil of lines through the intersection point induces the ruling of
$T_i\cap T_j$
. The pencil of lines through the intersection point induces the ruling of
![]() $\Sigma _2$
. It can be readily checked that the preimages
$\Sigma _2$
. It can be readily checked that the preimages
![]() $C_1^\pm , C_2^\pm $
of
$C_1^\pm , C_2^\pm $
of
![]() $C_1, C_2$
in
$C_1, C_2$
in
![]() $S_{ij}$
are all linearly equivalent to
$S_{ij}$
are all linearly equivalent to
![]() $2F+\Delta _0$
, since
$2F+\Delta _0$
, since
![]() $C_i^++C_i^-\sim 4F+2\Delta _0$
and
$C_i^++C_i^-\sim 4F+2\Delta _0$
and
![]() $C_i^{\pm }\cdot \Delta _0=0$
, where F is the divisor class of fibers and
$C_i^{\pm }\cdot \Delta _0=0$
, where F is the divisor class of fibers and
![]() $\Delta _0$
is the unique negative section with
$\Delta _0$
is the unique negative section with
![]() $\Delta _0^2=-2$
. Hence,
$\Delta _0^2=-2$
. Hence,
![]() $C_1^+\cdot C_2^+=C_1^+\cdot C_2^-=2$
and the splitting type of
$C_1^+\cdot C_2^+=C_1^+\cdot C_2^-=2$
and the splitting type of
![]() $(C_1, C_2; \mathcal {B})$
is
$(C_1, C_2; \mathcal {B})$
is
![]() $(2, 2)$
since
$(2, 2)$
since
![]() $C_i^{\pm }\cdot \Delta _0=0$
. Also, since
$C_i^{\pm }\cdot \Delta _0=0$
. Also, since
![]() $\varpi _{ij}$
and
$\varpi _{ij}$
and
![]() $\pi _{ij}|_{\pi _{ij}^{-1}(\mathcal {C})}$
are isomorphic outside
$\pi _{ij}|_{\pi _{ij}^{-1}(\mathcal {C})}$
are isomorphic outside
![]() $P_{ik}$
, this implies that the gluing data of
$P_{ik}$
, this implies that the gluing data of
![]() $\varpi _{ij}:\mathcal {C}^{\prime }_{ij}\rightarrow \mathcal {C}$
and
$\varpi _{ij}:\mathcal {C}^{\prime }_{ij}\rightarrow \mathcal {C}$
and
![]() $\mathcal {F}_{ij}:=\mathcal {O}_{\mathbb {P}^2}(1)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-P_{i1}-P_{i2}-P_{j1}-P_{j2})$
is
$\mathcal {F}_{ij}:=\mathcal {O}_{\mathbb {P}^2}(1)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-P_{i1}-P_{i2}-P_{j1}-P_{j2})$
is
![]() $(+,+,-,-)$
for a suitable choice of labels on the nodes
$(+,+,-,-)$
for a suitable choice of labels on the nodes
![]() $C_1\cap C_2$
. Note again that changing all of the signs in the gluing data gives isomorphic covers/sheaves, so the data
$C_1\cap C_2$
. Note again that changing all of the signs in the gluing data gives isomorphic covers/sheaves, so the data
![]() $(+, +, -, -)$
and
$(+, +, -, -)$
and
![]() $(-, -, +, +)$
give equivalent covers/sheaves. Let
$(-, -, +, +)$
give equivalent covers/sheaves. Let
![]() $Q_1, Q_2, Q_3, Q_4$
be the nodes of
$Q_1, Q_2, Q_3, Q_4$
be the nodes of
![]() $C_1+C_2$
and suppose that the gluing data of
$C_1+C_2$
and suppose that the gluing data of
![]() $\mathcal {F}_{12}$
is
$\mathcal {F}_{12}$
is
![]() $(+, +, -, -)$
for
$(+, +, -, -)$
for
![]() $(Q_1, Q_2, Q_3, Q_4)$
in this order. Since
$(Q_1, Q_2, Q_3, Q_4)$
in this order. Since
![]() $\mathcal {F}_{12}\otimes \mathcal {F}_{13}\cong \mathcal {F}_{23}$
and all of these sheaves have two “
$\mathcal {F}_{12}\otimes \mathcal {F}_{13}\cong \mathcal {F}_{23}$
and all of these sheaves have two “
![]() $+$
”s and two “
$+$
”s and two “
![]() $-$
”s in the gluing data and are nontrivial, we can assume that
$-$
”s in the gluing data and are nontrivial, we can assume that
![]() $\mathcal {F}_{12}, \mathcal {F}_{13}, \mathcal {F}_{23}$
are all distinct and the gluing data of
$\mathcal {F}_{12}, \mathcal {F}_{13}, \mathcal {F}_{23}$
are all distinct and the gluing data of
![]() $\mathcal {F}_{13}$
is
$\mathcal {F}_{13}$
is
![]() $(+, -, +, -)$
and the gluing data of
$(+, -, +, -)$
and the gluing data of
![]() $\mathcal {F}_{23}$
is
$\mathcal {F}_{23}$
is
![]() $(-, +, +, -)$
, after changing the labels of
$(-, +, +, -)$
, after changing the labels of
![]() $Q_3, Q_4$
if necessary. By the same argument, each triple
$Q_3, Q_4$
if necessary. By the same argument, each triple
![]() $\mathcal {F}_{ij}, \mathcal {F}_{jk}, \mathcal {F}_{ik}$
,
$\mathcal {F}_{ij}, \mathcal {F}_{jk}, \mathcal {F}_{ik}$
,
![]() $\{i, j, k\}\subset \{1, 2, 3, 4\}$
gives all three possible distinct invertible sheaves with two “
$\{i, j, k\}\subset \{1, 2, 3, 4\}$
gives all three possible distinct invertible sheaves with two “
![]() $+$
”s and two “
$+$
”s and two “
![]() $-$
”s in the gluing data. Moreover,
$-$
”s in the gluing data. Moreover,
![]() $\mathcal {F}_{ij}\not \cong \mathcal {F}_{ik}$
if
$\mathcal {F}_{ij}\not \cong \mathcal {F}_{ik}$
if
![]() $j\not =k$
. Furthermore, this implies that
$j\not =k$
. Furthermore, this implies that
![]() $\mathcal {F}_{ij}\cong \mathcal {F}_{kl}$
for
$\mathcal {F}_{ij}\cong \mathcal {F}_{kl}$
for
![]() $\{i, j, k, l\}=\{1, 2, 3, 4\}$
, as
$\{i, j, k, l\}=\{1, 2, 3, 4\}$
, as
![]() $\mathcal {F}_{kl}$
cannot be isomorphic to
$\mathcal {F}_{kl}$
cannot be isomorphic to
![]() $\mathcal {F}_{ik}$
or
$\mathcal {F}_{ik}$
or
![]() $\mathcal {F}_{jk}$
and must be isomorphic to the remaining
$\mathcal {F}_{jk}$
and must be isomorphic to the remaining
![]() $\mathcal {F}_{ij}$
in the triple
$\mathcal {F}_{ij}$
in the triple
![]() $\mathcal {F}_{ij}, \mathcal {F}_{jk}, \mathcal {F}_{ik}$
.
$\mathcal {F}_{ij}, \mathcal {F}_{jk}, \mathcal {F}_{ik}$
.
Remark 3.5 In Example 3.4,
![]() $\mathcal {O}_{\mathcal {C}}(2P_{i1}+2P_{i2})\cong \mathcal {L}|_{\mathcal {C}}\cong \omega _{\mathcal {C}}$
, where
$\mathcal {O}_{\mathcal {C}}(2P_{i1}+2P_{i2})\cong \mathcal {L}|_{\mathcal {C}}\cong \omega _{\mathcal {C}}$
, where
![]() $\omega _{\mathcal {C}}$
is the dualizing sheaf of
$\omega _{\mathcal {C}}$
is the dualizing sheaf of
![]() $\mathcal {C}$
. Hence,
$\mathcal {C}$
. Hence,
![]() $\mathcal {O}_{\mathcal {C}}(P_{i1}+P_{i2})$
is a theta characteristic of
$\mathcal {O}_{\mathcal {C}}(P_{i1}+P_{i2})$
is a theta characteristic of
![]() $\mathcal {C}$
(see [Reference Harris11]). Now,
$\mathcal {C}$
(see [Reference Harris11]). Now,
![]() ${\mathcal {F}_{ij}=\mathcal {L}|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-P_{i1}-P_{i2}-P_{j1}-P_{j2})\cong \mathcal {O}_{\mathcal {C}}((P_{i1}+P_{i2})-(P_{j1}+P_{j2}))}$
and is nothing but the difference between the odd theta characteristics
${\mathcal {F}_{ij}=\mathcal {L}|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-P_{i1}-P_{i2}-P_{j1}-P_{j2})\cong \mathcal {O}_{\mathcal {C}}((P_{i1}+P_{i2})-(P_{j1}+P_{j2}))}$
and is nothing but the difference between the odd theta characteristics
![]() $\mathcal {O}_{\mathcal {C}}(P_{i1}+P_{i2})$
and
$\mathcal {O}_{\mathcal {C}}(P_{i1}+P_{i2})$
and
![]() $\mathcal {O}_{\mathcal {C}}(P_{j1}+P_{j2})$
.
$\mathcal {O}_{\mathcal {C}}(P_{j1}+P_{j2})$
.
Remark 3.6 Since
![]() $\mathcal {F}_{ij}\cong \mathcal {F}_{kl}$
, we have
$\mathcal {F}_{ij}\cong \mathcal {F}_{kl}$
, we have
![]() $ \mathcal {F}_{ij}\otimes \mathcal {F}_{kl}\cong \mathcal {O}_{\mathcal {C}}, $
which gives
$ \mathcal {F}_{ij}\otimes \mathcal {F}_{kl}\cong \mathcal {O}_{\mathcal {C}}, $
which gives
 $$\begin{align*}\mathcal{O}_{\mathcal{C}}\left(\sum_{i=1}^4(P_{i1}+P_{i2})\right)\cong \mathcal{O}_{\mathbb{P}^2}(2)|_{\mathcal{C}}.\end{align*}$$
$$\begin{align*}\mathcal{O}_{\mathcal{C}}\left(\sum_{i=1}^4(P_{i1}+P_{i2})\right)\cong \mathcal{O}_{\mathbb{P}^2}(2)|_{\mathcal{C}}.\end{align*}$$
This implies Salmon’s theorem – namely, the eight points of tangency
![]() $\{P_{11}, \ldots , P_{42}\}$
lie on a conic. See [Reference Harris11, Theorem 3.3] for details. Also, another different proof can be found in [Reference Masuya12, Corollary 1.5].
$\{P_{11}, \ldots , P_{42}\}$
lie on a conic. See [Reference Harris11, Theorem 3.3] for details. Also, another different proof can be found in [Reference Masuya12, Corollary 1.5].
4 Unramified double covers of two conics induced by Poncelet transverses
Let
![]() $C_1, C_2$
be smooth conics intersecting transversely as before. In this section, we consider the unramified double covers of
$C_1, C_2$
be smooth conics intersecting transversely as before. In this section, we consider the unramified double covers of
![]() $\mathcal {C}=C_1+C_2$
induced by n-sided Poncelet transverses. We note that it is known that there exist
$\mathcal {C}=C_1+C_2$
induced by n-sided Poncelet transverses. We note that it is known that there exist
![]() $C_1, C_2$
intersecting transversely that admit an n-sided Poncelet transverse for any
$C_1, C_2$
intersecting transversely that admit an n-sided Poncelet transverse for any
![]() $n\geq 3$
(see [Reference Barth and Bauer9]).
$n\geq 3$
(see [Reference Barth and Bauer9]).
4.1 Degenerated Poncelet transverses
First, we study degenerated n-sided Poncelet transverses. Let
![]() $C_1, C_2$
be smooth conics intersecting transversely with an n-sided Poncelet transverse
$C_1, C_2$
be smooth conics intersecting transversely with an n-sided Poncelet transverse
![]() $\sqcap _{n}: (P_1, L_1), \ldots , (P_n, L_n)$
. If
$\sqcap _{n}: (P_1, L_1), \ldots , (P_n, L_n)$
. If
![]() $\sqcap _n$
is degenerated, there exists a pair
$\sqcap _n$
is degenerated, there exists a pair
![]() $(P_i, L_i)$
,
$(P_i, L_i)$
,
![]() $(P_j, L_j)$
(
$(P_j, L_j)$
(
![]() $i\not =j$
) such that either
$i\not =j$
) such that either
![]() $P_i=P_j$
or
$P_i=P_j$
or
![]() $L_i=L_j$
. We can assume
$L_i=L_j$
. We can assume
![]() $i<j$
without loss of generality. Note that
$i<j$
without loss of generality. Note that
![]() $(P_i, L_i)\not =(P_j, L_j)$
by the minimality of the period n.
$(P_i, L_i)\not =(P_j, L_j)$
by the minimality of the period n.
-
• Suppose
 $P_i=P_j$
. If
$P_i=P_j$
. If
 $P_i\in C_2$
, then there is only one unique line L passing through
$P_i\in C_2$
, then there is only one unique line L passing through
 $P_i$
and tangent to
$P_i$
and tangent to
 $C_2$
. Then
$C_2$
. Then
 $L_i=L_j$
, which contradicts the minimality of the period. Hence, we can assume
$L_i=L_j$
, which contradicts the minimality of the period. Hence, we can assume
 $P_i\not \in C_2$
and that there exist two distinct tangent lines
$P_i\not \in C_2$
and that there exist two distinct tangent lines
 $L_i'$
,
$L_i'$
,
 $L_i"$
, of
$L_i"$
, of
 $C_2$
passing through
$C_2$
passing through
 $P_i$
. Since
$P_i$
. Since
 $L_i\not =L_j$
by the minimality of the period, we have
$L_i\not =L_j$
by the minimality of the period, we have
 $\{L_i, L_j\}=\{L^{\prime }_i, L_i"\}$
. This implies that
$\{L_i, L_j\}=\{L^{\prime }_i, L_i"\}$
. This implies that
 $(P_i, L_i)$
,
$(P_i, L_i)$
,
 $(P_j, L_j)$
are consecutive in the sequence and are of the form
$(P_j, L_j)$
are consecutive in the sequence and are of the form
 $(P_i, L_i)$
,
$(P_i, L_i)$
,
 $(P_{i}, L_{i+1})$
; this can only occur if
$(P_{i}, L_{i+1})$
; this can only occur if
 $L_i$
is a tangent line of
$L_i$
is a tangent line of
 $C_1$
and hence a bitangent line to
$C_1$
and hence a bitangent line to
 $C_1+C_2$
.
$C_1+C_2$
. -
• Suppose
 $L_i=L_j$
. Then since
$L_i=L_j$
. Then since
 $P_i$
and
$P_i$
and
 $P_j$
lie on the same line, again we can assume that
$P_j$
lie on the same line, again we can assume that
 $(P_i, L_i)$
,
$(P_i, L_i)$
,
 $(P_j, L_j)$
are consecutive in the sequence and are of the form
$(P_j, L_j)$
are consecutive in the sequence and are of the form
 $(P_i, L_i)$
,
$(P_i, L_i)$
,
 $(P_{i+1}, L_i)$
. If
$(P_{i+1}, L_i)$
. If
 $P_{i+1} \not \in C_2$
, then there exist two distinct lines through
$P_{i+1} \not \in C_2$
, then there exist two distinct lines through
 $P_{i+1}$
tangent to
$P_{i+1}$
tangent to
 $C_2$
and
$C_2$
and
 $L_i\not =L_{i+1}$
, which contradicts
$L_i\not =L_{i+1}$
, which contradicts
 $L_i=L_j$
. Hence,
$L_i=L_j$
. Hence,
 $P_{i+1}\in C_2$
, and
$P_{i+1}\in C_2$
, and
 $L_i=L_j$
is the unique tangent line of
$L_i=L_j$
is the unique tangent line of
 $C_2$
passing through
$C_2$
passing through
 $P_{i+1}$
.
$P_{i+1}$
.
In both cases, the sequence is “reflected” at
![]() $(P_i, L_i)$
,
$(P_i, L_i)$
,
![]() $(P_{i+1}, L_{i+1})$
, and the points and lines leading up to this position appear in reverse order leading away. In order to be periodic, the sequence must be “reflected” once more to come back to
$(P_{i+1}, L_{i+1})$
, and the points and lines leading up to this position appear in reverse order leading away. In order to be periodic, the sequence must be “reflected” once more to come back to
![]() $(P_i, L_i)$
,
$(P_i, L_i)$
,
![]() $(P_{i+1}, L_{i+1})$
. A “reflection” only occurs in the above two cases; hence, if
$(P_{i+1}, L_{i+1})$
. A “reflection” only occurs in the above two cases; hence, if
![]() $\sqcap _n$
is degenerated, then it must contain exactly two lines that are either a bitangent line or a line tangent to
$\sqcap _n$
is degenerated, then it must contain exactly two lines that are either a bitangent line or a line tangent to
![]() $C_2$
at a point of
$C_2$
at a point of
![]() $C_1\cap C_2$
. A bitangent line will appear in the whole sequence only once, and the other lines will appear exactly twice. Therefore, we have the following:
$C_1\cap C_2$
. A bitangent line will appear in the whole sequence only once, and the other lines will appear exactly twice. Therefore, we have the following:
-
• If
 $n=2m$
, two cases can occur. In the first case,
$n=2m$
, two cases can occur. In the first case,
 $\sqcap _{2m}$
has two bitangent lines. The set of vertices consists of m distinct points, and the set of edges consists of two bitangents and
$\sqcap _{2m}$
has two bitangent lines. The set of vertices consists of m distinct points, and the set of edges consists of two bitangents and
 $m-1$
general lines. In this case, the transverse is of the form where
$m-1$
general lines. In this case, the transverse is of the form where $$\begin{align*}(P_1, L_1), \ldots, (P_m,L_m), (P_{m}, L_{m-1}),(P_{m-1}, L_{m-2}),\ldots, (P_{1}, L_{0}),\end{align*}$$
$$\begin{align*}(P_1, L_1), \ldots, (P_m,L_m), (P_{m}, L_{m-1}),(P_{m-1}, L_{m-2}),\ldots, (P_{1}, L_{0}),\end{align*}$$
 $L_0$
and
$L_0$
and
 $L_m$
are the bitangent lines, under a suitable choice of labels (see Figure 1 (a)). In the second case,
$L_m$
are the bitangent lines, under a suitable choice of labels (see Figure 1 (a)). In the second case,
 $\sqcap _{2m}$
has two lines each tangent to
$\sqcap _{2m}$
has two lines each tangent to
 $C_2$
at a point of
$C_2$
at a point of
 $C_1\cap C_2$
. In this case, the set of vertices consists of
$C_1\cap C_2$
. In this case, the set of vertices consists of
 $m+1$
distinct points, and the set of edges consists of the two lines each tangent to
$m+1$
distinct points, and the set of edges consists of the two lines each tangent to
 $C_2$
at a point of
$C_2$
at a point of
 $C_1\cap C_2$
and
$C_1\cap C_2$
and
 $m-2$
general lines. In this case, the transverse is of the form where
$m-2$
general lines. In this case, the transverse is of the form where $$\begin{align*}(P_1, L_1), \ldots, (P_m, L_m), (P_{m+1}, L_m), (P_m, L_{m-1}), \ldots, (P_3, L_2), (P_2, L_1), \end{align*}$$
$$\begin{align*}(P_1, L_1), \ldots, (P_m, L_m), (P_{m+1}, L_m), (P_m, L_{m-1}), \ldots, (P_3, L_2), (P_2, L_1), \end{align*}$$
 $P_1, P_{m+1}\in C_1\cap C_2$
and
$P_1, P_{m+1}\in C_1\cap C_2$
and
 $L_1$
and
$L_1$
and
 $L_m$
are the lines tangent to
$L_m$
are the lines tangent to
 $C_2$
at a point of
$C_2$
at a point of
 ${C_1\cap C_2}$
, under a suitable choice of labels (see Figure 1 (b)). There exist two degenerated
${C_1\cap C_2}$
, under a suitable choice of labels (see Figure 1 (b)). There exist two degenerated
 $2m$
-sided transverses of each kind.
$2m$
-sided transverses of each kind.
Figure 1 Three types of degenerated n-sided Poncelet transverses.
-
• If
 $n=2m+1$
,
$n=2m+1$
,
 $\sqcap _{2m+1}$
will have one bitangent line and one line tangent to
$\sqcap _{2m+1}$
will have one bitangent line and one line tangent to
 $C_2$
at a point of
$C_2$
at a point of
 $C_1\cap C_2$
. The set of vertices consists of
$C_1\cap C_2$
. The set of vertices consists of
 $m+1$
distinct points, and the set of edges consists of the bitangent line, the line tangent to
$m+1$
distinct points, and the set of edges consists of the bitangent line, the line tangent to
 $C_2$
at a point in
$C_2$
at a point in
 $C_1\cap C_2$
, and
$C_1\cap C_2$
, and
 $m-1$
general lines. The transverse is of the form where
$m-1$
general lines. The transverse is of the form where $$\begin{align*}(P_1, L_1), \ldots, (P_m, L_{m}), (P_{m+1}, L_{m}),(P_{m}, L_{m-1}) \ldots, (P_1, L_0), \end{align*}$$
$$\begin{align*}(P_1, L_1), \ldots, (P_m, L_{m}), (P_{m+1}, L_{m}),(P_{m}, L_{m-1}) \ldots, (P_1, L_0), \end{align*}$$
 $L_0$
is the bitangent line,
$L_0$
is the bitangent line,
 $P_{m+1}\in C_1\cap C_2$
, and
$P_{m+1}\in C_1\cap C_2$
, and
 $L_{m}$
is the line tangent to
$L_{m}$
is the line tangent to
 $C_2$
at
$C_2$
at
 $P_{m+1}$
, under a suitable choice of labels (see Figure 1 (c)). There exist four degenerated
$P_{m+1}$
, under a suitable choice of labels (see Figure 1 (c)). There exist four degenerated
 $2m+1$
-sided transverses of this kind.
$2m+1$
-sided transverses of this kind.
4.2 Deformation and degeneration of Poncelet transverses and line bundles of order two
Let
![]() $C_1, C_2$
be smooth conics intersecting transversely admitting a
$C_1, C_2$
be smooth conics intersecting transversely admitting a
![]() $2m$
-sided Poncelet transverse
$2m$
-sided Poncelet transverse
![]() $\sqcap _{2m}$
. In this subsection, we consider double covers of
$\sqcap _{2m}$
. In this subsection, we consider double covers of
![]() $\mathbb {P}^2$
branched along the lines of
$\mathbb {P}^2$
branched along the lines of
![]() $\sqcap _{2m}$
and its relation with the induced unramified double covers of
$\sqcap _{2m}$
and its relation with the induced unramified double covers of
![]() $\mathcal {C}=C_1+C_2$
. We study the unramified double cover through a degeneration argument, where we deform general
$\mathcal {C}=C_1+C_2$
. We study the unramified double cover through a degeneration argument, where we deform general
![]() $2m$
-sided Poncelet transverses to a degenerated transverse with two bitangent lines. Note that we do not consider the other type of degeneration, as it will not induce an unramified double cover of
$2m$
-sided Poncelet transverses to a degenerated transverse with two bitangent lines. Note that we do not consider the other type of degeneration, as it will not induce an unramified double cover of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Let
![]() $\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a general nondegenerated Poncelet transverse and let
$\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a general nondegenerated Poncelet transverse and let
![]() $\mathcal {P}_{2m}:=\sum _{i=1}^{2m}L_i$
. Let
$\mathcal {P}_{2m}:=\sum _{i=1}^{2m}L_i$
. Let
![]() $Q_i=C_2\cap L_i$
be the tangent points of
$Q_i=C_2\cap L_i$
be the tangent points of
![]() $L_i$
and
$L_i$
and
![]() $C_2$
(
$C_2$
(
![]() $i=1, \ldots , 2m$
). Let
$i=1, \ldots , 2m$
). Let
![]() $\pi _{\mathcal {P}}: S'\rightarrow \mathbb {P}^2$
be the double cover branched along
$\pi _{\mathcal {P}}: S'\rightarrow \mathbb {P}^2$
be the double cover branched along
![]() $\mathcal {P}_{2m}$
. Then, since
$\mathcal {P}_{2m}$
. Then, since
![]() $\mathcal {P}_{2m}$
has degree
$\mathcal {P}_{2m}$
has degree
![]() $2m$
and
$2m$
and
![]() $\mathcal {P}_{2m}|_{\mathcal {C}}=2(\sum _{i=1}^{2m} P_i+\sum _{j=1}^{2m} Q_j)$
,
$\mathcal {P}_{2m}|_{\mathcal {C}}=2(\sum _{i=1}^{2m} P_i+\sum _{j=1}^{2m} Q_j)$
,
![]() $\pi _{\mathcal {P}}$
induces an unramified double cover
$\pi _{\mathcal {P}}$
induces an unramified double cover
![]() $\varpi _{\mathcal {P}}: \mathcal {C}_{\mathcal {P}}'\rightarrow \mathcal {C}$
as in Section 3. The line bundle of order
$\varpi _{\mathcal {P}}: \mathcal {C}_{\mathcal {P}}'\rightarrow \mathcal {C}$
as in Section 3. The line bundle of order
![]() $2$
on
$2$
on
![]() $\mathcal {C}$
defining
$\mathcal {C}$
defining
![]() $\mathcal {C}^{\prime }_{\mathcal {P}}$
is
$\mathcal {C}^{\prime }_{\mathcal {P}}$
is
![]() $\mathcal {F}_{\mathcal {P}}:=\mathcal {O}_{\mathbb {P}^2}(m)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-\sum _{i=1}^{2m} P_i-\sum _{j=1}^{2m} Q_j)$
. We are interested in the structure of this double cover
$\mathcal {F}_{\mathcal {P}}:=\mathcal {O}_{\mathbb {P}^2}(m)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-\sum _{i=1}^{2m} P_i-\sum _{j=1}^{2m} Q_j)$
. We are interested in the structure of this double cover
![]() $\mathcal {C}^{\prime }_{\mathcal {P}}$
. By Theorem 1.1 (Poncelet’s closure theorem), when we continuously move
$\mathcal {C}^{\prime }_{\mathcal {P}}$
. By Theorem 1.1 (Poncelet’s closure theorem), when we continuously move
![]() $P_1$
on
$P_1$
on
![]() $C_1$
to a point
$C_1$
to a point
![]() $P'$
that is a tangent point of a bitangent line of
$P'$
that is a tangent point of a bitangent line of
![]() $\mathcal {C}=C_1+C_2$
, the
$\mathcal {C}=C_1+C_2$
, the
![]() $2m$
-sided Poncelet transverse originating at
$2m$
-sided Poncelet transverse originating at
![]() $P_1$
continuously deforms along with
$P_1$
continuously deforms along with
![]() $P_1$
to the degenerated Poncelet transverse originating at
$P_1$
to the degenerated Poncelet transverse originating at
![]() $P'$
. Let
$P'$
. Let
![]() $P^{\prime }_1=P'$
and let
$P^{\prime }_1=P'$
and let
be the degenerated transverse originating at
![]() $P_1'$
, where
$P_1'$
, where
![]() $L_0'$
and
$L_0'$
and
![]() $L_{m}'$
are bitangent lines of
$L_{m}'$
are bitangent lines of
![]() $\mathcal {C}=C_1+C_2$
. Let
$\mathcal {C}=C_1+C_2$
. Let
![]() $Q_i'=L^{\prime }_i\cap C_2$
(
$Q_i'=L^{\prime }_i\cap C_2$
(
![]() $i=0, \ldots , m$
) be the tangent points of
$i=0, \ldots , m$
) be the tangent points of
![]() $L^{\prime }_i$
and
$L^{\prime }_i$
and
![]() $C_2$
. The correspondence between the lines, vertices, and tangent points under the degeneration are as follows:
$C_2$
. The correspondence between the lines, vertices, and tangent points under the degeneration are as follows:
 $$ \begin{align*} P_i, P_{2m+1-i} &\rightarrow P^{\prime}_i \quad (i=1,\ldots, m),\\ L_i, L_{2m-i} &\rightarrow L^{\prime}_i \quad (i=1, \ldots, m-1), \quad L_m \rightarrow L^{\prime}_m, \quad L_{2m} \rightarrow L^{\prime}_0\\ Q_i, Q_{2m-i} &\rightarrow Q^{\prime}_i \quad (i=1, \ldots, m-1), \quad Q_m \rightarrow Q^{\prime}_m, \quad Q_{2m} \rightarrow Q^{\prime}_0 \end{align*} $$
$$ \begin{align*} P_i, P_{2m+1-i} &\rightarrow P^{\prime}_i \quad (i=1,\ldots, m),\\ L_i, L_{2m-i} &\rightarrow L^{\prime}_i \quad (i=1, \ldots, m-1), \quad L_m \rightarrow L^{\prime}_m, \quad L_{2m} \rightarrow L^{\prime}_0\\ Q_i, Q_{2m-i} &\rightarrow Q^{\prime}_i \quad (i=1, \ldots, m-1), \quad Q_m \rightarrow Q^{\prime}_m, \quad Q_{2m} \rightarrow Q^{\prime}_0 \end{align*} $$
Table 1
![]() $C_1+C_2$
and the degeneration of a
$C_1+C_2$
and the degeneration of a
![]() $6$
-sided Poncelet transverse.
$6$
-sided Poncelet transverse.

Here, the points
![]() $P_1, \ldots , P_{2m}$
and
$P_1, \ldots , P_{2m}$
and
![]() $Q_1, \ldots , Q_{2m}$
are continuously deformed on the smooth part of
$Q_1, \ldots , Q_{2m}$
are continuously deformed on the smooth part of
![]() $\mathcal {C}$
, while preserving the condition that
$\mathcal {C}$
, while preserving the condition that
![]() $\mathcal {O}_{\mathbb {P}^2}(m)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-\sum _{i=1}^{2m} P_i-\sum _{j=1}^{2m} Q_j)$
is of order
$\mathcal {O}_{\mathbb {P}^2}(m)|_{\mathcal {C}}\otimes \mathcal {O}_{\mathcal {C}}(-\sum _{i=1}^{2m} P_i-\sum _{j=1}^{2m} Q_j)$
is of order
![]() $2$
. However, the set of invertible sheaves of order
$2$
. However, the set of invertible sheaves of order
![]() $2$
of
$2$
of
![]() $\mathcal {C}$
is isomorphic to
$\mathcal {C}$
is isomorphic to
![]() $(\mathbb {Z}/2\mathbb {Z})^{\oplus 3}$
(see the discussions in Section 3 or [Reference Harris11, Section 3, 3a]) and is finite and discrete. By Lemma 3.2, the gluing data of the induced unramified double cover is constant under the deformation; hence, by Lemma 3.3, the gluing data of the invertible sheaves of order 2 must also be constant under the deformation, and the isomorphism classes of the sheaves
$(\mathbb {Z}/2\mathbb {Z})^{\oplus 3}$
(see the discussions in Section 3 or [Reference Harris11, Section 3, 3a]) and is finite and discrete. By Lemma 3.2, the gluing data of the induced unramified double cover is constant under the deformation; hence, by Lemma 3.3, the gluing data of the invertible sheaves of order 2 must also be constant under the deformation, and the isomorphism classes of the sheaves
![]() $\mathcal {F}_{\mathcal {P}}$
must be constant. Hence, we have
$\mathcal {F}_{\mathcal {P}}$
must be constant. Hence, we have
 $$ \begin{align*} \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes&\mathcal{O}_{\mathcal{C}}\left(-\sum_{i=1}^{2m} P_i-\sum_{j=1}^{2m} Q_j\right)\\ &\cong \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes \mathcal{O}_{\mathcal{C}}\left(-\sum _{i=1}^m 2P^{\prime}_i-\sum_{j=1}^{m-1} 2Q^{\prime}_j-Q^{\prime}_0-Q^{\prime}_{m}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes&\mathcal{O}_{\mathcal{C}}\left(-\sum_{i=1}^{2m} P_i-\sum_{j=1}^{2m} Q_j\right)\\ &\cong \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes \mathcal{O}_{\mathcal{C}}\left(-\sum _{i=1}^m 2P^{\prime}_i-\sum_{j=1}^{m-1} 2Q^{\prime}_j-Q^{\prime}_0-Q^{\prime}_{m}\right). \end{align*} $$
Furthermore, since
![]() $(L_1'+\cdots +L_{m-1}')|_{\mathcal {C}}=P_1'+\sum _{i=2}^{m-1}2P_i'+P_m'+\sum _{j=1}^{m-1} 2Q_j'$
and
$(L_1'+\cdots +L_{m-1}')|_{\mathcal {C}}=P_1'+\sum _{i=2}^{m-1}2P_i'+P_m'+\sum _{j=1}^{m-1} 2Q_j'$
and
![]() $\mathcal {O}_{\mathbb {P}_2}(m-1)|_{\mathcal {C}}\cong \mathcal {O}_{\mathcal {C}}(P_1'+\sum _{i=2}^{m-1}2P_i'+P_m'+\sum _{j=1}^{m-1} 2Q_j')$
, we have
$\mathcal {O}_{\mathbb {P}_2}(m-1)|_{\mathcal {C}}\cong \mathcal {O}_{\mathcal {C}}(P_1'+\sum _{i=2}^{m-1}2P_i'+P_m'+\sum _{j=1}^{m-1} 2Q_j')$
, we have
 $$ \begin{align*} \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes& \mathcal{O}_{\mathcal{C}}\left(-2\sum _{i=1}^m P^{\prime}_i-\sum_{j=1}^{m-1} 2Q^{\prime}_j-Q^{\prime}_0-Q^{\prime}_{m}\right)\\ &\cong \mathcal{O}_{\mathbb{P}^2}(1)|_{\mathcal{C}}\otimes \mathcal{O}_{\mathcal{C}}(- P^{\prime}_1-P^{\prime}_m-Q^{\prime}_0-Q^{\prime}_{m}). \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\mathbb{P}^2}(m)|_{\mathcal{C}}\otimes& \mathcal{O}_{\mathcal{C}}\left(-2\sum _{i=1}^m P^{\prime}_i-\sum_{j=1}^{m-1} 2Q^{\prime}_j-Q^{\prime}_0-Q^{\prime}_{m}\right)\\ &\cong \mathcal{O}_{\mathbb{P}^2}(1)|_{\mathcal{C}}\otimes \mathcal{O}_{\mathcal{C}}(- P^{\prime}_1-P^{\prime}_m-Q^{\prime}_0-Q^{\prime}_{m}). \end{align*} $$
The points
![]() $ P^{\prime }_1, Q^{\prime }_0$
are the tangent points of the bitangent line
$ P^{\prime }_1, Q^{\prime }_0$
are the tangent points of the bitangent line
![]() $L_0'$
, and the points
$L_0'$
, and the points
![]() $P^{\prime }_m,Q^{\prime }_{m}$
are the tangent points of the bitangent line
$P^{\prime }_m,Q^{\prime }_{m}$
are the tangent points of the bitangent line
![]() $L_{m}'$
. Hence, we see that the structures of
$L_{m}'$
. Hence, we see that the structures of
![]() $\mathcal {F}_{\mathcal {P}}$
and the associated unramified double cover
$\mathcal {F}_{\mathcal {P}}$
and the associated unramified double cover
![]() $\varpi _{\mathcal {P}}:\mathcal {C}^{\prime }_{\mathcal {P}}\rightarrow \mathcal {C}$
induced by
$\varpi _{\mathcal {P}}:\mathcal {C}^{\prime }_{\mathcal {P}}\rightarrow \mathcal {C}$
induced by
![]() $\pi _{\mathcal {P}}$
are identical to that of the double cover in Example 3.4 associated to the bitangent lines
$\pi _{\mathcal {P}}$
are identical to that of the double cover in Example 3.4 associated to the bitangent lines
![]() $L_0'+L_{m}'$
. Summing up these arguments, we have the following Lemma, where
$L_0'+L_{m}'$
. Summing up these arguments, we have the following Lemma, where
![]() $\varpi _{ij}$
is the unramified double cover of
$\varpi _{ij}$
is the unramified double cover of
![]() $\mathcal {C}$
induced by the double cover of
$\mathcal {C}$
induced by the double cover of
![]() $\mathbb {P}^2$
branched along
$\mathbb {P}^2$
branched along
![]() $T_i+T_j$
as defined in Example 3.4.
$T_i+T_j$
as defined in Example 3.4.
Lemma 4.1 Under the above settings and notation, let
![]() $T_1, T_2, T_3, T_4$
be the bitangent lines to
$T_1, T_2, T_3, T_4$
be the bitangent lines to
![]() $C_1, C_2$
labeled so that the pairs
$C_1, C_2$
labeled so that the pairs
![]() $T_1, T_2$
and
$T_1, T_2$
and
![]() $T_3, T_4$
each lie in the same degenerated
$T_3, T_4$
each lie in the same degenerated
![]() $2m$
-sided transverse. Then the unramified double covers
$2m$
-sided transverse. Then the unramified double covers
![]() $\varpi _{\mathcal {P}}$
,
$\varpi _{\mathcal {P}}$
,
![]() $\varpi _{12}$
,
$\varpi _{12}$
,
![]() $\varpi _{34}$
of
$\varpi _{34}$
of
![]() $\mathcal {C}=C_1+C_2$
are all isomorphic.
$\mathcal {C}=C_1+C_2$
are all isomorphic.
Remark 4.2 The isomorphism between
![]() $\varpi _{12}$
and
$\varpi _{12}$
and
![]() $\varpi _{34}$
has already been observed in Example 3.4, regardless of the existence of a
$\varpi _{34}$
has already been observed in Example 3.4, regardless of the existence of a
![]() $2m$
-sided Poncelet transverse.
$2m$
-sided Poncelet transverse.
5 Proof of Main Theorem
In this section, we prove Theorem 1.3. Let
![]() $C_1, C_2$
be smooth conics intersecting transversely that admit a
$C_1, C_2$
be smooth conics intersecting transversely that admit a
![]() $2m$
-sided Poncelet transverse. Let
$2m$
-sided Poncelet transverse. Let
![]() $T_1, T_2, T_3, T_4$
be bitangent lines of
$T_1, T_2, T_3, T_4$
be bitangent lines of
![]() $\mathcal {C}=C_1+C_2$
labeled so that the pairs
$\mathcal {C}=C_1+C_2$
labeled so that the pairs
![]() $T_1$
,
$T_1$
,
![]() $T_2$
and
$T_2$
and
![]() $T_3$
,
$T_3$
,
![]() $T_4$
each lie in the same degenerated
$T_4$
each lie in the same degenerated
![]() $2m$
-sided transverse. Let,
$2m$
-sided transverse. Let,
![]() $\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a nondegenerated transverse,
$\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a nondegenerated transverse,
![]() $\mathcal {P}_{2m}:=\sum _{i=1}^{2m}L_i$
and let
$\mathcal {P}_{2m}:=\sum _{i=1}^{2m}L_i$
and let
as in the Introduction.
Lemma 5.1 The combinatorial types
![]() $\mathop {\mathrm {Comb}}\nolimits (\mathcal {C}_{ij})$
of
$\mathop {\mathrm {Comb}}\nolimits (\mathcal {C}_{ij})$
of
![]() $\mathcal {C}_{ij}$
are the same for all
$\mathcal {C}_{ij}$
are the same for all
![]() $\{i, j\}\subset \{1, 2, 3, 4\}$
and any choice of nondegenerated transverse
$\{i, j\}\subset \{1, 2, 3, 4\}$
and any choice of nondegenerated transverse
![]() $\sqcap _{2m}$
.
$\sqcap _{2m}$
.
Proof Let
![]() $\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a nondegenerated transverse. Since all of the lines
$\sqcap _{2m}: (P_1, L_1), \ldots , (P_{2m}, L_{2m})$
be a nondegenerated transverse. Since all of the lines
![]() $L_1, \ldots , L_{2m}$
and
$L_1, \ldots , L_{2m}$
and
![]() $T_1, T_2, T_3, T_4$
are tangent lines of
$T_1, T_2, T_3, T_4$
are tangent lines of
![]() $\mathcal {C}_2$
, no three are concurrent. A line
$\mathcal {C}_2$
, no three are concurrent. A line
![]() $L_i$
and a bitangent
$L_i$
and a bitangent
![]() $T_j$
cannot intersect on
$T_j$
cannot intersect on
![]() $C_1$
, as we have assumed that
$C_1$
, as we have assumed that
![]() $L_i$
lies in a nondegenerated transverse and
$L_i$
lies in a nondegenerated transverse and
![]() $T_j$
lies in a degenerated transverse. They cannot intersect on
$T_j$
lies in a degenerated transverse. They cannot intersect on
![]() $C_2$
as well because they are distinct tangent lines of
$C_2$
as well because they are distinct tangent lines of
![]() $C_2$
. Hence, the combinatoral types are the same.
$C_2$
. Hence, the combinatoral types are the same.
Let
![]() $\mathcal {B}_{ij}:= \mathcal {P}_{2m}+T_i+T_j \quad (\{i, j\}\subset \{1, 2, 3, 4\})$
and let
$\mathcal {B}_{ij}:= \mathcal {P}_{2m}+T_i+T_j \quad (\{i, j\}\subset \{1, 2, 3, 4\})$
and let
![]() $\pi _{\mathcal {B}_{ij}}:S'\rightarrow \mathbb {P}^2$
be the double cover of
$\pi _{\mathcal {B}_{ij}}:S'\rightarrow \mathbb {P}^2$
be the double cover of
![]() $\mathbb {P}^2$
branched along
$\mathbb {P}^2$
branched along
![]() $\mathcal {B}_{ij}$
.
$\mathcal {B}_{ij}$
.
Lemma 5.2 Under the labeling above, the splitting type of
![]() $(C_1, C_2; \mathcal {B}_{ij})$
is
$(C_1, C_2; \mathcal {B}_{ij})$
is
![]() $(0,4)$
if
$(0,4)$
if
![]() $\{i, j\}=\{1, 2\}$
or
$\{i, j\}=\{1, 2\}$
or
![]() $\{3, 4\}$
and is
$\{3, 4\}$
and is
![]() $(2, 2)$
otherwise.
$(2, 2)$
otherwise.
Proof Since
![]() $\mathcal {B}_{ij}$
can be viewed as a sum of
$\mathcal {B}_{ij}$
can be viewed as a sum of
![]() $\mathcal {P}_{2m}$
and
$\mathcal {P}_{2m}$
and
![]() $(T_i+T_j)$
, by the discussions in Section 3, the cover
$(T_i+T_j)$
, by the discussions in Section 3, the cover
![]() $\pi _{\mathcal {B}_{ij}}$
induces an unramified double cover of
$\pi _{\mathcal {B}_{ij}}$
induces an unramified double cover of
![]() $\mathcal {C}=C_1+C_2$
, whose structure is given by the product of the covers
$\mathcal {C}=C_1+C_2$
, whose structure is given by the product of the covers
![]() $\varpi _{\mathcal {P}}$
of Section 4.2 and
$\varpi _{\mathcal {P}}$
of Section 4.2 and
![]() $\varpi _{ij}$
of Example 3.4. Then since
$\varpi _{ij}$
of Example 3.4. Then since
![]() $\varpi _{\mathcal {P}}$
,
$\varpi _{\mathcal {P}}$
,
![]() $\varpi _{12}$
,
$\varpi _{12}$
,
![]() $\varpi _{34}$
are isomorphic by Lemma 4.1,
$\varpi _{34}$
are isomorphic by Lemma 4.1,
![]() $\mathcal {B}_{ij}$
induces the trivial unramified double cover if
$\mathcal {B}_{ij}$
induces the trivial unramified double cover if
![]() $\{i, j\}=\{1, 2\}$
or
$\{i, j\}=\{1, 2\}$
or
![]() $\{3, 4\}$
, and otherwise induces a nontrivial unramified double cover with gluing data
$\{3, 4\}$
, and otherwise induces a nontrivial unramified double cover with gluing data
![]() $(+, +, -, -)$
for a suitable choice of labels of the nodes.
$(+, +, -, -)$
for a suitable choice of labels of the nodes.
Now, Lemma 5.1 and 5.2 together with Proposition 2.2 give the proof of Theorem 1.3.
Example 5.3 We give explicit equations of conics
![]() $C_1$
and
$C_1$
and
![]() $C_2$
admitting a 4-sided Poncelet transverse, and also an example of a Zariski pair of degree
$C_2$
admitting a 4-sided Poncelet transverse, and also an example of a Zariski pair of degree
![]() $10$
arising from the conics. We use
$10$
arising from the conics. We use
![]() $(x:y:z)$
as a system of homogeneous coordinates of
$(x:y:z)$
as a system of homogeneous coordinates of
![]() $\mathbb {P}^2$
. Let
$\mathbb {P}^2$
. Let
![]() $C_1$
and
$C_1$
and
![]() $C_2$
be two conics defined by the following equations:
$C_2$
be two conics defined by the following equations:
 $$ \begin{align*} C_1:& \ 4x^2-y^2-z^2=0, \\ C_2:& \ x^2-yz=0. \end{align*} $$
$$ \begin{align*} C_1:& \ 4x^2-y^2-z^2=0, \\ C_2:& \ x^2-yz=0. \end{align*} $$
The bitangent lines of
![]() $C_1+C_2$
are given as follows:
$C_1+C_2$
are given as follows:
 $$ \begin{align*} T_1:& \ \left(-\sqrt{-1}+\sqrt{3}\right) x -y - \left(\frac{1}{2}-\frac{\sqrt{-3}}{2}\right) z=0, \\ T_2: & \ \left(-\sqrt{-1}-\sqrt{3}\right) x - y - \left( \frac{1}{2}+\frac{\sqrt{-3}}{2}\right) z=0,\\ T_3: & \ \left(\sqrt{-1}-\sqrt{3}\right) x - y -\left(\frac{1}{2}-\frac{\sqrt{-3}}{2}\right) z=0,\\ T_4 : & \ \left(\sqrt{-1}+\sqrt{3}\right) x - y -\left(\frac{1}{2}+\frac{ \sqrt{-3}}{2}\right) z=0. \end{align*} $$
$$ \begin{align*} T_1:& \ \left(-\sqrt{-1}+\sqrt{3}\right) x -y - \left(\frac{1}{2}-\frac{\sqrt{-3}}{2}\right) z=0, \\ T_2: & \ \left(-\sqrt{-1}-\sqrt{3}\right) x - y - \left( \frac{1}{2}+\frac{\sqrt{-3}}{2}\right) z=0,\\ T_3: & \ \left(\sqrt{-1}-\sqrt{3}\right) x - y -\left(\frac{1}{2}-\frac{\sqrt{-3}}{2}\right) z=0,\\ T_4 : & \ \left(\sqrt{-1}+\sqrt{3}\right) x - y -\left(\frac{1}{2}+\frac{ \sqrt{-3}}{2}\right) z=0. \end{align*} $$
The tangent point of
![]() $C_1$
and
$C_1$
and
![]() $T_1$
is
$T_1$
is
![]() $P_1':=(\sqrt {-1}+\sqrt {3}:2+2\sqrt {-3}:4)$
. Let
$P_1':=(\sqrt {-1}+\sqrt {3}:2+2\sqrt {-3}:4)$
. Let
![]() $L_1'$
be the line defined by
$L_1'$
be the line defined by
![]() $2\sqrt {-1}x-y+z=0$
, which passes through
$2\sqrt {-1}x-y+z=0$
, which passes through
![]() $P_1'$
and is tangent to
$P_1'$
and is tangent to
![]() $C_2$
. The intersection point of
$C_2$
. The intersection point of
![]() $L_1'$
and
$L_1'$
and
![]() $C_1$
is
$C_1$
is
![]() $P_2'=(\sqrt {-1}-\sqrt {3}: 2-2\sqrt {-3}:4)$
, which coincides with the intersection point of
$P_2'=(\sqrt {-1}-\sqrt {3}: 2-2\sqrt {-3}:4)$
, which coincides with the intersection point of
![]() $T_2$
and
$T_2$
and
![]() $C_1$
. Now it is evident that the following sequence is a degenerated
$C_1$
. Now it is evident that the following sequence is a degenerated
![]() $4$
-sided Poncelet transverse:
$4$
-sided Poncelet transverse:
Hence, we have a
![]() $4$
-sided Poncelet transverse originating from any pair
$4$
-sided Poncelet transverse originating from any pair
![]() $(P_1,L_0)$
of a point
$(P_1,L_0)$
of a point
![]() $P_1\in C_1$
and a tangent line
$P_1\in C_1$
and a tangent line
![]() $L_0$
of
$L_0$
of
![]() $C_2$
passing through
$C_2$
passing through
![]() $P_1$
by Poncelet’s closure theorem. Note that since
$P_1$
by Poncelet’s closure theorem. Note that since
![]() $T_1$
and
$T_1$
and
![]() $T_2$
lie in a degenerated transverse,
$T_2$
lie in a degenerated transverse,
![]() $T_3$
and
$T_3$
and
![]() $T_4$
must also lie on the other degenerated transverse. By the above argument, if
$T_4$
must also lie on the other degenerated transverse. By the above argument, if
![]() $(i,j)\in \{(1,2), (3,4)\}$
and
$(i,j)\in \{(1,2), (3,4)\}$
and
![]() $(k,l)\notin \{(1,2), (3,4)\}$
, then the following pair of plane curves is a Zariski pair for the square
$(k,l)\notin \{(1,2), (3,4)\}$
, then the following pair of plane curves is a Zariski pair for the square
![]() $\mathcal {P}_4$
of any nondegenerated
$\mathcal {P}_4$
of any nondegenerated
![]() $4$
-sided Poncelet transverse:
$4$
-sided Poncelet transverse:
For example, the following
![]() $L_0,\dots ,L_3$
form a square
$L_0,\dots ,L_3$
form a square
![]() $\mathcal {P}_4$
of a nondegenerated
$\mathcal {P}_4$
of a nondegenerated
![]() $4$
-sided Poncelet transverse:
$4$
-sided Poncelet transverse:
 $$ \begin{align*} L_0:& \ z=0, & L_1: & \ 2x-y-z=0, \\ L_2:& \ y=0, & L_3: & \ 2x+y+z=0. \end{align*} $$
$$ \begin{align*} L_0:& \ z=0, & L_1: & \ 2x-y-z=0, \\ L_2:& \ y=0, & L_3: & \ 2x+y+z=0. \end{align*} $$