In glaciology, lowering of the surface of a melting snow layer is commonly accepted as a measure of ablation within the layer. For determining diurnal or even shorter period ablation rates, measurement of the fall in height of the snow surface as shown on ablation stakes, by ablatographs, or in the change in depth of holes punched in the snow is used almost exclusively. Yet even with extremely accurate measurements of the change in height with time of the snow surface, the problem of measuring the actual ablation, particularly for short periods, would be far from solved. The measurement of change in thickness of a snow layer is essentially a measure of the decrease in volume of the snow layer, whereas ablation, in its practical sense, is the decrease of mass within a snow layer. Setting the ablation equal to the decrease in thickness of a snow layer multiplied by a density factor implies that the snow density is constant both in time and space, an assumption for which there is little justification even for an over-ripe, melting snowpack.

The purpose in this discussion is to derive a simple expression from conservation of mass principles for changes of mass within a snow layer, and to point out the implications of the terms involved to the problem of measurements of ablation in a snow cover. In this discussion, ablation will be considered as the loss of water, in the liquid, solid or gaseous state, from a snow cover (corresponding to net ablation as defined by Ahlmann).

As a model for the analysis, a horizontal snow layer is considered of thickness h, and having a density ρ (mass of water per unit volume of snow), which is a function of depth z, though not necessarily a linear function. Then for a vertical column extending from the surface to the base of the snow cover and having unit cross-sectional area, the total mass of snow, M, within the column is given by:

(1)

For h and ρ functions of time, differentiation of (1) with respect to time yields:

(2)

where ρ_h is the snow density at the upper surface, h, of the snow layer.

If the discussion is restricted to cases in which 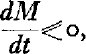equation (2) is then an expression for the rate of ablation per unit area in the snow layer. In this equation the term represents loss of mass at the snow surface through evaporation and downward percolation of water from the surface in excess of water reaching the surface through condensation and precipitation; and through surface lowering by compaction. The term 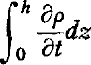represents changes of mass within the snow layer, being positive when sub-surface retention of water percolating downward from the surface and the effect of snow density increased by compaction exceed the flow of water out of the snow layer, and negative when these conditions are reversed.

In calculating ablation values from ablatograph or ablation stake data only the first term on the right in equation (2) is considered. This method of determining ablation is valid, therefore, only when the second term, associated with changes in snow density with time, is negligibly small or zero. Retention of melt water within a snow cover, which can lead to a significant increase of snow density with time, has been discussed by Ahlmann and Eriksson,Reference Ahlmann and Eriksson ¹ and Wallén.Reference Wallén ² In measurements of the ablation of snow on the Kársa Glacier, Wallén found values computed from sinking of the snow surface as measured on ablation stakes to be in the order of 15 per cent higher than values computed from changes in thickness and density of the snow measured in pits dug through the snow cover at different times. Because the snow had a temperature of 0° C. during the period of observation and the data showed snow density increasing with time, the discrepancy in values from the two methods of measurement could be explained either by compaction of the snow cover, or by deposition of melt water in the snow layers beneath the surface as suggested by Wallén. La Chapelle,Reference La Chapelle ³ in a similar investigation of snow ablation on the Taku Glacier, found ablation values computed from ablation stake data which were in the order of 20 per cent lower than values computed from snow thickness and density measurements made in pits at different times throughout the ablation season. Aside from possible errors in observations, the discrepancy could be explained by decrease in density of the snow as a result of sub-surface ablation.

It is not difficult to find a heat transfer process which could lead to sub-surface melting and, thereby, sub-surface ablation in a snow layer. From radiation absorption coefficients for snow determined experimentally by different observers,Reference Eckel and Tams ⁴ it appears-that 90 per cent of the solar radiation penetrating a snow cover is absorbed in a layer in the order of 10 to 50 cm. thick, depending on the physical characteristics of the snow. It follows that insolation absorbed by the snow can lead to melting through a comparable thickness of snow. An investigation of the surface heat exchange over snow on the Lemon Creek Glacier, Alaska, carried out by the writer in the summer of 1953 demonstrated that during a few periods when insolation was strong and heat transfer from the atmosphere to the snow negligibly small, ablation values computed from heat exchange data were consistently higher than values computed from measurements of the change in thickness of the snow layer. On the other hand, in one particular case when a sequence of relatively calm, sunny days was abruptly terminated by high winds and rain, ablation values computed from change in snow surface level were unreasonably large. This was clearly shown later in that the rate of lowering of the snow surface during the earliest hours of the storm was about 65 per cent higher than the rate of lowering later in the storm period when stronger winds, increased radiation to the snow and increased rainfall had led to an increase in the net energy transfer to the snow. Very probably, the surface layers of snow which had suffered a decrease in density during the calm, sunny period as the result of sub-surface ablation were later compacted by wind and rain in the early part of the storm.

Based on these considerations, it is concluded that measurement of lowering of the snow surface for purposes of determining short period ablation rates is quite insufficient, and in many situations computations of ablation which do not take into account density changes within the snow layer can contain excessive errors.

Other methods of ablation measurement must therefore be sought which consider density changes within a snow cover. Where the snow cover under consideration is not excessively deep and is underlain by solid ice, rock or soil, the problem is solved through use of a vertical coring instrument such as the Mt. Rose Sampler, with which it is possible to determine directly the change in mass in the snow layer through measurement of the total mass at regular intervals of time in a vertical column of unit cross-sectional area extending from the snow surface to the base of the snow cover. A different approach must necessarily be used in the case frequently encountered in glaciological studies where the snow layer is so deep as to make impractical frequent measurements of vertical cores through the entire layer.

On the other hand, the observer is often more interested in obtaining values of melting in the snow layer and evaporation from the surface in order to investigate their relationship to energy received by the snow from the atmosphere and sun. For this case, the snow density can be written:

(3)

where ρ _i is the ice density of the snow, defined here as the mass of solid ice per unit volume of snow, and ρ _w is the water density of the snow, defined as the mass of liquid water contained in a unit volume of snow. Substitution of (3) into (2) gives:

(4)

where the first two terms on the right express the change with time in the mass of ice contained within the vertical column of snow, and the last two terms the change in mass of liquid water within the column. When the sum of the first two terms is negative, it equals the net melting of ice per unit area in the snow layer, plus evaporation of ice that may occur at the surface.

For investigation of the energy balance of the snow layer, only the first two terms in (4) need to be measured. Where the snow layer overlies ice or firn, melting of the snow takes place between the upper surface and the maximum depth to which heat from the sun and atmosphere penetrates the snow. In this case the needed terms can be measured in a vertical column extending from the snow surface to a fixed horizon sufficiently far beneath the surface to remain below the maximum depth of sub-surface melting throughout the period for which measurements are made. To determine melting over periods less than a day’s time, the most practical method would be direct measurements of the change in mass of ice contained within a snow column from one observation to the next. This might be accomplished by using a vertical coring tube similar to a Mt. Rose Sampler for measuring the total mass of snow at the beginning and end of the observation period in a column between the surface and the above-mentioned sub-surface horizon, together with calorimetric measurements to calculate the ice density. The usefulness of this method would depend, of course, on finding a suitable means to identify the fixed lower horizon from one time of observation to the next.

With the present rapid development of methods for more precise measurements of the meteorological parameters associated with the energy transfer at a snow surface, it is becoming increasingly urgent that more effort be spent in developing new, more precise methods of ablation measurements, as well as the development of instruments to carry out these methods. As stated by Sharp,Reference Sharp and Ahlmann ⁵ “… some method is sorely needed for measuring ablation of snow and firn with an accuracy and reliability equivalent to that with which the meteorological factors are measured. This is not an easy task, but it is essential to an eventual balancing of the ablation equation.”