1.Introduction
A recent paper byReference Morland and Boulton Morland and Boulton (1975) presents an analytic solution and computer calculation of the stress in an isotropic elastic hump in plane strain under applied surface loads. The effects of glacier flow are modelled by assuming an idealized normal pressure distribution deduced from Reference NyeNye's (1969) wavy-bed sliding theory, ignoring the restriction to small slopes, On this basis the distribution of local maximum shear stress is determined in order to predict likely failure zones, and the global maximum shear stress is obtained to compare with a failure stress of any given material. The stress field is independent of the elastic moduli of the rock. This analysis is now complemented by including the effects of gravity on the stress field, and by making a more detailed examination of the stress field in relation to a Coulomb failure criterion. The body-force contribution was included in an analysis of flute formation on a horizontal bed by Reference Morris and MorlandMorris and Morland (1976), and for completeness we now incorporate an inclination of the mean bed line to the horizontal.
The Coulomb criterion is expressed as an inequality between a dimensionless failure stress S, which depends on the local stress and the friction angle ϕ, and a critical value Sc which depends only on the cohesive stress τ0, angle ϕ, pore-water pressure pw, and the chosen stress unit. Failure occurs when S exceeds Se. It is found that gravity influences the location of zones where S approaches its maximum value, and hence the likely regions of failure. However the gravity contribution has no significant effect on the maximum value of S attained, at least for the chosen hump profile and model pressure distribution, so will not seriously influence the predictions of failure. Essentially, the amplitude of the model pressure distribution far exceeds the variation of body-force stress through the depth of the hump, and the gravity terms are dominated by applied surface pressures.
Since the presence of pore-water pressure reduces the effective stress in the Coulomb criterion, the effect of pore pressure up to the ice overburden pressure is considered. However, it is found that for the adopted hump profile and model pressure distribution, Coulomb failure is unlikely in coherent rock except for glaciers with very high basal sliding velocities, implying a stable hump profile under the adopted conditions. A more skew hump, and corresponding pressure distribution, may lead to higher failure stress, or a jointed rock system to different and easier modes of failure. However, a more realistic determination of the applied pressure distribution, and possible tangential traction due to glacier flow over a hump with finite slope, is required before reliable predictions can be claimed.

Fig. 1. A moderately skew hump on a mean bed line inclined at angle δ to the horizontal n and s are unit vectors normal and tangential to the hump contour respectively, α is the local inclination of s to OX. The gravity force per unit mass, gk, acts vertically downwards.
2.Stress Field In The Elastic Hump
Consider a single plane hump on a mean bed line Ox inclined at angle δ to the horizontal (Fig. 1). The bed surface approaches Ox as x → ± ∞. Introduce dimensionless coordinates X = (X, Y) by
so that the hump amplitude is approximately unity in (X, Y) coordinates. The moderately skew hump shown in Figure 1 has a boundary defined by Im (ζ) = o in the conformai mapping

where z = X+iY, which is the hump used in theReference Morland and Boulton Morland and Boulton (1975) illustrations. Their theory and computer programme were developed for a class of rational mappings determining stress fields under conditions of zero body force and plane strain when the surface is subjected to normal and tangential tractions t n, t s vanishing at infinity. If α is the local inclination of the surface tangent to Ox, then
A gravity force per unit mass g k is now included, where
Introduce a stress unit C to normalize the applied pressure fluctuation due to the glacier flow, and let p0 be the overburden pressure on the bed line Ox, outside the hump, under depth h of ice. Then
where p is the ice density. If the stress σ is expressed in the form
so ∑ defines a dimensionless over-stress above an isotropic pressure P0, and assuming that there is an isotropic pressure p0 near the bed surface outside the influence of the hump loading, ∑ vanishes at the surface as X → ± ∞. Further, let

where Pr is the bedrock density, then ∑° is a self-equilibrating stress field (zero body-force) to which theReference Morland and Boulton Morland and Boulton (1975) theory applies. Note that Y, and hence (X . k), vanishes as X → ± ∞. If N, T are the normal and tangential tractions associated with ∑°, then


The case of δ = o (horizontal bed line) was used in an analysis of the formation of glacial flutes by Reference Morris and MorlandMorris and Morland (1976).
FollowingReference Morland and Boulton Morland and Boulton (1975) a model pressure fluctuation based onReference Nye Nye's (1969) theory, but ignoring the restriction to small slopes, is adopted, together with a crude cavitation approximation tn = o whenever the predicted normal traction becomes tensile. Thus

where for the hump surface given by Equation (2) the pressure fluctuation is approximately

on –1.87 ≼ X ≼ 2.93, zero outside the range, and has amplitude unity.
where η is the ice viscosity, U is the basal sliding velocity and λ is the wavelength of the hump, approximately 4.8α.Reference Nye Nye (1969) takes η = 3 × 1012 N s m−2, U = 3 × 10−7 m s−1, giving
Note that

for the stress unit given by Equation (13) and δ ≪ ½ π. Thus P0 < 1 for h < (102 → 103) m and cavitation occurs under these conditions. Also a regelation layer is assumed, to provide perfect slip:
If pr = 3 p ≈ 3 × 103 kg m−3,
If R is small, Equations (7) to (9) show that gravity effects are not significant. However, since R is proportional to λ2 and inversely proportional to U for a given hump profile, Equation (16) gives R = 0(1) if λ = 40 m, U = 3 × 10−7 m s−1 or if λ = 10 m and U =2 × 10−8 m s−l, both practical conditions. Note that the term in R of Equation (8) increases the normal traction N associated with σ° but has the opposite effect in the calculation of the actual overstress σ by Equation (7). The net effect can only be determined by calculated examples. By Equations (12) and (14) P0 is proportional to λ and inversely proportional to U. P0 increases under the conditions which lead Lo an increase in R. In fact, since a ≪ h,

for δ ≪½π Thus R = 0(1) implies P0 > 1 ; that is, the pressure fluctuation is too small for cavitation and Equation (10) applies everywhere, making Σ° and Σ independent of P0 for given R.
Consider a Coulomb failure criterion for the bedrock. Failure occurs if
where τo is the cohesive stress, pw the pore-water pressure, ϕ the friction angle (o < ϕ < ½π) and τ, σ are the shear and normal tractions on the failure planes which have normals inclined at angles ±(¼π – ½ϕ) to the maximum principal stress axis. If σ1, σ2 are the local principal stresses, then Σ has the same principal axes with principal values given by
Defining a dimensionless failure stress S by
Equation (18) becomes

S is determined everywhere by Σ and ϕ for a given hump and boundary loading, while Sc depends only on the Coulomb parameters and the stress unit C. Failure is initiated whenever S max max exceeds Sc . Pore-water pressure pw can theoretically range from zero to p0 when Sc takes its maximum and minimum values respectively.

However, the permeabilities of coherent rocks are very small (Reference Morris and JohnsonMorris and Johnson, 1967). The highest values for intact rock are = 5 × 10−6m s−1 (medium-grained sandstone), = 10−5m s−1 (oolitic limestone) and = 10−6 m s−1 (volcanic tuffs). Thus it is unlikely that Sc will be reduced to its minimum value by pore water within the voids of the coherent rock. Of course, well-jointed rock has a secondary and much higher permeability arising from the presence of open and continuous cracks and in this case “cleft water pressure” can reduce the strength of the rock significantly (Reference TerzaghiTerzaghi, 1962).
By construction Σ and , S max are of order unity, so failure can occur only if Sc is of order unity or less. Typical cohesive stresses are τ0 = 5 × 105 N m−2 (siltstone), (2 → 5) × 106 N m−2 (sandstone) and 107 N m−2 (granite). For h = 100 m the respective values of τ0/p0 are

Thus, even in the p w = p 0, failure is possible only when P0 ≼ 0(2) for siltstone, and much smaller for the other rocks, unless h ≫ 100 m. The corresponding friction angles are ϕ = 30°, 35° and 45°, so for p w = 0 the required factors are respectively

We have used Nye's theory for the sliding of ice over obstacles with small surface slopes to define P0, the ratio of the overburden pressure to the amplitude of the pressure variation across the hump, in terms of U, η and λ. However, the restrictions on P0 for failure to occur do not depend on the choice of sliding theory. Consideration of the overall equilibrium of the glacier indicates that it is unlikely that the amplitude of the pressure variation across a finite hump will be much greater than the overburden pressure. Thus we expect P0 = 0(1). Nye's theory gives P0 = p0 λ/2η U, which may take smaller values (Equation (14)). Larger h increases p0, and larger U decreases P0 for given p0, both effects decreasing Sc .
Since the stress field cannot be influenced significantly by the gravity terms unless R = 0(1), which implies P0 > 1 and hence Sc > 1, gravity will not affect failure conditions.
3.Illustrations
The stress fields in the elastic hump defined by Equation (2) have been calculated for various values of P0 and R in the case δ = o. In Figure 2 the variation of S max with P0 for ϕ = 30° and R – 0, 0.5, 1 and the variation of Sc with P0 for ϕ = 30°, pw = 0 and τ0/p0 = o, 0.5 are compared. Failure will occur if S max > Sc . A siltstone hump under 100 m of ice (r O/P 0 = 0.5) will fail if P0 ≼ 0.3 (R = o), P0 ≼ 0.45 ([R = 0.5) or P0 ≼ 0.65 [R = 1). The R = 1 curve is however not physically relevant for P0 ≼ 1. As h increases r0/p0 → o and failure can occur at higher values of P0 . The analogous curves for sandstone and granite are shown in Figures 3 and 4 respectively. In these cases also failure will only occur for low values of P0 when h = 100 m. Since from Nye's theory P0 is inversely proportional to U and proportional to λ, for a given value of p0, failure is most likely for high basal sliding velocity and a small hump.
Figures 2 to 4 show that S max increases with P0 to a level S0 at P0 = 1 and then remains constant at S0 . Below P0 = 1 the curve for R = O is not quite linear because the point of maximum stress moves from inside the hump to the surface of the down-stream flank. For R ≳ 0.2 the point of maximum stress is on the down-stream surface for all P 0.
The failure criterion (18) holds if P0 ≼ 1 and
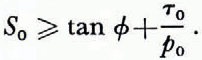
That is, failure occurs if the cohesive stress satisfies

Fig. 2. Smax and Se as functions of P0for ϕ = 30° and pw =.0. For a sillstone hump under 100 m of ice (τ0/p0 = 0.5) Smax > Se and failure will occur when P0 ≼ 0.3 (R – o), P0 ≼ 0.45 (R = 0.5) or P0 ≼ 0.65 (R = 1).

Fig. 3. Smax and Se as functions of P0 for ϕ = 35 and Pw = o. For a sandstone hump under 100 m of ice (τ0/p0 = 2) Smax > Se and failure will occur when P0 ≼ 0.04 (R = o), P0 ≼ 0.06 (R = 0.5) or P0 ≼ 0.09 (R = 1).

Fig. 4. Smax and Se as functions of P0 for ϕ = 45° and pw = o. For a granite hump under 100 m of ice (τ0/p0 ≈ 10) Smax > Se and failure will occur when P0 < 0.01 for R < 1.
when P0 ≼ 1. For P0 ≳ 1 smaller τ0 is required. Figure 5 shows the variation of τf with λ for ϕ; = 30°, pw = o and R – o (appropriate to low values of P0). Failure will occur if τt. Siltstone humps with τ0 = 5 × 105 N m−2 will fail if λ ≼ 3 m ((U = 3X 10−7), m s−1), λ ≼ 12 m (U = 10−6 m s−1) or λ ≼ 37 m (U = 3X 10−6 m s−1). A basal sliding velocity of U = 3 × 10−6 m s−1 is unusually fast for a normal (non-surging) temperate glacier to which the Nye theory is expected to apply. Analogous curves are shown for ϕ = 35° in Figure 6. Sandstone humps, with a minimum τ0 of 2 × 106 N m−2, will fail if λ ≼ 3 m (U = 10−6 m s−1) or λ ≼ 10 m (U = 3X 10−6). m s−1)

Fig. 5. .τf as a function of λ for ϕ = 30°, pw – o and R = 0. Failure occurs when τf > τ0. Siltstone humps will fail if λ < 3 m, (U = 3 × 10−6). m s−1), λ < 37 m (U = 3 × 10−6). m s−1).

Fig. 6. τf as a function of λ for ϕ = 30°, pw – o and R = 0. Failure occurs when τf > τ0.Sandstone humps will fail if λ < = 3 m (U = 10−6 m s−1) or λ < 10 m (U = 3 × 10−6 m s−1).
The region of the hump where failure is most likely to occur is shown for various values of P0 and R in Figures 7 to 10. Figure 7 shows the variation of 5 for ϕ = 35°, R = o and P0 = 0.5. The maximum value, Smax = 0.51, is not adjacent to the point of closure of the cavity as the previous analysis of this case (Reference Morland and BoultonMorland and Boulton, 1975) suggested, but deep within the down-stream flank of the hump. If R is increased to 0.5, about the largest physically reasonable value if P0 = 0.5, the maximum value of S increases slightly to 0.547 (Fig. 8) and is found on the down-stream surface just below the steepest portion but well up-stream of the point of closure of the cavity. Failure and subsequent removal of material in this region would tend to steepen the down-stream flank. Figure 9 shows the variation of S for ϕ; = 35°, R = 0 and Pa = 1. The maximum value of S is 0.872 and occurs on the surface just downstream of the point where the ice exerts minimum pressure on the rock. Increasing the value of R to 1 (Fig. 10) leads to an increase in the magnitude of Smax to 1.016. Its position does not change. Again any failure would tend to steepen the down-stream flank.

Fig. 7. The variation of S for ϕ 35. R o and P0 0.5.

Fig. 8. The variation of S for ϕ 35. R 0.5 and P0 0.5.

Fig. 9. Fig. 9. The variation of S for ϕ 35 . R 0 and P0 1.

Fig. 10. The variation of S for ϕ 35° , R = 1 and P0 = 1.
4.Conclusion
We have shown that in general the force exerted by a glacier on an obstacle of a given roche-moutonnée-like shape will not be sufficient to produce Coulomb failure if the rock is coherent. This profile and all other less skew profiles are stable unless jointing introduces an easier failure mechanism. Thus we follow Reference LewisLewis (1954) in suggesting that the typical “roche-moutonnéé” profile of obstacles on a glacier bed, from large stream-lined boulders to valley steps, cannot develop unless the rock is already jointed.
5.Acknowledgement
This investigation was pursued in connection with Natural Environment Research Council grant GR3/2680 “Flow of glaciers over deformable materials” held jointly with Dr G. S. Boulton in the School of Environmental Sciences.












