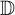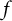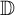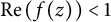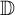1 Introduction
Bohr’s remarkable work in the year
![]() $1914$
on the power series in complex analysis has generated a lot of research activities in complex analysis and related areas. This work is popularly referred to as Bohr phenomenon. The phenomenon has been investigated in various function spaces. Throughout the article, we denote
$1914$
on the power series in complex analysis has generated a lot of research activities in complex analysis and related areas. This work is popularly referred to as Bohr phenomenon. The phenomenon has been investigated in various function spaces. Throughout the article, we denote
![]() $ \mathcal {A} $
be the class of all analytic functions
$ \mathcal {A} $
be the class of all analytic functions
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n $
defined on the unit disk
$ f(z)=\sum _{n=0}^{\infty }a_nz^n $
defined on the unit disk
![]() $ \mathbb {D}:=\{z\in \mathbb {C}:|z|<1\}$
. We define two subclasses
$ \mathbb {D}:=\{z\in \mathbb {C}:|z|<1\}$
. We define two subclasses
![]() $ \mathcal {B}:=\{f\in \mathcal {A} : |f(z)|\leq 1 \} $
and
$ \mathcal {B}:=\{f\in \mathcal {A} : |f(z)|\leq 1 \} $
and
![]() $ \mathcal {P}:=\{f\in \mathcal {A} : \mathrm {Re}\left (f(z)\right )< 1\} $
.
$ \mathcal {P}:=\{f\in \mathcal {A} : \mathrm {Re}\left (f(z)\right )< 1\} $
.
In
![]() $1914,$
the classical result related to the family
$1914,$
the classical result related to the family
![]() $ \mathcal {B} $
was discovered by Bohr [Reference Bohr18] as follows.
$ \mathcal {B} $
was discovered by Bohr [Reference Bohr18] as follows.
Theorem 1.1 [Reference Bohr18]
If
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
, then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
, then
 $$ \begin{align} M_f(r):=\sum_{n=0}^{\infty}|a_n|r^n\leq 1 \;\; \mbox{for}\;\; |z|=r\leq\frac{1}{3}. \end{align} $$
$$ \begin{align} M_f(r):=\sum_{n=0}^{\infty}|a_n|r^n\leq 1 \;\; \mbox{for}\;\; |z|=r\leq\frac{1}{3}. \end{align} $$
Bohr initially, shows the inequality (1.1) for
![]() $|z|=r\leq 1/6$
. Subsequently, the inequality (1.1) was improved for
$|z|=r\leq 1/6$
. Subsequently, the inequality (1.1) was improved for
![]() $|z|\leq 1/3$
by M. Riesz, I. Schur, and F. Wiener independently and they showed that the constant
$|z|\leq 1/3$
by M. Riesz, I. Schur, and F. Wiener independently and they showed that the constant
![]() $1/3$
cannot be improved. The constant
$1/3$
cannot be improved. The constant
![]() $1/3$
and the inequality (1.1) are called, respectively, the Bohr radius and the Bohr inequality for the class
$1/3$
and the inequality (1.1) are called, respectively, the Bohr radius and the Bohr inequality for the class
![]() $\mathcal {B}$
. Moreover, for
$\mathcal {B}$
. Moreover, for
it can be easily shown that
![]() $ M_{f_a}(r)>1 $
if, and only if,
$ M_{f_a}(r)>1 $
if, and only if,
![]() $ r>1/(1+2a) $
, and it is easy to see
$ r>1/(1+2a) $
, and it is easy to see
![]() $ a\rightarrow 1^{-} $
suggests that the constant
$ a\rightarrow 1^{-} $
suggests that the constant
![]() $ 1/3 $
is best possible.
$ 1/3 $
is best possible.
Initially, the problem was considered by Harald Bohr while working on the absolute convergence of the Dirichlet series of the form
![]() $ \sum a_nn^{-s} $
, but in recent years, it becomes an active area of research in modern function theory. In fact, this theorem gets much attention as it has been applied to the characterization problem of Banach algebra satisfying the von Neumann inequality [Reference Dixon21]. However, several other proofs of this interesting inequality were given in different articles (see [Reference Paulsen, Popescu and Singh36, Reference Sidon41, Reference Tomic42]). In
$ \sum a_nn^{-s} $
, but in recent years, it becomes an active area of research in modern function theory. In fact, this theorem gets much attention as it has been applied to the characterization problem of Banach algebra satisfying the von Neumann inequality [Reference Dixon21]. However, several other proofs of this interesting inequality were given in different articles (see [Reference Paulsen, Popescu and Singh36, Reference Sidon41, Reference Tomic42]). In
![]() $1997,$
Boas and Khavinson [Reference Boas and Khavinson17] first introduced the concept of the n-dimensional Bohr radius
$1997,$
Boas and Khavinson [Reference Boas and Khavinson17] first introduced the concept of the n-dimensional Bohr radius
![]() ${\mathcal K}^{\infty }_n$
and established the result: for every
${\mathcal K}^{\infty }_n$
and established the result: for every
![]() $n\in \mathbb {N},$
the n-dimensional Bohr radius
$n\in \mathbb {N},$
the n-dimensional Bohr radius
![]() ${\mathcal K}^{\infty }_n$
with
${\mathcal K}^{\infty }_n$
with
![]() $n\geq 2$
satisfies
$n\geq 2$
satisfies
 $$ \begin{align*} \dfrac{1}{3\sqrt{n}}<{\mathcal K}^{\infty}_n<2\sqrt{\dfrac{\log n}{n}}. \end{align*} $$
$$ \begin{align*} \dfrac{1}{3\sqrt{n}}<{\mathcal K}^{\infty}_n<2\sqrt{\dfrac{\log n}{n}}. \end{align*} $$
Such study concerning multidimensional Bohr inequality, by Boas and Khavinsion, was an incentive for many mathematicians to link the asymptotic behavior of
![]() ${\mathcal K}^{\infty }_n$
to various problems in analysis, for instance, geometry of Banach spaces, unconditional basic constant for spaces of polynomials, etc.
${\mathcal K}^{\infty }_n$
to various problems in analysis, for instance, geometry of Banach spaces, unconditional basic constant for spaces of polynomials, etc.
In the majorant series
![]() $\sum _{n=0}^{\infty }|a_n|r^n$
of the function
$\sum _{n=0}^{\infty }|a_n|r^n$
of the function
![]() $ f\in \mathcal {B} $
, the beginning terms play some significant role in the related discussion about the Bohr inequality. For instance, in the case of
$ f\in \mathcal {B} $
, the beginning terms play some significant role in the related discussion about the Bohr inequality. For instance, in the case of
![]() $|a_0|=0$
, Tomic [Reference Tomic42] has proved the inequality (1.1) for
$|a_0|=0$
, Tomic [Reference Tomic42] has proved the inequality (1.1) for
![]() $0\leq r \leq {1}/{2}$
and if the term
$0\leq r \leq {1}/{2}$
and if the term
![]() $|a_0|$
is replaced by
$|a_0|$
is replaced by
![]() $|a_0|^2$
, then the constant
$|a_0|^2$
, then the constant
![]() $1/3$
can be replaced by
$1/3$
can be replaced by
![]() $1/2$
. In addition, if
$1/2$
. In addition, if
![]() $|a_0|$
is replaced by
$|a_0|$
is replaced by
![]() $|f(z)|$
, then the constant
$|f(z)|$
, then the constant
![]() $1/3$
can be replaced by
$1/3$
can be replaced by
![]() $\sqrt {5}-2$
which is best possible (see [Reference Kayumov, Khammatova and Ponnusamy28, Reference Kayumov, Khammatova and Ponnusamy28]).
$\sqrt {5}-2$
which is best possible (see [Reference Kayumov, Khammatova and Ponnusamy28, Reference Kayumov, Khammatova and Ponnusamy28]).
An extension of the Bohr inequality has established by Paulsen et al. [Reference Paulsen, Popescu and Singh36] and the following sharp inequality for the class
![]() $\mathcal {P}$
are obtained.
$\mathcal {P}$
are obtained.
Theorem 1.2 [Reference Paulsen, Popescu and Singh36]
Suppose that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {P}.$
Then the following sharp inequality holds:
$f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {P}.$
Then the following sharp inequality holds:
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq\dfrac{1}{3}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq\dfrac{1}{3}. \end{align*} $$
It is generally known that the Bohr radius
![]() $ 1/3 $
remains valid in Theorem 1.1 even if the condition
$ 1/3 $
remains valid in Theorem 1.1 even if the condition
![]() $\mathrm {Re}\left (f(z)\right )<1 $
in
$\mathrm {Re}\left (f(z)\right )<1 $
in
![]() $ \mathbb {D} $
and
$ \mathbb {D} $
and
![]() $ a_0=f(0)\in [0,1) $
are substituted for the assumption on
$ a_0=f(0)\in [0,1) $
are substituted for the assumption on
![]() $ f $
. Actually, this condition shows that (see [Reference Duren22, Carathéodory’s Lemma, p. 41]) the coefficient bounds as
$ f $
. Actually, this condition shows that (see [Reference Duren22, Carathéodory’s Lemma, p. 41]) the coefficient bounds as
![]() $ |a_n|\leq 2(1-a_0) $
for all
$ |a_n|\leq 2(1-a_0) $
for all
![]() $ n\geq 1 $
and with this, the following sharp inequality holds (see [Reference Paulsen, Popescu and Singh36]):
$ n\geq 1 $
and with this, the following sharp inequality holds (see [Reference Paulsen, Popescu and Singh36]):
 $$ \begin{align*} a_0+\sum_{n=1}^{\infty}|a_n|r^n\leq a_0+2(1-a_0)\frac{r}{1-r}\leq 1\; \mbox{for}\; r\leq \frac{1}{3}. \end{align*} $$
$$ \begin{align*} a_0+\sum_{n=1}^{\infty}|a_n|r^n\leq a_0+2(1-a_0)\frac{r}{1-r}\leq 1\; \mbox{for}\; r\leq \frac{1}{3}. \end{align*} $$
For different aspects and some recent developments of the Bohr phenomenon for different classes of functions, we may refer to the articles [Reference Ahamed and Allu4–Reference Bénéteau, Dahlner and Khavinson15, Reference Dixon21, Reference Evdoridis, Ponnusamy and Rasila23, Reference Kumar30, Reference Lata and Singh31, Reference Liu, Shang and Xu35] and the references therein.
The exploration of the Bohr radius problem for subordinating families of analytic functions in
![]() $\mathbb {D}$
adds another interesting layer to the overall understanding of the Bohr phenomenon. For any two analytic functions f and g in
$\mathbb {D}$
adds another interesting layer to the overall understanding of the Bohr phenomenon. For any two analytic functions f and g in
![]() $\mathbb {D},$
the function f is said to be subordinate to
$\mathbb {D},$
the function f is said to be subordinate to
![]() $g,$
denoted by
$g,$
denoted by
![]() $f\prec g$
if there exist an
$f\prec g$
if there exist an
![]() $\omega \in \mathcal {B}$
satisfying
$\omega \in \mathcal {B}$
satisfying
![]() $\omega (0)=0$
and
$\omega (0)=0$
and
![]() $ f(z)=g(\omega (z)) $
in
$ f(z)=g(\omega (z)) $
in
![]() $z\in \mathbb {D}$
(see [Reference Duren22]).
$z\in \mathbb {D}$
(see [Reference Duren22]).
Throughout the article, we denote
![]() $S(g),$
the class of functions f subordinate to a function
$S(g),$
the class of functions f subordinate to a function
![]() $g.$
Many authors have studied Bohr phenomenon for functions in the class
$g.$
Many authors have studied Bohr phenomenon for functions in the class
![]() $S(g),$
where the function g belongs to different class (see [Reference Abu-Muhanna1, Reference Bhowmik and Das16, Reference Hamada24, Reference Ponnusamy, Vijayakumar and Wirths37]).
$S(g),$
where the function g belongs to different class (see [Reference Abu-Muhanna1, Reference Bhowmik and Das16, Reference Hamada24, Reference Ponnusamy, Vijayakumar and Wirths37]).
Our primary interest in this article is to establish sharp refined versions of Bohr-type inequalities for different classes of functions such as
![]() $ \mathcal {B} $
,
$ \mathcal {B} $
,
![]() $ \mathcal {P} $
, and
$ \mathcal {P} $
, and
![]() $ \mathcal {S}(g) $
, where g is a given function defined in
$ \mathcal {S}(g) $
, where g is a given function defined in
![]() $\mathbb {D}$
. The article is organized as follows: In Section 2, we establish a sharp Bohr-type inequalities for the class
$\mathbb {D}$
. The article is organized as follows: In Section 2, we establish a sharp Bohr-type inequalities for the class
![]() $\mathcal {B}$
with help of the planar integral
$\mathcal {B}$
with help of the planar integral
![]() $ S_r .$
In Section 3, we study refined version of Bohr-type inequality considering certain power of the initial coefficient for functions of the class
$ S_r .$
In Section 3, we study refined version of Bohr-type inequality considering certain power of the initial coefficient for functions of the class
![]() $ \mathcal {P} $
. Finally, in Section 4, we prove two results concerning refined versions of the Bohr inequality for the class
$ \mathcal {P} $
. Finally, in Section 4, we prove two results concerning refined versions of the Bohr inequality for the class
![]() $S(g)$
.
$S(g)$
.
2 Bohr-type inequalities for the class
 $ \mathcal {B} $
$ \mathcal {B} $
Inspired by the notion of Rogosinski’s inequality and Rogosinski’s radius investigated in [Reference Rogosinski38], Kayumov et al. [Reference Kayumov, Khammatova and Ponnusamy28] (see also [Reference Kayumov, Khammatova and Ponnusamy28]) obtained the following Bohr–Rogosinski inequality and Bohr–Rogosinski radius for the class
![]() $ \mathcal {B}.$
$ \mathcal {B}.$
Theorem 2.1 [Reference Kayumov, Khammatova and Ponnusamy28]
Suppose that
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then
 $$ \begin{align*} |f(z)|+\sum_{n=N}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq R_N, \end{align*} $$
$$ \begin{align*} |f(z)|+\sum_{n=N}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq R_N, \end{align*} $$
where
![]() $ R_N $
is the unique root of the equation
$ R_N $
is the unique root of the equation
![]() $ 2(1+r)r^N-(1-r)^2=0 $
in the interval
$ 2(1+r)r^N-(1-r)^2=0 $
in the interval
![]() $(0,1)$
. The radius
$(0,1)$
. The radius
![]() $ R_N $
is the best possible. Moreover,
$ R_N $
is the best possible. Moreover,
 $$ \begin{align*} |f(z)|^2+\sum_{n=N}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq R^{\prime}_N, \end{align*} $$
$$ \begin{align*} |f(z)|^2+\sum_{n=N}^{\infty}|a_n|r^n\leq 1\;\;\mbox{for}\;\; r\leq R^{\prime}_N, \end{align*} $$
where
![]() $ R^{\prime }_N $
is the unique root of the equation
$ R^{\prime }_N $
is the unique root of the equation
![]() $ (1+r)r^N-(1-r)^2=0 $
in the interval
$ (1+r)r^N-(1-r)^2=0 $
in the interval
![]() $(0,1)$
. The radius
$(0,1)$
. The radius
![]() $ R^{\prime }_N $
is the best possible.
$ R^{\prime }_N $
is the best possible.
In a number of articles (see [Reference Das20, Reference Liu, Liu and Ponnusamy32, Reference Liu and Ponnusamy33] and the references therein) have further refined and sometimes improved Theorem 2.1 for different classes of functions. Our objective in this section is to improve Theorem 2.1. In order to do that, let us recall some well-known formulations. Let f be holomorphic in
![]() $\mathbb D$
, and for
$\mathbb D$
, and for
![]() $0<r<1$
, let
$0<r<1$
, let
![]() $\mathbb D_r:=\{z\in \mathbb C: |z|<r\}$
. Throughout the article,
$\mathbb D_r:=\{z\in \mathbb C: |z|<r\}$
. Throughout the article,
![]() $S_r=S_r(f)$
denotes the planar integral
$S_r=S_r(f)$
denotes the planar integral
If
![]() $f(z)=\sum _{n=0}^\infty a_nz^n$
, than the quantity
$f(z)=\sum _{n=0}^\infty a_nz^n$
, than the quantity
![]() $ S_r $
has the following series representation:
$ S_r $
has the following series representation:
 $$ \begin{align*}S_r=\pi \sum_{n=1}^\infty n|a_n|^2 r^{2n}.\end{align*} $$
$$ \begin{align*}S_r=\pi \sum_{n=1}^\infty n|a_n|^2 r^{2n}.\end{align*} $$
In fact, if f is a univalent function, then
![]() $S_r$
is the area of
$S_r$
is the area of
![]() $f(\mathbb D_r)$
. The quantity
$f(\mathbb D_r)$
. The quantity
![]() $ S_r $
has a certain significant role in the study of improved versions of Bohr-type inequalities (see, e.g., [Reference Ahamed, Allu and Halder7, Reference Huang, Liu and Ponnusamy25, Reference Ismagilov, Kayumov and Ponnusamy27, Reference Liu, Liu and Ponnusamy32]). For example, Kayumov and Ponnusamy [Reference Kayumov and Ponnusamy29] have proved the following improved version of the Bohr inequality in terms of
$ S_r $
has a certain significant role in the study of improved versions of Bohr-type inequalities (see, e.g., [Reference Ahamed, Allu and Halder7, Reference Huang, Liu and Ponnusamy25, Reference Ismagilov, Kayumov and Ponnusamy27, Reference Liu, Liu and Ponnusamy32]). For example, Kayumov and Ponnusamy [Reference Kayumov and Ponnusamy29] have proved the following improved version of the Bohr inequality in terms of
![]() $ S_r $
.
$ S_r $
.
Theorem 2.2 [Reference Kayumov and Ponnusamy29]
Suppose that
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} .$
Then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} .$
Then
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+ \frac{16}{9} \left(\frac{S_{r}}{\pi}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{3} \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+ \frac{16}{9} \left(\frac{S_{r}}{\pi}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{3} \end{align*} $$
and the numbers
![]() $1/3$
,
$1/3$
,
![]() $16/9$
cannot be improved. Moreover,
$16/9$
cannot be improved. Moreover,
 $$ \begin{align*} |a_{0}|^{2}+\sum_{n=1}^{\infty}|a_n|r^n+ \frac{9}{8} \left(\frac{S_{r}}{\pi}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{2} \end{align*} $$
$$ \begin{align*} |a_{0}|^{2}+\sum_{n=1}^{\infty}|a_n|r^n+ \frac{9}{8} \left(\frac{S_{r}}{\pi}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{2} \end{align*} $$
and the numbers
![]() $1/2$
,
$1/2$
,
![]() $9/8$
cannot be improved.
$9/8$
cannot be improved.
In fact, Kayumov and Ponnusamy [Reference Kayumov, Khammatova and Ponnusamy28] have proved the following sharp inequality for the function
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}: $
$f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}: $
 $$ \begin{align} \frac{S_r}{\pi}=\sum_{n=1}^{\infty}n|a_n|^2r^{2n}\leq r^2\frac{(1-|a_0|^2)^2}{(1-|a_0|^2r^2)^2} \,\,\mbox{for}\,\, 0<r\leq1/\sqrt{2}. \end{align} $$
$$ \begin{align} \frac{S_r}{\pi}=\sum_{n=1}^{\infty}n|a_n|^2r^{2n}\leq r^2\frac{(1-|a_0|^2)^2}{(1-|a_0|^2r^2)^2} \,\,\mbox{for}\,\, 0<r\leq1/\sqrt{2}. \end{align} $$
Furthermore, Ismagilov et al. [Reference Ismagilov, Kayumov, Kayumov and Ponnusamy26] have observed that
 $$ \begin{align} 1-\dfrac{S_r}{\pi}\geq \dfrac{(1-r^2)(1-r^2|a_0|^4)}{(1-|a_0|^2r^2)^2}, \end{align} $$
$$ \begin{align} 1-\dfrac{S_r}{\pi}\geq \dfrac{(1-r^2)(1-r^2|a_0|^4)}{(1-|a_0|^2r^2)^2}, \end{align} $$
and hence, in view of (2.1) and (2.2), the following inequality can be obtained easily:
 $$ \begin{align} \dfrac{S_r}{\pi-S_r}\leq \dfrac{r^2(1-|a_0|^2)^2}{(1-r^2)(1-r^2|a_0|^4)}. \end{align} $$
$$ \begin{align} \dfrac{S_r}{\pi-S_r}\leq \dfrac{r^2(1-|a_0|^2)^2}{(1-r^2)(1-r^2|a_0|^4)}. \end{align} $$
In view of the upper bound of the quantity
![]() $ S_r/(\pi -S_r) $
, Theorem 2.2 is investigated further in [Reference Ismagilov, Kayumov, Kayumov and Ponnusamy26] and obtained the following sharp result replacing the quantity
$ S_r/(\pi -S_r) $
, Theorem 2.2 is investigated further in [Reference Ismagilov, Kayumov, Kayumov and Ponnusamy26] and obtained the following sharp result replacing the quantity
![]() $S_r/\pi $
by
$S_r/\pi $
by
![]() $S_r/(\pi -S_r)$
.
$S_r/(\pi -S_r)$
.
Theorem 2.3 [Reference Ismagilov, Kayumov, Kayumov and Ponnusamy26]
Suppose that
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\frac{16}{9} \left(\frac{S_{r}}{\pi-S_r}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{3} \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\frac{16}{9} \left(\frac{S_{r}}{\pi-S_r}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{3} \end{align*} $$
and the number
![]() $16/9$
cannot be improved. Moreover,
$16/9$
cannot be improved. Moreover,
 $$ \begin{align*} |a_{0}|^{2}+\sum_{n=1}^{\infty}|a_n|r^n+ \frac{9}{8} \left(\frac{S_{r}}{\pi-S_r}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{2} \end{align*} $$
$$ \begin{align*} |a_{0}|^{2}+\sum_{n=1}^{\infty}|a_n|r^n+ \frac{9}{8} \left(\frac{S_{r}}{\pi-S_r}\right) \leq 1 \quad \mbox{for} \quad r \leq \frac{1}{2} \end{align*} $$
and the number
![]() $9/8$
cannot be improved.
$9/8$
cannot be improved.
For recent development of Bohr-type inequalities with the quantity
![]() $S_r/(\pi -S_r)$
, we may refer to the article [Reference Ahamed and Ahammed3]. In fact, there is an ongoing research effort aimed at refining the Bohr inequality for the class
$S_r/(\pi -S_r)$
, we may refer to the article [Reference Ahamed and Ahammed3]. In fact, there is an ongoing research effort aimed at refining the Bohr inequality for the class
![]() $ \mathcal {B} $
, with the objective of finding sharp results. In this context, recently, Liu et al. [Reference Liu, Liu and Ponnusamy32] have studied refined Bohr inequality with various suitable settings and obtained the following result.
$ \mathcal {B} $
, with the objective of finding sharp results. In this context, recently, Liu et al. [Reference Liu, Liu and Ponnusamy32] have studied refined Bohr inequality with various suitable settings and obtained the following result.
Theorem 2.4 [Reference Liu, Liu and Ponnusamy32]
Suppose that
![]() $f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
$f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
 $$ \begin{align*} |f(z)|+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align*} $$
$$ \begin{align*} |f(z)|+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align*} $$
for
![]() $|z|=r \leq r_0=2/\left (3+|a_0|+\sqrt {5}(1+|a_0|)\right ).$
The radius
$|z|=r \leq r_0=2/\left (3+|a_0|+\sqrt {5}(1+|a_0|)\right ).$
The radius
![]() $r_0$
is best possible and
$r_0$
is best possible and
![]() $r_0>\sqrt {5}-2.$
Moreover,
$r_0>\sqrt {5}-2.$
Moreover,
 $$ \begin{align} |f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
$$ \begin{align} |f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
for
![]() $|z|=r\leq r^{\prime }_0,$
where
$|z|=r\leq r^{\prime }_0,$
where
![]() $r^{\prime }_0$
is the unique positive root of the equation
$r^{\prime }_0$
is the unique positive root of the equation
The radius
![]() $r^{\prime }_0$
is best possible and
$r^{\prime }_0$
is best possible and
![]() $1/3<r^{\prime }_0<1/\left (2+|a_0|\right ). $
$1/3<r^{\prime }_0<1/\left (2+|a_0|\right ). $
The above discussion motivates us to pose the following question in order to continue the study on the Bohr phenomenon for further improvement.
Question 2.1 Can we improve the inequality (2.4) in view of incorporating the nonnegative quantities
![]() $S_r/\pi $
and
$S_r/\pi $
and
![]() $S_r/(\pi -S_r)$
?
$S_r/(\pi -S_r)$
?
We have utilized the proof of techniques discussed in [Reference Ahamed and Ahammed3, Reference Ismagilov, Kayumov, Kayumov and Ponnusamy26, Reference Kayumov and Ponnusamy29] as inspiration to derive the following refined Bohr inequalities to answer the Question 2.1.
Theorem 2.5 Suppose that
![]() $f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
$f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
 $$ \begin{align} U_ 1(z,r):=|f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+\lambda\left(\dfrac{S_r}{\pi}\right)\leq 1 \end{align} $$
$$ \begin{align} U_ 1(z,r):=|f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+\lambda\left(\dfrac{S_r}{\pi}\right)\leq 1 \end{align} $$
for
![]() $r \leq 1/3,$
and the constant
$r \leq 1/3,$
and the constant
![]() $\lambda =8/9$
cannot be improved. Moreover,
$\lambda =8/9$
cannot be improved. Moreover,
 $$ \begin{align} U_2(z,r):=|f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+\lambda\left(\dfrac{S_r}{\pi-S_r}\right)\leq 1 \end{align} $$
$$ \begin{align} U_2(z,r):=|f(z)|^2+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+\lambda\left(\dfrac{S_r}{\pi-S_r}\right)\leq 1 \end{align} $$
for
![]() $r \leq 1/3,$
and the constant
$r \leq 1/3,$
and the constant
![]() $\lambda =8/9$
cannot be improved.
$\lambda =8/9$
cannot be improved.
Remark 2.1 The following observations are clear.
-
(i) If
 $ \lambda =0 $
, then the inequalities (2.5) and (2.6) coincide with the inequality (2.4), which shows that Theorem 2.5 improves Theorem 2.4 by improving (2.4).
$ \lambda =0 $
, then the inequalities (2.5) and (2.6) coincide with the inequality (2.4), which shows that Theorem 2.5 improves Theorem 2.4 by improving (2.4). -
(ii) The extension of the inequality (2.4) in two distinct cases is achieved by Theorem 2.5, which improves Theorem 2.4 for
 $ \lambda =8/9 $
.
$ \lambda =8/9 $
.
The proof of Theorem 2.5 relies heavily on the following two lemmas. The first lemma is established in [Reference Liu, Liu and Ponnusamy32] as a further refinement of Bohr-type inequalities, whereas the second lemma is well-known as “Schwarz–Pick lemma” used for the bounds of analytic function
![]() $ f $
and their first-order derivatives.
$ f $
and their first-order derivatives.
Lemma 2.1 [Reference Liu, Liu and Ponnusamy32]
Suppose that
![]() $ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then, for any N
$ f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then, for any N
![]() $\in \mathbb {N}$
, the following inequality holds:
$\in \mathbb {N}$
, the following inequality holds:
 $$ \begin{align*} \sum_{n=N}^{\infty}|a_n|r^n+sgn(t)\sum_{n=1}^{t}|a_n|^2\dfrac{r^N}{1-r}+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=t+1}^{\infty}|a_n|^2r^{2n}\leq \dfrac{(1-|a_0|^2)r^N}{1-r} \end{align*} $$
$$ \begin{align*} \sum_{n=N}^{\infty}|a_n|r^n+sgn(t)\sum_{n=1}^{t}|a_n|^2\dfrac{r^N}{1-r}+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=t+1}^{\infty}|a_n|^2r^{2n}\leq \dfrac{(1-|a_0|^2)r^N}{1-r} \end{align*} $$
for
![]() $ r\in [0,1),$
where
$ r\in [0,1),$
where
![]() $t=\lfloor {(N-1)/2}\rfloor $
.
$t=\lfloor {(N-1)/2}\rfloor $
.
Lemma 2.2 [Reference Ruscheweyh40]
(Schwarz–Pick lemma) Suppose that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then:
$f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B} $
. Then:
-
(i)
and the equality sign holds for distinct $$ \begin{align*} \dfrac{|f(z_1)-f(z_2)|}{|1-\overline{f(z_1)}f(z_2)|}\leq \dfrac{|z_1-z_2|}{|1-\overline{z_1}z_2|}\;\;\mbox{holds for } z_1,z_2\in \mathbb{D}, \end{align*} $$
$$ \begin{align*} \dfrac{|f(z_1)-f(z_2)|}{|1-\overline{f(z_1)}f(z_2)|}\leq \dfrac{|z_1-z_2|}{|1-\overline{z_1}z_2|}\;\;\mbox{holds for } z_1,z_2\in \mathbb{D}, \end{align*} $$
 $z_1,z_2\in \mathbb {D}$
if, and only if, f is a Möbius transformation.
$z_1,z_2\in \mathbb {D}$
if, and only if, f is a Möbius transformation.
-
(ii)
and the equality sign holds for some $$ \begin{align*} \;\;|f^\prime(z)|\leq \dfrac{1-|f(z)|^2}{1-|z|^2} \;\;\mbox{holds for}\;\; z\in\mathbb{D}, \end{align*} $$
$$ \begin{align*} \;\;|f^\prime(z)|\leq \dfrac{1-|f(z)|^2}{1-|z|^2} \;\;\mbox{holds for}\;\; z\in\mathbb{D}, \end{align*} $$
 $ z\in \mathbb {D} $
if, and only if, f is a Möbius transformation.
$ z\in \mathbb {D} $
if, and only if, f is a Möbius transformation.
Proof of Theorem 2.5
We consider the function
![]() $U_1(z,r)$
which is given by (2.5). Moreover, by applying the assumption of the result and the Schwarz–Pick lemma to the function f, it is easily obtain
$U_1(z,r)$
which is given by (2.5). Moreover, by applying the assumption of the result and the Schwarz–Pick lemma to the function f, it is easily obtain
By means of a basic computation involving the inequalities (2.1), (2.7), and Lemma 2.1 (with
![]() $N=1$
), it can be shown that
$N=1$
), it can be shown that
 $$ \begin{align*} U_1\left(z,r\right)&\leq \left(\dfrac{r+|a_0|}{1+r|a_0|}\right)^2+\dfrac{(1-|a_0|^2)r}{1-r}+\dfrac{8(1-|a_0|^2)^2r^2}{9(1-|a_0|^2r^2)^2}:=U^*_1(r). \end{align*} $$
$$ \begin{align*} U_1\left(z,r\right)&\leq \left(\dfrac{r+|a_0|}{1+r|a_0|}\right)^2+\dfrac{(1-|a_0|^2)r}{1-r}+\dfrac{8(1-|a_0|^2)^2r^2}{9(1-|a_0|^2r^2)^2}:=U^*_1(r). \end{align*} $$
It is easy to see that
![]() $U^*_1(r)$
is a monotonically increasing function of
$U^*_1(r)$
is a monotonically increasing function of
![]() $r,$
and therefore, it suffices to prove the inequality (2.5) for
$r,$
and therefore, it suffices to prove the inequality (2.5) for
![]() $r=1/3$
. For
$r=1/3$
. For
![]() $r=1/3,$
it can be seen through a simple calculation that
$r=1/3,$
it can be seen through a simple calculation that
 $$ \begin{align*} U^*_1(1/3)&=1-\dfrac{(1-|a_0|)^2(1+|a_0|)(47-2|a_0|-|a_0|^2)}{2(9-|a_0|^2)^2}\leq 1, \end{align*} $$
$$ \begin{align*} U^*_1(1/3)&=1-\dfrac{(1-|a_0|)^2(1+|a_0|)(47-2|a_0|-|a_0|^2)}{2(9-|a_0|^2)^2}\leq 1, \end{align*} $$
and, therefore, the desired inequality (2.5) holds for
![]() $r\leq 1/3$
and
$r\leq 1/3$
and
![]() $|a_0|\in [0,1).$
Next, we consider the function
$|a_0|\in [0,1).$
Next, we consider the function
![]() $U_2(z,r)$
which is given by (2.6). Using the inequalities (2.3) and (2.7), and in view of Lemma 2.1 (with
$U_2(z,r)$
which is given by (2.6). Using the inequalities (2.3) and (2.7), and in view of Lemma 2.1 (with
![]() $ N=1 $
), we obtain
$ N=1 $
), we obtain
 $$ \begin{align*} U_2(z,r)&\leq \left(\dfrac{r+|a_0|}{1+r|a_0|}\right)^2+\dfrac{(1-|a_0|^2)r}{1-r}+\dfrac{8(1-|a_0|^2)^2r^2}{9(1-r^2)(1-r^2|a_0|^4)}:=U^*_2(r). \end{align*} $$
$$ \begin{align*} U_2(z,r)&\leq \left(\dfrac{r+|a_0|}{1+r|a_0|}\right)^2+\dfrac{(1-|a_0|^2)r}{1-r}+\dfrac{8(1-|a_0|^2)^2r^2}{9(1-r^2)(1-r^2|a_0|^4)}:=U^*_2(r). \end{align*} $$
It suffices to show the inequality (2.6) for
![]() $r=1/3$
because
$r=1/3$
because
![]() $U^*_2(r)$
is an increasing function of r. For
$U^*_2(r)$
is an increasing function of r. For
![]() $r=1/3,$
by an easy computation, we obtain
$r=1/3,$
by an easy computation, we obtain
 $$ \begin{align*} U^*_2(1/3)&= 1-\dfrac{(1-|a_0|)^2(1+|a_0|)(45+24|a_0|+10|a_0|^2+8|a_0|^3+|a_0|^4)}{2(9-|a_0|^4)(3+|a_0|)^2}\leq1 \end{align*} $$
$$ \begin{align*} U^*_2(1/3)&= 1-\dfrac{(1-|a_0|)^2(1+|a_0|)(45+24|a_0|+10|a_0|^2+8|a_0|^3+|a_0|^4)}{2(9-|a_0|^4)(3+|a_0|)^2}\leq1 \end{align*} $$
and, therefore, the desire inequality (2.6) holds for
![]() $r\leq 1/3$
and
$r\leq 1/3$
and
![]() $|a_0|\in [0,1).$
In both the cases, the sharpness of the constant
$|a_0|\in [0,1).$
In both the cases, the sharpness of the constant
![]() $\lambda =8/9$
can be easily shown with the help of the function
$\lambda =8/9$
can be easily shown with the help of the function
![]() $f_a(z)=(a-z)/(1-az)$
,
$f_a(z)=(a-z)/(1-az)$
,
![]() $a\in (0,1)$
and hence, we omit the details.
$a\in (0,1)$
and hence, we omit the details.
3 Bohr-type inequalities for the class
 $ \mathcal {P} $
$ \mathcal {P} $
In geometric function theory, the subclass of the well-known class
![]() $\mathcal {S}$
that encompasses convex functions and starlike functions are named as
$\mathcal {S}$
that encompasses convex functions and starlike functions are named as
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {S}^*$
, respectively. Closely related to the classes
$\mathcal {S}^*$
, respectively. Closely related to the classes
![]() $ \mathcal {C} $
and
$ \mathcal {C} $
and
![]() $ \mathcal {S}^{*} $
is the class
$ \mathcal {S}^{*} $
is the class
![]() $ \mathcal {P} $
of all functions
$ \mathcal {P} $
of all functions
![]() $ \varphi $
analytic and having positive real part in
$ \varphi $
analytic and having positive real part in
![]() $ \mathbb {D} $
, with
$ \mathbb {D} $
, with
![]() $ \varphi (0)=1 $
and the function
$ \varphi (0)=1 $
and the function
![]() $ \varphi $
can be represented as Poisson–Stieltjes integral
$ \varphi $
can be represented as Poisson–Stieltjes integral
where
![]() $ d\mu (t)\geq 0 $
and
$ d\mu (t)\geq 0 $
and
![]() $ \int d\mu (t)=1 $
.
$ \int d\mu (t)=1 $
.
In 2022, Ponnusamy et al. [Reference Ponnusamy, Vijayakumar and Wirths37] further examined the Bohr inequality by replacing the unimodular boundedness of f by the condition Re
![]() $(f(z))<1$
and established the following sharp result.
$(f(z))<1$
and established the following sharp result.
Theorem 3.1 [Reference Ponnusamy, Vijayakumar and Wirths37]
Suppose that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {P}.$
Then
$f(z)=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {P}.$
Then
 $$ \begin{align} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
for
![]() $r\leq r_*,$
where
$r\leq r_*,$
where
![]() $r_*\approx 0.24683$
is the unique root of the equation
$r_*\approx 0.24683$
is the unique root of the equation
![]() $3r^3-5r^2-3r+1=0$
in the interval
$3r^3-5r^2-3r+1=0$
in the interval
![]() $(0,1).$
Moreover, for any
$(0,1).$
Moreover, for any
![]() $a_0\in (0,1),$
there exists a uniquely defined
$a_0\in (0,1),$
there exists a uniquely defined
![]() $r_0=r_0(a_0)\in (r_*,1/3) $
such that
$r_0=r_0(a_0)\in (r_*,1/3) $
such that
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1\;\;\mbox{for}\;\;r\in[0,r_0]. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1\;\;\mbox{for}\;\;r\in[0,r_0]. \end{align*} $$
The radius
![]() $r_0=r_0(a_0)$
can be computed as the solution of the equation
$r_0=r_0(a_0)$
can be computed as the solution of the equation
The result is sharp.
Since the initial coefficient
![]() $ |a_0| $
in the majorant series
$ |a_0| $
in the majorant series
![]() $M_f(r)= \sum _{n=0}^{\infty }|a_n|r^n $
, where
$M_f(r)= \sum _{n=0}^{\infty }|a_n|r^n $
, where
![]() $ f\in \mathcal {B} $
, plays some significant role in the study of Bohr radius, to determine the value corresponding to
$ f\in \mathcal {B} $
, plays some significant role in the study of Bohr radius, to determine the value corresponding to
![]() $ r_* $
, we are interested to obtain sharp version of the inequality (3.1) by considering general power of
$ r_* $
, we are interested to obtain sharp version of the inequality (3.1) by considering general power of
![]() $ |a_0| $
. Henceforth, in order to generalize Theorem 3.1, it is natural to find the answer to the following question.
$ |a_0| $
. Henceforth, in order to generalize Theorem 3.1, it is natural to find the answer to the following question.
Question 3.1 Can we prove the inequality (3.1) sharp for any
![]() $p\in \mathbb {N}$
if the initial term
$p\in \mathbb {N}$
if the initial term
![]() $ |a_0|$
is replaced by
$ |a_0|$
is replaced by
![]() $ |a_0|^p$
?
$ |a_0|^p$
?
We obtain the following result answering the Question 3.1.
Theorem 3.2 Let
![]() $f(z)$
be analytic function in
$f(z)$
be analytic function in
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n \in \mathcal {P}.$
Then, for any
$f(z)=\sum _{n=0}^{\infty }a_nz^n \in \mathcal {P}.$
Then, for any
![]() $p\in \mathbb {N},$
the following inequality holds:
$p\in \mathbb {N},$
the following inequality holds:
 $$ \begin{align} V_f(r):=|a_0|^p+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
$$ \begin{align} V_f(r):=|a_0|^p+\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq 1 \end{align} $$
for
![]() $r\leq r_*,$
where
$r\leq r_*,$
where
![]() $r_*\approx 0.24683$
is the unique root of the equation
$r_*\approx 0.24683$
is the unique root of the equation
in the interval
![]() $(0,1).$
The result is sharp.
$(0,1).$
The result is sharp.
We have the following remark.
Remark 3.1 In Theorem 3.2, the following observations are clear.
Proof of Theorem 3.2
To prove this result, we use the following lemma involving subordination.
Lemma 3.1 [Reference Ponnusamy, Vijayakumar and Wirths37]
Let
![]() $f(z)$
and
$f(z)$
and
![]() $g(z)$
be two analytic functions in
$g(z)$
be two analytic functions in
![]() $\mathbb {D}$
with the Taylor series expansions
$\mathbb {D}$
with the Taylor series expansions
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n$
and
$f(z)=\sum _{n=0}^{\infty }a_nz^n$
and
![]() $g(z)=\sum _{n=0}^{\infty }b_nz^n$
for
$g(z)=\sum _{n=0}^{\infty }b_nz^n$
for
![]() $z\in \mathbb {D}.$
If
$z\in \mathbb {D}.$
If
![]() $f(z)\prec g(z)$
, then
$f(z)\prec g(z)$
, then
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq \sum_{n=0}^{\infty}|b_n|r^n+\left(\dfrac{1}{1+|b_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n} \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq \sum_{n=0}^{\infty}|b_n|r^n+\left(\dfrac{1}{1+|b_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n} \end{align*} $$
for
![]() $r\leq 1/3.$
The number
$r\leq 1/3.$
The number
![]() $1/3$
cannot be improved.
$1/3$
cannot be improved.
Since
![]() $\mathrm {Re}\left (f(z)\right )<1,$
we may write the given condition as
$\mathrm {Re}\left (f(z)\right )<1,$
we may write the given condition as
 $$ \begin{align*}f(z)\prec g(z),\;\; g(z)=a_0-2(1-a_0)\dfrac{z}{1-z}=a_0-2(1-a_0)\sum_{n=1}^{\infty}z^n.\end{align*} $$
$$ \begin{align*}f(z)\prec g(z),\;\; g(z)=a_0-2(1-a_0)\dfrac{z}{1-z}=a_0-2(1-a_0)\sum_{n=1}^{\infty}z^n.\end{align*} $$
Here,
![]() $g(z)$
is a univalent function in
$g(z)$
is a univalent function in
![]() $\mathbb {D}$
onto the half-plane
$\mathbb {D}$
onto the half-plane
![]() $\{w:\mathrm {Re}(w)<1\}.$
According to the Lemma 3.1, if
$\{w:\mathrm {Re}(w)<1\}.$
According to the Lemma 3.1, if
![]() $g(z)=\sum _{n=0}^{\infty }b_nz^n,$
then it is sufficient to show that
$g(z)=\sum _{n=0}^{\infty }b_nz^n,$
then it is sufficient to show that
 $$ \begin{align*} V_g(r)=|b_0|^p+\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{1+|b_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}\leq1 \;\; \mbox{for}\;\; r\leq r_*, \end{align*} $$
$$ \begin{align*} V_g(r)=|b_0|^p+\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{1+|b_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}\leq1 \;\; \mbox{for}\;\; r\leq r_*, \end{align*} $$
where
![]() $r_*$
is as in the statement. For simplicity, let
$r_*$
is as in the statement. For simplicity, let
![]() $1-a_0=\mu $
so that
$1-a_0=\mu $
so that
![]() $a_0=1-\mu $
and
$a_0=1-\mu $
and
![]() $b_n=-2\mu $
for
$b_n=-2\mu $
for
![]() $n\geq 1.$
This gives for
$n\geq 1.$
This gives for
![]() $\mu \in [0,1]$
and
$\mu \in [0,1]$
and
![]() $r\in (0,1)$
that
$r\in (0,1)$
that
 $$ \begin{align*} V_g(r)&=(1-\mu)^p+2\mu \sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-\mu}+\dfrac{r}{1-r}\right)4{\mu}^2\sum_{n=1}^{\infty}r^{2n}\\&=1-\left(1-(1-\mu)^p-2\mu\dfrac{r}{1-r}-\dfrac{(1+r-r\mu)4{\mu}^2r^2}{(2-\mu)(1-r)(1-r^2)}\right)\\&=1-\mu\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+\dots+(1-\mu)^{p-1}-2\dfrac{r}{1-r}\right)\\&\quad+\dfrac{(1+r-r\mu)4{\mu}^2r^2}{(2-\mu)(1-r)(1-r^2)}\\&=1-\dfrac{\mu\Psi(\mu,r)}{(2-\mu)(1-r)(1-r^2)}, \end{align*} $$
$$ \begin{align*} V_g(r)&=(1-\mu)^p+2\mu \sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-\mu}+\dfrac{r}{1-r}\right)4{\mu}^2\sum_{n=1}^{\infty}r^{2n}\\&=1-\left(1-(1-\mu)^p-2\mu\dfrac{r}{1-r}-\dfrac{(1+r-r\mu)4{\mu}^2r^2}{(2-\mu)(1-r)(1-r^2)}\right)\\&=1-\mu\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+\dots+(1-\mu)^{p-1}-2\dfrac{r}{1-r}\right)\\&\quad+\dfrac{(1+r-r\mu)4{\mu}^2r^2}{(2-\mu)(1-r)(1-r^2)}\\&=1-\dfrac{\mu\Psi(\mu,r)}{(2-\mu)(1-r)(1-r^2)}, \end{align*} $$
where
 $$ \begin{align*} \Psi(\mu,r)&:=(1-r)(1-r^2)(2-\mu)\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+\dots+(1-\mu)^{p-1}\right)\\&\quad-2r(1-r^2)(2-\mu)-4\mu(1+r-r\mu)r^2. \end{align*} $$
$$ \begin{align*} \Psi(\mu,r)&:=(1-r)(1-r^2)(2-\mu)\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+\dots+(1-\mu)^{p-1}\right)\\&\quad-2r(1-r^2)(2-\mu)-4\mu(1+r-r\mu)r^2. \end{align*} $$
We claim that
![]() $\Psi (\mu ,r)\geq 0$
for every
$\Psi (\mu ,r)\geq 0$
for every
![]() $r\leq r_*$
and
$r\leq r_*$
and
![]() $\mu \in (0,1].$
For simplicity, set
$\mu \in (0,1].$
For simplicity, set
![]() $R(r)=(1-r)(1-r^2)$
and by a straightforward calculations, we obtain
$R(r)=(1-r)(1-r^2)$
and by a straightforward calculations, we obtain
 $$ \begin{align*} \dfrac{\partial\Psi(\mu,r)}{\partial\mu}&=-\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+(1-\mu)^4+\dots+(1-\mu)^{p-1}\right)R(r)\\&\quad+(2-\mu)R(r)\left(-1-2(1-\mu)-3(1-\mu)^2-\dots-(p-1)(1-\mu)^{p-2}\right)\\&\quad+2r(1-r^2)-4r^2(1+r)+8r^3\mu, \end{align*} $$
$$ \begin{align*} \dfrac{\partial\Psi(\mu,r)}{\partial\mu}&=-\left(1+(1-\mu)+(1-\mu)^2+(1-\mu)^3+(1-\mu)^4+\dots+(1-\mu)^{p-1}\right)R(r)\\&\quad+(2-\mu)R(r)\left(-1-2(1-\mu)-3(1-\mu)^2-\dots-(p-1)(1-\mu)^{p-2}\right)\\&\quad+2r(1-r^2)-4r^2(1+r)+8r^3\mu, \end{align*} $$
 $$ \begin{align*} \dfrac{{\partial}^2\Psi(\mu,r)}{{\partial}{\mu}^2}&=2\left(1+2(1-\mu)+3(1-\mu)^2+\dots+(p-1)(1-\mu)^{p-2}\right)R(r)\\&\quad+(2-\mu)R(r)\left(2+6(1-\mu)+12(1-\mu)^2\dots+(p-1)(p-2)(1-\mu)^{p-3}\right)\\&\quad+8r^3, \end{align*} $$
$$ \begin{align*} \dfrac{{\partial}^2\Psi(\mu,r)}{{\partial}{\mu}^2}&=2\left(1+2(1-\mu)+3(1-\mu)^2+\dots+(p-1)(1-\mu)^{p-2}\right)R(r)\\&\quad+(2-\mu)R(r)\left(2+6(1-\mu)+12(1-\mu)^2\dots+(p-1)(p-2)(1-\mu)^{p-3}\right)\\&\quad+8r^3, \end{align*} $$
and
 $$ \begin{align*} \dfrac{{\partial}^3\Psi(\mu,r)}{{\partial}{\mu}^3}&=-3R(r)\left(2+6(1-\mu)+\dots+(p-1)(p-2)(1-\mu)^{p-3}\right)\\&\quad-R(r)(2-\mu)\left(6+24(1-\mu)+\dots(p-1)(p-2)(p-3)(1-\mu)^{p-4}\right)\\&\leq0 \;\;\mbox{for all}\;\; \mu\in(0,1]. \end{align*} $$
$$ \begin{align*} \dfrac{{\partial}^3\Psi(\mu,r)}{{\partial}{\mu}^3}&=-3R(r)\left(2+6(1-\mu)+\dots+(p-1)(p-2)(1-\mu)^{p-3}\right)\\&\quad-R(r)(2-\mu)\left(6+24(1-\mu)+\dots(p-1)(p-2)(p-3)(1-\mu)^{p-4}\right)\\&\leq0 \;\;\mbox{for all}\;\; \mu\in(0,1]. \end{align*} $$
Thus, it is easy to see that
 $\dfrac {{\partial }^2\Psi (\mu ,r)}{{\partial }{\mu }^2}$
is a decreasing function of
$\dfrac {{\partial }^2\Psi (\mu ,r)}{{\partial }{\mu }^2}$
is a decreasing function of
![]() $\mu $
in
$\mu $
in
![]() $(0,1]$
, and hence,
$(0,1]$
, and hence,
 $$ \begin{align*} \dfrac{{\partial}^2\Psi(\mu,r)}{{\partial}{\mu}^2}\geq \dfrac{{\partial}^2\Psi(1,r)}{{\partial}{\mu}^2}=4R(r)+8r^3\geq0 \;\;\mbox{for all}\;\; r\in[0,1). \end{align*} $$
$$ \begin{align*} \dfrac{{\partial}^2\Psi(\mu,r)}{{\partial}{\mu}^2}\geq \dfrac{{\partial}^2\Psi(1,r)}{{\partial}{\mu}^2}=4R(r)+8r^3\geq0 \;\;\mbox{for all}\;\; r\in[0,1). \end{align*} $$
This shows that
 $\dfrac {\partial \Psi (\mu ,r)}{\partial \mu }$
is an increasing function of
$\dfrac {\partial \Psi (\mu ,r)}{\partial \mu }$
is an increasing function of
![]() $\mu $
in
$\mu $
in
![]() $(0,1]$
. Therefore, we obtain
$(0,1]$
. Therefore, we obtain
 $$ \begin{align*} \dfrac{{\partial}\Psi(\mu,r)}{{\partial}\mu}\leq \dfrac{{\partial}\Psi(1,r)}{{\partial}\mu}=-2+4r-2r^2\leq0 \;\;\mbox{for all}\;\; r\in[0,1). \end{align*} $$
$$ \begin{align*} \dfrac{{\partial}\Psi(\mu,r)}{{\partial}\mu}\leq \dfrac{{\partial}\Psi(1,r)}{{\partial}\mu}=-2+4r-2r^2\leq0 \;\;\mbox{for all}\;\; r\in[0,1). \end{align*} $$
Clearly,
where
![]() $r_*$
is given as in the statement of the theorem, and hence, the proof is complete.
$r_*$
is given as in the statement of the theorem, and hence, the proof is complete.
4 Bohr phenomenon for the class of subordinations
Studying the Bohr inequality for the class of subordination is an interesting and difficult exercise. In recent years, researchers are studying the Bohr phenomenon for such classes of functions and till date, the study continues. In [Reference Abu-Muhanna1], Abu-Muhanna showed the following sharp Bohr phenomenon for the subordinate class
![]() $S(g).$
$S(g).$
Theorem 4.1 [Reference Abu-Muhanna1]
Suppose g is a univalent function in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $f\in S(g)$
such that
$f\in S(g)$
such that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then
$f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then
 $$ \begin{align*} \sum_{n=1}^{\infty}|a_n|r^n\leq d\;\;\mbox{for}\;\; |z|=r\leq r_0=3-\sqrt{8}. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}|a_n|r^n\leq d\;\;\mbox{for}\;\; |z|=r\leq r_0=3-\sqrt{8}. \end{align*} $$
The radius
![]() $r_0$
is sharp for the Koebe function
$r_0$
is sharp for the Koebe function
![]() $f(z)=z/(1-z)^2$
.
$f(z)=z/(1-z)^2$
.
In [Reference Abu-Muhanna, Ali, Ng and Hasni2], Abu-Muhanna et al. established the results determining the Bohr radius for subordinating families of analytic functions and bounded harmonic mappings. In [Reference Liu, Ponnusamy and Wang34], Lie et al. studied two refined versions of the Bohr inequality and determine the Bohr radius for the derivatives of analytic functions associated with quasi-subordination. Bohr’s phenomenon for analytic functions subordinate to starlike or convex function is investigated by Hamada in [Reference Hamada24]. Recently, Ponnusamy et al. [Reference Ponnusamy, Vijayakumar and Wirths37] obtained the following refined versions of the Bohr-type inequalities.
Theorem 4.2 [Reference Ponnusamy, Vijayakumar and Wirths37]
Suppose that g is a univalent function in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $f\in S(g)$
such that
$f\in S(g)$
such that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then
$f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then
 $$ \begin{align} \sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq d \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}\leq d \end{align} $$
for
![]() $|z|=r<r^{\prime },$
where
$|z|=r<r^{\prime },$
where
![]() $r^{\prime }\approx 0.128445$
is the unique root of the equation
$r^{\prime }\approx 0.128445$
is the unique root of the equation
in the interval
![]() $(0,1),$
where
$(0,1),$
where
![]() $d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))<1.$
The sharpness of
$d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))<1.$
The sharpness of
![]() $r^{\prime }$
is shown by the Koebe function
$r^{\prime }$
is shown by the Koebe function
![]() $f(z)=z/(1-z)^2.$
$f(z)=z/(1-z)^2.$
Theorem 4.3 [Reference Ponnusamy, Vijayakumar and Wirths37]
Let
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n$
and g be analytic in
$f(z)=\sum _{n=0}^{\infty }a_nz^n$
and g be analytic in
![]() $\mathbb {D}$
such that g is univalent and convex in
$\mathbb {D}$
such that g is univalent and convex in
![]() $\mathbb {D}.$
Assume that
$\mathbb {D}.$
Assume that
![]() $f\in S(g)$
and
$f\in S(g)$
and
![]() $d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))\leq 1.$
Then the inequality (4.1) holds for all
$d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))\leq 1.$
Then the inequality (4.1) holds for all
![]() $r\leq r_*,$
where
$r\leq r_*,$
where
![]() $r_*\approx 0.24683$
is the unique root of the equation
$r_*\approx 0.24683$
is the unique root of the equation
![]() $3r^3-5r^2-3r+1=0$
in the interval
$3r^3-5r^2-3r+1=0$
in the interval
![]() $(0,1).$
Moreover, for any
$(0,1).$
Moreover, for any
![]() $d\in (0,1), $
there exists a uniquely defined
$d\in (0,1), $
there exists a uniquely defined
![]() $r_0(a_0)\in (r_*,1/3) $
such that the inequality (4.1) holds for all
$r_0(a_0)\in (r_*,1/3) $
such that the inequality (4.1) holds for all
![]() $r\in [0,r_0(a_0)].$
The radius
$r\in [0,r_0(a_0)].$
The radius
![]() $r_0(a_0)$
can be calculated as the solution of the equation
$r_0(a_0)$
can be calculated as the solution of the equation
![]() $4r^3d^2-(7r^3+3r^2-3r+1)d+6r^3-2r^2-6r+2=0.$
$4r^3d^2-(7r^3+3r^2-3r+1)d+6r^3-2r^2-6r+2=0.$
In the study of refined Bohr-type inequalities, finding different versions of refined Bohr-type inequalities and their sharpness is interesting in geometric function theory. Our aim in this section is to determine refined versions of Bohr-type inequalities for functions in the class
![]() $ S(g) $
. We now mention here refined versions of Bohr-type inequalities obtained recently by Liu et al. [Reference Liu, Liu and Ponnusamy32] for functions in the class
$ S(g) $
. We now mention here refined versions of Bohr-type inequalities obtained recently by Liu et al. [Reference Liu, Liu and Ponnusamy32] for functions in the class
![]() $ \mathcal {B} $
.
$ \mathcal {B} $
.
Theorem 4.4 [Reference Liu, Liu and Ponnusamy32]
Suppose that
![]() $f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
$f=\sum _{n=0}^{\infty }a_nz^n\in \mathcal {B}.$
Then
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|\leq 1\;\;\mbox{for}\;\; |z|=r\leq \dfrac{1}{5} \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|\leq 1\;\;\mbox{for}\;\; |z|=r\leq \dfrac{1}{5} \end{align*} $$
and the number
![]() $1/5$
cannot be improved. Moreover,
$1/5$
cannot be improved. Moreover,
 $$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|^2\leq 1\;\;\mbox{for}\;\; |z|=r\leq \dfrac{1}{3} \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}|a_n|r^n+\left(\dfrac{1}{1+|a_0|}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|^2\leq 1\;\;\mbox{for}\;\; |z|=r\leq \dfrac{1}{3} \end{align*} $$
if, and only if,
![]() $0\leq |a_0|\leq 4\sqrt {2}-5\approx 0.656854.$
$0\leq |a_0|\leq 4\sqrt {2}-5\approx 0.656854.$
To continue the research, our objective in this section is to establish the inequalities of Theorem 4.4 for the subordination class
![]() $S(g),$
where
$S(g),$
where
![]() $ g $
may be univalent or convex univalent in
$ g $
may be univalent or convex univalent in
![]() $ \mathbb {D} $
. Therefore, it is natural raise the following questions.
$ \mathbb {D} $
. Therefore, it is natural raise the following questions.
Question 4.1 Can we derive a sharp version of Theorem 4.4 for the class
![]() $S(g)$
when g is a univalent function in
$S(g)$
when g is a univalent function in
![]() $\mathbb {D}$
?
$\mathbb {D}$
?
Question 4.2 Can we derive a sharp version of Theorem 4.4 for the class
![]() $S(g) $
when g is the univalent and convex function in
$S(g) $
when g is the univalent and convex function in
![]() $\mathbb {D}$
?
$\mathbb {D}$
?
We obtain the following two results answering Questions 4.1 and 4.2, respectively.
Theorem 4.5 Let g be analytic and univalent function in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $f\in S(g)$
so that
$f\in S(g)$
so that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then the inequality
$f(z)=\sum _{n=0}^{\infty }a_nz^n.$
Then the inequality
 $$ \begin{align} X_{1,f}(r):=\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|\leq d \end{align} $$
$$ \begin{align} X_{1,f}(r):=\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|\leq d \end{align} $$
for
![]() $r\leq r_1,$
where
$r\leq r_1,$
where
![]() $r_1\approx 0.0888988$
is the unique root of the equation
$r_1\approx 0.0888988$
is the unique root of the equation
![]() $1-9r-27r^2+19r^3+3r^4-11r^5-9r^6+r^7=0 $
in the interval
$1-9r-27r^2+19r^3+3r^4-11r^5-9r^6+r^7=0 $
in the interval
![]() $(0,1).$
Moreover,
$(0,1).$
Moreover,
 $$ \begin{align} X_{2,f}(r):=\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|^2\leq d \end{align} $$
$$ \begin{align} X_{2,f}(r):=\sum_{n=1}^{\infty}|a_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|a_n|^2r^{2n}+|f(z)-a_0|^2\leq d \end{align} $$
for
![]() $r\leq r_2,$
where
$r\leq r_2,$
where
![]() $r_2\approx 0.10469$
is the unique root of the equation
$r_2\approx 0.10469$
is the unique root of the equation
in the interval
![]() $(0,1),$
where
$(0,1),$
where
![]() $d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))<1.$
The sharpness of
$d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))<1.$
The sharpness of
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are shown by the Koebe function
$r_2$
are shown by the Koebe function
![]() $f(z)=z/(1-z)^2.$
$f(z)=z/(1-z)^2.$
Theorem 4.6 Let g be analytic in
![]() $\mathbb {D}$
such that g is univalent and convex in
$\mathbb {D}$
such that g is univalent and convex in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $f\in S(g)$
so that
$f\in S(g)$
so that
![]() $f(z)=\sum _{n=0}^{\infty }a_nz^n$
. Then the inequality (4.2) holds for
$f(z)=\sum _{n=0}^{\infty }a_nz^n$
. Then the inequality (4.2) holds for
![]() $r\leq r_3,$
where
$r\leq r_3,$
where
![]() $r_3\approx 0.174789$
is the unique root of the equation
$r_3\approx 0.174789$
is the unique root of the equation
![]() $ 1-5r-5r^2+5r^3=0$
in the interval
$ 1-5r-5r^2+5r^3=0$
in the interval
![]() $(0,1).$
Moreover, the inequality (4.3) holds for
$(0,1).$
Moreover, the inequality (4.3) holds for
![]() $r\leq r_4,$
where
$r\leq r_4,$
where
![]() $r_4\approx 0.20473$
is the unique root of the equation
$r_4\approx 0.20473$
is the unique root of the equation
in the interval
![]() $(0,1),$
where
$(0,1),$
where
![]() $d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))\leq 1.$
$d=\mathrm{dist}(g(0),\partial g(\mathbb {D}))\leq 1.$
We now discuss the proof of Theorems 4.5 and 4.6.
Proof of Theorem 4.5
Let
![]() $f\prec g,$
where
$f\prec g,$
where
![]() $g(z)=\sum _{n=0}^{\infty }b_nz^n$
is a univalent mapping on
$g(z)=\sum _{n=0}^{\infty }b_nz^n$
is a univalent mapping on
![]() $\mathbb {D}$
onto a simply connected domain
$\mathbb {D}$
onto a simply connected domain
![]() $\Omega =g(\mathbb {D}).$
Then it is well known from the Koebe estimate and Rogosinski’s coefficient estimates for univalent functions that (see [Reference Branges19, Reference Rogosinski39])
$\Omega =g(\mathbb {D}).$
Then it is well known from the Koebe estimate and Rogosinski’s coefficient estimates for univalent functions that (see [Reference Branges19, Reference Rogosinski39])
where
![]() $d=\mathrm{dist}(g(0),\partial \Omega ).$
Also, the above first inequality gives
$d=\mathrm{dist}(g(0),\partial \Omega ).$
Also, the above first inequality gives
![]() $|b_n|\leq 4nd$
for
$|b_n|\leq 4nd$
for
![]() $n\geq 1.$
Since
$n\geq 1.$
Since
![]() $f\prec g,$
[Reference Bhowmik and Das16, Lemma 1] we see that
$f\prec g,$
[Reference Bhowmik and Das16, Lemma 1] we see that
 $$ \begin{align} |f(z)-a_0|=\left|\sum_{n=1}^{\infty}a_nz^n\right| \leq\sum_{n=1}^{\infty}|a_n|r^n\leq \sum_{n=1}^{\infty}|b_n|r^n\;\;\mbox{for}\;\; r\leq \dfrac{1}{3}. \end{align} $$
$$ \begin{align} |f(z)-a_0|=\left|\sum_{n=1}^{\infty}a_nz^n\right| \leq\sum_{n=1}^{\infty}|a_n|r^n\leq \sum_{n=1}^{\infty}|b_n|r^n\;\;\mbox{for}\;\; r\leq \dfrac{1}{3}. \end{align} $$
By the similar argument used in the proof of Theorem 4.2 and in view of (4.4) and Lemma 3.1, an easy computation shows that
 $$ \begin{align*} X_{1,g}(r)&\leq 8d\sum_{n=1}^{\infty}nr^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)16d^2\sum_{n=1}^{\infty}n^2r^{2n}\\&=d-d\left(\dfrac{1-10r+r^2}{(1-r)^2}-\dfrac{(1+r-rd)16dr^2(1+r^2)}{(1-r)(1-r^2)^3(2-d)}\right)\\&=d-\dfrac{dA_1(d,r)}{(1-r)(1-r^2)^3(2-d)}, \end{align*} $$
$$ \begin{align*} X_{1,g}(r)&\leq 8d\sum_{n=1}^{\infty}nr^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)16d^2\sum_{n=1}^{\infty}n^2r^{2n}\\&=d-d\left(\dfrac{1-10r+r^2}{(1-r)^2}-\dfrac{(1+r-rd)16dr^2(1+r^2)}{(1-r)(1-r^2)^3(2-d)}\right)\\&=d-\dfrac{dA_1(d,r)}{(1-r)(1-r^2)^3(2-d)}, \end{align*} $$
where
Our aim is to show that
![]() $A_1(d,r)\geq 0$
for every
$A_1(d,r)\geq 0$
for every
![]() $r\leq r_1$
and
$r\leq r_1$
and
![]() $d\in (0,1].$
We see that
$d\in (0,1].$
We see that
and thus,
![]() $\dfrac {\partial A_1(d,r)}{\partial d}$
is an increasing function of
$\dfrac {\partial A_1(d,r)}{\partial d}$
is an increasing function of
![]() $d.$
This gives
$d.$
This gives
for
![]() $ r\leq 0.120502 $
, and hence
$ r\leq 0.120502 $
, and hence
![]() $A_1(d,r)$
is a decreasing function of d in interval
$A_1(d,r)$
is a decreasing function of d in interval
![]() $(0,1]$
. Therefore,
$(0,1]$
. Therefore,
for all
![]() $ r\leq r_1 $
, where
$ r\leq r_1 $
, where
![]() $r_1\approx 0.0888988$
is the unique root in the interval
$r_1\approx 0.0888988$
is the unique root in the interval
![]() $(0,1)$
of the equation
$(0,1)$
of the equation
Moreover, in order to show the inequality (4.3), it is enough to show that
 $$ \begin{align*} X_{2,g}=\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}+\left(\sum_{n=1}^{\infty}|b_n|r^n\right)^2\leq d\;\;\mbox{for}\;\; r\leq r_2. \end{align*} $$
$$ \begin{align*} X_{2,g}=\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}+\left(\sum_{n=1}^{\infty}|b_n|r^n\right)^2\leq d\;\;\mbox{for}\;\; r\leq r_2. \end{align*} $$
Since
![]() $|b_n|\leq 4nd$
for
$|b_n|\leq 4nd$
for
![]() $n\geq 1,$
an easy computation shows that
$n\geq 1,$
an easy computation shows that
 $$ \begin{align*} X_{2,g}(r)&\leq 4d\sum_{n=1}^{\infty}nr^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)16d^2\sum_{n=1}^{\infty}n^2r^{2n}+16d^2\left(\sum_{n=1}^{\infty}nr^n\right)^2\\&=d-d\left(1-\dfrac{4r}{(1-r)^2}-\dfrac{(1+r-rd)16dr^2(1+r^2)}{(1-r)(1-r^2)^3(2-d)}-\dfrac{16dr^2}{(1-r)^4}\right)\\&=d-\dfrac{dA_2(d,r)}{(1-r)(1-r^2)^3(2-d)}, \end{align*} $$
$$ \begin{align*} X_{2,g}(r)&\leq 4d\sum_{n=1}^{\infty}nr^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)16d^2\sum_{n=1}^{\infty}n^2r^{2n}+16d^2\left(\sum_{n=1}^{\infty}nr^n\right)^2\\&=d-d\left(1-\dfrac{4r}{(1-r)^2}-\dfrac{(1+r-rd)16dr^2(1+r^2)}{(1-r)(1-r^2)^3(2-d)}-\dfrac{16dr^2}{(1-r)^4}\right)\\&=d-\dfrac{dA_2(d,r)}{(1-r)(1-r^2)^3(2-d)}, \end{align*} $$
where
 $$ \begin{align*} A_2(d,r)&:=(1-6r+r^2)(1-r)^2(1+r)^3(2-d)-16d(r^2+r^4)(1+r-dr)\\&\quad-16dr^2(1+r)^3(2-d). \end{align*} $$
$$ \begin{align*} A_2(d,r)&:=(1-6r+r^2)(1-r)^2(1+r)^3(2-d)-16d(r^2+r^4)(1+r-dr)\\&\quad-16dr^2(1+r)^3(2-d). \end{align*} $$
We claim that
![]() $A_2(d,r)\geq 0$
for every
$A_2(d,r)\geq 0$
for every
![]() $r\leq r_2$
and
$r\leq r_2$
and
![]() $d\in (0,1].$
It can be shown that
$d\in (0,1].$
It can be shown that
and hence,
![]() $\dfrac {\partial A_2(d,r)}{\partial d}$
is an increasing function of
$\dfrac {\partial A_2(d,r)}{\partial d}$
is an increasing function of
![]() $d.$
Evidently,
$d.$
Evidently,
for every
![]() $ r\leq 1 $
, and hence,
$ r\leq 1 $
, and hence,
![]() $A_2(d,r)$
is a decreasing function of d in interval
$A_2(d,r)$
is a decreasing function of d in interval
![]() $(0,1]$
. Therefore,
$(0,1]$
. Therefore,
for all
![]() $ r\leq r_2$
, where
$ r\leq r_2$
, where
![]() $r_2\approx 0.10469$
is the unique root of the equation
$r_2\approx 0.10469$
is the unique root of the equation
in the interval
![]() $(0,1).$
$(0,1).$
The sharpness of
![]() $r_1$
and
$r_1$
and
![]() $r_2 $
can be easily shown by the Koebe function
$r_2 $
can be easily shown by the Koebe function
![]() $f(z)=z/ (1-z)^2$
and hence, we omit the details.
$f(z)=z/ (1-z)^2$
and hence, we omit the details.
Proof of Theorem 4.6
Let
![]() $f\prec g,$
where
$f\prec g,$
where
![]() $g(z)=\sum _{n=0}^{\infty }b_nz^n$
is a univalent function on
$g(z)=\sum _{n=0}^{\infty }b_nz^n$
is a univalent function on
![]() $\mathbb {D}$
onto a convex domain
$\mathbb {D}$
onto a convex domain
![]() $\Omega =g(\mathbb {D}).$
Then it is well known from the growth estimate for convex functions and Rogosinski’s coefficient estimate (see [Reference Branges19, Reference Rogosinski39]) that
$\Omega =g(\mathbb {D}).$
Then it is well known from the growth estimate for convex functions and Rogosinski’s coefficient estimate (see [Reference Branges19, Reference Rogosinski39]) that
where
![]() $d=\mathrm{dist}(g(0),\partial \Omega ).$
It follows that
$d=\mathrm{dist}(g(0),\partial \Omega ).$
It follows that
![]() $|b_n|\leq 2d$
for
$|b_n|\leq 2d$
for
![]() $n\geq 1.$
Combining these inequalities and the inequality (4.4), we see that the desired inequality follows with the help of Lemma 3.1 if we able to show the inequality
$n\geq 1.$
Combining these inequalities and the inequality (4.4), we see that the desired inequality follows with the help of Lemma 3.1 if we able to show the inequality
 $$ \begin{align*} W_{1,g}(r):=2\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}\leq d\;\;\mbox{for}\;\; r\leq r_3. \end{align*} $$
$$ \begin{align*} W_{1,g}(r):=2\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}\leq d\;\;\mbox{for}\;\; r\leq r_3. \end{align*} $$
Since
![]() $|b_n|\leq 2d$
for
$|b_n|\leq 2d$
for
![]() $n\geq 1,$
we have
$n\geq 1,$
we have
 $$ \begin{align*} W_{1,g}(r)&\leq 4d\sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)4d^2\sum_{n=1}^{\infty}r^{2n}\\&=d-d\left(1-\dfrac{4r}{1-r}+\dfrac{(1+r-rd)4dr^2}{(1-r)(2-d)(1-r^2)}\right)\\&=d-\dfrac{d\Phi_1(d,r)}{(1-r)(1-r^2)(2-d)}, \end{align*} $$
$$ \begin{align*} W_{1,g}(r)&\leq 4d\sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)4d^2\sum_{n=1}^{\infty}r^{2n}\\&=d-d\left(1-\dfrac{4r}{1-r}+\dfrac{(1+r-rd)4dr^2}{(1-r)(2-d)(1-r^2)}\right)\\&=d-\dfrac{d\Phi_1(d,r)}{(1-r)(1-r^2)(2-d)}, \end{align*} $$
where
We claim that
![]() $\Phi _1(d,r)\geq 0$
for every
$\Phi _1(d,r)\geq 0$
for every
![]() $r\leq r_3$
and
$r\leq r_3$
and
![]() $d\in (0,1].$
We see that
$d\in (0,1].$
We see that
and thus,
![]() $\dfrac {\partial \Phi _1(d,r)}{\partial d}$
is an increasing function of
$\dfrac {\partial \Phi _1(d,r)}{\partial d}$
is an increasing function of
![]() $d.$
This gives
$d.$
This gives
for every
![]() $ r\leq 0.236068 $
, and hence
$ r\leq 0.236068 $
, and hence
![]() $\Phi _1(d,r)$
is a decreasing function of d in interval
$\Phi _1(d,r)$
is a decreasing function of d in interval
![]() $(0,1]$
. Therefore
$(0,1]$
. Therefore
where
![]() $r_3\approx 0.174789$
is the unique root of the equation
$r_3\approx 0.174789$
is the unique root of the equation
![]() $1-5r-5r^2+5r^3=0$
in the interval
$1-5r-5r^2+5r^3=0$
in the interval
![]() $(0,1).$
Moreover, for the inequality (4.3), it suffices to show that
$(0,1).$
Moreover, for the inequality (4.3), it suffices to show that
 $$ \begin{align*} W_{2,g}:=\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}+\left(\sum_{n=1}^{\infty}|b_n|r^n\right)^2\leq d. \end{align*} $$
$$ \begin{align*} W_{2,g}:=\sum_{n=1}^{\infty}|b_n|r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)\sum_{n=1}^{\infty}|b_n|^2r^{2n}+\left(\sum_{n=1}^{\infty}|b_n|r^n\right)^2\leq d. \end{align*} $$
Since
![]() $|b_n|\leq 2d$
for
$|b_n|\leq 2d$
for
![]() $n\geq 1,$
we have
$n\geq 1,$
we have
 $$ \begin{align*} W_{2,g}(r)&\leq 2d\sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)4d^2\sum_{n=1}^{\infty}r^{2n}+\left(2d\sum_{n=1}^{\infty}r^n\right)^2\\&=d-d\left(1-\dfrac{2r}{1-r}+\dfrac{(1+r-rd)4dr^2}{(1-r)(2-d)(1-r^2)}+\dfrac{4dr^2}{(1-r)^2}\right)\\&=d-\dfrac{d\Phi_2(d,r)}{(1-r)^2(1-r^2)(2-d)}, \end{align*} $$
$$ \begin{align*} W_{2,g}(r)&\leq 2d\sum_{n=1}^{\infty}r^n+\left(\dfrac{1}{2-d}+\dfrac{r}{1-r}\right)4d^2\sum_{n=1}^{\infty}r^{2n}+\left(2d\sum_{n=1}^{\infty}r^n\right)^2\\&=d-d\left(1-\dfrac{2r}{1-r}+\dfrac{(1+r-rd)4dr^2}{(1-r)(2-d)(1-r^2)}+\dfrac{4dr^2}{(1-r)^2}\right)\\&=d-\dfrac{d\Phi_2(d,r)}{(1-r)^2(1-r^2)(2-d)}, \end{align*} $$
where
Our aim is to show that
![]() $\Phi _2(d,r)\geq 0$
for every
$\Phi _2(d,r)\geq 0$
for every
![]() $r\leq r_4$
and
$r\leq r_4$
and
![]() $d\in (0,1].$
A simple computation shows that
$d\in (0,1].$
A simple computation shows that
which implies that
![]() $\dfrac {\partial \Phi _2(d,r)}{\partial d}$
is an increasing function of
$\dfrac {\partial \Phi _2(d,r)}{\partial d}$
is an increasing function of
![]() $d.$
This gives
$d.$
This gives
and hence
![]() $\Phi _2(d,r)$
is a decreasing function of d in interval
$\Phi _2(d,r)$
is a decreasing function of d in interval
![]() $(0,1]$
. Therefore,
$(0,1]$
. Therefore,
where
![]() $r_4\approx 0.20473$
is the unique root in the interval
$r_4\approx 0.20473$
is the unique root in the interval
![]() $(0,1)$
of the equation
$(0,1)$
of the equation
![]() $1-3r-9r^2-r^3=0.$
The sharpness of
$1-3r-9r^2-r^3=0.$
The sharpness of
![]() $r_3$
and
$r_3$
and
![]() $r_4 $
can be easily shown by the function
$r_4 $
can be easily shown by the function
![]() $f(z)=1/(1-z)$
and hence, we omit the details.
$f(z)=1/(1-z)$
and hence, we omit the details.
Acknowledgment
The authors extend their gratitude to the anonymous referees for their elaborate comments and suggestions, which significantly enhance the presentation of the article. The first author is supported by UGC-JRF (NTA Ref. No.: 201610135853), New Delhi, India.
Conflicts of interest
The authors declare that there is no conflicts of interest regarding the publication of this article.
Data availability statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.