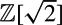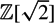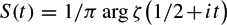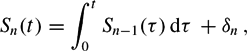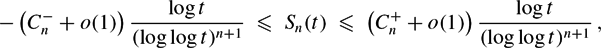Research Article
On the polar varieties of ruled hypersurfaces
-
- Published online by Cambridge University Press:
- 09 November 2016, pp. 193-204
-
- Article
- Export citation
Notes on weak units of group-like 1- and 2-stacks
-
- Published online by Cambridge University Press:
- 09 November 2016, pp. 205-220
-
- Article
- Export citation
The classification of rank 3 reflective hyperbolic lattices over
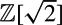 $\mathbb{Z}[\sqrt{2}]$
$\mathbb{Z}[\sqrt{2}]$
-
- Published online by Cambridge University Press:
- 09 December 2016, pp. 221-257
-
- Article
- Export citation
Bounding Sn(t) on the Riemann hypothesis
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 259-283
-
- Article
- Export citation
Local 𝔪-adic constancy of F-pure thresholds and test ideals
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 285-295
-
- Article
- Export citation
Generalised Dirichlet to Neumann maps for linear dispersive equations on half-line
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. 297-324
-
- Article
- Export citation
Derived invariance by syzygy complexes
-
- Published online by Cambridge University Press:
- 13 February 2017, pp. 325-343
-
- Article
- Export citation
On the tree-likeness of hyperbolic spaces
-
- Published online by Cambridge University Press:
- 10 April 2017, pp. 345-361
-
- Article
- Export citation
Crystallographic groups with trivial center and outer automorphism group
-
- Published online by Cambridge University Press:
- 06 March 2017, pp. 363-368
-
- Article
- Export citation
Equivariant smoothing of piecewise linear manifolds
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 369-380
-
- Article
- Export citation
Corrigendum
Corrigendum to “Decomposing locally compact groups into simple pieces” [Math. Proc. Camb. Phil. Soc. 150 (1) (2011) 97-128]
-
- Published online by Cambridge University Press:
- 21 November 2017, pp. 381-384
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 164 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 164 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation