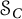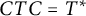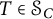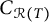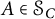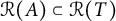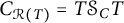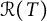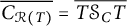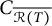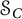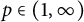1 Introduction
This paper is a continuation of a recent paper [Reference Wang and Zhu44], and aims to study the range inclusion and the diagonalization of complex symmetric operators. We start by recalling some terminology and basic facts.
1.1 Preliminaries
Throughout the following,
![]() ${\mathcal {H}}$
will always denote a separable, complex Hilbert space with an inner product
${\mathcal {H}}$
will always denote a separable, complex Hilbert space with an inner product
![]() $\langle \cdot ,\cdot \rangle $
. We let
$\langle \cdot ,\cdot \rangle $
. We let
![]() $\mathcal {B}({\mathcal {H}}_1,{\mathcal {H}}_2)$
denote the Banach space of all bounded linear operators from
$\mathcal {B}({\mathcal {H}}_1,{\mathcal {H}}_2)$
denote the Banach space of all bounded linear operators from
![]() ${\mathcal {H}}_1$
to
${\mathcal {H}}_1$
to
![]() ${\mathcal {H}}_2$
. We shall write
${\mathcal {H}}_2$
. We shall write
![]() $\mathcal {B(H)}$
instead of
$\mathcal {B(H)}$
instead of
![]() $\mathcal {B}({\mathcal {H}},{\mathcal {H}})$
. A map
$\mathcal {B}({\mathcal {H}},{\mathcal {H}})$
. A map
![]() $C:{\mathcal {H}} \rightarrow {\mathcal {H}}$
is called a conjugation if:
$C:{\mathcal {H}} \rightarrow {\mathcal {H}}$
is called a conjugation if:
-
(i) C is antilinear, i.e.,
 $C(\alpha x+y)=\overline {\alpha } C x+ Cy$
for
$C(\alpha x+y)=\overline {\alpha } C x+ Cy$
for
 $x,y\in {\mathcal {H}}$
and
$x,y\in {\mathcal {H}}$
and
 $\alpha \in \mathbb {C}$
,
$\alpha \in \mathbb {C}$
, -
(ii) C is invertible with
 $C^{-1}=C$
, and
$C^{-1}=C$
, and -
(iii)
 $\langle Cx, Cy\rangle =\langle y,x\rangle $
for all
$\langle Cx, Cy\rangle =\langle y,x\rangle $
for all
 $x, y\in {\mathcal {H}}$
.
$x, y\in {\mathcal {H}}$
.
An operator
![]() $T\in \mathcal {B(H)}$
is said to be complex symmetric (c.s.) if
$T\in \mathcal {B(H)}$
is said to be complex symmetric (c.s.) if
![]() $CTC=T^{*}$
for some conjugation C on
$CTC=T^{*}$
for some conjugation C on
![]() ${\mathcal {H}}$
; in this case, T is called C-symmetric. The general definition of a C-symmetric operator was first given in I. M. Glazman’s paper [Reference Glazman18], which combined with [Reference Glazman19] marks the foundation of the extension theory of C-symmetric differential operators. Glazman’s work was complemented in a series of papers such as [Reference Kalinina26, Reference Knowles28, Reference Li30, Reference Makarova32, Reference Race35, Reference Rayh and Tsekanovskii37], most of which were devoted to the existence and concrete descriptions of extensions of C-symmetric differential operators. The reader is referred to [Reference Zagorodnyuk47] and the references cited therein for more historical comments. Throughout the following, we let C denote a conjugation on
${\mathcal {H}}$
; in this case, T is called C-symmetric. The general definition of a C-symmetric operator was first given in I. M. Glazman’s paper [Reference Glazman18], which combined with [Reference Glazman19] marks the foundation of the extension theory of C-symmetric differential operators. Glazman’s work was complemented in a series of papers such as [Reference Kalinina26, Reference Knowles28, Reference Li30, Reference Makarova32, Reference Race35, Reference Rayh and Tsekanovskii37], most of which were devoted to the existence and concrete descriptions of extensions of C-symmetric differential operators. The reader is referred to [Reference Zagorodnyuk47] and the references cited therein for more historical comments. Throughout the following, we let C denote a conjugation on
![]() ${\mathcal {H}}$
unless otherwise stated, and let
${\mathcal {H}}$
unless otherwise stated, and let
![]() $\mathcal {S}_C$
denote the collection of all C-symmetric operators. The term “symmetric” stems from the fact that an operator T is complex symmetric if and only if there is an orthonormal basis
$\mathcal {S}_C$
denote the collection of all C-symmetric operators. The term “symmetric” stems from the fact that an operator T is complex symmetric if and only if there is an orthonormal basis
![]() $\{e_i\}$
of
$\{e_i\}$
of
![]() ${\mathcal {H}}$
such that T can be written as a (complex) symmetric matrix relative to
${\mathcal {H}}$
such that T can be written as a (complex) symmetric matrix relative to
![]() $\{e_i\}$
.
$\{e_i\}$
.
Now let us introduce the background of the general study of c.s. operators, initiated in [Reference Garcia and Putinar14, Reference Garcia and Putinar15]. In the finite-dimensional case, the class of c.s. operators, containing those operators induced by Toeplitz matrices and Hankel matrices, has been studied for many years. In fact, the study of c.s. operators has classical roots in the work on automorphic functions [Reference Hua24], projective geometry [Reference Jacobson25], quadratic forms [Reference Schur39], symplectic geometry [Reference Siegel40], and function theory [Reference Takagi42]. In the infinite-dimensional case, it is shown that the class of c.s. operators contains many important special operators, such as normal operators, binormal operators, truncated Toeplitz operators [Reference Sarason38], and many integration operators. People’s current interests in c.s. operators are greatly inspired by many results of S. Garcia, M. Putinar, and W. Wogen [Reference Garcia and Putinar14–Reference Garcia and Wogen16] as well as their connections to concrete operators [Reference Garcia10–Reference Garcia12] and applications to mathematical physics [Reference Garcia, Prodan and Putinar13, Reference Hai and Putinar20, Reference Prodan, Garcia and Putinar34].
Also, c.s. operators play an important role in the study of JB
![]() $^{*}$
-triples, a class of complex Banach spaces with well-behaved algebraic, geometric and holomorphic properties. This is due to the Jordan structure of
$^{*}$
-triples, a class of complex Banach spaces with well-behaved algebraic, geometric and holomorphic properties. This is due to the Jordan structure of
![]() $\mathcal {S}_C$
. In fact,
$\mathcal {S}_C$
. In fact,
![]() $\mathcal {S}_C$
is a weak operator closed subspace of
$\mathcal {S}_C$
is a weak operator closed subspace of
![]() $\mathcal {B(H)}$
, closed under the Jordan product
$\mathcal {B(H)}$
, closed under the Jordan product
![]() $\circ $
, defined by
$\circ $
, defined by
![]() $\mathcal {S}_C$
has been studied under the name of Hermitian type Cartan factors for many years. There are six types of Cartan factors, namely rectangular type, Hermitian type, symplectic type, triple spin factors, and two finite-dimensional exceptional Cartan factors. They originally arose in É. Cartan’s classification of finite-dimensional bounded symmetric domains (see [Reference Cartan2] or [Reference Chu3, Theorem 2.5.9]) and play an important role in the proof of the Gelfand–Naimark theorem for JB
$\mathcal {S}_C$
has been studied under the name of Hermitian type Cartan factors for many years. There are six types of Cartan factors, namely rectangular type, Hermitian type, symplectic type, triple spin factors, and two finite-dimensional exceptional Cartan factors. They originally arose in É. Cartan’s classification of finite-dimensional bounded symmetric domains (see [Reference Cartan2] or [Reference Chu3, Theorem 2.5.9]) and play an important role in the proof of the Gelfand–Naimark theorem for JB
![]() $^{*}$
-triples [Reference Friedman and Russo9].
$^{*}$
-triples [Reference Friedman and Russo9].
The present study is inspired by several interesting results concerning
![]() $\mathcal {S}_C$
, which suggest a rich structure of
$\mathcal {S}_C$
, which suggest a rich structure of
![]() $\mathcal {S}_C$
. In [Reference Garcia11], it was proved that each contraction
$\mathcal {S}_C$
. In [Reference Garcia11], it was proved that each contraction
![]() $T\in \mathcal {S}_C$
is the mean of two unitary operators in
$T\in \mathcal {S}_C$
is the mean of two unitary operators in
![]() $\mathcal {S}_C$
. In [Reference Wang and Zhu44], the authors classified Jordan ideals of
$\mathcal {S}_C$
. In [Reference Wang and Zhu44], the authors classified Jordan ideals of
![]() $\mathcal {S}_C$
, showing that Jordan ideals of
$\mathcal {S}_C$
, showing that Jordan ideals of
![]() $\mathcal {S}_C$
arise by intersection from associative ideals of
$\mathcal {S}_C$
arise by intersection from associative ideals of
![]() $\mathcal {B(H)}$
and hence are self-adjoint. Moreover, Jordan automorphisms of
$\mathcal {B(H)}$
and hence are self-adjoint. Moreover, Jordan automorphisms of
![]() $\mathcal {S}_C$
are shown to be induced by certain unitary operators. Also, it is proved that those Jordan invertible ones constitute a dense, path connected subset of
$\mathcal {S}_C$
are shown to be induced by certain unitary operators. Also, it is proved that those Jordan invertible ones constitute a dense, path connected subset of
![]() $\mathcal {S}_C$
. These results provide interesting contrasts between
$\mathcal {S}_C$
. These results provide interesting contrasts between
![]() $\mathcal {S}_C$
and
$\mathcal {S}_C$
and
![]() $\mathcal {B(H)}$
.
$\mathcal {B(H)}$
.
1.2 Range inclusion in
 $\mathcal {S}_C$
$\mathcal {S}_C$
The first aim of this paper is to characterize the range inclusion of operators in
![]() $\mathcal {S}_C$
, that is, given an operator
$\mathcal {S}_C$
, that is, given an operator
![]() $T\in \mathcal {S}_C$
, to characterize all those operators
$T\in \mathcal {S}_C$
, to characterize all those operators
![]() $A\in \mathcal {S}_C$
satisfying
$A\in \mathcal {S}_C$
satisfying
![]() $\mathcal {R}(A)\subseteq \mathcal {R}(T)$
, where
$\mathcal {R}(A)\subseteq \mathcal {R}(T)$
, where
![]() $\mathcal {R}(A)$
denotes the range of A.
$\mathcal {R}(A)$
denotes the range of A.
In [Reference Douglas6], R. Douglas proved the following classical result on the range inclusion for bounded linear operators on Hilbert spaces.
Theorem 1.1 [Reference Douglas6]
Let A and B be two bounded linear operators on
![]() ${\mathcal {H}}$
. Then the following statements are equivalent:
${\mathcal {H}}$
. Then the following statements are equivalent:
-
(i)
 $\mathcal {R}(A)\subseteq \mathcal {R} (B)$
;
$\mathcal {R}(A)\subseteq \mathcal {R} (B)$
; -
(ii)
 $AA^{*}\leq \lambda BB^{*}$
for some
$AA^{*}\leq \lambda BB^{*}$
for some
 $\lambda \geq 0$
;
$\lambda \geq 0$
; -
(iii)
 $A=BX$
for some operator
$A=BX$
for some operator
 $X\in \mathcal {B(H)}$
.
$X\in \mathcal {B(H)}$
.
The preceding result exhibits a close relationship among the notions of range inclusion, majorization, and factorization for bounded linear operators. In [Reference Embry7], M. R. Embry extended this result to Banach spaces and obtained that
![]() $A=XB$
for some bounded operator X on
$A=XB$
for some bounded operator X on
![]() $\mathcal {R} (B)$
if and only if
$\mathcal {R} (B)$
if and only if
![]() $\mathcal {R} (A')\subseteq \mathcal {R}(B')$
. Here,
$\mathcal {R} (A')\subseteq \mathcal {R}(B')$
. Here,
![]() $A'$
and
$A'$
and
![]() $B'$
denote, respectively, the adjoint of A and the adjoint of B. P. H. Wang and X. Zhang [Reference Wang and Zhang45] established some range inclusion theorems for non-archimedean Banach spaces over general valued fields.
$B'$
denote, respectively, the adjoint of A and the adjoint of B. P. H. Wang and X. Zhang [Reference Wang and Zhang45] established some range inclusion theorems for non-archimedean Banach spaces over general valued fields.
It is natural to ask whether there is a C-symmetric analogue of Douglas’ range inclusion theorem. Given a linear subspace
![]() ${\mathcal {M}}$
of
${\mathcal {M}}$
of
![]() ${\mathcal {H}}$
, we denote
${\mathcal {H}}$
, we denote
Let
![]() $T\in \mathcal {S}_C$
. We attempt to characterize
$T\in \mathcal {S}_C$
. We attempt to characterize
![]() $C_{\mathcal {R}(T)}$
. Note that
$C_{\mathcal {R}(T)}$
. Note that
![]() $\mathcal {S}_C$
is not closed in the usual operator multiplication, that is, given
$\mathcal {S}_C$
is not closed in the usual operator multiplication, that is, given
![]() $A,B\in \mathcal {S}_C$
,
$A,B\in \mathcal {S}_C$
,
![]() $\mathcal {R}(A)\subseteq \mathcal {R}(B)$
does not imply
$\mathcal {R}(A)\subseteq \mathcal {R}(B)$
does not imply
![]() $B=AX$
for some
$B=AX$
for some
![]() $X\in \mathcal {S}_C$
(see Example 2.5). So we turn to the quadratic product in
$X\in \mathcal {S}_C$
(see Example 2.5). So we turn to the quadratic product in
![]() $\mathcal {S}_C$
given by
$\mathcal {S}_C$
given by
![]() $(X,Y)\longmapsto XYX$
for
$(X,Y)\longmapsto XYX$
for
![]() $X,Y\in \mathcal {S}_C.$
For
$X,Y\in \mathcal {S}_C.$
For
![]() $T\in \mathcal {S}_C$
, it is easy to check that
$T\in \mathcal {S}_C$
, it is easy to check that
It is natural to ask whether the converse inclusion holds.
The first result of this paper is the following theorem, which provides a complete answer to the preceding question.
Theorem 1.2 If
![]() $T\in \mathcal {S}_C$
, then
$T\in \mathcal {S}_C$
, then
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
if and only if
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
if and only if
![]() $\mathcal {R}(T)$
is closed.
$\mathcal {R}(T)$
is closed.
The preceding result shows that if
![]() $T\in \mathcal {S}_C$
with non-closed range, then
$T\in \mathcal {S}_C$
with non-closed range, then
![]() $T\mathcal {S}_C T$
is properly contained in
$T\mathcal {S}_C T$
is properly contained in
![]() $C_{\mathcal {R}(T)}$
. However, by the following result, they always have the same norm closure.
$C_{\mathcal {R}(T)}$
. However, by the following result, they always have the same norm closure.
Theorem 1.3 If
![]() $T\in \mathcal {S}_C$
, then
$T\in \mathcal {S}_C$
, then
![]() $\overline {C_{\mathcal {R}(T)}}=\overline {T\mathcal {S}_C T}$
.
$\overline {C_{\mathcal {R}(T)}}=\overline {T\mathcal {S}_C T}$
.
By the preceding result, each
![]() $A\in \mathcal {S}_C$
with
$A\in \mathcal {S}_C$
with
![]() $\mathcal {R}(A)\subseteq {\mathcal {R}(T)}$
is a norm limit of operators with the form
$\mathcal {R}(A)\subseteq {\mathcal {R}(T)}$
is a norm limit of operators with the form
![]() $TXT$
for
$TXT$
for
![]() $X\in \mathcal {S}_C$
. Thus Theorem 1.3 can be viewed as an approximate range inclusion theorem for
$X\in \mathcal {S}_C$
. Thus Theorem 1.3 can be viewed as an approximate range inclusion theorem for
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
Given
![]() $A,B\in \mathcal {S}_C$
, it is interesting to compare the closure of
$A,B\in \mathcal {S}_C$
, it is interesting to compare the closure of
![]() $C_{\mathcal {R}(A)}$
with that of
$C_{\mathcal {R}(A)}$
with that of
![]() $C_{\mathcal {R}(B)}$
. To state our result, we introduce a notation. Let
$C_{\mathcal {R}(B)}$
. To state our result, we introduce a notation. Let
![]() $\mathcal {M},\mathcal {N}$
be two linear subspaces of
$\mathcal {M},\mathcal {N}$
be two linear subspaces of
![]() ${\mathcal {H}}$
. We write
${\mathcal {H}}$
. We write
![]() $\mathcal {M}\prec \mathcal {N}$
if for each closed subspace
$\mathcal {M}\prec \mathcal {N}$
if for each closed subspace
![]() $\mathcal {M}_1$
of
$\mathcal {M}_1$
of
![]() ${\mathcal {H}}$
contained in
${\mathcal {H}}$
contained in
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\varepsilon>0$
there exists a closed subspace
$\varepsilon>0$
there exists a closed subspace
![]() $\mathcal {N}_1$
of
$\mathcal {N}_1$
of
![]() ${\mathcal {H}}$
contained in
${\mathcal {H}}$
contained in
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\|P_{\mathcal {M}_1}-P_{\mathcal {N}_1}\|<\varepsilon $
, where
$\|P_{\mathcal {M}_1}-P_{\mathcal {N}_1}\|<\varepsilon $
, where
![]() $P_{\mathcal {M}_1}$
denotes the orthogonal projection of
$P_{\mathcal {M}_1}$
denotes the orthogonal projection of
![]() ${\mathcal {H}}$
onto
${\mathcal {H}}$
onto
![]() $\mathcal {M}_1$
.
$\mathcal {M}_1$
.
Theorem 1.4 If
![]() $A,B\in \mathcal {S}_C$
, then
$A,B\in \mathcal {S}_C$
, then
![]() $\overline {C_{\mathcal {R}(A)}}\subset \overline {C_{\mathcal {R}(B)}}$
if and only if
$\overline {C_{\mathcal {R}(A)}}\subset \overline {C_{\mathcal {R}(B)}}$
if and only if
![]() $\mathcal {R}(A)\prec \mathcal {R}(B)$
.
$\mathcal {R}(A)\prec \mathcal {R}(B)$
.
Hence,
![]() $\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
if and only if
$\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
if and only if
![]() $\mathcal {R}(A)\prec \mathcal {R}(B)$
and
$\mathcal {R}(A)\prec \mathcal {R}(B)$
and
![]() $\mathcal {R}(B)\prec \mathcal {R}(A)$
. Clearly,
$\mathcal {R}(B)\prec \mathcal {R}(A)$
. Clearly,
![]() $\mathcal {R}(A)=\mathcal {R}(B)$
implies
$\mathcal {R}(A)=\mathcal {R}(B)$
implies
![]() $\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
. In general, the converse does not hold (see Example 2.12).
$\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
. In general, the converse does not hold (see Example 2.12).
Inspired by Theorem 1.3, we are interested in characterizing the closure of
![]() $T\mathcal {S}_C T$
in several usual topologies for
$T\mathcal {S}_C T$
in several usual topologies for
![]() $T\in \mathcal {S}_C$
, such as the weak* topology, the strong operator topology (sot) and the weak operator topology (wot). Given a subset
$T\in \mathcal {S}_C$
, such as the weak* topology, the strong operator topology (sot) and the weak operator topology (wot). Given a subset
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() $\mathcal {B(H)}$
, we write
$\mathcal {B(H)}$
, we write
![]() $\overline {\mathcal {E}}^{w*}$
,
$\overline {\mathcal {E}}^{w*}$
, ![]() and
and ![]() to denote the the weak*-closure, the sot-closure and the wot-closure of
to denote the the weak*-closure, the sot-closure and the wot-closure of
![]() $\mathcal {E}$
, respectively.
$\mathcal {E}$
, respectively.
Theorem 1.5 If
![]() $T\in \mathcal {S}_C$
, then
$T\in \mathcal {S}_C$
, then
In view of the preceding results, it is natural to classify the inclusion relations among
![]() $T\mathcal {S}_C T, C_{\mathcal {R}(T)}$
,
$T\mathcal {S}_C T, C_{\mathcal {R}(T)}$
,
![]() $\overline {C_{\mathcal {R}(T)}}$
and
$\overline {C_{\mathcal {R}(T)}}$
and
![]() $C_{\overline {\mathcal {R}(T)}}$
for
$C_{\overline {\mathcal {R}(T)}}$
for
![]() $T\in \mathcal {S}_C$
. It is obvious that
$T\in \mathcal {S}_C$
. It is obvious that
In Section 2, we shall show that any two of these sets coincide if and only if T has a closed range (see Proposition 2.15).
1.3 Diagonalization in
 $\mathcal {S}_C$
$\mathcal {S}_C$
The other aim of this paper is to study the extension of the Weyl–von Neumann Theorem to
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
The Weyl–von Neumann Theorem, due to H. Weyl and J. von Neumann [Reference von Neumann33, Reference Weyl46], states that, after the addition of a compact (or even Hilbert–Schmidt) operator of arbitrarily small norm, a self-adjoint operator becomes a diagonal operator. Recall that an operator
![]() $T\in \mathcal {B(H)}$
is diagonal if there is an orthonormal basis for
$T\in \mathcal {B(H)}$
is diagonal if there is an orthonormal basis for
![]() ${\mathcal {H}}$
consisting of eigenvectors for T. In 1958, S. T. Kuroda [Reference Kuroda29] strengthened the result by proving that every self-adjoint operator is the sum of a diagonal operator and a compact operator with arbitrarily small Schatten p-norm for
${\mathcal {H}}$
consisting of eigenvectors for T. In 1958, S. T. Kuroda [Reference Kuroda29] strengthened the result by proving that every self-adjoint operator is the sum of a diagonal operator and a compact operator with arbitrarily small Schatten p-norm for
![]() $p\in (1,\infty )$
.
$p\in (1,\infty )$
.
We shall prove in Section 3 the following result, which can be viewed as an
![]() $\mathcal {S}_C$
-analogue of the Weyl–von Neumann Theorem.
$\mathcal {S}_C$
-analogue of the Weyl–von Neumann Theorem.
Theorem 1.6 Let
![]() $T\in \mathcal {S}_C$
be a self-adjoint operator. If
$T\in \mathcal {S}_C$
be a self-adjoint operator. If
![]() $p>1$
and
$p>1$
and
![]() $\varepsilon>0$
, then there is a diagonal, self-adjoint operator
$\varepsilon>0$
, then there is a diagonal, self-adjoint operator
![]() $D\in \mathcal {S}_C$
such that
$D\in \mathcal {S}_C$
such that
![]() $T-D$
lies in the Schatten p-class
$T-D$
lies in the Schatten p-class
![]() $\mathcal {B}_p\mathcal {(H)}$
and
$\mathcal {B}_p\mathcal {(H)}$
and
![]() $\|T-D\|_p<\varepsilon $
.
$\|T-D\|_p<\varepsilon $
.
Remark 1.7
-
(i) The proof of Theorem 1.6 is inspired by [Reference Conway4, Theorem 38.1]. The main difficulty stems from the fact that we always have to deal with not only the self-adjoint operator T but also the conjugation C at the same time.
-
(ii) By [Reference Kato27, Theorem 1], if A is a self-adjoint operator not purely singular, then A is not a trace class perturbation of any diagonal operator. Thus the preceding result does not hold for
 $p=1$
.
$p=1$
. -
(iii) I. D. Berg [Reference Berg1] and W. Sikonia [Reference Sikonia41] independently proved that each normal operator T on
 ${\mathcal {H}}$
is the sum of a diagonal operator and a compact one with arbitrarily small norm. The preceding result is sometimes called the Weyl–von Neumann–Berg Theorem. In [Reference Halmos22], P. R. Halmos gave a more perspicuous proof that reduces the normal case to the Hermitian one. As an application of Theorem 1.6, we shall prove that finite commuting normal operators in
${\mathcal {H}}$
is the sum of a diagonal operator and a compact one with arbitrarily small norm. The preceding result is sometimes called the Weyl–von Neumann–Berg Theorem. In [Reference Halmos22], P. R. Halmos gave a more perspicuous proof that reduces the normal case to the Hermitian one. As an application of Theorem 1.6, we shall prove that finite commuting normal operators in
 $\mathcal {S}_C$
can be simultaneously diagonalized (see Theorem 3.3).
$\mathcal {S}_C$
can be simultaneously diagonalized (see Theorem 3.3). -
(iv) In [Reference Voiculescu43], D. Voiculescu considered the simultaneous diagonalization of commuting self-adjoint operators and showed that if
 $T_1,\dots ,T_n (n\geq 2)$
are commuting self-adjoint operators and
$T_1,\dots ,T_n (n\geq 2)$
are commuting self-adjoint operators and
 $\varepsilon>0$
, then there exist n commuting self-adjoint diagonal operators
$\varepsilon>0$
, then there exist n commuting self-adjoint diagonal operators
 $D_1,\dots ,D_n$
such that
$D_1,\dots ,D_n$
such that
 $\|T_i-D_i\|_n<\varepsilon $
for all
$\|T_i-D_i\|_n<\varepsilon $
for all
 $i=1,\dots , n$
, where
$i=1,\dots , n$
, where
 $\|\cdot \|_n$
is the Schatten n-norm. We do not know whether Voiculescu’s result can be extended to the
$\|\cdot \|_n$
is the Schatten n-norm. We do not know whether Voiculescu’s result can be extended to the
 $\mathcal {S}_C$
-setting.
$\mathcal {S}_C$
-setting.
As another application of Theorem 1.6, we shall provide a result concerning the irreducible approximation in
![]() $\mathcal {S}_C$
, which shows that those irreducible ones in
$\mathcal {S}_C$
, which shows that those irreducible ones in
![]() $\mathcal {S}_C$
constitute a dense subset of
$\mathcal {S}_C$
constitute a dense subset of
![]() $\mathcal {S}_C$
(see Corollary 3.6). This is an
$\mathcal {S}_C$
(see Corollary 3.6). This is an
![]() $\mathcal {S}_C$
-analogue of Halmos’ irreducible approximation theorem [Reference Halmos21].
$\mathcal {S}_C$
-analogue of Halmos’ irreducible approximation theorem [Reference Halmos21].
The proofs of Theorems 1.2–1.5 will be given in Section 2. Section 3 is devoted to the proof of Theorem 1.6.
2 The range inclusion in
 $\mathcal {S}_C$
$\mathcal {S}_C$
The aim of this section is to give the proofs of Theorems 1.2–1.5.
2.1 Proof of Theorem 1.2
Before giving the proof of Theorem 1.2, we first make some preparations.
Given a bounded linear operator A, we denote by
![]() $\ker A$
the kernel of A.
$\ker A$
the kernel of A.
Lemma 2.1 Let
![]() $A, B\in \mathcal {S}_C$
. If
$A, B\in \mathcal {S}_C$
. If
![]() $\mathcal {R}(A)\subset \mathcal {R}(B)$
, then
$\mathcal {R}(A)\subset \mathcal {R}(B)$
, then
Proof Since
![]() $CAC=A^{*}$
and
$CAC=A^{*}$
and
![]() $CA^{*}C=A$
, one can see that
$CA^{*}C=A$
, one can see that
![]() $C(\mathcal {R}(A))=\mathcal {R}(A^{*})$
. Likewise, we have
$C(\mathcal {R}(A))=\mathcal {R}(A^{*})$
. Likewise, we have
![]() $C(\mathcal {R}(B))=\mathcal {R}(B^{*})$
. It follows immediately that
$C(\mathcal {R}(B))=\mathcal {R}(B^{*})$
. It follows immediately that
![]() $\mathcal {R}(A^{*})\subset \mathcal {R}(B^{*})$
. Thus
$\mathcal {R}(A^{*})\subset \mathcal {R}(B^{*})$
. Thus
![]() $\mathcal {R}(B^{*})^\bot \subset \mathcal {R}(A^{*})^\bot $
, that is,
$\mathcal {R}(B^{*})^\bot \subset \mathcal {R}(A^{*})^\bot $
, that is,
![]() $\ker {B}\subset \ker {A}$
.
$\ker {B}\subset \ker {A}$
.
On the other hand,
![]() $\mathcal {R}(A)\subset \mathcal {R}(B)$
implies
$\mathcal {R}(A)\subset \mathcal {R}(B)$
implies
![]() $\mathcal {R}(B)^{\bot }\subset \mathcal {R}(A)^{\bot }$
and, equivalently,
$\mathcal {R}(B)^{\bot }\subset \mathcal {R}(A)^{\bot }$
and, equivalently,
![]() $\ker {B^{*}}\subset \ker {A^{*}}.$
$\ker {B^{*}}\subset \ker {A^{*}}.$
Throughout the following, given a closed subspace
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() ${\mathcal {H}}$
, we denote by
${\mathcal {H}}$
, we denote by
![]() $P_{\mathcal {M}}$
the orthogonal projection of
$P_{\mathcal {M}}$
the orthogonal projection of
![]() ${\mathcal {H}}$
onto
${\mathcal {H}}$
onto
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
Proof of Theorem 1.2
“
![]() $\Longrightarrow $
”. Assume that
$\Longrightarrow $
”. Assume that
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. We shall show that
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. We shall show that
![]() $\mathcal {R}(T)$
is closed.
$\mathcal {R}(T)$
is closed.
Assume that
![]() $\{x_n\}_{n=1}^\infty \subset {\mathcal {H}}$
and
$\{x_n\}_{n=1}^\infty \subset {\mathcal {H}}$
and
![]() $Tx_n\rightarrow y_0\in {\mathcal {H}}$
. It suffices to show that
$Tx_n\rightarrow y_0\in {\mathcal {H}}$
. It suffices to show that
![]() $y_0\in \mathcal {R}(T)$
. Note that
$y_0\in \mathcal {R}(T)$
. Note that
![]() $T\in C_{\mathcal {R}(T)}$
. Thus there exists
$T\in C_{\mathcal {R}(T)}$
. Thus there exists
![]() $A\in \mathcal {S}_C$
such that
$A\in \mathcal {S}_C$
such that
![]() $T=TAT$
. Hence,
$T=TAT$
. Hence,
![]() $TATx_n\rightarrow y_0$
and
$TATx_n\rightarrow y_0$
and
![]() $TATx_n\rightarrow TAy_0$
, which implies
$TATx_n\rightarrow TAy_0$
, which implies
![]() $y_0=TAy_0\in \mathcal {R}(T).$
$y_0=TAy_0\in \mathcal {R}(T).$
“
![]() $\Longleftarrow $
”. Now assume that
$\Longleftarrow $
”. Now assume that
![]() $\mathcal {R}(T)$
is closed. Since
$\mathcal {R}(T)$
is closed. Since
![]() $T\mathcal {S}_C T \subseteq C_{\mathcal {R}(T)}$
is clear, it remains to show
$T\mathcal {S}_C T \subseteq C_{\mathcal {R}(T)}$
is clear, it remains to show
![]() $ C_{\mathcal {R}(T)} \subseteq T\mathcal {S}_C T$
.
$ C_{\mathcal {R}(T)} \subseteq T\mathcal {S}_C T$
.
Denote
![]() $\mathcal {N}=(\ker {T})^{\bot }$
and
$\mathcal {N}=(\ker {T})^{\bot }$
and
![]() $\mathcal {M}=\mathcal {R}(T)$
. For
$\mathcal {M}=\mathcal {R}(T)$
. For
![]() $x\in \mathcal {N}$
, define
$x\in \mathcal {N}$
, define
![]() $Fx=Tx$
. Since
$Fx=Tx$
. Since
![]() $\mathcal {M}$
is norm-closed, F is an invertible operator from
$\mathcal {M}$
is norm-closed, F is an invertible operator from
![]() $\mathcal {N}$
into
$\mathcal {N}$
into
![]() $\mathcal {M}$
. Define
$\mathcal {M}$
. Define
![]() $S=P_{\mathcal {N}}F^{-1}P_{\mathcal {M}}$
. One can verify that
$S=P_{\mathcal {N}}F^{-1}P_{\mathcal {M}}$
. One can verify that
![]() $TS=P_{\mathcal {M}}$
and
$TS=P_{\mathcal {M}}$
and
![]() $ST=P_{\mathcal {N}}$
.
$ST=P_{\mathcal {N}}$
.
Since
![]() $T\in \mathcal {S}_C$
, one can see that
$T\in \mathcal {S}_C$
, one can see that
![]() $C(\ker T)=\ker T^{*}$
, that is,
$C(\ker T)=\ker T^{*}$
, that is,
![]() $C(\mathcal {N}^\bot )=\mathcal {M}^\bot $
. Thus
$C(\mathcal {N}^\bot )=\mathcal {M}^\bot $
. Thus
![]() $C(\mathcal {N})=\mathcal {M}$
and
$C(\mathcal {N})=\mathcal {M}$
and
![]() $C(\mathcal {M})=\mathcal {N}$
. Denote
$C(\mathcal {M})=\mathcal {N}$
. Denote
![]() $C_1=C|_{\mathcal {M}}$
. Then
$C_1=C|_{\mathcal {M}}$
. Then
![]() $C_1:\mathcal {M}\longrightarrow \mathcal {N} $
is conjugate-linear, invertible, and isometric. One can check that
$C_1:\mathcal {M}\longrightarrow \mathcal {N} $
is conjugate-linear, invertible, and isometric. One can check that
![]() $Cx=C^{-1}x= C_1^{-1}x$
for all
$Cx=C^{-1}x= C_1^{-1}x$
for all
![]() $x\in \mathcal {N}.$
$x\in \mathcal {N}.$
Claim 1
![]() $C_1{(F^{-1})}^{*}=F^{-1}C_1^{-1}$
.
$C_1{(F^{-1})}^{*}=F^{-1}C_1^{-1}$
.
In fact, for any
![]() $x\in \mathcal { M} $
, note that
$x\in \mathcal { M} $
, note that
Thus
![]() $FC_1=C_1^{-1}F^{*}$
,
$FC_1=C_1^{-1}F^{*}$
,
![]() ${(F^{-1})}^{*}C_1=C_1^{-1} F^{-1}$
and
${(F^{-1})}^{*}C_1=C_1^{-1} F^{-1}$
and
![]() $C_1{(F^{-1})}^{*}= F^{-1}C_1^{-1}$
.
$C_1{(F^{-1})}^{*}= F^{-1}C_1^{-1}$
.
Claim 2
![]() $S\in \mathcal {S}_C.$
$S\in \mathcal {S}_C.$
For any
![]() $x\in {\mathcal {H}}$
, there is the unique decomposition
$x\in {\mathcal {H}}$
, there is the unique decomposition
![]() $x=x_1+x_2$
, where
$x=x_1+x_2$
, where
![]() $x_1\in \mathcal {N}$
and
$x_1\in \mathcal {N}$
and
![]() $x_2\in \mathcal {N}^{\bot }$
. So
$x_2\in \mathcal {N}^{\bot }$
. So
![]() $Cx_1\in \mathcal {M}$
and
$Cx_1\in \mathcal {M}$
and
![]() $Cx_2\in \mathcal {M}^{\bot }$
. By Claim 1, we have
$Cx_2\in \mathcal {M}^{\bot }$
. By Claim 1, we have
 $$ \begin{align*} CSCx&=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})(Cx_1+Cx_2)\\ &=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})Cx_1\\ &=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})C_1^{-1}x_1\\ &=C(P_{\mathcal{N}}F^{-1} C_1^{-1}x_1)\\ &=C_1^{-1} (F^{-1} C_1^{-1}x_1) \\ &=(C_1^{-1}F^{-1} C_1^{-1})x_1= {(F^{-1})}^{*} x_1\\ &= P_{\mathcal{M}}{(F^{-1})}^{*} P_{\mathcal{N}}x =S^{*}x. \end{align*} $$
$$ \begin{align*} CSCx&=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})(Cx_1+Cx_2)\\ &=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})Cx_1\\ &=C(P_{\mathcal{N}}F^{-1}P_{\mathcal{M}})C_1^{-1}x_1\\ &=C(P_{\mathcal{N}}F^{-1} C_1^{-1}x_1)\\ &=C_1^{-1} (F^{-1} C_1^{-1}x_1) \\ &=(C_1^{-1}F^{-1} C_1^{-1})x_1= {(F^{-1})}^{*} x_1\\ &= P_{\mathcal{M}}{(F^{-1})}^{*} P_{\mathcal{N}}x =S^{*}x. \end{align*} $$
This proves
![]() $S\in \mathcal {S}_C.$
$S\in \mathcal {S}_C.$
Set
![]() $X=SAS$
. Thus one can easily check that
$X=SAS$
. Thus one can easily check that
![]() $X\in \mathcal {S}_C$
. We shall prove that
$X\in \mathcal {S}_C$
. We shall prove that
![]() $TXT=A$
. Note that
$TXT=A$
. Note that
![]() $\mathcal {R}(A)\subset \mathcal {R} (T)= \mathcal {M}$
. It follows that
$\mathcal {R}(A)\subset \mathcal {R} (T)= \mathcal {M}$
. It follows that
It suffices to prove that
![]() $AP_{\mathcal {N}}=A$
, that is,
$AP_{\mathcal {N}}=A$
, that is,
![]() $A(I-P_{\mathcal {N}})=0$
.
$A(I-P_{\mathcal {N}})=0$
.
Since
![]() $\mathcal {R}(A)\subset \mathcal {R}(T)$
, it follows from Lemma 2.1 that
$\mathcal {R}(A)\subset \mathcal {R}(T)$
, it follows from Lemma 2.1 that
![]() $\ker {T}\subset \ker {A}$
. That is,
$\ker {T}\subset \ker {A}$
. That is,
![]() $\mathcal {N}^{\bot }\subset \ker A$
. Therefore we conclude that
$\mathcal {N}^{\bot }\subset \ker A$
. Therefore we conclude that
![]() $A(I-P_{\mathcal {N}})=0$
.
$A(I-P_{\mathcal {N}})=0$
.
Corollary 2.2 Let
![]() $T,A\in \mathcal {S}_C$
. If either
$T,A\in \mathcal {S}_C$
. If either
![]() $\mathcal {R}(T)$
or
$\mathcal {R}(T)$
or
![]() $\mathcal {R}(A)$
is closed, then
$\mathcal {R}(A)$
is closed, then
![]() $\mathcal {R}(A)\subset \mathcal {R}(T)$
if and only if
$\mathcal {R}(A)\subset \mathcal {R}(T)$
if and only if
![]() $A=TXT$
for some
$A=TXT$
for some
![]() $X\in \mathcal {S}_C$
.
$X\in \mathcal {S}_C$
.
Proof It suffices to prove the necessity.
“
![]() $\Longrightarrow $
”. By Theorem 1.2, we need only deal with the case that
$\Longrightarrow $
”. By Theorem 1.2, we need only deal with the case that
![]() $\mathcal {R}(A)$
is closed.
$\mathcal {R}(A)$
is closed.
Using Theorem 1.2 again, we can find
![]() $Z\in \mathcal {S}_C$
such that
$Z\in \mathcal {S}_C$
such that
![]() $A=AZA$
. Since
$A=AZA$
. Since
![]() $\mathcal {R} (A)\subset \mathcal {R} (T)$
, by Douglas’ range inclusion theorem,
$\mathcal {R} (A)\subset \mathcal {R} (T)$
, by Douglas’ range inclusion theorem,
![]() $A=TY$
for some
$A=TY$
for some
![]() $Y\in \mathcal {B(H)}$
. Noting that
$Y\in \mathcal {B(H)}$
. Noting that
![]() $A,T\in \mathcal {S}_C$
, we have
$A,T\in \mathcal {S}_C$
, we have
 $$ \begin{align*} A&=CA^{*}C=C(TY)^{*}C=CY^{*}T^{*}C\\ &=(CY^{*}C)(CT^{*}C)=(CY^{*}C)T. \end{align*} $$
$$ \begin{align*} A&=CA^{*}C=C(TY)^{*}C=CY^{*}T^{*}C\\ &=(CY^{*}C)(CT^{*}C)=(CY^{*}C)T. \end{align*} $$
Then
One can verify that
![]() $X:=YZ(CY^{*}C)\in \mathcal {S}_C$
, which completes the proof.
$X:=YZ(CY^{*}C)\in \mathcal {S}_C$
, which completes the proof.
Remark 2.3 The result of Corollary 2.2 is sharp. In fact, given any
![]() $T\in \mathcal {S}_C$
, it holds that
$T\in \mathcal {S}_C$
, it holds that
![]() $\mathcal {R}(T)\subset \mathcal {R}(T)$
; if, in addition,
$\mathcal {R}(T)\subset \mathcal {R}(T)$
; if, in addition,
![]() $\mathcal {R}(T)$
is not closed, then, by the proof for the necessity of Theorem 1.2, there exists no
$\mathcal {R}(T)$
is not closed, then, by the proof for the necessity of Theorem 1.2, there exists no
![]() $X\in \mathcal {B(H)}$
such that
$X\in \mathcal {B(H)}$
such that
![]() $TXT=T$
. Here, we provide a concrete example of complex symmetric operator with non-closed range.
$TXT=T$
. Here, we provide a concrete example of complex symmetric operator with non-closed range.
Let
![]() $\{e_n\}_{n=1}^\infty $
be an orthonormal basis of
$\{e_n\}_{n=1}^\infty $
be an orthonormal basis of
![]() ${\mathcal {H}}$
and
${\mathcal {H}}$
and
For
![]() $x=\sum _{n=1}^\infty \alpha _i e_i$
, define
$x=\sum _{n=1}^\infty \alpha _i e_i$
, define
![]() $Cx=\sum _{n=1}^\infty \overline {\alpha _i} e_i$
. Then C is a conjugation on
$Cx=\sum _{n=1}^\infty \overline {\alpha _i} e_i$
. Then C is a conjugation on
![]() ${\mathcal {H}}$
and one can check that
${\mathcal {H}}$
and one can check that
![]() $T\in \mathcal {S}_C$
. Clearly,
$T\in \mathcal {S}_C$
. Clearly,
![]() $\mathcal {R}(T)$
is not closed. If
$\mathcal {R}(T)$
is not closed. If
![]() $X\in \mathcal {S}_C$
and
$X\in \mathcal {S}_C$
and
![]() $T=TXT$
, then
$T=TXT$
, then
that is,
![]() $\langle Xe_n, e_n \rangle = n$
. Since n is arbitrary, we deduce that X is not bounded, a contradiction.
$\langle Xe_n, e_n \rangle = n$
. Since n is arbitrary, we deduce that X is not bounded, a contradiction.
For
![]() $e,f\in {\mathcal {H}}$
, we define an operator
$e,f\in {\mathcal {H}}$
, we define an operator
![]() $e\otimes f$
on
$e\otimes f$
on
![]() ${\mathcal {H}}$
as
${\mathcal {H}}$
as
Corollary 2.4 Let
![]() $T\in \mathcal {S}_C$
. If
$T\in \mathcal {S}_C$
. If
![]() $x,y\in \mathcal {R}(T)$
, then
$x,y\in \mathcal {R}(T)$
, then
Proof Denote
![]() $X=x\otimes (Cx)$
and
$X=x\otimes (Cx)$
and
![]() $Y=x\otimes (Cy)+y\otimes (Cx)$
. It is easy to verify that
$Y=x\otimes (Cy)+y\otimes (Cx)$
. It is easy to verify that
![]() $X\in \mathcal {S}_C$
and
$X\in \mathcal {S}_C$
and
![]() $\overline {\mathcal {R}(X)}=\mathcal {R}(X)\subset \mathcal {R}(T)$
. By Corollary 2.2, we have
$\overline {\mathcal {R}(X)}=\mathcal {R}(X)\subset \mathcal {R}(T)$
. By Corollary 2.2, we have
![]() $X\in T\mathcal {S}_C T$
. Likewise we have
$X\in T\mathcal {S}_C T$
. Likewise we have
![]() $Y\in T\mathcal {S}_C T$
.
$Y\in T\mathcal {S}_C T$
.
At the end of this subsection, we provide several illustrating examples.
The following example shows that Douglas’ range inclusion theorem does not hold for
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
Example 2.5 Let D be a conjugation on
![]() ${\mathcal {H}}$
and
${\mathcal {H}}$
and
 $$\begin{align*}A=\begin{bmatrix} 0&I\\ I&0 \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~,\ \ \ T=\begin{bmatrix} I&0\\ 0&-I \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~, \ \ \ C=\begin{bmatrix} D&0\\ 0&D \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~, \end{align*}$$
$$\begin{align*}A=\begin{bmatrix} 0&I\\ I&0 \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~,\ \ \ T=\begin{bmatrix} I&0\\ 0&-I \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~, \ \ \ C=\begin{bmatrix} D&0\\ 0&D \end{bmatrix}\begin{matrix} {\mathcal{H}}\\ {\mathcal{H}} \end{matrix}~, \end{align*}$$
where I is the identity operator on
![]() ${\mathcal {H}}$
. Then it is easy to check that C is a conjugation on
${\mathcal {H}}$
. Then it is easy to check that C is a conjugation on
![]() ${\mathcal {H}}\oplus {\mathcal {H}}$
,
${\mathcal {H}}\oplus {\mathcal {H}}$
,
![]() $A, T\in \mathcal {S}_C$
and
$A, T\in \mathcal {S}_C$
and
![]() $\mathcal {R}(A)\subset \mathcal {R}(T)$
.
$\mathcal {R}(A)\subset \mathcal {R}(T)$
.
If
![]() $X\in \mathcal {B}({\mathcal {H}}\oplus {\mathcal {H}})$
and
$X\in \mathcal {B}({\mathcal {H}}\oplus {\mathcal {H}})$
and
![]() $A=TX$
, then one can verify that
$A=TX$
, then one can verify that
 $$\begin{align*}X=T^{-1}A=\begin{bmatrix} 0&I\\ -I&0 \end{bmatrix}.\end{align*}$$
$$\begin{align*}X=T^{-1}A=\begin{bmatrix} 0&I\\ -I&0 \end{bmatrix}.\end{align*}$$
Clearly,
![]() $X\notin \mathcal {S}_C$
.
$X\notin \mathcal {S}_C$
.
The following example shows that Theorem 1.2 can not be extended to
![]() $\mathcal {B(H)}$
or general Jordan operator algebras.
$\mathcal {B(H)}$
or general Jordan operator algebras.
Example 2.6 Let
![]() $\mathcal {M}$
be a closed subspace of
$\mathcal {M}$
be a closed subspace of
![]() ${\mathcal {H}}$
with
${\mathcal {H}}$
with
![]() $\dim \mathcal {M}=\dim \mathcal {M}^{\bot }$
. Set
$\dim \mathcal {M}=\dim \mathcal {M}^{\bot }$
. Set
 $$\begin{align*}T=\begin{bmatrix} I_0&0\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix}\ \ \ \text{and} \ \ \ A=\begin{bmatrix} 0&B\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix}, \end{align*}$$
$$\begin{align*}T=\begin{bmatrix} I_0&0\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix}\ \ \ \text{and} \ \ \ A=\begin{bmatrix} 0&B\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix}, \end{align*}$$
where
![]() $I_0$
is the identity operator on
$I_0$
is the identity operator on
![]() $\mathcal {M}$
and B is an invertible operator from
$\mathcal {M}$
and B is an invertible operator from
![]() $\mathcal {M}^{\bot }$
onto
$\mathcal {M}^{\bot }$
onto
![]() $\mathcal {M}$
. Then
$\mathcal {M}$
. Then
![]() $\mathcal {R}(A)\subset \mathcal {R}(T)$
.
$\mathcal {R}(A)\subset \mathcal {R}(T)$
.
For any
![]() $X\in \mathcal {B(H)}$
with
$X\in \mathcal {B(H)}$
with
 $$\begin{align*}X= \begin{bmatrix} X_{1,1}&X_{1,2}\\ X_{2,1}&X_{2,2} \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix},\end{align*}$$
$$\begin{align*}X= \begin{bmatrix} X_{1,1}&X_{1,2}\\ X_{2,1}&X_{2,2} \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix},\end{align*}$$
one can check that
 $$\begin{align*}TXT= \begin{bmatrix} X_{1,1}&0\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix} \ne A.\end{align*}$$
$$\begin{align*}TXT= \begin{bmatrix} X_{1,1}&0\\ 0&0 \end{bmatrix}\begin{matrix} \mathcal{M} \\ \mathcal{M}^{\bot} \end{matrix} \ne A.\end{align*}$$
Hence,
![]() $A\ne TXT$
for any
$A\ne TXT$
for any
![]() $X\in \mathcal {B(H)}$
.
$X\in \mathcal {B(H)}$
.
2.2 Proof of Theorem 1.3
Let
![]() $\mathcal {M}$
be a closed subspace of
$\mathcal {M}$
be a closed subspace of
![]() ${\mathcal {H}}$
. A conjugate-linear map J on
${\mathcal {H}}$
. A conjugate-linear map J on
![]() ${\mathcal {H}}$
is called a partial conjugation supported on
${\mathcal {H}}$
is called a partial conjugation supported on
![]() $\mathcal {M}$
if
$\mathcal {M}$
if
![]() $\ker J = \mathcal {M}^\bot $
reduces J and
$\ker J = \mathcal {M}^\bot $
reduces J and
![]() $J|_{\mathcal {M}}$
is a conjugation.
$J|_{\mathcal {M}}$
is a conjugation.
Lemma 2.7 [Reference Garcia and Putinar15, Theorem 2]
Let
![]() $T\in \mathcal {B(H)}$
and C be a conjugation on
$T\in \mathcal {B(H)}$
and C be a conjugation on
![]() ${\mathcal {H}}$
. Then
${\mathcal {H}}$
. Then
![]() $T\in \mathcal {S}_C$
if and only if
$T\in \mathcal {S}_C$
if and only if
![]() $T=CJ|T|$
for some partial conjugation J supported on
$T=CJ|T|$
for some partial conjugation J supported on
![]() $\mathcal {R}(|T|)$
and commuting with
$\mathcal {R}(|T|)$
and commuting with
![]() $|T|$
.
$|T|$
.
Proof of Theorem 1.3
Since it is clear that
![]() $T\mathcal {S}_C T\subset C_{\mathcal {R}(T)}$
, it suffices to prove that
$T\mathcal {S}_C T\subset C_{\mathcal {R}(T)}$
, it suffices to prove that
![]() $C_{\mathcal {R}(T)}\subset \overline {T\mathcal {S}_C T}$
. Fix an operator A in
$C_{\mathcal {R}(T)}\subset \overline {T\mathcal {S}_C T}$
. Fix an operator A in
![]() $C_{\mathcal {R}(T)}$
. We shall prove that
$C_{\mathcal {R}(T)}$
. We shall prove that
![]() $A\in \overline {T \mathcal {S}_C T}$
. This follows readily from the following claim.
$A\in \overline {T \mathcal {S}_C T}$
. This follows readily from the following claim.
Claim Given
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $B\in \mathcal {S}_C$
with
$B\in \mathcal {S}_C$
with
![]() $\mathcal {R}(B)=\overline {\mathcal {R}(B)}\subset \mathcal {R}(A)$
such that
$\mathcal {R}(B)=\overline {\mathcal {R}(B)}\subset \mathcal {R}(A)$
such that
![]() $\|A-B\|<\varepsilon $
.
$\|A-B\|<\varepsilon $
.
In fact, if the preceding claim holds, then, by Corollary 2.2,
![]() $B\in T\mathcal {S}_C T$
and
$B\in T\mathcal {S}_C T$
and
![]() $\text {dist}(A, T\mathcal {S}_C T)<\varepsilon $
. Since
$\text {dist}(A, T\mathcal {S}_C T)<\varepsilon $
. Since
![]() $\varepsilon>0$
was arbitrary, we deduce that
$\varepsilon>0$
was arbitrary, we deduce that
![]() $A\in \overline {T\mathcal {S}_C T}$
.
$A\in \overline {T\mathcal {S}_C T}$
.
By Lemma 2.7,
![]() $A=CJP$
, where
$A=CJP$
, where
![]() $P=|A|$
and J is a partial conjugation supported on
$P=|A|$
and J is a partial conjugation supported on
![]() $\overline {\mathcal {R}(P)}$
with
$\overline {\mathcal {R}(P)}$
with
![]() $JP=PJ$
.
$JP=PJ$
.
Now we fix an
![]() $\varepsilon>0$
and define three functions
$\varepsilon>0$
and define three functions
![]() $f, g, h $
on
$f, g, h $
on
![]() $[0,\|A\|]$
as
$[0,\|A\|]$
as
 $$ \begin{align*}f(t)=\begin{cases} 0,& t\in[0,\varepsilon/2), \\ t,& t\in[\varepsilon/2, \|A\|],\end{cases} \ \ h(t)=\begin{cases} 0,& t\in[0,\varepsilon/2), \\ 1/t,& t\in[\varepsilon/2, \|A\|], \end{cases} \ \ \ g=fh.\end{align*} $$
$$ \begin{align*}f(t)=\begin{cases} 0,& t\in[0,\varepsilon/2), \\ t,& t\in[\varepsilon/2, \|A\|],\end{cases} \ \ h(t)=\begin{cases} 0,& t\in[0,\varepsilon/2), \\ 1/t,& t\in[\varepsilon/2, \|A\|], \end{cases} \ \ \ g=fh.\end{align*} $$
It is easy to see that:
-
(i)
 $f(P), g(P),$
and
$f(P), g(P),$
and
 $h(P)$
are positive operators commuting with J,
$h(P)$
are positive operators commuting with J, -
(ii)
 $g(P)$
is an orthogonal projection with
$g(P)$
is an orthogonal projection with
 $\mathcal {R}(f(P))=\mathcal {R}(g(P))=\mathcal {R}(h(P))$
, and
$\mathcal {R}(f(P))=\mathcal {R}(g(P))=\mathcal {R}(h(P))$
, and -
(iii)
 $\mathcal {R}(g(P))$
reduces J.
$\mathcal {R}(g(P))$
reduces J.
Define
![]() $\tilde {J}=Jg(P)$
. Then
$\tilde {J}=Jg(P)$
. Then
![]() $\tilde {J}$
is a partial anti-conjugation supported on
$\tilde {J}$
is a partial anti-conjugation supported on
![]() $\mathcal {R}(h(P))$
commuting with
$\mathcal {R}(h(P))$
commuting with
![]() $h(P)$
. Set
$h(P)$
. Set
![]() $B=CJf(P)$
. Note that
$B=CJf(P)$
. Note that
![]() $Jf(P)=\tilde {J}P$
. It follows that
$Jf(P)=\tilde {J}P$
. It follows that
![]() ${B=C\tilde {J}f(P)}$
. By Lemma 2.7, we have
${B=C\tilde {J}f(P)}$
. By Lemma 2.7, we have
![]() $B\in \mathcal {S}_C$
. Note that
$B\in \mathcal {S}_C$
. Note that
Since J is supported on
![]() $\overline {\mathcal {R}(P)}$
, it follows that
$\overline {\mathcal {R}(P)}$
, it follows that
Note that
This completes the proof.
The following result can be seen from the proof of Theorem 1.3.
Corollary 2.8 Let
![]() $T\in \mathcal {S}_C$
. Then, given
$T\in \mathcal {S}_C$
. Then, given
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $A\in \mathcal {S}_C$
with
$A\in \mathcal {S}_C$
with
![]() $\|T-A\|<\varepsilon $
such that
$\|T-A\|<\varepsilon $
such that
![]() $\mathcal {R}(A)=\overline {\mathcal {R}(A)}\subset \mathcal {R}(T)$
.
$\mathcal {R}(A)=\overline {\mathcal {R}(A)}\subset \mathcal {R}(T)$
.
2.3 Proof of Theorem 1.4
The aim of this subsection is to prove Theorem 1.4.
A subset
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() ${\mathcal {H}}$
is called an operator range if
${\mathcal {H}}$
is called an operator range if
![]() $\mathcal {E}=\mathcal {R}(A)$
for some
$\mathcal {E}=\mathcal {R}(A)$
for some
![]() $A\in \mathcal {B(H)}$
. We denote by
$A\in \mathcal {B(H)}$
. We denote by
![]() $\text {Ran}(\mathcal {H})$
the set of all operator ranges in
$\text {Ran}(\mathcal {H})$
the set of all operator ranges in
![]() ${\mathcal {H}}$
. Then, by [Reference Fillmore and Williams8, Section 2],
${\mathcal {H}}$
. Then, by [Reference Fillmore and Williams8, Section 2],
![]() $\text {Ran}(\mathcal {H})$
is a lattice.
$\text {Ran}(\mathcal {H})$
is a lattice.
The following lemma shows that each operator range can be attained in
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
Lemma 2.9 Given
![]() $T\in \mathcal {B(H)}$
, there exists
$T\in \mathcal {B(H)}$
, there exists
![]() $A\in \mathcal {S}_C$
with
$A\in \mathcal {S}_C$
with
![]() $\mathcal {R}(A)=\mathcal {R}(T)$
.
$\mathcal {R}(A)=\mathcal {R}(T)$
.
Proof Let
![]() $T=U|T|$
be the polar decomposition of T, where U is a partial isometry. So
$T=U|T|$
be the polar decomposition of T, where U is a partial isometry. So
![]() $\mathcal {R}(T)=\mathcal {R} (U|T|U^{*})$
.
$\mathcal {R}(T)=\mathcal {R} (U|T|U^{*})$
.
Denote
![]() $P=CU|T|U^{*}C$
. Clearly, P is positive and hence a complex symmetric operator. Then we can find a conjugation J on
$P=CU|T|U^{*}C$
. Clearly, P is positive and hence a complex symmetric operator. Then we can find a conjugation J on
![]() ${\mathcal {H}}$
so that
${\mathcal {H}}$
so that
![]() $JP=PJ$
. Set
$JP=PJ$
. Set
![]() $A=CJP$
. Then, by [Reference Gilbreath and Wogen17, Theorem 3.1],
$A=CJP$
. Then, by [Reference Gilbreath and Wogen17, Theorem 3.1],
![]() $A\in \mathcal {S}_C$
and
$A\in \mathcal {S}_C$
and
This ends the proof.
For
![]() $A\in \mathcal {B(H)}$
, we denote
$A\in \mathcal {B(H)}$
, we denote
![]() $A^t=CA^{*}C$
. Then it is easy to check the following.
$A^t=CA^{*}C$
. Then it is easy to check the following.
-
(a)
 $A\in \mathcal {S}_C$
if and only if
$A\in \mathcal {S}_C$
if and only if
 $A=A^t$
.
$A=A^t$
. -
(b)
 $A\mathcal {S}_C A^t\subset \mathcal {S}_C$
.
$A\mathcal {S}_C A^t\subset \mathcal {S}_C$
.
Proposition 2.10 If
![]() $A,B\in \mathcal {B(H)}$
, then the following are equivalent:
$A,B\in \mathcal {B(H)}$
, then the following are equivalent:
-
(i)
 $\mathcal {R}(A)\subset \mathcal {R}(B)$
;
$\mathcal {R}(A)\subset \mathcal {R}(B)$
; -
(ii)
 $C_{\mathcal {R}(A)}\subset C_{\mathcal {R}(B)}$
;
$C_{\mathcal {R}(A)}\subset C_{\mathcal {R}(B)}$
; -
(iii)
 $A\mathcal {S}_C A^t\subset B\mathcal {S}_C B^t$
.
$A\mathcal {S}_C A^t\subset B\mathcal {S}_C B^t$
.
Proof (i)
![]() $\Longrightarrow $
(ii). This is obvious.
$\Longrightarrow $
(ii). This is obvious.
(ii)
![]() $\Longrightarrow $
(i). For any
$\Longrightarrow $
(i). For any
![]() $x\in \mathcal {R}(A)$
, by Corollary 2.4, we have
$x\in \mathcal {R}(A)$
, by Corollary 2.4, we have
which implies
![]() $x\in \mathcal {R}(B)$
. Hence
$x\in \mathcal {R}(B)$
. Hence
![]() $\mathcal {R}(A)\subset \mathcal {R}(B)$
.
$\mathcal {R}(A)\subset \mathcal {R}(B)$
.
(i)
![]() $\Longrightarrow $
(iii). By Douglas’ range inclusion theorem,
$\Longrightarrow $
(iii). By Douglas’ range inclusion theorem,
![]() $\mathcal {R}(A)\subset \mathcal {R}(B)$
implies
$\mathcal {R}(A)\subset \mathcal {R}(B)$
implies
![]() $A=BZ$
for some
$A=BZ$
for some
![]() $Z\in \mathcal {B(H)}$
. Note that
$Z\in \mathcal {B(H)}$
. Note that
Thus, for any
![]() $X\in \mathcal {S}_C$
, we have
$X\in \mathcal {S}_C$
, we have
One can verify that
![]() $ZXZ^t\in \mathcal {S}_C$
. Thus
$ZXZ^t\in \mathcal {S}_C$
. Thus
![]() $AXA^t\in B\mathcal {S}_C B^t$
.
$AXA^t\in B\mathcal {S}_C B^t$
.
(iii)
![]() $\Longrightarrow $
(i). For
$\Longrightarrow $
(i). For
![]() $x\in {\mathcal {H}}$
, denote
$x\in {\mathcal {H}}$
, denote
![]() $y=Ax$
. We shall prove that
$y=Ax$
. We shall prove that
![]() $y\in \mathcal {R}(B)$
. Note that
$y\in \mathcal {R}(B)$
. Note that
 $$ \begin{align*} y\otimes (Cy)&=(Ax)\otimes(CAx)=(Ax)\otimes[(CAC)(Cx)]\\ &=A[x\otimes (Cx)](CAC)^{*} =A[x\otimes (Cx)]A^t\in A\mathcal{S}_C A^t. \end{align*} $$
$$ \begin{align*} y\otimes (Cy)&=(Ax)\otimes(CAx)=(Ax)\otimes[(CAC)(Cx)]\\ &=A[x\otimes (Cx)](CAC)^{*} =A[x\otimes (Cx)]A^t\in A\mathcal{S}_C A^t. \end{align*} $$
So
![]() $y\otimes (Cy)\in B\mathcal {S}_C B^t$
. Then
$y\otimes (Cy)\in B\mathcal {S}_C B^t$
. Then
![]() $y\otimes (Cy)=B X B^t$
for some
$y\otimes (Cy)=B X B^t$
for some
![]() $X\in \mathcal {S}_C$
. It follows that
$X\in \mathcal {S}_C$
. It follows that
![]() $y\in \mathcal {R}(B)$
.
$y\in \mathcal {R}(B)$
.
Corollary 2.11 If
![]() $T\in \mathcal {B(H)}$
, then
$T\in \mathcal {B(H)}$
, then
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T^t$
if and only if
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T^t$
if and only if
![]() $\mathcal {R}(T)=\overline {\mathcal {R}(T)}$
.
$\mathcal {R}(T)=\overline {\mathcal {R}(T)}$
.
Proof By Lemma 2.9, there exists
![]() $A\in \mathcal {S}_C$
with
$A\in \mathcal {S}_C$
with
![]() $\mathcal {R}(A)=\mathcal {R}(T)$
. Then
$\mathcal {R}(A)=\mathcal {R}(T)$
. Then
![]() $C_{\mathcal {R}(A)}=C_{\mathcal {R}(T)}$
and, by Proposition 2.10, we have
$C_{\mathcal {R}(A)}=C_{\mathcal {R}(T)}$
and, by Proposition 2.10, we have
Then
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T^t$
if and only if
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T^t$
if and only if
![]() $C_{\mathcal {R}(A)}=A\mathcal {S}_C A$
. The desired result follows readily from Theorem 1.2.
$C_{\mathcal {R}(A)}=A\mathcal {S}_C A$
. The desired result follows readily from Theorem 1.2.
Proof of Theorem 1.4
Denote
![]() ${\mathcal {M}}=\mathcal {R}(A)$
and
${\mathcal {M}}=\mathcal {R}(A)$
and
![]() $\mathcal {N}=\mathcal {R}(B)$
. By Theorem 1.3,
$\mathcal {N}=\mathcal {R}(B)$
. By Theorem 1.3,
![]() $\overline {A\mathcal {S}_C A}=\overline {C_{{\mathcal {M}}}}$
and
$\overline {A\mathcal {S}_C A}=\overline {C_{{\mathcal {M}}}}$
and
![]() $\overline {B\mathcal {S}_C B}=\overline {C_{\mathcal {N}}}$
.
$\overline {B\mathcal {S}_C B}=\overline {C_{\mathcal {N}}}$
.
“
![]() $\Longrightarrow $
”. Choose a closed subspace
$\Longrightarrow $
”. Choose a closed subspace
![]() $\mathcal {M}_1$
of
$\mathcal {M}_1$
of
![]() ${\mathcal {M}}$
and an orthonormal basis
${\mathcal {M}}$
and an orthonormal basis
![]() $\{e_i\}_{i\in \Lambda }$
of
$\{e_i\}_{i\in \Lambda }$
of
![]() $\mathcal {M}_1$
. Define
$\mathcal {M}_1$
. Define
![]() $U=\sum _{i\in \Lambda } e_i\otimes (ce:i)$
. Then one can check that
$U=\sum _{i\in \Lambda } e_i\otimes (ce:i)$
. Then one can check that
![]() $U\in \mathcal {S}_C$
is a partial isometry with
$U\in \mathcal {S}_C$
is a partial isometry with
![]() $\mathcal {R}(U)=\mathcal {M}_1$
, which implies
$\mathcal {R}(U)=\mathcal {M}_1$
, which implies
![]() $U\in C_{\mathcal {M}}\subset \overline {C_{\mathcal {N}}}$
. By the hypothesis, there exist
$U\in C_{\mathcal {M}}\subset \overline {C_{\mathcal {N}}}$
. By the hypothesis, there exist
![]() $X_n\in C_{\mathcal {N}}$
,
$X_n\in C_{\mathcal {N}}$
,
![]() $n\geq 1$
, such that
$n\geq 1$
, such that
![]() $X_n\rightarrow U$
.
$X_n\rightarrow U$
.
By Corollary 2.8, we can find
![]() $\{Y_n\}\subset \mathcal {S}_C$
with
$\{Y_n\}\subset \mathcal {S}_C$
with
![]() $\mathcal {R}(Y_n)=\overline {\mathcal {R}(Y_n)}\subset \mathcal {N}$
such that
$\mathcal {R}(Y_n)=\overline {\mathcal {R}(Y_n)}\subset \mathcal {N}$
such that
![]() $\|Y_n-X_n\|<\frac {1}{n}, n\geq 1$
. Then
$\|Y_n-X_n\|<\frac {1}{n}, n\geq 1$
. Then
![]() $Y_n\in C_{\mathcal {N}}$
and
$Y_n\in C_{\mathcal {N}}$
and
![]() $Y_n\rightarrow U$
. Furthermore, we have
$Y_n\rightarrow U$
. Furthermore, we have
![]() $Y_nY_n^{*}\rightarrow UU^{*}$
.
$Y_nY_n^{*}\rightarrow UU^{*}$
.
Note that
![]() $UU^{*}=P_{\mathcal {M}_1}$
and
$UU^{*}=P_{\mathcal {M}_1}$
and
![]() $\mathcal {R}(Y_nY_n^{*})=\mathcal {R}(Y_n)$
is closed,
$\mathcal {R}(Y_nY_n^{*})=\mathcal {R}(Y_n)$
is closed,
![]() $n\geq 1$
. There exists
$n\geq 1$
. There exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\sigma (Y_nY_n^{*})\subset \{0\}\cup [\delta , \infty )$
. Define a continuous function f on
$\sigma (Y_nY_n^{*})\subset \{0\}\cup [\delta , \infty )$
. Define a continuous function f on
![]() $\{0\}\cup (\delta /2, \infty )$
as
$\{0\}\cup (\delta /2, \infty )$
as
 $$ \begin{align*}f(t)=\begin{cases} 0,& t=0, \\ 1,& t\in(\delta/2, \infty).\end{cases}\end{align*} $$
$$ \begin{align*}f(t)=\begin{cases} 0,& t=0, \\ 1,& t\in(\delta/2, \infty).\end{cases}\end{align*} $$
Then
![]() $f(Y_nY_n^{*})\rightarrow f(UU^{*})=P_{\mathcal {M}_1}$
. Note that
$f(Y_nY_n^{*})\rightarrow f(UU^{*})=P_{\mathcal {M}_1}$
. Note that
![]() $f(Y_nY_n^{*})$
is an orthogonal projection with
$f(Y_nY_n^{*})$
is an orthogonal projection with
This proves the necessity.
“
![]() $\Longleftarrow $
”. Clearly, it suffices to prove
$\Longleftarrow $
”. Clearly, it suffices to prove
![]() $C_{{\mathcal {M}}}\subset \overline {C_{\mathcal {N}}}$
. By Corollary 2.8, it suffices to prove that any
$C_{{\mathcal {M}}}\subset \overline {C_{\mathcal {N}}}$
. By Corollary 2.8, it suffices to prove that any
![]() $X\in \mathcal {S}_C$
with
$X\in \mathcal {S}_C$
with
![]() $\mathcal {R}(X)=\overline {\mathcal {R}(X)}\subset {\mathcal {M}}$
satisfies
$\mathcal {R}(X)=\overline {\mathcal {R}(X)}\subset {\mathcal {M}}$
satisfies
![]() $X\in \overline {C_{\mathcal {N}}}$
.
$X\in \overline {C_{\mathcal {N}}}$
.
Denote
![]() $\mathcal {M}_1=\mathcal {R}(X)$
and, for convenience, we write P for
$\mathcal {M}_1=\mathcal {R}(X)$
and, for convenience, we write P for
![]() $P_{\mathcal {M}_1}$
. By Corollary 2.11, we have
$P_{\mathcal {M}_1}$
. By Corollary 2.11, we have
![]() $X\in C_{\mathcal {M}_1}=P\mathcal {S}_C P^t$
. So
$X\in C_{\mathcal {M}_1}=P\mathcal {S}_C P^t$
. So
![]() $X=PYP^t$
for some
$X=PYP^t$
for some
![]() $Y\in \mathcal {S}_C$
. On the other hand, by the hypothesis, we can find orthogonal projections
$Y\in \mathcal {S}_C$
. On the other hand, by the hypothesis, we can find orthogonal projections
![]() $\{P_n\}$
with
$\{P_n\}$
with
![]() $\mathcal {R}(P_n)\subset \mathcal {N}$
such that
$\mathcal {R}(P_n)\subset \mathcal {N}$
such that
![]() $P_n\rightarrow P$
. So
$P_n\rightarrow P$
. So
![]() $P_nYP_n^t\rightarrow PYP^t=X$
. Noting that
$P_nYP_n^t\rightarrow PYP^t=X$
. Noting that
![]() $P_nYP_n^t \in \mathcal {S}_C$
and
$P_nYP_n^t \in \mathcal {S}_C$
and
![]() $\mathcal {R}(P_nYP_n^t)\subset \mathcal {R}(P_n)\subset \mathcal {N}$
, we conclude that
$\mathcal {R}(P_nYP_n^t)\subset \mathcal {R}(P_n)\subset \mathcal {N}$
, we conclude that
![]() $P_nYP_n^t \in C_{\mathcal {N}}$
and
$P_nYP_n^t \in C_{\mathcal {N}}$
and
![]() $X\in \overline {C_{\mathcal {N}}}$
.
$X\in \overline {C_{\mathcal {N}}}$
.
Next, we determine
![]() $\overline {T\mathcal {S}_C T}$
for certain compact operators T.
$\overline {T\mathcal {S}_C T}$
for certain compact operators T.
Example 2.12 Let
![]() $\{e_n\}_{n=1}^\infty $
be an orthonormal basis of
$\{e_n\}_{n=1}^\infty $
be an orthonormal basis of
![]() ${\mathcal {H}}$
such that
${\mathcal {H}}$
such that
![]() $Ce_n=e_n, n=1,2,\dots $
. We define two diagonal operators on
$Ce_n=e_n, n=1,2,\dots $
. We define two diagonal operators on
![]() ${\mathcal {H}}$
as
${\mathcal {H}}$
as
 $$\begin{align*}A=\begin{bmatrix} 1&&&&\\ &\frac{1}{2^2}&&&\\ &&\frac{1}{3^2}&&\\ &&&\frac{1}{4^2}&\\ &&&&\ddots \end{bmatrix}\begin{matrix} e_1\\ e_2\\ e_3\\ e_4\\ \vdots \end{matrix} , \ \ \ \ B= \begin{bmatrix} 1&&&&\\ &\frac{1}{2 }&&&\\ &&\frac{1}{3 }&&\\ &&&\frac{1}{4 }&\\ &&&&\ddots \end{bmatrix}\begin{matrix} e_1\\ e_2\\ e_3\\ e_4\\ \vdots \end{matrix} .\end{align*}$$
$$\begin{align*}A=\begin{bmatrix} 1&&&&\\ &\frac{1}{2^2}&&&\\ &&\frac{1}{3^2}&&\\ &&&\frac{1}{4^2}&\\ &&&&\ddots \end{bmatrix}\begin{matrix} e_1\\ e_2\\ e_3\\ e_4\\ \vdots \end{matrix} , \ \ \ \ B= \begin{bmatrix} 1&&&&\\ &\frac{1}{2 }&&&\\ &&\frac{1}{3 }&&\\ &&&\frac{1}{4 }&\\ &&&&\ddots \end{bmatrix}\begin{matrix} e_1\\ e_2\\ e_3\\ e_4\\ \vdots \end{matrix} .\end{align*}$$
It is clear that
![]() $A,B\in \mathcal {S}_C$
and
$A,B\in \mathcal {S}_C$
and
![]() $A=B^2$
. Thus
$A=B^2$
. Thus
![]() $\mathcal {R}(A)\subset \mathcal {R}(B)$
. Noting that
$\mathcal {R}(A)\subset \mathcal {R}(B)$
. Noting that
we obtain
![]() $\mathcal {R}(A)\subsetneq \mathcal {R}(B).$
Next, we shall show that
$\mathcal {R}(A)\subsetneq \mathcal {R}(B).$
Next, we shall show that
![]() $\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
or, equivalently,
$\overline {C_{\mathcal {R}(A)}}=\overline {C_{\mathcal {R}(B)}}$
or, equivalently,
![]() $\overline {A\mathcal {S}_C A}=\overline {B\mathcal {S}_C B}$
.
$\overline {A\mathcal {S}_C A}=\overline {B\mathcal {S}_C B}$
.
Since it is clear that
![]() $[{A\mathcal {S}_C A}\cup {B\mathcal {S}_C B}]\subset [\mathcal {S}_C\cap \mathcal {K(H)}],$
where
$[{A\mathcal {S}_C A}\cup {B\mathcal {S}_C B}]\subset [\mathcal {S}_C\cap \mathcal {K(H)}],$
where
![]() $\mathcal {K(H)}$
is the ideal of operators in
$\mathcal {K(H)}$
is the ideal of operators in
![]() $\mathcal {B(H)}$
, it suffices to show
$\mathcal {B(H)}$
, it suffices to show
![]() $[\mathcal {S}_C\cap \mathcal {K(H)}]\subset [\overline {{A\mathcal {S}_C A}}\cap {\overline {B\mathcal {S}_C B}}]$
.
$[\mathcal {S}_C\cap \mathcal {K(H)}]\subset [\overline {{A\mathcal {S}_C A}}\cap {\overline {B\mathcal {S}_C B}}]$
.
Arbitrarily choose an operator
![]() $T\in \mathcal {S}_C\cap \mathcal {K(H)}$
. For each
$T\in \mathcal {S}_C\cap \mathcal {K(H)}$
. For each
![]() $n\geq 1$
, we let
$n\geq 1$
, we let
![]() $P_n$
denote the orthogonal projection of
$P_n$
denote the orthogonal projection of
![]() ${\mathcal {H}}$
onto
${\mathcal {H}}$
onto
![]() $\vee \{e_1,\dots ,e_n\}$
. Note that
$\vee \{e_1,\dots ,e_n\}$
. Note that
![]() $P_nTP_n\in \mathcal {S}_C$
with
$P_nTP_n\in \mathcal {S}_C$
with
By Corollary 2.2,
![]() $P_nTP_n\in C_{\mathcal {R}(A)}\cap C_{\mathcal {R}(B)}$
. Note that
$P_nTP_n\in C_{\mathcal {R}(A)}\cap C_{\mathcal {R}(B)}$
. Note that
![]() $P_nTP_n\rightarrow T$
. We obtain
$P_nTP_n\rightarrow T$
. We obtain
![]() $T\in \overline {{A\mathcal {S}_C A}}\cap {\overline {B\mathcal {S}_C B}}.$
Thus we have shown
$T\in \overline {{A\mathcal {S}_C A}}\cap {\overline {B\mathcal {S}_C B}}.$
Thus we have shown
Remark 2.13 Let
![]() $A,B\in \mathcal {B(H)}$
and C be defined as in the preceding example. Set
$A,B\in \mathcal {B(H)}$
and C be defined as in the preceding example. Set
Then one can see that
![]() $R,T\in {\mathcal S}_{\widetilde {C}}$
with
$R,T\in {\mathcal S}_{\widetilde {C}}$
with
![]() $\mathcal {R}(R)\nsubseteq \mathcal {R}(T) $
and
$\mathcal {R}(R)\nsubseteq \mathcal {R}(T) $
and
![]() $\mathcal {R}(T)\nsubseteq \mathcal {R}(R)$
. However, one can show that
$\mathcal {R}(T)\nsubseteq \mathcal {R}(R)$
. However, one can show that
![]() $\widetilde {C}_{\mathcal {R}(R)}$
and
$\widetilde {C}_{\mathcal {R}(R)}$
and
![]() $\widetilde {C}_{\mathcal {R}(T)}$
have the same norm closure.
$\widetilde {C}_{\mathcal {R}(T)}$
have the same norm closure.
2.4 Proof of Theorem 1.5
We first make some preparations.
Lemma 2.14 Let
![]() $\mathcal {M}$
be a subspace of
$\mathcal {M}$
be a subspace of
![]() ${\mathcal {H}}$
. Then
${\mathcal {H}}$
. Then
Proof One can easily check that
![]() $C_{\overline {\mathcal {M}}}$
is closed in the weak operator topology. It is clear that
$C_{\overline {\mathcal {M}}}$
is closed in the weak operator topology. It is clear that
So it suffices to prove
![]() $[C_{\overline {\mathcal {M}}}\cap \mathcal {K(H)}] \subset \overline { C_{\mathcal {M}}\cap \mathcal {K(H)} }$
.
$[C_{\overline {\mathcal {M}}}\cap \mathcal {K(H)}] \subset \overline { C_{\mathcal {M}}\cap \mathcal {K(H)} }$
.
Now assume that
![]() $A\in C_{\overline {\mathcal {M}}}\cap \mathcal {K(H)}$
. We shall prove
$A\in C_{\overline {\mathcal {M}}}\cap \mathcal {K(H)}$
. We shall prove
![]() $A\in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
. By [Reference Garcia and Putinar15, Theorem 3], A can be written as
$A\in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
. By [Reference Garcia and Putinar15, Theorem 3], A can be written as
where
![]() $e_n$
are certain orthonormal eigenvectors of
$e_n$
are certain orthonormal eigenvectors of
![]() $|A| =|AA^{*}|^{1/2}$
and the
$|A| =|AA^{*}|^{1/2}$
and the
![]() $\lambda _n$
are the nonzero eigenvalues of
$\lambda _n$
are the nonzero eigenvalues of
![]() $|A|$
, repeated according to multiplicity. Clearly,
$|A|$
, repeated according to multiplicity. Clearly,
![]() $\lambda _n\rightarrow 0$
and
$\lambda _n\rightarrow 0$
and
![]() $Ce_n\in \mathcal {R}(A)\subset \overline {\mathcal {M}}$
. Then
$Ce_n\in \mathcal {R}(A)\subset \overline {\mathcal {M}}$
. Then
 $$ \begin{align*}\sum_{n=1}^m \lambda_n(Ce_n)\otimes e_n\longrightarrow A\ \ \ \ \ \ (m\rightarrow\infty).\end{align*} $$
$$ \begin{align*}\sum_{n=1}^m \lambda_n(Ce_n)\otimes e_n\longrightarrow A\ \ \ \ \ \ (m\rightarrow\infty).\end{align*} $$
So it remains to prove that
![]() $(Ce_n)\otimes e_n\in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
for each
$(Ce_n)\otimes e_n\in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
for each
![]() $n\geq 1$
.
$n\geq 1$
.
Since
![]() $Ce_n\in \overline {{\mathcal {M}}}$
, there exists a sequence
$Ce_n\in \overline {{\mathcal {M}}}$
, there exists a sequence
![]() $\{x_k\}_{k=1}^\infty \subset {\mathcal {M}}$
converging to
$\{x_k\}_{k=1}^\infty \subset {\mathcal {M}}$
converging to
![]() $Ce_n$
. Clearly,
$Ce_n$
. Clearly,
![]() $x_k\otimes (Cx_k)\in C_{{\mathcal {M}}}\cap \mathcal {K(H)}$
for all
$x_k\otimes (Cx_k)\in C_{{\mathcal {M}}}\cap \mathcal {K(H)}$
for all
![]() $k\geq 1$
. Note that
$k\geq 1$
. Note that
![]() $\{x_k\otimes (Cx_k)\}$
converges to
$\{x_k\otimes (Cx_k)\}$
converges to
![]() ${(Ce_n)\otimes e_n}$
in the norm topology. We deduce that
${(Ce_n)\otimes e_n}$
in the norm topology. We deduce that
![]() $(Ce_n)\otimes e_n \in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
. Thus we complete the proof.
$(Ce_n)\otimes e_n \in \overline {C_{\mathcal {M}}\cap \mathcal {K(H)}}$
. Thus we complete the proof.
Proof of Theorem 1.5
We denote
![]() $\mathcal {M}={\mathcal {R}(T)}$
. It is trivial to see that
$\mathcal {M}={\mathcal {R}(T)}$
. It is trivial to see that
![]() $C_{\overline {{\mathcal {M}}}}$
is closed in both the weak operator topology and the weak* topology; moreover,
$C_{\overline {{\mathcal {M}}}}$
is closed in both the weak operator topology and the weak* topology; moreover,
On the other hand, since
![]() $C_{{\mathcal {M}}}$
is a subspace of
$C_{{\mathcal {M}}}$
is a subspace of
![]() $\mathcal {B(H)}$
, it is clear that
$\mathcal {B(H)}$
, it is clear that ![]() . Then it suffices to show
. Then it suffices to show
![]() $C_{\overline {{\mathcal {M}}}}\subset \overline {C_{{\mathcal {M}}}}^{w*}$
.
$C_{\overline {{\mathcal {M}}}}\subset \overline {C_{{\mathcal {M}}}}^{w*}$
.
We need only consider the case that
![]() $\mathcal {M}$
is not closed. In this case, we can choose an orthonormal basis
$\mathcal {M}$
is not closed. In this case, we can choose an orthonormal basis
![]() $\{e_i\}_{i=1}^\infty $
of
$\{e_i\}_{i=1}^\infty $
of
![]() $\overline {\mathcal {M}}$
. Define
$\overline {\mathcal {M}}$
. Define
![]() $U\in \mathcal {B(H)}$
as
$U\in \mathcal {B(H)}$
as
Thus U is a partial isometry lying in
![]() $\mathcal {S}_C$
,
$\mathcal {S}_C$
,
![]() $\mathcal {R}(U)=\overline {\mathcal {M}}$
and
$\mathcal {R}(U)=\overline {\mathcal {M}}$
and
![]() $(\ker U)^\bot =C(\overline {\mathcal {M}})$
. So
$(\ker U)^\bot =C(\overline {\mathcal {M}})$
. So
![]() $U\in C_{\overline {{\mathcal {M}}}}$
and it follows from Theorem 1.2 that
$U\in C_{\overline {{\mathcal {M}}}}$
and it follows from Theorem 1.2 that
![]() $C_{\overline {{\mathcal {M}}}}=U\mathcal {S}_C U$
.
$C_{\overline {{\mathcal {M}}}}=U\mathcal {S}_C U$
.
Fix an operator
![]() $A\in \mathcal {S}_C$
. Then it suffices to prove
$A\in \mathcal {S}_C$
. Then it suffices to prove
![]() $UAU\in \overline {C_{{\mathcal {M}}}}^{w*}$
.
$UAU\in \overline {C_{{\mathcal {M}}}}^{w*}$
.
For the conjugation C, there is an orthonormal basis
![]() $\{f_i\}$
of
$\{f_i\}$
of
![]() ${\mathcal {H}}$
such that
${\mathcal {H}}$
such that
![]() $Cf_i=f_i$
for all i (see [Reference Garcia, Prodan and Putinar13, Lemma 2.11]). For each
$Cf_i=f_i$
for all i (see [Reference Garcia, Prodan and Putinar13, Lemma 2.11]). For each
![]() $n\geq 1$
, set
$n\geq 1$
, set
![]() $P_n=\sum _{i=1}^nf_i\otimes f_i$
. It is easy to see
$P_n=\sum _{i=1}^nf_i\otimes f_i$
. It is easy to see
![]() $P_n\in \mathcal {S}_C$
. Noting that
$P_n\in \mathcal {S}_C$
. Noting that
![]() $P_nAP_n\in \mathcal {S}_C$
and, as
$P_nAP_n\in \mathcal {S}_C$
and, as
![]() $n\rightarrow \infty $
,
$n\rightarrow \infty $
,
![]() $P_nAP_n$
converges to A in the
$P_nAP_n$
converges to A in the ![]() . So
. So
![]() $UP_nAP_nU$
converges to
$UP_nAP_nU$
converges to
![]() $UAU$
in the
$UAU$
in the ![]() . Now it remains to prove the following claim.
. Now it remains to prove the following claim.
Claim
![]() $UP_nAP_nU\in \overline {C_{{\mathcal {M}}}}^{w*}$
for each
$UP_nAP_nU\in \overline {C_{{\mathcal {M}}}}^{w*}$
for each
![]() $n=1,2,\dots $
.
$n=1,2,\dots $
.
In fact, if the preceding claim holds, then, by [Reference Conway4, Proposition 20.3],
![]() $UAU\in \overline {C_{{\mathcal {M}}}}^{w*}$
.
$UAU\in \overline {C_{{\mathcal {M}}}}^{w*}$
.
Set
![]() $a_{j,i}=\langle Af_i, f_j\rangle $
for all
$a_{j,i}=\langle Af_i, f_j\rangle $
for all
![]() $i,j\in \{1,2,\dots \}$
. Since
$i,j\in \{1,2,\dots \}$
. Since
![]() $A\in \mathcal {S}_C$
, we have
$A\in \mathcal {S}_C$
, we have
![]() $a_{i,j}=a_{j,i}.$
Then
$a_{i,j}=a_{j,i}.$
Then
 $$ \begin{align*}P_nAP_n=\sum_{i=1}^n a_{i,i} f_i\otimes f_i +\sum_{1\leq i<j\leq n} a_{i,j}(f_i\otimes f_j+f_j\otimes f_i) \end{align*} $$
$$ \begin{align*}P_nAP_n=\sum_{i=1}^n a_{i,i} f_i\otimes f_i +\sum_{1\leq i<j\leq n} a_{i,j}(f_i\otimes f_j+f_j\otimes f_i) \end{align*} $$
and
 $$ \begin{align} &= \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (U^{*}f_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (U^{*}f_j)+(Uf_j)\otimes (U^{*}f_i)] \end{align} $$
$$ \begin{align} &= \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (U^{*}f_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (U^{*}f_j)+(Uf_j)\otimes (U^{*}f_i)] \end{align} $$
 $$ \begin{align} =& \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (U^{*}Cf_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (U^{*}Cf_j)+(Uf_j)\otimes (U^{*}Cf_i)] \end{align} $$
$$ \begin{align} =& \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (U^{*}Cf_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (U^{*}Cf_j)+(Uf_j)\otimes (U^{*}Cf_i)] \end{align} $$
 $$ \begin{align} =& \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (CUf_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (CUf_j)+(Uf_j)\otimes (CUf_i)]. \end{align} $$
$$ \begin{align} =& \sum_{i=1}^n a_{i,i} (Uf_i)\otimes (CUf_i) +\sum_{1\leq i<j\leq n} a_{i,j}[(Uf_i)\otimes (CUf_j)+(Uf_j)\otimes (CUf_i)]. \end{align} $$
Note that
![]() $Uf_i, Uf_j\in \mathcal {R}(U)=\overline {{\mathcal {M}}}$
.
$Uf_i, Uf_j\in \mathcal {R}(U)=\overline {{\mathcal {M}}}$
.
For any
![]() $x,y\in \overline {{\mathcal {M}}}$
, it follows from Lemma 2.14 that
$x,y\in \overline {{\mathcal {M}}}$
, it follows from Lemma 2.14 that
![]() $x\otimes (Cy)+y\otimes (Cx)\in \overline {C_{{\mathcal {M}}}}.$
In view of (1), we obtain
$x\otimes (Cy)+y\otimes (Cx)\in \overline {C_{{\mathcal {M}}}}.$
In view of (1), we obtain
![]() $UP_nAP_nU\in \overline {C_{{\mathcal {M}}}}\subset \overline {C_{{\mathcal {M}}}}^{w*}$
. This proves Claim and completes the proof.
$UP_nAP_nU\in \overline {C_{{\mathcal {M}}}}\subset \overline {C_{{\mathcal {M}}}}^{w*}$
. This proves Claim and completes the proof.
The following result classifies the inclusion relations among
![]() $T\mathcal {S}_C T, {C_{\mathcal {R}(T)}},\overline {C_{\mathcal {R}(T)}}$
and
$T\mathcal {S}_C T, {C_{\mathcal {R}(T)}},\overline {C_{\mathcal {R}(T)}}$
and
![]() $C_{\overline {\mathcal {R}(T)}}$
for
$C_{\overline {\mathcal {R}(T)}}$
for
![]() $T\in \mathcal {S}_C$
.
$T\in \mathcal {S}_C$
.
Proposition 2.15 For
![]() $T\in \mathcal {S}_C$
, the following are equivalent:
$T\in \mathcal {S}_C$
, the following are equivalent:
-
(i)
 $\mathcal {R}(T)=\overline {\mathcal {R}(T)}$
;
$\mathcal {R}(T)=\overline {\mathcal {R}(T)}$
; -
(ii)
 $C_{\mathcal {R}(T)}=\overline {C_{\mathcal {R}(T)}}$
;
$C_{\mathcal {R}(T)}=\overline {C_{\mathcal {R}(T)}}$
; -
(iii)
 ;
; -
(iv)
 $\overline {C_{\mathcal {R}(T)}}=C_{\overline {\mathcal {R}(T)}}$
;
$\overline {C_{\mathcal {R}(T)}}=C_{\overline {\mathcal {R}(T)}}$
; -
(v)
 $C_{\mathcal {R}(T)}=A\mathcal {S}_C A$
for some
$C_{\mathcal {R}(T)}=A\mathcal {S}_C A$
for some
 $A\in \mathcal {S}_C$
;
$A\in \mathcal {S}_C$
; -
(vi)
 $T\mathcal {S}_C T=C_{\mathcal {M}}$
for some subspace
$T\mathcal {S}_C T=C_{\mathcal {M}}$
for some subspace
 $\mathcal {M}$
of
$\mathcal {M}$
of
 ${\mathcal {H}}$
;
${\mathcal {H}}$
; -
(vii)
 $T\mathcal {S}_C T=\overline {T\mathcal {S}_C T}$
;
$T\mathcal {S}_C T=\overline {T\mathcal {S}_C T}$
; -
(viii)
 .
.
Proof “(i)
![]() $\Longrightarrow $
(iii), (iv) and (viii)”. Since
$\Longrightarrow $
(iii), (iv) and (viii)”. Since
![]() $\mathcal {R}(T)$
is norm-closed, one can easily verify that
$\mathcal {R}(T)$
is norm-closed, one can easily verify that
![]() $C_{\mathcal {R}(T)}$
is closed in the wot and, by Theorem 1.2, we have
$C_{\mathcal {R}(T)}$
is closed in the wot and, by Theorem 1.2, we have
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. Hence
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. Hence
![]() $T\mathcal {S}_C T$
is closed in the wot.
$T\mathcal {S}_C T$
is closed in the wot.
“(viii)
![]() $\Longrightarrow $
(vii)” and “(iii)
$\Longrightarrow $
(vii)” and “(iii)
![]() $\Longrightarrow $
(ii)”. Both are obvious.
$\Longrightarrow $
(ii)”. Both are obvious.
“(vii)
![]() $\Longrightarrow $
(i)”. Since
$\Longrightarrow $
(i)”. Since
![]() $T\mathcal {S}_C T$
is norm closed, by Theorem 1.3,
$T\mathcal {S}_C T$
is norm closed, by Theorem 1.3,
![]() $ T\mathcal {S}_C T= \overline {C_{\mathcal {R}(T)}} \supseteq C_{\mathcal {R}(T)} $
. Hence,
$ T\mathcal {S}_C T= \overline {C_{\mathcal {R}(T)}} \supseteq C_{\mathcal {R}(T)} $
. Hence,
![]() $T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
and, by Theorem 1.2,
$T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
and, by Theorem 1.2,
![]() $\mathcal {R}(T)$
is closed.
$\mathcal {R}(T)$
is closed.
“(ii)
![]() $\Longrightarrow $
(i)”. Choose an
$\Longrightarrow $
(i)”. Choose an
![]() $x\in \overline {\mathcal {R}(T)}$
. Then there exists a sequence
$x\in \overline {\mathcal {R}(T)}$
. Then there exists a sequence
![]() $\{x_n\}\in \mathcal {R}(T)$
converging to x. Clearly,
$\{x_n\}\in \mathcal {R}(T)$
converging to x. Clearly,
![]() $x_n\otimes (Cx_n)\in C_{\mathcal {R}(T)}$
for all n. Note that
$x_n\otimes (Cx_n)\in C_{\mathcal {R}(T)}$
for all n. Note that
![]() $\{x_n\otimes (Cx_n)\}$
converges to
$\{x_n\otimes (Cx_n)\}$
converges to
![]() $x\otimes (Cx)$
in norm. Since
$x\otimes (Cx)$
in norm. Since
![]() $C_{\mathcal {R}(T)}$
is norm-closed, we deduce that
$C_{\mathcal {R}(T)}$
is norm-closed, we deduce that
![]() $x\otimes (Cx)\in C_{\mathcal {R}(T)}$
. Thus
$x\otimes (Cx)\in C_{\mathcal {R}(T)}$
. Thus
![]() $x\in \mathcal {R}(T)$
. This shows that
$x\in \mathcal {R}(T)$
. This shows that
![]() ${\mathcal {R}(T)}=\overline {\mathcal {R}(T)}.$
${\mathcal {R}(T)}=\overline {\mathcal {R}(T)}.$
“(i)
![]() $\Longrightarrow $
(vi)”. By Theorem 1.2, we have
$\Longrightarrow $
(vi)”. By Theorem 1.2, we have
![]() $T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
.
$T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
.
“(vi)
![]() $\Longrightarrow $
(v)”. Assume that
$\Longrightarrow $
(v)”. Assume that
![]() $T\mathcal {S}_C T=C_{\mathcal {M}}$
for some subspace
$T\mathcal {S}_C T=C_{\mathcal {M}}$
for some subspace
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() ${\mathcal {H}}$
. It is clear that
${\mathcal {H}}$
. It is clear that
![]() $T\mathcal {S}_C T\subset C_{\mathcal {R}(T)}$
. So
$T\mathcal {S}_C T\subset C_{\mathcal {R}(T)}$
. So
![]() $C_{\mathcal {M}}\subset C_{\mathcal {R}(T)}$
. Then, for any
$C_{\mathcal {M}}\subset C_{\mathcal {R}(T)}$
. Then, for any
![]() $x\in \mathcal {M},$
we have
$x\in \mathcal {M},$
we have
![]() $x\otimes (Cx)\in C_{\mathcal {M}}\subset C_{\mathcal {R}(T)}$
and
$x\otimes (Cx)\in C_{\mathcal {M}}\subset C_{\mathcal {R}(T)}$
and
![]() $x\in \mathcal {R}(T)$
. This shows
$x\in \mathcal {R}(T)$
. This shows
![]() $\mathcal {M}\subset \mathcal {R}(T)$
.
$\mathcal {M}\subset \mathcal {R}(T)$
.
On the other hand, if
![]() $x\in \mathcal {R}(T)$
, then, by Corollary 2.4,
$x\in \mathcal {R}(T)$
, then, by Corollary 2.4,
![]() $x\otimes (Cx)\in T\mathcal {S}_C T=C_{\mathcal {M}}$
, which implies
$x\otimes (Cx)\in T\mathcal {S}_C T=C_{\mathcal {M}}$
, which implies
![]() $x\in \mathcal {M}$
. Hence
$x\in \mathcal {M}$
. Hence
![]() $\mathcal {R}(T)\subset \mathcal {M}$
. We conclude that
$\mathcal {R}(T)\subset \mathcal {M}$
. We conclude that
![]() $\mathcal {R}(T)=\mathcal {M}$
and
$\mathcal {R}(T)=\mathcal {M}$
and
![]() $T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
.
$T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
.
“(v)
![]() $\Longrightarrow $
(i)”. Assume that
$\Longrightarrow $
(i)”. Assume that
![]() $C_{\mathcal {R}(T)}=A\mathcal {S}_C A$
. Since
$C_{\mathcal {R}(T)}=A\mathcal {S}_C A$
. Since
![]() $A\mathcal {S}_C A\subset C_{\mathcal {R}(A)}$
, it follows that
$A\mathcal {S}_C A\subset C_{\mathcal {R}(A)}$
, it follows that
![]() $C_{\mathcal {R}(T)} \subset C_{\mathcal {R}(A)}$
. By Proposition 2.10, we have
$C_{\mathcal {R}(T)} \subset C_{\mathcal {R}(A)}$
. By Proposition 2.10, we have
![]() $ {\mathcal {R}(T)} \subset {\mathcal {R}(A)}$
.
$ {\mathcal {R}(T)} \subset {\mathcal {R}(A)}$
.
On the other hand, if
![]() $x\in \mathcal {R}(A)$
, then, by Corollary 2.4,
$x\in \mathcal {R}(A)$
, then, by Corollary 2.4,
![]() $x\otimes (Cx)\in A\mathcal {S}_C A=C_{\mathcal {R}(T)}$
, which implies
$x\otimes (Cx)\in A\mathcal {S}_C A=C_{\mathcal {R}(T)}$
, which implies
![]() $x\in \mathcal {R}(T)$
. Hence
$x\in \mathcal {R}(T)$
. Hence
![]() $ {\mathcal {R}(A)} \subset {\mathcal {R}(T)}$
and
$ {\mathcal {R}(A)} \subset {\mathcal {R}(T)}$
and
![]() ${\mathcal {R}(A)} ={\mathcal {R}(T)}$
. By Proposition 2.10, we have
${\mathcal {R}(A)} ={\mathcal {R}(T)}$
. By Proposition 2.10, we have
![]() $A\mathcal {S}_C A=T\mathcal {S}_C T$
. So
$A\mathcal {S}_C A=T\mathcal {S}_C T$
. So
![]() $C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. By Theorem 1.2, we deduce that
$C_{\mathcal {R}(T)}=T\mathcal {S}_C T$
. By Theorem 1.2, we deduce that
![]() $\mathcal {R}(T)$
is closed.
$\mathcal {R}(T)$
is closed.
“(iv)
![]() $\Longrightarrow $
(i)”. Denote
$\Longrightarrow $
(i)”. Denote
![]() ${\mathcal {M}}=\mathcal {R}(T)$
. We choose an orthonormal basis
${\mathcal {M}}=\mathcal {R}(T)$
. We choose an orthonormal basis
![]() $\{e_i\}_{i=1}^\infty $
of
$\{e_i\}_{i=1}^\infty $
of
![]() $\overline {\mathcal {M}}$
. Define
$\overline {\mathcal {M}}$
. Define
![]() $U\in \mathcal {B(H)}$
as
$U\in \mathcal {B(H)}$
as
Thus
![]() $U\in \mathcal {B(H)}$
is a partial isometry,
$U\in \mathcal {B(H)}$
is a partial isometry,
![]() $\mathcal {R}(U)=\overline {\mathcal {M}}$
and
$\mathcal {R}(U)=\overline {\mathcal {M}}$
and
![]() $ \mathcal {R}(U^{*})=(\ker U)^\bot =C(\overline {\mathcal {M}})$
. It is easy to check that
$ \mathcal {R}(U^{*})=(\ker U)^\bot =C(\overline {\mathcal {M}})$
. It is easy to check that
![]() $U\in \mathcal {S}_C$
. So
$U\in \mathcal {S}_C$
. So
![]() $U\in C_{\overline {\mathcal {M}}}$
.
$U\in C_{\overline {\mathcal {M}}}$
.
By the hypothesis, we can find
![]() $\{T_n\}\subset C_{\mathcal {M}}$
such that
$\{T_n\}\subset C_{\mathcal {M}}$
such that
![]() $T_n\longrightarrow U$
.
$T_n\longrightarrow U$
.
Since
![]() $\mathcal {R}(T_n)\subset \mathcal {M} \subset \overline {\mathcal {M}}=\mathcal {R}(U)$
, by Lemma 2.1, we have
$\mathcal {R}(T_n)\subset \mathcal {M} \subset \overline {\mathcal {M}}=\mathcal {R}(U)$
, by Lemma 2.1, we have
Denote
![]() $\widetilde {U}=U|_{C(\overline {\mathcal {M}})}$
and
$\widetilde {U}=U|_{C(\overline {\mathcal {M}})}$
and
![]() $\widetilde {T}_n=(T_n)|_{C(\overline {\mathcal {M}})}$
. Thus
$\widetilde {T}_n=(T_n)|_{C(\overline {\mathcal {M}})}$
. Thus
![]() $\widetilde {U},\widetilde {T}_n: C(\overline {\mathcal {M}})\rightarrow \overline {\mathcal {M}}$
are bounded linear operators and
$\widetilde {U},\widetilde {T}_n: C(\overline {\mathcal {M}})\rightarrow \overline {\mathcal {M}}$
are bounded linear operators and
![]() $\widetilde {U}$
is invertible.
$\widetilde {U}$
is invertible.
Since
![]() $T_n\rightarrow U$
, it follows that
$T_n\rightarrow U$
, it follows that
![]() $\widetilde {T}_n\rightarrow \widetilde {U}$
. By the stability of invertibility, we deduce that
$\widetilde {T}_n\rightarrow \widetilde {U}$
. By the stability of invertibility, we deduce that
![]() $\widetilde {T}_n$
is invertible for n large enough. This implies that
$\widetilde {T}_n$
is invertible for n large enough. This implies that
![]() $\mathcal {R}(T_n)=\mathcal {R}(\widetilde {T}_n)=\overline {\mathcal {M}}$
for n large enough. Since
$\mathcal {R}(T_n)=\mathcal {R}(\widetilde {T}_n)=\overline {\mathcal {M}}$
for n large enough. Since
![]() $\mathcal {R}(T_n)\subset \mathcal {M}$
, we obtain
$\mathcal {R}(T_n)\subset \mathcal {M}$
, we obtain
![]() $\overline {\mathcal {M}}=\mathcal {M}$
.
$\overline {\mathcal {M}}=\mathcal {M}$
.
Remark 2.16 By the preceding result and Theorem 1.2, if
![]() $T\in \mathcal {S}_C$
has a non-closed range, then
$T\in \mathcal {S}_C$
has a non-closed range, then
On the other hand, if T has a closed range, then all these sets coincide.
Corollary 2.17 Let
![]() $\mathcal {M}$
be a subspace of
$\mathcal {M}$
be a subspace of
![]() ${\mathcal {H}}$
. Then the following are equivalent:
${\mathcal {H}}$
. Then the following are equivalent:
-
(i)
 $C_{\mathcal {M}}=T\mathcal {S}_C T$
for some
$C_{\mathcal {M}}=T\mathcal {S}_C T$
for some
 $T\in \mathcal {S}_C$
;
$T\in \mathcal {S}_C$
; -
(ii)
 $C_{\mathcal {M}}$
is norm closed;
$C_{\mathcal {M}}$
is norm closed; -
(iii)
 $C_{\mathcal {M}}$
is wot closed;
$C_{\mathcal {M}}$
is wot closed; -
(iv)
 $\mathcal {M}=\overline {\mathcal {M}}$
.
$\mathcal {M}=\overline {\mathcal {M}}$
.
Proof The implications (iv)
![]() $\Longrightarrow $
(iii)
$\Longrightarrow $
(iii)
![]() $\Longrightarrow $
(ii) is obvious.
$\Longrightarrow $
(ii) is obvious.
“(ii)
![]() $\Longrightarrow $
(iv)”. Using a similar argument as in the proof for (ii)
$\Longrightarrow $
(iv)”. Using a similar argument as in the proof for (ii)
![]() $\Longrightarrow $
(i) of Proposition 2.15, one can see that
$\Longrightarrow $
(i) of Proposition 2.15, one can see that
![]() $\mathcal {M}$
is closed.
$\mathcal {M}$
is closed.
“(i)
![]() $\Longrightarrow $
(iv)”. Assume that
$\Longrightarrow $
(iv)”. Assume that
![]() $C_{\mathcal {M}}=T\mathcal {S}_C T$
for some
$C_{\mathcal {M}}=T\mathcal {S}_C T$
for some
![]() $T\in \mathcal {S}_C$
. From the proof for (vi)
$T\in \mathcal {S}_C$
. From the proof for (vi)
![]() $\Longrightarrow $
(v) in Proposition 2.15, one can see that
$\Longrightarrow $
(v) in Proposition 2.15, one can see that
![]() $T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
and
$T\mathcal {S}_C T=C_{\mathcal {R}(T)}$
and
![]() $\mathcal {M}=\mathcal {R}(T)$
. By Theorem 1.2, we deduce that
$\mathcal {M}=\mathcal {R}(T)$
. By Theorem 1.2, we deduce that
![]() ${\mathcal {M}}=\mathcal {R}(T)$
is closed.
${\mathcal {M}}=\mathcal {R}(T)$
is closed.
“(iv)
![]() $\Longrightarrow $
(i)”. By Lemma 2.9, we can choose an operator
$\Longrightarrow $
(i)”. By Lemma 2.9, we can choose an operator
![]() $T\in \mathcal {S}_C$
with
$T\in \mathcal {S}_C$
with
![]() $\mathcal {R}(T)={\mathcal {M}}$
. Then, by Theorem 1.2,
$\mathcal {R}(T)={\mathcal {M}}$
. Then, by Theorem 1.2,
![]() $T\mathcal {S}_C T=C_{\mathcal {R}(T)}=C_{\mathcal {M}}$
.
$T\mathcal {S}_C T=C_{\mathcal {R}(T)}=C_{\mathcal {M}}$
.
3 The diagonalization in
 $\mathcal {S}_C$
$\mathcal {S}_C$
The aim of this section is to study the diagonalization of normal operators in
![]() $\mathcal {S}_C$
and give the proof of Theorem 1.6.
$\mathcal {S}_C$
and give the proof of Theorem 1.6.
3.1 Proof of Theorem 1.6
We first give a key lemma.
Lemma 3.1 Let
![]() $T \in \mathcal {S}_C$
be a self-adjoint operator and
$T \in \mathcal {S}_C$
be a self-adjoint operator and
![]() $e\in {\mathcal {H}}$
. Then, given
$e\in {\mathcal {H}}$
. Then, given
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $p>1$
, there exist a finite-rank orthogonal projection
$p>1$
, there exist a finite-rank orthogonal projection
![]() $P\in \mathcal {S}_C$
with
$P\in \mathcal {S}_C$
with
![]() $e\in \mathcal {R}(P)$
and a finite-rank self-adjoint operator
$e\in \mathcal {R}(P)$
and a finite-rank self-adjoint operator
![]() $K\in \mathcal {S}_C$
with
$K\in \mathcal {S}_C$
with
![]() $\|K\|_p<\varepsilon $
such that
$\|K\|_p<\varepsilon $
such that
![]() $P(T+K)=(T+K)P$
.
$P(T+K)=(T+K)P$
.
Proof Let E be the projection-valued spectral measure for T and assume that
![]() $\sigma (T)\subset [a,b]$
. We fix a positive integer n. Then there exist pairwise disjoint Borel subsets
$\sigma (T)\subset [a,b]$
. We fix a positive integer n. Then there exist pairwise disjoint Borel subsets
![]() $\Delta _1,\Delta _2,\dots ,\Delta _n$
and
$\Delta _1,\Delta _2,\dots ,\Delta _n$
and
![]() $a_1,a_2,\dots ,a_n\in [a,b]$
such that
$a_1,a_2,\dots ,a_n\in [a,b]$
such that
For
![]() $i=1,2,\dots ,n$
, denote
$i=1,2,\dots ,n$
, denote
![]() ${\mathcal {H}}_i=\mathcal {R} (E(\Delta _i))$
. Then each
${\mathcal {H}}_i=\mathcal {R} (E(\Delta _i))$
. Then each
![]() ${\mathcal {H}}_i$
reduces T and
${\mathcal {H}}_i$
reduces T and
![]() ${\mathcal {H}}=\oplus _{i=1}^n{\mathcal {H}}_i$
. Put
${\mathcal {H}}=\oplus _{i=1}^n{\mathcal {H}}_i$
. Put
![]() $T_i=T|_{{\mathcal {H}}_i}$
. Then
$T_i=T|_{{\mathcal {H}}_i}$
. Then
![]() $T=\oplus _{i=1}^nT_i$
. For each i, choose
$T=\oplus _{i=1}^nT_i$
. For each i, choose
![]() $\lambda _i\in \Delta _i$
. Since
$\lambda _i\in \Delta _i$
. Since
![]() $\sigma (T_i)\subset \Delta _i^-$
, it follows that
$\sigma (T_i)\subset \Delta _i^-$
, it follows that
![]() $\|T_i-\lambda _i\|\leq (b-a)/n$
.
$\|T_i-\lambda _i\|\leq (b-a)/n$
.
Claim For each i with
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() ${\mathcal {H}}_i$
reduces C.
${\mathcal {H}}_i$
reduces C.
Fix an i with
![]() $i=1,\dots ,n$
. It suffices to prove
$i=1,\dots ,n$
. It suffices to prove
![]() $CE(\Delta _i)C=E(\Delta _i)$
. Note that there exists a sequence
$CE(\Delta _i)C=E(\Delta _i)$
. Note that there exists a sequence
![]() $\{p_k\}_{k=1}^\infty $
of polynomials with real coefficients such that
$\{p_k\}_{k=1}^\infty $
of polynomials with real coefficients such that
![]() $p_k(T)\rightarrow E(\Delta _i)$
in the strong operator topology. Since
$p_k(T)\rightarrow E(\Delta _i)$
in the strong operator topology. Since
![]() $Cp_k(T)C=p_k(T)$
for all k, it follows immediately that
$Cp_k(T)C=p_k(T)$
for all k, it follows immediately that
![]() $CE(\Delta _i)C=E(\Delta _i)$
. This proves the claim.
$CE(\Delta _i)C=E(\Delta _i)$
. This proves the claim.
For each i, denote
![]() $C_i=C|_{{\mathcal {H}}_i}$
. Then
$C_i=C|_{{\mathcal {H}}_i}$
. Then
![]() $C_i$
is a conjugation on
$C_i$
is a conjugation on
![]() ${\mathcal {H}}_i$
and, from
${\mathcal {H}}_i$
and, from
![]() $CTC=T^{*}=T$
, we obtain
$CTC=T^{*}=T$
, we obtain
![]() $C_iT_iC_i=T_i$
.
$C_iT_iC_i=T_i$
.
Since
![]() ${\mathcal {H}}=\oplus _{i=1}^n{\mathcal {H}}_i$
, we may assume that
${\mathcal {H}}=\oplus _{i=1}^n{\mathcal {H}}_i$
, we may assume that
![]() $e=\sum _{i=1}^n e_i$
with
$e=\sum _{i=1}^n e_i$
with
![]() $e_i\in {\mathcal {H}}_i$
. Then, by Claim,
$e_i\in {\mathcal {H}}_i$
. Then, by Claim,
![]() $Ce_i\in {\mathcal {H}}_i$
. For each i with
$Ce_i\in {\mathcal {H}}_i$
. For each i with
![]() $1\leq i\leq n$
, put
$1\leq i\leq n$
, put
![]() ${\mathcal {M}}_i=\vee \{e_i, Ce_i\}$
. Then
${\mathcal {M}}_i=\vee \{e_i, Ce_i\}$
. Then
![]() ${\mathcal {M}}_i$
is a subspace of
${\mathcal {M}}_i$
is a subspace of
![]() ${\mathcal {H}}_i$
, reducing C, and
${\mathcal {H}}_i$
, reducing C, and
![]() $1\leq \dim {\mathcal {M}}_i\leq 2$
. Then, relative to the decomposition
$1\leq \dim {\mathcal {M}}_i\leq 2$
. Then, relative to the decomposition
![]() ${\mathcal {H}}_i={\mathcal {M}}_i\oplus ({\mathcal {H}}_i\ominus {\mathcal {M}}_i)$
,
${\mathcal {H}}_i={\mathcal {M}}_i\oplus ({\mathcal {H}}_i\ominus {\mathcal {M}}_i)$
,
![]() $T_i$
can be written as
$T_i$
can be written as
 $$ \begin{align*}T_i=\begin{bmatrix} A_i&F_i\\ G_i&B_i \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
$$ \begin{align*}T_i=\begin{bmatrix} A_i&F_i\\ G_i&B_i \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
Note that
![]() $G_i=F_i^{*}$
, since
$G_i=F_i^{*}$
, since
![]() $T_i$
is self-adjoint.
$T_i$
is self-adjoint.
Since
![]() $C_i({\mathcal {M}}_i)={\mathcal {M}}_i$
, relative to the decomposition
$C_i({\mathcal {M}}_i)={\mathcal {M}}_i$
, relative to the decomposition
![]() ${\mathcal {H}}_i={\mathcal {M}}_i\oplus ({\mathcal {H}}_i\ominus {\mathcal {M}}_i)$
,
${\mathcal {H}}_i={\mathcal {M}}_i\oplus ({\mathcal {H}}_i\ominus {\mathcal {M}}_i)$
,
![]() $C_i$
can be written as
$C_i$
can be written as
 $$ \begin{align*}C_i=\begin{bmatrix} C_{i,1}&0\\ 0&C_{i,2} \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
$$ \begin{align*}C_i=\begin{bmatrix} C_{i,1}&0\\ 0&C_{i,2} \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
Then both
![]() $C_{i,1}$
and
$C_{i,1}$
and
![]() $C_{i,2}$
are conjugations. It follows readily from
$C_{i,2}$
are conjugations. It follows readily from
![]() $C_iT_iC_i=T_i$
that
$C_iT_iC_i=T_i$
that
![]() $C_iK_iC_i=K_i$
, where
$C_iK_iC_i=K_i$
, where
 $$ \begin{align*}K_i:=\begin{bmatrix} 0&F_i\\ G_i&0 \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
$$ \begin{align*}K_i:=\begin{bmatrix} 0&F_i\\ G_i&0 \end{bmatrix}\begin{matrix} {\mathcal{M}}_i\\ {\mathcal{H}}_i\ominus {\mathcal{M}}_i \end{matrix}.\end{align*} $$
Clearly,
![]() $K_i$
is self-adjoint,
$K_i$
is self-adjoint,
![]() $\text {rank} K_i\leq 4$
and
$\text {rank} K_i\leq 4$
and
 $$ \begin{align*} \|K_i\|&=\max\{ \|F_i\|, \|G_i\| \} \leq \left\|\begin{bmatrix} A_i-\lambda_i&F_i\\ G_i&B_i-\lambda_i \end{bmatrix}\right\| =\|T_i-\lambda_i\|\leq(b-a)/n. \end{align*} $$
$$ \begin{align*} \|K_i\|&=\max\{ \|F_i\|, \|G_i\| \} \leq \left\|\begin{bmatrix} A_i-\lambda_i&F_i\\ G_i&B_i-\lambda_i \end{bmatrix}\right\| =\|T_i-\lambda_i\|\leq(b-a)/n. \end{align*} $$
Set
![]() $K=-\oplus _{i=1}^n K_i$
. Thus K is a self-adjoint, finite-rank operator,
$K=-\oplus _{i=1}^n K_i$
. Thus K is a self-adjoint, finite-rank operator,
![]() $CKC=K$
,
$CKC=K$
,
and
where
![]() $q=1/(1-1/p)$
. Thus, for any
$q=1/(1-1/p)$
. Thus, for any
![]() $\varepsilon>0$
, there exists n large enough such that
$\varepsilon>0$
, there exists n large enough such that
![]() $\|K\|_p<\varepsilon $
.
$\|K\|_p<\varepsilon $
.
Denote by P the orthogonal projection of
![]() ${\mathcal {H}}$
onto
${\mathcal {H}}$
onto
![]() $\oplus _{i=1}^n {\mathcal {M}}_i$
. Thus
$\oplus _{i=1}^n {\mathcal {M}}_i$
. Thus
![]() $e\in \mathcal {R}(P)$
,
$e\in \mathcal {R}(P)$
,
![]() $\text {rank} P\leq 2n$
and
$\text {rank} P\leq 2n$
and
![]() $(T+K)P=P(T+K)$
; indeed,
$(T+K)P=P(T+K)$
; indeed,
Noting that
![]() $CPC=P$
and
$CPC=P$
and
![]() $CKC=K$
, that are,
$CKC=K$
, that are,
![]() $P,K\in \mathcal {S}_C$
, we complete the proof.
$P,K\in \mathcal {S}_C$
, we complete the proof.
Now we are going to prove Theorem 1.6.
Proof of Theorem 1.6
Since C is a conjugation, we can find an orthonormal basis
![]() $\{e_n\}_{n=1}^\infty $
of
$\{e_n\}_{n=1}^\infty $
of
![]() ${\mathcal {H}}$
such that
${\mathcal {H}}$
such that
![]() $Ce_n=e_n$
for all n.
$Ce_n=e_n$
for all n.
Now fix an
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $p>1$
. By Lemma 3.1, we can find a finite-rank, self-adjoint operator
$p>1$
. By Lemma 3.1, we can find a finite-rank, self-adjoint operator
![]() $K_1\in \mathcal {S}_C$
with
$K_1\in \mathcal {S}_C$
with
![]() $\|K_1\|_p<\varepsilon /2$
and a finite-rank orthogonal projection
$\|K_1\|_p<\varepsilon /2$
and a finite-rank orthogonal projection
![]() $P_1\in \mathcal {S}_C$
such that
$P_1\in \mathcal {S}_C$
such that
![]() $e_1\in \mathcal {R}(P_1)$
and
$e_1\in \mathcal {R}(P_1)$
and
![]() $P_1(T+K_1)=(T+K_1)P_1$
. Denote
$P_1(T+K_1)=(T+K_1)P_1$
. Denote
![]() ${\mathcal {H}}_1=\mathcal {R}(P_1)$
and
${\mathcal {H}}_1=\mathcal {R}(P_1)$
and
![]() $\widetilde {{\mathcal {H}}_1}={\mathcal {H}}\ominus {\mathcal {H}}_1$
. Then, with respect to the decomposition
$\widetilde {{\mathcal {H}}_1}={\mathcal {H}}\ominus {\mathcal {H}}_1$
. Then, with respect to the decomposition
![]() ${\mathcal {H}}={\mathcal {H}}_1\oplus \widetilde {{\mathcal {H}}_1}$
,
${\mathcal {H}}={\mathcal {H}}_1\oplus \widetilde {{\mathcal {H}}_1}$
,
 $$ \begin{align} T+K_1=\begin{bmatrix} T_1&0\\ 0& \widetilde{T_1} \end{bmatrix},\ \ \ C=\begin{bmatrix} C_1&0\\ 0& \widetilde{C_1} \end{bmatrix}, \end{align} $$
$$ \begin{align} T+K_1=\begin{bmatrix} T_1&0\\ 0& \widetilde{T_1} \end{bmatrix},\ \ \ C=\begin{bmatrix} C_1&0\\ 0& \widetilde{C_1} \end{bmatrix}, \end{align} $$
where
![]() $C_1T_1C_1=T_1$
and
$C_1T_1C_1=T_1$
and
![]() $\widetilde {C_1}\widetilde {T_1}\widetilde {C_1}=\widetilde {T_1}$
.
$\widetilde {C_1}\widetilde {T_1}\widetilde {C_1}=\widetilde {T_1}$
.
Now apply Lemma 3.1 again to the self-adjoint operator
![]() $\widetilde {T_1}$
and the vector
$\widetilde {T_1}$
and the vector
![]() $(I-P_1)e_2$
to get a finite-rank, self-adjoint operator
$(I-P_1)e_2$
to get a finite-rank, self-adjoint operator
![]() $\widetilde {K_2}\in \mathcal {S}_{\widetilde {C_1}}$
and two subspaces
$\widetilde {K_2}\in \mathcal {S}_{\widetilde {C_1}}$
and two subspaces
![]() ${\mathcal {H}}_2,\widetilde {{\mathcal {H}}_2}$
of
${\mathcal {H}}_2,\widetilde {{\mathcal {H}}_2}$
of
![]() $\widetilde {{\mathcal {H}}_1}$
such that
$\widetilde {{\mathcal {H}}_1}$
such that
and with respect to which
 $$\begin{align*}\widetilde{T_1}+\widetilde{K_2}=\begin{bmatrix} T_2&0\\ 0& \widetilde{T_2} \end{bmatrix},\ \ \ \widetilde{C_1}=\begin{bmatrix} C_2&0\\ 0& \widetilde{C_2} \end{bmatrix},\end{align*}$$
$$\begin{align*}\widetilde{T_1}+\widetilde{K_2}=\begin{bmatrix} T_2&0\\ 0& \widetilde{T_2} \end{bmatrix},\ \ \ \widetilde{C_1}=\begin{bmatrix} C_2&0\\ 0& \widetilde{C_2} \end{bmatrix},\end{align*}$$
where
![]() $C_2T_2C_2=T_2$
and
$C_2T_2C_2=T_2$
and
![]() $\widetilde {C_2}\widetilde {T_2}\widetilde {C_2}=\widetilde {T_2}$
. In view of (5), we can find a finite-rank, self-adjoint operator
$\widetilde {C_2}\widetilde {T_2}\widetilde {C_2}=\widetilde {T_2}$
. In view of (5), we can find a finite-rank, self-adjoint operator
![]() $K_2\in \mathcal {S}_C$
with
$K_2\in \mathcal {S}_C$
with
![]() $\|K_2\|_p<\varepsilon /4$
such that
$\|K_2\|_p<\varepsilon /4$
such that
 $$ \begin{align} T+K_1+K_2=\begin{bmatrix} T_1&0&0\\ 0&T_2&0\\ 0& 0&\widetilde{T_2} \end{bmatrix}\begin{matrix} {\mathcal{H}}_1\\ {\mathcal{H}}_2\\ \widetilde{{\mathcal{H}}_2} \end{matrix},\ \ \ C=\begin{bmatrix} C_1&0&0\\ 0&C_2&0\\ 0&0 &\widetilde{C_2} \end{bmatrix}\begin{matrix} {\mathcal{H}}_1\\ {\mathcal{H}}_2\\ \widetilde{{\mathcal{H}}_2} \end{matrix}. \end{align} $$
$$ \begin{align} T+K_1+K_2=\begin{bmatrix} T_1&0&0\\ 0&T_2&0\\ 0& 0&\widetilde{T_2} \end{bmatrix}\begin{matrix} {\mathcal{H}}_1\\ {\mathcal{H}}_2\\ \widetilde{{\mathcal{H}}_2} \end{matrix},\ \ \ C=\begin{bmatrix} C_1&0&0\\ 0&C_2&0\\ 0&0 &\widetilde{C_2} \end{bmatrix}\begin{matrix} {\mathcal{H}}_1\\ {\mathcal{H}}_2\\ \widetilde{{\mathcal{H}}_2} \end{matrix}. \end{align} $$
Note that
![]() $e_1,e_2\in {\mathcal {H}}_1\oplus {\mathcal {H}}_2$
,
$e_1,e_2\in {\mathcal {H}}_1\oplus {\mathcal {H}}_2$
,
![]() $C_iT_iC_i=T_i$
$C_iT_iC_i=T_i$
![]() $(i=1,2),$
and
$(i=1,2),$
and
![]() $\widetilde {C_2}\widetilde {T_2}\widetilde {C_2}=\widetilde {T_2}$
.
$\widetilde {C_2}\widetilde {T_2}\widetilde {C_2}=\widetilde {T_2}$
.
By induction, we can find a sequence of self-adjoint, finite-rank operators
![]() $\{K_i\}_{i=1}^\infty \subset \mathcal {S}_C$
and a sequence of pairwise orthogonal, finite-dimensional subspaces
$\{K_i\}_{i=1}^\infty \subset \mathcal {S}_C$
and a sequence of pairwise orthogonal, finite-dimensional subspaces
![]() $\{{\mathcal {H}}_i\}$
such that for each
$\{{\mathcal {H}}_i\}$
such that for each
![]() $n\geq 1,$
$n\geq 1,$
-
(i)
 $e_1,\dots ,e_n\in \oplus _{i=1}^n{\mathcal {H}}_i$
,
$e_1,\dots ,e_n\in \oplus _{i=1}^n{\mathcal {H}}_i$
, -
(ii)
 $\|K_n\|_p<\varepsilon /2^n$
, and
$\|K_n\|_p<\varepsilon /2^n$
, and -
(iii) relative to the decomposition
 ${\mathcal {H}}=(\oplus _{i=1}^n {\mathcal {H}}_i)\oplus \widetilde {{\mathcal {H}}_n}$
, (7)where
${\mathcal {H}}=(\oplus _{i=1}^n {\mathcal {H}}_i)\oplus \widetilde {{\mathcal {H}}_n}$
, (7)where $$ \begin{align} T+\sum_{i=1}^nK_i=(\oplus_{i=1}^n T_i)\oplus \widetilde{T_n},\ \ \ \ C=(\oplus_{i=1}^n C_i)\oplus \widetilde{C_n}, \end{align} $$
$$ \begin{align} T+\sum_{i=1}^nK_i=(\oplus_{i=1}^n T_i)\oplus \widetilde{T_n},\ \ \ \ C=(\oplus_{i=1}^n C_i)\oplus \widetilde{C_n}, \end{align} $$
 $\widetilde {{\mathcal {H}}_n}={\mathcal {H}}\ominus (\oplus _{i=1}^n {\mathcal {H}}_i)$
and
$\widetilde {{\mathcal {H}}_n}={\mathcal {H}}\ominus (\oplus _{i=1}^n {\mathcal {H}}_i)$
and  $$ \begin{align*}\widetilde{C_n}\widetilde{T_n}\widetilde{C_n}=\widetilde{T_n}, \ \ \ C_iT_iC_i=T_i, \ \ \ i=1,2,\dots, n. \end{align*} $$
$$ \begin{align*}\widetilde{C_n}\widetilde{T_n}\widetilde{C_n}=\widetilde{T_n}, \ \ \ C_iT_iC_i=T_i, \ \ \ i=1,2,\dots, n. \end{align*} $$
Since
![]() $\{e_i\}$
is an orthonormal basis of
$\{e_i\}$
is an orthonormal basis of
![]() ${\mathcal {H}}$
, it follows from statement (i) that
${\mathcal {H}}$
, it follows from statement (i) that
![]() ${\mathcal {H}}=\oplus _{i=1}^\infty {\mathcal {H}}_i$
and hence
${\mathcal {H}}=\oplus _{i=1}^\infty {\mathcal {H}}_i$
and hence
![]() $C=\oplus _{i=1}^\infty C_i$
. Set
$C=\oplus _{i=1}^\infty C_i$
. Set
![]() $K=\sum _{i=1}^\infty K_i$
. Then
$K=\sum _{i=1}^\infty K_i$
. Then
![]() $K\in \mathcal {B}_p\mathcal {(H)}$
is self-adjoint,
$K\in \mathcal {B}_p\mathcal {(H)}$
is self-adjoint,
![]() $\|K\|_p<\varepsilon $
and
$\|K\|_p<\varepsilon $
and
![]() $T+K=\oplus _{i=1}^\infty T_i$
. Note that each
$T+K=\oplus _{i=1}^\infty T_i$
. Note that each
![]() $T_i$
is self-adjoint and acting on a finite-dimensional space. Thus
$T_i$
is self-adjoint and acting on a finite-dimensional space. Thus
![]() $T+K$
is diagonal. Since
$T+K$
is diagonal. Since
![]() $C_iT_iC_i=T_i$
for all i, it follows that
$C_iT_iC_i=T_i$
for all i, it follows that
![]() $C(T+K)C=T+K$
. Set
$C(T+K)C=T+K$
. Set
![]() $D=T+K$
. This completes the proof.
$D=T+K$
. This completes the proof.
Corollary 3.2 Let T be a self-adjoint operator in
![]() $\mathcal {S}_C$
. Then, given
$\mathcal {S}_C$
. Then, given
![]() $\varepsilon>0$
, there exists a compact operator
$\varepsilon>0$
, there exists a compact operator
![]() $K\in \mathcal {S}_C$
with
$K\in \mathcal {S}_C$
with
![]() $\|K\|<\varepsilon $
such that
$\|K\|<\varepsilon $
such that
![]() $T+K$
is diagonal with
$T+K$
is diagonal with
![]() $\sigma (T+K)=\sigma (T)$
.
$\sigma (T+K)=\sigma (T)$
.
Proof Assume that
![]() $\sigma _p(T)=\{\lambda _i: i\in \Lambda \}$
. Set
$\sigma _p(T)=\{\lambda _i: i\in \Lambda \}$
. Set
Since T is self-adjoint, we deduce that
![]() ${\mathcal {H}}_0$
reduces T. Then
${\mathcal {H}}_0$
reduces T. Then
 $$ \begin{align*}T=\begin{bmatrix} T_0&0 \\ 0&T_1 \end{bmatrix}\begin{matrix} {\mathcal{H}}_0\\ {\mathcal{H}}_1 \end{matrix}.\end{align*} $$
$$ \begin{align*}T=\begin{bmatrix} T_0&0 \\ 0&T_1 \end{bmatrix}\begin{matrix} {\mathcal{H}}_0\\ {\mathcal{H}}_1 \end{matrix}.\end{align*} $$
Clearly,
![]() $T_0$
is diagonal and
$T_0$
is diagonal and
![]() $\sigma _p(T_1)=\emptyset $
. Since
$\sigma _p(T_1)=\emptyset $
. Since
![]() $CTC=C$
, one can see
$CTC=C$
, one can see
![]() $C({\mathcal {H}}_0)={\mathcal {H}}_0$
, which implies
$C({\mathcal {H}}_0)={\mathcal {H}}_0$
, which implies
![]() $C({\mathcal {H}}_1)={\mathcal {H}}_1$
and
$C({\mathcal {H}}_1)={\mathcal {H}}_1$
and
 $$ \begin{align*}C=\begin{bmatrix} C_0&0 \\ 0&C_1 \end{bmatrix}\begin{matrix} {\mathcal{H}}_0\\ {\mathcal{H}}_1 \end{matrix}.\end{align*} $$
$$ \begin{align*}C=\begin{bmatrix} C_0&0 \\ 0&C_1 \end{bmatrix}\begin{matrix} {\mathcal{H}}_0\\ {\mathcal{H}}_1 \end{matrix}.\end{align*} $$
It is easy to check that each
![]() $C_i$
is a conjugation and
$C_i$
is a conjugation and
![]() $T_i\in {\mathcal S}_{C_i}$
.
$T_i\in {\mathcal S}_{C_i}$
.
By Theorem 1.6, we can find
![]() $K_1\in {\mathcal S}_{C_1}$
with
$K_1\in {\mathcal S}_{C_1}$
with
![]() $\|K_1\|<\frac {\varepsilon }{2}$
such that
$\|K_1\|<\frac {\varepsilon }{2}$
such that
![]() $T_1+K_1$
is diagonal. Moreover, by the upper semi-continuity of spectrum, it can be required that
$T_1+K_1$
is diagonal. Moreover, by the upper semi-continuity of spectrum, it can be required that
![]() $\sigma (T_1+K_1)\subset \sigma (T_1)+B(0,\frac {\varepsilon }{2})$
.
$\sigma (T_1+K_1)\subset \sigma (T_1)+B(0,\frac {\varepsilon }{2})$
.
Since
![]() $T_1+K_1$
is diagonal, without loss of generality, we may assume that
$T_1+K_1$
is diagonal, without loss of generality, we may assume that
![]() $\sigma _p(T_1+K_1)=\{z_i: i\geq 1\}$
. Denote
$\sigma _p(T_1+K_1)=\{z_i: i\geq 1\}$
. Denote
![]() $\mathcal {K}_i=\ker (T_1+K_1-z_i)$
for
$\mathcal {K}_i=\ker (T_1+K_1-z_i)$
for
![]() $i\geq 1$
. Then
$i\geq 1$
. Then
relative to the decomposition
![]() ${\mathcal {H}}_1=\oplus _{i=1}^\infty \mathcal {K}_i$
, where
${\mathcal {H}}_1=\oplus _{i=1}^\infty \mathcal {K}_i$
, where
![]() $I_i$
is the identity operator on
$I_i$
is the identity operator on
![]() $\mathcal {K}_i$
. Since
$\mathcal {K}_i$
. Since
![]() $T_1+K_1\in \mathcal {S}_C$
is diagonal, it follows that
$T_1+K_1\in \mathcal {S}_C$
is diagonal, it follows that
Then each
![]() $\mathcal {K}_i$
reduces
$\mathcal {K}_i$
reduces
![]() $C_1$
. We may assume that
$C_1$
. We may assume that
![]() $C_1=\oplus _{i=1}^\infty C_i'$
, where
$C_1=\oplus _{i=1}^\infty C_i'$
, where
![]() $C_i'=C_1|_{\mathcal {K}_i}$
is a conjugation on
$C_i'=C_1|_{\mathcal {K}_i}$
is a conjugation on
![]() $\mathcal {K}_i$
.
$\mathcal {K}_i$
.
Fix an
![]() $i\geq 1$
. If
$i\geq 1$
. If
![]() $z_i\in \sigma (T_1)$
, then we set
$z_i\in \sigma (T_1)$
, then we set
![]() $\widetilde {z_i}=z_i$
. If
$\widetilde {z_i}=z_i$
. If
![]() $z_i\notin \sigma (T_1)$
, then
$z_i\notin \sigma (T_1)$
, then
![]() $z_i\notin \sigma _e(T_1)=\sigma _e(T_1+K_1)$
and hence
$z_i\notin \sigma _e(T_1)=\sigma _e(T_1+K_1)$
and hence
![]() $\dim \mathcal {K}_i<\infty $
; noting that
$\dim \mathcal {K}_i<\infty $
; noting that
![]() $z_i\in \sigma (T_1)+B(0,\frac {\varepsilon }{2})$
, we can find
$z_i\in \sigma (T_1)+B(0,\frac {\varepsilon }{2})$
, we can find
![]() $\widetilde {z_i}\in \sigma (T_1)$
such that
$\widetilde {z_i}\in \sigma (T_1)$
such that
![]() $|z_i-\widetilde {z_i}|=\text {dist}(z_i,\sigma (T_1))<\varepsilon /2$
.
$|z_i-\widetilde {z_i}|=\text {dist}(z_i,\sigma (T_1))<\varepsilon /2$
.
Set
![]() $K_2=\oplus _{i=1}^\infty (\widetilde {z_i}-z_i) I_i $
. Then
$K_2=\oplus _{i=1}^\infty (\widetilde {z_i}-z_i) I_i $
. Then
![]() $K_2\in {\mathcal S}_{C_1}$
,
$K_2\in {\mathcal S}_{C_1}$
,
![]() $\|K_2\|\leq \varepsilon /2$
and
$\|K_2\|\leq \varepsilon /2$
and
Clearly,
![]() $\sigma (T_1+K_1+K_2)=\{\widetilde {z_i}: i\geq 1 \}^-\subseteq \sigma (T_1)$
.
$\sigma (T_1+K_1+K_2)=\{\widetilde {z_i}: i\geq 1 \}^-\subseteq \sigma (T_1)$
.
Claim
![]() $K_2$
is compact.
$K_2$
is compact.
It suffices to show
![]() $\lim _i|z_i-\widetilde {z_i}|=0.$
Otherwise, we can choose a subsequence
$\lim _i|z_i-\widetilde {z_i}|=0.$
Otherwise, we can choose a subsequence
![]() $\{i_k\}_{k=1}^\infty $
of
$\{i_k\}_{k=1}^\infty $
of
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $z_{i_k}\notin \sigma (T_1)$
,
$z_{i_k}\notin \sigma (T_1)$
,
![]() $z_{i_k}\rightarrow z_0$
and
$z_{i_k}\rightarrow z_0$
and
Hence,
![]() $\text {dist}(z_{0},\sigma (T_1))>0$
and
$\text {dist}(z_{0},\sigma (T_1))>0$
and
a contradiction.
Set
![]() $K=0\oplus (K_1+K_2)$
. Then
$K=0\oplus (K_1+K_2)$
. Then
![]() $K\in \mathcal {S}_C$
is compact with
$K\in \mathcal {S}_C$
is compact with
![]() $\|K\|<\varepsilon $
and
$\|K\|<\varepsilon $
and
By the preceding discussion, we have
It remains to show
![]() $\sigma (T)\subset \sigma (T+K)$
.
$\sigma (T)\subset \sigma (T+K)$
.
Note that K is compact. Hence
If
![]() $z\in \sigma (T)\setminus \sigma _e(T)$
, then
$z\in \sigma (T)\setminus \sigma _e(T)$
, then
![]() $z\in \sigma _p(T)$
and
$z\in \sigma _p(T)$
and
![]() $z=\lambda _i\in \sigma (T_0)\subset \sigma (T+K)$
for some
$z=\lambda _i\in \sigma (T_0)\subset \sigma (T+K)$
for some
![]() $i\in \Lambda $
. Thus we have proved that
$i\in \Lambda $
. Thus we have proved that
![]() $\sigma (T)\subset \sigma (T+K)$
, which implies
$\sigma (T)\subset \sigma (T+K)$
, which implies
![]() $\sigma (T)= \sigma (T+K)$
.
$\sigma (T)= \sigma (T+K)$
.
Theorem 3.3 If
![]() $N_1, \dots ,N_n\in \mathcal {S}_C$
are commuting normal operators and
$N_1, \dots ,N_n\in \mathcal {S}_C$
are commuting normal operators and
![]() $\varepsilon>0$
, then there are commuting, diagonal operators
$\varepsilon>0$
, then there are commuting, diagonal operators
![]() $D_1$
,
$D_1$
,
![]() $\dots $
,
$\dots $
,
![]() $D_n\in \mathcal {S}_C$
such that
$D_n\in \mathcal {S}_C$
such that
![]() $N_i-D_i\in \mathcal {K(H)}$
and
$N_i-D_i\in \mathcal {K(H)}$
and
![]() $\|N_i-D_i\|<\varepsilon $
for all
$\|N_i-D_i\|<\varepsilon $
for all
![]() $ i=1,2,\dots ,n$
.
$ i=1,2,\dots ,n$
.
Proof Denote by
![]() ${\mathcal {A}}$
the von Neumann algebra generated by
${\mathcal {A}}$
the von Neumann algebra generated by
![]() $N_1$
,
$N_1$
,
![]() $\dots $
,
$\dots $
,
![]() $N_n$
. It is easy to see
$N_n$
. It is easy to see
![]() $\mathcal {A}\subset \mathcal {S}_C$
. By [Reference Davidson5, Lemma II.2.8], we can find a self-adjoint operator
$\mathcal {A}\subset \mathcal {S}_C$
. By [Reference Davidson5, Lemma II.2.8], we can find a self-adjoint operator
![]() $A\in \mathcal {B(H)}$
generating
$A\in \mathcal {B(H)}$
generating
![]() ${\mathcal {A}}$
and
${\mathcal {A}}$
and
![]() $N_1$
,
$N_1$
,
![]() $\dots $
,
$\dots $
,
![]() $N_n\in C^{*}(A)$
. Clearly,
$N_n\in C^{*}(A)$
. Clearly,
![]() $A\in \mathcal {S}_C$
. We can find continuous functions
$A\in \mathcal {S}_C$
. We can find continuous functions
![]() $f_1,\dots ,f_n$
on
$f_1,\dots ,f_n$
on
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $N_i=f_i(A)$
,
$N_i=f_i(A)$
,
![]() $i=1,\dots ,n.$
$i=1,\dots ,n.$
Now fix an
![]() $\varepsilon>0$
. In view of [Reference Conway4, Lemma 39.5], there exists
$\varepsilon>0$
. In view of [Reference Conway4, Lemma 39.5], there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\sup _{1\leq i\leq n}\|f_i(X)-f_i(Y)\|<\varepsilon $
for all self-adjoint operators
$\sup _{1\leq i\leq n}\|f_i(X)-f_i(Y)\|<\varepsilon $
for all self-adjoint operators
![]() $X,Y$
satisfying
$X,Y$
satisfying
![]() $\|X\|\leq \|A\|, \|Y\|\leq \|A\|$
and
$\|X\|\leq \|A\|, \|Y\|\leq \|A\|$
and
![]() $\|X-Y\|<\delta $
.
$\|X-Y\|<\delta $
.
By Corollary 3.2, we can find self-adjoint, diagonal
![]() $D\in \mathcal {S}_C$
with
$D\in \mathcal {S}_C$
with
![]() $\sigma (D)=\sigma (A)$
such that
$\sigma (D)=\sigma (A)$
such that
![]() $D-A\in \mathcal {K(H)}$
and
$D-A\in \mathcal {K(H)}$
and
![]() $\|D-A\|< \delta $
. Then
$\|D-A\|< \delta $
. Then
![]() $\|D\|=\|A\|$
and
$\|D\|=\|A\|$
and
Note that
![]() $f_1(D)$
,
$f_1(D)$
,
![]() $f_2(D)$
,
$f_2(D)$
,
![]() $\dots $
,
$\dots $
,
![]() $f_n(D)$
are commuting diagonal operators. Also, since
$f_n(D)$
are commuting diagonal operators. Also, since
![]() $D\in \mathcal {S}_C$
, it follows that
$D\in \mathcal {S}_C$
, it follows that
![]() $f_1(D),f_2(D)$
,
$f_1(D),f_2(D)$
,
![]() $\dots $
,
$\dots $
,
![]() $f_n(D)$
$f_n(D)$
![]() $\in $
$\in $
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
Note that
![]() $A-D\in \mathcal {K(H)}$
. Using the functional calculus for self-adjoint operators, one can easily prove that
$A-D\in \mathcal {K(H)}$
. Using the functional calculus for self-adjoint operators, one can easily prove that
![]() $f_i(A)-f_i(D)\in \mathcal {K(H)}$
,
$f_i(A)-f_i(D)\in \mathcal {K(H)}$
,
![]() $i=1,2,\dots ,n$
. This completes the proof.
$i=1,2,\dots ,n$
. This completes the proof.
Using a similar argument as in the proof of Corollary 3.2, one can prove the following.
Corollary 3.4 If
![]() $T\in \mathcal {S}_C$
is normal and
$T\in \mathcal {S}_C$
is normal and
![]() $\varepsilon>0$
, then there exists a diagonal operator
$\varepsilon>0$
, then there exists a diagonal operator
![]() $N\in \mathcal {S}_C$
such that
$N\in \mathcal {S}_C$
such that
![]() $\sigma (N)=\sigma (T)$
and
$\sigma (N)=\sigma (T)$
and
![]() $\|T-N\|<\varepsilon $
.
$\|T-N\|<\varepsilon $
.
3.2 Irreducible approximation
We conclude this paper with an application of Theorem 1.6 to the irreducible approximation in
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
By a classical approximation result of P. R. Halmos [Reference Halmos21], the set of irreducible operators is a dense
![]() $G_\delta $
set and hence a topologically large subset of
$G_\delta $
set and hence a topologically large subset of
![]() $\mathcal {B(H)}$
. H. Radjavi and P. Rosenthal [Reference Radjavi and Rosenthal36] gave a short proof of the density of irreducible operators in
$\mathcal {B(H)}$
. H. Radjavi and P. Rosenthal [Reference Radjavi and Rosenthal36] gave a short proof of the density of irreducible operators in
![]() $\mathcal {B(H)}$
. It can be seen from their proof that each operator has an arbitrarily small compact perturbation which is irreducible (see [Reference Herrero23, Lemma 4.33]).
$\mathcal {B(H)}$
. It can be seen from their proof that each operator has an arbitrarily small compact perturbation which is irreducible (see [Reference Herrero23, Lemma 4.33]).
In a recent paper [Reference Liu, Zhao and Zhu31], T. Liu, J. Y. Zhao, and the last author studied irreducible approximation of c.s. operators and obtained the following result.
Theorem 3.5 [Reference Liu, Zhao and Zhu31, Theorem 2.1]
Let
![]() $T\in \mathcal {S}_C$
and
$T\in \mathcal {S}_C$
and
![]() $T=A+\text {i}B$
, where
$T=A+\text {i}B$
, where
![]() $A,B$
are self-adjoint. If A or B is diagonal, then, given
$A,B$
are self-adjoint. If A or B is diagonal, then, given
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $K\in \mathcal {S}_C$
with
$K\in \mathcal {S}_C$
with
![]() $\|K\|<\varepsilon $
such that
$\|K\|<\varepsilon $
such that
![]() $T+K$
is irreducible.
$T+K$
is irreducible.
In addition, it can be required that K lies in the Schatten p-class and
![]() $\|K\|_p<\varepsilon $
. Using the preceding result, it was proved in [Reference Liu, Zhao and Zhu31] that each c.s. operator has a small perturbation being irreducible. Moreover, the following question was raised:
$\|K\|_p<\varepsilon $
. Using the preceding result, it was proved in [Reference Liu, Zhao and Zhu31] that each c.s. operator has a small perturbation being irreducible. Moreover, the following question was raised:
Is every complex symmetric operator a compact perturbation or a small compact perturbation of irreducible ones?
Using Theorems 1.6 and 3.5, one can see the following result, which combining Halmos’ result shows that those irreducible ones in
![]() $\mathcal {S}_C$
constitute a dense
$\mathcal {S}_C$
constitute a dense
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $\mathcal {S}_C$
.
$\mathcal {S}_C$
.
Corollary 3.6 Given
![]() $T\in \mathcal {S}_C$
,
$T\in \mathcal {S}_C$
,
![]() $p\in (1,\infty )$
and
$p\in (1,\infty )$
and
![]() $\varepsilon>0$
, there exists a compact operator
$\varepsilon>0$
, there exists a compact operator
![]() $K\in \mathcal {S}_C$
with
$K\in \mathcal {S}_C$
with
![]() $\|K\|_p<\varepsilon $
such that
$\|K\|_p<\varepsilon $
such that
![]() $T+K$
is irreducible.
$T+K$
is irreducible.
Acknowledgments
The authors are grateful to the referee for helpful comments and constructive suggestions concerning the manuscript.