Research Article
Forbidden intervals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1081-1099
-
- Article
- Export citation
Functional interpretation and inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1100-1120
-
- Article
- Export citation
Almost everywhere elimination of probability quantifiers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1121-1142
-
- Article
- Export citation
Some remarks on generic structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1143-1154
-
- Article
- Export citation
Incompatible Ω-Complete Theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1155-1170
-
- Article
- Export citation
Canonical rules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1171-1205
-
- Article
- Export citation
A note on defining transcendentals in function fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1206-1210
-
- Article
- Export citation
Approachability at the second successor of a singular cardinal
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1211-1224
-
- Article
- Export citation
Heirs of box types in polynomially bounded structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1225-1263
-
- Article
- Export citation
Promptness does not imply superlow cuppability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1264-1272
-
- Article
- Export citation
Independently axiomatizable ℒω1,ω theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1273-1286
-
- Article
- Export citation
Successors of singular cardinals and coloring theorems II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1287-1309
-
- Article
- Export citation
The strength of the rainbow Ramsey Theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1310-1324
-
- Article
- Export citation
d-computable categoricity for algebraic fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1325-1351
-
- Article
- Export citation
On computable self-embeddings of computable linear orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1352-1366
-
- Article
- Export citation
The modal μ-calculus hierarchy over restricted classes of transition systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1367-1400
-
- Article
- Export citation
Logical aspects of rates of convergence in metric spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1401-1428
-
- Article
- Export citation
First-order characterization of the radical of a finite group
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1429-1435
-
- Article
- Export citation
Correction
Corrigendum to: “On Lascar rank and Morley rank of definable groups in differentially closed fields”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1436-1437
-
- Article
- Export citation
Corrigendum to: “On the strength of Ramsey's Theorem for pairs”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1438-1439
-
- Article
- Export citation

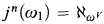 . So the Kunen result is striking in that it apparently allows strong ideals to exist above the conventional large cardinal limitations. The main result of this paper is that it is consistent (relative to a huge cardinal) that such ideals exist.
. So the Kunen result is striking in that it apparently allows strong ideals to exist above the conventional large cardinal limitations. The main result of this paper is that it is consistent (relative to a huge cardinal) that such ideals exist.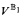 and
and 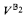 are generic extensions of
are generic extensions of  of
of