Many classical statements of set theory are settled by the existence of generic elementary embeddings that are analogous the elementary embeddings posited by large cardinals. [2] The embeddings analogous to measurable cardinals are determined by uniform, κ-complete precipitous ideals on cardinals κ. Stronger embeddings, analogous to those originating from supercompact or huge cardinals are encoded by normal fine ideals on sets such as [κ]<λ or [κ]λ.

The embeddings generated from these ideals are limited in ways analogous to conventional large cardinals. Explicitly, if j: V → M is a generic elementary embedding with critical point κ and λ supnЄωjn(κ) and the forcing yielding j is λ-saturated then j“λ+ ∉ M. (See [2].)

Ideals that yield embeddings that are analogous to strongly compact cardinals have more puzzling behavior and the analogy is not as straightforward. Some natural ideal properties of this kind have been shown to be inconsistent:

Theorem 1 (Kunen). There is no ω2-saturated, countably complete uniform ideal on any cardinal in the interval [ℵω, ℵω).

Generic embeddings that arise from countably complete, ω2-saturated ideals have the property that sup 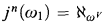. So the Kunen result is striking in that it apparently allows strong ideals to exist above the conventional large cardinal limitations. The main result of this paper is that it is consistent (relative to a huge cardinal) that such ideals exist.