Introduction
The ubiquitous aftermath of sudden explosive ice-shelf disintegration is a closely packed mass of ice-shelf fragments covering a sea-surface area that is conspicuously larger than the original area of the disintegrated ice shelf (Reference Rott, Skvarca and NaglerRott and others, 1996; Reference MacAyeal, Scambos, Hulbe and FahnestockMacAyeal and others, 2003; Reference Scambos, Hulbe, Fahnestock, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerScambos and others, 2003, Reference Scambos2009; Reference Braun and HumbertBraun and Humbert, 2009; Reference Braun, Humbert and MollBraun and others, 2009). Within the closely packed mass, ice-shelf fragments that retain the original firn-side up orientation can constitute less than one-quarter of the surface-area coverage (see figs 3 and 4 of Reference Scambos, Hulbe, Fahnestock, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerScambos and others, 2003), with the remainder of surface area covered by thin rectangular slivers of ice shelf that have capsized (rotated by 90˚) and ice rubble also likely formed by a capsize process, for example as time-lapse photographic observations of iceberg fragmentation in Greenlandic fjords attest (personal communication from J. Box, 2010; Reference Ahn and BoxAhn and Box, 2010; Reference Amundson, Fahnestock, Truffer, Brown, Lü thi and MotykaAmundson and others, 2010). This ubiquitous aftermath of explosive ice-shelf disintegration points to iceberg capsize as a likely driver of the immediate short-term mechanical processes involved in the disintegration.
A considerable amount of gravitational potential energy is released from the ice/water system when unstable icebergs capsize. As has been observed in both Antarctic and Greenlandic settings, iceberg calving and capsize generates impulsive surface gravity wave energy that can subsequently stimulate the calving of new icebergs (Reference Amundson, Truffer, Lüthi, Fahnestock, West and MotykaAmundson and others, 2008, Reference Amundson, Fahnestock, Truffer, Brown, Lü thi and Motyka2010; Reference NettlesNettles and others, 2008; Reference MacAyeal, Okal, Aster and BassisMacAyeal and others, 2009. Reference MacAyeal, Abbot and SergienkoMacAyeal and others (2011) show that the net energy released by capsize of an iceberg that is 300m thick and 150 m×1000m in horizontal dimension, comparable to icebergs capsized during the Wilkins Ice Shelf (Antarctica) events (Reference ScambosScambos and others, 2009), is ~3.5×1012 J, which is slightly less than the explosive energy yield of 1 kiloton of TNT (4.2×1012 J). Into what forms and into what proportions this gravitational potential energy is converted remains a subject of ongoing research. However, the fact that this energy conversion must be compressed into a short time because capsize takes on the order of tens to hundreds of seconds implies strongly that capsize may be the key energy source controlling ice-shelf collapse.
The question of how environmental forcing conditions cause ice shelves to be vulnerable to explosive disintegration remains of primary concern to glaciological science (Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000; Reference Van den BroekeVan den Broeke, 2005; Reference Vieli, Payne, Shepherd and DuVieli and others, 2007; Reference Glasser and ScambosGlasser and Scambos, 2008). This question, however, is not the central focus of this study. Instead, it focuses on the subsidiary question of how ice-shelf fragment capsize drives the explosive nature of the disintegration. Investigation of this subsidiary question sheds light on what specific conditions environmental forcing must achieve in order to cause disintegration (e.g. expressed in terms of fracture density and spacing, surrounding sea-ice conditions and basic properties of the ice shelf such as thickness, stress level and flow rate). Here we develop an idealized conceptual model of massed ice-shelf fragment capsize and explore its behavior and parameter sensitivities using computationally facilitated experiments.
Conceptual Model
We develop a conceptual model to explore the dynamics of massed ice-shelf fragment capsize from the idealized view expressed in Figure 1a. Restricting our idealization to two dimensions, the model consists of a large number of closely packed icebergs of rigid-body rheology and approximately rectangular cross section floating in sea water that is treated as purely hydrostatic, with no viscous or free-surface effects (i.e. the feedbacks between the icebergs and surface gravity waves are relegated to future study). In the initial state, at time t = 0, the icebergs are oriented upright, contained within an integrated (but fractured) ice shelf. A variably specified proportion of the icebergs are unstable in this orientation, as determined by their aspect ratio (vertical dimension divided by horizontal dimension). The fractures that separate the icebergs in the initial state are assumed to pre-exist, as we do not examine directly the process that induces initial fracture of the ice shelf into the pieces that subsequently capsize.
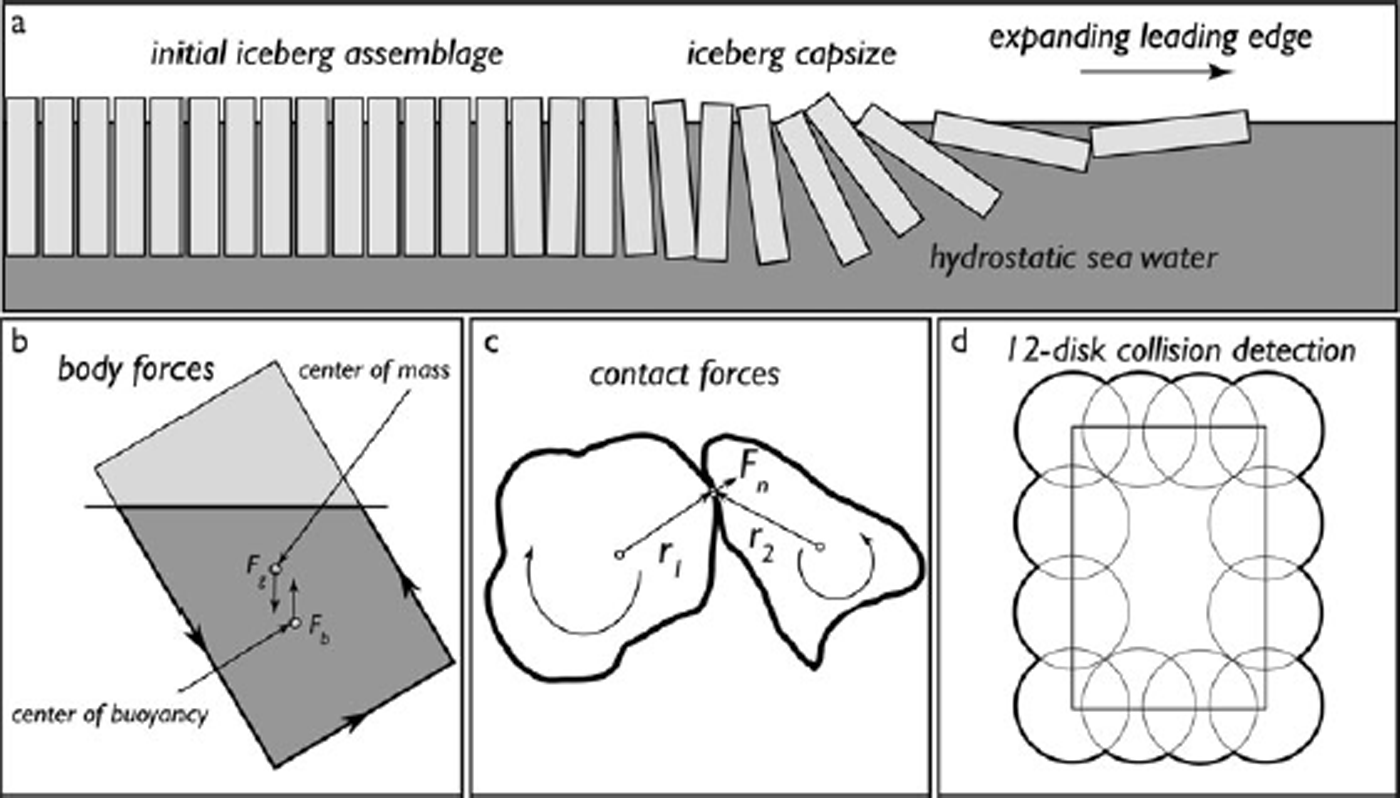
Fig. 1. Geometry of an idealized iceberg assemblage providing a conceptualization of the explosive phase of ice-shelf disintegration. (a) A runaway capsize of the assemblage leading to horizontal expansion of capsized icebergs across the open ocean surface (to the right). (b) The buoyant force on an iceberg is computed by determining the moments of the submerged portion of the iceberg. (c) Impulse associated with collision. (d) Our representation of the iceberg collision volume using 12 overlapping disks.
At the initial time, t = 0, a random infinitesimal perturbation to the angular velocity of each iceberg is used to initiate the subsequent behavior which is controlled by three basic processes: (1) buoyancy-driven rotation of individual icebergs (capsize); (2) iceberg-on-iceberg momentum and energy exchange (via collision); and (3) idealized dissipation. As we describe below, these three processes allow the evolution of a massed iceberg capsize, where energy is transferred from the static potential energy of the ice/water system into several forms of kinetic energy, rotational, translational and bobbing and rocking motions, that subsequently decay over time to evolve the system to a post-collapse quiescent state.
Although the conceptual model is highly idealized and the greatest possible simplification is embraced in its formulation, it is necessary to explore the behavior of the model via computation, as the large number of icebergs and their interactions are not amenable to exact analytic solution. The goal of the numerical treatment of the conceptual model, described below and in the Appendix, is to conduct two basic classes of experiments. The first class is performed to explore phenomenological similarities between the conceptual model and the immediate explosive part of ice-shelf disintegration. We conduct experiments to determine how quickly massed iceberg capsize can proceed and to determine the proportion of icebergs that have capsized as a function of time. Of particular interest in these experiments is the evaluation of energetic details describing how potential energy is converted into various forms of kinetic energy.
The second class of experiments is performed to explore the geometric conditions, i.e. the fracture spacing and its variability within a single ice shelf prior to collapse, necessary to facilitate the explosive character of ice-shelf disintegration. Numerous experiments are conducted where the mean aspect ratio (initial thickness to width) and heterogeneity (defined using a Gaussian distribution) characterizing the initial mass of icebergs are varied systematically. The result of these experiments is the construction of a conceptual phase diagram suggesting how the role of aspect ratio and heterogeneity impact the vulnerability of ice shelves to explosive disintegration.
Numerical Implementation
As shown in Figure 1, ice-shelf disintegration is conceptualized as beginning from an initially quiescent arrangement of approximately rectangular icebergs (having rounded corners, for reasons discussed below) packed into a tight mass that extends seaward from a fixed rigid wall (i.e. a first iceberg held fixed) to an ice front (i.e. a last iceberg that has only sea water facing it). The open ice-free ocean into which the mass of icebergs will expand by horizontal movement is assumed semi-infinite and quiescent at all times. The geometry of our initial simulations (Fig. 1a) is similar to a row of balanced dominoes (Van Leeuwen, 2010). However, unlike a row of dominoes which only tips under the application of sufficient force, icebergs in our simulations can be immediately unstable to tipping, depending on their aspect ratio (thickness to width), and so may provide the impetus to drive the tipping of other stable icebergs. The sea water in which the icebergs float is treated as a hydrostatic fluid with a permanently undisturbed free surface, so that the complexities of free-surface waves can be eliminated for initial study. The interactions among the icebergs and between the icebergs and the water are assumed to be frictionless, except for a linear drag law resisting horizontal iceberg motion that is designed to simplify the dissipative effects of viscous forces and surface-gravity-wave radiation.
Each iceberg is denoted by an index i, and has three degrees of freedom represented by the horizontal and vertical position of the center of mass (center of the iceberg cross-sectional area), xi and zi , respectively, and by the angle of tilt, θi , measured counterclockwise, with θi = 0 implying that the iceberg is upright in the initial orientation. Horizontal and vertical dimensions are rendered nondimensional by scaling the system using the initial iceberg width, w, which, unless otherwise specified, is assumed to be less than the initial iceberg thickness, l. For each iceberg, the forces of gravity, buoyancy and drag are resolved as indicated in Figure 1b and c and used to compute linear and angular accelerations ẍ i , z i and ӫ i . These accelerations are used to compute velocities (both linear and angular) which are then stepped forward through time, t, using a first-order backwards Euler scheme to determine the location and arrangement of the icebergs.
Collisions are treated as instantaneous solitary events, rather than by adding the contact forces to the determination of the acceleration. Collisions with ‘soft’ potentials (where repulsive forces scale with the degree of particle overlap) are usually the largest source of error in a simulation of interactions involving many bodies. This is because the potentials involved in two objects overlapping must be very stiff to properly model their material properties and so the timescale associated with collisions is the smallest timescale in the simulation. In order to resolve the collisions, the time-step, Δt, used must be smaller than this timescale or errors become sufficiently large as to violate the conservation laws of the system (momentum, energy and angular momentum). To avoid this computational difficulty, we choose to solve the collisions exactly (i.e. not using a ‘soft’ potential to represent repulsive forces) by assuming that they take place instantaneously and using the momentum and energy conservation principles to determine the exchanges during the collision directly. This means that we can use a much larger Δt and gain additional simplifications in the treatment of collisions that we discuss in the Appendix.
Within the simulation we use nondimensional variables so that the iceberg width, w, is defined to be 1 unit of length, and the acceleration due to gravity, g, is used to determine the corresponding unit of time: ![]() . For an iceberg 100m in width, this corresponds to a simulation time unit of about 3 s. Note that this is not the timescale for a single iceberg to capsize, it is simply the conversion between dimensionless simulation units and real units and encodes the scaling of iceberg capsize times with their width. In our simulations a single iceberg takes 45–100 time units to capsize depending on the magnitude of the initial disturbance, corresponding to 2–6 min for the 100m wide iceberg.
. For an iceberg 100m in width, this corresponds to a simulation time unit of about 3 s. Note that this is not the timescale for a single iceberg to capsize, it is simply the conversion between dimensionless simulation units and real units and encodes the scaling of iceberg capsize times with their width. In our simulations a single iceberg takes 45–100 time units to capsize depending on the magnitude of the initial disturbance, corresponding to 2–6 min for the 100m wide iceberg.
Gravity and buoyancy forces
Each iceberg has two body forces that act upon it continuously: (1) the gravitational force which operates at the center of mass; and (2) the buoyancy force which operates at the center of buoyancy (Fig. 1b). These forces lead to an energy-minimizing orientation with respect to the surface of the liquid in which the icebergs float (for an example in planetary morphology, see Reference Collins, Head, Pappalardo and SpaunCollins and others, 2000). We take the center of rotation of the icebergs to be their center of mass. In this way, gravity forces act downward at the center of mass and do not contribute a torque to the rotational dynamics. The mass of each iceberg (per unit of length in the unresolved dimension) is based on its cross-sectional area and on the density of ice, ρ i, which is assumed uniform and less than the density of water, ρ w. We discuss the calculation of the buoyancy forces in detail in the Appendix.
In addition, we implement a drag mechanism to represent the removal of energy from the moving icebergs by hydrodynamic and viscous effects. In general, icebergs moving through water will create turbulence and surface waves that damp their motion. We approximate this with a simple linear drag force ![]() on the center of mass that is proportional to velocity magnitude, and a corresponding drag torque
on the center of mass that is proportional to velocity magnitude, and a corresponding drag torque ![]() . The parameter ν then controls the magnitude of these dissipative forces in the simulation and is determined, as described below, in a manner to give decay rates similar to those observed in ice-melange-filled Greenlandic fjords.
. The parameter ν then controls the magnitude of these dissipative forces in the simulation and is determined, as described below, in a manner to give decay rates similar to those observed in ice-melange-filled Greenlandic fjords.
Contact forces and energy exchanges
Contact forces in rigid-body dynamics are generally treated by one of two methods. One method involves allowing the individual bodies to be slightly compressible and assigning a very stiff potential to the overlap between pairs of bodies, as in Reference Pöschel and BuchholtzPöschel and Buchholtz (1993), Reference PourninPournin (2005) and many others. The other method is to treat each collision as instantaneous and to use conservation laws to determine the velocities of the rigid bodies leaving the collision, as used in Reference Hoomans, Kuipers, Briel and van SwaaijHoomans and others (1996). We utilize the second method and treat collisions between icebergs as discrete events that transfer momentum and angular momentum through instantaneous impulses. In order to evaluate the contact impulse between a pair of colliding objects, we must assure that momentum and angular momentum are conserved and that the kinetic energy of the icebergs after collision KEf is proportional to the initial kinetic energy KEi according to the (dimensionless) Ecoefficient of restitution ε: Kf= εKEi.
Collision detection
Collisions between icebergs are handled computationally using techniques common to typical ‘discrete particle mechanics’ codes used for the study of sand flows and other phenomena (Reference Rycroft, Orpe and KudrollRycroft and others, 2009). We treat the icebergs as hard rectangular objects. When they collide, we generate momentum-conserving collisional impulses that instantaneously change the individual directions of motion. The collisions are partially inelastic, with the restitution coefficient, ε, defined above.
For rectangular particles such as our model icebergs, there is an ambiguity that may occur involving the perfectly sharp corners. For any size of Δt, there is a set of motions that would allow the corner of one colliding iceberg to temporarily penetrate the corner of the other iceberg. When determining how to handle this collision, the tip appears to be closer to the upper surface of the iceberg rather than the surface it initially crossed through, and an incorrect description of collision geometry (the normal vector) may be generated. This can cause spurious motions and is generally a problem for any infinitely sharp feature in a time-step-driven scheme.
We overcome this problem by representing the icebergs by a series of overlapping disks, so that corners are rounded (Fig. 1d). By doing so, we also gain the freedom, to be implemented in future study, to model shapes other than perfect rectangles with relative ease, i.e. we can use arrangement of disks to form arbitrary shapes. Because there may be a sensitivity of our results to the particular disk representation we choose, we have simulated the dynamics of our system for three disk counts (12, 28 and 60 disks) and have found that there are only small differences between 12 and 28 disks due to the different level of effective surface roughness of the icebergs. Fortunately, we find that there is little difference between the 28- and 60-disk representations at the aspect ratios we explored here (Fig. 2). Therefore, when not otherwise specified we use 28 disks to obtain all results presented. In future applications, the disk-representation parameterization used to represent arbitrary shapes should be monitored carefully to ensure adequate results.
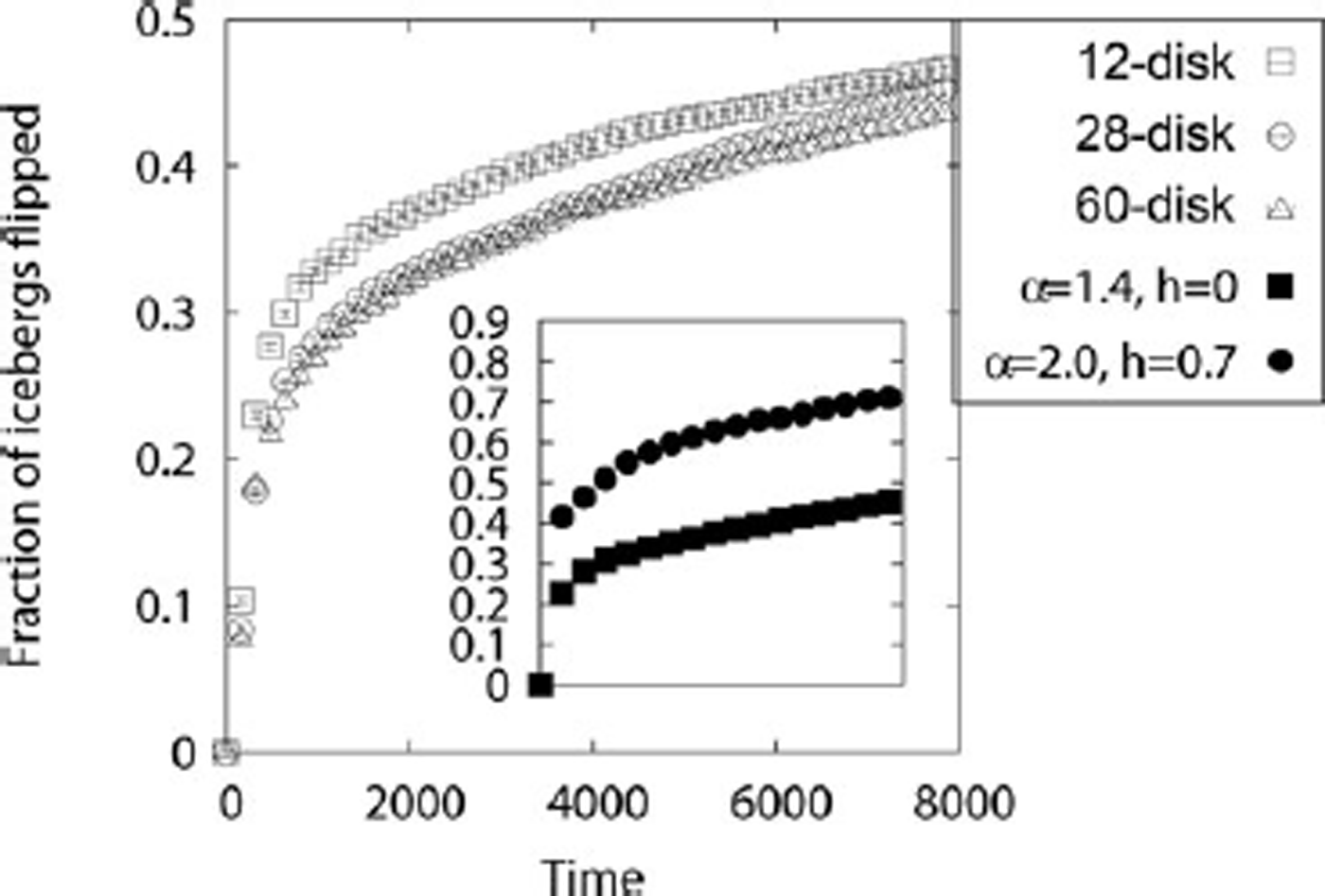
Fig. 2. The fraction of icebergs capsized by at least 45˚ as a function of time for a 12-, 28- and 60-disk representation for the αo = 1.4, h = 0 ice shelf. Each curve is averaged over eight simulation runs with different initial conditions. The error bars are determined from the standard deviation of the simulation results at each time. The inset shows a comparison between the αo = 1.4, h = 0 and the αo = 2.0, h = 0.7 iceberg assemblages, using the same scale on the x-axis.
Initial conditions
We initialize our simulations with 400 icebergs with various specified aspect ratios ![]() oriented in the initial ‘upright’ position. For rectangular icebergs, there are two important values of the aspect ratio. At an aspect ratio <1, iceberg capsize does not liberate energy, but rather consumes energy. These icebergs are globally stable. Between 1 and a critical aspect ratio α
c given by
oriented in the initial ‘upright’ position. For rectangular icebergs, there are two important values of the aspect ratio. At an aspect ratio <1, iceberg capsize does not liberate energy, but rather consumes energy. These icebergs are globally stable. Between 1 and a critical aspect ratio α
c given by
for typical values of ρ i and ρ w, a capsizing iceberg would release energy, but must first pass an energy barrier: a sufficient initial push is needed to cause the capsize to occur. For icebergs with α > α c, capsize proceeds automatically from any infinitesimal disturbance.
We seed the initial mass of icebergs with random small perturbations in their angular velocity to initiate the subsequent evolution. The randomness of the initial small perturbations introduces differences in the evolution of the experiments and these differences are evaluated (see below) to develop notions of fluctuation and uncertainty. The aspect ratios are generated randomly according to a heterogeneity parameter h, such that
where 03B7 is a Gaussian random variable with standard deviation 1 and αo is the mean aspect ratio. In the computations, we use α = max(αo (1 + hη), 0.1) to avoid α ≪ 1 and negative values.
The icebergs are initially stacked against the leftmost boundary of the simulation, which is treated as a rigid wall representing either the ice at the grounding line or the leading front of the remaining intact ice shelf. The icebergs are stacked such that there is a gap of S < 1 iceberg widths between them. Icebergs can capsize and flow freely to the unoccupied right side of the model domain. We place the icebergs so that they are initially in hydrostatic equilibrium to avoid giving the system a large initial bobbing motion.
Results
As described in the introduction, we wish to characterize both the phenomenology of the conceptual model and determine phase diagrams that describe how various parameter ranges facilitate massed iceberg capsize. The goals of studying the phenomenology are to: (1) see whether the behavior of the conceptual system has features in common with real ice-shelf disintegrations; and (2) determine how the behavior depends on parameters αo , h, ε, ν and S. The goal of determining phase diagrams is to attempt to simplify the understanding of how various parameter ranges influence the outcome of the conceptual model’s evolution. As the parameter space is quite large, we make parameter choices designed to generate representative results, not to represent an exhaustive study of sensitivity. In what follows, our particular choice of parameter values is a matter of expedience in order to seek concrete outcomes, and not a matter of whether the choice is particularly applicable to nature.
Parameter sensitivity analysis
With the above caveats, we perform a sensitivity analysis showing how the evolution of the conceptual model depends on the coefficient of restitution ε, the hydrodynamic damping ν, and the initial spacing between icebergs S. We choose an initial fiducial parameter point, S = 0.1, ε = 0.5 and ν = 0.01, to explore the surrounding parameter space. As common practice dictates, we vary one parameter at a time while holding the others constant. For the purpose of this analysis, we fix the geometry of the icebergs to minimize fluctuations between runs that would hide weak trends and so we choose αo = 1.4 with h = 0. The results are expressed using a single experimentally derived quantity, the fraction of icebergs that have flipped after 8000 time units, corresponding to about 7 hours of real time for icebergs 100 m in width. The results of our parameter search are presented in Figure 3a–c (a, b and c correspond to ε, ν and S, respectively).
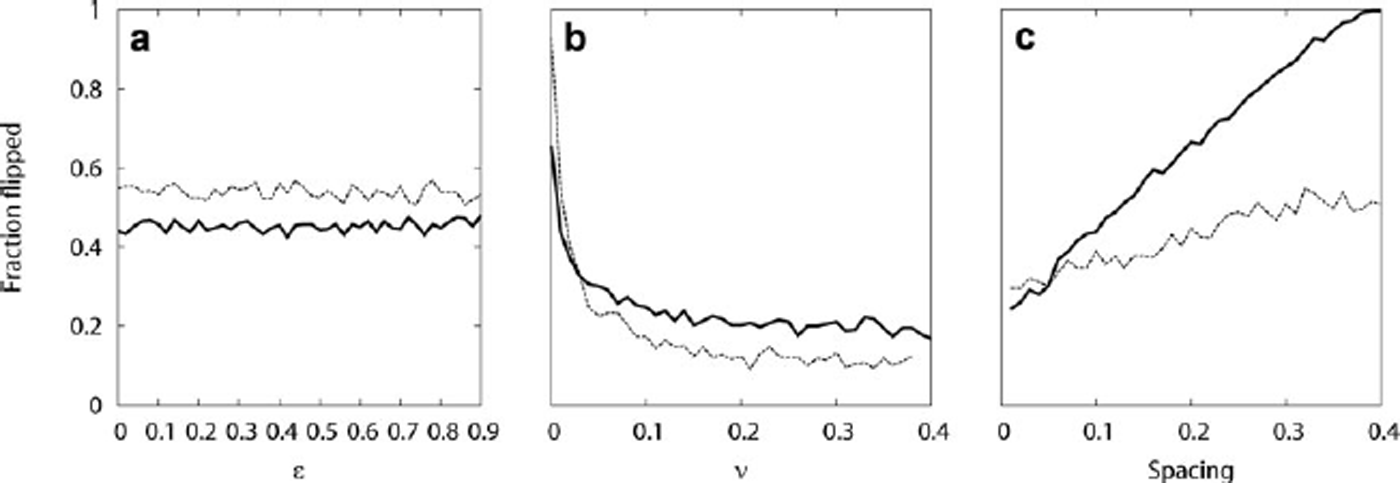
Fig. 3. The dependence of the fraction of icebergs capsized at t = 8000 (nondimensional time units) on the various model parameters: (a) the coefficient of restitution ε; (b) the hydrodynamic drag ν; and (c) the initial spacing S between icebergs. The solid line shows the results for a homogeneous iceberg assemblage αo = 1.4, h = 0. The dashed line shows the results for a slightly heterogeneous iceberg assemblage αo = 1.8, h = 0.2. The results do not depend significantly on the coefficient of restitution. The hydrodynamic drag strongly affects both cases, and the initial spacing only has a strong effect for the homogeneous near-critical iceberg assemblage.
Considering first the inelasticity, we find that there is no appreciable dependence on the choice of inelasticity of iceberg collisions. This can be understood by considering the role of inelasticity. If two icebergs are coming towards each other with some appreciable velocity, a highly inelastic collision will result in an outcome where the two icebergs are at rest relative to one another, whereas an elastic collision will result in both icebergs rebounding with equal but opposite relative motions. Within the bulk of the collapsed ice shelf, there is no room for the icebergs to rebound in a manner that does not immediately result in a second collision. This means that even small degrees of inelasticity, when applied over and over, quickly dissipate the energy of collisions and leave only slow toppling motions. A larger inelasticity would cause this to occur in fewer collisions, but within the ice shelf the time between collisions is much shorter than any other timescale of the system (the icebergs are basically in constant contact) and any amount of inelasticity is amplified into effectively perfect inelasticity.
The hydrodynamic damping, on the other hand, appears to have a strong effect on the results of the evolution. As the damping is increased, the massed capsize process is slowed significantly, so that at late times fewer icebergs have found their way free of the initial closely packed mass of icebergs. Roughly speaking, there are two regimes of behavior: that for very low damping and that for very high damping. In the high damping regime, the ice shelf slowly expands outward without introducing very much space between neighboring icebergs. The icebergs move apart just enough so that they are no longer in contact and then come to an immediate stop due to damping. In the low damping case, for values ν < 0.02, icebergs that capsize can propel others outwards explosively, creating staggered jumps of expansion and creating voids that free up space for other icebergs to capsize into.
The initial spacing between icebergs has a more subtle effect than the other parameters. For small values, it does not seem to significantly affect the fraction capsized at late times, but there is an increase towards 1 when the initial spacing is over half an iceberg width. This is basically tuning the collective effects (behaviors that occur only in the context of many iceberg-on-iceberg collisions) in the iceberg assembly. When the spacing is large, every iceberg can flip in place if it would normally do so without encountering any sort of hindrance from the rest of the ice shelf. When the spacing is small, icebergs are blocked from flipping until space is created by the expansion of the iceberg mass outward into open water.
Massed capsize phenomenology
The initial results of our simulations are reported here as a means of exploring several basic concepts of ice-shelf collapse and the influence of iceberg capsize on movement of dense masses of post-collapse ice-shelf fragments. The discussion is thus limited to basic qualitative phenomena, basic flow styles and timescales of motion.
In order to demonstrate the qualitative features of the collapse, we examine the dynamics of two particular experiments in detail, before systematically exploring the effect of variations in the aspect ratio and heterogeneity. The first experiment involves homogeneous icebergs just above the critical aspect ratio (αo = 1.4, h = 0). The second is a heterogeneous experiment composed of highly unstable icebergs with average aspect ratio αo = 1.8 and heterogeneity h = 0.7. We observe two modes of ‘collapse’ of the initial ordered iceberg arrangement. At short times, icebergs capsize wherever there is initial space to do so, including within the bulk of the initial mass of icebergs. However, once this initial instability is complete, the only way for the remaining uncapsized icebergs to capsize is for the mass of icebergs to expand horizontally into open water (Fig. 4). As the mass of icebergs expands, the rate at which icebergs capsize slows down and the system undergoes a period of evolution in which the rate of capsize and the rate of horizontal expansion into the open ocean are both relatively steady. Eventually, once all the icebergs have capsized, the mass of icebergs stops expanding as a result of the model’s dissipation. For the highly unstable experiment, the initial capsize is sufficiently energetic that the shelf does not stop expanding and the collapse proceeds quickly towards its end state.
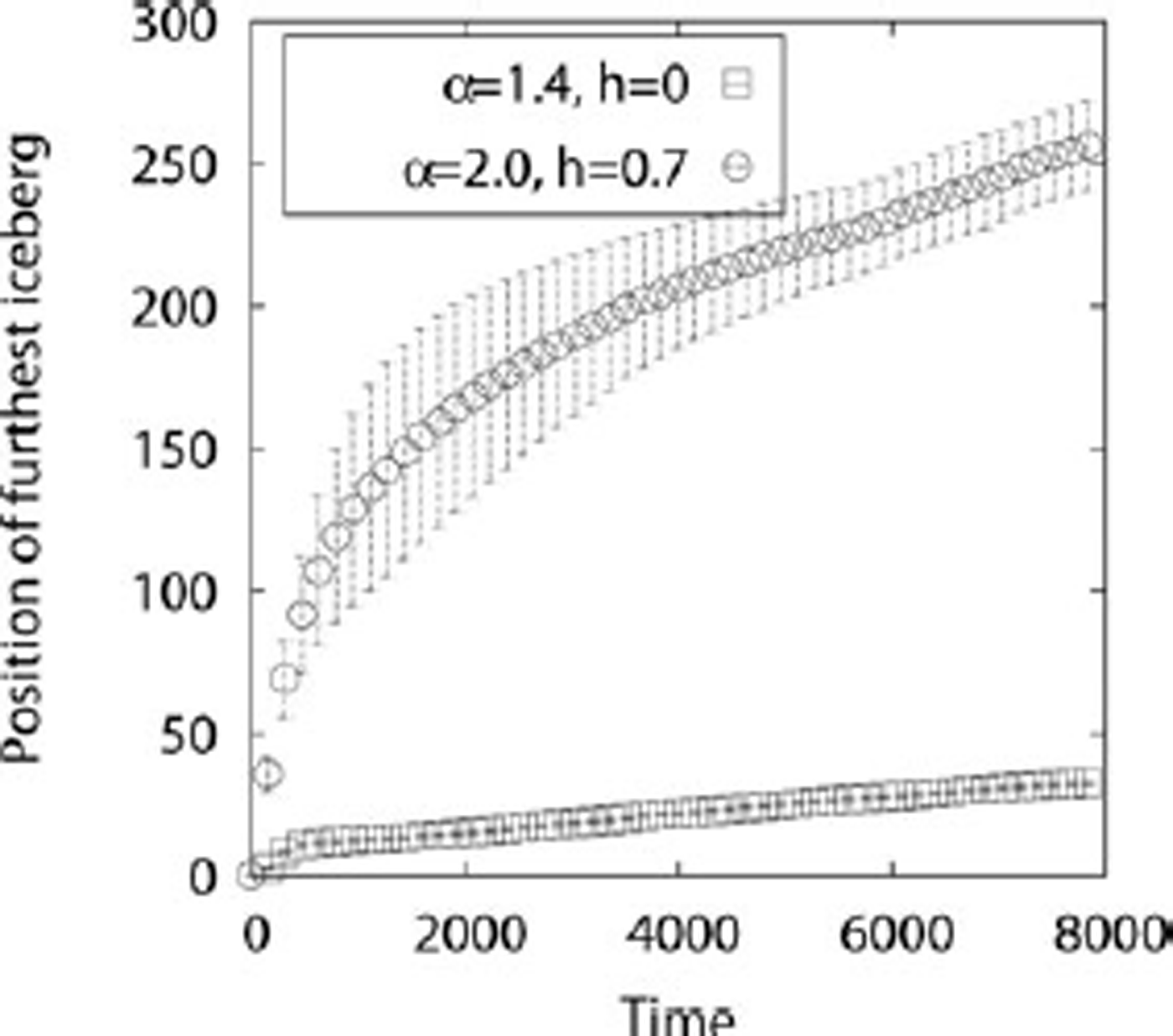
Fig. 4. Position of the seaward-most iceberg (nondimensional units) relative to its initial position averaged over eight runs of the simulation with different initial conditions and error bars determined from the standard deviation of the simulation results. The circles correspond to an iceberg assemblage composed of uniform blocks just above the critical aspect ratio (αo = 1.4, h = 0). The squares correspond to an iceberg assemblage composed of blocks with average aspect ratio αo = 2.0 and heterogeneity h = 0.7.
We plot the fraction of icebergs that have rotated by at least 45˚ as a function of time in the inset of Figure 2 and also the position of the leading edge of the mass of icebergs as a function of time in Figure 4. Both figures display error bars, which represent the expected fluctuation associated with the randomness of initial angular velocity perturbations given to each iceberg as an initial condition. Figure 5 depicts the local fractional density of capsized icebergs as a function of scaled position within the iceberg mass as a function of time for the first experiment.

Fig. 5. Fraction of icebergs capsized, f , as a function of the horizontal span of the icebergs at various times. These results are averaged over eight simulation runs. The results shown here are for the 60-disk representation of icebergs necessary for collision detection.
The evolution of the fraction of icebergs that have capsized as a function of time (Fig. 2) shows an initial period of rapid growth, corresponding to the initial capsize of icebergs that are surrounded by sufficient space to complete a rotation without having to push surrounding icebergs aside significantly. This initial evolution decays into a steady state after about t = 1000 (about 1 hour of physical time), signifying the new physical dynamic that represents a one-to-one relationship between iceberg capsize and the seaward expansion of the iceberg mass needed to make space for the capsized icebergs. This rapid growth of the fraction of icebergs capsized followed by a steady state seems to correspond qualitatively with the evolution of both the Larsen B and Wilkins ice-shelf collapse events. In both cases, the first appearance of blue ice covering the sea surface (denoting capsized or broken fragments) grew very quickly in the wake of initial calving of a few icebergs that constituted the seaward leading edge of the subsequent mass of icebergs (Reference ScambosScambos and others, 2009). A notable result of the simulations that was not anticipated from the limited observations of ice-shelf collapse is the fact that iceberg capsize evolves into a lengthy period of steady evolution after an initial period of relatively fast increase in the fraction of icebergs capsized.
In step with the fraction of capsized icebergs, the evolution of the position of the leading edge of the iceberg mass as a function of time (Fig. 4) shows an initial period of rapid expansion, corresponding to the initial capsize of icebergs, followed by a period of relatively steady expansion into the open ocean needed to make room for the steady-state growth in the fraction of icebergs that have capsized. Notable in this view of the system is the fact that a great deal of experiment-to-experiment variability (denoted by larger error bars) exists in the t < 2000 time period. Often in these experiments the leading iceberg is catapulted ahead by the collective flipping of the icebergs behind it. Thus, a large amount of energy is focused into the iceberg representing the furthest extent of expansion. The precise energy amount depends on which way each iceberg flips, something that is very sensitive to the random angular velocity perturbations given to the initial arrangement of icebergs. At longer times, these effects are smeared out as the rest of the ice sheet catches up with the leading seaward iceberg.
Heterogeneity: a variable catalyst
We now consider the effects of iceberg heterogeneity on the expansion of the iceberg assembly. If we consider an assembly that is fragmented into short wide blocks, we expect little flipping to occur. However, if there is a wide variation in the geometry of the blocks around this mean, some unstable blocks will tip and destabilize other blocks that are between aspect ratios of 1 and α c. In this case, where αo is below critical, we expect heterogeneity to be a destabilizing force.
On the other hand, if we have an iceberg arrangement that has many thick narrow blocks, then each block is driven by buoyancy to flip spontaneously and simply needs to make enough space to do so. In this case, heterogeneity will introduce blocks that are unusually stable and may isolate separate regions of the collapse from each other, preventing avalanching behavior. Thus we expect heterogeneity to be a stabilizing force if the mean aspect ratio is above critical.
If we assume a large initial spacing (in the absence of long-range hydrodynamic interactions), then each iceberg exists independently of the other icebergs. Therefore any given iceberg will capsize or fail to capsize based solely on its own properties and not the collective properties of the melange of icebergs. For an isolated iceberg we can predict precisely whether it will capsize: icebergs with α > α c will automatically capsize, whereas those with α < α c will not. We can use this to estimate how the fraction flipped, f , at late times should behave in the limit of large inter-iceberg spacing. If we have some distribution of iceberg aspect ratios given by P(α) dα then in this limit the fraction flipped is the portion of the distribution that lies above the critical aspect ratio:
For our simulations, we use a Gaussian-distributed set of aspect ratios with a mean αo and standard deviation hvo . Performing this integration we find the following features. If h = 0, the ice shelf goes from being completely stable to completely capsizing as α crosses the critical aspect ratio α c. In the vicinity of α c the eventual behavior of the system is highly sensitive to minute changes in the initial conditions.
At nonzero heterogeneity, however, this jump is smoothed out and the behavior of the ice shelf at late times changes gradually with the parameters αo and h. There appear to be three broad regions of behavior in this circumstance. The first is a region in which f is basically zero, i.e. 10–4 or smaller, and so most iceberg assemblages generated with these parameters would never evolve into a massed capsize that mimics ice-shelf disintegration. Outside this region, we can further refine the behavior by considering whether increasing heterogeneity stabilizes or destabilizes the iceberg assemblage. For αo < α c, heterogeneity introduces additional blocks above the critical aspect ratio that would not otherwise be and so the effect of increasing heterogeneity is to increase f and destabilize the ice shelf. For αo > α c, the entire shelf wishes to capsize at zero heterogeneity and so increased heterogeneity introduces a handful of stable icebergs, decreasing f.
In an attempt to develop a phase diagram where stability is plotted as a function of both αo and h, we experiment with a systematic range of the aspect ratio and heterogeneity. We cannot simulate until infinite time and so we choose a cutoff of 8000 time units or about 80 times the flipping time of a single iceberg. In the isolated iceberg limit this is well above the time it would take for the dynamics of every iceberg to play out. This is, however, not necessarily the case for dense iceberg assemblages in which collective effects seem to slow down the dynamics significantly.
We plot f as a function of αo and h in Figure 6. Qualitatively, the behavior can be separated into three cases: (1) the case in which no icebergs flip; (2) the case where heterogeneity has a stabilizing effect; and (3) the case where heterogeneity has a destabilizing effect. We have sketched the structure of the parameter space in a schematic phase diagram in Figure 7.

Fig. 6. The fraction of icebergs flipped, f , as a function of aspect ratio αo and heterogeneity h. In region 1 no icebergs are observed to capsize. Regions 2 and 3 indicate where heterogeneity has stabilizing (∂f /∂h < 0) and destabilizing (∂f =∂h > 0) effects, respectively. The solid line separating the regions is approximate and not calculated directly from the data.
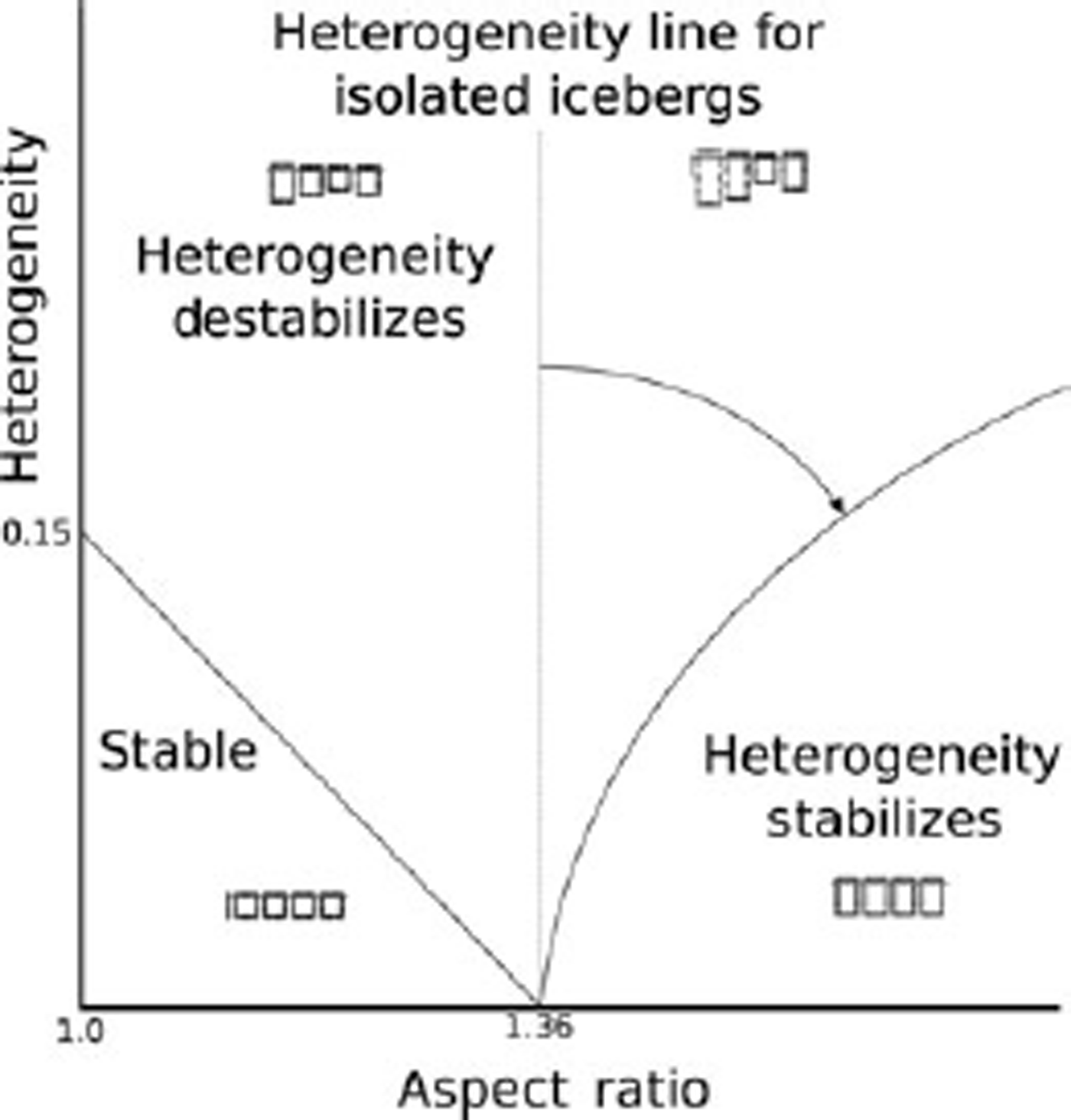
Fig. 7. Conceptual phase diagram showing the roles of iceberg aspect ratio and heterogeneity within the mass of icebergs on collapse stability. Unstable regions denote parameter ranges where initially random infinitesimal perturbations to the angular velocity of the icebergs can lead to capsize of the entire mass of icebergs.
We can see that collective effects change the results quantitatively at finite time. While a series of icebergs above the critical aspect ratio would all capsize in isolation, we find that the fraction flipped for such iceberg assemblages is not 100% when collective effects are introduced. Instead, there is a gradual slowing of the capsize process such that by the time we end our simulation ~30% of the unstable icebergs have still failed to capsize. Despite the quantitative differences, however, the qualitative features of this parameter space are mostly preserved.
However, one qualitative change is apparent: collective effects have introduced a bending to the line between stabilizing and destabilizing heterogeneity. As such, only small amounts of heterogeneity are stabilizing above the critical aspect ratio, but sufficiently large amounts turn the effect around and accelerate the collapse. This is likely due to the energy introduced by the capsize of very tall icebergs contributing to the overall expansion of the shelf in ways that overcome the additional introduction of lower aspect-ratio icebergs.
Conclusion
We have described an initial conceptual approach to exploring the dynamics associated with the immediate aftermath of ice-shelf collapse. The qualitative plausibility of the initial simulations presented above encourages the notion that it is possible to investigate the dynamics of the short time-span phenomena associated with explosive ice-shelf collapse using simple conceptual models that involve computations. Our experiments have revealed interesting connections between the distribution of post-collapse ice fragments and the dynamics of the ice expansion into the open ocean. We see situations in which a few large stable icebergs slow the collapse of an otherwise unstable shelf and situations in which a few large unstable icebergs enhance the collapse of an otherwise stable shelf. In all cases, the dense ice melange slows the process of expansion as packed unstable icebergs must make room by displacing the rest of the iceberg assemblage in order to overturn. These collective effects are responsible for the timescale of the expansion and the pattern of overturn in our simulations.
What is missing, of course, is a definitive set of observations, both of a qualitative and a quantitative nature, to which simulations of explosive ice-shelf collapse and the subsequent evolution of the ice-shelf fragment plume can be compared. We thus encourage future efforts to monitor any future collapse events with instruments and methods capable of discerning the various stages of evolution that may be compressed into a matter of hours.
Acknowledgements
This work is supported by the US National Science Foundation under grants ANT-0944193, OPP-0838811 and CMG-0934534. D.S. Abbot was supported by the T.C. Chamberlin Fellowship of the University of Chicago and the Canadian Institute for Advanced Research. We thank reviewers J. Johnson and T. Scambos and scientific editor L. Stearns for substantial help in clarifying the work presented here. The first author innovated the methods and performed the computations presented here. Co-authors, listed in alphabetical order, had significant but supportive roles.
Appendix: Computational Details
We include here the technical details of our computational implementation of the conceptual model of ice-shelf disintegration. The algorithm proceeds as follows. First, for each block, we determine the body forces upon that block due to its environment. These are the forces due to buoyancy, gravity and simplified hydrodynamic drag. The force and torque about the center of mass of each iceberg, F and τ, respectively, are evaluated using volume integration of the forces of gravity and buoyancy:
where g is the acceleration of gravity, ρ w is the density of sea water (assumed uniform), x and z are horizontal and vertical coordinates, respectively, r = (x – x cm) n x + (z – z cm) n z is the position vector of point (x, z) relative to the position of the center of mass, (x cm, z cm), and n x and n z are unit vectors in the x and z directions, respectively. We compute these integrals by first representing our icebergs as four line segments the equations of which we can determine based on the iceberg’s rotation from the vertical. We iterate through each line segment, computing its intersection with the water surface to determine if it is entirely above water, below water or crossing the water surface.
We then update the velocity and angular velocity of each block using a first-order Euler time-step. Using these new values, we then update the position and rotation with a first-order Euler time-step. Performing the updates in this order increases the stability of the Euler integrator without introducing additional computational cost or complexity to the procedure. The use of an Euler integrator is not critical to the performance of the computation since the determining limiting factor on time-step size is the stability of the collision algorithm. We show this in Figure 8 by examining the trajectory of a single iceberg for different time-steps. We use a value of 10–2 in our simulations in order to ensure that the collision scheme remains stable and does not generate persistent overlaps. At this time-step size, the error in vertical position of the single iceberg at t = 500 is about 0.01% and the continuous part of the dynamics is far below the threshold for numerical instability. A higher-order integrator could be used in place of the Euler scheme, but at these levels of error it would be an unnecessary increase in computational cost compared with other sources of error in the dynamics (e.g. collisional overlap).
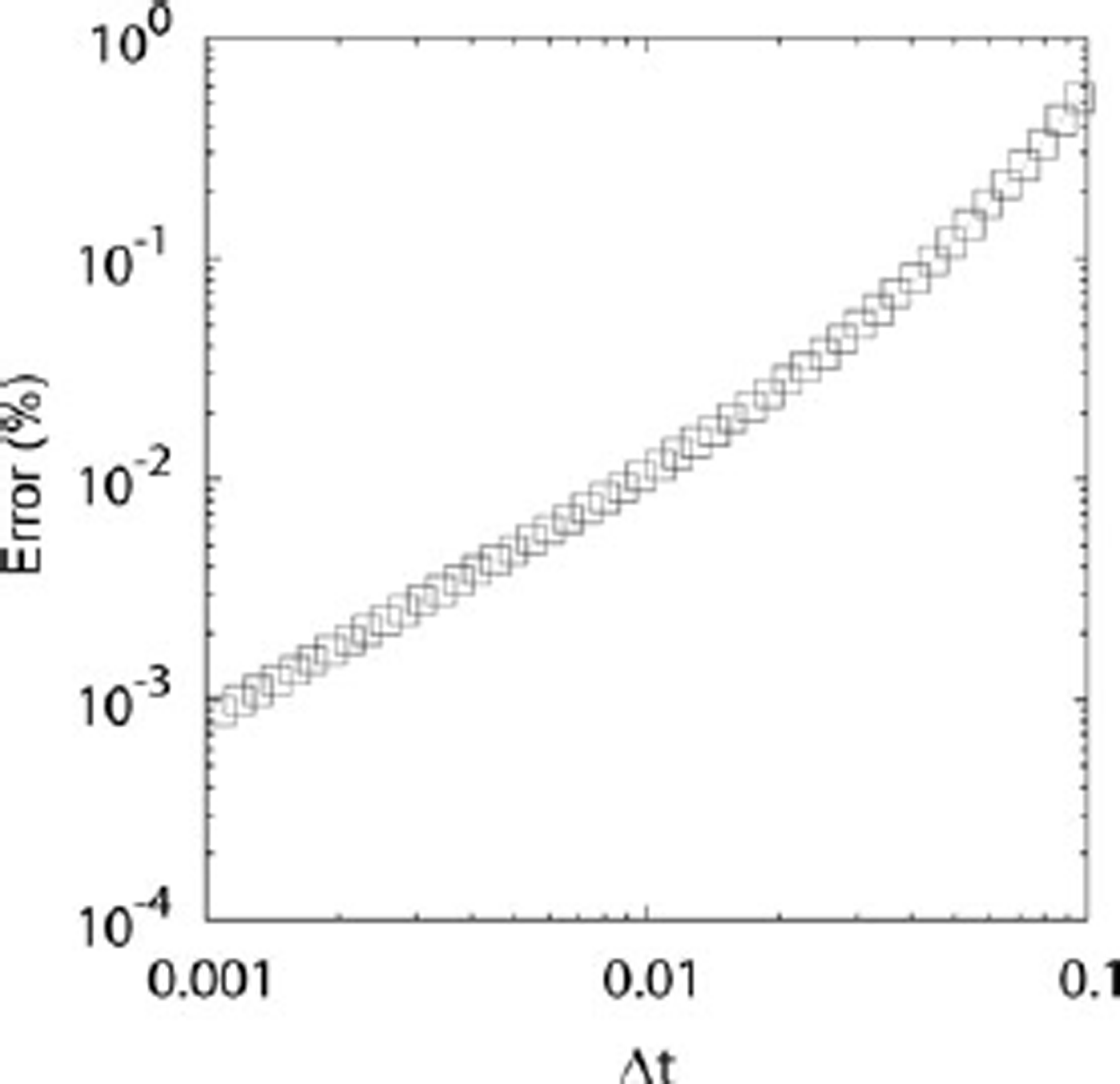
Fig. 8. The simulation error as a function of time-step when compared to a run at Δt = 10–4 for the dynamics of a single block. A single block of aspect ratio 1.4 is simulated from start until t = 500, at which point the final vertical position of the block is compared with that for time-step Δt = 10–4. Even at time-steps larger than those we use for the simulation, the error in the vertical position of the block is <1%.
In order to evaluate the contact normal impulse we need only know the positions of the iceberg centers of mass, the position and surface normal at the collision point, and the linear and angular velocities of the two icebergs as shown in Figure 1c. We must take into account that the contact points are moving, both due to translational momentum and the rotations of the objects. The relative motion of the two colliding objects, denoted by labels 1 and 2, at the contact point is
The post-collision velocities are expressed in general in Reference Hahn and BeachHahn (1988) as a function of the coefficient of restitution ε such that KEf = εKEi:
If we express all of the post-collisional velocities with respect to a collisional impulse acting along the normal direction F n then we can solve for the normal impulse:
where
is a reduced mass. If this impulse is negative, it implies that the collision in question is due to numerical error introducing an overlap between receding icebergs. For any such unphysical collisions we set the normal impulse to zero.
In order to determine the points of collision, we use a disk-based representation of the collision boundary. We evenly place a series of disks of radius r = 0.15 along the sides of each block. We choose a number of disks to cover the boundary without gaps for the largest aspect-ratio blocks in use. In order to determine efficiently which icebergs are at risk of collision, we sort the icebergs into a grid of size 2l where l is the length of the longest side of the icebergs in the simulation. In this way, collisions between icebergs are guaranteed to occur only between shared or neighboring cells.
We check for all possible overlaps between the component disks of each pair of icebergs that could collide. When an overlap is found, we generate a collision event using the point equidistant between the two disk centers for the location of collision, and the vector between the centers for the direction of the normal vector. With these parameters, we use the result of Equation (A5) to determine the velocity and angular velocity of the icebergs leaving the collision.
Because of the coefficient of restitution, when two icebergs collide during one time-step they move apart more slowly than they moved towards each other during the previous time-step. The consequence of this is that it may take multiple time-steps for an iceberg involved in a collision to stop being in a state of overlap with its collision partner. This can generate spurious collisions in subsequent time-steps. However, these spurious collisions can be distinguished from real collisions as the velocities of the icebergs are directed away from each other, leading to the calculated collision impulse being negative. That is, collisions which are spurious generate an attracting force between the two icebergs rather than a repulsive force. In order to prevent these spurious collisions from generating errors, we ignore any situation that generates a negative value of the contact impulse.










