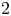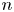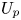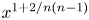1. Introduction
1.1 Background and statement of main theorem
The first ‘eigenvariety’ was constructed by Coleman and Mazur in [Reference Coleman and MazurCM98]. Now called the Coleman–Mazur eigencurve, it is a rigid analytic space parametrizing ![]() $p$-adic modular Hecke eigenforms with nonzero
$p$-adic modular Hecke eigenforms with nonzero ![]() $U_p$-eigenvalues. Since then, further work by numerous authors has resulted in a collection of eigenvarieties for
$U_p$-eigenvalues. Since then, further work by numerous authors has resulted in a collection of eigenvarieties for ![]() $p$-adic automorphic forms on various other groups. Particularly relevant for our purposes are the papers of Buzzard [Reference BuzzardBuz04, Reference BuzzardBuz07], Chenevier [Reference ChenevierChe04], and Bellaïche and Chenevier [Reference Bellaïche and ChenevierBC09], in which eigenvarieties are eventually constructed for
$p$-adic automorphic forms on various other groups. Particularly relevant for our purposes are the papers of Buzzard [Reference BuzzardBuz04, Reference BuzzardBuz07], Chenevier [Reference ChenevierChe04], and Bellaïche and Chenevier [Reference Bellaïche and ChenevierBC09], in which eigenvarieties are eventually constructed for ![]() $p$-adic automorphic forms on definite unitary groups of all ranks.
$p$-adic automorphic forms on definite unitary groups of all ranks.
For simplicity of notation in this introduction, let ![]() $p$ be an odd prime. We write
$p$ be an odd prime. We write ![]() $v$ for the
$v$ for the ![]() $p$-adic valuation and
$p$-adic valuation and ![]() $|\cdot |$ for the
$|\cdot |$ for the ![]() $p$-adic norm, normalized so that
$p$-adic norm, normalized so that ![]() $v(p)=1$ and
$v(p)=1$ and ![]() $|p|=p^{-1}$. A weight of a
$|p|=p^{-1}$. A weight of a ![]() $p$-adic modular form is a continuous character of
$p$-adic modular form is a continuous character of ![]() $\mathbb {Z}_p^\times$, and the weight space is the rigid analytic space
$\mathbb {Z}_p^\times$, and the weight space is the rigid analytic space ![]() $\mathscr {W}$ parametrizing such characters. The
$\mathscr {W}$ parametrizing such characters. The ![]() $T$-coordinate of a point
$T$-coordinate of a point ![]() $w\in \mathscr {W}$ is the value
$w\in \mathscr {W}$ is the value ![]() $T(w)=w(\exp (p))-1$; the space
$T(w)=w(\exp (p))-1$; the space ![]() $\mathscr {W}$ turns out to be a disjoint union of
$\mathscr {W}$ turns out to be a disjoint union of ![]() $p-1$ open unit discs with parameter
$p-1$ open unit discs with parameter ![]() $T$. For
$T$. For ![]() $r\in (0,1)$, we write
$r\in (0,1)$, we write ![]() $\mathscr {W}_{>r}$ for the rigid analytic subset of
$\mathscr {W}_{>r}$ for the rigid analytic subset of ![]() $\mathscr {W}$ where
$\mathscr {W}$ where ![]() $|T|>r$.
$|T|>r$.
We fix a tame level and let ![]() $\mathscr {Z}$ be the corresponding eigencurve. We let
$\mathscr {Z}$ be the corresponding eigencurve. We let ![]() $w:\mathscr {Z}\to \mathscr {W}$ be the map taking an eigenform to its weight,
$w:\mathscr {Z}\to \mathscr {W}$ be the map taking an eigenform to its weight, ![]() $a_p:\mathscr {Z}\to \mathbb {G}_m$ be the map taking an eigenform to its
$a_p:\mathscr {Z}\to \mathbb {G}_m$ be the map taking an eigenform to its ![]() $U_p$-eigenvalue, and
$U_p$-eigenvalue, and ![]() $\mathscr {Z}_{>r}$ be the preimage of
$\mathscr {Z}_{>r}$ be the preimage of ![]() $\mathscr {W}_{>r}$ in
$\mathscr {W}_{>r}$ in ![]() $\mathscr {Z}$. The following conjecture, sometimes called the ‘halo conjecture’, describes the geometry of the part of the eigencurve lying over the ‘boundary’ of weight space (i.e.
$\mathscr {Z}$. The following conjecture, sometimes called the ‘halo conjecture’, describes the geometry of the part of the eigencurve lying over the ‘boundary’ of weight space (i.e. ![]() $\mathscr {Z}_{>r}$ for
$\mathscr {Z}_{>r}$ for ![]() $r$ sufficiently close to
$r$ sufficiently close to ![]() $1$).
$1$).
Conjecture 1.1.1 (Coleman–Mazur–Buzzard–Kilford, as stated by Liu, Wan, and Xiao [Reference Liu, Wan and XiaoLWX17])
When ![]() $r\in (0,1)$ is sufficiently close to
$r\in (0,1)$ is sufficiently close to ![]() $1^-$, the following statements hold.
$1^-$, the following statements hold.
(i) The space
 $\mathscr {Z}_{>r}$ is a disjoint union of (countably infinitely many) connected components
$\mathscr {Z}_{>r}$ is a disjoint union of (countably infinitely many) connected components  $Z_1,Z_2,\dotsc,$ such that the weight map
$Z_1,Z_2,\dotsc,$ such that the weight map  $w:Z_n\to \mathscr {W}_{>r}$ is finite and flat for each
$w:Z_n\to \mathscr {W}_{>r}$ is finite and flat for each  $n$.
$n$.(ii) There exist nonnegative rational numbers
 $\alpha _1,\alpha _2,\dotsc \in \mathbb {Q}$ in non-decreasing order and tending to infinity such that, for each
$\alpha _1,\alpha _2,\dotsc \in \mathbb {Q}$ in non-decreasing order and tending to infinity such that, for each  $n$ and each point
$n$ and each point  $z\in Z_n$, we have
$z\in Z_n$, we have
 \[ |a_p(z)|=|T(w(z))|^{\alpha_n}. \]
\[ |a_p(z)|=|T(w(z))|^{\alpha_n}. \]
Note that part (ii) of Conjecture 1.1.1 implies that as one approaches the boundary, the slope ![]() $v(a_p(z))$ approaches
$v(a_p(z))$ approaches ![]() $0$ in proportion to
$0$ in proportion to ![]() $v(T(w(z)))$.
$v(T(w(z)))$.
Liu, Wan, and Xiao [Reference Liu, Wan and XiaoLWX17] proved the equivalent version of this conjecture for automorphic forms on definite quaternion algebras over ![]() $\mathbb {Q}$. The key step in their work is to obtain strong upper and lower bounds on the Newton polygon of the characteristic power series of the
$\mathbb {Q}$. The key step in their work is to obtain strong upper and lower bounds on the Newton polygon of the characteristic power series of the ![]() $U_p$-operator. For consistency with our discussion, we describe these bounds in the context of rank-
$U_p$-operator. For consistency with our discussion, we describe these bounds in the context of rank-![]() $2$ definite unitary groups over
$2$ definite unitary groups over ![]() $\mathbb {Q}$, for which the analysis is exactly the same.
$\mathbb {Q}$, for which the analysis is exactly the same.
Let ![]() $G$ be an algebraic group over
$G$ be an algebraic group over ![]() $\mathbb {Q}$ such that
$\mathbb {Q}$ such that ![]() $G(\mathbb {R})\cong U_n(\mathbb {R})$ and
$G(\mathbb {R})\cong U_n(\mathbb {R})$ and ![]() $G(\mathbb {Q}_p)\cong {GL}_n(\mathbb {Q}_p)$, and
$G(\mathbb {Q}_p)\cong {GL}_n(\mathbb {Q}_p)$, and ![]() $\mathscr {U}\subset G(\mathbb {A}_f)$ a compact open subgroup satisfying minor technical conditions. The corresponding eigenvariety
$\mathscr {U}\subset G(\mathbb {A}_f)$ a compact open subgroup satisfying minor technical conditions. The corresponding eigenvariety ![]() $\mathscr {Z}$ is now a rigid analytic space of dimension
$\mathscr {Z}$ is now a rigid analytic space of dimension ![]() $n-1$ lying over the weight space
$n-1$ lying over the weight space ![]() $\mathscr {W}$ parametrizing continuous characters of
$\mathscr {W}$ parametrizing continuous characters of ![]() $(\mathbb {Z}_p^\times )^{n-1}$. This
$(\mathbb {Z}_p^\times )^{n-1}$. This ![]() $\mathscr {W}$ is a disjoint union of
$\mathscr {W}$ is a disjoint union of ![]() $(p-1)^{n-1}$ open unit polydiscs of dimension
$(p-1)^{n-1}$ open unit polydiscs of dimension ![]() $n-1$ with parameters
$n-1$ with parameters ![]() $T_1,\dotsc,T_{n-1}$. Let
$T_1,\dotsc,T_{n-1}$. Let ![]() $\mathscr {S}_w(G,\mathscr {U})$ be the space of
$\mathscr {S}_w(G,\mathscr {U})$ be the space of ![]() $p$-adic automorphic forms on
$p$-adic automorphic forms on ![]() $G$ of weight
$G$ of weight ![]() $w$ and level
$w$ and level ![]() $\mathscr {U}$. Then Liu–Wan–Xiao showed that when
$\mathscr {U}$. Then Liu–Wan–Xiao showed that when ![]() $n=2$, the Newton polygon of
$n=2$, the Newton polygon of ![]() $\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ is shaped approximately like the curve
$\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ is shaped approximately like the curve ![]() $y=Av(T_1(w))x^2$, where
$y=Av(T_1(w))x^2$, where ![]() $A$ is a constant depending only on
$A$ is a constant depending only on ![]() $G$,
$G$, ![]() $\mathscr {U}$, and
$\mathscr {U}$, and ![]() $p$.
$p$.
In this paper, we generalize this bound to definite unitary groups of all ranks by showing that for arbitrary ![]() $n$, the Newton polygon of
$n$, the Newton polygon of ![]() $\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ is shaped approximately like
$\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ is shaped approximately like ![]() $y=Av(T_i(w))x^{1+2/{n(n-1)}}$, assuming that the
$y=Av(T_i(w))x^{1+2/{n(n-1)}}$, assuming that the ![]() $v(T_i(w))$ are not extremely different in size. A more precise statement follows.
$v(T_i(w))$ are not extremely different in size. A more precise statement follows.
Theorem 1.1.2
(i) There are constants
 $A_1,C>0$ (depending only on
$A_1,C>0$ (depending only on  $G$,
$G$,  $\mathscr {U}$, and
$\mathscr {U}$, and  $p$) such that for all
$p$) such that for all  $w$ such that each
$w$ such that each  $|T_i(w)|>1/p$, the Newton polygon of the power series
$|T_i(w)|>1/p$, the Newton polygon of the power series  $\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ lies above the curve
$\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ lies above the curve
 \[ y=\bigl(A_1x^{1+2/{n(n-1)}}-C\bigr)\min_iv(T_i(w)). \]
\[ y=\bigl(A_1x^{1+2/{n(n-1)}}-C\bigr)\min_iv(T_i(w)). \]
(ii) Suppose that
 $w(a_1,\dotsc,a_{n-1})=\prod _i a_i^{t_i}\chi _i(a_i)$, where
$w(a_1,\dotsc,a_{n-1})=\prod _i a_i^{t_i}\chi _i(a_i)$, where  $(t_1,\dotsc,t_{n-1})\in (\mathbb {Z}_{\ge 0})^{n-1}$ with
$(t_1,\dotsc,t_{n-1})\in (\mathbb {Z}_{\ge 0})^{n-1}$ with  $t_1\ge \dotsb \ge t_{n-1}$, and each
$t_1\ge \dotsb \ge t_{n-1}$, and each  $\chi _i$ is a finite character of conductor
$\chi _i$ is a finite character of conductor  $\operatorname {cond}(\chi _i)$ such that
$\operatorname {cond}(\chi _i)$ such that  $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all  $i\neq j$,
$i\neq j$,  $\operatorname {cond}(\chi _i)\ge 2$ if
$\operatorname {cond}(\chi _i)\ge 2$ if  $p\ge 3$, and
$p\ge 3$, and  $\operatorname {cond}(\chi _i)\ge 4$ if
$\operatorname {cond}(\chi _i)\ge 4$ if  $p=2$. Let
$p=2$. Let  $\chi _{(1)},\dotsc,\chi _{(n-1)}$ be the characters
$\chi _{(1)},\dotsc,\chi _{(n-1)}$ be the characters  $\chi _1,\dotsc,\chi _{n-1}$ reordered so that
$\chi _1,\dotsc,\chi _{n-1}$ reordered so that  $\operatorname {cond}(\chi _{(1)})\le \operatorname {cond}(\chi _{(2)})\le \dotsb \le \operatorname {cond}(\chi _{(n-1)})$, let
$\operatorname {cond}(\chi _{(1)})\le \operatorname {cond}(\chi _{(2)})\le \dotsb \le \operatorname {cond}(\chi _{(n-1)})$, let  $c_{(i)}=\operatorname {cond}(\chi _{(i)})$, and let
$c_{(i)}=\operatorname {cond}(\chi _{(i)})$, and let  $T_{(i)}=T(\chi _{(i)})$.
$T_{(i)}=T(\chi _{(i)})$.Then there is a constant
 $h$ (depending only on
$h$ (depending only on  $G$,
$G$,  $\mathscr {U}$, and
$\mathscr {U}$, and  $p$), a polynomial
$p$), a polynomial  $d_{t_1,\dotsc,t_{n-1}}$ of total degree
$d_{t_1,\dotsc,t_{n-1}}$ of total degree  ${n(n-1)}/2$ in the
${n(n-1)}/2$ in the  $t_i$, and a linear function
$t_i$, and a linear function  $l(t_1,\dotsc,t_{n-1})$ such that the Newton polygon of
$l(t_1,\dotsc,t_{n-1})$ such that the Newton polygon of  $\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ contains at least
segments of slope at most
$\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ contains at least
segments of slope at most \[ hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_{t_1,\dotsc,t_{n-1}} \]
\[ hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_{t_1,\dotsc,t_{n-1}} \]
 $l(t_1,\dotsc,t_{n-1})$, hence passes below the point
If for a given
$l(t_1,\dotsc,t_{n-1})$, hence passes below the point
If for a given \[ \biggl(hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_t,hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_tl(t)\biggr). \]
\[ \biggl(hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_t,hp^{c_{(1)}+2c_{(2)}+\dotsb+(n-1)c_{(n-1)}-{n(n-1)}/2}d_tl(t)\biggr). \]
 $\epsilon$, the
$\epsilon$, the  $t_i$ satisfy
$t_i$ satisfy  $t_i-t_{i+1}\ge \epsilon (t_j-t_{j+1})$ for all
$t_i-t_{i+1}\ge \epsilon (t_j-t_{j+1})$ for all  $i\neq j$, this point can also be written as
for
$i\neq j$, this point can also be written as
for \[ \biggl(x,A_2\bigl(v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\bigr)x^{1+2/{n(n-1)}}\biggr) \]
\[ \biggl(x,A_2\bigl(v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\bigr)x^{1+2/{n(n-1)}}\biggr) \]
 $x=hp^{c_{(1)}+2c_{(2)}+\dotsb +(n-1)c_{(n-1)}-{n(n-1)}/2}d_t$ and a constant
$x=hp^{c_{(1)}+2c_{(2)}+\dotsb +(n-1)c_{(n-1)}-{n(n-1)}/2}d_t$ and a constant  $A_2$ (depending additionally on
$A_2$ (depending additionally on  $\epsilon$). Note that, in particular,
$\epsilon$). Note that, in particular,
 \[ v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\le\max_i v(T_i). \]
\[ v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\le\max_i v(T_i). \]
Remark 1 It will be evident that the condition that ![]() $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all ![]() $i\neq j$ is not required for the proof to go through; it is just there to allow us to state the best and cleanest bound.
$i\neq j$ is not required for the proof to go through; it is just there to allow us to state the best and cleanest bound.
We also leverage Theorem 1.1.2 to prove two statements that may be more geometrically satisfying. First, we prove the following alternative version of the upper bound which provides infinitely many upper bound points on the same Newton polygon.
Theorem 1.1.3 Suppose that ![]() $w(a_1,\dotsc,a_{n-1})=\prod _i a_i^{t_i}\chi _i(a_i)$, where
$w(a_1,\dotsc,a_{n-1})=\prod _i a_i^{t_i}\chi _i(a_i)$, where ![]() $(t_1,\dotsc,t_{n-1})\in (\mathbb {Z}_{\ge 0})^{n-1}$ with
$(t_1,\dotsc,t_{n-1})\in (\mathbb {Z}_{\ge 0})^{n-1}$ with ![]() $t_1\ge \dotsb \ge t_{n-1}$, and each
$t_1\ge \dotsb \ge t_{n-1}$, and each ![]() $\chi _i$ is a finite character of conductor
$\chi _i$ is a finite character of conductor ![]() $c_i$ such that
$c_i$ such that ![]() $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all ![]() $i\neq j$. Then there is a constant
$i\neq j$. Then there is a constant ![]() $A_2$ such that for every radius
$A_2$ such that for every radius ![]() $r>0$, there is a weight
$r>0$, there is a weight ![]() $s$ such that
$s$ such that ![]() $|T_i(w)-T_i(s)|< r$ for all
$|T_i(w)-T_i(s)|< r$ for all ![]() $i$,
$i$, ![]() $|T_i(w)|=|T_i(s)|$ for all
$|T_i(w)|=|T_i(s)|$ for all ![]() $i$, and the Newton polygon of
$i$, and the Newton polygon of ![]() $\det (I-XU_p|\mathscr {S}_s(G,\mathscr {U}))$ lies below an infinite sequence of points (with
$\det (I-XU_p|\mathscr {S}_s(G,\mathscr {U}))$ lies below an infinite sequence of points (with ![]() $x$-coordinates going to
$x$-coordinates going to ![]() $\infty$) lying on the curve parametrized by
$\infty$) lying on the curve parametrized by
Again, keep in mind that the expression with the ![]() $T_{(i)}$ is at most
$T_{(i)}$ is at most ![]() $\max _i v(T_i(s))$.
$\max _i v(T_i(s))$.
Recall that the Newton polygon ![]() $NP(x)$ of
$NP(x)$ of ![]() $U_p$ at a given weight
$U_p$ at a given weight ![]() $s$ is a continuous, concave up piecewise linear function in the
$s$ is a continuous, concave up piecewise linear function in the ![]() $xy$-plane such that for every
$xy$-plane such that for every ![]() $\alpha \in \mathbb {Q}_{\ge 0}$, the horizontal length of the segment of
$\alpha \in \mathbb {Q}_{\ge 0}$, the horizontal length of the segment of ![]() $NP(x)$ of slope
$NP(x)$ of slope ![]() $\alpha$ equals the number of
$\alpha$ equals the number of ![]() $U_p$-eigenvalues among forms of weight
$U_p$-eigenvalues among forms of weight ![]() $s$ of
$s$ of ![]() $p$-adic valuation
$p$-adic valuation ![]() $\alpha$. Hence, Theorems 1.1.2 and 1.1.3 tell us the growth rate of the sizes of the eigenvalues of
$\alpha$. Hence, Theorems 1.1.2 and 1.1.3 tell us the growth rate of the sizes of the eigenvalues of ![]() $U_p$ at
$U_p$ at ![]() $s$. Specifically they tell us that we should expect the
$s$. Specifically they tell us that we should expect the ![]() $m$th smallest slope to be roughly of size
$m$th smallest slope to be roughly of size
Furthermore, the implicit constant should be proportional to the ![]() $v(T_i(s))$ (assuming they are not too different in size), so that the slope approaches
$v(T_i(s))$ (assuming they are not too different in size), so that the slope approaches ![]() $0$ as we approach the boundary of weight space, as part (ii) of Conjecture 1.1.1 implies for the dimension-
$0$ as we approach the boundary of weight space, as part (ii) of Conjecture 1.1.1 implies for the dimension-![]() $1$ case.
$1$ case.
We also use the lower bound of Theorem 1.1.2 to prove the following (vaguely stated) decomposition result for the boundary of the eigenvariety.
Theorem 1.1.4 Let ![]() $a_p:\mathscr {Z}\to \mathbb {G}_m$ be the map taking a point of
$a_p:\mathscr {Z}\to \mathbb {G}_m$ be the map taking a point of ![]() $\mathscr {Z}$ to its
$\mathscr {Z}$ to its ![]() $U_p$-eigenvalue. For
$U_p$-eigenvalue. For ![]() $\alpha \in \mathbb {R}_{\ge 0}$, let
$\alpha \in \mathbb {R}_{\ge 0}$, let ![]() $\mathscr {Z}(\alpha )$ be the subset of points
$\mathscr {Z}(\alpha )$ be the subset of points ![]() $z\in \mathscr {Z}$ such that
$z\in \mathscr {Z}$ such that ![]() $v(a_p(z))=\alpha v(T_i(z))$. Then over certain open subsets of the weight polydisc boundary where
$v(a_p(z))=\alpha v(T_i(z))$. Then over certain open subsets of the weight polydisc boundary where ![]() $v(T_i)$ is much smaller than all the other
$v(T_i)$ is much smaller than all the other ![]() $v(T_j)$,
$v(T_j)$, ![]() $\mathscr {Z}(\alpha )$ is disconnected from its complement in
$\mathscr {Z}(\alpha )$ is disconnected from its complement in ![]() $\mathscr {Z}$.
$\mathscr {Z}$.
(See Theorem 5.0.1 for the precise statement.) This is similar to the statement of part (i) of Conjecture 1.1.1, though weaker because the region over which we can prove that ![]() $\mathscr {Z}(\alpha )$ is disconnected from its complement depends on
$\mathscr {Z}(\alpha )$ is disconnected from its complement depends on ![]() $\alpha$, and becomes arbitrarily small as
$\alpha$, and becomes arbitrarily small as ![]() $\alpha$ goes to infinity. Hence, Theorems 1.1.2, 1.1.3, and 1.1.4 can all be seen as weak generalizations of Conjecture 1.1.1 to definite unitary groups of arbitrary rank.
$\alpha$ goes to infinity. Hence, Theorems 1.1.2, 1.1.3, and 1.1.4 can all be seen as weak generalizations of Conjecture 1.1.1 to definite unitary groups of arbitrary rank.
Historically, Conjecture 1.1.1 arose from a question of Coleman and Mazur [Reference Coleman and MazurCM98] and was suggested by a computation of Buzzard and Kilford [Reference Buzzard and KilfordBK05] for ![]() $p=2$ and tame level
$p=2$ and tame level ![]() $1$. Further explicit computations for small primes were later done by Roe [Reference RoeRoe14], Kilford [Reference KilfordKil08], and Kilford and McMurdy [Reference Kilford and McMurdyKM12]. The conjecture is given above in the form stated by Liu, Wan, and Xiao [Reference Liu, Wan and XiaoLWX17], whose proof for definite quaternion algebras builds on the work of Wan, Xiao, and Zhang [Reference Wan, Xiao and ZhangWXZ17]. Ren and Zhao [Reference Ren and ZhaoRZ22] have generalized much of Liu–Wan–Xiao's theorem to Hilbert modular forms for definite quaternion algebras over totally real fields in which
$1$. Further explicit computations for small primes were later done by Roe [Reference RoeRoe14], Kilford [Reference KilfordKil08], and Kilford and McMurdy [Reference Kilford and McMurdyKM12]. The conjecture is given above in the form stated by Liu, Wan, and Xiao [Reference Liu, Wan and XiaoLWX17], whose proof for definite quaternion algebras builds on the work of Wan, Xiao, and Zhang [Reference Wan, Xiao and ZhangWXZ17]. Ren and Zhao [Reference Ren and ZhaoRZ22] have generalized much of Liu–Wan–Xiao's theorem to Hilbert modular forms for definite quaternion algebras over totally real fields in which ![]() $p$ is totally split, Birkbeck [Reference BirkbeckBir21] has provided computational evidence for more general totally real fields, and Diao and Yao [Reference Diao and YaoDY23] have recently proven it for the original group
$p$ is totally split, Birkbeck [Reference BirkbeckBir21] has provided computational evidence for more general totally real fields, and Diao and Yao [Reference Diao and YaoDY23] have recently proven it for the original group ![]() ${GL}_2$. Statements of this nature can have far-reaching consequences for the arithmetic of modular forms; see, for example, [Reference Johansson and NewtonJN19b] or [Reference Newton and ThorneNT21], the latter of which uses the case
${GL}_2$. Statements of this nature can have far-reaching consequences for the arithmetic of modular forms; see, for example, [Reference Johansson and NewtonJN19b] or [Reference Newton and ThorneNT21], the latter of which uses the case ![]() $p=2$ of Conjecture 1.1.1 to prove automorphy lifting for symmetric power Galois representations.
$p=2$ of Conjecture 1.1.1 to prove automorphy lifting for symmetric power Galois representations.
As far as we know, there is little prior work on the shape of the Newton polygon of ![]() $\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ for any
$\det (I-XU_p|\mathscr {S}_w(G,\mathscr {U}))$ for any ![]() $G$ of rank greater than
$G$ of rank greater than ![]() $2$. The only prior result for general rank we have been able to find in the literature is Chenevier's weaker lower bound in [Reference ChenevierChe04] of the form
$2$. The only prior result for general rank we have been able to find in the literature is Chenevier's weaker lower bound in [Reference ChenevierChe04] of the form ![]() $y=Ax^{1+1/({2^n-n-1})}$, which applies only to the center of weight space. As late as 2018, Andreatta, Iovita, and Pilloni wrote [Reference Andreatta, Iovita and PilloniAIP18] that there were not even any conjectures about the actual shape of the Newton polygon for higher-dimensional eigenvarieties in the literature.
$y=Ax^{1+1/({2^n-n-1})}$, which applies only to the center of weight space. As late as 2018, Andreatta, Iovita, and Pilloni wrote [Reference Andreatta, Iovita and PilloniAIP18] that there were not even any conjectures about the actual shape of the Newton polygon for higher-dimensional eigenvarieties in the literature.
1.2 Proof outline
The proof of part (i) of Theorem 1.1.2 is an application of the method of Johansson and Newton [Reference Johansson and NewtonJN19a]. They construct families of automorphic forms extending over the boundary of weight space, to points in what can be viewed as an adic compactification of weight space, and show that the eigenvariety also extends to those points. (See also Gulotta [Reference GulottaGul19] for an analogous construction extending equidimensional eigenvarieties.) Consequently, we can compute the matrix coefficients of ![]() $U_p$ in an explicit basis for the space of forms over the ‘boundary weights’ given by monomials in the matrix coefficients of the dimension
$U_p$ in an explicit basis for the space of forms over the ‘boundary weights’ given by monomials in the matrix coefficients of the dimension ![]() ${n(n-1)}/2$ maximal lower unipotent subgroup of
${n(n-1)}/2$ maximal lower unipotent subgroup of ![]() ${GL}_n(\mathbb {Q}_p)$. Explicit bounds on those matrix coefficients arise directly from the proof of complete continuity of
${GL}_n(\mathbb {Q}_p)$. Explicit bounds on those matrix coefficients arise directly from the proof of complete continuity of ![]() $U_p$. In the case
$U_p$. In the case ![]() $n=2$, the procedure and output are identical to those of Liu–Wan–Xiao and Johansson–Newton.
$n=2$, the procedure and output are identical to those of Liu–Wan–Xiao and Johansson–Newton.
The proof of part (ii) of Theorem 1.1.2 requires a detailed analysis of ![]() $p$-adic automorphic representations which may be of independent interest. As in the proof of Proposition 3.22 of [Reference Liu, Wan and XiaoLWX17], we would like to carry out the following steps.
$p$-adic automorphic representations which may be of independent interest. As in the proof of Proposition 3.22 of [Reference Liu, Wan and XiaoLWX17], we would like to carry out the following steps.
(i) Construct a subspace
 $S$ of
$S$ of  $\mathscr {S}_w(G,\mathscr {U})$ of dimension
$\mathscr {S}_w(G,\mathscr {U})$ of dimension  $hp^{c_{(1)}+2c_{(2)}+\dotsb +(n-1)c_{(n-1)}-{n(n-1)}/2}d_t$ which can be thought of as the space of ‘classical forms of weight
$hp^{c_{(1)}+2c_{(2)}+\dotsb +(n-1)c_{(n-1)}-{n(n-1)}/2}d_t$ which can be thought of as the space of ‘classical forms of weight  $w$ and minimal level’.
$w$ and minimal level’.(ii) Prove that
 $U_p$ is injective on
$U_p$ is injective on  $S$, so that all eigenforms in
$S$, so that all eigenforms in  $S$ have finite slope.
$S$ have finite slope.(iii) Prove that finite-slope eigenforms in
 $S$ have slope bounded above by
$S$ have slope bounded above by  $l(t)$.
$l(t)$.
In general, it is a fact that a classical form ![]() $f$ is finite-slope if and only if the local component
$f$ is finite-slope if and only if the local component ![]() $\pi _{f,p}$ at
$\pi _{f,p}$ at ![]() $p$ of its associated automorphic representation is a principal series representation of
$p$ of its associated automorphic representation is a principal series representation of ![]() ${GL}_n(\mathbb {Q}_p)$. For
${GL}_n(\mathbb {Q}_p)$. For ![]() $n=2$ as in Liu–Wan–Xiao, the upper bound then follows from the fact that
$n=2$ as in Liu–Wan–Xiao, the upper bound then follows from the fact that ![]() $\pi _{f,p}$ is a principal series if the level of
$\pi _{f,p}$ is a principal series if the level of ![]() $f$ equals the conductor of its central character, which can be checked (as in Loeffler and Weinstein [Reference Loeffler and WeinsteinLW12]) by comparing its level to that of the new vectors in each of the three possible Bernstein–Zelevinsky classes of representations (principal series, special, and supercuspidal), those new vectors having been written down by Casselman [Reference CasselmanCas73]. The dimension of the space of such
$f$ equals the conductor of its central character, which can be checked (as in Loeffler and Weinstein [Reference Loeffler and WeinsteinLW12]) by comparing its level to that of the new vectors in each of the three possible Bernstein–Zelevinsky classes of representations (principal series, special, and supercuspidal), those new vectors having been written down by Casselman [Reference CasselmanCas73]. The dimension of the space of such ![]() $f$ is easy to count.
$f$ is easy to count.
To detect when ![]() $\pi _{f,p}$ is a principal series for all
$\pi _{f,p}$ is a principal series for all ![]() $n$ without brute-forcing through Bernstein–Zelevinsky classes, we use Roche's analysis of principal series types [Reference RocheRoc98]. (As a historical note, much of the analysis we rely on was already done for
$n$ without brute-forcing through Bernstein–Zelevinsky classes, we use Roche's analysis of principal series types [Reference RocheRoc98]. (As a historical note, much of the analysis we rely on was already done for ![]() ${GL}_n$ by Howe and Moy; see, e.g., [Reference Howe and MoyHM90]. For more information on types in general, see Fintzen [Reference FintzenFin21].) For a smooth character
${GL}_n$ by Howe and Moy; see, e.g., [Reference Howe and MoyHM90]. For more information on types in general, see Fintzen [Reference FintzenFin21].) For a smooth character ![]() $\chi$ of
$\chi$ of ![]() $T(\mathbb {Q}_p)$, Roche gives a subgroup
$T(\mathbb {Q}_p)$, Roche gives a subgroup ![]() $J\subset {GL}_n(\mathbb {Z}_p)$ and an extension of
$J\subset {GL}_n(\mathbb {Z}_p)$ and an extension of ![]() $\chi |_{T(\mathbb {Z}_p)}$ to
$\chi |_{T(\mathbb {Z}_p)}$ to ![]() $J$ such that an irreducible representation
$J$ such that an irreducible representation ![]() $\pi$ of
$\pi$ of ![]() ${GL}_n(\mathbb {Q}_p)$ is a principal series associated to an unramified twist of
${GL}_n(\mathbb {Q}_p)$ is a principal series associated to an unramified twist of ![]() $\chi$ if and only if
$\chi$ if and only if ![]() $\pi$ contains a vector on which
$\pi$ contains a vector on which ![]() $J$ acts by
$J$ acts by ![]() $\chi$, which we will call a
$\chi$, which we will call a ![]() $(J,\chi )$-vector.
$(J,\chi )$-vector.
To proceed, we construct a space of forms ![]() $S$ so that for any eigenform
$S$ so that for any eigenform ![]() $f\in S$,
$f\in S$, ![]() $\pi _{f,p}$ admits a nontrivial map from
$\pi _{f,p}$ admits a nontrivial map from ![]() $\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$, where
$\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$, where ![]() $\operatorname {Iw}_p$ is the subgroup of
$\operatorname {Iw}_p$ is the subgroup of ![]() ${GL}_n(\mathbb {Z}_p)$ of matrices that are upper triangular mod
${GL}_n(\mathbb {Z}_p)$ of matrices that are upper triangular mod ![]() $p$, hence contains a
$p$, hence contains a ![]() $(J,\chi )$-vector and is a principal series. The
$(J,\chi )$-vector and is a principal series. The ![]() $S$ we construct is not a priori a subspace of
$S$ we construct is not a priori a subspace of ![]() $\mathscr {S}_w(G,\mathscr {U})$, but we can show that it embeds into
$\mathscr {S}_w(G,\mathscr {U})$, but we can show that it embeds into ![]() $\mathscr {S}_w(G,\mathscr {U})$ using Emerton's locally analytic Jacquet functor. The dimension of
$\mathscr {S}_w(G,\mathscr {U})$ using Emerton's locally analytic Jacquet functor. The dimension of ![]() $S$ is proportional to the product of
$S$ is proportional to the product of ![]() $\dim \operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$, which is a function of the valuations
$\dim \operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$, which is a function of the valuations ![]() $v(T_i)$, and the dimension of the algebraic representation of
$v(T_i)$, and the dimension of the algebraic representation of ![]() ${GL}_n$ of highest weight corresponding to the algebraic part of
${GL}_n$ of highest weight corresponding to the algebraic part of ![]() $(T_1,\dotsc,T_{n-1})$, which is a polynomial of total degree
$(T_1,\dotsc,T_{n-1})$, which is a polynomial of total degree ![]() ${n(n-1)}/2$ in the weight parameters by a combinatorial calculation. This covers steps (i) and (ii). Then we do step (iii) by constructing companion forms
${n(n-1)}/2$ in the weight parameters by a combinatorial calculation. This covers steps (i) and (ii). Then we do step (iii) by constructing companion forms ![]() $f^w$ of
$f^w$ of ![]() $f$ for each
$f$ for each ![]() $w\in S_n$ such that the slopes of all the companion forms sum to
$w\in S_n$ such that the slopes of all the companion forms sum to ![]() $l(t)$.
$l(t)$.
We can also use ![]() $S$ to help understand the standard classical subspaces of
$S$ to help understand the standard classical subspaces of ![]() $\mathscr {S}_w(G,\mathscr {U})$. Specifically, when the pair
$\mathscr {S}_w(G,\mathscr {U})$. Specifically, when the pair ![]() $(J,\chi )$ arising from the weight
$(J,\chi )$ arising from the weight ![]() $w$ satisfies the additional technical condition that
$w$ satisfies the additional technical condition that ![]() $\operatorname {cond}(\chi _i)<2\operatorname {cond}(\chi _j)$ for all
$\operatorname {cond}(\chi _i)<2\operatorname {cond}(\chi _j)$ for all ![]() $i\neq j$ with
$i\neq j$ with ![]() $i,j\neq n$, we show by a Mackey theory calculation that
$i,j\neq n$, we show by a Mackey theory calculation that ![]() $\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$ is an irreducible representation of
$\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$ is an irreducible representation of ![]() $\operatorname {Iw}_p$. In this case,
$\operatorname {Iw}_p$. In this case, ![]() $S$ can be embedded into a classical subspace of
$S$ can be embedded into a classical subspace of ![]() $\mathscr {S}_w(G,\mathscr {U})$, and we can show the following.
$\mathscr {S}_w(G,\mathscr {U})$, and we can show the following.
Theorem 1.2.1 The space ![]() $S$ is precisely the space of finite-slope classical forms of weight
$S$ is precisely the space of finite-slope classical forms of weight ![]() $w$.
$w$.
To do this, we slightly refine the setup of the Bellaïche–Chenevier construction of the eigenvariety in order to precisely define the sense in which ![]() $S$ is ‘minimal level’. Consequently, our upper bound is the best possible with existing methods.
$S$ is ‘minimal level’. Consequently, our upper bound is the best possible with existing methods.
Note that the reason the Newton polygon upper bound resulting from this procedure fails to be sharp when ![]() $n>2$ is that it is obtained solely by bounding the slopes of all classical eigenforms, i.e. those in
$n>2$ is that it is obtained solely by bounding the slopes of all classical eigenforms, i.e. those in ![]() $S$. When
$S$. When ![]() $n=2$, the classical forms account for all of the smallest slopes in the Newton polygon, so our argument recovers Proposition 3.22 of [Reference Liu, Wan and XiaoLWX17] and, hence, their upper bound. When
$n=2$, the classical forms account for all of the smallest slopes in the Newton polygon, so our argument recovers Proposition 3.22 of [Reference Liu, Wan and XiaoLWX17] and, hence, their upper bound. When ![]() $n>2$, we expect there to exist nonclassical forms with small slopes which decrease the growth rate of the Newton polygon and which there is no known way to detect. We suspect that if there were a reliable way to find nonclassical forms with small slopes, combining it with our bounds would be sufficient to prove the full version of Conjecture 1.1.1 for all
$n>2$, we expect there to exist nonclassical forms with small slopes which decrease the growth rate of the Newton polygon and which there is no known way to detect. We suspect that if there were a reliable way to find nonclassical forms with small slopes, combining it with our bounds would be sufficient to prove the full version of Conjecture 1.1.1 for all ![]() $n$.
$n$.
1.3 Organization
In § 2, we describe the construction of the eigenvarieties we are interested in, primarily following Chenevier [Reference ChenevierChe04] and Bellaïche and Chenevier [Reference Bellaïche and ChenevierBC09], adding some extra details in places of particular importance to us. For example, we give a slightly more general definition of local analyticity of ![]() $p$-adic automorphic forms which allows different radii of analyticity for different coordinates and prove that it works, which aids in proving Theorem 1.2.1.
$p$-adic automorphic forms which allows different radii of analyticity for different coordinates and prove that it works, which aids in proving Theorem 1.2.1.
In § 3, we analyze the subspaces of classical automorphic forms of locally algebraic weights and the automorphic representations they generate, thus carrying out steps (i) and (ii), and proving Theorem 3.6.8, a precise version of Theorem 1.2.1.
In § 4, we carry out Johansson and Newton's method and step (iii) to prove Theorem 1.1.2 and Theorem 1.1.3.
Finally, in § 5, we state and prove a precise version of Theorem 1.1.4 and discuss other geometric consequences of Theorem 1.1.2. Unlike in the Liu–Wan–Xiao setting, for higher-dimensional eigenvarieties, the lower and upper bounds do not match at any point on the Newton polygon, and we cannot expect them to, because there exist (probably) nonclassical forms of slopes smaller than some classical forms. As a result, we cannot prove the equivalent of Conjecture 1.1.1 for these higher-dimensional eigenvarieties. However, we can prove that certain boundary sections of the eigenvariety decompose into many disconnected components (with the caveat that we cannot verify that those sections are nonempty, although in fact we expect them to be everything).
2. Bellaïche–Chenevier eigenvarieties for definite unitary groups
Let ![]() $p$ be a prime. Let
$p$ be a prime. Let ![]() $q=4$ if
$q=4$ if ![]() $p=2$ and
$p=2$ and ![]() $q=p$ otherwise. In this section, we go through the construction of eigenvarieties for definite unitary groups in the language of Chenevier and Bellaïche–Chenevier. In § 2.1, we define the groups and the spaces of
$q=p$ otherwise. In this section, we go through the construction of eigenvarieties for definite unitary groups in the language of Chenevier and Bellaïche–Chenevier. In § 2.1, we define the groups and the spaces of ![]() $p$-adic automorphic forms we are interested in, notably including the spaces of classical forms whose interpolation was the original motivation for this construction. In § 2.2, we describe the properties of the space of
$p$-adic automorphic forms we are interested in, notably including the spaces of classical forms whose interpolation was the original motivation for this construction. In § 2.2, we describe the properties of the space of ![]() $p$-adic weights. In § 2.3, we define certain coordinates on spaces of functions on the Iwahori subgroup
$p$-adic weights. In § 2.3, we define certain coordinates on spaces of functions on the Iwahori subgroup ![]() $\operatorname {Iw}_p$, using a convenient hybrid of the language of Chenevier and Bellaïche–Chenevier. In § 2.4, we introduce systematic notation for certain subgroups of
$\operatorname {Iw}_p$, using a convenient hybrid of the language of Chenevier and Bellaïche–Chenevier. In § 2.4, we introduce systematic notation for certain subgroups of ![]() $\operatorname {Iw}_p$. In § 2.5, we define the space of families of
$\operatorname {Iw}_p$. In § 2.5, we define the space of families of ![]() $p$-adic automorphic forms over weight space, along with subspaces of locally analytic families. In § 2.6, we define
$p$-adic automorphic forms over weight space, along with subspaces of locally analytic families. In § 2.6, we define ![]() $U_p$-operators and work through their various important properties in great detail. In § 2.7, we define the desired eigenvarieties.
$U_p$-operators and work through their various important properties in great detail. In § 2.7, we define the desired eigenvarieties.
2.1  $p$-adic automorphic forms
$p$-adic automorphic forms
Let ![]() $E$ be an imaginary quadratic field over
$E$ be an imaginary quadratic field over ![]() $\mathbb {Q}$, and
$\mathbb {Q}$, and ![]() $D$ a central simple
$D$ a central simple ![]() $E$-algebra of rank
$E$-algebra of rank ![]() $n^2$ which has an involution
$n^2$ which has an involution ![]() $x\mapsto x^*$ extending the nontrivial automorphism
$x\mapsto x^*$ extending the nontrivial automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $E$ over
$E$ over ![]() $\mathbb {Q}$ (for example,
$\mathbb {Q}$ (for example, ![]() $D$ could be
$D$ could be ![]() ${GL}_n(E)$, in which case
${GL}_n(E)$, in which case ![]() $x^*$ would be
$x^*$ would be ![]() $\sigma (x)^T$). Let
$\sigma (x)^T$). Let ![]() $G/\mathbb {Q}$ be the group whose
$G/\mathbb {Q}$ be the group whose ![]() $R$-points, for a
$R$-points, for a ![]() $\mathbb {Q}$-algebra
$\mathbb {Q}$-algebra ![]() $R$, are
$R$, are
Note that ![]() $G(\mathbb {Q}_p)$ is isomorphic to
$G(\mathbb {Q}_p)$ is isomorphic to ![]() ${GL}_n(\mathbb {Q}_p)$ if
${GL}_n(\mathbb {Q}_p)$ if ![]() $p$ is split in
$p$ is split in ![]() $E$ (since then
$E$ (since then ![]() $E_p\cong \mathbb {Q}_p\oplus \mathbb {Q}_p$ with
$E_p\cong \mathbb {Q}_p\oplus \mathbb {Q}_p$ with ![]() $\sigma$ switching factors) and to
$\sigma$ switching factors) and to ![]() $U_n(\mathbb {Q}_p)$ if
$U_n(\mathbb {Q}_p)$ if ![]() $p$ is inert in
$p$ is inert in ![]() $E$; we assume that
$E$; we assume that ![]() $p$ is split in
$p$ is split in ![]() $E$ and
$E$ and ![]() $G(\mathbb {Q}_p)\cong {GL}_n(\mathbb {Q}_p)$. In addition,
$G(\mathbb {Q}_p)\cong {GL}_n(\mathbb {Q}_p)$. In addition, ![]() $G(\mathbb {R})\cong U_{s,t}(\mathbb {R})$ for
$G(\mathbb {R})\cong U_{s,t}(\mathbb {R})$ for ![]() $(s,t)$ the signature of
$(s,t)$ the signature of ![]() $Q(x)=xx^*$; we assume that
$Q(x)=xx^*$; we assume that ![]() $Q(x)$ has signature
$Q(x)$ has signature ![]() $(n,0)$ or
$(n,0)$ or ![]() $(0,n)$, so that
$(0,n)$, so that ![]() $G(\mathbb {R})$ is compact.
$G(\mathbb {R})$ is compact.
As usual, we write ![]() $B$ and
$B$ and ![]() $\overline {B}$ for the upper and lower triangular Borel subgroups of
$\overline {B}$ for the upper and lower triangular Borel subgroups of ![]() ${GL}_n$, respectively,
${GL}_n$, respectively, ![]() $T$ for the diagonal torus, and
$T$ for the diagonal torus, and ![]() $N$ and
$N$ and ![]() $\overline {N}$ for the upper and lower unipotent subgroups of
$\overline {N}$ for the upper and lower unipotent subgroups of ![]() ${GL}_n$, respectively.
${GL}_n$, respectively.
Write ![]() $\mathbb {A}=\mathbb {A}_\mathbb {Q}$,
$\mathbb {A}=\mathbb {A}_\mathbb {Q}$, ![]() $\mathbb {A}_f$ for the finite adeles of
$\mathbb {A}_f$ for the finite adeles of ![]() $\mathbb {A}$, and
$\mathbb {A}$, and ![]() $\mathbb {A}_f^p$ for the finite adeles trivial at
$\mathbb {A}_f^p$ for the finite adeles trivial at ![]() $p$. Let
$p$. Let ![]() $\mathscr {U}$ be a compact open subgroup of
$\mathscr {U}$ be a compact open subgroup of ![]() $G(\mathbb {A}_f)$ of the form
$G(\mathbb {A}_f)$ of the form ![]() $\mathscr {U}_p\times \mathscr {U}^p$, where
$\mathscr {U}_p\times \mathscr {U}^p$, where ![]() $\mathscr {U}_p$ is a compact open subgroup of
$\mathscr {U}_p$ is a compact open subgroup of ![]() $G(\mathbb {Q}_p)$ (called the wild level structure) and
$G(\mathbb {Q}_p)$ (called the wild level structure) and ![]() $\mathscr {U}^p$ a compact open subgroup of
$\mathscr {U}^p$ a compact open subgroup of ![]() $G(\mathbb {A}_f^p)$ (called the tame level structure). We can now define
$G(\mathbb {A}_f^p)$ (called the tame level structure). We can now define ![]() $V$-valued automorphic forms for any
$V$-valued automorphic forms for any ![]() $\mathscr {U}_p$-module
$\mathscr {U}_p$-module ![]() $V$.
$V$.
In general, all our group and monoid actions will be left actions.
Definition 2.1.1 If ![]() $V$ is a
$V$ is a ![]() $k[\mathscr {U}_p]$-module for any field
$k[\mathscr {U}_p]$-module for any field ![]() $k$, write
$k$, write ![]() $V(G,\mathscr {U})$ for the
$V(G,\mathscr {U})$ for the ![]() $k$-vector space of maps
$k$-vector space of maps
such that ![]() $f(xu)=u_p^{-1}f(x)$ for all
$f(xu)=u_p^{-1}f(x)$ for all ![]() $x\in G(\mathbb {Q})\backslash G(\mathbb {A}_f)$ and
$x\in G(\mathbb {Q})\backslash G(\mathbb {A}_f)$ and ![]() $u\in \mathscr {U}$. Equivalently,
$u\in \mathscr {U}$. Equivalently,
where the action of ![]() $\mathscr {U}$ on
$\mathscr {U}$ on ![]() $\text {Hom}_{set}(G(\mathbb {Q})\backslash G(\mathbb {A}_f), k)$ is right translation and the action on
$\text {Hom}_{set}(G(\mathbb {Q})\backslash G(\mathbb {A}_f), k)$ is right translation and the action on ![]() $V$ is through
$V$ is through ![]() $\mathscr {U}_p$. For any submonoid
$\mathscr {U}_p$. For any submonoid ![]() $\mathscr {U}'\supseteq \mathscr {U}$ of
$\mathscr {U}'\supseteq \mathscr {U}$ of ![]() $G(\mathbb {A}_f)$ which has an action on
$G(\mathbb {A}_f)$ which has an action on ![]() $V$ that is trivial for
$V$ that is trivial for ![]() $\mathscr {U}$,
$\mathscr {U}$, ![]() $V(G,\mathscr {U})$ is a
$V(G,\mathscr {U})$ is a ![]() $\mathscr {U}'$-module with action
$\mathscr {U}'$-module with action ![]() $(uf)(x)=u_pf(xu)$.
$(uf)(x)=u_pf(xu)$.
We frequently express examples using the following notation: if ![]() $B\subseteq H$ are groups,
$B\subseteq H$ are groups, ![]() $R$ is a ring, and
$R$ is a ring, and ![]() $s:B\to R^\times$ is a character, let
$s:B\to R^\times$ is a character, let
and if ![]() $P$ is a property of some functions
$P$ is a property of some functions ![]() $f\in \operatorname {Ind}_B^Hs$ which is invariant under left translation by
$f\in \operatorname {Ind}_B^Hs$ which is invariant under left translation by ![]() $H$, let
$H$, let
Then ![]() $\operatorname {Ind}_B^{H,P}s$ is an
$\operatorname {Ind}_B^{H,P}s$ is an ![]() $R$-module with a (left) action of
$R$-module with a (left) action of ![]() $H$ given by
$H$ given by ![]() $(hf)(x)=f(h^{-1}x)$ for all
$(hf)(x)=f(h^{-1}x)$ for all ![]() $h,x\in H$. Note that our left/right conventions for induction are unusual for convenience.
$h,x\in H$. Note that our left/right conventions for induction are unusual for convenience.
For example, if ![]() $k$ is a field,
$k$ is a field, ![]() $t=(t_1,\dotsc,t_n)\in \mathbb {Z}^n$, and we write
$t=(t_1,\dotsc,t_n)\in \mathbb {Z}^n$, and we write ![]() $\operatorname {diag}(d_1,\dotsc,d_n)$ for the diagonal matrix with entries
$\operatorname {diag}(d_1,\dotsc,d_n)$ for the diagonal matrix with entries ![]() $d_1,\dotsc,d_n$ along the diagonal, we can interpret
$d_1,\dotsc,d_n$ along the diagonal, we can interpret ![]() $t$ as the character of the diagonal torus
$t$ as the character of the diagonal torus ![]() $T(k)$ of
$T(k)$ of ![]() ${GL}_n(k)$ taking
${GL}_n(k)$ taking ![]() $\operatorname {diag}(d_1,\dotsc,d_n)$ to
$\operatorname {diag}(d_1,\dotsc,d_n)$ to ![]() $\prod _{i=1}^n d_i^{t_i}$, and thus as the character of the upper triangular Borel
$\prod _{i=1}^n d_i^{t_i}$, and thus as the character of the upper triangular Borel ![]() $B(k)$ obtained by reducing to
$B(k)$ obtained by reducing to ![]() $T(k)$ and applying
$T(k)$ and applying ![]() $t$. In the event that
$t$. In the event that ![]() $t_1\ge \dotsb \ge t_n$, the
$t_1\ge \dotsb \ge t_n$, the ![]() $k$-vector space
$k$-vector space
where ‘alg’ stands for algebraic (i.e. ![]() $f:{GL}_n(k)\to k$ comes from an element of
$f:{GL}_n(k)\to k$ comes from an element of ![]() $k[{GL}_n]$), is the irreducible algebraic representation of
$k[{GL}_n]$), is the irreducible algebraic representation of ![]() ${GL}_n$ over
${GL}_n$ over ![]() $k$ of highest weight
$k$ of highest weight ![]() $t$ (see § 12.1.3 of [Reference Goodman and WallachGW09] and Proposition 2.2.1 of [Reference ChenevierChe04]). We call this representation
$t$ (see § 12.1.3 of [Reference Goodman and WallachGW09] and Proposition 2.2.1 of [Reference ChenevierChe04]). We call this representation ![]() $S_t(k)$. Then
$S_t(k)$. Then ![]() $S_t(k)(G,\mathscr {U})$ is the space of classical
$S_t(k)(G,\mathscr {U})$ is the space of classical ![]() $p$-adic automorphic forms on
$p$-adic automorphic forms on ![]() $G$ of weight
$G$ of weight ![]() $t$ and level
$t$ and level ![]() $\mathscr {U}$ with coefficients in
$\mathscr {U}$ with coefficients in ![]() $k$.
$k$.
One way to picture ![]() $V(G,\mathscr {U})$ is as follows. By the generalized finiteness of class groups (see Theorem 5.1 of [Reference BorelBor63]), the set
$V(G,\mathscr {U})$ is as follows. By the generalized finiteness of class groups (see Theorem 5.1 of [Reference BorelBor63]), the set ![]() $G(\mathbb {Q})\backslash G(\mathbb {A}_f)/\mathscr {U}$ is finite. Fix double coset representatives
$G(\mathbb {Q})\backslash G(\mathbb {A}_f)/\mathscr {U}$ is finite. Fix double coset representatives ![]() $x_1,\dotsc,x_h\in G(\mathbb {A}_f)$. Then we have an isomorphism
$x_1,\dotsc,x_h\in G(\mathbb {A}_f)$. Then we have an isomorphism
 \begin{align*} V(G,\mathscr{U}) & \xrightarrow{\sim} \bigoplus_{i=1}^h V^{x_i^{-1}G(\mathbb{Q})x_i\cap\mathscr{U}} \\ f & \mapsto (f(x_1),\dotsc,f(x_h)). \end{align*}
\begin{align*} V(G,\mathscr{U}) & \xrightarrow{\sim} \bigoplus_{i=1}^h V^{x_i^{-1}G(\mathbb{Q})x_i\cap\mathscr{U}} \\ f & \mapsto (f(x_1),\dotsc,f(x_h)). \end{align*}
Because ![]() $G(\mathbb {R})\cong U_n(\mathbb {R})$ is compact,
$G(\mathbb {R})\cong U_n(\mathbb {R})$ is compact, ![]() $G(\mathbb {Q})$ is discrete in
$G(\mathbb {Q})$ is discrete in ![]() $G(\mathbb {A}_f)$ (see, e.g., Proposition 1.4 of [Reference GrossGro99] or Proposition 3.1.2 of [Reference LoefflerLoe10]). Since, in addition,
$G(\mathbb {A}_f)$ (see, e.g., Proposition 1.4 of [Reference GrossGro99] or Proposition 3.1.2 of [Reference LoefflerLoe10]). Since, in addition, ![]() $\mathscr {U}$ is compact, the group
$\mathscr {U}$ is compact, the group ![]() $x_i^{-1}G(\mathbb {Q})x_i\cap \mathscr {U}$ is always finite, and it is trivial if
$x_i^{-1}G(\mathbb {Q})x_i\cap \mathscr {U}$ is always finite, and it is trivial if ![]() $\mathscr {U}^p$ is sufficiently small. (For example, by Proposition 4.1.1 of [Reference ChenevierChe04], there is an integer
$\mathscr {U}^p$ is sufficiently small. (For example, by Proposition 4.1.1 of [Reference ChenevierChe04], there is an integer ![]() $e_n$ depending only on
$e_n$ depending only on ![]() $n$ such that
$n$ such that ![]() $x_i^{-1}G(\mathbb {Q})x_i\cap \mathscr {U}$ is guaranteed to be trivial if the image of
$x_i^{-1}G(\mathbb {Q})x_i\cap \mathscr {U}$ is guaranteed to be trivial if the image of ![]() $\mathscr {U}^p$ in
$\mathscr {U}^p$ in ![]() $G(\mathbb {Q}_l)$ is contained in
$G(\mathbb {Q}_l)$ is contained in ![]() $\Gamma (l)=\{g\in {GL}_n(\mathbb {Z}_p)\mid g\equiv 1\pmod {l}\}$ for some prime
$\Gamma (l)=\{g\in {GL}_n(\mathbb {Z}_p)\mid g\equiv 1\pmod {l}\}$ for some prime ![]() $l\nmid e_n$.) It is this fact that makes the construction of the eigenvariety for
$l\nmid e_n$.) It is this fact that makes the construction of the eigenvariety for ![]() $G$ so sleek.
$G$ so sleek.
When convenient, we assume that ![]() $\mathscr {U}^p$ is sufficiently small (sometimes called ‘neat’ in the literature) and, thus,
$\mathscr {U}^p$ is sufficiently small (sometimes called ‘neat’ in the literature) and, thus, ![]() $V(G,\mathscr {U})\cong V^h$. As in Remark 2.14 of [Reference Liu, Wan and XiaoLWX17], this does not affect our results, because the eigenvariety for any
$V(G,\mathscr {U})\cong V^h$. As in Remark 2.14 of [Reference Liu, Wan and XiaoLWX17], this does not affect our results, because the eigenvariety for any ![]() $\mathscr {U}^p$ is a union of connected components of the eigenvariety for a sufficiently small subgroup of
$\mathscr {U}^p$ is a union of connected components of the eigenvariety for a sufficiently small subgroup of ![]() $\mathscr {U}^p$.
$\mathscr {U}^p$.
2.2 Weight space
A weight is a continuous character of ![]() $T(\mathbb {Z}_p)\cong (\mathbb {Z}_p^\times )^n$. Such a weight can be viewed as a character of
$T(\mathbb {Z}_p)\cong (\mathbb {Z}_p^\times )^n$. Such a weight can be viewed as a character of ![]() $B(\mathbb {Z}_p)$ by reduction to
$B(\mathbb {Z}_p)$ by reduction to ![]() $T(\mathbb {Z}_p)$. (In the introduction, we defined a weight instead to be a character of
$T(\mathbb {Z}_p)$. (In the introduction, we defined a weight instead to be a character of ![]() $(\mathbb {Z}_p^\times )^{n-1}$, that is, a character of
$(\mathbb {Z}_p^\times )^{n-1}$, that is, a character of ![]() $T(\mathbb {Z}_p)$ that is trivial on the last
$T(\mathbb {Z}_p)$ that is trivial on the last ![]() $\mathbb {Z}_p^\times$-factor. We will go back to restricting possible weights to the subset that is trivial on the last
$\mathbb {Z}_p^\times$-factor. We will go back to restricting possible weights to the subset that is trivial on the last ![]() $\mathbb {Z}_p^\times$-factor whenever it is convenient, because any character of
$\mathbb {Z}_p^\times$-factor whenever it is convenient, because any character of ![]() $T(\mathbb {Z}_p)$ can be twisted by a central character to one in this restricted subset, and central characters do not change spaces of automorphic forms in an interesting way.)
$T(\mathbb {Z}_p)$ can be twisted by a central character to one in this restricted subset, and central characters do not change spaces of automorphic forms in an interesting way.)
The weight space ![]() $\mathscr {W}^n$ is the rigid analytic space over
$\mathscr {W}^n$ is the rigid analytic space over ![]() $\mathbb {Q}_p$ such that for any affinoid
$\mathbb {Q}_p$ such that for any affinoid ![]() $\mathbb {Q}_p$-algebra
$\mathbb {Q}_p$-algebra ![]() $A$,
$A$, ![]() $\mathscr {W}^n(A)$ is the set of continuous characters
$\mathscr {W}^n(A)$ is the set of continuous characters ![]() $(\mathbb {Z}_p^\times )^n\to A^\times$. Let
$(\mathbb {Z}_p^\times )^n\to A^\times$. Let ![]() $\Delta ^n=((\mathbb {Z}/q\mathbb {Z})^\times )^n$. We have
$\Delta ^n=((\mathbb {Z}/q\mathbb {Z})^\times )^n$. We have
so an ![]() $A$-point of
$A$-point of ![]() $\mathscr {W}^n$ is determined by a character of
$\mathscr {W}^n$ is determined by a character of ![]() $\Delta ^n$ and a character of
$\Delta ^n$ and a character of ![]() $(1+q\mathbb {Z}_p)^n$. Furthermore, a character
$(1+q\mathbb {Z}_p)^n$. Furthermore, a character ![]() $s$ of
$s$ of ![]() $(1+q\mathbb {Z}_p)^n$ is determined by the values
$(1+q\mathbb {Z}_p)^n$ is determined by the values ![]() $T_i(s)=s(1,\dotsc,1,\exp (q),1,\dotsc,1)-1$ (where the
$T_i(s)=s(1,\dotsc,1,\exp (q),1,\dotsc,1)-1$ (where the ![]() $i$th entry is
$i$th entry is ![]() $\exp (q)$ and all the others are
$\exp (q)$ and all the others are ![]() $1$), since
$1$), since ![]() $\exp (q)$ topologically generates
$\exp (q)$ topologically generates ![]() $1+q\mathbb {Z}_p$. By Lemma 1 of [Reference BuzzardBuz04], the coordinates
$1+q\mathbb {Z}_p$. By Lemma 1 of [Reference BuzzardBuz04], the coordinates ![]() $(T_1,\dotsc,T_n)\in A^n$ come from an
$(T_1,\dotsc,T_n)\in A^n$ come from an ![]() $A$-point of
$A$-point of ![]() $\mathscr {W}^n$ precisely when they are topologically nilpotent. Thus
$\mathscr {W}^n$ precisely when they are topologically nilpotent. Thus ![]() $\mathscr {W}^n$ can be pictured as a finite disjoint union of
$\mathscr {W}^n$ can be pictured as a finite disjoint union of ![]() $\varphi (q)$ open unit polydiscs with coordinates
$\varphi (q)$ open unit polydiscs with coordinates ![]() $(T_1,\dotsc,T_n)$, one for each tame character of
$(T_1,\dotsc,T_n)$, one for each tame character of ![]() $\Delta ^n$.
$\Delta ^n$.
We use
to denote the universal character of ![]() $(\mathbb {Z}_p^\times )^n$ and
$(\mathbb {Z}_p^\times )^n$ and ![]() $\Lambda ^n$ to denote the Iwasawa algebra
$\Lambda ^n$ to denote the Iwasawa algebra
where ![]() $T_i=[(1,\dotsc,1,\exp (q),1,\dotsc,1)]-1$ with the
$T_i=[(1,\dotsc,1,\exp (q),1,\dotsc,1)]-1$ with the ![]() $\exp (q)$ in the
$\exp (q)$ in the ![]() $i$th position; then continuous homomorphisms
$i$th position; then continuous homomorphisms ![]() $\chi :\Lambda ^n\to A$ are in bijection with
$\chi :\Lambda ^n\to A$ are in bijection with ![]() $A$-points of
$A$-points of ![]() $\mathscr {W}^n$ via
$\mathscr {W}^n$ via ![]() $\chi \mapsto \chi \circ [\cdot ]$.
$\chi \mapsto \chi \circ [\cdot ]$.
Example 2.2.1 (Dominant algebraic weights)
If ![]() $t_1\ge \dotsb \ge t_n$ are integers, the algebraic character
$t_1\ge \dotsb \ge t_n$ are integers, the algebraic character ![]() $(d_1,\dotsc,d_n)\mapsto \prod _{i=1}^n d_i^{t_i}$ is a
$(d_1,\dotsc,d_n)\mapsto \prod _{i=1}^n d_i^{t_i}$ is a ![]() $\mathbb {Q}_p$-point of
$\mathbb {Q}_p$-point of ![]() $\mathscr {W}^n$ with
$\mathscr {W}^n$ with ![]() $T$-coordinates
$T$-coordinates
such that the valuation of ![]() $T_i=\exp (t_iq)-1$ is
$T_i=\exp (t_iq)-1$ is
We remark that the weight polydisc in which this character appears is determined by ![]() $(t_1,\dotsc,t_n)\pmod {\varphi (q)}$.
$(t_1,\dotsc,t_n)\pmod {\varphi (q)}$.
If ![]() $\chi :\mathbb {Z}_p^\times \to \mathbb {C}_p^\times$ is a finite-order character, we will borrow the following slightly nonstandard definition of the conductor
$\chi :\mathbb {Z}_p^\times \to \mathbb {C}_p^\times$ is a finite-order character, we will borrow the following slightly nonstandard definition of the conductor ![]() $\operatorname {cond}(\chi )$ of
$\operatorname {cond}(\chi )$ of ![]() $\chi$ from [Reference RocheRoc98, § 3]: it is the least positive integer
$\chi$ from [Reference RocheRoc98, § 3]: it is the least positive integer ![]() $n$ such that
$n$ such that ![]() $1+p^n\mathbb {Z}_p\subset \ker (\chi )$. Thus, the conductor of the trivial character is
$1+p^n\mathbb {Z}_p\subset \ker (\chi )$. Thus, the conductor of the trivial character is ![]() $1$ but the conductor of any other character is the same as with the usual definition.
$1$ but the conductor of any other character is the same as with the usual definition.
Example 2.2.2 (Locally algebraic weights)
If ![]() $t_1\ge \dotsb \ge t_n$ are integers and
$t_1\ge \dotsb \ge t_n$ are integers and ![]() $\chi _1,\dotsc,\chi _n$ are finite-order characters
$\chi _1,\dotsc,\chi _n$ are finite-order characters ![]() $\mathbb {Z}_p^\times \to \mathbb {C}_p^\times$, the ‘locally algebraic’ character
$\mathbb {Z}_p^\times \to \mathbb {C}_p^\times$, the ‘locally algebraic’ character
 \[ (d_1,\dotsc,d_n)\mapsto\prod_{i=1}^n\chi_i(d_i)d_i^{t_i} \]
\[ (d_1,\dotsc,d_n)\mapsto\prod_{i=1}^n\chi_i(d_i)d_i^{t_i} \]
is a ![]() $\mathbb {C}_p$-point of
$\mathbb {C}_p$-point of ![]() $\mathscr {W}^n$. If
$\mathscr {W}^n$. If ![]() $\chi _i$ is nontrivial with conductor
$\chi _i$ is nontrivial with conductor ![]() $c_i$, we have
$c_i$, we have
 \[
v(T_i)=v(\chi_i(\exp(q))\exp(t_iq)-1)=\begin{cases} v(t_iq)
& \text{ if }p>2 \text{ and }c_i=1, \\
\dfrac{q}{p^{c_i-1}(p-1)} & \text{ if } p>2 \text{ and }
c_i\ge2, \\ v(t_iq) & \text{ if }p=2 \text{ and
}c_i=3, \\
\dfrac{q}{p^{c_i-1}(p-1)}=\dfrac1{2^{c_i-3}} & \text{ if
}p=2 \text{ and }c_i\ge4. \end{cases} \]
\[
v(T_i)=v(\chi_i(\exp(q))\exp(t_iq)-1)=\begin{cases} v(t_iq)
& \text{ if }p>2 \text{ and }c_i=1, \\
\dfrac{q}{p^{c_i-1}(p-1)} & \text{ if } p>2 \text{ and }
c_i\ge2, \\ v(t_iq) & \text{ if }p=2 \text{ and
}c_i=3, \\
\dfrac{q}{p^{c_i-1}(p-1)}=\dfrac1{2^{c_i-3}} & \text{ if
}p=2 \text{ and }c_i\ge4. \end{cases} \]
For completeness, we quickly prove the second case; the others are similar. The value ![]() $\chi _i(\exp (q))=\chi _i(\exp (p))$ is a primitive
$\chi _i(\exp (q))=\chi _i(\exp (p))$ is a primitive ![]() $p^{c_i}$th root of unity, say
$p^{c_i}$th root of unity, say ![]() $\zeta _{p^{c_i}}$. Let
$\zeta _{p^{c_i}}$. Let
 \[ f(X)=\frac{X^{p^{c_i}}-1}{X^{p^{c_i-1}}-1}=\prod_{a\in(\mathbb{Z}/p^{c_i}\mathbb{Z})^\times}(X-\zeta_{p^{c_i}}^a)=X^{p^{c_i}-p^{c_i-1}}+X^{p^{c_i}-2p^{c_i-1}}+\dotsb+X^{p^{c_i-1}}+1. \]
\[ f(X)=\frac{X^{p^{c_i}}-1}{X^{p^{c_i-1}}-1}=\prod_{a\in(\mathbb{Z}/p^{c_i}\mathbb{Z})^\times}(X-\zeta_{p^{c_i}}^a)=X^{p^{c_i}-p^{c_i-1}}+X^{p^{c_i}-2p^{c_i-1}}+\dotsb+X^{p^{c_i-1}}+1. \]
Then ![]() $f(1)=p=\prod _{a\in (\mathbb {Z}/p^{c_i}\mathbb {Z})^\times }(1-\zeta _{p^{c_i}}^a)$. Each term in the product has the same valuation, since they are Galois conjugate, and there are
$f(1)=p=\prod _{a\in (\mathbb {Z}/p^{c_i}\mathbb {Z})^\times }(1-\zeta _{p^{c_i}}^a)$. Each term in the product has the same valuation, since they are Galois conjugate, and there are ![]() $p^{c_i-1}(p-1)$ such terms. Thus,
$p^{c_i-1}(p-1)$ such terms. Thus, ![]() $v(\chi _i(\exp (q))-1)=1/({p^{c_i-2}(p-1)})$. The factor of
$v(\chi _i(\exp (q))-1)=1/({p^{c_i-2}(p-1)})$. The factor of ![]() $\exp (t_iq)$ has no effect since it is
$\exp (t_iq)$ has no effect since it is ![]() $1\pmod {p}$.
$1\pmod {p}$.
In general, if ![]() $A$ is a Banach
$A$ is a Banach ![]() $\mathbb {Q}_p$-algebra, we say that a character
$\mathbb {Q}_p$-algebra, we say that a character ![]() $s:\mathbb {Z}_p^\times \to A^\times$ is
$s:\mathbb {Z}_p^\times \to A^\times$ is ![]() $c$-locally analytic if its restriction to
$c$-locally analytic if its restriction to ![]() $1+p^c\mathbb {Z}_p$ is given by a convergent power series with coefficients in
$1+p^c\mathbb {Z}_p$ is given by a convergent power series with coefficients in ![]() $A$. Every continuous character
$A$. Every continuous character ![]() $s$ is
$s$ is ![]() $c$-locally analytic for some
$c$-locally analytic for some ![]() $c$: let
$c$: let ![]() $T=s(\exp (q))-1$ and choose
$T=s(\exp (q))-1$ and choose ![]() $c$ such that
$c$ such that ![]() $|T^{q^{-1}p^c}|< q^{-1}$. Then we have
$|T^{q^{-1}p^c}|< q^{-1}$. Then we have
if this converges. But by our choice of ![]() $c$, we have
$c$, we have ![]() $|(1+T)^{q^{-1}p^c}-1|< q^{-1}$, and if
$|(1+T)^{q^{-1}p^c}-1|< q^{-1}$, and if ![]() $z\in (1+p^c\mathbb {Z}_p)$, then
$z\in (1+p^c\mathbb {Z}_p)$, then ![]() $|(1/{p^c})\log z|\le 1$. By Lemma 3.6.1 of [Reference ChenevierChe04], this expression is a convergent power series in
$|(1/{p^c})\log z|\le 1$. By Lemma 3.6.1 of [Reference ChenevierChe04], this expression is a convergent power series in ![]() $z$.
$z$.
Naturally, if ![]() $s:(\mathbb {Z}_p^\times )^n\to A^\times$ is a character, we say that it is
$s:(\mathbb {Z}_p^\times )^n\to A^\times$ is a character, we say that it is ![]() $(c_1,\dotsc,c_n)$-locally analytic if it is
$(c_1,\dotsc,c_n)$-locally analytic if it is ![]() $c_i$-locally analytic in the
$c_i$-locally analytic in the ![]() $i$th factor.
$i$th factor.
If ![]() $W$ is any open affinoid subset of
$W$ is any open affinoid subset of ![]() $\mathscr {W}$, we use
$\mathscr {W}$, we use
to denote the universal character of ![]() $(\mathbb {Z}_p^\times )^n$ with coefficients in
$(\mathbb {Z}_p^\times )^n$ with coefficients in ![]() $\mathscr {O}(W)$. Note that
$\mathscr {O}(W)$. Note that ![]() $[\cdot ]_W$ is
$[\cdot ]_W$ is ![]() $(c_1,\dotsc,c_n)$-locally analytic with
$(c_1,\dotsc,c_n)$-locally analytic with ![]() $c_i$ depending on
$c_i$ depending on ![]() $\max _{s\in W(\mathbb {C}_p)}|T_i(s)|$.
$\max _{s\in W(\mathbb {C}_p)}|T_i(s)|$.
2.3 Coordinates on spaces of functions on  $\operatorname {Iw}_p$
$\operatorname {Iw}_p$
If ![]() $A$ is an affinoid
$A$ is an affinoid ![]() $\mathbb {Q}_p$-algebra and
$\mathbb {Q}_p$-algebra and ![]() $s:(\mathbb {Z}_p^\times )^n\to A^\times$ is a weight, we can view any function
$s:(\mathbb {Z}_p^\times )^n\to A^\times$ is a weight, we can view any function ![]() $f\in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p}s$ as a function on
$f\in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p}s$ as a function on ![]() $\mathbb {Z}_p^{n(n-1)/2}$ by restricting
$\mathbb {Z}_p^{n(n-1)/2}$ by restricting ![]() $f$ to the lower unipotent subgroup
$f$ to the lower unipotent subgroup ![]() $\overline {N}$ and applying the map
$\overline {N}$ and applying the map
 \begin{align*} \mathbb{Z}_p^{n(n-1)/2} &\to \overline{N} \\ \underline{z}=(z_{ij})_{n\ge i>j\ge1} &\mapsto \overline{N}(\underline{z})= \begin{pmatrix} 1 & 0 & 0 & \dotsb & 0 \\ pz_{21} & 1 & 0 & \dotsb & 0 \\ pz_{31} & pz_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ pz_{n1} & pz_{n2} & pz_{n3} & \dotsb & 1 \end{pmatrix} \in \overline{N}. \end{align*}
\begin{align*} \mathbb{Z}_p^{n(n-1)/2} &\to \overline{N} \\ \underline{z}=(z_{ij})_{n\ge i>j\ge1} &\mapsto \overline{N}(\underline{z})= \begin{pmatrix} 1 & 0 & 0 & \dotsb & 0 \\ pz_{21} & 1 & 0 & \dotsb & 0 \\ pz_{31} & pz_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ pz_{n1} & pz_{n2} & pz_{n3} & \dotsb & 1 \end{pmatrix} \in \overline{N}. \end{align*}
We say that ![]() $f$ is continuous if it is continuous as a function on
$f$ is continuous if it is continuous as a function on ![]() $\mathbb {Z}_p^{n(n-1)/2}$ via
$\mathbb {Z}_p^{n(n-1)/2}$ via ![]() $\underline {z}\mapsto \overline {N}(\underline {z})$. Then
$\underline {z}\mapsto \overline {N}(\underline {z})$. Then ![]() $\mathscr {S}_s:=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}(s)$, where
$\mathscr {S}_s:=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}(s)$, where ![]() ${\rm cts}$ denotes continuous, is an
${\rm cts}$ denotes continuous, is an ![]() $A[\operatorname {Iw}_p]$-module. If
$A[\operatorname {Iw}_p]$-module. If ![]() $s^0:(\mathbb {Q}_p^\times )^n\to A^\times$ is the trivial extension of
$s^0:(\mathbb {Q}_p^\times )^n\to A^\times$ is the trivial extension of ![]() $s$ from
$s$ from ![]() $(\mathbb {Z}_p^\times )^n$ to
$(\mathbb {Z}_p^\times )^n$ to ![]() $(\mathbb {Q}_p^\times )^n$ (that is, we set
$(\mathbb {Q}_p^\times )^n$ (that is, we set ![]() $s^0(d)=1$ for any
$s^0(d)=1$ for any ![]() $d\in (\mathbb {Q}_p^\times )^n$ whose entries are powers of
$d\in (\mathbb {Q}_p^\times )^n$ whose entries are powers of ![]() $p$),
$p$), ![]() $\mathscr {S}_s$ is isomorphic to
$\mathscr {S}_s$ is isomorphic to ![]() $\operatorname {Ind}_{B(\mathbb {Q}_p)}^{B(\mathbb {Q}_p)\operatorname {Iw}_p,{\rm cts}}(s^0)$ by restriction of functions from
$\operatorname {Ind}_{B(\mathbb {Q}_p)}^{B(\mathbb {Q}_p)\operatorname {Iw}_p,{\rm cts}}(s^0)$ by restriction of functions from ![]() $B(\mathbb {Q}_p)\operatorname {Iw}_p$ to
$B(\mathbb {Q}_p)\operatorname {Iw}_p$ to ![]() $\operatorname {Iw}_p$. Consequently, it has an action by
$\operatorname {Iw}_p$. Consequently, it has an action by ![]() $B(\mathbb {Q}_p)\operatorname {Iw}_p$.
$B(\mathbb {Q}_p)\operatorname {Iw}_p$.
It will be useful to write out the natural action of ![]() $\operatorname {Iw}_p$ on
$\operatorname {Iw}_p$ on ![]() $f\in \mathscr {S}_s$ more explicitly in terms of the coordinates
$f\in \mathscr {S}_s$ more explicitly in terms of the coordinates ![]() $z_{ij}$. To do this, we interpret them as Plücker coordinates on
$z_{ij}$. To do this, we interpret them as Plücker coordinates on ![]() $\overline {N}(\underline {z})$. Recall that for any
$\overline {N}(\underline {z})$. Recall that for any ![]() $1\le j\le n$ and subset
$1\le j\le n$ and subset ![]() $\sigma$ of
$\sigma$ of ![]() $\{1,\dotsc,n\}$ with
$\{1,\dotsc,n\}$ with ![]() $\#\sigma =j$, the Plücker coordinate
$\#\sigma =j$, the Plücker coordinate ![]() $Z_{j,\sigma }$ associated to
$Z_{j,\sigma }$ associated to ![]() $(j,\sigma )$ is the algebraic function on
$(j,\sigma )$ is the algebraic function on ![]() ${GL}_n$ given by the determinant of the minor associated to the rows corresponding to
${GL}_n$ given by the determinant of the minor associated to the rows corresponding to ![]() $\sigma$ and the first
$\sigma$ and the first ![]() $j$ columns.
$j$ columns.
Give ![]() $\mathbb {Q}_p^n$ the standard basis
$\mathbb {Q}_p^n$ the standard basis ![]() $e_1,\dotsc,e_n$ and interpret elements of
$e_1,\dotsc,e_n$ and interpret elements of ![]() $\mathbb {Q}_p^n$ as horizontal vectors. Give
$\mathbb {Q}_p^n$ as horizontal vectors. Give ![]() $\wedge ^j(\mathbb {Q}_p^n)$ the corresponding standard basis
$\wedge ^j(\mathbb {Q}_p^n)$ the corresponding standard basis
ordered lexicographically, and again interpret elements of ![]() $\wedge ^j(\mathbb {Q}_p^n)$ as horizontal vectors. Let
$\wedge ^j(\mathbb {Q}_p^n)$ as horizontal vectors. Let ![]() $1_j=\{1,\dotsc,j\}$. If
$1_j=\{1,\dotsc,j\}$. If ![]() ${GL}_n(\mathbb {Q}_p)$ acts on
${GL}_n(\mathbb {Q}_p)$ acts on ![]() $\mathbb {Q}_p^n$ by right multiplication of horizontal vectors (the transpose of the standard action), and
$\mathbb {Q}_p^n$ by right multiplication of horizontal vectors (the transpose of the standard action), and ![]() $\iota _j:{GL}_n(\mathbb {Q}_p)\hookrightarrow {GL}(\wedge ^j(\mathbb {Q}_p^n))$ gives the induced action of
$\iota _j:{GL}_n(\mathbb {Q}_p)\hookrightarrow {GL}(\wedge ^j(\mathbb {Q}_p^n))$ gives the induced action of ![]() ${GL}_n(\mathbb {Q}_p)$ on
${GL}_n(\mathbb {Q}_p)$ on ![]() $\wedge ^j(\mathbb {Q}_p^n)$ (where again
$\wedge ^j(\mathbb {Q}_p^n)$ (where again ![]() ${GL}(\wedge ^j(\mathbb {Q}_p^n))$ acts on
${GL}(\wedge ^j(\mathbb {Q}_p^n))$ acts on ![]() $\wedge ^j(\mathbb {Q}_p^n)$ by right multiplication of horizontal vectors), then for
$\wedge ^j(\mathbb {Q}_p^n)$ by right multiplication of horizontal vectors), then for ![]() $x\in {GL}_n(\mathbb {Q}_p)$,
$x\in {GL}_n(\mathbb {Q}_p)$, ![]() $Z_{j,\sigma }(x)$ is the coefficient of
$Z_{j,\sigma }(x)$ is the coefficient of ![]() $e_{1_j}$ in
$e_{1_j}$ in ![]() $e_\sigma \cdot \iota _j(x)$, or the entry of
$e_\sigma \cdot \iota _j(x)$, or the entry of ![]() $\iota _j(x)$ in the
$\iota _j(x)$ in the ![]() $\sigma$th row and first column. If
$\sigma$th row and first column. If ![]() $b=(b_{ij})\in B(\mathbb {Q}_p)$,
$b=(b_{ij})\in B(\mathbb {Q}_p)$, ![]() $\iota _j(b)$ is also upper triangular, so the coefficient of
$\iota _j(b)$ is also upper triangular, so the coefficient of ![]() $e_{1_j}$ in
$e_{1_j}$ in ![]() $e_\sigma \cdot \iota _j(xb)=e_\sigma \cdot \iota _j(x)\cdot \iota _j(b)$ is
$e_\sigma \cdot \iota _j(xb)=e_\sigma \cdot \iota _j(x)\cdot \iota _j(b)$ is ![]() $Z_{j,\sigma }(x)$ times the top left entry of
$Z_{j,\sigma }(x)$ times the top left entry of ![]() $\iota _j(b)$, which is
$\iota _j(b)$, which is ![]() $b_{11}\dotsb b_{jj}=:t_j(b)$. That is, we have
$b_{11}\dotsb b_{jj}=:t_j(b)$. That is, we have
Thus, ![]() $Z_{j,\sigma }$ is invariant under right multiplication by
$Z_{j,\sigma }$ is invariant under right multiplication by ![]() $N$, and
$N$, and ![]() $Z_{j,\sigma /1}:=Z_{j,\sigma }/Z_{j,1_j}$ is invariant under right multiplication by
$Z_{j,\sigma /1}:=Z_{j,\sigma }/Z_{j,1_j}$ is invariant under right multiplication by ![]() $B$.
$B$.
If ![]() $u\in {GL}_n(\mathbb {Z}_p)$, we have
$u\in {GL}_n(\mathbb {Z}_p)$, we have ![]() $\iota _j(u^{-1}x)=\iota _j(u^{-1})\iota _j(x)$, so the entry of
$\iota _j(u^{-1}x)=\iota _j(u^{-1})\iota _j(x)$, so the entry of ![]() $\iota _j(u^{-1}x)$ in the
$\iota _j(u^{-1}x)$ in the ![]() $\sigma$th row and first column is a linear combination of all the entries of
$\sigma$th row and first column is a linear combination of all the entries of ![]() $\iota _j(x)$ in the first column. Hence, we can write
$\iota _j(x)$ in the first column. Hence, we can write
(note that ![]() $a_{j,\sigma,\tau }(u)\in \mathbb {Z}_p$, and if
$a_{j,\sigma,\tau }(u)\in \mathbb {Z}_p$, and if ![]() $u\in \operatorname {Iw}_p$, then
$u\in \operatorname {Iw}_p$, then ![]() $a_{j,1_j,1_j}(u)\in \mathbb {Z}_p^\times$), and
$a_{j,1_j,1_j}(u)\in \mathbb {Z}_p^\times$), and
 \[ Z_{j,\sigma/1}(u^{-1}x)=\frac{a_{j,\sigma,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,\sigma,\tau}(u)Z_{j,\tau/1}(x)}{a_{j,1_j,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,1_j,\tau}(u)Z_{j,\tau/1}(x)}. \]
\[ Z_{j,\sigma/1}(u^{-1}x)=\frac{a_{j,\sigma,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,\sigma,\tau}(u)Z_{j,\tau/1}(x)}{a_{j,1_j,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,1_j,\tau}(u)Z_{j,\tau/1}(x)}. \]
For ![]() $i\ge j$, let
$i\ge j$, let ![]() $\sigma _{ij}=\{1,\dotsc,j-1,i\}$ (so
$\sigma _{ij}=\{1,\dotsc,j-1,i\}$ (so ![]() $\sigma _{jj}=1_j$); then we can see that
$\sigma _{jj}=1_j$); then we can see that
 \[ Z_{j,\sigma_{ij}}(\overline{N}(\underline{z}))=\begin{cases} Z_{j,1_j}(\overline{N}(\underline{z}))=1 & \text{ if } i=j, \\ pz_{ij} & \text{ if } i>j. \end{cases} \]
\[ Z_{j,\sigma_{ij}}(\overline{N}(\underline{z}))=\begin{cases} Z_{j,1_j}(\overline{N}(\underline{z}))=1 & \text{ if } i=j, \\ pz_{ij} & \text{ if } i>j. \end{cases} \]
Thus, ![]() $z_{ij}$, or technically
$z_{ij}$, or technically ![]() $pz_{ij}$, is indeed a Plücker coordinate for
$pz_{ij}$, is indeed a Plücker coordinate for ![]() $\overline {N}(\underline {z})$ when
$\overline {N}(\underline {z})$ when ![]() $i>j$. Now using the Iwahori decomposition for
$i>j$. Now using the Iwahori decomposition for ![]() $\operatorname {Iw}_p$, let
$\operatorname {Iw}_p$, let
for some ![]() $\overline {N}(u,\underline {z})\in \overline {N}$,
$\overline {N}(u,\underline {z})\in \overline {N}$, ![]() $T(u,\underline {z})\in T$, and
$T(u,\underline {z})\in T$, and ![]() $N(u,\underline {z})\in N$. Let
$N(u,\underline {z})\in N$. Let ![]() $\underline {uz}=((uz)_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_p^{n(n-1)/2}$ be the preimage of
$\underline {uz}=((uz)_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_p^{n(n-1)/2}$ be the preimage of ![]() $\overline {N}(u,\underline {z})$ under
$\overline {N}(u,\underline {z})$ under ![]() $\mathbb {Z}_p^{n(n-1)/2}\to \overline {N}$, so that
$\mathbb {Z}_p^{n(n-1)/2}\to \overline {N}$, so that ![]() $\overline {N}(\underline {uz})=\overline {N}(u,\underline {z})$. Thus, if
$\overline {N}(\underline {uz})=\overline {N}(u,\underline {z})$. Thus, if ![]() $f\in \mathscr {S}_s$, we have
$f\in \mathscr {S}_s$, we have
 \begin{align*} (uf)(\overline{N}(\underline{z}))=f(u^{-1}\overline{N}(\underline{z})) &=f(\overline{N}(\underline{uz})T(u,\underline{z})N(u,\underline{z})) \\ &=s(T(u,\underline{z}))f(\overline{N}(\underline{uz})). \end{align*}
\begin{align*} (uf)(\overline{N}(\underline{z}))=f(u^{-1}\overline{N}(\underline{z})) &=f(\overline{N}(\underline{uz})T(u,\underline{z})N(u,\underline{z})) \\ &=s(T(u,\underline{z}))f(\overline{N}(\underline{uz})). \end{align*}
We wish to write ![]() $\underline {uz}$ and
$\underline {uz}$ and ![]() $T(u,\underline {z})$ in terms of
$T(u,\underline {z})$ in terms of ![]() $u$ and
$u$ and ![]() $\underline {z}$. But we have
$\underline {z}$. But we have
 \begin{align*} Z_{j,\sigma_{ij}}(u^{-1}\overline{N}(\underline{z})) &=Z_{j,\sigma_{ij}}(\overline{N}(\underline{uz})T(u,\underline{z})N(u,\underline{z})) \\ &=Z_{j,\sigma_{ij}}(\overline{N}(\underline{uz}))t_j(T(u,\underline{z})). \end{align*}
\begin{align*} Z_{j,\sigma_{ij}}(u^{-1}\overline{N}(\underline{z})) &=Z_{j,\sigma_{ij}}(\overline{N}(\underline{uz})T(u,\underline{z})N(u,\underline{z})) \\ &=Z_{j,\sigma_{ij}}(\overline{N}(\underline{uz}))t_j(T(u,\underline{z})). \end{align*}
Thus, in fact, setting ![]() $i=j$, we find
$i=j$, we find
where ![]() $Z_{j,\tau }(\overline {N}(\underline {z}))$ is, by definition, a polynomial in the variables
$Z_{j,\tau }(\overline {N}(\underline {z}))$ is, by definition, a polynomial in the variables ![]() $\{z_{kl}\}_{l\le j,k>l}$ with coefficients in
$\{z_{kl}\}_{l\le j,k>l}$ with coefficients in ![]() $p\mathbb {Z}_p$. Then when
$p\mathbb {Z}_p$. Then when ![]() $i>j$, we have
$i>j$, we have
so
 \[ p(uz)_{ij}=Z_{j,\sigma_{ij}/1}(u^{-1}\overline{N}(\underline{z}))=\frac{a_{j,\sigma,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,\sigma,\tau}(u)Z_{j,\tau/1}(\overline{N}(\underline{z}))}{a_{j,1_j,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,1_j,\tau}(u)Z_{j,\tau/1}(\overline{N}(\underline{z}))}, \]
\[ p(uz)_{ij}=Z_{j,\sigma_{ij}/1}(u^{-1}\overline{N}(\underline{z}))=\frac{a_{j,\sigma,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,\sigma,\tau}(u)Z_{j,\tau/1}(\overline{N}(\underline{z}))}{a_{j,1_j,1_j}+\sum_{\#\tau=j,\tau\neq 1_j}a_{j,1_j,\tau}(u)Z_{j,\tau/1}(\overline{N}(\underline{z}))}, \]
where ![]() $Z_{j,\tau /1}(\overline {N}(\underline {z}))$ is again a polynomial in the variables
$Z_{j,\tau /1}(\overline {N}(\underline {z}))$ is again a polynomial in the variables ![]() $\{z_{kl}\}_{l\le j,k>l}$ with coefficients in
$\{z_{kl}\}_{l\le j,k>l}$ with coefficients in ![]() $p\mathbb {Z}_p$.
$p\mathbb {Z}_p$.
2.4 Notation for subgroups of  $\operatorname {Iw}_p$
$\operatorname {Iw}_p$
Since we work with numerous subgroups of ![]() $\operatorname {Iw}_p$, we introduce some notation to identify them. If
$\operatorname {Iw}_p$, we introduce some notation to identify them. If ![]() $\underline {c}=(c_{ij})\in \mathbb {Z}_{\ge 0}^{n\times n}$ is any
$\underline {c}=(c_{ij})\in \mathbb {Z}_{\ge 0}^{n\times n}$ is any ![]() $n\times n$ matrix of nonnegative integers, we write
$n\times n$ matrix of nonnegative integers, we write
(where ![]() $\delta _{ij}$ is
$\delta _{ij}$ is ![]() $1$ if
$1$ if ![]() $i=j$ and
$i=j$ and ![]() $0$ otherwise). By Lemma 3.2 of [Reference RocheRoc98], when
$0$ otherwise). By Lemma 3.2 of [Reference RocheRoc98], when ![]() $\underline {c}$ satisfies
$\underline {c}$ satisfies ![]() $c_{ij}\le c_{ik}+c_{kj}$ for all
$c_{ij}\le c_{ik}+c_{kj}$ for all ![]() $i,j,k$ and
$i,j,k$ and ![]() $c_{ij}+c_{ji}\ge 1$ for all
$c_{ij}+c_{ji}\ge 1$ for all ![]() $i\neq j$, the set
$i\neq j$, the set ![]() $\Gamma (\underline {c})$ is closed under multiplication and inverses, hence is a group. Note that this means that if
$\Gamma (\underline {c})$ is closed under multiplication and inverses, hence is a group. Note that this means that if ![]() $\Gamma (\underline {c})$ is a group, then so is
$\Gamma (\underline {c})$ is a group, then so is ![]() $T(\mathbb {Z}_p)\Gamma (\underline {c})$. If we instead only have half a matrix of positive integers
$T(\mathbb {Z}_p)\Gamma (\underline {c})$. If we instead only have half a matrix of positive integers ![]() $\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$, we write
$\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$, we write
Definition 2.4.1 We say that ![]() $\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ is group-shaped if
$\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ is group-shaped if ![]() $c_{ij}\le c_{ik}+c_{kj}$ for all
$c_{ij}\le c_{ik}+c_{kj}$ for all ![]() $i,j,k$, where we set
$i,j,k$, where we set ![]() $c_{ab}$ to be
$c_{ab}$ to be ![]() $0$ if
$0$ if ![]() $a\le b$.
$a\le b$.
Thus, ![]() $\Gamma _1(\underline {c})$ and
$\Gamma _1(\underline {c})$ and ![]() $\Gamma _0(\underline {c})$ are subgroups whenever
$\Gamma _0(\underline {c})$ are subgroups whenever ![]() $\underline {c}$ is group-shaped.
$\underline {c}$ is group-shaped.
Definition 2.4.2 We call an ![]() $({n(n-1)}/{2})$-tuple
$({n(n-1)}/{2})$-tuple ![]() $\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ compatible with an
$\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ compatible with an ![]() $n$-tuple
$n$-tuple ![]() $(c_1,\dotsc,c_n)\in \mathbb {Z}_{>0}^n$ if
$(c_1,\dotsc,c_n)\in \mathbb {Z}_{>0}^n$ if ![]() $c_i\le \min \{c_{ij}|j< i\}\cup \{c_{ji}|j>i\}$ for all
$c_i\le \min \{c_{ij}|j< i\}\cup \{c_{ji}|j>i\}$ for all ![]() $i$. In this case, if we define
$i$. In this case, if we define ![]() $\underline {c}'\in \mathbb {Z}_{\ge 0}^{n\times n}$ by
$\underline {c}'\in \mathbb {Z}_{\ge 0}^{n\times n}$ by ![]() $c_{ij}'=c_{ij}$ for
$c_{ij}'=c_{ij}$ for ![]() $i>j$,
$i>j$, ![]() $c_{ii}'=c_i$, and
$c_{ii}'=c_i$, and ![]() $c_{ij}'=0$ for
$c_{ij}'=0$ for ![]() $i< j$, then
$i< j$, then ![]() $\Gamma (\underline {c}')$ is a group.
$\Gamma (\underline {c}')$ is a group.
Then we see that if ![]() $\chi =(\chi _1,\dotsc,\chi _n):T(\mathbb {Z}_p)\to \mathbb {C}^\times$ is a character of
$\chi =(\chi _1,\dotsc,\chi _n):T(\mathbb {Z}_p)\to \mathbb {C}^\times$ is a character of ![]() $T(\mathbb {Z}_p)$, and
$T(\mathbb {Z}_p)$, and ![]() $\underline {c}\in \mathbb {Z}_p^{n(n-1)/2}$,
$\underline {c}\in \mathbb {Z}_p^{n(n-1)/2}$, ![]() $\chi$ extends to a well-defined character of
$\chi$ extends to a well-defined character of ![]() $T(\mathbb {Z}_p)\Gamma _1(\underline {c})=\Gamma _0(\underline {c})$, trivial on
$T(\mathbb {Z}_p)\Gamma _1(\underline {c})=\Gamma _0(\underline {c})$, trivial on ![]() $\Gamma _1(\underline {c})$, whenever
$\Gamma _1(\underline {c})$, whenever ![]() $\underline {c}$ is compatible with
$\underline {c}$ is compatible with ![]() $(\operatorname {cond}(\chi _1),\dotsc,\operatorname {cond}(\chi _n))$.
$(\operatorname {cond}(\chi _1),\dotsc,\operatorname {cond}(\chi _n))$.
In the following calculations, whenever we write ![]() $\Gamma (\underline {c})$,
$\Gamma (\underline {c})$, ![]() $\Gamma _0(\underline {c})$, or
$\Gamma _0(\underline {c})$, or ![]() $\Gamma _1(\underline {c})$ for a matrix or half-matrix of nonnegative integers
$\Gamma _1(\underline {c})$ for a matrix or half-matrix of nonnegative integers ![]() $\underline {c}$, we implicitly assume that
$\underline {c}$, we implicitly assume that ![]() $\underline {c}$ has been chosen so that it is in fact a group.
$\underline {c}$ has been chosen so that it is in fact a group.
Depending on convenience, we may also overload the notation in the following ways. First, if ![]() $\underline {r}=(r_{ij})\in [0,1]^{n\times n}$ is any
$\underline {r}=(r_{ij})\in [0,1]^{n\times n}$ is any ![]() $n\times n$ matrix of real numbers in
$n\times n$ matrix of real numbers in ![]() $[0,1]$, we write
$[0,1]$, we write
Then ![]() $\Gamma (\underline {r})$ is a group whenever
$\Gamma (\underline {r})$ is a group whenever ![]() $r_{ij}\ge r_{ik}r_{kj}$ for all
$r_{ij}\ge r_{ik}r_{kj}$ for all ![]() $i,j,k$. We may define
$i,j,k$. We may define ![]() $\Gamma _1(\underline {r}),\Gamma _0(\underline {r})$ similarly. Second, if
$\Gamma _1(\underline {r}),\Gamma _0(\underline {r})$ similarly. Second, if ![]() $c\in \mathbb {Z}_{>0}$ is a single integer, we write
$c\in \mathbb {Z}_{>0}$ is a single integer, we write
This is always a group. We may define ![]() $\Gamma _1(c),\Gamma _0(c)$ similarly. Finally, if
$\Gamma _1(c),\Gamma _0(c)$ similarly. Finally, if ![]() $r$ is a single real number in
$r$ is a single real number in ![]() $[0,1]$, we write
$[0,1]$, we write ![]() $\Gamma (r),\Gamma _1(r),\Gamma _0(r)$ for the obvious final abuse of the same notation.
$\Gamma (r),\Gamma _1(r),\Gamma _0(r)$ for the obvious final abuse of the same notation.
2.5 The sheaf of  $p$-adic automorphic forms on weight space
$p$-adic automorphic forms on weight space
If ![]() $\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$, we say that
$\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{>0}^{n(n-1)/2}$, we say that ![]() $f\in \mathscr {S}_s$ is
$f\in \mathscr {S}_s$ is ![]() $\underline {c}$-locally analytic if, for any
$\underline {c}$-locally analytic if, for any ![]() $\underline {a}=(a_{ij})\in \mathbb {Z}_p^{n(n-1)/2}$, the restriction of
$\underline {a}=(a_{ij})\in \mathbb {Z}_p^{n(n-1)/2}$, the restriction of ![]() $f$ to
$f$ to
is given by a convergent power series in the variables ![]() $z_{ij}$ with coefficients in
$z_{ij}$ with coefficients in ![]() $A$.
$A$.
Definition 2.5.1 We call an ![]() $({n(n-1)}/2)$-tuple
$({n(n-1)}/2)$-tuple ![]() $\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$ analytic-shaped if we have
$\underline {c}=(c_{ij})_{n\ge i>j\ge 1}\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$ analytic-shaped if we have ![]() $c_{(j+1)j}=c_{(j+2)j}=\dotsb =c_{nj}$ for all
$c_{(j+1)j}=c_{(j+2)j}=\dotsb =c_{nj}$ for all ![]() $j$ and
$j$ and ![]() $c_{nj}\ge c_{n(j+1)}$ for all
$c_{nj}\ge c_{n(j+1)}$ for all ![]() $j$. (Note that if
$j$. (Note that if ![]() $\underline {c}$ is analytic-shaped it is also group-shaped.) We call
$\underline {c}$ is analytic-shaped it is also group-shaped.) We call ![]() $\underline {c}$ compatible with an
$\underline {c}$ compatible with an ![]() $n$-tuple
$n$-tuple ![]() $(c_1,\dotsc,c_n)\in \mathbb {Z}_{\ge 0}^n$ if
$(c_1,\dotsc,c_n)\in \mathbb {Z}_{\ge 0}^n$ if ![]() $c_j\le \min _{l\le j,k>l}c_{kl}$ for all
$c_j\le \min _{l\le j,k>l}c_{kl}$ for all ![]() $j$. That is, for each
$j$. That is, for each ![]() $j_0$, all the entries of
$j_0$, all the entries of ![]() $(c_{ij})$ corresponding to matrix entries appearing in or to the left of the
$(c_{ij})$ corresponding to matrix entries appearing in or to the left of the ![]() $j_0$th column should be at least
$j_0$th column should be at least ![]() $c_{j_0}$.
$c_{j_0}$.
Definition 2.5.2 If ![]() $\underline {c}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ is analytic-shaped, we say that
$\underline {c}\in \mathbb {Z}_{>0}^{n(n-1)/2}$ is analytic-shaped, we say that ![]() $s:(\mathbb {Z}_p^\times )^n\to A^\times$ is
$s:(\mathbb {Z}_p^\times )^n\to A^\times$ is ![]() $\underline {c}$-locally analytic if there is
$\underline {c}$-locally analytic if there is ![]() $(c_1,\dotsc,c_n)$ such that
$(c_1,\dotsc,c_n)$ such that ![]() $s$ is
$s$ is ![]() $(c_1,\dotsc,c_n)$-locally analytic and
$(c_1,\dotsc,c_n)$-locally analytic and ![]() $\underline {c}$ is compatible with
$\underline {c}$ is compatible with ![]() $(c_1,\dotsc,c_n)$.
$(c_1,\dotsc,c_n)$.
Proposition 2.5.3 If ![]() $s$ is
$s$ is ![]() $(c_1,\dotsc,c_n)$-locally analytic and
$(c_1,\dotsc,c_n)$-locally analytic and ![]() $f\in \mathscr {S}_s$ is
$f\in \mathscr {S}_s$ is ![]() $\underline {c}$-locally analytic for
$\underline {c}$-locally analytic for ![]() $\underline {c}$ analytic-shaped and compatible with
$\underline {c}$ analytic-shaped and compatible with ![]() $(c_1,\dotsc,c_n)$ (so that
$(c_1,\dotsc,c_n)$ (so that ![]() $s$ is
$s$ is ![]() $\underline {c}$-locally analytic), then
$\underline {c}$-locally analytic), then ![]() $uf$ is also
$uf$ is also ![]() $\underline {c}$-locally analytic for all
$\underline {c}$-locally analytic for all ![]() $u\in \operatorname {Iw}_p$.
$u\in \operatorname {Iw}_p$.
Proof. By the calculations in § 2.3, we have ![]() $(uf)(\overline {N}(\underline {z}))=s(T(u,\underline {z}))f(\overline {N}(\underline {uz}))$ where:
$(uf)(\overline {N}(\underline {z}))=s(T(u,\underline {z}))f(\overline {N}(\underline {uz}))$ where:
(i)
 $(uz)_{ij}$ is a power series in the variables
$(uz)_{ij}$ is a power series in the variables  $\{z_{kl}\}_{l\le j,k>l}$;
$\{z_{kl}\}_{l\le j,k>l}$;(ii) the
 $j$th diagonal entry of
$j$th diagonal entry of  $T(u,\underline {z})$, or
$T(u,\underline {z})$, or  ${t_j(T(u,\underline {z}))}/{t_{j-1}(T(u,\underline {z}))}$, is also a power series in the variables
${t_j(T(u,\underline {z}))}/{t_{j-1}(T(u,\underline {z}))}$, is also a power series in the variables  $\{z_{kl}\}_{l\le j,k>l}$.
$\{z_{kl}\}_{l\le j,k>l}$.
So if we restrict to ![]() $\underline {z}\in B(\underline {a},\underline {c})$, the coefficient
$\underline {z}\in B(\underline {a},\underline {c})$, the coefficient ![]() $(uz)_{ij}$ ranges over a ball of the form
$(uz)_{ij}$ ranges over a ball of the form ![]() $a_{ij}'+p^{\min _{l\le j,k>l}c_{kl}}\mathbb {Z}_p$; since
$a_{ij}'+p^{\min _{l\le j,k>l}c_{kl}}\mathbb {Z}_p$; since ![]() $\underline {c}$ is analytic-shaped, we have
$\underline {c}$ is analytic-shaped, we have ![]() $c_{ij}\le \min _{l\le j,k>l}c_{kl}$, and we conclude that
$c_{ij}\le \min _{l\le j,k>l}c_{kl}$, and we conclude that ![]() $\underline {uz}$ is also restricted to a ball of the form
$\underline {uz}$ is also restricted to a ball of the form ![]() $B(\underline {a}',\underline {c})$. Thus,
$B(\underline {a}',\underline {c})$. Thus, ![]() $f(\overline {N}(\underline {uz}))$ is analytic for
$f(\overline {N}(\underline {uz}))$ is analytic for ![]() $\underline {z}\in B(\underline {a},\underline {c})$. Similarly,
$\underline {z}\in B(\underline {a},\underline {c})$. Similarly, ![]() ${t_j(T(u,\underline {z}))}/{t_{j-1}(T(u,\underline {z}))}$ ranges over a ball of the form
${t_j(T(u,\underline {z}))}/{t_{j-1}(T(u,\underline {z}))}$ ranges over a ball of the form ![]() $a_{jj}''+p^{\min _{l\le j,k>l}c_{kl}}\mathbb {Z}_p$; since
$a_{jj}''+p^{\min _{l\le j,k>l}c_{kl}}\mathbb {Z}_p$; since ![]() $c_j\le \min _{l\le j,k>l}c_{kl}$ and
$c_j\le \min _{l\le j,k>l}c_{kl}$ and ![]() $s_j$ is analytic on
$s_j$ is analytic on ![]() $a_{jj}'+p^{c_j}\mathbb {Z}_p$, we conclude that
$a_{jj}'+p^{c_j}\mathbb {Z}_p$, we conclude that ![]() $s_j(T(u,\underline {z}))$ is analytic for
$s_j(T(u,\underline {z}))$ is analytic for ![]() $\underline {z}\in B(\underline {a},\underline {c})$. Thus,
$\underline {z}\in B(\underline {a},\underline {c})$. Thus, ![]() $(uf)(\overline {N}(\underline {z}))$ is analytic for
$(uf)(\overline {N}(\underline {z}))$ is analytic for ![]() $\underline {z}\in B(\underline {a},\underline {c})$, as desired.
$\underline {z}\in B(\underline {a},\underline {c})$, as desired.
By Proposition 2.5.3, if ![]() $s$ is
$s$ is ![]() $\underline {c}$-locally analytic with
$\underline {c}$-locally analytic with ![]() $\underline {c}$ analytic-shaped, the space
$\underline {c}$ analytic-shaped, the space ![]() $\mathscr {S}_{s,\underline {c}}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,\underline {c}\text {-loc.an.}}(s)$, where
$\mathscr {S}_{s,\underline {c}}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,\underline {c}\text {-loc.an.}}(s)$, where ![]() $\underline {c}\text {-loc.an.}$ denotes
$\underline {c}\text {-loc.an.}$ denotes ![]() $\underline {c}$-locally analytic, is well-defined and has an action by
$\underline {c}$-locally analytic, is well-defined and has an action by ![]() $\operatorname {Iw}_p$.
$\operatorname {Iw}_p$.
We let ![]() $\mathscr {S}=\mathscr {S}_{[\cdot ]}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}([\cdot ])$. If
$\mathscr {S}=\mathscr {S}_{[\cdot ]}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}([\cdot ])$. If ![]() $\mathscr {U}_p=\operatorname {Iw}_p$, we call
$\mathscr {U}_p=\operatorname {Iw}_p$, we call
the space of integral ![]() $p$-adic automorphic forms for
$p$-adic automorphic forms for ![]() $G$ of level
$G$ of level ![]() $\mathscr {U}$; it has an action by
$\mathscr {U}$; it has an action by ![]() $B(\mathbb {Q}_p)\mathscr {U}$. This gives a sheaf on
$B(\mathbb {Q}_p)\mathscr {U}$. This gives a sheaf on ![]() $\mathscr {W}$ whose fiber over
$\mathscr {W}$ whose fiber over ![]() $s$ is
$s$ is
Similarly, let ![]() $\mathscr {S}_{W,\underline {c}}=\mathscr {S}_{[\cdot ]_W,\underline {c}}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,\underline {c}\text {-loc.an.}}([\cdot ]_W)$ (for any
$\mathscr {S}_{W,\underline {c}}=\mathscr {S}_{[\cdot ]_W,\underline {c}}=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,\underline {c}\text {-loc.an.}}([\cdot ]_W)$ (for any ![]() $\underline {c}$ such that
$\underline {c}$ such that ![]() $[\cdot ]_W$ is
$[\cdot ]_W$ is ![]() $\underline {c}$-locally analytic). If
$\underline {c}$-locally analytic). If ![]() $\mathscr {U}_p=\operatorname {Iw}_p$, we call
$\mathscr {U}_p=\operatorname {Iw}_p$, we call
the space of ![]() $\underline {c}$-locally analytic
$\underline {c}$-locally analytic ![]() $p$-adic automorphic forms for
$p$-adic automorphic forms for ![]() $G$ of level
$G$ of level ![]() $\mathscr {U}$; we show in the next section that this does not have an action by
$\mathscr {U}$; we show in the next section that this does not have an action by ![]() $B(\mathbb {Q}_p)$, as some elements of
$B(\mathbb {Q}_p)$, as some elements of ![]() $B(\mathbb {Q}_p)$ do not preserve the radius of local analyticity (Remark 2), but it does have an action by a certain submonoid.
$B(\mathbb {Q}_p)$ do not preserve the radius of local analyticity (Remark 2), but it does have an action by a certain submonoid.
2.6 The operators  $U_p^a$
$U_p^a$
If ![]() $H$ is any locally compact, totally disconnected topological group, we write
$H$ is any locally compact, totally disconnected topological group, we write ![]() $\mathscr {H}(H)$ for the
$\mathscr {H}(H)$ for the ![]() $k$-algebra of compactly supported, locally constant
$k$-algebra of compactly supported, locally constant ![]() $k$-valued functions on
$k$-valued functions on ![]() $H$ with the convolution product
$H$ with the convolution product
where ![]() $\mu$ is a Haar measure on
$\mu$ is a Haar measure on ![]() $H$. This algebra usually has no identity, but many idempotents. If
$H$. This algebra usually has no identity, but many idempotents. If ![]() $K$ is a compact open subgroup of
$K$ is a compact open subgroup of ![]() $H$, the idempotent
$H$, the idempotent ![]() $e_K={\mathbb {1}_K}/{\mu (K)}$ projects
$e_K={\mathbb {1}_K}/{\mu (K)}$ projects ![]() $\mathscr {H}(H)$ onto the subalgebra
$\mathscr {H}(H)$ onto the subalgebra ![]() $\mathscr {H}(H// K)$ of functions that are both left- and right-invariant under
$\mathscr {H}(H// K)$ of functions that are both left- and right-invariant under ![]() $K$. If
$K$. If ![]() $V$ is a smooth
$V$ is a smooth ![]() $H$-module, it is an
$H$-module, it is an ![]() $\mathscr {H}(H)$-module via
$\mathscr {H}(H)$-module via
and, similarly, ![]() $V^K$ is an
$V^K$ is an ![]() $\mathscr {H}(H// K)$-module.
$\mathscr {H}(H// K)$-module.
In the particular case ![]() $H=B(\mathbb {Q}_p)\mathscr {U}$,
$H=B(\mathbb {Q}_p)\mathscr {U}$, ![]() $V=\mathscr {S}_s(G,\mathscr {U})$,
$V=\mathscr {S}_s(G,\mathscr {U})$, ![]() $K=\mathscr {U}$, we can rephrase this as follows. We sometimes write
$K=\mathscr {U}$, we can rephrase this as follows. We sometimes write ![]() $[\mathscr {U}\zeta \mathscr {U}]$ for the element
$[\mathscr {U}\zeta \mathscr {U}]$ for the element ![]() $\mathbb {1}_{\mathscr {U}\zeta \mathscr {U}}$ of
$\mathbb {1}_{\mathscr {U}\zeta \mathscr {U}}$ of ![]() $\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$. If
$\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$. If ![]() $\zeta _1,\dotsc,\zeta _r$ are left
$\zeta _1,\dotsc,\zeta _r$ are left ![]() $\mathscr {U}$-coset representatives of
$\mathscr {U}$-coset representatives of ![]() $\mathscr {U}\zeta \mathscr {U}$, so that
$\mathscr {U}\zeta \mathscr {U}$, so that
 \[ \mathscr{U}\zeta\mathscr{U}=\coprod_{i=1}^r\zeta_i\mathscr{U}, \]
\[ \mathscr{U}\zeta\mathscr{U}=\coprod_{i=1}^r\zeta_i\mathscr{U}, \]
then for any ![]() $\varphi \in \mathscr {S}_s(G,\mathscr {U})$ and
$\varphi \in \mathscr {S}_s(G,\mathscr {U})$ and ![]() $x\in G(\mathbb {Q})\backslash G(\mathbb {A}_f)$, we have
$x\in G(\mathbb {Q})\backslash G(\mathbb {A}_f)$, we have
 \begin{align*} [\mathscr{U}\zeta\mathscr{U}](\varphi)(x) &=\int_{G(\mathbb{A}_f)}[\mathscr{U}\zeta\mathscr{U}](g)\cdot(g.\varphi)(x)\,dg \\ &=\int_{\mathscr{U}\zeta\mathscr{U}}g_p\varphi(xg)\,dg= \sum_{i=1}^r(\zeta_i)_p.\varphi(x\zeta_i). \end{align*}
\begin{align*} [\mathscr{U}\zeta\mathscr{U}](\varphi)(x) &=\int_{G(\mathbb{A}_f)}[\mathscr{U}\zeta\mathscr{U}](g)\cdot(g.\varphi)(x)\,dg \\ &=\int_{\mathscr{U}\zeta\mathscr{U}}g_p\varphi(xg)\,dg= \sum_{i=1}^r(\zeta_i)_p.\varphi(x\zeta_i). \end{align*}
The following is Lemma 4.5.2 of [Reference ChenevierChe04] or Proposition 3.3.3 of [Reference LoefflerLoe10].
Lemma 2.6.1 Fix coset representatives ![]() $x_1,\dotsc,x_h$ of
$x_1,\dotsc,x_h$ of ![]() $G(\mathbb {Q})\backslash G(\mathbb {A}_f)/\mathscr {U}$ and, thus, an isomorphism
$G(\mathbb {Q})\backslash G(\mathbb {A}_f)/\mathscr {U}$ and, thus, an isomorphism ![]() $\mathscr {S}_s(G,\mathscr {U})\cong \mathscr {S}_s^h$. Then we have
$\mathscr {S}_s(G,\mathscr {U})\cong \mathscr {S}_s^h$. Then we have
 \[ [\mathscr{U}\zeta\mathscr{U}](\varphi)(x_j)=\sum_{k=1}^h\sum_{i\mid\zeta_i\in x_j^{-1}G(\mathbb{Q})x_k\mathscr{U}}(\zeta_iu_{ij}^{-1})_p.\varphi(x_k) \]
\[ [\mathscr{U}\zeta\mathscr{U}](\varphi)(x_j)=\sum_{k=1}^h\sum_{i\mid\zeta_i\in x_j^{-1}G(\mathbb{Q})x_k\mathscr{U}}(\zeta_iu_{ij}^{-1})_p.\varphi(x_k) \]
for some ![]() $u_{ij}\in \mathscr {U}$. That is, the action of
$u_{ij}\in \mathscr {U}$. That is, the action of ![]() $[\mathscr {U}\zeta \mathscr {U}]$ on
$[\mathscr {U}\zeta \mathscr {U}]$ on ![]() $\mathscr {S}_s(G,\mathscr {U})$ is of the form
$\mathscr {S}_s(G,\mathscr {U})$ is of the form ![]() $\sum T_j\circ \sigma _j$, where the
$\sum T_j\circ \sigma _j$, where the ![]() $\sigma _j$ are compositions of permutation operators on the entries of vectors in
$\sigma _j$ are compositions of permutation operators on the entries of vectors in ![]() $\mathscr {S}_s^h$ with projections onto one of the coordinates, and the
$\mathscr {S}_s^h$ with projections onto one of the coordinates, and the ![]() $T_j$ are diagonal translations of
$T_j$ are diagonal translations of ![]() $\mathscr {S}_s^h$ by elements of
$\mathscr {S}_s^h$ by elements of ![]() $\mathscr {U}\zeta \mathscr {U}$.
$\mathscr {U}\zeta \mathscr {U}$.
Proof. Write ![]() $x_j\zeta _i$ in the form
$x_j\zeta _i$ in the form ![]() $d_{ij}x_{k_{ij}}u_{ij}$ where
$d_{ij}x_{k_{ij}}u_{ij}$ where ![]() $d_{ij}\in G(\mathbb {Q})$ and
$d_{ij}\in G(\mathbb {Q})$ and ![]() $u_{ij}\in \mathscr {U}$. Then
$u_{ij}\in \mathscr {U}$. Then
 \begin{align*} [\mathscr{U}\zeta\mathscr{U}](\varphi)(x_j) &=\sum_{i=1}^r(\zeta_i)_p.\varphi(x_j\zeta_i) \\ &=\sum_{i=1}^r(\zeta_i)_p.\varphi(d_{ij}x_{k_{ij}}u_{ij})=\sum_{i=1}^r(\zeta_iu_{ij}^{-1})_p.\varphi(x_{k_{ij}}). \end{align*}
\begin{align*} [\mathscr{U}\zeta\mathscr{U}](\varphi)(x_j) &=\sum_{i=1}^r(\zeta_i)_p.\varphi(x_j\zeta_i) \\ &=\sum_{i=1}^r(\zeta_i)_p.\varphi(d_{ij}x_{k_{ij}}u_{ij})=\sum_{i=1}^r(\zeta_iu_{ij}^{-1})_p.\varphi(x_{k_{ij}}). \end{align*}
The values of ![]() $i$ for which
$i$ for which ![]() $k_{ij}=k$ are those for which
$k_{ij}=k$ are those for which ![]() $\zeta _i=x_j^{-1}dx_ku$ for some
$\zeta _i=x_j^{-1}dx_ku$ for some ![]() $d\in G(\mathbb {Q})$ and
$d\in G(\mathbb {Q})$ and ![]() $u\in \mathscr {U}$, that is,
$u\in \mathscr {U}$, that is, ![]() $\zeta _i\in x_j^{-1}G(\mathbb {Q})x_k\mathscr {U}$.
$\zeta _i\in x_j^{-1}G(\mathbb {Q})x_k\mathscr {U}$.
If ![]() $a=(a_1,\dotsc,a_n)\in \mathbb {Z}^n$, we write
$a=(a_1,\dotsc,a_n)\in \mathbb {Z}^n$, we write
and define the subgroup
and its submonoids
We frequently choose ![]() $\zeta$ to be an element of
$\zeta$ to be an element of ![]() $\Sigma ^-$. Let
$\Sigma ^-$. Let
Proposition 2.6.2 If ![]() $f\in \mathscr {S}_s$ and
$f\in \mathscr {S}_s$ and ![]() $a=(a_1,\dotsc,a_n)\in \mathbb {Z}^n$,
$a=(a_1,\dotsc,a_n)\in \mathbb {Z}^n$, ![]() $u^a$ acts on
$u^a$ acts on ![]() $f$ by
$f$ by ![]() $z_{ij}\mapsto p^{a_i-a_j}z_{ij}$.
$z_{ij}\mapsto p^{a_i-a_j}z_{ij}$.
Proof. We have
 \begin{align*} & f((u^a)^{-1}\overline{N}(z_{ij}))\\ & \quad =f\left( \begin{pmatrix}
p^{-a_1} & \dotsb & 0 \\ 0 & \vdots & 0 \\ 0 & \dotsb &
p^{-a_n} \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \dotsb &
0 \\ pz_{21} & 1 & 0 & \dotsb & 0 \\ pz_{31} & pz_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots
\\ pz_{n1} & pz_{n2} & pz_{n3} & \dotsb & 1 \end{pmatrix}
\right)\\ & \quad =f\begin{pmatrix} p^{-a_1} & 0 & 0 & \dotsb & 0
\\ p^{-a_2+1}z_{21} & p^{-a_2} & 0 & \dotsb & 0 \\
p^{-a_3+1}z_{31} & p^{-a_3+1}z_{32} & p^{-a_3} & \dotsb & 0
\\ \vdots & \vdots & \vdots & \vdots & \vdots \\
p^{-a_n+1}z_{n1} & p^{-a_n+1}z_{n2} & p^{-a_n+1}z_{n3} &
\dotsb & p^{-a_n} \end{pmatrix}\\ & \quad =f\left(\begin{pmatrix}
1 & 0 & 0 & \dotsb & 0 \\ p^{a_1-a_2+1}z_{21} & 1 & 0 &
\dotsb & 0 \\ p^{a_1-a_3+1}z_{31} & p^{a_2-a_3+1}z_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots
\\ p^{a_1-a_n+1}z_{n1} & p^{a_2-a_n+1}z_{n2} &
p^{a_3-a_n+1}z_{n3} & \dotsb & 1 \end{pmatrix}
\begin{pmatrix} p^{-a_1} & \dotsb & 0 \\ 0 & \vdots & 0 \\
0 & \dotsb & p^{-a_n} \end{pmatrix} \right)\\ & \quad =f(\overline{N}(p^{a_i-a_j}z_{ij}))s^0(u^a)=f(\overline{N}(p^{a_i-a_j}z_{ij})).
\end{align*}
\begin{align*} & f((u^a)^{-1}\overline{N}(z_{ij}))\\ & \quad =f\left( \begin{pmatrix}
p^{-a_1} & \dotsb & 0 \\ 0 & \vdots & 0 \\ 0 & \dotsb &
p^{-a_n} \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \dotsb &
0 \\ pz_{21} & 1 & 0 & \dotsb & 0 \\ pz_{31} & pz_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots
\\ pz_{n1} & pz_{n2} & pz_{n3} & \dotsb & 1 \end{pmatrix}
\right)\\ & \quad =f\begin{pmatrix} p^{-a_1} & 0 & 0 & \dotsb & 0
\\ p^{-a_2+1}z_{21} & p^{-a_2} & 0 & \dotsb & 0 \\
p^{-a_3+1}z_{31} & p^{-a_3+1}z_{32} & p^{-a_3} & \dotsb & 0
\\ \vdots & \vdots & \vdots & \vdots & \vdots \\
p^{-a_n+1}z_{n1} & p^{-a_n+1}z_{n2} & p^{-a_n+1}z_{n3} &
\dotsb & p^{-a_n} \end{pmatrix}\\ & \quad =f\left(\begin{pmatrix}
1 & 0 & 0 & \dotsb & 0 \\ p^{a_1-a_2+1}z_{21} & 1 & 0 &
\dotsb & 0 \\ p^{a_1-a_3+1}z_{31} & p^{a_2-a_3+1}z_{32} & 1 & \dotsb & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots
\\ p^{a_1-a_n+1}z_{n1} & p^{a_2-a_n+1}z_{n2} &
p^{a_3-a_n+1}z_{n3} & \dotsb & 1 \end{pmatrix}
\begin{pmatrix} p^{-a_1} & \dotsb & 0 \\ 0 & \vdots & 0 \\
0 & \dotsb & p^{-a_n} \end{pmatrix} \right)\\ & \quad =f(\overline{N}(p^{a_i-a_j}z_{ij}))s^0(u^a)=f(\overline{N}(p^{a_i-a_j}z_{ij})).
\end{align*}
Corollary 2.6.3 If ![]() $f\in \mathscr {S}_s$ is
$f\in \mathscr {S}_s$ is ![]() $\underline {c}$-locally analytic and
$\underline {c}$-locally analytic and ![]() $u^a\in \Sigma ^-$, then
$u^a\in \Sigma ^-$, then ![]() $u^af$ is also
$u^af$ is also ![]() $\underline {c}$-locally analytic. Thus, translation by
$\underline {c}$-locally analytic. Thus, translation by ![]() $\operatorname {Iw}_pu^a\operatorname {Iw}_p$ preserves
$\operatorname {Iw}_pu^a\operatorname {Iw}_p$ preserves ![]() $\mathscr {S}_{s,\underline {c}}$ (and, hence, by Lemma 2.6.1,
$\mathscr {S}_{s,\underline {c}}$ (and, hence, by Lemma 2.6.1, ![]() $U_p^a$ preserves
$U_p^a$ preserves ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$).
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$).
Proof. When ![]() $u^a\in \Sigma ^-$, we have
$u^a\in \Sigma ^-$, we have ![]() $a_i-a_j\ge 0$ for all
$a_i-a_j\ge 0$ for all ![]() $i>j$; thus, if
$i>j$; thus, if ![]() $(z_{ij})$ varies in a ball
$(z_{ij})$ varies in a ball ![]() $B(\underline {a},\underline {c})$, so does
$B(\underline {a},\underline {c})$, so does ![]() $(p^{a_i-a_j}z_{ij})=(u^az_{ij})$.
$(p^{a_i-a_j}z_{ij})=(u^az_{ij})$.
Let ![]() $\underline {c}^0\in \mathbb {Z}_{>0}^{n(n-1)/2}$ be minimal such that
$\underline {c}^0\in \mathbb {Z}_{>0}^{n(n-1)/2}$ be minimal such that ![]() $s$ is
$s$ is ![]() $\underline {c}^0$-locally analytic.
$\underline {c}^0$-locally analytic.
Corollary 2.6.4 If ![]() $f\in \mathscr {S}_s$ is
$f\in \mathscr {S}_s$ is ![]() $\underline {c}$-locally analytic and
$\underline {c}$-locally analytic and ![]() $u^a\in \Sigma ^{--}$, then
$u^a\in \Sigma ^{--}$, then ![]() $u^af$ is
$u^af$ is ![]() $\underline {c}^{--}:=(\max \{c_{ij}-1,c_{ij}^0\})$-locally analytic. Thus, translation by
$\underline {c}^{--}:=(\max \{c_{ij}-1,c_{ij}^0\})$-locally analytic. Thus, translation by ![]() $\operatorname {Iw}_pu^a\operatorname {Iw}_p$ takes
$\operatorname {Iw}_pu^a\operatorname {Iw}_p$ takes ![]() $\mathscr {S}_{s,\underline {c}}$ into
$\mathscr {S}_{s,\underline {c}}$ into ![]() $\mathscr {S}_{s,\underline {c}^{--}}$ (and, hence, by Lemma 2.6.1,
$\mathscr {S}_{s,\underline {c}^{--}}$ (and, hence, by Lemma 2.6.1, ![]() $U_p^a$ takes
$U_p^a$ takes ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$ into
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$ into ![]() $\mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})$).
$\mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})$).
Proof. When ![]() $u^a\in \Sigma ^{--}$, we have
$u^a\in \Sigma ^{--}$, we have ![]() $a_i-a_j>0$ for all
$a_i-a_j>0$ for all ![]() $i>j$; thus, if
$i>j$; thus, if ![]() $(z_{ij})$ varies in a ball
$(z_{ij})$ varies in a ball ![]() $B(\underline {a},\underline {c})$, then
$B(\underline {a},\underline {c})$, then ![]() $(p^{a_i-a_j}z_{ij})=(u^az_{ij})$ varies in a smaller ball
$(p^{a_i-a_j}z_{ij})=(u^az_{ij})$ varies in a smaller ball ![]() $B(\underline {a}',\underline {c+1})$, where
$B(\underline {a}',\underline {c+1})$, where ![]() $\underline {c+1}=(c_{ij}+1)_{n\ge i>j\ge 1}$.
$\underline {c+1}=(c_{ij}+1)_{n\ge i>j\ge 1}$.
Remark 2 Similarly, if ![]() $a_i< a_j$ for some
$a_i< a_j$ for some ![]() $i< j$, and
$i< j$, and ![]() $f\in \mathscr {S}_s$ is
$f\in \mathscr {S}_s$ is ![]() $\underline {c}$-locally analytic, then
$\underline {c}$-locally analytic, then ![]() $u^af$ need not be
$u^af$ need not be ![]() $\underline {c}$-locally analytic, because
$\underline {c}$-locally analytic, because ![]() $p^{a_i-a_j}z_{ij}$ varies in a larger ball than
$p^{a_i-a_j}z_{ij}$ varies in a larger ball than ![]() $z_{ij}$ does. This is why
$z_{ij}$ does. This is why ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$ does not have an action by
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$ does not have an action by ![]() $B(\mathbb {Q}_p)$ and we need to restrict to
$B(\mathbb {Q}_p)$ and we need to restrict to ![]() $\Sigma ^-$.
$\Sigma ^-$.
The space ![]() $\mathscr {S}_{s,\underline {c}}$ is an orthonormalizable
$\mathscr {S}_{s,\underline {c}}$ is an orthonormalizable ![]() $A$-module, for which we choose the following orthonormal basis: for each
$A$-module, for which we choose the following orthonormal basis: for each ![]() $\underline {a}\in \prod _{n\ge i>j\ge 1} \mathbb {Z}_p/p^{c_{ij}}\mathbb {Z}_p$, we choose the set of monomials
$\underline {a}\in \prod _{n\ge i>j\ge 1} \mathbb {Z}_p/p^{c_{ij}}\mathbb {Z}_p$, we choose the set of monomials ![]() $\prod _{n\ge i>j\ge 1}z_{ij}^{e_{ij}}$ as an orthonormal basis for the restriction of
$\prod _{n\ge i>j\ge 1}z_{ij}^{e_{ij}}$ as an orthonormal basis for the restriction of ![]() $\mathscr {S}_{s,\underline {c}}$ to
$\mathscr {S}_{s,\underline {c}}$ to ![]() $B(\underline {a},\underline {c})$; then for
$B(\underline {a},\underline {c})$; then for ![]() $\mathscr {S}_{s,\underline {c}}$, we may choose as orthonormal basis the set of monomials
$\mathscr {S}_{s,\underline {c}}$, we may choose as orthonormal basis the set of monomials ![]() $\prod _{n\ge i>j\ge 1}(z_{ij}^{\underline {a}})^{e_{ij}}$, with one copy for each
$\prod _{n\ge i>j\ge 1}(z_{ij}^{\underline {a}})^{e_{ij}}$, with one copy for each ![]() $\underline {a}\in \prod _{n\ge i>j\ge 1} \mathbb {Z}_p/p^{c_{ij}}\mathbb {Z}_p$, where
$\underline {a}\in \prod _{n\ge i>j\ge 1} \mathbb {Z}_p/p^{c_{ij}}\mathbb {Z}_p$, where ![]() $z_{ij}^{\underline {a}}$ is the function which equals
$z_{ij}^{\underline {a}}$ is the function which equals ![]() $z_{ij}$ on
$z_{ij}$ on ![]() $B(\underline {a},\underline {c})$ and
$B(\underline {a},\underline {c})$ and ![]() $0$ elsewhere.
$0$ elsewhere.
Corollary 2.6.5 When ![]() $a\in \Sigma ^{--}$, the operator of translation by
$a\in \Sigma ^{--}$, the operator of translation by ![]() $u^a$ acts completely continuously on
$u^a$ acts completely continuously on ![]() $\mathscr {S}_{s,\underline {c}}$, in the sense that it is a uniform limit of operators with finite-dimensional images. Thus, by Lemma 2.6.1,
$\mathscr {S}_{s,\underline {c}}$, in the sense that it is a uniform limit of operators with finite-dimensional images. Thus, by Lemma 2.6.1, ![]() $U_p^a$ is completely continuous on
$U_p^a$ is completely continuous on ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$.
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$.
Proof. By Proposition 2.6.2, ![]() $u^a$ scales
$u^a$ scales ![]() $\prod _{n\ge i>j\ge 1}(z_{ij}^{\underline {a}})^{e_{ij}}$ by
$\prod _{n\ge i>j\ge 1}(z_{ij}^{\underline {a}})^{e_{ij}}$ by ![]() $\prod _{n\ge i>j\ge 1}p^{(a_i-a_j)e_{ij}}$, which goes to
$\prod _{n\ge i>j\ge 1}p^{(a_i-a_j)e_{ij}}$, which goes to ![]() $\infty$ as any
$\infty$ as any ![]() $e_{ij}$ goes to
$e_{ij}$ goes to ![]() $\infty$. Furthermore, since the formulas in § 2.3 all have integer coefficients, it is clear that translation by
$\infty$. Furthermore, since the formulas in § 2.3 all have integer coefficients, it is clear that translation by ![]() $\operatorname {Iw}_p$ is norm
$\operatorname {Iw}_p$ is norm ![]() $1$.
$1$.
Since ![]() $U_p^a$ is completely continuous on
$U_p^a$ is completely continuous on ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$, for any
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$, for any ![]() $k$, the matrix of the action of
$k$, the matrix of the action of ![]() $U_p^a$ (in any basis) has a finite number of nonzero rows mod
$U_p^a$ (in any basis) has a finite number of nonzero rows mod ![]() $p^k$. Suppose that this matrix has
$p^k$. Suppose that this matrix has ![]() $r_k$ rows that are zero mod
$r_k$ rows that are zero mod ![]() $p^k$ but nonzero mod
$p^k$ but nonzero mod ![]() $p^{k+1}$. Then for any
$p^{k+1}$. Then for any ![]() $N\ge r_0+r_1+\dotsb +r_k$, the coefficient of
$N\ge r_0+r_1+\dotsb +r_k$, the coefficient of ![]() $X^N$ in the characteristic power series
$X^N$ in the characteristic power series
of ![]() $U_p^a$ acting on
$U_p^a$ acting on ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$, being a linear combination of minors of size
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$, being a linear combination of minors of size ![]() $N\ge r_0+r_1+\dotsb +r_k$, is divisible by
$N\ge r_0+r_1+\dotsb +r_k$, is divisible by ![]() $r_1+2r_2+\dotsb +kr_k$. Since this lower bound grows faster than any linear function of
$r_1+2r_2+\dotsb +kr_k$. Since this lower bound grows faster than any linear function of ![]() $N$,
$N$, ![]() $P_{s,\underline {c}}^a(X)$ is an entire function of
$P_{s,\underline {c}}^a(X)$ is an entire function of ![]() $X$.
$X$.
Proposition 2.6.6 The characteristic power series ![]() $P_{s,\underline {c}}^a(X)$ is independent of
$P_{s,\underline {c}}^a(X)$ is independent of ![]() $\underline {c}$. (So we henceforth call it
$\underline {c}$. (So we henceforth call it ![]() $P_s^a(X)$.)
$P_s^a(X)$.)
Proof. This follows from applying Corollary 2 of Proposition 7 of [Reference SerreSer62] to the map ![]() $U_p^a:\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})\to \mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})$ from Corollary 2.6.4 and the obvious inclusion
$U_p^a:\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})\to \mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})$ from Corollary 2.6.4 and the obvious inclusion ![]() $\mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})\hookrightarrow \mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$.
$\mathscr {S}_{s,\underline {c}^{--}}(G,\mathscr {U})\hookrightarrow \mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$.
Let ![]() $U_p^\Sigma$ be the subring of
$U_p^\Sigma$ be the subring of ![]() $\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$ generated by the elements
$\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$ generated by the elements ![]() $U_p^a$ for
$U_p^a$ for ![]() $a\in \Sigma ^-$ and their inverses (which exist, as discussed in [Reference Bellaïche and ChenevierBC09, § 6.4.1]). By Proposition 6.4.1 of [Reference Bellaïche and ChenevierBC09], the map from
$a\in \Sigma ^-$ and their inverses (which exist, as discussed in [Reference Bellaïche and ChenevierBC09, § 6.4.1]). By Proposition 6.4.1 of [Reference Bellaïche and ChenevierBC09], the map from ![]() $k[\Sigma ]$ to
$k[\Sigma ]$ to ![]() $U_p^\Sigma$ sending
$U_p^\Sigma$ sending ![]() $u^a$ to
$u^a$ to ![]() $U_p^b(U_p^c)^{-1}$ where
$U_p^b(U_p^c)^{-1}$ where ![]() $u^b,u^c$ are any elements of
$u^b,u^c$ are any elements of ![]() $\Sigma ^-$ such that
$\Sigma ^-$ such that ![]() $u^a=u^b(u^c)^{-1}$ is a well-defined isomorphism of rings. Thus, in particular,
$u^a=u^b(u^c)^{-1}$ is a well-defined isomorphism of rings. Thus, in particular, ![]() $U_p^\Sigma$ is abelian. Let
$U_p^\Sigma$ is abelian. Let ![]() $\mathscr {H}$ be a subalgebra of
$\mathscr {H}$ be a subalgebra of ![]() $\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$ given by the product of
$\mathscr {H}(G(\mathbb {A}_f)// \mathscr {U})$ given by the product of ![]() $\mathbb {Z}[U_p^\Sigma ]$ at
$\mathbb {Z}[U_p^\Sigma ]$ at ![]() $p$ and some commutative subalgebra of
$p$ and some commutative subalgebra of ![]() $\mathscr {H}(G(\mathbb {A}_f^p)// \mathscr {U}^p)$ away from
$\mathscr {H}(G(\mathbb {A}_f^p)// \mathscr {U}^p)$ away from ![]() $p$.
$p$.
We write ![]() $u_i$ for the image of
$u_i$ for the image of ![]() $\operatorname {diag}(1,\dotsc,1,p,1,\dotsc,1)\in k[\Sigma ]$ in
$\operatorname {diag}(1,\dotsc,1,p,1,\dotsc,1)\in k[\Sigma ]$ in ![]() $U_p^\Sigma$. If
$U_p^\Sigma$. If ![]() $f$ is an element of an
$f$ is an element of an ![]() $\mathscr {H}$-module
$\mathscr {H}$-module ![]() $S$ (such as
$S$ (such as ![]() $\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$) that is a generalized simultaneous eigenvector for
$\mathscr {S}_{s,\underline {c}}(G,\mathscr {U})$) that is a generalized simultaneous eigenvector for ![]() $\mathscr {H}$, let
$\mathscr {H}$, let ![]() $u_i(f)=\lambda _i f$. We call these the
$u_i(f)=\lambda _i f$. We call these the ![]() $\lambda$-values associated to
$\lambda$-values associated to ![]() $f$. We call the subspace generated by all the generalized simultaneous eigenvectors whose associated
$f$. We call the subspace generated by all the generalized simultaneous eigenvectors whose associated ![]() $\lambda$-values are nonzero the finite-slope subspace of
$\lambda$-values are nonzero the finite-slope subspace of ![]() $S$, and we denote it by
$S$, and we denote it by ![]() $S^{{\rm fs}}$.
$S^{{\rm fs}}$.
Unless otherwise specified, we will generally set ![]() $\mathscr {U}$ to be a compact open subgroup of
$\mathscr {U}$ to be a compact open subgroup of ![]() $G(\mathbb {A}_f)$ given by the product of
$G(\mathbb {A}_f)$ given by the product of ![]() $\operatorname {Iw}_p$ at
$\operatorname {Iw}_p$ at ![]() $p$ and a fixed tame level structure away from
$p$ and a fixed tame level structure away from ![]() $p$ chosen so that
$p$ chosen so that ![]() $x^{-1}G(\mathbb {Q})x\cap \mathscr {U}=1$ for all
$x^{-1}G(\mathbb {Q})x\cap \mathscr {U}=1$ for all ![]() $x$ (the condition of being ‘sufficiently small’ or ‘neat’ as described at the end of § 2.1). Call this subgroup
$x$ (the condition of being ‘sufficiently small’ or ‘neat’ as described at the end of § 2.1). Call this subgroup ![]() $U_0(p)$. (Note that for the same reason as in Proposition 3.1.2, our choice of
$U_0(p)$. (Note that for the same reason as in Proposition 3.1.2, our choice of ![]() $\operatorname {Iw}_p$ as the wild level structure does not actually affect
$\operatorname {Iw}_p$ as the wild level structure does not actually affect ![]() $P_s^a(X)$.)
$P_s^a(X)$.)
2.7 The eigenvariety
Given our setup so far, the eigenvariety is easy to define. For a given ![]() $u^a\in \Sigma ^{--}$, let
$u^a\in \Sigma ^{--}$, let ![]() $\mathscr {Z}^a$ be the subvariety of
$\mathscr {Z}^a$ be the subvariety of ![]() $\mathscr {W}\times \mathbb {G}_m$ which, in any subset
$\mathscr {W}\times \mathbb {G}_m$ which, in any subset ![]() $W\times \mathbb {G}_m$ where
$W\times \mathbb {G}_m$ where ![]() $W\subset \mathscr {W}$ is open affinoid, is cut out by the characteristic power series
$W\subset \mathscr {W}$ is open affinoid, is cut out by the characteristic power series ![]() $P_W^a(X)$ of
$P_W^a(X)$ of ![]() $U_p^a$ acting on
$U_p^a$ acting on ![]() $\mathscr {S}_W(G,U_0(p))$. Let
$\mathscr {S}_W(G,U_0(p))$. Let ![]() $w:\mathscr {Z}^a\to \mathscr {W}$ be the first projection (weight) map, and
$w:\mathscr {Z}^a\to \mathscr {W}$ be the first projection (weight) map, and ![]() $a_p^a:\mathscr {Z}^a\to \mathbb {G}_m$ the inverse of the second projection (
$a_p^a:\mathscr {Z}^a\to \mathbb {G}_m$ the inverse of the second projection (![]() $U_p^a$-eigenvalue) map. Then for any point
$U_p^a$-eigenvalue) map. Then for any point ![]() $z\in \mathscr {Z}^a$,
$z\in \mathscr {Z}^a$, ![]() $a_p^a(z)$ is a nonzero eigenvalue of
$a_p^a(z)$ is a nonzero eigenvalue of ![]() $U_p^a$ acting on
$U_p^a$ acting on ![]() $\mathscr {S}_{w(z)}(G,U_0(p))$, and for any
$\mathscr {S}_{w(z)}(G,U_0(p))$, and for any ![]() $w\in \mathscr {W}$, all nonzero eigenvalues of
$w\in \mathscr {W}$, all nonzero eigenvalues of ![]() $U_p^a$ acting on
$U_p^a$ acting on ![]() $\mathscr {S}_w(G,U_0(p))$ can be found in the fiber of
$\mathscr {S}_w(G,U_0(p))$ can be found in the fiber of ![]() $\mathscr {Z}^a$ over
$\mathscr {Z}^a$ over ![]() $w$. We call
$w$. We call ![]() $\mathscr {Z}^a$ the spectral variety associated to
$\mathscr {Z}^a$ the spectral variety associated to ![]() $U_p^a$.
$U_p^a$.
It is convenient to fix a particular choice of ![]() $u^a\in \Sigma ^{--}$; we choose
$u^a\in \Sigma ^{--}$; we choose ![]() $a=(n-1,n-2,\dotsc,1,0)$. From now on, we write
$a=(n-1,n-2,\dotsc,1,0)$. From now on, we write ![]() $U_p=U_p^{(n-1,n-2,\dotsc,1,0)}$ and
$U_p=U_p^{(n-1,n-2,\dotsc,1,0)}$ and ![]() $\mathscr {Z}=\mathscr {Z}^{(n-1,n-2,\dotsc,1,0)}$. We call an eigenform
$\mathscr {Z}=\mathscr {Z}^{(n-1,n-2,\dotsc,1,0)}$. We call an eigenform ![]() $f\in \mathscr {S}_w(G,U_0(p))$ finite-slope if
$f\in \mathscr {S}_w(G,U_0(p))$ finite-slope if ![]() $U_pf\neq 0$ (i.e. the valuation, or slope, of the
$U_pf\neq 0$ (i.e. the valuation, or slope, of the ![]() $U_p$-eigenvalue is finite, and
$U_p$-eigenvalue is finite, and ![]() $f$ appears on the eigenvariety), and infinite-slope otherwise.
$f$ appears on the eigenvariety), and infinite-slope otherwise.
Since ![]() $\mathscr {H}$ is commutative, we can construct the space
$\mathscr {H}$ is commutative, we can construct the space ![]() $\mathscr {D}$ whose points correspond to systems of eigenvalues of all Hecke operators in
$\mathscr {D}$ whose points correspond to systems of eigenvalues of all Hecke operators in ![]() $\mathscr {H}$, including in particular all
$\mathscr {H}$, including in particular all ![]() $U_p^a$ simultaneously, by simply taking
$U_p^a$ simultaneously, by simply taking ![]() $\mathscr {D}$ to be the finite cover of
$\mathscr {D}$ to be the finite cover of ![]() $\mathscr {Z}$ which, over an affinoid
$\mathscr {Z}$ which, over an affinoid ![]() $W\subset \mathscr {W}$, is given by the MaxSpec of the image of
$W\subset \mathscr {W}$, is given by the MaxSpec of the image of ![]() $\mathscr {H}\otimes \Lambda ^n$ in the endomorphism ring of
$\mathscr {H}\otimes \Lambda ^n$ in the endomorphism ring of ![]() $\mathscr {S}_W(G,U_0(p))$. Then
$\mathscr {S}_W(G,U_0(p))$. Then ![]() $\mathscr {D}$ inherits the weight map
$\mathscr {D}$ inherits the weight map ![]() $w:\mathscr {Z}^a\to \mathscr {W}$ and each eigenvalue map
$w:\mathscr {Z}^a\to \mathscr {W}$ and each eigenvalue map ![]() $a_p^a:\mathscr {D}\to \mathbb {G}^m$. Because
$a_p^a:\mathscr {D}\to \mathbb {G}^m$. Because ![]() $\mathscr {D}\to \mathscr {Z}^a$ is a finite map, in general the bounds and geometric properties we get for
$\mathscr {D}\to \mathscr {Z}^a$ is a finite map, in general the bounds and geometric properties we get for ![]() $\mathscr {Z}^a$ should also apply to
$\mathscr {Z}^a$ should also apply to ![]() $\mathscr {D}$. For this paper, we focus on the properties of
$\mathscr {D}$. For this paper, we focus on the properties of ![]() $\mathscr {Z}$ and/or
$\mathscr {Z}$ and/or ![]() $\mathscr {Z}^a$ for any fixed
$\mathscr {Z}^a$ for any fixed ![]() $a$.
$a$.
For additional details on properties of ![]() $\mathscr {Z}^a$ and
$\mathscr {Z}^a$ and ![]() $\mathscr {D}$ and their proofs, see [Reference ChenevierChe04] or [Reference BuzzardBuz07].
$\mathscr {D}$ and their proofs, see [Reference ChenevierChe04] or [Reference BuzzardBuz07].
3. Locally algebraic weights
In this section, we analyze classical automorphic forms of locally algebraic weights and their associated automorphic representations. In § 3.1, we define these spaces of classical forms and check their basic properties, including that they embed into the infinite-dimensional spaces of § 2.1. In § 3.2, we reproduce the Bellaïche–Chenevier slope criterion guaranteeing that a given form is classical, phrased to work for locally algebraic weights instead of just algebraic weights; while this is not directly needed for our purposes, it is useful to give a sense of where classical forms fit in among the world of all ![]() $p$-adic automorphic forms. In § 3.3, we explain the standard translation between classical forms and automorphic representations. In § 3.4, we analyze certain Iwahori subrepresentations that may appear in the local component at
$p$-adic automorphic forms. In § 3.3, we explain the standard translation between classical forms and automorphic representations. In § 3.4, we analyze certain Iwahori subrepresentations that may appear in the local component at ![]() $p$ of such an automorphic representation, including a particularly important irreducible subrepresentation. In § 3.5, we apply the work of Roche to a calculation of Hecke eigenvalues in ramified principal series. In § 3.6, we identify a subspace of forms whose associated automorphic representations have ramified principal series as their local components at
$p$ of such an automorphic representation, including a particularly important irreducible subrepresentation. In § 3.5, we apply the work of Roche to a calculation of Hecke eigenvalues in ramified principal series. In § 3.6, we identify a subspace of forms whose associated automorphic representations have ramified principal series as their local components at ![]() $p$, and compute their
$p$, and compute their ![]() $U_p$-eigenvalues in terms of the parameters of the corresponding principal series.
$U_p$-eigenvalues in terms of the parameters of the corresponding principal series.
3.1  $p$-adic automorphic forms of locally algebraic weights
$p$-adic automorphic forms of locally algebraic weights
In § 2.1, we defined classical forms of algebraic weights via the algebraic representation ![]() $S_t(k)$ of
$S_t(k)$ of ![]() ${GL}_n(\mathbb {Q}_p)$. This construction may be generalized to locally algebraic weights as follows. Let
${GL}_n(\mathbb {Q}_p)$. This construction may be generalized to locally algebraic weights as follows. Let ![]() $\chi =\chi _1\dotsb \chi _n$ be a finite character of
$\chi =\chi _1\dotsb \chi _n$ be a finite character of ![]() $(\mathbb {Z}_p^\times )^n$. Then
$(\mathbb {Z}_p^\times )^n$. Then ![]() $t\chi$ is a locally algebraic character of
$t\chi$ is a locally algebraic character of ![]() $(\mathbb {Z}_p^\times )^n$, in the sense that it is algebraic upon restriction to
$(\mathbb {Z}_p^\times )^n$, in the sense that it is algebraic upon restriction to ![]() $\prod _{i=1}^n(a_i+p^{c_i}\mathbb {Z}_p)$ for some choice of
$\prod _{i=1}^n(a_i+p^{c_i}\mathbb {Z}_p)$ for some choice of ![]() $c_i$ and any nonzero
$c_i$ and any nonzero ![]() $a_i$. Similarly to earlier notation, for a positive integer
$a_i$. Similarly to earlier notation, for a positive integer ![]() $c$, let
$c$, let
Then there are two equivalent definitions of the space
where ![]() $c\text {-loc.alg.}$ stands for
$c\text {-loc.alg.}$ stands for ![]() $c$-locally algebraic. The first is through the usual induction operator, as follows. We say that
$c$-locally algebraic. The first is through the usual induction operator, as follows. We say that ![]() $f\in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p}(t\chi )$ is
$f\in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p}(t\chi )$ is ![]() $c$-locally algebraic if it has an algebraic extension to
$c$-locally algebraic if it has an algebraic extension to ![]() $B(\underline {a},c)$ for all
$B(\underline {a},c)$ for all ![]() $\underline {a}\in \mathbb {Z}_p^{n(n-1)/2}$ of degree bounded as follows: writing
$\underline {a}\in \mathbb {Z}_p^{n(n-1)/2}$ of degree bounded as follows: writing ![]() $f$ as a polynomial in the variables
$f$ as a polynomial in the variables ![]() $Z_{i,k/1}$ as in § 2.3, we require that for each fixed
$Z_{i,k/1}$ as in § 2.3, we require that for each fixed ![]() $i$, the degree of
$i$, the degree of ![]() $f$ as a polynomial in all the variables
$f$ as a polynomial in all the variables ![]() $Z_{i,k/1}$ should be at most
$Z_{i,k/1}$ should be at most ![]() $t_i-t_{i+1}=:m_i$. As in Proposition 2.5.3, one can see using the formulas in § 2.3 that assuming
$t_i-t_{i+1}=:m_i$. As in Proposition 2.5.3, one can see using the formulas in § 2.3 that assuming ![]() $\operatorname {cond}(\chi _i)\le c$ for all
$\operatorname {cond}(\chi _i)\le c$ for all ![]() $i$, this condition is invariant under right translation by
$i$, this condition is invariant under right translation by ![]() $\operatorname {Iw}_p$.
$\operatorname {Iw}_p$.
The second definition, coming from the perspective of Loeffler [Reference LoefflerLoe10, § 2.5], is
Note that ![]() $\Gamma (c)$ is normal in
$\Gamma (c)$ is normal in ![]() $\operatorname {Iw}_p$ because it is the kernel of the reduction map from
$\operatorname {Iw}_p$ because it is the kernel of the reduction map from ![]() $\operatorname {Iw}_p$ to the corresponding group with coefficients in
$\operatorname {Iw}_p$ to the corresponding group with coefficients in ![]() $\mathbb {Z}_p/p^c\mathbb {Z}_p$.
$\mathbb {Z}_p/p^c\mathbb {Z}_p$.
Except for an annoying technical distinction which we discuss at the end of this subsection, the space ![]() $\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$ is the same (as an
$\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$ is the same (as an ![]() $\operatorname {Iw}_p$-representation) as the space
$\operatorname {Iw}_p$-representation) as the space ![]() $S_t(k)$ defined in § 2.1, since
$S_t(k)$ defined in § 2.1, since ![]() $\operatorname {Iw}_p$ is Zariski-dense in
$\operatorname {Iw}_p$ is Zariski-dense in ![]() ${GL}_n$. Let
${GL}_n$. Let ![]() $d_t=\dim \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$. We now check that the two definitions just given are actually equivalent.
$d_t=\dim \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$. We now check that the two definitions just given are actually equivalent.
Proposition 3.1.1 The natural map
 \begin{gather*} \biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)}^{\operatorname{Iw}_p,{\rm alg}}t\biggr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\Gamma(c)}\chi\biggr)\to \operatorname{Ind}_B^{\operatorname{Iw}_p,c\text{-loc.alg.}}(t\chi)\\ f\otimes g\mapsto fg \end{gather*}
\begin{gather*} \biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)}^{\operatorname{Iw}_p,{\rm alg}}t\biggr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\Gamma(c)}\chi\biggr)\to \operatorname{Ind}_B^{\operatorname{Iw}_p,c\text{-loc.alg.}}(t\chi)\\ f\otimes g\mapsto fg \end{gather*}
is an isomorphism.
Proof. To construct an inverse, let ![]() $\varphi \in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,c\text {-loc.alg.}}(t\chi )$. Let
$\varphi \in \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,c\text {-loc.alg.}}(t\chi )$. Let ![]() $\varphi _{{\rm alg}}:\operatorname {Iw}_p\to \mathbb {C}$ (the ‘algebraic part’ of
$\varphi _{{\rm alg}}:\operatorname {Iw}_p\to \mathbb {C}$ (the ‘algebraic part’ of ![]() $\phi$) be defined by
$\phi$) be defined by
for all ![]() $b\in B,\overline {n}\in \overline {N}\cap \operatorname {Iw}_p$, where
$b\in B,\overline {n}\in \overline {N}\cap \operatorname {Iw}_p$, where ![]() $\varphi '$ is the unique algebraic extension of
$\varphi '$ is the unique algebraic extension of ![]() $\varphi |_{\overline {N}\cap \Gamma (c)}$ to
$\varphi |_{\overline {N}\cap \Gamma (c)}$ to ![]() $\overline {N}\cap \operatorname {Iw}_p$. Let
$\overline {N}\cap \operatorname {Iw}_p$. Let ![]() $\varphi _{{\rm sm}}:\operatorname {Iw}_p/\operatorname {Iw}_p\cap \Gamma (c)\to \mathbb {C}$ (the ‘smooth part’ of
$\varphi _{{\rm sm}}:\operatorname {Iw}_p/\operatorname {Iw}_p\cap \Gamma (c)\to \mathbb {C}$ (the ‘smooth part’ of ![]() $\phi$) be defined by
$\phi$) be defined by
where ![]() $b,\overline {n}$ are any lifts of
$b,\overline {n}$ are any lifts of ![]() $\overline {b}\in B/B\cap \Gamma (c)$,
$\overline {b}\in B/B\cap \Gamma (c)$, ![]() $\overline {\overline {n}}\in (\overline {N}\cap \operatorname {Iw}_p)/(\overline {N}\cap \Gamma (c))$. Then we have
$\overline {\overline {n}}\in (\overline {N}\cap \operatorname {Iw}_p)/(\overline {N}\cap \Gamma (c))$. Then we have ![]() $\varphi _{{\rm alg}}\otimes \varphi _{{\rm sm}}\mapsto \varphi$, which suffices to prove surjectivity.
$\varphi _{{\rm alg}}\otimes \varphi _{{\rm sm}}\mapsto \varphi$, which suffices to prove surjectivity.
Injectivity follows from dimension counting: both sides have dimension ![]() $d_tp^{c\binom{n}{2}}$.
$d_tp^{c\binom{n}{2}}$.
Remark 3 There is a simple isomorphism of ![]() $\operatorname {Iw}_p$-representations
$\operatorname {Iw}_p$-representations
so we could just as easily have phrased this section in terms of ![]() $\operatorname {Ind}_{\Gamma _0(c)}^{\operatorname {Iw}_p}\chi$. For now, we have no particular reason to do this, but it may be more convenient for future work.
$\operatorname {Ind}_{\Gamma _0(c)}^{\operatorname {Iw}_p}\chi$. For now, we have no particular reason to do this, but it may be more convenient for future work.
We call
the space of classical ![]() $p$-adic automorphic forms on
$p$-adic automorphic forms on ![]() $G$ of weight
$G$ of weight ![]() $t\chi$, radius
$t\chi$, radius ![]() $c$, and level
$c$, and level ![]() $\mathscr {U}$. By the definitions, it embeds into
$\mathscr {U}$. By the definitions, it embeds into ![]() $\mathscr {S}_{t\chi }(G,\mathscr {U})$, and we call its image a classical subspace of
$\mathscr {S}_{t\chi }(G,\mathscr {U})$, and we call its image a classical subspace of ![]() $\mathscr {S}_{t\chi }(G,\mathscr {U})$. The following proposition is a quick generalization of part 4 of Lemma 4 of [Reference BuzzardBuz04].
$\mathscr {S}_{t\chi }(G,\mathscr {U})$. The following proposition is a quick generalization of part 4 of Lemma 4 of [Reference BuzzardBuz04].
Proposition 3.1.2 For any positive integers ![]() $c$,
$c$, ![]() $d$, and
$d$, and ![]() $e$ with
$e$ with ![]() $d\le e$ and
$d\le e$ and ![]() $c+d-e\ge 1$, we have a natural vector space isomorphism
$c+d-e\ge 1$, we have a natural vector space isomorphism
such that systems of ![]() $\mathscr {H}$-eigenvalues on the left (where
$\mathscr {H}$-eigenvalues on the left (where ![]() $\mathscr {H}$ is obtained with respect to
$\mathscr {H}$ is obtained with respect to ![]() $\mathscr {U}^p\Gamma _0(d)$) go to identical systems of
$\mathscr {U}^p\Gamma _0(d)$) go to identical systems of ![]() $\mathscr {H}$-eigenvalues on the right (where
$\mathscr {H}$-eigenvalues on the right (where ![]() $\mathscr {H}$ is obtained with respect to
$\mathscr {H}$ is obtained with respect to ![]() $\mathscr {U}^p\Gamma _0(e)$).
$\mathscr {U}^p\Gamma _0(e)$).
Proof. For the purposes of this proposition, let ![]() $X=G(\mathbb {Q})\backslash G(\mathbb {A}_f)$. The left-hand side is the subset of
$X=G(\mathbb {Q})\backslash G(\mathbb {A}_f)$. The left-hand side is the subset of
that remains invariant under a set of coset representatives ![]() $A$ for
$A$ for ![]() $\Gamma _0(e)\backslash \Gamma _0(d)$. This subset has a map by restriction of the second factor to
$\Gamma _0(e)\backslash \Gamma _0(d)$. This subset has a map by restriction of the second factor to
where ![]() $\mathscr {O}$ is the space of functions on
$\mathscr {O}$ is the space of functions on ![]() $B((p^{e-d}\mathbb {Z}_p)^{n(n-1)/2},c)$ that are algebraic on each ball
$B((p^{e-d}\mathbb {Z}_p)^{n(n-1)/2},c)$ that are algebraic on each ball ![]() $B(\underline {a},c)$. The map is an isomorphism: if
$B(\underline {a},c)$. The map is an isomorphism: if ![]() $\varphi \in (\text {Hom}(X,\mathbb {C}_p)\otimes \mathscr {O})^{\Gamma _0(e)}$, its inverse
$\varphi \in (\text {Hom}(X,\mathbb {C}_p)\otimes \mathscr {O})^{\Gamma _0(e)}$, its inverse ![]() $\psi$ may be defined by
$\psi$ may be defined by
In ![]() $\overline {N}(z)a^{-1}$,
$\overline {N}(z)a^{-1}$, ![]() $a$ should be interpreted as a coset representative for
$a$ should be interpreted as a coset representative for ![]() $\Gamma _0(e-d+1)\backslash \operatorname {Iw}_p$. Note that this inverse depends on the choice of coset representatives
$\Gamma _0(e-d+1)\backslash \operatorname {Iw}_p$. Note that this inverse depends on the choice of coset representatives ![]() $A$. Now
$A$. Now ![]() $B((p^{e-d}\mathbb {Z}_p)^{n(n-1)/2},c)$ is isomorphic to
$B((p^{e-d}\mathbb {Z}_p)^{n(n-1)/2},c)$ is isomorphic to ![]() $B(\mathbb {Z}_p^{n(n-1)/2},c+d-e)$ via multiplication by
$B(\mathbb {Z}_p^{n(n-1)/2},c+d-e)$ via multiplication by ![]() $p^{d-e}$, so
$p^{d-e}$, so ![]() $(\text {Hom}(X,\mathbb {C}_p)\otimes \mathscr {O})^{\Gamma _0(e)}$ is the desired right-hand side.
$(\text {Hom}(X,\mathbb {C}_p)\otimes \mathscr {O})^{\Gamma _0(e)}$ is the desired right-hand side.
To check that the Hecke operator action is preserved, it suffices to note that the Hecke operator action on the left-hand side can be calculated on its image in (1).
Corollary 3.1.3 For all positive integers ![]() $c$ and group-like
$c$ and group-like ![]() $\underline {d}\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$, we have a vector space embedding
$\underline {d}\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$, we have a vector space embedding
preserving systems of ![]() $\mathscr {H}$-eigenvalues.
$\mathscr {H}$-eigenvalues.
Proof. Let ![]() $d=\max d_{ij}$. Then we have an embedding
$d=\max d_{ij}$. Then we have an embedding
By Proposition 3.1.2, we have an isomorphism
The space on the right certainly embeds into ![]() $\mathscr {S}_{t\chi }(G,\mathscr {U}^p\operatorname {Iw}_p)=\mathscr {S}_{t\chi }(G,U_0(p))$ as discussed.
$\mathscr {S}_{t\chi }(G,\mathscr {U}^p\operatorname {Iw}_p)=\mathscr {S}_{t\chi }(G,U_0(p))$ as discussed.
For future reference, it will be important to note the following distinction between the space ![]() $S_{t,1}(G,U_0(p))$ defined here and the space
$S_{t,1}(G,U_0(p))$ defined here and the space ![]() $S_t(k)(G,U_0(p))$ of classical algebraic automorphic forms defined in § 2.1, which is that they are identical except for the normalization of the action of the
$S_t(k)(G,U_0(p))$ of classical algebraic automorphic forms defined in § 2.1, which is that they are identical except for the normalization of the action of the ![]() $U_p$-operator. This is because, as in the beginning of § 2.3, the action of
$U_p$-operator. This is because, as in the beginning of § 2.3, the action of ![]() $u^a$ on
$u^a$ on ![]() $S_t=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t=\operatorname {Ind}_{B(\mathbb {Q}_p)}^{B(\mathbb {Q}_p)\operatorname {Iw}_p,{\rm alg}}t^0$ implicitly arises from the extension of
$S_t=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t=\operatorname {Ind}_{B(\mathbb {Q}_p)}^{B(\mathbb {Q}_p)\operatorname {Iw}_p,{\rm alg}}t^0$ implicitly arises from the extension of ![]() $t$ to
$t$ to ![]() $t^0:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ where
$t^0:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ where ![]() $t^0(u^a)=1$, whereas the action of
$t^0(u^a)=1$, whereas the action of ![]() $u^a$ on
$u^a$ on ![]() $S_t(k)$ arises from the algebraic character
$S_t(k)$ arises from the algebraic character ![]() $t:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$, for which we can compute
$t:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$, for which we can compute ![]() $t(u^a)=p^{\sum _i a_it_i}$. Thus, we have
$t(u^a)=p^{\sum _i a_it_i}$. Thus, we have
3.2 A classicality theorem following Bellaïche–Chenevier
This is essentially Proposition 7.3.5 of [Reference Bellaïche and ChenevierBC09]. We just summarize the proof with modifications so that it also works for locally algebraic weights.
Theorem 3.2.1 Let ![]() $f\in \mathscr {S}_{t\chi }(G,\mathscr {U})$ where
$f\in \mathscr {S}_{t\chi }(G,\mathscr {U})$ where ![]() $t\chi =(t_1\chi _1,\dotsc, t_n\chi _n)$, in which the
$t\chi =(t_1\chi _1,\dotsc, t_n\chi _n)$, in which the ![]() $t_i$ are integers such that
$t_i$ are integers such that ![]() $t_1\ge \dotsb \ge t_n$ and the
$t_1\ge \dotsb \ge t_n$ and the ![]() $\chi _i$ are finite, such that
$\chi _i$ are finite, such that ![]() $f$ is an eigenform for all operators
$f$ is an eigenform for all operators ![]() $U_p^{(a_1,\dotsc,a_n)}$. Let
$U_p^{(a_1,\dotsc,a_n)}$. Let ![]() $\lambda _1,\dotsc,\lambda _{n-1}$ be the
$\lambda _1,\dotsc,\lambda _{n-1}$ be the ![]() $\lambda$-values associated to
$\lambda$-values associated to ![]() $f$ as defined at the end of § 2.6. If
$f$ as defined at the end of § 2.6. If
for all ![]() $i=1,\dotsc,n-1$, then
$i=1,\dotsc,n-1$, then ![]() $f$ is classical (i.e. lies in the image of
$f$ is classical (i.e. lies in the image of ![]() $S_{t\chi,c}(G,\mathscr {U})$ for any
$S_{t\chi,c}(G,\mathscr {U})$ for any ![]() $c$ such that this is well-defined).
$c$ such that this is well-defined).
Proof. Let ![]() $V=\mathbb {Q}_pv\oplus \mathbb {Q}_pR$ be a finite-dimensional vector space generated by a nonzero vector
$V=\mathbb {Q}_pv\oplus \mathbb {Q}_pR$ be a finite-dimensional vector space generated by a nonzero vector ![]() $v$ and a lattice
$v$ and a lattice ![]() $R$. In some basis whose first vector is
$R$. In some basis whose first vector is ![]() $v$, we define the following matrix groups, where a lowercase letter refers to a single matrix entry, an uppercase letter refers to a larger submatrix of the appropriate size, a number refers to a submatrix consisting of copies of that number of the appropriate size, and the subscript after the matrix refers to its coefficient ring:
$v$, we define the following matrix groups, where a lowercase letter refers to a single matrix entry, an uppercase letter refers to a larger submatrix of the appropriate size, a number refers to a submatrix consisting of copies of that number of the appropriate size, and the subscript after the matrix refers to its coefficient ring:
 \begin{gather*} H={GL}_{\mathbb{Q}_p}(V),\hspace{0.1in} P={\begin{pmatrix} {a} & {B} \\ {0} & {D}\end{pmatrix}}_{\mathbb{Q}_p}\subset H,\\ \overline{N}={\begin{pmatrix} {1} & {0} \\ {C} & {I_R}\end{pmatrix}}_{\mathbb{Z}_p},\hspace{0.1in} J={\begin{pmatrix} {a} & {B} \\ {pC} & {D}\end{pmatrix}}_{\mathbb{Z}_p}\subset {GL}_{\mathbb{Z}_p}(V). \end{gather*}
\begin{gather*} H={GL}_{\mathbb{Q}_p}(V),\hspace{0.1in} P={\begin{pmatrix} {a} & {B} \\ {0} & {D}\end{pmatrix}}_{\mathbb{Q}_p}\subset H,\\ \overline{N}={\begin{pmatrix} {1} & {0} \\ {C} & {I_R}\end{pmatrix}}_{\mathbb{Z}_p},\hspace{0.1in} J={\begin{pmatrix} {a} & {B} \\ {pC} & {D}\end{pmatrix}}_{\mathbb{Z}_p}\subset {GL}_{\mathbb{Z}_p}(V). \end{gather*}
In words, ![]() $P$ is the parabolic subgroup of
$P$ is the parabolic subgroup of ![]() ${GL}_{\mathbb {Q}_p}(V)$ stabilizing the line
${GL}_{\mathbb {Q}_p}(V)$ stabilizing the line ![]() $\mathbb {Q}_pv\subset V$,
$\mathbb {Q}_pv\subset V$, ![]() $\overline {N}$ is the unipotent radical of the opposite parabolic to
$\overline {N}$ is the unipotent radical of the opposite parabolic to ![]() $P$, and
$P$, and ![]() $J$ is the parahoric subgroup of
$J$ is the parahoric subgroup of ![]() ${GL}_{\mathbb {Z}_p}(V)$ associated to
${GL}_{\mathbb {Z}_p}(V)$ associated to ![]() $P$. We have an Iwasawa decomposition
$P$. We have an Iwasawa decomposition
 \[ J=(\overline{N}\cap J)\times(P\cap J)={\begin{pmatrix} {1} & {0} \\ {pC} & {I_R}\end{pmatrix}}_{\mathbb{Z}_p}\times{\begin{pmatrix} {a} & {B} \\ {0} & {D}\end{pmatrix}}_{\mathbb{Z}_p} \]
\[ J=(\overline{N}\cap J)\times(P\cap J)={\begin{pmatrix} {1} & {0} \\ {pC} & {I_R}\end{pmatrix}}_{\mathbb{Z}_p}\times{\begin{pmatrix} {a} & {B} \\ {0} & {D}\end{pmatrix}}_{\mathbb{Z}_p} \]
and an isomorphism ![]() $\alpha :\overline {N}\cap J\to R$ given by
$\alpha :\overline {N}\cap J\to R$ given by
We also write
 \begin{align*} \mathfrak{U}^-&=\left\{{\begin{pmatrix} {p^k} & {0} \\ {0} & {p^{k'}D}\end{pmatrix}}\mid k\ge k'\in\mathbb{Z}, D\in {GL}_{\mathbb{Z}_p}(R)\right\},\\ \mathfrak{U}^{--}&=\left\{{\begin{pmatrix} {p^k} & {0} \\ {0} & {p^{k'}D}\end{pmatrix}}\mid k> k'\in\mathbb{Z}, D\in {GL}_{\mathbb{Z}_p}(R)\right\}; \end{align*}
\begin{align*} \mathfrak{U}^-&=\left\{{\begin{pmatrix} {p^k} & {0} \\ {0} & {p^{k'}D}\end{pmatrix}}\mid k\ge k'\in\mathbb{Z}, D\in {GL}_{\mathbb{Z}_p}(R)\right\},\\ \mathfrak{U}^{--}&=\left\{{\begin{pmatrix} {p^k} & {0} \\ {0} & {p^{k'}D}\end{pmatrix}}\mid k> k'\in\mathbb{Z}, D\in {GL}_{\mathbb{Z}_p}(R)\right\}; \end{align*}
these are submonoids of ![]() $H={GL}_{\mathbb {Q}_p}(V)$. Finally, we write
$H={GL}_{\mathbb {Q}_p}(V)$. Finally, we write ![]() $\mathfrak {M}$ for the submonoid of
$\mathfrak {M}$ for the submonoid of ![]() $H$ generated by
$H$ generated by ![]() $\mathfrak {U}^-$ and
$\mathfrak {U}^-$ and ![]() $J$. Let
$J$. Let ![]() $\chi :P\to \mathbb {Q}_p^\times$ be the character of
$\chi :P\to \mathbb {Q}_p^\times$ be the character of ![]() $P$ acting on
$P$ acting on ![]() $\mathbb {Q}_p v$. We have a
$\mathbb {Q}_p v$. We have a ![]() $\mathbb {C}_p[H]$-equivariant isomorphism
$\mathbb {C}_p[H]$-equivariant isomorphism
 \begin{gather*} \operatorname{Sym}^m(V\otimes_{\mathbb{Q}_p}\mathbb{C}_p)^\vee\to \operatorname{Ind}_P^{H,{\rm alg}}(\chi^m)\\ \varphi\mapsto(h\mapsto\varphi(h(e))). \end{gather*}
\begin{gather*} \operatorname{Sym}^m(V\otimes_{\mathbb{Q}_p}\mathbb{C}_p)^\vee\to \operatorname{Ind}_P^{H,{\rm alg}}(\chi^m)\\ \varphi\mapsto(h\mapsto\varphi(h(e))). \end{gather*}
We get a natural ![]() $\mathfrak {M}$-equivariant map
$\mathfrak {M}$-equivariant map
by restriction. Let ![]() $\delta :\mathfrak {M}\to \mathbb {C}_p^\times$ be the character such that
$\delta :\mathfrak {M}\to \mathbb {C}_p^\times$ be the character such that ![]() $\delta (J)=1$ and
$\delta (J)=1$ and ![]() $\delta (u)=p^a$ if
$\delta (u)=p^a$ if
Let ![]() $e_1,\dotsc,e_n$ be the standard basis of
$e_1,\dotsc,e_n$ be the standard basis of ![]() $\mathbb {Q}_p^n$. Let
$\mathbb {Q}_p^n$. Let ![]() $V_i=\wedge ^i(\mathbb {Q}_p^n)$,
$V_i=\wedge ^i(\mathbb {Q}_p^n)$, ![]() $v_i=e_1\wedge e_1\wedge \dotsb \wedge e_i$,
$v_i=e_1\wedge e_1\wedge \dotsb \wedge e_i$, ![]() $m_i=t_i-t_{i+1}$ if
$m_i=t_i-t_{i+1}$ if ![]() $i< n$ and
$i< n$ and ![]() $m_n=t_n$, and
$m_n=t_n$, and ![]() $R_i$ be the
$R_i$ be the ![]() $\mathbb {Z}_p$-span of the elements
$\mathbb {Z}_p$-span of the elements ![]() $e_{j_1}\wedge \dotsb e_{j_i}$ with
$e_{j_1}\wedge \dotsb e_{j_i}$ with ![]() $j_1<\dotsb < j_i$ and
$j_1<\dotsb < j_i$ and ![]() $(j_1,\dotsc,j_i)\neq (1,\dotsc,i)$. Then for
$(j_1,\dotsc,j_i)\neq (1,\dotsc,i)$. Then for ![]() $i=1,\dotsc,n$, we get
$i=1,\dotsc,n$, we get
as defined above.
Write ![]() $S_i(\mathbb {C}_p)^\vee$ for the space
$S_i(\mathbb {C}_p)^\vee$ for the space ![]() $\operatorname {Ind}_{P_i}^{H_i,{\rm alg}}(\chi _i^{m_i})$ viewed as a representation of
$\operatorname {Ind}_{P_i}^{H_i,{\rm alg}}(\chi _i^{m_i})$ viewed as a representation of ![]() $G(\mathbb {Q}_p)$ via
$G(\mathbb {Q}_p)$ via ![]() $\wedge ^i:G(\mathbb {Q}_p)\to H_i$. Write
$\wedge ^i:G(\mathbb {Q}_p)\to H_i$. Write ![]() $\mathscr {S}_i(m_i)$ for the space
$\mathscr {S}_i(m_i)$ for the space ![]() $\operatorname {Ind}_{P_i}^{H_i,an}(\chi _i^{m_i})\otimes \delta _i^{m_i}$ viewed as a representation of
$\operatorname {Ind}_{P_i}^{H_i,an}(\chi _i^{m_i})\otimes \delta _i^{m_i}$ viewed as a representation of ![]() $\mathfrak {M}$ via
$\mathfrak {M}$ via ![]() $\wedge ^i$. We have surjections
$\wedge ^i$. We have surjections
 \begin{gather*} \bigotimes_{i=1}^mS_i(\mathbb{C}_p)^\vee\to S_t(\mathbb{C}_p)^\vee\\ \widehat{\bigotimes}_{i=1}^m \mathscr{S}_i(m_i)\to \mathscr{S}_t \end{gather*}
\begin{gather*} \bigotimes_{i=1}^mS_i(\mathbb{C}_p)^\vee\to S_t(\mathbb{C}_p)^\vee\\ \widehat{\bigotimes}_{i=1}^m \mathscr{S}_i(m_i)\to \mathscr{S}_t \end{gather*}
which are equivariant with respect to ![]() $G(\mathbb {Q}_p)$ and
$G(\mathbb {Q}_p)$ and ![]() $\mathfrak {M}$ respectively, both given by the formula
$\mathfrak {M}$ respectively, both given by the formula
 \[ (f_1,\dotsc,f_m)\mapsto\biggl(g\mapsto\prod_{i=1}^m f_i(\wedge^i(g))\biggr). \]
\[ (f_1,\dotsc,f_m)\mapsto\biggl(g\mapsto\prod_{i=1}^m f_i(\wedge^i(g))\biggr). \]
Let
 \begin{align*} Q &=\mathscr{S}_t/(S_t(\mathbb{C}_p)^\vee\otimes\delta_t)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr),\\ Q' &=\left. \widehat{\bigotimes}_{i=1}^m \mathscr{S}_i(m_i) \right/ \biggl(\bigotimes_{i=1}^mS_i(\mathbb{C}_p)^\vee\otimes\delta_i^{m_i}\biggr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr),\\ Q_i' &=\biggl(\widehat{\bigotimes}_{j\neq i}\mathscr{S}_j(m_j)\biggr)\otimes\bigl(\mathscr{S}_i(m_i)/S_i(\mathbb{C}_p)^\vee\otimes\delta_i^{m_i}\bigr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr). \end{align*}
\begin{align*} Q &=\mathscr{S}_t/(S_t(\mathbb{C}_p)^\vee\otimes\delta_t)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr),\\ Q' &=\left. \widehat{\bigotimes}_{i=1}^m \mathscr{S}_i(m_i) \right/ \biggl(\bigotimes_{i=1}^mS_i(\mathbb{C}_p)^\vee\otimes\delta_i^{m_i}\biggr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr),\\ Q_i' &=\biggl(\widehat{\bigotimes}_{j\neq i}\mathscr{S}_j(m_j)\biggr)\otimes\bigl(\mathscr{S}_i(m_i)/S_i(\mathbb{C}_p)^\vee\otimes\delta_i^{m_i}\bigr)\otimes\biggl(\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi\biggr). \end{align*}
Then we have a surjection
and an injection
 \[ Q'(G,\mathscr{U})\hookrightarrow\prod_{i=1}^n Q_i'(G,\mathscr{U}). \]
\[ Q'(G,\mathscr{U})\hookrightarrow\prod_{i=1}^n Q_i'(G,\mathscr{U}). \]
We wish to show that if ![]() $w\in Q(G,\mathscr {U})$ satisfies the hypotheses of the theorem, that is,
$w\in Q(G,\mathscr {U})$ satisfies the hypotheses of the theorem, that is, ![]() $u_i(w)=\lambda _i w$ with the
$u_i(w)=\lambda _i w$ with the ![]() $\lambda _i$ satisfying the given inequalities, then
$\lambda _i$ satisfying the given inequalities, then ![]() $w=0$. We can instead check this claim for
$w=0$. We can instead check this claim for ![]() $w'\in Q'(G,\mathscr {U})$ satisfying the same condition, and for this it suffices to check that the image
$w'\in Q'(G,\mathscr {U})$ satisfying the same condition, and for this it suffices to check that the image ![]() $w_i'$ of
$w_i'$ of ![]() $w'$ vanishes in
$w'$ vanishes in ![]() $Q_i'(G,\mathscr {U})$ for each
$Q_i'(G,\mathscr {U})$ for each ![]() $i$. Let
$i$. Let ![]() $U_i=({\prod _{j=1}^iu_i})/{p^{m_i+1}}$, so that
$U_i=({\prod _{j=1}^iu_i})/{p^{m_i+1}}$, so that ![]() $w_i'$ has
$w_i'$ has ![]() $U_i$-eigenvalue
$U_i$-eigenvalue ![]() $(({\lambda _1\lambda _2\dotsb \lambda _i})/{p^{m_i+1}})w$, which has norm
$(({\lambda _1\lambda _2\dotsb \lambda _i})/{p^{m_i+1}})w$, which has norm ![]() $>1$. Thus it suffices to check that
$>1$. Thus it suffices to check that ![]() $U_i$ has norm
$U_i$ has norm ![]() $\le 1$ on
$\le 1$ on ![]() $Q_i'(G,\mathscr {U})$, which follows from the claim that any element of the form
$Q_i'(G,\mathscr {U})$, which follows from the claim that any element of the form
 \[ \frac{g\bigl(\prod_{j=1}^iu_i\bigr)g'}{p^{m_i+1}} \]
\[ \frac{g\bigl(\prod_{j=1}^iu_i\bigr)g'}{p^{m_i+1}} \]
for ![]() $g,g'\in \operatorname {Iw}_p$ has norm
$g,g'\in \operatorname {Iw}_p$ has norm ![]() $\le 1$ on
$\le 1$ on ![]() $Q_i'$. This follows from Lemma 7.3.6 of [Reference Bellaïche and ChenevierBC09].
$Q_i'$. This follows from Lemma 7.3.6 of [Reference Bellaïche and ChenevierBC09].
3.3 Automorphic representations associated to automorphic forms of locally algebraic weights
Fix an isomorphism ![]() $\iota _p:\overline {\mathbb {Q}}_p\xrightarrow {\sim }\mathbb {C}$. Using
$\iota _p:\overline {\mathbb {Q}}_p\xrightarrow {\sim }\mathbb {C}$. Using ![]() $\iota _p$, we may view algebraic representations of
$\iota _p$, we may view algebraic representations of ![]() ${GL}_n$ over
${GL}_n$ over ![]() $\overline {\mathbb {Q}}_p$ as representations over
$\overline {\mathbb {Q}}_p$ as representations over ![]() $\mathbb {C}$, or vice versa. Let
$\mathbb {C}$, or vice versa. Let ![]() $f\in \mathscr {S}_{t\chi }(G,U_0(p))$ be a
$f\in \mathscr {S}_{t\chi }(G,U_0(p))$ be a ![]() $p$-adic automorphic form coming from some classical subspace
$p$-adic automorphic form coming from some classical subspace ![]() $S_{t\chi,c}(G,U_0(p))$. Let
$S_{t\chi,c}(G,U_0(p))$. Let ![]() $W=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,c-\text {loc.alg.}}(t\chi )$, so that
$W=\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,c-\text {loc.alg.}}(t\chi )$, so that ![]() $f$ is a function
$f$ is a function ![]() $G(\mathbb {Q})\backslash G(\mathbb {A}_f)\to W$. Following the proof of Proposition 3.8.1 of [Reference LoefflerLoe10], let
$G(\mathbb {Q})\backslash G(\mathbb {A}_f)\to W$. Following the proof of Proposition 3.8.1 of [Reference LoefflerLoe10], let ![]() $W=W^{{\rm sm},c}(\chi )\otimes S_t(\mathbb {C})$, where, as in § 3.1,
$W=W^{{\rm sm},c}(\chi )\otimes S_t(\mathbb {C})$, where, as in § 3.1,
 \begin{align*} W^{{\rm sm},c}(\chi) &=\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi, \\ S_t(\mathbb{C}) &=\operatorname{Ind}_{B(\mathbb{Z}_p)}^{\operatorname{Iw}_p,{\rm alg}}t, \end{align*}
\begin{align*} W^{{\rm sm},c}(\chi) &=\operatorname{Ind}_{B(\mathbb{Z}_p)/B(\mathbb{Z}_p)\cap \Gamma(c)}^{\operatorname{Iw}_p/\operatorname{Iw}_p\cap \Gamma(c)}\chi, \\ S_t(\mathbb{C}) &=\operatorname{Ind}_{B(\mathbb{Z}_p)}^{\operatorname{Iw}_p,{\rm alg}}t, \end{align*}
and let ![]() $\rho _{{\rm sm}},\rho _{{\rm alg}}$ denote the actions of
$\rho _{{\rm sm}},\rho _{{\rm alg}}$ denote the actions of ![]() $\operatorname {Iw}_p$ on
$\operatorname {Iw}_p$ on ![]() $W^{{\rm sm},c}(\chi )\otimes S_t(\mathbb {C})$ given by acting on only the first factor and only the second factor, respectively. Then we can define a function
$W^{{\rm sm},c}(\chi )\otimes S_t(\mathbb {C})$ given by acting on only the first factor and only the second factor, respectively. Then we can define a function ![]() $f_\infty :G(\mathbb {A})\to W$ by
$f_\infty :G(\mathbb {A})\to W$ by ![]() $f_\infty (g)=\rho _{{\rm alg}}(g_\infty ^{-1}\iota _p(g_p))f(g_f)$ which satisfies the relation
$f_\infty (g)=\rho _{{\rm alg}}(g_\infty ^{-1}\iota _p(g_p))f(g_f)$ which satisfies the relation
for all ![]() $u\in G(\mathbb {R})U_0(p)$. Equivalently,
$u\in G(\mathbb {R})U_0(p)$. Equivalently, ![]() $f_\infty$ can be viewed as the function
$f_\infty$ can be viewed as the function
which satisfies
for all ![]() $u\in U_0(p)$. Thus, for each
$u\in U_0(p)$. Thus, for each ![]() $\varphi \in W^{{\rm sm},c}(\chi )^\vee \otimes S_t(\mathbb {C})^\vee$, the function
$\varphi \in W^{{\rm sm},c}(\chi )^\vee \otimes S_t(\mathbb {C})^\vee$, the function ![]() $f_\infty ^\vee (\varphi,\cdot )$ is an element of
$f_\infty ^\vee (\varphi,\cdot )$ is an element of ![]() $C(G(\mathbb {Q})\backslash G(\mathbb {A}),\mathbb {C})$ which generates under right translation by
$C(G(\mathbb {Q})\backslash G(\mathbb {A}),\mathbb {C})$ which generates under right translation by ![]() $\operatorname {Iw}_p$ a representation containing an irreducible component of
$\operatorname {Iw}_p$ a representation containing an irreducible component of ![]() $W^{{\rm sm},c}(\chi )^\vee$. The right translates of
$W^{{\rm sm},c}(\chi )^\vee$. The right translates of ![]() $f_\infty ^\vee (\varphi,\cdot )$ under
$f_\infty ^\vee (\varphi,\cdot )$ under ![]() $G(\mathbb {A})$ generate an automorphic representation
$G(\mathbb {A})$ generate an automorphic representation ![]() $\pi _f$ of
$\pi _f$ of ![]() $G(\mathbb {A})$ which decomposes as a tensor product
$G(\mathbb {A})$ which decomposes as a tensor product ![]() $\bigotimes _p'\pi _{f,p}$. We are interested in describing the structure of
$\bigotimes _p'\pi _{f,p}$. We are interested in describing the structure of ![]() $\pi _{f,p}$.
$\pi _{f,p}$.
Note that this process is reversible: suppose given ![]() $\psi \in C(G(\mathbb {Q})\backslash G(\mathbb {A}),\mathbb {C})$ which generates a representation containing an irreducible component of
$\psi \in C(G(\mathbb {Q})\backslash G(\mathbb {A}),\mathbb {C})$ which generates a representation containing an irreducible component of ![]() $W^{{\rm sm},c}(\chi )^\vee$ under right translation by
$W^{{\rm sm},c}(\chi )^\vee$ under right translation by ![]() $\operatorname {Iw}_p$. Fixing
$\operatorname {Iw}_p$. Fixing ![]() $\varphi \in W^{{\rm sm},c}(\chi )^\vee \otimes S_t(\mathbb {C})^\vee$, we may recover the corresponding
$\varphi \in W^{{\rm sm},c}(\chi )^\vee \otimes S_t(\mathbb {C})^\vee$, we may recover the corresponding ![]() $f_\infty ^\vee$ such that
$f_\infty ^\vee$ such that ![]() $f_\infty ^\vee (\varphi,\cdot )=\psi$ by setting
$f_\infty ^\vee (\varphi,\cdot )=\psi$ by setting ![]() $f_\infty ^\vee (u_p\varphi,x)=\psi (xu_p)$ for all
$f_\infty ^\vee (u_p\varphi,x)=\psi (xu_p)$ for all ![]() $u_p\in \operatorname {Iw}_p$. Then from
$u_p\in \operatorname {Iw}_p$. Then from ![]() $f_\infty ^\vee$ we get
$f_\infty ^\vee$ we get ![]() $f_\infty :G(\mathbb {A})\to W$, and finally we get
$f_\infty :G(\mathbb {A})\to W$, and finally we get ![]() $f\in S_{t\chi,c}(G,U_0(p))$ by setting
$f\in S_{t\chi,c}(G,U_0(p))$ by setting ![]() $f(g_f)=\rho _{{\rm alg}}(\iota _p(g_p^{-1}))f_\infty (g_f)$ (where on the right-hand side
$f(g_f)=\rho _{{\rm alg}}(\iota _p(g_p^{-1}))f_\infty (g_f)$ (where on the right-hand side ![]() $g_f$ is the element of
$g_f$ is the element of ![]() $G(\mathbb {A})$ which equals
$G(\mathbb {A})$ which equals ![]() $g_f$ at the places in
$g_f$ at the places in ![]() $\mathbb {A}_f$ and
$\mathbb {A}_f$ and ![]() $1$ at
$1$ at ![]() $\infty$). Write
$\infty$). Write ![]() $f_\psi$ for the element of
$f_\psi$ for the element of ![]() $S_{t\chi,c}(G,U_0(p))$ associated to
$S_{t\chi,c}(G,U_0(p))$ associated to ![]() $\psi$ in this way.
$\psi$ in this way.
3.4 Structure of  $W^{{\rm sm},c}(\chi )$
$W^{{\rm sm},c}(\chi )$
We are interested in the representation
of ![]() $\operatorname {Iw}_p$. Note that there is an obvious embedding
$\operatorname {Iw}_p$. Note that there is an obvious embedding ![]() $W^{{\rm sm},c}(\chi )\hookrightarrow W^{{\rm sm},c+1}(\chi )$ which takes
$W^{{\rm sm},c}(\chi )\hookrightarrow W^{{\rm sm},c+1}(\chi )$ which takes ![]() $f\in W^{{\rm sm},c}(\chi )$ to the composition of
$f\in W^{{\rm sm},c}(\chi )$ to the composition of ![]() $f$ with the reduction map
$f$ with the reduction map ![]() $\operatorname {Iw}_p/\Gamma (c+1)\to \operatorname {Iw}_p/\Gamma (c)$.
$\operatorname {Iw}_p/\Gamma (c+1)\to \operatorname {Iw}_p/\Gamma (c)$.
Let ![]() $J$ be the compact open subgroup of
$J$ be the compact open subgroup of ![]() ${GL}_n(\mathbb {Q}_p)$ corresponding to
${GL}_n(\mathbb {Q}_p)$ corresponding to ![]() $\chi$ defined in § 3 of [Reference RocheRoc98]; we have
$\chi$ defined in § 3 of [Reference RocheRoc98]; we have ![]() $J=\Gamma (\underline {c})$ where
$J=\Gamma (\underline {c})$ where
 \[ c_{ij}=\begin{cases}
0 & \text{ if }i=j,\\
\left\lfloor\dfrac{\operatorname{cond}(\chi_i\chi_j^{-1})}2\right\rfloor
& \text{ if } i< j,\\
\left\lfloor\dfrac{\operatorname{cond}(\chi_i\chi_j^{-1})+1}2\right\rfloor
& \text{ if } i>j. \end{cases} \]
\[ c_{ij}=\begin{cases}
0 & \text{ if }i=j,\\
\left\lfloor\dfrac{\operatorname{cond}(\chi_i\chi_j^{-1})}2\right\rfloor
& \text{ if } i< j,\\
\left\lfloor\dfrac{\operatorname{cond}(\chi_i\chi_j^{-1})+1}2\right\rfloor
& \text{ if } i>j. \end{cases} \]
Then ![]() $\chi$ extends to a character of
$\chi$ extends to a character of ![]() $J$ which we will also call
$J$ which we will also call ![]() $\chi$; it is defined by the equation
$\chi$; it is defined by the equation ![]() $\chi (j^-jj^+)=\chi (j)$ when
$\chi (j^-jj^+)=\chi (j)$ when ![]() $j^-\in J\cap \overline {N}(\mathbb {Z}_p)$,
$j^-\in J\cap \overline {N}(\mathbb {Z}_p)$, ![]() $j\in T(\mathbb {Z}_p)$, and
$j\in T(\mathbb {Z}_p)$, and ![]() $j^+\in J\cap N(\mathbb {Z}_p)$. Let
$j^+\in J\cap N(\mathbb {Z}_p)$. Let ![]() $U^{{\rm sm}}(\chi ):=\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$.
$U^{{\rm sm}}(\chi ):=\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$.
Now note that ![]() $W^{{\rm sm},c}(\chi )$ contains the vector
$W^{{\rm sm},c}(\chi )$ contains the vector
 \[ f(\overline{x})=\begin{cases} \chi(j)\chi(b) & \text{ if }\overline{x}=\overline{j}\overline{b}\in\operatorname{Iw}_p/\Gamma(c)\text{ with }j\in J\text{ and }b\in B(\mathbb{Z}_p),\\ 0 & \text{otherwise.} \end{cases} \]
\[ f(\overline{x})=\begin{cases} \chi(j)\chi(b) & \text{ if }\overline{x}=\overline{j}\overline{b}\in\operatorname{Iw}_p/\Gamma(c)\text{ with }j\in J\text{ and }b\in B(\mathbb{Z}_p),\\ 0 & \text{otherwise.} \end{cases} \]
Note, furthermore, that for any ![]() $j\in J$ and
$j\in J$ and ![]() $\overline {x}\in \operatorname {Iw}_p/\Gamma (c)$, we have
$\overline {x}\in \operatorname {Iw}_p/\Gamma (c)$, we have
so that ![]() $f$ is
$f$ is ![]() $(J,\chi ^{-1})$-isotypic.
$(J,\chi ^{-1})$-isotypic.
Proposition 3.4.1 Assume ![]() $\chi =(\chi _1,\dotsc,\chi _n)$ satisfies:
$\chi =(\chi _1,\dotsc,\chi _n)$ satisfies:
(i) for all
 $i\neq j$,
$i\neq j$,  $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$; and
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$; and(ii) for all
 $i\neq j$ with
$i\neq j$ with  $i,j\neq n$,
$i,j\neq n$,  $\operatorname {cond}(\chi _i)<2\operatorname {cond}(\chi _j)$.
$\operatorname {cond}(\chi _i)<2\operatorname {cond}(\chi _j)$.
Then ![]() $U^{{\rm sm}}(\chi )$ is irreducible.
$U^{{\rm sm}}(\chi )$ is irreducible.
Proof. By Mackey's criterion, it is necessary and sufficient to show that for any ![]() $s\in \operatorname {Iw}_p\setminus J$, the characters
$s\in \operatorname {Iw}_p\setminus J$, the characters ![]() $\chi$ and
$\chi$ and ![]() $\chi ^s:j\mapsto \chi (sjs^{-1})$ are not identically equal on
$\chi ^s:j\mapsto \chi (sjs^{-1})$ are not identically equal on ![]() $J\cap s^{-1}Js$. If
$J\cap s^{-1}Js$. If ![]() $s\in \operatorname {Iw}_p\setminus J$, let
$s\in \operatorname {Iw}_p\setminus J$, let ![]() $t=s^{-1}$. Then there is a pair
$t=s^{-1}$. Then there is a pair ![]() $i\neq j$ such that
$i\neq j$ such that ![]() $t_{ji}$ is not divisible by
$t_{ji}$ is not divisible by ![]() $p^{c_{ji}}$. Among all such
$p^{c_{ji}}$. Among all such ![]() $i\neq j$, choose a pair such that either:
$i\neq j$, choose a pair such that either:
(a) among the integers
 $c_{kj}+c_{jk}-v(t_{jk})$,
$c_{kj}+c_{jk}-v(t_{jk})$,  $1\le k\le n$,
$1\le k\le n$,  $k\neq j$,
$k\neq j$,  $c_{ij}+c_{ji}-v(t_{ji})$ is the unique maximal one; or
$c_{ij}+c_{ji}-v(t_{ji})$ is the unique maximal one; or(b) if this is not possible, among the integers
 $c_{kj}+c_{jk}-v(t_{jk})$,
$c_{kj}+c_{jk}-v(t_{jk})$,  $1\le k\le n$,
$1\le k\le n$,  $k\neq j$,
$k\neq j$,  $c_{ij}+c_{ji}-v(t_{ji})$ is maximal and
$c_{ij}+c_{ji}-v(t_{ji})$ is maximal and  $i$ is minimal such that this is the case.
$i$ is minimal such that this is the case.
Let ![]() $x\in J$ be the identity except for the
$x\in J$ be the identity except for the ![]() $ij$th entry; let
$ij$th entry; let ![]() $x_{ij}=b$. Note that we must have
$x_{ij}=b$. Note that we must have ![]() $p^{c_{ij}}|b$. We show that we can choose
$p^{c_{ij}}|b$. We show that we can choose ![]() $b$ such that
$b$ such that ![]() $sxt\in J$ and
$sxt\in J$ and ![]() $1=\chi (x)\neq \chi (sxt)$ and, hence,
$1=\chi (x)\neq \chi (sxt)$ and, hence, ![]() $\chi (x)\neq \chi ^s(x)$, as desired.
$\chi (x)\neq \chi ^s(x)$, as desired.
The matrix ![]() $xt$ is the same as
$xt$ is the same as ![]() $t$ except for the
$t$ except for the ![]() $i$th row, which is
$i$th row, which is
The ![]() $kk$th entry of
$kk$th entry of ![]() $sxt$ is
$sxt$ is
Because of condition (i), one can check that for all ![]() $j\in J$, we have
$j\in J$, we have ![]() $\chi (j)=\chi _1(j_{11})\cdot \dotsb \cdot \chi _n(j_{nn})$. Thus, we wish to choose
$\chi (j)=\chi _1(j_{11})\cdot \dotsb \cdot \chi _n(j_{nn})$. Thus, we wish to choose ![]() $b$ such that
$b$ such that
Note that for all ![]() $k\neq i,j$, we have
$k\neq i,j$, we have
This is just because we chose ![]() $i,j$ such that
$i,j$ such that ![]() $c_{ij}+c_{ji}-v(t_{ji})\ge c_{jk}+c_{kj}-v(t_{jk})$, and such that if equality holds then
$c_{ij}+c_{ji}-v(t_{ji})\ge c_{jk}+c_{kj}-v(t_{jk})$, and such that if equality holds then ![]() $k>i$, in which case
$k>i$, in which case ![]() $v(s_{ki})\ge 1$ since
$v(s_{ki})\ge 1$ since ![]() $s\in \operatorname {Iw}_p$. Thus, if we choose
$s\in \operatorname {Iw}_p$. Thus, if we choose ![]() $b$ such that
$b$ such that ![]() $v(b)=c_{ij}+c_{ji}-v(t_{ji})-1\ge c_{ij}$, then we have
$v(b)=c_{ij}+c_{ji}-v(t_{ji})-1\ge c_{ij}$, then we have
for all ![]() $k\neq i,j$, hence
$k\neq i,j$, hence ![]() $\chi _k(1+bs_{ki}t_{jk})=1$. Then we have
$\chi _k(1+bs_{ki}t_{jk})=1$. Then we have
 \begin{align*} &\chi_1(1+bs_{1i}t_{j1})\dotsb\chi_i(1+bs_{ii}t_{ji})\dotsb\chi_j(1+bs_{ji}t_{jj})\dotsb\chi_n(1+bs_{ni}t_{jn})\\ &\qquad =\chi_i(1+bs_{ii}t_{ji})\chi_j(1+bs_{ji}t_{jj})=\chi_i(1+bs_{ii}t_{ji})\chi_j\biggl(1+b\biggl(\sum_{k\neq i}s_{ki}t_{jk}\biggr)\biggr) \end{align*}
\begin{align*} &\chi_1(1+bs_{1i}t_{j1})\dotsb\chi_i(1+bs_{ii}t_{ji})\dotsb\chi_j(1+bs_{ji}t_{jj})\dotsb\chi_n(1+bs_{ni}t_{jn})\\ &\qquad =\chi_i(1+bs_{ii}t_{ji})\chi_j(1+bs_{ji}t_{jj})=\chi_i(1+bs_{ii}t_{ji})\chi_j\biggl(1+b\biggl(\sum_{k\neq i}s_{ki}t_{jk}\biggr)\biggr) \end{align*}
since ![]() $v(bs_{ki}t_{jk})\ge \operatorname {cond}(\chi _j)$, but this is
$v(bs_{ki}t_{jk})\ge \operatorname {cond}(\chi _j)$, but this is
since ![]() $\sum _{k}s_{ki}t_{jk}=\sum _k t_{jk}s_{ki}=(ts)_{ji}=0$, and this can be rewritten as
$\sum _{k}s_{ki}t_{jk}=\sum _k t_{jk}s_{ki}=(ts)_{ji}=0$, and this can be rewritten as
because if ![]() $i>j$, then
$i>j$, then ![]() $v(b^2)\ge 2c_{ij}\ge c_{ij}+c_{ji}$, and if
$v(b^2)\ge 2c_{ij}\ge c_{ij}+c_{ji}$, and if ![]() $i< j$, then
$i< j$, then ![]() $v(b^2)\ge 2c_{ij}\ge c_{ij}+c_{ji}-1$ and
$v(b^2)\ge 2c_{ij}\ge c_{ij}+c_{ji}-1$ and ![]() $v(t_{ji})\ge 1$. But since
$v(t_{ji})\ge 1$. But since ![]() $v(b)< c_{ij}+c_{ji}-v(t_{ji})$, we have
$v(b)< c_{ij}+c_{ji}-v(t_{ji})$, we have ![]() $v(bs_{ii}t_{ji})<\operatorname {cond}(\chi _i\chi _j^{-1})$, so we can choose
$v(bs_{ii}t_{ji})<\operatorname {cond}(\chi _i\chi _j^{-1})$, so we can choose ![]() $b$ to make
$b$ to make ![]() $({\chi _i}/{\chi _j})(1+bs_{ii}t_{ji})\neq 1$.
$({\chi _i}/{\chi _j})(1+bs_{ii}t_{ji})\neq 1$.
Finally, we verify that for this choice of ![]() $b$, we actually have
$b$, we actually have ![]() $sxt\in J$. The
$sxt\in J$. The ![]() $kl$th entry of
$kl$th entry of ![]() $sbt$ is
$sbt$ is
We have
 \begin{align*} v(bs_{ki}t_{jl}) &=c_{ij}+c_{ji}-v(t_{ji})-1+v(s_{ki})+v(t_{jl}) \\ &=c_{ij}+c_{ji}-v(t_{ji})-(c_{lj}+c_{jl}-v(t_{jl}))+c_{lj}+c_{jl}-1+v(s_{ki}) \\ &\ge c_{lj}+c_{jl}-1+v(s_{ki})\ge c_{kl} \end{align*}
\begin{align*} v(bs_{ki}t_{jl}) &=c_{ij}+c_{ji}-v(t_{ji})-1+v(s_{ki})+v(t_{jl}) \\ &=c_{ij}+c_{ji}-v(t_{ji})-(c_{lj}+c_{jl}-v(t_{jl}))+c_{lj}+c_{jl}-1+v(s_{ki}) \\ &\ge c_{lj}+c_{jl}-1+v(s_{ki})\ge c_{kl} \end{align*}
by condition (ii).
Remark 4 We do not believe that either condition (i) or condition (ii) of Proposition 3.4.1 should be strictly necessary. Notably, most of the proof of Proposition 3.4.1 can be easily rephrased to avoid references to condition (i). Our only sticking point is the calculation of ![]() $\chi (j)$ in terms of
$\chi (j)$ in terms of ![]() $j_{11},\dotsc,j_{nn}$.
$j_{11},\dotsc,j_{nn}$.
We call ![]() $\chi$ ‘simple’ if it satisfies the conditions of Proposition 3.4.1. By Frobenius reciprocity, we conclude that if
$\chi$ ‘simple’ if it satisfies the conditions of Proposition 3.4.1. By Frobenius reciprocity, we conclude that if ![]() $\chi$ is simple,
$\chi$ is simple, ![]() $W^{{\rm sm},c}(\chi )$ contains
$W^{{\rm sm},c}(\chi )$ contains ![]() $U^{{\rm sm}}(\chi )$. Also note that if
$U^{{\rm sm}}(\chi )$. Also note that if ![]() $\chi$ satisfies condition (i), and the conductors of the nontrivial components of
$\chi$ satisfies condition (i), and the conductors of the nontrivial components of ![]() $\chi =(\chi _1,\dotsc,\chi _{n-1},1)$ are, in order from least to greatest,
$\chi =(\chi _1,\dotsc,\chi _{n-1},1)$ are, in order from least to greatest, ![]() $c_{(1)}\le c_{(2)}\le \dotsb \le c_{(n-1)}$, then the index of
$c_{(1)}\le c_{(2)}\le \dotsb \le c_{(n-1)}$, then the index of ![]() $J$ in
$J$ in ![]() $\operatorname {Iw}_p$ is
$\operatorname {Iw}_p$ is
and this is ![]() $\operatorname {rank}(U^{{\rm sm}}(\chi ))$. Thus, if
$\operatorname {rank}(U^{{\rm sm}}(\chi ))$. Thus, if ![]() $\chi$ is simple and
$\chi$ is simple and ![]() $\operatorname {cond}(\chi _i)=c$ for all
$\operatorname {cond}(\chi _i)=c$ for all ![]() $i\neq n$, then
$i\neq n$, then ![]() $W^{{\rm sm},c}(\chi )$ and
$W^{{\rm sm},c}(\chi )$ and ![]() $U^{{\rm sm}}(\chi )$ have the same dimension and must actually be isomorphic.
$U^{{\rm sm}}(\chi )$ have the same dimension and must actually be isomorphic.
3.5 Hecke eigenvalues of ramified principal series
The representations we are interested in will turn out to be ramified principal series of ![]() ${GL}_n(\mathbb {Q}_p)$, so we now cover the properties of these that we will need. To harmonize with the literature, for this section only, we use different conventions from the rest of the paper. If
${GL}_n(\mathbb {Q}_p)$, so we now cover the properties of these that we will need. To harmonize with the literature, for this section only, we use different conventions from the rest of the paper. If ![]() $\chi =(\chi _1,\dotsc,\chi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ is a smooth character of
$\chi =(\chi _1,\dotsc,\chi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ is a smooth character of ![]() $T(\mathbb {Q}_p)=(\mathbb {Q}_p^\times )^n$, we write
$T(\mathbb {Q}_p)=(\mathbb {Q}_p^\times )^n$, we write
for the representation of ![]() ${GL}_n(\mathbb {Q}_p)$ with the given underlying vector space and the right translation action of
${GL}_n(\mathbb {Q}_p)$ with the given underlying vector space and the right translation action of ![]() ${GL}_n(\mathbb {Q}_p)$. We let
${GL}_n(\mathbb {Q}_p)$. We let ![]() $\delta ^{1/2}:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ be the modulus character
$\delta ^{1/2}:(\mathbb {Q}_p^\times )^n\to \mathbb {C}$ be the modulus character
Then we define
The representation ![]() $\pi (\chi )$ is called the normalized parabolic induction of
$\pi (\chi )$ is called the normalized parabolic induction of ![]() $\chi$. Assume that for all
$\chi$. Assume that for all ![]() $i\neq j$, we have
$i\neq j$, we have ![]() $\chi _i(p)\neq \chi _j(p)p$. Let
$\chi _i(p)\neq \chi _j(p)p$. Let ![]() $J=\Gamma (\underline {c})$ be the subgroup defined at the beginning of § 3.4. Let
$J=\Gamma (\underline {c})$ be the subgroup defined at the beginning of § 3.4. Let ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ be the subspace of
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ be the subspace of ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p))$ generated by the functions
$\mathscr {H}({GL}_n(\mathbb {Q}_p))$ generated by the functions ![]() $\varphi :{GL}_n(\mathbb {Q}_p)\to \mathbb {C}$ satisfying
$\varphi :{GL}_n(\mathbb {Q}_p)\to \mathbb {C}$ satisfying ![]() $\varphi (j_1xj_2)=\chi (j_1)^{-1}\varphi (x)\chi (j_2)^{-1}$ for all
$\varphi (j_1xj_2)=\chi (j_1)^{-1}\varphi (x)\chi (j_2)^{-1}$ for all ![]() $j_1,j_2\in J$ and
$j_1,j_2\in J$ and ![]() $x\in {GL}_n(\mathbb {Q}_p)$.
$x\in {GL}_n(\mathbb {Q}_p)$.
Lemma 3.5.1 The ![]() $(J,\chi )$-isotypic piece of
$(J,\chi )$-isotypic piece of ![]() $\pi (\chi )$ is
$\pi (\chi )$ is ![]() $1$-dimensional.
$1$-dimensional.
Proof. By Theorem 6.3 of [Reference RocheRoc98], ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ is abelian. (To be precise, the theorem gives an isomorphism between
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ is abelian. (To be precise, the theorem gives an isomorphism between ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ and
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ and ![]() $\mathscr {H}(W_\chi ^0,S_\chi ^0)\otimes \mathbb {C}[\Omega _\chi ]$, where by our assumption that
$\mathscr {H}(W_\chi ^0,S_\chi ^0)\otimes \mathbb {C}[\Omega _\chi ]$, where by our assumption that ![]() $\chi _i(p)\neq \chi _j(p)p$ for
$\chi _i(p)\neq \chi _j(p)p$ for ![]() $i\neq j$, we have
$i\neq j$, we have ![]() $W_\chi ^0=S_\chi ^0=1$,
$W_\chi ^0=S_\chi ^0=1$, ![]() $\mathscr {H}(W_\chi ^0,S_\chi ^0)=\mathbb {C}$, and
$\mathscr {H}(W_\chi ^0,S_\chi ^0)=\mathbb {C}$, and ![]() $\Omega _\chi =\mathbb {Z}^n$.) Thus, the
$\Omega _\chi =\mathbb {Z}^n$.) Thus, the ![]() $(J,\chi )$-isotypic piece of
$(J,\chi )$-isotypic piece of ![]() $\pi (\chi )$ decomposes as a representation of
$\pi (\chi )$ decomposes as a representation of ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ into
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ into ![]() $1$-dimensional pieces. But by Theorem 9.2 of [Reference RocheRoc98], because
$1$-dimensional pieces. But by Theorem 9.2 of [Reference RocheRoc98], because ![]() $\pi (\chi )$ is irreducible, the
$\pi (\chi )$ is irreducible, the ![]() $(J,\chi )$-isotypic piece of
$(J,\chi )$-isotypic piece of ![]() $\pi (\chi )$ is irreducible as a representation of
$\pi (\chi )$ is irreducible as a representation of ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$. Thus, it is itself
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$. Thus, it is itself ![]() $1$-dimensional.
$1$-dimensional.
Lemma 3.5.2 If ![]() $a=(a_1,\dotsc,a_n)$ is such that
$a=(a_1,\dotsc,a_n)$ is such that ![]() $a_1\ge a_2\ge \dotsb \ge a_n$, the action of the element
$a_1\ge a_2\ge \dotsb \ge a_n$, the action of the element ![]() $[Ju^aJ]$ of
$[Ju^aJ]$ of ![]() $\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ corresponding to
$\mathscr {H}({GL}_n(\mathbb {Q}_p)// J,\chi )$ corresponding to ![]() $u^a=\operatorname {diag}(p^{a_1},\dotsc,p^{a_n})$ on the
$u^a=\operatorname {diag}(p^{a_1},\dotsc,p^{a_n})$ on the ![]() $(J,\chi )$-isotypic piece of
$(J,\chi )$-isotypic piece of ![]() $\pi (\chi )$ is multiplication by
$\pi (\chi )$ is multiplication by
Proof. The ![]() $(J,\chi )$-isotypic piece is generated by
$(J,\chi )$-isotypic piece is generated by
 \[ f(g)=\begin{cases} (\chi\delta^{1/2})(b)\chi(j) & \text{ if }g=bj\text{ with }b\in B(\mathbb{Q}_p)\text{ and }j\in J,\\ 0 & \text{otherwise.} \end{cases} \]
\[ f(g)=\begin{cases} (\chi\delta^{1/2})(b)\chi(j) & \text{ if }g=bj\text{ with }b\in B(\mathbb{Q}_p)\text{ and }j\in J,\\ 0 & \text{otherwise.} \end{cases} \]
This is just because this function ![]() $f$ satisfies the
$f$ satisfies the ![]() $(J,\chi )$-isotypic condition by construction, and is well-defined because
$(J,\chi )$-isotypic condition by construction, and is well-defined because ![]() $(\chi \delta ^{1/2})(b)=\chi (b)$ for any
$(\chi \delta ^{1/2})(b)=\chi (b)$ for any ![]() $b\in B\cap J$. We claim that
$b\in B\cap J$. We claim that
The lemma follows from this, because if ![]() $Ju^aJ=\coprod _{i=1}^rj_iu^aJ$, then
$Ju^aJ=\coprod _{i=1}^rj_iu^aJ$, then
 \[ ([Ju^aJ]f)(1)=\sum_{i=1}^r\chi(j_i)^{-1}f(j_iu^a)=\sum_{i=1}^r\chi(u^a)\delta^{1/2}(u^a)f(1)=\chi(u^a)\delta^{1/2}(u^a)^{-1}f(1) \]
\[ ([Ju^aJ]f)(1)=\sum_{i=1}^r\chi(j_i)^{-1}f(j_iu^a)=\sum_{i=1}^r\chi(u^a)\delta^{1/2}(u^a)f(1)=\chi(u^a)\delta^{1/2}(u^a)^{-1}f(1) \]
because ![]() $r=\delta (u^a)^{-1}$ (since the same calculation as in Proposition 2.6.2 shows that the index of
$r=\delta (u^a)^{-1}$ (since the same calculation as in Proposition 2.6.2 shows that the index of ![]() $J$ in
$J$ in ![]() $[(u^a)^{-1}Ju^a]J$ is
$[(u^a)^{-1}Ju^a]J$ is
To prove (2), first write ![]() $j=j^-j^0j^+$ where
$j=j^-j^0j^+$ where ![]() $j^-\in J\cap \overline {N}(\mathbb {Z}_p)$,
$j^-\in J\cap \overline {N}(\mathbb {Z}_p)$, ![]() $j^0\in T(\mathbb {Z}_p)$, and
$j^0\in T(\mathbb {Z}_p)$, and ![]() $j^+\in J\cap N(\mathbb {Z}_p)$. Then we have
$j^+\in J\cap N(\mathbb {Z}_p)$. Then we have ![]() $\chi (j)=\chi (j^0)$. Let
$\chi (j)=\chi (j^0)$. Let ![]() $j_1^+=j^0j^+(j^0)^{-1}$; then
$j_1^+=j^0j^+(j^0)^{-1}$; then ![]() $j_1^+\in J\cap N(\mathbb {Z}_p)$ as well, and
$j_1^+\in J\cap N(\mathbb {Z}_p)$ as well, and ![]() $j=j^-j_1^+j^0$. Use Lemmas 3.1 and 3.2 of [Reference RocheRoc98] to write
$j=j^-j_1^+j^0$. Use Lemmas 3.1 and 3.2 of [Reference RocheRoc98] to write ![]() $j^-j_1^+=j_2^+j_2^-c$, where
$j^-j_1^+=j_2^+j_2^-c$, where ![]() $j_2^+\in J\cap N(\mathbb {Z}_p)$,
$j_2^+\in J\cap N(\mathbb {Z}_p)$, ![]() $j_2^-\in J\cap \overline {N}(\mathbb {Z}_p)$, and
$j_2^-\in J\cap \overline {N}(\mathbb {Z}_p)$, and ![]() $c\in T(\mathbb {Z}_p)$ is a correction torus element in the kernel of
$c\in T(\mathbb {Z}_p)$ is a correction torus element in the kernel of ![]() $\chi$. Then we have
$\chi$. Then we have
We have ![]() $(u^a)^{-1}j_2^+u^a\in N(\mathbb {Q}_p)$, and by the same calculation as in Proposition 2.6.2, we have
$(u^a)^{-1}j_2^+u^a\in N(\mathbb {Q}_p)$, and by the same calculation as in Proposition 2.6.2, we have ![]() $(u^a)^{-1}j_2^-u^a\in J\cap \overline {N}(\mathbb {Z}_p)$. Therefore,
$(u^a)^{-1}j_2^-u^a\in J\cap \overline {N}(\mathbb {Z}_p)$. Therefore,
 \begin{align*} f(ju^a) &=f(u^a[(u^a)^{-1}j_2^+u^a][(u^a)^{-1}j_2^-u^a](j^0c)) \\ &=(\chi\delta^{1/2})(u^a[(u^a)^{-1}j_2^+u^a])\chi([(u^a)^{-1}j_2^-u^a](j^0c)) \\ &=(\chi\delta^{1/2})(u^a)\chi(j^0)=(\chi\delta^{1/2})(u^a)\chi(j), \end{align*}
\begin{align*} f(ju^a) &=f(u^a[(u^a)^{-1}j_2^+u^a][(u^a)^{-1}j_2^-u^a](j^0c)) \\ &=(\chi\delta^{1/2})(u^a[(u^a)^{-1}j_2^+u^a])\chi([(u^a)^{-1}j_2^-u^a](j^0c)) \\ &=(\chi\delta^{1/2})(u^a)\chi(j^0)=(\chi\delta^{1/2})(u^a)\chi(j), \end{align*}
as desired.
3.6 Structure of automorphic representations of locally algebraic weights
Let ![]() $f\in S_{t\chi,c}(G,U_0(p))$ be a classical eigenform, and let
$f\in S_{t\chi,c}(G,U_0(p))$ be a classical eigenform, and let ![]() $\pi _{f,p}$ be an irreducible component of the local component at
$\pi _{f,p}$ be an irreducible component of the local component at ![]() $p$ of the automorphic representation
$p$ of the automorphic representation ![]() $\pi _f$ associated to
$\pi _f$ associated to ![]() $f$ in § 3.3. We first verify a standard fundamental fact about the structure of
$f$ in § 3.3. We first verify a standard fundamental fact about the structure of ![]() $\pi _{f,p}$ for those
$\pi _{f,p}$ for those ![]() $f$ associated to points on the eigenvariety
$f$ associated to points on the eigenvariety ![]() $\mathscr {D}$.
$\mathscr {D}$.
Proposition 3.6.1 The eigenform ![]() $f$ may be associated to a classical point
$f$ may be associated to a classical point ![]() $x$ on
$x$ on ![]() $\mathscr {D}$ (equivalently,
$\mathscr {D}$ (equivalently, ![]() $f$ is finite-slope) if and only if
$f$ is finite-slope) if and only if ![]() $\pi _{f,p}$ has nonzero Jacquet module with respect to
$\pi _{f,p}$ has nonzero Jacquet module with respect to ![]() $B$ or, equivalently, is a subquotient of a principal series.
$B$ or, equivalently, is a subquotient of a principal series.
To show this, we use the following proposition of Casselman in [Reference CasselmanCas95] on canonical liftings. Recall the submonoid ![]() $\Sigma ^{--}$ from § 2.6. Also recall that, by definition, the Jacquet module of a representation
$\Sigma ^{--}$ from § 2.6. Also recall that, by definition, the Jacquet module of a representation ![]() $(\pi,V)$ of
$(\pi,V)$ of ![]() ${GL}_n(\mathbb {Q}_p)$ with respect to a parabolic subgroup
${GL}_n(\mathbb {Q}_p)$ with respect to a parabolic subgroup ![]() $P$ with Levi factorization
$P$ with Levi factorization ![]() $P=MN$ is the space
$P=MN$ is the space ![]() $V_N$ of
$V_N$ of ![]() $N$-coinvariants of
$N$-coinvariants of ![]() $V$, which is naturally a representation of
$V$, which is naturally a representation of ![]() $M$. (See [Reference CasselmanCas95, §§ 3 and 4] for more basic information about Jacquet modules.)
$M$. (See [Reference CasselmanCas95, §§ 3 and 4] for more basic information about Jacquet modules.)
Proposition 3.6.2 (Casselman [Proposition 4.1.4, Reference CasselmanCas95])
Let ![]() $(\pi,V)$ be an admissible representation of
$(\pi,V)$ be an admissible representation of ![]() ${GL}_n(\mathbb {Q}_p)$,
${GL}_n(\mathbb {Q}_p)$, ![]() $P=MN$ a parabolic subgroup with Levi factorization, and
$P=MN$ a parabolic subgroup with Levi factorization, and ![]() $K_0 =\overline {N}_0 M_0 N_0$ a compact open subgroup with Iwahori factorization. If
$K_0 =\overline {N}_0 M_0 N_0$ a compact open subgroup with Iwahori factorization. If ![]() $u^a\in \Sigma ^{--}$, then the projection from
$u^a\in \Sigma ^{--}$, then the projection from ![]() $V^{K_0}$ to
$V^{K_0}$ to ![]() $V_N^{M_0}$ given by
$V_N^{M_0}$ given by ![]() $[K_0u^aK_0]$ is a surjection. If
$[K_0u^aK_0]$ is a surjection. If ![]() $u^aN_1(u^a)^{-1}\subseteq N_0$, where
$u^aN_1(u^a)^{-1}\subseteq N_0$, where ![]() $N_1$ is a compact subgroup of
$N_1$ is a compact subgroup of ![]() $N$ such that
$N$ such that ![]() $V^{K_0}\cap V(N)\subseteq V(N_1)$, then the projection is an isomorphism.
$V^{K_0}\cap V(N)\subseteq V(N_1)$, then the projection is an isomorphism.
Proof of Proposition 3.6.1 We apply Proposition 3.6.2 with ![]() $P=B$ and
$P=B$ and ![]() $M=T$.
$M=T$.
Suppose ![]() $f$ is such that
$f$ is such that ![]() $\pi _{f,p}=(\pi,V)$ has nonzero Jacquet module. Let
$\pi _{f,p}=(\pi,V)$ has nonzero Jacquet module. Let ![]() $v\in V_N$ be a nonzero vector and let
$v\in V_N$ be a nonzero vector and let ![]() $M_0$ be a compact open subgroup of
$M_0$ be a compact open subgroup of ![]() $M$ fixing
$M$ fixing ![]() $v$. Let
$v$. Let ![]() $K_0$ be a compact open subgroup of
$K_0$ be a compact open subgroup of ![]() $G$ such that
$G$ such that ![]() $K_0\cap M=M_0$. By the proposition of Casselman,
$K_0\cap M=M_0$. By the proposition of Casselman, ![]() $[K_0u^aK_0]V$ surjects onto
$[K_0u^aK_0]V$ surjects onto ![]() $V_N^{M_0}\neq 0$, so is itself nonzero. Thus,
$V_N^{M_0}\neq 0$, so is itself nonzero. Thus, ![]() $[K_0u^aK_0]$ has some nonzero eigenvalue, corresponding to an eigenvector in
$[K_0u^aK_0]$ has some nonzero eigenvalue, corresponding to an eigenvector in ![]() $\pi _{f,p}$ which must be the image of an eigenform in
$\pi _{f,p}$ which must be the image of an eigenform in ![]() $S_{t\chi,c}(G,U_0(p))$ by the procedure of § 3.3.
$S_{t\chi,c}(G,U_0(p))$ by the procedure of § 3.3.
Now suppose in the other direction that ![]() $f$ is finite-slope. Then
$f$ is finite-slope. Then ![]() $\pi _{f,p}=(\pi,V)$ contains a vector
$\pi _{f,p}=(\pi,V)$ contains a vector ![]() $\operatorname {im}(f)$ with nonzero Hecke eigenvalue for
$\operatorname {im}(f)$ with nonzero Hecke eigenvalue for ![]() $[K_0u^aK_0]$ for some compact open subgroup
$[K_0u^aK_0]$ for some compact open subgroup ![]() $K_0$ and all
$K_0$ and all ![]() $a\in \Sigma ^-$. Choose a compact subgroup
$a\in \Sigma ^-$. Choose a compact subgroup ![]() $N_1$ of
$N_1$ of ![]() $N$ such that
$N$ such that ![]() $V^{K_0}\cap V(N)\subseteq V(N_1)$. We claim that for sufficiently large powers
$V^{K_0}\cap V(N)\subseteq V(N_1)$. We claim that for sufficiently large powers ![]() $(u^a)^k$ of
$(u^a)^k$ of ![]() $u^a$, we must have
$u^a$, we must have ![]() $(u^a)^k N_1(u^a)^{-k}\subseteq N_0$; this is just the effect of conjugation by
$(u^a)^k N_1(u^a)^{-k}\subseteq N_0$; this is just the effect of conjugation by ![]() $(u^a)^k$ on the
$(u^a)^k$ on the ![]() $ij$th entry of
$ij$th entry of ![]() $N_1$ is scaling by
$N_1$ is scaling by ![]() $p^{k(a_i-a_j)}$, and
$p^{k(a_i-a_j)}$, and ![]() $k(a_i-a_j)$ becomes arbitrarily large as
$k(a_i-a_j)$ becomes arbitrarily large as ![]() $k$ does. Then
$k$ does. Then ![]() $[K_0(u^a)^kK_0]V\cong V_N^{M_0}$, and we must have
$[K_0(u^a)^kK_0]V\cong V_N^{M_0}$, and we must have ![]() $V_N^{M_0}\neq 0$.
$V_N^{M_0}\neq 0$.
Now assume ![]() $\chi _n$ is trivial and let
$\chi _n$ is trivial and let ![]() $c_0=\max _{1\le i< n}\operatorname {cond}(\chi _i)$. Let
$c_0=\max _{1\le i< n}\operatorname {cond}(\chi _i)$. Let ![]() $(W^{{\rm sm},c_0}(\chi ))^\perp$ be the complement of
$(W^{{\rm sm},c_0}(\chi ))^\perp$ be the complement of ![]() $W^{{\rm sm},c_0}(\chi )$ in
$W^{{\rm sm},c_0}(\chi )$ in ![]() $W^{{\rm sm},c}(\chi )$. We now observe that as
$W^{{\rm sm},c}(\chi )$. We now observe that as ![]() $c$ goes to infinity, almost all eigenforms in
$c$ goes to infinity, almost all eigenforms in ![]() $S_{t\chi,c}(G,U_0(p))$ are infinite-slope.
$S_{t\chi,c}(G,U_0(p))$ are infinite-slope.
Proposition 3.6.3 Suppose that ![]() $f$ is an eigenform in
$f$ is an eigenform in
Then ![]() $U_pf=0$,
$U_pf=0$, ![]() $f$ is not associated to a point on the eigenvariety, and
$f$ is not associated to a point on the eigenvariety, and ![]() $\pi _{f,p}$ is not a subquotient of a principal series.
$\pi _{f,p}$ is not a subquotient of a principal series.
Proof. By Proposition 2.6.6, in order for ![]() $U_pf$ to be nonzero,
$U_pf$ to be nonzero, ![]() $f$ must lie in
$f$ must lie in ![]() $\mathscr {S}_{t\chi,c_0}(G,U_0(p))$. But the intersection of
$\mathscr {S}_{t\chi,c_0}(G,U_0(p))$. But the intersection of ![]() $\mathscr {S}_{t\chi,c_0}(G,U_0(p))$ with
$\mathscr {S}_{t\chi,c_0}(G,U_0(p))$ with ![]() $((W^{{\rm sm},c_0}(\chi ))^\perp \otimes S_t)(G,U_0(p))$ is trivial.
$((W^{{\rm sm},c_0}(\chi ))^\perp \otimes S_t)(G,U_0(p))$ is trivial.
Now recall the ![]() $\operatorname {Iw}_p$-representation
$\operatorname {Iw}_p$-representation ![]() $U^{{\rm sm}}(\chi ):=\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$ from the beginning of § 3.4. By the discussion at the end of § 3.4, if
$U^{{\rm sm}}(\chi ):=\operatorname {Ind}_J^{\operatorname {Iw}_p}\chi$ from the beginning of § 3.4. By the discussion at the end of § 3.4, if ![]() $\chi$ is simple,
$\chi$ is simple, ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is a subspace of
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is a subspace of ![]() $S_{t\chi,c}(G,U_0(p))$. Even if
$S_{t\chi,c}(G,U_0(p))$. Even if ![]() $\chi$ is not simple, the following is true.
$\chi$ is not simple, the following is true.
Proposition 3.6.4 There is a vector space embedding of ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))^{{\rm fs}}$ (as at the end of § 2.6) into
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))^{{\rm fs}}$ (as at the end of § 2.6) into ![]() $\mathscr {S}_{t\chi,c}(G,U_0(p))$ which preserves systems of
$\mathscr {S}_{t\chi,c}(G,U_0(p))$ which preserves systems of ![]() $\mathscr {H}$-eigenvalues.
$\mathscr {H}$-eigenvalues.
Proof. Let ![]() $\tilde {H}_{{\rm la}}^0$ be the space, as in Definition 3.2.3 of [Reference EmertonEme06b] and the discussion surrounding it, of continuous
$\tilde {H}_{{\rm la}}^0$ be the space, as in Definition 3.2.3 of [Reference EmertonEme06b] and the discussion surrounding it, of continuous ![]() $\overline {\mathbb {Q}}_p$-valued functions on
$\overline {\mathbb {Q}}_p$-valued functions on ![]() $G(\mathbb {Q})\backslash G(\mathbb {A})$ that are locally constant on cosets of
$G(\mathbb {Q})\backslash G(\mathbb {A})$ that are locally constant on cosets of ![]() $G(\mathbb {A}_f^p)$ and locally analytic on cosets of
$G(\mathbb {A}_f^p)$ and locally analytic on cosets of ![]() $G(\mathbb {Q}_p)$. Let
$G(\mathbb {Q}_p)$. Let ![]() $J_B$ be Emerton's locally analytic Jacquet module functor as constructed in [Reference EmertonEme06a]. Finally, let
$J_B$ be Emerton's locally analytic Jacquet module functor as constructed in [Reference EmertonEme06a]. Finally, let ![]() $e^p$ be the idempotent of
$e^p$ be the idempotent of ![]() $\mathscr {H}(G(\mathbb {A}))$ away from
$\mathscr {H}(G(\mathbb {A}))$ away from ![]() $p$ corresponding to the tame part of
$p$ corresponding to the tame part of ![]() $U_0(p)$. According to Proposition 3.10.3 of [Reference LoefflerLoe10],
$U_0(p)$. According to Proposition 3.10.3 of [Reference LoefflerLoe10], ![]() $\mathscr {S}_{t\chi,c}(G,U_0(p))^{{\rm fs}}$ is isomorphic as an
$\mathscr {S}_{t\chi,c}(G,U_0(p))^{{\rm fs}}$ is isomorphic as an ![]() $\mathscr {H}$-module to
$\mathscr {H}$-module to
where we write ![]() $(t\chi )$ for the representation of
$(t\chi )$ for the representation of ![]() $T(\mathbb {Z}_p)$ given by the character
$T(\mathbb {Z}_p)$ given by the character ![]() $t\chi$. (Note that Loeffer uses different conventions from us, hence writes
$t\chi$. (Note that Loeffer uses different conventions from us, hence writes ![]() $J_{\overline {B}}$ instead of
$J_{\overline {B}}$ instead of ![]() $J_B$.) For
$J_B$.) For ![]() $f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$, define
$f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$, define ![]() $f_\infty ^\vee :(U^{{\rm sm}}(\chi )\otimes S_t)^\vee \times G(\mathbb {Q})\backslash G(\mathbb {A})\to \mathbb {C}$ by the same construction as in § 3.3, with
$f_\infty ^\vee :(U^{{\rm sm}}(\chi )\otimes S_t)^\vee \times G(\mathbb {Q})\backslash G(\mathbb {A})\to \mathbb {C}$ by the same construction as in § 3.3, with ![]() $U^{{\rm sm}}(\chi )$ in place of
$U^{{\rm sm}}(\chi )$ in place of ![]() $W^{{\rm sm},c}(\chi )$. Then if
$W^{{\rm sm},c}(\chi )$. Then if ![]() $\varphi \in (U^{{\rm sm}}(\chi )\otimes S_t)^\vee$ is the vector taking an element of
$\varphi \in (U^{{\rm sm}}(\chi )\otimes S_t)^\vee$ is the vector taking an element of ![]() $U^{{\rm sm}}(\chi )\otimes S_t$ to its evaluation on
$U^{{\rm sm}}(\chi )\otimes S_t$ to its evaluation on ![]() $\operatorname {id}\in \operatorname {Iw}_p$, then
$\operatorname {id}\in \operatorname {Iw}_p$, then ![]() $f_\infty ^\vee (\varphi,\cdot )$ is a continuous
$f_\infty ^\vee (\varphi,\cdot )$ is a continuous ![]() $\mathbb {C}_p$-valued function on
$\mathbb {C}_p$-valued function on ![]() $G(\mathbb {Q})\backslash G(\mathbb {A})$ that is locally constant on cosets of
$G(\mathbb {Q})\backslash G(\mathbb {A})$ that is locally constant on cosets of ![]() $G(\mathbb {A}_f^p)$ and analytic on cosets of the compact open subgroup
$G(\mathbb {A}_f^p)$ and analytic on cosets of the compact open subgroup ![]() $J$ of
$J$ of ![]() $G(\mathbb {Q}_p)$. Thus, we get an inclusion
$G(\mathbb {Q}_p)$. Thus, we get an inclusion
 \begin{align*} (U^{{\rm sm}}(\chi)\otimes S_t)(G,U_0(p)) &\hookrightarrow \tilde{H}_{{\rm la}}^0 \\ f &\mapsto f_\infty^\vee(\varphi,\cdot). \end{align*}
\begin{align*} (U^{{\rm sm}}(\chi)\otimes S_t)(G,U_0(p)) &\hookrightarrow \tilde{H}_{{\rm la}}^0 \\ f &\mapsto f_\infty^\vee(\varphi,\cdot). \end{align*}
Let ![]() $\pi$ be the
$\pi$ be the ![]() $G(\mathbb {Q}_p)$-subrepresentation of
$G(\mathbb {Q}_p)$-subrepresentation of ![]() $\tilde {H}_{{\rm la}}^0$ generated by
$\tilde {H}_{{\rm la}}^0$ generated by ![]() $\operatorname {im}((U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p)))$. By Proposition 3.6.2, there is
$\operatorname {im}((U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p)))$. By Proposition 3.6.2, there is ![]() $a\in \Sigma ^{--}$ such that
$a\in \Sigma ^{--}$ such that ![]() $U_p^a$ gives an isomorphism
$U_p^a$ gives an isomorphism
Since ![]() $T(\mathbb {Z}_p)$ acts the same way on
$T(\mathbb {Z}_p)$ acts the same way on ![]() $J_B(\pi )$ and on
$J_B(\pi )$ and on ![]() $t\chi$, these identifications combine to an inclusion
$t\chi$, these identifications combine to an inclusion
Now it turns out that, in fact, all of ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is finite-slope.
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is finite-slope.
Proposition 3.6.5 Suppose that ![]() $f$ is an eigenform in
$f$ is an eigenform in ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Then
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Then ![]() $\pi _{f,p}$ is a subquotient of a principal series, in particular one of the form
$\pi _{f,p}$ is a subquotient of a principal series, in particular one of the form ![]() $\pi (\psi _1,\dotsc,\psi _n)$ where
$\pi (\psi _1,\dotsc,\psi _n)$ where ![]() $\psi _i:\mathbb {Q}_p^\times \to \mathbb {C}$ are characters of
$\psi _i:\mathbb {Q}_p^\times \to \mathbb {C}$ are characters of ![]() $\mathbb {Q}_p^\times$ whose restrictions to
$\mathbb {Q}_p^\times$ whose restrictions to ![]() $\mathbb {Z}_p^\times$ are the same as
$\mathbb {Z}_p^\times$ are the same as ![]() $\chi _1,\dotsc,\chi _n$ in some order.
$\chi _1,\dotsc,\chi _n$ in some order.
Proof. We know that ![]() $\pi _{f,p}$ is an irreducible subrepresentation of
$\pi _{f,p}$ is an irreducible subrepresentation of ![]() $C({GL}_n(\mathbb {Q}_p),\mathbb {C})$ whose restriction to
$C({GL}_n(\mathbb {Q}_p),\mathbb {C})$ whose restriction to ![]() $\Gamma _0(p)$ admits a nontrivial homomorphism from
$\Gamma _0(p)$ admits a nontrivial homomorphism from ![]() $(U^{{\rm sm}}(\chi ))^\vee$. By Frobenius reciprocity, the restriction of
$(U^{{\rm sm}}(\chi ))^\vee$. By Frobenius reciprocity, the restriction of ![]() $\pi _{f,p}$ to
$\pi _{f,p}$ to ![]() $J$ admits a nontrivial homomorphism from the representation of
$J$ admits a nontrivial homomorphism from the representation of ![]() $J$ given by
$J$ given by ![]() $\chi$; that is, it contains a
$\chi$; that is, it contains a ![]() $(J,\chi )$-isotypic vector. By Theorem 7.7 of [Reference RocheRoc98],
$(J,\chi )$-isotypic vector. By Theorem 7.7 of [Reference RocheRoc98], ![]() $\pi _{f,p}$ is a subquotient of
$\pi _{f,p}$ is a subquotient of ![]() $\pi (\psi _1,\dotsc,\psi _n)$.
$\pi (\psi _1,\dotsc,\psi _n)$.
Remark 5 If ![]() $\chi$ is simple, one can also prove Proposition 3.6.5 by noting that if
$\chi$ is simple, one can also prove Proposition 3.6.5 by noting that if ![]() $\pi _{f,p}$ admits a nontrivial homomorphism from the irreducible
$\pi _{f,p}$ admits a nontrivial homomorphism from the irreducible ![]() $(U^{{\rm sm}}(\chi ))^\vee$, it must, in fact, contain all of
$(U^{{\rm sm}}(\chi ))^\vee$, it must, in fact, contain all of ![]() $(U^{{\rm sm}}(\chi ))^\vee$, in particular the
$(U^{{\rm sm}}(\chi ))^\vee$, in particular the ![]() $(J,\chi )$-isotypic vector. (We are grateful to Jessica Fintzen for pointing out the more general proof above.)
$(J,\chi )$-isotypic vector. (We are grateful to Jessica Fintzen for pointing out the more general proof above.)
By Propositions 3.6.5 and 3.6.1, ![]() $U_p$ is injective on the space
$U_p$ is injective on the space ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Furthermore, for an eigenform
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Furthermore, for an eigenform ![]() $f$ in this space, it is possible to compute the eigenvalues of
$f$ in this space, it is possible to compute the eigenvalues of ![]() $U_p$ from the structure of
$U_p$ from the structure of ![]() $\pi _{f,p}$ or vice versa, as follows. From now on, for convenience, we sometimes refer to the algebraic weight
$\pi _{f,p}$ or vice versa, as follows. From now on, for convenience, we sometimes refer to the algebraic weight ![]() $(t_1,\dotsc,t_{n-1},0)$,
$(t_1,\dotsc,t_{n-1},0)$, ![]() $t_1\ge \dotsb \ge t_{n-1}$, by its successive differences
$t_1\ge \dotsb \ge t_{n-1}$, by its successive differences ![]() $m_1=t_1-t_2$,
$m_1=t_1-t_2$, ![]() $m_2=t_2-t_3,\ldots, m_{n-1}=t_{n-1}$.
$m_2=t_2-t_3,\ldots, m_{n-1}=t_{n-1}$.
Proposition 3.6.6 Suppose that ![]() $\chi _i(p)\neq \chi _j(p)p$ for all
$\chi _i(p)\neq \chi _j(p)p$ for all ![]() $i\neq j$, and
$i\neq j$, and ![]() $f$ is an eigenform in
$f$ is an eigenform in ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Suppose that we have
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$. Suppose that we have ![]() $\pi _{f,p}=\pi (\psi _1,\dotsc,\psi _n)$ (note that this is an equality because for such
$\pi _{f,p}=\pi (\psi _1,\dotsc,\psi _n)$ (note that this is an equality because for such ![]() $\chi$,
$\chi$, ![]() $\pi (\psi _1,\dotsc,\psi _n)$ is irreducible). The
$\pi (\psi _1,\dotsc,\psi _n)$ is irreducible). The ![]() $\lambda$-values associated to
$\lambda$-values associated to ![]() $x$ as in § 2.6 satisfy
$x$ as in § 2.6 satisfy
Proof. We are given that for all ![]() $u^a\in \Sigma ^-$, we have
$u^a\in \Sigma ^-$, we have ![]() $U_p^af=\lambda _1^{a_1}\dotsb \lambda _n^{a_n}f$. Since any eigenvector of
$U_p^af=\lambda _1^{a_1}\dotsb \lambda _n^{a_n}f$. Since any eigenvector of ![]() $U_p^a=[U_0(p)u^aU_0(p)]$ is also an eigenvector of
$U_p^a=[U_0(p)u^aU_0(p)]$ is also an eigenvector of ![]() $[Ju^aJ]$, we can calculate its eigenvalue using
$[Ju^aJ]$, we can calculate its eigenvalue using ![]() $[Ju^aJ]$ instead. Let
$[Ju^aJ]$ instead. Let
 \[ Ju^aJ=\coprod_{i=1}^r\zeta_iJ. \]
\[ Ju^aJ=\coprod_{i=1}^r\zeta_iJ. \]
Then for any ![]() $\varphi \in U^{{\rm sm}}(\chi )\otimes S_t$, we have
$\varphi \in U^{{\rm sm}}(\chi )\otimes S_t$, we have
 \begin{align*} (U_p^af)_\infty^\vee(\varphi,x) &=\varphi(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p))(U_p^af)(x_f)) \\ &=p^{-\sum a_it_i}\varphi\biggl(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p(\zeta_i)_p))\sum_{i=1}^r\rho_{{\rm sm}}((\zeta_i)_p)f(x\zeta_i)\biggr). \end{align*}
\begin{align*} (U_p^af)_\infty^\vee(\varphi,x) &=\varphi(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p))(U_p^af)(x_f)) \\ &=p^{-\sum a_it_i}\varphi\biggl(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p(\zeta_i)_p))\sum_{i=1}^r\rho_{{\rm sm}}((\zeta_i)_p)f(x\zeta_i)\biggr). \end{align*}
Choose ![]() $\varphi =\varphi _{{\rm sm}}\otimes \varphi _{{\rm alg}}$ so that
$\varphi =\varphi _{{\rm sm}}\otimes \varphi _{{\rm alg}}$ so that ![]() $\varphi _{{\rm sm}}$ is a
$\varphi _{{\rm sm}}$ is a ![]() $(J,\chi )$-isotypic vector in
$(J,\chi )$-isotypic vector in ![]() $U^{{\rm sm}}(\chi )$. Then, by definition,
$U^{{\rm sm}}(\chi )$. Then, by definition,
so
 \begin{align*} (U_p^af)_\infty^\vee(\varphi,x) &=p^{-\sum a_it_i}\sum_{i=1}^r\psi((\zeta_i)_p)\varphi\bigl(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p(\zeta_i)_p))f(x\zeta_i)\bigr)\\ &=p^{-\sum a_it_i}\sum_{i=1}^r\psi((\zeta_i)_p) f_\infty^\vee(\varphi,x\zeta_i). \end{align*}
\begin{align*} (U_p^af)_\infty^\vee(\varphi,x) &=p^{-\sum a_it_i}\sum_{i=1}^r\psi((\zeta_i)_p)\varphi\bigl(\rho_{{\rm alg}}(x_\infty^{-1}\iota_p(x_p(\zeta_i)_p))f(x\zeta_i)\bigr)\\ &=p^{-\sum a_it_i}\sum_{i=1}^r\psi((\zeta_i)_p) f_\infty^\vee(\varphi,x\zeta_i). \end{align*}
That is, we have
 \[ \sum_{i=1}^r\psi((\zeta_i)_p) f_\infty^\vee(\varphi,x\zeta_i)=p^{\sum a_it_i}\lambda_1^{a_1}\dotsb\lambda_n^{a_n}f_\infty^\vee(\varphi,x). \]
\[ \sum_{i=1}^r\psi((\zeta_i)_p) f_\infty^\vee(\varphi,x\zeta_i)=p^{\sum a_it_i}\lambda_1^{a_1}\dotsb\lambda_n^{a_n}f_\infty^\vee(\varphi,x). \]
Thus, the image of ![]() $f_\infty ^\vee (\varphi,\cdot )$ in
$f_\infty ^\vee (\varphi,\cdot )$ in ![]() $\pi _{f,p}$ is a
$\pi _{f,p}$ is a ![]() $J$-new vector (
$J$-new vector (![]() $\mathscr {H}(J,\psi )$-module). By Lemma 3.5.2, we have
$\mathscr {H}(J,\psi )$-module). By Lemma 3.5.2, we have
The proposition follows.
In summary, we have found a finite-slope subspace of ![]() $\mathscr {S}_{t\chi,c}(G,U_0(p))$ of rank
$\mathscr {S}_{t\chi,c}(G,U_0(p))$ of rank
where, as before, ![]() $d_t=\dim \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$,
$d_t=\dim \operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm alg}}t$, ![]() $h=\#(G(\mathbb {Q})\backslash G(\mathbb {A}_f)/U_0(p))$, and
$h=\#(G(\mathbb {Q})\backslash G(\mathbb {A}_f)/U_0(p))$, and ![]() $j(\chi )$ is defined as at the end of § 3.4. If
$j(\chi )$ is defined as at the end of § 3.4. If ![]() $\chi$ is simple, this subspace is contained in the classical space
$\chi$ is simple, this subspace is contained in the classical space ![]() $S_{t\chi,c}(G,U_0(p))$ and, furthermore, we can extend Proposition 3.6.3 to show that it accounts for all the finite-slope forms in
$S_{t\chi,c}(G,U_0(p))$ and, furthermore, we can extend Proposition 3.6.3 to show that it accounts for all the finite-slope forms in ![]() $S_{t\chi,c}(G,U_0(p))$.
$S_{t\chi,c}(G,U_0(p))$.
Proposition 3.6.7 Suppose that ![]() $\chi$ is simple and
$\chi$ is simple and ![]() $f$ is an eigenform in
$f$ is an eigenform in ![]() $(U^{{\rm sm}}(\chi )^\perp \otimes S_t)(G,U_0(p))\subset S_{t\chi,c}(G,U_0(p))$. Then
$(U^{{\rm sm}}(\chi )^\perp \otimes S_t)(G,U_0(p))\subset S_{t\chi,c}(G,U_0(p))$. Then ![]() $U_pf=0$,
$U_pf=0$, ![]() $f$ is not associated to a point on the eigenvariety, and
$f$ is not associated to a point on the eigenvariety, and ![]() $\pi _{f,p}$ is not a subquotient of a principal series.
$\pi _{f,p}$ is not a subquotient of a principal series.
Proof. Let ![]() $c_i=\operatorname {cond}(\chi _i)$, and first assume that
$c_i=\operatorname {cond}(\chi _i)$, and first assume that ![]() $c_1\ge \dotsb \ge c_{n-1}$. Then the tuple
$c_1\ge \dotsb \ge c_{n-1}$. Then the tuple ![]() $\underline {c}^0\in \mathbb {Z}_{>0}^{n(n-1)/2}$ associated to
$\underline {c}^0\in \mathbb {Z}_{>0}^{n(n-1)/2}$ associated to ![]() $\chi$ defined immediately before Corollary 2.6.4 satisfies
$\chi$ defined immediately before Corollary 2.6.4 satisfies ![]() $c_{ij}^0=c_i$ for all
$c_{ij}^0=c_i$ for all ![]() $i>j$. We claim that the intersection of
$i>j$. We claim that the intersection of ![]() $\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$ with
$\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$ with ![]() $S_{t\chi,c}(G,U_0(p))$ is precisely
$S_{t\chi,c}(G,U_0(p))$ is precisely ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$.
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$.
To show that ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is contained in
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is contained in ![]() $\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$, it suffices to note that
$\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$, it suffices to note that ![]() $U^{{\rm sm}}(\chi )\otimes S_t$ is contained in
$U^{{\rm sm}}(\chi )\otimes S_t$ is contained in ![]() $\mathscr {S}_{t\chi,\underline {c}^0}$, which is true because
$\mathscr {S}_{t\chi,\underline {c}^0}$, which is true because ![]() $f\otimes \varphi \in U^{{\rm sm}}(\chi )\otimes S_t$ is clearly contained in
$f\otimes \varphi \in U^{{\rm sm}}(\chi )\otimes S_t$ is clearly contained in ![]() $\mathscr {S}_{t\chi,\underline {c}^0}$ for the vector
$\mathscr {S}_{t\chi,\underline {c}^0}$ for the vector ![]() $f\in U^{{\rm sm}}(\chi )$ defined at the beginning of § 3.4 and any
$f\in U^{{\rm sm}}(\chi )$ defined at the beginning of § 3.4 and any ![]() $\varphi \in S_t$, and
$\varphi \in S_t$, and ![]() $U^{{\rm sm}}(\chi )\otimes S_t$ is irreducible.
$U^{{\rm sm}}(\chi )\otimes S_t$ is irreducible.
To show that ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ exhausts
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ exhausts ![]() $\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p)) \cap S_{t\chi,c}(G,U_0(p))$, we simply note that the latter space also has dimension
$\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p)) \cap S_{t\chi,c}(G,U_0(p))$, we simply note that the latter space also has dimension ![]() $hd_tp^{j(\chi )}$, since as a vector space it is
$hd_tp^{j(\chi )}$, since as a vector space it is ![]() $h$ copies of the locally algebraic vector subspace of
$h$ copies of the locally algebraic vector subspace of ![]() $\mathscr {S}_{t\chi,\underline {c}^0}$. By Proposition 2.6.6, in order for
$\mathscr {S}_{t\chi,\underline {c}^0}$. By Proposition 2.6.6, in order for ![]() $U_pf$ to be nonzero,
$U_pf$ to be nonzero, ![]() $f$ must lie in
$f$ must lie in ![]() $\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$; this completes the proof.
$\mathscr {S}_{t\chi,\underline {c}^0}(G,U_0(p))$; this completes the proof.
If the ![]() $c_i$ are not in decreasing order, by the beginning of § 4.2, the finite-slope subspace of
$c_i$ are not in decreasing order, by the beginning of § 4.2, the finite-slope subspace of ![]() $S_{t\chi,c}(G,U_0(p))$ has the same dimension as that of
$S_{t\chi,c}(G,U_0(p))$ has the same dimension as that of ![]() $S_{t\chi ^w,c}(G,U_0(p))$ where
$S_{t\chi ^w,c}(G,U_0(p))$ where ![]() $\chi ^w$ is
$\chi ^w$ is ![]() $\chi$ with the components rearranged so that the
$\chi$ with the components rearranged so that the ![]() $c_i$ are in decreasing order. This completes the argument for all
$c_i$ are in decreasing order. This completes the argument for all ![]() $\chi$ simple.
$\chi$ simple.
The combination of Propositions 3.6.5 and 3.6.7 gives us the following precise version of Theorem 1.2.1.
Theorem 3.6.8 If ![]() $\chi$ is simple, then the finite-slope classical subspace of
$\chi$ is simple, then the finite-slope classical subspace of ![]() $\mathscr {S}_{t\chi,c}(G,U_0(p))$ is precisely
$\mathscr {S}_{t\chi,c}(G,U_0(p))$ is precisely ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$.
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$.
4. Bounds on the Newton polygon
In this section, we prove Theorem 1.1.2. We prove part (i) in § 4.1 and part (ii) in § 4.2. In § 4.3, we prove a modified version of part (ii) which generates infinitely many upper bound points for the same Newton polygon.
Fix a character of ![]() $\Delta ^n$ and, thus, a particular polydisc in
$\Delta ^n$ and, thus, a particular polydisc in ![]() $\mathscr {W}^n$. Over the subset of this polydisc where
$\mathscr {W}^n$. Over the subset of this polydisc where ![]() $T_n=0$, we have
$T_n=0$, we have
with ![]() $c_0(T_1,\dotsc,T_{n-1})=1$. We want to bound the coefficients
$c_0(T_1,\dotsc,T_{n-1})=1$. We want to bound the coefficients ![]() $c_N(T_1,\dotsc,T_{n-1})$.
$c_N(T_1,\dotsc,T_{n-1})$.
4.1 A lower bound on the Newton polygon
We first summarize the theory of Johansson–Newton in [Reference Johansson and NewtonJN19a] that we will apply. As mentioned in § 1.2, they construct families of automorphic forms for various groups, including our definite unitary group ![]() $G$, over an extended weight space containing extra points at the boundary. We do not describe the extended weight space in more detail, since we only need to work with their families over the following subset of the standard weight space.
$G$, over an extended weight space containing extra points at the boundary. We do not describe the extended weight space in more detail, since we only need to work with their families over the following subset of the standard weight space.
Fix an index ![]() $a$, and consider the subset of our chosen polydisc in
$a$, and consider the subset of our chosen polydisc in ![]() $\mathscr {W}^n$ where:
$\mathscr {W}^n$ where:
(a)
 $|T_a|\ge 1/p$; and
$|T_a|\ge 1/p$; and(b)
 $|T_a|\ge |T_j|$ for all
$|T_a|\ge |T_j|$ for all  $j\neq a$.
$j\neq a$.
If ![]() $A$ is an affinoid
$A$ is an affinoid ![]() $\mathbb {Q}_p$-algebra, then
$\mathbb {Q}_p$-algebra, then ![]() $A$-points of
$A$-points of ![]() $\mathscr {W}^n$ lying in this subset are in bijection with continuous homomorphisms
$\mathscr {W}^n$ lying in this subset are in bijection with continuous homomorphisms ![]() $R\to A$, where
$R\to A$, where ![]() $R^\circ$ is the
$R^\circ$ is the ![]() $T_a$-adic completion of
$T_a$-adic completion of
and ![]() $R=R^\circ [1/T_a]$. Let
$R=R^\circ [1/T_a]$. Let ![]() $[\cdot ]_R:(\mathbb {Z}_p^\times )^n\to R^\times$ be the universal character with values in
$[\cdot ]_R:(\mathbb {Z}_p^\times )^n\to R^\times$ be the universal character with values in ![]() $R$.
$R$.
Johansson–Newton automorphic forms with coefficients in ![]() $R$ (i.e. families of automorphic forms over the subset of the boundary where the
$R$ (i.e. families of automorphic forms over the subset of the boundary where the ![]() $a$th coordinate is closest to the boundary) are defined as follows. Give
$a$th coordinate is closest to the boundary) are defined as follows. Give ![]() $R$ the norm
$R$ the norm ![]() $|r|=\inf \{p^{-n}\mid r\in T_a^n R_\eta ^\circ \}$. Let
$|r|=\inf \{p^{-n}\mid r\in T_a^n R_\eta ^\circ \}$. Let ![]() $\mathcal {D}$ be the continuous
$\mathcal {D}$ be the continuous ![]() $R$-dual of
$R$-dual of ![]() $\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}[\cdot ]_R$.
$\operatorname {Ind}_{B(\mathbb {Z}_p)}^{\operatorname {Iw}_p,{\rm cts}}[\cdot ]_R$. ![]() $\mathcal {D}$ is orthonormalizable with the following norm: choose topological generators
$\mathcal {D}$ is orthonormalizable with the following norm: choose topological generators ![]() $\overline {n}=(\overline {n}_1,\dotsc,\overline {n}_{n(n-1)/2})$ for
$\overline {n}=(\overline {n}_1,\dotsc,\overline {n}_{n(n-1)/2})$ for ![]() $\overline {N}$, for example the matrix coefficients
$\overline {N}$, for example the matrix coefficients ![]() $pz_{21},pz_{31},pz_{32},\dotsc,pz_{n(n-1)}$ of § 2.3. Let
$pz_{21},pz_{31},pz_{32},\dotsc,pz_{n(n-1)}$ of § 2.3. Let ![]() $\overline {\mathfrak {n}}_i\in \mathcal {D}$ be the Dirac distribution at
$\overline {\mathfrak {n}}_i\in \mathcal {D}$ be the Dirac distribution at ![]() $\overline {n}_i$ on
$\overline {n}_i$ on ![]() $\overline {N}$. For
$\overline {N}$. For ![]() $\eta =(\eta _1,\dotsc,\eta _{n(n-1)/2})\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$, write
$\eta =(\eta _1,\dotsc,\eta _{n(n-1)/2})\in \mathbb {Z}_{\ge 0}^{n(n-1)/2}$, write ![]() $\overline {\mathfrak {n}}^{\eta }:=\prod _{i=1}^{n(n-1)/2}\overline {\mathfrak {n}}_i^{\eta _i}$ and
$\overline {\mathfrak {n}}^{\eta }:=\prod _{i=1}^{n(n-1)/2}\overline {\mathfrak {n}}_i^{\eta _i}$ and ![]() $s(\eta )=\sum _{i=1}^{n(n-1)/2}\eta _i$ for short. Then
$s(\eta )=\sum _{i=1}^{n(n-1)/2}\eta _i$ for short. Then ![]() $\{\overline {\mathfrak {n}}^\eta \}_{\eta \in \mathbb {Z}^{n(n-1)/2}}$ is a basis for
$\{\overline {\mathfrak {n}}^\eta \}_{\eta \in \mathbb {Z}^{n(n-1)/2}}$ is a basis for ![]() $\mathcal {D}$, and the norm is
$\mathcal {D}$, and the norm is
 \[ \biggl\|\sum_\eta d_\eta\overline{\mathfrak{n}}^\eta\biggr\|_r=\sup_\eta|d_\eta|r^{s(\eta)}. \]
\[ \biggl\|\sum_\eta d_\eta\overline{\mathfrak{n}}^\eta\biggr\|_r=\sup_\eta|d_\eta|r^{s(\eta)}. \]
Let ![]() $\mathcal {D}^r$ be the completion of
$\mathcal {D}^r$ be the completion of ![]() $\mathcal {D}$ with respect to this norm. Then the space of Johansson–Newton automorphic forms with coefficients in
$\mathcal {D}$ with respect to this norm. Then the space of Johansson–Newton automorphic forms with coefficients in ![]() $R$ is
$R$ is ![]() $\mathcal {D}^{1/p}(G,U_0(p))$. See § 3.3 of [Reference Johansson and NewtonJN19a] for more details.
$\mathcal {D}^{1/p}(G,U_0(p))$. See § 3.3 of [Reference Johansson and NewtonJN19a] for more details.
Evidently, these automorphic forms are not exactly the same as ours, but this does not matter because eigenvarieties are essentially unique. In particular, Johansson and Newton prove (Remark 4.1.9 of [Reference Johansson and NewtonJN19a]) that if one constructs an eigenvariety using the action of ![]() $U_p$ on these automorphic forms, the result agrees with Hansen's construction in [Reference Hansen and NewtonHN17] over standard weight space. Hansen's construction (see the introduction to [Reference Hansen and NewtonHN17]) agrees with Loeffler's in [Reference LoefflerLoe10] when the latter applies (whenever
$U_p$ on these automorphic forms, the result agrees with Hansen's construction in [Reference Hansen and NewtonHN17] over standard weight space. Hansen's construction (see the introduction to [Reference Hansen and NewtonHN17]) agrees with Loeffler's in [Reference LoefflerLoe10] when the latter applies (whenever ![]() $G^{der}(\mathbb {R})$ is compact, which is certainly true for us). Loeffler's construction is the same as the one we use except for notational differences.
$G^{der}(\mathbb {R})$ is compact, which is certainly true for us). Loeffler's construction is the same as the one we use except for notational differences.
Consequently, the characteristic power series ![]() $\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N$ which we want to compute agrees with the characteristic power series of
$\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N$ which we want to compute agrees with the characteristic power series of ![]() $U_p$ acting on the space
$U_p$ acting on the space ![]() $\mathcal {D}^{1/p}(G,U_0(p))$.
$\mathcal {D}^{1/p}(G,U_0(p))$.
Finally, the characteristic power series of ![]() $U_p$ acting on
$U_p$ acting on ![]() $\mathcal {D}^{1/p}(G,U_0(p))$ can be computed using its matrix coefficients in the following explicit basis. According to the beginning of [Reference Johansson and NewtonJN19a, § 3.2],
$\mathcal {D}^{1/p}(G,U_0(p))$ can be computed using its matrix coefficients in the following explicit basis. According to the beginning of [Reference Johansson and NewtonJN19a, § 3.2], ![]() $\mathcal {D}^r$ has a potential orthonormal basis given by the elements
$\mathcal {D}^r$ has a potential orthonormal basis given by the elements
where
It follows that ![]() $\mathcal {D}^r(G,U_0(p))$ has a potential orthonormal basis given by the elements
$\mathcal {D}^r(G,U_0(p))$ has a potential orthonormal basis given by the elements
 \[ e_{r,\eta}^t:=(0,\dotsc,0,e_{r,\eta},0,\dotsc,0)\subset\bigoplus_{t=1}^h \mathcal{D}^r\cong\mathcal{D}^r(G,U_0(p)), \]
\[ e_{r,\eta}^t:=(0,\dotsc,0,e_{r,\eta},0,\dotsc,0)\subset\bigoplus_{t=1}^h \mathcal{D}^r\cong\mathcal{D}^r(G,U_0(p)), \]
where the ![]() $e_{r,\eta }$ is in the
$e_{r,\eta }$ is in the ![]() $t$th position. Furthermore, by Lemma 6.2.1 of [Reference Johansson and NewtonJN19a], we have
$t$th position. Furthermore, by Lemma 6.2.1 of [Reference Johansson and NewtonJN19a], we have
with
We may now proceed to prove part (i) of Theorem 1.1.2, which states the following.
Theorem 4.1.1 There are constants ![]() $A_1$,
$A_1$, ![]() $C$ (depending on
$C$ (depending on ![]() $n$,
$n$, ![]() $p$, and
$p$, and ![]() $h$) such that for all
$h$) such that for all ![]() $T_1,\dotsc,T_{n-1}$ such that all
$T_1,\dotsc,T_{n-1}$ such that all ![]() $|T_j|>\frac 1p$, the Newton polygon of
$|T_j|>\frac 1p$, the Newton polygon of ![]() $\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N$ lies above the points
$\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N$ lies above the points
for all ![]() $x$.
$x$.
Proof. We generalize the argument for the case ![]() $n=1$ given in Theorem 6.3.2 of [Reference Johansson and NewtonJN19a]. In the notation just defined, we have
$n=1$ given in Theorem 6.3.2 of [Reference Johansson and NewtonJN19a]. In the notation just defined, we have ![]() $n(p^{-1},T_a,\mu )=s(\mu )$ and
$n(p^{-1},T_a,\mu )=s(\mu )$ and ![]() $n(p^{-1/p},T_a,\mu )=\left \lfloor s(\mu )/p\right \rfloor$. Thus, Lemma 6.2.1 of [Reference Johansson and NewtonJN19a] says that
$n(p^{-1/p},T_a,\mu )=\left \lfloor s(\mu )/p\right \rfloor$. Thus, Lemma 6.2.1 of [Reference Johansson and NewtonJN19a] says that
with
Another way of saying this is that whenever ![]() $s(\mu )=N$, every matrix entry of
$s(\mu )=N$, every matrix entry of ![]() $U_p$ in the row
$U_p$ in the row ![]() $e_{r,\mu }^u$ has coefficient
$e_{r,\mu }^u$ has coefficient ![]() $a_\mu ^u$ divisible by
$a_\mu ^u$ divisible by ![]() $|T_a|^{N-\left \lfloor N/p\right \rfloor }$. There are
$|T_a|^{N-\left \lfloor N/p\right \rfloor }$. There are
choices of ![]() $u$ and
$u$ and ![]() $\mu$ such that
$\mu$ such that ![]() $s(\mu )=N$ and, hence, that many rows which we can guarantee are divisible by
$s(\mu )=N$ and, hence, that many rows which we can guarantee are divisible by ![]() $T_a^{N-\left \lfloor N/p\right \rfloor }$ (not counting rows which we can guarantee are divisible by higher powers of
$T_a^{N-\left \lfloor N/p\right \rfloor }$ (not counting rows which we can guarantee are divisible by higher powers of ![]() $T_a$). We conclude that
$T_a$). We conclude that ![]() $\operatorname {NP}(\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N)$ passes above the point
$\operatorname {NP}(\sum _{N\ge 0}c_N(T_1,\dotsc,T_{n-1})X^N)$ passes above the point
 \[ \biggl(h\sum_{N=0}^M\binom{N+n(n-1)/2-1}{n(n-1)/2-1},h\sum_{N=0}^M\binom{N+n(n-1)/2-1}{n(n-1)/2-1}(N-\left\lfloor N/p\right\rfloor)v(T_a)\biggr) \]
\[ \biggl(h\sum_{N=0}^M\binom{N+n(n-1)/2-1}{n(n-1)/2-1},h\sum_{N=0}^M\binom{N+n(n-1)/2-1}{n(n-1)/2-1}(N-\left\lfloor N/p\right\rfloor)v(T_a)\biggr) \]
for every integer ![]() $M\ge 0$. Since the
$M\ge 0$. Since the ![]() $x$-coordinate of the above expression is a polynomial in
$x$-coordinate of the above expression is a polynomial in ![]() $M$ of degree
$M$ of degree ![]() $n(n-1)/2$ and the
$n(n-1)/2$ and the ![]() $y$-coordinate is
$y$-coordinate is ![]() $v(T_a)$ times a polynomial in
$v(T_a)$ times a polynomial in ![]() $M$ of degree
$M$ of degree ![]() $n(n-1)/2+1$, the claim follows.
$n(n-1)/2+1$, the claim follows.
4.2 Systems of eigenvalues associated to classical points
A ‘refined principal series’ is a principal series representation ![]() $\pi$ of
$\pi$ of ![]() ${GL}_n(\mathbb {Q}_p)$ together with an ordered sequence of characters
${GL}_n(\mathbb {Q}_p)$ together with an ordered sequence of characters ![]() $(\psi _1,\dotsc,\psi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$ such that
$(\psi _1,\dotsc,\psi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$ such that ![]() $\pi \cong \pi (\psi _1,\dotsc,\psi _n)$. Thus, there are
$\pi \cong \pi (\psi _1,\dotsc,\psi _n)$. Thus, there are ![]() $n!$ possible refinements of each
$n!$ possible refinements of each ![]() $\pi$. The language comes from Galois representation theory. From our setup so far, it is easy to see that an eigenform
$\pi$. The language comes from Galois representation theory. From our setup so far, it is easy to see that an eigenform ![]() $f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is naturally associated to a particular refined principal series: the principal series
$f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is naturally associated to a particular refined principal series: the principal series ![]() $\pi _{f,p}$, together with, if
$\pi _{f,p}$, together with, if ![]() $f$ has
$f$ has ![]() $\lambda$-values
$\lambda$-values ![]() $\lambda _1,\dotsc,\lambda _n$, the ordered sequence
$\lambda _1,\dotsc,\lambda _n$, the ordered sequence ![]() $(\psi _1,\dotsc,\psi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$ such that
$(\psi _1,\dotsc,\psi _n):(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$ such that ![]() $\pi \cong \pi (\psi _1,\dotsc,\psi _n)$ and
$\pi \cong \pi (\psi _1,\dotsc,\psi _n)$ and ![]() $\lambda _i=p^{(n-1)/2-i+1-m_n-m_{n-1}-\dotsb -m_{n-i+1}}\psi _i(p)$. Also note that this refined principal series depends only on the point
$\lambda _i=p^{(n-1)/2-i+1-m_n-m_{n-1}-\dotsb -m_{n-i+1}}\psi _i(p)$. Also note that this refined principal series depends only on the point ![]() $x$ on
$x$ on ![]() $\mathscr {D}$ that
$\mathscr {D}$ that ![]() $f$ is associated to.
$f$ is associated to.
For a character ![]() $\chi :(\mathbb {Z}_p^\times )^n\to \mathbb {C}^\times$ or
$\chi :(\mathbb {Z}_p^\times )^n\to \mathbb {C}^\times$ or ![]() $\psi :(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$, and for any
$\psi :(\mathbb {Q}_p^\times )^n\to \mathbb {C}^\times$, and for any ![]() $w\in S_n$, we write
$w\in S_n$, we write ![]() $\chi ^w=(\chi _{w(1)},\dotsc,\chi _{w(n)})$, and
$\chi ^w=(\chi _{w(1)},\dotsc,\chi _{w(n)})$, and ![]() $\psi ^w$ similarly.
$\psi ^w$ similarly.
Now note that if ![]() $f_x\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is an eigenform associated (via Proposition 3.6.4) to a point
$f_x\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is an eigenform associated (via Proposition 3.6.4) to a point ![]() $x$ on
$x$ on ![]() $\mathscr {D}$ with associated refined principal series
$\mathscr {D}$ with associated refined principal series ![]() $(\pi (\psi ),\psi ^{\operatorname {id}})$, then the refined principal series
$(\pi (\psi ),\psi ^{\operatorname {id}})$, then the refined principal series ![]() $(\pi (\psi ),\psi ^w)$ is also associated to a point
$(\pi (\psi ),\psi ^w)$ is also associated to a point ![]() $x^w$ on
$x^w$ on ![]() $\mathscr {D}$ and a form
$\mathscr {D}$ and a form ![]() $f_x^w\in (U^{{\rm sm}}(\chi ^w)\otimes S_t)(G,U_0(p))$ (arising from the unique
$f_x^w\in (U^{{\rm sm}}(\chi ^w)\otimes S_t)(G,U_0(p))$ (arising from the unique ![]() $(J,\chi ^w)$-vector in
$(J,\chi ^w)$-vector in ![]() $\pi (\psi )$). The forms
$\pi (\psi )$). The forms ![]() $f_x^w$ are called companion forms of
$f_x^w$ are called companion forms of ![]() $f_x$. Having defined these companion forms, it is straightforward to show that the slopes appearing in
$f_x$. Having defined these companion forms, it is straightforward to show that the slopes appearing in ![]() $(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ are not only finite but bounded above by a linear function of
$(U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ are not only finite but bounded above by a linear function of ![]() $t$, as follows.
$t$, as follows.
Proposition 4.2.1 If ![]() $f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is a
$f\in (U^{{\rm sm}}(\chi )\otimes S_t)(G,U_0(p))$ is a ![]() $U_p^a$-eigenform with eigenvalue
$U_p^a$-eigenform with eigenvalue ![]() $a_p^{\operatorname {id}}$, and each companion form
$a_p^{\operatorname {id}}$, and each companion form ![]() $f^w$ has
$f^w$ has ![]() $U_p^a$-eigenvalue
$U_p^a$-eigenvalue ![]() $a_p^w$, then we have
$a_p^w$, then we have
where ![]() $l^a(t)$ is a linear function of
$l^a(t)$ is a linear function of ![]() $t_1,\dotsc,t_n$.
$t_1,\dotsc,t_n$.
In particular, let ![]() $l^{(n-1,n-2,\dotsc,0)}(t)=l(t)$. Suppose that
$l^{(n-1,n-2,\dotsc,0)}(t)=l(t)$. Suppose that ![]() $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i), \operatorname {cond} (\chi _j))$ for all
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i), \operatorname {cond} (\chi _j))$ for all ![]() $i\neq j$. Then for each
$i\neq j$. Then for each ![]() $w$, the Newton polygon of
$w$, the Newton polygon of
contains ![]() $hp^{j(\chi )}d_t$ slopes of size at most
$hp^{j(\chi )}d_t$ slopes of size at most ![]() $l(t)$, hence, in particular, passes below the point
$l(t)$, hence, in particular, passes below the point
Proof. Let ![]() $\pi _{f,p}=\pi (\psi _1,\dotsc,\psi _n)$. By Proposition 3.6.6, we have
$\pi _{f,p}=\pi (\psi _1,\dotsc,\psi _n)$. By Proposition 3.6.6, we have
The ![]() $\lambda$-values of
$\lambda$-values of ![]() $x^w$ are given by
$x^w$ are given by
for each ![]() $w\in S_n$. Then for
$w\in S_n$. Then for ![]() $a=(a_1,\dotsc,a_n)$, the
$a=(a_1,\dotsc,a_n)$, the ![]() $U_p^a$-eigenvalue associated to
$U_p^a$-eigenvalue associated to ![]() $x^w$ is
$x^w$ is
so the product of the ![]() $U_p^a$-eigenvalues associated to all the
$U_p^a$-eigenvalues associated to all the ![]() $x^w$ is
$x^w$ is
 \begin{align*}& p^{(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]}\biggl(\prod_i\psi_i(p)\biggr)^{(n-1)!\sum_ia_i}\\
& \quad=p^{(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]}\biggl(p^{nm_n+(n-1)m_{n-1}+\dotsb+m_1}\prod_i\lambda_i\biggr)^{(n-1)!\sum_ia_i}.
\end{align*}
\begin{align*}& p^{(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]}\biggl(\prod_i\psi_i(p)\biggr)^{(n-1)!\sum_ia_i}\\
& \quad=p^{(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]}\biggl(p^{nm_n+(n-1)m_{n-1}+\dotsb+m_1}\prod_i\lambda_i\biggr)^{(n-1)!\sum_ia_i}.
\end{align*}
But ![]() $\prod _i\lambda _i$ is the eigenvalue associated to the operator
$\prod _i\lambda _i$ is the eigenvalue associated to the operator ![]() $U_p^{(1,1,\dotsc,1)}$, which is just right translation by the central matrix
$U_p^{(1,1,\dotsc,1)}$, which is just right translation by the central matrix ![]() $\operatorname {diag}(p,p,\dotsc,p)$, which preserves
$\operatorname {diag}(p,p,\dotsc,p)$, which preserves ![]() $f$, so
$f$, so ![]() $\prod _i\lambda _i=1$. Thus, the sum of the valuations of the
$\prod _i\lambda _i=1$. Thus, the sum of the valuations of the ![]() $U_p^a$-eigenvalues associated to the companion points is
$U_p^a$-eigenvalues associated to the companion points is
 \begin{align*} &(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]\\ &\qquad +(nm_n+(n-1)m_{n-1}+\dotsb+m_1)(n-1)!\sum_ia_i\\ &\quad =(n-1)!\biggl(\sum_ia_{n-i+1}((n-1)/2-i+1)-\sum_j m_j(a_1+\dotsb+a_j)+\sum_j jm_j\biggl(\sum_i a_i\biggr)\biggr). \end{align*}
\begin{align*} &(n-1)!\sum_ia_{n-i+1}[(n-1)/2-i+1-m_n-m_{n-1}-\dotsb-m_{n-i+1}]\\ &\qquad +(nm_n+(n-1)m_{n-1}+\dotsb+m_1)(n-1)!\sum_ia_i\\ &\quad =(n-1)!\biggl(\sum_ia_{n-i+1}((n-1)/2-i+1)-\sum_j m_j(a_1+\dotsb+a_j)+\sum_j jm_j\biggl(\sum_i a_i\biggr)\biggr). \end{align*}
Defining ![]() $l^a(t)$ to be this last expression, we find that
$l^a(t)$ to be this last expression, we find that ![]() $\sum _{w\in S_n}v(a_p^w)=l^a(t)$ as desired.
$\sum _{w\in S_n}v(a_p^w)=l^a(t)$ as desired.
The conclusion that each individual ![]() $v(a_p^w)$ is bounded above by
$v(a_p^w)$ is bounded above by ![]() $l^a(t)$ follows because all the
$l^a(t)$ follows because all the ![]() $a_p^w$ are algebraic integers.
$a_p^w$ are algebraic integers.
Let ![]() $c_i=\operatorname {cond}(\chi _i)$, let
$c_i=\operatorname {cond}(\chi _i)$, let ![]() $\chi _{(1)},\dotsc,\chi _{(n-1)}$ be the characters
$\chi _{(1)},\dotsc,\chi _{(n-1)}$ be the characters ![]() $\chi _1,\dotsc,\chi _{n-1}$ reordered so that
$\chi _1,\dotsc,\chi _{n-1}$ reordered so that ![]() $\operatorname {cond}(\chi _{(1)})\le \operatorname {cond}(\chi _{(2)})\le \dotsb \le \operatorname {cond}(\chi _{(n-1)})$, let
$\operatorname {cond}(\chi _{(1)})\le \operatorname {cond}(\chi _{(2)})\le \dotsb \le \operatorname {cond}(\chi _{(n-1)})$, let ![]() $c_{(i)}=\operatorname {cond}(\chi _{(i)})$, and let
$c_{(i)}=\operatorname {cond}(\chi _{(i)})$, and let ![]() $T_{(i)}=T(\chi _{(i)})$. To get from Proposition 4.2.1 to the statement of Theorem 1.1.2, we just need to check that for all
$T_{(i)}=T(\chi _{(i)})$. To get from Proposition 4.2.1 to the statement of Theorem 1.1.2, we just need to check that for all ![]() $t$ and
$t$ and ![]() $\chi$ such that
$\chi$ such that ![]() $m_i\ge \epsilon m_j$ for all
$m_i\ge \epsilon m_j$ for all ![]() $i\neq j$ and
$i\neq j$ and ![]() $\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all
$\operatorname {cond}(\chi _i\chi _j^{-1})=\max (\operatorname {cond}(\chi _i),\operatorname {cond}(\chi _j))$ for all ![]() $i\neq j$,
$i\neq j$, ![]() $(hp^{j(\chi )}d_t, hp^{j(\chi )}d_tl(t))$ has the desired numerical qualities. First we check the size of
$(hp^{j(\chi )}d_t, hp^{j(\chi )}d_tl(t))$ has the desired numerical qualities. First we check the size of ![]() $d_t$.
$d_t$.
Proposition 4.2.2 The dimension ![]() $d_t$ is a polynomial of total degree
$d_t$ is a polynomial of total degree ![]() ${n(n-1)}/2$ in
${n(n-1)}/2$ in ![]() $m_1,\dotsc,m_{n-1}$.
$m_1,\dotsc,m_{n-1}$.
Proof. By Corollary 14.9 of [Reference Miller and SturmfelsMS04], ![]() $\operatorname {Ind}_{B(\mathbb {Z}_p)}^{{GL}_n(\mathbb {Z}_p),{\rm alg}}t$ has a basis indexed by chains in the poset described in [Reference Miller and SturmfelsMS04, § 14.2]. For a subset
$\operatorname {Ind}_{B(\mathbb {Z}_p)}^{{GL}_n(\mathbb {Z}_p),{\rm alg}}t$ has a basis indexed by chains in the poset described in [Reference Miller and SturmfelsMS04, § 14.2]. For a subset ![]() $\sigma$ of
$\sigma$ of ![]() $\{1,\dotsc,n\}$, let
$\{1,\dotsc,n\}$, let ![]() $f(\sigma )=\sum _{k\notin \sigma }(n+1-k)$. We claim that when you take one step down the poset,
$f(\sigma )=\sum _{k\notin \sigma }(n+1-k)$. We claim that when you take one step down the poset, ![]() $f(\sigma )$ goes down by
$f(\sigma )$ goes down by ![]() $1$. This is because, if
$1$. This is because, if ![]() $\sigma$ is one step below
$\sigma$ is one step below ![]() $\tau$, there are two possibilities. The first is that
$\tau$, there are two possibilities. The first is that ![]() $|\tau |=|\sigma |$ and there is some
$|\tau |=|\sigma |$ and there is some ![]() $i$ for which
$i$ for which ![]() $\sigma _i=\tau _i-1$ and
$\sigma _i=\tau _i-1$ and ![]() $\sigma _j=\tau _j$ for all
$\sigma _j=\tau _j$ for all ![]() $j$ with
$j$ with ![]() $j\neq i$; in this case the complements
$j\neq i$; in this case the complements ![]() $\sigma ^c$ and
$\sigma ^c$ and ![]() $\tau ^c$ are the same except for
$\tau ^c$ are the same except for ![]() $\sigma _i\in \tau ^c$ and
$\sigma _i\in \tau ^c$ and ![]() $\sigma _i+1=\tau _i\in \sigma ^c$, which contribute
$\sigma _i+1=\tau _i\in \sigma ^c$, which contribute ![]() $n-\sigma _i$ and
$n-\sigma _i$ and ![]() $n-\sigma _i-1$ to the sums
$n-\sigma _i-1$ to the sums ![]() $f(\sigma )$ and
$f(\sigma )$ and ![]() $f(\tau )$, so
$f(\tau )$, so ![]() $f(\sigma )=f(\tau )-1$. The second is that
$f(\sigma )=f(\tau )-1$. The second is that ![]() $|\sigma |=|\tau |+1$ and
$|\sigma |=|\tau |+1$ and ![]() $\sigma$ contains
$\sigma$ contains ![]() $n$ and
$n$ and ![]() $\tau$ does not, so again
$\tau$ does not, so again ![]() $f(\sigma )=f(\tau )-1$.
$f(\sigma )=f(\tau )-1$.
Thus, a maximal chain in this poset starts with ![]() $\{n\}$, which has
$\{n\}$, which has ![]() $f$-value
$f$-value ![]() $2+\dotsb +n={n(n+1)}/2-1$, and ends with
$2+\dotsb +n={n(n+1)}/2-1$, and ends with ![]() $\{1,2,\dotsc,n-1\}$, which has
$\{1,2,\dotsc,n-1\}$, which has ![]() $f$-value
$f$-value ![]() $1$; its length is therefore
$1$; its length is therefore ![]() ${n(n+1)}/2-1$. A leading term of
${n(n+1)}/2-1$. A leading term of ![]() $d_{m_1,\dotsc,m_{n-1},0}$ comes from distributing
$d_{m_1,\dotsc,m_{n-1},0}$ comes from distributing ![]() $m_1,\dotsc,m_{n-1}$ among corresponding variables in a maximal chain. Thus, it is a product
$m_1,\dotsc,m_{n-1}$ among corresponding variables in a maximal chain. Thus, it is a product ![]() $\prod \binom{m_i+c_i}{c_i}$ where the
$\prod \binom{m_i+c_i}{c_i}$ where the ![]() $c_i+1$ sum to
$c_i+1$ sum to ![]() ${n(n+1)}/2-1$; that is, the
${n(n+1)}/2-1$; that is, the ![]() $c_i$ sum to
$c_i$ sum to ![]() ${n(n+1)}/2-1-(n-1)={n(n-1)}/2$.
${n(n+1)}/2-1-(n-1)={n(n-1)}/2$.
Since ![]() $m_i\ge \epsilon m_j$ for all
$m_i\ge \epsilon m_j$ for all ![]() $i\neq j$, we can find some
$i\neq j$, we can find some ![]() $A_{\epsilon }$ such that
$A_{\epsilon }$ such that ![]() $l(t)\le A_{\epsilon }d_t^{2/{n(n-1)}}$ for all such
$l(t)\le A_{\epsilon }d_t^{2/{n(n-1)}}$ for all such ![]() $m_1,\dotsc,m_{n-1}$. Also, by the formula stated in Example 2.2.2, we have
$m_1,\dotsc,m_{n-1}$. Also, by the formula stated in Example 2.2.2, we have
for a constant ![]() $A_1$ (depending on
$A_1$ (depending on ![]() $p$). Thus, we have
$p$). Thus, we have
Thus, if we let ![]() $x=hp^{j(\chi )}d_t$ and
$x=hp^{j(\chi )}d_t$ and ![]() $y=hp^{j(\chi )}d_tl(t)$, we have
$y=hp^{j(\chi )}d_tl(t)$, we have
 \begin{align*} y&=\bigl(hp^{j(\chi)}d_t\bigr)^{1+2/{n(n-1)}}\bigl(hp^{j(\chi)}d_t\bigr)^{-2/{n(n-1)}}l(t)\\ &=A_3x^{1+2/{n(n-1)}}\bigl(p^{j(\chi)}\bigr)^{-2/{n(n-1)}}d_t^{-2/{n(n-1)}}l(t) \\ &\le A_4A_{\epsilon}x^{1+2/{n(n-1)}}\bigl(v(T_{(1)})^{-1}v(T_{(2)})^{-2}\dotsb v(T_{(n-1)})^{-(n-1)}\bigr)^{-2/{n(n-1)}}\\ &=A_5\bigl(v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\bigr)x^{1+2/{n(n-1)}}, \end{align*}
\begin{align*} y&=\bigl(hp^{j(\chi)}d_t\bigr)^{1+2/{n(n-1)}}\bigl(hp^{j(\chi)}d_t\bigr)^{-2/{n(n-1)}}l(t)\\ &=A_3x^{1+2/{n(n-1)}}\bigl(p^{j(\chi)}\bigr)^{-2/{n(n-1)}}d_t^{-2/{n(n-1)}}l(t) \\ &\le A_4A_{\epsilon}x^{1+2/{n(n-1)}}\bigl(v(T_{(1)})^{-1}v(T_{(2)})^{-2}\dotsb v(T_{(n-1)})^{-(n-1)}\bigr)^{-2/{n(n-1)}}\\ &=A_5\bigl(v(T_{(1)})^{{2}/{n(n-1)}}v(T_{(2)})^{({2\cdot 2})/{n(n-1)}}\dotsb v(T_{(n-1)})^{({2\cdot(n-1)})/{n(n-1)}}\bigr)x^{1+2/{n(n-1)}}, \end{align*}
where ![]() $A_5$ depends only on
$A_5$ depends only on ![]() $n$,
$n$, ![]() $p$,
$p$, ![]() $h$, and
$h$, and ![]() $\epsilon$, as desired. This proves part (ii) of Theorem 1.1.2.
$\epsilon$, as desired. This proves part (ii) of Theorem 1.1.2.
4.3 Combining upper bound points
We show that Theorem 1.1.3 is a natural consequence of part (ii) of Theorem 1.1.2. First we need the following lemma of Wan, which is stated in [Reference WanWan98] with ![]() $\mathbb {Z}_p$-coefficients but works identically with
$\mathbb {Z}_p$-coefficients but works identically with ![]() $\mathscr {O}_{\mathbb {C}_p}$-coefficients.
$\mathscr {O}_{\mathbb {C}_p}$-coefficients.
Lemma 4.3.1 (Wan [Reference WanWan98])
Let ![]() $Q_1(X),Q_2(X)$ be two elements in
$Q_1(X),Q_2(X)$ be two elements in ![]() $\mathscr {O}_{\mathbb {C}_p}[\kern-1pt[ X]\kern-1pt]$ with
$\mathscr {O}_{\mathbb {C}_p}[\kern-1pt[ X]\kern-1pt]$ with ![]() $Q_1(0)=Q_2(0)=1$. Let
$Q_1(0)=Q_2(0)=1$. Let ![]() $N_i(x)$ be the function on
$N_i(x)$ be the function on ![]() $\mathbb {R}_{\ge 0}$ whose graph is the Newton polygon of
$\mathbb {R}_{\ge 0}$ whose graph is the Newton polygon of ![]() $Q_i(X)$. Assume that
$Q_i(X)$. Assume that ![]() $\nu (x)$ is a strictly increasing continuous function on
$\nu (x)$ is a strictly increasing continuous function on ![]() $\mathbb {R}_{\ge 0}$ such that
$\mathbb {R}_{\ge 0}$ such that ![]() $\nu (0)\le 0$,
$\nu (0)\le 0$, ![]() $N_i(x)\ge x\nu (x)$ for
$N_i(x)\ge x\nu (x)$ for ![]() $1\le i\le 2$ and
$1\le i\le 2$ and ![]() $x\ge 1$, and
$x\ge 1$, and ![]() $\lim _{x\to \infty }\nu (x)=\infty$. Assume further that the function
$\lim _{x\to \infty }\nu (x)=\infty$. Assume further that the function ![]() $x\nu ^{-1}(x)$ is increasing on
$x\nu ^{-1}(x)$ is increasing on ![]() $\mathbb {R}_{>0}$, where
$\mathbb {R}_{>0}$, where ![]() $\nu ^{-1}(x)$ denotes the inverse function of
$\nu ^{-1}(x)$ denotes the inverse function of ![]() $\nu (x)$ defined at least on
$\nu (x)$ defined at least on ![]() $\mathbb {R}_{\ge 0}$. For
$\mathbb {R}_{\ge 0}$. For ![]() $x\ge 0$, we define the integer-valued increasing function
$x\ge 0$, we define the integer-valued increasing function ![]() $m_\nu (x)=\left \lfloor x\nu ^{-1}(x)\right \rfloor$. If the congruence
$m_\nu (x)=\left \lfloor x\nu ^{-1}(x)\right \rfloor$. If the congruence
holds for some ![]() $\alpha \ge 0$, then the two Newton polygons
$\alpha \ge 0$, then the two Newton polygons ![]() $N_i(x)$ coincide for all the sides with slopes at most
$N_i(x)$ coincide for all the sides with slopes at most ![]() $\alpha$.
$\alpha$.
Proof of Theorem 1.1.3 By Proposition 4.2.1, ![]() $\operatorname {NP}(t\chi )$ passes below the point
$\operatorname {NP}(t\chi )$ passes below the point
Note that the slope of ![]() $\operatorname {NP}(t\chi )$ at
$\operatorname {NP}(t\chi )$ at ![]() $x$-coordinate
$x$-coordinate ![]() $hp^{j(\chi )}d_t$ is at most
$hp^{j(\chi )}d_t$ is at most ![]() $l(t)$. We may apply Lemma 4.3.1 with
$l(t)$. We may apply Lemma 4.3.1 with ![]() $\nu (x)=A_1x^{2/{n(n-1)}}\min _iv(T(\chi _i))$, so that
$\nu (x)=A_1x^{2/{n(n-1)}}\min _iv(T(\chi _i))$, so that
 \[ m_\nu(x)\asymp \frac{x^{1+{n(n-1)}/2}}{\bigl(\min_iv(T(\chi_i))\bigr)^{{n(n-1)}/2}}. \]
\[ m_\nu(x)\asymp \frac{x^{1+{n(n-1)}/2}}{\bigl(\min_iv(T(\chi_i))\bigr)^{{n(n-1)}/2}}. \]
Let ![]() $t_i^{(1)}=t_i+(n-i)p^{m_\nu (l(t))+1}\varphi (q)$. By Lemma 4.3.1 applied to
$t_i^{(1)}=t_i+(n-i)p^{m_\nu (l(t))+1}\varphi (q)$. By Lemma 4.3.1 applied to ![]() $P(X,t\chi )$ and
$P(X,t\chi )$ and ![]() $P(X,t^{(1)}\chi )$, we find that
$P(X,t^{(1)}\chi )$, we find that ![]() $\operatorname {NP}(t^{(1)}\chi )$ also passes below this point. (The factor of
$\operatorname {NP}(t^{(1)}\chi )$ also passes below this point. (The factor of ![]() $\varphi (q)$ is to keep
$\varphi (q)$ is to keep ![]() $t_1^{(1)},\dotsc,t_{n-1}^{(1)}$ in the same equivalence class as
$t_1^{(1)},\dotsc,t_{n-1}^{(1)}$ in the same equivalence class as ![]() $t_1,\dotsc,t_{n-1}\pmod {\varphi (q)}$ so that they fall in the same weight polydisc; presumably it would also suffice to twist by an appropriate tame character instead.) However, by Corollary 4.2.1,
$t_1,\dotsc,t_{n-1}\pmod {\varphi (q)}$ so that they fall in the same weight polydisc; presumably it would also suffice to twist by an appropriate tame character instead.) However, by Corollary 4.2.1, ![]() $\operatorname {NP}(t^{(1)}\chi )$ also passes below
$\operatorname {NP}(t^{(1)}\chi )$ also passes below
Repeating this, we find a sequence ![]() $t=t^{(0)},t^{(1)},t^{(2)},\dotsc$ of dominant algebraic weights such that
$t=t^{(0)},t^{(1)},t^{(2)},\dotsc$ of dominant algebraic weights such that ![]() $\operatorname {NP}(t^{(k)}\chi )$ passes below
$\operatorname {NP}(t^{(k)}\chi )$ passes below
Evidently the ![]() $t^{(k)}$ approach a limit
$t^{(k)}$ approach a limit ![]() $t^\infty$, and
$t^\infty$, and ![]() $\operatorname {NP}(t^\infty \chi )$ passes below
$\operatorname {NP}(t^\infty \chi )$ passes below
for all ![]() $k$. The result follows as in the end of § 4.2. (Note that since
$k$. The result follows as in the end of § 4.2. (Note that since
if ![]() $m_i^{(k-1)}\ge \epsilon m_j^{(k-1)}$ for all
$m_i^{(k-1)}\ge \epsilon m_j^{(k-1)}$ for all ![]() $i\neq j$, the same is true for the
$i\neq j$, the same is true for the ![]() $m_i^{(k)}$.)
$m_i^{(k)}$.)
5. Geometry of the eigenvariety over the boundary of weight space
Fix an index ![]() $a$, and for any
$a$, and for any ![]() $\nu \in \mathbb {Q}$, let
$\nu \in \mathbb {Q}$, let ![]() $\mathscr {W}_{<\nu }$ be the admissible open subset of characters
$\mathscr {W}_{<\nu }$ be the admissible open subset of characters ![]() $w$ such that
$w$ such that ![]() $v(T_a(w))<\nu$ and
$v(T_a(w))<\nu$ and ![]() $v(T_a(w))<\nu v(T_j(w))$ for all
$v(T_a(w))<\nu v(T_j(w))$ for all ![]() $j\neq a$ (so, in particular,
$j\neq a$ (so, in particular, ![]() $v(T_a)=\min _i v(T_i)$). (We could also use
$v(T_a)=\min _i v(T_i)$). (We could also use ![]() $\mathscr {W}_{\le \nu }$, with the analogous definition; this would not only be admissible open, but would be a rational subdomain upon intersection with an affinoid subdomain of
$\mathscr {W}_{\le \nu }$, with the analogous definition; this would not only be admissible open, but would be a rational subdomain upon intersection with an affinoid subdomain of ![]() $\mathscr {W}$. See [Reference Baker, Conrad, Dasgupta, Teitelbaum and KedlayaBCD+08, Chapter 1, § 2] for more information about the rigid analytic Grothendieck topology on
$\mathscr {W}$. See [Reference Baker, Conrad, Dasgupta, Teitelbaum and KedlayaBCD+08, Chapter 1, § 2] for more information about the rigid analytic Grothendieck topology on ![]() $\mathscr {W}$.) let
$\mathscr {W}$.) let ![]() $\mathscr {Z}_{<\nu }$ be the preimage of
$\mathscr {Z}_{<\nu }$ be the preimage of ![]() $\mathscr {W}_{<\nu }$ in the eigencurve
$\mathscr {W}_{<\nu }$ in the eigencurve ![]() $\mathscr {Z}$. For any real number
$\mathscr {Z}$. For any real number ![]() $\alpha$, let
$\alpha$, let ![]() $X(<\alpha )$ be the subset of
$X(<\alpha )$ be the subset of ![]() $\mathscr {Z}$ of points
$\mathscr {Z}$ of points ![]() $x$ for which
$x$ for which ![]() $v(a_p(x))<\alpha v(T_a(w(x)))$, and define
$v(a_p(x))<\alpha v(T_a(w(x)))$, and define ![]() $X(=\alpha )$,
$X(=\alpha )$, ![]() $X(>\alpha )$ similarly.
$X(>\alpha )$ similarly.
As in the previous section, fix a polydisc in ![]() $\mathscr {W}$. For
$\mathscr {W}$. For ![]() $T=(T_1,\dotsc,T_{n-1})$ in the polydisc and
$T=(T_1,\dotsc,T_{n-1})$ in the polydisc and ![]() $m=(m_1,\dotsc,m_{n-1})\in \mathbb {Z}_{\ge 0}^{n-1}$, write
$m=(m_1,\dotsc,m_{n-1})\in \mathbb {Z}_{\ge 0}^{n-1}$, write ![]() $T^m=T_1^{m_1}\dotsb T_{n-1}^{m_{n-1}}$ for short. Let
$T^m=T_1^{m_1}\dotsb T_{n-1}^{m_{n-1}}$ for short. Let
where
 \[ c_N(T)=\sum_{m=(m_1,\dotsc,m_{n-1})\in\mathbb{Z}_{\ge0}^{n-1}}b_{N,m}T^m\in\mathbb{Z}_p[\kern-1pt[ T_1,\dotsc,T_{n-1}]\kern-1pt]. \]
\[ c_N(T)=\sum_{m=(m_1,\dotsc,m_{n-1})\in\mathbb{Z}_{\ge0}^{n-1}}b_{N,m}T^m\in\mathbb{Z}_p[\kern-1pt[ T_1,\dotsc,T_{n-1}]\kern-1pt]. \]
Let ![]() $y=\operatorname {NP}(T)(x)$ be the Newton polygon of
$y=\operatorname {NP}(T)(x)$ be the Newton polygon of ![]() $\sum _{N\ge 0}c_N(T)X^N$.
$\sum _{N\ge 0}c_N(T)X^N$.
For the following theorem, the only input we need is a lower bound for ![]() $y=\operatorname {NP}(T)(x)$ of the form
$y=\operatorname {NP}(T)(x)$ of the form ![]() $y=v(T_a)f(x)$ where
$y=v(T_a)f(x)$ where ![]() $f(x)$ is a convex function, which we have (with
$f(x)$ is a convex function, which we have (with ![]() $f(x)=A_1x^{1+2/{n(n-1)}}$) from part (i) of Theorem 1.1.2.
$f(x)=A_1x^{1+2/{n(n-1)}}$) from part (i) of Theorem 1.1.2.
Theorem 5.0.1 For every ![]() $\alpha \in \mathbb {R}_{\ge 0}$, there is some valuation
$\alpha \in \mathbb {R}_{\ge 0}$, there is some valuation ![]() $\nu (\alpha )>0$ such that
$\nu (\alpha )>0$ such that ![]() $X(=\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in
$X(=\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in ![]() $\mathscr {Z}_{<\nu (\alpha )}$.
$\mathscr {Z}_{<\nu (\alpha )}$.
Proof. Let ![]() $d(\alpha,T)$ be the number of slopes in
$d(\alpha,T)$ be the number of slopes in ![]() $y=\operatorname {NP}(T)(x)$ of value strictly less than
$y=\operatorname {NP}(T)(x)$ of value strictly less than ![]() $\alpha v(T_a)$ (that is to say, the dimension of
$\alpha v(T_a)$ (that is to say, the dimension of ![]() $\mathscr {S}_T(G,U_0(p))^{<\alpha v(T_a)}$). Assume
$\mathscr {S}_T(G,U_0(p))^{<\alpha v(T_a)}$). Assume ![]() $v(T_a)<1$.
$v(T_a)<1$.
We claim that the point ![]() $(d(\alpha,T),\operatorname {NP}(T)(d(\alpha,T)))$ lies inside the region bounded by the line
$(d(\alpha,T),\operatorname {NP}(T)(d(\alpha,T)))$ lies inside the region bounded by the line ![]() $y=\alpha v(T_a)x$ and the function
$y=\alpha v(T_a)x$ and the function ![]() $y=v(T_a)f(x)$. It lies below
$y=v(T_a)f(x)$. It lies below ![]() $y=\alpha v(T_a)x$ because all slopes of
$y=\alpha v(T_a)x$ because all slopes of ![]() $NP(T)$ up to
$NP(T)$ up to ![]() $d(\alpha,T)$ are less than
$d(\alpha,T)$ are less than ![]() $\alpha v(T_a)$. It lies above
$\alpha v(T_a)$. It lies above ![]() $y=v(T_a)f(x)$ because this is a lower bound for
$y=v(T_a)f(x)$ because this is a lower bound for ![]() $y=\operatorname {NP}(T)(x)$.
$y=\operatorname {NP}(T)(x)$.
This region lies inside the box whose lower left corner is ![]() $(0,0)$ and whose upper right corner is
$(0,0)$ and whose upper right corner is ![]() $(d(\alpha ),\alpha d(\alpha )v(T_a))$, where
$(d(\alpha ),\alpha d(\alpha )v(T_a))$, where ![]() $d(\alpha )$ is the nonzero solution to
$d(\alpha )$ is the nonzero solution to ![]() $\alpha x=f(x)$.
$\alpha x=f(x)$.
We have ![]() $(d(\alpha,T),\operatorname {NP}(T)(d(\alpha,T)))=(j,v(c_j(T)))$ for some
$(d(\alpha,T),\operatorname {NP}(T)(d(\alpha,T)))=(j,v(c_j(T)))$ for some ![]() $j$. This is a vertex of
$j$. This is a vertex of ![]() $y=\operatorname {NP}(T)(x)$. The vertex immediately preceding it is of the form
$y=\operatorname {NP}(T)(x)$. The vertex immediately preceding it is of the form ![]() $(i,v(c_i(T)))$ for some
$(i,v(c_i(T)))$ for some ![]() $i$. The slope between the two is
$i$. The slope between the two is
This is the largest slope of ![]() $y=\operatorname {NP}(T)(x)$ less than
$y=\operatorname {NP}(T)(x)$ less than ![]() $\alpha v(T_a)$. We have
$\alpha v(T_a)$. We have ![]() $1\le j-i\le d(\alpha )$.
$1\le j-i\le d(\alpha )$.
But ![]() $c_j(T)=\sum _{m\ge 0}b_{j,m}T^m$ is a sum of terms
$c_j(T)=\sum _{m\ge 0}b_{j,m}T^m$ is a sum of terms ![]() $b_{j,m}T^m$ where
$b_{j,m}T^m$ where ![]() $v(b_{j,m})$ is an integer and
$v(b_{j,m})$ is an integer and
Thus, ![]() $v(c_j(T))=\mu _j+\lambda _j^1v(T_1)+\dotsb +\lambda _j^{n-1}v(T_{n-1})$ where
$v(c_j(T))=\mu _j+\lambda _j^1v(T_1)+\dotsb +\lambda _j^{n-1}v(T_{n-1})$ where ![]() $\mu _j,\lambda _j^k$ are integers in the range
$\mu _j,\lambda _j^k$ are integers in the range ![]() $[0,\alpha d(\alpha )]$ (since
$[0,\alpha d(\alpha )]$ (since ![]() $v(c_j(T))\le \alpha d(\alpha )v(T_a)$). Similarly
$v(c_j(T))\le \alpha d(\alpha )v(T_a)$). Similarly ![]() $v(c_i(T))=\mu _i+\lambda _i^1v(T_1)+\dotsb +\lambda _i^{n-1}v(T_{n-1})$ where
$v(c_i(T))=\mu _i+\lambda _i^1v(T_1)+\dotsb +\lambda _i^{n-1}v(T_{n-1})$ where ![]() $\mu _i,\lambda _i^k\in [0,\alpha d(\alpha )]$ as well.
$\mu _i,\lambda _i^k\in [0,\alpha d(\alpha )]$ as well.
Assume that ![]() $v(T_a)<1/{\alpha d(\alpha )}$, so that
$v(T_a)<1/{\alpha d(\alpha )}$, so that ![]() $\alpha d(\alpha ) v(T_a)<1$ and, furthermore, that
$\alpha d(\alpha ) v(T_a)<1$ and, furthermore, that ![]() $v(T_a)<(1/{\alpha d(\alpha )})v(T_j)$ for all
$v(T_a)<(1/{\alpha d(\alpha )})v(T_j)$ for all ![]() $j\neq a$. Then in order to have
$j\neq a$. Then in order to have ![]() $v(c_i(T)),v(c_j(T))\le \alpha d(\alpha ) v(T_a)$, we must have
$v(c_i(T)),v(c_j(T))\le \alpha d(\alpha ) v(T_a)$, we must have ![]() $\mu _i=\mu _j=0$ and
$\mu _i=\mu _j=0$ and ![]() $\lambda ^k=0$ for all
$\lambda ^k=0$ for all ![]() $k\neq i$.
$k\neq i$.
Thus, the largest slope of ![]() $y=\operatorname {NP}(T)(x)$ less than
$y=\operatorname {NP}(T)(x)$ less than ![]() $\alpha v(T_a)$ is of the form
$\alpha v(T_a)$ is of the form ![]() $(({\lambda _j-\lambda _i})/({j-i})) v(T_a)$, where
$(({\lambda _j-\lambda _i})/({j-i})) v(T_a)$, where ![]() $\lambda _j-\lambda _i\in [0,\alpha d(\alpha )]$ and
$\lambda _j-\lambda _i\in [0,\alpha d(\alpha )]$ and ![]() $j-i\in [1,d(\alpha )]$. This is a finite, discrete set of points. Thus, the ratio of the largest slope of
$j-i\in [1,d(\alpha )]$. This is a finite, discrete set of points. Thus, the ratio of the largest slope of ![]() $y=\operatorname {NP}(T)(x)$ less than
$y=\operatorname {NP}(T)(x)$ less than ![]() $\alpha v(T_a)$ to
$\alpha v(T_a)$ to ![]() $v(T_a)$ is bounded away from
$v(T_a)$ is bounded away from ![]() $\alpha$ independently of
$\alpha$ independently of ![]() $T_a$.
$T_a$.
Setting ![]() $\nu (\alpha )<1/{\alpha d(\alpha )}$, we conclude that
$\nu (\alpha )<1/{\alpha d(\alpha )}$, we conclude that ![]() $X(<\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in
$X(<\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in ![]() $\mathscr {Z}_{<\nu (\alpha )}$.
$\mathscr {Z}_{<\nu (\alpha )}$.
This argument goes exactly the same if ![]() $X(<\alpha )$ is replaced by
$X(<\alpha )$ is replaced by ![]() $X(\le \alpha )$: either the smallest slope greater than
$X(\le \alpha )$: either the smallest slope greater than ![]() $\alpha$ is at least
$\alpha$ is at least ![]() $\alpha +1$, or, if not, the next endpoint is again trapped in a box whose area is at most linear in
$\alpha +1$, or, if not, the next endpoint is again trapped in a box whose area is at most linear in ![]() $v(T)$, and the same argument applies. Thus, we can choose
$v(T)$, and the same argument applies. Thus, we can choose ![]() $\nu (\alpha )$ such that
$\nu (\alpha )$ such that ![]() $X(=\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in
$X(=\alpha )_{<\nu (\alpha )}$ is disconnected from its complement in ![]() $\mathscr {Z}_{<\nu (\alpha )}$.
$\mathscr {Z}_{<\nu (\alpha )}$.
As Liu, Wan, and Xiao do in Theorem 3.19 of [Reference Liu, Wan and XiaoLWX17], we can also use part (i) of Theorem 1.1.2 to give a simple proof of the fact that the ordinary part of ![]() $\mathscr {Z}$ is finite and flat over
$\mathscr {Z}$ is finite and flat over ![]() $\mathscr {W}$ and disconnected from its complement.
$\mathscr {W}$ and disconnected from its complement.
Theorem 5.0.2 The subset ![]() $X(=0)$ is finite and flat over
$X(=0)$ is finite and flat over ![]() $\mathscr {W}$ and is a union of connected components of
$\mathscr {W}$ and is a union of connected components of ![]() $\mathscr {Z}$.
$\mathscr {Z}$.
Proof. The proof of Theorem 3.19 of [Reference Liu, Wan and XiaoLWX17] goes through almost word-for-word. By part (i) of Theorem 1.1.2, there is some maximal ![]() $N$ such that
$N$ such that ![]() $c_N(T_1,\dotsc,T_{n-1})$ is a unit in
$c_N(T_1,\dotsc,T_{n-1})$ is a unit in ![]() $\mathbb {Z}_p[\kern-1pt[ T_1,\dotsc,T_{n-1}]\kern-1pt]$ or, equivalently, the constant term of
$\mathbb {Z}_p[\kern-1pt[ T_1,\dotsc,T_{n-1}]\kern-1pt]$ or, equivalently, the constant term of ![]() $c_N(T_1,\dotsc,T_{n-1})$ is a unit in
$c_N(T_1,\dotsc,T_{n-1})$ is a unit in ![]() $\mathbb {Z}_p$. Then for each
$\mathbb {Z}_p$. Then for each ![]() $(T_1,\dotsc,T_{n-1})$, the Newton polygon of
$(T_1,\dotsc,T_{n-1})$, the Newton polygon of ![]() $\sum _{n=0}^\infty c_N(T_1,\dotsc,T_{n-1})X^N$ starts with
$\sum _{n=0}^\infty c_N(T_1,\dotsc,T_{n-1})X^N$ starts with ![]() $N$ segments of slope
$N$ segments of slope ![]() $0$ followed by a segment of slope at least
$0$ followed by a segment of slope at least ![]() $\max (1,B\min _j v(T_j))$ for some constant
$\max (1,B\min _j v(T_j))$ for some constant ![]() $B$. Since
$B$. Since ![]() $\max (1,B\min _j v(T_j))$ is uniformly bounded away from
$\max (1,B\min _j v(T_j))$ is uniformly bounded away from ![]() $0$ over any affinoid subdomain,
$0$ over any affinoid subdomain, ![]() $X(=0)$ is disconnected from its complement, and it is finite and flat of degree
$X(=0)$ is disconnected from its complement, and it is finite and flat of degree ![]() $N$.
$N$.
Acknowledgements
First and foremost, I would like to thank M. Kisin for suggesting this problem and providing years of advice about it and math in general. I am also grateful to T. Kaletha for pointing me to Roche's work on principal series types, J.-L. Kim for clearing up my confusion about new vectors, J. Fintzen for improving Proposition 3.6.5 (among other useful suggestions), and Y. Liu for helpful comments on a draft. I would also like to thank J. Bellaïche, J. Bergdall, C. Birkbeck, E. Knight, K. Shimizu, D. Yang, Z. Yao, and Y. Zhu for explaining various facts about eigenvarieties and representation theory to me, and G. Boxer, F. Calegari, M. Emerton, B. Gross, M. Harris, G. Henniart, M. Jeffs, D. Loeffler, B. Mazur, N. Sweeting, R. Taylor, P.-Y. Tsai, E. Urban, J. Weinstein, Y. Xu, and R. Zhou for various other helpful conversations.
Conflicts of Interest
None.