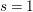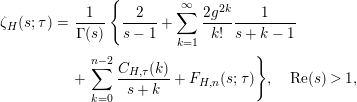1 Introduction
The spectrum of a Hamiltonian has been studied in both physics and mathematics, especially in spectral theory. One of the methods to do so is to make use of spectral zeta functions. For a
![]() $\mathbb{C}$
-Hilbert space
$\mathbb{C}$
-Hilbert space
![]() $V$
and a densely defined linear operator
$V$
and a densely defined linear operator
![]() $A:V\rightarrow V$
, the multiset of all eigenvalues of
$A:V\rightarrow V$
, the multiset of all eigenvalues of
![]() $A$
in
$A$
in
![]() $\mathbb{C}$
is denoted by
$\mathbb{C}$
is denoted by
![]() $\operatorname{Spec}(A)$
. If
$\operatorname{Spec}(A)$
. If
![]() $\operatorname{Spec}(A)$
is discrete, the spectral zeta function of
$\operatorname{Spec}(A)$
is discrete, the spectral zeta function of
![]() $A$
is defined as
$A$
is defined as
for
![]() $s\in \mathbb{C}$
if it makes sense. For example, it is well known that, for the harmonic oscillator
$s\in \mathbb{C}$
if it makes sense. For example, it is well known that, for the harmonic oscillator
![]() $h=\frac{1}{2}(-\unicode[STIX]{x2202}_{x}^{2}+x^{2})$
densely defined in
$h=\frac{1}{2}(-\unicode[STIX]{x2202}_{x}^{2}+x^{2})$
densely defined in
![]() $L^{2}(\mathbb{R})$
, the set
$L^{2}(\mathbb{R})$
, the set
![]() $\operatorname{Spec}(h)$
is given by
$\operatorname{Spec}(h)$
is given by
![]() $\{n+1/2\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 1. From this, the spectral zeta function of
$\{n+1/2\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 1. From this, the spectral zeta function of
![]() $h$
is of the form
$h$
is of the form
where
![]() $\unicode[STIX]{x1D701}(s)$
denotes the Riemann zeta function. This defining series is absolutely convergent for
$\unicode[STIX]{x1D701}(s)$
denotes the Riemann zeta function. This defining series is absolutely convergent for
![]() $\operatorname{Re}(s)>1$
, and has a meromorphic continuation to the whole
$\operatorname{Re}(s)>1$
, and has a meromorphic continuation to the whole
![]() $s$
-plane. Furthermore, the only pole
$s$
-plane. Furthermore, the only pole
![]() $s=1$
of
$s=1$
of
![]() $\unicode[STIX]{x1D701}_{h}(s)$
is simple, and
$\unicode[STIX]{x1D701}_{h}(s)$
is simple, and
![]() $\unicode[STIX]{x1D701}_{h}(-2n)=0$
holds for all nonnegative integers
$\unicode[STIX]{x1D701}_{h}(-2n)=0$
holds for all nonnegative integers
![]() $n$
. The points
$n$
. The points
![]() $0,-2,-4,-6,\ldots$
are called trivial zeros of
$0,-2,-4,-6,\ldots$
are called trivial zeros of
![]() $\unicode[STIX]{x1D701}_{h}(s)$
. The spectral zeta function
$\unicode[STIX]{x1D701}_{h}(s)$
. The spectral zeta function
![]() $\unicode[STIX]{x1D701}_{A}(s)$
for an operator
$\unicode[STIX]{x1D701}_{A}(s)$
for an operator
![]() $A$
encodes information on
$A$
encodes information on
![]() $\operatorname{Spec}(A)$
in its analytic properties. For example, as seen in applications to the Weyl law for
$\operatorname{Spec}(A)$
in its analytic properties. For example, as seen in applications to the Weyl law for
![]() $A$
, some pole of
$A$
, some pole of
![]() $\unicode[STIX]{x1D701}_{A}(s)$
with real part maximal is related to an asymptotic behavior of the spectral counting function of
$\unicode[STIX]{x1D701}_{A}(s)$
with real part maximal is related to an asymptotic behavior of the spectral counting function of
![]() $A$
:
$A$
:
(cf. [Reference Aramaki1], [Reference Parmeggiani18, Section 6.4] and [Reference Shubin29, Section 14]). In a quite general setting, Robert [Reference Robert27] studied spectral zeta functions for pseudodifferential operators in
![]() $\mathbb{R}^{n}$
, and later his result was generalized by Aramaki [Reference Aramaki1] to some infinite-dimensional situations. As a remarkable example of spectral zeta functions of matrix-valued pseudodifferential operators, we should mention that Ichinose and Wakayama [Reference Ichinose and Wakayama8] investigated very quantitatively the spectral zeta function
$\mathbb{R}^{n}$
, and later his result was generalized by Aramaki [Reference Aramaki1] to some infinite-dimensional situations. As a remarkable example of spectral zeta functions of matrix-valued pseudodifferential operators, we should mention that Ichinose and Wakayama [Reference Ichinose and Wakayama8] investigated very quantitatively the spectral zeta function
![]() $\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
of the noncommutative harmonic oscillator
$\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
of the noncommutative harmonic oscillator
densely defined in
![]() $L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
with
$L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
with
![]() $\unicode[STIX]{x1D6FC}>0$
and
$\unicode[STIX]{x1D6FC}>0$
and
![]() $\unicode[STIX]{x1D6FD}>0$
such that
$\unicode[STIX]{x1D6FD}>0$
such that
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1$
. In [Reference Ichinose and Wakayama8], they gave a meromorphic continuation of
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1$
. In [Reference Ichinose and Wakayama8], they gave a meromorphic continuation of
![]() $\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
to the whole
$\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
to the whole
![]() $s$
-plane and established a formula of
$s$
-plane and established a formula of
![]() $\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
, which includes information on its poles and trivial zeros. By the formula,
$\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
, which includes information on its poles and trivial zeros. By the formula,
![]() $\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
has the only one pole
$\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
has the only one pole
![]() $s=1$
, which is simple, and the following asymptotic formula holds:
$s=1$
, which is simple, and the following asymptotic formula holds:
Later, the formula in [Reference Ichinose and Wakayama8, Main theorem] was extended by Parmeggiani [Reference Parmeggiani18] to the case where
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
is replaced with a general globally elliptic
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
is replaced with a general globally elliptic
![]() $N\times N$
self-adjoint regular partial differential system with polynomial coefficients (PPDSs) in
$N\times N$
self-adjoint regular partial differential system with polynomial coefficients (PPDSs) in
![]() $\mathbb{R}^{n}$
of order
$\mathbb{R}^{n}$
of order
![]() $2$
(cf. [Reference Parmeggiani18, Theorem 7.2.1]). For more details for
$2$
(cf. [Reference Parmeggiani18, Theorem 7.2.1]). For more details for
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
, see [Reference Parmeggiani19].
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
, see [Reference Parmeggiani19].
In this paper, we explore fine analysis of the Hurwitz-type spectral zeta function for the quantum Rabi model with Hamiltonian
![]() $H=H_{\text{Rabi}}$
, and give a meromorphic continuation to
$H=H_{\text{Rabi}}$
, and give a meromorphic continuation to
![]() $\mathbb{C}$
and an asymptotic behavior of spectral counting function
$\mathbb{C}$
and an asymptotic behavior of spectral counting function
![]() $N_{H}(T)$
of
$N_{H}(T)$
of
![]() $H$
. Here, the quantum Rabi model is a model describing an interaction of light and matter of a two-level atom coupled to a single quantized photon of the electromagnetic field (cf. [Reference Braak and Anderssen3]). The Hamiltonian for the quantum Rabi model, which is called the Rabi Hamiltonian, is given by
$H$
. Here, the quantum Rabi model is a model describing an interaction of light and matter of a two-level atom coupled to a single quantized photon of the electromagnetic field (cf. [Reference Braak and Anderssen3]). The Hamiltonian for the quantum Rabi model, which is called the Rabi Hamiltonian, is given by
densely defined in
![]() $L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
. Here
$L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
. Here
![]() $\hbar$
is the Dirac constant,
$\hbar$
is the Dirac constant,
![]() $a$
and
$a$
and
![]() $a^{\dagger }$
are the annihilation and creation operators for a Bosonic mode of frequency
$a^{\dagger }$
are the annihilation and creation operators for a Bosonic mode of frequency
![]() $\unicode[STIX]{x1D714}>0$
, respectively, the symbols
$\unicode[STIX]{x1D714}>0$
, respectively, the symbols
![]() $\unicode[STIX]{x1D70E}_{x}$
,
$\unicode[STIX]{x1D70E}_{x}$
,
![]() $\unicode[STIX]{x1D70E}_{y}$
, and
$\unicode[STIX]{x1D70E}_{y}$
, and
![]() $\unicode[STIX]{x1D70E}_{z}$
are the Pauli matrices for the two-level system,
$\unicode[STIX]{x1D70E}_{z}$
are the Pauli matrices for the two-level system,
![]() $2\unicode[STIX]{x1D6E5}>0$
is the difference of the two-level energies, and
$2\unicode[STIX]{x1D6E5}>0$
is the difference of the two-level energies, and
![]() $g>0$
is the coupling constant for atom and photon. In [Reference Rabi23] and [Reference Rabi24], Rabi introduced originally a semiclassical model, and Jaynes and Cummings [Reference Jaynes and Cummings9] fully quantized the Rabi model as
$g>0$
is the coupling constant for atom and photon. In [Reference Rabi23] and [Reference Rabi24], Rabi introduced originally a semiclassical model, and Jaynes and Cummings [Reference Jaynes and Cummings9] fully quantized the Rabi model as
![]() $H$
. It is known that every
$H$
. It is known that every
![]() $\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)$
is real and one of the three forms:
$\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)$
is real and one of the three forms:
-
(1)
 $\unicode[STIX]{x1D706}=x_{n}^{\pm }-g^{2}$
with multiplicity
$\unicode[STIX]{x1D706}=x_{n}^{\pm }-g^{2}$
with multiplicity
 $1$
(nondegenerate), where
$1$
(nondegenerate), where
 $\{x_{n}^{+}\}_{n=1}^{\infty }$
and
$\{x_{n}^{+}\}_{n=1}^{\infty }$
and
 $\{x_{n}^{-}\}_{n=1}^{\infty }$
, which are contained in
$\{x_{n}^{-}\}_{n=1}^{\infty }$
, which are contained in
 $\mathbb{C}-\mathbb{Z}_{{\geqslant}0}$
, are the zeros of
$\mathbb{C}-\mathbb{Z}_{{\geqslant}0}$
, are the zeros of
 $G_{+}(x)$
and of
$G_{+}(x)$
and of
 $G_{-}(x)$
, respectively;
$G_{-}(x)$
, respectively; -
(2)
 $\unicode[STIX]{x1D706}=n-g^{2}$
for some
$\unicode[STIX]{x1D706}=n-g^{2}$
for some
 $n\in \mathbb{Z}_{{\geqslant}0}$
with multiplicity
$n\in \mathbb{Z}_{{\geqslant}0}$
with multiplicity
 $1$
(nondegenerate);
$1$
(nondegenerate); -
(3)
 $\unicode[STIX]{x1D706}=n-g^{2}$
for some
$\unicode[STIX]{x1D706}=n-g^{2}$
for some
 $n\in \mathbb{Z}_{{\geqslant}1}$
with multiplicity
$n\in \mathbb{Z}_{{\geqslant}1}$
with multiplicity
 $2$
(doubly degenerate);
$2$
(doubly degenerate);
(cf. [Reference Braak2, Reference Braak and Anderssen3, Reference Kuś16, Reference Maciejewski, Przybylska and Stachowiak17]). Here
![]() $G_{\pm }(x)$
is a meromorphic function with at most simple poles at all
$G_{\pm }(x)$
is a meromorphic function with at most simple poles at all
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
, which Braak [Reference Braak2] gave as power series satisfying
$n\in \mathbb{Z}_{{\geqslant}0}$
, which Braak [Reference Braak2] gave as power series satisfying
![]() $\operatorname{Spec}(H)-\{n-g^{2}\mid n\in \mathbb{Z}_{{\geqslant}0}\}=\{y-g^{2}\mid y\in \mathbb{R},~G_{+}(y)G_{-}(y)=0\}$
by explicitly describing recurrence equations for the coefficients of
$\operatorname{Spec}(H)-\{n-g^{2}\mid n\in \mathbb{Z}_{{\geqslant}0}\}=\{y-g^{2}\mid y\in \mathbb{R},~G_{+}(y)G_{-}(y)=0\}$
by explicitly describing recurrence equations for the coefficients of
![]() $G_{\pm }(x)$
. The eigenvalues in case (1) are called the regular spectrum, and those in cases (2) and (3) are called the exceptional spectrum. We should mention that Parmeggiani and Wakayama in [Reference Parmeggiani and Wakayama20] and [Reference Parmeggiani and Wakayama21] described a part of the spectrum of the noncommutative harmonic oscillators
$G_{\pm }(x)$
. The eigenvalues in case (1) are called the regular spectrum, and those in cases (2) and (3) are called the exceptional spectrum. We should mention that Parmeggiani and Wakayama in [Reference Parmeggiani and Wakayama20] and [Reference Parmeggiani and Wakayama21] described a part of the spectrum of the noncommutative harmonic oscillators
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
with
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
with
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1$
, which is similar to Braak’s work recalled as above.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1$
, which is similar to Braak’s work recalled as above.
Several mathematicians have studied the Rabi Hamiltonian
![]() $H$
and contributed theoretically to the field of quantum optics. As recent works, Hirokawa and Hiroshima [Reference Hirokawa and Hiroshima7] proved that the ground state energy for
$H$
and contributed theoretically to the field of quantum optics. As recent works, Hirokawa and Hiroshima [Reference Hirokawa and Hiroshima7] proved that the ground state energy for
![]() $H$
is nondegenerate (i.e., the smallest eigenvalue of
$H$
is nondegenerate (i.e., the smallest eigenvalue of
![]() $H$
has multiplicity 1), and that the ground state energy for
$H$
has multiplicity 1), and that the ground state energy for
![]() $H$
has no crossing for all
$H$
has no crossing for all
![]() $g$
and
$g$
and
![]() $\unicode[STIX]{x1D6E5}$
. By a representation theoretic approach, Wakayama and Yamasaki [Reference Wakayama and Yamasaki33] captured the doubly degenerate exceptional spectrum of
$\unicode[STIX]{x1D6E5}$
. By a representation theoretic approach, Wakayama and Yamasaki [Reference Wakayama and Yamasaki33] captured the doubly degenerate exceptional spectrum of
![]() $H$
via finite-dimensional representations of
$H$
via finite-dimensional representations of
![]() $\mathfrak{s}\mathfrak{l}_{2}(\mathbb{R})$
. Furthermore, Wakayama [Reference Wakayama32] pioneered a new relation between the noncommutative harmonic oscillator
$\mathfrak{s}\mathfrak{l}_{2}(\mathbb{R})$
. Furthermore, Wakayama [Reference Wakayama32] pioneered a new relation between the noncommutative harmonic oscillator
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
and the Rabi Hamiltonian
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
and the Rabi Hamiltonian
![]() $H$
, through a confluence process by Heun’s picture. Nevertheless it seems difficult to capture finer properties of the spectrum of
$H$
, through a confluence process by Heun’s picture. Nevertheless it seems difficult to capture finer properties of the spectrum of
![]() $H$
.
$H$
.
1.1 Main results
In what follows, we consider the Hurwitz-type spectral zeta function of
![]() $H$
$H$
for
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
. Throughout this paper, we normalize
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
. Throughout this paper, we normalize
![]() $H$
so that
$H$
so that
![]() $\hbar =\unicode[STIX]{x1D714}=1$
without loss of generality and both
$\hbar =\unicode[STIX]{x1D714}=1$
without loss of generality and both
![]() $g$
and
$g$
and
![]() $\unicode[STIX]{x1D6E5}$
are supposed to be arbitrary nonnegative real numbers. For the mathematical definition of
$\unicode[STIX]{x1D6E5}$
are supposed to be arbitrary nonnegative real numbers. For the mathematical definition of
![]() $H$
, see Section 2.2. Then, the defining series converges absolutely for
$H$
, see Section 2.2. Then, the defining series converges absolutely for
![]() $\operatorname{Re}(s)>1$
(see Proposition 3.1). We give its meromorphic continuation as follows by using the method of the parametrix of the heat equation investigated in [Reference Ichinose and Wakayama8].
$\operatorname{Re}(s)>1$
(see Proposition 3.1). We give its meromorphic continuation as follows by using the method of the parametrix of the heat equation investigated in [Reference Ichinose and Wakayama8].
Theorem 1.1. For any
![]() $g\geqslant 0$
,
$g\geqslant 0$
,
![]() $\unicode[STIX]{x1D6E5}\geqslant 0$
, and
$\unicode[STIX]{x1D6E5}\geqslant 0$
, and
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, we have the following.
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, we have the following.
-
(1) There exists an explicitly computable sequence
 $\{C_{H,\unicode[STIX]{x1D70F}}(k)\}_{k\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that, for any
$\{C_{H,\unicode[STIX]{x1D70F}}(k)\}_{k\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that, for any
 $n\geqslant 2$
, where
$n\geqslant 2$
, where $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\left\{\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{k=0}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{s+k}+F_{H,n}(s;\unicode[STIX]{x1D70F})\right\}\!,\quad \operatorname{Re}(s)>1,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\left\{\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{k=0}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{s+k}+F_{H,n}(s;\unicode[STIX]{x1D70F})\right\}\!,\quad \operatorname{Re}(s)>1,\nonumber\end{eqnarray}$$
 $F_{H,n}(s;\unicode[STIX]{x1D70F})$
is a holomorphic function on
$F_{H,n}(s;\unicode[STIX]{x1D70F})$
is a holomorphic function on
 $\operatorname{Re}(s)>-n/2$
. In particular,
$\operatorname{Re}(s)>-n/2$
. In particular,
 $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
has a meromorphic continuation to
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
has a meromorphic continuation to
 $\mathbb{C}$
. Moreover, it is holomorphic on
$\mathbb{C}$
. Moreover, it is holomorphic on
 $\mathbb{C}$
except for the only one simple pole
$\mathbb{C}$
except for the only one simple pole
 $s=1$
with the residue
$s=1$
with the residue
 $\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=2$
.
$\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=2$
.
-
(2) We have
 $C_{H,\unicode[STIX]{x1D70F}}(k)\in \mathbb{Q}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
for any
$C_{H,\unicode[STIX]{x1D70F}}(k)\in \mathbb{Q}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
for any
 $k\in \mathbb{Z}_{{\geqslant}0}$
.
$k\in \mathbb{Z}_{{\geqslant}0}$
.
Theorem 1.1(1) solves Wakayama’s conjecture on a meromorphic continuation of
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
(see [Reference Wakayama and Nishii31, Section 3]), and is regarded as an analogue of [Reference Parmeggiani18, Theorem 7.2.1] and [Reference Ichinose and Wakayama8, Main theorem]. We remark that [Reference Parmeggiani18, Theorem 7.1.1], which is a special case of [Reference Robert27], cannot be applied to the Rabi Hamiltonian
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
(see [Reference Wakayama and Nishii31, Section 3]), and is regarded as an analogue of [Reference Parmeggiani18, Theorem 7.2.1] and [Reference Ichinose and Wakayama8, Main theorem]. We remark that [Reference Parmeggiani18, Theorem 7.1.1], which is a special case of [Reference Robert27], cannot be applied to the Rabi Hamiltonian
![]() $H$
since
$H$
since
![]() $H$
is not classical in the sense of [Reference Parmeggiani18, Definition 3.2.19] although the noncommutative harmonic oscillator
$H$
is not classical in the sense of [Reference Parmeggiani18, Definition 3.2.19] although the noncommutative harmonic oscillator
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
is classical. By a general result [Reference Robert27, Théorèmes (6.3) et (6.4)] by Robert, we can obtain a meromorphicity of
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
is classical. By a general result [Reference Robert27, Théorèmes (6.3) et (6.4)] by Robert, we can obtain a meromorphicity of
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
and its poles are contained in
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
and its poles are contained in
![]() $\{1\}\cup \{1/2-j\mid j\in \mathbb{Z}_{{\geqslant}0}\}$
. However, Robert’s method by the parametrix of the resolvent does not seem to work well in order to eliminate
$\{1\}\cup \{1/2-j\mid j\in \mathbb{Z}_{{\geqslant}0}\}$
. However, Robert’s method by the parametrix of the resolvent does not seem to work well in order to eliminate
![]() $s=1/2-j$
with
$s=1/2-j$
with
![]() $j\in \mathbb{Z}_{{\geqslant}0}$
from the possible poles.
$j\in \mathbb{Z}_{{\geqslant}0}$
from the possible poles.
As for Theorem 1.1(2), we introduce a generalization of Bernoulli polynomials as follows. By our proof of Theorem 1.1(1), we obtain that a polynomial
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)\in \mathbb{C}[g,\unicode[STIX]{x1D6E5},x]$
for every
$R_{k}(g,\unicode[STIX]{x1D6E5};x)\in \mathbb{C}[g,\unicode[STIX]{x1D6E5},x]$
for every
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
can be defined by the relation
$k\in \mathbb{Z}_{{\geqslant}1}$
can be defined by the relation
Then, Theorem 1.1(2) implies that
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)\in \mathbb{Q}[g^{2},\unicode[STIX]{x1D6E5}^{2},x]$
. If
$R_{k}(g,\unicode[STIX]{x1D6E5};x)\in \mathbb{Q}[g^{2},\unicode[STIX]{x1D6E5}^{2},x]$
. If
![]() $g=\unicode[STIX]{x1D6E5}=0$
, the polynomial
$g=\unicode[STIX]{x1D6E5}=0$
, the polynomial
![]() $R_{k}(0,0;x)$
coincides with
$R_{k}(0,0;x)$
coincides with
![]() $B_{k}(x)$
for every
$B_{k}(x)$
for every
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
, where
$k\in \mathbb{Z}_{{\geqslant}1}$
, where
![]() $B_{k}(x)$
is the
$B_{k}(x)$
is the
![]() $k$
th Bernoulli polynomial defined by
$k$
th Bernoulli polynomial defined by
Thus we call
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
the
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
the
![]() $k$
th Rabi–Bernoulli polynomial. As in the case of
$k$
th Rabi–Bernoulli polynomial. As in the case of
![]() $B_{k}(x)$
, the polynomial
$B_{k}(x)$
, the polynomial
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic, all the coefficients of
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic, all the coefficients of
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
are rational, and its degree with respect to
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
are rational, and its degree with respect to
![]() $x$
equals exactly
$x$
equals exactly
![]() $k$
(see Proposition 5.3). Although we can compute explicitly Rabi–Bernoulli polynomials by definition and integration, it seems difficult to give simple formulas of them. We might expect some number theoretic properties of quantum Rabi models, as Kimoto and Wakayama extracted from noncommutative harmonic oscillators
$k$
(see Proposition 5.3). Although we can compute explicitly Rabi–Bernoulli polynomials by definition and integration, it seems difficult to give simple formulas of them. We might expect some number theoretic properties of quantum Rabi models, as Kimoto and Wakayama extracted from noncommutative harmonic oscillators
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
via (higher) Apéry-like numbersFootnote
1
encoded in special values of
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
via (higher) Apéry-like numbersFootnote
1
encoded in special values of
![]() $\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
(cf. [Reference Kimoto10–Reference Kimoto and Wakayama15]).
$\unicode[STIX]{x1D701}_{Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}}(s)$
(cf. [Reference Kimoto10–Reference Kimoto and Wakayama15]).
Braak in [Reference Braak2] conjectured that the interval
![]() $[n-g^{2},n+1-g^{2}]$
for every
$[n-g^{2},n+1-g^{2}]$
for every
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
contains at most two eigenvalues of
$n\in \mathbb{Z}_{{\geqslant}0}$
contains at most two eigenvalues of
![]() $H$
, that the interval
$H$
, that the interval
![]() $[n,n+1]$
for every
$[n,n+1]$
for every
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
has at most two zeros of
$n\in \mathbb{Z}_{{\geqslant}0}$
has at most two zeros of
![]() $G_{+}(x)G_{-}(x)$
, that two intervals containing no zeros are not adjacent, and that two intervals containing two zeros are also not adjacent. As an application of Theorem 1.1, we have the Weyl law for
$G_{+}(x)G_{-}(x)$
, that two intervals containing no zeros are not adjacent, and that two intervals containing two zeros are also not adjacent. As an application of Theorem 1.1, we have the Weyl law for
![]() $H$
by using Tauberian theorem (cf. [Reference Aramaki1, Theorem 1.1] and [Reference Ichinose and Wakayama8, Corollary 2.6]).
$H$
by using Tauberian theorem (cf. [Reference Aramaki1, Theorem 1.1] and [Reference Ichinose and Wakayama8, Corollary 2.6]).
Corollary 1.2. We have
This corollary supports Braak’s conjecture.
Here is a remark on zeta regularized products. The zeta regularized product of
![]() $\operatorname{Spec}(A)$
for an operator
$\operatorname{Spec}(A)$
for an operator
![]() $A$
is defined by
$A$
is defined by
if
![]() $\unicode[STIX]{x1D701}_{A}(s)$
is analytically continued to a function holomorphic around
$\unicode[STIX]{x1D701}_{A}(s)$
is analytically continued to a function holomorphic around
![]() $s=0$
. The zeta regularized product of
$s=0$
. The zeta regularized product of
![]() $\operatorname{Spec}(A)$
is applied to the existence of an entire function whose zeros coincide with
$\operatorname{Spec}(A)$
is applied to the existence of an entire function whose zeros coincide with
![]() $\operatorname{Spec}(A)$
as a multiset, and plays a pivotal role as a functional determinant
$\operatorname{Spec}(A)$
as a multiset, and plays a pivotal role as a functional determinant ![]() (cf. [Reference Ray and Singer25], [Reference Ray and Singer26] and [Reference Voros30]). Wakayama [Reference Wakayama and Nishii31, Conjecture 1] conjectured that
(cf. [Reference Ray and Singer25], [Reference Ray and Singer26] and [Reference Voros30]). Wakayama [Reference Wakayama and Nishii31, Conjecture 1] conjectured that
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
would be meromorphic or holomorphic at
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
would be meromorphic or holomorphic at
![]() $s=0$
. Since
$s=0$
. Since
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is holomorphic at
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is holomorphic at
![]() $s=0$
by Theorem 1.1 (or [Reference Robert27, Théorème (6.4), a)]), we can actually define the zeta regularized product
$s=0$
by Theorem 1.1 (or [Reference Robert27, Théorème (6.4), a)]), we can actually define the zeta regularized product ![]() as an entire function by [Reference Quine, Heydari and Song22, Theorem 1]. A formula of
as an entire function by [Reference Quine, Heydari and Song22, Theorem 1]. A formula of ![]() using
using
![]() $F_{H,n}(s;\unicode[STIX]{x1D70F})$
is given in Proposition 5.2. The comparison of
$F_{H,n}(s;\unicode[STIX]{x1D70F})$
is given in Proposition 5.2. The comparison of ![]() with
with
![]() $G_{+}(z+g^{2})G_{-}(z+g^{2})$
may be an interesting problem (cf. [Reference Wakayama and Nishii31, Conjecture 1]).
$G_{+}(z+g^{2})G_{-}(z+g^{2})$
may be an interesting problem (cf. [Reference Wakayama and Nishii31, Conjecture 1]).
This paper is organized as follows. After fixing our notation, we explain the Rabi Hamiltonians
![]() $H$
defined for any
$H$
defined for any
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}\geqslant 0$
describing the quantum Rabi models in Section 2, referring mainly to [Reference Helffer6], [Reference Parmeggiani18] and [Reference Shubin29]. In the same section, a lower bound of
$\unicode[STIX]{x1D6E5}\geqslant 0$
describing the quantum Rabi models in Section 2, referring mainly to [Reference Helffer6], [Reference Parmeggiani18] and [Reference Shubin29]. In the same section, a lower bound of
![]() $\operatorname{Spec}(H)$
is given in Lemma 2.2, and the maximal domain of
$\operatorname{Spec}(H)$
is given in Lemma 2.2, and the maximal domain of
![]() $H$
is given as
$H$
is given as
![]() $B^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
, where
$B^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}$
, where
![]() $B^{2}(\mathbb{R})$
is a Shubin–Sobolev space originally introduced by Shubin [Reference Shubin29, Section 25] (the Russian version of [Reference Shubin29] was published in 1978). The convergence of the spectral zeta functions for the quantum Rabi models is discussed in Section 3. In the rest of Sections 3 and 4, we explore the method of the parametrix of the heat equation from [Reference Ichinose and Wakayama8], by which a meromorphic continuation of
$B^{2}(\mathbb{R})$
is a Shubin–Sobolev space originally introduced by Shubin [Reference Shubin29, Section 25] (the Russian version of [Reference Shubin29] was published in 1978). The convergence of the spectral zeta functions for the quantum Rabi models is discussed in Section 3. In the rest of Sections 3 and 4, we explore the method of the parametrix of the heat equation from [Reference Ichinose and Wakayama8], by which a meromorphic continuation of
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is given in Section 5. The method is a finer analysis of the trace
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is given in Section 5. The method is a finer analysis of the trace
![]() $\operatorname{Tr}K(t)$
of the heat operator
$\operatorname{Tr}K(t)$
of the heat operator
![]() $K(t)=e^{-t(H+\unicode[STIX]{x1D70F}I)}$
for any
$K(t)=e^{-t(H+\unicode[STIX]{x1D70F}I)}$
for any
![]() $t>0$
and sufficiently large
$t>0$
and sufficiently large
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
. In Section 3, the heat operator
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
. In Section 3, the heat operator
![]() $K(t)$
is decomposed into the finite sum of explicitly computable operators
$K(t)$
is decomposed into the finite sum of explicitly computable operators
![]() $K_{m}(t)$
over
$K_{m}(t)$
over
![]() $m=1,\ldots ,n$
and the residual operator
$m=1,\ldots ,n$
and the residual operator
![]() $R_{n+1}(t)$
(see (3.2)). In the same section,
$R_{n+1}(t)$
(see (3.2)). In the same section,
![]() $K_{1}(t)$
is made explicit and
$K_{1}(t)$
is made explicit and
![]() $\operatorname{Tr}R_{n+1}(t)$
is estimated. In Section 4, we give the asymptotic series expansion of
$\operatorname{Tr}R_{n+1}(t)$
is estimated. In Section 4, we give the asymptotic series expansion of
![]() $\operatorname{Tr}K_{m}(t)$
for
$\operatorname{Tr}K_{m}(t)$
for
![]() $m\geqslant 2$
as
$m\geqslant 2$
as
![]() $t\rightarrow +0$
in Theorem 4.1 with the aid of the asymptotic series of
$t\rightarrow +0$
in Theorem 4.1 with the aid of the asymptotic series of
![]() $e^{ixy/t}$
as
$e^{ixy/t}$
as
![]() $t\rightarrow +0$
in Lemma 4.2. The vanishing results of coefficients of the asymptotic series of
$t\rightarrow +0$
in Lemma 4.2. The vanishing results of coefficients of the asymptotic series of
![]() $\operatorname{Tr}K_{m}(t)$
, Lemmas 4.6–4.9, are key ingredients of proving Theorem 4.1. Finally, we prove Theorem 1.1(1) in Section 5. Theorem 1.1(2) is also proved in Section 5.2 by a rationality of
$\operatorname{Tr}K_{m}(t)$
, Lemmas 4.6–4.9, are key ingredients of proving Theorem 4.1. Finally, we prove Theorem 1.1(1) in Section 5. Theorem 1.1(2) is also proved in Section 5.2 by a rationality of
![]() $C_{H,\unicode[STIX]{x1D70F}}(k)$
(see Theorem 5.4). Lemmas 4.6–4.9 on vanishing results are effectively used to prove Theorem 1.1(2). The first, second, and third Rabi–Bernoulli polynomials
$C_{H,\unicode[STIX]{x1D70F}}(k)$
(see Theorem 5.4). Lemmas 4.6–4.9 on vanishing results are effectively used to prove Theorem 1.1(2). The first, second, and third Rabi–Bernoulli polynomials
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for
![]() $k\in \{1,2,3\}$
are explicitly computed in Section 6. For treating some matrix-valued exponential functions
$k\in \{1,2,3\}$
are explicitly computed in Section 6. For treating some matrix-valued exponential functions
![]() $t\mapsto \exp (tX)$
for some 2-by-2 square matrices
$t\mapsto \exp (tX)$
for some 2-by-2 square matrices
![]() $X$
, the commutativity of two matrices
$X$
, the commutativity of two matrices
![]() $[\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!]$
and
$[\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!]$
and
![]() $[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
matches our computation from Sections 3–5, while such a treatment is difficult in the case of the noncommutative harmonic oscillator
$[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
matches our computation from Sections 3–5, while such a treatment is difficult in the case of the noncommutative harmonic oscillator
![]() $Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
[Reference Ichinose and Wakayama8], which is described by noncommutative matrices
$Q_{(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}$
[Reference Ichinose and Wakayama8], which is described by noncommutative matrices
![]() $[\!\begin{smallmatrix}\unicode[STIX]{x1D6FC} & 0\\ 0 & \unicode[STIX]{x1D6FD}\end{smallmatrix}\!]$
and
$[\!\begin{smallmatrix}\unicode[STIX]{x1D6FC} & 0\\ 0 & \unicode[STIX]{x1D6FD}\end{smallmatrix}\!]$
and
![]() $[\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!]$
. However, difficulty in the case of the quantum Rabi models seems to be inherent in the simultaneous use of three matrices
$[\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!]$
. However, difficulty in the case of the quantum Rabi models seems to be inherent in the simultaneous use of three matrices
![]() $[\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!]$
,
$[\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!]$
,
![]() $[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
, and
$[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
, and
![]() $[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
, among which
$[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
, among which
![]() $[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
and
$[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
and
![]() $[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
are noncommutative.
$[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
are noncommutative.
2 Preliminaries
2.1 Notation
For any
![]() $a\in \mathbb{Z}$
, let
$a\in \mathbb{Z}$
, let
![]() $\mathbb{Z}_{{\geqslant}a}$
denote the set of all
$\mathbb{Z}_{{\geqslant}a}$
denote the set of all
![]() $n\in \mathbb{Z}$
such that
$n\in \mathbb{Z}$
such that
![]() $n\geqslant a$
. For complex-valued functions
$n\geqslant a$
. For complex-valued functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
on a set
$f_{2}$
on a set
![]() $X$
, we write
$X$
, we write
![]() $f_{1}(t)={\mathcal{O}}(f_{2}(t))$
if there exists a constant
$f_{1}(t)={\mathcal{O}}(f_{2}(t))$
if there exists a constant
![]() $C>0$
such that
$C>0$
such that
![]() $|f_{1}(t)|\leqslant C|f_{2}(t)|$
for all
$|f_{1}(t)|\leqslant C|f_{2}(t)|$
for all
![]() $t\in X$
. We write
$t\in X$
. We write
![]() $f_{1}(t)\asymp f_{2}(t)$
if both
$f_{1}(t)\asymp f_{2}(t)$
if both
![]() $f_{1}(t)={\mathcal{O}}(f_{2}(t))$
and
$f_{1}(t)={\mathcal{O}}(f_{2}(t))$
and
![]() $f_{2}(t)={\mathcal{O}}(f_{1}(t))$
hold. Furthermore, if
$f_{2}(t)={\mathcal{O}}(f_{1}(t))$
hold. Furthermore, if
![]() $X=\{t\in \mathbb{R}\mid t>0\}$
, we write
$X=\{t\in \mathbb{R}\mid t>0\}$
, we write
![]() $f_{1}(t)\sim f_{2}(t)(t\rightarrow \infty )$
for
$f_{1}(t)\sim f_{2}(t)(t\rightarrow \infty )$
for
![]() $\lim _{t\rightarrow \infty }f_{1}(t)/f_{2}(t)=1$
. We also write
$\lim _{t\rightarrow \infty }f_{1}(t)/f_{2}(t)=1$
. We also write
if there exists a positive constant
![]() $C_{N}$
for every
$C_{N}$
for every
![]() $N\in \mathbb{Z}_{{\geqslant}0}$
such that
$N\in \mathbb{Z}_{{\geqslant}0}$
such that
Let
![]() ${\mathcal{S}}(\mathbb{R})$
be the Schwartz space on
${\mathcal{S}}(\mathbb{R})$
be the Schwartz space on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $\unicode[STIX]{x1D6FF}(x-a):{\mathcal{S}}(\mathbb{R})\rightarrow \mathbb{C}$
the Dirac delta distribution supported at
$\unicode[STIX]{x1D6FF}(x-a):{\mathcal{S}}(\mathbb{R})\rightarrow \mathbb{C}$
the Dirac delta distribution supported at
![]() $a\in \mathbb{R}$
. By abuse of notation,
$a\in \mathbb{R}$
. By abuse of notation,
![]() $\unicode[STIX]{x1D6FF}(x-a)$
is used as if it is an integrand.
$\unicode[STIX]{x1D6FF}(x-a)$
is used as if it is an integrand.
For a
![]() $\mathbb{C}$
-Hilbert space
$\mathbb{C}$
-Hilbert space
![]() $V$
and a densely defined linear operator
$V$
and a densely defined linear operator
![]() $A:V\rightarrow V$
, let
$A:V\rightarrow V$
, let
![]() $\operatorname{Spec}(A)$
denote the multiset of eigenvalues of
$\operatorname{Spec}(A)$
denote the multiset of eigenvalues of
![]() $A$
in
$A$
in
![]() $\mathbb{C}$
. Suppose that
$\mathbb{C}$
. Suppose that
![]() $\operatorname{Spec}(A)$
is discrete. Then, the norms
$\operatorname{Spec}(A)$
is discrete. Then, the norms
![]() $\Vert A\Vert _{p}$
on
$\Vert A\Vert _{p}$
on
![]() $V$
for
$V$
for
![]() $p\in \{1,2\}$
are defined by
$p\in \{1,2\}$
are defined by
as long as they make sense. For any
![]() $N\in \{1,2\}$
, we set
$N\in \{1,2\}$
, we set
![]() $L^{2}(\mathbb{R};\mathbb{C}^{N})=L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{N}$
. The natural
$L^{2}(\mathbb{R};\mathbb{C}^{N})=L^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{N}$
. The natural
![]() $L^{2}$
-inner product on
$L^{2}$
-inner product on
![]() $L^{2}(\mathbb{R})$
is denoted by
$L^{2}(\mathbb{R})$
is denoted by
![]() $\langle \cdot ,\cdot \rangle _{L^{2}}$
. Then, we endow
$\langle \cdot ,\cdot \rangle _{L^{2}}$
. Then, we endow
![]() $L^{2}(\mathbb{R};\mathbb{C}^{2})$
with the
$L^{2}(\mathbb{R};\mathbb{C}^{2})$
with the
![]() $L^{2}$
-inner product
$L^{2}$
-inner product
![]() $\langle \cdot ,\cdot \rangle$
defined by
$\langle \cdot ,\cdot \rangle$
defined by
for any
![]() $u_{1},u_{2},u_{1}^{\prime },u_{2}^{\prime }\in L^{2}(\mathbb{R})$
. We note that the Schwartz space
$u_{1},u_{2},u_{1}^{\prime },u_{2}^{\prime }\in L^{2}(\mathbb{R})$
. We note that the Schwartz space
![]() ${\mathcal{S}}(\mathbb{R};\mathbb{C}^{N})={\mathcal{S}}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{N}$
on
${\mathcal{S}}(\mathbb{R};\mathbb{C}^{N})={\mathcal{S}}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{N}$
on
![]() $\mathbb{R}$
is densely embedded in
$\mathbb{R}$
is densely embedded in
![]() $L^{2}(\mathbb{R};\mathbb{C}^{N})$
for any
$L^{2}(\mathbb{R};\mathbb{C}^{N})$
for any
![]() $N\in \{1,2\}$
. If
$N\in \{1,2\}$
. If
![]() $A:L^{2}(\mathbb{R};\mathbb{C}^{N})\rightarrow L^{2}(\mathbb{R};\mathbb{C}^{N})$
for
$A:L^{2}(\mathbb{R};\mathbb{C}^{N})\rightarrow L^{2}(\mathbb{R};\mathbb{C}^{N})$
for
![]() $N\in \{1,2\}$
is a densely defined differential operator, then a dense domain of
$N\in \{1,2\}$
is a densely defined differential operator, then a dense domain of
![]() $A$
is supposed to be the maximal domain
$A$
is supposed to be the maximal domain
![]() ${\mathcal{D}}(A)$
defined by
${\mathcal{D}}(A)$
defined by
where
![]() $Au$
is the derivative of
$Au$
is the derivative of
![]() $u$
as a tempered distribution on
$u$
as a tempered distribution on
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
2.2 Quantum Rabi models
Throughout this paper, we use the following 2-by-2 complex matrices
We note the relations
![]() $IW=WI$
,
$IW=WI$
,
![]() $IL=LI$
, and
$IL=LI$
, and
![]() $LW=-WL$
.
$LW=-WL$
.
For real numbers
![]() $\hbar >0$
,
$\hbar >0$
,
![]() $\unicode[STIX]{x1D714}>0$
,
$\unicode[STIX]{x1D714}>0$
,
![]() $g\geqslant 0$
, and
$g\geqslant 0$
, and
![]() $\unicode[STIX]{x1D6E5}\geqslant 0$
, let us define the Rabi Hamiltonian
$\unicode[STIX]{x1D6E5}\geqslant 0$
, let us define the Rabi Hamiltonian
![]() $H$
densely defined in
$H$
densely defined in
![]() $L^{2}(\mathbb{R};\mathbb{C}^{2})$
by
$L^{2}(\mathbb{R};\mathbb{C}^{2})$
by
where
 $$\begin{eqnarray}\displaystyle a=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\hbar }}x+\sqrt{\frac{\hbar }{\unicode[STIX]{x1D714}}}\unicode[STIX]{x2202}_{x}\right), & & \displaystyle \nonumber\\ \displaystyle a^{\dagger }=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\hbar }}x-\sqrt{\frac{\hbar }{\unicode[STIX]{x1D714}}}\unicode[STIX]{x2202}_{x}\right), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\hbar }}x+\sqrt{\frac{\hbar }{\unicode[STIX]{x1D714}}}\unicode[STIX]{x2202}_{x}\right), & & \displaystyle \nonumber\\ \displaystyle a^{\dagger }=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\hbar }}x-\sqrt{\frac{\hbar }{\unicode[STIX]{x1D714}}}\unicode[STIX]{x2202}_{x}\right), & & \displaystyle \nonumber\end{eqnarray}$$
![]() $\unicode[STIX]{x1D70E}_{z}=[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
and
$\unicode[STIX]{x1D70E}_{z}=[\!\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix}\!]$
and
![]() $\unicode[STIX]{x1D70E}_{x}=[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
. Throughout this paper, we normalize
$\unicode[STIX]{x1D70E}_{x}=[\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!]$
. Throughout this paper, we normalize
![]() $H$
so that
$H$
so that
![]() $\hbar =\unicode[STIX]{x1D714}=1$
without loss of generality, and use the following expression:
$\hbar =\unicode[STIX]{x1D714}=1$
without loss of generality, and use the following expression:
which is the Weyl quantization of
Then the operator
![]() $H:L^{2}(\mathbb{R};\mathbb{C}^{2})\rightarrow L^{2}(\mathbb{R};\mathbb{C}^{2})$
is unbounded, closed, and symmetric (cf. [Reference Parmeggiani18, pp. 8–9]). Besides,
$H:L^{2}(\mathbb{R};\mathbb{C}^{2})\rightarrow L^{2}(\mathbb{R};\mathbb{C}^{2})$
is unbounded, closed, and symmetric (cf. [Reference Parmeggiani18, pp. 8–9]). Besides,
![]() $H$
is a global pseudodifferential operator of order 2 and elliptic in the sense of [Reference Parmeggiani18, Definition 3.2.19], that is,
$H$
is a global pseudodifferential operator of order 2 and elliptic in the sense of [Reference Parmeggiani18, Definition 3.2.19], that is,
![]() $|\text{det}\,H(x,\unicode[STIX]{x1D709})|\sim \sqrt{1+x^{2}+\unicode[STIX]{x1D709}^{2}}^{4},(x^{2}+\unicode[STIX]{x1D709}^{2}\rightarrow \infty )$
. We remark that
$|\text{det}\,H(x,\unicode[STIX]{x1D709})|\sim \sqrt{1+x^{2}+\unicode[STIX]{x1D709}^{2}}^{4},(x^{2}+\unicode[STIX]{x1D709}^{2}\rightarrow \infty )$
. We remark that
![]() $H$
is not classical but semiregular classical in the sense of [Reference Parmeggiani18, Definition 3.2.19 and Remark 3.2.4], and that
$H$
is not classical but semiregular classical in the sense of [Reference Parmeggiani18, Definition 3.2.19 and Remark 3.2.4], and that
![]() $H$
is actually classical in the sense of [Reference Helffer6, Définition 1.5.1]. Here, when we use “classical” in the sense of [Reference Helffer6, Définition 1.5.1], we need to generalize notions for scalar-valued pseudodifferential operators in [Reference Helffer6, Chapitre 1] to matrix-valued ones. However, this procedure is easy to perform by referring to [Reference Parmeggiani18, Chapter 3].
$H$
is actually classical in the sense of [Reference Helffer6, Définition 1.5.1]. Here, when we use “classical” in the sense of [Reference Helffer6, Définition 1.5.1], we need to generalize notions for scalar-valued pseudodifferential operators in [Reference Helffer6, Chapitre 1] to matrix-valued ones. However, this procedure is easy to perform by referring to [Reference Parmeggiani18, Chapter 3].
Proposition 2.1. The operator
![]() $H$
is self-adjoint.
$H$
is self-adjoint.
Proof. Since
![]() $H$
is formally self-adjoint, the assertion follows from [Reference Parmeggiani18, Proposition 3.3.10].◻
$H$
is formally self-adjoint, the assertion follows from [Reference Parmeggiani18, Proposition 3.3.10].◻
Proposition 2.2. All eigenvalues
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $H$
satisfy
$H$
satisfy
![]() $\unicode[STIX]{x1D706}\geqslant -g^{2}-\unicode[STIX]{x1D6E5}$
. In particular, for any
$\unicode[STIX]{x1D706}\geqslant -g^{2}-\unicode[STIX]{x1D6E5}$
. In particular, for any
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, the operator
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, the operator
![]() $H+\unicode[STIX]{x1D70F}I$
is positive.
$H+\unicode[STIX]{x1D70F}I$
is positive.
Proof. First, we see
for any
![]() $v\in {\mathcal{S}}(\mathbb{R})$
by the proof of [Reference Parmeggiani18, Theorem 2.2.1].
$v\in {\mathcal{S}}(\mathbb{R})$
by the proof of [Reference Parmeggiani18, Theorem 2.2.1].
Let us take any
![]() $\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)$
. Then
$\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)$
. Then
![]() $\unicode[STIX]{x1D706}$
is real by the self-adjointness of
$\unicode[STIX]{x1D706}$
is real by the self-adjointness of
![]() $H$
. Set
$H$
. Set
![]() $H^{\prime }=UHU^{-1}$
with
$H^{\prime }=UHU^{-1}$
with
 $$\begin{eqnarray}U=\left[\begin{array}{@{}cc@{}}\displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{2}}\\ -\displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{2}}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}U=\left[\begin{array}{@{}cc@{}}\displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{2}}\\ -\displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{2}}\end{array}\right].\end{eqnarray}$$
Then,
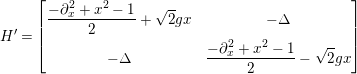 $$\begin{eqnarray}\displaystyle H^{\prime }=\left[\begin{array}{@{}cc@{}}\displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+x^{2}-1}{2}+\sqrt{2}gx & -\unicode[STIX]{x1D6E5}\\ -\unicode[STIX]{x1D6E5} & \displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+x^{2}-1}{2}-\sqrt{2}gx\end{array}\right] & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{\prime }=\left[\begin{array}{@{}cc@{}}\displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+x^{2}-1}{2}+\sqrt{2}gx & -\unicode[STIX]{x1D6E5}\\ -\unicode[STIX]{x1D6E5} & \displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+x^{2}-1}{2}-\sqrt{2}gx\end{array}\right] & & \displaystyle\end{eqnarray}$$
holds by noting
![]() $ULU^{-1}=-W$
and
$ULU^{-1}=-W$
and
![]() $UWU^{-1}=L$
(cf. [Reference Hirokawa and Hiroshima7, (3.1)]). Since
$UWU^{-1}=L$
(cf. [Reference Hirokawa and Hiroshima7, (3.1)]). Since
![]() $\operatorname{Spec}(H)$
coincides with
$\operatorname{Spec}(H)$
coincides with
![]() $\operatorname{Spec}(H^{\prime })$
as a multiset,
$\operatorname{Spec}(H^{\prime })$
as a multiset,
![]() $\unicode[STIX]{x1D706}$
is contained in
$\unicode[STIX]{x1D706}$
is contained in
![]() $\operatorname{Spec}(H^{\prime })$
. Put
$\operatorname{Spec}(H^{\prime })$
. Put
Let
![]() $u=^{t}(u_{1},u_{2})$
be a fixed eigenvector with
$u=^{t}(u_{1},u_{2})$
be a fixed eigenvector with
![]() $H^{\prime }u=\unicode[STIX]{x1D706}u$
. We note that
$H^{\prime }u=\unicode[STIX]{x1D706}u$
. We note that
![]() $u$
is taken as an element of
$u$
is taken as an element of
![]() ${\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
by [Reference Helffer6, (1.9.2)]. By virtue of the inequality
${\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
by [Reference Helffer6, (1.9.2)]. By virtue of the inequality
![]() $\langle D_{\pm }u,u\rangle \geqslant -g^{2}\langle u,u\rangle$
by (2.2), a direct computation gives us
$\langle D_{\pm }u,u\rangle \geqslant -g^{2}\langle u,u\rangle$
by (2.2), a direct computation gives us
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}\langle u,u\rangle =\left\langle \left[\begin{array}{@{}cc@{}}D_{+} & -\unicode[STIX]{x1D6E5}\\ -\unicode[STIX]{x1D6E5} & D_{-}\end{array}\right]u,u\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\langle D_{+}u_{1},u_{1}\rangle _{L^{2}}+\langle D_{-}u_{2},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}\langle u_{1},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}\langle u_{2},u_{1}\rangle _{L^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant -g^{2}\langle u_{1},u_{1}\rangle _{L^{2}}-g^{2}\langle u_{2},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}(\Vert u_{1}+u_{2}\Vert _{L^{2}}^{2}-\Vert u_{1}\Vert _{L^{2}}^{2}-\Vert u_{2}\Vert _{L^{2}}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant -g^{2}(\Vert u_{1}\Vert _{L^{2}}^{2}+\Vert u_{2}\Vert _{L^{2}}^{2})-\unicode[STIX]{x1D6E5}(\Vert u_{1}\Vert _{L^{2}}^{2}+\Vert u_{2}\Vert _{L^{2}}^{2})=(-g^{2}-\unicode[STIX]{x1D6E5})\langle u,u\rangle ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}\langle u,u\rangle =\left\langle \left[\begin{array}{@{}cc@{}}D_{+} & -\unicode[STIX]{x1D6E5}\\ -\unicode[STIX]{x1D6E5} & D_{-}\end{array}\right]u,u\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\langle D_{+}u_{1},u_{1}\rangle _{L^{2}}+\langle D_{-}u_{2},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}\langle u_{1},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}\langle u_{2},u_{1}\rangle _{L^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant -g^{2}\langle u_{1},u_{1}\rangle _{L^{2}}-g^{2}\langle u_{2},u_{2}\rangle _{L^{2}}-\unicode[STIX]{x1D6E5}(\Vert u_{1}+u_{2}\Vert _{L^{2}}^{2}-\Vert u_{1}\Vert _{L^{2}}^{2}-\Vert u_{2}\Vert _{L^{2}}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant -g^{2}(\Vert u_{1}\Vert _{L^{2}}^{2}+\Vert u_{2}\Vert _{L^{2}}^{2})-\unicode[STIX]{x1D6E5}(\Vert u_{1}\Vert _{L^{2}}^{2}+\Vert u_{2}\Vert _{L^{2}}^{2})=(-g^{2}-\unicode[STIX]{x1D6E5})\langle u,u\rangle ,\nonumber\end{eqnarray}$$
where
![]() $||\cdot ||_{L^{2}}$
is the
$||\cdot ||_{L^{2}}$
is the
![]() $L^{2}$
-norm on
$L^{2}$
-norm on
![]() $L^{2}(\mathbb{R})$
induced from
$L^{2}(\mathbb{R})$
induced from
![]() $\langle \cdot ,\cdot \rangle _{L^{2}}$
. This completes the proof.◻
$\langle \cdot ,\cdot \rangle _{L^{2}}$
. This completes the proof.◻
Set
![]() $\unicode[STIX]{x1D6EC}^{2}=1+x^{2}-\unicode[STIX]{x2202}_{x}^{2}$
and
$\unicode[STIX]{x1D6EC}^{2}=1+x^{2}-\unicode[STIX]{x2202}_{x}^{2}$
and
![]() $B^{2}(\mathbb{R})=\{u\in {\mathcal{S}}^{\prime }(\mathbb{R})\mid \unicode[STIX]{x1D6EC}^{2}u\in L^{2}(\mathbb{R})\}$
, where
$B^{2}(\mathbb{R})=\{u\in {\mathcal{S}}^{\prime }(\mathbb{R})\mid \unicode[STIX]{x1D6EC}^{2}u\in L^{2}(\mathbb{R})\}$
, where
![]() ${\mathcal{S}}^{\prime }(\mathbb{R})$
denotes the space of tempered distributions on
${\mathcal{S}}^{\prime }(\mathbb{R})$
denotes the space of tempered distributions on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $\unicode[STIX]{x1D6EC}^{2}u$
is the differential of
$\unicode[STIX]{x1D6EC}^{2}u$
is the differential of
![]() $u$
as a tempered distribution. Then
$u$
as a tempered distribution. Then
![]() $B^{2}(\mathbb{R})$
is called a Shubin–Sobolev space (cf. [Reference Shubin29, Section 25]). The Shubin–Sobolev space
$B^{2}(\mathbb{R})$
is called a Shubin–Sobolev space (cf. [Reference Shubin29, Section 25]). The Shubin–Sobolev space
![]() $B^{2}(\mathbb{R})$
contains
$B^{2}(\mathbb{R})$
contains
![]() ${\mathcal{S}}(\mathbb{R})$
obviously and has a Hilbert space structure with inner product
${\mathcal{S}}(\mathbb{R})$
obviously and has a Hilbert space structure with inner product
![]() $(u_{1},u_{2})_{B^{2}}=(\unicode[STIX]{x1D6EC}^{2}u_{1},\unicode[STIX]{x1D6EC}^{2}u_{2})_{L^{2}}$
for any
$(u_{1},u_{2})_{B^{2}}=(\unicode[STIX]{x1D6EC}^{2}u_{1},\unicode[STIX]{x1D6EC}^{2}u_{2})_{L^{2}}$
for any
![]() $u_{1},u_{2}\in B^{2}(\mathbb{R})$
. The space
$u_{1},u_{2}\in B^{2}(\mathbb{R})$
. The space
![]() $B^{2}(\mathbb{R})$
is dense and compactly embedded in
$B^{2}(\mathbb{R})$
is dense and compactly embedded in
![]() $L^{2}(\mathbb{R})$
by [Reference Shubin29, Proposition 25.4] (see also [Reference Helffer6, Proposition 1.6.11] and [Reference Parmeggiani18, Proposition 3.2.26]).
$L^{2}(\mathbb{R})$
by [Reference Shubin29, Proposition 25.4] (see also [Reference Helffer6, Proposition 1.6.11] and [Reference Parmeggiani18, Proposition 3.2.26]).
Proposition 2.3. We have
![]() ${\mathcal{D}}(H)=B^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}.$
${\mathcal{D}}(H)=B^{2}(\mathbb{R})\otimes _{\mathbb{C}}\mathbb{C}^{2}.$
Proof. As we see that
![]() $H$
is a globally elliptic pseudodifferential operator of order 2 and that
$H$
is a globally elliptic pseudodifferential operator of order 2 and that
![]() $H$
is classical in the sense of [Reference Helffer6, Définition 1.5.1], we obtain the assertion by [Reference Helffer6, Théorème 1.6.4] (see also [Reference Parmeggiani18, Lemma 3.3.9]).◻
$H$
is classical in the sense of [Reference Helffer6, Définition 1.5.1], we obtain the assertion by [Reference Helffer6, Théorème 1.6.4] (see also [Reference Parmeggiani18, Lemma 3.3.9]).◻
Remark.
By Proposition 2.3, the operator
![]() $H$
has a compact resolvent, and hence the spectrum of
$H$
has a compact resolvent, and hence the spectrum of
![]() $H$
coincides with the set
$H$
coincides with the set
![]() $\operatorname{Spec}(H)$
of the eigenvalues of
$\operatorname{Spec}(H)$
of the eigenvalues of
![]() $H$
as a multiset, that is, the continuous and the residual spectra of
$H$
as a multiset, that is, the continuous and the residual spectra of
![]() $H$
are empty (cf. [Reference Schmüdgen28, Proposition 2.11] or [Reference Shubin29, Theorem 26.3]). In particular,
$H$
are empty (cf. [Reference Schmüdgen28, Proposition 2.11] or [Reference Shubin29, Theorem 26.3]). In particular,
![]() $\operatorname{Spec}(H)$
is discrete. Such a discreteness also follows from the location of zeros of
$\operatorname{Spec}(H)$
is discrete. Such a discreteness also follows from the location of zeros of
![]() $G_{+}(x)G_{-}(x)$
constructed in [Reference Braak2].
$G_{+}(x)G_{-}(x)$
constructed in [Reference Braak2].
Lemma 2.4. Let
![]() $\unicode[STIX]{x1D70F}$
be a real number such that
$\unicode[STIX]{x1D70F}$
be a real number such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
and let
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
and let
![]() $0<\unicode[STIX]{x1D706}_{1}^{\prime }\leqslant \unicode[STIX]{x1D706}_{2}^{\prime }\leqslant \unicode[STIX]{x1D706}_{3}^{\prime }\leqslant \cdots \leqslant \unicode[STIX]{x1D706}_{n}^{\prime }\leqslant \cdots \,$
be the sequence of all eigenvalues of
$0<\unicode[STIX]{x1D706}_{1}^{\prime }\leqslant \unicode[STIX]{x1D706}_{2}^{\prime }\leqslant \unicode[STIX]{x1D706}_{3}^{\prime }\leqslant \cdots \leqslant \unicode[STIX]{x1D706}_{n}^{\prime }\leqslant \cdots \,$
be the sequence of all eigenvalues of
![]() $H+\unicode[STIX]{x1D70F}I$
. Then, we have
$H+\unicode[STIX]{x1D70F}I$
. Then, we have
![]() $\unicode[STIX]{x1D706}_{n}^{\prime }\asymp n$
.
$\unicode[STIX]{x1D706}_{n}^{\prime }\asymp n$
.
Proof. Let
![]() $H^{\prime }$
denote the Hamiltonian given by (2.3). By
$H^{\prime }$
denote the Hamiltonian given by (2.3). By
![]() $\operatorname{Spec}(H)=\operatorname{Spec}(H^{\prime })$
as a multiset, we may consider
$\operatorname{Spec}(H)=\operatorname{Spec}(H^{\prime })$
as a multiset, we may consider
![]() $H^{\prime }$
instead of
$H^{\prime }$
instead of
![]() $H$
. Put
$H$
. Put
as an operator in
![]() $L^{2}(\mathbb{R};\mathbb{C}^{2})$
whose domain is
$L^{2}(\mathbb{R};\mathbb{C}^{2})$
whose domain is
![]() ${\mathcal{D}}(H^{\prime })$
. Then,
${\mathcal{D}}(H^{\prime })$
. Then,
 $$\begin{eqnarray}B=\!\left[\begin{array}{@{}cc@{}}\displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+(x+\sqrt{2}g)^{2}}{2}-1/2-g^{2}+\unicode[STIX]{x1D70F} & 0\\ 0 & \displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+(x-\sqrt{2}g)^{2}}{2}-1/2-g^{2}+\unicode[STIX]{x1D70F}\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}B=\!\left[\begin{array}{@{}cc@{}}\displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+(x+\sqrt{2}g)^{2}}{2}-1/2-g^{2}+\unicode[STIX]{x1D70F} & 0\\ 0 & \displaystyle \frac{-\unicode[STIX]{x2202}_{x}^{2}+(x-\sqrt{2}g)^{2}}{2}-1/2-g^{2}+\unicode[STIX]{x1D70F}\end{array}\right]\end{eqnarray}$$
is a positive self-adjoint operator and its
![]() $n$
th eigenvalue
$n$
th eigenvalue
![]() $\unicode[STIX]{x1D706}_{n}(B)$
satisfies
$\unicode[STIX]{x1D706}_{n}(B)$
satisfies
![]() $\unicode[STIX]{x1D706}_{n}(B)\asymp n$
as
$\unicode[STIX]{x1D706}_{n}(B)\asymp n$
as
![]() $n\rightarrow \infty$
. Since the canonical injection
$n\rightarrow \infty$
. Since the canonical injection
![]() ${\mathcal{D}}(H^{\prime })={\mathcal{D}}(H){\hookrightarrow}L^{2}(\mathbb{R};\mathbb{C}^{2})$
is compact by Proposition 2.3, both
${\mathcal{D}}(H^{\prime })={\mathcal{D}}(H){\hookrightarrow}L^{2}(\mathbb{R};\mathbb{C}^{2})$
is compact by Proposition 2.3, both
![]() $H^{\prime }$
and
$H^{\prime }$
and
![]() $B$
have compact resolvents. By
$B$
have compact resolvents. By
![]() $H^{\prime }=B-\unicode[STIX]{x1D6E5}W$
, we easily have
$H^{\prime }=B-\unicode[STIX]{x1D6E5}W$
, we easily have
for all
![]() $u\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
, where
$u\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
, where
![]() $||\cdot ||$
is the
$||\cdot ||$
is the
![]() $L^{2}$
-norm on
$L^{2}$
-norm on
![]() $L^{2}(\mathbb{R};\mathbb{C}^{2})$
induced from
$L^{2}(\mathbb{R};\mathbb{C}^{2})$
induced from
![]() $\langle \cdot ,\cdot \rangle$
. Similarly we have also
$\langle \cdot ,\cdot \rangle$
. Similarly we have also
![]() $\Vert Bu\Vert ^{2}\leqslant 2(1+\unicode[STIX]{x1D6E5}^{2})(\Vert H^{\prime }u\Vert ^{2}+\Vert u\Vert ^{2})$
for all
$\Vert Bu\Vert ^{2}\leqslant 2(1+\unicode[STIX]{x1D6E5}^{2})(\Vert H^{\prime }u\Vert ^{2}+\Vert u\Vert ^{2})$
for all
![]() $u\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
. Therefore, by applying [Reference Parmeggiani18, Proposition 4.2.2] to
$u\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
. Therefore, by applying [Reference Parmeggiani18, Proposition 4.2.2] to
![]() $H^{\prime }$
and
$H^{\prime }$
and
![]() $B$
, we obtain the desired assertion.◻
$B$
, we obtain the desired assertion.◻
3 Spectral zeta functions
For any
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
, the Hurwitz-type spectral zeta function of the Rabi Hamiltonian
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
, the Hurwitz-type spectral zeta function of the Rabi Hamiltonian
![]() $H$
is given as the formal series
$H$
is given as the formal series
We check the convergence for some suitable choices of
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $s$
. The following is a consequence from Lemma 2.4.
$s$
. The following is a consequence from Lemma 2.4.
Proposition 3.1. For any fixed
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}-\operatorname{Spec}(-H)$
, the series
$\unicode[STIX]{x1D70F}\in \mathbb{C}-\operatorname{Spec}(-H)$
, the series
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
converges absolutely for
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
converges absolutely for
![]() $\operatorname{Re}(s)>1$
. Furthermore, the series
$\operatorname{Re}(s)>1$
. Furthermore, the series
![]() $\unicode[STIX]{x1D701}(1;\unicode[STIX]{x1D70F})$
is divergent.
$\unicode[STIX]{x1D701}(1;\unicode[STIX]{x1D70F})$
is divergent.
For the Rabi Hamiltonian
![]() $H$
and
$H$
and
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
, we consider the heat operator
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
, we consider the heat operator
![]() $K(t)=e^{-t(H+\unicode[STIX]{x1D70F}I)}$
on
$K(t)=e^{-t(H+\unicode[STIX]{x1D70F}I)}$
on
![]() $t>0$
. From now on, we fix
$t>0$
. From now on, we fix
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}.$
By Propositions 2.1 and 2.2,
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}.$
By Propositions 2.1 and 2.2,
![]() $H+\unicode[STIX]{x1D70F}I$
is a self-adjoint operator and all its eigenvalues are positive. Hence the Hurwitz-type spectral zeta function of
$H+\unicode[STIX]{x1D70F}I$
is a self-adjoint operator and all its eigenvalues are positive. Hence the Hurwitz-type spectral zeta function of
![]() $H$
has an integral expression
$H$
has an integral expression
as long as the integral on the left-hand side is absolutely convergent. Set
Lemma 3.2. The integral
![]() $Z_{0}(s)$
converges absolutely for
$Z_{0}(s)$
converges absolutely for
![]() $\operatorname{Re}(s)>1$
, and the integral
$\operatorname{Re}(s)>1$
, and the integral
![]() $Z_{\infty }(s)$
converges absolutely for all
$Z_{\infty }(s)$
converges absolutely for all
![]() $s\in \mathbb{C}$
. In particular, the function
$s\in \mathbb{C}$
. In particular, the function
![]() $Z_{\infty }(s)$
has an analytic continuation to
$Z_{\infty }(s)$
has an analytic continuation to
![]() $\mathbb{C}$
. Furthermore, the integral
$\mathbb{C}$
. Furthermore, the integral
![]() $\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
converges absolutely for
$\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
converges absolutely for
![]() $\operatorname{Re}(s)>1$
and we have
$\operatorname{Re}(s)>1$
and we have
Proof. We follow the method given in the proof of [Reference Ichinose and Wakayama8, Proposition 2.1]. We remark that
 $$\begin{eqnarray}\displaystyle \operatorname{Tr}K(t) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})t}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{\{(1+\unicode[STIX]{x1D716})/e\}^{1+\unicode[STIX]{x1D716}}}{\{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})t\}^{1+\unicode[STIX]{x1D716}}}\nonumber\\ \displaystyle & = & \displaystyle \{(1+\unicode[STIX]{x1D716})/e\}^{1+\unicode[STIX]{x1D716}}\unicode[STIX]{x1D701}_{H}(1+\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})t^{-1-\unicode[STIX]{x1D716}}<\infty \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Tr}K(t) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})t}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{\{(1+\unicode[STIX]{x1D716})/e\}^{1+\unicode[STIX]{x1D716}}}{\{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})t\}^{1+\unicode[STIX]{x1D716}}}\nonumber\\ \displaystyle & = & \displaystyle \{(1+\unicode[STIX]{x1D716})/e\}^{1+\unicode[STIX]{x1D716}}\unicode[STIX]{x1D701}_{H}(1+\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})t^{-1-\unicode[STIX]{x1D716}}<\infty \nonumber\end{eqnarray}$$
for any
![]() $\unicode[STIX]{x1D716}>0$
, where we use Proposition 3.1 and the inequality
$\unicode[STIX]{x1D716}>0$
, where we use Proposition 3.1 and the inequality
![]() $e^{-b}\leqslant (a/e)^{a}b^{-a}$
for all
$e^{-b}\leqslant (a/e)^{a}b^{-a}$
for all
![]() $a,b>0$
. Thus it is obvious that
$a,b>0$
. Thus it is obvious that
![]() $Z_{0}(s)$
converges absolutely for
$Z_{0}(s)$
converges absolutely for
![]() $\operatorname{Re}(s)>1$
. Put
$\operatorname{Re}(s)>1$
. Put
![]() $\unicode[STIX]{x1D70E}=\operatorname{Re}(s)$
and take
$\unicode[STIX]{x1D70E}=\operatorname{Re}(s)$
and take
![]() $a\in \mathbb{R}$
such that
$a\in \mathbb{R}$
such that
![]() $a>\max (\unicode[STIX]{x1D70E},1)$
. Then,
$a>\max (\unicode[STIX]{x1D70E},1)$
. Then,
 $$\begin{eqnarray}\displaystyle \int _{1}^{\infty }|t^{s-1}\operatorname{Tr}K(t)|\,dt & {\leqslant} & \displaystyle \int _{1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{(a/e)^{a}}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{a}}t^{-a}\times t^{\unicode[STIX]{x1D70E}-1}\,dt\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}_{H}(a;\unicode[STIX]{x1D70F})\int _{1}^{\infty }t^{\unicode[STIX]{x1D70E}-a-1}\,dt<\infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{1}^{\infty }|t^{s-1}\operatorname{Tr}K(t)|\,dt & {\leqslant} & \displaystyle \int _{1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{(a/e)^{a}}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{a}}t^{-a}\times t^{\unicode[STIX]{x1D70E}-1}\,dt\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}_{H}(a;\unicode[STIX]{x1D70F})\int _{1}^{\infty }t^{\unicode[STIX]{x1D70E}-a-1}\,dt<\infty .\nonumber\end{eqnarray}$$
Equalities (3.1) follow from
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(s)\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{-s} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\int _{0}^{\infty }e^{-t}\left(\frac{t}{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F}}\right)^{s}\frac{dt}{t}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-(\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D706})t}t^{s}\frac{dt}{t}=\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(s)\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{-s} & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\int _{0}^{\infty }e^{-t}\left(\frac{t}{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F}}\right)^{s}\frac{dt}{t}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-(\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D706})t}t^{s}\frac{dt}{t}=\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt.\nonumber\end{eqnarray}$$
The change of integrals and series is justified when
![]() $\operatorname{Re}(s)>1$
.◻
$\operatorname{Re}(s)>1$
.◻
For the operator
![]() $H+\unicode[STIX]{x1D70F}I$
, we define an operator
$H+\unicode[STIX]{x1D70F}I$
, we define an operator
![]() $K_{1}(t)$
and its kernel
$K_{1}(t)$
and its kernel
![]() $K_{1}(t,x,y)$
by
$K_{1}(t,x,y)$
by
 $$\begin{eqnarray}\displaystyle & & \displaystyle (K_{1}(t)f)(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]f(y)\,dy\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }K_{1}(t,x,y)f(y)\,dy\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (K_{1}(t)f)(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]f(y)\,dy\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }K_{1}(t,x,y)f(y)\,dy\nonumber\end{eqnarray}$$
for any
![]() $f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
. We set
$f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
. We set
![]() $R_{2}(t)=K(t)-K_{1}(t)$
. Then the equation
$R_{2}(t)=K(t)-K_{1}(t)$
. Then the equation
![]() $(\unicode[STIX]{x2202}_{t}+H+\unicode[STIX]{x1D70F}I)K_{1}(t)+(\unicode[STIX]{x2202}_{t}+H+\unicode[STIX]{x1D70F}I)R_{2}(t)=0$
holds. Furthermore, we set
$(\unicode[STIX]{x2202}_{t}+H+\unicode[STIX]{x1D70F}I)K_{1}(t)+(\unicode[STIX]{x2202}_{t}+H+\unicode[STIX]{x1D70F}I)R_{2}(t)=0$
holds. Furthermore, we set
![]() $F(t,x,y)=(\unicode[STIX]{x2202}_{t}+H_{x}+\unicode[STIX]{x1D70F}I)R_{2}(t,x,y)=-(\unicode[STIX]{x2202}_{t}+H_{x}+\unicode[STIX]{x1D70F}I)K_{1}(t,x,y)$
, where
$F(t,x,y)=(\unicode[STIX]{x2202}_{t}+H_{x}+\unicode[STIX]{x1D70F}I)R_{2}(t,x,y)=-(\unicode[STIX]{x2202}_{t}+H_{x}+\unicode[STIX]{x1D70F}I)K_{1}(t,x,y)$
, where
![]() $H_{x}$
is the operator
$H_{x}$
is the operator
![]() $H$
acting on the
$H$
acting on the
![]() $x$
-variables. By
$x$
-variables. By
![]() $K_{1}(t,x,y)\rightarrow \unicode[STIX]{x1D6FF}(x-y)I$
as
$K_{1}(t,x,y)\rightarrow \unicode[STIX]{x1D6FF}(x-y)I$
as
![]() $t\rightarrow +0$
, we have easily
$t\rightarrow +0$
, we have easily
![]() $R_{2}(t)\rightarrow 0I$
as
$R_{2}(t)\rightarrow 0I$
as
![]() $t\rightarrow +0$
. Therefore, by Duhamel’s principle (cf. [Reference Courant and Hilbert4, pp. 202–204]), we have the following expression
$t\rightarrow +0$
. Therefore, by Duhamel’s principle (cf. [Reference Courant and Hilbert4, pp. 202–204]), we have the following expression
where we put
![]() $(F(u)f)(x)=\int _{-\infty }^{\infty }F(u,x,y)f(y)\,dy$
for any
$(F(u)f)(x)=\int _{-\infty }^{\infty }F(u,x,y)f(y)\,dy$
for any
![]() $f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
.
$f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
.
Lemma 3.3. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle F(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\left[\frac{y^{2}-x^{2}}{2}I+\sqrt{2}g(y-x)W\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709}-\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left[\left(\unicode[STIX]{x1D70F}-\frac{1}{2}\right)I+\unicode[STIX]{x1D6E5}L\right]\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\left[\frac{y^{2}-x^{2}}{2}I+\sqrt{2}g(y-x)W\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709}-\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left[\left(\unicode[STIX]{x1D70F}-\frac{1}{2}\right)I+\unicode[STIX]{x1D6E5}L\right]\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709}.\nonumber\end{eqnarray}$$
Proof. It follows from the definition of
![]() $K_{1}(t,x,y)$
and the expression
$K_{1}(t,x,y)$
and the expression
![]() $\int _{-\infty }^{\infty }F(t,x,y)f(y)\,dy=\int _{-\infty }^{\infty }(-\unicode[STIX]{x2202}_{t}-H-\unicode[STIX]{x1D70F}I)K_{1}(t,x,y)f(y)\,dy$
for any
$\int _{-\infty }^{\infty }F(t,x,y)f(y)\,dy=\int _{-\infty }^{\infty }(-\unicode[STIX]{x2202}_{t}-H-\unicode[STIX]{x1D70F}I)K_{1}(t,x,y)f(y)\,dy$
for any
![]() $f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
.◻
$f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
.◻
The function
![]() $\operatorname{Tr}K_{1}(t)$
is analyzed as follows.
$\operatorname{Tr}K_{1}(t)$
is analyzed as follows.
Lemma 3.4. We have the following formulas:
 $$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Tr}K_{1}(t)=\frac{2e^{g^{2}t}}{t},\quad t>0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{0}^{1}t^{s-1}\operatorname{Tr}K_{1}(t)\,dt=\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1},\quad \operatorname{Re}(s)>1. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Tr}K_{1}(t)=\frac{2e^{g^{2}t}}{t},\quad t>0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{0}^{1}t^{s-1}\operatorname{Tr}K_{1}(t)\,dt=\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1},\quad \operatorname{Re}(s)>1. & \displaystyle \nonumber\end{eqnarray}$$
Proof. Since
![]() $I$
and
$I$
and
![]() $W$
are commutative, by [Reference Gradshteyn and Ryzhik5, 3.323, 2.
$W$
are commutative, by [Reference Gradshteyn and Ryzhik5, 3.323, 2.
![]() $^{10}$
], the function
$^{10}$
], the function
![]() $K_{1}(t,x,y)$
can be described as
$K_{1}(t,x,y)$
can be described as
 $$\begin{eqnarray}\displaystyle & & \displaystyle K_{1}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{i(x-y)\unicode[STIX]{x1D709}}\exp \left(-\frac{t\unicode[STIX]{x1D709}^{2}}{2}I\right)\,d\unicode[STIX]{x1D709}\times \exp \left(-\frac{ty^{2}}{2}I\right)\exp (-\sqrt{2}gtyW)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle K_{1}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{i(x-y)\unicode[STIX]{x1D709}}\exp \left(-\frac{t\unicode[STIX]{x1D709}^{2}}{2}I\right)\,d\unicode[STIX]{x1D709}\times \exp \left(-\frac{ty^{2}}{2}I\right)\exp (-\sqrt{2}gtyW)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW).\nonumber\end{eqnarray}$$
Hence we obtain
 $$\begin{eqnarray}\displaystyle \operatorname{Tr}K_{1}(t) & = & \displaystyle \int _{-\infty }^{\infty }\operatorname{tr}K_{1}(t,x,x)\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\int _{-\infty }^{\infty }e^{-tx^{2}/2}2\cosh (\sqrt{2}gtx)\,dx=\frac{2e^{g^{2}t}}{t},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Tr}K_{1}(t) & = & \displaystyle \int _{-\infty }^{\infty }\operatorname{tr}K_{1}(t,x,x)\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\int _{-\infty }^{\infty }e^{-tx^{2}/2}2\cosh (\sqrt{2}gtx)\,dx=\frac{2e^{g^{2}t}}{t},\nonumber\end{eqnarray}$$
where we use [Reference Gradshteyn and Ryzhik5, 3.546.2]. This completes the proof. ◻
3.1 Estimates of residual operators
Set
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{1}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\frac{y^{2}-x^{2}}{2}I\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{2}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\sqrt{2}g(y-x)W\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{3}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}(-\unicode[STIX]{x1D6E5})L\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{4}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)I\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{1}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\frac{y^{2}-x^{2}}{2}I\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{2}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\sqrt{2}g(y-x)W\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{3}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}(-\unicode[STIX]{x1D6E5})L\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\\ \displaystyle & & \displaystyle F_{4}(t,x,y)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }e^{i(x-y)\unicode[STIX]{x1D709}}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)I\exp \left[-t\left(\frac{\unicode[STIX]{x1D709}^{2}+y^{2}}{2}I+\sqrt{2}gyW\right)\right]d\unicode[STIX]{x1D709},\nonumber\end{eqnarray}$$
and
![]() $F_{j}(t)=\int _{-\infty }^{\infty }F_{j}(t,x,y)f(y)\,dy$
for any
$F_{j}(t)=\int _{-\infty }^{\infty }F_{j}(t,x,y)f(y)\,dy$
for any
![]() $f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
and any
$f\in {\mathcal{S}}(\mathbb{R};\mathbb{C}^{2})$
and any
![]() $j\in \{1,2,3,4\}$
. Then we see
$j\in \{1,2,3,4\}$
. Then we see
and
We have the following by the same computation as in Lemma 3.4.
Lemma 3.5. We have the following explicit formulas:
 $$\begin{eqnarray}\displaystyle F_{1}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\frac{y^{2}-x^{2}}{2}Ie^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{2}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\sqrt{2}g(y-x)We^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{3}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}(-\unicode[STIX]{x1D6E5})Le^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{4}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)Ie^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{1}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\frac{y^{2}-x^{2}}{2}Ie^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{2}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\sqrt{2}g(y-x)We^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{3}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}(-\unicode[STIX]{x1D6E5})Le^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW), & & \displaystyle \nonumber\\ \displaystyle F_{4}(t,x,y)=\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}t}}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)Ie^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW). & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 3.6. For
![]() $0<t<1$
, we have
$0<t<1$
, we have
![]() $\Vert F_{1}(t)+F_{2}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
and
$\Vert F_{1}(t)+F_{2}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
and
![]() $\Vert F_{3}(t)+F_{4}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
.
$\Vert F_{3}(t)+F_{4}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
.
Proof. Set
![]() $\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}-1/2$
,
$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}-1/2$
,
![]() $F_{-}(t,x,y)=F_{3}(t,x,y)+F_{4}(t,x,y)$
, and
$F_{-}(t,x,y)=F_{3}(t,x,y)+F_{4}(t,x,y)$
, and
![]() $F_{-}(t)=F_{3}(t)+F_{4}(t)$
. Since the adjoint operator
$F_{-}(t)=F_{3}(t)+F_{4}(t)$
. Since the adjoint operator
![]() $F_{-}(t)^{\ast }$
of
$F_{-}(t)^{\ast }$
of
![]() $F_{-}(t)$
is given by
$F_{-}(t)$
is given by
![]() $(F_{-}(t)^{\ast }f)(x)=\int _{-\infty }^{\infty }\overline{F_{-}(t,y,x)}f(y)\,dy$
, by noting
$(F_{-}(t)^{\ast }f)(x)=\int _{-\infty }^{\infty }\overline{F_{-}(t,y,x)}f(y)\,dy$
, by noting
![]() $WL=-LW$
and Lemma 3.5, we obtain
$WL=-LW$
and Lemma 3.5, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert F_{-}(t)\Vert _{2}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Tr}(F_{-}(t)^{\ast }F_{-}(t))=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}F_{-}(t,x,y)\overline{F_{-}(t,x,y)}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}\left[\frac{1}{2\unicode[STIX]{x1D70B}t}(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW)\vphantom{\frac{1}{2\unicode[STIX]{x1D70B}t}}\right]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\operatorname{tr}[\,(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)(\unicode[STIX]{x1D70F}^{\prime }\exp (-\sqrt{2}gtyW)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6E5}L\exp (\sqrt{2}gtyW))\exp (-\sqrt{2}gtyW)]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}[(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)(\unicode[STIX]{x1D70F}^{\prime }\exp (-2\sqrt{2}gtyW)+\unicode[STIX]{x1D6E5}L)]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\times 2\{{\unicode[STIX]{x1D70F}^{\prime }}^{2}\cosh (2\sqrt{2}gty)+\unicode[STIX]{x1D6E5}^{2}\}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{{\unicode[STIX]{x1D70F}^{\prime }}^{2}}{\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\cosh (2\sqrt{2}gty)\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D6E5}^{2}}{\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\,dy\,dx,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert F_{-}(t)\Vert _{2}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Tr}(F_{-}(t)^{\ast }F_{-}(t))=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}F_{-}(t,x,y)\overline{F_{-}(t,x,y)}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}\left[\frac{1}{2\unicode[STIX]{x1D70B}t}(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)e^{-(x-y)^{2}/2t-ty^{2}/2}\exp (-\sqrt{2}gtyW)\vphantom{\frac{1}{2\unicode[STIX]{x1D70B}t}}\right]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\operatorname{tr}[\,(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)(\unicode[STIX]{x1D70F}^{\prime }\exp (-\sqrt{2}gtyW)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6E5}L\exp (\sqrt{2}gtyW))\exp (-\sqrt{2}gtyW)]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}[(\unicode[STIX]{x1D70F}^{\prime }I+\unicode[STIX]{x1D6E5}L)(\unicode[STIX]{x1D70F}^{\prime }\exp (-2\sqrt{2}gtyW)+\unicode[STIX]{x1D6E5}L)]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\times 2\{{\unicode[STIX]{x1D70F}^{\prime }}^{2}\cosh (2\sqrt{2}gty)+\unicode[STIX]{x1D6E5}^{2}\}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{{\unicode[STIX]{x1D70F}^{\prime }}^{2}}{\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\cosh (2\sqrt{2}gty)\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D6E5}^{2}}{\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\,dy\,dx,\nonumber\end{eqnarray}$$
and hence we have
![]() $\Vert F_{-}(t)\Vert _{2}^{2}=t^{-1}({\unicode[STIX]{x1D70F}^{\prime }}^{2}e^{2g^{2}t}+\unicode[STIX]{x1D6E5}^{2})$
by the formulas
$\Vert F_{-}(t)\Vert _{2}^{2}=t^{-1}({\unicode[STIX]{x1D70F}^{\prime }}^{2}e^{2g^{2}t}+\unicode[STIX]{x1D6E5}^{2})$
by the formulas
 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\,dy\,dx=\unicode[STIX]{x1D70B}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}e^{\pm 2\sqrt{2}gty}\,dy\,dx=\unicode[STIX]{x1D70B}e^{2g^{2}t}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}\,dy\,dx=\unicode[STIX]{x1D70B}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x-y)^{2}/t-ty^{2}}e^{\pm 2\sqrt{2}gty}\,dy\,dx=\unicode[STIX]{x1D70B}e^{2g^{2}t}. & \displaystyle \nonumber\end{eqnarray}$$
Next we set
![]() $F_{+}(t)=F_{1}(t)+F_{2}(t)$
and
$F_{+}(t)=F_{1}(t)+F_{2}(t)$
and
![]() $F_{+}(t,x,y)=F_{1}(t,x,y)+F_{2}(t,x,y)$
. Combining
$F_{+}(t,x,y)=F_{1}(t,x,y)+F_{2}(t,x,y)$
. Combining
![]() $IW=WI$
with Lemma 3.5, we obtain
$IW=WI$
with Lemma 3.5, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert F_{+}(t)\Vert _{2}^{2}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}F_{+}(t,x,y)\overline{F_{+}(t,x,y)}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}\operatorname{tr}\left[\left\{\frac{y^{2}-x^{2}}{2}I+\sqrt{2}g(y-x)W\right\}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left.e^{-(x-y)^{2}/t-ty^{2}}\exp (-2\sqrt{2}gtyW)\right]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\times \left[\left\{\frac{y^{2}-x^{2}}{2}+\sqrt{2}g(y-x)\right\}^{2}e^{-2\sqrt{2}gty}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\left\{\frac{y^{2}-x^{2}}{2}-\sqrt{2}g(y-x)\right\}^{2}e^{2\sqrt{2}gty}\right]\,dy\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert F_{+}(t)\Vert _{2}^{2}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\operatorname{tr}F_{+}(t,x,y)\overline{F_{+}(t,x,y)}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}\operatorname{tr}\left[\left\{\frac{y^{2}-x^{2}}{2}I+\sqrt{2}g(y-x)W\right\}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left.e^{-(x-y)^{2}/t-ty^{2}}\exp (-2\sqrt{2}gtyW)\right]\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\times \left[\left\{\frac{y^{2}-x^{2}}{2}+\sqrt{2}g(y-x)\right\}^{2}e^{-2\sqrt{2}gty}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\left\{\frac{y^{2}-x^{2}}{2}-\sqrt{2}g(y-x)\right\}^{2}e^{2\sqrt{2}gty}\right]\,dy\,dx.\nonumber\end{eqnarray}$$
Hence
![]() $\Vert F_{+}(t)\Vert _{2}^{2}={\mathcal{O}}(t^{-1})$
follows from
$\Vert F_{+}(t)\Vert _{2}^{2}={\mathcal{O}}(t^{-1})$
follows from
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\left\{\frac{y^{2}-x^{2}}{2}\pm \sqrt{2}g(x-y)\right\}^{2}e^{\mp 2\sqrt{2}gty}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-u^{2}-v^{2}}\frac{u^{2}}{4}(tu+2v\pm 2\sqrt{2}g\sqrt{t})^{2}e^{\pm 2\sqrt{2}g\sqrt{t}v}\,du\,dv\nonumber\\ \displaystyle & & \displaystyle \quad ={\mathcal{O}}(t^{-1}).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{1}{2\unicode[STIX]{x1D70B}t}e^{-(x-y)^{2}/t-ty^{2}}\left\{\frac{y^{2}-x^{2}}{2}\pm \sqrt{2}g(x-y)\right\}^{2}e^{\mp 2\sqrt{2}gty}\,dy\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}t}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-u^{2}-v^{2}}\frac{u^{2}}{4}(tu+2v\pm 2\sqrt{2}g\sqrt{t})^{2}e^{\pm 2\sqrt{2}g\sqrt{t}v}\,du\,dv\nonumber\\ \displaystyle & & \displaystyle \quad ={\mathcal{O}}(t^{-1}).\square\nonumber\end{eqnarray}$$
Set
 $$\begin{eqnarray}\displaystyle K_{m}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{m-2}}\nonumber\\ \displaystyle & & \displaystyle \!\!\times \,K_{1}(t-u_{1}-\cdots u_{m-1})F(u_{m-1})F(u_{m-2})\cdots F(u_{1})\,du_{m-1}\cdots du_{1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{m}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{m-2}}\nonumber\\ \displaystyle & & \displaystyle \!\!\times \,K_{1}(t-u_{1}-\cdots u_{m-1})F(u_{m-1})F(u_{m-2})\cdots F(u_{1})\,du_{m-1}\cdots du_{1}\nonumber\end{eqnarray}$$
for
![]() $m\geqslant 2$
and
$m\geqslant 2$
and
 $$\begin{eqnarray}\displaystyle R_{n+1}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{n-1}}K(t-u_{1}-\cdots u_{n})\nonumber\\ \displaystyle & & \displaystyle \times \,F(u_{n})F(u_{n-1})\cdots F(u_{1})\,du_{n}\,du_{n-1}\cdots du_{1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{n+1}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{n-1}}K(t-u_{1}-\cdots u_{n})\nonumber\\ \displaystyle & & \displaystyle \times \,F(u_{n})F(u_{n-1})\cdots F(u_{1})\,du_{n}\,du_{n-1}\cdots du_{1}\nonumber\end{eqnarray}$$
for
![]() $n\geqslant 2$
, respectively. Then, by the same argument in [Reference Ichinose and Wakayama8, pp. 704–705], we decompose
$n\geqslant 2$
, respectively. Then, by the same argument in [Reference Ichinose and Wakayama8, pp. 704–705], we decompose
![]() $K(t)$
as
$K(t)$
as
Lemma 3.7. For any
![]() $\unicode[STIX]{x1D716}\in (0,1/2)$
, there exists a positive constant
$\unicode[STIX]{x1D716}\in (0,1/2)$
, there exists a positive constant
![]() $C=C(g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F},\unicode[STIX]{x1D716})$
such that
$C=C(g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F},\unicode[STIX]{x1D716})$
such that
 $$\begin{eqnarray}\displaystyle & \displaystyle |\text{Tr}\,R_{2}(t)|\leqslant Ct^{-\unicode[STIX]{x1D716}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle |\text{Tr}\,R_{n+1}(t)|\leqslant C^{n}\frac{\unicode[STIX]{x1D70B}^{n/2}}{\unicode[STIX]{x1D6E4}(n/2+1)}t^{n/2} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle |\text{Tr}\,R_{2}(t)|\leqslant Ct^{-\unicode[STIX]{x1D716}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle |\text{Tr}\,R_{n+1}(t)|\leqslant C^{n}\frac{\unicode[STIX]{x1D70B}^{n/2}}{\unicode[STIX]{x1D6E4}(n/2+1)}t^{n/2} & \displaystyle \nonumber\end{eqnarray}$$
for any
![]() $t\in (0,1)$
and any
$t\in (0,1)$
and any
![]() $n\in \mathbb{Z}_{{\geqslant}2}$
.
$n\in \mathbb{Z}_{{\geqslant}2}$
.
Proof. We follow the method in [Reference Ichinose and Wakayama8, Proposition 2.3]. For any
![]() $t>0$
,
$t>0$
,
![]() $u\in (0,t)$
, and
$u\in (0,t)$
, and
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \!\!\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}\Vert _{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-2(t-u)(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left(\frac{1+2\unicode[STIX]{x1D716}}{e}\right)^{(1+2\unicode[STIX]{x1D716})/2}\!\left(\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{1}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{1+2\unicode[STIX]{x1D716}}}\!\right)^{1/2}\!2^{-(1+2\unicode[STIX]{x1D716})/2}(t-u)^{-(1+2\unicode[STIX]{x1D716})/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{1+2\unicode[STIX]{x1D716}}{e}\right)^{(1+2\unicode[STIX]{x1D716})/2}\unicode[STIX]{x1D701}_{H}(1+2\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})^{1/2}2^{-(1+2\unicode[STIX]{x1D716})/2}(t-u)^{-(1+2\unicode[STIX]{x1D716})/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \!\!\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}\Vert _{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}e^{-2(t-u)(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left(\frac{1+2\unicode[STIX]{x1D716}}{e}\right)^{(1+2\unicode[STIX]{x1D716})/2}\!\left(\mathop{\sum }_{\unicode[STIX]{x1D706}\in \operatorname{Spec}(H)}\frac{1}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70F})^{1+2\unicode[STIX]{x1D716}}}\!\right)^{1/2}\!2^{-(1+2\unicode[STIX]{x1D716})/2}(t-u)^{-(1+2\unicode[STIX]{x1D716})/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{1+2\unicode[STIX]{x1D716}}{e}\right)^{(1+2\unicode[STIX]{x1D716})/2}\unicode[STIX]{x1D701}_{H}(1+2\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})^{1/2}2^{-(1+2\unicode[STIX]{x1D716})/2}(t-u)^{-(1+2\unicode[STIX]{x1D716})/2}.\nonumber\end{eqnarray}$$
We note that
![]() $\unicode[STIX]{x1D701}_{H}(1+2\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})$
is convergent by Proposition 3.1. By virtue of Lemma 3.6, we have
$\unicode[STIX]{x1D701}_{H}(1+2\unicode[STIX]{x1D716};\unicode[STIX]{x1D70F})$
is convergent by Proposition 3.1. By virtue of Lemma 3.6, we have
![]() $\Vert F(t)\Vert _{2}\leqslant \Vert F_{1}(t)+F_{2}(t)\Vert _{2}+\Vert F_{3}(t)+F_{4}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
. Then, we estimate
$\Vert F(t)\Vert _{2}\leqslant \Vert F_{1}(t)+F_{2}(t)\Vert _{2}+\Vert F_{3}(t)+F_{4}(t)\Vert _{2}={\mathcal{O}}(t^{-1/2})$
. Then, we estimate
![]() $\operatorname{Tr}R_{2}(t)=\int _{0}^{t}\operatorname{Tr}(e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u))\,du$
as
$\operatorname{Tr}R_{2}(t)=\int _{0}^{t}\operatorname{Tr}(e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u))\,du$
as
 $$\begin{eqnarray}\displaystyle |\text{Tr}\,R_{2}(t)| & = & \displaystyle \int _{0}^{t}|\text{Tr}(e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u))|\,du\leqslant \int _{0}^{t}\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u)\Vert _{1}\,du\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{0}^{t}\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}\Vert _{2}\Vert F(u)\Vert _{2}\,du\leqslant C\int _{0}^{t}(t-u)^{-1/2-\unicode[STIX]{x1D716}}u^{-1/2}\,du\nonumber\\ \displaystyle & = & \displaystyle Ct^{-\unicode[STIX]{x1D716}}B(1/2-\unicode[STIX]{x1D716},1/2),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{Tr}\,R_{2}(t)| & = & \displaystyle \int _{0}^{t}|\text{Tr}(e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u))|\,du\leqslant \int _{0}^{t}\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}F(u)\Vert _{1}\,du\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{0}^{t}\Vert e^{-(t-u)(H+\unicode[STIX]{x1D70F}I)}\Vert _{2}\Vert F(u)\Vert _{2}\,du\leqslant C\int _{0}^{t}(t-u)^{-1/2-\unicode[STIX]{x1D716}}u^{-1/2}\,du\nonumber\\ \displaystyle & = & \displaystyle Ct^{-\unicode[STIX]{x1D716}}B(1/2-\unicode[STIX]{x1D716},1/2),\nonumber\end{eqnarray}$$
where
![]() $C=C(g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F},\unicode[STIX]{x1D716})$
is a positive constant depending only on
$C=C(g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F},\unicode[STIX]{x1D716})$
is a positive constant depending only on
![]() $g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F}$
, and
$g,\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D70F}$
, and
![]() $\unicode[STIX]{x1D716}$
. From this,
$\unicode[STIX]{x1D716}$
. From this,
![]() $|\text{Tr}\,R_{n+1}(t)|$
for
$|\text{Tr}\,R_{n+1}(t)|$
for
![]() $n\geqslant 2$
is majorized as
$n\geqslant 2$
is majorized as
![]() $|\text{Tr}\,R_{n+1}(t)|\leqslant C^{n}t^{n/2}\frac{\unicode[STIX]{x1D70B}^{n/2}}{\unicode[STIX]{x1D6E4}(n/2+1)}$
in the same way as [Reference Ichinose and Wakayama8, Proposition 2.3].◻
$|\text{Tr}\,R_{n+1}(t)|\leqslant C^{n}t^{n/2}\frac{\unicode[STIX]{x1D70B}^{n/2}}{\unicode[STIX]{x1D6E4}(n/2+1)}$
in the same way as [Reference Ichinose and Wakayama8, Proposition 2.3].◻
4 Asymptotic expansions
In this section, we give the asymptotic series of
![]() $\operatorname{Tr}K_{m}(t)$
as
$\operatorname{Tr}K_{m}(t)$
as
![]() $t\rightarrow +0$
, which is used in Section 5. Recall that
$t\rightarrow +0$
, which is used in Section 5. Recall that
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
is fixed so that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
is fixed so that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
as in Section 3. The main result in this section is the following.
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
as in Section 3. The main result in this section is the following.
Theorem 4.1. For any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
, there exists a sequence
$m\in \mathbb{Z}_{{\geqslant}2}$
, there exists a sequence
![]() $\{c_{q}^{(m)}\}_{q\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that
$\{c_{q}^{(m)}\}_{q\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that
Moreover, we have
![]() $c_{q}^{(m)}=0$
if
$c_{q}^{(m)}=0$
if
![]() $q<m-2$
.
$q<m-2$
.
For
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
and
$m\in \mathbb{Z}_{{\geqslant}2}$
and
![]() $\unicode[STIX]{x1D716}=(\unicode[STIX]{x1D716}_{j})_{j=1,\ldots ,m-1}\in \{1,2,3,4\}^{m-1}$
, we set
$\unicode[STIX]{x1D716}=(\unicode[STIX]{x1D716}_{j})_{j=1,\ldots ,m-1}\in \{1,2,3,4\}^{m-1}$
, we set
 $$\begin{eqnarray}\displaystyle K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{m-2}}K_{1}(t-u_{1}-\cdots -u_{m-1})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(u_{m-1})F_{\unicode[STIX]{x1D716}_{m-2}}(u_{m-2})\cdots F_{\unicode[STIX]{x1D716}_{2}}(u_{2})F_{\unicode[STIX]{x1D716}_{1}}(u_{1})\,du_{m-1}\cdots du_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle \int _{0}^{t}\int _{0}^{t-u_{1}}\cdots \int _{0}^{t-u_{1}-\cdots -u_{m-2}}K_{1}(t-u_{1}-\cdots -u_{m-1})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(u_{m-1})F_{\unicode[STIX]{x1D716}_{m-2}}(u_{m-2})\cdots F_{\unicode[STIX]{x1D716}_{2}}(u_{2})F_{\unicode[STIX]{x1D716}_{1}}(u_{1})\,du_{m-1}\cdots du_{1}.\nonumber\end{eqnarray}$$
Then
![]() $K_{m}(t)$
is decomposed as
$K_{m}(t)$
is decomposed as
Therefore, we only have to consider an asymptotic behavior of
![]() $\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)$
for each
$\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)$
for each
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
. By the change of variables
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
. By the change of variables
![]() $u_{j}=tu_{j}^{\prime }$
, it holds that
$u_{j}=tu_{j}^{\prime }$
, it holds that
 $$\begin{eqnarray}\displaystyle K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle t^{m-1}\int _{0}^{1}\int _{0}^{1-u_{1}^{\prime }}\cdots \int _{0}^{1-u_{1}^{\prime }-\cdots -u_{m-2}^{\prime }}K_{1}(t(1-u_{1}^{\prime }-\cdots -u_{m-1}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(tu_{m-1}^{\prime })F_{\unicode[STIX]{x1D716}_{m-2}}(tu_{m-2}^{\prime })\cdots F_{\unicode[STIX]{x1D716}_{2}}(tu_{2}^{\prime })F_{\unicode[STIX]{x1D716}_{1}}(tu_{1}^{\prime })\,du_{m-1}^{\prime }\cdots du_{1}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle t^{m-1}\int _{0}^{1}\int _{0}^{1-u_{1}^{\prime }}\cdots \int _{0}^{1-u_{1}^{\prime }-\cdots -u_{m-2}^{\prime }}K_{1}(t(1-u_{1}^{\prime }-\cdots -u_{m-1}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(tu_{m-1}^{\prime })F_{\unicode[STIX]{x1D716}_{m-2}}(tu_{m-2}^{\prime })\cdots F_{\unicode[STIX]{x1D716}_{2}}(tu_{2}^{\prime })F_{\unicode[STIX]{x1D716}_{1}}(tu_{1}^{\prime })\,du_{m-1}^{\prime }\cdots du_{1}^{\prime }.\nonumber\end{eqnarray}$$
By putting
![]() $D_{m-1}=\{u\in \mathbb{R}^{m-1}\mid u_{j}\geqslant 0(\forall j=1,\ldots ,m-1),\sum _{j=1}^{m-1}u_{j}\leqslant 1\}$
, we have
$D_{m-1}=\{u\in \mathbb{R}^{m-1}\mid u_{j}\geqslant 0(\forall j=1,\ldots ,m-1),\sum _{j=1}^{m-1}u_{j}\leqslant 1\}$
, we have
 $$\begin{eqnarray}\displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle t^{m-1}\int _{D_{m-1}}\,du\int _{z_{0}\in \mathbb{R}}\operatorname{tr}\int _{(z_{1},\ldots ,z_{m-1})\in \mathbb{R}^{m-1}}\nonumber\\ \displaystyle & & \displaystyle \times \,K_{1}(t(1-u_{1}-\cdots -u_{m-1}),z_{0},z_{m-1})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(tu_{m-1},z_{m-1},z_{m-2})\cdots F_{\unicode[STIX]{x1D716}_{2}}(tu_{2},z_{2},z_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,F_{\unicode[STIX]{x1D716}_{1}}(tu_{1},z_{1},z_{0})\,dz_{0}\,dz_{1}\cdots dz_{m-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t) & = & \displaystyle t^{m-1}\int _{D_{m-1}}\,du\int _{z_{0}\in \mathbb{R}}\operatorname{tr}\int _{(z_{1},\ldots ,z_{m-1})\in \mathbb{R}^{m-1}}\nonumber\\ \displaystyle & & \displaystyle \times \,K_{1}(t(1-u_{1}-\cdots -u_{m-1}),z_{0},z_{m-1})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{\unicode[STIX]{x1D716}_{m-1}}(tu_{m-1},z_{m-1},z_{m-2})\cdots F_{\unicode[STIX]{x1D716}_{2}}(tu_{2},z_{2},z_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,F_{\unicode[STIX]{x1D716}_{1}}(tu_{1},z_{1},z_{0})\,dz_{0}\,dz_{1}\cdots dz_{m-1}.\nonumber\end{eqnarray}$$
By the definition of
![]() $F_{\unicode[STIX]{x1D716}}(t,x,y)$
for
$F_{\unicode[STIX]{x1D716}}(t,x,y)$
for
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
and by the change of variables
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
and by the change of variables
![]() $\sqrt{t}z_{j}\leftrightarrow z_{j}$
and
$\sqrt{t}z_{j}\leftrightarrow z_{j}$
and
![]() $\sqrt{t}\unicode[STIX]{x1D709}_{j}\leftrightarrow \unicode[STIX]{x1D709}_{j}$
, the integral above is transformed to
$\sqrt{t}\unicode[STIX]{x1D709}_{j}\leftrightarrow \unicode[STIX]{x1D709}_{j}$
, the integral above is transformed to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad =t^{-1}\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\frac{1}{(2\unicode[STIX]{x1D70B})^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{i[(z_{0}-z_{m-1})\unicode[STIX]{x1D709}_{m}+(z_{m-1}-z_{m-2})\unicode[STIX]{x1D709}_{m-1}+\cdots +(z_{1}-z_{0})\unicode[STIX]{x1D709}_{1}]/t}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[e^{-(1-u_{1}-\cdots -u_{m-1})[((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{m-1}W]}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1}/\sqrt{t},z_{j}/\sqrt{t})e^{-u_{j}[((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{j-1}W]}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =t^{-1-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\frac{1}{(2\unicode[STIX]{x1D70B})^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}e^{i(z_{j}-z_{j-1})(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})/t}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[e^{-(1-u_{1}-\cdots -u_{m-1})[((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{m-1}W]}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}[((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{j-1}W]}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad =t^{-1}\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\frac{1}{(2\unicode[STIX]{x1D70B})^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{i[(z_{0}-z_{m-1})\unicode[STIX]{x1D709}_{m}+(z_{m-1}-z_{m-2})\unicode[STIX]{x1D709}_{m-1}+\cdots +(z_{1}-z_{0})\unicode[STIX]{x1D709}_{1}]/t}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[e^{-(1-u_{1}-\cdots -u_{m-1})[((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{m-1}W]}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1}/\sqrt{t},z_{j}/\sqrt{t})e^{-u_{j}[((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{j-1}W]}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =t^{-1-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\frac{1}{(2\unicode[STIX]{x1D70B})^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}e^{i(z_{j}-z_{j-1})(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})/t}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[e^{-(1-u_{1}-\cdots -u_{m-1})[((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{m-1}W]}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}[((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I+\sqrt{2}g\sqrt{t}z_{j-1}W]}\right].\end{eqnarray}$$
Here we put
![]() $r_{j}(\unicode[STIX]{x1D716})=\#\{j\in \{1,\ldots ,m-1\}\mid \unicode[STIX]{x1D716}_{j}=k\}$
for each
$r_{j}(\unicode[STIX]{x1D716})=\#\{j\in \{1,\ldots ,m-1\}\mid \unicode[STIX]{x1D716}_{j}=k\}$
for each
![]() $k\in \{1,2,3,4\}$
,
$k\in \{1,2,3,4\}$
,
![]() $T_{1}(x,y)=\frac{x^{2}-y^{2}}{2}I$
,
$T_{1}(x,y)=\frac{x^{2}-y^{2}}{2}I$
,
![]() $T_{2}(x,y)=\sqrt{2}g(x-y)W$
,
$T_{2}(x,y)=\sqrt{2}g(x-y)W$
,
![]() $T_{3}(x,y)=-\unicode[STIX]{x1D6E5}L$
,
$T_{3}(x,y)=-\unicode[STIX]{x1D6E5}L$
,
![]() $T_{4}(x,y)=(1/2-\unicode[STIX]{x1D70F})I$
, and
$T_{4}(x,y)=(1/2-\unicode[STIX]{x1D70F})I$
, and
 $$\begin{eqnarray}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A_{j}=A_{m-1}\cdots A_{1}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A_{j}=A_{m-1}\cdots A_{1}\end{eqnarray}$$
for any 2-by-2 matrices
![]() $A_{1},\ldots ,A_{m-1}$
. In order to expand integral (4.1), we use the following given in [Reference Ichinose and Wakayama8, Lemma 3.3].
$A_{1},\ldots ,A_{m-1}$
. In order to expand integral (4.1), we use the following given in [Reference Ichinose and Wakayama8, Lemma 3.3].
Lemma 4.2. The function
![]() $(x,y)\mapsto e^{ixy/t}$
has the asymptotic series
$(x,y)\mapsto e^{ixy/t}$
has the asymptotic series
as a tempered distribution in
![]() $\mathbb{R}^{2}$
.
$\mathbb{R}^{2}$
.
From this lemma (or [Reference Ichinose and Wakayama8, (4.7)]), by integration by parts, (4.1) is expanded as
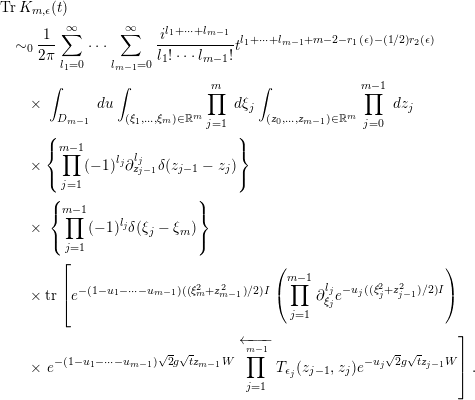 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{0}\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}e^{-(1-u_{1}-\cdots -u_{m-1})((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I}\left(\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{j}}^{l_{j}}e^{-u_{j}((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.e^{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}\sqrt{2}g\sqrt{t}z_{j-1}W}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{0}\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}e^{-(1-u_{1}-\cdots -u_{m-1})((\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2)I}\left(\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{j}}^{l_{j}}e^{-u_{j}((\unicode[STIX]{x1D709}_{j}^{2}+z_{j-1}^{2})/2)I}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.e^{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}\sqrt{2}g\sqrt{t}z_{j-1}W}\right].\end{eqnarray}$$
Here, we remark that the symbol
![]() $\unicode[STIX]{x1D6FF}(z_{j}-z_{j-1})$
is always replaced with
$\unicode[STIX]{x1D6FF}(z_{j}-z_{j-1})$
is always replaced with
![]() $\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})$
throughout this paper when
$\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})$
throughout this paper when
![]() $\unicode[STIX]{x2202}_{z_{j}}^{l_{j}}$
is transformed to
$\unicode[STIX]{x2202}_{z_{j}}^{l_{j}}$
is transformed to
![]() $(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}$
by integration by parts. (The symbol
$(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}$
by integration by parts. (The symbol
![]() $\unicode[STIX]{x1D6FF}(z_{j}-z_{j-1})$
used in [Reference Ichinose and Wakayama8, (4.8), (4.17b), (4.18), (4.19), (4.21), the first (4.22), and (4,23)] should be replaced with
$\unicode[STIX]{x1D6FF}(z_{j}-z_{j-1})$
used in [Reference Ichinose and Wakayama8, (4.8), (4.17b), (4.18), (4.19), (4.21), the first (4.22), and (4,23)] should be replaced with
![]() $\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})$
if it is regarded as a tempered distribution supported at
$\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})$
if it is regarded as a tempered distribution supported at
![]() $z_{j}$
.)
$z_{j}$
.)
Let us further analyze some factors in the integrand above. The following is obvious.
Lemma 4.3. For any
![]() $l\in \mathbb{Z}_{{\geqslant}0}$
and
$l\in \mathbb{Z}_{{\geqslant}0}$
and
![]() $u\in (0,1)$
, we have
$u\in (0,1)$
, we have
where
![]() $H_{l}(x)$
is the
$H_{l}(x)$
is the
![]() $l$
th Hermite polynomial defined by
$l$
th Hermite polynomial defined by
![]() $H_{l}(x)=(-1)^{l}e^{x^{2}}(\unicode[STIX]{x2202}_{x}^{l}e^{-x^{2}})$
.
$H_{l}(x)=(-1)^{l}e^{x^{2}}(\unicode[STIX]{x2202}_{x}^{l}e^{-x^{2}})$
.
Let us consider a transformation of the ordered product
 $$\begin{eqnarray}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}\sqrt{2}g\sqrt{t}z_{j-1}W}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})e^{-u_{j}\sqrt{2}g\sqrt{t}z_{j-1}W}.\end{eqnarray}$$
By the definition of
![]() $T_{\unicode[STIX]{x1D716}_{j}}(x,y)$
, the product as above is described as
$T_{\unicode[STIX]{x1D716}_{j}}(x,y)$
, the product as above is described as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}\frac{z_{j-1}^{2}-z_{j}^{2}}{2}\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}\left(-\unicode[STIX]{x1D70F}+\frac{1}{2}\right)^{r_{4}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{tr}\left[\exp (-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})e^{-\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W}\right]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}\frac{z_{j-1}^{2}-z_{j}^{2}}{2}\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}\left(-\unicode[STIX]{x1D70F}+\frac{1}{2}\right)^{r_{4}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{tr}\left[\exp (-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})e^{-\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W}\right]\nonumber\end{eqnarray}$$
with
![]() $A(1)=A(4)=I$
,
$A(1)=A(4)=I$
,
![]() $A(2)=W$
, and
$A(2)=W$
, and
![]() $A(3)=L$
. In the oriented product, we cannot shift all terms of the form
$A(3)=L$
. In the oriented product, we cannot shift all terms of the form
![]() $e^{aW}$
$e^{aW}$
![]() $(a\in \mathbb{R})$
into the left because of the noncommutativity of
$(a\in \mathbb{R})$
into the left because of the noncommutativity of
![]() $L$
and
$L$
and
![]() $W$
. However, we can define a mapping
$W$
. However, we can define a mapping
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}:\{1,\ldots ,m-1\}\rightarrow \{0,1\}$
by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}:\{1,\ldots ,m-1\}\rightarrow \{0,1\}$
by
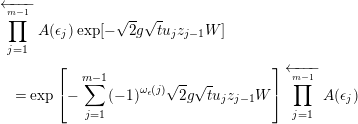 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\exp [-\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W]\nonumber\\ \displaystyle & & \displaystyle \quad =\exp \left[-\mathop{\sum }_{j=1}^{m-1}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W\right]\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\exp [-\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W]\nonumber\\ \displaystyle & & \displaystyle \quad =\exp \left[-\mathop{\sum }_{j=1}^{m-1}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\sqrt{2}g\sqrt{t}u_{j}z_{j-1}W\right]\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\end{eqnarray}$$
because of
![]() $WL=-LW$
. Set
$WL=-LW$
. Set
 $$\begin{eqnarray}A(\unicode[STIX]{x1D716})=\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j}).\end{eqnarray}$$
$$\begin{eqnarray}A(\unicode[STIX]{x1D716})=\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j}).\end{eqnarray}$$
Lemma 4.4. We have
 $$\begin{eqnarray}\displaystyle A(\unicode[STIX]{x1D716})\in \left\{\begin{array}{@{}ll@{}}\{\pm I\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is even and }r_{3}(\unicode[STIX]{x1D716})\text{ is even}),\\ \{\pm W\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is odd and }r_{3}(\unicode[STIX]{x1D716})\text{ is even}),\\ \{\pm L\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is even and }r_{3}(\unicode[STIX]{x1D716})\text{ is odd}),\\ \{\pm LW\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is odd and }r_{3}(\unicode[STIX]{x1D716})\text{ is odd}).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A(\unicode[STIX]{x1D716})\in \left\{\begin{array}{@{}ll@{}}\{\pm I\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is even and }r_{3}(\unicode[STIX]{x1D716})\text{ is even}),\\ \{\pm W\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is odd and }r_{3}(\unicode[STIX]{x1D716})\text{ is even}),\\ \{\pm L\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is even and }r_{3}(\unicode[STIX]{x1D716})\text{ is odd}),\\ \{\pm LW\}\quad & (\text{if }r_{2}(\unicode[STIX]{x1D716})\text{ is odd and }r_{3}(\unicode[STIX]{x1D716})\text{ is odd}).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. It follows immediately from the relations
![]() $W^{2}=L^{2}=I$
and
$W^{2}=L^{2}=I$
and
![]() $WL=-LW$
.◻
$WL=-LW$
.◻
By using the mapping
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}$
and the Maclaurin expansion
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}$
and the Maclaurin expansion
for
![]() $a\in \mathbb{R}$
and
$a\in \mathbb{R}$
and
![]() $t>0$
, the right-hand side of (4.2) is rewritten as
$t>0$
, the right-hand side of (4.2) is rewritten as
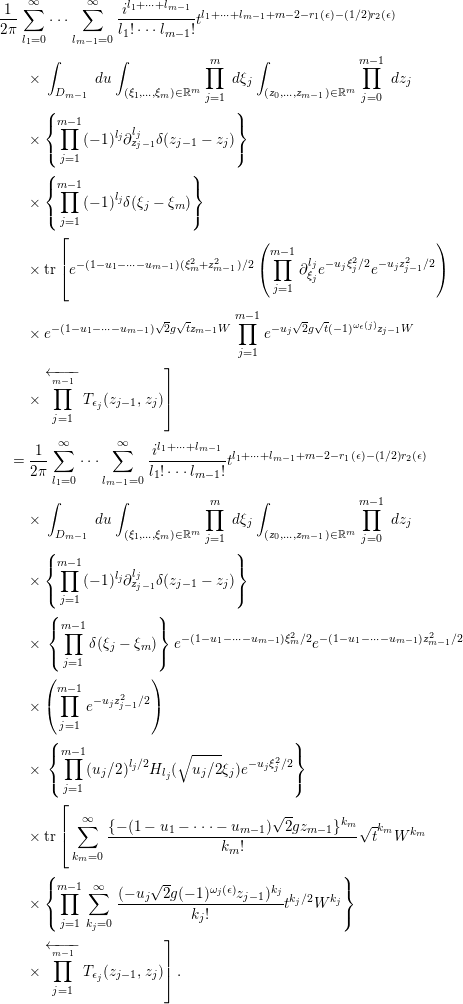 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}e^{-(1-u_{1}-\cdots -u_{m-1})(\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2}\left(\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{j}}^{l_{j}}e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}e^{-u_{j}z_{j-1}^{2}/2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W}\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}\sqrt{2}g\sqrt{t}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}z_{j-1}W}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})\unicode[STIX]{x1D709}_{m}^{2}/2}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}_{j})e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}\mathop{\sum }_{k_{m}=0}^{\infty }\frac{\{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}gz_{m-1}\}^{k_{m}}}{k_{m}!}\sqrt{t}^{k_{m}}W^{k_{m}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}\mathop{\sum }_{k_{j}=0}^{\infty }\frac{(-u_{j}\sqrt{2}g(-1)^{\unicode[STIX]{x1D714}_{j}(\unicode[STIX]{x1D716})}z_{j-1})^{k_{j}}}{k_{j}!}t^{k_{j}/2}W^{k_{j}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}e^{-(1-u_{1}-\cdots -u_{m-1})(\unicode[STIX]{x1D709}_{m}^{2}+z_{m-1}^{2})/2}\left(\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{j}}^{l_{j}}e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}e^{-u_{j}z_{j-1}^{2}/2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}g\sqrt{t}z_{m-1}W}\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}\sqrt{2}g\sqrt{t}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}z_{j-1}W}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}}\mathop{\sum }_{l_{1}=0}^{\infty }\cdots \mathop{\sum }_{l_{m-1}=0}^{\infty }\frac{i^{l_{1}+\cdots +l_{m-1}}}{l_{1}!\cdots l_{m-1}!}t^{l_{1}+\cdots +l_{m-1}+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})\unicode[STIX]{x1D709}_{m}^{2}/2}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}_{j})e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\operatorname{tr}\left[\vphantom{\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}}\mathop{\sum }_{k_{m}=0}^{\infty }\frac{\{-(1-u_{1}-\cdots -u_{m-1})\sqrt{2}gz_{m-1}\}^{k_{m}}}{k_{m}!}\sqrt{t}^{k_{m}}W^{k_{m}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}\mathop{\sum }_{k_{j}=0}^{\infty }\frac{(-u_{j}\sqrt{2}g(-1)^{\unicode[STIX]{x1D714}_{j}(\unicode[STIX]{x1D716})}z_{j-1})^{k_{j}}}{k_{j}!}t^{k_{j}/2}W^{k_{j}}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}T_{\unicode[STIX]{x1D716}_{j}}(z_{j-1},z_{j})\right].\end{eqnarray}$$
As a consequence, by noting
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})\unicode[STIX]{x1D709}_{m}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}_{j})e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in \mathbb{R}^{m}}\mathop{\prod }_{j=1}^{m}\,d\unicode[STIX]{x1D709}_{j}\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{j}-\unicode[STIX]{x1D709}_{m})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})\unicode[STIX]{x1D709}_{m}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}_{j})e^{-u_{j}\unicode[STIX]{x1D709}_{j}^{2}/2}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\end{eqnarray}$$
and the analysis made so far, we have the following asymptotic series.
Theorem 4.5. For any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
and
$m\in \mathbb{Z}_{{\geqslant}2}$
and
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, we have
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, we have
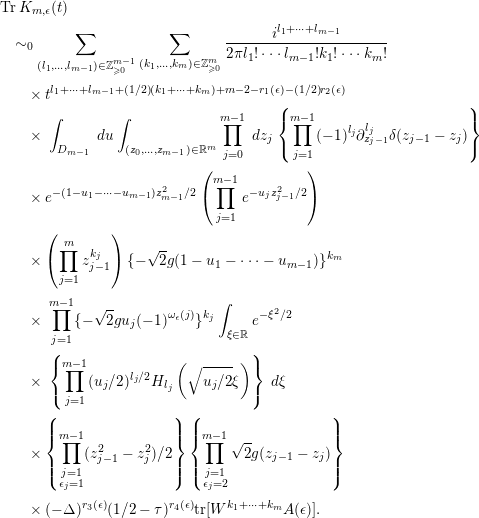 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{0}\mathop{\sum }_{(l_{1},\ldots ,l_{m-1})\in \mathbb{Z}_{{\geqslant}0}^{m-1}}\mathop{\sum }_{(k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{m}}\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{l_{1}+\cdots +l_{m-1}+(1/2)(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m}z_{j-1}^{k_{j}}\right)\{-\sqrt{2}g(1-u_{1}-\cdots -u_{m-1})\}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\{-\sqrt{2}gu_{j}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\}^{k_{j}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}\left(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}\right)\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}(z_{j-1}^{2}-z_{j}^{2})/2\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{0}\mathop{\sum }_{(l_{1},\ldots ,l_{m-1})\in \mathbb{Z}_{{\geqslant}0}^{m-1}}\mathop{\sum }_{(k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{m}}\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{l_{1}+\cdots +l_{m-1}+(1/2)(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m}z_{j-1}^{k_{j}}\right)\{-\sqrt{2}g(1-u_{1}-\cdots -u_{m-1})\}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\{-\sqrt{2}gu_{j}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\}^{k_{j}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}\left(\sqrt{u_{j}/2}\unicode[STIX]{x1D709}\right)\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}(z_{j-1}^{2}-z_{j}^{2})/2\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\end{eqnarray}$$
Here
![]() $r_{k}(\unicode[STIX]{x1D716})$
is the cardinality of
$r_{k}(\unicode[STIX]{x1D716})$
is the cardinality of
![]() $\{j\in \{1,\ldots ,m-1\}\mid \unicode[STIX]{x1D716}_{j}=k\}$
for each
$\{j\in \{1,\ldots ,m-1\}\mid \unicode[STIX]{x1D716}_{j}=k\}$
for each
![]() $k\in \{1,2,3,4\}$
, a mapping
$k\in \{1,2,3,4\}$
, a mapping
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}:\{1,\ldots ,m-1\}\rightarrow \{0,1\}$
is defined by (4.3), the function
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}:\{1,\ldots ,m-1\}\rightarrow \{0,1\}$
is defined by (4.3), the function
![]() $H_{l_{j}}(x)$
is the
$H_{l_{j}}(x)$
is the
![]() $l_{j}$
th Hermite polynomial defined in Lemma 4.3, and we set
$l_{j}$
th Hermite polynomial defined in Lemma 4.3, and we set
 $$\begin{eqnarray}A(\unicode[STIX]{x1D716})=\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\end{eqnarray}$$
$$\begin{eqnarray}A(\unicode[STIX]{x1D716})=\mathop{\prod }_{j=1}^{\xleftarrow[{m-1}]{}}A(\unicode[STIX]{x1D716}_{j})\end{eqnarray}$$
with
![]() $A(1)=A(4)=I$
,
$A(1)=A(4)=I$
,
![]() $A(2)=W$
, and
$A(2)=W$
, and
![]() $A(3)=L$
.
$A(3)=L$
.
Let
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
be the coefficient of
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
be the coefficient of
in (4.5). Then, we obtain the following series of vanishing results.
Lemma 4.6. The coefficient
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
vanishes if
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
vanishes if
![]() $l_{1}+\cdots +l_{m-1}$
is odd.
$l_{1}+\cdots +l_{m-1}$
is odd.
Proof. If
![]() $l_{1}+\cdots +l_{m-1}$
is odd, by
$l_{1}+\cdots +l_{m-1}$
is odd, by
![]() $H_{l_{j}}(-x)=(-1)^{l_{j}}H_{l_{j}}(x)$
the product
$H_{l_{j}}(-x)=(-1)^{l_{j}}H_{l_{j}}(x)$
the product
![]() $\prod _{j=1}^{m-1}H_{l_{j}}(x)$
is an odd function in
$\prod _{j=1}^{m-1}H_{l_{j}}(x)$
is an odd function in
![]() $x$
, and hence we have
$x$
, and hence we have
This completes the proof. ◻
Lemma 4.7. The coefficient
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
vanishes if
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
vanishes if
![]() $k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
is odd. In particular, any coefficients of
$k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
is odd. In particular, any coefficients of
![]() $\sqrt{t}^{2k+1}$
of
$\sqrt{t}^{2k+1}$
of
![]() $\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)$
for any
$\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)$
for any
![]() $k\in \mathbb{Z}_{{\geqslant}0}$
vanish.
$k\in \mathbb{Z}_{{\geqslant}0}$
vanish.
Proof. If
![]() $k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
is odd, Lemma 4.4 yields that
$k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
is odd, Lemma 4.4 yields that
![]() $W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})$
is equal to
$W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})$
is equal to
![]() $\pm W$
or
$\pm W$
or
![]() $\pm LW$
, whose trace is zero. This completes the proof.◻
$\pm LW$
, whose trace is zero. This completes the proof.◻
Lemma 4.8. We have
![]() $\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)=0$
if
$\operatorname{Tr}K_{m,\unicode[STIX]{x1D716}}(t)=0$
if
![]() $r_{3}(\unicode[STIX]{x1D716})$
is odd.
$r_{3}(\unicode[STIX]{x1D716})$
is odd.
Proof. If
![]() $r_{3}(\unicode[STIX]{x1D716})$
is odd, for any
$r_{3}(\unicode[STIX]{x1D716})$
is odd, for any
![]() $(k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{m}$
, by Lemma 4.4,
$(k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{m}$
, by Lemma 4.4,
![]() $W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})$
is equal to
$W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})$
is equal to
![]() $\pm L$
or
$\pm L$
or
![]() $\pm LW$
, whose trace is zero. From this and (4.5), we have the desired assertion.◻
$\pm LW$
, whose trace is zero. From this and (4.5), we have the desired assertion.◻
Lemma 4.9. We have
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
if there exists
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
if there exists
![]() $j\in \{1.\ldots ,m-1\}$
such that
$j\in \{1.\ldots ,m-1\}$
such that
![]() $\unicode[STIX]{x1D716}_{j}\in \{1,2\}$
and
$\unicode[STIX]{x1D716}_{j}\in \{1,2\}$
and
![]() $l_{j}=0$
. In particular, we have
$l_{j}=0$
. In particular, we have
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
if
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
if
![]() $l_{1}+\cdots +l_{m-1}<r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})$
.
$l_{1}+\cdots +l_{m-1}<r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})$
.
Proof. We obtain the assertion by noting the factor
![]() $\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})(z_{j-1}-z_{j})$
.◻
$\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})(z_{j-1}-z_{j})$
.◻
By Lemmas 4.6–4.8, we have the following.
Lemma 4.10. For any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
,
$m\in \mathbb{Z}_{{\geqslant}2}$
,
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
,
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
,
![]() $(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
$(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\int _{D_{m-1}}\,du\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m}z_{j-1}^{k_{j}}\right)\{-\sqrt{2}g(1-u_{1}-\cdots -u_{m-1})\}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\{-\sqrt{2}gu_{j}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\}^{k_{j}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}(z_{j-1}^{2}-z_{j}^{2})/2\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\int _{D_{m-1}}\,du\int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=1}^{m-1}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}\left(\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\mathop{\prod }_{j=1}^{m}z_{j-1}^{k_{j}}\right)\{-\sqrt{2}g(1-u_{1}-\cdots -u_{m-1})\}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{j=1}^{m-1}\{-\sqrt{2}gu_{j}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)}\}^{k_{j}}\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=1}}^{m-1}(z_{j-1}^{2}-z_{j}^{2})/2\right\}\left\{\mathop{\prod }_{\substack{ j=1 \\ \unicode[STIX]{x1D716}_{j}=2}}^{m-1}\sqrt{2}g(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\nonumber\end{eqnarray}$$
Moreover, it is an element of
![]() $\mathbb{R}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
.
$\mathbb{R}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
.
Proof. By Lemmas 4.6–4.8, we may assume that
![]() $l_{1}+\cdots +l_{m-1}$
,
$l_{1}+\cdots +l_{m-1}$
,
![]() $k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
and
$k_{1}+\cdots +k_{m}-r_{2}(\unicode[STIX]{x1D716})$
and
![]() $r_{3}(\unicode[STIX]{x1D716})$
are all even. Then, the assertion follows from
$r_{3}(\unicode[STIX]{x1D716})$
are all even. Then, the assertion follows from
![]() $\prod _{j=1}^{m-1}(-1)^{l_{j}}=1$
,
$\prod _{j=1}^{m-1}(-1)^{l_{j}}=1$
,
![]() $i^{l_{1}+\cdots +l_{m-1}}\in \{\pm 1\}$
and
$i^{l_{1}+\cdots +l_{m-1}}\in \{\pm 1\}$
and
![]() $(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}=\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}$
.◻
$(-\unicode[STIX]{x1D6E5})^{r_{3}(\unicode[STIX]{x1D716})}=\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}$
.◻
Proof of Theorem 4.1.
Let us take any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
,
$m\in \mathbb{Z}_{{\geqslant}2}$
,
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
, and
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
, and
![]() $q\in \frac{1}{2}\mathbb{Z}$
, and set
$q\in \frac{1}{2}\mathbb{Z}$
, and set
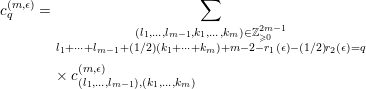 $$\begin{eqnarray}\displaystyle c_{q}^{(m,\unicode[STIX]{x1D716})} & = & \displaystyle \mathop{\sum }_{\substack{ (l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1} \\ l_{1}+\cdots +l_{m-1}+(1/2)(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=q}}\nonumber\\ \displaystyle & & \displaystyle \times \,c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{q}^{(m,\unicode[STIX]{x1D716})} & = & \displaystyle \mathop{\sum }_{\substack{ (l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1} \\ l_{1}+\cdots +l_{m-1}+(1/2)(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=q}}\nonumber\\ \displaystyle & & \displaystyle \times \,c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\end{eqnarray}$$
and
By virtue of Lemma 4.7, we have
![]() $c_{q}^{(m,\unicode[STIX]{x1D716})}=0$
unless
$c_{q}^{(m,\unicode[STIX]{x1D716})}=0$
unless
![]() $q\in \mathbb{Z}$
. Moreover, if
$q\in \mathbb{Z}$
. Moreover, if
![]() $l_{1}+\cdots +l_{m-1}+\frac{1}{2}(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})<m-2$
, we have
$l_{1}+\cdots +l_{m-1}+\frac{1}{2}(k_{1}+\cdots +k_{m})+m-2-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})<m-2$
, we have
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
with the aid of Lemma 4.9. Thus we obtain
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}=0$
with the aid of Lemma 4.9. Thus we obtain
![]() $c_{q}^{(m,\unicode[STIX]{x1D716})}=0$
if
$c_{q}^{(m,\unicode[STIX]{x1D716})}=0$
if
![]() $q<m-2$
. This completes the proof.◻
$q<m-2$
. This completes the proof.◻
5 Meromorphic continuations
In this section, we prove Theorem 1.1. Recall that
![]() $\unicode[STIX]{x1D70F}$
is any fixed real number such that
$\unicode[STIX]{x1D70F}$
is any fixed real number such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
as in Section 3. Theorem 1.1(1) is a consequence of the following theorem.
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
as in Section 3. Theorem 1.1(1) is a consequence of the following theorem.
Theorem 5.1. There exists a sequence
![]() $\{C_{H,\unicode[STIX]{x1D70F}}(k)\}_{k\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that
$\{C_{H,\unicode[STIX]{x1D70F}}(k)\}_{k\in \mathbb{Z}_{{\geqslant}0}}$
of complex numbers such that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\left\{\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{k=0}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{s+k}+h_{1}(s)+h_{2}(s)+Z_{\infty }(s)\right\}\!,\quad \operatorname{Re}(s)>1\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}(s)}\left\{\frac{2}{s-1}+\mathop{\sum }_{k=1}^{\infty }\frac{2g^{2k}}{k!}\frac{1}{s+k-1}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{k=0}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{s+k}+h_{1}(s)+h_{2}(s)+Z_{\infty }(s)\right\}\!,\quad \operatorname{Re}(s)>1\nonumber\end{eqnarray}$$
for any
![]() $n\in \mathbb{Z}_{{\geqslant}2}$
. Here,
$n\in \mathbb{Z}_{{\geqslant}2}$
. Here,
![]() $Z_{\infty }(s)$
is the entire function treated in Lemma 3.2,
$Z_{\infty }(s)$
is the entire function treated in Lemma 3.2,
![]() $h_{1}(s)$
is a holomorphic function on
$h_{1}(s)$
is a holomorphic function on
![]() $\operatorname{Re}(s)>-n$
such that
$\operatorname{Re}(s)>-n$
such that
![]() $h_{1}(s)={\mathcal{O}}(1/(\operatorname{Re}(s)+n))$
on the region
$h_{1}(s)={\mathcal{O}}(1/(\operatorname{Re}(s)+n))$
on the region
![]() $\operatorname{Re}(s)>-n$
, and
$\operatorname{Re}(s)>-n$
, and
![]() $h_{2}(s)$
is a holomorphic function on
$h_{2}(s)$
is a holomorphic function on
![]() $\operatorname{Re}(s)>-n/2$
such that
$\operatorname{Re}(s)>-n/2$
such that
![]() $h_{2}(s)={\mathcal{O}}(1/(\operatorname{Re}(s)+n/2))$
on the region
$h_{2}(s)={\mathcal{O}}(1/(\operatorname{Re}(s)+n/2))$
on the region
![]() $\operatorname{Re}(s)>-n/2$
.
$\operatorname{Re}(s)>-n/2$
.
In particular,
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
has a meromorphic continuation to
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
has a meromorphic continuation to
![]() $\mathbb{C}$
and is holomorphic on
$\mathbb{C}$
and is holomorphic on
![]() $\mathbb{C}-\{1\}$
. Furthermore,
$\mathbb{C}-\{1\}$
. Furthermore,
![]() $s=1$
is a simple pole with
$s=1$
is a simple pole with
![]() $\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=2$
.
$\operatorname{Res}_{s=1}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=2$
.
Proof. Recall
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=(1/\unicode[STIX]{x1D6E4}(s))\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
. Since
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})=(1/\unicode[STIX]{x1D6E4}(s))\int _{0}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
. Since
![]() $Z_{\infty }(t)=\int _{1}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
is entire by Lemma 3.2, we only have to consider
$Z_{\infty }(t)=\int _{1}^{\infty }t^{s-1}\operatorname{Tr}K(t)\,dt$
is entire by Lemma 3.2, we only have to consider
![]() $\int _{0}^{1}t^{s-1}\operatorname{Tr}K(t)\,dt$
. As for the first term of (3.2), Lemma 3.4 yields that
$\int _{0}^{1}t^{s-1}\operatorname{Tr}K(t)\,dt$
. As for the first term of (3.2), Lemma 3.4 yields that
is entire. As for the third term of (3.2), by Lemma 3.7, the integral
![]() $\int _{0}^{1}|t^{s-1}\operatorname{Tr}R_{n+1}(t)|\,dt$
for
$\int _{0}^{1}|t^{s-1}\operatorname{Tr}R_{n+1}(t)|\,dt$
for
![]() $\operatorname{Re}(s)>-n/2$
is majorized by
$\operatorname{Re}(s)>-n/2$
is majorized by
up to a positive constant, and hence the function
![]() $h_{2}(s)=\int _{0}^{1}t^{s-1}\operatorname{Tr}R_{n+1}(t)\,dt$
is holomorphic on
$h_{2}(s)=\int _{0}^{1}t^{s-1}\operatorname{Tr}R_{n+1}(t)\,dt$
is holomorphic on
![]() $\operatorname{Re}(s)>-n/2$
. By setting
$\operatorname{Re}(s)>-n/2$
. By setting
Theorem 4.1 gives us
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t) & = & \displaystyle \mathop{\sum }_{m=2}^{n}\mathop{\sum }_{q=m-2}^{n-2}c_{q}^{(m)}t^{q}+{\mathcal{O}}(t^{n-1})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}+{\mathcal{O}}(t^{n-1}),\quad (t\rightarrow +0).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t) & = & \displaystyle \mathop{\sum }_{m=2}^{n}\mathop{\sum }_{q=m-2}^{n-2}c_{q}^{(m)}t^{q}+{\mathcal{O}}(t^{n-1})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}+{\mathcal{O}}(t^{n-1}),\quad (t\rightarrow +0).\nonumber\end{eqnarray}$$
Then the integral of the second term of (3.2) is evaluated as
 $$\begin{eqnarray}\displaystyle \int _{0}^{1}t^{s-1}\mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t)\,dt & = & \displaystyle \int _{0}^{1}t^{s-1}\mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}\,dt\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{1}t^{s-1}\left\{\mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t)-\mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}\right\}dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{1}t^{s-1}\mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t)\,dt & = & \displaystyle \int _{0}^{1}t^{s-1}\mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}\,dt\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{1}t^{s-1}\left\{\mathop{\sum }_{m=2}^{n}\operatorname{Tr}K_{m}(t)-\mathop{\sum }_{k=0}^{n-2}C_{H,\unicode[STIX]{x1D70F}}(k)t^{k}\right\}dt.\nonumber\end{eqnarray}$$
As the first term is evaluated as
![]() $\sum _{k=0}^{n-2}(C_{H,\unicode[STIX]{x1D70F}}(k)/(s+k))$
and the second term as above is majorized by
$\sum _{k=0}^{n-2}(C_{H,\unicode[STIX]{x1D70F}}(k)/(s+k))$
and the second term as above is majorized by
up to a positive constant when
![]() $\operatorname{Re}(s)>-n$
, the integral
$\operatorname{Re}(s)>-n$
, the integral
is holomorphic on
![]() $\operatorname{Re}(s)>-n$
. As a consequence, we have the theorem.◻
$\operatorname{Re}(s)>-n$
. As a consequence, we have the theorem.◻
By Theorem 5.1, the function
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is holomorphic at
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
is holomorphic at
![]() $s=0$
for any
$s=0$
for any
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
. Thus,
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
. Thus, ![]() can be defined for any
can be defined for any
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
by [Reference Quine, Heydari and Song22, Theorem 1]. Here is a formula of the zeta regularized product of
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
by [Reference Quine, Heydari and Song22, Theorem 1]. Here is a formula of the zeta regularized product of
![]() $\operatorname{Spec}(H+\unicode[STIX]{x1D70F}I)$
.
$\operatorname{Spec}(H+\unicode[STIX]{x1D70F}I)$
.
Proposition 5.2. For any
![]() $n\in \mathbb{Z}_{{\geqslant}2}$
and any real number
$n\in \mathbb{Z}_{{\geqslant}2}$
and any real number
![]() $\unicode[STIX]{x1D70F}$
such that
$\unicode[STIX]{x1D70F}$
such that
![]() $\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, we have
$\unicode[STIX]{x1D70F}>g^{2}+\unicode[STIX]{x1D6E5}$
, we have

where
![]() $\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is Euler’s constant.
$\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6E4}^{\prime }(1)$
is Euler’s constant.
Proof. By using Theorem 1.1(1), a direct computation gives us
 $$\begin{eqnarray}\displaystyle \frac{d}{ds}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})|_{s=0} & = & \displaystyle -2+\mathop{\sum }_{k=2}^{\infty }\frac{2g^{2k}}{k!(k-1)}+\unicode[STIX]{x1D6FE}\{2g^{2}+C_{H,\unicode[STIX]{x1D70F}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=1}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{k}+F_{H,n}(0;\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d}{ds}\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})|_{s=0} & = & \displaystyle -2+\mathop{\sum }_{k=2}^{\infty }\frac{2g^{2k}}{k!(k-1)}+\unicode[STIX]{x1D6FE}\{2g^{2}+C_{H,\unicode[STIX]{x1D70F}}(0)\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=1}^{n-2}\frac{C_{H,\unicode[STIX]{x1D70F}}(k)}{k}+F_{H,n}(0;\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
We shall compute
![]() $C_{H,\unicode[STIX]{x1D70F}}(0)$
. By (4.6), (4.7), and (5.1),
$C_{H,\unicode[STIX]{x1D70F}}(0)$
. By (4.6), (4.7), and (5.1),
![]() $C_{H,\unicode[STIX]{x1D70F}}(0)$
is expressed as
$C_{H,\unicode[STIX]{x1D70F}}(0)$
is expressed as
![]() $C_{H,\unicode[STIX]{x1D70F}}(0)=c_{0}^{(2)}=\sum _{\unicode[STIX]{x1D716}=1}^{4}c_{0}^{(2,\unicode[STIX]{x1D716})}$
with
$C_{H,\unicode[STIX]{x1D70F}}(0)=c_{0}^{(2)}=\sum _{\unicode[STIX]{x1D716}=1}^{4}c_{0}^{(2,\unicode[STIX]{x1D716})}$
with
 $$\begin{eqnarray}c_{0}^{(2,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ (l,k_{1},k_{2})\in \mathbb{Z}_{{\geqslant}0}^{3} \\ l+(1/2)(k_{1}+k_{2})-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=0}}c_{l,(k_{1},k_{2})}^{(2,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
$$\begin{eqnarray}c_{0}^{(2,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ (l,k_{1},k_{2})\in \mathbb{Z}_{{\geqslant}0}^{3} \\ l+(1/2)(k_{1}+k_{2})-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=0}}c_{l,(k_{1},k_{2})}^{(2,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}\in \{1,2\}$
, we have
$\unicode[STIX]{x1D716}\in \{1,2\}$
, we have
![]() $c_{0}^{(2,1)}=c_{0}^{(2,2)}=0$
by Lemma 6.1 below. For
$c_{0}^{(2,1)}=c_{0}^{(2,2)}=0$
by Lemma 6.1 below. For
![]() $\unicode[STIX]{x1D716}=3$
, Lemma 4.8 yields
$\unicode[STIX]{x1D716}=3$
, Lemma 4.8 yields
![]() $c_{0}^{(2,3)}=0$
. For
$c_{0}^{(2,3)}=0$
. For
![]() $\unicode[STIX]{x1D716}=4$
, we have
$\unicode[STIX]{x1D716}=4$
, we have
![]() $c_{0}^{(2,4)}=1-2\unicode[STIX]{x1D70F}$
by the proof of Proposition 5.3 below. Hence, we obtain
$c_{0}^{(2,4)}=1-2\unicode[STIX]{x1D70F}$
by the proof of Proposition 5.3 below. Hence, we obtain
![]() $C_{H,\unicode[STIX]{x1D70F}}(0)=1-2\unicode[STIX]{x1D70F}$
.◻
$C_{H,\unicode[STIX]{x1D70F}}(0)=1-2\unicode[STIX]{x1D70F}$
.◻
5.1 Simple examples
We give an example of
![]() $\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
in terms of the Hurwitz zeta function
$\unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F})$
in terms of the Hurwitz zeta function
![]() $\unicode[STIX]{x1D701}(s;a)=\sum _{n=0}^{\infty }(n+a)^{-s}$
for
$\unicode[STIX]{x1D701}(s;a)=\sum _{n=0}^{\infty }(n+a)^{-s}$
for
![]() $a>0$
.
$a>0$
.
The case
![]() $\unicode[STIX]{x1D6E5}=0$
: In the case
$\unicode[STIX]{x1D6E5}=0$
: In the case
![]() $\unicode[STIX]{x1D6E5}=0$
, we consider
$\unicode[STIX]{x1D6E5}=0$
, we consider
![]() $H^{\prime }$
defined in (2.3) instead of
$H^{\prime }$
defined in (2.3) instead of
![]() $H$
. We have
$H$
. We have
![]() $H^{\prime }=B-\unicode[STIX]{x1D70F}I$
, where
$H^{\prime }=B-\unicode[STIX]{x1D70F}I$
, where
![]() $B$
is the operator defined in the proof of Lemma 2.4. Hence we have
$B$
is the operator defined in the proof of Lemma 2.4. Hence we have
![]() $\operatorname{Spec}(H)=\operatorname{Spec}(B-\unicode[STIX]{x1D70F}I)=\{n-g^{2}\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 2 and
$\operatorname{Spec}(H)=\operatorname{Spec}(B-\unicode[STIX]{x1D70F}I)=\{n-g^{2}\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 2 and
From this, the
![]() $k$
th Rabi–Bernoulli polynomial, which is defined by (1.1), is given by
$k$
th Rabi–Bernoulli polynomial, which is defined by (1.1), is given by
![]() $R_{k}(g,0;x)=B_{k}(x-g^{2})$
for any
$R_{k}(g,0;x)=B_{k}(x-g^{2})$
for any
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
, where
$k\in \mathbb{Z}_{{\geqslant}1}$
, where
![]() $B_{k}(x)$
is the
$B_{k}(x)$
is the
![]() $k$
th Bernoulli polynomial as in the Introduction.
$k$
th Bernoulli polynomial as in the Introduction.
The case
![]() $g=0$
: Another simple example is the case
$g=0$
: Another simple example is the case
![]() $g=0$
. Assume
$g=0$
. Assume
![]() $\unicode[STIX]{x1D6E5}>0$
. In this case, the expression
$\unicode[STIX]{x1D6E5}>0$
. In this case, the expression
gives us
![]() $\operatorname{Spec}(H)=\{n+\unicode[STIX]{x1D6E5}\mid n\in \mathbb{Z}_{{\geqslant}0}\}\cup \{n-\unicode[STIX]{x1D6E5}\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 1. As a result, we obtain
$\operatorname{Spec}(H)=\{n+\unicode[STIX]{x1D6E5}\mid n\in \mathbb{Z}_{{\geqslant}0}\}\cup \{n-\unicode[STIX]{x1D6E5}\mid n\in \mathbb{Z}_{{\geqslant}0}\}$
with multiplicity 1. As a result, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(n+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D70F})^{s}}+\mathop{\sum }_{n=0}^{\infty }\frac{1}{(n-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D70F})^{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}(s;\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D701}(s;\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D6E5})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{H}(s;\unicode[STIX]{x1D70F}) & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(n+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D70F})^{s}}+\mathop{\sum }_{n=0}^{\infty }\frac{1}{(n-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D70F})^{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}(s;\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D701}(s;\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D6E5})\nonumber\end{eqnarray}$$
and
![]() $R_{k}(0,\unicode[STIX]{x1D6E5};x)=\frac{1}{2}(B_{k}(x+\unicode[STIX]{x1D6E5})+B_{k}(x-\unicode[STIX]{x1D6E5}))$
for any
$R_{k}(0,\unicode[STIX]{x1D6E5};x)=\frac{1}{2}(B_{k}(x+\unicode[STIX]{x1D6E5})+B_{k}(x-\unicode[STIX]{x1D6E5}))$
for any
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
.
$k\in \mathbb{Z}_{{\geqslant}1}$
.
As we see as above,
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic and its degree is equal to
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic and its degree is equal to
![]() $k$
as a polynomial in
$k$
as a polynomial in
![]() $x$
when
$x$
when
![]() $g=0$
or
$g=0$
or
![]() $\unicode[STIX]{x1D6E5}=0$
. We have the following for general
$\unicode[STIX]{x1D6E5}=0$
. We have the following for general
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}\geqslant 0$
.
$\unicode[STIX]{x1D6E5}\geqslant 0$
.
Proposition 5.3. For any
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
, the degree of
$k\in \mathbb{Z}_{{\geqslant}1}$
, the degree of
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
with respect to
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
with respect to
![]() $x$
is equal to
$x$
is equal to
![]() $k$
. Furthermore,
$k$
. Furthermore,
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic as a polynomial in
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
is monic as a polynomial in
![]() $x$
.
$x$
.
Proof. By (5.1), it suffices to analyze
![]() $C_{H,\unicode[STIX]{x1D70F}}(k)=\sum _{m=2}^{k+2}c_{k}^{(m)}$
. With the aid of (4.6) and (4.7), it suffices to study the term for
$C_{H,\unicode[STIX]{x1D70F}}(k)=\sum _{m=2}^{k+2}c_{k}^{(m)}$
. With the aid of (4.6) and (4.7), it suffices to study the term for
![]() $\unicode[STIX]{x1D716}=(4,\ldots ,4)\in \{1,2,3,4\}^{k+1}$
appearing in
$\unicode[STIX]{x1D716}=(4,\ldots ,4)\in \{1,2,3,4\}^{k+1}$
appearing in
![]() $c_{k}^{(k+2)}$
. Put
$c_{k}^{(k+2)}$
. Put
![]() $\mathbf{0}_{m-1}=(0,\ldots ,0)\in \mathbb{Z}_{{\geqslant}0}^{m-1}$
and
$\mathbf{0}_{m-1}=(0,\ldots ,0)\in \mathbb{Z}_{{\geqslant}0}^{m-1}$
and
![]() $\mathbf{4}_{m-1}=(4,\ldots ,4)\in \{1,2,3,4\}^{m-1}$
for any
$\mathbf{4}_{m-1}=(4,\ldots ,4)\in \{1,2,3,4\}^{m-1}$
for any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
. By Lemma 4.10, we easily obtain
$m\in \mathbb{Z}_{{\geqslant}2}$
. By Lemma 4.10, we easily obtain
and thus we are done. ◻
5.2 Rationality of coefficients
In this subsection, we shall prove Theorem 1.1(2) by combining (4.6), (4.7), and (5.1) with the following theorem.
Theorem 5.4. For any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
,
$m\in \mathbb{Z}_{{\geqslant}2}$
,
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
![]() $(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
$(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
We remark that
![]() $C_{H,\unicode[STIX]{x1D70F}}(k)\in \mathbb{R}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
is obvious from combining (4.6), (4.7), and (5.1) with Lemma 4.10. The following two lemmas will be used later in order to prove Theorem 5.4.
$C_{H,\unicode[STIX]{x1D70F}}(k)\in \mathbb{R}[g^{2},\unicode[STIX]{x1D6E5}^{2},\unicode[STIX]{x1D70F}]$
is obvious from combining (4.6), (4.7), and (5.1) with Lemma 4.10. The following two lemmas will be used later in order to prove Theorem 5.4.
Lemma 5.5. For any polynomial
![]() $P(u_{1},\ldots ,u_{m-1},\unicode[STIX]{x1D709})\in \mathbb{Q}[u_{1},\ldots ,u_{m-1},\unicode[STIX]{x1D709}]$
, we have
$P(u_{1},\ldots ,u_{m-1},\unicode[STIX]{x1D709})\in \mathbb{Q}[u_{1},\ldots ,u_{m-1},\unicode[STIX]{x1D709}]$
, we have
Proof. By the formula
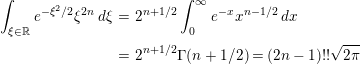 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\unicode[STIX]{x1D709}^{2n}\,d\unicode[STIX]{x1D709} & = & \displaystyle 2^{n+1/2}\int _{0}^{\infty }e^{-x}x^{n-1/2}\,dx\nonumber\\ \displaystyle & = & \displaystyle 2^{n+1/2}\unicode[STIX]{x1D6E4}(n+1/2)=(2n-1)!!\sqrt{2\unicode[STIX]{x1D70B}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\unicode[STIX]{x1D709}^{2n}\,d\unicode[STIX]{x1D709} & = & \displaystyle 2^{n+1/2}\int _{0}^{\infty }e^{-x}x^{n-1/2}\,dx\nonumber\\ \displaystyle & = & \displaystyle 2^{n+1/2}\unicode[STIX]{x1D6E4}(n+1/2)=(2n-1)!!\sqrt{2\unicode[STIX]{x1D70B}}\end{eqnarray}$$
for any
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
, we obtain the desired assertion.◻
$n\in \mathbb{Z}_{{\geqslant}0}$
, we obtain the desired assertion.◻
Lemma 5.6. For any polynomial
![]() $P(u_{1},\ldots ,u_{m-1})\in \mathbb{Q}[u_{1},\ldots ,u_{m-1}]$
, we have
$P(u_{1},\ldots ,u_{m-1})\in \mathbb{Q}[u_{1},\ldots ,u_{m-1}]$
, we have
where
![]() $D_{m-1}$
is the subset of
$D_{m-1}$
is the subset of
![]() $\mathbb{R}^{m-1}$
defined in Section 4.
$\mathbb{R}^{m-1}$
defined in Section 4.
Proof. The assertion follows from the formula
 $$\begin{eqnarray}\displaystyle \int _{D_{m-1}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{a_{j}}\right)\,du_{m-1}\cdots du_{1}=\frac{\mathop{\prod }_{j=1}^{m-1}a_{j}!}{(\mathop{\sum }_{j=1}^{m-1}a_{j}+m-1)!}\in \mathbb{Q} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{D_{m-1}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{a_{j}}\right)\,du_{m-1}\cdots du_{1}=\frac{\mathop{\prod }_{j=1}^{m-1}a_{j}!}{(\mathop{\sum }_{j=1}^{m-1}a_{j}+m-1)!}\in \mathbb{Q} & & \displaystyle \nonumber\end{eqnarray}$$
for any
![]() $(a_{1},\ldots ,a_{m-1})\in \mathbb{Z}_{{\geqslant}0}^{m-1}$
(cf. [Reference Gradshteyn and Ryzhik5,
$(a_{1},\ldots ,a_{m-1})\in \mathbb{Z}_{{\geqslant}0}^{m-1}$
(cf. [Reference Gradshteyn and Ryzhik5,
![]() $4.634^{8}$
]).◻
$4.634^{8}$
]).◻
Let us take any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
,
$m\in \mathbb{Z}_{{\geqslant}2}$
,
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
![]() $(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
. We may assume that
$(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
. We may assume that
![]() $l_{1}+\cdots +l_{m-1}$
,
$l_{1}+\cdots +l_{m-1}$
,
![]() $k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})$
, and
$k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})$
, and
![]() $r_{3}(\unicode[STIX]{x1D716})$
are all even by Lemmas 4.6–4.8.
$r_{3}(\unicode[STIX]{x1D716})$
are all even by Lemmas 4.6–4.8.
We show a refined formula of
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
. Set
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
. Set
![]() $D_{1}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},1}$
,
$D_{1}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},1}$
,
![]() $D_{2}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},2}$
, and
$D_{2}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},2}$
, and
![]() $D_{34}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},3}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},4}$
for any
$D_{34}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},3}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716},4}$
for any
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
, where
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}$
, where
![]() $\unicode[STIX]{x1D6FF}_{a,b}$
is the Kronecker delta. For our purpose, we calculate the following integral appearing in the formula of
$\unicode[STIX]{x1D6FF}_{a,b}$
is the Kronecker delta. For our purpose, we calculate the following integral appearing in the formula of
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
in Lemma 4.10:
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
in Lemma 4.10:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\left(\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\right)e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\{D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{0},\ldots ,z_{m-1})\in \mathbb{R}^{m}}\left(\mathop{\prod }_{j=0}^{m-1}\,dz_{j}\right)e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{j=1}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\mathop{\prod }_{j=1}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\{D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\}.\end{eqnarray}$$
First, let us consider the
![]() $z_{0}$
-integral. By a direct computation, we have
$z_{0}$
-integral. By a direct computation, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{0}\in \mathbb{R}}\,dz_{0}\unicode[STIX]{x1D6FF}(z_{0}-z_{1})\unicode[STIX]{x2202}_{z_{0}}^{l_{1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,[e^{-u_{1}z_{0}^{2}/2}z_{0}^{k_{1}}\{D_{1}(\unicode[STIX]{x1D716}_{1})(z_{0}^{2}-z_{1}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{1})(z_{0}-z_{1})+D_{34}(\unicode[STIX]{x1D716}_{1})\}]\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{z_{0}\in \mathbb{R}}\unicode[STIX]{x1D6FF}(z_{0}-z_{1})e^{-u_{1}z_{0}^{2}/2}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{0})\,dz_{0}=e^{-u_{1}z_{1}^{2}/2}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{0}\in \mathbb{R}}\,dz_{0}\unicode[STIX]{x1D6FF}(z_{0}-z_{1})\unicode[STIX]{x2202}_{z_{0}}^{l_{1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,[e^{-u_{1}z_{0}^{2}/2}z_{0}^{k_{1}}\{D_{1}(\unicode[STIX]{x1D716}_{1})(z_{0}^{2}-z_{1}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{1})(z_{0}-z_{1})+D_{34}(\unicode[STIX]{x1D716}_{1})\}]\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{z_{0}\in \mathbb{R}}\unicode[STIX]{x1D6FF}(z_{0}-z_{1})e^{-u_{1}z_{0}^{2}/2}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{0})\,dz_{0}=e^{-u_{1}z_{1}^{2}/2}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1}),\nonumber\end{eqnarray}$$
where we set
 $$\begin{eqnarray}\displaystyle & & \displaystyle P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{a=0}^{l_{1}}\binom{l_{1}}{a}(-1)^{l_{1}-a}(u_{1}/2)^{(l_{1}-a)/2}H_{l_{1}-a}(\sqrt{u_{1}/2}z_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left[\frac{k_{1}!}{(k_{1}-a)!}z_{0}^{k_{1}-a}\{D_{1}(\unicode[STIX]{x1D716}_{1})(z_{0}^{2}-z_{1}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{1})(z_{0}-z_{1})+D_{34}(\unicode[STIX]{x1D716}_{1})\}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\binom{a}{1}\frac{k_{1}!}{(k_{1}-a+1)!}z_{0}^{k_{1}-a+1}\{D_{1}(\unicode[STIX]{x1D716}_{1})z_{0}+D_{2}(\unicode[STIX]{x1D716}_{1})\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\binom{a}{2}\frac{k_{1}!}{(k-a+2)!}z_{0}^{k_{1}-a+2}D_{1}(\unicode[STIX]{x1D716}_{1})\right]\bigg|_{z_{0}=z_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{a=0}^{l_{1}}\binom{l_{1}}{a}(-1)^{l_{1}-a}(u_{1}/2)^{(l_{1}-a)/2}H_{l_{1}-a}(\sqrt{u_{1}/2}z_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left[\frac{k_{1}!}{(k_{1}-a)!}z_{0}^{k_{1}-a}\{D_{1}(\unicode[STIX]{x1D716}_{1})(z_{0}^{2}-z_{1}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{1})(z_{0}-z_{1})+D_{34}(\unicode[STIX]{x1D716}_{1})\}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\binom{a}{1}\frac{k_{1}!}{(k_{1}-a+1)!}z_{0}^{k_{1}-a+1}\{D_{1}(\unicode[STIX]{x1D716}_{1})z_{0}+D_{2}(\unicode[STIX]{x1D716}_{1})\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\binom{a}{2}\frac{k_{1}!}{(k-a+2)!}z_{0}^{k_{1}-a+2}D_{1}(\unicode[STIX]{x1D716}_{1})\right]\bigg|_{z_{0}=z_{1}}.\end{eqnarray}$$
Then,
![]() $P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})\in \mathbb{Q}[u_{1},z_{1}]$
follows easily. Thus, (5.3) is evaluated as
$P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})\in \mathbb{Q}[u_{1},z_{1}]$
follows easily. Thus, (5.3) is evaluated as
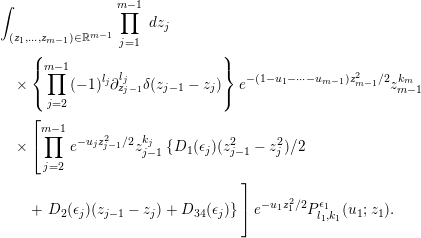 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{1},\ldots ,z_{m-1})\in \mathbb{R}^{m-1}}\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \quad \times \left\{\mathop{\prod }_{j=2}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \left[\mathop{\prod }_{j=2}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\{\!D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\!\}\right]e^{-u_{1}z_{1}^{2}/2}P_{l_{1},k_{1}}^{\unicode[STIX]{x1D716}_{1}}(u_{1};z_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{1},\ldots ,z_{m-1})\in \mathbb{R}^{m-1}}\mathop{\prod }_{j=1}^{m-1}\,dz_{j}\nonumber\\ \displaystyle & & \displaystyle \quad \times \left\{\mathop{\prod }_{j=2}^{m-1}(-1)^{l_{j}}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \left[\mathop{\prod }_{j=2}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\{\!D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\!\}\right]e^{-u_{1}z_{1}^{2}/2}P_{l_{1},k_{1}}^{\unicode[STIX]{x1D716}_{1}}(u_{1};z_{1}).\end{eqnarray}$$
Next let us consider the
![]() $z_{1}$
-integral
$z_{1}$
-integral
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{1}\in \mathbb{R}}\unicode[STIX]{x1D6FF}(z_{2}-z_{1})\unicode[STIX]{x2202}_{z_{1}}^{l_{2}} [e^{-(u_{1}+u_{2})z_{1}^{2}/2}z_{1}^{k_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\{D_{1}(\unicode[STIX]{x1D716}_{2})(z_{1}^{2}-z_{2}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{2})(z_{1}-z_{2})+D_{34}(\unicode[STIX]{x1D716}_{2})\}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})]\,dz_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{1}\in \mathbb{R}}\unicode[STIX]{x1D6FF}(z_{2}-z_{1})\unicode[STIX]{x2202}_{z_{1}}^{l_{2}} [e^{-(u_{1}+u_{2})z_{1}^{2}/2}z_{1}^{k_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\{D_{1}(\unicode[STIX]{x1D716}_{2})(z_{1}^{2}-z_{2}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{2})(z_{1}-z_{2})+D_{34}(\unicode[STIX]{x1D716}_{2})\}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})]\,dz_{1}.\nonumber\end{eqnarray}$$
We set
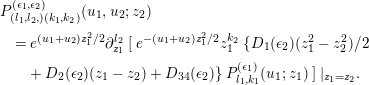 $$\begin{eqnarray}\displaystyle & & \displaystyle P_{(l_{1},l_{2},)(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =e^{(u_{1}+u_{2})z_{1}^{2}/2}\unicode[STIX]{x2202}_{z_{1}}^{l_{2}} [e^{-(u_{1}+u_{2})z_{1}^{2}/2}z_{1}^{k_{2}}\{\!D_{1}(\unicode[STIX]{x1D716}_{2})(z_{1}^{2}-z_{2}^{2})/2\nonumber\\ \displaystyle & & \displaystyle \qquad +\,D_{2}(\unicode[STIX]{x1D716}_{2})(z_{1}-z_{2})+D_{34}(\unicode[STIX]{x1D716}_{2})\!\}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})]|_{z_{1}=z_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P_{(l_{1},l_{2},)(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =e^{(u_{1}+u_{2})z_{1}^{2}/2}\unicode[STIX]{x2202}_{z_{1}}^{l_{2}} [e^{-(u_{1}+u_{2})z_{1}^{2}/2}z_{1}^{k_{2}}\{\!D_{1}(\unicode[STIX]{x1D716}_{2})(z_{1}^{2}-z_{2}^{2})/2\nonumber\\ \displaystyle & & \displaystyle \qquad +\,D_{2}(\unicode[STIX]{x1D716}_{2})(z_{1}-z_{2})+D_{34}(\unicode[STIX]{x1D716}_{2})\!\}P_{l_{1},k_{1}}^{(\unicode[STIX]{x1D716}_{1})}(u_{1};z_{1})]|_{z_{1}=z_{2}}.\end{eqnarray}$$
Then,
![]() $P_{(l_{1},l_{2},)(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2})$
is contained in
$P_{(l_{1},l_{2},)(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2})$
is contained in
![]() $\mathbb{Q}[u_{1},u_{2},z_{2}]$
. Thus (5.5) is transformed to
$\mathbb{Q}[u_{1},u_{2},z_{2}]$
. Thus (5.5) is transformed to
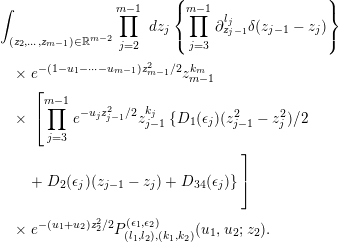 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{2},\ldots ,z_{m-1})\in \mathbb{R}^{m-2}}\mathop{\prod }_{j=2}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=3}^{m-1}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left[\mathop{\prod }_{j=3}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\{\!D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\!\}\right]\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e^{-(u_{1}+u_{2})z_{2}^{2}/2}P_{(l_{1},l_{2}),(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(z_{2},\ldots ,z_{m-1})\in \mathbb{R}^{m-2}}\mathop{\prod }_{j=2}^{m-1}\,dz_{j}\left\{\mathop{\prod }_{j=3}^{m-1}\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j}}\unicode[STIX]{x1D6FF}(z_{j-1}-z_{j})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left[\mathop{\prod }_{j=3}^{m-1}e^{-u_{j}z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\{\!D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{j})\!\}\right]\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e^{-(u_{1}+u_{2})z_{2}^{2}/2}P_{(l_{1},l_{2}),(k_{1},k_{2})}^{(\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2})}(u_{1},u_{2};z_{2}).\end{eqnarray}$$
In general, we define a polynomial
![]() $P_{(l_{1},\ldots ,l_{j}),(k_{1},\ldots ,k_{j})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j})}(u_{1},\ldots ,u_{j};z_{j})\in \mathbb{Q}[u_{1},\ldots ,u_{j},z_{j}]$
by (5.4) and the recurrence relation
$P_{(l_{1},\ldots ,l_{j}),(k_{1},\ldots ,k_{j})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j})}(u_{1},\ldots ,u_{j};z_{j})\in \mathbb{Q}[u_{1},\ldots ,u_{j},z_{j}]$
by (5.4) and the recurrence relation
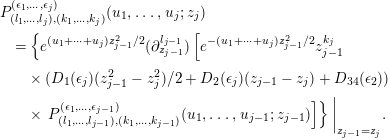 $$\begin{eqnarray}\displaystyle & & \displaystyle P_{(l_{1},\ldots ,l_{j}),(k_{1},\ldots ,k_{j})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j})}(u_{1},\ldots ,u_{j};z_{j})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{e^{(u_{1}+\cdots +u_{j})z_{j-1}^{2}/2}(\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j-1}})\left[e^{-(u_{1}+\cdots +u_{j})z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{2}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left.P_{(l_{1},\ldots ,l_{j-1}),(k_{1},\ldots ,k_{j-1})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j-1})}(u_{1},\ldots ,u_{j-1};z_{j-1})\right]\right\}\bigg|_{z_{j-1}=z_{j}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P_{(l_{1},\ldots ,l_{j}),(k_{1},\ldots ,k_{j})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j})}(u_{1},\ldots ,u_{j};z_{j})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{e^{(u_{1}+\cdots +u_{j})z_{j-1}^{2}/2}(\unicode[STIX]{x2202}_{z_{j-1}}^{l_{j-1}})\left[e^{-(u_{1}+\cdots +u_{j})z_{j-1}^{2}/2}z_{j-1}^{k_{j}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(D_{1}(\unicode[STIX]{x1D716}_{j})(z_{j-1}^{2}-z_{j}^{2})/2+D_{2}(\unicode[STIX]{x1D716}_{j})(z_{j-1}-z_{j})+D_{34}(\unicode[STIX]{x1D716}_{2}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left.P_{(l_{1},\ldots ,l_{j-1}),(k_{1},\ldots ,k_{j-1})}^{(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{j-1})}(u_{1},\ldots ,u_{j-1};z_{j-1})\right]\right\}\bigg|_{z_{j-1}=z_{j}}.\end{eqnarray}$$
In a similar fashion to computations for (5.5) and (5.7), integral (5.3) can be described as
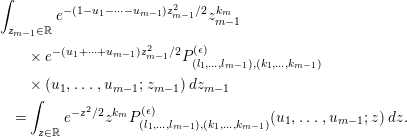 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{m-1}\in \mathbb{R}}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(u_{1}+\cdots +u_{m-1})z_{m-1}^{2}/2}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(u_{1},\ldots ,u_{m-1};z_{m-1})\,dz_{m-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z_{m-1}\in \mathbb{R}}e^{-(1-u_{1}-\cdots -u_{m-1})z_{m-1}^{2}/2}z_{m-1}^{k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{-(u_{1}+\cdots +u_{m-1})z_{m-1}^{2}/2}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(u_{1},\ldots ,u_{m-1};z_{m-1})\,dz_{m-1}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz.\end{eqnarray}$$
Hence we obtain the following refined expression of Lemma 4.10.
Lemma 5.7. For any
![]() $m\in \mathbb{Z}_{{\geqslant}2}$
,
$m\in \mathbb{Z}_{{\geqslant}2}$
,
![]() $\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
$\unicode[STIX]{x1D716}\in \{1,2,3,4\}^{m-1}$
, and
![]() $(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
$(l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m})\in \mathbb{Z}_{{\geqslant}0}^{2m-1}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)k_{j}}\right\}(-1)^{k_{1}+\cdots +k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{l_{1}+\cdots +l_{m-1}}}{2\unicode[STIX]{x1D70B}l_{1}!\cdots l_{m-1}!k_{1}!\cdots k_{m}!}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{D_{m-1}}\,du(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\left\{\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\right\}\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{m-1}(-1)^{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}}(j)k_{j}}\right\}(-1)^{k_{1}+\cdots +k_{m}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}[W^{k_{1}+\cdots +k_{m}}A(\unicode[STIX]{x1D716})].\nonumber\end{eqnarray}$$
Here
![]() $P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\in \mathbb{Q}[u_{1},\ldots ,u_{m-1},z]$
is the polynomial determined by (5.4) and (5.8).
$P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\in \mathbb{Q}[u_{1},\ldots ,u_{m-1},z]$
is the polynomial determined by (5.4) and (5.8).
Proof of Theorem 5.4.
It is obvious that
from the fact that
![]() $H_{l_{j}}$
is an even (resp. odd) function if
$H_{l_{j}}$
is an even (resp. odd) function if
![]() $l_{j}$
is even (resp. odd). Combining this with Lemma 5.5, there exists a polynomial
$l_{j}$
is even (resp. odd). Combining this with Lemma 5.5, there exists a polynomial
![]() $Q_{1}(u_{1},\ldots ,u_{m-1})$
such that
$Q_{1}(u_{1},\ldots ,u_{m-1})$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \quad =\sqrt{2\unicode[STIX]{x1D70B}}Q_{1}(u_{1},\ldots ,u_{m-1})\in \sqrt{2\unicode[STIX]{x1D70B}}\mathbb{Q}[u_{1},\ldots ,u_{m-1}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\mathop{\prod }_{j=1}^{m-1}(u_{j}/2)^{l_{j}/2}H_{l_{j}}(\sqrt{u_{j}/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & & \displaystyle \quad =\sqrt{2\unicode[STIX]{x1D70B}}Q_{1}(u_{1},\ldots ,u_{m-1})\in \sqrt{2\unicode[STIX]{x1D70B}}\mathbb{Q}[u_{1},\ldots ,u_{m-1}].\nonumber\end{eqnarray}$$
Thus, by Lemma 5.7, the coefficient
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
is contained in
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
is contained in
 $$\begin{eqnarray}\displaystyle & & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\int _{D_{m-1}}\,du(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\sqrt{2\unicode[STIX]{x1D70B}}Q_{1}(u_{1},\ldots ,u_{m-1})\times (\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\int _{D_{m-1}}\,du(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\sqrt{2\unicode[STIX]{x1D70B}}Q_{1}(u_{1},\ldots ,u_{m-1})\times (\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}.\nonumber\end{eqnarray}$$
Moreover, by Lemma 5.5, there exists a polynomial
![]() $Q_{2}(u_{1},\ldots ,u_{m-1})$
such that
$Q_{2}(u_{1},\ldots ,u_{m-1})$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \quad =\sqrt{2\unicode[STIX]{x1D70B}}Q_{2}(u_{1},\ldots ,u_{m-1})\in \sqrt{2\unicode[STIX]{x1D70B}}\mathbb{Q}[u_{1},\ldots ,u_{m-1}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{k_{m}}P_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m-1})}^{(\unicode[STIX]{x1D716})}(u_{1},\ldots ,u_{m-1};z)\,dz\nonumber\\ \displaystyle & & \displaystyle \quad =\sqrt{2\unicode[STIX]{x1D70B}}Q_{2}(u_{1},\ldots ,u_{m-1})\in \sqrt{2\unicode[STIX]{x1D70B}}\mathbb{Q}[u_{1},\ldots ,u_{m-1}].\nonumber\end{eqnarray}$$
Finally,
![]() $c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
is contained in
$c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}$
is contained in
 $$\begin{eqnarray}\displaystyle & & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\sqrt{2\unicode[STIX]{x1D70B}}^{2}\int _{D_{m-1}}(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{2}Q_{j}(u_{1},\ldots ,u_{m-1})\right\}\,du_{m-1}\cdots du_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}\nonumber\\ \displaystyle & & \displaystyle \quad \subset \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\sqrt{2\unicode[STIX]{x1D70B}}^{2}\int _{D_{m-1}}(1-u_{1}-\cdots -u_{m-1})^{k_{m}}\left(\mathop{\prod }_{j=1}^{m-1}u_{j}^{k_{j}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{\mathop{\prod }_{j=1}^{2}Q_{j}(u_{1},\ldots ,u_{m-1})\right\}\,du_{m-1}\cdots du_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}\nonumber\\ \displaystyle & & \displaystyle \quad \subset \,(\sqrt{2}g)^{k_{1}+\cdots +k_{m}+r_{2}(\unicode[STIX]{x1D716})}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\mathbb{Q}\nonumber\end{eqnarray}$$
by virtue of Lemma 5.6. Consequently, we obtain Theorem 5.4. ◻
6 Examples of Rabi–Bernoulli polynomials
It seems difficult to give a simple formula of
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for a general
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for a general
![]() $k\in \mathbb{Z}_{{\geqslant}1}$
, although we can explicitly compute it for any fixed
$k\in \mathbb{Z}_{{\geqslant}1}$
, although we can explicitly compute it for any fixed
![]() $k$
by definition. In this section, we give simple formulas of
$k$
by definition. In this section, we give simple formulas of
![]() $R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for
$R_{k}(g,\unicode[STIX]{x1D6E5};x)$
for
![]() $k\in \{1,2,3\}$
. By Proposition 5.2, the first Rabi–Bernoulli polynomial is given by
$k\in \{1,2,3\}$
. By Proposition 5.2, the first Rabi–Bernoulli polynomial is given by
![]() $R_{1}(g,\unicode[STIX]{x1D6E5};x)=x-1/2-g^{2}=B_{1}(x-g^{2})$
.
$R_{1}(g,\unicode[STIX]{x1D6E5};x)=x-1/2-g^{2}=B_{1}(x-g^{2})$
.
For preparation, we give another vanishing result on
![]() $\operatorname{Tr}K_{2,\unicode[STIX]{x1D716}}(t)$
in addition to Lemmas 4.6–4.9. By Lemma 4.8, we have
$\operatorname{Tr}K_{2,\unicode[STIX]{x1D716}}(t)$
in addition to Lemmas 4.6–4.9. By Lemma 4.8, we have
![]() $\operatorname{Tr}K_{2,3}(t)=0$
for
$\operatorname{Tr}K_{2,3}(t)=0$
for
![]() $\unicode[STIX]{x1D716}=3$
, that is,
$\unicode[STIX]{x1D716}=3$
, that is,
![]() $c_{q}^{(2,3)}=0$
for all
$c_{q}^{(2,3)}=0$
for all
![]() $q\in \mathbb{Z}_{{\geqslant}0}$
. Such a vanishing is still true for
$q\in \mathbb{Z}_{{\geqslant}0}$
. Such a vanishing is still true for
![]() $\unicode[STIX]{x1D716}\in \{1,2\}$
.
$\unicode[STIX]{x1D716}\in \{1,2\}$
.
Lemma 6.1. We have
![]() $\operatorname{Tr}K_{2,1}(t)=0$
and
$\operatorname{Tr}K_{2,1}(t)=0$
and
![]() $\operatorname{Tr}K_{2,2}(t)=0.$
In particular, we have
$\operatorname{Tr}K_{2,2}(t)=0.$
In particular, we have
![]() $c_{q}^{(2,1)}=c_{q}^{(2,2)}=0$
for any
$c_{q}^{(2,1)}=c_{q}^{(2,2)}=0$
for any
![]() $q\in \mathbb{Z}_{{\geqslant}0}$
. In particular,
$q\in \mathbb{Z}_{{\geqslant}0}$
. In particular,
![]() $\operatorname{Tr}K_{2}(t)=\operatorname{Tr}K_{2,4}(t)$
holds.
$\operatorname{Tr}K_{2}(t)=\operatorname{Tr}K_{2,4}(t)$
holds.
Proof. We give a proof only in the case
![]() $\unicode[STIX]{x1D716}=1$
. The case
$\unicode[STIX]{x1D716}=1$
. The case
![]() $\unicode[STIX]{x1D716}=2$
is proved in a similar fashion. By using Lemmas 3.4 and 3.5, the trace of
$\unicode[STIX]{x1D716}=2$
is proved in a similar fashion. By using Lemmas 3.4 and 3.5, the trace of
![]() $K_{2,1}(t)$
is evaluated as
$K_{2,1}(t)$
is evaluated as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{2,1}(t)=\int _{0}^{t}\,du\int _{(z_{0},z_{1})\in \mathbb{R}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{tr}\left[\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}(t-u)}}e^{-(z_{0}-z_{1})^{2}/2(t-u)-(t-u)z_{1}^{2}/2}\exp (-\sqrt{2}g(t-u)z_{1}W)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \times \left.\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}u}}\frac{z_{0}^{2}-z_{1}^{2}}{2}e^{-(z_{1}-z_{0})^{2}/2u-uz_{0}^{2}/2}\exp (-\sqrt{2}guz_{0}W)\right]dz_{0}\,dz_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Tr}K_{2,1}(t)=\int _{0}^{t}\,du\int _{(z_{0},z_{1})\in \mathbb{R}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\operatorname{tr}\left[\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}(t-u)}}e^{-(z_{0}-z_{1})^{2}/2(t-u)-(t-u)z_{1}^{2}/2}\exp (-\sqrt{2}g(t-u)z_{1}W)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \times \left.\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}u}}\frac{z_{0}^{2}-z_{1}^{2}}{2}e^{-(z_{1}-z_{0})^{2}/2u-uz_{0}^{2}/2}\exp (-\sqrt{2}guz_{0}W)\right]dz_{0}\,dz_{1}.\nonumber\end{eqnarray}$$
By the change of variables
![]() $(z_{0},z_{1})\mapsto (z_{1},z_{0})$
and
$(z_{0},z_{1})\mapsto (z_{1},z_{0})$
and
![]() $u\mapsto t-u$
, we obtain
$u\mapsto t-u$
, we obtain
![]() $\operatorname{Tr}K_{2,1}(t)=-\operatorname{Tr}K_{2,1}(t)$
. This completes the proof.◻
$\operatorname{Tr}K_{2,1}(t)=-\operatorname{Tr}K_{2,1}(t)$
. This completes the proof.◻
A simple formula for
![]() $k=2$
is given by a direct computation as follows.
$k=2$
is given by a direct computation as follows.
Proposition 6.2. We have
Proof. We shall compute
![]() $C_{H,\unicode[STIX]{x1D70F}}(1)=c_{1}^{(2)}+c_{1}^{(3)}$
. First, we observe the first term
$C_{H,\unicode[STIX]{x1D70F}}(1)=c_{1}^{(2)}+c_{1}^{(3)}$
. First, we observe the first term
![]() $c_{1}^{(2)}=\sum _{\unicode[STIX]{x1D716}=1}^{4}c_{1}^{(2,\unicode[STIX]{x1D716})}$
. By (4.7), we have
$c_{1}^{(2)}=\sum _{\unicode[STIX]{x1D716}=1}^{4}c_{1}^{(2,\unicode[STIX]{x1D716})}$
. By (4.7), we have
 $$\begin{eqnarray}c_{1}^{(2,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ (l_{1},k_{1},k_{2})\in \mathbb{Z}_{{\geqslant}0}^{3} \\ l_{1}+(1/2)(k_{1}+k_{2})-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=1}}c_{l_{1},(k_{1},k_{2})}^{(2,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
$$\begin{eqnarray}c_{1}^{(2,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ (l_{1},k_{1},k_{2})\in \mathbb{Z}_{{\geqslant}0}^{3} \\ l_{1}+(1/2)(k_{1}+k_{2})-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=1}}c_{l_{1},(k_{1},k_{2})}^{(2,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
In the case of
![]() $\unicode[STIX]{x1D716}\in \{1,2\}$
, both values
$\unicode[STIX]{x1D716}\in \{1,2\}$
, both values
![]() $c_{1}^{(2,1)}$
and
$c_{1}^{(2,1)}$
and
![]() $c_{1}^{(2,2)}$
vanish by Lemma 6.1. For
$c_{1}^{(2,2)}$
vanish by Lemma 6.1. For
![]() $\unicode[STIX]{x1D716}=3$
, we have
$\unicode[STIX]{x1D716}=3$
, we have
![]() $c_{l_{1},(k_{1},k_{2})}^{(2,3)}=0$
by Lemma 4.8. For
$c_{l_{1},(k_{1},k_{2})}^{(2,3)}=0$
by Lemma 4.8. For
![]() $\unicode[STIX]{x1D716}=4$
, the integer
$\unicode[STIX]{x1D716}=4$
, the integer
![]() $l_{1}$
in
$l_{1}$
in
![]() $c_{l_{1},(k_{1},k_{2})}^{(2,4)}$
satisfies
$c_{l_{1},(k_{1},k_{2})}^{(2,4)}$
satisfies
![]() $l_{1}\in \{0,1\}$
. In the case of
$l_{1}\in \{0,1\}$
. In the case of
![]() $l_{1}=1$
, the value
$l_{1}=1$
, the value
![]() $c_{1,(k_{1},k_{2})}^{(2,4)}$
vanishes by Lemma 4.6. When
$c_{1,(k_{1},k_{2})}^{(2,4)}$
vanishes by Lemma 4.6. When
![]() $l_{1}=0$
, by noting
$l_{1}=0$
, by noting
![]() $k_{1}+k_{2}=2$
, we have
$k_{1}+k_{2}=2$
, we have
 $$\begin{eqnarray}\displaystyle c_{0,(k_{1},k_{2})}^{(2,4)} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!}\int _{0}^{1}\,du\int _{z_{0}\in \mathbb{R}}e^{-z_{0}^{2}/2}z_{0}^{2}\,dz_{0}\{-\sqrt{2}g(1-u)\}^{k_{2}}(-\sqrt{2}gu)^{k_{1}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{k_{1}!k_{2}!}B(k_{1}+1,k_{2}+1)2g^{2}(1-2\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(k_{1}+k_{2}+1)!}2g^{2}(1-2\unicode[STIX]{x1D70F})=\frac{1}{3}g^{2}(1-2\unicode[STIX]{x1D70F}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{0,(k_{1},k_{2})}^{(2,4)} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!}\int _{0}^{1}\,du\int _{z_{0}\in \mathbb{R}}e^{-z_{0}^{2}/2}z_{0}^{2}\,dz_{0}\{-\sqrt{2}g(1-u)\}^{k_{2}}(-\sqrt{2}gu)^{k_{1}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{k_{1}!k_{2}!}B(k_{1}+1,k_{2}+1)2g^{2}(1-2\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(k_{1}+k_{2}+1)!}2g^{2}(1-2\unicode[STIX]{x1D70F})=\frac{1}{3}g^{2}(1-2\unicode[STIX]{x1D70F}),\nonumber\end{eqnarray}$$
which leads us to
![]() $c_{1}^{(2,4)}=c_{0,(0,2)}^{(2,4)}+c_{0,(1,1)}^{(2,4)}+c_{0,(2,0)}^{(2,4)}=g^{2}(1-2\unicode[STIX]{x1D70F})$
. By the argument as above, we finally obtain
$c_{1}^{(2,4)}=c_{0,(0,2)}^{(2,4)}+c_{0,(1,1)}^{(2,4)}+c_{0,(2,0)}^{(2,4)}=g^{2}(1-2\unicode[STIX]{x1D70F})$
. By the argument as above, we finally obtain
Next let us consider the case
![]() $m=3$
. In this case, with the aid of Lemmas 4.6–4.8 and (4.7), only the following cases survive among all
$m=3$
. In this case, with the aid of Lemmas 4.6–4.8 and (4.7), only the following cases survive among all
![]() $c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,\unicode[STIX]{x1D716})}$
such that
$c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,\unicode[STIX]{x1D716})}$
such that
![]() $l_{1}+l_{2}+\frac{k_{1}+k_{2}+k_{3}}{2}-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})=0$
:
$l_{1}+l_{2}+\frac{k_{1}+k_{2}+k_{3}}{2}-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})=0$
:
-
(1)
 $\unicode[STIX]{x1D716}\in \{(3,3),(4,4)\}$
and
$\unicode[STIX]{x1D716}\in \{(3,3),(4,4)\}$
and
 $l_{1}=l_{2}=k_{1}=k_{2}=k_{3}=0$
.
$l_{1}=l_{2}=k_{1}=k_{2}=k_{3}=0$
. -
(2)
 $\unicode[STIX]{x1D716}=(1,1)$
,
$\unicode[STIX]{x1D716}=(1,1)$
,
 $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
 $k_{1}=k_{2}=k_{3}=0$
.
$k_{1}=k_{2}=k_{3}=0$
.
In case (1), the coefficient involved is evaluated as
 $$\begin{eqnarray}\displaystyle c_{(0,0),(0,0,0)}^{(3,\unicode[STIX]{x1D716})} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\int _{0}^{1}\,du_{1}\int _{0}^{1-u_{1}}\,du_{2}\int _{z_{0}\in \mathbb{R}}e^{-z_{0}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(0,0),(0,0,0)}^{(3,\unicode[STIX]{x1D716})} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}\int _{0}^{1}\,du_{1}\int _{0}^{1-u_{1}}\,du_{2}\int _{z_{0}\in \mathbb{R}}e^{-z_{0}^{2}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}.\nonumber\end{eqnarray}$$
In case (2), we have
![]() $P_{(1,1),(0,0)}^{3,(1,1)}(u_{1},u_{2};z)=z^{2}$
by (5.4) and (5.6). Thus, Lemma 5.7 yields
$P_{(1,1),(0,0)}^{3,(1,1)}(u_{1},u_{2};z)=z^{2}$
by (5.4) and (5.6). Thus, Lemma 5.7 yields
 $$\begin{eqnarray}\displaystyle c_{(1,1),(0,0,0)}^{(3,(1,1))} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{0}^{1}\,du_{1}\int _{0}^{1-u_{1}}\,du_{2}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}\operatorname{tr}(I)=-1/12\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(1,1),(0,0,0)}^{(3,(1,1))} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{0}^{1}\,du_{1}\int _{0}^{1-u_{1}}\,du_{2}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}\operatorname{tr}(I)=-1/12\nonumber\end{eqnarray}$$
with the aid of (5.2). Hence,
holds. As a consequence, we obtain the desired assertion by (6.1) and (6.2).◻
Next let us compute the third Rabi–Bernoulli polynomial
![]() $R_{3}(g,\unicode[STIX]{x1D6E5};x)$
. By definition,
$R_{3}(g,\unicode[STIX]{x1D6E5};x)$
. By definition,
![]() $R_{3}(g,\unicode[STIX]{x1D6E5};\unicode[STIX]{x1D70F})=-g^{6}-3C_{H,\unicode[STIX]{x1D70F}}(2)$
and
$R_{3}(g,\unicode[STIX]{x1D6E5};\unicode[STIX]{x1D70F})=-g^{6}-3C_{H,\unicode[STIX]{x1D70F}}(2)$
and
![]() $C_{H,\unicode[STIX]{x1D70F}}(2)=c_{2}^{(2)}+c_{2}^{(3)}+c_{2}^{(4)}$
hold with
$C_{H,\unicode[STIX]{x1D70F}}(2)=c_{2}^{(2)}+c_{2}^{(3)}+c_{2}^{(4)}$
hold with
and
 $$\begin{eqnarray}c_{2}^{(m,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m}\in \mathbb{Z}_{{\geqslant}0} \\ l_{1}+\cdots +l_{m-1}+(k_{1}+\cdots +k_{m})/2+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=2}}c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{(m,\unicode[STIX]{x1D716})}=\mathop{\sum }_{\substack{ l_{1},\ldots ,l_{m-1},k_{1},\ldots ,k_{m}\in \mathbb{Z}_{{\geqslant}0} \\ l_{1}+\cdots +l_{m-1}+(k_{1}+\cdots +k_{m})/2+m-2-r_{1}(\unicode[STIX]{x1D716})-(1/2)r_{2}(\unicode[STIX]{x1D716})=2}}c_{(l_{1},\ldots ,l_{m-1}),(k_{1},\ldots ,k_{m})}^{(m,\unicode[STIX]{x1D716})}.\end{eqnarray}$$
Lemma 6.3. We have
Proof. By Lemmas 4.8 and 6.1, we easily have
![]() $c_{2}^{(2,\unicode[STIX]{x1D716})}=0$
for any
$c_{2}^{(2,\unicode[STIX]{x1D716})}=0$
for any
![]() $\unicode[STIX]{x1D716}\in \{1,2,3\}$
. When
$\unicode[STIX]{x1D716}\in \{1,2,3\}$
. When
![]() $\unicode[STIX]{x1D716}=4$
, by Lemma 4.6,
$\unicode[STIX]{x1D716}=4$
, by Lemma 4.6,
![]() $(l_{1},k_{1},k_{2})$
in
$(l_{1},k_{1},k_{2})$
in
![]() $c_{l_{1},(k_{1},k_{2})}^{(2,4)}\neq 0$
satisfies
$c_{l_{1},(k_{1},k_{2})}^{(2,4)}\neq 0$
satisfies
![]() $l_{1}\in \{0,2\}$
and
$l_{1}\in \{0,2\}$
and
![]() $k_{1}+k_{2}=4-2l_{1}$
. If
$k_{1}+k_{2}=4-2l_{1}$
. If
![]() $l_{1}=0$
and
$l_{1}=0$
and
![]() $k_{1}+k_{2}=4$
, we have
$k_{1}+k_{2}=4$
, we have
 $$\begin{eqnarray}\displaystyle c_{0,(k_{1},k_{2})}^{(2,4)} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!}\int _{0}^{1}\,du(1-u)^{k_{2}}u^{k_{1}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{4}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{4}(-1)^{4}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{g^{4}}{5}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{0,(k_{1},k_{2})}^{(2,4)} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!}\int _{0}^{1}\,du(1-u)^{k_{2}}u^{k_{1}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{4}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{4}(-1)^{4}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{g^{4}}{5}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\nonumber\end{eqnarray}$$
If
![]() $l_{1}=2$
and
$l_{1}=2$
and
![]() $k_{1}=k_{2}=0$
, we have
$k_{1}=k_{2}=0$
, we have
 $$\begin{eqnarray}\displaystyle c_{2,(0,0)}^{(2,4)} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{0}^{1}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}P_{2,0}^{(4)}(u;z)\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}(u/2)H_{2}(\sqrt{u/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{30}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{2,(0,0)}^{(2,4)} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{0}^{1}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}P_{2,0}^{(4)}(u;z)\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}(u/2)H_{2}(\sqrt{u/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{30}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right),\nonumber\end{eqnarray}$$
where we use
![]() $P_{2,0}^{(4)}(u;z)=(u/2)H_{2}(\sqrt{u/2}z)=u(uz^{2}-1)$
. Hence we obtain
$P_{2,0}^{(4)}(u;z)=(u/2)H_{2}(\sqrt{u/2}z)=u(uz^{2}-1)$
. Hence we obtain
 $$\begin{eqnarray}\displaystyle c_{2}^{(2,4)}=\mathop{\sum }_{\substack{ k_{1},k_{2}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}=4}}\frac{g^{4}}{5}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)-\frac{1}{30}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)=\left(g^{4}-\frac{1}{30}\right)\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\square & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{2}^{(2,4)}=\mathop{\sum }_{\substack{ k_{1},k_{2}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}=4}}\frac{g^{4}}{5}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)-\frac{1}{30}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)=\left(g^{4}-\frac{1}{30}\right)\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\square & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 6.4. We have
Proof. We give a proof by computing
![]() $c_{2}^{(3,\unicode[STIX]{x1D716})}$
for all
$c_{2}^{(3,\unicode[STIX]{x1D716})}$
for all
![]() $\unicode[STIX]{x1D716}$
. By Lemma 4.8, we only have to consider the cases
$\unicode[STIX]{x1D716}$
. By Lemma 4.8, we only have to consider the cases
![]() $\unicode[STIX]{x1D716}=(1,1)$
,
$\unicode[STIX]{x1D716}=(1,1)$
,
![]() $(1,2)$
,
$(1,2)$
,
![]() $(1,4)$
,
$(1,4)$
,
![]() $(2,1)$
,
$(2,1)$
,
![]() $(2,2)$
,
$(2,2)$
,
![]() $(2,4)$
,
$(2,4)$
,
![]() $(3,3)$
,
$(3,3)$
,
![]() $(4,1)$
,
$(4,1)$
,
![]() $(4,2)$
,
$(4,2)$
,
![]() $(4,4)$
. We shall give expressions of all
$(4,4)$
. We shall give expressions of all
![]() $c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,\unicode[STIX]{x1D716})}$
such that
$c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,\unicode[STIX]{x1D716})}$
such that
![]() $l_{1}+l_{2}+\frac{k_{1}+k_{2}+k_{3}}{2}+1-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})=2$
in the following way.
$l_{1}+l_{2}+\frac{k_{1}+k_{2}+k_{3}}{2}+1-r_{1}(\unicode[STIX]{x1D716})-\frac{1}{2}r_{2}(\unicode[STIX]{x1D716})=2$
in the following way.
For
![]() $\unicode[STIX]{x1D716}=(1,1)$
, we may assume
$\unicode[STIX]{x1D716}=(1,1)$
, we may assume
![]() $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
![]() $k_{1}+k_{2}+k_{3}=2$
by Lemmas 4.6 and 4.9, and thus we compute
$k_{1}+k_{2}+k_{3}=2$
by Lemmas 4.6 and 4.9, and thus we compute
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(1,1))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{4}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{(k_{1}+1)(k_{2}+1)}{60}g^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(1,1))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{4}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{(k_{1}+1)(k_{2}+1)}{60}g^{2}.\nonumber\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}c_{2}^{(3,(1,1))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=2}}\frac{-(k_{1}+1)(k_{2}+1)}{60}g^{2}=-\frac{1}{4}g^{2}.\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{(3,(1,1))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=2}}\frac{-(k_{1}+1)(k_{2}+1)}{60}g^{2}=-\frac{1}{4}g^{2}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}=(1,2)$
, the numbers
$\unicode[STIX]{x1D716}=(1,2)$
, the numbers
![]() $(l_{1},l_{2})$
and
$(l_{1},l_{2})$
and
![]() $(k_{1},k_{2},k_{3})$
satisfy
$(k_{1},k_{2},k_{3})$
satisfy
![]() $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
![]() $k_{1}+k_{2}+k_{3}=1$
by Lemmas 4.6 and 4.9. Then, we have
$k_{1}+k_{2}+k_{3}=1$
by Lemmas 4.6 and 4.9. Then, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(1,2))}\nonumber\\ \displaystyle & & \displaystyle \quad =(2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(-1)^{1}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(1,2))}\nonumber\\ \displaystyle & & \displaystyle \quad =(2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(-1)^{1}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}\nonumber\end{eqnarray}$$
with the aid of
![]() $P_{(1,1),(k_{1},k_{2})}^{(2,1)}(u_{1},u_{2};z_{2})=z_{2}^{k_{1}+k_{2}+1}$
. Hence we obtain
$P_{(1,1),(k_{1},k_{2})}^{(2,1)}(u_{1},u_{2};z_{2})=z_{2}^{k_{1}+k_{2}+1}$
. Hence we obtain
 $$\begin{eqnarray}c_{2}^{(3,(1,2))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=1}}\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}=\frac{1}{6}g^{2}.\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{(3,(1,2))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=1}}\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}=\frac{1}{6}g^{2}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}=(1,4)$
, we may assume
$\unicode[STIX]{x1D716}=(1,4)$
, we may assume
![]() $(l_{1},l_{2})$
and
$(l_{1},l_{2})$
and
![]() $(k_{1},k_{2},k_{3})$
satisfy
$(k_{1},k_{2},k_{3})$
satisfy
![]() $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
![]() $(k_{1},k_{2},k_{3})=\mathbf{0}_{3}$
by Lemmas 4.6 and 4.9. By noting
$(k_{1},k_{2},k_{3})=\mathbf{0}_{3}$
by Lemmas 4.6 and 4.9. By noting
![]() $P_{(1,1),\mathbf{0}_{2}}^{(1,4)}(u_{1},u_{2};z_{2})=1-(u_{1}+u_{2})z_{2}^{2}$
and
$P_{(1,1),\mathbf{0}_{2}}^{(1,4)}(u_{1},u_{2};z_{2})=1-(u_{1}+u_{2})z_{2}^{2}$
and
![]() $P_{(2,0),\mathbf{0}_{2}}^{(1,4)}(u_{1},u_{2};z_{2})=1-2u_{1}z_{2}^{2}$
, we have
$P_{(2,0),\mathbf{0}_{2}}^{(1,4)}(u_{1},u_{2};z_{2})=1-2u_{1}z_{2}^{2}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(1,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(1-u_{1}z^{2}-u_{2}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=-\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(1,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(1-u_{1}z^{2}-u_{2}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=-\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(2,0),\mathbf{0}_{3}}^{(3,(1,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(1-2u_{1}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(2,0),\mathbf{0}_{3}}^{(3,(1,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(1-2u_{1}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right).\nonumber\end{eqnarray}$$
Hence we obtain
![]() $c_{2}^{(3,(1,4))}=0$
.
$c_{2}^{(3,(1,4))}=0$
.
For
![]() $\unicode[STIX]{x1D716}=(2,1)$
, we may assume
$\unicode[STIX]{x1D716}=(2,1)$
, we may assume
![]() $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
![]() $k_{1}+k_{2}+k_{3}=1$
by Lemmas 4.6 and 4.9. By a direct computation, we have
$k_{1}+k_{2}+k_{3}=1$
by Lemmas 4.6 and 4.9. By a direct computation, we have
 $$\begin{eqnarray}\displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(2,1))} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(-1)(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}+1)(k_{2}+1)}{30}g^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(1,1),(k_{1},k_{2},k_{3})}^{(3,(2,1))} & = & \displaystyle (2\unicode[STIX]{x1D70B})^{-1}i^{2}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(-1)(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}+1)(k_{2}+1)}{30}g^{2},\nonumber\end{eqnarray}$$
and hence we obtain
 $$\begin{eqnarray}c_{2}^{3,(2,1)}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=1}}\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}=\frac{1}{6}g^{2}.\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{3,(2,1)}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=1}}\frac{(k_{1}+1)(k_{2}+1)}{30}g^{2}=\frac{1}{6}g^{2}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}=(2,2)$
, we may assume
$\unicode[STIX]{x1D716}=(2,2)$
, we may assume
![]() $l_{1}=l_{2}=1$
and
$l_{1}=l_{2}=1$
and
![]() $k_{1}=k_{2}=k_{3}=0$
by Lemmas 4.6 and 4.9. Noting
$k_{1}=k_{2}=k_{3}=0$
by Lemmas 4.6 and 4.9. Noting
![]() $P_{(1,1),(0,0)}^{(2,2)}(u_{1},u_{2};z)=1$
, we obtain
$P_{(1,1),(0,0)}^{(2,2)}(u_{1},u_{2};z)=1$
, we obtain
 $$\begin{eqnarray}\displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(2,2))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{6}g^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(2,2))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{6}g^{2}.\nonumber\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}=(2,4)$
, all
$\unicode[STIX]{x1D716}=(2,4)$
, all
![]() $c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,(2,4))}$
concerned vanish by Lemmas 4.6 and 4.9.
$c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,(2,4))}$
concerned vanish by Lemmas 4.6 and 4.9.
For
![]() $\unicode[STIX]{x1D716}=(3,3)$
, we may assume
$\unicode[STIX]{x1D716}=(3,3)$
, we may assume
![]() $l_{1}=l_{2}=0$
and
$l_{1}=l_{2}=0$
and
![]() $k_{1}+k_{2}+k_{3}=2$
. Then we have
$k_{1}+k_{2}+k_{3}=2$
. Then we have
 $$\begin{eqnarray}\displaystyle c_{(0,0),(k_{1},k_{2},k_{3})}^{(3,(3,3))} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\left\{\mathop{\prod }_{j=1}^{2}(-1)^{\unicode[STIX]{x1D714}_{(3,3)}(j)k_{j}}\right\}(\sqrt{2}g)^{2}\unicode[STIX]{x1D6E5}^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{6}g^{2}\unicode[STIX]{x1D6E5}^{2}(-1)^{k_{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(0,0),(k_{1},k_{2},k_{3})}^{(3,(3,3))} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\left\{\mathop{\prod }_{j=1}^{2}(-1)^{\unicode[STIX]{x1D714}_{(3,3)}(j)k_{j}}\right\}(\sqrt{2}g)^{2}\unicode[STIX]{x1D6E5}^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{6}g^{2}\unicode[STIX]{x1D6E5}^{2}(-1)^{k_{2}},\nonumber\end{eqnarray}$$
and hence we obtain
 $$\begin{eqnarray}c_{2}^{(3,(3,3))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=2}}\frac{1}{6}(-1)^{k_{2}}g^{2}\unicode[STIX]{x1D6E5}^{2}=\frac{1}{3}g^{2}\unicode[STIX]{x1D6E5}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{(3,(3,3))}=\mathop{\sum }_{\substack{ k_{1},k_{2},k_{3}\in \mathbb{Z}_{{\geqslant}0} \\ k_{1}+k_{2}+k_{3}=2}}\frac{1}{6}(-1)^{k_{2}}g^{2}\unicode[STIX]{x1D6E5}^{2}=\frac{1}{3}g^{2}\unicode[STIX]{x1D6E5}^{2}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D716}=(4,1)$
, we may assume
$\unicode[STIX]{x1D716}=(4,1)$
, we may assume
![]() $l_{1}+l_{2}=2$
and
$l_{1}+l_{2}=2$
and
![]() $(k_{1},k_{2},k_{3})=\mathbf{0}_{3}$
by Lemma 4.6. Furthermore, we may assume
$(k_{1},k_{2},k_{3})=\mathbf{0}_{3}$
by Lemma 4.6. Furthermore, we may assume
![]() $l_{2}\neq 0$
by Lemma 4.9. Then, a direct computation gives us
$l_{2}\neq 0$
by Lemma 4.9. Then, a direct computation gives us
 $$\begin{eqnarray}\displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(4,1))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(-u_{1}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=\frac{1}{30}(1/2-\unicode[STIX]{x1D70F})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(1,1),\mathbf{0}_{3}}^{(3,(4,1))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}(-u_{1}z^{2})\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)=\frac{1}{30}(1/2-\unicode[STIX]{x1D70F})\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle c_{(0,2),\mathbf{0}_{3}}^{(3,(4,1))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\{1-2(u_{1}+u_{2})z^{2}\}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}(u_{2}/2)H_{2}(\sqrt{u_{2}/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{30}(1/2-\unicode[STIX]{x1D70F}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(0,2),\mathbf{0}_{3}}^{(3,(4,1))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}2!}\int _{D_{2}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\{1-2(u_{1}+u_{2})z^{2}\}\,dz\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}(u_{2}/2)H_{2}(\sqrt{u_{2}/2}\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{30}(1/2-\unicode[STIX]{x1D70F}),\nonumber\end{eqnarray}$$
and hence we obtain
![]() $c_{2}^{(3,(4,1))}=0$
. For
$c_{2}^{(3,(4,1))}=0$
. For
![]() $\unicode[STIX]{x1D716}=(4,2)$
, all
$\unicode[STIX]{x1D716}=(4,2)$
, all
![]() $c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,(4,2))}$
concerned vanish in the same way as in the case
$c_{(l_{1},l_{2}),(k_{1},k_{2},k_{3})}^{(3,(4,2))}$
concerned vanish in the same way as in the case
![]() $\unicode[STIX]{x1D716}=(2,4)$
. For
$\unicode[STIX]{x1D716}=(2,4)$
. For
![]() $\unicode[STIX]{x1D716}=(4,4)$
, we may assume
$\unicode[STIX]{x1D716}=(4,4)$
, we may assume
![]() $l_{1}=l_{2}=0$
and
$l_{1}=l_{2}=0$
and
![]() $k_{1}+k_{2}+k_{3}=2$
by Lemma 4.6, and a direct computation gives us
$k_{1}+k_{2}+k_{3}=2$
by Lemma 4.6, and a direct computation gives us
 $$\begin{eqnarray}\displaystyle & & \displaystyle c_{(0,0),(k_{1},k_{2},k_{3})}^{(3,(4,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}(1/2-\unicode[STIX]{x1D70F})^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{6}g^{2}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle c_{(0,0),(k_{1},k_{2},k_{3})}^{(3,(4,4))}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}k_{1}!k_{2}!k_{3}!}\int _{D_{2}}\,du(1-u_{1}-u_{2})^{k_{3}}u_{1}^{k_{1}}u_{2}^{k_{2}}\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}(\sqrt{2}g)^{2}(1/2-\unicode[STIX]{x1D70F})^{2}\operatorname{tr}(I)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{6}g^{2}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)^{2}.\nonumber\end{eqnarray}$$
Thus we have
![]() $c_{2}^{(3,(4,4))}=g^{2}(1/2-\unicode[STIX]{x1D70F})^{2}$
.
$c_{2}^{(3,(4,4))}=g^{2}(1/2-\unicode[STIX]{x1D70F})^{2}$
.
Finally, by the consideration as above, we obtain the formula as desired. ◻
Lemma 6.5. We have
Proof. Consider
![]() $c_{(l_{1},l_{2},l_{3}),(k_{1},k_{2},k_{3},k_{4})}^{(4,\unicode[STIX]{x1D716})}$
. We may assume
$c_{(l_{1},l_{2},l_{3}),(k_{1},k_{2},k_{3},k_{4})}^{(4,\unicode[STIX]{x1D716})}$
. We may assume
![]() $r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})=0$
, by which
$r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})=0$
, by which
![]() $\unicode[STIX]{x1D716}\in \{3,4\}^{3}$
holds, and also that
$\unicode[STIX]{x1D716}\in \{3,4\}^{3}$
holds, and also that
![]() $r_{3}(\unicode[STIX]{x1D716})$
is even by Lemma 4.8. A direct computation gives us
$r_{3}(\unicode[STIX]{x1D716})$
is even by Lemma 4.8. A direct computation gives us
 $$\begin{eqnarray}\displaystyle c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,\unicode[STIX]{x1D716})} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}}\int _{D_{3}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}A(\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{3}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)^{r_{4}(\unicode[STIX]{x1D716})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,\unicode[STIX]{x1D716})} & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}}\int _{D_{3}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}\,d\unicode[STIX]{x1D709}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}(1/2-\unicode[STIX]{x1D70F})^{r_{4}(\unicode[STIX]{x1D716})}\operatorname{tr}A(\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{3}\unicode[STIX]{x1D6E5}^{r_{3}(\unicode[STIX]{x1D716})}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)^{r_{4}(\unicode[STIX]{x1D716})}.\nonumber\end{eqnarray}$$
Thus we obtain
![]() $c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(4,4,4))}=\frac{1}{3}(\frac{1}{2}-\unicode[STIX]{x1D70F})^{3}$
and
$c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(4,4,4))}=\frac{1}{3}(\frac{1}{2}-\unicode[STIX]{x1D70F})^{3}$
and
![]() $c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(4,3,3))}=c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(3,4,3))}=c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(3,3,4))}=\frac{1}{3}\unicode[STIX]{x1D6E5}^{2}(\frac{1}{2}-\unicode[STIX]{x1D70F}).$
If
$c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(4,3,3))}=c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(3,4,3))}=c_{\mathbf{0}_{3},\mathbf{0}_{4}}^{(4,(3,3,4))}=\frac{1}{3}\unicode[STIX]{x1D6E5}^{2}(\frac{1}{2}-\unicode[STIX]{x1D70F}).$
If
![]() $r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})\in \{1,3\}$
, then all
$r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})\in \{1,3\}$
, then all
![]() $c_{(l_{1},l_{2},l_{3}),(k_{1},k_{2},k_{3},k_{4})}^{(4,\unicode[STIX]{x1D716})}$
vanish by Lemmas 4.6 and 4.9. If
$c_{(l_{1},l_{2},l_{3}),(k_{1},k_{2},k_{3},k_{4})}^{(4,\unicode[STIX]{x1D716})}$
vanish by Lemmas 4.6 and 4.9. If
![]() $r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})=2$
, the only case
$r_{1}(\unicode[STIX]{x1D716})+r_{2}(\unicode[STIX]{x1D716})=2$
, the only case
![]() $r_{1}(\unicode[STIX]{x1D716})=2$
,
$r_{1}(\unicode[STIX]{x1D716})=2$
,
![]() $r_{2}(\unicode[STIX]{x1D716})=0$
survives, and in such a case, by Lemmas 4.6 and 4.9, it is sufficient to consider the only case
$r_{2}(\unicode[STIX]{x1D716})=0$
survives, and in such a case, by Lemmas 4.6 and 4.9, it is sufficient to consider the only case
![]() $((l_{1},l_{2},l_{3}),\unicode[STIX]{x1D716})\in \{((1,1,0),(1,1,4)),((1,0,1),(1,4,1)),((0,1,1),(4,1,1))\}$
and
$((l_{1},l_{2},l_{3}),\unicode[STIX]{x1D716})\in \{((1,1,0),(1,1,4)),((1,0,1),(1,4,1)),((0,1,1),(4,1,1))\}$
and
![]() $(k_{1},k_{2},k_{3},k_{4})=\mathbf{0}_{4}$
. A direct computation gives us
$(k_{1},k_{2},k_{3},k_{4})=\mathbf{0}_{4}$
. A direct computation gives us
 $$\begin{eqnarray}\displaystyle c_{(1,1,0),\mathbf{0}_{4}}^{(4,(1,1,4))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{3}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{(1,1,0),\mathbf{0}_{4}}^{(4,(1,1,4))} & = & \displaystyle \frac{i^{2}}{2\unicode[STIX]{x1D70B}}\int _{D_{3}}\,du\int _{z\in \mathbb{R}}e^{-z^{2}/2}z^{2}\,dz\int _{\unicode[STIX]{x1D709}\in \mathbb{R}}e^{-\unicode[STIX]{x1D709}^{2}/2}u_{1}u_{2}\unicode[STIX]{x1D709}^{2}\,d\unicode[STIX]{x1D709}(1/2-\unicode[STIX]{x1D70F})\operatorname{tr}(I)\nonumber\\ \displaystyle & = & \displaystyle -\,\frac{1}{60}\left(\frac{1}{2}-\unicode[STIX]{x1D70F}\right)\nonumber\end{eqnarray}$$
with the aid of
![]() $P_{(1,1,0),\mathbf{0}_{3}}^{(1,1,4)}(u_{1},u_{2},u_{3};z)=z^{2}$
, and in a similar fashion, we obtain
$P_{(1,1,0),\mathbf{0}_{3}}^{(1,1,4)}(u_{1},u_{2},u_{3};z)=z^{2}$
, and in a similar fashion, we obtain
![]() $c_{(1,0,1),\mathbf{0}_{4}}^{(4,(1,4,1))}=c_{(0,1,1),\mathbf{0}_{4}}^{(4,(4,1,1))}=-\frac{1}{60}(\frac{1}{2}-\unicode[STIX]{x1D70F}).$
Finally, we have the formula as desired.◻
$c_{(1,0,1),\mathbf{0}_{4}}^{(4,(1,4,1))}=c_{(0,1,1),\mathbf{0}_{4}}^{(4,(4,1,1))}=-\frac{1}{60}(\frac{1}{2}-\unicode[STIX]{x1D70F}).$
Finally, we have the formula as desired.◻
Proposition 6.6. We have
 $$\begin{eqnarray}\displaystyle R_{3}(g,\unicode[STIX]{x1D6E5};x) & = & \displaystyle x^{3}-\left(3g^{2}+\frac{3}{2}\right)x^{2}+\left(3g^{4}+3g^{2}+3\unicode[STIX]{x1D6E5}^{2}+\frac{1}{2}\right)x-g^{6}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3}{2}g^{4}-\frac{1}{2}g^{2}-\frac{3}{2}\unicode[STIX]{x1D6E5}^{2}-g^{2}\unicode[STIX]{x1D6E5}^{2}\nonumber\\ \displaystyle & = & \displaystyle B_{3}(x-g^{2})+3\unicode[STIX]{x1D6E5}^{2}B_{1}(x-g^{2})+2g^{2}\unicode[STIX]{x1D6E5}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{3}(g,\unicode[STIX]{x1D6E5};x) & = & \displaystyle x^{3}-\left(3g^{2}+\frac{3}{2}\right)x^{2}+\left(3g^{4}+3g^{2}+3\unicode[STIX]{x1D6E5}^{2}+\frac{1}{2}\right)x-g^{6}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3}{2}g^{4}-\frac{1}{2}g^{2}-\frac{3}{2}\unicode[STIX]{x1D6E5}^{2}-g^{2}\unicode[STIX]{x1D6E5}^{2}\nonumber\\ \displaystyle & = & \displaystyle B_{3}(x-g^{2})+3\unicode[STIX]{x1D6E5}^{2}B_{1}(x-g^{2})+2g^{2}\unicode[STIX]{x1D6E5}^{2}.\nonumber\end{eqnarray}$$
Acknowledgments
The author would like to thank Professor Masato Wakayama for giving him the interest in spectral zeta functions and the quantum Rabi models, and a lot of useful comments and suggestions. He would also like to thank Professor Kazufumi Kimoto for fruitful discussion and for informing him about papers [Reference Kimoto, van Dijk and Wakayama11] and [Reference Kimoto, Wakayama, Dito, Moriyoshi, Natsume and Watamura14], and preprints [Reference Kimoto10] and [Reference Kimoto and Wakayama15]. Thanks are also due to Professor Yoshinori Yamasaki for useful comments and careful reading of the earlier draft. The author would like to thank Cid Reyes-Bustos for pointing out grammatical errors and Professor Fumio Hiroshima for useful discussion.