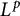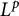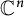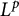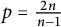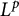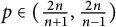1 Introduction
Let
$\Omega $
be a domain in the complex Euclidean space
$\mathbb C^n$
. Let
$dV$
denote the Lebesgue measure. The Bergman projection
$P_\Omega $
is the orthogonal projection from
$L^2(\Omega )$
onto the Bergman space
$A^2(\Omega )$
, the space of all square-integrable holomorphic functions. Associated with
$P_\Omega $
, there is a unique function
$K_\Omega $
on
$\Omega \times \Omega $
such that for any
$f\in L^2(\Omega )$
:
$$ \begin{align} P_\Omega(f)(z)=\int_{\Omega}K_\Omega(z;\bar w)f(w)dV(w). \end{align} $$
The positive Bergman operator
$P^+_{\Omega }$
is given by
$$ \begin{align} P^+_\Omega(f)(z)=\int_{\Omega}|K_\Omega(z;\bar w)|f(w)dV(w). \end{align} $$
By its definition, the Bergman projection is
$L^2$
bounded. An active area of research in several complex variables and harmonic analysis considers the
$L^p$
regularity of
$P_\Omega $
for
$p\neq 2$
. In particular, people are interested in the connection between the boundary geometry of pseudoconvex domains and the
$L^p$
behavior of the projection. On a wide class of domains, the Bergman projection is
$L^p$
regular for all
$1<p<\infty $
(see, for instance, [Reference Barrett and ŞahutoğluBŞ12, Reference Charpentier and DupainCD06, Reference Ehsani and LiebEL08, Reference FeffermanFef74, Reference McNealMcN89, Reference McNealMcN94a, Reference McNealMcN94b, Reference McNeal and SteinMS94, Reference Nagel, Rosay, Stein and WaingerNRSW88, Reference Phong and SteinPS77]). On some other domains, the projection has only a finite range of mapping regularity (see, for example, [Reference Bender, Chakrabarti, Edholm and MainkarBCEM22, Reference ChenChe17, Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20, Reference Chakrabarti and ZeytuncuCZ16, Reference Edholm and McNealEM16, Reference Edholm and McNealEM17, Reference ZeytuncuZey13]). We also refer to [Reference ZeytuncuZey20] for a survey on the problem.
In this article, we focus on the Bergman projection on the symmetrized polydisc
$\mathbb G^n$
. Let
$\mathbb D^n$
denote the polydisc in
$\mathbb C^n$
. Let
$\Phi _n$
be the rational holomorphic mapping on
$\mathbb C^n$
given by
$\Phi _n(w_1,\dots ,w_n)=(p_1(w),\dots , p_n(w)),$
where
$p_j(w)$
is the symmetric polynomial in w of degree j:
$$\begin{align*}p_j(w_1,w_2,\dots,w_n)=\sum_{k_1<k_2<\dots<k_j}w_{k_1}w_{k_2}\dots w_{k_j}. \end{align*}$$
The symmetrized polydisc
$\mathbb G^n$
is the image of
$\mathbb D^n$
under
$\Phi _n$
:
$$ \begin{align} \mathbb G^n:=\{(p_1(w),\dots,p_n(w)):w\in \mathbb D^n\}. \end{align} $$
When
$n=2$
, the symmetrized bidisc
$$ \begin{align}\mathbb G:=\mathbb G^2=\{(w_1+w_2,w_1w_2):(w_1,w_2)\in \mathbb D^2\} \end{align} $$
serves as an interesting example in several complex variables. It is a first known example of many phenomena. We list some of them here below:
-
• The Lempert theorem may hold on bounded pseudoconvex domains that are not biholomorphically equivalent to any convex domains [Reference Agler and YoungAY04].
-
• Bounded
$\mathbb C$
-convex domains are not necessarily biholomorphically equivalent to convex ones [Reference Nikolov, Pflug and ZwonekNPZ08].
See also [Reference Agler, Lykova and YoungALY18, Reference Agler and YoungAY00, Reference SarkarSar15] for some recent work on
$\mathbb G$
.
In addition, the symmetrized polydisc
$\mathbb G^n$
also serves as an example of a quotient domain and is biholomorphically equivalent to
$\mathbb D^n/\mathcal S_n,$
where
$\mathcal S_n$
is the group of permutations of n coordinate variables in
$\mathbb C^n$
. See [Reference Dall’Ara and MonguzziDM23, Reference GhoshGho21] for some recent studies regarding Bergman projections over quotient domains of the form
$\Omega /G$
.
Partially due to
$\mathbb G^2$
’s interesting properties, the
$L^p$
regularity of
$P_{\mathbb G^2}$
and
$P_{\mathbb G^n}$
has also attracted attention in recent years. In [Reference Chen, Krantz and YuanCKY20], Chen, Krantz, and Yuan showed that
$P_{\mathbb G^n}$
is
$L^p$
bounded for
$p\in (1+\frac {n-1}{\sqrt {n^2-1}},1+\frac {\sqrt {n^2-1}}{n-1})$
. Later, Chen, Jin, and Yuan [Reference Chen, Jin and YuanCJY20] improved the
$L^p$
regular range of
$P_{\mathbb G}$
to
$({4}/{3},4)$
and established the Sobolev estimates for
$P_{\mathbb G}$
. While preparing this article, the authors were informed of a discrepancy between the arXiv version of [Reference Chen, Jin and YuanCJY20] and the version those authors submitted to a journal for publication. In a recent update of [Reference Chen, Jin and YuanCJY20] posted to the arXiv, the range of
$L^p$
regularity for the symmetrized polydisc is at least
$(\frac {2n}{n+1},\frac {2n}{n-1})$
, see [Reference Chen, Jin and YuanCJY23, Remark 1.5]. The main idea in the proof of these results is to use Bell’s transformation formula [Reference BellBel81] to reformulate the
$L^p$
regularity problem of
$P_{\mathbb G^n}$
into a weighted
$L^p$
regularity problem of
$P_{\mathbb D^n}$
over a weighted
$L^p$
space of antisymmetric functions. Yet, the precise
$L^p$
regular range for
$P_{\mathbb G^n}$
was not previously known.
There are mainly two challenges on obtaining the sharp
$L^p$
estimates of
$P_{\mathbb G^n}$
: 1. the complexity of the Jacobian of
$(p_1,\dots ,p_n)$
for large n dimension makes estimations complicated. 2. The cancellation caused by integrating antisymmetric functions creates obstacles to precisely analyze the (un)boundedness of the operator. To us, the second issue is more crucial and distinguishes the problem on
$\mathbb G^n$
from other settings like the Hartogs triangle. Actually, this issue leads to an interesting yet nontrivial weighted inequality problem in harmonic analysis. We elaborate below using a simple analogical example:
Let T be a singular integral operator on
$L^p(\mathbb R^2)$
. Set
$$ \begin{align*}L^p_{\text{anti}}(\mathbb R^2,|x_1-x_2|^a):=\{f\in L^p(\mathbb R^2,|x_1-x_2|^a):f(x_1,x_2)=-f(x_2,x_1)\}. \end{align*} $$
For which p is the operator T bounded on
$L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
?
From the classical weighted theory, the singularity of the weight function
$|x_1-x_2|^a$
over the line
$\{x_1=x_2\}$
may cause unboundedness issue for T over
$L^p(\mathbb R^2,|x_1-x_2|^a)$
. On the other hand, the antisymmetry property
$f(x_1,x_2)=-f(x_2,x_1)$
implies that for any
$U\subseteq \mathbb R,$
$$ \begin{align*}\int_{U\times U}fdV=0,\end{align*} $$
suggesting possible better behavior of T on the subspace
$L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
than on the entire weighted
$L^p$
space. Nevertheless, the usual harmonic analysis methods for weighted
$L^p$
cannot be directly applied to this subspace case.
In this article, we overcome these issues on
$\mathbb G^n$
and give the precise
$L^p$
regular range for
$P_{\mathbb G^n}$
and
$P^+_{\mathbb G^n}$
:
Theorem 1.1
$P_{\mathbb G^n}$
and
$P^+_{\mathbb G^n}$
are
$L^p$
bounded if and only if
$p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
.
When
$n=2$
,
$P_{\mathbb G}$
is
$L^p$
bounded if and only if
$p\in (\frac {4}{3},4)$
. In contrast to this result, Dall’Ara and Monguzzi [Reference Dall’Ara and MonguzziDM23] recently showed that, if one replaces
$\mathbb D^2$
by unit ball
$\mathbb B_2$
in (1.4), the Bergman projection over the newly formed domain
$\{(w_1+w_2, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
will possess completely different
$L^p$
mapping properties. In particular, they proved the following:
Set
$D_{2^k}:=\{(w_1^{2^k}+w_2^{2^k}, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
with
$k\in \mathbb N\cup \{0\}$
. Then the Bergman projection on
$D_{2^k}$
is
$L^p$
bounded for all
$p\in (1,\infty )$
.
Our computations suggest that the distinction between results on
$\mathbb G$
and
$D_{2^k}$
is caused by the product structure of
$\mathbb D^2$
. It is yet to be investigated on what exact geometric property of these domains will determine the
$L^p$
mapping behaviors of the projection over them.
Our proof strategy of Theorems 1.1 can be summarized as follows:
-
(1) Similar to [Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20], we reformulate Theorem 1.1 into a weighted
$L^p$
regularity result of
$P_{\mathbb D^n}$
for antisymmetric functions on the polydisc
$\mathbb D^n$
(see Theorems 2.4 and 2.3). -
(2) We prove in detail the
$L^p$
boundedness results for
$p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
using known weighted estimates on the polydisc (see Theorem 2.3, Section 3, and [Reference Chen, Jin and YuanCJY23, Remark 1.5]). -
(3) To obtain the unboundedness result for the case
$p=\frac {2n}{n-1}$
, we decompose
$P_{\mathbb D^n}$
into the sum of two operators
$T^n_1$
and
$T^n_2$
(see (4.5) and (4.6)), where
$T^n_1=0$
and
$T^n_2=P_{\mathbb D^n}$
over spaces of antisymmetric functions (see Lemmas 4.1 and 4.3). -
(4) By using
$T^n_2$
, we further reduce the (un)boundedness problem of
$P_{\mathbb D^n}$
over a space of antisymmetric functions into a problem about an operator
$\tilde T^n$
over a different space of symmetric functions. Finally, we provide examples for the unboundedness of
$\tilde T^n$
there (see Theorems 4.2 and 4.4 and their proofs).
We remark that the decomposition
$P_{\mathbb D^n}=T^n_1+T^n_2$
is crucial in our proof. Using the kernel function of
$T^n_2$
, we are able to “cancel out” part of the weight of the space, transform the problem from an antisymmetric function space to a symmetric one, and reduce norm computation difficulty in n-dimensional case all at once.
Our article is organized as follows: In Section 2, we provide known lemmas and reduce
$L^p$
estimates of
$P_{\mathbb G^n}$
and
$P^+_{\mathbb G^n}$
into weighted
$L^p$
estimates of
$P_{\mathbb D^n}$
for (anti)symmetric functions. In Section 3, we recall the known weighted
$L^p$
norm estimates of
$P_{\mathbb D}$
and give a detailed proof for the
$L^p$
boundedness result for
$P_{\mathbb G^n}$
and
$P^+_{\mathbb G^n}$
. In Section 4, we present the decomposition of
$P_{\mathbb D^n}$
and examples for the
$L^p$
irregularity of
$P_{\mathbb G^n}$
for
$p=\frac {2n}{n-1}$
. In Section 5, we point out some directions for future research.
Given functions of several variables f and g, we use
$f\lesssim g$
to denote that
$f\leq Cg$
for a constant C. If
$f\lesssim g$
and
$g\lesssim f$
, then we say f is comparable to g and write
$f\approx g$
.
2 Pull back from
$\mathbb G^n$
to
$\mathbb D^n$
This section focuses on reformulating the
$L^p$
regularity of
$P_{\mathbb G^n}$
into a problem on the polydisc
${\mathbb D}^n$
. Most of the lemmas and results were included in [Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20]. We provide proofs here for completeness of our article.
2.1 From
$\mathbb G^n$
to
$\mathbb D^n$
Recall that
$\Phi _n(w)=(p_1(w),p_2(w),\dots ,p_n(w)),$
where
$$\begin{align*}p_j(w_1,w_2,\dots,w_n)=\sum_{k_1<k_2<\dots<k_j}w_{k_1}w_{k_2}\dots w_{k_j}. \end{align*}$$
Then
$\Phi _n$
is a ramified rational proper covering map of order
$n!$
with complex holomorphic Jacobian
$$ \begin{align*}J_{\mathbb C}\Phi_n=\prod_{j<k}(w_j-w_k)\end{align*} $$
(see, for example, [Reference Chen, Krantz and YuanCKY20]). Let
$h\in L^p(\mathbb G^n)$
. Via a change of variables, the estimate
$$\begin{align*}\|P_{\mathbb G^n}(h)\|_{L^p(\mathbb G^n)}\lesssim \|h\|_{L^p(\mathbb G^n)} \end{align*}$$
is equivalent to
$$ \begin{align} \|P_{\mathbb G^n}(h)\circ\Phi_n\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^2)}\lesssim \|h\circ\Phi_n\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^2)}. \end{align} $$
Using the Bell’s transformation formula [Reference BellBel81],
$$\begin{align*}P_{\mathbb D^n}(J_{\mathbb C}\Phi_n\cdot(h\circ \Phi_n))=J_{\mathbb C}\Phi\cdot (P_{\mathbb G^n}(h)\circ \Phi_n),\end{align*}$$
(2.1) becomes the following weighted estimate:
$$ \begin{align} \|P_{\mathbb D^n}(J_{\mathbb C}\Phi_n\cdot(h\circ \Phi_n))\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p})}\lesssim \|J_{\mathbb C}\Phi_n\cdot h\circ \Phi_n\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p})}. \end{align} $$
By Bell’s transformation formula for the Bergman kernel,
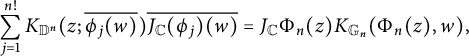$$\begin{align*}\sum_{j=1}^{n!}K_{\mathbb D^n}(z; \overline {\phi_j(w)})\overline {J_{\mathbb C}(\phi_j)(w)}=J_{\mathbb C}\Phi_n(z)K_{\mathbb G_n}(\Phi_n(z),w), \end{align*}$$
where
$\phi _j$
are the
$n!$
local inverses of
$\Phi $
. Therefore, to show the estimate
$$\begin{align*}\|P^+_{\mathbb G^n}(h)\|_{L^p(\mathbb G^n)}\lesssim \|h\|_{L^p(\mathbb G^n)},\end{align*}$$
it is sufficient to prove that
$$ \begin{align}\|P^+_{\mathbb D^n}(|J_{\mathbb C}\Phi_n|\cdot(h\circ \Phi_n))\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p})}\lesssim \||J_{\mathbb C}\Phi_n|\cdot h\circ \Phi\|_{L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p})}.\end{align} $$
Let
$\mathcal S_n$
denote the family of all permutations of
$\{z_1,\dots ,z_n\}$
. Since
$\Phi _n$
is invariant under any permutation, the function
$h\circ \Phi _n$
also inherits symmetry properties. To clearly describe them, we give several definitions below. For
$j,k\in \{1,\dots ,n\}$
with
$j<k$
, we let
$\tau _{j,k}$
denote the 2-cycle in
$\mathcal S_n$
that interchanges
$z_j$
and
$z_k$
. For
$j=1,\dots ,n$
, we will also abuse the notation for
$\tau \in \mathcal S_n$
and let
$\tau (j)$
denote the index such that
$\tau (z_j)=z_{\tau (j)}$
.
Definition 2.1 Let f be a function on
$\mathbb D^n$
.
-
(1) f is called
$(j,k)$
symmetric if
$f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
, and is called symmetric if
$f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
$j\neq k$
. -
(2) f is called
$(j,k)$
antisymmetric if
$f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
and is called antisymmetric if
$f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
$j\neq k$
.
By the above definition,
$h\circ \Phi _n$
is symmetric while
$J_{\mathbb C}\Phi _n$
is antisymmetric. Therefore, the function
$J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is antisymmetric and
$|J_{\mathbb C}\Phi _n|\cdot h\circ \Phi _n$
is symmetric. It’s also not hard to see that
$P_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
and
$P^+_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
are antisymmetric and
$P^+_{\mathbb D^n}(|J_{\mathbb C}\Phi _n|\cdot (h\circ \Phi _n))$
is symmetric. Set
$$ \begin{align} &L^p_{\text{anti}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p}):=\{f\in L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p}):f \text{ is antisymmetric}\}, \end{align} $$
$$ \begin{align} &L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p}):=\{f\in L^p(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2-p}):f \text{ is symmetric}\}. \end{align} $$
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
and
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
turn out to be equivalent to
$L^p(\mathbb G^n)$
.
The next lemma gives the norm equivalence of
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, and
$L^p(\mathbb G^n)$
. When
$p=2$
, this lemma can be viewed as a special case of [Reference TrybulaTry13, Theorem 1].
Lemma 2.2 The following statements are true:
-
(1)
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
$L^p(\mathbb G^n)$
via the mapping: (2.6)
$$ \begin{align} f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi}\right)\circ \phi_j. \end{align} $$
-
(2)
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
$L^p(\mathbb G^n)$
via the mapping: (2.7)
$$ \begin{align}f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{|J_{\mathbb C}\Phi_n|}\right)\circ \phi_j. \end{align} $$
Proof We prove the statement for
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. The proof for
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is similar. We begin by showing that the mapping in (2.6) is norm preserving. Since f is antisymmetric, the function
$\frac {f}{J_{\mathbb C}\Phi _n}$
is symmetric. Thus,
$\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _j=\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _k$
for any
$j,k$
and
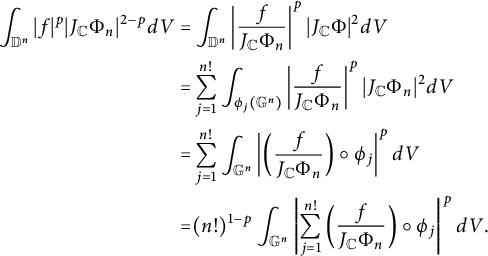$$ \begin{align*}\int_{\mathbb D^n}|f|^p|J_{\mathbb C}\Phi_n|^{2-p}dV=&\int_{\mathbb D^n}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\phi_j(\mathbb G^n)}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi_n|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\mathbb G^n}\left|\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV\\=&(n!)^{1-p}\int_{\mathbb G^n}\left|\sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV.\end{align*} $$
Note also that
$h\mapsto \frac {1}{n!}J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is the inverse of (2.6), the mapping in (2.6) is onto which completes the proof.
By Lemma 2.2 and the fact that
$|P_{\mathbb G^n}(f)(z)|\leq P^+_{\mathbb G^n}(|f|)(z)$
, the next two theorems are sufficient to yield Theorem 1.1.
Theorem 2.3
$P_{\mathbb D^n}$
and
$P^+_{\mathbb D^n}$
are bounded on
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
.
Theorem 2.3 appears as [Reference Chen, Jin and YuanCJY23, Remark 1.5] with the same range of p.
Theorem 2.4
$P_{\mathbb D^n}$
is unbounded on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$p=\frac {2n}{n-1}$
.
Last, we reference below the Forelli–Rudin estimates on
$\mathbb D$
which will be used in the proof of Theorem 2.4 (see, for example, [Reference ZhuZhu05] for its proof).
Lemma 2.5 (Forelli–Rudin)
For
$\epsilon <1$
and
$z\in \mathbb D$
, let
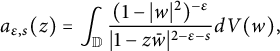$$ \begin{align} a_{\epsilon,s}(z)=\int_{\mathbb D}\frac{(1-|w|^2)^{-\epsilon}}{|1-z\bar w |^{2-\epsilon-s}}dV(w), \end{align} $$
Then:
-
(1) for
$s>0$
,
$a_{\epsilon ,s}(z)$
is bounded on
$\mathbb D$
; -
(2) for
$s=0$
,
$a_{\epsilon ,s}(z)$
is comparable to the function
$-\log (1-|z|^2)$
; -
(3) for
$s<0$
,
$a_{\epsilon ,s}(z)$
is comparable to the function
$(1-|z|^2)^{s}$
.
3 Proof of Theorem 2.3
While [Reference Chen, Jin and YuanCJY23, Remark 1.5] sketches the proof of Theorem 2.3, here we provide all the relevant details to make the article self-contained (see also [Reference Zhang and YuanZY, Corollary 6.1]). The main ingredient of the weighted norm estimates of the positive Bergman operator
$P^+_{\mathbb D}$
over weighted
$L^p$
spaces. On the unit disc
$\mathbb D$
, the boundedness of
$P_{\mathbb D}$
and
$P^+_{\mathbb D}$
on weighted
$L^p$
spaces is closely related to the Bekollé–Bonami constant of weight functions. Let
$T_z$
denote the Carleson tent over z in the unit disc
$\mathbb D$
defined as below:
-
•
$T_z:=\left \{w\in \mathbb D:\left |1-\bar w\frac {z}{|z|}\right |<1-|z|\right \}$
for
$z\neq 0$
, and -
•
$T_z:= \mathbb D$
for
$z=0$
.
Bekollé and Bonami [Reference Bekollé and BonamiBB78] characterized weighted
$L^p$
spaces where
$P_{\mathbb D}$
and
$P^+_{\mathbb D}$
are bounded:
Theorem 3.1 (Bekollé–Bonami [Reference Bekollé and BonamiBB78])
Let the weight
$u(w)$
be a positive, locally integrable function on the unit disc
$\mathbb D$
. Let
$1<p<\infty $
. Then the following conditions are equivalent:
-
(1)
$P:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded. -
(2)
$P^+:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded. -
(3) The Bekollé–Bonami constant
is finite.
$$ \begin{align*} B_p(u):=\sup_{z\in \mathbb D}\frac{\int_{T_z}u(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1} \end{align*} $$
Using dyadic harmonic analysis technique, various authors established quantitative weighted
$L^p$
norm estimates of the Bergman projection (see [Reference Huo and WickHW20b, Reference Huo, Wagner and WickHWW21, Reference Pott and RegueraPR13, Reference Rahm, Tchoundja and WickRTW17]).
Theorem 3.2 [Reference Rahm, Tchoundja and WickRTW17, Lemma 15]
Let the weight function u be positive, locally integrable on
$\mathbb D$
. Then for
$p\in (1,\infty )$
,
$$\begin{align*}\|P_{\mathbb D}\|_{L^p(\mathbb D,u)}\leq \|P^+_{\mathbb D}\|_{L^p(\mathbb D,u)}\lesssim \left(B_p(u)\right)^{\max\{1,(p-1)^{-1}\}}.\end{align*}$$
Lemma 3.3 For a fixed point
$a\in \mathbb D$
, let
$u_p(w)=|a-w|^{2-p}$
. Then for any
$p\in (4/3,4)$
,
$B_p(u_p)\lesssim 1,$
where the upper bound is independent of a. Moreover, if we choose arbitrary m points
$a_1,\dots ,a_m$
in
$\mathbb D$
, and set
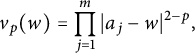$$ \begin{align*}v_p(w)=\prod_{j=1}^{m}|a_j-w|^{2-p},\end{align*} $$
then for any
$p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
,
$B_p(v_p)\lesssim 1$
. Here, the upper bounds may depend on constants m and p but are independent of
$a_j$
.
Proof We first consider the case of the weight
$u_p$
. Note that
$u_p$
and
$u_p^{-1/(p-1)}$
are integrable on
$\mathbb D$
if and only if
$p\in (\frac {4}{3},4)$
. Then, it is enough to show that
$B_p(|a-w|^{b})\lesssim 1$
with an upper bound independent of a if both
$u_p$
and
$u_p^{-1/(p-1)}$
are integrable on
$\mathbb D$
. We consider the integral of
$u_p$
and
$u_p^{-1/(p-1)}$
over
$T_z$
for arbitrary
$z\in \mathbb D$
. Notice that
$T_z=\mathbb D\cap \{w:|w-\frac {z}{|z|}|<1-|z|\}$
is the intersection set of the unit disc
$\mathbb D$
and the disc centered at the point
$z/|z|$
with Euclidean radius
$1 -|z|$
. A geometric consideration then yields that the Lebesgue measure
$V(T_z)$
of
$T_z$
is comparable to
$(1-|z|)^2$
.
If
$|a-z|<3(1-|z|)$
, then
$T_z$
is contained in a ball
$B_a$
given by
$$\begin{align*}B_a=\{w\in \mathbb C: |w-a|<5(1-|z|)\}.\end{align*}$$
Thus,
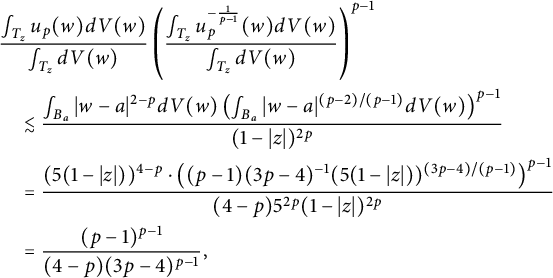$$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\&\quad \lesssim \frac{\int_{B_a}|w-a|^{2-p} dV(w)\left(\int_{B_a}|w-a|^{(p-2)/(p-1)} dV(w)\right)^{p-1}}{(1-|z|)^{2p}}\\&\quad =\frac{(5(1-|z|))^{4-p}\cdot \left((p-1)(3p-4)^{-1}(5(1-|z|))^{(3p-4)/(p-1)}\right)^{p-1}}{(4-p)5^{2p}(1-|z|)^{2p}}\\&\quad =\frac{(p-1)^{p-1}}{(4-p)(3p-4)^{p-1}}, \end{align*} $$
provided
$u_p$
and
$u_p^{-1/(p-1)}$
are integrable. If
$|a-z|\geq 3(1-|z|)$
, then
$ |a-w|\approx |a-z|$
for all
$w\in T_z$
and hence
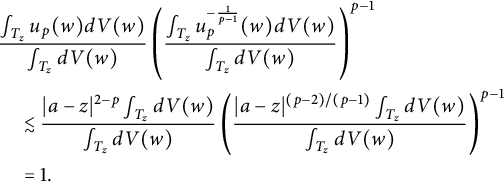$$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \frac{|a-z|^{2-p}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\left(\frac{|a-z|^{(p-2)/(p-1)}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad =1. \end{align*} $$
Since the upper bound obtained in both cases are independent of the choice of a and
$T_z$
, we conclude that
$B_p(u_p)$
is bounded above by a constant if and only if
$p\in (4/3,4)$
and the upper bound is independent of
$a_j$
.
Now we turn to the case of weight
$v_p(w)=\prod _{j=1}^{m}|a_j-w|^{2-p}$
. By a similar proof as above,
$B_p(|a-w|^{(2-p)m})\lesssim 1$
for any
$p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
where the upper bound is independent of a. Using Hölder’s inequality, we obtain for any
$z\in \mathbb D$
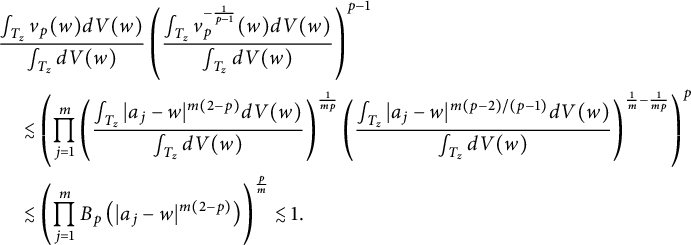$$ \begin{align*} &\frac{\int_{T_z}v_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}v_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \left(\prod_{j=1}^{m}\left(\frac{\int_{T_z} |a_j-w|^{m(2-p)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{mp}}\left(\frac{\int_{T_z} |a_j-w|^{m(p-2)/(p-1)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{m}-\frac{1}{mp}}\right)^p\\& \quad \lesssim \left(\prod_{j=1}^{m}B_p\left(|a_j-w|^{m(2-p)}\right)\right)^{\frac{p}{m}}\lesssim 1. \end{align*} $$
Therefore,
$B_p(v_p)\lesssim 1$
with upper bound independent of points
$a_j$
.
With Lemma 3.3, we are ready to show Theorem 2.3:
Proof of Theorem 2.3
Since
$|P_{\mathbb D^n}(h)(z)|\leq P^+_{\mathbb D^n}(|h|)(z)$
for any
$h\in L^p(\mathbb D^n, |J_{\mathbb C}\Phi _n|^{2-p})$
, it suffices to show the boundedness for
$P^+_{\mathbb D^n}$
. Note that
$J_{\mathbb C}\Phi _n(w)$
consists of
$n-1$
many factors of each variable
$w_j$
. When integrating with respect to the single variable
$w_j$
, only these
$n-1$
factors matter in
$J_{\mathbb C}\Phi _n(w)$
. Thus the boundedness of
$P^+_{\mathbb D^n}$
on
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
follows from Fubini and Lemma 3.3 with
$m=n-1$
.
4 Proof of Theorem 2.4
We will first prove the theorem for the case
$n=2$
, clearly illustrating the decomposition we use for
$P_{\mathbb D^2}$
. Then we dive into the case for general n where the decomposition procedure and estimations are more complicated yet the same strategy applies.
4.1 The case for
$n=2$
Note that
$J_{\mathbb C}\Phi _2=w_1-w_2$
. To prove Theorem 2.4, we consider the decomposition
$P_{\mathbb D^2}=T^2_1+T^2_2$
where
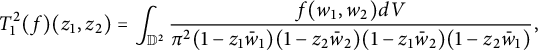$$ \begin{align} T^2_1(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)(1-z_2\bar w_2)(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
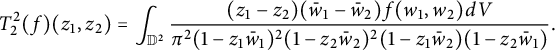$$ \begin{align} T^2_2(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{(z_1-z_2)(\bar w_1-\bar w_2)f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}. \end{align} $$
Lemma 4.1
$T^2_1$
is a zero operator on
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
.
Proof Note that
$T^2_1(f)(z_1,z_2)$
is symmetric by its definition. For any
$f\in L^p_{\text {anti}}(\mathbb D^2, |w_1-w_2|^{2-p})$
,
$$ \begin{align*}T^2_1(f)(z_1,z_2)=T^2_1(-f)(z_2,z_1)=-T^2_1(f)(z_1,z_2),\end{align*} $$
which implies
$T^2_1(f)= 0$
.
By Lemma 4.1,
$P_{\mathbb D^2}=T^2_2$
on
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
. So, Theorem 2.4 can be further reduced into the following statement in the case
$n=2$
.
Theorem 4.2
$T^2_2$
is unbounded on
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
for
$p=4=\frac {2\times 2}{2-1}$
.
Proof Let
$\tilde T^2$
denote the operator given as follows:
$$\begin{align*}\tilde T^2(h)(z):=(J_{\mathbb C}\Phi_2(z))^{-1}T_2(h\bar J_{\mathbb C}\Phi_2)(z).\end{align*}$$
Then
$$ \begin{align} \tilde T^2(h)(z)&=\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2h(w)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
and
$\|T^2_2\|_{L^p_{\text {anti}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2-p})}=\|\tilde T^2\|_{L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
$\tilde T^2$
is unbounded on
$L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
for
$p=4$
. For
$s\in [\frac {1}{2},1)$
, we set
$$ \begin{align*}h_s(w)=\frac{1}{\pi(1-sw_1)^2}+\frac{1}{\pi(1-sw_2)^2}.\end{align*} $$
Then
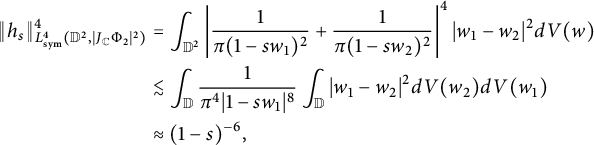$$ \begin{align*} \|h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}&=\int_{\mathbb D^2}\left|\frac{1}{\pi(1-sw_1)^2}+\frac{1}{\pi(1-sw_2)^2}\right|^4| w_1- w_2|^2dV(w)\\&\lesssim\int_{\mathbb D}\frac{1}{\pi^{4}|1-sw_1|^{8}}\int_{\mathbb D}| w_1- w_2|^{2}dV(w_2)dV(w_1) \\&\approx (1-s)^{-6}, \end{align*} $$
where the last equality follows from the Forelli–Rudin estimates (2.8). Note that the kernel function of
$\tilde {T}^2$
is anti-holomorphic in w variables and
$h_s$
can be expressed in terms the conjugate of the Bergman kernels:
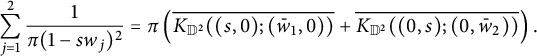$$ \begin{align*} \sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}={\pi}\left(\overline{K_{\mathbb D^2}((s,0);(\bar w_1,0))}+\overline{K_{\mathbb D^2}((0,s);(0,\bar w_2))}\right). \end{align*} $$
The reproducing property of the Bergman projection implies:
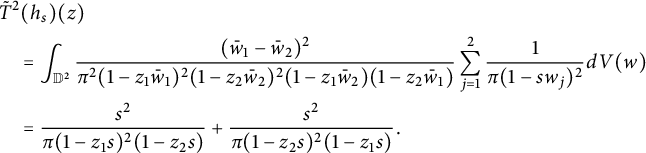$$ \begin{align*} &\tilde T^2(h_s)(z)\\& \quad =\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}\sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}dV(w)\\& \quad =\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}. \end{align*} $$
Thus
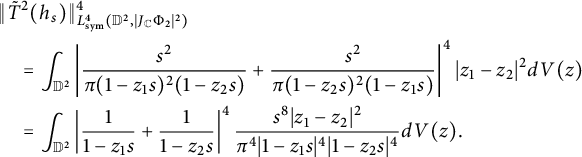$$ \begin{align} &\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}\right|^4|z_1-z_2|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z). \end{align} $$
For fixed
$s<1$
, set
$U(s)=\{z\in \mathbb D: \text {Arg}(1-zs)\in \left (-\frac {\pi }{6},\frac {\pi }{6}\right )\}$
. Then for
$z_1,z_2\in U(s)$
,
$$\begin{align*}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|\geq \frac{1}{2|1-z_1s|}.\end{align*}$$
Applying this inequality to (4.4) gives
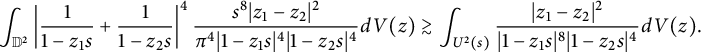$$ \begin{align*} &\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z)\gtrsim\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z).\end{align*} $$
Since
$$\begin{align*}\frac{z_1-z_2}{(1-z_1s)(1-z_2s)}=\frac{1}{s(1-z_1s)}-\frac{1}{s(1-z_2s)}, \end{align*}$$
we have
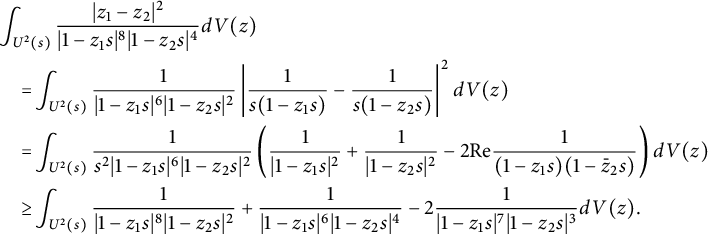$$ \begin{align*}\kern-3pt &\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z)\\& \quad =\!\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^2}\left|\frac{1}{s(1-z_1s)}- \frac{1}{s(1-z_2s)}\right|^2dV(z) \\& \quad =\!\int_{U^2(s)}\frac{1}{s^2|1-z_1s|^6|1-z_2s|^2}\left(\frac{1}{|1-z_1s|^2}+\frac{1}{|1-z_2s|^2}-2\text{Re} \frac{1}{(1-z_1s)(1-\bar z_2 s)}\right)dV(z)\\& \quad \geq\! \int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}+\frac{1}{|1-z_1s|^6|1-z_2s|^4}-2 \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z). \end{align*} $$
By realizing that
$|1-zs|=s|\frac {1}{s}-z|$
and applying polar coordinates, one can obtain the following Forelli–Rudin estimates (2.8) on
$U(s)$
.
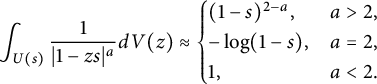$$\begin{align*}\int_{U(s)}\frac{1}{|1-zs|^a}dV(z)\approx\begin{cases} (1-s)^{2-a},& a>2,\\ -\log(1-s),& a=2,\\ 1,&a<2. \end{cases}\end{align*}$$
We leave the details of its proof to readers as an exercise. Using these estimates,
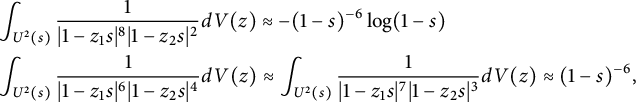$$ \begin{align*} &\int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}dV(z)\approx -(1-s)^{-6}\log(1-s)\\ &\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^4}dV(z)\approx \int_{U^2(s)} \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z)\approx (1-s)^{-6}, \end{align*} $$
which implies that
$\|\tilde T^2(h_s)\|^4_{L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}\approx -(1-s)^{-6}\log (1-s)$
.
As
$s\to 1$
,
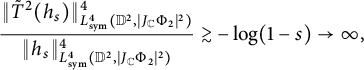$$\begin{align*}\frac{\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}{\| h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}\gtrsim-\log(1-s)\to \infty, \end{align*}$$
proving that
$\tilde T^2$
is unbounded on
$L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
.
4.2 The case for general n
Like the case
$n=2$
, our proof for general n also involves a decomposition of
$P_{\mathbb D^n}$
into operators
$T^n_1$
and
$T^n_2$
.
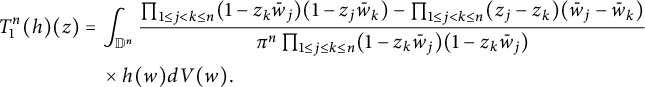$$ \begin{align} T^n_{1}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)-\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_k\bar w_j)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
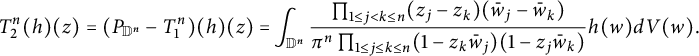$$ \begin{align} T^n_{2}(h)(z)&=(P_{\mathbb D^n}-T^n_{1})(h)(z)=\!\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}h(w)dV(w).\nonumber\\ \end{align} $$
Lemma 4.3
$T^n_1$
is a zero operator on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
Proof Recall that
$\tau _{j,k}$
is the permutation that interchanges variables
$w_j$
and
$w_k$
, and a kernel function
$K(z;\bar w)$
on
$\mathbb D^n\times \mathbb D^n$
is called
$(j,k)$
-symmetric in w if
$K(z;\bar w)=K(z;\bar \tau _{j,k}(w))$
. If
$K(z;\bar w)$
is
$(j,k)$
-symmetric in
$\bar w$
, then for any antisymmetric
$f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, we have
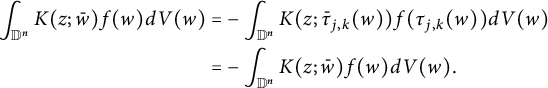$$ \begin{align*} \int_{\mathbb D^n}K(z;\bar w)f(w)dV(w)&=-\int_{\mathbb D^n}K(z;\bar\tau_{j,k} (w))f(\tau_{j,k}(w))dV(w)\\&=-\int_{\mathbb D^n}K(z;\bar w)f(w)dV(w). \end{align*} $$
Thus operators with
$(j,k)$
-symmetric kernel functions in w annihilate
$ L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
For
$l=1,\dots ,n$
, we define the operator
$P_l$
to be as follows:
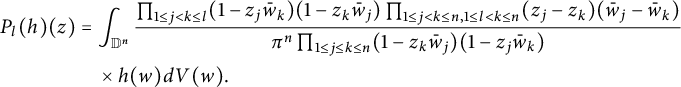$$ \begin{align} P_{l}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq l}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{1\leq j<k\leq n,1\leq l< k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
Then
$P_1=T^n_2$
and
$P_n=P_{\mathbb D^n}$
. We claim that
$P_{\mathbb D^n}=P_{l}$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for all
$l=1,\dots ,n$
. Then
$T^n_1=P_{\mathbb D^n}-P_1=0$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. We prove the claim by induction on l.
Let
$K_l$
denote the kernel function of
$P_l$
. When
$l=2$
,
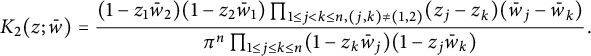$$ \begin{align*} K_{2}(z;\bar w)&=\frac{(1-z_1\bar w_2)(1-z_2\bar w_1)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}. \end{align*} $$
Then
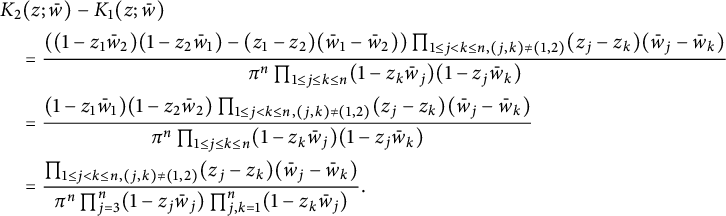$$ \begin{align*}&K_{2}(z;\bar w)-K_{1}(z;\bar w)\\& \quad = \frac{((1-z_1\bar w_2)(1-z_2\bar w_1)-(z_1-z_2)(\bar w_1-\bar w_2))\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{(1-z_1\bar w_1)(1-z_2\bar w_2)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j=3}^n(1-z_j\bar w_j)\prod_{j,k=1}^n(1-z_k\bar w_j)}. \end{align*} $$
It is not hard to check that
$K_{2}-K_{1}$
is
$(1,2)$
-symmetric in w which shows that
$P_{1}=P_2$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
Suppose that
$P_{1}=P_l$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$l=m$
. We show that
$P_{m+1}=P_m$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. Let
$\mathcal R_m$
denote the power set
$$\begin{align*}\mathcal R_m:=\{\mathcal I:\mathcal I\subseteq \{1,2,\dots,m\}\}. \end{align*}$$
Given
$\mathcal I\in \mathcal R_m$
, let
$|\mathcal I|$
denote the cardinality of
$\mathcal I$
. For simplicity of notation, we set
$a_{j,k}=1-z_j\bar w_k$
and
$b_{j,k}=(z_j-z_k)(\bar w_j-\bar w_k)$
. Then for
$j\neq k$
,
$a_{j,k}a_{k,j}=a_{j,j}a_{kk}+b_{j,k}.$
Note that
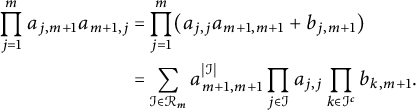$$ \begin{align*} \prod_{j=1}^{m}a_{j,m+1} a_{m+1,j}=& \prod_{j=1}^{m}(a_{j,j} a_{m+1,m+1}+b_{j,m+1})\\ =& \sum_{\mathcal I\in \mathcal R_m}a_{m+1,m+1}^{|\mathcal I|}\prod_{j\in\mathcal I}a_{j,j} \prod_{k\in \mathcal I^c}b_{k,m+1}. \end{align*} $$
We set
$$\begin{align*}p_{\mathcal I}(z;\bar w):=a_{m+1,m+1}^{|\mathcal I|}\prod_{j\in\mathcal I}a_{j,j} \prod_{k\in \mathcal I^c}b_{k,m+1}.\end{align*}$$
Then
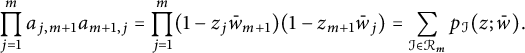$$ \begin{align*}\prod_{j=1}^{m}a_{j,m+1}a_{m+1,j}=\prod_{j=1}^{m}(1-z_j\bar w_{m+1})(1-z_{m+1}\bar w_j)=\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w).\end{align*} $$
Let
$K_m$
and
$K_{m+1}$
be the kernel function of
$P_m$
and
$P_{m+1}$
, respectively, as in (4.7). Let
$K_{m,\mathcal I}$
denote the kernel function
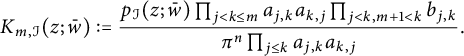$$\begin{align*}K_{m,\mathcal I}(z;\bar w):=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*}$$
We can express
$K_m$
and
$K_{m+1}$
in terms of
$K_{m,\mathcal I}(z;\bar w)$
:
$$ \begin{align*} K_m(z;\bar w)&=\frac{\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k, m<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\ &=\frac{p_{\emptyset}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k, m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=K_{m,\emptyset}(z;\bar w), \end{align*} $$
and
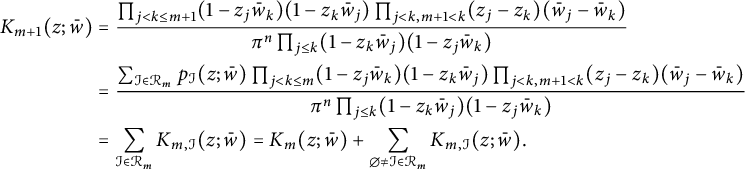$$ \begin{align*} K_{m+1}(z;\bar w)&=\frac{\prod_{j<k\leq m+1}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\frac{\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\sum_{\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w)=K_{m}(z;\bar w)+\sum_{\emptyset\neq\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w). \end{align*} $$
We show that for any nonempty
$\mathcal I\in \mathcal R_m$
,
$K_{m,\mathcal I}$
is a linear combination of
$(j,k)$
-symmetric kernel functions. Then for antisymmetric
$f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
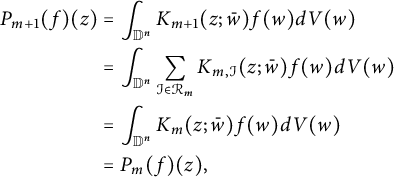$$ \begin{align*} P_{m+1}(f)(z)&=\int_{\mathbb D^n}K_{m+1}(z;\bar w)f(w)dV(w)\\&=\int_{\mathbb D^n}\sum_{\mathcal I\in\mathcal R_m}K_{m,\mathcal I}(z;\bar w)f(w)dV(w)\\ &=\int_{\mathbb D^n}K_{m}(z;\bar w)f(w)dV(w)\\ &=P_{m}(f)(z), \end{align*} $$
which completes the induction and the proof of the lemma. When
$|\mathcal I|>1$
, there exists
$j_1,j_2\in \mathcal I$
, and
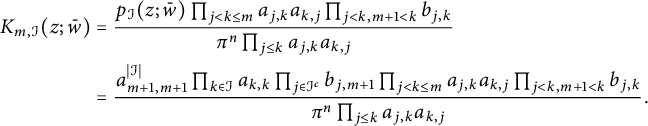$$ \begin{align*} K_{m,\mathcal I}(z;\bar w)&=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=\frac{a_{m+1,m+1}^{|\mathcal I|}\prod_{k\in\mathcal I}a_{k,k} \prod_{j\in \mathcal I^c}b_{j,m+1}\prod_{ j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*} $$
It’s easy to see that
$K_{m,\mathcal I}(z;\bar w)$
is
$(j_1,j_2)$
-symmetric.
Now we turn to consider the case when
$\mathcal I=\{j_0\}$
. Without loss of generality, we let
$j_0=1$
.
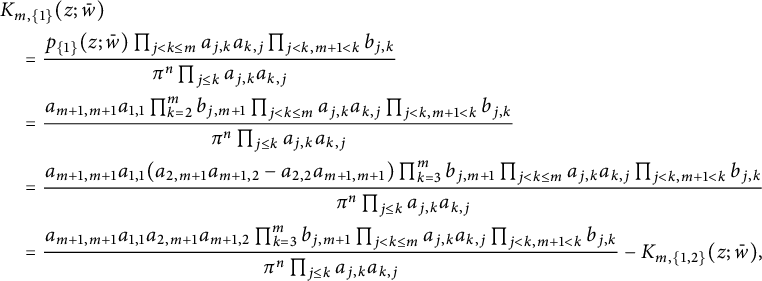$$ \begin{align*}&K_{m,\{1\}}(z;\bar w)\\& \quad =\frac{p_{\{1\}}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} \prod_{k=2}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} (a_{2,m+1}a_{m+1,2}-a_{2,2}a_{m+1,m+1})\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}-K_{m,\{1,2\}}(z;\bar w), \end{align*} $$
where
$K_{m,\{1,2\}}(z;\bar w)$
is
$(1,2)$
-symmetric in w.
Since
$b_{3,m+1}=a_{3,m+1}a_{m+1,3}-a_{3,3}a_{m+1,m+1}$
, we have
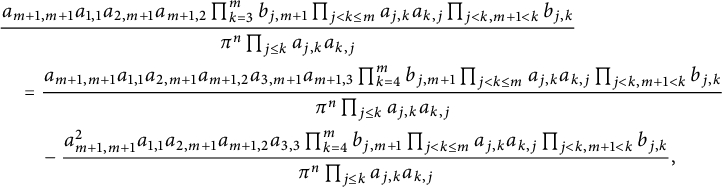$$ \begin{align*} &\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,m+1}a_{m+1,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \qquad -\frac{a^2_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}, \end{align*} $$
where the negative term above is
$(1,3)$
-symmetric in w. Repeating the above process using the identity
$b_{j,m+1}=a_{j,m+1}a_{m+1,j}-a_{j,j}a_{m+1,m+1}$
until no
$b_{j,m+1}$
term left, we obtain
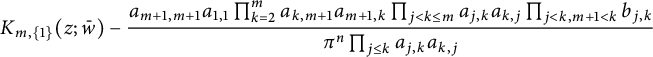$$ \begin{align*} K_{m,\{1\}}(z;\bar w)-\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*} $$
is a linear combination of functions that are
$(1,j)$
-symmetric in w. Since the function
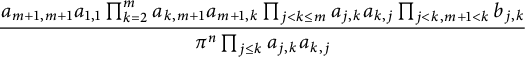$$\begin{align*}\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*}$$
is
$(1,m+1)$
-symmetric in w, we are done.
Since
$T^n_2=P_{\mathbb D^n}$
on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p}|)$
, the next theorem implies Theorem 2.4 for general n.
Theorem 4.4
$T^n_2$
is unbounded on
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$p=\frac {2n}{n-1}$
.
Proof The proof for the case
$n>2$
follows from a similar argument as in the proof of Theorem 4.2. Let
$\tilde T^n$
denote the operator given as follows:
$$\begin{align*}\tilde T^n(h)(z):=(J_{\mathbb C}\Phi_n(z))^{-1}T^n_2(h\bar J_{\mathbb C}\Phi_n)(z). \end{align*}$$
Then
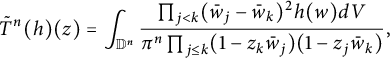$$ \begin{align} \tilde T^n(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{j<k}(\bar w_j-\bar w_k)^2h(w)dV}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}, \end{align} $$
and
$\|T^n_2\|_{L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}=\|\tilde T^n\|_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
$\tilde T^n$
is unbounded on
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
$p=\frac {2n}{n-1}$
.
Recall that
$\mathcal S_n$
is the set of all permutations of
$\{z_1,\dots ,z_n\}$
. For
$s\in (0,1)$
, we set
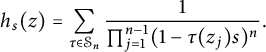$$ \begin{align*}h_s(z)=\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(z_j)s)^n}.\end{align*} $$
Then
$h_s$
is a symmetric function with
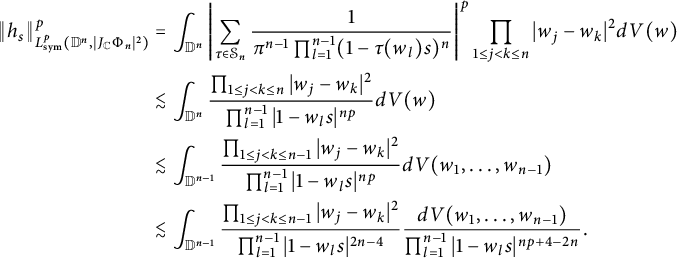$$ \begin{align} \|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber&=\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\pi^{n-1}\prod_{l=1}^{n-1}(1-\tau(w_l)s)^n}\right|^p\prod_{1\leq j<k\leq n }| w_j- w_k|^2dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w_1,\dots,w_{n-1})\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{dV(w_1,\dots,w_{n-1})}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}. \end{align} $$
To evaluate the integral above, we need an
$(n-2)$
-step procedure to eliminate the numerator of the integrand, i.e., we rewrite
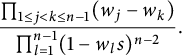$$\begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}.\end{align*}$$
Step 1. Recall that by partial fractions:
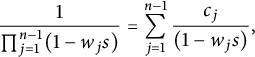$$ \begin{align*}\frac{1}{\prod_{j=1}^{n-1}(1-w_js)}=\sum_{j=1}^{n-1}\frac{c_j}{(1-w_js)},\end{align*} $$
where
$c_j=\frac {1}{s^{n-2}\prod _{k=1,k\neq j}^{n-1}({w_j}-{w_k})}$
. Then
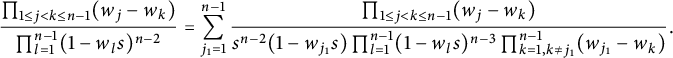$$ \begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}&=\sum_{j_1=1}^{n-1}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}. \end{align*} $$
Step 2. Now we focus on the
$j_1$
th term in the sum above:
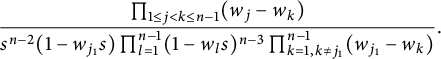$$ \begin{align*}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}.\end{align*} $$
Applying the partial fractions yields
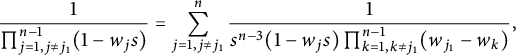$$ \begin{align*}\frac{1}{\prod_{j=1,j\neq j_1}^{n-1}(1-w_js)}=\sum_{j=1,j\neq j_1}^{n}\frac{1}{s^{n-3}(1- w_js)\prod_{k=1,k\neq j_1}^{n-1}(w_{j_1}-w_{k})},\end{align*} $$
and
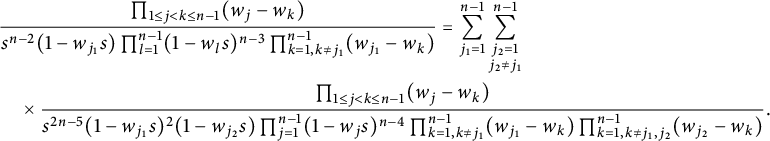$$ \begin{align*} &\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})}=\sum_{j_1=1}^{n-1}\sum_{\substack{j_2=1\\j_2\neq j_1}}^{n-1}\\& \quad \times \frac{\prod_{1\leq j<k\leq n-1}( w_j-w_k)}{s^{2n-5}(1-{w}_{j_1}s)^2(1-{w}_{j_2}s)\prod_{j=1}^{n-1}(1-w_js)^{n-4}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})\prod_{{k=1,k\neq j_1,j_2}}^{n-1}({w_{j_2}}-{w_k})}. \end{align*} $$
Step 3. As in Step 2, we turn to the term with sub-indices
$(j_1,j_2)$
in the sum above and continue the process by doing partial fractions to
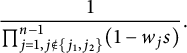$$ \begin{align*}\frac{1}{\prod_{j=1,j\notin \{j_1,j_2\}}^{n-1}(1- w_js)}.\end{align*} $$
Repeat this process. Then after
$n-2$
steps, we obtain
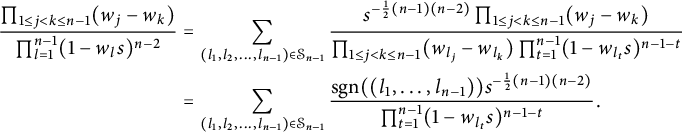$$ \begin{align} \frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}\nonumber&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{s^{-\frac{1}{2}(n-1)(n-2)}\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{1\leq j<k\leq n-1}(w_{l_j}- w_{l_k})\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}\nonumber\\&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{\text{sgn}((l_1,\dots,l_{n-1}))s^{-\frac{1}{2}(n-1)(n-2)}}{\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}. \end{align} $$
Here,
$\text {sgn}((l_1,\dots ,l_{n-1}))$
is the sign of the permutation
$(l_1,\dots ,l_{n-1})$
.
Applying this identity to (4.9) and using the triangle inequality, we obtain
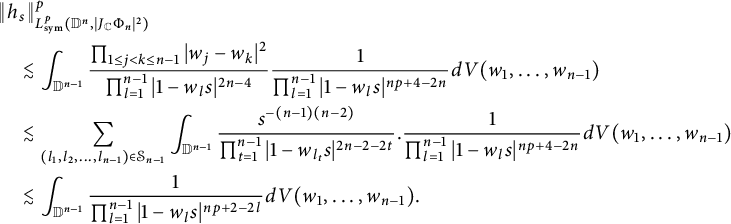$$ \begin{align} &\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\int_{\mathbb D^{n-1}}\frac{s^{-(n-1)(n-2)}}{\prod_{t=1}^{n-1}|1- w_{l_t}s|^{2n-2-2t}}.\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1}).\nonumber\\ \end{align} $$
For
$p=\frac {2n}{n-1}$
,
$np+2-2l\geq np+2-2(n-1)>2$
. Thus the Forelli–Rudin estimates (2.8) imply
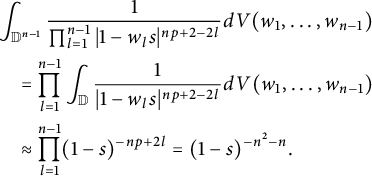$$ \begin{align} &\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad =\prod_{l=1}^{n-1}\int_{\mathbb D}\frac{1}{|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \approx \prod_{l=1}^{n-1}(1-s)^{-np+2l}=(1-s)^{-n^2-n}. \end{align} $$
Hence
$ \|h_s\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\lesssim (1-s)^{-n^2-n}.$
Now we turn to compute
$\tilde T^n(h_s)$
. Let I denote the identity operator. For the variable
$w_j$
, let
$\mathcal D_{w_j}$
denote the partial differential operator
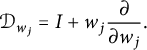$$\begin{align*}\mathcal D_{w_j}=I+w_j\frac{\partial}{\partial w_j}.\end{align*}$$
For any
$k\in \mathbb N$
and holomorphic function
$f(w)=\sum _{\alpha \in \mathbb N^n} c_{\alpha }w^{\alpha }$
on
$\mathbb D^n$
,
$$\begin{align*}(\mathcal D_{w_j})^kf(w)=\sum_{\alpha\in \mathbb N^n} c_{\alpha}(\alpha_j+1)^kw^\alpha.\end{align*}$$
For each integer
$k>2$
,
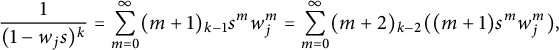$$ \begin{align*}\frac{1}{(1-w_js)^k}=\sum_{m=0}^{\infty}(m+1)_{k-1}s^mw_j^m=\sum_{m=0}^{\infty}(m+2)_{k-2}((m+1)s^mw_j^m),\end{align*} $$
where the Pochhammer symbol
$(m+2)_{k-2}=(m+2)\dot (m+3)\dots (m+k-1)$
is a polynomial in m of degree
$k-2$
. Thus, there exists a polynomial
$q_{k-2}$
of degree
$k-2$
such that
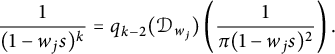$$ \begin{align*}\frac{1}{(1-w_js)^k}=q_{k-2}(\mathcal D_{w_j})\left(\frac{1}{\pi(1-w_js)^2}\right).\end{align*} $$
For holomorphic functions
$f,g$
on
$\mathbb D^n$
with
$f(w)=\sum _{\alpha }c_{\alpha }w^\alpha $
and
$g(w)=\sum _{\alpha }d_{\alpha }w^\alpha $
,
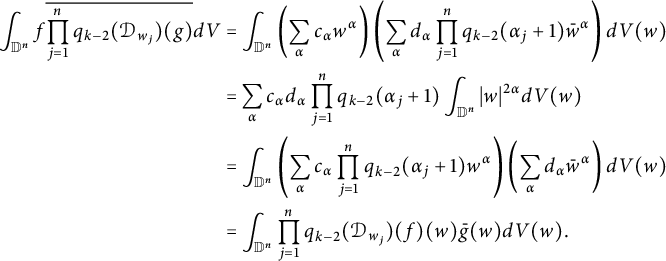$$ \begin{align} \int_{\mathbb D^n}f\overline{\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(g)}dV=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\bar w^\alpha\right)dV(w)\nonumber\\=&\sum_{\alpha}c_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\int_{\mathbb D^n}|w|^{2\alpha}dV(w)\nonumber\\=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\bar w^\alpha\right)dV(w)\nonumber\\=&\int_{\mathbb D^n}\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(f)(w)\bar g(w)dV(w). \end{align} $$
Therefore, we have
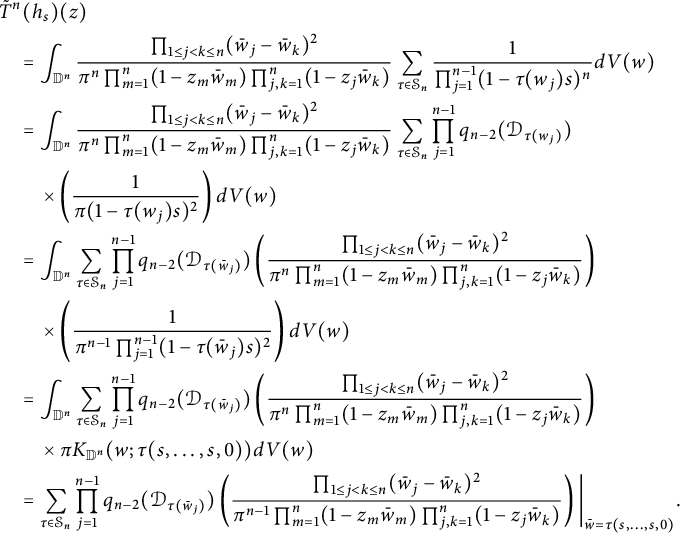$$ \begin{align*} &\tilde T^n(h_s)(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(w_j)s)^n}dV(w)\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(w_j)})\\& \qquad \times \left(\frac{1}{\pi(1-\tau(w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \left(\frac{1}{\pi^{n-1}\prod_{j=1}^{n-1}(1-\tau(\bar w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \pi K_{\mathbb D^n}(w;\tau(s,\dots,s,0))dV(w) \\& \quad =\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}. \end{align*} $$
We claim that there is a constant
$c_n$
such that
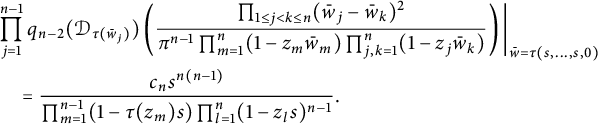$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
By symmetry, it suffices to show (4.14) for the case when
$\tau $
is the identity map, i.e.,
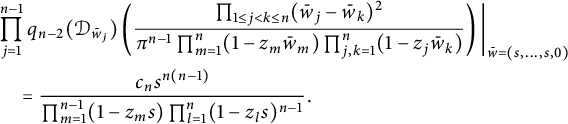$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}}.\end{align} $$
Set
$\bar \partial _j=\frac {\partial }{\partial \bar w_j}$
. For a multi-index
$\mathbf l=(l_1,\dots ,l_{n})$
, set
$\bar \partial ^{\mathbf l}=\bar \partial _1^{l_1}\dots \bar \partial _n^{l_n}$
. Then by the product rule,
$\mathcal D_{\bar w_j}^k=\sum _{l=0}^{k}c_{k,l}\bar w_j^l\bar \partial ^l_j$
. Therefore
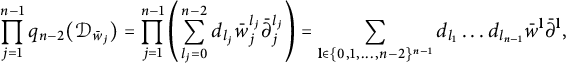$$ \begin{align*}\prod_{j=1}^{n-1}q_{n-2}(\mathcal D_{\bar w_j})=\prod_{j=1}^{n-1}\left(\sum_{l_j=0}^{n-2}d_{l_j} \bar w_j^{l_j}\bar \partial^{l_j}_j\right)=\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l},\end{align*} $$
for some constants
$d_{l_j}$
. Note that for
$\mathbf l=(l_1,\dots ,l_{n-1})\in \{0,1,\dots , n-2\}^{n-1}$
,
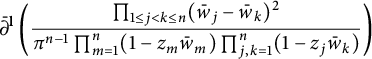$$ \begin{align*}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\end{align*} $$
can be expressed as a linear combination of terms of the form
$$\begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bar \partial^{\mathbf l-\mathbf m}\left(\frac{1}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right),\end{align*}$$
where
$\mathbf m=(m_1,\dots ,m_{n-1})$
with
$m_j\leq l_j$
for all j and
$\mathbf l-\mathbf m=(l_1-m_1,\dots ,l_{n-1}-m_{n-1})$
.
Since
$l_j\leq n-2$
for each j, the sum
$$ \begin{align*}|\mathbf m|=\sum m_j\leq \sum l_j\leq (n-1)(n-2).\end{align*} $$
Thus, the polynomial
$\bar \partial ^{\mathbf m}\left ({\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right )$
is of total degree
$n(n-1)-|\mathbf m|$
which is at least
$n(n-1)-(n-1)(n-2)=2(n-1)$
. Note also that for
$\bar w=(s,\dots ,s,0)$
, the factor
$(\bar w_j-\bar w_k)\neq 0$
if and only if either j or k equals n. It is not hard to see that the polynomial
$\prod _{k=1}^{n-1}(\bar w_k-\bar w_n)^2$
is the only divisor of
$\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2$
that has degree at least
$2(n-1)$
and does not vanish at
$(s,\dots ,s,0)$
. Hence,
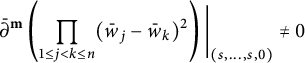$$ \begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}\neq 0\end{align*} $$
if and only if
$|\mathbf m|=(n-2)(n-1)$
, i.e.,
$\mathbf m=(n-2,\dots ,n-2)$
. In this case, we have
$$ \begin{align*}\prod_{j=1}^{n-1}\bar \partial_j^{n-2}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}=c_n\prod_{k=1}^{n-1}(\bar w_k-\bar w_n)^2|_{(s,\dots,s,0)}=c_ns^{2n-2}\end{align*} $$
for some constant
$c_n$
. Therefore,
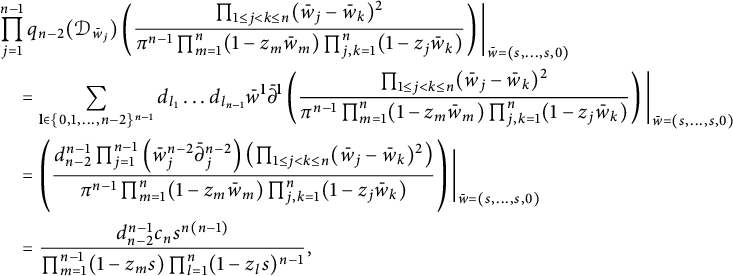$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\left(\frac{d_{n-2}^{n-1}\prod_{j=1}^{n-1}\left(\bar w_j^{n-2}\bar \partial_j^{n-2}\right)\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}},\nonumber\\ \end{align} $$
which proves the claim (4.15) and gives
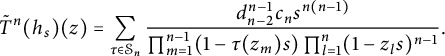$$ \begin{align} \tilde T^n(h_s)(z)=\sum_{\tau\in\mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
We next compute the norm of
$\tilde T^n(h_s)$
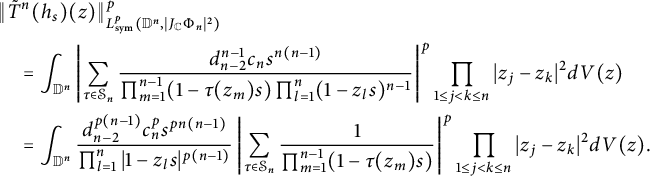$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z).\nonumber\\ \end{align} $$
Set
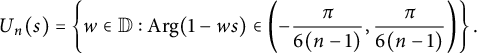$$ \begin{align*}U_n(s)=\left\{w\in \mathbb D: \text{Arg}(1-ws)\in \left(-\frac{\pi}{6(n-1)},\frac{\pi}{6(n-1)}\right)\right\}.\end{align*} $$
Then for any
$z=(z_1,\dots ,z_n)\in (U_n(s))^n$
and
$\tau \in \mathcal S_n$
,
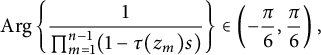$$\begin{align*}\text{Arg}\left\{\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right\}\in \left(-\frac{\pi}{6},\frac{\pi}{6}\right),\end{align*}$$
which yields that
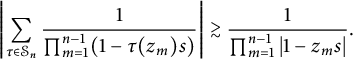$$\begin{align*}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|\gtrsim \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|}.\end{align*}$$
Using this inequality, we have
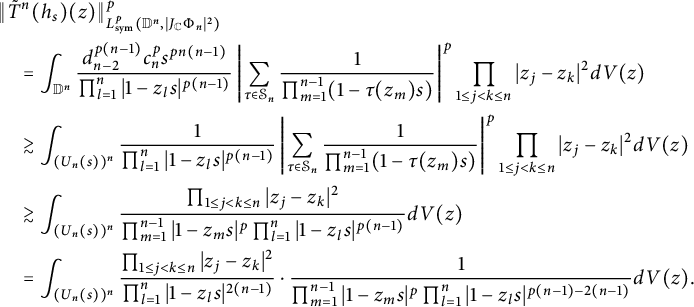$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{1}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)}}dV(z)\nonumber\\& \quad =\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z).\nonumber\\ \end{align} $$
By a similar
$(n-1)$
-step partial fraction procedure, we obtain the following analogue of (4.10)
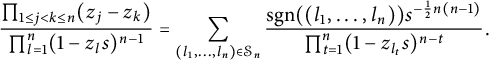$$\begin{align*}\frac{\prod_{1\leq j<k\leq n }(z_j- z_k)}{\prod_{l=1}^n(1-z_ls)^{n-1}}=\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))s^{-\frac{1}{2}n(n-1)}}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}.\end{align*}$$
Hence (4.19) becomes
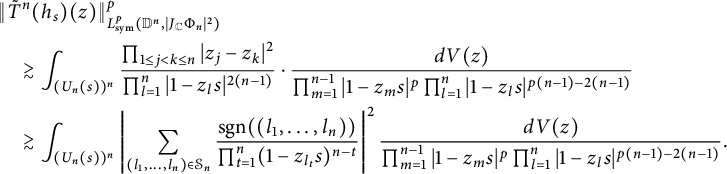$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}\nonumber\\& \quad \gtrsim \int_{(U_n(s))^n}\left|\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}\right|^2\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}.\nonumber\\ \end{align} $$
We further restrict our region of integration to obtain more precise estimates. For
$j\in \{1,\dots ,n\}$
and
$s\in (1-(5n!)^{-2n},1)$
, we set
$$\begin{align*}U_n(s,j)=U_n(s)\bigcap\left\{z:(5n!)^{2j}(1-s)<\left|z-\frac{1}{s}\right|<1\right\},\end{align*}$$
and set
$\mathbf U(s)=U_n(s,1)\times U_n(s,2)\times \dots \times U_n(s,n).$
It is worth noting that we implement a positive lower bound
$1-(5n!)^{-2n}$
for s here so that
$U_n(s,j)$
is nonempty and
$\mathbf U(s)$
is asymmetric in its components. As the reader will see, we need this extra restriction for s but not when
$n=2$
since in higher dimensions, the desired integral estimates cannot be achieved solely by Forelli–Rudin estimate. The asymmetry of
$\mathbf U(s)$
is also used.
By a polar coordinate computation,
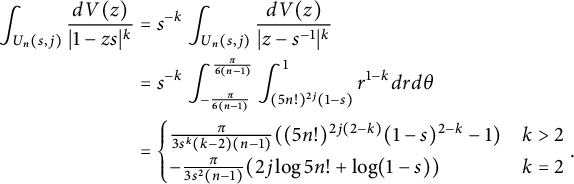$$ \begin{align} \int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}&=s^{-k}\int_{U_n(s,j)}\frac{dV(z)}{|z-s^{-1}|^k}\nonumber\\&=s^{-k}\int_{-\frac{\pi}{6(n-1)}}^{\frac{\pi}{6(n-1)}}\int_{(5n!)^{2j}(1-s)}^{1}r^{1-k}drd\theta\nonumber\\&=\begin{cases} \frac{\pi}{3s^k(k-2)(n-1)}((5n!)^{2j(2-k)}(1-s)^{2-k}-1)& k>2\\ -\frac{\pi}{3s^2(n-1)}(2j\log 5n!+\log(1-s))& k=2 \end{cases}.\end{align} $$
For functions
$f(s)$
and
$g(s)$
, we write
$f(s)\sim g(s)$
if
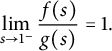$$\begin{align*}\lim_{s\to 1^-}\frac{f(s)}{g(s)}=1.\end{align*}$$
Then, (4.21) yields
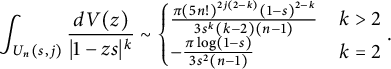$$ \begin{align}\int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}\sim \begin{cases} \frac{\pi(5n!)^{2j(2-k)}(1-s)^{2-k}}{3s^k(k-2)(n-1)}& k>2\\ -\frac{\pi\log(1-s)}{3s^2(n-1)}& k=2 \end{cases}.\end{align} $$
Recall that for
$\tau \in \mathcal S_n$
, we let
$\tau (j)$
be the index satisfying
$z_{\tau (j)}=\tau (z_j)$
. For
$p=\frac {2n}{n-1}$
, the triangle inequality and Cauchy–Schwarz inequality implies
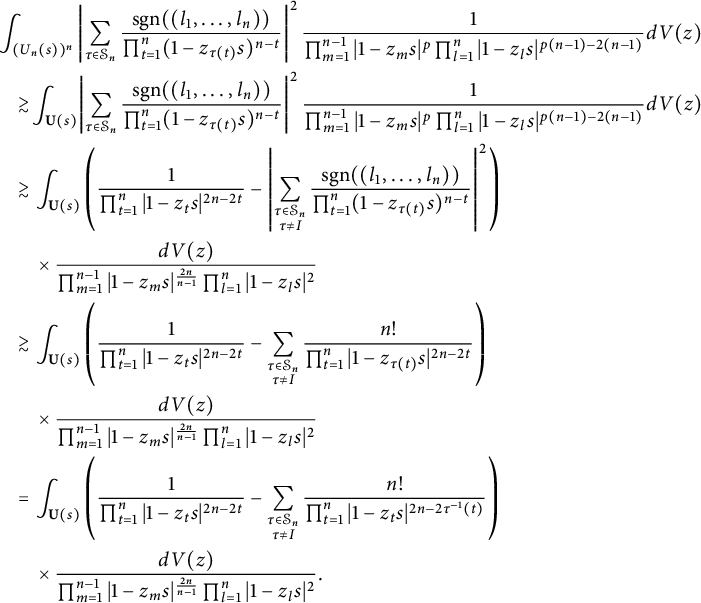$$ \begin{align*} &\!\!\int_{(U_n(s))^n}\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\!\int_{\mathbf U(s)}\!\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2 \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\left|\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_{\tau(t)}s|^{2n-2t}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!=\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}. \end{align*} $$
We claim that in the integral above, the first term will dominate the rest terms, and thus determines the size of the entire integral. We start by showing that the first term dominates the sum of those terms with
$\tau ^{-1}(n)\neq n$
. Note that
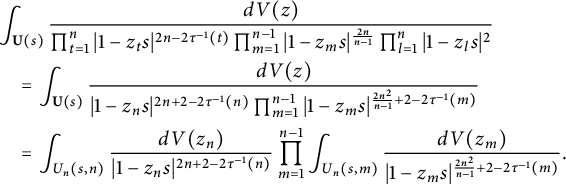$$ \begin{align} &\int_{\mathbf U(s)}\frac{dV(z)}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad = \int_{\mathbf U(s)}\frac{dV(z)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\nonumber\\& \quad = \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}. \end{align} $$
Since
$1\leq m\leq n-1$
, the denominator factor
$|1-z_ms|$
in (4.23) has power strictly greater than 2. The factor
$|1-z_ns|$
has power 2 only if
$\tau ^{-1}(n)=n$
, or equivalently
$\tau (z_n)=z_n$
. By the Forelli–Rudin estimates (2.8) and the fact that
$\{\tau ^{-1}(1),\dots ,\tau ^{-1}(n)\}=\{1,\dots ,n\}$
,
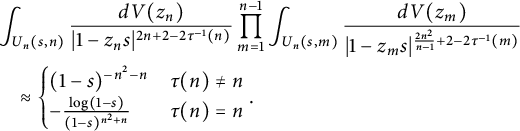$$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}} \nonumber\\& \quad \approx\begin{cases} (1-s)^{-n^2-n}& \tau(n)\neq n\\ -\frac{\log(1-s)}{(1-s)^{n^2+n}}& \tau(n)=n \end{cases}. \end{align} $$
Thus, for s sufficiently close to
$1$
, the integral in (4.23) with
$\tau (n)=n$
dominates the ones with
$\tau (n)\neq n$
. Therefore, we can further assume that
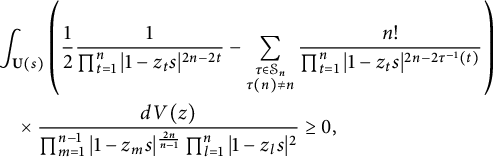$$\begin{align*}&\int_{\mathbf U(s)}\left(\frac{1}{2}\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau(n)\neq n}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \quad \times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^2}\geq0, \end{align*}$$
which implies
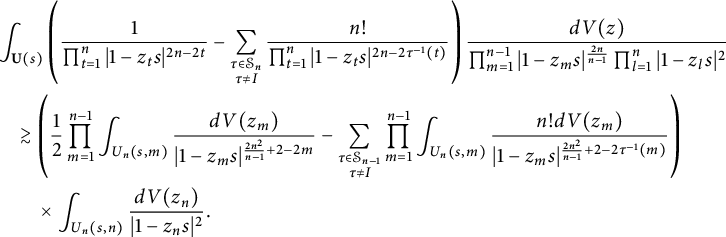$$ \begin{align} &\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad \gtrsim\left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\substack{\tau\in\mathcal S_{n-1}\\ \tau\neq I}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \qquad \times \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}. \nonumber\\ \end{align} $$
Now we turn to show that the positive term in the last line of (4.25) also dominates the rest terms. Since all these terms share the same
$z_n$
part, the estimate (4.24) is no longer able to distinguish one from another. Thus here, we will make use of the asymmetry of
$\mathbf U(s)$
in
$z_j$
variables to prove the claim.
By (4.22), we have
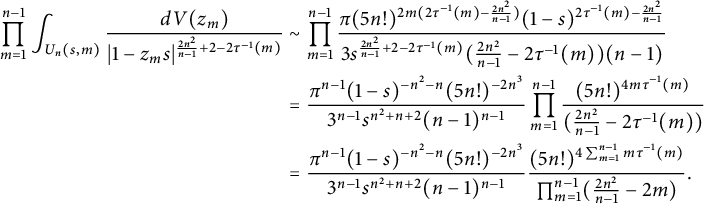$$ \begin{align} \prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}&\sim\prod_{m=1}^{n-1} \frac{\pi(5n!)^{2m(2\tau^{-1}(m)-\frac{2n^2}{n-1})}(1-s)^{2\tau^{-1}(m)-\frac{2n^2}{n-1}}}{3s^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)} (\frac{2n^2}{n-1}-2\tau^{-1}(m))(n-1)}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}} \prod_{m=1}^{n-1}\frac{(5n!)^{4m\tau^{-1}(m)}}{(\frac{2n^2}{n-1}-2\tau^{-1}(m))}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}}\frac{(5n!)^{4\sum_{m=1}^{n-1}m \tau^{-1}(m)}}{\prod_{m=1}^{n-1}(\frac{2n^2}{n-1}-2m)}. \end{align} $$
Hence, for any permutation
$\tau \in \mathcal S_{n-1}$
with
$\tau \neq I$
,
$$ \begin{align} \frac{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}}{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}}&\sim(5n!)^{4\sum_{m=1}^{n-1}(m^2-m\tau^{-1}(m))}\geq (4n!)^4. \end{align} $$
Here
$\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))\geq 1$
follows by Cauchy–Schwarz inequality and the fact that the sum
$\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))$
is an integer. Substituting these estimates into (4.25), we finally obtain
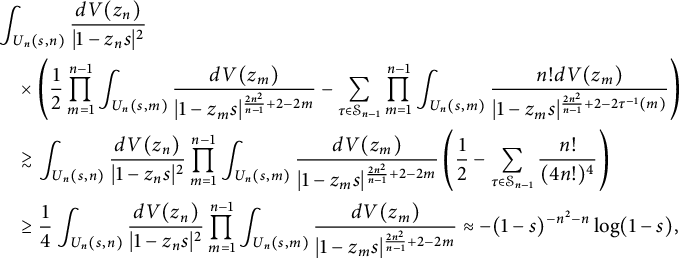$$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\nonumber\\& \quad \times \left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\tau\in\mathcal S_{n-1}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \quad \gtrsim \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\left(\frac{1}{2}-\sum_{\tau\in\mathcal S_{n-1}}\frac{n!}{(4n!)^{4}}\right) \nonumber\\& \quad \geq \frac{1}{4} \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\approx-(1-s)^{-n^2-n}\log(1-s),\nonumber\\ \end{align} $$
which implies that
$\| \tilde T^n(h_s)\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\gtrsim -(1-s)^{-n^2-n}\log (1-s)$
. Thus
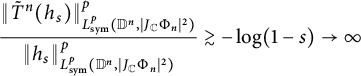$$\begin{align*}\frac{\| \tilde T^n(h_s)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}{\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}\gtrsim-\log(1-s)\to \infty \end{align*}$$
as
$s\to 1$
, proving that
$\tilde T^n$
is unbounded on
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
$p=\frac {2n}{n-1}$
.
5 Some remarks
1. In [Reference Huo and WickHW20a], we studied weak-type estimates of the Bergman projection on the Hartogs triangle and showed the projection is of weak-type
$(4,4)$
but not of weak-type
$(\frac {4}{3},\frac {4}{3})$
. These results together with the Marcinkiewicz interpolation also recover the sharp
$L^p$
regular range
$(\frac {4}{3},4)$
for the projection on the Hartogs triangle. Similarly, weak-type
$(p,p)$
estimates of
$P_{\mathbb G^n}$
when
$p=\frac {2n}{n\pm 1}$
could lead to an alternative approach for Theorem 1.1.
2. In [Reference Chen, Jin and YuanCJY23], Chen, Jin, and Yuan obtained the Sobolev
$L^p$
boundedness for
$P_{\mathbb G}$
from
$W^{k,p}(\mathbb G)$
to some weighted
$W^{k,p}$
spaces for
$p>2$
. With
$L^p$
irregularity results obtained for
$P_{\mathbb G^n}$
, it would be interesting to investigate the
$W^{k,p}$
(ir)regularity for
$P_{\mathbb G^n}$
. In addition to estimates for
$P_{\mathbb G^n}$
, one may further consider
$L^p$
boundedness and compactness of operators that are related to the Bergman projection, such as Toeplitz operators and Hankel operators.
3. The symmetrized polydisc
$\mathbb G^n$
can be viewed as the quotient domain
$\mathbb D^n/\mathcal S_n$
, where
$\mathcal S_n$
is the group of permutations of variables acting on
$\mathbb D^n$
. It is interesting to see whether our method can be generalized to obtain similar results on other quotient domains of
$\mathbb D^n$
. For instance, the
$L^p$
norm of
$P_{\mathbb G^n}$
is equivalent to the
$L^p$
norm of
$P_{\mathbb D^n}$
over
${L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}$
, a subspace of
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
that is related to
$\mathcal S_n$
. On this subspace, we are able to construct the operator
$T^n_2$
which equals
$P_{\mathbb D^n}$
. It is interesting to see if such a proving strategy can be abstracted to work for general quotient domains.
Acknowledgments
The authors would like to thank Gian Maria Dall’Ara, Yuan Yuan, Yuan Zhang, Włodzimierz Zwonek, and the anonymous referee for their valuable comments and suggestions.
