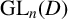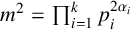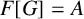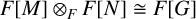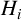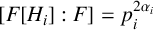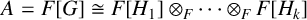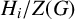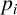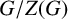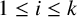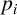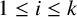1 Introduction
The multiplicative group of a noncommutative division ring has been investigated in various papers by Amitsur [Reference Amitsur3], Herstein [Reference Herstein13, Reference Herstein14], Hua [Reference Hua15, Reference Hua16], Huzurbazar [Reference Huzurbazar17] and Scott [Reference Scott23, Reference Scott24]. Given a noncommutative division ring D with centre
$Z(D) = F$
, the structure of the skew linear group
$\mathrm {GL}_n(D)$
for
$n \geq 1$
is generally unknown. A good account of the most important results concerning skew linear groups can be found in [Reference Shirvani and Wehrfritz25], as well as in [Reference Suprunenko26] particularly for linear groups. For instance, it is shown in [Reference Hazrat and Wadsworth12] that there is a close connection between the question of the existence of maximal subgroups in the multiplicative group of a finite-dimensional division algebra and Albert’s conjecture concerning the cyclicity of division algebras of prime degree. In this direction, in [Reference Mahdavi-Hezavehi and Tignol20], it is shown that when D is a central division F-algebra of prime degree p, then D is cyclic if and only if
$D^*$
contains a nonabelian soluble subgroup. Furthermore, a theorem of Albert (see [Reference Draxl6, page 87]) asserts that D is cyclic if
$D^*/F^*$
contains an element of order p.
The structure of locally nilpotent subgroups of
$\mathrm {GL}_n(D)$
is studied in many papers. The basic structure of locally nilpotent skew linear groups over a locally finite-dimensional division algebra was studied by Zaleeskii [Reference Zaleeskii30]. One important problem raised by Zaleeskii remains open, namely, is every locally nilpotent subgroup of
$\mathrm {GL}_n(D)$
hypercentral. In [Reference Garascuk10], Garascuk proved a theorem that shows this question has a positive answer in the case where
$[D:F]< \infty $
. A treatment of such results which is both more elaborate and more refined may be found in [Reference Dixon4, Reference Shirvani and Wehrfritz25–Reference Wehrfritz29]. For example, it is shown in [Reference Wehrfritz29] that when H is a locally nilpotent normal subgroup of the absolutely irreducible skew linear group G, then H is centre-by-locally-finite and
$G/C_G(H)$
is periodic. In special cases, the structure of maximal subgroups of
$\mathrm {GL}_n(D)$
has been investigated (see [Reference Akbari, Ebrahimian, Momenaee Kermani and Salehi Golsefidy1, Reference Akbari, Mahdavi-Hezavehi and Mahmudi2, Reference Dorbidi, Fallah-Moghaddam and Mahdavi-Hezavehi5, Reference Ebrahimian7, Reference Fallah-Moghaddam9]). For instance, it is shown in [Reference Akbari, Ebrahimian, Momenaee Kermani and Salehi Golsefidy1] that when D is a finite-dimensional division ring with infinite centre F and M is a locally nilpotent maximal subgroup of
$\mathrm {GL}_n(D)$
, then M is an abelian group. Also, by [Reference Shirvani and Wehrfritz25, Theorem 3.3.8], when D is an F-central locally finite-dimensional division algebra, every locally nilpotent subgroup of
$\mathrm {GL}_n(D)$
is soluble.
Another important property of locally nilpotent subgroups arises in crossed product constructions. Let R be a ring, S a subring of R and G a group of units of R normalising S such that
$R=S[G]$
. Suppose that
$N=S\cap G$
is a normal subgroup of G and
$R=\oplus _{t \in T} tS$
, where T is some transversal of N to G. Set
$H=G/N$
. We summarise this construction by saying that
$(R, S, G, H)$
is a crossed product. Sometimes, we say that R is a crossed product of S by H. Let
$\mathcal {O}$
be the class of all groups H such that every crossed product of a division ring by H is an Ore domain. In [Reference Shirvani and Wehrfritz25, Remark 1.4.4], it is shown that the group ring
$EG$
is an Ore domain for any division ring E and any torsion-free locally nilpotent group G. In addition, any hyper torsion-free locally nilpotent group is in
$\mathcal {O}$
.
Let D be an F-central division algebra and G a subgroup of
$\mathrm {GL}_n(D)$
. The F-algebra of G, that is, the F-subalgebra generated by elements of G over F in
$M_n(D)$
is denoted by
$F[G]$
. Further, G is absolutely irreducible if
$F[G]=M_n(D)$
. When
$M_n(D)$
is a crossed product over a maximal subfield K, from [Reference Draxl6, page 92],
$K/F$
is Galois and we can write
$M_n(D)=\oplus _{\sigma \in \mathrm {Gal}(K/F)}Ke_{\sigma }$
, where
$e_{\sigma }\in \mathrm {GL}_n(D)$
and for each
$x\in K$
and
$\sigma \in \mathrm {Gal}(K/F)$
, there exists
$\sigma (x)\in K$
such that
$e_{\sigma }x=\sigma (x)e_{\sigma }$
. Several recent papers investigate the group theoretical properties which give useful tools to realise maximal Galois subfields of central simple algebras in terms of absolutely irreducible subgroups (see [Reference Akbari, Ebrahimian, Momenaee Kermani and Salehi Golsefidy1, Reference Ebrahimian, Kiani and Mahdavi-Hezavehi8, Reference Fallah-Moghaddam9, Reference Hazrat, Mahdavi-Hezavehi and Motiee11, Reference Keshavarzipour and Mahdavi-Hezavehi18–Reference Mahdavi-Hezavehi and Tignol20]).
We say a group G is a central product of two of its subgroups M and N if
$G=MN$
and
$M\subseteq C_G(N)$
. In fact, a central product of two groups is a quotient group of
$M\times N$
. If F is a field and
$FG$
denotes the group algebra of G, then it is well known that
$FM\otimes _F FN\cong F(M\times N)$
. We prove a similar result for skew linear groups. Let A be an F-central simple algebra of degree
$n^2=\prod _{i=1}^k p_i^{2\alpha _i}$
and G be a subgroup of the unit group of A such that
$F[G]=A$
. We prove that if G is a central product of two of its subgroups M and N, then
$F[M]\otimes _F F[N]\cong F[G]$
. Also, if G is locally nilpotent, then G is a central product of subgroups
$H_i$
, where
$[F[H_i]:F]=p_i^{2\alpha _i}$
,
$A=F[G]\cong F[H_1]\otimes _F \cdots \otimes _F F[H_k]$
and
$H_i/Z(G)$
is the Sylow
$p_i$
-subgroup of
$G/Z(G)$
for
$1\leq i\leq k$
. Additionally, there is an element of order
$p_i$
in F for
$1\leq i\leq k$
.
2 Notation and conventions
We recall here some of the notation that we will need throughout this article. Given a subset S and a subring K of a ring R, the subring generated by K and S is denoted by
$K[S].$
The unit group of R is written as
$R^*$
. For a group G and subset
$S\subset G$
, we denote by
$Z(G)$
and
$C_G(S)$
the centre and the centraliser of S in G and the same notation is applied for R. We use
$N_G(S)$
for the normaliser of S in G and
$G'$
for the derived subgroup of G. A group G is a central product of its subgroups
$H_1,\ldots ,H_k$
if
$G=H_1\cdots H_k$
and
$H_i\subseteq C_G(H_j)$
for each
$i\neq j$
.
Let F be a field, and A and B be two unital F-algebras. Let H be a subgroup of
$A^*$
and G be a subgroup of
$B^*$
. We define
$H\otimes _F G$
by
$$ \begin{align*}H\otimes_F G=\{a\otimes b \mid a\in H, b\in G\}.\end{align*} $$
Note that
$(a\otimes b)^{-1}=a^{-1}\otimes b^{-1}$
, so it is easily checked that
$H\otimes _F G$
is a subgroup of
$(A\otimes B)^*$
. Also,
$F[H]\otimes _F F[G]=F[H\otimes _F G]$
in
$A\otimes _F B$
.
Given a division ring D with centre F and a subgroup G of
$\mathrm {GL}_n(D)$
, the space of column n-vectors
$V=D^n$
over D is a
$G\text {--}D$
bimodule; G is called irreducible, completely reducible or reducible according to whether V is irreducible, completely reducible or reducible as a
$G\text {--}D$
bimodule.
An irreducible group G is said to be imprimitive if for some integer
$m\geq 2,$
there exist subspaces
$V_1,\ldots ,V_m$
of V such that
$V=\oplus _{i=1}^m V_i$
and for any
$g\in G$
, the mapping
$V_i\rightarrow gV_i$
is a permutation of the set
$\{V_1,\ldots ,V_m\}$
; otherwise, G is called primitive.
The following important results on central simple algebras will be used later.
Theorem 2.1 (Double centraliser theorem; [Reference Draxl6, page 43]).
Let
$B\subseteq A$
be simple rings such that
$K:=Z(A)=Z(B)$
. Then,
$A\cong B\otimes _K C_A(B)$
whenever
$[B:K]$
is finite.
Theorem 2.2 (Centraliser theorem; [Reference Draxl6, page 42]).
Let B be a simple subring of a simple ring A,
$ K:=Z(A)\subseteq Z(B)$
and
$n:=[B:K]$
be finite. Then:
-
(1)
$C_A(B)\otimes _K M_n(K) \cong A \otimes _K B^{\mathrm {op}}$
; -
(2)
$C_A(B)$
is a simple ring; -
(3)
$Z(C_A(B))=Z(B)$
; -
(4)
$C_A(C_A(B))=B$
; -
(5) if
$L:=Z(B)$
and
$r:=[L:K]$
, then
$A \otimes _K L \cong M_r(B) \otimes _L C_A(B) $
; -
(6) A is a free left (right)
$C_A(B)$
-module of unique rank n; -
(7) if, in addition to the above assumptions,
$m:=[A:K]$
is also finite, then A is a free left (right) B-module of unique rank
$m/n=[C_A(B):K]$
.
Theorem 2.3 [Reference Draxl6, page 30].
Let
$A,B$
be K-algebras,
$K:=Z(A)\subseteq Z(B)$
a field and either
$[A:K]$
or
$[B:K]$
finite. Then,
$A\otimes _K B$
is a simple ring if and only if A and B are simple rings.
3 Central products of skew linear groups and tensor products of central simple algebras
In this section, we prove a theorem which relates a central decomposition of an absolutely irreducible group G to the tensor product decomposition of
$F[G]$
.
It is well known that every finite dimensional division algebra is isomorphic to a tensor product of division algebras of prime power degree [Reference Draxl6, page 68]. Since each central simple algebra is isomorphic to some
$M_n(D)$
, we easily obtain the following result.
Lemma 3.1. Let A be an F-central simple algebra of degree
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$
. Then,
$A\cong A_1\otimes _F\cdots \otimes _F A_k$
, where
$A_i$
is a unique (up to isomorphism) F-central simple algebra of degree
$p_i^{2\alpha _i}$
.
Additionally, we have the following easy lemma.
Lemma 3.2. Let
$A,B$
be two F-central simple algebras, and
$M\leq A^*$
and
$N\leq B^*$
. Then, M and N are absolutely irreducible if and only if
$M\otimes _F N$
is an absolutely irreducible subgroup of
$A\otimes _F B$
.
Lemma 3.3. Let F be a field,
$A,B$
be two unital F-algebras and
$a\in A,b\in B$
. Then,
$a\otimes b=1\otimes 1$
if and only if
$a,b \in F$
and
$ab=1$
.
Proof. First, if
$a,b \in F$
and
$ab=1$
, then
$a\otimes b=ab\otimes 1=1\otimes 1$
.
Conversely, assume
$a\otimes b=1\otimes 1$
. It is clear that
$a\neq 0$
and
$b\neq 0$
. First, assume that
$a,b \notin F^*$
. Then,
$\{1,a\}$
is an F-linearly independent set in A and
$\{1,b\}$
is an F-linearly independent set in B. By [Reference Draxl6, Theorem 4.3],
$\{a\otimes b,1\otimes 1\}$
is an F-linearly independent set in
$A\otimes _F B$
. Therefore,
$a\otimes b \neq 1\otimes 1$
. Next, assume that
$a \notin F^*$
and
$ b\in F^*$
. Then,
$ab\notin F^*$
and
$\{1,ab\}$
is an F-linearly independent set in B. Thus,
$\{1\otimes ab,1\otimes 1\}$
is an F-linearly independent set in
$A\otimes _F B$
and
$a\otimes b=1\otimes ab\neq 1\otimes 1$
. When
$b \notin F^*$
and
$ a\in F^*$
, the proof is similar. We conclude that if
$a\otimes b=1\otimes 1$
, then
$a,b \in F^*$
. Now, we have
$1\otimes 1=a\otimes b=ab\otimes 1=ab(1\otimes 1)$
. Consequently,
$ab=1$
, as we desired.
The following result shows that any absolutely irreducible skew linear group can be viewed as an absolutely irreducible linear group.
Proposition 3.4. Let F be a field and D be a finite dimensional F-central division algebra such that
$[D:F]=n^2$
. Let K be a maximal subfield of D and G be an absolutely irreducible subgroup of
$\mathrm {GL}_m(D)$
. Then,
$M_m(D)\otimes K\cong M_{mn}(K)$
and
$G\otimes _F 1$
is an absolutely irreducible subgroup of
$U(M_m(D)\otimes _F K)\cong \mathrm {GL}_{nm}(K)$
isomorphic to G.
Proof. By [Reference Pierce21, Propositions 13.5 and 13.3], there exists a maximal subfield K of D such that
$[D:K]=[K:F]=n$
and
$D\otimes _F K\cong M_n(K)$
. Therefore,
$M_m(D)\otimes _F K\cong M_m(F)\otimes _F(D\otimes _F K)\cong (M_m(F)\otimes _F M_n(F))\otimes _F K \cong M_{mn}(K)$
. Now, by Lemma 3.3, the map
$\phi : G\rightarrow G\otimes _F 1$
given by
$\phi (g)=g\otimes 1$
is an isomorphism. However, G is an absolutely irreducible subgroup of
$\mathrm {GL}_m(D)$
, so
$F[G]=M_m(D)$
. Also,
$M_m(D)\otimes _F K=F[G]\otimes _F K=K[G\otimes _F K^*]\subseteq K[G\otimes _F 1]\subseteq M_m(D)\otimes _F K$
. Consequently,
$K[G\otimes _F 1]=M_m(D)\otimes _F K$
. This means
$G\otimes _F 1$
is an absolutely irreducible subgroup of
$\mathrm {GL}_m(D)\otimes _F K^*$
isomorphic to G. In addition, G is isomorphic to an absolutely irreducible subgroup of
$\mathrm {GL}_{nm}(K)$
.
Corollary 3.5. Let F be a field and D be a finite dimensional F-central division algebra. Assume that G is a subgroup of
$\mathrm {GL}_m(D)$
such that
$F[G]$
is a simple ring. Then, there exists an absolutely irreducible linear group H isomorphic to G.
Theorem 3.6 [Reference Shirvani and Wehrfritz25, page 7].
Let F be a field, D a locally finite-dimensional division F-algebra and G a subgroup of
$\mathrm {GL}_n(D)$
. Set
$R=F[G]\subseteq M_n(D)$
.
-
(1) If G is completely reducible, then R is semisimple Artinian.
-
(2) If G is irreducible, then R is simple Artinian.
Using Theorem 3.6, we obtain the following result.
Corollary 3.7. Let F be a field and D be a finite dimensional F-central division algebra. If G is an irreducible subgroup of
$\mathrm {GL}_m(D)$
, then there exists an absolutely irreducible linear group H isomorphic to G.
When F is a field, a subgroup G of
$\mathrm {GL}_n(F)$
is said to be absolutely irreducible if it is an irreducible subgroup of
$\mathrm {GL}_n(K)$
for any extension K of F. Hence, we obtain the following result.
Corollary 3.8. Let F be a field and D be a finite dimensional F-central division algebra. If G is an irreducible subgroup of
$\mathrm {GL}_m(D)$
such that either G is irreducible or
$F[G]$
is a simple ring, then there exists an algebraically closed field
$\Omega $
and an irreducible
$\Omega $
-linear group H isomorphic to G.
Theorem 3.9 [Reference Shirvani and Wehrfritz25, page 8].
Let F be a field, D a division F-algebra and G a subgroup of
$\mathrm {GL}_n(D)$
. Set
$R=F[G]\subseteq M_n(D)$
.
-
(1) If R is semiprime (for example, if R is semisimple Artinian), then G is isomorphic to a completely reducible subgroup of
$\mathrm {GL}_n(D)$
. -
(2) If R is simple Artinian, then for some
$m\leq n$
, the group G is isomorphic to an irreducible subgroup of
$\mathrm {GL}_m(D)$
.
Using Theorem 3.9, we obtain the following result.
Corollary 3.10. Let F be a field and D be a finite dimensional F-central division algebra such that
$[D:F]=n^2$
. Let
$A=M_m(D)\subseteq M_{n^2m}(F)=B$
be an F-central simple algebra. If G is a subgroup of
$\mathrm {GL}_m(D)$
such that either G is irreducible or
$F[G]$
is a simple ring, then for some
$s\leq mn^2$
, the group G is isomorphic to an irreducible subgroup of
$\mathrm {GL}_{s}(F)$
.
Theorem 3.11 [Reference Suprunenko26, page 111].
Let V be a finite dimensional linear space over a division ring D and G an irreducible subgroup of
$\mathrm {GL}(V)$
which can be represented in the form
$G=HF$
, where H and F are elementwise permutable normal subgroups of G. Then, the irreducible components of
$H(F)$
are pairwise equivalent.
Proposition 3.12. Let F be a field and D be a finite dimensional F-central division algebra. Assume that G is an absolutely irreducible subgroup of
$\mathrm {GL}_n(D)$
. If
$G=MN$
is a central product decomposition of G, then
$F[M]\otimes _F F[N]\cong F[G]$
and under this isomorphism,
$M\otimes _F N\cong G$
. Additionally,
$F[M]$
and
$F[N]$
are F-central division algebras.
Proof. By [Reference Shirvani and Wehrfritz25, Theorem 1.2.1], G is irreducible. Using [Reference Shirvani and Wehrfritz25, Theorem 1.1.7] and Theorem 3.11, we conclude that M is a homogeneous completely irreducible subgroup. So Theorem 3.11 implies
$D^n\cong V^m$
, where V is an irreducible
$M-D$
bimodule. Hence,
$F[N]\subseteq A=C_{M_n(D)}(M)=\mathrm {End}_{M-D}(D^n)\cong M_m(E)$
, where
$E=\mathrm {End}_{M-D}(V)$
is a division ring by Schur’s lemma. Note that
$F[N]\otimes F[M]\leq A\otimes _F C_{M_n(D)}(A)$
. Hence, by the centraliser theorem,
$[F[M]:F]FN]:F]\leq [A:F][C_{M_n(D)}(A):F]=n^2[D:F]$
. Furthermore,
$F[M],F[N]\subseteq F[G]$
implies that there is a surjective homomorphism f from
$F[N]\otimes _F F[M]$
onto
$F[G]{\kern-1pt}={\kern-1pt}M_n(D)$
such that
$f(a\otimes b){\kern-1pt}={\kern-1pt}ab$
for each
$a{\kern-1pt}\in{\kern-1pt} M,b{\kern-1pt}\in{\kern-1pt} N$
. So
$F[M]\otimes _F F[N]\cong F[G]$
by dimension counting. It is clear that
$\overline {f}$
, the restriction of f to
$M\otimes _F N$
, is a surjective homomorphism on G. If
$\overline {f}(a\otimes b)=ab=1$
, then
$a=b^{-1}\in M\cap N\subseteq Z(G)\subseteq F$
. Hence,
$a\otimes b=b^{-1}\otimes b=1\otimes b^{-1}b=1\otimes 1$
. So,
$\ker (\overline {f})$
is trivial and
$\overline {f}$
is an isomorphism from
$M\otimes _F N$
to G. Consequently,
$F[M]$
and
$F[N]$
are F-central division algebras by Theorem 2.3.
The following example shows that the above result is not true in semisimple rings.
Example 3.13. Let
$A=F\times F$
,
$G=\{(1,1),(1,-1),(-1,1),(-1,-1)\}$
,
$M=\{(1,1), (1,-1)\},N=\{(1,1),(-1,1)\}$
. Then, G is a central product of M and N. However,
$ [F[M]\otimes _F F[N]:F]=4$
. So
$F[M]\otimes _F F[N]\ncong F[G]=A$
.
Next we introduce some notation from [Reference Suprunenko26]. Let V be a finite dimensional linear space over a division ring D and G a completely irreducible subgroup of
$\mathrm {GL}(V)$
. Let
$D^n=V=L_1\oplus \cdots \oplus L_r $
and suppose that
$L_i$
is a G-invariant G-irreducible subspace of V for
$1\leq i\leq r$
. We determine the irreducible components of G, that is, the irreducible representations
$d_i$
of the form
$$ \begin{align*}d_i:G\rightarrow \text{GL}(L_i), \quad g\rightarrow g\mid L_i, \quad i=1, \ldots, r.\end{align*} $$
By [Reference Suprunenko26, Lemma 13.1], the irreducible components
$d_i$
and
$d_j$
of G are equivalent if and only if there exists a module isomorphism
$\Psi : L_i\rightarrow L_j$
such that for any
$y \in G$
,
$$ \begin{align*}d_j(y)=\Psi d_1(y)\Psi^{-1}.\end{align*} $$
In addition, these representations are equivalent if and only if the modules
$L_i$
and
$L_j$
have respective bases
$B_1 $
and
$B_2$
such that for any
$y\in G$
, the matrix of the endomorphism
$d_i(y)$
in
$B_1$
is the same as that of
$d_j(y)$
in
$B_2$
. This observation gives the following result.
Lemma 3.14. Let G be a completely irreducible subgroup of
$\mathrm {GL}_n(D)$
such that the irreducible components of G are pairwise equivalent. Let r be the degree of an irreducible component of G and
$n=rs$
. Then, there is an isomorphism f with
$f:M_n(D)\longrightarrow M_r(D)\otimes _F M_s(F)$
and an irreducible subgroup H of
$\mathrm {GL}_r(D)$
such that
$f(G)=H\otimes \{1\}$
.
4 Locally nilpotent subgroups of
$\textrm {GL}_n(D)$
In this section, we prove that every absolutely irreducible locally nilpotent subgroup of
$\mathrm {GL}_n(D)$
is a central product of some of its subgroups which gives a decomposition of
$M_n(D)$
as a tensor product of central simple algebras of prime power degree. First, we recall the following general results which play a key role in proving our main theorems.
Theorem 4.1 [Reference Suprunenko26, page 216].
Let F be an arbitrary field and G be an absolutely irreducible locally nilpotent subgroup of
$\mathrm {GL}_n(F)$
. Then,
$G/Z(G) $
is periodic and
$\pi (G/Z(G))=\pi (n)$
.
Theorem 4.2 [Reference Wehrfritz29].
Let H be a locally nilpotent normal subgroup of the absolutely irreducible skew linear group G. Then, H is centre-by-locally finite and
$G/C_G(H)$
is periodic.
Theorem 4.3 [Reference Robinson22, page 342].
Let G be a locally nilpotent group. Then, the elements of finite order in G form a fully invariant subgroup T (the torsion subgroup of G) such that
$G/T$
is torsion and T is a direct product of p-groups.
Theorem 4.4 [Reference Dorbidi, Fallah-Moghaddam and Mahdavi-Hezavehi5].
Let N be a normal subgroup in a primitive subgroup M of
$\mathrm {GL}_n(D)$
. Then:
-
(1)
$F[N]$
is a prime ring; -
(2)
$C_{M_n(D)}(N)$
is a simple Artinian ring; -
(3) if
$C_{M_n(D)}(N)$
is a division ring, then N is irreducible.
Theorem 4.5 [Reference Keshavarzipour and Mahdavi-Hezavehi18].
Let D be a finite dimensional F-central division algebra. Then,
$M_m(D)$
is a crossed product over a maximal subfield if and only if there exists an absolutely irreducible subgroup G of
$M_m(D)$
and a normal abelian subgroup A of G such that
$C_G(A)=A$
and
$F[A]$
contains no zero divisor.
Theorem 4.6. Let
$A=M_n(D)$
be an F-central simple algebra of degree
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$
and G be an absolutely irreducible locally nilpotent subgroup
$A^*$
. Then:
-
(1)
$G/Z(G) $
is locally finite and
$\pi (G/Z(G))=\pi (m)$
; -
(2)
$G/Z(G) $
is a p-group for some prime p if and only if m is a pth power.
Proof. (1) By Theorem 4.2, G is centre-by-locally finite. Let K be a maximal subfield of D. By Proposition 3.4, G is isomorphic to an absolutely irreducible subgroup of
$\mathrm {GL}_{m}(K)$
. Now, Theorem 4.1 asserts that
$\pi (G/Z(G))=\pi (m)$
.
(2) This statement is clear from item (1).
Corollary 4.7. Let
$A=M_n(D)$
be an F-central simple algebra of degree
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$
and G be an absolutely irreducible locally nilpotent subgroup of
$A^*$
. Then:
-
(1)
$G/Z(G) $
is locally finite and
$\pi (G/Z(G))=\pi (m^2/[C_{M_n(D)}:F])\subseteq \pi (m)$
; -
(2) if
$G/Z(G) $
is a p-group for some prime p, then
$[F[G]:F]$
is a pth power; -
(3) if m is a pth power for some prime p, then
$G/Z(G) $
is a p-group.
Proof. By Theorem 3.6,
$F[G]$
is a simple ring. From the centraliser theorem,
$[F[G]:F][C_{M_n(D)}:F]=m^2$
. The reminder of the proof is similar to the proof of Theorem 4.6.
Now we are ready to prove the main theorem of this article.
Theorem 4.8. Let
$A=M_n(D)$
be an F-central simple algebra of degree
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$
and G be an absolutely irreducible locally nilpotent subgroup
$A^*$
. Then:
-
(1)
$G/Z(G)$
is the internal direct product of
${H_1}/{Z(G)},\ldots , {H_k}/{Z(G)}$
, where
$H_i/Z(G)$
is the Sylow
$p_i$
-subgroup of
$G/Z(G)$
; -
(2) G is the central product of
$H_1,\ldots ,H_k$
; -
(3)
$A=F[G]\cong F[H_1]\otimes _F \cdots \otimes _F F[H_k]$
and
$G\cong H_1\otimes _F \cdots \otimes _F H_k $
under this isomorphism and, for each i,
$A_i=F[H_i]$
is an F-central simple algebra and
$[F[H_i]:F]={p_i}^{2\alpha _i}$
.
Proof. (1) The statement follows from Theorems 4.3 and 4.6.
(2) Let
$i \neq j$
and take
$a \in H_i,b \in H_j$
. Then,
$ab=\lambda ba$
with
$\lambda \in Z(G) \subseteq F^*$
. Now,
$a^{{p_i}^\gamma } \in F^*$
and
$b^{{p_j}^\delta }\in F^*$
, so
$\lambda ^{{p_i}^\gamma }=\lambda ^{{p_j}^\delta }=1$
, which gives
$\lambda =1$
and
$ab=ba$
. So,
$H_i\subseteq C_G(H_j)$
and G is the central product of
$H_1,\ldots ,H_k$
.
(3) This statement follows from Proposition 3.12 and induction on k.
Corollary 4.9. Keep the notation and assumptions of Theorem 4.8. If
$n=1$
and
$F[H_i]=D_i$
, then
$D\cong D_1\otimes _F \cdots \otimes _F D_k$
, where
$i(D_i)={p_i}^{\alpha _i}$
.
Using [Reference Kiani and Ramezan-Nassab19, Theorem 2.4], we have the following proposition.
Proposition 4.10. Keep the notation and assumptions of Theorem 4.8. Then,
$F[G]=M_n(D)$
is a crossed product over a maximal subfield K if and only if for each i,
$F[H_i]$
is a crossed product over a maximal subfield
$K_i$
. In addition, under these circumstances,
$K\cong K_1 \otimes _F\cdots \otimes _F K_k$
and
$\mathrm {Gal}(K/F)\cong \mathrm {Gal}(K_1/F)\times \cdots \times \mathrm {Gal}(K_k/F). $
Theorem 4.11. Let D be an F-central finite dimensional division algebra. Assume that G be a primitive absolutely irreducible locally nilpotent subgroup of
$\mathrm {GL}_n(D)$
. Then,
$M_n(D)$
is a crossed product over a maximal subfield K. With the notation and assumptions of Theorem 4.8:
-
(1) there exists an abelian normal subgroup S of G such that
$G/S$
and
$\mathrm {Gal}(K/F)$
are finite nilpotent groups and
$\mathrm {Gal}(K/F)\cong N_{\mathrm {GL}_n(D)}(K^*)/K^*\cong G/S$
; -
(2) for each i, there exists an abelian subgroup
$A_i$
of
$H_i$
such that
$F[H_i]$
is a crossed product over a maximal subfield
$K_i$
and, in addition,
$H_i/A_i$
and
$Gal(K_i/F)$
are finite nilpotent groups and
$\mathrm {Gal}(K_i/F)\cong N_{F[H_i]^*}(K_i^*)/K_i^*\cong H_i/A_i$
; -
(3)
$S\cong A_1\otimes _F \cdots \otimes _F A_k $
,
$K\cong K_1\otimes _F \cdots \otimes _F K_k $
and
$S=A_1 \cdots A_k $
.
Proof. By [Reference Shirvani and Wehrfritz25, Theorem 3.3.8], G is soluble. Now, using [Reference Suprunenko26, Theorem 6, page 135], G contains a maximal abelian normal subgroup, say S, such that
$|G/S|< \infty $
. By Theorem 4.4,
$K=F[S]$
is a field and by a result in [Reference Garascuk10], G is hypercentral. Hence, by an exercise from [Reference Robinson22, page 354], we conclude that every maximal abelian normal subgroup of G is self-centralising. Now, using Theorem 4.5, we conclude that
$M_n(D)$
is a crossed product over a maximal subfield K. By a result of [Reference Draxl6, page 92],
$K/F$
is Galois and we can write
$M_n(D)=\oplus _{\sigma \in \mathrm {Gal}(K/F)}Ke_{\sigma }$
, where
$e_{\sigma }\in \mathrm {GL}_n(D)$
and for each
$x\in K$
and
$\sigma \in \mathrm {Gal}(K/F)$
, there exists
$\sigma (x)\in K$
such that
$e_{\sigma }x=\sigma (x)e_{\sigma }$
. So,
$e_{\sigma }\in N_{\mathrm {GL}_n(D)}(K^*)$
. Now, using the Skolem–Noether theorem [Reference Draxl6, page 39] and the fact that
$C_{M_n(D)}(K)=K$
, we obtain
$\mathrm {Gal}(K/F)\cong N_{\mathrm {GL}_n(D)}(K^*)/K^*$
. However, consider the homomorphism
$\sigma : G\rightarrow \mathrm {Gal}(K/F)$
given by
$\sigma (x)=f_x$
, where
$f_x(k)=xkx^{-1}$
for
$k\in K$
. Clearly,
$\ker (\sigma )=C_G(K)$
. Since
$S\subseteq C_G(K)\subseteq C_G(S)=S$
, we have
$C_G(K)=S$
. Choose an element
$a \in \mathrm {Fix}(\mathrm {Im}\, \sigma )$
. For any
$x\in G$
, we have
$f_x(a)=a$
and hence
$xa=ax$
. This shows that
$\mathrm {Fix}(\mathrm {Im}\, \sigma )\subseteq C_K(G)\subseteq C_{M_n(D)}(G)=F$
. Hence,
$F=\mathrm {Fix}(\mathrm {Im}\, \sigma )$
and
$\sigma $
is surjective. Therefore,
$\mathrm {Gal}(K/F)\cong G/S$
, as we claimed.
The proof is completed by using Theorem 4.8 and Proposition 4.10.
We can immediately deduce the following theorem.
Theorem 4.12. Let D be an F-central finite dimensional division algebra such that
$[D:F]=i(D)^2=\prod _{i=1}^k{p_i}^{2\alpha _i}$
. If
$D^*$
contains an absolutely irreducible locally nilpotent subgroup G, then D is a crossed product over a maximal subfield K. With the notation and assumptions of Theorems 4.8 and 4.11,
$D\cong D_1\otimes _F \cdots \otimes _F D_k$
, where
$F[H_i]=D_i$
and
$D_i$
is a crossed product over a maximal subfield
$K_i$
.
Proposition 4.13. Let
$A=M_n(D)$
be an F-central simple algebra of degree
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$
and G be an absolutely irreducible locally nilpotent subgroup
$A^*$
. Then, there is an element of order
$p_i$
in F for
$1\leq i\leq k$
.
Proof. Keep the notation and assumptions of Theorem 4.8, so that
$[F[H_i]:F]={p_i}^{2\alpha _i}$
. Since
$F[H_i]$
is a central simple algebra,
$F[H_i]\cong M_{{p_i}^{\beta _i}}(D_i)$
, where
$D_i$
is an F-central division algebra of degree a power of
$p_i$
. Assume that
$K_i$
is a maximal subfield of
$D_i$
. By [Reference Suprunenko26, Theorem 27.6] and Proposition 3.4,
$K_i$
contains an element b, say, of order
$p_i$
. Now,
$[F(b):F]\leq p_i-1$
and
$[F(b):F]\mid [K_i:F]$
. However,
$[K_i:F]$
is a power of
$p_i$
, which implies
$[F[b]:F]=1$
, that is,
$b\in F$
.
Proposition 4.14. Let D be an F-central finite dimensional division algebra and suppose that for
$p \in \pi (n)$
, there is an element of order p in F, when
$n>1$
. Then,
$\mathrm {GL}_n(D)$
contains a finite irreducible nonabelian nilpotent subgroup G such that
$F[G]=M_n(F)\subseteq M_n(D)$
.
Proof. By [Reference Suprunenko26, Theorem 27.6], there exists a finite nilpotent subgroup G of
$\mathrm {GL}_n(F)$
such that
$F[G]=M_n(F)\subseteq M_n(D)$
. We show that G is an irreducible subgroup of
$\mathrm {GL}_n(D)$
. In contrast, assume that G is reducible in
$\mathrm {GL}_n(D)$
. By [Reference Shirvani and Wehrfritz25, Theorem 1.1.1], there exists a matrix
$P \in \mathrm {GL}_n(D)$
such that
$$ \begin{align*}P(F[G])P^{-1}\subseteq\left[\begin{matrix} M_r(D) & B \\ 0_{(n-s)\times r} & M_{n-s}(D)\\ \end{matrix}\right].\end{align*} $$
This means that we can define a homomorphism from
$M_n(F)$
to
$M_r(D)$
. However,
$M_n(F)$
is a simple ring. Hence, this map is an injection. This contradicts [Reference Shirvani and Wehrfritz25, Theorem 1.1.9], which asserts that the matrix ring
$M_r(D)$
contains at most r nonzero pairwise orthogonal idempotents.
Example 4.15. The multiplicative group of the real quaternion division algebra contains the quaternion group which is an absolutely irreducible
$2$
-group. By [Reference Ebrahimian, Kiani and Mahdavi-Hezavehi8, Corollary 3.5], if D is a noncommutative finite dimensional F-central division algebra and
$D^*$
contains an absolutely irreducible finite p-subgroup for some prime p, then D is a nilpotent crossed product with
$[D : F] = 2^m$
for some
$m \in \mathbb {N}$
.
Acknowledgements
The first author thanks the Research Council of the Farhangian University for support. The second author is indebted to the Research Council of University of Jiroft for support.
