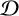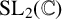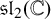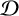1 Introduction
1.1 Overview
Jantzen filtrations arise in many situations in representation theory. The Jantzen filtration of a Verma module over a semisimple Lie algebra provides information on characters (the Jantzen sum formula) [Reference JantzenJan79], and gives representation-theoretic significance to coefficients of Kazhdan–Lusztig polynomials (the Jantzen conjectures) [Reference Beilinson, Bernstein and Gel’fandBB93]. The Jantzen filtration of a Weyl module over a reductive algebraic group of positive characteristic is a helpful tool in the notoriously difficult problem of determining irreducible characters [Reference JantzenJan79]. Jantzen filtrations also play a critical role in the unitary algorithm of [Reference Adams, van Leeuwen, Trapa and VoganAvLTV20], which determines the irreducible unitary representations of a real reductive group.
Though the utility of Jantzen filtrations in applications is primarily algebraic (providing information about characters or multiplicities of representations), establishing deep properties of the Jantzen filtration usually requires a geometric incarnation due to Beilinson and Bernstein. In [Reference Beilinson, Bernstein and Gel’fandBB93], Beilinson and Bernstein introduce a
![]() $\mathcal {D}$
-module version of the Jantzen filtration, which provides them with powerful geometric tools to analyze its structure. The constructions in [Reference Beilinson, Bernstein and Gel’fandBB93] require technical and deep machinery in the theory of
$\mathcal {D}$
-module version of the Jantzen filtration, which provides them with powerful geometric tools to analyze its structure. The constructions in [Reference Beilinson, Bernstein and Gel’fandBB93] require technical and deep machinery in the theory of
![]() $\mathcal {D}$
-modules, and as such, may not be easily accessible to a reader unfamiliar with this geometric approach to representation theory. However, the persistent utility of Beilinson and Bernstein’s results indicates that the geometric Jantzen filtration is a critical tool.
$\mathcal {D}$
-modules, and as such, may not be easily accessible to a reader unfamiliar with this geometric approach to representation theory. However, the persistent utility of Beilinson and Bernstein’s results indicates that the geometric Jantzen filtration is a critical tool.
In our experience, it is often enlightening, insightful, and nontrivial to describe a difficult construction in a simple example. The purpose of this paper is to illustrate the construction of Beilinson and Bernstein in the simplest nontrivial example. In doing this, we include simplified proofs of Beilinson and Bernstein’s results for the Lie algebra
![]() $\mathfrak {sl}_2(\mathbb {C})$
and detailed computations that do not appear in the original paper.
$\mathfrak {sl}_2(\mathbb {C})$
and detailed computations that do not appear in the original paper.
The main contribution of our example is to provide algebraic insight into a fundamental geometric construction. Beilinson–Bernstein localization is a powerful bridge between representation theory and algebraic geometry, which has provided geometric proofs of several important algebraic theorems. This strategy of using geometric tools to approach algebraic problems is effective, but it has a drawback—without deep knowledge of the geometry involved, the algebraist using these results is left without a sense of what is happening under the hood and, as a result, geometric results are often used as black boxes.
Our approach in this paper is to shine light into the black box by providing a series of algebraic snapshots of a geometric computation. We do this by computing the global sections of the
![]() $\mathcal {D}$
-modules that arise at each step in the computation and illustrating the corresponding
$\mathcal {D}$
-modules that arise at each step in the computation and illustrating the corresponding
![]() $\mathfrak {sl}_2(\mathbb {C})$
-representations. Here we mean ‘illustrate’ in the most literal sense—we include eight figures in which we draw precise pictures of these representations. Our hope is that by giving a concrete visual description, we are able to provide readers with algebraic intuition for the general construction.
$\mathfrak {sl}_2(\mathbb {C})$
-representations. Here we mean ‘illustrate’ in the most literal sense—we include eight figures in which we draw precise pictures of these representations. Our hope is that by giving a concrete visual description, we are able to provide readers with algebraic intuition for the general construction.
This paper is concerned with the example of
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {C})$
. However, some amount of general theory is helpful to set the scene. We dedicate the remainder of the introduction to orienting the reader with the necessary general theory.
$\operatorname {\mathrm {SL}}_2(\mathbb {C})$
. However, some amount of general theory is helpful to set the scene. We dedicate the remainder of the introduction to orienting the reader with the necessary general theory.
1.2 The algebraic Jantzen filtration
Let
![]() $\mathfrak {g}\supset \mathfrak {b} \supset \mathfrak {h}$
be a complex semisimple Lie algebra, a Borel subalgebra, and a Cartan subalgebra, respectively. Denote by
$\mathfrak {g}\supset \mathfrak {b} \supset \mathfrak {h}$
be a complex semisimple Lie algebra, a Borel subalgebra, and a Cartan subalgebra, respectively. Denote by
![]() $\mathfrak {n} = [\mathfrak {b},\mathfrak {b}]$
the nilradical of
$\mathfrak {n} = [\mathfrak {b},\mathfrak {b}]$
the nilradical of
![]() $\mathfrak {b}$
and by
$\mathfrak {b}$
and by
![]() $\overline {\mathfrak {b}}$
the opposite Borel subalgebra. Given a weight
$\overline {\mathfrak {b}}$
the opposite Borel subalgebra. Given a weight
![]() $\lambda \in \mathfrak {h}^*$
, let
$\lambda \in \mathfrak {h}^*$
, let
![]() $M(\lambda ) = \mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {U}(\mathfrak {b})} \mathbb {C}_\lambda $
be the corresponding Verma module,
$M(\lambda ) = \mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {U}(\mathfrak {b})} \mathbb {C}_\lambda $
be the corresponding Verma module,
![]() $I(\lambda )$
the corresponding dual Verma module (defined to be the direct sum of the weight spaces in the
$I(\lambda )$
the corresponding dual Verma module (defined to be the direct sum of the weight spaces in the
![]() $\mathfrak {g}$
-module
$\mathfrak {g}$
-module
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {U}(\overline {\mathfrak {b}})}(\mathcal {U}(\mathfrak {g}), \mathbb {C}_\lambda )$
), and
$\operatorname {\mathrm {Hom}}_{\mathcal {U}(\overline {\mathfrak {b}})}(\mathcal {U}(\mathfrak {g}), \mathbb {C}_\lambda )$
), and
the canonical
![]() $\mathfrak {g}$
-module homomorphism from
$\mathfrak {g}$
-module homomorphism from
![]() $M(\lambda )$
to
$M(\lambda )$
to
![]() $I(\lambda )$
.
$I(\lambda )$
.
The algebraic Jantzen filtration of
![]() $M(\lambda )$
involves a deformation of the above set-up in a specified direction
$M(\lambda )$
involves a deformation of the above set-up in a specified direction
![]() $\gamma \in \mathfrak {h}^*$
. The deformation is constructed as follows. Given
$\gamma \in \mathfrak {h}^*$
. The deformation is constructed as follows. Given
![]() ${\gamma \in \mathfrak {h}^*}$
, let
${\gamma \in \mathfrak {h}^*}$
, let
![]() $T=\mathcal {O}(\mathbb {C} \gamma )$
be the ring of regular functions on the line
$T=\mathcal {O}(\mathbb {C} \gamma )$
be the ring of regular functions on the line
![]() $\mathbb {C} \gamma \subset \mathfrak {h}^*$
. This can be identified with a polynomial ring
$\mathbb {C} \gamma \subset \mathfrak {h}^*$
. This can be identified with a polynomial ring
![]() $\mathbb {C}[s]$
. Denote by
$\mathbb {C}[s]$
. Denote by
![]() $A=T_{(s)}$
the local ring of T at the prime ideal
$A=T_{(s)}$
the local ring of T at the prime ideal
![]() $(s)$
.
$(s)$
.
We use the ring A to construct the corresponding deformed Verma module, defined to be the
![]() $(\mathfrak {g},A)$
-bimodule
$(\mathfrak {g},A)$
-bimodule
where
![]() $A_\lambda =A$
is the
$A_\lambda =A$
is the
![]() $(\mathfrak {h}, A)$
bimodule given by
$(\mathfrak {h}, A)$
bimodule given by
for
![]() $h \in \mathfrak {h}$
,
$h \in \mathfrak {h}$
,
![]() $a \in A$
, extended trivially to
$a \in A$
, extended trivially to
![]() $U(\mathfrak {b})$
. Equation (1-1) demonstrates that
$U(\mathfrak {b})$
. Equation (1-1) demonstrates that
![]() $M_A(\lambda )$
is a ‘deformation of
$M_A(\lambda )$
is a ‘deformation of
![]() $M(\lambda )$
in the direction
$M(\lambda )$
in the direction
![]() $\gamma $
’.
$\gamma $
’.
Similarly, the deformed dual Verma module
![]() $I_A(\lambda )$
is defined to be the sum of deformed weight spaces (see (2-52)) in the
$I_A(\lambda )$
is defined to be the sum of deformed weight spaces (see (2-52)) in the
![]() $(\mathfrak {g},A)$
-bimodule
$(\mathfrak {g},A)$
-bimodule
There is a canonical
![]() $(\mathfrak {g},A)$
-module homomorphism
$(\mathfrak {g},A)$
-module homomorphism
Setting
![]() $s=0$
recovers the usual Verma and dual Verma modules, and the canonical morphism
$s=0$
recovers the usual Verma and dual Verma modules, and the canonical morphism
![]() $\psi $
.
$\psi $
.
The A-submodules
![]() $s^iM_A(\lambda )$
and
$s^iM_A(\lambda )$
and
![]() $s^iI_A(\lambda )$
are
$s^iI_A(\lambda )$
are
![]() $\mathfrak {g}$
-stable for all i, so both
$\mathfrak {g}$
-stable for all i, so both
![]() $M_A(\lambda )$
and
$M_A(\lambda )$
and
![]() $I_A(\lambda )$
have
$I_A(\lambda )$
have
![]() $(\mathfrak {g},A)$
-module filtrations given by powers of s. The Jantzen filtration of
$(\mathfrak {g},A)$
-module filtrations given by powers of s. The Jantzen filtration of
![]() $M_A(\lambda )$
is the filtration obtained by pulling back the filtration of
$M_A(\lambda )$
is the filtration obtained by pulling back the filtration of
![]() $I_A(\lambda )$
by powers of s along the canonical homomorphism
$I_A(\lambda )$
by powers of s along the canonical homomorphism
![]() $\psi _A$
(see (1-2)). Setting
$\psi _A$
(see (1-2)). Setting
![]() $s=0$
recovers a filtration of
$s=0$
recovers a filtration of
![]() $M(\lambda )$
. This is the algebraic Jantzen filtration of the Verma module
$M(\lambda )$
. This is the algebraic Jantzen filtration of the Verma module
![]() $M(\lambda )$
. Analogous constructions yield Jantzen filtrations of the Weyl modules and principal series representations mentioned in Section 1.1 [Reference Beilinson, Bernstein and Gel’fandBB93, Reference JantzenJan79]. Because we focus on Verma modules in our example, we do not define these other Jantzen filtrations precisely.
$M(\lambda )$
. Analogous constructions yield Jantzen filtrations of the Weyl modules and principal series representations mentioned in Section 1.1 [Reference Beilinson, Bernstein and Gel’fandBB93, Reference JantzenJan79]. Because we focus on Verma modules in our example, we do not define these other Jantzen filtrations precisely.
Remark 1.1 (Computability of Jantzen filtration).
The algebraic Jantzen filtration is traditionally formulated in terms of a contravariant form, which explicitly realizes the canonical map between
![]() $M(\lambda )$
and
$M(\lambda )$
and
![]() $I(\lambda )$
. See, for example, [Reference JantzenJan79, Reference ShapovalovSha72]. This explicit realization makes the filtration directly computable, which is useful in applications. In contrast, other important representation-theoretic filtrations, such as composition series, are known to exist, but are much more difficult to compute algorithmically.
$I(\lambda )$
. See, for example, [Reference JantzenJan79, Reference ShapovalovSha72]. This explicit realization makes the filtration directly computable, which is useful in applications. In contrast, other important representation-theoretic filtrations, such as composition series, are known to exist, but are much more difficult to compute algorithmically.
For
![]() $\mathfrak {g} = \mathfrak {sl}_2(\mathbb {C})$
, the Jantzen filtration coincides with the composition series, as our computations in Section 2 illustrate. However, for larger Lie algebras (already starting at
$\mathfrak {g} = \mathfrak {sl}_2(\mathbb {C})$
, the Jantzen filtration coincides with the composition series, as our computations in Section 2 illustrate. However, for larger Lie algebras (already starting at
![]() $\mathfrak {sl}_3(\mathbb {C})$
), the Jantzen filtration differs from the composition series, and carries fundamental information about Verma modules and related representations. Jantzen conjectured [Reference JantzenJan79, Section 5.17] that for
$\mathfrak {sl}_3(\mathbb {C})$
), the Jantzen filtration differs from the composition series, and carries fundamental information about Verma modules and related representations. Jantzen conjectured [Reference JantzenJan79, Section 5.17] that for
![]() $\gamma = \rho $
(the half-sum of positive roots), the Jantzen filtration satisfies the following properties.
$\gamma = \rho $
(the half-sum of positive roots), the Jantzen filtration satisfies the following properties.
-
(1) Embeddings of Verma modules
 $M(\mu ) \hookrightarrow M(\lambda )$
are strict for Jantzen filtrations.
$M(\mu ) \hookrightarrow M(\lambda )$
are strict for Jantzen filtrations. -
(2) The Jantzen filtration coincides with the socle filtration. In particular, the filtration layers are semisimple.
Subsequent work by Barbasch [Reference BarbaschBar83], Gabber and Joseph [Reference Gabber and JosephGJ81], and others revealed that Jantzen’s conjectures have deep consequences. In particular, Jantzen’s conjectures imply a stronger version of Kazhdan and Lusztig’s famous conjecture on composition series multiplicities of Verma modules [Reference Kazhdan and LusztigKL79]: multiplicities of simple modules in layers of the Jantzen filtration are given by coefficients of a corresponding Kazhdan–Lusztig polynomial.
Kazhdan and Lusztig’s original multiplicity conjecture was proven by Beilinson and Bernstein in [Reference Beilinson and BernsteinBB81] using
![]() $\mathcal {D}$
-module techniques. A proof of Jantzen’s conjectures did not appear until 12 years later in [Reference Beilinson, Bernstein and Gel’fandBB93], using a significant extension of the geometric techniques used in [Reference Beilinson and BernsteinBB81]. In the following section, we outline their approach.
$\mathcal {D}$
-module techniques. A proof of Jantzen’s conjectures did not appear until 12 years later in [Reference Beilinson, Bernstein and Gel’fandBB93], using a significant extension of the geometric techniques used in [Reference Beilinson and BernsteinBB81]. In the following section, we outline their approach.
Remark 1.2 (Algebraic proof of Jantzen’s conjectures).
In [Reference WilliamsonWil16], Williamson provided an alternate proof of Jantzen’s conjectures using Soergel bimodule techniques, following previous work of Soergel and Kübel [Reference KübelKüb12a, Reference KübelKüb12b, Reference SoergelSoe08]. Williamson’s proof holds for Verma modules, whereas Beilinson and Bernstein’s proof also holds for more general Harish-Chandra modules.
Remark 1.3 (Deformation direction).
The definition of the algebraic Jantzen filtration relies on a choice of deformation direction
![]() $\gamma \in \mathfrak {h}^*$
, which also has a geometric manifestation in Beilinson and Bernstein’s construction. It is clear from the definitions that this direction should be nondegenerate; that is, that it should not lie on any root hyperplanes. However, it was a long-standing problem (raised in [Reference Beilinson, Bernstein and Gel’fandBB93]) as to whether the deformation direction need be dominant. Williamson showed in [Reference WilliamsonWil16] that it does, giving examples of nondominant deformation directions resulting in different filtrations for Lie algebras as small as
$\gamma \in \mathfrak {h}^*$
, which also has a geometric manifestation in Beilinson and Bernstein’s construction. It is clear from the definitions that this direction should be nondegenerate; that is, that it should not lie on any root hyperplanes. However, it was a long-standing problem (raised in [Reference Beilinson, Bernstein and Gel’fandBB93]) as to whether the deformation direction need be dominant. Williamson showed in [Reference WilliamsonWil16] that it does, giving examples of nondominant deformation directions resulting in different filtrations for Lie algebras as small as
![]() $\mathfrak {g}=\mathfrak {sl}_4(\mathbb {C})$
.
$\mathfrak {g}=\mathfrak {sl}_4(\mathbb {C})$
.
1.3 The geometric Jantzen filtration
Beilinson and Bernstein’s approach to the Jantzen conjectures is to relate the algebraic Jantzen filtration to a natural geometric filtration on the corresponding
![]() $\mathcal {D}$
-module under Beilinson–Bernstein localization. They then argue that this geometric Jantzen filtration coincides with the weight filtration on the
$\mathcal {D}$
-module under Beilinson–Bernstein localization. They then argue that this geometric Jantzen filtration coincides with the weight filtration on the
![]() $\mathcal {D}$
-module, providing them access to powerful techniques in weight theory. In this section, we outline Beilinson and Bernstein’s construction. More details can be found in [Reference Beilinson, Bernstein and Gel’fandBB93].
$\mathcal {D}$
-module, providing them access to powerful techniques in weight theory. In this section, we outline Beilinson and Bernstein’s construction. More details can be found in [Reference Beilinson, Bernstein and Gel’fandBB93].
1.3.1 Monodromy filtrations
Geometric Jantzen filtrations are intimately related to monodromy filtrations. Given an object A in an abelian category
![]() $\mathcal {A}$
and a nilpotent endomorphism
$\mathcal {A}$
and a nilpotent endomorphism
![]() $s \in \operatorname {\mathrm {End}}_{\mathcal {A}}(A)$
, the monodromy filtration of A is defined to be the unique increasing exhaustive filtration
$s \in \operatorname {\mathrm {End}}_{\mathcal {A}}(A)$
, the monodromy filtration of A is defined to be the unique increasing exhaustive filtration
![]() $\mu ^\bullet $
on A such that
$\mu ^\bullet $
on A such that
![]() $s\mu ^n \subset \mu ^{n-2}$
, and for
$s\mu ^n \subset \mu ^{n-2}$
, and for
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $s^k$
induces an isomorphism
$s^k$
induces an isomorphism
![]() $\mathrm {gr}_\mu ^k A \simeq \mathrm {gr}_\mu ^{-k} A.$
$\mathrm {gr}_\mu ^k A \simeq \mathrm {gr}_\mu ^{-k} A.$
The monodromy filtration of A induces a filtration
![]() $J_{!}^\bullet $
on
$J_{!}^\bullet $
on
![]() $\ker s $
and a filtration
$\ker s $
and a filtration
![]() $J_+^\bullet $
on
$J_+^\bullet $
on
![]() $\operatorname {\mathrm {coker}} s$
in the natural way. Moreover, on
$\operatorname {\mathrm {coker}} s$
in the natural way. Moreover, on
![]() $\ker s$
and
$\ker s$
and
![]() $\operatorname {\mathrm {coker}} s $
, the monodromy filtration can be described explicitly in terms of powers of s. Namely,
$\operatorname {\mathrm {coker}} s $
, the monodromy filtration can be described explicitly in terms of powers of s. Namely,
where it is taken that
![]() $\operatorname {\mbox {im }} s^i = A$
for
$\operatorname {\mbox {im }} s^i = A$
for
![]() $i \leq 0$
and
$i \leq 0$
and
![]() $\ker s^i=0$
for
$\ker s^i=0$
for
![]() $i\leq 0$
[Reference Beilinson, Bernstein and Gel’fandBB93, Section 4.1]. (See also [Reference DeligneDel80, Section 1.6].)
$i\leq 0$
[Reference Beilinson, Bernstein and Gel’fandBB93, Section 4.1]. (See also [Reference DeligneDel80, Section 1.6].)
1.3.2 Geometric Jantzen filtrations
Certain
![]() $\mathcal {D}$
-modules come equipped with nilpotent endomorphisms, and thus acquire monodromy filtrations. In particular, the maximal extension functor provides a recipe for constructing
$\mathcal {D}$
-modules come equipped with nilpotent endomorphisms, and thus acquire monodromy filtrations. In particular, the maximal extension functor provides a recipe for constructing
![]() $\mathcal {D}$
-modules with nilpotent endomorphisms from
$\mathcal {D}$
-modules with nilpotent endomorphisms from
![]() $\mathcal {D}$
-modules on open subvarieties using a deformation procedure. (See Section 2.4 for the precise definition of this functor.)
$\mathcal {D}$
-modules on open subvarieties using a deformation procedure. (See Section 2.4 for the precise definition of this functor.)
More precisely, if Y is a smooth algebraic variety with a fixed regular function
![]() $f: Y \rightarrow \mathbb {A}^1$
, the maximal extension
$f: Y \rightarrow \mathbb {A}^1$
, the maximal extension
![]() $\Xi _f \mathcal {M}_U$
of a holonomic
$\Xi _f \mathcal {M}_U$
of a holonomic
![]() $\mathcal {D}_U$
-module
$\mathcal {D}_U$
-module
![]() $\mathcal {M}_U$
on
$\mathcal {M}_U$
on
![]() ${U=f^{-1}(\mathbb {A}^1 - \{0\})}$
is constructed by deforming
${U=f^{-1}(\mathbb {A}^1 - \{0\})}$
is constructed by deforming
![]() $\mathcal {M}_U$
by the ring
$\mathcal {M}_U$
by the ring
![]() $\mathbb {C}[s]/s^n$
using the function f, then pushing forward the deformed
$\mathbb {C}[s]/s^n$
using the function f, then pushing forward the deformed
![]() $\mathcal {M}_U$
along the inclusion map
$\mathcal {M}_U$
along the inclusion map
![]() $j:U \hookrightarrow Y$
. The resulting
$j:U \hookrightarrow Y$
. The resulting
![]() $\mathcal {D}_Y$
-module is an object in the abelian category of holonomic
$\mathcal {D}_Y$
-module is an object in the abelian category of holonomic
![]() $\mathcal {D}_Y$
-modules, which has a natural nilpotent endomorphism s arising from the deformation of
$\mathcal {D}_Y$
-modules, which has a natural nilpotent endomorphism s arising from the deformation of
![]() $\mathcal {M}_U$
. Hence, it has a monodromy filtration.
$\mathcal {M}_U$
. Hence, it has a monodromy filtration.
The construction of the maximal extension functor guarantees that
and
so the (nondeformed)
![]() $!$
-standard and
$!$
-standard and
![]() $+$
-standard
$+$
-standard
![]() $\mathcal {D}_Y$
-modules
$\mathcal {D}_Y$
-modules
![]() $j_! \mathcal {M}_U$
and
$j_! \mathcal {M}_U$
and
![]() $j_+ \mathcal {M}_U$
appear as sub and quotient modules of the maximal extension
$j_+ \mathcal {M}_U$
appear as sub and quotient modules of the maximal extension
![]() $\Xi _f \mathcal {M}_U$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1]. In this way, we obtain filtrations of the
$\Xi _f \mathcal {M}_U$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1]. In this way, we obtain filtrations of the
![]() $\mathcal {D}_Y$
-modules
$\mathcal {D}_Y$
-modules
![]() $j_! \mathcal {M}_U$
and
$j_! \mathcal {M}_U$
and
![]() $j_+ \mathcal {M}_U$
from the monodromy filtration of
$j_+ \mathcal {M}_U$
from the monodromy filtration of
![]() $\Xi _f \mathcal {M}_U$
. These are the geometric Jantzen filtrations.
$\Xi _f \mathcal {M}_U$
. These are the geometric Jantzen filtrations.
Note that analogously to the algebraic Jantzen filtration, the geometric Jantzen filtration depends on a choice of deformation parameter, given by the regular function
![]() $f:Y \rightarrow \mathbb {A}^1$
. Moreover, the explicit realization in equation (1-3) in terms of powers of s means that like the algebraic Jantzen filtration, the geometric Jantzen filtration is explicitly computable.
$f:Y \rightarrow \mathbb {A}^1$
. Moreover, the explicit realization in equation (1-3) in terms of powers of s means that like the algebraic Jantzen filtration, the geometric Jantzen filtration is explicitly computable.
1.3.3 Geometric Jantzen filtrations on Harish-Chandra sheaves
The
![]() $\mathcal {D}$
-modules corresponding to Verma modules and dual Verma modules under Beilinson–Bernstein localization can be made to fit into the framework of Section 1.3.2, and thus acquire geometric Jantzen filtrations. Such
$\mathcal {D}$
-modules corresponding to Verma modules and dual Verma modules under Beilinson–Bernstein localization can be made to fit into the framework of Section 1.3.2, and thus acquire geometric Jantzen filtrations. Such
![]() $\mathcal {D}$
-modules manifest as Harish-Chandra sheaves, which are a class of
$\mathcal {D}$
-modules manifest as Harish-Chandra sheaves, which are a class of
![]() $\mathcal {D}$
-modules equivariant with respect to a certain group action. We explain this connection below.
$\mathcal {D}$
-modules equivariant with respect to a certain group action. We explain this connection below.
Let G be the simply connected semisimple Lie group associated to
![]() $\mathfrak {g}$
,
$\mathfrak {g}$
,
![]() $B\subset G$
the Borel subgroup corresponding to
$B\subset G$
the Borel subgroup corresponding to
![]() $\mathfrak {b}$
, and
$\mathfrak {b}$
, and
![]() $N \subset B$
its unipotent radical. Set
$N \subset B$
its unipotent radical. Set
![]() $H:=B/N$
to be the abstract maximal torus of G [Reference Chriss and GinzburgCG97, Lemma 6.1.1], and identify
$H:=B/N$
to be the abstract maximal torus of G [Reference Chriss and GinzburgCG97, Lemma 6.1.1], and identify
![]() $\mathfrak {h}$
with
$\mathfrak {h}$
with
![]() $\operatorname {\mathrm {Lie}} H$
. Let
$\operatorname {\mathrm {Lie}} H$
. Let
![]() $\widetilde {X}:=G/N$
be the base affine space and
$\widetilde {X}:=G/N$
be the base affine space and
![]() $X:=G/B$
the flag variety. The projection
$X:=G/B$
the flag variety. The projection
![]() $\pi : \widetilde {X} \rightarrow X$
is a principal G-equivariant H-bundle with respect to the right action of H on
$\pi : \widetilde {X} \rightarrow X$
is a principal G-equivariant H-bundle with respect to the right action of H on
![]() $\widetilde {X}$
by right multiplication.
$\widetilde {X}$
by right multiplication.
Remark 1.4 (H-monodromic
 $\mathcal {D}_{\widetilde {X}}$
-modules).
$\mathcal {D}_{\widetilde {X}}$
-modules).
In [Reference Beilinson, Bernstein and Gel’fandBB93], Beilinson and Bernstein work with H-monodromic
![]() $\mathcal {D}$
-modules on the base affine space
$\mathcal {D}$
-modules on the base affine space
![]() $\widetilde {X}$
instead of modules over sheaves of twisted differential operators (TDOs) on the flag variety X, as they do in [Reference Beilinson and BernsteinBB81]. Working over
$\widetilde {X}$
instead of modules over sheaves of twisted differential operators (TDOs) on the flag variety X, as they do in [Reference Beilinson and BernsteinBB81]. Working over
![]() $\widetilde {X}$
has several advantages: it allows one to study entire families of representations at once (see Figures 1 and 2 in Section 2.3 for an illustration of this phenomenon), and it allows one to study
$\widetilde {X}$
has several advantages: it allows one to study entire families of representations at once (see Figures 1 and 2 in Section 2.3 for an illustration of this phenomenon), and it allows one to study
![]() $\mathfrak {g}$
-modules with generalized infinitesimal characters. In contrast, modules over TDOs can only be used to study
$\mathfrak {g}$
-modules with generalized infinitesimal characters. In contrast, modules over TDOs can only be used to study
![]() $\mathfrak {g}$
-modules with strict infinitesimal character. There is a precise relationship between H-monodromic
$\mathfrak {g}$
-modules with strict infinitesimal character. There is a precise relationship between H-monodromic
![]() $\mathcal {D}_{\widetilde {X}}$
-modules and modules over TDOs; see Remark 2.5.
$\mathcal {D}_{\widetilde {X}}$
-modules and modules over TDOs; see Remark 2.5.
For an N-orbit (that is, a Bruhat cell) Q in X, denote by
![]() $\widetilde {Q} = \pi ^{-1}(Q)$
the corresponding union of N-orbits in
$\widetilde {Q} = \pi ^{-1}(Q)$
the corresponding union of N-orbits in
![]() $\widetilde {X}$
. A choice of dominant regular integral weight
$\widetilde {X}$
. A choice of dominant regular integral weight
![]() $\gamma \in \mathfrak {h}^*$
(the ‘deformation direction’) determines a regular function
$\gamma \in \mathfrak {h}^*$
(the ‘deformation direction’) determines a regular function
![]() $ f_\gamma : \overline {\widetilde {Q}}\rightarrow \mathbb {A}^1$
on the closure of
$ f_\gamma : \overline {\widetilde {Q}}\rightarrow \mathbb {A}^1$
on the closure of
![]() $\widetilde {Q}$
such that
$\widetilde {Q}$
such that
![]() $f_\gamma ^{-1}(\mathbb {A}^1 - \{0\}) = \widetilde {Q}$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 3.5.1]. This function extends to a regular function on
$f_\gamma ^{-1}(\mathbb {A}^1 - \{0\}) = \widetilde {Q}$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 3.5.1]. This function extends to a regular function on
![]() $\widetilde {X}$
, which, by the process outlined in Section 1.3.2, determines a maximal extension functor
$\widetilde {X}$
, which, by the process outlined in Section 1.3.2, determines a maximal extension functor
![]() $\Xi _{f_\gamma }:\mathcal {M}_{\mathrm {hol}}(\mathcal {D}_U) \rightarrow \mathcal {M}_{\mathrm {hol}}(\mathcal {D}_{\widetilde {X}})$
. Here, U is the preimage in
$\Xi _{f_\gamma }:\mathcal {M}_{\mathrm {hol}}(\mathcal {D}_U) \rightarrow \mathcal {M}_{\mathrm {hol}}(\mathcal {D}_{\widetilde {X}})$
. Here, U is the preimage in
![]() $\widetilde {X}$
of
$\widetilde {X}$
of
![]() $\mathbb {A}^1 - \{0\}$
under the extension of
$\mathbb {A}^1 - \{0\}$
under the extension of
![]() $f_\gamma $
. Restricting
$f_\gamma $
. Restricting
![]() $\Xi _{f_\gamma }$
to the category of holonomic
$\Xi _{f_\gamma }$
to the category of holonomic
![]() $\mathcal {D}_U$
-modules supported on
$\mathcal {D}_U$
-modules supported on
![]() $\widetilde {Q}$
results in a functor
$\widetilde {Q}$
results in a functor
Let
![]() $\mathcal {O}_{\widetilde {Q}}$
be the structure sheaf on
$\mathcal {O}_{\widetilde {Q}}$
be the structure sheaf on
![]() $\widetilde {Q}$
and
$\widetilde {Q}$
and
![]() $j_{\widetilde {Q}}: \widetilde {Q} \hookrightarrow \overline {\widetilde {Q}}$
the inclusion of
$j_{\widetilde {Q}}: \widetilde {Q} \hookrightarrow \overline {\widetilde {Q}}$
the inclusion of
![]() $\widetilde {Q}$
into its closure. Via the construction in Section 1.3.2, the modules
$\widetilde {Q}$
into its closure. Via the construction in Section 1.3.2, the modules
![]() $j_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
and
$j_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
and
![]() $j_{\widetilde {Q}+}\mathcal {O}_{\widetilde {Q}}$
acquire from
$j_{\widetilde {Q}+}\mathcal {O}_{\widetilde {Q}}$
acquire from
![]() $\Xi _{f_\gamma }\mathcal {O}_{\widetilde {Q}}$
geometric Jantzen filtrations. Because
$\Xi _{f_\gamma }\mathcal {O}_{\widetilde {Q}}$
geometric Jantzen filtrations. Because
![]() $\overline {\widetilde {Q}}$
is closed in
$\overline {\widetilde {Q}}$
is closed in
![]() $\widetilde {X}$
, a theorem of Kashiwara [Reference MiličićMil, Theorem 12.6] allows one to lift these filtrations to filtrations of the standard N-equivariant
$\widetilde {X}$
, a theorem of Kashiwara [Reference MiličićMil, Theorem 12.6] allows one to lift these filtrations to filtrations of the standard N-equivariant
![]() $\mathcal {D}_{\widetilde {X}}$
-modules
$\mathcal {D}_{\widetilde {X}}$
-modules
![]() $i_{\widetilde {Q}!} \mathcal {O}_{\widetilde {Q}}$
and
$i_{\widetilde {Q}!} \mathcal {O}_{\widetilde {Q}}$
and
![]() $i_{\widetilde {Q}+} \mathcal {O}_{\widetilde {Q}}$
, for
$i_{\widetilde {Q}+} \mathcal {O}_{\widetilde {Q}}$
, for
![]() $i_{\widetilde {Q}}: \widetilde {Q} \hookrightarrow \widetilde {X}$
the inclusion.
$i_{\widetilde {Q}}: \widetilde {Q} \hookrightarrow \widetilde {X}$
the inclusion.
There is a natural map
obtained by differentiating the G-action on
![]() $\widetilde {X}$
that endows global sections of
$\widetilde {X}$
that endows global sections of
![]() $\mathcal {D}_{\widetilde {X}}$
-modules with the structure of
$\mathcal {D}_{\widetilde {X}}$
-modules with the structure of
![]() $\mathcal {U}(\mathfrak {g})$
-modules. In Section 2.1, we explicitly compute this map for
$\mathcal {U}(\mathfrak {g})$
-modules. In Section 2.1, we explicitly compute this map for
![]() $\mathfrak {sl}_2(\mathbb {C})$
. As
$\mathfrak {sl}_2(\mathbb {C})$
. As
![]() $\mathcal {U}(\mathfrak {g})$
-modules, the global sections of
$\mathcal {U}(\mathfrak {g})$
-modules, the global sections of
![]() $i_{\widetilde {Q}!} \mathcal {O}_{\widetilde {Q}}$
and
$i_{\widetilde {Q}!} \mathcal {O}_{\widetilde {Q}}$
and
![]() $i_{\widetilde {Q}+} \mathcal {O}_{\widetilde {Q}}$
are direct sums of all integral Verma modules and dual Verma modules, respectively. In Section 2.3, we illustrate this structure in our example.
$i_{\widetilde {Q}+} \mathcal {O}_{\widetilde {Q}}$
are direct sums of all integral Verma modules and dual Verma modules, respectively. In Section 2.3, we illustrate this structure in our example.
Remark 1.5 (Other Harish-Chandra pairs).
Note that this construction works for many Harish-Chandra pairs
![]() $(\mathfrak {g},K)$
, not just the pair
$(\mathfrak {g},K)$
, not just the pair
![]() $(\mathfrak {g},N)$
. In [Reference Beilinson, Bernstein and Gel’fandBB93, Section 3.4], the specific conditions on K necessary for such a construction to hold are discussed. In particular, these constructions can be applied to any symmetric pair [Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 3.5.2], so they can be used in the study of admissible representations of real reductive groups.
$(\mathfrak {g},N)$
. In [Reference Beilinson, Bernstein and Gel’fandBB93, Section 3.4], the specific conditions on K necessary for such a construction to hold are discussed. In particular, these constructions can be applied to any symmetric pair [Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 3.5.2], so they can be used in the study of admissible representations of real reductive groups.
Remark 1.6 (Comparison with [Reference RomanovRom21]).
It is interesting to contrast the computations of the current paper to those in Romanov’s previous paper [Reference RomanovRom21], whose goal was to illustrate four families of
![]() $\mathcal {D}$
-modules corresponding to well-known families of representations (finite-dimensional, Verma/dual Verma, principal series, and Whittaker). Our approach in the current paper is to study all integral Verma/dual Verma modules simultaneously by working over base affine space, as explained above. In contrast, [Reference RomanovRom21, Section 6] analyzes Verma/dual Verma modules one at a time using modules over varying TDOs on the flag variety. (Compare Figures 1 and 2 to [Reference RomanovRom21, Figures 2 and 3].) Our techniques in this paper are not specific to Verma modules: by working over base affine space, we could recover each family of examples in [Reference RomanovRom21] using a single H-monodromic
$\mathcal {D}$
-modules corresponding to well-known families of representations (finite-dimensional, Verma/dual Verma, principal series, and Whittaker). Our approach in the current paper is to study all integral Verma/dual Verma modules simultaneously by working over base affine space, as explained above. In contrast, [Reference RomanovRom21, Section 6] analyzes Verma/dual Verma modules one at a time using modules over varying TDOs on the flag variety. (Compare Figures 1 and 2 to [Reference RomanovRom21, Figures 2 and 3].) Our techniques in this paper are not specific to Verma modules: by working over base affine space, we could recover each family of examples in [Reference RomanovRom21] using a single H-monodromic
![]() $\mathcal {D}$
-module.
$\mathcal {D}$
-module.
Our current approach is not merely stylistic—it is necessary for our goal. Because the deformed Verma modules arising in the construction of the Jantzen filtration do not have a strict infinitesimal character as Verma modules do, they cannot be studied as modules over TDOs on the flag variety. However, deformed Verma modules can be approximated by
![]() $\mathfrak {g}$
-modules with generalized infinitesimal characters (see Section 2.4.1, and, in particular, (2-43) and (2-42)), so a
$\mathfrak {g}$
-modules with generalized infinitesimal characters (see Section 2.4.1, and, in particular, (2-43) and (2-42)), so a
![]() $\mathcal {D}$
-module approach to their study must necessarily work over
$\mathcal {D}$
-module approach to their study must necessarily work over
![]() $\widetilde {X}$
instead of X; see Remark 1.4.
$\widetilde {X}$
instead of X; see Remark 1.4.
1.3.4 Relationship between monodromy and weight filtrations
The geometric Jantzen filtration of
![]() $i_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
constructed in the previous section is computable via (1-3), but it is not clear that it should satisfy the properties of Jantzen’s conjectures. The key idea of Beilinson and Bernstein’s proof is to relate the monodromy filtration on
$i_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
constructed in the previous section is computable via (1-3), but it is not clear that it should satisfy the properties of Jantzen’s conjectures. The key idea of Beilinson and Bernstein’s proof is to relate the monodromy filtration on
![]() $\Xi _{f_\gamma } \mathcal {O}_{\widetilde {Q}}$
to the weight filtration on the corresponding perverse sheaf under the Riemann–Hilbert correspondence, which has strong functoriality and semisimplicity properties.
$\Xi _{f_\gamma } \mathcal {O}_{\widetilde {Q}}$
to the weight filtration on the corresponding perverse sheaf under the Riemann–Hilbert correspondence, which has strong functoriality and semisimplicity properties.
Weight filtrations on objects in derived categories of constructible
![]() $\mathbb {Q}_\ell $
-sheaves are a deep generalization of filtrations on cohomology rings of algebraic varieties. Explicitly constructing weight filtrations is extremely difficult outside of the most basic examples, but they can be shown to exist for complexes built from simple examples via sheaf functors. In particular, the perverse sheaf corresponding to the maximal extension
$\mathbb {Q}_\ell $
-sheaves are a deep generalization of filtrations on cohomology rings of algebraic varieties. Explicitly constructing weight filtrations is extremely difficult outside of the most basic examples, but they can be shown to exist for complexes built from simple examples via sheaf functors. In particular, the perverse sheaf corresponding to the maximal extension
![]() $\Xi _{f_\gamma } \mathcal {O}_{\widetilde {Q}}$
admits a ‘mixed structure’, and hence a weight filtration, as it is the quotient of a push-forward of a
$\Xi _{f_\gamma } \mathcal {O}_{\widetilde {Q}}$
admits a ‘mixed structure’, and hence a weight filtration, as it is the quotient of a push-forward of a
![]() $\mathcal {D}$
-module of ‘geometric origin’.
$\mathcal {D}$
-module of ‘geometric origin’.
Remark 1.7. Beilinson and Bernstein’s results could also be formulated in the more modern language of Saito’s mixed Hodge modules [Reference SaitoSai88, Reference SaitoSai90], but because the initial draft of their paper was written in 1986 before Saito’s work was published, they instead used the technology of mixed
![]() $\ell $
-adic sheaves [Reference DeligneDel80].
$\ell $
-adic sheaves [Reference DeligneDel80].
Beilinson and Bernstein’s strategy was to use a theorem of Gabber [Reference Beilinson, Bernstein and Gel’fandBB93, Theorem 5.1.2], which establishes that on a perverse sheaf obtained by a nearby cycles functor (of which the maximal extension functor is a special instance), the monodromy filtration agrees with the weight filtration. Passing Gabber’s theorem to
![]() $\mathcal {D}$
-modules via the Riemann–Hilbert correspondence lets them conclude that the geometric Jantzen filtration on
$\mathcal {D}$
-modules via the Riemann–Hilbert correspondence lets them conclude that the geometric Jantzen filtration on
![]() $i_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
agrees with the weight filtration.
$i_{\widetilde {Q}!}\mathcal {O}_{\widetilde {Q}}$
agrees with the weight filtration.
Weight filtrations have two important properties: (1) they are functorial with respect to morphisms of mixed perverse sheaves; and (2) the associated graded object is semisimple. These properties are exactly what is needed to prove Jantzen’s conjectures: the functoriality implies the strictness of the Jantzen filtration with respect to embeddings of Verma modules, and the semisimplicity of the associated graded object implies (with some additional pointwise purity arguments) the agreement of the Jantzen filtration with the socle filtration.
The power of Beilinson and Bernstein’s proof comes from the connection between two very different filtrations—the Jantzen filtration, which is explicitly computable but has no obvious structure, and the weight filtration, which is very difficult to compute but satisfies remarkable properties.
1.4 Relationship between algebraic and geometric Jantzen filtrations
Beilinson and Bernstein’s proof of Jantzen’s conjectures relies on the fact that the geometric and algebraic Jantzen filtrations align under the global sections functor. Though both constructions involve similar ingredients, such as deformations and relationships between standard and costandard objects, it is not immediately obvious from the definitions that they should yield the same filtration on Verma modules. This crucial relationship is given minimal justification in [Reference Beilinson, Bernstein and Gel’fandBB93].
Because of the critical nature of this relationship, we dedicate Section 2.6 of our paper to explicitly describing the relationship between the two filtrations for
![]() $\mathfrak {sl}_2(\mathbb {C})$
, and illustrating it for a fixed infinitesimal character in Figure 8. Our arguments easily generalize to any Lie algebra.
$\mathfrak {sl}_2(\mathbb {C})$
, and illustrating it for a fixed infinitesimal character in Figure 8. Our arguments easily generalize to any Lie algebra.
1.5 Structure of the paper
The remainder of the paper is dedicated to the computation of the geometric Jantzen filtration for the Lie algebra
![]() $\mathfrak {sl}_2(\mathbb {C})$
. The computation is structured as follows.
$\mathfrak {sl}_2(\mathbb {C})$
. The computation is structured as follows.
Section 2.1: We establish an algebra homomorphism from the extended universal enveloping algebra to global differential operators on base affine space. This algebra homomorphism is what allows us to view the global sections of
![]() $\mathcal {D}_{\widetilde {X}}$
-modules as modules over the (extended) universal enveloping algebra.
$\mathcal {D}_{\widetilde {X}}$
-modules as modules over the (extended) universal enveloping algebra.
Section 2.2: We give some background on H-monodromic
![]() $\mathcal {D}_X$
-modules, and explain their relationship to modules over twisted sheaves of differential operators.
$\mathcal {D}_X$
-modules, and explain their relationship to modules over twisted sheaves of differential operators.
Section 2.3: We introduce the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules whose global sections contain Verma modules and dual Verma modules—these are the
$\mathcal {D}_{\widetilde {X}}$
-modules whose global sections contain Verma modules and dual Verma modules—these are the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules that we endow with geometric Jantzen filtrations. We illustrate the
$\mathcal {D}_{\widetilde {X}}$
-modules that we endow with geometric Jantzen filtrations. We illustrate the
![]() $\mathfrak {sl}_2(\mathbb {C})$
-module structure on their global sections in Figures 1 and 2.
$\mathfrak {sl}_2(\mathbb {C})$
-module structure on their global sections in Figures 1 and 2.
Section 2.4: We introduce the maximal extension functor, which gives the deformation necessary for the Jantzen filtration. We compute the maximal extension of the structure sheaf on an open subset of
![]() $\widetilde {X}$
, and illustrate in Figures 3 and 4 how deformed Verma modules and deformed dual Verma modules arise geometrically. We illustrate in Figures 5 and 6 the global sections of the maximal extension, identifying them with the big projective in category
$\widetilde {X}$
, and illustrate in Figures 3 and 4 how deformed Verma modules and deformed dual Verma modules arise geometrically. We illustrate in Figures 5 and 6 the global sections of the maximal extension, identifying them with the big projective in category
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Section 2.5: We define the geometric Jantzen filtration using monodromy filtrations. We compute the monodromy filtration of the maximal extension, and illustrate its global sections in Figure 7. This specializes to the geometric Jantzen filtration on certain sub- and quotient sheaves.
Section 2.6: We introduce the algebraic Jantzen filtration on a Verma module in Section 2.6.1, then explain why the global sections of the geometric Jantzen filtration align with the algebraic Jantzen filtration in Section 2.6.2. Figure 8 illustrates this relationship in our example.
2 Example
Now we proceed with our example. For the remainder of this paper, set
![]() $G = \operatorname {\mathrm {SL}}_2(\mathbb {C})$
, and fix subgroups
$G = \operatorname {\mathrm {SL}}_2(\mathbb {C})$
, and fix subgroups
 $$ \begin{align*} B= \bigg\{ \begin{pmatrix} a & b \\ 0 & a^{-1} \end{pmatrix}\, \Bigg|\ a\in\mathbb{C}^*,\,b\in\mathbb{C} \bigg\}, \quad N = \bigg\{ \begin{pmatrix} 1 & b \\ 0 & 1 \end{pmatrix}\, \Bigg|\ b \in \mathbb{C} \bigg\} \end{align*} $$
$$ \begin{align*} B= \bigg\{ \begin{pmatrix} a & b \\ 0 & a^{-1} \end{pmatrix}\, \Bigg|\ a\in\mathbb{C}^*,\,b\in\mathbb{C} \bigg\}, \quad N = \bigg\{ \begin{pmatrix} 1 & b \\ 0 & 1 \end{pmatrix}\, \Bigg|\ b \in \mathbb{C} \bigg\} \end{align*} $$
and
 $$ \begin{align*} H = \bigg\{ \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix}\, \Bigg|\ a \in \mathbb{C}^* \bigg\}. \end{align*} $$
$$ \begin{align*} H = \bigg\{ \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix}\, \Bigg|\ a \in \mathbb{C}^* \bigg\}. \end{align*} $$
Let
![]() $\mathfrak {g}$
,
$\mathfrak {g}$
,
![]() $\mathfrak {b}$
,
$\mathfrak {b}$
,
![]() $\mathfrak {n}$
, and
$\mathfrak {n}$
, and
![]() $\mathfrak {h}$
be the corresponding Lie algebras, and
$\mathfrak {h}$
be the corresponding Lie algebras, and
![]() $\bar {\mathfrak {n}}$
the opposite nilpotent subalgebra to
$\bar {\mathfrak {n}}$
the opposite nilpotent subalgebra to
![]() $\mathfrak {n}$
. Denote by
$\mathfrak {n}$
. Denote by
 $$ \begin{align} e = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, \quad f = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \quad \text{and} \quad h = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\end{align} $$
$$ \begin{align} e = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, \quad f = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \quad \text{and} \quad h = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\end{align} $$
the standard basis elements of
![]() $\mathfrak {g}$
, so
$\mathfrak {g}$
, so
![]() $\mathfrak {n} = \mathbb {C} e$
,
$\mathfrak {n} = \mathbb {C} e$
,
![]() $\mathfrak {h} = \mathbb {C} h$
, and
$\mathfrak {h} = \mathbb {C} h$
, and
![]() $\bar {\mathfrak {n}} = \mathbb {C} f$
. Denote by
$\bar {\mathfrak {n}} = \mathbb {C} f$
. Denote by
![]() $\mathcal {Z}(\mathfrak {g})$
the center of the universal enveloping algebra
$\mathcal {Z}(\mathfrak {g})$
the center of the universal enveloping algebra
![]() $\mathcal {U}(\mathfrak {g})$
. The algebra
$\mathcal {U}(\mathfrak {g})$
. The algebra
![]() $\mathcal {Z}(\mathfrak {g})$
is generated by the Casimir element
$\mathcal {Z}(\mathfrak {g})$
is generated by the Casimir element
Let
be the projection onto the first coordinate of the direct sum decomposition
The restriction of
![]() $\gamma _{\mathrm {HC}}$
to
$\gamma _{\mathrm {HC}}$
to
![]() $\mathcal {Z}(\mathfrak {g})$
is an algebra homomorphism.
$\mathcal {Z}(\mathfrak {g})$
is an algebra homomorphism.
Set
![]() $X=G/B$
and
$X=G/B$
and
![]() $\widetilde {X} = G/N$
. Then, X is the flag variety of
$\widetilde {X} = G/N$
. Then, X is the flag variety of
![]() $\mathfrak {g}$
, and we refer to
$\mathfrak {g}$
, and we refer to
![]() $\widetilde {X}$
as base affine space. We identify X with the complex projective line
$\widetilde {X}$
as base affine space. We identify X with the complex projective line
![]() $\mathbb {C}\mathbb {P}^1$
via
$\mathbb {C}\mathbb {P}^1$
via
 $$ \begin{align} \begin{pmatrix}x_1&*\\x_2&*\end{pmatrix}B\mapsto(x_1:x_2), \end{align} $$
$$ \begin{align} \begin{pmatrix}x_1&*\\x_2&*\end{pmatrix}B\mapsto(x_1:x_2), \end{align} $$
and
![]() $\widetilde {X}$
with
$\widetilde {X}$
with
![]() $\mathbb {C}^2 \backslash \{(0,0)\}$
via
$\mathbb {C}^2 \backslash \{(0,0)\}$
via
 $$ \begin{align} \begin{pmatrix}x_1&*\\x_2&*\end{pmatrix}N\mapsto(x_1,x_2). \end{align} $$
$$ \begin{align} \begin{pmatrix}x_1&*\\x_2&*\end{pmatrix}N\mapsto(x_1,x_2). \end{align} $$
There are left actions of G on X and
![]() $\widetilde {X}$
by left multiplication. Under the identifications (2-4) and (2-5), these actions are given by
$\widetilde {X}$
by left multiplication. Under the identifications (2-4) and (2-5), these actions are given by
 $$ \begin{align*} \begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot(x_1:x_2)=(ax_1+bx_2:cx_1+dx_2) \end{align*} $$
$$ \begin{align*} \begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot(x_1:x_2)=(ax_1+bx_2:cx_1+dx_2) \end{align*} $$
and
 $$ \begin{align} \begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot(x_1,x_2)=(ax_1+bx_2,cx_1+dx_2). \end{align} $$
$$ \begin{align} \begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot(x_1,x_2)=(ax_1+bx_2,cx_1+dx_2). \end{align} $$
Because H normalizes N, there is also a right action of H on
![]() $G/N$
by right multiplication. Under the identification (2-5), this action is given by
$G/N$
by right multiplication. Under the identification (2-5), this action is given by
 $$ \begin{align} (x_1,x_2)\cdot\begin{pmatrix}a&0\\0&a^{-1}\end{pmatrix}=(ax_1,ax_2). \end{align} $$
$$ \begin{align} (x_1,x_2)\cdot\begin{pmatrix}a&0\\0&a^{-1}\end{pmatrix}=(ax_1,ax_2). \end{align} $$
The natural G-equivariant quotient map
is an H-torsor over X. In the language of [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5], this provides an ‘H-monodromic structure’ on X.
For an algebraic variety Y, we denote by
![]() $\mathcal {O}_Y$
the structure sheaf on Y, and by
$\mathcal {O}_Y$
the structure sheaf on Y, and by
![]() $\mathcal {O}(Y) = \Gamma (Y, \mathcal {O}_Y)$
the algebra of global regular functions. We denote by
$\mathcal {O}(Y) = \Gamma (Y, \mathcal {O}_Y)$
the algebra of global regular functions. We denote by
![]() $\mathcal {D}_Y$
the sheaf of differential operators on Y, and
$\mathcal {D}_Y$
the sheaf of differential operators on Y, and
![]() $\mathcal {D}(Y) = \Gamma (Y, \mathcal {D}_Y)$
the global differential operators.
$\mathcal {D}(Y) = \Gamma (Y, \mathcal {D}_Y)$
the global differential operators.
Base affine space
![]() $\widetilde {X}$
is a quasi-affine variety, with affine closure
$\widetilde {X}$
is a quasi-affine variety, with affine closure
![]() $\overline {\widetilde {X}} = \mathbb {A}^2$
. Throughout this text, we make use the following facts about quasi-affine varieties. Let Y be an irreducible quasi-affine variety, openly embedded in an affine variety
$\overline {\widetilde {X}} = \mathbb {A}^2$
. Throughout this text, we make use the following facts about quasi-affine varieties. Let Y be an irreducible quasi-affine variety, openly embedded in an affine variety
![]() $\overline {Y}$
.
$\overline {Y}$
.
-
• If Y is normal with
 $\mathrm {codim}_{\overline {Y}}(\overline {Y} \backslash Y) \geq 2$
, then
$\mathrm {codim}_{\overline {Y}}(\overline {Y} \backslash Y) \geq 2$
, then
 $\mathcal {O}(Y) = \mathcal {O}(\overline {Y})$
and
$\mathcal {O}(Y) = \mathcal {O}(\overline {Y})$
and
 $\mathcal {D}(Y) =\mathcal {D}(\overline {Y})$
[Reference Levasseur and StaffordLS06, Section 2]. (In particular, for
$\mathcal {D}(Y) =\mathcal {D}(\overline {Y})$
[Reference Levasseur and StaffordLS06, Section 2]. (In particular, for
 $Y = \widetilde {X}$
, this implies that global differential operators are nothing more than the Weyl algebra in two variables.)
$Y = \widetilde {X}$
, this implies that global differential operators are nothing more than the Weyl algebra in two variables.) -
• Because the variety
 $\overline {Y}$
is affine, it is also D-affine, meaning that the global sections functor induces an equivalence of categories between the category of quasi-coherent
$\overline {Y}$
is affine, it is also D-affine, meaning that the global sections functor induces an equivalence of categories between the category of quasi-coherent
 $\mathcal {D}_{\overline {Y}}$
-modules and the category of modules over
$\mathcal {D}_{\overline {Y}}$
-modules and the category of modules over
 $\mathcal {D}(\overline {Y})$
.
$\mathcal {D}(\overline {Y})$
. -
• Since the inclusion
 $i: Y \rightarrow \overline {Y}$
is an open immersion, the restriction functor
$i: Y \rightarrow \overline {Y}$
is an open immersion, the restriction functor
 $i^+$
on the corresponding categories of
$i^+$
on the corresponding categories of
 $\mathcal {D}$
-modules is exact, and commutes with pushforwards from open affine subvarieties [Reference MiličićMil, Remark 3.1].
$\mathcal {D}$
-modules is exact, and commutes with pushforwards from open affine subvarieties [Reference MiličićMil, Remark 3.1].
The facts listed above allow us to move freely between
![]() $\mathcal {D}_{\widetilde {X}}$
-modules and
$\mathcal {D}_{\widetilde {X}}$
-modules and
![]() $\mathcal {D}(\mathbb {A}^2)$
-modules. We do this periodically in computations.
$\mathcal {D}(\mathbb {A}^2)$
-modules. We do this periodically in computations.
Remark 2.1. Outside of
![]() $\mathfrak {sl}_2(\mathbb {C})$
, the global differential operators on base affine space are no longer given by the Weyl algebra. For a Lie algebra
$\mathfrak {sl}_2(\mathbb {C})$
, the global differential operators on base affine space are no longer given by the Weyl algebra. For a Lie algebra
![]() $\mathfrak {g} \neq \mathfrak {sl}_2(\mathbb {C})^m$
, the affine closure of the corresponding base affine space is singular, and the ring of global differential operators can be quite complicated; see, for example, [Reference Levasseur and StaffordLS06].
$\mathfrak {g} \neq \mathfrak {sl}_2(\mathbb {C})^m$
, the affine closure of the corresponding base affine space is singular, and the ring of global differential operators can be quite complicated; see, for example, [Reference Levasseur and StaffordLS06].
2.1 The map
 $\mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {Z}(\mathfrak {g})} \mathcal {U}(\mathfrak {h}) \rightarrow \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
$\mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {Z}(\mathfrak {g})} \mathcal {U}(\mathfrak {h}) \rightarrow \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
Our strategy for gaining intuition about the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules arising in the construction of the Jantzen filtration is to illustrate the
$\mathcal {D}_{\widetilde {X}}$
-modules arising in the construction of the Jantzen filtration is to illustrate the
![]() $\mathfrak {g}$
-module structure on their global sections. This gives us an algebraic snapshot as to what is happening at each step in the construction sketched in Section 1.3. The first step is to differentiate the actions (2-6) and (2-7) to obtain a map
$\mathfrak {g}$
-module structure on their global sections. This gives us an algebraic snapshot as to what is happening at each step in the construction sketched in Section 1.3. The first step is to differentiate the actions (2-6) and (2-7) to obtain a map
![]() $\mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {Z}(\mathfrak {g})} \mathcal {U}(\mathfrak {h}) \rightarrow \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
. This map provides the
$\mathcal {U}(\mathfrak {g}) \otimes _{\mathcal {Z}(\mathfrak {g})} \mathcal {U}(\mathfrak {h}) \rightarrow \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
. This map provides the
![]() $\mathfrak {g}$
-module structure on the global sections of
$\mathfrak {g}$
-module structure on the global sections of
![]() $\mathcal {D}_{\widetilde {X}}$
-modules. We dedicate this section to the computation of this map.
$\mathcal {D}_{\widetilde {X}}$
-modules. We dedicate this section to the computation of this map.
By differentiating the left action of G in (2-6), we obtain an algebra homomorphism
given by the formula
for
![]() $g \in G$
,
$g \in G$
,
![]() $f \in \Gamma (\widetilde {X}, \mathcal {O}_{ \widetilde {X}})$
,
$f \in \Gamma (\widetilde {X}, \mathcal {O}_{ \widetilde {X}})$
,
![]() $x \in \widetilde {X}$
. Computing the image of the basis (2-1) under the homomorphism (2-9) is straightforward. For example, the image of e is given by the following computation using (2-6):
$x \in \widetilde {X}$
. Computing the image of the basis (2-1) under the homomorphism (2-9) is straightforward. For example, the image of e is given by the following computation using (2-6):
 $$ \begin{align*} e \cdot f(x_1, x_2) &= \frac{d}{dt} \bigg|_{t=0} f \left( \begin{pmatrix} 1 & -t \\ 0 & 1 \end{pmatrix} \cdot (x_1, x_2 ) \right) \\ &= \frac{d}{dt} \bigg|_{t=0} f(x_1 - t x_2, x_2) \\ &= - x_2 \partial_1 f(x_1, x_2). \end{align*} $$
$$ \begin{align*} e \cdot f(x_1, x_2) &= \frac{d}{dt} \bigg|_{t=0} f \left( \begin{pmatrix} 1 & -t \\ 0 & 1 \end{pmatrix} \cdot (x_1, x_2 ) \right) \\ &= \frac{d}{dt} \bigg|_{t=0} f(x_1 - t x_2, x_2) \\ &= - x_2 \partial_1 f(x_1, x_2). \end{align*} $$
Similar computations determine the images of f and h:
It is also useful to compute the image of the Casimir element (2-2) under the homomorphism L:
Similarly, the right action of H determines an algebra homomorphism
Under this homomorphism, h is sent to the Euler operator
Combining the homomorphisms L in (2-9) and R in (2-12), we obtain an algebra homomorphism
Lemma 2.2. The homomorphism (2-14) factors through the quotient
where
![]() $\mathcal {Z}(\mathfrak {g})$
acts on
$\mathcal {Z}(\mathfrak {g})$
acts on
![]() $\mathcal {U}(\mathfrak {h})$
via the Harish-Chandra projection
$\mathcal {U}(\mathfrak {h})$
via the Harish-Chandra projection
![]() $\gamma _{\mathrm {HC}}$
in (2-3).
$\gamma _{\mathrm {HC}}$
in (2-3).
Proof. Direct computation shows that the images of
![]() $\Omega \otimes 1$
and
$\Omega \otimes 1$
and
![]() $1 \otimes \gamma _{\mathrm {HC}}(\Omega )$
agree. Indeed,
$1 \otimes \gamma _{\mathrm {HC}}(\Omega )$
agree. Indeed,
 $$ \begin{align*} 1 \otimes \gamma_{\mathrm{HC}}(\Omega) = 1 \otimes (h^2 + 2h) \mapsto &R_h^2 + 2 R_h \\ &=(x_1 \partial_1 + x_2 \partial_2)^2 + 2(x_1 \partial_1 + x_2 \partial_2) \\ &=x_1^2 \partial _1^2 + 3 x_1 \partial_1 + 2 x_1 x_2 \partial_1 \partial_2 + x_2^2 \partial_x^2 + 3 x_2 \partial_x \\ &= L_\Omega.\\[-2.8pc] \end{align*} $$
$$ \begin{align*} 1 \otimes \gamma_{\mathrm{HC}}(\Omega) = 1 \otimes (h^2 + 2h) \mapsto &R_h^2 + 2 R_h \\ &=(x_1 \partial_1 + x_2 \partial_2)^2 + 2(x_1 \partial_1 + x_2 \partial_2) \\ &=x_1^2 \partial _1^2 + 3 x_1 \partial_1 + 2 x_1 x_2 \partial_1 \partial_2 + x_2^2 \partial_x^2 + 3 x_2 \partial_x \\ &= L_\Omega.\\[-2.8pc] \end{align*} $$
We refer to the algebra
![]() $\widetilde {\mathcal {U}}$
as the extended universal enveloping algebra. By Lemma 2.2, we have an algebra homomorphism
$\widetilde {\mathcal {U}}$
as the extended universal enveloping algebra. By Lemma 2.2, we have an algebra homomorphism
Global sections of
![]() $\mathcal {D}_{\widetilde {X}}$
-modules have the structure of
$\mathcal {D}_{\widetilde {X}}$
-modules have the structure of
![]() $\widetilde {\mathcal {U}}$
-modules via
$\widetilde {\mathcal {U}}$
-modules via
![]() $\alpha .$
$\alpha .$
2.2 Monodromic
 $\mathcal {D}_{X}$
-modules
$\mathcal {D}_{X}$
-modules
The
![]() $\mathcal {D}$
-modules that play a role in our story have an additional structure: they are ‘H-monodromic’. It is necessary for our purposes to work with H-monodromic
$\mathcal {D}$
-modules that play a role in our story have an additional structure: they are ‘H-monodromic’. It is necessary for our purposes to work with H-monodromic
![]() $\mathcal {D}$
-modules on base affine space instead of
$\mathcal {D}$
-modules on base affine space instead of
![]() $\mathcal {D}$
-modules on the flag variety. This is due to the fact that the
$\mathcal {D}$
-modules on the flag variety. This is due to the fact that the
![]() $\mathfrak {g}$
-modules in the construction of the Jantzen filtration have generalized infinitesimal characters, so they do not arise as global sections of modules over twisted sheaves of differential operators on the flag variety.
$\mathfrak {g}$
-modules in the construction of the Jantzen filtration have generalized infinitesimal characters, so they do not arise as global sections of modules over twisted sheaves of differential operators on the flag variety.
The machinery of H-monodromic
![]() $\mathcal {D}$
-modules is rather technical, and the details of the construction are not strictly necessary for our computation of the Jantzen filtration below. However, we thought that it would be useful to describe this construction in a specific example to illustrate that the equivalences established in [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5] are quite clear for
$\mathcal {D}$
-modules is rather technical, and the details of the construction are not strictly necessary for our computation of the Jantzen filtration below. However, we thought that it would be useful to describe this construction in a specific example to illustrate that the equivalences established in [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5] are quite clear for
![]() $\mathfrak {sl}_2(\mathbb {C})$
. In this section, we describe the construction of H-monodromic
$\mathfrak {sl}_2(\mathbb {C})$
. In this section, we describe the construction of H-monodromic
![]() $\mathcal {D}$
-modules for
$\mathcal {D}$
-modules for
![]() $\mathfrak {sl}_2(\mathbb {\mathbb {C}})$
and explain how it relates to representations of Lie algebras. More details on the general construction can be found in [Reference Beilinson, Bernstein and Gel’fandBB93, Reference Beilinson and GinzburgBG99].
$\mathfrak {sl}_2(\mathbb {\mathbb {C}})$
and explain how it relates to representations of Lie algebras. More details on the general construction can be found in [Reference Beilinson, Bernstein and Gel’fandBB93, Reference Beilinson and GinzburgBG99].
A weakly H-equivariant
![]() $\mathcal {D}_{\widetilde {X}}$
-module is an H-equivariant sheaf
$\mathcal {D}_{\widetilde {X}}$
-module is an H-equivariant sheaf
![]() $\mathcal {V}$
equipped with a
$\mathcal {V}$
equipped with a
![]() $\mathcal {D}_{\widetilde {X}}$
-module structure so that the isomorphism
$\mathcal {D}_{\widetilde {X}}$
-module structure so that the isomorphism
![]() $\mathrm {act}^*\mathcal {V} \rightarrow p^* \mathcal {V}$
given by the equivariant sheaf structure on
$\mathrm {act}^*\mathcal {V} \rightarrow p^* \mathcal {V}$
given by the equivariant sheaf structure on
![]() $\mathcal {V}$
is a morphism of
$\mathcal {V}$
is a morphism of
![]() $\mathcal {D}_{\widetilde {X}} \boxtimes \mathcal {O}_H$
-modules. Here,
$\mathcal {D}_{\widetilde {X}} \boxtimes \mathcal {O}_H$
-modules. Here,
![]() $\mathrm {act}:\widetilde {X} \times H \rightarrow \widetilde {X}$
is the action map and
$\mathrm {act}:\widetilde {X} \times H \rightarrow \widetilde {X}$
is the action map and
![]() $p: \widetilde {X} \times H \rightarrow \widetilde {X}$
is the projection map. For a reference on weakly equivariant
$p: \widetilde {X} \times H \rightarrow \widetilde {X}$
is the projection map. For a reference on weakly equivariant
![]() $\mathcal {D}$
-modules, see [Reference Miličić, Pandžić, Tirao, Vogan and WolfMP98, Section 4].
$\mathcal {D}$
-modules, see [Reference Miličić, Pandžić, Tirao, Vogan and WolfMP98, Section 4].
Definition 2.3. An H-monodromic
![]() $\mathcal {D}_X$
-module is a weakly H-equivariant
$\mathcal {D}_X$
-module is a weakly H-equivariant
![]() $\mathcal {D}_{\widetilde {X}}$
-module.
$\mathcal {D}_{\widetilde {X}}$
-module.
There is an equivalent characterization of H-monodromic
![]() $\mathcal {D}_X$
-modules in terms of H-invariant differential operators, which is established in [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5.2]. This perspective makes the structures of our examples more transparent, so we take this approach to monodromicity. Below we describe the construction for
$\mathcal {D}_X$
-modules in terms of H-invariant differential operators, which is established in [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5.2]. This perspective makes the structures of our examples more transparent, so we take this approach to monodromicity. Below we describe the construction for
![]() $\mathfrak {g}=\mathfrak {sl}_2(\mathbb {C})$
.
$\mathfrak {g}=\mathfrak {sl}_2(\mathbb {C})$
.
The right H-action in (2-7) induces a left H-action on
![]() $\mathcal {O}_{\widetilde {X}}$
and
$\mathcal {O}_{\widetilde {X}}$
and
![]() $\mathcal {D}_{\widetilde {X}}$
. The H-action on
$\mathcal {D}_{\widetilde {X}}$
. The H-action on
![]() $\mathcal {D}_{\widetilde {X}}$
satisfies the following relation: for
$\mathcal {D}_{\widetilde {X}}$
satisfies the following relation: for
![]() $g \in H$
,
$g \in H$
,
![]() $\theta \in \mathcal {D}_{\widetilde {X}}$
, and
$\theta \in \mathcal {D}_{\widetilde {X}}$
, and
![]() $f \in \mathcal {O}_{\widetilde {X}}$
,
$f \in \mathcal {O}_{\widetilde {X}}$
,
The H-action on
![]() $\mathcal {D}_{\widetilde {X}}$
induces an H-action on the sheaf
$\mathcal {D}_{\widetilde {X}}$
induces an H-action on the sheaf
![]() $\pi _*(\mathcal {D}_{\widetilde {X}})$
by algebra automorphisms, where
$\pi _*(\mathcal {D}_{\widetilde {X}})$
by algebra automorphisms, where
![]() $\pi :\widetilde {X}\rightarrow X$
is the quotient map (2-8). Here,
$\pi :\widetilde {X}\rightarrow X$
is the quotient map (2-8). Here,
![]() $\pi _*$
is the
$\pi _*$
is the
![]() $\mathcal {O}$
-module direct image. Denote the sheaf of H-invariant sections of
$\mathcal {O}$
-module direct image. Denote the sheaf of H-invariant sections of
![]() $\pi _*\mathcal {D}_{\widetilde {X}}$
by
$\pi _*\mathcal {D}_{\widetilde {X}}$
by
This is a sheaf of algebras on X. Explicitly, on an open set
![]() $U \subseteq X$
,
$U \subseteq X$
,
Note that because
![]() $\pi $
is an H-torsor,
$\pi $
is an H-torsor,
![]() $\pi ^{-1}(U)$
is H-stable for any set U, so this construction is well defined.
$\pi ^{-1}(U)$
is H-stable for any set U, so this construction is well defined.
Let
![]() $\mathcal {M}(\mathcal {D}_{\widetilde {X}}, H)_{\mathrm {weak}}$
be the category of weakly H-equivariant
$\mathcal {M}(\mathcal {D}_{\widetilde {X}}, H)_{\mathrm {weak}}$
be the category of weakly H-equivariant
![]() $\mathcal {D}_{\widetilde {X}}$
-modules, and
$\mathcal {D}_{\widetilde {X}}$
-modules, and
![]() $\mathcal {M}(\widetilde {\mathcal {D}})$
be the category of
$\mathcal {M}(\widetilde {\mathcal {D}})$
be the category of
![]() $\widetilde {\mathcal {D}}$
-modules. By [Reference Beilinson, Bernstein and Gel’fandBB93, Sections 1.8.9, 2.5.2], there is an equivalence of categories
$\widetilde {\mathcal {D}}$
-modules. By [Reference Beilinson, Bernstein and Gel’fandBB93, Sections 1.8.9, 2.5.2], there is an equivalence of categories
Hence, we can study monodromic
![]() $\mathcal {D}_X$
-modules by instead considering
$\mathcal {D}_X$
-modules by instead considering
![]() $\widetilde {\mathcal {D}}$
-modules. For the remainder of the paper, we take this to be our definition of monodromicity.
$\widetilde {\mathcal {D}}$
-modules. For the remainder of the paper, we take this to be our definition of monodromicity.
Definition 2.4. An H-monodromic
![]() $\mathcal {D}_X$
-module is a
$\mathcal {D}_X$
-module is a
![]() $\widetilde {\mathcal {D}}$
-module, where
$\widetilde {\mathcal {D}}$
-module, where
![]() $\widetilde {\mathcal {D}}$
is as in (2-18).
$\widetilde {\mathcal {D}}$
is as in (2-18).
Remark 2.5 (Relationship to twisted differential operators).
The sheaf
![]() $\widetilde {\mathcal {D}}$
is a sheaf of
$\widetilde {\mathcal {D}}$
is a sheaf of
![]() $S(\mathfrak {h})$
-algebras. In our example, the
$S(\mathfrak {h})$
-algebras. In our example, the
![]() $S(\mathfrak {h})$
-action is given by multiplication by the operator
$S(\mathfrak {h})$
-action is given by multiplication by the operator
![]() $R_h$
in (2-13). In particular, we can consider
$R_h$
in (2-13). In particular, we can consider
![]() $S(\mathfrak {h})$
as a subsheaf of
$S(\mathfrak {h})$
as a subsheaf of
![]() $\widetilde {\mathcal {D}}$
. In fact, it is the center [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5]. For
$\widetilde {\mathcal {D}}$
. In fact, it is the center [Reference Beilinson, Bernstein and Gel’fandBB93, Section 2.5]. For
![]() $\lambda \in \mathfrak {h}^*$
, denote by
$\lambda \in \mathfrak {h}^*$
, denote by
![]() $\mathfrak {m}_\lambda \subset S(\mathfrak {h})$
the corresponding maximal ideal. The sheaf
$\mathfrak {m}_\lambda \subset S(\mathfrak {h})$
the corresponding maximal ideal. The sheaf
![]() $\mathcal {D}_\lambda := \widetilde {\mathcal {D}}/ \mathfrak {m}_\lambda \widetilde {\mathcal {D}}$
is a twisted sheaf of differential operators (TDOs) on X. Hence,
$\mathcal {D}_\lambda := \widetilde {\mathcal {D}}/ \mathfrak {m}_\lambda \widetilde {\mathcal {D}}$
is a twisted sheaf of differential operators (TDOs) on X. Hence,
![]() $\widetilde {\mathcal {D}}$
-modules on which
$\widetilde {\mathcal {D}}$
-modules on which
![]() $R_h$
acts by eigenvalue
$R_h$
acts by eigenvalue
![]() $\lambda $
can be naturally identified with modules over the TDO
$\lambda $
can be naturally identified with modules over the TDO
![]() $\mathcal {D}_\lambda $
.
$\mathcal {D}_\lambda $
.
Modules over
![]() $\widetilde {\mathcal {D}}$
are directly related to modules over the extended universal enveloping algebra (2-15) via the global sections functor. The relationship is as follows. Because the left G-action and right H-action commute, the differential operators
$\widetilde {\mathcal {D}}$
are directly related to modules over the extended universal enveloping algebra (2-15) via the global sections functor. The relationship is as follows. Because the left G-action and right H-action commute, the differential operators
![]() $L_e, L_f,$
and
$L_e, L_f,$
and
![]() $L_h$
in (2-10) are H-invariant. This can also be shown via direct computation using (2-10) and (2-13). Hence, the image of the homomorphism (2-16) is contained in H-invariant differential operators:
$L_h$
in (2-10) are H-invariant. This can also be shown via direct computation using (2-10) and (2-13). Hence, the image of the homomorphism (2-16) is contained in H-invariant differential operators:
Composing
![]() $\alpha $
with
$\alpha $
with
![]() $\Gamma (\pi _*)$
, we obtain a map
$\Gamma (\pi _*)$
, we obtain a map
Theorem 2.6 [Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 3.2.2].
The map (2-21) is an isomorphism.
Proof. The theorem holds for general
![]() $\mathfrak {g}$
. We prove the theorem for
$\mathfrak {g}$
. We prove the theorem for
![]() $\mathfrak {g}=\mathfrak {sl}_2(\mathbb {C})$
by direct computation.
$\mathfrak {g}=\mathfrak {sl}_2(\mathbb {C})$
by direct computation.
We start by describing the sheaves
![]() $\pi _*\mathcal {D}_{\widetilde {X}}$
and
$\pi _*\mathcal {D}_{\widetilde {X}}$
and
![]() $\widetilde {\mathcal {D}}$
on
$\widetilde {\mathcal {D}}$
on
![]() $X=\mathbb {C} \mathbb {P} ^1$
by describing them on the open patches
$X=\mathbb {C} \mathbb {P} ^1$
by describing them on the open patches
and giving gluing conditions. Set
where
![]() $V(f(x_1, x_2))$
denotes the vanishing of the polynomial
$V(f(x_1, x_2))$
denotes the vanishing of the polynomial
![]() $f(x_1, x_2)$
. By definition,
$f(x_1, x_2)$
. By definition,
with obvious gluing conditions.
Using (2-17), we conclude that the H-action on
![]() $\mathcal {D}_{\widetilde {X}}$
is given by the local formulas
$\mathcal {D}_{\widetilde {X}}$
is given by the local formulas
where
![]() $g \in H$
is regarded as an element of
$g \in H$
is regarded as an element of
![]() $\mathbb {C}^\times $
under the identification
$\mathbb {C}^\times $
under the identification
 $$ \begin{align*} H \simeq \mathbb{C}^\times, \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix} \mapsto a. \end{align*} $$
$$ \begin{align*} H \simeq \mathbb{C}^\times, \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix} \mapsto a. \end{align*} $$
From this, we obtain a local description of
![]() $\widetilde {\mathcal {D}}$
, using (2-19):
$\widetilde {\mathcal {D}}$
, using (2-19):
Hence, the global sections are given by
Now, it is clear that
so the operators
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
generate
$R_h$
generate
![]() $\Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})^H$
. Since
$\Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})^H$
. Since
![]() $e\otimes 1, f \otimes 1, h \otimes 1$
and
$e\otimes 1, f \otimes 1, h \otimes 1$
and
![]() $1 \otimes h$
generate
$1 \otimes h$
generate
![]() $\widetilde {\mathcal {U}}$
, this shows that the map (2-21) is surjective. Direct computations establish that
$\widetilde {\mathcal {U}}$
, this shows that the map (2-21) is surjective. Direct computations establish that
Combining these computations with the fact that
![]() $L_e,L_f,L_h$
, and
$L_e,L_f,L_h$
, and
![]() $R_h$
are linearly independent shows that the relations satisfied by
$R_h$
are linearly independent shows that the relations satisfied by
![]() $L_e, L_f, L_h,$
and
$L_e, L_f, L_h,$
and
![]() $R_h$
are precisely those satisfied by
$R_h$
are precisely those satisfied by
![]() $e\otimes 1,f\otimes 1,h\otimes 1$
, and
$e\otimes 1,f\otimes 1,h\otimes 1$
, and
![]() $1\otimes h.$
Therefore, the map (2-21) is also injective.
$1\otimes h.$
Therefore, the map (2-21) is also injective.
The relationships described in this section can be summarized with the following commuting diagrams.

The composition of the top two arrows and the right-most arrow is the equivalence (2-20). (See [Reference Beilinson, Bernstein and Gel’fandBB93, Sections 1.8.9, 2.5.3] for more details.)
2.3 Verma modules and dual Verma modules
Using the map (2-16) constructed in Section 2.1, we can describe the
![]() $\widetilde {\mathcal {U}}$
-module structure on various classes of
$\widetilde {\mathcal {U}}$
-module structure on various classes of
![]() $\mathcal {D}_{\widetilde {X}}$
-modules. We start by examining the
$\mathcal {D}_{\widetilde {X}}$
-modules. We start by examining the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules
$\mathcal {D}_{\widetilde {X}}$
-modules
![]() $j_+\mathcal {O}_U$
and
$j_+\mathcal {O}_U$
and
![]() $j_!\mathcal {O}_U$
, where
$j_!\mathcal {O}_U$
, where
![]() $j:U \hookrightarrow \widetilde {X}$
is inclusion of the open union of N-orbits
$j:U \hookrightarrow \widetilde {X}$
is inclusion of the open union of N-orbits
Here the
![]() $+$
and
$+$
and
![]() $!$
indicate the
$!$
indicate the
![]() $\mathcal {D}$
-module push-forward functors; see [Reference MiličićMil]. These are the
$\mathcal {D}$
-module push-forward functors; see [Reference MiličićMil]. These are the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules that are eventually endowed with geometric Jantzen filtrations in Section 2.5. In this section, we describe the
$\mathcal {D}_{\widetilde {X}}$
-modules that are eventually endowed with geometric Jantzen filtrations in Section 2.5. In this section, we describe the
![]() $\widetilde {\mathcal {U}}$
-module structure on
$\widetilde {\mathcal {U}}$
-module structure on
![]() $\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
and
$\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
and
![]() $\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
.
$\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
.
Because j is an open embedding, the
![]() $\mathcal {D}_{\widetilde {X}}$
-module
$\mathcal {D}_{\widetilde {X}}$
-module
![]() $j_+\mathcal {O}_U$
is just the sheaf
$j_+\mathcal {O}_U$
is just the sheaf
![]() $\mathcal {O}_U$
with
$\mathcal {O}_U$
with
![]() $\mathcal {D}_{\widetilde {X}}$
-module structure given by the restriction of
$\mathcal {D}_{\widetilde {X}}$
-module structure given by the restriction of
![]() $\mathcal {D}_U$
to
$\mathcal {D}_U$
to
![]() $\mathcal {D}_{\widetilde {X}} \subseteq \mathcal {D}_U$
. Hence, the global sections of
$\mathcal {D}_{\widetilde {X}} \subseteq \mathcal {D}_U$
. Hence, the global sections of
![]() $j_+\mathcal {O}_U$
can be identified with the ring
$j_+\mathcal {O}_U$
can be identified with the ring

Figure 1 Dual Verma modules arise as global sections of
![]() $j_+\mathcal {O}_U$
.
$j_+\mathcal {O}_U$
.
The operators
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
from (2-10) and (2-13) act on monomials
$R_h$
from (2-10) and (2-13) act on monomials
![]() $x_1^m x_2^n$
for
$x_1^m x_2^n$
for
![]() $m \geq 0$
,
$m \geq 0$
,
![]() $n \in \mathbb {Z}$
by the formulas
$n \in \mathbb {Z}$
by the formulas
Using (2-23)–(2-26), we can illustrate the
![]() $\widetilde {\mathcal {U}}$
-module structure on
$\widetilde {\mathcal {U}}$
-module structure on
![]() $\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
using nodes and colored arrows. We do this in Figure 1. The monomials
$\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
using nodes and colored arrows. We do this in Figure 1. The monomials
![]() $x_1^m x_2^n$
for
$x_1^m x_2^n$
for
![]() $m \in \mathbb {Z}_{\geq 0}$
and
$m \in \mathbb {Z}_{\geq 0}$
and
![]() $n \in \mathbb {Z}$
form a basis for
$n \in \mathbb {Z}$
form a basis for
![]() $\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
. The green (dashed) arrows illustrate the action of the operator
$\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
. The green (dashed) arrows illustrate the action of the operator
![]() $ L_e$
on basis elements, the red (dotted) arrows the action of
$ L_e$
on basis elements, the red (dotted) arrows the action of
![]() $L_f$
, and the blue (solid) arrows the action of
$L_f$
, and the blue (solid) arrows the action of
![]() $L_h$
. If an operator acts by zero, no arrow is included. The
$L_h$
. If an operator acts by zero, no arrow is included. The
![]() $R_h$
-eigenspaces are highlighted in gray, with corresponding eigenvalues listed below.
$R_h$
-eigenspaces are highlighted in gray, with corresponding eigenvalues listed below.
Remark 2.7. We make the following observations about the
![]() $\mathcal {D}_{\widetilde {X}}$
-module
$\mathcal {D}_{\widetilde {X}}$
-module
![]() $j_+\mathcal {O}_U$
and its global sections.
$j_+\mathcal {O}_U$
and its global sections.
-
(1) As a
 $\widetilde {\mathcal {U}}$
-module,
$\widetilde {\mathcal {U}}$
-module,
 $\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
decomposes into a direct sum of submodules, each of which is an
$\Gamma (\widetilde {X}, j_+\mathcal {O}_U)$
decomposes into a direct sum of submodules, each of which is an
 $R_h$
-eigenspace corresponding to an integer eigenvalue:
$R_h$
-eigenspace corresponding to an integer eigenvalue:  $$ \begin{align*} \Gamma(\widetilde{X}, j_+ \mathcal{O}_U) = \bigoplus_{n \in \mathbb{Z}} \Gamma(\widetilde{X}, j_+ \mathcal{O}_U)_n. \end{align*} $$
$$ \begin{align*} \Gamma(\widetilde{X}, j_+ \mathcal{O}_U) = \bigoplus_{n \in \mathbb{Z}} \Gamma(\widetilde{X}, j_+ \mathcal{O}_U)_n. \end{align*} $$
In Figure 1, these eigenspaces are highlighted in gray.
-
(2) As a
 $\mathcal {U}(\mathfrak {g})$
-module, the
$\mathcal {U}(\mathfrak {g})$
-module, the
 $R_h$
-eigenspace
$R_h$
-eigenspace
 $\Gamma (\widetilde {X}, j_+\mathcal {O}_U)_n$
of eigenvalue n is isomorphic to the dual Verma module of highest weight n. In particular, it is irreducible if
$\Gamma (\widetilde {X}, j_+\mathcal {O}_U)_n$
of eigenvalue n is isomorphic to the dual Verma module of highest weight n. In particular, it is irreducible if
 $n<0$
, and it has a unique irreducible finite-dimensional submodule if
$n<0$
, and it has a unique irreducible finite-dimensional submodule if
 $n \geq 0$
.
$n \geq 0$
. -
(3) The sheaf
 $\pi _*j_+\mathcal {O}_U$
is a monodromic
$\pi _*j_+\mathcal {O}_U$
is a monodromic
 $\mathcal {D}_X$
-module because it admits an action of
$\mathcal {D}_X$
-module because it admits an action of
 $\widetilde {\mathcal {D}}$
(Definition 2.4). For each positive integer n,
$\widetilde {\mathcal {D}}$
(Definition 2.4). For each positive integer n,
 $\pi _*j_+\mathcal {O}_{U}$
has a subsheaf
$\pi _*j_+\mathcal {O}_{U}$
has a subsheaf
 $(\pi _*j_+\mathcal {O}_{U})_n$
on which
$(\pi _*j_+\mathcal {O}_{U})_n$
on which
 $R_h$
acts locally by the eigenvalue n. These subsheaves are
$R_h$
acts locally by the eigenvalue n. These subsheaves are
 $\mathcal {D}_n$
-modules, where
$\mathcal {D}_n$
-modules, where
 $\mathcal {D}_n$
is the twisted sheaf of differential operators as defined in Remark 2.5. These are exactly the
$\mathcal {D}_n$
is the twisted sheaf of differential operators as defined in Remark 2.5. These are exactly the
 $\mathcal {D}_n$
-modules appearing in [Reference RomanovRom21, Section 6, Figure 4].
$\mathcal {D}_n$
-modules appearing in [Reference RomanovRom21, Section 6, Figure 4].
Next we describe
![]() $\Gamma (\widetilde {X}, j_!\mathcal {O}_{\widetilde {X}})$
. This is slightly more involved. By definition,
$\Gamma (\widetilde {X}, j_!\mathcal {O}_{\widetilde {X}})$
. This is slightly more involved. By definition,
where
![]() $\mathbb {D}$
denotes the holonomic duality functor. Explicitly, for a smooth algebraic variety Y and a holonomic
$\mathbb {D}$
denotes the holonomic duality functor. Explicitly, for a smooth algebraic variety Y and a holonomic
![]() $\mathcal {D}_Y$
-module
$\mathcal {D}_Y$
-module
![]() $\mathcal {V}$
,
$\mathcal {V}$
,
This is a well-defined functor from the category of holonomic
![]() $\mathcal {D}_Y$
-modules to itself [Reference Hotta, Takeuchi and TanisakiHTT08, Corollary 2.6.8].
$\mathcal {D}_Y$
-modules to itself [Reference Hotta, Takeuchi and TanisakiHTT08, Corollary 2.6.8].
The first two steps of the composition in (2-27) are straightforward to compute. The right
![]() $\mathcal {D}_U$
-module
$\mathcal {D}_U$
-module
![]() $\mathbb {D}_U \mathcal {O}_U$
is just the sheaf
$\mathbb {D}_U \mathcal {O}_U$
is just the sheaf
![]() $\mathcal {O}_U$
, viewed as a right
$\mathcal {O}_U$
, viewed as a right
![]() $\mathcal {D}_U$
-module via the natural right action. Then, since j is an open immersion,
$\mathcal {D}_U$
-module via the natural right action. Then, since j is an open immersion,
![]() $j_+ \mathbb {D}_U \mathcal {O}_U$
is the sheaf
$j_+ \mathbb {D}_U \mathcal {O}_U$
is the sheaf
![]() $\mathcal {O}_U$
with right
$\mathcal {O}_U$
with right
![]() $\mathcal {D}_{\widetilde {X}}$
-module structure given by restriction to
$\mathcal {D}_{\widetilde {X}}$
-module structure given by restriction to
![]() $\mathcal {D}_{\widetilde {X}} \subset \mathcal {D}_U$
.
$\mathcal {D}_{\widetilde {X}} \subset \mathcal {D}_U$
.
To apply
![]() $\mathbb {D}_{\widetilde {X}}$
to
$\mathbb {D}_{\widetilde {X}}$
to
![]() $j_+ \mathbb {D}_U \mathcal {O}_U$
, we must take a projective resolution of
$j_+ \mathbb {D}_U \mathcal {O}_U$
, we must take a projective resolution of
![]() $j_+\mathbb {D}_U \mathcal {O}_U$
. First, we make the identification
$j_+\mathbb {D}_U \mathcal {O}_U$
. First, we make the identification
We take the following free (hence, projective) resolution of
![]() $\langle \partial _1, \partial _2 \rangle \mathcal {D}_U \backslash \mathcal {D}_U$
:
$\langle \partial _1, \partial _2 \rangle \mathcal {D}_U \backslash \mathcal {D}_U$
:
where the maps are defined by
 $$ \begin{align*} \epsilon: 1 &\mapsto x_2^{-1}, \\ d_0: (\theta_1, \theta_2) &\mapsto \partial_1 \theta_1 - x_2 \partial_2 \theta_2, \\ d_1: 1 &\mapsto (x_2 \partial_2, \partial_1). \end{align*} $$
$$ \begin{align*} \epsilon: 1 &\mapsto x_2^{-1}, \\ d_0: (\theta_1, \theta_2) &\mapsto \partial_1 \theta_1 - x_2 \partial_2 \theta_2, \\ d_1: 1 &\mapsto (x_2 \partial_2, \partial_1). \end{align*} $$
Applying
![]() $\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}}, r}( - , \mathcal {D}_{\widetilde {X}})$
to this complex, we obtain the complex
$\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}}, r}( - , \mathcal {D}_{\widetilde {X}})$
to this complex, we obtain the complex
where
![]() $d_i^*$
sends a morphism f to
$d_i^*$
sends a morphism f to
![]() $f \circ d_i$
.
$f \circ d_i$
.
Because the module
![]() $j_+\mathbb {D}_U \mathcal {O}_U$
is holonomic, the complex (2-29) only has nonzero cohomology in degree
$j_+\mathbb {D}_U \mathcal {O}_U$
is holonomic, the complex (2-29) only has nonzero cohomology in degree
![]() $2$
. This can also be seen by direct computation. By identifying
$2$
. This can also be seen by direct computation. By identifying
![]() $\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}},r}(\mathcal {D}_{\widetilde {X}}, \mathcal {D}_{\widetilde {X}}) \simeq \mathcal {D}_{\widetilde {X}}$
via
$\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}},r}(\mathcal {D}_{\widetilde {X}}, \mathcal {D}_{\widetilde {X}}) \simeq \mathcal {D}_{\widetilde {X}}$
via
![]() $f \mapsto f(1)$
and
$f \mapsto f(1)$
and
![]() $\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}},r}(\mathcal {D}_{\widetilde {X}}\oplus \mathcal {D}_{\widetilde {X}}, \mathcal {D}_{\widetilde {X}}) \simeq \mathcal {D}_{\widetilde {X}} \oplus \mathcal {D}_{\widetilde {X}}$
via
$\mathrm {Hom}_{\mathcal {D}_{\widetilde {X}},r}(\mathcal {D}_{\widetilde {X}}\oplus \mathcal {D}_{\widetilde {X}}, \mathcal {D}_{\widetilde {X}}) \simeq \mathcal {D}_{\widetilde {X}} \oplus \mathcal {D}_{\widetilde {X}}$
via
![]() $ f \mapsto (f(1,0), f(0,1))$
, we see that
$ f \mapsto (f(1,0), f(0,1))$
, we see that
Hence,
Now we can describe the global sections of
![]() $j_! \mathcal {O}_U$
and illustrate their
$j_! \mathcal {O}_U$
and illustrate their
![]() $\widetilde {\mathcal {U}}$
-module structure, as we did for
$\widetilde {\mathcal {U}}$
-module structure, as we did for
![]() $\mathcal {O}_{\widetilde {X}}$
and
$\mathcal {O}_{\widetilde {X}}$
and
![]() $j_+\mathcal {O}_U$
. The monomials
$j_+\mathcal {O}_U$
. The monomials
![]() $x_1^m x_2^n$
and
$x_1^m x_2^n$
and
![]() $x_1^m \partial _2^n$
for
$x_1^m \partial _2^n$
for
![]() $m, n \geq 0$
form a basis for
$m, n \geq 0$
form a basis for
![]() $\Gamma (\widetilde {X}, j_! \mathcal {O}_U)$
. The action of
$\Gamma (\widetilde {X}, j_! \mathcal {O}_U)$
. The action of
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
on
$R_h$
on
![]() $x^m_1 x_2^n$
for
$x^m_1 x_2^n$
for
![]() $m \geq 0$
and
$m \geq 0$
and
![]() $n> 0$
is given by (2-23)–(2-26). The action of
$n> 0$
is given by (2-23)–(2-26). The action of
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
on
$R_h$
on
![]() $x^m_1 \partial _2^n$
for
$x^m_1 \partial _2^n$
for
![]() $m \geq 0$
and
$m \geq 0$
and
![]() $n> 0$
is given by
$n> 0$
is given by
The action of
![]() $L_e$
on
$L_e$
on
![]() $x_1^m$
is given by (2-23), the action of
$x_1^m$
is given by (2-23), the action of
![]() $L_f$
on
$L_f$
on
![]() $x_1^m$
is given by (2-30), and the actions of
$x_1^m$
is given by (2-30), and the actions of
![]() $L_h$
and
$L_h$
and
![]() $R_h$
on
$R_h$
on
![]() $x^m$
are given by either (2-25)–(2-26) or (2-31)–(2-32).
$x^m$
are given by either (2-25)–(2-26) or (2-31)–(2-32).
We illustrate the
![]() $\widetilde {\mathcal {U}}$
-module structure of
$\widetilde {\mathcal {U}}$
-module structure of
![]() $\Gamma (\widetilde {X}, j_! \mathcal {O}_U)$
in Figure 2. The colors (line-styles) indicate the same operators as in the earlier example: green (dashed) is
$\Gamma (\widetilde {X}, j_! \mathcal {O}_U)$
in Figure 2. The colors (line-styles) indicate the same operators as in the earlier example: green (dashed) is
![]() $L_e$
, red (dotted) is
$L_e$
, red (dotted) is
![]() $L_f$
, blue (solid) is
$L_f$
, blue (solid) is
![]() $L_h$
, and
$L_h$
, and
![]() $R_h$
-eigenspaces are highlighted in gray, with corresponding eigenvalues listed below.
$R_h$
-eigenspaces are highlighted in gray, with corresponding eigenvalues listed below.

Figure 2 Verma modules arise as global sections of
![]() $j_!\mathcal {O}_U$
.
$j_!\mathcal {O}_U$
.
Remark 2.8. We make the following observations about
![]() $\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
.
$\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
.
-
(1) As a
 $\widetilde {\mathcal {U}}$
-module,
$\widetilde {\mathcal {U}}$
-module,
 $\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
decomposes into a direct sum of submodules, each of which is an
$\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
decomposes into a direct sum of submodules, each of which is an
 $R_h$
-eigenspace corresponding to an integer eigenvalue. Again, these eigenspaces are highlighted in gray.
$R_h$
-eigenspace corresponding to an integer eigenvalue. Again, these eigenspaces are highlighted in gray. -
(2) As a
 $\mathcal {U}(\mathfrak {g})$
-module, the
$\mathcal {U}(\mathfrak {g})$
-module, the
 $R_h$
-eigenspace of
$R_h$
-eigenspace of
 $\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
of eigenvalue n is isomorphic to the Verma module of highest weight n. In particular, it is irreducible if
$\Gamma (\widetilde {X}, j_!\mathcal {O}_U)$
of eigenvalue n is isomorphic to the Verma module of highest weight n. In particular, it is irreducible if
 $n<0$
, and it has a unique irreducible finite-dimensional quotient if
$n<0$
, and it has a unique irreducible finite-dimensional quotient if
 $n \geq 0$
.
$n \geq 0$
. -
(3) The sheaf
 $\pi _*j_!\mathcal {O}_U$
is an H-monodromic
$\pi _*j_!\mathcal {O}_U$
is an H-monodromic
 $\mathcal {D}_X$
-module. For each positive integer n,
$\mathcal {D}_X$
-module. For each positive integer n,
 $\pi _*j_!\mathcal {O}_{U}$
has a subsheaf
$\pi _*j_!\mathcal {O}_{U}$
has a subsheaf
 $(\pi _*j_!\mathcal {O}_{U})_n$
on which
$(\pi _*j_!\mathcal {O}_{U})_n$
on which
 $R_h$
acts locally by the eigenvalue n. These subsheaves are modules over the TDO
$R_h$
acts locally by the eigenvalue n. These subsheaves are modules over the TDO
 $\mathcal {D}_n$
(Remark 2.5). These are exactly the
$\mathcal {D}_n$
(Remark 2.5). These are exactly the
 $\mathcal {D}_n$
-modules appearing in [Reference RomanovRom21, Section 6, Figure 3].
$\mathcal {D}_n$
-modules appearing in [Reference RomanovRom21, Section 6, Figure 3].
2.4 The maximal extension
 $\Xi _\rho \mathcal {O}_U$
$\Xi _\rho \mathcal {O}_U$
To describe the geometric Jantzen filtrations on the
![]() $\mathcal {D}_{\widetilde {X}}$
-modules
$\mathcal {D}_{\widetilde {X}}$
-modules
![]() $j_!\mathcal {O}_U$
and
$j_!\mathcal {O}_U$
and
![]() $j_+\mathcal {O}_U$
, it is necessary to introduce the maximal extension functor
$j_+\mathcal {O}_U$
, it is necessary to introduce the maximal extension functor
This functor (defined in (2-36) below) extends
![]() $j_+$
and
$j_+$
and
![]() $j_!$
(see (2-37)–(2-38)), so it is a natural way to study both modules
$j_!$
(see (2-37)–(2-38)), so it is a natural way to study both modules
![]() $j_!\mathcal {O}_U$
and
$j_!\mathcal {O}_U$
and
![]() $j_+\mathcal {O}_U$
at once. In this section, we give the construction of
$j_+\mathcal {O}_U$
at once. In this section, we give the construction of
![]() $\Xi _\rho $
, then describe the
$\Xi _\rho $
, then describe the
![]() $\widetilde {\mathcal {U}}$
-module structure on
$\widetilde {\mathcal {U}}$
-module structure on
![]() $\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
.
$\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
.
To start, we recall the construction of maximal extension for
![]() $\mathcal {D}$
-modules, which is a special case of the construction in [Reference BeilinsonBei87], which produces the maximal extension and nearby cycle functors. Let Y be a smooth variety,
$\mathcal {D}$
-modules, which is a special case of the construction in [Reference BeilinsonBei87], which produces the maximal extension and nearby cycle functors. Let Y be a smooth variety,
![]() $f:Y \rightarrow \mathbb {A}^1$
a regular function, and
$f:Y \rightarrow \mathbb {A}^1$
a regular function, and
the corresponding open-closed decomposition of Y. For
![]() $n \in \mathbb {N}$
, denote by
$n \in \mathbb {N}$
, denote by
the free rank-1
![]() $\mathcal {O}_{\mathbb {A}^1 - \{0\}} \otimes \mathbb {C}[s]/s^n$
-module generated by the symbol
$\mathcal {O}_{\mathbb {A}^1 - \{0\}} \otimes \mathbb {C}[s]/s^n$
-module generated by the symbol
![]() $t^s$
. The action
$t^s$
. The action
![]() $\partial _t \cdot t^s = st^{-1}t^s$
gives
$\partial _t \cdot t^s = st^{-1}t^s$
gives
![]() $I^{(n)}$
the structure of a
$I^{(n)}$
the structure of a
![]() $\mathcal {D}_{\mathbb {A}^1-\{0\}}$
-module. Any
$\mathcal {D}_{\mathbb {A}^1-\{0\}}$
-module. Any
![]() $\mathcal {D}_U$
-module
$\mathcal {D}_U$
-module
![]() $\mathcal {M}_U$
can be deformed using
$\mathcal {M}_U$
can be deformed using
![]() $I^{(n)}$
: set
$I^{(n)}$
: set
to be the
![]() $\mathcal {D}_U$
-module obtained by twisting
$\mathcal {D}_U$
-module obtained by twisting
![]() $\mathcal {M}_U$
by
$\mathcal {M}_U$
by
![]() $I^{(n)}$
. Note that
$I^{(n)}$
. Note that
![]() $f^s\mathcal {M}_U^{(1)} = \mathcal {M}_U$
, and that both
$f^s\mathcal {M}_U^{(1)} = \mathcal {M}_U$
, and that both
![]() $I^{(n)}$
and
$I^{(n)}$
and
![]() $f^s\mathcal {M}_U^{(n)}$
have a natural action by
$f^s\mathcal {M}_U^{(n)}$
have a natural action by
![]() $s \in \mathbb {C}[s]/s^n$
.
$s \in \mathbb {C}[s]/s^n$
.
Assume that
![]() $\mathcal {M}_U$
is holonomic. Denote by
$\mathcal {M}_U$
is holonomic. Denote by
the canonical map between the
![]() $!$
and
$!$
and
![]() $+$
pushforwards, and
$+$
pushforwards, and
the composition of
![]() $\mathrm {can}$
with multiplication by s. For large enough n, the cokernel of
$\mathrm {can}$
with multiplication by s. For large enough n, the cokernel of
![]() $s^1(n)$
stabilizes; that is,
$s^1(n)$
stabilizes; that is,
![]() $\operatorname {\mathrm {coker}} s^1(n) = \operatorname {\mathrm {coker}} s^1(n+k)$
for all
$\operatorname {\mathrm {coker}} s^1(n) = \operatorname {\mathrm {coker}} s^1(n+k)$
for all
![]() $k>0$
. For
$k>0$
. For
![]() $n\gg 0$
, define the
$n\gg 0$
, define the
![]() $\mathcal {D}_Y$
-module
$\mathcal {D}_Y$
-module
called the maximal extension of
![]() $\mathcal {M}_U$
. By construction, this module comes equipped with the nilpotent endomorphism s. The corresponding functor
$\mathcal {M}_U$
. By construction, this module comes equipped with the nilpotent endomorphism s. The corresponding functor
is exact [Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1(i)]. Moreover, there are canonical short exact sequences [Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1(ii)’]
with
![]() $j_! = \ker (s: \Xi _f \rightarrow \Xi _f)$
and
$j_! = \ker (s: \Xi _f \rightarrow \Xi _f)$
and
![]() $j_+ = \operatorname {\mathrm {coker}}(s: \Xi _f \rightarrow \Xi _f)$
.
$j_+ = \operatorname {\mathrm {coker}}(s: \Xi _f \rightarrow \Xi _f)$
.
Now, we apply this general construction in the setting of our example. Let
![]() $\widetilde {X}$
and U be as above (see (2-5) and (2-22)), and let
$\widetilde {X}$
and U be as above (see (2-5) and (2-22)), and let
![]() $f_\rho $
be the function
$f_\rho $
be the function
This choice of function corresponds to the deformation direction
![]() $\rho \in \mathfrak {h}^*$
; see Remarks 1.3 and 2.10.
$\rho \in \mathfrak {h}^*$
; see Remarks 1.3 and 2.10.
For a variety Y, set
We compute the maximal extension
![]() $\Xi _{\rho }\mathcal {O}_U:= \Xi _{f_\rho } \mathcal {O}_U$
of the structure sheaf
$\Xi _{\rho }\mathcal {O}_U:= \Xi _{f_\rho } \mathcal {O}_U$
of the structure sheaf
![]() $\mathcal {O}_U$
using the construction above, then describe the
$\mathcal {O}_U$
using the construction above, then describe the
![]() $\widetilde {\mathcal {U}}$
-module structure on its global sections. To clarify the exposition, we list each step as a subsection.
$\widetilde {\mathcal {U}}$
-module structure on its global sections. To clarify the exposition, we list each step as a subsection.
2.4.1 Step 1: Deformation
Let
![]() $I^{(n)}$
be as in (2-34). The deformed version of
$I^{(n)}$
be as in (2-34). The deformed version of
![]() $\mathcal {O}_U$
is
$\mathcal {O}_U$
is
The global sections of
![]() $f^s \mathcal {O}_U^{(n)}$
are
$f^s \mathcal {O}_U^{(n)}$
are
where the differentials
![]() $\partial _1,\partial _2 \in \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
act on the generator
$\partial _1,\partial _2 \in \Gamma (\widetilde {X}, \mathcal {D}_{\widetilde {X}})$
act on the generator
![]() $t^s$
by
$t^s$
by
Alternatively, we can identify
![]() $f^s \mathcal {O}_U^{(n)}$
with a quotient of
$f^s \mathcal {O}_U^{(n)}$
with a quotient of
![]() $\mathcal {A}_U$
:
$\mathcal {A}_U$
:
Both descriptions are useful below.
2.4.2 Step 2:
 $+$
-pushforward
$+$
-pushforward
Because
![]() $j: U \hookrightarrow \widetilde {X}$
is an open embedding, the
$j: U \hookrightarrow \widetilde {X}$
is an open embedding, the
![]() $\mathcal {D}_{\widetilde {X}}$
-module
$\mathcal {D}_{\widetilde {X}}$
-module
![]() $j_+ f^s \mathcal {O}_U^{(n)}$
is the sheaf
$j_+ f^s \mathcal {O}_U^{(n)}$
is the sheaf
![]() $f^s \mathcal {O}_U^{(n)}$
with
$f^s \mathcal {O}_U^{(n)}$
with
![]() $\mathcal {D}_{\widetilde {X}}$
-module structure given by restriction to
$\mathcal {D}_{\widetilde {X}}$
-module structure given by restriction to
![]() $\mathcal {D}_{\widetilde {X}} \subset \mathcal {D}_U$
. Under the identification (2-40),
$\mathcal {D}_{\widetilde {X}} \subset \mathcal {D}_U$
. Under the identification (2-40),
with
![]() $\mathcal {D}_{\widetilde {X}}$
-action given by left multiplication.
$\mathcal {D}_{\widetilde {X}}$
-action given by left multiplication.
It is interesting to examine the
![]() $\widetilde {\mathcal {U}}$
-module structure on the global sections of this module. The operators
$\widetilde {\mathcal {U}}$
-module structure on the global sections of this module. The operators
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
in (2-10), (2-13) act on the monomial basis elements of (2-39) by the following formulas:
$R_h$
in (2-10), (2-13) act on the monomial basis elements of (2-39) by the following formulas:
The resulting
![]() $\widetilde {\mathcal {U}}$
-module has a natural filtration given by powers of s, and it decomposes into a direct sum of submodules spanned by monomials
$\widetilde {\mathcal {U}}$
-module has a natural filtration given by powers of s, and it decomposes into a direct sum of submodules spanned by monomials
![]() $\{x_1^k x_2^\ell s^m t^s\}$
for fixed integers
$\{x_1^k x_2^\ell s^m t^s\}$
for fixed integers
![]() $k + \ell $
. Each of these submodules has the structure of a deformed dual Verma module, as illustrated in Figure 3 for
$k + \ell $
. Each of these submodules has the structure of a deformed dual Verma module, as illustrated in Figure 3 for
![]() $k + \ell = 0$
. Note that in Figure 3, we omit the generator
$k + \ell = 0$
. Note that in Figure 3, we omit the generator
![]() $t^s$
and the arrows corresponding to the
$t^s$
and the arrows corresponding to the
![]() $R_h$
-action for clarity.
$R_h$
-action for clarity.

Figure 3 Deformed dual Verma modules arise as global sections of
![]() $j_+f^s\mathcal {O}_U^{(n)}$
.
$j_+f^s\mathcal {O}_U^{(n)}$
.
Moreover, one can compute that the Casimir element
![]() $L_\Omega $
in (2-11) acts by
$L_\Omega $
in (2-11) acts by
Since s is nilpotent, we can see from this computation that a high enough power of the operator
annihilates any monomial basis element. (Here,
![]() $\gamma _{\mathrm {HC}}$
is the Harish-Chandra projection in (2-3).) Hence, the global sections of the submodules of
$\gamma _{\mathrm {HC}}$
is the Harish-Chandra projection in (2-3).) Hence, the global sections of the submodules of
![]() $j_+ f^s \mathcal {O}_U ^{(n)}$
spanned by monomials
$j_+ f^s \mathcal {O}_U ^{(n)}$
spanned by monomials
![]() $\{x_1^k x_2^\ell s^m t^s\}$
for fixed integers
$\{x_1^k x_2^\ell s^m t^s\}$
for fixed integers
![]() $k + \ell $
have generalized, but not strict, infinitesimal character.
$k + \ell $
have generalized, but not strict, infinitesimal character.
2.4.3 Step 3:
 $!$
-pushforward
$!$
-pushforward
Recall that
![]() $j_! = \mathbb {D}_{\widetilde {X}} \circ j_+ \circ \mathbb {D}_U$
, where
$j_! = \mathbb {D}_{\widetilde {X}} \circ j_+ \circ \mathbb {D}_U$
, where
![]() $\mathbb {D}$
denotes holonomic duality, as in (2-28). We begin by computing the right
$\mathbb {D}$
denotes holonomic duality, as in (2-28). We begin by computing the right
![]() $\mathcal {D}_U$
-module
$\mathcal {D}_U$
-module
![]() $\mathbb {D}_U f^s \mathcal {O}_U^{(n)}$
by taking a projective resolution of
$\mathbb {D}_U f^s \mathcal {O}_U^{(n)}$
by taking a projective resolution of
![]() $f^s \mathcal {O}_U^{(n)}$
as a left
$f^s \mathcal {O}_U^{(n)}$
as a left
![]() $\mathcal {A}_U$
-module. This is straightforward using the description (2-39). The complex
$\mathcal {A}_U$
-module. This is straightforward using the description (2-39). The complex
where
![]() $\epsilon $
is the canonical quotient map,
$\epsilon $
is the canonical quotient map,
![]() $d_0$
sends
$d_0$
sends
![]() $(\theta _1, \theta _2) \in \mathcal {A}_U \oplus \mathcal {A}_U$
to
$(\theta _1, \theta _2) \in \mathcal {A}_U \oplus \mathcal {A}_U$
to
![]() $\theta _1 \partial _1 - \theta _2 (x_2 \partial _2 -s)$
, and
$\theta _1 \partial _1 - \theta _2 (x_2 \partial _2 -s)$
, and
![]() $d_1$
sends
$d_1$
sends
![]() $1 \mapsto (x_2 \partial _2 - s, \partial _1)$
, is a free resolution of the left
$1 \mapsto (x_2 \partial _2 - s, \partial _1)$
, is a free resolution of the left
![]() $\mathcal {A}_U$
-module
$\mathcal {A}_U$
-module
![]() $f^s \mathcal {O}_U^{(n)}$
. Applying the functor
$f^s \mathcal {O}_U^{(n)}$
. Applying the functor
![]() $\mathrm {Hom}_{\mathcal {A}_U}( - , \mathcal {A}_U)$
and making the natural identification
$\mathrm {Hom}_{\mathcal {A}_U}( - , \mathcal {A}_U)$
and making the natural identification
of right
![]() $\mathcal {A}_U$
-modules, we see that
$\mathcal {A}_U$
-modules, we see that
Here,
![]() $d_i^* (\varphi ) = \varphi \circ d_i$
for an appropriate homomorphism
$d_i^* (\varphi ) = \varphi \circ d_i$
for an appropriate homomorphism
![]() $\varphi $
, and the right
$\varphi $
, and the right
![]() $\mathcal {A}_U$
-module structure is given by right multiplication.
$\mathcal {A}_U$
-module structure is given by right multiplication.
To finish the computation of
![]() $j_! f^s \mathcal {O}_U^{(n)}$
, we must take a projective resolution of this module. We do so following a similar process to the
$j_! f^s \mathcal {O}_U^{(n)}$
, we must take a projective resolution of this module. We do so following a similar process to the
![]() $!$
-pushforward computation in Section 2.3. Denote by I the right ideal
$!$
-pushforward computation in Section 2.3. Denote by I the right ideal
![]() $\langle \partial _1, x_2 \partial _2 - s \rangle \mathcal {A}_U$
in
$\langle \partial _1, x_2 \partial _2 - s \rangle \mathcal {A}_U$
in
![]() $\mathcal {A}_U$
. The complex
$\mathcal {A}_U$
. The complex
with maps given by
 $$ \begin{align*} \,\epsilon: 1 &\mapsto Ix_2^{-1};\\d_0: (\theta_1, \theta_2) &\mapsto x_2 \partial_1 \theta_1 - (x_2^2 \partial_2 - x_2 s) \theta_2;\\d_1: 1 &\mapsto (x_2 \partial_2 - s, \partial_1) \end{align*} $$
$$ \begin{align*} \,\epsilon: 1 &\mapsto Ix_2^{-1};\\d_0: (\theta_1, \theta_2) &\mapsto x_2 \partial_1 \theta_1 - (x_2^2 \partial_2 - x_2 s) \theta_2;\\d_1: 1 &\mapsto (x_2 \partial_2 - s, \partial_1) \end{align*} $$
is a free resolution of
![]() $\mathbb {D}_U f^s \mathcal {O}_U^{(n)}$
by right
$\mathbb {D}_U f^s \mathcal {O}_U^{(n)}$
by right
![]() $\mathcal {A}_{\widetilde {X}}$
-modules. Applying
$\mathcal {A}_{\widetilde {X}}$
-modules. Applying
![]() $\mathrm {Hom}_{\mathcal {A}_{\widetilde {X}}, r}( - , \mathcal {A}_{\widetilde {X}})$
and making the natural identifications as above,
$\mathrm {Hom}_{\mathcal {A}_{\widetilde {X}}, r}( - , \mathcal {A}_{\widetilde {X}})$
and making the natural identifications as above,
The left
![]() $\mathcal {A}_{\widetilde {X}}$
-module structure is given by left multiplication.
$\mathcal {A}_{\widetilde {X}}$
-module structure is given by left multiplication.
Again, it is interesting to examine the
![]() $\widetilde {\mathcal {U}}$
-module structure on the global sections of this module. The global sections of
$\widetilde {\mathcal {U}}$
-module structure on the global sections of this module. The global sections of
![]() $j_! f^s \mathcal {O}_U^{(n)}$
are spanned by monomials
$j_! f^s \mathcal {O}_U^{(n)}$
are spanned by monomials
![]() $x_1^k x_2^{\ell } s^m$
for
$x_1^k x_2^{\ell } s^m$
for
![]() $k, \ell \geq 0$
and
$k, \ell \geq 0$
and
![]() $0 \leq m < n$
, and
$0 \leq m < n$
, and
![]() $x_1^a \partial _2^ b s^m$
for
$x_1^a \partial _2^ b s^m$
for
![]() $a, b \geq 0$
and
$a, b \geq 0$
and
![]() $0 \leq m < n$
. For
$0 \leq m < n$
. For
![]() $\ell>0$
, the
$\ell>0$
, the
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
-actions on the monomials
$R_h$
-actions on the monomials
![]() $x_1^k x_2^{\ell } s^m$
are as in (2-41)–(2-44) (where we identify the generator
$x_1^k x_2^{\ell } s^m$
are as in (2-41)–(2-44) (where we identify the generator
![]() $t^s$
of
$t^s$
of
![]() $j_+ f^s \mathcal {O}_U^{(n)}$
with the coset containing
$j_+ f^s \mathcal {O}_U^{(n)}$
with the coset containing
![]() $1$
in
$1$
in
![]() $j_!f^s \mathcal {O}_U^{(n)}$
), and the actions on the monomials
$j_!f^s \mathcal {O}_U^{(n)}$
), and the actions on the monomials
![]() $x_1^a \partial _2^ b s^m$
are given by the following formulas:
$x_1^a \partial _2^ b s^m$
are given by the following formulas:
 $$ \begin{align*} L_e \cdot x_1^a \partial_2^ b s^m &= a(b - 1 - s) x_1^{a-1} \partial_2 ^{b-1} s^m;\\L_f \cdot x_1^a \partial_2^ b s^m &= -x_1^{a+1} \partial_2^{b+1} s^m; \end{align*} $$
$$ \begin{align*} L_e \cdot x_1^a \partial_2^ b s^m &= a(b - 1 - s) x_1^{a-1} \partial_2 ^{b-1} s^m;\\L_f \cdot x_1^a \partial_2^ b s^m &= -x_1^{a+1} \partial_2^{b+1} s^m; \end{align*} $$
For
![]() $\ell =b= 0$
, the actions of
$\ell =b= 0$
, the actions of
![]() $L_h$
and
$L_h$
and
![]() $R_h$
are as in (2-47)–(2-48), and the actions of
$R_h$
are as in (2-47)–(2-48), and the actions of
![]() $L_e$
and
$L_e$
and
![]() $L_f$
are given by
$L_f$
are given by
As in Section 2.4.2, this
![]() $\widetilde {\mathcal {U}}$
-module has an n-step filtration by powers of s, and decomposes into a direct sum of
$\widetilde {\mathcal {U}}$
-module has an n-step filtration by powers of s, and decomposes into a direct sum of
![]() $\widetilde {\mathcal {U}}$
-submodules, each spanned by the set of monomials
$\widetilde {\mathcal {U}}$
-submodules, each spanned by the set of monomials
![]() $\{x_1^k x_2^{\ell } s^m\}$
and
$\{x_1^k x_2^{\ell } s^m\}$
and
![]() $\{x_1^a \partial _2^ b s^m\}$
such that
$\{x_1^a \partial _2^ b s^m\}$
such that
![]() $k + \ell = a-b$
is a fixed integer. For
$k + \ell = a-b$
is a fixed integer. For
![]() $k + \ell = a-b=\lambda $
, this submodule is isomorphic to a deformed Verma module of highest weight
$k + \ell = a-b=\lambda $
, this submodule is isomorphic to a deformed Verma module of highest weight
![]() $\lambda $
. We illustrate the module corresponding to
$\lambda $
. We illustrate the module corresponding to
![]() $\lambda = 0$
in Figure 4.
$\lambda = 0$
in Figure 4.

Figure 4 Deformed Verma modules arise as global sections of
![]() $j_!f^s\mathcal {O}_U^{(n)}$
.
$j_!f^s\mathcal {O}_U^{(n)}$
.
2.4.4 Step 4: Image of the canonical map
Set
![]() $I_U = \mathcal {A}_U \langle \partial _1, x_2 \partial _2 - s \rangle $
and
$I_U = \mathcal {A}_U \langle \partial _1, x_2 \partial _2 - s \rangle $
and
![]() $I_{\widetilde {X}} = \mathcal {A}_{\widetilde {X}} \langle \partial _1, x_2 \partial _2 - s \rangle $
to be the left ideals generated by the operators
$I_{\widetilde {X}} = \mathcal {A}_{\widetilde {X}} \langle \partial _1, x_2 \partial _2 - s \rangle $
to be the left ideals generated by the operators
![]() $\partial _1$
and
$\partial _1$
and
![]() $x_2 \partial _2 - s$
in
$x_2 \partial _2 - s$
in
![]() $\mathcal {A}_U$
and
$\mathcal {A}_U$
and
![]() $\mathcal {A}_{\widetilde {X}}$
, respectively. The canonical map between the
$\mathcal {A}_{\widetilde {X}}$
, respectively. The canonical map between the
![]() $!$
- and
$!$
- and
![]() $+$
-pushforwards is given by
$+$
-pushforwards is given by
 $$ \begin{align*} j_! f^s \mathcal{O}_U^{(n)} = \mathcal{A}_{\widetilde{X}} / I_{\widetilde{X}} &\xrightarrow{\mathrm{can}} \mathcal{A}_U / I_U =j_+ f^s \mathcal{O}_U^{(n)} \\ 1I_{\widetilde{X}} &\longmapsto 1 I_U. \end{align*} $$
$$ \begin{align*} j_! f^s \mathcal{O}_U^{(n)} = \mathcal{A}_{\widetilde{X}} / I_{\widetilde{X}} &\xrightarrow{\mathrm{can}} \mathcal{A}_U / I_U =j_+ f^s \mathcal{O}_U^{(n)} \\ 1I_{\widetilde{X}} &\longmapsto 1 I_U. \end{align*} $$
Since
![]() $1\mathcal {A}_{\widetilde {X}}$
generates
$1\mathcal {A}_{\widetilde {X}}$
generates
![]() $j_! f^s \mathcal {O}_U^{(n)}$
as an
$j_! f^s \mathcal {O}_U^{(n)}$
as an
![]() $\mathcal {A}_{\widetilde {X}}$
-module, its image completely determines the morphism
$\mathcal {A}_{\widetilde {X}}$
-module, its image completely determines the morphism
![]() $\mathrm {can}$
. On the monomial basis elements
$\mathrm {can}$
. On the monomial basis elements
![]() $x_1^k x_2^\ell s^m$
and
$x_1^k x_2^\ell s^m$
and
![]() $x_1^k \partial _2^\ell s^m$
of
$x_1^k \partial _2^\ell s^m$
of
![]() $j_! f^s \mathcal {O}_U^{(n)}$
, the canonical map acts by
$j_! f^s \mathcal {O}_U^{(n)}$
, the canonical map acts by
for
![]() $b>1$
. For
$b>1$
. For
![]() $b=1$
,
$b=1$
, ![]() .
.
The image of the morphism
![]() $\mathrm {can}$
is the
$\mathrm {can}$
is the
![]() $\mathcal {A}_{\widetilde {X}}$
-submodule
$\mathcal {A}_{\widetilde {X}}$
-submodule
In the description of the global sections of
![]() $j_+ f^s \mathcal {O}_U^{(n)}$
in (2-39), the global sections of
$j_+ f^s \mathcal {O}_U^{(n)}$
in (2-39), the global sections of
![]() $\operatorname {\mbox {im }} (\mathrm {can})$
can be identified with
$\operatorname {\mbox {im }} (\mathrm {can})$
can be identified with
2.4.5 Step 5: The maximal extension
Composing the canonical map
![]() $\mathrm {can}$
with s gives
$\mathrm {can}$
with s gives
The global sections of the image of
![]() $s^1(n)$
(as a submodule of (2-39)) are
$s^1(n)$
(as a submodule of (2-39)) are
This gives us an explicit description of
![]() $\Xi _\rho \mathcal {O}_U = \operatorname {\mathrm {coker}} s^1(n)$
:
$\Xi _\rho \mathcal {O}_U = \operatorname {\mathrm {coker}} s^1(n)$
:
 $$ \begin{align} \Gamma(\widetilde{X}, \Xi_\rho \mathcal{O}_U) &= (\mathbb{C}[x_1, x_2, x_2^{-1}] \otimes \mathbb{C}[s]/s^n ) t^s / \Gamma(\widetilde{X}, \operatorname{\mbox{im }} s^1(n))\nonumber\\ &= ( \mathbb{C}[x_1, x_2, x_2^{-1}] \otimes \mathbb{C}[s]/s^2 )t^s / ( \mathbb{C}[x_1, x_2]\otimes s \mathbb{C}[s]/s^2 )t^s. \end{align} $$
$$ \begin{align} \Gamma(\widetilde{X}, \Xi_\rho \mathcal{O}_U) &= (\mathbb{C}[x_1, x_2, x_2^{-1}] \otimes \mathbb{C}[s]/s^n ) t^s / \Gamma(\widetilde{X}, \operatorname{\mbox{im }} s^1(n))\nonumber\\ &= ( \mathbb{C}[x_1, x_2, x_2^{-1}] \otimes \mathbb{C}[s]/s^2 )t^s / ( \mathbb{C}[x_1, x_2]\otimes s \mathbb{C}[s]/s^2 )t^s. \end{align} $$

Figure 5 Caricature of the maximal extension
![]() $\Xi _\rho \mathcal {O}_U$
.
$\Xi _\rho \mathcal {O}_U$
.
A caricature of the
![]() $\Gamma (\widetilde {X}, \mathcal {A}_{\widetilde {X}})$
-module (2-51) is illustrated as in Figure 5. It has two layers, corresponding to the two nonzero powers of s, and action by s moves layers up. As vector spaces, the bottom layer is isomorphic to
$\Gamma (\widetilde {X}, \mathcal {A}_{\widetilde {X}})$
-module (2-51) is illustrated as in Figure 5. It has two layers, corresponding to the two nonzero powers of s, and action by s moves layers up. As vector spaces, the bottom layer is isomorphic to
![]() $\mathbb {C}[x_1, x_2, x_2^{-1}]$
and the top layer to
$\mathbb {C}[x_1, x_2, x_2^{-1}]$
and the top layer to
![]() $sx_2^{-1} \mathbb {C}[x_1, x_2^{-1}]$
.
$sx_2^{-1} \mathbb {C}[x_1, x_2^{-1}]$
.
Our final step is to examine the
![]() $\widetilde {\mathcal {U}}$
-module structure on
$\widetilde {\mathcal {U}}$
-module structure on
![]() $\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
. The module (2-51) has a basis given by monomials
$\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
. The module (2-51) has a basis given by monomials
![]() $x_1^k x_2^\ell t^s$
for
$x_1^k x_2^\ell t^s$
for
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $\ell \in \mathbb {Z}$
, and
$\ell \in \mathbb {Z}$
, and
![]() $x_1^k x_2^\ell s t^s$
for
$x_1^k x_2^\ell s t^s$
for
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $\ell \in \mathbb {Z}_{< 0}$
. The actions of the operators
$\ell \in \mathbb {Z}_{< 0}$
. The actions of the operators
![]() $L_e, L_f, L_h$
, and
$L_e, L_f, L_h$
, and
![]() $R_h$
in (2-10) on these monomials are given by applying the formulas (2-41)–(2-44) and taking the image of the resulting monomials in the quotient (2-51).
$R_h$
in (2-10) on these monomials are given by applying the formulas (2-41)–(2-44) and taking the image of the resulting monomials in the quotient (2-51).
The
![]() $\widetilde {\mathcal {U}}$
-module
$\widetilde {\mathcal {U}}$
-module
![]() $\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
splits into a direct sum of submodules spanned by monomials
$\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
splits into a direct sum of submodules spanned by monomials
![]() $x_1^k x_2^\ell t^s$
and
$x_1^k x_2^\ell t^s$
and
![]() $x_1^k x_2^\ell s t^s$
such that
$x_1^k x_2^\ell s t^s$
such that
![]() $k + \ell $
is a fixed integer. We illustrate the submodule for
$k + \ell $
is a fixed integer. We illustrate the submodule for
![]() $k + \ell = 0$
in Figure 6. For clarity, we drop the generator
$k + \ell = 0$
in Figure 6. For clarity, we drop the generator
![]() $t^s$
from our notation in Figure 6. If
$t^s$
from our notation in Figure 6. If
![]() $\lambda \geq 0$
, the submodule corresponding to the integer
$\lambda \geq 0$
, the submodule corresponding to the integer
![]() $\lambda = k + \ell $
has the Verma module of highest weight
$\lambda = k + \ell $
has the Verma module of highest weight
![]() $\lambda $
as a submodule, and the dual Verma module corresponding to
$\lambda $
as a submodule, and the dual Verma module corresponding to
![]() $\lambda $
as a quotient. As a
$\lambda $
as a quotient. As a
![]() $\mathcal {U}(\mathfrak {g})$
-module, it is isomorphic to the big projective module
$\mathcal {U}(\mathfrak {g})$
-module, it is isomorphic to the big projective module
![]() $P(w_0\lambda )$
in the corresponding block of category
$P(w_0\lambda )$
in the corresponding block of category
![]() $\mathcal {O}$
. (The big projective module is the projective cover of the irreducible highest-weight module
$\mathcal {O}$
. (The big projective module is the projective cover of the irreducible highest-weight module
![]() $L(w_0 \lambda )$
, where
$L(w_0 \lambda )$
, where
![]() $w_0$
is the longest element of the Weyl group. It is the longest indecomposable projective object in the block
$w_0$
is the longest element of the Weyl group. It is the longest indecomposable projective object in the block
![]() $\mathcal {O}_\lambda $
of category
$\mathcal {O}_\lambda $
of category
![]() $\mathcal {O}$
[Reference HumphreysHum08, Section 3.12].)
$\mathcal {O}$
[Reference HumphreysHum08, Section 3.12].)

Figure 6 Big projective modules arise as global sections of slices of
![]() $\Xi _\rho \mathcal {O}_U$
.
$\Xi _\rho \mathcal {O}_U$
.
2.5 The monodromy filtration and the geometric Jantzen filtration
The maximal extension
![]() $\Xi _\rho \mathcal {O}_U$
naturally comes equipped with a nilpotent endomorphism s, giving it a corresponding monodromy filtration. This is the source of the geometric Jantzen filtrations on
$\Xi _\rho \mathcal {O}_U$
naturally comes equipped with a nilpotent endomorphism s, giving it a corresponding monodromy filtration. This is the source of the geometric Jantzen filtrations on
![]() $j_!\mathcal {O}_U$
and
$j_!\mathcal {O}_U$
and
![]() $j_+\mathcal {O}_U$
. In this section, we use the monodromy filtration on
$j_+\mathcal {O}_U$
. In this section, we use the monodromy filtration on
![]() $\Xi _\rho \mathcal {O}_U$
to compute the geometric Jantzen filtration on
$\Xi _\rho \mathcal {O}_U$
to compute the geometric Jantzen filtration on
![]() $j_!\mathcal {O}_U$
. Using the computations of Section 2.4, we then describe the corresponding
$j_!\mathcal {O}_U$
. Using the computations of Section 2.4, we then describe the corresponding
![]() $\widetilde {\mathcal {U}}$
-module filtration on global sections.
$\widetilde {\mathcal {U}}$
-module filtration on global sections.
We begin by recalling monodromy filtrations in abelian categories, following [Reference DeligneDel80, Section 1.6]. Given an object A in an abelian category
![]() $\mathcal {A}$
and a nilpotent endomorphism
$\mathcal {A}$
and a nilpotent endomorphism
![]() $s: A \rightarrow A$
, it follows from the Jacobson–Morosov theorem [Reference DeligneDel80, Proposition 1.6.1] that there exists a unique increasing exhaustive filtration
$s: A \rightarrow A$
, it follows from the Jacobson–Morosov theorem [Reference DeligneDel80, Proposition 1.6.1] that there exists a unique increasing exhaustive filtration
![]() $\mu ^\bullet $
on A such that
$\mu ^\bullet $
on A such that
![]() $s\mu ^n \subset \mu ^{n-2}$
, and for
$s\mu ^n \subset \mu ^{n-2}$
, and for
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $s^k$
induces an isomorphism
$s^k$
induces an isomorphism
![]() $\mathrm {gr}_\mu ^k A \simeq \mathrm {gr}_\mu ^{-k} A.$
This unique filtration is called the monodromy filtration of A.
$\mathrm {gr}_\mu ^k A \simeq \mathrm {gr}_\mu ^{-k} A.$
This unique filtration is called the monodromy filtration of A.
Following Deligne’s proof in [Reference DeligneDel80, Section 1.6], the monodromy filtration can be described explicitly in terms of powers of
![]() $s.$
Namely, if we set
$s.$
Namely, if we set
 $$ \begin{align*} \mathscr{K}^p A: = \begin{cases} \ker s^{p+1} & \text{for } p \geq 0; \\ 0 & \text{for } p<0 \end{cases} \end{align*} $$
$$ \begin{align*} \mathscr{K}^p A: = \begin{cases} \ker s^{p+1} & \text{for } p \geq 0; \\ 0 & \text{for } p<0 \end{cases} \end{align*} $$
to be the kernel filtration of A and
 $$ \begin{align*} \mathscr{I}^q A:= \begin{cases} \operatorname{\mbox{im }} s^q & \text{for } q>0; \\ A & \text{for } q \leq 0, \end{cases} \end{align*} $$
$$ \begin{align*} \mathscr{I}^q A:= \begin{cases} \operatorname{\mbox{im }} s^q & \text{for } q>0; \\ A & \text{for } q \leq 0, \end{cases} \end{align*} $$
to be the image filtration of A, then
![]() $\mu ^\bullet $
is the convolution of the kernel and image filtrations; that is,
$\mu ^\bullet $
is the convolution of the kernel and image filtrations; that is,
 $$ \begin{align} \mu^r = \sum_{p-q = r} \mathscr{K}^p \cap \mathscr{I}^q. \end{align} $$
$$ \begin{align} \mu^r = \sum_{p-q = r} \mathscr{K}^p \cap \mathscr{I}^q. \end{align} $$
The monodromy filtration
![]() $\mu ^\bullet $
induces filtrations
$\mu ^\bullet $
induces filtrations
![]() $J_!^\bullet $
on
$J_!^\bullet $
on
![]() $\ker s$
and
$\ker s$
and
![]() $J_+^\bullet $
on
$J_+^\bullet $
on
![]() $\operatorname {\mathrm {coker}} s$
. By (2-52), these can be seen to be
$\operatorname {\mathrm {coker}} s$
. By (2-52), these can be seen to be
In the setting of holonomic
![]() $\mathcal {D}$
-modules, the filtrations
$\mathcal {D}$
-modules, the filtrations
![]() $J_!^\bullet $
and
$J_!^\bullet $
and
![]() $J_+^\bullet $
define the geometric Jantzen filtrations.
$J_+^\bullet $
define the geometric Jantzen filtrations.
Definition 2.9. Let Y be a smooth variety, f a regular function on Y and
![]() $U=f^{-1}(\mathbb {A}^1 - \{0\})$
as in (2-34). For a holonomic
$U=f^{-1}(\mathbb {A}^1 - \{0\})$
as in (2-34). For a holonomic
![]() $\mathcal {D}_U$
-module
$\mathcal {D}_U$
-module
![]() $\mathcal {M}_U$
, recall that
$\mathcal {M}_U$
, recall that
![]() $j_! \mathcal {M}_U = \ker (s: \Xi _f \mathcal {M}_U \rightarrow \Xi _f \mathcal {M}_U)$
and
$j_! \mathcal {M}_U = \ker (s: \Xi _f \mathcal {M}_U \rightarrow \Xi _f \mathcal {M}_U)$
and
![]() $j_+ \mathcal {M}_U= \operatorname {\mathrm {coker}}(s: \Xi _f \mathcal {M}_U \rightarrow \Xi _f \mathcal {M}_U)$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1]. The filtrations
$j_+ \mathcal {M}_U= \operatorname {\mathrm {coker}}(s: \Xi _f \mathcal {M}_U \rightarrow \Xi _f \mathcal {M}_U)$
[Reference Beilinson, Bernstein and Gel’fandBB93, Lemma 4.2.1]. The filtrations
![]() $J_!^\bullet $
of
$J_!^\bullet $
of
![]() $j_!\mathcal {M}_U$
and
$j_!\mathcal {M}_U$
and
![]() $J_+^\bullet $
of
$J_+^\bullet $
of
![]() $j_+ \mathcal {M}_U$
are called the geometric Jantzen filtrations.
$j_+ \mathcal {M}_U$
are called the geometric Jantzen filtrations.
Now we return to our running example. The monodromy filtration
![]() $\mu ^\bullet $
on
$\mu ^\bullet $
on
![]() $\Xi _\rho \mathcal {O}_U$
is
$\Xi _\rho \mathcal {O}_U$
is
Restricting this to
![]() $\ker s = j_! \mathcal {O}_U$
, we obtain the geometric Jantzen filtration of
$\ker s = j_! \mathcal {O}_U$
, we obtain the geometric Jantzen filtration of
![]() $j_! \mathcal {O}_U$
:
$j_! \mathcal {O}_U$
:
The induced filtration on
![]() $\operatorname {\mathrm {coker}} s = j_+ \mathcal {O}_U$
gives the geometric Jantzen filtration on
$\operatorname {\mathrm {coker}} s = j_+ \mathcal {O}_U$
gives the geometric Jantzen filtration on
![]() $j_+ \mathcal {O}_U$
:
$j_+ \mathcal {O}_U$
:
Remark 2.10 (Geometric deformation direction).
There are other choices of regular functions on
![]() $\widetilde {X}$
that we could have used in the construction of these filtrations. In particular, if
$\widetilde {X}$
that we could have used in the construction of these filtrations. In particular, if
![]() $\gamma \in \mathfrak {h}^*$
is dominant and integral such that
$\gamma \in \mathfrak {h}^*$
is dominant and integral such that
![]() $\gamma (h)=n$
for
$\gamma (h)=n$
for
![]() $n \in \mathbb {Z}_{> 0}$
, then the function
$n \in \mathbb {Z}_{> 0}$
, then the function
![]() $f_{\gamma }:(x_1, x_2) \mapsto x_2^n$
can be used to define an intermediate extension functor
$f_{\gamma }:(x_1, x_2) \mapsto x_2^n$
can be used to define an intermediate extension functor
![]() $\Xi _{f_\gamma }$
and corresponding Jantzen filtrations. Beilinson and Bernstein establish that all such
$\Xi _{f_\gamma }$
and corresponding Jantzen filtrations. Beilinson and Bernstein establish that all such
![]() $f_\gamma $
lead to the same filtration. For general Lie algebras
$f_\gamma $
lead to the same filtration. For general Lie algebras
![]() $\mathfrak {g}$
, the construction can also be done for other choices of meromorphic functions on
$\mathfrak {g}$
, the construction can also be done for other choices of meromorphic functions on
![]() $\widetilde {X}$
, but it is unclear geometrically whether these result in different filtrations [Reference Beilinson, Bernstein and Gel’fandBB93, Section 4.3]. This is comparable to the dependence on deformation direction in the algebraic Jantzen filtration; see Remark 1.3.
$\widetilde {X}$
, but it is unclear geometrically whether these result in different filtrations [Reference Beilinson, Bernstein and Gel’fandBB93, Section 4.3]. This is comparable to the dependence on deformation direction in the algebraic Jantzen filtration; see Remark 1.3.
Using the computations in Section 2.4, we can examine the
![]() $\widetilde {\mathcal {U}}$
-module filtrations that we obtain on global sections. Recall that
$\widetilde {\mathcal {U}}$
-module filtrations that we obtain on global sections. Recall that
![]() $\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
decomposes into a direct sum of submodules spanned by monomials
$\Gamma (\widetilde {X}, \Xi _\rho \mathcal {O}_U)$
decomposes into a direct sum of submodules spanned by monomials
![]() $x_1^k x_2^\ell t^s$
and
$x_1^k x_2^\ell t^s$
and
![]() $x_1^k x_2^\ell s t^s$
such that
$x_1^k x_2^\ell s t^s$
such that
![]() $k + \ell $
is a fixed nonnegative integer. Figure 6 illustrates the submodule corresponding to
$k + \ell $
is a fixed nonnegative integer. Figure 6 illustrates the submodule corresponding to
![]() $k + \ell = 0$
. Looking at this figure, it is clear that
$k + \ell = 0$
. Looking at this figure, it is clear that
![]() $\ker s = \mathrm {span}\{ x_1^k x_2^\ell s t^s, t^s \}$
is isomorphic to the Verma module of highest weight
$\ker s = \mathrm {span}\{ x_1^k x_2^\ell s t^s, t^s \}$
is isomorphic to the Verma module of highest weight
![]() $0$
, and
$0$
, and
![]() $\operatorname {\mathrm {coker}} s = \mathrm {span}\{x_1^k x_2^\ell t^s\}$
is isomorphic to the corresponding dual Verma module. Moreover, the global sections of the monodromy filtration on
$\operatorname {\mathrm {coker}} s = \mathrm {span}\{x_1^k x_2^\ell t^s\}$
is isomorphic to the corresponding dual Verma module. Moreover, the global sections of the monodromy filtration on
![]() $\Xi _\rho \mathcal {O}_U$
restricted to the submodule corresponding to
$\Xi _\rho \mathcal {O}_U$
restricted to the submodule corresponding to
![]() $k + \ell = \lambda $
is the composition series of the corresponding big projective module
$k + \ell = \lambda $
is the composition series of the corresponding big projective module
![]() $P( w_0\lambda )$
when
$P( w_0\lambda )$
when
![]() $\lambda \geq 0$
. This is illustrated in Figure 7 for
$\lambda \geq 0$
. This is illustrated in Figure 7 for
![]() $\lambda = 0$
. We conclude that the filtrations on the Verma module
$\lambda = 0$
. We conclude that the filtrations on the Verma module
![]() $M(\lambda )$
and dual Verma module
$M(\lambda )$
and dual Verma module
![]() $I(\lambda )$
obtained by taking global sections of the geometric Jantzen filtrations are the composition series. Note that this is an
$I(\lambda )$
obtained by taking global sections of the geometric Jantzen filtrations are the composition series. Note that this is an
![]() $\mathfrak {sl}_2(\mathbb {C})$
phenomenon. For larger groups, this procedure yields a filtration different from the composition series.
$\mathfrak {sl}_2(\mathbb {C})$
phenomenon. For larger groups, this procedure yields a filtration different from the composition series.

Figure 7 Global sections of the monodromy filtration on
![]() $\Xi _\rho \mathcal {O}_U$
are the composition series of the big projective module.
$\Xi _\rho \mathcal {O}_U$
are the composition series of the big projective module.
2.6 Relation to the algebraic Jantzen filtration
The geometric Jantzen filtrations described above have an algebraic analogue, due to Jantzen [Reference JantzenJan79]. In this section, we recall the construction of the algebraic Jantzen filtration of a Verma module, then explain its relation with the geometric construction in Section 2.5.
2.6.1 The algebraic Jantzen filtration
We follow [Reference SoergelSoe08]. Another nice reference for Jantzen filtrations is [Reference Iohara and KogaIK11].
Let
![]() $\mathfrak {g}$
be a complex semisimple Lie algebra,
$\mathfrak {g}$
be a complex semisimple Lie algebra,
![]() $\mathfrak {b}$
a fixed Borel subalgebra,
$\mathfrak {b}$
a fixed Borel subalgebra,
![]() $\mathfrak {n} = [\mathfrak {b}, \mathfrak {b}]$
the nilpotent radical of
$\mathfrak {n} = [\mathfrak {b}, \mathfrak {b}]$
the nilpotent radical of
![]() $\mathfrak {b}$
, and
$\mathfrak {b}$
, and
![]() $\mathfrak {h}$
a Cartan subalgebra so that
$\mathfrak {h}$
a Cartan subalgebra so that
![]() $\mathfrak {b}= \mathfrak {h} \oplus \mathfrak {n}$
. Denote by
$\mathfrak {b}= \mathfrak {h} \oplus \mathfrak {n}$
. Denote by
![]() $\bar {\mathfrak {b}}$
the opposite Borel subalgebra to
$\bar {\mathfrak {b}}$
the opposite Borel subalgebra to
![]() $\mathfrak {b}$
. For
$\mathfrak {b}$
. For
![]() $\lambda \in \mathfrak {h}^*$
, denote the Verma module of highest weight
$\lambda \in \mathfrak {h}^*$
, denote the Verma module of highest weight
![]() $\lambda $
by
$\lambda $
by
Denote by
![]() $I(\lambda )$
the corresponding dual Verma module, defined to be the direct sum of weight spaces in
$I(\lambda )$
the corresponding dual Verma module, defined to be the direct sum of weight spaces in
Set
![]() $T = \mathcal {O}(\mathbb {C}\rho )$
to be the ring of regular functions on the line
$T = \mathcal {O}(\mathbb {C}\rho )$
to be the ring of regular functions on the line
![]() $\mathbb {C} \rho \subset \mathfrak {h}^*$
, where
$\mathbb {C} \rho \subset \mathfrak {h}^*$
, where
![]() $\rho $
is the half-sum of positive roots in the root system determined by
$\rho $
is the half-sum of positive roots in the root system determined by
![]() $\mathfrak {b}$
. A choice of linear functional
$\mathfrak {b}$
. A choice of linear functional
![]() $s: \mathbb {C} \rho \rightarrow \mathbb {C}$
gives an isomorphism
$s: \mathbb {C} \rho \rightarrow \mathbb {C}$
gives an isomorphism
![]() $T \simeq \mathbb {C}[s]$
. Fix such an identification. Set
$T \simeq \mathbb {C}[s]$
. Fix such an identification. Set
![]() $A:=T_{(s)}$
to be the local
$A:=T_{(s)}$
to be the local
![]() $\mathbb {C}$
-algebra obtained from T by inverting all polynomials not divisible by s, and
$\mathbb {C}$
-algebra obtained from T by inverting all polynomials not divisible by s, and
to be the composition of the restriction map
![]() $\mathcal {O}(\mathfrak {h}^*) \rightarrow T$
with the inclusion
$\mathcal {O}(\mathfrak {h}^*) \rightarrow T$
with the inclusion
![]() $T \hookrightarrow A$
. Note that under the identification
$T \hookrightarrow A$
. Note that under the identification
![]() $\mathcal {U}(\mathfrak {h}) \simeq \mathcal {O}(\mathfrak {h}^*)$
,
$\mathcal {U}(\mathfrak {h}) \simeq \mathcal {O}(\mathfrak {h}^*)$
,
![]() $\varphi (\mathfrak {h}) \subseteq (s)$
, the unique maximal ideal of A.
$\varphi (\mathfrak {h}) \subseteq (s)$
, the unique maximal ideal of A.
Let V be a
![]() $(\mathfrak {g},A)$
-bimodule on which the right and left actions of
$(\mathfrak {g},A)$
-bimodule on which the right and left actions of
![]() $\mathbb {C}$
agree. The deformed weight space
$\mathbb {C}$
agree. The deformed weight space
![]() $V^\mu $
of V corresponding to a weight
$V^\mu $
of V corresponding to a weight
![]() $\mu $
is the subspace
$\mu $
is the subspace
The direct sum of all deformed weight spaces of V is a
![]() $(\mathfrak {g},A)$
-submodule of V [Reference SoergelSoe08, Section 2.3].
$(\mathfrak {g},A)$
-submodule of V [Reference SoergelSoe08, Section 2.3].
For
![]() $\lambda \in \mathfrak {h}^*$
, the deformed Verma module corresponding to
$\lambda \in \mathfrak {h}^*$
, the deformed Verma module corresponding to
![]() $\lambda $
is the
$\lambda $
is the
![]() $(\mathfrak {g},A)$
-bimodule
$(\mathfrak {g},A)$
-bimodule
where the
![]() $\mathcal {U}(\mathfrak {b})$
-module structure on
$\mathcal {U}(\mathfrak {b})$
-module structure on
![]() $A_\lambda $
is given by extending the
$A_\lambda $
is given by extending the
![]() $\mathfrak {h}$
-action
$\mathfrak {h}$
-action
trivially to
![]() $\mathfrak {b}$
. Here,
$\mathfrak {b}$
. Here,
![]() $h \in \mathfrak {h}$
,
$h \in \mathfrak {h}$
,
![]() $a \in A$
, and
$a \in A$
, and
![]() $\varphi $
is as in (2-54). The deformed Verma module
$\varphi $
is as in (2-54). The deformed Verma module
![]() $M_A(\lambda )$
is equal to the direct sum of its deformed weight spaces.
$M_A(\lambda )$
is equal to the direct sum of its deformed weight spaces.
The deformed dual Verma module
![]() $I_A(\lambda )$
corresponding to
$I_A(\lambda )$
corresponding to
![]() $\lambda $
is the direct sum of deformed weight spaces in the
$\lambda $
is the direct sum of deformed weight spaces in the
![]() $(\mathfrak {g},A)$
-bimodule
$(\mathfrak {g},A)$
-bimodule
There is a canonical isomorphism [Reference SoergelSoe08, Proposition 2.12]
Under this isomorphism,
![]() $1 \in A$
distinguishes a canonical
$1 \in A$
distinguishes a canonical
![]() $(\mathfrak {g},A)$
-bimodule homomorphism
$(\mathfrak {g},A)$
-bimodule homomorphism
For any A-module M, there is a descending A-module filtration
![]() $M^i:=s^iM$
with associated grading
$M^i:=s^iM$
with associated grading
![]() $gr^iM = M^i/M^{i+1}$
. Hence, there is a reduction map
$gr^iM = M^i/M^{i+1}$
. Hence, there is a reduction map
For
![]() $M_A(\lambda )$
and
$M_A(\lambda )$
and
![]() $I_A(\lambda )$
, the layers of this filtration are
$I_A(\lambda )$
, the layers of this filtration are
![]() $\mathfrak {g}$
-stable, so we obtain surjective
$\mathfrak {g}$
-stable, so we obtain surjective
![]() $\mathfrak {g}$
-module homomorphisms
$\mathfrak {g}$
-module homomorphisms
Pulling back the filtration above along the canonical map
![]() $\psi _{A, \lambda }$
in (2-57) gives a
$\psi _{A, \lambda }$
in (2-57) gives a
![]() $(\mathfrak {g}, A)$
-bimodule filtration of
$(\mathfrak {g}, A)$
-bimodule filtration of
![]() $M_A(\lambda )$
.
$M_A(\lambda )$
.
Definition 2.11. The algebraic Jantzen filtration of
![]() $M_A(\lambda )$
is the
$M_A(\lambda )$
is the
![]() $(\mathfrak {g}, A)$
-bimodule filtration
$(\mathfrak {g}, A)$
-bimodule filtration
where
![]() $\psi _{A, \lambda }$
is the canonical map (2-54). By applying the reduction map in (2-58) to the filtration layers, we obtain a filtration
$\psi _{A, \lambda }$
is the canonical map (2-54). By applying the reduction map in (2-58) to the filtration layers, we obtain a filtration
![]() $M(\lambda )^\bullet $
of
$M(\lambda )^\bullet $
of
![]() $M(\lambda )$
.
$M(\lambda )$
.
2.6.2 Relationship between algebraic and geometric Jantzen filtrations
Though the constructions seem quite different at first glance, the geometric Jantzen filtration in Section 2.5 aligns with the algebraic Jantzen filtration described in Section 2.6.1 under the global sections functor. In this final section, we illustrate this relationship through our running example.
Recall the canonical map (2-35):
As illustrated in Figures 3 and 4, the global sections of
![]() $j_!f^s \mathcal {O}_U^{(n)}$
and
$j_!f^s \mathcal {O}_U^{(n)}$
and
![]() $j_+ f^s \mathcal {O}_U^{(n)}$
decompose into direct sums of deformed dual Verma and Verma modules, respectively. The global sections of
$j_+ f^s \mathcal {O}_U^{(n)}$
decompose into direct sums of deformed dual Verma and Verma modules, respectively. The global sections of
![]() $\mathrm {can}$
are the direct sum of
$\mathrm {can}$
are the direct sum of
![]() $\psi _{A,\lambda }$
in (2-57) for all integral
$\psi _{A,\lambda }$
in (2-57) for all integral
![]() $\lambda $
.
$\lambda $
.
Remark 2.12. To be more precise, the submodules of
![]() $\Gamma (\widetilde {X}, j_!f^s \mathcal {O}_U^{(n)})$
and
$\Gamma (\widetilde {X}, j_!f^s \mathcal {O}_U^{(n)})$
and
![]() $\Gamma (\widetilde {X}, j_+ f^s \mathcal {O}_U^{(n)})$
corresponding to an integer
$\Gamma (\widetilde {X}, j_+ f^s \mathcal {O}_U^{(n)})$
corresponding to an integer
![]() $\lambda $
are truncated versions of
$\lambda $
are truncated versions of
![]() $M_A(\lambda )$
in (2-56) and
$M_A(\lambda )$
in (2-56) and
![]() $I_A(\lambda )$
in (2-56) obtained by taking a quotient so that
$I_A(\lambda )$
in (2-56) obtained by taking a quotient so that
![]() $s^n = 0$
.
$s^n = 0$
.
There are two natural filtrations of
![]() $j_! \mathcal {O}_U$
that we have described using this set-up.
$j_! \mathcal {O}_U$
that we have described using this set-up.
Filtration 1: (algebraic Jantzen filtration)
We obtain a filtration of
![]() $j_! f^s \mathcal {O}_U^{(n)}$
by pulling back the ‘powers of s’ filtration along
$j_! f^s \mathcal {O}_U^{(n)}$
by pulling back the ‘powers of s’ filtration along
![]() $\mathrm {can}$
. This induces a filtration on the quotient
$\mathrm {can}$
. This induces a filtration on the quotient
This is exactly the
![]() $\mathcal {D}$
-module analogue of the algebraic Jantzen filtration described in Section 2.6.1. On global sections, it is the filtration
$\mathcal {D}$
-module analogue of the algebraic Jantzen filtration described in Section 2.6.1. On global sections, it is the filtration
Filtration 2: (geometric Jantzen filtration)
There is a unique monodromy filtration on
![]() $\Xi _\rho \mathcal {O}_U = \operatorname {\mathrm {coker}} (s \circ \mathrm {can})$
. Restricting this to the kernel of s, we obtain a filtration on
$\Xi _\rho \mathcal {O}_U = \operatorname {\mathrm {coker}} (s \circ \mathrm {can})$
. Restricting this to the kernel of s, we obtain a filtration on
This is the geometric Jantzen filtration. It can be realized explicitly in terms of the image of powers of s using (2-53). On global sections, this gives

Figure 8 Relationship between the algebraic and geometric Jantzen filtrations.
It is helpful to see these filtrations in a picture. Figure 8 illustrates the set-up when restricted to the submodule corresponding to
![]() $\lambda = 0$
.
$\lambda = 0$
.
The map
![]() $\mathrm {can}$
is described on basis elements in (2-49). Computing these actions for
$\mathrm {can}$
is described on basis elements in (2-49). Computing these actions for
![]() $\lambda = 0$
, we see in Figure 8 that
$\lambda = 0$
, we see in Figure 8 that
![]() $\mathrm {can}$
fixes the right-most column and sends any other monomial on the left to a linear combination of monomials directly above the corresponding monomial on the right. The image of
$\mathrm {can}$
fixes the right-most column and sends any other monomial on the left to a linear combination of monomials directly above the corresponding monomial on the right. The image of
![]() $s_1(n)=s \circ \mathrm {can}$
in (2-50) is highlighted in gray. The quotient by this image is the maximal extension, which is outlined in the black box. The quotient in (2-59) is highlighted in blue (darker shading) in the left hand module, and the submodule in (2-61) is highlighted in blue (darker shading) in the right-hand module.
$s_1(n)=s \circ \mathrm {can}$
in (2-50) is highlighted in gray. The quotient by this image is the maximal extension, which is outlined in the black box. The quotient in (2-59) is highlighted in blue (darker shading) in the left hand module, and the submodule in (2-61) is highlighted in blue (darker shading) in the right-hand module.
We see that there are two copies of
![]() $j_! \mathcal {O}_U$
(each highlighted in blue (darker shading) in Figure 8) in this set-up: one as a quotient of the left-hand module
$j_! \mathcal {O}_U$
(each highlighted in blue (darker shading) in Figure 8) in this set-up: one as a quotient of the left-hand module
![]() $j_! f^s \mathcal {O}_U^{(n)}$
, and one as a submodule of a quotient of the right-hand module
$j_! f^s \mathcal {O}_U^{(n)}$
, and one as a submodule of a quotient of the right-hand module
![]() $j_+ f^s \mathcal {O}_U^{(n)}$
. These two copies can be naturally identified as follows.
$j_+ f^s \mathcal {O}_U^{(n)}$
. These two copies can be naturally identified as follows.
Because the submodule
![]() $s j_! f^s \mathcal {O}_U^{(n)}$
is in the kernel of the composition of
$s j_! f^s \mathcal {O}_U^{(n)}$
is in the kernel of the composition of
![]() $\mathrm {can}$
with the quotient
$\mathrm {can}$
with the quotient
![]() $j_! f^s \mathcal {O}_U^{(n)} \rightarrow \operatorname {\mathrm {coker}}( s \circ \mathrm {can}) = \Xi _\rho \mathcal {O}_U$
, the map
$j_! f^s \mathcal {O}_U^{(n)} \rightarrow \operatorname {\mathrm {coker}}( s \circ \mathrm {can}) = \Xi _\rho \mathcal {O}_U$
, the map
![]() $\mathrm {can}$
descends to a map on the quotient:
$\mathrm {can}$
descends to a map on the quotient:
By construction, the map
![]() $\overline {\mathrm {can}}$
is injective. Its image is exactly
$\overline {\mathrm {can}}$
is injective. Its image is exactly
![]() $\ker (s: \Xi _\rho \mathcal {O}_U \rightarrow \Xi _\rho \mathcal {O}_U)$
. This is immediately apparent in Figure 8. Hence,
$\ker (s: \Xi _\rho \mathcal {O}_U \rightarrow \Xi _\rho \mathcal {O}_U)$
. This is immediately apparent in Figure 8. Hence,
![]() $\overline {\mathrm {can}}$
provides an explicit isomorphism that can be used to identify the two copies of
$\overline {\mathrm {can}}$
provides an explicit isomorphism that can be used to identify the two copies of
![]() $j_! \mathcal {O}_U$
. Under this identification, the algebraic Jantzen filtration in (2-60) and the geometric Jantzen filtration in (2-62) clearly align.
$j_! \mathcal {O}_U$
. Under this identification, the algebraic Jantzen filtration in (2-60) and the geometric Jantzen filtration in (2-62) clearly align.
Acknowledgements
This paper arose from computations in the first author’s honors thesis at the University of New South Wales. We would like to thank the referee for helpful suggestions, which greatly improved the readability of the paper. The first author would like to thank Daniel Chan, who influenced his interests in this topic, and broadened his understanding of the various geometric techniques used in this paper. The second author would like to thank Jens Eberhardt, Adam Brown, and Geordie Williamson for many hours of conversations about Jantzen filtrations, which contributed significantly to her understanding.