Article contents
Energy flux and high-order statistics of hydrodynamic turbulence
Published online by Cambridge University Press: 15 November 2023
Abstract
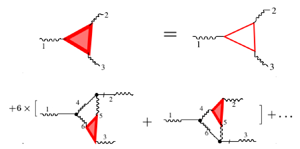
We use the Dyson–Wyld diagrammatic technique to analyse the infinite series for the correlation functions of the velocity in hydrodynamic turbulence. We demonstrate the fundamental role played by the triple correlator of the velocity in determining the entire statistics of the hydrodynamic turbulence. All higher-order correlation functions are expressed through the triple correlator. This is shown through the suggested triangular re-summation of the infinite diagrammatic series for multi-point correlation functions. The triangular re-summation is the next logical step after the Dyson–Wyld line re-summation for the Green's function and the double correlator. In particular, it allows us to explain why the inverse cascade of the two-dimensional hydrodynamic turbulence is close to Gaussian. Since the triple correlator dictates the flux of energy  $\varepsilon$ through the scales, we support the Kolmogorov-1941 idea that
$\varepsilon$ through the scales, we support the Kolmogorov-1941 idea that  $\varepsilon$ is one of the main characteristics of hydrodynamic turbulence.
$\varepsilon$ is one of the main characteristics of hydrodynamic turbulence.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by



