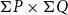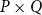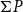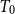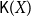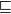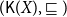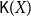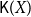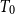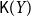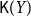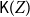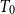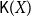Soft sets were introduced as a means to study objects that are not defined in an absolute way and have found applications in numerous areas of mathematics, decision theory, and in statistical applications. Soft topological spaces were first considered in Shabir and Naz ((2011). Computers & Mathematics with Applications 61 (7) 1786–1799) and soft separation axioms for soft topological spaces were studied in El-Shafei et al. ((2018). Filomat 32 (13) 4755–4771), El-Shafei and Al-Shami ((2020). Computational and Applied Mathematics 39 (3) 1–17), Al-shami ((2021). Mathematical Problems in Engineering 2021). In this paper, we introduce the effective versions of soft separation axioms. Specifically, we focus our attention on computable u-soft and computable p-soft separation axioms and investigate various relations between them. We also compare the effective and classical versions of these soft separation axioms.

The study of the sobriety of Scott spaces has got a relatively long history in domain theory. Lawson and Hoffmann independently proved that the Scott space of every continuous directed complete poset (usually called domain) is sober. Johnstone constructed the first directed complete poset whose Scott space is non-sober. Soon after, Isbell gave a complete lattice with a non-sober Scott space. Based on Isbell’s example, Xu, Xi, and Zhao showed that there is even a complete Heyting algebra whose Scott space is non-sober. Achim Jung then asked whether every countable complete lattice has a sober Scott space. The main aim of this paper is to answer Jung’s problem by constructing a countable complete lattice whose Scott space is non-sober. This lattice is then modified to obtain a countable distributive complete lattice with a non-sober Scott space. In addition, we prove that the topology of the product space $\Sigma P\times \Sigma Q$ coincides with the Scott topology of the product poset $P\times Q$ if the set Id(P) and Id(Q) of all incremental ideals of posets P and Q are both countable. Based on this, it is deduced that a directed complete poset P has a sober Scott space, if Id(P) is countable and $\Sigma P$ is coherent and well filtered. In particular, every complete lattice L with Id(L) countable has a sober Scott space.

For a 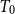$T_0$ space X, let 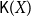$\mathsf{K}(X)$ be the poset of all nonempty compact saturated subsets of X endowed with the Smyth order 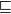$\sqsubseteq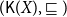$. $(\mathsf{K}(X), \sqsubseteq)$ (shortly 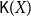$\mathsf{K}(X)$) is called the Smyth power poset of X. In this paper, we mainly discuss some basic properties of the Scott topology on Smyth power posets. It is proved that for a well-filtered space X, its Smyth power poset 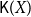$\mathsf{K}(X)$ with the Scott topology is still well-filtered, and a 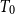$T_0$ space Y is well-filtered iff the Smyth power poset 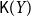$\mathsf{K}(Y)$ with the Scott topology is well-filtered and the upper Vietoris topology is coarser than the Scott topology on 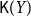$\mathsf{K}(Y)$. A sober space Z is constructed for which the Smyth power poset 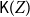$\mathsf{K}(Z)$ with the Scott topology is not sober. A few sufficient conditions are given for a 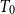$T_0$ space X under which its Smyth power poset 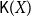$\mathsf{K}(X)$ with the Scott topology is sober. Some other properties, such as local compactness, first-countability, Rudin property and well-filtered determinedness, of Smyth power spaces, and the Scott topology on Smyth power posets, are also investigated.