Article contents
Scott topology on Smyth power posets
Published online by Cambridge University Press: 27 July 2023
Abstract
For a 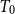 $T_0$ space X, let
$T_0$ space X, let 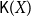 $\mathsf{K}(X)$ be the poset of all nonempty compact saturated subsets of X endowed with the Smyth order
$\mathsf{K}(X)$ be the poset of all nonempty compact saturated subsets of X endowed with the Smyth order 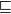 $\sqsubseteq$.
$\sqsubseteq$. 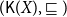 $(\mathsf{K}(X), \sqsubseteq)$ (shortly
$(\mathsf{K}(X), \sqsubseteq)$ (shortly 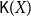 $\mathsf{K}(X)$) is called the Smyth power poset of X. In this paper, we mainly discuss some basic properties of the Scott topology on Smyth power posets. It is proved that for a well-filtered space X, its Smyth power poset
$\mathsf{K}(X)$) is called the Smyth power poset of X. In this paper, we mainly discuss some basic properties of the Scott topology on Smyth power posets. It is proved that for a well-filtered space X, its Smyth power poset 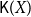 $\mathsf{K}(X)$ with the Scott topology is still well-filtered, and a
$\mathsf{K}(X)$ with the Scott topology is still well-filtered, and a 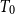 $T_0$ space Y is well-filtered iff the Smyth power poset
$T_0$ space Y is well-filtered iff the Smyth power poset 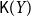 $\mathsf{K}(Y)$ with the Scott topology is well-filtered and the upper Vietoris topology is coarser than the Scott topology on
$\mathsf{K}(Y)$ with the Scott topology is well-filtered and the upper Vietoris topology is coarser than the Scott topology on 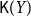 $\mathsf{K}(Y)$. A sober space Z is constructed for which the Smyth power poset
$\mathsf{K}(Y)$. A sober space Z is constructed for which the Smyth power poset 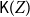 $\mathsf{K}(Z)$ with the Scott topology is not sober. A few sufficient conditions are given for a
$\mathsf{K}(Z)$ with the Scott topology is not sober. A few sufficient conditions are given for a 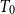 $T_0$ space X under which its Smyth power poset
$T_0$ space X under which its Smyth power poset 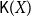 $\mathsf{K}(X)$ with the Scott topology is sober. Some other properties, such as local compactness, first-countability, Rudin property and well-filtered determinedness, of Smyth power spaces, and the Scott topology on Smyth power posets, are also investigated.
$\mathsf{K}(X)$ with the Scott topology is sober. Some other properties, such as local compactness, first-countability, Rudin property and well-filtered determinedness, of Smyth power spaces, and the Scott topology on Smyth power posets, are also investigated.
Keywords
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
This research was supported by the National Natural Science Foundation of China (Nos. 12071199, 12071188, 11661057).
Dedicated to Professor Dana Scott on the occasion of his 90th birthday
References
- 2
- Cited by



