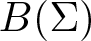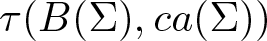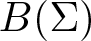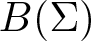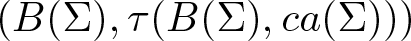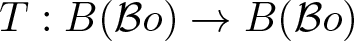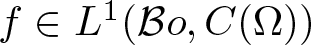1. Introduction and preliminaries
Let Σ be a σ-algebra of subsets of a set Ω and ![]() $B(\Sigma)$ be the Banach space of all bounded Σ-measurable scalar functions on Ω, equipped with the uniform norm
$B(\Sigma)$ be the Banach space of all bounded Σ-measurable scalar functions on Ω, equipped with the uniform norm ![]() $\|\cdot\|_\infty$. We assume that the field of scalars is either the set of real numbers or the set of complex numbers.
$\|\cdot\|_\infty$. We assume that the field of scalars is either the set of real numbers or the set of complex numbers.
Let ![]() $ba(\Sigma)$ denote the Banach space of all bounded additive scalar-valued measures λ on Σ, equipped the total variation norm
$ba(\Sigma)$ denote the Banach space of all bounded additive scalar-valued measures λ on Σ, equipped the total variation norm ![]() $\|\lambda\|:=|\lambda|(\Omega).$ The Banach dual
$\|\lambda\|:=|\lambda|(\Omega).$ The Banach dual ![]() $B(\Sigma)'$ of
$B(\Sigma)'$ of ![]() $B(\Sigma)$ can be identified with
$B(\Sigma)$ can be identified with ![]() $ba(\Sigma)$ throughout the mapping
$ba(\Sigma)$ throughout the mapping
where  $\Phi_\lambda(u):=\int_\Omega u(\omega)\,d\lambda$ for
$\Phi_\lambda(u):=\int_\Omega u(\omega)\,d\lambda$ for ![]() $u\in B(\Sigma)$ and
$u\in B(\Sigma)$ and ![]() $\|\Phi_\lambda\|=\|\lambda\|$. Let
$\|\Phi_\lambda\|=\|\lambda\|$. Let ![]() $ca(\Sigma)$ denote the closed subspace of
$ca(\Sigma)$ denote the closed subspace of ![]() $\,ba(\Sigma)$ consisting of all countably additive members of
$\,ba(\Sigma)$ consisting of all countably additive members of ![]() $ba(\Sigma)$.
$ba(\Sigma)$.
From now on we assume that ![]() $(E,\|\cdot\|_E)$ is a Banach space and
$(E,\|\cdot\|_E)$ is a Banach space and ![]() $(E',\|\cdot\|_{E'})$ denotes its dual. Assume that
$(E',\|\cdot\|_{E'})$ denotes its dual. Assume that ![]() $m:\Sigma\rightarrow E$ is a finitely additive measure. By
$m:\Sigma\rightarrow E$ is a finitely additive measure. By ![]() $|m|(A)$ (resp.
$|m|(A)$ (resp. ![]() $\|m\|(A)$) we denote the variation (resp. semivariation) of m on A (see [Reference Diestel and Uhl7, Definition 4, p. 2]). Then
$\|m\|(A)$) we denote the variation (resp. semivariation) of m on A (see [Reference Diestel and Uhl7, Definition 4, p. 2]). Then ![]() $\|m\|(A)\leq|m|(A)$ for
$\|m\|(A)\leq|m|(A)$ for ![]() $A\in\Sigma$.
$A\in\Sigma$.
If ![]() $T:B(\Sigma)\rightarrow E$ is a bounded linear operator, let
$T:B(\Sigma)\rightarrow E$ is a bounded linear operator, let
Then,  $T(u)=\int_\Omega u(\omega)dm_T$ and
$T(u)=\int_\Omega u(\omega)dm_T$ and ![]() $\|T\|=\|m_T\|(\Omega)$ (see [Reference Diestel and Uhl7, Theorem 13, p. 6]).
$\|T\|=\|m_T\|(\Omega)$ (see [Reference Diestel and Uhl7, Theorem 13, p. 6]).
Different classes of linear operators ![]() $T:B(\Sigma)\rightarrow E$ (weakly compact, absolutely summing, nuclear, integral, σ-smooth) have been studied in numerous papers (see [Reference Diestel5], [Reference Diestel6], [Reference Diestel and Uhl7], [Reference Graves and Ruess11], [Reference Nowak18], [Reference Nowak17]).
$T:B(\Sigma)\rightarrow E$ (weakly compact, absolutely summing, nuclear, integral, σ-smooth) have been studied in numerous papers (see [Reference Diestel5], [Reference Diestel6], [Reference Diestel and Uhl7], [Reference Graves and Ruess11], [Reference Nowak18], [Reference Nowak17]).
For ![]() $\mu\in ca(\Sigma)^+$, let
$\mu\in ca(\Sigma)^+$, let ![]() $L^1(\mu,E)$ denote the Banach space of µ-equivalence classes of all E-valued Bochner µ-integrable functions f on Ω, equipped with norm
$L^1(\mu,E)$ denote the Banach space of µ-equivalence classes of all E-valued Bochner µ-integrable functions f on Ω, equipped with norm  $\|f\|_1:=\int_\Omega\|f(\omega)\|_E \,d\mu$.
$\|f\|_1:=\int_\Omega\|f(\omega)\|_E \,d\mu$.
Following [Reference Tong26] we can consider a class of linear operators on ![]() $B(\Sigma)$.
$B(\Sigma)$.
Definition 1.1. We say that a linear operator ![]() $T:B(\Sigma)\rightarrow E$ is Bochner representable if there exist a measure
$T:B(\Sigma)\rightarrow E$ is Bochner representable if there exist a measure ![]() $\mu\in ca(\Sigma)^+$ and a function
$\mu\in ca(\Sigma)^+$ and a function ![]() $f\in L^1(\mu,E)$ so that
$f\in L^1(\mu,E)$ so that
 \begin{equation*}
T(u)=\int_\Omega u(\omega)\,f(\omega)\,d\mu,\quad\mbox{for all } \ u\in B(\Sigma).
\end{equation*}
\begin{equation*}
T(u)=\int_\Omega u(\omega)\,f(\omega)\,d\mu,\quad\mbox{for all } \ u\in B(\Sigma).
\end{equation*}The concept of nuclear operators between Banach spaces in due to Grothendieck [Reference Grothendieck12], [Reference Grothendieck13] (see also [Reference Yosida28, p. 279], [Reference Pietsch21, Chap. 3], [Reference Pietsch22], [Reference Diestel and Uhl7, Chap. 6], [Reference Drewnowski9, Chap. 5], [Reference Sofi25], [Reference Ryan23]).
Recall (see [Reference Yosida28, p. 279], [Reference Sofi25]) that a linear operator ![]() $T:B(\Sigma)\rightarrow E$ between Banach spaces
$T:B(\Sigma)\rightarrow E$ between Banach spaces ![]() $B(\Sigma)$ and E is said to be nuclear if there exist a bounded sequence
$B(\Sigma)$ and E is said to be nuclear if there exist a bounded sequence ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ba(\Sigma)$, a bounded sequence
$ba(\Sigma)$, a bounded sequence ![]() $(e_n)$ in E and a sequence
$(e_n)$ in E and a sequence ![]() $(\alpha_n)\in\ell^1$ so that
$(\alpha_n)\in\ell^1$ so that
 \begin{equation}
T(u)=\sum^\infty_{n=1}\alpha_n \Phi_{\lambda_n}(u)\,e_n,\quad\mbox{for all} \ u\in B(\Sigma).
\end{equation}
\begin{equation}
T(u)=\sum^\infty_{n=1}\alpha_n \Phi_{\lambda_n}(u)\,e_n,\quad\mbox{for all} \ u\in B(\Sigma).
\end{equation}Then the nuclear norm of T is defined by
 \begin{equation*}
\|T\|_{nuc}:=\inf\left\{\sum^\infty_{n=1} |\alpha_n|\,|\lambda_n|\,(\Omega)\,
\|e_n\|_E\right\},
\end{equation*}
\begin{equation*}
\|T\|_{nuc}:=\inf\left\{\sum^\infty_{n=1} |\alpha_n|\,|\lambda_n|\,(\Omega)\,
\|e_n\|_E\right\},
\end{equation*} where the infimum is taken over all sequences ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ba(\Sigma)$ and
$ba(\Sigma)$ and ![]() $(e_n)$ in E and
$(e_n)$ in E and ![]() $(\alpha_n)\in\ell^1$ such that T admits a representation (1.1).
$(\alpha_n)\in\ell^1$ such that T admits a representation (1.1).
Let ![]() ${\cal L}(B(\Sigma),E)$ denote the Banach space of all bounded linear operators from
${\cal L}(B(\Sigma),E)$ denote the Banach space of all bounded linear operators from ![]() $B(\Sigma)$ to E, equipped with the operator norm. Then in view of (1.1), we have
$B(\Sigma)$ to E, equipped with the operator norm. Then in view of (1.1), we have
 \begin{equation*}
T=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}\otimes\,e_n \ \ \mbox{in} \ \
{\cal L}(B(\Sigma),E),
\end{equation*}
\begin{equation*}
T=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}\otimes\,e_n \ \ \mbox{in} \ \
{\cal L}(B(\Sigma),E),
\end{equation*} where ![]() $(\alpha_n\Phi_{\lambda_n}\otimes\,e_n)(u)=\alpha_n\Phi_{\lambda_n}(u)\,e_n$ for
$(\alpha_n\Phi_{\lambda_n}\otimes\,e_n)(u)=\alpha_n\Phi_{\lambda_n}(u)\,e_n$ for ![]() $u\in B(\Sigma)$.
$u\in B(\Sigma)$.
It is known that the space ![]() ${\cal N}(B(\Sigma),E)$ of all nuclear operators between
${\cal N}(B(\Sigma),E)$ of all nuclear operators between ![]() $B(\Sigma)$ and E (equipped with the nuclear norm
$B(\Sigma)$ and E (equipped with the nuclear norm ![]() $\|\cdot\|_{nuc}$) is a Banach space (see [Reference Pietsch21, 3.1, Proposition, p. 51]).
$\|\cdot\|_{nuc}$) is a Banach space (see [Reference Pietsch21, 3.1, Proposition, p. 51]).
Due to Diestel [Reference Diestel5, Theorem 9] a bounded linear operator ![]() $T:B(\Sigma)\rightarrow E$ is nuclear if and only if mT has an approximate Radon-Nikodym derivative with respect to its variation.
$T:B(\Sigma)\rightarrow E$ is nuclear if and only if mT has an approximate Radon-Nikodym derivative with respect to its variation.
According to [Reference Nowak18, Definition 2.1] we have
Definition 1.2. A linear operator ![]() $T:B(\Sigma)\rightarrow E$ is said to be σ-smooth if
$T:B(\Sigma)\rightarrow E$ is said to be σ-smooth if ![]() $\|T(u_n)\|_E\rightarrow 0$ whenever
$\|T(u_n)\|_E\rightarrow 0$ whenever ![]() $(u_n)$ is a uniformly bounded sequence in
$(u_n)$ is a uniformly bounded sequence in ![]() $B(\Sigma)$ such that
$B(\Sigma)$ such that ![]() $u_n(\omega)\rightarrow 0$ for each
$u_n(\omega)\rightarrow 0$ for each ![]() $\omega\in\Omega$.
$\omega\in\Omega$.
By ![]() $\tau(B(\Sigma),ca(\Sigma))$ we denote the natural Mackey topology on
$\tau(B(\Sigma),ca(\Sigma))$ we denote the natural Mackey topology on ![]() $B(\Sigma)$. Note that
$B(\Sigma)$. Note that ![]() $(B(\Sigma),\tau(B(\Sigma),$
$(B(\Sigma),\tau(B(\Sigma),$ ![]() $ca(\Sigma)))$ is a generalized DF-space, that is,
$ca(\Sigma)))$ is a generalized DF-space, that is, ![]() $\tau(B(\Sigma),ca(\Sigma))$ is the finest locally convex topology agreeing with itself on norm-bounded sets in
$\tau(B(\Sigma),ca(\Sigma))$ is the finest locally convex topology agreeing with itself on norm-bounded sets in ![]() $B(\Sigma)$ (see [Reference Khurana16], [Reference Nowak18], [Reference Nowak17], [Reference Graves and Ruess11]).
$B(\Sigma)$ (see [Reference Khurana16], [Reference Nowak18], [Reference Nowak17], [Reference Graves and Ruess11]).
The following characterization of σ-smooth operators ![]() $T:B(\Sigma)\rightarrow E$ will be useful (see [Reference Nowak18, Proposition 2.2], [Reference Nowak17, Proposition 3.1]).
$T:B(\Sigma)\rightarrow E$ will be useful (see [Reference Nowak18, Proposition 2.2], [Reference Nowak17, Proposition 3.1]).
Proposition 1.1. For a bounded linear operator ![]() $T:B(\Sigma)\rightarrow E$, the following statements are equivalent:
$T:B(\Sigma)\rightarrow E$, the following statements are equivalent:
(i) T is σ-smooth.
(ii) T is
 $(\tau(B(\Sigma),ca(\Sigma)),\|\cdot\|_E)$-continuous.
$(\tau(B(\Sigma),ca(\Sigma)),\|\cdot\|_E)$-continuous.(iii)
 $m_T:\Sigma\rightarrow E$ is a countably additive measure.
$m_T:\Sigma\rightarrow E$ is a countably additive measure.
In this paper, we show that a linear operator ![]() $T:B(\Sigma)\rightarrow E$ is Bochner representable if and only if T is a nuclear σ-smooth operator and if and only if T is a nuclear operator between the locally convex space
$T:B(\Sigma)\rightarrow E$ is Bochner representable if and only if T is a nuclear σ-smooth operator and if and only if T is a nuclear operator between the locally convex space ![]() $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E (see Corollary 2.5 below). We derive a formula for the trace of a Bochner representable operator
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E (see Corollary 2.5 below). We derive a formula for the trace of a Bochner representable operator ![]() $T:B({\cal B} o)\rightarrow B({\cal B} o)$ generated by a function
$T:B({\cal B} o)\rightarrow B({\cal B} o)$ generated by a function ![]() $f\in L^1({\cal B} o, C(\Omega))$, where Ω is a compact Hausdorff space (see Corollary 3.1 below).
$f\in L^1({\cal B} o, C(\Omega))$, where Ω is a compact Hausdorff space (see Corollary 3.1 below).
2. Nuclearity of Bochner representable operators on  $B(\Sigma)$
$B(\Sigma)$
We will need the following result (see [Reference Khurana16, Theorem 3], [Reference Nowak20, Proposition 13 and Corollary 14]).
Proposition 2.1. For a subset ![]() ${\cal M}$ of
${\cal M}$ of ![]() $ca(\Sigma)$, the following statements are equivalent:
$ca(\Sigma)$, the following statements are equivalent:
(i) The family
 $\{\Phi_\lambda:\lambda\in{\cal M}\}$ is
$\{\Phi_\lambda:\lambda\in{\cal M}\}$ is  $\tau(B(\Sigma),ca(\Sigma))$-equicontinuous.
$\tau(B(\Sigma),ca(\Sigma))$-equicontinuous.(ii)
 $\sup_{\lambda\in{\cal M}}\|\lambda\| \lt \infty$ and
$\sup_{\lambda\in{\cal M}}\|\lambda\| \lt \infty$ and  ${\cal M}$ is uniformly countably additive.
${\cal M}$ is uniformly countably additive.
Grothendieck carried over the concept of nuclear operators to locally convex spaces [Reference Grothendieck12], [Reference Grothendieck13] (see also [Reference Yosida28, p. 289–293], [Reference Jarchow15, pp. 376–378], [Reference Schaefer24, Chap. 3, § 7], [Reference Trèves27, § 47]). Following [Reference Schaefer24, Chap. 3, § 7], [Reference Trèves27, § 47] and using Proposition 2.1 we have the following definition.
Definition 2.1. A linear operator ![]() $T:B(\Sigma)\rightarrow E$ between the locally convex space
$T:B(\Sigma)\rightarrow E$ between the locally convex space ![]() $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and a Banach space E is said to be nuclear if there exist a bounded and uniformly countably additive sequence
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and a Banach space E is said to be nuclear if there exist a bounded and uniformly countably additive sequence ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ca(\Sigma)$, a bounded sequence
$ca(\Sigma)$, a bounded sequence ![]() $(e_n)$ in E and a sequence
$(e_n)$ in E and a sequence ![]() $(\alpha_n)\in\ell^1$ such that
$(\alpha_n)\in\ell^1$ such that
 \begin{equation}
T(u)=\sum^\infty_{n=1}\alpha_n\left(\int_\Omega u(\omega)\, d\lambda_n\right)e_n \ \
\rm{for\, all}\ \ u\in B(\Sigma).
\end{equation}
\begin{equation}
T(u)=\sum^\infty_{n=1}\alpha_n\left(\int_\Omega u(\omega)\, d\lambda_n\right)e_n \ \
\rm{for\, all}\ \ u\in B(\Sigma).
\end{equation} Then ![]() $T:B(\Sigma)\rightarrow E$ is
$T:B(\Sigma)\rightarrow E$ is ![]() $(\tau(B(\Sigma),ca(\Sigma)),\|\cdot\|_E)$-compact, that is, T(V) is relatively norm compact in E for some
$(\tau(B(\Sigma),ca(\Sigma)),\|\cdot\|_E)$-compact, that is, T(V) is relatively norm compact in E for some ![]() $\tau(B(\Sigma),ca(\Sigma))$-neighbourhood V of 0 in
$\tau(B(\Sigma),ca(\Sigma))$-neighbourhood V of 0 in ![]() $B(\Sigma)$ (see [Reference Schaefer24, Chap. 3, § 7, Corollary 1], [Reference Trèves27, Theorem 47.3]). Hence T is
$B(\Sigma)$ (see [Reference Schaefer24, Chap. 3, § 7, Corollary 1], [Reference Trèves27, Theorem 47.3]). Hence T is ![]() $(\tau(B(\Sigma),ca(\Sigma)),$
$(\tau(B(\Sigma),ca(\Sigma)),$ ![]() $\|\cdot\|_E)$-continuous.
$\|\cdot\|_E)$-continuous.
Let us put
 \begin{equation*}
\|T\|_{\tau-nuc}:=\inf\left\{\sum^\infty_{n=1}
|\alpha_n|\,|\lambda_n|\,(\Omega)\,\|e_n\|_E\right\},
\end{equation*}
\begin{equation*}
\|T\|_{\tau-nuc}:=\inf\left\{\sum^\infty_{n=1}
|\alpha_n|\,|\lambda_n|\,(\Omega)\,\|e_n\|_E\right\},
\end{equation*} where the infimum is taken over all sequences ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ca(\Sigma)$ and
$ca(\Sigma)$ and ![]() $(e_n)$ in E and
$(e_n)$ in E and ![]() $(\alpha_n)\in\ell^1$ such that T admits a representation (2.1).
$(\alpha_n)\in\ell^1$ such that T admits a representation (2.1).
According to [Reference Nowak19, Theorem 2.1] and Proposition 1.1 we have the following characterization of nuclear σ-smooth operators ![]() $T:B(\Sigma)\rightarrow E$.
$T:B(\Sigma)\rightarrow E$.
Theorem 2.2. Assume that ![]() $T:B(\Sigma)\rightarrow E$ is a σ-smooth operator. Then the following statements are equivalent:
$T:B(\Sigma)\rightarrow E$ is a σ-smooth operator. Then the following statements are equivalent:
(i) T is a nuclear operator between the Banach spaces
 $B(\Sigma)$ and E.
$B(\Sigma)$ and E.(ii)
 $|m_T|(\Omega) \lt \infty$ and mT has a
$|m_T|(\Omega) \lt \infty$ and mT has a  $|m_T|$-Bochner integrable derivative, that is, there exists a function
$|m_T|$-Bochner integrable derivative, that is, there exists a function  $f\in L^1(|m_T|,E)$ so that
$f\in L^1(|m_T|,E)$ so that  $m_T(A)=\int_Af(\omega)\,d|m_T|$ for all
$m_T(A)=\int_Af(\omega)\,d|m_T|$ for all  $A\in\Sigma$.
$A\in\Sigma$.(iii)
 $|m_T|(\Omega) \lt \infty$ and T is a
$|m_T|(\Omega) \lt \infty$ and T is a  $|m_T|$-Bochner integrable kernel, that is, there exists a function
$|m_T|$-Bochner integrable kernel, that is, there exists a function  $f\in L^1(|m_T|,E)$ so that
$f\in L^1(|m_T|,E)$ so that  $T(u)=\int_{\Omega}u(\omega)f(\omega)\,d|m_T|$ for all
$T(u)=\int_{\Omega}u(\omega)f(\omega)\,d|m_T|$ for all  $u\in B(\Sigma)$.
$u\in B(\Sigma)$.(iv) T is a nuclear operator between the locally convex space
 $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
In this case, ![]() $\|T\|_{nuc}=\|T\|_{\tau-nuc}=|m_T|(\Omega)$.
$\|T\|_{nuc}=\|T\|_{\tau-nuc}=|m_T|(\Omega)$.
Making us of [Reference Dinculeanu8, Sect.2, F, Theorem 30, p. 26] we have the following result.
Lemma 2.3. For ![]() $\mu\in ca(\Sigma)^+$ and
$\mu\in ca(\Sigma)^+$ and ![]() $f\in L^1(\mu,E)$, let us put
$f\in L^1(\mu,E)$, let us put
 \begin{equation*}
\lambda(A):=\int_A\|f(\omega)\|_E\,d\mu,\quad\mbox{for all}\ \ A\in\Sigma,
\end{equation*}
\begin{equation*}
\lambda(A):=\int_A\|f(\omega)\|_E\,d\mu,\quad\mbox{for all}\ \ A\in\Sigma,
\end{equation*}and
Then ![]() $h_f\in L^1(\lambda, E)$ and
$h_f\in L^1(\lambda, E)$ and
 \begin{equation*}
\int_{\Omega}u(\omega)h_f(\omega)\,d\lambda=\int_{\Omega}u(\omega)f(\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*}
\begin{equation*}
\int_{\Omega}u(\omega)h_f(\omega)\,d\lambda=\int_{\Omega}u(\omega)f(\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*} In particular,  $\int_Ah_f(\omega)\,d\lambda=\int_Af(\omega)\,d\mu$ for all
$\int_Ah_f(\omega)\,d\lambda=\int_Af(\omega)\,d\mu$ for all ![]() $A\in\Sigma$.
$A\in\Sigma$.
Theorem 2.4. Assume that ![]() $T:B(\Sigma)\rightarrow E$ is a Bochner representable operator. Then T is a nuclear operator between the locally convex space
$T:B(\Sigma)\rightarrow E$ is a Bochner representable operator. Then T is a nuclear operator between the locally convex space ![]() $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
Proof. There exists a measure ![]() $\mu\in ca(\Sigma)^+$ and a function
$\mu\in ca(\Sigma)^+$ and a function ![]() $f\in L^1(\mu,E)$ so that
$f\in L^1(\mu,E)$ so that
 \begin{equation*}
T(u)=\int_\Omega u(\omega)f(\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*}
\begin{equation*}
T(u)=\int_\Omega u(\omega)f(\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*}Hence
 \begin{equation*}
m_T(A)=\int_A f(\omega)\,d\mu\ \ \mbox{and}\ \ |m_T|(A)=\int_A\|f(\omega)\|_E\,d\mu,\quad \mbox{for all}\ \ A\in\Sigma,
\end{equation*}
\begin{equation*}
m_T(A)=\int_A f(\omega)\,d\mu\ \ \mbox{and}\ \ |m_T|(A)=\int_A\|f(\omega)\|_E\,d\mu,\quad \mbox{for all}\ \ A\in\Sigma,
\end{equation*}where mT is a countably additive measure (see [Reference Diestel and Uhl7, Theorem 4, p. 46]), and in view of Proposition 1.1 T is σ-smooth. Hence using Lemma 2.3 we get
 \begin{equation*}
m_T(A)=\int_Af(\omega)\,d\mu=\int_Ah_f(\omega)\,d|m_T|,\quad \mbox{for all}\ \ A\in\Sigma,
\end{equation*}
\begin{equation*}
m_T(A)=\int_Af(\omega)\,d\mu=\int_Ah_f(\omega)\,d|m_T|,\quad \mbox{for all}\ \ A\in\Sigma,
\end{equation*} where ![]() $h_f\in L^1(|m_T|,E)$. By Theorem 2.2 we derive that T is a nuclear operator between the locally convex space
$h_f\in L^1(|m_T|,E)$. By Theorem 2.2 we derive that T is a nuclear operator between the locally convex space ![]() $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
In view of Theorem 2.4 and Theorem 2.2 we can obtain the following characterization of Bochner representable operators ![]() $T:B(\Sigma)\rightarrow E$.
$T:B(\Sigma)\rightarrow E$.
Theorem 2.5. For a linear operator ![]() $T:B(\Sigma)\rightarrow E$, the following statements are equivalent:
$T:B(\Sigma)\rightarrow E$, the following statements are equivalent:
(i) T is a Bochner representable operator.
(ii) T is a nuclear operator between the locally convex space
 $(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.
$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E.(iii) T is a σ-smooth nuclear operator between the Banach spaces
 $B(\Sigma)$ and E.
$B(\Sigma)$ and E.
As a consequence of Theorem 2.4 and Theorem 2.2, we get
Corollary 2.6. Assume that ![]() $T:B(\Sigma)\rightarrow E$ is a Bochner representable operator. Then the mapping
$T:B(\Sigma)\rightarrow E$ is a Bochner representable operator. Then the mapping
is a nuclear operator and ![]() $\|T^*\|_{nuc}=\|T\|_{nuc}=|m_T|(\Omega)$.
$\|T^*\|_{nuc}=\|T\|_{nuc}=|m_T|(\Omega)$.
Proof. Let ɛ > 0 be given. In view of Theorem 2.4 and Theorem 2.2 there exist a bounded and uniformly countably additive sequence ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ca(\Sigma)$, a bounded sequence
$ca(\Sigma)$, a bounded sequence ![]() $(e_n)$ in E and
$(e_n)$ in E and ![]() $(\alpha_n)\in\ell^1$ so that
$(\alpha_n)\in\ell^1$ so that
 \begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n \Phi_{\lambda_n}(u)\,e_n,\quad \mbox{for all} \ \ u\in B(\Sigma)
\end{equation*}
\begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n \Phi_{\lambda_n}(u)\,e_n,\quad \mbox{for all} \ \ u\in B(\Sigma)
\end{equation*}and
 \begin{equation}
\sum^\infty_{n=1}|\alpha_n|\;|\lambda_n|(\Omega)\;\|e_n\|_E\leq |m_T|(\Omega)+\varepsilon.
\end{equation}
\begin{equation}
\sum^\infty_{n=1}|\alpha_n|\;|\lambda_n|(\Omega)\;\|e_n\|_E\leq |m_T|(\Omega)+\varepsilon.
\end{equation} One can show that for each ![]() $e'\in E'$, we have
$e'\in E'$, we have
 \begin{equation*}
e'\circ T=\sum^\infty_{n=1}\alpha_n\,e'(e_n)\Phi_{\lambda_n} \ \ \mbox{in}\ \ B(\Sigma)'.
\end{equation*}
\begin{equation*}
e'\circ T=\sum^\infty_{n=1}\alpha_n\,e'(e_n)\Phi_{\lambda_n} \ \ \mbox{in}\ \ B(\Sigma)'.
\end{equation*} Moreover, for each ![]() $e'\in E'$, we have
$e'\in E'$, we have ![]() $e'\circ m_T\in ca(\Sigma)$ and
$e'\circ m_T\in ca(\Sigma)$ and
 \begin{equation*}
(e'\circ T)(u)=\int_\Omega u(\omega)\,d(e'\circ m_T) ,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*}
\begin{equation*}
(e'\circ T)(u)=\int_\Omega u(\omega)\,d(e'\circ m_T) ,\quad \mbox{for all}\ \ u\in B(\Sigma).
\end{equation*} Let ![]() $i:E\rightarrow E^{\prime\prime}$ stand for the canonical isometry, that is,
$i:E\rightarrow E^{\prime\prime}$ stand for the canonical isometry, that is, ![]() $i(e)(e')=e'(e)$ for
$i(e)(e')=e'(e)$ for ![]() $e\in E$,
$e\in E$, ![]() $e'\in E'$ and
$e'\in E'$ and ![]() $\|i(e)\|_{E^{\prime\prime}}=\|e\|_E$. Hence for each
$\|i(e)\|_{E^{\prime\prime}}=\|e\|_E$. Hence for each ![]() $e'\in E'$, we get
$e'\in E'$, we get
 \begin{equation*}
T^*(e') = e'\circ m_T =\Phi^{-1}(e'\circ T)=
\sum^\infty_{n=1}\alpha_n\,i(e_n)(e')\,\lambda_n.
\end{equation*}
\begin{equation*}
T^*(e') = e'\circ m_T =\Phi^{-1}(e'\circ T)=
\sum^\infty_{n=1}\alpha_n\,i(e_n)(e')\,\lambda_n.
\end{equation*} This means that ![]() $T^*$ is a nuclear operator and by (2.5) we get
$T^*$ is a nuclear operator and by (2.5) we get ![]() $\|T^*\|_{nuc}\le|m_T|(\Omega)$.
$\|T^*\|_{nuc}\le|m_T|(\Omega)$.
Now, we shall show that
Let ɛ > 0 be given. Since ![]() $T^*$ is a nuclear operator, there exist a bounded sequence
$T^*$ is a nuclear operator, there exist a bounded sequence ![]() $(e^{\prime\prime}_n)$ in E ʹʹ, a bounded sequence
$(e^{\prime\prime}_n)$ in E ʹʹ, a bounded sequence ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ca(\Sigma)$ and
$ca(\Sigma)$ and ![]() $(\alpha_n)\in\ell^1$ so that
$(\alpha_n)\in\ell^1$ so that
 \begin{equation*}
T^*(e')=\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e')\,\lambda_n\ \ \mbox{for}\ \ e'\in E'
\end{equation*}
\begin{equation*}
T^*(e')=\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e')\,\lambda_n\ \ \mbox{for}\ \ e'\in E'
\end{equation*}and
 \begin{equation}
\sum_{n=1}^\infty|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}|\lambda_n|(\Omega)\le\|T^*\|_{nuc}+\varepsilon.
\end{equation}
\begin{equation}
\sum_{n=1}^\infty|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}|\lambda_n|(\Omega)\le\|T^*\|_{nuc}+\varepsilon.
\end{equation} Then for ![]() $A\in\Sigma$, we obtain
$A\in\Sigma$, we obtain
 \begin{equation*}
(e'\circ m_T)(A)=T^*(e')(A)=\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e')\,\lambda_n(A).
\end{equation*}
\begin{equation*}
(e'\circ m_T)(A)=T^*(e')(A)=\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e')\,\lambda_n(A).
\end{equation*} Moreover, by the Hahn-Banach theorem for every ![]() $A\in\Sigma$, there exists
$A\in\Sigma$, there exists ![]() $e'_A\in E'$ with
$e'_A\in E'$ with ![]() $\|e'_A\|_{E'}=1$ such that
$\|e'_A\|_{E'}=1$ such that ![]() $\|m_T(A)\|_E=|(e'_A\circ m_T)(A)|$. Hence, if Π is a finite Σ-partition of Ω, then using (2.6) we have
$\|m_T(A)\|_E=|(e'_A\circ m_T)(A)|$. Hence, if Π is a finite Σ-partition of Ω, then using (2.6) we have
 \begin{equation*}
\begin{array}{l}
\displaystyle\sum_{A\in\Pi}\|m_T(A)\|_E=\sum_{A\in\Pi}|(e'_A\circ m_T)(A)|=\sum_{A\in\Pi}\left|\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e'_A)\,\lambda_n(A)\right|\\[6mm]
\displaystyle\leq\sum_{A\in\Pi}\left(\sum^\infty_{n=1}|\alpha_n|\,|e^{\prime\prime}_n(e'_A)|\,|\lambda_n(A)|\right)\leq\sum^\infty_{n=1}\left(|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}\sum_{A\in\Pi}|\lambda_n(A)|\right)\\[6mm]
\displaystyle\leq\sum^\infty_{n=1}|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}|\lambda_n|(\Omega)\le\|T^*\|_{nuc}+\varepsilon.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{l}
\displaystyle\sum_{A\in\Pi}\|m_T(A)\|_E=\sum_{A\in\Pi}|(e'_A\circ m_T)(A)|=\sum_{A\in\Pi}\left|\sum_{n=1}^\infty\alpha_n\,e^{\prime\prime}_n(e'_A)\,\lambda_n(A)\right|\\[6mm]
\displaystyle\leq\sum_{A\in\Pi}\left(\sum^\infty_{n=1}|\alpha_n|\,|e^{\prime\prime}_n(e'_A)|\,|\lambda_n(A)|\right)\leq\sum^\infty_{n=1}\left(|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}\sum_{A\in\Pi}|\lambda_n(A)|\right)\\[6mm]
\displaystyle\leq\sum^\infty_{n=1}|\alpha_n|\|e^{\prime\prime}_n\|_{E^{\prime\prime}}|\lambda_n|(\Omega)\le\|T^*\|_{nuc}+\varepsilon.
\end{array}
\end{equation*} Since ɛ > 0 is arbitrary, we get ![]() $|m_T|(\Omega)\le\|T^*\|_{nuc}$ and finally
$|m_T|(\Omega)\le\|T^*\|_{nuc}$ and finally ![]() $\|T^*\|_{nuc}=|m_T|(\Omega)=\|T\|_{nuc}$.
$\|T^*\|_{nuc}=|m_T|(\Omega)=\|T\|_{nuc}$.
3. Traces of Bochner representable operators
Formulas for the traces of kernel operators on Banach function spaces (in particular, ![]() $L^p(\mu)$-spaces) have been the object of much study (see [Reference Grothendieck14], [Reference Brislawn2], [Reference Delgado4], [Reference Gohberg, Goldberg and Krupnik10], [Reference Pietsch22]).
$L^p(\mu)$-spaces) have been the object of much study (see [Reference Grothendieck14], [Reference Brislawn2], [Reference Delgado4], [Reference Gohberg, Goldberg and Krupnik10], [Reference Pietsch22]).
Grothendieck [Reference Grothendieck13, Chap. I, p. 165] showed that the notion of ‘trace’ can be defined for nuclear operators in Banach spaces with the approximation property (see [Reference Pietsch22, 4.6.2, Lemma, pp. 210–211]).
Recall that a Banach space ![]() $(X,\|\cdot\|_X)$ has the approximation property if for every compact subset K of X and every ɛ > 0 there exists a bounded finite rank operator
$(X,\|\cdot\|_X)$ has the approximation property if for every compact subset K of X and every ɛ > 0 there exists a bounded finite rank operator ![]() $S:X\rightarrow X$ such that
$S:X\rightarrow X$ such that ![]() $\|x-S(x)\|_X\leq\varepsilon$ for every
$\|x-S(x)\|_X\leq\varepsilon$ for every ![]() $x\in K$ (see [Reference Ryan23, Chap. 4, p. 72], [Reference Diestel and Uhl7, Definition 1, p. 238]).
$x\in K$ (see [Reference Ryan23, Chap. 4, p. 72], [Reference Diestel and Uhl7, Definition 1, p. 238]).
Note that the Banach space ![]() $B(\Sigma)$ has the approximation property. Assume first that
$B(\Sigma)$ has the approximation property. Assume first that ![]() $B(\Sigma)$ is the Banach lattice of all bounded Σ-measurable real functions on Ω. Since
$B(\Sigma)$ is the Banach lattice of all bounded Σ-measurable real functions on Ω. Since ![]() $(B(\Sigma),\|\cdot\|_\infty)$ is an AM-space with the unit
$(B(\Sigma),\|\cdot\|_\infty)$ is an AM-space with the unit ![]() $\mathbb{1}_\Omega$, due to the Kakutani-Bohnenblust-M. and S. Krein theorem (see [Reference Aliprantis and Burkinshaw1, Theorem 3.40])
$\mathbb{1}_\Omega$, due to the Kakutani-Bohnenblust-M. and S. Krein theorem (see [Reference Aliprantis and Burkinshaw1, Theorem 3.40]) ![]() $B(\Sigma)$ is lattice isometric to some C(K)-space for a unique (up to homeomorphism) compact Hausdorff space K in such a way that
$B(\Sigma)$ is lattice isometric to some C(K)-space for a unique (up to homeomorphism) compact Hausdorff space K in such a way that ![]() $\mathbb{1}_\Omega$ is identified with
$\mathbb{1}_\Omega$ is identified with ![]() $\mathbb{1}_K$. This follows that
$\mathbb{1}_K$. This follows that ![]() $B(\Sigma)$ has the approximation property because C(K) has the approximation property (see [Reference Ryan23, Example 4.2]). For the Banach space
$B(\Sigma)$ has the approximation property because C(K) has the approximation property (see [Reference Ryan23, Example 4.2]). For the Banach space ![]() $B(\Sigma)$ of complex-valued functions on Ω, one has to consider real and imaginary parts separate.
$B(\Sigma)$ of complex-valued functions on Ω, one has to consider real and imaginary parts separate.
Assume that ![]() $T:B(\Sigma)\rightarrow B(\Sigma)$ is a nuclear operator, that is, there exist a bounded sequence
$T:B(\Sigma)\rightarrow B(\Sigma)$ is a nuclear operator, that is, there exist a bounded sequence ![]() $(\lambda_n)$ in
$(\lambda_n)$ in ![]() $ba(\Sigma)$, a bounded sequence
$ba(\Sigma)$, a bounded sequence ![]() $(w_n)$ in
$(w_n)$ in ![]() $B(\Sigma)$ and
$B(\Sigma)$ and ![]() $(\alpha_n)\in\ell^1$ so that
$(\alpha_n)\in\ell^1$ so that
 \begin{equation}
T=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}\otimes w_n \ \ \mbox{in} \ \
{\cal L}(B(\Sigma),B(\Sigma)).
\end{equation}
\begin{equation}
T=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}\otimes w_n \ \ \mbox{in} \ \
{\cal L}(B(\Sigma),B(\Sigma)).
\end{equation}Then the trace of T is given by
 \begin{equation*}
{\rm tr}\,T:=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}(w_n)=\sum^\infty_{n=1}\alpha_n\int_\Omega
w_n(\omega)\,d\lambda_n,
\end{equation*}
\begin{equation*}
{\rm tr}\,T:=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}(w_n)=\sum^\infty_{n=1}\alpha_n\int_\Omega
w_n(\omega)\,d\lambda_n,
\end{equation*}and it does not depend on the special choice of the nuclear representation (3.1) of T (see [Reference Gohberg, Goldberg and Krupnik10, Chap. 5, Theorem 1.2], [Reference Pietsch22, Lemma, pp. 210–211]).
From now on we assume that ![]() $(\Omega,{\cal T})$ is a compact Hausdorff space and
$(\Omega,{\cal T})$ is a compact Hausdorff space and ![]() ${\cal B} o$ denotes the σ-algebra of Borel sets in Ω. Then
${\cal B} o$ denotes the σ-algebra of Borel sets in Ω. Then ![]() $C(\Omega)\subset B({\cal B} o)$.
$C(\Omega)\subset B({\cal B} o)$.
Assume that a measure ![]() $\mu\in ca^+({\cal B} o)$ is strictly positive, that is, for all
$\mu\in ca^+({\cal B} o)$ is strictly positive, that is, for all ![]() $U\in{\cal T}$ with
$U\in{\cal T}$ with ![]() $U\neq \emptyset$,
$U\neq \emptyset$, ![]() $\mu(U) \gt 0$. Then
$\mu(U) \gt 0$. Then ![]() $L^1(\mu,C(\Omega))\subset L^1(\mu,B({\cal B} o))$.
$L^1(\mu,C(\Omega))\subset L^1(\mu,B({\cal B} o))$.
Corollary 3.1. Assume that ![]() $T:B({\cal B} o)\rightarrow B({\cal B} o)$ is a Bochner representable operator such that
$T:B({\cal B} o)\rightarrow B({\cal B} o)$ is a Bochner representable operator such that
 \begin{equation*}
T(u)=\int_\Omega u(\omega)\,f(\omega)\,d\mu,\quad \mbox{for all} \ u\in B({\cal B} o),
\end{equation*}
\begin{equation*}
T(u)=\int_\Omega u(\omega)\,f(\omega)\,d\mu,\quad \mbox{for all} \ u\in B({\cal B} o),
\end{equation*} where ![]() $f\in L^1(\mu, C(\Omega))$. Then T has a well-defined trace
$f\in L^1(\mu, C(\Omega))$. Then T has a well-defined trace
 \begin{equation*}
{\rm tr}\,T=\int_\Omega f(\omega)(\omega)\,d\mu.
\end{equation*}
\begin{equation*}
{\rm tr}\,T=\int_\Omega f(\omega)(\omega)\,d\mu.
\end{equation*}Proof. Let ![]() $L^1(\mu)\,\hat{\otimes}\,C(\Omega)$ denote the projective tensor product of
$L^1(\mu)\,\hat{\otimes}\,C(\Omega)$ denote the projective tensor product of ![]() $L^1(\mu)$ and
$L^1(\mu)$ and ![]() $C(\Omega)$, equipped with the completed norm π (see [Reference Diestel and Uhl7, p. 227], [Reference Ryan23, p. 17]). Note that for
$C(\Omega)$, equipped with the completed norm π (see [Reference Diestel and Uhl7, p. 227], [Reference Ryan23, p. 17]). Note that for ![]() $z\in L^1(\mu)\,\hat{\otimes}\, C(\Omega)$, we have
$z\in L^1(\mu)\,\hat{\otimes}\, C(\Omega)$, we have
 \begin{equation*}
\pi(z)=\inf\left\{\sum^\infty_{n=1}|\alpha_n|\,\|v_n\|_1\|w_n\|_\infty\right\},
\end{equation*}
\begin{equation*}
\pi(z)=\inf\left\{\sum^\infty_{n=1}|\alpha_n|\,\|v_n\|_1\|w_n\|_\infty\right\},
\end{equation*} where the infimum is taken over all sequences ![]() $(v_n)$ in
$(v_n)$ in ![]() $L^1(\mu)$ and
$L^1(\mu)$ and ![]() $(w_n)$ in
$(w_n)$ in ![]() $C(\Omega)$ with
$C(\Omega)$ with ![]() $\lim_n\|v_n\|_1=0=\lim_n\|w_n\|_\infty$ and
$\lim_n\|v_n\|_1=0=\lim_n\|w_n\|_\infty$ and ![]() $(\alpha_n)\in\ell^1$ such that
$(\alpha_n)\in\ell^1$ such that ![]() $z=\sum^\infty_{n=1}\alpha_n\,v_n\otimes w_n$ in π-norm (see [Reference Ryan23, Proposition 2.8, pp. 21–22]).
$z=\sum^\infty_{n=1}\alpha_n\,v_n\otimes w_n$ in π-norm (see [Reference Ryan23, Proposition 2.8, pp. 21–22]).
It is known that ![]() $L^1(\mu)\,\hat{\otimes}\, C(\Omega)$ is isometrically isomorphic to the Banach space
$L^1(\mu)\,\hat{\otimes}\, C(\Omega)$ is isometrically isomorphic to the Banach space ![]() $(L^1(\mu,C(\Omega)),\|\cdot\|_1)$ by the isometry J, defined by:
$(L^1(\mu,C(\Omega)),\|\cdot\|_1)$ by the isometry J, defined by:
(see [Reference Diestel and Uhl7, Example 10, p. 228], [Reference Ryan23, Example 2.19, p. 29]). Then there exist sequences ![]() $(v_n)$ in
$(v_n)$ in ![]() $L^1(\mu)$ and
$L^1(\mu)$ and ![]() $(w_n)$ in
$(w_n)$ in ![]() $C(\Omega)$ with
$C(\Omega)$ with ![]() $\lim_n\|v_n\|_1=0=\lim_n\|w_n\|_\infty$ and
$\lim_n\|v_n\|_1=0=\lim_n\|w_n\|_\infty$ and ![]() $(\alpha_n)\in\ell^1$ such that
$(\alpha_n)\in\ell^1$ such that
 \begin{equation*}
J^{-1}(f)=\sum^\infty_{n=1}\alpha_n\,v_n\otimes w_n \ \ \mbox{in} \
\big(L^1(\mu)\,\hat{\otimes} \,C(\Omega), \pi\big).
\end{equation*}
\begin{equation*}
J^{-1}(f)=\sum^\infty_{n=1}\alpha_n\,v_n\otimes w_n \ \ \mbox{in} \
\big(L^1(\mu)\,\hat{\otimes} \,C(\Omega), \pi\big).
\end{equation*}Thus it follows that
 \begin{equation*}
f=J\left(\sum^\infty_{n=1}\alpha_n v_n\otimes w_n\right)=\sum^\infty_{n=1}
\alpha_n v_n(\cdot)\, w_n \ \ \mbox{in} \ \ L^1(\mu,C(\Omega)),
\end{equation*}
\begin{equation*}
f=J\left(\sum^\infty_{n=1}\alpha_n v_n\otimes w_n\right)=\sum^\infty_{n=1}
\alpha_n v_n(\cdot)\, w_n \ \ \mbox{in} \ \ L^1(\mu,C(\Omega)),
\end{equation*}and hence
 \begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n\left(\int_\Omega u(\omega)\,v_n(\omega)\,d\mu\right)
w_n,\quad \mbox{for all} \ \ u\in B(\Sigma).
\end{equation*}
\begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n\left(\int_\Omega u(\omega)\,v_n(\omega)\,d\mu\right)
w_n,\quad \mbox{for all} \ \ u\in B(\Sigma).
\end{equation*} For ![]() $n\in\mathbb{N}$, let
$n\in\mathbb{N}$, let
 \begin{equation*}
\lambda_n(A):=\int_A v_n(\omega)\,d\mu,\quad \mbox{for all} \ \ A\in\Sigma.
\end{equation*}
\begin{equation*}
\lambda_n(A):=\int_A v_n(\omega)\,d\mu,\quad \mbox{for all} \ \ A\in\Sigma.
\end{equation*} Note that ![]() $\lambda_n\in ca(\Sigma)$ and
$\lambda_n\in ca(\Sigma)$ and ![]() $|\lambda_n|(\Omega)=\|v_n\|_1$ and hence
$|\lambda_n|(\Omega)=\|v_n\|_1$ and hence ![]() $\lim\lambda_n(A)=0$ for all
$\lim\lambda_n(A)=0$ for all ![]() $A\in\Sigma$. By the Nikodym convergence theorem (see [Reference Drewnowski9, Theorem 8.6]), the family
$A\in\Sigma$. By the Nikodym convergence theorem (see [Reference Drewnowski9, Theorem 8.6]), the family ![]() $\{\lambda_n:n\in\mathbb{N}\}$ is uniformly countably additive.
$\{\lambda_n:n\in\mathbb{N}\}$ is uniformly countably additive.
Since  $\Phi_{\lambda_n}(u)=\int_\Omega u(\omega)\,d\lambda_n=\int_\Omega u(\omega)\,v_n(\omega)\,d\mu$ for all
$\Phi_{\lambda_n}(u)=\int_\Omega u(\omega)\,d\lambda_n=\int_\Omega u(\omega)\,v_n(\omega)\,d\mu$ for all ![]() $u\in B(\Sigma)$ (see [Reference Conway3, Theorem 8C, p. 380]), we get
$u\in B(\Sigma)$ (see [Reference Conway3, Theorem 8C, p. 380]), we get
 \begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}(u)w_n,\quad \mbox{for all} \ \ u\in B(\Sigma),
\end{equation*}
\begin{equation*}
T(u)=\sum^\infty_{n=1}\alpha_n\Phi_{\lambda_n}(u)w_n,\quad \mbox{for all} \ \ u\in B(\Sigma),
\end{equation*}that is,
 \begin{equation*}
T=\sum_{n=1}^\infty\alpha_n\Phi_{\lambda_n}\otimes w_n\ \ \mbox{in}\ \ {\cal L}(B(\Sigma),B(\Sigma)).
\end{equation*}
\begin{equation*}
T=\sum_{n=1}^\infty\alpha_n\Phi_{\lambda_n}\otimes w_n\ \ \mbox{in}\ \ {\cal L}(B(\Sigma),B(\Sigma)).
\end{equation*}Hence
 \begin{equation*}
{\rm tr}\,T=\sum_{n=1}^\infty\alpha_n\Phi_{\lambda_n}(w_n)=\sum_{n=1}^\infty\alpha_n\int_\Omega w_n(\omega)\,v_n(\omega)\,d\mu.
\end{equation*}
\begin{equation*}
{\rm tr}\,T=\sum_{n=1}^\infty\alpha_n\Phi_{\lambda_n}(w_n)=\sum_{n=1}^\infty\alpha_n\int_\Omega w_n(\omega)\,v_n(\omega)\,d\mu.
\end{equation*} For ![]() $n\in\mathbb{N}$, let
$n\in\mathbb{N}$, let ![]() $f_n=\sum_{i=1}^n\alpha_i\,v_i(\cdot)\,w_i$. Hence
$f_n=\sum_{i=1}^n\alpha_i\,v_i(\cdot)\,w_i$. Hence  $\int_\Omega\|f(\omega)-f_n(\omega)\|_\infty\,d\mu\rightarrow 0$. Thus we get,
$\int_\Omega\|f(\omega)-f_n(\omega)\|_\infty\,d\mu\rightarrow 0$. Thus we get,
 \begin{equation*}
\begin{array}{l}
\displaystyle \left|\int_\Omega f(\omega)(\omega)\,d\mu-\sum^n_{i=1}\alpha_i\int_\Omega v_i(\omega)\,
w_i(\omega)\,d\mu\right|\\[5mm]
\displaystyle \leq \int_\Omega\left|\left(f(\omega)(\omega)-\sum^n_{i=1}\alpha_i v_i(\omega)\,w_i(\omega)\right)
\right|d\mu \leq \int_\Omega\|f(\omega)-f_n(\omega)\|_\infty \,d\mu.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{l}
\displaystyle \left|\int_\Omega f(\omega)(\omega)\,d\mu-\sum^n_{i=1}\alpha_i\int_\Omega v_i(\omega)\,
w_i(\omega)\,d\mu\right|\\[5mm]
\displaystyle \leq \int_\Omega\left|\left(f(\omega)(\omega)-\sum^n_{i=1}\alpha_i v_i(\omega)\,w_i(\omega)\right)
\right|d\mu \leq \int_\Omega\|f(\omega)-f_n(\omega)\|_\infty \,d\mu.
\end{array}
\end{equation*} Let ![]() $g\in L^1(\mu,C(\Omega))$ be another function representing T, that is,
$g\in L^1(\mu,C(\Omega))$ be another function representing T, that is,
 \begin{equation*}
T(u)(t)=\int_\Omega u(\omega)\,f(\omega)(t)\,d\mu(\omega)=\int_\Omega u(\omega)\,g(\omega)(t)\,d\mu(\omega)\ \ \mbox{for}\ \ u\in B({\cal B} o).
\end{equation*}
\begin{equation*}
T(u)(t)=\int_\Omega u(\omega)\,f(\omega)(t)\,d\mu(\omega)=\int_\Omega u(\omega)\,g(\omega)(t)\,d\mu(\omega)\ \ \mbox{for}\ \ u\in B({\cal B} o).
\end{equation*} Denote ![]() $h(\omega)(t):=f(\omega)(t)-g(\omega)(t)$ for
$h(\omega)(t):=f(\omega)(t)-g(\omega)(t)$ for ![]() $\omega,t\in\Omega$. Then for every
$\omega,t\in\Omega$. Then for every ![]() $A\in{\cal B} o$ and
$A\in{\cal B} o$ and ![]() $u=\mathbb{1}_A$ we obtain
$u=\mathbb{1}_A$ we obtain
 \begin{equation*}
\int_A h(\omega)(t)\,d\mu(\omega)=0 \ \ \mbox{for all}\ \ t\in\Omega.
\end{equation*}
\begin{equation*}
\int_A h(\omega)(t)\,d\mu(\omega)=0 \ \ \mbox{for all}\ \ t\in\Omega.
\end{equation*} Hence for every ![]() $t\in\Omega$,
$t\in\Omega$, ![]() $h(\cdot)(t)=0$ µ-a.e and it follows that
$h(\cdot)(t)=0$ µ-a.e and it follows that
 \begin{equation}
\int_\Omega\left(\int_\Omega |h(\omega)(t)|\,d\mu(\omega)\right)\,d\mu(t)=0.
\end{equation}
\begin{equation}
\int_\Omega\left(\int_\Omega |h(\omega)(t)|\,d\mu(\omega)\right)\,d\mu(t)=0.
\end{equation}We shall show that
 \begin{equation*}
\int_\Omega h(\omega)(\omega)\,d\mu(\omega)=0.
\end{equation*}
\begin{equation*}
\int_\Omega h(\omega)(\omega)\,d\mu(\omega)=0.
\end{equation*} For indirect proof suppose that  $\left|\int_\Omega h(\omega)(\omega)\,d\mu(\omega)\right| \gt 0$. Then there exists
$\left|\int_\Omega h(\omega)(\omega)\,d\mu(\omega)\right| \gt 0$. Then there exists ![]() $A\in{\cal B} o$,
$A\in{\cal B} o$, ![]() $\mu(A)\neq 0$ such that
$\mu(A)\neq 0$ such that ![]() $h(\omega)(\omega) \gt 0$ or
$h(\omega)(\omega) \gt 0$ or ![]() $h(\omega)(\omega) \lt 0 $ for
$h(\omega)(\omega) \lt 0 $ for ![]() $\omega\in A$. Without loss of generality, let
$\omega\in A$. Without loss of generality, let ![]() $h(\omega)(\omega) \gt 0$ for
$h(\omega)(\omega) \gt 0$ for ![]() $\omega\in A$. Since for
$\omega\in A$. Since for ![]() $\omega\in\Omega$ we have
$\omega\in\Omega$ we have ![]() $h(\omega)\in C(\Omega)$, then there exists a neighbourhood Hω of
$h(\omega)\in C(\Omega)$, then there exists a neighbourhood Hω of ![]() $\omega\in A$ such that
$\omega\in A$ such that
Since µ is strictly positive, then for every ![]() $\omega\in A$,
$\omega\in A$, ![]() $\mu(H_\omega) \gt 0$ and hence
$\mu(H_\omega) \gt 0$ and hence
 \begin{equation*}
\int_{H_\omega}h(\omega)(t)\,d\mu(t) \gt 0.
\end{equation*}
\begin{equation*}
\int_{H_\omega}h(\omega)(t)\,d\mu(t) \gt 0.
\end{equation*} Let ![]() $\omega_0\in A$ be given. Then, we have
$\omega_0\in A$ be given. Then, we have
 \begin{equation*}
\int_{\Omega}|h(\omega_0)(t)|\,d\mu(t)\ge\int_{\bigcup H_\omega}|h(\omega_0)(t)|\,d\mu(t)\ge\int_{H_{\omega_0}}|h(\omega_0)(t)|\,d\mu(t) \gt 0.
\end{equation*}
\begin{equation*}
\int_{\Omega}|h(\omega_0)(t)|\,d\mu(t)\ge\int_{\bigcup H_\omega}|h(\omega_0)(t)|\,d\mu(t)\ge\int_{H_{\omega_0}}|h(\omega_0)(t)|\,d\mu(t) \gt 0.
\end{equation*}Since ω 0 is arbitrary, it follows that
 \begin{equation*}
\int_\Omega\left(\int_\Omega |h(\omega)(t)|\,d\mu(t)\right)\,d\mu(\omega) \gt 0
\end{equation*}
\begin{equation*}
\int_\Omega\left(\int_\Omega |h(\omega)(t)|\,d\mu(t)\right)\,d\mu(\omega) \gt 0
\end{equation*}and, in view of Hille’s theorem (see [Reference Dinculeanu8, § 1, Theorem 36, p. 16]), this is in contradiction with (3.2). Hence we finally get
 \begin{equation*}
\int_\Omega h(\omega)(\omega)\,d\mu(\omega)=0.
\end{equation*}
\begin{equation*}
\int_\Omega h(\omega)(\omega)\,d\mu(\omega)=0.
\end{equation*} Thus this follows that the trace of T is well defined and  ${\rm tr}\,T=\int_\Omega f(\omega)(\omega)\,d\mu$.
${\rm tr}\,T=\int_\Omega f(\omega)(\omega)\,d\mu$.
Grothendieck [Reference Grothendieck14] showed that if Ω is a compact Hausdorff space with a positive Borel measure µ on Ω and ![]() $k(\cdot,\cdot)\in C(\Omega\times\Omega)$, then the kernel operator
$k(\cdot,\cdot)\in C(\Omega\times\Omega)$, then the kernel operator ![]() $T_k:C(\Omega)\rightarrow C(\Omega)$ defined by:
$T_k:C(\Omega)\rightarrow C(\Omega)$ defined by:
 \begin{equation*}
T_k(u):=\int_\Omega u(\omega)\,k(\cdot,\omega)\,d\mu \ \ \mbox{for} \ \ u\in C(\Omega),
\end{equation*}
\begin{equation*}
T_k(u):=\int_\Omega u(\omega)\,k(\cdot,\omega)\,d\mu \ \ \mbox{for} \ \ u\in C(\Omega),
\end{equation*} is nuclear and has a well-defined trace  ${\rm tr}\,T_k=\int_\Omega k(\omega,\omega)\,d\mu$ (see [Reference Grothendieck14], [Reference Pietsch22, 6.6.2, Theorem, p. 274]).
${\rm tr}\,T_k=\int_\Omega k(\omega,\omega)\,d\mu$ (see [Reference Grothendieck14], [Reference Pietsch22, 6.6.2, Theorem, p. 274]).
Now, we can extend this formula for the trace of kernel operators ![]() $T_k:B({\cal B} o)\rightarrow B({\cal B} o)$.
$T_k:B({\cal B} o)\rightarrow B({\cal B} o)$.
Let ![]() $k(\cdot,\cdot)\in C(\Omega\times\Omega)$. Hence for every
$k(\cdot,\cdot)\in C(\Omega\times\Omega)$. Hence for every ![]() $\omega\in\Omega$,
$\omega\in\Omega$, ![]() $k(\cdot,\omega)\in C(\Omega)$. Let
$k(\cdot,\omega)\in C(\Omega)$. Let ![]() $C(\Omega, C(\Omega))$ denote the Banach space of all continuous functions
$C(\Omega, C(\Omega))$ denote the Banach space of all continuous functions ![]() $f:\Omega\rightarrow C(\Omega)$, equipped with the uniform norm
$f:\Omega\rightarrow C(\Omega)$, equipped with the uniform norm ![]() $\|\cdot\|_\infty$.
$\|\cdot\|_\infty$.
Assume that ![]() $\mu\in ca({\cal B} o)^+$. Let
$\mu\in ca({\cal B} o)^+$. Let ![]() ${\cal L}^\infty(\mu, C(\Omega))$ denote the space of all µ-measurable functions
${\cal L}^\infty(\mu, C(\Omega))$ denote the space of all µ-measurable functions ![]() $g:\Omega\rightarrow C(\Omega)$ such that
$g:\Omega\rightarrow C(\Omega)$ such that ![]() $\mu-{\rm ess }\sup\|g(\omega)\|_\infty \lt \infty$. In view of the Pettis measurability theorem (see [Reference Diestel and Uhl7, Theorem 2, p. 42]), we have
$\mu-{\rm ess }\sup\|g(\omega)\|_\infty \lt \infty$. In view of the Pettis measurability theorem (see [Reference Diestel and Uhl7, Theorem 2, p. 42]), we have
and the space ![]() ${\cal L}^\infty(\mu, C(\Omega))$ can be embedded in the space
${\cal L}^\infty(\mu, C(\Omega))$ can be embedded in the space ![]() $L^1(\mu, C(\Omega))$ such that with each function from
$L^1(\mu, C(\Omega))$ such that with each function from ![]() ${\cal L}^\infty(\mu, C(\Omega))$ is associated its µ-equivalence class in
${\cal L}^\infty(\mu, C(\Omega))$ is associated its µ-equivalence class in ![]() $L^1(\mu, C(\Omega))$.
$L^1(\mu, C(\Omega))$.
It is well known (see [Reference Pietsch22, 6.1.4, p. 243]) that the function:
is bounded and continuous. Then in view of (3.3), ![]() $f\in{\cal L}^\infty(\mu, C(\Omega))$. Hence its µ-equivalence class belongs to
$f\in{\cal L}^\infty(\mu, C(\Omega))$. Hence its µ-equivalence class belongs to ![]() $L^1(\mu,C(\Omega))$. Thus it follows that one can define the kernel operator
$L^1(\mu,C(\Omega))$. Thus it follows that one can define the kernel operator ![]() $T_k: B({\cal B} o)\rightarrow B({\cal B} o)$ by
$T_k: B({\cal B} o)\rightarrow B({\cal B} o)$ by
 \begin{equation*}
T_k(u):=\int_\Omega u(\omega)\,k(\cdot,\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B({\cal B} o).
\end{equation*}
\begin{equation*}
T_k(u):=\int_\Omega u(\omega)\,k(\cdot,\omega)\,d\mu,\quad \mbox{for all}\ \ u\in B({\cal B} o).
\end{equation*} For ![]() $t\in\Omega$, let
$t\in\Omega$, let ![]() $\Phi_t(u)=u(t)$ for all
$\Phi_t(u)=u(t)$ for all ![]() $u\in B({\cal B} o)$. Then
$u\in B({\cal B} o)$. Then ![]() $\Phi_t\in C(\Omega)'$ and using Hille’s theorem, for all
$\Phi_t\in C(\Omega)'$ and using Hille’s theorem, for all ![]() $u\in B({\cal B} o)$,
$u\in B({\cal B} o)$, ![]() $t\in\Omega$, we get
$t\in\Omega$, we get
 \begin{equation*}
T_k(u)(t)=\int_\Omega u(\omega)\,\Phi_t(k(\cdot,\omega))\,d\mu=\int_\Omega u(\omega)\,k(t,\omega)\,d\mu.
\end{equation*}
\begin{equation*}
T_k(u)(t)=\int_\Omega u(\omega)\,\Phi_t(k(\cdot,\omega))\,d\mu=\int_\Omega u(\omega)\,k(t,\omega)\,d\mu.
\end{equation*}As a consequence of Theorem 2.2 and Corollary 3.1, we get
Corollary 3.2. The kernel operator ![]() $T_k:B({\cal B} o)\rightarrow B({\cal B} o)$ is nuclear σ-smooth and
$T_k:B({\cal B} o)\rightarrow B({\cal B} o)$ is nuclear σ-smooth and
 \begin{equation*}
{\rm tr}\,T_k=\int_\Omega k(\omega,\omega)\,d\mu.
\end{equation*}
\begin{equation*}
{\rm tr}\,T_k=\int_\Omega k(\omega,\omega)\,d\mu.
\end{equation*}