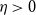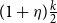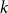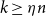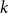1. Introduction
A typical question in extremal graph theory is whether information on the degree sequence of a graph
![]() $G$
can be used to find some specific subgraph in
$G$
can be used to find some specific subgraph in
![]() $G$
. A famous example is Dirac’s theorem [Reference Dirac9], which states that any
$G$
. A famous example is Dirac’s theorem [Reference Dirac9], which states that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
of minimum degree
$G$
of minimum degree
![]() $\delta (G)\ge \frac{n}{2}$
contains a spanning cycle. A minimum degree of at least
$\delta (G)\ge \frac{n}{2}$
contains a spanning cycle. A minimum degree of at least
![]() $\frac{n-1}{2}$
guarantees a spanning path. Such a result also holds for shorter paths: Already Dirac, as well as Erdős and Gallai, observed that if a graph
$\frac{n-1}{2}$
guarantees a spanning path. Such a result also holds for shorter paths: Already Dirac, as well as Erdős and Gallai, observed that if a graph
![]() $G$
has a connected component with at least
$G$
has a connected component with at least
![]() $k+1$
vertices and
$k+1$
vertices and
![]() $\delta (G)\geq \frac k2$
, then
$\delta (G)\geq \frac k2$
, then
![]() $G$
contains a
$G$
contains a
![]() $k$
-edge path (see [Reference Erdős and Gallai10]). Note that we need to require that
$k$
-edge path (see [Reference Erdős and Gallai10]). Note that we need to require that
![]() $G$
has a sufficiently large component as otherwise
$G$
has a sufficiently large component as otherwise
![]() $G$
could be the disjoint union of complete graphs of order
$G$
could be the disjoint union of complete graphs of order
![]() $k$
.
$k$
.
Considering the same question for oriented graphs
![]() $D$
, we replace the minimum degree with the minimum semidegree
$D$
, we replace the minimum degree with the minimum semidegree
![]() $\delta ^0(D)$
, which is defined as the minimum over all the in- and all the out-degrees of the vertices. Note that any oriented graph of minimum semidegree
$\delta ^0(D)$
, which is defined as the minimum over all the in- and all the out-degrees of the vertices. Note that any oriented graph of minimum semidegree
![]() $\delta ^0(D) \gt \frac k2$
has an underlying connected graph on more than
$\delta ^0(D) \gt \frac k2$
has an underlying connected graph on more than
![]() $k$
vertices (and therefore, no extra condition on large components will be necessary). Jackson [Reference Jackson15] showed that every oriented graph
$k$
vertices (and therefore, no extra condition on large components will be necessary). Jackson [Reference Jackson15] showed that every oriented graph
![]() $D$
with
$D$
with
![]() $\delta ^0(D) \gt \frac k2$
contains the directed path on
$\delta ^0(D) \gt \frac k2$
contains the directed path on
![]() $k$
edges, which is best possible. The first author conjectured that this result extends to any orientation of the path.
$k$
edges, which is best possible. The first author conjectured that this result extends to any orientation of the path.
Conjecture 1.1. [Reference Stein, Raigoroskii and Rassias29] Every oriented graph
![]() $D$
with
$D$
with
![]() $\delta ^0(D) \gt \frac k2$
contains every oriented path on
$\delta ^0(D) \gt \frac k2$
contains every oriented path on
![]() $k$
edges.
$k$
edges.
This conjecture is best possible for odd
![]() $k$
, as a regular tournament on
$k$
, as a regular tournament on
![]() $k$
vertices does not contain any oriented path with
$k$
vertices does not contain any oriented path with
![]() $k$
edges. A different example works for antidirected paths, that is, oriented paths whose edges alternate directions (more generally, an antidirected graph is an oriented graph having no
$k$
edges. A different example works for antidirected paths, that is, oriented paths whose edges alternate directions (more generally, an antidirected graph is an oriented graph having no
![]() $2$
-edge directed path). Note that in an
$2$
-edge directed path). Note that in an
![]() $\ell$
-blow-up of the directed triangle (where each vertex is replaced with
$\ell$
-blow-up of the directed triangle (where each vertex is replaced with
![]() $\ell$
independent vertices), any longest antidirected path can only cover
$\ell$
independent vertices), any longest antidirected path can only cover
![]() $2\ell$
vertices.
$2\ell$
vertices.
It is known [Reference Klimošová and Stein22] that if
![]() $\delta ^0(D)\gt \frac{3k-2}{4}$
, then the oriented graph
$\delta ^0(D)\gt \frac{3k-2}{4}$
, then the oriented graph
![]() $D$
contains each antipath with
$D$
contains each antipath with
![]() $k$
edges. Further, if we replace the bound with
$k$
edges. Further, if we replace the bound with
![]() $\delta ^0(D) \ge k$
, Conjecture 1.1 becomes very easy (a greedy embedding strategy suffices). This strategy also works if we wish to find a
$\delta ^0(D) \ge k$
, Conjecture 1.1 becomes very easy (a greedy embedding strategy suffices). This strategy also works if we wish to find a
![]() $k$
-edge oriented tree instead of an
$k$
-edge oriented tree instead of an
![]() $k$
-edge oriented path. Moreover, in this case we cannot do any better: In the
$k$
-edge oriented path. Moreover, in this case we cannot do any better: In the
![]() $(k-1)$
-blow-up of a directed triangle, each vertex has semidegree
$(k-1)$
-blow-up of a directed triangle, each vertex has semidegree
![]() $k-1$
, but no antidirected star with
$k-1$
, but no antidirected star with
![]() $k$
edges is present. However, the antidirected star is very unbalanced. The situation might be different for balanced antidirected trees
$k$
edges is present. However, the antidirected star is very unbalanced. The situation might be different for balanced antidirected trees
![]() $T$
, that is, those that have as many vertices of in-degree
$T$
, that is, those that have as many vertices of in-degree
![]() $0$
as of out-degree
$0$
as of out-degree
![]() $0$
. We suspect that these trees appear whenever the host oriented graph
$0$
. We suspect that these trees appear whenever the host oriented graph
![]() $D$
has minimum semidegree greater than
$D$
has minimum semidegree greater than
![]() $\frac k2$
.
$\frac k2$
.
We show that this is asymptotically true if
![]() $D$
is dense and
$D$
is dense and
![]() $T$
is large and has bounded maximum degree, where the maximum degree
$T$
is large and has bounded maximum degree, where the maximum degree
![]() $\Delta (T)$
of an oriented tree
$\Delta (T)$
of an oriented tree
![]() $T$
is defined as the maximum degree of the underlying undirected tree.
$T$
is defined as the maximum degree of the underlying undirected tree.
Theorem 1.2.
For all
![]() $\eta \in (0,1)$
and
$\eta \in (0,1)$
and
![]() $c\in \mathbb N$
there is
$c\in \mathbb N$
there is
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $k\geq \eta n$
, every oriented graph
$k\geq \eta n$
, every oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains every balanced antidirected tree
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains every balanced antidirected tree
![]() $T$
with
$T$
with
![]() $k$
edges and with
$k$
edges and with
![]() $\Delta (T)\leq (\!\log (n))^c$
.
$\Delta (T)\leq (\!\log (n))^c$
.
Instead of Theorem 1.2 we will prove a slightly stronger version, namely Theorem 5.2. This is necessary for a later application of the result in the proof of Theorem 1.9 below. Theorem 5.2 allows us to specify a subset of
![]() $V(D)$
where the root of
$V(D)$
where the root of
![]() $T$
will be mapped, a feature that might be of independent interest.
$T$
will be mapped, a feature that might be of independent interest.
Theorem 1.2 can be interpreted as a version for smaller trees of a recent result by Kathapurkar and Montgomery [Reference Kathapurkar and Montgomery17] (and the preceding result in [Reference Mycroft and Naia27]). In [Reference Kathapurkar and Montgomery17] it is shown that for each
![]() $\eta \gt 0$
, there is some
$\eta \gt 0$
, there is some
![]() $c \gt 0$
such that every sufficiently large
$c \gt 0$
such that every sufficiently large
![]() $n$
-vertex directed graph with minimum semidegree at least
$n$
-vertex directed graph with minimum semidegree at least
![]() $(\frac 12 + \eta )n$
contains a copy of every
$(\frac 12 + \eta )n$
contains a copy of every
![]() $n$
-vertex oriented tree whose underlying maximum degree is at most
$n$
-vertex oriented tree whose underlying maximum degree is at most
![]() $c\frac n{\log n}$
. This generalises a well-known theorem of Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi23] for graphs. The result from [Reference Kathapurkar and Montgomery17] cannot hold for smaller trees and accordingly smaller semidegree without adding further conditions, because of the example of the antidirected star from above.
$c\frac n{\log n}$
. This generalises a well-known theorem of Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi23] for graphs. The result from [Reference Kathapurkar and Montgomery17] cannot hold for smaller trees and accordingly smaller semidegree without adding further conditions, because of the example of the antidirected star from above.
Turning back to our original question for oriented paths, note that Theorem 1.2 immediately implies that Conjecture 1.1 holds asymptotically for large antidirected paths in large graphs. (If the path is not balanced, we can extend it by one vertex and apply Theorem 1.2 with a sufficiently smaller
![]() $\eta$
.)
$\eta$
.)
Corollary 1.3.
For all
![]() $\eta \in (0,1)$
there is
$\eta \in (0,1)$
there is
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $k\geq \eta n$
every oriented graph
$k\geq \eta n$
every oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains every antidirected path with
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains every antidirected path with
![]() $k$
edges.
$k$
edges.
How about asking for oriented cycles instead of oriented paths or trees? Keevash, Kühn, and Osthus [Reference Keevash, Kühn and Osthus18] showed that every sufficiently large
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $G$
of minimum semidegree
$G$
of minimum semidegree
![]() $\delta ^0(G)\geq \frac{3n}8$
contains a directed Hamilton cycle, and Kelly [Reference Kelly19] showed that asymptotically, the same bound guarantees any orientation of a Hamilton cycle. Kelly, Kühn, and Osthus [Reference Kelly, Kühn and Osthus20] extended this to a pancyclicity result, proving that every oriented graph
$\delta ^0(G)\geq \frac{3n}8$
contains a directed Hamilton cycle, and Kelly [Reference Kelly19] showed that asymptotically, the same bound guarantees any orientation of a Hamilton cycle. Kelly, Kühn, and Osthus [Reference Kelly, Kühn and Osthus20] extended this to a pancyclicity result, proving that every oriented graph
![]() $D$
of minimum semidegree
$D$
of minimum semidegree
![]() $\delta ^0(D)\geq \frac{3n}8+o(n)$
contains every orientation of every cycle (of any length between
$\delta ^0(D)\geq \frac{3n}8+o(n)$
contains every orientation of every cycle (of any length between
![]() $3$
and
$3$
and
![]() $n$
). These authors also show that for cycles of constant length the bounds can be improved, but the improvement depends on the cycle type: the number of forward edges minus the number of backwards edges of the cycle. For some cycle types and lengths, a semidegree exceeding
$n$
). These authors also show that for cycles of constant length the bounds can be improved, but the improvement depends on the cycle type: the number of forward edges minus the number of backwards edges of the cycle. For some cycle types and lengths, a semidegree exceeding
![]() $\frac n3$
is necessary: for instance, if
$\frac n3$
is necessary: for instance, if
![]() $3$
does not divide
$3$
does not divide
![]() $k$
, a blowup of the directed triangle has minimum semidegree
$k$
, a blowup of the directed triangle has minimum semidegree
![]() $\frac n3$
but does not contain a directed
$\frac n3$
but does not contain a directed
![]() $C_k$
. For cycle type
$C_k$
. For cycle type
![]() $0$
the bound on the minimum semidegree can be much lower: For each
$0$
the bound on the minimum semidegree can be much lower: For each
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $\eta \gt 0$
every large enough
$\eta \gt 0$
every large enough
![]() $n$
-vertex oriented graph of minimum semidegree at least
$n$
-vertex oriented graph of minimum semidegree at least
![]() $\eta n$
contains all oriented cycles of length at most
$\eta n$
contains all oriented cycles of length at most
![]() $k$
and cycle type
$k$
and cycle type
![]() $0$
[Reference Kelly, Kühn and Osthus20].
$0$
[Reference Kelly, Kühn and Osthus20].
As antidirected cycles have cycle type
![]() $0$
, the discussion from the previous paragraph implies that we can find short antidirected cycles with a minimum semidegree of
$0$
, the discussion from the previous paragraph implies that we can find short antidirected cycles with a minimum semidegree of
![]() $\eta n$
and antidirected cycles of any length with a minimum semidegree exceeding
$\eta n$
and antidirected cycles of any length with a minimum semidegree exceeding
![]() $\delta ^0(D)\geq \frac{3n}8+o(n)$
. In light of Theorem 1.2 it seems natural to suspect that an intermediate bound on the minimum semidegree could suffice for antidirected cycles of medium length. This is indeed possible, as our next result shows.
$\delta ^0(D)\geq \frac{3n}8+o(n)$
. In light of Theorem 1.2 it seems natural to suspect that an intermediate bound on the minimum semidegree could suffice for antidirected cycles of medium length. This is indeed possible, as our next result shows.
Theorem 1.4.
For all
![]() $\eta \in (0,1)$
there is
$\eta \in (0,1)$
there is
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $k\geq \eta n$
, every oriented graph
$k\geq \eta n$
, every oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains any antidirected cycle of length at most
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains any antidirected cycle of length at most
![]() $k$
.
$k$
.
We will in fact prove a more general result, Theorem 1.7 below. Theorem 1.7 focuses on embedding antidirected subdivisions of complete graphs. Before stating Theorem 1.7, let us review the history of (oriented) subdivisions in (oriented) graphs of high minimum (semi)degree.
For undirected graphs, Mader [Reference Mader26] proved that there is a function
![]() $g(h)$
such that every graph with minimum degree at least
$g(h)$
such that every graph with minimum degree at least
![]() $g(h)$
contains a subdivision of the complete graph
$g(h)$
contains a subdivision of the complete graph
![]() $K_h$
. Thomassen [Reference Thomassen32] showed that a direct translation of this result to digraphs is not true: For every function
$K_h$
. Thomassen [Reference Thomassen32] showed that a direct translation of this result to digraphs is not true: For every function
![]() $g(h)$
there is a digraph of minimum outdegree
$g(h)$
there is a digraph of minimum outdegree
![]() $g(h)$
that does not contain a subdivision of the complete digraph on
$g(h)$
that does not contain a subdivision of the complete digraph on
![]() $h\ge 3$
vertices. (A subdivision of a digraph
$h\ge 3$
vertices. (A subdivision of a digraph
![]() $D$
substitutes each edge of
$D$
substitutes each edge of
![]() $D$
with a directed path.) Mader [Reference Mader25] modified Thomassen’s construction showing that the same is true if we replace the minimum outdegree with the minimum semidegree. Crucially, the constructed digraphs have no even directed cycles (which appear in subdivisions of
$D$
with a directed path.) Mader [Reference Mader25] modified Thomassen’s construction showing that the same is true if we replace the minimum outdegree with the minimum semidegree. Crucially, the constructed digraphs have no even directed cycles (which appear in subdivisions of
![]() $K_3$
). Following these discoveries, Mader suggested to replace the subdivision of the complete digraph with the transitive tournament, that is, the tournament without directed cycles. He conjectured the following.
$K_3$
). Following these discoveries, Mader suggested to replace the subdivision of the complete digraph with the transitive tournament, that is, the tournament without directed cycles. He conjectured the following.
Conjecture 1.5 (Mader [Reference Mader25]). There is a function
![]() $f(h)$
such that every digraph of minimum outdegree at least
$f(h)$
such that every digraph of minimum outdegree at least
![]() $f(h)$
contains a subdivision of the transitive tournament of order
$f(h)$
contains a subdivision of the transitive tournament of order
![]() $h$
.
$h$
.
This conjecture is open even for
![]() $h=5$
. Recently, there has been much activity on variants of Conjecture 1.5, see for instance [Reference Aboulker, Cohen, Havet, Lochet, Moura and Thomassé1, Reference Cohen, Havet, Lochet and Nisse8, Reference Girão, Popielarz and Snyder11, Reference Gishboliner, Steiner and Szabó12, Reference Gishboliner, Steiner and Szabó13, Reference Jagger16, Reference Kühn, Osthus and Young24, Reference Scott28, Reference Steiner30]. Aboulker, Cohen, Havet, Lochet, Moura, and Thomassé [Reference Aboulker, Cohen, Havet, Lochet, Moura and Thomassé1] observed that Conjecture 1.5 is equivalent to the following conjecture.
$h=5$
. Recently, there has been much activity on variants of Conjecture 1.5, see for instance [Reference Aboulker, Cohen, Havet, Lochet, Moura and Thomassé1, Reference Cohen, Havet, Lochet and Nisse8, Reference Girão, Popielarz and Snyder11, Reference Gishboliner, Steiner and Szabó12, Reference Gishboliner, Steiner and Szabó13, Reference Jagger16, Reference Kühn, Osthus and Young24, Reference Scott28, Reference Steiner30]. Aboulker, Cohen, Havet, Lochet, Moura, and Thomassé [Reference Aboulker, Cohen, Havet, Lochet, Moura and Thomassé1] observed that Conjecture 1.5 is equivalent to the following conjecture.
Conjecture 1.6. [Reference Aboulker, Cohen, Havet, Lochet, Moura and Thomassé1] There is a function
![]() $f(h)$
such that every digraph of minimum semidegree at least
$f(h)$
such that every digraph of minimum semidegree at least
![]() $f(h)$
contains a subdivision of a transitive tournament of order
$f(h)$
contains a subdivision of a transitive tournament of order
![]() $h$
.
$h$
.
We will show a result along the lines of Conjectures 1.5 and 1.6 for oriented graphs. Namely, we will prove that any oriented graph of large minimum semidegree contains an antidirected orientation of a subdivision of a complete graph
![]() $K_h$
, where
$K_h$
, where
![]() $h$
cannot be too large. We can even choose the lengths of the antidirected paths in the subdivision, as long as the very short paths do not span a cycle. To make this more precise, we need some notation.
$h$
cannot be too large. We can even choose the lengths of the antidirected paths in the subdivision, as long as the very short paths do not span a cycle. To make this more precise, we need some notation.
For
![]() $h,k\in \mathbb N$
, consider a subdivision of
$h,k\in \mathbb N$
, consider a subdivision of
![]() $K_h$
where each edge
$K_h$
where each edge
![]() $e\in E(K_h)$
is substituted by a path of length
$e\in E(K_h)$
is substituted by a path of length
![]() $g(e)$
, with
$g(e)$
, with
![]() $\sum _{e\in E(K_h)}g(e)=k$
. Call any antidirected orientation of this graph a
$\sum _{e\in E(K_h)}g(e)=k$
. Call any antidirected orientation of this graph a
![]() $k$
-edge antisubdivision of
$k$
-edge antisubdivision of
![]() $K_h$
. If furthermore the edges of
$K_h$
. If furthermore the edges of
![]() $K_h$
with
$K_h$
with
![]() $g(e)\lt 3$
induce a forest in
$g(e)\lt 3$
induce a forest in
![]() $K_h$
, we say the
$K_h$
, we say the
![]() $k$
-edge antisubdivision is long. Note that in particular, if all edges of
$k$
-edge antisubdivision is long. Note that in particular, if all edges of
![]() $K_h$
are substituted with paths of length at least 3, the resulting antisubdivision is long.
$K_h$
are substituted with paths of length at least 3, the resulting antisubdivision is long.
Theorem 1.7.
For all
![]() $\eta \in (0,1)$
there are
$\eta \in (0,1)$
there are
![]() $n_0\in \mathbb N$
and
$n_0\in \mathbb N$
and
![]() $\gamma \gt 0$
such that for each
$\gamma \gt 0$
such that for each
![]() $n\ge n_0$
, each
$n\ge n_0$
, each
![]() $h\le \gamma \sqrt n$
and each
$h\le \gamma \sqrt n$
and each
![]() $k\ge \eta n$
the following holds. Every oriented graph
$k\ge \eta n$
the following holds. Every oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains each long
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
contains each long
![]() $k$
-edge antisubdivision of
$k$
-edge antisubdivision of
![]() $K_h$
.
$K_h$
.
As indicated above, Theorem 1.7 quickly implies Theorem 1.4.Footnote 1
Let us now turn back to oriented trees. Looking for parameters related to the appearance of certain oriented trees in a digraph, a natural alternative to the minimum semidegree is the edge density. In 1970, Graham [Reference Graham14] confirmed a conjecture he attributes to Erdős: for every antidirected tree
![]() $T$
there is a constant
$T$
there is a constant
![]() $c_T$
such that every sufficiently large directed graph
$c_T$
such that every sufficiently large directed graph
![]() $D$
on
$D$
on
![]() $n$
vertices and with at least
$n$
vertices and with at least
![]() $c_Tn$
edges contains
$c_Tn$
edges contains
![]() $T$
. A similar statement does not hold for other oriented trees: A bipartite graph on sets
$T$
. A similar statement does not hold for other oriented trees: A bipartite graph on sets
![]() $A$
and
$A$
and
![]() $B$
, with every edge oriented from
$B$
, with every edge oriented from
![]() $A$
to
$A$
to
![]() $B$
, has
$B$
, has
![]() $|A||B|$
edges, and only has antidirected subgraphs [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2, Reference Burr7].
$|A||B|$
edges, and only has antidirected subgraphs [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2, Reference Burr7].
In 1982, Burr [Reference Burr7] gave an improvement of Graham’s result: Every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $D$
with more than
$D$
with more than
![]() $4kn$
edges contains each antidirected tree
$4kn$
edges contains each antidirected tree
![]() $T$
on
$T$
on
![]() $k$
edges. He obtains this result by greedily embedding
$k$
edges. He obtains this result by greedily embedding
![]() $T$
into a suitable bipartite subgraph of
$T$
into a suitable bipartite subgraph of
![]() $D$
. Burr states that the bound
$D$
. Burr states that the bound
![]() $4kn$
on the number of edges can ‘almost certainly be made rather smaller’ and provides an example where
$4kn$
on the number of edges can ‘almost certainly be made rather smaller’ and provides an example where
![]() $(k-1)n$
edges are not sufficient: The
$(k-1)n$
edges are not sufficient: The
![]() $k$
-edge star with all edges directed outwards, and the complete bipartite graph
$k$
-edge star with all edges directed outwards, and the complete bipartite graph
![]() $K_{k-2,k-2}$
with half of the edges oriented in either direction in an appropriate way (one can also take the
$K_{k-2,k-2}$
with half of the edges oriented in either direction in an appropriate way (one can also take the
![]() $(k-1)$
-blow-up of the directed triangle). In 2013, Addario-Berry, Havet, Linhares Sales, Reed, and Thomassé [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2] formulated a conjecture which states that
$(k-1)$
-blow-up of the directed triangle). In 2013, Addario-Berry, Havet, Linhares Sales, Reed, and Thomassé [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2] formulated a conjecture which states that
![]() $(k-1)n$
is the correct bound.
$(k-1)n$
is the correct bound.
Conjecture 1.8. [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2] Every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $D$
with more than
$D$
with more than
![]() $(k-1)n$
edges contains each antidirected tree on
$(k-1)n$
edges contains each antidirected tree on
![]() $k$
edges.
$k$
edges.
The authors of [Reference Addario-Berry, Havet, Linhares Sales, Reed and Thomassé2] prove this conjecture for antidirected trees of diameter at most 3 and point out that it implies the well-known Erdős–Sós conjecture for graphs. If the digraph
![]() $D$
from Conjecture 1.8 is an oriented graph, it is known [Reference Klimošová and Stein22] that about
$D$
from Conjecture 1.8 is an oriented graph, it is known [Reference Klimošová and Stein22] that about
![]() $\frac 32 (k-1)n$
edges are sufficient to find all antidirected paths on
$\frac 32 (k-1)n$
edges are sufficient to find all antidirected paths on
![]() $k$
edges.
$k$
edges.
We show that Conjecture 1.8 is approximately true in oriented graphs for all balanced antidirected trees of bounded maximum degree.
Theorem 1.9.
For all
![]() $\eta \in (0,1)$
and
$\eta \in (0,1)$
and
![]() $c\in \mathbb N$
, there is
$c\in \mathbb N$
, there is
![]() $n_0\in \mathbb N$
such that for every
$n_0\in \mathbb N$
such that for every
![]() $n\ge n_0$
and every
$n\ge n_0$
and every
![]() $k\ge \eta n$
, every
$k\ge \eta n$
, every
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $D$
with more than
$D$
with more than
![]() $(1 + \eta )(k-1)n$
edges contains each balanced antidirected tree
$(1 + \eta )(k-1)n$
edges contains each balanced antidirected tree
![]() $T$
with
$T$
with
![]() $k$
edges and
$k$
edges and
![]() $\Delta (T)\leq (\!\log (n))^c$
.
$\Delta (T)\leq (\!\log (n))^c$
.
In particular, Conjecture 1.8 holds asymptotically for long antidirected paths in oriented graphs. Moreover, Theorem 1.9 implies the asymptotic bound
![]() $2(k-1)n$
for digraphs (as any digraph can be turned into an oriented graph by deleting at most half the edges).
$2(k-1)n$
for digraphs (as any digraph can be turned into an oriented graph by deleting at most half the edges).
The paper is organised as follows. We start with a sketch of the proofs of Theorems 1.4, 1.7 and 1.9 in Section 2. We then go through some preliminaries in Section 3. We give the proof of Theorem 1.4 in Section 5. We prove Theorem 1.7 in Section 6, and Theorem 1.9 in Section 7. In Section 8, we discuss some open questions.
2. Proof sketches
2.1. Connected antimatchings
Fundamental to our proofs is the concept of a connected antimatching: this is a set
![]() $M$
of disjoint edges in an oriented graph
$M$
of disjoint edges in an oriented graph
![]() $D$
such that every pair of edges in
$D$
such that every pair of edges in
![]() $M$
is connected by an antidirected walk in
$M$
is connected by an antidirected walk in
![]() $D$
(see Definition 4.5). Section 4 is dedicated to connected antimatchings. First, we will prove that any oriented graph of large minimum semidegree contains a large connected antimatching
$D$
(see Definition 4.5). Section 4 is dedicated to connected antimatchings. First, we will prove that any oriented graph of large minimum semidegree contains a large connected antimatching
![]() $M$
. Second, we will show that we can choose such an antimatching
$M$
. Second, we will show that we can choose such an antimatching
![]() $M$
in a way that the edges of
$M$
in a way that the edges of
![]() $M$
lie at bounded distance
$M$
lie at bounded distance
![]() $d$
from each other.
$d$
from each other.
2.2. Sketch of the proof of Theorem 1.4
Given an oriented graph
![]() $D$
and an antidirected tree
$D$
and an antidirected tree
![]() $T$
fulfilling the conditions of the theorem, we apply the digraph regularity lemma to
$T$
fulfilling the conditions of the theorem, we apply the digraph regularity lemma to
![]() $D$
to find a partition into a bounded number of clusters. The reduced oriented graph
$D$
to find a partition into a bounded number of clusters. The reduced oriented graph
![]() $R$
maintains the condition on the minimum semidegree and thus has a large connected antimatching whose edges lie at bounded distance from each other. (In particular, the clusters covered by
$R$
maintains the condition on the minimum semidegree and thus has a large connected antimatching whose edges lie at bounded distance from each other. (In particular, the clusters covered by
![]() $M$
can accommodate all of
$M$
can accommodate all of
![]() $T$
.)
$T$
.)
Now we turn to our antidirected tree
![]() $T$
. We decompose
$T$
. We decompose
![]() $T$
into a family
$T$
into a family
![]() $\mathcal{T}$
of small subtrees (for details see Section 3.2). As we prove in Section 3.3, it is possible to assign the trees in
$\mathcal{T}$
of small subtrees (for details see Section 3.2). As we prove in Section 3.3, it is possible to assign the trees in
![]() $\mathcal{T}$
to edges of
$\mathcal{T}$
to edges of
![]() $M$
in a way that they will fit comfortably into the corresponding clusters.
$M$
in a way that they will fit comfortably into the corresponding clusters.

Figure 1. Regularise
![]() $D$
to obtain
$D$
to obtain
![]() $R$
, with a connected antimatching marked in bold.
$R$
, with a connected antimatching marked in bold.

Figure 2. Embedding a small antidirected tree
![]() $S$
in
$S$
in
![]() $D$
.
$D$
.
We now embed
![]() $T$
as follows. We go through the decomposition of
$T$
as follows. We go through the decomposition of
![]() $T$
, embedding one small tree at a time, always keeping the embedded part connected in (the underlying tree of)
$T$
, embedding one small tree at a time, always keeping the embedded part connected in (the underlying tree of)
![]() $T$
. We embed the first
$T$
. We embed the first
![]() $d$
levels of each small tree
$d$
levels of each small tree
![]() $S$
into the clusters of an antiwalk in the reduced oriented graph that starts at the already embedded parent of the root of
$S$
into the clusters of an antiwalk in the reduced oriented graph that starts at the already embedded parent of the root of
![]() $S$
and leads to the edge
$S$
and leads to the edge
![]() $CD$
of
$CD$
of
![]() $M$
that was assigned to
$M$
that was assigned to
![]() $S$
. All later levels of
$S$
. All later levels of
![]() $S$
are embedded into clusters
$S$
are embedded into clusters
![]() $C$
and
$C$
and
![]() $D$
. Since
$D$
. Since
![]() $T$
has bounded maximum degree, the union of first
$T$
has bounded maximum degree, the union of first
![]() $d$
levels of the trees in
$d$
levels of the trees in
![]() $\mathcal{T}$
is very small, and therefore it is not a problem if the first
$\mathcal{T}$
is very small, and therefore it is not a problem if the first
![]() $d$
levels of
$d$
levels of
![]() $S$
are embedded outside the edge
$S$
are embedded outside the edge
![]() $CD$
. After going through all
$CD$
. After going through all
![]() $S$
, we have finished the embedding of
$S$
, we have finished the embedding of
![]() $T$
. See Figures1 and 2 for an illustration.
$T$
. See Figures1 and 2 for an illustration.
2.3. Sketch of the proof of Theorem 1.7
Let a long
![]() $k$
-antisubdivision of
$k$
-antisubdivision of
![]() $K_h$
be given, together with an oriented graph
$K_h$
be given, together with an oriented graph
![]() $D$
satisfying the conditions of the theorem. Since the antisubdivision is long, we can choose a set
$D$
satisfying the conditions of the theorem. Since the antisubdivision is long, we can choose a set
![]() $\mathcal P$
of long antidirected paths of the antisubdivision such that deleting two inner vertices of each of the antidirected paths in
$\mathcal P$
of long antidirected paths of the antisubdivision such that deleting two inner vertices of each of the antidirected paths in
![]() $\mathcal P$
leaves us with an antidirected tree
$\mathcal P$
leaves us with an antidirected tree
![]() $T$
.
$T$
.
As in the proof of Theorem 1.2, we find a connected antimatching
![]() $M$
in the reduced oriented graph of
$M$
in the reduced oriented graph of
![]() $D$
(see Section 4 for details). We embed
$D$
(see Section 4 for details). We embed
![]() $T$
with the help of
$T$
with the help of
![]() $M$
as follows. Fixing one edge
$M$
as follows. Fixing one edge
![]() $e$
of
$e$
of
![]() $M$
, we embed the branch vertices of the antisubdivision into the clusters corresponding to
$M$
, we embed the branch vertices of the antisubdivision into the clusters corresponding to
![]() $e$
. We embed the long antipaths into clusters corresponding to
$e$
. We embed the long antipaths into clusters corresponding to
![]() $e$
and to other edges of
$e$
and to other edges of
![]() $M$
, with the first and last vertices on these antipaths going to clusters on antidirected paths in the reduced oriented graph that connect the edges of
$M$
, with the first and last vertices on these antipaths going to clusters on antidirected paths in the reduced oriented graph that connect the edges of
![]() $M$
.
$M$
.
We finish the embedding by adding the two deleted vertices on the paths from
![]() $\mathcal P$
. Their neighbours were embedded into the clusters corresponding to the edge
$\mathcal P$
. Their neighbours were embedded into the clusters corresponding to the edge
![]() $e$
and regularity allows us to connect them by a
$e$
and regularity allows us to connect them by a
![]() $3$
-edge path on unused vertices. This finishes the embedding of the antisubdivision.
$3$
-edge path on unused vertices. This finishes the embedding of the antisubdivision.
2.4. Sketch of the proof of Theorem 1.9
Given the antidirected tree
![]() $T$
and the oriented graph
$T$
and the oriented graph
![]() $D$
as in the theorem, we start by finding an oriented subgraph
$D$
as in the theorem, we start by finding an oriented subgraph
![]() $D'$
of
$D'$
of
![]() $D$
where each vertex has either out-degree at least
$D$
where each vertex has either out-degree at least
![]() $\frac k2$
or out-degree
$\frac k2$
or out-degree
![]() $0$
, and either in-degree at least
$0$
, and either in-degree at least
![]() $\frac k2$
or in-degree
$\frac k2$
or in-degree
![]() $0$
. Moreover,
$0$
. Moreover,
![]() $D'$
has at least one edge.
$D'$
has at least one edge.
We then transform
![]() $D'$
into an oriented graph
$D'$
into an oriented graph
![]() $D''$
which has minimum semidegree exceeding
$D''$
which has minimum semidegree exceeding
![]() $\frac k2$
. More precisely,
$\frac k2$
. More precisely,
![]() $D''$
consists of four copies of
$D''$
consists of four copies of
![]() $D'$
, two of them with all edges reversed, glued together appropriately.
$D'$
, two of them with all edges reversed, glued together appropriately.
We now need Theorem 5.2, a variation of Theorem 1.2 which allows us to embed
![]() $T$
into
$T$
into
![]() $D''$
, guaranteeing that the root of
$D''$
, guaranteeing that the root of
![]() $T$
is embedded in a small set of
$T$
is embedded in a small set of
![]() $V(D)$
which we can choose before the embedding. We choose to have the root
$V(D)$
which we can choose before the embedding. We choose to have the root
![]() $v$
of
$v$
of
![]() $T$
embedded in a vertex
$T$
embedded in a vertex
![]() $w$
of one of the original copies of
$w$
of one of the original copies of
![]() $D$
(i.e. a copy with edges in the original orientation). We can further ensure that one of the edges at
$D$
(i.e. a copy with edges in the original orientation). We can further ensure that one of the edges at
![]() $v$
is embedded into an edge having the original orientation of
$v$
is embedded into an edge having the original orientation of
![]() $D$
. Then it is not hard to deduce that all of
$D$
. Then it is not hard to deduce that all of
![]() $T$
was embedded into an original copy of
$T$
was embedded into an original copy of
![]() $D$
, and therefore,
$D$
, and therefore,
![]() $T$
is contained in
$T$
is contained in
![]() $D$
.
$D$
.
3. Preliminaries
3.1. Basic digraph notation
A digraph is a pair of sets
![]() $(V,E)$
, where the elements of
$(V,E)$
, where the elements of
![]() $V$
are called vertices and
$V$
are called vertices and
![]() $E$
is a set of ordered pairs of distinct vertices in
$E$
is a set of ordered pairs of distinct vertices in
![]() $V$
, called edges. An oriented graph is a digraph that allows at most one edge between a pair of vertices.
$V$
, called edges. An oriented graph is a digraph that allows at most one edge between a pair of vertices.
The edges of a digraph
![]() $D$
are directed, and we will write
$D$
are directed, and we will write
![]() $uv$
for an edge that is directed from
$uv$
for an edge that is directed from
![]() $u$
to
$u$
to
![]() $v$
. While a digraph may have both edges
$v$
. While a digraph may have both edges
![]() $uv,vu$
for any pair of vertices
$uv,vu$
for any pair of vertices
![]() $u, v$
, an oriented graph has at most one of these edges. The out-degree
$u, v$
, an oriented graph has at most one of these edges. The out-degree
![]() $\delta ^+(v)$
of a vertex
$\delta ^+(v)$
of a vertex
![]() $v$
is the number of edges coming out of
$v$
is the number of edges coming out of
![]() $v$
, and the in-degree
$v$
, and the in-degree
![]() $\delta ^-(v)$
is defined analogously. The minimum semidegree
$\delta ^-(v)$
is defined analogously. The minimum semidegree
![]() $\delta ^0(D)$
of a digraph is the minimum over the out-degrees and the in-degrees of all vertices in
$\delta ^0(D)$
of a digraph is the minimum over the out-degrees and the in-degrees of all vertices in
![]() $D$
.
$D$
.
We denote by
![]() ${V_{\text{in}}}(D)$
the set of all vertices of
${V_{\text{in}}}(D)$
the set of all vertices of
![]() $D$
that have no outgoing edges, while
$D$
that have no outgoing edges, while
![]() $V_{\text{out}}(D)$
is the set of all vertices of
$V_{\text{out}}(D)$
is the set of all vertices of
![]() $D$
that have no incoming edges. A digraph
$D$
that have no incoming edges. A digraph
![]() $D$
is antidirected if
$D$
is antidirected if
![]() $V(D)={V_{\text{in}}}(D)\cup V_{\text{out}}(D)$
. If the underlying undirected graph of
$V(D)={V_{\text{in}}}(D)\cup V_{\text{out}}(D)$
. If the underlying undirected graph of
![]() $D$
is a tree, we also call
$D$
is a tree, we also call
![]() $D$
an antitree. Antipaths and anticycles are defined analogously. Note that anticycles are even. The length of an antipath or anticycle is the number of edges in it.
$D$
an antitree. Antipaths and anticycles are defined analogously. Note that anticycles are even. The length of an antipath or anticycle is the number of edges in it.
An antiwalk (or antidirected walk) is a sequence of edges that alternate directions, but we usually denote it by writing the sequence of the corresponding vertices. Note that an antiwalk may repeat vertices and edges, and a repeated vertex
![]() $v$
may have both outgoing and incoming edges in the antiwalk. The length of an antiwalk is the length of the corresponding sequence of edges. For instance, the antiwalk
$v$
may have both outgoing and incoming edges in the antiwalk. The length of an antiwalk is the length of the corresponding sequence of edges. For instance, the antiwalk
![]() $abab$
has length
$abab$
has length
![]() $3$
, while having only one edge.
$3$
, while having only one edge.
Finally, an antitree
![]() $T$
is balanced if
$T$
is balanced if
![]() $|V_{\text{in}}(T)|=|V_{\text{out}}(T)|$
. Note that antipaths of odd length are balanced.
$|V_{\text{in}}(T)|=|V_{\text{out}}(T)|$
. Note that antipaths of odd length are balanced.
3.2. Tree decompositions
In our proof of the main theorem, we will have to partition the given antitree into smaller trees. It will be enough to define this decomposition for undirected trees, as we can apply it later to the underlying graph of our antitree. This type of decomposition appeared in the literature already in the 1990’s, for instance in [Reference Ajtai, Komlós and Szemerédi3]. Here we use a version from [Reference Besomi, Pavez-Signé and Stein6]:
Definition 3.1 (
![]() $\beta$
-decomposition). Let
$\beta$
-decomposition). Let
![]() $\beta \in (0,1)$
, and let
$\beta \in (0,1)$
, and let
![]() $T$
be a tree on
$T$
be a tree on
![]() $k+1$
vertices, rooted at
$k+1$
vertices, rooted at
![]() $r$
. If there are a set
$r$
. If there are a set
![]() $W\subseteq V(T)$
and a family
$W\subseteq V(T)$
and a family
![]() $\mathcal{T}$
of disjoint rooted trees such that
$\mathcal{T}$
of disjoint rooted trees such that
-
(i)
 $r\in W$
;
$r\in W$
; -
(ii)
 $\mathcal{T}$
consists of the components of
$\mathcal{T}$
consists of the components of
 $T-W$
, and each
$T-W$
, and each
 $S\in \mathcal{T}$
is rooted at the vertex closest to the root of
$S\in \mathcal{T}$
is rooted at the vertex closest to the root of
 $T$
;
$T$
; -
(iii)
 $|S|\leq \beta k$
for each
$|S|\leq \beta k$
for each
 $S\in \mathcal{T}$
; and
$S\in \mathcal{T}$
; and
-
(iv)
 $|W| \le \frac 1\beta + 2$
,
$|W| \le \frac 1\beta + 2$
,
then the pair
![]() $(W,\mathcal{T})$
is called a
$(W,\mathcal{T})$
is called a
![]() $\beta$
-decomposition of
$\beta$
-decomposition of
![]() $T$
.
$T$
.
Lemma 3.2. [Reference Besomi, Pavez-Signé and Stein6] Let
![]() $\beta \in (0,1)$
, and let
$\beta \in (0,1)$
, and let
![]() $T$
be a tree on
$T$
be a tree on
![]() $k+1$
vertices, rooted at
$k+1$
vertices, rooted at
![]() $r$
. Then there is a
$r$
. Then there is a
![]() $\beta$
-decomposition
$\beta$
-decomposition
![]() $(W,\mathcal{T})$
of
$(W,\mathcal{T})$
of
![]() $T$
.
$T$
.
Let us see what happens to a balanced tree
![]() $T$
if we remove some vertices from the upper levels of the trees
$T$
if we remove some vertices from the upper levels of the trees
![]() $S\in \mathcal T$
of the tree-decomposition of
$S\in \mathcal T$
of the tree-decomposition of
![]() $T$
. We first define what exactly we wish to remove. As usual, the
$T$
. We first define what exactly we wish to remove. As usual, the
![]() $j$
th level of a tree
$j$
th level of a tree
![]() $S$
contains every vertex in
$S$
contains every vertex in
![]() $S$
that has distance
$S$
that has distance
![]() $j$
to the root of
$j$
to the root of
![]() $S$
.
$S$
.
Definition 3.3 (
![]() $Lev_m(S)$
,
$Lev_m(S)$
,
![]() $L_m(T)$
). Given
$L_m(T)$
). Given
![]() $j\in \mathbb N$
and a
$j\in \mathbb N$
and a
![]() $\beta$
-decomposition
$\beta$
-decomposition
![]() $(W, \mathcal{T})$
of a tree
$(W, \mathcal{T})$
of a tree
![]() $T$
, define
$T$
, define
![]() $Lev_j(S)$
as the union of the first
$Lev_j(S)$
as the union of the first
![]() $j$
levels of
$j$
levels of
![]() $S\in \mathcal{T}$
. Set
$S\in \mathcal{T}$
. Set
![]() $L_j(T; (W, \mathcal{T}) )=\bigcup _{S\in \mathcal{T}}Lev_j(S)$
, and write shorthand
$L_j(T; (W, \mathcal{T}) )=\bigcup _{S\in \mathcal{T}}Lev_j(S)$
, and write shorthand
![]() $L_j(T)$
if
$L_j(T)$
if
![]() $(W, \mathcal{T})$
is clear from the context.
$(W, \mathcal{T})$
is clear from the context.
We show now that after removing
![]() $L_j(T)$
from
$L_j(T)$
from
![]() $T$
for some bounded
$T$
for some bounded
![]() $j$
, the remainder of
$j$
, the remainder of
![]() $T$
is still relatively well balanced.
$T$
is still relatively well balanced.
Lemma 3.4.
Let
![]() $k, j\in \mathbb{N}^+$
,
$k, j\in \mathbb{N}^+$
,
![]() $\alpha, \beta \in (0, \frac 12)$
. Let
$\alpha, \beta \in (0, \frac 12)$
. Let
![]() $T$
be a balanced rooted antitree with
$T$
be a balanced rooted antitree with
![]() $k$
edges such that
$k$
edges such that
![]() $\Delta (T)\leq (\frac{\alpha \beta k}8)^{\frac 1{j+1}}$
. Let
$\Delta (T)\leq (\frac{\alpha \beta k}8)^{\frac 1{j+1}}$
. Let
![]() $(W,\mathcal{T})$
be a
$(W,\mathcal{T})$
be a
![]() $\beta$
-decomposition of
$\beta$
-decomposition of
![]() $T$
. Then,
$T$
. Then,
![]() $(1-\alpha )p_T \leq q_T \leq (1+ \alpha )p_T$
, where
$(1-\alpha )p_T \leq q_T \leq (1+ \alpha )p_T$
, where
Proof. Note that
![]() $L_j(T)$
is contained in the union of the balls of radius
$L_j(T)$
is contained in the union of the balls of radius
![]() $j$
centred at the vertices of
$j$
centred at the vertices of
![]() $W$
. Thus
$W$
. Thus
As
![]() $T$
is balanced, we easily deduce the desired inequalities.
$T$
is balanced, we easily deduce the desired inequalities.
3.3. Packing trees into edges
Once the given antitree is cut into small pieces
![]() $S$
, and we shaved off their first levels
$S$
, and we shaved off their first levels
![]() $L_j$
, the details of which are described in Section 3.2, we will have to decide how to pack the remainder of the small pieces into the edges of the connected antimatching of the reduced oriented graph. The following lemma shows how to allocate all of the
$L_j$
, the details of which are described in Section 3.2, we will have to decide how to pack the remainder of the small pieces into the edges of the connected antimatching of the reduced oriented graph. The following lemma shows how to allocate all of the
![]() $S\setminus L_j(T)$
.
$S\setminus L_j(T)$
.
Lemma 3.5.
Let
![]() $m, t\in \mathbb{N}$
,
$m, t\in \mathbb{N}$
,
![]() $\alpha \gt 0$
and let
$\alpha \gt 0$
and let
![]() $(p_i, q_i)_{i\in I}\subseteq \mathbb{N}^2$
be a family such that:
$(p_i, q_i)_{i\in I}\subseteq \mathbb{N}^2$
be a family such that:
-
(a)
 $(1-\alpha )\sum _{i\in I} p_i \leq \sum _{i\in I} q_i \leq (1+\alpha )\sum _{i\in I} p_i$
,
$(1-\alpha )\sum _{i\in I} p_i \leq \sum _{i\in I} q_i \leq (1+\alpha )\sum _{i\in I} p_i$
, -
(b)
 $p_i + q_i \leq \alpha m$
, for all
$p_i + q_i \leq \alpha m$
, for all
 $i\in I$
, and
$i\in I$
, and
-
(c)
 $\max \{\sum _{i\in I} p_i, \sum _{i\in I} q_i\} \lt (1-10\alpha )mt$
.
$\max \{\sum _{i\in I} p_i, \sum _{i\in I} q_i\} \lt (1-10\alpha )mt$
.
Then there is a partition
![]() $\mathcal{J}$
of
$\mathcal{J}$
of
![]() $I$
of size
$I$
of size
![]() $t$
such that for every
$t$
such that for every
![]() $J\in \mathcal{J}$
,
$J\in \mathcal{J}$
,
 \begin{equation*}\sum _{j\in J} p_j \leq (1-7\alpha )m { \ and \ } \sum _{j\in J} q_j \leq (1-7\alpha )m.\end{equation*}
\begin{equation*}\sum _{j\in J} p_j \leq (1-7\alpha )m { \ and \ } \sum _{j\in J} q_j \leq (1-7\alpha )m.\end{equation*}
Proof. For every
![]() $i\in I$
, set
$i\in I$
, set
![]() $\delta _i\;:\!=\;p_i-q_i$
and for every
$\delta _i\;:\!=\;p_i-q_i$
and for every
![]() $S\subseteq I$
, define
$S\subseteq I$
, define
![]() $\delta _S: = \sum _{i\in S} \delta _i$
. Let
$\delta _S: = \sum _{i\in S} \delta _i$
. Let
![]() $A_1, \ldots, A_t\subseteq I$
be disjoint sets such that for every
$A_1, \ldots, A_t\subseteq I$
be disjoint sets such that for every
![]() $j\in [t]$
,
$j\in [t]$
,
and such that, under these conditions,
![]() $R\;:\!=\;I\setminus (A_1\cup \ldots \cup A_t)$
is minimised. Note that for each
$R\;:\!=\;I\setminus (A_1\cup \ldots \cup A_t)$
is minimised. Note that for each
![]() $j\in R$
there is an index
$j\in R$
there is an index
![]() $k(j)\in [t]$
such that
$k(j)\in [t]$
such that
since otherwise, using the fact that
![]() $p_j\le \alpha m$
by (b), we have
$p_j\le \alpha m$
by (b), we have
a contradiction to (c). Next, we claim that
To see (3), suppose there are
![]() $a,b\in R$
with
$a,b\in R$
with
![]() $\delta _a\delta _b \lt 0$
. Say
$\delta _a\delta _b \lt 0$
. Say
![]() $p_a\geq p_b$
. Then there is an index
$p_a\geq p_b$
. Then there is an index
![]() $k(a)$
such that (2) holds with
$k(a)$
such that (2) holds with
![]() $j=a$
, and since
$j=a$
, and since
![]() $p_a\ge p_b$
, the inequality also holds when substituting
$p_a\ge p_b$
, the inequality also holds when substituting
![]() $p_a$
with
$p_a$
with
![]() $p_b$
. Moreover, since
$p_b$
. Moreover, since
![]() $a\in R$
, we know that neither
$a\in R$
, we know that neither
![]() $a$
nor
$a$
nor
![]() $b$
can be added to
$b$
can be added to
![]() $A_{k(a)}$
without violating (1), and thus
$A_{k(a)}$
without violating (1), and thus
However,
![]() $\delta _{A_{k(a)}} \in [{-}\alpha m, \alpha m]$
by (ii). So, since we assumed that
$\delta _{A_{k(a)}} \in [{-}\alpha m, \alpha m]$
by (ii). So, since we assumed that
![]() $\delta _a\delta _b\lt 0$
, it must be that
$\delta _a\delta _b\lt 0$
, it must be that
![]() $|\delta _a|+|\delta _b|\gt 2\alpha m$
. But this contradicts (b). We proved (3), which enables us to split the rest of the proof into two cases.
$|\delta _a|+|\delta _b|\gt 2\alpha m$
. But this contradicts (b). We proved (3), which enables us to split the rest of the proof into two cases.
Case 1:
![]() $\delta _i\ge 0$
for all
$\delta _i\ge 0$
for all
![]() $i\in R$
. For
$i\in R$
. For
![]() $k\in [t]$
, we let
$k\in [t]$
, we let
![]() $A^{\prime}_k\supseteq A_k$
be disjoint sets such that
$A^{\prime}_k\supseteq A_k$
be disjoint sets such that
![]() $\sum _{i\in A^{\prime}_k} p_i \leq (1-9\alpha )m$
for every
$\sum _{i\in A^{\prime}_k} p_i \leq (1-9\alpha )m$
for every
![]() $k\in [t]$
, and thus also,
$k\in [t]$
, and thus also,
Similarly as for (2), we can show that for each
![]() $j\in R'\;:\!=\;I\setminus (A^{\prime}_1\cup \ldots \cup A^{\prime}_t)$
there is an index
$j\in R'\;:\!=\;I\setminus (A^{\prime}_1\cup \ldots \cup A^{\prime}_t)$
there is an index
![]() $k'(j)\in [t]$
with
$k'(j)\in [t]$
with
![]() $ p_j+\sum _{i\in A^{\prime}_{k_p(j)}} p_i \leq (1-9\alpha )m$
, and thus, by (4),
$ p_j+\sum _{i\in A^{\prime}_{k_p(j)}} p_i \leq (1-9\alpha )m$
, and thus, by (4),
![]() $q_j+\sum _{i\in A^{\prime}_{k_p(j)}} q_i \leq (1-9\alpha )m$
. So
$q_j+\sum _{i\in A^{\prime}_{k_p(j)}} q_i \leq (1-9\alpha )m$
. So
![]() $R'=\emptyset$
, and we are done, taking
$R'=\emptyset$
, and we are done, taking
![]() $\mathcal{J}= \{A^{\prime}_1, \ldots, A^{\prime}_t\}$
.
$\mathcal{J}= \{A^{\prime}_1, \ldots, A^{\prime}_t\}$
.
Case 2:
![]() $\delta _i\le 0$
for all
$\delta _i\le 0$
for all
![]() $i\in R$
. We proceed as in Case 1, but choose sets
$i\in R$
. We proceed as in Case 1, but choose sets
![]() $A^{\prime}_k\supseteq A_k$
such that
$A^{\prime}_k\supseteq A_k$
such that
![]() $\sum _{i\in A^{\prime}_k} q_i \leq (1-9\alpha )m$
for every
$\sum _{i\in A^{\prime}_k} q_i \leq (1-9\alpha )m$
for every
![]() $k\in [t]$
. The rest of the argument is similar.
$k\in [t]$
. The rest of the argument is similar.
3.4. Diregularity
We will use the regularity method which goes back to Szemerédi’s work from the 1970’s [Reference Szemerédi31]. We will need regularity for oriented graphs, but start introducing the concept for undirected graphs. Let
![]() $G$
be a graph, let
$G$
be a graph, let
![]() $\varepsilon \gt 0$
and let
$\varepsilon \gt 0$
and let
![]() $A,B$
be two disjoint subsets of
$A,B$
be two disjoint subsets of
![]() $V(G)$
. The density of the pair
$V(G)$
. The density of the pair
![]() $(A,B)$
is
$(A,B)$
is
![]() $d(A,B)=\frac{|E(A,B)|}{|A|\cdot |B|}$
, with
$d(A,B)=\frac{|E(A,B)|}{|A|\cdot |B|}$
, with
![]() $|E(A,B)|$
denoting the number of edges between
$|E(A,B)|$
denoting the number of edges between
![]() $A$
and
$A$
and
![]() $B$
. The pair
$B$
. The pair
![]() $(A,B)$
is
$(A,B)$
is
![]() $\varepsilon$
-regular if
$\varepsilon$
-regular if
![]() $|d(X,Y)-d(A,B)|\lt \varepsilon$
for every
$|d(X,Y)-d(A,B)|\lt \varepsilon$
for every
![]() $X\subseteq A$
and
$X\subseteq A$
and
![]() $Y\subseteq B$
satisfying
$Y\subseteq B$
satisfying
![]() $|X|\gt \varepsilon |A|$
and
$|X|\gt \varepsilon |A|$
and
![]() $|Y|\gt \varepsilon |B|$
.
$|Y|\gt \varepsilon |B|$
.
Let
![]() $(A,B)$
be an
$(A,B)$
be an
![]() $\varepsilon$
-regular pair of density
$\varepsilon$
-regular pair of density
![]() $d$
and let
$d$
and let
![]() $Y\subseteq B$
be such that
$Y\subseteq B$
be such that
![]() $|Y|\gt \varepsilon |B|$
. A vertex
$|Y|\gt \varepsilon |B|$
. A vertex
![]() $x\in A$
is called
$x\in A$
is called
![]() $\varepsilon$
-typical (or simply typical) with respect to
$\varepsilon$
-typical (or simply typical) with respect to
![]() $Y$
if it has more than
$Y$
if it has more than
![]() $(d-\varepsilon )|Y|$
neighbours in
$(d-\varepsilon )|Y|$
neighbours in
![]() $Y$
. It is well known and easy to prove that
$Y$
. It is well known and easy to prove that
![]() $A$
has at most
$A$
has at most
![]() $\varepsilon |A|$
vertices that are not typical with respect to
$\varepsilon |A|$
vertices that are not typical with respect to
![]() $Y$
.
$Y$
.
A partition
![]() $\{V_0, \ldots, V_k\}$
of
$\{V_0, \ldots, V_k\}$
of
![]() $V(G)$
is called an
$V(G)$
is called an
![]() $\varepsilon$
-regular partition of
$\varepsilon$
-regular partition of
![]() $G$
if
$G$
if
-
(i)
 $|V_0|\leq \varepsilon |V|$
,
$|V_0|\leq \varepsilon |V|$
, -
(ii)
 $|V_1| = \ldots = |V_k|$
,
$|V_1| = \ldots = |V_k|$
, -
(iii) all but at most
 $\varepsilon k^2$
of the pairs
$\varepsilon k^2$
of the pairs
 $(V_i, V_j)$
, with
$(V_i, V_j)$
, with
 $1\leq i \lt j\leq k$
, are
$1\leq i \lt j\leq k$
, are
 $\varepsilon$
-regular.
$\varepsilon$
-regular.
Let
![]() $D$
be a digraph and let
$D$
be a digraph and let
![]() $A,B\subseteq V(D)$
disjoint. We denote by
$A,B\subseteq V(D)$
disjoint. We denote by
![]() $(A,B)$
the oriented subgraph of
$(A,B)$
the oriented subgraph of
![]() $D$
with vertex set
$D$
with vertex set
![]() $A\cup B$
and every edge directed from
$A\cup B$
and every edge directed from
![]() $A$
to
$A$
to
![]() $B$
in
$B$
in
![]() $D$
. In this case, we say the pair
$D$
. In this case, we say the pair
![]() $(A,B)$
is
$(A,B)$
is
![]() $\varepsilon$
-regular if the underlying graph is
$\varepsilon$
-regular if the underlying graph is
![]() $\varepsilon$
-regular. With these notions and based on the Szemerédi’s Regularity Lemma for graphs without orientation [Reference Szemerédi31], we show its version for digraphs as stated by Alon and Shapira in [Reference Alon and Shapira4]:
$\varepsilon$
-regular. With these notions and based on the Szemerédi’s Regularity Lemma for graphs without orientation [Reference Szemerédi31], we show its version for digraphs as stated by Alon and Shapira in [Reference Alon and Shapira4]:
Lemma 3.6 (Degree form of the Diregularity Lemma [Reference Alon and Shapira4]). For all
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
![]() $m_0\in \mathbb N$
, there are
$m_0\in \mathbb N$
, there are
![]() $M_0, n_0\in \mathbb N$
such that for each
$M_0, n_0\in \mathbb N$
such that for each
![]() $d\in [0,1]$
and for each digraph
$d\in [0,1]$
and for each digraph
![]() $D$
on
$D$
on
![]() $n\geq n_0$
vertices there are a partition of
$n\geq n_0$
vertices there are a partition of
![]() $V(D)$
into sets
$V(D)$
into sets
![]() $V_0, V_1, \ldots, V_k$
and a spanning subdigraph
$V_0, V_1, \ldots, V_k$
and a spanning subdigraph
![]() $D'$
of
$D'$
of
![]() $D$
, called the regularised digraph, such that the following holds:
$D$
, called the regularised digraph, such that the following holds:
 $m_0 \leq k \leq M_0$
,
$m_0 \leq k \leq M_0$
, $|V_0| \leq \varepsilon n$
and
$|V_0| \leq \varepsilon n$
and
 $|V_1| = \dotsc = |V_k| \;=\!:\; m$
,
$|V_1| = \dotsc = |V_k| \;=\!:\; m$
, $d_{D'}^+ (x) \gt d_D^+(x) - (d+\varepsilon )n$
for all vertices
$d_{D'}^+ (x) \gt d_D^+(x) - (d+\varepsilon )n$
for all vertices
 $x\in D$
,
$x\in D$
, $d_{D'}^- (x) \gt d_D^-(x) - (d+\varepsilon )n$
for all vertices
$d_{D'}^- (x) \gt d_D^-(x) - (d+\varepsilon )n$
for all vertices
 $x\in V(D)$
,
$x\in V(D)$
,for all
 $1\leq i\lt j\leq k$
and
$1\leq i\lt j\leq k$
and
 $i\neq j$
, the bipartite graph
$i\neq j$
, the bipartite graph
 $(V_i, V_j)_{D'}$
whose vertex classes are
$(V_i, V_j)_{D'}$
whose vertex classes are
 $V_i$
and
$V_i$
and
 $V_j$
and whose edge set consists of all the
$V_j$
and whose edge set consists of all the
 $V_i$
-
$V_i$
-
 $V_j$
edges in
$V_j$
edges in
 $D'$
is
$D'$
is
 $\varepsilon$
-regular and has density either 0 or at least
$\varepsilon$
-regular and has density either 0 or at least
 $d$
,
$d$
,for all
 $1\leq i \leq k$
the digraph
$1\leq i \leq k$
the digraph
 $D'[V_i]$
is empty.
$D'[V_i]$
is empty.
Given a regularised digraph
![]() $D'$
with clusters
$D'$
with clusters
![]() $V_1, \ldots, V_t$
, the reduced digraph
$V_1, \ldots, V_t$
, the reduced digraph
![]() $R$
is a digraph with vertices
$R$
is a digraph with vertices
![]() $V_1, \ldots, V_t$
such that the edge
$V_1, \ldots, V_t$
such that the edge
![]() $V_iV_j$
exists only if
$V_iV_j$
exists only if
![]() $D'$
contains a
$D'$
contains a
![]() $V_i$
-
$V_i$
-
![]() $V_j$
edge. Observe that,
$V_j$
edge. Observe that,
![]() $R$
need not be an oriented graph, even if
$R$
need not be an oriented graph, even if
![]() $D'$
is. However, it is possible [Reference Kelly, Kühn and Osthus21] to discard appropriate edges from the reduced digraph to find an oriented spanning subgraph
$D'$
is. However, it is possible [Reference Kelly, Kühn and Osthus21] to discard appropriate edges from the reduced digraph to find an oriented spanning subgraph
![]() $R'$
of
$R'$
of
![]() $R$
that preserves the minimum semidegree of the original oriented graph
$R$
that preserves the minimum semidegree of the original oriented graph
![]() $D$
(proportionally to the order of the reduced digraph). The new oriented graph
$D$
(proportionally to the order of the reduced digraph). The new oriented graph
![]() $R'$
is called the reduced oriented graph. This result is formalised in the following lemma.
$R'$
is called the reduced oriented graph. This result is formalised in the following lemma.
Lemma 3.7 (see [Reference Kelly, Kühn and Osthus21]). Let
![]() $\varepsilon, d\in [0,1]$
,
$\varepsilon, d\in [0,1]$
,
![]() $m_0\in \mathbb N$
, let
$m_0\in \mathbb N$
, let
![]() $G$
be a large enough oriented graph and let
$G$
be a large enough oriented graph and let
![]() $R'$
be the reduced digraph obtained by applying the Lemma 3.6 to
$R'$
be the reduced digraph obtained by applying the Lemma 3.6 to
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon, m_0$
and
$\varepsilon, m_0$
and
![]() $d$
. Then,
$d$
. Then,
![]() $R'$
has a spanning oriented subgraph
$R'$
has a spanning oriented subgraph
![]() $R$
with
$R$
with
-
(i)
 $\delta ^+(R) \geq \left(\frac{\delta ^+(G)}{|G|} - (3\varepsilon +d)\right)|R|,$
$\delta ^+(R) \geq \left(\frac{\delta ^+(G)}{|G|} - (3\varepsilon +d)\right)|R|,$
-
(ii)
 $\delta ^-(R) \geq \left(\frac{\delta ^-(G)}{|G|} - (3\varepsilon +d)\right)|R|.$
$\delta ^-(R) \geq \left(\frac{\delta ^-(G)}{|G|} - (3\varepsilon +d)\right)|R|.$
This oriented graph
![]() $R$
is called the
$R$
is called the
![]() $(\varepsilon, d)$
-reduced oriented graph.
$(\varepsilon, d)$
-reduced oriented graph.
3.5. Embedding small trees in antiwalks
We now show how to embed a small tree into an antiwalk of the reduced oriented graph. This will be useful for embedding the first levels of a piece
![]() $S$
of the decomposition of our antitree
$S$
of the decomposition of our antitree
![]() $T$
into an antiwalk leading to a suitable edge
$T$
into an antiwalk leading to a suitable edge
![]() $a_ib_i$
of the connected antimatching. The edge
$a_ib_i$
of the connected antimatching. The edge
![]() $a_ib_i$
will accommodate the rest of
$a_ib_i$
will accommodate the rest of
![]() $S$
.
$S$
.
We start with a convenient definition, expressing that the orientations of the small tree
![]() $S$
and the antiwalk coincide.
$S$
and the antiwalk coincide.
Definition 3.8 (Consistent antiwalk and antitree). Let
![]() $P$
be a non-trivial antiwalk and let
$P$
be a non-trivial antiwalk and let
![]() $T$
be a rooted antitree. We say
$T$
be a rooted antitree. We say
![]() $P$
and
$P$
and
![]() $T$
are consistent if one of the following holds:
$T$
are consistent if one of the following holds:
-
(i)
 $r(T)\in V_{\text{out}}(T)$
and
$r(T)\in V_{\text{out}}(T)$
and
 $P$
starts with an out-edge, or
$P$
starts with an out-edge, or
-
(ii)
 $r(T)\in V_{\text{in}}(T)$
and
$r(T)\in V_{\text{in}}(T)$
and
 $P$
starts with an in-edge.
$P$
starts with an in-edge.
Now we embed an antitree into a consistent antiwalk of a reduced digraph. A very similar result for undirected graphs was proved in [Reference Besomi, Pavez-Signé and Stein6].
Lemma 3.9.
Let
![]() $\varepsilon \in (0, \frac{1}{4})$
,
$\varepsilon \in (0, \frac{1}{4})$
,
![]() $m,h\in \mathbb{N}$
. Let
$m,h\in \mathbb{N}$
. Let
![]() $P=Q_0 \ldots Q_{h-1}Q_{h}$
be an antiwalk in an
$P=Q_0 \ldots Q_{h-1}Q_{h}$
be an antiwalk in an
![]() $(\varepsilon, 2\sqrt{\varepsilon })$
-reduced oriented graph
$(\varepsilon, 2\sqrt{\varepsilon })$
-reduced oriented graph
![]() $R$
of an oriented graph
$R$
of an oriented graph
![]() $D$
, where clusters have size
$D$
, where clusters have size
![]() $m$
. For
$m$
. For
![]() $0\leq i\leq h$
, let
$0\leq i\leq h$
, let
![]() $Z_i\subseteq Q_i$
be such that
$Z_i\subseteq Q_i$
be such that
![]() $|Z_i|\geq 3\sqrt{\varepsilon } m$
if
$|Z_i|\geq 3\sqrt{\varepsilon } m$
if
![]() $i\neq 0$
and
$i\neq 0$
and
![]() $|Z_0|\geq 3{\varepsilon } m$
. For
$|Z_0|\geq 3{\varepsilon } m$
. For
![]() $i=h-1, h$
, let
$i=h-1, h$
, let
![]() $X_{i}\subseteq Q_{i}\setminus Z_{i}$
with
$X_{i}\subseteq Q_{i}\setminus Z_{i}$
with
![]() $|X_i|\gt 3\sqrt \varepsilon m$
. Let
$|X_i|\gt 3\sqrt \varepsilon m$
. Let
![]() $S$
be a rooted antitree with
$S$
be a rooted antitree with
![]() $|S|\lt \frac \varepsilon{10} m$
such that
$|S|\lt \frac \varepsilon{10} m$
such that
![]() $P$
and
$P$
and
![]() $S$
are consistent. Then there is an embedding
$S$
are consistent. Then there is an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $S$
into
$S$
into
![]() $D$
such that
$D$
such that
-
(a) for each
 $i\le h$
, and for each
$i\le h$
, and for each
 $v$
from the
$v$
from the
 $i$
th level of
$i$
th level of
 $S$
,
$S$
,
 $\varphi (v)\in Z_i$
and
$\varphi (v)\in Z_i$
and
 $\varphi (v)$
is typical with respect to
$\varphi (v)$
is typical with respect to
 $Z_{i+1}$
(or with respect to
$Z_{i+1}$
(or with respect to
 $Z_{i-1}$
if
$Z_{i-1}$
if
 $i=h$
), and
$i=h$
), and
-
(b) for each
 $i\gt h$
, and for each
$i\gt h$
, and for each
 $v$
from the
$v$
from the
 $i$
th level of
$i$
th level of
 $S$
,
$S$
,
 $\varphi (v)\in X_{h-1}$
is typical with respect to
$\varphi (v)\in X_{h-1}$
is typical with respect to
 $X_{h}$
if
$X_{h}$
if
 $i-h$
is odd, and
$i-h$
is odd, and
 $\varphi (v)\in X_{h}$
is typical with respect to
$\varphi (v)\in X_{h}$
is typical with respect to
 $X_{h-1}$
if
$X_{h-1}$
if
 $i-h$
is even.
$i-h$
is even.
Proof. Let
![]() $r(S)$
be the root of
$r(S)$
be the root of
![]() $S$
and denote the embedding by
$S$
and denote the embedding by
![]() $\phi\; :\; V(S) \longrightarrow \cup _{i=0}^{h} Q_i$
. Suppose that
$\phi\; :\; V(S) \longrightarrow \cup _{i=0}^{h} Q_i$
. Suppose that
![]() $Q_0Q_1\in E(R)$
, and
$Q_0Q_1\in E(R)$
, and
![]() $r(S)\in V_{\text{out}}(S)$
, the other case is analogous.
$r(S)\in V_{\text{out}}(S)$
, the other case is analogous.
We embed
![]() $r(S)$
in a typical vertex of
$r(S)$
in a typical vertex of
![]() $Z_0$
with respect to
$Z_0$
with respect to
![]() $Z_1$
, and then embed successively, for
$Z_1$
, and then embed successively, for
![]() $i\lt h$
, the vertices from the
$i\lt h$
, the vertices from the
![]() $i$
th level into vertices from
$i$
th level into vertices from
![]() $Z_i$
that are typical to
$Z_i$
that are typical to
![]() $Z_{i+1}$
. (This is possible since we embed at most
$Z_{i+1}$
. (This is possible since we embed at most
![]() $|S|\lt \frac \varepsilon{10} m$
vertices in total, and since
$|S|\lt \frac \varepsilon{10} m$
vertices in total, and since
![]() $|Z_i|\geq 3\sqrt{\varepsilon }m$
for all
$|Z_i|\geq 3\sqrt{\varepsilon }m$
for all
![]() $i$
, while there are less than
$i$
, while there are less than
![]() $\varepsilon m$
atypical vertices in each
$\varepsilon m$
atypical vertices in each
![]() $Z_i$
.) For the vertices from the
$Z_i$
.) For the vertices from the
![]() $h$
th level we take care that their images are typical with respect to both
$h$
th level we take care that their images are typical with respect to both
![]() $Z_{h-1}$
and
$Z_{h-1}$
and
![]() $X_{h-1}$
. The vertices from later levels are embedded alternatingly into
$X_{h-1}$
. The vertices from later levels are embedded alternatingly into
![]() $X_{h-1}$
and
$X_{h-1}$
and
![]() $X_h$
, and we take care that their images are typical with respect to both
$X_h$
, and we take care that their images are typical with respect to both
![]() $Z_{h}$
and
$Z_{h}$
and
![]() $X_{h}$
, or both
$X_{h}$
, or both
![]() $Z_{h-1}$
and
$Z_{h-1}$
and
![]() $X_{h-1}$
, respectively.
$X_{h-1}$
, respectively.
4. Connected antimatchings
In this section we introduce the concept of a connected antimatching, which is central to our proof. We also prove two lemmas (Lemmas 4.6 and 4.8) relating the minimum semidegree of an oriented graph
![]() $D$
to the existence and size of a connected antimatching in
$D$
to the existence and size of a connected antimatching in
![]() $D$
, whose edges are not too distant from each other.
$D$
, whose edges are not too distant from each other.
Before we can introduce the notion of a connected antimatching, we need some preliminary definitions.
Definition 4.1 (in-vertex and out-vertex of an antiwalk). Let
![]() $P$
be an antiwalk, and let
$P$
be an antiwalk, and let
![]() $v\in V(P)$
. We call
$v\in V(P)$
. We call
![]() $v$
an out-vertex of
$v$
an out-vertex of
![]() $P$
if
$P$
if
![]() $P=v$
or
$P=v$
or
![]() $P$
has one or more edges of the form
$P$
has one or more edges of the form
![]() $vx$
. We call
$vx$
. We call
![]() $v$
an in-vertex of
$v$
an in-vertex of
![]() $P$
if
$P$
if
![]() $P=v$
or
$P=v$
or
![]() $P$
has one or more edges of the form
$P$
has one or more edges of the form
![]() $xv$
.
$xv$
.
Note that also in non-trivial walks a vertex can be both an in- and an out-vertex.
Definition 4.2 (out-walk; out-in-walk; out-out-walk). Let
![]() $C$
be an oriented graph with
$C$
be an oriented graph with
![]() $a,z\in V(C)$
. A non-trivial antiwalk
$a,z\in V(C)$
. A non-trivial antiwalk
![]() $P$
starting in
$P$
starting in
![]() $a$
and ending in
$a$
and ending in
![]() $z$
whose first edge is directed away from
$z$
whose first edge is directed away from
![]() $a$
is called an out-walk from
$a$
is called an out-walk from
![]() $a$
to
$a$
to
![]() $z$
. Call
$z$
. Call
![]() $P$
an out-in-walk if its last edge is directed towards
$P$
an out-in-walk if its last edge is directed towards
![]() $z$
, and an out-out-walk otherwise. Also call a trivial walk an out-out-walk.
$z$
, and an out-out-walk otherwise. Also call a trivial walk an out-out-walk.
Definition 4.3 (
![]() $In(C,a)$
;
$In(C,a)$
;
![]() $Out(C,a)$
). Let
$Out(C,a)$
). Let
![]() $C$
be an oriented graph with
$C$
be an oriented graph with
![]() $a\in V(C)$
. Then
$a\in V(C)$
. Then
![]() $\textrm{In}(C,a)$
is the set of all
$\textrm{In}(C,a)$
is the set of all
![]() $z\in V(C)$
such that there is an out-in-walk from
$z\in V(C)$
such that there is an out-in-walk from
![]() $a$
to
$a$
to
![]() $z$
, and
$z$
, and
![]() $\textrm{Out}(C,a)$
is the set of all
$\textrm{Out}(C,a)$
is the set of all
![]() $z\in V(C)$
such that there is an out-out-walk from
$z\in V(C)$
such that there is an out-out-walk from
![]() $a$
to
$a$
to
![]() $z$
.
$z$
.
Observe that
![]() $\textrm{In}(C,a)$
and
$\textrm{In}(C,a)$
and
![]() $\textrm{Out}(C,a)$
are not necessarily disjoint.
$\textrm{Out}(C,a)$
are not necessarily disjoint.
Definition 4.4 (anticonnected oriented graph). Let
![]() $C$
be an oriented graph with
$C$
be an oriented graph with
![]() $a\in V(C)$
. We say
$a\in V(C)$
. We say
![]() $(C,a)$
is anticonnected if
$(C,a)$
is anticonnected if
![]() $V(C)=\textrm{In}(C,a) \cup \textrm{Out}(C,a)$
.
$V(C)=\textrm{In}(C,a) \cup \textrm{Out}(C,a)$
.
Definition 4.5 (connected antimatching). Call
![]() $M=\{a_ib_i\}_{1\leq i\leq m}$
a connected antimatching of size
$M=\{a_ib_i\}_{1\leq i\leq m}$
a connected antimatching of size
![]() $m$
in an oriented graph
$m$
in an oriented graph
![]() $D$
if
$D$
if
![]() $M$
is a matching in the underlying graph of
$M$
is a matching in the underlying graph of
![]() $D$
and if
$D$
and if
![]() $a_i\in \textrm{Out}(D,a_1)$
for every
$a_i\in \textrm{Out}(D,a_1)$
for every
![]() $1\leq i\leq m$
. We write
$1\leq i\leq m$
. We write
![]() $V(M)$
for the set of all vertices covered by
$V(M)$
for the set of all vertices covered by
![]() $M$
.
$M$
.
Our first lemma of this section links the size of a connected antimatching in an oriented graph with its minimum semidegree. We can even choose a vertex to be included in the antimatching, as an outvertex of a matching edge (of course, by inverting all direction we could also choose it as an invertex).
Lemma 4.6.
Let
![]() $t\in \mathbb N^+$
, let
$t\in \mathbb N^+$
, let
![]() $D$
be an oriented graph with
$D$
be an oriented graph with
![]() $\delta ^0(D) \geq t$
, and let
$\delta ^0(D) \geq t$
, and let
![]() $w\in V(D)$
. Then
$w\in V(D)$
. Then
![]() $D$
has a connected antimatching
$D$
has a connected antimatching
![]() $M=\{a_ib_i\}_{1\leq i\leq t}$
of size
$M=\{a_ib_i\}_{1\leq i\leq t}$
of size
![]() $t$
, with
$t$
, with
![]() $w=a_1$
.
$w=a_1$
.
Proof. Let
![]() $M=\{a_ib_i\}_{1\leq i\leq m}$
be a connected antimatching of maximum size in
$M=\{a_ib_i\}_{1\leq i\leq m}$
be a connected antimatching of maximum size in
![]() $D$
with the property that
$D$
with the property that
![]() $w=a_1$
. Note that
$w=a_1$
. Note that
![]() $m \geq 1$
, because any single edge constitutes a connected antimatching. For contradiction, we assume that
$m \geq 1$
, because any single edge constitutes a connected antimatching. For contradiction, we assume that
![]() $m \lt t$
. Let
$m \lt t$
. Let
![]() $C$
be the largest induced subdigraph of
$C$
be the largest induced subdigraph of
![]() $D$
such that
$D$
such that
-
(a)
 $M\subseteq E(C)$
$M\subseteq E(C)$
-
(b)
 $a_i\in \textrm{Out}(C,a_1)$
for every
$a_i\in \textrm{Out}(C,a_1)$
for every
 $1\leq i\leq m$
and
$1\leq i\leq m$
and -
(c)
 $(C, a_1)$
is anticonnected.
$(C, a_1)$
is anticonnected.
We claim that
Indeed, let
![]() $v\in \textrm{In}(C,a_1)$
and suppose that there is a vertex
$v\in \textrm{In}(C,a_1)$
and suppose that there is a vertex
![]() $x\in N^-(v)\setminus V(C)$
. By definition of
$x\in N^-(v)\setminus V(C)$
. By definition of
![]() $\textrm{In}(C,a_1)$
, the digraph
$\textrm{In}(C,a_1)$
, the digraph
![]() $C$
contains an out-in-walk
$C$
contains an out-in-walk
![]() $P_v$
from
$P_v$
from
![]() $a_1$
to
$a_1$
to
![]() $v$
. Then
$v$
. Then
![]() $P_v$
and the edge
$P_v$
and the edge
![]() $xv$
form an out-out-walk from
$xv$
form an out-out-walk from
![]() $a_1$
to
$a_1$
to
![]() $x$
. Thus, adding the vertex
$x$
. Thus, adding the vertex
![]() $x$
and the edge
$x$
and the edge
![]() $xv$
to
$xv$
to
![]() $C$
, we obtain a subdigraph
$C$
, we obtain a subdigraph
![]() $C'$
of
$C'$
of
![]() $D$
that is larger than
$D$
that is larger than
![]() $C$
and fulfils (i)-(iii), a contradiction. The proof for
$C$
and fulfils (i)-(iii), a contradiction. The proof for
![]() $v\in \textrm{Out}(C,a_1)$
is analogous. This proves (5).
$v\in \textrm{Out}(C,a_1)$
is analogous. This proves (5).
Now, we show that
In order to see (6), let
![]() $v\in \textrm{In}(C,a_1)\setminus V(M)$
, and let
$v\in \textrm{In}(C,a_1)\setminus V(M)$
, and let
![]() $x\in N^-(v)$
. By (5), we know that
$x\in N^-(v)$
. By (5), we know that
![]() $x\in V(C)$
. For contradiction, assume
$x\in V(C)$
. For contradiction, assume
![]() $x\notin V(M)$
. Define
$x\notin V(M)$
. Define
![]() $a_{m+1} \;:\!=\; x$
,
$a_{m+1} \;:\!=\; x$
,
![]() $b_{m+1} \;:\!=\; v$
and set
$b_{m+1} \;:\!=\; v$
and set
![]() $M'\;:\!=\;\{a_ib_i\}_{1\leq i\leq m+1}$
. Consider an out-in-walk from
$M'\;:\!=\;\{a_ib_i\}_{1\leq i\leq m+1}$
. Consider an out-in-walk from
![]() $a_1$
to
$a_1$
to
![]() $v$
and add the edge
$v$
and add the edge
![]() $xv$
at the end to see that
$xv$
at the end to see that
![]() $x\in \textrm{Out}(C,a_1)$
. So
$x\in \textrm{Out}(C,a_1)$
. So
![]() $M'$
is a connected antimatching of size
$M'$
is a connected antimatching of size
![]() $m+1$
, with
$m+1$
, with
![]() $w=a_1$
, a contradiction to the choice of
$w=a_1$
, a contradiction to the choice of
![]() $M$
. We can proceed similarly for
$M$
. We can proceed similarly for
![]() $v\in \textrm{Out}(C,a_1)\setminus V(M)$
. This proves (6).
$v\in \textrm{Out}(C,a_1)\setminus V(M)$
. This proves (6).
Next, we claim that
To prove (7) by contradiction, we start by considering a vertex
![]() $u$
in
$u$
in
![]() $V(C)\setminus V(M)$
. Since
$V(C)\setminus V(M)$
. Since
![]() $\delta ^0(D) \geq t$
and because of (6), we know that if
$\delta ^0(D) \geq t$
and because of (6), we know that if
![]() $u\in \textrm{In}(C,a_1)$
, then
$u\in \textrm{In}(C,a_1)$
, then
![]() $u$
has at least
$u$
has at least
![]() $t$
in-neighbours in
$t$
in-neighbours in
![]() $V(M)$
, and if
$V(M)$
, and if
![]() $u\in \textrm{Out}(C,a_1)$
, then
$u\in \textrm{Out}(C,a_1)$
, then
![]() $u$
at least
$u$
at least
![]() $t$
out-neighbours in
$t$
out-neighbours in
![]() $V(M)$
. Now suppose there are two distinct vertices in
$V(M)$
. Now suppose there are two distinct vertices in
![]() $V(C)\setminus V(M)$
. Since we assume that
$V(C)\setminus V(M)$
. Since we assume that
![]() $|M|\lt t$
, there are distinct
$|M|\lt t$
, there are distinct
![]() $u_1,u_2\in V(C)\setminus V(M)$
, edges
$u_1,u_2\in V(C)\setminus V(M)$
, edges
![]() $e_1, e_2\in E(C)$
, an index
$e_1, e_2\in E(C)$
, an index
![]() $j\le t-1$
and an edge
$j\le t-1$
and an edge
![]() $v_1v_2\;:\!=\;a_jb_j\in M$
such that for each
$v_1v_2\;:\!=\;a_jb_j\in M$
such that for each
![]() $i=1,2$
one of the following holds:
$i=1,2$
one of the following holds:
 $u_i\in \textrm{In}(C,a_1)$
and
$u_i\in \textrm{In}(C,a_1)$
and
 $e_i=v_iu_i$
, or
$e_i=v_iu_i$
, or $u_i\in \textrm{Out}(C,a_1)$
and
$u_i\in \textrm{Out}(C,a_1)$
and
 $e_i=u_iv_i$
, or
$e_i=u_iv_i$
, or
If possible, choose
![]() $j\neq 1$
, and if that is not possible try to choose
$j\neq 1$
, and if that is not possible try to choose
![]() $u_1$
in a way that
$u_1$
in a way that
![]() $e_1=a_1u_1$
.
$e_1=a_1u_1$
.
Obtain
![]() $M'$
from
$M'$
from
![]() $M$
by adding
$M$
by adding
![]() $e_1$
and
$e_1$
and
![]() $e_2$
to
$e_2$
to
![]() $M$
and removing
$M$
and removing
![]() $e_3$
. Note that for
$e_3$
. Note that for
![]() $i=1,2$
, if
$i=1,2$
, if
![]() $e_i=u_iv_i$
then
$e_i=u_iv_i$
then
![]() $u_i\in \textrm{Out}(C,a_1)$
, and furthermore, if
$u_i\in \textrm{Out}(C,a_1)$
, and furthermore, if
![]() $e_i=v_iu_i$
then
$e_i=v_iu_i$
then
![]() $u_i\in \textrm{In}(C,a_1)$
, which means that
$u_i\in \textrm{In}(C,a_1)$
, which means that
![]() $u_i$
is reachable by an out-in-walk from
$u_i$
is reachable by an out-in-walk from
![]() $a_1$
, to which we can add the edge
$a_1$
, to which we can add the edge
![]() $v_iu_i$
to obtain an out-out-walk from
$v_iu_i$
to obtain an out-out-walk from
![]() $a_1$
to
$a_1$
to
![]() $v_i$
, implying that
$v_i$
, implying that
![]() $v_i\in \textrm{Out}(C,a_1)$
. So, in the case that
$v_i\in \textrm{Out}(C,a_1)$
. So, in the case that
![]() $j\neq 1$
, and in the case that
$j\neq 1$
, and in the case that
![]() $j=1$
and
$j=1$
and
![]() $e_1=v_1u_1$
, we know that
$e_1=v_1u_1$
, we know that
![]() $M'$
is a connected antimatching which is larger than
$M'$
is a connected antimatching which is larger than
![]() $M$
, with
$M$
, with
![]() $w$
being the outvertex of a matching edge we can call
$w$
being the outvertex of a matching edge we can call
![]() $a_1b_1$
. This is a contradiction to the choice of
$a_1b_1$
. This is a contradiction to the choice of
![]() $M$
. Thus
$M$
. Thus
![]() $j=1$
and
$j=1$
and
![]() $e_1=u_1a_1$
.
$e_1=u_1a_1$
.
Note that the fact that
![]() $j=1$
implies that both
$j=1$
implies that both
![]() $u_1$
and
$u_1$
and
![]() $u_2$
have only
$u_2$
have only
![]() $t-2$
out- or in-neighbours in
$t-2$
out- or in-neighbours in
![]() $V(M)\setminus \{a_1, b_1\}$
, where we count out-neighbours for
$V(M)\setminus \{a_1, b_1\}$
, where we count out-neighbours for
![]() $u_i$
if
$u_i$
if
![]() $u_i\in \textrm{Out}(C,a_1)$
and in-neighbours otherwise. Thus both are connected by edges to both of
$u_i\in \textrm{Out}(C,a_1)$
and in-neighbours otherwise. Thus both are connected by edges to both of
![]() $a_1, b_1$
. Since we would have chosen
$a_1, b_1$
. Since we would have chosen
![]() $e_1=a_1u_1$
if that was possible for a choice of
$e_1=a_1u_1$
if that was possible for a choice of
![]() $u_1$
, we know that both
$u_1$
, we know that both
![]() $u_1$
,
$u_1$
,
![]() $u_2$
are in-neighbours of
$u_2$
are in-neighbours of
![]() $a_1$
, in fact,
$a_1$
, in fact,
![]() $a_1$
has no out-neighbours outside
$a_1$
has no out-neighbours outside
![]() $V(M)$
. So, because of our bound on the minimum semidegree,
$V(M)$
. So, because of our bound on the minimum semidegree,
![]() $a_1$
has at least
$a_1$
has at least
![]() $t-1$
out-neighbours in
$t-1$
out-neighbours in
![]() $V(M)\setminus \{a_1, b_1\}$
. As the outdegree of
$V(M)\setminus \{a_1, b_1\}$
. As the outdegree of
![]() $u_1$
into
$u_1$
into
![]() $V(M)\setminus \{a_1, b_1\}$
is at least
$V(M)\setminus \{a_1, b_1\}$
is at least
![]() $t-2$
, we find an edge
$t-2$
, we find an edge
![]() $a_jb_j\in M$
, with
$a_jb_j\in M$
, with
![]() $j\neq 1$
, such that
$j\neq 1$
, such that
![]() $a_1a_j, u_1b_j\in E(D)$
or
$a_1a_j, u_1b_j\in E(D)$
or
![]() $a_1b_j, u_1a_j\in E(D)$
. Adding these two edges and
$a_1b_j, u_1a_j\in E(D)$
. Adding these two edges and
![]() $e_2$
to
$e_2$
to
![]() $M$
while deleting
$M$
while deleting
![]() $a_1b_1$
and
$a_1b_1$
and
![]() $a_jb_j$
gives a connected antimatching
$a_jb_j$
gives a connected antimatching
![]() $M''$
, which is larger than
$M''$
, which is larger than
![]() $M$
, and where
$M$
, and where
![]() $a_1=w$
(choosing the corresponding edge as
$a_1=w$
(choosing the corresponding edge as
![]() $a_1b_1$
). Therefore, inequality (7) holds.
$a_1b_1$
). Therefore, inequality (7) holds.
By (7), and since we assume
![]() $M$
to have at most
$M$
to have at most
![]() $t-1$
edges, we see that
$t-1$
edges, we see that
Now, by (5), the out-neighbourhood of
![]() $a_1$
is contained in
$a_1$
is contained in
![]() $V(C)$
and thus is a subset of
$V(C)$
and thus is a subset of
![]() $\textrm{In}(C,a_1)$
. Similarly, the in-neighbourhood of
$\textrm{In}(C,a_1)$
. Similarly, the in-neighbourhood of
![]() $b_1$
is a subset of
$b_1$
is a subset of
![]() $\textrm{Out}(C,a_1)$
. Considering the minimum semidegree of
$\textrm{Out}(C,a_1)$
. Considering the minimum semidegree of
![]() $D$
, we deduce that
$D$
, we deduce that
By (8), we conclude
![]() $\textrm{In}(C,a_1) \cap \textrm{Out}(C,a_1) \neq \emptyset$
and thus contains a vertex
$\textrm{In}(C,a_1) \cap \textrm{Out}(C,a_1) \neq \emptyset$
and thus contains a vertex
![]() $v$
. Because of (5), both the in-neighbourhood and the out-neighbourhood of
$v$
. Because of (5), both the in-neighbourhood and the out-neighbourhood of
![]() $v$
are contained in
$v$
are contained in
![]() $C$
. As each of these two disjoint sets has at least
$C$
. As each of these two disjoint sets has at least
![]() $t$
elements,
$t$
elements,
![]() $C$
has at least
$C$
has at least
![]() $2t$
vertices, a contradiction to (8).
$2t$
vertices, a contradiction to (8).
For the next lemma, we need another definition.
Definition 4.7 (out-out-distance
![]() $\textrm{ood}(a,a')$
; out-in-distance
$\textrm{ood}(a,a')$
; out-in-distance
![]() $\textrm{oid}(a,a')$
). In an oriented graph
$\textrm{oid}(a,a')$
). In an oriented graph
![]() $D$
, the out-out-distance
$D$
, the out-out-distance
![]() $\textrm{ood}(a,a')$
between two vertices
$\textrm{ood}(a,a')$
between two vertices
![]() $a, a'\in V(D)$
is the length of the shortest out-out-walk from
$a, a'\in V(D)$
is the length of the shortest out-out-walk from
![]() $a$
to
$a$
to
![]() $a'$
, if such a walk exists. Otherwise
$a'$
, if such a walk exists. Otherwise
![]() $\textrm{ood}(a,a')=\infty$
.
$\textrm{ood}(a,a')=\infty$
.
Similarly, the out-in-distance
![]() $\textrm{oid}(a,a')$
between two vertices
$\textrm{oid}(a,a')$
between two vertices
![]() $a, a'\in V(D)$
is the length of the shortest out-in-walk from
$a, a'\in V(D)$
is the length of the shortest out-in-walk from
![]() $a$
to
$a$
to
![]() $a'$
, if such a walk exists, and otherwise
$a'$
, if such a walk exists, and otherwise
![]() $\textrm{oid}(a,a')=\infty$
.
$\textrm{oid}(a,a')=\infty$
.
Observe that
![]() $\textrm{ood}(a,a)=0$
and for edges
$\textrm{ood}(a,a)=0$
and for edges
![]() $ab,a'b'$
of a connected antimatching,
$ab,a'b'$
of a connected antimatching,
![]() $\textrm{ood}(a,a')$
is finite by definition. For use in the proof of the following lemma, we define
$\textrm{ood}(a,a')$
is finite by definition. For use in the proof of the following lemma, we define
![]() $\textrm{ood}(M)=\sum _{i=2}^{d} \textrm{ood}(a_1, a_i)$
, where
$\textrm{ood}(M)=\sum _{i=2}^{d} \textrm{ood}(a_1, a_i)$
, where
![]() $M = \{a_ib_i\}_{1\leq i\leq t}$
is a connected antimatching.
$M = \{a_ib_i\}_{1\leq i\leq t}$
is a connected antimatching.
Lemma 4.8.
Let
![]() $t\in \mathbb N$
and let
$t\in \mathbb N$
and let
![]() $D$
be an oriented graph with
$D$
be an oriented graph with
![]() $\delta ^0(D)\geq t$
. Let
$\delta ^0(D)\geq t$
. Let
![]() $w\in V(D)$
. Then
$w\in V(D)$
. Then
![]() $D$
contains a connected antimatching
$D$
contains a connected antimatching
![]() $M = \{a_ib_i\}_{1\leq i\leq t}$
, with
$M = \{a_ib_i\}_{1\leq i\leq t}$
, with
![]() $w=a_1$
, and such that for every
$w=a_1$
, and such that for every
![]() $1\leq i\leq t$
,
$1\leq i\leq t$
,
![]() $\textrm{ood}(a_1, a_i) \leq 8t$
.
$\textrm{ood}(a_1, a_i) \leq 8t$
.
Proof. By Lemma 4.6, we know that
![]() $D$
contains a connected antimatching
$D$
contains a connected antimatching
![]() $M'=\{a^{\prime}_ib^{\prime}_i\}_{1\leq i\leq t}$
with
$M'=\{a^{\prime}_ib^{\prime}_i\}_{1\leq i\leq t}$
with
![]() $w=a^{\prime}_1$
. Among all such antimatchings choose
$w=a^{\prime}_1$
. Among all such antimatchings choose
![]() $M=\{a_ib_i\}_{1\leq i\leq t}$
such that
$M=\{a_ib_i\}_{1\leq i\leq t}$
such that
![]() $\textrm{ood}(M)$
is minimised. For the sake of contradiction, suppose there exists
$\textrm{ood}(M)$
is minimised. For the sake of contradiction, suppose there exists
![]() $k$
with
$k$
with
![]() $2\le k\le t$
such that
$2\le k\le t$
such that
![]() $\textrm{ood}(a_1, a_k)\gt 8d$
. Let
$\textrm{ood}(a_1, a_k)\gt 8d$
. Let
![]() $P$
be a shortest out-out-walk from
$P$
be a shortest out-out-walk from
![]() $a_1$
to
$a_1$
to
![]() $a_k$
. We claim that
$a_k$
. We claim that
Indeed, suppose vertex
![]() $v$
appears at least twice as an in-vertex on
$v$
appears at least twice as an in-vertex on
![]() $P$
. Then there are distinct vertices
$P$
. Then there are distinct vertices
![]() $x,y\in V(D)$
such that
$x,y\in V(D)$
such that
![]() $P=P_1xvP_2yvP_3$
(where the each of paths
$P=P_1xvP_2yvP_3$
(where the each of paths
![]() $P_i$
is allowed to be empty). The antiwalk
$P_i$
is allowed to be empty). The antiwalk
![]() $P_1xvP_3$
is shorter than
$P_1xvP_3$
is shorter than
![]() $P$
, a contradiction to the choice of
$P$
, a contradiction to the choice of
![]() $P$
. We can argue similarly if
$P$
. We can argue similarly if
![]() $v$
appears twice on
$v$
appears twice on
![]() $P$
as an out-vertex. This proves (9).
$P$
as an out-vertex. This proves (9).
From (9) it follows that
![]() $P$
does not repeat edges. Therefore, and since we assumed that
$P$
does not repeat edges. Therefore, and since we assumed that
![]() $P$
has length greater than
$P$
has length greater than
![]() $8t$
, we know that
$8t$
, we know that
By (9), every
![]() $a_i$
is incident to at most 4 edges in
$a_i$
is incident to at most 4 edges in
![]() $P$
. The same holds for every
$P$
. The same holds for every
![]() $b_i$
. So at most
$b_i$
. So at most
![]() $8t$
edges have one of their extremes on
$8t$
edges have one of their extremes on
![]() $M$
, and hence, by (10), there is an edge
$M$
, and hence, by (10), there is an edge
![]() $xy$
on
$xy$
on
![]() $P$
such that
$P$
such that
![]() $x,y\notin V(M)$
. Replacing
$x,y\notin V(M)$
. Replacing
![]() $a_kb_k$
with
$a_kb_k$
with
![]() $xy$
in
$xy$
in
![]() $M$
, we obtain a connected antimatching
$M$
, we obtain a connected antimatching
![]() $M'$
of size
$M'$
of size
![]() $t$
with
$t$
with
![]() $\textrm{ood}(M')\lt \textrm{ood}(M)$
, a contradiction to the choice of
$\textrm{ood}(M')\lt \textrm{ood}(M)$
, a contradiction to the choice of
![]() $M$
.
$M$
.
5. Antitrees: The proof of Theorem 1.2
Instead of Theorem 1.2, we will prove a slightly stronger result, namely Theorem 5.2 below. The additional properties of Theorem 5.2 will be necessary for the proof of Theorem 1.9.
Let us define the following shorthand notation.
Definition 5.1.
For digraphs
![]() $A$
and
$A$
and
![]() $D$
, we write
$D$
, we write
![]() $A\subseteq _\gamma D$
if for each set
$A\subseteq _\gamma D$
if for each set
![]() $V^*\subseteq V(D)$
of size at least
$V^*\subseteq V(D)$
of size at least
![]() $\gamma |V(D)|$
and for each
$\gamma |V(D)|$
and for each
![]() $x\in V(A)$
, there is an embedding of
$x\in V(A)$
, there is an embedding of
![]() $A$
in
$A$
in
![]() $D$
with
$D$
with
![]() $x$
mapped to
$x$
mapped to
![]() $V^*$
.
$V^*$
.
Here is the result that immediately implies Theorem 1.2.
Theorem 5.2.
For all
![]() $\eta \in (0,1)$
,
$\eta \in (0,1)$
,
![]() $c\in \mathbb N$
there is
$c\in \mathbb N$
there is
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $k\geq \eta n$
the following holds for every oriented graph
$k\geq \eta n$
the following holds for every oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices and every balanced antidirected tree
$n$
vertices and every balanced antidirected tree
![]() $T$
with
$T$
with
![]() $k$
edges. If
$k$
edges. If
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
and
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
and
![]() $\Delta (T)\leq (\!\log (n))^c$
, then
$\Delta (T)\leq (\!\log (n))^c$
, then
![]() $T\subseteq _\eta D$
.
$T\subseteq _\eta D$
.
In the remainder of this section, we prove Theorem 5.2.
Proof of Theorem
5.2
. We will first define our constants, then prepare the given digraph
![]() $D$
and the antitree
$D$
and the antitree
![]() $T$
and finally proceed to embed
$T$
and finally proceed to embed
![]() $T$
in
$T$
in
![]() $D$
.
$D$
.
Setting the constants. We define our constants
![]() $\varepsilon, \beta$
and
$\varepsilon, \beta$
and
![]() $n_0$
so that
$n_0$
so that
More precisely, given
![]() $\eta$
and
$\eta$
and
![]() $c$
, we set
$c$
, we set
![]() $\varepsilon \;:\!=\; \frac{\eta ^2}{10^5}$
. Lemma 3.6 with input
$\varepsilon \;:\!=\; \frac{\eta ^2}{10^5}$
. Lemma 3.6 with input
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $m_0\;:\!=\;\lceil \frac 1\varepsilon \rceil$
gives constants
$m_0\;:\!=\;\lceil \frac 1\varepsilon \rceil$
gives constants
![]() $n^{\prime}_0$
and
$n^{\prime}_0$
and
![]() $M_0$
such that we can apply the lemma to digraphs on
$M_0$
such that we can apply the lemma to digraphs on
![]() $n\geq n^{\prime}_0$
vertices. Set
$n\geq n^{\prime}_0$
vertices. Set
![]() $\beta \;:\!=\;\frac{\varepsilon }{100 M_0}$
, and choose
$\beta \;:\!=\;\frac{\varepsilon }{100 M_0}$
, and choose
![]() $n_0\ge n^{\prime}_0$
such that
$n_0\ge n^{\prime}_0$
such that
Finally, let
![]() $n\geq n_0$
and let
$n\geq n_0$
and let
![]() $k\geq \eta n$
.
$k\geq \eta n$
.
Objective. Let
![]() $D$
be an oriented graph
$D$
be an oriented graph
![]() $D$
on
$D$
on
![]() $n$
vertices, with
$n$
vertices, with
![]() $\delta ^0 (D)\gt (1 + \eta )\frac k2$
. Let
$\delta ^0 (D)\gt (1 + \eta )\frac k2$
. Let
![]() $T$
be a balanced antidirected tree
$T$
be a balanced antidirected tree
![]() $T$
with
$T$
with
![]() $k$
edges, with
$k$
edges, with
![]() $\Delta (T)\leq (\!\log (n))^c$
. We need to show that for every
$\Delta (T)\leq (\!\log (n))^c$
. We need to show that for every
![]() $V^*\subseteq V(D)$
with
$V^*\subseteq V(D)$
with
![]() $|V^*|\ge \eta n$
, the antitree
$|V^*|\ge \eta n$
, the antitree
![]() $T$
can be embedded in
$T$
can be embedded in
![]() $D$
, with
$D$
, with
![]() $x$
embedded in
$x$
embedded in
![]() $V^*$
.
$V^*$
.
So let such
![]() $V^*\subseteq V(D)$
and
$V^*\subseteq V(D)$
and
![]() $x\in V(T)$
be given. Note that we can assume that
$x\in V(T)$
be given. Note that we can assume that
![]() $x\in V_{\text{out}}(T)$
, as otherwise we could switch the orientations of
$x\in V_{\text{out}}(T)$
, as otherwise we could switch the orientations of
![]() $D$
and of
$D$
and of
![]() $T$
, which would move
$T$
, which would move
![]() $x$
to
$x$
to
![]() $\textrm{Out}(T)$
. Once
$\textrm{Out}(T)$
. Once
![]() $T$
is embedded, we switch all orientations back to normal.
$T$
is embedded, we switch all orientations back to normal.
Preparing the oriented graph
![]() $D$
. We apply Lemma 3.6 with
$D$
. We apply Lemma 3.6 with
![]() $d=2\sqrt{\varepsilon }$
to obtain
$d=2\sqrt{\varepsilon }$
to obtain
![]() $D'$
, a digraph with
$D'$
, a digraph with
![]() $r\leq M_0$
clusters
$r\leq M_0$
clusters
![]() $C_1, \ldots, C_r$
of the same size
$C_1, \ldots, C_r$
of the same size
![]() $m$
, and with
$m$
, and with
![]() $\delta ^0(D') \gt (1+\frac \eta 2)\frac k2$
. We divide each cluster of
$\delta ^0(D') \gt (1+\frac \eta 2)\frac k2$
. We divide each cluster of
![]() $D'$
into two slices,
$D'$
into two slices,
![]() $C_i^1$
and
$C_i^1$
and
![]() $C_i^2$
of sizes
$C_i^2$
of sizes
Note that at least one of the clusters
![]() $C_i$
contains at least
$C_i$
contains at least
![]() $\eta |C_i|$
vertices from
$\eta |C_i|$
vertices from
![]() $V^*$
. Let
$V^*$
. Let
![]() $C^*$
be such a cluster.
$C^*$
be such a cluster.
Let
![]() $R$
be the reduced oriented graph of
$R$
be the reduced oriented graph of
![]() $D'$
given by Lemma 3.7, on vertices
$D'$
given by Lemma 3.7, on vertices
![]() $C_1, \ldots, C_r$
, of minimum semidegree greater than
$C_1, \ldots, C_r$
, of minimum semidegree greater than
By Lemma 4.8,
![]() $R$
has a connected antimatching
$R$
has a connected antimatching
![]() $M=\{a_ib_i\}_{i=1}^t$
such that
$M=\{a_ib_i\}_{i=1}^t$
such that
and such that
![]() $C^*=C_{a_1}$
, where here and later we write
$C^*=C_{a_1}$
, where here and later we write
![]() $C_{a_i}$
(resp.
$C_{a_i}$
(resp.
![]() $C_{b_i}$
) for the cluster corresponding to
$C_{b_i}$
) for the cluster corresponding to
![]() $a_i$
(resp.
$a_i$
(resp.
![]() $b_i$
) in our reduced oriented graph
$b_i$
) in our reduced oriented graph
![]() $R$
, for every antimatching edge
$R$
, for every antimatching edge
![]() $a_ib_i\in M$
.
$a_ib_i\in M$
.
Preparing the antitree
![]() $T$
. Note that because of (11), and since we assume that
$T$
. Note that because of (11), and since we assume that
![]() $\Delta (T)\le \log n$
,
$\Delta (T)\le \log n$
,
We root
![]() $T$
at the
$T$
at the
![]() $x$
. By Lemma 3.2, there is a
$x$
. By Lemma 3.2, there is a
![]() $\beta$
-decomposition
$\beta$
-decomposition
![]() $(W,\mathcal{T}')$
of the underlying undirected tree of
$(W,\mathcal{T}')$
of the underlying undirected tree of
![]() $T$
, with
$T$
, with
![]() $|W|\lt \frac 1\beta + 2\le \frac 2\beta$
. Let
$|W|\lt \frac 1\beta + 2\le \frac 2\beta$
. Let
![]() $\mathcal{T}$
denote the set of oriented subtrees of
$\mathcal{T}$
denote the set of oriented subtrees of
![]() $T$
corresponding to
$T$
corresponding to
![]() $\mathcal{T}'$
. For each
$\mathcal{T}'$
. For each
![]() $S\in \mathcal{T}$
, we define
$S\in \mathcal{T}$
, we define
We claim that the family
![]() $(p_S, q_S)_{S\in \mathcal{T}}$
satisfies the conditions of Lemma 3.5 with
$(p_S, q_S)_{S\in \mathcal{T}}$
satisfies the conditions of Lemma 3.5 with
![]() $\sqrt{\varepsilon }$
playing the role of
$\sqrt{\varepsilon }$
playing the role of
![]() $\alpha$
. Indeed, Lemma 3.5
$\alpha$
. Indeed, Lemma 3.5
![]() $(a)$
holds by Lemma 3.4, because of (14), and since
$(a)$
holds by Lemma 3.4, because of (14), and since
![]() $t\ge M_0$
. As
$t\ge M_0$
. As
![]() $(W,\mathcal{T}')$
is a
$(W,\mathcal{T}')$
is a
![]() $\beta$
-decomposition, and by our choice of
$\beta$
-decomposition, and by our choice of
![]() $\beta$
, we know that
$\beta$
, we know that
for each
![]() $S\in \mathcal T$
, and thus, Lemma 3.5
$S\in \mathcal T$
, and thus, Lemma 3.5
![]() $(b)$
holds. Finally Lemma 3.5
$(b)$
holds. Finally Lemma 3.5
![]() $(c)$
is true because
$(c)$
is true because
![]() $T$
is balanced, and thus, by our choice of
$T$
is balanced, and thus, by our choice of
![]() $t$
, and since
$t$
, and since
![]() $|W|\ge 1$
,
$|W|\ge 1$
,
 \begin{align*} \max \left\{\sum _{S\in \mathcal{T}} p_S, \sum _{S\in \mathcal{T}} q_S \right\} &\leq \frac{k}{2}\le (1-10\sqrt \varepsilon )^2(1-\varepsilon )(1+\frac \eta 2)\frac k2 \\ &\le (1-10\sqrt \varepsilon )^2(1-\varepsilon )\frac n{r} t \le (1-10\sqrt \varepsilon )|C_{a_1}^2|t. \end{align*}
\begin{align*} \max \left\{\sum _{S\in \mathcal{T}} p_S, \sum _{S\in \mathcal{T}} q_S \right\} &\leq \frac{k}{2}\le (1-10\sqrt \varepsilon )^2(1-\varepsilon )(1+\frac \eta 2)\frac k2 \\ &\le (1-10\sqrt \varepsilon )^2(1-\varepsilon )\frac n{r} t \le (1-10\sqrt \varepsilon )|C_{a_1}^2|t. \end{align*}
So Lemma 3.5, gives a partition
![]() $\{P_j\}_{j=1}^{t}$
of
$\{P_j\}_{j=1}^{t}$
of
![]() $\mathcal{T}$
, such that for every
$\mathcal{T}$
, such that for every
![]() $j\in [t]$
,
$j\in [t]$
,
 \begin{equation} \max \left\{\sum _{i\in P_j} p_i, \sum _{i\in P_j} q_i \right\}\leq (1-7\sqrt{\varepsilon })|C_{a_1}^2|. \end{equation}
\begin{equation} \max \left\{\sum _{i\in P_j} p_i, \sum _{i\in P_j} q_i \right\}\leq (1-7\sqrt{\varepsilon })|C_{a_1}^2|. \end{equation}
For convenience, let us also define, for each
![]() $S\in \mathcal T$
, the set
$S\in \mathcal T$
, the set
![]() $W_S$
. This set contains all vertices from
$W_S$
. This set contains all vertices from
![]() $W$
whose path to
$W$
whose path to
![]() $r(T)=x$
passes through
$r(T)=x$
passes through
![]() $S$
before passing through any other
$S$
before passing through any other
![]() $S'\in \mathcal T$
. That is,
$S'\in \mathcal T$
. That is,
![]() $W_S$
contains all children of
$W_S$
contains all children of
![]() $S$
in
$S$
in
![]() $W$
, as well as their children in
$W$
, as well as their children in
![]() $W$
, etcetera. Similarly, we define
$W$
, etcetera. Similarly, we define
![]() $W_{r(T)}$
as the set of all vertices from
$W_{r(T)}$
as the set of all vertices from
![]() $W$
whose path to
$W$
whose path to
![]() $r(T)$
does not meet any tree from
$r(T)$
does not meet any tree from
![]() $\mathcal T$
.
$\mathcal T$
.
Idea of the embedding procedure. The process starts with embedding
![]() $r(T)=x$
into
$r(T)=x$
into
![]() $C^*$
. Then we embed the vertices from
$C^*$
. Then we embed the vertices from
![]() $W_{r(T)}$
into
$W_{r(T)}$
into
![]() $C_{a_1}^1\cup C_{b_1}^1$
.
$C_{a_1}^1\cup C_{b_1}^1$
.
After that, in every step of the process, we will embed some
![]() $S\in \mathcal{T}$
, say with
$S\in \mathcal{T}$
, say with
![]() $S\in P_j$
, together with the set
$S\in P_j$
, together with the set
![]() $W_S$
. We choose
$W_S$
. We choose
![]() $S$
such that the parent of its root
$S$
such that the parent of its root
![]() $r(S)$
is already embedded, say in cluster
$r(S)$
is already embedded, say in cluster
![]() $C$
. As
$C$
. As
![]() $C$
itself or a neighbouring cluster
$C$
itself or a neighbouring cluster
![]() $C'$
lies at out-out-distance at most
$C'$
lies at out-out-distance at most
![]() $8t$
to
$8t$
to
![]() $C_{a_1}$
in
$C_{a_1}$
in
![]() $R$
, there is a short antiwalk
$R$
, there is a short antiwalk
![]() $P$
from
$P$
from
![]() $C$
or from
$C$
or from
![]() $CC'$
to
$CC'$
to
![]() $C_{a_j}$
. We embed the first
$C_{a_j}$
. We embed the first
![]() $16t+2$
levels of
$16t+2$
levels of
![]() $T[S\cup W_S]$
into the
$T[S\cup W_S]$
into the
![]() $Q^1$
-slices of clusters
$Q^1$
-slices of clusters
![]() $Q$
of
$Q$
of
![]() $P$
, and the rest into
$P$
, and the rest into
![]() $C_{a_j}^2, C_{b_j}^2$
.
$C_{a_j}^2, C_{b_j}^2$
.
The bound on the maximum degree of
![]() $T$
ensures that only few vertices in total go to clusters from connecting antiwalks
$T$
ensures that only few vertices in total go to clusters from connecting antiwalks
![]() $P$
. Therefore,
$P$
. Therefore,
![]() $T$
will be mainly embedded into the edges from
$T$
will be mainly embedded into the edges from
![]() $M$
, where we have control on how space is allocated.
$M$
, where we have control on how space is allocated.
The embedding. Let us make this sketch more precise. Let
![]() $V_1 = \bigcup _{i=1}^r C_i^1$
and
$V_1 = \bigcup _{i=1}^r C_i^1$
and
![]() $V_2 = \bigcup _{i=1}^r C_i^2$
. Embed
$V_2 = \bigcup _{i=1}^r C_i^2$
. Embed
![]() $r(T)=x$
in a vertex of
$r(T)=x$
in a vertex of
![]() $C^*\cap W=C_{a_1}\cap W$
that is typical to
$C^*\cap W=C_{a_1}\cap W$
that is typical to
![]() $C_{b_1}^1$
. We next embed all of
$C_{b_1}^1$
. We next embed all of
![]() $W_{r(T)}$
into
$W_{r(T)}$
into
![]() $C_{a_1}^1\cup C_{b_1}^1$
. This can be done levelwise, in each step choosing vertices that are typical with respect to
$C_{a_1}^1\cup C_{b_1}^1$
. This can be done levelwise, in each step choosing vertices that are typical with respect to
![]() $C_{a_1}^1$
or
$C_{a_1}^1$
or
![]() $C_{b_1}^1$
, respectively. As
$C_{b_1}^1$
, respectively. As
![]() $W_{r(T)}$
has at most
$W_{r(T)}$
has at most
![]() $\frac 2\beta$
vertices, we can embed all of
$\frac 2\beta$
vertices, we can embed all of
![]() $W_{r(T)}$
without a problem.
$W_{r(T)}$
without a problem.
We now go through the antitrees
![]() $S\in \mathcal{T}$
and embed
$S\in \mathcal{T}$
and embed
![]() $S$
together with
$S$
together with
![]() $W_S$
in
$W_S$
in
![]() $ W$
. We do this in an ordered way, so that when starting to work with
$ W$
. We do this in an ordered way, so that when starting to work with
![]() $S$
, the parent of
$S$
, the parent of
![]() $r(S)$
is already embedded. We will show that at every step of the process, that is, for each
$r(S)$
is already embedded. We will show that at every step of the process, that is, for each
![]() $S\in \mathcal{T}$
, the following conditions are met:
$S\in \mathcal{T}$
, the following conditions are met:
-
(a)
 $Lev_{16t+2}(T[S\cup W_S])$
is embedded into
$Lev_{16t+2}(T[S\cup W_S])$
is embedded into
 $V_1$
, and the rest of
$V_1$
, and the rest of
 $T[S\cup W_S]$
is embedded into
$T[S\cup W_S]$
is embedded into
 $V_2$
,
$V_2$
, -
(b) if
 $S\in P_j$
, then
$S\in P_j$
, then
 $V_{\text{out}}(T[S\cup W_S])\setminus Lev_{16t+2}(T[S\cup W_S])$
is embedded into
$V_{\text{out}}(T[S\cup W_S])\setminus Lev_{16t+2}(T[S\cup W_S])$
is embedded into
 $C_{a_j}^2$
and
$C_{a_j}^2$
and
 $V_{\text{in}}(T[S\cup W_S])\setminus Lev_{16t+2}(T[S\cup W_S])$
is embedded into
$V_{\text{in}}(T[S\cup W_S])\setminus Lev_{16t+2}(T[S\cup W_S])$
is embedded into
 $C_{b_j}^2$
,
$C_{b_j}^2$
, -
(c) every vertex in
 $V_{\text{out}}(T[S\cup W_S])$
is embedded in a cluster
$V_{\text{out}}(T[S\cup W_S])$
is embedded in a cluster
 $C_v$
corresponding to a vertex
$C_v$
corresponding to a vertex
 $v$
with
$v$
with
 $\textrm{ood} (a_1,v)\le 8t$
,
$\textrm{ood} (a_1,v)\le 8t$
, -
(d) every vertex in
 $V_{\text{in}}(T[S\cup W_S])$
is embedded in a cluster
$V_{\text{in}}(T[S\cup W_S])$
is embedded in a cluster
 $C_v$
corresponding to a vertex
$C_v$
corresponding to a vertex
 $v$
with
$v$
with
 $\textrm{oid} (a_1,v)\le 8t$
, and
$\textrm{oid} (a_1,v)\le 8t$
, and -
(e) for every
 $w\in W$
, if the image of
$w\in W$
, if the image of
 $w$
lies in cluster
$w$
lies in cluster
 $C$
then it is typical with respect to
$C$
then it is typical with respect to
 $(C')^1$
for some neighbour
$(C')^1$
for some neighbour
 $C'$
of
$C'$
of
 $C$
.
$C$
.
Assume now we are in a step of the process and about to embed
![]() $T[S\cup W_S]$
for some
$T[S\cup W_S]$
for some
![]() $S\in \mathcal{T}$
. Let
$S\in \mathcal{T}$
. Let
![]() $j\in [t]$
be such that
$j\in [t]$
be such that
![]() $S\in P_j$
. Observe that the parent of
$S\in P_j$
. Observe that the parent of
![]() $r(S)$
is already embedded in a vertex
$r(S)$
is already embedded in a vertex
![]() $w$
of a cluster
$w$
of a cluster
![]() $C$
so that
$C$
so that
![]() $w$
is typical to
$w$
is typical to
![]() $(C')^1$
for some neighbour
$(C')^1$
for some neighbour
![]() $C'$
of cluster
$C'$
of cluster
![]() $C$
, by (e).
$C$
, by (e).
First assume that
![]() $r(S)\in V_{\text{out}}(S)$
. Then the parent of
$r(S)\in V_{\text{out}}(S)$
. Then the parent of
![]() $r(S)$
is an in-neighbour of
$r(S)$
is an in-neighbour of
![]() $r(S)$
. Because of (c) and (13), there is an out-out-walk
$r(S)$
. Because of (c) and (13), there is an out-out-walk
![]() $P''$
of (even) length at most
$P''$
of (even) length at most
![]() $16t$
starting at
$16t$
starting at
![]() $C$
and ending at
$C$
and ending at
![]() $C_{a_j}$
. We add the cluster
$C_{a_j}$
. We add the cluster
![]() $C_{b_j}$
at the end and the cluster
$C_{b_j}$
at the end and the cluster
![]() $C'$
at the beginning to obtain an antiwalk
$C'$
at the beginning to obtain an antiwalk
![]() $P'$
of length at most
$P'$
of length at most
![]() $16t+2$
. We obtain an antiwalk
$16t+2$
. We obtain an antiwalk
![]() $P$
of length exactly
$P$
of length exactly
![]() $16t+2$
by repeating two subsequent vertices of
$16t+2$
by repeating two subsequent vertices of
![]() $P'$
an appropriate number of times. Note that
$P'$
an appropriate number of times. Note that
![]() $P$
and
$P$
and
![]() $T[S\cup W_S]$
are consistent.
$T[S\cup W_S]$
are consistent.
Now, if
![]() $r(S)\in V_{\text{in}}(S)$
, we proceed analogously, only that here,
$r(S)\in V_{\text{in}}(S)$
, we proceed analogously, only that here,
![]() $P''$
is an in-in-walk of length at most
$P''$
is an in-in-walk of length at most
![]() $16t-1$
, and when constructing
$16t-1$
, and when constructing
![]() $P'$
, we add the antiwalk
$P'$
, we add the antiwalk
![]() $C_{b_j}C_{a_j}$
at the end. That gives an in-out-walk
$C_{b_j}C_{a_j}$
at the end. That gives an in-out-walk
![]() $P$
of length exactly
$P$
of length exactly
![]() $16t+2$
that is consistent with
$16t+2$
that is consistent with
![]() $T[S\cup W_S]$
.
$T[S\cup W_S]$
.
Observe that
![]() $|S\cup W|\lt \frac \varepsilon{10} m$
. Set
$|S\cup W|\lt \frac \varepsilon{10} m$
. Set
![]() $h\;:\!=\;16t+2$
, and let
$h\;:\!=\;16t+2$
, and let
![]() $X_{h-1}$
and
$X_{h-1}$
and
![]() $X_{h}$
be the sets of all unoccupied vertices of the last two clusters on
$X_{h}$
be the sets of all unoccupied vertices of the last two clusters on
![]() $P$
. By (a), the only vertices embedded in
$P$
. By (a), the only vertices embedded in
![]() $C_{a_j}^2\cup C_{b_j}^2$
are vertices from
$C_{a_j}^2\cup C_{b_j}^2$
are vertices from
![]() $W$
and antitrees from
$W$
and antitrees from
![]() $P_j$
without their first
$P_j$
without their first
![]() $16t+2$
levels. By (12) and (15), we conclude that
$16t+2$
levels. By (12) and (15), we conclude that
We will use Lemma 3.9 to embed
![]() $T[S\cup W_S]$
into
$T[S\cup W_S]$
into
![]() $P$
. For this, let
$P$
. For this, let
![]() $Z_0$
be the set of all unused out-neighbours (if
$Z_0$
be the set of all unused out-neighbours (if
![]() $r(S)\in V_{\text{out}}(S)$
) or in-neighbours (if
$r(S)\in V_{\text{out}}(S)$
) or in-neighbours (if
![]() $r(S)\in V_{\text{out}}(S)$
) of
$r(S)\in V_{\text{out}}(S)$
) of
![]() $w$
in
$w$
in
![]() $C'$
. For
$C'$
. For
![]() $1\le i\leq h$
, let
$1\le i\leq h$
, let
![]() $Z_i$
be the set of all unused vertices of
$Z_i$
be the set of all unused vertices of
![]() $Q^1$
, where
$Q^1$
, where
![]() $Q$
is the
$Q$
is the
![]() $(i+1)$
th vertex on
$(i+1)$
th vertex on
![]() $P$
. By (a), any used vertex in
$P$
. By (a), any used vertex in
![]() $Q^1$
lies in
$Q^1$
lies in
![]() $L_{16t+2}(T)\cup W$
, and this set contains at most
$L_{16t+2}(T)\cup W$
, and this set contains at most
vertices, where we used (14) for the third inequality. So, since by (12), the neighbourhood of
![]() $w$
in
$w$
in
![]() $(C')^1$
is at least
$(C')^1$
is at least
![]() $d\cdot |(C')^1|\ge 2\sqrt \varepsilon \cdot 9\sqrt \varepsilon |C'| \ge 18 \varepsilon m$
, we conclude that
$d\cdot |(C')^1|\ge 2\sqrt \varepsilon \cdot 9\sqrt \varepsilon |C'| \ge 18 \varepsilon m$
, we conclude that
![]() $|Z_1|\gt 3{\varepsilon }m$
and similarly, we see that
$|Z_1|\gt 3{\varepsilon }m$
and similarly, we see that
![]() $|Z_i|\gt 3\sqrt{\varepsilon }m$
for
$|Z_i|\gt 3\sqrt{\varepsilon }m$
for
![]() $1\le i\leq h$
. Thus, we can apply Lemma 3.9 to embed
$1\le i\leq h$
. Thus, we can apply Lemma 3.9 to embed
![]() $T[S\cup W_S]$
. Observe that conditions (a)–(e) are satisfied after embedding
$T[S\cup W_S]$
. Observe that conditions (a)–(e) are satisfied after embedding
![]() $S$
.
$S$
.
After embedding
![]() $T[S\cup W_S]$
for each
$T[S\cup W_S]$
for each
![]() $S\in \mathcal T$
in this way, we have embedded all of
$S\in \mathcal T$
in this way, we have embedded all of
![]() $T$
, with
$T$
, with
![]() $x$
embedded in
$x$
embedded in
![]() $V^*$
, which finishes the proof.
$V^*$
, which finishes the proof.
6. Antisubdivisions of
 $K_h$
: The proof of Theorem 1.7
$K_h$
: The proof of Theorem 1.7
The proof of Theorem 1.7 is similar to the proof of Theorem 1.2, with the difference that we only need the connected antimatching in the reduced oriented graph, and then do the embedding ‘by hand’.
6.1. Preparation
We choose our constants as in the proof of Theorem 1.2, in particular ensuring that
![]() $n_0\ge 100\varepsilon ^{-1}M_0^3$
. In addition, we set
$n_0\ge 100\varepsilon ^{-1}M_0^3$
. In addition, we set
We now prepare the oriented graph in the same way as for Theorem 1.2. In the reduced oriented graph of
![]() $D$
, we use Lemma 4.6 to find a connected antimatching
$D$
, we use Lemma 4.6 to find a connected antimatching
![]() $M=\{a_ib_i\}_{1\le i\le t}$
of convenient size
$M=\{a_ib_i\}_{1\le i\le t}$
of convenient size
![]() $t$
. We split each cluster
$t$
. We split each cluster
![]() $C$
into two slices
$C$
into two slices
![]() $C^1$
and
$C^1$
and
![]() $C^2$
, where
$C^2$
, where
![]() $C^1$
only contains about a
$C^1$
only contains about a
![]() $10\sqrt \varepsilon$
portion of the vertices of
$10\sqrt \varepsilon$
portion of the vertices of
![]() $C$
.
$C$
.
Let a long
![]() $k$
-edge antisubdivision
$k$
-edge antisubdivision
![]() $H$
of
$H$
of
![]() $K_h$
be given, that is, a set
$K_h$
be given, that is, a set
![]() $X=x_1,\ldots, x_h$
of vertices, and antipaths
$X=x_1,\ldots, x_h$
of vertices, and antipaths
![]() $P_{i,j}$
connecting
$P_{i,j}$
connecting
![]() $x_i$
with
$x_i$
with
![]() $x_j$
, for each
$x_j$
, for each
![]() $1\le i\lt j\le h$
. For each two-edge path
$1\le i\lt j\le h$
. For each two-edge path
![]() $P_{i,j}$
we add the middle vertex
$P_{i,j}$
we add the middle vertex
![]() $x_{i,j}$
to
$x_{i,j}$
to
![]() $X$
. Call the obtained set
$X$
. Call the obtained set
![]() $X'$
. By assumption,
$X'$
. By assumption,
![]() $X'$
induces a forest in
$X'$
induces a forest in
![]() $K_h$
. Choose a subset of
$K_h$
. Choose a subset of
so that together with
![]() $X'$
, they induce a tree in
$X'$
, they induce a tree in
![]() $K_h$
. For all other paths
$K_h$
. For all other paths
![]() $P_{i,j}$
we choose a subpath
$P_{i,j}$
we choose a subpath
![]() $Q_{i,j}\subseteq P_{i,j}$
of length
$Q_{i,j}\subseteq P_{i,j}$
of length
![]() $3$
. Let
$3$
. Let
![]() $\mathcal Q$
be the set of all such paths
$\mathcal Q$
be the set of all such paths
![]() $Q_{i,j}$
, and let
$Q_{i,j}$
, and let
![]() $Y$
be the set of their endvertices. Note that
$Y$
be the set of their endvertices. Note that
![]() $T=K_h-(\bigcup _{Q_{i,j}\in \mathcal Q}V(Q_{i,j})\setminus Y)$
is an antitree. We root
$T=K_h-(\bigcup _{Q_{i,j}\in \mathcal Q}V(Q_{i,j})\setminus Y)$
is an antitree. We root
![]() $T$
at
$T$
at
![]() $x_1$
.
$x_1$
.
Let
![]() $Z$
be the set of all vertices on paths in
$Z$
be the set of all vertices on paths in
![]() $T$
between vertices of
$T$
between vertices of
![]() $X\cup Y$
that have length at most
$X\cup Y$
that have length at most
![]() $M_0$
. Set
$M_0$
. Set
![]() $W=X'\cup Y\cup Z$
, and note that
$W=X'\cup Y\cup Z$
, and note that
![]() $W$
naturally partitions into two sets:
$W$
naturally partitions into two sets:
![]() $W_{in}=W\cap{V_{\text{in}}}(H)$
and
$W_{in}=W\cap{V_{\text{in}}}(H)$
and
![]() $W_{out}=W\cap V_{\text{out}}(H)$
. Observe that there are at most
$W_{out}=W\cap V_{\text{out}}(H)$
. Observe that there are at most
![]() $\frac{h^2}2$
paths
$\frac{h^2}2$
paths
![]() $P_{i,j}$
of length at least
$P_{i,j}$
of length at least
![]() $3$
, and thus
$3$
, and thus
Also note that each component of
![]() $T- W$
is a long path (longer than
$T- W$
is a long path (longer than
![]() $M_0$
). Let
$M_0$
). Let
![]() $\mathcal P$
be the set of all these components.
$\mathcal P$
be the set of all these components.
6.2. Embedding of
 $T$
$T$
We first give quick overview of the embedding of
![]() $T$
, the details are given further below. First, we embed the root
$T$
, the details are given further below. First, we embed the root
![]() $x_1$
into
$x_1$
into
![]() $C_{a_1}\cup C_{b_1}$
. Then at each step, we embed either a vertex from
$C_{a_1}\cup C_{b_1}$
. Then at each step, we embed either a vertex from
![]() $W$
or a path from
$W$
or a path from
![]() $\mathcal P$
whose parent is already embedded. All vertices of
$\mathcal P$
whose parent is already embedded. All vertices of
![]() $W$
are embedded into
$W$
are embedded into
![]() $C_{a_1}^1\cup C_{b_1}^1$
, and the paths from
$C_{a_1}^1\cup C_{b_1}^1$
, and the paths from
![]() $\mathcal P$
are embedded mainly into the
$\mathcal P$
are embedded mainly into the
![]() $C^2$
-slices of clusters corresponding to edges of
$C^2$
-slices of clusters corresponding to edges of
![]() $M$
. For this, we use the edges of the antimatching
$M$
. For this, we use the edges of the antimatching
![]() $M$
(including
$M$
(including
![]() $a_1b_1$
although this is not crucial) in an ordered way, and when one edge is sufficiently used, we go to the next edge of
$a_1b_1$
although this is not crucial) in an ordered way, and when one edge is sufficiently used, we go to the next edge of
![]() $M$
. For the connections between
$M$
. For the connections between
![]() $C_{a_i}\cup C_{b_i}$
and
$C_{a_i}\cup C_{b_i}$
and
![]() $C_{a_j}\cup C_{b_j}$
we use the slices
$C_{a_j}\cup C_{b_j}$
we use the slices
![]() $C^1$
. At all times, vertices are embedded into typical vertices with respect to the unused part of the slice
$C^1$
. At all times, vertices are embedded into typical vertices with respect to the unused part of the slice
![]() $C^2$
to be used in the next step, or with respect to the slice
$C^2$
to be used in the next step, or with respect to the slice
![]() $C^1$
to be used in the future for children. The details of the embedding of
$C^1$
to be used in the future for children. The details of the embedding of
![]() $W$
are given in the next paragraph, and the details for the paths from
$W$
are given in the next paragraph, and the details for the paths from
![]() $\mathcal P$
are given in the subsequent paragraph.
$\mathcal P$
are given in the subsequent paragraph.
The vertices of
![]() $W$
are embedded into
$W$
are embedded into
![]() $C_{a_1}^1\cup C_{b_1}^1$
, as mentioned above. Namely, each
$C_{a_1}^1\cup C_{b_1}^1$
, as mentioned above. Namely, each
![]() $w\in W$
(in particular
$w\in W$
(in particular
![]() $x_1$
) is embedded into
$x_1$
) is embedded into
![]() $C_{a_1}^1$
if
$C_{a_1}^1$
if
![]() $w\in W_{out}$
and
$w\in W_{out}$
and
![]() $w$
is embedded into
$w$
is embedded into
![]() $C_{b_1}^1$
if
$C_{b_1}^1$
if
![]() $w\in W_{in}$
. Every time we embed a vertex from
$w\in W_{in}$
. Every time we embed a vertex from
![]() $W$
into
$W$
into
![]() $C_{a_1}^1$
, we make sure its image is typical with respect to
$C_{a_1}^1$
, we make sure its image is typical with respect to
![]() $C_{b_1}^1$
, and every time we embed a vertex from
$C_{b_1}^1$
, and every time we embed a vertex from
![]() $W$
into
$W$
into
![]() $C_{b_1}^1$
, we make sure its image is typical with respect to
$C_{b_1}^1$
, we make sure its image is typical with respect to
![]() $C_{a_1}^1$
. By (17), the set
$C_{a_1}^1$
. By (17), the set
![]() $W$
is small enough to easily fit into
$W$
is small enough to easily fit into
![]() $C_{a_1}^1\cup C_{b_1}^1$
. It is also much smaller than a typical neighbourhood in
$C_{a_1}^1\cup C_{b_1}^1$
. It is also much smaller than a typical neighbourhood in
![]() $C_{a_1}^1$
or in
$C_{a_1}^1$
or in
![]() $C_{b_1}^1$
, and therefore, it is not a problem if a vertex from
$C_{b_1}^1$
, and therefore, it is not a problem if a vertex from
![]() $W$
is embedded much earlier than some of its children (as long as we ensure the children are embedded into
$W$
is embedded much earlier than some of its children (as long as we ensure the children are embedded into
![]() $C^1$
-slices). For a more precise analysis, see below.
$C^1$
-slices). For a more precise analysis, see below.
Let us now turn to the paths from
![]() $\mathcal P$
. As mentioned above, these paths are embedded mainly into the
$\mathcal P$
. As mentioned above, these paths are embedded mainly into the
![]() $C^2$
-slices of clusters corresponding to edges of the antimatching
$C^2$
-slices of clusters corresponding to edges of the antimatching
![]() $M$
. However, the first vertex
$M$
. However, the first vertex
![]() $s$
of such a path
$s$
of such a path
![]() $S$
goes to either
$S$
goes to either
![]() $C_{a_1}^1$
or
$C_{a_1}^1$
or
![]() $C_{b_1}^1$
(depending on the image of its parent), and we choose for the image of
$C_{b_1}^1$
(depending on the image of its parent), and we choose for the image of
![]() $s$
a vertex that is typical with respect to
$s$
a vertex that is typical with respect to
![]() $C_0^1$
where
$C_0^1$
where
![]() $C_0$
is the first cluster on a path
$C_0$
is the first cluster on a path
![]() $P$
from
$P$
from
![]() $C_{a_1}$
, or from
$C_{a_1}$
, or from
![]() $C_{b_1}$
, to the clusters
$C_{b_1}$
, to the clusters
![]() $C_{a_j}$
and
$C_{a_j}$
and
![]() $C_{b_j}$
we plan to use for
$C_{b_j}$
we plan to use for
![]() $S$
. We embed the next vertices of
$S$
. We embed the next vertices of
![]() $S$
along
$S$
along
![]() $P$
, always into
$P$
, always into
![]() $C^1$
-slices, always typical to the next slice until we reach
$C^1$
-slices, always typical to the next slice until we reach
![]() $C_{a_j}\cup C_{b_j}$
(after at most
$C_{a_j}\cup C_{b_j}$
(after at most
![]() $M_0$
steps). Then we switch to the slices
$M_0$
steps). Then we switch to the slices
![]() $C_{a_j}^2$
and
$C_{a_j}^2$
and
![]() $C_{b_j}^2$
. Now, every vertex is embedded into a typical vertex with respect to the unused part of
$C_{b_j}^2$
. Now, every vertex is embedded into a typical vertex with respect to the unused part of
![]() $C_{a_j}^2$
or of
$C_{a_j}^2$
or of
![]() $C_{b_j}^2$
. If necessary, we move from
$C_{b_j}^2$
. If necessary, we move from
![]() $C_{a_j}\cup C_{b_j}$
to
$C_{a_j}\cup C_{b_j}$
to
![]() $C_{a_{j+1}}\cup C_{b_{j+1}}$
(using at most
$C_{a_{j+1}}\cup C_{b_{j+1}}$
(using at most
![]() $M_0$
vertices which are embedded into
$M_0$
vertices which are embedded into
![]() $C^1$
-slices on a suitable path). We keep moving to subsequent
$C^1$
-slices on a suitable path). We keep moving to subsequent
![]() $C_{a_i}\cup C_{b_i}$
’s if necessary. When we reach the last vertices on
$C_{a_i}\cup C_{b_i}$
’s if necessary. When we reach the last vertices on
![]() $S$
, we start moving back to
$S$
, we start moving back to
![]() $C_{a_1}\cup C_{b_1}$
, through the
$C_{a_1}\cup C_{b_1}$
, through the
![]() $C^1$
-slices on a path of length at most
$C^1$
-slices on a path of length at most
![]() $M_0$
. We reach
$M_0$
. We reach
![]() $C_{a_1}\cup C_{b_1}$
and embed the last vertex of
$C_{a_1}\cup C_{b_1}$
and embed the last vertex of
![]() $S$
into a typical vertex with respect to
$S$
into a typical vertex with respect to
![]() $C_{a_1}^1$
or to
$C_{a_1}^1$
or to
![]() $C_{b_1}^1$
. If
$C_{b_1}^1$
. If
![]() $S$
has a child in
$S$
has a child in
![]() $W$
, this child can be embedded now, or later in the process.
$W$
, this child can be embedded now, or later in the process.
Let us analyse the embedding procedure to see that
![]() $T$
can indeed be embedded in this way. First, we note that the size of
$T$
can indeed be embedded in this way. First, we note that the size of
![]() $M$
is sufficient, and the
$M$
is sufficient, and the
![]() $C^2$
-slices are large enough so that all the paths from
$C^2$
-slices are large enough so that all the paths from
![]() $\mathcal P$
can be embedded without a problem. Second, we observe that we used the
$\mathcal P$
can be embedded without a problem. Second, we observe that we used the
![]() $C^1$
-slices exclusively for
$C^1$
-slices exclusively for
![]() $W$
, for the first
$W$
, for the first
![]() $\le M_0$
and last
$\le M_0$
and last
![]() $\le M_0$
vertices on a long path, and for moving from one edge
$\le M_0$
vertices on a long path, and for moving from one edge
![]() $a_jb_j$
to the next edge
$a_jb_j$
to the next edge
![]() $a_{j+1}b_{j+1}$
. So the number of vertices embedded into the
$a_{j+1}b_{j+1}$
. So the number of vertices embedded into the
![]() $C^1$
-slices is at most
$C^1$
-slices is at most
![]() $|W|+2M_0\cdot h^2+M_0\cdot t$
. Because of (17) and since
$|W|+2M_0\cdot h^2+M_0\cdot t$
. Because of (17) and since
![]() $t\le M_0$
, this number is bounded from above by
$t\le M_0$
, this number is bounded from above by
So, whenever are about to embed a vertex into a
![]() $C^1$
-slice, it is enough to know that the image of its parent was chosen typical with respect to the whole slice (as a typical neighbourhood in the slice has at least
$C^1$
-slice, it is enough to know that the image of its parent was chosen typical with respect to the whole slice (as a typical neighbourhood in the slice has at least
![]() $18\varepsilon m$
vertices). We can thus embed all of
$18\varepsilon m$
vertices). We can thus embed all of
![]() $T$
.
$T$
.
6.3. Embedding interior vertices on paths from
 $\mathcal Q$
$\mathcal Q$
It only remains to embed the two middle vertices
![]() $q_{i,j}$
,
$q_{i,j}$
,
![]() $q^{\prime}_{i,j}$
of the paths
$q^{\prime}_{i,j}$
of the paths
![]() $Q_{i,j}$
, which we do successively, in any order. Say the neighbour of
$Q_{i,j}$
, which we do successively, in any order. Say the neighbour of
![]() $q_{i,j}$
was embedded in
$q_{i,j}$
was embedded in
![]() $v\in C^1_{a_1}$
, and the neighbour of
$v\in C^1_{a_1}$
, and the neighbour of
![]() $q^{\prime}_{i,j}$
was embedded in
$q^{\prime}_{i,j}$
was embedded in
![]() $v'\in C^1_{b_1}$
. We consider the neighbourhood
$v'\in C^1_{b_1}$
. We consider the neighbourhood
![]() $N_1$
of the image of
$N_1$
of the image of
![]() $v$
in the unused part of
$v$
in the unused part of
![]() $C^1_{b_1}$
and the neighbourhood
$C^1_{b_1}$
and the neighbourhood
![]() $N_2$
of the image of
$N_2$
of the image of
![]() $v'$
in the unused part of
$v'$
in the unused part of
![]() $C^1_{a_1}$
. Since at most
$C^1_{a_1}$
. Since at most
![]() $ \frac \varepsilon 2 m+h^2\le \varepsilon |C^1_{a_1}|$
vertices of
$ \frac \varepsilon 2 m+h^2\le \varepsilon |C^1_{a_1}|$
vertices of
![]() $C^1_{a_1}$
and
$C^1_{a_1}$
and
![]() $C^1_{b_1}$
have been used so far, we know that
$C^1_{b_1}$
have been used so far, we know that
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are sufficiently large to ensure that there is an edge
$N_2$
are sufficiently large to ensure that there is an edge
![]() $ww'$
we can use. We complete the embedding by mapping
$ww'$
we can use. We complete the embedding by mapping
![]() $v$
and
$v$
and
![]() $v'$
to
$v'$
to
![]() $w$
and
$w$
and
![]() $w'$
.
$w'$
.
7. Edge density: The proof of Theorem 1.9
In order to prove Theorem 1.9 we will need a lemma that allows us to rewrite the condition on the edge density as a condition on a parameter that is very similar to the semidegree, and which we will call the minimum pseudo-semidegree. Define the minimum pseudo-semidegree
![]() $\bar \delta ^0(D)$
of a digraph
$\bar \delta ^0(D)$
of a digraph
![]() $D$
with at least one edge as the minimum
$D$
with at least one edge as the minimum
![]() $d$
such that for each vertex
$d$
such that for each vertex
![]() $v\in V(D)$
we have
$v\in V(D)$
we have
![]() $\delta ^+(v), \delta ^-(v)\in \{0\}\cup [d,\infty )$
. The minimum pseudo-semidegree of an empty digraph is
$\delta ^+(v), \delta ^-(v)\in \{0\}\cup [d,\infty )$
. The minimum pseudo-semidegree of an empty digraph is
![]() $0$
.
$0$
.
Lemma 7.1.
Let
![]() $k\in \mathbb N^+$
. If a digraph
$k\in \mathbb N^+$
. If a digraph
![]() $D$
has more than
$D$
has more than
![]() $(k-1)|V(D)|$
edges, then it contains a digraph
$(k-1)|V(D)|$
edges, then it contains a digraph
![]() $D'$
with
$D'$
with
![]() $\bar \delta ^0(D')\ge \frac k2$
.
$\bar \delta ^0(D')\ge \frac k2$
.
Proof. Note that the vertices of
![]() $D$
have, on average, in-degree greater than
$D$
have, on average, in-degree greater than
![]() $k-1$
and out-degree greater than
$k-1$
and out-degree greater than
![]() $k-1$
. Consider the following folklore construction of an auxiliary bipartite graph
$k-1$
. Consider the following folklore construction of an auxiliary bipartite graph
![]() $B$
associated to the digraph
$B$
associated to the digraph
![]() $D$
: first, divide each vertex
$D$
: first, divide each vertex
![]() $v\in V(D)$
into two vertices
$v\in V(D)$
into two vertices
![]() $v_{in}$
and
$v_{in}$
and
![]() $v_{out}$
, letting
$v_{out}$
, letting
![]() $v_{in}$
be adjacent to all edges ending at
$v_{in}$
be adjacent to all edges ending at
![]() $v$
, and letting
$v$
, and letting
![]() $v_{out}$
be adjacent to all edges starting at
$v_{out}$
be adjacent to all edges starting at
![]() $v$
; second, omit all directions on edges.
$v$
; second, omit all directions on edges.
Then the average degree of
![]() $B$
is greater than
$B$
is greater than
![]() $k-1$
, and a standard argument shows that
$k-1$
, and a standard argument shows that
![]() $B$
has a non-empty subgraph
$B$
has a non-empty subgraph
![]() $B'$
of minimum degree at least
$B'$
of minimum degree at least
![]() $\frac{k}2$
(for this, it suffices to successively delete edges of degree at most
$\frac{k}2$
(for this, it suffices to successively delete edges of degree at most
![]() $\frac{k-1}2$
and to calculate that we have not deleted the entire graph). Translating
$\frac{k-1}2$
and to calculate that we have not deleted the entire graph). Translating
![]() $B'$
back to the digraph setting, we see that
$B'$
back to the digraph setting, we see that
![]() $D$
has a subdigraph
$D$
has a subdigraph
![]() $D'$
, such that
$D'$
, such that
![]() $D'$
minimum pseudo-semidegree at least
$D'$
minimum pseudo-semidegree at least
![]() $\frac{k}2$
, which is as desired.
$\frac{k}2$
, which is as desired.
The next auxiliary result states that the minimum semidegree and the minimum pseudo-semidegree are practically equivalent for the purposes of finding antidirected subgraphs
![]() $A$
in oriented graphs
$A$
in oriented graphs
![]() $D$
, if there is some control over the placement of
$D$
, if there is some control over the placement of
![]() $A$
in
$A$
in
![]() $D$
.
$D$
.
Say an oriented graph is weakly connected if its underlying graph is connected. Recall that the notation
![]() $\subseteq _\gamma$
is given Definition 5.1.
$\subseteq _\gamma$
is given Definition 5.1.
Lemma 7.2.
For any weakly connected antidirected graph
![]() $A$
and for any
$A$
and for any
![]() $\ell, n_0\in \mathbb N$
, the following holds. If for each oriented graph
$\ell, n_0\in \mathbb N$
, the following holds. If for each oriented graph
![]() $D$
on at least
$D$
on at least
![]() $n_0$
vertices with
$n_0$
vertices with
![]() $\delta ^0(D)\ge \ell$
we have
$\delta ^0(D)\ge \ell$
we have
![]() $A\subseteq _{1/8} D$
, then each oriented graph
$A\subseteq _{1/8} D$
, then each oriented graph
![]() $D'$
on at least
$D'$
on at least
![]() $n_0$
vertices with
$n_0$
vertices with
![]() $\bar \delta ^0(D')\ge \ell$
contains
$\bar \delta ^0(D')\ge \ell$
contains
![]() $A$
.
$A$
.
Proof. Given
![]() $A$
,
$A$
,
![]() $\ell$
, and
$\ell$
, and
![]() $n_0$
, let
$n_0$
, let
![]() $D'$
be an oriented graph on at least
$D'$
be an oriented graph on at least
![]() $n_0$
vertices with
$n_0$
vertices with
![]() $\bar \delta ^0(D')\ge \ell$
. Assume that
$\bar \delta ^0(D')\ge \ell$
. Assume that
![]() $|V_{\text{out}}(D')|\ge |{V_{\text{in}}}(D')|$
(the other case is analogous). Then
$|V_{\text{out}}(D')|\ge |{V_{\text{in}}}(D')|$
(the other case is analogous). Then
We will construct an auxiliary oriented graph
![]() $D$
to which the hypothesis of the lemma can be applied. Take four copies
$D$
to which the hypothesis of the lemma can be applied. Take four copies
![]() $D_1, D_2, D_3, D_4$
of
$D_1, D_2, D_3, D_4$
of
![]() $D'$
. Let
$D'$
. Let
![]() $A_i=V_{\text{out}}(D_i)$
and
$A_i=V_{\text{out}}(D_i)$
and
![]() $B_i={V_{\text{in}}}(D_i)$
for
$B_i={V_{\text{in}}}(D_i)$
for
![]() $i=1,\ldots 4$
. For
$i=1,\ldots 4$
. For
![]() $i=1,3$
, identify the vertices of
$i=1,3$
, identify the vertices of
![]() $A_i$
with the vertices of
$A_i$
with the vertices of
![]() $A_{i+1}$
, and the vertices of
$A_{i+1}$
, and the vertices of
![]() $B_i$
with the vertices of
$B_i$
with the vertices of
![]() $B_{i-1}$
(addition modulo
$B_{i-1}$
(addition modulo
![]() $4$
). Finally, reverse all directions on edges in copies
$4$
). Finally, reverse all directions on edges in copies
![]() $D_2$
and
$D_2$
and
![]() $D_4$
. For an illustration, see Fig. 3.
$D_4$
. For an illustration, see Fig. 3.

Figure 3. Construction of
![]() $D$
from
$D$
from
![]() $D'$
in the proof of Lemma 7.2.
$D'$
in the proof of Lemma 7.2.
Note that the obtained digraph
![]() $D$
is an oriented graph and has more than
$D$
is an oriented graph and has more than
![]() $n_0$
vertices. Also note that
$n_0$
vertices. Also note that
![]() $\delta ^0(D)\ge \ell$
, since all vertices in
$\delta ^0(D)\ge \ell$
, since all vertices in
![]() $D_i\setminus (A_i\cup B_i)$
maintain their semidegree, the vertices in
$D_i\setminus (A_i\cup B_i)$
maintain their semidegree, the vertices in
![]() $A_i=A_{i+1}$
have at least
$A_i=A_{i+1}$
have at least
![]() $\ell$
out-neighbours in
$\ell$
out-neighbours in
![]() $D_i$
and at least
$D_i$
and at least
![]() $\ell$
in-neighbours in
$\ell$
in-neighbours in
![]() $D_{i+1}$
, for
$D_{i+1}$
, for
![]() $i=1,3$
, and a similar statement holds for the vertices in the sets
$i=1,3$
, and a similar statement holds for the vertices in the sets
![]() $B_i$
.
$B_i$
.
We choose
![]() $V^*$
as the set of all vertices in
$V^*$
as the set of all vertices in
![]() $V(D_1)\setminus B_1$
. Note that
$V(D_1)\setminus B_1$
. Note that
![]() $|V^*|\ge \frac{|V(D_1)|}2$
and therefore
$|V^*|\ge \frac{|V(D_1)|}2$
and therefore
![]() $|V^*|\ge \frac{|V(D)|}8$
. We let
$|V^*|\ge \frac{|V(D)|}8$
. We let
![]() $xx'$
be any edge of
$xx'$
be any edge of
![]() $A$
(directed from
$A$
(directed from
![]() $x$
to
$x$
to
![]() $x'$
). By the hypothesis of the lemma, we find an embedding of
$x'$
). By the hypothesis of the lemma, we find an embedding of
![]() $A$
into
$A$
into
![]() $D$
, with
$D$
, with
![]() $x$
embedded into some vertex
$x$
embedded into some vertex
![]() $v^*\in V^*$
.
$v^*\in V^*$
.
We claim that
Then, as
![]() $D_1$
is a copy of
$D_1$
is a copy of
![]() $D'$
(with the original directions on the edges), we can conclude that
$D'$
(with the original directions on the edges), we can conclude that
![]() $A$
is a subdigraph of
$A$
is a subdigraph of
![]() $D'$
.
$D'$
.
So all that remains is to prove (18). Proceeding by contradiction, we assume otherwise, that is, we assume there is a vertex
![]() $z\in V(A)$
whose image does not lie in
$z\in V(A)$
whose image does not lie in
![]() $V(D_1)$
. Then the underlying graph of
$V(D_1)$
. Then the underlying graph of
![]() $A$
, which is connected by assumption, contains a path from
$A$
, which is connected by assumption, contains a path from
![]() $x$
to
$x$
to
![]() $z$
. So
$z$
. So
![]() $A$
, which is antidirected, contains an antipath
$A$
, which is antidirected, contains an antipath
![]() $xy_1y_2\ldots y_hz$
from
$xy_1y_2\ldots y_hz$
from
![]() $x$
to
$x$
to
![]() $z$
. Since
$z$
. Since
![]() $xx'$
is an edge of
$xx'$
is an edge of
![]() $A$
, we know that the edge
$A$
, we know that the edge
![]() $xy_1$
is directed from
$xy_1$
is directed from
![]() $x$
to
$x$
to
![]() $y_1$
.
$y_1$
.
Recall that
![]() $x$
is embedded in
$x$
is embedded in
![]() $v^*\in V^*=V(D_1)\setminus B_1$
. This location of
$v^*\in V^*=V(D_1)\setminus B_1$
. This location of
![]() $v^*$
ensures that all out-neighbours of
$v^*$
ensures that all out-neighbours of
![]() $v^*$
are in
$v^*$
are in
![]() $D_1$
. More specifically, by the definition of
$D_1$
. More specifically, by the definition of
![]() $A_1$
, all out-neighbours of
$A_1$
, all out-neighbours of
![]() $v^*$
are in
$v^*$
are in
![]() $D_1\setminus A_1$
. In particular,
$D_1\setminus A_1$
. In particular,
![]() $y_1$
is embedded in a vertex
$y_1$
is embedded in a vertex
![]() $w_1$
of
$w_1$
of
![]() $D_1\setminus A_1$
. This in turn ensures that all in-neighbours of
$D_1\setminus A_1$
. This in turn ensures that all in-neighbours of
![]() $w_1$
are in
$w_1$
are in
![]() $D_1\setminus B_1$
. In particular,
$D_1\setminus B_1$
. In particular,
![]() $y_2$
is embedded in a vertex
$y_2$
is embedded in a vertex
![]() $w_2$
of
$w_2$
of
![]() $D_1\setminus B_1$
. Continuing to argue in this manner, we see that all
$D_1\setminus B_1$
. Continuing to argue in this manner, we see that all
![]() $y_i$
and also
$y_i$
and also
![]() $z$
are embedded in
$z$
are embedded in
![]() $V(D_1)$
. This proves (18), and thus completes the proof of the lemma.
$V(D_1)$
. This proves (18), and thus completes the proof of the lemma.
Remark 7.3.
We remark that Lemma 7.2 also holds if both
![]() $D$
and
$D$
and
![]() $D'$
are directed graphs instead of oriented graphs. However, since Theorem
5.2
only holds for oriented graphs of high minimum semidegree, we need the lemma in the form it is written.
$D'$
are directed graphs instead of oriented graphs. However, since Theorem
5.2
only holds for oriented graphs of high minimum semidegree, we need the lemma in the form it is written.
Remark 7.4.
Observe that in Lemma 7.2 it is essential to require that a vertex of
![]() $A$
can be mapped to a specific set in
$A$
can be mapped to a specific set in
![]() $D$
: If we left out this requirement, then we might find a copy of
$D$
: If we left out this requirement, then we might find a copy of
![]() $A$
in
$A$
in
![]() $D_2$
instead of in
$D_2$
instead of in
![]() $D_1$
. Thus in
$D_1$
. Thus in
![]() $D'$
we would only get a copy of
$D'$
we would only get a copy of
![]() $A$
with all directions reversed.
$A$
with all directions reversed.
We are ready to prove Theorem 1.9.
Proof of Theorem
1.9
. Given
![]() $\eta$
and
$\eta$
and
![]() $c$
from Theorem 1.9, we note that we may assume that
$c$
from Theorem 1.9, we note that we may assume that
![]() $\eta \le 1/8$
. Let
$\eta \le 1/8$
. Let
![]() $n_0$
be given by Theorem 5.2 for input
$n_0$
be given by Theorem 5.2 for input
![]() $\eta$
and
$\eta$
and
![]() $c$
.
$c$
.
Now, let
![]() $n\ge n_0$
and
$n\ge n_0$
and
![]() $k\ge \eta n$
, and let
$k\ge \eta n$
, and let
![]() $D$
be an oriented graph on
$D$
be an oriented graph on
![]() $n$
vertices with
$n$
vertices with
![]() $|E(D)|\gt (1+\eta )(k-1)|V(D)|$
. Let
$|E(D)|\gt (1+\eta )(k-1)|V(D)|$
. Let
![]() $T$
be a balanced antitree with
$T$
be a balanced antitree with
![]() $k$
edges and
$k$
edges and
![]() $\Delta (T)\le (\!\log n)^c$
. We need to show that
$\Delta (T)\le (\!\log n)^c$
. We need to show that
![]() $T\subseteq D$
.
$T\subseteq D$
.
Apply Lemma 7.1 to
![]() $D$
to obtain an oriented graph
$D$
to obtain an oriented graph
![]() $D'\subseteq D$
with
$D'\subseteq D$
with
![]() $\bar \delta ^0(D)\ge (1+\eta )\frac k2$
. Use Lemma 7.2 and Theorem 5.2 to see that
$\bar \delta ^0(D)\ge (1+\eta )\frac k2$
. Use Lemma 7.2 and Theorem 5.2 to see that
![]() $T$
can be embedded in
$T$
can be embedded in
![]() $D'$
. As
$D'$
. As
![]() $D'\subseteq D$
, we see that
$D'\subseteq D$
, we see that
![]() $T\subseteq D$
.
$T\subseteq D$
.
8. Conclusion
8.1. Oriented trees in digraphs
Any digraph
![]() $D$
with a minimum semidegree of at least
$D$
with a minimum semidegree of at least
![]() $k$
contains every orientation of every tree with
$k$
contains every orientation of every tree with
![]() $k$
edges, by a greedy embedding argument. This bound cannot be lowered, not even if we are only looking for oriented paths, as the disjoint union of complete digraphs of order
$k$
edges, by a greedy embedding argument. This bound cannot be lowered, not even if we are only looking for oriented paths, as the disjoint union of complete digraphs of order
![]() $k$
has minimum semidegree
$k$
has minimum semidegree
![]() $k-1$
but no
$k-1$
but no
![]() $k$
-edge oriented path. Perhaps an additional condition, for instance on the maximum semidegree of
$k$
-edge oriented path. Perhaps an additional condition, for instance on the maximum semidegree of
![]() $D$
, or requiring
$D$
, or requiring
![]() $D$
to be weakly connected and sufficiently large, combined with a lower bound on the semidegree of
$D$
to be weakly connected and sufficiently large, combined with a lower bound on the semidegree of
![]() $D$
could give a variant of Corollary 1.3 for digraphs.
$D$
could give a variant of Corollary 1.3 for digraphs.
8.2. Oriented trees in oriented graphs
In the introduction, we saw the example of a
![]() $k$
-edge star with all edges directed outwards, which is not contained in, for instance, the
$k$
-edge star with all edges directed outwards, which is not contained in, for instance, the
![]() $(k-1)$
-blow-up of the directed triangle, although this graph has minimum semidegree
$(k-1)$
-blow-up of the directed triangle, although this graph has minimum semidegree
![]() $k-1$
. We overcame this difficulty in Theorem 1.2 by concentrating on balanced antitrees. Another possibility, which was suggested in [Reference Stein, Raigoroskii and Rassias29], could be to add an extra condition on the oriented graph
$k-1$
. We overcame this difficulty in Theorem 1.2 by concentrating on balanced antitrees. Another possibility, which was suggested in [Reference Stein, Raigoroskii and Rassias29], could be to add an extra condition on the oriented graph
![]() $D$
, for instance a condition on the maximum semidegree of
$D$
, for instance a condition on the maximum semidegree of
![]() $D$
, with the hope of guaranteeing all
$D$
, with the hope of guaranteeing all
![]() $k$
-edge antitrees, or even all
$k$
-edge antitrees, or even all
![]() $k$
-edge oriented trees. Such a condition has been successfully used in the undirected graph setting (see e.g. [Reference Besomi, Pavez-Signé and Stein5]).
$k$
-edge oriented trees. Such a condition has been successfully used in the undirected graph setting (see e.g. [Reference Besomi, Pavez-Signé and Stein5]).
8.3. Oriented subdivisions
Perhaps Theorem 1.7 extends to other orientations of subdivisions of the complete graph. For instance, one could ask whether there is a function
![]() $f(h)$
such that every oriented graph of minimum semidegree at least
$f(h)$
such that every oriented graph of minimum semidegree at least
![]() $f(h)$
contains an orientation of a subdivision of
$f(h)$
contains an orientation of a subdivision of
![]() $K_h$
, where each path changes directions only a bounded number of times. This would be implied by Conjecture 1.6.
$K_h$
, where each path changes directions only a bounded number of times. This would be implied by Conjecture 1.6.
Acknowledgements
The first author would like to thank Matthias Kriesell for pointing out Conjecture 1.5, and suggesting it might be possible to prove a result along the lines of Theorem 1.7.
MS acknowledges support by ANID Fondecyt RegularGrant 1221905, by FAPESP-ANID Investigación Conjunta grant 2019/13364-7, by RandNET (RISEproject H2020-EU.1.3.3) and by ANID PIA CMM FB210005.
CZG acknowledges support by the Universityof Birmingham, by RandNET (RISE project H2020-EU.1.3.3) and by ANID PIA CMM FB210005.