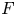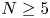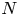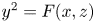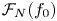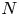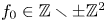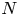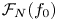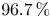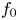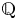1. Introduction
Let ![]() $F$ be a separable integral binary form of degree
$F$ be a separable integral binary form of degree ![]() $N \geq 5$. When
$N \geq 5$. When ![]() $N = 2n$ is even, the subscheme
$N = 2n$ is even, the subscheme ![]() $C_F$ of the weighted projective plane
$C_F$ of the weighted projective plane ![]() $\mathbb {P}_\mathbb {Q}^2(1,n,1)$ cut out by the equation
$\mathbb {P}_\mathbb {Q}^2(1,n,1)$ cut out by the equation ![]() $y^2 = F(x,z)$ is known as a hyperelliptic curve, and by Faltings’ theorem (see [Reference FaltingsFal83, Satz 7]), the curve
$y^2 = F(x,z)$ is known as a hyperelliptic curve, and by Faltings’ theorem (see [Reference FaltingsFal83, Satz 7]), the curve ![]() $C_F$ has only finitely many rational points. In [Reference BhargavaBha13, Theorem 1], Bhargava established the following ‘strong asymptotic form’ of Faltings’ theorem for hyperelliptic curves: when integral binary
$C_F$ has only finitely many rational points. In [Reference BhargavaBha13, Theorem 1], Bhargava established the following ‘strong asymptotic form’ of Faltings’ theorem for hyperelliptic curves: when integral binary ![]() $N$-ic forms are ordered by height, the density of forms
$N$-ic forms are ordered by height, the density of forms ![]() $F$ such that the curve
$F$ such that the curve ![]() $C_F$ has a rational point is
$C_F$ has a rational point is ![]() $o(2^{-n})$. In other words, most even-degree binary forms fail to represent a square.
$o(2^{-n})$. In other words, most even-degree binary forms fail to represent a square.
When ![]() $N= 2n+1$ is odd, the equation
$N= 2n+1$ is odd, the equation ![]() $y^2 = F(x,z)$ is called superelliptic. In contrast with the case of hyperelliptic curves, the problem of studying rational solutions to superelliptic equations is trivial: given any pair
$y^2 = F(x,z)$ is called superelliptic. In contrast with the case of hyperelliptic curves, the problem of studying rational solutions to superelliptic equations is trivial: given any pair ![]() $(x_0,z_0) \in \mathbb {Q}^2$, the triple
$(x_0,z_0) \in \mathbb {Q}^2$, the triple
is a solution to the equation ![]() $y^2 = F(x,z)$ and, in fact, the subscheme
$y^2 = F(x,z)$ and, in fact, the subscheme ![]() $S_F \subset \mathbb {P}_\mathbb {Q}^2(2,2n+1,2)$ cut out by this equation is isomorphic to
$S_F \subset \mathbb {P}_\mathbb {Q}^2(2,2n+1,2)$ cut out by this equation is isomorphic to ![]() $\mathbb {P}_{\mathbb {Q}}^1$. On the other hand, the problem of studying primitive integer solutions, triples
$\mathbb {P}_{\mathbb {Q}}^1$. On the other hand, the problem of studying primitive integer solutions, triples ![]() $(x_0,y_0,z_0) \in \mathbb {Z}^3$ such that
$(x_0,y_0,z_0) \in \mathbb {Z}^3$ such that ![]() $y_0^2 = F(x_0,z_0)$ and
$y_0^2 = F(x_0,z_0)$ and ![]() $\gcd (x_0,z_0) = 1$, is considerably more interesting. For instance, a result of Darmon and Granville states that
$\gcd (x_0,z_0) = 1$, is considerably more interesting. For instance, a result of Darmon and Granville states that ![]() $y^2 = F(x,z)$ has only finitely many primitive integer solutions (see [Reference Darmon and GranvilleDG95, Theorem 1
$y^2 = F(x,z)$ has only finitely many primitive integer solutions (see [Reference Darmon and GranvilleDG95, Theorem 1![]() $'$]). Given this analogue of Faltings’ theorem, it is natural to expect that an analogue of Bhargava's strong asymptotic form holds for primitive integer solutions to superelliptic equations. The purpose of this paper is to prove this expectation, i.e. that most integral odd-degree binary forms fail to primitively represent a square.
$'$]). Given this analogue of Faltings’ theorem, it is natural to expect that an analogue of Bhargava's strong asymptotic form holds for primitive integer solutions to superelliptic equations. The purpose of this paper is to prove this expectation, i.e. that most integral odd-degree binary forms fail to primitively represent a square.
1.1 Superelliptic stacky curves
In the rest of the paper, it will be convenient to reinterpret primitive integer solutions to the superelliptic equation ![]() $y^2 = F(x,z)$ as integral points on a certain stacky curve, which we denote by
$y^2 = F(x,z)$ as integral points on a certain stacky curve, which we denote by ![]() $\mathscr {S}_F$ and define as follows. Consider the punctured affine surface
$\mathscr {S}_F$ and define as follows. Consider the punctured affine surface
The group ![]() $\mathbb {G}_m$ acts by scaling on
$\mathbb {G}_m$ acts by scaling on ![]() $\widetilde {S}_F$ via
$\widetilde {S}_F$ via ![]() $\lambda \cdot (x_0,y_0,z_0) = (\lambda ^2 \cdot x_0,\lambda ^{2n+1} \cdot y_0, \lambda ^2 \cdot z_0)$. The map
$\lambda \cdot (x_0,y_0,z_0) = (\lambda ^2 \cdot x_0,\lambda ^{2n+1} \cdot y_0, \lambda ^2 \cdot z_0)$. The map ![]() $\widetilde {S}_F \to \mathbb {P}_\mathbb {Z}^1$ defined by
$\widetilde {S}_F \to \mathbb {P}_\mathbb {Z}^1$ defined by ![]() $(x,y,z) \to [x : z]$ is
$(x,y,z) \to [x : z]$ is ![]() $\mathbb {G}_m$-equivariant, and the field of
$\mathbb {G}_m$-equivariant, and the field of ![]() $\mathbb {G}_m$-invariant rational functions on
$\mathbb {G}_m$-invariant rational functions on ![]() $\widetilde {S}_F$ is generated by
$\widetilde {S}_F$ is generated by ![]() $x/z$, so the scheme quotient
$x/z$, so the scheme quotient ![]() $\widetilde {S}_F/\mathbb {G}_m$ is isomorphic to
$\widetilde {S}_F/\mathbb {G}_m$ is isomorphic to ![]() $\mathbb {P}_\mathbb {Z}^1$. The associated stack quotient
$\mathbb {P}_\mathbb {Z}^1$. The associated stack quotient ![]() $\mathscr {S}_F := [\widetilde {S}_F / \mathbb {G}_m]$ is a stacky curve with coarse moduli space
$\mathscr {S}_F := [\widetilde {S}_F / \mathbb {G}_m]$ is a stacky curve with coarse moduli space ![]() $\mathbb {P}^1_\mathbb {Z}$. The
$\mathbb {P}^1_\mathbb {Z}$. The ![]() $\mathbb {G}_m$-action on
$\mathbb {G}_m$-action on ![]() $\widetilde {S}_F$ has a nontrivial stabilizer isomorphic to the group scheme
$\widetilde {S}_F$ has a nontrivial stabilizer isomorphic to the group scheme ![]() $\mu _2$ if and only if
$\mu _2$ if and only if ![]() $y = 0$, so
$y = 0$, so ![]() $\mathscr {S}_F$ has a ‘
$\mathscr {S}_F$ has a ‘![]() $\tfrac {1}{2}$-point’ at each of the
$\tfrac {1}{2}$-point’ at each of the ![]() $2n+1$ distinct roots of
$2n+1$ distinct roots of ![]() $F$ over the algebraic closure.
$F$ over the algebraic closure.
Let ![]() $R$ be a principal ideal domain. We say that a triple
$R$ be a principal ideal domain. We say that a triple ![]() $(x_0, y_0, z_0) \in R^3$ is an
$(x_0, y_0, z_0) \in R^3$ is an ![]() $R$-primitive solution to
$R$-primitive solution to ![]() $y^2 = F(x,z)$ if
$y^2 = F(x,z)$ if ![]() $y_0^2 = F(x_0,z_0)$ and
$y_0^2 = F(x_0,z_0)$ and ![]() $Rx_0 + Rz_0 = R$. The set of
$Rx_0 + Rz_0 = R$. The set of ![]() $R$-primitive solutions to
$R$-primitive solutions to ![]() $y^2 = F(x,z)$ is readily seen to be in bijection with the set
$y^2 = F(x,z)$ is readily seen to be in bijection with the set ![]() $\widetilde {S}_F(R)$ of morphisms
$\widetilde {S}_F(R)$ of morphisms ![]() $\operatorname {Spec} R \to \widetilde {S}_F$ (i.e.
$\operatorname {Spec} R \to \widetilde {S}_F$ (i.e. ![]() $R$-points of
$R$-points of ![]() $\widetilde {S}_F\!$), which in turn corresponds bijectively with the set
$\widetilde {S}_F\!$), which in turn corresponds bijectively with the set ![]() $\mathscr {S}_F(R)$: indeed, specifying a map
$\mathscr {S}_F(R)$: indeed, specifying a map ![]() $\operatorname {Spec} R \to \mathscr {S}_F$ is definitionally equivalent to specifying a map
$\operatorname {Spec} R \to \mathscr {S}_F$ is definitionally equivalent to specifying a map ![]() $L \to \widetilde {S}_F$, where
$L \to \widetilde {S}_F$, where ![]() $L$ is a torsor of
$L$ is a torsor of ![]() $\operatorname {Spec} R$ by
$\operatorname {Spec} R$ by ![]() $\mathbb {G}_m$, but
$\mathbb {G}_m$, but ![]() $\operatorname {Spec} R$ has no nontrivial
$\operatorname {Spec} R$ has no nontrivial ![]() $\mathbb {G}_m$-torsors. In what follows, we abuse notation by writing
$\mathbb {G}_m$-torsors. In what follows, we abuse notation by writing ![]() $\mathscr {S}_F(R)$ for the set of
$\mathscr {S}_F(R)$ for the set of ![]() $R$-primitive solutions to
$R$-primitive solutions to ![]() $y^2 = F(x,z)$, regardless of whether
$y^2 = F(x,z)$, regardless of whether ![]() $F$ is separable.
$F$ is separable.
1.2 Main results
Our results concern families of superelliptic equations ![]() $y^2 = F(x,z)$ of degree
$y^2 = F(x,z)$ of degree ![]() $2n+1 \geq 3$ having fixed leading coefficient
$2n+1 \geq 3$ having fixed leading coefficient ![]() $f_0 := F(1,0) \in \mathbb {Z} \smallsetminus \{0\}$. Suppose that
$f_0 := F(1,0) \in \mathbb {Z} \smallsetminus \{0\}$. Suppose that ![]() $|f_0|$ is not a square, let
$|f_0|$ is not a square, let ![]() $|f_0| = m^2\kappa$, where
$|f_0| = m^2\kappa$, where ![]() $m,\kappa \in \mathbb {Z}$ and
$m,\kappa \in \mathbb {Z}$ and ![]() $\kappa$ is squarefree, and define the following quantities:
$\kappa$ is squarefree, and define the following quantities:
 \[ \mu_{f_0} := \prod_{p \mid \kappa}\bigg(\frac{1}{p^2} + \frac{p-1}{p^{n+1}}\bigg) \quad \text{and} \quad \mu_{f_0}' := \prod_{p \mid \kappa} \bigg(1 - \frac{1}{p^{2p+1}}\bigg). \]
\[ \mu_{f_0} := \prod_{p \mid \kappa}\bigg(\frac{1}{p^2} + \frac{p-1}{p^{n+1}}\bigg) \quad \text{and} \quad \mu_{f_0}' := \prod_{p \mid \kappa} \bigg(1 - \frac{1}{p^{2p+1}}\bigg). \]
For a ![]() $\mathbb {Z}$-algebra
$\mathbb {Z}$-algebra ![]() $R$, we write
$R$, we write ![]() $\mathscr {F}_{2n+1}(f_0, R) \subset R[x,z]$ for the set of binary forms of degree
$\mathscr {F}_{2n+1}(f_0, R) \subset R[x,z]$ for the set of binary forms of degree ![]() ${2n+1}$ with leading coefficient equal to
${2n+1}$ with leading coefficient equal to ![]() $f_0$; when
$f_0$; when ![]() $R = \mathbb {Z}$, we abbreviate
$R = \mathbb {Z}$, we abbreviate ![]() $\mathscr {F}_{2n+1}(f_0,\mathbb {Z})$ as
$\mathscr {F}_{2n+1}(f_0,\mathbb {Z})$ as ![]() $\mathscr {F}_{2n+1}(f_0)$. For simplicity, we sometimes write
$\mathscr {F}_{2n+1}(f_0)$. For simplicity, we sometimes write ![]() $\mathscr {F}_{2n+1}(f_0)$ to mean the family of superelliptic equations or superelliptic stacky curves defined by the forms in
$\mathscr {F}_{2n+1}(f_0)$ to mean the family of superelliptic equations or superelliptic stacky curves defined by the forms in ![]() $\mathscr {F}_{2n+1}(f_0)$. The height
$\mathscr {F}_{2n+1}(f_0)$. The height ![]() $H(F)$ of a binary form
$H(F)$ of a binary form ![]() $F(x,z) = \sum _{i = 0}^{2n+1} f_i x^{2n+1-i}z^i \in \mathscr {F}_{2n+1}(f_0)$ is defined as follows:
$F(x,z) = \sum _{i = 0}^{2n+1} f_i x^{2n+1-i}z^i \in \mathscr {F}_{2n+1}(f_0)$ is defined as follows:
With this setup, we prove the following analogue for superelliptic stacky curves of [Reference BhargavaBha13, Theorem 1].
Theorem 1 Let ![]() $f_0$ be a non-square integer. For every sufficiently large
$f_0$ be a non-square integer. For every sufficiently large ![]() $n$, most superelliptic stacky curves in the family
$n$, most superelliptic stacky curves in the family ![]() $\mathscr {F}_{2n+1}(f_0)$ have no primitive integer solutions. More precisely, we proceed as follows.
$\mathscr {F}_{2n+1}(f_0)$ have no primitive integer solutions. More precisely, we proceed as follows.
(a) Suppose
 $2 \nmid f_0$. For every
$2 \nmid f_0$. For every  $n \geq 5$, a positive proportion of forms
$n \geq 5$, a positive proportion of forms  $F \in \mathscr {F}_{2n+1}(f_0)$, when ordered by height, have the property that
$F \in \mathscr {F}_{2n+1}(f_0)$, when ordered by height, have the property that  $\mathscr {S}_F(\mathbb {Z}) = \varnothing$. Moreover, the lower density of forms
$\mathscr {S}_F(\mathbb {Z}) = \varnothing$. Moreover, the lower density of forms  $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that  $\mathscr {S}_F(\mathbb {Z}) = \varnothing$ is at least
$\mathscr {S}_F(\mathbb {Z}) = \varnothing$ is at least  $1 - \mu _{f_0} + o(2^{-n})$.
$1 - \mu _{f_0} + o(2^{-n})$.(b) Suppose
 $2 \mid f_0$. The lower density of forms
$2 \mid f_0$. The lower density of forms  $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that  $\mathscr {S}_F(\mathbb {Z}) = \varnothing$ is at least
$\mathscr {S}_F(\mathbb {Z}) = \varnothing$ is at least  $1 - \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers
$1 - \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers  $\varepsilon _1,\varepsilon _2 > 0$.
$\varepsilon _1,\varepsilon _2 > 0$.
As indicated by Table 1, the quantity ![]() $1-\mu _{f_0}$, which by Theorem 1 constitutes a lower bound on the density of insoluble equations in
$1-\mu _{f_0}$, which by Theorem 1 constitutes a lower bound on the density of insoluble equations in ![]() $\mathscr {F}_{2n+1}(f_0)$ in the large-
$\mathscr {F}_{2n+1}(f_0)$ in the large-![]() $n$ limit, rapidly approaches
$n$ limit, rapidly approaches ![]() $1$ as the number of prime factors of
$1$ as the number of prime factors of ![]() $\kappa$ grows. Furthermore, the method used to prove Theorem 1 can be easily adapted to obtain a similar result when the family
$\kappa$ grows. Furthermore, the method used to prove Theorem 1 can be easily adapted to obtain a similar result when the family ![]() $\mathscr {F}_{2n+1}(f_0)$ is replaced by any subfamily defined by congruence conditions modulo finitely many prime powers.
$\mathscr {F}_{2n+1}(f_0)$ is replaced by any subfamily defined by congruence conditions modulo finitely many prime powers.
Table 1. The strength of the limiting lower bounds ![]() $\lim _{n \to \infty }1 - \mu _{f_0}$ (respectively,
$\lim _{n \to \infty }1 - \mu _{f_0}$ (respectively, ![]() $\lim _{n \to \infty } \mu _{f_0}' - \mu _{f_0}$) on the density of insoluble superelliptic equations given by Theorem 1 (respectively, on the density of superelliptic equations having a Brauer–Manin obstruction to solubility given by Theorem 2).
$\lim _{n \to \infty } \mu _{f_0}' - \mu _{f_0}$) on the density of insoluble superelliptic equations given by Theorem 1 (respectively, on the density of superelliptic equations having a Brauer–Manin obstruction to solubility given by Theorem 2).

Note that Theorem 1 is subject to the condition that ![]() $|f_0|$ is not a square. When
$|f_0|$ is not a square. When ![]() $|f_0|$ is a square, every form
$|f_0|$ is a square, every form ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ is such that
$F \in \mathscr {F}_{2n+1}(f_0)$ is such that ![]() $y^2 = F(x,z)$ has a trivial solution, namely
$y^2 = F(x,z)$ has a trivial solution, namely ![]() $(x,y,z) = (\operatorname {sign}(f_0),\sqrt {|f_0|},0)$. We expect that for most
$(x,y,z) = (\operatorname {sign}(f_0),\sqrt {|f_0|},0)$. We expect that for most ![]() $F \in \mathscr {F}_{2n+1}(f_0)$, the equation
$F \in \mathscr {F}_{2n+1}(f_0)$, the equation ![]() $y^2 = F(x,z)$ has no solutions other than the trivial one. The presence of the trivial solution renders this expectation difficult to prove: e.g. to obtain the analogous result for rational points on monic odd-degree hyperelliptic curves, Poonen and Stoll [Reference Poonen and StollPS14] combined work of Bhargava and Gross [Reference Bhargava and GrossBG13] on equidistribution of the
$y^2 = F(x,z)$ has no solutions other than the trivial one. The presence of the trivial solution renders this expectation difficult to prove: e.g. to obtain the analogous result for rational points on monic odd-degree hyperelliptic curves, Poonen and Stoll [Reference Poonen and StollPS14] combined work of Bhargava and Gross [Reference Bhargava and GrossBG13] on equidistribution of the ![]() $2$-Selmer elements of the Jacobians of these curves with a variant of Chabauty's method (cf. [Reference Shankar and WangSW18], in which Shankar and Wang treat the even-degree case, as well as the work of Thorne and Romano [Reference Romano and ThorneRT21] and Laga [Reference LagaLag21], which prove similar theorems for certain families of non-hyperelliptic curves). To the author's knowledge, analogues of the notion of Selmer group and of Chabauty's method remain to be formulated for superelliptic stacky curves.
$2$-Selmer elements of the Jacobians of these curves with a variant of Chabauty's method (cf. [Reference Shankar and WangSW18], in which Shankar and Wang treat the even-degree case, as well as the work of Thorne and Romano [Reference Romano and ThorneRT21] and Laga [Reference LagaLag21], which prove similar theorems for certain families of non-hyperelliptic curves). To the author's knowledge, analogues of the notion of Selmer group and of Chabauty's method remain to be formulated for superelliptic stacky curves.
In the course of proving Theorem 1, we actually prove the stronger statement that most superelliptic stacky curves have a ![]() $2$-descent obstruction to having an integral point. Since these stacky curves typically have integral points everywhere locally, it follows that most of them fail the Hasse principle (i.e. do not have a
$2$-descent obstruction to having an integral point. Since these stacky curves typically have integral points everywhere locally, it follows that most of them fail the Hasse principle (i.e. do not have a ![]() $\mathbb {Z}$-point despite having a
$\mathbb {Z}$-point despite having a ![]() $\mathbb {Z}_v$-point for every place
$\mathbb {Z}_v$-point for every place ![]() $v$ of
$v$ of ![]() $\mathbb {Q}$) due to a
$\mathbb {Q}$) due to a ![]() $2$-descent obstruction. Upon showing that such a
$2$-descent obstruction. Upon showing that such a ![]() $2$-descent obstruction yields a case of the Brauer–Manin obstruction, we obtain the following analogue for superelliptic stacky curves of [Reference BhargavaBha13, Corollary 4]Footnote 1 (see also the work of Thorne [Reference ThorneTho15] and Thorne and Romano [Reference Romano and ThorneRT18], which prove similar theorems for certain families of non-hyperelliptic curves).
$2$-descent obstruction yields a case of the Brauer–Manin obstruction, we obtain the following analogue for superelliptic stacky curves of [Reference BhargavaBha13, Corollary 4]Footnote 1 (see also the work of Thorne [Reference ThorneTho15] and Thorne and Romano [Reference Romano and ThorneRT18], which prove similar theorems for certain families of non-hyperelliptic curves).
Theorem 2 Let ![]() $f_0$ be a non-square integer. The lower density of forms
$f_0$ be a non-square integer. The lower density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$, when ordered by height, such that the stacky curve
$F \in \mathscr {F}_{2n+1}(f_0)$, when ordered by height, such that the stacky curve ![]() $\mathscr {S}_F$ fails the Hasse principle due to the Brauer–Manin obstruction is at least
$\mathscr {S}_F$ fails the Hasse principle due to the Brauer–Manin obstruction is at least ![]() $\mu _{f_0}' - \mu _{f_0} + o(2^{-n})$ if
$\mu _{f_0}' - \mu _{f_0} + o(2^{-n})$ if ![]() $2 \nmid f_0$ and is at least
$2 \nmid f_0$ and is at least ![]() $\mu _{f_0}' - \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some
$\mu _{f_0}' - \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some ![]() $\varepsilon _1,\varepsilon _2 > 0$ if
$\varepsilon _1,\varepsilon _2 > 0$ if ![]() $2 \mid f_0$.
$2 \mid f_0$.
The proportion ![]() $\mu _{f_0}'-\mu _{f_0}$, which can be thought of as a lower bound on the density of superelliptic equations with leading coefficient
$\mu _{f_0}'-\mu _{f_0}$, which can be thought of as a lower bound on the density of superelliptic equations with leading coefficient ![]() $f_0$ having a Brauer–Manin obstruction to solubility in the large-
$f_0$ having a Brauer–Manin obstruction to solubility in the large-![]() $n$ limit, approaches
$n$ limit, approaches ![]() $\approx 96.7\,\%$ as the number of prime factors of
$\approx 96.7\,\%$ as the number of prime factors of ![]() $\kappa$ grows; see Table 1.
$\kappa$ grows; see Table 1.
The genus of a stacky curve can be defined in terms of the Euler characteristic of an orbifold curve; see [Reference DarmonDar97, section entitled ‘Orbifolds, and the topology of ![]() $M$-curves’]. In [Reference Bhargava and PoonenBP19], Bhargava and Poonen prove that all (suitably defined) stacky curves
$M$-curves’]. In [Reference Bhargava and PoonenBP19], Bhargava and Poonen prove that all (suitably defined) stacky curves ![]() $S$ of genus less than
$S$ of genus less than ![]() $\frac {1}{2}$ over
$\frac {1}{2}$ over ![]() $\mathbb {Z}$ satisfy the Hasse principle; i.e. if
$\mathbb {Z}$ satisfy the Hasse principle; i.e. if ![]() $S(\mathbb {R}) \neq \varnothing$ and
$S(\mathbb {R}) \neq \varnothing$ and ![]() $S(\mathbb {Z}_p) \neq \varnothing$ for every prime
$S(\mathbb {Z}_p) \neq \varnothing$ for every prime ![]() $p \in \mathbb {Z}$, then
$p \in \mathbb {Z}$, then ![]() $S(\mathbb {Z}) \neq \varnothing$. On the other hand, there is no guarantee that a stacky curve of genus at least
$S(\mathbb {Z}) \neq \varnothing$. On the other hand, there is no guarantee that a stacky curve of genus at least ![]() $\frac {1}{2}$ satisfies the Hasse principle: indeed, for any separable integral binary form
$\frac {1}{2}$ satisfies the Hasse principle: indeed, for any separable integral binary form ![]() $F$ of degree
$F$ of degree ![]() $2n+1 \geq 3$, the genus of the associated stacky curve
$2n+1 \geq 3$, the genus of the associated stacky curve ![]() $\mathscr {S}_F$ is given by
$\mathscr {S}_F$ is given by ![]() $({2n+1})/{4} > \frac {1}{2}$, and Theorem 2 demonstrates that these stacky curves often fail the Hasse principle.
$({2n+1})/{4} > \frac {1}{2}$, and Theorem 2 demonstrates that these stacky curves often fail the Hasse principle.
1.3 Method of proof
Our strategy is to transform the problem of counting soluble superelliptic equations into one of counting integral orbits of a certain representation by devising a suitable orbit construction. In § 3, we prove that elements of ![]() $\mathscr {S}_F(\mathbb {Z})$ naturally give rise to certain square roots of the ideal class of the inverse different of a ring
$\mathscr {S}_F(\mathbb {Z})$ naturally give rise to certain square roots of the ideal class of the inverse different of a ring ![]() $R_F$ associated to the form
$R_F$ associated to the form ![]() $F$. Via a parametrization that we introduced in [Reference SwaminathanSwa23], these square roots correspond to certain integral orbits for the action of the split odd special orthogonal group
$F$. Via a parametrization that we introduced in [Reference SwaminathanSwa23], these square roots correspond to certain integral orbits for the action of the split odd special orthogonal group ![]() $G$ on a space
$G$ on a space ![]() $V$ of self-adjoint operators
$V$ of self-adjoint operators ![]() $T$, where the characteristic polynomial of
$T$, where the characteristic polynomial of ![]() $T$ is equal to the monicized form
$T$ is equal to the monicized form ![]() $F_{\operatorname {mon}}(x,1) := ({1}/{f_0}) \cdot F(x,f_0z)$.
$F_{\operatorname {mon}}(x,1) := ({1}/{f_0}) \cdot F(x,f_0z)$.
The parametrization in [Reference SwaminathanSwa23] is explicitly leading-coefficient-dependent and is, thus, particularly well-suited for applications concerning binary forms with fixed leading coefficient. By generalizing an equidistribution argument that we developed in joint work with Bhargava and Shankar (see [Reference Bhargava, Shankar and SwaminathanBSS21], where we used the very same parametrization to determine the second moment of the size of the ![]() $2$-Selmer group of elliptic curves), one can average the bounds in Theorems 1 and 2 over all leading coefficients and, thus, deduce analogues of these theorems for the full family of superelliptic equations of given degree. In this paper, we fix the leading coefficient for two reasons: doing so simplifies the orbit-counting and allows us to prove a stronger result, that within each thin subfamily of superelliptic equations with fixed leading coefficient, most members fail the Hasse principle.
$2$-Selmer group of elliptic curves), one can average the bounds in Theorems 1 and 2 over all leading coefficients and, thus, deduce analogues of these theorems for the full family of superelliptic equations of given degree. In this paper, we fix the leading coefficient for two reasons: doing so simplifies the orbit-counting and allows us to prove a stronger result, that within each thin subfamily of superelliptic equations with fixed leading coefficient, most members fail the Hasse principle.
In § 2, we discuss the representation of ![]() $G$ on
$G$ on ![]() $V$, the orbits of which also correspond to
$V$, the orbits of which also correspond to ![]() $2$-Selmer elements of the Jacobians of monic odd-degree hyperelliptic curves (see the work of Bhargava and Gross [Reference Bhargava and GrossBG13]), we define the ring
$2$-Selmer elements of the Jacobians of monic odd-degree hyperelliptic curves (see the work of Bhargava and Gross [Reference Bhargava and GrossBG13]), we define the ring ![]() $R_F$, and we recall the parametrization from [Reference SwaminathanSwa23]. In § 4, we prove Theorem 1 in a series of three steps. First, in § 4.2, we adapt results of Bhargava and Gross (see [Reference Bhargava and GrossBG13, § 10]) to obtain a bound on the number of
$R_F$, and we recall the parametrization from [Reference SwaminathanSwa23]. In § 4, we prove Theorem 1 in a series of three steps. First, in § 4.2, we adapt results of Bhargava and Gross (see [Reference Bhargava and GrossBG13, § 10]) to obtain a bound on the number of ![]() $G(\mathbb {Z})$-orbits on
$G(\mathbb {Z})$-orbits on ![]() $V(\mathbb {Z})$ satisfying local conditions. Second, in § 4.3–4.6, we bound the local volume of the set of elements in
$V(\mathbb {Z})$ satisfying local conditions. Second, in § 4.3–4.6, we bound the local volume of the set of elements in ![]() $V(\mathbb {Z}_v)$ that arise from
$V(\mathbb {Z}_v)$ that arise from ![]() $\mathbb {Z}_v$-primitive solutions via the orbit construction in § 3 for each place
$\mathbb {Z}_v$-primitive solutions via the orbit construction in § 3 for each place ![]() $v$ of
$v$ of ![]() $\mathbb {Q}$. This is the most technical step of the proof, and we handle it in a series of subsections as follows.
$\mathbb {Q}$. This is the most technical step of the proof, and we handle it in a series of subsections as follows.
– In § 4.3, we take
 $v = \infty$ and show that the relevant local volume contributes a factor of
$v = \infty$ and show that the relevant local volume contributes a factor of  $O(2^n)$ to the final bound.
$O(2^n)$ to the final bound.– In § 4.4, we take
 $v = p \nmid 2f_0$ and obtain a bound on the relevant local volume; later, in § 4.7, we show that the product of this bound over all
$v = p \nmid 2f_0$ and obtain a bound on the relevant local volume; later, in § 4.7, we show that the product of this bound over all  $p \nmid 2f_0$ contributes a factor of
$p \nmid 2f_0$ contributes a factor of  $O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ to the final bound; this constitutes part of the saving when
$O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ to the final bound; this constitutes part of the saving when  $2 \nmid f_0$ and all of the saving when
$2 \nmid f_0$ and all of the saving when  $2 \mid f_0$.
$2 \mid f_0$.– In § 4.5, we take
 $v = 2 \nmid f_0$ and show that the relevant local volume contributes a factor of
$v = 2 \nmid f_0$ and show that the relevant local volume contributes a factor of  $O(2^{-2n})$ to the final bound; this constitutes most of the saving when
$O(2^{-2n})$ to the final bound; this constitutes most of the saving when  $2 \nmid f_0$.
$2 \nmid f_0$.– In § 4.6, we take
 $v = p \mid f_0$ and show that the relevant local volume contributes a factor of
$v = p \mid f_0$ and show that the relevant local volume contributes a factor of  $O(1)$ to the final bound.
$O(1)$ to the final bound.
The main idea for the savings obtained in §§ 4.4 and 4.5 is that the number of solutions to ![]() $y^2 = F(x,z)$ modulo an integer
$y^2 = F(x,z)$ modulo an integer ![]() $k$ is at most
$k$ is at most ![]() $\#\mathbb {P}^1(\mathbb {Z}/k\mathbb {Z})$, which, for
$\#\mathbb {P}^1(\mathbb {Z}/k\mathbb {Z})$, which, for ![]() $k$ small relative to the degree
$k$ small relative to the degree ![]() $n$, is typically smaller than the total number of
$n$, is typically smaller than the total number of ![]() $G(\mathbb {Z}/k\mathbb {Z})$-orbits having characteristic polynomial
$G(\mathbb {Z}/k\mathbb {Z})$-orbits having characteristic polynomial ![]() $F_{\mathrm {mon}}$; for example, when
$F_{\mathrm {mon}}$; for example, when ![]() $k = p \nmid f_0$ is an odd prime, this number of orbits is
$k = p \nmid f_0$ is an odd prime, this number of orbits is ![]() $\asymp 2^m$, where
$\asymp 2^m$, where ![]() $m$ is the number of distinct irreducible factors of
$m$ is the number of distinct irreducible factors of ![]() $F_{\mathrm {mon}}$ modulo
$F_{\mathrm {mon}}$ modulo ![]() $p$. Third, in § 4.7, we combine the results of the first two steps to complete the proof of Theorem 1. Finally, in § 5, we define the notions of
$p$. Third, in § 4.7, we combine the results of the first two steps to complete the proof of Theorem 1. Finally, in § 5, we define the notions of ![]() $2$-descent obstruction and Brauer–Manin obstruction for superelliptic stacky curves, and we prove Theorem 2.
$2$-descent obstruction and Brauer–Manin obstruction for superelliptic stacky curves, and we prove Theorem 2.
2. Algebraic preliminaries
In this section, we recall several algebraic notions that feature in our construction of orbits from integral points on superelliptic stacky curves. We begin in § 2.1 by introducing the representation of ![]() $G$ on
$G$ on ![]() $V$. Then, in § 2.2, we define the ring
$V$. Then, in § 2.2, we define the ring ![]() $R_F$ associated to a binary form
$R_F$ associated to a binary form ![]() $F$, and in § 2.3, we recall a parametrization from [Reference SwaminathanSwa23] of square roots of the ideal class of the inverse different of
$F$, and in § 2.3, we recall a parametrization from [Reference SwaminathanSwa23] of square roots of the ideal class of the inverse different of ![]() $R_F$. We finish in § 2.4 by describing the parametrization over fields.
$R_F$. We finish in § 2.4 by describing the parametrization over fields.
2.1 A representation of the split odd special orthogonal group
Let ![]() $W$ be the
$W$ be the ![]() $\mathbb {Z}$-lattice of rank
$\mathbb {Z}$-lattice of rank ![]() $2n+1$ equipped with a nondegenerate symmetric bilinear form
$2n+1$ equipped with a nondegenerate symmetric bilinear form ![]() $[-,-] \colon W \times W \to \mathbb {Z}$ that has signature
$[-,-] \colon W \times W \to \mathbb {Z}$ that has signature ![]() $(n+1,n)$ after extending scalars to
$(n+1,n)$ after extending scalars to ![]() $\mathbb {R}$. By [Reference SerreSer73, Chapter V]), the lattice
$\mathbb {R}$. By [Reference SerreSer73, Chapter V]), the lattice ![]() $W$ is unique up to isomorphism over
$W$ is unique up to isomorphism over ![]() $\mathbb {Z}$, and there is a
$\mathbb {Z}$, and there is a ![]() $\mathbb {Z}$-basis
$\mathbb {Z}$-basis
such that ![]() $[e_i, e_j] = [e_i',e_j'] = [e_i,u]= [e_i',u]= 0$,
$[e_i, e_j] = [e_i',e_j'] = [e_i,u]= [e_i',u]= 0$, ![]() $[e_i, e_j'] = \delta _{ij}$, and
$[e_i, e_j'] = \delta _{ij}$, and ![]() $[u,u] = 1$ for all relevant pairs
$[u,u] = 1$ for all relevant pairs ![]() $(i,j)$. We denote by
$(i,j)$. We denote by ![]() $A_0$ the matrix of
$A_0$ the matrix of ![]() $[-,-]$ with respect to the basis (3).
$[-,-]$ with respect to the basis (3).
For a ![]() $\mathbb {Z}$-algebra
$\mathbb {Z}$-algebra ![]() $R$, let
$R$, let ![]() $W_R := W \otimes _\mathbb {Z} R$. For a field
$W_R := W \otimes _\mathbb {Z} R$. For a field ![]() $k$ of characteristic not equal to
$k$ of characteristic not equal to ![]() $2$, the
$2$, the ![]() $k$-vector space
$k$-vector space ![]() $W_k$ equipped with the bilinear form
$W_k$ equipped with the bilinear form ![]() $[-,-]$ is called the split orthogonal space of dimension
$[-,-]$ is called the split orthogonal space of dimension ![]() $2n+1$ and determinant
$2n+1$ and determinant ![]() $(-1)^n$ over
$(-1)^n$ over ![]() $k$ and is unique up to
$k$ and is unique up to ![]() $k$-isomorphism [Reference Milnor and HusemollerMH73, § 6]. The space
$k$-isomorphism [Reference Milnor and HusemollerMH73, § 6]. The space ![]() $W_k$ is called ‘split’ because it is a nondegenerate quadratic space containing a maximal isotropic subspace (defined over
$W_k$ is called ‘split’ because it is a nondegenerate quadratic space containing a maximal isotropic subspace (defined over ![]() $k$) for the bilinear form
$k$) for the bilinear form ![]() $[-,-]$.
$[-,-]$.
Let ![]() $T \in \operatorname {End}_R(W_R)$. Recall that the adjoint transformation
$T \in \operatorname {End}_R(W_R)$. Recall that the adjoint transformation ![]() $T^{\dagger} \in \operatorname {End}_R(W_R)$ of
$T^{\dagger} \in \operatorname {End}_R(W_R)$ of ![]() $T$ with respect to the form
$T$ with respect to the form ![]() $[-,-]$ is determined by the formula
$[-,-]$ is determined by the formula ![]() $[Tv, w] = [v, T^{\dagger} w]$ for all
$[Tv, w] = [v, T^{\dagger} w]$ for all ![]() $v,w \in W_R$, and that
$v,w \in W_R$, and that ![]() $T$ is said to be self-adjoint if
$T$ is said to be self-adjoint if ![]() $T = T^{\dagger}$. If
$T = T^{\dagger}$. If ![]() $T$ is expressed as a matrix with respect to the basis (3), then
$T$ is expressed as a matrix with respect to the basis (3), then ![]() $T$ is self-adjoint with respect to the form
$T$ is self-adjoint with respect to the form ![]() $[-,-]$ if and only if
$[-,-]$ if and only if ![]() $T^TA_0 = A_0T$.
$T^TA_0 = A_0T$.
Let ![]() $V$ be the affine space defined over
$V$ be the affine space defined over ![]() $\operatorname {Spec} \mathbb {Z}$ whose
$\operatorname {Spec} \mathbb {Z}$ whose ![]() $R$-points are given by
$R$-points are given by
for any ![]() $\mathbb {Z}$-algebra
$\mathbb {Z}$-algebra ![]() $R$. An
$R$. An ![]() $R$-automorphism
$R$-automorphism ![]() $g \in \operatorname {Aut}_R(W_R)$ is called orthogonal with respect to the form
$g \in \operatorname {Aut}_R(W_R)$ is called orthogonal with respect to the form ![]() $[-,-]$ if
$[-,-]$ if ![]() $[g(v),g(w)] = [v,w]$ for all
$[g(v),g(w)] = [v,w]$ for all ![]() $v,w \in W_R$. If
$v,w \in W_R$. If ![]() $g$ is expressed as a matrix with respect to the basis (3), then
$g$ is expressed as a matrix with respect to the basis (3), then ![]() $g$ is orthogonal with respect to the form
$g$ is orthogonal with respect to the form ![]() $[-,-]$ if and only if
$[-,-]$ if and only if ![]() $g^TA_0g = A_0$. Let
$g^TA_0g = A_0$. Let ![]() $G := \operatorname {SO}(W)$ be the group scheme defined over
$G := \operatorname {SO}(W)$ be the group scheme defined over ![]() $\operatorname {Spec} \mathbb {Z}$ whose
$\operatorname {Spec} \mathbb {Z}$ whose ![]() $R$-points are given by
$R$-points are given by
for any ![]() $\mathbb {Z}$-algebra
$\mathbb {Z}$-algebra ![]() $R$. The group scheme
$R$. The group scheme ![]() $G$ is known as the split odd special orthogonal group of the lattice
$G$ is known as the split odd special orthogonal group of the lattice ![]() $W$, and it acts on
$W$, and it acts on ![]() $V$ by conjugation: for
$V$ by conjugation: for ![]() $g \in G(R)$ and
$g \in G(R)$ and ![]() $T \in V(R)$, the map
$T \in V(R)$, the map ![]() $gTg^{-1} \in \operatorname {End}_R(W_R)$ is readily checked to be self-adjoint with respect to
$gTg^{-1} \in \operatorname {End}_R(W_R)$ is readily checked to be self-adjoint with respect to ![]() $[-,-]$ and is therefore an element of
$[-,-]$ and is therefore an element of ![]() $V(R)$. We thus obtain a linear representation
$V(R)$. We thus obtain a linear representation ![]() $G \to \operatorname {GL}(V)$ of dimension
$G \to \operatorname {GL}(V)$ of dimension ![]() $\dim V = 2n^2 + 3n + 1$.
$\dim V = 2n^2 + 3n + 1$.
Since ![]() $G$ acts on
$G$ acts on ![]() $V$ by conjugation, the characteristic polynomial
$V$ by conjugation, the characteristic polynomial
 \[ \operatorname{ch}(T) := \det(x \cdot \operatorname{id} - T) = x^{2n+1} + \sum_{i = 1}^{2n+1} c_i x^{2n+1-i} \in R[x] \]
\[ \operatorname{ch}(T) := \det(x \cdot \operatorname{id} - T) = x^{2n+1} + \sum_{i = 1}^{2n+1} c_i x^{2n+1-i} \in R[x] \]
is invariant under the action of ![]() $G(R)$ for each
$G(R)$ for each ![]() $T \in V(R)$. In fact, by [Reference BourbakiBou75, § 8.3, part (VI) of § 13.2], the coefficients
$T \in V(R)$. In fact, by [Reference BourbakiBou75, § 8.3, part (VI) of § 13.2], the coefficients ![]() $c_1, \ldots, c_{2n+1}$, which have respective degrees
$c_1, \ldots, c_{2n+1}$, which have respective degrees ![]() $1, \ldots, 2n+1$, freely generate the ring of
$1, \ldots, 2n+1$, freely generate the ring of ![]() $G$-invariant functions on
$G$-invariant functions on ![]() $V$.
$V$.
2.2 Rings associated to binary forms
For the rest of § 2, let ![]() $R$ be a principal ideal domain (we typically take
$R$ be a principal ideal domain (we typically take ![]() $R$ to be
$R$ to be ![]() $\mathbb {Z}$,
$\mathbb {Z}$, ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $\mathbb {Z}_p$,
$\mathbb {Z}_p$, ![]() $\mathbb {Z}/p\mathbb {Z}$, or
$\mathbb {Z}/p\mathbb {Z}$, or ![]() $\mathbb {Q}_p$, where
$\mathbb {Q}_p$, where ![]() $p \in \mathbb {Z}$ is a prime), and let
$p \in \mathbb {Z}$ is a prime), and let ![]() $k$ be the fraction field of
$k$ be the fraction field of ![]() $R$. Let
$R$. Let ![]() $n \geq 1$, and let
$n \geq 1$, and let
 \[ F(x,z) = \sum_{i = 0}^{2n+1} f_i x^{2n+1-i}z^i \in R[x,z] \]
\[ F(x,z) = \sum_{i = 0}^{2n+1} f_i x^{2n+1-i}z^i \in R[x,z] \]
be a separable binary form of degree ![]() $2n+1$ with leading coefficient
$2n+1$ with leading coefficient ![]() $f_0 \in R\smallsetminus \{0\}$.
$f_0 \in R\smallsetminus \{0\}$.
Consider the étale ![]() $k$-algebra
$k$-algebra
Let ![]() $\theta$ denote the image of
$\theta$ denote the image of ![]() $x$ in
$x$ in ![]() $K_F$. For each
$K_F$. For each ![]() $i \in \{1, \ldots, 2n\}$, let
$i \in \{1, \ldots, 2n\}$, let ![]() $p_i$ be the polynomial defined by
$p_i$ be the polynomial defined by
 \[ p_i(t) := \sum_{j = 0}^{i-1} f_j t^{i-j}, \]
\[ p_i(t) := \sum_{j = 0}^{i-1} f_j t^{i-j}, \]
and let ![]() $\zeta _i := p_i(\theta )$. To the binary form
$\zeta _i := p_i(\theta )$. To the binary form ![]() $F$, there is a naturally associated free
$F$, there is a naturally associated free ![]() $R$-submodule
$R$-submodule ![]() $R_F \subset K_F$ having rank
$R_F \subset K_F$ having rank ![]() $2n+1$ and
$2n+1$ and ![]() $R$-basis given by
$R$-basis given by
The module ![]() $R_F$ is of significant interest in its own right and has been studied extensively in the literature. In [Reference Birch and MerrimanBM72, proof of Lemma 3], Birch and Merriman proved that the discriminant of
$R_F$ is of significant interest in its own right and has been studied extensively in the literature. In [Reference Birch and MerrimanBM72, proof of Lemma 3], Birch and Merriman proved that the discriminant of ![]() $F$ is equal to the discriminant of
$F$ is equal to the discriminant of ![]() $R_F$, and in [Reference NakagawaNak89, Proposition 1.1], Nakagawa proved that
$R_F$, and in [Reference NakagawaNak89, Proposition 1.1], Nakagawa proved that ![]() $R_F$ is actually a ring (and, hence, an order in
$R_F$ is actually a ring (and, hence, an order in ![]() $K_F\!$) having multiplication table
$K_F\!$) having multiplication table
 \begin{equation} \zeta_i\zeta_j = \sum_{k = j+1}^{\min\{i+j,2n+1\}} f_{i+j-k}\zeta_k - \sum_{k = \max\{i+j-(2n+1),1\}}^i f_{i+j-k}\zeta_k, \end{equation}
\begin{equation} \zeta_i\zeta_j = \sum_{k = j+1}^{\min\{i+j,2n+1\}} f_{i+j-k}\zeta_k - \sum_{k = \max\{i+j-(2n+1),1\}}^i f_{i+j-k}\zeta_k, \end{equation}
where ![]() $1 \leq i \leq j \leq 2n$ and we take
$1 \leq i \leq j \leq 2n$ and we take ![]() $\zeta _0 = 1$ and
$\zeta _0 = 1$ and ![]() $\zeta _{2n+1} = -f_{2n+1}$ for the sake of convenience. (To be clear, these results of Nakagawa are stated for the case of irreducible
$\zeta _{2n+1} = -f_{2n+1}$ for the sake of convenience. (To be clear, these results of Nakagawa are stated for the case of irreducible ![]() $F$, but as noted in [Reference WoodWoo11, § 2.1], their proofs continue to hold when
$F$, but as noted in [Reference WoodWoo11, § 2.1], their proofs continue to hold when ![]() $F$ is not irreducible.)
$F$ is not irreducible.)
Also contained in ![]() $K_F$ is a natural family of free
$K_F$ is a natural family of free ![]() $R$-submodules
$R$-submodules ![]() $I_F^j$ of rank
$I_F^j$ of rank ![]() $2n+1$ for each
$2n+1$ for each ![]() $j \in \{0, \ldots, 2n\}$, having
$j \in \{0, \ldots, 2n\}$, having ![]() $R$-basis given by
$R$-basis given by
Note that ![]() $I_F^0 = R_F$ is the unit ideal. By [Reference WoodWoo11, Proposition A.1], each
$I_F^0 = R_F$ is the unit ideal. By [Reference WoodWoo11, Proposition A.1], each ![]() $I_F^j$ is an
$I_F^j$ is an ![]() $R_F$-module and, hence, a fractional ideal of
$R_F$-module and, hence, a fractional ideal of ![]() $R_F$; moreover, the notation
$R_F$; moreover, the notation ![]() $I_F^j$ makes sense, because
$I_F^j$ makes sense, because ![]() $I_F^j$ is equal to the
$I_F^j$ is equal to the ![]() $j$th power of
$j$th power of ![]() $I_F^1$. By [Reference WoodWoo11, Proposition A.4], the fractional ideals
$I_F^1$. By [Reference WoodWoo11, Proposition A.4], the fractional ideals ![]() $I_F^j$ are invertible precisely when the form
$I_F^j$ are invertible precisely when the form ![]() $F$ is primitive, in the sense that
$F$ is primitive, in the sense that ![]() $\sum _{i = 0}^{2n+1}Rf_i = R$. It is a result of Simon (see [Reference SimonSim08, Proposition 14]; cf. [Reference WoodWoo11, Theorem 2.4]) that
$\sum _{i = 0}^{2n+1}Rf_i = R$. It is a result of Simon (see [Reference SimonSim08, Proposition 14]; cf. [Reference WoodWoo11, Theorem 2.4]) that
represents the ideal class of the inverse different of ![]() $R_F$.
$R_F$.
Given a fractional ideal ![]() $I$ of
$I$ of ![]() $R_F$ having a specified basis (i.e. a based fractional ideal), the norm of
$R_F$ having a specified basis (i.e. a based fractional ideal), the norm of ![]() $I$, denoted by
$I$, denoted by ![]() $\operatorname {N}(I)$, is defined to be the determinant of the
$\operatorname {N}(I)$, is defined to be the determinant of the ![]() $k$-linear transformation taking the basis of
$k$-linear transformation taking the basis of ![]() $I$ to the basis of
$I$ to the basis of ![]() $R_F$ in (4). It is easy to check that
$R_F$ in (4). It is easy to check that ![]() $\operatorname {N}(I_F^j) = f_0^{-j}$ for each
$\operatorname {N}(I_F^j) = f_0^{-j}$ for each ![]() $j$ with respect to the basis in (6). The norm of
$j$ with respect to the basis in (6). The norm of ![]() $\kappa \in K_F^\times$ is
$\kappa \in K_F^\times$ is ![]() $\operatorname {N}(\kappa ) := \operatorname {N}(\kappa \cdot I_F^0)$ with respect to the basis
$\operatorname {N}(\kappa ) := \operatorname {N}(\kappa \cdot I_F^0)$ with respect to the basis ![]() $\langle \kappa, \kappa \cdot \zeta _1, \ldots, \kappa \cdot \zeta _{2n}\rangle$ of
$\langle \kappa, \kappa \cdot \zeta _1, \ldots, \kappa \cdot \zeta _{2n}\rangle$ of ![]() $\kappa \cdot I_F^0$. Note that we have the multiplicativity relation
$\kappa \cdot I_F^0$. Note that we have the multiplicativity relation
for any ![]() $\kappa \in K_F^\times$ and fractional ideal
$\kappa \in K_F^\times$ and fractional ideal ![]() $I$ of
$I$ of ![]() $R_F$ with a specified basis.
$R_F$ with a specified basis.
We now explain how the objects ![]() $K_F$,
$K_F$, ![]() $R_F$, and
$R_F$, and ![]() $I_F^j$ transform under the action of
$I_F^j$ transform under the action of ![]() $\gamma \in \operatorname {SL}_2(R)$ on binary forms of degree
$\gamma \in \operatorname {SL}_2(R)$ on binary forms of degree ![]() $2n+1$ defined by
$2n+1$ defined by ![]() $\gamma \cdot F = F((x,z) \cdot \gamma )$. If
$\gamma \cdot F = F((x,z) \cdot \gamma )$. If ![]() $F' = \gamma \cdot F$, then
$F' = \gamma \cdot F$, then ![]() $\gamma$ induces an isomorphism
$\gamma$ induces an isomorphism ![]() $K_F \simeq K_{F'}$, under which the rings
$K_F \simeq K_{F'}$, under which the rings ![]() $R_F$ and
$R_F$ and ![]() $R_{F'}$ happen to be identified with each other (see [Reference NakagawaNak89, Proposition 1.2] for a direct proof and [Reference WoodWoo11, § 2.3] for a geometric argument). On the other hand, the ideals
$R_{F'}$ happen to be identified with each other (see [Reference NakagawaNak89, Proposition 1.2] for a direct proof and [Reference WoodWoo11, § 2.3] for a geometric argument). On the other hand, the ideals ![]() $I_F^j$ and
$I_F^j$ and ![]() $I_{F'}^j$ are isomorphic as
$I_{F'}^j$ are isomorphic as ![]() $R_F$-modules but may not necessarily be identified under the isomorphism
$R_F$-modules but may not necessarily be identified under the isomorphism ![]() $K_F \simeq K_F'$. Indeed, as explained in [Reference BhargavaBha13, (7)], these ideals are related by the following explicit rule: if
$K_F \simeq K_F'$. Indeed, as explained in [Reference BhargavaBha13, (7)], these ideals are related by the following explicit rule: if ![]() $\gamma = [\begin{smallmatrix} a & b \\ c & d\end{smallmatrix}]$, then for each
$\gamma = [\begin{smallmatrix} a & b \\ c & d\end{smallmatrix}]$, then for each ![]() $j \in \{0, \ldots, 2n\}$, the composition
$j \in \{0, \ldots, 2n\}$, the composition

is an injective map of ![]() $R_F$-modules having image equal to
$R_F$-modules having image equal to ![]() $I_{F'}^{j}$, where
$I_{F'}^{j}$, where ![]() $\phi _{j,\gamma }$ sends each
$\phi _{j,\gamma }$ sends each ![]() $\delta \in I_F^j$ to
$\delta \in I_F^j$ to ![]() $(-b\theta +a)^{-j} \cdot \delta \in K_F$. When
$(-b\theta +a)^{-j} \cdot \delta \in K_F$. When ![]() $j = 0$, we recover the identification of
$j = 0$, we recover the identification of ![]() $R_F = I_F^0$ with
$R_F = I_F^0$ with ![]() $R_{F'} = I_{F'}^0$ from (
$R_{F'} = I_{F'}^0$ from (
).
2.3 Parametrization of square roots of the class of  $J_F$
$J_F$
We say that a based fractional ideal ![]() $I$ of
$I$ of ![]() $R_F$ is a square root of the class of the inverse different if there exists
$R_F$ is a square root of the class of the inverse different if there exists ![]() $\delta \in K_F^\times$ such that
$\delta \in K_F^\times$ such that
We now recall an orbit parametrization for such square roots that we introduced in [Reference SwaminathanSwa23]. To do this, let ![]() $\widetilde {H}_F$ be the set of pairs
$\widetilde {H}_F$ be the set of pairs ![]() $(I, \delta )$ satisfying (9). Let
$(I, \delta )$ satisfying (9). Let ![]() $H_F = \widetilde {H}_F/ \sim$, where the equivalence relation
$H_F = \widetilde {H}_F/ \sim$, where the equivalence relation ![]() $\sim$ is defined as follows:
$\sim$ is defined as follows: ![]() $(I_1, \delta _1) \sim (I_2, \delta _2)$ if and only if there exists
$(I_1, \delta _1) \sim (I_2, \delta _2)$ if and only if there exists ![]() $\kappa \in K_F^\times$ such that the based fractional ideals
$\kappa \in K_F^\times$ such that the based fractional ideals ![]() $I_1$ and
$I_1$ and ![]() $\kappa \cdot I_2$ are equal up to an
$\kappa \cdot I_2$ are equal up to an ![]() $\operatorname {SL}_{2n+1}(R)$-change-of-basis and such that
$\operatorname {SL}_{2n+1}(R)$-change-of-basis and such that ![]() $\alpha _1 = \kappa ^2 \cdot \alpha _2$. Now, take
$\alpha _1 = \kappa ^2 \cdot \alpha _2$. Now, take ![]() $(I, \delta ) \in H_F$, and consider the symmetric bilinear form:
$(I, \delta ) \in H_F$, and consider the symmetric bilinear form:
Let ![]() $\pi _{2n-1},\pi _{2n} \in \operatorname {Hom}_{R}(J_F,R)$ be the maps defined on the
$\pi _{2n-1},\pi _{2n} \in \operatorname {Hom}_{R}(J_F,R)$ be the maps defined on the ![]() $R$-basis (6) of
$R$-basis (6) of ![]() $J_F$ by
$J_F$ by
 \begin{align*} \pi_{2n-1}(\theta^{2n-1}) - 1 &= \pi_{2n-1}(\zeta_{2n}) = \pi_{2n-1}(\theta^i) = 0 \quad\text{for each } i \in \{0, \ldots, 2n-2\} ,\\ \pi_{2n}(\zeta_{2n}) + 1 &= \pi_{2n}(\theta^i) = 0 \quad\text{for each } i \in \{0, \ldots, 2n-1\}. \end{align*}
\begin{align*} \pi_{2n-1}(\theta^{2n-1}) - 1 &= \pi_{2n-1}(\zeta_{2n}) = \pi_{2n-1}(\theta^i) = 0 \quad\text{for each } i \in \{0, \ldots, 2n-2\} ,\\ \pi_{2n}(\zeta_{2n}) + 1 &= \pi_{2n}(\theta^i) = 0 \quad\text{for each } i \in \{0, \ldots, 2n-1\}. \end{align*}
Let ![]() $A$ and
$A$ and ![]() $B$ respectively denote the matrices representing the symmetric bilinear forms
$B$ respectively denote the matrices representing the symmetric bilinear forms ![]() $\pi _{2n} \circ \langle -, - \rangle \colon I \times I \to R$ and
$\pi _{2n} \circ \langle -, - \rangle \colon I \times I \to R$ and ![]() $\pi _{2n-1} \circ \langle -, - \rangle \colon I \times I \to R$ with respect to the
$\pi _{2n-1} \circ \langle -, - \rangle \colon I \times I \to R$ with respect to the ![]() $R$-basis of
$R$-basis of ![]() $I$, and observe that
$I$, and observe that ![]() $A$ and
$A$ and ![]() $B$ are symmetric of dimension
$B$ are symmetric of dimension ![]() $(2n+1) \times (2n+1)$ and have entries in
$(2n+1) \times (2n+1)$ and have entries in ![]() $R$. We have, thus, constructed a map of sets
$R$. We have, thus, constructed a map of sets
where by ![]() $R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ we mean the space of pairs of
$R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ we mean the space of pairs of ![]() $(2n+1) \times (2n+1)$ symmetric matrices with entries in
$(2n+1) \times (2n+1)$ symmetric matrices with entries in ![]() $R$. The following result characterizes the map
$R$. The following result characterizes the map ![]() $\mathsf {orb}_F$.
$\mathsf {orb}_F$.
Theorem 3 [Reference SwaminathanSwa23, Theorems 14 and 18, Propositions 17 and 20]
The map ![]() $\mathsf {orb}_F$ defines a bijection from
$\mathsf {orb}_F$ defines a bijection from ![]() $H_F$ to the set of all those
$H_F$ to the set of all those ![]() $\operatorname {SL}_{2n+1}(R)$-orbits of pairs
$\operatorname {SL}_{2n+1}(R)$-orbits of pairs ![]() $(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ such that:
$(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ such that:
(a)
 $(-1)^n \cdot \det (x \cdot A + z \cdot B) = F_{\operatorname {mon}}(x,z) := ({1}/{f_0})\cdot F(x,f_0z)$; and
$(-1)^n \cdot \det (x \cdot A + z \cdot B) = F_{\operatorname {mon}}(x,z) := ({1}/{f_0})\cdot F(x,f_0z)$; and(b)
 $p_i(({1}/{f_0}) \cdot -A^{-1}B)$ is a matrix with entries in
$p_i(({1}/{f_0}) \cdot -A^{-1}B)$ is a matrix with entries in  $R$ for each
$R$ for each  $i \in \{1, \ldots, 2n\}$.
$i \in \{1, \ldots, 2n\}$.
Moreover, for any ![]() $(I, \delta ) \in H_F$, the stabilizer in
$(I, \delta ) \in H_F$, the stabilizer in ![]() $\operatorname {SL}_{2n+1}(R)$ of
$\operatorname {SL}_{2n+1}(R)$ of ![]() $\mathsf {orb}_F(I, \delta )$ contains a subgroup isomorphic to the group
$\mathsf {orb}_F(I, \delta )$ contains a subgroup isomorphic to the group ![]() $R_F^\times [2]_{\operatorname {N}\equiv 1} := \{\rho \in R_F^\times : \rho ^2 = 1 = \operatorname {N}(\rho )\}$.
$R_F^\times [2]_{\operatorname {N}\equiv 1} := \{\rho \in R_F^\times : \rho ^2 = 1 = \operatorname {N}(\rho )\}$.
For the purposes of this paper, it turns out (see Lemma 11) that we only need the restriction of the parametrization in Theorem 3 to those pairs ![]() $(A,B)$ such that
$(A,B)$ such that ![]() $A$ defines a split quadratic form over
$A$ defines a split quadratic form over ![]() $k$. This restricted parametrization can be expressed in terms of the action of
$k$. This restricted parametrization can be expressed in terms of the action of ![]() $G(R)$ on
$G(R)$ on ![]() $V(R)$. Indeed, suppose we are given a pair
$V(R)$. Indeed, suppose we are given a pair ![]() $(A,B) \in R^2 \otimes _{R} \operatorname {Sym}_2 R^{2n+1}$ such that the invariant form
$(A,B) \in R^2 \otimes _{R} \operatorname {Sym}_2 R^{2n+1}$ such that the invariant form ![]() $\det (x \cdot A + z \cdot B)$ of
$\det (x \cdot A + z \cdot B)$ of ![]() $(A,B)$ is equal to
$(A,B)$ is equal to ![]() $(-1)^n \cdot F_{\operatorname {mon}}(x,z)$ and such that
$(-1)^n \cdot F_{\operatorname {mon}}(x,z)$ and such that ![]() $A$ defines a quadratic form that is split over
$A$ defines a quadratic form that is split over ![]() $k$. Then there exists
$k$. Then there exists ![]() $g \in \operatorname {GL}_{2n+1}(R)$ satisfying
$g \in \operatorname {GL}_{2n+1}(R)$ satisfying ![]() $gAg^T = A_0$ (by the uniqueness statement in the first paragraph of § 2.1), and the matrix
$gAg^T = A_0$ (by the uniqueness statement in the first paragraph of § 2.1), and the matrix ![]() $T = (g^T)^{-1}\cdot -A^{-1}B \cdot g^T$ is self-adjoint with respect to the matrix
$T = (g^T)^{-1}\cdot -A^{-1}B \cdot g^T$ is self-adjoint with respect to the matrix ![]() $A_0$ and has characteristic polynomial
$A_0$ and has characteristic polynomial ![]() $F_{\operatorname {mon}}(x,1)$. We thus obtain the following correspondence, the proof of which is immediate.
$F_{\operatorname {mon}}(x,1)$. We thus obtain the following correspondence, the proof of which is immediate.
Proposition 4 The map ![]() $(A,B) \mapsto T$ described above defines a natural bijection from the set of
$(A,B) \mapsto T$ described above defines a natural bijection from the set of ![]() $\operatorname {SL}_{2n+1}(R)$-orbits on pairs
$\operatorname {SL}_{2n+1}(R)$-orbits on pairs ![]() $(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ with invariant form
$(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ with invariant form ![]() $(-1)^n \cdot F_{\operatorname {mon}}$ such that
$(-1)^n \cdot F_{\operatorname {mon}}$ such that ![]() $A$ defines a split quadratic form over
$A$ defines a split quadratic form over ![]() $k$ to the set of
$k$ to the set of ![]() $G(R)$-orbits on
$G(R)$-orbits on ![]() $V(R)$ with characteristic polynomial
$V(R)$ with characteristic polynomial ![]() $F_{\operatorname {mon}}(x,1)$. Under this bijection, we have that
$F_{\operatorname {mon}}(x,1)$. Under this bijection, we have that ![]() $\operatorname {Stab}_{\operatorname {SL}_{2n+1}(R)}(A,B) = \operatorname {Stab}_{G(R)}(T)$.
$\operatorname {Stab}_{\operatorname {SL}_{2n+1}(R)}(A,B) = \operatorname {Stab}_{G(R)}(T)$.
Remark 5 As explained in [Reference SwaminathanSwa23, § 2.2], the proof of Theorem 3 is inspired by [Reference WoodWoo14], where Wood derives a similar parametrization in which the multiplication table of a fractional ideal of ![]() $R_F$ gives rise to a pair of symmetric matrices with invariant form equal to
$R_F$ gives rise to a pair of symmetric matrices with invariant form equal to ![]() $F$ (up to a sign). In [Reference BhargavaBha13, § 2], Bhargava uses Wood's parametrization to prove analogues of Theorems 1 and 2 for rational points on hyperelliptic curves.
$F$ (up to a sign). In [Reference BhargavaBha13, § 2], Bhargava uses Wood's parametrization to prove analogues of Theorems 1 and 2 for rational points on hyperelliptic curves.
2.4 Orbits over fields
When ![]() $R = k$ is a field, the parametrization in Theorem 3 simplifies considerably. Indeed, every fractional ideal of
$R = k$ is a field, the parametrization in Theorem 3 simplifies considerably. Indeed, every fractional ideal of ![]() $R_F = K_F$ is equal to
$R_F = K_F$ is equal to ![]() $K_F$, so every element of
$K_F$, so every element of ![]() $H_F$ is of the form
$H_F$ is of the form ![]() $(K_F,\delta )$, where
$(K_F,\delta )$, where ![]() $f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1} := \{ \rho \in K_F^\times : \operatorname {N}(\rho ) \in k^{\times 2}\}/K_F^{\times 2}$. Moreover, condition
$f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1} := \{ \rho \in K_F^\times : \operatorname {N}(\rho ) \in k^{\times 2}\}/K_F^{\times 2}$. Moreover, condition ![]() $\mathrm {(b)}$ in Theorem 3 holds trivially in this case, implying that every
$\mathrm {(b)}$ in Theorem 3 holds trivially in this case, implying that every ![]() $\operatorname {SL}_{2n+1}(k)$-orbit on
$\operatorname {SL}_{2n+1}(k)$-orbit on ![]() $k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form
$k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form ![]() $F_{\operatorname {mon}}(x,1)$ arises from an element of
$F_{\operatorname {mon}}(x,1)$ arises from an element of ![]() $H_F$. We thus obtain the following result, which gives a convenient description of the orbits of
$H_F$. We thus obtain the following result, which gives a convenient description of the orbits of ![]() $\operatorname {SL}_{2n+1}(k)$ on
$\operatorname {SL}_{2n+1}(k)$ on ![]() $k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ that arise via the parametrization.
$k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ that arise via the parametrization.
Proposition 6 [Reference SwaminathanSwa23, Proposition 36]
When ![]() $R = k$ is a field, the set of
$R = k$ is a field, the set of ![]() $\operatorname {SL}_{2n+1}(k)$-orbits on
$\operatorname {SL}_{2n+1}(k)$-orbits on ![]() $k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form
$k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form ![]() $F_{\operatorname {mon}}$ is in bijection with the set
$F_{\operatorname {mon}}$ is in bijection with the set ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$. Under this bijection, the orbit corresponding to the pair
$(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$. Under this bijection, the orbit corresponding to the pair ![]() $(K_F, \delta ) \in H_F$ is sent to
$(K_F, \delta ) \in H_F$ is sent to ![]() $f_0 \cdot \delta$.
$f_0 \cdot \delta$.
In what follows, we say that an orbit of ![]() $\operatorname {SL}_{2n+1}(k)$ on
$\operatorname {SL}_{2n+1}(k)$ on ![]() $k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ (or of
$k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ (or of ![]() $G(k)$ on
$G(k)$ on ![]() $V(k)$) is distinguished if it corresponds to
$V(k)$) is distinguished if it corresponds to ![]() $1 \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ under the bijection of Proposition 6. In geometric terms, the orbit of a pair
$1 \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ under the bijection of Proposition 6. In geometric terms, the orbit of a pair ![]() $(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ is distinguished if and only if
$(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ is distinguished if and only if ![]() $A$ and
$A$ and ![]() $B$ share a maximal isotropic space defined over
$B$ share a maximal isotropic space defined over ![]() $k$ (see [Reference Bhargava and GrossBG13, § 4]).
$k$ (see [Reference Bhargava and GrossBG13, § 4]).
For ease of notation, write ![]() $f = F_{\operatorname {mon}}$. Given any
$f = F_{\operatorname {mon}}$. Given any ![]() $(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form
$(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form ![]() $f$, we may regard
$f$, we may regard ![]() $A$ and
$A$ and ![]() $B$ as quadratic forms cutting out a pair of quadric hypersurfaces
$B$ as quadratic forms cutting out a pair of quadric hypersurfaces ![]() $Q_A$ and
$Q_A$ and ![]() $Q_B$ in
$Q_B$ in ![]() $\mathbb {P}_k^{2n}$. Let
$\mathbb {P}_k^{2n}$. Let ![]() $\mathscr {F}_{(A,B)}$ denote the Fano scheme parametrizing
$\mathscr {F}_{(A,B)}$ denote the Fano scheme parametrizing ![]() $(n-1)$-dimensional linear spaces contained in the base locus
$(n-1)$-dimensional linear spaces contained in the base locus ![]() $Q_A \cap Q_B$ of the pencil of quadric hypersurfaces spanned by
$Q_A \cap Q_B$ of the pencil of quadric hypersurfaces spanned by ![]() $Q_A$ and
$Q_A$ and ![]() $Q_B$. The following proposition states that
$Q_B$. The following proposition states that ![]() $\mathscr {F}_{(A,B)}$ is a torsor of the Jacobian of
$\mathscr {F}_{(A,B)}$ is a torsor of the Jacobian of ![]() $\mathscr {S}_F$.
$\mathscr {S}_F$.
Proposition 7 Let ![]() $(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form
$(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n+1}$ with invariant form ![]() $f$. Then, if
$f$. Then, if ![]() $\#k$ is sufficiently large,
$\#k$ is sufficiently large, ![]() $\mathscr {F}_{(A,B)}$ is a torsor over
$\mathscr {F}_{(A,B)}$ is a torsor over ![]() $k$ of the Jacobian of the stacky curve
$k$ of the Jacobian of the stacky curve ![]() $\mathscr {S}_F$.
$\mathscr {S}_F$.
Proof. The Jacobian of a stacky curve ![]() $\mathscr {X}$ is defined to be the
$\mathscr {X}$ is defined to be the ![]() $0$th-degree component
$0$th-degree component ![]() $\operatorname {Pic}^0(\mathscr {X})$ of the group
$\operatorname {Pic}^0(\mathscr {X})$ of the group ![]() $\operatorname {Pic}(\mathscr {X})$ of divisors on
$\operatorname {Pic}(\mathscr {X})$ of divisors on ![]() $\mathscr {X}$ modulo principal divisors. Let
$\mathscr {X}$ modulo principal divisors. Let ![]() $k_{\operatorname {sep}}$ be a separable closure of
$k_{\operatorname {sep}}$ be a separable closure of ![]() $k$, and let
$k$, and let ![]() $\theta _1, \ldots, \theta _{2n+1} \in \mathbb {P}^1_k(k_{\operatorname {sep}})$ be the roots of
$\theta _1, \ldots, \theta _{2n+1} \in \mathbb {P}^1_k(k_{\operatorname {sep}})$ be the roots of ![]() $F$. Applying the correspondence between isomorphism classes of line bundles and divisor classes to [Reference Candelori and CameronCC17, proof of Proposition 2.2] yields that
$F$. Applying the correspondence between isomorphism classes of line bundles and divisor classes to [Reference Candelori and CameronCC17, proof of Proposition 2.2] yields that ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ is the group generated by the classes of the divisors
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ is the group generated by the classes of the divisors ![]() $(\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j)$ subject to the relations
$(\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j)$ subject to the relations ![]() $2 \cdot (\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j) = 0$ for
$2 \cdot (\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j) = 0$ for ![]() $1 \leq i < j \leq 2n+1$; i.e. we have
$1 \leq i < j \leq 2n+1$; i.e. we have
There is a natural right action of the absolute Galois group ![]() $G_k := \operatorname {Gal}(k_{\operatorname {sep}}/k)$ on
$G_k := \operatorname {Gal}(k_{\operatorname {sep}}/k)$ on ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$: for
$\operatorname {Pic}^0(\mathscr {S}_F\!)$: for ![]() $\sigma \in G_k$, we have
$\sigma \in G_k$, we have ![]() $(\tfrac {1}{2} \theta _i - \tfrac {1}{2} \theta _i) \cdot \sigma = (\tfrac {1}{2} (\sigma ^{-1} \cdot \theta _i) - \tfrac {1}{2} (\sigma ^{-1} \cdot \theta _j))$.
$(\tfrac {1}{2} \theta _i - \tfrac {1}{2} \theta _i) \cdot \sigma = (\tfrac {1}{2} (\sigma ^{-1} \cdot \theta _i) - \tfrac {1}{2} (\sigma ^{-1} \cdot \theta _j))$.
A result of Wang (see [Reference WangWan18, Corollary 2.5]) implies that, as long as ![]() $\#k$ is sufficiently large, the Fano scheme
$\#k$ is sufficiently large, the Fano scheme ![]() $\mathscr {F}_{(A,B)}$ is a torsor over
$\mathscr {F}_{(A,B)}$ is a torsor over ![]() $k$ of the
$k$ of the ![]() $2$-torsion subgroup
$2$-torsion subgroup ![]() $J[2]$ of the Jacobian
$J[2]$ of the Jacobian ![]() $J$ of the monic odd-degree hyperelliptic curve
$J$ of the monic odd-degree hyperelliptic curve ![]() $y^2 = f(x,1)$. Thus, to prove that
$y^2 = f(x,1)$. Thus, to prove that ![]() $\mathscr {F}_{(A,B)}$ is a torsor of
$\mathscr {F}_{(A,B)}$ is a torsor of ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$, it suffices to show that there is a
$\operatorname {Pic}^0(\mathscr {S}_F\!)$, it suffices to show that there is a ![]() $G_k$-equivariant isomorphism
$G_k$-equivariant isomorphism ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!) \simeq J[2]$. But this is clear: the divisor classes
$\operatorname {Pic}^0(\mathscr {S}_F\!) \simeq J[2]$. But this is clear: the divisor classes ![]() $(\theta _i - \theta _j)$ for
$(\theta _i - \theta _j)$ for ![]() $1 \leq i < j \leq 2n+1$ generate
$1 \leq i < j \leq 2n+1$ generate ![]() $J[2](k_{\operatorname {sep}})$ over
$J[2](k_{\operatorname {sep}})$ over ![]() $\mathbb {Z}/2\mathbb {Z}$.
$\mathbb {Z}/2\mathbb {Z}$.
Note, in particular, that the ![]() $\operatorname {SL}_{2n+1}(k)$-orbit of
$\operatorname {SL}_{2n+1}(k)$-orbit of ![]() $(A,B)$ is distinguished if and only if
$(A,B)$ is distinguished if and only if ![]() $\mathscr {F}_{(A,B)}$ is the trivial torsor of the Jacobian of
$\mathscr {F}_{(A,B)}$ is the trivial torsor of the Jacobian of ![]() $\mathscr {S}_F$ (which happens if and only if
$\mathscr {S}_F$ (which happens if and only if ![]() $\mathscr {F}_{(A,B)}(k) \neq \varnothing$).
$\mathscr {F}_{(A,B)}(k) \neq \varnothing$).
Remark 8 As it happens, Proposition 7 admits an analogue for pencils of even-dimensional quadric hypersurfaces; see the work of Wang [Reference WangWan18] (generalizing previous work of Reid [Reference ReidRei72, Theorem 4.8]), showing that the Fano scheme of maximal linear spaces in the base locus of a pencil of quadric hypersurfaces generated by a pair ![]() $(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n}$ is a torsor of the Jacobian of the hyperelliptic curve cut out by the equation
$(A,B) \in k^2 \otimes _k \operatorname {Sym}_2 k^{2n}$ is a torsor of the Jacobian of the hyperelliptic curve cut out by the equation ![]() $y^2 = (-1)^n \cdot \det (x \cdot A+ z \cdot B)$.
$y^2 = (-1)^n \cdot \det (x \cdot A+ z \cdot B)$.
We conclude this section by explaining how to visualize the simply transitive action of ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ on
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ on ![]() $\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$ from Proposition 7. For each
$\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$ from Proposition 7. For each ![]() $i \in \{1, \ldots, 2n+1\}$, let
$i \in \{1, \ldots, 2n+1\}$, let ![]() $Q_i$ be the singular fiber lying over the point
$Q_i$ be the singular fiber lying over the point ![]() $\theta _i$ in the pencil of quadrics spanned by
$\theta _i$ in the pencil of quadrics spanned by ![]() $Q_A$ and
$Q_A$ and ![]() $Q_B$. Suppose that
$Q_B$. Suppose that ![]() $T$ is generic, so that each of the quadrics
$T$ is generic, so that each of the quadrics ![]() $Q_i$ is a simple cone with cone point
$Q_i$ is a simple cone with cone point ![]() $q_i$. Let
$q_i$. Let ![]() $\mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) = \{p_1, \ldots, p_{2^{2n}}\}$, and for each
$\mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) = \{p_1, \ldots, p_{2^{2n}}\}$, and for each ![]() $\ell \in \{1, \ldots, 2^{2n}\}$, let
$\ell \in \{1, \ldots, 2^{2n}\}$, let ![]() $\overline {p}_\ell$ denote the corresponding linear subspace of
$\overline {p}_\ell$ denote the corresponding linear subspace of ![]() $\mathbb {P}_{k_{\operatorname {sep}}}^{2n}$. We illustrate this setup in the case where
$\mathbb {P}_{k_{\operatorname {sep}}}^{2n}$. We illustrate this setup in the case where ![]() $n = 1$ in Figure 1.
$n = 1$ in Figure 1.

Figure 1. The pencil of conics spanned by ![]() $Q_A$ and
$Q_A$ and ![]() $Q_B$ in
$Q_B$ in ![]() $\mathbb {P}_{k_{\operatorname {sep}}}^2$, with singular fibers
$\mathbb {P}_{k_{\operatorname {sep}}}^2$, with singular fibers ![]() $Q_1$,
$Q_1$, ![]() $Q_2$, and
$Q_2$, and ![]() $Q_3$ having cone points
$Q_3$ having cone points ![]() $q_1$,
$q_1$, ![]() $q_2$, and
$q_2$, and ![]() $q_3$, respectively. In this case,
$q_3$, respectively. In this case, ![]() $\mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) = Q_A \cap Q_B = \{p_1, p_2, p_3, p_4\}$. The dashed arrows display the action of the degree-
$\mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) = Q_A \cap Q_B = \{p_1, p_2, p_3, p_4\}$. The dashed arrows display the action of the degree-![]() $0$ divisor
$0$ divisor ![]() $(\tfrac {1}{2}\theta _1 - \tfrac {1}{2}\theta _2)$ on
$(\tfrac {1}{2}\theta _1 - \tfrac {1}{2}\theta _2)$ on ![]() $\mathscr {F}_{(A,B)}$.
$\mathscr {F}_{(A,B)}$.
We define an action of ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ on
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ on ![]() $\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$ by first specifying how each
$\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$ by first specifying how each ![]() $(\tfrac {1}{2}\theta _i)$ acts on
$(\tfrac {1}{2}\theta _i)$ acts on ![]() $\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$. Let
$\mathscr {F}_{(A,B)}(k_{\operatorname {sep}})$. Let ![]() $L_{i\ell } \subset \mathbb {P}_{k_{\operatorname {sep}}}^{2n}$ be the linear span of the
$L_{i\ell } \subset \mathbb {P}_{k_{\operatorname {sep}}}^{2n}$ be the linear span of the ![]() $(n-1)$-plane
$(n-1)$-plane ![]() $\overline {p}_\ell$ and the point
$\overline {p}_\ell$ and the point ![]() $q_i$ for each pair
$q_i$ for each pair ![]() $(i,\ell )$. By [Reference ReidRei72, Theorem 3.8], there exists precisely one element
$(i,\ell )$. By [Reference ReidRei72, Theorem 3.8], there exists precisely one element ![]() $p_{i(\ell )} \in \mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) \smallsetminus \{p_\ell \}$ such that
$p_{i(\ell )} \in \mathscr {F}_{(A,B)}(k_{\operatorname {sep}}) \smallsetminus \{p_\ell \}$ such that ![]() $\overline {p}_{i(\ell )} \subset L_{i\ell }$. For each
$\overline {p}_{i(\ell )} \subset L_{i\ell }$. For each ![]() $i$, let
$i$, let ![]() $(\tfrac {1}{2}\theta _i)$ act on
$(\tfrac {1}{2}\theta _i)$ act on ![]() $\mathscr {F}_{(A,B)}$ by swapping
$\mathscr {F}_{(A,B)}$ by swapping ![]() $p_\ell$ and
$p_\ell$ and ![]() $p_{i(\ell )}$ for each
$p_{i(\ell )}$ for each ![]() $\ell$. Then for each pair
$\ell$. Then for each pair ![]() $(i,j)$, the divisor
$(i,j)$, the divisor ![]() $(\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j)$ acts on
$(\tfrac {1}{2}\theta _i - \tfrac {1}{2}\theta _j)$ acts on ![]() $\mathscr {F}_{(A,B)}$ by swapping
$\mathscr {F}_{(A,B)}$ by swapping ![]() $p_\ell$ with
$p_\ell$ with ![]() $p_{i(j(\ell ))} = p_{j(i(\ell ))}$ for each
$p_{i(j(\ell ))} = p_{j(i(\ell ))}$ for each ![]() $\ell$. When
$\ell$. When ![]() $n = 1$, for example, the divisor
$n = 1$, for example, the divisor ![]() $(\tfrac {1}{2}\theta _1 - \tfrac {1}{2}\theta _2)$ acts on
$(\tfrac {1}{2}\theta _1 - \tfrac {1}{2}\theta _2)$ acts on ![]() $\mathscr {F}_{(A,B)}$ by sending
$\mathscr {F}_{(A,B)}$ by sending ![]() $(p_1, p_2, p_3, p_4)$ to
$(p_1, p_2, p_3, p_4)$ to ![]() $(p_3, p_4, p_1, p_2)$, as we demonstrate in Figure 1.
$(p_3, p_4, p_1, p_2)$, as we demonstrate in Figure 1.
3. Construction of an integral orbit from a primitive integer solution
Take ![]() $R$ and
$R$ and ![]() $F$ as in § 2.2, and assume that
$F$ as in § 2.2, and assume that ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $0$. In § 3.1, we prove that points
$0$. In § 3.1, we prove that points ![]() $(x_0,y_0,z_0) \in \mathscr {S}_F(R)$ give rise to certain orbits of
$(x_0,y_0,z_0) \in \mathscr {S}_F(R)$ give rise to certain orbits of ![]() $G(R)$ on
$G(R)$ on ![]() $V(R)$ with characteristic polynomial
$V(R)$ with characteristic polynomial ![]() $F_{\mathrm {mon}}(x,1)$. To produce the desired orbit, it suffices by Theorem 3 and Proposition 4 to construct a pair
$F_{\mathrm {mon}}(x,1)$. To produce the desired orbit, it suffices by Theorem 3 and Proposition 4 to construct a pair ![]() $(I, \delta ) \in H_F$ such that the matrix
$(I, \delta ) \in H_F$ such that the matrix ![]() $A$ that arises defines a split quadratic form over
$A$ that arises defines a split quadratic form over ![]() $k$. Our construction extends a result of Simon, who constructs the desired pair
$k$. Our construction extends a result of Simon, who constructs the desired pair ![]() $(I,\delta )$ under the following special conditions:
$(I,\delta )$ under the following special conditions: ![]() $F$ is primitive and irreducible and
$F$ is primitive and irreducible and ![]() $y_0$ is coprime to the index of
$y_0$ is coprime to the index of ![]() $R_F$ in its integral closure (see [Reference SimonSim08, Corollary 4]). We finish in § 3.2 by describing when the orbits arising from the construction are distinguished.
$R_F$ in its integral closure (see [Reference SimonSim08, Corollary 4]). We finish in § 3.2 by describing when the orbits arising from the construction are distinguished.
3.1 The construction
Let ![]() $(x_0,y_0,z_0) \in \mathscr {S}_F(R)$. For convenience, we say that the point
$(x_0,y_0,z_0) \in \mathscr {S}_F(R)$. For convenience, we say that the point ![]() $(x_0, y_0, z_0)$ is a Weierstrass point if
$(x_0, y_0, z_0)$ is a Weierstrass point if ![]() $y_0 = 0$ and a non-Weierstrass point otherwise. Note that if
$y_0 = 0$ and a non-Weierstrass point otherwise. Note that if ![]() $y_0 = 0$, then
$y_0 = 0$, then ![]() $z_0 \neq 0$ because
$z_0 \neq 0$ because ![]() $f_0 \neq 0$, so the binary form
$f_0 \neq 0$, so the binary form ![]() $F$ factors uniquely as
$F$ factors uniquely as
where ![]() $\widetilde {F} \in R[x,z]$ is a binary form of degree
$\widetilde {F} \in R[x,z]$ is a binary form of degree ![]() $2n$ with leading coefficient equal to
$2n$ with leading coefficient equal to ![]() $f_0$.
$f_0$.
We start by transforming the pair ![]() $(x_0, z_0)$ into a pair with simpler coordinates by constructing a suitable
$(x_0, z_0)$ into a pair with simpler coordinates by constructing a suitable ![]() $\gamma \in \operatorname {SL}_2(R)$ such that
$\gamma \in \operatorname {SL}_2(R)$ such that ![]() $(x_0, z_0) \cdot \gamma = (0,1)$. Let
$(x_0, z_0) \cdot \gamma = (0,1)$. Let ![]() $b_0, d_0 \in R$ be any elements such that
$b_0, d_0 \in R$ be any elements such that ![]() $b_0x_0 + d_0z_0 = 1$ (such
$b_0x_0 + d_0z_0 = 1$ (such ![]() $b_0, d_0$ exist since
$b_0, d_0$ exist since ![]() $Rx_0 + Rz_0 = R$). We claim that there exists
$Rx_0 + Rz_0 = R$). We claim that there exists ![]() $t \in R$ such that
$t \in R$ such that ![]() $(d_0 -t x_0) + \theta (b_0 + t z_0) \in K_F^\times$. Indeed, if we were to have
$(d_0 -t x_0) + \theta (b_0 + t z_0) \in K_F^\times$. Indeed, if we were to have ![]() $(d_0 -t x_0) + \theta (b_0 + t z_0) \in K_F \smallsetminus K_F^\times$, then the pair
$(d_0 -t x_0) + \theta (b_0 + t z_0) \in K_F \smallsetminus K_F^\times$, then the pair ![]() $(x,z) = (d_0 - tx_0,-b_0 - t z_0)$ is a root of the equation
$(x,z) = (d_0 - tx_0,-b_0 - t z_0)$ is a root of the equation ![]() $F(x,z) = 0$, which has finitely many roots up to scaling, implying that we can choose
$F(x,z) = 0$, which has finitely many roots up to scaling, implying that we can choose ![]() $t$ to avoid this outcome (since
$t$ to avoid this outcome (since ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $0$). Take any such
$0$). Take any such ![]() $t \in R$, let
$t \in R$, let ![]() $b = b_0 + t z_0$ and
$b = b_0 + t z_0$ and ![]() $d = d_0 - t x_0$, and let
$d = d_0 - t x_0$, and let ![]() $\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]$. Now, let
$\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]$. Now, let ![]() $F'$ be defined by
$F'$ be defined by
 \[ F'(x,z) = F ((x,z) \cdot \gamma^{-1}) = \sum_{i = 0}^{2n+1} f_i' x^{2n+1-i}z^i \in R[x,z]. \]
\[ F'(x,z) = F ((x,z) \cdot \gamma^{-1}) = \sum_{i = 0}^{2n+1} f_i' x^{2n+1-i}z^i \in R[x,z]. \]
Note that ![]() $f_{2n+1}' = y_0^2$ and that
$f_{2n+1}' = y_0^2$ and that ![]() $f_0' \neq 0$ since
$f_0' \neq 0$ since ![]() $f_0' = f_0 \cdot \operatorname {N}(d + \theta b)$. If
$f_0' = f_0 \cdot \operatorname {N}(d + \theta b)$. If ![]() $y_0 = 0$, the binary form
$y_0 = 0$, the binary form ![]() $F'$ factors uniquely as
$F'$ factors uniquely as
where ![]() $\widetilde {F}' \in R[x,z]$ is a binary form of degree
$\widetilde {F}' \in R[x,z]$ is a binary form of degree ![]() $2n$ with leading coefficient equal to
$2n$ with leading coefficient equal to ![]() $f_0'$; further observe that
$f_0'$; further observe that ![]() $f_{2n}' = \widetilde {F}(x_0,z_0) \neq 0$ because
$f_{2n}' = \widetilde {F}(x_0,z_0) \neq 0$ because ![]() $F$ is separable. Let
$F$ is separable. Let ![]() $\theta ' = (-x_0 + \theta z_0)/(d+\theta b)$ be the root of
$\theta ' = (-x_0 + \theta z_0)/(d+\theta b)$ be the root of ![]() $F'(x,1)$ in
$F'(x,1)$ in ![]() $K_{F'} = K_F$, and consider the free rank-
$K_{F'} = K_F$, and consider the free rank-![]() $(2n+1)$
$(2n+1)$ ![]() $R$-submodule
$R$-submodule ![]() $I' \subset K_{F'}$ defined by
$I' \subset K_{F'}$ defined by
 \begin{equation} I' := R\langle \xi, \theta', \ldots, {\theta'}^n, \zeta_{n+1}', \ldots, \zeta_{2n}'\rangle, \quad \text{where } \xi :=\begin{cases} y_0 & \text{if $y_0 \neq 0$,} \\ \zeta_{2n}'+f_{2n}' & \text{if $y_0 = 0$.} \end{cases} \end{equation}
\begin{equation} I' := R\langle \xi, \theta', \ldots, {\theta'}^n, \zeta_{n+1}', \ldots, \zeta_{2n}'\rangle, \quad \text{where } \xi :=\begin{cases} y_0 & \text{if $y_0 \neq 0$,} \\ \zeta_{2n}'+f_{2n}' & \text{if $y_0 = 0$.} \end{cases} \end{equation}
Observe that the ![]() $R$-module
$R$-module ![]() $I'$ is a fractional ideal of
$I'$ is a fractional ideal of ![]() $R_{F'}$ that resembles the fractional ideal
$R_{F'}$ that resembles the fractional ideal ![]() $I_{F'}^n$, the only difference between them being that the basis element
$I_{F'}^n$, the only difference between them being that the basis element ![]() $1 \in I_{F'}^n$ is replaced by
$1 \in I_{F'}^n$ is replaced by ![]() $\xi \in I'$.
$\xi \in I'$.
Lemma 9 We have that
 \[ {I'}^2 \subset \delta' \cdot J_{F'}, \quad \text{where } \delta' := \begin{cases} -\theta' & \text{if $y_0 \neq 0$,}\\ \widetilde{F}'(\theta',1)-\theta' & \text{if $y_0 = 0$}\end{cases} \]
\[ {I'}^2 \subset \delta' \cdot J_{F'}, \quad \text{where } \delta' := \begin{cases} -\theta' & \text{if $y_0 \neq 0$,}\\ \widetilde{F}'(\theta',1)-\theta' & \text{if $y_0 = 0$}\end{cases} \]
and that ![]() $\operatorname {N}(I')^2 = \operatorname {N}(\delta ') \cdot \operatorname {N}(J_{F'})$.
$\operatorname {N}(I')^2 = \operatorname {N}(\delta ') \cdot \operatorname {N}(J_{F'})$.
Proof. Recall from (6) that the fractional ideal ![]() $J_{F'}$ has the
$J_{F'}$ has the ![]() $\mathbb {Z}$-basis
$\mathbb {Z}$-basis
To prove the claimed containment, it suffices to check that when each of the pairwise products of the basis elements of ![]() $I'$ in (12) is divided by
$I'$ in (12) is divided by ![]() $\delta '$, what results is an element of
$\delta '$, what results is an element of ![]() $J_{F'}$. We have the following computations:
$J_{F'}$. We have the following computations:
 \begin{align*} \xi^2/\delta' & =
\zeta_{2n}' + f_{2n}', & & \\ (\xi \cdot
{\theta'}^i)/\delta' & = -y_0 {\theta'}^{i-1} & & \text{for
$i \in \{1, \ldots, n\}$} ,\\ (\xi \cdot
\zeta_j')/\delta' & = -y_0 \zeta_{j-1}' - y_0 f_{j-1}' & &
\text{for }j \in \{n+1, \ldots, 2n\}, \\
({\theta'}^i \cdot {\theta'}^j)/\delta' & =
-{\theta'}^{i+j-1} & & \text{for }i,j \in \{1, \ldots, n\}
,\\ ({\theta'}^i \cdot \zeta_j')/\delta' & =
-{\theta}'^{i-1} \zeta_j' & & \text{for }i \in \{1, \ldots,
n\},\,j \in \{n+1, \ldots, 2n\}, \\ (\zeta_i'\cdot
\zeta_j')/\delta' & =
-\zeta_i'\zeta_{j-1}'-f_{j-1}'\zeta_i' & & \text{for }i,j
\in \{n+1, \ldots, 2n\}.
\end{align*}
\begin{align*} \xi^2/\delta' & =
\zeta_{2n}' + f_{2n}', & & \\ (\xi \cdot
{\theta'}^i)/\delta' & = -y_0 {\theta'}^{i-1} & & \text{for
$i \in \{1, \ldots, n\}$} ,\\ (\xi \cdot
\zeta_j')/\delta' & = -y_0 \zeta_{j-1}' - y_0 f_{j-1}' & &
\text{for }j \in \{n+1, \ldots, 2n\}, \\
({\theta'}^i \cdot {\theta'}^j)/\delta' & =
-{\theta'}^{i+j-1} & & \text{for }i,j \in \{1, \ldots, n\}
,\\ ({\theta'}^i \cdot \zeta_j')/\delta' & =
-{\theta}'^{i-1} \zeta_j' & & \text{for }i \in \{1, \ldots,
n\},\,j \in \{n+1, \ldots, 2n\}, \\ (\zeta_i'\cdot
\zeta_j')/\delta' & =
-\zeta_i'\zeta_{j-1}'-f_{j-1}'\zeta_i' & & \text{for }i,j
\in \{n+1, \ldots, 2n\}.
\end{align*}
Using the fact that ![]() $\zeta _i' \in R_{F'}$ for each
$\zeta _i' \in R_{F'}$ for each ![]() $i \in \{0, \ldots, 2n+1\}$ together with the fact that
$i \in \{0, \ldots, 2n+1\}$ together with the fact that ![]() $J_{F'}$ is closed under multiplication by elements in
$J_{F'}$ is closed under multiplication by elements in ![]() $R_{F'}$, one readily verifies that each of the expressions obtained on the right-hand side above is an element of
$R_{F'}$, one readily verifies that each of the expressions obtained on the right-hand side above is an element of ![]() $J_{F'}$. Crucially, these expressions do not depend in piecewise fashion on the value of
$J_{F'}$. Crucially, these expressions do not depend in piecewise fashion on the value of ![]() $y_0$, even though
$y_0$, even though ![]() $\xi$ and
$\xi$ and ![]() $\delta '$ do (see Remark 12).
$\delta '$ do (see Remark 12).
As for the second part of the lemma, using ![]() $\operatorname {N}(I_{F'}^n) = {f_0'}^{-n}$, we find that
$\operatorname {N}(I_{F'}^n) = {f_0'}^{-n}$, we find that ![]() $\operatorname {N}(I') = \widetilde {\xi } \cdot {f_0'}^{-n}$, where
$\operatorname {N}(I') = \widetilde {\xi } \cdot {f_0'}^{-n}$, where ![]() $\widetilde {\xi } = \xi = y_0$ if
$\widetilde {\xi } = \xi = y_0$ if ![]() $y_0 \neq 0$ and
$y_0 \neq 0$ and ![]() $\widetilde {\xi } = \xi -\zeta _{2n}' = f_{2n}'$ if
$\widetilde {\xi } = \xi -\zeta _{2n}' = f_{2n}'$ if ![]() $y_0 = 0$. Moreover, a calculation reveals that
$y_0 = 0$. Moreover, a calculation reveals that ![]() $\operatorname {N}(\delta ') = \widetilde {\xi }^2 \cdot {f_0'}^{-1}$. Combining these norm calculations, we deduce that
$\operatorname {N}(\delta ') = \widetilde {\xi }^2 \cdot {f_0'}^{-1}$. Combining these norm calculations, we deduce that
We now transform ![]() $I'$ and
$I'$ and ![]() $\delta '$ back from
$\delta '$ back from ![]() $R_{F'}$ to
$R_{F'}$ to ![]() $R_F$. Recall from (8) that
$R_F$. Recall from (8) that
where we can invert ![]() $-b\theta ' + z_0$ because its inverse is equal to
$-b\theta ' + z_0$ because its inverse is equal to ![]() $d + \theta b$. Since
$d + \theta b$. Since ![]() $I'$ resembles
$I'$ resembles ![]() $I_{F'}^n$, it makes sense to consider the fractional ideal
$I_{F'}^n$, it makes sense to consider the fractional ideal
which has norm given by
where we used the multiplicativity relation (7). Similarly, let ![]() $\delta \in K_F^\times$ be defined as follows:
$\delta \in K_F^\times$ be defined as follows:
 \begin{equation} \delta := \phi_{1,\gamma}(\delta') = \frac{\delta'}{-b\theta'+z_0} = \begin{cases} x_0 - \theta z_0 & \text{if $y_0 \neq 0$,} \\ \widetilde{F}(z_0\theta, z_0) + (x_0 - \theta z_0) & \text{if $y_0 = 0$.} \end{cases} \end{equation}
\begin{equation} \delta := \phi_{1,\gamma}(\delta') = \frac{\delta'}{-b\theta'+z_0} = \begin{cases} x_0 - \theta z_0 & \text{if $y_0 \neq 0$,} \\ \widetilde{F}(z_0\theta, z_0) + (x_0 - \theta z_0) & \text{if $y_0 = 0$.} \end{cases} \end{equation}It then follows from Lemma 9 that
where in the last step above, we used the fact that
Note that ![]() $\operatorname {N}(I)^2 = \operatorname {N}(\delta ) \cdot \operatorname {N}(J_{F}\!)$ (this can be verified directly from (14) and (15), but it also follows from the fact that
$\operatorname {N}(I)^2 = \operatorname {N}(\delta ) \cdot \operatorname {N}(J_{F}\!)$ (this can be verified directly from (14) and (15), but it also follows from the fact that ![]() $\operatorname {N}(I')^2 = \operatorname {N}(\delta ') \cdot \operatorname {N}(J_{F'})$ by Lemma 9).
$\operatorname {N}(I')^2 = \operatorname {N}(\delta ') \cdot \operatorname {N}(J_{F'})$ by Lemma 9).
Lemma 10 The fractional ideal ![]() $I$ is well-defined, in the sense that it does not depend on the choice of
$I$ is well-defined, in the sense that it does not depend on the choice of ![]() $\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]\in \operatorname {SL}_2(R)$ satisfying
$\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]\in \operatorname {SL}_2(R)$ satisfying ![]() $(x_0, z_0) \cdot \gamma = (0,1)$ and
$(x_0, z_0) \cdot \gamma = (0,1)$ and ![]() $d + \theta b \in K_F^\times$.
$d + \theta b \in K_F^\times$.
Proof. Let ![]() $\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]\in \operatorname {SL}_2(R)$ satisfying
$\gamma = [\begin{smallmatrix} z_0 & b\\ -x_0 & d\end{smallmatrix}]\in \operatorname {SL}_2(R)$ satisfying ![]() $(x_0, z_0) \cdot \gamma = (0,1)$ and
$(x_0, z_0) \cdot \gamma = (0,1)$ and ![]() $d + \theta b \in K_F^\times$ as above. Any other
$d + \theta b \in K_F^\times$ as above. Any other ![]() $\check {\gamma } \in \operatorname {SL}_2(R)$ satisfying
$\check {\gamma } \in \operatorname {SL}_2(R)$ satisfying ![]() $(x_0,z_0) \cdot \check {\gamma }$ to
$(x_0,z_0) \cdot \check {\gamma }$ to ![]() $(0,1)$ is a right-translate of
$(0,1)$ is a right-translate of ![]() $\gamma$ by an element of the stabilizer of
$\gamma$ by an element of the stabilizer of ![]() $(0,1)$, which is the group of unipotent matrices
$(0,1)$, which is the group of unipotent matrices ![]() $M_t = [\begin{smallmatrix} 1 & t \\ 0 & 1 \end{smallmatrix} ]$ for
$M_t = [\begin{smallmatrix} 1 & t \\ 0 & 1 \end{smallmatrix} ]$ for ![]() $t \in R$. Thus, take
$t \in R$. Thus, take ![]() $t \in R$, and let
$t \in R$, and let
Let ![]() $\check {F}(x,z) = F((x,z) \cdot \check {\gamma }^{-1}) = \sum _{i = 0}^{2n+1} \check {f}_i x^{2n+1-i}z^i$, and let
$\check {F}(x,z) = F((x,z) \cdot \check {\gamma }^{-1}) = \sum _{i = 0}^{2n+1} \check {f}_i x^{2n+1-i}z^i$, and let ![]() $\check {\theta }$ be the root of
$\check {\theta }$ be the root of ![]() $\check {F}(x,1)$ in
$\check {F}(x,1)$ in ![]() $K_F$. Assume that
$K_F$. Assume that ![]() $t$ has been chosen so that
$t$ has been chosen so that ![]() $(d-t x_0) + \theta (b+tz_0) \in K_F^\times$, and note that
$(d-t x_0) + \theta (b+tz_0) \in K_F^\times$, and note that
Just as we associated a pair ![]() $(I', \delta ')$ to
$(I', \delta ')$ to ![]() $\gamma$, we can associate a pair
$\gamma$, we can associate a pair ![]() $(\check {I}, \check {\delta })$ to
$(\check {I}, \check {\delta })$ to ![]() $\check {\gamma }$ satisfying the analogous properties
$\check {\gamma }$ satisfying the analogous properties ![]() $\check {I}^2 \subset \check {\delta } \cdot J_{\check {F}}$ and
$\check {I}^2 \subset \check {\delta } \cdot J_{\check {F}}$ and ![]() $\operatorname {N}(\check {I})^2 = \operatorname {N}(\check {\delta }) \cdot \operatorname {N}(J_{\check {F}})$. To prove the lemma, it suffices to show that
$\operatorname {N}(\check {I})^2 = \operatorname {N}(\check {\delta }) \cdot \operatorname {N}(J_{\check {F}})$. To prove the lemma, it suffices to show that
The second equality in (18) is readily deduced by inspecting (15); as for the first equality, note that it is equivalent to the following:
Using (17), we find that the fraction in parentheses in (19) is equal to ![]() $1+t \theta '$. Now, observe that we can express the ideals
$1+t \theta '$. Now, observe that we can express the ideals ![]() $I'$ and
$I'$ and ![]() $\check {I}$ as
$\check {I}$ as
where ![]() $\widetilde {\xi } = y_0$ if
$\widetilde {\xi } = y_0$ if ![]() $y_0 \neq 0$ and
$y_0 \neq 0$ and ![]() $\widetilde {\xi } = f_{2n}' = \check {f}_{2n}$ if
$\widetilde {\xi } = f_{2n}' = \check {f}_{2n}$ if ![]() $y_0 = 0$. Upon combining (19) and (20), we find that
$y_0 = 0$. Upon combining (19) and (20), we find that
 \begin{align*} (1 + t \theta')^n \cdot \widetilde{I} & = R\langle (1+t \theta')^n \cdot \widetilde{\xi} , ((1+t\theta') \widetilde{\theta}) \cdot ((1+t\theta')I_{\widetilde{F}})^{n-1}\rangle \\ & = R\langle(1+t\theta')^n \cdot \widetilde{\xi}, \theta' \cdot I_{F'}^{n-1} \rangle = I', \end{align*}
\begin{align*} (1 + t \theta')^n \cdot \widetilde{I} & = R\langle (1+t \theta')^n \cdot \widetilde{\xi} , ((1+t\theta') \widetilde{\theta}) \cdot ((1+t\theta')I_{\widetilde{F}})^{n-1}\rangle \\ & = R\langle(1+t\theta')^n \cdot \widetilde{\xi}, \theta' \cdot I_{F'}^{n-1} \rangle = I', \end{align*}
where the last step above follows because ![]() ${\theta '}^i \in I'$ for each
${\theta '}^i \in I'$ for each ![]() $i \in \{0, \ldots, n\}$.
$i \in \{0, \ldots, n\}$.
By applying the correspondence in Theorem 3 to the pair ![]() $(I, \delta )$ constructed above, we see that the point
$(I, \delta )$ constructed above, we see that the point ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(R)$ gives rise to a pair
$(x_0, y_0, z_0) \in \mathscr {S}_F(R)$ gives rise to a pair ![]() $(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ with invariant form
$(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ with invariant form ![]() $(-1)^n \cdot F_{\operatorname {mon}}$. To complete the construction, it remains to verify that
$(-1)^n \cdot F_{\operatorname {mon}}$. To complete the construction, it remains to verify that ![]() $A$ is split.
$A$ is split.
Lemma 11 The matrix ![]() $A$ defines a split quadratic form over
$A$ defines a split quadratic form over ![]() $k$.
$k$.
Proof. It suffices to exhibit an ![]() $n$-dimensional isotropic space
$n$-dimensional isotropic space ![]() $X$ over
$X$ over ![]() $k$ for the quadratic form defined by
$k$ for the quadratic form defined by ![]() $A$. We claim that
$A$. We claim that
does the job. Indeed, since ![]() $F$ is separable, the elements
$F$ is separable, the elements ![]() $\theta ^i(x_0 - \theta z_0)$ for
$\theta ^i(x_0 - \theta z_0)$ for ![]() $i \in \{0, \ldots, n-1\}$ are linearly independent over
$i \in \{0, \ldots, n-1\}$ are linearly independent over ![]() $k$: if
$k$: if ![]() $y_0 \neq 0$, then this follows because the elements
$y_0 \neq 0$, then this follows because the elements ![]() $\theta ^i \in K_F$ for
$\theta ^i \in K_F$ for ![]() $i \in \{0, \ldots, n-1\}$ are linearly independent and
$i \in \{0, \ldots, n-1\}$ are linearly independent and ![]() $x_0 - \theta z_0$ is an invertible element of
$x_0 - \theta z_0$ is an invertible element of ![]() $K_F$; if
$K_F$; if ![]() $y_0 = 0$, then this follows because the elements
$y_0 = 0$, then this follows because the elements ![]() $\theta ^i \in K_{\widetilde {F}}$ for
$\theta ^i \in K_{\widetilde {F}}$ for ![]() $i \in \{0, \ldots, n-1\}$ are linearly independent and
$i \in \{0, \ldots, n-1\}$ are linearly independent and ![]() $x_0 - \theta z_0$ is an invertible element of
$x_0 - \theta z_0$ is an invertible element of ![]() $K_{\widetilde {F}}$. Thus, we have that
$K_{\widetilde {F}}$. Thus, we have that ![]() $\dim _k X = n$. Moreover, note that
$\dim _k X = n$. Moreover, note that
for any ![]() $i,j \in \{0, \ldots, n-1\}$.
$i,j \in \{0, \ldots, n-1\}$.
Remark 12 We defined the pair ![]() $(I,\delta )$ in piecewise fashion, according as
$(I,\delta )$ in piecewise fashion, according as ![]() $y_0 \neq 0$ or
$y_0 \neq 0$ or ![]() $y_0 = 0$. The resulting pair
$y_0 = 0$. The resulting pair ![]() $(A,B)$ nevertheless admits a ‘functorial’ definition: indeed, the entries of
$(A,B)$ nevertheless admits a ‘functorial’ definition: indeed, the entries of ![]() $A$ and
$A$ and ![]() $B$ are polynomial functions in
$B$ are polynomial functions in ![]() $x_0, y_0, z_0, b, d$ and the coefficients of
$x_0, y_0, z_0, b, d$ and the coefficients of ![]() $F$. Thus, if our purpose was simply to construct orbits from integral points, we could have carried out the construction for
$F$. Thus, if our purpose was simply to construct orbits from integral points, we could have carried out the construction for ![]() $y_0 \neq 0$ and specialized the resulting pair of matrices to the case
$y_0 \neq 0$ and specialized the resulting pair of matrices to the case ![]() $y_0 = 0$. However, our proofs of Theorems 1 and 2 require knowledge of the element
$y_0 = 0$. However, our proofs of Theorems 1 and 2 require knowledge of the element ![]() $\delta \in K_F^\times$ corresponding to the orbit arising from an integral point, and it is difficult to reverse-engineer
$\delta \in K_F^\times$ corresponding to the orbit arising from an integral point, and it is difficult to reverse-engineer ![]() $\delta$ from a representative
$\delta$ from a representative ![]() $(A,B)$ of such an orbit.
$(A,B)$ of such an orbit.
In [Reference BhargavaBha13, § 2], Bhargava establishes an analogous construction for rational points on hyperelliptic curves, one that takes a non-Weierstrass point on a degree-![]() $2n$ hyperelliptic curve
$2n$ hyperelliptic curve ![]() $y^2 = F(x,z)$ and produces a pair
$y^2 = F(x,z)$ and produces a pair ![]() $(I, \delta )$ of a fractional ideal
$(I, \delta )$ of a fractional ideal ![]() $I$ and
$I$ and ![]() $\delta \in K_F^\times$ such that
$\delta \in K_F^\times$ such that ![]() $I^2 \subset \delta \cdot I_F^{2n-3}$ and
$I^2 \subset \delta \cdot I_F^{2n-3}$ and ![]() $\operatorname {N}(I)^2 = \operatorname {N}(\delta ) \cdot \operatorname {N}(I_F^{2n-3})$. By a parametrization due to Wood (see [Reference WoodWoo14, Theorem 5.7]), the pair
$\operatorname {N}(I)^2 = \operatorname {N}(\delta ) \cdot \operatorname {N}(I_F^{2n-3})$. By a parametrization due to Wood (see [Reference WoodWoo14, Theorem 5.7]), the pair ![]() $(I,\delta )$ gives rise to a pair
$(I,\delta )$ gives rise to a pair ![]() $(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n}$ such that
$(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n}$ such that ![]() $\det (x \cdot A + z \cdot B) = (-1)^n \cdot F(x,z)$. To handle Weierstrass points, Bhargava uses the aforementioned specialization trick but does not determine the element
$\det (x \cdot A + z \cdot B) = (-1)^n \cdot F(x,z)$. To handle Weierstrass points, Bhargava uses the aforementioned specialization trick but does not determine the element ![]() $\delta \in K_F^\times$ corresponding to the specialized orbit, even though this data seems necessary for the proofs of [Reference BhargavaBha13, Theorem 3 and Corollary 4] to go through.Footnote 2 We note here that the piecewise construction of the pair
$\delta \in K_F^\times$ corresponding to the specialized orbit, even though this data seems necessary for the proofs of [Reference BhargavaBha13, Theorem 3 and Corollary 4] to go through.Footnote 2 We note here that the piecewise construction of the pair ![]() $(I,\delta )$ given in this section can be modified to work for hyperelliptic curves, thus yielding complete proofs of [Reference BhargavaBha13, Theorem 3 and Corollary 4].
$(I,\delta )$ given in this section can be modified to work for hyperelliptic curves, thus yielding complete proofs of [Reference BhargavaBha13, Theorem 3 and Corollary 4].
Remark 13 That the invariant form of the pair ![]() $(A,B)$ is equal to
$(A,B)$ is equal to ![]() $(-1)^n \cdot F_{\operatorname {mon}}$, that
$(-1)^n \cdot F_{\operatorname {mon}}$, that ![]() $A$ defines a split quadratic form, and that the stabilizer of
$A$ defines a split quadratic form, and that the stabilizer of ![]() $(A,B)$ contains a subgroup isomorphic to
$(A,B)$ contains a subgroup isomorphic to ![]() $R_F^\times [2]$ are properties that hold formally. Thus, if we replace
$R_F^\times [2]$ are properties that hold formally. Thus, if we replace ![]() $R$ with any base ring and
$R$ with any base ring and ![]() $F \in R[x,z]$ is any binary form of degree
$F \in R[x,z]$ is any binary form of degree ![]() $2n+1$, any
$2n+1$, any ![]() $R$-primitive solution
$R$-primitive solution ![]() $(x,y,z) = (x_0,y_0,z_0) \in R^3$ to the superelliptic equation
$(x,y,z) = (x_0,y_0,z_0) \in R^3$ to the superelliptic equation ![]() $y^2 = F(x,z)$ gives rise to a pair of matrices
$y^2 = F(x,z)$ gives rise to a pair of matrices ![]() $(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ such that the invariant form is
$(A,B) \in R^2 \otimes _R \operatorname {Sym}_2 R^{2n+1}$ such that the invariant form is ![]() $F_{\operatorname {mon}}$ and such that the stabilizer in
$F_{\operatorname {mon}}$ and such that the stabilizer in ![]() $\operatorname {SL}_{2n+1}(R)$ contains a subgroup isomorphic to
$\operatorname {SL}_{2n+1}(R)$ contains a subgroup isomorphic to ![]() $R_F^\times [2]_{\operatorname {N}\equiv 1}$. If the base ring
$R_F^\times [2]_{\operatorname {N}\equiv 1}$. If the base ring ![]() $R$ is an integral domain, then
$R$ is an integral domain, then ![]() $A$ defines a split quadratic form over the fraction field
$A$ defines a split quadratic form over the fraction field ![]() $k$ of
$k$ of ![]() $R$. Note that these properties hold even if we do not assume that
$R$. Note that these properties hold even if we do not assume that ![]() $f_0 \neq 0$, that
$f_0 \neq 0$, that ![]() $F$ is separable, and that
$F$ is separable, and that ![]() $k$ has characteristic
$k$ has characteristic ![]() $0$, despite the fact that we used these assumptions to derive the construction.
$0$, despite the fact that we used these assumptions to derive the construction.
3.2 Distinguished points
We say that a point ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(R)$ is distinguished if its associated
$(x_0, y_0, z_0) \in \mathscr {S}_F(R)$ is distinguished if its associated ![]() $G(k)$-orbit is distinguished. Note that Proposition 6 implies that
$G(k)$-orbit is distinguished. Note that Proposition 6 implies that ![]() $(x_0, y_0, z_0)$ is distinguished if and only if
$(x_0, y_0, z_0)$ is distinguished if and only if ![]() $f_0 \cdot (x_0 - \theta z_0)$ is a square in
$f_0 \cdot (x_0 - \theta z_0)$ is a square in ![]() $K_F^\times$.
$K_F^\times$.
When ![]() $f_0$ is a multiple of a perfect square by a unit
$f_0$ is a multiple of a perfect square by a unit ![]() $u \in R^\times$,
$u \in R^\times$, ![]() $\mathscr {S}_F$ has a trivial
$\mathscr {S}_F$ has a trivial ![]() $R$-point, namely
$R$-point, namely ![]() $(u,\sqrt {u^{2n+1} \cdot f_0},0)$. Since
$(u,\sqrt {u^{2n+1} \cdot f_0},0)$. Since ![]() $f_0\cdot (u - \theta \cdot 0) = u \cdot f_0 \in K_F^{\times 2}$, the orbits associated to these trivial solutions are always distinguished. Whether a primitive integer solution is distinguished is not necessarily invariant under replacing
$f_0\cdot (u - \theta \cdot 0) = u \cdot f_0 \in K_F^{\times 2}$, the orbits associated to these trivial solutions are always distinguished. Whether a primitive integer solution is distinguished is not necessarily invariant under replacing ![]() $F$ with an
$F$ with an ![]() $\operatorname {SL}_2(R)$-translate. Indeed, suppose
$\operatorname {SL}_2(R)$-translate. Indeed, suppose ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(R)$, take
$(x_0, y_0, z_0) \in \mathscr {S}_F(R)$, take ![]() $\gamma \in \operatorname {SL}_2(R)$ such that
$\gamma \in \operatorname {SL}_2(R)$ such that ![]() $(x_0, z_0) \cdot \gamma = (1,0)$, and let
$(x_0, z_0) \cdot \gamma = (1,0)$, and let ![]() $F'(x,z) = F((x,z) \cdot \gamma ^{-1})$. Then the point
$F'(x,z) = F((x,z) \cdot \gamma ^{-1})$. Then the point ![]() $(1,y_0,0) \in \mathscr {S}_{F'}(R)$ is distinguished, regardless of whether the point
$(1,y_0,0) \in \mathscr {S}_{F'}(R)$ is distinguished, regardless of whether the point ![]() $(x_0,y_0,z_0) \in \mathscr {S}_F(R)$ is distinguished. Nevertheless, whether a solution is distinguished is always preserved under replacing
$(x_0,y_0,z_0) \in \mathscr {S}_F(R)$ is distinguished. Nevertheless, whether a solution is distinguished is always preserved under replacing ![]() $F$ with a translate by a unipotent matrix of the form
$F$ with a translate by a unipotent matrix of the form ![]() $M_t^T$ for
$M_t^T$ for ![]() $t \in R$.
$t \in R$.
Now take ![]() $R = \mathbb {Z}$. When
$R = \mathbb {Z}$. When ![]() $|f_0|$ is not a perfect square, we show in [Reference SwaminathanSwa23, § 3.3] that the non-square factors of
$|f_0|$ is not a perfect square, we show in [Reference SwaminathanSwa23, § 3.3] that the non-square factors of ![]() $|f_0|$ tend to obstruct the distinguished
$|f_0|$ tend to obstruct the distinguished ![]() $G(\mathbb {Q})$-orbit from arising via the map
$G(\mathbb {Q})$-orbit from arising via the map ![]() $\mathsf {orb}_F$ defined in § 2.3. More precisely, we have the following result, which states that there are strong limitations on the forms
$\mathsf {orb}_F$ defined in § 2.3. More precisely, we have the following result, which states that there are strong limitations on the forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ for which some point of
$F \in \mathscr {F}_{2n+1}(f_0)$ for which some point of ![]() $\mathscr {S}_F(\mathbb {Z})$ is distinguished:
$\mathscr {S}_F(\mathbb {Z})$ is distinguished:
Theorem 14 Let ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ be separable, and suppose that there exists a point of
$F \in \mathscr {F}_{2n+1}(f_0)$ be separable, and suppose that there exists a point of ![]() $\mathscr {S}_F(\mathbb {Z})$ giving rise to the distinguished
$\mathscr {S}_F(\mathbb {Z})$ giving rise to the distinguished ![]() $G(\mathbb {Q})$-orbit via the construction in § 3. Then one of the following two mutually exclusive possibilities holds for each prime
$G(\mathbb {Q})$-orbit via the construction in § 3. Then one of the following two mutually exclusive possibilities holds for each prime ![]() $p \mid \kappa$:
$p \mid \kappa$:
(a)
 $R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is not the maximal order in
$R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is not the maximal order in  $K_F \otimes _\mathbb {Q} \mathbb {Q}_p$; or
$K_F \otimes _\mathbb {Q} \mathbb {Q}_p$; or(b)
 $R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is the maximal order in
$R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is the maximal order in  $K_F \otimes _\mathbb {Q} \mathbb {Q}_p$ and
$K_F \otimes _\mathbb {Q} \mathbb {Q}_p$ and  $F/z$ is a unit multiple of a square modulo
$F/z$ is a unit multiple of a square modulo  $p$.
$p$.
Moreover, the density of binary forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that one of the conditions
$F \in \mathscr {F}_{2n+1}(f_0)$ such that one of the conditions ![]() $(\mathrm {a})$ or
$(\mathrm {a})$ or ![]() $(\mathrm {b})$ holds for every prime
$(\mathrm {b})$ holds for every prime ![]() $p \mid \kappa$ is equal to
$p \mid \kappa$ is equal to ![]() $\mu _{f_0} := \prod _{p \mid \kappa }({1}/{p^2} + ({p-1})/{p^{n+1}})$.
$\mu _{f_0} := \prod _{p \mid \kappa }({1}/{p^2} + ({p-1})/{p^{n+1}})$.
Proof. Let ![]() $p \mid \kappa$. By [Reference SwaminathanSwa23, Proposition 40], if
$p \mid \kappa$. By [Reference SwaminathanSwa23, Proposition 40], if ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ is such that some element of the image of
$F \in \mathscr {F}_{2n+1}(f_0)$ is such that some element of the image of ![]() $\mathsf {orb}_F$ has distinguished
$\mathsf {orb}_F$ has distinguished ![]() $G(\mathbb {Q}_p)$-orbit, then one of conditions (a) or (b) in the theorem statement holds. By [Reference Ash, Brakenhoff and ZarrabiABZ07, Proposition 3.5], the
$G(\mathbb {Q}_p)$-orbit, then one of conditions (a) or (b) in the theorem statement holds. By [Reference Ash, Brakenhoff and ZarrabiABZ07, Proposition 3.5], the ![]() $p$-adic density of
$p$-adic density of ![]() $F \in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ satisfying condition (a) is
$F \in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ satisfying condition (a) is ![]() $p^{-2}$, and it follows from [Reference SwaminathanSwa23, Proposition 41] that the
$p^{-2}$, and it follows from [Reference SwaminathanSwa23, Proposition 41] that the ![]() $p$-adic density of
$p$-adic density of ![]() $F\in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ satisfying condition (b) is
$F\in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ satisfying condition (b) is ![]() $p^{-n-1}(p-1)$. The theorem follows by combining these density calculations.
$p^{-n-1}(p-1)$. The theorem follows by combining these density calculations.
Theorem 14 implies that points of ![]() $\mathscr {S}_F(\mathbb {Z})$ often fail to be distinguished, a fact that is crucial for the proofs of Theorems 1 and 2, because the geometry-of-numbers results from [Reference Bhargava and GrossBG13, § 9] that we apply in § 4 to count orbits of
$\mathscr {S}_F(\mathbb {Z})$ often fail to be distinguished, a fact that is crucial for the proofs of Theorems 1 and 2, because the geometry-of-numbers results from [Reference Bhargava and GrossBG13, § 9] that we apply in § 4 to count orbits of ![]() $G(\mathbb {Z})$ on
$G(\mathbb {Z})$ on ![]() $V(\mathbb {Z})$ only give us a count of the non-distinguished orbits.
$V(\mathbb {Z})$ only give us a count of the non-distinguished orbits.
4. Proof of Theorem 1
The purpose of this section is to give a proof of our first main result, namely Theorem 1.
4.1 Outline of the proof
Let ![]() $\delta$ be the upper density of forms
$\delta$ be the upper density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$, enumerated by height, such that
$F \in \mathscr {F}_{2n+1}(f_0)$, enumerated by height, such that ![]() $\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. Proving Theorem 1 amounts to obtaining an upper bound on
$\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. Proving Theorem 1 amounts to obtaining an upper bound on ![]() $\delta$.
$\delta$.
To this end, let ![]() $\mathscr {F}_{2n+1}^*(f_0)$ be the subset of all
$\mathscr {F}_{2n+1}^*(f_0)$ be the subset of all ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ satisfying both conditions in Theorem 14 for every prime
$F \in \mathscr {F}_{2n+1}(f_0)$ satisfying both conditions in Theorem 14 for every prime ![]() $p \mid \kappa$; note that the complement of
$p \mid \kappa$; note that the complement of ![]() $\mathscr {F}_{2n+1}^*(f_0)$ consists entirely of binary forms for which the distinguished orbit does not arise from a primitive integer solution. Moreover, let
$\mathscr {F}_{2n+1}^*(f_0)$ consists entirely of binary forms for which the distinguished orbit does not arise from a primitive integer solution. Moreover, let ![]() $\mathscr {P}$ denote the (
$\mathscr {P}$ denote the (![]() $G(\mathbb {Z})$-invariant) subset of integral elements of
$G(\mathbb {Z})$-invariant) subset of integral elements of ![]() $V(\mathbb {Z})$ that arise via the construction in § 3.1 from separable forms
$V(\mathbb {Z})$ that arise via the construction in § 3.1 from separable forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$. By partitioning
$F \in \mathscr {F}_{2n+1}(f_0)$. By partitioning ![]() $\mathscr {F}_{2n+1}(f_0)$ into
$\mathscr {F}_{2n+1}(f_0)$ into ![]() $\mathscr {F}_{2n+1}^*(f_0)$ and its complement, we see that
$\mathscr {F}_{2n+1}^*(f_0)$ and its complement, we see that ![]() $\delta$ can be bounded as follows:
$\delta$ can be bounded as follows:
where we say that ![]() $T$ is irreducible if
$T$ is irreducible if ![]() $\operatorname {ch}(T)$ is separable and the
$\operatorname {ch}(T)$ is separable and the ![]() $G(\mathbb {Q})$-orbit of
$G(\mathbb {Q})$-orbit of ![]() $T$ is non-distinguished.
$T$ is non-distinguished.
The first term on the right-hand side of (21) constitutes the trivial bound for the density of forms ![]() $F \in \mathscr {F}_{2n+1}^*(f_0)$ such that
$F \in \mathscr {F}_{2n+1}^*(f_0)$ such that ![]() $\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. Computing this first term is straightforward. Indeed, the first term in the numerator and the denominator are respectively given by
$\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. Computing this first term is straightforward. Indeed, the first term in the numerator and the denominator are respectively given by
The second term in the numerator on the right-hand side of (21) means ‘the number of ![]() $G(\mathbb {Q})$-equivalence classes of irreducible elements
$G(\mathbb {Q})$-equivalence classes of irreducible elements ![]() $T \in \mathscr {P}$ of height less than
$T \in \mathscr {P}$ of height less than ![]() $X$’, and this constitutes a bound on the number forms
$X$’, and this constitutes a bound on the number forms ![]() $F \in \mathscr {F}_{2n+1}(f_0) \smallsetminus \mathscr {F}_{2n+1}^*(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0) \smallsetminus \mathscr {F}_{2n+1}^*(f_0)$ such that ![]() $\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. It is hard to describe
$\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. It is hard to describe ![]() $\mathscr {P}$ explicitly and, hence, to obtain a precise asymptotic for this second term. But
$\mathscr {P}$ explicitly and, hence, to obtain a precise asymptotic for this second term. But ![]() $\mathscr {P}$ is contained within a subset of
$\mathscr {P}$ is contained within a subset of ![]() $V(\mathbb {Z})$ defined by local conditions: indeed, we have
$V(\mathbb {Z})$ defined by local conditions: indeed, we have
where for each place ![]() $v$ of
$v$ of ![]() $\mathbb {Q}$, we write
$\mathbb {Q}$, we write ![]() $\mathscr {P}_v$ for the subset of
$\mathscr {P}_v$ for the subset of ![]() $V(\mathbb {Z}_v)$ that arises via the construction in § 3.1 from separable forms
$V(\mathbb {Z}_v)$ that arises via the construction in § 3.1 from separable forms ![]() $F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_v)$. Thus, the second term in the numerator on the right-hand side of (21) is bounded by the following quantity:
$F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_v)$. Thus, the second term in the numerator on the right-hand side of (21) is bounded by the following quantity:
The rest of this section is devoted to bounding (24). We desire a bound of order ![]() $o(f_0^{-2n^2-n} \cdot 2^{-n})$ when
$o(f_0^{-2n^2-n} \cdot 2^{-n})$ when ![]() $2 \nmid f_0$ and a bound of order
$2 \nmid f_0$ and a bound of order ![]() $O(f_0^{-2n^2-n} \cdot 2^{-\varepsilon _1 n^{\varepsilon _2}})$ when
$O(f_0^{-2n^2-n} \cdot 2^{-\varepsilon _1 n^{\varepsilon _2}})$ when ![]() $2 \mid f_0$. We obtain bounds of these magnitudes by means of the following steps.
$2 \mid f_0$. We obtain bounds of these magnitudes by means of the following steps.
(A) In § 4.2, we adapt results of Bhargava–Gross [Reference Bhargava and GrossBG13] to obtain an asymptotic upper bound for the number of irreducible orbits of ![]() $G(\mathbb {Z})$ on
$G(\mathbb {Z})$ on ![]() $V(\mathbb {Z})$ of bounded height, where the orbits are counted with respect to a weight function
$V(\mathbb {Z})$ of bounded height, where the orbits are counted with respect to a weight function ![]() $\phi$ defined by infinitely many local conditions (see Theorem 16). By choosing the weight function
$\phi$ defined by infinitely many local conditions (see Theorem 16). By choosing the weight function ![]() $\phi$ appropriately, so that it picks out orbits belonging to
$\phi$ appropriately, so that it picks out orbits belonging to ![]() $\mathscr {P}_v$ for every place
$\mathscr {P}_v$ for every place ![]() $v$ and counts each
$v$ and counts each ![]() $G(\mathbb {Q})$-equivalence class of integral orbits just once, we obtain an upper bound for the quantity (24). This bound is expressed a product of local mass formulas, one for each place of
$G(\mathbb {Q})$-equivalence class of integral orbits just once, we obtain an upper bound for the quantity (24). This bound is expressed a product of local mass formulas, one for each place of ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
(B) Proving Theorem 1 then amounts to bounding each of the local mass formulas obtained in step (A) (in other words, we must control the ‘size’ of ![]() $\mathscr {P}_v$ for each
$\mathscr {P}_v$ for each ![]() $v$).
$v$).
– In § 4.3, we bound the mass at
 $\infty$ by working over
$\infty$ by working over  $\mathbb {R}$ (see Proposition 18). The mass at
$\mathbb {R}$ (see Proposition 18). The mass at  $\infty$ contributes a factor of
$\infty$ contributes a factor of  $O(2^n \cdot X^{({n+1})/{2n}})$ to the bound.
$O(2^n \cdot X^{({n+1})/{2n}})$ to the bound.– In § 4.4, we bound the mass at
 $p$ when
$p$ when  $2 \neq p \nmid f_0$ by working over
$2 \neq p \nmid f_0$ by working over  $\mathbb {Z}/p\mathbb {Z}$ (see Proposition 22). As we later show in § 4.7, the masses at these primes together contribute a factor of
$\mathbb {Z}/p\mathbb {Z}$ (see Proposition 22). As we later show in § 4.7, the masses at these primes together contribute a factor of  $O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ to the bound. This constitutes a small part of the saving when
$O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ to the bound. This constitutes a small part of the saving when  $2 \nmid f_0$ and the entire saving when
$2 \nmid f_0$ and the entire saving when  $2 \mid f_0$.
$2 \mid f_0$.– In § 4.5, we bound the mass at
 $p$ when
$p$ when  $2 = p \nmid f_0$ by working over
$2 = p \nmid f_0$ by working over  $\mathbb {Z}/8\mathbb {Z}$ (see Proposition 26). In this case, the mass at
$\mathbb {Z}/8\mathbb {Z}$ (see Proposition 26). In this case, the mass at  $2$ contributes a factor of
$2$ contributes a factor of  $O(2^{-2n})$ to the bound, which constitutes most of the saving.
$O(2^{-2n})$ to the bound, which constitutes most of the saving.– In § 4.6, we bound the mass at
 $p$ when
$p$ when  $p \mid f_0$ by working over
$p \mid f_0$ by working over  $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and  $\mathbb {Z}_p$ (see Propositions 30 and 33). In this case, the mass at
$\mathbb {Z}_p$ (see Propositions 30 and 33). In this case, the mass at  $p$ contributes to the bound a factor of
$p$ contributes to the bound a factor of  $O(|f_0|_p^{2n^2+n})$ when
$O(|f_0|_p^{2n^2+n})$ when  $p \neq 2$ and
$p \neq 2$ and  $O(2^{-n} \cdot |f_0|_2^{2n^2+n})$ when
$O(2^{-n} \cdot |f_0|_2^{2n^2+n})$ when  $p = 2$.
$p = 2$.
(C) The final step is to combine the bounds obtained in steps (A) and (B) and to simplify the result. We do this in § 4.7.
4.2 Step (A): counting irreducible integral orbits of bounded height
For a monic polynomial ![]() $f = x^{2n+1} + \sum _{i = 1}^{2n+1} c_i \cdot x^{2n+1-i} \in \mathbb {Z}[x]$, let the height of
$f = x^{2n+1} + \sum _{i = 1}^{2n+1} c_i \cdot x^{2n+1-i} \in \mathbb {Z}[x]$, let the height of ![]() $f$ be defined by
$f$ be defined by ![]() $H(f) := H(c_1, \ldots, c_{2n+1}) := \max \{|c_i|^{2n(2n+1)/i} : i = 1, \ldots, 2n+1\}$. For an element
$H(f) := H(c_1, \ldots, c_{2n+1}) := \max \{|c_i|^{2n(2n+1)/i} : i = 1, \ldots, 2n+1\}$. For an element ![]() $T \in V(\mathbb {Z})$, let the height of (the
$T \in V(\mathbb {Z})$, let the height of (the ![]() $G(\mathbb {Z})$-orbit of)
$G(\mathbb {Z})$-orbit of) ![]() $T$ be defined by
$T$ be defined by ![]() $H(T) = H(\operatorname {ch}(T))$.
$H(T) = H(\operatorname {ch}(T))$.
Fix ![]() $m \in \{0, \ldots, n\}$, and define
$m \in \{0, \ldots, n\}$, and define ![]() $\mathscr {I}(m) \subset \mathscr {F}_{2n+1}(1,\mathbb {R})$ to be the set of separable monic degree-
$\mathscr {I}(m) \subset \mathscr {F}_{2n+1}(1,\mathbb {R})$ to be the set of separable monic degree-![]() $(2n+1)$ polynomials over
$(2n+1)$ polynomials over ![]() $\mathbb {R}$ having exactly
$\mathbb {R}$ having exactly ![]() $2m+1$ real roots. Let
$2m+1$ real roots. Let ![]() $\mathscr {B} \subset \operatorname {ch}^{-1}(\mathscr {I}(m)) \subset V(\mathbb {R})$ be a measurable subset closed under the action of
$\mathscr {B} \subset \operatorname {ch}^{-1}(\mathscr {I}(m)) \subset V(\mathbb {R})$ be a measurable subset closed under the action of ![]() $G(\mathbb {R})$. Let
$G(\mathbb {R})$. Let ![]() $N(V(\mathbb {Z}) \cap \mathscr {B}; X)$ denote the number of
$N(V(\mathbb {Z}) \cap \mathscr {B}; X)$ denote the number of ![]() $G(\mathbb {Z})$-orbits of irreducible elements
$G(\mathbb {Z})$-orbits of irreducible elements ![]() $T \in V(\mathbb {Z}) \cap \mathscr {B}$ satisfying
$T \in V(\mathbb {Z}) \cap \mathscr {B}$ satisfying ![]() $H(T) < X$. Then we have the following adaptation of [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)], giving an asymptotic for
$H(T) < X$. Then we have the following adaptation of [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)], giving an asymptotic for ![]() $N(V(\mathbb {Z}) \cap \mathscr {B}; X)$.
$N(V(\mathbb {Z}) \cap \mathscr {B}; X)$.
Theorem 15 There exists an absolute constant ![]() $\mathscr {J} \in \mathbb {Q}^\times$ such that
$\mathscr {J} \in \mathbb {Q}^\times$ such that
 \begin{align*} N(V(\mathbb{Z}) \cap \mathscr{B}; X)
&= \frac{1}{2^{m+n}} \cdot |\mathscr{J}| \cdot
\operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \\
&\quad \cdot \int_{\substack{f \in \mathscr{I}(m) \\ H(f) < X}}
\#\bigg(\frac{\mathscr{B} \cap
\operatorname{ch}^{-1}(f)}{G(\mathbb{R})}\bigg)\, df +
o(X^{({n+1})/{2n}}), \end{align*}
\begin{align*} N(V(\mathbb{Z}) \cap \mathscr{B}; X)
&= \frac{1}{2^{m+n}} \cdot |\mathscr{J}| \cdot
\operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \\
&\quad \cdot \int_{\substack{f \in \mathscr{I}(m) \\ H(f) < X}}
\#\bigg(\frac{\mathscr{B} \cap
\operatorname{ch}^{-1}(f)}{G(\mathbb{R})}\bigg)\, df +
o(X^{({n+1})/{2n}}), \end{align*}
where the fundamental volume ![]() $\operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ is computed with respect to a differential
$\operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ is computed with respect to a differential ![]() $\omega$ that generates the rank-
$\omega$ that generates the rank-![]() $1$ module of top-degree differentials of
$1$ module of top-degree differentials of ![]() $G$ over
$G$ over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Proof. In [Reference Bhargava and GrossBG13], Bhargava and Gross work with the subrepresentation ![]() $V' \subset V$ consisting of the traceless operators in
$V' \subset V$ consisting of the traceless operators in ![]() $V$. Such traceless operators have characteristic polynomial with the coefficient
$V$. Such traceless operators have characteristic polynomial with the coefficient ![]() $c_1$ of the term
$c_1$ of the term ![]() $x^{2n}$ equal to
$x^{2n}$ equal to ![]() $0$. They prove that
$0$. They prove that ![]() $N(V'(\mathbb {Z}) \cap \mathscr {B}; X)$ is given by a formula (see [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)]) that is almost identical to the formula in the statement of Theorem 15, except that the value of
$N(V'(\mathbb {Z}) \cap \mathscr {B}; X)$ is given by a formula (see [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)]) that is almost identical to the formula in the statement of Theorem 15, except that the value of ![]() $\mathscr {J}$ may be different and the integral runs over polynomials with coefficients
$\mathscr {J}$ may be different and the integral runs over polynomials with coefficients ![]() $(0, c_2, \ldots, c_{2n+1})$ in
$(0, c_2, \ldots, c_{2n+1})$ in ![]() $\mathscr {I}(m)$. By simply lifting the restriction that
$\mathscr {I}(m)$. By simply lifting the restriction that ![]() $c_1 = 0$, it is not hard to check that the proof of [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)] carries over with minimal modifications to prove Theorem 15.
$c_1 = 0$, it is not hard to check that the proof of [Reference Bhargava and GrossBG13, Theorem 10.1 and (10.27)] carries over with minimal modifications to prove Theorem 15.
The following result generalizes Theorem 15 by giving an upper bound on the number of integral orbits of height up to ![]() $X$, where the orbits are weighted by a function defined by local conditions.
$X$, where the orbits are weighted by a function defined by local conditions.
Theorem 16 (Cf. [Reference Bhargava and GrossBG13, Theorem 10.12])
Let ![]() $\phi \colon V(\mathbb {Z}) \to [0,1] \subset \mathbb {R}$ be a function such that there exists a function
$\phi \colon V(\mathbb {Z}) \to [0,1] \subset \mathbb {R}$ be a function such that there exists a function ![]() $\phi _p \colon V(\mathbb {Z}_p) \to [0,1]$ for each prime
$\phi _p \colon V(\mathbb {Z}_p) \to [0,1]$ for each prime ![]() $p$ satisfying the following conditions:
$p$ satisfying the following conditions:
– for all
 $T \in V(\mathbb {Z})$, the product
$T \in V(\mathbb {Z})$, the product  $\prod _{p} \phi _p(T)$ converges to
$\prod _{p} \phi _p(T)$ converges to  $\phi (T)$; and
$\phi (T)$; and– for each
 $p$, the function
$p$, the function  $\phi _p$ is locally constant outside a closed set
$\phi _p$ is locally constant outside a closed set  $S_p \subset V(\mathbb {Z}_p)$ of measure
$S_p \subset V(\mathbb {Z}_p)$ of measure  $0$.
$0$.
Let ![]() $N_\phi (V(\mathbb {Z}) \cap \mathscr {B}; X)$ denote the number of
$N_\phi (V(\mathbb {Z}) \cap \mathscr {B}; X)$ denote the number of ![]() $G(\mathbb {Z})$-orbits of irreducible elements
$G(\mathbb {Z})$-orbits of irreducible elements ![]() $T \in V(\mathbb {Z}) \cap \mathscr {B}$ satisfying
$T \in V(\mathbb {Z}) \cap \mathscr {B}$ satisfying ![]() $H(T) < X$, where each orbit
$H(T) < X$, where each orbit ![]() $G(\mathbb {Z}) \cdot T$ is counted with weight
$G(\mathbb {Z}) \cdot T$ is counted with weight ![]() $\phi (T) := \prod _p \phi _p(T)$. Then
$\phi (T) := \prod _p \phi _p(T)$. Then
 \[ N_\phi(V(\mathbb{Z}) \cap \mathscr{B}; X) \leq N(V(\mathbb{Z}) \cap \mathscr{B}; X) \cdot \prod_{p} \int_{T \in V(\mathbb{Z}_p)} \phi_p(T)\,dT + o(X^{({n+1})/{2n}}). \]
\[ N_\phi(V(\mathbb{Z}) \cap \mathscr{B}; X) \leq N(V(\mathbb{Z}) \cap \mathscr{B}; X) \cdot \prod_{p} \int_{T \in V(\mathbb{Z}_p)} \phi_p(T)\,dT + o(X^{({n+1})/{2n}}). \]
Proof. The proof is identical to the first half of the proof of [Reference Bhargava and ShankarBS15, Theorem 2.21] (note that the ‘accep-table’ hypothesis in [Reference Bhargava and ShankarBS15, Theorem 2.21] is not needed for the upper bound in Theorem 16).
To apply Theorem 16 to bound (24), we need to choose the local weight functions ![]() $\phi _p$ appropriately. Given
$\phi _p$ appropriately. Given ![]() $T \in V(\mathbb {Z})$, denote by
$T \in V(\mathbb {Z})$, denote by ![]() $m(T)$ the quantity
$m(T)$ the quantity
 \[ m(T) := \sum_{T' \in \mathscr{O}(T)} \frac{\#\operatorname{Stab}_\mathbb{Q}(T')}{\#\operatorname{Stab}_\mathbb{Z}(T')} = \sum_{T' \in \mathscr{O}(T)} \frac{\#\operatorname{Stab}_\mathbb{Q}(T)}{\#\operatorname{Stab}_\mathbb{Z}(T')}, \]
\[ m(T) := \sum_{T' \in \mathscr{O}(T)} \frac{\#\operatorname{Stab}_\mathbb{Q}(T')}{\#\operatorname{Stab}_\mathbb{Z}(T')} = \sum_{T' \in \mathscr{O}(T)} \frac{\#\operatorname{Stab}_\mathbb{Q}(T)}{\#\operatorname{Stab}_\mathbb{Z}(T')}, \]
where ![]() $\mathscr {O}(T)$ denotes a set of representatives for the action of
$\mathscr {O}(T)$ denotes a set of representatives for the action of ![]() $G(\mathbb {Z})$ on the
$G(\mathbb {Z})$ on the ![]() $G(\mathbb {Q})$-orbit of
$G(\mathbb {Q})$-orbit of ![]() $T$, and where
$T$, and where ![]() $\operatorname {Stab}_\mathbb {Q}(T')$ and
$\operatorname {Stab}_\mathbb {Q}(T')$ and ![]() $\operatorname {Stab}_\mathbb {Z}(T')$ respectively denote the stabilizers of
$\operatorname {Stab}_\mathbb {Z}(T')$ respectively denote the stabilizers of ![]() $T'$ in
$T'$ in ![]() $G(\mathbb {Q})$ and
$G(\mathbb {Q})$ and ![]() $G(\mathbb {Z})$. By [Reference Bhargava and GrossBG13, Proposition 10.8], counting
$G(\mathbb {Z})$. By [Reference Bhargava and GrossBG13, Proposition 10.8], counting ![]() $G(\mathbb {Q})$-orbits on
$G(\mathbb {Q})$-orbits on ![]() $V(\mathbb {Z})$ is, up to a negligible error, no different from counting
$V(\mathbb {Z})$ is, up to a negligible error, no different from counting ![]() $G(\mathbb {Z})$-orbits on
$G(\mathbb {Z})$-orbits on ![]() $V(\mathbb {Z})$, where the
$V(\mathbb {Z})$, where the ![]() $G(\mathbb {Z})$-orbit of
$G(\mathbb {Z})$-orbit of ![]() $T \in V(\mathbb {Z})$ is weighted by
$T \in V(\mathbb {Z})$ is weighted by ![]() $1/m(T)$.
$1/m(T)$.
The weight ![]() $m(T)$ can be expressed as a product over primes
$m(T)$ can be expressed as a product over primes ![]() $p$ of local weights
$p$ of local weights ![]() $m_p(T)$. Indeed, as stated in [Reference Bhargava and GrossBG13, (11.3)], we have that
$m_p(T)$. Indeed, as stated in [Reference Bhargava and GrossBG13, (11.3)], we have that
 \begin{equation} m(T) = \prod_{p} m_p(T), \quad \text{where } m_p(T) := \sum_{T' \in \mathscr{O}_p(T)} \frac{\#\operatorname{Stab}_{\mathbb{Q}_p}(T)}{\#\operatorname{Stab}_{\mathbb{Z}_p}(T')}, \end{equation}
\begin{equation} m(T) = \prod_{p} m_p(T), \quad \text{where } m_p(T) := \sum_{T' \in \mathscr{O}_p(T)} \frac{\#\operatorname{Stab}_{\mathbb{Q}_p}(T)}{\#\operatorname{Stab}_{\mathbb{Z}_p}(T')}, \end{equation}
where ![]() $\mathscr {O}_p(T)$ denotes a set of representatives for the action of
$\mathscr {O}_p(T)$ denotes a set of representatives for the action of ![]() $G(\mathbb {Z}_p)$ on the
$G(\mathbb {Z}_p)$ on the ![]() $G(\mathbb {Q}_p)$-orbit of
$G(\mathbb {Q}_p)$-orbit of ![]() $T$, and where
$T$, and where ![]() $\operatorname {Stab}_{\mathbb {Q}_p}(T')$ and
$\operatorname {Stab}_{\mathbb {Q}_p}(T')$ and ![]() $\operatorname {Stab}_{\mathbb {Z}_p}(T')$ denote the stabilizers of
$\operatorname {Stab}_{\mathbb {Z}_p}(T')$ denote the stabilizers of ![]() $T'$ in
$T'$ in ![]() $G(\mathbb {Q}_p)$ and
$G(\mathbb {Q}_p)$ and ![]() $G(\mathbb {Z}_p)$, respectively.
$G(\mathbb {Z}_p)$, respectively.
For each prime ![]() $p$, let
$p$, let ![]() $\psi _p \colon V(\mathbb {Z}_p) \to \{0,1\} \subset \mathbb {R}$ be the indicator function of elements
$\psi _p \colon V(\mathbb {Z}_p) \to \{0,1\} \subset \mathbb {R}$ be the indicator function of elements ![]() $T \in \mathscr {P}_p$ such that
$T \in \mathscr {P}_p$ such that ![]() $\operatorname {ch}(T)$ is separable. Then upon taking
$\operatorname {ch}(T)$ is separable. Then upon taking ![]() $\phi _p = \psi _p/m_p$ for each
$\phi _p = \psi _p/m_p$ for each ![]() $p$, Theorems 15 and 16 together imply the following.
$p$, Theorems 15 and 16 together imply the following.
Proposition 17 We have that (24) is bounded above by
 \begin{align} & \sum_{m = 0}^n \frac{1}{2^{m+n}} \cdot |\mathscr{J}| \cdot \operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \cdot\int_{\substack{f \in \mathscr{I}(m) \nonumber\\
H(f) < X}} \#\bigg(\frac{\mathscr{P}_\infty \cap \operatorname{ch}^{-1}(f)}{G(\mathbb{R})}\bigg) df \nonumber\\ & \quad \cdot \prod_{p} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}dT + o(X^{({n+1})/{2n}}). \end{align}
\begin{align} & \sum_{m = 0}^n \frac{1}{2^{m+n}} \cdot |\mathscr{J}| \cdot \operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \cdot\int_{\substack{f \in \mathscr{I}(m) \nonumber\\
H(f) < X}} \#\bigg(\frac{\mathscr{P}_\infty \cap \operatorname{ch}^{-1}(f)}{G(\mathbb{R})}\bigg) df \nonumber\\ & \quad \cdot \prod_{p} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}dT + o(X^{({n+1})/{2n}}). \end{align} In what follows, we call the sum over ![]() $m$ on the first line of (26) the mass at
$m$ on the first line of (26) the mass at ![]() $\infty$, and we call the integral over
$\infty$, and we call the integral over ![]() $V(\mathbb {Z}_p)$ on the second line of (26) the mass at
$V(\mathbb {Z}_p)$ on the second line of (26) the mass at ![]() $p$.
$p$.
4.3 Step (B): bounding the mass at  $\infty$
$\infty$
In this section, we prove the following result, which shows that the mass at ![]() $\infty$ in (26) is bounded by
$\infty$ in (26) is bounded by ![]() $O(2^n \cdot X^{({n+1})/{2n}})$.
$O(2^n \cdot X^{({n+1})/{2n}})$.
Proposition 18 The mass at ![]() $\infty$ in (26) is
$\infty$ in (26) is
 \[ \leq 3 \cdot 2^{n} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{H(f) < X} df. \]
\[ \leq 3 \cdot 2^{n} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{H(f) < X} df. \]
Proof. We start with the following lemma, where we derive an upper bound on the factor ![]() $|\mathscr {J}| \cdot \operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ that occurs in the mass at
$|\mathscr {J}| \cdot \operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ that occurs in the mass at ![]() $\infty$.
$\infty$.
Lemma 19 We have that
 \[ |\mathscr{J}|\cdot \operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \leq 2^{2n+1} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})}. \]
\[ |\mathscr{J}|\cdot \operatorname{Vol}(G(\mathbb{Z}) \backslash G(\mathbb{R})) \leq 2^{2n+1} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})}. \]
Proof. Let ![]() $R = \mathbb {C}$,
$R = \mathbb {C}$, ![]() $\mathbb {R}$, or
$\mathbb {R}$, or ![]() $\mathbb {Z}_p$ where
$\mathbb {Z}_p$ where ![]() $p$ is a prime. Let
$p$ is a prime. Let ![]() $\mathscr {R} \subset R^{2n+1}$ be any open subset, and let
$\mathscr {R} \subset R^{2n+1}$ be any open subset, and let ![]() $s \colon \mathscr {R} \to V(R)$ be a continuous function such that the characteristic polynomial of
$s \colon \mathscr {R} \to V(R)$ be a continuous function such that the characteristic polynomial of ![]() $s(c_1, \ldots, c_{2n+1})$ is given by
$s(c_1, \ldots, c_{2n+1})$ is given by ![]() $x^{2n+1} + \sum _{i = 1}^{2n+1} c_ix^{2n+1-i}$ for every
$x^{2n+1} + \sum _{i = 1}^{2n+1} c_ix^{2n+1-i}$ for every ![]() $(c_1, \ldots, c_{2n+1}) \in \mathscr {R}$. The constant
$(c_1, \ldots, c_{2n+1}) \in \mathscr {R}$. The constant ![]() $\mathscr {J}$ arises as a multiplicative factor in the following change-of-measure formula.
$\mathscr {J}$ arises as a multiplicative factor in the following change-of-measure formula.
Lemma 20 For any measurable function ![]() $\phi$ on
$\phi$ on ![]() $V(R)$, we have
$V(R)$, we have
where we regard ![]() $G(R) \cdot s(\mathscr {R})$ as a multiset,
$G(R) \cdot s(\mathscr {R})$ as a multiset, ![]() $|-|$ denotes the standard absolute value on
$|-|$ denotes the standard absolute value on ![]() $R$,
$R$, ![]() $dT$ is the Euclidean measure on
$dT$ is the Euclidean measure on ![]() $V(R)$, and
$V(R)$, and ![]() $dr$ is the restriction to
$dr$ is the restriction to ![]() $\mathscr {R}$ of the Euclidean measure on
$\mathscr {R}$ of the Euclidean measure on ![]() $R^{2n+1}$.
$R^{2n+1}$.
Proof of Lemma 20 The proof is identical to that of [Reference Bhargava and ShankarBS15, Proposition 3.11].
In particular, the constant ![]() $\mathscr {J}$ is independent of the choices of
$\mathscr {J}$ is independent of the choices of ![]() $R = \mathbb {C}$,
$R = \mathbb {C}$, ![]() $\mathbb {R}$, or
$\mathbb {R}$, or ![]() $\mathbb {Z}_p$ and of the region
$\mathbb {Z}_p$ and of the region ![]() $\mathscr {R}$ and the functions
$\mathscr {R}$ and the functions ![]() $s$ and
$s$ and ![]() $\phi$. Thus, to compute
$\phi$. Thus, to compute ![]() $|\mathscr {J}|$, we can make the following convenient choices: take
$|\mathscr {J}|$, we can make the following convenient choices: take ![]() $R = \mathbb {Z}_p$, so that
$R = \mathbb {Z}_p$, so that ![]() $|-| = |-|_p$; take
$|-| = |-|_p$; take
 \[ \mathscr{R} = \bigg\{(c_1, \ldots,
c_{2n+1}) \in \mathbb{Z}_p^{2n+1} : x^{2n+1} + \sum_{i =
1}^{2n+1} c_i x^{2n+1-i} \equiv f\ ({\rm mod}\ p)\bigg\}
\]
\[ \mathscr{R} = \bigg\{(c_1, \ldots,
c_{2n+1}) \in \mathbb{Z}_p^{2n+1} : x^{2n+1} + \sum_{i =
1}^{2n+1} c_i x^{2n+1-i} \equiv f\ ({\rm mod}\ p)\bigg\}
\]
for a fixed monic irreducible degree-![]() $(2n+1)$ polynomial
$(2n+1)$ polynomial ![]() $f \in (\mathbb {Z}/p\mathbb {Z})[x]$; letting
$f \in (\mathbb {Z}/p\mathbb {Z})[x]$; letting ![]() $\Sigma _f := \{T \in V(\mathbb {Z}_p) : \operatorname {ch}(T) \equiv f \pmod p\}$, take
$\Sigma _f := \{T \in V(\mathbb {Z}_p) : \operatorname {ch}(T) \equiv f \pmod p\}$, take ![]() $s$ to be any continuous right-inverse to the function that sends
$s$ to be any continuous right-inverse to the function that sends ![]() $T \in \Sigma _f$ to the list of coefficients of
$T \in \Sigma _f$ to the list of coefficients of ![]() $\operatorname {ch}(T)$; and take
$\operatorname {ch}(T)$; and take ![]() $\phi$ to be the function that sends
$\phi$ to be the function that sends ![]() $T \in \Sigma _f$ to
$T \in \Sigma _f$ to ![]() ${1}/{\#\operatorname {Stab}(T)}$, where
${1}/{\#\operatorname {Stab}(T)}$, where ![]() $\operatorname {Stab}(T) \subset G(\mathbb {Z}_p)$ is the stabilizer of
$\operatorname {Stab}(T) \subset G(\mathbb {Z}_p)$ is the stabilizer of ![]() $T$, and sends
$T$, and sends ![]() $T \in V(\mathbb {Z}_p) \smallsetminus \Sigma _f$ to
$T \in V(\mathbb {Z}_p) \smallsetminus \Sigma _f$ to ![]() $0$. The existence of the right-inverse
$0$. The existence of the right-inverse ![]() $s$ is well-known; see, e.g., [Reference Shankar, Siad, Swaminathan and VarmaSSSV21, § 3.3].
$s$ is well-known; see, e.g., [Reference Shankar, Siad, Swaminathan and VarmaSSSV21, § 3.3].
Because ![]() $\phi$ is
$\phi$ is ![]() $G(\mathbb {Z}_p)$-invariant, Lemma 20 yields that for the above convenient choices, we have, on the one hand, that the
$G(\mathbb {Z}_p)$-invariant, Lemma 20 yields that for the above convenient choices, we have, on the one hand, that the ![]() $p$-adic density of
$p$-adic density of ![]() $\Sigma _f$ is
$\Sigma _f$ is
 \begin{align}
\operatorname{Vol}(\Sigma_f) := \int_{T \in
\Sigma_f} dT & = \int_{T \in G(\mathbb{Z}_p) \cdot
s(\mathscr{R})} \frac{1}{\#\operatorname{Stab}(T)}\, dT
\nonumber\\ & = |\mathscr{J}|_p \cdot
\operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{f'\equiv
f\,(\operatorname{mod} p)}\sum_{\substack{T \in
G(\mathbb{Z}_p)\backslash\Sigma_f \nonumber\\
\operatorname{ch}(T) = f'}}
\frac{1}{\#\operatorname{Stab}(T)}\, dr.
\end{align}
\begin{align}
\operatorname{Vol}(\Sigma_f) := \int_{T \in
\Sigma_f} dT & = \int_{T \in G(\mathbb{Z}_p) \cdot
s(\mathscr{R})} \frac{1}{\#\operatorname{Stab}(T)}\, dT
\nonumber\\ & = |\mathscr{J}|_p \cdot
\operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{f'\equiv
f\,(\operatorname{mod} p)}\sum_{\substack{T \in
G(\mathbb{Z}_p)\backslash\Sigma_f \nonumber\\
\operatorname{ch}(T) = f'}}
\frac{1}{\#\operatorname{Stab}(T)}\, dr.
\end{align}
First suppose ![]() $p \neq 2$. We now compute the sum in the integrand in (27). Because we chose
$p \neq 2$. We now compute the sum in the integrand in (27). Because we chose ![]() $f$ to be irreducible over
$f$ to be irreducible over ![]() $\mathbb {Z}/p\mathbb {Z}$, the ring
$\mathbb {Z}/p\mathbb {Z}$, the ring ![]() $R_{f'} := \mathbb {Z}_p[x]/(f')$ is the maximal order in its field of fractions
$R_{f'} := \mathbb {Z}_p[x]/(f')$ is the maximal order in its field of fractions ![]() $K_{f'}$, and it is, in fact, the unique local ring of rank
$K_{f'}$, and it is, in fact, the unique local ring of rank ![]() $2n+1$ over
$2n+1$ over ![]() $\mathbb {Z}_p$ having residue field
$\mathbb {Z}_p$ having residue field ![]() $\mathbb {F}_{p^{2n+1}}$ (hence,
$\mathbb {F}_{p^{2n+1}}$ (hence, ![]() $R_{f'}$ does not depend on the choice of
$R_{f'}$ does not depend on the choice of ![]() $f'$). Then by [Reference SwaminathanSwa23, (63)], there is precisely one
$f'$). Then by [Reference SwaminathanSwa23, (63)], there is precisely one ![]() $G(\mathbb {Z}_p)$-orbit with characteristic polynomial
$G(\mathbb {Z}_p)$-orbit with characteristic polynomial ![]() $f'$, and the size of the stabilizer of this orbit is equal to
$f'$, and the size of the stabilizer of this orbit is equal to ![]() $\#R_{f'}^\times [2]_{\operatorname {N}\equiv 1} = 1$. Thus, we find that
$\#R_{f'}^\times [2]_{\operatorname {N}\equiv 1} = 1$. Thus, we find that
 \begin{equation} \sum_{\substack{T \in G(\mathbb{Z}_p)\backslash\Sigma_f \\ \operatorname{ch}(T) = f'}} \frac{1}{\#\operatorname{Stab}(T)} = 1. \end{equation}
\begin{equation} \sum_{\substack{T \in G(\mathbb{Z}_p)\backslash\Sigma_f \\ \operatorname{ch}(T) = f'}} \frac{1}{\#\operatorname{Stab}(T)} = 1. \end{equation}Combining (27) and (28) yields that
Let ![]() $\overline {\Sigma }_f := \{T \in V(\mathbb {Z}/p\mathbb {Z}) : \operatorname {ch}(T) = f\}$. Then the mod-
$\overline {\Sigma }_f := \{T \in V(\mathbb {Z}/p\mathbb {Z}) : \operatorname {ch}(T) = f\}$. Then the mod-![]() $p$ reduction map
$p$ reduction map ![]() $\Sigma _f \to \overline {\Sigma }_f$ is surjective, and we have by [Reference Bhargava and GrossBG13, § 6.1] that
$\Sigma _f \to \overline {\Sigma }_f$ is surjective, and we have by [Reference Bhargava and GrossBG13, § 6.1] that ![]() $\#\overline {\Sigma }_f = \#G(\mathbb {Z}/p\mathbb {Z})$. Thus, we have, on the other hand, that
$\#\overline {\Sigma }_f = \#G(\mathbb {Z}/p\mathbb {Z})$. Thus, we have, on the other hand, that
Equating (29) and (30) yields that
when ![]() $p \neq 2$, where the last equality follows from the fact that the group
$p \neq 2$, where the last equality follows from the fact that the group ![]() $G$ is smooth over
$G$ is smooth over ![]() $\mathbb {Z}_p$ when
$\mathbb {Z}_p$ when ![]() $p \neq 2$.
$p \neq 2$.
Next, suppose ![]() $p = 2$. We now derive an upper bound on the sum in the integrand in (27). By [Reference SwaminathanSwa22, Proposition 59], the number of
$p = 2$. We now derive an upper bound on the sum in the integrand in (27). By [Reference SwaminathanSwa22, Proposition 59], the number of ![]() $G(\mathbb {Z}_2)$-orbits with characteristic polynomial
$G(\mathbb {Z}_2)$-orbits with characteristic polynomial ![]() $f'$ is equal to
$f'$ is equal to ![]() $2^{n-1}(2^n+1)$. The size of the stabilizer of any such orbit is equal to
$2^{n-1}(2^n+1)$. The size of the stabilizer of any such orbit is equal to ![]() $\#R_{f'}^\times [2]_{\operatorname {N}\equiv 1} = 1$, so we find that
$\#R_{f'}^\times [2]_{\operatorname {N}\equiv 1} = 1$, so we find that
 \begin{equation} \sum_{\substack{T \in G(\mathbb{Z}_p)\backslash\Sigma_f \\ \operatorname{ch}(T) = f'}} \frac{1}{\#\operatorname{Stab}(T)} = 2^{n-1}(2^n+1). \end{equation}
\begin{equation} \sum_{\substack{T \in G(\mathbb{Z}_p)\backslash\Sigma_f \\ \operatorname{ch}(T) = f'}} \frac{1}{\#\operatorname{Stab}(T)} = 2^{n-1}(2^n+1). \end{equation}Combining (27) and (32) yields that
Let ![]() $\overline {\Sigma }_f = \{T \in V(\mathbb {Z}/2\mathbb {Z}) : \operatorname {ch}(T) = f\}$. Then the mod-
$\overline {\Sigma }_f = \{T \in V(\mathbb {Z}/2\mathbb {Z}) : \operatorname {ch}(T) = f\}$. Then the mod-![]() $2$ reduction map
$2$ reduction map ![]() $\Sigma _f \to \overline {\Sigma }_f$ is surjective, and by Propositions 4 and 6, the action of
$\Sigma _f \to \overline {\Sigma }_f$ is surjective, and by Propositions 4 and 6, the action of ![]() $G(\mathbb {Z}/2\mathbb {Z})$ on
$G(\mathbb {Z}/2\mathbb {Z})$ on ![]() $\overline {\Sigma }_f$ is simply transitive, so
$\overline {\Sigma }_f$ is simply transitive, so ![]() $\#\overline {\Sigma }_f = \#G(\mathbb {Z}/2\mathbb {Z})$. Thus, we have, on the other hand, that
$\#\overline {\Sigma }_f = \#G(\mathbb {Z}/2\mathbb {Z})$. Thus, we have, on the other hand, that
Combining (33) and (34) yields that
Since ![]() $G$ is not smooth over
$G$ is not smooth over ![]() $\mathbb {Z}_2$, computing
$\mathbb {Z}_2$, computing ![]() $\operatorname {Vol}(G(\mathbb {Z}_2))$ is far more complicated, but we do not need to know the value of
$\operatorname {Vol}(G(\mathbb {Z}_2))$ is far more complicated, but we do not need to know the value of ![]() $\operatorname {Vol}(G(\mathbb {Z}_2))$ for our purpose. The value of
$\operatorname {Vol}(G(\mathbb {Z}_2))$ for our purpose. The value of ![]() $\#G(\mathbb {Z}/2\mathbb {Z})$ is given in [Reference ChoCho15, § 6] to be
$\#G(\mathbb {Z}/2\mathbb {Z})$ is given in [Reference ChoCho15, § 6] to be ![]() $\#G(\mathbb {Z}/2\mathbb {Z}) = 2^{n^2} \cdot \prod _{i = 1}^n (2^{2i}-1)$, so it follows that
$\#G(\mathbb {Z}/2\mathbb {Z}) = 2^{n^2} \cdot \prod _{i = 1}^n (2^{2i}-1)$, so it follows that
 \begin{equation} \frac{2^{2n^2-1}(2^n+1)}{\#G(\mathbb{Z}/2\mathbb{Z})} = (2^{-1} + 2^{-n-1}) \cdot \prod_{i = 1}^n (1 - 2^{-2i})^{-1} \leq 1. \end{equation}
\begin{equation} \frac{2^{2n^2-1}(2^n+1)}{\#G(\mathbb{Z}/2\mathbb{Z})} = (2^{-1} + 2^{-n-1}) \cdot \prod_{i = 1}^n (1 - 2^{-2i})^{-1} \leq 1. \end{equation}Now, applying the identity
along with the Tamagawa number identity (see [Reference LanglandsLan66])
and combining them with (31), (35), and (36) completes the proof of Lemma 19.
Next, in the following lemma, we compute the integrand in the integral over ![]() $f$.
$f$.
Lemma 21 Let ![]() $F \in \mathscr {F}_{2n+1}(f_0,\mathbb {R})$, and suppose that
$F \in \mathscr {F}_{2n+1}(f_0,\mathbb {R})$, and suppose that ![]() $F$ has exactly
$F$ has exactly ![]() $2m+1$ real roots. Then there are exactly
$2m+1$ real roots. Then there are exactly ![]() $2m+1$ orbits of
$2m+1$ orbits of ![]() $G(\mathbb {R})$ on
$G(\mathbb {R})$ on ![]() $V(\mathbb {R})$ that arise from points in
$V(\mathbb {R})$ that arise from points in ![]() $\mathscr {S}_F(\mathbb {R})$. In particular, the integrand in the integral in the mass at
$\mathscr {S}_F(\mathbb {R})$. In particular, the integrand in the integral in the mass at ![]() $\infty$ in (26) is a constant with value
$\infty$ in (26) is a constant with value ![]() $2m+1$.
$2m+1$.
Proof. Let ![]() $f(x) = F_{\operatorname {mon}}(x,1)$, and let the real roots of
$f(x) = F_{\operatorname {mon}}(x,1)$, and let the real roots of ![]() $f$ be given in increasing order by
$f$ be given in increasing order by ![]() $\lambda _1 < \cdots < \lambda _{2m+1}$. We now compute the number of orbits of
$\lambda _1 < \cdots < \lambda _{2m+1}$. We now compute the number of orbits of ![]() $G(\mathbb {R})$ on
$G(\mathbb {R})$ on ![]() $V(\mathbb {R})$ having characteristic polynomial
$V(\mathbb {R})$ having characteristic polynomial ![]() $f$ that arise from points in
$f$ that arise from points in ![]() $\mathscr {S}_F(\mathbb {R})$ via the construction in § 3. The
$\mathscr {S}_F(\mathbb {R})$ via the construction in § 3. The ![]() $G(\mathbb {R})$-orbit associated to a point
$G(\mathbb {R})$-orbit associated to a point ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(\mathbb {R})$ is identified via the correspondence in Proposition 6 with some
$(x_0, y_0, z_0) \in \mathscr {S}_F(\mathbb {R})$ is identified via the correspondence in Proposition 6 with some ![]() $f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$. If
$f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$. If ![]() $y_0 \neq 0$, this class is represented by a sequence of the form
$y_0 \neq 0$, this class is represented by a sequence of the form
Otherwise, if ![]() $y_0 = 0$, then
$y_0 = 0$, then ![]() ${x_0}/{z_0} = \lambda _j$ for some
${x_0}/{z_0} = \lambda _j$ for some ![]() $j$; letting
$j$; letting ![]() $\widetilde {F}$ be as in (11), we see that the class
$\widetilde {F}$ be as in (11), we see that the class ![]() $f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ is represented by a sequence of the form
$f_0 \cdot \delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ is represented by a sequence of the form
where the term ![]() $f_0 \cdot \widetilde {F}(x_0, z_0)$ in (40) replaces the term
$f_0 \cdot \widetilde {F}(x_0, z_0)$ in (40) replaces the term ![]() $f_0(x_0 - \lambda _j z_0)$ in (39). The class in
$f_0(x_0 - \lambda _j z_0)$ in (39). The class in ![]() $(K_F^{\times }/K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the sequence in (39) or in (40) is given by the sequence of signs of its first
$(K_F^{\times }/K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the sequence in (39) or in (40) is given by the sequence of signs of its first ![]() $2m+1$ terms. Because
$2m+1$ terms. Because ![]() $\operatorname {N}(b_j) > 0$ for every
$\operatorname {N}(b_j) > 0$ for every ![]() $j$, the condition that
$j$, the condition that ![]() $\operatorname {N}(f_0 \cdot \delta )$ is a square in
$\operatorname {N}(f_0 \cdot \delta )$ is a square in ![]() $\mathbb {R}^\times$ is equivalent to the condition that
$\mathbb {R}^\times$ is equivalent to the condition that ![]() $\prod _{i = 1}^{2m+1} f_0(x_0 - \lambda _i z_0) > 0$ if
$\prod _{i = 1}^{2m+1} f_0(x_0 - \lambda _i z_0) > 0$ if ![]() $y_0 \neq 0$ and
$y_0 \neq 0$ and ![]() $(f_0 \cdot \widetilde {F}(x_0,z_0)) \cdot \prod _{\substack {i = 1 \\ i \neq j}}^{2m+1} f_0(x_0 - \lambda _i z_0) > 0$ if
$(f_0 \cdot \widetilde {F}(x_0,z_0)) \cdot \prod _{\substack {i = 1 \\ i \neq j}}^{2m+1} f_0(x_0 - \lambda _i z_0) > 0$ if ![]() $y_0 = 0$. We now split into cases based on the signs of
$y_0 = 0$. We now split into cases based on the signs of ![]() $f_0$ and
$f_0$ and ![]() $z_0$.
$z_0$.
Case 1a: ![]() $f_0 > 0$,
$f_0 > 0$, ![]() $z_0 > 0$. First suppose
$z_0 > 0$. First suppose ![]() $y_0 \neq 0$. In this case, the sign of
$y_0 \neq 0$. In this case, the sign of ![]() $f_0(x_0 - \lambda _i z_0)$ is equal to the sign of
$f_0(x_0 - \lambda _i z_0)$ is equal to the sign of ![]() $(x_0/z_0) - \lambda _i$. The possible sequences of signs of the
$(x_0/z_0) - \lambda _i$. The possible sequences of signs of the ![]() $f_0(x_0 - \lambda _i z_0)$ are therefore
$f_0(x_0 - \lambda _i z_0)$ are therefore
giving a total of ![]() $m+1$ orbits. We label the sign sequences in (41) from left to right by an index
$m+1$ orbits. We label the sign sequences in (41) from left to right by an index ![]() $\tau$ that runs from
$\tau$ that runs from ![]() $1$ up to
$1$ up to ![]() $m+1$. If
$m+1$. If ![]() $y_0 = 0$ and
$y_0 = 0$ and ![]() ${x_0}/{z_0} = \lambda _j$, then because
${x_0}/{z_0} = \lambda _j$, then because ![]() $\lambda _i < \lambda _j$ when
$\lambda _i < \lambda _j$ when ![]() $i < j$ and
$i < j$ and ![]() $\lambda _i > \lambda _j$ when
$\lambda _i > \lambda _j$ when ![]() $i > j$, we obtain the same sign sequences as those listed in (41).
$i > j$, we obtain the same sign sequences as those listed in (41).
Case 1b: ![]() $f_0 > 0$,
$f_0 > 0$, ![]() $z_0 < 0$. First suppose
$z_0 < 0$. First suppose ![]() $y_0 \neq 0$. In this case, the sign of
$y_0 \neq 0$. In this case, the sign of ![]() $f_0(x_0 - \lambda _i z_0)$ is equal to the opposite of the sign of
$f_0(x_0 - \lambda _i z_0)$ is equal to the opposite of the sign of ![]() $(x_0/z_0) - \lambda _i$. The possible sequences of signs of the
$(x_0/z_0) - \lambda _i$. The possible sequences of signs of the ![]() $f_0(x_0 - \lambda _i z_0)$ are, therefore,
$f_0(x_0 - \lambda _i z_0)$ are, therefore,
giving a total of ![]() $m+1$ orbits. We label the sign sequences in (42) from left to right by an index
$m+1$ orbits. We label the sign sequences in (42) from left to right by an index ![]() $\tau$ that runs from
$\tau$ that runs from ![]() $m+1$ up to
$m+1$ up to ![]() $2m+1$. (Note that the first sign sequence in (42) is the same as the last sign sequence in (41), which is why they share the same value of
$2m+1$. (Note that the first sign sequence in (42) is the same as the last sign sequence in (41), which is why they share the same value of ![]() $\tau$.) If
$\tau$.) If ![]() $y_0 = 0$, we again obtain the same sign sequences as those listed in (42).
$y_0 = 0$, we again obtain the same sign sequences as those listed in (42).
Case 2a: ![]() $f_0 < 0$,
$f_0 < 0$, ![]() $z_0 > 0$. The possible sign sequences are the same as those listed in (42), and we likewise label them from left to right by an index
$z_0 > 0$. The possible sign sequences are the same as those listed in (42), and we likewise label them from left to right by an index ![]() $\tau$ that runs from
$\tau$ that runs from ![]() $m+1$ up to
$m+1$ up to ![]() $2m+1$.
$2m+1$.
Case 2b: ![]() $f_0 < 0$,
$f_0 < 0$, ![]() $z_0 < 0$. The possible sign sequences are the same as those listed in (41), and we likewise label them from left to right by an index
$z_0 < 0$. The possible sign sequences are the same as those listed in (41), and we likewise label them from left to right by an index ![]() $\tau$ that runs from
$\tau$ that runs from ![]() $1$ up to
$1$ up to ![]() $m+1$.
$m+1$.
Substituting the results of Lemmas 19 and 21 into the mass at ![]() $\infty$ in (26), we deduce that this mass is bounded by
$\infty$ in (26), we deduce that this mass is bounded by
 \begin{align} \leq \sum_{m = 0}^n \frac{1}{2^{m+n}} \cdot 2^{2n+1} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{\substack{f \in \mathscr{I}(m) \\ H(f) < X}} (2m+1)\, df \leq 3 \cdot 2^{n} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{H(f) < X} df, \end{align}
\begin{align} \leq \sum_{m = 0}^n \frac{1}{2^{m+n}} \cdot 2^{2n+1} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{\substack{f \in \mathscr{I}(m) \\ H(f) < X}} (2m+1)\, df \leq 3 \cdot 2^{n} \cdot \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \cdot \int_{H(f) < X} df, \end{align}as necessary. This completes the proof of Proposition 18.
4.4 Step (B): bounding the mass at  $p$ when
$p$ when  $2 \neq p \nmid f_0$
$2 \neq p \nmid f_0$
Let ![]() $\mathscr {I}_p(m)$ denote the set of monic degree-
$\mathscr {I}_p(m)$ denote the set of monic degree-![]() $(2n+1)$ polynomials over
$(2n+1)$ polynomials over ![]() $\mathbb {Z}/p\mathbb {Z}$ (not necessarily separable) having
$\mathbb {Z}/p\mathbb {Z}$ (not necessarily separable) having ![]() $m$ distinct irreducible factors. When
$m$ distinct irreducible factors. When ![]() $2 \neq p \nmid f_0$, we obtain the following result, which bounds the mass at
$2 \neq p \nmid f_0$, we obtain the following result, which bounds the mass at ![]() $p$ in (26).
$p$ in (26).
Proposition 22 For each prime ![]() $p \nmid 2f_0$, we have that
$p \nmid 2f_0$, we have that
 \[ \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT \leq \min\bigg\{1,\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#G(\mathbb{Z}/p\mathbb{Z})}{p^{2n^2+n}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\}. \]
\[ \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT \leq \min\bigg\{1,\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#G(\mathbb{Z}/p\mathbb{Z})}{p^{2n^2+n}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\}. \]
Remark 23 As we later show in § 4.7, combining the bound in Proposition 22 over all primes ![]() $p \nmid 2f_0$ yields a total saving of
$p \nmid 2f_0$ yields a total saving of ![]() $O(2^{-\varepsilon _1 n^{\varepsilon _2}})$.
$O(2^{-\varepsilon _1 n^{\varepsilon _2}})$.
Proof of Proposition 22 Given a monic degree-![]() $(2n+1)$ polynomial
$(2n+1)$ polynomial ![]() $f$ over
$f$ over ![]() $\mathbb {Z}/p\mathbb {Z}$, let
$\mathbb {Z}/p\mathbb {Z}$, let ![]() $\overline {\Sigma }_f^{\operatorname {sol}} \subset V(\mathbb {Z}/p\mathbb {Z})$ denote the mod-
$\overline {\Sigma }_f^{\operatorname {sol}} \subset V(\mathbb {Z}/p\mathbb {Z})$ denote the mod-![]() $p$ reduction of the subset
$p$ reduction of the subset ![]() $\{T \in \mathscr {P}_p : \operatorname {ch}(T) \equiv f \pmod p\}$. Because
$\{T \in \mathscr {P}_p : \operatorname {ch}(T) \equiv f \pmod p\}$. Because ![]() $G$ is smooth over
$G$ is smooth over ![]() $\mathbb {Z}_p$, the map
$\mathbb {Z}_p$, the map ![]() $G(\mathbb {Z}_p) \to G(\mathbb {Z}/p\mathbb {Z})$ is surjective, implying that
$G(\mathbb {Z}_p) \to G(\mathbb {Z}/p\mathbb {Z})$ is surjective, implying that ![]() $\overline {\Sigma }_f^{\operatorname {sol}}$ is
$\overline {\Sigma }_f^{\operatorname {sol}}$ is ![]() $G(\mathbb {Z}/p\mathbb {Z})$-invariant. Then, since
$G(\mathbb {Z}/p\mathbb {Z})$-invariant. Then, since ![]() $m_p(T) \geq 1$, we have
$m_p(T) \geq 1$, we have
 \begin{align} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT &\leq \int_{T \in \mathscr{P}_p} dT\nonumber\\ & \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \frac{\#\overline{\Sigma}_f^{\operatorname{sol}}}{p^{\dim V}} = \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \sum_{T \in G(\mathbb{Z}/p\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{\#\mathscr{O}(T)}{p^{2n^2+3n+1}}, \end{align}
\begin{align} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT &\leq \int_{T \in \mathscr{P}_p} dT\nonumber\\ & \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \frac{\#\overline{\Sigma}_f^{\operatorname{sol}}}{p^{\dim V}} = \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \sum_{T \in G(\mathbb{Z}/p\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{\#\mathscr{O}(T)}{p^{2n^2+3n+1}}, \end{align}
where for each ![]() $T \in V(\mathbb {Z}/p\mathbb {Z})$, we denote by
$T \in V(\mathbb {Z}/p\mathbb {Z})$, we denote by ![]() $\mathscr {O}(T)$ the
$\mathscr {O}(T)$ the ![]() $G(\mathbb {Z}/p\mathbb {Z})$-orbit of
$G(\mathbb {Z}/p\mathbb {Z})$-orbit of ![]() $T$. Let
$T$. Let ![]() $\operatorname {Stab}(T) \subset G(\mathbb {Z}/p\mathbb {Z})$ denote the stabilizer of
$\operatorname {Stab}(T) \subset G(\mathbb {Z}/p\mathbb {Z})$ denote the stabilizer of ![]() $T$. Substituting
$T$. Substituting ![]() $\#\mathscr {O}(T) = \#G(\mathbb {Z}/p\mathbb {Z})/\#\operatorname {Stab}(T)$ into (44) yields that
$\#\mathscr {O}(T) = \#G(\mathbb {Z}/p\mathbb {Z})/\#\operatorname {Stab}(T)$ into (44) yields that
 \begin{equation} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \sum_{T \in G(\mathbb{Z}/p\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{1}{\#\operatorname{Stab}(T)}\cdot \frac{\#G(\mathbb{Z}/p\mathbb{Z})}{p^{2n^2+3n+1}}. \end{equation}
\begin{equation} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_p(T)}{m_p(T)}\, dT \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_p(m)} \sum_{T \in G(\mathbb{Z}/p\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{1}{\#\operatorname{Stab}(T)}\cdot \frac{\#G(\mathbb{Z}/p\mathbb{Z})}{p^{2n^2+3n+1}}. \end{equation}
The following lemma gives a formula for ![]() $\#\operatorname {Stab}(T)$ that is independent of
$\#\operatorname {Stab}(T)$ that is independent of ![]() $f \in \mathscr {I}_p(m)$.
$f \in \mathscr {I}_p(m)$.
Lemma 24 For ![]() $T \in \overline {\Sigma }_f^{\operatorname {sol}}$, we have that
$T \in \overline {\Sigma }_f^{\operatorname {sol}}$, we have that ![]() $\#\operatorname {Stab}(T) = 2^{m-1}$.
$\#\operatorname {Stab}(T) = 2^{m-1}$.
Proof of Lemma 24 Let ![]() $K_f = (\mathbb {Z}/p\mathbb {Z})[x]/(f)$. By Proposition 4,
$K_f = (\mathbb {Z}/p\mathbb {Z})[x]/(f)$. By Proposition 4, ![]() $\#\operatorname {Stab}(T) = \#K_f^\times [2]_{\operatorname {N}\equiv 1}$. Letting
$\#\operatorname {Stab}(T) = \#K_f^\times [2]_{\operatorname {N}\equiv 1}$. Letting ![]() $f$ split over
$f$ split over ![]() $\mathbb {Z}/p\mathbb {Z}$ as
$\mathbb {Z}/p\mathbb {Z}$ as ![]() $f(x) = \prod _{i = 1}^m f_i(x)^{n_i}$, where the
$f(x) = \prod _{i = 1}^m f_i(x)^{n_i}$, where the ![]() $f_i$ are distinct and irreducible, we have that
$f_i$ are distinct and irreducible, we have that ![]() $K_f \simeq \prod _{i = 1}^m (\mathbb {Z}/p\mathbb {Z})[x]/(f_i^{n_i})$. Consequently,
$K_f \simeq \prod _{i = 1}^m (\mathbb {Z}/p\mathbb {Z})[x]/(f_i^{n_i})$. Consequently, ![]() $K_f^\times [2]$ contains the
$K_f^\times [2]$ contains the ![]() $2^m$ elements of the form
$2^m$ elements of the form ![]() $(\pm 1, \ldots, \pm 1)$. Exactly half of these elements have norm
$(\pm 1, \ldots, \pm 1)$. Exactly half of these elements have norm ![]() $1$, so
$1$, so ![]() $\#K_f^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
$\#K_f^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
To bound the right-hand side of (45), it remains to control the number of ![]() $G(\mathbb {Z}/p\mathbb {Z})$-orbits on
$G(\mathbb {Z}/p\mathbb {Z})$-orbits on ![]() $\overline {\Sigma }_f^{\operatorname {sol}}$. But there can only be as many orbits as there are points in
$\overline {\Sigma }_f^{\operatorname {sol}}$. But there can only be as many orbits as there are points in ![]() $\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, which has size
$\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, which has size ![]() $p+1$. Combining this observation with (45) and Lemma 24 yields the proposition.
$p+1$. Combining this observation with (45) and Lemma 24 yields the proposition.
Remark 25 It is well-known (see [Reference Bhargava and GrossBG13, § 6.1]) that for each odd prime ![]() $p$, we have
$p$, we have
 \begin{equation} \#G(\mathbb{Z}/p\mathbb{Z}) = p^{n^2} \cdot \prod_{i = 1}^n (p^{2i}-1) \leq p^{2n^2+n}. \end{equation}
\begin{equation} \#G(\mathbb{Z}/p\mathbb{Z}) = p^{n^2} \cdot \prod_{i = 1}^n (p^{2i}-1) \leq p^{2n^2+n}. \end{equation}
Further note that ![]() $\operatorname {Vol}(G(\mathbb {Z}_p)) = \#G(\mathbb {Z}/p\mathbb {Z})/p^{2n^2+n}$.
$\operatorname {Vol}(G(\mathbb {Z}_p)) = \#G(\mathbb {Z}/p\mathbb {Z})/p^{2n^2+n}$.
4.5 Step (B): bounding the mass at  $2$ when
$2$ when  $2 \nmid f_0$
$2 \nmid f_0$
Here, it turns out to be ineffective to work over ![]() $\mathbb {Z}/2\mathbb {Z}$ or even
$\mathbb {Z}/2\mathbb {Z}$ or even ![]() $\mathbb {Z}/4\mathbb {Z}$; instead, we work over
$\mathbb {Z}/4\mathbb {Z}$; instead, we work over ![]() $\mathbb {Z}/8\mathbb {Z}$. Let
$\mathbb {Z}/8\mathbb {Z}$. Let ![]() $\mathscr {I}_8(m)$ denote the set of monic degree-
$\mathscr {I}_8(m)$ denote the set of monic degree-![]() $(2n+1)$ polynomials in
$(2n+1)$ polynomials in ![]() $(\mathbb {Z}/8\mathbb {Z})[x]$ having
$(\mathbb {Z}/8\mathbb {Z})[x]$ having ![]() $m$ distinct irreducible factors over
$m$ distinct irreducible factors over ![]() $\mathbb {Z}/2\mathbb {Z}$. When
$\mathbb {Z}/2\mathbb {Z}$. When ![]() $2 = p \nmid f_0$, we obtain the following result, which shows that the mass at
$2 = p \nmid f_0$, we obtain the following result, which shows that the mass at ![]() $2$ in (26) contributes a saving of
$2$ in (26) contributes a saving of ![]() $O(2^{-2n})$.
$O(2^{-2n})$.
Proposition 26 We have that
 \[ \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT \leq \min\bigg\{1,\sum_{m = 1}^{2n+1} \frac{12}{2^{2n+m-1}} \cdot 2 \cdot \frac{\#\mathscr{I}_8(m)}{8^{2n+1}}\bigg\}. \]
\[ \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT \leq \min\bigg\{1,\sum_{m = 1}^{2n+1} \frac{12}{2^{2n+m-1}} \cdot 2 \cdot \frac{\#\mathscr{I}_8(m)}{8^{2n+1}}\bigg\}. \]
Proof. Given a monic degree-![]() $(2n+1)$ polynomial
$(2n+1)$ polynomial ![]() $f$ over
$f$ over ![]() $\mathbb {Z}/8\mathbb {Z}$, let
$\mathbb {Z}/8\mathbb {Z}$, let ![]() $\overline {\Sigma }_f^{\operatorname {sol}} \subset V(\mathbb {Z}/8\mathbb {Z})$ denote the closure under the action of
$\overline {\Sigma }_f^{\operatorname {sol}} \subset V(\mathbb {Z}/8\mathbb {Z})$ denote the closure under the action of ![]() $G(\mathbb {Z}/8\mathbb {Z})$ of the mod-
$G(\mathbb {Z}/8\mathbb {Z})$ of the mod-![]() $8$ reduction of the subset
$8$ reduction of the subset ![]() $\{T \in \mathscr {P}_2 : \operatorname {ch}(T) \equiv f \pmod 8\}$ (note that this subset may not be a priori
$\{T \in \mathscr {P}_2 : \operatorname {ch}(T) \equiv f \pmod 8\}$ (note that this subset may not be a priori ![]() $G(\mathbb {Z}/8\mathbb {Z})$-invariant, because
$G(\mathbb {Z}/8\mathbb {Z})$-invariant, because ![]() $G$ is not smooth over
$G$ is not smooth over ![]() $\mathbb {Z}_2$ and the map
$\mathbb {Z}_2$ and the map ![]() $G(\mathbb {Z}_2) \to G(\mathbb {Z}/8\mathbb {Z})$ is not surjective). Then we have
$G(\mathbb {Z}_2) \to G(\mathbb {Z}/8\mathbb {Z})$ is not surjective). Then we have
 \begin{align} \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT & \leq \int_{T \in \mathscr{P}_2} dT \nonumber\\ & \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_8(m)} \frac{\#\overline{\Sigma}_f^{\operatorname{sol}}}{8^{\dim V}} = \sum_{m = 1}^{2n+1}\sum_{f \in \mathscr{I}_8(m)} \sum_{T \in G(\mathbb{Z}/8\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{\#\mathscr{O}(T)}{8^{2n^2+3n+1}}, \end{align}
\begin{align} \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT & \leq \int_{T \in \mathscr{P}_2} dT \nonumber\\ & \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_8(m)} \frac{\#\overline{\Sigma}_f^{\operatorname{sol}}}{8^{\dim V}} = \sum_{m = 1}^{2n+1}\sum_{f \in \mathscr{I}_8(m)} \sum_{T \in G(\mathbb{Z}/8\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{\#\mathscr{O}(T)}{8^{2n^2+3n+1}}, \end{align}
where for each ![]() $T \in V(\mathbb {Z}/8\mathbb {Z})$, we denote by
$T \in V(\mathbb {Z}/8\mathbb {Z})$, we denote by ![]() $\mathscr {O}(T)$ the
$\mathscr {O}(T)$ the ![]() $G(\mathbb {Z}/8\mathbb {Z})$-orbit of
$G(\mathbb {Z}/8\mathbb {Z})$-orbit of ![]() $T$. Let
$T$. Let ![]() $\operatorname {Stab}(T) \subset G(\mathbb {Z}/8\mathbb {Z})$ denote the stabilizer of
$\operatorname {Stab}(T) \subset G(\mathbb {Z}/8\mathbb {Z})$ denote the stabilizer of ![]() $T$. Substituting
$T$. Substituting ![]() $\#\mathscr {O}(T) = \#G(\mathbb {Z}/8\mathbb {Z})/\#\operatorname {Stab}(T)$ into (47) yields that
$\#\mathscr {O}(T) = \#G(\mathbb {Z}/8\mathbb {Z})/\#\operatorname {Stab}(T)$ into (47) yields that
 \begin{equation} \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_8(m)} \sum_{T \in G(\mathbb{Z}/8\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{1}{\#\operatorname{Stab}(T)}\cdot \frac{\#G(\mathbb{Z}/8\mathbb{Z})}{8^{2n^2+3n+1}}. \end{equation}
\begin{equation} \int_{T \in V(\mathbb{Z}_2)} \frac{\psi_2(T)}{m_2(T)}\, dT \leq \sum_{m = 1}^{2n+1} \sum_{f \in \mathscr{I}_8(m)} \sum_{T \in G(\mathbb{Z}/8\mathbb{Z})\backslash \overline{\Sigma}_f^{\operatorname{sol}}} \frac{1}{\#\operatorname{Stab}(T)}\cdot \frac{\#G(\mathbb{Z}/8\mathbb{Z})}{8^{2n^2+3n+1}}. \end{equation}
The following lemma gives a lower bound for ![]() $\#\operatorname {Stab}(T)$ that is independent of
$\#\operatorname {Stab}(T)$ that is independent of ![]() $f \in \mathscr {I}_8(m)$.
$f \in \mathscr {I}_8(m)$.
Lemma 27 For ![]() $T \in \overline {\Sigma }_f^{\operatorname {sol}}$, we have that
$T \in \overline {\Sigma }_f^{\operatorname {sol}}$, we have that ![]() $\#\operatorname {Stab}(T) \geq 2^{2n+m-1}$.
$\#\operatorname {Stab}(T) \geq 2^{2n+m-1}$.
Proof of Lemma 27 Let ![]() $R_f = (\mathbb {Z}/8\mathbb {Z})[x]/(f)$. By Remark 13,
$R_f = (\mathbb {Z}/8\mathbb {Z})[x]/(f)$. By Remark 13, ![]() $\operatorname {Stab}(T)$ contains a subgroup isomorphic to
$\operatorname {Stab}(T)$ contains a subgroup isomorphic to ![]() $R_f^\times [2]_{\operatorname {N}\equiv 1} := \{\rho \in R_f^\times : \rho ^2 = 1 = \operatorname {N}(\rho )\}$. Let
$R_f^\times [2]_{\operatorname {N}\equiv 1} := \{\rho \in R_f^\times : \rho ^2 = 1 = \operatorname {N}(\rho )\}$. Let ![]() $f$ split over
$f$ split over ![]() $\mathbb {Z}/8\mathbb {Z}$ as
$\mathbb {Z}/8\mathbb {Z}$ as ![]() $f(x) = \prod _{i = 1}^m f_i(x)$, where the
$f(x) = \prod _{i = 1}^m f_i(x)$, where the ![]() $f_i$ have the property that their mod-
$f_i$ have the property that their mod-![]() $2$ reductions are powers of distinct irreducible polynomials. Then it follows from [Reference Lei and PoulinLP20, Theorem 7] together with the Chinese remainder theorem that
$2$ reductions are powers of distinct irreducible polynomials. Then it follows from [Reference Lei and PoulinLP20, Theorem 7] together with the Chinese remainder theorem that ![]() $R_f \simeq \prod _{i = 1}^m (\mathbb {Z}/8\mathbb {Z})[x]/(f_i)$, and
$R_f \simeq \prod _{i = 1}^m (\mathbb {Z}/8\mathbb {Z})[x]/(f_i)$, and ![]() $R_f^\times [2]$ contains the
$R_f^\times [2]$ contains the ![]() $2^{2n+m+1}$ elements of the form
$2^{2n+m+1}$ elements of the form
 \[ \bigg(\ldots, \rho_0 + \sum_{j = 1}^{d_i-1} \rho_j\theta_i^j, \ldots\bigg) \in \prod_{i = 1}^m (\mathbb{Z}/8\mathbb{Z})[x]/(f_i), \]
\[ \bigg(\ldots, \rho_0 + \sum_{j = 1}^{d_i-1} \rho_j\theta_i^j, \ldots\bigg) \in \prod_{i = 1}^m (\mathbb{Z}/8\mathbb{Z})[x]/(f_i), \]
where ![]() $\rho _0$ is any element of
$\rho _0$ is any element of ![]() $(\mathbb {Z}/8\mathbb {Z})^\times$ and
$(\mathbb {Z}/8\mathbb {Z})^\times$ and ![]() $\rho _j$ is any element of
$\rho _j$ is any element of ![]() $\{0,4\} \subset \mathbb {Z}/8\mathbb {Z}$ for each
$\{0,4\} \subset \mathbb {Z}/8\mathbb {Z}$ for each ![]() $j$,
$j$, ![]() $\theta _i$ is the image of
$\theta _i$ is the image of ![]() $x$ in
$x$ in ![]() $(\mathbb {Z}/8\mathbb {Z})[x]/(f_i)$, and
$(\mathbb {Z}/8\mathbb {Z})[x]/(f_i)$, and ![]() $d_i = \deg f_i$ for each
$d_i = \deg f_i$ for each ![]() $i$. At least
$i$. At least ![]() $\frac {1}{4}$ of these elements have norm
$\frac {1}{4}$ of these elements have norm ![]() $1$, so
$1$, so ![]() $\#\operatorname {Stab}(T) \geq \#R_F^\times [2]_{\operatorname {N}\equiv 1} \geq 2^{2n+m-1}$.
$\#\operatorname {Stab}(T) \geq \#R_F^\times [2]_{\operatorname {N}\equiv 1} \geq 2^{2n+m-1}$.
Let ![]() $\widehat {G}$ be the split odd orthogonal group scheme, defined in the same way as
$\widehat {G}$ be the split odd orthogonal group scheme, defined in the same way as ![]() $G$ but without the determinant-
$G$ but without the determinant-![]() $1$ condition. Observe that the determinant map
$1$ condition. Observe that the determinant map ![]() $\operatorname {det} \colon \widehat {G}(\mathbb {Z}/8\mathbb {Z}) \to (\mathbb {Z}/8\mathbb {Z})^\times$ is surjective: for each
$\operatorname {det} \colon \widehat {G}(\mathbb {Z}/8\mathbb {Z}) \to (\mathbb {Z}/8\mathbb {Z})^\times$ is surjective: for each ![]() $\sigma \in (\mathbb {Z}/8\mathbb {Z})^\times$, the diagonal matrix with row-
$\sigma \in (\mathbb {Z}/8\mathbb {Z})^\times$, the diagonal matrix with row-![]() $(n+1)$, column-
$(n+1)$, column-![]() $(n+1)$ entry equal to
$(n+1)$ entry equal to ![]() $\sigma$ and all other diagonal entries equal to
$\sigma$ and all other diagonal entries equal to ![]() $1$ is orthogonal with respect to
$1$ is orthogonal with respect to ![]() $A_0$ and has determinant
$A_0$ and has determinant ![]() $\sigma$. Combining this observation with the computation of
$\sigma$. Combining this observation with the computation of ![]() $\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$ in Proposition 28 (to follow) yields
$\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$ in Proposition 28 (to follow) yields
To bound the right-hand side of (48), it remains to control the number of ![]() $G(\mathbb {Z}/8\mathbb {Z})$-orbits on
$G(\mathbb {Z}/8\mathbb {Z})$-orbits on ![]() $\overline {\Sigma }_f^{\operatorname {sol}}$. But there can only be as many orbits as there are points in
$\overline {\Sigma }_f^{\operatorname {sol}}$. But there can only be as many orbits as there are points in ![]() $\mathbb {P}^1(\mathbb {Z}/8\mathbb {Z})$, which has size
$\mathbb {P}^1(\mathbb {Z}/8\mathbb {Z})$, which has size ![]() $12$. Combining this observation with (48), Lemma 27, Proposition 28, and (49) yields the proposition.
$12$. Combining this observation with (48), Lemma 27, Proposition 28, and (49) yields the proposition.
In the following proposition, we determine the value of ![]() $\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$, which was used in (49).
$\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$, which was used in (49).
Proposition 28 We have that
 \[ \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = 2^{5n^2+3n+3}\cdot(2^n-1)\cdot\prod_{i = 1}^{n-1}(2^{2i}-1) \]
\[ \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = 2^{5n^2+3n+3}\cdot(2^n-1)\cdot\prod_{i = 1}^{n-1}(2^{2i}-1) \]
when ![]() $n \geq 1$, and
$n \geq 1$, and ![]() $\#\widehat {G}(\mathbb {Z}/8\mathbb {Z}) = 4$ when
$\#\widehat {G}(\mathbb {Z}/8\mathbb {Z}) = 4$ when ![]() $n = 0$.
$n = 0$.
Proof. We apply the recursive formula for computing sizes of orthogonal groups modulo ![]() $8$ given in [Reference ReinerRei56, § 4.1.3]. The first step is to diagonalize
$8$ given in [Reference ReinerRei56, § 4.1.3]. The first step is to diagonalize ![]() $A_0$. One readily verifies that there exists
$A_0$. One readily verifies that there exists ![]() $g_1 \in \operatorname {GL}_{2n+1}(\mathbb {Z})$ such that
$g_1 \in \operatorname {GL}_{2n+1}(\mathbb {Z})$ such that ![]() $g_1A_0g_1^T$ is equal to the diagonal matrix with first
$g_1A_0g_1^T$ is equal to the diagonal matrix with first ![]() $n+1$ diagonal entries equal to
$n+1$ diagonal entries equal to ![]() $1$ and remaining
$1$ and remaining ![]() $n$ diagonal entries equal to
$n$ diagonal entries equal to ![]() $-1$. By [Reference JonesJon44, proof of Lemma 3], there exists
$-1$. By [Reference JonesJon44, proof of Lemma 3], there exists ![]() $g_2 \in \operatorname {GL}_{2n+1}(\mathbb {Z}_2)$ such that
$g_2 \in \operatorname {GL}_{2n+1}(\mathbb {Z}_2)$ such that ![]() $g_2g_1A_0g_1^Tg_2^T$ is equivalent modulo
$g_2g_1A_0g_1^Tg_2^T$ is equivalent modulo ![]() $8$ to the following diagonal matrix:
$8$ to the following diagonal matrix:
 \begin{equation} \left[\begin{array}{cccccc} 1 & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 & 0 & 0 \\ 0 & \cdots & 0 & a_1 & 0 & 0 \\ 0 & \cdots & 0 & 0 & a_2 & 0 \\ 0 & \cdots & 0 & 0 & 0 & a_3 \end{array}\right], \quad \text{where} \ (a_1, a_2, a_3) = \begin{cases} (1,1,1) & \text{if $2n+1 \equiv 1 \pmod 8$,} \\ (1,1,7) & \text{if $2n+1 \equiv 3 \pmod 8$,} \\ (1,3,3) & \text{if $2n+1 \equiv 5 \pmod 8$,} \\ (3,3,7) & \text{if $2n+1 \equiv 7 \pmod 8$} \end{cases}. \end{equation}
\begin{equation} \left[\begin{array}{cccccc} 1 & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 & 0 & 0 \\ 0 & \cdots & 0 & a_1 & 0 & 0 \\ 0 & \cdots & 0 & 0 & a_2 & 0 \\ 0 & \cdots & 0 & 0 & 0 & a_3 \end{array}\right], \quad \text{where} \ (a_1, a_2, a_3) = \begin{cases} (1,1,1) & \text{if $2n+1 \equiv 1 \pmod 8$,} \\ (1,1,7) & \text{if $2n+1 \equiv 3 \pmod 8$,} \\ (1,3,3) & \text{if $2n+1 \equiv 5 \pmod 8$,} \\ (3,3,7) & \text{if $2n+1 \equiv 7 \pmod 8$} \end{cases}. \end{equation}Using (50) together with the recursive formula displayed in [Reference ReinerRei56, § 4.1.3] yields that
 \begin{align} \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = \prod_{j = 1}^{2n+1} \bigg(8^j+4^{j+1}\cdot f(u_{2n+1-j})+2(4\sqrt{2})^j \cdot \cos\bigg(\frac{\pi}{4} K_{2n+1-j}\bigg)-8 \cdot 4^jh(u_{2n+1-j})\bigg), \end{align}
\begin{align} \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = \prod_{j = 1}^{2n+1} \bigg(8^j+4^{j+1}\cdot f(u_{2n+1-j})+2(4\sqrt{2})^j \cdot \cos\bigg(\frac{\pi}{4} K_{2n+1-j}\bigg)-8 \cdot 4^jh(u_{2n+1-j})\bigg), \end{align}
where the functions ![]() $f$ and
$f$ and ![]() $h$ are defined by
$h$ are defined by
 \[ f(u_i) = \begin{cases} 1 & \text{if $u_i \equiv 0 \pmod 8$,} \\ -1 & \text{if $u_i \equiv 4 \pmod 8$,} \\ 0 & \text{otherwise} \end{cases} \quad \text{and} \quad h(u_i) = \begin{cases} 1 & \text{if $i < 2n$ and $u_i \equiv 0 \pmod 8$,} \\ 0 & \text{otherwise} \end{cases} \]
\[ f(u_i) = \begin{cases} 1 & \text{if $u_i \equiv 0 \pmod 8$,} \\ -1 & \text{if $u_i \equiv 4 \pmod 8$,} \\ 0 & \text{otherwise} \end{cases} \quad \text{and} \quad h(u_i) = \begin{cases} 1 & \text{if $i < 2n$ and $u_i \equiv 0 \pmod 8$,} \\ 0 & \text{otherwise} \end{cases} \]
and where the quantities ![]() $u_i$ and
$u_i$ and ![]() $h_i$ are given as follows.
$h_i$ are given as follows.
Case 1: ![]() $(a_1, a_2, a_3) = (1,1,1)$. We have that
$(a_1, a_2, a_3) = (1,1,1)$. We have that
Case 2: ![]() $(a_1, a_2, a_3) = (1,1,7)$. We have that
$(a_1, a_2, a_3) = (1,1,7)$. We have that
 \begin{equation} u_{2n+1-j} = \begin{cases} j+5 & \text{if $j \geq 2$,} \\ 0 & \text{if $j = 1$,} \end{cases}\quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-4 & \text{if $j \geq 2$,}\\ -15 & \text{if $j = 1$.} \end{cases} \end{equation}
\begin{equation} u_{2n+1-j} = \begin{cases} j+5 & \text{if $j \geq 2$,} \\ 0 & \text{if $j = 1$,} \end{cases}\quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-4 & \text{if $j \geq 2$,}\\ -15 & \text{if $j = 1$.} \end{cases} \end{equation}
Case 3: ![]() $(a_1, a_2, a_3) = (1,3,3)$. We have that
$(a_1, a_2, a_3) = (1,3,3)$. We have that
 \begin{equation} u_{2n+1-j} = \begin{cases} j+3 & \text{if $j \geq 3$,} \\ 3 & \text{if $j = 2$,} \\ 0 & \text{if $j = 1$,} \end{cases} \quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-6 & \text{if $j \geq 3$,} \\ -8 & \text{if $j = 2$,} \\ -7 & \text{if $j = 1$.} \end{cases} \end{equation}
\begin{equation} u_{2n+1-j} = \begin{cases} j+3 & \text{if $j \geq 3$,} \\ 3 & \text{if $j = 2$,} \\ 0 & \text{if $j = 1$,} \end{cases} \quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-6 & \text{if $j \geq 3$,} \\ -8 & \text{if $j = 2$,} \\ -7 & \text{if $j = 1$.} \end{cases} \end{equation}
Case 4: ![]() $(a_1, a_2, a_3) = (3,3,7)$. We have that
$(a_1, a_2, a_3) = (3,3,7)$. We have that
 \begin{equation} u_{2n+1-j} = \begin{cases} j+9 & \text{if $j \geq 4$,} \\ 10 & \text{if $j = 3$,} \\ 7 & \text{if $j = 2$,} \\ 0 & \text{if $j = 1$,} \end{cases} \quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-8 & \text{if $j \geq 4$,} \\ -9 & \text{if $j = 3$,} \\ -8 & \text{if $j = 2$,} \\ -15 & \text{if $j = 1$.} \end{cases} \end{equation}
\begin{equation} u_{2n+1-j} = \begin{cases} j+9 & \text{if $j \geq 4$,} \\ 10 & \text{if $j = 3$,} \\ 7 & \text{if $j = 2$,} \\ 0 & \text{if $j = 1$,} \end{cases} \quad \text{and} \quad K_{2n+1-j} = \begin{cases} j-8 & \text{if $j \geq 4$,} \\ -9 & \text{if $j = 3$,} \\ -8 & \text{if $j = 2$,} \\ -15 & \text{if $j = 1$.} \end{cases} \end{equation}Substituting (52)–(55) into (51) and simplifying yields the desired formula.
We can also compute ![]() $\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$ by comparing two different formulas for a quantity known as ‘the
$\#\widehat {G}(\mathbb {Z}/8\mathbb {Z})$ by comparing two different formulas for a quantity known as ‘the ![]() $2$-adic density of the quadratic lattice’ defined by the matrix
$2$-adic density of the quadratic lattice’ defined by the matrix ![]() $A_0$, which is up to normalization the same as the
$A_0$, which is up to normalization the same as the ![]() $2$-adic volume of
$2$-adic volume of ![]() $G(\mathbb {Z}_2)$ with respect to Haar measure. We denote this quantity by
$G(\mathbb {Z}_2)$ with respect to Haar measure. We denote this quantity by ![]() $\alpha _2$. One of the two formulas for
$\alpha _2$. One of the two formulas for ![]() $\alpha _2$ is given in [Reference ChoCho15], where Cho constructs a smooth model of the group scheme
$\alpha _2$ is given in [Reference ChoCho15], where Cho constructs a smooth model of the group scheme ![]() $G$ over
$G$ over ![]() $\mathbb {Z}_2$. Letting
$\mathbb {Z}_2$. Letting ![]() $\widetilde {G}$ denote the special fiber of this smooth model, one can show by applying [Reference ChoCho15, Lemma 4.2, Remark 4.3, and Theorem 5.2] that
$\widetilde {G}$ denote the special fiber of this smooth model, one can show by applying [Reference ChoCho15, Lemma 4.2, Remark 4.3, and Theorem 5.2] that
where ![]() $\operatorname {SO}_{2n}$ denotes the special orthogonal group on a
$\operatorname {SO}_{2n}$ denotes the special orthogonal group on a ![]() $2n$-dimensional split orthogonal space. To be precise,
$2n$-dimensional split orthogonal space. To be precise, ![]() $\alpha _2$ is defined in [Reference ChoCho15] to be
$\alpha _2$ is defined in [Reference ChoCho15] to be ![]() $1/2$ of the quantity in (56), to account for the number of connected components of
$1/2$ of the quantity in (56), to account for the number of connected components of ![]() $G$ in
$G$ in ![]() $\widehat {G}$. However, we have removed this factor of
$\widehat {G}$. However, we have removed this factor of ![]() $1/2$ to make the definition of
$1/2$ to make the definition of ![]() $\alpha _2$ consistent with that given by Conway and Sloane in [Reference Conway and SloaneCS88, § 12], who define
$\alpha _2$ consistent with that given by Conway and Sloane in [Reference Conway and SloaneCS88, § 12], who define ![]() $\alpha _2$ by
$\alpha _2$ by
 \begin{equation} \alpha_2 = \frac{\#\widehat{G}(\mathbb{Z}/2^r\mathbb{Z})}{(2^r)^{2n^2 + n}} \end{equation}
\begin{equation} \alpha_2 = \frac{\#\widehat{G}(\mathbb{Z}/2^r\mathbb{Z})}{(2^r)^{2n^2 + n}} \end{equation}
for any sufficiently large positive integer ![]() $r$. It follows from [Reference KitaokaKit93, Proposition 5.6.1(ii) and proof of Lemma 5.6.5] that we can take
$r$. It follows from [Reference KitaokaKit93, Proposition 5.6.1(ii) and proof of Lemma 5.6.5] that we can take ![]() $r = 3$ in (57). Comparing (56) and (57) together with the fact that
$r = 3$ in (57). Comparing (56) and (57) together with the fact that ![]() $\#\operatorname {SO}_{2n}(\mathbb {Z}/2\mathbb {Z}) = 2^{n^2-n}\cdot (2^n-1)\cdot \prod _{i = 1}^{n-1}(2^{2i}-1)$ for
$\#\operatorname {SO}_{2n}(\mathbb {Z}/2\mathbb {Z}) = 2^{n^2-n}\cdot (2^n-1)\cdot \prod _{i = 1}^{n-1}(2^{2i}-1)$ for ![]() $n \geq 1$ (see [Reference ChoCho15, § 6]) yields that
$n \geq 1$ (see [Reference ChoCho15, § 6]) yields that
 \[ \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = 2^{4n^2+4n+3} \cdot \#\operatorname{SO}_{2n}(\mathbb{Z}/2\mathbb{Z}) = 2^{5n^2+3n+3}\cdot(2^n-1)\cdot\prod_{i = 1}^{n-1}(2^{2i}-1). \]
\[ \#\widehat{G}(\mathbb{Z}/8\mathbb{Z}) = 2^{4n^2+4n+3} \cdot \#\operatorname{SO}_{2n}(\mathbb{Z}/2\mathbb{Z}) = 2^{5n^2+3n+3}\cdot(2^n-1)\cdot\prod_{i = 1}^{n-1}(2^{2i}-1). \]
Remark 29 The strategy for the second proof of Proposition 28 can likewise be used to obtain a formula for ![]() $\#\widehat {G}(\mathbb {Z}/2^r\mathbb {Z})$ for each
$\#\widehat {G}(\mathbb {Z}/2^r\mathbb {Z})$ for each ![]() $r \geq 3$.
$r \geq 3$.
4.6 Step (B): bounding the mass at  $p$ when
$p$ when  $p \mid f_0$
$p \mid f_0$
When ![]() $p \nmid f_0$, Propositions 22 and 26 give sufficiently good control on the size of
$p \nmid f_0$, Propositions 22 and 26 give sufficiently good control on the size of ![]() $\mathscr {P}_p$. But when
$\mathscr {P}_p$. But when ![]() $p \mid f_0$, the bounds in Propositions 22 and 26 do not suffice. Indeed, since proving Theorems 1 and 2 involves averaging over monicizations of forms in
$p \mid f_0$, the bounds in Propositions 22 and 26 do not suffice. Indeed, since proving Theorems 1 and 2 involves averaging over monicizations of forms in ![]() $\mathscr {F}_{2n+1}(f_0)$, we must obtain a bound that decays with
$\mathscr {F}_{2n+1}(f_0)$, we must obtain a bound that decays with ![]() $|f_0|_p$ at least as fast as
$|f_0|_p$ at least as fast as ![]() $|f_0|_p^{2n^2+n}$, which is the
$|f_0|_p^{2n^2+n}$, which is the ![]() $p$-adic density of the set of monicizations of forms in
$p$-adic density of the set of monicizations of forms in ![]() $\mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$.
$\mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$.
In this section, we bound the mass at ![]() $p$ for primes
$p$ for primes ![]() $p \mid f_0$ by controlling the number of orbits of
$p \mid f_0$ by controlling the number of orbits of ![]() $G(\mathbb {Q}_p)$ on
$G(\mathbb {Q}_p)$ on ![]() $V(\mathbb {Q}_p)$ that can arise from points of
$V(\mathbb {Q}_p)$ that can arise from points of ![]() $\mathscr {S}_F(\mathbb {Z}_p)$. Specifically, we obtain the following result, which shows that the mass at
$\mathscr {S}_F(\mathbb {Z}_p)$. Specifically, we obtain the following result, which shows that the mass at ![]() $p$ is bounded by
$p$ is bounded by ![]() $O(|f_0|_p^{2n^2+n})$ when
$O(|f_0|_p^{2n^2+n})$ when ![]() $p \neq 2$ and by
$p \neq 2$ and by ![]() $O(2^{-n} \cdot |f_0|_2^{2n^2+n})$ when
$O(2^{-n} \cdot |f_0|_2^{2n^2+n})$ when ![]() $p = 2$.
$p = 2$.
Proposition 30 For each prime ![]() $p \mid f_0$, we have that
$p \mid f_0$, we have that
 \begin{align*} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}(T)}{m_p(T)}\, dT & \leq \begin{cases} 4 \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot |f_0|_p^{2n^2+n}, & \text{if $p \neq 2$,} \\ 8 \cdot 2^n \cdot |\mathscr{J}|_2 \cdot \operatorname{Vol}(G(\mathbb{Z}_2)) \cdot |f_0|_2^{2n^2+n}, & \text{if $p = 2$.} \end{cases} \end{align*}
\begin{align*} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}(T)}{m_p(T)}\, dT & \leq \begin{cases} 4 \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot |f_0|_p^{2n^2+n}, & \text{if $p \neq 2$,} \\ 8 \cdot 2^n \cdot |\mathscr{J}|_2 \cdot \operatorname{Vol}(G(\mathbb{Z}_2)) \cdot |f_0|_2^{2n^2+n}, & \text{if $p = 2$.} \end{cases} \end{align*}
Proof. We start with the following lemma, which gives a convenient formula for the mass at ![]() $p$.
$p$.
Lemma 31 Let ![]() $\varphi$ be a continuous
$\varphi$ be a continuous ![]() $G(\mathbb {Q}_p)$-invariant function on
$G(\mathbb {Q}_p)$-invariant function on ![]() $V(\mathbb {Z}_p)$ such that every element
$V(\mathbb {Z}_p)$ such that every element ![]() $T \in V(\mathbb {Z}_p)$ in the support of
$T \in V(\mathbb {Z}_p)$ in the support of ![]() $\varphi$ is separable. Then we have
$\varphi$ is separable. Then we have
 \begin{align*} & \int_{T \in V(\mathbb{Z}_p)} \frac{\varphi(T)}{m_p(T)}\, dT \\ & \quad =|\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{\substack{(c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1} \\ }} \sum_{\substack{T \in G(\mathbb{Q}_p)\backslash V(\mathbb{Z}_p) \\ \operatorname{ch}(T) = x^{2n+1} + c_1x^{2n}+\cdots+c_{2n+1}}}\frac{\varphi(T)}{\#\operatorname{Stab}_{\mathbb{Q}_p}(T)}\,\,dc_1\cdots dc_{2n+1}, \end{align*}
\begin{align*} & \int_{T \in V(\mathbb{Z}_p)} \frac{\varphi(T)}{m_p(T)}\, dT \\ & \quad =|\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{\substack{(c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1} \\ }} \sum_{\substack{T \in G(\mathbb{Q}_p)\backslash V(\mathbb{Z}_p) \\ \operatorname{ch}(T) = x^{2n+1} + c_1x^{2n}+\cdots+c_{2n+1}}}\frac{\varphi(T)}{\#\operatorname{Stab}_{\mathbb{Q}_p}(T)}\,\,dc_1\cdots dc_{2n+1}, \end{align*}
where ![]() $\mathscr {J} \in \mathbb {Q}$ is the same constant that appears in Theorem 15.
$\mathscr {J} \in \mathbb {Q}$ is the same constant that appears in Theorem 15.
Proof of Lemma 31 The proof is identical to that of [Reference Bhargava and GrossBG13, Corollary 11.3].
To evaluate the sum within the integral that occurs in the formula given by Lemma 31, we utilize the following lemma.
Lemma 32 Let ![]() $p$ be an odd (respectively, even) prime, and suppose that
$p$ be an odd (respectively, even) prime, and suppose that ![]() $F \in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ splits as a product
$F \in \mathscr {F}_{2n+1}(f_0,\mathbb {Z}_p)$ splits as a product ![]() $m$ distinct irreducible factors over
$m$ distinct irreducible factors over ![]() $\mathbb {Z}_p$. Then there are at most
$\mathbb {Z}_p$. Then there are at most ![]() $2^{m+1}$ (respectively,
$2^{m+1}$ (respectively, ![]() $2^{n+m+2})$ orbits of
$2^{n+m+2})$ orbits of ![]() $G(\mathbb {Q}_p)$ on
$G(\mathbb {Q}_p)$ on ![]() $V(\mathbb {Q}_p)$ arising from points of
$V(\mathbb {Q}_p)$ arising from points of ![]() $\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3. The size of the stabilizer in
$\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3. The size of the stabilizer in ![]() $G(\mathbb {Q}_p)$ of any such orbit is at least
$G(\mathbb {Q}_p)$ of any such orbit is at least ![]() $\#K_F^{\times }[2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
$\#K_F^{\times }[2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
Proof of Lemma 32 By Proposition 6, it suffices to bound the number of elements of ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the form
$(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the form ![]() $f_0 \cdot \delta$, where
$f_0 \cdot \delta$, where ![]() $\delta \in K_F^\times$ is the second coordinate of a pair
$\delta \in K_F^\times$ is the second coordinate of a pair ![]() $(I,\delta ) \in H_F$ arising from a points of
$(I,\delta ) \in H_F$ arising from a points of ![]() $\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3.
$\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3.
Fix ![]() $z_0 \in \mathbb {Z}_p$, and consider the monic odd-degree hyperelliptic curve
$z_0 \in \mathbb {Z}_p$, and consider the monic odd-degree hyperelliptic curve ![]() $C_{F,z_0}$ of genus
$C_{F,z_0}$ of genus ![]() $n$ over
$n$ over ![]() $\mathbb {Q}_p$ defined by the affine equation
$\mathbb {Q}_p$ defined by the affine equation ![]() $C_{F,z_0} \colon y^2 = F_{\operatorname {mon}}(x, z_0)$. Note that
$C_{F,z_0} \colon y^2 = F_{\operatorname {mon}}(x, z_0)$. Note that ![]() $C_{F,z_0}$ is a quadratic twist of
$C_{F,z_0}$ is a quadratic twist of ![]() $C_{F,1}$ and that for
$C_{F,1}$ and that for ![]() $z_0' \in \mathbb {Z}_p$, the curves
$z_0' \in \mathbb {Z}_p$, the curves ![]() $C_{F,z_0}$ and
$C_{F,z_0}$ and ![]() $C_{F,z_0'}$ are isomorphic over
$C_{F,z_0'}$ are isomorphic over ![]() $\mathbb {Q}_p$ when
$\mathbb {Q}_p$ when ![]() $z_0$ and
$z_0$ and ![]() $z_0'$ represent the same class in
$z_0'$ represent the same class in ![]() $\mathbb {Q}_p^\times /\mathbb {Q}_p^{\times 2}$. Let
$\mathbb {Q}_p^\times /\mathbb {Q}_p^{\times 2}$. Let ![]() $\{\eta _1, \ldots, \eta _\ell \} \subset \mathbb {Z}_p$ denote a complete set of representatives of elements of
$\{\eta _1, \ldots, \eta _\ell \} \subset \mathbb {Z}_p$ denote a complete set of representatives of elements of ![]() $\mathbb {Q}_p^\times /\mathbb {Q}_p^{\times 2}$, and note that we can take
$\mathbb {Q}_p^\times /\mathbb {Q}_p^{\times 2}$, and note that we can take ![]() $\ell = 4$ when
$\ell = 4$ when ![]() $p$ is odd and
$p$ is odd and ![]() $\ell = 8$ when
$\ell = 8$ when ![]() $p = 2$. Then each
$p = 2$. Then each ![]() $C_{F,z_0}$ is isomorphic to one of
$C_{F,z_0}$ is isomorphic to one of ![]() $C_{F,\eta _1}, \ldots, C_{F, \eta _\ell }$.
$C_{F,\eta _1}, \ldots, C_{F, \eta _\ell }$.
Let ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(\mathbb {Z}_p)$ giving rise to a pair
$(x_0, y_0, z_0) \in \mathscr {S}_F(\mathbb {Z}_p)$ giving rise to a pair ![]() $(I,\delta )$. Then the point
$(I,\delta )$. Then the point ![]() $(f_0x_0, y_0)$ is a
$(f_0x_0, y_0)$ is a ![]() $\mathbb {Q}_p$-rational point on the curve
$\mathbb {Q}_p$-rational point on the curve ![]() $C_{F,z_0}$ and, hence, is identified with a
$C_{F,z_0}$ and, hence, is identified with a ![]() $\mathbb {Q}_p$-rational point
$\mathbb {Q}_p$-rational point ![]() $(x_0',y_0')$ on one of the curves
$(x_0',y_0')$ on one of the curves ![]() $C_{F,\eta _i}$. In [Reference Bhargava and GrossBG13, § 5], Bhargava and Gross show that points in
$C_{F,\eta _i}$. In [Reference Bhargava and GrossBG13, § 5], Bhargava and Gross show that points in ![]() $C_{F,\eta _i}(\mathbb {Q}_p)$ naturally give rise to orbits of
$C_{F,\eta _i}(\mathbb {Q}_p)$ naturally give rise to orbits of ![]() $G(\mathbb {Q}_p)$ on
$G(\mathbb {Q}_p)$ on ![]() $V(\mathbb {Q}_p)$ having characteristic polynomial
$V(\mathbb {Q}_p)$ having characteristic polynomial ![]() $F_{\operatorname {mon}}(x, \eta _i)$. Under the construction of Bhargava and Gross, points of
$F_{\operatorname {mon}}(x, \eta _i)$. Under the construction of Bhargava and Gross, points of ![]() $C_{F,\eta _i}(\mathbb {Q}_p)$ give rise to
$C_{F,\eta _i}(\mathbb {Q}_p)$ give rise to ![]() $G(\mathbb {Q}_p)$-orbits on
$G(\mathbb {Q}_p)$-orbits on ![]() $V(\mathbb {Q}_p)$ via the following composition:
$V(\mathbb {Q}_p)$ via the following composition:
where ![]() $J_i$ denotes the Jacobian of
$J_i$ denotes the Jacobian of ![]() $C_{F,\eta _i}$ and where we identify the set of
$C_{F,\eta _i}$ and where we identify the set of ![]() $G(\mathbb {Q}_p)$-orbits on
$G(\mathbb {Q}_p)$-orbits on ![]() $V(\mathbb {Q}_p)$ having characteristic polynomial
$V(\mathbb {Q}_p)$ having characteristic polynomial ![]() $F_{\operatorname {mon}}(x,z_0)$ with
$F_{\operatorname {mon}}(x,z_0)$ with ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ via Proposition 6. The composite map in (58) is known as the Cassels map, and was first studied by Cassels in [Reference CasselsCas83].
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ via Proposition 6. The composite map in (58) is known as the Cassels map, and was first studied by Cassels in [Reference CasselsCas83].
Let ![]() $\theta ' \in K_F$ be the image of
$\theta ' \in K_F$ be the image of ![]() $x$ under the identification
$x$ under the identification ![]() $\mathbb {Q}_p[x]/F_{\operatorname {mon}}(x, 1) \simeq K_F$. If
$\mathbb {Q}_p[x]/F_{\operatorname {mon}}(x, 1) \simeq K_F$. If ![]() $y_0 = 0$, then
$y_0 = 0$, then ![]() $F_{\operatorname {mon}}(x,\eta _i\cdot z)$ factors uniquely as
$F_{\operatorname {mon}}(x,\eta _i\cdot z)$ factors uniquely as
where ![]() $\widetilde {F}_{\operatorname {mon}} \in \mathscr {F}_{2n}(1, \mathbb {Z}_p)$. (The notation
$\widetilde {F}_{\operatorname {mon}} \in \mathscr {F}_{2n}(1, \mathbb {Z}_p)$. (The notation ![]() $\widetilde {F}_{\operatorname {mon}}$ makes sense, because
$\widetilde {F}_{\operatorname {mon}}$ makes sense, because ![]() $\widetilde {F}_{\operatorname {mon}}$ is indeed the monicized form of
$\widetilde {F}_{\operatorname {mon}}$ is indeed the monicized form of ![]() $\widetilde {F}$ as defined in (11).) Using the explicit description of the Cassels map stated in [Reference Bruin and StollBS09, § 2], one finds that the point
$\widetilde {F}$ as defined in (11).) Using the explicit description of the Cassels map stated in [Reference Bruin and StollBS09, § 2], one finds that the point ![]() $(x_0', c') \in C_{F,\eta _i}(\mathbb {Q}_p)$ gives rise to the class
$(x_0', c') \in C_{F,\eta _i}(\mathbb {Q}_p)$ gives rise to the class
 \begin{align*}
\left.\begin{array}{ll@{}} x_0' - \theta' \eta_i & \text{if $y_0 \neq 0$,} \\
\widetilde{F}_{\operatorname{mon}}(\theta' \eta_i, \eta_i) + (x_0' - \theta' \eta_i) & \text{if $y_0 = 0$}\end{array}\right\}
\equiv f_0 \cdot \delta \in (K_F^\times/K_F^{\times 2})_{\operatorname{N}\equiv1}. \end{align*}
\begin{align*}
\left.\begin{array}{ll@{}} x_0' - \theta' \eta_i & \text{if $y_0 \neq 0$,} \\
\widetilde{F}_{\operatorname{mon}}(\theta' \eta_i, \eta_i) + (x_0' - \theta' \eta_i) & \text{if $y_0 = 0$}\end{array}\right\}
\equiv f_0 \cdot \delta \in (K_F^\times/K_F^{\times 2})_{\operatorname{N}\equiv1}. \end{align*}
Meanwhile, by Proposition 6, the class in ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ corresponding to
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ corresponding to ![]() $(x_0,y_0, z_0) \in \mathscr {S}_F(\mathbb {Z}_p)$ is also
$(x_0,y_0, z_0) \in \mathscr {S}_F(\mathbb {Z}_p)$ is also ![]() $f_0 \cdot \delta$. Thus, the number of elements of
$f_0 \cdot \delta$. Thus, the number of elements of ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the form
$(K_F^\times /K_F^{\times 2})_{\operatorname {N} \equiv 1}$ of the form ![]() $f_0 \cdot \delta$ arising form points of
$f_0 \cdot \delta$ arising form points of ![]() $\mathscr {S}_F(\mathbb {Z}_p)$ is bounded above by the total number of
$\mathscr {S}_F(\mathbb {Z}_p)$ is bounded above by the total number of ![]() $G(\mathbb {Q}_p)$-orbits on
$G(\mathbb {Q}_p)$-orbits on ![]() $V(\mathbb {Q}_p)$ arising from
$V(\mathbb {Q}_p)$ arising from ![]() $\mathbb {Q}_p$-rational points on any one of the finitely many curves
$\mathbb {Q}_p$-rational points on any one of the finitely many curves ![]() $C_{F,\eta _1}, \ldots, C_{F, \eta _\ell }$. By [Reference Bhargava and GrossBG13, § 6.2], the number of
$C_{F,\eta _1}, \ldots, C_{F, \eta _\ell }$. By [Reference Bhargava and GrossBG13, § 6.2], the number of ![]() $G(\mathbb {Q}_p)$-orbits on
$G(\mathbb {Q}_p)$-orbits on ![]() $V(\mathbb {Q}_p)$ arising from each
$V(\mathbb {Q}_p)$ arising from each ![]() $C_{F,\eta _i}$ is at most
$C_{F,\eta _i}$ is at most ![]() $2^{m_i-1}$ when
$2^{m_i-1}$ when ![]() $p$ is odd (respectively,
$p$ is odd (respectively, ![]() $2^{n+m_i-1}$ when
$2^{n+m_i-1}$ when ![]() $p = 2$), where
$p = 2$), where ![]() $m_i$ is the number of distinct irreducible factors of
$m_i$ is the number of distinct irreducible factors of ![]() $F_{\operatorname {mon}}(x,\eta _i)$. But clearly
$F_{\operatorname {mon}}(x,\eta _i)$. But clearly ![]() $m_i = m$ for each
$m_i = m$ for each ![]() $i$, so we get the desired upper bound of
$i$, so we get the desired upper bound of ![]() $\ell \cdot 2^{m-1}$ when
$\ell \cdot 2^{m-1}$ when ![]() $p$ is odd (respectively,
$p$ is odd (respectively, ![]() $2^{n+m-1}$ when
$2^{n+m-1}$ when ![]() $p = 2$).
$p = 2$).
As for the statement about stabilizers, by Theorem 3, the stabilizer of any orbit arising via ![]() $\mathsf {orb}_F$ contains a subgroup isomorphic to
$\mathsf {orb}_F$ contains a subgroup isomorphic to ![]() $K_F^\times [2]_{\operatorname {N}\equiv 1}$, which has size
$K_F^\times [2]_{\operatorname {N}\equiv 1}$, which has size ![]() $\#K_F^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
$\#K_F^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
If ![]() $p \neq 2$, combining Lemmas 31 and 32 along with (31) yields that
$p \neq 2$, combining Lemmas 31 and 32 along with (31) yields that
 \begin{align*} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}(T)}{m_p(T)}\, dT & \leq |\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{\substack{\vec{c} = (c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1} \\ f_0^{i-1} \mid c_i \text{ for every }i }} \frac{2^{m(\vec{c})+1}}{2^{m(\vec{c})-1}}\,dc_1\cdots dc_{2n+1} \\ & = 4 \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot |f_0|_p^{2n^2+n}, \end{align*}
\begin{align*} \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}(T)}{m_p(T)}\, dT & \leq |\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot \int_{\substack{\vec{c} = (c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1} \\ f_0^{i-1} \mid c_i \text{ for every }i }} \frac{2^{m(\vec{c})+1}}{2^{m(\vec{c})-1}}\,dc_1\cdots dc_{2n+1} \\ & = 4 \cdot \operatorname{Vol}(G(\mathbb{Z}_p)) \cdot |f_0|_p^{2n^2+n}, \end{align*}
as necessary, where ![]() $m(\vec {c})$ is the number of irreducible factors of the polynomial
$m(\vec {c})$ is the number of irreducible factors of the polynomial ![]() $x^{2n+1}+\sum _{i = 1}^{2n+1} c_i \cdot x^{2n+1-i} \in \mathbb {Z}_p[x]$. The case where
$x^{2n+1}+\sum _{i = 1}^{2n+1} c_i \cdot x^{2n+1-i} \in \mathbb {Z}_p[x]$. The case where ![]() $p = 2$ may be deduced analogously.
$p = 2$ may be deduced analogously.
This completes the proof of Proposition 30.
Now, let ![]() $p$ be an odd prime. If we restrict our consideration to those forms
$p$ be an odd prime. If we restrict our consideration to those forms ![]() $F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that
$F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that ![]() $R_F$ is maximal, we can do better than the bound in Proposition 30. Indeed, let
$R_F$ is maximal, we can do better than the bound in Proposition 30. Indeed, let ![]() $\mu _p^{\rm max}(f_0)$ denote the
$\mu _p^{\rm max}(f_0)$ denote the ![]() $p$-adic density of
$p$-adic density of ![]() $F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that
$F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that ![]() $R_F$ is maximal, and let
$R_F$ is maximal, and let ![]() $\psi _p^{\rm max} \colon V(\mathbb {Z}_p) \to \{0,1\} \subset \mathbb {R}$ denote the indicator function of elements
$\psi _p^{\rm max} \colon V(\mathbb {Z}_p) \to \{0,1\} \subset \mathbb {R}$ denote the indicator function of elements ![]() $T \in \mathscr {P}_p$ that arise from points
$T \in \mathscr {P}_p$ that arise from points ![]() $\mathscr {S}_F(\mathbb {Z}_p)$ for a form
$\mathscr {S}_F(\mathbb {Z}_p)$ for a form ![]() $F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that
$F \in \mathscr {F}_{2n+1}(f_0, \mathbb {Z}_p)$ such that ![]() $R_F$ is maximal. Then we have the following result.
$R_F$ is maximal. Then we have the following result.
Proposition 33 For each prime ![]() $p \mid f_0$, we have that
$p \mid f_0$, we have that
Proof. It follows from Lemma 31 that
 \begin{align}
& \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}^{\rm max}(T)}{m_p(T)}\, dT
\leq |\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p))\nonumber\\
& \quad \cdot \int_{\substack{(c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1}}}
\sum_{\substack{T \in G(\mathbb{Z}_p)\backslash V(\mathbb{Z}_p) \\ \operatorname{ch}(T) = x^{2n+1} + c_1x^{2n}+\cdots+c_{2n+1}}}
\frac{\psi_p^{\rm max}(T)}{\#\operatorname{Stab}_{\mathbb{Z}_p}(T)}\,\,dc_1\cdots dc_{2n+1}. \end{align}
\begin{align}
& \int_{T \in V(\mathbb{Z}_p)} \frac{\psi_{p}^{\rm max}(T)}{m_p(T)}\, dT
\leq |\mathscr{J}|_p \cdot \operatorname{Vol}(G(\mathbb{Z}_p))\nonumber\\
& \quad \cdot \int_{\substack{(c_1, \ldots, c_{2n+1}) \in \mathbb{Z}_p^{2n+1}}}
\sum_{\substack{T \in G(\mathbb{Z}_p)\backslash V(\mathbb{Z}_p) \\ \operatorname{ch}(T) = x^{2n+1} + c_1x^{2n}+\cdots+c_{2n+1}}}
\frac{\psi_p^{\rm max}(T)}{\#\operatorname{Stab}_{\mathbb{Z}_p}(T)}\,\,dc_1\cdots dc_{2n+1}. \end{align}
When ![]() $F$ is such that
$F$ is such that ![]() $R_F$ is the maximal order in
$R_F$ is the maximal order in ![]() $K_F$, we have the following analogue of Lemma 32 bounding the number of orbits over
$K_F$, we have the following analogue of Lemma 32 bounding the number of orbits over ![]() $\mathbb {Z}_p$ arising from points in
$\mathbb {Z}_p$ arising from points in ![]() $\mathscr {S}_F(\mathbb {Z}_p)$.
$\mathscr {S}_F(\mathbb {Z}_p)$.
Lemma 34 Let ![]() $p$ be an odd prime, and suppose that
$p$ be an odd prime, and suppose that ![]() $R_F$ is maximal in
$R_F$ is maximal in ![]() $K_F$. Then there are at most
$K_F$. Then there are at most ![]() $2^{m-1}$ orbits of
$2^{m-1}$ orbits of ![]() $G(\mathbb {Z}_p)$ on
$G(\mathbb {Z}_p)$ on ![]() $V(\mathbb {Z}_p)$ arising from points of
$V(\mathbb {Z}_p)$ arising from points of ![]() $\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3. The size of the stabilizer in
$\mathscr {S}_F(\mathbb {Z}_p)$ via the construction in § 3. The size of the stabilizer in ![]() $G(\mathbb {Z}_p)$ of any such orbit is
$G(\mathbb {Z}_p)$ of any such orbit is ![]() $2^{m-1}$.
$2^{m-1}$.
Proof of Lemma 34 By [Reference SwaminathanSwa23, Theorem 30], the number of ![]() $G(\mathbb {Z}_p)$-orbits on
$G(\mathbb {Z}_p)$-orbits on ![]() $V(\mathbb {Z}_p)$ arising from elements of
$V(\mathbb {Z}_p)$ arising from elements of ![]() $H_F$ via the correspondence in Theorem 3 is equal to
$H_F$ via the correspondence in Theorem 3 is equal to ![]() $\#(R_F ^\times /R_F^{\times 2})_{\operatorname {N}\equiv 1}=2^{m-1}$. By Theorem 3, the stabilizer of any such orbit has size
$\#(R_F ^\times /R_F^{\times 2})_{\operatorname {N}\equiv 1}=2^{m-1}$. By Theorem 3, the stabilizer of any such orbit has size ![]() $\#R_F^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
$\#R_F^\times [2]_{\operatorname {N}\equiv 1} = 2^{m-1}$.
Proposition 33 now follows by substituting the result of Lemma 34 into the bound in (59).
4.7 Step (C): finishing the proof
We can now apply Theorem 16 and Propositions 18, 22, 26, and 30 to obtain a bound on (26) and, hence, on (24); combining the result with (22) and (23) gives a bound on ![]() $\delta$ via (21). Then, simplifying the result, we draw the following conclusions.
$\delta$ via (21). Then, simplifying the result, we draw the following conclusions.
Case 1: ![]() $2 \nmid f_0$. When
$2 \nmid f_0$. When ![]() $2 \nmid f_0$, we have
$2 \nmid f_0$, we have
 \begin{equation} \delta - \mu_{f_0} \ll 2^n \cdot 2^{-2n} \cdot \prod_{p \nmid 2f_0}\min\bigg\{\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})},\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\},\end{equation}
\begin{equation} \delta - \mu_{f_0} \ll 2^n \cdot 2^{-2n} \cdot \prod_{p \nmid 2f_0}\min\bigg\{\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})},\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\},\end{equation}
where the mass at ![]() $\infty$ contributes
$\infty$ contributes ![]() $O(2^n)$, the mass at
$O(2^n)$, the mass at ![]() $2$ contributes
$2$ contributes ![]() $O(2^{-2n})$, and the masses at primes dividing
$O(2^{-2n})$, and the masses at primes dividing ![]() $f_0$ contribute
$f_0$ contribute ![]() $O(1)$.
$O(1)$.
We now bound the product of the masses at primes not dividing ![]() $2f_0$, proving that they contribute
$2f_0$, proving that they contribute ![]() $O(2^{-\varepsilon _1 n^{\varepsilon _2}})$. The following lemma allows us to bound the factors at primes less than a small power of the degree
$O(2^{-\varepsilon _1 n^{\varepsilon _2}})$. The following lemma allows us to bound the factors at primes less than a small power of the degree ![]() $2n+1$.
$2n+1$.
Lemma 35 We have for each fixed ![]() $A \in (0,1/3) \subset \mathbb {R}$ that
$A \in (0,1/3) \subset \mathbb {R}$ that
 \[ \prod_{ 3 \leq p \leq (2n+1)^A}\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \ll 2^{-\varepsilon_1 n^{\varepsilon_2}}, \]
\[ \prod_{ 3 \leq p \leq (2n+1)^A}\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \ll 2^{-\varepsilon_1 n^{\varepsilon_2}}, \]
where ![]() $\varepsilon _1, \varepsilon _2 > 0$ are real numbers that may depend on
$\varepsilon _1, \varepsilon _2 > 0$ are real numbers that may depend on ![]() $A$.
$A$.
Proof. We first estimate each factor in the product over primes. We split the sum at the prime ![]() $p$ into two ranges, one for
$p$ into two ranges, one for ![]() $m \leq \frac {1}{2}\log (2n+1)$ and one for
$m \leq \frac {1}{2}\log (2n+1)$ and one for ![]() $m > \frac {1}{2}\log (2n+1)$. We bound the sum over
$m > \frac {1}{2}\log (2n+1)$. We bound the sum over ![]() $m > \frac {1}{2}\log (2n+1)$ as follows:
$m > \frac {1}{2}\log (2n+1)$ as follows:
 \begin{equation} \sum_{\frac{1}{2}\log(2n+1) < m \leq 2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \leq \sum_{\frac{1}{2}\log(2n+1) < m \leq 2n+1} \frac{p+1}{2^{m-1}} \leq \frac{2(p+1)}{\sqrt{2n+1}}.\end{equation}
\begin{equation} \sum_{\frac{1}{2}\log(2n+1) < m \leq 2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \leq \sum_{\frac{1}{2}\log(2n+1) < m \leq 2n+1} \frac{p+1}{2^{m-1}} \leq \frac{2(p+1)}{\sqrt{2n+1}}.\end{equation}
For the sum over ![]() $m < \frac {1}{2}\log (2n+1)$, we rely on the following result of Afshar and Porritt.Footnote 3
$m < \frac {1}{2}\log (2n+1)$, we rely on the following result of Afshar and Porritt.Footnote 3
Theorem 36 [Reference Afshar and PorrittAP19, Remark 2.11]
Let ![]() $p$ be a prime, and let
$p$ be a prime, and let ![]() $1 \leq m \leq \log (2n+1)$. Then we have the following uniform estimate:
$1 \leq m \leq \log (2n+1)$. Then we have the following uniform estimate:
where the implied constant is absolute (i.e. does not depend on ![]() $p$), and where the function
$p$), and where the function ![]() $D_p$ is defined as follows. Letting
$D_p$ is defined as follows. Letting ![]() $\mathscr {I} \subset (\mathbb {Z}/p\mathbb {Z})[x]$ be the set of all monic irreducible polynomials, we have
$\mathscr {I} \subset (\mathbb {Z}/p\mathbb {Z})[x]$ be the set of all monic irreducible polynomials, we have
 \[ D_p(z) = \frac{E(1/p,z)}{\Gamma(1+z)}, \quad \text{where } E(x,z) = \prod_{f \in \mathscr{I}} \bigg(1 + \frac{zx^{\deg f}}{1-x^{\deg f}}\bigg)\cdot (1 - x^{\deg f})^z. \]
\[ D_p(z) = \frac{E(1/p,z)}{\Gamma(1+z)}, \quad \text{where } E(x,z) = \prod_{f \in \mathscr{I}} \bigg(1 + \frac{zx^{\deg f}}{1-x^{\deg f}}\bigg)\cdot (1 - x^{\deg f})^z. \]
We now turn the very careful estimate in Theorem 36 into a more easily usable form. First, note that for any ![]() $x \in (0,1/2) \subset \mathbb {R}$ and
$x \in (0,1/2) \subset \mathbb {R}$ and ![]() $z \in (0,1)$ we have
$z \in (0,1)$ we have
By Carlitz's theorem (see [Reference CarlitzCar32]), there are exactly ![]() $p^{d-1}$ monic separable polynomials of degree
$p^{d-1}$ monic separable polynomials of degree ![]() $d$ over
$d$ over ![]() $\mathbb {Z}/p\mathbb {Z}$, and hence at most
$\mathbb {Z}/p\mathbb {Z}$, and hence at most ![]() $p^{d-1}$ monic irreducible polynomials of degree
$p^{d-1}$ monic irreducible polynomials of degree ![]() $d$ over
$d$ over ![]() $\mathbb {Z}/p\mathbb {Z}$. Using this together with (62), we deduce that
$\mathbb {Z}/p\mathbb {Z}$. Using this together with (62), we deduce that
 \begin{equation} E(1/p,z) \leq \prod_{f \in \mathscr{I}} (1 + p^{-2 \deg f}) \leq \prod_{d = 1}^\infty (1 + p^{-2 d})^{p^{d-1}}. \end{equation}
\begin{equation} E(1/p,z) \leq \prod_{f \in \mathscr{I}} (1 + p^{-2 \deg f}) \leq \prod_{d = 1}^\infty (1 + p^{-2 d})^{p^{d-1}}. \end{equation}
To estimate the right-hand side of (63), we take its logarithm and apply the bound ![]() $\log (1+x) \leq x$ (which holds for
$\log (1+x) \leq x$ (which holds for ![]() $x > -1$):
$x > -1$):
 \begin{equation} \log\bigg(\prod_{d = 1}^\infty (1+p^{-2d})^{p^{d-1}}\bigg) = \sum_{d = 1}^\infty p^{d-1} \cdot \log(1+p^{-2d}) \leq \sum_{d = 1}^\infty p^{d-1} \cdot p^{-2d} = \frac{1}{p(p-1)}. \end{equation}
\begin{equation} \log\bigg(\prod_{d = 1}^\infty (1+p^{-2d})^{p^{d-1}}\bigg) = \sum_{d = 1}^\infty p^{d-1} \cdot \log(1+p^{-2d}) \leq \sum_{d = 1}^\infty p^{d-1} \cdot p^{-2d} = \frac{1}{p(p-1)}. \end{equation}
Taking ![]() $p = 2$ in (64) and using the fact that
$p = 2$ in (64) and using the fact that ![]() $\Gamma (1+z) > 1/2$, we have for any prime
$\Gamma (1+z) > 1/2$, we have for any prime ![]() $p$, any
$p$, any ![]() $1 \leq m \leq \log (2n+1)$, and all sufficiently large
$1 \leq m \leq \log (2n+1)$, and all sufficiently large ![]() $n$ that
$n$ that
where ![]() $e$ denotes the usual base of the natural logarithm. Upon combining (61), (65), and Theorem 36, we find for all sufficiently large
$e$ denotes the usual base of the natural logarithm. Upon combining (61), (65), and Theorem 36, we find for all sufficiently large ![]() $n$ that
$n$ that
 \begin{align} \sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} & \leq \frac{2(p+1)}{\sqrt{2n+1}} + \sum_{1 \leq m \leq \frac{1}{2}\log(2n+1)} \frac{4(p+1)}{(2n+1)} \cdot \frac{(\frac{1}{2}\log (2n+1))^{m-1}}{(m-1)!} \nonumber\\ & \leq \frac{2(p+1)}{\sqrt{2n+1}} +\frac{4(p+1)}{2n+1} \cdot e^{\frac{1}{2}\log(2n+1)} = \frac{6p+6}{\sqrt{2n+1}} \leq \frac{8p}{\sqrt{2n+1}}, \end{align}
\begin{align} \sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} & \leq \frac{2(p+1)}{\sqrt{2n+1}} + \sum_{1 \leq m \leq \frac{1}{2}\log(2n+1)} \frac{4(p+1)}{(2n+1)} \cdot \frac{(\frac{1}{2}\log (2n+1))^{m-1}}{(m-1)!} \nonumber\\ & \leq \frac{2(p+1)}{\sqrt{2n+1}} +\frac{4(p+1)}{2n+1} \cdot e^{\frac{1}{2}\log(2n+1)} = \frac{6p+6}{\sqrt{2n+1}} \leq \frac{8p}{\sqrt{2n+1}}, \end{align}
where we have used the fact that ![]() $\sum _{i = 0}^N ({x^i}/{i!}) \leq e^x$ for any
$\sum _{i = 0}^N ({x^i}/{i!}) \leq e^x$ for any ![]() $x > 0$ and integer
$x > 0$ and integer ![]() $N \geq 0$. By Erds’ proof of Bertrand's postulate, we have
$N \geq 0$. By Erds’ proof of Bertrand's postulate, we have ![]() $\prod _{p < N} < 4^N$ for any
$\prod _{p < N} < 4^N$ for any ![]() $N \geq 3$. By the prime number theorem, for any
$N \geq 3$. By the prime number theorem, for any ![]() $\varepsilon > 0$, there exists an integer
$\varepsilon > 0$, there exists an integer ![]() $N > 0$ such that for all
$N > 0$ such that for all ![]() $N' > N$, the number of primes less than or equal to
$N' > N$, the number of primes less than or equal to ![]() $N'$ is at least
$N'$ is at least ![]() $(1-\varepsilon ) \cdot ({N'}/{\log N'})$ and is at most
$(1-\varepsilon ) \cdot ({N'}/{\log N'})$ and is at most ![]() $(1+\varepsilon ) \cdot ({N'}/{\log N'})$. Combining this fact with (66), we find for any fixed
$(1+\varepsilon ) \cdot ({N'}/{\log N'})$. Combining this fact with (66), we find for any fixed ![]() $A < 1/3$ and all sufficiently large
$A < 1/3$ and all sufficiently large ![]() $n$ (where ‘large’ depends on
$n$ (where ‘large’ depends on ![]() $A$ and
$A$ and ![]() $\varepsilon$) that
$\varepsilon$) that
 \[ \prod_{ 3 \leq p \leq (2n+1)^A}\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \leq \frac{8^{(1+\varepsilon) \cdot ({(2n+1)^A}/{A \log (2n+1)})} \cdot 4^{(2n+1)^A}}{(\sqrt{2n+1})^{(1-\varepsilon) \cdot ({(2n+1)^A}/{A \log(2n+1)})}} \ll 2^{-\varepsilon_1 n^{\varepsilon_2}}, \]
\[ \prod_{ 3 \leq p \leq (2n+1)^A}\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}} \leq \frac{8^{(1+\varepsilon) \cdot ({(2n+1)^A}/{A \log (2n+1)})} \cdot 4^{(2n+1)^A}}{(\sqrt{2n+1})^{(1-\varepsilon) \cdot ({(2n+1)^A}/{A \log(2n+1)})}} \ll 2^{-\varepsilon_1 n^{\varepsilon_2}}, \]
for some real numbers ![]() $\varepsilon _2, \varepsilon _2 > 0$.
$\varepsilon _2, \varepsilon _2 > 0$.
The following lemma allows us to bound the factors at the remaining primes.
Lemma 37 We have that
 \[ \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \ll 1, \]
\[ \prod_{p > 2} \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \ll 1, \]
where the implied constant does not depend on ![]() $n$.
$n$.
Proof. From (46), it follows that
 \begin{equation} \log \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} = \sum_{i = 1}^n -\log(1-p^{-2i}) \leq 2 \cdot \sum_{i = 1}^n p^{-2i} \leq \frac{2}{p^2-1}, \end{equation}
\begin{equation} \log \frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} = \sum_{i = 1}^n -\log(1-p^{-2i}) \leq 2 \cdot \sum_{i = 1}^n p^{-2i} \leq \frac{2}{p^2-1}, \end{equation}
where we have applied the bound ![]() $-\log (1-x) \leq 2x$, which holds for
$-\log (1-x) \leq 2x$, which holds for ![]() $x \in (0,1/2) \subset \mathbb {R}$. It is not hard to check (by comparing derivatives) that
$x \in (0,1/2) \subset \mathbb {R}$. It is not hard to check (by comparing derivatives) that ![]() ${2}/({p^2-1}) \leq \log (1 + p^{-{3}/{2}})$ for each
${2}/({p^2-1}) \leq \log (1 + p^{-{3}/{2}})$ for each ![]() $p \geq 5$. Thus,
$p \geq 5$. Thus,
 \[ \prod_{p >
2}\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \leq
\frac{e^{{1}/{4}}}{(1+2^{-{3}/{2}})(1 +
3^{-{3}/{2}})} \cdot \prod_{p} (1 + p^{-{3}/{2}})
\ll 1. \]
\[ \prod_{p >
2}\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} \leq
\frac{e^{{1}/{4}}}{(1+2^{-{3}/{2}})(1 +
3^{-{3}/{2}})} \cdot \prod_{p} (1 + p^{-{3}/{2}})
\ll 1. \]
It follows from Lemmas 35 and 37 that the factor at the odd primes not dividing ![]() $f_0$ is
$f_0$ is ![]() $O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers
$O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers ![]() $\varepsilon _1, \varepsilon _2 > 0$, so by (60), we have
$\varepsilon _1, \varepsilon _2 > 0$, so by (60), we have ![]() $\delta = \mu _{f_0} + o(2^{-n})$. This completes the proof of the second statement in part (a) of Theorem 1.
$\delta = \mu _{f_0} + o(2^{-n})$. This completes the proof of the second statement in part (a) of Theorem 1.
We now determine the smallest ![]() $n$ for which our method yields that a positive proportion of superelliptic stacky curves in
$n$ for which our method yields that a positive proportion of superelliptic stacky curves in ![]() $\mathscr {F}_{2n+1}(f_0)$ are insoluble. To this end, let
$\mathscr {F}_{2n+1}(f_0)$ are insoluble. To this end, let ![]() $\mathscr {F}_{2n+1}^{\rm max}(f_0)$ be the set of forms
$\mathscr {F}_{2n+1}^{\rm max}(f_0)$ be the set of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that ![]() $R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is the maximal order in
$R_F \otimes _\mathbb {Z} \mathbb {Z}_p$ is the maximal order in ![]() $K_F \otimes _\mathbb {Q} \mathbb {Q}_p$ for every prime
$K_F \otimes _\mathbb {Q} \mathbb {Q}_p$ for every prime ![]() $p \mid f_0$ and such that condition (b) in Theorem 14 fails for some prime
$p \mid f_0$ and such that condition (b) in Theorem 14 fails for some prime ![]() $p \mid \kappa$. Let
$p \mid \kappa$. Let ![]() $\delta _{\rm max}$ be the upper density of forms
$\delta _{\rm max}$ be the upper density of forms ![]() $F \in \mathscr {F}_{2n+1}^{\rm max}(f_0)$, enumerated by height, such that
$F \in \mathscr {F}_{2n+1}^{\rm max}(f_0)$, enumerated by height, such that ![]() $\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. For each prime
$\mathscr {S}_F(\mathbb {Z}) \neq \varnothing$. For each prime ![]() $p \mid f_0$, instead of applying Proposition 30, we can apply Proposition 33, which yields the following explicit bound on
$p \mid f_0$, instead of applying Proposition 30, we can apply Proposition 33, which yields the following explicit bound on ![]() $\delta _{\rm max}$:
$\delta _{\rm max}$:
 \[\delta_{{\rm max}} \leq 3 \cdot 2^n \cdot
\bigg(\sum_{m = 1}^{2n+1} \frac{12}{2^{2n+m-1}} \cdot \frac{\#G(\mathbb{Z}/8\mathbb{Z})}{8^{2n^2+n}} \cdot \frac{\#\mathscr{I}_8(m)}{8^{2n+1}} \bigg) \cdot
\prod_{p > 2}\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})}.\]
\[\delta_{{\rm max}} \leq 3 \cdot 2^n \cdot
\bigg(\sum_{m = 1}^{2n+1} \frac{12}{2^{2n+m-1}} \cdot \frac{\#G(\mathbb{Z}/8\mathbb{Z})}{8^{2n^2+n}} \cdot \frac{\#\mathscr{I}_8(m)}{8^{2n+1}} \bigg) \cdot
\prod_{p > 2}\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})}.\]
Upon applying the estimate ![]() $\#\mathscr {I}_8(m)/8^{2n+1} \leq 1$, we deduce that
$\#\mathscr {I}_8(m)/8^{2n+1} \leq 1$, we deduce that ![]() $\delta _{\rm max} < 2^{7-n} \leq 1$ whenever
$\delta _{\rm max} < 2^{7-n} \leq 1$ whenever ![]() ${n \geq 7}$. By explicitly computing
${n \geq 7}$. By explicitly computing ![]() ${\#\mathscr {I}_8(m)}/{8^{2n+1}}$ in Sage for
${\#\mathscr {I}_8(m)}/{8^{2n+1}}$ in Sage for ![]() $n < 7$, one can check that we also have
$n < 7$, one can check that we also have ![]() $\delta _{\rm max} < 1$ when
$\delta _{\rm max} < 1$ when ![]() $n \in \{5, 6\}$. Since the density of
$n \in \{5, 6\}$. Since the density of ![]() $\mathscr {F}_{2n+1}^{\rm max}(f_0)$ in
$\mathscr {F}_{2n+1}^{\rm max}(f_0)$ in ![]() $\mathscr {F}_{2n+1}(f_0)$ is positive, this completes the proof of the first statement in part (a) of Theorem 1.
$\mathscr {F}_{2n+1}(f_0)$ is positive, this completes the proof of the first statement in part (a) of Theorem 1.
Case 2: ![]() $2 \mid f_0$. When
$2 \mid f_0$. When ![]() $2 \mid f_0$, we bound the mass at
$2 \mid f_0$, we bound the mass at ![]() $\infty$ slightly differently: specifically, we do not use the bound on
$\infty$ slightly differently: specifically, we do not use the bound on ![]() $|\mathscr {J}| \cdot \operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ given by Lemma 19. Doing so, and applying the identities (37) and (38), we obtain
$|\mathscr {J}| \cdot \operatorname {Vol}(G(\mathbb {Z}) \backslash G(\mathbb {R}))$ given by Lemma 19. Doing so, and applying the identities (37) and (38), we obtain
 \begin{equation} \delta - \mu_{f_0} \ll 2^{-n} \cdot 2^n \cdot \prod_{\substack{p \nmid f_0}}\min \bigg\{\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} ,\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\},\end{equation}
\begin{equation} \delta - \mu_{f_0} \ll 2^{-n} \cdot 2^n \cdot \prod_{\substack{p \nmid f_0}}\min \bigg\{\frac{p^{2n^2+n}}{\#G(\mathbb{Z}/p\mathbb{Z})} ,\sum_{m = 1}^{2n+1} \frac{p+1}{2^{m-1}} \cdot \frac{\#\mathscr{I}_p(m)}{p^{2n+1}}\bigg\},\end{equation}
where the implied constant is independent of ![]() $n$. In (68), the mass at
$n$. In (68), the mass at ![]() $\infty$ contributes
$\infty$ contributes ![]() $O(2^{-n})$ (as the Jacobian factors at all places have canceled out), the mass at
$O(2^{-n})$ (as the Jacobian factors at all places have canceled out), the mass at ![]() $2$ contributes
$2$ contributes ![]() $O(2^{n})$, and the masses at primes dividing
$O(2^{n})$, and the masses at primes dividing ![]() $f_0$ contribute
$f_0$ contribute ![]() $O(1)$. It follows from Lemmas 35 and 37 that the factor at the primes not dividing
$O(1)$. It follows from Lemmas 35 and 37 that the factor at the primes not dividing ![]() $f_0$ is
$f_0$ is ![]() $O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers
$O(2^{-\varepsilon _1n^{\varepsilon _2}})$ for some real numbers ![]() $\varepsilon _1, \varepsilon _2 > 0$, so
$\varepsilon _1, \varepsilon _2 > 0$, so ![]() $\delta = \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ in this case. This completes the proof of part (b) of Theorem 1.
$\delta = \mu _{f_0} + O(2^{-\varepsilon _1n^{\varepsilon _2}})$ in this case. This completes the proof of part (b) of Theorem 1.
5. Obstruction to the Hasse principle and the proof of Theorem 2
In this section, we study how often superelliptic stacky curves satisfy the Hasse principle using the method of descent. Specifically, we describe ![]() $2$-coverings of superelliptic stacky curves, and we modify the proof of Theorem 1 to show that superelliptic stacky curves often have no locally soluble
$2$-coverings of superelliptic stacky curves, and we modify the proof of Theorem 1 to show that superelliptic stacky curves often have no locally soluble ![]() $2$-coverings and, thus, fail the Hasse principle. Upon showing that such a
$2$-coverings and, thus, fail the Hasse principle. Upon showing that such a ![]() $2$-covering obstruction to solubility is a special case of the Brauer–Manin obstruction, we obtain Theorem 2.
$2$-covering obstruction to solubility is a special case of the Brauer–Manin obstruction, we obtain Theorem 2.
5.1 Defining the Brauer–Manin obstruction for  $\mathscr {S}_F$
$\mathscr {S}_F$
Let ![]() $F$ be a separable integral binary form of degree
$F$ be a separable integral binary form of degree ![]() $2n+1 \geq 3$. While a suitable theory of Brauer–Manin obstruction for stacks remains to be developed, such a theory is not required in the context of superelliptic stacky curves. Indeed, we can exploit the fact that the stack
$2n+1 \geq 3$. While a suitable theory of Brauer–Manin obstruction for stacks remains to be developed, such a theory is not required in the context of superelliptic stacky curves. Indeed, we can exploit the fact that the stack ![]() $\mathscr {S}_F$ is defined as a quotient of the punctured affine surface
$\mathscr {S}_F$ is defined as a quotient of the punctured affine surface ![]() $\widetilde {S}_F$ (see (2)), where the usual theory of the Brauer–Manin obstruction for varieties applies.
$\widetilde {S}_F$ (see (2)), where the usual theory of the Brauer–Manin obstruction for varieties applies.
Let ![]() $\widetilde {S}_{F,\mathbb {Q}} = \widetilde {S}_F \otimes _{\mathbb {Z}} \mathbb {Q}$, and let
$\widetilde {S}_{F,\mathbb {Q}} = \widetilde {S}_F \otimes _{\mathbb {Z}} \mathbb {Q}$, and let ![]() $\widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$ denote the usual Brauer–Manin set of the
$\widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$ denote the usual Brauer–Manin set of the ![]() $\mathbb {Q}$-variety
$\mathbb {Q}$-variety ![]() $\widetilde {S}_{F,\mathbb {Q}}$ (see [Reference Cao, Demarche and XuCDX19, § 1] for the definition). Let
$\widetilde {S}_{F,\mathbb {Q}}$ (see [Reference Cao, Demarche and XuCDX19, § 1] for the definition). Let
be the set of adelic points of ![]() $\widetilde {S}_F$ that are integral in every place (i.e. the set of everywhere-primitive adelic solutions to the superelliptic equation
$\widetilde {S}_F$ that are integral in every place (i.e. the set of everywhere-primitive adelic solutions to the superelliptic equation ![]() $y^2 = F(x,z)$, or equivalently, the set of everywhere-integral adelic points on the stacky curve
$y^2 = F(x,z)$, or equivalently, the set of everywhere-integral adelic points on the stacky curve ![]() $\mathscr {S}_F\!$). With this notation in place, we define the Brauer–Manin set of
$\mathscr {S}_F\!$). With this notation in place, we define the Brauer–Manin set of ![]() $\mathscr {S}_F$ by
$\mathscr {S}_F$ by
and we say that ![]() $\mathscr {S}_F$ has a Brauer–Manin obstruction to having an integral point if its Brauer–Manin set is empty (i.e. if
$\mathscr {S}_F$ has a Brauer–Manin obstruction to having an integral point if its Brauer–Manin set is empty (i.e. if ![]() $\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}} = \varnothing$).
$\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}} = \varnothing$).
Because we have defined ![]() $\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$ as a subset of
$\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$ as a subset of ![]() $\widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$, we can use the method of descent as laid out for open varieties in [Reference Cao, Demarche and XuCDX19] to obtain a set-theoretic ‘upper bound’ on
$\widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$, we can use the method of descent as laid out for open varieties in [Reference Cao, Demarche and XuCDX19] to obtain a set-theoretic ‘upper bound’ on ![]() $\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$. Indeed, suppose that we have a torsor
$\mathscr {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {Br}}$. Indeed, suppose that we have a torsor ![]() $f \colon Z \to \widetilde {S}_{F,\mathbb {Q}}$ by a group of multiplicative type or connected algebraic group
$f \colon Z \to \widetilde {S}_{F,\mathbb {Q}}$ by a group of multiplicative type or connected algebraic group ![]() $\Gamma$ (all defined over
$\Gamma$ (all defined over ![]() $\mathbb {Q}$). Let
$\mathbb {Q}$). Let
be the descent set of ![]() $f$, where
$f$, where ![]() $f^\sigma \colon Z^\sigma \to \widetilde {S}_{F,\mathbb {Q}}$ is the twist of
$f^\sigma \colon Z^\sigma \to \widetilde {S}_{F,\mathbb {Q}}$ is the twist of ![]() $f \colon Z \to \widetilde {S}_{F,\mathbb {Q}}$ by a
$f \colon Z \to \widetilde {S}_{F,\mathbb {Q}}$ by a ![]() $1$-cocycle representing
$1$-cocycle representing ![]() $\sigma \in H^1(G_\mathbb {Q}, \Gamma (\overline {\mathbb {Q}}))$. Since
$\sigma \in H^1(G_\mathbb {Q}, \Gamma (\overline {\mathbb {Q}}))$. Since ![]() $\widetilde {S}_{F,\mathbb {Q}}$ is smooth and geometrically integral, Theorem 1.1 of [Reference Cao, Demarche and XuCDX19] implies that
$\widetilde {S}_{F,\mathbb {Q}}$ is smooth and geometrically integral, Theorem 1.1 of [Reference Cao, Demarche and XuCDX19] implies that
It follows from (70) and (72) that ![]() $\mathscr {S}_F$ has a Brauer–Manin obstruction to having an integral point if it has an obstruction to descent by
$\mathscr {S}_F$ has a Brauer–Manin obstruction to having an integral point if it has an obstruction to descent by ![]() $\Gamma$-torsors in the sense that
$\Gamma$-torsors in the sense that ![]() $\widetilde {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {int}} \cap \widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^f = \varnothing$.
$\widetilde {S}_F(\mathbb {A}_\mathbb {Q})^{\operatorname {int}} \cap \widetilde {S}_{F,\mathbb {Q}}(\mathbb {A}_\mathbb {Q})^f = \varnothing$.
5.2  $2$-coverings
$2$-coverings
Let ![]() $k$ be a field of characteristic not equal to
$k$ be a field of characteristic not equal to ![]() $2$, let
$2$, let ![]() $f_0 \in k^\times$, and let
$f_0 \in k^\times$, and let ![]() $F \in \mathscr {F}_{2n+1}(f_0,k)$ be separable. Let
$F \in \mathscr {F}_{2n+1}(f_0,k)$ be separable. Let ![]() $\theta _1, \ldots, \theta _{2n+1} \in k_{\operatorname {sep}}$ be the distinct roots of the polynomial
$\theta _1, \ldots, \theta _{2n+1} \in k_{\operatorname {sep}}$ be the distinct roots of the polynomial ![]() $F(x,1)$, and for each
$F(x,1)$, and for each ![]() $\sigma \in G_k$ and
$\sigma \in G_k$ and ![]() $i \in \{1, \ldots, 2n+1\}$, let
$i \in \{1, \ldots, 2n+1\}$, let ![]() $\sigma (i) \in \{1, \ldots, 2n+1\}$ be defined by
$\sigma (i) \in \{1, \ldots, 2n+1\}$ be defined by ![]() $\theta _{\sigma (i)} = \sigma (\theta _i)$. Let
$\theta _{\sigma (i)} = \sigma (\theta _i)$. Let ![]() $\widetilde {S}_F$ and
$\widetilde {S}_F$ and ![]() $\mathscr {S}_F$ denote the corresponding punctured affine surface and stacky curve (which are now defined over
$\mathscr {S}_F$ denote the corresponding punctured affine surface and stacky curve (which are now defined over ![]() $k$, as opposed to
$k$, as opposed to ![]() $\mathbb {Z}$), respectively. In this section, we specialize the discussion of descent in § 5.1 to the case where
$\mathbb {Z}$), respectively. In this section, we specialize the discussion of descent in § 5.1 to the case where ![]() $\Gamma$ is equal to the Jacobian
$\Gamma$ is equal to the Jacobian ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ of
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ of ![]() $\mathscr {S}_F$. Note that
$\mathscr {S}_F$. Note that ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ is a group of multiplicative type, because over
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ is a group of multiplicative type, because over ![]() $k_{\operatorname {sep}}$, it is isomorphic to a finite product of copies of
$k_{\operatorname {sep}}$, it is isomorphic to a finite product of copies of ![]() $\mathbb {Z}/2\mathbb {Z}$ and is thus diagonalizable. Consequently, we can apply (72) to
$\mathbb {Z}/2\mathbb {Z}$ and is thus diagonalizable. Consequently, we can apply (72) to ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$-torsors.
$\operatorname {Pic}^0(\mathscr {S}_F\!)$-torsors.
A Galois étale covering defined over ![]() $k$ with Galois group isomorphic to
$k$ with Galois group isomorphic to ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ as
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ as ![]() $G_k$-modules is called a
$G_k$-modules is called a ![]() $2$-covering. Our strategy for describing the
$2$-covering. Our strategy for describing the ![]() $2$-coverings of
$2$-coverings of ![]() $\widetilde {S}_{F}$ is to describe the
$\widetilde {S}_{F}$ is to describe the ![]() $2$-coverings of
$2$-coverings of ![]() $\mathscr {S}_F$ and pull back along the quotient map
$\mathscr {S}_F$ and pull back along the quotient map ![]() $\widetilde {S}_{F} \to [\widetilde {S}_F/\mathbb {G}_m] = \mathscr {S}_{F}$. We now briefly recall the results of [Reference Bruin and FlynnBF05, § 5], in which Bruin and Flynn explicitly construct all
$\widetilde {S}_{F} \to [\widetilde {S}_F/\mathbb {G}_m] = \mathscr {S}_{F}$. We now briefly recall the results of [Reference Bruin and FlynnBF05, § 5], in which Bruin and Flynn explicitly construct all ![]() $2$-coverings of
$2$-coverings of ![]() $\mathscr {S}_{F}$ up to isomorphism over
$\mathscr {S}_{F}$ up to isomorphism over ![]() $k$ (see also [Reference BruinBru02, § 3]). Consider the projective space
$k$ (see also [Reference BruinBru02, § 3]). Consider the projective space ![]() $\mathbb {P}_k^{2n}$ with homogeneous coordinates
$\mathbb {P}_k^{2n}$ with homogeneous coordinates ![]() $[Z_1 : \cdots : Z_{2n+1}]$ such that
$[Z_1 : \cdots : Z_{2n+1}]$ such that ![]() $G_k$ acts on
$G_k$ acts on ![]() $Z_i$ by
$Z_i$ by ![]() $\sigma \cdot Z_i = Z_{\sigma (i)}$. The distinguished covering is defined to be the closed subscheme
$\sigma \cdot Z_i = Z_{\sigma (i)}$. The distinguished covering is defined to be the closed subscheme ![]() $C^1 \subset \mathbb {P}_k^{2n}$ cut out by the homogeneous ideal
$C^1 \subset \mathbb {P}_k^{2n}$ cut out by the homogeneous ideal
Let ![]() $\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ be the map defined by
$\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ be the map defined by
 \[ \pi^1([Z_1 : \cdots : Z_{2n+1}]) = \frac{\theta_j Z_i^2 - \theta_i Z_j^2}{Z_i^2 - Z_j^2} \]
\[ \pi^1([Z_1 : \cdots : Z_{2n+1}]) = \frac{\theta_j Z_i^2 - \theta_i Z_j^2}{Z_i^2 - Z_j^2} \]
for any distinct ![]() $i,j \in \{1, \ldots, 2n+1\}$. For each class
$i,j \in \{1, \ldots, 2n+1\}$. For each class ![]() $\delta \in H^1(G_k, \operatorname {Pic}^0(\mathscr {S}_F\!))$, the twist of
$\delta \in H^1(G_k, \operatorname {Pic}^0(\mathscr {S}_F\!))$, the twist of ![]() $\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ by
$\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ by ![]() $\delta$ is given explicitly as follows. By [Reference Bhargava and GrossBG13, last paragraphs of §§ 4.2 and 5.1],
$\delta$ is given explicitly as follows. By [Reference Bhargava and GrossBG13, last paragraphs of §§ 4.2 and 5.1], ![]() $H^1(G_\mathbb {Q}, \operatorname {Pic}^0(\mathscr {S}_F\!))$ can be identified with
$H^1(G_\mathbb {Q}, \operatorname {Pic}^0(\mathscr {S}_F\!))$ can be identified with ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, so we may think of
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, so we may think of ![]() $\delta$ as being an element of
$\delta$ as being an element of ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$. Let
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$. Let ![]() $(\delta _1, \ldots, \delta _{2n+1})$ be the image of
$(\delta _1, \ldots, \delta _{2n+1})$ be the image of ![]() $\delta$ under the map
$\delta$ under the map ![]() $K_F^\times /K_F^{\times 2} \to ((k_{\operatorname {sep}})^\times /(k_{\operatorname {sep}})^{\times 2})^{2n+1}$ given by taking the product of the distinct embeddings of each field component of
$K_F^\times /K_F^{\times 2} \to ((k_{\operatorname {sep}})^\times /(k_{\operatorname {sep}})^{\times 2})^{2n+1}$ given by taking the product of the distinct embeddings of each field component of ![]() $K_F$ into
$K_F$ into ![]() $k_{\operatorname {sep}}$. Then the twist of
$k_{\operatorname {sep}}$. Then the twist of ![]() $C^1$ by
$C^1$ by ![]() $\delta$ is the closed subscheme
$\delta$ is the closed subscheme ![]() $C^\delta \subset \mathbb {P}_k^{2n}$ cut out by the homogeneous ideal
$C^\delta \subset \mathbb {P}_k^{2n}$ cut out by the homogeneous ideal
and the twist of ![]() $\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ is the map
$\pi ^1 \colon C^1 \to \mathbb {P}_k^1$ is the map ![]() $\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$ defined by
$\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$ defined by
 \[ \pi^\delta([Z_1 : \cdots : Z_{2n+1}]) = \frac{\theta_j \delta_i Z_i^2 - \theta_i \delta_j Z_j^2}{\delta_iZ_i^2 - \delta_jZ_j^2} \]
\[ \pi^\delta([Z_1 : \cdots : Z_{2n+1}]) = \frac{\theta_j \delta_i Z_i^2 - \theta_i \delta_j Z_j^2}{\delta_iZ_i^2 - \delta_jZ_j^2} \]
for any distinct ![]() $i,j \in \{1, \ldots, 2n+1\}$. The following theorem enumerates the basic properties of the maps
$i,j \in \{1, \ldots, 2n+1\}$. The following theorem enumerates the basic properties of the maps ![]() $\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$.
$\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$.
Theorem 38 ([Reference Bruin and FlynnBF05, Lemma 5.10] and [Reference BruinBru02, § 3.1])
With notation as above, we have:
(a) for each
 $\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, the scheme
$\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, the scheme  $C_\delta$ is a smooth, geometrically irreducible, projective curve of genus
$C_\delta$ is a smooth, geometrically irreducible, projective curve of genus  $n \cdot 2^{2n-1} - 3 \cdot 2^{2n-2} + 1$;
$n \cdot 2^{2n-1} - 3 \cdot 2^{2n-2} + 1$;(b) the action of
 $G_k$ leaves both
$G_k$ leaves both  $I^\delta$ and
$I^\delta$ and  $\pi ^\delta$ invariant, so the map
$\pi ^\delta$ invariant, so the map  $\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$ is defined over
$\pi ^\delta \colon C^\delta \to \mathbb {P}_k^1$ is defined over  $k$;
$k$;(c) the map
 $\pi ^\delta$ is a covering map with Galois group generated by the automorphisms
$\pi ^\delta$ is a covering map with Galois group generated by the automorphisms  $\tau _i \colon C^\delta \to C^\delta$ defined by
$\tau _i \colon C^\delta \to C^\delta$ defined by  $Z_i \to -Z_i$ for each
$Z_i \to -Z_i$ for each  $i \in \{1, \ldots, 2n+1\}$; and
$i \in \{1, \ldots, 2n+1\}$; and(d) we have that
 $\deg \pi ^\delta = 2^{2n}$, that
$\deg \pi ^\delta = 2^{2n}$, that  $\# (\pi ^{\delta })^{-1}(\theta _i) = 2^{2n-1}$, and that
$\# (\pi ^{\delta })^{-1}(\theta _i) = 2^{2n-1}$, and that  $\#(\pi ^\delta )^{-1}(\alpha ) = 2^{2n}$ for each
$\#(\pi ^\delta )^{-1}(\alpha ) = 2^{2n}$ for each  $\alpha \in \mathbb {P}_k^1(k_{\operatorname {sep}}) \smallsetminus \{\theta _1, \ldots, \theta _{2n+1}\}$.
$\alpha \in \mathbb {P}_k^1(k_{\operatorname {sep}}) \smallsetminus \{\theta _1, \ldots, \theta _{2n+1}\}$.
We now demonstrate that the map ![]() $\pi ^\delta$ can actually be thought of as a
$\pi ^\delta$ can actually be thought of as a ![]() $2$-covering
$2$-covering ![]() $\pi ^\delta \colon C^\delta \to \mathscr {S}_F$.
$\pi ^\delta \colon C^\delta \to \mathscr {S}_F$.
Proposition 39 For any ![]() $\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, the map
$\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, the map ![]() $\pi ^\delta$ factors through the coarse moduli map
$\pi ^\delta$ factors through the coarse moduli map ![]() $\mathscr {S}_F \to \mathbb {P}_k^1$ to give a
$\mathscr {S}_F \to \mathbb {P}_k^1$ to give a ![]() $2$-covering
$2$-covering ![]() $\pi ^\delta \colon C^\delta \to \mathscr {S}_F$.
$\pi ^\delta \colon C^\delta \to \mathscr {S}_F$.
Proof. Recall that a finite étale cover of ![]() $\mathscr {S}_F$ is the pullback via
$\mathscr {S}_F$ is the pullback via ![]() $\mathscr {S}_F \to \mathbb {P}_k^1$ of a finite cover of its coarse moduli space
$\mathscr {S}_F \to \mathbb {P}_k^1$ of a finite cover of its coarse moduli space ![]() $\mathbb {P}_k^1$ that is ramified with ramification index
$\mathbb {P}_k^1$ that is ramified with ramification index ![]() $2$ at every point in the preimage of
$2$ at every point in the preimage of ![]() $\theta _i \in \mathbb {P}_k^1(k_{\operatorname {sep}})$ for each
$\theta _i \in \mathbb {P}_k^1(k_{\operatorname {sep}})$ for each ![]() $i$ (to account for the fact that
$i$ (to account for the fact that ![]() $\mathscr {S}_F$ has a
$\mathscr {S}_F$ has a ![]() $\frac {1}{2}$-point at each
$\frac {1}{2}$-point at each ![]() $\theta _i$) and unramified everywhere else. It follows from part (d) of Theorem 38 that the branch locus of the map
$\theta _i$) and unramified everywhere else. It follows from part (d) of Theorem 38 that the branch locus of the map ![]() $\pi ^\delta$ consists precisely of the points
$\pi ^\delta$ consists precisely of the points ![]() $\theta _i$ and that each point in
$\theta _i$ and that each point in ![]() $(\pi ^{\delta })^{-1}(\theta _i)$ has ramification index
$(\pi ^{\delta })^{-1}(\theta _i)$ has ramification index ![]() $2$. Thus, the map
$2$. Thus, the map ![]() $\pi ^\delta$ factors through the stacky curve
$\pi ^\delta$ factors through the stacky curve ![]() $\mathscr {S}_F$, giving an étale map
$\mathscr {S}_F$, giving an étale map ![]() $\pi ^{\delta } \colon C^{\delta } \to \mathscr {S}_F$.
$\pi ^{\delta } \colon C^{\delta } \to \mathscr {S}_F$.
By parts (b) and (c) of Theorem 38, to prove that ![]() $\pi ^{\delta }$ is a
$\pi ^{\delta }$ is a ![]() $2$-covering of
$2$-covering of ![]() $\mathscr {S}_F$ over
$\mathscr {S}_F$ over ![]() $k$, it suffices to show that the group generated by the automorphisms
$k$, it suffices to show that the group generated by the automorphisms ![]() $\tau _i$ is isomorphic to
$\tau _i$ is isomorphic to ![]() $\operatorname {Pic}^0(\mathscr {S}_F\!)$ as
$\operatorname {Pic}^0(\mathscr {S}_F\!)$ as ![]() $G_k$-modules. Let
$G_k$-modules. Let ![]() $J$ denote the Jacobian of the monic odd-degree hyperelliptic curve
$J$ denote the Jacobian of the monic odd-degree hyperelliptic curve ![]() $y^2 = F_{\operatorname {mon}}(x,1)$. We claim that the map
$y^2 = F_{\operatorname {mon}}(x,1)$. We claim that the map ![]() $\tau _i \mapsto (\theta _i - \infty ) \in J[2](k_{\operatorname {sep}})$ defines a
$\tau _i \mapsto (\theta _i - \infty ) \in J[2](k_{\operatorname {sep}})$ defines a ![]() $G_k$-equivariant isomorphism of groups. To see why this claim holds, note that the group generated by the automorphisms
$G_k$-equivariant isomorphism of groups. To see why this claim holds, note that the group generated by the automorphisms ![]() $\tau _i$ is isomorphic to
$\tau _i$ is isomorphic to
 \[ (\mathbb{Z}/2\mathbb{Z})\langle \tau_1, \ldots, \tau_{2n+1}\rangle\bigg/ \bigg(\prod_{i = 1}^{2n+1} \tau_i = 1\bigg) \]
\[ (\mathbb{Z}/2\mathbb{Z})\langle \tau_1, \ldots, \tau_{2n+1}\rangle\bigg/ \bigg(\prod_{i = 1}^{2n+1} \tau_i = 1\bigg) \]
and the action of ![]() $\sigma \in G_k$ on
$\sigma \in G_k$ on ![]() $\tau _i$ is given by
$\tau _i$ is given by ![]() $\sigma \cdot \tau _i = \tau _{\sigma ^{-1}(i)}$, because the action of
$\sigma \cdot \tau _i = \tau _{\sigma ^{-1}(i)}$, because the action of ![]() $\sigma$ on
$\sigma$ on ![]() $Z_i$ is defined to be
$Z_i$ is defined to be ![]() $\sigma (Z_i) = Z_{\sigma (i)}$. On the other hand, we have that
$\sigma (Z_i) = Z_{\sigma (i)}$. On the other hand, we have that
 \[ J[2](k_{\operatorname{sep}})= (\mathbb{Z}/2\mathbb{Z})\langle (\theta_1 - \infty), \ldots, (\theta_{2n+1} - \infty)\rangle\bigg/\bigg(\sum_{i = 1}^{2n+1} (\theta_i - \infty)\bigg) \]
\[ J[2](k_{\operatorname{sep}})= (\mathbb{Z}/2\mathbb{Z})\langle (\theta_1 - \infty), \ldots, (\theta_{2n+1} - \infty)\rangle\bigg/\bigg(\sum_{i = 1}^{2n+1} (\theta_i - \infty)\bigg) \]
and the action of ![]() $\sigma \in G_k$ on
$\sigma \in G_k$ on ![]() $(\theta _i - \infty )$ is
$(\theta _i - \infty )$ is ![]() $(\theta _i - \infty ) \cdot \sigma = (\sigma ^{-1} \cdot \theta _i - \sigma ^{-1} \cdot \infty ) = (\theta _{\sigma ^{-1}(i)} - \infty )$. Thus, we have the claim. The proposition now follows from the fact that
$(\theta _i - \infty ) \cdot \sigma = (\sigma ^{-1} \cdot \theta _i - \sigma ^{-1} \cdot \infty ) = (\theta _{\sigma ^{-1}(i)} - \infty )$. Thus, we have the claim. The proposition now follows from the fact that ![]() $J[2] \simeq \operatorname {Pic}^0(\mathscr {S}_{F}\!)$ as
$J[2] \simeq \operatorname {Pic}^0(\mathscr {S}_{F}\!)$ as ![]() $G_k$-modules (see the proof of Proposition 7).
$G_k$-modules (see the proof of Proposition 7).
Remark 40 Note that two coverings ![]() $\pi ^{\delta _1} \colon C^{\delta _1} \to \mathscr {S}_F$ and
$\pi ^{\delta _1} \colon C^{\delta _1} \to \mathscr {S}_F$ and ![]() $\pi ^{\delta _2} \colon C^{\delta _2} \to \mathscr {S}_F$ are isomorphic (as coverings of
$\pi ^{\delta _2} \colon C^{\delta _2} \to \mathscr {S}_F$ are isomorphic (as coverings of ![]() $\mathscr {S}_F$ defined over
$\mathscr {S}_F$ defined over ![]() $k$) if and only if
$k$) if and only if ![]() $\delta _1$ and
$\delta _1$ and ![]() $\delta _2$ represent the same class in
$\delta _2$ represent the same class in ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$.
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$.
Let ![]() $(x_0, y_0, z_0) \in \mathscr {S}_F(k)$, and let
$(x_0, y_0, z_0) \in \mathscr {S}_F(k)$, and let ![]() $\delta \in K_F^\times$ be the element associated to the point
$\delta \in K_F^\times$ be the element associated to the point ![]() $(x_0, y_0, z_0)$ via the construction in § 3. By (15), we have that
$(x_0, y_0, z_0)$ via the construction in § 3. By (15), we have that
 \[ \delta = \begin{cases} x_0 - \theta z_0 & \text{if $y_0 \neq 0$,} \\ \widetilde{F}(z_0\theta, z_0) + (x_0 - \theta z_0) & \text{if $y_0 = 0$,} \end{cases} \]
\[ \delta = \begin{cases} x_0 - \theta z_0 & \text{if $y_0 \neq 0$,} \\ \widetilde{F}(z_0\theta, z_0) + (x_0 - \theta z_0) & \text{if $y_0 = 0$,} \end{cases} \]
where ![]() $\widetilde {F}$ is as in (11). With this notation, we have the following result, which tells us which
$\widetilde {F}$ is as in (11). With this notation, we have the following result, which tells us which ![]() $2$-covering of
$2$-covering of ![]() $\mathscr {S}_F$ has the property that
$\mathscr {S}_F$ has the property that ![]() $(x_0, y_0, z_0)$ lies in the image of its
$(x_0, y_0, z_0)$ lies in the image of its ![]() $k$-rational points.
$k$-rational points.
Lemma 41 We have that ![]() $(x_0, y_0, z_0) \in \pi ^{f_0\cdot \delta }(C^{f_0\cdot \delta }(k)) \subset \mathscr {S}_F(k)$.
$(x_0, y_0, z_0) \in \pi ^{f_0\cdot \delta }(C^{f_0\cdot \delta }(k)) \subset \mathscr {S}_F(k)$.
Proof. First suppose ![]() $y_0 \neq 0$. By construction, the point
$y_0 \neq 0$. By construction, the point ![]() $[1: 1 : \cdots : 1] \in C^{f_0 \cdot \delta }(k)$ satisfies
$[1: 1 : \cdots : 1] \in C^{f_0 \cdot \delta }(k)$ satisfies
 \begin{align} \pi^{f_0 \cdot \delta}([1: 1 : \cdots : 1]) & = \frac{\theta_j (f_0 \cdot\delta_i) - \theta_i (f_0 \cdot \delta_j)}{f_0 \cdot \delta_i - f_0 \cdot \delta_j} = \frac{\theta_j \cdot f_0(x_0 - \theta_i z_0) - \theta_i \cdot f_0( x_0 - \theta_j z_0)}{f_0(x_0 - \theta_i z_0) - f_0( x_0 - \theta_j z_0)} \nonumber\\ & = [x_0 : z_0] \in \mathbb{P}_k^1(k) = \mathscr{S}_F(k). \end{align}
\begin{align} \pi^{f_0 \cdot \delta}([1: 1 : \cdots : 1]) & = \frac{\theta_j (f_0 \cdot\delta_i) - \theta_i (f_0 \cdot \delta_j)}{f_0 \cdot \delta_i - f_0 \cdot \delta_j} = \frac{\theta_j \cdot f_0(x_0 - \theta_i z_0) - \theta_i \cdot f_0( x_0 - \theta_j z_0)}{f_0(x_0 - \theta_i z_0) - f_0( x_0 - \theta_j z_0)} \nonumber\\ & = [x_0 : z_0] \in \mathbb{P}_k^1(k) = \mathscr{S}_F(k). \end{align}
Now suppose ![]() $y_0 = 0$. Then one readily checks that the calculation in (73) goes through by replacing
$y_0 = 0$. Then one readily checks that the calculation in (73) goes through by replacing ![]() $[1 : 1 : \cdots : 1]$ with the point
$[1 : 1 : \cdots : 1]$ with the point ![]() $[0 : 1 : 1 : \cdots : 1] \in C^{f_0 \cdot \delta }(k)$.
$[0 : 1 : 1 : \cdots : 1] \in C^{f_0 \cdot \delta }(k)$.
We have, thus, completed our description of the ![]() $2$-coverings of
$2$-coverings of ![]() $\mathscr {S}_F$. The
$\mathscr {S}_F$. The ![]() $2$-coverings of
$2$-coverings of ![]() $\widetilde {S}_F$ are precisely the pullbacks of the coverings
$\widetilde {S}_F$ are precisely the pullbacks of the coverings ![]() $\pi ^\delta \colon C^\delta \to \mathscr {S}_F$ via the quotient map
$\pi ^\delta \colon C^\delta \to \mathscr {S}_F$ via the quotient map ![]() $\widetilde {S}_F \to \mathscr {S}_F$.
$\widetilde {S}_F \to \mathscr {S}_F$.
5.3 Proof of Theorem 2
Let ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ be irreducible, let
$F \in \mathscr {F}_{2n+1}(f_0)$ be irreducible, let ![]() $\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, and consider the associated
$\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$, and consider the associated ![]() $2$-covering
$2$-covering ![]() $\pi ^\delta \colon C^\delta \to \mathscr {S}_F$ over
$\pi ^\delta \colon C^\delta \to \mathscr {S}_F$ over ![]() $\mathbb {Q}$. We say that the
$\mathbb {Q}$. We say that the ![]() $2$-covering
$2$-covering ![]() $\pi ^\delta$ is locally soluble if for every place
$\pi ^\delta$ is locally soluble if for every place ![]() $v$ of
$v$ of ![]() $\mathbb {Q}$, there exists a point
$\mathbb {Q}$, there exists a point ![]() $P_v \in \mathscr {S}_F(\mathbb {Z}_v)$ such that the number
$P_v \in \mathscr {S}_F(\mathbb {Z}_v)$ such that the number ![]() $\delta _v$ associated to
$\delta _v$ associated to ![]() $P_v$ via (15) is such that
$P_v$ via (15) is such that ![]() $f_0 \cdot \delta _v$ is equal to the image of
$f_0 \cdot \delta _v$ is equal to the image of ![]() $\delta$ under the natural map
$\delta$ under the natural map ![]() $(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1} \to ((K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^\times /(K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^{\times 2})_{\operatorname {N}\equiv 1}$. (Note that, in this situation,
$(K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1} \to ((K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^\times /(K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^{\times 2})_{\operatorname {N}\equiv 1}$. (Note that, in this situation, ![]() $P_v \in \pi ^\delta (C^\delta (\mathbb {Q}_v))$ by Lemma 41.) Just as Bruin and Stoll did for hyperelliptic curves in [Reference Bruin and StollBS09, § 2], we define the fake
$P_v \in \pi ^\delta (C^\delta (\mathbb {Q}_v))$ by Lemma 41.) Just as Bruin and Stoll did for hyperelliptic curves in [Reference Bruin and StollBS09, § 2], we define the fake ![]() $2$-Selmer set
$2$-Selmer set ![]() $\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) \subset (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ to be the set of locally soluble
$\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) \subset (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$ to be the set of locally soluble ![]() $2$-coverings of
$2$-coverings of ![]() $\mathscr {S}_F$.
$\mathscr {S}_F$.
We claim that each element ![]() $\delta \in \operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!)$ gives rise to an orbit of
$\delta \in \operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!)$ gives rise to an orbit of ![]() $G(\mathbb {Z})$ on
$G(\mathbb {Z})$ on ![]() $V(\mathbb {Z})$, the associated
$V(\mathbb {Z})$, the associated ![]() $G(\mathbb {Q})$-orbit of which is represented by the class
$G(\mathbb {Q})$-orbit of which is represented by the class ![]() $\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$. For each place
$\delta \in (K_F^\times /K_F^{\times 2})_{\operatorname {N}\equiv 1}$. For each place ![]() $v$, let
$v$, let ![]() $P_v \in \mathscr {S}_F(\mathbb {Z}_v) \cap \pi ^\delta (C^\delta (\mathbb {Q}_v))$. Then via the construction in § 3,
$P_v \in \mathscr {S}_F(\mathbb {Z}_v) \cap \pi ^\delta (C^\delta (\mathbb {Q}_v))$. Then via the construction in § 3, ![]() $P_v$ naturally gives rise to an orbit of
$P_v$ naturally gives rise to an orbit of ![]() $G(\mathbb {Z}_v)$ on
$G(\mathbb {Z}_v)$ on ![]() $V(\mathbb {Z}_v)$, the associated
$V(\mathbb {Z}_v)$, the associated ![]() $G(\mathbb {Q}_v)$-orbit of which is represented by the class
$G(\mathbb {Q}_v)$-orbit of which is represented by the class ![]() $\delta \in ((K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^\times /(K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^{\times 2})_{\operatorname {N}\equiv 1}$. Since the algebraic group
$\delta \in ((K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^\times /(K_F\otimes _\mathbb {Q} \mathbb {Q}_v)^{\times 2})_{\operatorname {N}\equiv 1}$. Since the algebraic group ![]() $G$ has class number equal to
$G$ has class number equal to ![]() $1$, and since the orbit of
$1$, and since the orbit of ![]() $G(\mathbb {Q}_v)$ on
$G(\mathbb {Q}_v)$ on ![]() $V(\mathbb {Q}_v)$ associated to
$V(\mathbb {Q}_v)$ associated to ![]() $\delta$ has a representative over
$\delta$ has a representative over ![]() $\mathbb {Z}_v$ for every place
$\mathbb {Z}_v$ for every place ![]() $v$, it follows that the orbit of
$v$, it follows that the orbit of ![]() $G(\mathbb {Q})$ on
$G(\mathbb {Q})$ on ![]() $V(\mathbb {Q})$ has representative over
$V(\mathbb {Q})$ has representative over ![]() $\mathbb {Z}$. Thus, we have the claim.
$\mathbb {Z}$. Thus, we have the claim.
In the next lemma, we relate the fake ![]() $2$-Selmer set to the Brauer–Manin obstruction.
$2$-Selmer set to the Brauer–Manin obstruction.
Lemma 42 If ![]() $\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$, then
$\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$, then ![]() $\mathscr {S}_F$ has a Brauer–Manin obstruction to having a
$\mathscr {S}_F$ has a Brauer–Manin obstruction to having a ![]() $\mathbb {Z}$-point.
$\mathbb {Z}$-point.
Proof. Let ![]() $\pi \colon C \to \widetilde {S}_{F,\mathbb {Q}}$ be any
$\pi \colon C \to \widetilde {S}_{F,\mathbb {Q}}$ be any ![]() $2$-covering. We have by (69)–(72) that
$2$-covering. We have by (69)–(72) that
 \begin{align*} \mathscr{S}_F(\mathbb{A}_\mathbb{Q})^{\operatorname{Br}} & \subset \widetilde{S}_F(\mathbb{A}_\mathbb{Q})^{\operatorname{int}} \cap \widetilde{S}_{F,\mathbb{Q}}(\mathbb{A}_\mathbb{Q})^\pi = \bigg(\prod_{v} \mathscr{S}_F(\mathbb{Z}_v)\bigg) \cap \biggl(\bigcup_{\delta \in H^1(G_\mathbb{Q}, \operatorname{Pic}^0(\mathscr{S}_F\!)(\overline{\mathbb{Q}}))} \pi^\delta(C^\delta(\mathbb{A}_\mathbb{Q})) \biggr) \\ & \subset \bigcup_{\delta \in \operatorname{Sel}_{\operatorname{fake}}^2(\mathscr{S}_F\!)} \pi^\delta(C^\delta(\mathbb{A}_\mathbb{Q})), \end{align*}
\begin{align*} \mathscr{S}_F(\mathbb{A}_\mathbb{Q})^{\operatorname{Br}} & \subset \widetilde{S}_F(\mathbb{A}_\mathbb{Q})^{\operatorname{int}} \cap \widetilde{S}_{F,\mathbb{Q}}(\mathbb{A}_\mathbb{Q})^\pi = \bigg(\prod_{v} \mathscr{S}_F(\mathbb{Z}_v)\bigg) \cap \biggl(\bigcup_{\delta \in H^1(G_\mathbb{Q}, \operatorname{Pic}^0(\mathscr{S}_F\!)(\overline{\mathbb{Q}}))} \pi^\delta(C^\delta(\mathbb{A}_\mathbb{Q})) \biggr) \\ & \subset \bigcup_{\delta \in \operatorname{Sel}_{\operatorname{fake}}^2(\mathscr{S}_F\!)} \pi^\delta(C^\delta(\mathbb{A}_\mathbb{Q})), \end{align*}
and clearly the last union above is empty if ![]() $\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$.
$\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$.
In proving Theorem 1, we imposed local conditions on ![]() $V(\mathbb {Z})$ to sieve to the orbits that arise from local points at each place. By definition, the exact same local conditions define orbits that arise from elements of fake
$V(\mathbb {Z})$ to sieve to the orbits that arise from local points at each place. By definition, the exact same local conditions define orbits that arise from elements of fake ![]() $2$-Selmer sets. Moreover, if
$2$-Selmer sets. Moreover, if ![]() $F \in \mathscr {F}_{2n+1}(f_0) \smallsetminus \mathscr {F}_{2n+1}^*(f_0)$, Theorem 14 implies that the distinguished covering is not everywhere locally soluble. Thus, by the argument in § 4, we have the following result.
$F \in \mathscr {F}_{2n+1}(f_0) \smallsetminus \mathscr {F}_{2n+1}^*(f_0)$, Theorem 14 implies that the distinguished covering is not everywhere locally soluble. Thus, by the argument in § 4, we have the following result.
Theorem 43 The upper density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that ![]() $\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) \neq \varnothing$ is at most
$\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) \neq \varnothing$ is at most ![]() $\mu _{f_0} + o(2^{-n})$ when
$\mu _{f_0} + o(2^{-n})$ when ![]() $2 \nmid f_0$ and at most
$2 \nmid f_0$ and at most ![]() $\mu _{f_0} + O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ for some
$\mu _{f_0} + O(2^{-\varepsilon _1 n^{\varepsilon _2}})$ for some ![]() $\varepsilon _1, \varepsilon _2 > 0$ when
$\varepsilon _1, \varepsilon _2 > 0$ when ![]() $2 \mid f_0$.
$2 \mid f_0$.
To prove Theorem 2, it remains to determine how often it is that the stacky curves ![]() $\mathscr {S}_F$ have integral points everywhere locally. We do so as follows.
$\mathscr {S}_F$ have integral points everywhere locally. We do so as follows.
Lemma 44 The density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that ![]() $\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place
$\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place ![]() $v$ is at least
$v$ is at least ![]() $\mu _{f_0}' + O(2^{-2n})$.
$\mu _{f_0}' + O(2^{-2n})$.
Proof. By (1), we always have ![]() $\mathscr {S}_F(\mathbb {R}) \neq \varnothing$. If there is no prime
$\mathscr {S}_F(\mathbb {R}) \neq \varnothing$. If there is no prime ![]() $p \mid \kappa$ such that
$p \mid \kappa$ such that ![]() $F(x_0,z_0) = 0$ for every
$F(x_0,z_0) = 0$ for every ![]() $[x_0 : z_0] \in \mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, then for any prime
$[x_0 : z_0] \in \mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, then for any prime ![]() $p \mid \kappa$, there exists a pair
$p \mid \kappa$, there exists a pair ![]() $(x_0, z_0) \in \mathbb {Z}^2$ such that
$(x_0, z_0) \in \mathbb {Z}^2$ such that ![]() $\gcd (x_0, z_0) = \gcd (F(x_0, z_0),p) = 1$, so
$\gcd (x_0, z_0) = \gcd (F(x_0, z_0),p) = 1$, so ![]() $(x_0 \cdot F(x_0, z_0), F(x_0, z_0)^{n+1}, z_0 \cdot F(x_0, z_0)) \in \mathscr {S}_F(\mathbb {Z}_p)$. On the other hand, if
$(x_0 \cdot F(x_0, z_0), F(x_0, z_0)^{n+1}, z_0 \cdot F(x_0, z_0)) \in \mathscr {S}_F(\mathbb {Z}_p)$. On the other hand, if ![]() $p \mid \kappa$ and the mod-
$p \mid \kappa$ and the mod-![]() $p$ reduction of
$p$ reduction of ![]() $F$ has a simple zero at some point of
$F$ has a simple zero at some point of ![]() $\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, then
$\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$, then ![]() $\mathscr {S}_F$ has a Weierstrass point over
$\mathscr {S}_F$ has a Weierstrass point over ![]() $\mathbb {Z}_p$ and is, thus, soluble. Moreover, for any prime
$\mathbb {Z}_p$ and is, thus, soluble. Moreover, for any prime ![]() $p$ such that
$p$ such that ![]() $p \nmid \kappa$ but
$p \nmid \kappa$ but ![]() $p \mid f_0$, we have
$p \mid f_0$, we have ![]() $(\kappa,f_0^{{1}/{2}}\kappa ^{({2n+1})/{2}},0) \in \mathscr {S}_F(\mathbb {Z}_p)$, and for any prime
$(\kappa,f_0^{{1}/{2}}\kappa ^{({2n+1})/{2}},0) \in \mathscr {S}_F(\mathbb {Z}_p)$, and for any prime ![]() $p \nmid f_0$, we have
$p \nmid f_0$, we have ![]() $(f_0, f_0^{n+1},0) \in \mathscr {S}_F(\mathbb {Z}_p)$.
$(f_0, f_0^{n+1},0) \in \mathscr {S}_F(\mathbb {Z}_p)$.
If ![]() $p \mid \kappa$, the
$p \mid \kappa$, the ![]() $p$-adic density of forms
$p$-adic density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that the mod-
$F \in \mathscr {F}_{2n+1}(f_0)$ such that the mod-![]() $p$ reduction of
$p$ reduction of ![]() $F$ has a zero of multiplicity greater than
$F$ has a zero of multiplicity greater than ![]() $1$ at each point of
$1$ at each point of ![]() $\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$ is
$\mathbb {P}^1(\mathbb {Z}/p\mathbb {Z})$ is ![]() $p^{-2p-1}$ if
$p^{-2p-1}$ if ![]() $2p+2 < 2n+1$ and
$2p+2 < 2n+1$ and ![]() $p^{-2n-1}$ otherwise. Thus, the density of forms
$p^{-2n-1}$ otherwise. Thus, the density of forms ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ such that
$F \in \mathscr {F}_{2n+1}(f_0)$ such that ![]() $\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place
$\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place ![]() $v$ is at least
$v$ is at least ![]() $\prod _{p \mid \kappa } (1 - p^{-2p-1} - p^{-2n-1}) = \mu _{f_0}' + O(2^{-2n})$.
$\prod _{p \mid \kappa } (1 - p^{-2p-1} - p^{-2n-1}) = \mu _{f_0}' + O(2^{-2n})$.
It follows from Theorem 43 and Lemma 44 that for all sufficiently large ![]() $n$, a positive proportion of
$n$, a positive proportion of ![]() $F \in \mathscr {F}_{2n+1}(f_0)$ are such that
$F \in \mathscr {F}_{2n+1}(f_0)$ are such that ![]() $\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$ and
$\operatorname {Sel}_{\operatorname {fake}}^2(\mathscr {S}_F\!) = \varnothing$ and ![]() $\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place
$\mathscr {S}_F(\mathbb {Z}_v) \neq \varnothing$ for every place ![]() $v$. Indeed,
$v$. Indeed,
 \[ (1 - \mu_{f_0}) + (\mu_{f_0}' + O(2^{-2n})) = 1 - \prod_{p \mid \kappa} \frac{1}{p^2} + \prod_{p \mid \kappa} \bigg(1 - \frac{1}{p^{2p+1}}\bigg) + O(2^{-n}), \]
\[ (1 - \mu_{f_0}) + (\mu_{f_0}' + O(2^{-2n})) = 1 - \prod_{p \mid \kappa} \frac{1}{p^2} + \prod_{p \mid \kappa} \bigg(1 - \frac{1}{p^{2p+1}}\bigg) + O(2^{-n}), \]
which is clearly greater than ![]() $1$ for every sufficiently large
$1$ for every sufficiently large ![]() $n$. Theorem 2 now follows from Lemma 42.
$n$. Theorem 2 now follows from Lemma 42.
Acknowledgements
It is a pleasure to thank M. Bhargava for suggesting the questions that led to this paper and for providing invaluable advice and encouragement. We are immensely grateful to N. Bruin, S. Cho, B. Gross, B. Poonen, P. Sarnak, A. Shankar, M. Stoll, D. Zureick-Brown, and J. Wang for answering our questions and for sharing their insights. We thank the anonymous referee for providing numerous helpful comments and suggesting several revisions that have improved the readability of the paper. We also thank L. Alpöge, J. Harris, A. Landesman, D. Loughran, A. Patel, B. Romano, E. Sofos, J. Tao, and M. Wood for helpful discussions.
Funding
This research was supported by the Paul and Daisy Soros Fellowship and the NSF Graduate Research Fellowship.
Conflicts of interest
None.