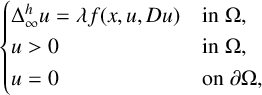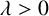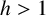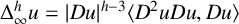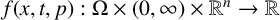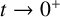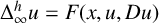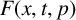1. Introduction
In this paper, we consider the singular boundary value problem
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{{in}}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega,\\ u=0 \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{{in}}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega,\\ u=0 \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
where the domain
![]() $\Omega \subseteq \mathbb {R}^{n}$
,
$\Omega \subseteq \mathbb {R}^{n}$
,
![]() $\lambda>0$
is a parameter and
$\lambda>0$
is a parameter and
 $$ \begin{align*} \Delta_\infty^h u:= |Du|^{h-3}\langle D^2uDu,Du \rangle =|Du|^{h-3}\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j},\quad h>1 \end{align*} $$
$$ \begin{align*} \Delta_\infty^h u:= |Du|^{h-3}\langle D^2uDu,Du \rangle =|Du|^{h-3}\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j},\quad h>1 \end{align*} $$
is the h-homogeneous quasilinear operator associated with the infinity Laplacian. The nonlinear term
![]() $f(x,t,p):\Omega \times (0,\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and may exhibit singularity at
$f(x,t,p):\Omega \times (0,\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and may exhibit singularity at
![]() $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
When
![]() $h = 3$
, the operator is the infinity Laplacian
$h = 3$
, the operator is the infinity Laplacian
 $$ \begin{align*} \Delta_\infty u:= \langle D^{2}uDu,Du \rangle =\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j}, \end{align*} $$
$$ \begin{align*} \Delta_\infty u:= \langle D^{2}uDu,Du \rangle =\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j}, \end{align*} $$
which was first introduced by Aronsson in the study of the absolutely minimizing Lipschitz extension (AMLE) [Reference Aronsson2–Reference Aronsson5] in the 1960s. The infinity Laplacian is quasilinear and highly degenerate, and the solutions are usually understood in the viscosity sense. See for example Crandall et al. [Reference Crandall, Ishii and Lions18]. In [Reference Jensen24], Jensen proved that the AMLE functions are equivalent to the infinity harmonic functions (viscosity solutions to the homogeneous infinity Laplacian equation
![]() $\Delta _{\infty }u=0$
) and also proved the existence and uniqueness of AMLE. In [Reference Crandall, Evans and Gariepy16], Crandall et al. showed that the infinity harmonic functions can be compared with linear cones that can be regarded as the fundamental solution of the equation
$\Delta _{\infty }u=0$
) and also proved the existence and uniqueness of AMLE. In [Reference Crandall, Evans and Gariepy16], Crandall et al. showed that the infinity harmonic functions can be compared with linear cones that can be regarded as the fundamental solution of the equation
![]() $\Delta _{\infty }u=0.$
For more results on the infinity harmonic functions, one can see [Reference Armstrong and Smart1, Reference Crandall and Evans15, Reference Crandall, Gunnarsson and Wang17].
$\Delta _{\infty }u=0.$
For more results on the infinity harmonic functions, one can see [Reference Armstrong and Smart1, Reference Crandall and Evans15, Reference Crandall, Gunnarsson and Wang17].
When
![]() $h = 1$
, the operator is the normalized infinity Laplacian
$h = 1$
, the operator is the normalized infinity Laplacian
 $$ \begin{align*} \Delta_\infty^{N} u:= |Du|^{-2}\langle D^{2}uDu,Du \rangle =|Du|^{-2}\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j}. \end{align*} $$
$$ \begin{align*} \Delta_\infty^{N} u:= |Du|^{-2}\langle D^{2}uDu,Du \rangle =|Du|^{-2}\sum_{i,j=1}^{n} \frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j} \frac{\partial^{2} u}{\partial x_i\partial x_j}. \end{align*} $$
Peres et al. [Reference Peres, Schramm, Sheffield and Wilson38] discovered a wonderful connection between the Dirichlet problem corresponding to the normalized infinity Laplacian and a random game named ‘tug-of-war’. The game is played by two players and the token is initially at any point
![]() $x_{0}\in \Omega $
. When the game starts, the two players take turns to move the token arbitrarily and the length of the movement is not greater than
$x_{0}\in \Omega $
. When the game starts, the two players take turns to move the token arbitrarily and the length of the movement is not greater than
![]() $\varepsilon>0$
. When one of the players moves the token to the point
$\varepsilon>0$
. When one of the players moves the token to the point
![]() $x\in \partial \Omega $
, the game is over and the players are rewarded or punished through the running payoff function f and the final payoff function g. As
$x\in \partial \Omega $
, the game is over and the players are rewarded or punished through the running payoff function f and the final payoff function g. As
![]() $\varepsilon \rightarrow 0$
, Peres et al. proved that the continuum value function of the game is the unique viscosity solution of the problem
$\varepsilon \rightarrow 0$
, Peres et al. proved that the continuum value function of the game is the unique viscosity solution of the problem
 $$ \begin{align} \begin{cases} \Delta_\infty^N u=f(x) &\mathrm{in}\; \Omega, \\ u=g &\mathrm{on} \;\partial\Omega \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^N u=f(x) &\mathrm{in}\; \Omega, \\ u=g &\mathrm{on} \;\partial\Omega \end{cases} \end{align} $$
for the continuous functions
![]() $f \; (|f|>0)$
and
$f \; (|f|>0)$
and
![]() $g.$
Lu and Wang [Reference Lu and Wang32] established the existence and uniqueness of the solution for the problem (1-2) based on partial differential equation methods. The normalized infinity Laplacian equations related to some ‘tug-of-war’ game have attracted increasingly more interest. The normalized infinity Laplacian with a transport term
$g.$
Lu and Wang [Reference Lu and Wang32] established the existence and uniqueness of the solution for the problem (1-2) based on partial differential equation methods. The normalized infinity Laplacian equations related to some ‘tug-of-war’ game have attracted increasingly more interest. The normalized infinity Laplacian with a transport term
 $$ \begin{align*} \begin{cases} \Delta_\infty^N u+\langle\xi,Du\rangle=0 &\mathrm{in}\; \Omega, \\ u=g &\mathrm{on} \;\partial\Omega \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_\infty^N u+\langle\xi,Du\rangle=0 &\mathrm{in}\; \Omega, \\ u=g &\mathrm{on} \;\partial\Omega \end{cases} \end{align*} $$
was first studied by L
![]() $\mathrm {\acute {o}}$
pez-Soriano et al. [Reference López-Soriano, Navarro-Climent and Rossi30]. When
$\mathrm {\acute {o}}$
pez-Soriano et al. [Reference López-Soriano, Navarro-Climent and Rossi30]. When
![]() $\xi $
is a continuous gradient vector field, they obtained the existence and uniqueness of the viscosity solutions. When
$\xi $
is a continuous gradient vector field, they obtained the existence and uniqueness of the viscosity solutions. When
![]() $\xi $
is Lipschitz continuous but not necessarily a gradient, they established the existence of viscosity solutions using ‘tug-of-war’ game arguments. In addition, Peres et al. [Reference Peres, Pete and Somersille37] introduced a biased ‘tug-of-war’ and showed the existence and uniqueness of viscosity solutions under the continuous Dirichlet boundary condition for the
$\xi $
is Lipschitz continuous but not necessarily a gradient, they established the existence of viscosity solutions using ‘tug-of-war’ game arguments. In addition, Peres et al. [Reference Peres, Pete and Somersille37] introduced a biased ‘tug-of-war’ and showed the existence and uniqueness of viscosity solutions under the continuous Dirichlet boundary condition for the
![]() $\beta $
-biased infinity Laplacian equation
$\beta $
-biased infinity Laplacian equation
where
![]() $\beta \in \mathbb {R}$
is a fixed constant denoting the bias. If
$\beta \in \mathbb {R}$
is a fixed constant denoting the bias. If
![]() $\beta =0$
, (1-3) reduces to the unbiased case.
$\beta =0$
, (1-3) reduces to the unbiased case.
In [Reference Lu and Wang31], Lu and Wang showed the existence and uniqueness of viscosity solutions for the inhomogeneous Dirichlet problem
 $$ \begin{align*} \begin{cases} \Delta_\infty u=f(x) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_\infty u=f(x) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
when the nonhomogeneous term f has one sign. Bhattacharya and Mohammed [Reference Bhattacharya and Mohammed7] studied the existence and nonexistence of viscosity solutions to the Dirichlet problem
 $$ \begin{align*} \begin{cases} \Delta_\infty u=f(x,u) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_\infty u=f(x,u) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
where f has sign and monotonicity restrictions. In [Reference Bhattacharya and Mohammed8], they presented some structure conditions on f and established the existence results without sign and monotonicity restrictions. Liu and Yang [Reference Liu and Yang29] gave existence and uniqueness results of viscosity solutions of the nonhomogeneous problem
 $$ \begin{align*} \begin{cases} \Delta_\infty^{h} u=f(x) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_\infty^{h} u=f(x) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
where
![]() $1\leq h\leq 3$
. In [Reference Li and Liu26], Li and Liu established the existence of viscosity solutions of the Dirichlet problem
$1\leq h\leq 3$
. In [Reference Li and Liu26], Li and Liu established the existence of viscosity solutions of the Dirichlet problem
 $$ \begin{align*} \begin{cases} \Delta_\infty^{h} u=f(x,u) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_\infty^{h} u=f(x,u) \quad &\mathrm{in}\; \Omega, \\ u=g \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$
when the right-hand side
![]() $f(x,t)$
is nondecreasing in t and nonincreasing in t. For other studies on the infinity Laplacian operator, one can refer to [Reference Liu27, Reference Mebrate and Mohammed33, Reference Mebrate and Mohammed34].
$f(x,t)$
is nondecreasing in t and nonincreasing in t. For other studies on the infinity Laplacian operator, one can refer to [Reference Liu27, Reference Mebrate and Mohammed33, Reference Mebrate and Mohammed34].
Over the years, the singular boundary value problem for the partial differential equation has attracted much attention and the earliest study on the singular boundary value problem was introduced by Fulks and Maybee in [Reference Fulks and Maybee21]. They studied the physical problem about heat conduction in electrically conducting materials. Let
![]() $\Omega \subseteq \mathbb {R}^{3}$
be occupied by an electrical conductor. Then each point
$\Omega \subseteq \mathbb {R}^{3}$
be occupied by an electrical conductor. Then each point
![]() $x\in \Omega $
becomes a source of heat when a current is passing through
$x\in \Omega $
becomes a source of heat when a current is passing through
![]() $\Omega $
. Suppose that the function
$\Omega $
. Suppose that the function
![]() $E(x,t)$
describes the local voltage drop in
$E(x,t)$
describes the local voltage drop in
![]() $\Omega $
and
$\Omega $
and
![]() $\sigma (u)$
is the electrical resistivity, where u is the temperature. According to the resistance heat generation formula,
$\sigma (u)$
is the electrical resistivity, where u is the temperature. According to the resistance heat generation formula,
![]() ${E^{2}(x,t)}\backslash {\sigma (u)}$
denotes the rate of generation of heat at any point x and time t. Let c and
${E^{2}(x,t)}\backslash {\sigma (u)}$
denotes the rate of generation of heat at any point x and time t. Let c and
![]() $\kappa $
be the specific heat and thermal conductivity of
$\kappa $
be the specific heat and thermal conductivity of
![]() $\Omega $
, respectively, which can be taken as constant. Then the temperature u at the point
$\Omega $
, respectively, which can be taken as constant. Then the temperature u at the point
![]() $x\in \Omega $
and time t satisfies
$x\in \Omega $
and time t satisfies
 $$ \begin{align} cu_{t}-\kappa\Delta u=\frac{E^{2}(x,t)}{\sigma(u)}. \end{align} $$
$$ \begin{align} cu_{t}-\kappa\Delta u=\frac{E^{2}(x,t)}{\sigma(u)}. \end{align} $$
In one simple case, one can take
![]() $\sigma (u)=\alpha u$
, where
$\sigma (u)=\alpha u$
, where
![]() $\alpha $
is a positive constant. It is obvious that
$\alpha $
is a positive constant. It is obvious that
![]() $\sigma (u)\rightarrow 0$
as
$\sigma (u)\rightarrow 0$
as
![]() $u\rightarrow 0$
. Thus, (1-4) is singular since the right-hand side becomes unbounded at
$u\rightarrow 0$
. Thus, (1-4) is singular since the right-hand side becomes unbounded at
![]() $u=0$
. This physical problem naturally leads to the study of the singular problem related to the parabolic Laplacian equation
$u=0$
. This physical problem naturally leads to the study of the singular problem related to the parabolic Laplacian equation
where
![]() $a^2={\kappa }/{c}$
and
$a^2={\kappa }/{c}$
and
![]() $F(x,t,u)={E^{2}(x,t)}/{c\sigma (u)}$
. The singular boundary value problems can be widely applied in non-Newtonian fluids, boundary layer phenomena for viscous fluids and chemical heterogeneous catalysts [Reference Diaz, Morel and Oswald19, Reference Esteban and Vásquez20, Reference Gomes22].
$F(x,t,u)={E^{2}(x,t)}/{c\sigma (u)}$
. The singular boundary value problems can be widely applied in non-Newtonian fluids, boundary layer phenomena for viscous fluids and chemical heterogeneous catalysts [Reference Diaz, Morel and Oswald19, Reference Esteban and Vásquez20, Reference Gomes22].
It is worth noting that
![]() $\Delta _{\infty }^{N}u=|Du|^{-2}\Delta _{\infty }u$
reduces to
$\Delta _{\infty }^{N}u=|Du|^{-2}\Delta _{\infty }u$
reduces to
![]() $\Delta u$
when the dimension is one. Therefore, it is natural to study the singular boundary value problems related to the infinity Laplacian. Bhattacharya and Mohammed [Reference Bhattacharya and Mohammed7] considered the singular boundary value problem
$\Delta u$
when the dimension is one. Therefore, it is natural to study the singular boundary value problems related to the infinity Laplacian. Bhattacharya and Mohammed [Reference Bhattacharya and Mohammed7] considered the singular boundary value problem
 $$ \begin{align} \begin{cases} -\Delta_\infty u=b(x)h(u) \quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} -\Delta_\infty u=b(x)h(u) \quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align} $$
where
![]() $b\in C(\Omega )\cap L^{\infty }(\Omega )$
is a positive function in
$b\in C(\Omega )\cap L^{\infty }(\Omega )$
is a positive function in
![]() $\Omega $
, and
$\Omega $
, and
![]() $h\in C(0,\infty )$
is positive and may exhibit singularity at zero, in other words,
$h\in C(0,\infty )$
is positive and may exhibit singularity at zero, in other words,
![]() $h(t)\rightarrow \infty $
as
$h(t)\rightarrow \infty $
as
![]() $t\rightarrow 0^{+}$
. They gave the existence, uniqueness and asymptotic behaviour of the positive viscosity solution of Problem (1-5). In [Reference Biset and Mohammed10], Biset and Mohammed extended the existence results of viscosity solutions to the singular boundary value problem
$t\rightarrow 0^{+}$
. They gave the existence, uniqueness and asymptotic behaviour of the positive viscosity solution of Problem (1-5). In [Reference Biset and Mohammed10], Biset and Mohammed extended the existence results of viscosity solutions to the singular boundary value problem
 $$ \begin{align*} \begin{cases} -\Delta_\infty u=\lambda f(x,u) \quad &\mathrm{in}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} -\Delta_\infty u=\lambda f(x,u) \quad &\mathrm{in}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega \end{cases} \end{align*} $$
in a bounded domain
![]() $\Omega $
as well as in the whole Euclidean space, where
$\Omega $
as well as in the whole Euclidean space, where
![]() $\lambda>0$
is a parameter. In [Reference Li and Liu26], Li and Liu established the existence, uniqueness and the asymptotic estimate of the viscosity solution to the singular boundary value problem
$\lambda>0$
is a parameter. In [Reference Li and Liu26], Li and Liu established the existence, uniqueness and the asymptotic estimate of the viscosity solution to the singular boundary value problem
 $$ \begin{align*} \begin{cases} -\Delta_\infty^h u=b(x)g(u) \quad &\mathrm{in}\; \Omega, \\ u>0 \quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} -\Delta_\infty^h u=b(x)g(u) \quad &\mathrm{in}\; \Omega, \\ u>0 \quad &\mathrm{in}\; \Omega, \\ u=0 \quad\quad &\mathrm{on} \;\partial\Omega. \end{cases} \end{align*} $$
For other studies of the singular boundary value problems, one can refer to [Reference Mohammed35, Reference Mohammed36, Reference Santos39].
Inspired by these works, we study the singular boundary value problem (1-1) of the strongly degenerate operator
![]() $\Delta _\infty ^h u$
. For all cases
$\Delta _\infty ^h u$
. For all cases
![]() $h>1,$
we prove that
$h>1,$
we prove that
![]() $\Delta_\infty^h$
share a common theory. Let us point out that, unlike the case
$\Delta_\infty^h$
share a common theory. Let us point out that, unlike the case
![]() $h = 1,$
the operator
$h = 1,$
the operator
![]() $ \Delta _\infty ^h $
is quasilinear even in dimension 1. Therefore, we must make subtle analysis. Our main results are as follows.
$ \Delta _\infty ^h $
is quasilinear even in dimension 1. Therefore, we must make subtle analysis. Our main results are as follows.
We first give the comparison principle for the following general equation:
Theorem 1.1. Let
![]() $\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain. Suppose that the function
$\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain. Suppose that the function
![]() $F(x,t,p)\in C(\Omega \times \mathbb {R}\times \mathbb {R}^{n})$
is negative and nondecreasing in t, and the map
$F(x,t,p)\in C(\Omega \times \mathbb {R}\times \mathbb {R}^{n})$
is negative and nondecreasing in t, and the map
![]() $\tau \mapsto F(x,t,\tau p)$
is nondecreasing in
$\tau \mapsto F(x,t,\tau p)$
is nondecreasing in
![]() $[1,\rho )$
for each
$[1,\rho )$
for each
![]() $(x,t,p)\in \Omega \times \mathbb {R}\times \mathbb {R}^{n}$
, where
$(x,t,p)\in \Omega \times \mathbb {R}\times \mathbb {R}^{n}$
, where
![]() $\rho>1$
. Assume that
$\rho>1$
. Assume that
![]() $u\in C(\overline {\Omega })$
and
$u\in C(\overline {\Omega })$
and
![]() $v\in C(\overline {\Omega })$
satisfy
$v\in C(\overline {\Omega })$
satisfy
and
in the viscosity sense, respectively. If
![]() $u\leq v$
on
$u\leq v$
on
![]() $\partial \Omega $
, then
$\partial \Omega $
, then
![]() $u\leq v$
in
$u\leq v$
in
![]() $\Omega $
.
$\Omega $
.
The proof of the comparison principle Theorem 1.1 is based on the double variables method in viscosity solution theory. If the nonhomogeneous term
![]() $F(x,u,Du)$
is independent of the gradient
$F(x,u,Du)$
is independent of the gradient
![]() $Du,$
Li and Liu proved the comparison principle for the equation
$Du,$
Li and Liu proved the comparison principle for the equation
![]() $\Delta _\infty ^h u= F(x,u)$
in [Reference Li and Liu25]. However, due to the strong degeneracy of the operator
$\Delta _\infty ^h u= F(x,u)$
in [Reference Li and Liu25]. However, due to the strong degeneracy of the operator
![]() $ \Delta _\infty ^h $
and the dependence of p of the nonlinear term
$ \Delta _\infty ^h $
and the dependence of p of the nonlinear term
![]() $F(x,t,p),$
we must perturb twice to make Jensen’s method useful [Reference Jensen24]. In [Reference Li and Liu25], they also established the existence of the boundary blow-up viscosity solution and analysed the boundary asymptotic behaviour of the blow-up solutions based on the comparison principle and Karamata’s regular variation theory, which was first introduced by Cîrstea and R
$F(x,t,p),$
we must perturb twice to make Jensen’s method useful [Reference Jensen24]. In [Reference Li and Liu25], they also established the existence of the boundary blow-up viscosity solution and analysed the boundary asymptotic behaviour of the blow-up solutions based on the comparison principle and Karamata’s regular variation theory, which was first introduced by Cîrstea and R
![]() $\check{\mathrm{a}}$
dulescu [Reference Cîrstea and Rǎdulescu11–Reference Cîrstea and Rǎdulescu13].
$\check{\mathrm{a}}$
dulescu [Reference Cîrstea and Rǎdulescu11–Reference Cîrstea and Rǎdulescu13].
Theorem 1.2. Let
![]() $\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain and
$\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain and
![]() $\varphi \in C(\partial \Omega )$
. Assume that
$\varphi \in C(\partial \Omega )$
. Assume that
![]() $F:\Omega \times \mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and satisfies
$F:\Omega \times \mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and satisfies
for every compact interval
![]() $I\subseteq \mathbb {R}.$
Suppose that
$I\subseteq \mathbb {R}.$
Suppose that
![]() $u_{*}\in C(\overline {\Omega })$
is a viscosity subsolution and
$u_{*}\in C(\overline {\Omega })$
is a viscosity subsolution and
![]() $u^{*}\in C(\overline {\Omega })$
is a viscosity supersolution of
$u^{*}\in C(\overline {\Omega })$
is a viscosity supersolution of
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=F(x,u,Du) \quad &\text{in } \Omega, \\ u=\varphi \quad &\text{on } \partial\Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=F(x,u,Du) \quad &\text{in } \Omega, \\ u=\varphi \quad &\text{on } \partial\Omega, \end{cases} \end{align} $$
in
![]() $\Omega $
. If
$\Omega $
. If
![]() $u_{*}\leq u^{*}$
in
$u_{*}\leq u^{*}$
in
![]() $\Omega $
, then the problem (1-8) admits a viscosity solution
$\Omega $
, then the problem (1-8) admits a viscosity solution
![]() $u\in C(\overline {\Omega })$
such that
$u\in C(\overline {\Omega })$
such that
![]() $u_{*}\leq u\leq u^{*}$
in
$u_{*}\leq u\leq u^{*}$
in
![]() $\Omega $
.
$\Omega $
.
Theorem 1.2 gives the existence of the viscosity solution of (1-8) when the nonlinear
![]() $F(x,t,p)$
is bounded in Condition (1-7) for the class of operators
$F(x,t,p)$
is bounded in Condition (1-7) for the class of operators
![]() $\Delta _{\infty }^{h}$
with a parameter
$\Delta _{\infty }^{h}$
with a parameter
![]() $h> 1. $
The method is based on the standard Perron idea. Let us point out that, unlike the case
$h> 1. $
The method is based on the standard Perron idea. Let us point out that, unlike the case
![]() $h = 1$
, the operator
$h = 1$
, the operator
![]() $\Delta _{\infty }^{h}$
is quasilinear even in dimension one. Hence, we must make subtle analysis. During this procedure, the construction of barrier functions is more complicated. This observation is very important for the study of the existence.
$\Delta _{\infty }^{h}$
is quasilinear even in dimension one. Hence, we must make subtle analysis. During this procedure, the construction of barrier functions is more complicated. This observation is very important for the study of the existence.
Obviously, taking
![]() $F(x,u,Du)=\lambda f(x,u,Du),$
one can immediately get the existence result of Problem (1-1) if
$F(x,u,Du)=\lambda f(x,u,Du),$
one can immediately get the existence result of Problem (1-1) if
![]() $f(x,u,Du)$
is bounded, that is
$f(x,u,Du)$
is bounded, that is
![]() $\sup \nolimits _{\Omega \times I\times \mathbb {R}^{n}}|f(x,u,Du)|<\infty $
. Now we turn to the singular boundary problem (1-1). That is,
$\sup \nolimits _{\Omega \times I\times \mathbb {R}^{n}}|f(x,u,Du)|<\infty $
. Now we turn to the singular boundary problem (1-1). That is,
![]() $f(x,t,p)$
may exhibit the singularity when
$f(x,t,p)$
may exhibit the singularity when
![]() $ t\rightarrow 0^{+}$
. We need some basic assumptions on the singular nonlinear term
$ t\rightarrow 0^{+}$
. We need some basic assumptions on the singular nonlinear term
![]() $f(x,t,p)$
to construct a viscosity subsolution and supersolution.
$f(x,t,p)$
to construct a viscosity subsolution and supersolution.
Let
![]() $\mathbb {R}^{+}:=(0,\infty )$
and
$\mathbb {R}^{+}:=(0,\infty )$
and
![]() $f(x,t,p):\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function that satisfies the following conditions.
$f(x,t,p):\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function that satisfies the following conditions.
(F-1): There are
![]() $t_{0}\in \mathbb {R}^{+}$
and two continuous functions
$t_{0}\in \mathbb {R}^{+}$
and two continuous functions
![]() $k:(0,t_{0})\rightarrow \mathbb {R}^{+}$
and
$k:(0,t_{0})\rightarrow \mathbb {R}^{+}$
and
![]() $a:\overline {\Omega }\rightarrow \mathbb {R}^{+}$
such that
$a:\overline {\Omega }\rightarrow \mathbb {R}^{+}$
such that
(F-2): There are two continuous functions
![]() $g:\mathbb {R}^{+}\rightarrow \mathbb {R}^{+}$
and
$g:\mathbb {R}^{+}\rightarrow \mathbb {R}^{+}$
and
![]() $b:\Omega \rightarrow \mathbb {R}^{+}$
such that
$b:\Omega \rightarrow \mathbb {R}^{+}$
such that
Now we define the following notation in connection with the functions k and g:
We always assume that
![]() $0<k_{0}\leq \infty $
.
$0<k_{0}\leq \infty $
.
Furthermore, we assume that the function b in Condition (F-2) above satisfies the following condition.
(B-w): The following problem:
 $$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\mathrm{{in}}\; \Omega, \\ w>0 \quad &\mathrm{in}\; \Omega,\\ w=0 \quad &\mathrm{on} \; \partial\Omega \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\mathrm{{in}}\; \Omega, \\ w>0 \quad &\mathrm{in}\; \Omega,\\ w=0 \quad &\mathrm{on} \; \partial\Omega \end{cases} \end{align} $$
admits a viscosity solution
![]() $w_{\Omega }\in C(\overline {\Omega })$
. When the function
$w_{\Omega }\in C(\overline {\Omega })$
. When the function
![]() $b\in C(\Omega )$
is positive, the existence of the Problem (1-10) has been established by Li and Liu (see [Reference Li and Liu26]).
$b\in C(\Omega )$
is positive, the existence of the Problem (1-10) has been established by Li and Liu (see [Reference Li and Liu26]).
To investigate the existence of the viscosity solutions to the singular boundary value problem (1-1), one key is to find a viscosity subsolution. Due to the nonlinear term
![]() $f(x,t,p)$
on the right-hand side, it is difficult to construct a viscosity subsolution. Here we adopt the principal eigenfunction for the following eigenvalue problem:
$f(x,t,p)$
on the right-hand side, it is difficult to construct a viscosity subsolution. Here we adopt the principal eigenfunction for the following eigenvalue problem:
 $$ \begin{align} \begin{cases} \Delta_\infty^h u+\mu a(x)u^{h}=0 \quad &\mathrm{{in}}\; \Omega, \\ u=0 \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u+\mu a(x)u^{h}=0 \quad &\mathrm{{in}}\; \Omega, \\ u=0 \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
where
![]() $\Omega $
is a bounded domain and
$\Omega $
is a bounded domain and
![]() $a(x)$
is a positive continuous function in
$a(x)$
is a positive continuous function in
![]() $\overline {\Omega }.$
Liu et al. [Reference Liu, Tian and Zhao28] established the existence of a positive principal eigenfunction
$\overline {\Omega }.$
Liu et al. [Reference Liu, Tian and Zhao28] established the existence of a positive principal eigenfunction
![]() $\Phi _{\Omega }$
and gave a characteristic for the principal eigenvalue
$\Phi _{\Omega }$
and gave a characteristic for the principal eigenvalue
![]() $\Lambda _{1}(\Omega )$
of Problem (1-11). Additionally, it is obvious that
$\Lambda _{1}(\Omega )$
of Problem (1-11). Additionally, it is obvious that
![]() $\Lambda _{1}(\Omega _{1})\geq \Lambda _{1}(\Omega _{2})$
if
$\Lambda _{1}(\Omega _{1})\geq \Lambda _{1}(\Omega _{2})$
if
![]() $\Omega _{1}\subseteq \Omega _{2}$
. Since the principal Dirichlet-eigenvalue
$\Omega _{1}\subseteq \Omega _{2}$
. Since the principal Dirichlet-eigenvalue
![]() $\Lambda _{1}(\Omega )$
and the corresponding eigenfunction
$\Lambda _{1}(\Omega )$
and the corresponding eigenfunction
![]() $\Phi _{\Omega }$
are both positive, we need the positivity of
$\Phi _{\Omega }$
are both positive, we need the positivity of
![]() $k_0$
as in (1-9) to construct an appropriate viscosity subsolution and then Perron’s method guarantees the existence of viscosity solutions to the singular boundary problem (1-1).
$k_0$
as in (1-9) to construct an appropriate viscosity subsolution and then Perron’s method guarantees the existence of viscosity solutions to the singular boundary problem (1-1).
Theorem 1.3. Let
![]() $ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
$ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
![]() $f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function. If f satisfies the conditions (F-1), (F-2) and b satisfies the condition (B-w), then there exists a constant
$f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function. If f satisfies the conditions (F-1), (F-2) and b satisfies the condition (B-w), then there exists a constant
![]() $\lambda _\Omega ^\ast $
depending on
$\lambda _\Omega ^\ast $
depending on
![]() $ \Omega , g_{\infty }$
and
$ \Omega , g_{\infty }$
and
![]() $\|w_{\Omega }\|_{\infty }$
such that Problem (1-1) admits a viscosity solution
$\|w_{\Omega }\|_{\infty }$
such that Problem (1-1) admits a viscosity solution
![]() $u=u_{\lambda }\in C(\overline {\Omega })$
for any
$u=u_{\lambda }\in C(\overline {\Omega })$
for any
![]() $\lambda $
with
$\lambda $
with
![]() $\Lambda _{1}(\Omega )k_{0}^{-1}<\lambda <\lambda _{\Omega }^{\ast }$
.
$\Lambda _{1}(\Omega )k_{0}^{-1}<\lambda <\lambda _{\Omega }^{\ast }$
.
Theorem 1.3 shows the existence of the viscosity solution of the singular boundary value problem (1-1) when the parameter
![]() $\lambda $
is lying in an appropriate range, that is
$\lambda $
is lying in an appropriate range, that is
![]() $\Lambda _{1}(\Omega )k_{0}^{-1}<\lambda <\lambda _{\Omega }^{\ast }.$
To overcome the difficulty of the singularity of Problem (1-1), we construct the appropriate cut-off function and then use the comparison principle, compactness analysis and Perron’s method to establish the existence of the viscosity solution. Due to the high degeneracy and quasilinearity of the operator
$\Lambda _{1}(\Omega )k_{0}^{-1}<\lambda <\lambda _{\Omega }^{\ast }.$
To overcome the difficulty of the singularity of Problem (1-1), we construct the appropriate cut-off function and then use the comparison principle, compactness analysis and Perron’s method to establish the existence of the viscosity solution. Due to the high degeneracy and quasilinearity of the operator
![]() $\Delta _\infty ^h$
and the singularity of the nonlinear term
$\Delta _\infty ^h$
and the singularity of the nonlinear term
![]() $f(x,t,p)$
, we cannot follow the scheme in [Reference Biset, Mebrate and Mohammed9]. To overcome this difficulty, we propose conditions (F-1) and (F-2) and then construct a suitable viscosity supersolution of Problem (1-10). However, we invoke the positive eigenfunction of the eigenvalue problem (1-11) to construct an appropriate viscosity subsolution to Problem (1-1). Then by the standard Perron method, we can obtain the existence of the viscosity solution of the singular boundary value problem.
$f(x,t,p)$
, we cannot follow the scheme in [Reference Biset, Mebrate and Mohammed9]. To overcome this difficulty, we propose conditions (F-1) and (F-2) and then construct a suitable viscosity supersolution of Problem (1-10). However, we invoke the positive eigenfunction of the eigenvalue problem (1-11) to construct an appropriate viscosity subsolution to Problem (1-1). Then by the standard Perron method, we can obtain the existence of the viscosity solution of the singular boundary value problem.
With Theorem 1.3 in hand, we can establish the existence result of the singular problem in the entire Euclidean space by the approximation procedure. Due to the strong degeneracy of the operator, we need the following additional monotone condition (F-3) on the nonlinear term
![]() $f(x,t,p)$
. Note that it would be interesting to consider the singular problem on unbounded domains other than
$f(x,t,p)$
. Note that it would be interesting to consider the singular problem on unbounded domains other than
![]() $\mathbb {R}^n.$
$\mathbb {R}^n.$
(F-3): For any
![]() $(x,t,p)\in \Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}$
, the function
$(x,t,p)\in \Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}$
, the function
![]() $t\rightarrow {f(x,t,tp)}/{a(x)t^{h}}$
is nondecreasing in t, where the function
$t\rightarrow {f(x,t,tp)}/{a(x)t^{h}}$
is nondecreasing in t, where the function
![]() $a(x)$
is the one in (F-1).
$a(x)$
is the one in (F-1).
Theorem 1.4. Let f satisfy the conditions (F-1), (F-2) and (F-3) in
![]() $\mathbb {R}^{n}$
, where b satisfies the condition (B-w). Then for any
$\mathbb {R}^{n}$
, where b satisfies the condition (B-w). Then for any
![]() $\lambda $
with
$\lambda $
with
![]() $\Lambda _{1}(B(O,1))k_{0}^{-1}<\lambda <\lambda ^{*}$
, the problem
$\Lambda _{1}(B(O,1))k_{0}^{-1}<\lambda <\lambda ^{*}$
, the problem
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\text{in } \mathbb{R}^{n}, \\ u>0 \quad &\text{in } \mathbb{R}^{n}, \\ u(x)\rightarrow 0 \quad &\text{as } |x|\rightarrow\infty \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\text{in } \mathbb{R}^{n}, \\ u>0 \quad &\text{in } \mathbb{R}^{n}, \\ u(x)\rightarrow 0 \quad &\text{as } |x|\rightarrow\infty \end{cases} \end{align} $$
admits a viscosity solution
![]() $u=u_{\lambda }\in C(\mathbb {R}^{n})$
, where
$u=u_{\lambda }\in C(\mathbb {R}^{n})$
, where
![]() $\Lambda _{1}(B(O,1))$
is the principal eigenvalue of Problem (1-11) on the unit ball
$\Lambda _{1}(B(O,1))$
is the principal eigenvalue of Problem (1-11) on the unit ball
![]() $\Omega =B(O,1)$
.
$\Omega =B(O,1)$
.
The paper is organized as follows. In Section 2, we give the definition of the viscosity solutions and establish the comparison principle by the double variables method based on viscosity solutions theory. In Section 3, we prove the existence of the viscosity solutions to the boundary value problem by Perron’s method if the nonlinear term on the right-hand side is bounded. In Section 4, we establish the existence of the viscosity solution of the singular boundary problem (1-1) in a bounded domain
![]() $\Omega $
by truncation and Perron’s method. In Section 5, we extend the existence result to the entire Euclidean space by the approximation procedure.
$\Omega $
by truncation and Perron’s method. In Section 5, we extend the existence result to the entire Euclidean space by the approximation procedure.
2. Comparison principle
In this section, we first give the definition of viscosity solutions to the general equation
where
![]() $F:\Omega \times \mathbb {R}\times \mathbb {R} ^n \rightarrow \mathbb {R}$
is continuous. Then we establish the comparison principle by the perturbation method based on viscosity solutions theory.
$F:\Omega \times \mathbb {R}\times \mathbb {R} ^n \rightarrow \mathbb {R}$
is continuous. Then we establish the comparison principle by the perturbation method based on viscosity solutions theory.
Since the operator
![]() $\Delta _{\infty }^{h}$
is highly degenerate and singular at the points where the gradient vanishes, one should give an appropriate explanation at these points. Here we adopt the viscosity solutions based on the semicontinuous extension [Reference Crandall, Ishii and Lions18, Reference Ishii23]. Note that one can rewrite (2-1) as
$\Delta _{\infty }^{h}$
is highly degenerate and singular at the points where the gradient vanishes, one should give an appropriate explanation at these points. Here we adopt the viscosity solutions based on the semicontinuous extension [Reference Crandall, Ishii and Lions18, Reference Ishii23]. Note that one can rewrite (2-1) as
where
![]() $G_{h}:\mathbb {S}\times (\mathbb {R}^{n}\setminus \{0\})\rightarrow \mathbb {R}, G_{h}(X,p):=|p|^{h-3}(Xp)\cdot p$
and
$G_{h}:\mathbb {S}\times (\mathbb {R}^{n}\setminus \{0\})\rightarrow \mathbb {R}, G_{h}(X,p):=|p|^{h-3}(Xp)\cdot p$
and
![]() $\mathbb {S}$
is the set of all
$\mathbb {S}$
is the set of all
![]() $n\times n$
real symmetric matrices. When
$n\times n$
real symmetric matrices. When
![]() $h>1$
, we have
$h>1$
, we have
![]() $\lim \nolimits _{p\rightarrow 0}G_{h}(X,p)=0$
for any
$\lim \nolimits _{p\rightarrow 0}G_{h}(X,p)=0$
for any
![]() $X\in \mathbb {S}$
. Thus, we can define the following continuous extension of
$X\in \mathbb {S}$
. Thus, we can define the following continuous extension of
![]() $G_{h}$
:
$G_{h}$
:
 $$ \begin{align*} \overline{G}_{h}(X,p)=\begin{cases} G_{h}(X,p) \quad &\mathrm{if}\; p\neq 0, \\ 0 \quad\quad &\mathrm{if} \; p=0. \end{cases} \end{align*} $$
$$ \begin{align*} \overline{G}_{h}(X,p)=\begin{cases} G_{h}(X,p) \quad &\mathrm{if}\; p\neq 0, \\ 0 \quad\quad &\mathrm{if} \; p=0. \end{cases} \end{align*} $$
Now we give the definition of viscosity solutions to (2-1).
Definition 2.1. Let
![]() $\Omega \subseteq \mathbb {R}^{n}$
be a domain. An upper semicontinuous (USC) function u defined in
$\Omega \subseteq \mathbb {R}^{n}$
be a domain. An upper semicontinuous (USC) function u defined in
![]() $\Omega $
is said to be a viscosity subsolution of (2-1) if and only if for every
$\Omega $
is said to be a viscosity subsolution of (2-1) if and only if for every
![]() $x_{0}\in \Omega $
and
$x_{0}\in \Omega $
and
![]() $\varphi \in C^{2}(\Omega )$
such that
$\varphi \in C^{2}(\Omega )$
such that
![]() $u(x_{0})=\varphi (x_{0})$
and
$u(x_{0})=\varphi (x_{0})$
and
![]() $u(x)\leq \varphi (x)$
for all
$u(x)\leq \varphi (x)$
for all
![]() $x\in \Omega $
near
$x\in \Omega $
near
![]() $x_{0}$
, there holds
$x_{0}$
, there holds
Similarly, a lower semicontinuous (LSC) function u defined in
![]() $\Omega $
is said to be a viscosity supersolution of (2-1) if and only if for every
$\Omega $
is said to be a viscosity supersolution of (2-1) if and only if for every
![]() $x_{0}\in \Omega $
and
$x_{0}\in \Omega $
and
![]() $\varphi \in C^{2}(\Omega )$
such that
$\varphi \in C^{2}(\Omega )$
such that
![]() $u(x_{0})=\varphi (x_{0})$
and
$u(x_{0})=\varphi (x_{0})$
and
![]() $u(x)\geq \varphi (x)$
for all
$u(x)\geq \varphi (x)$
for all
![]() $x\in \Omega $
near
$x\in \Omega $
near
![]() $x_{0}$
, there holds
$x_{0}$
, there holds
If a continuous function
![]() $u\in C(\Omega )$
is both a viscosity supersolution and a viscosity subsolution of (2-1), then we say that u is a viscosity solution of (2-1).
$u\in C(\Omega )$
is both a viscosity supersolution and a viscosity subsolution of (2-1), then we say that u is a viscosity solution of (2-1).
Note that one can give the definition of viscosity subsolutions and viscosity supersolutions equivalently by super-jets and sub-jets. We first recall the definition of super-jets and sub-jets, and then give an equivalent definition of viscosity subsolutions and viscosity supersolutions. One can see the details in for example [Reference Crandall, Ishii and Lions18].
Definition 2.2. The second-order super-jet of
![]() $u\in \mathrm {{USC}} (\Omega )$
at
$u\in \mathrm {{USC}} (\Omega )$
at
![]() $x_{0}\in \Omega $
is the set
$x_{0}\in \Omega $
is the set
and the closure of
![]() $\mathcal {J}^{2,+}u(x_{0})$
is
$\mathcal {J}^{2,+}u(x_{0})$
is
 $$ \begin{align*} \overline{\mathcal{J}}^{2,+}u(x_{0}):=\Big\{&(p,X)\in \mathbb{R}^{n}\times\mathbb{S} :\text{there exists } (x_{n},p_{n}, X_{n})\in \Omega \times \mathbb{R}^{n}\times\mathbb{S} \text{ such that }\\ &(p_{n}, X_{n})\in \mathcal{J}^{2,+}u(x_{n})\text{ and } (x_{n},u(x_{n}),p_{n},X_{n}) \rightarrow(x_{0},u(x_{0}),p,X)\Big\}. \end{align*} $$
$$ \begin{align*} \overline{\mathcal{J}}^{2,+}u(x_{0}):=\Big\{&(p,X)\in \mathbb{R}^{n}\times\mathbb{S} :\text{there exists } (x_{n},p_{n}, X_{n})\in \Omega \times \mathbb{R}^{n}\times\mathbb{S} \text{ such that }\\ &(p_{n}, X_{n})\in \mathcal{J}^{2,+}u(x_{n})\text{ and } (x_{n},u(x_{n}),p_{n},X_{n}) \rightarrow(x_{0},u(x_{0}),p,X)\Big\}. \end{align*} $$
Similarly, the second-order sub-jet of
![]() $u\in \mathrm {{LSC}} (\Omega )$
at
$u\in \mathrm {{LSC}} (\Omega )$
at
![]() $x_{0}\in \Omega $
is the set
$x_{0}\in \Omega $
is the set
and the closure of
![]() $\mathcal {J}^{2,-}u(x_{0})$
is
$\mathcal {J}^{2,-}u(x_{0})$
is
 $$ \begin{align*} \overline{\mathcal{J}}^{2,-}u(x_{0}):=\Big\{&(p,X)\in \mathbb{R}^{n}\times\mathbb{S} :\text{there exists } (x_{n},p_{n}, X_{n})\in \Omega \times \mathbb{R}^{n}\times\mathbb{S} \text{ such that }\\ &(p_{n}, X_{n})\in \mathcal{J}^{2,-}u(x_{n})\text{ and } (x_{n},u(x_{n}),p_{n},X_{n}) \rightarrow(x_{0},u(x_{0}),p,X)\Big\}. \end{align*} $$
$$ \begin{align*} \overline{\mathcal{J}}^{2,-}u(x_{0}):=\Big\{&(p,X)\in \mathbb{R}^{n}\times\mathbb{S} :\text{there exists } (x_{n},p_{n}, X_{n})\in \Omega \times \mathbb{R}^{n}\times\mathbb{S} \text{ such that }\\ &(p_{n}, X_{n})\in \mathcal{J}^{2,-}u(x_{n})\text{ and } (x_{n},u(x_{n}),p_{n},X_{n}) \rightarrow(x_{0},u(x_{0}),p,X)\Big\}. \end{align*} $$
Definition 2.3. We say that
![]() $u\in \mathrm {{USC}}(\Omega )$
is a viscosity subsolution of (2-1) if
$u\in \mathrm {{USC}}(\Omega )$
is a viscosity subsolution of (2-1) if
Similarly, we say that
![]() $u\in \mathrm {{LSC}}(\Omega )$
is a viscosity supersolution of (2-1) if
$u\in \mathrm {{LSC}}(\Omega )$
is a viscosity supersolution of (2-1) if
If a continuous function
![]() $u\in C(\Omega ) $
is both a viscosity supersolution and viscosity subsolution of (2-1), we say that u is a viscosity solution of (2-1).
$u\in C(\Omega ) $
is both a viscosity supersolution and viscosity subsolution of (2-1), we say that u is a viscosity solution of (2-1).
By the definition of the viscosity subsolution (supersolution), one can easily get the following results.
Remark 2.4.
![]() $(1)$
If
$(1)$
If
![]() $u_{1}, u_{2}$
are viscosity subsolutions of (2-1), then
$u_{1}, u_{2}$
are viscosity subsolutions of (2-1), then
![]() $\max \{u_{1}, u_{2}\}$
is a viscosity subsolution of (2-1) as well.
$\max \{u_{1}, u_{2}\}$
is a viscosity subsolution of (2-1) as well.
![]() $(2)$
If
$(2)$
If
![]() $u_{1}, u_{2}$
are viscosity supersolutions of (2-1), then
$u_{1}, u_{2}$
are viscosity supersolutions of (2-1), then
![]() $\min \{u_{1}, u_{2}\}$
is a viscosity supersolution of (2-1) as well.
$\min \{u_{1}, u_{2}\}$
is a viscosity supersolution of (2-1) as well.
Now we give the local Lipschitz continuity of a viscosity solution to
![]() $\Delta _{\infty }^{h}u= \alpha ,$
where
$\Delta _{\infty }^{h}u= \alpha ,$
where
![]() $\alpha $
is a constant. For more regularity results of infinity Laplacian equations, one can see [Reference Bhattacharya and Mohammed8, Reference Lu and Wang31].
$\alpha $
is a constant. For more regularity results of infinity Laplacian equations, one can see [Reference Bhattacharya and Mohammed8, Reference Lu and Wang31].
Lemma 2.5. Let
![]() $\alpha $
be a constant. If
$\alpha $
be a constant. If
![]() $u\in C(\Omega )\bigcap L^{\infty }(\Omega )$
satisfies
$u\in C(\Omega )\bigcap L^{\infty }(\Omega )$
satisfies
![]() $\Delta _{\infty }^{h}u\geq \alpha $
in the viscosity sense, then u is locally Lipschitz continuous in
$\Delta _{\infty }^{h}u\geq \alpha $
in the viscosity sense, then u is locally Lipschitz continuous in
![]() $\Omega $
. Moreover, for any given
$\Omega $
. Moreover, for any given
![]() $x_{0}\in \Omega $
, there exists a constant C such that
$x_{0}\in \Omega $
, there exists a constant C such that
where C depends on
![]() $x_{0}, \mathrm {diam}(\Omega ), |\alpha |$
and
$x_{0}, \mathrm {diam}(\Omega ), |\alpha |$
and
![]() $\|u\|_{L^{\infty }(\Omega )}$
. A similar result holds if u satisfies
$\|u\|_{L^{\infty }(\Omega )}$
. A similar result holds if u satisfies
![]() $\Delta _{\infty }^{h}u\leq \alpha $
.
$\Delta _{\infty }^{h}u\leq \alpha $
.
Proof. Let
![]() $d(x_0):=\mathrm {dist}(x_0,\partial \Omega )$
for each
$d(x_0):=\mathrm {dist}(x_0,\partial \Omega )$
for each
![]() $x_0\in \Omega $
. Set
$x_0\in \Omega $
. Set
where
![]() $M:=\max \nolimits _\Omega u$
and
$M:=\max \nolimits _\Omega u$
and
![]() $m:=\min \nolimits _\Omega u$
. For all
$m:=\min \nolimits _\Omega u$
. For all
![]() $y\in B_{{d(x_0)}/{3}}(x_0)$
, we consider the function
$y\in B_{{d(x_0)}/{3}}(x_0)$
, we consider the function
where
![]() $k:= k(x_0)$
is defined in (2-2). Note that
$k:= k(x_0)$
is defined in (2-2). Note that
![]() $\psi \in C^{\infty }(\mathbb {R}^{n}-\{y\})$
. For
$\psi \in C^{\infty }(\mathbb {R}^{n}-\{y\})$
. For
![]() $x\neq y$
,
$x\neq y$
,
Since
![]() $k\geq 1+|\alpha |\mathrm {diam}(\Omega )$
, we see that
$k\geq 1+|\alpha |\mathrm {diam}(\Omega )$
, we see that
![]() $\Delta _{\infty }^{h}\psi \leq \alpha $
in
$\Delta _{\infty }^{h}\psi \leq \alpha $
in
![]() $\Omega \setminus \{y\}$
. Note that
$\Omega \setminus \{y\}$
. Note that
![]() $d(y)\geq {2d(x_0)}/{3}$
for any
$d(y)\geq {2d(x_0)}/{3}$
for any
![]() $y\in B_{{d(x_0)}/{3}}(x_0)$
. For any
$y\in B_{{d(x_0)}/{3}}(x_0)$
. For any
![]() $x\in \partial B_{d(y)}(y)$
,
$x\in \partial B_{d(y)}(y)$
,
 $$ \begin{align*} \begin{aligned} \psi(x)&=u(y)+kd(y)-\frac{|\alpha|}{2}d^{2}(y)\\ &\geq m+\frac{d(x_0)}{2}\left(k-\frac{|\alpha|}{2}d(y)\right)\\ &\geq m+\frac{d(x_0)}{2}\left(k-\frac{|\alpha|}{2}\mathrm{diam}(\Omega)\right)\geq M\geq u(x), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi(x)&=u(y)+kd(y)-\frac{|\alpha|}{2}d^{2}(y)\\ &\geq m+\frac{d(x_0)}{2}\left(k-\frac{|\alpha|}{2}d(y)\right)\\ &\geq m+\frac{d(x_0)}{2}\left(k-\frac{|\alpha|}{2}\mathrm{diam}(\Omega)\right)\geq M\geq u(x), \end{aligned} \end{align*} $$
where we use (2-2). Therefore,
![]() $u\leq \psi $
on
$u\leq \psi $
on
![]() $\partial (B_{d(y)}(y)\setminus \{y\})$
. Since
$\partial (B_{d(y)}(y)\setminus \{y\})$
. Since
![]() $\Delta _{\infty }^{h}\psi \leq \alpha $
and
$\Delta _{\infty }^{h}\psi \leq \alpha $
and
![]() $\Delta _{\infty }^{h}u\geq \alpha $
in
$\Delta _{\infty }^{h}u\geq \alpha $
in
![]() $B_{d(y)}(y)\setminus \{y\}$
, by the comparison principle in [Reference Li and Liu25], we have
$B_{d(y)}(y)\setminus \{y\}$
, by the comparison principle in [Reference Li and Liu25], we have
![]() $u\leq \psi $
in
$u\leq \psi $
in
![]() $B_{d(y)}(y)$
. Thus, for any
$B_{d(y)}(y)$
. Thus, for any
![]() $y\in B_{{d(x_0)}/{3}}(x_0)$
and any
$y\in B_{{d(x_0)}/{3}}(x_0)$
and any
![]() $z\in B_{d(y)}(y)$
,
$z\in B_{d(y)}(y)$
,
For any
![]() $p\in B_{{d(x_0)}/{3}}(x_0)$
, one has
$p\in B_{{d(x_0)}/{3}}(x_0)$
, one has
![]() $B_{{d(x_0)}/{3}}(x_0)\subseteq B_{d(p)}(p)$
. According to (2-3), for any
$B_{{d(x_0)}/{3}}(x_0)\subseteq B_{d(p)}(p)$
. According to (2-3), for any
![]() $x, y\in B_{{d(x_0)}/{3}}(x_0),$
$x, y\in B_{{d(x_0)}/{3}}(x_0),$
and
That is,
Thus, for a given
![]() $x_{0}\in \Omega $
,
$x_{0}\in \Omega $
,
where C depends on
![]() $x_{0}, \mathrm {diam}(\Omega ), |\alpha |$
and
$x_{0}, \mathrm {diam}(\Omega ), |\alpha |$
and
![]() $\|u\|_{L^{\infty }(\Omega )}$
.
$\|u\|_{L^{\infty }(\Omega )}$
.
Now we recall the maximum principle of infinity harmonic functions [Reference Aronsson, Crandall and Juutinen6, Reference Crandall14].
Lemma 2.6. If
![]() $u\in C(\overline {\Omega })$
satisfies
$u\in C(\overline {\Omega })$
satisfies
![]() $\Delta _{\infty }u\geq 0$
in the viscosity sense, then u attains its maximum only on the boundary
$\Delta _{\infty }u\geq 0$
in the viscosity sense, then u attains its maximum only on the boundary
![]() $\partial \Omega $
unless u is a constant.
$\partial \Omega $
unless u is a constant.
Proof of Theorem 1.1.
Define
Since
![]() $F(x,t,p)$
is negative, nondecreasing in t and
$F(x,t,p)$
is negative, nondecreasing in t and
![]() $\tau \rightarrow F(x,t,\tau p)$
is nondecreasing in
$\tau \rightarrow F(x,t,\tau p)$
is nondecreasing in
![]() $[1,\rho )$
,
$[1,\rho )$
,
 $$ \begin{align*} \Delta_\infty^h v_{\varepsilon}&=(1+\varepsilon)^{h}\Delta_\infty^h v\\ &\leq(1+\varepsilon)^{h}F(x,v,Dv)\\ &\leq(1+\varepsilon)^{h}F(x,v_{\varepsilon},Dv_{\varepsilon})\\ &< F(x,v_{\varepsilon},Dv_{\varepsilon}) \end{align*} $$
$$ \begin{align*} \Delta_\infty^h v_{\varepsilon}&=(1+\varepsilon)^{h}\Delta_\infty^h v\\ &\leq(1+\varepsilon)^{h}F(x,v,Dv)\\ &\leq(1+\varepsilon)^{h}F(x,v_{\varepsilon},Dv_{\varepsilon})\\ &< F(x,v_{\varepsilon},Dv_{\varepsilon}) \end{align*} $$
in the viscosity sense. That is,
![]() $v_{\varepsilon }$
is a viscosity supersolution of (1-6).
$v_{\varepsilon }$
is a viscosity supersolution of (1-6).
Next we want to show
![]() $u\leq v_{\varepsilon }$
in
$u\leq v_{\varepsilon }$
in
![]() $\Omega $
. Suppose in contrast that
$\Omega $
. Suppose in contrast that
![]() $u>v_{\varepsilon }$
at some point
$u>v_{\varepsilon }$
at some point
![]() $x_{0}\in \Omega $
and
$x_{0}\in \Omega $
and
According to [Reference Crandall, Ishii and Lions18], we double the variables
Suppose that
![]() $w_{j}$
attains its maximum at
$w_{j}$
attains its maximum at
![]() $(x_{j},y_{j})\in \overline {\Omega }\times \overline {\Omega }$
. According to [Reference Crandall, Ishii and Lions18, Proposition 3.7],
$(x_{j},y_{j})\in \overline {\Omega }\times \overline {\Omega }$
. According to [Reference Crandall, Ishii and Lions18, Proposition 3.7],
 $$ \begin{align*} \lim\limits_{j\rightarrow \infty}{M_{j}}=\lim\limits_{j\rightarrow\infty}\bigg(u(x_{j})- v_{\varepsilon}(y_{j})-\frac{j|x_{j}-y_{j}|^4}{4}\bigg)=M \end{align*} $$
$$ \begin{align*} \lim\limits_{j\rightarrow \infty}{M_{j}}=\lim\limits_{j\rightarrow\infty}\bigg(u(x_{j})- v_{\varepsilon}(y_{j})-\frac{j|x_{j}-y_{j}|^4}{4}\bigg)=M \end{align*} $$
and
 $$ \begin{align*} \lim\limits_{j\rightarrow\infty}\frac{j|x_{j}-y_{j}|^4}{4}=0. \end{align*} $$
$$ \begin{align*} \lim\limits_{j\rightarrow\infty}\frac{j|x_{j}-y_{j}|^4}{4}=0. \end{align*} $$
It is clear that
![]() $x_{j}\rightarrow x_{0}, y_{j}\rightarrow x_{0}$
as
$x_{j}\rightarrow x_{0}, y_{j}\rightarrow x_{0}$
as
![]() $j\rightarrow \infty $
. Since
$j\rightarrow \infty $
. Since
![]() $ M>0\geq \sup \nolimits _{\partial \Omega }(u-v_{\varepsilon })$
, there exists an open set
$ M>0\geq \sup \nolimits _{\partial \Omega }(u-v_{\varepsilon })$
, there exists an open set
![]() $\Omega _{0}$
such that
$\Omega _{0}$
such that
![]() $x_{0},x_{j}$
and
$x_{0},x_{j}$
and
![]() $y_{j}\in \Omega _{0}\subseteq \Omega $
as
$y_{j}\in \Omega _{0}\subseteq \Omega $
as
![]() $j\rightarrow \infty $
.
$j\rightarrow \infty $
.
Let
 $$ \begin{align*} \varphi(x)=\frac{j|x-y_{j}|^4}{4} , \quad\psi(y)=-\frac{j|x_{j}-y|^4}{4}. \end{align*} $$
$$ \begin{align*} \varphi(x)=\frac{j|x-y_{j}|^4}{4} , \quad\psi(y)=-\frac{j|x_{j}-y|^4}{4}. \end{align*} $$
It is obvious that the function
![]() $u-\varphi $
has a local maximum at
$u-\varphi $
has a local maximum at
![]() $x_{j}$
and
$x_{j}$
and
![]() $v_{\varepsilon }-\psi $
has a local minimum at
$v_{\varepsilon }-\psi $
has a local minimum at
![]() $y_{j}$
.
$y_{j}$
.
We consider the following two cases: either
![]() $x_{j}= y_{j}$
or
$x_{j}= y_{j}$
or
![]() $x_{j}\neq y_{j}$
for j large enough.
$x_{j}\neq y_{j}$
for j large enough.
Case 1: If
![]() $x_{j}= y_{j}$
, we have
$x_{j}= y_{j}$
, we have
![]() $D\psi (y_{j})=0 $
and
$D\psi (y_{j})=0 $
and
![]() $D^{2}\psi (y_{j})=0$
. Since
$D^{2}\psi (y_{j})=0$
. Since
![]() $v_{\varepsilon }$
is a viscosity supersolution,
$v_{\varepsilon }$
is a viscosity supersolution,
which contradicts
![]() $F<0$
.
$F<0$
.
Case 2: If
![]() $x_{j}\neq y_{j}$
, we use jets and the maximum principle for semicontinuous functions [Reference Crandall, Ishii and Lions18, Theorem 3.2]. There exist
$x_{j}\neq y_{j}$
, we use jets and the maximum principle for semicontinuous functions [Reference Crandall, Ishii and Lions18, Theorem 3.2]. There exist
![]() $n\times n$
symmetric matrices
$n\times n$
symmetric matrices
![]() $X_{j}$
and
$X_{j}$
and
![]() $Y_{j}$
such that
$Y_{j}$
such that
![]() $X_{j}\leq Y_{j}$
and
$X_{j}\leq Y_{j}$
and
where
![]() $p_{j}=j|x_{j}-y_{j}|^{2}(x_{j}-y_{j})$
. By the definitions of the viscosity subsolution and supersolution, since
$p_{j}=j|x_{j}-y_{j}|^{2}(x_{j}-y_{j})$
. By the definitions of the viscosity subsolution and supersolution, since
![]() $\Delta _\infty ^h u\geq F(x,u,Du)$
and
$\Delta _\infty ^h u\geq F(x,u,Du)$
and
![]() $\Delta _\infty ^h v_{\varepsilon }\leq (1+\varepsilon )^{h} F(x,v_{\varepsilon },Dv_{\varepsilon })$
in the viscosity sense,
$\Delta _\infty ^h v_{\varepsilon }\leq (1+\varepsilon )^{h} F(x,v_{\varepsilon },Dv_{\varepsilon })$
in the viscosity sense,
 $$ \begin{align} 0&\leq|p_{j}|^{h-3}\langle X_{j}p_{j},p_{j}\rangle -F(x_{j},u(x_{j}),p_{j})\nonumber\\ &\leq|p_{j}|^{h-3}\langle Y_{j}p_{j},p_{j} \rangle -F(x_{j},u(x_{j}),p_{j})\nonumber\\ &\leq (1+\varepsilon)^{h}F(y_{j},v_{\varepsilon}(y_{j}),p_{j}) -F(x_{j},u(x_{j}),p_{j}). \end{align} $$
$$ \begin{align} 0&\leq|p_{j}|^{h-3}\langle X_{j}p_{j},p_{j}\rangle -F(x_{j},u(x_{j}),p_{j})\nonumber\\ &\leq|p_{j}|^{h-3}\langle Y_{j}p_{j},p_{j} \rangle -F(x_{j},u(x_{j}),p_{j})\nonumber\\ &\leq (1+\varepsilon)^{h}F(y_{j},v_{\varepsilon}(y_{j}),p_{j}) -F(x_{j},u(x_{j}),p_{j}). \end{align} $$
Since
![]() $w_{j}$
attains its maximum at
$w_{j}$
attains its maximum at
![]() $(x_{j},y_{j})\in \overline {\Omega }\times \overline {\Omega }$
,
$(x_{j},y_{j})\in \overline {\Omega }\times \overline {\Omega }$
,
 $$ \begin{align} u(x)-v_{\varepsilon}(y)-\frac{j}{4}|x-y|^4\leq u(x_{j})- v_{\varepsilon}(y_{j})-\frac{j|x_{j}-y_{j}|^4}{4}\quad \text{for all } x,y\in\overline{\Omega}. \end{align} $$
$$ \begin{align} u(x)-v_{\varepsilon}(y)-\frac{j}{4}|x-y|^4\leq u(x_{j})- v_{\varepsilon}(y_{j})-\frac{j|x_{j}-y_{j}|^4}{4}\quad \text{for all } x,y\in\overline{\Omega}. \end{align} $$
Since
![]() $v_{\varepsilon }$
is a viscosity supersolution, we see that
$v_{\varepsilon }$
is a viscosity supersolution, we see that
![]() $v_\varepsilon $
is locally Lipschitz continuous by Lemma 2.5. Taking
$v_\varepsilon $
is locally Lipschitz continuous by Lemma 2.5. Taking
![]() $x=y=x_j$
in (2-5),
$x=y=x_j$
in (2-5),
 $$ \begin{align*} \frac{j|x_{j}-y_{j}|^4}{4}\leq v_{\varepsilon}(x_{j})-v_{\varepsilon}(y_{j})\leq L|x_{j}-y_{j}|, \end{align*} $$
$$ \begin{align*} \frac{j|x_{j}-y_{j}|^4}{4}\leq v_{\varepsilon}(x_{j})-v_{\varepsilon}(y_{j})\leq L|x_{j}-y_{j}|, \end{align*} $$
where L is the Lipschitz constant of
![]() $v_\varepsilon $
. Thus,
$v_\varepsilon $
. Thus,
 $$ \begin{align*} \frac{j|x_{j}-y_{j}|^3}{4}\leq L. \end{align*} $$
$$ \begin{align*} \frac{j|x_{j}-y_{j}|^3}{4}\leq L. \end{align*} $$
Upon taking a subsequence if necessary, we can assume that
![]() $p_j\rightarrow p$
. Taking the limit in (2-4),
$p_j\rightarrow p$
. Taking the limit in (2-4),
Thus,
Since
![]() $F(x,t,p)$
is nondecreasing in t and
$F(x,t,p)$
is nondecreasing in t and
![]() $u(x_{0})>v_{\varepsilon }(x_{0})$
,
$u(x_{0})>v_{\varepsilon }(x_{0})$
,
which contradicts (2-6).
Thus, we have
![]() $u\leq v_{\varepsilon }$
in
$u\leq v_{\varepsilon }$
in
![]() $\Omega $
. Letting
$\Omega $
. Letting
![]() $\varepsilon \rightarrow 0$
, we obtain
$\varepsilon \rightarrow 0$
, we obtain
![]() $u\leq v$
in
$u\leq v$
in
![]() $\Omega $
.
$\Omega $
.
Remark 2.7. If
![]() $F(x,t,p)>0$
,
$F(x,t,p)>0$
,
![]() $F(x,t,p)$
is nondecreasing in t and
$F(x,t,p)$
is nondecreasing in t and
![]() $\tau \rightarrow F(x,t,\tau p)$
is nonincreasing in
$\tau \rightarrow F(x,t,\tau p)$
is nonincreasing in
![]() $(\rho , 1]$
for each
$(\rho , 1]$
for each
![]() $(x,t,p)\in \Omega \times \mathbb {R}\times \mathbb {R}^{n}$
, where
$(x,t,p)\in \Omega \times \mathbb {R}\times \mathbb {R}^{n}$
, where
![]() $0<\rho <1$
, then the comparison principle still holds if we perturb the supersolution v to
$0<\rho <1$
, then the comparison principle still holds if we perturb the supersolution v to
![]() $v_\varepsilon =v(1-\varepsilon )+\varepsilon \sup \nolimits _{\overline {\Omega }}v$
, where
$v_\varepsilon =v(1-\varepsilon )+\varepsilon \sup \nolimits _{\overline {\Omega }}v$
, where
![]() $0<\varepsilon <1-\rho $
.
$0<\varepsilon <1-\rho $
.
3. Existence when nonlinear term
 $\mathbf {sup}{_{{\boldsymbol\Omega }\times I\times {\mathbb {R}}^{n}}|F(x,t,p)|<\infty }$
$\mathbf {sup}{_{{\boldsymbol\Omega }\times I\times {\mathbb {R}}^{n}}|F(x,t,p)|<\infty }$
In this section, we want to establish the existence of viscosity solutions of the boundary value problem (1-8) when the nonlinear term
![]() $F(x,t,p)$
is bounded, that is,
$F(x,t,p)$
is bounded, that is,
![]() $\sup \nolimits _{\Omega \times I\times \mathbb {R}^{n}}|F(x,t,p)|<\infty .$
The method is based on the standard Perron idea, but we must make subtle analysis due to the strong degeneracy of the operator
$\sup \nolimits _{\Omega \times I\times \mathbb {R}^{n}}|F(x,t,p)|<\infty .$
The method is based on the standard Perron idea, but we must make subtle analysis due to the strong degeneracy of the operator
![]() $\Delta _\infty ^h. $
$\Delta _\infty ^h. $
Proof of Theorem 1.2.
Let
Here
![]() $\mathbb {T}$
is nonempty since
$\mathbb {T}$
is nonempty since
![]() $u_{*}\in \mathbb {T}.$
$u_{*}\in \mathbb {T}.$
Let
Setting
![]() $v_{*}:=\inf \nolimits _{\Omega }u_{*}$
and
$v_{*}:=\inf \nolimits _{\Omega }u_{*}$
and
![]() $v^{*}:=\sup \nolimits _{\Omega }u^{*},$
$v^{*}:=\sup \nolimits _{\Omega }u^{*},$
Step 1. We show that u is a viscosity subsolution. Let
![]() $\psi \in C^{2}(\Omega )$
and
$\psi \in C^{2}(\Omega )$
and
![]() $u-\psi $
have a local maximum at
$u-\psi $
have a local maximum at
![]() $x_{0}\in \Omega .$
Then there exists some small ball
$x_{0}\in \Omega .$
Then there exists some small ball
![]() $B_{\rho }(x_{0})\subseteq \Omega $
such that
$B_{\rho }(x_{0})\subseteq \Omega $
such that
![]() $u(x)-\psi (x)\leq u(x_{0})-\psi (x_{0})$
for any
$u(x)-\psi (x)\leq u(x_{0})-\psi (x_{0})$
for any
![]() $x\in B_{\rho }(x_{0}).$
We want to show
$x\in B_{\rho }(x_{0}).$
We want to show
According to (3-1),
![]() $u(x_{0})=\sup \nolimits _{\alpha \in \mathbb {T}}\alpha (x_{0})$
. We fix
$u(x_{0})=\sup \nolimits _{\alpha \in \mathbb {T}}\alpha (x_{0})$
. We fix
![]() $0<\delta <\rho ^{2(h+1)}$
and pick a sequence
$0<\delta <\rho ^{2(h+1)}$
and pick a sequence
![]() $\{\alpha _{k}\}$
in
$\{\alpha _{k}\}$
in
![]() $\mathbb {T}$
such that
$\mathbb {T}$
such that
![]() $u(x_{0})-\alpha _{k}(x_{0})<{\delta }/{k}$
for each positive integer k. Clearly,
$u(x_{0})-\alpha _{k}(x_{0})<{\delta }/{k}$
for each positive integer k. Clearly,
That is,
Therefore,
for all
![]() $x\in B_{\rho }(x_{0})\backslash \overline {B}_{({\delta }/{k})^{1/[2(h+1)]}}(x_{0}).$
This implies that
$x\in B_{\rho }(x_{0})\backslash \overline {B}_{({\delta }/{k})^{1/[2(h+1)]}}(x_{0}).$
This implies that
![]() $\alpha _{k}(x)-[\psi (x)+ |x-x_{0}|^{2(h+1)}]$
attains its maximum at some point
$\alpha _{k}(x)-[\psi (x)+ |x-x_{0}|^{2(h+1)}]$
attains its maximum at some point
![]() $x_{k} \in \overline {B}_{({\delta }/{k})^{1/[2(h+1)]}}(x_{0})$
. In particular,
$x_{k} \in \overline {B}_{({\delta }/{k})^{1/[2(h+1)]}}(x_{0})$
. In particular,
Let
![]() $\psi _{0}(x):=\psi (x)+|x-x_{0}|^{2(h+1)}.$
By a direct calculation,
$\psi _{0}(x):=\psi (x)+|x-x_{0}|^{2(h+1)}.$
By a direct calculation,
where we use
![]() $\alpha _{k}\in \mathbb {T}.$
Combining (3-2) and (3-3),
$\alpha _{k}\in \mathbb {T}.$
Combining (3-2) and (3-3),
which implies
![]() $\lim \nolimits _{k\rightarrow \infty }\alpha _{k}(x_{k})=u(x_{0})$
. Letting
$\lim \nolimits _{k\rightarrow \infty }\alpha _{k}(x_{k})=u(x_{0})$
. Letting
![]() $k\rightarrow \infty $
in (3-4),
$k\rightarrow \infty $
in (3-4),
Therefore, u is a viscosity subsolution.
Step 2. We want to show
![]() $u\in C(\overline {\Omega })$
and
$u\in C(\overline {\Omega })$
and
![]() $u=\varphi $
on
$u=\varphi $
on
![]() $\partial \Omega $
. Take two constants
$\partial \Omega $
. Take two constants
![]() $C_{*}<0<C^{*}$
such that
$C_{*}<0<C^{*}$
such that
and
Since u is a viscosity subsolution of
![]() $\Delta _\infty ^h u=F(x,u,Du)$
and
$\Delta _\infty ^h u=F(x,u,Du)$
and
![]() $F(x,u,Du)$
is bounded, u is locally Lipschitz in
$F(x,u,Du)$
is bounded, u is locally Lipschitz in
![]() $\Omega $
by Lemma 2.5. Now we proceed to show that u is continuous on
$\Omega $
by Lemma 2.5. Now we proceed to show that u is continuous on
![]() $\partial \Omega $
and
$\partial \Omega $
and
![]() $u=\varphi $
on
$u=\varphi $
on
![]() $\partial \Omega $
. By [Reference Li and Liu26], there exist
$\partial \Omega $
. By [Reference Li and Liu26], there exist
![]() $\alpha _{*},\beta ^{*}\in C(\overline {\Omega })$
such that
$\alpha _{*},\beta ^{*}\in C(\overline {\Omega })$
such that
Since
![]() $\Delta _\infty ^h u^{*}\leq C^{*}$
and
$\Delta _\infty ^h u^{*}\leq C^{*}$
and
![]() $\alpha _{*}\leq u^{*}$
on
$\alpha _{*}\leq u^{*}$
on
![]() $\partial \Omega $
, we have
$\partial \Omega $
, we have
![]() $\alpha _{*}\leq u^{*}$
in
$\alpha _{*}\leq u^{*}$
in
![]() $\Omega $
by the comparison principle (see Remark 2.7). Similarly, we have
$\Omega $
by the comparison principle (see Remark 2.7). Similarly, we have
![]() $u_{*}\leq \beta ^{*}$
in
$u_{*}\leq \beta ^{*}$
in
![]() $\Omega $
. Let
$\Omega $
. Let
Then
![]() $\hat {\alpha }\in C(\overline {\Omega }), \hat {\beta }\in C(\overline {\Omega })$
, and
$\hat {\alpha }\in C(\overline {\Omega }), \hat {\beta }\in C(\overline {\Omega })$
, and
Note that
![]() $\alpha _{*}$
and
$\alpha _{*}$
and
![]() $\beta ^{*}$
are a viscosity subsolution and a viscosity supersolution of (1-8), respectively. By Remark 2.4, we conclude that
$\beta ^{*}$
are a viscosity subsolution and a viscosity supersolution of (1-8), respectively. By Remark 2.4, we conclude that
![]() $\hat {\alpha }$
and
$\hat {\alpha }$
and
![]() $\hat {\beta }$
are a viscosity subsolution and a viscosity supersolution of (1-8), respectively. Thus,
$\hat {\beta }$
are a viscosity subsolution and a viscosity supersolution of (1-8), respectively. Thus,
![]() $\hat {\alpha }\in \mathbb {T}$
and
$\hat {\alpha }\in \mathbb {T}$
and
![]() $\hat {\alpha }\leq u$
in
$\hat {\alpha }\leq u$
in
![]() $\overline {\Omega }$
. For any
$\overline {\Omega }$
. For any
![]() $z\in \mathbb {T}$
, we have
$z\in \mathbb {T}$
, we have
![]() $z\leq u^{*}$
in
$z\leq u^{*}$
in
![]() $\overline {\Omega }$
. Additionally, by the comparison principle, we also have
$\overline {\Omega }$
. Additionally, by the comparison principle, we also have
![]() $z\leq \beta ^{*}$
in
$z\leq \beta ^{*}$
in
![]() $\overline {\Omega }$
. Therefore,
$\overline {\Omega }$
. Therefore,
![]() $z\leq \hat {\beta }$
in
$z\leq \hat {\beta }$
in
![]() $\overline {\Omega }$
. This implies
$\overline {\Omega }$
. This implies
![]() $u \leq \hat {\beta }$
in
$u \leq \hat {\beta }$
in
![]() $\overline {\Omega }$
. Then we have
$\overline {\Omega }$
. Then we have
![]() $\hat {\alpha }\leq u \leq \hat {\beta }$
in
$\hat {\alpha }\leq u \leq \hat {\beta }$
in
![]() $\overline {\Omega }$
.
$\overline {\Omega }$
.
Since
![]() $\hat {\alpha }, \hat {\beta }\in C(\overline {\Omega })$
and
$\hat {\alpha }, \hat {\beta }\in C(\overline {\Omega })$
and
![]() $\hat {\alpha }=\hat {\beta }=\varphi $
on
$\hat {\alpha }=\hat {\beta }=\varphi $
on
![]() $\partial \Omega $
, it follows that
$\partial \Omega $
, it follows that
![]() $u\in C(\overline {\Omega })$
and
$u\in C(\overline {\Omega })$
and
![]() $u=\varphi $
on
$u=\varphi $
on
![]() $\partial \Omega $
.
$\partial \Omega $
.
Step 3. We show that u is a viscosity supersolution. Suppose that it does not hold. Then there exists a point
![]() $x_{0}\in \Omega $
and a function
$x_{0}\in \Omega $
and a function
![]() $\psi \in C^{2}(\Omega )$
such that
$\psi \in C^{2}(\Omega )$
such that
![]() $u-\psi $
has a local minimum at
$u-\psi $
has a local minimum at
![]() $x_{0},$
but
$x_{0},$
but
Suppose that
![]() $u(x_{0})=u^{*}(x_{0})$
. Then for any x near
$u(x_{0})=u^{*}(x_{0})$
. Then for any x near
![]() $x_{0}$
,
$x_{0}$
,
Since
![]() $u^{*}$
is a viscosity supersolution,
$u^{*}$
is a viscosity supersolution,
which is contrary to (3-5).
Now suppose that
![]() $u(x_{0})<u^{*}(x_{0})$
. Let
$u(x_{0})<u^{*}(x_{0})$
. Let
![]() $d(x_{0}):=\mathrm {dist} (x_{0},\partial \Omega )$
. For any
$d(x_{0}):=\mathrm {dist} (x_{0},\partial \Omega )$
. For any
![]() $x\in B_{\rho }(x_{0})$
,
$x\in B_{\rho }(x_{0})$
,
Define
![]() $\phi (x):=\psi (x)+(u(x_{0})-\psi (x_{0})).$
For any
$\phi (x):=\psi (x)+(u(x_{0})-\psi (x_{0})).$
For any
![]() $x\in B_{\rho }(x_{0})$
,
$x\in B_{\rho }(x_{0})$
,
Since
![]() $F(x,t,p)$
is continuous, one can take
$F(x,t,p)$
is continuous, one can take
![]() $0<\varepsilon _{0}<\min \{1,\rho ,({d(x_{0})}/{2})^{4(h+1)}\}$
small enough such that
$0<\varepsilon _{0}<\min \{1,\rho ,({d(x_{0})}/{2})^{4(h+1)}\}$
small enough such that
For
![]() $0<\varepsilon \leq \varepsilon _{0}$
, define
$0<\varepsilon \leq \varepsilon _{0}$
, define
![]() $\phi _{\varepsilon }(x):=\phi (x)-\sqrt {\varepsilon }|x-x_{0}|^{2(h+1)}+\varepsilon $
. By a direct computation,
$\phi _{\varepsilon }(x):=\phi (x)-\sqrt {\varepsilon }|x-x_{0}|^{2(h+1)}+\varepsilon $
. By a direct computation,
Thus, by (3-6),
We claim that there exists a small
![]() $\varepsilon _{1}$
, with
$\varepsilon _{1}$
, with
![]() $0<\varepsilon _{1}<\varepsilon _{0}$
, such that
$0<\varepsilon _{1}<\varepsilon _{0}$
, such that
Suppose that our claim does not hold. Then for each small
![]() $\varepsilon>0$
, there exists an
$\varepsilon>0$
, there exists an
![]() $x_{\varepsilon }\in B_{\varepsilon ^{1/[4(h+1)]}}(x_{0})$
such that
$x_{\varepsilon }\in B_{\varepsilon ^{1/[4(h+1)]}}(x_{0})$
such that
![]() $\Delta _{\infty }^{h}\phi _{\varepsilon }(x_{\varepsilon }) \leq F(x_{\varepsilon },\phi _{\varepsilon }(x_{\varepsilon }),D\phi _{\varepsilon }(x_{\varepsilon }))$
. Since
$\Delta _{\infty }^{h}\phi _{\varepsilon }(x_{\varepsilon }) \leq F(x_{\varepsilon },\phi _{\varepsilon }(x_{\varepsilon }),D\phi _{\varepsilon }(x_{\varepsilon }))$
. Since
![]() $x_{\varepsilon }\rightarrow x_{0}$
as
$x_{\varepsilon }\rightarrow x_{0}$
as
![]() $\varepsilon \rightarrow 0$
, we observe that
$\varepsilon \rightarrow 0$
, we observe that
We conclude that
![]() $\Delta _{\infty }^{h}\phi (x_{0})\leq F(x_{0},\phi (x_{0}),D\phi (x_{0})),$
which is a contradiction and the claim is proved.
$\Delta _{\infty }^{h}\phi (x_{0})\leq F(x_{0},\phi (x_{0}),D\phi (x_{0})),$
which is a contradiction and the claim is proved.
Since
![]() $\phi (x_{0})=u(x_{0})<u^{*}(x_{0})$
, we can suppose that
$\phi (x_{0})=u(x_{0})<u^{*}(x_{0})$
, we can suppose that
![]() $\varepsilon _{1}$
is small enough and for all
$\varepsilon _{1}$
is small enough and for all
![]() $x\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})$
,
$x\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})$
,
![]() $\phi (x)\leq \phi _{\varepsilon _{1}}(x) \leq u^{*}(x)$
. Since
$\phi (x)\leq \phi _{\varepsilon _{1}}(x) \leq u^{*}(x)$
. Since
![]() $u(x_{0})<u(x_{0})+\varepsilon _{1}=\phi (x_{0})+\varepsilon _{1} =\phi _{\varepsilon _{1}}(x_{0})$
, there exists
$u(x_{0})<u(x_{0})+\varepsilon _{1}=\phi (x_{0})+\varepsilon _{1} =\phi _{\varepsilon _{1}}(x_{0})$
, there exists
![]() $0<s_{1}<\varepsilon _{1}^{1/[4(h+1)]}$
such that
$0<s_{1}<\varepsilon _{1}^{1/[4(h+1)]}$
such that
![]() $u(x)<\phi _{\varepsilon _{1}}(x)$
for all
$u(x)<\phi _{\varepsilon _{1}}(x)$
for all
![]() $x\in B_{s_{1}}(x_{0})$
. We note that
$x\in B_{s_{1}}(x_{0})$
. We note that
and
 $$ \begin{align*} &u(x)-\phi_{\varepsilon_{1}}(x)=u(x)-\phi(x) +\sqrt{\varepsilon_{1}}|x-x_{0}|^{2(h+1)}-\varepsilon_{1}>0\\ &\quad\text{for all } x\in B_{\rho}(x_{0})\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}} (x_{0}). \end{align*} $$
$$ \begin{align*} &u(x)-\phi_{\varepsilon_{1}}(x)=u(x)-\phi(x) +\sqrt{\varepsilon_{1}}|x-x_{0}|^{2(h+1)}-\varepsilon_{1}>0\\ &\quad\text{for all } x\in B_{\rho}(x_{0})\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}} (x_{0}). \end{align*} $$
To sum up,
 $$ \begin{align} \begin{cases} (1)\;\Delta_\infty^h \phi_{\varepsilon_{1}}(x)>F(x,\phi_{\varepsilon_{1}}(x),D\phi_{\varepsilon_{1}}(x)) \quad &\text{for all } x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}), \\ (2)\;\phi_{\varepsilon_{1}}(x)<u^{*}(x)\quad &\text{for all } x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}),\\ (3)\;u(x)<\phi_{\varepsilon_{1}}(x) \quad &\text{for all } x\in B_{s_{1}}(x_{0}),\\ (4)\;u(x)>\phi_{\varepsilon_{1}}(x) \quad &\text{for all } x\in B_{\rho}(x_{0})\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (1)\;\Delta_\infty^h \phi_{\varepsilon_{1}}(x)>F(x,\phi_{\varepsilon_{1}}(x),D\phi_{\varepsilon_{1}}(x)) \quad &\text{for all } x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}), \\ (2)\;\phi_{\varepsilon_{1}}(x)<u^{*}(x)\quad &\text{for all } x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}),\\ (3)\;u(x)<\phi_{\varepsilon_{1}}(x) \quad &\text{for all } x\in B_{s_{1}}(x_{0}),\\ (4)\;u(x)>\phi_{\varepsilon_{1}}(x) \quad &\text{for all } x\in B_{\rho}(x_{0})\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}). \end{cases} \end{align} $$
Now define
 $$ \begin{align*} \hat{u}(x)=\begin{cases} u(x)\quad &\mathrm{if}\; x\in\; \Omega\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}), \\ \sup\{\phi_{\varepsilon_{1}}(x),u(x)\}\quad &\mathrm{if}\; x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}). \end{cases} \end{align*} $$
$$ \begin{align*} \hat{u}(x)=\begin{cases} u(x)\quad &\mathrm{if}\; x\in\; \Omega\backslash \overline{B}_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}), \\ \sup\{\phi_{\varepsilon_{1}}(x),u(x)\}\quad &\mathrm{if}\; x\in B_{\varepsilon_{1}^{1/[4(h+1)]}}(x_{0}). \end{cases} \end{align*} $$
It is obvious that
![]() $\hat {u}\in C(\overline {\Omega })$
and
$\hat {u}\in C(\overline {\Omega })$
and
![]() $u_{*}\leq u\leq \hat {u}\leq u^{*}$
in
$u_{*}\leq u\leq \hat {u}\leq u^{*}$
in
![]() $\Omega $
. Next we want to show that
$\Omega $
. Next we want to show that
![]() $\hat {u}\in \mathbb {T}$
. Take
$\hat {u}\in \mathbb {T}$
. Take
![]() $\hat {\psi }\in C^{2}(\Omega )$
such that
$\hat {\psi }\in C^{2}(\Omega )$
such that
![]() $\hat {u}-\hat {\psi }$
has a local maximum at some point
$\hat {u}-\hat {\psi }$
has a local maximum at some point
![]() $y\in \Omega $
, that is,
$y\in \Omega $
, that is,
![]() $\hat {u}(x)-\hat {\psi }(x)\leq \hat {u}(y)-\hat {\psi }(y)$
for x in some ball
$\hat {u}(x)-\hat {\psi }(x)\leq \hat {u}(y)-\hat {\psi }(y)$
for x in some ball
![]() $B_{\delta }(y)$
. It is clear that
$B_{\delta }(y)$
. It is clear that
![]() $\hat {u}(y)=u(y)$
or
$\hat {u}(y)=u(y)$
or
![]() $\hat {u}(y)=\phi _{\varepsilon _{1}}(y)$
. If
$\hat {u}(y)=\phi _{\varepsilon _{1}}(y)$
. If
![]() $\hat {u}(y)=u(y)$
, we note that
$\hat {u}(y)=u(y)$
, we note that
![]() $u\leq \hat {u}$
in
$u\leq \hat {u}$
in
![]() $\Omega $
. For all
$\Omega $
. For all
![]() $x\in B_{\delta }(y)$
,
$x\in B_{\delta }(y)$
,
Thus,
![]() $u-\hat {\psi }$
has a local maximum at y. Since u is a viscosity subsolution, we have
$u-\hat {\psi }$
has a local maximum at y. Since u is a viscosity subsolution, we have
![]() $\Delta _{\infty }^{h}\hat {\psi }(y)\geq F(y,u(y),D\hat {\psi }(y))=F(y,\hat {u}(y),D\hat {\psi }(y))$
. If
$\Delta _{\infty }^{h}\hat {\psi }(y)\geq F(y,u(y),D\hat {\psi }(y))=F(y,\hat {u}(y),D\hat {\psi }(y))$
. If
![]() $\hat {u}(y)=\phi _{\varepsilon _{1}}(y)$
, we can see that
$\hat {u}(y)=\phi _{\varepsilon _{1}}(y)$
, we can see that
![]() $u(y)<\phi _{\varepsilon _{1}}(y)$
. According to (3-7)(4), we have
$u(y)<\phi _{\varepsilon _{1}}(y)$
. According to (3-7)(4), we have
![]() $y\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})$
. Then note that
$y\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})$
. Then note that
![]() $\phi _{\varepsilon _{1}}\leq \hat {u}$
and for any
$\phi _{\varepsilon _{1}}\leq \hat {u}$
and for any
![]() $x\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})\bigcap B_{\delta }(y)$
,
$x\in B_{\varepsilon _{1}^{1/[4(h+1)]}}(x_{0})\bigcap B_{\delta }(y)$
,
Thus,
![]() $\phi _{\varepsilon _{1}}-\hat {\psi }$
has a local maximum at y. This implies that
$\phi _{\varepsilon _{1}}-\hat {\psi }$
has a local maximum at y. This implies that
![]() $\Delta _{\infty }^{h}\phi _{\varepsilon _{1}}(y)\leq \Delta _{\infty }^{h}\hat {\psi }(y)$
. Together with (3-7)(1), one has
$\Delta _{\infty }^{h}\phi _{\varepsilon _{1}}(y)\leq \Delta _{\infty }^{h}\hat {\psi }(y)$
. Together with (3-7)(1), one has
![]() $\Delta _{\infty }^{h}\hat {\psi }(y)\geq F(y,\phi _{\varepsilon _{1}}(y),D\phi _{\varepsilon _{1}}(y)) =F(y,\hat {u}(y),D\hat {\psi }(y))$
. In any case, we show that
$\Delta _{\infty }^{h}\hat {\psi }(y)\geq F(y,\phi _{\varepsilon _{1}}(y),D\phi _{\varepsilon _{1}}(y)) =F(y,\hat {u}(y),D\hat {\psi }(y))$
. In any case, we show that
![]() $\hat {u}$
is a viscosity subsolution, that is,
$\hat {u}$
is a viscosity subsolution, that is,
![]() $\hat {u}\in \mathbb {T}$
. By (3-7)(3), we see that
$\hat {u}\in \mathbb {T}$
. By (3-7)(3), we see that
![]() $\hat {u}=\phi _{\varepsilon _{1}}>u$
in
$\hat {u}=\phi _{\varepsilon _{1}}>u$
in
![]() $B_{s_{1}}(x_{0})$
, which contradicts the definition of u. Therefore, u is a viscosity supersolution.
$B_{s_{1}}(x_{0})$
, which contradicts the definition of u. Therefore, u is a viscosity supersolution.
We have completed the proof that u is a viscosity solution to Problem (1-8) in
![]() $\Omega $
.
$\Omega $
.
4. Singular boundary value problem in a bounded domain
In this section, we are devoted to the existence of the viscosity solution of the singular boundary value problem. The key is to deal with the singularity of the term
![]() $F(x,u,Du).$
We choose an appropriate cut-off function and combine the truncation, compactness method and Theorem 1.2 to deal with the difficulty. We consider the following problem:
$F(x,u,Du).$
We choose an appropriate cut-off function and combine the truncation, compactness method and Theorem 1.2 to deal with the difficulty. We consider the following problem:
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=F(x,u,Du) \quad &\mathrm{in}\; \Omega, \\ u=\varphi \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=F(x,u,Du) \quad &\mathrm{in}\; \Omega, \\ u=\varphi \quad &\mathrm{on} \; \partial\Omega, \end{cases} \end{align} $$
where
![]() $\Omega \subseteq \mathbb {R}^{n}$
,
$\Omega \subseteq \mathbb {R}^{n}$
,
![]() $F:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and
$F:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and
![]() $\varphi \in C(\partial \Omega )$
is nonnegative. Note that
$\varphi \in C(\partial \Omega )$
is nonnegative. Note that
![]() $\varphi \equiv 0$
is possible and that
$\varphi \equiv 0$
is possible and that
![]() $F(x,t,p)$
may exhibit singularity at
$F(x,t,p)$
may exhibit singularity at
![]() $t=0$
. The corresponding theorem is as follows.
$t=0$
. The corresponding theorem is as follows.
Theorem 4.1. Let
![]() $\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain,
$\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain,
![]() $F:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function and
$F:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function and
![]() $\varphi \in C(\partial \Omega )$
be nonnegative. If
$\varphi \in C(\partial \Omega )$
be nonnegative. If
![]() $\underline {u}\in C(\overline {\Omega })$
and
$\underline {u}\in C(\overline {\Omega })$
and
![]() $\overline {u}\in C(\overline {\Omega })$
are a viscosity subsolution and a viscosity supersolution of (4-1) in
$\overline {u}\in C(\overline {\Omega })$
are a viscosity subsolution and a viscosity supersolution of (4-1) in
![]() $\Omega $
, respectively, such that
$\Omega $
, respectively, such that
![]() $0<\underline {u}\leq \overline {u}$
in
$0<\underline {u}\leq \overline {u}$
in
![]() $\Omega $
and
$\Omega $
and
![]() $\underline {u}=\varphi =\overline {u}$
on
$\underline {u}=\varphi =\overline {u}$
on
![]() $\partial \Omega $
, then Problem (4-1) admits a viscosity solution
$\partial \Omega $
, then Problem (4-1) admits a viscosity solution
![]() $u\in C(\overline {\Omega })$
such that
$u\in C(\overline {\Omega })$
such that
![]() $\underline {u}\leq u\leq \overline {u}$
in
$\underline {u}\leq u\leq \overline {u}$
in
![]() $\overline {\Omega }$
.
$\overline {\Omega }$
.
Proof. Define the cut-off function
![]() $\hat {F}(x,t,p):\Omega \times \mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
by
$\hat {F}(x,t,p):\Omega \times \mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
by
 $$ \begin{align} \hat{F}(x,t,p)=\begin{cases} F(x,t,p)\quad &\mathrm{for} \ t\geq \underline{u}(x), \\ F(x,\underline{u}(x),p)\quad &\mathrm{for} \ t<\underline{u}(x). \end{cases} \end{align} $$
$$ \begin{align} \hat{F}(x,t,p)=\begin{cases} F(x,t,p)\quad &\mathrm{for} \ t\geq \underline{u}(x), \\ F(x,\underline{u}(x),p)\quad &\mathrm{for} \ t<\underline{u}(x). \end{cases} \end{align} $$
Since
![]() $\underline {u}>0$
in
$\underline {u}>0$
in
![]() $\Omega $
, we have
$\Omega $
, we have
![]() $\underset {\Omega \times I\times \mathbb {R}^{n}}\sup |\hat {F}(x,t,p)|<\infty $
for any compact interval
$\underset {\Omega \times I\times \mathbb {R}^{n}}\sup |\hat {F}(x,t,p)|<\infty $
for any compact interval
![]() $I\subseteq \mathbb {R}$
. Let
$I\subseteq \mathbb {R}$
. Let
![]() $\{\Omega _{j}\}$
be a sequence of sub-domains of
$\{\Omega _{j}\}$
be a sequence of sub-domains of
![]() $\Omega $
such that
$\Omega $
such that
 $$ \begin{align*} \Omega_{j}\Subset\Omega_{j+1}\quad \text{and} \quad\Omega=\bigcup_{k=1}^{\infty}\Omega_{k}, \quad (j=1,2,\ldots). \end{align*} $$
$$ \begin{align*} \Omega_{j}\Subset\Omega_{j+1}\quad \text{and} \quad\Omega=\bigcup_{k=1}^{\infty}\Omega_{k}, \quad (j=1,2,\ldots). \end{align*} $$
For each positive integer j, we consider the following Dirichlet problem:
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=\hat{F}(x,u,Du) \quad &\mathrm{in}\; \Omega_{j}, \\ u=\underline{u} \quad &\mathrm{on} \; \partial\Omega_{j}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=\hat{F}(x,u,Du) \quad &\mathrm{in}\; \Omega_{j}, \\ u=\underline{u} \quad &\mathrm{on} \; \partial\Omega_{j}. \end{cases} \end{align} $$
Since
![]() $\overline {u}$
is a viscosity supersolution of (4-1) and
$\overline {u}$
is a viscosity supersolution of (4-1) and
![]() $0<\underline {u}\leq \overline {u}$
in
$0<\underline {u}\leq \overline {u}$
in
![]() $\Omega $
,
$\Omega $
,
in the viscosity sense, where we use (4-2). That is,
![]() $\overline {u}$
is a viscosity supersolution of (4-3) in
$\overline {u}$
is a viscosity supersolution of (4-3) in
![]() $\Omega _{j}$
for each positive integer j. Similarly,
$\Omega _{j}$
for each positive integer j. Similarly,
![]() $\underline {u}$
is a viscosity subsolution of (4-3) in
$\underline {u}$
is a viscosity subsolution of (4-3) in
![]() $\Omega _{j}$
. Since
$\Omega _{j}$
. Since
![]() $\underline {u}\leq \overline {u}$
in
$\underline {u}\leq \overline {u}$
in
![]() $\Omega $
, according to Theorem 1.2, we can find a viscosity solution
$\Omega $
, according to Theorem 1.2, we can find a viscosity solution
![]() $\tilde {u}_{j}\in C(\overline {\Omega }_{j})$
of (4-3) such that
$\tilde {u}_{j}\in C(\overline {\Omega }_{j})$
of (4-3) such that
![]() $\underline {u}\leq \tilde {u}_{j}\leq \overline {u}$
in
$\underline {u}\leq \tilde {u}_{j}\leq \overline {u}$
in
![]() $\overline {\Omega }_{j}$
. We extend
$\overline {\Omega }_{j}$
. We extend
![]() $u_{j}$
to
$u_{j}$
to
![]() $\overline {\Omega }$
by defining
$\overline {\Omega }$
by defining
 $$ \begin{align*} u_{j}=\begin{cases} \tilde{u}_{j} \quad &\mathrm{in}\; \Omega_{j}, \\ \underline{u} \quad &\mathrm{on} \; \overline{\Omega}\setminus\Omega_{j}. \end{cases} \end{align*} $$
$$ \begin{align*} u_{j}=\begin{cases} \tilde{u}_{j} \quad &\mathrm{in}\; \Omega_{j}, \\ \underline{u} \quad &\mathrm{on} \; \overline{\Omega}\setminus\Omega_{j}. \end{cases} \end{align*} $$
Then we obtain a sequence
![]() $\{u_{j}\}$
in
$\{u_{j}\}$
in
![]() $C(\overline {\Omega })$
with
$C(\overline {\Omega })$
with
![]() $\underline {u}\leq u_{j}\leq \overline {u}$
in
$\underline {u}\leq u_{j}\leq \overline {u}$
in
![]() $\overline {\Omega }$
for all j. In particular,
$\overline {\Omega }$
for all j. In particular,
![]() $\{u_{j}\}$
is uniformly bounded in
$\{u_{j}\}$
is uniformly bounded in
![]() $\overline {\Omega }$
. We also note that
$\overline {\Omega }$
. We also note that
![]() $\{u_{j}\}$
is locally Lipschitz continuous in
$\{u_{j}\}$
is locally Lipschitz continuous in
![]() $\Omega $
from Lemma 2.5. Thus,
$\Omega $
from Lemma 2.5. Thus,
![]() $\{u_{j}\}$
is equicontinuous. Therefore, there exists a subsequence of
$\{u_{j}\}$
is equicontinuous. Therefore, there exists a subsequence of
![]() $\{u_{j}\}$
that converges locally uniformly to some
$\{u_{j}\}$
that converges locally uniformly to some
![]() $u\in C(\Omega )$
. Since
$u\in C(\Omega )$
. Since
![]() $\underline {u}\leq u\leq \overline {u}$
in
$\underline {u}\leq u\leq \overline {u}$
in
![]() $\overline {\Omega }$
and
$\overline {\Omega }$
and
![]() $\underline {u}=u=\overline {u}$
on
$\underline {u}=u=\overline {u}$
on
![]() $\partial \Omega $
, we have
$\partial \Omega $
, we have
![]() $u\in C(\overline {\Omega })$
.
$u\in C(\overline {\Omega })$
.
By (4-2) and
![]() $u\geq \underline {u}> 0$
in
$u\geq \underline {u}> 0$
in
![]() $\Omega $
, we have
$\Omega $
, we have
![]() $\hat {F}(x,u,Du)=F(x,u,Du)$
in
$\hat {F}(x,u,Du)=F(x,u,Du)$
in
![]() $\Omega $
. If we want to show that u is a viscosity solution of
$\Omega $
. If we want to show that u is a viscosity solution of
![]() $\Delta _\infty ^h u=F(x,u,Du)$
, we only need to show that u is a viscosity solution of
$\Delta _\infty ^h u=F(x,u,Du)$
, we only need to show that u is a viscosity solution of
![]() $\Delta _\infty ^h u=\hat {F}(x,u,Du)$
in
$\Delta _\infty ^h u=\hat {F}(x,u,Du)$
in
![]() $\Omega $
. First, we show
$\Omega $
. First, we show
![]() $\Delta _\infty ^h u\leq \hat {F}(x,u,Du)$
in the viscosity sense.
$\Delta _\infty ^h u\leq \hat {F}(x,u,Du)$
in the viscosity sense.
Suppose that
![]() $\psi \in C^{2}(\Omega )$
and
$\psi \in C^{2}(\Omega )$
and
![]() $u-\psi $
has a local minimum at some
$u-\psi $
has a local minimum at some
![]() $x_{0}\in \Omega $
. Then,
$x_{0}\in \Omega $
. Then,
where
![]() $x\in B_{r}(x_{0})\Subset \Omega _{l}$
for some small
$x\in B_{r}(x_{0})\Subset \Omega _{l}$
for some small
![]() $r>0$
and some positive integer l. Fix
$r>0$
and some positive integer l. Fix
![]() $\varepsilon>0$
small enough and let
$\varepsilon>0$
small enough and let
![]() $x_{j}\in \overline {B}_{r}(x_{0})$
be a point of minimum of
$x_{j}\in \overline {B}_{r}(x_{0})$
be a point of minimum of
Then,
Since
![]() $x_{j}\in \overline {B}_{r}(x_{0})$
, we assume that
$x_{j}\in \overline {B}_{r}(x_{0})$
, we assume that
![]() $x_{j}\rightarrow \hat {x}$
for some
$x_{j}\rightarrow \hat {x}$
for some
![]() $\hat {x}\in \overline {B}_{r}(x_{0})$
. Taking the limit in (4-4) as
$\hat {x}\in \overline {B}_{r}(x_{0})$
. Taking the limit in (4-4) as
![]() $j\rightarrow \infty $
,
$j\rightarrow \infty $
,
Therefore,
This yields
![]() $\hat {x}=x_{0}$
. Since
$\hat {x}=x_{0}$
. Since
![]() $u_{j}$
is a viscosity solution of (4-3) and
$u_{j}$
is a viscosity solution of (4-3) and
![]() $x_{j}$
is a point of minimum of
$x_{j}$
is a point of minimum of
![]() $u_{j}(x)-(\psi (x)-{\varepsilon }/{2}|x-x_{0}|^{2})$
in
$u_{j}(x)-(\psi (x)-{\varepsilon }/{2}|x-x_{0}|^{2})$
in
![]() $B_{r}(x_{0})$
, we take
$B_{r}(x_{0})$
, we take
![]() $\phi _{\varepsilon }(x):=\psi (x)-{\varepsilon }/{2}|x-x_{0}|^{2}$
as a test function. Then,
$\phi _{\varepsilon }(x):=\psi (x)-{\varepsilon }/{2}|x-x_{0}|^{2}$
as a test function. Then,
Recalling that
![]() $u_{j}\rightarrow u$
uniformly in
$u_{j}\rightarrow u$
uniformly in
![]() $B_{r}(x_{0})$
and taking the limit as
$B_{r}(x_{0})$
and taking the limit as
![]() $j\rightarrow \infty $
,
$j\rightarrow \infty $
,
Letting
![]() $\varepsilon \rightarrow 0$
,
$\varepsilon \rightarrow 0$
,
that is, u is a viscosity supersolution of (4-3). Thus, u is a viscosity supersolution of (4-1).
Similarly, one can prove that u satisfies
![]() $\Delta _\infty ^h u\geq \hat {F }(x,u,Du)$
in the viscosity sense. We leave it to the reader.
$\Delta _\infty ^h u\geq \hat {F }(x,u,Du)$
in the viscosity sense. We leave it to the reader.
By Theorem 4.1, we can get the following corollary immediately.
Corollary 4.2. Let
![]() $\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain and
$\Omega \subseteq \mathbb {R}^{n}$
be a bounded domain and
![]() $\lambda> 0$
be a parameter. Suppose that
$\lambda> 0$
be a parameter. Suppose that
![]() $f(x,t,p):\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and may exhibit singularity at
$f(x,t,p):\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
is a continuous function and may exhibit singularity at
![]() $t=0$
. If
$t=0$
. If
![]() $\underline {u}\in C(\overline {\Omega })$
and
$\underline {u}\in C(\overline {\Omega })$
and
![]() $\overline {u}\in C(\overline {\Omega })$
are a viscosity subsolution and a viscosity supersolution of
$\overline {u}\in C(\overline {\Omega })$
are a viscosity subsolution and a viscosity supersolution of
respectively, such that
![]() $0<\underline {u}\leq \overline {u}$
in
$0<\underline {u}\leq \overline {u}$
in
![]() $\Omega $
and
$\Omega $
and
![]() $\underline {u}=0=\overline {u}$
on
$\underline {u}=0=\overline {u}$
on
![]() $\partial \Omega $
, then (4-5) admits a viscosity solution
$\partial \Omega $
, then (4-5) admits a viscosity solution
![]() $u\in C(\overline {\Omega })$
such that
$u\in C(\overline {\Omega })$
such that
![]() $\underline {u}\leq u\leq \overline {u}$
in
$\underline {u}\leq u\leq \overline {u}$
in
![]() $\overline {\Omega }$
.
$\overline {\Omega }$
.
If we take
![]() $F(x,u,Du)=\lambda f(x,u,Du), $
where
$F(x,u,Du)=\lambda f(x,u,Du), $
where
![]() $\lambda>0$
and f satisfies conditions (F-1), (F-2), then by Corollary 4.2, the existence of a viscosity solution reduces to finding a viscosity supersolution and subsolution.
$\lambda>0$
and f satisfies conditions (F-1), (F-2), then by Corollary 4.2, the existence of a viscosity solution reduces to finding a viscosity supersolution and subsolution.
Lemma 4.3. Let
![]() $ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
$ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
![]() $f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function. If f satisfies Condition (F-2) and b satisfies (B-w), then there exists a constant
$f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function. If f satisfies Condition (F-2) and b satisfies (B-w), then there exists a constant
![]() $\lambda _\Omega ^\ast $
depending on
$\lambda _\Omega ^\ast $
depending on
![]() $ \Omega , g_{\infty }$
and
$ \Omega , g_{\infty }$
and
![]() $\|w_{\Omega }\|_{\infty }$
such that Problem (1-1) admits a viscosity supersolution
$\|w_{\Omega }\|_{\infty }$
such that Problem (1-1) admits a viscosity supersolution
![]() $v_{\Omega ,\lambda }\in C(\overline {\Omega })$
for any
$v_{\Omega ,\lambda }\in C(\overline {\Omega })$
for any
![]() $\lambda $
with
$\lambda $
with
![]() $0<\lambda <\lambda _{\Omega }^{\ast }$
. Moreover,
$0<\lambda <\lambda _{\Omega }^{\ast }$
. Moreover,
![]() $v_{\Omega ,\lambda }$
satisfies
$v_{\Omega ,\lambda }$
satisfies
Proof. Define a continuous function
![]() $G:\mathbb {R}^{+}\times \mathbb {R}^{+}\rightarrow \mathbb {R}^{+}$
$G:\mathbb {R}^{+}\times \mathbb {R}^{+}\rightarrow \mathbb {R}^{+}$
 $$ \begin{align*} G(t,\tau) := \begin{cases} t ^{h}\underset{t\leq s\leq \tau }\sup g(s) s^{-h} & 0<t\leq \tau , \\ t ^{h} g(\tau) \tau^{-h} & 0<\tau \leq t. \end{cases} \end{align*} $$
$$ \begin{align*} G(t,\tau) := \begin{cases} t ^{h}\underset{t\leq s\leq \tau }\sup g(s) s^{-h} & 0<t\leq \tau , \\ t ^{h} g(\tau) \tau^{-h} & 0<\tau \leq t. \end{cases} \end{align*} $$
It is easy to see that
![]() $G(t, \tau ) t^{-h}$
is nonincreasing in t. Let
$G(t, \tau ) t^{-h}$
is nonincreasing in t. Let
 $$ \begin{align} \Gamma(t)=\frac{2}{t} \int_{t / 2}^t \frac{G(s, t)}{s^h} \,ds,\quad t>0. \end{align} $$
$$ \begin{align} \Gamma(t)=\frac{2}{t} \int_{t / 2}^t \frac{G(s, t)}{s^h} \,ds,\quad t>0. \end{align} $$
Noting that
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $C^1$
function,
$C^1$
function,
 $$ \begin{align*} \begin{aligned} \Gamma'(t) &=-\frac{2}{t^2} \int_{t/2}^t \frac{G(s, t)}{s^h}\,ds +\frac{2}{t}\bigg(\frac{G(t,t)}{t^h}-\frac{1}{2} \frac{G(t / 2, t)}{(t / 2)^h}\bigg) \\ & \leq-\frac{1}{t} \frac{G(t, t)}{t^h}+\frac{2}{t} \frac{G(t, t)}{t^h} -\frac{1}{t} \frac{G(t / 2, t)}{(t / 2)^h} \\ &=\frac{1}{t}\bigg( \frac{G(t, t)}{t^h}- \frac{G(t / 2, t)}{(t / 2)^h} \bigg)\\ & \leq 0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Gamma'(t) &=-\frac{2}{t^2} \int_{t/2}^t \frac{G(s, t)}{s^h}\,ds +\frac{2}{t}\bigg(\frac{G(t,t)}{t^h}-\frac{1}{2} \frac{G(t / 2, t)}{(t / 2)^h}\bigg) \\ & \leq-\frac{1}{t} \frac{G(t, t)}{t^h}+\frac{2}{t} \frac{G(t, t)}{t^h} -\frac{1}{t} \frac{G(t / 2, t)}{(t / 2)^h} \\ &=\frac{1}{t}\bigg( \frac{G(t, t)}{t^h}- \frac{G(t / 2, t)}{(t / 2)^h} \bigg)\\ & \leq 0. \end{aligned} \end{align*} $$
Hence,
![]() $\Gamma $
is a nonincreasing function in
$\Gamma $
is a nonincreasing function in
![]() $\mathbb {R}^{+}$
. It is obvious that
$\mathbb {R}^{+}$
. It is obvious that
 $$ \begin{align} \frac{g(t)}{t^{h}} =\frac{G(t,t)}{t^{h}}\leq\Gamma(t) \leq \frac{G(\frac{t}{2},t)}{(\frac{t}{2})^{h}} =\sup_{({t}/{2})\leq s \leq t}\frac{g(s)}{s^{h}}\leq\sup_{({t}/{2})\leq s < \infty}\frac{g(s)}{s^{h}}. \end{align} $$
$$ \begin{align} \frac{g(t)}{t^{h}} =\frac{G(t,t)}{t^{h}}\leq\Gamma(t) \leq \frac{G(\frac{t}{2},t)}{(\frac{t}{2})^{h}} =\sup_{({t}/{2})\leq s \leq t}\frac{g(s)}{s^{h}}\leq\sup_{({t}/{2})\leq s < \infty}\frac{g(s)}{s^{h}}. \end{align} $$
Therefore,
Now we suppose that
![]() $0<g_{\infty }<\infty $
and, in this case, we define
$0<g_{\infty }<\infty $
and, in this case, we define
 $$ \begin{align} \lambda_{\Omega}^{\ast}:=\frac{1}{g_{\infty}\|w_{\Omega}\|_{\infty}^{h}}. \end{align} $$
$$ \begin{align} \lambda_{\Omega}^{\ast}:=\frac{1}{g_{\infty}\|w_{\Omega}\|_{\infty}^{h}}. \end{align} $$
For
![]() $0<\lambda <\lambda _{\Omega }^{\ast }$
,
$0<\lambda <\lambda _{\Omega }^{\ast }$
,
 $$ \begin{align*} \lim_{t\rightarrow\infty}\Gamma(t) =\frac{1}{\lambda_{\Omega}^{\ast}\|w_{\Omega}\|_{\infty}^{h}} <\frac{1}{\lambda\|w_{\Omega}\|_{\infty}^{h}}. \end{align*} $$
$$ \begin{align*} \lim_{t\rightarrow\infty}\Gamma(t) =\frac{1}{\lambda_{\Omega}^{\ast}\|w_{\Omega}\|_{\infty}^{h}} <\frac{1}{\lambda\|w_{\Omega}\|_{\infty}^{h}}. \end{align*} $$
Consider the function
 $$ \begin{align*} \Psi(t):=\int_{0}^{t}\frac{1}{\sqrt[h]{\Gamma(s)}} ds ,\quad t>0. \end{align*} $$
$$ \begin{align*} \Psi(t):=\int_{0}^{t}\frac{1}{\sqrt[h]{\Gamma(s)}} ds ,\quad t>0. \end{align*} $$
We have
 $$ \begin{align*} \lim_{t\rightarrow\infty}\frac{\Psi(t)}{t}=\lim_{t\rightarrow\infty}\Psi'(t) =\lim_{t\rightarrow\infty}\frac{1}{\sqrt[h]{\Gamma(t)}}>\sqrt[h]{\lambda} \|w_{\Omega}\|_{\infty}. \end{align*} $$
$$ \begin{align*} \lim_{t\rightarrow\infty}\frac{\Psi(t)}{t}=\lim_{t\rightarrow\infty}\Psi'(t) =\lim_{t\rightarrow\infty}\frac{1}{\sqrt[h]{\Gamma(t)}}>\sqrt[h]{\lambda} \|w_{\Omega}\|_{\infty}. \end{align*} $$
Thus, we can find
![]() $\theta \geq 1$
large enough such that
$\theta \geq 1$
large enough such that
In the other case, we suppose
![]() $g_{\infty }=\infty $
. One can verify that
$g_{\infty }=\infty $
. One can verify that
Set
 $$ \begin{align} \lambda_{\Omega}^{\ast}:=\bigg(\frac{\alpha_{\ast}}{\|w_{\Omega}\|_{\infty}}\bigg)^{h}. \end{align} $$
$$ \begin{align} \lambda_{\Omega}^{\ast}:=\bigg(\frac{\alpha_{\ast}}{\|w_{\Omega}\|_{\infty}}\bigg)^{h}. \end{align} $$
Then for
![]() $0<\lambda <\lambda _{\Omega }^{\ast },$
$0<\lambda <\lambda _{\Omega }^{\ast },$
Therefore, there exists
![]() $\gamma _{\infty }\geq 1$
, depending on
$\gamma _{\infty }\geq 1$
, depending on
![]() $\lambda $
, such that
$\lambda $
, such that
 $$ \begin{align} \sqrt[h]{\lambda}\|w_{\Omega}\|_{\infty}<\frac{\Psi(\gamma_{\infty})}{\gamma_{\infty}}. \end{align} $$
$$ \begin{align} \sqrt[h]{\lambda}\|w_{\Omega}\|_{\infty}<\frac{\Psi(\gamma_{\infty})}{\gamma_{\infty}}. \end{align} $$
Hence, by (4-10) and (4-12), there exists
![]() $\theta \geq 1$
such that
$\theta \geq 1$
such that
Let
![]() $\Phi $
be the inverse of
$\Phi $
be the inverse of
![]() $\Psi $
, that is,
$\Psi $
, that is,
![]() $\Phi $
satisfies
$\Phi $
satisfies
 $$ \begin{align*} \int_{0}^{\Phi(t)}\frac{1}{\sqrt[h]{\Gamma(s)}}\,ds =t, \quad t\geq0. \end{align*} $$
$$ \begin{align*} \int_{0}^{\Phi(t)}\frac{1}{\sqrt[h]{\Gamma(s)}}\,ds =t, \quad t\geq0. \end{align*} $$
Define
It is clear that
![]() $v_{\Omega ,\lambda }>0$
in
$v_{\Omega ,\lambda }>0$
in
![]() $\Omega $
and
$\Omega $
and
![]() $v_{\Omega ,\lambda }=0$
on
$v_{\Omega ,\lambda }=0$
on
![]() $\partial \Omega $
.
$\partial \Omega $
.
Next we want to show that
![]() $v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1). Let
$v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1). Let
![]() $x_{0}\in \Omega $
and
$x_{0}\in \Omega $
and
![]() $\varphi \in C^{2}(\Omega )$
such that
$\varphi \in C^{2}(\Omega )$
such that
![]() $v_{\Omega ,\lambda }-\varphi $
has a local minimum at
$v_{\Omega ,\lambda }-\varphi $
has a local minimum at
![]() $x_{0}\in \Omega $
. Without loss of generality, we can suppose that
$x_{0}\in \Omega $
. Without loss of generality, we can suppose that
![]() $x_{0}$
is a global minimum point of
$x_{0}$
is a global minimum point of
![]() $v_{\Omega ,\lambda }-\varphi $
in
$v_{\Omega ,\lambda }-\varphi $
in
![]() $\Omega $
and
$\Omega $
and
![]() $v_{\Omega ,\lambda }(x_{0})=\varphi (x_{0})$
. Setting
$v_{\Omega ,\lambda }(x_{0})=\varphi (x_{0})$
. Setting
 $$ \begin{align*} \eta(x):=\frac{1}{\theta\sqrt[h]{\lambda}}\Psi(\varphi)\in C^{2}(\Omega), \end{align*} $$
$$ \begin{align*} \eta(x):=\frac{1}{\theta\sqrt[h]{\lambda}}\Psi(\varphi)\in C^{2}(\Omega), \end{align*} $$
we have
![]() $w_{\Omega }(x_{0})=\eta (x_{0})$
and
$w_{\Omega }(x_{0})=\eta (x_{0})$
and
![]() $w_{\Omega }-\eta $
has a minimum at
$w_{\Omega }-\eta $
has a minimum at
![]() $x_{0}$
. Since
$x_{0}$
. Since
![]() $w_{\Omega }$
is a viscosity supersolution of Problem (1-10),
$w_{\Omega }$
is a viscosity supersolution of Problem (1-10),
Since
![]() $\Psi '(\varphi )>0$
and
$\Psi '(\varphi )>0$
and
![]() $\Psi "(\varphi )\geq 0$
, one can easily check that
$\Psi "(\varphi )\geq 0$
, one can easily check that
 $$ \begin{align*} \begin{aligned} \Delta_{\infty}^{h}\eta &=\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h} (\Psi"(\varphi)[\Psi'(\varphi)]^{h-1}|D\varphi|^{h+1} +[\Psi'(\varphi)]^{h}\Delta_{\infty}^{h}\varphi) \\ &\geq\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h}[\Psi'(\varphi)]^{h}\Delta_{\infty}^{h}\varphi\\ &=\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h} \frac{1}{\Gamma(\varphi)}\Delta_{\infty}^{h}\varphi. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Delta_{\infty}^{h}\eta &=\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h} (\Psi"(\varphi)[\Psi'(\varphi)]^{h-1}|D\varphi|^{h+1} +[\Psi'(\varphi)]^{h}\Delta_{\infty}^{h}\varphi) \\ &\geq\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h}[\Psi'(\varphi)]^{h}\Delta_{\infty}^{h}\varphi\\ &=\bigg(\frac{1}{\theta\sqrt[h]{\lambda}}\bigg)^{h} \frac{1}{\Gamma(\varphi)}\Delta_{\infty}^{h}\varphi. \end{aligned} \end{align*} $$
Then we have the following inequalities at
![]() $x_{0}$
$x_{0}$
 $$ \begin{align} \Delta_{\infty}^{h}\varphi &\leq(\theta\sqrt[h]{\lambda})^{h}\Gamma(\varphi) \Delta_{\infty}^{h}\eta\nonumber\\ &\leq-b(\theta\sqrt[h]{\lambda})^{h}\Gamma(\varphi)\nonumber\\ &\leq-b(\theta\sqrt[h]{\lambda})^{h}\bigg(\frac{g(\varphi)}{\varphi^{h}}\bigg)\nonumber\\ &=-\lambda b\bigg(\frac{\theta}{\varphi}\bigg)^{h}g(\varphi)\nonumber\\ &\leq-\lambda bg(\varphi)\nonumber\\ &\leq\lambda f(x_{0},\varphi,D\varphi), \end{align} $$
$$ \begin{align} \Delta_{\infty}^{h}\varphi &\leq(\theta\sqrt[h]{\lambda})^{h}\Gamma(\varphi) \Delta_{\infty}^{h}\eta\nonumber\\ &\leq-b(\theta\sqrt[h]{\lambda})^{h}\Gamma(\varphi)\nonumber\\ &\leq-b(\theta\sqrt[h]{\lambda})^{h}\bigg(\frac{g(\varphi)}{\varphi^{h}}\bigg)\nonumber\\ &=-\lambda b\bigg(\frac{\theta}{\varphi}\bigg)^{h}g(\varphi)\nonumber\\ &\leq-\lambda bg(\varphi)\nonumber\\ &\leq\lambda f(x_{0},\varphi,D\varphi), \end{align} $$
where we use (4-8) and
![]() $\varphi (x_0)=v_{\Omega ,\lambda }(x_0)=\Phi (\theta \sqrt [h]{\lambda }w_{\Omega }(x_0)) \leq \Phi (\theta \sqrt [h]{\lambda }\|w_{\Omega }\|_{\infty })\leq \theta $
. This shows that
$\varphi (x_0)=v_{\Omega ,\lambda }(x_0)=\Phi (\theta \sqrt [h]{\lambda }w_{\Omega }(x_0)) \leq \Phi (\theta \sqrt [h]{\lambda }\|w_{\Omega }\|_{\infty })\leq \theta $
. This shows that
![]() $v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1).
$v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1).
Finally, since
![]() $\theta \geq 1$
, it follows from (4-15) that
$\theta \geq 1$
, it follows from (4-15) that
![]() $\Delta _{\infty }^{h}\varphi \leq -\lambda b(x)\Gamma (\varphi )$
. Therefore,
$\Delta _{\infty }^{h}\varphi \leq -\lambda b(x)\Gamma (\varphi )$
. Therefore,
Remark 4.4. If
![]() $g_{\infty }=0$
, then Problem (1-1) admits a positive supersolution for any
$g_{\infty }=0$
, then Problem (1-1) admits a positive supersolution for any
![]() $0<\lambda <\infty $
, provided that the hypotheses in Lemma 4.3 hold.
$0<\lambda <\infty $
, provided that the hypotheses in Lemma 4.3 hold.
Now we proceed to construct a positive viscosity subsolution to Problem (1-1).
Lemma 4.5. Let
![]() $ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
$ \Omega \subseteq \mathbb {R}^n$
be a bounded domain and
![]() $f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function satisfying Condition (F-1). Then for any
$f:\Omega \times \mathbb {R}^{+}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$
be a continuous function satisfying Condition (F-1). Then for any
![]() $\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
, Problem (1-1) admits a positive viscosity subsolution
$\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
, Problem (1-1) admits a positive viscosity subsolution
![]() $\phi _{\Omega ,\lambda }\in C(\overline {\Omega })$
.
$\phi _{\Omega ,\lambda }\in C(\overline {\Omega })$
.
Proof. Fix
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
. First, if the constant
$\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
. First, if the constant
![]() $0<k_{0}<\infty $
, where
$0<k_{0}<\infty $
, where
![]() $k_{0}$
is defined in (1-9), then there exists a
$k_{0}$
is defined in (1-9), then there exists a
![]() $\delta :=\delta (\lambda )$
with
$\delta :=\delta (\lambda )$
with
![]() $0<\delta <t_{0}$
such that
$0<\delta <t_{0}$
such that
 $$ \begin{align*} k(t)\geq\bigg(\frac{\Lambda_{1}(\Omega)k_{0}^{-1}}{\lambda}\bigg)k_{0}t^{h} =\frac{\Lambda_{1}(\Omega)}{\lambda}t^{h}\quad\text{for all } 0<t\leq\delta. \end{align*} $$
$$ \begin{align*} k(t)\geq\bigg(\frac{\Lambda_{1}(\Omega)k_{0}^{-1}}{\lambda}\bigg)k_{0}t^{h} =\frac{\Lambda_{1}(\Omega)}{\lambda}t^{h}\quad\text{for all } 0<t\leq\delta. \end{align*} $$
However, if
![]() $k_{0}=\infty $
, then for any
$k_{0}=\infty $
, then for any
![]() $\lambda>0 $
, there exists
$\lambda>0 $
, there exists
![]() $0<\delta <t_{0}$
such that
$0<\delta <t_{0}$
such that
In any case, let
![]() $\phi _{\Omega ,\lambda }$
be a positive eigenfunction of Problem (1-11) corresponding to the principal eigenvalue
$\phi _{\Omega ,\lambda }$
be a positive eigenfunction of Problem (1-11) corresponding to the principal eigenvalue
![]() $\Lambda _{1}(\Omega )$
such that
$\Lambda _{1}(\Omega )$
such that
![]() $0<\phi _{\Omega ,\lambda }\leq \min \{1,\delta (\lambda )\}$
in
$0<\phi _{\Omega ,\lambda }\leq \min \{1,\delta (\lambda )\}$
in
![]() $\Omega $
. Then under the assumption on
$\Omega $
. Then under the assumption on
![]() $\lambda $
and condition (F-1),
$\lambda $
and condition (F-1),
in
![]() $\Omega $
. This shows that
$\Omega $
. This shows that
![]() $\phi _{\Omega ,\lambda }$
is a viscosity subsolution of Problem (1-1).
$\phi _{\Omega ,\lambda }$
is a viscosity subsolution of Problem (1-1).
Now we establish the existence of a viscosity solution of Problem (1-1) by Perron’s method.
Proof of Theorem 1.3.
When
![]() $\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
, according to Lemma 4.5, we have a viscosity subsolution
$\lambda>\Lambda _{1}(\Omega )k_{0}^{-1}$
, according to Lemma 4.5, we have a viscosity subsolution
![]() $\phi _{\Omega ,\lambda }$
of Problem (1-1) and
$\phi _{\Omega ,\lambda }$
of Problem (1-1) and
![]() $\phi _{\Omega ,\lambda }\leq 1$
in
$\phi _{\Omega ,\lambda }\leq 1$
in
![]() $\Omega $
. Then,
$\Omega $
. Then,
 $$ \begin{align*} \begin{aligned} \Delta_{\infty}^{h}\phi_{\Omega,\lambda}&\geq \lambda f(x,\phi_{\Omega,\lambda},D\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)g(\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)\phi_{\Omega,\lambda}^{h}\Gamma(\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)\Gamma(\phi_{\Omega,\lambda}) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Delta_{\infty}^{h}\phi_{\Omega,\lambda}&\geq \lambda f(x,\phi_{\Omega,\lambda},D\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)g(\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)\phi_{\Omega,\lambda}^{h}\Gamma(\phi_{\Omega,\lambda})\\ &\geq -\lambda b(x)\Gamma(\phi_{\Omega,\lambda}) \end{aligned} \end{align*} $$
in the viscosity sense, where
![]() $\Gamma $
is the function defined in (4-7).
$\Gamma $
is the function defined in (4-7).
When
![]() $0<\lambda <\lambda _{\Omega }^{\ast }$
, according to Lemma 4.3, we know that
$0<\lambda <\lambda _{\Omega }^{\ast }$
, according to Lemma 4.3, we know that
![]() $v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1) and satisfies (4-6).
$v_{\Omega ,\lambda }$
is a viscosity supersolution of Problem (1-1) and satisfies (4-6).
Now we claim that
![]() $\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
$\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
![]() $\Omega $
. Assume that
$\Omega $
. Assume that
![]() $\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
is not valid. Let
$\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
is not valid. Let
Since
![]() $\Gamma $
is nonincreasing,
$\Gamma $
is nonincreasing,
Then in
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
According to the comparison principle (Theorem 1.1), we see that
![]() $\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
$\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
![]() $\mathbb {D}$
, which is a contradiction.
$\mathbb {D}$
, which is a contradiction.
Furthermore, we see that
![]() $0<\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
$0<\phi _{\Omega ,\lambda }\leq v_{\Omega ,\lambda }$
in
![]() $\Omega $
and
$\Omega $
and
![]() $\phi _{\Omega ,\lambda }(x)=v_{\Omega ,\lambda }=0$
on
$\phi _{\Omega ,\lambda }(x)=v_{\Omega ,\lambda }=0$
on
![]() $\partial \Omega $
. By Corollary 4.2, we conclude that Problem (1-1) admits a viscosity solution
$\partial \Omega $
. By Corollary 4.2, we conclude that Problem (1-1) admits a viscosity solution
![]() $u\in C(\overline {\Omega })$
such that
$u\in C(\overline {\Omega })$
such that
![]() $\phi _{\Omega ,\lambda }\leq u\leq v_{\Omega ,\lambda }$
in
$\phi _{\Omega ,\lambda }\leq u\leq v_{\Omega ,\lambda }$
in
![]() $\overline {\Omega }$
.
$\overline {\Omega }$
.
5. Singular problem in the entire Euclidean space
In this section, we consider Problem (1-12) and establish the existence of viscosity solutions in the entire Euclidean space.
First, we show that Condition (B-w) holds when
![]() $\Omega =\mathbb {R}^{n}$
. To prove this we recall the following lemma in [Reference Liu and Yang29].
$\Omega =\mathbb {R}^{n}$
. To prove this we recall the following lemma in [Reference Liu and Yang29].
Lemma 5.1. For any fixed constant
![]() $a\neq 0,$
the equation
$a\neq 0,$
the equation
![]() $\Delta _\infty ^h w=2a$
admits a viscosity solution
$\Delta _\infty ^h w=2a$
admits a viscosity solution
in
![]() $D(x_0,B)=\{x\in \mathbb {R}^{n}:2a|x-x_0|>-B \; \mathrm {{ and }} \; x\neq x_0\},$
where
$D(x_0,B)=\{x\in \mathbb {R}^{n}:2a|x-x_0|>-B \; \mathrm {{ and }} \; x\neq x_0\},$
where
![]() $ B,\; C$
are arbitrary constants.
$ B,\; C$
are arbitrary constants.
Now, we establish the existence of the viscosity solution of Problem (1-10) when
![]() $\Omega =\mathbb {R}^{n}$
.
$\Omega =\mathbb {R}^{n}$
.
Lemma 5.2. Let
![]() $b(x)\in C(\mathbb {R}^{n})$
be positive and bounded. Then the problem
$b(x)\in C(\mathbb {R}^{n})$
be positive and bounded. Then the problem
 $$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\text{in }\mathbb{R}^{n}, \\ w(x)\rightarrow 0 \quad &\text{as } |x|\rightarrow\infty \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\text{in }\mathbb{R}^{n}, \\ w(x)\rightarrow 0 \quad &\text{as } |x|\rightarrow\infty \end{cases} \end{align} $$
admits a viscosity solution
![]() $w:=w_{\mathbb {R}^{n}}$
.
$w:=w_{\mathbb {R}^{n}}$
.
Proof. Let
![]() $B_{r}:=B(O,r)$
be the ball of radius r centred at the origin O. By [Reference Li and Liu26], we note that the problem
$B_{r}:=B(O,r)$
be the ball of radius r centred at the origin O. By [Reference Li and Liu26], we note that the problem
 $$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\mathrm{{in}}\; B_r, \\ w>0 \quad &\mathrm{in}\; B_r,\\ w=0 \quad &\mathrm{on} \; \partial B_r \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h w=-b(x) \quad &\mathrm{{in}}\; B_r, \\ w>0 \quad &\mathrm{in}\; B_r,\\ w=0 \quad &\mathrm{on} \; \partial B_r \end{cases} \end{align} $$
admits a viscosity solution
![]() $w_r$
. Taking
$w_r$
. Taking
![]() $2a=\inf \nolimits _{\mathbb {R}^{n}}(-b(x))$
in Lemma 5.1, it is obvious that
$2a=\inf \nolimits _{\mathbb {R}^{n}}(-b(x))$
in Lemma 5.1, it is obvious that
![]() $v_{x_{0},BC}(x)$
is a viscosity supersolution of the equation
$v_{x_{0},BC}(x)$
is a viscosity supersolution of the equation
![]() $\Delta _\infty ^h w=-b(x)$
in
$\Delta _\infty ^h w=-b(x)$
in
![]() $B_r$
. Then,
$B_r$
. Then,
This implies that the sequence
![]() $\{w_{r}\}$
is uniformly bounded in
$\{w_{r}\}$
is uniformly bounded in
![]() $\mathbb {R}^{n}$
. According to Lemma 2.5, we note that the sequence
$\mathbb {R}^{n}$
. According to Lemma 2.5, we note that the sequence
![]() $\{w_{r}\}$
is locally uniformly Lipschitz. Therefore,
$\{w_{r}\}$
is locally uniformly Lipschitz. Therefore,
![]() $\{w_{r}\}$
is equicontinuous. Then we can obtain a subsequence that converges locally uniformly to some w and
$\{w_{r}\}$
is equicontinuous. Then we can obtain a subsequence that converges locally uniformly to some w and
![]() $0<w\leq v_{x_{0},BC}(x)$
in
$0<w\leq v_{x_{0},BC}(x)$
in
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
Then we want to show that w is a viscosity solution of
![]() $\Delta _\infty ^h w=-b(x)$
in
$\Delta _\infty ^h w=-b(x)$
in
![]() $\mathbb {R}^{n}$
. We can use the similar argument to the one in the proof of Theorem 4.1. First, we show
$\mathbb {R}^{n}$
. We can use the similar argument to the one in the proof of Theorem 4.1. First, we show
![]() $\Delta _\infty ^h w\leq -b(x)$
in the viscosity sense.
$\Delta _\infty ^h w\leq -b(x)$
in the viscosity sense.
Let
![]() $\varphi \in C^{2}(\mathbb {R}^{n})$
and suppose
$\varphi \in C^{2}(\mathbb {R}^{n})$
and suppose
![]() $w-\varphi $
has a local minimum at some
$w-\varphi $
has a local minimum at some
![]() $x_{0}\in \mathbb {R}^{n}$
, that is,
$x_{0}\in \mathbb {R}^{n}$
, that is,
for some small
![]() $\delta>0$
and some positive integer s. We take
$\delta>0$
and some positive integer s. We take
![]() $\varepsilon>0$
small enough and let
$\varepsilon>0$
small enough and let
![]() $x_{r}\in \overline {B}_{\delta }(x_{0})$
be a point of minimum of
$x_{r}\in \overline {B}_{\delta }(x_{0})$
be a point of minimum of
Then,
We can assume that
![]() $x_{r}\rightarrow \hat {x}$
for some
$x_{r}\rightarrow \hat {x}$
for some
![]() $\hat {x}\in \overline {B}_{r}(x_{0})$
. As
$\hat {x}\in \overline {B}_{r}(x_{0})$
. As
![]() $r\rightarrow \infty $
, it follows from (5-3) that
$r\rightarrow \infty $
, it follows from (5-3) that
That is,
This implies
![]() $\hat {x}=x_{0}$
. Since
$\hat {x}=x_{0}$
. Since
![]() $w_{r}$
is a viscosity solution of (5-2) and
$w_{r}$
is a viscosity solution of (5-2) and
![]() $x_{r}$
is a point of minimum of
$x_{r}$
is a point of minimum of
![]() $w_{r}(x)-(\varphi (x)- \frac {\varepsilon }{2}|x-x_{0}|^{2})$
in
$w_{r}(x)-(\varphi (x)- \frac {\varepsilon }{2}|x-x_{0}|^{2})$
in
![]() $B_{r}(x_{0})$
, we take a test function
$B_{r}(x_{0})$
, we take a test function
![]() $\phi _{\varepsilon }(x):=\varphi (x)- \frac {\varepsilon }{2}|x-x_{0}|^{2}$
. Then,
$\phi _{\varepsilon }(x):=\varphi (x)- \frac {\varepsilon }{2}|x-x_{0}|^{2}$
. Then,
Taking the limit as
![]() $r\rightarrow \infty $
,
$r\rightarrow \infty $
,
Letting
![]() $\varepsilon \rightarrow 0$
,
$\varepsilon \rightarrow 0$
,
that is, w is a viscosity supersolution of
![]() $\Delta _\infty ^h w=-b(x)$
in
$\Delta _\infty ^h w=-b(x)$
in
![]() $\mathbb {R}^{n}$
. Similarly, one can prove that w is a viscosity subsolution of
$\mathbb {R}^{n}$
. Similarly, one can prove that w is a viscosity subsolution of
![]() $\Delta _\infty ^h w=-b(x)$
in
$\Delta _\infty ^h w=-b(x)$
in
![]() $\mathbb {R}^{n}$
. Clearly,
$\mathbb {R}^{n}$
. Clearly,
![]() $w(x)\rightarrow 0$
as
$w(x)\rightarrow 0$
as
![]() $|x|\rightarrow \infty $
. Therefore, w is a viscosity solution of (5-1).
$|x|\rightarrow \infty $
. Therefore, w is a viscosity solution of (5-1).
By the comparison principle, we have
![]() $w_{\Omega }\leq w_{\mathbb {R}^{n}}$
in
$w_{\Omega }\leq w_{\mathbb {R}^{n}}$
in
![]() $\Omega $
. Furthermore, according to Definitions (4-9) and (4-11), we see that
$\Omega $
. Furthermore, according to Definitions (4-9) and (4-11), we see that
![]() $\lambda _{\mathbb {R}^{n}}^{*}\leq \lambda _{\Omega }^{*}$
. Then for
$\lambda _{\mathbb {R}^{n}}^{*}\leq \lambda _{\Omega }^{*}$
. Then for
![]() $0<\lambda <\lambda _{\mathbb {R}^{n}}^{*}$
, we have
$0<\lambda <\lambda _{\mathbb {R}^{n}}^{*}$
, we have
![]() $v_{\Omega ,\lambda }\leq v_{\lambda }$
in
$v_{\Omega ,\lambda }\leq v_{\lambda }$
in
![]() $\Omega $
according to Definition (4-14), where
$\Omega $
according to Definition (4-14), where
![]() $v_{\lambda }:=v_{\mathbb {R}^{n},\lambda }$
is a viscosity supersolution of Problem (1-12) in
$v_{\lambda }:=v_{\mathbb {R}^{n},\lambda }$
is a viscosity supersolution of Problem (1-12) in
![]() $\mathbb {R}^{n}$
. Thus, we have
$\mathbb {R}^{n}$
. Thus, we have
![]() $0< u_{\Omega ,\lambda }\leq v_{\lambda }$
in
$0< u_{\Omega ,\lambda }\leq v_{\lambda }$
in
![]() $\Omega $
, where
$\Omega $
, where
![]() $u_{\Omega ,\lambda }$
is the viscosity solution of Problem (1-1) in
$u_{\Omega ,\lambda }$
is the viscosity solution of Problem (1-1) in
![]() $\Omega $
.
$\Omega $
.
Now, we give the proof of the existence result by an approximation procedure in the entire Euclidean space.
Proof of Theorem 1.4.
Let
![]() $\lambda ^{*}:=\lambda _{\mathbb {R}^{n}}^{*}$
be the positive constant in Theorem 1.3 corresponding to
$\lambda ^{*}:=\lambda _{\mathbb {R}^{n}}^{*}$
be the positive constant in Theorem 1.3 corresponding to
![]() $\Omega =\mathbb {R}^{n}$
and
$\Omega =\mathbb {R}^{n}$
and
![]() $\Lambda _{1}(B(O,1))k_{0}^{-1}<\lambda <\lambda ^{*}$
. For each positive integer k, let
$\Lambda _{1}(B(O,1))k_{0}^{-1}<\lambda <\lambda ^{*}$
. For each positive integer k, let
![]() $B_{k}:=B(O,k)$
be the ball of radius k centred at the origin O. Since
$B_{k}:=B(O,k)$
be the ball of radius k centred at the origin O. Since
![]() $\Lambda _{1}(B(O,k))\leq \Lambda _{1}(B(O,1))$
and
$\Lambda _{1}(B(O,k))\leq \Lambda _{1}(B(O,1))$
and
![]() $\lambda ^{*}\leq \lambda _{B(O,k)}^{*}$
, we have
$\lambda ^{*}\leq \lambda _{B(O,k)}^{*}$
, we have
![]() $\Lambda _{1}(B(O,k))k_{0}^{-1}<\lambda <\lambda _{B(O,k)}^{*}$
. Since f satisfies Conditions (F-1), (F-2) and b satisfies (B-w) in
$\Lambda _{1}(B(O,k))k_{0}^{-1}<\lambda <\lambda _{B(O,k)}^{*}$
. Since f satisfies Conditions (F-1), (F-2) and b satisfies (B-w) in
![]() $\Omega =B(O,k)$
, by Theorem 1.3, we obtain a viscosity solution
$\Omega =B(O,k)$
, by Theorem 1.3, we obtain a viscosity solution
![]() $u_{k}:=u_{B_{k},\lambda }\in C(\overline {B}_{k}) (k=1,2,\ldots )$
of the singular boundary value problem
$u_{k}:=u_{B_{k},\lambda }\in C(\overline {B}_{k}) (k=1,2,\ldots )$
of the singular boundary value problem
 $$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{in}\; B_{k}, \\ u(x)=0 \quad &\mathrm{on} \; \partial B_{k}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{in}\; B_{k}, \\ u(x)=0 \quad &\mathrm{on} \; \partial B_{k}. \end{cases} \end{align} $$
Letting
![]() $v_{\lambda }$
be a viscosity supersolution of Problem (1-12) given by the method in Lemma 4.3 in
$v_{\lambda }$
be a viscosity supersolution of Problem (1-12) given by the method in Lemma 4.3 in
![]() $\Omega =\mathbb {R}^{n},$
$\Omega =\mathbb {R}^{n},$
Equation (5-5) shows that the sequence
![]() $\{u_{k}\}$
is uniformly bounded in
$\{u_{k}\}$
is uniformly bounded in
![]() $\mathbb {R}^{n}$
. According to Lemma 2.5, we see that the sequence
$\mathbb {R}^{n}$
. According to Lemma 2.5, we see that the sequence
![]() $\{u_{k}\}$
is locally uniformly Lipschitz. Thus,
$\{u_{k}\}$
is locally uniformly Lipschitz. Thus,
![]() $\{u_{k}\}$
is equicontinuous. Then we can obtain a subsequence that converges locally uniformly to some
$\{u_{k}\}$
is equicontinuous. Then we can obtain a subsequence that converges locally uniformly to some
![]() $u_{\lambda }\in C(\mathbb {R}^{n})$
and
$u_{\lambda }\in C(\mathbb {R}^{n})$
and
![]() $0\leq u_{\lambda }\leq v_{\lambda }$
in
$0\leq u_{\lambda }\leq v_{\lambda }$
in
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
Next, for a given positive integer l, let
![]() $\varphi _{l}:=\varphi _{B_{l}}$
be an eigenfunction of Problem (1-11) corresponding to the principal eigenvalue
$\varphi _{l}:=\varphi _{B_{l}}$
be an eigenfunction of Problem (1-11) corresponding to the principal eigenvalue
![]() $\Lambda _{1}(B(O,l))$
on the ball
$\Lambda _{1}(B(O,l))$
on the ball
![]() $B_{l}:=B(O,l)$
. For any viscosity solution
$B_{l}:=B(O,l)$
. For any viscosity solution
![]() $u_{k}$
of (5-4), we want to show that
$u_{k}$
of (5-4), we want to show that
For each
![]() $(x,t,p)\in \mathbb {R}^{n}\times \mathbb {R}^{+}\times \mathbb {R}^{n}$
, let
$(x,t,p)\in \mathbb {R}^{n}\times \mathbb {R}^{+}\times \mathbb {R}^{n}$
, let
 $$ \begin{align*} \hat{f}(x,t,p)=\frac{f(x,e^{t},e^{t}p)}{a(x)(e^{t})^{h}}. \end{align*} $$
$$ \begin{align*} \hat{f}(x,t,p)=\frac{f(x,e^{t},e^{t}p)}{a(x)(e^{t})^{h}}. \end{align*} $$
For convenience, we set
![]() $\Lambda _{1}:=\Lambda _{1}(B(O,1))$
and
$\Lambda _{1}:=\Lambda _{1}(B(O,1))$
and
![]() $\Lambda _{l}:=\Lambda _{1}(B(O,l))$
. Note that
$\Lambda _{l}:=\Lambda _{1}(B(O,l))$
. Note that
where
![]() $k_{0}$
is defined in (1-9) and
$k_{0}$
is defined in (1-9) and
![]() $k_{0}^{-1}$
is interpreted to be zero if
$k_{0}^{-1}$
is interpreted to be zero if
![]() $k_{0}=\infty $
. Fix
$k_{0}=\infty $
. Fix
![]() $\tau $
such that
$\tau $
such that
Then by the definition of
![]() $k_{0}$
, there exists
$k_{0}$
, there exists
![]() $0<t^{*}:=t^{*}(\lambda )\leq t_{0}$
such that
$0<t^{*}:=t^{*}(\lambda )\leq t_{0}$
such that
![]() $k(t)\geq (\frac {\tau }{\lambda })t^{h}$
for
$k(t)\geq (\frac {\tau }{\lambda })t^{h}$
for
![]() $0<t<t^{*}$
. Thus,
$0<t<t^{*}$
. Thus,
Therefore,
Suppose that
![]() $\varphi _{l}$
has been normalized so that
$\varphi _{l}$
has been normalized so that
![]() $0<\varphi _{l}\leq t^{*}$
in
$0<\varphi _{l}\leq t^{*}$
in
![]() $B_{l}$
. Suppose that Inequality (5-6) is not true. Since
$B_{l}$
. Suppose that Inequality (5-6) is not true. Since
![]() $u_{k}\geq \varphi _{l}$
on
$u_{k}\geq \varphi _{l}$
on
![]() $\partial B_{l}$
, it follows that
$\partial B_{l}$
, it follows that
![]() $\frac {\varphi _{l}}{u_{k}}$
attains its maximum in
$\frac {\varphi _{l}}{u_{k}}$
attains its maximum in
![]() $B_{l}$
. Since
$B_{l}$
. Since
![]() $u_{k}$
and
$u_{k}$
and
![]() $\varphi _{l}$
are positive in
$\varphi _{l}$
are positive in
![]() $ B_{l}$
, we see that
$ B_{l}$
, we see that
attains its positive maximum at some point
![]() $x_{0}\in B_{l}$
. Set
$x_{0}\in B_{l}$
. Set
By direct calculations,
 $$ \begin{align} \Delta_\infty^h \alpha=-\frac{1}{\varphi_{l}^{h+1}}|D\varphi_{l}|^{h+1}+\frac{1}{\varphi_{l}^{h}}\Delta_\infty^h \varphi_{l} =-|D\alpha|^{h+1}-\Lambda_{l}a, \end{align} $$
$$ \begin{align} \Delta_\infty^h \alpha=-\frac{1}{\varphi_{l}^{h+1}}|D\varphi_{l}|^{h+1}+\frac{1}{\varphi_{l}^{h}}\Delta_\infty^h \varphi_{l} =-|D\alpha|^{h+1}-\Lambda_{l}a, \end{align} $$
 $$ \begin{align} \Delta_\infty^h \beta=-\frac{1}{u_{k}^{h+1}}|Du_{k}|^{h+1}+\frac{1}{u_{k}^{h}}\Delta_\infty^h u_{k} =-|D\beta|^{h+1}+\frac{\lambda f(x,e^{\beta},e^{\beta}D\beta)}{(e^{\,\beta})^{h}}. \end{align} $$
$$ \begin{align} \Delta_\infty^h \beta=-\frac{1}{u_{k}^{h+1}}|Du_{k}|^{h+1}+\frac{1}{u_{k}^{h}}\Delta_\infty^h u_{k} =-|D\beta|^{h+1}+\frac{\lambda f(x,e^{\beta},e^{\beta}D\beta)}{(e^{\,\beta})^{h}}. \end{align} $$
Therefore,
 $$ \begin{align*} \Delta_\infty^h \alpha+|D\alpha|^{h+1}=-a\Lambda_{l} \quad \mathrm{and} \quad \Delta_\infty^h \beta+|D\beta|^{h+1}=\frac{\lambda f(x,e^{\beta},e^{\beta}D\beta)}{(e^{\,\beta})^{h}}. \end{align*} $$
$$ \begin{align*} \Delta_\infty^h \alpha+|D\alpha|^{h+1}=-a\Lambda_{l} \quad \mathrm{and} \quad \Delta_\infty^h \beta+|D\beta|^{h+1}=\frac{\lambda f(x,e^{\beta},e^{\beta}D\beta)}{(e^{\,\beta})^{h}}. \end{align*} $$
Note that
has a positive maximum in
![]() $\overline {B}_{l}$
, that is,
$\overline {B}_{l}$
, that is,
![]() $M:=\max \nolimits _{\overline {B}_{l}}(\alpha -\beta )>0$
. Define
$M:=\max \nolimits _{\overline {B}_{l}}(\alpha -\beta )>0$
. Define
Let
Without loss of generality, we can assume that the sequence
![]() $\{(x_{\varepsilon },y_{\varepsilon })\}$
converges to
$\{(x_{\varepsilon },y_{\varepsilon })\}$
converges to
![]() $(z,z)\in \overline {B}_{l}\times \overline {B}_{l}$
as
$(z,z)\in \overline {B}_{l}\times \overline {B}_{l}$
as
![]() $\varepsilon \rightarrow 0$
, where
$\varepsilon \rightarrow 0$
, where
![]() $M=(\alpha -\beta )(z)$
. Since
$M=(\alpha -\beta )(z)$
. Since
![]() $M>0$
, we must have
$M>0$
, we must have
![]() $z\in B_{l}$
. Then we can suppose that
$z\in B_{l}$
. Then we can suppose that
![]() $(x_{\varepsilon },y_{\varepsilon })\in B_{l}$
for sufficiently small
$(x_{\varepsilon },y_{\varepsilon })\in B_{l}$
for sufficiently small
![]() $\varepsilon>0$
. According to the maximum principle in [Reference Crandall, Ishii and Lions18, Reference Ishii23], there are
$\varepsilon>0$
. According to the maximum principle in [Reference Crandall, Ishii and Lions18, Reference Ishii23], there are
![]() $n\times n$
symmetric matrices
$n\times n$
symmetric matrices
![]() $X_{\varepsilon }, Y_{\varepsilon }\in \mathbb {S}$
such that
$X_{\varepsilon }, Y_{\varepsilon }\in \mathbb {S}$
such that
and
 $$ \begin{align} -\frac{3}{\varepsilon}\left({\begin{array}{cc}I&0\\0&I\\ \end{array}}\right) \leq \left({\begin{array}{cc}X_{\varepsilon}&0\\0&-Y_{\varepsilon}\\ \end{array}}\right) \leq \frac{3}{\varepsilon}\left({\begin{array}{cc}I&-I\\-I&I\\ \end{array}}\right), \end{align} $$
$$ \begin{align} -\frac{3}{\varepsilon}\left({\begin{array}{cc}I&0\\0&I\\ \end{array}}\right) \leq \left({\begin{array}{cc}X_{\varepsilon}&0\\0&-Y_{\varepsilon}\\ \end{array}}\right) \leq \frac{3}{\varepsilon}\left({\begin{array}{cc}I&-I\\-I&I\\ \end{array}}\right), \end{align} $$
where
![]() $\eta _{\varepsilon }:=\frac {1}{\varepsilon }(x_{\varepsilon }-y_{\varepsilon })$
. Following from Inequality (5-11), we have
$\eta _{\varepsilon }:=\frac {1}{\varepsilon }(x_{\varepsilon }-y_{\varepsilon })$
. Following from Inequality (5-11), we have
![]() $X_{\varepsilon }\leq Y_{\varepsilon }$
. Applying the definitions of the viscosity subsolution and viscosity supersolution to (5-9) and (5-10), respectively,
$X_{\varepsilon }\leq Y_{\varepsilon }$
. Applying the definitions of the viscosity subsolution and viscosity supersolution to (5-9) and (5-10), respectively,
 $$ \begin{align*} &-\Lambda_{l}a(x_{\varepsilon})\leq\langle X_{\varepsilon}\eta_{\varepsilon},\eta_{\varepsilon}\rangle |\eta_{\varepsilon}|^{h-3}+|\eta_{\varepsilon}|^{h+1} \quad \mathrm{and} \\ &\qquad\langle Y_{\varepsilon}\eta_{\varepsilon},\eta_{\varepsilon}\rangle |\eta_{\varepsilon}|^{h-3} +|\eta_{\varepsilon}|^{h+1}\leq \frac{\lambda f(y_{\varepsilon},e^{\beta},e^{\beta}\eta_{\varepsilon})} {(e^{\,\beta})^{h}}. \end{align*} $$
$$ \begin{align*} &-\Lambda_{l}a(x_{\varepsilon})\leq\langle X_{\varepsilon}\eta_{\varepsilon},\eta_{\varepsilon}\rangle |\eta_{\varepsilon}|^{h-3}+|\eta_{\varepsilon}|^{h+1} \quad \mathrm{and} \\ &\qquad\langle Y_{\varepsilon}\eta_{\varepsilon},\eta_{\varepsilon}\rangle |\eta_{\varepsilon}|^{h-3} +|\eta_{\varepsilon}|^{h+1}\leq \frac{\lambda f(y_{\varepsilon},e^{\beta},e^{\beta}\eta_{\varepsilon})} {(e^{\,\beta})^{h}}. \end{align*} $$
Since
![]() $X_{\varepsilon }\leq Y_{\varepsilon }$
,
$X_{\varepsilon }\leq Y_{\varepsilon }$
,
 $$ \begin{align*} \frac{\lambda f(y_{\varepsilon},e^{\beta},e^{\beta}\eta_{\varepsilon})}{(e^{\,\beta})^{h}} \geq -\Lambda_{l}a(x_{\varepsilon}). \end{align*} $$
$$ \begin{align*} \frac{\lambda f(y_{\varepsilon},e^{\beta},e^{\beta}\eta_{\varepsilon})}{(e^{\,\beta})^{h}} \geq -\Lambda_{l}a(x_{\varepsilon}). \end{align*} $$
As
![]() $\varepsilon \rightarrow 0$
, we get the inequality
$\varepsilon \rightarrow 0$
, we get the inequality
 $$ \begin{align*} \frac{\lambda f(z,e^{\beta}(z),e^{\beta}(z)\eta_{\varepsilon})}{(e^{\beta}(z))^{h}}\geq -\Lambda_{l}a(z). \end{align*} $$
$$ \begin{align*} \frac{\lambda f(z,e^{\beta}(z),e^{\beta}(z)\eta_{\varepsilon})}{(e^{\beta}(z))^{h}}\geq -\Lambda_{l}a(z). \end{align*} $$
Therefore,
By the assumption
![]() $\varphi _{l}(z)>u_{k}(z)$
and since
$\varphi _{l}(z)>u_{k}(z)$
and since
![]() $\hat {f}(x,t,p)$
is nondecreasing in t, we conclude that
$\hat {f}(x,t,p)$
is nondecreasing in t, we conclude that
Together with Inequality (5-8),
Inequality (5-12) is an obvious contradiction to (5-7). Thus, the claim that
![]() $u_{k}\geq \varphi _{l}$
in
$u_{k}\geq \varphi _{l}$
in
![]() $B(O,l)$
for all
$B(O,l)$
for all
![]() $k>l$
holds.
$k>l$
holds.
Then,
As a consequence of this inequality, we have
![]() $0<\varphi _{l}\leq u_{\lambda }$
in
$0<\varphi _{l}\leq u_{\lambda }$
in
![]() $B(O,l)$
. Thus,
$B(O,l)$
. Thus,
Since l is arbitrary, we conclude that
![]() $0<u_{\lambda }\leq v_{\lambda }$
in
$0<u_{\lambda }\leq v_{\lambda }$
in
![]() $\mathbb {R}^{n}$
. By a similar argument to the one used in the proof of Theorem 4.1, we can show that
$\mathbb {R}^{n}$
. By a similar argument to the one used in the proof of Theorem 4.1, we can show that
![]() $u_{\lambda }$
is a viscosity solution of Problem (1-12). Clearly,
$u_{\lambda }$
is a viscosity solution of Problem (1-12). Clearly,
![]() $u(x)\rightarrow 0$
as
$u(x)\rightarrow 0$
as
![]() $|x|\rightarrow \infty $
.
$|x|\rightarrow \infty $
.
Acknowledgements
The authors would like to thank the anonymous referee for their careful reading of the manuscript and useful suggestions and comments.