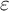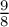1 Introduction
1.1 Presentation of the problem and related results
In this article, we study 2-D incompressible Navier-Stokes equations in a thin domain where the aspect ratio and the Reynolds number have certain constraints:
 $$ \begin{align} \left\{ \begin{aligned} &\partial_{t} U+U \cdot \nabla U-\varepsilon^{2} (\partial_x^2+\eta\partial_y^2) U+\nabla P=0,\\ &\mbox{div}~ U=0,\\ &U|_{y=0}=U|_{y=\varepsilon}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_{t} U+U \cdot \nabla U-\varepsilon^{2} (\partial_x^2+\eta\partial_y^2) U+\nabla P=0,\\ &\mbox{div}~ U=0,\\ &U|_{y=0}=U|_{y=\varepsilon}=0, \end{aligned} \right. \end{align} $$
where
![]() $t\geq 0, (x,y)\in \mathcal {S}^{\varepsilon }=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<\varepsilon \right \}.$
Here,
$t\geq 0, (x,y)\in \mathcal {S}^{\varepsilon }=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<\varepsilon \right \}.$
Here,
![]() $U(t,x,y), P(t,x,y)$
stand for the velocity and pressure function, respectively, and
$U(t,x,y), P(t,x,y)$
stand for the velocity and pressure function, respectively, and
![]() $\eta $
is a positive constant independent of
$\eta $
is a positive constant independent of
![]() $\varepsilon $
. The width of domain
$\varepsilon $
. The width of domain
![]() $\mathcal {S}^{\varepsilon }$
is
$\mathcal {S}^{\varepsilon }$
is
![]() $\varepsilon ,$
and the boundary condition in (1.1) corresponds to the non-slip condition at the walls
$\varepsilon ,$
and the boundary condition in (1.1) corresponds to the non-slip condition at the walls
![]() $y = 0, \varepsilon .$
In addition, the system is prescribed with the initial data of the form
$y = 0, \varepsilon .$
In addition, the system is prescribed with the initial data of the form
This is a classical model with applications to oceanography, meteorology and geophysical flows, where the vertical dimension of the domain is very small compared with the horizontal dimension of the domain.
To study the process
![]() $\varepsilon \to 0$
, we first fix the domain independent of
$\varepsilon \to 0$
, we first fix the domain independent of
![]() $\varepsilon $
. Here, we rescale the system (1.1) as follows:
$\varepsilon $
. Here, we rescale the system (1.1) as follows:
We put above relations into (1.1), and then (1.1) is reduced to a scaled anisotropic Navier-Stokes system:
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u^{\varepsilon}+u^{\varepsilon}\partial_x u^{\varepsilon}+v^{\varepsilon}\partial_y u^{\varepsilon}-\varepsilon^2\partial_x^2 u^{\varepsilon}-\eta\partial_y^2 u^{\varepsilon}+\partial_x p^{\varepsilon}=0,\\ &\varepsilon^2(\partial_t v^{\varepsilon}+u^{\varepsilon}\partial_x v^{\varepsilon}+v^{\varepsilon}\partial_y v^{\varepsilon}-\varepsilon^2\partial_x^2 v^{\varepsilon}-\eta\partial_y^2 v^{\varepsilon})+\partial_y p^{\varepsilon}=0,\\ &\partial_x u^{\varepsilon}+\partial_y v^{\varepsilon}=0,\\ &(u^{\varepsilon},v^{\varepsilon})|_{y=0,1}=0,\\ &(u^{\varepsilon},v^{\varepsilon})|_{t=0}=(u_0,v_0) , \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u^{\varepsilon}+u^{\varepsilon}\partial_x u^{\varepsilon}+v^{\varepsilon}\partial_y u^{\varepsilon}-\varepsilon^2\partial_x^2 u^{\varepsilon}-\eta\partial_y^2 u^{\varepsilon}+\partial_x p^{\varepsilon}=0,\\ &\varepsilon^2(\partial_t v^{\varepsilon}+u^{\varepsilon}\partial_x v^{\varepsilon}+v^{\varepsilon}\partial_y v^{\varepsilon}-\varepsilon^2\partial_x^2 v^{\varepsilon}-\eta\partial_y^2 v^{\varepsilon})+\partial_y p^{\varepsilon}=0,\\ &\partial_x u^{\varepsilon}+\partial_y v^{\varepsilon}=0,\\ &(u^{\varepsilon},v^{\varepsilon})|_{y=0,1}=0,\\ &(u^{\varepsilon},v^{\varepsilon})|_{t=0}=(u_0,v_0) , \end{aligned} \right. \end{align} $$
where
![]() $(x,y)\in \mathcal {S}=\left \{(x, y) \in \mathbb {T}\times (0,1) \right \}$
.
$(x,y)\in \mathcal {S}=\left \{(x, y) \in \mathbb {T}\times (0,1) \right \}$
.
To simplify the notations, we take
![]() $\eta =1$
in this paper and denote
$\eta =1$
in this paper and denote
![]() $\Delta _{\varepsilon }=\varepsilon ^2\partial _x^2+\partial _y^2$
.
$\Delta _{\varepsilon }=\varepsilon ^2\partial _x^2+\partial _y^2$
.
Formally, taking
![]() $\varepsilon \to 0$
in (1.3), we derive the hydrostatic Navier-Stokes/Prandtl system (see [Reference Lagrée and Lorthois22, Reference Renardy31]):
$\varepsilon \to 0$
in (1.3), we derive the hydrostatic Navier-Stokes/Prandtl system (see [Reference Lagrée and Lorthois22, Reference Renardy31]):
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u_p+u_p\partial_x u_p+v_p\partial_y u_p-\eta\partial_y^2 u_p+\partial_x p_p=0\quad \text{ in } \mathcal{S} \times (0, \infty),\\ &\partial_y p_p=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &\partial_x u_p+\partial_y v_p=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &(u_p,v_p)|_{y=0,1}=0,\\ &u_p|_{t=0}=u_0 \quad \text{ in }\,\, \mathcal{S}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u_p+u_p\partial_x u_p+v_p\partial_y u_p-\eta\partial_y^2 u_p+\partial_x p_p=0\quad \text{ in } \mathcal{S} \times (0, \infty),\\ &\partial_y p_p=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &\partial_x u_p+\partial_y v_p=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &(u_p,v_p)|_{y=0,1}=0,\\ &u_p|_{t=0}=u_0 \quad \text{ in }\,\, \mathcal{S}. \end{aligned} \right. \end{align} $$
This paper aims to justify the limit from the scaled anisotropic Navier-Stokes system (1.3) to the hydrostatic Navier-Stokes/Prandtl system (1.4) for a class of convex data in the optimal Gevrey class with index
![]() $\gamma =\frac 32$
.
$\gamma =\frac 32$
.
Before presenting the precise statement of the main result in this paper, we recall some results on system (1.4). If
![]() $\eta =0$
in the system (1.4), we get the hydrostatic Euler system:
$\eta =0$
in the system (1.4), we get the hydrostatic Euler system:
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u+u\partial_x u+v\partial_y u +\partial_x p=0\quad \text{ in } \mathcal{S} \times (0, \infty) ,\\ &\partial_y p=0\quad \text{ in } \mathcal{S} \times (0, \infty) ,\\ &\partial_x u+\partial_y v=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &v|_{y=0,1}=0,\\ &u|_{t=0}=u_0 \quad \text{ in }\,\, \mathcal{S}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u+u\partial_x u+v\partial_y u +\partial_x p=0\quad \text{ in } \mathcal{S} \times (0, \infty) ,\\ &\partial_y p=0\quad \text{ in } \mathcal{S} \times (0, \infty) ,\\ &\partial_x u+\partial_y v=0 \quad \text{ in } \mathcal{S} \times (0, \infty),\\ &v|_{y=0,1}=0,\\ &u|_{t=0}=u_0 \quad \text{ in }\,\, \mathcal{S}. \end{aligned} \right. \end{align} $$
There is a lot of research on the system (1.5), and readers can refer to [Reference Brenier3, Reference Brenier4, Reference Cao, Ibrahim, Nakanishi and Titi5, Reference Grenier16, Reference Kukavica, Temam, Vicol and Ziane20, Reference Kukavica, Masmoudi, Vicol and Wong19, Reference Masmoudi and Wong26, Reference Renardy31, Reference Wong38]. Renardy [Reference Renardy31] proved the linearization of (1.5) has a growth like
![]() $e^{|k|t}$
if the initial data is not uniform convexity (or concavity) with respect to the variable y. Local well-posedness in the analytic setting was established in [Reference Kukavica, Temam, Vicol and Ziane20]. Under the convexity condition, Masmoudi and Wong [Reference Masmoudi and Wong26] got the well-posedness of (1.5) in the Sobolev space.
$e^{|k|t}$
if the initial data is not uniform convexity (or concavity) with respect to the variable y. Local well-posedness in the analytic setting was established in [Reference Kukavica, Temam, Vicol and Ziane20]. Under the convexity condition, Masmoudi and Wong [Reference Masmoudi and Wong26] got the well-posedness of (1.5) in the Sobolev space.
Next, we recall some results on the well-posedness of the hydrostatic Navier-Stokes/Prandtl system (1.4). Similar to the classical Prandtl equation, (1.4) loses one derivative because of the term
![]() $v_p\partial _y u_p$
. Paicu, Zhang and Zhang [Reference Paicu, Zhang and Zhang30] obtained the global well-posedness of system (1.4) when the initial data is small in the analytical space. Meanwhile, Renardy [Reference Renardy31] also proved that the linearization of the hydrostatic Navier-Stokes equations at certain parallel shear flows is ill-posed and may have a growth
$v_p\partial _y u_p$
. Paicu, Zhang and Zhang [Reference Paicu, Zhang and Zhang30] obtained the global well-posedness of system (1.4) when the initial data is small in the analytical space. Meanwhile, Renardy [Reference Renardy31] also proved that the linearization of the hydrostatic Navier-Stokes equations at certain parallel shear flows is ill-posed and may have a growth
![]() $e^{|k|t}$
which is the same as (1.5) when the initial data is not convex. Thus, to obtain well-posedness results that break through the analytic space, one may need the convexity condition on the velocity. For that, under the convexity condition, Gérard-Varet, Masmoudi and Vicol proved (1.4) is local well-posedness in the Gevrey class with index
$e^{|k|t}$
which is the same as (1.5) when the initial data is not convex. Thus, to obtain well-posedness results that break through the analytic space, one may need the convexity condition on the velocity. For that, under the convexity condition, Gérard-Varet, Masmoudi and Vicol proved (1.4) is local well-posedness in the Gevrey class with index
![]() $9/8$
in [Reference Gérard-Varet, Masmoudi and Vicol15]. In [Reference Gérard-Varet, Masmoudi and Vicol15], they first derive the vorticity equations
$9/8$
in [Reference Gérard-Varet, Masmoudi and Vicol15]. In [Reference Gérard-Varet, Masmoudi and Vicol15], they first derive the vorticity equations
![]() $\omega =\partial _y u$
:
$\omega =\partial _y u$
:
where the worst term is
![]() $\partial _x v$
leading to one derivative loss. Then, they use the ‘hydrostatic trick’ which means that they take the inner product with
$\partial _x v$
leading to one derivative loss. Then, they use the ‘hydrostatic trick’ which means that they take the inner product with
![]() $\partial _x \omega /\partial _y \omega $
(
$\partial _x \omega /\partial _y \omega $
(
![]() $\partial _y\omega \geq c_0>0$
) instead of
$\partial _y\omega \geq c_0>0$
) instead of
![]() $\partial _x \omega $
to take advantage of the cancellation:
$\partial _x \omega $
to take advantage of the cancellation:
 $$ \begin{align*} \int \partial_x v\partial_y \omega\cdot \frac{\partial_x \omega}{\partial_y \omega}=\int \partial_x v\partial_x \omega=-\int \partial_x\partial_y v\partial_x u=0. \end{align*} $$
$$ \begin{align*} \int \partial_x v\partial_y \omega\cdot \frac{\partial_x \omega}{\partial_y \omega}=\int \partial_x v\partial_x \omega=-\int \partial_x\partial_y v\partial_x u=0. \end{align*} $$
Such an idea was used previously in [Reference Masmoudi and Wong26]. To close the energy estimates, the ‘hydrostatic trick’ is not enough due to the ‘bad’ boundary condition of
![]() $\omega $
$\omega $
 $$ \begin{align*} \partial_y\omega|_{y=0}=-\partial_x \int_0^1 u^2dy+\cdots, \end{align*} $$
$$ \begin{align*} \partial_y\omega|_{y=0}=-\partial_x \int_0^1 u^2dy+\cdots, \end{align*} $$
which loses one derivative too. To overcome that, [Reference Gérard-Varet, Masmoudi and Vicol15] introduce the following decomposition:
where
![]() $\omega ^{bl}$
is the boundary corrector which satisfies that
$\omega ^{bl}$
is the boundary corrector which satisfies that
 $$ \begin{align*} \partial_t \omega^{bl}-\partial_{y}^2\omega^{bl}=0,\quad \partial_y\omega^{bl}|_{y=0}=-\partial_x \int_0^1 u^2dy. \end{align*} $$
$$ \begin{align*} \partial_t \omega^{bl}-\partial_{y}^2\omega^{bl}=0,\quad \partial_y\omega^{bl}|_{y=0}=-\partial_x \int_0^1 u^2dy. \end{align*} $$
Following the above decomposition, [Reference Gérard-Varet, Masmoudi and Vicol15] obtain the well-posedness results of (1.4) in the Gevrey class with index
![]() $\gamma =\frac 98$
.
$\gamma =\frac 98$
.
To search the best functional space for the system (1.4), based on the Tollmien-Schlichting instabilities for Navier-Stokes [Reference Grenier, Guo and Nguyen17], Gérard-Varet, Masmoudi and Vicol also give the following conjecture: ‘Our conjecture - based on a formal parallel with Tollmien-Schlichting instabilities for Navier-Stokes [18] - is that the best exponent possible should be
![]() $\gamma =\frac 32$
, but the such result is for the time being out of reach’.
$\gamma =\frac 32$
, but the such result is for the time being out of reach’.
While studying the anisotropic Navier-Stokes system (1.3) and the hydrostatic Navier-Stokes/Prandtl system (1.4), another important problem is to justify the inviscid limit. Under the analytical setting, Paicu, Zhang and Zhang [Reference Paicu, Zhang and Zhang30] justified the limit from (1.3) to (1.4). Based on the work [Reference Gérard-Varet, Masmoudi and Vicol15], we [Reference Wang, Wang and Zhang35] justified the limit in the Gevrey class with index
![]() $\gamma =\frac 98$
.
$\gamma =\frac 98$
.
In this paper, we aim to prove the conjecture of Gérard-Varet, Masmoudi and Vicol. To do that, we use some ideas from the classical inviscid limit theory. Next, we recall the recent development of the classical Prandtl equation and the inviscid limit theory.
There are a lot of papers studying the well-posedness of the Prandtl equation in some special functional space. For monotonic initial data, [Reference Oleinik29, Reference Alexandre, Wang, Xu and Yang1, Reference Masmoudi and Wong27] used a different method to get the local existence and uniqueness of classical solutions to the Prandtl equation in Sobolev space. Without monotonic condition, [Reference Lombardo, Cannone and Sammartino24, Reference Sammartino and Caflisch32] proved that the Prandtl equation is well-posedness in the analytic class; [Reference Gérard-Varet and Masmoudi14, Reference Li and Yang23, Reference Chen, Wang and Zhang6] proved the well-posedness of the Prandtl equations in the Gevrey class for a class of concave initial data. Without any structure assumption, Dietert and Gérard-Varet [Reference Dietert and Gérard-Varet8] proved well-posedness in the Gevrey space with index
![]() $\gamma =2$
. According to [Reference Gérard-Varet and Dormy10],
$\gamma =2$
. According to [Reference Gérard-Varet and Dormy10],
![]() $\gamma =2$
may be the optimal index for the well-posedness theory. For more results on the Prandtl equation, see [Reference Grenier and Nguyen18, Reference Wang37, Reference Wang, Xin and Zang36, Reference Xiao and Xin39, Reference Xin and Zhang40].
$\gamma =2$
may be the optimal index for the well-posedness theory. For more results on the Prandtl equation, see [Reference Grenier and Nguyen18, Reference Wang37, Reference Wang, Xin and Zang36, Reference Xiao and Xin39, Reference Xin and Zhang40].
On the inviscid limit problem, we refer to [Reference Sammartino and Caflisch33, Reference Wang, Wang and Zhang34, Reference Kukavica, Vicol and Wang21, Reference Nguyen and Nguyen28, Reference Maekawa25, Reference Fei, Tao and Zhang9] for the analytical class. Note that going from analytic to Gevrey data is a challenging problem. The first result in the Gevrey class is given by [Reference Gérard-Varet, Maekawa and Masmoudi12]. Gérard-Varet, Masmoudi and Maekawa [Reference Gérard-Varet, Maekawa and Masmoudi12] proved the stability of the Prandtl expansion for the perturbations in the Gevrey class when
![]() $U^{BL}(t, Y)$
is a monotone and concave function where the boundary layer is the shear type like
$U^{BL}(t, Y)$
is a monotone and concave function where the boundary layer is the shear type like
where
![]() $\nu $
is the viscosity coefficient. Later, Chen, Wu and Zhang [Reference Chen, Wu and Zhang7] improved the results in [Reference Gérard-Varet, Maekawa and Masmoudi12] to get the
$\nu $
is the viscosity coefficient. Later, Chen, Wu and Zhang [Reference Chen, Wu and Zhang7] improved the results in [Reference Gérard-Varet, Maekawa and Masmoudi12] to get the
![]() $L^2\cap L^{\infty }$
stability. Very recently, Gérard-Varet, Masmoudi and Maekawa [Reference Gérard-Varet, Maekawa and Masmoudi13] used a very clever decomposition to get the optimal Prandtl expansion around the concave boundary layer. Their results generalized the one obtained in [Reference Gérard-Varet, Maekawa and Masmoudi12, Reference Chen, Wu and Zhang7], which restricted to expansions of shear flow type. In their paper, they decompose the stream function
$L^2\cap L^{\infty }$
stability. Very recently, Gérard-Varet, Masmoudi and Maekawa [Reference Gérard-Varet, Maekawa and Masmoudi13] used a very clever decomposition to get the optimal Prandtl expansion around the concave boundary layer. Their results generalized the one obtained in [Reference Gérard-Varet, Maekawa and Masmoudi12, Reference Chen, Wu and Zhang7], which restricted to expansions of shear flow type. In their paper, they decompose the stream function
![]() $\phi $
as follows:
$\phi $
as follows:
where
![]() $\phi _{slip}$
enjoys a “good” boundary condition and
$\phi _{slip}$
enjoys a “good” boundary condition and
![]() $\phi _{bc}$
is a corrector which recover the boundary condition. This kind of decomposition is also used in [Reference Chen, Wu and Zhang7]. To estimate
$\phi _{bc}$
is a corrector which recover the boundary condition. This kind of decomposition is also used in [Reference Chen, Wu and Zhang7]. To estimate
![]() $\phi _{bc}$
, they also need the following decomposition
$\phi _{bc}$
, they also need the following decomposition
where
![]() $\phi _{bc, S}$
satisfies the Stokes equation,
$\phi _{bc, S}$
satisfies the Stokes equation,
![]() $\phi _{bc, T}$
is to correct the stretching term with ‘good’ boundary condition and
$\phi _{bc, T}$
is to correct the stretching term with ‘good’ boundary condition and
![]() $\phi _{bc, R}$
solves formally the same system as
$\phi _{bc, R}$
solves formally the same system as
![]() $\phi _{slip}$
. In this paper, we apply the decomposition in [Reference Gérard-Varet, Maekawa and Masmoudi13] to justify the limit from (1.3) to (1.4).
$\phi _{slip}$
. In this paper, we apply the decomposition in [Reference Gérard-Varet, Maekawa and Masmoudi13] to justify the limit from (1.3) to (1.4).
1.2 Statement of the main results
Before starting the main results, we give some assumptions on the initial data. Assume that initial data belong to the following Gevrey class:
where
![]() $H^{r,s}$
is the anisotropic Sobolev space defined by
$H^{r,s}$
is the anisotropic Sobolev space defined by
More precisely, we consider the initial data of the form
which satisfies the compatibility conditions
 $$ \begin{align} &\int_0^1\partial_x u_0dy=0,\quad \partial_y^2u_0|_{y=0,1}=\int_0^1(-\partial_xu_0^2+\partial_y^2 u_0)-\int_{\mathcal{S}}\partial_y^2 u_0 dxdy.\qquad\quad\ \end{align} $$
$$ \begin{align} &\int_0^1\partial_x u_0dy=0,\quad \partial_y^2u_0|_{y=0,1}=\int_0^1(-\partial_xu_0^2+\partial_y^2 u_0)-\int_{\mathcal{S}}\partial_y^2 u_0 dxdy.\qquad\quad\ \end{align} $$
Moreover, we assume the initial velocity satisfies the convex condition
Now, we are in the position to state the main results of our paper.
Theorem 1.1. Let initial data
![]() $u_0$
satisfy (1.6)-(1.9). Then there exist
$u_0$
satisfy (1.6)-(1.9). Then there exist
![]() $T>0$
and
$T>0$
and
![]() $C> 0$
independent of
$C> 0$
independent of
![]() $\varepsilon $
such that there exists a unique solution of the scaled anisotropic Navier–Stokes equations (1.3) in
$\varepsilon $
such that there exists a unique solution of the scaled anisotropic Navier–Stokes equations (1.3) in
![]() $[0,T]$
, which satisfies that for any
$[0,T]$
, which satisfies that for any
![]() $t\in [0,T],$
it holds that
$t\in [0,T],$
it holds that
where
![]() $(u_p, v_p)$
is the solution to (1.4).
$(u_p, v_p)$
is the solution to (1.4).
Remark 1.2. Although we do not give the proof that the system (1.4) is well-posedness in Gevrey class
![]() $\frac 32$
, one can follow the proof of Theorem 1.1 to obtain the well-posedness. To avoid repeatability in the proof, we omit the details. Actually, the main difference between
$\frac 32$
, one can follow the proof of Theorem 1.1 to obtain the well-posedness. To avoid repeatability in the proof, we omit the details. Actually, the main difference between
![]() $\varepsilon =0$
and
$\varepsilon =0$
and
![]() $\varepsilon \neq 0$
is on the construction boundary corrector
$\varepsilon \neq 0$
is on the construction boundary corrector
![]() $\phi _{bc,S}$
, and readers can find more details in Remark 8.1.
$\phi _{bc,S}$
, and readers can find more details in Remark 8.1.
Remark 1.3. In the recent work [Reference Gérard-Varet, Iyer and Maekawa11], they established the well-posedness of the linearized Hydrostatic Navier-Stokes system around shear flow in Gevrey class
![]() $\frac 32$
. In our present work, we consider the general nonlinear system and focus on the inviscid limit problem.
$\frac 32$
. In our present work, we consider the general nonlinear system and focus on the inviscid limit problem.
1.3 Sketch of the proof
In this subsection, we sketch the main ingredients in our proof.
-
(1) Introduce the error equations. In Section 3, we deduce the error equations. We introduce the error
 $$ \begin{align*} u^R=u^{\varepsilon}-u^p,\quad v^R=v^{\varepsilon}-v^p, \quad p^R=p^{\varepsilon}-p^p, \end{align*} $$
$$ \begin{align*} u^R=u^{\varepsilon}-u^p,\quad v^R=v^{\varepsilon}-v^p, \quad p^R=p^{\varepsilon}-p^p, \end{align*} $$
which satisfies
(1.10) $$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-{\Delta_{\varepsilon} u^R}+v^R\partial_y u^p+\partial_x p^R=\cdots,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R)+\partial_y p^R=\cdots. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-{\Delta_{\varepsilon} u^R}+v^R\partial_y u^p+\partial_x p^R=\cdots,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R)+\partial_y p^R=\cdots. \end{aligned} \right. \end{align} $$
Here,
 $(u^p, v^p, p^p)$
is an approximate solution given in (3.1). The key point in this paper is to obtain the uniform estimate (in
$(u^p, v^p, p^p)$
is an approximate solution given in (3.1). The key point in this paper is to obtain the uniform estimate (in
 $\varepsilon $
) of
$\varepsilon $
) of
 $(u^R, \varepsilon v^R)$
in the Gevrey class with index
$(u^R, \varepsilon v^R)$
in the Gevrey class with index
 $\gamma =\frac 32.$
In view of (1.10), since
$\gamma =\frac 32.$
In view of (1.10), since
 $v^R$
is controlled via the relation
$v^R$
is controlled via the relation
 $v^R=-\int _0^y \partial _x u^R dy'$
, the main difficulty comes from the term
$v^R=-\int _0^y \partial _x u^R dy'$
, the main difficulty comes from the term
 $v^R\partial _y u^p$
, which loses one tangential derivative. In [Reference Wang, Wang and Zhang35], we justify the limit in Gevrey class
$v^R\partial _y u^p$
, which loses one tangential derivative. In [Reference Wang, Wang and Zhang35], we justify the limit in Gevrey class
 $\frac 98.$
For the data in the Gevrey class with optimal index
$\frac 98.$
For the data in the Gevrey class with optimal index
 $\gamma =\frac 32$
, we need to introduce new ideas.
$\gamma =\frac 32$
, we need to introduce new ideas. -
(2) Introduce the vorticity formulation. In order to eliminate
 $p^R,$
we introduce vorticity
$p^R,$
we introduce vorticity
 $\omega ^R=-\varepsilon ^2\partial _x v^R+\partial _y u^R$
and rewrite the equation of
$\omega ^R=-\varepsilon ^2\partial _x v^R+\partial _y u^R$
and rewrite the equation of
 $\omega ^R$
by stream function
$\omega ^R$
by stream function
 $\phi $
which satisfies
$\phi $
which satisfies  $$ \begin{align*} v^R=-\partial_x\phi, \quad u^R=\partial_y \phi+C(t), \quad C(t)=\frac1{2\pi}\int_{{\mathcal S}} u^Rdxdy. \end{align*} $$
$$ \begin{align*} v^R=-\partial_x\phi, \quad u^R=\partial_y \phi+C(t), \quad C(t)=\frac1{2\pi}\int_{{\mathcal S}} u^Rdxdy. \end{align*} $$
Thus, we get
(1.11) $$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon} \phi-\partial_x\phi\partial_y \omega^p=\cdots,\qquad (x,y)\in\mathcal{S},\\ &\phi|_{y=0,1}=0, \quad \partial_y\phi|_{y=0,1}=C(t),\qquad x\in\mathbb{T}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon} \phi-\partial_x\phi\partial_y \omega^p=\cdots,\qquad (x,y)\in\mathcal{S},\\ &\phi|_{y=0,1}=0, \quad \partial_y\phi|_{y=0,1}=C(t),\qquad x\in\mathbb{T}. \end{aligned} \right. \end{align} $$
We notice the term
 $\partial _x\phi \partial _y \omega ^p$
also loses one tangential derivative. But under the convexity condition
$\partial _x\phi \partial _y \omega ^p$
also loses one tangential derivative. But under the convexity condition
 $\partial _y\omega ^p\geq c_0>0,$
one can use the ‘hydrostatic trick’ to deal with this term. Testing
$\partial _y\omega ^p\geq c_0>0,$
one can use the ‘hydrostatic trick’ to deal with this term. Testing
 $\frac {\omega ^R}{\partial _y\omega ^p}$
to the (1.11) instead of
$\frac {\omega ^R}{\partial _y\omega ^p}$
to the (1.11) instead of
 $\omega ^R,$
we have the following cancellation:
$\omega ^R,$
we have the following cancellation:  $$ \begin{align*} -\int_{{\mathcal S}}\partial_x\phi \partial_y\omega^p \cdot\frac{\omega^R}{\partial_y\omega^p}dxdy=-\int_{{\mathcal S}}\partial_x\phi \triangle_{\varepsilon} \phi dxdy=\int_{{\mathcal S}}\partial_x|\nabla_{\varepsilon}\phi|^2 dxdy=0, \end{align*} $$
$$ \begin{align*} -\int_{{\mathcal S}}\partial_x\phi \partial_y\omega^p \cdot\frac{\omega^R}{\partial_y\omega^p}dxdy=-\int_{{\mathcal S}}\partial_x\phi \triangle_{\varepsilon} \phi dxdy=\int_{{\mathcal S}}\partial_x|\nabla_{\varepsilon}\phi|^2 dxdy=0, \end{align*} $$
where we use
 $\phi |_{y=0,1}=0.$
However, the boundary condition of
$\phi |_{y=0,1}=0.$
However, the boundary condition of
 $\phi $
is
$\phi $
is
 $\partial _y\phi |_{y=0,1}= C(t)$
, which brings an essential difficulty.
$\partial _y\phi |_{y=0,1}= C(t)$
, which brings an essential difficulty.By the energy estimates, taking the inner product in
 $X^{r}$
(the definition is given in section 2) with
$X^{r}$
(the definition is given in section 2) with
 $-\partial _t\phi ,$
we get (1.12)
$-\partial _t\phi ,$
we get (1.12) $$ \begin{align} &\sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\| \Delta_{\varepsilon}\phi(s)\|_{X^2}^2) \end{align} $$
$$ \begin{align} &\sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\| \Delta_{\varepsilon}\phi(s)\|_{X^2}^2) \end{align} $$
 $$\begin{align*}\leq &\ C\int_0^t(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\| \nabla_{\varepsilon}\phi\|_{X^2}^2+\cdots)ds,\end{align*}$$
$$\begin{align*}\leq &\ C\int_0^t(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\| \nabla_{\varepsilon}\phi\|_{X^2}^2+\cdots)ds,\end{align*}$$
where
 $\varphi (y)=y(1-y).$
All we need to do is to control
$\varphi (y)=y(1-y).$
All we need to do is to control
 $\varepsilon ^{-1}\|\varphi \Delta _{\varepsilon }\phi \|_{X^2}$
and
$\varepsilon ^{-1}\|\varphi \Delta _{\varepsilon }\phi \|_{X^2}$
and
 $\varepsilon ^{-1}\|\nabla _{\varepsilon }\phi \|_{X^2}$
by the left-hand side of (1.12).
$\varepsilon ^{-1}\|\nabla _{\varepsilon }\phi \|_{X^2}$
by the left-hand side of (1.12).Motivated by [Reference Gérard-Varet, Maekawa and Masmoudi13], we expect to achieve that by a decomposition of stream function,
 $\phi =\phi _{slip}+\phi _{bc}$
in Gevrey
$\phi =\phi _{slip}+\phi _{bc}$
in Gevrey
 $\frac 32$
regularity. Here,
$\frac 32$
regularity. Here,
 $\phi _{slip}$
enjoys a ‘good’ boundary condition and
$\phi _{slip}$
enjoys a ‘good’ boundary condition and
 $\phi _{bc}$
is a corrector which recovers the boundary condition. In the following, we present the decomposition precisely.
$\phi _{bc}$
is a corrector which recovers the boundary condition. In the following, we present the decomposition precisely. -
(3) Gevrey estimate under artificial boundary conditions.
 $\phi _{slip}$
enjoying a good boundary condition is defined by (1.13)
$\phi _{slip}$
enjoying a good boundary condition is defined by (1.13) $$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\omega_{slip}-\partial_x\phi_{slip}\partial_y \omega^p=\cdots,\qquad (x,y)\in\mathcal{S}\\ &\phi_{slip}|_{y=0,1}=0, \quad \omega_{slip}|_{y=0,1}=0,\qquad x\in\mathbb{T}, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\omega_{slip}-\partial_x\phi_{slip}\partial_y \omega^p=\cdots,\qquad (x,y)\in\mathcal{S}\\ &\phi_{slip}|_{y=0,1}=0, \quad \omega_{slip}|_{y=0,1}=0,\qquad x\in\mathbb{T}, \end{aligned} \right. \end{align} $$
where
 $\omega _{slip}=\Delta _{\varepsilon }\phi _{slip}.$
By ‘hydrostatic trick’ and Navier-slip boundary conditions, we obtain (1.14)
$\omega _{slip}=\Delta _{\varepsilon }\phi _{slip}.$
By ‘hydrostatic trick’ and Navier-slip boundary conditions, we obtain (1.14) $$ \begin{align} \lambda\int_0^t (\|\omega_{slip}\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds\leq \frac{C}{\lambda}\int_0^t\| \varepsilon\Delta_{\varepsilon}\phi \|_{X^{2}}^2 ds+\cdots. \end{align} $$
$$ \begin{align} \lambda\int_0^t (\|\omega_{slip}\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds\leq \frac{C}{\lambda}\int_0^t\| \varepsilon\Delta_{\varepsilon}\phi \|_{X^{2}}^2 ds+\cdots. \end{align} $$
The full study of the Orr-Sommerfeld formulation (1.13) with Navier-slip boundary conditions is given in Section 7.
-
(4) Recovery the non-slip boundary condition. In Step (3), we use the slip boundary condition, not the real boundary condition
 $\partial _y\phi |_{y=0, 1}=C(t).$
To recover the boundary condition, we introduce the following system: (1.15)
$\partial _y\phi |_{y=0, 1}=C(t).$
To recover the boundary condition, we introduce the following system: (1.15) $$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}-\partial_x\phi_{bc}\partial_y \omega^p=0, \qquad (x,y)\in\mathcal{S}\\ &\phi_{bc}|_{y=0,1}=0, \quad \partial_y\phi_{bc}|_{y=i}=h^i,\qquad x\in\mathbb{T}, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}-\partial_x\phi_{bc}\partial_y \omega^p=0, \qquad (x,y)\in\mathcal{S}\\ &\phi_{bc}|_{y=0,1}=0, \quad \partial_y\phi_{bc}|_{y=i}=h^i,\qquad x\in\mathbb{T}, \end{aligned} \right. \end{align} $$
where
 $\omega _{bc}=\Delta _{\varepsilon } \phi _{bc}$
and
$\omega _{bc}=\Delta _{\varepsilon } \phi _{bc}$
and
 $i=0,1.$
And we need to choose a suitable
$i=0,1.$
And we need to choose a suitable
 $h^i$
such that
$h^i$
such that  $$ \begin{align*} \partial_y \phi_{bc}|_{y=0,1}=-\partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
$$ \begin{align*} \partial_y \phi_{bc}|_{y=0,1}=-\partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
Next, we give the main idea for proving the existence of
 $h^i$
:
$h^i$
:-
1. We define
 $\phi _{bc,S}=\phi _{bc,S}^0+\phi _{bc,S}^1$
, where
$\phi _{bc,S}=\phi _{bc,S}^0+\phi _{bc,S}^1$
, where
 $\phi _{bc,S}^i$
solve (1.16)
$\phi _{bc,S}^i$
solve (1.16) $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^i_{bc, S}=0,\\ &\phi^i_{bc, S}|_{y=i}=0,\quad \partial_y\phi^i_{bc, S}|_{y=i}=h^i,\\ &\phi^i_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^i_{bc, S}=0,\\ &\phi^i_{bc, S}|_{y=i}=0,\quad \partial_y\phi^i_{bc, S}|_{y=i}=h^i,\\ &\phi^i_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
where
 $x\in \mathbb {T}$
,
$x\in \mathbb {T}$
,
 $y\in (0,+\infty )$
for
$y\in (0,+\infty )$
for
 $i=0$
and
$i=0$
and
 $y\in (-\infty ,1)$
for
$y\in (-\infty ,1)$
for
 $i=1.$
Taking Fourier transformation on t and x, we can write the precise expression of the solution to obtain the Gevrey estimate for
$i=1.$
Taking Fourier transformation on t and x, we can write the precise expression of the solution to obtain the Gevrey estimate for
 $\phi _{bc,S}^i$
: (1.17)
$\phi _{bc,S}^i$
: (1.17) $$ \begin{align} &\int_0^t\|\nabla_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac{5}{2}}_i}^2+\|\varphi^i\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac52}_i}^2 + \|\partial_x\phi^i_{bc,S}\|_{X^{\frac53}}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
$$ \begin{align} &\int_0^t\|\nabla_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac{5}{2}}_i}^2+\|\varphi^i\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac52}_i}^2 + \|\partial_x\phi^i_{bc,S}\|_{X^{\frac53}}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
where
 $\varphi ^0(y)=y,~\varphi ^1(y)=1-y.$
Compared with the decomposition in [Reference Wang, Wang and Zhang35], we get more regularity of
$\varphi ^0(y)=y,~\varphi ^1(y)=1-y.$
Compared with the decomposition in [Reference Wang, Wang and Zhang35], we get more regularity of
 $\partial _x\phi ^i_{bc,S}$
, which is a key point to get the optimal Gevrey regularity. The details for this step are given in Section 8.1.
$\partial _x\phi ^i_{bc,S}$
, which is a key point to get the optimal Gevrey regularity. The details for this step are given in Section 8.1. -
2. We correct the nonlocal term constructed in the above step by considering the following equations:
(1.18) $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^i_{bc, R}-\partial_x\phi_{bc,R}^i\partial_y\omega^p=\partial_x\phi_{bc,S}^i\partial_y\omega^p,\quad (x,y)\in {\mathcal S}\\ &\phi^i_{bc, R}|_{t=0}=0, \quad (x,y)\in {\mathcal S} \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^i_{bc, R}-\partial_x\phi_{bc,R}^i\partial_y\omega^p=\partial_x\phi_{bc,S}^i\partial_y\omega^p,\quad (x,y)\in {\mathcal S}\\ &\phi^i_{bc, R}|_{t=0}=0, \quad (x,y)\in {\mathcal S} \end{aligned} \right. \end{align} $$
with Navier-slip conditions. By the same process as Step (3) and combining with the sharp estimate (1.17) to get an estimate for
 $\phi ^i_{bc,R},$
(1.19)
$\phi ^i_{bc,R},$
(1.19) $$ \begin{align} \lambda\int_0^t \|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds&+\int_0^t (\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2+|\partial_y\phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2)ds \end{align} $$
$$ \begin{align} \lambda\int_0^t \|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds&+\int_0^t (\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2+|\partial_y\phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2)ds \end{align} $$
 $$\begin{align*}\leq&\frac{C}{\lambda^{\frac12}} \int_0^t|h^i|_{X^{\frac73}}^2ds+\cdots,\nonumber \qquad t\in[0, T]. \end{align*}$$
$$\begin{align*}\leq&\frac{C}{\lambda^{\frac12}} \int_0^t|h^i|_{X^{\frac73}}^2ds+\cdots,\nonumber \qquad t\in[0, T]. \end{align*}$$
More details are given in Section 8.3.
-
3. We define
 $\phi _{bc}=\phi _{bc,S}+\phi _{bc,R}$
, where
$\phi _{bc}=\phi _{bc,S}+\phi _{bc,R}$
, where
 $\phi _{bc,S}=\sum _{i=0, 1}\phi ^i_{bc,S} $
and
$\phi _{bc,S}=\sum _{i=0, 1}\phi ^i_{bc,S} $
and
 $\phi _{bc,R}=\sum _{i=0, 1}\phi ^i_{bc,R}$
, which solves system (1.15). To match the boundary condition on the derivative of
$\phi _{bc,R}=\sum _{i=0, 1}\phi ^i_{bc,R}$
, which solves system (1.15). To match the boundary condition on the derivative of
 $\partial _y\phi |_{y=0,1}=C(t)$
, we need
$\partial _y\phi |_{y=0,1}=C(t)$
, we need  $$ \begin{align*} \partial_y\phi_{bc,S}|_{y=0,1}+\partial_y\phi_{bc,R}|_{y=0,1}=\partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
$$ \begin{align*} \partial_y\phi_{bc,S}|_{y=0,1}+\partial_y\phi_{bc,R}|_{y=0,1}=\partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
On one hand,
 $\phi _{bc,S}$
and
$\phi _{bc,S}$
and
 $\phi _{bc,R}$
are defined by
$\phi _{bc,R}$
are defined by
 $h^i$
. We define a
$h^i$
. We define a
 $0$
-order operator
$0$
-order operator
 $R_{bc}$
given in (8.71) such that
$R_{bc}$
given in (8.71) such that  $$ \begin{align*} (1+R_{bc}) h^i= - \partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
$$ \begin{align*} (1+R_{bc}) h^i= - \partial_y\phi_{slip}|_{y=0,1}+C(t). \end{align*} $$
Moreover, by the estimate in Step 1 and Step 2, we can get
 $$ \begin{align*} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq&\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac 73}}^2ds, \end{align*} $$
$$ \begin{align*} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq&\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac 73}}^2ds, \end{align*} $$
which means that
 $(1+R_{bc})$
is an invertible operator when
$(1+R_{bc})$
is an invertible operator when
 $\lambda $
is large. That means that
$\lambda $
is large. That means that
 $\phi _{bc,S}$
and
$\phi _{bc,S}$
and
 $\phi _{bc,R}$
are well-defined and (1.15) is well-posedness. Details are given in Section 8.4.
$\phi _{bc,R}$
are well-defined and (1.15) is well-posedness. Details are given in Section 8.4.Due to the transport terms, we need to introduce a new auxiliary function
 $\phi _{bc, T}$
between Step 1 and Step 2. For more details, see Section 8.2.
$\phi _{bc, T}$
between Step 1 and Step 2. For more details, see Section 8.2.
-
-
(5) Close the energy estimates (1.12). Summing estimates (1.17) and (1.19) in Step (4), we get an estimate for
 $\phi _{bc}:$
which along with (1.14), we have
$\phi _{bc}:$
which along with (1.14), we have $$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\phi_{bc}\|_{X^{\frac{7}{3}}}^2+\|\varphi\Delta_{\varepsilon}\phi_{bc}\|_{X^{\frac 73}}^2ds\leq &\ \frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds\\ \leq &\ C\int_0^t |\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}ds+\cdots, \end{align*} $$
and then we put the above estimate into (1.12) to close the estimate for system (1.11).
$$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\phi_{bc}\|_{X^{\frac{7}{3}}}^2+\|\varphi\Delta_{\varepsilon}\phi_{bc}\|_{X^{\frac 73}}^2ds\leq &\ \frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds\\ \leq &\ C\int_0^t |\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}ds+\cdots, \end{align*} $$
and then we put the above estimate into (1.12) to close the estimate for system (1.11). $$ \begin{align*} \int_0^t (\|\varphi\omega\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2)ds\leq \frac{C}{\lambda}\int_0^t\| \varepsilon\Delta_{\varepsilon}\phi \|_{X^{2}}^2 ds+\cdots, \end{align*} $$
$$ \begin{align*} \int_0^t (\|\varphi\omega\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2)ds\leq \frac{C}{\lambda}\int_0^t\| \varepsilon\Delta_{\varepsilon}\phi \|_{X^{2}}^2 ds+\cdots, \end{align*} $$
1.4 Notations
-
–
 $\mathcal {S}^{\varepsilon }=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<\varepsilon \right \}$
and
$\mathcal {S}^{\varepsilon }=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<\varepsilon \right \}$
and
 $\mathcal {S}=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<1\right \}.$
$\mathcal {S}=\left \{(x, y) \in \mathbb {T}\times \mathbb {R} : 0<y<1\right \}.$
-
–
 $\nabla _{\varepsilon }=(\varepsilon \partial _x, \partial _y)$
and
$\nabla _{\varepsilon }=(\varepsilon \partial _x, \partial _y)$
and
 $\Delta _{\varepsilon }=\varepsilon ^2 \partial _x^2+\partial _y^2$
.
$\Delta _{\varepsilon }=\varepsilon ^2 \partial _x^2+\partial _y^2$
. -
– Vorticity of Prandtl part
 $\omega ^p$
is defined by
$\omega ^p$
is defined by
 $ \omega ^p=\partial _y u^p$
.
$ \omega ^p=\partial _y u^p$
. -
– Vorticity of reminder part
 $\omega ^R=\Delta _{\varepsilon } \phi $
is defined by
$\omega ^R=\Delta _{\varepsilon } \phi $
is defined by
 $\omega ^R=\varepsilon ^2\partial _x v^R-\partial _y u^R$
. In this paper, we also define
$\omega ^R=\varepsilon ^2\partial _x v^R-\partial _y u^R$
. In this paper, we also define
 $\omega ^i_{bc, j}=\Delta _{\varepsilon } \phi _{bc, j}^i$
, where
$\omega ^i_{bc, j}=\Delta _{\varepsilon } \phi _{bc, j}^i$
, where
 $i=0, 1$
and
$i=0, 1$
and
 $j\in \{R, T\}$
$j\in \{R, T\}$
-
– Cut-off functions
 $\varphi (y)=y(1-y)$
and
$\varphi (y)=y(1-y)$
and
 $\varphi ^i(y)=i+(-1)^iy$
.
$\varphi ^i(y)=i+(-1)^iy$
. -
–
 $C(t)=\frac 1{2\pi }\int _{{\mathcal S}} u^Rdxdy$
.
$C(t)=\frac 1{2\pi }\int _{{\mathcal S}} u^Rdxdy$
. -
– The Fourier transform of
 $f_{\Phi }$
is defined by
$f_{\Phi }$
is defined by
 $e^{(1-\lambda t)\langle k\rangle ^{\frac 23}} \widehat {f}(k)$
.
$e^{(1-\lambda t)\langle k\rangle ^{\frac 23}} \widehat {f}(k)$
.
2 Gevrey norms and preliminary lemmas
At the beginning of this section, we define the functional space
![]() $X^r$
and the Gevrey class. First, we define
$X^r$
and the Gevrey class. First, we define
where
![]() $\tau (t)\ge 0$
. Moreover, it is easy to get that
$\tau (t)\ge 0$
. Moreover, it is easy to get that
![]() $\Phi (t,k)$
satisfies the subadditive inequality
$\Phi (t,k)$
satisfies the subadditive inequality
Now, we are in the position to define
![]() $X^r_{\tau }$
, which is defined by
$X^r_{\tau }$
, which is defined by
We say that a function f belongs to the Gevrey class
![]() $\frac 32$
if
$\frac 32$
if
![]() $\|f\|_{X^r_{\tau }}<+\infty $
.
$\|f\|_{X^r_{\tau }}<+\infty $
.
Moreover, we need to deal with some Gevrey class functions defined on the boundary. Thus, we introduce the following functional space:
where f depends on variable x.
By the definition of
![]() $X^r_{\tau }$
, it is easy to see that if
$X^r_{\tau }$
, it is easy to see that if
![]() $r'\geq r,$
then
$r'\geq r,$
then
![]() $\|\cdot \|_{X^{r'}_{\tau }}\geq \|\cdot \|_{X^{r}_{\tau }}.$
For simplicity, we drop subscript
$\|\cdot \|_{X^{r'}_{\tau }}\geq \|\cdot \|_{X^{r}_{\tau }}.$
For simplicity, we drop subscript
![]() $\tau $
in the notations
$\tau $
in the notations
![]() $\|f\|_{X^r_{\tau }}, |f|_{X^r_{\tau }}$
etc. In the sequel, we always take
$\|f\|_{X^r_{\tau }}, |f|_{X^r_{\tau }}$
etc. In the sequel, we always take
with
![]() $\lambda \geq 1$
determined later. Thus, if we take t small enough, we have
$\lambda \geq 1$
determined later. Thus, if we take t small enough, we have
![]() $\tau>0$
.
$\tau>0$
.
In the following, we present some lemmas on product estimates in the Gevrey class and the readers can refer to Lemmas 2.1–2.3 in [Reference Wang, Wang and Zhang34] for details. The first lemma is the commutator estimate in Sobolev space:
Lemma 2.1. Let
![]() $r\ge 0,~s_1>\frac 32$
,
$r\ge 0,~s_1>\frac 32$
,
![]() $s>\frac 12$
and
$s>\frac 12$
and
![]() $0\leq \delta \leq 1$
. Then it holds that
$0\leq \delta \leq 1$
. Then it holds that
In the Gevrey class, we have the following:
Lemma 2.2. Let
![]() $r\ge 0$
and
$r\ge 0$
and
![]() $s> \frac 12$
. Then it holds that
$s> \frac 12$
. Then it holds that
For the commutator in the Gevrey class, we have the following:
Lemma 2.3. Let
![]() $r\ge 0,~s_1>\frac 32$
,
$r\ge 0,~s_1>\frac 32$
,
![]() $s>\frac 12$
and
$s>\frac 12$
and
![]() $0\leq \delta \leq 1$
. Then it holds that
$0\leq \delta \leq 1$
. Then it holds that
3 Approximate equations and Error equations
3.1 Approximate equations
By the Hilbert asymptotic method, we can obtain the approximate solutions. We define approximate solutions as the following:
 $$ \begin{align} \left\{ \begin{aligned} u^p(t,x,y)=&\ u_p^0(t,x,y)+\varepsilon^2u_p^2(t,x,y),\\ v^p(t,x,y)=&\ v_p^0(t,x,y)+\varepsilon^2v_p^2(t,x,y),\\ p^p(t,x,y)=&\ p_p^0(t,x,y)+\varepsilon^2p_p^2(t,x,y), \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} u^p(t,x,y)=&\ u_p^0(t,x,y)+\varepsilon^2u_p^2(t,x,y),\\ v^p(t,x,y)=&\ v_p^0(t,x,y)+\varepsilon^2v_p^2(t,x,y),\\ p^p(t,x,y)=&\ p_p^0(t,x,y)+\varepsilon^2p_p^2(t,x,y), \end{aligned} \right. \end{align} $$
where
![]() $(u_p^0, v_p^0, p_p^0)$
satisfies equation (1.4) and
$(u_p^0, v_p^0, p_p^0)$
satisfies equation (1.4) and
![]() $(u_p^2, v_p^2, p_p^2)$
satisfies equation
$(u_p^2, v_p^2, p_p^2)$
satisfies equation
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u_p^2+ u_p^0\partial_x u_p^2+v_p^0\partial_y u_p^2+u_p^2\partial_x u_p^0+v_p^2\partial_y u_p^0+\partial_x p_p^2-\partial^2_y u_p^2=-\partial_x^2 u_p^0,\\ &\partial_y p_p^2=-(\partial_t v_p^0+u_p^0\partial_x v_p^0+v_p^0\partial_y v_p^0-\partial_y^2v_p^0),\\ &\partial_x u_p^2+\partial_y v_p^2=0,\\ &(u_p^2, v_p^2)|_{y=0,1}=0,\\ &u_p^2|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u_p^2+ u_p^0\partial_x u_p^2+v_p^0\partial_y u_p^2+u_p^2\partial_x u_p^0+v_p^2\partial_y u_p^0+\partial_x p_p^2-\partial^2_y u_p^2=-\partial_x^2 u_p^0,\\ &\partial_y p_p^2=-(\partial_t v_p^0+u_p^0\partial_x v_p^0+v_p^0\partial_y v_p^0-\partial_y^2v_p^0),\\ &\partial_x u_p^2+\partial_y v_p^2=0,\\ &(u_p^2, v_p^2)|_{y=0,1}=0,\\ &u_p^2|_{t=0}=0. \end{aligned} \right. \end{align} $$
We point here that
![]() $(u_p^1, v_p^1, p_p^1)=0$
by matching the equation of order
$(u_p^1, v_p^1, p_p^1)=0$
by matching the equation of order
![]() $\varepsilon $
. Based on the equation of
$\varepsilon $
. Based on the equation of
![]() $(u_p^0, v_p^0, p_p^0)$
and
$(u_p^0, v_p^0, p_p^0)$
and
![]() $(u_p^2, v_p^2, p_p^2)$
, we deduce the approximate solution
$(u_p^2, v_p^2, p_p^2)$
, we deduce the approximate solution
![]() $(u^p, v^p, p^p)$
which satisfies the following equation:
$(u^p, v^p, p^p)$
which satisfies the following equation:
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u^p+u^p\partial_x u^p+v^p\partial_y u^p+\partial_x p^p-\Delta_{\varepsilon} u^p=-R_1,\\ &\varepsilon^2(\partial_t v^p+u^p\partial_x v^p+v^p\partial_y v^p-\Delta_{\varepsilon} v^p)+\partial_y p^p=-R_2,\\ &\partial_x u^p+\partial_y v^p=0,\\ &(u^p, v^p)|_{y=0,1}=0,\\ &(u^p, v^p)|_{t=0}=(u_0, v_0), \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u^p+u^p\partial_x u^p+v^p\partial_y u^p+\partial_x p^p-\Delta_{\varepsilon} u^p=-R_1,\\ &\varepsilon^2(\partial_t v^p+u^p\partial_x v^p+v^p\partial_y v^p-\Delta_{\varepsilon} v^p)+\partial_y p^p=-R_2,\\ &\partial_x u^p+\partial_y v^p=0,\\ &(u^p, v^p)|_{y=0,1}=0,\\ &(u^p, v^p)|_{t=0}=(u_0, v_0), \end{aligned} \right. \end{align} $$
where reminder
![]() $(R_1, R_2)$
is given by
$(R_1, R_2)$
is given by
By the definition of
![]() $R_1$
and
$R_1$
and
![]() $R_2$
, it is easy to get that
$R_2$
, it is easy to get that
3.2 Equations of error functions
We define error functions
![]() $(u^R, v^R, p^R)$
:
$(u^R, v^R, p^R)$
:
It is easy to deduce the system of error functions:
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-\Delta_{\varepsilon} u^R+\partial_x p^R+u^{\varepsilon}\partial_x u^R+u^R\partial_x u^p+v^{\varepsilon}\partial_y u^R+v^R\partial_y u^p=R_1,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R+u^{\varepsilon}\partial_x v^R+u^R\partial_x v^p+v^{\varepsilon}\partial_y v^R+v^R\partial_y v^p)+\partial_y p^R=R_2,\\ &\partial_x u^R+\partial_y v^R=0,\\ &(u^R,v^R)|_{y=0}=(u^R,v^R)|_{y=1}=0,\\ &(u^R,v^R)|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-\Delta_{\varepsilon} u^R+\partial_x p^R+u^{\varepsilon}\partial_x u^R+u^R\partial_x u^p+v^{\varepsilon}\partial_y u^R+v^R\partial_y u^p=R_1,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R+u^{\varepsilon}\partial_x v^R+u^R\partial_x v^p+v^{\varepsilon}\partial_y v^R+v^R\partial_y v^p)+\partial_y p^R=R_2,\\ &\partial_x u^R+\partial_y v^R=0,\\ &(u^R,v^R)|_{y=0}=(u^R,v^R)|_{y=1}=0,\\ &(u^R,v^R)|_{t=0}=0. \end{aligned} \right. \end{align} $$
For convenience, we rewrite (3.6) as
 $$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-{\Delta_{\varepsilon} u^R}+u^p\partial_x u^R+u^R\partial_x u^p+v^R\partial_y u^p+v^p\partial_y u^R+\partial_x p^R=\mathcal{N}_u+R_1,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R+u^p\partial_x v^R+u^R\partial_x v^p+v^R\partial_y v^p+v^p\partial_y v^R)+\partial_y p^R=\varepsilon^2\mathcal{N}_v+R_2,\\ &\partial_x u^R+\partial_y v^R=0 ,\\ &(u^R,v^R)|_{y=0}=(u^R,v^R)|_{y=1}=0,\\ &(u^R,v^R)|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\partial_t u^R-{\Delta_{\varepsilon} u^R}+u^p\partial_x u^R+u^R\partial_x u^p+v^R\partial_y u^p+v^p\partial_y u^R+\partial_x p^R=\mathcal{N}_u+R_1,\\ &\varepsilon^2(\partial_t v^R-\Delta_{\varepsilon} v^R+u^p\partial_x v^R+u^R\partial_x v^p+v^R\partial_y v^p+v^p\partial_y v^R)+\partial_y p^R=\varepsilon^2\mathcal{N}_v+R_2,\\ &\partial_x u^R+\partial_y v^R=0 ,\\ &(u^R,v^R)|_{y=0}=(u^R,v^R)|_{y=1}=0,\\ &(u^R,v^R)|_{t=0}=0. \end{aligned} \right. \end{align} $$
Here,
![]() $(\mathcal {N}_u,\mathcal {N}_v)$
is a nonlinear term given by
$(\mathcal {N}_u,\mathcal {N}_v)$
is a nonlinear term given by
Based on the above system, we get the equations of the vorticity
![]() $\omega ^R=\partial _y u^R-\varepsilon ^2 \partial _x v^R$
:
$\omega ^R=\partial _y u^R-\varepsilon ^2 \partial _x v^R$
:
 $$ \begin{align} &\partial_t \omega^R-\Delta_{\varepsilon}\omega^R+u^p\partial_x \omega^R+u^R\partial_x \omega^p+v^p\partial_y \omega^R+v^R\partial_y \omega^p\\&\quad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v+\varepsilon^2 f_1+f_2,\nonumber \end{align} $$
$$ \begin{align} &\partial_t \omega^R-\Delta_{\varepsilon}\omega^R+u^p\partial_x \omega^R+u^R\partial_x \omega^p+v^p\partial_y \omega^R+v^R\partial_y \omega^p\\&\quad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v+\varepsilon^2 f_1+f_2,\nonumber \end{align} $$
where
![]() $f_1, f_2$
are defined by
$f_1, f_2$
are defined by
Moreover, following the calculations in [Reference Wang, Wang and Zhang34], we can obtain the boundary conditions of
![]() $\omega ^R$
:
$\omega ^R$
:
where
3.3 Equations of stream function
Thanks to
![]() $\partial _x u^R+\partial _yv^R=0$
and
$\partial _x u^R+\partial _yv^R=0$
and
![]() $v^R|_{y=0,1}=0$
, there exists a stream function
$v^R|_{y=0,1}=0$
, there exists a stream function
![]() $\phi $
satisfying the following system:
$\phi $
satisfying the following system:
Since
![]() $\int _{\mathbb {T}} v^Rdx=0,$
the function
$\int _{\mathbb {T}} v^Rdx=0,$
the function
![]() $\phi $
is periodic in x. Thanks to
$\phi $
is periodic in x. Thanks to
![]() $\partial _x\phi |_{y=0,1}=0$
and
$\partial _x\phi |_{y=0,1}=0$
and
![]() $\phi (1,x)-\phi (0,x)=0$
, we may assume that
$\phi (1,x)-\phi (0,x)=0$
, we may assume that
![]() $\phi |_{y=0,1}=0$
. Thus, there holds that
$\phi |_{y=0,1}=0$
. Thus, there holds that
Taking (3.18) and (3.19) into (3.9) and using the boundary condition
![]() $(u^R, v^R)|_{y=0,1}=0$
, we obtain
$(u^R, v^R)|_{y=0,1}=0$
, we obtain
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi+u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi+\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p\\ &\qquad\qquad\qquad\qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi|_{y=0,1}=0,\quad \partial_y\phi|_{y=0,1}=C(t), \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi+u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi+\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p\\ &\qquad\qquad\qquad\qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi|_{y=0,1}=0,\quad \partial_y\phi|_{y=0,1}=C(t), \end{aligned} \right. \end{align} $$
where
![]() $C(t)=\frac 1{2\pi }\int _{{\mathcal S}} u^Rdxdy$
and
$C(t)=\frac 1{2\pi }\int _{{\mathcal S}} u^Rdxdy$
and
![]() $(\mathcal {N}_u, \mathcal {N}_v), ~f_1, ~f_2$
are given in (3.8), (3.10) and (3.11).
$(\mathcal {N}_u, \mathcal {N}_v), ~f_1, ~f_2$
are given in (3.8), (3.10) and (3.11).
At the end of the subsection, we state some elliptic estimates which can be obtained by classical theory. First, by elliptic estimate and Hardy inequality, we have
where
![]() $\varphi (y)=y(1-y)$
and
$\varphi (y)=y(1-y)$
and
![]() $\nabla _{\varepsilon }=(\partial _y,\varepsilon \partial _x).$
Indeed, taking the
$\nabla _{\varepsilon }=(\partial _y,\varepsilon \partial _x).$
Indeed, taking the
![]() $L^2$
inner product with
$L^2$
inner product with
![]() $-\phi $
in (3.19) and integrating by parts, we use boundary condition
$-\phi $
in (3.19) and integrating by parts, we use boundary condition
![]() $\phi |_{y={0,1}}=0$
and the Hardy inequality to have
$\phi |_{y={0,1}}=0$
and the Hardy inequality to have
Since
![]() $(u^R,v^R)$
satisfies the elliptic equations
$(u^R,v^R)$
satisfies the elliptic equations
 $$ \begin{align*} \left\{ \begin{array}{ll} \Delta_{\varepsilon} u^R=\partial_y\omega^R,\\ u^R|_{y=0,1}=0, \end{array} \right. \qquad \left\{ \begin{array}{ll} \Delta_{\varepsilon} v^R=-\partial_x \omega^R,\\ v^R|_{y=0,1}=0, \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} \Delta_{\varepsilon} u^R=\partial_y\omega^R,\\ u^R|_{y=0,1}=0, \end{array} \right. \qquad \left\{ \begin{array}{ll} \Delta_{\varepsilon} v^R=-\partial_x \omega^R,\\ v^R|_{y=0,1}=0, \end{array} \right. \end{align*} $$
we arrive at
for any
![]() $r\geq 0.$
$r\geq 0.$
4 Estimate of
 $\nabla _{\varepsilon }\phi $
and
$\nabla _{\varepsilon }\phi $
and
 $\Delta _{\varepsilon }\phi $
in the Gevrey space
$\Delta _{\varepsilon }\phi $
in the Gevrey space
Before giving the estimate of
![]() $\nabla _{\varepsilon }\phi $
and
$\nabla _{\varepsilon }\phi $
and
![]() $\Delta _{\varepsilon }\phi $
, we need the estimates of the reminder terms
$\Delta _{\varepsilon }\phi $
, we need the estimates of the reminder terms
![]() $R_1$
and
$R_1$
and
![]() $R_2$
which are defined by the approximate solution
$R_2$
which are defined by the approximate solution
![]() $u^p$
and
$u^p$
and
![]() $v^p$
. For
$v^p$
. For
![]() $(u^p, v^p),$
we have the following bound:
$(u^p, v^p),$
we have the following bound:
Lemma 4.1. Let initial data
![]() $u_0$
of (1.4) satisfy (1.6)-(1.9). There exists a time
$u_0$
of (1.4) satisfy (1.6)-(1.9). There exists a time
![]() $T_p$
such that
$T_p$
such that
![]() $(u_p^i, v_p^i),~i=0,2$
defined in (1.4) and (3.2) have the following estimates:
$(u_p^i, v_p^i),~i=0,2$
defined in (1.4) and (3.2) have the following estimates:
 $$ \begin{align*} &\|v_p^0\|_{X^{11}}+\|(u_p^0, \varepsilon v_p^0)\|_{X^{12}}+\|\partial_y u_p^0\|_{X^{12}}+\|\partial_y^3 u_p^0\|_{X^8}\leq C, \\ &\|v_p^2\|_{X^9}+\|(u_p^2, \varepsilon v_p^2)\|_{X^{10}}+\|\partial_y u_p^2\|_{X^{10}}+\|\partial_y^3 u_p^2\|_{X^6}\leq C, \end{align*} $$
$$ \begin{align*} &\|v_p^0\|_{X^{11}}+\|(u_p^0, \varepsilon v_p^0)\|_{X^{12}}+\|\partial_y u_p^0\|_{X^{12}}+\|\partial_y^3 u_p^0\|_{X^8}\leq C, \\ &\|v_p^2\|_{X^9}+\|(u_p^2, \varepsilon v_p^2)\|_{X^{10}}+\|\partial_y u_p^2\|_{X^{10}}+\|\partial_y^3 u_p^2\|_{X^6}\leq C, \end{align*} $$
for
![]() $t\in [0, T_p]$
.
$t\in [0, T_p]$
.
Moreover, according to (3.1), it holds that
and
Proof. Here, the key of this lemma is to prove that (1.4) is well-posedness in the Gevrey class
![]() $\frac 32$
which is the conjecture in [Reference Gérard-Varet, Masmoudi and Vicol15]. If we set
$\frac 32$
which is the conjecture in [Reference Gérard-Varet, Masmoudi and Vicol15]. If we set
![]() $\varepsilon =0$
and follow the step-by-step process in this paper, we can get the conjecture proved. Here, to avoid repeatability, we leave the proof to the readers.
$\varepsilon =0$
and follow the step-by-step process in this paper, we can get the conjecture proved. Here, to avoid repeatability, we leave the proof to the readers.
Then, by the definition of
![]() $(R_1, R_2)$
in (3.4)-(3.5), using Lemma 2.2, we get the following:
$(R_1, R_2)$
in (3.4)-(3.5), using Lemma 2.2, we get the following:
Lemma 4.2. It holds that
Now, we state our main result in this section:
Proposition 4.3. There exist
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
and
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
and
![]() $\lambda _0\geq 1,$
such that for any
$\lambda _0\geq 1,$
such that for any
![]() $t\in [0,T]$
and
$t\in [0,T]$
and
![]() $\lambda \geq \lambda _0,$
it holds that
$\lambda \geq \lambda _0,$
it holds that
 $$ \begin{align*} &\sup_{s\in[0,t]}\Big(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2\Big) +\int_0^t \Big(\|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}+\|\nabla_{\varepsilon}\omega^R\|^2_{L^2}\Big)ds\\ \leq &\ C\int_0^t\Big(\varepsilon^{-2}\|\varphi \triangle_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2+\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8\Big)ds, \end{align*} $$
$$ \begin{align*} &\sup_{s\in[0,t]}\Big(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2\Big) +\int_0^t \Big(\|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}+\|\nabla_{\varepsilon}\omega^R\|^2_{L^2}\Big)ds\\ \leq &\ C\int_0^t\Big(\varepsilon^{-2}\|\varphi \triangle_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2+\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8\Big)ds, \end{align*} $$
where
![]() $\Delta _{\varepsilon }\phi =\omega ^R$
,
$\Delta _{\varepsilon }\phi =\omega ^R$
,
![]() $\varphi (y)=y(1-y)$
and C is a constant independent of
$\varphi (y)=y(1-y)$
and C is a constant independent of
![]() $\varepsilon $
.
$\varepsilon $
.
Proof. Acting
![]() $e^{\Phi (t, D_x)}$
on the both sides of the first equation of (3.20), we get
$e^{\Phi (t, D_x)}$
on the both sides of the first equation of (3.20), we get
 $$ \begin{align*} (\partial_t+\lambda\langle D_x\rangle^{\frac23} &-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{\Phi}+(u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi)_{\Phi}+(\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p)_{\Phi}\\ &=\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}+(\varepsilon^2 f_1+f_2)_{\Phi} -C(t)\partial_x \omega^p_{\Phi}. \end{align*} $$
$$ \begin{align*} (\partial_t+\lambda\langle D_x\rangle^{\frac23} &-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{\Phi}+(u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi)_{\Phi}+(\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p)_{\Phi}\\ &=\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}+(\varepsilon^2 f_1+f_2)_{\Phi} -C(t)\partial_x \omega^p_{\Phi}. \end{align*} $$
Taking
![]() $H^{2,0}$
inner product with
$H^{2,0}$
inner product with
![]() $-\partial _t\phi _{\Phi }$
and using boundary conditions
$-\partial _t\phi _{\Phi }$
and using boundary conditions
we integrate by parts to arrive at
 $$ \begin{align} &\frac12\frac{d}{dt}(\lambda\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2)+\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}^2-\Big\langle \Delta_{\varepsilon}\phi_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^{2}_x}\Big|_{y=0}^{y=1}\\=&\ \Big\langle (u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi)_{\Phi},\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}}+\Big\langle (\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p)_{\Phi},\partial_t\phi_{\Phi}\Big\rangle_{H^{2,0}} \nonumber\\ &+\Big\langle \partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}}+\Big\langle (\varepsilon^2 f_1+f_2)_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}} \nonumber\\ &-\Big\langle C(t)\partial_x \omega^p_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}} \nonumber\\ =\ &I_1+\cdots+I_5. \nonumber \end{align} $$
$$ \begin{align} &\frac12\frac{d}{dt}(\lambda\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2)+\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}^2-\Big\langle \Delta_{\varepsilon}\phi_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^{2}_x}\Big|_{y=0}^{y=1}\\=&\ \Big\langle (u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi)_{\Phi},\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}}+\Big\langle (\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p)_{\Phi},\partial_t\phi_{\Phi}\Big\rangle_{H^{2,0}} \nonumber\\ &+\Big\langle \partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}}+\Big\langle (\varepsilon^2 f_1+f_2)_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}} \nonumber\\ &-\Big\langle C(t)\partial_x \omega^p_{\Phi},-\partial_t\phi_{\Phi} \Big\rangle_{H^{2,0}} \nonumber\\ =\ &I_1+\cdots+I_5. \nonumber \end{align} $$
First, let’s estimate
![]() $I_i,~i=1,\cdots , 5$
term by term.
$I_i,~i=1,\cdots , 5$
term by term.
![]() $\underline {\mathrm {Estimate \ of} \ I_1.}$
Since divergence free condition
$\underline {\mathrm {Estimate \ of} \ I_1.}$
Since divergence free condition
![]() $\partial _x u^p+\partial _y v^p=0,$
we get
$\partial _x u^p+\partial _y v^p=0,$
we get
According to
![]() $(u^p, v^p)|_{y=0,1}=0,$
we use integration by parts and Lemma 2.2 to have
$(u^p, v^p)|_{y=0,1}=0,$
we use integration by parts and Lemma 2.2 to have
 $$ \begin{align*} I_1=&\ -\Big\langle (u^p\Delta_{\varepsilon}\phi)_{\Phi},\partial_t\partial_x\phi_{\Phi} \Big\rangle_{H^{2,0}}-\Big\langle (v^p\Delta_{\varepsilon}\phi)_{\Phi},\partial_t\partial_y\phi_{\Phi} \Big\rangle_{H^{2,0}}\\ \leq &\ C\Big\||\frac{u^p}{\varphi}|_{X^2}|\varphi\Delta_{\varepsilon}\phi|_{X^2}\Big\|_{L^2_y}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\Big\||\frac{v^p}{\varphi}|_{X^2}|\varphi\Delta_{\varepsilon}\phi|_{X^2}\Big\|_{L^2_y}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\||\frac{u^p}{\varphi}|_{X^2}\|_{L^{\infty}_y}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\Big\||\frac{v^p}{\varphi}|_{X^2}\|_{L^{\infty}_y}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\varepsilon^{-1}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
$$ \begin{align*} I_1=&\ -\Big\langle (u^p\Delta_{\varepsilon}\phi)_{\Phi},\partial_t\partial_x\phi_{\Phi} \Big\rangle_{H^{2,0}}-\Big\langle (v^p\Delta_{\varepsilon}\phi)_{\Phi},\partial_t\partial_y\phi_{\Phi} \Big\rangle_{H^{2,0}}\\ \leq &\ C\Big\||\frac{u^p}{\varphi}|_{X^2}|\varphi\Delta_{\varepsilon}\phi|_{X^2}\Big\|_{L^2_y}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\Big\||\frac{v^p}{\varphi}|_{X^2}|\varphi\Delta_{\varepsilon}\phi|_{X^2}\Big\|_{L^2_y}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\||\frac{u^p}{\varphi}|_{X^2}\|_{L^{\infty}_y}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\Big\||\frac{v^p}{\varphi}|_{X^2}\|_{L^{\infty}_y}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\varepsilon^{-1}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_2.}$
Similarly, we write
$\underline {\mathrm {Estimate \ of} \ I_2.}$
Similarly, we write
Then, along with
![]() $\phi |_{y=0,1}=0$
, we use integration by parts and Lemma 2.2 to deduce
$\phi |_{y=0,1}=0$
, we use integration by parts and Lemma 2.2 to deduce
 $$ \begin{align*} I_2=&\ \Big\langle\partial_x(\partial_y\phi\omega^p)_{\Phi}-\partial_y(\partial_x\phi_{\Phi} \omega^p)_{\Phi},\partial_t\phi_{\Phi}\Big\rangle_{H^{2,0}}\\ =&\ -\Big\langle(\partial_y\phi\omega^p)_{\Phi},\partial_t\partial_x\phi_{\Phi}\Big\rangle_{H^{2,0}}+\Big\langle(\partial_x\phi \omega^p)_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^{2,0}}\\ \leq &\ C\||\omega^p|_{X^2}\|_{L^{\infty}_y}\|\partial_y \phi\|_{X^2}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\||\omega^p|_{X^2}\|_{L^{\infty}_y}\|\partial_x \phi\|_{X^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\varepsilon^{-1}\|\nabla_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
$$ \begin{align*} I_2=&\ \Big\langle\partial_x(\partial_y\phi\omega^p)_{\Phi}-\partial_y(\partial_x\phi_{\Phi} \omega^p)_{\Phi},\partial_t\phi_{\Phi}\Big\rangle_{H^{2,0}}\\ =&\ -\Big\langle(\partial_y\phi\omega^p)_{\Phi},\partial_t\partial_x\phi_{\Phi}\Big\rangle_{H^{2,0}}+\Big\langle(\partial_x\phi \omega^p)_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^{2,0}}\\ \leq &\ C\||\omega^p|_{X^2}\|_{L^{\infty}_y}\|\partial_y \phi\|_{X^2}\|\partial_t\partial_x\phi_{\Phi}\|_{H^{2,0}}+C\||\omega^p|_{X^2}\|_{L^{\infty}_y}\|\partial_x \phi\|_{X^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C\varepsilon^{-1}\|\nabla_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_3.}$
Due to
$\underline {\mathrm {Estimate \ of} \ I_3.}$
Due to
![]() $\phi |_{y=0,1}=0,$
taking integration by parts, it yields that
$\phi |_{y=0,1}=0,$
taking integration by parts, it yields that
![]() $\underline {\mathrm {Estimate \ of} \ I_4.}$
Recall
$\underline {\mathrm {Estimate \ of} \ I_4.}$
Recall
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in (3.10)-(3.11). According to (3.22) and Lemma 4.2, we have
$f_2$
in (3.10)-(3.11). According to (3.22) and Lemma 4.2, we have
 $$ \begin{align*} I_4\leq &\ C(\|\varepsilon^2 f_1\|_{X^2}+\|f_2\|_{X^2})\|\partial_t\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C(\varepsilon^2\|u^R\|_{X^2}+\varepsilon\|\varepsilon v^R\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C(\varepsilon\|\Delta_{\varepsilon}\phi\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
$$ \begin{align*} I_4\leq &\ C(\|\varepsilon^2 f_1\|_{X^2}+\|f_2\|_{X^2})\|\partial_t\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C(\varepsilon^2\|u^R\|_{X^2}+\varepsilon\|\varepsilon v^R\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ \leq &\ C(\varepsilon\|\Delta_{\varepsilon}\phi\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_5.}$
Poincaré inequality implies
$\underline {\mathrm {Estimate \ of} \ I_5.}$
Poincaré inequality implies
for
![]() $\phi |_{y=0,1}=0.$
Since
$\phi |_{y=0,1}=0.$
Since
we get
Collecting
![]() $I_1-I_5$
together, it holds that
$I_1-I_5$
together, it holds that
 $$ \begin{align} I_1+\cdots+I_5\leq &\ C\varepsilon^{-1}\| \varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}+C \varepsilon^{-1}\|\nabla_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}\nonumber\\ &+C\|(\mathcal{N}_u, \varepsilon \mathcal{N}_v)\|_{X^2} \|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}+C\|\Delta_{\varepsilon} \phi\|_{L^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ &+C(\varepsilon\|\Delta_{\varepsilon}\phi\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}} \nonumber\\ \leq &\ \frac1{10}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}^2+C\Big(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2\Big)\nonumber \\ &+C\Big(\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}+\varepsilon^8\Big).\nonumber \end{align} $$
$$ \begin{align} I_1+\cdots+I_5\leq &\ C\varepsilon^{-1}\| \varphi\Delta_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}+C \varepsilon^{-1}\|\nabla_{\varepsilon}\phi\|_{X^2}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}\nonumber\\ &+C\|(\mathcal{N}_u, \varepsilon \mathcal{N}_v)\|_{X^2} \|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}+C\|\Delta_{\varepsilon} \phi\|_{L^2}\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}}\\ &+C(\varepsilon\|\Delta_{\varepsilon}\phi\|_{X^2}+\varepsilon^4)\|\partial_t\partial_y\phi_{\Phi}\|_{H^{2,0}} \nonumber\\ \leq &\ \frac1{10}\|\partial_t\nabla_{\varepsilon}\phi_{\Phi}\|_{H^{2,0}}^2+C\Big(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2\Big)\nonumber \\ &+C\Big(\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}+\varepsilon^8\Big).\nonumber \end{align} $$
Next, we focus on the boundary term
![]() $\Big \langle \Delta _{\varepsilon }\phi _{\Phi },\partial _t\partial _y\phi _{\Phi }\Big \rangle _{H^{2}_x}\Big |_{y=0}^{y=1}$
. First, we give the estimate of
$\Big \langle \Delta _{\varepsilon }\phi _{\Phi },\partial _t\partial _y\phi _{\Phi }\Big \rangle _{H^{2}_x}\Big |_{y=0}^{y=1}$
. First, we give the estimate of
![]() $C'(t)$
:
$C'(t)$
:
which gives
Owing to
where
![]() $\delta (k)$
is a Dirac function and
$\delta (k)$
is a Dirac function and
![]() $k\in \mathbb {Z},$
we have
$k\in \mathbb {Z},$
we have
 $$ \begin{align*} \Big\langle \Delta_{\varepsilon}\phi_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}=&\ \Big\langle \Delta_{\varepsilon}\phi\Big|_{y=0}^{y=1},C'(t)\Big\rangle_{L^2_x}=\Big\langle \int_0^1\partial_y\Delta_{\varepsilon}\phi dy,C'(t)\Big\rangle_{L^2_x}\\ \leq &\ CC'(t)\|\partial_y\omega^R\|_{L^2}\leq C\|\partial_y\omega^R\|_{L^2}^2, \end{align*} $$
$$ \begin{align*} \Big\langle \Delta_{\varepsilon}\phi_{\Phi},\partial_t\partial_y\phi_{\Phi}\Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}=&\ \Big\langle \Delta_{\varepsilon}\phi\Big|_{y=0}^{y=1},C'(t)\Big\rangle_{L^2_x}=\Big\langle \int_0^1\partial_y\Delta_{\varepsilon}\phi dy,C'(t)\Big\rangle_{L^2_x}\\ \leq &\ CC'(t)\|\partial_y\omega^R\|_{L^2}\leq C\|\partial_y\omega^R\|_{L^2}^2, \end{align*} $$
where we used (4.3) in the last step.
Putting the above estimate and (4.2) into (4.1), we get
 $$ \begin{align} &\frac12\frac{d}{dt}(\lambda\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2)\nonumber\\ &\quad\leq C\Big(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2+\|\partial_y\omega^R\|^2_{L^2}+\varepsilon^8\Big). \end{align} $$
$$ \begin{align} &\frac12\frac{d}{dt}(\lambda\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2)\nonumber\\ &\quad\leq C\Big(\varepsilon^{-2}\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2+\varepsilon^{-2}\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{X^2}^2+\|\Delta_{\varepsilon}\phi\|_{X^2}^2+\|\partial_y\omega^R\|^2_{L^2}+\varepsilon^8\Big). \end{align} $$
Next, we give the estimates of
![]() $\|\partial _y\omega ^R\|^2_{L^2}$
. First, we recall the equation of
$\|\partial _y\omega ^R\|^2_{L^2}$
. First, we recall the equation of
![]() $\omega ^R$
:
$\omega ^R$
:
 $$ \begin{align} &\partial_t \omega^R-\Delta_{\varepsilon}\omega^R+u^p\partial_x \omega^R+u^R\partial_x \omega^p+v^p\partial_y \omega^R+v^R\partial_y \omega^p \\&\quad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v+\varepsilon^2 f_1+f_2,\nonumber\end{align} $$
$$ \begin{align} &\partial_t \omega^R-\Delta_{\varepsilon}\omega^R+u^p\partial_x \omega^R+u^R\partial_x \omega^p+v^p\partial_y \omega^R+v^R\partial_y \omega^p \\&\quad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v+\varepsilon^2 f_1+f_2,\nonumber\end{align} $$
with boundary conditions
where
![]() $f_1,~f_2, f$
and
$f_1,~f_2, f$
and
![]() $\mathcal {N}$
are given in (3.10)-(3.16).
$\mathcal {N}$
are given in (3.10)-(3.16).
Taking the
![]() $L^2$
inner product with
$L^2$
inner product with
![]() $\omega ^R$
on (4.5) and integration by parts, it follows from
$\omega ^R$
on (4.5) and integration by parts, it follows from
![]() $(\mathcal {N}_u,\varepsilon \mathcal {N}_v)|_{y=0,1}=0$
and
$(\mathcal {N}_u,\varepsilon \mathcal {N}_v)|_{y=0,1}=0$
and
![]() $(u^p, v^p)|_{y=0,1}=0$
to obtain
$(u^p, v^p)|_{y=0,1}=0$
to obtain
 $$ \begin{align} \frac12\frac{d}{dt}\|\omega^R\|_{L^2}^2+&\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2-\int_{\mathbb{T}}\partial_y\omega^R \omega^Rdx\Big|_{y=0}^{y=1}\\\leq &\ C\|(u^R, v^R)\|_{L^2}\| \omega^R\|_{L^2}+C \|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{L^2}\|\nabla_{\varepsilon}\omega^R\|_{L^2}\nonumber\\ &+C(\|\varepsilon^2 u^R\|_{L^2} + \|\varepsilon^2v^R\|_{L^2} + \varepsilon^4)\|\omega^R\|_{L^2}\nonumber\\ \leq &\ \frac1{10}\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2+C(\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\omega^R\|_{H^{1,0}}^2+\varepsilon^8).\notag \end{align} $$
$$ \begin{align} \frac12\frac{d}{dt}\|\omega^R\|_{L^2}^2+&\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2-\int_{\mathbb{T}}\partial_y\omega^R \omega^Rdx\Big|_{y=0}^{y=1}\\\leq &\ C\|(u^R, v^R)\|_{L^2}\| \omega^R\|_{L^2}+C \|(\mathcal{N}_u, \varepsilon\mathcal{N}_v)\|_{L^2}\|\nabla_{\varepsilon}\omega^R\|_{L^2}\nonumber\\ &+C(\|\varepsilon^2 u^R\|_{L^2} + \|\varepsilon^2v^R\|_{L^2} + \varepsilon^4)\|\omega^R\|_{L^2}\nonumber\\ \leq &\ \frac1{10}\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2+C(\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\omega^R\|_{H^{1,0}}^2+\varepsilon^8).\notag \end{align} $$
For the boundary term, we use (4.6)-(4.7) to write
 $$ \begin{align*} \int_{\mathbb{T}}\partial_y\omega^R \omega^Rdx\Big|_{y=0}^{y=1}= &\int_{\mathbb{T}} \Big(\varepsilon|D|\omega^R|_{y=1}+\partial_y (\Delta_{\varepsilon,D})^{-1} (f-\mathcal{N})|_{y=1}+C(t)\Big)\omega^R|_{y=1} dx\\ &-\int_{\mathbb{T}}\Big(-\varepsilon|D|\omega^R|_{y=0}+\partial_y (\Delta_{\varepsilon,D})^{-1}(f-\mathcal{N})|_{y=0}+C(t)\Big)\omega^R|_{y=0} dx\\ =&\ \int_{\mathbb{T}}(\varepsilon|D|\omega^R~\omega^R)|_{y=0,1}dx+C(t)\int_{\mathbb{T}}\omega^R|_{y=0}^{y=1}dx\\ &+\int_{\mathcal{S}}\partial_y\Big(\partial_y(\Delta_{\varepsilon,D})^{-1}(f-\mathcal{N})\omega^R\Big)dxdy=B_1+B_2+B_3. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{T}}\partial_y\omega^R \omega^Rdx\Big|_{y=0}^{y=1}= &\int_{\mathbb{T}} \Big(\varepsilon|D|\omega^R|_{y=1}+\partial_y (\Delta_{\varepsilon,D})^{-1} (f-\mathcal{N})|_{y=1}+C(t)\Big)\omega^R|_{y=1} dx\\ &-\int_{\mathbb{T}}\Big(-\varepsilon|D|\omega^R|_{y=0}+\partial_y (\Delta_{\varepsilon,D})^{-1}(f-\mathcal{N})|_{y=0}+C(t)\Big)\omega^R|_{y=0} dx\\ =&\ \int_{\mathbb{T}}(\varepsilon|D|\omega^R~\omega^R)|_{y=0,1}dx+C(t)\int_{\mathbb{T}}\omega^R|_{y=0}^{y=1}dx\\ &+\int_{\mathcal{S}}\partial_y\Big(\partial_y(\Delta_{\varepsilon,D})^{-1}(f-\mathcal{N})\omega^R\Big)dxdy=B_1+B_2+B_3. \end{align*} $$
Let
![]() $y_0\in [0,1]$
so that
$y_0\in [0,1]$
so that
Then, along with Gagliardo-Nirenberg inequality
it infers that
 $$ \begin{align*} B_1=&\ \int_{y_0}^1\partial_y(\varepsilon|D|\omega^R\omega^R)dxdy+\int_{y_0}^0\partial_y(\varepsilon|D|\omega^R\omega^R)dxdy+2\int_{\mathbb{T}}(\varepsilon|D|\omega^R~\omega^R)|_{y=y_0}dx\\ \leq &\ C\|\varepsilon|D|\omega^R\|_{L^2}\|\partial_y\omega^R\|_{L^2}+C\|\varepsilon|D|\omega^{R}\|_{L^2}\|\omega^R\|_{L^{\infty}_y(L^2_x)}\\ \leq &\ C\varepsilon\|\omega^R\|_{H^{1,0}}^2+C\varepsilon\|\partial_y\omega^R\|_{L^2}^2. \end{align*} $$
$$ \begin{align*} B_1=&\ \int_{y_0}^1\partial_y(\varepsilon|D|\omega^R\omega^R)dxdy+\int_{y_0}^0\partial_y(\varepsilon|D|\omega^R\omega^R)dxdy+2\int_{\mathbb{T}}(\varepsilon|D|\omega^R~\omega^R)|_{y=y_0}dx\\ \leq &\ C\|\varepsilon|D|\omega^R\|_{L^2}\|\partial_y\omega^R\|_{L^2}+C\|\varepsilon|D|\omega^{R}\|_{L^2}\|\omega^R\|_{L^{\infty}_y(L^2_x)}\\ \leq &\ C\varepsilon\|\omega^R\|_{H^{1,0}}^2+C\varepsilon\|\partial_y\omega^R\|_{L^2}^2. \end{align*} $$
Similarly, we use (4.9) and
![]() $|C(t)|\leq C\|u^R\|_{L^2}\leq C\|\omega ^R\|_{L^2}$
to have
$|C(t)|\leq C\|u^R\|_{L^2}\leq C\|\omega ^R\|_{L^2}$
to have
 $$ \begin{align*} B_2\leq &\ C|C(t)|\|\omega^R\|_{L^{\infty}_y(L^2_x)}\leq C\|\omega^R\|_{L^2}^{\frac32}(\|\omega^R\|_{L^2}^{\frac12}+\|\partial_y\omega^R\|_{L^2}^{\frac12)}\\ \leq &\ \frac1{10}\|\partial_y\omega^R\|_{L^2}^2+C\|\omega^R\|_{L^2}^2. \end{align*} $$
$$ \begin{align*} B_2\leq &\ C|C(t)|\|\omega^R\|_{L^{\infty}_y(L^2_x)}\leq C\|\omega^R\|_{L^2}^{\frac32}(\|\omega^R\|_{L^2}^{\frac12}+\|\partial_y\omega^R\|_{L^2}^{\frac12)}\\ \leq &\ \frac1{10}\|\partial_y\omega^R\|_{L^2}^2+C\|\omega^R\|_{L^2}^2. \end{align*} $$
All we have left is to do
![]() $B_3.$
With the fact that operator
$B_3.$
With the fact that operator
![]() $\partial _y(\triangle _{\varepsilon ,D})^{-1},~\partial _y(\triangle _{\varepsilon ,D})^{-1}(\partial _y,\varepsilon \partial _x)$
and
$\partial _y(\triangle _{\varepsilon ,D})^{-1},~\partial _y(\triangle _{\varepsilon ,D})^{-1}(\partial _y,\varepsilon \partial _x)$
and
![]() $\partial _y^2(\triangle _{\varepsilon ,D})^{-1}$
are bounded from
$\partial _y^2(\triangle _{\varepsilon ,D})^{-1}$
are bounded from
![]() $L^2\to L^2,$
we have
$L^2\to L^2,$
we have
 $$ \begin{align*} B_3=&\ \int_{\mathcal{S}}\partial_y^2(\triangle_{\varepsilon,D})^{-1}(f-\mathcal{N})\omega^Rdxdy+\int_{\mathcal{S}}\partial_y(\triangle_{\varepsilon,D})^{-1}\partial_y(v^p\omega^R)\partial_y\omega^Rdxdy\\ &+\int_{\mathcal{S}}\partial_y(\triangle_{\varepsilon,D})^{-1}(f-\partial_y(v^p\omega^R)-\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v)\partial_y\omega^Rdxdy\\ \leq &\ C\|f-\mathcal{N}\|_{L^2}\|\omega^R\|_{L^2}+C\|v^p\omega^R\|_{L^2}\|\partial_y\omega^R\|_{L^2}\\ &+C(\|f-\partial_y(v^p\omega^R)\|_{L^2}+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2})\|\partial_y\omega^R\|_{L^2}. \end{align*} $$
$$ \begin{align*} B_3=&\ \int_{\mathcal{S}}\partial_y^2(\triangle_{\varepsilon,D})^{-1}(f-\mathcal{N})\omega^Rdxdy+\int_{\mathcal{S}}\partial_y(\triangle_{\varepsilon,D})^{-1}\partial_y(v^p\omega^R)\partial_y\omega^Rdxdy\\ &+\int_{\mathcal{S}}\partial_y(\triangle_{\varepsilon,D})^{-1}(f-\partial_y(v^p\omega^R)-\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v)\partial_y\omega^Rdxdy\\ \leq &\ C\|f-\mathcal{N}\|_{L^2}\|\omega^R\|_{L^2}+C\|v^p\omega^R\|_{L^2}\|\partial_y\omega^R\|_{L^2}\\ &+C(\|f-\partial_y(v^p\omega^R)\|_{L^2}+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2})\|\partial_y\omega^R\|_{L^2}. \end{align*} $$
According to the definition of (3.16) and (3.15), we have
 $$ \begin{align*} \|f\|_{L^2}\leq &\ C(\|\partial_x\omega^R\|_{L^2}+\|\partial_y\omega^R\|_{L^2}+\|(u^R, v^R)\|_{L^2}+\varepsilon^4)\\ \leq &\ C(\|\omega^R\|_{H^{1,0}}+\|\partial_y\omega^R\|_{L^2}+\varepsilon^4), \end{align*} $$
$$ \begin{align*} \|f\|_{L^2}\leq &\ C(\|\partial_x\omega^R\|_{L^2}+\|\partial_y\omega^R\|_{L^2}+\|(u^R, v^R)\|_{L^2}+\varepsilon^4)\\ \leq &\ C(\|\omega^R\|_{H^{1,0}}+\|\partial_y\omega^R\|_{L^2}+\varepsilon^4), \end{align*} $$
and
 $$ \begin{align*} \|f-\partial_y(v^p\omega^R)\|_{L^2}\leq &\ C(\|\partial_x\omega^R\|_{L^2}+\|(u^R, v^R)\|_{L^2}+\varepsilon^4)\\ \leq &\ C(\|\omega^R\|_{H^{1,0}}+\varepsilon^4), \end{align*} $$
$$ \begin{align*} \|f-\partial_y(v^p\omega^R)\|_{L^2}\leq &\ C(\|\partial_x\omega^R\|_{L^2}+\|(u^R, v^R)\|_{L^2}+\varepsilon^4)\\ \leq &\ C(\|\omega^R\|_{H^{1,0}}+\varepsilon^4), \end{align*} $$
which give that
 $$ \begin{align*} B_3\leq &\ C(\|\omega^R\|_{H^{1,0}}+\|\partial_y\omega^R\|_{L^2}+\|\mathcal{N}\|_{L^2}+\varepsilon^4)\|\omega^R\|_{L^2}\\ &+C(\|\omega^R\|_{H^{1,0}}+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}+\varepsilon^4)\|\partial_y\omega^R\|_{L^2}\\ \leq & \ \frac1{10}\|\partial_y\omega^R\|_{L^2}^2+C(\|\omega^R\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8). \end{align*} $$
$$ \begin{align*} B_3\leq &\ C(\|\omega^R\|_{H^{1,0}}+\|\partial_y\omega^R\|_{L^2}+\|\mathcal{N}\|_{L^2}+\varepsilon^4)\|\omega^R\|_{L^2}\\ &+C(\|\omega^R\|_{H^{1,0}}+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}+\varepsilon^4)\|\partial_y\omega^R\|_{L^2}\\ \leq & \ \frac1{10}\|\partial_y\omega^R\|_{L^2}^2+C(\|\omega^R\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8). \end{align*} $$
Summarizing
![]() $B_1-B_3$
together, we obtain
$B_1-B_3$
together, we obtain
Substituting (4.10) into (4.8), we take
![]() $\varepsilon $
small enough to arrive at
$\varepsilon $
small enough to arrive at
 $$ \begin{align*} \frac12\frac{d}{dt}\|\omega^R\|_{L^2}^2+&\frac12\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2\\ \nonumber \leq &\ C(\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\omega^R\|_{H^{1,0}}^2+\varepsilon^8)\\ \nonumber &+C(\|\omega^R\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8)\\ \nonumber \leq &\ C(\|\Delta_{\varepsilon}\phi\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8). \end{align*} $$
$$ \begin{align*} \frac12\frac{d}{dt}\|\omega^R\|_{L^2}^2+&\frac12\|\nabla_{\varepsilon}\omega^R\|_{L^2}^2\\ \nonumber \leq &\ C(\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\omega^R\|_{H^{1,0}}^2+\varepsilon^8)\\ \nonumber &+C(\|\omega^R\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8)\\ \nonumber \leq &\ C(\|\Delta_{\varepsilon}\phi\|_{H^{1,0}}^2+\|(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\|\mathcal{N}\|_{L^2}^2+\varepsilon^8). \end{align*} $$
Bring the above estimate into (4.4) and integrate time from
![]() $0$
to t to get the desired results.
$0$
to t to get the desired results.
5 Sketch the proof to Theorem 1.1
In this section, we shall sketch the proof of Theorem 1.1. In the paper, we use the continued argument. Here, we define
5.1 The key a priori estimates
In this subsection, we shall present the key a priori estimates used in the proof of Theorem 1.1.
By Proposition 4.3, we need the estimates of
![]() $\int _0^t (\|\nabla _{\varepsilon }\phi \|_{X^2}^2+\|\varphi \Delta _{\varepsilon }\phi \|_{X^2}^2)ds$
to close the energy.
$\int _0^t (\|\nabla _{\varepsilon }\phi \|_{X^2}^2+\|\varphi \Delta _{\varepsilon }\phi \|_{X^2}^2)ds$
to close the energy.
Proposition 5.1. Let
![]() $\phi $
be the solution of (3.20). Then there exists
$\phi $
be the solution of (3.20). Then there exists
![]() $\lambda _0\geq 1$
and
$\lambda _0\geq 1$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for
![]() $\lambda \geq \lambda _0$
and
$\lambda \geq \lambda _0$
and
![]() $t\in [0, T]$
, it holds that
$t\in [0, T]$
, it holds that
 $$ \begin{align} \int_0^t (\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2)ds\leq &\ C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds, \end{align} $$
$$ \begin{align} \int_0^t (\|\nabla_{\varepsilon}\phi\|_{X^2}^2+\|\varphi\Delta_{\varepsilon}\phi\|_{X^2}^2)ds\leq &\ C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds, \end{align} $$
with
![]() $t\in [0, T]$
.
$t\in [0, T]$
.
The proof of the above proposition is the main part of this paper, and we prove it in Section 6.
5.2 Proof of Theorem 1.1
Before we prove Theorem 1.1, we first give the estimates for the nonlinear terms:
Proposition 5.2. Under the assumption (5.1), there holds that
 $$ \begin{align} \int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds\leq &\ C\varepsilon^4\int_0^t\|\omega^R\|_{X^2}^2ds, \end{align} $$
$$ \begin{align} \int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds\leq &\ C\varepsilon^4\int_0^t\|\omega^R\|_{X^2}^2ds, \end{align} $$
 $$ \begin{align} \int_0^t\|\mathcal{N}\|_{L^2}^2ds\leq &\ C\varepsilon^4\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds, \end{align} $$
$$ \begin{align} \int_0^t\|\mathcal{N}\|_{L^2}^2ds\leq &\ C\varepsilon^4\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds, \end{align} $$
where
![]() $t\in [0, T^*]$
.
$t\in [0, T^*]$
.
Proof. By the definition of
![]() $\mathcal {N}_u,$
we have
$\mathcal {N}_u,$
we have
 $$ \begin{align*} \int_0^t\|\mathcal{N}_u\|_{X^2}^2ds\leq \int_0^t\|u^R\partial_x u^R\|_{X^2}^2ds+\int_0^t\|v^R\partial_y u^R\|_{X^2}^2ds=I_1+I_2. \end{align*} $$
$$ \begin{align*} \int_0^t\|\mathcal{N}_u\|_{X^2}^2ds\leq \int_0^t\|u^R\partial_x u^R\|_{X^2}^2ds+\int_0^t\|v^R\partial_y u^R\|_{X^2}^2ds=I_1+I_2. \end{align*} $$
It follows from Lemma 2.2 and (3.22) that
 $$ \begin{align*} I_1\leq &\ C\int_0^t \|\frac{u^R_{\Phi}}{\varepsilon}\|_{L^{\infty}_y(H^2_x)}^2\|\varepsilon\partial_x u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t \|u^R\|_{X^2}(\|u^R\|_{X^2}+\|\partial_y u^R\|_{X^2})\|\varepsilon\partial_x u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t \|\omega^R\|_{X^2}^4ds, \end{align*} $$
$$ \begin{align*} I_1\leq &\ C\int_0^t \|\frac{u^R_{\Phi}}{\varepsilon}\|_{L^{\infty}_y(H^2_x)}^2\|\varepsilon\partial_x u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t \|u^R\|_{X^2}(\|u^R\|_{X^2}+\|\partial_y u^R\|_{X^2})\|\varepsilon\partial_x u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t \|\omega^R\|_{X^2}^4ds, \end{align*} $$
where we use the Gagliardo-Nirenberg inequality (4.9) in the second step.
Similarly, we use Lemma 2.2 and (3.22) to deduce
 $$ \begin{align*} I_2\leq &\ C\int_0^t\|v^R_{\Phi}\|_{L^{\infty}_y(H^2_x)}^2\|\partial_y u^R\|_{X^2}^2ds \leq C\varepsilon^{-2}\int_0^t\|\varepsilon\partial_xu^R\|_{X^2}^2\|\partial_y u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t\|\omega^R\|_{X^2}^4ds, \end{align*} $$
$$ \begin{align*} I_2\leq &\ C\int_0^t\|v^R_{\Phi}\|_{L^{\infty}_y(H^2_x)}^2\|\partial_y u^R\|_{X^2}^2ds \leq C\varepsilon^{-2}\int_0^t\|\varepsilon\partial_xu^R\|_{X^2}^2\|\partial_y u^R\|_{X^2}^2ds\\ \leq &\ C\varepsilon^{-2}\int_0^t\|\omega^R\|_{X^2}^4ds, \end{align*} $$
where we use
![]() $v^R=-\int _0^y \partial _x u^R dy'$
in the second step.
$v^R=-\int _0^y \partial _x u^R dy'$
in the second step.
Collecting
![]() $I_1$
and
$I_1$
and
![]() $I_2$
together and using (5.1), it holds that
$I_2$
together and using (5.1), it holds that
 $$ \begin{align*} \int_0^t\|\mathcal{N}_u\|_{X^2}^2ds\leq C\varepsilon^{-2}\int_0^t\|\omega^R\|_{X^2}^4ds\leq C\varepsilon^4\int_0^t\|\omega^R\|_{X^2}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\mathcal{N}_u\|_{X^2}^2ds\leq C\varepsilon^{-2}\int_0^t\|\omega^R\|_{X^2}^4ds\leq C\varepsilon^4\int_0^t\|\omega^R\|_{X^2}^2ds. \end{align*} $$
The estimate for
![]() $\varepsilon \mathcal {N}_v$
is obtained by changing
$\varepsilon \mathcal {N}_v$
is obtained by changing
![]() $u^R$
into
$u^R$
into
![]() $\varepsilon v^R$
in the above argument and we omit details. Thus, we obtain (5.3).
$\varepsilon v^R$
in the above argument and we omit details. Thus, we obtain (5.3).
For (5.4), we use the definition of
![]() $\mathcal {N}$
to have
$\mathcal {N}$
to have
 $$ \begin{align*} \int_0^t\|\mathcal{N}\|_{L^2}^2ds\leq &\ \int_0^t\|u^R\partial_x \omega^R\|_{L^2}^2ds+\int_0^t\| v^R\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ \varepsilon^{-2}\int_0^t\|u^R\|_{L^{\infty}_y(H^1_x)}^2\|\varepsilon\partial_x \omega^R\|_{L^2}^2ds+\int_0^t\| v^R\|_{L^{\infty}_y(H^1_x)}^2\|\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^{-2}\int_0^t\|\omega^R\|_{H^{1,0}}^2\|\varepsilon\partial_x \omega^R\|_{L^2}^2ds+C\int_0^t\| \omega^R\|_{H^{2,0}}^2\|\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^{-2}\sup_{s\in[0,t]}\|\omega^R\|_{X^2}^2\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^4\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds \end{align*} $$
$$ \begin{align*} \int_0^t\|\mathcal{N}\|_{L^2}^2ds\leq &\ \int_0^t\|u^R\partial_x \omega^R\|_{L^2}^2ds+\int_0^t\| v^R\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ \varepsilon^{-2}\int_0^t\|u^R\|_{L^{\infty}_y(H^1_x)}^2\|\varepsilon\partial_x \omega^R\|_{L^2}^2ds+\int_0^t\| v^R\|_{L^{\infty}_y(H^1_x)}^2\|\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^{-2}\int_0^t\|\omega^R\|_{H^{1,0}}^2\|\varepsilon\partial_x \omega^R\|_{L^2}^2ds+C\int_0^t\| \omega^R\|_{H^{2,0}}^2\|\partial_y\omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^{-2}\sup_{s\in[0,t]}\|\omega^R\|_{X^2}^2\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds\\[5pt] \leq &\ C\varepsilon^4\int_0^t\|\nabla_{\varepsilon} \omega^R\|_{L^2}^2ds \end{align*} $$
With Proposition 5.1 and Proposition 5.2 in hand, we are in the position to prove Theorem 1.1. By Proposition 4.3, Proposition 5.1 and Proposition 5.2, we get
 $$ \begin{align*} \sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2) +\int_0^t \|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}\leq Ct \varepsilon^6+C\int_0^t \|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2ds, \end{align*} $$
$$ \begin{align*} \sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2) +\int_0^t \|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}\leq Ct \varepsilon^6+C\int_0^t \|\Delta_{\varepsilon}\phi(s)\|_{X^2}^2ds, \end{align*} $$
for
![]() $t\in [0,T].$
By the Gronwall inequality and choosing a small
$t\in [0,T].$
By the Gronwall inequality and choosing a small
![]() $T<\min \{T_p, \frac {1}{2\lambda }\}$
, we get that
$T<\min \{T_p, \frac {1}{2\lambda }\}$
, we get that
 $$ \begin{align*} \sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\omega^R\|_{X^2}^2) +\int_0^t \|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}\leq \frac{\mathfrak{C}}{2} \varepsilon^6. \end{align*} $$
$$ \begin{align*} \sup_{s\in[0,t]}(\lambda\|\nabla_{\varepsilon}\phi(s)\|_{X^{\frac73}}^2+\|\omega^R\|_{X^2}^2) +\int_0^t \|\partial_t \nabla_{\varepsilon}\phi_{\Phi}\|^2_{H^{2,0}}\leq \frac{\mathfrak{C}}{2} \varepsilon^6. \end{align*} $$
By the Sobolev embedding theorem and Lemma 4.1, we get Theorem 1.1 proved.
6 The proof of Proposition 5.1
All we have left is to prove Proposition 5.1. To prove that, we first give the following decomposition of
![]() $\phi $
:
$\phi $
:
where
![]() $\phi _{slip}$
satisfies that
$\phi _{slip}$
satisfies that
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{slip}+u^p\partial_x \Delta_{\varepsilon}\phi_{slip}+v^p\partial_y \Delta_{\varepsilon}\phi_{slip}+\partial_y\phi_{slip}\partial_x \omega^p-\partial_x\phi_{slip}\partial_y \omega^p\\ &\qquad\qquad\qquad\qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi_{slip}|_{y=0,1}=0,\quad \Delta_{\varepsilon}\phi_{slip}|_{y=0,1}=0,\\ &\phi_{slip}|_{t=0}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{slip}+u^p\partial_x \Delta_{\varepsilon}\phi_{slip}+v^p\partial_y \Delta_{\varepsilon}\phi_{slip}+\partial_y\phi_{slip}\partial_x \omega^p-\partial_x\phi_{slip}\partial_y \omega^p\\ &\qquad\qquad\qquad\qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi_{slip}|_{y=0,1}=0,\quad \Delta_{\varepsilon}\phi_{slip}|_{y=0,1}=0,\\ &\phi_{slip}|_{t=0}=0, \end{aligned} \right. \end{align} $$
and
![]() $\phi _{bc}$
satisfies that
$\phi _{bc}$
satisfies that
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p-\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t)\\ &\phi_{bc}|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p-\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t)\\ &\phi_{bc}|_{t=0}=0. \end{aligned} \right. \end{align} $$
To prove Proposition 5.1, we need the estimates of
![]() $\phi _{slip}$
and
$\phi _{slip}$
and
![]() $\phi _{bc}$
. First, we notice that
$\phi _{bc}$
. First, we notice that
![]() $\phi _{slip}$
has a good boundary condition. We use the ‘hydrostatic trick’ method to get its estimates. The proof of the following proposition is given in Section 7.
$\phi _{slip}$
has a good boundary condition. We use the ‘hydrostatic trick’ method to get its estimates. The proof of the following proposition is given in Section 7.
Proposition 6.1. There exists
![]() $\lambda _0>1$
and
$\lambda _0>1$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
![]() $t\in [0,T]$
,
$t\in [0,T]$
,
![]() $\lambda \geq \lambda _0$
, there holds that
$\lambda \geq \lambda _0$
, there holds that
 $$ \begin{align*} \|\Delta_{\varepsilon}\phi_{slip}\|_{X^{2}}^2+&\lambda\int_0^t (\|\Delta_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds+\int_0^t\|\nabla_{\varepsilon}\Delta_{\varepsilon}\phi_{slip}\|_{X^{2}}^2ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|(C(t),\varepsilon^2 f_1,f_2)\|_{X^{\frac53}}^2 ds. \end{align*} $$
$$ \begin{align*} \|\Delta_{\varepsilon}\phi_{slip}\|_{X^{2}}^2+&\lambda\int_0^t (\|\Delta_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds+\int_0^t\|\nabla_{\varepsilon}\Delta_{\varepsilon}\phi_{slip}\|_{X^{2}}^2ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|(C(t),\varepsilon^2 f_1,f_2)\|_{X^{\frac53}}^2 ds. \end{align*} $$
The estimates of
![]() $\phi _{bc}$
are much more difficult. Here, we state the main results on it:
$\phi _{bc}$
are much more difficult. Here, we state the main results on it:
Proposition 6.2. There exists
![]() $\lambda _0>1$
and
$\lambda _0>1$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
![]() $t\in [0,T]$
,
$t\in [0,T]$
,
![]() $\lambda \geq \lambda _0$
, there holds that
$\lambda \geq \lambda _0$
, there holds that
 $$ \begin{align} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2+\|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq &\ \frac{C}{\lambda^{\frac12}}\int_0^t \Big(|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}+|C(s)|^2\Big)ds, \end{align} $$
$$ \begin{align} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2+\|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq &\ \frac{C}{\lambda^{\frac12}}\int_0^t \Big(|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}+|C(s)|^2\Big)ds, \end{align} $$
where C is a universal constant.
The proof of Proposition 6.2 is given in Section 8.
Based on the above two propositions, we are in the position to prove Proposition 5.1. First, we give the estimates of
![]() $\|u^R\|_{L^2}$
which are used to control the
$\|u^R\|_{L^2}$
which are used to control the
![]() $C(t)$
.
$C(t)$
.
Lemma 6.3. There exist
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
and
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
and
![]() $\lambda _0\geq 1$
such that for
$\lambda _0\geq 1$
such that for
![]() $t\in [0,T]$
and
$t\in [0,T]$
and
![]() $\lambda \geq \lambda _0,$
it holds that
$\lambda \geq \lambda _0,$
it holds that
 $$ \begin{align} \|e^{(1-\lambda t)}(u^R,\varepsilon v^R)\|_{L^2}^2+&\lambda\int_0^t\|e^{(1-\lambda s)}(u^R,\varepsilon v^R)\|_{L^2}^2ds+\int_0^t\|e^{(1-\lambda s)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2ds\\ \nonumber \leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|\nabla_{\varepsilon}\phi\|_{X^2}^2ds. \end{align} $$
$$ \begin{align} \|e^{(1-\lambda t)}(u^R,\varepsilon v^R)\|_{L^2}^2+&\lambda\int_0^t\|e^{(1-\lambda s)}(u^R,\varepsilon v^R)\|_{L^2}^2ds+\int_0^t\|e^{(1-\lambda s)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2ds\\ \nonumber \leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|\nabla_{\varepsilon}\phi\|_{X^2}^2ds. \end{align} $$
Remark 6.4. We use weighted quantity
![]() $\|e^{(1-\lambda t)}(u^R,\varepsilon v^R)\|_{L^2}$
instead of
$\|e^{(1-\lambda t)}(u^R,\varepsilon v^R)\|_{L^2}$
instead of
![]() $\|(u^R,\varepsilon v^R)\|_{L^2}$
to obtain a small constant factor in front of
$\|(u^R,\varepsilon v^R)\|_{L^2}$
to obtain a small constant factor in front of
![]() $\int _0^t\|\nabla _{\varepsilon }\phi \|_{X^2}^2ds$
in (6.5).
$\int _0^t\|\nabla _{\varepsilon }\phi \|_{X^2}^2ds$
in (6.5).
Proof. Taking the
![]() $L^2$
inner product with
$L^2$
inner product with
![]() $e^{2(1-\lambda t)}u^R$
in the first equation of (3.7) and with
$e^{2(1-\lambda t)}u^R$
in the first equation of (3.7) and with
![]() $e^{2(1-\lambda t)}v^R$
in the second equation of (3.7), we use the fact
$e^{2(1-\lambda t)}v^R$
in the second equation of (3.7), we use the fact
and integrate by parts by boundary condition
![]() $(u^R, v^R)|_{y=0,1}=0$
to yield
$(u^R, v^R)|_{y=0,1}=0$
to yield
 $$ \begin{align*} \frac12\frac{d}{dt}&\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+\lambda\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+\|e^{(1-\lambda t)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2\\ \leq &\ C(\|e^{(1-\lambda t)}(u^R, v^R)\|_{L^2}+\|e^{(1-\lambda t)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}+\|(R_1, R_2)\|_{L^2})\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}\\ \leq &\ \frac{\lambda}{2}\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+C(\|e^{(1-\lambda t)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)+\frac{C}{\lambda}\|e^{(1-\lambda t)}\partial_x u^R\|_{L^2}^2, \end{align*} $$
$$ \begin{align*} \frac12\frac{d}{dt}&\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+\lambda\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+\|e^{(1-\lambda t)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2\\ \leq &\ C(\|e^{(1-\lambda t)}(u^R, v^R)\|_{L^2}+\|e^{(1-\lambda t)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}+\|(R_1, R_2)\|_{L^2})\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}\\ \leq &\ \frac{\lambda}{2}\|e^{(1-\lambda t)}(u^R, \varepsilon v^R)\|_{L^2}^2+C(\|e^{(1-\lambda t)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)+\frac{C}{\lambda}\|e^{(1-\lambda t)}\partial_x u^R\|_{L^2}^2, \end{align*} $$
where we write
![]() $v^R=-\int _0^y \partial _x u^Rdy'$
and use the fact
$v^R=-\int _0^y \partial _x u^Rdy'$
and use the fact
![]() $\partial _xu^p+\partial _y v^p=0 $
to eliminate the transport term and
$\partial _xu^p+\partial _y v^p=0 $
to eliminate the transport term and
![]() $\partial _xu^R+\partial _y v^R=0 $
to eliminate the pressure term, respectively.
$\partial _xu^R+\partial _y v^R=0 $
to eliminate the pressure term, respectively.
Afterwards, integrating time from
![]() $0$
to t and using
$0$
to t and using
![]() $\partial _x u^R=-\partial _x \partial _y\phi $
, we obtain
$\partial _x u^R=-\partial _x \partial _y\phi $
, we obtain
 $$ \begin{align*} \|e^{(1-\lambda t)}(u^R,\varepsilon v^R)(t)\|_{L^2}^2+&\lambda\int_0^t\|e^{(1-\lambda s)}(u^R,\varepsilon v^R)\|_{L^2}^2ds+\int_0^t\|e^{(1-\lambda s)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2ds\\ \leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|e^{(1-\lambda s)}\partial_x \partial_y\phi\|_{L^2}^2ds. \end{align*} $$
$$ \begin{align*} \|e^{(1-\lambda t)}(u^R,\varepsilon v^R)(t)\|_{L^2}^2+&\lambda\int_0^t\|e^{(1-\lambda s)}(u^R,\varepsilon v^R)\|_{L^2}^2ds+\int_0^t\|e^{(1-\lambda s)}\nabla_{\varepsilon}(u^R,\varepsilon v^R)\|_{L^2}^2ds\\ \leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|e^{(1-\lambda s)}\partial_x \partial_y\phi\|_{L^2}^2ds. \end{align*} $$
Finally, we use
![]() $\|e^{(1-\lambda s)}\partial _x\partial _y\phi \|_{L^2}\leq C\|\nabla _{\varepsilon }\phi \|_{X^2}$
to complete the proof.
$\|e^{(1-\lambda s)}\partial _x\partial _y\phi \|_{L^2}\leq C\|\nabla _{\varepsilon }\phi \|_{X^2}$
to complete the proof.
Proof of Proposition 5.1
Now, we give the proof Proposition 5.1. We divide this proof into two parts.
![]() $\underline {\mathrm {Estimates \ of } \ \int _0^t \|\nabla _{\varepsilon }\phi \|_{X^2}^2.}$
Since
$\underline {\mathrm {Estimates \ of } \ \int _0^t \|\nabla _{\varepsilon }\phi \|_{X^2}^2.}$
Since
by Lemma 6.3, we ensure
 $$ \begin{align} |C(t)|^2\leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|\nabla_{\varepsilon}\phi\|_{X^2}^2ds. \end{align} $$
$$ \begin{align} |C(t)|^2\leq &\ C\int_0^t(\|e^{(1-\lambda s)}(\mathcal{N}_u,\varepsilon\mathcal{N}_v)\|_{L^2}^2+\varepsilon^8)ds+\frac{C}{\lambda}\int_0^t\|\nabla_{\varepsilon}\phi\|_{X^2}^2ds. \end{align} $$
By the definition of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, we obtain that
$f_2$
, we obtain that
 $$ \begin{align*} &\int_0^t \|f_1\|_{X^{\frac 53}}^2+\|f_2\|_{X^{\frac 53}}^2ds\leq C\int_0^t (\|\varepsilon \triangle_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds, \end{align*} $$
$$ \begin{align*} &\int_0^t \|f_1\|_{X^{\frac 53}}^2+\|f_2\|_{X^{\frac 53}}^2ds\leq C\int_0^t (\|\varepsilon \triangle_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds, \end{align*} $$
and we get
 $$ \begin{align} \lambda\int_0^t (\|\Delta_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+&\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\Big(|C(t)|^2+\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds\Big).\nonumber \end{align} $$
$$ \begin{align} \lambda\int_0^t (\|\Delta_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+&\|\nabla_{\varepsilon}\phi_{slip}\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2)ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\Big(|C(t)|^2+\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds\Big).\nonumber \end{align} $$
Then, it follows
![]() $\phi =\phi _{slip}+\phi _{bc}$
and (6.4) to deduce
$\phi =\phi _{slip}+\phi _{bc}$
and (6.4) to deduce
 $$ \begin{align} \int_0^t \|\nabla_{\varepsilon}\phi\|_{X^2}^2ds\leq &\ \int_0^t \|\nabla_{\varepsilon}\phi_{slip}\|_{X^2}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc}\|_{X^2}^2ds\\\leq &\ \frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda^2}\Big(\int_0^t \|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8ds\Big) \nonumber\\ &+\frac{C}{\lambda^{\frac12}}\int_0^t |\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2 ds+\frac{C}{\lambda^{\frac12}}|C(t)|^2,\nonumber\\ \leq &\ \frac{C}{\lambda^{\frac12}}|C(t)|^2+\frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda^2}\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds .\nonumber \end{align} $$
$$ \begin{align} \int_0^t \|\nabla_{\varepsilon}\phi\|_{X^2}^2ds\leq &\ \int_0^t \|\nabla_{\varepsilon}\phi_{slip}\|_{X^2}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc}\|_{X^2}^2ds\\\leq &\ \frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda^2}\Big(\int_0^t \|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8ds\Big) \nonumber\\ &+\frac{C}{\lambda^{\frac12}}\int_0^t |\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|_{X^{\frac73}}^2 ds+\frac{C}{\lambda^{\frac12}}|C(t)|^2,\nonumber\\ \leq &\ \frac{C}{\lambda^{\frac12}}|C(t)|^2+\frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda^2}\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds .\nonumber \end{align} $$
Plusing (6.6) and above estimates together and taking
![]() $\lambda $
large enough, we get
$\lambda $
large enough, we get
 $$ \begin{align} |C(t)|^2+ \int_0^t \|\nabla_{\varepsilon}\phi\|_{X^2}^2ds \leq C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+C\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align} $$
$$ \begin{align} |C(t)|^2+ \int_0^t \|\nabla_{\varepsilon}\phi\|_{X^2}^2ds \leq C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+C\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align} $$
![]() $\underline {\mathrm {Estimates \ of } \ \int _0^t\|\varphi \triangle _{\varepsilon }\phi \|_{X^2}^2.}$
$\underline {\mathrm {Estimates \ of } \ \int _0^t\|\varphi \triangle _{\varepsilon }\phi \|_{X^2}^2.}$
It follows from (6.7) and (6.9) that
 $$ \begin{align*} \int_0^t\|\Delta_{\varepsilon}\phi_{slip}\|_{X^2}^2ds\leq &\ \frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\Big(|C(t)|^2+\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds\Big)\\ \leq &\ \frac{C}{\lambda}\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\Delta_{\varepsilon}\phi_{slip}\|_{X^2}^2ds\leq &\ \frac{C}{\lambda}\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\Big(|C(t)|^2+\int_0^t (\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds\Big)\\ \leq &\ \frac{C}{\lambda}\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
Applying Proposition 6.2 again, we get
 $$ \begin{align*} \int_0^t\|\varphi\Delta_{\varepsilon}\phi_{bc}\|_{X^2}^2ds\leq C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\varphi\Delta_{\varepsilon}\phi_{bc}\|_{X^2}^2ds\leq C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
Combining the above two estimates, we get
 $$ \begin{align*} \int_0^t\|\varphi\Delta_{\varepsilon}\phi \|_{X^2}^2ds\leq C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\varphi\Delta_{\varepsilon}\phi \|_{X^2}^2ds\leq C\int_0^t(\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2+\|\varepsilon \Delta_{\varepsilon} \phi\|_{X^{\frac 53}}^2+\varepsilon^8)ds. \end{align*} $$
By now, we get the desired results.
7 Vorticity estimates under artificial boundary condition: Proof of Proposition 6.1
In this section, we give the proof of Proposition 6.1. To simplify the notation, we drop the subscript in the system (6.2):
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi+u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi+\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p\\ &\qquad \qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi|_{y=0,1}=0,\quad \Delta_{\varepsilon}\phi|_{y=0,1}=0,\\ &\phi|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi+u^p\partial_x \Delta_{\varepsilon}\phi+v^p\partial_y \Delta_{\varepsilon}\phi+\partial_y\phi\partial_x \omega^p-\partial_x\phi\partial_y \omega^p\\ &\qquad \qquad\qquad=\partial_y \mathcal{N}_u-\varepsilon^2\partial_x \mathcal{N}_v +\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p,\\ &\phi|_{y=0,1}=0,\quad \Delta_{\varepsilon}\phi|_{y=0,1}=0,\\ &\phi|_{t=0}=0. \end{aligned} \right. \end{align} $$
The goal in this section is to establish a uniform (in
![]() $\varepsilon $
) estimate of vorticity
$\varepsilon $
) estimate of vorticity
![]() $\omega =\triangle _{\varepsilon }\phi .$
$\omega =\triangle _{\varepsilon }\phi .$
Proposition 7.1. There exists
![]() $\lambda _0>0$
and
$\lambda _0>0$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
![]() $t\in [0,T]$
,
$t\in [0,T]$
,
![]() $\lambda \geq \lambda _0$
, the following holds:
$\lambda \geq \lambda _0$
, the following holds:
 $$ \begin{align*} \|\omega(t)\|_{X^{2}}^2+&\lambda\int_0^t (\|\omega\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi|_{y=0,1}|_{X^{\frac73}}^2)ds+\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1, f_2,C(t)\|_{X^{\frac53}}^2 ds. \end{align*} $$
$$ \begin{align*} \|\omega(t)\|_{X^{2}}^2+&\lambda\int_0^t (\|\omega\|_{X^{\frac73}}^2+\|\nabla_{\varepsilon}\phi\|_{X^{\frac73}}^2+|\nabla_{\varepsilon}\phi|_{y=0,1}|_{X^{\frac73}}^2)ds+\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\\ \leq &\ C\int_0^t\|(\mathcal{N}_u,\varepsilon \mathcal{N}_v)\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1, f_2,C(t)\|_{X^{\frac53}}^2 ds. \end{align*} $$
Proof. By Lemma 4.1, we have
Hence, we use the ‘hydrostatic trick’ to get the desired results. First, acting operator
![]() $e^{\Phi (t,D_x)}$
on the first equation of (6.2), we get
$e^{\Phi (t,D_x)}$
on the first equation of (6.2), we get
 $$ \begin{align} &(\partial_t+\lambda\langle D_x\rangle^{\frac23} -\Delta_{\varepsilon})\omega_{\Phi}+u^p\partial_x \omega_{\Phi}+v^p\partial_y\omega_{\Phi}-\partial_x\phi_{\Phi}\partial_y \omega^p \\&\qquad=-(\partial_y\phi\partial_x \omega^p)_{\Phi}-[e^{\Phi(t,D_x)},u^p\partial_x ] \omega-[e^{\Phi(t,D_x)},v^p\partial_y ] \omega \nonumber\\ &\qquad\quad+[e^{\Phi(t,D_x)},\partial_y\omega^p ]\partial_x \phi +\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}+(\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p)_{\Phi}.\nonumber\end{align} $$
$$ \begin{align} &(\partial_t+\lambda\langle D_x\rangle^{\frac23} -\Delta_{\varepsilon})\omega_{\Phi}+u^p\partial_x \omega_{\Phi}+v^p\partial_y\omega_{\Phi}-\partial_x\phi_{\Phi}\partial_y \omega^p \\&\qquad=-(\partial_y\phi\partial_x \omega^p)_{\Phi}-[e^{\Phi(t,D_x)},u^p\partial_x ] \omega-[e^{\Phi(t,D_x)},v^p\partial_y ] \omega \nonumber\\ &\qquad\quad+[e^{\Phi(t,D_x)},\partial_y\omega^p ]\partial_x \phi +\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}+(\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p)_{\Phi}.\nonumber\end{align} $$
In view of (7.2), the terrible term comes from
![]() $\partial _x\phi _{\Phi }\partial _y \omega ^p,$
which loses one tangential derivative. In order to overcome the derivative loss, we take
$\partial _x\phi _{\Phi }\partial _y \omega ^p,$
which loses one tangential derivative. In order to overcome the derivative loss, we take
![]() $\langle D_x\rangle ^2$
on the (7.2) and then take the
$\langle D_x\rangle ^2$
on the (7.2) and then take the
![]() $L^2$
inner product with
$L^2$
inner product with
![]() $\frac {\langle D_x\rangle ^2\omega _{\Phi }}{\partial _y\omega ^p}$
to obtain that
$\frac {\langle D_x\rangle ^2\omega _{\Phi }}{\partial _y\omega ^p}$
to obtain that
 $$ \begin{align*} \frac12\frac{d}{dt}&\Big\|\frac{\langle D_x\rangle^2\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2+\lambda\Big\|\frac{\langle D_x\rangle^{\frac73}\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2+\Big\|\frac{\nabla_{\varepsilon}\langle D_x\rangle^2\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2\\ =&\ -\int_{\mathcal{S}}\langle D_x\rangle^2\omega_{\Phi}\cdot(\varepsilon\partial_x,\partial_y)\frac{1}{\partial_y\omega^p}\cdot (\varepsilon\partial_x,\partial_y)\langle D_x\rangle^2\omega_{\Phi} dxdy\\ &+\int_{\mathcal{S}}|\langle D_x\rangle^2\omega_{\Phi}|^2\Big(\partial_x(\frac{u^p}{\partial_y\omega^p})+\partial_y(\frac{v^p}{\partial_y\omega^p})\Big)dxdy-\int_{\mathcal{S}}\big[\langle D_x\rangle^2,u^p\partial_x+v^p\partial_y\big]\omega_{\Phi} ~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &-\int_{\mathcal{S}}\langle D_x\rangle^2(\partial_y\phi\partial_x\omega^p)_{\Phi}~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy+\int_{\mathcal{S}}[\langle D_x\rangle^2,\partial_y\omega^p]\partial_x\phi_{\Phi}~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ & +\int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\phi_{\Phi}\langle D_x\rangle^2\omega_{\Phi} dxdy -\int_{\mathcal{S}}\langle D_x\rangle^2\Big([e^{\Phi(t,D_x)},u^p\partial_x ] \omega \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &-\int_{\mathcal{S}}\langle D_x\rangle^2\Big( [e^{\Phi(t,D_x)},v^p\partial_y ] \omega \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2\Big( [e^{\Phi(t,D_x)}, \partial_y \omega^p] \partial_x \phi \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2\Big(\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}\Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2(\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p)_{\Phi}~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ =&\ T^0+\cdots T^{10}. \end{align*} $$
$$ \begin{align*} \frac12\frac{d}{dt}&\Big\|\frac{\langle D_x\rangle^2\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2+\lambda\Big\|\frac{\langle D_x\rangle^{\frac73}\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2+\Big\|\frac{\nabla_{\varepsilon}\langle D_x\rangle^2\omega_{\Phi}}{\sqrt{\partial_y\omega^p}}\Big\|_{L^2}^2\\ =&\ -\int_{\mathcal{S}}\langle D_x\rangle^2\omega_{\Phi}\cdot(\varepsilon\partial_x,\partial_y)\frac{1}{\partial_y\omega^p}\cdot (\varepsilon\partial_x,\partial_y)\langle D_x\rangle^2\omega_{\Phi} dxdy\\ &+\int_{\mathcal{S}}|\langle D_x\rangle^2\omega_{\Phi}|^2\Big(\partial_x(\frac{u^p}{\partial_y\omega^p})+\partial_y(\frac{v^p}{\partial_y\omega^p})\Big)dxdy-\int_{\mathcal{S}}\big[\langle D_x\rangle^2,u^p\partial_x+v^p\partial_y\big]\omega_{\Phi} ~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &-\int_{\mathcal{S}}\langle D_x\rangle^2(\partial_y\phi\partial_x\omega^p)_{\Phi}~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy+\int_{\mathcal{S}}[\langle D_x\rangle^2,\partial_y\omega^p]\partial_x\phi_{\Phi}~\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ & +\int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\phi_{\Phi}\langle D_x\rangle^2\omega_{\Phi} dxdy -\int_{\mathcal{S}}\langle D_x\rangle^2\Big([e^{\Phi(t,D_x)},u^p\partial_x ] \omega \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &-\int_{\mathcal{S}}\langle D_x\rangle^2\Big( [e^{\Phi(t,D_x)},v^p\partial_y ] \omega \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2\Big( [e^{\Phi(t,D_x)}, \partial_y \omega^p] \partial_x \phi \Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2\Big(\partial_y (\mathcal{N}_u)_{\Phi}-\varepsilon^2\partial_x (\mathcal{N}_v)_{\Phi}\Big)~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ &+\int_{\mathcal{S}}\langle D_x\rangle^2(\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p)_{\Phi}~ \frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}dxdy\\ =&\ T^0+\cdots T^{10}. \end{align*} $$
The boundary term is zero due to artificial boundary condition
![]() $\omega |_{y=0,1}=\Delta _{\varepsilon }\phi |_{y=0,1}=0.$
Integrating on
$\omega |_{y=0,1}=\Delta _{\varepsilon }\phi |_{y=0,1}=0.$
Integrating on
![]() $[0,t)$
with
$[0,t)$
with
![]() $t\leq T$
and using
$t\leq T$
and using
![]() $\partial _y\omega ^p\geq c_0$
, we obtain
$\partial _y\omega ^p\geq c_0$
, we obtain
 $$ \begin{align*} \|\omega(t)\|_{X^{2}}^2+2\lambda\int_0^t \|\omega\|_{X^{\frac73}}^2ds+2\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\leq C\int_0^t|T^0|+\cdots+|T^{10}|ds. \end{align*} $$
$$ \begin{align*} \|\omega(t)\|_{X^{2}}^2+2\lambda\int_0^t \|\omega\|_{X^{\frac73}}^2ds+2\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\leq C\int_0^t|T^0|+\cdots+|T^{10}|ds. \end{align*} $$
Now, we estimate
![]() $T^i, i=0,\cdots , 10$
one by one.
$T^i, i=0,\cdots , 10$
one by one.
![]() $\underline {\mathrm {Estimate \ of } \ T^0 \ \mathrm {and} \ T^1.}$
Since
$\underline {\mathrm {Estimate \ of } \ T^0 \ \mathrm {and} \ T^1.}$
Since
![]() $\partial _y\omega ^p\geq c_0>0$
and Lemma 4.1 imply
$\partial _y\omega ^p\geq c_0>0$
and Lemma 4.1 imply
it is easy to see
![]() $\underline {\mathrm {Estimate \ of} \ T^2 \ \mathrm {and} \ T^4.}$
By using Lemma 2.1, we get
$\underline {\mathrm {Estimate \ of} \ T^2 \ \mathrm {and} \ T^4.}$
By using Lemma 2.1, we get
 $$ \begin{align*} &\|[\langle D_x\rangle^2,u^p\partial_x+v^p\partial_y\big]\omega_{\Phi}\|_{L^2}\leq C(\|\omega\|_{X^2}+\|\partial_y\omega\|_{X^2}),\\ &\|[\langle D_x\rangle^2,\partial_y\omega^p]\partial_x\phi_{\Phi}\|_{L^2}\leq C\|\phi\|_{X^2}\leq C\|\partial_y\phi\|_{X^2}, \end{align*} $$
$$ \begin{align*} &\|[\langle D_x\rangle^2,u^p\partial_x+v^p\partial_y\big]\omega_{\Phi}\|_{L^2}\leq C(\|\omega\|_{X^2}+\|\partial_y\omega\|_{X^2}),\\ &\|[\langle D_x\rangle^2,\partial_y\omega^p]\partial_x\phi_{\Phi}\|_{L^2}\leq C\|\phi\|_{X^2}\leq C\|\partial_y\phi\|_{X^2}, \end{align*} $$
where we used the Poincaré inequality and
![]() $\phi |_{y=0,1}=0$
to ensure
$\phi |_{y=0,1}=0$
to ensure
in the last step.
According to
classical elliptic estimate and (7.3) imply
which gives
Therefore, it follows from
![]() $\partial _y\omega ^p\geq c_0>0$
to get
$\partial _y\omega ^p\geq c_0>0$
to get
![]() $\underline {\mathrm {Estimate \ of} \ T_3.}$
Using Lemma 2.2 and (7.5), it shows
$\underline {\mathrm {Estimate \ of} \ T_3.}$
Using Lemma 2.2 and (7.5), it shows
![]() $\underline {\mathrm {Estimate \ of} \ T^.}$
This term is a troubling term because it loses one tangential derivative. However, the hydrostatic trick implies
$\underline {\mathrm {Estimate \ of} \ T^.}$
This term is a troubling term because it loses one tangential derivative. However, the hydrostatic trick implies
 $$ \begin{align*} T^5=&\ \int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\phi_{\Phi}\langle D_x\rangle^2\Delta_{\varepsilon}\phi_{\Phi} dxdy=-\int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\nabla_{\varepsilon}\phi_{\Phi}\langle D_x\rangle^2\nabla_{\varepsilon}\phi_{\Phi} dxdy\\ =&\ -\frac12\int_{\mathcal{S}} \partial_x|\langle D_x\rangle^2\nabla_{\varepsilon}\phi_{\Phi}|^2 dxdy=0, \end{align*} $$
$$ \begin{align*} T^5=&\ \int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\phi_{\Phi}\langle D_x\rangle^2\Delta_{\varepsilon}\phi_{\Phi} dxdy=-\int_{\mathcal{S}} \langle D_x\rangle^2 \partial_x\nabla_{\varepsilon}\phi_{\Phi}\langle D_x\rangle^2\nabla_{\varepsilon}\phi_{\Phi} dxdy\\ =&\ -\frac12\int_{\mathcal{S}} \partial_x|\langle D_x\rangle^2\nabla_{\varepsilon}\phi_{\Phi}|^2 dxdy=0, \end{align*} $$
by using
![]() $\phi |_{y=0,1}=0.$
$\phi |_{y=0,1}=0.$
![]() $\underline {\mathrm {Estimate \ of} \ T^6, T^7 \ \mathrm {and}\ T^8.}$
Let’s estimate commutators by Lemma 2.3. Since
$\underline {\mathrm {Estimate \ of} \ T^6, T^7 \ \mathrm {and}\ T^8.}$
Let’s estimate commutators by Lemma 2.3. Since
![]() $\partial _y\omega ^p\geq c_0>0,$
we use Lemma 2.3 to ensure that
$\partial _y\omega ^p\geq c_0>0,$
we use Lemma 2.3 to ensure that
 $$ \begin{align*} |T^6|\leq &\ C\|(u^p\partial_x\omega)_{\Phi}-u^p\partial_x\omega_{\Phi} \|_{H^{2-\frac13,0}}\|\omega\|_{X^{\frac73}}\leq C\|\omega\|_{X^{2+1-\frac13-\frac13}}\|\omega\|_{X^{\frac73}}=C\|\omega\|_{X^{\frac73}}^2,\\ |T^7|\leq &\ C\|\partial_y\omega\|_{X^2}\|\omega\|_{X^2},\\ |T^8|\leq &\ C\|(\partial_x\phi\partial_y\omega^p)_{\Phi}-\partial_x\phi_{\Phi}\partial_y\omega^p\|_{H^{2-\frac13}}\|\omega\|_{X^{\frac73}}\leq C\|\partial_x\phi\|_{X^{2-\frac13-\frac13}}\|\omega\|_{X^{\frac73}}\leq C\|\phi\|_{X^{\frac73}}\|\omega\|_{X^{\frac73}}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq C\|\omega\|_{X^{\frac73}}^2. \end{align*} $$
$$ \begin{align*} |T^6|\leq &\ C\|(u^p\partial_x\omega)_{\Phi}-u^p\partial_x\omega_{\Phi} \|_{H^{2-\frac13,0}}\|\omega\|_{X^{\frac73}}\leq C\|\omega\|_{X^{2+1-\frac13-\frac13}}\|\omega\|_{X^{\frac73}}=C\|\omega\|_{X^{\frac73}}^2,\\ |T^7|\leq &\ C\|\partial_y\omega\|_{X^2}\|\omega\|_{X^2},\\ |T^8|\leq &\ C\|(\partial_x\phi\partial_y\omega^p)_{\Phi}-\partial_x\phi_{\Phi}\partial_y\omega^p\|_{H^{2-\frac13}}\|\omega\|_{X^{\frac73}}\leq C\|\partial_x\phi\|_{X^{2-\frac13-\frac13}}\|\omega\|_{X^{\frac73}}\leq C\|\phi\|_{X^{\frac73}}\|\omega\|_{X^{\frac73}}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq C\|\omega\|_{X^{\frac73}}^2. \end{align*} $$
Here, we use (7.3) and (7.5) in the last estimate.
![]() $\underline {\mathrm {Estimate \ of} \ T^9 \ \mbox {and} \ T^{10}.}$
Integration by parts and boundary condition
$\underline {\mathrm {Estimate \ of} \ T^9 \ \mbox {and} \ T^{10}.}$
Integration by parts and boundary condition
![]() $\omega |_{y=0,1}=0$
give that
$\omega |_{y=0,1}=0$
give that
 $$ \begin{align*} |T^9|=&\ \int_{\mathcal{S}}\langle D_x\rangle^2(\mathcal{N}_u,\varepsilon \mathcal{N}_v)_{\Phi}\cdot \nabla_{\varepsilon}\Big(\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}\Big)dxdy\\ \leq &\ C\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}(\|\omega\|_{X^2}+\|\nabla_{\varepsilon}\omega\|_{X^2}). \end{align*} $$
$$ \begin{align*} |T^9|=&\ \int_{\mathcal{S}}\langle D_x\rangle^2(\mathcal{N}_u,\varepsilon \mathcal{N}_v)_{\Phi}\cdot \nabla_{\varepsilon}\Big(\frac{\langle D_x\rangle^2\omega_{\Phi}}{\partial_y\omega^p}\Big)dxdy\\ \leq &\ C\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}(\|\omega\|_{X^2}+\|\nabla_{\varepsilon}\omega\|_{X^2}). \end{align*} $$
However, using the Hölder inequality, we get
Collecting
![]() $T^0-T^{10}$
together, we finally obtain
$T^0-T^{10}$
together, we finally obtain
 $$ \begin{align*} \int_0^t|T^0|+\cdots+|T^{10}|ds\leq &\ C\int_0^t\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}(\|\nabla_{\varepsilon}\omega\|_{X^2}+\|\omega\|_{X^2})\\ &+\|\omega\|_{X^{\frac73}}(\|\omega\|_{X^{\frac73}}+\|\nabla_{\varepsilon}\omega\|_{X^2}+\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}})ds\\ \leq &\frac1{10}\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^2}^2ds+C\int_0^t\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}^2ds\\ &+(C+\frac{\lambda}{4})\int_0^t\|\omega\|_{X^{\frac73}}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}}^2 ds. \end{align*} $$
$$ \begin{align*} \int_0^t|T^0|+\cdots+|T^{10}|ds\leq &\ C\int_0^t\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}(\|\nabla_{\varepsilon}\omega\|_{X^2}+\|\omega\|_{X^2})\\ &+\|\omega\|_{X^{\frac73}}(\|\omega\|_{X^{\frac73}}+\|\nabla_{\varepsilon}\omega\|_{X^2}+\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}})ds\\ \leq &\frac1{10}\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^2}^2ds+C\int_0^t\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}^2ds\\ &+(C+\frac{\lambda}{4})\int_0^t\|\omega\|_{X^{\frac73}}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}}^2 ds. \end{align*} $$
Taking
![]() $\lambda $
large enough, we deduce
$\lambda $
large enough, we deduce
 $$ \begin{align} &\|\omega(t)\|_{X^{2}}^2+\lambda\int_0^t \|\omega\|_{X^{\frac73}}^2ds+\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\\\leq &\ C\int_0^t(\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}}^2 ds. \nonumber \end{align} $$
$$ \begin{align} &\|\omega(t)\|_{X^{2}}^2+\lambda\int_0^t \|\omega\|_{X^{\frac73}}^2ds+\int_0^t\|\nabla_{\varepsilon}\omega\|_{X^{2}}^2ds\\\leq &\ C\int_0^t(\|\mathcal{N}_u,\varepsilon \mathcal{N}_v\|_{X^2}^2ds+\frac{C}{\lambda}\int_0^t\|\varepsilon^2 f_1+f_2-C(t)\partial_x\omega^p\|_{X^{\frac53}}^2 ds. \nonumber \end{align} $$
However, (7.5) gives
Calderon-Zygmund inequality and Gagliardo-Nirenberg inequality (4.9) imply
8 Construction of the boundary corrector: Proof of Proposition 6.2
In the previous section, we construct a solution to the Orr-Sommerfeld equation with artificial boundary conditions: we replace condition
![]() $\partial _y\phi |_{y=0,1}=0$
by
$\partial _y\phi |_{y=0,1}=0$
by
![]() $\Delta _{\varepsilon }\phi |_{y=0,1}=0.$
To go back to the original system, we need to correct Neumann’s condition. Thus, we define
$\Delta _{\varepsilon }\phi |_{y=0,1}=0.$
To go back to the original system, we need to correct Neumann’s condition. Thus, we define
![]() $\phi _{bc}$
which satisfies the following system:
$\phi _{bc}$
which satisfies the following system:
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p -\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t),\\ &\phi|_{t=0}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p -\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0,1}=- \partial_y\phi_{slip}|_{y=0,1}+C(t),\\ &\phi|_{t=0}=0, \end{aligned} \right. \end{align} $$
To estimate
![]() $\phi _{bc}$
, we use the following decomposition:
$\phi _{bc}$
, we use the following decomposition:
The definitions and estimates of
![]() $\phi _{bc, S}, \phi _{bc, T}$
and
$\phi _{bc, S}, \phi _{bc, T}$
and
![]() $\phi _{bc, R}$
are given in the following subsections.
$\phi _{bc, R}$
are given in the following subsections.
8.1 The estimates of
 $\phi _{bc, S}$
: Stokes equation
$\phi _{bc, S}$
: Stokes equation
In this subsection, we deal with
![]() $\phi _{bc, S}$
.
$\phi _{bc, S}$
.
Because of two boundaries
![]() $y=0$
and
$y=0$
and
![]() $y=1$
, we define
$y=1$
, we define
where
![]() $\phi ^0_{bc, S}$
satisfies the following Stokes equation:
$\phi ^0_{bc, S}$
satisfies the following Stokes equation:
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^0_{bc, S}=0,\quad (x, y)\in \mathbb{T}\times (0,+\infty)\\ &\phi^0_{bc, S}|_{y=0}=0,\quad \partial_y\phi^0_{bc, S}|_{y=0}=h^0,\\ &\phi^0_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^0_{bc, S}=0,\quad (x, y)\in \mathbb{T}\times (0,+\infty)\\ &\phi^0_{bc, S}|_{y=0}=0,\quad \partial_y\phi^0_{bc, S}|_{y=0}=h^0,\\ &\phi^0_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
and
![]() $\phi ^1_{bc, S}$
satisfies the following Stokes equation:
$\phi ^1_{bc, S}$
satisfies the following Stokes equation:
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^1_{bc, S}=0,\quad (x, y)\in \mathbb{T}\times (-\infty,1)\\ &\phi^1_{bc, S}|_{y=1}=0,\quad \partial_y\phi^1_{bc, S}|_{y=1}=h^1,\\ &\phi^1_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t -\Delta_{\varepsilon})\Delta_{\varepsilon}\phi^1_{bc, S}=0,\quad (x, y)\in \mathbb{T}\times (-\infty,1)\\ &\phi^1_{bc, S}|_{y=1}=0,\quad \partial_y\phi^1_{bc, S}|_{y=1}=h^1,\\ &\phi^1_{bc, S}|_{t=0}=0, \end{aligned} \right. \end{align} $$
where
![]() $t\in [0,T]$
. Here,
$t\in [0,T]$
. Here,
![]() $(h^0,h^1)$
is a given boundary data satisfying
$(h^0,h^1)$
is a given boundary data satisfying
![]() $(h^0(t), h^1(t))=0$
for
$(h^0(t), h^1(t))=0$
for
![]() $t=0$
and
$t=0$
and
![]() $t\geq T.$
Here, we point out that
$t\geq T.$
Here, we point out that
![]() $h^i$
is defined by
$h^i$
is defined by
where the operator
![]() $\mathcal {A}$
is a zero-order operator which is defined later.
$\mathcal {A}$
is a zero-order operator which is defined later.
In the following, we only give the process for
![]() $\phi ^0_{bc, S}.$
The case of
$\phi ^0_{bc, S}.$
The case of
![]() $\phi ^1_{bc, S}$
is almost the same and we leave details to readers.
$\phi ^1_{bc, S}$
is almost the same and we leave details to readers.
At first, we give zero extension of
![]() $\phi ^0_{bc, S}$
and
$\phi ^0_{bc, S}$
and
![]() $h^0$
with
$h^0$
with
![]() $t\leq 0$
such that we can take a Fourier transform in
$t\leq 0$
such that we can take a Fourier transform in
![]() $t.$
Let
$t.$
Let
![]() $\widehat {\phi ^0_{bc, S}}=\widehat {\phi ^0_{bc, S}}(\zeta , k, y)$
be the Fourier transform of
$\widehat {\phi ^0_{bc, S}}=\widehat {\phi ^0_{bc, S}}(\zeta , k, y)$
be the Fourier transform of
![]() $\phi ^0_{bc, S}$
on x and t. Then
$\phi ^0_{bc, S}$
on x and t. Then
![]() $\widehat {(\phi ^0_{bc, S})_{\Phi }}$
satisfies the ODE:
$\widehat {(\phi ^0_{bc, S})_{\Phi }}$
satisfies the ODE:
 $$ \begin{align} \left\{ \begin{aligned} &-(\partial_y^2-\varepsilon^2|k|^2)^2\widehat{(\phi^0_{bc, S})_{\Phi}}+(i\zeta+\lambda{\langle k\rangle}^{\frac23})(\partial_y^2-\varepsilon^2|k|^2)\widehat{(\phi^0_{bc, S})_{\Phi}}=0,\quad y>0,\\ &\widehat{(\phi^0_{bc, S})_{\Phi}}|_{y=0}=0,\quad \partial_y\widehat{(\phi^0_{bc, S})_{\Phi}}|_{y=0}=\widehat{h^0_{\Phi}}, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &-(\partial_y^2-\varepsilon^2|k|^2)^2\widehat{(\phi^0_{bc, S})_{\Phi}}+(i\zeta+\lambda{\langle k\rangle}^{\frac23})(\partial_y^2-\varepsilon^2|k|^2)\widehat{(\phi^0_{bc, S})_{\Phi}}=0,\quad y>0,\\ &\widehat{(\phi^0_{bc, S})_{\Phi}}|_{y=0}=0,\quad \partial_y\widehat{(\phi^0_{bc, S})_{\Phi}}|_{y=0}=\widehat{h^0_{\Phi}}, \end{aligned} \right. \end{align} $$
where
![]() $\zeta \in \mathbb {R}$
and
$\zeta \in \mathbb {R}$
and
![]() $k\in \mathbb {Z}.$
Assuming the decay of
$k\in \mathbb {Z}.$
Assuming the decay of
![]() $(|k|\phi ^0_{bc, S},\partial _y\phi ^0_{bc, S})$
and the boundedness of
$(|k|\phi ^0_{bc, S},\partial _y\phi ^0_{bc, S})$
and the boundedness of
![]() $\partial _y\phi ^0_{bc, S},$
we obtain the formula
$\partial _y\phi ^0_{bc, S},$
we obtain the formula
 $$ \begin{align} \widehat{(\phi^0_{bc, S})_{\Phi}}(\zeta, k, y)=&\ -\frac{e^{-\gamma y}-e^{-\varepsilon |k|y}}{\gamma-\varepsilon|k|}\widehat{h^0_{\Phi}}(\zeta, k),\quad y>0 \end{align} $$
$$ \begin{align} \widehat{(\phi^0_{bc, S})_{\Phi}}(\zeta, k, y)=&\ -\frac{e^{-\gamma y}-e^{-\varepsilon |k|y}}{\gamma-\varepsilon|k|}\widehat{h^0_{\Phi}}(\zeta, k),\quad y>0 \end{align} $$
where the square root is taken so that the real part is positive, and it follows that
This inequality will be used frequently. It is easy to calculate that
The formula (8.8) will be used in estimating velocity and (8.9) will be used in estimating vorticity. With the same process above, we get the formula for
![]() $\widehat {(\phi ^1_{bc, S})_{\Phi }}:$
$\widehat {(\phi ^1_{bc, S})_{\Phi }}:$
 $$ \begin{align} \widehat{(\phi^1_{bc, S})_{\Phi}}(\zeta, k, y)=\frac{e^{-\gamma(1-y)}-e^{-\varepsilon |k|(1-y)}}{\gamma-\varepsilon |k|}\widehat{h^1_{\Phi}}(\zeta,k),\quad y<1, \end{align} $$
$$ \begin{align} \widehat{(\phi^1_{bc, S})_{\Phi}}(\zeta, k, y)=\frac{e^{-\gamma(1-y)}-e^{-\varepsilon |k|(1-y)}}{\gamma-\varepsilon |k|}\widehat{h^1_{\Phi}}(\zeta,k),\quad y<1, \end{align} $$
with
![]() $\gamma $
given in (8.6). It is easy to see
$\gamma $
given in (8.6). It is easy to see
Remark 8.1. For
![]() $\varepsilon =0$
in (8.2),
$\varepsilon =0$
in (8.2),
![]() $\triangle _0=\partial _y^2.$
$\triangle _0=\partial _y^2.$
 $$ \begin{align} \widehat{(\phi^0_{bc, S})_{\Phi}}(\zeta, k, y)=-\frac{\widehat{h^0_{\Phi}}}{\gamma_0}(e^{-\gamma_0 y}-1),\quad \gamma_0=\sqrt{\lambda{\langle k\rangle}^{\frac{2}{3}} + i\zeta} \end{align} $$
$$ \begin{align} \widehat{(\phi^0_{bc, S})_{\Phi}}(\zeta, k, y)=-\frac{\widehat{h^0_{\Phi}}}{\gamma_0}(e^{-\gamma_0 y}-1),\quad \gamma_0=\sqrt{\lambda{\langle k\rangle}^{\frac{2}{3}} + i\zeta} \end{align} $$
solves (8.4) with
![]() $\varepsilon =0$
and
$\varepsilon =0$
and
![]() $\widehat {(\phi ^0_{bc, S})_{\Phi }}$
holds
$\widehat {(\phi ^0_{bc, S})_{\Phi }}$
holds
![]() $\lim _{y\to +\infty }=\frac {\widehat {h^0_{\Phi }}}{\gamma _0}.$
Though
$\lim _{y\to +\infty }=\frac {\widehat {h^0_{\Phi }}}{\gamma _0}.$
Though
![]() $\widehat {(\phi ^0_{bc, S})_{\Phi }}$
does not tend to zero as y tends to infinity, the solution
$\widehat {(\phi ^0_{bc, S})_{\Phi }}$
does not tend to zero as y tends to infinity, the solution
![]() $\widehat {(\phi ^0_{bc, S})_{\Phi }}$
is only used to correct the boundary condition near
$\widehat {(\phi ^0_{bc, S})_{\Phi }}$
is only used to correct the boundary condition near
![]() $y=0$
, and we do not care about its value at infinity. It is easy to deduce
$y=0$
, and we do not care about its value at infinity. It is easy to deduce
and we find these two terms decay to zero as y tends to infinity. By the same method, we can get another solution near
![]() $y=1:$
$y=1:$
 $$ \begin{align} \widehat{(\phi^1_{bc, S})_{\Phi}}(\zeta, k, y)=\frac{\widehat{h^0_{\Phi}}}{\gamma_0}(e^{-\gamma_0 (1-y)}-1). \end{align} $$
$$ \begin{align} \widehat{(\phi^1_{bc, S})_{\Phi}}(\zeta, k, y)=\frac{\widehat{h^0_{\Phi}}}{\gamma_0}(e^{-\gamma_0 (1-y)}-1). \end{align} $$
These constructions are the main difference between
![]() $\varepsilon =0$
and
$\varepsilon =0$
and
![]() $\varepsilon \neq 0,$
but they enjoy the same properties stated below.
$\varepsilon \neq 0,$
but they enjoy the same properties stated below.
Lemma 8.2. Let
![]() $\phi ^i_{bc,S}$
be the solution of (8.2). It holds that
$\phi ^i_{bc,S}$
be the solution of (8.2). It holds that
 $$ \begin{align} \sum_{k\in\mathbb{Z}}\|(\varepsilon|k|\widehat{(\phi^i_{bc, S})_{\Phi}},\partial_y\widehat{(\phi^i_{bc, S})_{\Phi}})\|_{L^2_{\zeta,y}} \leq & \frac{C}{\lambda^{\frac14}}\sum_{k\in\mathbb{Z}}\|{\langle k\rangle}^{-\frac16}\widehat{h^i_{\Phi}}\|_{L^2_{\zeta}} , \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}}\|(\varepsilon|k|\widehat{(\phi^i_{bc, S})_{\Phi}},\partial_y\widehat{(\phi^i_{bc, S})_{\Phi}})\|_{L^2_{\zeta,y}} \leq & \frac{C}{\lambda^{\frac14}}\sum_{k\in\mathbb{Z}}\|{\langle k\rangle}^{-\frac16}\widehat{h^i_{\Phi}}\|_{L^2_{\zeta}} , \end{align} $$
where
![]() $i=0,1$
and
$i=0,1$
and
![]() $L^2_{\zeta , y}=l^2_{\zeta }(L^2_{y}(0,+\infty ))$
for
$L^2_{\zeta , y}=l^2_{\zeta }(L^2_{y}(0,+\infty ))$
for
![]() $i=0$
and
$i=0$
and
![]() $L^2_{\zeta , y}=l^2_{\zeta }(L^2_y(-\infty ,1))$
for
$L^2_{\zeta , y}=l^2_{\zeta }(L^2_y(-\infty ,1))$
for
![]() $i=1.$
$i=1.$
It is also held that
 $$ \begin{align} \sum_{k\in\mathbb{Z}}\|k\widehat{(\phi^i_{bc, S})_{\Phi}}\|_{L^2_{\zeta,y}} \leq & \frac{C}{\lambda^{\frac12}}\|k{\langle k\rangle}^{-\frac13} \widehat{h^i_{\Phi}}\|_{L^2_{\zeta}} , \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}}\|k\widehat{(\phi^i_{bc, S})_{\Phi}}\|_{L^2_{\zeta,y}} \leq & \frac{C}{\lambda^{\frac12}}\|k{\langle k\rangle}^{-\frac13} \widehat{h^i_{\Phi}}\|_{L^2_{\zeta}} , \end{align} $$
where
![]() $i=0,1$
and
$i=0,1$
and
![]() $L^2_{\zeta , y}=l^2_{\zeta }(L^2_{y}(0,1)).$
$L^2_{\zeta , y}=l^2_{\zeta }(L^2_{y}(0,1)).$
Proof. We only give the proof for
![]() $i=0.$
The case
$i=0.$
The case
![]() $i=1$
is almost the same, and we omit details to readers.
$i=1$
is almost the same, and we omit details to readers.
(8.16) follows from (8.5), (8.8) and the Plancherel theorem by observing the estimate for multipliers
 $$ \begin{align} \qquad\qquad\quad\ \qquad\qquad\|e^{-{\mathbf{Re}}(\gamma)y}\|_{L^2_{y}(0,\infty)}\leq & \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}, \end{align} $$
$$ \begin{align} \qquad\qquad\quad\ \qquad\qquad\|e^{-{\mathbf{Re}}(\gamma)y}\|_{L^2_{y}(0,\infty)}\leq & \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}, \end{align} $$
 $$ \begin{align} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align} $$
$$ \begin{align} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align} $$
The estimate (8.18) is a direct consequence of
 $$ \begin{align} {\mathbf{Re}}(\gamma)\geq \frac{1}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align} $$
$$ \begin{align} {\mathbf{Re}}(\gamma)\geq \frac{1}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align} $$
For (8.19), we divide it into two cases: 1.
![]() $\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
, and 2.
$\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
, and 2.
![]() $\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}.$
In case 1,
$\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}.$
In case 1,
 $$ \begin{align*} \Big|\gamma-\varepsilon|k|\Big|\geq \frac{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}{C}, \end{align*} $$
$$ \begin{align*} \Big|\gamma-\varepsilon|k|\Big|\geq \frac{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}{C}, \end{align*} $$
which implies
 $$ \begin{align*} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot|\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\frac{C}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\|\varepsilon|k|e^{-\varepsilon|k|y}\|_{L^2_y(0,+\infty)}\\ \leq &\ C\frac{(\varepsilon|k|)^{\frac12}}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\leq \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align*} $$
$$ \begin{align*} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot|\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\frac{C}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\|\varepsilon|k|e^{-\varepsilon|k|y}\|_{L^2_y(0,+\infty)}\\ \leq &\ C\frac{(\varepsilon|k|)^{\frac12}}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\leq \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align*} $$
In case 2, we use the bound
for
![]() ${\mathbf {Re}}(z)>0,$
which implies that
${\mathbf {Re}}(z)>0,$
which implies that
 $$ \begin{align*} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\|y\varepsilon|k|e^{-\varepsilon|k|y}\|_{L^2_y(0,+\infty)}\leq \frac{C}{(\varepsilon|k|)^{\frac12}}\leq \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align*} $$
$$ \begin{align*} \|\varepsilon|k|\cdot e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,+\infty)}\leq &\|y\varepsilon|k|e^{-\varepsilon|k|y}\|_{L^2_y(0,+\infty)}\leq \frac{C}{(\varepsilon|k|)^{\frac12}}\leq \frac{C}{\lambda^{\frac14}{\langle k\rangle}^{\frac16}}. \end{align*} $$
Combining cases 1–2, we complete (8.19), which yields (8.16). The estimate (8.17) is proved by using (8.5), Placherel theorem and
 $$ \begin{align} \|e^{-\varepsilon|k|y}\cdot|\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq &\frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align} $$
$$ \begin{align} \|e^{-\varepsilon|k|y}\cdot|\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq &\frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align} $$
Indeed, note that the integral interval is
![]() $y\in (0,1)$
and we also divide it into
$y\in (0,1)$
and we also divide it into
![]() $\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
and
$\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
and
![]() $\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}.$
When
$\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}.$
When
![]() $\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13},$
the similar argument above gives that
$\varepsilon |k|\geq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13},$
the similar argument above gives that
 $$ \begin{align} \|e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq \frac{C}{\lambda^{\frac34}{\langle k\rangle}^{\frac12}}. \end{align} $$
$$ \begin{align} \|e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq \frac{C}{\lambda^{\frac34}{\langle k\rangle}^{\frac12}}. \end{align} $$
When
![]() $\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
( with
$\varepsilon |k|\leq \frac 12\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}$
( with
![]() $\varepsilon |k|\ll 1$
), we compute as
$\varepsilon |k|\ll 1$
), we compute as
 $$ \begin{align*} \|e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq C\|\frac{1}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\|_{L^2_y(0,1)}\leq \frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align*} $$
$$ \begin{align*} \|e^{-\varepsilon|k|y}\cdot |\frac{1-e^{-(\gamma-\varepsilon|k|)y}}{\gamma-\varepsilon|k|}|\|_{L^2_y(0,1)}\leq C\|\frac{1}{\varepsilon|k|+\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\|_{L^2_y(0,1)}\leq \frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}. \end{align*} $$
The finite interval
![]() $(0,1)$
is essential here. Thus, we complete this lemma.
$(0,1)$
is essential here. Thus, we complete this lemma.
To express this clearly, we introduce norms related to
![]() $y>0$
and
$y>0$
and
![]() $y<1$
, respectively. For any function f, we define
$y<1$
, respectively. For any function f, we define
where
![]() $I_0=(0,+\infty )$
and
$I_0=(0,+\infty )$
and
![]() $I_1=(-\infty ,1).$
It is obvious to see
$I_1=(-\infty ,1).$
It is obvious to see
![]() $\|\cdot \|_{X^r}\leq \|\cdot \|_{X^r_i}$
for any
$\|\cdot \|_{X^r}\leq \|\cdot \|_{X^r_i}$
for any
![]() $i=0,1.$
Using Lemma 8.2 above, we can deduce the estimate for
$i=0,1.$
Using Lemma 8.2 above, we can deduce the estimate for
![]() $\nabla _{\varepsilon }\phi ^i,$
where
$\nabla _{\varepsilon }\phi ^i,$
where
![]() $i=0,1.$
$i=0,1.$
Proposition 8.3. Let
![]() $\phi ^i_{bc,S}$
be the solution of (8.2). It holds that
$\phi ^i_{bc,S}$
be the solution of (8.2). It holds that
 $$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
$$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
 $$ \begin{align} \int_0^t\|\partial_x\phi^i_{bc,S}\|_{X^{\frac{5}{3}}}^2ds\leq \frac{C}{\lambda}\int_0^t|\partial_x h^i|_{X^{\frac43}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\|\partial_x\phi^i_{bc,S}\|_{X^{\frac{5}{3}}}^2ds\leq \frac{C}{\lambda}\int_0^t|\partial_x h^i|_{X^{\frac43}}^2ds. \end{align} $$
Next, we give the estimate to the boundary term
![]() $\phi ^0_{bc,S}|_{y=1}$
and
$\phi ^0_{bc,S}|_{y=1}$
and
![]() $\phi ^1_{bc,S}|_{y=0.}$
$\phi ^1_{bc,S}|_{y=0.}$
Lemma 8.4. For any
![]() $M\geq 0$
and
$M\geq 0$
and
![]() $i=0,1,$
it holds that
$i=0,1,$
it holds that
 $$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\phi^i_{bc,S}|_{y=1-i}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{r}}^2ds, \end{align} $$
$$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\phi^i_{bc,S}|_{y=1-i}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{r}}^2ds, \end{align} $$
and
 $$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\partial_y\phi^i_{bc,S}|_{y=1-i}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{r}}^2ds, \end{align} $$
$$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\partial_y\phi^i_{bc,S}|_{y=1-i}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{r}}^2ds, \end{align} $$
for any
![]() $r\geq 0.$
$r\geq 0.$
Proof. We only give the proof for the case
![]() $i=0$
; the case
$i=0$
; the case
![]() $i=1$
is similar and we omit details to readers. Taking
$i=1$
is similar and we omit details to readers. Taking
![]() $y=1$
in (8.5) and using
$y=1$
in (8.5) and using
 $$ \begin{align} \Big|(\varepsilon|k|)^M \cdot e^{-\varepsilon|k|} \cdot \frac{e^{-(\gamma-\varepsilon|k|)}-1}{\gamma-\varepsilon|k|}\Big|\leq \frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}, \end{align} $$
$$ \begin{align} \Big|(\varepsilon|k|)^M \cdot e^{-\varepsilon|k|} \cdot \frac{e^{-(\gamma-\varepsilon|k|)}-1}{\gamma-\varepsilon|k|}\Big|\leq \frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}}, \end{align} $$
we get
 $$ \begin{align*} \int_0^t|(\varepsilon|k|)^M\phi^0_{bc,S}|_{y=1}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^0|_{X^{r}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t|(\varepsilon|k|)^M\phi^0_{bc,S}|_{y=1}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^0|_{X^{r}}^2ds. \end{align*} $$
However, we refer to (8.8) and take
![]() $y=1$
in it by noticing
$y=1$
in it by noticing
 $$ \begin{align*} \Big|e^{-{\mathbf{Re}}(\gamma)}(\varepsilon|k|)^M\Big|\leq &\Big|e^{-\frac12\varepsilon|k|}(\varepsilon|k|)^Me^{-\frac12\lambda^{\frac12}{\langle k\rangle}^{\frac16}}\Big|\leq Ce^{-\frac12\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\leq \frac{C}{(\lambda{\langle k\rangle}^{\frac23})^{N/2}}, \end{align*} $$
$$ \begin{align*} \Big|e^{-{\mathbf{Re}}(\gamma)}(\varepsilon|k|)^M\Big|\leq &\Big|e^{-\frac12\varepsilon|k|}(\varepsilon|k|)^Me^{-\frac12\lambda^{\frac12}{\langle k\rangle}^{\frac16}}\Big|\leq Ce^{-\frac12\lambda^{\frac12}{\langle k\rangle}^{\frac13}}\leq \frac{C}{(\lambda{\langle k\rangle}^{\frac23})^{N/2}}, \end{align*} $$
for any
![]() $N\geq 0$
, and combining with (8.28) to deduce
$N\geq 0$
, and combining with (8.28) to deduce
 $$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\partial_y\phi^0_{bc,S}|_{y=1}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^0|_{X^{r}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t|(\varepsilon\partial_x)^M\partial_y\phi^0_{bc,S}|_{y=1}|_{X^{r+\frac13}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^0|_{X^{r}}^2ds. \end{align} $$
Thus, we finish our proof.
At the end of this subsection, we give some weight estimates of vorticity
![]() $\omega ^i_{bc,S}=\Delta _{\varepsilon }\phi ^i_{bc,S}$
. Denote
$\omega ^i_{bc,S}=\Delta _{\varepsilon }\phi ^i_{bc,S}$
. Denote
Proposition 8.5. It holds that
As a consequence, we get for
![]() $\theta '\in [-\frac 12,2]$
$\theta '\in [-\frac 12,2]$
 $$ \begin{align*} \int_0^t \|(\varphi^i)^{1+\theta'} \omega^i_{bc,S}\|_{X^{\frac73+\frac13(\theta'+\frac12)}_i}^2+\|(\varphi^i)^{2+\theta'}(\partial_y,\varepsilon|k|)\omega^i_{bc,S}\|_{X^{\frac73+\frac13(\theta'+\frac12)}_i}^2ds\leq \frac{C}{\lambda^{\frac12+\theta'}}\int_0^t |h^i|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \|(\varphi^i)^{1+\theta'} \omega^i_{bc,S}\|_{X^{\frac73+\frac13(\theta'+\frac12)}_i}^2+\|(\varphi^i)^{2+\theta'}(\partial_y,\varepsilon|k|)\omega^i_{bc,S}\|_{X^{\frac73+\frac13(\theta'+\frac12)}_i}^2ds\leq \frac{C}{\lambda^{\frac12+\theta'}}\int_0^t |h^i|_{X^{\frac73}}^2ds. \end{align*} $$
Proof. The result is obtained by using formula (8.6), (8.9) and (8.12), the Plancherel theorem and by observing that multiplier
![]() $\varphi ^i(y)$
gains
$\varphi ^i(y)$
gains
![]() $\frac {1}{\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}}$
. More precisely,
$\frac {1}{\lambda ^{\frac 12}{\langle k\rangle }^{\frac 13}}$
. More precisely,
 $$ \begin{align*} \|(\varphi^i)^{1+m}|\gamma|e^{-{\mathbf{Re}}(\gamma)\varphi^i}\|_{L^2_y(I_i)}\leq (\frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}})^{m+\frac12}. \end{align*} $$
$$ \begin{align*} \|(\varphi^i)^{1+m}|\gamma|e^{-{\mathbf{Re}}(\gamma)\varphi^i}\|_{L^2_y(I_i)}\leq (\frac{C}{\lambda^{\frac12}{\langle k\rangle}^{\frac13}})^{m+\frac12}. \end{align*} $$
Thus, we complete the proof.
Based on the above proposition, we have more estimates on
![]() $\omega ^i_{bc,S}$
:
$\omega ^i_{bc,S}$
:
Proposition 8.6. Let
![]() $\theta \in [0,2].$
It holds that
$\theta \in [0,2].$
It holds that
 $$ \begin{align} &\int_0^t\|\varphi^i\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2+ \|(\varphi^i)^2\partial_y\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
$$ \begin{align} &\int_0^t\|\varphi^i\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2+ \|(\varphi^i)^2\partial_y\Delta_{\varepsilon}\phi^i_{bc,S}\|_{X^{\frac73+\frac16}_i}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
 $$ \begin{align} &\int_0^t\|\langle D_x\rangle^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}(\partial_x\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^2_i}^2ds\leq \frac{C}{\lambda^{\theta+1}} \int_0^t|h^i|_{X^{\frac73}}^2ds,\qquad\qquad\!\!\!\!\! \end{align} $$
$$ \begin{align} &\int_0^t\|\langle D_x\rangle^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}(\partial_x\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^2_i}^2ds\leq \frac{C}{\lambda^{\theta+1}} \int_0^t|h^i|_{X^{\frac73}}^2ds,\qquad\qquad\!\!\!\!\! \end{align} $$
 $$ \begin{align} &\int_0^t\|\langle D_x\rangle^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}(\partial_y\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^2_i}^2ds\leq \frac{C}{\lambda^{\theta}}\int_0^t|h^i|_{X^{\frac53}}^2ds.\qquad\qquad \end{align} $$
$$ \begin{align} &\int_0^t\|\langle D_x\rangle^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}(\partial_y\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^2_i}^2ds\leq \frac{C}{\lambda^{\theta}}\int_0^t|h^i|_{X^{\frac53}}^2ds.\qquad\qquad \end{align} $$
Proof. (8.32) is a direct result of Lemma 8.5 by taking
![]() $\theta =0.$
It is easy to check
$\theta =0.$
It is easy to check
 $$ \begin{align*} \|{\langle k\rangle}^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}k\widehat{\Delta_{\varepsilon}(\phi^i_{bc,S})_{\Phi}}\|_{L^2_y(I_i)}\leq C\frac{{\langle k\rangle}^{\frac23+\frac{\theta}{3}}}{(\lambda^{\frac12}{\langle k\rangle}^{\frac13})^{\theta+\frac12+\frac12}}|\widehat{h^i_{\Phi}}|=\frac{C{\langle k\rangle}^{\frac13}}{\lambda^{\frac12(\theta+1)}}|\widehat{h^i_{\Phi}}| \end{align*} $$
$$ \begin{align*} \|{\langle k\rangle}^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}k\widehat{\Delta_{\varepsilon}(\phi^i_{bc,S})_{\Phi}}\|_{L^2_y(I_i)}\leq C\frac{{\langle k\rangle}^{\frac23+\frac{\theta}{3}}}{(\lambda^{\frac12}{\langle k\rangle}^{\frac13})^{\theta+\frac12+\frac12}}|\widehat{h^i_{\Phi}}|=\frac{C{\langle k\rangle}^{\frac13}}{\lambda^{\frac12(\theta+1)}}|\widehat{h^i_{\Phi}}| \end{align*} $$
by taking
![]() $\theta '=\theta +\frac 12$
in Lemma 8.5 and completing (8.33). Similarly, we check
$\theta '=\theta +\frac 12$
in Lemma 8.5 and completing (8.33). Similarly, we check
 $$ \begin{align*} \|{\langle k\rangle}^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}\partial_y\widehat{\Delta_{\varepsilon}(\phi^i_{bc,S})_{\Phi}}\|_{L^2_y(I_i)}\leq \frac{C{\langle k\rangle}^{\frac{\theta}{3}-\frac13}}{\lambda^{\frac{\theta}{2}}{\langle k\rangle}^{\frac{\theta}{3}}}|\widehat{h^i_{\Phi}}| \leq \frac{C}{\lambda^{\frac{\theta}{2}}{\langle k\rangle}^{\frac13}}|\widehat{h^i_{\Phi}}| \end{align*} $$
$$ \begin{align*} \|{\langle k\rangle}^{\frac{\theta}{3}-\frac13}(\varphi^i)^{\theta+\frac32}\partial_y\widehat{\Delta_{\varepsilon}(\phi^i_{bc,S})_{\Phi}}\|_{L^2_y(I_i)}\leq \frac{C{\langle k\rangle}^{\frac{\theta}{3}-\frac13}}{\lambda^{\frac{\theta}{2}}{\langle k\rangle}^{\frac{\theta}{3}}}|\widehat{h^i_{\Phi}}| \leq \frac{C}{\lambda^{\frac{\theta}{2}}{\langle k\rangle}^{\frac13}}|\widehat{h^i_{\Phi}}| \end{align*} $$
by taking
![]() $\theta '=\theta -\frac 12$
in Lemma 8.5 to completing (8.34).
$\theta '=\theta -\frac 12$
in Lemma 8.5 to completing (8.34).
8.2 The estimates of
 $\phi _{bc, T}$
: vorticity transport estimate
$\phi _{bc, T}$
: vorticity transport estimate
![]() $\phi _{bc, T}$
is defined by
$\phi _{bc, T}$
is defined by
where
![]() $\phi ^0_{bc, T}$
is defined by
$\phi ^0_{bc, T}$
is defined by

and
![]() $\phi ^1_{bc, T}$
is defined by
$\phi ^1_{bc, T}$
is defined by

We need to emphasize that we extend
![]() $(u^p, v^p)$
to
$(u^p, v^p)$
to
![]() $y\in \mathbb {R}$
by zero, which means that
$y\in \mathbb {R}$
by zero, which means that
![]() $(u^p, v^p)=0$
when
$(u^p, v^p)=0$
when
![]() $y\in \mathbb {R}\setminus [0,1].$
$y\in \mathbb {R}\setminus [0,1].$
Before we give the estimates of
![]() $\phi ^i_{bc, T}$
, we use Proposition 8.6 and
$\phi ^i_{bc, T}$
, we use Proposition 8.6 and
![]() $(u^p, v^p)|_{y=0,1}=0$
to get that
$(u^p, v^p)|_{y=0,1}=0$
to get that
 $$ \begin{align} \int_0^t\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2ds\leq &\ C\int_0^t\|(\varphi^i)^{\frac32+\theta}(\partial_x\Delta_{\varepsilon}\phi^i_{bc,S} +\partial_y\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2ds\\\leq &\ C\int_0^t|h^i|_{X^{\frac73}}^2ds, \nonumber \end{align} $$
$$ \begin{align} \int_0^t\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2ds\leq &\ C\int_0^t\|(\varphi^i)^{\frac32+\theta}(\partial_x\Delta_{\varepsilon}\phi^i_{bc,S} +\partial_y\Delta_{\varepsilon}\phi^i_{bc,S})\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2ds\\\leq &\ C\int_0^t|h^i|_{X^{\frac73}}^2ds, \nonumber \end{align} $$
where
![]() $\theta =0,1,2$
.
$\theta =0,1,2$
.
We are in the position to give the estimates of
![]() $\phi ^i_{bc,T}$
:
$\phi ^i_{bc,T}$
:
Proposition 8.7. Let
![]() $\theta =0,1,2$
and
$\theta =0,1,2$
and
![]() $i=0,1$
. There exists
$i=0,1$
. There exists
![]() $\lambda _0>1$
and
$\lambda _0>1$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
![]() $t\in [0,T]$
,
$t\in [0,T]$
,
![]() $\lambda \geq \lambda _0$
, it holds that
$\lambda \geq \lambda _0$
, it holds that
 $$ \begin{align*} &\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+\lambda\int_0^t\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2ds\\ &\qquad+\int_0^t\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2ds\leq \frac{C}{\lambda^{\frac12}} \int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} &\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+\lambda\int_0^t\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2ds\\ &\qquad+\int_0^t\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2ds\leq \frac{C}{\lambda^{\frac12}} \int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align*} $$
where
![]() $\Delta _{\varepsilon }\phi ^i_{bc,T}=\omega ^i_{bc,T}$
and
$\Delta _{\varepsilon }\phi ^i_{bc,T}=\omega ^i_{bc,T}$
and
![]() $\varphi ^i$
is given in (8.30).
$\varphi ^i$
is given in (8.30).
Proof. Acting
![]() $e^{\Phi (t,D_x)}$
on the first equation of (8.35), we obtain
$e^{\Phi (t,D_x)}$
on the first equation of (8.35), we obtain
 $$ \begin{align} (\partial_t+&\lambda\langle D_x\rangle^{\frac23} -\Delta_{\varepsilon})(\omega^i_{bc,T})_{\Phi}+u^p \partial_x(\omega^i_{bc,T})_{\Phi}+v^p\partial_y(\omega^i_{bc,T})_{\Phi}\\ &+\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)+\Big((v^p\partial_y\omega^i_{bc,T})_{\Phi}-v^p\partial_y(\omega^i_{bc,T})_{\Phi}\Big)=H^i_{\Phi}.\nonumber \end{align} $$
$$ \begin{align} (\partial_t+&\lambda\langle D_x\rangle^{\frac23} -\Delta_{\varepsilon})(\omega^i_{bc,T})_{\Phi}+u^p \partial_x(\omega^i_{bc,T})_{\Phi}+v^p\partial_y(\omega^i_{bc,T})_{\Phi}\\ &+\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)+\Big((v^p\partial_y\omega^i_{bc,T})_{\Phi}-v^p\partial_y(\omega^i_{bc,T})_{\Phi}\Big)=H^i_{\Phi}.\nonumber \end{align} $$
Then, taking the
![]() $L^2_y(I_i;H^{\frac {11}{6}+\frac {\theta }3}_x)$
inner product with
$L^2_y(I_i;H^{\frac {11}{6}+\frac {\theta }3}_x)$
inner product with
![]() $(\varphi ^i)^{2\theta }(\omega ^i_{bc,T})_{\Phi }$
, we get by using
$(\varphi ^i)^{2\theta }(\omega ^i_{bc,T})_{\Phi }$
, we get by using
![]() $\omega ^i_{bc,T}|_{y=i}=0,~\partial _xu^p+\partial _y v^p=0$
and integrating by parts that
$\omega ^i_{bc,T}|_{y=i}=0,~\partial _xu^p+\partial _y v^p=0$
and integrating by parts that
 $$ \begin{align*} \frac12\frac{d}{dt}&\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+\lambda\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\\ =&\ -\int_{\mathcal{S}_i}(\varphi^i)^{2\theta}[\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3},u^p\partial_x+v^p\partial_y](\omega^i_{bc,T})_{\Phi}~ \langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi} dxdy\\ &+\frac12\int_{\mathcal{S}_i}\partial_y \big((\varphi^i)^{2\theta}\big) v^p|\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}|^2dxdy\\ &-\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ &-\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\Big((v^p\partial_y\omega^i_{bc,T})_{\Phi}-v^p\partial_y(\omega^i_{bc,T})_{\Phi}\Big)~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ &-\int_{\mathcal{S}_i} \partial_y \big((\varphi^i)^{2\theta}\big) \langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\partial_y(\omega^i_{bc,T})_{\Phi}~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi} dxdy\\ &+\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}H^i_{\Phi}~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ =&\ I_1^i+\cdots+I_6^i, \end{align*} $$
$$ \begin{align*} \frac12\frac{d}{dt}&\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+\lambda\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\\ =&\ -\int_{\mathcal{S}_i}(\varphi^i)^{2\theta}[\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3},u^p\partial_x+v^p\partial_y](\omega^i_{bc,T})_{\Phi}~ \langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi} dxdy\\ &+\frac12\int_{\mathcal{S}_i}\partial_y \big((\varphi^i)^{2\theta}\big) v^p|\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}|^2dxdy\\ &-\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ &-\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\Big((v^p\partial_y\omega^i_{bc,T})_{\Phi}-v^p\partial_y(\omega^i_{bc,T})_{\Phi}\Big)~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ &-\int_{\mathcal{S}_i} \partial_y \big((\varphi^i)^{2\theta}\big) \langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}\partial_y(\omega^i_{bc,T})_{\Phi}~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi} dxdy\\ &+\int_{\mathcal{S}_i}\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}H^i_{\Phi}~\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{2\theta} dxdy\\ =&\ I_1^i+\cdots+I_6^i, \end{align*} $$
where
![]() $\mathcal {S}_i=\mathbb {T}\times I_i.$
Integrating on
$\mathcal {S}_i=\mathbb {T}\times I_i.$
Integrating on
![]() $[0,t)$
with
$[0,t)$
with
![]() $t\leq T$
, we obtain
$t\leq T$
, we obtain
 $$ \begin{align} \|(\varphi^i)^{\theta}\omega^i_{bc,T}(t)\|_{X^{\frac{11}{6}+ \frac{\theta}3}_i}^2+&2\lambda\int_0^t\|(\varphi^i)^{\theta} \omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2ds+2\int_0^t\|(\varphi^i)^{\theta} \nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2ds\\\leq &2\int_0^t|I_1^i|+\cdots+ |I_6^i| ds.\nonumber \end{align} $$
$$ \begin{align} \|(\varphi^i)^{\theta}\omega^i_{bc,T}(t)\|_{X^{\frac{11}{6}+ \frac{\theta}3}_i}^2+&2\lambda\int_0^t\|(\varphi^i)^{\theta} \omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2ds+2\int_0^t\|(\varphi^i)^{\theta} \nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2ds\\\leq &2\int_0^t|I_1^i|+\cdots+ |I_6^i| ds.\nonumber \end{align} $$
Now, we estimate
![]() $I_j^i,~j=1,\cdots ,6$
term by term.
$I_j^i,~j=1,\cdots ,6$
term by term.
![]() $\underline {\mathrm {Estimate \ of} \ I_1^i.}$
It follows from Lemma 2.1 that
$\underline {\mathrm {Estimate \ of} \ I_1^i.}$
It follows from Lemma 2.1 that
which deduces that
 $$ \begin{align*} |I_1^i|\leq &\ C(\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}+\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i})\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq &\frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+ C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
$$ \begin{align*} |I_1^i|\leq &\ C(\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}+\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i})\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq &\frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+ C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_2^i.}$
Thanks to
$\underline {\mathrm {Estimate \ of} \ I_2^i.}$
Thanks to
by using
![]() $v^p|_{y=i}=0,$
it is obvious to see
$v^p|_{y=i}=0,$
it is obvious to see
![]() $\underline {\mathrm {Estimate \ of} \ I_3^i.}$
Applying Lemma 2.3, we find
$\underline {\mathrm {Estimate \ of} \ I_3^i.}$
Applying Lemma 2.3, we find
 $$ \begin{align*} |I_3^i|\leq &\|(\varphi^i)^{\theta}\langle D_x\rangle^{\frac{9}{6}+\frac{\theta}3}\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)\|_{L^2_y(I_i; L^2_x)}\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}\\ \leq &\ C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
$$ \begin{align*} |I_3^i|\leq &\|(\varphi^i)^{\theta}\langle D_x\rangle^{\frac{9}{6}+\frac{\theta}3}\Big((u^p\partial_x\omega^i_{bc,T})_{\Phi}-u^p\partial_x(\omega^i_{bc,T})_{\Phi}\Big)\|_{L^2_y(I_i; L^2_x)}\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}\\ \leq &\ C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_4^i.}$
Applying Lemma 2.2, we get
$\underline {\mathrm {Estimate \ of} \ I_4^i.}$
Applying Lemma 2.2, we get
 $$ \begin{align*} |I_4^i|\leq &\ C\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq & \frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
$$ \begin{align*} |I_4^i|\leq &\ C\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq & \frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+C\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_5^i.}$
By the fact
$\underline {\mathrm {Estimate \ of} \ I_5^i.}$
By the fact
we have
 $$ \begin{align*} |I_5^i|\leq &\ C\theta\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq &\frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+C\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
$$ \begin{align*} |I_5^i|\leq &\ C\theta\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}\\ \leq &\frac1{10}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+C\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2. \end{align*} $$
![]() $\underline {\mathrm {Estimate \ of} \ I_6^i.}$
It follows from
$\underline {\mathrm {Estimate \ of} \ I_6^i.}$
It follows from
 $$ \begin{align*} &\|\langle D_x\rangle^{2+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta-\frac12}\|_{L^2_y(I_i; L^2_x)}\\&\quad\leq \|\langle D_x\rangle^{\frac{13}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\|\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta-1}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\\ &\quad\leq \|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^{\frac12}\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^{\frac12}, \end{align*} $$
$$ \begin{align*} &\|\langle D_x\rangle^{2+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta-\frac12}\|_{L^2_y(I_i; L^2_x)}\\&\quad\leq \|\langle D_x\rangle^{\frac{13}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\|\langle D_x\rangle^{\frac{11}{6}+\frac{\theta}3}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{\theta-1}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\\ &\quad\leq \|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^{\frac12}\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^{\frac12}, \end{align*} $$
for
![]() $\theta =1,2$
and
$\theta =1,2$
and
 $$ \begin{align*} \|\langle D_x\rangle^{2}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{-\frac12}\|_{L^2_y(I_i; L^2_x)}\leq &\|\langle D_x\rangle^{\frac{13}{6}}(\omega^i_{bc,T})_{\Phi}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\|\langle D_x\rangle^{\frac{11}{6}}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{-1}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\\ \leq &\ C\|\omega^i_{bc,T}\|_{X^{\frac{13}{6}}_i}^{\frac12} \|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^{\frac12}, \end{align*} $$
$$ \begin{align*} \|\langle D_x\rangle^{2}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{-\frac12}\|_{L^2_y(I_i; L^2_x)}\leq &\|\langle D_x\rangle^{\frac{13}{6}}(\omega^i_{bc,T})_{\Phi}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\|\langle D_x\rangle^{\frac{11}{6}}(\omega^i_{bc,T})_{\Phi}(\varphi^i)^{-1}\|_{L^2_y(I_i; L^2_x)}^{\frac12}\\ \leq &\ C\|\omega^i_{bc,T}\|_{X^{\frac{13}{6}}_i}^{\frac12} \|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^{\frac12}, \end{align*} $$
by using Hardy inequality for
![]() $\theta =0.$
Therefore, we get for
$\theta =0.$
Therefore, we get for
![]() $\theta =0,1,2$
that
$\theta =0,1,2$
that
 $$ \begin{align*} |I_6^i|\leq &\ C\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}\times \|(\varphi^i)^{\theta}\omega^i_{bc, T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^{\frac12} \times \left\{ \begin{aligned} \|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^{\frac12},\quad \theta=1,2,\\ \|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^{\frac12},\quad \theta=0, \end{aligned} \right. \\ \leq &\frac1{10}\|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^2+\frac{\lambda}{4}\Big(\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\frac{\theta^2} 2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\Big)+\frac{C}{\lambda^{\frac12}}\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2. \end{align*} $$
$$ \begin{align*} |I_6^i|\leq &\ C\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}\times \|(\varphi^i)^{\theta}\omega^i_{bc, T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^{\frac12} \times \left\{ \begin{aligned} \|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^{\frac12},\quad \theta=1,2,\\ \|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^{\frac12},\quad \theta=0, \end{aligned} \right. \\ \leq &\frac1{10}\|\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}}_i}^2+\frac{\lambda}{4}\Big(\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\frac{\theta^2} 2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\Big)+\frac{C}{\lambda^{\frac12}}\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2. \end{align*} $$
Putting
![]() $I_1^i-I_6^i$
together, we have
$I_1^i-I_6^i$
together, we have
 $$ \begin{align*} |I_1^i|+\cdots+|I_6^i|\leq &\frac1{2}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+(C+\frac{\lambda}{4})\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\frac{\lambda}{8}\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\\ &+\frac{C}{\lambda^{\frac12}}\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2. \end{align*} $$
$$ \begin{align*} |I_1^i|+\cdots+|I_6^i|\leq &\frac1{2}\|(\varphi^i)^{\theta}\partial_y\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2+(C+\frac{\lambda}{4})\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}_i}^2+\frac{\lambda}{8}\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}_i}^2\\ &+\frac{C}{\lambda^{\frac12}}\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}_i}^2. \end{align*} $$
Then we insert them into (8.39) and take
![]() $\lambda $
large enough to obtain
$\lambda $
large enough to obtain
 $$ \begin{align*} \|(\varphi^i)^{\theta}\omega^i_{bc,T}(t)\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2+&\frac32\lambda\int_0^t\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}}^2ds+\int_0^t\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}}^2+\frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac{7}{3}}}^2ds+\frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds, \end{align*} $$
$$ \begin{align*} \|(\varphi^i)^{\theta}\omega^i_{bc,T}(t)\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2+&\frac32\lambda\int_0^t\|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}}^2ds+\int_0^t\|(\varphi^i)^{\theta}\nabla_{\varepsilon}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t\|(\varphi^i)^{\frac12+\theta}H^i\|_{X^{\frac{5}{3}+\frac{\theta}{3}}}^2+\frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac{7}{3}}}^2ds+\frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds, \end{align*} $$
where we use (8.37) in the last step.
All we have left to do is to control the last term of the above inequality. For that, we rewrite it as follows:
 $$ \begin{align*} \frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds &\leq \frac{\lambda}{2} \sum_{\theta=1}^2\int_0^t \|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta-1}3}}^2ds\\ &=\frac{\lambda}{2} \sum_{\theta=0}^1\int_0^t \|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}}^2ds. \end{align*} $$
$$ \begin{align*} \frac{\lambda}{8}\int_0^t\theta^2\|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{11}{6}+\frac{\theta}3}}^2ds &\leq \frac{\lambda}{2} \sum_{\theta=1}^2\int_0^t \|(\varphi^i)^{\theta-1}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta-1}3}}^2ds\\ &=\frac{\lambda}{2} \sum_{\theta=0}^1\int_0^t \|(\varphi^i)^{\theta}\omega^i_{bc,T}\|_{X^{\frac{13}{6}+\frac{\theta}3}}^2ds. \end{align*} $$
Combing all the above estimates, we get the desired results.
Based on estimates of
![]() $\omega _{bc, T}^i$
, we use the elliptic equation to get the estimates of
$\omega _{bc, T}^i$
, we use the elliptic equation to get the estimates of
![]() $\phi ^i_{bc,T}$
.
$\phi ^i_{bc,T}$
.
Corollary 8.8. There exists
![]() $\lambda _0>1$
and
$\lambda _0>1$
and
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
such that for all
![]() $t\in [0,T]$
,
$t\in [0,T]$
,
![]() $\lambda \geq \lambda _0$
, it holds that
$\lambda \geq \lambda _0$
, it holds that
 $$ \begin{align} &\int_0^t\Big(\|\nabla_{\varepsilon}\phi^i_{bc,T}\|_{X^{\frac73+\frac16}}^2 + |\partial_y\phi^i_{bc,T}|_{y=0,1}|_{X^{\frac73}}^2 + \|\partial_x\phi^i_{bc,T}\|_{X^{\frac{5}{3}}}^2+|\phi^i_{bc,T}|_{y=1-i}|_{X^{\frac{8}{3}}}^2 \Big)ds\nonumber\\&\quad\leq \frac{C}{\lambda } \int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} &\int_0^t\Big(\|\nabla_{\varepsilon}\phi^i_{bc,T}\|_{X^{\frac73+\frac16}}^2 + |\partial_y\phi^i_{bc,T}|_{y=0,1}|_{X^{\frac73}}^2 + \|\partial_x\phi^i_{bc,T}\|_{X^{\frac{5}{3}}}^2+|\phi^i_{bc,T}|_{y=1-i}|_{X^{\frac{8}{3}}}^2 \Big)ds\nonumber\\&\quad\leq \frac{C}{\lambda } \int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
Proof. Here, we only give the proof of the case
![]() $i=0$
. The case
$i=0$
. The case
![]() $i=1$
is the same.
$i=1$
is the same.
We recall the elliptic equation
for
![]() $y>0$
. Then we take the
$y>0$
. Then we take the
![]() $X^{r}_0$
inner product with
$X^{r}_0$
inner product with
![]() $\phi ^0_{bc,T}$
and use the Hardy inequality to get
$\phi ^0_{bc,T}$
and use the Hardy inequality to get
 $$ \begin{align*} \|\nabla_{\varepsilon}\phi^0_{bc,T}\|_{X^{r}_0}^2\leq \|\varphi^0\omega^0_{bc,T}\|_{X^{r}_0}\|\frac{\phi^0_{bc,T}}{\varphi^0}\|_{X^{r}_0}\leq C\|\varphi^0\omega^0_{bc,T}\|_{X^{r}_0}\|\partial_y\phi^0_{bc,T}\|_{X^{r}_0}, \end{align*} $$
$$ \begin{align*} \|\nabla_{\varepsilon}\phi^0_{bc,T}\|_{X^{r}_0}^2\leq \|\varphi^0\omega^0_{bc,T}\|_{X^{r}_0}\|\frac{\phi^0_{bc,T}}{\varphi^0}\|_{X^{r}_0}\leq C\|\varphi^0\omega^0_{bc,T}\|_{X^{r}_0}\|\partial_y\phi^0_{bc,T}\|_{X^{r}_0}, \end{align*} $$
which implies
for
![]() $r\geq 0.$
By Proposition 8.7, we get
$r\geq 0.$
By Proposition 8.7, we get
 $$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi^0_{bc,T}\|_{X^{\frac52}_0}^2ds\leq &\int_0^t\|\varphi^0\omega^0_{bc,T}\|_{X^{\frac52}_0}^2ds\leq \frac{C}{\lambda^{\frac32}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi^0_{bc,T}\|_{X^{\frac52}_0}^2ds\leq &\int_0^t\|\varphi^0\omega^0_{bc,T}\|_{X^{\frac52}_0}^2ds\leq \frac{C}{\lambda^{\frac32}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align} $$
For the boundary term, using the interpolation inequality, we get
 $$ \begin{align*} |\partial_y\phi^0_{bc,T}|_{y=0,1}|_{X^{\frac73}}\leq &\ C\|\partial_y\phi^0_{bc,T}\|_{X^{\frac52}_0}^{\frac12}\|\partial_y^2\phi^0_{bc,T}\|_{X^{\frac{13}6}_0}^{\frac12}\\ \leq &\ C\|\varphi^0\omega^0_{bc,T}\|_{X^{\frac52}_0}^{\frac12}\|\omega^0_{bc,T}\|_{X^{\frac{13}6}_0}^{\frac12}, \end{align*} $$
$$ \begin{align*} |\partial_y\phi^0_{bc,T}|_{y=0,1}|_{X^{\frac73}}\leq &\ C\|\partial_y\phi^0_{bc,T}\|_{X^{\frac52}_0}^{\frac12}\|\partial_y^2\phi^0_{bc,T}\|_{X^{\frac{13}6}_0}^{\frac12}\\ \leq &\ C\|\varphi^0\omega^0_{bc,T}\|_{X^{\frac52}_0}^{\frac12}\|\omega^0_{bc,T}\|_{X^{\frac{13}6}_0}^{\frac12}, \end{align*} $$
where we use (8.43) and the Calderon-Zygmund inequality in the last step. Along with Proposition 8.7, we arrive at
 $$ \begin{align} \int_0^t|\partial_y\phi^i_{bc,T}|_{y=0,1}|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t|\partial_y\phi^i_{bc,T}|_{y=0,1}|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
Next, we deal with the term
![]() $\|\partial _x\phi ^0_{bc,T}\|_{X^{\frac {5}{3}}}$
. Taking the Fourier transform in x to (8.42), we write the solution
$\|\partial _x\phi ^0_{bc,T}\|_{X^{\frac {5}{3}}}$
. Taking the Fourier transform in x to (8.42), we write the solution
 $$ \begin{align} \widehat{\phi}^0_{bc,T}(k,y)=\int_0^y e^{-\varepsilon|k|(y-y')}\int_{y'}^{+\infty}e^{-\varepsilon|k|(y"-y')}\widehat{\omega}^0_{bc,T}(k, y")d y" dy'. \end{align} $$
$$ \begin{align} \widehat{\phi}^0_{bc,T}(k,y)=\int_0^y e^{-\varepsilon|k|(y-y')}\int_{y'}^{+\infty}e^{-\varepsilon|k|(y"-y')}\widehat{\omega}^0_{bc,T}(k, y")d y" dy'. \end{align} $$
Then we have
 $$ \begin{align*} |\widehat{\phi}^0_{bc,T}(k,y)|\leq &\int_0^y\int_{y'}^{+\infty}|\widehat{\omega}^0_{bc,T}(k, y")|d y" dy'. \end{align*} $$
$$ \begin{align*} |\widehat{\phi}^0_{bc,T}(k,y)|\leq &\int_0^y\int_{y'}^{+\infty}|\widehat{\omega}^0_{bc,T}(k, y")|d y" dy'. \end{align*} $$
Decomposing the integral
![]() $\int _0^y$
into
$\int _0^y$
into
![]() $\int _0^{\min \{y,{\langle k\rangle }^{-\frac 13}\}}$
and
$\int _0^{\min \{y,{\langle k\rangle }^{-\frac 13}\}}$
and
![]() $\int _{\min \{y,{\langle k\rangle }^{-\frac 13}\}}^y$
, it follows from the Hölder inequality that
$\int _{\min \{y,{\langle k\rangle }^{-\frac 13}\}}^y$
, it follows from the Hölder inequality that
We take summation
![]() $\sum _{k\in \mathbb {Z}}$
and use the Plancherel theorem to deduce
$\sum _{k\in \mathbb {Z}}$
and use the Plancherel theorem to deduce
Thus, we get that
 $$ \begin{align} \int_0^t\Big(\|\partial_x\phi^i_{bc,T}\|_{X^{\frac{5}{3}}}^2+|\phi^i_{bc,T}|_{y=1-i}|_{X^{\frac{8}{3}}}^2\Big) ds\leq &\ C\int_0^t\|\varphi^i\omega^i_{bc,T}\|_{X^{\frac52}_i}^2ds+C\int_0^t\|(\varphi^i)^2\omega^i_{bc,T}\|_{X^{\frac{17}{6}}_i}^2ds\\ \nonumber \leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\Big(\|\partial_x\phi^i_{bc,T}\|_{X^{\frac{5}{3}}}^2+|\phi^i_{bc,T}|_{y=1-i}|_{X^{\frac{8}{3}}}^2\Big) ds\leq &\ C\int_0^t\|\varphi^i\omega^i_{bc,T}\|_{X^{\frac52}_i}^2ds+C\int_0^t\|(\varphi^i)^2\omega^i_{bc,T}\|_{X^{\frac{17}{6}}_i}^2ds\\ \nonumber \leq &\frac{C}{\lambda}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
Collecting (8.44), (8.45) and (8.48) together, we get the corollary proved.
8.3 The estimates of
 $\phi _{bc, R}$
: full construction of boundary corrector
$\phi _{bc, R}$
: full construction of boundary corrector
All we have left is the term
![]() $\phi _{bc, R}$
. Like the previous argument, we define
$\phi _{bc, R}$
. Like the previous argument, we define
where
![]() $\phi ^i_{bc, R}$
satisfies that
$\phi ^i_{bc, R}$
satisfies that

and

For simplicity, denote
![]() $\omega _{bc,R}^i=\Delta _{\varepsilon } \phi ^i_{bc,R}$
, which has the following relationship:
$\omega _{bc,R}^i=\Delta _{\varepsilon } \phi ^i_{bc,R}$
, which has the following relationship:
 $$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \phi_{bc,R}^0=\omega_{bc,R}^0,\\ &\phi_{bc,R}^0|_{y=0}=0,\quad \phi_{bc,R}^0|_{y=1}=f^0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \phi_{bc,R}^0=\omega_{bc,R}^0,\\ &\phi_{bc,R}^0|_{y=0}=0,\quad \phi_{bc,R}^0|_{y=1}=f^0, \end{aligned} \right. \end{align} $$
and
 $$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \phi_{bc,R}^1=\omega_{bc,R}^1,\\ &\phi_{bc,R}^1|_{y=0}=f^1,\quad \phi_{bc,R}^1|_{y=1}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \phi_{bc,R}^1=\omega_{bc,R}^1,\\ &\phi_{bc,R}^1|_{y=0}=f^1,\quad \phi_{bc,R}^1|_{y=1}=0, \end{aligned} \right. \end{align} $$
where
To homogenize boundary conditions, we introduce
where
![]() $\widetilde {\phi }_{bc,R}^0$
satisfies
$\widetilde {\phi }_{bc,R}^0$
satisfies
 $$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \widetilde{\phi}_{bc,R}^0=\omega_{bc,R}^0+\Delta_{\varepsilon} g^0,\\ & \widetilde{\phi}_{bc,R}^0|_{y=0,1}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \widetilde{\phi}_{bc,R}^0=\omega_{bc,R}^0+\Delta_{\varepsilon} g^0,\\ & \widetilde{\phi}_{bc,R}^0|_{y=0,1}=0, \end{aligned} \right. \end{align} $$
where
Similarly, we introduce
and
![]() $\widetilde {\phi }_2^1$
satisfies
$\widetilde {\phi }_2^1$
satisfies
 $$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \widetilde{\phi}_{bc,R}^1=\omega_{bc,R}^1+\Delta_{\varepsilon} g^1,\\ &\widetilde{\phi}_{bc,R}^1|_{y=0,1}=0, \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\Delta_{\varepsilon} \widetilde{\phi}_{bc,R}^1=\omega_{bc,R}^1+\Delta_{\varepsilon} g^1,\\ &\widetilde{\phi}_{bc,R}^1|_{y=0,1}=0, \end{aligned} \right. \end{align} $$
where
First, we give some elliptic estimates.
Lemma 8.9. Let
![]() $(f^0, f^1)$
,
$(f^0, f^1)$
,
![]() $(g^0, g^1)$
– introduced in (8.53)–(8.54), (8.55) and (8.58). It holds that
$(g^0, g^1)$
– introduced in (8.53)–(8.54), (8.55) and (8.58). It holds that
 $$ \begin{align} \int_0^t\Big(|f^i|_{X^{\frac83}}^2+ \|\nabla_{\varepsilon} g^i\|_{X^{\frac52}}^2+\|\Delta_{\varepsilon} g^i\|_{X^{\frac52}}^2\Big)ds\leq & \frac{C}{\lambda^{\frac12}}\int_0^t|h^{i}|_{X^{\frac73}}^2ds \end{align} $$
$$ \begin{align} \int_0^t\Big(|f^i|_{X^{\frac83}}^2+ \|\nabla_{\varepsilon} g^i\|_{X^{\frac52}}^2+\|\Delta_{\varepsilon} g^i\|_{X^{\frac52}}^2\Big)ds\leq & \frac{C}{\lambda^{\frac12}}\int_0^t|h^{i}|_{X^{\frac73}}^2ds \end{align} $$
for
![]() $i=0,1.$
$i=0,1.$
Moreover,
![]() $\phi _{bc,R}^i~(i=0,1)$
has the following estimates:
$\phi _{bc,R}^i~(i=0,1)$
has the following estimates:
 $$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds. \end{align} $$
Proof. Here we only prove the case
![]() $i=0.$
The case
$i=0.$
The case
![]() $i=1$
is almost the same, and we omit details to readers. We first give the proof for
$i=1$
is almost the same, and we omit details to readers. We first give the proof for
![]() $f^0$
. By the definition of
$f^0$
. By the definition of
![]() $f^0$
, we get
$f^0$
, we get
 $$ \begin{align*} \int_0^t|f^0|_{X^{\frac83}}^2ds\leq \int_0^t|\phi^0_{bc,S}|_{y=1}|_{X^{\frac83}}^2 ds+ \int_0^t|\phi^0_{bc,T}|_{y=1}|_{X^{\frac83}}^2 ds \leq \frac{C}{\lambda}\int_0^t|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} \int_0^t|f^0|_{X^{\frac83}}^2ds\leq \int_0^t|\phi^0_{bc,S}|_{y=1}|_{X^{\frac83}}^2 ds+ \int_0^t|\phi^0_{bc,T}|_{y=1}|_{X^{\frac83}}^2 ds \leq \frac{C}{\lambda}\int_0^t|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
where we used Lemma 8.4 and Corollary 8.8.
For
![]() $g^0$
, by Corollary 8.8, Proposition 8.3, we have
$g^0$
, by Corollary 8.8, Proposition 8.3, we have
 $$ \begin{align*} \int_0^t\|\nabla_{\varepsilon} g^0\|_{X^{\frac52}}^2ds &\leq \int_0^t\Big( \|\nabla_{\varepsilon}\phi_{bc,S}^0\|_{X^{\frac52}} + \|\nabla_{\varepsilon}\phi_{bc,T}^0\|_{X^{\frac52}} + \|\phi_{bc,S}^0\|_{X^{\frac83}} + \|\phi_{bc,T}^0\|_{X^{\frac83}}\Big)ds\\ &\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\nabla_{\varepsilon} g^0\|_{X^{\frac52}}^2ds &\leq \int_0^t\Big( \|\nabla_{\varepsilon}\phi_{bc,S}^0\|_{X^{\frac52}} + \|\nabla_{\varepsilon}\phi_{bc,T}^0\|_{X^{\frac52}} + \|\phi_{bc,S}^0\|_{X^{\frac83}} + \|\phi_{bc,T}^0\|_{X^{\frac83}}\Big)ds\\ &\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
On one hand, using Proposition 8.3, Proposition 8.5, Corollary 8.8 and Proposition 8.7, we get
 $$ \begin{align*} &\!\int_0^t\!\!\Big(\|y\Delta_{\varepsilon}\phi^0_{bc,S}\|_{X^{\frac52}}^2+\|\partial_y\phi^0_{bc,S}\|_{X^{\frac52}}^2 +\|y\Delta_{\varepsilon}\phi^0_{bc,T}\|_{X^{\frac52}}^2+\|\partial_y\phi^0_{bc,T}\|_{X^{\frac52}}^2\Big)ds\leq \frac{C}{\lambda^{\frac12}}\!\int_0^t\!|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} &\!\int_0^t\!\!\Big(\|y\Delta_{\varepsilon}\phi^0_{bc,S}\|_{X^{\frac52}}^2+\|\partial_y\phi^0_{bc,S}\|_{X^{\frac52}}^2 +\|y\Delta_{\varepsilon}\phi^0_{bc,T}\|_{X^{\frac52}}^2+\|\partial_y\phi^0_{bc,T}\|_{X^{\frac52}}^2\Big)ds\leq \frac{C}{\lambda^{\frac12}}\!\int_0^t\!|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
which implies that
 $$ \begin{align*} \int_0^t \|\Delta_{\varepsilon} g^0\|_{X^{\frac52}}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \|\Delta_{\varepsilon} g^0\|_{X^{\frac52}}^2ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
At last, we prove (8.62). Taking the
![]() $X^{\frac 73}$
inner product with
$X^{\frac 73}$
inner product with
![]() $\widetilde {\phi }_{bc,R}^0$
toward (8.56), we use integration by parts and then integrate time from
$\widetilde {\phi }_{bc,R}^0$
toward (8.56), we use integration by parts and then integrate time from
![]() $0$
to t that
$0$
to t that
 $$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds=-\int_0^t\langle \omega_{bc,R}^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds+\int_0^t\langle \Delta_{\varepsilon} g^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds=-\int_0^t\langle \omega_{bc,R}^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds+\int_0^t\langle \Delta_{\varepsilon} g^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds. \end{align*} $$
Due to
![]() $ \widetilde {\phi }_{bc,R}^0|_{y=0,1}=0,$
we use the Poincaré inequality to imply
$ \widetilde {\phi }_{bc,R}^0|_{y=0,1}=0,$
we use the Poincaré inequality to imply
 $$ \begin{align} \int_0^t\langle \omega_{bc,R}^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds\leq &\frac1{10}\int_0^t\|\partial_y\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}ds+ C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\langle \omega_{bc,R}^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds\leq &\frac1{10}\int_0^t\|\partial_y\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}ds+ C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align} $$
According to (8.61), we get
 $$ \begin{align} \int_0^t\langle \Delta_{\varepsilon} g^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds\leq &\int_0^t\|\Delta_{\varepsilon} g^0\|_{X^{\frac73}}\|\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}} ds\\ \nonumber \leq & \frac1{10}\int_0^t\|\partial_y\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}} ^2 ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\langle \Delta_{\varepsilon} g^0,\widetilde{\phi}_{bc,R}^0\rangle_{X^{\frac73}}ds\leq &\int_0^t\|\Delta_{\varepsilon} g^0\|_{X^{\frac73}}\|\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}} ds\\ \nonumber \leq & \frac1{10}\int_0^t\|\partial_y\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}} ^2 ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align} $$
Combining (8.63) and (8.64), we deduce
 $$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align*} $$
Bringing
![]() $\nabla _{\varepsilon }\phi _{bc,R}^0=\nabla _{\varepsilon }\widetilde {\phi }_{bc,R}^0-\nabla _{\varepsilon } g^0$
into the above inequality, we obtain
$\nabla _{\varepsilon }\phi _{bc,R}^0=\nabla _{\varepsilon }\widetilde {\phi }_{bc,R}^0-\nabla _{\varepsilon } g^0$
into the above inequality, we obtain
 $$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\phi_{bc,R}^0\|_{X^{\frac73}}^2ds\leq &\int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds+\int_0^t\|\nabla_{\varepsilon} g^0\|_{X^{\frac73}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t\|\nabla_{\varepsilon}\phi_{bc,R}^0\|_{X^{\frac73}}^2ds\leq &\int_0^t\|\nabla_{\varepsilon}\widetilde{\phi}_{bc,R}^0\|_{X^{\frac73}}^2ds+\int_0^t\|\nabla_{\varepsilon} g^0\|_{X^{\frac73}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds. \end{align*} $$
By now, we finish the proof.
In order to estimate the right-hand side of (8.49) and (8.50) and the boundary term, we need the following results:
Lemma 8.10. For
![]() $i=0,1,$
we have that
$i=0,1,$
we have that
 $$ \begin{align} \int_0^t\Big(\|\partial_x(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2+\|\partial_y (\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2\Big) ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
$$ \begin{align} \int_0^t\Big(\|\partial_x(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2+\|\partial_y (\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2\Big) ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
 $$ \begin{align} \int_0^t |\partial_y \phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
$$ \begin{align} \int_0^t |\partial_y \phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \end{align} $$
 $$ \begin{align} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^i)_{\Phi},\partial_y(\phi_{bc,R}^i)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^i)_{\Phi},\partial_y(\phi_{bc,R}^i)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align} $$
Proof. Here, we only prove the case
![]() $i=0.$
The case
$i=0.$
The case
![]() $i=1$
is almost the same, and we omit details to readers.
$i=1$
is almost the same, and we omit details to readers.
By Proposition 8.3 and Corollary 8.8, we get (8.65) proved.
Next, we deal with the boundary term. A direct calculation gives that
 $$ \begin{align*} \partial_y\phi_{bc,R}^0|_{y=1}=&\ (\partial_y\widetilde{\phi}_{bc,R}^0-\partial_yg^0)|_{y=1}\\ =&\ \partial_y\widetilde{\phi}_{bc,R}^0|_{y=1}-(\partial_y\phi^0_{bc,S}+\partial_y\phi^0_{bc,T})|_{y=1}-(\phi^0_{bc,S}+\phi^0_{bc,T})|_{y=1}, \end{align*} $$
$$ \begin{align*} \partial_y\phi_{bc,R}^0|_{y=1}=&\ (\partial_y\widetilde{\phi}_{bc,R}^0-\partial_yg^0)|_{y=1}\\ =&\ \partial_y\widetilde{\phi}_{bc,R}^0|_{y=1}-(\partial_y\phi^0_{bc,S}+\partial_y\phi^0_{bc,T})|_{y=1}-(\phi^0_{bc,S}+\phi^0_{bc,T})|_{y=1}, \end{align*} $$
and
due to
![]() $\phi _{bc, S}^0|_{y=0}=\phi _{bc, T}^0|_{y=0}=0.$
$\phi _{bc, S}^0|_{y=0}=\phi _{bc, T}^0|_{y=0}=0.$
By Corollary 8.8, we get
 $$ \begin{align*} \int_0^t|\partial_y\widetilde{\phi}_{bc, R}^0|_{y=0,1}|_{X^{\frac73}}^2ds \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t(\|\omega_{bc, R}^0\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon} g^0\|_{X^{\frac73}}^2)ds\\ \leq &\ C\int_0^t\|\omega_{bc, R}^0\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} \int_0^t|\partial_y\widetilde{\phi}_{bc, R}^0|_{y=0,1}|_{X^{\frac73}}^2ds \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds+C\int_0^t(\|\omega_{bc, R}^0\|_{X^{\frac73}}^2+\|\Delta_{\varepsilon} g^0\|_{X^{\frac73}}^2)ds\\ \leq &\ C\int_0^t\|\omega_{bc, R}^0\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds, \end{align*} $$
where we use an elliptic estimate and the Calderon-Zygmund inequality
For the last estimate, we use (8.66) and (8.61) to imply
 $$ \begin{align*} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^0)_{\Phi},\partial_y(\phi_{bc,R}^0)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t|(\phi_{bc,S}^0+\phi_{bc,T}^0)|_{y=1}|_{X^{\frac83}}|\partial_y \phi_{bc,R}^0|_{y=1}|_{X^{\frac73}}ds\\ \leq &\ C\int_0^t|f^0|_{X^{\frac83}}|\partial_y \phi_{bc,R}^0|_{y=1}|_{X^{\frac73}}ds\\ \leq &\ C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^0)_{\Phi},\partial_y(\phi_{bc,R}^0)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t|(\phi_{bc,S}^0+\phi_{bc,T}^0)|_{y=1}|_{X^{\frac83}}|\partial_y \phi_{bc,R}^0|_{y=1}|_{X^{\frac73}}ds\\ \leq &\ C\int_0^t|f^0|_{X^{\frac83}}|\partial_y \phi_{bc,R}^0|_{y=1}|_{X^{\frac73}}ds\\ \leq &\ C\int_0^t\|\omega_{bc,R}^0\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^0|_{X^{\frac73}}^2ds. \end{align*} $$
Here, we complete this lemma.
We are coming to the main part of this section. We shall give the estimate for the system (8.49) and (8.50).
Proposition 8.11. Let
![]() $\phi _{bc,R}^0$
and
$\phi _{bc,R}^0$
and
![]() $\phi _{bc,R}^1$
be the solution of (8.49) and (8.50), respectively, and
$\phi _{bc,R}^1$
be the solution of (8.49) and (8.50), respectively, and
![]() $\omega _{bc,R}^i=\Delta _{\varepsilon } \phi _{bc,R}^i$
for
$\omega _{bc,R}^i=\Delta _{\varepsilon } \phi _{bc,R}^i$
for
![]() $i=0,1.$
Then, for every
$i=0,1.$
Then, for every
![]() $i=0,1$
, it holds that
$i=0,1$
, it holds that
 $$ \begin{align*} \|\omega_{bc,R}^i(t)\|_{X^{2}}^2+&\lambda\int_0^t \|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\int_0^t (\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2+|\partial_y\phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2)ds+\kern-1pt\int_0^t\kern-1pt\|\nabla_{\varepsilon}\omega_{bc,R}^i\|_{X^{2}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \qquad t\in[0, T], \end{align*} $$
$$ \begin{align*} \|\omega_{bc,R}^i(t)\|_{X^{2}}^2+&\lambda\int_0^t \|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\int_0^t (\|\nabla_{\varepsilon}\phi_{bc,R}^i\|_{X^{\frac73}}^2+|\partial_y\phi_{bc,R}^i|_{y=0,1}|_{X^{\frac73}}^2)ds+\kern-1pt\int_0^t\kern-1pt\|\nabla_{\varepsilon}\omega_{bc,R}^i\|_{X^{2}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds, \qquad t\in[0, T], \end{align*} $$
where
![]() $0<T<\min \{T_p, \frac {1}{2\lambda }\}$
.
$0<T<\min \{T_p, \frac {1}{2\lambda }\}$
.
Proof. The result mainly comes from the process of Proposition 7.1. Here we take
![]() $(\mathcal {N}_u, \varepsilon \mathcal {N}_v)=0$
and
$(\mathcal {N}_u, \varepsilon \mathcal {N}_v)=0$
and
![]() $\varepsilon ^2 f_1+f_2-C(t)\partial _x\omega ^p$
is replaced by
$\varepsilon ^2 f_1+f_2-C(t)\partial _x\omega ^p$
is replaced by
![]() $G^i=-\partial _y(\phi _{bc,S}^i+\phi _{bc,T}^i)\partial _x\omega ^p+\partial _x(\phi _{bc,S}^i+\phi _{bc,T}^i)\partial _y\omega ^p$
for
$G^i=-\partial _y(\phi _{bc,S}^i+\phi _{bc,T}^i)\partial _x\omega ^p+\partial _x(\phi _{bc,S}^i+\phi _{bc,T}^i)\partial _y\omega ^p$
for
![]() $i=0,1.$
In order to estimate the source term
$i=0,1.$
In order to estimate the source term
![]() $\int _0^t \|G^i\|_{X^{\frac 53}}^2ds$
, using Lemma 8.10 and product estimate in Lemma 2.2, we get
$\int _0^t \|G^i\|_{X^{\frac 53}}^2ds$
, using Lemma 8.10 and product estimate in Lemma 2.2, we get
 $$ \begin{align*} \int_0^t \|G^i\|_{X^{\frac53}}^2ds\leq &\ C\int_0^t \|\partial_y(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2ds+C\int_0^t \|\partial_x(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \|G^i\|_{X^{\frac53}}^2ds\leq &\ C\int_0^t \|\partial_y(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2ds+C\int_0^t \|\partial_x(\phi_{bc,S}^i+\phi_{bc,T}^i)\|_{X^{\frac53}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align*} $$
The only difference comes from the boundary conditions
which are not zero compared with equation (6.2). We review
![]() $T^5$
in Propoposition 7.1. After integration by parts, the boundary term is left. More precisely, we need to estimate
$T^5$
in Propoposition 7.1. After integration by parts, the boundary term is left. More precisely, we need to estimate
![]() $\int _0^t \Big \langle \partial _x(\phi _{bc,R}^i)_{\Phi },\partial _y(\phi _{bc,R}^i)_{\Phi } \Big \rangle _{H^2_x}\Big |_{y=0}^{y=1}ds.$
According to Lemma 8.10, we have
$\int _0^t \Big \langle \partial _x(\phi _{bc,R}^i)_{\Phi },\partial _y(\phi _{bc,R}^i)_{\Phi } \Big \rangle _{H^2_x}\Big |_{y=0}^{y=1}ds.$
According to Lemma 8.10, we have
 $$ \begin{align*} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^i)_{\Phi},\partial_y(\phi_{bc,R}^i)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \Big\langle \partial_x(\phi_{bc,R}^i)_{\Phi},\partial_y(\phi_{bc,R}^i)_{\Phi} \Big\rangle_{H^2_x}\Big|_{y=0}^{y=1}ds\leq &\ C\int_0^t\|\omega_{bc,R}^i\|_{X^{\frac73}}^2ds+\frac{C}{\lambda^{\frac12}}\int_0^t|h^i|_{X^{\frac73}}^2ds. \end{align*} $$
Here, we take
![]() $\lambda $
large enough to complete the proof.
$\lambda $
large enough to complete the proof.
8.4 Proof of Proposition 6.2
In this subsection, we combine all the above estimates to finish the proof of Proposition 6.2. Recalling the definition of
![]() $\phi _{bc}$
:
$\phi _{bc}$
:
we get that
 $$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p-\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0}=h^0+R_{bc}^{00} +R_{bc}^{01} ,\quad \partial_y\phi_{bc}|_{y=1}=h^1+R_{bc}^{10} +R_{bc}^{11} ,\\ &\phi_{bc}|_{t=0}=0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(\partial_t-\Delta_{\varepsilon})\Delta_{\varepsilon}\phi_{bc}+u^p\partial_x \Delta_{\varepsilon}\phi_{bc}+v^p\partial_y \Delta_{\varepsilon}\phi_{bc}+\partial_y\phi_{bc}\partial_x \omega^p-\partial_x\phi_{bc}\partial_y \omega^p=0,\\ &\phi_{bc}|_{y=0,1}=0,\quad \partial_y\phi_{bc}|_{y=0}=h^0+R_{bc}^{00} +R_{bc}^{01} ,\quad \partial_y\phi_{bc}|_{y=1}=h^1+R_{bc}^{10} +R_{bc}^{11} ,\\ &\phi_{bc}|_{t=0}=0. \end{aligned} \right. \end{align} $$
Here,
![]() $R_{bc}^{ji}~ (j=0,1,~i=0,1)$
are linear operators and are defined by
$R_{bc}^{ji}~ (j=0,1,~i=0,1)$
are linear operators and are defined by
 $$ \begin{align*} R_{bc}^{00}=&\ \big(\partial_y\phi_{bc, T}^0 +\partial_y\phi_{bc, R}^0\big) |_{y=0},\\ R_{bc}^{01}=&\ \big(\partial_y\phi_{bc, S}^1 +\partial_y\phi_{bc, T}^1 +\partial_y \phi_{bc, R}^1\big) |_{y=0},\\ R_{bc}^{10}=&\ \big(\partial_y\phi_{bc, S}^0 +\partial_y\phi_{bc, T}^0 +\partial_y\phi_{bc, R}^0\big) |_{y=1},\\ R_{bc}^{11}=&\ \big(\partial_y\phi_{bc, T}^1 +\partial_y \phi_{bc, R}^1\big)|_{y=1}. \end{align*} $$
$$ \begin{align*} R_{bc}^{00}=&\ \big(\partial_y\phi_{bc, T}^0 +\partial_y\phi_{bc, R}^0\big) |_{y=0},\\ R_{bc}^{01}=&\ \big(\partial_y\phi_{bc, S}^1 +\partial_y\phi_{bc, T}^1 +\partial_y \phi_{bc, R}^1\big) |_{y=0},\\ R_{bc}^{10}=&\ \big(\partial_y\phi_{bc, S}^0 +\partial_y\phi_{bc, T}^0 +\partial_y\phi_{bc, R}^0\big) |_{y=1},\\ R_{bc}^{11}=&\ \big(\partial_y\phi_{bc, T}^1 +\partial_y \phi_{bc, R}^1\big)|_{y=1}. \end{align*} $$
Compared with the system (8.1), we need to find
![]() $(h^0, h^1)$
such that
$(h^0, h^1)$
such that
 $$ \begin{align} \left\{ \begin{aligned} h^0+R_{bc}^{00} +R_{bc}^{01} =- \partial_y\phi_{slip}|_{y=0}+C(t),\\ h^1+R_{bc}^{10} +R_{bc}^{01} =- \partial_y\phi_{slip}|_{y=1}+C(t) \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} h^0+R_{bc}^{00} +R_{bc}^{01} =- \partial_y\phi_{slip}|_{y=0}+C(t),\\ h^1+R_{bc}^{10} +R_{bc}^{01} =- \partial_y\phi_{slip}|_{y=1}+C(t) \end{aligned} \right. \end{align} $$
hold. To do that, we define an operator
![]() $R_{bc}[h^0, h^1],$
which is defined by
$R_{bc}[h^0, h^1],$
which is defined by
 $$ \begin{align} R_{bc}[h^0, h^1]= \left(\begin{array}{@{}cc@{}}R_{bc}^{00} & R_{bc}^{01} \\R_{bc}^{10} & R_{bc}^{11} \end{array}\right), \end{align} $$
$$ \begin{align} R_{bc}[h^0, h^1]= \left(\begin{array}{@{}cc@{}}R_{bc}^{00} & R_{bc}^{01} \\R_{bc}^{10} & R_{bc}^{11} \end{array}\right), \end{align} $$
which is a
![]() $2\times 2$
matrix operator and is well-defined on the Banach space
$2\times 2$
matrix operator and is well-defined on the Banach space
 $$ \begin{align} Z_{bc}=\{(h^0, h^1)\in L^2(0,t; L^2)| \int_0^t|(h^0, h^1)|^2_{X^{\frac73}}ds<+\infty\}. \end{align} $$
$$ \begin{align} Z_{bc}=\{(h^0, h^1)\in L^2(0,t; L^2)| \int_0^t|(h^0, h^1)|^2_{X^{\frac73}}ds<+\infty\}. \end{align} $$
Proposition 8.12. There exists
![]() $\lambda _0\geq 1$
such that if
$\lambda _0\geq 1$
such that if
![]() $\lambda \geq \lambda _0$
, the map
$\lambda \geq \lambda _0$
, the map
![]() $R_{bc}: Z_{bc}\to Z_{bc}$
defined by (8.71) satisfies
$R_{bc}: Z_{bc}\to Z_{bc}$
defined by (8.71) satisfies
 $$ \begin{align} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac73}}^2ds. \end{align} $$
$$ \begin{align} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac73}}^2ds. \end{align} $$
Hence, the operator
![]() $I+R_{bc}$
is invertible in
$I+R_{bc}$
is invertible in
![]() $Z_{bc}$
. Moreover, there exists
$Z_{bc}$
. Moreover, there exists
![]() $(h_0, h_1)\in Z_{bc}$
such that (8.70) holds and
$(h_0, h_1)\in Z_{bc}$
such that (8.70) holds and
![]() $(h_0, h_1)$
is defined by
$(h_0, h_1)$
is defined by
Proof. First, by Lemma 8.4, Proposition 8.8, Corollary 8.7 and Proposition 8.11, it is easy to get
 $$ \begin{align*} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t\Big|R_{bc}[h^0, h^1]\Big|_{X^{\frac73}}^2 ds\leq \frac{C}{\lambda^{\frac12}}\int_0^t|(h^0,h^1)|_{X^{\frac73}}^2ds. \end{align*} $$
Taking
![]() $\lambda $
large enough, we get that the operator
$\lambda $
large enough, we get that the operator
![]() $I+R_{bc}$
is invertible in
$I+R_{bc}$
is invertible in
![]() $Z_{bc}$
. Thus, there exists
$Z_{bc}$
. Thus, there exists
![]() $(h_0, h_1)\in Z_{bc}$
such that (8.70) holds.
$(h_0, h_1)\in Z_{bc}$
such that (8.70) holds.
Let’s continue to prove Proposition 6.2. According to Proposition 8.3, Proposition 8.6, Corollary 8.8 and Proposition 8.11, we get by (8.68) that
 $$ \begin{align*} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2ds\leq &\int_0^t \|\nabla_{\varepsilon}\phi_{bc,S} \|_{X^{\frac52}}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc,T} \|_{X^{\frac52}}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc,R} \|_{X^{\frac73}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2ds\leq &\int_0^t \|\nabla_{\varepsilon}\phi_{bc,S} \|_{X^{\frac52}}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc,T} \|_{X^{\frac52}}^2ds+\int_0^t \|\nabla_{\varepsilon}\phi_{bc,R} \|_{X^{\frac73}}^2ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds, \end{align*} $$
and
 $$ \begin{align*} \int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq & \int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc,S}\|^2_{X^{\frac52}}ds+\int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc,T}\|^2_{X^{\frac52}}ds+\int_0^t \| \Delta_{\varepsilon} \phi_{bc,R}\|^2_{X^{\frac73}}ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds, \end{align*} $$
$$ \begin{align*} \int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq & \int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc,S}\|^2_{X^{\frac52}}ds+\int_0^t \|\varphi \Delta_{\varepsilon} \phi_{bc,T}\|^2_{X^{\frac52}}ds+\int_0^t \| \Delta_{\varepsilon} \phi_{bc,R}\|^2_{X^{\frac73}}ds\\ \leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds, \end{align*} $$
which imply
 $$ \begin{align*} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2+\|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds. \end{align*} $$
$$ \begin{align*} \int_0^t \|\nabla_{\varepsilon}\phi_{bc} \|_{X^{\frac73}}^2+\|\varphi \Delta_{\varepsilon} \phi_{bc}\|^2_{X^2}ds\leq &\frac{C}{\lambda^{\frac12}}\int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds. \end{align*} $$
Due to Proposition 8.12 and taking
![]() $\mathcal {A}=(I+R_{bc})^{-1},$
we know
$\mathcal {A}=(I+R_{bc})^{-1},$
we know
![]() $\mathcal {A}$
is a zero-order bounded operator in
$\mathcal {A}$
is a zero-order bounded operator in
![]() $Z_{bc}$
and obtain
$Z_{bc}$
and obtain
 $$ \begin{align*} \int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds=&\ \int_0^t|\mathcal{A}(- \partial_y\phi_{slip}|_{y=0}+C(s), - \partial_y\phi_{slip}|_{y=1}+C(s))|_{X^{\frac73}}^2ds\\ \leq &\ C\int_0^t \Big(|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}+|C(s)|^2\Big)ds, \end{align*} $$
$$ \begin{align*} \int_0^t|(h^0, h^1)|_{X^{\frac73}}^2ds=&\ \int_0^t|\mathcal{A}(- \partial_y\phi_{slip}|_{y=0}+C(s), - \partial_y\phi_{slip}|_{y=1}+C(s))|_{X^{\frac73}}^2ds\\ \leq &\ C\int_0^t \Big(|\nabla_{\varepsilon}\phi_{slip}|_{y=0,1}|^2_{X^{\frac73}}+|C(s)|^2\Big)ds, \end{align*} $$
which finishes this proposition.
Acknowledgements
The authors would like to thank Professor Zhifei Zhang for the valuable discussions and suggestions. C. Wang is partially supported by the NSF of China under Grant 12071008. Y. Wang is partially supported by NSF of China under Grant 12101431 and the Sichuan Youth Science and Technology Foundation No. 21CXTD0076.
Competing Interests
The author declares none.