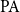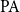1. Introduction
Partial combinatory algebra (pca) generalizes the setting of classical combinatory algebra (ca) to structures with a partial application operator. The first entry in the literature is Feferman (Reference Feferman and Crossley1975), which is surprisingly late, some fifty years after the invention of combinatory algebra and the closely related lambda calculus, although the concept of a pca existed before that (see Section 5). Apart from this connection with lambda calculus, pcas have played a notable part in constructive mathematics. At the end of Section 2 below, we list a number of key examples of pcas, and say something about their role in various settings.
Since the application operator in pcas is partial, they can often be naturally represented as c.e. structures in the sense of Selivanov (Reference Selivanov, Cooper and Goncharov2003) and Khoussainov (Reference Khoussainov and Manea2018). The computable structure theory of pcas as partial c.e. structures was recently studied by Fokina and Terwijn (Reference Fokina and Terwijn2024). Since pcas can be seen as abstract models of computation, it is only natural to consider their complexity as algebraic structures from the viewpoint of computability theory. At least for countable pcas, there is a straightforward definition of their complexity in terms of the complexity of a presentation, as in computable model theory. Below we formulate this using numberings (Definition 3.1). Some of the complexity of pcas was studied earlier in Shafer and Terwijn (Reference Shafer and Terwijn2021) and Golov and Terwijn (Reference Golov and Terwijn2023). In the current paper, we focus on the complexity of completions, and in particular of completions of what is called Kleene’s first model
![]() $\mathcal{K}_1$
, with application defined in terms of partial computable functions on the natural numbers.
$\mathcal{K}_1$
, with application defined in terms of partial computable functions on the natural numbers.
A completion of a pca is a total pca (i.e. a combinatory algebra in the classical sense, in which applications are always defined) in which the pca can be embedded. Not every pca has a completion, as was first proved in Klop (Reference Klop1982). On the other hand, Kleene’s
![]() $\mathcal{K}_1$
does have a completion. This follows from the sufficient condition for completability given in Bethke et al. (Reference Bethke, Klop and de Vrijer1996). This yields a certain term model
$\mathcal{K}_1$
does have a completion. This follows from the sufficient condition for completability given in Bethke et al. (Reference Bethke, Klop and de Vrijer1996). This yields a certain term model
![]() $T(\omega )/\!\!\sim$
as a completion of
$T(\omega )/\!\!\sim$
as a completion of
![]() $\mathcal{K}_1$
. In Section 5 below, we will discuss how Scott’s graph model, which is another important example of a pca, can also be seen as a (weak) completion of
$\mathcal{K}_1$
. In Section 5 below, we will discuss how Scott’s graph model, which is another important example of a pca, can also be seen as a (weak) completion of
![]() $\mathcal{K}_1$
. We note, however, that these completions of
$\mathcal{K}_1$
. We note, however, that these completions of
![]() $\mathcal{K}_1$
have high complexity, which brings up the question of what the optimal complexity of such a completion could be. Although no computable completions of
$\mathcal{K}_1$
have high complexity, which brings up the question of what the optimal complexity of such a completion could be. Although no computable completions of
![]() $\mathcal{K}_1$
exist (cf. Theorem 5.2 and the remarks following it), we show that there exist completions of
$\mathcal{K}_1$
exist (cf. Theorem 5.2 and the remarks following it), we show that there exist completions of
![]() $\mathcal{K}_1$
of low Turing degree (Theorem 5.3). Such completions are close to computable in the sense that the complexity of their halting problem is the same as the standard halting problem.
$\mathcal{K}_1$
of low Turing degree (Theorem 5.3). Such completions are close to computable in the sense that the complexity of their halting problem is the same as the standard halting problem.
All this suggests a connection with complete extensions of Peano arithmetic, for which a similar story exists. Note, however, that we are talking here about pcas, that is, the models of a theory, rather than the theory itself. Nevertheless, in Section 6, we show that indeed there is a connection. Finally, in Section 7, we discuss the complexity of pcas resulting from nonstandard models of
![]() $\mathrm{PA}$
.
$\mathrm{PA}$
.
Our notation from computability theory is mostly standard. For unexplained notions, we refer to Odifreddi (Reference Odifreddi1989) or Soare (Reference Soare1987). In particular,
![]() $\omega$
denotes the natural numbers, and
$\omega$
denotes the natural numbers, and
![]() $\varphi _e$
the
$\varphi _e$
the
![]() $e$
-th partial computable (p.c.) function. For any set
$e$
-th partial computable (p.c.) function. For any set
![]() $A$
,
$A$
,
![]() $A'$
denotes the Turing jump of
$A'$
denotes the Turing jump of
![]() $A$
, and in particular
$A$
, and in particular
![]() $\emptyset '$
denotes the halting problem.
$\emptyset '$
denotes the halting problem.
2. Partial Combinatory Algebras
To make the paper self-contained, we briefly review the basic definitions from partial combinatory algebra. Our presentation follows van Oosten (Reference van Oosten2008).
A partial applicative structure (pas) is a set
![]() $\mathcal{A}$
together with a partial map
$\mathcal{A}$
together with a partial map
![]() $\cdot$
from
$\cdot$
from
![]() $\mathcal{A}\times \mathcal{A}$
to
$\mathcal{A}\times \mathcal{A}$
to
![]() $\mathcal{A}$
. We usually write
$\mathcal{A}$
. We usually write
![]() $ab$
instead of
$ab$
instead of
![]() $a\cdot b$
, and think of this as “
$a\cdot b$
, and think of this as “
![]() $a$
applied to
$a$
applied to
![]() $b$
.” If this is defined, we denote this by
$b$
.” If this is defined, we denote this by
![]() $ab\!\downarrow$
. By convention, application associates to the left, so we write
$ab\!\downarrow$
. By convention, application associates to the left, so we write
![]() $abc$
instead of
$abc$
instead of
![]() $(ab)c$
. Terms over
$(ab)c$
. Terms over
![]() $\mathcal{A}$
are built from elements of
$\mathcal{A}$
are built from elements of
![]() $\mathcal{A}$
, variables, and application. If
$\mathcal{A}$
, variables, and application. If
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are terms, then so is
$t_2$
are terms, then so is
![]() $t_1t_2$
. If
$t_1t_2$
. If
![]() $t(x_1,\ldots, x_n)$
is a term with variables
$t(x_1,\ldots, x_n)$
is a term with variables
![]() $x_i$
, and
$x_i$
, and
![]() $a_1,\ldots, a_n \in \mathcal{A}$
, then
$a_1,\ldots, a_n \in \mathcal{A}$
, then
![]() $t(a_1,\ldots, a_n)$
is the term obtained by substituting the
$t(a_1,\ldots, a_n)$
is the term obtained by substituting the
![]() $a_i$
for the
$a_i$
for the
![]() $x_i$
. For closed terms (i.e. terms without variables)
$x_i$
. For closed terms (i.e. terms without variables)
![]() $t$
and
$t$
and
![]() $s$
, we write
$s$
, we write
![]() $t \simeq s$
if either both are undefined, or both are defined and equal. Here application is strict in the sense that for
$t \simeq s$
if either both are undefined, or both are defined and equal. Here application is strict in the sense that for
![]() $t_1t_2$
to be defined, it is required that both
$t_1t_2$
to be defined, it is required that both
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are defined.
$t_2$
are defined.
Definition 2.1.
A pas
![]() $\mathcal{A}$
is called combinatory complete if for any term
$\mathcal{A}$
is called combinatory complete if for any term
![]() $t(x_1,\ldots, x_n,x)$
,
$t(x_1,\ldots, x_n,x)$
,
![]() $n\geqslant 0$
, with free variables among
$n\geqslant 0$
, with free variables among
![]() $x_1,\ldots, x_n,x$
, there exists
$x_1,\ldots, x_n,x$
, there exists
![]() $b\in \mathcal{A}$
such that for all
$b\in \mathcal{A}$
such that for all
![]() $a_1,\ldots, a_n,a\in \mathcal{A}$
,
$a_1,\ldots, a_n,a\in \mathcal{A}$
,
-
(i)
 $ba_1\cdots a_n\!\downarrow$
,
$ba_1\cdots a_n\!\downarrow$
, -
(ii)
 $ba_1\cdots a_n a \simeq t(a_1,\ldots, a_n,a)$
.
$ba_1\cdots a_n a \simeq t(a_1,\ldots, a_n,a)$
.
A pas
![]() $\mathcal{A}$
is a pca if it is combinatory complete. A ca is a pca for which the application operator is total.
$\mathcal{A}$
is a pca if it is combinatory complete. A ca is a pca for which the application operator is total.
Combinatory completeness of pcas can be characterized by the existence of combinators
![]() $k$
and
$k$
and
![]() $s$
, just as in classical ca and lambda calculus. In van Oosten (Reference van Oosten2008), it is stated that the following theorem is “essentially due to Feferman (Reference Feferman and Crossley1975).”
$s$
, just as in classical ca and lambda calculus. In van Oosten (Reference van Oosten2008), it is stated that the following theorem is “essentially due to Feferman (Reference Feferman and Crossley1975).”
Theorem 2.2. (Feferman) A pas
![]() $\mathcal{A}$
is a pca if and only if it has elements
$\mathcal{A}$
is a pca if and only if it has elements
![]() $k$
and
$k$
and
![]() $s$
with the following properties for all
$s$
with the following properties for all
![]() $a,b,c\in \mathcal{A}$
:
$a,b,c\in \mathcal{A}$
:
-
•
 $ka\!\downarrow$
and
$ka\!\downarrow$
and
 $kab = a$
,
$kab = a$
, -
•
 $sab\!\downarrow$
and
$sab\!\downarrow$
and
 $sabc \simeq ac(bc)$
.
$sabc \simeq ac(bc)$
.
In the following, we will always assume that our pcas are nontrivial, that is, have more than one element. This automatically implies that they are infinite and have
![]() $k\neq s$
.
$k\neq s$
.
The prime example of a pca is Kleene’s first model
![]() $\mathcal{K}_1$
that was already mentioned in the introduction. This is a model defined on the natural numbers, with application
$\mathcal{K}_1$
that was already mentioned in the introduction. This is a model defined on the natural numbers, with application
Thus
![]() $\mathcal{K}_1$
models the setting of classical computability theory. We can also relativize this to an arbitrary oracle
$\mathcal{K}_1$
models the setting of classical computability theory. We can also relativize this to an arbitrary oracle
![]() $X$
, thus obtaining the relativized pca
$X$
, thus obtaining the relativized pca
![]() $\mathcal{K}_1^X$
.
$\mathcal{K}_1^X$
.
Kleene’s second model
![]() $\mathcal{K}_2$
, from the book Kleene and Vesley (Reference Kleene and Vesley1965), is a pca defined on Baire space
$\mathcal{K}_2$
, from the book Kleene and Vesley (Reference Kleene and Vesley1965), is a pca defined on Baire space
![]() $\omega ^\omega$
. Application
$\omega ^\omega$
. Application
![]() $\alpha \cdot \beta$
in this model can be informally described as applying the continuous functional with code
$\alpha \cdot \beta$
in this model can be informally described as applying the continuous functional with code
![]() $\alpha$
to the real
$\alpha$
to the real
![]() $\beta$
. The original coding of
$\beta$
. The original coding of
![]() $\mathcal{K}_2$
is a bit cumbersome, but it is essentially equivalent to
$\mathcal{K}_2$
is a bit cumbersome, but it is essentially equivalent to
where
![]() $\Phi _e$
is the
$\Phi _e$
is the
![]() $e$
-th Turing functional, and the application is understood to be defined if the RHS is total. This coding, used in Shafer and Terwijn (Reference Shafer and Terwijn2021), is easier to work with. See the appendix of Golov and Terwijn (Reference Golov and Terwijn2023) for a proof (and precise statement) of the equivalence with the original coding.
$e$
-th Turing functional, and the application is understood to be defined if the RHS is total. This coding, used in Shafer and Terwijn (Reference Shafer and Terwijn2021), is easier to work with. See the appendix of Golov and Terwijn (Reference Golov and Terwijn2023) for a proof (and precise statement) of the equivalence with the original coding.
An interesting variant of
![]() $\mathcal{K}_2$
, called the van Oosten model, is obtained by extending the domain to include partial functions, cf. van Oosten (Reference van Oosten, Cooper and Truss1999).
$\mathcal{K}_2$
, called the van Oosten model, is obtained by extending the domain to include partial functions, cf. van Oosten (Reference van Oosten, Cooper and Truss1999).
![]() $\mathcal{K}_2$
is uncountable, but restricting attention to computable sequences gives a countable pca
$\mathcal{K}_2$
is uncountable, but restricting attention to computable sequences gives a countable pca
![]() $\mathcal{K}_2^{\mathrm{eff}}$
. Similarly, restricting to
$\mathcal{K}_2^{\mathrm{eff}}$
. Similarly, restricting to
![]() $X$
-computable sequences gives a pca
$X$
-computable sequences gives a pca
![]() $\mathcal{K}_2^X$
for every
$\mathcal{K}_2^X$
for every
![]() $X$
. In Golov and Terwijn (Reference Golov and Terwijn2023), the relations between these and other pcas are studied using embeddings.
$X$
. In Golov and Terwijn (Reference Golov and Terwijn2023), the relations between these and other pcas are studied using embeddings.
Many other examples of pcas can be found in the literature. For example, pcas have been extensively used in constructive mathematics, see Beeson (Reference Beeson1985), Troelstra and van Dalen (Reference Troelstra and van Dalen1988). In particular, they have been used as a basis for models of constructive set theory, as in McCarty (Reference McCarty1986), Rathjen (Reference Rathjen2006), and Frittaion and Rathjen (Reference Frittaion and Rathjen2021). Pcas are also pivotal in the categorical treatment of realizability, cf. van Oosten (Reference van Oosten2008, Chapter 2) where they serve as a basis for realizability toposes. In particular, Hyland’s famous effective topos is the realizability topos of
![]() $\mathcal{K}_1$
. For a categorical characterization of pcas, see Cockett and Hofstra (Reference Cockett and Hofstra2008) (extending early work of Longo and Moggi Reference Longo, Moggi, Chytil and Koubek1984); for a discussion of pcas in the context of oracles see Kihara (Reference Kihara2022).
$\mathcal{K}_1$
. For a categorical characterization of pcas, see Cockett and Hofstra (Reference Cockett and Hofstra2008) (extending early work of Longo and Moggi Reference Longo, Moggi, Chytil and Koubek1984); for a discussion of pcas in the context of oracles see Kihara (Reference Kihara2022).
A pca that has been particularly important in connection with ca and lambda calculus is Scott’s graph model (Scott Reference Scott and Kanger1975). This pca is a model of the lambda calculus (see Barendregt Reference Barendregt1984), and it is also closely related to the enumeration degrees in computability theory, cf. Odifreddi (Reference Odifreddi1999). We will discuss this model in Section 5, where we also explain how the restriction of this model to the c.e. sets can be seen as a completion of
![]() $\mathcal{K}_1$
.
$\mathcal{K}_1$
.
3. Effective Presentations of Pcas
Below, we will call a ca
![]() $\mathcal{A}$
$\mathcal{A}$
![]() $Y$
-computable if
$Y$
-computable if
![]() $\mathcal{A}$
has a representation such that the application
$\mathcal{A}$
has a representation such that the application
![]() $\cdot$
in
$\cdot$
in
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-computable. We will also require that equality on
$Y$
-computable. We will also require that equality on
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-decidable. The following definition (similar to notions used in Golov and Terwijn Reference Golov and Terwijn2023) makes this precise, using numberings to represent
$Y$
-decidable. The following definition (similar to notions used in Golov and Terwijn Reference Golov and Terwijn2023) makes this precise, using numberings to represent
![]() $\mathcal{A}$
. Recall that a numbering is a surjective function
$\mathcal{A}$
. Recall that a numbering is a surjective function
![]() $\gamma :\omega \to \mathcal{A}$
. We think of
$\gamma :\omega \to \mathcal{A}$
. We think of
![]() $n\in \omega$
as a code for
$n\in \omega$
as a code for
![]() $\gamma (n)\in \mathcal{A}$
.
$\gamma (n)\in \mathcal{A}$
.
Definition 3.1.
Let
![]() $\mathcal{A}$
be a pca and
$\mathcal{A}$
be a pca and
![]() $Y\subseteq \omega$
. We call
$Y\subseteq \omega$
. We call
![]() $\mathcal{A}$
partial
$\mathcal{A}$
partial
![]() $Y$
-computable if there exist a numbering
$Y$
-computable if there exist a numbering
![]() $\gamma :\omega \to \mathcal{A}$
and a partial
$\gamma :\omega \to \mathcal{A}$
and a partial
![]() $Y$
-computable function
$Y$
-computable function
![]() $\psi$
such that for all
$\psi$
such that for all
![]() $n$
and
$n$
and
![]() $m$
,
$m$
,
![]() $\gamma (n)\cdot \gamma (m)\!\downarrow$
in
$\gamma (n)\cdot \gamma (m)\!\downarrow$
in
![]() $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
![]() $\psi (n,m)\!\downarrow$
, and
$\psi (n,m)\!\downarrow$
, and
We also require that equality on
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-decidable, meaning that the set
$Y$
-decidable, meaning that the set
![]() $\{(n,m)\mid \gamma (n)=\gamma (m)\}$
is
$\{(n,m)\mid \gamma (n)=\gamma (m)\}$
is
![]() $Y$
-computable. If
$Y$
-computable. If
![]() $\mathcal{A}$
is total, i.e., a ca, then
$\mathcal{A}$
is total, i.e., a ca, then
![]() $\psi$
is total, and we simply call
$\psi$
is total, and we simply call
![]() $\mathcal{A}$
$\mathcal{A}$
![]() $Y$
-computable. (This is consistent with Definition 3.2 below.)
$Y$
-computable. (This is consistent with Definition 3.2 below.)
Notice that the numbering
![]() $\gamma$
in Definition 3.1 is not required to be computable in any way. Also, nontrivial combinatorial algebras are never computable, cf. Barendregt (Reference Barendregt1984, 5.1.15).
$\gamma$
in Definition 3.1 is not required to be computable in any way. Also, nontrivial combinatorial algebras are never computable, cf. Barendregt (Reference Barendregt1984, 5.1.15).
Definition 3.1 focuses on representing application in a pca as a p.c. function. For the record, we also mention another way to define effective representations.
Definition 3.2.
We call a pca
![]() $\mathcal{A}$
$\mathcal{A}$
![]() $Y$
-c.e. if there exist a numbering
$Y$
-c.e. if there exist a numbering
![]() $\gamma :\omega \to \mathcal{A}$
such that the set
$\gamma :\omega \to \mathcal{A}$
such that the set
is
![]() $Y$
-c.e. Again we also require that equality on
$Y$
-c.e. Again we also require that equality on
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-decidable, meaning that the set
$Y$
-decidable, meaning that the set
![]() $\{(n,m)\mid \gamma (n)=\gamma (m)\}$
is
$\{(n,m)\mid \gamma (n)=\gamma (m)\}$
is
![]() $Y$
-computable. We call
$Y$
-computable. We call
![]() $\mathcal{A}$
$\mathcal{A}$
![]() $Y$
-computable if the set (2) is
$Y$
-computable if the set (2) is
![]() $Y$
-computable.
Footnote
1
$Y$
-computable.
Footnote
1
As an example, note that
![]() $\mathcal{K}_1$
is p.c. in the sense that
$\mathcal{K}_1$
is p.c. in the sense that
![]() $a\cdot b$
is a p.c. function on
$a\cdot b$
is a p.c. function on
![]() $\omega$
, and that
$\omega$
, and that
![]() $\mathcal{K}_1$
is c.e. in the sense that
$\mathcal{K}_1$
is c.e. in the sense that
![]() $a\cdot b\!\downarrow = c$
is a c.e. relation. We note here that the two definitions are equivalent:
$a\cdot b\!\downarrow = c$
is a c.e. relation. We note here that the two definitions are equivalent:
Proposition 3.3.
A pca is partial
![]() $Y$
-computable if and only if it is
$Y$
-computable if and only if it is
![]() $Y$
-c.e.
$Y$
-c.e.
Proof.
We always have c.e. implies p.c.: Given
![]() $n,m$
, search for
$n,m$
, search for
![]() $k$
such that
$k$
such that
![]() $(n,m,k)$
is in the set (2), and define
$(n,m,k)$
is in the set (2), and define
![]() $\psi (n,m)$
to be the least
$\psi (n,m)$
to be the least
![]() $k$
found. (Note that
$k$
found. (Note that
![]() $\gamma$
need not be injective, so there may be multiple such
$\gamma$
need not be injective, so there may be multiple such
![]() $k$
.) Then Equation (1) holds for
$k$
.) Then Equation (1) holds for
![]() $\psi (n,m)$
.
$\psi (n,m)$
.
The converse direction uses the condition that equality on
![]() $\mathcal{A}$
is decidable. Given
$\mathcal{A}$
is decidable. Given
![]() $\mathcal{A}$
p.c. and
$\mathcal{A}$
p.c. and
![]() $\psi$
satisfying (1), enumerate
$\psi$
satisfying (1), enumerate
![]() $(n,m,k)$
if
$(n,m,k)$
if
![]() $\psi (n,m)\!\downarrow$
and
$\psi (n,m)\!\downarrow$
and
![]() $\gamma (k) = \gamma (\psi (n,m))$
. This gives an enumeration of Equation (2).
$\gamma (k) = \gamma (\psi (n,m))$
. This gives an enumeration of Equation (2).
Note that the above definitions are in the spirit of the c.e. structures in Selivanov (Reference Selivanov, Cooper and Goncharov2003), where they are called positive structures. These are defined as structures in which the predicates are c.e., and the functions are computable. The latter makes sense for total functions, but in the case of pcas, we are dealing with a partial application operator, in which case it is natural to have this as a c.e. function.
For pcas on
![]() $\omega$
(i.e. with
$\omega$
(i.e. with
![]() $\gamma :\omega \to \mathcal{A}$
the identity), we have that equality on
$\gamma :\omega \to \mathcal{A}$
the identity), we have that equality on
![]() $\mathcal{A}$
is decidable, so the two notions of pca are equivalent. This is the type of pca that was used in Fokina and Terwijn (Reference Fokina and Terwijn2024). Without the condition that equality on
$\mathcal{A}$
is decidable, so the two notions of pca are equivalent. This is the type of pca that was used in Fokina and Terwijn (Reference Fokina and Terwijn2024). Without the condition that equality on
![]() $\mathcal{A}$
is decidable (or c.e.), it is not clear that the two definitions are equivalent in general, though we do not know of an example of a pca that is p.c. but not c.e.
$\mathcal{A}$
is decidable (or c.e.), it is not clear that the two definitions are equivalent in general, though we do not know of an example of a pca that is p.c. but not c.e.
Finally, in the case of a
![]() $Y$
-computable pca or ca
$Y$
-computable pca or ca
![]() $\mathcal{A}$
(which is what we will mostly use below), the requirement that equality on
$\mathcal{A}$
(which is what we will mostly use below), the requirement that equality on
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-decidable actually follows from the fact that Equation (2) is
$Y$
-decidable actually follows from the fact that Equation (2) is
![]() $Y$
-computable, namely let
$Y$
-computable, namely let
![]() $n$
be such that
$n$
be such that
![]() $\gamma (n)$
is the identity (which exists in any pca).
$\gamma (n)$
is the identity (which exists in any pca).
4. Embeddings and Isomorphisms
There are at least three notions of embedding for pcas, depending on what structure is required to be preserved. For example, the choice of the combinators
![]() $k$
and
$k$
and
![]() $s$
from Theorem 2.2 can be regarded as part of the structure or not. For instance, Zoethout (Reference Zoethout2022, p. 33) does not consider
$s$
from Theorem 2.2 can be regarded as part of the structure or not. For instance, Zoethout (Reference Zoethout2022, p. 33) does not consider
![]() $k$
and
$k$
and
![]() $s$
to be part of the structure of a pca. We have the following notions of embedding of pcas:
$s$
to be part of the structure of a pca. We have the following notions of embedding of pcas:
-
• Only preserve applications. This notion was studied in Bethke (Reference Bethke1988), Asperti and Ciabattoni (Reference Asperti and Ciabattoni1997), Shafer and Terwijn (Reference Shafer and Terwijn2021), and Golov and Terwijn (Reference Golov and Terwijn2023).
-
• Besides applications, also preserve
 $k$
and
$k$
and
 $s$
, for a particular choice of these combinators. This stronger notion was studied in Bethke et al. (Reference Bethke, Klop and de Vrijer1996, Reference Bethke, Klop and de Vrijer1999).
$s$
, for a particular choice of these combinators. This stronger notion was studied in Bethke et al. (Reference Bethke, Klop and de Vrijer1996, Reference Bethke, Klop and de Vrijer1999). -
• There is an even weaker notion of embedding, using the notion of applicative morphism, that was introduced in Longley (Reference Longley1994), see also Longley and Normann (Reference Longley and Normann2015). Applicative morphisms do not have to preserve applications; instead, there have to be terms in the codomain that simulate applications in the domain. This notion is useful in realizability theory, see van Oosten (Reference van Oosten2008).
Our primary interest here is the notion of embedding where
![]() $k$
and
$k$
and
![]() $s$
are not considered part of the signature, but we will also be using the stronger notion of embedding, especially when we talk about completions. To distinguish the two, we will refer to them as weak and strong embeddings. (In Golov and Terwijn Reference Golov and Terwijn2023, weak embeddings were simply called embeddings.) To distinguish applications in different pcas, we also write
$s$
are not considered part of the signature, but we will also be using the stronger notion of embedding, especially when we talk about completions. To distinguish the two, we will refer to them as weak and strong embeddings. (In Golov and Terwijn Reference Golov and Terwijn2023, weak embeddings were simply called embeddings.) To distinguish applications in different pcas, we also write
![]() $\mathcal{A}\models a\cdot b\!\downarrow$
if this application is defined in
$\mathcal{A}\models a\cdot b\!\downarrow$
if this application is defined in
![]() $\mathcal{A}$
.
$\mathcal{A}$
.
Definition 4.1.
For given pcas
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
, an injection
$\mathcal{B}$
, an injection
![]() $f: \mathcal{A} \to \mathcal{B}$
is a weak embedding if for all
$f: \mathcal{A} \to \mathcal{B}$
is a weak embedding if for all
![]() $a, b \in \mathcal{A}$
,
$a, b \in \mathcal{A}$
,
If
![]() $\mathcal{A}$
embeds into
$\mathcal{A}$
embeds into
![]() $\mathcal{B}$
, in this way we write
$\mathcal{B}$
, in this way we write
![]() $\mathcal{A}\hookrightarrow \mathcal{B}$
. If in addition to (3), for a specific choice of combinators
$\mathcal{A}\hookrightarrow \mathcal{B}$
. If in addition to (3), for a specific choice of combinators
![]() $k$
and
$k$
and
![]() $s$
of
$s$
of
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $f(k)$
and
$f(k)$
and
![]() $f(s)$
serve as combinators for
$f(s)$
serve as combinators for
![]() $\mathcal{B}$
, we call
$\mathcal{B}$
, we call
![]() $f$
a strong embedding.
$f$
a strong embedding.
A (total) ca
![]() $\mathcal{B}$
is called a weak completion of
$\mathcal{B}$
is called a weak completion of
![]() $\mathcal{A}$
if there exists a weak embedding
$\mathcal{A}$
if there exists a weak embedding
![]() $\mathcal{A} \hookrightarrow \mathcal{B}$
. If the embedding is strong, we call
$\mathcal{A} \hookrightarrow \mathcal{B}$
. If the embedding is strong, we call
![]() $\mathcal{B}$
a strong completion.
$\mathcal{B}$
a strong completion.
Two pcas
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are isomorphic, denoted by
$\mathcal{B}$
are isomorphic, denoted by
![]() $\mathcal{A}\cong \mathcal{B}$
, if there exists a bijection
$\mathcal{A}\cong \mathcal{B}$
, if there exists a bijection
![]() $f:\mathcal{A}\rightarrow \mathcal{B}$
such that for all
$f:\mathcal{A}\rightarrow \mathcal{B}$
such that for all
![]() $a,b\in \mathcal{A}$
,
$a,b\in \mathcal{A}$
,
![]() $ab\!\downarrow$
if and only if
$ab\!\downarrow$
if and only if
![]() $f(a)f(b)\!\downarrow$
, and in this case
$f(a)f(b)\!\downarrow$
, and in this case
Besides the term completion, in the literature also the term extension is used. Bethke et al. (Reference Bethke, Klop and de Vrijer1999, Definition 1.5) call a pca
![]() $\mathcal{B}$
an extension of a pca
$\mathcal{B}$
an extension of a pca
![]() $\mathcal{A}$
if
$\mathcal{A}$
if
![]() $\mathcal{A} \subseteq \mathcal{B}$
, the application
$\mathcal{A} \subseteq \mathcal{B}$
, the application
![]() $\cdot _{\mathcal{A}}$
in
$\cdot _{\mathcal{A}}$
in
![]() $\mathcal{A}$
is the restriction of application
$\mathcal{A}$
is the restriction of application
![]() $\cdot _{\mathcal{B}}$
in
$\cdot _{\mathcal{B}}$
in
![]() $\mathcal{B}$
to the domain of
$\mathcal{B}$
to the domain of
![]() $\cdot _{\mathcal{A}}$
, and
$\cdot _{\mathcal{A}}$
, and
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $\mathcal{A}$
both have the same combinators
$\mathcal{A}$
both have the same combinators
![]() $k$
and
$k$
and
![]() $s$
as in Theorem 2.2.
$s$
as in Theorem 2.2.
Now suppose that
![]() $f:\mathcal{A}\hookrightarrow \mathcal{B}$
is a strong embedding. Then
$f:\mathcal{A}\hookrightarrow \mathcal{B}$
is a strong embedding. Then
![]() $f(\mathcal{A})\subseteq \mathcal{B}$
is an extension in the above sense, where both
$f(\mathcal{A})\subseteq \mathcal{B}$
is an extension in the above sense, where both
![]() $f(\mathcal{A})$
and
$f(\mathcal{A})$
and
![]() $\mathcal{B}$
have combinators
$\mathcal{B}$
have combinators
![]() $f(k)$
and
$f(k)$
and
![]() $f(s)$
. Note that
$f(s)$
. Note that
![]() $\mathcal{A} \cong f(\mathcal{A})$
if we define application in
$\mathcal{A} \cong f(\mathcal{A})$
if we define application in
![]() $f(\mathcal{A})$
by
$f(\mathcal{A})$
by
![]() $f(\mathcal{A})\models f(a)\cdot f(b) \!\downarrow =f(c)$
if and only if
$f(\mathcal{A})\models f(a)\cdot f(b) \!\downarrow =f(c)$
if and only if
![]() $\mathcal{A}\models a \cdot b\!\downarrow = c$
. So we see that total extensions and completions amount to the same thing, provided that in both cases we have to specify whether to also fix
$\mathcal{A}\models a \cdot b\!\downarrow = c$
. So we see that total extensions and completions amount to the same thing, provided that in both cases we have to specify whether to also fix
![]() $s$
and
$s$
and
![]() $k$
or not.
$k$
or not.
In Terwijn (Reference Terwijn2023), it is shown that weak and strong embeddability and completions are different: There exists a pca that is weakly completable, but not strongly completable.Footnote 2
5. Complexity of Completions of
 $\mathcal{K}_1$
$\mathcal{K}_1$
It was an important open question in the 1970s whether every pca has a strong completion. The question was raised by Barendregt, Mitschke, and Scott, and discussed at a meeting in Swansea in 1974, cf. Bethke et al. (Reference Bethke, Klop and de Vrijer1999). (Note that this predates Feferman’s paper Feferman Reference Feferman and Crossley1975.) A negative answer was obtained by Klop (Reference Klop1982), see also Bethke et al. (Reference Bethke, Klop and de Vrijer1999). Other examples of incompletable pcas can be found in Bethke (Reference Bethke1987) and Bethke and Klop (Reference Bethke, Klop, Dowek, Heering, Meinke and Möller1996).
In contrast to these examples,
![]() $\mathcal{K}_1$
does have strong completions. This follows from the criterion given in Bethke et al. (Reference Bethke, Klop and de Vrijer1996) about the existence of unique head-normal forms, which is satisfied in
$\mathcal{K}_1$
does have strong completions. This follows from the criterion given in Bethke et al. (Reference Bethke, Klop and de Vrijer1996) about the existence of unique head-normal forms, which is satisfied in
![]() $\mathcal{K}_1$
. The completion of
$\mathcal{K}_1$
. The completion of
![]() $\mathcal{K}_1$
resulting from this is a certain term model
$\mathcal{K}_1$
resulting from this is a certain term model
![]() $T(\omega )/\!\!\sim$
. On the face of it, the equivalence relation
$T(\omega )/\!\!\sim$
. On the face of it, the equivalence relation
![]() $\sim$
is not computable, since it is essentially equivalence of terms in
$\sim$
is not computable, since it is essentially equivalence of terms in
![]() $\mathcal{K}_1$
. That indeed it cannot be computable follows from Theorem 5.2, and also from the fact that computable combinatorial algebras do not exist.
$\mathcal{K}_1$
. That indeed it cannot be computable follows from Theorem 5.2, and also from the fact that computable combinatorial algebras do not exist.
We now discuss how another famous pca can be seen as a completion of
![]() $\mathcal{K}_1$
. Scott’s graph model
$\mathcal{K}_1$
. Scott’s graph model
![]() $\mathcal{G}$
is a pca defined on the power set
$\mathcal{G}$
is a pca defined on the power set
![]() $\mathcal{P}(\omega )$
, with application defined by
$\mathcal{P}(\omega )$
, with application defined by
Here
![]() $D_u$
as always denotes the finite set with canonical code
$D_u$
as always denotes the finite set with canonical code
![]() $u$
, and
$u$
, and
![]() $\langle \cdot, \cdot \rangle$
denotes an effective pairing function.
$\langle \cdot, \cdot \rangle$
denotes an effective pairing function.
![]() $\mathcal{E}$
is defined as the restriction of
$\mathcal{E}$
is defined as the restriction of
![]() $\mathcal{G}$
to the c.e. sets. That
$\mathcal{G}$
to the c.e. sets. That
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $\mathcal{E}$
are (total) cas is implicit in Scott (Reference Scott and Kanger1975). Note the close connection with enumeration reducibility (cf. Odifreddi Reference Odifreddi1999, XIV): For all sets
$\mathcal{E}$
are (total) cas is implicit in Scott (Reference Scott and Kanger1975). Note the close connection with enumeration reducibility (cf. Odifreddi Reference Odifreddi1999, XIV): For all sets
![]() $Y$
and
$Y$
and
![]() $Z$
,
$Z$
,
![]() $Z\leqslant _e Y$
is equivalent with
$Z\leqslant _e Y$
is equivalent with
![]() $X\cdot Y = Z$
for some c.e. set
$X\cdot Y = Z$
for some c.e. set
![]() $X$
.
$X$
.
In Golov and Terwijn (Reference Golov and Terwijn2023, Corollary 7.5, it was shown that
![]() $\mathcal{K}_1 \hookrightarrow \mathcal{E}$
, so that we can see
$\mathcal{K}_1 \hookrightarrow \mathcal{E}$
, so that we can see
![]() $\mathcal{E}$
as a weak completion of
$\mathcal{E}$
as a weak completion of
![]() $\mathcal{K}_1$
. Note that equality on
$\mathcal{K}_1$
. Note that equality on
![]() $\mathcal{E}$
is equality of c.e. sets, which is
$\mathcal{E}$
is equality of c.e. sets, which is
![]() $\Pi ^0_2$
-complete when we represent c.e. sets by their indices.Footnote
3
So this is more complicated than equality in the term model
$\Pi ^0_2$
-complete when we represent c.e. sets by their indices.Footnote
3
So this is more complicated than equality in the term model
![]() $T(\omega )/\!\!\sim$
.
$T(\omega )/\!\!\sim$
.
We can see
![]() $\mathcal{E}$
as a combination of
$\mathcal{E}$
as a combination of
![]() $\mathcal{K}_1$
and
$\mathcal{K}_1$
and
![]() $\mathcal{K}_2$
. Indeed we have
$\mathcal{K}_2$
. Indeed we have
(the latter by Golov and Terwijn Reference Golov and Terwijn2023, Corollary 6.2, so that we can view
![]() $\mathcal{E}$
as a kind of middle ground between Kleene’s models. This combination famously gives a model of the
$\mathcal{E}$
as a kind of middle ground between Kleene’s models. This combination famously gives a model of the
![]() $\lambda$
-calculus, as shown in Scott (Reference Scott and Kanger1975), see Odifreddi (Reference Odifreddi1999, XIV.4).
$\lambda$
-calculus, as shown in Scott (Reference Scott and Kanger1975), see Odifreddi (Reference Odifreddi1999, XIV.4).
Below, we use that for an embedding
![]() $f:\mathcal{K}_1\hookrightarrow \mathcal{A}$
of
$f:\mathcal{K}_1\hookrightarrow \mathcal{A}$
of
![]() $\mathcal{K}_1$
into a pca
$\mathcal{K}_1$
into a pca
![]() $\mathcal{A}$
, it suffices to know the value of
$\mathcal{A}$
, it suffices to know the value of
![]() $f$
on finitely many elements. This observation was also used in Golov and Terwijn (Reference Golov and Terwijn2023, Theorem 4.1), and it can be used to bypass the fact that embeddings such as
$f$
on finitely many elements. This observation was also used in Golov and Terwijn (Reference Golov and Terwijn2023, Theorem 4.1), and it can be used to bypass the fact that embeddings such as
![]() $f$
do not have to be computable. Below we give a somewhat simpler version of this trick, using the following lemma.
$f$
do not have to be computable. Below we give a somewhat simpler version of this trick, using the following lemma.
Lemma 5.1.
There exist elements
![]() $t_n\in \mathcal{K}_1$
,
$t_n\in \mathcal{K}_1$
,
![]() $n\geqslant 1$
, such that for all
$n\geqslant 1$
, such that for all
![]() $n$
and
$n$
and
![]() $m$
,
$m$
,
 \begin{align*} t_n \cdot m = \begin{cases} n & \textrm{if}\ m=0 \\ t_{n+1} & \textrm{if}\ m\gt 0. \end{cases} \end{align*}
\begin{align*} t_n \cdot m = \begin{cases} n & \textrm{if}\ m=0 \\ t_{n+1} & \textrm{if}\ m\gt 0. \end{cases} \end{align*}
Proof.
By the recursion theorem, let
![]() $d\in \omega$
be a code such that
$d\in \omega$
be a code such that
 \begin{align*} \varphi _d(n,m) = \begin{cases} n & \text{if $m=0$} \\ S^1_1(d,n+1) & \text{if $m\gt 0$.} \end{cases} \end{align*}
\begin{align*} \varphi _d(n,m) = \begin{cases} n & \text{if $m=0$} \\ S^1_1(d,n+1) & \text{if $m\gt 0$.} \end{cases} \end{align*}
Here
![]() $S^1_1$
is the primitive recursive function from the S-m-n-theorem. Define
$S^1_1$
is the primitive recursive function from the S-m-n-theorem. Define
![]() $t_n = S^1_1(d,n)$
. W.l.o.g. we may assume
$t_n = S^1_1(d,n)$
. W.l.o.g. we may assume
![]() $t_n\gt 0$
for all
$t_n\gt 0$
for all
![]() $n$
. Then
$n$
. Then
![]() $\varphi _{t_n}(m) = \varphi _{S^1_1(d,n)}(m) = \varphi _d(n,m) = t_{n+1}$
for
$\varphi _{t_n}(m) = \varphi _{S^1_1(d,n)}(m) = \varphi _d(n,m) = t_{n+1}$
for
![]() $m\gt 0$
and equal to
$m\gt 0$
and equal to
![]() $n$
otherwise.
$n$
otherwise.
In Golov and Terwijn (Reference Golov and Terwijn2023, Corollary 4.2, it was proved that if
![]() $\mathcal{K}_1^X\hookrightarrow \mathcal{A}$
is a weak embedding of
$\mathcal{K}_1^X\hookrightarrow \mathcal{A}$
is a weak embedding of
![]() $\mathcal{K}_1^X$
into a pca
$\mathcal{K}_1^X$
into a pca
![]() $\mathcal{A}$
with
$\mathcal{A}$
with
![]() $Y$
-c.e. inequality, then
$Y$
-c.e. inequality, then
![]() $X\leqslant _T Y$
. We obtain a stronger conclusion when we assume that
$X\leqslant _T Y$
. We obtain a stronger conclusion when we assume that
![]() $\mathcal{A}$
is total and
$\mathcal{A}$
is total and
![]() $Y$
-computable.
$Y$
-computable.
Theorem 5.2.
Suppose
![]() $\mathcal{A}$
is a
$\mathcal{A}$
is a
![]() $Y$
-computable combinatorial algebra, and that
$Y$
-computable combinatorial algebra, and that
![]() $f:\mathcal{K}_1^X\hookrightarrow \mathcal{A}$
is a weak embedding. Then
$f:\mathcal{K}_1^X\hookrightarrow \mathcal{A}$
is a weak embedding. Then
![]() $X \lt _T Y$
.
$X \lt _T Y$
.
Proof.
The successor function
![]() $S$
in
$S$
in
![]() $\mathcal{K}_1$
satisfies
$\mathcal{K}_1$
satisfies
![]() $S^n(0)=n$
, but we need an element
$S^n(0)=n$
, but we need an element
![]() $t$
such that the
$t$
such that the
![]() $n$
-fold application
$n$
-fold application
![]() $t\cdot \ldots \cdot t\cdot 0$
equals
$t\cdot \ldots \cdot t\cdot 0$
equals
![]() $n$
, with the convention that application associates to the left, not to the right. Let
$n$
, with the convention that application associates to the left, not to the right. Let
![]() $t = t_1$
be as in Lemma 5.1. Then for the
$t = t_1$
be as in Lemma 5.1. Then for the
![]() $n$
-fold application, we have
$n$
-fold application, we have
![]() $t\cdot \ldots \cdot t\cdot 0 = t_n \cdot 0 = n$
for every
$t\cdot \ldots \cdot t\cdot 0 = t_n \cdot 0 = n$
for every
![]() $n\gt 0$
. Since
$n\gt 0$
. Since
![]() $f$
is an embedding, we obtain from this
$f$
is an embedding, we obtain from this
with the applications repeated
![]() $n$
times. So we see that the image of
$n$
times. So we see that the image of
![]() $f$
is completely determined by
$f$
is completely determined by
![]() $f(t)$
and
$f(t)$
and
![]() $f(0)$
.
$f(0)$
.
To show that
![]() $Y\not \leqslant _T X$
, let
$Y\not \leqslant _T X$
, let
![]() $A$
,
$A$
,
![]() $B$
be a
$B$
be a
![]() $X$
-computably inseparable pair of
$X$
-computably inseparable pair of
![]() $X$
-c.e. sets, and let
$X$
-c.e. sets, and let
![]() $e$
be a code such that for all
$e$
be a code such that for all
![]() $x$
,
$x$
,
 \begin{align*} \varphi _e^X(x) = \begin{cases} 0 & \text{if $x\in A$} \\ 1 & \text{if $x\in B$} \\ \uparrow & \text{otherwise}. \end{cases} \end{align*}
\begin{align*} \varphi _e^X(x) = \begin{cases} 0 & \text{if $x\in A$} \\ 1 & \text{if $x\in B$} \\ \uparrow & \text{otherwise}. \end{cases} \end{align*}
Then we have in particular that
Since
![]() $\mathcal{A}$
is total, for every
$\mathcal{A}$
is total, for every
![]() $x$
the application
$x$
the application
![]() $f(e)\cdot f(x)$
is always defined in
$f(e)\cdot f(x)$
is always defined in
![]() $\mathcal{A}$
, and by Equation (4), it is equal to a term containing only
$\mathcal{A}$
, and by Equation (4), it is equal to a term containing only
![]() $f(t)$
,
$f(t)$
,
![]() $f(0)$
, and application. Because
$f(0)$
, and application. Because
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-computable, we can compute a code of
$Y$
-computable, we can compute a code of
![]() $f(e)\cdot f(x)$
effectively from
$f(e)\cdot f(x)$
effectively from
![]() $x$
. (All we need is
$x$
. (All we need is
![]() $e$
, and codes of
$e$
, and codes of
![]() $f(t)$
and
$f(t)$
and
![]() $f(0)$
, all of which are fixed.) Furthermore, since the definition of
$f(0)$
, all of which are fixed.) Furthermore, since the definition of
![]() $Y$
-computable pca entails that equality on
$Y$
-computable pca entails that equality on
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-decidable, we can decide with
$Y$
-decidable, we can decide with
![]() $Y$
whether
$Y$
whether
![]() $f(e)\cdot f(x)$
is equal to
$f(e)\cdot f(x)$
is equal to
![]() $f(0)$
or
$f(0)$
or
![]() $f(1)$
or not. It follows that the set
$f(1)$
or not. It follows that the set
![]() $C = \{x \mid \mathcal{A}\models f(e)\cdot f(x) = f(0)\}$
is
$C = \{x \mid \mathcal{A}\models f(e)\cdot f(x) = f(0)\}$
is
![]() $Y$
-computable and separates
$Y$
-computable and separates
![]() $A$
and
$A$
and
![]() $B$
, and since
$B$
, and since
![]() $A$
and
$A$
and
![]() $B$
have no
$B$
have no
![]() $X$
-computable separation
$X$
-computable separation
![]() $Y$
is not
$Y$
is not
![]() $X$
-computable.
$X$
-computable.
That
![]() $X\leqslant _T Y$
can be shown using a very similar argument. Instead of
$X\leqslant _T Y$
can be shown using a very similar argument. Instead of
![]() $\varphi _e^X$
above, use the characteristic function
$\varphi _e^X$
above, use the characteristic function
![]() $\varphi _d^X(x)$
which is
$\varphi _d^X(x)$
which is
![]() $0$
if
$0$
if
![]() $x\in X$
and
$x\in X$
and
![]() $1$
if
$1$
if
![]() $x\notin X$
. Then the rest of the argument above, replacing
$x\notin X$
. Then the rest of the argument above, replacing
![]() $e$
with
$e$
with
![]() $d$
, shows that
$d$
, shows that
![]() $X$
is
$X$
is
![]() $Y$
-computable. So we have
$Y$
-computable. So we have
![]() $Y\not \leqslant _T X$
and
$Y\not \leqslant _T X$
and
![]() $X\leqslant _T Y$
, hence
$X\leqslant _T Y$
, hence
![]() $X\lt _T Y$
.
$X\lt _T Y$
.
From Theorem 5.2, we see that, in particular,
![]() $\mathcal{K}_1$
does not have a computable weak completion, which also follows from the fact that combinatorial algebras are never computable, see Barendregt (Reference Barendregt1984, 5.1.15). We now show that this is optimal, namely that there exist completions of low Turing degree. (Recall that
$\mathcal{K}_1$
does not have a computable weak completion, which also follows from the fact that combinatorial algebras are never computable, see Barendregt (Reference Barendregt1984, 5.1.15). We now show that this is optimal, namely that there exist completions of low Turing degree. (Recall that
![]() $Y$
is low if
$Y$
is low if
![]() $Y'\leqslant _T \emptyset '$
).
$Y'\leqslant _T \emptyset '$
).
Theorem 5.3.
There exists a strong completion
![]() $\mathcal{A}$
of
$\mathcal{A}$
of
![]() $\mathcal{K}_1$
of low Turing degree, that is,
$\mathcal{K}_1$
of low Turing degree, that is,
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $Y$
-computable such that
$Y$
-computable such that
![]() $Y$
is low.
$Y$
is low.
Proof.
The outline of the proof is as follows. We first define a first-order base theory
![]() $\mathrm{Cmpl}$
such that each model of
$\mathrm{Cmpl}$
such that each model of
![]() $\mathrm{Cmpl}$
gives rise to a strong completion of
$\mathrm{Cmpl}$
gives rise to a strong completion of
![]() $\mathcal{K}_1$
. The theory
$\mathcal{K}_1$
. The theory
![]() $\mathrm{Cmpl}$
will be consistent because we already know that
$\mathrm{Cmpl}$
will be consistent because we already know that
![]() $\mathcal{K}_1$
has strong completions. We then use standard recursion theory to obtain a complete and consistent extension of
$\mathcal{K}_1$
has strong completions. We then use standard recursion theory to obtain a complete and consistent extension of
![]() $\mathrm{Cmpl}$
of low degree. This does not immediately give a completion of
$\mathrm{Cmpl}$
of low degree. This does not immediately give a completion of
![]() $\mathcal{K}_1$
of low degree, but we use a model-theoretic argument to obtain a completion of the desired complexity.
$\mathcal{K}_1$
of low degree, but we use a model-theoretic argument to obtain a completion of the desired complexity.
The language of
![]() $\mathrm{Cmpl}$
is two-sorted,Footnote
4
with a predicate
$\mathrm{Cmpl}$
is two-sorted,Footnote
4
with a predicate
![]() $N(x)$
intended to range over natural numbers, and a predicate
$N(x)$
intended to range over natural numbers, and a predicate
![]() $A(x)$
intended to range over a pca
$A(x)$
intended to range over a pca
![]() $\mathcal{A}$
that is a completion of
$\mathcal{A}$
that is a completion of
![]() $\mathcal{K}_1$
. Furthermore, the language has a function symbol
$\mathcal{K}_1$
. Furthermore, the language has a function symbol
![]() $f$
with the intended meaning that
$f$
with the intended meaning that
![]() $f:\mathcal{K}_1\to \mathcal{A}$
is a strong embedding. The language for the sort
$f:\mathcal{K}_1\to \mathcal{A}$
is a strong embedding. The language for the sort
![]() $N$
is the same as the language of arithmetic, and for this sort, we take the axioms of
$N$
is the same as the language of arithmetic, and for this sort, we take the axioms of
![]() $\mathrm{PA}$
. The language of the sort
$\mathrm{PA}$
. The language of the sort
![]() $A$
is that of pcas, with one function symbol
$A$
is that of pcas, with one function symbol
![]() $\cdot$
for application in
$\cdot$
for application in
![]() $\mathcal{A}$
. Since
$\mathcal{A}$
. Since
![]() $\cdot$
will be required to be total we add it as a function symbol, rather than as a relation symbol, which would have been more appropriate for a partial operation. By arithmetization, we may assume that expressions of the form
$\cdot$
will be required to be total we add it as a function symbol, rather than as a relation symbol, which would have been more appropriate for a partial operation. By arithmetization, we may assume that expressions of the form
![]() $\varphi _a(b)\!\downarrow =c$
are directly expressible for the sort
$\varphi _a(b)\!\downarrow =c$
are directly expressible for the sort
![]() $N$
for all standard numbers
$N$
for all standard numbers
![]() $a,b,c\in \omega$
, where we represent a number
$a,b,c\in \omega$
, where we represent a number
![]() $n\in \omega$
by the term
$n\in \omega$
by the term
![]() $S^n(0)$
.
$S^n(0)$
.
So as axioms of
![]() $\mathrm{Cmpl}$
, we have the following:
$\mathrm{Cmpl}$
, we have the following:
-
• The axioms of
 $\mathrm{PA}$
for the sort
$\mathrm{PA}$
for the sort
 $N$
(i.e. all axioms relative to
$N$
(i.e. all axioms relative to
 $N$
).
$N$
). -
• Axioms expressing that
 $f$
is an embedding from
$f$
is an embedding from
 $\mathcal{K}_1$
to
$\mathcal{K}_1$
to
 $\mathcal{A}$
:
$\mathcal{A}$
:
-
−
 $\forall a \in N (f(a)\in A)$
.
$\forall a \in N (f(a)\in A)$
. -
−
 $\forall a,b \in N(f(a)=f(b) \rightarrow a=b)$
.
$\forall a,b \in N(f(a)=f(b) \rightarrow a=b)$
. -
− For all
 $a,b,c\in \omega$
, we have an axiom(5)Note that the LHS can be expressed for the sort
$a,b,c\in \omega$
, we have an axiom(5)Note that the LHS can be expressed for the sort \begin{equation} \mathcal{K}_1 \models a\cdot b\!\downarrow =c \;\Longrightarrow \; \mathcal{A} \models f(a)\cdot f(b) = f(c). \end{equation}
\begin{equation} \mathcal{K}_1 \models a\cdot b\!\downarrow =c \;\Longrightarrow \; \mathcal{A} \models f(a)\cdot f(b) = f(c). \end{equation}
 $N$
using the language of arithmetic, using terms
$N$
using the language of arithmetic, using terms
 $S^n(0)$
to express the natural number
$S^n(0)$
to express the natural number
 $n$
, and the RHS can be expressed for the sort
$n$
, and the RHS can be expressed for the sort
 $A$
.
$A$
.
-
• To ensure that
 $f$
is a strong embedding, we fix standard combinators
$f$
is a strong embedding, we fix standard combinators
 $s$
and
$s$
and
 $k$
in
$k$
in
 $\mathcal{K}_1$
satisfying the axioms of Theorem 2.2. Note that these can be expressed for the sort
$\mathcal{K}_1$
satisfying the axioms of Theorem 2.2. Note that these can be expressed for the sort
 $N$
. Also, note that
$N$
. Also, note that
 $s$
and
$s$
and
 $k$
are just standard numbers, so we do not need to add them to the signature. Next, we add axioms expressing that
$k$
are just standard numbers, so we do not need to add them to the signature. Next, we add axioms expressing that
 $f(s)$
and
$f(s)$
and
 $f(k)$
also satisfy the axioms of Theorem 2.2, but now for the sort
$f(k)$
also satisfy the axioms of Theorem 2.2, but now for the sort
 $A$
. The existence of these combinators
$A$
. The existence of these combinators
 $f(s)$
and
$f(s)$
and
 $f(k)$
automatically ensures that
$f(k)$
automatically ensures that
 $\mathcal{A}$
forms a pca. The fact that
$\mathcal{A}$
forms a pca. The fact that
 $\mathcal{A}$
should be total is handled by the fact that application is a function symbol in the language, so no explicit axiom is needed for this.
$\mathcal{A}$
should be total is handled by the fact that application is a function symbol in the language, so no explicit axiom is needed for this.
Taken together, the axioms of
![]() $\mathrm{Cmpl}$
express that
$\mathrm{Cmpl}$
express that
![]() $f$
is a strong embedding from
$f$
is a strong embedding from
![]() $\mathcal{K}_1$
to
$\mathcal{K}_1$
to
![]() $\mathcal{A}$
. Every model
$\mathcal{A}$
. Every model
![]() $M$
of
$M$
of
![]() $\mathrm{Cmpl}$
gives a strong completion of
$\mathrm{Cmpl}$
gives a strong completion of
![]() $\mathcal{K}_1$
as follows. Denote by
$\mathcal{K}_1$
as follows. Denote by
![]() $M \upharpoonright N$
and
$M \upharpoonright N$
and
![]() $M \upharpoonright A$
the part of
$M \upharpoonright A$
the part of
![]() $M$
restricted to the sorts
$M$
restricted to the sorts
![]() $N$
and
$N$
and
![]() $A$
. Then
$A$
. Then
![]() $M \upharpoonright N$
is a model of
$M \upharpoonright N$
is a model of
![]() $\mathrm{PA}$
and
$\mathrm{PA}$
and
![]() $\mathcal{A}=M \upharpoonright A$
is a pca. Furthermore, the restriction of
$\mathcal{A}=M \upharpoonright A$
is a pca. Furthermore, the restriction of
![]() $f^M$
to the standard numbers
$f^M$
to the standard numbers
![]() $n\in \omega$
is an injection of
$n\in \omega$
is an injection of
![]() $\omega$
into
$\omega$
into
![]() $\mathcal{A}$
, which, by Equation (5), is an embedding of
$\mathcal{A}$
, which, by Equation (5), is an embedding of
![]() $\mathcal{K}_1$
, which is strong because
$\mathcal{K}_1$
, which is strong because
![]() $f(s)$
and
$f(s)$
and
![]() $f(k)$
satisfy the axioms of Theorem 2.2. The values of
$f(k)$
satisfy the axioms of Theorem 2.2. The values of
![]() $f^M$
on possible nonstandard elements of
$f^M$
on possible nonstandard elements of
![]() $M \upharpoonright N$
are irrelevant.
$M \upharpoonright N$
are irrelevant.
Since
![]() $\mathrm{Cmpl}$
is a computable axiomatization, by a result of Shoenfield (cf. Cenzer Reference Cenzer and Griffor1999, Theorem 6.1), the set of complete and consistent extensions of it can be represented as a
$\mathrm{Cmpl}$
is a computable axiomatization, by a result of Shoenfield (cf. Cenzer Reference Cenzer and Griffor1999, Theorem 6.1), the set of complete and consistent extensions of it can be represented as a
![]() $\Pi ^0_1$
-class, that is, there is a computable tree
$\Pi ^0_1$
-class, that is, there is a computable tree
![]() $T \subseteq 2^{\lt \omega }$
such that the set of infinite paths
$T \subseteq 2^{\lt \omega }$
such that the set of infinite paths
![]() $[T]$
consists of all complete and consistent extensions of
$[T]$
consists of all complete and consistent extensions of
![]() $\mathrm{Cmpl}$
. (We encode sentences by natural numbers, so that paths in
$\mathrm{Cmpl}$
. (We encode sentences by natural numbers, so that paths in
![]() $2^\omega$
correspond to sets of sentences.) Note that the theory
$2^\omega$
correspond to sets of sentences.) Note that the theory
![]() $\mathrm{Cmpl}$
is consistent because we know by Bethke et al. (Reference Bethke, Klop and de Vrijer1996) that there exists a strong completion of
$\mathrm{Cmpl}$
is consistent because we know by Bethke et al. (Reference Bethke, Klop and de Vrijer1996) that there exists a strong completion of
![]() $\mathcal{K}_1$
. In particular, the tree
$\mathcal{K}_1$
. In particular, the tree
![]() $T$
is infinite, and
$T$
is infinite, and
![]() $[T]$
is nonempty. By the Low Basis Theorem (Jockusch and Soare Reference Jockusch and Soare1972),
$[T]$
is nonempty. By the Low Basis Theorem (Jockusch and Soare Reference Jockusch and Soare1972),
![]() $T$
has a path of low Turing degree, which gives us a complete and consistent extension
$T$
has a path of low Turing degree, which gives us a complete and consistent extension
![]() $X$
of
$X$
of
![]() $\mathrm{Cmpl}$
of low degree.
$\mathrm{Cmpl}$
of low degree.
Since
![]() $X$
is consistent, it has a model
$X$
is consistent, it has a model
![]() $M$
by the completeness theorem, and by the remarks above
$M$
by the completeness theorem, and by the remarks above
![]() $M$
defines a strong completion of
$M$
defines a strong completion of
![]() $\mathcal{K}_1$
, namely
$\mathcal{K}_1$
, namely
![]() $M \upharpoonright A$
. However, there is no guarantee that this completion is
$M \upharpoonright A$
. However, there is no guarantee that this completion is
![]() $X$
-computable. But we do not need all of
$X$
-computable. But we do not need all of
![]() $M \upharpoonright A$
; it suffices to consider the smaller pca
$M \upharpoonright A$
; it suffices to consider the smaller pca
![]() $\mathcal{A}$
consisting of all terms built from
$\mathcal{A}$
consisting of all terms built from
![]() $f(n)$
for standard numbers
$f(n)$
for standard numbers
![]() $n\in \omega$
(represented as terms
$n\in \omega$
(represented as terms
![]() $S^n(0))$
, and application. Note that
$S^n(0))$
, and application. Note that
![]() $\mathcal{A}$
is a pca because of the presence of
$\mathcal{A}$
is a pca because of the presence of
![]() $f(s)$
and
$f(s)$
and
![]() $f(k)$
, and
$f(k)$
, and
![]() $\mathcal{A}$
is total since for
$\mathcal{A}$
is total since for
![]() $u$
and
$u$
and
![]() $v$
of the given form,
$v$
of the given form,
![]() $u\cdot v$
is again of this form. Not every element of
$u\cdot v$
is again of this form. Not every element of
![]() $\mathcal{A}$
is of the form
$\mathcal{A}$
is of the form
![]() $f(n$
), for example, it has terms
$f(n$
), for example, it has terms
![]() $f(a)\cdot f(b)$
such that
$f(a)\cdot f(b)$
such that
![]() $\varphi _a(b)\!\uparrow$
. The pca
$\varphi _a(b)\!\uparrow$
. The pca
![]() $\mathcal{A}$
is a sub-pca of
$\mathcal{A}$
is a sub-pca of
![]() $M \upharpoonright A$
in the sense of Shafer and Terwijn (Reference Shafer and Terwijn2021). To finish the proof of the theorem, we note that
$M \upharpoonright A$
in the sense of Shafer and Terwijn (Reference Shafer and Terwijn2021). To finish the proof of the theorem, we note that
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $X$
-computable. Namely, given to terms
$X$
-computable. Namely, given to terms
![]() $u$
and
$u$
and
![]() $v$
of the form above, we can simply compute their application as the term
$v$
of the form above, we can simply compute their application as the term
![]() $u\cdot v$
. Equality of terms in
$u\cdot v$
. Equality of terms in
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $X$
-decidable because the theory
$X$
-decidable because the theory
![]() $X$
is complete and thus contains all equalities
$X$
is complete and thus contains all equalities
![]() $u=v$
and
$u=v$
and
![]() $u\neq v$
of such terms. So the sub-pca
$u\neq v$
of such terms. So the sub-pca
![]() $\mathcal{A}$
of
$\mathcal{A}$
of
![]() $M \upharpoonright A$
is total and
$M \upharpoonright A$
is total and
![]() $X$
-computable, and hence of low degree since
$X$
-computable, and hence of low degree since
![]() $X$
is low.
$X$
is low.
6. Complete Extensions of
 $\mathrm{PA}$
$\mathrm{PA}$
Following modern terminology, we call a Turing degree a PA degree if it is the degree of a complete extension of Peano arithmetic (cf. Downey and Hirschfeldt Reference Downey and Hirschfeldt2010, p. 84). We will simply call a set PA-complete if it has PA degree.
In this section, we show that every (strong or weak) completion of
![]() $\mathcal{K}_1$
computes a PA degree, and vice versa. Since there exist PA-complete sets of low degree (Downey and Hirschfeldt Reference Downey and Hirschfeldt2010, p. 87), Theorem 5.3 follows from the statement of this equivalence; however, this does not make the proof of Theorem 5.3 superfluous, since the tree
$\mathcal{K}_1$
computes a PA degree, and vice versa. Since there exist PA-complete sets of low degree (Downey and Hirschfeldt Reference Downey and Hirschfeldt2010, p. 87), Theorem 5.3 follows from the statement of this equivalence; however, this does not make the proof of Theorem 5.3 superfluous, since the tree
![]() $T$
from its proof is used in the proof of the equivalence.
$T$
from its proof is used in the proof of the equivalence.
Proposition 6.1.
Every PA-complete set computes a strong completion of
![]() $\mathcal{K}_1$
.
$\mathcal{K}_1$
.
Proof.
By results of Scott and Solovay (cf. Odifreddi Reference Odifreddi1989, V.5.36), a set
![]() $Y$
is PA-complete if and only if it can compute an element of every nonempty
$Y$
is PA-complete if and only if it can compute an element of every nonempty
![]() $\Pi ^0_1$
-class. In particular,
$\Pi ^0_1$
-class. In particular,
![]() $Y$
can compute an element of
$Y$
can compute an element of
![]() $[T]$
for the computable tree
$[T]$
for the computable tree
![]() $T$
from the proof of Theorem 5.3. By the rest of the proof of Theorem 5.3, this implies that
$T$
from the proof of Theorem 5.3. By the rest of the proof of Theorem 5.3, this implies that
![]() $Y$
computes a strong completion of
$Y$
computes a strong completion of
![]() $\mathcal{K}_1$
, namely the term model defined at the end of the proof.
$\mathcal{K}_1$
, namely the term model defined at the end of the proof.
The following result strengthens Theorem 5.2.
Theorem 6.2.
Suppose
![]() $\mathcal{A}$
is a
$\mathcal{A}$
is a
![]() $Y$
-computable combinatorial algebra, and that
$Y$
-computable combinatorial algebra, and that
![]() $f:\mathcal{K}_1\hookrightarrow \mathcal{A}$
is a weak embedding. Then
$f:\mathcal{K}_1\hookrightarrow \mathcal{A}$
is a weak embedding. Then
![]() $Y$
is PA-complete.
$Y$
is PA-complete.
Proof.
According to Jockusch and Soare (Reference Jockusch and Soare1972), a set is PA-complete if and only if it can compute a separation of an effectively inseparable pair of c.e. sets. (See also Downey and Hirschfeldt Reference Downey and Hirschfeldt2010, p. 86.) Now let
![]() $A$
,
$A$
,
![]() $B$
be a pair of effectively inseparable c.e. sets, for example, we can take the provable and refutable sentences of PA (Odifreddi Reference Odifreddi1989, p. 513). Then the proof of Theorem 5.2 shows that
$B$
be a pair of effectively inseparable c.e. sets, for example, we can take the provable and refutable sentences of PA (Odifreddi Reference Odifreddi1989, p. 513). Then the proof of Theorem 5.2 shows that
![]() $Y$
computes a separation of
$Y$
computes a separation of
![]() $A$
and
$A$
and
![]() $B$
, and hence
$B$
, and hence
![]() $Y$
is PA-complete.
$Y$
is PA-complete.
Putting Proposition 6.1 and Theorem 6.2 together, we obtain the following characterization:
Corollary 6.3.
The following are equivalent for any set
![]() $A$
:
$A$
:
-
(i)
 $A$
computes a weak completion of
$A$
computes a weak completion of
 $\mathcal{K}_1$
,
$\mathcal{K}_1$
, -
(ii)
 $A$
computes a strong completion of
$A$
computes a strong completion of
 $\mathcal{K}_1$
,
$\mathcal{K}_1$
, -
(iii)
 $A$
is PA-complete.
$A$
is PA-complete.
In the case of PA degrees, more is known, namely that they are closed upwards. We do not know whether the degrees of (weak or strong) completions of
![]() $\mathcal{K}_1$
are also upwards closed.
$\mathcal{K}_1$
are also upwards closed.
7. Nonstandard Models of
 $\mathrm{PA}$
$\mathrm{PA}$
As mentioned in Beeson (Reference Beeson1985, VI.2.5) and van Oosten (Reference van Oosten2008), every model
![]() $M$
of Peano Arithmetic
$M$
of Peano Arithmetic
![]() $\mathrm{PA}$
defines a pca on
$\mathrm{PA}$
defines a pca on
![]() $M$
, with application defined by
$M$
, with application defined by
for all
![]() $a,b,c\in M$
. By restricting Equation (6) to standard numbers
$a,b,c\in M$
. By restricting Equation (6) to standard numbers
![]() $a,b,c\in \omega$
, we obtain a pca on
$a,b,c\in \omega$
, we obtain a pca on
![]() $\omega$
, which we will call
$\omega$
, which we will call
![]() $\mathcal{K}_1(M)$
. Note that
$\mathcal{K}_1(M)$
. Note that
![]() $\mathcal{K}_1(M)$
is just Kleene’s first model
$\mathcal{K}_1(M)$
is just Kleene’s first model
![]() $\mathcal{K}_1$
“inside
$\mathcal{K}_1$
“inside
![]() $M$
.” It is a pca because we can pick combinators
$M$
.” It is a pca because we can pick combinators
![]() $k,s \in \mathcal{K}_1$
as in Theorem 2.2 such that
$k,s \in \mathcal{K}_1$
as in Theorem 2.2 such that
![]() $\mathrm{PA}$
proves that they have the required properties.
$\mathrm{PA}$
proves that they have the required properties.
Note that for
![]() $a,b,c\in \omega$
we have that
$a,b,c\in \omega$
we have that
![]() $a\cdot b\!\downarrow = c$
in
$a\cdot b\!\downarrow = c$
in
![]() $\mathcal{K}_1$
if and only if
$\mathcal{K}_1$
if and only if
![]() $\exists y(T(a,b,y) \wedge U(y)=c)$
, where
$\exists y(T(a,b,y) \wedge U(y)=c)$
, where
![]() $T$
and
$T$
and
![]() $U$
are the primitive recursive predicate and function from Kleene’s normal form theorem (cf. Odifreddi Reference Odifreddi1989). In a nonstandard model
$U$
are the primitive recursive predicate and function from Kleene’s normal form theorem (cf. Odifreddi Reference Odifreddi1989). In a nonstandard model
![]() $M$
, this
$M$
, this
![]() $y$
can be nonstandard, so that more computations converge than in reality. In particular, in general, we have
$y$
can be nonstandard, so that more computations converge than in reality. In particular, in general, we have
but not conversely. For example, consider a model
![]() $M$
of
$M$
of
![]() $\mathrm{PA} + \neg \mathrm{con}(\mathrm{PA})$
, where
$\mathrm{PA} + \neg \mathrm{con}(\mathrm{PA})$
, where
![]() $\mathrm{con}(\mathrm{PA})$
expresses the consistency of
$\mathrm{con}(\mathrm{PA})$
expresses the consistency of
![]() $\mathrm{PA}$
. Such models exist by Gödel’s second incompleteness theorem. If we consider the p.c. function
$\mathrm{PA}$
. Such models exist by Gödel’s second incompleteness theorem. If we consider the p.c. function
![]() $\varphi _a$
that on input
$\varphi _a$
that on input
![]() $b$
searches for a proof of an inconsistency in
$b$
searches for a proof of an inconsistency in
![]() $\mathrm{PA}$
, then the computation
$\mathrm{PA}$
, then the computation
![]() $a\cdot b$
will converge in
$a\cdot b$
will converge in
![]() $\mathcal{K}_1(M)$
, but not in
$\mathcal{K}_1(M)$
, but not in
![]() $\mathcal{K}_1$
(assuming
$\mathcal{K}_1$
(assuming
![]() $\mathrm{PA}$
is consistent).
$\mathrm{PA}$
is consistent).
Note that by Equation (7), we have an embedding
![]() $\mathcal{K}_1 \hookrightarrow \mathcal{K}_1(M)$
for every model
$\mathcal{K}_1 \hookrightarrow \mathcal{K}_1(M)$
for every model
![]() $M$
of
$M$
of
![]() $\mathrm{PA}$
. This is in fact a strong embedding, as the same combinators
$\mathrm{PA}$
. This is in fact a strong embedding, as the same combinators
![]() $s$
and
$s$
and
![]() $k$
can be used in
$k$
can be used in
![]() $\mathcal{K}_1(M)$
.
$\mathcal{K}_1(M)$
.
Since
![]() $\mathrm{PA}$
proves that certain p.c. functions are nontotal, any model of
$\mathrm{PA}$
proves that certain p.c. functions are nontotal, any model of
![]() $\mathrm{PA}$
has nontotal p.c. functions. This remains true if we restrict to standard numbers, that is, there are standard numbers
$\mathrm{PA}$
has nontotal p.c. functions. This remains true if we restrict to standard numbers, that is, there are standard numbers
![]() $e,n\in \omega$
such that
$e,n\in \omega$
such that
![]() $\mathrm{PA}$
proves that
$\mathrm{PA}$
proves that
![]() $\varphi _e(n)$
never halts. In particular, we see that
$\varphi _e(n)$
never halts. In particular, we see that
![]() $\mathcal{K}_1(M)$
is never a total pca (i.e. a ca). Therefore, we have:
$\mathcal{K}_1(M)$
is never a total pca (i.e. a ca). Therefore, we have:
Proposition 7.1.
![]() $\mathcal{K}_1(M)$
is never a weak completion of
$\mathcal{K}_1(M)$
is never a weak completion of
![]() $\mathcal{K}_1$
.
$\mathcal{K}_1$
.
By Tennenbaum’s theorem (cf. Boolos and Jeffrey Reference Boolos and Jeffrey1974), there are no computable nonstandard models of
![]() $\mathrm{PA}$
. More precisely, there are no nonstandard models in which
$\mathrm{PA}$
. More precisely, there are no nonstandard models in which
![]() $+$
is computable. (This is an extension of Tennenbaum’s theorem due to Kreisel.) It follows that there are also no nonstandard models that are c.e., because
$+$
is computable. (This is an extension of Tennenbaum’s theorem due to Kreisel.) It follows that there are also no nonstandard models that are c.e., because
![]() $+$
is a total operation, and in a c.e. model, it would actually be computable, contradicting Kreisel’s result. So it would seem that the pcas
$+$
is a total operation, and in a c.e. model, it would actually be computable, contradicting Kreisel’s result. So it would seem that the pcas
![]() $\mathcal{K}_1(M)$
for nonstandard models
$\mathcal{K}_1(M)$
for nonstandard models
![]() $M$
cannot be used for the problems about c.e. pcas discussed in computable structure theory (see Fokina and Terwijn Reference Fokina and Terwijn2024). However, for models
$M$
cannot be used for the problems about c.e. pcas discussed in computable structure theory (see Fokina and Terwijn Reference Fokina and Terwijn2024). However, for models
![]() $M_0$
and
$M_0$
and
![]() $M_1$
of
$M_1$
of
![]() $\mathrm{PA}$
, we do not have in general that
$\mathrm{PA}$
, we do not have in general that
To see this, let
![]() $M_0=\omega$
be the standard model, and let
$M_0=\omega$
be the standard model, and let
![]() $M_1$
be a nonstandard model that has the same first-order theory as
$M_1$
be a nonstandard model that has the same first-order theory as
![]() $\omega$
(which exists by the compactness theorem). Then
$\omega$
(which exists by the compactness theorem). Then
![]() $M_0 \not \cong M_1$
, but
$M_0 \not \cong M_1$
, but
![]() $\mathcal{K}_1(M_0) = \mathcal{K}_1(M_1) = \mathcal{K}_1$
.
$\mathcal{K}_1(M_0) = \mathcal{K}_1(M_1) = \mathcal{K}_1$
.
In particular, we see that it is possible that
![]() $\mathcal{K}_1(M)$
is c.e. (in the sense of Definition 3.2) for a nonstandard model
$\mathcal{K}_1(M)$
is c.e. (in the sense of Definition 3.2) for a nonstandard model
![]() $M$
of
$M$
of
![]() $\mathrm{PA}$
. This prompts the following question:
$\mathrm{PA}$
. This prompts the following question:
Question 7.2.
What are the possible c.e. degrees for such
![]() $\mathcal{K}_1(M)$
aaaa can
$\mathcal{K}_1(M)$
aaaa can
![]() $\mathcal{K}_1(M)$
be c.e. but not equal to
$\mathcal{K}_1(M)$
be c.e. but not equal to
![]() $\mathcal{K}_1$
aaaa
$\mathcal{K}_1$
aaaa
In the following, we note that though
![]() $\mathcal{K}_1(M)$
is always noncomputable, it can have low degree (if we do not require that it is also c.e.).
$\mathcal{K}_1(M)$
is always noncomputable, it can have low degree (if we do not require that it is also c.e.).
Proposition 7.3.
![]() $\mathcal{K}_1(M)$
is always noncomputable.
$\mathcal{K}_1(M)$
is always noncomputable.
Proof. Consider the computably inseparable pair of sets
Now consider the set
![]() $C = \{x\in \omega \mid \mathcal{K}_1(M) \models x\cdot x\!\downarrow =0\}$
.
$C = \{x\in \omega \mid \mathcal{K}_1(M) \models x\cdot x\!\downarrow =0\}$
.
![]() $C$
is computable from
$C$
is computable from
![]() $\mathcal{K}_1(M)$
, and it follows from Equation (7) that it separates
$\mathcal{K}_1(M)$
, and it follows from Equation (7) that it separates
![]() $A$
and
$A$
and
![]() $B$
, from which it follows immediately that
$B$
, from which it follows immediately that
![]() $\mathcal{K}_1(M)$
cannot be computable.
$\mathcal{K}_1(M)$
cannot be computable.
Proposition 7.4.
![]() $\mathcal{K}_1(M)$
can have low Turing degree.
$\mathcal{K}_1(M)$
can have low Turing degree.
Proof.
We have to show that there exists a model
![]() $M$
and a low set
$M$
and a low set
![]() $Y$
such that
$Y$
such that
![]() $\mathcal{K}_1(M)$
is
$\mathcal{K}_1(M)$
is
![]() $Y$
-computable (in the sense of Definition 3.2), that is, such that the set
$Y$
-computable (in the sense of Definition 3.2), that is, such that the set
is
![]() $Y$
-computable. According to Jockusch and Soare, there exists a complete and consistent extension
$Y$
-computable. According to Jockusch and Soare, there exists a complete and consistent extension
![]() $X$
of
$X$
of
![]() $\mathrm{PA}$
of low Turing degree. Let
$\mathrm{PA}$
of low Turing degree. Let
![]() $M$
be a model with theory
$M$
be a model with theory
![]() $X$
. We can identify the set
$X$
. We can identify the set
![]() $Z$
with the set of sentences
$Z$
with the set of sentences
![]() $a\cdot b\!\downarrow = c$
that hold in
$a\cdot b\!\downarrow = c$
that hold in
![]() $M$
. Since
$M$
. Since
![]() $Z$
is then just a subset of
$Z$
is then just a subset of
![]() $X$
consisting of sentences of a specific form, there is a computable set
$X$
consisting of sentences of a specific form, there is a computable set
![]() $R$
such that
$R$
such that
![]() $Z = R\cap X$
, and we have
$Z = R\cap X$
, and we have
![]() $(R\cap X)' \leqslant _T X'\leqslant _T \emptyset '$
so that
$(R\cap X)' \leqslant _T X'\leqslant _T \emptyset '$
so that
![]() $Z$
is low.
$Z$
is low.
Competing interests
The author declares none.