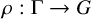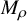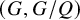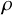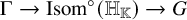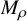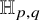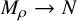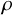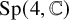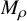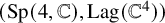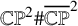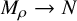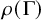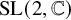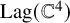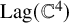1 Introduction
A
![]() $(G,X)$
–manifold is a topological manifold that is locally modelled on a G–homogeneous space X. This means that the manifold is equipped with local charts with values in a model space X and transition functions with values in a Lie group G acting transitively on X. The theory of
$(G,X)$
–manifold is a topological manifold that is locally modelled on a G–homogeneous space X. This means that the manifold is equipped with local charts with values in a model space X and transition functions with values in a Lie group G acting transitively on X. The theory of
![]() $(G,X)$
–manifolds plays an important role in Thurston’s geometrization program, but extends far beyond it. In particular,
$(G,X)$
–manifolds plays an important role in Thurston’s geometrization program, but extends far beyond it. In particular,
![]() $(G,X)$
–structures capture many geometric structures beyond Riemannian metrics – for example, projective or affine structures on manifolds.
$(G,X)$
–structures capture many geometric structures beyond Riemannian metrics – for example, projective or affine structures on manifolds.
The simplest examples of
![]() $(G,X)$
–manifolds are quotients of X by a discrete subgroup of G acting freely and properly discontinuously – the complete
$(G,X)$
–manifolds are quotients of X by a discrete subgroup of G acting freely and properly discontinuously – the complete
![]() $(G,X)$
–manifolds. A larger class of examples arises more generally from quotients of an open domain
$(G,X)$
–manifolds. A larger class of examples arises more generally from quotients of an open domain
![]() $\Omega $
of X. These are sometimes called Kleinian
$\Omega $
of X. These are sometimes called Kleinian
![]() $(G,X)$
–manifolds.
$(G,X)$
–manifolds.
The terminology Kleinian comes from the theory of Kleinian groups. A Kleinian group
![]() $\Gamma $
is a (non-elementary) discrete subgroup of isometries of the hyperbolic
$\Gamma $
is a (non-elementary) discrete subgroup of isometries of the hyperbolic
![]() $3$
–space
$3$
–space
![]() ${\mathbb H}^3$
. Its action on the boundary at infinity
${\mathbb H}^3$
. Its action on the boundary at infinity
![]() $\partial _\infty {\mathbb H}^3 \simeq \mathbb {CP}^1$
has a minimal invariant limit set
$\partial _\infty {\mathbb H}^3 \simeq \mathbb {CP}^1$
has a minimal invariant limit set
![]() $\Lambda _\Gamma $
and is properly discontinuous on the complement
$\Lambda _\Gamma $
and is properly discontinuous on the complement
![]() $\Omega _\Gamma $
, called the domain of discontinuity. The quotient
$\Omega _\Gamma $
, called the domain of discontinuity. The quotient
![]() $\Gamma \backslash \Omega _\Gamma $
is (at least when
$\Gamma \backslash \Omega _\Gamma $
is (at least when
![]() $\Gamma $
is torsion-free) a Riemann surface equipped with a complex projective structure. The group
$\Gamma $
is torsion-free) a Riemann surface equipped with a complex projective structure. The group
![]() $\Gamma $
is convex-cocompact when the action of
$\Gamma $
is convex-cocompact when the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() ${\mathbb H}^3 \sqcup \Omega _\Gamma $
is cocompact. The quotient then gives a conformal compactification of the hyperbolic
${\mathbb H}^3 \sqcup \Omega _\Gamma $
is cocompact. The quotient then gives a conformal compactification of the hyperbolic
![]() $3$
–manifold
$3$
–manifold
![]() $\Gamma \backslash {\mathbb H}^3$
. Convex-cocompact Kleinian groups and the corresponding hyperbolic
$\Gamma \backslash {\mathbb H}^3$
. Convex-cocompact Kleinian groups and the corresponding hyperbolic
![]() $3$
–manifolds play a central role in Thurston’s hyperbolization theorem.
$3$
–manifolds play a central role in Thurston’s hyperbolization theorem.
In recent years, the theory of convex-cocompact subgroups in rank one Lie groups has been generalized to the higher rank setting through the theory of Anosov representations, introduced by Labourie [Reference LabourieLab06] and, more generally, by Guichard–Wienhard [Reference Guichard and WienhardGW12]. A strong connection between Anosov representations and
![]() $(G,X)$
–manifolds has been established through the construction of domains of discontinuity by Guichard–Wienhard [Reference Guichard and WienhardGW12] and then by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18].
$(G,X)$
–manifolds has been established through the construction of domains of discontinuity by Guichard–Wienhard [Reference Guichard and WienhardGW12] and then by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18].
Let G be a semisimple Lie group and P a parabolic subgroup of G. Informally, a P–Anosov representation of a Gromov hyperbolic group
![]() $\Gamma $
into G is a homomorphism
$\Gamma $
into G is a homomorphism
![]() $\rho :\Gamma \to G$
that admits a
$\rho :\Gamma \to G$
that admits a
![]() $\rho $
–equivariant continuous embedding of the boundary at infinity
$\rho $
–equivariant continuous embedding of the boundary at infinity
![]() $\partial _\infty \Gamma $
of
$\partial _\infty \Gamma $
of
![]() $\Gamma $
into the flag variety
$\Gamma $
into the flag variety
![]() $G/P$
, which preserves the dynamics of the action of
$G/P$
, which preserves the dynamics of the action of
![]() $\Gamma $
on its boundary (see Definition 2.1). Anosov representations are quasi-isometric embeddings and are stable under small perturbations. Guichard–Wienhard proved in [Reference Guichard and WienhardGW12] that, for some parabolic subgroup Q (possibly different from P), a P–Anosov representation
$\Gamma $
on its boundary (see Definition 2.1). Anosov representations are quasi-isometric embeddings and are stable under small perturbations. Guichard–Wienhard proved in [Reference Guichard and WienhardGW12] that, for some parabolic subgroup Q (possibly different from P), a P–Anosov representation
![]() $\rho : \Gamma \to G$
defines a properly discontinuous and cocompact action of
$\rho : \Gamma \to G$
defines a properly discontinuous and cocompact action of
![]() $\Gamma $
on an open subset
$\Gamma $
on an open subset
![]() $\Omega _\rho \subset G/Q$
, which is the complement of a disjoint union of Schubert subvarieties parametrized by
$\Omega _\rho \subset G/Q$
, which is the complement of a disjoint union of Schubert subvarieties parametrized by
![]() $\partial _\infty \Gamma $
(see Definition 2.4). The precise parabolic subgroups Q for which this construction works have been systematically described by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18]. We call the domains of discontinuity
$\partial _\infty \Gamma $
(see Definition 2.4). The precise parabolic subgroups Q for which this construction works have been systematically described by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18]. We call the domains of discontinuity
![]() $\Omega _\rho $
obtained by their constructions flag domains of discontinuity.
$\Omega _\rho $
obtained by their constructions flag domains of discontinuity.
This associates to an Anosov representation
![]() $\rho \colon \thinspace \Gamma \to G$
of a torsion-free group
$\rho \colon \thinspace \Gamma \to G$
of a torsion-free group
![]() $\Gamma $
a closed manifold
$\Gamma $
a closed manifold
![]() $M_\rho = \Gamma \backslash \Omega _\rho $
equipped with a Kleinian
$M_\rho = \Gamma \backslash \Omega _\rho $
equipped with a Kleinian
![]() $(G,G/Q)$
–structure. Even though the topological type of
$(G,G/Q)$
–structure. Even though the topological type of
![]() $M_\rho $
only depends on the connected component of
$M_\rho $
only depends on the connected component of
![]() $\rho $
in the space of P–Anosov representations [Reference Guichard and WienhardGW12], it is very difficult to determine the topology of
$\rho $
in the space of P–Anosov representations [Reference Guichard and WienhardGW12], it is very difficult to determine the topology of
![]() $M_\rho $
. Even in the case of convex-cocompact subgroups of a hyperbolic space of dimension
$M_\rho $
. Even in the case of convex-cocompact subgroups of a hyperbolic space of dimension
![]() $\geq 4$
, the topology of
$\geq 4$
, the topology of
![]() $M_\rho $
is still very mysterious, and many wild phenomena can occur (see Section 1.4 for an example with a surface group), suggesting that a systematic answer is impossible. Nonetheless, important classes of examples of Anosov representations arise from deformations of uniform lattices in Lie groups of real rank
$M_\rho $
is still very mysterious, and many wild phenomena can occur (see Section 1.4 for an example with a surface group), suggesting that a systematic answer is impossible. Nonetheless, important classes of examples of Anosov representations arise from deformations of uniform lattices in Lie groups of real rank
![]() $1$
into a higher rank Lie group. For such representations, the topology of
$1$
into a higher rank Lie group. For such representations, the topology of
![]() $M_\rho $
becomes more tractable.
$M_\rho $
becomes more tractable.
1.1 Part 1: Deformations of rank 1 lattices
In the first part of the paper, we prove a general fibration theorem for the quotients of flag domains of discontinuity associated to Anosov deformations of a rank
![]() $1$
lattice into a higher rank Lie group.
$1$
lattice into a higher rank Lie group.
Let H be a connected semisimple Lie group of real rank
![]() $1$
with finite center, and
$1$
with finite center, and
![]() $\Gamma $
a torsion-free uniform lattice in H. Denote by
$\Gamma $
a torsion-free uniform lattice in H. Denote by
![]() $\rho _0\colon \thinspace \Gamma \to H$
the identity representation. Let G be a connected semisimple Lie group with finite center, and
$\rho _0\colon \thinspace \Gamma \to H$
the identity representation. Let G be a connected semisimple Lie group with finite center, and
![]() $\iota \colon \thinspace H \to G$
a faithful representation. Then
$\iota \colon \thinspace H \to G$
a faithful representation. Then
![]() $\iota \circ \rho _0$
is a P–Anosov representation of
$\iota \circ \rho _0$
is a P–Anosov representation of
![]() $\Gamma $
in G for some parabolic subgroup P: we will call
$\Gamma $
in G for some parabolic subgroup P: we will call
![]() $\iota \circ \rho _0$
an
$\iota \circ \rho _0$
an
![]() $\iota $
–lattice representation. The set
$\iota $
–lattice representation. The set
![]() $\mathrm {Anosov}_{P}(\Gamma ,G)$
of P–Anosov representations of
$\mathrm {Anosov}_{P}(\Gamma ,G)$
of P–Anosov representations of
![]() $\Gamma $
into G is an open subset of
$\Gamma $
into G is an open subset of
![]() $\operatorname {Hom}(\Gamma , G)$
containing the
$\operatorname {Hom}(\Gamma , G)$
containing the
![]() $\iota $
–lattice representation
$\iota $
–lattice representation
![]() $\iota \circ \rho _0$
. We call a representation
$\iota \circ \rho _0$
. We call a representation
![]() $\rho :\Gamma \to G$
a P–Anosov deformation of
$\rho :\Gamma \to G$
a P–Anosov deformation of
![]() $\iota \circ \rho _0$
if
$\iota \circ \rho _0$
if
![]() $\rho $
belongs to the connected component of
$\rho $
belongs to the connected component of
![]() $\iota \circ \rho _0$
in
$\iota \circ \rho _0$
in
![]() $\mathrm {Anosov}_P(\Gamma ,G)$
.
$\mathrm {Anosov}_P(\Gamma ,G)$
.
Let us now fix any parabolic subgroup Q of G such that P–Anosov representations in G admit a cocompact flag domain of discontinuity in
![]() $G/Q$
. For
$G/Q$
. For
![]() $\rho \in \mathrm {Anosov}_{P}(\Gamma ,G)$
, we denote the domain by
$\rho \in \mathrm {Anosov}_{P}(\Gamma ,G)$
, we denote the domain by
![]() $\Omega _\rho \subset G/Q$
and the closed quotient manifold by
$\Omega _\rho \subset G/Q$
and the closed quotient manifold by
![]() $M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
. Finally, we denote by
$M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
. Finally, we denote by
![]() $S_H$
the symmetric space of H. Our first main result is the following:
$S_H$
the symmetric space of H. Our first main result is the following:
Theorem A (see Theorem 3.1).
For
![]() $H,\Gamma ,G,\iota ,P,Q$
as above, let
$H,\Gamma ,G,\iota ,P,Q$
as above, let
![]() $\rho :\Gamma \rightarrow G$
be a P–Anosov deformation of
$\rho :\Gamma \rightarrow G$
be a P–Anosov deformation of
![]() $\iota \circ \rho _0$
. Then
$\iota \circ \rho _0$
. Then
![]() $\Omega _\rho $
admits a smooth
$\Omega _\rho $
admits a smooth
![]() $\Gamma $
–equivariant fibration onto
$\Gamma $
–equivariant fibration onto
![]() $S_H$
. In particular,
$S_H$
. In particular,
![]() $M_\rho $
is a smooth fiber bundle over the negatively curved locally symmetric space
$M_\rho $
is a smooth fiber bundle over the negatively curved locally symmetric space
![]() $\Gamma \backslash S_H$
, and
$\Gamma \backslash S_H$
, and
![]() $\Omega _\rho $
deformation retracts to a closed manifold of dimension
$\Omega _\rho $
deformation retracts to a closed manifold of dimension
![]() $\dim (G/Q)-\dim (S_H)$
.
$\dim (G/Q)-\dim (S_H)$
.
This theorem was obtained independently by Davalo [Reference DavaloDav24] with different methods (see Section 1.3). It comes with companion theorems (see Theorem 3.3 and Corollary 3.4 below) that describe the structure group and the invariants of the fiber bundle.
Let us emphasize that Theorem A applies to every (!) cocompact flag domain of discontinuity. Even for a given representation, and a given flag variety, there can be many different cocompact flag domains of discontinuity (see [Reference SteckerSte18]). The theorem further applies when we consider the representation
![]() $\rho :\Gamma \rightarrow G \rightarrow G'$
as an Ansosov representation into a larger Lie group, and all the flag domains of discontinuity constructed in flag varieties of
$\rho :\Gamma \rightarrow G \rightarrow G'$
as an Ansosov representation into a larger Lie group, and all the flag domains of discontinuity constructed in flag varieties of
![]() $G'$
. See [Reference Guichard and WienhardGW12] and [Reference Guichard, Gueritaud, Kassel and WienhardGGKW17] for examples of how one can play around with such embeddings into larger groups.
$G'$
. See [Reference Guichard and WienhardGW12] and [Reference Guichard, Gueritaud, Kassel and WienhardGGKW17] for examples of how one can play around with such embeddings into larger groups.
An important source of applications of Theorem A is when an entire connected component of the representation variety
![]() $\operatorname {Hom}(\Gamma , G)$
consists of Anosov representations. For fundamental groups of closed surfaces with negative Euler characteristic (which we call surface groups from now on), such components are called higher rank Teichmüller components, and most of them contain representations that factor through a compact extension of
$\operatorname {Hom}(\Gamma , G)$
consists of Anosov representations. For fundamental groups of closed surfaces with negative Euler characteristic (which we call surface groups from now on), such components are called higher rank Teichmüller components, and most of them contain representations that factor through a compact extension of
![]() $\mathrm {PSL}(2,\mathbb R)$
. Therefore, Theorem A gives a positive answer to [Reference WienhardWie18, Conjecture 13] in most cases, as well as a complete answer to a conjecture by Dumas–Sanders [Reference Dumas and SandersDS20, Conjecture 1.1]. More precisely, we have the following.
$\mathrm {PSL}(2,\mathbb R)$
. Therefore, Theorem A gives a positive answer to [Reference WienhardWie18, Conjecture 13] in most cases, as well as a complete answer to a conjecture by Dumas–Sanders [Reference Dumas and SandersDS20, Conjecture 1.1]. More precisely, we have the following.
Corollary B. Let
![]() $\Gamma = \pi _1(\Sigma )$
be a surface group, and
$\Gamma = \pi _1(\Sigma )$
be a surface group, and
![]() $\mathcal {C}\subset \operatorname {Hom}(\Gamma , G)$
be a higher rank Teichmüller component that contains a twisted Fuchsian representation. Then for every representation
$\mathcal {C}\subset \operatorname {Hom}(\Gamma , G)$
be a higher rank Teichmüller component that contains a twisted Fuchsian representation. Then for every representation
![]() $\rho \in \mathcal C$
, every parabolic subgroup Q and every cocompact flag domain of discontinuity
$\rho \in \mathcal C$
, every parabolic subgroup Q and every cocompact flag domain of discontinuity
![]() $\Omega _\rho \subset G/Q$
, the quotient manifold
$\Omega _\rho \subset G/Q$
, the quotient manifold
![]() $M = \rho (\pi _1(\Sigma )) \backslash \Omega $
is homeomorphic to a fiber bundle
$M = \rho (\pi _1(\Sigma )) \backslash \Omega $
is homeomorphic to a fiber bundle
![]() $M\to \Sigma $
. In particular, the composition
$M\to \Sigma $
. In particular, the composition
![]() $\pi _1(M) \to \pi _1(\Sigma ) \overset {\rho }{\to } G$
is the holonomy of a Kleinian
$\pi _1(M) \to \pi _1(\Sigma ) \overset {\rho }{\to } G$
is the holonomy of a Kleinian
![]() $(G,G/Q)$
–structure on M.
$(G,G/Q)$
–structure on M.
Let us mention a list of interesting examples for which Theorem A and Corollary B apply.
-
1. Hitchin components. Let
 $\Gamma = \pi _1(\Sigma )$
be a surface group and G a split real simple linear group. The group
$\Gamma = \pi _1(\Sigma )$
be a surface group and G a split real simple linear group. The group
 $H = \mathrm {SL}(2,\mathbb R)$
admits a principal representation
$H = \mathrm {SL}(2,\mathbb R)$
admits a principal representation
 $\iota _0:H \rightarrow G$
. Given a Fuchsian representation
$\iota _0:H \rightarrow G$
. Given a Fuchsian representation
 $\rho _0:\Gamma \rightarrow H$
, the composition
$\rho _0:\Gamma \rightarrow H$
, the composition
 $\iota _0\circ \rho _0$
is called a principal Fuchsian representation in G. The representations of the connected component of
$\iota _0\circ \rho _0$
is called a principal Fuchsian representation in G. The representations of the connected component of
 $\iota _0\circ \rho _0$
in
$\iota _0\circ \rho _0$
in
 $\mathrm {Hom}(\Gamma ,G)$
are called Hitchin representations. Hitchin representations are Anosov with respect to the minimal parabolic subgroup
$\mathrm {Hom}(\Gamma ,G)$
are called Hitchin representations. Hitchin representations are Anosov with respect to the minimal parabolic subgroup
 $P_{min}<G$
or, equivalently, with respect to any parabolic subgroup
$P_{min}<G$
or, equivalently, with respect to any parabolic subgroup
 $P<G$
[Reference LabourieLab06, Reference Fock and GoncharovFG06]. They are thus P–Anosov deformations of the lattice representation
$P<G$
[Reference LabourieLab06, Reference Fock and GoncharovFG06]. They are thus P–Anosov deformations of the lattice representation
 $\iota _0\circ \rho _0$
, and Theorem A applies.
$\iota _0\circ \rho _0$
, and Theorem A applies. -
2. P–quasi-Hitchin representations. Theorem A also applies to deformations of Hitchin representations into complex Lie groups. For this, we embed G into its complexification
 $G_{{\mathbb C}}$
, and we consider the principal Fuchsian representation
$G_{{\mathbb C}}$
, and we consider the principal Fuchsian representation
 $\iota _0\circ \rho _0:\Gamma \to G <G_{{\mathbb C}}$
as taking values in
$\iota _0\circ \rho _0:\Gamma \to G <G_{{\mathbb C}}$
as taking values in
 $G_{{\mathbb C}}$
. This representation is Anosov with respect to any parabolic subgroup
$G_{{\mathbb C}}$
. This representation is Anosov with respect to any parabolic subgroup
 $P_{{\mathbb C}} < G_{{\mathbb C}}$
. However, not every continuous deformation of
$P_{{\mathbb C}} < G_{{\mathbb C}}$
. However, not every continuous deformation of
 $\iota _0\circ \rho _0$
will be Anosov. We define the set of P–quasi-Hitchin representation to be the connected component of the space of P–Anosov representations in
$\iota _0\circ \rho _0$
will be Anosov. We define the set of P–quasi-Hitchin representation to be the connected component of the space of P–Anosov representations in
 $G_{{\mathbb C}}$
containing the principal Fuchsian representations. When
$G_{{\mathbb C}}$
containing the principal Fuchsian representations. When
 $G = \mathrm {PSL}(2,\mathbb R)$
, this is precisely the set of quasi-Fuchsian representations. Note that, in higher rank, this set might depend on the choice of parabolic subgroup P.
$G = \mathrm {PSL}(2,\mathbb R)$
, this is precisely the set of quasi-Fuchsian representations. Note that, in higher rank, this set might depend on the choice of parabolic subgroup P.The geometry of
 $P_{min}$
–quasi-Hitchin representations in
$P_{min}$
–quasi-Hitchin representations in
 $\mathrm {PSL}(n,{{\mathbb C}})$
has been studied by Dumas–Sanders [Reference Dumas and SandersDS20]. In particular, they proved that flag domains of discontinuity
$\mathrm {PSL}(n,{{\mathbb C}})$
has been studied by Dumas–Sanders [Reference Dumas and SandersDS20]. In particular, they proved that flag domains of discontinuity
 $\Omega _\rho $
satisfy a Poincaré duality of rank
$\Omega _\rho $
satisfy a Poincaré duality of rank
 $\dim (G/Q)-2$
and computed the cohomology of
$\dim (G/Q)-2$
and computed the cohomology of
 $M_\rho $
. They conjectured that
$M_\rho $
. They conjectured that
 $M_\rho $
admits a fibration over the surface
$M_\rho $
admits a fibration over the surface
 $\Sigma $
. Theorem A applies in this situation and thus gives a positive answer to their conjecture.
$\Sigma $
. Theorem A applies in this situation and thus gives a positive answer to their conjecture. -
3. Positive representations. The Hitchin component is one example of a higher rank Teichmüller component. Other examples are formed by maximal representations, and more generally by spaces of
 $\Theta $
–positive representations introduced in [Reference Guichard and WienhardGW18, Reference Guichard and WienhardGW]. Here,
$\Theta $
–positive representations introduced in [Reference Guichard and WienhardGW18, Reference Guichard and WienhardGW]. Here,
 $\Theta $
is a subset of the set of simple roots
$\Theta $
is a subset of the set of simple roots
 $\Delta $
. Hitchin representations are
$\Delta $
. Hitchin representations are
 $\Delta $
–positive representations. Maximal representations into Hermitian groups of tube type are
$\Delta $
–positive representations. Maximal representations into Hermitian groups of tube type are
 $\{\alpha \}$
–positive for a specific choice of
$\{\alpha \}$
–positive for a specific choice of
 $\alpha \in \Delta $
. There are two further families of Lie groups that admit
$\alpha \in \Delta $
. There are two further families of Lie groups that admit
 $\Theta $
–positive structures and
$\Theta $
–positive structures and
 $\Theta $
–positive representations. When G is a Lie group carrying a
$\Theta $
–positive representations. When G is a Lie group carrying a
 $\Theta $
–positive structure, then there is a special simple three-dimensional
$\Theta $
–positive structure, then there is a special simple three-dimensional
 $\Theta $
–principal subgroup in G; see [Reference Guichard and WienhardGW]. Contrary to the principal subgroup of a split real Lie group, this H might have a compact centralizer, so there is a compact extension H of the
$\Theta $
–principal subgroup in G; see [Reference Guichard and WienhardGW]. Contrary to the principal subgroup of a split real Lie group, this H might have a compact centralizer, so there is a compact extension H of the
 $\Theta $
–principal subgroup that embeds into G. We choose a discrete and faithful representation
$\Theta $
–principal subgroup that embeds into G. We choose a discrete and faithful representation
 $\rho _0:\pi _1(\Sigma ) \rightarrow H$
and call
$\rho _0:\pi _1(\Sigma ) \rightarrow H$
and call
 $\iota \circ \rho _0:\pi _1(\Sigma ) \to G$
a twisted
$\iota \circ \rho _0:\pi _1(\Sigma ) \to G$
a twisted
 $\Theta $
–principal embedding. This representation is
$\Theta $
–principal embedding. This representation is
 $P_\Theta $
–Anosov, where
$P_\Theta $
–Anosov, where
 $P_\Theta $
is the parabolic subgroup determined by
$P_\Theta $
is the parabolic subgroup determined by
 $\Theta $
. In fact, any deformation of
$\Theta $
. In fact, any deformation of
 $\iota \circ \rho _0$
is
$\iota \circ \rho _0$
is
 $P_\Theta $
–Anosov [Reference Guichard, Labourie and WienhardGLW, Reference Beyrer, Guichard, Labourie, Pozzetti and WienhardBGL+24], and thus, Theorem A applies.
$P_\Theta $
–Anosov [Reference Guichard, Labourie and WienhardGLW, Reference Beyrer, Guichard, Labourie, Pozzetti and WienhardBGL+24], and thus, Theorem A applies.Note that there are cases where not every
 $\Theta $
–positive representation arises from a deformation of a principal or
$\Theta $
–positive representation arises from a deformation of a principal or
 $\Theta $
–principal Fuchsian representation. In particular, when
$\Theta $
–principal Fuchsian representation. In particular, when
 $G = {\mathrm {Sp}}(4,\mathbb R), \mathrm {SO}(2,3), \mathrm {SO}(n,n+1)$
, there are connected components of the space of
$G = {\mathrm {Sp}}(4,\mathbb R), \mathrm {SO}(2,3), \mathrm {SO}(n,n+1)$
, there are connected components of the space of
 $\Theta $
–positive representations where every representation is Zariski-dense. In particular, Theorem A does not apply to these components. When
$\Theta $
–positive representations where every representation is Zariski-dense. In particular, Theorem A does not apply to these components. When
 $G = {\mathrm {Sp}}(4,\mathbb R), \mathrm {SO}(2,3)$
, it has been proven by other means that the quotient manifolds
$G = {\mathrm {Sp}}(4,\mathbb R), \mathrm {SO}(2,3)$
, it has been proven by other means that the quotient manifolds
 $M_\rho $
are fiber bundles over
$M_\rho $
are fiber bundles over
 $\Sigma $
; see the discussion in Section 1.3.
$\Sigma $
; see the discussion in Section 1.3. -
4. P–quasi-positive representations. Similarly to the discussion of quasi-Hitchin representations, when G admits a
 $\Theta $
–positive structure, we can embed G into its complexification
$\Theta $
–positive structure, we can embed G into its complexification
 $G_{\mathbb C}$
, and any
$G_{\mathbb C}$
, and any
 $\Theta $
–positive representation
$\Theta $
–positive representation
 $\rho :\pi _1(\Sigma ) \to G <G_{\mathbb C}$
will be P–Anosov for a set of parabolic subgroups determined by
$\rho :\pi _1(\Sigma ) \to G <G_{\mathbb C}$
will be P–Anosov for a set of parabolic subgroups determined by
 $\Theta $
. Thus, we can define the set of P–quasi-positive representations as the connected components of the space of P–Anosov representations into
$\Theta $
. Thus, we can define the set of P–quasi-positive representations as the connected components of the space of P–Anosov representations into
 $G_{\mathbb C}$
containing a
$G_{\mathbb C}$
containing a
 $\Theta $
–positive representation into G. Theorem A then applies to the components of P–quasi-positive representations that contain a twisted
$\Theta $
–positive representation into G. Theorem A then applies to the components of P–quasi-positive representations that contain a twisted
 $\Theta $
–principal embedding.
$\Theta $
–principal embedding.Applications of Theorem A are not limited to representations of surface groups. There are notably interesting examples of Anosov deformations of fundamental groups of higher dimensional hyperbolic manifolds.
-
5. Convex divisible representations. The fundamental group
 $\pi _1(M)$
of a closed hyperbolic manifold of dimension
$\pi _1(M)$
of a closed hyperbolic manifold of dimension
 $d\geq 3$
has a natural discrete and faithful embedding
$d\geq 3$
has a natural discrete and faithful embedding
 $\rho _0: \pi _1(M) \to \mathrm {SO}(d,1)\simeq \operatorname {Isom}(\mathbb H^d)$
. In many examples,
$\rho _0: \pi _1(M) \to \mathrm {SO}(d,1)\simeq \operatorname {Isom}(\mathbb H^d)$
. In many examples,
 $\rho _0$
can be deformed into
$\rho _0$
can be deformed into
 $\mathrm {SL}(d+1,{\mathbb R})$
. All such continuous deformations are Anosov (see Section 2.4 for details), so Theorem A applies to all such deformations, as well as further small deformations in
$\mathrm {SL}(d+1,{\mathbb R})$
. All such continuous deformations are Anosov (see Section 2.4 for details), so Theorem A applies to all such deformations, as well as further small deformations in
 $\mathrm {SL}(d+1,{{\mathbb C}})$
.
$\mathrm {SL}(d+1,{{\mathbb C}})$
. -
6.
 ${\mathbb H}^{p,q}$
-convex-cocompact representations. Similarly, the representation
${\mathbb H}^{p,q}$
-convex-cocompact representations. Similarly, the representation
 $\rho _0$
can often be continuously deformed into
$\rho _0$
can often be continuously deformed into
 $\mathrm {SO}(d, d')$
,
$\mathrm {SO}(d, d')$
,
 $d'\geq 2$
, and every such deformation remains Anosov (see Section 2.4 for details). Theorem A thus applies to all such deformations, as well as further small deformations into
$d'\geq 2$
, and every such deformation remains Anosov (see Section 2.4 for details). Theorem A thus applies to all such deformations, as well as further small deformations into
 $\mathrm {SO}(d+d', {{\mathbb C}})$
.
$\mathrm {SO}(d+d', {{\mathbb C}})$
.
Even if we know that
![]() $M_\rho $
is a fiber bundle over the locally symmetric space
$M_\rho $
is a fiber bundle over the locally symmetric space
![]() $\Gamma \backslash S_H$
, it seems difficult in general to determine precisely the topology of the fiber. Explicit descriptions of the fibers have been given in some cases; see Section 1.3. In fact, the main reason why such a general result as Theorem A has been previously overlooked seems to be that, in interesting low dimensional situations, there are explicit and natural H–equivariant fibrations from
$\Gamma \backslash S_H$
, it seems difficult in general to determine precisely the topology of the fiber. Explicit descriptions of the fibers have been given in some cases; see Section 1.3. In fact, the main reason why such a general result as Theorem A has been previously overlooked seems to be that, in interesting low dimensional situations, there are explicit and natural H–equivariant fibrations from
![]() $\Omega $
to
$\Omega $
to
![]() $S_H$
which are not smooth and whose fibers are not manifolds.
$S_H$
which are not smooth and whose fibers are not manifolds.
In the proof of Theorem A, the assumption that
![]() $\rho $
is a P–Anosov deformation of a rank one lattice is used crucially in order to reduce to the ‘Fuchsian’ case. Indeed, Guichard–Wienhard proved that the topology of
$\rho $
is a P–Anosov deformation of a rank one lattice is used crucially in order to reduce to the ‘Fuchsian’ case. Indeed, Guichard–Wienhard proved that the topology of
![]() $M_\rho $
is invariant under continuous deformation of
$M_\rho $
is invariant under continuous deformation of
![]() $\rho $
in
$\rho $
in
![]() $\mathrm {Anosov}_P(\Gamma ,G)$
. We can thus assume without loss of generality that
$\mathrm {Anosov}_P(\Gamma ,G)$
. We can thus assume without loss of generality that
![]() $\rho = \iota \circ \rho _0$
. In that case, the domain
$\rho = \iota \circ \rho _0$
. In that case, the domain
![]() $\Omega _\rho $
is H–invariant, and our main theorem follows from the following general result:
$\Omega _\rho $
is H–invariant, and our main theorem follows from the following general result:
Lemma C (See Lemma 3.5).
Let X be a smooth manifold with a proper action of a semisimple Lie group H. Then there exists a smooth H–equivariant fibration from X to the symmetric space
![]() $S_H$
.
$S_H$
.
Though this fairly general lemma sounds like a classical result, it seems to have been overlooked by people in the field. To prove it, we fix an arbitrary torsion-free uniform lattice
![]() $\Gamma \subset H$
, choose a smooth
$\Gamma \subset H$
, choose a smooth
![]() $\Gamma $
–equivariant map from X to
$\Gamma $
–equivariant map from X to
![]() $S_H$
, and then take a barycentric average of f under some action of H.
$S_H$
, and then take a barycentric average of f under some action of H.
A more precise version of Theorem A (see Theorem 3.3 and Corollary 3.4) shows that
![]() $M_\rho $
is a fiber bundle over
$M_\rho $
is a fiber bundle over
![]() $\Gamma \backslash S_H$
associated to an explicit principal K–bundle, where K is a maximal compact subgroup of H. In order to complete the description of
$\Gamma \backslash S_H$
associated to an explicit principal K–bundle, where K is a maximal compact subgroup of H. In order to complete the description of
![]() $M_\rho $
, the only missing element is the topology of the fiber. The topology of the fiber has been determined in some cases; see Section 1.3. In the second part of the paper, we determine the fiber in a special low-dimensional case.
$M_\rho $
, the only missing element is the topology of the fiber. The topology of the fiber has been determined in some cases; see Section 1.3. In the second part of the paper, we determine the fiber in a special low-dimensional case.
1.2 Part 2: Symplectic quasi-Hitchin representations
In the second part of the paper, we focus on P–quasi-Hitchin representations into
![]() $\mathrm {PSp}(4,{\mathbb C})$
, where P is the stabilizer of a line in
$\mathrm {PSp}(4,{\mathbb C})$
, where P is the stabilizer of a line in
![]() $\mathbb {CP}^3$
. Let
$\mathbb {CP}^3$
. Let
![]() $\Gamma $
be the fundamental group of a closed surface
$\Gamma $
be the fundamental group of a closed surface
![]() $\Sigma $
of genus
$\Sigma $
of genus
![]() $g\geq 2$
, embedded as a uniform lattice in
$g\geq 2$
, embedded as a uniform lattice in
![]() $H= \mathrm {PSL}(2,{\mathbb R})$
via a Fuchsian representation
$H= \mathrm {PSL}(2,{\mathbb R})$
via a Fuchsian representation
![]() $\rho _0$
. Let
$\rho _0$
. Let
![]() $\iota _0\colon \thinspace \mathrm {PSL}(2,{\mathbb R})\to \mathrm {PSp}(4,{\mathbb C})$
be the principal representation. We see
$\iota _0\colon \thinspace \mathrm {PSL}(2,{\mathbb R})\to \mathrm {PSp}(4,{\mathbb C})$
be the principal representation. We see
![]() $\iota _0\circ \rho _0$
as a P–Anosov representation, and we consider P–quasi-Hitchin representations (i.e., P–Anosov deformations of
$\iota _0\circ \rho _0$
as a P–Anosov representation, and we consider P–quasi-Hitchin representations (i.e., P–Anosov deformations of
![]() $\iota _0\circ \rho _0$
).
$\iota _0\circ \rho _0$
).
Guichard and Wienhard [Reference Guichard and WienhardGW12] show that P–quasi-Hitchin representations
![]() $\rho \colon \thinspace \pi _1(\Sigma )\to \mathrm {Sp}(4,{\mathbb C})$
admit cocompact domains of discontinuity
$\rho \colon \thinspace \pi _1(\Sigma )\to \mathrm {Sp}(4,{\mathbb C})$
admit cocompact domains of discontinuity
![]() $\Omega _\rho $
in the space
$\Omega _\rho $
in the space
![]() ${\mathrm {Lag}}({\mathbb C}^{4})$
of Lagrangian subspaces of
${\mathrm {Lag}}({\mathbb C}^{4})$
of Lagrangian subspaces of
![]() ${\mathbb C}^{4}$
, of complex dimension
${\mathbb C}^{4}$
, of complex dimension
![]() $3$
. We write as before
$3$
. We write as before
![]() $M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
. By topological invariance
$M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
. By topological invariance
![]() $M_\rho $
is diffeomorphic to
$M_\rho $
is diffeomorphic to
![]() $M_{\iota _0\circ \rho _0}$
, and Theorem A tells us that this manifold is a smooth fiber bundle over the hyperbolic surface
$M_{\iota _0\circ \rho _0}$
, and Theorem A tells us that this manifold is a smooth fiber bundle over the hyperbolic surface
![]() $\Sigma = \Gamma \backslash {\mathbb H}^2$
.
$\Sigma = \Gamma \backslash {\mathbb H}^2$
.
We prove the following theorem:
Theorem D. Let
![]() $\rho $
be a P–quasi-Hitchin representation of a surface group
$\rho $
be a P–quasi-Hitchin representation of a surface group
![]() $\Gamma = \pi _1(\Sigma )$
into
$\Gamma = \pi _1(\Sigma )$
into
![]() $\mathrm {PSp}(4,{\mathbb C})$
, and let
$\mathrm {PSp}(4,{\mathbb C})$
, and let
![]() $\Omega _\rho $
be its flag domain of discontinuity in the space of complex Lagrangians. Then
$\Omega _\rho $
be its flag domain of discontinuity in the space of complex Lagrangians. Then
![]() $M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
is a smooth fiber bundle over
$M_\rho = \rho (\Gamma ) \backslash \Omega _\rho $
is a smooth fiber bundle over
![]() $\Sigma $
with fiber homeomorphic to
$\Sigma $
with fiber homeomorphic to
![]() $\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
.
$\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
.
Remark 1.1. Theorem D does not say anything about the diffeomorphism type of the fiber. This question is still open, and it is particularly interesting. The question whether
![]() $\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
admits exotic smooth structures is open, and it is an important question in the study of smooth
$\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
admits exotic smooth structures is open, and it is an important question in the study of smooth
![]() $4$
–manifolds.
$4$
–manifolds.
The domain of discontinuity
![]() $\Omega _\rho \subset {\mathrm {Lag}}({\mathbb C}^{2n})$
is of particular interest in the context of potential generalizations of Bers’ double uniformization for higher rank Teichmüller spaces. In the case when
$\Omega _\rho \subset {\mathrm {Lag}}({\mathbb C}^{2n})$
is of particular interest in the context of potential generalizations of Bers’ double uniformization for higher rank Teichmüller spaces. In the case when
![]() $n=1$
and
$n=1$
and
![]() $\rho $
is a Fuchsian representation,
$\rho $
is a Fuchsian representation,
![]() $\Omega _\rho $
is the disjoint union of the upper and the lower half disc; if
$\Omega _\rho $
is the disjoint union of the upper and the lower half disc; if
![]() $\rho $
is a quasi-Fuchsian representation it is precisely the complement of the limit set, and thus consists of two connected components, whose quotients give rise to the two conformal structures associated to a quasi-Fuchsian representation. For general n and
$\rho $
is a quasi-Fuchsian representation it is precisely the complement of the limit set, and thus consists of two connected components, whose quotients give rise to the two conformal structures associated to a quasi-Fuchsian representation. For general n and
![]() $\rho $
a Hitchin representation into
$\rho $
a Hitchin representation into
![]() $\mathrm {PSp}(2n,\mathbb R)$
, the domain of discontinuity
$\mathrm {PSp}(2n,\mathbb R)$
, the domain of discontinuity
![]() $\Omega _\rho $
contains two copies of the symmetric space associated to
$\Omega _\rho $
contains two copies of the symmetric space associated to
![]() $\mathrm {PSp}(2n,\mathbb R)$
, a copy of the Siegel upper half space, and a copy of the Siegel lower half space, which are exchanged by the complex conjugation. However, it also contains other strata, (e.g., all the pseudo-Riemannian symmetric spaces
$\mathrm {PSp}(2n,\mathbb R)$
, a copy of the Siegel upper half space, and a copy of the Siegel lower half space, which are exchanged by the complex conjugation. However, it also contains other strata, (e.g., all the pseudo-Riemannian symmetric spaces
![]() $\mathrm {PSp}(2n,\mathbb R)/\mathrm {PSU}(p,q)$
,
$\mathrm {PSp}(2n,\mathbb R)/\mathrm {PSU}(p,q)$
,
![]() $p+q=n$
), which are permuted by the complex conjugation. (For a more detailed discussion, see [Reference WienhardWie16].) The fact that for
$p+q=n$
), which are permuted by the complex conjugation. (For a more detailed discussion, see [Reference WienhardWie16].) The fact that for
![]() $\mathrm {PSp}(4,{\mathbb C})$
the fiber is
$\mathrm {PSp}(4,{\mathbb C})$
the fiber is
![]() $\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
appears to be quite interesting in this respect.
$\mathbb {CP}^2 \# \overline {\mathbb {CP}}^2$
appears to be quite interesting in this respect.
In order to prove Theorem D, we actually have to take quite a bit of a detour. We first give a natural geometric construction of an H–equivariant continuous fibration
![]() $\pi $
from
$\pi $
from
![]() $\Omega _{\iota _0\circ \rho _0}$
to
$\Omega _{\iota _0\circ \rho _0}$
to
![]() ${\mathbb H}^2$
. The map
${\mathbb H}^2$
. The map
![]() $\pi $
is not smooth, and its fiber F is singular. Nevertheless, the fiber F is homotopy equivalent to the fiber
$\pi $
is not smooth, and its fiber F is singular. Nevertheless, the fiber F is homotopy equivalent to the fiber
![]() $F'$
of a smooth equivariant fibration since both are retractions of
$F'$
of a smooth equivariant fibration since both are retractions of
![]() $\Omega _{\iota _0\circ \rho _0}$
. By carefully studying F, we can determine its second cohomology and the intersection form on it. Finally, using the classification of smooth
$\Omega _{\iota _0\circ \rho _0}$
. By carefully studying F, we can determine its second cohomology and the intersection form on it. Finally, using the classification of smooth
![]() $4$
–manifolds due to Whitehead, Milnor, Milnor–Hausemoller, Freedman, Serre and Donaldson, we deduce the homeomorphism type of
$4$
–manifolds due to Whitehead, Milnor, Milnor–Hausemoller, Freedman, Serre and Donaldson, we deduce the homeomorphism type of
![]() $F'$
(which has the same second homology group) and prove the theorem.
$F'$
(which has the same second homology group) and prove the theorem.
1.3 Related works and perspectives
The topology of flag domains of discontinuity and their quotient manifolds
![]() $M_\rho $
for Anosov representations
$M_\rho $
for Anosov representations
![]() $\rho $
have been studied before in special examples, mainly for Anosov representations of a surface group
$\rho $
have been studied before in special examples, mainly for Anosov representations of a surface group
![]() $\pi _1(\Sigma )$
. We review these results here.
$\pi _1(\Sigma )$
. We review these results here.
In [Reference Guichard and WienhardGW08], Guichard–Wienhard constructed flag domains of discontinuity in
![]() $\mathbb R\mathbb {P}^3$
for Hitchin representations into
$\mathbb R\mathbb {P}^3$
for Hitchin representations into
![]() $\mathrm {PSL}(4,\mathbb R)$
and
$\mathrm {PSL}(4,\mathbb R)$
and
![]() $\mathrm {PSp}(4,\mathbb R)$
. These domains of discontinuity have two connected components
$\mathrm {PSp}(4,\mathbb R)$
. These domains of discontinuity have two connected components
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
. They showed that the quotient manifold
$\Omega _2$
. They showed that the quotient manifold
![]() $\pi _1(\Sigma ) \backslash \Omega _1$
is homeomorphic to the unit tangent bundle
$\pi _1(\Sigma ) \backslash \Omega _1$
is homeomorphic to the unit tangent bundle
![]() $T^1S$
of the surface and in fact gives rise to convex foliated projective structures of
$T^1S$
of the surface and in fact gives rise to convex foliated projective structures of
![]() $T^1S$
. The quotient manifold
$T^1S$
. The quotient manifold
![]() $\pi _1(S) \backslash \Omega _2$
is a quotient of
$\pi _1(S) \backslash \Omega _2$
is a quotient of
![]() $T^1S$
by
$T^1S$
by
![]() $\mathbb {Z}/3\mathbb {Z}$
. They also show that deformations of quasi-Fuchsian representations (in
$\mathbb {Z}/3\mathbb {Z}$
. They also show that deformations of quasi-Fuchsian representations (in
![]() $\mathrm {PSL}(2,{\mathbb C})\cong \operatorname {PO}(3,1)$
) into
$\mathrm {PSL}(2,{\mathbb C})\cong \operatorname {PO}(3,1)$
) into
![]() $\mathrm {PSL}(4,\mathbb R)$
give rise to projective structures on
$\mathrm {PSL}(4,\mathbb R)$
give rise to projective structures on
![]() $T^1 S$
.
$T^1 S$
.
The study of Hitchin representations in
![]() $\mathrm {PSL}(4,\mathbb R)$
and
$\mathrm {PSL}(4,\mathbb R)$
and
![]() $\mathrm {PSp}(4,\mathbb R)$
and their domains of discontinuity in
$\mathrm {PSp}(4,\mathbb R)$
and their domains of discontinuity in
![]() $\mathbb R\mathbb {P}^3$
can be carried out also for lattices in
$\mathbb R\mathbb {P}^3$
can be carried out also for lattices in
![]() $\mathrm {PSL}(2,{\mathbb R})$
that have torsion; see Alessandrini–Lee–Schaffhauser [Reference Alessandrini, Lee and SchaffhauserALS23]. There, they show that in this case, the quotient
$\mathrm {PSL}(2,{\mathbb R})$
that have torsion; see Alessandrini–Lee–Schaffhauser [Reference Alessandrini, Lee and SchaffhauserALS23]. There, they show that in this case, the quotient
![]() $\mathbb R\mathbb {P}^3$
-manifolds are homeomorphic to certain Seifert-fibered
$\mathbb R\mathbb {P}^3$
-manifolds are homeomorphic to certain Seifert-fibered
![]() $3$
–manifolds that depend on the lattice.
$3$
–manifolds that depend on the lattice.
In [Reference Guichard and WienhardGW12], determining part of the cohomology of the flag domains of discontinuity played a key role in showing that the action of
![]() $\rho (\Gamma )$
on
$\rho (\Gamma )$
on
![]() $\Omega _\rho $
is cocompact. They describe several explicit examples of such flag domains of discontinuity – among them, some where
$\Omega _\rho $
is cocompact. They describe several explicit examples of such flag domains of discontinuity – among them, some where
![]() $M_\rho $
are in fact compact Clifford–Klein forms. For maximal representations in the symplectic group, and for the domain of discontinuity in
$M_\rho $
are in fact compact Clifford–Klein forms. For maximal representations in the symplectic group, and for the domain of discontinuity in
![]() $\mathbb R\mathbb {P}^{2n-1}$
, they announced that
$\mathbb R\mathbb {P}^{2n-1}$
, they announced that
![]() $M_\rho $
is a fiber bundle over S with fiber
$M_\rho $
is a fiber bundle over S with fiber
![]() $\mathrm {O}(n)/\mathrm {O}(n-2)$
. This in particular also applies to the components of the space of maximal representations into
$\mathrm {O}(n)/\mathrm {O}(n-2)$
. This in particular also applies to the components of the space of maximal representations into
![]() $\mathrm {PSp}(4,\mathbb R)$
where all representations are Zariski-dense. This result lead them to conjecture that the quotient manifold
$\mathrm {PSp}(4,\mathbb R)$
where all representations are Zariski-dense. This result lead them to conjecture that the quotient manifold
![]() $M_\rho $
is a compact fibre bundle over
$M_\rho $
is a compact fibre bundle over
![]() $\Sigma $
for all higher Teichmüller spaces; see [Reference WienhardWie18, Conjecture 13].
$\Sigma $
for all higher Teichmüller spaces; see [Reference WienhardWie18, Conjecture 13].
When
![]() $\rho $
is a quasi-Hitchin representation into a complex group G, Dumas–Sanders [Reference Dumas and SandersDS20] computed the cohomology ring of
$\rho $
is a quasi-Hitchin representation into a complex group G, Dumas–Sanders [Reference Dumas and SandersDS20] computed the cohomology ring of
![]() $\Omega _\rho $
and
$\Omega _\rho $
and
![]() $M_\rho $
for all choices of parabolic subgroups and balanced ideals. They found that the cohomology of
$M_\rho $
for all choices of parabolic subgroups and balanced ideals. They found that the cohomology of
![]() $M_\rho $
is the tensor product of the cohomology of
$M_\rho $
is the tensor product of the cohomology of
![]() $\Sigma $
with the cohomology of
$\Sigma $
with the cohomology of
![]() $\Omega _\rho $
and that, under their hypothesis,
$\Omega _\rho $
and that, under their hypothesis,
![]() $\Omega _\rho $
is a Poincaré duality space. They remarked that this is compatible with
$\Omega _\rho $
is a Poincaré duality space. They remarked that this is compatible with
![]() $M_\rho $
being a fiber bundle on
$M_\rho $
being a fiber bundle on
![]() $\Sigma $
, and they stated a conjecture [Reference Dumas and SandersDS20, Conjecture 1.1] that is a special case of our Theorem A. Interestingly, in their conjecture, they stated that
$\Sigma $
, and they stated a conjecture [Reference Dumas and SandersDS20, Conjecture 1.1] that is a special case of our Theorem A. Interestingly, in their conjecture, they stated that
![]() $M_\rho $
is a continuous fiber bundle over
$M_\rho $
is a continuous fiber bundle over
![]() $\Sigma $
because in some examples available at the time, the known fibrations were only continuous, but not smooth. They verified their conjecture in the special case when
$\Sigma $
because in some examples available at the time, the known fibrations were only continuous, but not smooth. They verified their conjecture in the special case when
![]() $G=\mathrm {SL}(3,{{\mathbb C}})$
and
$G=\mathrm {SL}(3,{{\mathbb C}})$
and
![]() $G/Q$
is the full flag variety.
$G/Q$
is the full flag variety.
When
![]() $G = \mathrm {SL}(2n,\mathbb {K})$
with
$G = \mathrm {SL}(2n,\mathbb {K})$
with
![]() $\mathbb {K} = {\mathbb R}$
or
$\mathbb {K} = {\mathbb R}$
or
![]() ${{\mathbb C}}$
,
${{\mathbb C}}$
,
![]() $\iota $
is the principal representation and
$\iota $
is the principal representation and
![]() $G/Q$
is
$G/Q$
is
![]() $\mathbb {KP}^{2n-1}$
, Alessandrini–Davalo–Li [Reference Alessandrini, Davalo and LiADL24] proved that M is a fiber bundle over
$\mathbb {KP}^{2n-1}$
, Alessandrini–Davalo–Li [Reference Alessandrini, Davalo and LiADL24] proved that M is a fiber bundle over
![]() $\Sigma $
with structure group
$\Sigma $
with structure group
![]() $\mathrm {SO}(2)$
, described the topology of the fiber, and computed the Euler class of the underline
$\mathrm {SO}(2)$
, described the topology of the fiber, and computed the Euler class of the underline
![]() $\mathrm {SO}(2)$
-bundle. They used Higgs bundles, as described in the survey paper [Reference AlessandriniAle19]. In a paper in preparation, Alessandrini–Li [Reference Alessandrini and LiAL] extend some of these results to the case when
$\mathrm {SO}(2)$
-bundle. They used Higgs bundles, as described in the survey paper [Reference AlessandriniAle19]. In a paper in preparation, Alessandrini–Li [Reference Alessandrini and LiAL] extend some of these results to the case when
![]() $G = \mathrm {SL}(n,\mathbb {K})$
and
$G = \mathrm {SL}(n,\mathbb {K})$
and
![]() $G/Q$
is a partial flag manifold parametrizing flags consisting of lines and hyperplanes, and when
$G/Q$
is a partial flag manifold parametrizing flags consisting of lines and hyperplanes, and when
![]() $G = \mathrm {SL}(4n+3,{\mathbb R})$
,
$G = \mathrm {SL}(4n+3,{\mathbb R})$
,
![]() $G/Q = {\mathbb S}^{4n+2}$
, and M is the manifold constructed by Stecker–Treib [Reference Stecker and TreibST18].
$G/Q = {\mathbb S}^{4n+2}$
, and M is the manifold constructed by Stecker–Treib [Reference Stecker and TreibST18].
In [Reference Collier, Tholozan and ToulisseCTT19], Collier–Tholozan–Toulisse studied the case where
![]() $\rho : \pi _1(\Sigma ) \to \mathrm {SO}(2,n+1)$
is a maximal representation of a closed surface group. Such representations admit a flag domain of discontinuity
$\rho : \pi _1(\Sigma ) \to \mathrm {SO}(2,n+1)$
is a maximal representation of a closed surface group. Such representations admit a flag domain of discontinuity
![]() $\Omega _\rho $
in the space of totally isotropic planes in
$\Omega _\rho $
in the space of totally isotropic planes in
![]() ${\mathbb R}^{2,n+1}$
. The authors prove that such maximal representations come with an equivariant spacelike embedding of
${\mathbb R}^{2,n+1}$
. The authors prove that such maximal representations come with an equivariant spacelike embedding of
![]() ${\mathbb H}^2$
into the pseudo-hyperbolic space
${\mathbb H}^2$
into the pseudo-hyperbolic space
![]() ${\mathbb H}^{2,n}$
and that the domain
${\mathbb H}^{2,n}$
and that the domain
![]() $\Omega _\rho $
fibers
$\Omega _\rho $
fibers
![]() $\rho $
–equivariantly over this spacelike disk, and deduce that
$\rho $
–equivariantly over this spacelike disk, and deduce that
![]() $M_\rho $
is a homogeneous fiber bundle over
$M_\rho $
is a homogeneous fiber bundle over
![]() $\Sigma $
with fiber a Stiefel manifold. The topological invariants of this fiber bundle turn out to depend on the connected component of
$\Sigma $
with fiber a Stiefel manifold. The topological invariants of this fiber bundle turn out to depend on the connected component of
![]() $\rho $
as the set of maximal representations. In particular, for
$\rho $
as the set of maximal representations. In particular, for
![]() $n=3$
, one obtains circle bundles over
$n=3$
, one obtains circle bundles over
![]() $\Sigma $
whose Euler class varies with the connected component of maximal representations. Interestingly, there are connected components of the set of maximal representations into
$\Sigma $
whose Euler class varies with the connected component of maximal representations. Interestingly, there are connected components of the set of maximal representations into
![]() $\mathrm {SO}(2,3)$
that do not contain a representation factoring through
$\mathrm {SO}(2,3)$
that do not contain a representation factoring through
![]() $\mathrm {PSL}(2,{\mathbb R})$
. For these representations, the fibration of
$\mathrm {PSL}(2,{\mathbb R})$
. For these representations, the fibration of
![]() $M_\rho $
over
$M_\rho $
over
![]() $\Sigma $
is not given by Theorem A.
$\Sigma $
is not given by Theorem A.
More generally, let
![]() $\Gamma $
be a
$\Gamma $
be a
![]() $\mathbb H^{p,q}$
-convex-cocompact subgroup of
$\mathbb H^{p,q}$
-convex-cocompact subgroup of
![]() $\mathrm {SO}(p,q+1)$
and
$\mathrm {SO}(p,q+1)$
and
![]() $\rho : \Gamma \to \mathrm {SO}(p,q+1)$
. Then
$\rho : \Gamma \to \mathrm {SO}(p,q+1)$
. Then
![]() $\Gamma $
admits a Guichard–Wienhard domain of discontinuity
$\Gamma $
admits a Guichard–Wienhard domain of discontinuity
![]() $\Omega _\rho $
in
$\Omega _\rho $
in
![]() $\mathrm {SO}(p,q+1)/Q$
, where Q is the stabilizer of a maximal isotropic subspace of
$\mathrm {SO}(p,q+1)/Q$
, where Q is the stabilizer of a maximal isotropic subspace of
![]() ${\mathbb R}^{p,q+1}$
. If
${\mathbb R}^{p,q+1}$
. If
![]() $\partial _\infty \Gamma $
is a
$\partial _\infty \Gamma $
is a
![]() $p-1$
-sphere, Seppi, Smith and Toulisse recently proved that
$p-1$
-sphere, Seppi, Smith and Toulisse recently proved that
![]() $\Gamma $
is virtually the fundamental group of an aspherical p-manifold M and that
$\Gamma $
is virtually the fundamental group of an aspherical p-manifold M and that
![]() $\Gamma \backslash \Omega _\rho $
is a smooth fiber bundle over M [Reference SeppiSST23]. Interestingly here, the group
$\Gamma \backslash \Omega _\rho $
is a smooth fiber bundle over M [Reference SeppiSST23]. Interestingly here, the group
![]() $\Gamma $
need not be isomorphic to a rank one lattice (see [Reference Monclair, Schlenker and TholozanMST23]).
$\Gamma $
need not be isomorphic to a rank one lattice (see [Reference Monclair, Schlenker and TholozanMST23]).
Finally, let us mention that Theorem A was obtained independently by Davalo [Reference DavaloDav24] with a different method. With the notations above, Davalo associates to a point in
![]() $\Omega _{\iota \circ \rho _0}$
a Buseman function on the symmetric space of G and shows that the restriction of this Buseman function to the symmetric space of H admits a unique critical point. The equivariant fibration derived from this construction is somewhat more explicit than the one in our proof of Theorem A, and its fibers can be expressed as real projective algebraic varieties. Nevertheless, their topology remains difficult to grasp, even in some low-dimensional cases such as the one studied in the second part of the paper.
$\Omega _{\iota \circ \rho _0}$
a Buseman function on the symmetric space of G and shows that the restriction of this Buseman function to the symmetric space of H admits a unique critical point. The equivariant fibration derived from this construction is somewhat more explicit than the one in our proof of Theorem A, and its fibers can be expressed as real projective algebraic varieties. Nevertheless, their topology remains difficult to grasp, even in some low-dimensional cases such as the one studied in the second part of the paper.
1.4 Wild Kleinian groups
A crucial hypothesis in our Theorem A is that the representation is a deformation of an
![]() $\iota $
–lattice representation. We report on an example, by Gromov–Lawson–Thurston [Reference Gromov, Lawson and ThurstonGLT88], showing that this hypothesis is indeed necessary. They show that one can obtain wild convex-cocompact embeddings of a surface group
$\iota $
–lattice representation. We report on an example, by Gromov–Lawson–Thurston [Reference Gromov, Lawson and ThurstonGLT88], showing that this hypothesis is indeed necessary. They show that one can obtain wild convex-cocompact embeddings of a surface group
![]() $\Gamma = \pi _1(\Sigma )$
into
$\Gamma = \pi _1(\Sigma )$
into
![]() $\operatorname {Isom}({\mathbb H}^4)$
from a ‘twisted necklace’ of
$\operatorname {Isom}({\mathbb H}^4)$
from a ‘twisted necklace’ of
![]() $2$
–spheres in
$2$
–spheres in
![]() $\partial _\infty {\mathbb H}^4$
. They construct such convex-cocompact representations for which
$\partial _\infty {\mathbb H}^4$
. They construct such convex-cocompact representations for which
![]() $M_\rho $
is a nontrivial circle bundle over
$M_\rho $
is a nontrivial circle bundle over
![]() $\Sigma $
. Again, by topological invariance, such
$\Sigma $
. Again, by topological invariance, such
![]() $\rho $
cannot be deformed to a Fuchsian representation within the domain of convex-cocompact representations. Such examples were also obtained independently by Kapovich [Reference KapovichKap89].
$\rho $
cannot be deformed to a Fuchsian representation within the domain of convex-cocompact representations. Such examples were also obtained independently by Kapovich [Reference KapovichKap89].
Gromov–Lawson–Thurston also point out that, starting from a knotted necklace, one obtains a convex-cocompact representation whose limit set is a wild knot. The associated conformal
![]() $3$
–manifold
$3$
–manifold
![]() $M_\rho $
is then obtained by gluing a circle bundle over a surface with boundary with one or several knot complements. These examples do not fiber over the surface
$M_\rho $
is then obtained by gluing a circle bundle over a surface with boundary with one or several knot complements. These examples do not fiber over the surface
![]() $\Sigma $
and their domains of discontinuity have infinitely generated fundamental group, showing that Theorem A cannot be true in general for Anosov representations which are not Fuchsian deformations.
$\Sigma $
and their domains of discontinuity have infinitely generated fundamental group, showing that Theorem A cannot be true in general for Anosov representations which are not Fuchsian deformations.
For more examples of convex-cocompact subgroups of
![]() $\operatorname {Isom}({\mathbb H}^n)$
with ‘wild’ limit set (e.g., Antoine’s necklace of Alexander’s horned sphere), we refer to the survey of Kapovich [Reference KapovichKap08].
$\operatorname {Isom}({\mathbb H}^n)$
with ‘wild’ limit set (e.g., Antoine’s necklace of Alexander’s horned sphere), we refer to the survey of Kapovich [Reference KapovichKap08].
Outline of the paper
In Section 2, we review the required background on Anosov representations and their domains of discontinuity. Section 3 is dedicated to the proof of Theorem A. These form the first part of the paper.
The second part of the paper focuses on quasi-Hitchin representations in
![]() ${\mathrm {Sp}}(4,{\mathbb C})$
. In Section 4, we describe the action of
${\mathrm {Sp}}(4,{\mathbb C})$
. In Section 4, we describe the action of
![]() $\mathrm {PSL}(2,{{\mathbb C}})$
on the
$\mathrm {PSL}(2,{{\mathbb C}})$
on the
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
and identify the Lagrangian Grassmannian to the space of (possibly degenerate) regular ideal tetrahedra in
${\mathrm {Lag}}({{\mathbb C}}^4)$
and identify the Lagrangian Grassmannian to the space of (possibly degenerate) regular ideal tetrahedra in
![]() ${\mathbb H}^3$
. Using this point of view, we construct a
${\mathbb H}^3$
. Using this point of view, we construct a
![]() $\mathrm {PSL}(2,{\mathbb R})$
–equivariant ‘projection’ from
$\mathrm {PSL}(2,{\mathbb R})$
–equivariant ‘projection’ from
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
to
${\mathrm {Lag}}({{\mathbb C}}^4)$
to
![]() $\overline {{\mathbb H}^2}$
that we study more closely in Section 5. In Section 6, we carefully study the topology of the fiber F of this projection. In particular, we compute the intersection form on its second cohomology group and conclude the proof of Theorem D using the topological classification of simply connected
$\overline {{\mathbb H}^2}$
that we study more closely in Section 5. In Section 6, we carefully study the topology of the fiber F of this projection. In particular, we compute the intersection form on its second cohomology group and conclude the proof of Theorem D using the topological classification of simply connected
![]() $4$
–manifolds.
$4$
–manifolds.
Part I Topology of the quotient of the domain of discontinuity
2 Anosov representations
In this section, we recall the notion of Anosov representation, originally introduced in [Reference LabourieLab06, Reference Guichard and WienhardGW12], and we discuss several interesting examples. We then review the construction of their flag domains of discontinuity, based on [Reference Guichard and WienhardGW12, Reference Kapovich, Leeb and PortiKLP18].
2.1 Definition and properties
There are several equivalent definitions of Anosov representations in literature; see [Reference LabourieLab06, Reference Guichard and WienhardGW12, Reference Kapovich, Leeb and PortiKLP17, Reference Guichard, Gueritaud, Kassel and WienhardGGKW17, Reference Bochi, Potrie and SambarinoBPS19, Reference Kassel and PotrieKP22]. Here, we will describe the one that is more suitable for our aims. Let G be a connected semisimple Lie group with finite center and P a parabolic subgroup of G that is conjugate to its opposite parabolic subgroup
![]() $P^{\textit {op}}$
. Two points p and q in
$P^{\textit {op}}$
. Two points p and q in
![]() $G/P$
are called transverse if there exists
$G/P$
are called transverse if there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $g\operatorname {\mathrm {Stab}}_G(p) g^{-1} = P$
and
$g\operatorname {\mathrm {Stab}}_G(p) g^{-1} = P$
and
![]() $g\operatorname {\mathrm {Stab}}_G(q)g^{-1} = P^{\textit {op}}$
.
$g\operatorname {\mathrm {Stab}}_G(q)g^{-1} = P^{\textit {op}}$
.
Let now
![]() $\Gamma $
be a finitely generated hyperbolic group with Gromov boundary
$\Gamma $
be a finitely generated hyperbolic group with Gromov boundary
![]() $\partial _\infty \Gamma $
.
$\partial _\infty \Gamma $
.
Definition 2.1. A representation
![]() $\rho \colon \thinspace \Gamma \to G$
is P–Anosov if there exists a continuous,
$\rho \colon \thinspace \Gamma \to G$
is P–Anosov if there exists a continuous,
![]() $\rho $
–equivariant map
$\rho $
–equivariant map
that is
-
• transverse (i.e.,
 $\xi _\rho (x)$
and
$\xi _\rho (x)$
and
 $\xi _\rho (y)$
are transverse for all
$\xi _\rho (y)$
are transverse for all
 $x \neq y \in \partial _\infty \Gamma $
);
$x \neq y \in \partial _\infty \Gamma $
); -
• strongly dynamics preserving (i.e., for any sequence
 $(\gamma _n)_{n\in {\mathbb N}} \in \Gamma ^{\mathbb N}$
with
$(\gamma _n)_{n\in {\mathbb N}} \in \Gamma ^{\mathbb N}$
with
 $\gamma _n \underset {n\to +\infty }{\longrightarrow } \gamma _+ \in \partial _\infty \Gamma $
and
$\gamma _n \underset {n\to +\infty }{\longrightarrow } \gamma _+ \in \partial _\infty \Gamma $
and
 $\gamma _n^{-1} \underset {n\to +\infty }{\longrightarrow } \gamma _- \in \partial _\infty \Gamma $
, for all
$\gamma _n^{-1} \underset {n\to +\infty }{\longrightarrow } \gamma _- \in \partial _\infty \Gamma $
, for all $$\begin{align*}\rho(\gamma_n)\cdot p \underset{n\to +\infty}{\longrightarrow} \xi_\rho(\gamma_+)\end{align*}$$
$$\begin{align*}\rho(\gamma_n)\cdot p \underset{n\to +\infty}{\longrightarrow} \xi_\rho(\gamma_+)\end{align*}$$
 $p\in G/P$
transverse to
$p\in G/P$
transverse to
 $\xi _\rho (\gamma _-)$
).
$\xi _\rho (\gamma _-)$
).
A subgroup
![]() $\Gamma $
of G is called Anosov if it is hyperbolic and the inclusion
$\Gamma $
of G is called Anosov if it is hyperbolic and the inclusion
![]() $\Gamma \hookrightarrow G$
is Anosov with respect to some proper parabolic subgroup P of G.
$\Gamma \hookrightarrow G$
is Anosov with respect to some proper parabolic subgroup P of G.
We denote by
![]() $\mathrm {Anosov}_P(\Gamma ,G)$
the subset of
$\mathrm {Anosov}_P(\Gamma ,G)$
the subset of
![]() $\mathrm {Hom}(\Gamma ,G)$
consisting of P–Anosov representations. Note that P–Anosov representations are discrete and have finite kernel. In this paper, we will only work with groups
$\mathrm {Hom}(\Gamma ,G)$
consisting of P–Anosov representations. Note that P–Anosov representations are discrete and have finite kernel. In this paper, we will only work with groups
![]() $\Gamma $
that are torsion-free. For such groups, P–Anosov representations are thus discrete and faithful.
$\Gamma $
that are torsion-free. For such groups, P–Anosov representations are thus discrete and faithful.
One of the most important properties of Anosov representations is their structural stablility (i.e.,
![]() $\mathrm {Anosov}_P(\Gamma ,G)$
is open in
$\mathrm {Anosov}_P(\Gamma ,G)$
is open in
![]() $\mathrm {Hom}(\Gamma ,G)$
). Structural stability gives a way to construct several Anosov representations as small deformations of a fixed Anosov representation. This is a major source of examples, as we will discuss in Section 2.2.
$\mathrm {Hom}(\Gamma ,G)$
). Structural stability gives a way to construct several Anosov representations as small deformations of a fixed Anosov representation. This is a major source of examples, as we will discuss in Section 2.2.
Another important property of P–Anosov representations is that they admit cocompact domains of discontinuity in boundaries of G (i.e., in homogeneous spaces
![]() $G/Q$
, where Q is a proper parabolic subgroup of G), possibly different from P. We will discuss this property in Section 2.5.
$G/Q$
, where Q is a proper parabolic subgroup of G), possibly different from P. We will discuss this property in Section 2.5.
2.2 Construction of Anosov representations via deformation
Let us fix a connected semisimple Lie group H of real rank
![]() $1$
with finite center, and let
$1$
with finite center, and let
![]() $K \subset H$
be its maximal compact subgroup. The symmetric space
$K \subset H$
be its maximal compact subgroup. The symmetric space
![]() $S_H = H/K$
has strictly negative sectional curvature and is thus Gromov hyperbolic. Recall that a uniform lattice
$S_H = H/K$
has strictly negative sectional curvature and is thus Gromov hyperbolic. Recall that a uniform lattice
![]() $\Gamma < H$
is a discrete cocompact subgroup of H. Any such lattice is quasi-isometric to
$\Gamma < H$
is a discrete cocompact subgroup of H. Any such lattice is quasi-isometric to
![]() $S_H$
and is thus a hyperbolic group. Moreover, H has a unique conjugacy class of parabolic subgroups
$S_H$
and is thus a hyperbolic group. Moreover, H has a unique conjugacy class of parabolic subgroups
![]() $P_H$
. By Guichard–Wienhard [Reference Guichard and WienhardGW12, Thm 5.15],
$P_H$
. By Guichard–Wienhard [Reference Guichard and WienhardGW12, Thm 5.15],
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $P_H$
–Anosov subgroup of H. We will always assume that
$P_H$
–Anosov subgroup of H. We will always assume that
![]() $\Gamma $
is torsion-free, which is always virtually true by Selberg’s lemma.
$\Gamma $
is torsion-free, which is always virtually true by Selberg’s lemma.
Remark 2.2. Note that the Anosov subgroups of a real rank
![]() $1$
Lie group H are precisely its quasi-isometrically embedded (equivalently: quasi-convex, or convex-cocompact) subgroups.
$1$
Lie group H are precisely its quasi-isometrically embedded (equivalently: quasi-convex, or convex-cocompact) subgroups.
An important case is when H is a compact extensionFootnote
1
of
![]() $\mathrm {PSL}(2,\mathbb R)$
(i.e., H admits a surjective morphism to
$\mathrm {PSL}(2,\mathbb R)$
(i.e., H admits a surjective morphism to
![]() $\mathrm {PSL}(2,\mathbb R)$
with compact kernel). In that case,
$\mathrm {PSL}(2,\mathbb R)$
with compact kernel). In that case,
![]() $S_H$
is the hyperbolic plane
$S_H$
is the hyperbolic plane
![]() ${\mathbb H}^2$
, and a torsion-free cocompact lattice
${\mathbb H}^2$
, and a torsion-free cocompact lattice
![]() $\Gamma $
in H is a surface group (i.e.,
$\Gamma $
in H is a surface group (i.e.,
![]() $\Gamma = \pi _1(\Sigma )$
, where
$\Gamma = \pi _1(\Sigma )$
, where
![]() $\Sigma $
is a closed orientable surface of genus
$\Sigma $
is a closed orientable surface of genus
![]() $g \geq 2$
). A representation
$g \geq 2$
). A representation
![]() $\rho _0:\pi _1(\Sigma ) \rightarrow \mathrm {PSL}(2,{\mathbb R})$
is called Fuchsian if it is discrete and faithful (in which case
$\rho _0:\pi _1(\Sigma ) \rightarrow \mathrm {PSL}(2,{\mathbb R})$
is called Fuchsian if it is discrete and faithful (in which case
![]() $\rho _0(\pi _1(\Sigma )) \backslash {\mathbb H}^2$
is a closed hyperbolic surface diffeomorphic to
$\rho _0(\pi _1(\Sigma )) \backslash {\mathbb H}^2$
is a closed hyperbolic surface diffeomorphic to
![]() $\Sigma $
). Similarly, a discrete and faithful representation into a compact extension H of
$\Sigma $
). Similarly, a discrete and faithful representation into a compact extension H of
![]() $\mathrm {PSL}(2,{\mathbb R})$
will be called a twisted Fuchsian representation. It is the case if and only if its projection to
$\mathrm {PSL}(2,{\mathbb R})$
will be called a twisted Fuchsian representation. It is the case if and only if its projection to
![]() $\mathrm {PSL}(2,{\mathbb R})$
is Fuchsian.
$\mathrm {PSL}(2,{\mathbb R})$
is Fuchsian.
Other interesting cases arise when H is (a compact extension of)
![]() $\operatorname {PO}_0(1,n)$
or
$\operatorname {PO}_0(1,n)$
or
![]() $\mathrm {PU}(1,n)$
, in which cases the symmetric space
$\mathrm {PU}(1,n)$
, in which cases the symmetric space
![]() $S_H$
is respectively the real hyperbolic space
$S_H$
is respectively the real hyperbolic space
![]() ${\mathbb H}^n = {\mathbb H}^n_{{\mathbb R}}$
and the complex hyperbolic space
${\mathbb H}^n = {\mathbb H}^n_{{\mathbb R}}$
and the complex hyperbolic space
![]() ${\mathbb H}^n_{{{\mathbb C}}}$
. The group
${\mathbb H}^n_{{{\mathbb C}}}$
. The group
![]() $\Gamma $
is then the fundamental group of a closed real hyperbolic or complex hyperbolic manifold. The other Lie groups of real rank
$\Gamma $
is then the fundamental group of a closed real hyperbolic or complex hyperbolic manifold. The other Lie groups of real rank
![]() $1$
(namely,
$1$
(namely,
![]() ${\mathrm {Sp}}(1,n)$
and
${\mathrm {Sp}}(1,n)$
and
![]() $\mathrm F_4^{-20}$
) are slightly less interesting for this paper since their lattices are superrigid (see below). Still, our Theorem A applies also to them.
$\mathrm F_4^{-20}$
) are slightly less interesting for this paper since their lattices are superrigid (see below). Still, our Theorem A applies also to them.
Let us fix a uniform torsion-free lattice
![]() $\Gamma \subset H$
and an embedding
$\Gamma \subset H$
and an embedding
![]() $\iota :H \rightarrow G$
, where G is a connected semisimple Lie group G with finite center. By Guichard–Wienhard [Reference Guichard and WienhardGW12, Prop. 4.7], the representation
$\iota :H \rightarrow G$
, where G is a connected semisimple Lie group G with finite center. By Guichard–Wienhard [Reference Guichard and WienhardGW12, Prop. 4.7], the representation
![]() $\iota \circ \rho _0 : \Gamma \rightarrow G$
is P–Anosov for certain parabolic subgroups P of G (depending only on G, H and
$\iota \circ \rho _0 : \Gamma \rightarrow G$
is P–Anosov for certain parabolic subgroups P of G (depending only on G, H and
![]() $\iota $
). We will call such a representation an
$\iota $
). We will call such a representation an
![]() $\iota $
–lattice representation of
$\iota $
–lattice representation of
![]() $\Gamma $
in G.
$\Gamma $
in G.
When H is
![]() $\mathrm {PSL}(2,{\mathbb R})$
, the representation
$\mathrm {PSL}(2,{\mathbb R})$
, the representation
![]() $\iota \circ \rho _0 : \pi _1(\Sigma ) \rightarrow G$
will be called an
$\iota \circ \rho _0 : \pi _1(\Sigma ) \rightarrow G$
will be called an
![]() $\iota $
–Fuchsian representation in G. Similarly, when H is a compact extension of
$\iota $
–Fuchsian representation in G. Similarly, when H is a compact extension of
![]() $\mathrm {PSL}(2,{\mathbb R})$
,
$\mathrm {PSL}(2,{\mathbb R})$
,
![]() $\iota \circ \rho _0$
will be called a twisted
$\iota \circ \rho _0$
will be called a twisted
![]() $\iota $
–Fuchsian representation in G.
$\iota $
–Fuchsian representation in G.
Using the property of structural stability, we can deform the representation
![]() $\iota \circ \rho _0$
, obtaining an open subset of
$\iota \circ \rho _0$
, obtaining an open subset of
![]() $\mathrm {Hom}(\Gamma ,G)$
entirely consisting of P–Anosov representations of
$\mathrm {Hom}(\Gamma ,G)$
entirely consisting of P–Anosov representations of
![]() $\Gamma $
in G. In the following, we denote by
$\Gamma $
in G. In the following, we denote by
![]() $\mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
the connected component of
$\mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
the connected component of
![]() $\mathrm {Anosov}_{P}(\Gamma ,G)$
that contains the representation
$\mathrm {Anosov}_{P}(\Gamma ,G)$
that contains the representation
![]() $\iota \circ \rho _0$
. We will say that a representation of
$\iota \circ \rho _0$
. We will say that a representation of
![]() $\Gamma $
is a P–Anosov deformation of a lattice representation if it belongs to one of the connected components
$\Gamma $
is a P–Anosov deformation of a lattice representation if it belongs to one of the connected components
![]() $\mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
. In the special case when H is a compact extension of
$\mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
. In the special case when H is a compact extension of
![]() $\mathrm {PSL}(2,{\mathbb R})$
, such representations will be called P–Anosov deformations of a twisted
$\mathrm {PSL}(2,{\mathbb R})$
, such representations will be called P–Anosov deformations of a twisted
![]() $\iota $
–Fuchsian representation.
$\iota $
–Fuchsian representation.
For this paper, we are particularly interested in P–Anosov deformations of lattice representations because our Theorem A applies to this special class of Anosov representations. It is a special class, but it is also rather general since most known Anosov representations fall in this class. This is mainly because this is the easiest way to construct Anosov representations.
Now, we want to describe the most important examples of such representations. The main source of examples of interesting deformations of lattice representations come from the case when H is a compact extension of
![]() $PSL(2,{\mathbb R})$
(i.e., the case of surface groups). These examples are discussed in Section 2.3. The other important source of examples is the case of uniform lattices in
$PSL(2,{\mathbb R})$
(i.e., the case of surface groups). These examples are discussed in Section 2.3. The other important source of examples is the case of uniform lattices in
![]() $\operatorname {PO}_0(d,1)$
(i.e., fundamental groups of closed hyperbolic d–manifolds). These examples are discussed in Section 2.4.
$\operatorname {PO}_0(d,1)$
(i.e., fundamental groups of closed hyperbolic d–manifolds). These examples are discussed in Section 2.4.
Lattices in
![]() $\mathrm {PU}(d,1)$
exhibit more rigid behaviour; see [Reference KlinglerKli11] and references therein. Still, some of them admit interesting Zariski dense deformations into higher rank Lie groups, but very few examples are known. When
$\mathrm {PU}(d,1)$
exhibit more rigid behaviour; see [Reference KlinglerKli11] and references therein. Still, some of them admit interesting Zariski dense deformations into higher rank Lie groups, but very few examples are known. When
![]() $H \simeq {\mathrm {Sp}}(d,1)$
or
$H \simeq {\mathrm {Sp}}(d,1)$
or
![]() $\mathrm F_4^{-20}$
, by a theorem of Corlette [Reference CorletteCor92],
$\mathrm F_4^{-20}$
, by a theorem of Corlette [Reference CorletteCor92],
![]() $\Gamma $
is superrigid. In particular, there are no nontrivial deformations of
$\Gamma $
is superrigid. In particular, there are no nontrivial deformations of
![]() $\iota \circ \rho _0 : \Gamma \rightarrow G$
.
$\iota \circ \rho _0 : \Gamma \rightarrow G$
.
Remark 2.3. All the arguments in this Section 2.2 are more general than the way we presented them. The hypothesis that
![]() $\Gamma $
is torsion-free is not really needed, and we can also replace the assumption that
$\Gamma $
is torsion-free is not really needed, and we can also replace the assumption that
![]() $\Gamma $
is a uniform lattice in H with the more general assumption that
$\Gamma $
is a uniform lattice in H with the more general assumption that
![]() $\Gamma $
is a convex-cocompact subgroup of H. Also in this higher generality, embeddings of H in other groups G allow to construct open subsets of Anosov representations in G. In our discussion, however, we restricted our attention to torsion-free uniform lattices for additional clarity and because our Theorem A works in this special case.
$\Gamma $
is a convex-cocompact subgroup of H. Also in this higher generality, embeddings of H in other groups G allow to construct open subsets of Anosov representations in G. In our discussion, however, we restricted our attention to torsion-free uniform lattices for additional clarity and because our Theorem A works in this special case.
2.3 Anosov representations of surface groups
The case of surface groups is the one that is best understood. When H is a compact extension of
![]() $\mathrm {PSL}(2,{\mathbb R})$
, Lie theory gives a classification of all representations
$\mathrm {PSL}(2,{\mathbb R})$
, Lie theory gives a classification of all representations
![]() $\iota : H \rightarrow G$
, for a simple group G. Most of the time, twisted
$\iota : H \rightarrow G$
, for a simple group G. Most of the time, twisted
![]() $\iota $
–Fuchsian representations into G admit small deformations with Zariski dense image.
$\iota $
–Fuchsian representations into G admit small deformations with Zariski dense image.
In special cases, for particular twisted
![]() $\iota $
–Fuchsian representations into G, all deformations (not just small ones) are Anosov. This phenomenon gives rise to the so-called higher rank Teichmüller components, defined as connected components of the representation variety
$\iota $
–Fuchsian representations into G, all deformations (not just small ones) are Anosov. This phenomenon gives rise to the so-called higher rank Teichmüller components, defined as connected components of the representation variety
![]() $\mathrm {Hom}(\pi _1(S),G)/G$
that consist entirely of discrete and faithful representations. They generalize many aspects of classical Teichmüller spaces, which can be seen as connected components of
$\mathrm {Hom}(\pi _1(S),G)/G$
that consist entirely of discrete and faithful representations. They generalize many aspects of classical Teichmüller spaces, which can be seen as connected components of
![]() $\mathrm {Hom}(\pi _1(S),\mathrm {PSL}(2,{\mathbb R}))/\mathrm {PSL}(2,{\mathbb R})$
. An interesting feature for us is that most higher Teichmüller components consist of deformations of twisted
$\mathrm {Hom}(\pi _1(S),\mathrm {PSL}(2,{\mathbb R}))/\mathrm {PSL}(2,{\mathbb R})$
. An interesting feature for us is that most higher Teichmüller components consist of deformations of twisted
![]() $\iota $
–Fuchsian representations.
$\iota $
–Fuchsian representations.
There are four families of higher rank Teichmüller spaces (see Guichard–Wienhard [Reference Guichard and WienhardGW]). The first family consists of Hitchin representations, introduced by Hitchin [Reference HitchinHit87]. In fact, Labourie’s original motivation for defining Anosov representations in [Reference LabourieLab06] was showing that Hitchin representations form higher rank Teichmüller components. Hitchin representations are defined when G is a split real simple Lie group. Then G admits a special conjugacy class of representations
![]() $\iota _0:\mathrm {SL}(2,{\mathbb R}) \rightarrow G$
called the principal representation. For this choice, the representation
$\iota _0:\mathrm {SL}(2,{\mathbb R}) \rightarrow G$
called the principal representation. For this choice, the representation
![]() $\iota _0 \circ \rho _0$
is called a principal Fuchsian representation in G, and it is Anosov with respect to the minimal parabolic subgroups
$\iota _0 \circ \rho _0$
is called a principal Fuchsian representation in G, and it is Anosov with respect to the minimal parabolic subgroups
![]() $P_{min}$
. Hitchin components are the connected components containing a principal Fuchsian representation. In particular, any Hitchin representation is a deformation of a principal Fuchsian representation.
$P_{min}$
. Hitchin components are the connected components containing a principal Fuchsian representation. In particular, any Hitchin representation is a deformation of a principal Fuchsian representation.
The second family consists of Maximal representations, which are defined when G is a real simple Lie group of Hermitian type [Reference Burger, Iozzi and WienhardBIW10]. Maximal representations are in general only Anosov with respect to a particular maximal parabolic subgroup. Most maximal representations are deformations of twisted
![]() $\iota $
–Fuchsian representations, but for G locally isomorphic to
$\iota $
–Fuchsian representations, but for G locally isomorphic to
![]() ${\mathrm {Sp}}(4,{\mathbb R})$
, there exist connected components in the space of maximal representations where every representation is Zariski dense [Reference GothenGot01, Reference Guichard and WienhardGW10, Reference Bradlow, García-Prada and GothenBGPG12].
${\mathrm {Sp}}(4,{\mathbb R})$
, there exist connected components in the space of maximal representations where every representation is Zariski dense [Reference GothenGot01, Reference Guichard and WienhardGW10, Reference Bradlow, García-Prada and GothenBGPG12].
The other two families of higher Teichmüller components arise from the notion of
![]() $\Theta $
–positivity introduced in [Reference Guichard and WienhardGW18, Reference Guichard and WienhardGW, Reference Guichard, Labourie and WienhardGLW], which leads to the notion of positive representations. Hitchin representations and maximal representations are positive representations, but there are two further families of Lie groups admitting positive representations, Lie groups locally isomorphic to
$\Theta $
–positivity introduced in [Reference Guichard and WienhardGW18, Reference Guichard and WienhardGW, Reference Guichard, Labourie and WienhardGLW], which leads to the notion of positive representations. Hitchin representations and maximal representations are positive representations, but there are two further families of Lie groups admitting positive representations, Lie groups locally isomorphic to
![]() $\mathrm {SO}(p,q)$
, as well as an exceptional family. With a positive structure comes again a special representation
$\mathrm {SO}(p,q)$
, as well as an exceptional family. With a positive structure comes again a special representation
![]() $\mathrm {SL}(2,{\mathbb R}) \rightarrow G$
. This representation might have a compact centralizer, so there is a compact extension H of
$\mathrm {SL}(2,{\mathbb R}) \rightarrow G$
. This representation might have a compact centralizer, so there is a compact extension H of
![]() $\mathrm {SL}(2,{\mathbb R})$
that embeds into G; this is the representation
$\mathrm {SL}(2,{\mathbb R})$
that embeds into G; this is the representation
![]() $\iota $
. From the classification of the connected components of positive representations, we see that deformations of twisted
$\iota $
. From the classification of the connected components of positive representations, we see that deformations of twisted
![]() $\iota $
–Fuchsian representations account for most of the connected components; exceptions occur only for
$\iota $
–Fuchsian representations account for most of the connected components; exceptions occur only for
![]() $\mathrm {SO}(p,p+1)$
. See [Reference Guichard and WienhardGW18], Guichard–Labourie–Wienhard [Reference Guichard, Labourie and WienhardGLW], Collier [Reference CollierCol15], Aparicio-Arroyo–Bradlow–Collier–Garcia-Prada–Gothen–Oliveira [Reference Aparicio-Arroyo, Bradlow, Collier, Garcia-Prada, Gothen and OliveiraAABC+19], Bradlow–Collier–Garcia-Prada–Gothen–Oliveira [Reference Bradlow, Collier, García-Prada, Gothen and OliveiraBCGP+], Beyrer–Pozzetti [Reference Beyrer and Beatrice PozzettiBP], Beyrer–Guichard–Labourie–Pozzetti–Wienhard [Reference Beyrer, Guichard, Labourie, Pozzetti and WienhardBGL+24] for more details on positive representations.
$\mathrm {SO}(p,p+1)$
. See [Reference Guichard and WienhardGW18], Guichard–Labourie–Wienhard [Reference Guichard, Labourie and WienhardGLW], Collier [Reference CollierCol15], Aparicio-Arroyo–Bradlow–Collier–Garcia-Prada–Gothen–Oliveira [Reference Aparicio-Arroyo, Bradlow, Collier, Garcia-Prada, Gothen and OliveiraAABC+19], Bradlow–Collier–Garcia-Prada–Gothen–Oliveira [Reference Bradlow, Collier, García-Prada, Gothen and OliveiraBCGP+], Beyrer–Pozzetti [Reference Beyrer and Beatrice PozzettiBP], Beyrer–Guichard–Labourie–Pozzetti–Wienhard [Reference Beyrer, Guichard, Labourie, Pozzetti and WienhardBGL+24] for more details on positive representations.
Given a representation
![]() $\rho \colon \thinspace \pi _1(\Sigma ) \to G$
in a higher Teichmüller space, we can embed G into its complexification
$\rho \colon \thinspace \pi _1(\Sigma ) \to G$
in a higher Teichmüller space, we can embed G into its complexification
![]() $G_{{\mathbb C}}$
. If
$G_{{\mathbb C}}$
. If
![]() $\rho $
is Anosov with respect to a parabolic subgroup P, the composition will be Anosov with respect to the parabolic
$\rho $
is Anosov with respect to a parabolic subgroup P, the composition will be Anosov with respect to the parabolic
![]() $P_{{\mathbb C}}<G_{{\mathbb C}}$
. In the complex group not every deformation will be discrete and faithful, but we can consider the space of Anosov representations
$P_{{\mathbb C}}<G_{{\mathbb C}}$
. In the complex group not every deformation will be discrete and faithful, but we can consider the space of Anosov representations
![]() $\mathrm {Anosov}_{P_{{\mathbb C}}}(\pi _1(\Sigma ),G_{{\mathbb C}})$
and the connected component of this space containing
$\mathrm {Anosov}_{P_{{\mathbb C}}}(\pi _1(\Sigma ),G_{{\mathbb C}})$
and the connected component of this space containing
![]() $\rho : \pi _1(\Sigma ) \to G < G_{{\mathbb C}}$
. This generalizes the notion of quasi-Fuchsian representation into
$\rho : \pi _1(\Sigma ) \to G < G_{{\mathbb C}}$
. This generalizes the notion of quasi-Fuchsian representation into
![]() $\mathrm {PSL}(2,{{\mathbb C}})$
to this higher rank setting. Of particular interest to us will be the connected component of
$\mathrm {PSL}(2,{{\mathbb C}})$
to this higher rank setting. Of particular interest to us will be the connected component of
![]() $\mathrm {Anosov}_{P_{{\mathbb C}}}(\pi _1(\Sigma ),G_{{\mathbb C}})$
which contains the principal Fuchsian representation
$\mathrm {Anosov}_{P_{{\mathbb C}}}(\pi _1(\Sigma ),G_{{\mathbb C}})$
which contains the principal Fuchsian representation
![]() $\iota _0 \circ \rho _0$
. We call this set the quasi-Hitchin space and representations therein quasi-Hitchin representations. Theorem A applies in particular to quasi-Hitchin representations, and Theorem D focuses on quasi-Hitchin representations for
$\iota _0 \circ \rho _0$
. We call this set the quasi-Hitchin space and representations therein quasi-Hitchin representations. Theorem A applies in particular to quasi-Hitchin representations, and Theorem D focuses on quasi-Hitchin representations for
![]() $G_{{\mathbb C}} = {\mathrm {Sp}}(4,{{\mathbb C}})$
$G_{{\mathbb C}} = {\mathrm {Sp}}(4,{{\mathbb C}})$
2.4 Fundamental groups of hyperbolic manifolds
As mentioned in the introduction, applications of Theorem A are not limited to representations of surface groups. There are indeed interesting classes of Anosov deformations of fundamental groups of closed hyperbolic manifolds of higher dimension.
Let
![]() $\Gamma = \pi _1(M)$
be the fundamental group of a closed orientable hyperbolic manifold of dimension
$\Gamma = \pi _1(M)$
be the fundamental group of a closed orientable hyperbolic manifold of dimension
![]() $d\geq 3$
. Then
$d\geq 3$
. Then
![]() $\Gamma $
identifies with a uniform torsion-free lattice in
$\Gamma $
identifies with a uniform torsion-free lattice in
![]() $\mathrm {SO}_0(d,1) \simeq \operatorname {Isom}_+(\mathbb H^d)$
via a representation
$\mathrm {SO}_0(d,1) \simeq \operatorname {Isom}_+(\mathbb H^d)$
via a representation
![]() $\rho _0 : \Gamma \to \mathrm {SO}_0(p,1)$
. One can construct in every dimension many examples where M contains an embedded totally geodesic hypersurface. There is then a general ‘bending’ procedure that allows one to deform the representation
$\rho _0 : \Gamma \to \mathrm {SO}_0(p,1)$
. One can construct in every dimension many examples where M contains an embedded totally geodesic hypersurface. There is then a general ‘bending’ procedure that allows one to deform the representation
![]() $\rho _0$
into a higher rank Lie group. We mention two particularly interesting examples.
$\rho _0$
into a higher rank Lie group. We mention two particularly interesting examples.
Representations dividing a convex set. In a series of four papers, Benoist developed the theory of divisible convex sets – that is, proper convex subsets of a real projective space admitting a cocompact action of a discrete group of projective transformations. In particular, taking
![]() $\iota : \mathrm {SO}_0(d,1) \to \mathrm {SL}(d+1,\mathbb R)$
to be the standard representation, Benoist proved in [Reference BenoistBen05] that any continous deformation
$\iota : \mathrm {SO}_0(d,1) \to \mathrm {SL}(d+1,\mathbb R)$
to be the standard representation, Benoist proved in [Reference BenoistBen05] that any continous deformation
![]() $\rho : \Gamma \to \mathrm {SL}(d+1,{\mathbb R})$
of
$\rho : \Gamma \to \mathrm {SL}(d+1,{\mathbb R})$
of
![]() $\iota \circ \rho _0$
is discrete, faithful and acts properly discontinuously and cocompactly on an open strictly convex domain
$\iota \circ \rho _0$
is discrete, faithful and acts properly discontinuously and cocompactly on an open strictly convex domain
![]() $\Omega _\rho $
of the projective space
$\Omega _\rho $
of the projective space
![]() $\mathbb{RP}^d$
. It follows (see [Reference Guichard and WienhardGW12, Proposition 6.1]) that any continuous deformation of
$\mathbb{RP}^d$
. It follows (see [Reference Guichard and WienhardGW12, Proposition 6.1]) that any continuous deformation of
![]() $\iota \circ \rho _0$
is
$\iota \circ \rho _0$
is
![]() $P_{1,d}$
-Anosov.
$P_{1,d}$
-Anosov.
The domain
![]() $\Omega _\rho \subset \mathbb R\mathbb {P}^{d}$
is a flag domain of discontinuity whose quotient is easily described:
$\Omega _\rho \subset \mathbb R\mathbb {P}^{d}$
is a flag domain of discontinuity whose quotient is easily described:
![]() $\Omega _\rho $
is contractible and
$\Omega _\rho $
is contractible and
![]() $\rho (\Gamma )\backslash \Omega _\rho $
is diffeomorphic to M. However, it is not the only flag domain of discontinuity one can associate to a convex divisible representation. There are many flag domains of discontinuity in other flag varieties of
$\rho (\Gamma )\backslash \Omega _\rho $
is diffeomorphic to M. However, it is not the only flag domain of discontinuity one can associate to a convex divisible representation. There are many flag domains of discontinuity in other flag varieties of
![]() $\mathrm {SL}(d+1,{\mathbb R})$
, as well as flag domains of discontinuities in
$\mathrm {SL}(d+1,{\mathbb R})$
, as well as flag domains of discontinuities in
![]() $G'/Q' $
when we embed
$G'/Q' $
when we embed
![]() $\mathrm {SL}(d+1,{\mathbb R})$
into a larger Lie group
$\mathrm {SL}(d+1,{\mathbb R})$
into a larger Lie group
![]() $G'$
. The topology of these domains of discontinuity can be more complicated. Theorem A applies to all these domains of discontinuity, as long as
$G'$
. The topology of these domains of discontinuity can be more complicated. Theorem A applies to all these domains of discontinuity, as long as
![]() $\rho $
is in the same connected component (of Anosov representations) as
$\rho $
is in the same connected component (of Anosov representations) as
![]() $\iota \circ \rho _0$
.
$\iota \circ \rho _0$
.
AdS quasi-Fuchsian and
![]() $\mathbf {\mathbb H^{p,q}}$
-convex-cocompact representations. Similarly, consider the embedding
$\mathbf {\mathbb H^{p,q}}$
-convex-cocompact representations. Similarly, consider the embedding
![]() $\iota : \mathrm {SO}_0(d,1) \to \mathrm {SO}(d,2)$
. Barbot and Mérigot proved in [Reference Barbot and MérigotBM12] and [Reference BarbotBar15] that any continuous deformation
$\iota : \mathrm {SO}_0(d,1) \to \mathrm {SO}(d,2)$
. Barbot and Mérigot proved in [Reference Barbot and MérigotBM12] and [Reference BarbotBar15] that any continuous deformation
![]() $\rho $
of
$\rho $
of
![]() $\iota \circ \rho _0$
into
$\iota \circ \rho _0$
into
![]() $\mathrm {SO}(d,2)$
is P-Anosov, where P is the stabilizer of an isotropic line. Moreover,
$\mathrm {SO}(d,2)$
is P-Anosov, where P is the stabilizer of an isotropic line. Moreover,
![]() $\rho $
acts properly discontinuously on a convex domain
$\rho $
acts properly discontinuously on a convex domain
![]() $\Omega _\rho $
contained in the anti-de Sitter space of dimension
$\Omega _\rho $
contained in the anti-de Sitter space of dimension
![]() $d+1$
, and the quotient
$d+1$
, and the quotient
![]() $\rho (\Gamma )\backslash \Omega _\rho $
is a globally hyperbolic Cauchy compact anti-de Sitter spacetime. Barbot and Mérigot call these representations AdS-quasi-Fuchsian. Our main theorem applies to these representations.
$\rho (\Gamma )\backslash \Omega _\rho $
is a globally hyperbolic Cauchy compact anti-de Sitter spacetime. Barbot and Mérigot call these representations AdS-quasi-Fuchsian. Our main theorem applies to these representations.
Recently, these results have been generalized to deformations of
![]() $\iota \circ \rho _0$
, for
$\iota \circ \rho _0$
, for
![]() $\iota : \mathrm {SO}_0(d,1) \to \mathrm {SO}(d,d')$
the standard embedding: Beyrer and Kassel proved in [Reference Beyrer and KasselBK23] that any continuous deformation into
$\iota : \mathrm {SO}_0(d,1) \to \mathrm {SO}(d,d')$
the standard embedding: Beyrer and Kassel proved in [Reference Beyrer and KasselBK23] that any continuous deformation into
![]() $\mathrm {SO}(d,d')$
is P-Anosov and
$\mathrm {SO}(d,d')$
is P-Anosov and
![]() $\mathbb H^{d,d'-1}$
-convex-cocompact in the sense of [Reference Danciger, Guéritaud and KasselDGK18]. Our theorem applies to these deformations, which again exist in many examples. Such groups have in particular a cocompact flag domain of discontinuity in the space of maximal totally isotropic subspaces of
$\mathbb H^{d,d'-1}$
-convex-cocompact in the sense of [Reference Danciger, Guéritaud and KasselDGK18]. Our theorem applies to these deformations, which again exist in many examples. Such groups have in particular a cocompact flag domain of discontinuity in the space of maximal totally isotropic subspaces of
![]() ${\mathbb R}^{d,d'}$
. The topology of this domain is described in the recent paper [Reference SeppiSST23].Footnote
2
${\mathbb R}^{d,d'}$
. The topology of this domain is described in the recent paper [Reference SeppiSST23].Footnote
2
Complex deformations. Note finally that whenever
![]() $\iota \circ \rho _0$
admits deformations into a real linear algebraic group G, it also admits deformations into its complexification
$\iota \circ \rho _0$
admits deformations into a real linear algebraic group G, it also admits deformations into its complexification
![]() $G_{{\mathbb C}}$
which are not real. For instance, the above examples admit respectively Anosov deformations in
$G_{{\mathbb C}}$
which are not real. For instance, the above examples admit respectively Anosov deformations in
![]() $\mathrm {SL}(d+1,{{\mathbb C}})$
and
$\mathrm {SL}(d+1,{{\mathbb C}})$
and
![]() $\mathrm {SO}(d+d',{{\mathbb C}})$
. Theorem A applies to such complex deformations as well.
$\mathrm {SO}(d+d',{{\mathbb C}})$
. Theorem A applies to such complex deformations as well.
2.5 Domains of discontinuity
A P–Anosov representation
![]() $\rho \colon \thinspace \Gamma \to G$
acts on all homogeneous spaces
$\rho \colon \thinspace \Gamma \to G$
acts on all homogeneous spaces
![]() $G/Q$
, where Q is a proper parabolic subgroup. The theory of domains of discontinuity, introduced by Guichard–Wienhard [Reference Guichard and WienhardGW12] and further developed by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18], gives conditions for the existence of a
$G/Q$
, where Q is a proper parabolic subgroup. The theory of domains of discontinuity, introduced by Guichard–Wienhard [Reference Guichard and WienhardGW12] and further developed by Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18], gives conditions for the existence of a
![]() $\rho $
–invariant open subset
$\rho $
–invariant open subset
![]() $\Omega \subset G/Q$
where the action is properly discontinuous and/or cocompact. We sketch very briefly this construction here and refer the reader to [Reference Kapovich, Leeb and PortiKLP18] for details.
$\Omega \subset G/Q$
where the action is properly discontinuous and/or cocompact. We sketch very briefly this construction here and refer the reader to [Reference Kapovich, Leeb and PortiKLP18] for details.
The action of P on
![]() $G/Q$
has finitely many orbits which are labelled by elements of
$G/Q$
has finitely many orbits which are labelled by elements of
![]() $W_P \backslash W/W_Q$
, where W is the Weyl group of G and
$W_P \backslash W/W_Q$
, where W is the Weyl group of G and
![]() $W_P, W_Q$
are the subgroups corresponding to P and Q. A subset I of
$W_P, W_Q$
are the subgroups corresponding to P and Q. A subset I of
![]() $W_P \backslash W/W_Q$
corresponds to a P–invariant subset
$W_P \backslash W/W_Q$
corresponds to a P–invariant subset
![]() $K_I$
of
$K_I$
of
![]() $G/Q$
(consisting of the union of the orbits labelled by elements of I). The set
$G/Q$
(consisting of the union of the orbits labelled by elements of I). The set
![]() $K_I$
is closed if and only if I is an ideal for the Bruhat order on W.
$K_I$
is closed if and only if I is an ideal for the Bruhat order on W.
Given
![]() $x = gP\in G/P$
, set
$x = gP\in G/P$
, set
![]() $K_I(x) = g K_I$
(this is well-defined since
$K_I(x) = g K_I$
(this is well-defined since
![]() $K_I$
is P–invariant). The I–thickening of a subset
$K_I$
is P–invariant). The I–thickening of a subset
![]() $A\subset G/P$
is the set
$A\subset G/P$
is the set
![]() $K_I(A) = \bigcup _{x\in A} K_I(x)$
. Finally, an ideal is called balanced if
$K_I(A) = \bigcup _{x\in A} K_I(x)$
. Finally, an ideal is called balanced if
![]() $I \cap -I = \emptyset $
and
$I \cap -I = \emptyset $
and
![]() $I\cup -I = W_P\backslash W /W_Q$
.
$I\cup -I = W_P\backslash W /W_Q$
.
Now, let
![]() $\Gamma $
be a hyperbolic group,
$\Gamma $
be a hyperbolic group,
![]() $\rho \colon \thinspace \Gamma \to G$
a P–Anosov representation and
$\rho \colon \thinspace \Gamma \to G$
a P–Anosov representation and
![]() $\xi _\rho \colon \thinspace \partial _\infty \Gamma \to G/P$
the associated boundary map.
$\xi _\rho \colon \thinspace \partial _\infty \Gamma \to G/P$
the associated boundary map.
Theorem 2.4 (Kapovich–Leeb–Porti, [Reference Kapovich, Leeb and PortiKLP18]).
If
![]() $I \subset W_P\backslash W /W_Q$
is a balanced ideal, then
$I \subset W_P\backslash W /W_Q$
is a balanced ideal, then
![]() $\Gamma $
acts properly discontinuously and cocompactly on the domain
$\Gamma $
acts properly discontinuously and cocompactly on the domain
Remark 2.5. If the ideal satisfies
![]() $I\cup -I = W_P\backslash W /W_Q$
, the construction still gives rise to a domain of discontinuity, but then the action of
$I\cup -I = W_P\backslash W /W_Q$
, the construction still gives rise to a domain of discontinuity, but then the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Omega _{\rho ,I}$
is not necessarily cocompact.
$\Omega _{\rho ,I}$
is not necessarily cocompact.
Remark 2.6. The domain
![]() $\Omega _{\rho ,I}$
could a priori be empty, but this requires the topological dimension of
$\Omega _{\rho ,I}$
could a priori be empty, but this requires the topological dimension of
![]() $\partial _\infty \Gamma $
to equal the codimension of
$\partial _\infty \Gamma $
to equal the codimension of
![]() $K_I$
, which is quite exceptional. In particular, one can always find a nonempty cocompact flag domain of discontinuity after embedding G into a larger group
$K_I$
, which is quite exceptional. In particular, one can always find a nonempty cocompact flag domain of discontinuity after embedding G into a larger group
![]() $G'$
(see [Reference Guichard and WienhardGW12, Remark 1.10]).
$G'$
(see [Reference Guichard and WienhardGW12, Remark 1.10]).
When
![]() $\Gamma $
is a uniform lattice in a rank
$\Gamma $
is a uniform lattice in a rank
![]() $1$
subgroup H of G, these domains of discontinuity are actually preserved by the group H:
$1$
subgroup H of G, these domains of discontinuity are actually preserved by the group H:
Lemma 2.7. Assume
![]() $\Gamma $
is a uniform lattice in a rank
$\Gamma $
is a uniform lattice in a rank
![]() $1$
Lie group H and
$1$
Lie group H and
![]() $\rho = \iota \circ \rho _0$
, where
$\rho = \iota \circ \rho _0$
, where
![]() $\rho _0: \Gamma \to H$
is the inclusion and
$\rho _0: \Gamma \to H$
is the inclusion and
![]() $\iota $
is an embedding of H into G. Then H preserves
$\iota $
is an embedding of H into G. Then H preserves
![]() $\Omega _{\rho ,I}$
and acts properly on it.
$\Omega _{\rho ,I}$
and acts properly on it.
Proof. In this situation, the boundary map
![]() $\xi _\rho $
is actually H-equivariant. Hence, its image is H-invariant and so is the domain
$\xi _\rho $
is actually H-equivariant. Hence, its image is H-invariant and so is the domain
![]() $\Omega _{\rho ,I}$
(which only depends on the image of
$\Omega _{\rho ,I}$
(which only depends on the image of
![]() $\xi _\rho $
). Now, the properness of the action of H follows from the proper discontinuity of the action of
$\xi _\rho $
). Now, the properness of the action of H follows from the proper discontinuity of the action of
![]() $\Gamma $
as a consequence of a general topological fact (Proposition 2.8 below).
$\Gamma $
as a consequence of a general topological fact (Proposition 2.8 below).
Proposition 2.8. Let X be a manifold equipped with a smooth action of H and
![]() $\Gamma $
a uniform lattice in H. Then H acts properly on X if and only if
$\Gamma $
a uniform lattice in H. Then H acts properly on X if and only if
![]() $\Gamma $
acts properly discontinuously. In that case, the action of
$\Gamma $
acts properly discontinuously. In that case, the action of
![]() $\Gamma $
is cocompact if and only if the action of H is.
$\Gamma $
is cocompact if and only if the action of H is.
Proof. Now, let C be a compact subset of H such that
![]() $\Gamma C = H$
. Let D be any compact subset of
$\Gamma C = H$
. Let D be any compact subset of
![]() $\Omega _{\rho ,I}$
.
$\Omega _{\rho ,I}$
.
Assume
![]() $\Gamma $
is properly discontinuous. The set
$\Gamma $
is properly discontinuous. The set
is contained in
![]() $FC$
, where
$FC$
, where
Since
![]() $C\cdot D$
is compact, F is finite by proper discontinuity of
$C\cdot D$
is compact, F is finite by proper discontinuity of
![]() $\Gamma $
. Hence,
$\Gamma $
. Hence,
![]() $FC$
is compact, proving the properness of the action of H.
$FC$
is compact, proving the properness of the action of H.
Conversely, if H is properly discontinuous, the set
is the intersection of
![]() $\Gamma $
with a compact subset of H, which is thus finite since
$\Gamma $
with a compact subset of H, which is thus finite since
![]() $\Gamma $
is discrete.
$\Gamma $
is discrete.
Assume some compact subset D of X satisfies
![]() $\Gamma \cdot D = X$
. Then obviously
$\Gamma \cdot D = X$
. Then obviously
![]() $H\cdot D= X$
. Conversely, assume
$H\cdot D= X$
. Conversely, assume
![]() $H\cdot D = X$
. Then
$H\cdot D = X$
. Then
![]() $\Gamma \cdot (C\cdot D) = H$
and
$\Gamma \cdot (C\cdot D) = H$
and
![]() $C\cdot D$
is compact. This proves that cocompactness of
$C\cdot D$
is compact. This proves that cocompactness of
![]() $\Gamma $
and H are equivalent.
$\Gamma $
and H are equivalent.
Remark 2.9. The construction of domains of discontinuity was further generalized by Stecker–Treib [Reference Stecker and TreibST18], who extended it to the case where Q is an oriented parabolic subgroup (i.e., a subgroup of G lying between a parabolic subgroup and its identity component). The corresponding homogeneous space
![]() $G/Q$
is called an oriented flag variety. Stecker–Treib [Reference Stecker and TreibST18] give conditions for the existence of (possibly cocompact) domains of discontinuity on
$G/Q$
is called an oriented flag variety. Stecker–Treib [Reference Stecker and TreibST18] give conditions for the existence of (possibly cocompact) domains of discontinuity on
![]() $G/Q$
. This generalization is interesting because some new cocompact domains of discontinuity arise that are not lifts of domains of discontinuity in the corresponding unoriented flag varieties. We refer the reader to Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18] and Stecker–Treib [Reference Stecker and TreibST18] for more details. The previous lemma and all the results of Part I apply to these domains as well.
$G/Q$
. This generalization is interesting because some new cocompact domains of discontinuity arise that are not lifts of domains of discontinuity in the corresponding unoriented flag varieties. We refer the reader to Kapovich–Leeb–Porti [Reference Kapovich, Leeb and PortiKLP18] and Stecker–Treib [Reference Stecker and TreibST18] for more details. The previous lemma and all the results of Part I apply to these domains as well.
In order to illustrate the theory, let us now describe the example that will be studied in detail in Part II of this paper. Consider the case where the group G is
![]() ${\mathrm {Sp}}(2n,\mathbb {K})$
, where
${\mathrm {Sp}}(2n,\mathbb {K})$
, where
![]() $\mathbb {K}$
can be
$\mathbb {K}$
can be
![]() ${\mathbb R}$
of
${\mathbb R}$
of
![]() ${{\mathbb C}}$
, and the parabolic subgroup P is the stabilizer of a point in
${{\mathbb C}}$
, and the parabolic subgroup P is the stabilizer of a point in
![]() $\mathbb {KP}^{2n-1}$
. In this case,
$\mathbb {KP}^{2n-1}$
. In this case,
![]() $G/P=\mathbb {KP}^{2n-1}$
. Every P–Anosov representation
$G/P=\mathbb {KP}^{2n-1}$
. Every P–Anosov representation
![]() $\rho \colon \thinspace \Gamma \to {\mathrm {Sp}}(2n,\mathbb {K})$
has an associated
$\rho \colon \thinspace \Gamma \to {\mathrm {Sp}}(2n,\mathbb {K})$
has an associated
![]() $\rho $
–equivariant map
$\rho $
–equivariant map
We now consider as second parabolic subgroup Q the stabilizer of a Lagrangian subspace in
![]() $\mathbb {K}^{2n}$
. Then
$\mathbb {K}^{2n}$
. Then
![]() $G/Q$
is the Lagrangian Grassmannian
$G/Q$
is the Lagrangian Grassmannian
![]() ${\mathrm {Lag}}(\mathbb {K}^{2n})$
(i.e., the space of all the Lagrangian subspaces of
${\mathrm {Lag}}(\mathbb {K}^{2n})$
(i.e., the space of all the Lagrangian subspaces of
![]() $\mathbb {K}^{2n}$
). The action of P on
$\mathbb {K}^{2n}$
). The action of P on
![]() $G/Q$
has only two orbits: a closed orbit consisting of Lagrangian subspaces containing the line fixed by P, and its complement which is open. In this case,
$G/Q$
has only two orbits: a closed orbit consisting of Lagrangian subspaces containing the line fixed by P, and its complement which is open. In this case,
![]() $W_P \backslash W/W_Q$
has only two elements and admits a unique nontrivial ideal I, for which
$W_P \backslash W/W_Q$
has only two elements and admits a unique nontrivial ideal I, for which
![]() $K_I$
is the closed P–orbit. This ideal is balanced.
$K_I$
is the closed P–orbit. This ideal is balanced.
For each line
![]() $\ell \in \mathbb {KP}^{2n-1}$
, we have
$\ell \in \mathbb {KP}^{2n-1}$
, we have
and we define the subset
Guichard and Wienhard [Reference Guichard and WienhardGW12] showed that the complement
is a cocompact domain of discontinuity for
![]() $\rho $
. Recall that
$\rho $
. Recall that
![]() $\Gamma $
acts freely since it is torsion-free, so we have that
$\Gamma $
acts freely since it is torsion-free, so we have that
is a closed manifold endowed with a geometric structure modelled on the parabolic geometry
![]() $(G, G/Q) = \left ({\mathrm {Sp}}(2n,\mathbb {K}), {\mathrm {Lag}}(\mathbb {K}^{2n})\right )$
. Determining the topology of this quotient manifold (and more general such constructions) is a main focus of this paper.
$(G, G/Q) = \left ({\mathrm {Sp}}(2n,\mathbb {K}), {\mathrm {Lag}}(\mathbb {K}^{2n})\right )$
. Determining the topology of this quotient manifold (and more general such constructions) is a main focus of this paper.
2.6 Deformations
Consider one of our spaces
![]() $\mathcal {A} = \mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
, defined in Section 2.2. Let Q be a parabolic subgroup and I a balanced ideal of
$\mathcal {A} = \mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
, defined in Section 2.2. Let Q be a parabolic subgroup and I a balanced ideal of
![]() $W_P \backslash W /W_Q$
. For every representation
$W_P \backslash W /W_Q$
. For every representation
![]() $\rho \in \mathcal {A}$
, we obtain a closed manifold
$\rho \in \mathcal {A}$
, we obtain a closed manifold
![]() $M_{\rho ,I} = \rho (\Gamma ) \backslash \Omega _{\rho ,I}$
endowed with a geometric structure locally modelled on the parabolic geometry
$M_{\rho ,I} = \rho (\Gamma ) \backslash \Omega _{\rho ,I}$
endowed with a geometric structure locally modelled on the parabolic geometry
![]() $(G, G/Q)$
, and whose holonomy factors throughFootnote
3
the representation
$(G, G/Q)$
, and whose holonomy factors throughFootnote
3
the representation
![]() $\rho $
.
$\rho $
.
Theorem 2.10 (Guichard–Wienhard, [Reference Guichard and WienhardGW12]).
Let
![]() $\rho $
be a P–Anosov representation of a hyperbolic group
$\rho $
be a P–Anosov representation of a hyperbolic group
![]() $\Gamma $
into a semisimple Lie group G and let
$\Gamma $
into a semisimple Lie group G and let
![]() $\rho '$
be a P–Anosov deformation of
$\rho '$
be a P–Anosov deformation of
![]() $\rho $
. Then for any parabolic subgroup Q of G and any balanced ideal I of
$\rho $
. Then for any parabolic subgroup Q of G and any balanced ideal I of
![]() $W_P\backslash W/W_Q$
, there exists a smooth
$W_P\backslash W/W_Q$
, there exists a smooth
![]() $(\rho ,\rho ')$
–equivariant diffeomorphism from
$(\rho ,\rho ')$
–equivariant diffeomorphism from
![]() $\Omega _{\rho ,I}$
to
$\Omega _{\rho ,I}$
to
![]() $\Omega _{\rho ',I}$
. In particular,
$\Omega _{\rho ',I}$
. In particular,
![]() $M_{\rho ,I}$
and
$M_{\rho ,I}$
and
![]() $M_{\rho ',I}$
are diffeomorphic.
$M_{\rho ',I}$
are diffeomorphic.
Remark 2.11. The theorem also applies to the quotients of domains of discontinuity constructed by Stecker–Treib in oriented flag varieties. More generally, it essentially follows from Ehresmann’s fibration theorem that a smooth family of closed
![]() $(G,X)$
–manifolds is locally topologically trivial.
$(G,X)$
–manifolds is locally topologically trivial.
For a
![]() $\rho \in \mathcal {A} = \mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
, the topology of
$\rho \in \mathcal {A} = \mathrm {Anosov}_{P,\iota ,\rho _0}(\Gamma ,G)$
, the topology of
![]() $M_{\rho ,I}$
does not depend on
$M_{\rho ,I}$
does not depend on
![]() $\rho $
; hence, we can denote this smooth manifold by
$\rho $
; hence, we can denote this smooth manifold by
![]() $M_{\rho _0,\iota ,I}$
. Thus, the space
$M_{\rho _0,\iota ,I}$
. Thus, the space
![]() $\mathcal {A}$
can be seen as a deformation space for a family of
$\mathcal {A}$
can be seen as a deformation space for a family of
![]() $(G,G/Q)$
–structures on a the fixed closed manifold
$(G,G/Q)$
–structures on a the fixed closed manifold
![]() $M_{\rho _0,\iota ,I}$
. This is particularly interesting for higher rank Teichmüller spaces because it gives a nice geometric interpretation of these spaces. It is also interesting for the theory of geometric structures on manifolds because it gives several interesting examples of closed manifolds with a large deformation space of geometric structures.
$M_{\rho _0,\iota ,I}$
. This is particularly interesting for higher rank Teichmüller spaces because it gives a nice geometric interpretation of these spaces. It is also interesting for the theory of geometric structures on manifolds because it gives several interesting examples of closed manifolds with a large deformation space of geometric structures.
3 Topology of the quotient
3.1 General statement
We can now rephrase Theorem A, which describes the topology of
![]() $M_{\rho _0,\iota ,I}$
constructed from an Anosov deformation of an
$M_{\rho _0,\iota ,I}$
constructed from an Anosov deformation of an
![]() $\iota $
–lattice representation.
$\iota $
–lattice representation.
Let us fix a connected semisimple Lie group H of real rank
![]() $1$
with finite center, a uniform torsion-free lattice
$1$
with finite center, a uniform torsion-free lattice
![]() $\Gamma \subset H$
and a representation
$\Gamma \subset H$
and a representation
![]() $\iota $
of H into some connected semisimple Lie group G with finite center. Denote by
$\iota $
of H into some connected semisimple Lie group G with finite center. Denote by
![]() $\rho _0$
the inclusion of
$\rho _0$
the inclusion of
![]() $\Gamma $
into H, let P be a parabolic subgroup of G such that
$\Gamma $
into H, let P be a parabolic subgroup of G such that
![]() $\iota \circ \rho _0$
is P–Anosov, and let
$\iota \circ \rho _0$
is P–Anosov, and let
![]() $\rho $
be a P–Anosov deformation of
$\rho $
be a P–Anosov deformation of
![]() $\iota \circ \rho _0$
. Finally, let
$\iota \circ \rho _0$
. Finally, let
![]() ${S_H}$
denote the symmetric space of H.
${S_H}$
denote the symmetric space of H.
Theorem 3.1. For every parabolic subgroup Q of G and every balanced ideal I of
![]() $W_P \backslash W/W_Q$
, the domain
$W_P \backslash W/W_Q$
, the domain
![]() $\Omega _{\rho ,I}$
is a smooth
$\Omega _{\rho ,I}$
is a smooth
![]() $\Gamma $
–equivariant fiber bundle over the symmetric space
$\Gamma $
–equivariant fiber bundle over the symmetric space
![]() ${S_H}$
, with fiber a closed manifold
${S_H}$
, with fiber a closed manifold
![]() $\mathfrak F$
. In particular,
$\mathfrak F$
. In particular,
![]() $\Omega _{\rho ,I}$
deformation retracts to
$\Omega _{\rho ,I}$
deformation retracts to
![]() $\mathfrak F$
and the manifold
$\mathfrak F$
and the manifold
![]() $M_{\rho _0,\iota ,I} = \Gamma \backslash \Omega _{\rho ,I}$
is a fiber bundle over the locally symmetric space
$M_{\rho _0,\iota ,I} = \Gamma \backslash \Omega _{\rho ,I}$
is a fiber bundle over the locally symmetric space
![]() $\Gamma \backslash {S_H}$
with fiber
$\Gamma \backslash {S_H}$
with fiber
![]() $\mathfrak F$
.
$\mathfrak F$
.
In fact, one can say a bit more on the structure of this bundle. For this, let us recall the notion of fiber bundle associated to a principal bundle. Let K be a Lie group,
![]() $T\to B$
a principal K-bundle and
$T\to B$
a principal K-bundle and
![]() $\mathfrak F$
a smooth manifold equipped with a smooth action of K.
$\mathfrak F$
a smooth manifold equipped with a smooth action of K.
Definition 3.2. Let
![]() $\mathfrak E$
denote the quotient of
$\mathfrak E$
denote the quotient of
![]() $T \times \mathfrak F$
by the diagonal action of K. Then the projection
$T \times \mathfrak F$
by the diagonal action of K. Then the projection
![]() $T \times \mathfrak F \to T$
factors to a smooth fibration
$T \times \mathfrak F \to T$
factors to a smooth fibration
![]() $\mathfrak E\to B$
with fibers diffeomorphic to
$\mathfrak E\to B$
with fibers diffeomorphic to
![]() $\mathfrak F$
. This fiber bundle is called the
$\mathfrak F$
. This fiber bundle is called the
![]() $\mathfrak F$
-bundle associated to T.
$\mathfrak F$
-bundle associated to T.
Theorem 3.3. In the setting of Theorem 3.1, the manifold
![]() $\mathfrak F$
admits a smooth action of the compact subgroup K, and the manifold
$\mathfrak F$
admits a smooth action of the compact subgroup K, and the manifold
![]() $M_{\rho _0,\iota ,I}$
is the
$M_{\rho _0,\iota ,I}$
is the
![]() $\mathfrak F$
–bundle over
$\mathfrak F$
–bundle over
![]() $\Gamma \backslash {S_H}$
associated to the principal K–bundle
$\Gamma \backslash {S_H}$
associated to the principal K–bundle
In the previous theorem, the bundle
![]() $\Gamma \backslash H \to \Gamma \backslash {S_H}$
must be thought of as an explicit object that depends only on the lattice
$\Gamma \backslash H \to \Gamma \backslash {S_H}$
must be thought of as an explicit object that depends only on the lattice
![]() $\Gamma $
. For example, when
$\Gamma $
. For example, when
![]() $H = PO_0(n,1)$
,
$H = PO_0(n,1)$
,
![]() $\Gamma \backslash {S_H}$
is a closed hyperbolic manifold,
$\Gamma \backslash {S_H}$
is a closed hyperbolic manifold,
![]() $\Gamma $
is its fundamental group, and the bundle
$\Gamma $
is its fundamental group, and the bundle
![]() $\Gamma \backslash H \to \Gamma \backslash {S_H}$
is its frame bundle.
$\Gamma \backslash H \to \Gamma \backslash {S_H}$
is its frame bundle.
In the special case when H is a compact extension of
![]() $\mathrm {PSL}(2,{\mathbb R})$
, these theorems take an even more explicit form. In this case,
$\mathrm {PSL}(2,{\mathbb R})$
, these theorems take an even more explicit form. In this case,
![]() $S_H = \mathbb {H}^2$
is the hyperbolic plane, the group
$S_H = \mathbb {H}^2$
is the hyperbolic plane, the group
![]() $\Gamma = \pi _1(\Sigma )$
is a surface group, and
$\Gamma = \pi _1(\Sigma )$
is a surface group, and
![]() $\Gamma \backslash \mathbb {H}^2$
is the surface
$\Gamma \backslash \mathbb {H}^2$
is the surface
![]() $\Sigma $
. The principal bundle
$\Sigma $
. The principal bundle
depends on the extension H. For example, when
![]() $H = \mathrm {PSL}(2,{\mathbb R})$
, this bundle is a circle bundle isomorphic to the unit tangent bundle of
$H = \mathrm {PSL}(2,{\mathbb R})$
, this bundle is a circle bundle isomorphic to the unit tangent bundle of
![]() $\Sigma $
(i.e., a circle bundle with Euler class
$\Sigma $
(i.e., a circle bundle with Euler class
![]() $2g-2$
). When
$2g-2$
). When
![]() $H = \mathrm {SL}(2,{\mathbb R})$
, this bundle is the double cover of the unit tangent bundle of
$H = \mathrm {SL}(2,{\mathbb R})$
, this bundle is the double cover of the unit tangent bundle of
![]() $\Sigma $
(i.e., a circle bundle with Euler class
$\Sigma $
(i.e., a circle bundle with Euler class
![]() $g-1$
). For all the interesting groups H, it is possible to understand this bundle explicitly. We will now restate the previous theorems in the case when
$g-1$
). For all the interesting groups H, it is possible to understand this bundle explicitly. We will now restate the previous theorems in the case when
![]() $H = \mathrm {SL}(2,{\mathbb R})$
.
$H = \mathrm {SL}(2,{\mathbb R})$
.
Corollary 3.4. Let
![]() $H = \mathrm {SL}(2,{\mathbb R})$
, P be a parabolic subgroup of G, Q another parabolic subgroup and I a balanced ideal of
$H = \mathrm {SL}(2,{\mathbb R})$
, P be a parabolic subgroup of G, Q another parabolic subgroup and I a balanced ideal of
![]() $W_Q\backslash W/W_P$
. Let
$W_Q\backslash W/W_P$
. Let
![]() $\rho $
be a P–Anosov deformation of an
$\rho $
be a P–Anosov deformation of an
![]() $\iota $
–Fuchsian representation of a surface group
$\iota $
–Fuchsian representation of a surface group
![]() $\pi _1(\Sigma )$
. Then
$\pi _1(\Sigma )$
. Then
-
•
 $\Omega _{\rho ,I}$
retracts to a closed submanifold
$\Omega _{\rho ,I}$
retracts to a closed submanifold
 $\mathfrak F$
of codimension
$\mathfrak F$
of codimension
 $2$
carrying a smooth circle action.
$2$
carrying a smooth circle action. -
• The quotient
 $\rho (\pi _1(\Sigma )) \backslash \Omega _{\rho ,I}$
is diffeomorphic to a fiber bundle over
$\rho (\pi _1(\Sigma )) \backslash \Omega _{\rho ,I}$
is diffeomorphic to a fiber bundle over
 $\Sigma $
with fiber
$\Sigma $
with fiber
 $\mathfrak F$
. This is the
$\mathfrak F$
. This is the
 $\mathfrak F$
–bundle associated to the principal circle bundle of Euler class
$\mathfrak F$
–bundle associated to the principal circle bundle of Euler class
 $g-1$
over
$g-1$
over
 $\Sigma $
.
$\Sigma $
.
One of the main applications of this corollary is for (quasi)-Hitchin representations. Recall that Hitchin representations are deformations of
![]() $\iota _0 \circ \rho _0$
where
$\iota _0 \circ \rho _0$
where
![]() $\rho _0: \pi _1(\Sigma )\to \mathrm {SL}(2,{\mathbb R})$
is a Fuchsian representation and
$\rho _0: \pi _1(\Sigma )\to \mathrm {SL}(2,{\mathbb R})$
is a Fuchsian representation and
![]() $\iota _0$
is the principal representation of
$\iota _0$
is the principal representation of
![]() $\mathrm {SL}(2,{\mathbb R})$
into a real split semisimple Lie group G, and quasi-Hitchin representations are their
$\mathrm {SL}(2,{\mathbb R})$
into a real split semisimple Lie group G, and quasi-Hitchin representations are their
![]() $P_{\min }$
–Anosov deformations into its complexification
$P_{\min }$
–Anosov deformations into its complexification
![]() $G_{{\mathbb C}}$
.
$G_{{\mathbb C}}$
.
We can also apply Theorems 3.1 and 3.3 to the positive representations that are Anosov deformations of twisted
![]() $\iota $
–Fuchsian representations. As discussed in Section 2.3, almost all the positive representations in the classical groups are of this type, with the only exception of the exceptional components in
$\iota $
–Fuchsian representations. As discussed in Section 2.3, almost all the positive representations in the classical groups are of this type, with the only exception of the exceptional components in
![]() ${\mathrm {Sp}}(4,{\mathbb R})$
and
${\mathrm {Sp}}(4,{\mathbb R})$
and
![]() $\mathrm {SO}(p,p+1)$
. In order to apply our results to positive representations, we need to consider the group
$\mathrm {SO}(p,p+1)$
. In order to apply our results to positive representations, we need to consider the group
![]() $H = \mathrm {SL}(2,{\mathbb R}) \times C$
for a certain compact subgroup C. The statement is similar to Corollary 3.4, except that the structure group of the bundle is now
$H = \mathrm {SL}(2,{\mathbb R}) \times C$
for a certain compact subgroup C. The statement is similar to Corollary 3.4, except that the structure group of the bundle is now
![]() $\mathrm {SO}(2)\times C$
. The invariants that characterize the bundle are the Euler class and the characteristic classes of the C component of
$\mathrm {SO}(2)\times C$
. The invariants that characterize the bundle are the Euler class and the characteristic classes of the C component of
![]() $\rho _0$
.
$\rho _0$
.
3.2 Proof of the theorems
A key hypothesis in Theorem 3.1 is the assumption that
![]() $\rho $
is a P–Anosov deformation of an
$\rho $
is a P–Anosov deformation of an
![]() $\iota $
–Fuchsian representation
$\iota $
–Fuchsian representation
![]() $\iota \circ \rho _0$
. Indeed, by Guichard–Wienhard’s Theorem 2.10, the topology of
$\iota \circ \rho _0$
. Indeed, by Guichard–Wienhard’s Theorem 2.10, the topology of
![]() $M_{\rho ,I}$
does not change, and we only have to determine it for
$M_{\rho ,I}$
does not change, and we only have to determine it for
![]() $\rho = \iota \circ \rho _0$
. The key result for the proof is thus the following.
$\rho = \iota \circ \rho _0$
. The key result for the proof is thus the following.
Lemma 3.5. Let H be a semisimple Lie group with finite center, and
![]() $K \subset H$
be its maximal compact subgroup. Let X be a manifold with a proper action of H. Then there exists an H–equivariant smooth fibration
$K \subset H$
be its maximal compact subgroup. Let X be a manifold with a proper action of H. Then there exists an H–equivariant smooth fibration
where
![]() $S_H$
denotes the symmetric space of H.
$S_H$
denotes the symmetric space of H.
For the proof, we use the fact that the symmetric space
![]() $S_H = H/K$
has non-positive curvature. We need the notion of barycenter: Given a finite measure of compact support
$S_H = H/K$
has non-positive curvature. We need the notion of barycenter: Given a finite measure of compact support
![]() $\nu $
on
$\nu $
on
![]() $S_H$
, we consider the function
$S_H$
, we consider the function
defined by
Since
![]() $S_H$
has non-positive curvature, the squared distance function is smooth (as push-forward of the squared norm under the exponential map), the distance function is convex (see [Reference Ballmann, Gromov and SchroederBGS85, Thm 1.3]), and hence the squared distance function is strongly convex. This implies that the function b is strongly convex, and since it is also proper, it has a unique critical point, which is a global minimum. Moreover, the Hessian of b at the global minimum is positive definite. The barycenter
$S_H$
has non-positive curvature, the squared distance function is smooth (as push-forward of the squared norm under the exponential map), the distance function is convex (see [Reference Ballmann, Gromov and SchroederBGS85, Thm 1.3]), and hence the squared distance function is strongly convex. This implies that the function b is strongly convex, and since it is also proper, it has a unique critical point, which is a global minimum. Moreover, the Hessian of b at the global minimum is positive definite. The barycenter
![]() $\mathrm {Bar}\{\nu \}$
of
$\mathrm {Bar}\{\nu \}$
of
![]() $\nu $
is defined to be the unique critical point of b.
$\nu $
is defined to be the unique critical point of b.
Proof of Lemma 3.5.
We choose a torsion-free uniform lattice
![]() $\Gamma $
in H. This always exists. See, for example, Borel and Harish–Chandra [Reference Borel and ChandraBHC62]. Then
$\Gamma $
in H. This always exists. See, for example, Borel and Harish–Chandra [Reference Borel and ChandraBHC62]. Then
![]() $\Gamma $
acts freely and properly discontinuously on X (see Proposition 2.8); hence, the quotient
$\Gamma $
acts freely and properly discontinuously on X (see Proposition 2.8); hence, the quotient
![]() $\Gamma \backslash X$
is a manifold. Then
$\Gamma \backslash X$
is a manifold. Then
![]() $\Gamma $
is isomorphic to the quotient
$\Gamma $
is isomorphic to the quotient
![]() $\pi _1(\Gamma \backslash X)/\pi _1(X)$
, and we have a homomorphism
$\pi _1(\Gamma \backslash X)/\pi _1(X)$
, and we have a homomorphism
![]() $\psi \colon \thinspace \pi _1(\Gamma \backslash X) \to \Gamma = \pi _1(\Gamma \backslash S_H)$
. Since
$\psi \colon \thinspace \pi _1(\Gamma \backslash X) \to \Gamma = \pi _1(\Gamma \backslash S_H)$
. Since
![]() $S_H$
is contractible, there exists a map
$S_H$
is contractible, there exists a map
![]() $\Gamma \backslash X \to \Gamma \backslash S_H$
inducing
$\Gamma \backslash X \to \Gamma \backslash S_H$
inducing
![]() $\psi $
(for the details, [Reference AlessandriniAle03, Prop. 13]). A priori this map is only continuous, but since smooth maps are dense in the space of continuous maps between compact manifolds, we can assume that the map is smooth. Lifting this map, we obtain a smooth
$\psi $
(for the details, [Reference AlessandriniAle03, Prop. 13]). A priori this map is only continuous, but since smooth maps are dense in the space of continuous maps between compact manifolds, we can assume that the map is smooth. Lifting this map, we obtain a smooth
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
This allows us to define, for all
![]() $x\in X$
, a smooth map
$x\in X$
, a smooth map
![]() $F^x\colon \thinspace H \to S_H$
by
$F^x\colon \thinspace H \to S_H$
by
Since f is
![]() $\Gamma $
–equivariant, we have that
$\Gamma $
–equivariant, we have that
![]() $F^x(g\gamma )= F^x(g)$
for all
$F^x(g\gamma )= F^x(g)$
for all
![]() $\gamma \in \Gamma $
. Hence,
$\gamma \in \Gamma $
. Hence,
![]() $F^x$
descends to a continuous map
$F^x$
descends to a continuous map
![]() $\overline {F}^x: H/\Gamma \to S_H$
.
$\overline {F}^x: H/\Gamma \to S_H$
.
Note that we have
We can finally define a map
![]() $\bar f\colon \thinspace X \to S_H$
as follows:
$\bar f\colon \thinspace X \to S_H$
as follows:
where
![]() $\mu $
is the Haar measure on
$\mu $
is the Haar measure on
![]() $H/\Gamma $
,
$H/\Gamma $
,
![]() $\overline {F}^x_*\mu $
its push-forward by
$\overline {F}^x_*\mu $
its push-forward by
![]() $\overline {F}^x$
, and
$\overline {F}^x$
, and
![]() $\mathrm {Bar}$
is the barycenter of a finite measure with compact support, as defined above. Note that the image of
$\mathrm {Bar}$
is the barycenter of a finite measure with compact support, as defined above. Note that the image of
![]() $\overline {F}^x$
is compact since
$\overline {F}^x$
is compact since
![]() $H/\Gamma $
is compact; hence,
$H/\Gamma $
is compact; hence,
![]() $\overline {F}^x_*\mu $
does have compact support.
$\overline {F}^x_*\mu $
does have compact support.
We claim that
![]() $\bar f$
is H–equivariant. Indeed, for
$\bar f$
is H–equivariant. Indeed, for
![]() $x\in X$
and
$x\in X$
and
![]() $g\in H$
, we have
$g\in H$
, we have
 $$ \begin{align*} \bar f(gx) &= \mathrm{Bar} \{ \overline{F}^{gx}_*\mu\} \\ &= \mathrm{Bar}\{g_* \overline{F}^x_* g^{-1}_* \mu\} \quad \textrm{by (1)}\\ &= \mathrm{Bar}\{g_* \overline{F}^x_* \mu \} \quad \textrm{by left invariance of the Haar measure}\\ &= g\cdot \mathrm{Bar}\{\overline{F}^x_* \mu \} \quad \textrm{by equivariance of the barycenter map}\\ &= g\cdot \bar f(x). \end{align*} $$
$$ \begin{align*} \bar f(gx) &= \mathrm{Bar} \{ \overline{F}^{gx}_*\mu\} \\ &= \mathrm{Bar}\{g_* \overline{F}^x_* g^{-1}_* \mu\} \quad \textrm{by (1)}\\ &= \mathrm{Bar}\{g_* \overline{F}^x_* \mu \} \quad \textrm{by left invariance of the Haar measure}\\ &= g\cdot \mathrm{Bar}\{\overline{F}^x_* \mu \} \quad \textrm{by equivariance of the barycenter map}\\ &= g\cdot \bar f(x). \end{align*} $$
The rest follows from the two lemmas below. Lemma 3.6 guarantees that the map
![]() $\bar {f}$
is smooth, and Lemma 3.7 shows that it is an Ehresmann fibration.
$\bar {f}$
is smooth, and Lemma 3.7 shows that it is an Ehresmann fibration.
Lemma 3.6. The map
![]() $\bar f$
, constructed in the proof of Lemma 3.5, is smooth.
$\bar f$
, constructed in the proof of Lemma 3.5, is smooth.
Proof. For every
![]() $x\in X$
,
$x\in X$
,
![]() $\bar {f}(x)$
is the unique critical point of the function
$\bar {f}(x)$
is the unique critical point of the function
where the measure
![]() $\nu $
is the push-forward
$\nu $
is the push-forward
![]() $\nu = \overline {F}^x_* \mu $
. By the change-of-variable formula, this can be written as
$\nu = \overline {F}^x_* \mu $
. By the change-of-variable formula, this can be written as
In this setting, the function b depends on the parameter x. To make this more explicit, we write it as
![]() $b(x,y)$
, a smooth function of two variables
$b(x,y)$
, a smooth function of two variables
![]() $x \in X$
and
$x \in X$
and
![]() $y \in S_H$
. We consider the differential of b with respect to y:
$y \in S_H$
. We consider the differential of b with respect to y:
Let us fix an
![]() $x_0 \in X$
and the corresponding
$x_0 \in X$
and the corresponding
![]() $y_0 = \bar {f}(x_0) \in S_H$
. We choose local coordinates on a small neighborhood U of
$y_0 = \bar {f}(x_0) \in S_H$
. We choose local coordinates on a small neighborhood U of
![]() $y_0$
in
$y_0$
in
![]() $S_H$
. This trivializes the cotangent bundle on U:
$S_H$
. This trivializes the cotangent bundle on U:
![]() $T^* U \simeq U \times {\mathbb R}^k$
, where
$T^* U \simeq U \times {\mathbb R}^k$
, where
![]() $k = \dim (S_H)$
. Let
$k = \dim (S_H)$
. Let
![]() $\pi _2: T^* U \rightarrow {\mathbb R}^k$
denote the projection onto the second factor. Now we consider the composition
$\pi _2: T^* U \rightarrow {\mathbb R}^k$
denote the projection onto the second factor. Now we consider the composition
Now, for all x close enough to
![]() $x_0$
, the pairs
$x_0$
, the pairs
![]() $(x,\bar {f}(x))$
are precisely the solutions to the equation
$(x,\bar {f}(x))$
are precisely the solutions to the equation
We can now apply the implicit function theorem to the function
![]() $\pi _2 \circ \beta (x,y)$
. Consider a tangent vector to
$\pi _2 \circ \beta (x,y)$
. Consider a tangent vector to
![]() $X\times U$
of the form
$X\times U$
of the form
![]() $(0,u)$
at a point
$(0,u)$
at a point
![]() $(x,\bar {f}(x))$
. Then we have
$(x,\bar {f}(x))$
. Then we have
where
![]() $\mathrm {Hess}_y b{\bar f(x)}(u,v)$
denotes the Hessian of the function
$\mathrm {Hess}_y b{\bar f(x)}(u,v)$
denotes the Hessian of the function
![]() $b(x,\cdot )$
at the point
$b(x,\cdot )$
at the point
![]() $\bar f(x)$
(recall that the Hessian of a function at critical point is well-defined independently of the local coordinate). Since
$\bar f(x)$
(recall that the Hessian of a function at critical point is well-defined independently of the local coordinate). Since
![]() $b(x,\cdot )$
is strongly convex,
$b(x,\cdot )$
is strongly convex,
![]() $\mathrm {Hess}_y b{\bar f(x)}$
is positive definite, and the differential of
$\mathrm {Hess}_y b{\bar f(x)}$
is positive definite, and the differential of
![]() $\pi _2$
in the y direction is an isomorphism from
$\pi _2$
in the y direction is an isomorphism from
![]() $T_{\bar f(x)} U$
to
$T_{\bar f(x)} U$
to
![]() $T^*_{\bar f(x)} U = {\mathbb R}^k$
. Hence,
$T^*_{\bar f(x)} U = {\mathbb R}^k$
. Hence,
![]() $\pi _2$
is a submersion, and the set
$\pi _2$
is a submersion, and the set
![]() $\{(x,\bar f(x))\} = \pi _2^{-1}(0)$
is the graph of a smooth function.
$\{(x,\bar f(x))\} = \pi _2^{-1}(0)$
is the graph of a smooth function.
Lemma 3.7. Let H be a Lie group, and let
![]() $X, Y$
be manifolds equipped with smooth H-actions, where the action on Y is transitive. Denote by L the stabilizer in H of a point of Y, and identify Y with
$X, Y$
be manifolds equipped with smooth H-actions, where the action on Y is transitive. Denote by L the stabilizer in H of a point of Y, and identify Y with
![]() $H/L$
. Then, every H–equivariant map
$H/L$
. Then, every H–equivariant map
![]() $\phi :X \rightarrow Y$
is a smooth fiber bundle, associated to the principal L-bundle
$\phi :X \rightarrow Y$
is a smooth fiber bundle, associated to the principal L-bundle
![]() $H\mapsto H/L$
(in the sense of Definition 3.2).
$H\mapsto H/L$
(in the sense of Definition 3.2).
Proof. First note that, by homogeneity of Y, the map
![]() $\phi $
needs to be onto. We will construct a local trivialization around every point
$\phi $
needs to be onto. We will construct a local trivialization around every point
![]() $y \in Y$
. We choose the subgroup L as the stabilizer of y. Hence, L is acting on the fiber
$y \in Y$
. We choose the subgroup L as the stabilizer of y. Hence, L is acting on the fiber
![]() $F = \phi ^{-1}(y)$
. Let U be a neighborhood of y in Y that trivializes the bundle
$F = \phi ^{-1}(y)$
. Let U be a neighborhood of y in Y that trivializes the bundle
![]() $H \rightarrow H/L$
. The trivialization is a map
$H \rightarrow H/L$
. The trivialization is a map
![]() $t:U \times L \rightarrow H$
.
$t:U \times L \rightarrow H$
.
A trivialization of
![]() $\phi $
over U is given by the map
$\phi $
over U is given by the map
where e is the identity of H. Clearly,
![]() $\phi (T(u,f)) = u$
, because
$\phi (T(u,f)) = u$
, because
![]() $t(u,e)$
sends y to u. The map T is
$t(u,e)$
sends y to u. The map T is
![]() $1$
–
$1$
–
![]() $1$
because if
$1$
because if
![]() $t(u,e)f = t(u',e)f'$
, then
$t(u,e)f = t(u',e)f'$
, then
![]() $u = u'$
because
$u = u'$
because
![]() $\phi (T(u,f))=u$
, and then by multiplying by
$\phi (T(u,f))=u$
, and then by multiplying by
![]() $t(u,e)^{-1}$
, we see that
$t(u,e)^{-1}$
, we see that
![]() $f=f'$
. We can also see that the map T is onto
$f=f'$
. We can also see that the map T is onto
![]() $\phi ^{-1}(U)$
because given
$\phi ^{-1}(U)$
because given
![]() $x \in \phi ^{-1}(U)$
, let
$x \in \phi ^{-1}(U)$
, let
![]() $f = t(\phi (x),e)^{-1}x \in F$
, and then
$f = t(\phi (x),e)^{-1}x \in F$
, and then
![]() $x = T(\phi (x),f)$
.
$x = T(\phi (x),f)$
.
The construction above shows that every atlas for the bundle
![]() $H \rightarrow H/L$
induces an atlas for the bundle
$H \rightarrow H/L$
induces an atlas for the bundle
![]() $\phi : X \rightarrow Y$
. It is easy to check that the two atlases have the same transition functions, and hence, the two bundles are associated.
$\phi : X \rightarrow Y$
. It is easy to check that the two atlases have the same transition functions, and hence, the two bundles are associated.
The following Proposition 3.8 is similar to Theorems 3.1 and 3.3, but the difference is that it can be applied to domains of discontinuity that are not necessarily cocompact. Anyway, if the domain is not cocompact, our conclusion only holds for
![]() $\iota $
–lattice representations, but does not automatically extend to their deformations. After that, we will add the hypothesis that the domain of discontinuity is cocompact and prove the full Theorems 3.1 and 3.3 for their deformations.
$\iota $
–lattice representations, but does not automatically extend to their deformations. After that, we will add the hypothesis that the domain of discontinuity is cocompact and prove the full Theorems 3.1 and 3.3 for their deformations.
Proposition 3.8. Let H be a connected semisimple Lie group with finite center of real rank
![]() $1$
,
$1$
,
![]() $K \subset H$
a maximal compact subgroup, and
$K \subset H$
a maximal compact subgroup, and
![]() $S_H = H/K$
the symmetric space for H. Let
$S_H = H/K$
the symmetric space for H. Let
![]() $\rho _0:\Gamma \rightarrow H$
be the inclusion of a torsion-free uniform lattice in H. Let G be a connected semi-simple Lie group with finite center, and
$\rho _0:\Gamma \rightarrow H$
be the inclusion of a torsion-free uniform lattice in H. Let G be a connected semi-simple Lie group with finite center, and
![]() $\iota :H \rightarrow G$
be a representation. Let
$\iota :H \rightarrow G$
be a representation. Let
![]() $P < G$
be a parabolic subgroup of G such that the representation
$P < G$
be a parabolic subgroup of G such that the representation
![]() $\rho = \iota \circ \rho _0$
is P–Anosov.
$\rho = \iota \circ \rho _0$
is P–Anosov.
Let Q be a parabolic subgroup of G and
![]() $\Omega _{\rho ,I} \subset G/Q$
a domain of discontinuity for
$\Omega _{\rho ,I} \subset G/Q$
a domain of discontinuity for
![]() $\rho $
constructed from a thickening of a (not necessarily balanced) ideal I. Let
$\rho $
constructed from a thickening of a (not necessarily balanced) ideal I. Let
![]() $M_{\rho ,I} = \rho \backslash \Omega _{\rho ,I}$
be the quotient manifold.
$M_{\rho ,I} = \rho \backslash \Omega _{\rho ,I}$
be the quotient manifold.
Then
![]() $M_{\rho ,I}$
is diffeomorphic to a smooth fiber bundle over
$M_{\rho ,I}$
is diffeomorphic to a smooth fiber bundle over
![]() $S_\Gamma $
. The fiber F of the bundle is homotopically equivalent to the domain
$S_\Gamma $
. The fiber F of the bundle is homotopically equivalent to the domain
![]() $\Omega _\rho $
and carries a K–action that gives the bundle a structure of K–bundle. The bundle is isomorphic to the K–bundle associated to the K–principal bundle
$\Omega _\rho $
and carries a K–action that gives the bundle a structure of K–bundle. The bundle is isomorphic to the K–bundle associated to the K–principal bundle
![]() $\Gamma \backslash H \rightarrow \Gamma \backslash S_H$
via a change of fiber.
$\Gamma \backslash H \rightarrow \Gamma \backslash S_H$
via a change of fiber.
Proof. As we saw in Section 2.2, it was proved in Guichard–Wienhard [Reference Guichard and WienhardGW12, Prop. 4.7] that the representation
![]() $\rho $
is P–Anosov for a certain family of parabolic subgroups described there.
$\rho $
is P–Anosov for a certain family of parabolic subgroups described there.
Since
![]() $\Gamma $
is a uniform lattice in H, the group H preserves the domain of discontinuity
$\Gamma $
is a uniform lattice in H, the group H preserves the domain of discontinuity
![]() $\Omega _\rho $
and acts properly on it by Lemma 2.7. Applying Lemmas 3.5 and 3.7 with
$\Omega _\rho $
and acts properly on it by Lemma 2.7. Applying Lemmas 3.5 and 3.7 with
![]() $X= \Omega _\rho $
and
$X= \Omega _\rho $
and
![]() $Y= S_H$
, we get a smooth H–equivariant fiber bundle map from
$Y= S_H$
, we get a smooth H–equivariant fiber bundle map from
![]() $\Omega _\rho $
to
$\Omega _\rho $
to
![]() $S_H$
, which factors to a smooth fiber bundle map from M to
$S_H$
, which factors to a smooth fiber bundle map from M to
![]() $S_\Gamma $
.
$S_\Gamma $
.
Proof of Theorems 3.1 and 3.3.
In Proposition 3.8, we have already proved the theorem for twisted
![]() $\iota $
–Fuchsian and for lattice representations. Now, since we are assuming that the domain of discontinuity is cocompact, it follows from Theorem 2.10 that the topology of M is constant in
$\iota $
–Fuchsian and for lattice representations. Now, since we are assuming that the domain of discontinuity is cocompact, it follows from Theorem 2.10 that the topology of M is constant in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Part II
Quasi-Hitchin representations into
![]() $\mathbf {{\mathrm {Sp}}(4,{{\mathbb C}})}$
$\mathbf {{\mathrm {Sp}}(4,{{\mathbb C}})}$
In the second part of the paper, we will focus on quasi-Hitchin representations into
![]() $G = {\mathrm {Sp}}(4,{{\mathbb C}})$
. We fix the principal representation
$G = {\mathrm {Sp}}(4,{{\mathbb C}})$
. We fix the principal representation
![]() $\iota _0 \colon \thinspace \mathrm {SL}(2, {\mathbb R}) \to G$
and a Fuchsian representation
$\iota _0 \colon \thinspace \mathrm {SL}(2, {\mathbb R}) \to G$
and a Fuchsian representation
![]() $\rho _0 \colon \thinspace \pi _1(\Sigma ) \to \mathrm {SL}(2, {\mathbb R})$
. The principal Fuchsian representation
$\rho _0 \colon \thinspace \pi _1(\Sigma ) \to \mathrm {SL}(2, {\mathbb R})$
. The principal Fuchsian representation
![]() $\iota _0\circ \rho _0$
is Anosov with reference to every parabolic subgroup P of G. Recall that a P–quasi-Hitchin representation is a P–Anosov deformation of
$\iota _0\circ \rho _0$
is Anosov with reference to every parabolic subgroup P of G. Recall that a P–quasi-Hitchin representation is a P–Anosov deformation of
![]() $\iota _0\circ \rho _0$
. Our aim is to determine the topology of the quotient manifolds of the cocompact domains of discontinuity for these representations.
$\iota _0\circ \rho _0$
. Our aim is to determine the topology of the quotient manifolds of the cocompact domains of discontinuity for these representations.
The group
![]() ${\mathrm {Sp}}(4,{{\mathbb C}})$
has (up to conjugation) three different proper parabolic subgroups, so there are three flag varieties for us to consider: the projective space
${\mathrm {Sp}}(4,{{\mathbb C}})$
has (up to conjugation) three different proper parabolic subgroups, so there are three flag varieties for us to consider: the projective space
![]() $\mathbb {CP}^3$
, the Lagrangian Grassmannian
$\mathbb {CP}^3$
, the Lagrangian Grassmannian
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
, and the full flag variety, which consists of full isotropic flags (i.e., pairs consisting of a line in
${\mathrm {Lag}}({{\mathbb C}}^4)$
, and the full flag variety, which consists of full isotropic flags (i.e., pairs consisting of a line in
![]() ${{\mathbb C}}^4$
and a Lagrangian subspace of
${{\mathbb C}}^4$
and a Lagrangian subspace of
![]() ${{\mathbb C}}^4$
containing that line). The principal Fuchsian representation
${{\mathbb C}}^4$
containing that line). The principal Fuchsian representation
![]() $\iota _0\circ \rho _0$
admits four cocompact domains of discontinuity constructed by a balanced thickening: one in the projective space
$\iota _0\circ \rho _0$
admits four cocompact domains of discontinuity constructed by a balanced thickening: one in the projective space
![]() $\mathbb {CP}^3$
, one in the Lagrangian Grassmannian
$\mathbb {CP}^3$
, one in the Lagrangian Grassmannian
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
(whose construction is described in Section 2.5), and two in the isotropic full flag variety. The two domains of discontinuity in the isotropic full flags variety are in fact the pullback of the two domains in
${\mathrm {Lag}}({{\mathbb C}}^4)$
(whose construction is described in Section 2.5), and two in the isotropic full flag variety. The two domains of discontinuity in the isotropic full flags variety are in fact the pullback of the two domains in
![]() $\mathbb {CP}^3$
and in
$\mathbb {CP}^3$
and in
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
under the natural projection from the full flag variety to the partial flag varieties; hence, they can be understood from a description of the latter two. The domain of discontinuity in
${\mathrm {Lag}}({{\mathbb C}}^4)$
under the natural projection from the full flag variety to the partial flag varieties; hence, they can be understood from a description of the latter two. The domain of discontinuity in
![]() $\mathbb {CP}^3$
was described in Alessandrini–Davalo–Li [Reference Alessandrini, Davalo and LiADL24, Corol. 10.2], where it is proved that the quotient manifold M is diffeomorphic to a fiber bundle over the surface
$\mathbb {CP}^3$
was described in Alessandrini–Davalo–Li [Reference Alessandrini, Davalo and LiADL24, Corol. 10.2], where it is proved that the quotient manifold M is diffeomorphic to a fiber bundle over the surface
![]() $\Sigma $
with fiber
$\Sigma $
with fiber
![]() $\mathbb {S}^2 \times \mathbb {S}^2$
.
$\mathbb {S}^2 \times \mathbb {S}^2$
.
The only cocompact domain of discontinuity that is not yet understood is the one in
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
. The second part of this paper is devoted to the description of this domain and its quotient manifold. In fact, the domain of discontinuity in the Lagrangian Grassmannian is of particular interest because it contains two copies of the symmetric space associated to
${\mathrm {Lag}}({{\mathbb C}}^4)$
. The second part of this paper is devoted to the description of this domain and its quotient manifold. In fact, the domain of discontinuity in the Lagrangian Grassmannian is of particular interest because it contains two copies of the symmetric space associated to
![]() ${\mathrm {Sp}}(4,{\mathbb R})$
: the Siegel upper half space and the Siegel lower half space; see [Reference WienhardWie16]. This is very reminiscent of the situation for quasi-Fuchsian representations, and we hope that a good understanding of the domain of discontinuity and its quotient manifold might help to shed some light on possible generalizations of the Bers’ double uniformization theorem for quasi-Hitchin representations.
${\mathrm {Sp}}(4,{\mathbb R})$
: the Siegel upper half space and the Siegel lower half space; see [Reference WienhardWie16]. This is very reminiscent of the situation for quasi-Fuchsian representations, and we hope that a good understanding of the domain of discontinuity and its quotient manifold might help to shed some light on possible generalizations of the Bers’ double uniformization theorem for quasi-Hitchin representations.
The construction of the domain of discontinuity in
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
, described in Section 2.5, only uses the fact that the representation is Anosov with respect to P, where P is the stabilizer of a point in
${\mathrm {Lag}}({{\mathbb C}}^4)$
, described in Section 2.5, only uses the fact that the representation is Anosov with respect to P, where P is the stabilizer of a point in
![]() $\mathbb {CP}^3$
. We will thus consider a representation
$\mathbb {CP}^3$
. We will thus consider a representation
![]() $\rho $
in the quasi-Hitchin space
$\rho $
in the quasi-Hitchin space
![]() $\mathrm {QHit}_{P}(\Sigma , {\mathrm {Sp}}(4,{{\mathbb C}})) := \mathrm {Anosov}_{P,\iota _0,\rho _0}(\pi _1(\Sigma ),{\mathrm {Sp}}(4,{{\mathbb C}}))$
.
$\mathrm {QHit}_{P}(\Sigma , {\mathrm {Sp}}(4,{{\mathbb C}})) := \mathrm {Anosov}_{P,\iota _0,\rho _0}(\pi _1(\Sigma ),{\mathrm {Sp}}(4,{{\mathbb C}}))$
.
There is a unique nontrivial ideal I, which allows us to define a cocompact domain of discontinuity
![]() $\Omega _{\rho ,I}$
, with quotient manifold
$\Omega _{\rho ,I}$
, with quotient manifold
![]() $M_{\rho ,I}$
; see Section 2.5. Since, by Theorem 2.10, the topology of the quotient manifold does not depend on
$M_{\rho ,I}$
; see Section 2.5. Since, by Theorem 2.10, the topology of the quotient manifold does not depend on
![]() $\rho $
, we can restrict our attention to the case when
$\rho $
, we can restrict our attention to the case when
![]() $\rho = \iota _0\circ \rho _0$
. With the representation fixed once for all, we will denote the domain of discontinuity and the quotient manifold simply by
$\rho = \iota _0\circ \rho _0$
. With the representation fixed once for all, we will denote the domain of discontinuity and the quotient manifold simply by
![]() $\Omega $
and M, instead of
$\Omega $
and M, instead of
![]() $\Omega _{\rho ,I}$
and
$\Omega _{\rho ,I}$
and
![]() $M_{\rho ,I}$
.
$M_{\rho ,I}$
.
Our Theorem A gives smooth fibrations
In this second part of the paper, we will study the fiber
![]() $\mathfrak {F} = \mathfrak {F}_p$
of these maps and prove Theorem D, which states that
$\mathfrak {F} = \mathfrak {F}_p$
of these maps and prove Theorem D, which states that
![]() $\mathfrak {F}$
is homeomorphic to the
$\mathfrak {F}$
is homeomorphic to the
![]() $4$
–manifold
$4$
–manifold
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
.
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
.
Our strategy will be to describe a new
![]() $\rho $
–equivariant fibration
$\rho $
–equivariant fibration
which is not smooth, but has a more geometric definition and for which the fiber
![]() $F = F_q$
is easier to understand. This new fiber F is not a manifold, but it is homotopically equivalent to the domain of discontinuity
$F = F_q$
is easier to understand. This new fiber F is not a manifold, but it is homotopically equivalent to the domain of discontinuity
![]() $\Omega $
; hence, F is homotopically equivalent to the smooth fiber
$\Omega $
; hence, F is homotopically equivalent to the smooth fiber
![]() $\mathfrak {F}$
. We will see that F is simply connected, and hence
$\mathfrak {F}$
. We will see that F is simply connected, and hence
![]() $\mathfrak {F}$
is a simply connected
$\mathfrak {F}$
is a simply connected
![]() $4$
–manifold. A smooth simply connected
$4$
–manifold. A smooth simply connected
![]() $4$
–manifold is determined up to homeomorphism by its homotopy type; hence, we can determine
$4$
–manifold is determined up to homeomorphism by its homotopy type; hence, we can determine
![]() $\mathfrak {F}$
by computing the homotopy invariants of F.
$\mathfrak {F}$
by computing the homotopy invariants of F.
In order to define the fibration q, we will study the action of
![]() $\mathrm {SL}(2,{{\mathbb C}})$
on the Lagrangian Grassmannian
$\mathrm {SL}(2,{{\mathbb C}})$
on the Lagrangian Grassmannian
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
induced by the principal representation
${\mathrm {Lag}}({{\mathbb C}}^4)$
induced by the principal representation
![]() $\iota _0$
. In Section 4, we will discuss the
$\iota _0$
. In Section 4, we will discuss the
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–orbits in
$\mathrm {SL}(2,{{\mathbb C}})$
–orbits in
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
, and this discussion will allow us to define q at the end of the section. In Section 5, we will study the fiber F, and in Section 6, we will use our results on the topology of F to understand
$\mathrm {Lag}({{\mathbb C}}^{4})$
, and this discussion will allow us to define q at the end of the section. In Section 5, we will study the fiber F, and in Section 6, we will use our results on the topology of F to understand
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
4 Lagrangians as regular ideal tetrahedra
In this section, we will study the action of
![]() $\mathrm {SL}(2,{{\mathbb C}})$
on
$\mathrm {SL}(2,{{\mathbb C}})$
on
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
and its orbits. This will allow us to define the projection
$\mathrm {Lag}({{\mathbb C}}^{4})$
and its orbits. This will allow us to define the projection
![]() $q\colon \thinspace \Omega \to {\mathbb H}^2$
explicitly.
$q\colon \thinspace \Omega \to {\mathbb H}^2$
explicitly.
4.1 Lagrangian subspaces in
 ${{\mathbb C}}^{2n}$
${{\mathbb C}}^{2n}$
Let
![]() $\mathbb {K}$
be
$\mathbb {K}$
be
![]() ${\mathbb R}$
or
${\mathbb R}$
or
![]() ${{\mathbb C}}$
, and let
${{\mathbb C}}$
, and let
![]() $V_{n, \mathbb {K}} = \mathbb {K}^{(2n-1)}[X, Y]$
be the space of homogeneous polynomials of degree
$V_{n, \mathbb {K}} = \mathbb {K}^{(2n-1)}[X, Y]$
be the space of homogeneous polynomials of degree
![]() $2n-1$
in the variables X and Y. We fix an explicit basis of
$2n-1$
in the variables X and Y. We fix an explicit basis of
![]() $V_{n, \mathbb {K}}$
given by the polynomials
$V_{n, \mathbb {K}}$
given by the polynomials
![]() $P_k = X^{2n-1-k}Y^k$
for
$P_k = X^{2n-1-k}Y^k$
for
![]() $k = 0, \ldots , 2n-1$
. In particular,
$k = 0, \ldots , 2n-1$
. In particular,
![]() $\dim (V_{n, \mathbb {K}}) = 2n$
. We remark that
$\dim (V_{n, \mathbb {K}}) = 2n$
. We remark that
![]() $V_{n, \mathbb {K}} = \mathrm {Sym}^{2n-1}(V_{1, \mathbb {K}})$
, or, in words, that
$V_{n, \mathbb {K}} = \mathrm {Sym}^{2n-1}(V_{1, \mathbb {K}})$
, or, in words, that
![]() $V_{n, \mathbb {K}}$
is the
$V_{n, \mathbb {K}}$
is the
![]() $(2n-1)$
-st symmetric power of
$(2n-1)$
-st symmetric power of
![]() $V_{1, \mathbb {K}}$
.
$V_{1, \mathbb {K}}$
.
We endow
![]() $V_{1, \mathbb {K}}$
with the symplectic form
$V_{1, \mathbb {K}}$
with the symplectic form
![]() $\omega _{1, \mathbb {K}}$
determined by
$\omega _{1, \mathbb {K}}$
determined by
![]() $\omega _{1, \mathbb {K}}(X,Y) = 1$
. This induces a symplectic form
$\omega _{1, \mathbb {K}}(X,Y) = 1$
. This induces a symplectic form
![]() $\omega _{n, \mathbb {K}} = \mathrm {Sym}^{2n-1}\omega _{1, \mathbb {K}}$
on
$\omega _{n, \mathbb {K}} = \mathrm {Sym}^{2n-1}\omega _{1, \mathbb {K}}$
on
![]() $V_{n, \mathbb {K}}$
. Explicitly, this symplectic form is determined by the following formulae:
$V_{n, \mathbb {K}}$
. Explicitly, this symplectic form is determined by the following formulae:
 $$\begin{align*}\left\{ \begin{array}{ll} \omega_{n, \mathbb{K}}(P_k, P_l) = 0 & \mbox{if } k+l \neq 2n-1 \\ \omega_{n, \mathbb{K}}(P_k, P_{2n-1-k}) = (-1)^k \ \frac{k! (2n-1-k)!}{(2n-1)!}. & \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{ll} \omega_{n, \mathbb{K}}(P_k, P_l) = 0 & \mbox{if } k+l \neq 2n-1 \\ \omega_{n, \mathbb{K}}(P_k, P_{2n-1-k}) = (-1)^k \ \frac{k! (2n-1-k)!}{(2n-1)!}. & \end{array} \right. \end{align*}$$
Here, we are mainly interested in the case
![]() $n=2$
, where these formulae can be written more explicitly:
$n=2$
, where these formulae can be written more explicitly:
 $$ \begin{align} \left\{ \begin{array}{ll} \omega_{2, \mathbb{K}}(X^3, Y^3) = 1 \,,\\ \omega_{2, \mathbb{K}}(X^2 Y, X Y^2) = -\frac{1}{3} \,, & \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} \omega_{2, \mathbb{K}}(X^3, Y^3) = 1 \,,\\ \omega_{2, \mathbb{K}}(X^2 Y, X Y^2) = -\frac{1}{3} \,, & \end{array} \right. \end{align} $$
all other pairings being zero.
The group
![]() ${\mathrm {Sp}}(V_{1, \mathbb {K}}, \omega _{1, \mathbb {K}}) \cong {\mathrm {Sp}}(2, \mathbb {K}) \cong \mathrm {SL}(2, \mathbb {K})$
acts, via symmetric power, on
${\mathrm {Sp}}(V_{1, \mathbb {K}}, \omega _{1, \mathbb {K}}) \cong {\mathrm {Sp}}(2, \mathbb {K}) \cong \mathrm {SL}(2, \mathbb {K})$
acts, via symmetric power, on
![]() $V_{n, \mathbb {K}}$
, and this action preserves the symplectic form
$V_{n, \mathbb {K}}$
, and this action preserves the symplectic form
![]() $\omega _{n, \mathbb {K}}$
. This defines a representation
$\omega _{n, \mathbb {K}}$
. This defines a representation
that is irreducible: the principal representation in
![]() ${\mathrm {Sp}}(2n,\mathbb {K})$
. This representation induces an action of
${\mathrm {Sp}}(2n,\mathbb {K})$
. This representation induces an action of
![]() $\mathrm {SL}(2, \mathbb {K})$
on the projective space
$\mathrm {SL}(2, \mathbb {K})$
on the projective space
![]() $\mathbb {P}(\mathbb {K}^{(2n-1)}[X, Y]) \cong \mathbb {K}\mathbb {P}^{2n-1}$
. This action can be described explicitly by considering how
$\mathbb {P}(\mathbb {K}^{(2n-1)}[X, Y]) \cong \mathbb {K}\mathbb {P}^{2n-1}$
. This action can be described explicitly by considering how
![]() $\mathrm {SL}(2, \mathbb {K})$
moves the
$\mathrm {SL}(2, \mathbb {K})$
moves the
![]() $2n-1$
roots of a polynomial.
$2n-1$
roots of a polynomial.
A vector subspace
![]() $L \subset V_{n, \mathbb {K}}$
is called isotropic if
$L \subset V_{n, \mathbb {K}}$
is called isotropic if
![]() $L \subset L^{\perp _{\omega _{n, \mathbb {K}}}}$
, where
$L \subset L^{\perp _{\omega _{n, \mathbb {K}}}}$
, where
![]() $L^{\perp _{\omega _{n, \mathbb {K}}}}$
is the orthogonal complement with respect to
$L^{\perp _{\omega _{n, \mathbb {K}}}}$
is the orthogonal complement with respect to
![]() $\omega _{n, \mathbb {K}}$
. An isotropic subspace
$\omega _{n, \mathbb {K}}$
. An isotropic subspace
![]() $L \subset V_{n,\mathbb {K}}$
is maximal if it has dimension n, or equivalently if
$L \subset V_{n,\mathbb {K}}$
is maximal if it has dimension n, or equivalently if
![]() $L = L^{\perp _{\omega _{n, \mathbb {K}}}}$
. In this case, L is called a Lagrangian subspace. Using the fact that
$L = L^{\perp _{\omega _{n, \mathbb {K}}}}$
. In this case, L is called a Lagrangian subspace. Using the fact that
![]() $\omega _{n, \mathbb {K}}$
is skew-symmetric, we can see that all the subspaces of
$\omega _{n, \mathbb {K}}$
is skew-symmetric, we can see that all the subspaces of
![]() $V_{n, \mathbb {K}}$
of dimension one are isotropic, and hence, the space of
$V_{n, \mathbb {K}}$
of dimension one are isotropic, and hence, the space of
![]() $1$
–dimensional isotropic subspaces can be identified with the projective space
$1$
–dimensional isotropic subspaces can be identified with the projective space
![]() $\mathbb {P}(V_{n, \mathbb {K}})$
. We denote the space of n–dimensional Lagrangian subspaces of
$\mathbb {P}(V_{n, \mathbb {K}})$
. We denote the space of n–dimensional Lagrangian subspaces of
![]() $V_{n, \mathbb {K}}$
by
$V_{n, \mathbb {K}}$
by
![]() $\mathrm {Lag}(V_{n,\mathbb {K}})$
, and we will call it the Lagrangian Grassmannian. We can think of it as a subspace of the Grassmannian of n–dimensional subspaces in
$\mathrm {Lag}(V_{n,\mathbb {K}})$
, and we will call it the Lagrangian Grassmannian. We can think of it as a subspace of the Grassmannian of n–dimensional subspaces in
![]() $V_{n, \mathbb {K}}$
. The representation
$V_{n, \mathbb {K}}$
. The representation
![]() $\iota _0$
induces an action of
$\iota _0$
induces an action of
![]() $\mathrm {SL}(2, \mathbb {K})$
on
$\mathrm {SL}(2, \mathbb {K})$
on
![]() $\mathrm {Lag}(V_{n, \mathbb {K}})$
.
$\mathrm {Lag}(V_{n, \mathbb {K}})$
.
One last thing we want to recall about this Lagrangian Grassmanian is its topology. There are different ways to describe the topology, but the way we will mostly use in this paper is via the subspace topology inherited from the Grassmanian space, whose topology can be described using the Plücker map or Plücker coordinates. In our case, the Plücker map is an embedding of the Grassmanian of n–planes in
![]() $V_{n, \mathbb {K}}$
into the projectivization of the n-th exterior power of
$V_{n, \mathbb {K}}$
into the projectivization of the n-th exterior power of
![]() $V_{n, \mathbb {K}}$
:
$V_{n, \mathbb {K}}$
:
which realizes
![]() $\mathrm {Gr}(n,V_{n, \mathbb {K}})$
as an algebraic variety, since the image consists of the intersection of a number of quadrics defined by the Plücker relations. To write these relations, we need to be more precise. Given
$\mathrm {Gr}(n,V_{n, \mathbb {K}})$
as an algebraic variety, since the image consists of the intersection of a number of quadrics defined by the Plücker relations. To write these relations, we need to be more precise. Given
![]() $W \in \mathrm {Gr}(n,V_{n, \mathbb {K}})$
, choose a basis
$W \in \mathrm {Gr}(n,V_{n, \mathbb {K}})$
, choose a basis
![]() $W_1, W_2, \ldots , W_n$
of W consisting of column vectors. Let
$W_1, W_2, \ldots , W_n$
of W consisting of column vectors. Let
![]() $\widehat {W}$
be the
$\widehat {W}$
be the
![]() $(2n) \times n$
matrix whose columns are
$(2n) \times n$
matrix whose columns are
![]() $W_1, W_2, \ldots , W_n$
. For any ordered sequence
$W_1, W_2, \ldots , W_n$
. For any ordered sequence
![]() $1 \leq i_1 < i_2 < \cdots < i_n\leq 2n$
of n integers, let
$1 \leq i_1 < i_2 < \cdots < i_n\leq 2n$
of n integers, let
![]() $W_{i_1, \ldots , i_n}$
be the determinant of the
$W_{i_1, \ldots , i_n}$
be the determinant of the
![]() $n \times n$
matrix given by the rows
$n \times n$
matrix given by the rows
![]() $i_1, \ldots , i_n$
of
$i_1, \ldots , i_n$
of
![]() $\widehat {W}$
. The numbers
$\widehat {W}$
. The numbers
![]() $W_{i_1, \ldots , i_n}$
are projective coordinates for W, and they satisfy the following relations:
$W_{i_1, \ldots , i_n}$
are projective coordinates for W, and they satisfy the following relations:
 $$\begin{align*}\sum_{l=1}^{n+1} W_{i_1, \ldots, i_{n-1}, j_l} W_{j_1, \ldots,\hat{j}_l, \ldots j_{n+1}} = 0\,,\end{align*}$$
$$\begin{align*}\sum_{l=1}^{n+1} W_{i_1, \ldots, i_{n-1}, j_l} W_{j_1, \ldots,\hat{j}_l, \ldots j_{n+1}} = 0\,,\end{align*}$$
for
![]() $1 \leq i_1 < i_2 < \cdots < i_{n-1}\leq 2n$
and
$1 \leq i_1 < i_2 < \cdots < i_{n-1}\leq 2n$
and
![]() $1 \leq j_1 < j_2 < \cdots < j_{n+1}\leq 2n$
and where
$1 \leq j_1 < j_2 < \cdots < j_{n+1}\leq 2n$
and where
![]() $\hat {j}_l$
denotes the fact that the
$\hat {j}_l$
denotes the fact that the
![]() $j_l$
term is omitted. For example, in the case
$j_l$
term is omitted. For example, in the case
![]() $n = 2$
, which will be the main focus of the article, we will have coordinates
$n = 2$
, which will be the main focus of the article, we will have coordinates
![]() $W_{1, 2}$
,
$W_{1, 2}$
,
![]() $W_{1, 3}$
,
$W_{1, 3}$
,
![]() $W_{1, 4}$
,
$W_{1, 4}$
,
![]() $W_{2, 3}$
,
$W_{2, 3}$
,
![]() $W_{2, 4}$
and
$W_{2, 4}$
and
![]() $W_{3, 4}$
, with the relation
$W_{3, 4}$
, with the relation
The condition that the space W is Lagrangian gives one additional polynomial equation, so that
![]() ${\mathrm {Lag}}({{\mathbb C}}^4)$
is a projective variety of complex dimension
${\mathrm {Lag}}({{\mathbb C}}^4)$
is a projective variety of complex dimension
![]() $3$
.
$3$
.
4.2
 $\mathrm {SL}(2,{{\mathbb C}})$
–orbits of
$\mathrm {SL}(2,{{\mathbb C}})$
–orbits of
 $\mathrm {Lag}({{\mathbb C}}^{4})$
$\mathrm {Lag}({{\mathbb C}}^{4})$
From now on, we focus on dimension
![]() $4$
. So, let
$4$
. So, let
![]() $V_{\mathbb {K}} = \mathbb {K}^{(3)}[X, Y] \cong \mathbb {K}^4$
be the symplectic space of homogeneous polynomials of degree
$V_{\mathbb {K}} = \mathbb {K}^{(3)}[X, Y] \cong \mathbb {K}^4$
be the symplectic space of homogeneous polynomials of degree
![]() $3$
in X and Y, equipped with the symplectic form
$3$
in X and Y, equipped with the symplectic form
![]() $\omega _{\mathbb {K}} = \omega _{2, \mathbb {K}}$
defined above. We define the Veronese embeddings
$\omega _{\mathbb {K}} = \omega _{2, \mathbb {K}}$
defined above. We define the Veronese embeddings
by
 $$ \begin{align*} \begin{aligned} \xi^1_{{\mathbb C}}([a:b]) &:= \langle (bX-aY)^3 \rangle\in {{\mathbb C}}\mathbb{P}^3\\ \xi^2_{{\mathbb C}}([a:b]) &:= \langle (bX-aY)^3, (dX-cY)(bX-aY)^2\rangle \in \mathrm{Lag}({{\mathbb C}}^4), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \xi^1_{{\mathbb C}}([a:b]) &:= \langle (bX-aY)^3 \rangle\in {{\mathbb C}}\mathbb{P}^3\\ \xi^2_{{\mathbb C}}([a:b]) &:= \langle (bX-aY)^3, (dX-cY)(bX-aY)^2\rangle \in \mathrm{Lag}({{\mathbb C}}^4), \end{aligned} \end{align*} $$
where
![]() $[c:d]$
is any point chosen in
$[c:d]$
is any point chosen in
![]() ${{\mathbb C}}\mathbb {P}^1 \setminus \{[a:b]\}$
. The Lagrangian
${{\mathbb C}}\mathbb {P}^1 \setminus \{[a:b]\}$
. The Lagrangian
![]() $\xi ^2_{{\mathbb C}}([a:b])$
does not depend on the choice of
$\xi ^2_{{\mathbb C}}([a:b])$
does not depend on the choice of
![]() $[c:d]$
. Let
$[c:d]$
. Let
Similar to Section 2.5, for a line
![]() $\ell \in \mathbb {CP}^{3}$
, we define
$\ell \in \mathbb {CP}^{3}$
, we define
We now introduce the set
More explicitly, we can write
that is,
![]() $K_{{{\mathbb C}}}$
is the set of Lagrangian subspaces that contain a polynomial with a triple complex root.
$K_{{{\mathbb C}}}$
is the set of Lagrangian subspaces that contain a polynomial with a triple complex root.
Lemma 4.1.
![]() $K_{{{\mathbb C}}}$
is the set of Lagrangians
$K_{{{\mathbb C}}}$
is the set of Lagrangians
![]() $W \in \mathrm {Lag}({{\mathbb C}}^{4})$
with a common root; that is,
$W \in \mathrm {Lag}({{\mathbb C}}^{4})$
with a common root; that is,
Proof. Let
![]() $W \in K_{{{\mathbb C}}}$
. We know that it contains an element with a triple root. By acting with
$W \in K_{{{\mathbb C}}}$
. We know that it contains an element with a triple root. By acting with
![]() $\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the triple root is zero – in other words, that
$\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the triple root is zero – in other words, that
![]() $X^3 \in W$
. Let
$X^3 \in W$
. Let
![]() $p\in W$
. We can write
$p\in W$
. We can write
![]() $p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. Since W is isotropic, we know that
$p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. Since W is isotropic, we know that
![]() $\omega _{2,{{\mathbb C}}}(X^3,p) = 0$
, and hence, by (2), we see that
$\omega _{2,{{\mathbb C}}}(X^3,p) = 0$
, and hence, by (2), we see that
![]() $d=0$
. Hence, zero is a common root of every element of W.
$d=0$
. Hence, zero is a common root of every element of W.
Conversely, assume that all elements of W have a common root. By acting with
![]() $\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the common root is zero, and hence, all elements of W are of the form
$\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the common root is zero, and hence, all elements of W are of the form
![]() $p = a X^3 + bX^2Y + c XY^2$
. By (2),
$p = a X^3 + bX^2Y + c XY^2$
. By (2),
Hence, all polynomials in W have the same ratio
![]() $\frac {b}{c}$
(which can be infinite if
$\frac {b}{c}$
(which can be infinite if
![]() $c=0$
). Given a basis
$c=0$
). Given a basis
![]() $p_1, p_2$
of W, we can multiply one of them by a scalar to make sure they have the same coefficients
$p_1, p_2$
of W, we can multiply one of them by a scalar to make sure they have the same coefficients
![]() $b,c$
. Then
$b,c$
. Then
![]() $p_1 - p_2$
is a multiple of
$p_1 - p_2$
is a multiple of
![]() $X^3$
, and hence, W has an element with a triple root.
$X^3$
, and hence, W has an element with a triple root.
We can now prove the following:
Proposition 4.2.
![]() $K_{{{\mathbb C}}}$
is in bijection with
$K_{{{\mathbb C}}}$
is in bijection with
![]() ${{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1$
.
${{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1$
.
Proof. We construct an explicit bijection
defined by
 $$\begin{align*}g(([a:b], [c:d])) = \left\{ \begin{array}{ll} \xi^2_{{\mathbb C}}([a:b]) & \mbox{if } [a:b] = [c:d]\\ \langle (bX-aY)^3, (dX-cY)^2 (bX-aY) \rangle & \mbox{if } [a:b] \neq [c:d] \end{array} \right.\end{align*}$$
$$\begin{align*}g(([a:b], [c:d])) = \left\{ \begin{array}{ll} \xi^2_{{\mathbb C}}([a:b]) & \mbox{if } [a:b] = [c:d]\\ \langle (bX-aY)^3, (dX-cY)^2 (bX-aY) \rangle & \mbox{if } [a:b] \neq [c:d] \end{array} \right.\end{align*}$$
Easy calculations show that the map g is well-defined and bijective.
Remark 4.3 (The space
 $K_{{\mathbb R}}$
).
$K_{{\mathbb R}}$
).
The space
is precisely the space
![]() $K_{\rho ,I}$
in Section 2.5; hence,
$K_{\rho ,I}$
in Section 2.5; hence,
![]() $\Omega = {\mathrm {Lag}}({{\mathbb C}}^{4}) \setminus K_{\mathbb R}$
. Note that
$\Omega = {\mathrm {Lag}}({{\mathbb C}}^{4}) \setminus K_{\mathbb R}$
. Note that
corresponds to the set of Lagrangian subspaces with a triple real root
![]() $[a:b] \in {\mathbb R}\mathbb {P}^1$
. We thus see that
$[a:b] \in {\mathbb R}\mathbb {P}^1$
. We thus see that
or, more precisely,
![]() $K_{{\mathbb R}} = g({\mathbb R}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^2))$
.
$K_{{\mathbb R}} = g({\mathbb R}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^2))$
.
Remark 4.4 (Generalisation to
 $\mathrm {Lag}({{\mathbb C}}^{2n})$
).
$\mathrm {Lag}({{\mathbb C}}^{2n})$
).
The second factor
![]() ${{\mathbb C}}\mathbb {P}^1$
in the maps above should be interpreted as
${{\mathbb C}}\mathbb {P}^1$
in the maps above should be interpreted as
![]() $\mathrm {Lag}({{\mathbb C}}^2)$
. In fact, in more generality, we can prove that, for any dimension,
$\mathrm {Lag}({{\mathbb C}}^2)$
. In fact, in more generality, we can prove that, for any dimension,
![]() $K_{{{\mathbb C}}} \cong {{\mathbb C}}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^{2(n-1)})$
and
$K_{{{\mathbb C}}} \cong {{\mathbb C}}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^{2(n-1)})$
and
![]() $K_{{\mathbb R}} \cong {\mathbb R}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^{2(n-1)}).$
$K_{{\mathbb R}} \cong {\mathbb R}\mathbb {P}^1 \times \mathrm {Lag}({{\mathbb C}}^{2(n-1)}).$
Lemma 4.5. Every Lagrangian W contains a polynomial
with a double root
![]() $[a:b] \in {{\mathbb C}}\mathbb {P}^1$
and a single root
$[a:b] \in {{\mathbb C}}\mathbb {P}^1$
and a single root
![]() $[c:d]\neq [a:b]\in {{\mathbb C}}\mathbb {P}^1$
.
$[c:d]\neq [a:b]\in {{\mathbb C}}\mathbb {P}^1$
.
Proof. If W has a polynomial with a triple root, then
![]() $W\in K_{{\mathbb C}}$
, and we saw above that these Lagrangians also contain a polynomial with a double root and a single root. If W does not contain a polynomial with a triple root but has a polynomial with a double root, the third root must be distinct, and hence, we are done.
$W\in K_{{\mathbb C}}$
, and we saw above that these Lagrangians also contain a polynomial with a double root and a single root. If W does not contain a polynomial with a triple root but has a polynomial with a double root, the third root must be distinct, and hence, we are done.
Assume now that W has a polynomial with three distinct roots. Acting with
![]() $\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the three roots are
$\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the three roots are
![]() $[-1:1], [0:1], [1:0]$
, and hence that
$[-1:1], [0:1], [1:0]$
, and hence that
![]() $XY(X+Y)=X^2Y + XY^2 \in W$
. Let
$XY(X+Y)=X^2Y + XY^2 \in W$
. Let
![]() $p\in W$
,
$p\in W$
,
![]() $p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. By (2), we have
$p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. By (2), we have
which implies that
![]() $b=c$
. Hence,
$b=c$
. Hence,
![]() $W = \left <XY(X+Y), a X^3 + d Y^3\right>$
, and W is determined by
$W = \left <XY(X+Y), a X^3 + d Y^3\right>$
, and W is determined by
![]() $[a:d]$
. The other elements of W are scalar multiples of the ones of the form
$[a:d]$
. The other elements of W are scalar multiples of the ones of the form
We want to find elements with a double root. We can find them using the discriminant. The discriminant
![]() $\Delta $
of a degree–
$\Delta $
of a degree–
![]() $3$
polynomial
$3$
polynomial
![]() $\alpha x^3+\beta x^2y +\gamma xy^2 +\delta y^3$
is defined by
$\alpha x^3+\beta x^2y +\gamma xy^2 +\delta y^3$
is defined by
and polynomials with a double root correspond to the zeros of the discriminant. In our case, we have
A non-constant polynomial has always at least one solution over the complex numbers; hence, for every value of a and d, we can find a
![]() $\beta $
such that q has a double root.
$\beta $
such that q has a double root.
The next statement summarizes the results of this subsection, describing the three orbits of the
![]() $\mathrm {SL}(2, {{\mathbb C}})$
–action.
$\mathrm {SL}(2, {{\mathbb C}})$
–action.
Theorem 4.6. There are three
![]() $\mathrm {SL}(2, {{\mathbb C}})$
–orbits in
$\mathrm {SL}(2, {{\mathbb C}})$
–orbits in
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
:
$\mathrm {Lag}({{\mathbb C}}^{4})$
:
-
•
 $\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X^2 Y \rangle $
is the only closed orbit, and it is in bijection with the diagonal
$\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X^2 Y \rangle $
is the only closed orbit, and it is in bijection with the diagonal
 $\Delta \subset K_{{\mathbb C}} \cong {{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1$
.
$\Delta \subset K_{{\mathbb C}} \cong {{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1$
. -
•
 $K_{{{\mathbb C}}} \setminus \xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X Y^2 \rangle $
is not open nor closed, and it is in bijection with
$K_{{{\mathbb C}}} \setminus \xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X Y^2 \rangle $
is not open nor closed, and it is in bijection with
 ${{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
.
${{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
. -
•
 $\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}} = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^2Y, X^3 + Y^3\rangle $
is the only open orbit.
$\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}} = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^2Y, X^3 + Y^3\rangle $
is the only open orbit.
Proof. We have already discussed above the bijection
![]() $g\colon \thinspace {{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1 \stackrel {\cong }{\longrightarrow } K_{{{\mathbb C}}}$
. From the discussion above, you can see that
$g\colon \thinspace {{\mathbb C}}\mathbb {P}^1 \times {{\mathbb C}}\mathbb {P}^1 \stackrel {\cong }{\longrightarrow } K_{{{\mathbb C}}}$
. From the discussion above, you can see that
-
•
 $\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X^2 Y \rangle $
corresponds to Lagrangians all of whose polynomials share a common double root;
$\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X^2 Y \rangle $
corresponds to Lagrangians all of whose polynomials share a common double root; -
•
 $K_{{{\mathbb C}}} \setminus \xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X Y^2 \rangle $
corresponds to Lagrangians all of whose polynomials share a common single root.
$K_{{{\mathbb C}}} \setminus \xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^3, X Y^2 \rangle $
corresponds to Lagrangians all of whose polynomials share a common single root.
Since
![]() $\xi ^2_{{\mathbb C}}$
is an embedding,
$\xi ^2_{{\mathbb C}}$
is an embedding,
![]() $\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) \cong {{\mathbb C}}\mathbb {P}^1$
is closed.
$\xi ^2_{{\mathbb C}}({{\mathbb C}}\mathbb {P}^1) \cong {{\mathbb C}}\mathbb {P}^1$
is closed.
To complete the proof, we need to show that
![]() $\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}}$
is one
$\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}}$
is one
![]() $\mathrm {SL}(2, {{\mathbb C}})$
orbit. Given
$\mathrm {SL}(2, {{\mathbb C}})$
orbit. Given
![]() $W \not \in K_{{{\mathbb C}}}$
, by Lemma 4.5, W contains a polynomial with a double root and a single root. Acting with a matrix in
$W \not \in K_{{{\mathbb C}}}$
, by Lemma 4.5, W contains a polynomial with a double root and a single root. Acting with a matrix in
![]() $\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the roots are
$\mathrm {SL}(2,{{\mathbb C}})$
, we can assume that the roots are
![]() $[0:1]$
and
$[0:1]$
and
![]() $[1:0]$
(i.e., that
$[1:0]$
(i.e., that
![]() $X^2 Y \in W$
). Let
$X^2 Y \in W$
). Let
![]() $p\in W$
,
$p\in W$
,
![]() $p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. By (2), we have
$p = a X^3 + bX^2Y + c XY^2 + d Y^3$
. By (2), we have
which implies that
![]() $c=0$
. Hence,
$c=0$
. Hence,
![]() $W = \left <X^2Y, a X^3 + d Y^3\right>$
. Now we act again with a matrix
$W = \left <X^2Y, a X^3 + d Y^3\right>$
. Now we act again with a matrix
![]() $A \in \mathrm {SL}(2,{{\mathbb C}})$
. We choose
$A \in \mathrm {SL}(2,{{\mathbb C}})$
. We choose
![]() $\alpha = \sqrt [6]{\tfrac {d}{a}}$
, one of the 6 complex roots, and we consider the matrix
$\alpha = \sqrt [6]{\tfrac {d}{a}}$
, one of the 6 complex roots, and we consider the matrix
 $$\begin{align*}A = \begin{pmatrix} \alpha & 0 \\ 0 & \alpha^{-1} \end{pmatrix} \end{align*}$$
$$\begin{align*}A = \begin{pmatrix} \alpha & 0 \\ 0 & \alpha^{-1} \end{pmatrix} \end{align*}$$
When acting on
![]() ${{\mathbb C}}\mathbb {P}^1$
, A fixes
${{\mathbb C}}\mathbb {P}^1$
, A fixes
![]() $[0:1]$
and
$[0:1]$
and
![]() $[1:0]$
and hence sends
$[1:0]$
and hence sends
![]() $X^2 Y$
to one of its multiples. Moreover, A sends
$X^2 Y$
to one of its multiples. Moreover, A sends
![]() $a X^3 + d Y^3$
to a multiple of
$a X^3 + d Y^3$
to a multiple of
![]() $X^3 + Y^3$
. Hence,
$X^3 + Y^3$
. Hence,
![]() $A \cdot W = \left <X^2Y, X^3 + Y^3\right>$
, and this proves that
$A \cdot W = \left <X^2Y, X^3 + Y^3\right>$
, and this proves that
4.3 The space of regular ideal tetrahedra
Recall that an ideal hyperbolic tetrahedron in
![]() $\mathbb {H}^3$
is called regular when all the dihedral angles are equal to each other (and equal to
$\mathbb {H}^3$
is called regular when all the dihedral angles are equal to each other (and equal to
![]() $\frac {\pi }{3}$
). These tetrahedra can also be characterized by their volume or their cross-ratio, since a tetrahedron is regular if and only if it has maximal volume, if and only if the cross-ratio of its vertices is
$\frac {\pi }{3}$
). These tetrahedra can also be characterized by their volume or their cross-ratio, since a tetrahedron is regular if and only if it has maximal volume, if and only if the cross-ratio of its vertices is
![]() $\frac {1-\sqrt {3}i}{2}.$
Recall that given
$\frac {1-\sqrt {3}i}{2}.$
Recall that given
![]() $4$
points
$4$
points
![]() $z_1, z_2, z_3, z_4$
in
$z_1, z_2, z_3, z_4$
in
![]() ${{\mathbb C}}\mathbb {P}^1$
, here seen as the boundary at infinity of
${{\mathbb C}}\mathbb {P}^1$
, here seen as the boundary at infinity of
![]() $\mathbb {H}^3$
, we define their cross-ratio as
$\mathbb {H}^3$
, we define their cross-ratio as
Equivalently,
![]() $[z_1, z_2, z_3, z_4] = A z_4$
, where
$[z_1, z_2, z_3, z_4] = A z_4$
, where
![]() $A \in \mathrm {PSL}(2,{{\mathbb C}})$
is defined by
$A \in \mathrm {PSL}(2,{{\mathbb C}})$
is defined by
![]() $A z_1 = \infty , Az_2 = 0$
, and
$A z_1 = \infty , Az_2 = 0$
, and
![]() $A z_3 = 1$
. When computing the cross-ratio of the vertices of a tetrahedron, we use the orientation of
$A z_3 = 1$
. When computing the cross-ratio of the vertices of a tetrahedron, we use the orientation of
![]() $\mathbb {H}^3$
, and we choose the order of the vertices in a way that is compatible with the orientation. More precisely, if
$\mathbb {H}^3$
, and we choose the order of the vertices in a way that is compatible with the orientation. More precisely, if
![]() $z_1$
is a vertex, the other three vertices lie on the boundary of a copy of the hyperbolic plane. When watched from
$z_1$
is a vertex, the other three vertices lie on the boundary of a copy of the hyperbolic plane. When watched from
![]() $z_1$
, we require that the vertices
$z_1$
, we require that the vertices
![]() $z_2, z_3, z_4$
rotate in the clockwise direction. Note that if you change the order of the points, in a way that is still compatible with the orientation of
$z_2, z_3, z_4$
rotate in the clockwise direction. Note that if you change the order of the points, in a way that is still compatible with the orientation of
![]() $\mathbb {H}^3$
as explained, then the cross-ratio z can become
$\mathbb {H}^3$
as explained, then the cross-ratio z can become
![]() $1-\frac {1}{z}$
or
$1-\frac {1}{z}$
or
![]() $\frac {1}{1-z}$
. However, if
$\frac {1}{1-z}$
. However, if
![]() $z_0 = \frac {1-\sqrt {3}i}{2}$
, then
$z_0 = \frac {1-\sqrt {3}i}{2}$
, then
![]() $z_0 = 1-\frac {1}{z_0} = \frac {1}{1-z_0}$
, so the characterization of regular tetrahedra in terms of cross-ratio does not depend on the chosen order of the vertices when calculating the cross-ratio, as it should be. We will discuss more properties of regular ideal hyperbolic tetrahedra in Section 5.1.
$z_0 = 1-\frac {1}{z_0} = \frac {1}{1-z_0}$
, so the characterization of regular tetrahedra in terms of cross-ratio does not depend on the chosen order of the vertices when calculating the cross-ratio, as it should be. We will discuss more properties of regular ideal hyperbolic tetrahedra in Section 5.1.
We will denote by
![]() $\mathfrak {T}_{{\mathbb H}^3}$
the space of regular ideal hyperbolic tetrahedra in
$\mathfrak {T}_{{\mathbb H}^3}$
the space of regular ideal hyperbolic tetrahedra in
![]() $\mathbb {H}^3$
. In order to define a topology on
$\mathbb {H}^3$
. In order to define a topology on
![]() $\mathfrak {T}_{{\mathbb H}^3}$
, we embed it in the symmetric product
$\mathfrak {T}_{{\mathbb H}^3}$
, we embed it in the symmetric product
The group
![]() $\mathrm {SL}(2,{{\mathbb C}})$
acts transitively on
$\mathrm {SL}(2,{{\mathbb C}})$
acts transitively on
![]() $\mathfrak {T}_{{\mathbb H}^3}$
via hyperbolic isometries. Moreover, the action of
$\mathfrak {T}_{{\mathbb H}^3}$
via hyperbolic isometries. Moreover, the action of
![]() $\mathrm {SL}(2,{{\mathbb C}})$
on
$\mathrm {SL}(2,{{\mathbb C}})$
on
![]() ${{\mathbb C}}\mathbb {P}^1$
gives a way to extend this action to the whole symmetric product.
${{\mathbb C}}\mathbb {P}^1$
gives a way to extend this action to the whole symmetric product.
The homogeneous space
![]() $\mathfrak {T}_{{\mathbb H}^3}$
is open but not closed in the symmetric product. We will now describe its closure; this gives an
$\mathfrak {T}_{{\mathbb H}^3}$
is open but not closed in the symmetric product. We will now describe its closure; this gives an
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–invariant compactification of
$\mathrm {SL}(2,{{\mathbb C}})$
–invariant compactification of
![]() $\mathfrak {T}_{{\mathbb H}^3}$
.
$\mathfrak {T}_{{\mathbb H}^3}$
.
Proposition 4.7. The topological frontier of
![]() $\mathfrak {T}_{{\mathbb H}^3}$
in
$\mathfrak {T}_{{\mathbb H}^3}$
in
![]() $\mathrm {Sym}^4\left ({{\mathbb C}}\mathbb {P}^1\right )$
consists of all the points in the symmetric product where one element has multiplicity at least 3. Hence, the frontier is homeomorphic to
$\mathrm {Sym}^4\left ({{\mathbb C}}\mathbb {P}^1\right )$
consists of all the points in the symmetric product where one element has multiplicity at least 3. Hence, the frontier is homeomorphic to
![]() ${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, where the first coordinate contains the element with high multiplicity.
${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, where the first coordinate contains the element with high multiplicity.
Proof. Given a regular ideal tetrahedron T, denote by
![]() $b\in {\mathbb H}^3$
its barycenter. The 4 lines from b to the 4 vertices meet at b, each pair of lines with the same angle, that we will denote here by
$b\in {\mathbb H}^3$
its barycenter. The 4 lines from b to the 4 vertices meet at b, each pair of lines with the same angle, that we will denote here by
![]() $\alpha $
. Note that
$\alpha $
. Note that
![]() $\tfrac {\pi }{2} < \alpha < \pi $
. Denote by
$\tfrac {\pi }{2} < \alpha < \pi $
. Denote by
![]() $\beta = \frac {1}{2}(\pi -\alpha )$
, where
$\beta = \frac {1}{2}(\pi -\alpha )$
, where
![]() $0 < \beta < \tfrac {\pi }{4}$
.
$0 < \beta < \tfrac {\pi }{4}$
.
We construct the distance d as in Figure 1: Given a plane P passing through b, we construct the cone with angle
![]() $\beta $
from P, and we consider the plane
$\beta $
from P, and we consider the plane
![]() $P'$
tangent to the cone at infinity. The distance d is defined as the distance between the two planes P and
$P'$
tangent to the cone at infinity. The distance d is defined as the distance between the two planes P and
![]() $P'$
. The quantities
$P'$
. The quantities
![]() $\alpha , \beta $
and d can be made explicit, but we do not need their explicit values here.
$\alpha , \beta $
and d can be made explicit, but we do not need their explicit values here.

Figure 1 The distance d between the two geodesics.
We claim that given a regular ideal tetrahedron with barycenter contained in the open half-space below P, then at most one of its vertices can be in the closed half-space above
![]() $P'$
, and the other three vertices must lie in the open half-space below
$P'$
, and the other three vertices must lie in the open half-space below
![]() $P'$
. This is because of the way we have chosen the distance d between P and
$P'$
. This is because of the way we have chosen the distance d between P and
![]() $P'$
. Assume that a regular ideal tetrahedron has barycenter at O, in the open half-space below P. Assume by contradiction that at least two of its vertices are in the closed half-space above
$P'$
. Assume that a regular ideal tetrahedron has barycenter at O, in the open half-space below P. Assume by contradiction that at least two of its vertices are in the closed half-space above
![]() $P'$
. Then the line between the two vertices lies entirely in the closed half-space above
$P'$
. Then the line between the two vertices lies entirely in the closed half-space above
![]() $P'$
, but it must be at distance d from O, a contradiction.
$P'$
, but it must be at distance d from O, a contradiction.
Now consider a sequence of regular ideal tetrahedra that converges to a point of the symmetric product that does not represent a regular ideal tetrahedron. The barycenters of the tetrahedra of the sequence are unbounded in
![]() ${\mathbb H}^3$
; otherwise, a subsequence would converge to a regular ideal tetrahedron. Up to subsequences, we can assume that the barycenters of the tetrahedra converge to a point
${\mathbb H}^3$
; otherwise, a subsequence would converge to a regular ideal tetrahedron. Up to subsequences, we can assume that the barycenters of the tetrahedra converge to a point
![]() $x \in \mathbb {CP}^1$
.
$x \in \mathbb {CP}^1$
.
We consider a small ball in
![]() $\mathbb {CP}^1$
containing x. This small ball bounds a plane
$\mathbb {CP}^1$
containing x. This small ball bounds a plane
![]() $P'$
. Let P denote a plane whose boundary lies in the ball and whose distance from
$P'$
. Let P denote a plane whose boundary lies in the ball and whose distance from
![]() $P'$
is at least d. For all the tetrahedra in our subsequence whose barycenter lies in the half-space bounded by P, we know from the considerations above that at least three of their vertices lie in the half-space bounded by
$P'$
is at least d. For all the tetrahedra in our subsequence whose barycenter lies in the half-space bounded by P, we know from the considerations above that at least three of their vertices lie in the half-space bounded by
![]() $P'$
.
$P'$
.
This shows that for our subsequence, at least three of the vertices of the tetrahedra converge to the same point x, while the fourth vertices are free to go anywhere. Again up to subsequences, we can assume that the fourth vertices are also converging to some point in
![]() $\mathbb {CP}^1$
.
$\mathbb {CP}^1$
.
This implies that the limit of our original sequence has an element with multiplicity at least
![]() $3$
.
$3$
.
We will call the points of the frontier degenerate tetrahedra. We will denote the compactified space by
![]() $\mathfrak {T}_{\overline {{\mathbb H}^3}}$
. This space carries a natural
$\mathfrak {T}_{\overline {{\mathbb H}^3}}$
. This space carries a natural
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–action and can be described as
$\mathrm {SL}(2,{{\mathbb C}})$
–action and can be described as
We can now state the main result for this section, which identifies the
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–action on
$\mathrm {SL}(2,{{\mathbb C}})$
–action on
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
with the one on
$\mathrm {Lag}({{\mathbb C}}^{4})$
with the one on
![]() $\mathfrak {T}_{\overline {{\mathbb H}^3}}$
. This will be a key step in the proof of Theorem D.
$\mathfrak {T}_{\overline {{\mathbb H}^3}}$
. This will be a key step in the proof of Theorem D.
In order to do this, we will use Theorem 4.6, but we still need to identify the unique open
![]() $\mathrm {SL}(2, {{\mathbb C}})$
–orbit in
$\mathrm {SL}(2, {{\mathbb C}})$
–orbit in
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
with the space
$\mathrm {Lag}({{\mathbb C}}^{4})$
with the space
![]() $\mathfrak {T}_{{\mathbb H}^3}$
, and verify the the map between the two spaces is continuous.
$\mathfrak {T}_{{\mathbb H}^3}$
, and verify the the map between the two spaces is continuous.
Theorem 4.8. The space
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
is
$\mathrm {Lag}({{\mathbb C}}^{4})$
is
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–equivariantly homeomorphic to the space
$\mathrm {SL}(2,{{\mathbb C}})$
–equivariantly homeomorphic to the space
Proof. We will construct an equivariant homeomorphism between the two spaces. Since both spaces are compact Hausdorff, it will be enough to check that the equivariant map is a continuous bijection. As a first step, we will show that
![]() $\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}} = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^2Y, X^3 + Y^3\rangle $
is in bijection with the space
$\mathrm {Lag}({{\mathbb C}}^{4}) \setminus K_{{{\mathbb C}}} = \mathrm {SL}(2, {{\mathbb C}}) \cdot \langle X^2Y, X^3 + Y^3\rangle $
is in bijection with the space
![]() $\mathfrak {T}_{{\mathbb H}^3}$
of regular ideal hyperbolic tetrahedra in
$\mathfrak {T}_{{\mathbb H}^3}$
of regular ideal hyperbolic tetrahedra in
![]() $\mathbb {H}^3$
.
$\mathbb {H}^3$
.
Consider the Lagrangian subspace
![]() $W=\langle X^2Y, X^3 + Y^3\rangle $
. We will see that it contains exactly
$W=\langle X^2Y, X^3 + Y^3\rangle $
. We will see that it contains exactly
![]() $4$
‘special’ polynomials which have a double root. To find them, we use the discriminant as in the proof of Lemma 4.5. The elements of W are of the form
$4$
‘special’ polynomials which have a double root. To find them, we use the discriminant as in the proof of Lemma 4.5. The elements of W are of the form
hence, the discriminant is
We have that
![]() $\Delta (q)= 0$
if and only if
$\Delta (q)= 0$
if and only if
-
1.
 $[\alpha :\beta ]=[0:1]$
;
$[\alpha :\beta ]=[0:1]$
; -
2.
 $[\alpha :\beta ] = \left [-\frac {\sqrt [3]{4}}{3}:1\right ]$
;
$[\alpha :\beta ] = \left [-\frac {\sqrt [3]{4}}{3}:1\right ]$
; -
3.
 $[\alpha :\beta ] = \left [\frac {1}{3\sqrt [3]{2}}- i \frac {1}{\sqrt [3]{2}\sqrt {3}}:1\right ]$
;
$[\alpha :\beta ] = \left [\frac {1}{3\sqrt [3]{2}}- i \frac {1}{\sqrt [3]{2}\sqrt {3}}:1\right ]$
; -
4.
 $[\alpha :\beta ] = \left [\frac {1}{3\sqrt [3]{2}}+ i \frac {1}{\sqrt [3]{2}\sqrt {3}}:1\right ]$
.
$[\alpha :\beta ] = \left [\frac {1}{3\sqrt [3]{2}}+ i \frac {1}{\sqrt [3]{2}\sqrt {3}}:1\right ]$
.
The associated polynomials have double and single roots, respectively, given by
-
1.
 $0$
and
$0$
and
 $\infty $
;
$\infty $
; -
2.
 $\sqrt [3]{2}$
and
$\sqrt [3]{2}$
and
 $-\frac {1}{\sqrt [3]{4}}$
;
$-\frac {1}{\sqrt [3]{4}}$
; -
3.
 $\frac {-1-i\sqrt {3}}{\sqrt [3]{4}}$
and
$\frac {-1-i\sqrt {3}}{\sqrt [3]{4}}$
and
 $\frac {1+i\sqrt {3}}{2\sqrt [3]{4}}$
;
$\frac {1+i\sqrt {3}}{2\sqrt [3]{4}}$
; -
4.
 $\frac {-1+i\sqrt {3}}{\sqrt [3]{4}}$
and
$\frac {-1+i\sqrt {3}}{\sqrt [3]{4}}$
and
 $\frac {1-i\sqrt {3}}{2\sqrt [3]{4}}$
.
$\frac {1-i\sqrt {3}}{2\sqrt [3]{4}}$
.
The vertices corresponding to the
![]() $4$
double roots define an ideal hyperbolic tetrahedron
$4$
double roots define an ideal hyperbolic tetrahedron
![]() $T = \left \{ 0,\sqrt [3]{2},\frac {-1-i\sqrt {3}}{\sqrt [3]{4}}, \frac {-1+i\sqrt {3}}{\sqrt [3]{4}}\right \}$
, and the vertices corresponding to the
$T = \left \{ 0,\sqrt [3]{2},\frac {-1-i\sqrt {3}}{\sqrt [3]{4}}, \frac {-1+i\sqrt {3}}{\sqrt [3]{4}}\right \}$
, and the vertices corresponding to the
![]() $4$
single roots define a ‘dual’ ideal hyperbolic tetrahedron
$4$
single roots define a ‘dual’ ideal hyperbolic tetrahedron
![]() $T_{dual} = \left \{\infty ,-\frac {1}{\sqrt [3]{4}}, \frac {1+i\sqrt {3}}{2\sqrt [3]{4}}, \frac {1-i\sqrt {3}}{2\sqrt [3]{4}} \right \}$
. The tetrahedron
$T_{dual} = \left \{\infty ,-\frac {1}{\sqrt [3]{4}}, \frac {1+i\sqrt {3}}{2\sqrt [3]{4}}, \frac {1-i\sqrt {3}}{2\sqrt [3]{4}} \right \}$
. The tetrahedron
![]() $T_{dual}$
is the image of T by the central symmetry centered at the barycenter of T. A simple calculation shows that the cross-ratio of the vertices of T and
$T_{dual}$
is the image of T by the central symmetry centered at the barycenter of T. A simple calculation shows that the cross-ratio of the vertices of T and
![]() $T_{dual}$
are equal to
$T_{dual}$
are equal to
![]() $\frac {1-\sqrt {3}i}{2}$
:
$\frac {1-\sqrt {3}i}{2}$
:
 $$\begin{align*}\left[ 0, \sqrt[3]{2}, \frac{-1+i\sqrt{3}}{\sqrt[3]{4}}, \frac{-1-i\sqrt{3}}{\sqrt[3]{4}} \right] = \left[\infty, -\frac{1}{\sqrt[3]{4}}, \frac{1+i\sqrt{3}}{2\sqrt[3]{4}}, \frac{1-i\sqrt{3}}{2\sqrt[3]{4}} \right] = \frac{1-\sqrt{3}i}{2}.\end{align*}$$
$$\begin{align*}\left[ 0, \sqrt[3]{2}, \frac{-1+i\sqrt{3}}{\sqrt[3]{4}}, \frac{-1-i\sqrt{3}}{\sqrt[3]{4}} \right] = \left[\infty, -\frac{1}{\sqrt[3]{4}}, \frac{1+i\sqrt{3}}{2\sqrt[3]{4}}, \frac{1-i\sqrt{3}}{2\sqrt[3]{4}} \right] = \frac{1-\sqrt{3}i}{2}.\end{align*}$$
Hence, T and
![]() $T_{dual}$
are regular ideal hyperbolic tetrahedra, as we wanted to prove. Notice that in the computation of the cross-ratio for T, we changed the order of the vertices to make sure it is compatible with the orientation of
$T_{dual}$
are regular ideal hyperbolic tetrahedra, as we wanted to prove. Notice that in the computation of the cross-ratio for T, we changed the order of the vertices to make sure it is compatible with the orientation of
![]() $\mathbb {H}^3$
.
$\mathbb {H}^3$
.
Now we want to see that the bijections described above are actually homeomorphisms. Remember also that the topology of
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
can be described by considering
$\mathrm {Lag}({{\mathbb C}}^{4})$
can be described by considering
![]() $\mathrm {Lag}({{\mathbb C}}^{4}) \subset \mathrm {Gr}(2, {{\mathbb C}}^{4})$
and using the Plücker coordinates for the topology of
$\mathrm {Lag}({{\mathbb C}}^{4}) \subset \mathrm {Gr}(2, {{\mathbb C}}^{4})$
and using the Plücker coordinates for the topology of
![]() $ \mathrm {Gr}(2, {{\mathbb C}}^{4})$
.
$ \mathrm {Gr}(2, {{\mathbb C}}^{4})$
.
To prove this result, we will extend the map g, defined above, to a map
and check that the map is a homeomorphism.
Given a tetrahedron
![]() $T = \{v_1, \ldots , v_4\} \in \mathfrak {T}_{{\mathbb H}^3}$
, we define the dual tetrahedron
$T = \{v_1, \ldots , v_4\} \in \mathfrak {T}_{{\mathbb H}^3}$
, we define the dual tetrahedron
![]() $T_{dual} = \{v_1^{dual}, \ldots , v_4^{dual}\}$
as the tetrahedron (also in
$T_{dual} = \{v_1^{dual}, \ldots , v_4^{dual}\}$
as the tetrahedron (also in
![]() $\mathfrak {T}_{{\mathbb H}^3}$
) with vertices
$\mathfrak {T}_{{\mathbb H}^3}$
) with vertices
![]() $v_i^{dual}$
such that
$v_i^{dual}$
such that
![]() $v_i$
, the barycenter b of T and
$v_i$
, the barycenter b of T and
![]() $v_i^{dual}$
lie on the same geodesic for
$v_i^{dual}$
lie on the same geodesic for
![]() $i = 1, \ldots , 4$
. Let
$i = 1, \ldots , 4$
. Let
![]() $v_i$
and
$v_i$
and
![]() $v_j$
be two distinct vertices of T. If we let
$v_j$
be two distinct vertices of T. If we let
![]() $v_i = [a_1: b_1] \in {{\mathbb C}}\mathbb {P}^1$
,
$v_i = [a_1: b_1] \in {{\mathbb C}}\mathbb {P}^1$
,
![]() $v_i^{dual} = [c_1: d_1] \in {{\mathbb C}}\mathbb {P}^1$
,
$v_i^{dual} = [c_1: d_1] \in {{\mathbb C}}\mathbb {P}^1$
,
![]() $v_j = [a_2: b_2] \in {{\mathbb C}}\mathbb {P}^1$
, and
$v_j = [a_2: b_2] \in {{\mathbb C}}\mathbb {P}^1$
, and
![]() $v_j^{dual} = [c_2: d_2] \in {{\mathbb C}}\mathbb {P}^1$
, then the Lagrangian subspace associated to T is
$v_j^{dual} = [c_2: d_2] \in {{\mathbb C}}\mathbb {P}^1$
, then the Lagrangian subspace associated to T is
Its Plücker coordinates are
-
•
 $W_{1,2} = -b_1^2d_1(b_2^2c_2+2a_2b_2d_2) + b_2^2d_2 (b_1^2c_1+2a_1b_1d_1)$
;
$W_{1,2} = -b_1^2d_1(b_2^2c_2+2a_2b_2d_2) + b_2^2d_2 (b_1^2c_1+2a_1b_1d_1)$
; -
•
 $W_{1,3} = b_1^2d_1(a_2^2d_2+2a_2b_2c_2) - b_2^2d_2 (a_1^2d_1+2a_1b_1c_1)$
;
$W_{1,3} = b_1^2d_1(a_2^2d_2+2a_2b_2c_2) - b_2^2d_2 (a_1^2d_1+2a_1b_1c_1)$
; -
•
 $W_{1,4} = -b_1^2d_1a_2^2c_2 + b_2^2d_2a_1^2c_1$
;
$W_{1,4} = -b_1^2d_1a_2^2c_2 + b_2^2d_2a_1^2c_1$
; -
•
 $W_{2,3} = -(b_1^2c_1+2a_1b_1d_1)(a_2^2d_2+2a_2b_2c_2) + (b_2^2c_2+2a_2b_2d_2)(a_1^2d_1+2a_1b_1c_1)$
;
$W_{2,3} = -(b_1^2c_1+2a_1b_1d_1)(a_2^2d_2+2a_2b_2c_2) + (b_2^2c_2+2a_2b_2d_2)(a_1^2d_1+2a_1b_1c_1)$
; -
•
 $W_{2,4} = a_2^2c_2 (b_1^2c_1+2a_1b_1d_1) - a_1^2c_1 (b_2^2c_2+2a_2b_2d_2)$
;
$W_{2,4} = a_2^2c_2 (b_1^2c_1+2a_1b_1d_1) - a_1^2c_1 (b_2^2c_2+2a_2b_2d_2)$
; -
•
 $W_{3,4} = -a_2^2c_2 (a_1^2d_1+2a_1b_1c_1) + a_1^2c_1(a_2^2d_2+2a_2b_2c_2)$
.
$W_{3,4} = -a_2^2c_2 (a_1^2d_1+2a_1b_1c_1) + a_1^2c_1(a_2^2d_2+2a_2b_2c_2)$
.
Similarly, given a point
![]() $([a:b], [c:d]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
, where
$([a:b], [c:d]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
, where
![]() $\Delta = \{([a:b], [a:b]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1\}$
is the diagonal, then the associated Lagrangian subspace is
$\Delta = \{([a:b], [a:b]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1\}$
is the diagonal, then the associated Lagrangian subspace is
which has Plücker coordinates
-
•
 $U_{1,2} = 2b^3 d (bc-ad)$
;
$U_{1,2} = 2b^3 d (bc-ad)$
; -
•
 $U_{1,3} = b^2(3ad+bc)(bc-ad)$
;
$U_{1,3} = b^2(3ad+bc)(bc-ad)$
; -
•
 $U_{1,4} = -ba(bc+ad)(bc-ad)$
;
$U_{1,4} = -ba(bc+ad)(bc-ad)$
; -
•
 $U_{2,3} = -3ba(bc+ad)(bc-ad)$
;
$U_{2,3} = -3ba(bc+ad)(bc-ad)$
; -
•
 $U_{2,4} = a^2 (ad+3bc)(bc-ad)$
;
$U_{2,4} = a^2 (ad+3bc)(bc-ad)$
; -
•
 $U_{3,4} = -2a^3c (bc-ad)$
.
$U_{3,4} = -2a^3c (bc-ad)$
.
Lastly, given a point
![]() $([a:b], [a:b]) \in \Delta \subset {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, the associated Lagrangian subspace is
$([a:b], [a:b]) \in \Delta \subset {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, the associated Lagrangian subspace is
for
![]() $[c:d]\neq [a:b]\in {{\mathbb C}}\mathbb {P}^1$
, and Z has Plücker coordinates
$[c:d]\neq [a:b]\in {{\mathbb C}}\mathbb {P}^1$
, and Z has Plücker coordinates
-
•
 $Z_{1,2} = - 2b^4 (bc-ad)$
;
$Z_{1,2} = - 2b^4 (bc-ad)$
; -
•
 $Z_{1,3} = 2ab^3(bc-ad)$
;
$Z_{1,3} = 2ab^3(bc-ad)$
; -
•
 $Z_{1,4} = -a^2b^2(bc-ad)$
;
$Z_{1,4} = -a^2b^2(bc-ad)$
; -
•
 $Z_{2,3} = -3a^2b^2(bc-ad)$
;
$Z_{2,3} = -3a^2b^2(bc-ad)$
; -
•
 $Z_{2,4} = 2a^3b (bc-ad)$
;
$Z_{2,4} = 2a^3b (bc-ad)$
; -
•
 $Z_{3,4} = -a^4 (bc-ad)$
.
$Z_{3,4} = -a^4 (bc-ad)$
.
We saw in Proposition 4.7 that when a sequence of tetrahedra in
![]() $\mathfrak {T}_{{\mathbb H}^3}$
degenerates, their barycenters converge to a point in
$\mathfrak {T}_{{\mathbb H}^3}$
degenerates, their barycenters converge to a point in
![]() ${{\mathbb C}}\mathbb {P}^1$
. In that case, at least three vertices will converge to the same point in
${{\mathbb C}}\mathbb {P}^1$
. In that case, at least three vertices will converge to the same point in
![]() ${{\mathbb C}}\mathbb {P}^1$
, so tetrahedra can only degenerate to points in
${{\mathbb C}}\mathbb {P}^1$
, so tetrahedra can only degenerate to points in
![]() ${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, that is
${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, that is
![]() ${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 = \partial \mathfrak {T}_{{\mathbb H}^3}$
.
${{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 = \partial \mathfrak {T}_{{\mathbb H}^3}$
.
We can now see that
![]() $g|_{{{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1}$
and
$g|_{{{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1}$
and
![]() $g|_{\mathfrak {T}_{{\mathbb H}^3}}$
are continuous. For the first case, we only have to consider the expression of the Plücker coordinates and look at the case
$g|_{\mathfrak {T}_{{\mathbb H}^3}}$
are continuous. For the first case, we only have to consider the expression of the Plücker coordinates and look at the case
![]() $([a_n:b_n], [c_n:d_n]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
such that
$([a_n:b_n], [c_n:d_n]) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
such that
![]() $([a_n:b_n], [c_n:d_n]) \to ([a:b], [a:b]) \in \Delta $
. In particular, we can do the calculations in the case that
$([a_n:b_n], [c_n:d_n]) \to ([a:b], [a:b]) \in \Delta $
. In particular, we can do the calculations in the case that
![]() $[a:b]= [0:1]\in {{\mathbb C}}\mathbb {P}^1$
. If we denote
$[a:b]= [0:1]\in {{\mathbb C}}\mathbb {P}^1$
. If we denote
![]() $U_{i, j}^n$
the Plücker coordinates associated to
$U_{i, j}^n$
the Plücker coordinates associated to
![]() $F\left (([a_n:b_n], [c_n:d_n])\right )$
, we can see that the only nonzero coordinate in the limit is
$F\left (([a_n:b_n], [c_n:d_n])\right )$
, we can see that the only nonzero coordinate in the limit is
![]() $U_{1,2}^n$
, as we wanted. For the second case
$U_{1,2}^n$
, as we wanted. For the second case
![]() $g|_{\mathfrak {T}_{{\mathbb H}^3}}$
, again, we only have to consider the expression of the Plücker coordinates in term of the vertices of the tetrahedra. Hence, we are left with the discussion of converging sequences
$g|_{\mathfrak {T}_{{\mathbb H}^3}}$
, again, we only have to consider the expression of the Plücker coordinates in term of the vertices of the tetrahedra. Hence, we are left with the discussion of converging sequences
![]() $\{T_n\}$
of tetrahedra in
$\{T_n\}$
of tetrahedra in
![]() $\mathfrak {T}_{{\mathbb H}^3}$
such that
$\mathfrak {T}_{{\mathbb H}^3}$
such that
![]() $T_n \to T_\infty \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
. We have two possibilities:
$T_n \to T_\infty \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
. We have two possibilities:
-
•
 $T_\infty = ([a:b], [c:d])\in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
.
$T_\infty = ([a:b], [c:d])\in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1 \setminus \Delta $
. -
•
 $T_\infty = ([a:b], [a:b])\in \Delta $
.
$T_\infty = ([a:b], [a:b])\in \Delta $
.
In the first case, three vertices of the tetrahedron
![]() $\{T_n\}$
and all the dual vertices of the tetrahedron
$\{T_n\}$
and all the dual vertices of the tetrahedron
![]() $\{T_n^{dual}\}$
converge to
$\{T_n^{dual}\}$
converge to
![]() $[a:b] \in {{\mathbb C}}\mathbb {P}^1$
, while in the second case, all the four vertices of the tetrahedron
$[a:b] \in {{\mathbb C}}\mathbb {P}^1$
, while in the second case, all the four vertices of the tetrahedron
![]() $\{T_n\}$
and at least three dual vertices of the tetrahedron
$\{T_n\}$
and at least three dual vertices of the tetrahedron
![]() $\{T_n^{dual}\}$
converge to
$\{T_n^{dual}\}$
converge to
![]() $[a:b] \in {{\mathbb C}}\mathbb {P}^1$
. In particular, in the first case we, choose vertices
$[a:b] \in {{\mathbb C}}\mathbb {P}^1$
. In particular, in the first case we, choose vertices
![]() $v_i^n = [a_1^n: b_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
$v_i^n = [a_1^n: b_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
![]() $v_j^n = [a_2^n: b_2^n] \in {{\mathbb C}}\mathbb {P}^1$
of
$v_j^n = [a_2^n: b_2^n] \in {{\mathbb C}}\mathbb {P}^1$
of
![]() $T_n$
with dual vertices
$T_n$
with dual vertices
![]() $(v_i^n)^{dual} = [c_1^n: d_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
$(v_i^n)^{dual} = [c_1^n: d_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
![]() $(v_j^n)^{dual} = [c_2^n: d_2^n] \in {{\mathbb C}}\mathbb {P}^1$
, such that
$(v_j^n)^{dual} = [c_2^n: d_2^n] \in {{\mathbb C}}\mathbb {P}^1$
, such that
-
•
 $[a_1^n:b_1^n]\to [a:b]$
;
$[a_1^n:b_1^n]\to [a:b]$
; -
•
 $[c_1^n:d_1^n]\to [a:b]$
;
$[c_1^n:d_1^n]\to [a:b]$
; -
•
 $[a_2^n:b_2^n]\to [c:d]$
;
$[a_2^n:b_2^n]\to [c:d]$
; -
•
 $[c_2^n:d_2^n]\to [a:b]$
.
$[c_2^n:d_2^n]\to [a:b]$
.
We can also assume
![]() $[a:b]= [0:1]$
and
$[a:b]= [0:1]$
and
![]() $[c:d]= [1:0]$
. If we denote
$[c:d]= [1:0]$
. If we denote
![]() $W_{i, j}^n$
the Plücker coordinates associated to
$W_{i, j}^n$
the Plücker coordinates associated to
![]() $g\left (T_n\right )$
, we can see that the only nonzero coordinate in the limit is
$g\left (T_n\right )$
, we can see that the only nonzero coordinate in the limit is
![]() $W_{1,3}^n$
, as we wanted.
$W_{1,3}^n$
, as we wanted.
In the second case, we choose vertices
![]() $v_i^n = [a_1^n: b_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
$v_i^n = [a_1^n: b_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
![]() $v_j^n = [a_2^n: b_2^n] \in {{\mathbb C}}\mathbb {P}^1$
of
$v_j^n = [a_2^n: b_2^n] \in {{\mathbb C}}\mathbb {P}^1$
of
![]() $T_n$
with dual vertices
$T_n$
with dual vertices
![]() $(v_i^n)^{dual} = [c_1^n: d_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
$(v_i^n)^{dual} = [c_1^n: d_1^n] \in {{\mathbb C}}\mathbb {P}^1$
and
![]() $(v_j^n)^{dual} = [c_2^n: d_2^n] \in {{\mathbb C}}\mathbb {P}^1$
, such that
$(v_j^n)^{dual} = [c_2^n: d_2^n] \in {{\mathbb C}}\mathbb {P}^1$
, such that
-
•
 $[a_1^n:b_1^n]\to [a:b]$
;
$[a_1^n:b_1^n]\to [a:b]$
; -
•
 $[a_2^n:b_2^n]\to [a:b]$
.
$[a_2^n:b_2^n]\to [a:b]$
.
Again, we can assume
![]() $[a:b]= [0:1]$
. Let’s denote
$[a:b]= [0:1]$
. Let’s denote
![]() $W_{i, j}^n$
the Plücker coordinates associated to
$W_{i, j}^n$
the Plücker coordinates associated to
![]() $F\left (T_n\right )$
. We have two cases:
$F\left (T_n\right )$
. We have two cases:
-
• At least one of the sequences
 $[c_1^n:d_1^n]$
or
$[c_1^n:d_1^n]$
or
 $[c_2^n:d_2^n]$
do not converge to
$[c_2^n:d_2^n]$
do not converge to
 $[a:b]$
. Then we can see that the only nonzero coordinate in the limit is
$[a:b]$
. Then we can see that the only nonzero coordinate in the limit is
 $W_{1,2}^n$
, as we wanted.
$W_{1,2}^n$
, as we wanted. -
• If both
 $[c_1^n:d_1^n], [c_2^n:d_2^n]$
converge to
$[c_1^n:d_1^n], [c_2^n:d_2^n]$
converge to
 $[a:b]$
, then we need to be more careful and analyze the rate of convergence, but after diving all coordinates by
$[a:b]$
, then we need to be more careful and analyze the rate of convergence, but after diving all coordinates by
 $c_1^n$
or
$c_1^n$
or
 $c_2^n$
, we can see that the only nonzero coordinate in the limit is
$c_2^n$
, we can see that the only nonzero coordinate in the limit is
 $W_{1,2}^n$
, as we wanted.
$W_{1,2}^n$
, as we wanted.
In the following, we will denote by
the
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–equivariant map defined in the previous theorem.
$\mathrm {SL}(2,{{\mathbb C}})$
–equivariant map defined in the previous theorem.
4.4 The domain
 $\Omega \subset \mathrm {Lag}({{\mathbb C}}^{4})$
$\Omega \subset \mathrm {Lag}({{\mathbb C}}^{4})$
We will use the barycenters of the tetrahedra to describe interesting subsets of
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
. The barycenter of a regular ideal tetrahedron is a standard notion in hyperbolic geometry. For a degenerate tetrahedron, determined by a pair
$\mathrm {Lag}({{\mathbb C}}^{4})$
. The barycenter of a regular ideal tetrahedron is a standard notion in hyperbolic geometry. For a degenerate tetrahedron, determined by a pair
![]() $(x,y) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, we define the barycenter as its first coordinate, here x. Recall that, when seen as an element of the symmetric product, the first coordinate is the point of
$(x,y) \in {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
, we define the barycenter as its first coordinate, here x. Recall that, when seen as an element of the symmetric product, the first coordinate is the point of
![]() $\mathbb {CP}^1$
that appears with higher multiplicity.
$\mathbb {CP}^1$
that appears with higher multiplicity.
We now introduce the map
that sends a (possibly degenerate) tetrahedron to its barycenter. This map is continuous: this follows from the same arguments we used in the proof of Proposition 4.7. In the rest of the paper, we will use a special notation for the inverse images of sets of
![]() $\overline {{\mathbb H}^3}$
under this map: if
$\overline {{\mathbb H}^3}$
under this map: if
![]() $S \subset \overline {{\mathbb H}^3}$
is any subset, we will denote by
$S \subset \overline {{\mathbb H}^3}$
is any subset, we will denote by
![]() $\mathfrak {T}_{S}$
the set
$\mathfrak {T}_{S}$
the set
So, for example, we can denote the compactification of
![]() $\mathfrak {T}_{{\mathbb H}^3}$
as
$\mathfrak {T}_{{\mathbb H}^3}$
as
where
![]() $\mathfrak {T}_{\mathbb {CP}^1} \simeq {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
is the set of degenerate tetrahedra. By considering the map
$\mathfrak {T}_{\mathbb {CP}^1} \simeq {{\mathbb C}}\mathbb {P}^1\times {{\mathbb C}}\mathbb {P}^1$
is the set of degenerate tetrahedra. By considering the map
![]() $Q:= \pi _{\beta } \circ g^{-1}$
we obtain the following:
$Q:= \pi _{\beta } \circ g^{-1}$
we obtain the following:
Corollary 4.9. There is a continuous
![]() $\mathrm {SL}(2,{{\mathbb C}})$
–equivariant projection
$\mathrm {SL}(2,{{\mathbb C}})$
–equivariant projection
This corollary will help us to understand the action of
![]() $\mathrm {SL}(2,{{\mathbb C}})$
on
$\mathrm {SL}(2,{{\mathbb C}})$
on
![]() $\mathrm {Lag}({{\mathbb C}}^{4})$
because we understand very well the action on
$\mathrm {Lag}({{\mathbb C}}^{4})$
because we understand very well the action on
![]() $\overline {{\mathbb H}^3}$
. We will now show an example of how this works. We restrict our attention to the action of
$\overline {{\mathbb H}^3}$
. We will now show an example of how this works. We restrict our attention to the action of
![]() $\mathrm {SL}(2,{\mathbb R}) < \mathrm {SL}(2,{{\mathbb C}})$
. This smaller subgroup preserves a copy of
$\mathrm {SL}(2,{\mathbb R}) < \mathrm {SL}(2,{{\mathbb C}})$
. This smaller subgroup preserves a copy of
![]() ${\mathbb H}^2 \subset {\mathbb H}^3$
and of its boundary
${\mathbb H}^2 \subset {\mathbb H}^3$
and of its boundary
![]() $\mathbb {RP}^1 \subset \mathbb {CP}^1$
. We define the map
$\mathbb {RP}^1 \subset \mathbb {CP}^1$
. We define the map
as the orthogonal projection into the hyperbolic plane
![]() $\mathcal {P}$
bounded by
$\mathcal {P}$
bounded by
![]() ${\mathbb R}\mathbb {P}^1\subset {{\mathbb C}}\mathbb {P}^1$
. This map is only
${\mathbb R}\mathbb {P}^1\subset {{\mathbb C}}\mathbb {P}^1$
. This map is only
![]() $\mathrm {SL}(2,{\mathbb R})$
–equivariant. By composition, we obtain a projection
$\mathrm {SL}(2,{\mathbb R})$
–equivariant. By composition, we obtain a projection
By Remark 4.3, the inverse image of
![]() ${\mathbb R}\mathbb {P}^1 = \partial {\mathbb H}^2$
is the set
${\mathbb R}\mathbb {P}^1 = \partial {\mathbb H}^2$
is the set
![]() $K_{\mathbb R}$
, and the inverse image of
$K_{\mathbb R}$
, and the inverse image of
![]() ${\mathbb H}^2$
is the set
${\mathbb H}^2$
is the set
Restricting the map
![]() $\pi _{\mathcal {P}} \circ Q$
to
$\pi _{\mathcal {P}} \circ Q$
to
![]() $\Omega $
, we obtain
$\Omega $
, we obtain
an
![]() $\mathrm {SL}(2,{\mathbb R})$
–equivariant map from
$\mathrm {SL}(2,{\mathbb R})$
–equivariant map from
![]() $\Omega $
to
$\Omega $
to
![]() ${\mathbb H}^2$
, which is a fiber bundle by Lemma 3.7. Notice that the map q is proper, because it is the restriction of the map
${\mathbb H}^2$
, which is a fiber bundle by Lemma 3.7. Notice that the map q is proper, because it is the restriction of the map
![]() $\pi _{\mathcal {P}} \circ Q$
which is defined on a compact space.
$\pi _{\mathcal {P}} \circ Q$
which is defined on a compact space.
We will identify
![]() ${\mathbb H}^2$
with the hyperbolic plane
${\mathbb H}^2$
with the hyperbolic plane
![]() $\mathcal {P} \subset {\mathbb H}^3$
. We denote by
$\mathcal {P} \subset {\mathbb H}^3$
. We denote by
![]() $\mathcal {O} \in {\mathbb H}^2 \subset {\mathbb H}^3$
the point
$\mathcal {O} \in {\mathbb H}^2 \subset {\mathbb H}^3$
the point
![]() $\mathcal {O} = (0, 1)\in {{\mathbb C}} \times {\mathbb R}_{>0}$
, and by F the fiber of q over this point:
$\mathcal {O} = (0, 1)\in {{\mathbb C}} \times {\mathbb R}_{>0}$
, and by F the fiber of q over this point:
Since
![]() $q\colon \thinspace \Omega \to {\mathbb H}^2$
is a fiber bundle over a contractible base, we conclude the following result:
$q\colon \thinspace \Omega \to {\mathbb H}^2$
is a fiber bundle over a contractible base, we conclude the following result:
Corollary 4.10. The space
![]() $\Omega $
is homeomorphic to the product
$\Omega $
is homeomorphic to the product
![]() $F \times {\mathbb H}^2$
; hence,
$F \times {\mathbb H}^2$
; hence,
![]() $\Omega $
deformation retracts to F.
$\Omega $
deformation retracts to F.
In the following sections, we will describe the topology of F. Since F is homotopy equivalent to
![]() $\Omega $
, and
$\Omega $
, and
![]() $\Omega $
is homotopically equivalent to our smooth fiber
$\Omega $
is homotopically equivalent to our smooth fiber
![]() $\mathfrak {F}$
, the information we will find about F will allow us to determine
$\mathfrak {F}$
, the information we will find about F will allow us to determine
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
5 Description of the fiber from the tetrahedra
We consider the geodesic
![]() $\overline {\ell }:= \pi _{\mathcal {P}}^{-1}(\mathcal {O})$
, where
$\overline {\ell }:= \pi _{\mathcal {P}}^{-1}(\mathcal {O})$
, where
![]() $\pi _{\mathcal {P}}\colon \thinspace \overline {{\mathbb H}^3}\to \overline {{\mathbb H}^2}$
is the orthogonal projection, and
$\pi _{\mathcal {P}}\colon \thinspace \overline {{\mathbb H}^3}\to \overline {{\mathbb H}^2}$
is the orthogonal projection, and
![]() $\mathcal {O} \in {\mathbb H}^2$
is the point introduced at the end of the previous section. The geodesic
$\mathcal {O} \in {\mathbb H}^2$
is the point introduced at the end of the previous section. The geodesic
![]() $\overline {\ell }$
joins the points at infinity i and
$\overline {\ell }$
joins the points at infinity i and
![]() $-i$
. We denote
$-i$
. We denote
![]() $\ell := \overline {\ell } \cap {\mathbb H}^3$
, so we have
$\ell := \overline {\ell } \cap {\mathbb H}^3$
, so we have
![]() $\overline {\ell } = \ell \cup \{\pm i\}$
. We denote by
$\overline {\ell } = \ell \cup \{\pm i\}$
. We denote by
![]() $\ell ^+$
the ray of
$\ell ^+$
the ray of
![]() $\ell $
from
$\ell $
from
![]() $\mathcal {O}$
to i, and by
$\mathcal {O}$
to i, and by
![]() $\ell ^-$
the ray from
$\ell ^-$
the ray from
![]() $\mathcal {O}$
to
$\mathcal {O}$
to
![]() $-i$
. In both cases,
$-i$
. In both cases,
![]() $\mathcal {O}$
is included, and
$\mathcal {O}$
is included, and
![]() $\pm i$
is not. Similarly, we denote by
$\pm i$
is not. Similarly, we denote by
![]() $\overline {\ell ^+}$
and
$\overline {\ell ^+}$
and
![]() $\overline {\ell ^-}$
the compactified rays that include
$\overline {\ell ^-}$
the compactified rays that include
![]() $\pm i$
.
$\pm i$
.
We will identify
![]() $\overline {\ell }$
with the segment
$\overline {\ell }$
with the segment
![]() $[-\infty , \infty ]$
via the homeomorphism
$[-\infty , \infty ]$
via the homeomorphism
defined by the following properties:
-
•
 $\eta (\mathcal {O}) = 0$
,
$\eta (\mathcal {O}) = 0$
, -
•
 $\eta (\pm i) = \pm \infty $
,
$\eta (\pm i) = \pm \infty $
, -
• for every
 $x \in \ell ^+$
,
$x \in \ell ^+$
,
 $\eta (x) = d_{{\mathbb H}^3}(\mathcal {O}, x)$
, and
$\eta (x) = d_{{\mathbb H}^3}(\mathcal {O}, x)$
, and -
• for any
 $x \in \ell ^-$
,
$x \in \ell ^-$
,
 $\eta (x) = -d_{{\mathbb H}^3}(\mathcal {O}, x)$
.
$\eta (x) = -d_{{\mathbb H}^3}(\mathcal {O}, x)$
.
We define the space
![]() $\mathfrak {T}_{\overline {\ell }}$
consisting of (possibly degenerate) tetrahedra with (possibly degenerate) barycenter on the geodesic
$\mathfrak {T}_{\overline {\ell }}$
consisting of (possibly degenerate) tetrahedra with (possibly degenerate) barycenter on the geodesic
![]() $\overline {\ell }$
. This space is homeomorphic to the fiber F: recall that in Theorem 4.8, we constructed an explicit homeomorphism from the space of (unlabelled) regular ideal tetrahedra to the Lagrangian Grassmannian
$\overline {\ell }$
. This space is homeomorphic to the fiber F: recall that in Theorem 4.8, we constructed an explicit homeomorphism from the space of (unlabelled) regular ideal tetrahedra to the Lagrangian Grassmannian
Then, the fiber
![]() $F = q^{-1}(\mathcal {O}) \subset \Omega \subset \mathrm {Lag}({{\mathbb C}}^{4})$
for the projection
$F = q^{-1}(\mathcal {O}) \subset \Omega \subset \mathrm {Lag}({{\mathbb C}}^{4})$
for the projection
![]() $q = \pi _{\mathcal {P}} \circ Q|_{\Omega }\colon \thinspace \Omega \to {\mathbb H}^2$
is exactly the image
$q = \pi _{\mathcal {P}} \circ Q|_{\Omega }\colon \thinspace \Omega \to {\mathbb H}^2$
is exactly the image
![]() $g(\mathfrak {T}_{\overline {\ell }})$
.
$g(\mathfrak {T}_{\overline {\ell }})$
.
Our main aim in this section will be to describe the space
![]() $\mathfrak {T}_{\overline {\ell }}$
. It will be useful to distinguish between three subsets: the open subset
$\mathfrak {T}_{\overline {\ell }}$
. It will be useful to distinguish between three subsets: the open subset
![]() $\mathfrak {T}_\ell $
consisting of tetrahedra with barycenter in
$\mathfrak {T}_\ell $
consisting of tetrahedra with barycenter in
![]() $\ell $
, and the closed subsets
$\ell $
, and the closed subsets
![]() $\mathfrak {T}_i$
and
$\mathfrak {T}_i$
and
![]() $\mathfrak {T}_{-i}$
consisting of degenerate tetrahedra with barycenter in i or
$\mathfrak {T}_{-i}$
consisting of degenerate tetrahedra with barycenter in i or
![]() $-i$
, respectively.
$-i$
, respectively.
We have that
The space
![]() $\mathfrak {T}_\ell $
will be described in Section 5.1. The shape of each of the three pieces,
$\mathfrak {T}_\ell $
will be described in Section 5.1. The shape of each of the three pieces,
![]() $\mathfrak {T}_\ell , \mathfrak {T}_i, \mathfrak {T}_{-i}$
is easy to understand. The most interesting thing is to describe how they are glued together, which is done in Section 5.2.
$\mathfrak {T}_\ell , \mathfrak {T}_i, \mathfrak {T}_{-i}$
is easy to understand. The most interesting thing is to describe how they are glued together, which is done in Section 5.2.
We consider the upper half space model
![]() ${\mathbb H}^3 = {{\mathbb C}} \times {\mathbb R}_{>0}$
of hyperbolic space. In this model, the compactified hyperbolic space is
${\mathbb H}^3 = {{\mathbb C}} \times {\mathbb R}_{>0}$
of hyperbolic space. In this model, the compactified hyperbolic space is
![]() $\overline {{\mathbb H}^3} = {{\mathbb C}} \times {\mathbb R}_{\geq 0} \cup \{\infty \}$
, and its boundary is
$\overline {{\mathbb H}^3} = {{\mathbb C}} \times {\mathbb R}_{\geq 0} \cup \{\infty \}$
, and its boundary is
![]() $\partial {\mathbb H}^3 = {{\mathbb C}} \times \{0\} \cup \{\infty \} = {{\mathbb C}}\mathbb {P}^1$
. In the following, with a slight abuse of notation, we will simply use complex numbers (or
$\partial {\mathbb H}^3 = {{\mathbb C}} \times \{0\} \cup \{\infty \} = {{\mathbb C}}\mathbb {P}^1$
. In the following, with a slight abuse of notation, we will simply use complex numbers (or
![]() $\infty $
) to denote points of
$\infty $
) to denote points of
![]() $\partial {\mathbb H}^3 = \mathbb {CP}^1$
. We identify
$\partial {\mathbb H}^3 = \mathbb {CP}^1$
. We identify
![]() ${\mathbb H}^2$
with the plane
${\mathbb H}^2$
with the plane
![]() $\mathcal {P} = {\mathbb R} \times {\mathbb R}_{>0} \subset {\mathbb H}^3$
whose boundary is
$\mathcal {P} = {\mathbb R} \times {\mathbb R}_{>0} \subset {\mathbb H}^3$
whose boundary is
![]() $\partial {\mathbb H}^2 = {\mathbb R}\mathbb {P}^1 \subset {{\mathbb C}}\mathbb {P}^1$
. Note that
$\partial {\mathbb H}^2 = {\mathbb R}\mathbb {P}^1 \subset {{\mathbb C}}\mathbb {P}^1$
. Note that
![]() $\mathrm {PSL}(2, {\mathbb R})$
acts preserving
$\mathrm {PSL}(2, {\mathbb R})$
acts preserving
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
5.1 Tetrahedra with a fixed barycenter
For any
![]() $c\in {\mathbb H}^3$
, let
$c\in {\mathbb H}^3$
, let
![]() $\mathfrak {T}_c$
be the set of regular ideal unlabelled tetrahedra with barycenter c. All the spaces
$\mathfrak {T}_c$
be the set of regular ideal unlabelled tetrahedra with barycenter c. All the spaces
![]() $\mathfrak {T}_c$
are homeomorphic to each other. The space
$\mathfrak {T}_c$
are homeomorphic to each other. The space
![]() $\mathfrak {T}_\ell $
is homeomorphic to
$\mathfrak {T}_\ell $
is homeomorphic to
![]() $\mathfrak {T}_c \times {\mathbb R}$
for any choice of c. We will now describe
$\mathfrak {T}_c \times {\mathbb R}$
for any choice of c. We will now describe
![]() $\mathfrak {T}_c$
.
$\mathfrak {T}_c$
.
Note that for all
![]() $c\in \ell $
, the space
$c\in \ell $
, the space
![]() $\mathfrak {T}_c$
is homeomorphic to
$\mathfrak {T}_c$
is homeomorphic to
This is a Seifert fibered space — an orbifold–
![]() ${\mathbb S}^1$
–bundle over the
${\mathbb S}^1$
–bundle over the
![]() $2$
–orbifold
$2$
–orbifold
![]() ${\mathbb S}^2(2, 3, 3) = {\mathbb S}^2 / A_4$
— and it corresponds to the space described by Martelli [Reference MartelliMar22] in the second line of Table 10.6 for
${\mathbb S}^2(2, 3, 3) = {\mathbb S}^2 / A_4$
— and it corresponds to the space described by Martelli [Reference MartelliMar22] in the second line of Table 10.6 for
![]() $q = -2$
. The structure of Seifert fibered manifold of
$q = -2$
. The structure of Seifert fibered manifold of
![]() $\mathfrak {T}_c$
can be described geometrically.
$\mathfrak {T}_c$
can be described geometrically.
Consider the action of
![]() $\mathrm {SO}(2)$
on
$\mathrm {SO}(2)$
on
![]() ${\mathbb H}^3$
via rotations that fix
${\mathbb H}^3$
via rotations that fix
![]() $\ell $
. Since we are assuming that
$\ell $
. Since we are assuming that
![]() $c\in \ell $
, this induces an action of
$c\in \ell $
, this induces an action of
![]() $\mathrm {SO}(2)$
on
$\mathrm {SO}(2)$
on
![]() $\mathfrak {T}_c$
. The orbits of this action are the fibers of the Seifert fibration. The three circles associated with the three singular fibers correspond to tetrahedra (with barycenter at the point c) with special symmetries:
$\mathfrak {T}_c$
. The orbits of this action are the fibers of the Seifert fibration. The three circles associated with the three singular fibers correspond to tetrahedra (with barycenter at the point c) with special symmetries:
-
(i) the circles associated with the order–
 $3$
cone points correspond to tetrahedra in
$3$
cone points correspond to tetrahedra in
 $\mathfrak {T}_c$
with one vertex in
$\mathfrak {T}_c$
with one vertex in
 $-i$
or i, respectively,
$-i$
or i, respectively, -
(ii) the circle associated with the order–
 $2$
cone point corresponds to tetrahedra in
$2$
cone point corresponds to tetrahedra in
 $\mathfrak {T}_c$
with two sides orthogonal to
$\mathfrak {T}_c$
with two sides orthogonal to
 $\ell $
.
$\ell $
.
We want to decompose
![]() $\mathfrak {T}_c$
in two sets:
$\mathfrak {T}_c$
in two sets:
As above, we denote by
![]() $\ell ^+_c$
the ray of
$\ell ^+_c$
the ray of
![]() $\ell $
from c to i, and by
$\ell $
from c to i, and by
![]() $\ell ^-_c$
the ray from c to
$\ell ^-_c$
the ray from c to
![]() $-i$
. In both cases, c is included, and
$-i$
. In both cases, c is included, and
![]() $\pm i$
are not. Similarly, we denote by
$\pm i$
are not. Similarly, we denote by
![]() $\overline {\ell ^+_c}$
and
$\overline {\ell ^+_c}$
and
![]() $\overline {\ell ^-_c}$
the compactified rays that include
$\overline {\ell ^-_c}$
the compactified rays that include
![]() $\pm i$
. The boundary of the tetrahedra in the family in
$\pm i$
. The boundary of the tetrahedra in the family in
![]() $(ii)$
(with order–
$(ii)$
(with order–
![]() $2$
symmetry) will intersect
$2$
symmetry) will intersect
![]() $\ell $
in two points: one in
$\ell $
in two points: one in
![]() $\ell ^-_c$
(which we will denote
$\ell ^-_c$
(which we will denote
![]() $A_{c}$
) and the other in
$A_{c}$
) and the other in
![]() $\ell ^+_c$
. Let
$\ell ^+_c$
. Let
![]() $B_{c}$
be the point in
$B_{c}$
be the point in
![]() $\ell ^-_c$
between
$\ell ^-_c$
between
![]() $-i$
and
$-i$
and
![]() $A_c$
and at (hyperbolic) distance
$A_c$
and at (hyperbolic) distance
![]() $1$
from
$1$
from
![]() $A_{c}$
. Let
$A_{c}$
. Let
![]() $C_{c}$
be circle in
$C_{c}$
be circle in
![]() ${{\mathbb C}}\mathbb {P}^1$
that bounds the plane in
${{\mathbb C}}\mathbb {P}^1$
that bounds the plane in
![]() ${\mathbb H}^3$
orthogonal to
${\mathbb H}^3$
orthogonal to
![]() $\ell $
and intersecting it at
$\ell $
and intersecting it at
![]() $B_c$
and let
$B_c$
and let
![]() $D_{c}$
(resp.
$D_{c}$
(resp.
![]() $\overline {D_{c}}$
) be the open (resp. closed) disk in
$\overline {D_{c}}$
) be the open (resp. closed) disk in
![]() ${{\mathbb C}}\mathbb {P}^1$
with boundary
${{\mathbb C}}\mathbb {P}^1$
with boundary
![]() $C_{c}$
and containing
$C_{c}$
and containing
![]() $-i$
.
$-i$
.
With this notation, we can define
![]() $\mathfrak {T}_{c}^{\uparrow }, \mathfrak {T}_{c}^{\downarrow }$
as follows:
$\mathfrak {T}_{c}^{\uparrow }, \mathfrak {T}_{c}^{\downarrow }$
as follows:
-
•
 $\mathfrak {T}_{c}^{\uparrow }$
is the set of tetrahedra in
$\mathfrak {T}_{c}^{\uparrow }$
is the set of tetrahedra in
 $\mathfrak {T}_c$
such that all vertices are in
$\mathfrak {T}_c$
such that all vertices are in
 ${{\mathbb C}}\mathbb {P}^1 \setminus D_{c}$
;
${{\mathbb C}}\mathbb {P}^1 \setminus D_{c}$
; -
•
 $\mathfrak {T}_{c}^{\downarrow }$
is the set of tetrahedra in
$\mathfrak {T}_{c}^{\downarrow }$
is the set of tetrahedra in
 $\mathfrak {T}_c$
such that one of their vertices is in
$\mathfrak {T}_c$
such that one of their vertices is in
 $D_{c}$
.
$D_{c}$
.
The set
![]() $\mathfrak {T}_{c}^{\uparrow }$
is closed, and the set
$\mathfrak {T}_{c}^{\uparrow }$
is closed, and the set
![]() $\mathfrak {T}_{c}^{\downarrow }$
is open. They share a common boundary
$\mathfrak {T}_{c}^{\downarrow }$
is open. They share a common boundary
![]() $\partial \mathfrak {T}_{c}^{\uparrow } = \partial \mathfrak {T}_{c}^{\downarrow }$
, the set of tetrahedra in
$\partial \mathfrak {T}_{c}^{\uparrow } = \partial \mathfrak {T}_{c}^{\downarrow }$
, the set of tetrahedra in
![]() $\mathfrak {T}_c$
such that one of their vertices is in
$\mathfrak {T}_c$
such that one of their vertices is in
![]() $C_{c}$
. This decomposition is motivated by the following property:
$C_{c}$
. This decomposition is motivated by the following property:
Proposition 5.1. For every
![]() $c \in \ell $
and for every
$c \in \ell $
and for every
![]() $T \in \overline {\mathfrak {T}_{c}^{\downarrow }}$
, the tetrahedron T has exactly one vertex in
$T \in \overline {\mathfrak {T}_{c}^{\downarrow }}$
, the tetrahedron T has exactly one vertex in
![]() $\overline {D_{c}}$
.
$\overline {D_{c}}$
.
Proof. The proof is elementary, but it requires several computations. We will break it into three claims and a main argument following the claims.
Claim 1: The (hyperbolic) distance between the barycenter and the faces of a regular tetrahedron
![]() $T \in \mathfrak {T}_{{\mathbb H}^3}$
is
$T \in \mathfrak {T}_{{\mathbb H}^3}$
is
![]() $\ln {\sqrt {2}}$
. To see that, we consider the tetrahedron T with vertices
$\ln {\sqrt {2}}$
. To see that, we consider the tetrahedron T with vertices
![]() $\{\infty , -1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}\}$
. We can check that T is regular by calculating the cross-ratio
$\{\infty , -1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}\}$
. We can check that T is regular by calculating the cross-ratio
![]() $[\infty , -1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}]$
. The barycenter of this tetrahedron is
$[\infty , -1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}]$
. The barycenter of this tetrahedron is
![]() $(0, 0, \sqrt {2})$
, which corresponds to the point of intersection between the geodesic passing through
$(0, 0, \sqrt {2})$
, which corresponds to the point of intersection between the geodesic passing through
![]() $0$
and
$0$
and
![]() $\infty $
and the geodesic passing through
$\infty $
and the geodesic passing through
![]() $-1$
and orthogonal to the plane
$-1$
and orthogonal to the plane
![]() $\{x = \frac {1}{2}\}$
in
$\{x = \frac {1}{2}\}$
in
![]() ${\mathbb H}^3$
(which is the plane containing
${\mathbb H}^3$
(which is the plane containing
![]() $\infty $
,
$\infty $
,
![]() $\frac {1+\sqrt {3}i}{2}$
and
$\frac {1+\sqrt {3}i}{2}$
and
![]() $\frac {1-\sqrt {3}i}{2}$
). It is easy now to see that the (hyperbolic) distance between the barycenter and the face of T passing trough
$\frac {1-\sqrt {3}i}{2}$
). It is easy now to see that the (hyperbolic) distance between the barycenter and the face of T passing trough
![]() $\{-1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}\}$
is
$\{-1, \frac {1+\sqrt {3}i}{2}, \frac {1-\sqrt {3}i}{2}\}$
is
![]() $\ln {\sqrt {2}}$
.
$\ln {\sqrt {2}}$
.
Claim 2: Given a tetrahedron with with order–
![]() $2$
symmetry, the (hyperbolic) distance between its barycenter c and the point
$2$
symmetry, the (hyperbolic) distance between its barycenter c and the point
![]() $A_c$
is
$A_c$
is
![]() $\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
. To prove this, we consider the tetrahedron
$\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
. To prove this, we consider the tetrahedron
![]() $T = \{1, -1, (2-\sqrt {3})i, -(2-\sqrt {3})i\}$
. The barycenter of this tetrahedron is
$T = \{1, -1, (2-\sqrt {3})i, -(2-\sqrt {3})i\}$
. The barycenter of this tetrahedron is
![]() $(0, 0, \tfrac {1}{2}(\sqrt {6}-\sqrt {2}))$
, and the distance between the barycenter and the geodesic between
$(0, 0, \tfrac {1}{2}(\sqrt {6}-\sqrt {2}))$
, and the distance between the barycenter and the geodesic between
![]() $1$
and
$1$
and
![]() $-1$
is
$-1$
is
![]() $\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
.
$\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
.
Claim 3: Consider two points
![]() $O, P \in \mathbb {H}^3$
, and let d be their distance, the length of the segment
$O, P \in \mathbb {H}^3$
, and let d be their distance, the length of the segment
![]() $OP$
. Let C be the plane passing through P and perpendicular to
$OP$
. Let C be the plane passing through P and perpendicular to
![]() $OP$
. Let I be a point of
$OP$
. Let I be a point of
![]() ${{\mathbb C}}\mathbb {P}^1$
at the boundary of C. The angle
${{\mathbb C}}\mathbb {P}^1$
at the boundary of C. The angle
![]() $\theta $
between the segment
$\theta $
between the segment
![]() $OP$
and the ray
$OP$
and the ray
![]() $OI$
depends only on d, and it is given by the function
$OI$
depends only on d, and it is given by the function
![]() $F(d)$
defined by
$F(d)$
defined by
This is actually a 2-dimensional question; all the computations can be made in the Poincaré disc model of the hyperbolic plane. We choose O as the center of the disc, and P, to be determined later, will lie on the positive real axis. Using the angle
![]() $\theta $
as a parameter, we write the point
$\theta $
as a parameter, we write the point
![]() $I = \cos \theta + i \sin \theta $
. We compute the geodesic passing through I and
$I = \cos \theta + i \sin \theta $
. We compute the geodesic passing through I and
![]() $\bar {I}$
, and this determines the position of the point P. An elementary computation gives the formula.
$\bar {I}$
, and this determines the position of the point P. An elementary computation gives the formula.
Now we go back to the statement to prove. Let
![]() $c \in \ell $
, and let
$c \in \ell $
, and let
![]() $T \in \partial \mathfrak {T}_{c}^{\downarrow }$
be a tetrahedron with one vertex
$T \in \partial \mathfrak {T}_{c}^{\downarrow }$
be a tetrahedron with one vertex
![]() $v_T$
on the circle
$v_T$
on the circle
![]() $C_{c}$
. Then the other three vertices of T (different from
$C_{c}$
. Then the other three vertices of T (different from
![]() $v_T$
) lie on a circle
$v_T$
) lie on a circle
![]() $C_T$
, spanning a disc
$C_T$
, spanning a disc
![]() $D_T$
in
$D_T$
in
![]() ${{\mathbb C}}\mathbb {P}^1$
. The plane bounded by
${{\mathbb C}}\mathbb {P}^1$
. The plane bounded by
![]() $C_T$
is perpendicular to the geodesic between
$C_T$
is perpendicular to the geodesic between
![]() $v_T$
and c and intersecting it at the point at distance
$v_T$
and c and intersecting it at the point at distance
![]() $\mathrm {ln}\sqrt {2}$
(by Claim 1) from c and farthest from
$\mathrm {ln}\sqrt {2}$
(by Claim 1) from c and farthest from
![]() $v_T$
. Then, in order to prove the result above, we just have to check that the circle
$v_T$
. Then, in order to prove the result above, we just have to check that the circle
![]() $C_T$
does not intersect
$C_T$
does not intersect
![]() $\overline {D}_{c}$
. This can be checked with a computation in the plane S containing
$\overline {D}_{c}$
. This can be checked with a computation in the plane S containing
![]() $\ell $
and
$\ell $
and
![]() $v_T$
. The plane S intersects
$v_T$
. The plane S intersects
![]() $C_c$
in two points,
$C_c$
in two points,
![]() $v_T$
and
$v_T$
and
![]() $P_1$
. The distance between c and
$P_1$
. The distance between c and
![]() $B_c$
is
$B_c$
is
![]() $d_1 = 1+\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
, by Claim 2; hence, by Claim 3, the angle between
$d_1 = 1+\ln \left (\tfrac {1}{2}(\sqrt {6}+\sqrt {2})\right )$
, by Claim 2; hence, by Claim 3, the angle between
![]() $v_T$
and
$v_T$
and
![]() $P_1$
, seen from c, is
$P_1$
, seen from c, is
![]() $2 F(d_1) \simeq 0.752\dots $
. The intersection between the plane S and
$2 F(d_1) \simeq 0.752\dots $
. The intersection between the plane S and
![]() $C_T$
is two points; we denote the
$C_T$
is two points; we denote the
![]() $P_2$
the one closest to
$P_2$
the one closest to
![]() $P_1$
. The angle between
$P_1$
. The angle between
![]() $v_T$
and
$v_T$
and
![]() $P_2$
, seen from c, is
$P_2$
, seen from c, is
![]() $\pi - F(\ln \sqrt {2}) \simeq 1.91\dots $
, by Claim 1 and 3. Since this is larger than
$\pi - F(\ln \sqrt {2}) \simeq 1.91\dots $
, by Claim 1 and 3. Since this is larger than
![]() $2 F(d_1)$
, the circle
$2 F(d_1)$
, the circle
![]() $C_T$
does not intersect
$C_T$
does not intersect
![]() $\overline {D}_{c}$
.
$\overline {D}_{c}$
.
We can describe more precisely the topology of
![]() $\mathfrak {T}_{c}^{\uparrow }$
and
$\mathfrak {T}_{c}^{\uparrow }$
and
![]() $\mathfrak {T}_{c}^{\downarrow }$
.
$\mathfrak {T}_{c}^{\downarrow }$
.
Proposition 5.2.
![]() $\mathfrak {T}_{c}^{\uparrow }$
is homeomorphic to the complement of an open tubular neighborhood of a
$\mathfrak {T}_{c}^{\uparrow }$
is homeomorphic to the complement of an open tubular neighborhood of a
![]() $(2, 3)$
–torus knot (or, equivalently, a trefoil knot);
$(2, 3)$
–torus knot (or, equivalently, a trefoil knot);
Proof. Since we know that
![]() $\mathfrak {T}_{c} \cong \mathrm {SO}(3)/A_4$
, its Seifert structure is well known; see, for example, the second line of Table 10.6 in Martelli [Reference MartelliMar22] with
$\mathfrak {T}_{c} \cong \mathrm {SO}(3)/A_4$
, its Seifert structure is well known; see, for example, the second line of Table 10.6 in Martelli [Reference MartelliMar22] with
![]() $q = -2$
. In order to prove the first claim, we need to understand the Seifert structure of the trefoil knot complement. This is described in Moser [Reference MoserMos71]. We can easily see that it is the same as the one of
$q = -2$
. In order to prove the first claim, we need to understand the Seifert structure of the trefoil knot complement. This is described in Moser [Reference MoserMos71]. We can easily see that it is the same as the one of
![]() $\mathfrak {T}_{c}^{\uparrow }$
.
$\mathfrak {T}_{c}^{\uparrow }$
.
Proposition 5.3.
![]() $\mathfrak {T}_{c}^{\downarrow }$
is homeomorphic to an open solid torus
$\mathfrak {T}_{c}^{\downarrow }$
is homeomorphic to an open solid torus
![]() $\mathbb {D} \times \mathbb {S}^1$
, where
$\mathbb {D} \times \mathbb {S}^1$
, where
![]() $\mathbb {D}$
is an open disc in
$\mathbb {D}$
is an open disc in
![]() ${{\mathbb C}}$
. More precisely, there are explicit coordinates
${{\mathbb C}}$
. More precisely, there are explicit coordinates
where
![]() $D_c$
is the disc defined before Proposition 5.1.
$D_c$
is the disc defined before Proposition 5.1.
Proof. We will describe explicit coordinates for
![]() $\mathfrak {T}_{c}^{\downarrow }$
as we will need them in the following section. We will parametrize
$\mathfrak {T}_{c}^{\downarrow }$
as we will need them in the following section. We will parametrize
![]() $\mathfrak {T}_{c}^{\downarrow }$
with
$\mathfrak {T}_{c}^{\downarrow }$
with
![]() $D_c \times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
, where
$D_c \times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
, where
![]() ${\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
is a circle with a parameter that ranges between
${\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
is a circle with a parameter that ranges between
![]() $0$
and
$0$
and
![]() $\frac {2\pi }{3}$
, and we recall that
$\frac {2\pi }{3}$
, and we recall that
![]() $D_c$
is an open disc in
$D_c$
is an open disc in
![]() ${{\mathbb C}}\mathbb {P}^1$
containing the point
${{\mathbb C}}\mathbb {P}^1$
containing the point
![]() $-i$
. Removing the point
$-i$
. Removing the point
![]() $-i$
, we obtain an anulus
$-i$
, we obtain an anulus
![]() $\mathbb {A} = D_c \setminus \{-i\}$
, which we will parametrize with polar coordinates; that is, we will write it as
$\mathbb {A} = D_c \setminus \{-i\}$
, which we will parametrize with polar coordinates; that is, we will write it as
Geometrically, we will consider the family
![]() $\mathcal {F}$
of hyperbolic half-planes bounded by the line
$\mathcal {F}$
of hyperbolic half-planes bounded by the line
![]() $\ell $
. These half-planes are orthogonal to the plane bounded by
$\ell $
. These half-planes are orthogonal to the plane bounded by
![]() ${\mathbb R}\mathbb {P}^1$
. We denote by
${\mathbb R}\mathbb {P}^1$
. We denote by
![]() $\mathcal {F}_0$
the half-plane in
$\mathcal {F}_0$
the half-plane in
![]() $\mathcal {F}$
that contains the point
$\mathcal {F}$
that contains the point
![]() $0 \in {\mathbb R}\mathbb {P}^1$
. Every
$0 \in {\mathbb R}\mathbb {P}^1$
. Every
![]() $z \in \mathbb {A}$
lies in exactly one half-plane in
$z \in \mathbb {A}$
lies in exactly one half-plane in
![]() $\mathcal {F}$
, denoted by
$\mathcal {F}$
, denoted by
![]() $\mathcal {F}_z$
. Define
$\mathcal {F}_z$
. Define
![]() $\alpha (z) \in {\mathbb S}^1$
as the angle between
$\alpha (z) \in {\mathbb S}^1$
as the angle between
![]() $\mathcal {F}_0$
and
$\mathcal {F}_0$
and
![]() $\mathcal {F}_z$
, in the clockwise direction, and
$\mathcal {F}_z$
, in the clockwise direction, and
![]() $\rho (z) \in (0,1)$
as the angle between the line
$\rho (z) \in (0,1)$
as the angle between the line
![]() $\ell $
and the line
$\ell $
and the line
![]() $cz$
as seen from the point c. The angle
$cz$
as seen from the point c. The angle
![]() $\rho (z)$
needs to be rescaled suitably so that it ranges between
$\rho (z)$
needs to be rescaled suitably so that it ranges between
![]() $0$
and
$0$
and
![]() $1$
when z moves in
$1$
when z moves in
![]() $D_c$
. This describes the coordinates
$D_c$
. This describes the coordinates
We first consider the family
![]() $\mathfrak {T}_{c}^{\downarrow , 3}$
of the tetrahedra in
$\mathfrak {T}_{c}^{\downarrow , 3}$
of the tetrahedra in
![]() $\mathfrak {T}_c^{\downarrow }$
with bottom vertex in
$\mathfrak {T}_c^{\downarrow }$
with bottom vertex in
![]() $-i$
. This is one of the families of tetrahedra with the order–
$-i$
. This is one of the families of tetrahedra with the order–
![]() $3$
symmetry. They form the core of the solid torus and will be parametrized by
$3$
symmetry. They form the core of the solid torus and will be parametrized by
![]() $\{-i\} \times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
in the following way: if v is another vertex of a tetrahedron
$\{-i\} \times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
in the following way: if v is another vertex of a tetrahedron
![]() $T \in \mathfrak {T}_{c}^{\downarrow , 3}$
, we associate to T the angle
$T \in \mathfrak {T}_{c}^{\downarrow , 3}$
, we associate to T the angle
![]() $\theta _T$
between the half-plane
$\theta _T$
between the half-plane
![]() $\mathcal {F}_0$
and
$\mathcal {F}_0$
and
![]() $\mathcal {F}_v$
, in the clockwise direction, reduced modulo
$\mathcal {F}_v$
, in the clockwise direction, reduced modulo
![]() $\frac {2\pi }{3}\mathbb {Z}$
.
$\frac {2\pi }{3}\mathbb {Z}$
.
The complement of this family (i.e., the space
![]() $\mathfrak {T}_{c}^{\downarrow }\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
) will be parametrized by
$\mathfrak {T}_{c}^{\downarrow }\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
) will be parametrized by
![]() $\mathbb {A}\times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
as follows. If
$\mathbb {A}\times {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
as follows. If
![]() $T \in \overline {\mathfrak {T}_c^{\downarrow }}\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
, let
$T \in \overline {\mathfrak {T}_c^{\downarrow }}\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
, let
![]() $v_T$
be the unique vertex of T in
$v_T$
be the unique vertex of T in
![]() $D_{c}\setminus \{-i\} = \mathbb {A}$
. The point
$D_{c}\setminus \{-i\} = \mathbb {A}$
. The point
![]() $v_T$
will be the coordinate of T in
$v_T$
will be the coordinate of T in
![]() $\mathbb {A}$
. We now define the coordinate
$\mathbb {A}$
. We now define the coordinate
![]() $\theta _T \in {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
. Once
$\theta _T \in {\mathbb R}/(\frac {2\pi }{3}\mathbb {Z})$
. Once
![]() $v_T$
is fixed (and c is fixed), the other three vertices lie on a circle
$v_T$
is fixed (and c is fixed), the other three vertices lie on a circle
![]() $C_T$
. Let
$C_T$
. Let
![]() $w_T$
be the point where
$w_T$
be the point where
![]() $C_T$
meets the half-plane
$C_T$
meets the half-plane
![]() $\mathcal {F}_{v_T}$
. Define the angle
$\mathcal {F}_{v_T}$
. Define the angle
![]() $\beta (T)$
as the angle between the half-plane bounded by
$\beta (T)$
as the angle between the half-plane bounded by
![]() $v_T, c$
and containing
$v_T, c$
and containing
![]() $w_T$
and the half-plane bounded by
$w_T$
and the half-plane bounded by
![]() $v_T,c$
and containing another vertex of T, in the clockwise direction, modulo
$v_T,c$
and containing another vertex of T, in the clockwise direction, modulo
![]() $\frac {2\pi }{3}\mathbb {Z}$
. The angle
$\frac {2\pi }{3}\mathbb {Z}$
. The angle
![]() $\theta _T$
is defined as
$\theta _T$
is defined as
![]() $\theta _T = \beta (T)+\alpha (v_T)$
. This gives a parametrization
$\theta _T = \beta (T)+\alpha (v_T)$
. This gives a parametrization
When the parametrizations of the two parts
![]() $\mathfrak {T}_{c}^{\downarrow , 3}$
and
$\mathfrak {T}_{c}^{\downarrow , 3}$
and
![]() $\mathfrak {T}_{c}^{\downarrow }\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
are put together, they give a homeomorphism
$\mathfrak {T}_{c}^{\downarrow }\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
are put together, they give a homeomorphism
The fact that the joint map is continuous follows from the geometric definition: let’s consider a sequence
![]() $T_n\in \overline {\mathfrak {T}_c^{\downarrow }}\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
such that
$T_n\in \overline {\mathfrak {T}_c^{\downarrow }}\setminus \mathfrak {T}_{c}^{\downarrow , 3}$
such that
![]() $T_n\to T\in \mathfrak {T}_{c}^{\downarrow , 3}$
. Up to a rotation by an isometry that stabilizes
$T_n\to T\in \mathfrak {T}_{c}^{\downarrow , 3}$
. Up to a rotation by an isometry that stabilizes
![]() $\ell $
, we can assume that T corresponds to the parameters
$\ell $
, we can assume that T corresponds to the parameters
![]() $(-i,0)$
(i.e., that one of its vertices lies on the half-plane
$(-i,0)$
(i.e., that one of its vertices lies on the half-plane
![]() $\mathcal {F}_0$
). Since
$\mathcal {F}_0$
). Since
![]() $T_n\to T$
, we know that
$T_n\to T$
, we know that
![]() $v_{T_n} \to -i$
. We only have to prove that
$v_{T_n} \to -i$
. We only have to prove that
![]() $\beta (T_n)+\alpha (v_{T_n}) \to 0$
. To see this, notice that the half-plane bounded by
$\beta (T_n)+\alpha (v_{T_n}) \to 0$
. To see this, notice that the half-plane bounded by
![]() $v_{T_n}, c$
and containing
$v_{T_n}, c$
and containing
![]() $w_{T_n}$
is getting closer and closer to
$w_{T_n}$
is getting closer and closer to
![]() $\mathcal {F}_{v_{T_n}}$
. One of the vertices of
$\mathcal {F}_{v_{T_n}}$
. One of the vertices of
![]() $T_n$
is getting closer and closer to the half-plane
$T_n$
is getting closer and closer to the half-plane
![]() $\mathcal {F}_0$
; hence, the half-plane bounded by
$\mathcal {F}_0$
; hence, the half-plane bounded by
![]() $v_{T_n},c$
and containing this other vertex of
$v_{T_n},c$
and containing this other vertex of
![]() $T_n$
is getting closer and closer to
$T_n$
is getting closer and closer to
![]() $\mathcal {F}_0$
. Hence, the angle
$\mathcal {F}_0$
. Hence, the angle
![]() $\beta (T_n)$
is getting closer and closer to
$\beta (T_n)$
is getting closer and closer to
![]() $-\alpha (V_{T_n})$
(modulo
$-\alpha (V_{T_n})$
(modulo
![]() $\tfrac {2\pi }{3}\mathbb {Z}$
) and this implies that
$\tfrac {2\pi }{3}\mathbb {Z}$
) and this implies that
![]() $\theta _{T_n}$
is approaching
$\theta _{T_n}$
is approaching
![]() $0$
.
$0$
.
5.2 Description of the construction
In this section, we are going to study the topology of the space
![]() $\mathfrak {T}_{\overline {\ell }}$
and prove that it is homeomorphic to a certain quotient
$\mathfrak {T}_{\overline {\ell }}$
and prove that it is homeomorphic to a certain quotient
![]() $\mathfrak {T}_{\mathcal {O}} \times [-\infty , +\infty ] / \sim $
, where
$\mathfrak {T}_{\mathcal {O}} \times [-\infty , +\infty ] / \sim $
, where
![]() $\mathcal {O} = \ell \cap \mathcal {P} \in \ell $
.
$\mathcal {O} = \ell \cap \mathcal {P} \in \ell $
.
In order to define the construction, we need to use the following maps:
-
•
 $\iota \colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the reflection in the plane
$\iota \colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the reflection in the plane
 $\mathcal {P}$
with boundary
$\mathcal {P}$
with boundary
 ${\mathbb R}\mathbb {P}^1 \subset {{\mathbb C}}\mathbb {P}^1$
.
${\mathbb R}\mathbb {P}^1 \subset {{\mathbb C}}\mathbb {P}^1$
. -
•
 $L_{\lambda }^+\colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the hyperbolic isometry of
$L_{\lambda }^+\colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the hyperbolic isometry of
 ${\mathbb H}^3$
with axis
${\mathbb H}^3$
with axis
 $\ell $
and translation length
$\ell $
and translation length
 $\lambda \in {\mathbb R}_{>0}$
and attracting fixed point i;
$\lambda \in {\mathbb R}_{>0}$
and attracting fixed point i; -
•
 $L_{\lambda }^-\colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the hyperbolic isometry of
$L_{\lambda }^-\colon \thinspace \overline {{\mathbb H}^3} \to \overline {{\mathbb H}^3}$
is the hyperbolic isometry of
 ${\mathbb H}^3$
with axis
${\mathbb H}^3$
with axis
 $\ell $
and translation length
$\ell $
and translation length
 $\lambda \in {\mathbb R}_{>0}$
and attracting fixed point
$\lambda \in {\mathbb R}_{>0}$
and attracting fixed point
 $-i$
.
$-i$
.
In the following, we will use the decomposition
![]() $\mathfrak {T}_c = \mathfrak {T}_{c}^{\uparrow } \cup \mathfrak {T}_{c}^{\downarrow }$
, described before Proposition 5.1. We will also use the notations
$\mathfrak {T}_c = \mathfrak {T}_{c}^{\uparrow } \cup \mathfrak {T}_{c}^{\downarrow }$
, described before Proposition 5.1. We will also use the notations
![]() $A_c, B_c, C_c, D_c$
introduced there.
$A_c, B_c, C_c, D_c$
introduced there.
The isometry
![]() $L_{\lambda }^+$
can be used to move a tetrahedron in
$L_{\lambda }^+$
can be used to move a tetrahedron in
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
Proposition 5.4. The transformations
![]() $L_{\lambda }^{\pm }$
satisfy the following properties:
$L_{\lambda }^{\pm }$
satisfy the following properties:
-
1.
 $L_{\lambda }^{\pm }(\mathfrak {T}_c) = \mathfrak {T}_{L_{\lambda }^{\pm }(c)}$
;
$L_{\lambda }^{\pm }(\mathfrak {T}_c) = \mathfrak {T}_{L_{\lambda }^{\pm }(c)}$
; -
2.
 $L_{\lambda }^{\pm }(B_{c}) = B_{L_{\lambda }^{\pm }(c)}$
.
$L_{\lambda }^{\pm }(B_{c}) = B_{L_{\lambda }^{\pm }(c)}$
.
Together with the
![]() $L_\lambda ^+$
, we will also need a companion map that we will denote by
$L_\lambda ^+$
, we will also need a companion map that we will denote by
![]() $M_\lambda $
. This will be, for every
$M_\lambda $
. This will be, for every
![]() $c\in \ell $
, the map
$c\in \ell $
, the map
that moves the barycenter of the tetrahedra along
![]() $\ell $
according to
$\ell $
according to
![]() $L_\lambda ^+$
, but does not move the bottom vertex in
$L_\lambda ^+$
, but does not move the bottom vertex in
![]() $\overline {D_c}$
. In order to define
$\overline {D_c}$
. In order to define
![]() $M_{\lambda }$
, we use the coordinates on
$M_{\lambda }$
, we use the coordinates on
![]() $\mathfrak {T}_c^{\downarrow }$
described in the proof of Proposition 5.3. The map
$\mathfrak {T}_c^{\downarrow }$
described in the proof of Proposition 5.3. The map
![]() $M_\lambda $
is defined as follows: For every tetrahedron
$M_\lambda $
is defined as follows: For every tetrahedron
![]() $T \in \overline {\mathfrak {T}_{c}^{\downarrow }}$
, let
$T \in \overline {\mathfrak {T}_{c}^{\downarrow }}$
, let
![]() $M_{\lambda }(T)$
be the tetrahedron in
$M_{\lambda }(T)$
be the tetrahedron in
![]() $\mathfrak {T}_{L_{\lambda }^+(c)}^{\downarrow }$
with barycenter in
$\mathfrak {T}_{L_{\lambda }^+(c)}^{\downarrow }$
with barycenter in
![]() $L_{\lambda }^+(c)$
, same ‘bottom’ vertex
$L_{\lambda }^+(c)$
, same ‘bottom’ vertex
![]() $v_T$
and same angle
$v_T$
and same angle
![]() $\theta _T$
. Notice that in the special case when
$\theta _T$
. Notice that in the special case when
![]() $T\in \mathfrak {T}_{c}^{\downarrow ,3}$
, then
$T\in \mathfrak {T}_{c}^{\downarrow ,3}$
, then
![]() $M_{\lambda }(T) = L_{\lambda }^+(T)$
, but for tetrahedra outside
$M_{\lambda }(T) = L_{\lambda }^+(T)$
, but for tetrahedra outside
![]() $\mathfrak {T}_{c}^{\downarrow ,3}$
,
$\mathfrak {T}_{c}^{\downarrow ,3}$
,
![]() $M_{\lambda }$
and
$M_{\lambda }$
and
![]() $L_{\lambda }^+$
can be very different. By Proposition 5.3, the map
$L_{\lambda }^+$
can be very different. By Proposition 5.3, the map
![]() $M_{\lambda }$
is continuous on
$M_{\lambda }$
is continuous on
![]() $\overline {\mathfrak {T}_{c}^{\downarrow }}$
.
$\overline {\mathfrak {T}_{c}^{\downarrow }}$
.
We will need the definition of a function
![]() $h\colon \thinspace {{\mathbb C}}\mathbb {P}^1 \to [-\infty , +\infty ]$
, called the height of z. If
$h\colon \thinspace {{\mathbb C}}\mathbb {P}^1 \to [-\infty , +\infty ]$
, called the height of z. If
![]() $z \in \{\pm i\}$
, we define
$z \in \{\pm i\}$
, we define
![]() $h_i := +\infty $
and
$h_i := +\infty $
and
![]() $h_{-i} := -\infty $
. For every point
$h_{-i} := -\infty $
. For every point
![]() $z \in {{\mathbb C}}\mathbb {P}^1 \setminus \{\pm i\}$
, consider the unique hyperbolic plane perpendicular to
$z \in {{\mathbb C}}\mathbb {P}^1 \setminus \{\pm i\}$
, consider the unique hyperbolic plane perpendicular to
![]() $\ell $
and containing z in its boundary, and denote by d the intersection of this plane with
$\ell $
and containing z in its boundary, and denote by d the intersection of this plane with
![]() $\ell $
. Denote by
$\ell $
. Denote by
![]() $h_z := \eta (d)\in {\mathbb R}$
.
$h_z := \eta (d)\in {\mathbb R}$
.
For every tetrahedron in F, we denote by
![]() $b_T$
its barycenter. For every
$b_T$
its barycenter. For every
![]() $c \in \ell $
and for every tetrahedron in
$c \in \ell $
and for every tetrahedron in
![]() $\overline {\mathfrak {T}_c^{\downarrow }}$
, we denote by
$\overline {\mathfrak {T}_c^{\downarrow }}$
, we denote by
![]() $v_T$
the unique vertex of T in
$v_T$
the unique vertex of T in
![]() $\overline {D_{c}}$
and by
$\overline {D_{c}}$
and by
![]() $h_T$
the height
$h_T$
the height
![]() $h_{v_T}$
.
$h_{v_T}$
.
We can now state the main result of the section.
Theorem 5.5. There is a continuous surjective map
such that
-
1. For all
 $T\in \mathfrak {T}_{\mathcal {O}}$
, and
$T\in \mathfrak {T}_{\mathcal {O}}$
, and
 $s\in [-\infty ,+\infty ]$
,
$s\in [-\infty ,+\infty ]$
,
 $\Phi (T,-s) = \iota (\Phi (\iota (T),s))$
;
$\Phi (T,-s) = \iota (\Phi (\iota (T),s))$
; -
2. For all
 $T \in \mathfrak {T}_{\mathcal {O}}$
,
$T \in \mathfrak {T}_{\mathcal {O}}$
,
 $\Phi (T,0) = T$
;
$\Phi (T,0) = T$
; -
3. For all
 $T \in \mathfrak {T}_{\mathcal {O}}$
, and
$T \in \mathfrak {T}_{\mathcal {O}}$
, and
 $s \in [0,+\infty )$
,
$s \in [0,+\infty )$
,
 $\Phi (T,s) \in \{T \in \mathfrak {T} \mid b_T \in \ell ^+\}$
;
$\Phi (T,s) \in \{T \in \mathfrak {T} \mid b_T \in \ell ^+\}$
; -
4. The restriction
is a homeomorphism; $$\begin{align*}\Phi|_{\mathfrak{T}_{\mathcal{O}} \times (-\infty, +\infty)}\colon\thinspace \mathfrak{T}_{\mathcal{O}} \times (-\infty, +\infty) \to \mathfrak{T}_\ell\end{align*}$$
$$\begin{align*}\Phi|_{\mathfrak{T}_{\mathcal{O}} \times (-\infty, +\infty)}\colon\thinspace \mathfrak{T}_{\mathcal{O}} \times (-\infty, +\infty) \to \mathfrak{T}_\ell\end{align*}$$
-
5.
 $\Phi (\mathfrak {T}_{\mathcal {O}}^{\uparrow }\times \{+\infty \}) = \{(+ i, + i)\} \in \mathfrak {T}_i$
;
$\Phi (\mathfrak {T}_{\mathcal {O}}^{\uparrow }\times \{+\infty \}) = \{(+ i, + i)\} \in \mathfrak {T}_i$
; -
6. The restriction
 $\Phi _{+\infty }:=\Phi |_{\mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \}} \colon \thinspace \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \} \to \mathfrak {T}_i \setminus \{(+ i, + i)\}$
is surjective;
$\Phi _{+\infty }:=\Phi |_{\mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \}} \colon \thinspace \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \} \to \mathfrak {T}_i \setminus \{(+ i, + i)\}$
is surjective; -
7. Consider the function f defined by
 $$\begin{align*}f\colon\thinspace(-\infty, \eta(B_{\mathcal{O}}))\to (-\infty, +\infty)\end{align*}$$
$$\begin{align*}f\colon\thinspace(-\infty, \eta(B_{\mathcal{O}}))\to (-\infty, +\infty)\end{align*}$$
 $$\begin{align*}f(v) = v + \frac{1}{\eta(B_{\mathcal{O}}) - v} = \frac{v^2 - \eta(B_{\mathcal{O}}) v -1}{v - \eta(B_{\mathcal{O}})} .\end{align*}$$
$$\begin{align*}f(v) = v + \frac{1}{\eta(B_{\mathcal{O}}) - v} = \frac{v^2 - \eta(B_{\mathcal{O}}) v -1}{v - \eta(B_{\mathcal{O}})} .\end{align*}$$
Then f is a strictly increasing homeomorphism. For every
 $z \in {{\mathbb C}}\mathbb {P}^1$
with
$z \in {{\mathbb C}}\mathbb {P}^1$
with
 $h_z < \eta (B_{\mathcal {O}})$
, the f-uplift of z is the point
$h_z < \eta (B_{\mathcal {O}})$
, the f-uplift of z is the point
 $z^f := L^+_{\lambda }(z)$
, where
$z^f := L^+_{\lambda }(z)$
, where
 $\lambda = f(h_z)-h_z$
. When
$\lambda = f(h_z)-h_z$
. When
 $z = -i$
,
$z = -i$
,
 $z^f := -i$
. In this way,
$z^f := -i$
. In this way,
 $h_{z^f} = f(h_z)$
.
$h_{z^f} = f(h_z)$
. -
8. When
 $z \in {{\mathbb C}}\mathbb {P}^1 \setminus \{i\}$
, the fiber of
$z \in {{\mathbb C}}\mathbb {P}^1 \setminus \{i\}$
, the fiber of
 $\Phi $
at the point
$\Phi $
at the point
 $(i,z) \in \mathfrak {T}_i$
is the circle consisting of all the tetrahedra with a fixed vertex
$(i,z) \in \mathfrak {T}_i$
is the circle consisting of all the tetrahedra with a fixed vertex $$\begin{align*}\Phi^{-1}(i, z) = \{\ (T,+\infty) \mid T \in \mathfrak{T}_{\mathcal{O}}^{\downarrow}, \ \ (v_T)^f = z \ \}.\end{align*}$$
$$\begin{align*}\Phi^{-1}(i, z) = \{\ (T,+\infty) \mid T \in \mathfrak{T}_{\mathcal{O}}^{\downarrow}, \ \ (v_T)^f = z \ \}.\end{align*}$$
 $v_T \in D_{c}$
.
$v_T \in D_{c}$
.
Proof. For the proof we first construct
with the property that for all
![]() $T \in \mathfrak {T}_{\mathcal {O}}$
,
$T \in \mathfrak {T}_{\mathcal {O}}$
,
![]() $\Phi ^+(T,0) = T$
. Then, we will define
$\Phi ^+(T,0) = T$
. Then, we will define
by the formula
The map
![]() $\Phi $
will be obtained by glueing
$\Phi $
will be obtained by glueing
![]() $\Phi ^+$
and
$\Phi ^+$
and
![]() $\Phi ^-$
.
$\Phi ^-$
.
We will now discuss the construction of
![]() $\Phi ^+$
. First of all, we notice that property (7) is an easy computation. Moreover, f satisfies the properties
$\Phi ^+$
. First of all, we notice that property (7) is an easy computation. Moreover, f satisfies the properties
-
(a)
 $f(v)> v$
.
$f(v)> v$
. -
(b)
 $\widehat {f}(v) := f(v)-v = \frac {1}{\eta (B_{\mathcal {O}})-v}$
is strictly increasing and tends to
$\widehat {f}(v) := f(v)-v = \frac {1}{\eta (B_{\mathcal {O}})-v}$
is strictly increasing and tends to
 $+\infty $
when
$+\infty $
when
 $v \to \eta (B_{\mathcal {O}})$
.
$v \to \eta (B_{\mathcal {O}})$
.
We define
![]() $\Phi ^+$
as follows:
$\Phi ^+$
as follows:
-
• If
 $(T, \infty )\in \mathfrak {T}_{\mathcal {O}}^{\uparrow } \times \{+\infty \}$
, then
$(T, \infty )\in \mathfrak {T}_{\mathcal {O}}^{\uparrow } \times \{+\infty \}$
, then
 $\Phi ^+((T, \infty )) := (+i, +i)$
.
$\Phi ^+((T, \infty )) := (+i, +i)$
. -
• If
 $(T, \infty )\in \mathfrak {T}_{\mathcal {O}}^{\downarrow }\times \{+\infty \}$
, then
$(T, \infty )\in \mathfrak {T}_{\mathcal {O}}^{\downarrow }\times \{+\infty \}$
, then
 $\Phi ^+((T, \infty )) := L^+_{f(h_T) - h_T}(v_T)$
.
$\Phi ^+((T, \infty )) := L^+_{f(h_T) - h_T}(v_T)$
. -
• If
 $(T, s)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }\times [0, +\infty )$
, then
$(T, s)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }\times [0, +\infty )$
, then
 $\Phi ^+((T, s)) := L^+_{s}(T)$
.
$\Phi ^+((T, s)) := L^+_{s}(T)$
. -
• If
 $(T, s)\in \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times [0, +\infty )$
, then
$(T, s)\in \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times [0, +\infty )$
, then  $$ \begin{align*}\Phi^+((T, s)) := \left\{ \begin{array}{ll} L^+_{s}(T) & \mbox{if } s \leq f(h_T) - h_T \\ M_{s - f(h_T) + h_T} \circ L^+_{f(h_T) - h_T}(T) & \mbox{if } s \geq f(h_T) - h_T, \end{array} \right.\end{align*} $$
$$ \begin{align*}\Phi^+((T, s)) := \left\{ \begin{array}{ll} L^+_{s}(T) & \mbox{if } s \leq f(h_T) - h_T \\ M_{s - f(h_T) + h_T} \circ L^+_{f(h_T) - h_T}(T) & \mbox{if } s \geq f(h_T) - h_T, \end{array} \right.\end{align*} $$
where the map
![]() $M_{\lambda }$
is the one defined before the theorem. In order to better understand the map
$M_{\lambda }$
is the one defined before the theorem. In order to better understand the map
![]() $\Phi ^+$
, consider, for every
$\Phi ^+$
, consider, for every
![]() $s \in [0, \infty ]$
, the map represented in Figure 2, defined by
$s \in [0, \infty ]$
, the map represented in Figure 2, defined by
 $$\begin{align*}\rho_s(v) = \mathrm{min}\{v + s, f(v)\}= \begin{cases} v + s &\text{ if } v+s \leq f(v) \\ f(v) &\text{ if } v+s \geq f(v). \end{cases}.\end{align*}$$
$$\begin{align*}\rho_s(v) = \mathrm{min}\{v + s, f(v)\}= \begin{cases} v + s &\text{ if } v+s \leq f(v) \\ f(v) &\text{ if } v+s \geq f(v). \end{cases}.\end{align*}$$
Note that for any
![]() $T \in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
and
$T \in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
and
![]() $s \in [0, +\infty )$
,
$s \in [0, +\infty )$
,
![]() $\Phi ^+((T, s))$
is a tetrahedron
$\Phi ^+((T, s))$
is a tetrahedron
![]() $T'$
with height
$T'$
with height
![]() $h_{T'} = \rho _s(h_T)$
.
$h_{T'} = \rho _s(h_T)$
.

Figure 2 The functions
![]() $y = v+s$
,
$y = v+s$
,
![]() $y = f(v)$
and (in red)
$y = f(v)$
and (in red)
![]() $y = \mathfrak {T}_s(v) = \mathrm {min}\{v+s, f(v)\}$
.
$y = \mathfrak {T}_s(v) = \mathrm {min}\{v+s, f(v)\}$
.
We can now check that for any
![]() $t \in \mathfrak {T}_{\mathcal {O}}$
, we have that
$t \in \mathfrak {T}_{\mathcal {O}}$
, we have that
![]() $\Phi ^+ (T, 0) = L^+_{0}(T) = T = \Phi ^- (T, 0)$
, so we can combine the maps
$\Phi ^+ (T, 0) = L^+_{0}(T) = T = \Phi ^- (T, 0)$
, so we can combine the maps
![]() $\Phi ^+$
and
$\Phi ^+$
and
![]() $\Phi ^-$
into the map
$\Phi ^-$
into the map
![]() $\Phi $
we wanted. This calculation also shows that
$\Phi $
we wanted. This calculation also shows that
![]() $\Phi $
satisfies properties
$\Phi $
satisfies properties
![]() $(1)$
and
$(1)$
and
![]() $(2)$
. From the definition, we can also see that
$(2)$
. From the definition, we can also see that
![]() $\Phi ^+$
satisfies property
$\Phi ^+$
satisfies property
![]() $(5)$
.
$(5)$
.
Claim 5.6. The map
![]() $\Phi $
satisfies property (4); that is, the restriction
$\Phi $
satisfies property (4); that is, the restriction
is a homeomorphism.
Proof. For the surjectivity, let
![]() $T \in \mathfrak {T}_{c_s}$
, where
$T \in \mathfrak {T}_{c_s}$
, where
![]() $c_s \in \ell ^+$
. Let
$c_s \in \ell ^+$
. Let
![]() $s = \eta (c_s)\in [0, +\infty )$
.
$s = \eta (c_s)\in [0, +\infty )$
.
-
• If
 $T \in \mathfrak {T}_{c_s}^{\uparrow }$
, let
$T \in \mathfrak {T}_{c_s}^{\uparrow }$
, let
 $\widehat {T}=L^{-}_s(T)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. Then
$\widehat {T}=L^{-}_s(T)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. Then
 $\Phi ^+(\widehat {T}, s) = T$
.
$\Phi ^+(\widehat {T}, s) = T$
. -
• If
 $T \in \mathfrak {T}_{c_s}^{\downarrow }\setminus \mathfrak {T}_{c_s}^{\downarrow ,3}$
, let
$T \in \mathfrak {T}_{c_s}^{\downarrow }\setminus \mathfrak {T}_{c_s}^{\downarrow ,3}$
, let
 $h = \rho _s^{-1}(h_T)$
. We need to use the parametrization of
$h = \rho _s^{-1}(h_T)$
. We need to use the parametrization of
 $\mathfrak {T}_{c_s}^{\downarrow }$
described in the definition of the map
$\mathfrak {T}_{c_s}^{\downarrow }$
described in the definition of the map
 $M_{\lambda }$
. Let
$M_{\lambda }$
. Let
 $\widehat {T}$
be the (unique) tetrahedra in
$\widehat {T}$
be the (unique) tetrahedra in
 $\mathfrak {T}_{\mathcal {O}}$
such that
$\mathfrak {T}_{\mathcal {O}}$
such that
 $h_{\widehat {T}}= h$
and such that
$h_{\widehat {T}}= h$
and such that
 $\theta _{\widehat {T}} = \theta _{T}$
. Then again we can see that
$\theta _{\widehat {T}} = \theta _{T}$
. Then again we can see that
 $\Phi ^+(\widehat {T}, s) = T$
.
$\Phi ^+(\widehat {T}, s) = T$
. -
• If
 $T \in \mathfrak {T}_{c_s}^{\downarrow ,3}$
, let
$T \in \mathfrak {T}_{c_s}^{\downarrow ,3}$
, let
 $\widehat {T}=L^{-}_s(T)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. Then
$\widehat {T}=L^{-}_s(T)\in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. Then
 $\Phi ^+(\widehat {T}, s) = T$
.
$\Phi ^+(\widehat {T}, s) = T$
.
For the injectivity, let
![]() $T, T' \in \mathfrak {T}_{\mathcal {O}}$
and
$T, T' \in \mathfrak {T}_{\mathcal {O}}$
and
![]() $s, s' \in [0, +\infty )$
such that
$s, s' \in [0, +\infty )$
such that
![]() $\Phi ^+(T, s) = \Phi ^+(T', s') = \widehat {T}$
. Since the image is the same, the two image tetrahedra have the same barycenter, so
$\Phi ^+(T, s) = \Phi ^+(T', s') = \widehat {T}$
. Since the image is the same, the two image tetrahedra have the same barycenter, so
![]() $s = s'$
. Also, since the map
$s = s'$
. Also, since the map
![]() $\Phi ^+$
does not change the ‘type’ of the tetrahedra (that is,
$\Phi ^+$
does not change the ‘type’ of the tetrahedra (that is,
![]() $\mathfrak {T}_{c}^{\uparrow }$
or
$\mathfrak {T}_{c}^{\uparrow }$
or
![]() $\mathfrak {T}_{c_s}^{\downarrow }$
), we have two cases: either
$\mathfrak {T}_{c_s}^{\downarrow }$
), we have two cases: either
![]() $T, T' \in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
or
$T, T' \in \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
or
![]() $T, T' \in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
.
$T, T' \in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
.
-
• In the first case, the fact that
 $L_s^{+}$
is an isometry implies that
$L_s^{+}$
is an isometry implies that
 $T = T'$
.
$T = T'$
. -
• In the second case, we have that
 $h_T = h_{T'} = \rho _s^{-1}(h_{\widehat {T}})$
. Now we have two possibilities: either
$h_T = h_{T'} = \rho _s^{-1}(h_{\widehat {T}})$
. Now we have two possibilities: either
 $s \leq f(h_T) - h_T$
or
$s \leq f(h_T) - h_T$
or
 $s \geq f(h_T) - h_T$
.
$s \geq f(h_T) - h_T$
.-
1. If
 $s \leq f(h_T) - h_T$
, then we use again the fact that
$s \leq f(h_T) - h_T$
, then we use again the fact that
 $L_s^{+}$
is injective to see that
$L_s^{+}$
is injective to see that
 $T = T'$
.
$T = T'$
. -
2. If
 $s \geq f(h_T) - h_T$
, then we use again the fact that the map
$s \geq f(h_T) - h_T$
, then we use again the fact that the map
 $M_{s - f(h_T) + h_T} L_{f(h_T) - h_T}^{+}$
is injective to conclude that
$M_{s - f(h_T) + h_T} L_{f(h_T) - h_T}^{+}$
is injective to conclude that
 $T = T'$
.
$T = T'$
.
-
Since all the maps we use are continuous, we only need to check the continuity at points in
![]() $\mathfrak {T}_{\mathcal {O}}^{\uparrow } \cap \overline {\mathfrak {T}_{\mathcal {O}}^{\downarrow }}$
– that is, at tetrahedra T such that
$\mathfrak {T}_{\mathcal {O}}^{\uparrow } \cap \overline {\mathfrak {T}_{\mathcal {O}}^{\downarrow }}$
– that is, at tetrahedra T such that
![]() $h_T = \eta (B_{\mathcal {O}})$
. Since
$h_T = \eta (B_{\mathcal {O}})$
. Since
![]() $f(\eta (B_{\mathcal {O}})) = + \infty $
, then we are always in the case
$f(\eta (B_{\mathcal {O}})) = + \infty $
, then we are always in the case
![]() $s \leq f(h_T) - h_T$
, so
$s \leq f(h_T) - h_T$
, so
![]() $\Phi ^+(T, s) = L^+_{s}(T)$
.
$\Phi ^+(T, s) = L^+_{s}(T)$
.
Claim 5.7. The map
![]() $\Phi $
satisfies property (6) – that is, the restriction
$\Phi $
satisfies property (6) – that is, the restriction
![]() $\Phi _{+\infty }:=\Phi |_{\mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \}} \colon \thinspace \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \} \to \mathfrak {T}_i \setminus \{(+i,+i)\}$
is surjective.
$\Phi _{+\infty }:=\Phi |_{\mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \}} \colon \thinspace \mathfrak {T}_{\mathcal {O}}^{\downarrow } \times \{+\infty \} \to \mathfrak {T}_i \setminus \{(+i,+i)\}$
is surjective.
This also shows, together with Claim 5.6, that
![]() $\Phi $
is surjective.
$\Phi $
is surjective.
Proof. Given a point
![]() $(i,z)\in \{+ i\} \times ({{\mathbb C}}\mathbb {P}^1\setminus \{+ i\})$
, since the function f is a homeomorphism, we can find a point
$(i,z)\in \{+ i\} \times ({{\mathbb C}}\mathbb {P}^1\setminus \{+ i\})$
, since the function f is a homeomorphism, we can find a point
![]() $v \in {{\mathbb C}}\mathbb {P}^1$
such that
$v \in {{\mathbb C}}\mathbb {P}^1$
such that
![]() $f(h_v) = h_z$
and such that
$f(h_v) = h_z$
and such that
![]() $v^f = z$
. Let
$v^f = z$
. Let
![]() $T \in \mathfrak {T}_{\mathcal {O}}$
be such that
$T \in \mathfrak {T}_{\mathcal {O}}$
be such that
![]() $v_T = v$
. Then T is necessarily in
$v_T = v$
. Then T is necessarily in
![]() $\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
. By definition of the map
$\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
. By definition of the map
![]() $\Phi ^+$
,
$\Phi ^+$
,
![]() $\Phi ^+(T) = (i,z)$
.
$\Phi ^+(T) = (i,z)$
.
Now, we only have to prove the following:
Claim 5.8. The map
![]() $\Phi ^+$
is continuous.
$\Phi ^+$
is continuous.
Proof. The continuity on
![]() $\mathfrak {T}_{\mathcal {O}} \times [0,+\infty )$
was established in Claim 5.6. The continuity on
$\mathfrak {T}_{\mathcal {O}} \times [0,+\infty )$
was established in Claim 5.6. The continuity on
![]() $\mathfrak {T}_{\mathcal {O}} \times \{+\infty \}$
is clear from the definition. So, in order to check the continuity of
$\mathfrak {T}_{\mathcal {O}} \times \{+\infty \}$
is clear from the definition. So, in order to check the continuity of
![]() $\Phi ^+$
, it suffices to check the continuity for sequences
$\Phi ^+$
, it suffices to check the continuity for sequences
![]() $(T_n, s_n) \in \mathfrak {T}_{\mathcal {O}} \times [0, +\infty )$
such that
$(T_n, s_n) \in \mathfrak {T}_{\mathcal {O}} \times [0, +\infty )$
such that
![]() $T_n \to T$
and
$T_n \to T$
and
![]() $s_n \to +\infty $
. We have three cases:
$s_n \to +\infty $
. We have three cases:
-
(1) If T is in the interior part of
 $\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
, then we can assume that all the
$\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
, then we can assume that all the
 $T_n$
are also in
$T_n$
are also in
 $\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. From the definition of the map, because all the
$\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. From the definition of the map, because all the $$ \begin{align*}\Phi^+(T_n,s_n) = L^+_{s_n}(T_n) \to (+i,+i) = \Phi^+(T,+\infty),\end{align*} $$
$$ \begin{align*}\Phi^+(T_n,s_n) = L^+_{s_n}(T_n) \to (+i,+i) = \Phi^+(T,+\infty),\end{align*} $$
 $T_n$
are in
$T_n$
are in
 $\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
.
$\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
.
-
(2) If
 $T\in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
, then we can assume that all the
$T\in \mathfrak {T}_{\mathcal {O}}^{\downarrow }$
, then we can assume that all the
 $T_n$
are also in
$T_n$
are also in
 $\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
. Since
$\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
. Since
 $T_n \to T$
, when n is big enough, we can assume that
$T_n \to T$
, when n is big enough, we can assume that
 $h_{T_n}$
is close enough to
$h_{T_n}$
is close enough to
 $h_T$
. Hence, when n is big enough, we can assume that
$h_T$
. Hence, when n is big enough, we can assume that
 $s_n \geq f(h_{T_n}) - h_{T_n}$
. From the definition, we have
$s_n \geq f(h_{T_n}) - h_{T_n}$
. From the definition, we have  $$ \begin{align*}\Phi^+(T_n, s_n) = M_{s_n - f(h_{T_n}) + h_{T_n}} \circ L^+_{f(h_{T_n}) - h_{T_n}}(T_n).\end{align*} $$
$$ \begin{align*}\Phi^+(T_n, s_n) = M_{s_n - f(h_{T_n}) + h_{T_n}} \circ L^+_{f(h_{T_n}) - h_{T_n}}(T_n).\end{align*} $$
This is a tetrahedron
 $T_n'$
with vertex
$T_n'$
with vertex
 $v_{T_n'}$
equal to
$v_{T_n'}$
equal to
 $L^+_{f(h_{T_n}) - h_{T_n}}(v_{T_n})$
. Hence, the sequence
$L^+_{f(h_{T_n}) - h_{T_n}}(v_{T_n})$
. Hence, the sequence
 $\Phi ^+(T_n, s_n)$
converges to
$\Phi ^+(T_n, s_n)$
converges to
 $\Phi ^+(T, +\infty ) = L^+_{f(h_{T}) - h_{T}}(v_{T})$
.
$\Phi ^+(T, +\infty ) = L^+_{f(h_{T}) - h_{T}}(v_{T})$
. -
(3) Finally, we assume that
 $T \in \partial \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. If a subsequence of
$T \in \partial \mathfrak {T}_{\mathcal {O}}^{\uparrow }$
. If a subsequence of
 $T_n$
lies in
$T_n$
lies in
 $\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
, we can conclude that subsequence converges to
$\mathfrak {T}_{\mathcal {O}}^{\uparrow }$
, we can conclude that subsequence converges to
 $(i,i)$
as in part (1). Now let’s assume that all the
$(i,i)$
as in part (1). Now let’s assume that all the
 $T_n$
s are in
$T_n$
s are in
 $\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
, and write
$\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
, and write
 $T_n' = \Phi ^+(T_n, s_n)$
. Then,
$T_n' = \Phi ^+(T_n, s_n)$
. Then,
 $h_{T_n} \to +\infty $
and also
$h_{T_n} \to +\infty $
and also
 $f(h_{T_n}) - h_{T_n} \to +\infty $
; hence, for big enough n, we can assume that
$f(h_{T_n}) - h_{T_n} \to +\infty $
; hence, for big enough n, we can assume that
 $s_n$
is as big as we want, and
$s_n$
is as big as we want, and
 $f(h_{T_n}) - h_{T_n}$
is as big as we want. From this, we see that
$f(h_{T_n}) - h_{T_n}$
is as big as we want. From this, we see that
 $h_{T_n'}$
becomes as big as we want; hence,
$h_{T_n'}$
becomes as big as we want; hence,
 $T_n' \to (+i,+i)$
.
$T_n' \to (+i,+i)$
.
This concludes the proof of the theorem.
On
![]() $\mathfrak {T}_{\mathcal {O}} \times [-\infty , +\infty ]$
, we consider the following equivalence relation: for
$\mathfrak {T}_{\mathcal {O}} \times [-\infty , +\infty ]$
, we consider the following equivalence relation: for
![]() $T,T' \in \mathfrak {T}_{\mathcal {O}}$
and
$T,T' \in \mathfrak {T}_{\mathcal {O}}$
and
![]() $t,t' \in [-\infty , +\infty ]$
,
$t,t' \in [-\infty , +\infty ]$
,
 $$\begin{align*}(T,t) \sim (T',t') \Leftrightarrow \begin{cases} T,T' \in \mathfrak{T}_{\mathcal{O}}^{\uparrow}, t=t'=+\infty, \text{ or} \\ T,T' \in \iota(\mathfrak{T}_{\mathcal{O}}^{\uparrow}), t=t'=-\infty, \text{ or} \\ T,T' \in \mathfrak{T}_{\mathcal{O}}^{\downarrow}, v_T = v_{T'}, t=t'=+\infty, \text{ or} \\ T,T' \in \iota(\mathfrak{T}_{\mathcal{O}}^{\downarrow}), v_{\iota(T)} = v_{\iota(T')}, t=t'=-\infty, \text{ or} \\ T=T', t=t'. \end{cases} \end{align*}$$
$$\begin{align*}(T,t) \sim (T',t') \Leftrightarrow \begin{cases} T,T' \in \mathfrak{T}_{\mathcal{O}}^{\uparrow}, t=t'=+\infty, \text{ or} \\ T,T' \in \iota(\mathfrak{T}_{\mathcal{O}}^{\uparrow}), t=t'=-\infty, \text{ or} \\ T,T' \in \mathfrak{T}_{\mathcal{O}}^{\downarrow}, v_T = v_{T'}, t=t'=+\infty, \text{ or} \\ T,T' \in \iota(\mathfrak{T}_{\mathcal{O}}^{\downarrow}), v_{\iota(T)} = v_{\iota(T')}, t=t'=-\infty, \text{ or} \\ T=T', t=t'. \end{cases} \end{align*}$$
Corollary 5.9. The map
![]() $\Phi $
from Theorem 5.5 descends to a homeomorphism
$\Phi $
from Theorem 5.5 descends to a homeomorphism
Proof. The description of the fibers of the map
![]() $\Phi $
given in Theorem 5.5 guarantees that the map descends to the quotient. It is continuous and onto because
$\Phi $
given in Theorem 5.5 guarantees that the map descends to the quotient. It is continuous and onto because
![]() $\Phi $
is continuous and onto. It is
$\Phi $
is continuous and onto. It is
![]() $1$
–
$1$
–
![]() $1$
, again from the description of the fibers. It is a homeomorphism because it is a bijective continuous map from a compact space to a Hausdorff space. This concludes the proof.
$1$
, again from the description of the fibers. It is a homeomorphism because it is a bijective continuous map from a compact space to a Hausdorff space. This concludes the proof.
6 Topology of the fiber
In this section, we continue the study of the fiber
![]() $F= q^{-1}(\mathcal {O})$
of the projection
$F= q^{-1}(\mathcal {O})$
of the projection
![]() $q \colon \thinspace \Omega \to {\mathbb H}^2$
, where
$q \colon \thinspace \Omega \to {\mathbb H}^2$
, where
![]() $\mathcal {O} = (0, 1)\in {{\mathbb C}} \times {\mathbb R}_{>0}$
. In the end, we will use the study of the topology of F to describe the homeomorphism type of the smooth fiber
$\mathcal {O} = (0, 1)\in {{\mathbb C}} \times {\mathbb R}_{>0}$
. In the end, we will use the study of the topology of F to describe the homeomorphism type of the smooth fiber
![]() $\mathfrak {F}$
. We start by analyzing the structure of
$\mathfrak {F}$
. We start by analyzing the structure of
![]() $\mathfrak {T}_{\overline {\ell }}$
in a bit more detail.
$\mathfrak {T}_{\overline {\ell }}$
in a bit more detail.
6.1 Singularities of the fiber F
The space
![]() $F \cong \mathfrak {T}_{\overline {\ell }}$
is not a manifold. We will show in this subsection that it has four singular points, and all the other points have neighborhoods homeomorphic to
$F \cong \mathfrak {T}_{\overline {\ell }}$
is not a manifold. We will show in this subsection that it has four singular points, and all the other points have neighborhoods homeomorphic to
![]() ${\mathbb R}^4$
. The four singular points are
${\mathbb R}^4$
. The four singular points are
![]() $(+i,+i), (+i,-i) \in \mathfrak {T}_i$
and
$(+i,+i), (+i,-i) \in \mathfrak {T}_i$
and
![]() $(-i,-i), (-i,+i) \in \mathfrak {T}_{-i}$
. Two of them,
$(-i,-i), (-i,+i) \in \mathfrak {T}_{-i}$
. Two of them,
![]() $(+i,-i)$
and
$(+i,-i)$
and
![]() $(-i,+i)$
, are ‘mild singularities’ – they are orbifold points with isotropy group
$(-i,+i)$
, are ‘mild singularities’ – they are orbifold points with isotropy group
![]() $\mathbb {Z}_3$
. The other two singular points,
$\mathbb {Z}_3$
. The other two singular points,
![]() $(+i,+i)$
and
$(+i,+i)$
and
![]() $(-i,-i)$
, are more complicated singularities, and a small neighborhood of these points looks like the cone over a closed
$(-i,-i)$
, are more complicated singularities, and a small neighborhood of these points looks like the cone over a closed
![]() $3$
–manifold that is a Dehn filling of the trefoil knot. All such Dehn fillings are described in Moser [Reference MoserMos71]. As a consequence, we will prove Corollary 6.3, stating that the fibration q is not a smooth map.
$3$
–manifold that is a Dehn filling of the trefoil knot. All such Dehn fillings are described in Moser [Reference MoserMos71]. As a consequence, we will prove Corollary 6.3, stating that the fibration q is not a smooth map.
We already know, by part (4) of Theorem 5.5, that
![]() $\mathfrak {T}_{\ell }$
is a manifold. We will now describe a neighborhood of the points of
$\mathfrak {T}_{\ell }$
is a manifold. We will now describe a neighborhood of the points of
![]() $\mathfrak {T}_i$
and
$\mathfrak {T}_i$
and
![]() $\mathfrak {T}_{-i}$
. We only need to discuss
$\mathfrak {T}_{-i}$
. We only need to discuss
![]() $\mathfrak {T}_i$
because we have the orientation reversing homeomorphism
$\mathfrak {T}_i$
because we have the orientation reversing homeomorphism
![]() $\iota $
that exchanges
$\iota $
that exchanges
![]() $\mathfrak {T}_{-i}$
with
$\mathfrak {T}_{-i}$
with
![]() $\mathfrak {T}_i$
.
$\mathfrak {T}_i$
.
We first describe the ‘mild’ singular points and the manifold points.
Proposition 6.1. Every point
![]() $\mathfrak {T}_i$
, except from the two points
$\mathfrak {T}_i$
, except from the two points
![]() $(+i,+i)$
and
$(+i,+i)$
and
![]() $(+i,-i)$
, has a neighborhood in
$(+i,-i)$
, has a neighborhood in
![]() $\mathfrak {T}_{\overline {\ell }}$
that is homeomorphic to
$\mathfrak {T}_{\overline {\ell }}$
that is homeomorphic to
![]() ${\mathbb R}^4$
. The point
${\mathbb R}^4$
. The point
![]() $(+i,-i)$
has a neighborhood in
$(+i,-i)$
has a neighborhood in
![]() $\mathfrak {T}_{\overline {\ell }}$
that is homeomorphic to
$\mathfrak {T}_{\overline {\ell }}$
that is homeomorphic to
![]() ${\mathbb R}^4$
modded out by a linear action of
${\mathbb R}^4$
modded out by a linear action of
![]() $\mathbb {Z}_3$
.
$\mathbb {Z}_3$
.
Proof. A labelled tetrahedron is a tuple
![]() $(T,v_1,v_2,v_3,v_4)$
, where T is a regular ideal tetrahedron and
$(T,v_1,v_2,v_3,v_4)$
, where T is a regular ideal tetrahedron and
![]() $\{v_1,v_2,v_3,v_4\}$
is the set of vertices of T. We say that the labelling is even if when watching from the vertex
$\{v_1,v_2,v_3,v_4\}$
is the set of vertices of T. We say that the labelling is even if when watching from the vertex
![]() $v_1$
, the vertices
$v_1$
, the vertices
![]() $v_2,v_3,v_4$
appear in counter-clockwise cyclic order. The labelling is odd otherwise. An even labelled tetrahedron is determined by its baricenter
$v_2,v_3,v_4$
appear in counter-clockwise cyclic order. The labelling is odd otherwise. An even labelled tetrahedron is determined by its baricenter
![]() $b_T$
and the first two vertices
$b_T$
and the first two vertices
![]() $v_1, v_2$
. The vertices
$v_1, v_2$
. The vertices
![]() $v_3$
and
$v_3$
and
![]() $v_4$
are determined by these data.
$v_4$
are determined by these data.
We denote by
![]() $\mathfrak {T}_{\mathcal {O}}^{even}$
the set of all even labelled tetrahedra with barycenter in
$\mathfrak {T}_{\mathcal {O}}^{even}$
the set of all even labelled tetrahedra with barycenter in
![]() $\mathcal {O}$
. The group
$\mathcal {O}$
. The group
![]() $A_4$
acts on
$A_4$
acts on
![]() $\mathfrak {T}_{\mathcal {O}}^{even}$
in the following way: if
$\mathfrak {T}_{\mathcal {O}}^{even}$
in the following way: if
![]() $\sigma \in A_4$
, define
$\sigma \in A_4$
, define
We have a natural forgetful map
that is
![]() $12 : 1$
. This map identifies
$12 : 1$
. This map identifies
![]() $\mathfrak {T}_{\mathcal {O}}$
with a quotient:
$\mathfrak {T}_{\mathcal {O}}$
with a quotient:
The space
![]() $\mathfrak {T}_{\mathcal {O}}^{even}$
is homeomorphic to
$\mathfrak {T}_{\mathcal {O}}^{even}$
is homeomorphic to
![]() $SO(3) \simeq {\mathbb R}\mathbb {P}^3 \simeq T^1(\mathbb {S}^2)$
. To explicitly see the homeomorphism between
$SO(3) \simeq {\mathbb R}\mathbb {P}^3 \simeq T^1(\mathbb {S}^2)$
. To explicitly see the homeomorphism between
![]() $\mathfrak {T}_{\mathcal {O}}^{even}$
and
$\mathfrak {T}_{\mathcal {O}}^{even}$
and
![]() $T^1(\mathbb {S}^2)$
, notice that we can see
$T^1(\mathbb {S}^2)$
, notice that we can see
![]() $v_1$
as a point of
$v_1$
as a point of
![]() $\mathbb {S}^2$
, identify the circle where the other three vertices lie with the tangent circle at
$\mathbb {S}^2$
, identify the circle where the other three vertices lie with the tangent circle at
![]() $v_1$
, and then see
$v_1$
, and then see
![]() $v_2$
as a unit tangent vector to the point
$v_2$
as a unit tangent vector to the point
![]() $v_1$
. An interesting consequence is that
$v_1$
. An interesting consequence is that
![]() $\mathfrak {T}_{\mathcal {O}} \simeq SO(3)/A_4$
.
$\mathfrak {T}_{\mathcal {O}} \simeq SO(3)/A_4$
.
We define the open subset
![]() $\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
as
$\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
as
The subset
![]() $\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
is not preserved by the action of
$\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
is not preserved by the action of
![]() $A_4$
. Only the subgroup of
$A_4$
. Only the subgroup of
![]() $A_4$
that fixes
$A_4$
that fixes
![]() $1$
acts there. This subgroup is isomorphic to
$1$
acts there. This subgroup is isomorphic to
![]() $\mathbb {Z}_3$
.
$\mathbb {Z}_3$
.
The restriction of r to
![]() $\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
gives a
$\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }$
gives a
![]() $3:1$
map
$3:1$
map
that identifies
![]() $\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
with a quotient
$\mathfrak {T}_{\mathcal {O}}^{\downarrow }$
with a quotient
We now apply a construction called mapping cylinder to
![]() $\mathfrak {T}_{\mathcal {O}}^{even}$
. The mapping cylinder of
$\mathfrak {T}_{\mathcal {O}}^{even}$
. The mapping cylinder of
![]() $p\colon \thinspace T^1(\mathbb {S}^2) \to \mathbb {S}^2$
is the space
$p\colon \thinspace T^1(\mathbb {S}^2) \to \mathbb {S}^2$
is the space
where
![]() $\sim $
is defined by
$\sim $
is defined by
![]() $(y, 0) \sim p(y)$
. Note that
$(y, 0) \sim p(y)$
. Note that
![]() $M_p$
corresponds to the unit disk bundle of
$M_p$
corresponds to the unit disk bundle of
![]() ${\mathbb S}^2$
, and its boundary is the unit tangent bundle
${\mathbb S}^2$
, and its boundary is the unit tangent bundle
![]() $\partial M_p \cong T^1(\mathbb {S}^2) \cong {\mathbb R}\mathbb {P}^3 \cong \mathrm {SO}(3)$
. In particular,
$\partial M_p \cong T^1(\mathbb {S}^2) \cong {\mathbb R}\mathbb {P}^3 \cong \mathrm {SO}(3)$
. In particular,
![]() $M_p$
is a manifold with boundary.
$M_p$
is a manifold with boundary.
We now take its double; that is, we glue two copies of
![]() $M_p$
along their boundary via the identity map:
$M_p$
along their boundary via the identity map:
The space M is clearly a manifold, and it is not hard to see that it is indeed homeomorphic to the manifold
![]() ${\mathbb S}^2 \times {\mathbb S}^2$
, even if we will not need this fact here.
${\mathbb S}^2 \times {\mathbb S}^2$
, even if we will not need this fact here.
Now, it is also clear from the definition that we have a map
This map identifies M with the quotient
where the equivalence relation
![]() $\sim $
identifies all the labelled tetrahedra in
$\sim $
identifies all the labelled tetrahedra in
![]() $\mathfrak {T}_{\mathcal {O}}^{even} \times \{\infty \}$
that have the same vertex
$\mathfrak {T}_{\mathcal {O}}^{even} \times \{\infty \}$
that have the same vertex
![]() $v_1$
and, similarly, identifies all the labelled tetrahedra in
$v_1$
and, similarly, identifies all the labelled tetrahedra in
![]() $\mathfrak {T}_{\mathcal {O}}^{even} \times \{-\infty \}$
that have the same vertex
$\mathfrak {T}_{\mathcal {O}}^{even} \times \{-\infty \}$
that have the same vertex
![]() $v_1$
.
$v_1$
.
Now, let’s consider the following open subset of
![]() $\mathfrak {T}_{\mathcal {O}}^{even} \times [-\infty ,\infty ]$
:
$\mathfrak {T}_{\mathcal {O}}^{even} \times [-\infty ,\infty ]$
:
The image
![]() $\Psi (U)$
is an open subset of M; hence, it is a manifold.
$\Psi (U)$
is an open subset of M; hence, it is a manifold.
Now let’s consider again the
![]() $3:1$
map
$3:1$
map
![]() $r_|: {\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }} \rightarrow \mathfrak {T}^{\downarrow }_{\mathcal {O}}$
. This induces the map
$r_|: {\mathfrak {T}_{\mathcal {O}}^{even, \downarrow }} \rightarrow \mathfrak {T}^{\downarrow }_{\mathcal {O}}$
. This induces the map
where
![]() $\Phi $
is the map from Theorem 5.5. The image of this map is an open subset V of F that contains
$\Phi $
is the map from Theorem 5.5. The image of this map is an open subset V of F that contains
![]() $\mathfrak {T}_i \setminus \{(+i,+i)\}$
. Moreover, V is homeomorphic with the quotient
$\mathfrak {T}_i \setminus \{(+i,+i)\}$
. Moreover, V is homeomorphic with the quotient
![]() $\Psi (U)$
by the action of the group
$\Psi (U)$
by the action of the group
![]() $\mathbb {Z}_3$
. This shows that all the points of
$\mathbb {Z}_3$
. This shows that all the points of
![]() $\mathfrak {T}_i \setminus \{(+i,+i),(+i,-i)\}$
are manifold points in F, and that the point
$\mathfrak {T}_i \setminus \{(+i,+i),(+i,-i)\}$
are manifold points in F, and that the point
![]() $(+i,-i)$
is an orbifold point with group
$(+i,-i)$
is an orbifold point with group
![]() $\mathbb {Z}_3$
.
$\mathbb {Z}_3$
.
We now describe a neighborhood of the singular point
![]() $(+i,+i)$
.
$(+i,+i)$
.
Proposition 6.2. The point
![]() $(+i,+i)$
has a neighborhood in
$(+i,+i)$
has a neighborhood in
![]() $\mathfrak {T}$
that is homeomorphic to the cone
$\mathfrak {T}$
that is homeomorphic to the cone
![]() $C(M)$
over a closed
$C(M)$
over a closed
![]() $3$
–manifold M, where M is a Dehn filling of the complement of the trefoil knot.
$3$
–manifold M, where M is a Dehn filling of the complement of the trefoil knot.
Note that all the possible Dehn fillings of the trefoil knot are described in [Reference MoserMos71].
Proof. Using the notation of Section 5.1, Let
![]() $\beta _{\mathcal {O}}' = \beta _{\mathcal {O}}-1$
, and consider the disc
$\beta _{\mathcal {O}}' = \beta _{\mathcal {O}}-1$
, and consider the disc
![]() $D_{\beta _{\mathcal {O}}'}$
, an open disc in
$D_{\beta _{\mathcal {O}}'}$
, an open disc in
![]() ${{\mathbb C}}\mathbb {P}^1$
contained in
${{\mathbb C}}\mathbb {P}^1$
contained in
![]() $D_{\beta _{\mathcal {O}}}$
. We define the closed subset
$D_{\beta _{\mathcal {O}}}$
. We define the closed subset
![]() $\mathfrak {T}_{\mathcal {O}}^*$
of
$\mathfrak {T}_{\mathcal {O}}^*$
of
![]() $\mathfrak {T}_{\mathcal {O}}$
as the set of tetrahedra in
$\mathfrak {T}_{\mathcal {O}}$
as the set of tetrahedra in
![]() $\mathfrak {T}_{\mathcal {O}}$
such that all vertices are in
$\mathfrak {T}_{\mathcal {O}}$
such that all vertices are in
![]() ${{\mathbb C}}\mathbb {P}^1 \setminus D_{\beta _{c}'}$
. This is a closed neighborhood of
${{\mathbb C}}\mathbb {P}^1 \setminus D_{\beta _{c}'}$
. This is a closed neighborhood of
![]() $\mathfrak {T}_{\mathcal {O}}^\uparrow $
, and it is homeomorphic to
$\mathfrak {T}_{\mathcal {O}}^\uparrow $
, and it is homeomorphic to
![]() $\mathfrak {T}_{\mathcal {O}}^\uparrow $
.
$\mathfrak {T}_{\mathcal {O}}^\uparrow $
.
Now consider the set
where
![]() $\Phi $
is the map from Theorem 5.5. The set U is a closed neighborhood of
$\Phi $
is the map from Theorem 5.5. The set U is a closed neighborhood of
![]() $(+i,+i)$
in F, and it is easy to see that U is a cone with center in
$(+i,+i)$
in F, and it is easy to see that U is a cone with center in
![]() $(+i,+i)$
over the boundary
$(+i,+i)$
over the boundary
![]() $\partial U$
. We only need to prove that
$\partial U$
. We only need to prove that
![]() $\partial U$
is homeomorphic to a Dehn filling of the trefoil knot complement.
$\partial U$
is homeomorphic to a Dehn filling of the trefoil knot complement.
The boundary
![]() $\partial U$
is the union of two pieces,
$\partial U$
is the union of two pieces,
![]() $\Phi (\mathfrak {T}_{\mathcal {O}}^* \times \{0\})$
and
$\Phi (\mathfrak {T}_{\mathcal {O}}^* \times \{0\})$
and
![]() $\Phi (\partial \mathfrak {T}_{\mathcal {O}}^* \times [0,+\infty ])$
. The first piece,
$\Phi (\partial \mathfrak {T}_{\mathcal {O}}^* \times [0,+\infty ])$
. The first piece,
![]() $\Phi (\mathfrak {T}_{\mathcal {O}}^* \times \{0\})$
, is homeomorphic to
$\Phi (\mathfrak {T}_{\mathcal {O}}^* \times \{0\})$
, is homeomorphic to
![]() $\mathfrak {T}_{\mathcal {O}}^*$
(i.e. homeomorphic to
$\mathfrak {T}_{\mathcal {O}}^*$
(i.e. homeomorphic to
![]() $\mathfrak {T}_{\mathcal {O}}^\uparrow $
), and by Proposition 5.2, this is homeomorphic to the trefoil knot complement. The second piece is homeomorphic to a solid torus: indeed,
$\mathfrak {T}_{\mathcal {O}}^\uparrow $
), and by Proposition 5.2, this is homeomorphic to the trefoil knot complement. The second piece is homeomorphic to a solid torus: indeed,
![]() $\partial \mathfrak {T}_{\mathcal {O}}^*$
is a torus,
$\partial \mathfrak {T}_{\mathcal {O}}^*$
is a torus,
![]() $\Phi (\partial \mathfrak {T}_{\mathcal {O}} \times [0,+\infty ))$
is homeomorphic to a torus times
$\Phi (\partial \mathfrak {T}_{\mathcal {O}} \times [0,+\infty ))$
is homeomorphic to a torus times
![]() $[0,+\infty )$
, and
$[0,+\infty )$
, and
![]() $\Phi (\partial \mathfrak {T}_{\mathcal {O}} \times \{+\infty \})$
is a circle that completes the solid torus.
$\Phi (\partial \mathfrak {T}_{\mathcal {O}} \times \{+\infty \})$
is a circle that completes the solid torus.
From this, we can see that
![]() $\partial U$
is a Dehn filling of the trefoil knot complement.
$\partial U$
is a Dehn filling of the trefoil knot complement.
Corollary 6.3. The fiber bundle
![]() $q\colon \thinspace \Omega \to {\mathbb H}^2$
is not smooth.
$q\colon \thinspace \Omega \to {\mathbb H}^2$
is not smooth.
Proof. The map q is
![]() $SL(2,{\mathbb R})$
–equivariant. If it were smooth, it would have some regular values, and by
$SL(2,{\mathbb R})$
–equivariant. If it were smooth, it would have some regular values, and by
![]() $SL(2,{\mathbb R})$
–equivariance, all the values would be regular. Hence, it would be a submersion, and this would imply that the fiber would be a smooth manifold, which is impossible because it has four singular points.
$SL(2,{\mathbb R})$
–equivariance, all the values would be regular. Hence, it would be a submersion, and this would imply that the fiber would be a smooth manifold, which is impossible because it has four singular points.
6.2 Cohomology of the fiber F
In this section, we will study the cohomology of
![]() $\mathfrak {T}_{\overline {\ell }} \cong F$
, and this will determine the cohomology for
$\mathfrak {T}_{\overline {\ell }} \cong F$
, and this will determine the cohomology for
![]() $\mathfrak {F}$
. In particular, we will reprove a result of Dumas–Sanders [Reference Dumas and SandersDS20]. The proof will include calculations that we will need in later proofs:
$\mathfrak {F}$
. In particular, we will reprove a result of Dumas–Sanders [Reference Dumas and SandersDS20]. The proof will include calculations that we will need in later proofs:
Proposition 6.4 (Theorem C in [Reference Dumas and SandersDS20]).
F is a Poincaré duality space; it is simply connected, and its homology is given by
-
•
 $H^0(F;\mathbb {Z}) \cong \mathbb {Z}$
;
$H^0(F;\mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^1(F;\mathbb {Z}) = H^3(F;\mathbb {Z}) = 0$
;
$H^1(F;\mathbb {Z}) = H^3(F;\mathbb {Z}) = 0$
; -
•
 $H^2(F;\mathbb {Z}) \cong \mathbb {Z} \oplus \mathbb {Z}$
;
$H^2(F;\mathbb {Z}) \cong \mathbb {Z} \oplus \mathbb {Z}$
; -
•
 $H^4(F; \mathbb {Z}) \cong \mathbb {Z}$
;
$H^4(F; \mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^i(F;\mathbb {Z}) =0$
for all
$H^i(F;\mathbb {Z}) =0$
for all
 $i> 4$
.
$i> 4$
.
Moreover, for each
![]() $i= 0, \ldots , 4$
, there is a natural isomorphism
$i= 0, \ldots , 4$
, there is a natural isomorphism
![]() $H^i(F; \mathbb {Z}) \cong H_{4-i}(F; \mathbb {Z})$
.
$H^i(F; \mathbb {Z}) \cong H_{4-i}(F; \mathbb {Z})$
.
To prove Proposition 6.4, we work again with
![]() $\mathfrak {T}_{\overline {\ell }}$
. We will write
$\mathfrak {T}_{\overline {\ell }}$
. We will write
![]() $\mathfrak {T}_{\overline {\ell }}$
as a union of two open sets
$\mathfrak {T}_{\overline {\ell }}$
as a union of two open sets
Let
The first thing we have to prove is the following:
Proposition 6.5. The open set A deformation retracts to
Similarly, B deformation retracts to
Proof. Denote by
![]() $\kappa = (\kappa _1,\kappa _2)$
the inverse of the map
$\kappa = (\kappa _1,\kappa _2)$
the inverse of the map
which is a homeomorphism by Theorem 5.5. So for
![]() $x \in A \setminus \mathfrak {T}_i$
,
$x \in A \setminus \mathfrak {T}_i$
,
![]() $\kappa _1(x) \in \mathfrak {T}_{\mathcal {O}}$
,
$\kappa _1(x) \in \mathfrak {T}_{\mathcal {O}}$
,
![]() $\kappa _2(x) \in (-1,+\infty )$
, and
$\kappa _2(x) \in (-1,+\infty )$
, and
![]() $\Phi (\kappa _1(x),\kappa _2(x)) = x$
. Here,
$\Phi (\kappa _1(x),\kappa _2(x)) = x$
. Here,
![]() $\kappa _2(x) = \eta (b_x)$
. We write the retraction as
$\kappa _2(x) = \eta (b_x)$
. We write the retraction as
 $$\begin{align*}H(x,t) := \begin{cases} x & \text{ if } x\in \mathfrak{T}_i\\ \Phi(\kappa_1(x),\kappa_2(x)+t) & \text{ if } x\in A \setminus \mathfrak{T}_i. \end{cases} \end{align*}$$
$$\begin{align*}H(x,t) := \begin{cases} x & \text{ if } x\in \mathfrak{T}_i\\ \Phi(\kappa_1(x),\kappa_2(x)+t) & \text{ if } x\in A \setminus \mathfrak{T}_i. \end{cases} \end{align*}$$
It is easy to check that H is a retraction by deformation; that is, H is continuous,
![]() $H(\cdot ,0)$
is the identity on A,
$H(\cdot ,0)$
is the identity on A,
![]() $H(x,+\infty ) \in \mathfrak {T}_i$
and for all
$H(x,+\infty ) \in \mathfrak {T}_i$
and for all
![]() $x \in \mathfrak {T}_i, H(x,t) = x$
.
$x \in \mathfrak {T}_i, H(x,t) = x$
.
We will also use the following version of Poincaré Duality to calculate the homology of the intersection Y. Note that we use the convention that homology and cohomology groups of negative dimension are zero, so the duality statement includes the fact that all the nontrivial homology and cohomology of M lies in the dimension range from
![]() $0$
to n.
$0$
to n.
Theorem 6.6 (Poincaré Duality, see Hatcher [Reference HatcherHat02, page 231]).
Let M be a closed orientable n–manifold. Then
-
1.
 $H_k(M;\mathbb {Z})$
and
$H_k(M;\mathbb {Z})$
and
 $H^{n-k}(M;\mathbb {Z})$
are isomorphic.
$H^{n-k}(M;\mathbb {Z})$
are isomorphic. -
2. Modulo their torsion subgroups,
 $H_k(M;\mathbb {Z})$
and
$H_k(M;\mathbb {Z})$
and
 $H_{n-k}(M;\mathbb {Z})$
are isomorphic.
$H_{n-k}(M;\mathbb {Z})$
are isomorphic. -
3. The torsion subgroups of
 $H_{k}(M;\mathbb {Z})$
and
$H_{k}(M;\mathbb {Z})$
and
 $H_{n-k-1}(M;\mathbb {Z})$
are isomorphic for
$H_{n-k-1}(M;\mathbb {Z})$
are isomorphic for
 $k = 0, \ldots , 4$
.
$k = 0, \ldots , 4$
.
Proof of Proposition 6.4.
The fact that F is a Poincaré duality space follows from the fact that F is homotopically equivalent to the smooth manifold
![]() $\mathfrak {F}$
, since both are homotopically equivalent to
$\mathfrak {F}$
, since both are homotopically equivalent to
![]() $\Omega $
, as proven in Corollary 4.10 and Theorem 3.1. Since F and
$\Omega $
, as proven in Corollary 4.10 and Theorem 3.1. Since F and
![]() $\mathfrak {T}_{\overline {\ell }}$
are homeomorphic, this also tells us that
$\mathfrak {T}_{\overline {\ell }}$
are homeomorphic, this also tells us that
![]() $\mathfrak {T}_{\overline {\ell }}$
is a Poincaré duality space.
$\mathfrak {T}_{\overline {\ell }}$
is a Poincaré duality space.
For the second part of the result, we will study the homology and cohomology of
![]() $\mathfrak {T}_{\overline {\ell }}$
, which will suffice to conclude. Through all the proof, we will use the decomposition above for
$\mathfrak {T}_{\overline {\ell }}$
, which will suffice to conclude. Through all the proof, we will use the decomposition above for
![]() $\mathfrak {T}_{\overline {\ell }} = A \cup B$
and
$\mathfrak {T}_{\overline {\ell }} = A \cup B$
and
![]() $Y = A\cap B$
. Using Proposition 6.5 and the definitions, we can see the following homotopy equivalences:
$Y = A\cap B$
. Using Proposition 6.5 and the definitions, we can see the following homotopy equivalences:
-
•
 $A, B \simeq {\mathbb S}^2$
, and
$A, B \simeq {\mathbb S}^2$
, and -
•
 $Y \simeq \mathrm {SO}(3)/A_4$
.
$Y \simeq \mathrm {SO}(3)/A_4$
.
The simple connectivity of
![]() $\mathfrak {T}_{\overline {\ell }}$
follows from Seifert–Van Kampen theorem and the decomposition
$\mathfrak {T}_{\overline {\ell }}$
follows from Seifert–Van Kampen theorem and the decomposition
![]() $\mathfrak {T}_{\overline {\ell }} = A \cup B$
described above. Proposition 6.5 shows that the groups
$\mathfrak {T}_{\overline {\ell }} = A \cup B$
described above. Proposition 6.5 shows that the groups
![]() $\pi _1(A)$
and
$\pi _1(A)$
and
![]() $\pi _1(B)$
are trivial, and hence that
$\pi _1(B)$
are trivial, and hence that
![]() $\pi _1(\mathfrak {T}_{\overline {\ell }})$
is trivial as well. Since
$\pi _1(\mathfrak {T}_{\overline {\ell }})$
is trivial as well. Since
![]() $\mathfrak {T}_{\overline {\ell }}$
is connected, this proves that
$\mathfrak {T}_{\overline {\ell }}$
is connected, this proves that
![]() $\mathfrak {T}_{\overline {\ell }}$
is simply connected.
$\mathfrak {T}_{\overline {\ell }}$
is simply connected.
In order to compute the cohomology of
![]() $\mathfrak {T}_{\overline {\ell }}$
, we will use the Mayer–Vietoris sequence. We know the cohomology of A and B:
$\mathfrak {T}_{\overline {\ell }}$
, we will use the Mayer–Vietoris sequence. We know the cohomology of A and B:
-
•
 $H^0(A;\mathbb {Z}) \cong H^0(B;\mathbb {Z}) \cong \mathbb {Z}$
;
$H^0(A;\mathbb {Z}) \cong H^0(B;\mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^2(A;\mathbb {Z}) \cong H^2(B;\mathbb {Z}) \cong \mathbb {Z}$
;
$H^2(A;\mathbb {Z}) \cong H^2(B;\mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^i(A;\mathbb {Z}) = H^i(B;\mathbb {Z}) =0$
for
$H^i(A;\mathbb {Z}) = H^i(B;\mathbb {Z}) =0$
for
 $i = 1$
and for all
$i = 1$
and for all
 $i> 2$
.
$i> 2$
.
In order to compute the cohomology of Y, we remember that it deformation retracts to
![]() $\mathrm {SO}(3)/A_4$
, which is a Seifert-fibered manifold described in the second line of Table 10.6 in Martelli [Reference MartelliMar22] with
$\mathrm {SO}(3)/A_4$
, which is a Seifert-fibered manifold described in the second line of Table 10.6 in Martelli [Reference MartelliMar22] with
![]() $q = -2$
. Hence, the cohomology for Y is
$q = -2$
. Hence, the cohomology for Y is
-
•
 $H^0(Y;\mathbb {Z})\cong \mathbb {Z}$
;
$H^0(Y;\mathbb {Z})\cong \mathbb {Z}$
; -
•
 $H^1(Y;\mathbb {Z}) = 0$
;
$H^1(Y;\mathbb {Z}) = 0$
; -
•
 $H^2(Y;\mathbb {Z}) \cong \mathbb {Z}_3$
;
$H^2(Y;\mathbb {Z}) \cong \mathbb {Z}_3$
; -
•
 $H^3(Y;\mathbb {Z}) \cong \mathbb {Z}$
;
$H^3(Y;\mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^i(Y;\mathbb {Z}) =0$
for all
$H^i(Y;\mathbb {Z}) =0$
for all
 $i> 3$
.
$i> 3$
.
Since Y is connected, we have
![]() $H_0(Y;\mathbb {Z}) \cong H^3(Y;\mathbb {Z})\cong \mathbb {Z}$
, and since it is a manifold, and hence a Poincaré duality space, we have that
$H_0(Y;\mathbb {Z}) \cong H^3(Y;\mathbb {Z})\cong \mathbb {Z}$
, and since it is a manifold, and hence a Poincaré duality space, we have that
![]() $H_3(Y;\mathbb {Z}) \cong H^0(Y;\mathbb {Z}) \cong \mathbb {Z}$
. From Martelli [Reference MartelliMar22], we can see that
$H_3(Y;\mathbb {Z}) \cong H^0(Y;\mathbb {Z}) \cong \mathbb {Z}$
. From Martelli [Reference MartelliMar22], we can see that
![]() $H_1(Y;\mathbb {Z}) \cong H^2(Y;\mathbb {Z}) \cong \mathbb {Z}_3$
. Finally, again using Poincaré duality (see Theorem 6.6 with
$H_1(Y;\mathbb {Z}) \cong H^2(Y;\mathbb {Z}) \cong \mathbb {Z}_3$
. Finally, again using Poincaré duality (see Theorem 6.6 with
![]() $n = 3$
), we can see that
$n = 3$
), we can see that
![]() $H_2(Y;\mathbb {Z}) \cong H^1(Y;\mathbb {Z})$
is free (because its torsion subgroup is isomorphic to the one of
$H_2(Y;\mathbb {Z}) \cong H^1(Y;\mathbb {Z})$
is free (because its torsion subgroup is isomorphic to the one of
![]() $H_0(Y;\mathbb {Z})$
), and that
$H_0(Y;\mathbb {Z})$
), and that
![]() $H_2(Y;\mathbb {Z}) = H^1(Y;\mathbb {Z}) = 0$
(because
$H_2(Y;\mathbb {Z}) = H^1(Y;\mathbb {Z}) = 0$
(because
![]() $H_1(Y;\mathbb {Z})\cong \mathbb {Z}_3$
and, modulo their torsion subgroups,
$H_1(Y;\mathbb {Z})\cong \mathbb {Z}_3$
and, modulo their torsion subgroups,
![]() $H_1(M;\mathbb {Z})$
and
$H_1(M;\mathbb {Z})$
and
![]() $H_{2}(M;\mathbb {Z})$
are isomorphic).
$H_{2}(M;\mathbb {Z})$
are isomorphic).
Now we are ready to compute the cohomology of
![]() $\mathfrak {T}_{\overline {\ell }}$
. We have
$\mathfrak {T}_{\overline {\ell }}$
. We have
-
•
 $H^0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z}$
;
$H^0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z}$
; -
•
 $H^1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z} ) = 0$
;
$H^1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z} ) = 0$
; -
•
 $H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z} \oplus \mathbb {Z}$
;
$H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z} \oplus \mathbb {Z}$
; -
•
 $H^4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z}$
;
$H^4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z}$
; -
•
 $H^i(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) =0$
for all
$H^i(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) =0$
for all
 $i> 4$
.
$i> 4$
.
Since
![]() $\mathfrak {T}_{\overline {\ell }}$
is connected, we have
$\mathfrak {T}_{\overline {\ell }}$
is connected, we have
![]() $H_0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong H^4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z}$
. Using Theorem 6.6, we can see that
$H_0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong H^4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong \mathbb {Z}$
. Using Theorem 6.6, we can see that
![]() $H_4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong H_0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z}$
, that
$H_4(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong H_0(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z}$
, that
![]() $H_1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H_3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = 0$
, and that
$H_1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H_3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^1(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = H^3(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) = 0$
, and that
![]() $H_2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
is free abelian. We now use the following exact sequence coming from the Mayer–Vietoris sequence to see that
$H_2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z}) \cong H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
is free abelian. We now use the following exact sequence coming from the Mayer–Vietoris sequence to see that
![]() $H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z} \oplus \mathbb {Z}$
.
$H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})\cong \mathbb {Z} \oplus \mathbb {Z}$
.
As we said, using the fact that F is homeomorphic to
![]() $\mathfrak {T}_{\overline {\ell }}$
via the map
$\mathfrak {T}_{\overline {\ell }}$
via the map
![]() $g^{-1}$
, the result follows.
$g^{-1}$
, the result follows.
6.3 The homeomorphism type of
 $\mathfrak {F}$
$\mathfrak {F}$
In this section, we will prove the following result:
Proposition 6.7.
![]() $\mathfrak {F}$
is homeomorphic to
$\mathfrak {F}$
is homeomorphic to
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
, and F and
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
, and F and
![]() $\mathfrak {T}_{\overline {\ell }}$
are homotopically equivalent to
$\mathfrak {T}_{\overline {\ell }}$
are homotopically equivalent to
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
.
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
.
For the proof, we need deep classification theorems of simply connected smooth
![]() $4$
–manifolds due to Whitehead, Milnor, Milnor–Hausemoller, Freedman, Serre and Donaldson, which use their intersection form. The intersection form for a closed oriented
$4$
–manifolds due to Whitehead, Milnor, Milnor–Hausemoller, Freedman, Serre and Donaldson, which use their intersection form. The intersection form for a closed oriented
![]() $4$
–manifold N is the map
$4$
–manifold N is the map
defined by
![]() $Q_N(\alpha , \beta ) : = (\alpha \smile \beta ) [N],$
where
$Q_N(\alpha , \beta ) : = (\alpha \smile \beta ) [N],$
where
![]() $\alpha , \beta \in H^2(N, \mathbb {Z})$
and
$\alpha , \beta \in H^2(N, \mathbb {Z})$
and
![]() $\smile $
denotes the cohomological cup product of
$\smile $
denotes the cohomological cup product of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and
$\beta $
and
![]() $[N]\in H_4(N;\mathbb {Z})$
is the fundamental class. See Scorpan [Reference ScorpanSco05, Chap. 3] for a more detailed discussion.
$[N]\in H_4(N;\mathbb {Z})$
is the fundamental class. See Scorpan [Reference ScorpanSco05, Chap. 3] for a more detailed discussion.
This definition of the intersection form only uses the cup product, and this is well defined for all topological spaces, including our singular space
![]() $\mathfrak {T}_{\overline {\ell }}$
. In our proof, we want to compute the intersection form of the smooth
$\mathfrak {T}_{\overline {\ell }}$
. In our proof, we want to compute the intersection form of the smooth
![]() $4$
–manifold
$4$
–manifold
![]() $\mathfrak {F}$
, and we will do this by computing the cup product of the homotopically equivalent space
$\mathfrak {F}$
, and we will do this by computing the cup product of the homotopically equivalent space
![]() $\mathfrak {T}_{\overline {\ell }}$
.
$\mathfrak {T}_{\overline {\ell }}$
.
Recall the following definitions:
-
• The intersection form
 $Q_N$
is called unimodular if the matrix representing
$Q_N$
is called unimodular if the matrix representing
 $Q_N$
is invertible over
$Q_N$
is invertible over
 $\mathbb {Z}$
.
$\mathbb {Z}$
. -
• The rank of
 $Q_N$
is defined as
$Q_N$
is defined as
 $\mathrm {rank}(Q_N):= \mathrm {dim}_{\mathbb {Z}} H^2(N; \mathbb {Z})$
.
$\mathrm {rank}(Q_N):= \mathrm {dim}_{\mathbb {Z}} H^2(N; \mathbb {Z})$
. -
• The signature of
 $Q_N$
as where
$Q_N$
as where $$ \begin{align*}\mathrm{sign}(Q_N): = \mathrm{dim}_{\mathbb{Z}} H^2_+(N; \mathbb{Z}) - \mathrm{dim}_{\mathbb{Z}} H^2_-(N; \mathbb{Z}),\end{align*} $$
$$ \begin{align*}\mathrm{sign}(Q_N): = \mathrm{dim}_{\mathbb{Z}} H^2_+(N; \mathbb{Z}) - \mathrm{dim}_{\mathbb{Z}} H^2_-(N; \mathbb{Z}),\end{align*} $$
 $H^2_+(N; \mathbb {Z})$
(resp.
$H^2_+(N; \mathbb {Z})$
(resp.
 $H^2_-(N; \mathbb {Z})$
) is defined as the maximal positive-definite (resp. negative-definite) subspace for
$H^2_-(N; \mathbb {Z})$
) is defined as the maximal positive-definite (resp. negative-definite) subspace for
 $Q_N$
.
$Q_N$
.
-
• The definiteness of
 $Q_N$
can be positive definite, negative definite or indefinite. We say that
$Q_N$
can be positive definite, negative definite or indefinite. We say that
 $Q_N$
is positive-definite if for all nonzero
$Q_N$
is positive-definite if for all nonzero
 $\alpha $
, we have
$\alpha $
, we have
 $Q_N(\alpha , \alpha )> 0$
, and negative-definite if for all nonzero
$Q_N(\alpha , \alpha )> 0$
, and negative-definite if for all nonzero
 $\alpha $
, we have
$\alpha $
, we have
 $Q_N(\alpha , \alpha ) < 0$
. If there exists classes
$Q_N(\alpha , \alpha ) < 0$
. If there exists classes
 $\alpha $
, and
$\alpha $
, and
 $\beta $
such that
$\beta $
such that
 $Q_N(\alpha , \alpha )> 0$
and
$Q_N(\alpha , \alpha )> 0$
and
 $Q_N(\beta , \beta )< 0$
, then
$Q_N(\beta , \beta )< 0$
, then
 $Q_N$
is called indefinite.
$Q_N$
is called indefinite. -
• The parity of
 $Q_N$
can be even or odd. We say that
$Q_N$
can be even or odd. We say that
 $Q_N$
is even if for all classes
$Q_N$
is even if for all classes
 $\alpha $
, we have
$\alpha $
, we have
 $Q_N(\alpha , \alpha )$
is even. Otherwise, we say that
$Q_N(\alpha , \alpha )$
is even. Otherwise, we say that
 $Q_N$
is odd.
$Q_N$
is odd.
As proven in Scorpan [Reference ScorpanSco05, Sec. 3.2], the intersection form
![]() $Q_N$
of a
$Q_N$
of a
![]() $4$
–manifold is always unimodular. In addition, the intersection form satisfies the following properties: given two
$4$
–manifold is always unimodular. In addition, the intersection form satisfies the following properties: given two
![]() $4$
–manifolds
$4$
–manifolds
![]() $N_1$
and
$N_1$
and
![]() $N_2$
, we have
$N_2$
, we have
-
•
 $Q_{\overline {N}} = -Q_N,$
where
$Q_{\overline {N}} = -Q_N,$
where
 $\overline {N}$
is N with opposite orientation.
$\overline {N}$
is N with opposite orientation. -
•
 $Q_{N_1 \# N_2} = Q_{N_1} \oplus Q_{N_2}$
, where
$Q_{N_1 \# N_2} = Q_{N_1} \oplus Q_{N_2}$
, where
 $N_1 \# N_2$
is the connected sum of
$N_1 \# N_2$
is the connected sum of
 $N_1$
and
$N_1$
and
 $N_2$
.
$N_2$
.
Example 6.8. In Scorpan [Reference ScorpanSco05, Sec. 3.2], one can see the details of the calculations of the intersection forms for
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
and
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
and
![]() $\mathbb {S}^2 \times \mathbb {S}^2$
which are simply-connected
$\mathbb {S}^2 \times \mathbb {S}^2$
which are simply-connected
![]() $4$
–manifolds with their intersection forms of rank
$4$
–manifolds with their intersection forms of rank
![]() $2$
and indefinite signature. The parity is odd for
$2$
and indefinite signature. The parity is odd for
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
, and even for
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
, and even for
![]() $\mathbb {S}^2 \times \mathbb {S}^2$
. In fact, their intersection forms are given by
$\mathbb {S}^2 \times \mathbb {S}^2$
. In fact, their intersection forms are given by
-
•
 $Q_{{{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2} = \begin {bmatrix} 1 & 0\\ 0 & -1 \end {bmatrix}$
,
$Q_{{{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2} = \begin {bmatrix} 1 & 0\\ 0 & -1 \end {bmatrix}$
, -
•
 $Q_{\mathbb {S}^2 \times \mathbb {S}^2} = \begin {bmatrix} 0 & 1\\ 1 & 0 \end {bmatrix}$
.
$Q_{\mathbb {S}^2 \times \mathbb {S}^2} = \begin {bmatrix} 0 & 1\\ 1 & 0 \end {bmatrix}$
.
We will use the following classification theorems of smooth
![]() $4$
–manifolds, due to Serre, Freedman and Donaldson:
$4$
–manifolds, due to Serre, Freedman and Donaldson:
Theorem 6.9 (Serre, Freedman, Donaldson).
Two smooth simply-connected
![]() $4$
–manifolds are homeomorphic if and only if their intersection forms have the same rank, signature, and parity.
$4$
–manifolds are homeomorphic if and only if their intersection forms have the same rank, signature, and parity.
Theorem 6.10 (Freedman’s Classification Theorem [Reference FreedmanFre82]).
For any integral symmetric unimodular form Q, there is a closed simply-connected topological
![]() $4$
–manifold that has Q as its intersection form.
$4$
–manifold that has Q as its intersection form.
-
• If Q is even, there is exactly one such manifold.
-
• If Q is odd, there are exactly two such manifolds, at least one of which does not admit any smooth structures.
Proof of Theorem 6.7.
First, since F,
![]() $\mathfrak {T}_{\overline {\ell }}$
and
$\mathfrak {T}_{\overline {\ell }}$
and
![]() $\mathfrak {F}$
are homotopically equivalent, their intersection forms are isomorphic. Since our description of
$\mathfrak {F}$
are homotopically equivalent, their intersection forms are isomorphic. Since our description of
![]() $\mathfrak {T}_{\overline {\ell }}$
is more concrete, we will discuss
$\mathfrak {T}_{\overline {\ell }}$
is more concrete, we will discuss
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
and use that discussion to find the homeomorphism type of
$Q_{\mathfrak {T}_{\overline {\ell }}}$
and use that discussion to find the homeomorphism type of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
First, we know that the rank of
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
is
$Q_{\mathfrak {T}_{\overline {\ell }}}$
is
![]() $2$
because
$2$
because
![]() $H^2(\mathfrak {T}_{\overline {\ell }}; \mathbb {Z})\cong \mathbb {Z} \oplus \mathbb {Z}$
.
$H^2(\mathfrak {T}_{\overline {\ell }}; \mathbb {Z})\cong \mathbb {Z} \oplus \mathbb {Z}$
.
Second, since there is a self-homeomorphism r of
![]() $\mathfrak {T}_{\overline {\ell }}$
reversing the orientation, and since the sign satisfies the following property:
$\mathfrak {T}_{\overline {\ell }}$
reversing the orientation, and since the sign satisfies the following property:
![]() $\mathrm {sign}(Q_N) = -\mathrm {sign}(Q_{\overline {N}}),$
where
$\mathrm {sign}(Q_N) = -\mathrm {sign}(Q_{\overline {N}}),$
where
![]() $\overline {N}$
is N with opposite orientation, we can see that the signature of the intersection form is
$\overline {N}$
is N with opposite orientation, we can see that the signature of the intersection form is
![]() $\mathrm {sign}(Q_{\mathfrak {T}_{\overline {\ell }}}) = 0$
, and hence,
$\mathrm {sign}(Q_{\mathfrak {T}_{\overline {\ell }}}) = 0$
, and hence,
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
is indefinite.
$Q_{\mathfrak {T}_{\overline {\ell }}}$
is indefinite.
Let us show that
 $Q_{\mathfrak {T}_{\overline {\ell }}} = \begin {bmatrix} 1 & 0\\ 0 & -1 \end {bmatrix}$
in an appropriate basis.
$Q_{\mathfrak {T}_{\overline {\ell }}} = \begin {bmatrix} 1 & 0\\ 0 & -1 \end {bmatrix}$
in an appropriate basis.
From the Mayer–Vietoris sequence in cohomology, we have
Let r be the orientation reversing involution of
![]() $\mathfrak {T}_{\overline {\ell }}$
. We have that
$\mathfrak {T}_{\overline {\ell }}$
. We have that
![]() $r(A) = B$
. The two maps
$r(A) = B$
. The two maps
![]() $H^2(A;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
and
$H^2(A;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
and
![]() $H^2(B;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
are either both zero or both nonzero. By the Mayer-Vietoris sequence, the map
$H^2(B;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
are either both zero or both nonzero. By the Mayer-Vietoris sequence, the map
![]() $H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z})\to H^2(Y;\mathbb {Z})$
is onto; hence, the two maps are both nonzero. We choose the generators of
$H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z})\to H^2(Y;\mathbb {Z})$
is onto; hence, the two maps are both nonzero. We choose the generators of
![]() $H^2(A;\mathbb {Z})$
and
$H^2(A;\mathbb {Z})$
and
![]() $H^2(B;\mathbb {Z})$
such that both generators map to
$H^2(B;\mathbb {Z})$
such that both generators map to
![]() $1$
in
$1$
in
![]() $H^2(Y;\mathbb {Z}) = Z_3$
. The map
$H^2(Y;\mathbb {Z}) = Z_3$
. The map
![]() $\zeta \colon \thinspace H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
can then be written as
$\zeta \colon \thinspace H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z}) \to H^2(Y;\mathbb {Z})$
can then be written as
Hence, the Mayer–Vietoris sequence and the injective map
![]() $\mu \colon \thinspace H^2(\mathfrak {T}_{\overline {\ell }}) \to H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z})$
identifies
$\mu \colon \thinspace H^2(\mathfrak {T}_{\overline {\ell }}) \to H^2(A;\mathbb {Z}) \oplus H^2(B;\mathbb {Z})$
identifies
![]() $H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
with the subgroup
$H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
with the subgroup
A basis of
![]() $H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
is given by the elements
$H^2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
is given by the elements
![]() $v=(2,1)$
and
$v=(2,1)$
and
![]() $w=(1,2)$
. We now express
$w=(1,2)$
. We now express
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
as a matrix in this basis:
$Q_{\mathfrak {T}_{\overline {\ell }}}$
as a matrix in this basis:
 $$\begin{align*}Q_{\mathfrak{T}_{\overline{\ell}}} = \begin{pmatrix} x & z\\ z & y. \end{pmatrix} \end{align*}$$
$$\begin{align*}Q_{\mathfrak{T}_{\overline{\ell}}} = \begin{pmatrix} x & z\\ z & y. \end{pmatrix} \end{align*}$$
In order to compute
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
, we consider the elements
$Q_{\mathfrak {T}_{\overline {\ell }}}$
, we consider the elements
![]() $(3,0) = 2v-w$
and
$(3,0) = 2v-w$
and
![]() $(0,3) = 2w-v$
. These two elements are
$(0,3) = 2w-v$
. These two elements are
![]() $Q_{\mathfrak {T}_{\overline {\ell }}}$
–orthogonal because A and B retract to disjoint
$Q_{\mathfrak {T}_{\overline {\ell }}}$
–orthogonal because A and B retract to disjoint
![]() $2$
–cycles in
$2$
–cycles in
![]() $H_2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
, and we have that
$H_2(\mathfrak {T}_{\overline {\ell }};\mathbb {Z})$
, and we have that
![]() $(3,0)$
maps to
$(3,0)$
maps to
![]() $0$
in
$0$
in
![]() $H^2(B;\mathbb {Z})$
and
$H^2(B;\mathbb {Z})$
and
![]() $(0,3)$
maps to
$(0,3)$
maps to
![]() $0$
in
$0$
in
![]() $H^2(A;\mathbb {Z})$
. We have
$H^2(A;\mathbb {Z})$
. We have
where
![]() $q \in \mathbb {Z}$
is the norm of
$q \in \mathbb {Z}$
is the norm of
![]() $(3,0)$
. The norm of
$(3,0)$
. The norm of
![]() $(0,3)$
is then
$(0,3)$
is then
![]() $-q$
because
$-q$
because
![]() $r(3,0) = (0,\pm 3)$
, and r reverses the orientation.
$r(3,0) = (0,\pm 3)$
, and r reverses the orientation.
The determinant of the
![]() $3 \times 3$
matrix of the coefficients is
$3 \times 3$
matrix of the coefficients is
![]() $27 \neq 0$
; hence, the system of equations has at most one solution. An explicit solution is given by
$27 \neq 0$
; hence, the system of equations has at most one solution. An explicit solution is given by
![]() $x = \frac {q}{3}, y = -\frac {q}{3}, z=0$
. Since Q is unimodular, this implies
$x = \frac {q}{3}, y = -\frac {q}{3}, z=0$
. Since Q is unimodular, this implies
![]() $q = \pm 3$
and we conclude that
$q = \pm 3$
and we conclude that
 $$\begin{align*}Q_{\mathfrak{T}_{\overline{\ell}}} = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}Q_{\mathfrak{T}_{\overline{\ell}}} = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}. \end{align*}$$
Since
![]() $\mathfrak {T}_{\overline {\ell }}$
and
$\mathfrak {T}_{\overline {\ell }}$
and
![]() $\mathfrak F$
are homotopy equivalent, we have proven that
$\mathfrak F$
are homotopy equivalent, we have proven that
![]() $\mathfrak F$
has the same intersection matrix as
$\mathfrak F$
has the same intersection matrix as
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
. Since
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
. Since
![]() $\mathfrak F$
is smooth, Freedman’s Classification Theorem tells us that
$\mathfrak F$
is smooth, Freedman’s Classification Theorem tells us that
![]() $\mathfrak F$
is homeomorphic to
$\mathfrak F$
is homeomorphic to
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
(hence that
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
(hence that
![]() $\mathfrak {T}_{\overline {\ell }}$
and F are homotopy equivalent to
$\mathfrak {T}_{\overline {\ell }}$
and F are homotopy equivalent to
![]() ${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
).
${{\mathbb C}}\mathbb {P}^2 \# \overline {{{\mathbb C}}\mathbb {P}}^2$
).
Acknowledgements
The authors would like to thank Renato Bettiol, David Dumas, Steve Kerckhoff, Qiongling Li, Tom Mark, Tye Lidman, Andy Sanders and Florian Stecker for interesting conversations related to the paper, and Colin Davalo for sharing a preprint of his results. We are also very grateful to the referees for their valuable suggestions which greatly improved the paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
We acknowledge support from U.S. National Science Foundation grants DMS 1107452, 1107263, 1107367 ‘RNMS: GEometric structures And Representation varieties’ (the GEAR Network). S.M. was partially supported by U.S. National Science Foundation grants DMS-1848346 (NSF CAREER). N.T. acknowledges support from the CNRS International Emerging Action program. A.W. was suported by the European Research Council under ERC-Consolidator Grant grant 614733 and ERC-Advanced Grant 101018839, as well as by the DFG through the project 338644254 (SPP2026). A.W. thanks the Hector Fellow Academy for support, and the Institute of Advanced Study, Princeton, for its hopsitality.