1. Introduction
The paper by Schmid (Reference Schmid2010) stands out as the only paper in the Journal of Fluid Mechanics to be the subject of two Focus of Fluids articles. The initial article, authored by Henningson (Reference Henningson2010), focused on the potential implications of the work. Now, after 14 years, we reflect on the enduring impact of the paper and why it was selected as the most significant paper in the Journal of Fluid Mechanics published in the century of volumes 601–700.
Schmid (Reference Schmid2010) introduced dynamic mode decomposition (DMD), which was initially presented at the 2008 APS-DFD meeting (Schmid & Sesterhenn Reference Schmid and Sesterhenn2008). The DMD approach serves as a factorization and dimensionality reduction technique for sequential data streams. Essentially, it provides a means to analyse and extract dynamic behaviour from time-series data, particularly within the context of dynamical systems and fluid dynamics. It represents an equation-free, data-driven approach aimed at identifying spatial and temporal patterns or modes within the data.
The rapid adoption and success of DMD in fluid mechanics since Schmid (Reference Schmid2010) has likely coincided with the concurrent rise of data science and the rapid development of time-resolved, planar and volumetric velocity field measurement techniques (particle image velocimetry and its variants) and numerical simulations (direct numerical simulations and large-eddy simulations). These techniques provide the necessary input to DMD, as described by Schmid (Reference Schmid2010), in the form of constant-sampling-rate time-series data.
2. Overview
The fundamental aspects of the DMD approach are depicted in figure 1. The time-series data are arranged into a data (snapshot) matrix 
$\boldsymbol {D}$ where each column represents a snapshot of the system at a specific time. The aim is to produce a decomposition of this data matrix into three matrices capturing spatial structures ($\boldsymbol {\varPhi }$), the amplitudes (${\rm {diag}}(\boldsymbol {\xi })$) and temporal dynamics ($\boldsymbol {C}$).
Figure 1. Dynamic mode decomposition: (a) factorization and (b) dimensionality reduction. Adapted with permission from Schmid (Reference Schmid2022).
The reduced-order representation detailed in figure 1(b) may be obtained by manually selecting modes that correspond to large amplitudes and/or frequencies of interest, or via algorithmic methods such as the sparsity-promoting DMD variant developed in Jovanović, Schmid & Nichols (Reference Jovanović, Schmid and Nichols2014). This reduced subset aims to capture the dominant dynamics of the system. The selected (dynamic) modes depict spatial patterns or structures evolving over time, with each mode representing a specific oscillatory behaviour or dynamic feature of the system. Furthermore, the eigenvalues associated with each dynamic mode are produced by the DMD algorithm, providing insights into the growth or decay rates of the respective modes.
The DMD approach is closely associated with Koopman analysis, a technique used in dynamical systems theory. Specifically, DMD produces the best (least-squares) fit linear dynamical system to the nonlinear dynamical system generating the data; its dynamic modes are approximations of Koopman modes (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009). Hence, DMD provides a straightforward and powerful algorithm for computing Koopman eigenfunctions and their associated eigenvalues (Brunton et al. Reference Brunton, Budišić, Kaiser and Kutz2022), which can be further enhanced through the use of nonlinear transformations of the original data (Williams, Kevrekidis & Rowley Reference Williams, Kevrekidis and Rowley2015). Moreover, as pointed out by Henningson (Reference Henningson2010), the dynamic modes of DMD simplify to global linear eigenmodes for linearized problems or to Fourier modes for (nonlinear) periodic problems.
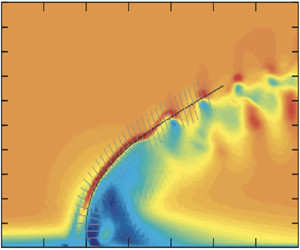
The DMD methodology is well suited for analysing flows where the processed data capture relevant temporal and/or spatial scales of the dynamic process. Schmid (Reference Schmid2022) presents an illustrative example demonstrating its effectiveness in complex flows, particularly in describing the evolution of structures along curved trajectories in space. For instance, as depicted in figure 2, a turbulent jet in cross-flow exhibits a breakdown of vortical structures developing along a curved counterrotating vortex pair. Streamline-based DMD analysis reveals this phenomenon by projecting the three-dimensional velocity fields into in-plane and plane-normal components along the curved streamline and incorporating these data into the DMD data matrix.
Figure 2. Jet in cross-flow. (a) Isocontour of $Q$ for representative snapshot. (b) Layout of the spatial slices normal to the base-flow streamline. (c) First dominant dynamic mode from streamline-based DMD analysis of the spatial evolution of fluid structures along the counterrotating vortex sheet. Velocity vectors shown in black and vorticity contours in red–grey colour in a plane normal to the base-flow streamline emanating from the jet exit. Adapted with permission from Schmid (Reference Schmid2022).
While DMD has predominantly been utilized in fluid mechanical studies for flow-field analysis, its application extends to various other domains, including thermal, reactive, acoustic or fluid-structural time-series data. In addition to serving as a diagnostic tool through low-rank spatiotemporal features, DMD facilitates state estimation and future-state prediction, paving the way for its application in purely data-driven control strategies (Kutz et al. Reference Kutz, Brunton, Brunton and Proctor2016). These attributes, coupled with the approach's versatility in handling a variety of evolution processes and data formats, underscore the broad appeal and utility of DMD.
3. Broader applications and future
Schmid (Reference Schmid2022) provides a comprehensive review of recent advancements in DMD, emphasizing its strengths while also recognizing its limitations. Since DMD is limited to linear analysis, it may struggle to capture nonlinear transients and strong nonlinearity effects. It can also face robustness challenges when dealing with noisy or insufficient data, which are usually unknowns, as well as sparse measurements or data with sub-Nyquist sampling. Consequently, considerable attention has been directed towards extending, generalizing and improving DMD, making it an active area of ongoing research (Kutz et al. Reference Kutz, Brunton, Brunton and Proctor2016; Schmid Reference Schmid2022).
The utility of the DMD approach, relying solely on data without the need for an underlying model or governing equations, has led to its rapid adoption across numerous fields beyond fluid mechanics. Examples range from its utilization in the analysis and forecasting of highway traffic (Avila & Mezić Reference Avila and Mezić2020) to its application in facial recognition schemes. In this latter context, DMD's capability to represent the temporal information of an entire video as a single image with dimensions similar to those of the video's constituent images serves as a critical preprocessing step, enabling efficient detection of spoof samples (Tirunagari et al. Reference Tirunagari, Poh, Windridge, Iorliam, Suki and Ho2015). Furthermore, DMD finds application in medicine, such as in the real-time forecasting of tumour ablation treatment simulations (Bourantas et al. Reference Bourantas, Ghommem, Kagadis, Katsanos, Loukopoulos, Burganos and Nikiforidis2014), and in robotics, where Berger et al. (Reference Berger, Sastuba, Vogt, Jung and Ben Amor2015) integrated DMD with machine learning to detect, estimate and compensate for external perturbations using only input from standard sensors. Numerous other application areas, as described by Schmid (Reference Schmid2022), extend to neuroscience, epidemiology, medical imaging, climate science, oceanography and financial engineering.
The above list of application areas is far from complete and will only continue to grow. Indeed, the citation numbers of Schmid (Reference Schmid2010) continue to increase exponentially year on year. This growth is unlikely to halt anytime soon, especially given the incorporation of DMD into many modern machine learning approaches (Brunton, Noack & Koumoutsakos Reference Brunton, Noack and Koumoutsakos2020), whose uptake in research has been staggering. Coupled with the ever-growing generation of data, in both quality and quantity, this trend ensures that the impact of data-centric techniques such as DMD will only continue to expand.
$Q$ for representative snapshot. (b) Layout of the spatial slices normal to the base-flow streamline. (c) First dominant dynamic mode from streamline-based DMD analysis of the spatial evolution of fluid structures along the counterrotating vortex sheet. Velocity vectors shown in black and vorticity contours in red–grey colour in a plane normal to the base-flow streamline emanating from the jet exit. Adapted with permission from Schmid (2022).
You have
Access
Open access
1. Introduction
The paper by Schmid (Reference Schmid2010) stands out as the only paper in the Journal of Fluid Mechanics to be the subject of two Focus of Fluids articles. The initial article, authored by Henningson (Reference Henningson2010), focused on the potential implications of the work. Now, after 14 years, we reflect on the enduring impact of the paper and why it was selected as the most significant paper in the Journal of Fluid Mechanics published in the century of volumes 601–700.
Schmid (Reference Schmid2010) introduced dynamic mode decomposition (DMD), which was initially presented at the 2008 APS-DFD meeting (Schmid & Sesterhenn Reference Schmid and Sesterhenn2008). The DMD approach serves as a factorization and dimensionality reduction technique for sequential data streams. Essentially, it provides a means to analyse and extract dynamic behaviour from time-series data, particularly within the context of dynamical systems and fluid dynamics. It represents an equation-free, data-driven approach aimed at identifying spatial and temporal patterns or modes within the data.
The rapid adoption and success of DMD in fluid mechanics since Schmid (Reference Schmid2010) has likely coincided with the concurrent rise of data science and the rapid development of time-resolved, planar and volumetric velocity field measurement techniques (particle image velocimetry and its variants) and numerical simulations (direct numerical simulations and large-eddy simulations). These techniques provide the necessary input to DMD, as described by Schmid (Reference Schmid2010), in the form of constant-sampling-rate time-series data.
2. Overview
The fundamental aspects of the DMD approach are depicted in figure 1. The time-series data are arranged into a data (snapshot) matrix
$\boldsymbol {D}$ where each column represents a snapshot of the system at a specific time. The aim is to produce a decomposition of this data matrix into three matrices capturing spatial structures (
$\boldsymbol {\varPhi }$), the amplitudes (
${\rm {diag}}(\boldsymbol {\xi })$) and temporal dynamics (
$\boldsymbol {C}$).
Figure 1. Dynamic mode decomposition: (a) factorization and (b) dimensionality reduction. Adapted with permission from Schmid (Reference Schmid2022).
The reduced-order representation detailed in figure 1(b) may be obtained by manually selecting modes that correspond to large amplitudes and/or frequencies of interest, or via algorithmic methods such as the sparsity-promoting DMD variant developed in Jovanović, Schmid & Nichols (Reference Jovanović, Schmid and Nichols2014). This reduced subset aims to capture the dominant dynamics of the system. The selected (dynamic) modes depict spatial patterns or structures evolving over time, with each mode representing a specific oscillatory behaviour or dynamic feature of the system. Furthermore, the eigenvalues associated with each dynamic mode are produced by the DMD algorithm, providing insights into the growth or decay rates of the respective modes.
The DMD approach is closely associated with Koopman analysis, a technique used in dynamical systems theory. Specifically, DMD produces the best (least-squares) fit linear dynamical system to the nonlinear dynamical system generating the data; its dynamic modes are approximations of Koopman modes (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009). Hence, DMD provides a straightforward and powerful algorithm for computing Koopman eigenfunctions and their associated eigenvalues (Brunton et al. Reference Brunton, Budišić, Kaiser and Kutz2022), which can be further enhanced through the use of nonlinear transformations of the original data (Williams, Kevrekidis & Rowley Reference Williams, Kevrekidis and Rowley2015). Moreover, as pointed out by Henningson (Reference Henningson2010), the dynamic modes of DMD simplify to global linear eigenmodes for linearized problems or to Fourier modes for (nonlinear) periodic problems.
The DMD methodology is well suited for analysing flows where the processed data capture relevant temporal and/or spatial scales of the dynamic process. Schmid (Reference Schmid2022) presents an illustrative example demonstrating its effectiveness in complex flows, particularly in describing the evolution of structures along curved trajectories in space. For instance, as depicted in figure 2, a turbulent jet in cross-flow exhibits a breakdown of vortical structures developing along a curved counterrotating vortex pair. Streamline-based DMD analysis reveals this phenomenon by projecting the three-dimensional velocity fields into in-plane and plane-normal components along the curved streamline and incorporating these data into the DMD data matrix.
Figure 2. Jet in cross-flow. (a) Isocontour of
$Q$ for representative snapshot. (b) Layout of the spatial slices normal to the base-flow streamline. (c) First dominant dynamic mode from streamline-based DMD analysis of the spatial evolution of fluid structures along the counterrotating vortex sheet. Velocity vectors shown in black and vorticity contours in red–grey colour in a plane normal to the base-flow streamline emanating from the jet exit. Adapted with permission from Schmid (Reference Schmid2022).
While DMD has predominantly been utilized in fluid mechanical studies for flow-field analysis, its application extends to various other domains, including thermal, reactive, acoustic or fluid-structural time-series data. In addition to serving as a diagnostic tool through low-rank spatiotemporal features, DMD facilitates state estimation and future-state prediction, paving the way for its application in purely data-driven control strategies (Kutz et al. Reference Kutz, Brunton, Brunton and Proctor2016). These attributes, coupled with the approach's versatility in handling a variety of evolution processes and data formats, underscore the broad appeal and utility of DMD.
3. Broader applications and future
Schmid (Reference Schmid2022) provides a comprehensive review of recent advancements in DMD, emphasizing its strengths while also recognizing its limitations. Since DMD is limited to linear analysis, it may struggle to capture nonlinear transients and strong nonlinearity effects. It can also face robustness challenges when dealing with noisy or insufficient data, which are usually unknowns, as well as sparse measurements or data with sub-Nyquist sampling. Consequently, considerable attention has been directed towards extending, generalizing and improving DMD, making it an active area of ongoing research (Kutz et al. Reference Kutz, Brunton, Brunton and Proctor2016; Schmid Reference Schmid2022).
The utility of the DMD approach, relying solely on data without the need for an underlying model or governing equations, has led to its rapid adoption across numerous fields beyond fluid mechanics. Examples range from its utilization in the analysis and forecasting of highway traffic (Avila & Mezić Reference Avila and Mezić2020) to its application in facial recognition schemes. In this latter context, DMD's capability to represent the temporal information of an entire video as a single image with dimensions similar to those of the video's constituent images serves as a critical preprocessing step, enabling efficient detection of spoof samples (Tirunagari et al. Reference Tirunagari, Poh, Windridge, Iorliam, Suki and Ho2015). Furthermore, DMD finds application in medicine, such as in the real-time forecasting of tumour ablation treatment simulations (Bourantas et al. Reference Bourantas, Ghommem, Kagadis, Katsanos, Loukopoulos, Burganos and Nikiforidis2014), and in robotics, where Berger et al. (Reference Berger, Sastuba, Vogt, Jung and Ben Amor2015) integrated DMD with machine learning to detect, estimate and compensate for external perturbations using only input from standard sensors. Numerous other application areas, as described by Schmid (Reference Schmid2022), extend to neuroscience, epidemiology, medical imaging, climate science, oceanography and financial engineering.
The above list of application areas is far from complete and will only continue to grow. Indeed, the citation numbers of Schmid (Reference Schmid2010) continue to increase exponentially year on year. This growth is unlikely to halt anytime soon, especially given the incorporation of DMD into many modern machine learning approaches (Brunton, Noack & Koumoutsakos Reference Brunton, Noack and Koumoutsakos2020), whose uptake in research has been staggering. Coupled with the ever-growing generation of data, in both quality and quantity, this trend ensures that the impact of data-centric techniques such as DMD will only continue to expand.
Acknowledgements
I wish to thank Dr S. Illingworth and Dr S. Dawson for their informative insights and helpful discussions, and the ONR (grant N62909-23-1-2068) for financial support.
Declaration of interests
The author reports no conflict of interest.