We consider the problem of tracking a Brownian motion by a process of bounded variation, in such a way as to minimize total expected cost of both ‘action' and ‘deviation from a target state 0'. The former is proportional to the amount of control exerted to date, while the latter is being measured by a function which can be viewed, for simplicity, as quadratic. We discuss the discounted, stationary and finite-horizon variants of the problem. The answer to all three questions takes the form of exerting control in a singular manner, in order not to exit from a certain region. Explicit solutions are found for the first and second questions, while the third is reduced to an appropriate optimal stopping problem. This reduction yields properties, as well as global upper and lower bounds, for the associated moving boundary. The pertinent Abelian and ergodic relationships for the corresponding value functions are also derived.

Let Y(t) be a pure birth process. If a maximum likelihood estimator of the birth intensity is desired and the number n of observational points and the last observation T are given in advance, it is shown that equidistant sampling is not an optimal procedure. Properties of ‘optimal' designs and the corresponding maximum likelihood estimators are investigated and compared with equidistant and continuous sampling.

Recently the authors introduced the concept of Markov decision drift processes. A Markov decision drift process can be seen as a straightforward generalization of a Markov decision process with continuous time parameter. In this paper we investigate the existence of stationary average optimal policies for Markov decision drift processes. Using a well-known Abelian theorem we derive sufficient conditions, which guarantee that a ‘limit point' of a sequence of discounted optimal policies with the discounting factor approaching 1 is an average optimal policy. An alternative set of sufficient conditions is obtained for the case in which the discounted optimal policies generate regenerative stochastic processes. The latter set of conditions is easier to verify in several applications. The results of this paper are also applicable to Markov decision processes with discrete or continuous time parameter and to semi-Markov decision processes. In this sense they generalize some well-known results for Markov decision processes with finite or compact action space. Applications to an M/M/1 queueing model and a maintenance replacement model are given. It is shown that under certain conditions on the model parameters the average optimal policy for the M/M/1 queueing model is monotone non-decreasing (as a function of the number of waiting customers) with respect to the service intensity and monotone non-increasing with respect to the arrival intensity. For the maintenance replacement model we prove the average optimality of a bang-bang type policy. Special attention is paid to the computation of the optimal control parameters.

Techniques for studying the reliability of simple series or parallel systems are well known. This paper is concerned with more complicated systems in which the load on failed elements is transmitted to unfailed elements according to some load-sharing rule. The emphasis is on local load sharing, and in particular on a specific load-sharing rule introduced by Harlow and Phoenix for fibrous composites. Earlier results are reviewed and improved techniques for approximating the probability of failure and the size effect are derived.

A large deviation theorem of the Cramér–Petrov type and a ranking limit theorem of Loève are used to derive an approximation for the statistical distribution of the failure time of fibrous materials. For that, fibrous materials are modeled as a series of independent and identical bundles of parallel filaments and the asymptotic distribution of their failure time is determined in terms of statistical characteristics of the individual filaments, as both the number of filaments in each bundle and the number of bundles in the chain grow large simultaneously. 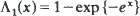While keeping the number n of filaments in each bundle fixed and increasing only the chain length k leads to a Weibull limiting distribution for the failure time, letting both increase in such a way that log k(n) = o(n), we show that the limit distribution is for 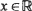. Since fibrous materials which are both long and have many filaments prevail, the result is of importance in the materials science area since refined approximations to failure-time distributions can be achieved.

Queueing systems which can be formulated as Markov renewal processes with basic transitions of three types, ‘arrivals', ‘departures' and ‘feedbacks' are examined. The filtering procedure developed for Markov renewal processes by Çinlar (1969) is applied to such queueing models to show that the queue-length processes embedded at any of the ‘arrival', ‘departure', ‘feedback', ‘input', ‘output' or ‘external' transition epochs are also Markov renewal. In this part we focus attention on the derivation of stationary and limiting distributions (when they exist) for each of the embedded discrete-time processes, the embedded Markov chains. These results are applied to birth–death queues with instantaneous state-dependent feedback including the special cases of M/M/1/N and M/M/1 queues with instantaneous Bernoulli feedback.

In this part we extend and particularise results developed by the author in Part I (pp. 349–375) for a class of queueing systems which can be formulated as Markov renewal processes. We examine those models where the basic transition consists of only two types: ‘arrivals' and ‘departures'. The ‘arrival lobby' and ‘departure lobby' queue-length processes are shown, using the results of Part I to be Markov renewal. Whereas the initial study focused attention on the behaviour of the embedded discrete-time Markov chains, in this paper we examine, in detail, the embedded continuous-time semi-Markov processes. The limiting distributions of the queue-length processes in both continuous and discrete time are derived and interrelationships between them are examined in the case of continuous-time birth–death queues including the M/M/1/M and M/M/1 variants. Results for discrete-time birth–death queues are also derived.

We study the queue GI/M/s with customers of m different types. An arriving customer is of type i with probability pi and the types of different customers are independent. A customer of type i requires a service time which is exponentially distributed with parameter bi. This model is equivalent to the queue GI/Hm/s, where Hm denotes a mixture of m different exponential distributions. We are primarily interested in the distributions of waiting times and queue lengths. Using a probabilistic argument we reduce the problem to the solution of a system of Wiener-Hopf-type equations. This system is solved by a factorization method. Thus we obtain explicit results for the stationary distributions of waiting times and queue lengths.

Waiting-time distributions for M/G/1 systems with priority dependent on class, order of arrival, service length, etc., are difficult to obtain. For single-server multipurpose processors the difficulties are compounded. A certain ergodic post-arrival depletion time is shown to be a true maximum for all delay times of interest. Explicit numerical evaluation of the distribution of this time is available. A heavy-traffic distribution for this time is shown to provide a simple and useful engineering tool with good results and insensitivity to service-time distribution even at modest traffic intensity levels. The relationship to the diffusion approximation for heavy traffic is described.

A particular queue, the general arrival, general service-time, infinite-server queue (GA/G/∞), is introduced and certain of its properties studied. Motivated by a life situation in which the interarrival times for service converge to 0, a different sort of regularity condition (involving a tail property of random measures) is imposed on the arrival process to prove various limit theorems. There are similarities to heavy-traffic theory.

In this note we establish an inequality between the maximal coefficient of correlation and the φ -mixing coefficient which is symmetric in its arguments. Motivated by this inequality, we introduce a mixing coefficient which is the product of two φ -mixing coefficients.

We also study an invariance principle under conditions imposed on this new mixing coefficient. As a consequence of this result it follows that the invariance principle holds when either the direct-time process or its time-reversed process is φ -mixing; when both processes are φ-mixing the invariance principle holds for sequences of L2-integrable random variables under a mixing rate weaker than that used by Ibragimov.

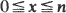Consider first-passage percolation on the square lattice. Hammersley and Welsh, who introduced the subject in 1965, conjectured that the expected minimum travel time from (0, 0) to (n, 0) along paths contained in the cylinder is always non-decreasing in n. However, when the bonds have time-coordinate 1 with probability p and 0 with probability 1 – p (0 < P < 1), then, for p sufficiently small, we get a counterexample.

Consider a processor-sharing queue placed in a quasi-reversible network in equilibrium. This note explains why the expected sojourn time of a customer in such a queue is proportional to his service time.